Электричество и магнетизм
Решение. Емкость прежнего конденсатора, чьими обкладками были сферы радиусами дается формулой (2.18):
Как видно из рисунка, новый конденсатор представляет собой последовательное соединение двух сферических конденсаторов: образованного сферами радиусами (его емкость обозначим как ) и (его емкость будет ). Имеем по той же формуле:
|
(2.30) |
Для емкости последовательно соединенных конденсаторов получаем теперь
Емкость нового конденсатора оказалась больше емкости первоначального.
Аналитическая формула для емкости такой батареи имеет вид:
|
(2. |
При бесконечно тонкой внутренней сфере заряды на ее поверхностях скомпенсируют друг друга, и мы должны получить формулу для емкости конденсатора без внутренней оболочки. Так оно и следует из формулы (2.31) при . В обратном предельном случае, когда стенки внутренней оболочки близки к обкладкам первоначального конденсатора, получается формула для емкости двух последовательно соединенных плоских конденсаторов.
Конденсаторы нашли широкое практическое применение, особенно в радиотехнике. Некоторые типы конденсаторов показаны на рис. 2.18.
Рис. 2.18. Различные типы конденсаторов, применяемых в технике: 1 — конденсаторы постоянной емкости; 2 — конденсатор переменной емкости
Дополнительная информация
http://www.elektropolus.com/condensator/type.php — типы конденсаторов;
http://gete.ru/post_1212414212.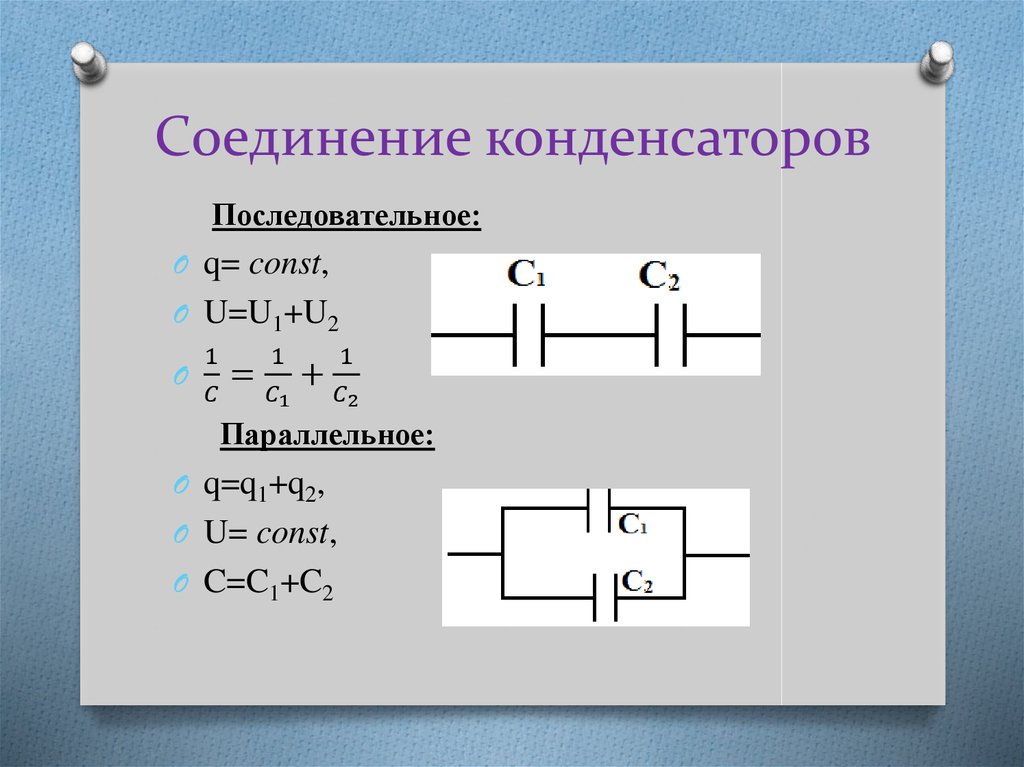 html — классификация и маркировка конденсаторов;
html — классификация и маркировка конденсаторов;
http://www.chipdip.ru/video.aspx?vid=ID000274696&tag=dielectric — видео «Конструкция электролитического алюминиевого конденсатора»;
http://www.symmetron.ru/articles/tantalum_replacement.shtml — керамические конденсаторы большой емкости;
http://radiobooka.ru/radio_nach/kak_sdelat_kondensator.phtml — как сделать конденсатор своими руками;
http://chipinfo.ru/literature/radio/194701/p54-57.html — статья «Переменные конденсаторы»;
http://www.eham.net/articles/5217 — переменный конденсатор своими руками;
http://www.kpsec.freeuk.com/components/capac.htm — коденсаторы, переменные конденсаторы;
http://qrx.narod.ru/arhn/e_d.htm — бесконтактные емкостные датчики;
http://www.lionprecision.com/capacitive-sensors/index.html — обзор емкостных датчиков;
http://pda-reader.ru/93 — принципы работы сенсорных экранов;
http://pcavto.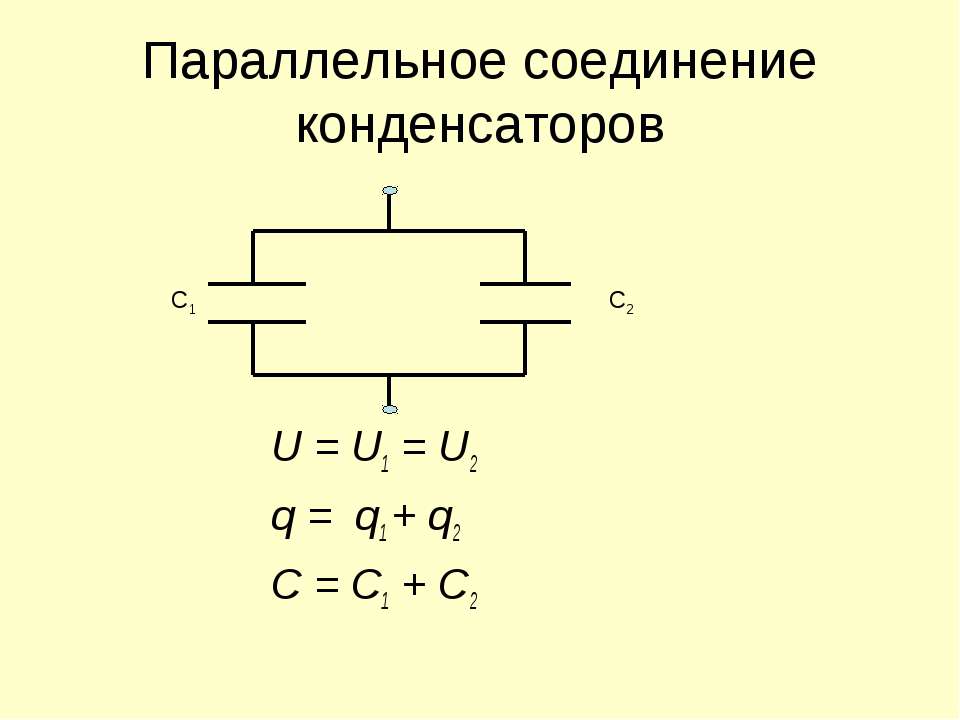 ru/kak-eto-rabotaet/printscipyi-rabotyi-sensornyix-ekranov-touch-screen.html — как работают сенсорные экраны разных типов.
ru/kak-eto-rabotaet/printscipyi-rabotyi-sensornyix-ekranov-touch-screen.html — как работают сенсорные экраны разных типов.
ПАРАЛЛЕЛЬНОЕ И ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ КОНДЕНСАТОРОВ
Когда в нашем распоряжении нет конденсатора нужной емкости или напряжение на конденсаторе превышает допускаемое, возникает необходимость использовать параллельное и последовательное соединение конденсаторов.
Последовательное соединение конденсаторов
Сообщим равные по величине разноименные заряды крайним обкладкам (внешним электродам) цепочке из двух последовательно соединенных конденсаторов с емкостью С1 и С2.
В результате взаимодействия зарядов на соединенных проводником внутренних обкладках возникнут также равные по величине и обратные по знаку заряды, так что на каждой из четырех обкладок будут одинаковые по величине заряды Q. Согласно формуле C = Q/U напряжения между обкладками каждого конденсатора будут:
U = Q/C1 и U2 = Q/C2,
т. е. при различных значениях емкостей напряжения на конденсаторах будут различны.
Сложив напряжения U1 и U2, мы получим напряжение U между внешними обкладками (напряжение на зажимах цепочки). Таким образом,
U = U1 + U2. (1-9)
Подставив в выражение (1-9) вместо напряжений отношение зарядов к емкостям, получим:
Q/C = Q/C1 + Q/C2
где С — общая или эквивалентная емкость.
Сокращая на Q, будем иметь:
1/C = 1/C1 + 1/C2, (1-10)
откуда емкость конденсатора, заменяющая цепочку, или общая емкость двух последовательно соединенных конденсаторов.
1/C = C2 + C1 / C1C2 или C = C1C2 / C1+C2 (1-11)
В случае последовательного соединения трех конденсаторов общую емкость можно найти из формулы, аналогичной (1-10):
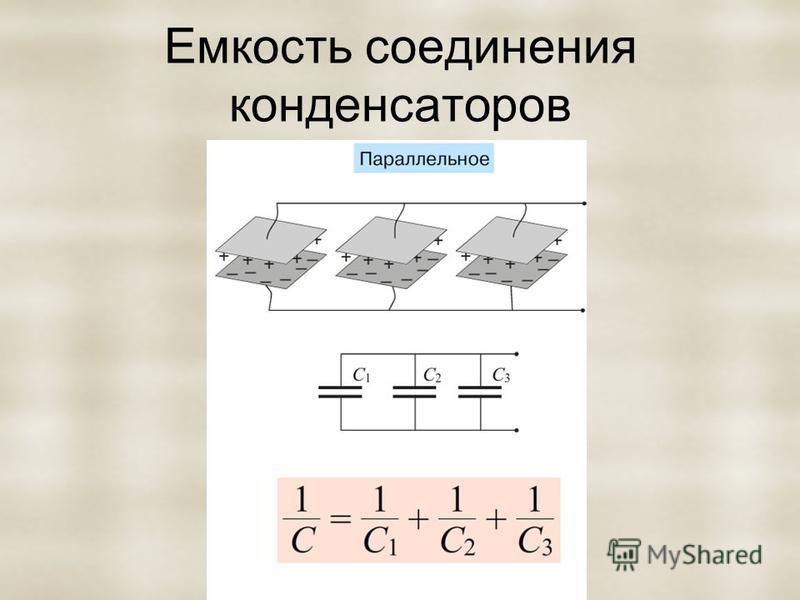
1/C = 1/C1 + 1/C2 + 1/C3 (1-12)
Тем же путем можно вычислить общую емкость любого числа последовательно соединенных конденсаторов.
Параллельное соединение конденсаторов
При параллельном соединении, например, трех конденсаторов (рис. 1-11) получаются две группы обкладок разных конденсаторов.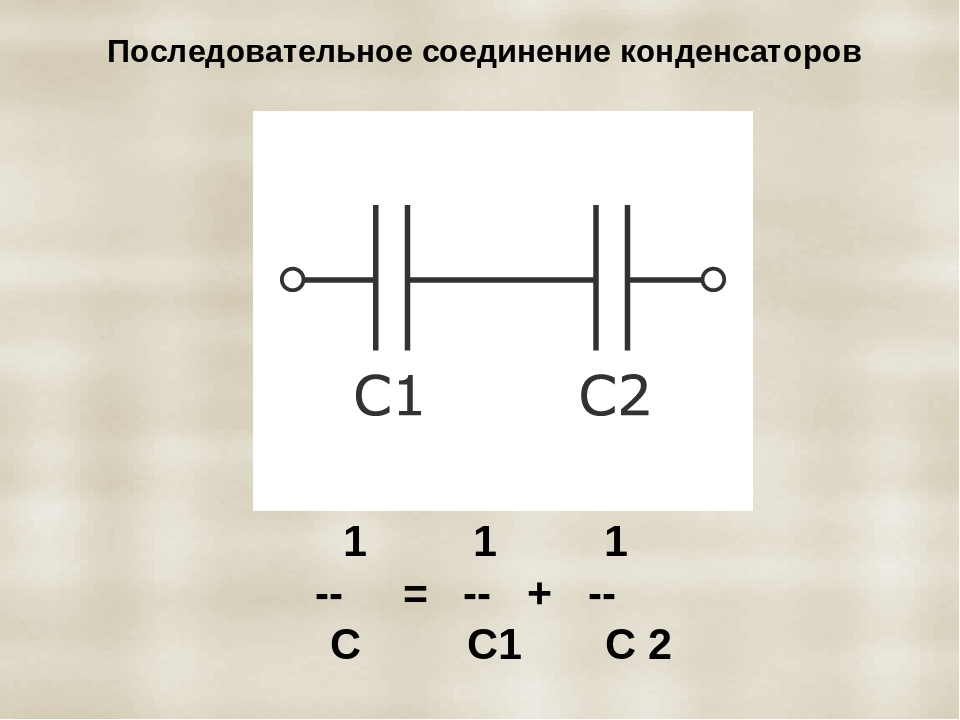 Каждая группа обкладок представляет собой равнопотенциальное проводящее тело, поэтому разности потенциалов (или напряжения) между обкладками отдельных конденсаторов будут одинаковы. Заряды на обкладках при неодинаковых емкостях конденсаторов имеют разные значения:
Каждая группа обкладок представляет собой равнопотенциальное проводящее тело, поэтому разности потенциалов (или напряжения) между обкладками отдельных конденсаторов будут одинаковы. Заряды на обкладках при неодинаковых емкостях конденсаторов имеют разные значения:
Ql = C1U; Q2 = C2U; Q3 = C3U.
Заряд на группе объединенных обкладок
Q = Q1 + Q2 + Q3,
откуда емкость конденсатора, заменяющего три параллельно соединенных конденсатора, или общая емкость
С = Q/U = Q1 + Q2 + Q3/U = C1 + C2 + C3, (1-13)
т. е. равна сумме емкостей отдельных конденсаторов. Это и есть формула при параллельном соединение конденсаторов.
При другом числе параллельно соединенных конденсаторов общая емкость вычисляется аналогично.
Пример:
Определить общую емкость двух конденсаторов при последовательном и параллельном их соединении, если С1 = 2 мкф, а С2 = 4 мкф.
Емкость при последовательном соединении
C = C1C2/C1+C2 = 2×4/2+4 = 1,33 мкф.
Емкость при параллельном соединении
С = С1 + С2 = 2 + 4 = 6 мкф.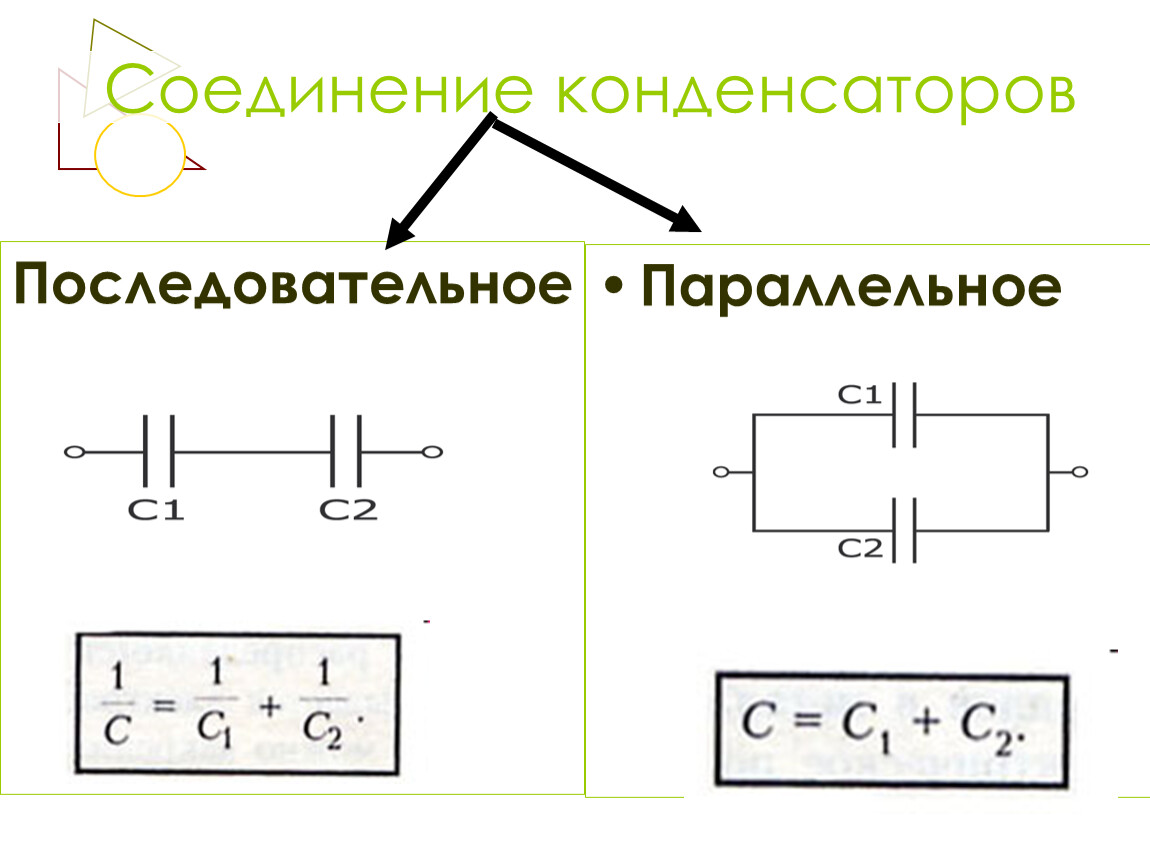
Видеофильм о последовательном и параллельном их соединении конденсаторов смотрите ниже:
Калькулятор емкости последовательного соединения конденсаторов • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения
Калькулятор позволяет рассчитать емкость нескольких конденсаторов, соединенных последовательно.
Пример. Рассчитать эквивалентную емкость двух соединенных последовательно конденсаторов 10 мкФ и 5 мкФ.
Входные данные
Добавить конденсатор
Выходные данные
Эквивалентная емкость
C микрофарад (мкФ)
Введите значения емкости в поля C1 и C 2, добавьте при необходимости новые поля, выберите единицы емкости (одинаковые для всех полей ввода) в фарадах (Ф), миллифарадах (мФ), микрофарадах (мкФ), пикофарадах (пФ), нанофарадах (нФ) и нажмите на кнопку Рассчитать.
1 мФ = 0,001 Ф. 1 мкФ = 0,000001 = 10⁻⁶ Ф. 1 нФ = 0,000000001 = 10⁻⁹ Ф. 1 пФ = 0,000000000001 = 10⁻¹² Ф.
В соответствии со вторым правилом Кирхгофа, падения напряжения V₁, V₂ and V₃ на каждом из конденсаторов в группе из трех соединенных последовательно конденсаторов в общем случае различные и общая разность потенциалов V равна их сумме:
По определению емкости и с учетом того, что заряд Q группы последовательно соединенных конденсаторов является общим для всех конденсаторов, эквивалентная емкость Ceq всех трех конденсаторов, соединенных последовательно, определяется как
или
Для группы из n соединенных последовательно конденсаторов эквивалентная емкость Ceq равна величине, обратной сумме величин, обратных емкостям отдельных конденсаторов:
или
Эта формула для Ceq и используется для расчетов в этом калькуляторе. Например, общая емкость соединенных последовательно трех конденсаторов емкостью 10, 15 and 20 мкФ будет равна 4,62 мкФ:
Если конденсаторов только два, то их общая емкость определяется по формуле
или
Если имеется n соединенных последовательно конденсаторов с емкостью C, их эквивалентная емкость равна
Отметим, что для расчета общей емкости нескольких соединенных последовательно конденсаторов используется та же формула, что и для расчета общего сопротивления параллельно соединенных резисторов.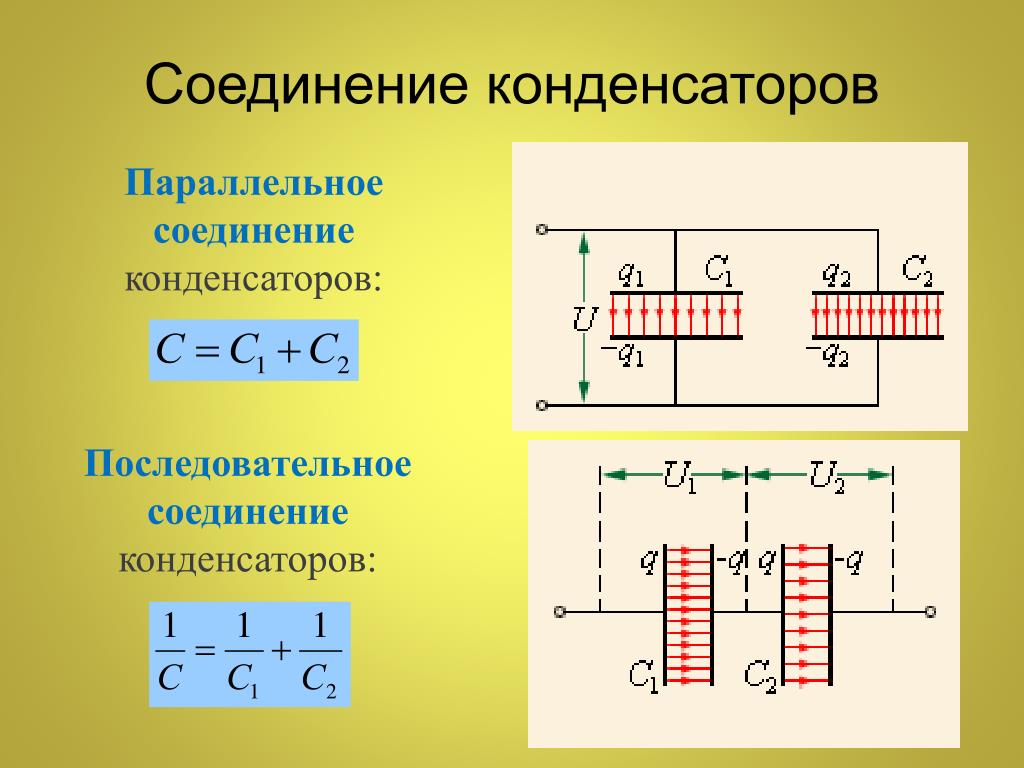
Отметим также, что общая емкость группы из любого количества последовательно соединенных конденсаторов всегда будет меньше, чем емкость самого маленького конденсатора, а добавление конденсаторов в группу всегда приводит к уменьшению емкости.
Конденсаторы на печатной плате
Отдельного упоминания заслуживает падение напряжения на каждом конденсаторе в группе последовательно соединенных конденсаторов. Если все конденсаторы в группе имеют одинаковую номинальную емкость, падение напряжения на них скорее всего будет разным, так как конденсаторы в реальности будут иметь разную емкость и разный ток утечки. На конденсаторе с наименьшей емкостью будет наибольшее падение напряжения и, таким образом, он будет самым слабым звеном этой цепи.
Выравнивающие резисторы уменьшают разброс напряжений на отдельных конденсаторах
Для получения более равномерного распределения напряжений параллельно конденсаторам включают выравнивающие резисторы. Эти резисторы работают как делители напряжения, уменьшающие разброс напряжений на отдельных конденсаторах.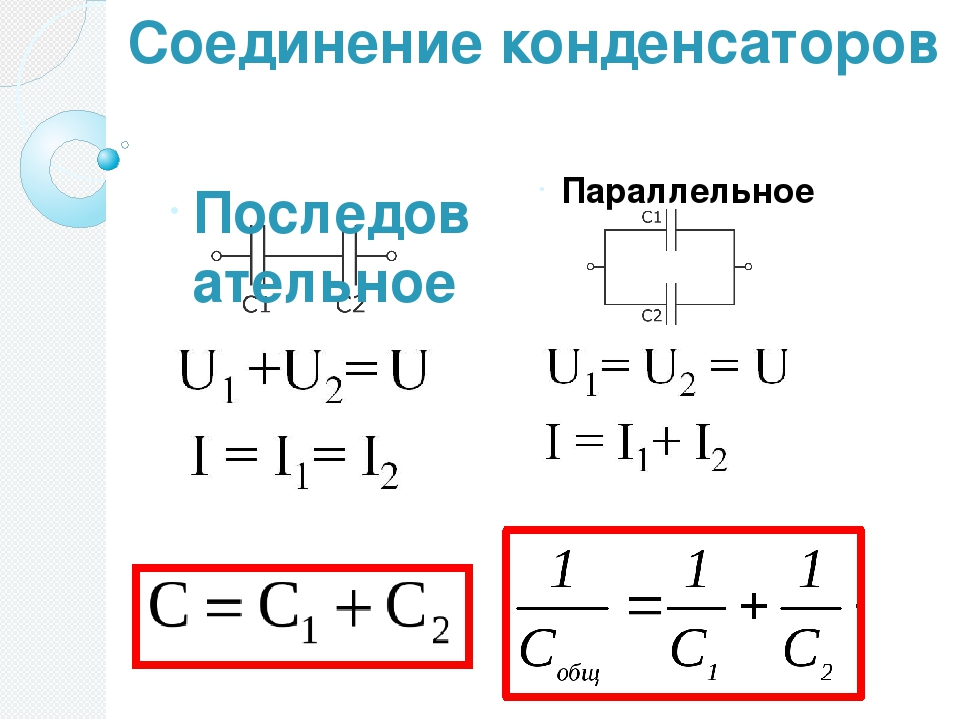 Но даже с этими резисторами все равно для последовательного включения следует выбирать конденсаторы с большим запасом по рабочему напряжению.
Но даже с этими резисторами все равно для последовательного включения следует выбирать конденсаторы с большим запасом по рабочему напряжению.
Если несколько конденсаторов соединены параллельно, разность потенциалов V на группе конденсаторов равна разности потенциалов соединительных проводов группы. Общий заряд Q разделяется между конденсаторами и если их емкости различны, то заряды на отдельных конденсаторах Q₁, Q₂ and Q₃ тоже будут различными. Общий заряд определяется как
Конденсаторы, соединенные параллельно
По определению емкости, эквивалентная емкость группы конденсаторов равна
отсюда
или
Для группы n включенных параллельно конденсаторов
То есть, если несколько конденсаторов включены параллельно, их эквивалентная емкость определяется путем сложения емкостей всех конденсаторов в группе.
Возможно, вы заметили, что конденсаторы ведут себя противоположно резисторам: если резисторы соединены последовательно, их общее сопротивление всегда будет выше сопротивлений отдельных резисторов, а в случае конденсаторов всё происходит с точностью до наоборот.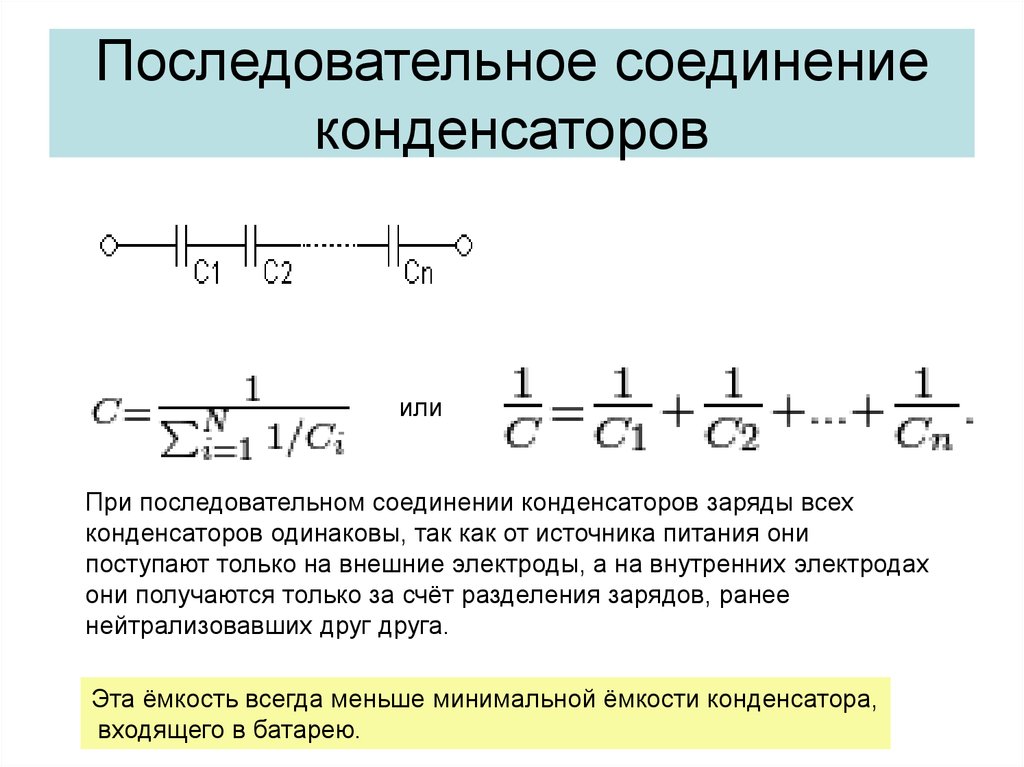
Конденсаторы на печатной плате
Автор статьи: Анатолий Золотков
Последовательное и параллельное соединение конденсаторов
Соединение конденсаторов в электрической цепи может быть последовательным,
параллельным и последовательно-пареллельным (смешанным).
Если провести аналогию между соединением конденсаторов и соединением резисторов , то стоит отметить,
что формулы расчета общей емкости и общего сопротивления идентичны, только между разными типами соединений:
Формула Cобщ при параллельном соединении конденсаторов = формула Rобщ
при последовательном соединении резисторов.
Формула Cобщ при последовательном соединении конденсаторов = формула Rобщ при
параллельном соединении резисторов.
- Cобщ — общая емкость
- Rобщ — общее сопротивление
Параллельное соединение конденсаторов
Параллельное соединение конденсаторов — это соединение при котором конденсаторы соединяются собой обоими контактами.
В результате к одной точке может быть присоединено несколько конденсаторов.
При параллельном соединении формируется один большой конденсатор с площадью обкладок,
равной сумме площадей обкладок всех отдельных компонентов. Поскольку емкость конденсаторов прямо
пропорциональна площади обкладок, общая емкость Собщ при параллельном соединении равняется сумме
емкостей всех конденсаторов в цепи.
Параллельное соединение конденсаторов
Напряжение при параллельном соединении
На все параллельно соединенные конденсаторы падает одинаковое напряжение. Так происходит,
потому что существует всего лишь две точки, между которыми может быть разность потенциалов (напряжение).
Другими словами, можно сказать что при параллельном соединении все конденсаторы подключены к одному источнику напряжения.
Падение напряжения при параллельном соединении
Ток при параллельном соединении
Ток конденсатора во время переходного периода зависит от его емкости и изменения напряжения:
- ic — ток конденсатора
- C — Емкость конденсатора
- ΔVC/Δt – Скорость изменения напряжения
При параллельном соединении через каждый конденсатор
потечет одельный ток, в зависимости от емкости конденсатора:
Ток при параллельном соединении
Последовательное соединение конденсаторов
Последовательное соединение конденсаторов – это соединение двух или более конденсаторов
в форме цепи, в которой каждый отдельный конденсатор соединяется с другим
отдельным конденсатором только в одной точке.
Последовательное соединение конденсаторов
Ток при последовательном соединении
Ток (iC), заряжающий последовательную цепь конденсаторов,
будет одинаковым для всех конденсаторов, поскольку у
него есть только один возможный путь прохождения:
Вследствие того что через все последовательно соединенные конденсаторы течет одинаковый ток,
количество накопленого электрического заряда для каждого конденсатора будет одинаковым, независимо
от его емкости. Так происходит, потому что электрический заряд, накапливаемый на обкладке любого
конденсатора, должен прийти с обкладки примыкающего конденсатора.
Таким образом, последовательно соединенные конденсаторы
имеют одинаковый электрический заряд:
Посмотрим на последовательную цепь из трех конденсаторов на рисунке выше. Правая обкладка первого конденсатора
С1 соединяется с левой второго конденсатора С2, у которого правая обкладка соединяется с левой третьего конденсатора С3.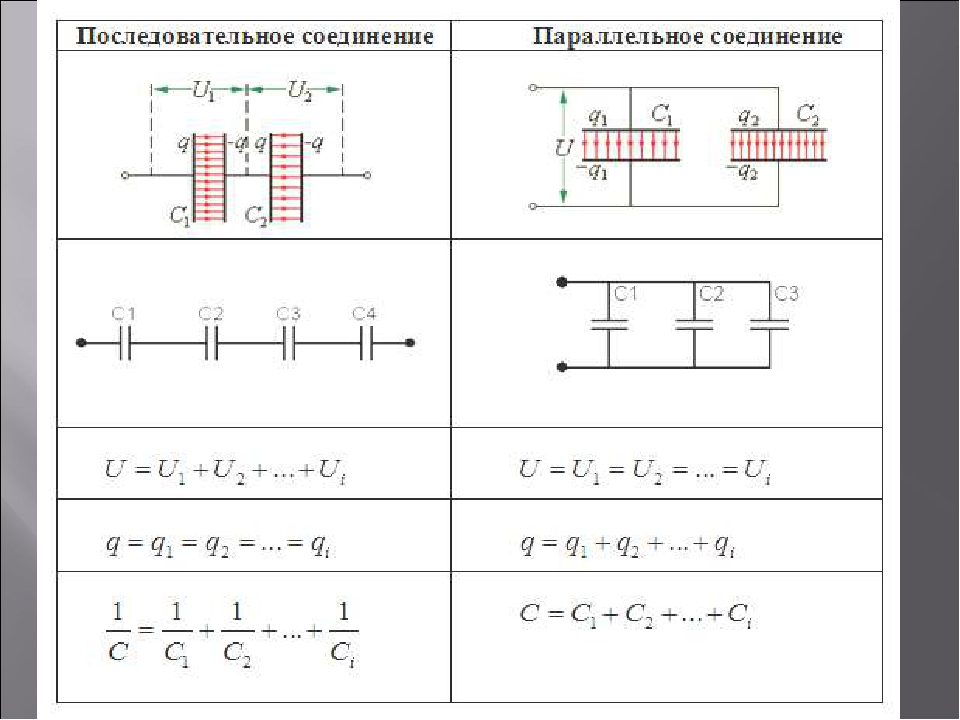
Это означает, что в режиме постоянного тока конденсатор С2 электрически изолирован от общей цепи.
В итогое эффективная площадь обкладок уменьшается до площади обкладок самого маленького конденсатора.
Это объясняется тем, что как только обкладки наименшей площади заполнятся электрическим зарядом,
данный конденсатор перестанет пропускать ток. В результате ток прекратиться во всей цепи,
и процесс зарядки остальных конденсаторов также прекратится.
При последовательном соединении общее расстояние между обкладками увеличивается
до суммы расстояний между обкладками всех конденсаторов.
Таким образом, последовательная цепь формирует один большой конденсатор с площадью обкладок элемента
с наименьшей емкостью, и расстоянием между обкладками, равному сумме всех расстояний в цепи.
Площадь и расстояние между обкладками при последовательном соединении
Падение напряжения и общая емкость при последовательном соединении
На каждый отдельный конденсатор в последовательной цепи падает разное напряжение.
Поскольку емкость обратно пропрциональна напряжению (С = Q/V), то чем меньше емкость
конденсатора, тем большее напряжение на него упадет.
Применим закон Кирхгофа для напряжения в последовательной цепи из трех конденсаторов:
Падение напряжения при последовательном соединении
Емкость конденсатора прямо пропорциональна его заряду и обратно пропорциональна
его напряжению — C = Q/V. Как уже упоминалось выше, последовательно соединенные
конденсаторы имеют одинаковый электрический заряд — Qобщ = Q1 = Q2 = Q3.
Следовательно:
Разделив все выражение на Qобщ мы получим уравнение для
общей емкости при последовательном соединении:
Из данного уравнения можно легко вывести формулу общей емкости
для любого частного случая последовательного соединения.
Например, общая емкость для трех конденсаторов:
Общая емкость для двух конденсаторов:
Смешанное соединение конденсаторов
Если в цепи есть и последовательное и параллельное соединение, то такую цепь называют смешанной
или последовательно-параллельной. Тем не менее, смешанное соединение может иметь
Тем не менее, смешанное соединение может иметь
как последовательный, так и параллельный характер.
Смешанное соединение конденсаторов
Общая емкость смешанного соединения конденсаторов
Чтобы посчитать общую емкость смешанного соединения конденсаторов, следуют такому же алгоритму,
как и при расчете общего сопротивления смешанного соединения резисторов.
- Цепь разбивают на участки с только пареллельным или только последовательным соединением
- Вычисляют общую емкость для каждого отдельного участка.
- Вычисляют общую емкость для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 2:
Преобразование смешанного соединения в параллельное
Зачем все это нужно?
Вполне справедливым может оказаться вопрос, для чего надо соединять конденсаторы
последовательно, если общая емкость будет меньше? Скорее всего, первым что приходит
в голову — это чтобы получить новый эквивалентный конденсатор с меньшей емкостью.
Но в производстве микросхем вряд ли будут делать подобное, поскольку, во -первых,
обычно нужно экономить место на печатной плате, а во-вторых, нет смысла тратить деньги
на два компонента или больше, если можно купить один с требуемой емкостью.
Но если в параллельном или последовательном соединении конденсаторов
еще есть хоть какая-то логика, то кому вообще нужно смешанное?
Дело в том, что емкостью, то есть способностью накапливать электрический заряд,
обладает любое тело в природе, даже человеческое. Если мы говорим о электрической цепи,
то все ее элементы на практике обладают емкостью, и их можно представить как конденсаторы.
Часто такую емкость еще называют паразитической, потому как она создает разного рода помехи.
Например, у нас есть какая-то электронная цепь с множеством различных компонентов,
которая принимает сигнал, обрабатывает его определенным образом и выдает на выход результат.
Известно, что время задержки сигнала, в основном, зависит от паразитической емкости электронных
компонентов схемы. Поскольку должно пройти время зарядки паразитической емкости,
прежде чем она начнет пропускать сигнал. Если мы хотим узнать время задержки,
нужно посчитать общую емкость всех компонентов, конвертировав их в цепь из конденсаторов.
Параллельное и последовательное соединение конденсаторов
В предыдущих статьях были рассмотрены вопросы работы и характеристики конденсаторов. Сейчас Я расскажу о всех методах соединения конденсаторов для подключения в схему. Сразу скажу, что в жизни практически везде, за исключением редких случаев используется только параллельная схема подключения.
Следует знать, что в цепи переменного тока конденсатор выступает еще как емкостное сопротивление. При чем с увеличением величины емкости конденсатора- уменьшается сопротивление в цепи переменного тока.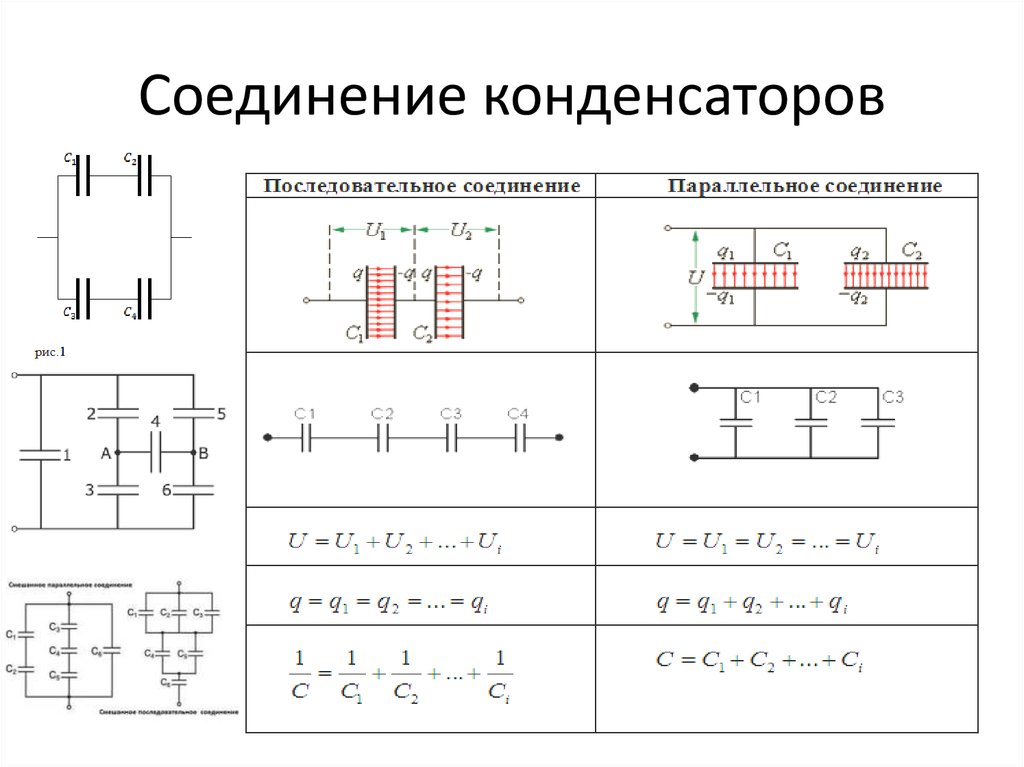
Параллельное соединение конденсаторов
При параллельной схеме подключения все обкладки конденсаторов соединяются в две группы, причем один вывод с каждого конденсатора соединяется в одну группу с другими, а второй — в другую. Наглядный пример параллельного соединения и схема на картинке.
Все параллельно соединенные конденсаторы подключаются к одному источнику напряжения, поэтому существует на них две точки разности потенциалов или напряжения. На всех выводах конденсаторов будет абсолютно одинаковое напряжение.
При подключении параллельно все конденсаторы вместе, образуют принципиально одну емкость, величина которой будет равняться сумме всех емкостей подключенных в цепи конденсаторов.При параллельном подключении через каждый из конденсаторов потечет разный ток, который будет зависеть от величины емкости каждого из них. Чем выше емкость, тем больший ток потечет через неё.
Параллельное соединение очень часто встречается в жизни. С его помощью можно из группы конденсаторов собрать любую необходимую емкость. Например, для запуска 3 фазного электродвигателя в однофазной сети 220 Вольт в результате расчетов Вы получили что необходима рабочая емкость 125 мкФ. Такой емкости конденсаторов Вы не найдете в продаже. Для того, что бы получить необходимую емкость придется купить и соединить параллельно 3 конденсатора один на 100 мкФ, второй- на 20, и третий на 5 мкФ.
С его помощью можно из группы конденсаторов собрать любую необходимую емкость. Например, для запуска 3 фазного электродвигателя в однофазной сети 220 Вольт в результате расчетов Вы получили что необходима рабочая емкость 125 мкФ. Такой емкости конденсаторов Вы не найдете в продаже. Для того, что бы получить необходимую емкость придется купить и соединить параллельно 3 конденсатора один на 100 мкФ, второй- на 20, и третий на 5 мкФ.
Соединение конденсаторов последовательно
При последовательном соединении конденсаторов каждая из обкладок соединяется только в одной точке с одной обкладкой другого конденсатора. Получается цепочка конденсаторов. Крайние два вывода подключаются к источнику тока, в результате чего происходит перераспределение между ними электрических зарядов. Заряды на всех промежуточных обкладках одинаковые величине с чередованием по знаку.
Через все соединенные конденсаторы последовательно протекает одинаковой величины ток, потому что у него нет другого пути прохождения.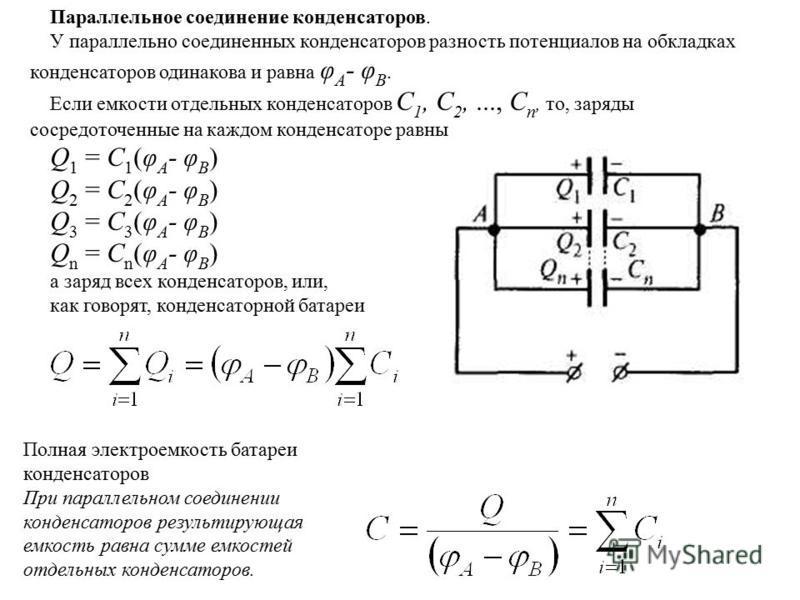
Общая же емкость будет ограничиваться площадью обкладок самого маленького по величине, потому что как только зарядится полностью конденсатор с самой маленькой емкостью- вся цепочка перестанет пропускать ток и заряд остальных прервется. Высчитывается же емкость по этой формуле:Но при последовательном соединении увеличивается расстояние (или изоляция) между обкладками до величины равной сумме расстояний между обкладками всех последовательно подключенных конденсаторов. Например, если взять два конденсатора с рабочим напряжением 200 Вольт и соединить последовательно, то изоляция между их обкладками сможет выдержать 1000 Вольт при подключении в схему.
Из выше сказанного можно сделать вывод, что последовательно соединять необходимо:
- Для получения эквивалентного меньшего по емкости конденсатора.
- Если необходима емкость, работающая на более высоких напряжениях.
- Для создания емкостного делителя напряжения, который позволяет получить меньшей величины напряжение из более высокого.

Практически, для получения первого и второго достаточно просто купить один конденсатор с необходимой величиной емкости или рабочим напряжением. Поэтому данный метод соединения в жизни не встречается.
Смешанное соединение конденсаторов
Встречается смешанное соединение только на различных платах. Для него характерно наличие в одной цепи параллельного и последовательного соединения конденсаторов. При чем смешанное соединение может быть как последовательного, так параллельного характера.
В жизни подробные знания о смешанном соединении могут только пригодится радиолюбителям, поэтому не буду на этом подробно останавливаться.
Из следующей статьи Вы узнаете как правильно проверить и определить емкость конденсатора.
способы, правила, формулы. Вычисление падений напряжения на конденсаторах
Конденсаторы, как и резисторы, можно соединять последовательно и параллельно. Рассмотрим соединение конденсаторов: для чего применяются каждая из схем, и их итоговые характеристики.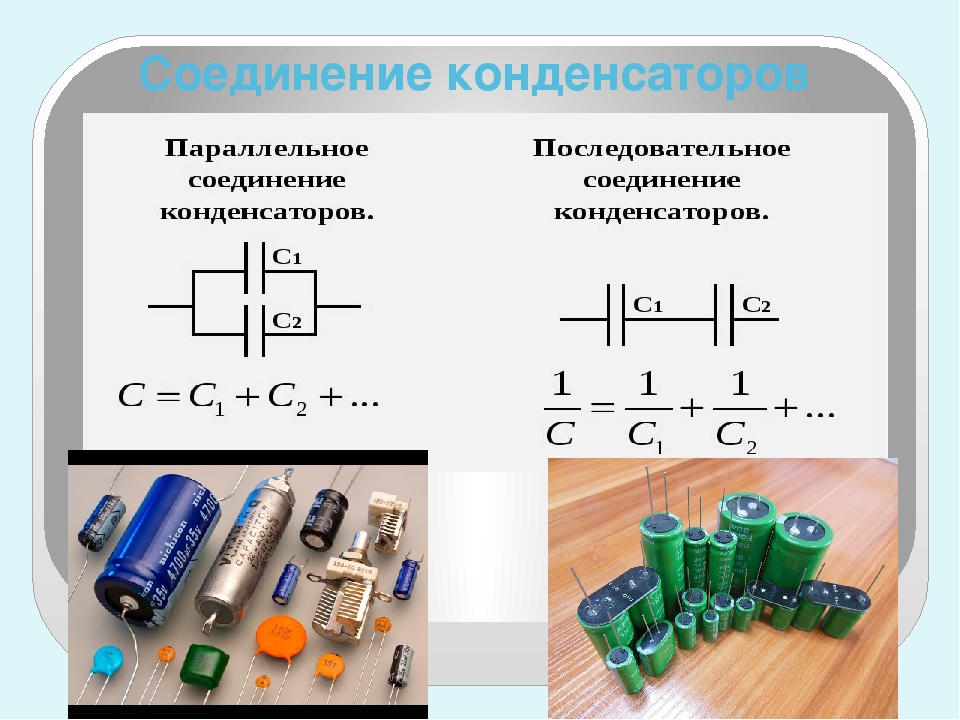
Эта схема – самая распространенная. В ней обкладки конденсаторов соединяются между собой, образуя эквивалентную емкость, равную сумме соединяемых емкостей.
При параллельном соединении электролитических конденсаторов необходимо, чтобы между собой соединялись выводы одной полярности.
Особенность такого соединения – одинаковое напряжение на всех соединяемых конденсаторах
. Номинальное напряжение группы параллельно соединенных конденсаторов равно рабочему напряжению конденсатора группы, у которого оно минимально.
Токи через конденсаторы группы протекают разные: через конденсатор с большей емкостью потечет больший ток.
На практике параллельное соединение применяется для получения емкости нужной величины, когда она выходит за границы диапазона, выпускаемого промышленностью, или не укладываются в стандартный ряд емкостей. В системах регулирования коэффициента мощности (cos ϕ) изменение емкости происходит за счет автоматического подключения или отключения конденсаторов в параллель.
При последовательном соединении обкладки конденсатором соединяются друг к другу, образуя цепочку. Крайние обкладки подключаются к источнику, а ток по всем конденсаторам группы потечет одинаковый.
Эквивалентная емкость последовательно соединенных конденсаторов ограничена самой маленькой емкостью в группе. Объясняется это тем, что как только она полностью зарядится, ток прекратится. Подсчитать общую емкость двух последовательно соединенных конденсаторов можно по формуле
Но применение последовательного соединения для получения нестандартных номиналов емкостей не так распространено, как параллельного.
При последовательном соединении напряжение источника питания распределяется между конденсаторами группы. Это позволяет получить батарею конденсаторов, рассчитанную на большее напряжение
, чем номинальное напряжение входящих в нее компонентов. Так из дешевых и небольших по размерам конденсаторов изготавливаются блоки, выдерживающие высокие напряжения.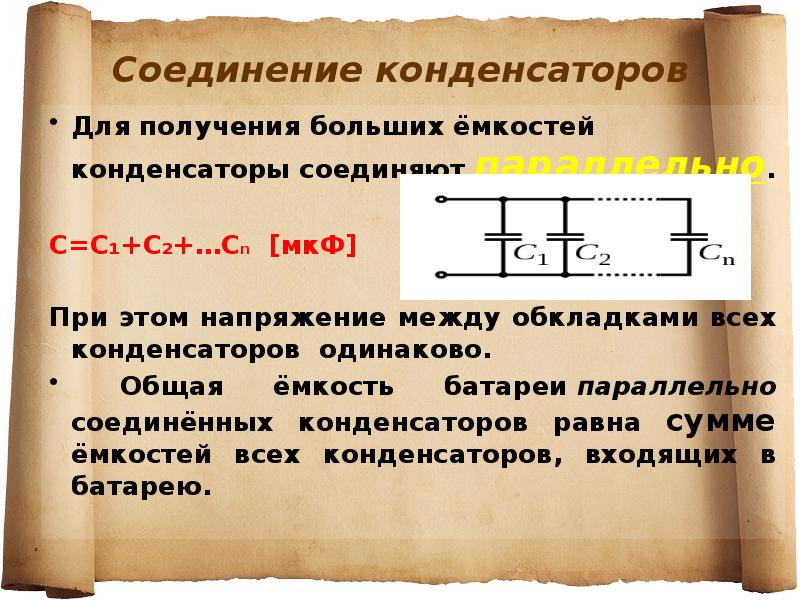
Еще одна область применения последовательного соединения конденсаторов связана с перераспределением напряжений между ними. Если емкости одинаковы, напряжение делится пополам, если нет – на конденсаторе большей емкости напряжение получается большим. Устройство, работающее на этом принципе, называют емкостным делителем напряжения
.
Смешанное соединение конденсаторов
Такие схемы существуют, но в устройствах специального назначения, требующие высокой точности получения величины емкости, а также для их точной настройки.
1 мФ = 0,001 Ф. 1 мкФ = 0,000001 = 10⁻⁶ Ф. 1 нФ = 0,000000001 = 10⁻⁹ Ф. 1 пФ = 0,000000000001 = 10⁻¹² Ф.
В соответствии со вторым правилом Кирхгофа, падения напряжения V₁
, V₂
and V₃
на каждом из конденсаторов в группе из трех соединенных последовательно конденсаторов в общем случае различные и общая разность потенциалов V
равна их сумме:
По определению емкости и с учетом того, что заряд Q
группы последовательно соединенных конденсаторов является общим для всех конденсаторов, эквивалентная емкость C
eq всех трех конденсаторов, соединенных последовательно, определяется как
Для группы из n
соединенных последовательно конденсаторов эквивалентная емкость C
eq равна величине, обратной сумме величин, обратных емкостям отдельных конденсаторов:
Эта формула для C
eq и используется для расчетов в этом калькуляторе. Например, общая емкость соединенных последовательно трех конденсаторов емкостью 10, 15 and 20 мкФ будет равна 4,62 мкФ:
Например, общая емкость соединенных последовательно трех конденсаторов емкостью 10, 15 and 20 мкФ будет равна 4,62 мкФ:
Если конденсаторов только два, то их общая емкость определяется по формуле
Если имеется n
соединенных последовательно конденсаторов с емкостью C
, их эквивалентная емкость равна
Отметим, что для расчета общей емкости нескольких соединенных последовательно конденсаторов используется та же формула, что и для расчета общего сопротивления параллельно соединенных резисторов .
Отметим также, что общая емкость группы из любого количества последовательно соединенных конденсаторов всегда будет меньше, чем емкость самого маленького конденсатора, а добавление конденсаторов в группу всегда приводит к уменьшению емкости.
Отдельного упоминания заслуживает падение напряжения на каждом конденсаторе в группе последовательно соединенных конденсаторов. Если все конденсаторы в группе имеют одинаковую номинальную емкость, падение напряжения на них скорее всего будет разным, так как конденсаторы в реальности будут иметь разную емкость и разный ток утечки.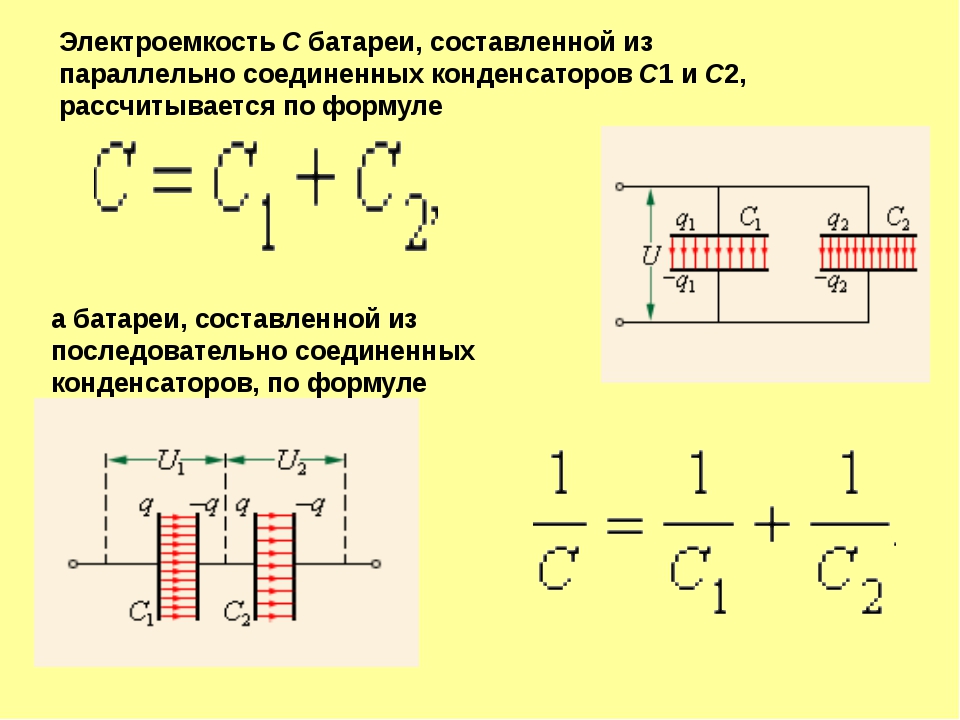 На конденсаторе с наименьшей емкостью будет наибольшее падение напряжения и, таким образом, он будет самым слабым звеном этой цепи.
На конденсаторе с наименьшей емкостью будет наибольшее падение напряжения и, таким образом, он будет самым слабым звеном этой цепи.
Для получения более равномерного распределения напряжений параллельно конденсаторам включают выравнивающие резисторы. Эти резисторы работают как делители напряжения, уменьшающие разброс напряжений на отдельных конденсаторах. Но даже с этими резисторами все равно для последовательного включения следует выбирать конденсаторы с большим запасом по рабочему напряжению.
Если несколько конденсаторов соединены параллельно
, разность потенциалов V
на группе конденсаторов равна разности потенциалов соединительных проводов группы. Общий заряд Q
разделяется между конденсаторами и если их емкости различны, то заряды на отдельных конденсаторах Q₁
, Q₂
and Q₃
тоже будут различными. Общий заряд определяется как
У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”
Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?
Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное
и последовательное
.
В реальности это выглядит так:
Параллельное соединение
Принципиальная схема параллельного соединения
Последовательное соединение
Принципиальная схема последовательного соединения
Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.
Но на практике вам вряд ли это пригодиться.
Как рассчитать общую ёмкость соединённых конденсаторов?
Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.
Общая ёмкость параллельно соединённых конденсаторов:
С 1 – ёмкость первого;
С 2 – ёмкость второго;
С 3 – ёмкость третьего;
С N – ёмкость N
-ого конденсатора;
C общ – суммарная ёмкость составного конденсатора.
Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!
Внимание!
Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C 1
, C 2
в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!
Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте .
Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте .
Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:
Внимание!
Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается .
Или то же самое, но более понятно:
Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.
В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:
Здесь, вместо буквы M
ставиться количество конденсаторов, а C 1
– его ёмкость.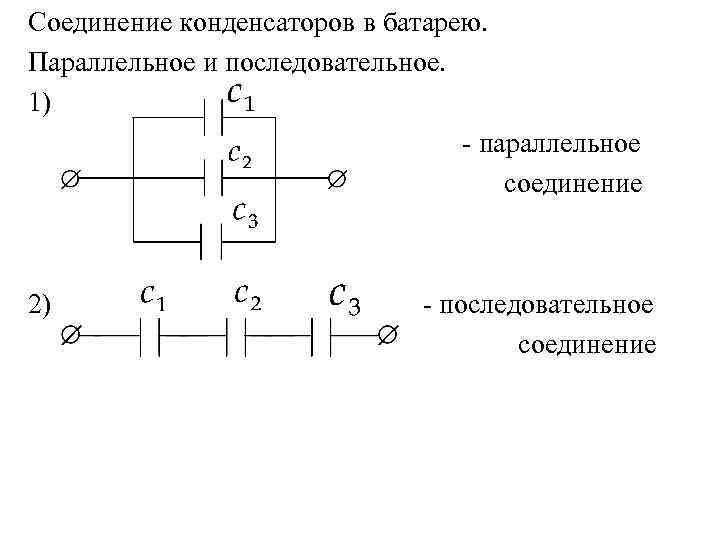
Стоит также запомнить простое правило:
При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.
Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.
Не будем пускать слов по ветру, а проверим конденсатор , замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.
Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+
и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).
Замер ёмкости при последовательном соединении
Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)
А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).
фото).
Измерение ёмкости при параллельном соединении
Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).
Что ещё необходимо знать, чтобы правильно соединять конденсаторы?
Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.
При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.
Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.
Для электролитических конденсаторов.
Последовательное соединение электролитов
Схема последовательного соединения
Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.
То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.
Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.
Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены:)
Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!
Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы , могут соединяться последовательно или параллельно.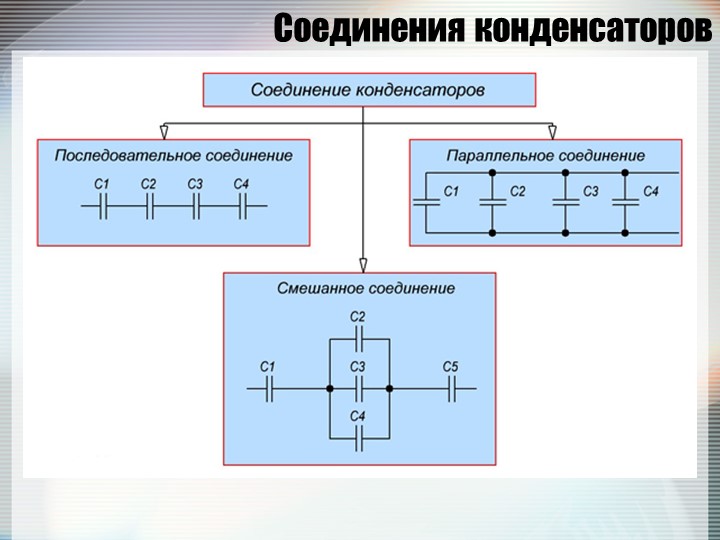 Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.
Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.
При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику ЭДС/тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.
Напряжение на данном участке цепи соотносятся следующим образом:
Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:
Сократив выражение на Q, получим знакомую формулу:
Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:
При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.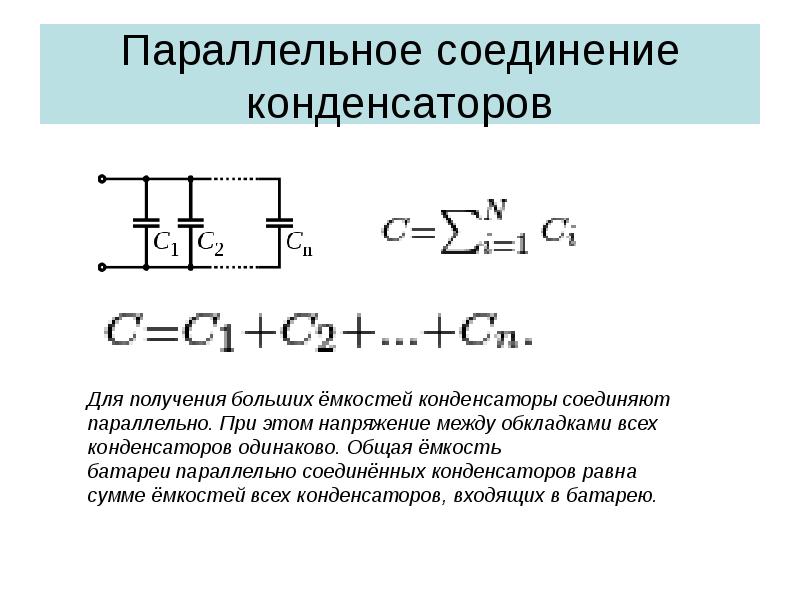
Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:
Так как заряд конденсатора
А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов
Пример 1
Какова результирующая емкость 4 конденсаторов включенных последовательно и параллельно, если известно что С 1 = 10 мкФ, C 2 = 2 мкФ, C 3 = 5 мкФ, а C 4 = 1 мкФ?
При последовательном соединении общая емкость равна:
При параллельном соединении общая емкость равна:
Пример 2
Определить результирующую емкость группы конденсаторов подключенных последовательно-параллельно, если известно, что С 1 = 7 мкФ, С 2 = 2 мкФ, С 3 = 1 мкФ.
Рис.2
U=U 1 =U 2 =U 3
Общий
заряд Q
всех
конденсаторов
Общая
емкость С,
или
емкость батареи, параллельно включенных
конденсаторов равна сумме емкостей
этих конденсаторов.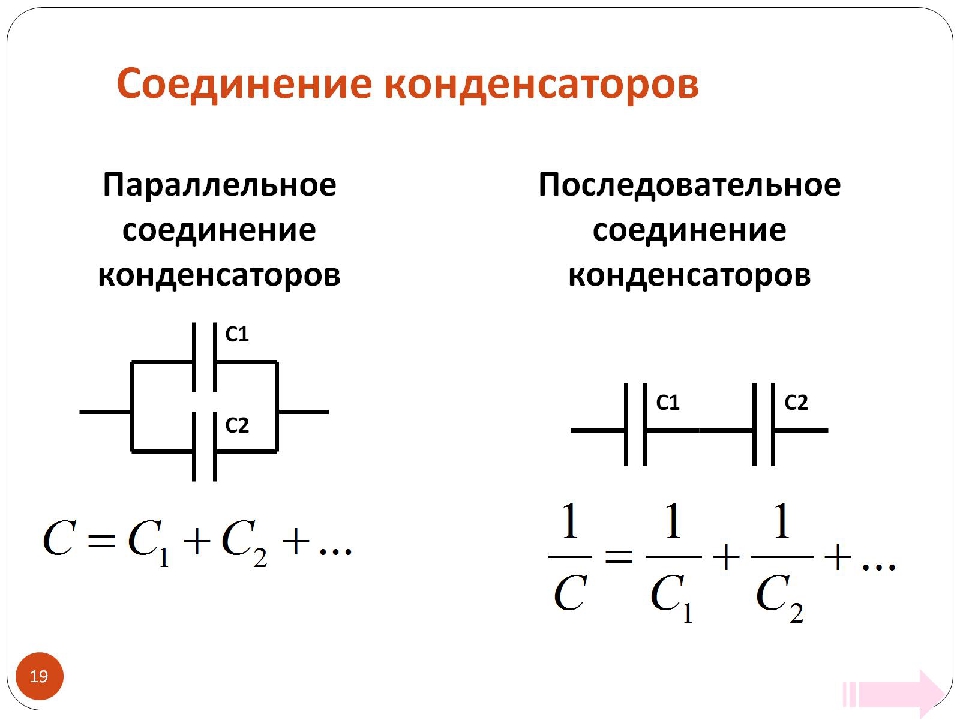
Параллельное
подключение конденсатора к группе
других включенных конденсаторов
увеличивает общую емкость батареи этих
конденсаторов. Следовательно, параллельное
соединение конденсаторов применяется
для увеличения емкости.
4)Если
параллельно включены т
одинаковых
конденсаторов емкостью С´ каждый,
то общая (эквивалентная) емкость батареи
этих конденсаторов может быть определена
выражением
Последовательное соединение конденсаторов
Рис.3
На
обкладках последовательно соединенных
конденсаторов, подключенных к источнику
постоянного тока с напряжением U
,
появятся
заряды одинаковые по величине с
противоположными знаками.
Напряжение на
конденсаторах распределяется обратно
пропорционально емкостям конденсаторов:
Обратная величина
общей емкости последовательно соединенных
конденсаторов равна сумме обратных
величин емкостей этих конденсаторов.
При последовательном
включении двух конденсаторов их общая
емкость определяется следующим
выражением:
Если
в цепь включены последовательно п
одинаковых
конденсаторов емкостью С
каждый,
то общая емкость этих конденсаторов:
Из
(14) видно, что, чем больше конденсаторов
п
соединено
последовательно, тем меньше будет их
общая емкость С,
т.
е. последовательное включение
конденсаторов приводит к уменьшению
общей емкости батареи конденсаторов.
На
практике может оказаться, что допустимое
рабочее напряжение U
p
конденсатора
меньше напряжения, на которое
необходимо подключить конденсатор.
Если этот конденсатор подключить на
такое напряжение, то он выйдет из строя,
так как будет пробит диэлектрик. Если
же последовательно включить несколько
конденсаторов, то напряжение распределится
между ними и на каждом конденсаторе
напряжение окажется меньше его
допустимого рабочего U
p
.
Следовательно,
последовательное
соединение конденсаторов применяют
для того, чтобы напряжение на каждом
конденсаторе не превышало его рабочего
напряжения
U
p
.
Смешанное соединение конденсаторов
Смешанное соединение
(последовательно-параллельное)
конденсаторов применяют тогда, когда
необходимо увеличить емкость и
рабочее напряжение батареи конденсаторов.
Рассмотрим смешанное
соединение конденсаторов на нижеприведенных
примерах.
Энергия
конденсаторов
где Q
—
заряд конденсатора или конденсаторов,
к которым приложено напряжение U
;
С
—
электрическая емкость конденсатора
или батареи соединенных конденсаторов,
к которой приложено напряжение U
.
Таким образом,
конденсаторы служат для накопления и
сохранения электрического поля и
его энергии.
15.
Дайте
определение
понятиям
трех лучевая звезда и треугольник
сопротивлений. Запишите формулы для
преобразования трех лучевой звезды
сопротивлений в треугольник
сопротивлений
и наоборот. Преобразуйте схему к двум
узлам (Рисунок 5)
Рисунок 5- Схема
электрическая
6.СХЕМЫ ЗАМЕЩЕНИЯ
Для облегчения расчета составляется
схема замещения электрической цепи, т.
е. схема, отображающая свойства цепи
при определенных условиях.
На схеме замещения изображают все
элементы, влиянием которых на результат
расчета нельзя пренебречь, и указывают
также электрические соединения между
ними, которые имеются в цепи.
1.Схемы замещения элементов электрических
цепей
На расчетных схемах источник энергии
можно представить ЭДС без внутреннего
сопротивления, если это сопротивление
мало по сравнению с сопротивлением
приемника (рис. 3.13,6).
Приr= 0
внутреннее падение напряженияUо
= 0, поэтому
напряжение на зажимах источника
при любом токе равно
ЭДС: U
=
E
=
const.
В некоторых случаях источник электрической
энергии на расчетной схеме заменяют
другой (эквивалентной) схемой (рис. 3.14,
а),
где вместо ЭДСЕ
источник
характеризуется его током короткого
замыканияI K ,
а вместо внутреннего сопротивления
в расчет вводится внутренняя проводимостьg
=1/
r
.
Возможность такой замены можно доказать,
разделив равенство (3.1) на r:
U
/
r
=
E
/
r
—
I
,
где U
/
r
=
Io
-некоторый ток,
равный отношению напряжения на зажимах
источника к внутреннему сопротивлению;E
/
r
=
I
K
— ток короткого замыкания источника;
Вводя новые обозначения, получим
равенство I
K
=
Io
+
I
,
которому удовлетворяет эквивалентная
схема рис. 3.14,а.
3.14,а.
В этом случае при любой величине
напряжения на зажимах; источника его
ток остается равным току короткого
замыкания (рис. 3.14,6):
Источник с неизменным током, не зависящим
от внешнего сопротивления, называют
источником тока.
Один и тот же источник электрической
энергии может быть заменен в расчетной
схеме источником ЭДС или источником
тока.
Физика — 11
• Общая ёмкость цепи, состоящей из последовательно соединенных n конденсаторов одинаковой ёмкости, в n раз меньше ёмкости одного конденсатора:
Cпосл = C
n.
• Напряжение и энергия последовательно соединенных конденсаторов обратно пропорциональны их электрическим ёмкостям:
U = q
C => U1
U2= C2
C1;
W = q2
2C => W1
W2= C2
C1
Параллельное соединение конденсаторов
При параллельном соединении положительно заряженные пластины всех конденсаторов соединяют в одной точке, а отрицательно заряженные пластины в другой точке (d).
• Общий заряд параллельно соединенных конденсаторов равен сумме зарядов отдельных конденсаторов:
q = q1 + q2
• Напряжения на концах параллельно соединенных конденсаторов одинаковы:
U1 = U2 = U
• Общая электроёмкость батареи параллельно соединенных конденсаторов равна сумме электроёмкостей отдельных конденсаторов:
Cпар = C1 + C2.
•Общая электроёмкость n числа параллельно соединенных одинаковых конденсаторов в n раз больше электроёмкости одного конденсатора:
Cпар = nC.
• Электрические заряды и энергии параллельно соединенных конденсаторов прямо пропорциональны их электроёмкостям:
q = UC => q1
q2
= C1
C2;
W= CU2
2 => W1
W2= C1
C2.
конденсаторов последовательно и параллельно
конденсаторов последовательно и параллельно
Далее: Энергия в конденсаторах
Up: Емкость
Предыдущая: Диэлектрики
Конденсаторы — один из стандартных компонентов электронных схем.
Кроме того, часто встречаются сложные комбинации конденсаторов.
в практических схемах. Это,
поэтому полезно иметь набор правил для определения эквивалентной емкости
некоторого общего расположения конденсаторов.Оказывается, всегда можно найти
эквивалентная емкость при повторном
применение двух простых правил . Эти правила относятся к подключенным конденсаторам.
последовательно и параллельно.
Рассмотрим два конденсатора, подключенных параллельно : , т. Е. , с
положительно заряженные пластины подключены к общему « входному » проводу, а отрицательно
заряженные пластины присоединены к общему « выходному » проводу — см. рис.15. Какая эквивалентная емкость?
рис.15. Какая эквивалентная емкость?
между входным и выходным проводами? В этом случае потенциал
разница между двумя конденсаторами одинакова и равна
разность потенциалов между входным и выходным проводами. Общий заряд
однако, хранящиеся в двух конденсаторах делятся между
конденсаторы, так как он должен распределяться так, чтобы напряжение на
два то же самое. Поскольку конденсаторы могут иметь разную емкость, и,
и сборы тоже могут быть разными.Эквивалентная емкость
пары конденсаторов — это просто соотношение, где
— общий накопленный заряд. Это следует из того
| (113) |
давая
| (114) |
Здесь мы воспользовались тем фактом, что напряжение является общим для всех трех
конденсаторы. Таким образом, правило таково:
Таким образом, правило таково:
Эквивалентная емкость двух конденсаторов, соединенных параллельно
представляет собой сумму отдельных емкостей.
Для конденсаторов, соединенных параллельно, уравнение. (114) обобщает на
.
Рассмотрим два конденсатора, подключенных в серию : , т. Е. , в линию так, что
положительная пластина одного прикреплена к отрицательной пластине другого — см.
Рис.16.
Фактически, предположим, что положительная обкладка конденсатора 1 подключена
к проводу « вход » отрицательная обкладка конденсатора 1 подключается к
положительная пластина конденсатора 2 и отрицательная пластина конденсатора
2 подключается к проводу « выход ».Какая эквивалентная емкость между входными и выходными проводами?
В этом случае важно понимать, что заряд, хранящийся в
два конденсатора одинаковые. Это легче всего увидеть, если рассмотреть
Это легче всего увидеть, если рассмотреть
« внутренние » пластины: , т.е. , отрицательная пластина конденсатора 1 и
положительная пластина конденсатора 2. Эти пластины физически отключены.
от остальной части схемы, поэтому общий заряд на них должен
остается постоянным. Если предположить, что кажется разумным, что эти пластины несут нулевой заряд
когда к двум конденсаторам приложена нулевая разность потенциалов, следует
что при наличии ненулевой разности потенциалов заряд на положительном
пластина конденсатора 2 должна быть уравновешена равным и противоположным зарядом
на отрицательной пластине конденсатора 1.Поскольку отрицательная пластина
Конденсатор 1 несет заряд, положительная пластина должна нести заряд.
Аналогичным образом, поскольку положительная пластина конденсатора 2 несет заряд,
отрицательная пластина должна нести заряд. В итоге оба конденсатора
обладают таким же накопленным зарядом. Потенциал падает, и
два конденсатора, как правило, разные. Однако сумма этих
падение равняется общему падению потенциала, приложенному на входе и выходе
провода: т. е. ,. Эквивалентная емкость пары
е. ,. Эквивалентная емкость пары
конденсаторы снова
.Таким образом,
| (115) |
давая
| (116) |
Здесь мы использовали тот факт, что заряд является общим для всех трех
конденсаторы.
Следовательно, правило таково:
Величина, обратная эквивалентной емкости двух конденсаторов, подключенных в
серия — это сумма обратных величин отдельных емкостей.
Для конденсаторов, соединенных последовательно, уравнение.(116) обобщает на
Далее: Энергия в конденсаторах
Up: Емкость
Предыдущая: Диэлектрики
2007-07-14
конденсаторов параллельно | Приложения
Конденсаторы, как и другие электрические элементы, могут подключаться к другим элементам последовательно или параллельно. Иногда бывает полезно подключить несколько конденсаторов параллельно, чтобы получился функциональный блок, подобный показанному на рисунке.В таких случаях важно знать эквивалентную емкость блока параллельного подключения. В этой статье мы сосредоточимся на анализе параллельного соединения конденсаторов и возможных сферах применения таких схем.
Иногда бывает полезно подключить несколько конденсаторов параллельно, чтобы получился функциональный блок, подобный показанному на рисунке.В таких случаях важно знать эквивалентную емкость блока параллельного подключения. В этой статье мы сосредоточимся на анализе параллельного соединения конденсаторов и возможных сферах применения таких схем.
Анализ
Все конденсаторы в параллельном соединении имеют одинаковое напряжение на них, что означает:
, где от V 1 до V n представляют напряжение на каждом соответствующем конденсаторе. Это напряжение равно напряжению, приложенному к параллельному соединению конденсаторов через входные провода.Однако количество заряда, накопленного на каждом конденсаторе, не одинаково и зависит от емкости каждого конденсатора по формуле:
, где Q n — количество заряда, накопленного на конденсаторе, C n — это емкость конденсатора, а V n — напряжение, приложенное к конденсатору, которое равно напряжению, приложенному ко всей параллели.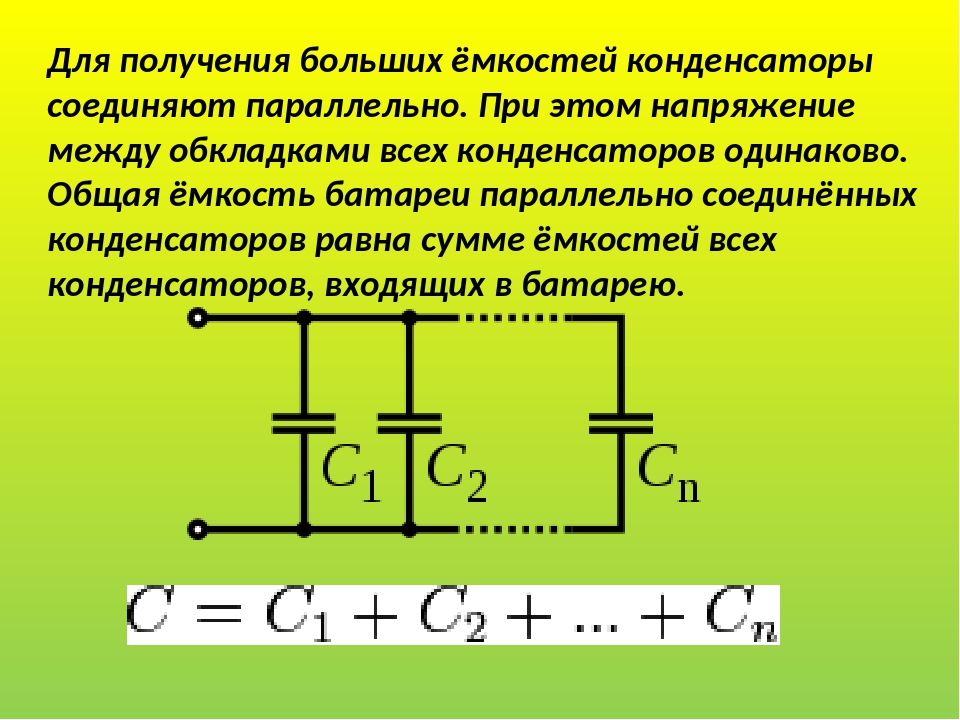 блок подключения. Общее количество заряда, которое хранится в блоке конденсаторов, обозначается Q и делится между всеми конденсаторами, присутствующими в этой цепи.Это представлено:
блок подключения. Общее количество заряда, которое хранится в блоке конденсаторов, обозначается Q и делится между всеми конденсаторами, присутствующими в этой цепи.Это представлено:
Следующее уравнение используется для определения эквивалентной емкости при параллельном соединении нескольких конденсаторов:
, где C eq — эквивалентная емкость параллельного соединения конденсаторов, V — напряжение, приложенное к конденсаторам через входные провода, а Q 1 — Q n представляют собой заряды, накопленные на каждом соответствующем конденсаторе. Это подводит нас к важному выводу, что:
, что означает, что эквивалентная емкость при параллельном соединении конденсаторов равна сумме индивидуальных емкостей.Этот результат также интуитивно понятен — конденсаторы, включенные параллельно, можно рассматривать как один конденсатор, площадь пластин которого равна сумме площадей пластин отдельных конденсаторов.
Приложения
Конденсаторы — это устройства, предназначенные для хранения электрической энергии в виде электрического заряда. При параллельном подключении нескольких конденсаторов полученная схема может хранить больше энергии, поскольку эквивалентная емкость является суммой отдельных емкостей всех задействованных конденсаторов.Этот эффект используется в некоторых приложениях.
При параллельном подключении нескольких конденсаторов полученная схема может хранить больше энергии, поскольку эквивалентная емкость является суммой отдельных емкостей всех задействованных конденсаторов.Этот эффект используется в некоторых приложениях.
Источники питания постоянного тока
Одним из примеров являются источники постоянного тока, которые иногда используют несколько параллельных конденсаторов, чтобы лучше фильтровать выходной сигнал и устранять пульсации переменного тока. Используя этот подход, можно использовать конденсаторы меньшего размера, которые имеют превосходные характеристики пульсации, при этом получая более высокие значения емкости.
Более высокие значения емкости
Для некоторых приложений просто требуются значения емкости, которые намного выше, чем могут предложить коммерчески доступные конденсаторы.В таких приложениях используются конденсаторные батареи. Одним из примеров являются конденсаторные батареи, используемые для коррекции коэффициента мощности с индуктивными нагрузками. Другим примером являются батареи накопителей энергии, которые заявлены для использования в автомобильной промышленности, а именно KERS (система рекуперации кинетической энергии), используемая для рекуперативного торможения в больших транспортных средствах, таких как трамваи, а также в гибридных автомобилях.
Другим примером являются батареи накопителей энергии, которые заявлены для использования в автомобильной промышленности, а именно KERS (система рекуперации кинетической энергии), используемая для рекуперативного торможения в больших транспортных средствах, таких как трамваи, а также в гибридных автомобилях.
Импульсные нагрузки
Одна лаборатория с сильным магнитным полем приводит в действие самый мощный в мире магнит, способный создавать магнитное поле почти 100 тесла за счет хранения энергии в конденсаторной батарее.Накопленная энергия высвобождается через магнитную катушку за очень короткое время, создавая очень мощное магнитное поле.
В любом случае конденсаторные батареи могут достигать очень высоких значений емкости. При использовании нескольких суперконденсаторов, соединенных параллельно, достижимы емкости в несколько десятков килофарад, особенно с учетом того, что суперконденсаторы способны достигать значений емкости более 2000 фарад.
Ограничения конструкции
При параллельном подключении конденсаторов следует помнить о некоторых моментах. Во-первых, максимальное номинальное напряжение при параллельном соединении конденсаторов равно минимальному номинальному напряжению всех конденсаторов, используемых в системе. Таким образом, если несколько конденсаторов номиналом 500 В подключены параллельно конденсатору на 100 В, максимальное номинальное напряжение всей системы составляет всего 100 В, поскольку одинаковое напряжение применяется ко всем конденсаторам в параллельной цепи.
Во-первых, максимальное номинальное напряжение при параллельном соединении конденсаторов равно минимальному номинальному напряжению всех конденсаторов, используемых в системе. Таким образом, если несколько конденсаторов номиналом 500 В подключены параллельно конденсатору на 100 В, максимальное номинальное напряжение всей системы составляет всего 100 В, поскольку одинаковое напряжение применяется ко всем конденсаторам в параллельной цепи.
Безопасность
Еще один момент, о котором следует помнить, заключается в том, что батареи конденсаторов могут быть опасными из-за количества хранимой энергии и того факта, что конденсаторы могут высвобождать накопленную энергию за очень короткое время.Эта накопленная энергия иногда может вызвать серьезные травмы или повреждение электропроводки и устройств в случае случайного короткого замыкания.
Емкостное реактивное сопротивление
— Как найти последовательные и параллельные конденсаторы
Найдите емкостное реактивное сопротивление цепи с последовательными или параллельными конденсаторами, используя этот простой двухэтапный процесс.

Шаг 1. Найдите общую емкость цепи
Предположим, у нас есть три конденсатора, 12 Ф, 20 Ф и 30 Ф, подключенных к источнику с частотой 60 Гц.Каково полное емкостное реактивное сопротивление (X C ) при последовательном или параллельном подключении?
1А. Для конденсаторов серии
Когда конденсаторы соединены последовательно, общая емкость меньше, чем любая из отдельных емкостей последовательных конденсаторов. Если два или более конденсатора соединены последовательно, общий эффект будет таким, как у одного (эквивалентного) конденсатора, имеющего в сумме расстояние между пластинами отдельных конденсаторов.
Конденсаторы серии Пример:
1/12 = 0,083, 1/20 = 0,050, 1/30 = 0,033
0,083 + 0,050 + 0,033 = 0,166
1 / 0,163 = 6,02 мкФ
Примечание: математические расчеты упрощены для целей иллюстрации. Для более точных чисел воспользуйтесь калькулятором.
Для более точных чисел воспользуйтесь калькулятором.
1Б. Для параллельных конденсаторов
При параллельном подключении конденсаторов общая емкость складывается из емкостей отдельных конденсаторов.Если два или более конденсатора соединены параллельно, общий эффект будет таким, как у одного эквивалентного конденсатора, имеющего сумму площадей пластин отдельных конденсаторов.
Параллельные конденсаторы Пример:
12 + 20 + 30 = 62 мкФ
Шаг 2: Определите емкостное реактивное сопротивление
Как и сопротивление, реактивное сопротивление измеряется в Ом, но ему присваивается символ X, чтобы отличить его от чисто резистивного значения R, и поскольку рассматриваемый компонент является конденсатором, реактивное сопротивление конденсатора называется емкостным реактивным сопротивлением (X C ) который измеряется в Ом.
Поскольку конденсаторы заряжаются и разряжаются пропорционально скорости изменения напряжения на них, чем быстрее изменяется напряжение, тем больше тока течет. Точно так же, чем медленнее изменяется напряжение, тем меньше будет протекать ток. Это означает, что реактивное сопротивление конденсатора переменного тока «обратно пропорционально» частоте источника питания.
Точно так же, чем медленнее изменяется напряжение, тем меньше будет протекать ток. Это означает, что реактивное сопротивление конденсатора переменного тока «обратно пропорционально» частоте источника питания.
X C — емкостное реактивное сопротивление в омах, f — частота в герцах и C — емкость переменного тока в фарадах. Очень важно преобразовать наш пример из микрофарад в фарады, чтобы получить правильный результат!
1 мкФ = 0,000001 F
60 Гц Серия Пример:
6,02 мкФ = 0,000006 Ф (упрощенно)
2 х 3,14 х 60 х 0,000006 = 0,0022608
1 / 0,0022608 = 442,32 Ом
60 Гц Параллельный Пример:
62 мкФ = 0,000062 F
2 х 3.14 х 60 х 0,000062 = 0,0233616
1 / 0,0233616 = 42,805 Ом
Теперь посмотрим, что произойдет при изменении частоты на 400 Гц :
Серия 400 Гц Пример:
2 х 3,14 х 400 х 0,000006 = 0,015072
1 / 0,015072 = 66,34 Ом
Параллельный 400 Гц Пример:
2 х 3,14 х 400 х 0,000062 = 0,155744
1 / 0,155744 = 6,42 Ом
Полезные ссылки
8.
 3: Последовательные и параллельные конденсаторы
3: Последовательные и параллельные конденсаторы
Несколько конденсаторов могут быть соединены вместе для использования в различных приложениях. Несколько подключений конденсаторов ведут себя как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения. Конденсаторы могут быть организованы в два простых и распространенных типа соединений, известных как серия и параллельно , для которых мы можем легко вычислить общую емкость.Эти две основные комбинации, последовательная и параллельная, также могут использоваться как часть более сложных соединений.
Серия конденсаторов
На рисунке \ (\ PageIndex {1} \) показано последовательное сочетание трех конденсаторов, расположенных в ряд внутри схемы. Как и в случае любого конденсатора, емкость комбинации связана как с зарядом, так и с напряжением:
\ [C = \ dfrac {Q} {V}. \]
\]
Когда эта последовательная комбинация подключена к аккумулятору с напряжением В, , каждый из конденсаторов получает идентичный заряд Q .Чтобы объяснить, сначала обратите внимание, что заряд на пластине, подключенной к положительной клемме батареи, равен \ (+ Q \), а заряд на пластине, подключенной к отрицательной клемме, равен \ (- Q \). Затем на других пластинах индуцируются заряды, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю. Однако падение потенциала \ (V_1 = Q / C_1 \) на одном конденсаторе может отличаться от падения потенциала \ (V_2 = Q / C_2 \) на другом конденсаторе, потому что, как правило, конденсаторы могут иметь разные емкости.Последовательная комбинация двух или трех конденсаторов напоминает один конденсатор с меньшей емкостью. Как правило, любое количество последовательно соединенных конденсаторов эквивалентно одному конденсатору, емкость которого (называемая эквивалентной емкостью ) меньше наименьшей из емкостей в последовательной комбинации. Заряд этого эквивалентного конденсатора такой же, как заряд любого конденсатора в последовательной комбинации: то есть все конденсаторы последовательной комбинации имеют одинаковый заряд .Это происходит из-за сохранения заряда в цепи. Когда заряд Q в последовательной цепи удаляется с пластины первого конденсатора (который мы обозначаем как \ (- Q \)), он должен быть помещен на пластину второго конденсатора (который мы обозначаем как \ ( + Q \)) и т. Д.
Заряд этого эквивалентного конденсатора такой же, как заряд любого конденсатора в последовательной комбинации: то есть все конденсаторы последовательной комбинации имеют одинаковый заряд .Это происходит из-за сохранения заряда в цепи. Когда заряд Q в последовательной цепи удаляется с пластины первого конденсатора (который мы обозначаем как \ (- Q \)), он должен быть помещен на пластину второго конденсатора (который мы обозначаем как \ ( + Q \)) и т. Д.
Рисунок \ (\ PageIndex {1} \): (a) Три конденсатора соединены последовательно. Величина заряда на каждой пластине равна Q. (b) Сеть конденсаторов на (a) эквивалентна одному конденсатору, который имеет меньшую емкость, чем любая из отдельных емкостей на (a), а заряд на его пластинах равен В.
Мы можем найти выражение для полной (эквивалентной) емкости, рассматривая напряжения на отдельных конденсаторах. Потенциалы на конденсаторах 1, 2 и 3 равны, соответственно, \ (V_1 = Q / C_1 \), \ (V_2 = Q / C_2 \) и \ (V_3 = Q / C_3 \). Эти потенциалы должны в сумме равняться напряжению батареи, давая следующий баланс потенциалов:
Эти потенциалы должны в сумме равняться напряжению батареи, давая следующий баланс потенциалов:
\ [V = V_1 + V_2 + V_3. \]
Потенциал \ (V \) измеряется на эквивалентном конденсаторе, который держит заряд \ (Q \) и имеет эквивалентную емкость \ (C_S \).Вводя выражения для \ (V_1 \), \ (V_2 \) и \ (V_3 \), получаем
\ [\ dfrac {Q} {C_S} = \ dfrac {Q} {C_1} + \ dfrac {Q} {C_2} + \ dfrac {Q} {C_3}. \]
Отменяя заряд Q , мы получаем выражение, содержащее эквивалентную емкость \ (C_S \) трех последовательно соединенных конденсаторов:
\ [\ dfrac {1} {C_S} = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3}. \]
Это выражение можно обобщить для любого количества конденсаторов в последовательной сети.
Комбинация серии
Для конденсаторов, соединенных последовательно, эквивалентная емкость, обратная величине, равна сумме обратных величин индивидуальных емкостей:
\ [\ dfrac {1} {C_S} = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3} + \ dots \ label {capseries} \]
Пример \ (\ PageIndex {1} \): эквивалентная емкость последовательной сети
Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их отдельные емкости равны \ (1.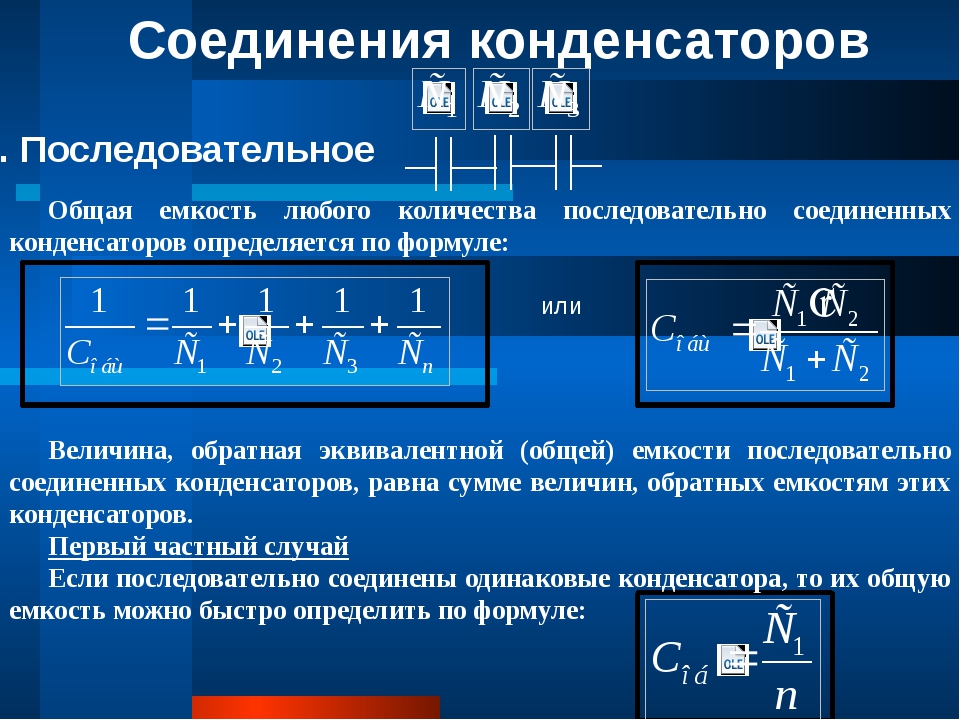 000 мкФ \), \ (5.000 мкФ \) и \ (8.000 мкФ \).
000 мкФ \), \ (5.000 мкФ \) и \ (8.000 мкФ \).
Стратегия
Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение \ ref {capseries} с тремя членами.
Раствор
Вводим указанные емкости в уравнение \ ref {capseries}:
\ [\ begin {align *} \ dfrac {1} {C_S} & = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3} \\ [4pt] & = \ dfrac {1} {1.000 \ mu F} + \ dfrac {1} {5.000 \ mu F} + \ dfrac {1} {8.000 \ mu F} \\ [4pt] & = \ dfrac {1.325} {\ mu F}. \ End {align *} \]
Теперь инвертируем этот результат и получаем
\ [\ begin {align *} C_S & = \ dfrac {\ mu F} {1.325} \\ [4pt] & = 0.755 \ mu F. \ end {align *} \ nonumber \]
Значение
Обратите внимание, что в последовательной сети конденсаторов эквивалентная емкость всегда меньше наименьшей отдельной емкости в сети.
Параллельная комбинация конденсаторов
Параллельная комбинация трех конденсаторов, одна пластина каждого конденсатора подключена к одной стороне цепи, а другая пластина подключена к другой стороне, показана на рисунке \ (\ PageIndex {2a} \).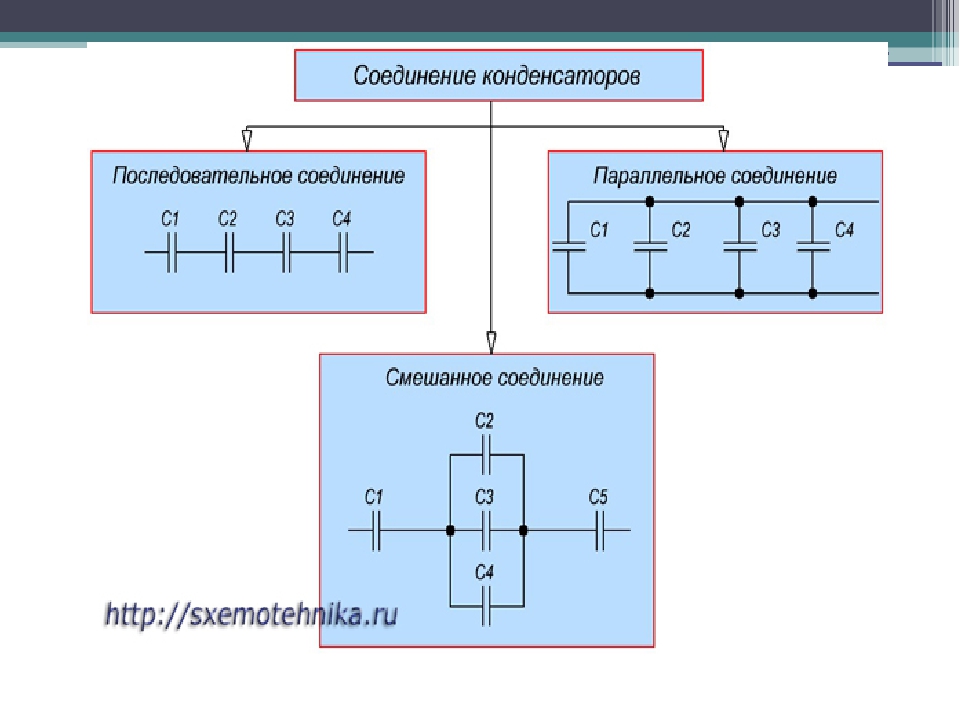 Поскольку конденсаторы подключены параллельно, , все они имеют одинаковое напряжение V на своих пластинах . Однако каждый конденсатор в параллельной сети может накапливать свой заряд. Чтобы найти эквивалентную емкость \ (C_p \) параллельной сети, отметим, что общий заряд Q , хранящийся в сети, является суммой всех отдельных зарядов:
Поскольку конденсаторы подключены параллельно, , все они имеют одинаковое напряжение V на своих пластинах . Однако каждый конденсатор в параллельной сети может накапливать свой заряд. Чтобы найти эквивалентную емкость \ (C_p \) параллельной сети, отметим, что общий заряд Q , хранящийся в сети, является суммой всех отдельных зарядов:
\ [Q = Q_1 + Q_2 + Q_3. \]
В левой части этого уравнения используется соотношение \ (Q = C_pV \), которое выполняется для всей сети.В правой части уравнения мы используем соотношения \ (Q_1 = C_1 V \), \ (Q_2 = C_2V \) и \ (Q_3 = C_3V \) для трех конденсаторов в сети. Таким образом получаем
\ [C_pV = C_1V + C_2V + C_3V. \]
Это уравнение в упрощенном виде представляет собой выражение для эквивалентной емкости параллельной сети из трех конденсаторов:
\ [C_p = C_1 + C_2 + C_3. \]
Это выражение легко обобщается на любое количество конденсаторов, включенных параллельно в сеть.
Параллельная комбинация
Для конденсаторов, соединенных параллельно, эквивалентная (полезная) емкость представляет собой сумму всех индивидуальных емкостей в сети,
\ [C_p = C_1 + C_2 + C_3 + … \ label {capparallel} \]
Рисунок \ (\ PageIndex {2} \): (a) Три конденсатора подключены параллельно. Каждый конденсатор подключен напрямую к батарее. (b) Заряд эквивалентного конденсатора представляет собой сумму зарядов отдельных конденсаторов.
Пример \ (\ PageIndex {2} \): эквивалентная емкость параллельной сети
Найдите чистую емкость для трех конденсаторов, соединенных параллельно, учитывая, что их индивидуальные емкости равны \ (1.0 \ mu F \), \ (5.0 \ mu F \) и \ (8.0 \ mu F \).
Стратегия
Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение \ ref {capparallel} с тремя членами.
Раствор
Ввод заданных емкостей в уравнение \ ref {capparallel} дает
\ [\ begin {align *} C_p & = C_1 + C_2 + C_3 \\ [4pt] & = 1.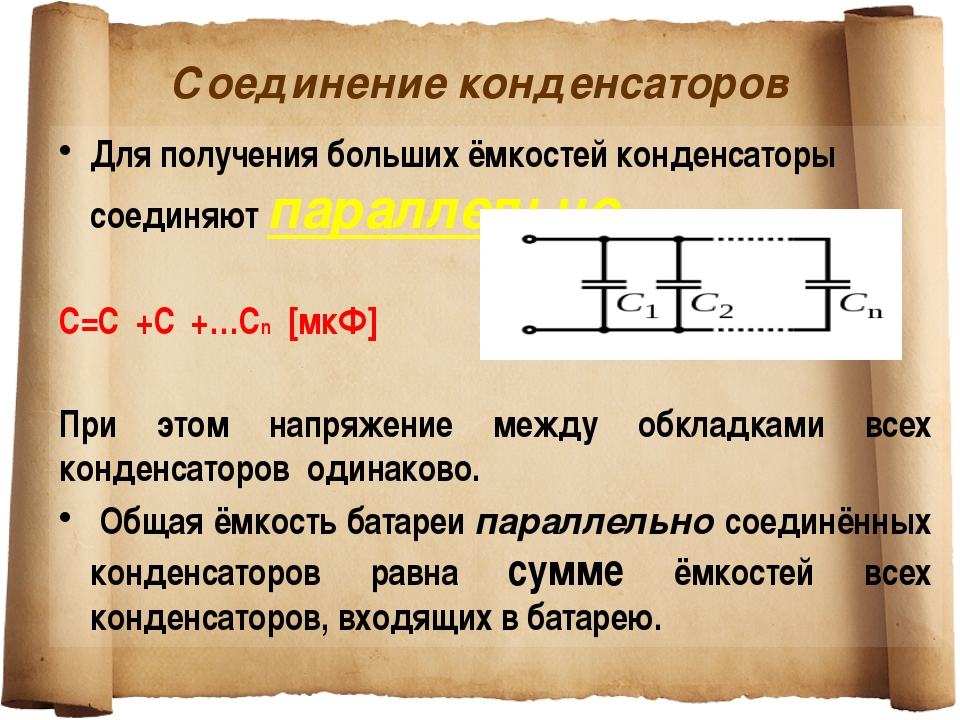 0 \ mu F + 5.0 \ mu F + 8.0 \ mu F \\ [4pt] & = 14.0 \ mu F.\ end {align *} \]
0 \ mu F + 5.0 \ mu F + 8.0 \ mu F \\ [4pt] & = 14.0 \ mu F.\ end {align *} \]
Значение
Обратите внимание, что в параллельной сети конденсаторов эквивалентная емкость всегда больше, чем любая из отдельных емкостей в сети.
Конденсаторные сети обычно представляют собой комбинацию последовательных и параллельных соединений, как показано на Рисунке \ (\ PageIndex {3} \). Чтобы найти чистую емкость таких комбинаций, мы определяем части, которые содержат только последовательные или только параллельные соединения, и находим их эквивалентные емкости.Мы повторяем этот процесс, пока не сможем определить эквивалентную емкость всей сети. Следующий пример иллюстрирует этот процесс.
Рисунок \ (\ PageIndex {3} \): (a) Эта схема содержит как последовательные, так и параллельные соединения конденсаторов. (б) \ (C_1 \) и \ (C_2 \) идут последовательно; их эквивалентная емкость \ (C_S \) c) Эквивалентная емкость \ (C_S \) подключена параллельно с \ (C_3 \).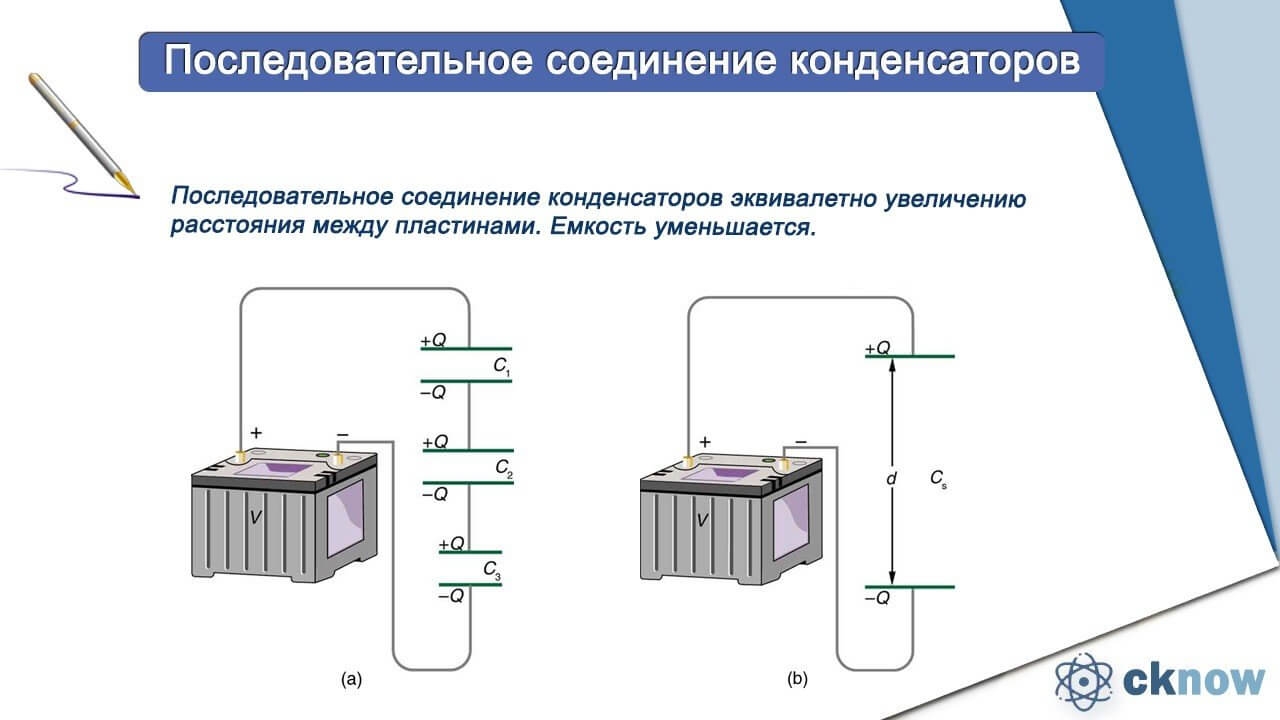 Таким образом, эквивалентная емкость всей сети является суммой \ (C_S \) и \ (C_3 \).
Таким образом, эквивалентная емкость всей сети является суммой \ (C_S \) и \ (C_3 \).
Пример \ (\ PageIndex {3} \): эквивалентная емкость сети
Найдите общую емкость комбинации конденсаторов, показанной на рисунке \ (\ PageIndex {3} \). Предположим, что емкости известны с точностью до трех десятичных знаков (\ (C_1 = 1.000 мкФ, C_2 = 5.000 мкФ, C_3 = 8.000 мкФ \)). Округлите ответ до трех десятичных знаков.
Стратегия
Сначала мы определяем, какие конденсаторы включены последовательно, а какие — параллельно. Конденсаторы \ (C_1 \) и \ (C_2 \) включены последовательно.Их комбинация, помеченная \ (C_S \), параллельна \ (C_3 \).
Раствор
Поскольку \ (C_1 \) и \ (C_2 \) включены последовательно, их эквивалентная емкость \ (C_S \) получается с помощью уравнения \ ref {capseries}:
\ [\ begin {align *} \ dfrac {1} {C_S} & = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} \\ [4pt] & = \ dfrac {1} {1.000 \ mu F} + \ dfrac {1} {5. 000 \ mu F} \\ [4pt] & = \ dfrac {1.200} {\ mu F} \ end {align *} \]
000 \ mu F} \\ [4pt] & = \ dfrac {1.200} {\ mu F} \ end {align *} \]
Для этого
\ [C_S = 0,833 \ mu F. \ nonumber \]
Емкость \ (C_S \) соединена параллельно с третьей емкостью \ (C_3 \), поэтому мы используем уравнение \ ref {capparallel}, чтобы найти эквивалентную емкость C всей сети:
\ [\ begin {align *} C & = C_S + C_3 \\ [4pt] & = 0.833 \ mu F + 8.000 \ mu F \\ [4pt] & = 8.833 \ mu F. \ end {align *} \]
Сеть конденсаторов
Определите чистую емкость C комбинации конденсаторов, показанной на рисунке \ (\ PageIndex {4} \), когда емкости равны \ (C_1 = 12,0 мкФ, C_2 = 2,0 мкФ \) и \ (C_3 = 4,0 мкФ \). Когда на комбинации поддерживается разность потенциалов 12,0 В, найдите заряд и напряжение на каждом конденсаторе.
Рисунок \ (\ PageIndex {4} \): (a) Комбинация конденсаторов.(b) Эквивалентная комбинация из двух конденсаторов. Стратегия
Сначала мы вычисляем чистую емкость \ (C_ {23} \) параллельного соединения \ (C_2 \) и \ (C_3 \).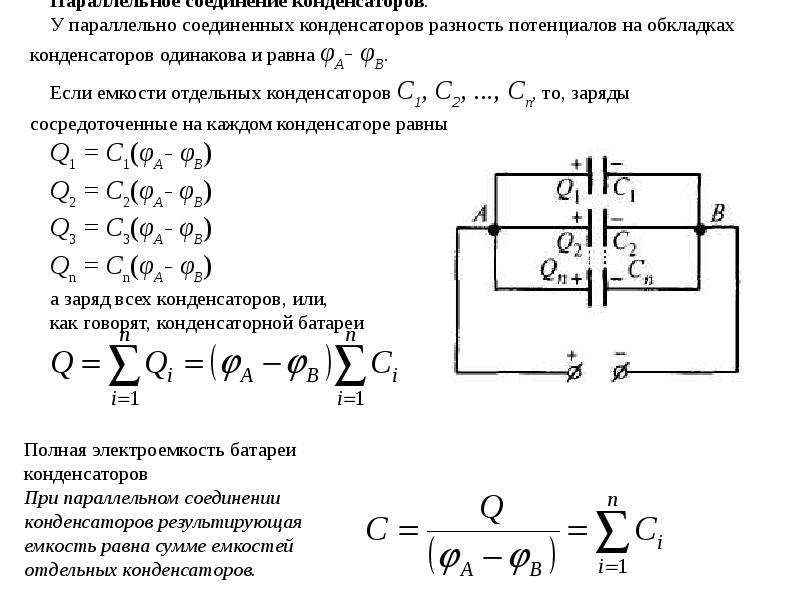 Тогда C — это чистая емкость последовательного соединения \ (C_1 \) и \ (C_ {23} \). Мы используем соотношение \ (C = Q / V \), чтобы найти заряды \ (Q_1, Q_2 \) и \ (Q_3 \), а также напряжения \ (V_1, V_2 \) и \ (V_3 \) на конденсаторы 1, 2 и 3 соответственно.
Тогда C — это чистая емкость последовательного соединения \ (C_1 \) и \ (C_ {23} \). Мы используем соотношение \ (C = Q / V \), чтобы найти заряды \ (Q_1, Q_2 \) и \ (Q_3 \), а также напряжения \ (V_1, V_2 \) и \ (V_3 \) на конденсаторы 1, 2 и 3 соответственно.
Решение Эквивалентная емкость для \ (C_2 \) и \ (C_3 \) составляет
\ [C_ {23} = C_2 + C_3 = 2.0 мк F + 4,0 мк F = 6,0 мк F. \]
Вся комбинация из трех конденсаторов эквивалентна двум последовательным конденсаторам,
\ [\ dfrac {1} {C} = \ dfrac {1} {12.0 \ mu F} + \ dfrac {1} {6.0 \ mu F} = \ dfrac {1} {4.0 \ mu F} \ Rightarrow C = 4,0 мкм F. \]
Рассмотрим эквивалентную комбинацию из двух конденсаторов на рисунке \ (\ PageIndex {2b} \). Поскольку конденсаторы включены последовательно, они имеют одинаковый заряд, \ (Q_1 = Q_ {23} \). Кроме того, конденсаторы разделяют разность потенциалов 12,0 В, поэтому
\ [12.0 V = V_1 + V_ {23} = \ dfrac {Q_1} {C_1} + \ dfrac {Q_ {23}} {C_ {23}} = \ dfrac {Q_1} {12. 0 \ mu F} + \ dfrac {Q_1 } {6.0 \ mu F} \ Rightarrow Q_1 = 48.0 \ mu C. \]
0 \ mu F} + \ dfrac {Q_1 } {6.0 \ mu F} \ Rightarrow Q_1 = 48.0 \ mu C. \]
Теперь разность потенциалов на конденсаторе 1 равна
.
\ [V_1 = \ dfrac {Q_1} {C_1} = \ dfrac {48,0 \ mu C} {12,0 \ mu F} = 4,0 В. \]
Поскольку конденсаторы 2 и 3 подключены параллельно, они имеют одинаковую разность потенциалов:
\ [V_2 = V_3 = 12,0 В — 4,0 В = 8,0 В. \]
Следовательно, заряды на этих двух конденсаторах равны, соответственно,
\ [Q_2 = C_2V_2 = (2.0 мкФ) (8,0 В) = 16,0 мкФ, \]
\ [Q_3 = C_3V_3 = (4,0 мкФ) (8,0 В) = 32,0 мкФ \]
Значимость Как и ожидалось, чистая плата за параллельную комбинацию \ (C_2 \) и \ (C_3 \) составляет \ (Q_ {23} = Q_2 + Q_3 = 48,0 \ mu C. \)
Упражнение \ (\ PageIndex {1} \)
Определите чистую емкость C каждой сети конденсаторов, показанной ниже. Предположим, что \ (C_1 = 1,0 пФ, C_2 = 2,0 пФ, C_3 = 4,0 пФ \) и \ (C_4 = 5,0 пФ \). Найдите заряд на каждом конденсаторе, предполагая, что разность потенциалов равна 12. 0 В в каждой сети.
0 В в каждой сети.
- Ответьте на
\ (C = 0,86 пФ, Q_1 = 10 пКл, Q_2 = 3,4 пКл, Q_3 = 6,8 пКл \)
- Ответ б
\ (C = 2,3 пФ, Q_1 = 12 пКл, Q_2 = Q_3 = 16 пКл \)
- Ответ c
\ (C = 2,3 пФ, Q_1 = 9,0 пКл, Q_2 = 18 пКл, Q_3 = 12 пКл, Q_4 = 15 пКл \)
4.2 Последовательные и параллельные конденсаторы — Введение в электричество, магнетизм и схемы
ЦЕЛИ ОБУЧЕНИЯ
К концу этого раздела вы сможете:
- Объясните, как определить эквивалентную емкость конденсаторов, соединенных последовательно и параллельно
- Вычислить разность потенциалов на пластинах и заряд на пластинах конденсатора в сети и определить полезную емкость сети конденсаторов.
Несколько конденсаторов могут быть соединены вместе для использования в различных приложениях.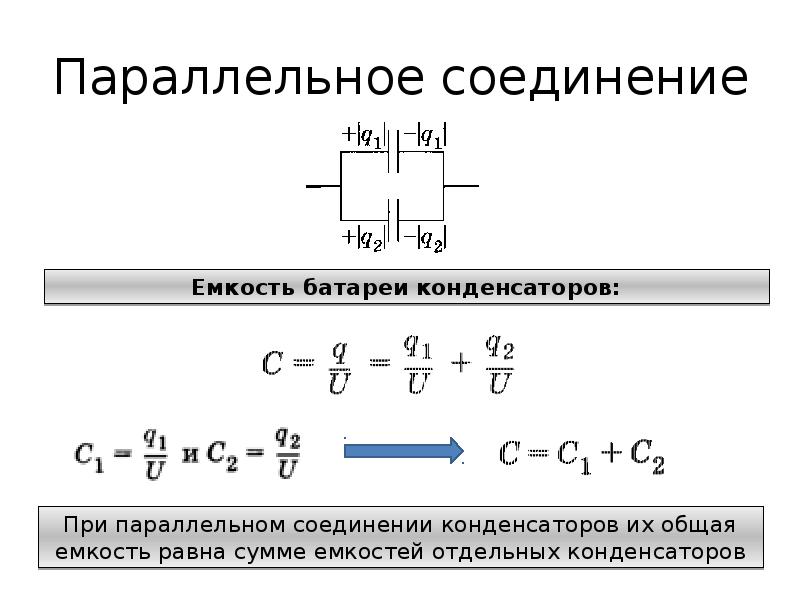 Несколько подключений конденсаторов ведут себя как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения. Конденсаторы могут быть организованы в два простых и распространенных типа соединений, известных как серии и параллельно , для которых мы можем легко вычислить общую емкость. Эти две основные комбинации, последовательная и параллельная, также могут использоваться как часть более сложных соединений.
Несколько подключений конденсаторов ведут себя как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения. Конденсаторы могут быть организованы в два простых и распространенных типа соединений, известных как серии и параллельно , для которых мы можем легко вычислить общую емкость. Эти две основные комбинации, последовательная и параллельная, также могут использоваться как часть более сложных соединений.
Серия конденсаторов
Рисунок 4.2.1 иллюстрирует последовательную комбинацию трех конденсаторов, расположенных в ряд внутри схемы. Как и в случае любого конденсатора, емкость комбинации связана с зарядом и напряжением с помощью уравнения 4.1.1. Когда эта последовательная комбинация подключена к аккумулятору с напряжением В, , каждый из конденсаторов получает одинаковый заряд. Чтобы объяснить, сначала обратите внимание, что заряд на пластине, подключенной к положительной клемме аккумулятора, есть, а заряд на пластине, подключенной к отрицательной клемме. Затем на других пластинах индуцируются заряды, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю. Однако падение потенциала на одном конденсаторе может отличаться от падения потенциала на другом конденсаторе, потому что, как правило, конденсаторы могут иметь разные емкости. Последовательная комбинация двух или трех конденсаторов напоминает один конденсатор с меньшей емкостью. Как правило, любое количество последовательно соединенных конденсаторов эквивалентно одному конденсатору, емкость которого (называемая эквивалентной емкостью ) меньше наименьшей из емкостей в последовательной комбинации.Заряд этого эквивалентного конденсатора такой же, как заряд любого конденсатора в последовательной комбинации: то есть , все конденсаторы последовательной комбинации имеют одинаковый заряд . Это происходит из-за сохранения заряда в цепи. Когда заряд в последовательной цепи снимается с пластины первого конденсатора (который мы обозначаем как), он должен быть помещен на пластину второго конденсатора (который мы обозначаем как), и так далее.
Затем на других пластинах индуцируются заряды, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю. Однако падение потенциала на одном конденсаторе может отличаться от падения потенциала на другом конденсаторе, потому что, как правило, конденсаторы могут иметь разные емкости. Последовательная комбинация двух или трех конденсаторов напоминает один конденсатор с меньшей емкостью. Как правило, любое количество последовательно соединенных конденсаторов эквивалентно одному конденсатору, емкость которого (называемая эквивалентной емкостью ) меньше наименьшей из емкостей в последовательной комбинации.Заряд этого эквивалентного конденсатора такой же, как заряд любого конденсатора в последовательной комбинации: то есть , все конденсаторы последовательной комбинации имеют одинаковый заряд . Это происходит из-за сохранения заряда в цепи. Когда заряд в последовательной цепи снимается с пластины первого конденсатора (который мы обозначаем как), он должен быть помещен на пластину второго конденсатора (который мы обозначаем как), и так далее.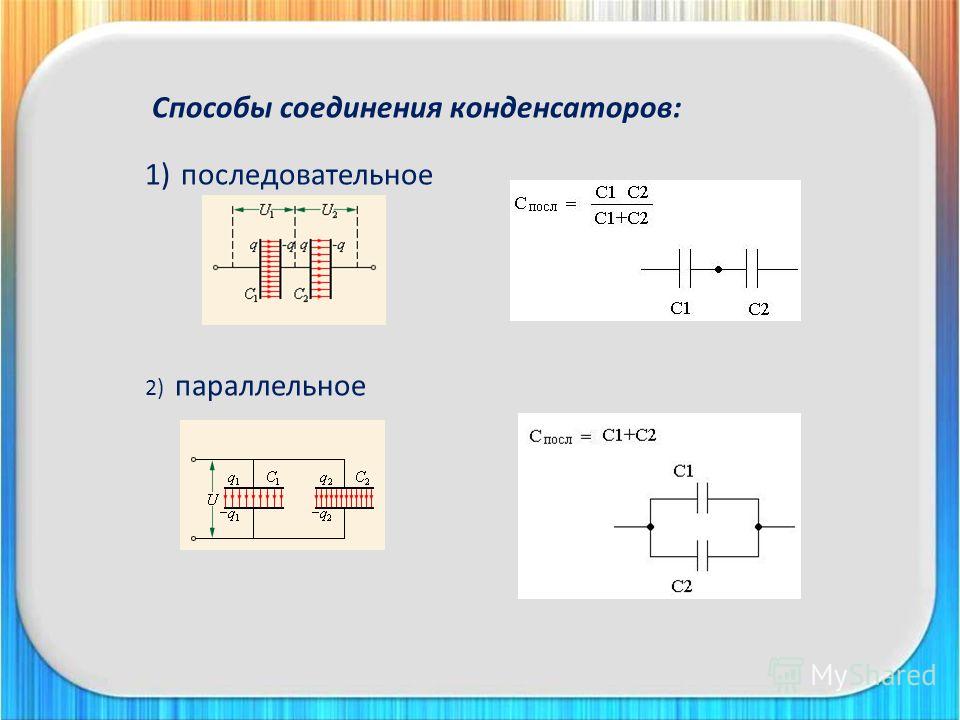
(рисунок 4.2.1)
Рисунок 4.2.1 (a) Три конденсатора соединены последовательно. Величина заряда на каждой пластине. (б) Сеть конденсаторов в (а) эквивалентна одному конденсатору, который имеет меньшую емкость, чем любая из отдельных емкостей в (а), и заряд на его пластинах равен.
Мы можем найти выражение для полной (эквивалентной) емкости, рассматривая напряжения на отдельных конденсаторах. Потенциалы на конденсаторах, и равны, соответственно,, и ,. Эти потенциалы должны в сумме равняться напряжению батареи, давая следующий баланс потенциалов:
Потенциал измеряется на эквивалентном конденсаторе, который держит заряд и имеет эквивалентную емкость.Вводя выражения для, и, получаем
Отменяя заряд, получаем выражение, содержащее эквивалентную емкость трех последовательно соединенных конденсаторов:
Это выражение можно обобщить для любого количества конденсаторов в последовательной сети.
КОМБИНАЦИЯ СЕРИИ
Для конденсаторов, соединенных последовательным соединением , величина, обратная эквивалентной емкости, является суммой обратных величин индивидуальных емкостей:
(4.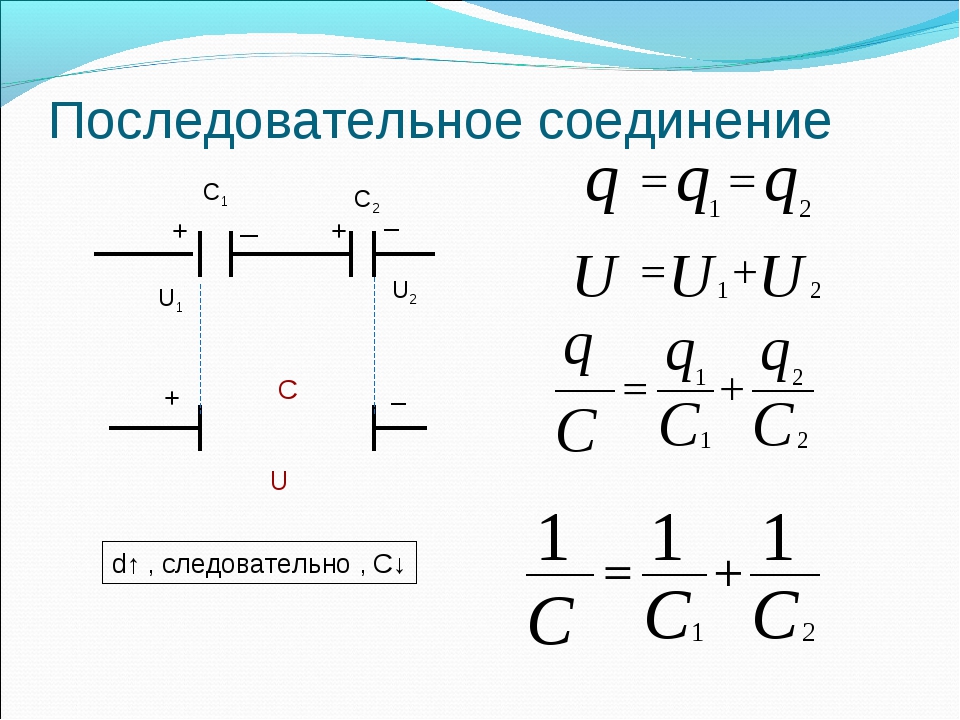 2.1)
2.1)
ПРИМЕР 4.2.1
Эквивалентная емкость последовательной сети
Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их отдельные емкости равны, и.
Стратегия
Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение 4.2.1 с тремя членами.
Решение
Вводим заданные емкости в уравнение 4.2.1:
Теперь инвертируем этот результат и получаем.
Значение
Обратите внимание, что в последовательной сети конденсаторов эквивалентная емкость всегда меньше наименьшей отдельной емкости в сети.
Параллельная комбинация конденсаторов
Параллельная комбинация трех конденсаторов, одна пластина каждого конденсатора подключена к одной стороне цепи, а другая пластина подключена к другой стороне, показана на рисунке 4.2.2 (а). Поскольку конденсаторы соединены параллельно, , все они имеют одинаковое напряжение на своих пластинах .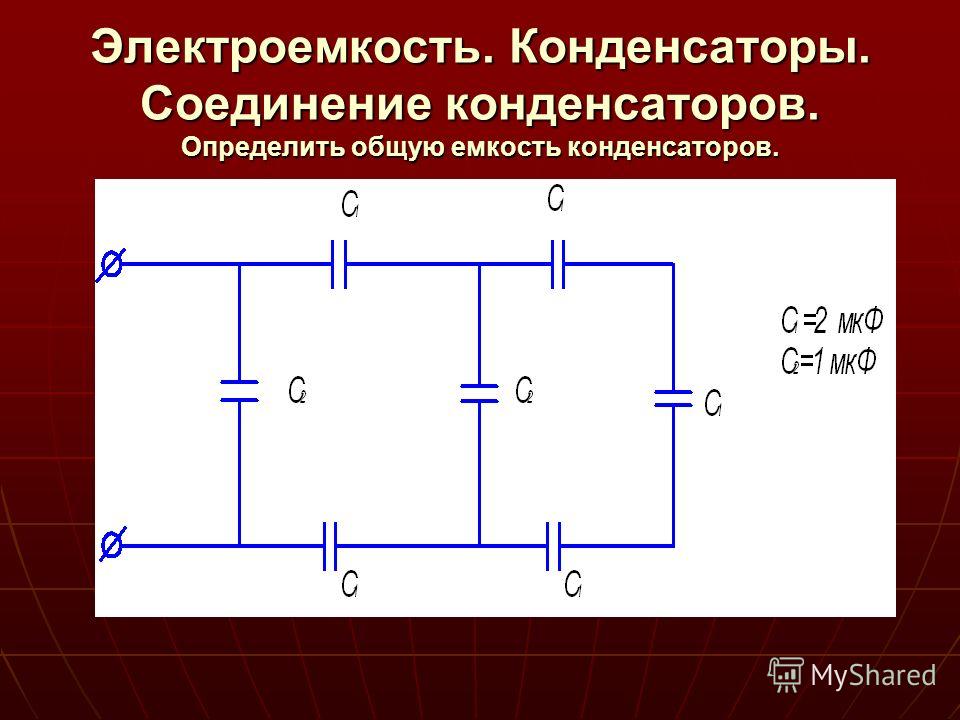 Однако каждый конденсатор в параллельной сети может накапливать свой заряд. Чтобы найти эквивалентную емкость параллельной сети, отметим, что общий заряд, накопленный в сети, представляет собой сумму всех отдельных зарядов:
Однако каждый конденсатор в параллельной сети может накапливать свой заряд. Чтобы найти эквивалентную емкость параллельной сети, отметим, что общий заряд, накопленный в сети, представляет собой сумму всех отдельных зарядов:
В левой части этого уравнения используется соотношение, которое справедливо для всей сети. В правой части уравнения мы используем соотношения, и для трех конденсаторов в сети.Таким образом получаем
Это уравнение в упрощенном виде представляет собой выражение для эквивалентной емкости параллельной сети из трех конденсаторов:
Это выражение легко обобщается на любое количество конденсаторов, включенных параллельно в сеть.
ПАРАЛЛЕЛЬНАЯ КОМБИНАЦИЯ
Для конденсаторов, соединенных в параллельную комбинацию , эквивалентная (полезная) емкость представляет собой сумму всех индивидуальных емкостей в сети,
(4.2.2)
(рисунок 4.2.2)
Рисунок 4. 2.2 (a) Три конденсатора подключены параллельно. Каждый конденсатор подключен напрямую к батарее. (b) Заряд эквивалентного конденсатора представляет собой сумму зарядов отдельных конденсаторов.
2.2 (a) Три конденсатора подключены параллельно. Каждый конденсатор подключен напрямую к батарее. (b) Заряд эквивалентного конденсатора представляет собой сумму зарядов отдельных конденсаторов.
ПРИМЕР 4.2.2
Эквивалентная емкость параллельной сети
Найдите полезную емкость для трех конденсаторов, соединенных параллельно, учитывая их индивидуальные емкости, и.
Стратегия
Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение 4.2.2 с тремя членами.
Решение
Ввод заданных емкостей в уравнение 4.2.2 дает
Значение
Обратите внимание, что в параллельной сети конденсаторов эквивалентная емкость всегда больше, чем любая из отдельных емкостей в сети.
Конденсаторные сети обычно представляют собой комбинацию последовательных и параллельных соединений, как показано на Рисунке 4.2.3. Чтобы найти чистую емкость таких комбинаций, мы определяем части, которые содержат только последовательные или только параллельные соединения, и находим их эквивалентные емкости. Мы повторяем этот процесс, пока не сможем определить эквивалентную емкость всей сети. Следующий пример иллюстрирует этот процесс.
Мы повторяем этот процесс, пока не сможем определить эквивалентную емкость всей сети. Следующий пример иллюстрирует этот процесс.
(рисунок 4.2.3)
ПРИМЕР 4.2.4
Сеть конденсаторов
Определите полезную емкость комбинации конденсаторов, показанной на Рисунке 4.2.4 при емкостях,,. Когда в комбинации сохраняется разность потенциалов, найдите заряд и напряжение на каждом конденсаторе.
(рисунок 4.2.4)
Рисунок 4.2.4 (a) Комбинация конденсаторов. (b) Эквивалентная комбинация из двух конденсаторов.
Стратегия
Сначала мы вычисляем полезную емкость параллельного соединения и. Тогда — чистая емкость последовательного соединения и. Мы используем соотношение, чтобы найти заряды, и, и напряжения,, и на конденсаторах, и, соответственно.
Решение
Эквивалентная емкость для и составляет
Вся комбинация из трех конденсаторов эквивалентна двум последовательным конденсаторам,
Рассмотрим эквивалентную комбинацию из двух конденсаторов на рис. 4.2.4 (b). Поскольку конденсаторы включены последовательно, они имеют одинаковый заряд. Кроме того, конденсаторы разделяют разность потенциалов, поэтому
4.2.4 (b). Поскольку конденсаторы включены последовательно, они имеют одинаковый заряд. Кроме того, конденсаторы разделяют разность потенциалов, поэтому
Теперь разность потенциалов на конденсаторе
.
Поскольку конденсаторы и подключены параллельно, они имеют одинаковую разность потенциалов:
Следовательно, заряды на этих двух конденсаторах равны, соответственно,
Значение
Как и ожидалось, чистая плата за параллельную комбинацию и составляет.
ПРОВЕРЬТЕ ПОНИМАНИЕ 4.5
Кандела Цитаты
CC лицензионный контент, конкретная атрибуция
- Загрузите бесплатно по адресу http://cnx.org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
Последовательные и параллельные конденсаторы
Последовательные конденсаторы
Давайте подключим n из конденсаторов последовательно . Через эту последовательную комбинацию конденсаторов подается напряжение V вольт.
Через эту последовательную комбинацию конденсаторов подается напряжение V вольт.
Рассмотрим емкость конденсаторов C 1 , C 2 , C 3 …… .C n соответственно, а эквивалентная емкость последовательной комбинации конденсаторов равна C. Падения напряжения на конденсаторах равны считаются V 1 , V 2 , V 3 …… .V n соответственно.
Теперь, если Q кулонов будет зарядом, передаваемым от источника через эти конденсаторы, тогда,
Поскольку заряд, накопленный в каждом конденсаторе и I, вся последовательная комбинация конденсаторов будет одинаковой, и это рассматривается как Q.
Теперь уравнение (i) можно записать как:
Параллельные конденсаторы
Конденсатор предназначен для хранения энергии в форме своего электрического поля, то есть электростатической энергии. Когда возникает необходимость в увеличении емкости накопления электростатической энергии, требуется подходящий конденсатор с увеличенной емкостью.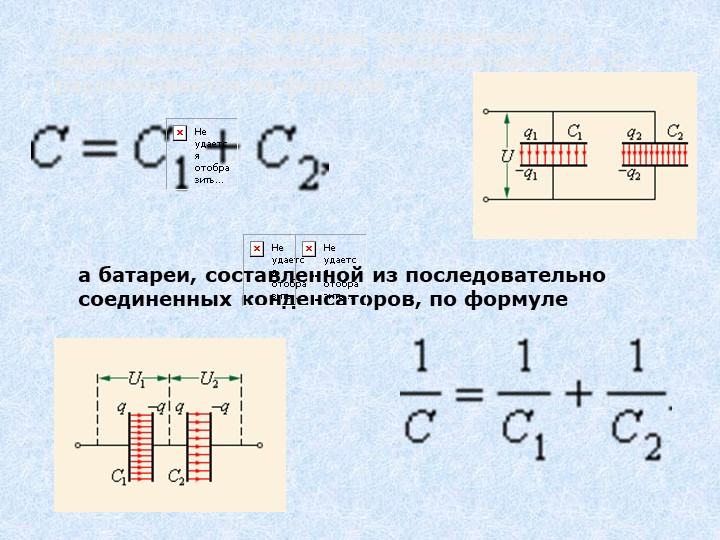 Конденсатор состоит из двух металлических пластин, соединенных параллельно и разделенных диэлектрической средой, такой как стекло, слюда, керамика и т. Д. Диэлектрик обеспечивает непроводящую среду между пластинами и обладает уникальной способностью удерживать заряд, а также способностью конденсатора для хранения заряда определяется как емкость конденсатора.Когда к пластинам конденсатора подключается источник напряжения, на одной пластине осаждается положительный заряд, а на другой — отрицательный. Общая сумма накопленного заряда (q) прямо пропорциональна источнику напряжения (В), так что,
Конденсатор состоит из двух металлических пластин, соединенных параллельно и разделенных диэлектрической средой, такой как стекло, слюда, керамика и т. Д. Диэлектрик обеспечивает непроводящую среду между пластинами и обладает уникальной способностью удерживать заряд, а также способностью конденсатора для хранения заряда определяется как емкость конденсатора.Когда к пластинам конденсатора подключается источник напряжения, на одной пластине осаждается положительный заряд, а на другой — отрицательный. Общая сумма накопленного заряда (q) прямо пропорциональна источнику напряжения (В), так что,
Где, C — константа пропорциональности, то есть емкость. Его значение зависит от физических размеров конденсатора.
Где ε = диэлектрическая проницаемость, A = эффективная площадь пластины и d = расстояние между пластинами.
Чтобы увеличить значение емкости конденсатора, два или более конденсатора подключаются параллельно как две одинаковые пластины, соединенные вместе, затем их эффективная площадь перекрытия складывается с постоянным интервалом между ними, и, следовательно, их эквивалентное значение емкости становится равным удвоение (C ∝ A) индивидуальной емкости. Конденсаторная батарея используется в различных производственных и перерабатывающих отраслях и включает в себя конденсаторы, включенные параллельно, чтобы обеспечить требуемую емкость, требуемую путем регулирования соединения конденсаторов, подключенных параллельно, и, таким образом, она эффективно используется в качестве статического компенсатора для баланса реактивной мощности. в компенсации энергосистемы. Когда два конденсатора подключены параллельно, тогда напряжение (В) на каждом конденсаторе одинаковое, т.е. (V экв = V a = V b ) и ток (i экв ) делится на две части i а и я б .Как известно,
Конденсаторная батарея используется в различных производственных и перерабатывающих отраслях и включает в себя конденсаторы, включенные параллельно, чтобы обеспечить требуемую емкость, требуемую путем регулирования соединения конденсаторов, подключенных параллельно, и, таким образом, она эффективно используется в качестве статического компенсатора для баланса реактивной мощности. в компенсации энергосистемы. Когда два конденсатора подключены параллельно, тогда напряжение (В) на каждом конденсаторе одинаковое, т.е. (V экв = V a = V b ) и ток (i экв ) делится на две части i а и я б .Как известно,
Подставляя значение q из уравнения (1) в уравнение выше,
Последний член становится равным нулю (поскольку емкость конденсатора постоянна). Следовательно,
Применение закона Кирхгофа по току на входящем узле параллельного соединения
В итоге мы получаем,
Следовательно, всякий раз, когда n конденсаторов подключаются параллельно, эквивалентная емкость всего соединения определяется следующим уравнением, которое похоже на аналогичное эквивалентному сопротивлению резисторов при последовательном включении.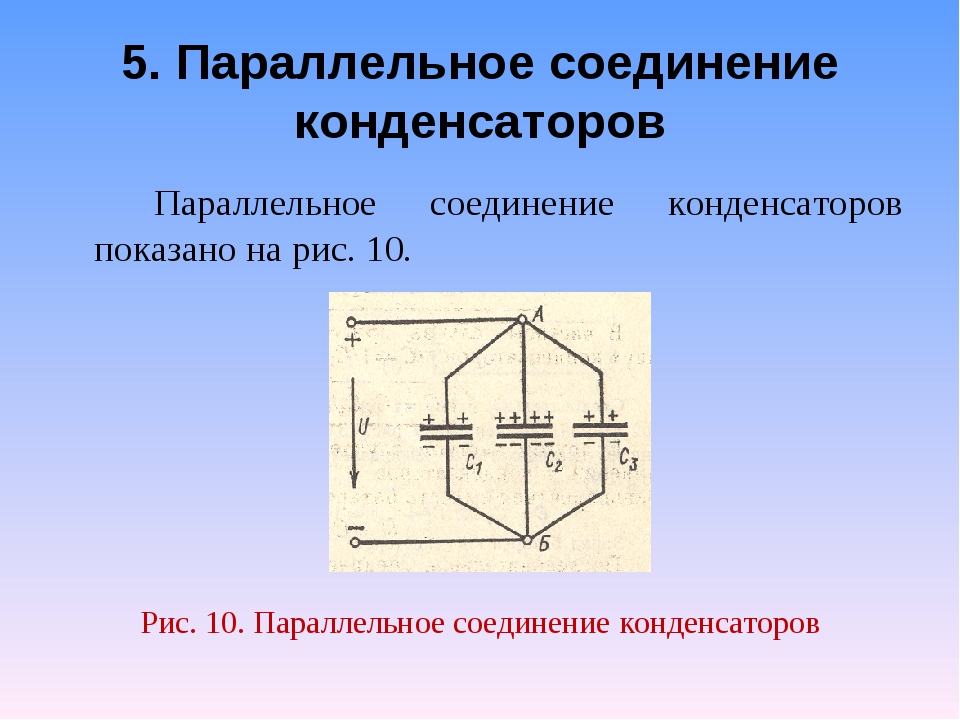
Метод определения выражения эквивалентной емкости параллельного конденсатора
Подключим n конденсаторов параллельно через источник напряжения V вольт.
Рассмотрим емкость конденсаторов C 1 , C 2 , C 3 … ..C n соответственно, а эквивалентная емкость комбинации конденсаторов равна C. Как и у конденсаторы подключаются параллельно , вроде ток заряда в каждом конденсаторе будет одинаковым.Общий заряд параллельной комбинации будет разделен в каждом конденсаторе в соответствии с его значением емкости, но напряжение на каждом конденсаторе будет одинаковым, а в установившемся режиме оно точно равно приложенному напряжению.
Где, Q 1 , Q 2 , Q 3 , …… .Q n — заряд конденсатора C 1 , C 2 , C 3 … .. C n соответственно.
Теперь уравнение (2) можно записать как:
Последовательные и параллельные конденсаторы
Последовательные и параллельные конденсаторы
Последовательные и параллельные конденсаторы
Конденсатор — это устройство для хранения разделенного заряда и
поэтому накапливается электростатическая потенциальная энергия. Цепи часто содержат
Цепи часто содержат
более одного конденсатора.
Рассмотрим два конденсатора в
параллельно , как показано справа
Когда батарея подключена, электроны будут течь до тех пор, пока потенциал
точка A совпадает с потенциалом положительной клеммы аккумулятора и
потенциал точки B равен потенциалу отрицательной клеммы
аккумулятор. Таким образом, разность потенциалов между пластинами обоих конденсаторов равна
V A — V B = V bat .Имеем C 1 = Q 1 / V bat
и C 2 = Q 2 / V bat , где Q 1 —
заряд конденсатора C 1 , а Q 2 — заряд конденсатора
С 2 . Пусть C — эквивалентная емкость двух конденсаторов в
параллельно, то есть C = Q / V bat , где Q = Q 1 + Q 2 . Тогда C = (Q 1 + Q 2 ) / V bat = C 1 + C 2 .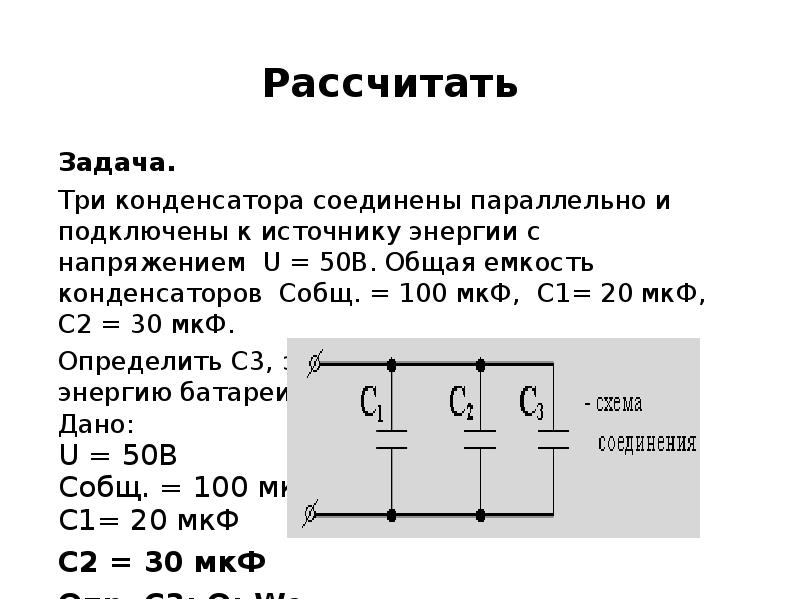
Для конденсаторов, включенных параллельно, емкости добавляют.
Для более двух конденсаторов
имеем
C = C 1 + C 2 + C 3 + C 4 + ….
Рассмотрим два конденсатора серии , как показано справа.
Пусть Q представляет собой общий заряд на верхней пластине C 1 ,
который затем индуцирует заряд -Q на своей нижней пластине. Заряд на
нижняя пластина C 2 будет -Q, что, в свою очередь, вызывает заряд
+ Q на верхней пластине, как показано.
Пусть V 1 и V 2 представляют разности потенциалов
между обкладками конденсаторов С 1 и С 2 соответственно. потом
V 1 + V 2 = V bat , или (Q / C 1 ) + (Q / C 2 )
= Q / C или (1 / C 1 ) + (1 / C 2 ) = 1 / C. Более двух
конденсаторы последовательно имеем
1 / C = 1 / C 1 + 1 / C 2 +
1 / C 3 + 1 / C 4 +. …
…
где C — эквивалентная емкость двух конденсаторов.
Для конденсаторов, включенных последовательно, величина, обратная их
эквивалентная емкость равна сумме обратных величин их индивидуальных
емкости.
Проблема:
Какую общую емкость можно получить, подключив 5 мкФ и 8 мкФ
конденсатор вместе?
Решение:
- Рассуждение:
Мы можем подключать конденсаторы последовательно или параллельно.
Чтобы получить наибольшую емкость, мы
необходимо подключить конденсаторы параллельно.
Чтобы получить наименьшую емкость, мы должны подключить
конденсаторы последовательно. - Детали расчета:
Параллельное подключение конденсаторов:
C наибольший = (5 + 8) мкФ
= 13 мкФ.
Последовательное соединение конденсаторов.
1 / C наименьшее = (1/5 + 1/8) (мкФ) -1 =
13 / (40 мкФ) = 0,325 / мкФ.
C наименьший = 40/13 мкФ = 3.077 мкФ.
.

 31)
31)