Закон сохранения энергии, общая форма. Полная энергия: механическая, кинетическая, потенциальная. Формулировка, формулы
Тестирование онлайн
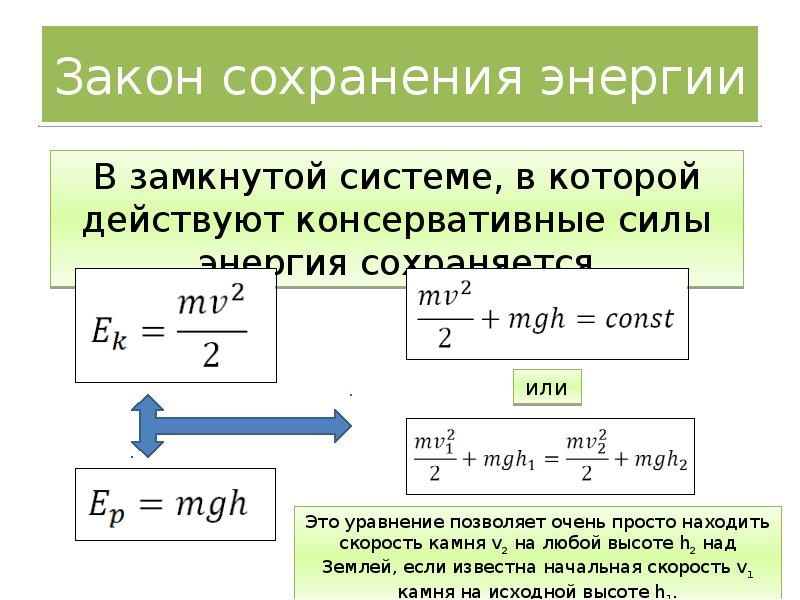
Закон сохранения энергии
Полная механическая энергия замкнутой системы тел остается неизменной
Закон сохранения энергии можно представить в виде
Если между телами действуют силы трения, то закон сохранения энергии видоизменяется. Изменение полной механической энергии равно работе сил трения
Рассмотрим свободное падение тела с некоторой высоты h2. Тело еще не движется (допустим, мы его держим), скорость равна нулю, кинетическая энергия равна нулю. Потенциальная энергия максимальная, так как сейчас тело находится выше всего от земли, чем в состоянии 2 или 3.
В состоянии 2 тело обладает кинетической энергией (так как уже развило скорость), но при этом потенциальная энергия уменьшилась, так как h3 меньше h2. Часть потенциальной энергии перешло в кинетическую.
Состояние 3 — это состояние перед самой остановкой. Тело как бы только-только дотронулось до земли, при этом скорость максимальная. Тело обладает максимальной кинетической энергией. Потенциальная энергия равна нулю (тело находится на земле).
Полные механические энергии равны между собой , если пренебрегать силой сопротивления воздуха. Например, максимальная потенциальная энергия в состоянии 1 равна максимальной кинетической энергии в состоянии 3.
А куда потом исчезает кинетическая энергия? Исчезает бесследно? Опыт показывает, что механическое движение никогда не исчезает бесследно и никогда оно не возникает само собой. Во время торможения тела произошло нагревание поверхностей. В результате действия сил трения кинетическая энергия не исчезла, а превратилась во внутреннюю энергию теплового движения молекул.
При любых физических взаимодействиях энергия не возникает и не исчезает, а только превращается из одной формы в другую.
Главное запомнить
1) Суть закона сохранения энергии
Закон сохранения энергии — это.
 .. Что такое Закон сохранения энергии?
.. Что такое Закон сохранения энергии?
Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии.
С фундаментальной точки зрения, согласно теореме Нётер, закон сохранения энергии является следствием однородности времени, то есть независимостью законов физики от момента времени, в который рассматривается система. В этом смысле закон сохранения энергии является универсальным, то есть присущим системам самой разной физической природы. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря различающимся для разных систем.
В различных разделах физики по историческим причинам закон сохранения энергии формулировался независимо, в связи с чем были введены различные виды энергии. Говорят, что возможен переход энергии одного типа в другой, но полная энергия системы, равная сумме отдельных видов энергий, сохраняется. Ввиду условности деления энергии на различные виды, такое деление не всегда может быть произведено однозначно.
Для каждого вида энергии закон сохранения может иметь свою, отличающуюся от универсальной, формулировку. Например, в классической механике был сформулирован закон сохранения механической энергии, в термодинамике — первое начало термодинамики, а в электродинамике — теорема Пойнтинга.
С математической точки зрения закон сохранения энергии эквивалентен утверждению, что система дифференциальных уравнений, описывающая динамику данной физической системы, обладает первым интегралом движения, связанным с симметричностью уравнений относительно сдвига во времени.
Фундаментальный смысл закона
Фундаментальный смысл закона сохранения энергии раскрывается теоремой Нётер. Согласно этой теореме каждый закон сохранения однозначно соответствует той или иной симметрии уравнений, описывающих физическую систему. В частности, закон сохранения энергии эквивалентен однородности времени, то есть независимости всех законов, описывающих систему, от момента времени, в который система рассматривается.
Согласно этой теореме каждый закон сохранения однозначно соответствует той или иной симметрии уравнений, описывающих физическую систему. В частности, закон сохранения энергии эквивалентен однородности времени, то есть независимости всех законов, описывающих систему, от момента времени, в который система рассматривается.
Вывод этого утверждения может быть произведён, например, на основе лагранжева формализма[1]. Если время однородно, то функция Лагранжа, описывающая систему, не зависит явно от времени, поэтому полная её производная по времени имеет вид:
Здесь — функция Лагранжа, — обобщённые координаты и их первые и вторые производные по времени соответственно. Воспользовавшись уравнениями Лагранжа, заменим производные на выражение :
Перепишем последнее выражение в виде
Сумма, стоящая в скобках, по определению называется энергией системы и в силу равенства нулю полной производной от неё по времени она является интегралом движения (то есть сохраняется).
Частные формы закона сохранения энергии
Классическая механика
Формулировка
В ньютоновской механике формулируется частный случай закона сохранения энергии — Закон сохранения механической энергии, звучащий следующим образом[2]
Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.
Проще говоря, при отсутствии диссипативных сил (например, сил трения) механическая энергия не возникает из ничего и не может исчезнуть никуда.
Примеры
Классическим примером этого утверждения являются пружинный или математический маятники с пренебрежимо малым затуханием. В случае пружинного маятника в процессе колебаний потенциальная энергия деформированной пружины (имеющая максимум в крайних положениях груза) переходит в кинетическую энергию груза (достигающую максимума в момент прохождения грузом положения равновесия) и обратно[3]. В случае математического маятника[4] аналогично ведёт себя потенциальная энергия груза в поле силы тяжести.
В случае математического маятника[4] аналогично ведёт себя потенциальная энергия груза в поле силы тяжести.
Вывод из уравнений Ньютона
Закон сохранения механической энергии может быть выведен из второго закона Ньютона[5], если учесть, что в консервативной системе все силы, действующие на тело, потенциальны и, следовательно, могут быть представлены в виде
- ,
где — потенциальная энергия материальной точки ( — радиус-вектор точки пространства). В этом случае второй закон Ньютона для одной частицы имеет вид
- ,
где — масса частицы, — вектор её скорости. Скалярно домножив обе части данного уравнения на скорость частицы и приняв во внимание, что , можно получить
Путём элементарных операций это выражение может быть приведено к следующему виду
Отсюда непосредственно следует, что выражение, стоящее под знаком дифференцирования по времени, сохраняется. Это выражение и называется механической энергией материальной точки.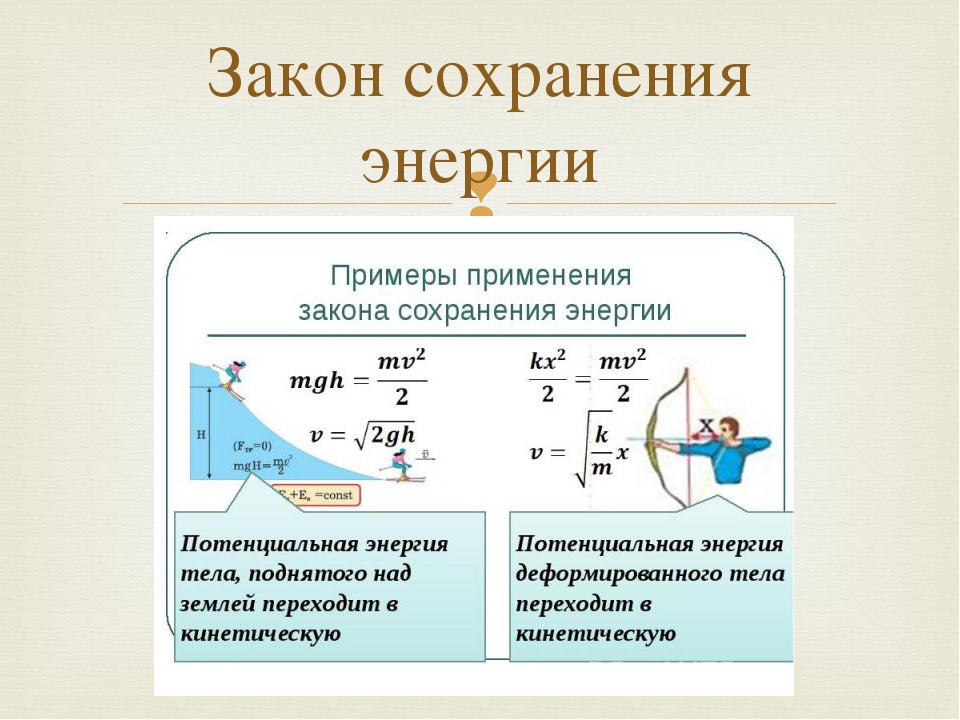 Первый член в сумме отвечает кинетической энергии, второй — потенциальной.
Первый член в сумме отвечает кинетической энергии, второй — потенциальной.
Этот вывод может быть легко обобщён на систему материальных точек[2].
Термодинамика
В термодинамике исторически закон сохранения формулируется в виде первого принципа термодинамики:
Изменение внутренней энергии термодинамической системы при переходе её из одного состояния в другое равно сумме работы внешних сил над системой и количества теплоты, переданного системе, и не зависит от способа, которым осуществляется этот переход
или альтернативно[6]:
Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил
В математической формулировке это может быть выражено следующим образом:
- ,
где введены обозначения — количество теплоты, полученное системой, — изменение внутренней энергии системы, — работа, совершённая системой.
Закон сохранения энергии, в частности, утверждает, что не существует вечных двигателей первого рода, то есть невозможны такие процессы, единственным результатом которых было бы производство работы без каких-либо изменений в других телах[6].
Гидродинамика
В гидродинамике идеальной жидкости закон сохранения энергии традиционно формулируется в виде уравнения Бернулли: вдоль линий тока остаётся постоянной сумма[7]
Здесь введены следующие обозначения: — скорость потока жидкости, — тепловая функция жидкости, — ускорение свободного падения, — координата точки в направлении силы тяжести. Если внутренняя энергия жидкости не меняется (жидкость не нагревается и не охлаждается), то уравнение Бернулли может быть переписано в виде[8]
где — давление жидкости, — плотность жидкости. Для несжимаемой жидкости плотность является постоянной величиной, поэтому в последнем уравнении может быть выполнено интегрирование[8]:
Электродинамика
В электродинамике закон сохранения энергии исторически формулируется в виде теоремы Пойнтинга[9][10](иногда также называемой теоремой Умова—Пойнтинга[11]), связывающей плотность потока электромагнитной энергии с плотностью электромагнитной энергии и плотностью джоулевых потерь. В словесной форме теорема может быть сформулирована следующим образом:
В словесной форме теорема может быть сформулирована следующим образом:
Изменение электромагнитной энергии, заключённой в неком объёме, за некий интервал времени равно потоку электромагнитной энергии через поверхность, ограничивающую данный объём, и количеству тепловой энергии, выделившейся в данном объёме, взятой с обратным знаком.
Математически это выражается в виде (здесь и ниже в разделе использована Гауссова система единиц)
где — некий объём, — поверхность, ограничивающая этот объём,
- — плотность электромагнитной энергии,
- — вектор Пойнтинга,
— плотность тока, — напряжённость электрического поля, — индукция электрического поля, — напряжённость магнитного поля, — индукция магнитного поля.
Этот же закон математически может быть записан в дифференциальной форме:
Нелинейная оптика
Основная статья: Соотношения Мэнли — Роу
В нелинейной оптике рассматривается распространение оптического (и вообще электромагнитного) излучения в среде с учётом многоквантового взаимодействия этого излучения с веществом среды. В частности, широкий круг исследований посвящён задачам так называемых трёх- и четырёхволновоого взаимодействий, в которых происходит взаимодействие соответственно трёх или четырёх квантов излучения. Поскольку каждый отдельный акт такого взаимодействия подчиняется законам сохранения энергии и импульса, существует возможность сформулировать достаточно общие соотношения между макроскопическими параметрами взаимодействующих волн. Эти соотношения носят название соотношений Мэнли — Роу.
В частности, широкий круг исследований посвящён задачам так называемых трёх- и четырёхволновоого взаимодействий, в которых происходит взаимодействие соответственно трёх или четырёх квантов излучения. Поскольку каждый отдельный акт такого взаимодействия подчиняется законам сохранения энергии и импульса, существует возможность сформулировать достаточно общие соотношения между макроскопическими параметрами взаимодействующих волн. Эти соотношения носят название соотношений Мэнли — Роу.
В качестве примера рассмотрим явление сложения частот света: генерацию в нелинейной среде излучения с частотой , равной сумме частот двух других волн и . Этот процесс является частным случаем трёхволновых процессов: при взаимодействии двух квантов исходных волн с веществом они поглощаются с испусканием третьего кванта. Согласно закону сохранения энергии, сумма энергий двух исходных квантов должна быть равна энергии нового кванта:
Из этого равенства непосредственно следует одно из соотношений Мэнли — Роу:
- ,
которое, собственно, и выражает тот факт, что частота генерируемого излучения равна сумме частот двух исходных волн.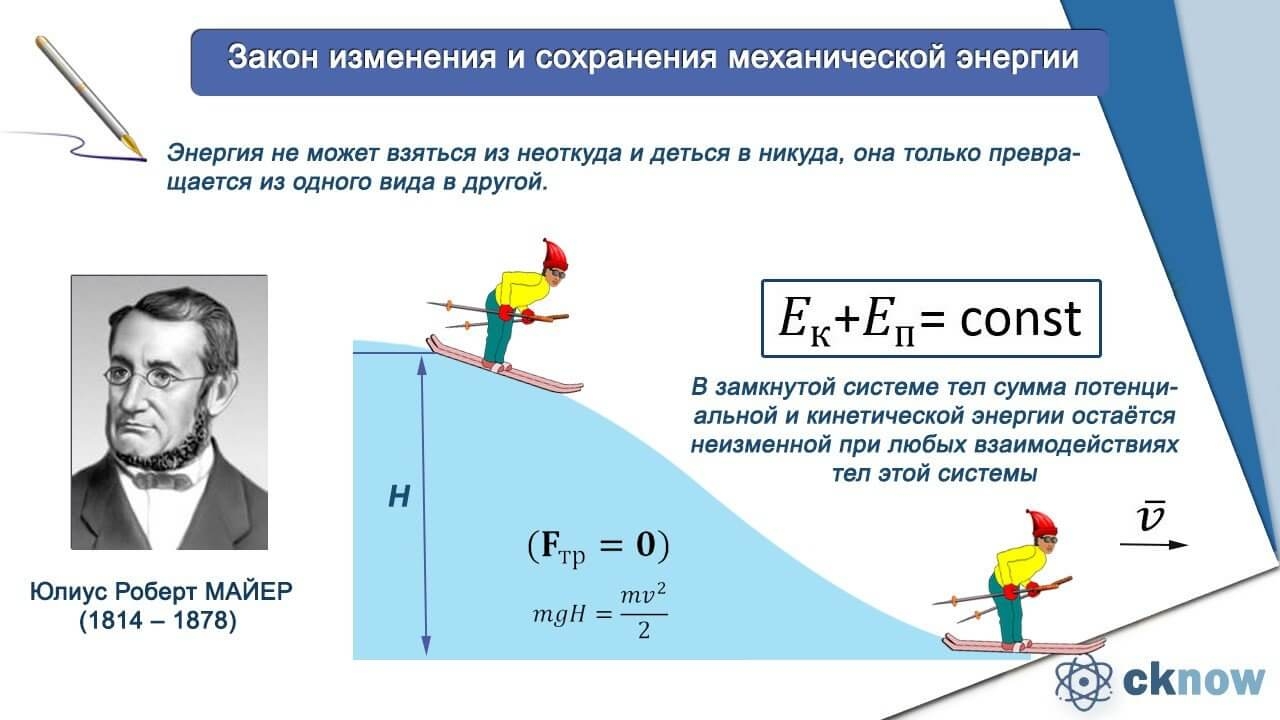
Релятивистская механика
В релятивистской механике вводится понятие 4-вектора энергии-импульса (или просто четырёхимпульса)[12]. Его введение позволяет записать законы сохранения канонического импульса и энергии в единой форме, которая к тому же является лоренц-ковариантной, то есть не меняется при переходе из одной инерциальной системы отсчёта в другую. Например, при движении заряженной материальной точки в электромагнитном поле ковариантная форма закона сохранения имеет вид
- ,
где — канонический четырёхимпульс частицы, — четырёхимпульс частицы, — энергия частицы, — четырёхвектор потенциала электромагнитного поля , — электрический заряд и масса частицы, — собственное время частицы.
Также важным является тот факт, что даже при невыполнении закона сохранения энергии-импульса (например, в открытой системе) сохраняется модуль этого 4-вектора, с точностью до размерного множителя имеющий смысл энергии покоя частицы[12]:
Квантовая механика
В квантовой механике также возможно формулирование закона сохранения энергии для изолированной системы. Так, в шредингеровском представлении при отсутствии внешних переменных полей гамильтониан системы не зависит от времени и можно показать[13], что волновая функция, отвечающая решению уравнения Шредингера, может быть представлена в виде:
Так, в шредингеровском представлении при отсутствии внешних переменных полей гамильтониан системы не зависит от времени и можно показать[13], что волновая функция, отвечающая решению уравнения Шредингера, может быть представлена в виде:
Здесь — волновая функция системы, — совокупность переменных, от которых зависит состояние системы в данном представлении, — собственные функции и собственные значения оператора Гамильтона, — постоянная Планка, — некоторые постоянные комплексные коэффициенты, характеризующие состояние системы. По определению средней энергией квантовой системы, описываемой волновой функцией, называется интеграл
где — гамильтониан системы. Несложно видеть, что этот интеграл не зависит от времени:
где также использовано свойство ортонормированности собственных функций гамильтониана[14]. Таким образом, энергия замкнутой системы сохраняется.
Следует, однако, отметить, что по сравнению с классической механикой у квантового закона сохранения энергии имеется одно существенное отличие. Дело в том, что для экспериментальной проверки выполнения закона необходимо провести измерение, представляющее собой взаимодействие исследуемой системы с неким прибором. В процессе измерения система, вообще говоря, более не является изолированной и её энергия может не сохраняться (происходит обмен энергией с прибором). В рамках классической физики, однако, это влияние прибора всегда может быть сделано сколь угодно малым, в то время как в квантовой механике имеются фундаментальные ограничения на то, насколько малым может быть возмущение системы в процессе измерения. Это приводит к так называемому принципу неопределённости Гейзенберга, который в математической формулировке может быть выражен в следующем виде:
Дело в том, что для экспериментальной проверки выполнения закона необходимо провести измерение, представляющее собой взаимодействие исследуемой системы с неким прибором. В процессе измерения система, вообще говоря, более не является изолированной и её энергия может не сохраняться (происходит обмен энергией с прибором). В рамках классической физики, однако, это влияние прибора всегда может быть сделано сколь угодно малым, в то время как в квантовой механике имеются фундаментальные ограничения на то, насколько малым может быть возмущение системы в процессе измерения. Это приводит к так называемому принципу неопределённости Гейзенберга, который в математической формулировке может быть выражен в следующем виде:
- ,
где имеет смысл среднеквадратичного отклонения измеренного значения энергии от среднего значения при проведении серии измерений, — продолжительность взаимодействия системы с прибором в каждом из измерений.
В связи с наличием этого фундаментального ограничения на точность измерений в квантовой механике часто говорят о законе сохранения средней энергии (в смысле среднего значения энергии, полученного в результате серии измерений).
Общая теория относительности
Основная статья: Проблема законов сохранения в общей теории относительности
Являясь обобщением специальной теории относительности, общая теория относительности пользуется обобщением понятия четырёхимпульса — тензором энергии-импульса. Закон сохранения формулируется для тензора энергии-импульса системы и в математической форме имеет вид[15]
где точка с запятой выражает ковариантную производную.
В общей теории относительности закон сохранения энергии, строго говоря, выполняется только локально. Связано это с тем фактом, что этот закон является следствием однородности времени, в то время как в общей теории относительности время неоднородно и испытывает изменения в зависимости от наличия тел и полей в пространстве-времени. Следует отметить, что при должным образом определённом псевдотензоре энергии-импульса гравитационного поля можно добиться сохранения полной энергии гравитационно взаимодействующих тел и полей, включая гравитационное[16]. Однако на данный момент не существует общепризнанного способа введения энергии гравитационного поля, поскольку все предложенные варианты обладают теми или иными недостатками. Например, энергия гравитационного поля принципиально не может быть определена как тензор относительно общих преобразований координат[17].
Однако на данный момент не существует общепризнанного способа введения энергии гравитационного поля, поскольку все предложенные варианты обладают теми или иными недостатками. Например, энергия гравитационного поля принципиально не может быть определена как тензор относительно общих преобразований координат[17].
История открытия
История до XIX века
Философские предпосылки к открытию закона были заложены ещё античными философами. Ясную, хотя ещё не количественную, формулировку дал в «Началах философии» (1644) Рене Декарт[18]:
Когда одно тело сталкивается с другим, оно может сообщить ему лишь столько движения, сколько само одновременно потеряет, и отнять у него лишь столько, насколько оно увеличит своё собственное движение.
Аналогичную точку зрения выразил в XVIII веке М. В. Ломоносов[19]. В письме к Эйлеру он формулирует свой «всеобщий естественный закон» (5 июля 1748 года), повторяя его в диссертации «Рассуждение о твердости и жидкости тел» (1760)[20][21]:
Все перемены, в натуре случающиеся, такого суть состояния, что сколько чего у одного тела отнимется, столько присовокупится к другому, так ежели где убудет несколько материи, то умножится в другом месте… Сей всеобщий естественный закон простирается и в самые правила движения, ибо тело, движущее своею силою другое, столько же оные у себя теряет, сколько сообщает другому, которое от него движение получает[22].
XIX век
Одним из первых экспериментов, подтверждавших закон сохранения энергии, был эксперимент Жозефа Луи Гей-Люссака, проведённый в 1807 году. Пытаясь доказать, что теплоёмкость газа зависит от объёма, он изучал расширение газа в пустоту и обнаружил, что при этом его температура не изменяется. Однако, объяснить этот факт ему не удалось[19].
В начале XIX века рядом экспериментов было показано, что электрический ток может оказывать химическое, тепловое, магнитное и электродинамическое действия. Такое многообразие подвигло М. Фарадея выразить мнение, заключающееся в том, что различные формы, в которых проявляются силы материи, имеют общее происхождение, то есть могут превращаться друг в друга[23]. Эта точка зрения, по своей сути, предвосхищает закон сохранения энергии.
Сади Карно
Сади Карно — французский физик, выполнивший первые работы по установлению количественой связи между работой и теплотой.
Первые работы по установлению количественной связи между совершённой работой и выделившейся теплотой были проведены Сади Карно[23]. В 1824 году им была опубликована небольшая брошюра «Размышления о движущей силе огня и о машинах, способных развивать эту силу» (фр. Réflexions sur la puissance motrice du feu et sur les machines propres а développer cette puissance[24]), которая вначале не получила большой известности, и была случайно обнаружена Клапейроном через 10 лет после издания. Клапейрон придал изложению Карно современную аналитическую и графическую форму и переопубликовал работу под тем же названием в журнале «Journal de l’Ecole Polytechnique». Позднее была также перепечатана в «Анналах Поггендорфа». После ранней смерти Карно от холеры остались дневники, которые были опубликованы его братом. В них, в частности, Карно пишет[25]:
В 1824 году им была опубликована небольшая брошюра «Размышления о движущей силе огня и о машинах, способных развивать эту силу» (фр. Réflexions sur la puissance motrice du feu et sur les machines propres а développer cette puissance[24]), которая вначале не получила большой известности, и была случайно обнаружена Клапейроном через 10 лет после издания. Клапейрон придал изложению Карно современную аналитическую и графическую форму и переопубликовал работу под тем же названием в журнале «Journal de l’Ecole Polytechnique». Позднее была также перепечатана в «Анналах Поггендорфа». После ранней смерти Карно от холеры остались дневники, которые были опубликованы его братом. В них, в частности, Карно пишет[25]:
|
Доподлинно неизвестно, какие именно размышления привели Карно к этому выводу, но по своей сути они являются аналогичными современным представлениям о том, что совершённая над телом работа переходит в его внутреннюю энергию, то есть теплоту. Также в дневниках Карно пишет[26]:
|
Однако, ему не удалось найти более точное количественное соотношение между совершённой работой и выделившимся теплом.
Джеймс Джоуль
Установка Джоуля для измерения механического эквивалента тепла. Груз, расположенный справа, заставлял лопасти, погруженные в воду, вращаться, в результате чего вода нагревалась.
Количественное доказательство закона было дано Джеймсом Джоулем в ряде классических опытов. Он помещал в сосуд с водой соленоид с железным сердечником, вращающийся в поле электромагнита. Джоуль измерял количество теплоты, выделявшееся в результате трения в катушке, в случаях замкнутой и разомкнутой обмотки электромагнита. Сравнивая эти величины он пришёл к выводу, что выделяемое количество теплоты пропорционально квадрату силы тока и создаётся механическими силами. Далее Джоуль усовершенствовал установку, заменив вращение катушки рукой на вращение, производимое падающим грузом. Это позволило связать величину выделяемого тепла с изменением энергии груза[19][27]:
Далее Джоуль усовершенствовал установку, заменив вращение катушки рукой на вращение, производимое падающим грузом. Это позволило связать величину выделяемого тепла с изменением энергии груза[19][27]:
|
Эти результаты были изложены на физико-математической секции Британской ассоциации в его работе 1843 года «О тепловом эффекте магнитоэлектричества и механическом значении тепла»[28].
В работах 1847—1850 годов Джоуль даёт ещё более точный механический эквивалент тепла. Им использовался металлический калориметр, установленный на деревянной скамье. Внутри калориметра находилась ось с расположенными на ней лопастями. На боковых стенках калориметра располагались ряды пластинок, препятствовавшие движению воды, но не задевавшие лопасти. На ось снаружи калориметра наматывалась нить с двумя свисающими концами, к которым были прикреплены грузы. В экспериментах измерялось количество теплоты, выделяемое при вращении оси из-за трения. Это количество теплоты сравнивалось с изменением положения грузов и силой, действующей на них.
Роберт Майер
Роберт Майер первым выдвинул гипотезу об универсальности закона сохранения энергии
Первым осознал и сформулировал всеобщность закона сохранения энергии немецкий врач Роберт Майер[19]. При исследовании законов функционирования человека у него возник вопрос, не изменится ли количество теплоты, выделяемое организмом при переработке пищи, если он при этом будет совершать работу. Если количество теплоты не изменялось бы, то из того же количества пищи можно было бы получать больше тепла путём перевода работы в тепло (например, через трение). Если же количество теплоты изменяется, то, следовательно, работа и тепло должны быть как-то связаны между собой и с процессом переработки пищи. Подобные рассуждения привели Майера к формулированию закона сохранения энергии в качественной форме[23]:
Если количество теплоты не изменялось бы, то из того же количества пищи можно было бы получать больше тепла путём перевода работы в тепло (например, через трение). Если же количество теплоты изменяется, то, следовательно, работа и тепло должны быть как-то связаны между собой и с процессом переработки пищи. Подобные рассуждения привели Майера к формулированию закона сохранения энергии в качественной форме[23]:
Движение, теплота, и, как мы намерены показать в дальнейшем, электричество представляют собой явления, которые могут быть сведены к единой силе, которые изменяются друг другом и переходят друг в друга по определенным законам
Ему же принадлежит обобщение закона сохранения энергии на астрономические тела. Майер утверждает, что тепло, которое поступает на Землю от Солнца, должна сопровождаться химическими превращениями или механической работой на Солнце:
Всеобщий закон природы, не допускающий никаких исключений, гласит, что для образования тепла необходима известная затрата.
Эту затрату, как бы разнообразна она ни была, всегда можно свести к двум главным категориям, а именно, она сводится либо к химическому материалу, либо к механической работе
Свои мысли Майер изложил в работе 1841 года «О количественном и качественном определении сил»[29], которую послал сначала в ведущий на тот момент журнал «Annalen der Physik und Chemie», где она была отклонена главным редактором журнала Иоганном Поггендорфом, после чего статья была опубликована в «Annalen der Chemie und Pharmacie», где оставалась незамеченной до 1862 года, когда её обнаружил Клаузиус.
Герман Гельмгольц
Герман Гельмгольц первым ввёл представление о потенциальной энергии
Рассуждения Майера и опыты Джоуля доказали эквивалентность механической работы и теплоты, показав, что количество выделяемой теплоты равно совершённой работе и наоборот, однако, формулировку в точных терминах закону сохранения энергии первым дал Герман Гельмгольц[23]. В отличие от своих предшественников, Гельмгольц связывал закон сохранения энергии с невозможностью существования вечных двигателей[30]. В своих рассуждениях он шёл от механистической концепции устройства материи, представляя её как совокупность большого количество материальных точек, взаимодействующих между собой посредством центральных сил. Исходя из такой модели, Гельмгольц свёл все виды сил (позднее получивших название видов энергии) к двум большим типам: живым силам движущихся тел (кинетической энергии в современном понимании) и силам напряжения (потенциальной энергии). Закон сохранения этих сил был им сформулирован в следующем виде[31]:
В отличие от своих предшественников, Гельмгольц связывал закон сохранения энергии с невозможностью существования вечных двигателей[30]. В своих рассуждениях он шёл от механистической концепции устройства материи, представляя её как совокупность большого количество материальных точек, взаимодействующих между собой посредством центральных сил. Исходя из такой модели, Гельмгольц свёл все виды сил (позднее получивших название видов энергии) к двум большим типам: живым силам движущихся тел (кинетической энергии в современном понимании) и силам напряжения (потенциальной энергии). Закон сохранения этих сил был им сформулирован в следующем виде[31]:
|
В этой цитате под живой силой Гельмгольц понимает кинетическую энергию материальных точек, а под силой напряжения — потенциальную. Мерой произведённой работы Гельмгольц предложил считать половину величины mq² (где m — масса точки, q — её скорость) и выразил сформулированный закон в следующей математической форме[31]:
понимая под и скорости тела в положениях и соответственно, а под — «величину силы, которая действует по направлению r» и «считается положительной, если имеется притяжение, и отрицательной, если наблюдается отталкивание…»[30] Таким образом, главным нововведением Гельмгольца стало введение понятия потенциальных сил и потенциальной энергии, что позволило в дальнейшем обобщить закон сохранения энергии на все разделы физики. В частности, опираясь на закон сохранения энергии, он вывел закон электромагнитной индукции Фарадея.
В частности, опираясь на закон сохранения энергии, он вывел закон электромагнитной индукции Фарадея.
Введение термина «энергия»
Переход от понятия «живой силы» к понятию «энергии» произошёл в начале второй половине XIX века и был связан с тем, что понятие силы уже было занято в ньютоновской механике. Само понятие энергии в этом смысле было введено ещё в 1807 году Томасом Юнгом в его «Курсе лекций по естественной философии и механическому искусству» (англ. «A course of lectures on natural philosophy and the mechanical arts»)[32][33]. Первое строгое определение энергии дал Уильям Томсон в 1852 году в работе «Динамическая теория тепла»[23][34]:
Под энергией материальной системы в определённом состоянии мы понимаем измеренную в механических единицах работы сумму всех действий, которые производятся вне системы, когда она переходит из этого состояния любым способом в произвольно выбранное нулевое состояние
Оригинальный текст (англ.
)
«mechanical energy of a body in a given state,» will denote the mechanical value of the effects the body would produce in passing from the state in which it is given, to the standard state
Философское значение закона
Открытие закона сохранения энергии оказало влияние не только на развитие физических наук, но и на философию XIX века. С именем Роберта Майера связано возникновение так называемого естественно-научного энергетизма — мировоззрения, сводящего всё существующее и происходящее к энергии, её движению и взаимопревращению. В частности, материя и дух в этом представлении являются формами проявления энергии. Главным представителем этого направления энергетизма является немецкий химик Вильгельм Оствальд, высшим императивом философии которого стал лозунг «Не растрачивай понапрасну никакую энергию, используй её!»[35]
Примечания
- ↑ Ландау, Л. Д., Лифшиц, Е. М. Механика. — Издание 4-е, исправленное.
 — М.: Наука, 1988. — С. 25. — 215 с. — («Теоретическая физика», том I). — ISBN 5-02-013850-9
— М.: Наука, 1988. — С. 25. — 215 с. — («Теоретическая физика», том I). — ISBN 5-02-013850-9 - ↑ 1 2 Савельев И. В. Глава 3. Работа и энергия // Курс общей физики. Механика. — 4-е изд. — М.: Наука, 1970. — С. 89—99. — ISBN 5-17-002963-2
- ↑ Савельев И. В. Глава 9. Колебательное движение // Курс общей физики. Механика. — 4-е изд. — М.: Наука, 1970. — С. 228—229. — ISBN 5-17-002963-2
- ↑ Савельев И. В. Глава 9. Колебательное движение // Курс общей физики. Механика. — 4-е изд. — М.: Наука, 1970. — С. 234—235. — ISBN 5-17-002963-2
- ↑ Сивухин Д. В. Общий курс физики. — М.: Наука, 1979. — Т. I. Механика. — С. 123—147. — 520 с.
- ↑ 1 2 Сивухин Д. В. Общий курс физики. — Т. II. Термодинамика и молекулярная физика. — С. 37—41.
- ↑ Ландау, Л. Д., Лифшиц, Е. М. Гидродинамика. — М., 1986.
 — С. 24—25. — («Теоретическая физика», том VI).
— С. 24—25. — («Теоретическая физика», том VI). - ↑ 1 2 Г. Ламб Гидродинамика. — М., Л.: Гос. изд. технико-теоретической литературы, 1947. — С. 36—38. — 928 с. — 8000 экз.
- ↑ J. D. Jackson. Classical Electrodynamics. — 2nd Ed. — John Wiley & Sons, Inc., 1975. — С. 189—190. — 848 с. — ISBN 047143132X
- ↑ И. Е. Тамм §92. Теорема Пойнтинга. Поток энергии // Основы теории электричества. — 10-е изд., испр. — М.: Наука. Гл. ред. физ.-мат. лит., 1989. — С. 346—351. — 504 с. — 25 500 экз. — ISBN 5-02-014244-1
- ↑ Сивухин Д. В. Общий курс физики. — М.: Наука, 1977. — Т. III. Электричество. — С. 364. — 688 с.
- ↑ 1 2 Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — С. 45—49. — («Теоретическая физика», том II). — ISBN 5-02-014420-7
- ↑ Д. И. Блохинцев.
 Основы квантовой механики. — 7-е изд., стер. — СПб.: Издательство «Лань», 2004. — С. 125—127. — 672 с. — 2000 экз. — ISBN 5-8114-0554-5
Основы квантовой механики. — 7-е изд., стер. — СПб.: Издательство «Лань», 2004. — С. 125—127. — 672 с. — 2000 экз. — ISBN 5-8114-0554-5 - ↑ Д. И. Блохинцев. Основы квантовой механики. — 7-е изд., стер. — СПб.: Издательство «Лань», 2004. — С. 94—97. — 672 с. — 2000 экз. — ISBN 5-8114-0554-5
- ↑ Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — С. 352. — («Теоретическая физика», том II). — ISBN 5-02-014420-7
- ↑ Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — С. 362—368. — («Теоретическая физика», том II). — ISBN 5-02-014420-7
- ↑ А. В. Петров. Законы сохранения в ОТО и их приложения. Конспект лекций.
- ↑ Кудрявцев П. С. Курс истории физики. — М.: Просвещение, 1974. — Т. I (глава VI). — С. 148.
- ↑ 1 2 3 4 100 великих научных открытий / Д.
 К. Самин. — М.: Вече, 2002. — С. 90—93. — 480 с. — 25 000 экз. — ISBN 5-7838-1085-1
К. Самин. — М.: Вече, 2002. — С. 90—93. — 480 с. — 25 000 экз. — ISBN 5-7838-1085-1 - ↑ Михаил Васильевич Ломоносов. Избранные произведения в 2-х томах. М.: Наука. 1986
- ↑ Фигуровский Н. А. Очерк общей истории химии. От древнейших времен до начала XIX в. — М.: Наука, 1969
- ↑ В латинском тексте письма говорится о сохранении движения — в русском переводе речь идет о сохранении силы. В письме М. В. Ломоносов впервые объединяет в одной формулировке законы сохранения материи и движения и называет это «всеобщим естественным законом».
- ↑ 1 2 3 4 5 В. М. Дуков История формулировки закона сохранения энергии (рус.) // Физика : Учебно-методическая газета. — М.: Издательский дом «Первое сентября», 2002. — № 31/02.
- ↑ Sadi Carnot. Réflexions sur la puissance motrice du feu et sur les machines propres а développer cette puissance.
 — 1824. — 102 с. (русский перевод В. Р. Бурсиана и Ю. А. Круткова: Размышления о движущей силе огня и о машинах, способных развивать эту силу на сайте nature.web.ru)
— 1824. — 102 с. (русский перевод В. Р. Бурсиана и Ю. А. Круткова: Размышления о движущей силе огня и о машинах, способных развивать эту силу на сайте nature.web.ru) - ↑ Sadi Carnot. Réflexions sur la puissance motrice du feu, et sur les machines propres à développer oette puissance. — Paris: Gauthier-Villar, Imprimeur-Libraire, 1878. — С. 94. — 102 с.
- ↑ Sadi Carnot. Réflexions sur la puissance motrice du feu, et sur les machines propres à développer oette puissance. — Paris: Gauthier-Villar, Imprimeur-Libraire, 1878. — С. 95. — 102 с.
- ↑ Donald S. L. Cardwell. James Joule: A Biography. — Manchester University Press, 1991. — С. 57. — 333 с. — ISBN 0-7190-3479-5
- ↑ James Prescott Joule. On the Calorific Effects of Magneto-Electricity, and on the Mechanical Value of Heat. — 1843. — 32 с.
- ↑ von J. R. Mayer Bemerkungen über die Kräfte der unbelebten Natur (нем.) // Annalen der Chemie und Pharmacie.
 — 1842. — Т. 42. — С. 233—240.
— 1842. — Т. 42. — С. 233—240. - ↑ 1 2 Кудрявцев, П. С. Открытие закона сохранения и превращения энергии // Курс истории физики. — 2-е изд., испр. и доп. — М.: Просвещение, 1982. — 448 с.
- ↑ 1 2 Hermann von Helmholtz. Über die Erhaltung der Kraft. — Berlin: Druck und Verlag von G. Reimer, 1847. — С. 17. — 72 с.
- ↑ Thomas Young. A course of lectures on natural philosophy and the mechanical arts: in two volumes. — London: Joseph Johnson, 1807. — Т. Vol. 1. — 796 с.
- ↑ Thomas Young. A course of lectures on natural philosophy and the mechanical arts: in two volumes. — London: Joseph Johnson, 1807. — Т. Vol. 2. — 738 с.
- ↑ William Thomson Kelvin. On the dynamical theory of heat. — 1852.
- ↑ Энергетизм // Философский энциклопедический словарь. — 2010.
Литература
Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа. / / Законы сохранения в механике. Механическая работа, мощность, энергия, закон сохранения импульса, закон сохранения энергии, равновесие твердых тел Поделиться:
Поиск в инженерном справочнике DPVA. Введите свой запрос: | ||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||
|
1. |
Превращения энергии
|
1 |
|
2. |
Нагревание при сжигании топлива
|
2,9 |
|
3. 
|
КПД нагревательной установки
|
2 |
|
4. |
Нагревание за счёт сгорания топлива
|
2 |
|
5. 
|
КПД нагревательной установки
|
3 |
|
6. |
Нагревание при падении на землю
|
4 |
|
7. 
|
В котле
|
4 |
|
8. |
Нагревание при падении с высоты
|
4 |
|
9. 
|
Мощность двигателей самолёта
|
5 |
|
10. |
Реактивный лайнер
|
5 |
|
11. 
|
Паровой молот
|
5 |
|
12. |
Измерение температуры воды
|
5 |
|
13. 
|
Охлаждение энергетической установки
|
6 |
Секрет сохранения энергии. Как черпать ресурс в работе?
ГлавнаяИнформационный каналНаша командаСекрет сохранения энергии. Как черпать ресурс в работе?
09.08.2021
Мы проводим на работе большую часть нашей жизни: изо дня в день решаем сложные задачи, выстраиваем отношения с коллегами, а в выходные пытаемся настроиться на новую рабочую неделю. Как в таком сумасшедшем графике оставаться в ресурсе, быть продуктивным и, что самое главное, научиться черпать энергию из самой работы?
Как в таком сумасшедшем графике оставаться в ресурсе, быть продуктивным и, что самое главное, научиться черпать энергию из самой работы?
— Среди сотрудников я наблюдаю поведенческие признаки потери энергии: снижение продуктивности, стереотипное негибкое поведение, уклонение от какого-то нового содержания работ. Но самая сложная ситуация — когда состояние доходит до соматических признаков: высокая утомляемость, нарушения сна, обострение болезней и прочие неприятности. Вот почему так важно уметь восполнять энергию вовремя и не доводить до физического истощения свой организм, — рассказала руководитель Управления по развитию приоритетных рекрутинговых программ Елена Спиридонова.
Сотрудники Правительства Москвы поделились с нами своими секретами восполнения энергии, рассказали, почему вдохновлены своей деятельностью и как помогают другим сотрудникам и подчиненным восстановить ресурсы.
Делать дела не для себя
Анзор Алисултанов, заместитель префекта ЮЗАО
— Энергия — в удовольствии от выполненной работы и от полученного результата. Например, во время реновации мы видели весь процесс и участвовали в нем — от возникновения идеи до момента переселения людей, которые счастливы и довольны новым жильем. Это определенная победа, что сделал доброе дело не для себя, от этого наполняешься энергией. Когда есть возможность, я занимаюсь спортом, хожу в зал, а также встречаюсь и общаюсь с друзьями. Но у меня лучшее лекарство от выгорания — сон и новые проекты. Когда появляется новая задача, выгорание уходит на второй план, она начинает аккумулировать силы, нервы, здоровье. В нашей организации сумасшедший ритм работы — 24/7, поэтому важно сохранять не только свою, но и энергию сотрудников, чтобы они были эффективны: по-человечески относиться к каждому, помогать добрым словом или поддержкой, в каких-то ситуациях перейти в неформальную обстановку. Например, сегодня отпустить человека пораньше, но при этом знать, что при других обстоятельствах он выйдет и будет работать.
Например, во время реновации мы видели весь процесс и участвовали в нем — от возникновения идеи до момента переселения людей, которые счастливы и довольны новым жильем. Это определенная победа, что сделал доброе дело не для себя, от этого наполняешься энергией. Когда есть возможность, я занимаюсь спортом, хожу в зал, а также встречаюсь и общаюсь с друзьями. Но у меня лучшее лекарство от выгорания — сон и новые проекты. Когда появляется новая задача, выгорание уходит на второй план, она начинает аккумулировать силы, нервы, здоровье. В нашей организации сумасшедший ритм работы — 24/7, поэтому важно сохранять не только свою, но и энергию сотрудников, чтобы они были эффективны: по-человечески относиться к каждому, помогать добрым словом или поддержкой, в каких-то ситуациях перейти в неформальную обстановку. Например, сегодня отпустить человека пораньше, но при этом знать, что при других обстоятельствах он выйдет и будет работать.
Общение как источник энергии
Анастасия Лебедь, начальник управления госслужбы и кадров префектуры ЦАО
— Мне дает энергию любимая работа. За 21 год поменялись и система госслужбы, и работа кадровых отделов. Но я по-прежнему люблю общаться с людьми, выстраивать грамотные коммуникации, решать проблемы. Общение — мой источник. В конце рабочего дня я точно знаю, что сделано, какие вопросы решены, — и это мое вдохновение. Безусловно, семья меня поддерживает, и в окружении с родными я также черпаю энергию. А последние два месяца я стала заниматься спортом — хожу в фитнес-клуб. Также один из моих секретов — я стараюсь всегда ложиться спать не позже 11, чтобы был полноценный сон. Это важно и для моих подчиненных: иногда просто нужно дать человеку отоспаться. Но к каждому я подбираю индивидуальный подход. Например, если я вижу, что сотрудник близок к выгоранию, то в первую очередь необходимо с ним поговорить, выяснить причину. Для кого-то важно просто побеседовать, почувствовать поддержку со стороны руководства, а есть те, кто просит не отправлять в отпуск, для них именно работа — это положительные эмоции.
За 21 год поменялись и система госслужбы, и работа кадровых отделов. Но я по-прежнему люблю общаться с людьми, выстраивать грамотные коммуникации, решать проблемы. Общение — мой источник. В конце рабочего дня я точно знаю, что сделано, какие вопросы решены, — и это мое вдохновение. Безусловно, семья меня поддерживает, и в окружении с родными я также черпаю энергию. А последние два месяца я стала заниматься спортом — хожу в фитнес-клуб. Также один из моих секретов — я стараюсь всегда ложиться спать не позже 11, чтобы был полноценный сон. Это важно и для моих подчиненных: иногда просто нужно дать человеку отоспаться. Но к каждому я подбираю индивидуальный подход. Например, если я вижу, что сотрудник близок к выгоранию, то в первую очередь необходимо с ним поговорить, выяснить причину. Для кого-то важно просто побеседовать, почувствовать поддержку со стороны руководства, а есть те, кто просит не отправлять в отпуск, для них именно работа — это положительные эмоции.
Смена деятельности как секрет сохранения энергии
Мария Подгорная, начальник отдела госслужбы и кадров МАДИ
— Работа занимает большую часть жизни и она же дает энергию: отдача, опыт, пусть даже плохой — иногда это даже лучше. Важна балансировка деятельности, чтобы избежать выгорания. Лично меня расслабляет и переключает рисование, а также домашние дела и заботы. В работе с подчиненными я использую тот же принцип: когда я вижу, что человек теряет интерес, то стараюсь переключить его на другие проекты. Я подбираю занятие, не отходя от деятельности отдела, под конкретного сотрудника. Важен индивидуальный подход! Мне важно, чтобы человек развивался и продолжал работать.
Важна балансировка деятельности, чтобы избежать выгорания. Лично меня расслабляет и переключает рисование, а также домашние дела и заботы. В работе с подчиненными я использую тот же принцип: когда я вижу, что человек теряет интерес, то стараюсь переключить его на другие проекты. Я подбираю занятие, не отходя от деятельности отдела, под конкретного сотрудника. Важен индивидуальный подход! Мне важно, чтобы человек развивался и продолжал работать.
Помимо наших советов, что делать, когда ваш энергетический запал в организации начал угасать, руководитель Управления по развитию приоритетных рекрутинговых программ Елена Спиридонова поделилась несколькими своими лайфхаками для восполнения энергии в течение рабочего дня.
— Не забывайте пить воду
Наш организм состоит из воды на 60—80% от массы тела. Пейте именно воду: она участвует в регуляции теплообмена, синтезе энергии. Современные научные исследования доказывают, что потребление достаточного количества воды на 15% улучшает активность мозга, она стимулирует когнитивные функции человека.
— Работайте с открытым окном
Проветривая помещение, мы снижаем концентрацию углекислого газа, который связывают с рабочим переутомлением.
— Делайте 15-минутную зарядку
Исследования доказывают, что у офисных сотрудников, занимающихся мини-зарядкой по несколько минут в день, из-за разгона лимфы и крови, а также дополнительного насыщения мозга кислородом улучшается настроение, повышаются когнитивные способности, устраняется чувство усталости.
— Используйте самоподдержку
Большинство сотрудников Правительства Москвы — перфекционисты. Все поставленные задачи мы хотим довести до идеала. Но в сутках только 24 часа. Если что-то не получается в течение рабочего дня, вы не успеваете сделать дополнительный фронт работ — похвалите себя за уже реализованные подзадачи. Находите возможность хвалить себя почаще, даже за незначительный успех.
— Проведите ревизию закончившегося рабочего дня
Незавершенные дела провоцируют тревогу, которая отнимает у нас энергию. Мысли об оставшихся «долгах», накопившихся в течение рабочего дня, будут нас преследовать и дома. Проведите ревизию, составьте краткий список того, с чего стоит начать завтрашний день. Градус тревоги снизится.
Мысли об оставшихся «долгах», накопившихся в течение рабочего дня, будут нас преследовать и дома. Проведите ревизию, составьте краткий список того, с чего стоит начать завтрашний день. Градус тревоги снизится.
Работа становится той частью, без которой сотрудникам Правительства Москвы представить свою жизнь уже сложно. Благодаря балансу в виде новых интересных проектов, вовлеченных людей, любви к работе, семье, спорту, интересным хобби происходит постоянный энергообмен. Заряжаться дома — и с новыми силами идти на работу. Получать удовольствие от работы — и с удовлетворением возвращаться домой. Это и есть закон сохранения энергии!
Возврат к списку
Мифы современной физики. Законы сохранения / Хабр
Продолжение. Начало
тут
и
тут
:
В этот раз мы замахнемся на святое: на законы сохранения, в том числе на закон сохранения энергии. Правда, вечного двигателя я вам не обещаю.
Закон сохранения энергии имеет такой ореол святости, что практически любой человек напрягается, услышав, что с ним не все хорошо. Между тем, энергия сохраняется в механике, в квантовой механике и даже в СТО – Специальной Теории Относительности. Но… не в ОТО – Общей Теории Относительности. Однако сказать, что энергия не сохраняется, тоже нельзя. Вначале разберемся,
Между тем, энергия сохраняется в механике, в квантовой механике и даже в СТО – Специальной Теории Относительности. Но… не в ОТО – Общей Теории Относительности. Однако сказать, что энергия не сохраняется, тоже нельзя. Вначале разберемся,
Что же такое – сохраняться?
Вот мы положили в мешок два шара, синий и красный. Через какое-то время достали их. Ага, было два шара, и стало два шара, шары
сохраняются
в мешке! Так выглядит пространственно — временная картина этого эксперимента:
Однако с количеством шаров все просто – все наблюдатели, как бы они ни двигались, согласятся с тем, что шаров – два. А как быть с энергией? Вот, например, я стою около дома весом 1000 тонн. Кинетическая энергия его в моей системе отсчета равна нулю. Теперь я пойду от дома со скоростью 1 метр в секунду. В моей системе отсчета дом приобрел огромную энергию! Как я, слабый человек, мог дать дому такую энергию всего одним шагом?
Если вы внимательно следили за руками, то, несомненно, заметили, что я совершил грязный хак. Считал энергию вначале в одной системе отсчёта, а потом нагло перескочил в другую. Так делать нельзя. Для энергии состояние до и состояние после должно быть привязано к одной и той же системе отсчета.
Считал энергию вначале в одной системе отсчёта, а потом нагло перескочил в другую. Так делать нельзя. Для энергии состояние до и состояние после должно быть привязано к одной и той же системе отсчета.
Для нашей картинки с шарами это означает, что дно и крышка цилиндра (в общем случае любой фигуры) должны быть параллельны друг другу. А вот с этим в искривленном пространстве плохо: как вы помните, в искривленном пространстве могут быть много параллельных или не быть ни одной! Хуже того, пространство может быть таким кривым, что туда вообще не вписать такую фигуру!
Или время закольцовано – и понятия до и после не вполне определены. Таким образом, в ОТО не то, чтобы энергия не сохраняется, а само понятие “сохраняться” плохо определено.
Канонический пример несохранения энергии
Мы все знаем, что Вселенная расширяется. Когда ее линейный размер увеличивается в 10 раз, то ее объем увеличивается в 1000 раз, и плотность обычного вещества (ведь атомы – это шарики, и все наблюдатели согласны с тем, сколько их) падает тоже в 1000 раз
А вот плотность излучения, в частности реликтового излучения, падает в 10000 раз – помимо того, что фотоны рассеялись в большем объеме, каждый из них еще и покраснел. То есть плотность вещества падает как третья степень, а излучения – как четвертая.
То есть плотность вещества падает как третья степень, а излучения – как четвертая.
У этого есть интересное следствие – если мы будем двигаться в прошлое, то плотность излучения будет расти быстрее, чем плотность материи, и мы можем дойти до периода, когда плотностью и давлением обычной материи можно будет вообще пренебречь. Гравитация в основном создавалась давлением фотонного газа.
Следует заметить, что космологическая точка зрения – “вся вселенная в такое-то время”, несмотря на ее интуитивную понятность и полезность, для каждого времени после Большого Взрыва образует в пространстве-времени кривую поверхность, то есть не является валидной системой отсчета.
Можно ли поднять себя за волосы?
Спойлер: ДА. Импульс, как вы догадались, тоже не сохраняется. Вы можете погуглить по словам Swimming in space. Вот видео, как это выглядит. Конечно, практической ценности в этом почти нет, но все равно интересно.
Законы сохранения энергии — Электронный учебник по законам сохранения
Если тело некоторой массы m двигалось под действием приложенных сил, и его скорость изменилась от до то силы совершили определенную работу A.
Работа всех приложенных сил равна работе равнодействующей силы
| Работа равнодействующей силы. .A = F1s cos α1 + F2s cos α2 = F1ss + F2ss = Fрss = Fрs cos α |
Между изменением скорости тела и работой, совершенной приложенными к телу силами, существует связь. Эту связь проще всего установить, рассматривая движение тела вдоль прямой линии под действием постоянной силы В этом случае векторы силы перемещения скорости и ускорения направлены вдоль одной прямой, и тело совершает прямолинейное равноускоренное движение. Направив координатную ось вдоль прямой движения, можно рассматривать F, s, υ и a как алгебраические величины (положительные или отрицательные в зависимости от направления соответствующего вектора). Тогда работу силы можно записать как A = Fs. При равноускоренном движении перемещение s выражается формулой
При равноускоренном движении перемещение s выражается формулой
Отсюда следует, что
Это выражение показывает, что работа, совершенная силой (или равнодействующей всех сил), связана с изменением квадрата скорости (а не самой скорости).
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:
Работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии.
Это утверждение называют теоремой о кинетической энергии. Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения.
Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:
Если тело движется со скоростью то для его полной остановки необходимо совершить работу
В физике наряду с кинетической энергией или энергией движения важную роль играет понятие потенциальной энергии или энергии взаимодействия тел.
Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения и определяется только начальным и конечным положениями тела. Такие силы называются консервативными.
Работа консервативных сил на замкнутой траектории равна нулю. Это утверждение поясняет рисунок ниже
Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.
Работа консервативной силы A1a2 = A1b2. Работа на замкнутой траекторииA = A1a2 + A2b1 = A1a2 – A1b2 = 0 |
Если тело перемещается вблизи поверхности Земли, то на него действует постоянная по величине и направлению сила тяжести Работа этой силы зависит только от вертикального перемещения тела. На любом участке пути работу силы тяжести можно записать в проекциях вектора перемещения на ось OY, направленную вертикально вверх:
На любом участке пути работу силы тяжести можно записать в проекциях вектора перемещения на ось OY, направленную вертикально вверх:
| ΔA = Fт Δs cos α = –mgΔs y, |
где Fт = Fтy = –mg – проекция силы тяжести, Δsy – проекция вектора перемещения. При подъеме тела вверх сила тяжести совершает отрицательную работу, так как Δsy > 0. Если тело переместилось из точки, расположенной на высоте h1, в точку, расположенную на высоте h2 от начала координатной оси OY , то сила тяжести совершила работу
| A = –mg (h2 – h1) = –(mgh2 – mgh1). |
Работа силы тяжести |
Эта работа равна изменению некоторой физической величины mgh, взятому с противоположным знаком. Эту физическую величину называют потенциальной энергией тела в поле силы тяжести
Эту физическую величину называют потенциальной энергией тела в поле силы тяжести
Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень.
Если рассматривать движение тел в поле тяготения Земли на значительных расстояниях от нее, то при определении потенциальной энергии необходимо принимать во внимание зависимость силы тяготения от расстояния до центра Земли (закон всемирного тяготени). Для сил всемирного тяготения потенциальную энергию удобно отсчитывать от бесконечно удаленной точки, т. е. полагать потенциальную энергию тела в бесконечно удаленной точке равной нулю. Формула, выражающая потенциальную энергию тела массой m на расстоянии rот центра Земли, имеет вид:
где M – масса Земли, G – гравитационная постоянная.
Понятие потенциальной энергии можно ввести и для силы упругости. Эта сила также обладает свойством консервативности. Растягивая (или сжимая) пружину, мы можем делать это различными способами.
Можно просто удлинить пружину на величину x, или сначала удлинить ее на 2x, а затем уменьшить удлинение до значения x и т. д. Во всех этих случаях сила упругости совершает одну и ту же работу, которая зависит только от удлинения пружины x в конечном состоянии, если первоначально пружина была недеформирована. Эта работа равна работе внешней силы A, взятой с противоположным знаком :
где k – жесткость пружины. Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, т. е. сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Потенциальной энергией пружины (или любого упруго деформированного тела) называют величину
Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией.
Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x1, тогда при переходе в новое состояние с удлинением x2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком:
Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой посредством сил упругости.
Свойством консервативности наряду с силой тяжести и силой упругости обладают некоторые другие виды сил, например, сила электростатического взаимодействия между заряженными телами. Сила трения не обладает этим свойством. Работа силы трения зависит от пройденного пути. Понятие потенциальной энергии для силы трения вводить нельзя.
|
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.
Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.
Пример применения закона сохранения энергии – нахождение минимальной прочности легкой нерастяжимой нити, удерживающей тело массой m при его вращении в вертикальной плоскости (задача Х. Гюйгенса). Рис. 1.20.1 поясняет решение этой задачи.
К задаче Христиана Гюйгенса. – сила натяжения нити в нижней точке траектории – сила натяжения нити в нижней точке траектории |
Закон сохранения энергии для тела в верхней и нижней точках траектории записывается в виде:
Обратим внимание на то, что сила натяжения нити всегда перпендикулярна скорости тела; поэтому она не совершает работы.
При минимальной скорости вращения натяжение нити в верхней точке равно нулю и, следовательно, центростремительное ускорение телу в верхней точке сообщается только силой тяжести:
Из этих соотношений следует:
Центростремительное ускорение в нижней точке создается силами и направленными в противоположные стороны:
Отсюда следует, что при минимальной скорости тела в верхней точке натяжение нити в нижней точке будет по модулю равно
Прочность нити должна, очевидно, превышать это значение.
Очень важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач.
В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими консервативными силами действуют силы трения или силы сопротивления среды.
Сила трения не является консервативной. Работа силы трения зависит от длины пути.
Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).
При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую.
Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.
Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии
Один из проектов «вечного двигателя». Почему эта машина не будет работать? |
История хранит немалое число проектов «вечного двигателя». В некоторых из них ошибки «изобретателя» очевидны, в других эти ошибки замаскированы сложной конструкцией прибора, и бывает очень непросто понять, почему эта машина не будет работать. Бесплодные попытки создания «вечного двигателя» продолжаются и в наше время. Все эти попытки обречены на неудачу, так как закон сохранения и превращения энергии «запрещает» получение работы без затраты энергии.
Сохранение энергии
Сохранение энергии — фундаментальное понятие физики.
вместе с
сохранение массы
и
сохранение количества движения.
В некоторой проблемной области количество энергии остается постоянным.
и энергия не создается и не разрушается. Энергия может быть преобразована из
одна форма в другую (потенциальная энергия может быть преобразована в кинетическую
энергия), но полная энергия внутри домена остается фиксированной.
Термодинамика — это раздел физики
который имеет дело с энергией и работой системы.Как упоминалось на
слайд свойств газа, термодинамика
только с крупномасштабным откликом системы, который мы можем наблюдать
и измерить в экспериментах. В ракетостроении мы больше всех
интересуется термодинамикой при изучении
двигательные установки
и понимание высокоскоростных потоков.
На некоторых отдельных слайдах мы обсудили
состояние статического газа,
свойства
которые определяют состояние, а
первый закон
термодинамики применительно к любой системе в целом.
На этом слайде мы выводим полезную форму уравнения сохранения энергии
для газа, начиная с первого закона термодинамики.Если называть внутреннюю энергию газа E , то
работа, выполняемая газом W , и тепло, передаваемое газу Q ,
тогда первый закон термодинамики указывает, что между состоянием «1» и
состояние «2»:
E2 — E1 = Q — W
Аэрокосмические инженеры обычно упрощают термодинамический анализ
с использованием интенсивных переменных; переменные, не зависящие от
масса газа. Мы называем эти переменные
конкретный
переменные. Мы создаем «конкретную» переменную, беря свойство, чье
значение зависит от массы системы и деления ее на массу
системы.Многие из государственных свойств, перечисленных на этом слайде,
например работа и внутренняя энергия зависят от общей массы газа.
Мы будем использовать «специфические» версии этих переменных.
Инженеры обычно используют строчные буквы для обозначения «конкретных».
версия переменной. Тогда наше первое уравнение закона становится:
e2 — e1 = q — w
Поскольку мы рассматриваем движущийся газ, мы добавляем термин удельной кинетической энергии
к внутренней энергии на левой стороне. 2) / 2
2) / 2
и уравнение первого закона становится:
e2 — e1 + k2 — k1 = q — w
Есть две части конкретной работы для
движущийся газ.Некоторые работы, называемые работы на валу (wsh) , являются
используется для перемещения жидкости или вращения вала, в то время как остальная часть
работа идет на изменение состояния
газ. Для
давление p и
удельный объем v , работа дана по:
w = (p * v) 2 — (p * v) 1 + wsh
Подставляя:
e2 — e1 + k2 — k1 = q — (p * v) 2 + (p * v) 1 — wsh
Если мы проведем небольшую алгебру по первому закону термодинамики,
мы можем начать группировать некоторые члены уравнений.2/2
Полная удельная энтальпия аналогична полному давлению в
Уравнение Бернулли; оба выражения
включают «статическое» значение плюс половину квадрата
скорость.
Последняя, наиболее полезная форма уравнения энергии:
дано в красной рамке.
ht2 — ht1 = q — wsh
Для компрессора или
силовая турбина, внешнего тепла нет
поток в газ и член «q» установлен равным нулю. в
в
горелки, никаких работ не производится и «wsh»
срок установлен на ноль.
Действия:
Экскурсии с гидом
Навигация ..
- Руководство для начинающих Домашняя страница
Закон сохранения энергии — обзор
2 КОНСТИТУТИВНЫЕ УРАВНЕНИЯ
Хорошо известно, что в термодинамике есть два основных закона, которые играют важную роль почти во всех вопросах, связанных с термодинамикой.
Первый закон (закон сохранения энергии) имеет следующий вид
(a) ρe˙ = σ: ɛ˙ + r − divq
где ρ обозначает объемную плотность, e обозначает удельную внутреннюю энергию, r — объемная плотность внутреннего тепловыделения, σ и ɛ — тензоры напряжений и деформаций соответственно, а q — вектор теплового потока.
Второй закон, известный как принцип приращения энтропии, может быть записан как
(b) ρs˙ − rT + divqT≥0
, где T — абсолютная температура, а s — удельная энтропия. Для удобства введем функцию свободной энергии
Для удобства введем функцию свободной энергии
(c) ψ = e − Ts
Подставляя (c) в (a) и (b), получаем
(1) σ: ɛ˙ − ρ (ψ˙ + sT˙) −ρTs˙ + r − divq = 0
и
(2) σ: ɛ˙ − ρ (ψ˙ + sT˙) −q⋅gradTT≥0
где уравнение (2) называется неравенство Клаузиуса-Дюгема.
В термодинамике есть некоторые переменные состояния элементов, такие как температура, давление и т. Д., Которые отражают макроскопические средние эффекты движения большого количества частиц. Существуют также функции состояния, такие как удельная энтропия, удельная внутренняя энергия, которые являются функциями переменных состояния элемента и зависят только от текущего термодинамического состояния, а не от путей его достижения. Введение функций состояния устанавливает теорию внутренних переменных состояния.Пригожин [12] разработал теорию необратимых химических реакций. Био [3] был первым исследователем, который применил теорию для представления необратимых неупругих деформаций сплошной среды.
Отметив, что удельная внутренняя энергия e и удельная энтропия s являются функциями состояния, мы можем сделать вывод, что введенная функция свободной энергии ψ также является функцией состояния, которая может быть выражена набором переменных состояния. Следует отметить, что выбор переменных состояния в ψ важен, поскольку он связан с достоверностью описанного термодинамического состояния.Как показано авторами в другой статье [13], когда упрочнение материалов изотропно, достаточно описать неупругую деформацию с помощью подходящего набора переменных внутреннего состояния, как это делают большинство авторов; Однако, если происходит анизотропное упрочнение, мы должны, помимо набора переменных внутреннего состояния, выбрать неупругую деформацию в качестве независимой переменной, чтобы полностью охарактеризовать неупругую деформацию. Таким образом, с общей точки зрения функция свободной энергии ψ должна быть выражена как
(3) ψ = ψ (ɛe, ɛin, vk, T)
, где ɛ e и T — тензор упругих деформаций и переменная температуры, соответственно, которая может отражать обратимый процесс упругой и термической деформации.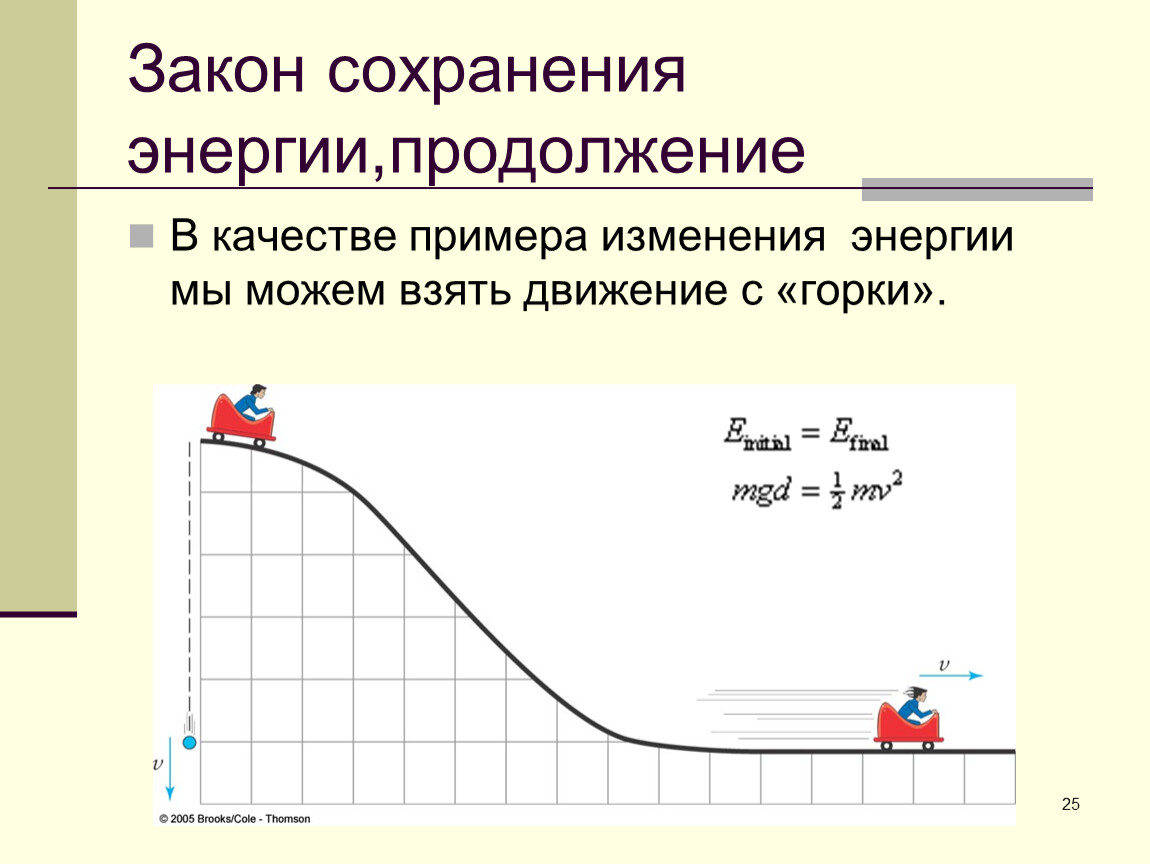 ɛ в — тензор неупругой деформации, а v k ( k = 1,2, …, n ) — переменные внутреннего состояния n , v k могут быть скалярами, векторами или тензорами в соответствии с рассматриваемой проблемой. Для простоты v k — это скаляры в этой статье.
ɛ в — тензор неупругой деформации, а v k ( k = 1,2, …, n ) — переменные внутреннего состояния n , v k могут быть скалярами, векторами или тензорами в соответствии с рассматриваемой проблемой. Для простоты v k — это скаляры в этой статье.
Подставляя (3) в (1) и (2) и отмечая, что ɛ = ɛ e + ɛ в , получаем
(4) (σ − ρ∂ψ∂ɛe): ɛ˙e + (σ −ρ∂ψ∂ɛin): ɛ˙in − ρ (s + ∂ψ∂T) T˙ − ρ∂ψ∂vkv˙k + r − ρTs˙ − divq = 0
(5) (σ − ρ∂ψ ∂ɛe): ɛ˙e + (σ − ρ∂ψ∂ɛin): ɛ˙in − ρ (s + ∂ψ∂T) T˙ − ρ∂ψ∂vkv˙k − q⋅gradTT≥0
Некоторые из члены в (4) и (5) можно исключить, если отметить, что ɛ e и T являются управляемыми переменными.Прежде всего, пусть деформация будет чисто упругой, а процесс нагружения будет настолько медленным, чтобы его можно было рассматривать как изотермический, таким образом, ɛ˙in = 0, T˙ = 0, v˙k = 0, gradT = 0. Поскольку неравенство (5) выполняется независимо от любого конкретного ɛ˙e, отсюда следует, что
Поскольку неравенство (5) выполняется независимо от любого конкретного ɛ˙e, отсюда следует, что
(6) σ = ρ∂ψ∂ɛe
Теперь рассмотрим термическую деформацию, при которой только T изменяется равномерно везде, тогда ɛ˙ in = 0, v˙k = 0, grad T = 0, из (5) также имеем
(7) s = −∂ψ∂T
, таким образом (4) и (5) уменьшаются до
(8) (σ − ρ∂ψ∂ɛin): ɛ˙in − ρ∂ψ∂vkv˙k + r − ρTs˙ − divq = 0
и
(9) (σ − ρ∂ψ∂ɛin) : ɛ˙in − ρ∂ψ∂vkv˙k − q⋅gradTT≥0
(6) и (7) являются определяющими уравнениями, (8) — уравнением теплопередачи, а (9) — неравенством диссипации.Очевидно, что общее количество производных уравнений меньше количества неизвестных переменных.
Для решения термодинамической задачи при заданных граничных и начальных условиях необходимо искать дополнительные уравнения в дополнение к указанным выше определяющим соотношениям и уравнению теплопередачи. С этой целью давайте сначала определим понятие термодинамических связанных сил. Связанная с термодинамикой сила — это величина, которая, действуя на переменные потока, производит работу рассеяния.В термодинамике континуума переменными потока являются тензор скорости деформации, скорости переменных внутреннего состояния и вектор теплового потока. Согласно приведенному выше определению и отмечая, что правая часть неравенства (9) представляет собой полную рассеиваемую энергию, мы можем называть следующие «силы», связанные с их переменными
Связанная с термодинамикой сила — это величина, которая, действуя на переменные потока, производит работу рассеяния.В термодинамике континуума переменными потока являются тензор скорости деформации, скорости переменных внутреннего состояния и вектор теплового потока. Согласно приведенному выше определению и отмечая, что правая часть неравенства (9) представляет собой полную рассеиваемую энергию, мы можем называть следующие «силы», связанные с их переменными
(10) σin = σ − ρ∂ψ∂ɛin
(11) Ak = −ρ∂ψ∂vk (k = 1,2, ⋯, n)
(12) G = −gradTT
таким образом неравенство диссипации (9) принимает вид
(13) σin: ɛ˙in + Akv˙k + G⋅q≥0
, который показывает, что полная работа рассеяния, выполняемая соответствующими силами на их термодинамические переменные, никогда не будет отрицательной.Работа равна нулю тогда и только тогда, когда процесс обратим.
Очень интересно отметить из (9), что это σ в , а не полное напряжение σ, которое определяется как сила, связанная с неупругой деформацией, когда ɛ в выбирается в качестве независимой переменной. Второй член ρ — ∂ψ∂ɛin в правой части (10) объясняется как кинематическая переменная X , когда имеет место анизотропное упрочнение [13]. Очевидно, что результат сводится к результату, полученному другими авторами, когда неупругая деформация ɛ в явно не входит в функцию свободной энергии ψ, что соответствует случаю, когда происходит только изотропное упрочнение.
Второй член ρ — ∂ψ∂ɛin в правой части (10) объясняется как кинематическая переменная X , когда имеет место анизотропное упрочнение [13]. Очевидно, что результат сводится к результату, полученному другими авторами, когда неупругая деформация ɛ в явно не входит в функцию свободной энергии ψ, что соответствует случаю, когда происходит только изотропное упрочнение.
Отменен ли закон сохранения энергии? — Проблема 79: Катализаторы
.
Физика часто сбивает с толку, но один принцип кажется твердым: закон сохранения энергии. В мире есть то, что называется «энергией», количество которой никогда не меняется. Он может менять свою форму или переходить от одного тела к другому, но его общее количество остается постоянным. От этого закона зависит все, от арки удачного футбольного мяча до мурлыканья автомобильного двигателя. Это делает энергию драгоценным товаром, который считается, накапливается и за нее борются.
Квантовый мир неопределен; атрибуты, такие как энергия, нечеткие или нечеткие.
Мы, физики, узнали, что наши тела не просто используют энергию, но состоят из нее. Формула Эйнштейна E = mc 2 определяет массу как форму энергии, которая может быть преобразована в другие формы (например, с помощью ядерной бомбы) или создана из этих форм (в коллайдере частиц). Формула укрепляет нашу интуицию о том, что энергия — это основной материал, из которого сделаны вещи.Когда кто-то углубляется в физику, он также узнает, что законы сохранения тесно связаны с симметриями, что впервые осознала немецкий математик Эмми Нётер почти столетие назад. Энергия сохраняется, потому что законы природы симметричны во времени — они не меняются от момента к моменту.
Но физика не была бы физикой, если бы она не подвергала себя постоянному сомнению. Вскоре после того, как Эйнштейн вывел свою знаменитую формулу, он начал создавать теорию гравитации, свою общую теорию относительности.Сохранение энергии стало немного рискованным. Хотя отдельные наблюдатели могут измерить плотность энергии непосредственно вокруг себя и подтвердить, что полная энергия локализованных систем остается постоянной, невозможно определить общую энергию, которая строго сохраняется. Может показаться странным, что можно определить локальное количество энергии, а не глобальное. И это.
Может показаться странным, что можно определить локальное количество энергии, а не глобальное. И это.
Также по физике
Наука о оружии из «Звездных войн»
Патрик Джонсон
Если вы уже являетесь поклонником «Звездных войн», вы знаете, что события происходят в далекой-далекой галактике, поэтому законы физики все равно должны применяться.С другой стороны, это явно художественные произведения; is … ПОДРОБНЕЕ
Наша собственная расширяющаяся Вселенная — хороший пример этой странности. Плотность энергии материи уменьшается обратно пропорционально объему пространства. Например, галактики расходятся, так что их меньше в заданном объеме в соответствии с законом сохранения энергии. Но плотность энергии звездного света и других форм излучения уменьшается с большей скоростью. Их энергия теряется. Это не переходит в какую-либо другую форму.Это допустимо, потому что расширяющаяся Вселенная не симметрична во времени; его рост отличает прошлое от будущего. Итак, общая теория относительности затрудняет утверждение, что энергия — это фундаментальный материал, из которого состоит все остальное.
Итак, общая теория относительности затрудняет утверждение, что энергия — это фундаментальный материал, из которого состоит все остальное.
Это только начало. Рассмотрим другую теорию, которая произвела революцию в физике 20 века, квантовую механику. Квантовый мир неопределен; атрибуты, такие как энергия, нечеткие или нечеткие. Хуже того, у теории есть очень серьезный концептуальный недостаток, который необходимо принимать во внимание при рассмотрении окончательной судьбы сохранения энергии.
Физика не была бы физикой, если бы она не задавала себе постоянных вопросов.
А именно, квантовая механика включает два различных и несовместимых рецепта для определения того, как частица или система частиц эволюционируют во времени. Первый применяется, когда за системой не наблюдают, второй — когда за ней наблюдают. Теория неясна, какой рецепт использовать. Что именно составляет измерение или наблюдение? Нужно задействовать сознательное существо? Может ли блоха произвести замер? Вирус? Эта проблема известна как проблема измерения, которую, как отмечали различные критики, следует называть проблемой реальности: в теории неясно, что существует «снаружи» независимо от нашего восприятия.
Как обсуждал Тим Модлин из Нью-Йоркского университета, подходы к решению проблемы бывают трех типов. 1 Добавляются так называемые скрытые переменные — ингредиенты, выходящие за рамки того, что предоставляет обычная квантовая теория, — чтобы обеспечить более полное описание состояния системы. Наиболее известным примером является теория де Бройля – Бома, которая предполагает, что помимо волновой функции существуют частицы, которые имеют определенные положения, которые стандартный квантовый формализм не фиксирует.Волновая функция просто ведет их, как овчарка.
Второй вид подхода постулирует случайный процесс, который сводит на нет неопределенность системы и устраняет ее нечеткость. Третье решение связано с множеством вселенных. То, что мы называем измерением, каким-то образом соответствует разделению нашей Вселенной на множество ветвей, каждая из которых соответствует каждому возможному результату. Все эти идеи обходятся без проблемного рецепта измерения. Ни у кого нет проблем, но это то, что есть.
Ни у кого нет проблем, но это то, что есть.
В этом году Модлин, Элиас Окон из Национального автономного университета Мексики и я решили изучить судьбу законов сохранения в этих трех подходах. 2 Наш анализ включал общие соображения, а также различные мысленные эксперименты.
Рассмотрим стандартный эксперимент, в котором квантовая система, состоящая, например, из нескольких фотонов, превращается в характерную комбинацию квантового типа, известную как «суперпозиция» двух путей. Это приводит к ситуациям, которые на классическом уровне соответствуют разным значениям энергии.Один путь ведет фотоны в далекую галактику и обратно, заставляя их терять энергию из-за космического расширения. Другой путь не предполагает изменения их изначальной энергии. Согласно центральному принципу квантовой теории, каждый фотон идет обоими путями.
Темная энергия — это своего рода совокупная память обо всех нарушениях локального сохранения энергии, имевших место в истории Вселенной.
Стандартная история в квантовой физике состоит в том, что любое несохранение может быть объяснено путем учета энергии, подаваемой или поглощаемой измерительным прибором.Мы исключаем эту возможность, используя другой квантовый эффект, запутанность, чтобы мы могли проводить измерения удаленно.
Три подхода к интерпретации предлагают разные объяснения того, что происходит с энергией. В теориях спонтанного коллапса система через достаточно долгое время подвергается внезапному коллапсу до одного из значений энергии, что приводит к ее несохранению. В подходе де Бройля – Бома любое понятие энергии, имеющее хоть какую-то возможность сохранения в целом, должно включать как частицы, так и ведущую волновую функцию.Волновая функция разделяется, а затем воссоединяется в лаборатории, и интерференция, возникающая при воссоединении, заставляет фотоны вести себя таким образом, что энергия не сохраняется. В настройке многих миров средняя энергия всех ветвей, на которые делится мир, может сохраняться, но энергия каждой ветви сохраняется. С точки зрения каждой ветви происходящее происходит точно так же, как и в теориях коллапса.
С точки зрения каждой ветви происходящее происходит точно так же, как и в теориях коллапса.
Короче говоря, мы пришли к выводу, что ни одна схема не предлагает разумного определения глобальной энергии системы, которая строго сохраняется.Ни один из них не предлагал понятия локального сохранения энергии — что плохо, потому что общая теория относительности требует, чтобы локальное сохранение энергии было внутренне непротиворечивым.
Для примирения квантовой механики и общей теории относительности потребуется квантовая теория гравитации. Физики категорически не согласны с тем, как будет выглядеть такая теория, но большинство согласны в одном: понятие пространства-времени исчезнет на фундаментальном уровне квантовой гравитации. В этом случае законы сохранения полностью теряют свою актуальность.Как можно сказать, что определенная величина не меняется со временем, если на фундаментальном уровне времени нет?
На практическом уровне ожидается, что отклонения от строгого сохранения будут незначительными и не помогут решить конкретные проблемы, с которыми мы, люди, сталкиваемся с энергией. Но для многих теоретиков любое нарушение кощунственно. Тем не менее, компенсация может быть.
Но для многих теоретиков любое нарушение кощунственно. Тем не менее, компенсация может быть.
Тибо Джоссет и Алехандро Перес из Университета Марселя, Джеймс Бьоркен из Стэнфордского университета и я показали, что модификация общей теории относительности (первоначально рассмотренная самим Эйнштейном) допускает небольшие отклонения от локального сохранения энергии. 3-5 И такая теория может предложить путь к разрешению одной из самых больших загадок современной науки: темной энергии.
Темная энергия — таинственный компонент Вселенной — около 70 процентов ее общего содержания, — который вызывает ускорение ее расширения. Согласно нашему анализу, темная энергия — это своего рода совокупная память обо всех нарушениях локального сохранения энергии, которые имели место в истории Вселенной. В одной из рассматриваемых конкретных моделей прогнозируемое значение совершенно естественным образом совпадает с наблюдениями.
Конечно, ситуация далека от урегулирования. Исследование этих и связанных с ними вопросов все еще находится в зачаточном состоянии. Но когда мы снова посмотрим на принцип, который раньше считали само собой разумеющимся, мы ожидаем, что будем и дальше удивляться его последствиям.
Но когда мы снова посмотрим на принцип, который раньше считали само собой разумеющимся, мы ожидаем, что будем и дальше удивляться его последствиям.
Дэниел Сударкси — физик-теоретик Национального автономного университета Мексики в Мехико. Он сосредотачивается на взаимодействии общей теории относительности Эйнштейна и квантовой физики, ища ключи к разгадке более глубокой теории, которую можно раскрыть, сосредоточив внимание на точках трения.
Ссылки
1. Модлин, Т. Три проблемы измерения. Topoi 14 , 7-15 (1995).
2. Модлин Т., Окон Э. и Сударский Д. О статусе законов сохранения в физике: последствия для полуклассической гравитации. arXiv: 1910.06473 (2019).
3. Джоссет Т., Перес А. и Сударский Д. Темная энергия от нарушения закона сохранения энергии. Physical Review Letters 118 , 021102 (2017).
4. Перес, А., Сударский, Д., & Бьоркен, Дж. Д. Микроскопическая модель эмерджентной космологической постоянной. Международный журнал современной физики D 27 , 1846002 (2018).
Международный журнал современной физики D 27 , 1846002 (2018).
5. Перес, А., Сударский, Д. Темная энергия из дискретности квантовой гравитации. Physical Review Letters 122 , 221302 (2019).
Изображение: patpitchaya / Shutterstock
8. СОХРАНЕНИЕ ЭНЕРГИИ
8. СОХРАНЕНИЕ ЭНЕРГИИ
В этой главе мы обсудим сохранение энергии.Законы сохранения
в физике можно выразить в очень простой форме:
«Рассмотрим систему частиц, полностью изолированную от внешнего воздействия.
Поскольку частицы движутся и взаимодействуют друг с другом, возникают определенные
свойства системы, которые не меняются »
Вкратце мы можем выразить это как
X = константа
в котором X — сохраняющееся свойство.
Масса, свисающая с потолка, будет иметь кинетическую энергию, равную нулю.Если
шнур порвется, масса будет быстро увеличивать свою кинетическую энергию. Этот
Этот
кинетическая энергия каким-то образом накапливалась в массе, когда она висела на
потолок: энергия была скрыта, но может снова появиться в виде кинетической
энергия. Накопленная энергия называется потенциальной энергией . Сохранение
энергия говорит нам, что полная энергия системы сохраняется , а в
в этом случае сумма кинетической и потенциальной энергии должна быть постоянной. Этот
означает, что каждое изменение кинетической энергии системы должно быть
с равным, но противоположным изменением потенциальной энергии :
[Дельта] U + [Дельта] K = 0
и
E = U + K = постоянная
Теорема работы-энергии, обсуждаемая в главе 7, связывает количество
работа W на изменение кинетической энергии системы
W = [Delta] K
Изменение потенциальной энергии системы теперь можно связать с
объем работы, проделанной в системе
[Delta] U = — [Delta] K = — W
что будет определением потенциальной энергии.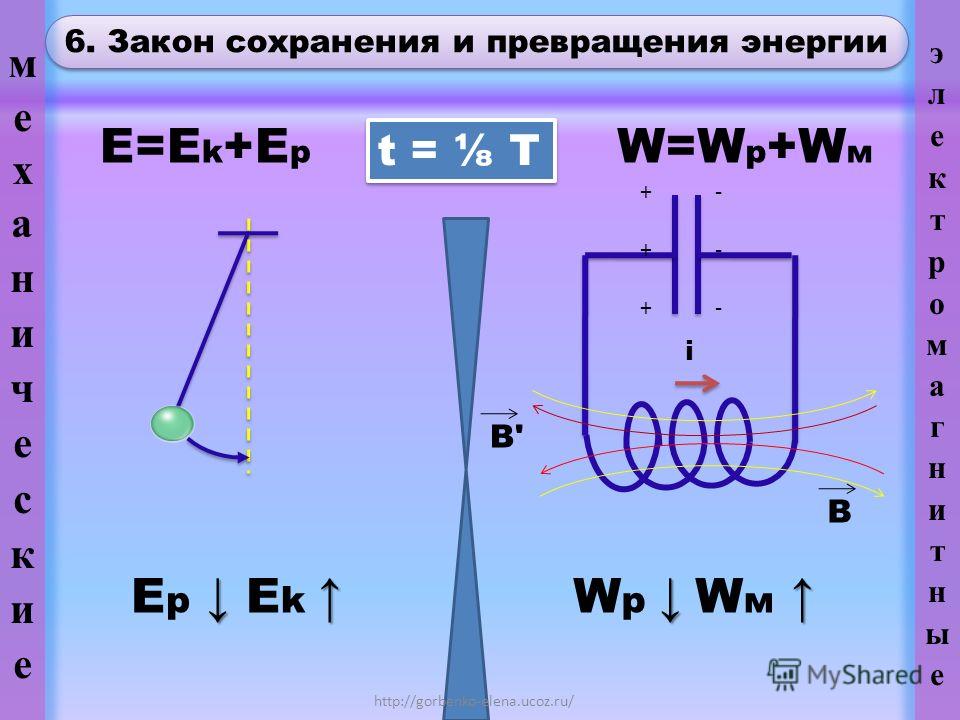 Единица
Единица
потенциальная энергия — Джоуль (Дж).
Потенциальная энергия U может быть получена из приложенной силы F
и
где U (x 0 ) — потенциальная энергия системы на ее
выбранная эталонная конфигурация. Получается, что меняется только в
потенциальная энергия важна , а мы можем присвоить произвольную
нулевое значение потенциальной энергии системы, когда она находится в эталонном состоянии.
конфигурация .
Иногда функция потенциальной энергии U (x) известна. Сила
ответственный за этот потенциал может быть получен
Мы продолжим обсуждение некоторых примеров сохранения
энергия.
8.2.1. Пружина усилие
Силу, прилагаемую пружиной к массе m, можно рассчитать с помощью
Закон Гука
F (x) = — k x
где k — жесткость пружины, а x — величина, на которую
пружина растягивается (x> 0) или сжимается (x <0). Когда движущийся объект
Когда движущийся объект
впадает в расслабленную пружину, она замедляется, на мгновение останавливается, прежде чем
ускорение в направлении, противоположном его первоначальному направлению (см. рис.
8.1). Пока объект замедляется, он сжимает пружину. Как
пружина сжимается, кинетическая энергия блока передается постепенно
к источнику, где он хранится как потенциальная энергия. Потенциальная энергия
пружина в расслабленном положении считается нулевой. Потенциальная энергия
пружины в любом другом состоянии можно получить из закона Гука
Предположим, что полная энергия системы шарик-пружина равна E.Сохранение
энергии говорит нам
Обратите внимание, что объем работы, выполняемой пружиной на блоке после нее
возвращается в исходное положение — ноль.
Рисунок 8.1. Преобразование кинетической энергии в потенциальную и
наоборот.
Пример задачи 8-4
Пружина пружинного пистолета сжимается на расстояние d от своего расслабленного состояния. А
А
мяч, если в ствол вложена масса m.С какой скоростью мяч покинет
ствол после выстрела?
Предположим, что E i — это механическая энергия системы, когда пружина
сжат. Поскольку система изначально находится в состоянии покоя, полная энергия равна
потенциальная энергия сжатой пружины:
В тот момент, когда шар покидает ствол, пружина находится в своем положении.
расслабленное положение, и его потенциальная энергия равна нулю. Полная энергия при этом
точка — это просто кинетическая энергия движущейся массы:
Для сохранения энергии требуется, чтобы E i = E f .Это означает
Теперь мы можем рассчитать скорость мяча
Пример задачи 1
Предположим, что шар на рисунке 8.1 имеет начальную скорость v 0 .
и масса m. Если жесткость пружины равна k, то каково максимальное сжатие
Если жесткость пружины равна k, то каково максимальное сжатие
весна ?
В исходной ситуации пружина находится в расслабленном положении (U = 0).В
полная энергия системы шарик-пружина равна
Максимальное сжатие пружины произойдет, когда шар находится на
отдых. В этот момент кинетическая энергия системы равна нулю (K = 0) и
общая энергия системы равна
Сохранение энергии говорит нам, что E i = E f , и
таким образом
и
8.2.2. Гравитационная сила
Шар, движущийся вверх в гравитационном поле Земли
потеряет кинетическую энергию и на мгновение остановится в своей наивысшей точке.
Затем мяч меняет направление, постепенно восстанавливая свою кинетическую энергию.
что было потеряно на пути вверх. Когда мяч достигает начальной точки, он
будет иметь кинетическую энергию, равную его начальной кинетической энергии. Проделанная работа
Проделанная работа
гравитационная сила на шаре отрицательна при движении вверх
пока он идет вниз.Работа, выполненная, когда мяч возвращается в
его исходное положение равно нулю.
Потенциальная энергия за счет силы тяжести может быть вычислена
где потенциальная энергия при y = 0 определена равной нулю.
Сохранение энергии для системы земля-шар теперь показывает
Это уравнение справедливо также для шара, движущегося в двух или трех измерениях.
Поскольку F g перпендикулярно горизонтальному направлению, работа проделана
эта сила на шаре равна нулю для смещения по оси x и / или
z-направление.При расчете изменения гравитационного потенциала
энергии объекта, необходимо только смещение в вертикальном направлении.
рассматриваться.
Пример задачи 8-3
Ребенок с массой m выходит из состояния покоя на вершине изогнутой водной горки,
высота h над уровнем бассейна. Какая скорость у ребенка при
Какая скорость у ребенка при
она проецируется в бассейн? Предположим, что ползун не имеет трения.
Начальная энергия состоит только из потенциальной энергии (так как ребенок находится на
в остальном кинетическая энергия равна нулю)
E i = m g h
где мы приняли потенциальную энергию на уровне бассейна равной нулю.В
внизу слайда потенциальная энергия равна нулю, а конечная энергия
состоит только из кинетической энергии
Для сохранения энергии необходимо, чтобы
E i = E f
Таким образом
или
8.2.3. Сила трения
Блок массы m, спроецированный на шероховатую поверхность, будет
остановлено кинетической силой трения.Нет возможности вернуть
исходная кинетическая энергия блока после того, как сила трения довела его до
отдых. Направленное крупномасштабное движение блока преобразовано в
Направленное крупномасштабное движение блока преобразовано в
кинетическая энергия беспорядочно направленных движущихся атомов, составляющих блок, и
самолет. Мы не можем связать потенциальную энергию с силой трения.
Если потенциальная энергия может быть связана с силой, мы называем силу
консервативный .Примерами консервативных сил являются сила пружины и
гравитационная сила. Если потенциальная энергия не может быть связана с
силу, мы называем эту силу неконсервативной . Пример — трение
сила. Альтернативные тесты консервативного характера силы:
1. Сила консервативна, если работа, которую она совершает с частицей, которая движется через
поездка туда и обратно равна нулю; в противном случае сила неконсервативна. В
Требование нулевой работы для поездки туда и обратно не выполняется за счет силы трения.
2. Сила консервативна, если работа, совершаемая ею над движущейся частицей
между двумя точками одинаково для всех путей, соединяющих эти точки;
в противном случае это неконсервативно.
Тест 1 и тест 2 эквивалентны. Например, предположим, что работа, проделанная для
путь туда и обратно от A до B и обратно до A (см. рисунок 8.2) равен нулю. Это означает
тот
Рисунок 8.2. Частица в пути туда и обратно из А в Б, обратно в А и из А
в пункт B двумя разными маршрутами.
W AB, 1 + W BA, 2 = 0
или
W AB, 1 = — W BA, 2
Работа, выполняемая силой на каждом сегменте, меняет знак, если мы вернемся
направление
W AB, 2 = — W BA, 2
Это соотношение можно использовать, чтобы показать, что
W AB, 1 = W AB, 2
это именно то, что утверждает тест 2 (работа, выполняемая силой на
объект зависит только от начальной и конечной позиции объекта, а не от
выбранный путь).
На рисунке 8.3 показаны две возможные траектории, чтобы добраться из пункта А в пункт Б.
работа, совершаемая на объекте силой тяжести для траектории 1 и для
траектория 2? Произведенная работа при перемещении массы по маршруту 1 равна
.
Альтернативный маршрут (маршрут 2) состоит из движения по горизонтали.
направление, за которым следует один в вертикальном направлении. Для любого движения в
В горизонтальной плоскости сила тяжести перпендикулярна смещению.Следовательно, работа, совершаемая гравитационной силой, равна нулю. Для движения
по вертикали движению противодействует сила тяжести. Работа
за счет силы тяжести
Рисунок 8.3. Две возможные траектории из пункта А в пункт Б.
Суммарная работа, совершаемая гравитационной силой над объектом, когда он
перемещен из A в B по маршруту 2, поэтому
что равно W 1 .
График потенциальной энергии как функции координаты x говорит нам о многом.
о движении объекта (см., например, рис. 8.12 в книге Хэллидея,
Резник и Уокер). Дифференцируя U (x), мы можем получить силу, действующую на
объект
В отсутствие трения сохраняется сохранение механической энергии.
и
U (x) + K = E
Поскольку кинетическая энергия не может быть отрицательной, частица может быть только
в тех регионах, для которых E — U равно нулю или положительно.Точки, в которых E —
U = K = 0 называются точками поворота. Кривая потенциальной энергии
(Рисунок 8.12 у Холлидея, Резника и Уокера) показывает несколько локальных максимумов и
минимумы. Сила в каждом из этих максимумов и минимумов равна нулю. Точка — это
положение устойчивого равновесия, если потенциальная энергия при этом имеет минимум
точки (в этом случае небольшие смещения в любом направлении приведут к
сила, которая толкает частицу обратно в положение стабильной
равновесие).Точки неустойчивого равновесия проявляются как максимумы в потенциале
кривая энергии (если частица немного смещена от положения
неустойчивое равновесие, силы, действующие на него, будут стремиться толкать частицу
еще дальше).
Если мы посмотрим на систему блок-пружина, колеблющуюся на шероховатой поверхности, мы
видим, что амплитуда движения непрерывно уменьшается. Из-за
сила трения, механическая энергия больше не сохраняется.Если мы посмотрим на
система, на которую действуют несколько консервативных сил, помимо трения
сила. Всего по системе проделано
что равно изменению кинетической энергии системы
(теорема работы-энергии). Каждую консервативную силу можно отождествить с
потенциальная энергия и
Теперь мы можем переписать выражение для изменения кинетической энергии
системы
Работа, совершаемая силой трения, равна изменению
механическая энергия системы.
При наличии неконсервативных сил механическая энергия преобразуется
во внутреннюю энергию U int (или тепловую энергию):
[Delta] U int = — W f
При таком определении внутренней энергии работа-энергия
теорему можно переписать как
что является законом сохранения энергии. Прописью
Прописью
«Энергия может быть преобразована из одного вида в другой в изолированной системе.
но его нельзя создать или уничтожить; полная энергия системы всегда
остается постоянным.»
Пример задачи 8-8
Шарикоподшипник массой m запускается вертикально вниз с высоты h.
с начальной скоростью v 0 (см. рис. 8.4). Он зарывается в
песок на глубине d. Какая средняя восходящая сила сопротивления f действует на песок?
воздействовать на мяч, когда дело касается отдыха?
Рисунок 8.4. Пример задачи 5.
Работа, совершаемая силой трения f, определяется по формуле
.
Начальная механическая энергия системы равна
.
Конечная механическая энергия системы состоит только из
потенциальная энергия (K f = 0)
E f = U f = m g (- d) = — m g d
Изменение механической энергии
которая должна быть равна работе, совершаемой на подшипнике фрикционным
сила
Теперь можно рассчитать силу трения f
Пример задачи 2
Блок массой m запускается по наклонной плоскости (см. Рис.
Рис.
8.5) с начальной скоростью v 0 . Он проходит расстояние d вверх по
плоскости, на мгновение останавливается, а затем скользит обратно в нижнюю часть
самолет. Какова величина кинетической силы трения, действующей на
блок, пока он движется? Какая будет скорость, когда блок
возвращается в исходное положение.
Работа, совершаемая силой трения, равна изменению механической
энергия системы. Потенциальная энергия в начале координат принимается равной нулю.Следовательно, начальная механическая энергия системы — это просто кинетическая энергия.
энергия блока
Рисунок 8.5. Пример задачи 2.
Конечная механическая энергия (на максимальной высоте) — это всего лишь потенциальная
энергия блока на высоте h:
E f = m g h = m g d sin ([theta])
Изменение механической энергии
Работа, совершаемая на блоке силой трения, составляет
W f = — f d
и должен быть равен [Delta] E. Таким образом
Таким образом
Теперь можно получить силу трения f
Когда блок возвращается в исходное положение, сила трения снова действует.
работа на блоке. Суммарная работа силы трения на блоке равна
сейчас
W f = — 2 f d
Это должно быть равно изменению механической энергии системы.
Когда блок возвращается в начало координат, его потенциал не меняется.
энергия.Изменение механической энергии системы происходит из-за изменения
в скорости блока:
Теперь можно рассчитать конечную скорость блока
Отправляйте комментарии, вопросы и / или предложения по электронной почте по адресу [email protected] и / или посетите домашнюю страницу Фрэнка Вольфса.
Можно ли нарушить закон сохранения энергии?
[1]
История физики / GUO Yi-ling, Chen Huijun ed Издательство: Пекин: Издательство Университета Цинхуа, 1993. 7.
7.
[2]
Theoretical Mechanics counseling and problem sets; Author: Gao Yunfeng, Li Junfeng, ed. Gao Yunfeng. Junfeng; Publisher: Beijing Tsinghua University Press.
[3]
Физика; Автор: Чжу Фэн, редактор; Издатель: Beijing Tsinghua University Press.
[4]
Антивещество — абсолютное зеркало мира; Автор: Гордон — Фрейзер; Пресса: Шанхайская научно-техническая образовательная пресса.
Закон сохранения энергии | Заявление и примеры
Полная энергия изолированной системы остается постоянной во времени. Колыбель Ньютона. Устройство, демонстрирующее закон сохранения механической энергии и количества движения.
Энергия может быть определена как способность выполнять работу . Он может существовать в различных формах и быть преобразован из одного типа энергии в другой сотнями способов.
Например, сжигание бензина в автомобилях — это процесс преобразования энергии, на который мы полагаемся. Химическая энергия в бензине — это преобразованная в тепловую энергию , затем преобразованную в механическую энергию , которая заставляет автомобиль двигаться. Механическая энергия была преобразована в кинетическую энергию . Когда мы используем тормоза для остановки автомобиля, эта кинетическая энергия преобразуется посредством трения обратно в тепло или тепловую энергию .
Следствием закона сохранения энергии является то, что вечный двигатель первого типа, который производит работу без ввода энергии, не может существовать.
Концепция энергосбережения широко используется во многих областях. В этой статье обсуждаются следующие области:
Закон сохранения энергии в классической физике
Сохранение механической энергии
Во-первых, был сформулирован принцип сохранения механической энергии :
Общая механическая энергия энергия (определяемая как сумма ее потенциальной и кинетической энергий) частицы, на которую действуют только консервативные силы , является постоянной .
Изолированная система — это система, в которой никакая внешняя сила не вызывает изменения энергии. Если на объект действуют только консервативных сил и U является функцией потенциальной энергии для общей консервативной силы, то:
E мех = U + K
Потенциальная энергия U зависит от положения объекта, на который действует консервативная сила.
Определяется как способность объекта выполнять работу и увеличивается по мере того, как объект перемещается в направлении, противоположном силе.
Потенциальная энергия , связанная с системой, состоящей из Земли и ближайшей частицы, равна гравитационной потенциальной энергии .
Кинетическая энергия, K , зависит от скорости объекта и представляет собой способность движущегося объекта выполнять работу с другими объектами при столкновении с ними.
K = ½ mv 2
В приведенном выше определении ( E mech = U + K ) предполагается, что система свободна от трения и других не консервативные силы . Разница между консервативной и неконсервативной силой состоит в том, что когда консервативная сила перемещает объект из одной точки в другую, работа, выполняемая консервативной силой, не зависит от пути.
В любой реальной ситуации присутствуют силы трения, и другие неконсервативные силы. Тем не менее, их влияние на систему настолько мало, что принцип сохранения механической энергии может использоваться во многих случаях как хорошее приближение. Например, сила трения является неконсервативной силой, потому что она снижает механическую энергию в системе.
Обратите внимание, что неконсервативные силы не всегда снижают механическую энергию. Неконсервативная сила изменяет механическую энергию.Некоторые силы увеличивают общую механическую энергию, например сила, создаваемая двигателем или двигателем, которая также является неконсервативной силой.
“Пример
Предположим, что маятник (шар массы m, подвешенный на веревке длиной L , которую мы подтянули вверх, так что высота шара составляет H 
Освобождаем его от покоя. Как быстро он движется внизу?
Маятник достигает наибольшей кинетической энергии и наименьшей потенциальной энергии в вертикальном положении , потому что он будет иметь наибольшую скорость и в этой точке будет ближе к Земле. С другой стороны, у него будет наименьшая кинетическая энергия и наибольшая потенциальная энергия в крайних положениях его поворота, , потому что он имеет нулевую скорость и находится дальше всего от Земли в этих точках.
Если амплитуда ограничена небольшими колебаниями, период T простого маятника, время берется за полный цикл, составляет:
, где L — длина маятника, а г — местное ускорение свободного падения. Для небольших качелей период качания примерно одинаков для качелей разного размера. То есть период не зависит от амплитуды .
Закон сохранения энергии — Неконсервативные силы
Теперь мы учтем неконсервативных сил , таких как трение, поскольку они важны в реальных ситуациях.Например, снова рассмотрим маятник, но на этот раз включим сопротивление воздуха . Маятник замедлится из-за трения. В этом и других естественных процессах механическая энергия (сумма кинетической и потенциальной энергий) не остается постоянной , а уменьшается. Поскольку силы трения уменьшают механическую энергию (но не полную энергию), они называются неконсервативными силами (или диссипативными силами ).Но в девятнадцатом веке было продемонстрировано , что полная энергия сохраняется в любом процессе . В случае маятника вся его начальная кинетическая энергия преобразуется в тепловую энергию.
Для каждого типа силы, консервативной или неконсервативной, всегда можно было определить тип энергии, который соответствует работе, совершаемой такой силой. И экспериментально было обнаружено, что полная энергия E всегда остается постоянной. Общий закон сохранения энергии можно сформулировать следующим образом:
И экспериментально было обнаружено, что полная энергия E всегда остается постоянной. Общий закон сохранения энергии можно сформулировать следующим образом:
Полная энергия E системы (сумма ее механической энергии и ее внутренней энергии, включая тепловую) может изменяться только в зависимости от количества переданной энергии. в систему или из нее.
Сохранение импульса и энергии при столкновениях
Использование законов сохранения импульса и энергии также очень важно при столкновениях частиц . Это очень мощное правило, потому что оно может позволить нам определить результаты столкновения, не зная подробностей столкновения. Закон сохранения импульса гласит, что полный импульс сохраняется при столкновении двух объектов, таких как бильярдные шары.Предположение о сохранении импульса и кинетической энергии делает возможным вычисление конечных скоростей в столкновениях двух тел. На этом этапе мы должны различать два типа столкновений:
На этом этапе мы должны различать два типа столкновений:
- Упругие столкновения
- Неупругие столкновения
Упругие столкновения
A Совершенно упругое столкновение определяется как столкновение, в котором нет. чистое преобразование кинетической энергии в другие формы (например, тепло или шум).В течение короткого момента, в течение которого два объекта находятся в контакте, некоторая (или вся) энергия мгновенно сохраняется в форме упругой потенциальной энергии . Но если мы сравним полную кинетическую энергию непосредственно перед столкновением с полной кинетической энергией сразу после столкновения, они окажутся одинаковыми. Мы говорим, что общая кинетическая энергия сохраняется .
- Крупномасштабные взаимодействия между спутниками и планетами идеально эластичны , как и гравитационные взаимодействия типа рогатки (также известные как планетарный поворот или гравитационный маневр).

- Столкновения между очень твердыми сферами могут быть почти упругими , поэтому полезно рассчитать предельный случай упругого столкновения.
- Столкновения в идеальных газах приближаются к идеально упругим столкновениям, как и рассеивающие взаимодействия субатомных частиц, отклоняемых электромагнитной силой.
- Резерфордовское рассеяние — это упругое рассеяние заряженных частиц также под действием электромагнитной силы.
- Реакция рассеяния нейтрона на ядре также может быть упругой, но в этом случае нейтрон отклоняется сильной ядерной силой.
“Уравнения
Предположим, что одномерное упругое столкновение двух объектов, объекта A и объекта B. Эти два объекта движутся со скоростями v A и v B, вдоль Ось x до столкновения. После столкновения их скорости равны v’A и v’B . Сохранение полного импульса требует, чтобы полный импульс до столкновения был таким же, как полный импульс после столкновения.Аналогично, сохранение полной кинетической энергии требует, чтобы полная кинетическая энергия обоих объектов до столкновения была такой же, как полная кинетическая энергия после столкновения. Оба закона могут быть выражены в уравнениях:
Сохранение полного импульса требует, чтобы полный импульс до столкновения был таким же, как полный импульс после столкновения.Аналогично, сохранение полной кинетической энергии требует, чтобы полная кинетическая энергия обоих объектов до столкновения была такой же, как полная кинетическая энергия после столкновения. Оба закона могут быть выражены в уравнениях:
Относительная скорость двух объектов после столкновения имеет такую же величину (но в противоположном направлении), как до столкновения, независимо от массы .
Упругое ядерное столкновение
См. Также: замедлители нейтронов
Известно, что нейтроны деления играют важную роль в любой системе цепной реакции.Все нейтроны, образующиеся при делении, рождаются как быстрых нейтронов с высокой кинетической энергией. Прежде чем такие нейтроны смогут эффективно вызвать дополнительное деление, они должны быть замедлены столкновениями с ядрами в замедлителе реактора.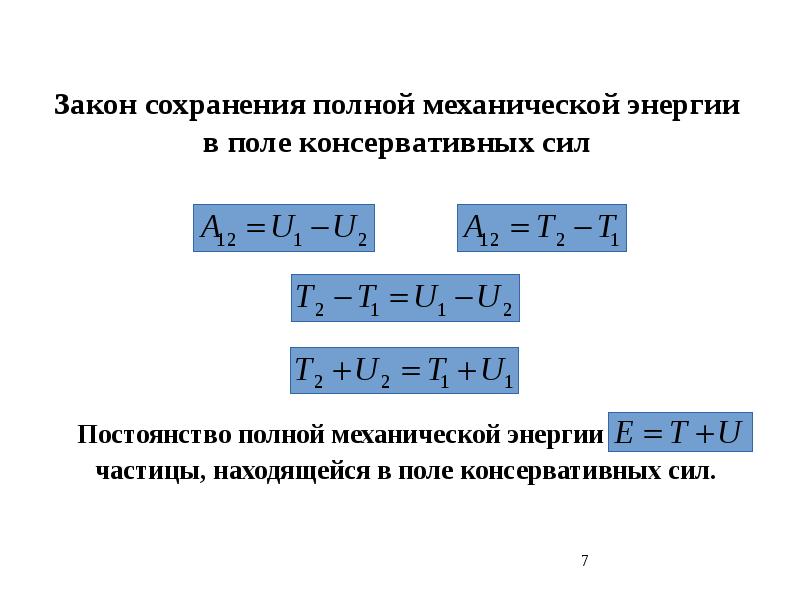 Вероятность деления U-235 становится очень большой при тепловых энергиях медленных нейтронов. Этот факт подразумевает увеличение коэффициента размножения реактора (т.е. для поддержания цепной реакции требуется более низкое обогащение топлива).
Вероятность деления U-235 становится очень большой при тепловых энергиях медленных нейтронов. Этот факт подразумевает увеличение коэффициента размножения реактора (т.е. для поддержания цепной реакции требуется более низкое обогащение топлива).
Нейтроны, выделяющиеся при делении со средней энергией 2 МэВ в реакторе в среднем претерпевают многих столкновений (упругих или неупругих), прежде чем они будут поглощены.Во время реакции рассеяния часть кинетической энергии нейтрона передается ядру . Можно вывести следующее уравнение для массы ядра мишени или замедлителя (M), энергии падающего нейтрона (E i ) и энергии рассеянного нейтрона (E s ), используя законы сохранения импульса и энергии и аналогия соударений бильярдных шаров для упругого рассеяния.
где A — атомное массовое число, в случае водорода (A = 1) в качестве ядра-мишени, падающий нейтрон может быть полностью остановлен . Но это работает, когда нейтрон полностью меняет направление (т. Е. Рассеивается на 180 °). В действительности направление рассеяния колеблется от 0 до 180 °, а передаваемая энергия также колеблется от 0% до максимума. Поэтому средняя энергия рассеянного нейтрона принимается как среднее значение энергий с углами рассеяния 0 и 180 °.
Но это работает, когда нейтрон полностью меняет направление (т. Е. Рассеивается на 180 °). В действительности направление рассеяния колеблется от 0 до 180 °, а передаваемая энергия также колеблется от 0% до максимума. Поэтому средняя энергия рассеянного нейтрона принимается как среднее значение энергий с углами рассеяния 0 и 180 °.
Кроме того, полезно работать с логарифмическими величинами . Следовательно, можно определить логарифмический декремент энергии на столкновение (ξ) как ключевую материальную константу, описывающую перенос энергии во время замедления нейтрона.ξ не зависит от энергии, а зависит только от A и определяется следующим образом: Для тяжелых ядер-мишеней ξ может быть аппроксимировано следующей формулой: Из этих уравнений легко определить количество столкновений, необходимых для замедления нейтрон от, например, от 2 МэВ до 1 эВ .
Пример: Определите количество столкновений, необходимых для термализации нейтронов с энергией 2 МэВ в углероде.
ξ УГЛЕРОД = 0,158
N ( 2МэВ → 1эВ ) = ln 2⋅10 6 / ξ = 14.5 / 0,158 = 92 Таблица среднего логарифмического декремента энергии некоторых элементов.
Для смеси изотопов:
Пример: Упругое ядерное столкновение
Нейтрон (n) с массой 1,01 u движется со скоростью 3,60 x 10 4 м / с взаимодействует с Углерод (C) ядро ( m C = 12.00 u ) первоначально в состоянии покоя при упругом лобовом столкновении .
Каковы скорости нейтрона и ядра углерода после столкновения?
Решение:
Это упругое лобовое столкновение двух объектов с неравными массами .Мы должны использовать законы сохранения количества движения и кинетической энергии и применить их к нашей системе двух частиц.
Мы можем решить эту систему уравнений или использовать уравнение, полученное в предыдущем разделе. Это уравнение утверждает, что относительная скорость двух объектов после столкновения имеет ту же величину (но в противоположном направлении), что и до столкновения, независимо от массы.
Это уравнение утверждает, что относительная скорость двух объектов после столкновения имеет ту же величину (но в противоположном направлении), что и до столкновения, независимо от массы.
Знак минус для v ’говорит нам, что нейтрон рассеивает назад ядра углерода, потому что ядро углерода значительно тяжелее.С другой стороны, его скорость меньше его начальной скорости. Этот процесс известен как замедление нейтронов , и существенно зависит от массы ядер замедлителя.
Неупругие столкновения
Неупругие столкновения — это когда часть кинетической энергии изменяется на некоторую другую форму энергии при столкновении. Любое макроскопическое столкновение между объектами преобразует некоторую кинетическую энергию во внутреннюю энергию и другие формы энергии, поэтому никакие крупномасштабные столкновения не являются идеально упругими . Например, при столкновении общих тел, таких как две машины, некоторая энергия всегда передается от кинетической энергии к другим формам энергии, таким как тепловая энергия или энергия звука . Неупругое столкновение двух тел всегда связано с потерей кинетической энергии системы. Наибольшие потери происходят, если тела слипаются, и в этом случае столкновение называется полностью неупругим столкновением . Таким образом, кинетическая энергия системы равна , не сохраняется , тогда как общая энергия сохраняется , как того требует общий принцип сохранения энергии. Импульс сохраняется при неупругих столкновениях , но невозможно отследить кинетическую энергию во время столкновения, поскольку часть ее преобразуется в другие формы энергии.
Например, при столкновении общих тел, таких как две машины, некоторая энергия всегда передается от кинетической энергии к другим формам энергии, таким как тепловая энергия или энергия звука . Неупругое столкновение двух тел всегда связано с потерей кинетической энергии системы. Наибольшие потери происходят, если тела слипаются, и в этом случае столкновение называется полностью неупругим столкновением . Таким образом, кинетическая энергия системы равна , не сохраняется , тогда как общая энергия сохраняется , как того требует общий принцип сохранения энергии. Импульс сохраняется при неупругих столкновениях , но невозможно отследить кинетическую энергию во время столкновения, поскольку часть ее преобразуется в другие формы энергии.
В ядерной физике неупругое столкновение — это когда падающая частица заставляет ядро ударить, чтобы возбудиться или разрушиться. Глубоконеупругое рассеяние — это метод исследования структуры субатомных частиц во многом так же, как Резерфорд исследовал внутреннюю часть атома (см. Рассеяние Резерфорда).
Глубоконеупругое рассеяние — это метод исследования структуры субатомных частиц во многом так же, как Резерфорд исследовал внутреннюю часть атома (см. Рассеяние Резерфорда).
В ядерных реакторах неупругие столкновения играют важную роль в процессе замедления нейтронов . Неупругое рассеяние играет важную роль в замедлении нейтронов, особенно при высоких энергиях и на тяжелых ядрах . Неупругое рассеяние происходит выше пороговой энергии . Эта пороговая энергия превышает энергию первого возбужденного состояния ядра-мишени (из-за законов сохранения) и определяется следующей формулой:
E t = ((A +1) / A) * ε 1
где E t — неупругая пороговая энергия , и ε 1 — энергия первого возбужденного состояния . Таким образом, особенно данные рассеяния 238 U , основного компонента ядерного топлива в промышленных энергетических реакторах, являются одними из наиболее важных данных при расчетах переноса нейтронов в активной зоне реактора.
Таким образом, особенно данные рассеяния 238 U , основного компонента ядерного топлива в промышленных энергетических реакторах, являются одними из наиболее важных данных при расчетах переноса нейтронов в активной зоне реактора.
Пример: баллистический маятник
Баллистический маятник — это своего рода «трансформатор», меняющий высокую скорость легкого объекта (пули) на низкую скорость массивного объекта.
Баллистический маятник — это устройство для измерения скорости снаряда, например пули .Баллистический маятник — это своего рода «трансформатор», меняющий высокую скорость легкого объекта (пули) на низкую скорость массивного объекта (блока). Когда пуля попадает в блок, ее импульс передается блоку. Импульс пули можно определить по амплитуде качания маятника .
Когда пуля встраивается в блок, это происходит так быстро, что блок не перемещается заметно. Поддерживающие струны остаются почти вертикальными, поэтому незначительная внешняя горизонтальная сила действует на систему пуля-блок, и горизонтальная составляющая импульса сохраняется . Однако механическая энергия не сохраняется на этом этапе, потому что неконсервативная сила действительно работает (сила трения между пулей и блоком).
Однако механическая энергия не сохраняется на этом этапе, потому что неконсервативная сила действительно работает (сила трения между пулей и блоком).
На втором этапе пуля и блок движутся вместе. Единственными силами, действующими на эту систему, являются гравитация (консервативная сила) и натяжение струн (которые не работают). Таким образом, при повороте блока сохраняется механической энергии . Импульс не сохраняется на этом этапе , потому что существует чистая внешняя сила (силы тяжести и натяжения струны не отменяются, когда струны наклонены).
Уравнения, управляющие баллистическим маятником
На первом этапе сохраняется импульс , и, следовательно:
, где v — начальная скорость снаряда массой
68 м P P 90 . v ’ — скорость блока и встроенного снаряда (оба имеют массу m P + m B ) сразу после столкновения, прежде чем они существенно переместятся.
На втором этапе сохраняется механической энергии .Мы выбираем y = 0, когда маятник висит вертикально, а затем y = h, когда блок и встроенная снарядная система достигают своей максимальной высоты. Система раскачивается и останавливается на мгновение на высоте y, где ее кинетическая энергия равна нулю, а потенциальная энергия равна (m P + m B ) gh . Таким образом, мы запишем закон сохранения энергии:
, который является начальной скоростью снаряда и нашим конечным результатом.
Если использовать реалистичные числа:
- м P = 5 г
- м B = 2 кг
- h = 3 см
- v =?
, тогда мы имеем:
Сохранение энергии в механике жидкостей — принцип Бернулли
Закон сохранения энергии также можно использовать при анализе текущих жидкостей .
Уравнение Бернулли можно рассматривать как утверждение принципа сохранения энергии , подходящего для текущих жидкостей. Это одно из самых важных и полезных уравнений в механике жидкости . Он ставит в соотношение давление и скорость в невязком несжимаемом потоке . Общее уравнение энергии упрощается до:
Это одно из самых важных и полезных уравнений в механике жидкости . Он ставит в соотношение давление и скорость в невязком несжимаемом потоке . Общее уравнение энергии упрощается до:
Это уравнение является самым известным в гидродинамике . Уравнение Бернулли описывает качественное поведение текущей жидкости, которое обычно обозначается эффектом Бернулли .Этот эффект вызывает понижение давления жидкости в областях, где скорость потока увеличивается. Это понижение давления в сужении пути потока может показаться нелогичным, но кажется менее очевидным, если учесть, что давление составляет , плотность энергии . В высокоскоростном потоке через сужение кинетическая энергия должна увеличиваться за счет энергии давления . Размеры членов в уравнении — кинетическая энергия на единицу объема.Вышеприведенное уравнение предполагает, что на жидкость не действуют неконсервативные силы (например, силы трения). Это очень сильное предположение.
Это очень сильное предположение.
Расширенное уравнение Бернулли
Уравнение Бернулли можно модифицировать, чтобы учесть приростов и потерь напора , вызванных внешними силами и неконсервативными силами . Полученное уравнение, называемое расширенным уравнением Бернулли , полезно при решении большинства задач потока жидкости.Следующее уравнение является одной из форм расширенного уравнения Бернулли.
где:
- h = высота над контрольным уровнем (м)
- v = средняя скорость жидкости (м / с)
- p = давление жидкости (Па)
- H насос = добавленный напор насосом (м)
- H трение = потеря напора из-за гидравлического трения (м)
- g = ускорение свободного падения (м / с 2 )
Гидравлическая линия уклона и общий напор для труб постоянного диаметра с трением.В реальном трубопроводе возникают потери энергии из-за трения — их необходимо учитывать, поскольку они могут быть очень значительными.
Потеря напора (или потеря давления) из-за трения жидкости (H трение ) представляет собой энергию, используемую для преодоления трения, вызванного стенками трубы. Потеря напора, возникающая в трубах, зависит от скорости потока , диаметра трубы, длины и и коэффициента трения на основе шероховатости трубы и числа Рейнольдса потока.Система трубопроводов, содержащая множество фитингов и соединений, схождение труб, расхождение, повороты, шероховатость поверхности и другие физические свойства также увеличивают потерю напора гидравлической системы.
Хотя потеря напора представляет собой потерю энергии , она не представляет собой потерю общей энергии жидкости. Полная энергия жидкости сохраняется как следствие закона сохранения энергии . В действительности потеря напора из-за трения приводит к эквивалентному увеличению на внутренней энергии (повышению температуры) жидкости.
Это явление также можно наблюдать в случае насосов теплоносителя реактора. Как правило, насосы теплоносителя реактора очень мощные, они могут потреблять от до 6 МВт каждый, , и поэтому их можно использовать для нагрева теплоносителя первого контура перед запуском реактора, например, от 30 ° C при холодной нулевой мощности (CZP). до 290 ° C при горячем нуле мощности (HZP).
Сохранение энергии в термодинамике — первый закон термодинамики
В термодинамике, понятие энергии расширено, чтобы учесть другие наблюдаемые изменения.Принцип сохранения энергии расширен, чтобы включить широкий спектр способов взаимодействия систем с окружающей средой. Единственные способы изменения энергии замкнутой системы — это передача энергии работой или теплом . Кроме того, основываясь на экспериментах Джоуля и других, фундаментальный аспект концепции энергии состоит в том, что энергии сохраняется. Этот принцип известен как первый закон термодинамики . Первый закон термодинамики можно записать в различных формах:
Словами:
Физическая схема четырех основных устройств, используемых в цикле Ренкина и основных передачах энергии.
Форма уравнения:
∆E int = Q — W
где E int представляет внутреннюю энергию материала, которая зависит только от материала . состояние (температура, давление и объем), Q — это чистое тепло , добавленное к системе, и W — чистая работа , выполненная системой. Мы должны быть осторожны и последовательны в соблюдении соглашений о знаках для Q и W.Поскольку W в уравнении — это работа, выполняемая системой, то, если работа выполняется в системе, W будет отрицательным, а E int увеличится.
Аналогично, Q положительно для тепла, добавляемого в систему, поэтому Q отрицательно, если тепло покидает систему. Это говорит нам следующее: внутренняя энергия системы имеет тенденцию увеличиваться, если система поглощает тепло или если в системе совершается положительная работа. И наоборот, внутренняя энергия имеет тенденцию уменьшаться, если система теряет тепло или если в системе совершается отрицательная работа.Он должен быть добавлен. Q и W зависят от пути, а E int не зависит от пути.
Дифференциальная форма:
dE int = dQ — dW
Внутренняя энергия E int системы имеет тенденцию увеличиваться, если энергия добавляется как тепло Q, и имеет тенденцию уменьшаться, если энергия теряется как работа W выполняется системой.
Открытая система — Закрытая система — Изолированная система
Тепло и / или работа могут быть направлены в или из контрольного объема .Но для удобства и в качестве стандартного соглашения здесь представлен чистый обмен энергией, при этом предполагается, что чистый теплообмен осуществляется в систему, а сеть — вне системы. Если никакая масса не пересекает границу, , но работает и / или нагревается, система называется «закрытой» системой . Если масса, работа и тепло не пересекают границу (то есть, обмен энергией происходит только внутри системы), система называется изолированной системой .Изолированные и закрытые системы — это не что иное, как специализированные корпуса открытой системы .
Сохранение энергии в электрических цепях
Закон напряжения Кирхгофа (KVL)
Закон сохранения энергии также может быть использован при анализе электрических цепей . При анализе электрических цепей принцип сохранения энергии составляет основу закона, известного как закон напряжения Кирхгофа (или второй закон Кирхгофа ) в честь немецкого физика Густава Роберта Кирхгофа.
Закон Кирхгофа по напряжению гласит:
Алгебраическая сумма напряжений (падающих или возрастающих), возникающих при прохождении любого контура цепи в указанном направлении, должна быть равна нулю.
Алгебраическая сумма напряжений (падающих или возрастающих), возникающих при прохождении любого контура цепи в указанном направлении, должна быть равна нулю.
Проще говоря, изменения напряжения в любом замкнутом контуре должны в сумме равняться нулю. Сумма повышений напряжения равна сумме падений напряжения в контуре.Независимо от того, какой путь вы пройдете через электрическую цепь, если вы вернетесь в исходную точку, вы должны измерить то же напряжение, ограничивая чистое изменение вокруг контура равным нулю.
Поскольку напряжение составляет электрической потенциальной энергии на единицу заряда, закон напряжения может быть следствием сохранения энергии . Это правило эквивалентно утверждению, что каждая точка горы имеет только одну высоту над уровнем моря. Если вы начнете с любой точки и вернетесь к ней после обхода горы, алгебраическая сумма изменений высоты, с которыми вы столкнетесь, должна быть равна нулю.
Закон напряжения имеет большое практическое применение при анализе электрических цепей. Он используется в сочетании с текущим законом во многих задачах анализа цепей.
Сохранение энергии в химических реакциях
Концепция сохранения энергии также широко используется в химии . Химические реакции определяются законами термодинамики . В термодинамике внутренняя энергия системы — это энергия, содержащаяся в системе, за исключением кинетической энергии движения системы в целом и потенциальной энергии системы в целом, обусловленной внешними силовыми полями.
В термодинамике внутренняя энергия включает поступательную кинетическую энергию молекул (в случае газов), кинетическую энергию, обусловленную вращением на молекул относительно их центров масс, и кинетическая энергия, связанная с колебательными движениями внутри молекул.
В химических реакциях энергия накапливается в химических связях между атомами, составляющими молекулы. Накопитель энергии на атомном уровне включает энергию, связанную с электронными орбитальными состояниями. Независимо от того, поглощает ли химическая реакция или высвобождает энергию, общего изменения количества энергии во время реакции не происходит. Это из-за закона сохранения энергии , который гласит:
Энергия не может быть создана или уничтожена . Энергия может менять форму во время химической реакции .
Например, энергия может измениться с химической на тепловую, когда газ горит в печи.Точное количество энергии остается после реакции, как и раньше. Это верно для всех химических реакций.
В эндотермической реакции продукты содержат больше химической энергии, чем реагенты. В экзотермической реакции верно обратное. Продукты содержат меньше химической энергии, чем реагенты. Избыточная энергия обычно выделяется в окружающую среду, когда происходит реакция.
Пример: сжигание водорода
В пламени чистого газообразного водорода, горящего в воздухе, водород (h3) реагирует с кислородом (O2) с образованием воды (h3O) и выделяет энергию.
Рассмотрим горение водорода на воздухе. В пламени чистого газообразного водорода, горящего в воздухе, водород (H 2 ) реагирует с кислородом (O 2 ) с образованием воды (H 2 O) и выделяет энергию .
Энергетически процесс может потребовать энергии для диссоциации H 2 и O 2 , но затем связывание H 2 O возвращает систему в связанное состояние с отрицательным потенциалом .Оно на отрицательнее, чем на , чем связанные состояния реагентов, и образование двух молекул воды, следовательно, является экзотермической реакцией , которая выделяет 5,7 эВ энергии.
2H 2 (г) + O 2 (г) → 2H 2 O (г)
Энергетический баланс до и после реакции можно схематически проиллюстрировать с помощью состояния, в котором все атомы находятся в free взят за эталон для энергии.
Закон сохранения массы-энергии — эквивалентность массы-энергии
В начале 20 века понятие массы претерпело радикальный пересмотр.Масса утратила абсолютность . Один из поразительных результатов теории относительности Эйнштейна состоит в том, что масса и энергия эквивалентны и конвертируются друг в друга. Эквивалентность массы и энергии описывается знаменитой формулой Эйнштейна E = mc 2 . Другими словами, энергия равна массе , умноженной на квадрата скорости света . Поскольку скорость света — это очень большое число, формула подразумевает, что любое небольшое количество вещества содержит очень большое количество энергии.Масса объекта считалась эквивалентной энергии, взаимопревращаемой с энергией и значительно увеличивающейся на чрезвычайно высоких скоростях, близких к скорости света. Под полной энергией объекта понималась его масса покоя на и увеличение массы на , вызванное увеличением кинетической энергии на .
В специальной теории относительности определенные типы материи могут быть созданы или уничтожены . Тем не менее, масса и энергия, связанные с такой материей , остаются неизменными в количестве во всех этих процессах.Было обнаружено, что масса покоя атомного ядра заметно меньше, чем сумма масс покоя составляющих его протонов, нейтронов и электронов . Масса больше не считалась неизменной в закрытой системе. Разница — это мера энергии связи ядра, которая удерживает ядро вместе. Согласно соотношению Эйнштейна ( E = mc 2 ), эта энергия связи пропорциональна этой разнице масс, известной как дефект массы .
“Пример:
Вычислите дефект массы ядра 63 Cu , если фактическая масса 63 Cu в основном ядерном состоянии составляет 62, ед.
63 Ядро Cu имеет 29 протонов и также имеет (63 — 29) 34 нейтрона.
Масса протона 1.00728 u, и нейтрона 1.00867 u .
Общая масса равна: 29 протонов x (1,00728 ед / протон) + 34 нейтрона x (1,00867 ед / нейтрон) = 63.50590 u
Дефект массы равен Δm = 63,50590 u — 62, u = 0,59223 u
Преобразуйте дефект массы в энергию (энергию связи ядра).
(0,59223 ед. / Ядро) x (1,6606 x 10 -27 кг / ед.) = 9,8346 x 10 -28 кг / ядро
ΔE = Δmc 2 9Δ0003
( 9,8346 x 10 -28 кг / ядро) x (2,9979 x 10 8 м / с) 2 = 8.8387 x 10 -11 Дж / ядро
Энергия, вычисленная в предыдущем примере, равна энергия связи ядра . Однако энергия связи ядра может быть выражена в кДж / моль (для лучшего понимания).
Рассчитайте ядерную энергию связи 1 моля 63 Cu:
(8,8387 x 10 -11 Дж / ядро) x (1 кДж / 1000 Дж) x (6,022 x 10 23 ядер / моль) = 5,3227 x 10 10 кДж / моль ядер.
Один моль 63 Cu (~ 63 грамма) связан с энергией связи ядра (5.3227 x 10 10 кДж / моль), что эквивалентно:
- 14,8 миллиона киловатт-часов (≈ 15 ГВт · ч)
- 336 100 американских галлонов автомобильного бензина
“Пример:
Рассчитайте дефект массы активной зоны реактора 3000 МВт th после одного года эксплуатации.
Средняя извлекаемая энергия на одно деление составляет около 200 МэВ , то есть полная энергия за вычетом энергии излучаемых антинейтрино.
Скорость реакции на все 3000 МВт th активная зона реактора составляет около 9,33 × 10 19 делений в секунду .
Общее выделение энергии в джоулях составляет:
200 × 10 6 (эВ) x 1,602 × 10 -19 (Дж / эВ) x 9,33 × 10 19 (с — 1 ) x 31,5 × 10 6 (секунды в году) = 9,4 × 10 16 Дж / год
Дефект массы рассчитывается как:
Δm = ΔE / c 2
Δm = 9.4 × 10 16 / (2,9979 x 10 8 ) 2 = 1,046 кг
Это означает, что в типичной активной зоне реактора мощностью 3000 МВтт около 1 килограмма вещества превращается в чистую энергию.
Обратите внимание, что типичная годовая нагрузка урана для активной зоны реактора мощностью 3000 МВт тепл. составляет примерно 20 тонн из обогащенного урана (т.е. примерно 22,7 тонны UO 2 ). Вся активная зона реактора может содержать около 80 тонн обогащенного урана.
Дефект массы непосредственно из E = mc
2
Дефект массы можно рассчитать непосредственно из соотношения Эйнштейна ( E = mc 2 ) как:
Δm = ΔE / c 2
Δm = 3000 × 10 6 (W = Дж / с) x 31,5 × 10 6 (секунды в году) / (2,9979 x 10 8 ) 2 = 1,051 кг
Кривая энергии связи ядра.
Источник: hyperphysics.phy-astr.gsu.edu
Во время ядерного расщепления или ядерного синтеза некоторая часть массы ядра превращается в огромное количество энергии.Таким образом, эта масса удаляется из общей массы исходных частиц, и масса отсутствует в получившемся ядре. Энергии связи ядер огромны, и они в миллион раз больше, чем энергии связи электронов атомов.
Как правило, как в химических реакциях , , так и в ядерных реакциях происходит некоторое преобразование между массой покоя и энергией, так что продукты обычно имеют меньшую или большую массу, чем реагенты. Следовательно, новый принцип сохранения — сохранение энергии массы .
См. Также: Энергия, выделяемая при делении
Сохранение энергии в ядерных реакциях
При анализе ядерных реакций мы должны применять общий закон сохранения энергии массы. Согласно этому закону, масса и энергия эквивалентны и преобразуются друг в друга. Это один из поразительных результатов теории относительности Эйнштейна . Это эквивалент массы и энергии описывается знаменитой формулой Эйнштейна E = mc 2 .
Как правило, как в химических реакциях , , так и в ядерных реакциях происходит некоторое преобразование между массой покоя и энергией, так что продукты обычно имеют меньшую или большую массу, чем реагенты. В общем, полная (релятивистская) энергия должна быть сохранена. Следовательно, «недостающая» масса покоя должна снова появиться в виде кинетической энергии, высвобождаемой в реакции. Разница — это мера энергии связи ядра, которая удерживает ядро вместе.
Энергии связи ядер огромны и в миллион раз превышают энергии связи электронов атомов.Q-значение DT-реакции синтеза
Энергетика ядерных реакций определяется значением Q- этой реакции. Q-значение реакции определяется как разность между суммой масс исходных реагентов и суммой масс конечных продуктов в единицах энергии (обычно в МэВ).
Рассмотрим типичную реакцию, в которой снаряд a и цель A попадают в два продукта, B и b.Это также может быть выражено в обозначениях, которые мы использовали до сих пор, a + A → B + b , или даже в более компактных обозначениях, A (a, b) B .
См. Также: E = mc 2
Значение Q этой реакции определяется как:
Q = [m a + m A — (m b + m B )] c 2
, что соответствует избыточной кинетической энергии конечных продуктов:
Q =
T конечный — T начальный
= T b + T B — (T 9011 9011 9011 9011 9011 9011 A )
Для реакций, в которых наблюдается увеличение кинетической энергии продуктов, Q положительно .Положительные Q-реакции называются экзотермическими (или экзергическими ). Имеется чистое высвобождение энергии, поскольку кинетическая энергия конечного состояния больше, чем кинетическая энергия начального состояния.
Для реакций, в которых наблюдается уменьшение кинетической энергии продуктов, Q отрицательно . Отрицательные Q-реакции являются эндотермическими (или эндоэргическими ), и они требуют ввода чистой энергии.
См. Также: Калькулятор Q-value.
Пример: экзотермическая реакция — DT Fusion
Значение Q реакции DT-синтеза
Реакция DT-синтеза дейтерия и трития особенно интересна из-за ее потенциала обеспечения энергии в будущем. Рассчитайте значение Q реакции .
3T (d, n) 4He
Атомные массы реагентов и продуктов составляют:
м ( 3 T) = 3,0160 а.е.м.
м ( 2 D) = 2,0141 а.е.м.
м ( 1 n) = 1.0087 а.е.м.
м ( 4 He) = 4,0026 а.е.м.
Используя эквивалентность массы и энергии, мы получаем Q-значение этой реакции как:
Q = {(3.0160 + 2.0141) [amu] — (1.0087 + 4.0026) [а. кинетика и в субкритический контроль .Особенно в ядерных реакторах с замедлителем D 2 O (реакторы CANDU) или отражателями из Be (некоторые экспериментальные реакторы). Нейтроны также могут образовываться в реакциях (γ, n), , и поэтому их обычно называют фотонейтронами .
Фотон высокой энергии (гамма-излучение) может при определенных условиях выбросить нейтрон из ядра. Это происходит, когда его энергия превышает энергию связи нейтрона в ядре. Большинство ядер имеют энергию связи выше 6 МэВ , что выше энергии большинства гамма-лучей от деления.С другой стороны, несколько ядер с достаточно низкой энергией связи представляют практический интерес . Это 2 D, 9 Be , 6 Li, 7 Li и 13 C. Как видно из таблицы, нижний порог имеет 9 Be с 1.666 МэВ и 2 D с 2.226 МэВ . Нуклиды с низкими пороговыми энергиями фотораспада
.
В случае дейтерия нейтроны могут образовываться при взаимодействии гамма-лучей (с минимальной энергией 2.22 МэВ) с дейтерием:
Q-значение реакции рассчитано ниже:
Атомные массы реагента и продуктов составляют:
м ( 2 D) = 2,01363 а.е.м.
м ( 1 n) = 1,00866 а.е.м.
м ( 1 H) = 1,00728 а.е.м.
Используя эквивалент массы и энергии, мы получаем значение Q этой реакции как:
Q = {2,01363 [а.е.м.] — ( 1,00866 + 1,00728) [а.е.м.]} x 931,481 [МэВ / а.е.м.]
= -0,00231 x 931.481 = -2,15 МэВ
Энергия , выделяемая в ядерной реакции , может проявляться в основном одним из трех способов:
- Кинетическая энергия продуктов
- Эмиссия гамма-лучей . Гамма-лучи излучаются нестабильными ядрами при их переходе из высокоэнергетического состояния в более низкое состояние, известное как гамма-распад.
- Метастабильное состояние . Некоторая энергия может оставаться в ядре в виде метастабильного энергетического уровня.
Небольшое количество энергии может также выделяться в виде рентгеновских лучей.Как правило, продукты ядерных реакций могут иметь разные атомные номера, и поэтому конфигурация их электронных оболочек отличается от реагентов. Поскольку электронов перестраивают сами и опускаются на более низкие энергетические уровни, могут испускаться рентгеновские лучи внутреннего перехода (рентгеновские лучи с точно определенными линиями излучения).
Сохранение энергии при делении ядер
В целом, деление ядер приводит к высвобождению огромных количеств энергии .Количество энергии сильно зависит от ядра, которое должно делиться, а также сильно зависит от кинетической энергии падающего нейтрона. Для расчета мощности реактора необходимо точно идентифицировать отдельные составляющие этой энергии . Во-первых, важно различать — полную высвобождаемую энергию, , и — энергию, которая может быть восстановлена в реакторе .
Полная энергия, выделяемая при делении, может быть рассчитана на основе энергий связи исходного ядра-мишени, которое должно делиться, и энергий связи продуктов деления.Но не всю полную энергию можно восстановить в реакторе. Например, около 10 МэВ выделяется в виде нейтрино (фактически, антинейтрино). Поскольку нейтрино слабо взаимодействуют (с чрезвычайно низким сечением любого взаимодействия), они не вносят вклад в энергию, которая может быть восстановлена в реакторе.
См. Также: Энергия, выделяемая при делении.
“Пример:
Рассчитайте дефект массы активной зоны реактора 3000MW th после одного года эксплуатации.
Средняя извлекаемая энергия на одно деление составляет около 200 МэВ , то есть полная энергия за вычетом энергии излучаемых антинейтрино.
Скорость реакции на все 3000 МВт th активная зона реактора составляет около 9,33 × 10 19 делений в секунду .
Общее выделение энергии в джоулях составляет:
200 × 10 6 (эВ) x 1,602 × 10 -19 (Дж / эВ) x 9,33 × 10 19 (с — 1 ) х 31.5 × 10 6 (секунды в году) = 9,4 × 10 16 Дж / год
Дефект массы рассчитывается как:
Δm = ΔE / c 2
Δm = 9,4 × 10 16 / (2,9979 x 10 8 ) 2 = 1,046 кг
Это означает, что в типичной активной зоне реактора мощностью 3000 МВт тепл. Около 1 кг вещества превращается в чистую энергию.
Обратите внимание, что типичная годовая нагрузка урана для активной зоны реактора мощностью 3000 МВт тепл. Составляет около 20 тонн из обогащенного урана (т.е., около 22,7 т УО 2 ). Вся активная зона реактора может содержать около 80 тонн обогащенного урана.
Дефект массы непосредственно из E = mc
2
Дефект массы можно рассчитать непосредственно из соотношения Эйнштейна ( E = mc 2 ) как:
Δm = ΔE / c 2
Δm = 3000 × 10 6 (W = Дж / с) x 31,5 × 10 6 (секунд в году) / (2,9979 x 10 8 ) 2 = 1,051 кг
Энергосбережение в бета-распаде — Открытие нейтрино
Бета-распад (β-распад) — это радиоактивный распад, при котором бета-частица и соответствующее нейтрино испускаются из ядра атома. Бета-излучение состоит из бета-частиц высокой энергии . Во время бета-распада испускаются высокоскоростные электронов или позитронов. Из-за испускания бета-распада нейтрон превращается в протон за счет испускания электрона. И наоборот, протон превращается в нейтрон при испускании позитрона, тем самым меняя тип нуклида. Бета-распад ядра C-14.
Открытие нейтрино
Изучение бета-распада дало первое физическое свидетельство существования нейтрино .Открытие нейтрино основано на законе сохранения энергии в процессе бета-распада.
Полученная частица (альфа-частица или фотон) имеет узкое энергетическое распределение как в альфа-, так и в гамма-распаде. Частица несет энергию от разницы между начальным и конечным состояниями ядра. Например, в случае альфа-распада, когда родительское ядро спонтанно разрушается с образованием дочернего ядра и альфа-частицы, сумма масс двух продуктов не совсем равна массе исходного ядра (см. Дефект массы ).В результате закона сохранения энергии эта разница проявляется в виде кинетической энергии альфа-частицы . Поскольку одни и те же частицы появляются как продукты при каждом разрушении определенного родительского ядра, разница масс должна быть всегда одинаковой , а кинетическая энергия альфа-частиц также всегда должна быть одинаковой. Другими словами, пучок альфа-частиц должен быть моноэнергетическим .
Ожидалось, что те же соображения будут справедливы для родительского ядра, распадающегося на дочернее ядро и бета-частицы .Поскольку только электрон и отскакивающее дочернее ядро наблюдали бета-распад, процесс первоначально предполагался как двухчастичный процесс , очень похожий на альфа-распад. Казалось бы разумным предположить, что бета-частицы также образуют моноэнергетический пучок .
Чтобы продемонстрировать энергетику двухчастичного бета-распада, рассмотрим бета-распад, при котором электрон испускается, а родительское ядро покоится. Сохранение энергии требует:
Поскольку электрон — гораздо более легкая частица, ожидалось, что он унесет большую часть выделяемой энергии, которая будет иметь уникальное значение T e- .Форма этой кривой энергии зависит от того, какая часть энергии реакции (значение Q — количество энергии, выделяемой реакцией) переносится электроном или нейтрино.
Но на самом деле все было иначе . Однако спектр бета-частиц, измеренный Лизой Мейтнер и Отто Ханом в 1911 году и Жаном Данишем в 1913 году, показал несколько линий на диффузном фоне. Более того, практически все испускаемые бета-частицы имеют энергии ниже предсказываемых законом сохранения энергии при двухчастичных распадах. Электроны, испускаемые при бета-распаде, имеют непрерывный, а не дискретный спектр. , казалось, противоречит закону сохранения энергии, в соответствии с текущим предположением, что бета-распад — это простое излучение электрона из ядра. Когда это было впервые замечено, казалось, что это угрожает существованию одного из важнейших законов сохранения в физике !
Чтобы учесть это выделение энергии, Паули предположил (в 1931 году), что в процессе распада испускалась другая частица , позже названная Ферми нейтрино .Было ясно, что эта статья должна быть очень проницательной и что для сохранения электрического заряда нейтрино должно быть электрически нейтральным. Это могло бы объяснить, почему эту частицу было так трудно обнаружить. Термин нейтрино происходит от итальянского, что означает «маленький нейтральный», а нейтрино обозначаются греческой буквой ν (nu) . В процессе бета-распада нейтрино несет недостающую энергию, а также в этом процессе закон сохранения энергии остается в силе .
Сохранение механической энергии
Начиная с ньютоновской системы описания движения — объектов, взаимодействий, законов Ньютона — и задавая вопрос, «какая часть 2-го закона Ньютона говорит нам, как объект изменяет свою скорость (независимо от направления)», мы были вынуждены ввести понятие кинетической энергии — ½ мВ 2 . Теорема работы-энергии (второй закон Ньютона для объекта, отмеченного смещением объекта) привела нас к введению идеи потенциальной энергии — энергии места.Это привело нас к тому, что мы увидели силы взаимодействия как способ «хранения» кинетической энергии таким образом, чтобы она потенциально могла быть восстановлена в результате сил, которые объекты оказывают друг на друга в силу их относительного местоположения. Таким образом, кинетическая энергия объекта, брошенного вверх, «хранится» в большем смещении объекта от земли. Кинетическая энергия объекта, приближающегося к пружине, «хранится» в сжатии пружины. По мере приближения одного положительного заряда к другому он замедляется и «накапливает» свою кинетическую энергию в непосредственной близости от другого заряда.
Мы определяем потенциальную энергию как отрицательную часть работы, совершаемой силой над объектом, и перемещаем ее на другую сторону уравнения работы-энергии, рассматривая эффект силы, действующей на расстоянии, как новый вид энергия. Мы смогли сделать это для трех сил, которые мы изучили: гравитации, электричества и пружин. Поскольку мы интерпретируем нормальные силы и силы натяжения как своего рода очень жесткую силу пружины (см. Модуль Юнга), мы, вероятно, можем определить потенциальные энергии и для них (хотя обычно мы не беспокоимся по разным причинам).А как насчет других наших сил? Наши силы сопротивления?
Консервативные и неконсервативные силы
Оказывается, мы не можем определить потенциальные энергии, связанные с силами сопротивления. Мы можем увидеть это на макроуровне, вспомнив условие, необходимое для превращения работы в потенциальную энергию: работа, совершаемая силой, должна быть обратимой. Если он уменьшал KE в одном направлении, ему приходилось восстанавливать его, когда объект перемещался назад. Добытая энергия заняла место .Маркер, который позволил нам понять, что это происходит, заключался в том, что работа зависела только от начальной и конечной позиций, а не от того, что происходило между ними. Таким образом, если вы измените направление, вы измените знак работы и вернете PE, когда вы измените направление. Силы, для которых это работает, называются , , консервативными, .
Это требование не выполняется для сил сопротивления трения, вязкости и сопротивления. Для двух относительно движущихся объектов, которые оказывают друг на друга силы сопротивления, эти силы всегда указывают, чтобы противодействовать относительному движению.В результате работа отрицательна — сила и смещение противоположны (и cos 180 ° = -1), поэтому она поглощает KE. Если вы попытаетесь повернуть движение вспять, силы тоже обратятся, и работа останется отрицательной. Он продолжает пожирать KE вместо того, чтобы восстанавливать его. Подобные силы, работу которых нельзя описать как изменение потенциальной энергии, называются неконсервативными .
Самый простой пример — блок, скользящий по столу. Если я толкну его, блок соскользнет, но трение о стол замедлит его и остановит.Если я толкну его в другую сторону, трение все равно замедлит его, а не ускорит, восстанавливая украденную энергию. Таким образом, работу, совершаемую этими силами, нельзя описать как изменение потенциальной энергии.
Теорема работы-энергии с PE
Ну ладно. PE сделал вещи красивыми и дал нам хороший способ думать о движении, но мы все еще можем написать теорему работы-энергии, разделив консервативные и неконсервативные силы. Мы записываем работу, проделанную консервативными силами, как PE, а работу, проделанную неконсервативными силами, оставляем как работу.{net} _ {неконсервативно} \ cdot \ overrightarrow {\ Delta r} $$
Это, конечно, только уравнение энергии для одного объекта, и ему назначаются PE, предполагая, что другие объекты, вызывающие у нашего объекта ощущение консервативных сил, не двигаются значительно. Если они это сделают, нам придется сложить уравнения энергии для двух объектов и назначить только один PE, поскольку он действительно принадлежит взаимодействию, а не объекту.
Закон сохранения
Это уравнение дает нам закон сохранения и условия, при которых его можно использовать.2 + U_f $$
где «i» обозначает переменную в начальном состоянии, «f» обозначает переменные в конечном состоянии, а U представляет собой сумму всех потенциальных энергий — гравитационной, электрической и пружинной.
Если у нас есть система взаимодействующих объектов, которые взаимодействуют только с консервативными силами *, мы можем сложить отдельные теоремы работы-энергии. (Мы должны быть осторожны и подсчитывать взаимодействия между парой объектов только один раз.) Результат —
Принцип сохранения механической энергии (многие объекты) : Когда набор объектов, i = 1 ,.j U_ {ij} \ bigg] = 0 $$
, где $ U_ {ij} $ представляет собой сумму всех потенциальных энергий — гравитационной, электрической и пружинной — между объектами i и j.
Когда это полезно?
Такой способ описания движения как обмена между кинетической и потенциальной энергиями особенно полезен, когда выполняются условия принципа и когда нас не волнует время. Если вы скользите по горке (почти) без трения и хотите знать, с какой скоростью вы едете, когда доберетесь до нее, но не заботитесь о том, сколько времени это займет, — сохранение механической энергии скажет вам.Если вы бросаете мяч прямо вверх с определенной скоростью и хотите знать, как высоко он летит, но не заботитесь о том, когда он туда попадет, сохранение механической энергии скажет вам об этом.
В принципе, сохранение механической энергии полезно, когда вы хотите найти, как коррелируют положение и скорость, и вы можете игнорировать силы сопротивления.
Что на самом деле происходит?
О чем это на самом деле? Мы, , знаем, , что общая энергия сохраняется. Чем отличается эта теорема о «механической энергии»? Что происходит с нашими силами сопротивления?
Хотя мы знаем, что энергия сохраняется, когда мы определили все возможные формы, не все формы энергии одинаково полезны.Во время всего нашего обсуждения концепции движения Ньютона мы говорили о движении объектов. Поскольку мы знаем, что объекты состоят из молекул, это говорит нам о том, что все молекулы объекта движутся когерентно . Вот что мы подразумеваем под механической энергией . Когда трение или сопротивление истощает кинетическую энергию макроскопического объекта, то что оно делает, так это преобразование когерентной механической энергии объекта в некогерентные случайные движения молекул объекта.Когда KE объекта истощается, все его молекулы могут двигаться быстрее (его температура немного повышается), но они движутся в разные стороны. Нелегко снова сделать эти движения связными. В дальнейшем мы изучим, что происходит с потерянной энергией (тепловой энергией) и когда ее можно восстановить в виде когерентного макроскопического движения (свободной энергии).
* Этот процесс сложнее, чем кажется, и сложнее, чем в случае обобщения сохранения импульса на многие объекты. Это связано с тем, что PE включает в себя относительные положения объектов, поэтому требуется сложное преобразование координат, прежде чем PE могут быть правильно построены.


 Обратно: при исчезновении теплоты всегда возникает движущая сила
Обратно: при исчезновении теплоты всегда возникает движущая сила )
) 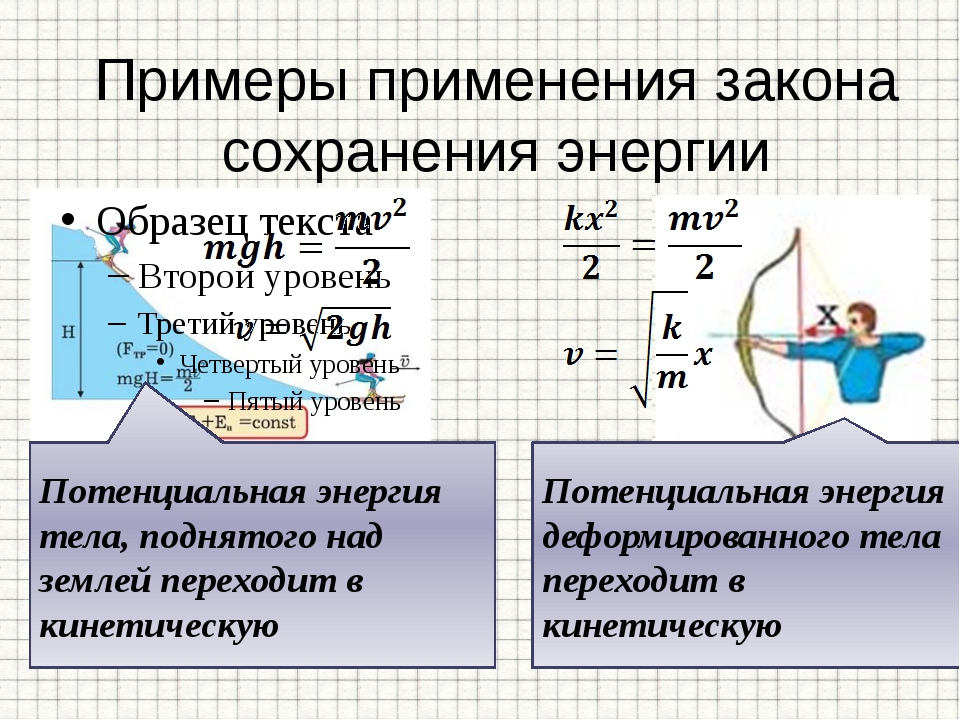 Эту затрату, как бы разнообразна она ни была, всегда можно свести к двум главным категориям, а именно, она сводится либо к химическому материалу, либо к механической работе
Эту затрату, как бы разнообразна она ни была, всегда можно свести к двум главным категориям, а именно, она сводится либо к химическому материалу, либо к механической работе Таким образом, всегда сумма живой силы и силы напряжения постоянна.
Таким образом, всегда сумма живой силы и силы напряжения постоянна. )
)  — М.: Наука, 1988. — С. 25. — 215 с. — («Теоретическая физика», том I). — ISBN 5-02-013850-9
— М.: Наука, 1988. — С. 25. — 215 с. — («Теоретическая физика», том I). — ISBN 5-02-013850-9 — С. 24—25. — («Теоретическая физика», том VI).
— С. 24—25. — («Теоретическая физика», том VI). Основы квантовой механики. — 7-е изд., стер. — СПб.: Издательство «Лань», 2004. — С. 125—127. — 672 с. — 2000 экз. — ISBN 5-8114-0554-5
Основы квантовой механики. — 7-е изд., стер. — СПб.: Издательство «Лань», 2004. — С. 125—127. — 672 с. — 2000 экз. — ISBN 5-8114-0554-5 К. Самин. — М.: Вече, 2002. — С. 90—93. — 480 с. — 25 000 экз. — ISBN 5-7838-1085-1
К. Самин. — М.: Вече, 2002. — С. 90—93. — 480 с. — 25 000 экз. — ISBN 5-7838-1085-1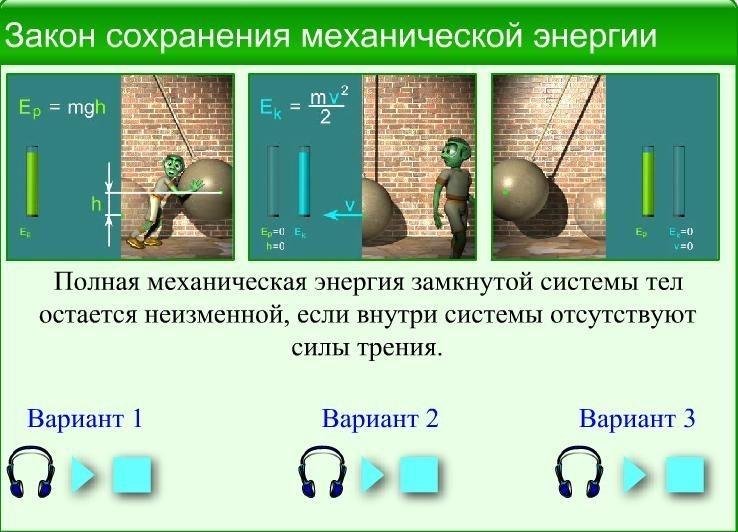 — 1824. — 102 с. (русский перевод В. Р. Бурсиана и Ю. А. Круткова: Размышления о движущей силе огня и о машинах, способных развивать эту силу на сайте nature.web.ru)
— 1824. — 102 с. (русский перевод В. Р. Бурсиана и Ю. А. Круткова: Размышления о движущей силе огня и о машинах, способных развивать эту силу на сайте nature.web.ru)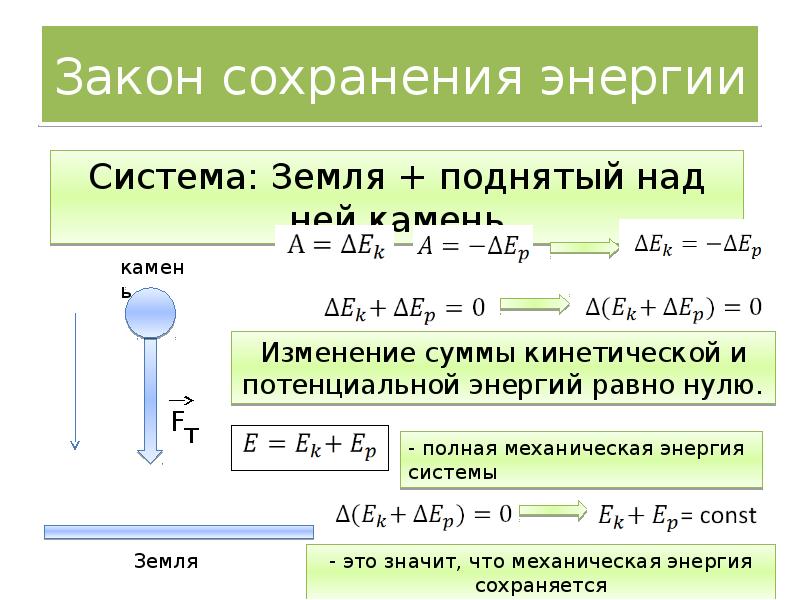 — 1842. — Т. 42. — С. 233—240.
— 1842. — Т. 42. — С. 233—240. Механическая работа, мощность, энергия, закон сохранения импульса, закон сохранения энергии, равновесие твердых тел
Механическая работа, мощность, энергия, закон сохранения импульса, закон сохранения энергии, равновесие твердых тел Введите свой запрос:
Введите свой запрос: Физика, 8 класс: уроки, тесты, задания.
Физика, 8 класс: уроки, тесты, задания.