Урок 1. механические колебания — Физика — 11 класс
Физика, 11 класс
Урок 1. Механические колебания
Перечень вопросов, рассматриваемых на уроке:
Механические колебания;
Виды механических колебаний;
Характеристики колебательных движений;
Явление резонанса.
Глоссарий по теме
Механические колебания – это физические процессы, точно или приблизительно повторяющиеся через одинаковые интервалы времени.
Колебания, происходящие под действием внутренних сил в колебательной системе, называют свободными.
Вынужденные колебания – это колебания, происходящие под действием внешней периодически меняющейся силы.
Амплитуда – это наибольшее смещение колеблющейся величины от положения равновесия.
Период – это время одного полного колебания.
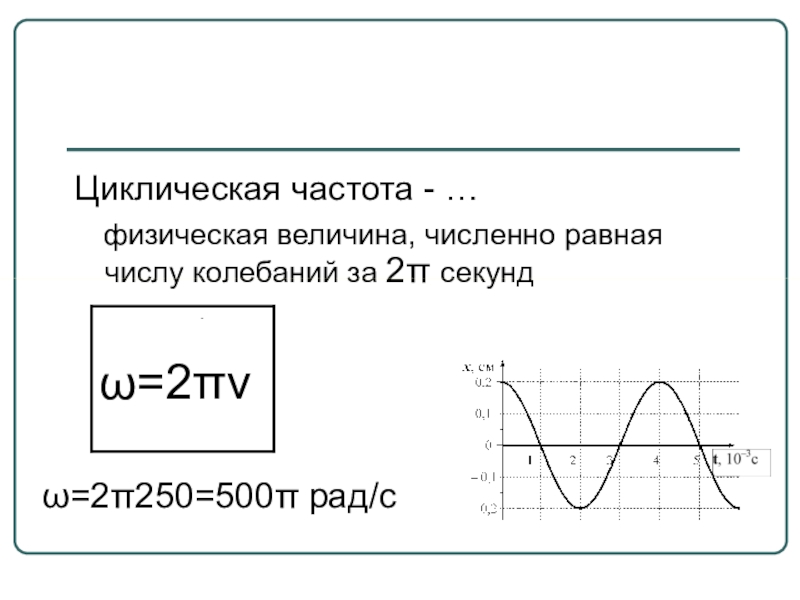
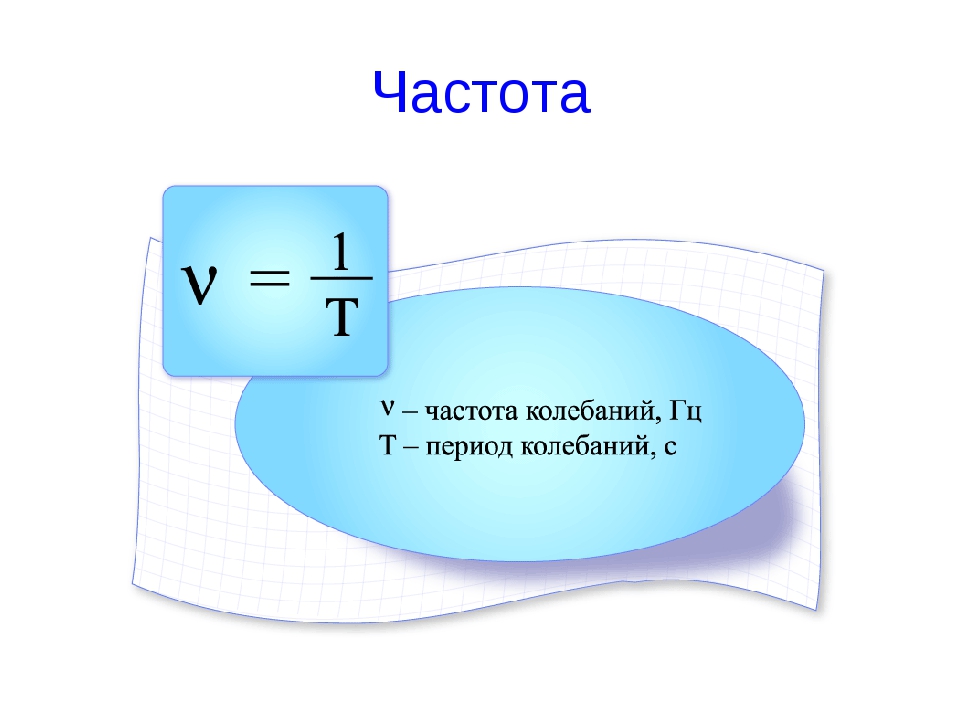
Частота колебаний – это число колебаний за единицу времени.
Фаза колебаний – это физическая величина определяющая отклонение колеблющейся величины от положения равновесия в данный момент времени.
Резонанс – это явление резкого возрастания амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы, действующей на систему с частотой свободных колебаний.
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 53 – 73.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2009. – С. 59 – 61.
- Степанова. Г.Н. Сборник задач по физике. 10-11 класс. М., Просвещение 1999 г.
- Е.А. Марон, А.Е. Марон. Контрольные работы по физике. М., Просвещение, 2004
Основное содержание урока
Мир удивителен и многообразен. Мы каждый день наблюдаем разные движения тел. Все мы видели, как раскачивается ветка на ветру, лодка на волнах, качели, деревья при ветре. Чем эти движения отличаются от движения тележки движущейся прямолинейно? Мы видим, что в отличие от движения тележки движущейся прямолинейно, движения всех этих тел повторяются через определенный промежуток времени.
Механические колебания – это физические процессы, точно или приблизительно повторяющиеся через одинаковые интервалы времени.
Колебания играют огромную роль в нашей жизни. Примерами колебаний в нашем организме являются биение сердца, движение голосовых связок. Колебания происходят и в жизни нашей планеты (приливы, отливы, землетрясения) и в астрономических явлениях (пульсации звезд). Одним из грозных явлений природы является землетрясение – колебание земной поверхности. Строители рассчитывают возводимые ими сооружения на устойчивость при землетрясении.
Без знания законов колебаний нельзя было бы создать, телевидение, радио и многие современные устройства и машины. Неучтенные колебания могут привести к разрушению сложных технических сооружений и вызвать серьезные заболевания человека. Все это делает необходимым их всестороннее изучение.
Основным признаком колебательного движения является его периодичность. Колеблющееся тело за одно колебание дважды проходит положение равновесия. Колебания характеризуются такими величинами как период, частота, амплитуда и фаза колебаний.
Колебания характеризуются такими величинами как период, частота, амплитуда и фаза колебаний.
Амплитуда – это наибольшее смещение колеблющейся величины от положения равновесия.
При малых амплитудах путь пройденный телом за одно полное колебание равен примерно четырем амплитудам.
Промежуток времени, в течение которого тело совершает одно полное колебание, называют периодом колебаний.
Период – это время одного полного колебания.
Чтобы найти период колебаний нужно разделить время колебаний на число колебаний.
[T] = 1с
Частота колебаний – это число колебаний за единицу времени.
[v] = 1 Гц (герц)
Единица частоты названа в честь немецкого ученого Г. Герца.
Фаза колебаний – это физическая величина определяющая отклонение колеблющейся величины от положения равновесия в данный момент времени.
[ω] = 1 рад/ с
Во всех колебательных системах действуют силы, стремящиеся вернуть тело в состояние устойчивого равновесия. Существуют несколько типов маятников: нитяные и, пружинные и т.д. Под словом «маятник» понимают твердое тело способное совершать колебания под действием приложенных сил около неподвижной точки или вокруг оси.
Существуют несколько типов маятников: нитяные и, пружинные и т.д. Под словом «маятник» понимают твердое тело способное совершать колебания под действием приложенных сил около неподвижной точки или вокруг оси.
Мы с вами будем рассматривать пружинный и математический маятники.
Пружинный маятник. Колебательная система в этом случае представляет собой тело, прикрепленное к пружине. Колебания в таком маятнике возникают под действием силы упругости пружины и силы тяжести.
Период колебаний пружинного маятника:
T- период колебаний пружинного маятника
m – масса подвешенного груза
𝑘 – жесткость пружины
Математический маятник.
Математический маятник – это материальная точка, подвешенная на длинной нерастяжимой нити.
Математический маятник — это идеализированная модель. Реальный маятник можно считать математическим, если длина нити много больше размеров подвешенного тела и масса нити ничтожна по сравнению с массой тела. Колебания такого маятника происходят под действием силы натяжения нити и силы тяжести. Формула для расчета периода колебаний математического маятника была выведена Гюйгенсом.
Колебания такого маятника происходят под действием силы натяжения нити и силы тяжести. Формула для расчета периода колебаний математического маятника была выведена Гюйгенсом.
T – период колебаний математического маятника
𝑙 – длина нити маятника
𝑔 – ускорение свободного падения
Гюйгенс доказал, что период малых колебаний маятника не зависят от времени. Используя это свойство, названное изохронностью маятника Гюйгенс в тысяча шестьсот пятьдесят седьмом году, сконструировал первые маятниковые часы. Это свойство маятника было открыто 19-летним Галилеем более чем за 20 лет до открытия Гюйгенса. Наблюдая за тем, как раскачиваются в соборе светильники, подвешенные на нитях одинаковой длины, он заметил, что их период колебаний не зависит от времени. Наручных часов тогда не было, и юный Галилей пришёл к решению, которое для многих поколений будет служить образцом блеска и остроумия человеческой мысли: он сравнил колебания маятника с частотой биения собственного сердца.
Гармоническими являются колебания, происходящие под действием силы пропорциональной смещению колеблющейся точки и направленной противоположно этому смещению. Уравнение гармонических колебаний:
x – координата колеблющейся величины
– амплитуда колебаний
ω — циклическая частота
При наличии сил трения в системе колебания затухают. Амплитуда колебаний в этом случае со временем уменьшается. Иногда возникает необходимость в гашении колебаний, к примеру колебания кузова, на рессорах при езде на автомобиле. Для гашения колебаний применяют специальные амортизаторы. С кузовом связывают поршень, который при колебаниях движется в цилиндре, заполненном жидкостью. Большое сопротивление жидкости приводит к гашению колебаний.
Колебания, происходящие под действием внешней периодической силы, называются вынужденными.
Если частота изменения внешней силы не равна частоте свободных колебаний системы, то внешняя сила будет действовать не в такт со свободными колебаниями самой системы. В этом случае амплитуда колебаний будет определяться максимальным значением действующей на систему внешней силы.
В этом случае амплитуда колебаний будет определяться максимальным значением действующей на систему внешней силы.
Если частота изменения внешней силы совпадет с частотой свободных колебаний, то будет наблюдаться резкое возрастание амплитуды колебаний, так как внешняя сила в этом случае будет действовать в такт со свободными колебаниями этой системы.
ω — частота изменения внешней силы.
ω0 – частота свободных колебаний системы.
Впервые явление резонанса было описано Галилеем. Явление резонанса играет большую роль в природе, технике и науке. Большинство сооружений и машин обладая определенной упругостью, способно совершать свободные колебания. Поэтому внешние периодические воздействия могут вызвать их резонанс, что может стать причиной катастроф. Известно много случаев, когда источником опасных колебаний были люди, идущие в ногу. Так, в 1831 году в городе Манчестер при прохождении по мосту колонны солдат строевым шагом мост разрушился. Аналогичный случай был в г. Петербурге в 1905 году. При прохождении моста через реку Фонтанка эскадроном гвардейской кавалерии мост обрушился. Для предотвращения резонансных явлений используют разные способы гашения вынужденных колебаний. Один способ состоит в изменении частоты свободных колебаний в системе. Другой способ состоит в увеличении силы трения в системе: чем больше сила трения, тем меньше амплитуда резонансных колебаний
Петербурге в 1905 году. При прохождении моста через реку Фонтанка эскадроном гвардейской кавалерии мост обрушился. Для предотвращения резонансных явлений используют разные способы гашения вынужденных колебаний. Один способ состоит в изменении частоты свободных колебаний в системе. Другой способ состоит в увеличении силы трения в системе: чем больше сила трения, тем меньше амплитуда резонансных колебаний
Разбор тренировочных заданий
1. Найдите массу груза, который на пружине жесткостью 250 Н/м делает 20 колебаний за 16 с.
Дано:
𝑘=250 Н/м
N= 20
t= 16 с
_______
m=?
Решение:
Напишем формулу периода пружинного маятника
T=2π√(m/k)
Из этой формулы выразим массу
Период колебаний груза найдём через время колебаний и число колебаний по формуле:
Подставляем числовые значения величин
T=0,8 с.
Следовательно масса равна:
m=4 кг
Ответ: m=4 кг
2. На нити подвешен шарик массой 0,1 кг. Шарик отклонили на высоту 2,5 см (по отношению к положению равновесия) и отпустили. Определите максимальную скорость шарика.
На нити подвешен шарик массой 0,1 кг. Шарик отклонили на высоту 2,5 см (по отношению к положению равновесия) и отпустили. Определите максимальную скорость шарика.
Дано:
m= 0,1 кг
h=2,5 см = 0.025 м
_________
vm=?
Решение:
Скорость колеблющегося шарика максимальна в момент прохождения положения равновесия.
Для решения задачи применим закон сохранения энергии:
Подставляем числовые значения величин:
Ответ:
|
1. |
Связь частоты с периодом колебаний
|
1 |
|
2. 
|
Период колебаний
|
1 |
|
3. |
Частота колебаний
|
1 |
|
4. 
|
Связь периода колебаний с частотой
|
2 |
|
5. |
Насекомые
|
2 |
|
6. 
|
Сколько взмахов?
|
3 |
|
7. |
Перемещение и путь
|
4 |
|
8. 
|
Максимальная скорость
|
4 |
|
9. |
Неполное колебание
|
6 |
Глава 11.
 Механические колебания и волны
Механические колебания и волны
Колебательным называется любое периодически повторяющееся движение. Поэтому зависимости координаты и скорости тела от времени при колебаниях описываются периодическими функциями времени. В школьном курсе физики рассматриваются такие колебания, в которых зависимости и скорости тела представляют собой тригонометрические функции , или их комбинацию, где — некоторое число. Такие колебания на-зываются гармоническими (функции и часто называют гармоническими функциями). Для решения задач на колебания, входящих в программу единого государственного экзамена по физике, нужно знать определения основных характеристик колебательного движения: амплитуды, периода, частоты, круговой (или циклической) частоты и фазы колебаний. Дадим эти определения и свяжем перечисленные величины с параметрами зависимости координаты тела от времени , которая в случае гармонических колебаний всегда может быть представлена в виде
(11. |
где , и — некоторые числа.
Амплитудой колебаний называется максимальное отклонение колеблющегося тела от положения равновесия. Поскольку максимальное и минимальное значение косинуса в (11.1) равно ±1, то амплитуда колебаний тела, совершающего колебания (11.1), равна величине . Период колебаний — это минимальное время, через которое движение тела повторяется. Для зависимости (11.1) период можно установить из следующих соображений. Косинус — периодическая функция с периодом . Поэтому движение полностью повторяется через такое значение , что . Отсюда получаем
(11.2) |
Частотой колебаний тела называется число колебаний, совершаемых в единицу времени. Очевидно, что частота колебаний связана с периодом колебаний по формуле
(11.3) |
Круговой (или циклической) частотой колебаний называется число колебаний, совершаемых за единиц времени. Из формулы (11.3) заключаем, что круговой частотой является величина из формулы (11.1).
Из формулы (11.3) заключаем, что круговой частотой является величина из формулы (11.1).
Фазой колебаний называется аргумент тригонометрической функции, описывающей зависимость координаты от времени. Из формулы (11.1) видим, что фаза колебаний тела, движение которого описывается зависимостью (11.1), равна . Значение фазы колебаний в момент времени = 0 называется начальной фазой. Для зависимости (11.1) начальная фаза колебаний равна величине . Очевидно, начальная фаза колебаний зависит от выбора начала отсчета времени (момента = 0), которое всегда является условным. Изменением начала отсчета времени начальная фаза колебаний всегда может быть «сделана» равной нулю, а синус в формуле (11.1) «превращен» в косинус или наоборот.
В программу единого государственного экзамена входит также знание формул для частоты колебаний пружинного и математического маятников. Пружинным маятником принято называть тело, которое может совершать колебания на гладкой горизонтальной поверхности под действием пружины, второй конец которой закреплен (левый рисунок). Математическим маятником называется массивное тело, размерами которого можно пренебречь, совершающее колебания на длинной, невесомой и нерастяжимой нити (правый рисунок). Название этой системы – «математический маятник» связано с тем, что она представляет собой абстрактную математическую модель реального (физического) маятника. Необходимо помнить формулы для периода (или частоты) колебаний пружинного и математического маятников. Для пружинного маятника
Математическим маятником называется массивное тело, размерами которого можно пренебречь, совершающее колебания на длинной, невесомой и нерастяжимой нити (правый рисунок). Название этой системы – «математический маятник» связано с тем, что она представляет собой абстрактную математическую модель реального (физического) маятника. Необходимо помнить формулы для периода (или частоты) колебаний пружинного и математического маятников. Для пружинного маятника
(11.4) |
где — коэффициент жесткости пружины, — масса груза. Период колебаний математического маятника определяется следующим соотношением
(11.5) |
где — длина нити, — ускорение свободного падения. Рассмотрим применение этих определений и законов на примере решения задач.
Чтобы найти циклическую частоту колебаний груза в задаче 11. 1.1 найдем сначала период колебаний, а затем воспользуемся формулой (11.2). Поскольку 10 м 28 с — это 628 с, и за это время груз совершает 100 колебаний, период колебаний груза равен 6,28 с. Поэтому циклическая частота колебаний равна 1 c-1 (ответ 2). В задаче 11.1.2 груз за 600 с совершил 60 колебаний, поэтому частота колебаний — 0,1 с-1 (ответ 1).
1.1 найдем сначала период колебаний, а затем воспользуемся формулой (11.2). Поскольку 10 м 28 с — это 628 с, и за это время груз совершает 100 колебаний, период колебаний груза равен 6,28 с. Поэтому циклическая частота колебаний равна 1 c-1 (ответ 2). В задаче 11.1.2 груз за 600 с совершил 60 колебаний, поэтому частота колебаний — 0,1 с-1 (ответ 1).
Чтобы понять, какой путь пройдет груз за 2,5 периода (задача 11.1.3), проследим за его движением. Через период груз вернется назад в точку максимального отклонения, совершив полное колебание. Поэтому за это время груз пройдет расстояние, равное четырем амплитудам: до положения равновесия — одна амплитуда, от положения равновесия до точки максимального отклонения в другую сторону — вторая, назад в положение равновесия — третья, из положения равновесия в начальную точку — четвертая. За второй период груз снова пройдет четыре амплитуды, а за оставшиеся половину периода — две амплитуды.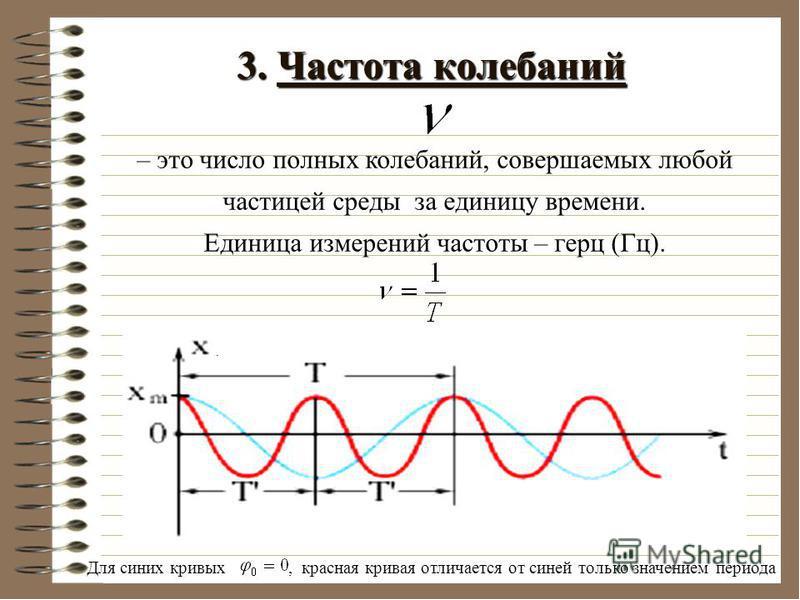 Поэтому пройденный путь равен десяти амплитудам (ответ 4).
Поэтому пройденный путь равен десяти амплитудам (ответ 4).
Величина перемещения тела — расстояние от начальной точки до конечной. За 2,5 периода в задаче 11.1.4 тело успеет совершить два полных и половину полного колебания, т.е. окажется на максимальном отклонении, но с другой стороны от положения равновесия. Поэтому величина перемещения равна двум амплитудам (ответ 3).
По определению фаза колебаний — это аргумент тригонометрической функции, которой описывается зависимость координаты колеблющегося тела от времени. Поэтому правильный ответ в задаче 11.1.5 — 3.
Период — это время полного колебания. Это значит, что возвращение тела назад в ту же точку, из которой тело начало движение, еще не означает, что прошел период: тело должно вернуться в ту же точку с той же скоростью. Например, тело, начав колебания из положения равновесия, за период успеет отклониться на максимальную величину в одну сторону, вернуться назад, отклонится на максимум в другую сторону и снова вернуться назад. Поэтому за период тело успеет два раза отклониться на максимальную величину от положения равновесия и вернуться обратно. Следовательно, на прохождение от положения равновесия до точки максимального отклонения (задача 11.1.6) тело затрачивает четвертую часть периода (ответ 3).
Поэтому за период тело успеет два раза отклониться на максимальную величину от положения равновесия и вернуться обратно. Следовательно, на прохождение от положения равновесия до точки максимального отклонения (задача 11.1.6) тело затрачивает четвертую часть периода (ответ 3).
Гармоническими называются такие колебания, при которых зависимость координаты колеблющегося тела от времени описывается тригонометрической (синус или косинус) функцией времени. В задаче 11.1.7 таковыми являются функции и , несмотря на то, что входящие в них параметры обозначены как 2 и 2. Функция же — тригонометрическая функция квадрата времени. Поэтому гармоническими являются колебания только величин и (ответ 4).
При гармонических колебаниях скорость тела изменяется по закону , где — амплитуда колебаний скорости (начало отсчета времени выбрано так, чтобы начальная фаза колебаний равнялась бы нулю). Отсюда находим зависимость кинетической энергии тела от времени (задача 11. 1.8). Используя далее известную тригонометрическую формулу, получаем
1.8). Используя далее известную тригонометрическую формулу, получаем
Из этой формулы следует, что кинетическая энергия тела изменяется при гармонических колебаниях также по гармоническому закону, но с удвоенной частотой (ответ 2).
За соотношением между кинетической энергий груза и потенциальной энергией пружины (задача 11.1.9) легко проследить из следующих соображений. Когда тело отклонено на максимальную величину от положения равновесия, скорость тела равна нулю, и, следовательно, потенциальная энергия пружины больше кинетической энергии груза. Напротив, когда тело проходит положение равновесия, потенциальная энергия пружины равна нулю, и, следовательно, кинетическая энергия больше потенциальной. Поэтому между прохождением положения равновесия и максимальным отклонением кинетическая и потенциальная энергия один раз сравниваются. А поскольку за период тело четыре раза проходит от положения равновесия до максимального отклонения или обратно, то за период кинетическая энергия груза и потенциальная энергия пружины сравниваются друг с другом четыре раза (ответ 2).
Амплитуду колебаний скорости (задача 11.1.10) проще всего найти по закону сохранения энергии. В точке максимального отклонения энергия колебательной системы равна потенциальной энергии пружины , где — коэффициент жесткости пружины, — амплитуда колебаний. При прохождении положения равновесия энергия тела равна кинетической энергии , где — масса тела, — скорость тела при прохождении положения равновесия, которая является максимальной скоростью тела в процессе колебаний и, следовательно, представляет собой амплитуду колебаний скорости. Приравнивая эти энергии, находим
(ответ 1), где использовано выражение для круговой частоты колебаний груза на пружине:
По формуле (11.4) получаем в задаче 11.2.1
(ответ 4).
Из формулы (11.5) заключаем (задача 11. 2.2), что от массы математического маятника его период не зависит, а при увеличении длины в 4 раза период колебаний увеличивается в 2 раза (ответ 1).
2.2), что от массы математического маятника его период не зависит, а при увеличении длины в 4 раза период колебаний увеличивается в 2 раза (ответ 1).
Часы — это колебательный процесс, который используется для измерения интервалов времени (задача 11.2.3). Слова часы «спешат» означают, что период этого процесса меньше того, каким он должен быть. Поэтому для уточнения хода этих часов необходимо увеличить период процесса. Согласно формуле (11.5) для увеличения периода колебаний математического маятника необходимо увеличить его длину (ответ 3).
Чтобы найти амплитуду колебаний в задаче 11.2.4, необходимо представить зависимость координаты тела от времени в виде одной тригонометрической функции. Для данной в условии функции это можно сделать с помощью введения дополнительного угла. Умножая и деля эту функцию на и используя формулу сложения тригонометрических функций, получим
где — такой угол, что . Из этой формулы следует, что амплитуда колебаний тела — (ответ 4).
Из этой формулы следует, что амплитуда колебаний тела — (ответ 4).
В задаче 11.2.5 имеем при см. Откуда см (ответ 2).
Задачи 11.2.6 и 11.2.7 посвящены механическим волнам. Волна – некоторый колебательный процесс, который может распространяться в среде. При этом каждая точка среды совершает колебания около определенного положения и в среднем не перемещается в пространстве. Волна характеризуется периодом (или связанной с ним частотой ), скоростью и длиной волны , которая определяется как минимальное расстояние между точками, колеблющимися в одинаковой фазе. Для решения задач ЕГЭ по этой теме необходимо помнить формулу, дающую связь между параметрами волны
(11.6) |
которую легко запомнить, поскольку эта связь имеет такой же вид как обычное соотношение между расстоянием, скоростью и временем. Например, в задаче 11.2. 6 по формуле (11.6) находим длину волны м (ответ 2).
6 по формуле (11.6) находим длину волны м (ответ 2).
Как следует из рисунка в задаче 11.2.7 длина волны, распространяющейся по шнуру, равна м. Поэтому по формуле (11.6) имеем Гц (ответ 4).
Поскольку в момент максимального отклонения пружинного маятника, механическая энергия системы равна потенциальной энергии пружины, то
где — амплитуда колебаний, — жесткость пружины. Поэтому при увеличении механической энергии пружинного маятника в 2 раза амплитуда колебаний увеличилась в раз (задача 11.2.8 – ответ 1).
Используя известную тригонометрическую формулу, получим в задаче 11.2.9
Эта зависимость представляет собой гармоническую функцию, но колеблющуюся вокруг точки . Амплитудой этих колебаний является множитель перед косинусом — (так как сам косинус меняется в интервале от -1 до 1).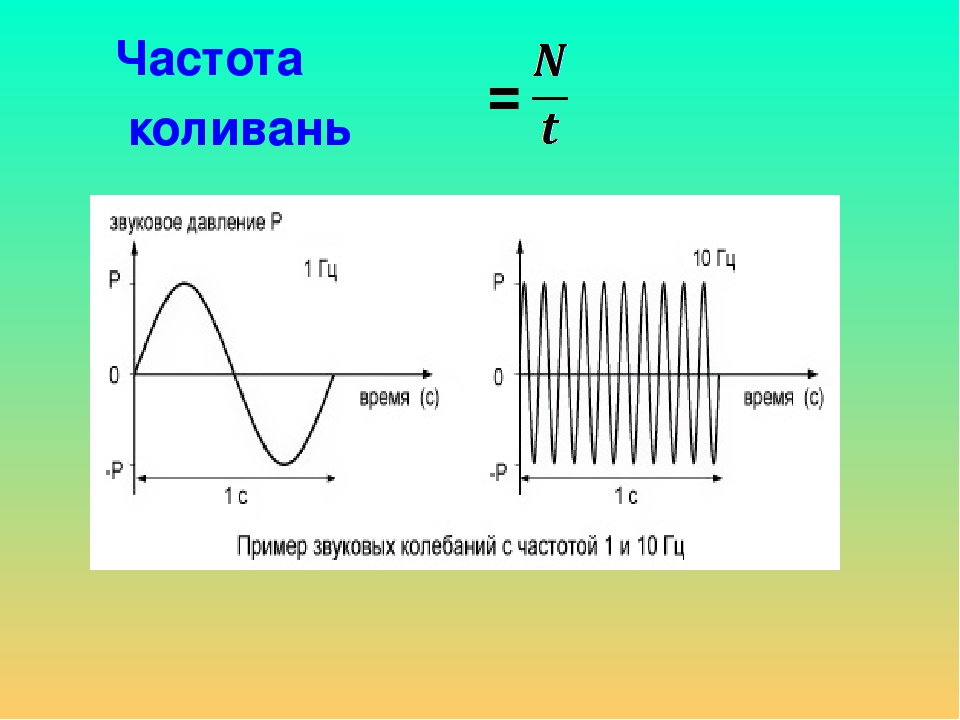 Циклической частотой — величина (ответ 4).
Циклической частотой — величина (ответ 4).
Вертикальный пружинный маятник отличается от горизонтального (задача 11.2.10) наличием силы тяжести. Однако сила тяжести приводит только к сдвигу положения равновесия маятника, а возвращающая сила по прежнему будет зависеть от смещения маятника от положения равновесия по закону (так как возвращающей силой будет разность силы упругости и постоянной силы тяжести). Поэтому период колебаний груза на вертикальной и горизонтальной пружине — одинаков (конечно, при условии, что и сам груз и пружины одинаковы). Правильный ответ в задаче — 3.
Колебания — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Гармонические колебания
К оглавлению…
В технике и окружающем нас мире часто приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными. Колебаниями называют изменения физической величины, происходящие по определенному закону во времени. Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения.
Колебаниями называют изменения физической величины, происходящие по определенному закону во времени. Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения.
Механическими колебаниями называют движения тел, повторяющиеся точно через одинаковые промежутки времени. Примерами простых колебательных систем могут служить груз на пружине или математический маятник. Для существования в системе гармонических колебаний необходимо, чтобы у нее было положение устойчивого равновесия, то есть такое положение, при выведении из которого на систему начала бы действовать возвращающая сила.
Механические колебания, как и колебательные процессы любой другой физической природы, могут быть свободными и вынужденными. Свободные колебания совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания маятника являются свободными колебаниями. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными.
Свободные колебания совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания маятника являются свободными колебаниями. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными.
Простейшим видом колебательного процесса являются колебания, происходящие по закону синуса или косинуса, называемые гармоническими колебаниями. Уравнение описывающее физические системы способные совершать гармонические колебания с циклической частотой ω0 задаётся следующим образом:
Решение предыдущего уравнения является уравнением движения для гармонических колебаний, которое имеет вид:
где: x – смещение тела от положение равновесия, A – амплитуда колебаний, то есть максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний (ω = 2Π/T), t – время. Величина, стоящая под знаком косинуса: φ = ωt + φ0, называется фазой гармонического процесса. Смысл фазы колебаний: стадия, в которой колебание находится в данный момент времени. При t = 0 получаем, что φ = φ0, поэтому φ0 называют начальной фазой (то есть той стадией, из которой начиналось колебание).
Величина, стоящая под знаком косинуса: φ = ωt + φ0, называется фазой гармонического процесса. Смысл фазы колебаний: стадия, в которой колебание находится в данный момент времени. При t = 0 получаем, что φ = φ0, поэтому φ0 называют начальной фазой (то есть той стадией, из которой начиналось колебание).
Минимальный интервал времени, через который происходит повторение движения тела, называется периодом колебаний T. Если же количество колебаний N, а их время t, то период находится как:
Физическая величина, обратная периоду колебаний, называется частотой колебаний:
Частота колебаний ν показывает, сколько колебаний совершается за 1 с. Единица частоты – Герц (Гц). Частота колебаний связана с циклической частотой ω и периодом колебаний T соотношениями:
Зависимость скорости от времени при гармонических механических колебаниях выражается следующей формулой:
Максимальное значение скорости при гармонических механических колебаниях:
Максимальные по модулю значения скорости υm = ωA достигаются в те моменты времени, когда тело проходит через положения равновесия (x = 0). Аналогичным образом определяется ускорение a = ax тела при гармонических колебаниях. Зависимость ускорения от времени при гармонических механических колебаниях:
Аналогичным образом определяется ускорение a = ax тела при гармонических колебаниях. Зависимость ускорения от времени при гармонических механических колебаниях:
Максимальное значение ускорения при механических гармонических колебаниях:
Знак минус в предыдущем выражении означает, что ускорение a(t) всегда имеет знак, противоположный знаку смещения x(t), и, следовательно, возвращает тело в начальное положение (x = 0), т.е. заставляет тело совершать гармонические колебания.
Следует обратить внимание на то, что:
- физические свойства колебательной системы определяют только собственную частоту колебаний ω0 или период T.
- Такие параметры процесса колебаний, как амплитуда A = xm и начальная фаза φ0, определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени, т.
 е. начальными условиями.
е. начальными условиями. - При колебательном движении тело за время, равное периоду, проходит путь, равный 4 амплитудам. При этом тело возвращается в исходную точку, то есть перемещение тела будет равно нулю. Следовательно, путь равный амплитуде тело пройдет за время равное четверти периода.
Чтобы определить, когда в уравнение колебаний подставлять синус, а когда косинус, нужно обратить внимание на следующие факторы:
- Проще всего, если в условии задачи колебания названы синусоидальными или косинусоидальными.
- Если сказано, что тело толкнули из положения равновесия – берем синус с начальной фазой, равной нулю.
- Если сказано, что тело отклонили и отпустили – косинус с начальной фазой, равной нулю.
- Если тело толкнули из отклоненного от положения равновесия состояния, то начальная фаза не равна нолю, а брать можно и синус и косинус.
Математический маятник
К оглавлению…
Математическим маятником называют тело небольших размеров, подвешенное на тонкой, длинной и нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. Только в случае малых колебаний математический маятник является гармоническим осциллятором, то есть системой, способной совершать гармонические (по закону sin или cos) колебания. Практически такое приближение справедливо для углов порядка 5–10°. Колебания маятника при больших амплитудах не являются гармоническими.
Только в случае малых колебаний математический маятник является гармоническим осциллятором, то есть системой, способной совершать гармонические (по закону sin или cos) колебания. Практически такое приближение справедливо для углов порядка 5–10°. Колебания маятника при больших амплитудах не являются гармоническими.
Циклическая частота колебаний математического маятника рассчитывается по формуле:
Период колебаний математического маятника:
Полученная формула называется формулой Гюйгенса и выполняется, когда точка подвеса маятника неподвижна. Важно запомнить, что период малых колебаний математического маятника не зависит от амплитуды колебаний. Такое свойство маятника называется изохронностью. Как и для любой другой системы, совершающей механические гармонические колебания, для математического маятника выполняются следующие соотношения:
- Путь от положения равновесия до крайней точки (или обратно) проходится за четверть периода.

- Путь от крайней точки до половины амплитуды (или обратно) проходится за одну шестую периода.
- Путь от положения равновесия до половины амплитуды (или обратно) проходится за одну двенадцатую долю периода.
Пружинный маятник
К оглавлению…
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению. Таким свойством обладает сила упругости.
Таким образом, груз некоторой массы m, прикрепленный к пружине жесткости k, второй конец которой закреплен неподвижно, составляют систему, способную совершать в отсутствие трения свободные гармонические колебания. Груз на пружине называют пружинным маятником.
Циклическая частота колебаний пружинного маятника рассчитывается по формуле:
Период колебаний пружинного маятника:
При малых амплитудах период колебаний пружинного маятника не зависит от амплитуды (как и у математического маятника). При горизонтальном расположении системы пружина–груз сила тяжести, приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину x0, равную:
А колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты ω0 и периода колебаний T справедливы и в этом случае. Таким образом, полученная формула для периода колебаний груза на пружине остается справедливой во всех случаях, независимо от направления колебаний, движения опоры, действия внешних постоянных сил.
При свободных механических колебаниях кинетическая и потенциальная энергии периодически изменяются. При максимальном отклонении тела от положения равновесия его скорость, а, следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на пружине потенциальная энергия – это энергия упругой деформации пружины. Для математического маятника – это энергия в поле тяготения Земли.
При максимальном отклонении тела от положения равновесия его скорость, а, следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на пружине потенциальная энергия – это энергия упругой деформации пружины. Для математического маятника – это энергия в поле тяготения Земли.
Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. Тело проскакивает положение равновесия по инерции. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией (как правило, потенциальную энергию в положении равновесия полагают равной нулю). Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и так далее.
Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот. Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной. При этом, максимальное значение кинетической энергии при механических гармонических колебаниях задаётся формулой:
Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной. При этом, максимальное значение кинетической энергии при механических гармонических колебаниях задаётся формулой:
Максимальное значение потенциальной энергии при механических гармонических колебаниях пружинного маятника:
Взаимосвязь энергетических характеристик механического колебательного процесса (полная механическая энергия равна максимальным значениям кинетической и потенциальной энергий, а также сумме кинетической и потенциальной энергий в произвольный момент времени):
Механические волны
К оглавлению…
Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной.
Механические волны бывают разных видов. Если при распространении волны частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, такая волна называется поперечной. Если смещение частиц среды происходит в направлении распространения волны, такая волна называется продольной.
Как в поперечных, так и в продольных волнах не происходит переноса вещества в направлении распространения волны. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой.
Характерной особенностью механических волн является то, что они распространяются в материальных средах (твердых, жидких или газообразных). Существуют немеханические волны, которые способны распространяться и в пустоте (например, световые, т.е. электромагнитные волны могут распространяться в вакууме).
- Продольные механические волны могут распространяться в любых средах – твердых, жидких и газообразных.

- Поперечные волны не могут существовать в жидкой или газообразной средах.
Значительный интерес для практики представляют простые гармонические или синусоидальные волны. Они характеризуются амплитудой A колебания частиц, частотой ν и длиной волны λ. Синусоидальные волны распространяются в однородных средах с некоторой постоянной скоростью υ.
Длиной волны λ называют расстояние между двумя соседними точками, колеблющимися в одинаковых фазах. Расстояние, равное длине волны λ, волна пробегает за время равное периоду T, следовательно, длина волны может быть рассчитана по формуле:
где: υ – скорость распространения волны. При переходе волны из одной среды в другую длина волны и скорость ее распространения меняются. Неизменными остаются только частота и период волны.
Разность фаз колебаний двух точек волны, расстояние между которыми l рассчитывается по формуле:
Электрический контур
К оглавлению. ..
..
В электрических цепях, так же, как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный LC-контур. В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими. Энергетические характеристики и их взаимосвязь при колебаниях в электрическом контуре:
Период гармонических колебаний в электрическом колебательном контуре определяется по формуле:
Циклическая частота колебаний в электрическом колебательном контуре:
Зависимость заряда на конденсаторе от времени при колебаниях в электрическом контуре описывается законом:
Зависимость электрического тока протекающего через катушку индуктивности от времени при колебаниях в электрическом контуре:
Зависимость напряжения на конденсаторе от времени при колебаниях в электрическом контуре:
Максимальное значение силы тока при гармонических колебаниях в электрическом контуре может быть рассчитано по формуле:
Максимальное значение напряжения на конденсаторе при гармонических колебаниях в электрическом контуре:
Все реальные контура содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в теплоту, выделяющуюся на резисторе, и колебания становятся затухающими.
Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в теплоту, выделяющуюся на резисторе, и колебания становятся затухающими.
Переменный ток. Трансформатор
К оглавлению…
Основная часть электроэнергии в мире в настоящее время вырабатывается генераторами переменного тока, создающими синусоидальное напряжение. Они позволяют наиболее просто и экономно осуществлять передачу, распределение и использование электрической энергии.
Устройство, предназначенное для превращения механической энергии в энергию переменного тока, называется генератором переменного тока. Он характеризуется переменным напряжением U(t) (индуцированной ЭДС) на его клеммах. В основу работы генератора переменного тока положено явление электромагнитной индукции.
Переменным током называется электрический ток, который изменяется с течением времени по гармоническому закону. Величины U0, I0 = U0/R называются амплитудными значениями напряжения и силы тока. Значения напряжения U(t) и силы тока I(t), зависящие от времени, называют мгновенными.
Величины U0, I0 = U0/R называются амплитудными значениями напряжения и силы тока. Значения напряжения U(t) и силы тока I(t), зависящие от времени, называют мгновенными.
Переменный ток характеризуется действующими значениями силы тока и напряжения. Действующим (эффективным) значением переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделил бы в единицу времени такое же количество теплоты, что и данный переменный ток. Для переменного тока действующее значение силы тока может быть рассчитано по формуле:
Аналогично можно ввести действующее (эффективное) значение и для напряжения, рассчитываемое по формуле:
Таким образом, выражения для мощности постоянного тока остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:
Обратите внимание, что если идет речь о напряжении или силе переменного тока, то (если не сказано иного) имеется в виду именно действующее значение. Так, 220В – это действующее напряжение в домашней электросети.
Так, 220В – это действующее напряжение в домашней электросети.
Конденсатор в цепи переменного тока
Строго говоря, конденсатор ток не проводит (в том смысле, что носители заряда через него не протекают). Поэтому, если конденсатор подключен в цепь постоянного тока, то сила тока в любой момент времени в любой точке цепи равна нулю. При подключении в цепь переменного тока из-за постоянного изменения ЭДС конденсатор перезаряжается. Ток через него по-прежнему не течет, но ток в цепи существует. Поэтому условно говорят, что конденсатор проводит переменный ток. В этом случае вводится понятие сопротивления конденсатора в цепи переменного тока (или емкостного сопротивления). Это сопротивление определяется выражением:
Обратите внимание, что емкостное сопротивление зависит от частоты переменного тока. Оно в корне отличается от привычного нам сопротивления R. Так, на сопротивлении R выделяется теплота (поэтому его часто называют активным), а на емкостном сопротивлении теплота не выделяется. Активное сопротивление связано со взаимодействием носителей заряда при протекании тока, а емкостное – с процессами перезарядки конденсатора.
Активное сопротивление связано со взаимодействием носителей заряда при протекании тока, а емкостное – с процессами перезарядки конденсатора.
Катушка индуктивности в цепи переменного тока
При протекании переменного тока в катушке возникает явление самоиндукции, и, следовательно, ЭДС. Из-за этого напряжение и сила тока в катушке не совпадают по фазе (когда сила тока равна нулю, напряжение имеет максимальное значение и наоборот). Из-за такого несовпадения средняя тепловая мощность, выделяющаяся в катушке, равна нулю. В этом случае вводится понятие сопротивления катушки в цепи переменного тока (или индуктивного сопротивления). Это сопротивление определяется выражением:
Обратите внимание, что индуктивное сопротивление зависит от частоты переменного тока. Как и емкостное сопротивление, оно отличается от сопротивления R. Как и на емкостном сопротивлении, на индуктивном сопротивлении теплота не выделяется. Индуктивное сопротивление связано с явлением самоиндукции в катушке.
Трансформаторы
Среди приборов переменного тока, нашедших широкое применение в технике, значительное место занимают трансформаторы. Принцип действия трансформаторов, применяемых для повышения или понижения напряжения переменного тока, основан на явлении электромагнитной индукции. Простейший трансформатор состоит из сердечника замкнутой формы, на который намотаны две обмотки: первичная и вторичная. Первичная обмотка подсоединяется к источнику переменного тока с некоторым напряжением U1, а вторичная обмотка подключается к нагрузке, на которой появляется напряжение U2. При этом, если число витков в первичной обмотке равно n1, а во вторичной n2, то выполняется следующее соотношение:
Коэффициент трансформации вычисляется по формуле:
Если трансформатор идеальный, то выполняется следующее соотношение (мощности на входе и выходе равны):
В неидеальном трансформаторе вводится понятие КПД:
Электромагнитные волны
К оглавлению. ..
..
Электромагнитные волны – это распространяющееся в пространстве и во времени электромагнитное поле. Электромагнитные волны поперечны – векторы электрической напряженности и магнитной индукции перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны. Электромагнитные волны распространяются в веществе с конечной скоростью, которая может быть рассчитана по формуле:
где: ε и μ – диэлектрическая и магнитная проницаемости вещества, ε0 и μ0 – электрическая и магнитная постоянные: ε0 = 8,85419·10–12 Ф/м, μ0 = 1,25664·10–6 Гн/м. Скорость электромагнитных волн в вакууме (где ε = μ = 1) постоянна и равна с = 3∙108 м/с, она также может быть вычислена по формуле:
Скорость распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных. Если электромагнитная волна распространяется в какой-либо среде, то скорость ее распространения также выражается следующим соотношением:
Если электромагнитная волна распространяется в какой-либо среде, то скорость ее распространения также выражается следующим соотношением:
где: n – показатель преломления вещества – физическая величина, показывающая во сколько раз скорость света в среде меньше чем в вакууме. Показатель преломления, как видно из предыдущих формул, может быть рассчитан следующим образом:
- Электромагнитные волны переносят энергию. При распространении волн возникает поток электромагнитной энергии.
- Электромагнитные волны могут возбуждаться только ускоренно движущимися зарядами. Цепи постоянного тока, в которых носители заряда движутся с неизменной скоростью, не являются источником электромагнитных волн. А вот цепи, в которых протекает переменный ток, т.е. такие цепи в которых носители заряда постоянно меняют направление своего движения, т.е. двигаются с ускорением – являются источником электромагнитных волн. В современной радиотехнике излучение электромагнитных волн производится с помощью антенн различных конструкций, в которых возбуждаются быстропеременные токи.

Длина волны — формулы, измерение, определение
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Волна: продольная и поперечная
Начнем с того, что волна — это распространение колебания в пространстве.
Волны бывают механическими и электромагнитными.
Механические волны — это те волны, колебания которых можно почувствовать физически, потому что они распространяются в упругой среде.
- Например, звук. Когда звук распространяется внутри какого-либо вещества, мы можем ощутить его прикосновением.
Представьте, что вы стоите на железнодорожных путях. Нет, вы не Анна Каренина, вы — экспериментатор.
Если к вам приближается поезд, вы рано или поздно его услышите. Вернее, услышите, как только звуковая волна со скоростью 𝑣 = 330 м/с достигнет ваших ушей. 8 м/с. И источники у них разные.
8 м/с. И источники у них разные.
Волны также принято делить на продольные и поперечные:
Продольные — это те волны, у которых колебание происходит вдоль направления распространения волны.
- Дрожание окон во время грома или сейсмические волны (землетрясения) — это пример продольных волн.
Поперечные — волны, у которых колебание происходит поперек направления распространения волны.
- Представьте, что вы запустили волну из людей на стадионе — она будет поперечной.
- Видимый свет и дрожание гитарной струны — тоже поперечные волны.
Морская волна — продольная или поперечная?
На самом деле в ней есть и продольная, и поперечная составляющие, поэтому ее нельзя отнести к конкретному типу.
Длина волны: определение и расчет
Конечно, у любой волны есть характеристики. Одна из таких характеристик — это длина волны.
Одна из таких характеристик — это длина волны.
- λ — длина волны [м]
Длиной волны называется расстояние между двумя точками этой волны, колеблющихся в одной фазе. Если проще, то это расстояние между двумя «гребнями».
Еще длиной волны можно назвать расстояние, пройденное волной, за один период колебания.
Период — это время, за которое происходит одно колебание. То есть, если дано время распространения волны и количество колебаний, можно рассчитать период.
Формула периода колебания волны T = t/N T — период [с] t — время [с] N — количество колебаний [-] |
Курсы подготовки к ОГЭ по физике помогут снять стресс перед экзаменом и получить высокий балл.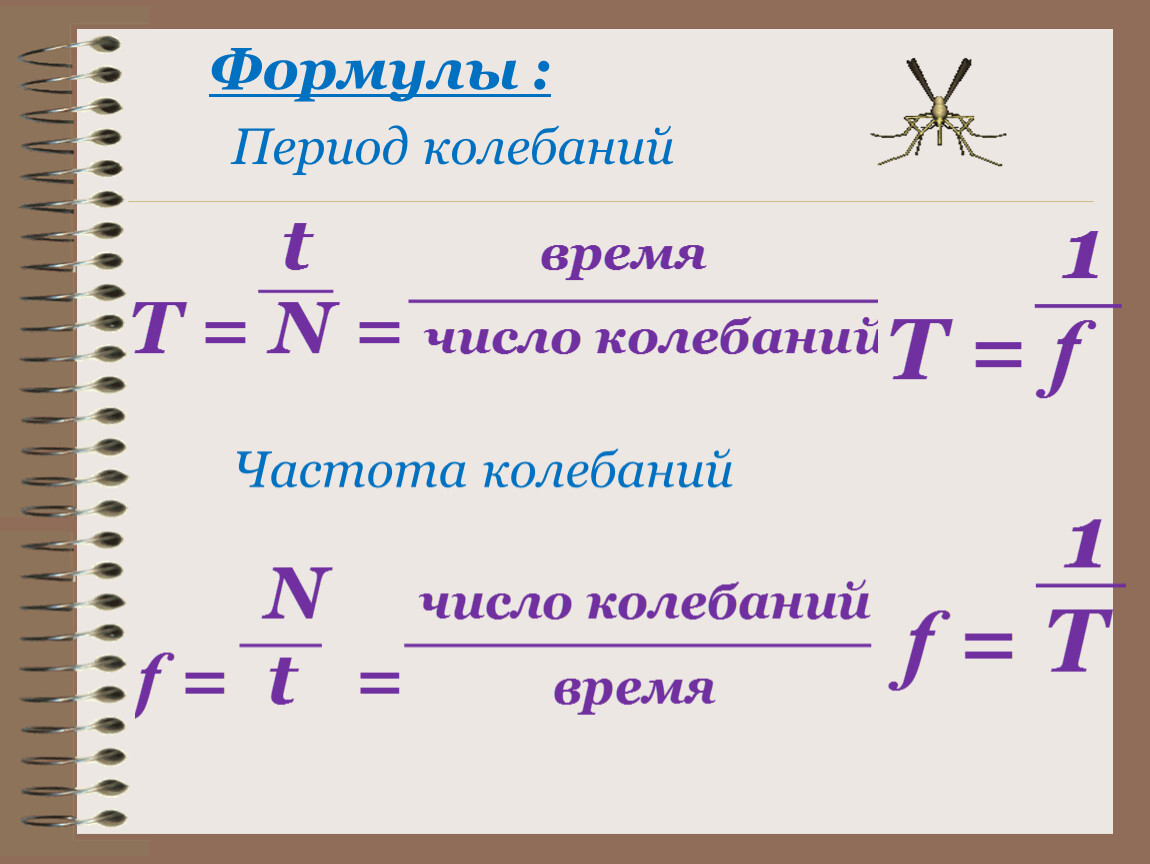
Связь со скоростью
Чтобы вывести формулу скорости через длину волны, нужно вспомнить формулу скорости из кинематики — это раздел физики, в котором изучается движение тел без учета внешнего воздействия).
Формула скорости 𝑣 = S/t 𝑣 — скорость [м/с] S — путь [м] t — время [с] |
Переходя к волнам, можно провести следующие аналогии:
- путь — длина волны
- время — период
А для скорости даже аналогия не нужна — скорость и Африке скорость.
Формула скорости волны 𝑣 = λ/T 𝑣 — скорость [м/с] λ — длина волны [м] T — период [с] |
Задачка
Лодка совершает колебания на волнах. За 40 с она совершила 10 колебаний. Какова скорость распространения волны, если расстояние между соседними гребнями волны равно 1 м?
За 40 с она совершила 10 колебаний. Какова скорость распространения волны, если расстояние между соседними гребнями волны равно 1 м?
Решение:
- Возьмем формулу скорости:
- Нам известна длина волны, но не дан период. Период вычисляется по формуле:
- Теперь подставляем величины в формулу
𝑣 = λ/T
T = t/N
T = 40/10 = 4 с
𝑣 = λ/T
𝑣 = ¼ = 0,25 м/с
Ответ: 𝑣 = 0,25 м/с
Резонанс
Если громко говорить в одном помещении с гитарой — можно услышать, как на ней начал играть призрак. На самом деле частота струны совпала с частотой голоса и возник резонанс.
На графике ниже можно увидеть, что на некоторой частоте резко увеличивается амплитуда. Эта частота называется частотой резонанса.
Частота — это величина, обратная периоду. Она показывает, за какое время происходит одно колебание.
Она показывает, за какое время происходит одно колебание.
Формула частоты ν = N/t ν — частота [Гц] t — время [с] N — количество колебаний [-] |
В мире существует очень много историй про то, как солдаты шли в ногу по мосту, он впал в резонанс и все провалились. А вот еще одна история про гидрологов — как говорится, из первых уст🙂
Команда гидрологов — специалистов по внутренним водам — работала на Алтае и изучала местную реку. Через реку был протянут веревочный мост, а по центру моста стояла лебедка, которая помогает поднять пробу воды из речки, не спускаясь до нее.
В один из дней экспедиции начался сильный, почти штормовой, ветер. Исследователи работали на мосту, а когда поняли, что находиться на веревочной конструкции в такой сильный ветер небезопасно, начали с него уходить. Как только последний человек из команды сделал шаг с моста на землю, мост вместе с лебедкой разнесло в щепки. Это произошло из-за того, что частота ветра совпала с собственной частотой раскачивающегося моста. Хорошо, что история закончилась именно так.
Как только последний человек из команды сделал шаг с моста на землю, мост вместе с лебедкой разнесло в щепки. Это произошло из-за того, что частота ветра совпала с собственной частотой раскачивающегося моста. Хорошо, что история закончилась именно так.
Объяснение загадочного поведения камертона с помощью численного моделирования
Если ударить по камертону и прижать его к поверхности стола, максимальная частота излучаемого звука удваивается. Такое загадочное поведение сбивает многих людей с толку. В этой заметке мы раскроем эту «тайну» с помощью численного моделирования, а также расскажем некоторые интересные факты о камертонах.
«Загадочное» поведение камертона
В недавнем видео, вышедшем на YouTube-канале standupmaths, популяризаторы науки Matt Parker и Hugh Hunt обсуждали и демонстрировали подобный феномен камертона. Когда вы ударяете по камертону и прижимаете его к поверхности стола, кажется, что частота удваивается. Как оказалось, объяснение этой загадки можно свести к задаче о нелинейной механике твёрдого тела.
Как звук достигает наших ушей?
Когда вы держите в руках «работающий» камертон, вибрация ножек приводит к колебанию воздуха вокруг них. Волны давления распространяются в воздухе в виде звука. Вы можете их даже услышать, однако такое преобразование механических вибраций в акустическое давление не очень эффективно.
Когда вы прикладываете стержень камертона к столу, его аксиальные колебания передаются на поверхность. Эти колебания гораздо меньше, чем поперечное движение ножек, однако плоская поверхность стола является намного более эффективным излучателем звука, нежели тонкие ножки камертона. В данном случае поверхность стола будет выступать в роли большой диафрагмы громкоговорителя.
Фотография нашего камертона.
Для исследования этого интересного явления мы создали численную модель для вибрационного анализа камертона. Модель воссоздает камертон, который один из моих коллег хранит у себя в сумке. Тон устройства соответствует эталонной ноте «ля» первой октавы (A4, 440 Hz), материал — нержавеющая сталь, общая длина порядка 12 см.
Для начала давайте взглянем на смещения в камертона на первой собственной моде:
Форма моды камертона на основной частоте.
Если мы подробней посмотрим на возникающие смещения, то увидим, что, хотя основное движение ножек происходит в поперечном направлении (в направлении оси x на изображении выше), присутствуют также и небольшие вертикальные смещения (в направлении оси z), которые состоят из двух частей:
- Изгиб ножек сопровождается движением вверх-вниз, которое линейно изменяется по поперечному сечению ножки
- Стержень камертона в основном совершает жёсткое аксиальное смещение, которое необходимо для удержания центра масс в фиксированном положении по второму закону Ньютона
Смещения визуализированы на рисунке ниже. Мода нормирована, так что максимальное общее смещение равно 1. Максимальное аксиальное смещение равно 0.03, смещение в стержне составляет 0.01.
Векторы общего смещения на первой собственной моде.
Векторы смещения только в аксиальном направлении. Обратите внимание, что графики нормированы по разному. Центр тяжести обозначен голубой сферой.
Теперь давайте перейдём к моделированию излучения звука. Для того, чтобы рассчитать уровень звукового давления в окружающем воздухе, проведен расчет связанных акустических процессов на основе метода граничных элементов. Амплитуду вибраций на краях ножек укажем равной 1 мм. Это примерное максимально допустимое значения для камертона, чтобы он не был перегружен возникающими механическими напряжениями.
Как видно из рисунка ниже, интенсивность звука быстро уменьшается по мере удаления от камертона, а также имеет высокую степень направленности. На самом деле: если вы повернёте камертон вокруг своей оси на 45 градусов около уха, то вы ничего не услышите. Это действительно поражает!
Уровень звукового давления (dB) и диаграмма направленности излучения (график-вставка) вокруг камертона.
Теперь добавим к модели деревянную поверхность стола толщиной 2 см. Длина и ширина равна 1 м. Стол закреплён на углах. Стержень камертона соприкасается со столом в центре. Как можно видеть из графика ниже, уровень звукового давления довольно высокий в большей части воздушной области над столом и за ним.
Длина и ширина равна 1 м. Стол закреплён на углах. Стержень камертона соприкасается со столом в центре. Как можно видеть из графика ниже, уровень звукового давления довольно высокий в большей части воздушной области над столом и за ним.
Уровень звукового давления над столом для случая стержня, соприкасающегося с ним.
Для сравнения построим график уровня звукового давления для случая, когда стержень держут в воздухе. Как мы видим, разница довольна существенная. Уровень звукового давления стал очень низким, кроме области в непосредственной близи от камертона. Такое распределение соответствует опыту с камертонами, показанному в оригинальном видео на YouTube.
Уровень звукового давления вокруг камертона в воздухе (без стола).
Является ли удвоенная частота собственной?
До сих пор мы не касались первоначального вопроса: Почему частота вибраций камертона, расположенного на столе, удваивается? Одним из возможных объяснений может быть то, что существует собственная частота, для которой основные смещения в основном происходят в вертикальном направлении. 2}\sqrt{\dfrac{EI}{\rho A}}
2}\sqrt{\dfrac{EI}{\rho A}}
Она в 6.27 раза больше, чем основная частота. Как мы видим, это не может стать причиной удвоения частоты. Однако, также существуют и другие формы мод, помимо симметричного изгиба. Может ли одна из них определять удвоение частоты?
Это маловероятно по двум причинам. Первая причина в том, что удвоение частоты наблюдается в камертонах различной формы. Было бы большим совпадением, если бы у всех них собственная мода была ровно вдвое больше основной собственной частоты. Вторая причина заключается в том, что несимметричные собственные моды имеют большое поперечное смещение в области стержня, где камертон удерживают. Таким образом, подобные собственные моды сильно бы затухали от прикосновения руки и имели бы маленькую амплитуду. Один из таких режимов на собственной частоте 1242 Гц представлен на анимации ниже.
Анимации первой собственной моды камертона на частоте 440 Hz, поперечной собственной моды на частоте 1242 Hz и второй собственной моды на частоте 2774 Hz.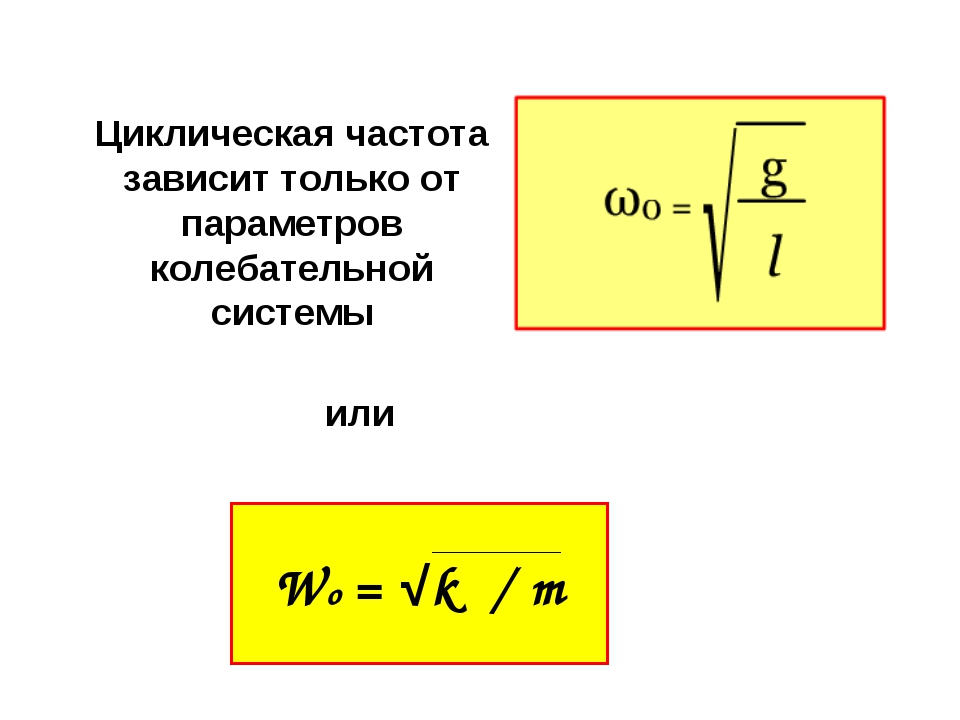
Вероятная причина «загадочного» поведения камертона
Давайте немного подытожим, что мы на данный момент знаем о феномене удвоения частоты. Так как данное явление происходит только тогда, когда мы прижимаем камертон к столу, вибрации на удвоенной частоте включают большое аксиальное смещение в стержне. Также, на основании данных спектроанализатора (вы можете скачать это приложение на свой телефон) можно сделать вывод, что уровень вибраций на двойной частоте относительно быстро угасает. Т.е. существует переход обратно к основной частоте.
Зависимость от амплитуды колебаний предполагает наличие нелинейностей. Аксиальное смещение стержня говорит о том, что он компенсирует изменение положения центра масс ножек.
Не вдаваясь в математические подробности, для изгибающейся консольной балки можно определить расстояние смещения центра масс вниз относительно первоначальной длины L по следующей формуле:
\dfrac{\delta Z}{L} = \beta \left ( \dfrac{a}{L} \right)^2
Здесь a — поперечное смещение края, коэффициент β ≈ 0. 2 \mathrm 80 \, mm = 0.0025 \, mm
2 \mathrm 80 \, mm = 0.0025 \, mm
Масса стержня гораздо меньше, чем масса ножек, поэтому он должен смещаться ещё больше, чтобы общий центр тяжести оставался неподвижным. По формуле амплитуда колебаний стержня равна 0.005 мм. Эту величину можно сравнить с численными экспериментами, о которых мы рассказывали выше. Линейная (440 Гц) компонента аксиального смещения равна отношению a/100, в нашем примере — это 0.01 мм.
В реальности, камертон представляет из себя гораздо более сложную систему, чем обычная консольная балка. Область соединения стержня и ножек также будет влиять на результаты. Для нашего камертона амплитуда смещений второго порядка на самом деле будет меньше половины от рассчитанного приближённо значения 0.005 мм.
Тем не менее, амплитуда аксиального смещения, которое вызвано движением массы второго порядка, является значительной. Однако, если мы рассматриваем излучение звука, то нам важна скорость, а не смещение. Таким образом, если амплитуды смещения равны на частотах 440 Гц и 880 Гц, то скорость на двойной частоте будет в два раза больше, чем на основной.
Поскольку амплитуда аксиальных колебаний на частоте 440 Гц пропорциональна амплитуде смещения ножки а, а на частоте 880 Гц пропорциональна a2, необходимо ударить по камертону достаточно сильно, чтобы заметить эффект удвоения частоты. По мере затухания вибраций относительный вклад нелинейного члена уменьшается. Это хорошо видно на спектроанализаторе.
Данный процесс можно подробно проанализировать, выполнив динамический расчет во временной области с учетом геометрической нелинейности. Горизонтальные поверхности ножек возбуждаются симметричным импульсом и камертон начинает свободно вибрировать. По графику видно, что горизонтальные вибрации ножек почти синусоидальны на частоте 440 Гц, в то время как смещение стержня вверх и вниз явно нелинейно. Это происходит из-за того, что вклад компоненты смещения на частоте 440 Гц синхронен со смещением стержня, а на частоте 880 Гц — нет, таким образом, возникают дополнительные смещения вверх.
Из-за нелинейности системы вибрации периодичны не полностью. Даже амплитуда смещений ножек может изменяться от периода к периоду.
Даже амплитуда смещений ножек может изменяться от периода к периоду.
Синим графиком показано поперечное смещение на конце ножки, зелёным — вертикальное смещение в нижней части стержня.
Если разложить смещение стержня в частотный спектр с помощью быстрого Фурье-преобразования (FFT), то мы увидим два главных пика на частотах 440 Гц и 880 Гц. Также есть небольшой третий пик в окрестности второй изгибной моды.
Разложение вертикального смещения стержня в частотный спектр с помощью быстрого Фурье-преобразования.
Чтобы реально увидеть вклад компоненты вибраций второго порядка на частоте 880 Гц, давайте вычтем компоненту вибраций стержня, которая синфазна вибрациям ножек камертона, из общего смещения стержня. На графике ниже это смещение изображено красной линией.
Общее аксиальное смещение (синяя линия), вибрация ножек камертона, пропорциональная смещению стержня (пунктирная зелёная линия) и смещение второго порядка (красная линия).
Как мы выполнили подобное преобразование? Из расчёта на собственные частоты мы получили значение амплитуды аксиального смещения стержня, которое равно примерно 1% от величины поперечного смещения ножек (если быть совсем точными то 0.92%). На графике выше пунктирная зелёная линия в 0.0092 раза больше, чем смещение на конце ножек (эта зависимость не показана на графике). Данную кривую можно рассматривать, как линейную компоненту на частоте 440 Гц, которая имеет более-менее гармоническую синусоидальную форму. Затем эта величина вычитается из общего смещения стержня и получается красная кривая. Данный график равен нулю в момент, когда ножки камертона не изогнуты, и дважды за период достигает своего амплитудного значения, когда ножки максимально изогнуты внутрь или наружу.
На самом деле, красная кривая очень похожа на график функции sin2(ωt). Как мы уже упоминали выше, так как это график смещения, он пропорционален квадрату смещения ножки. Используем известное тригонометрическое тождество \sin^2(\omega t) = \dfrac{1-\cos(2 \omega t)}{2}. Встречайте удвоенную частоту!
Встречайте удвоенную частоту!
Различные камертоны
В комментах к оригинальному видео отметили, что некоторые камертоны работают лучше других, а в некоторых вообще трудно уловить явление удвоения частоты. Как уже говорилось выше, для начала необходимо достаточно сильно ударить по камертону, чтобы попасть в нелинейный режим. К тому же, различная геометрия будет влиять на соотношение амплитуд для двух видов вибраций.
К примеру, если масса ножек будет намного больше стержня, то это вызовет большие смещения удвоенной частоты, так как в этом случае стержень должен будет больше перемещаться, чтобы центр тяжести оставался неизменным. В камертоне с тонкими ножками будет большее соотношение амплитуды к длине (a/L), что приведёт к увеличению нелинейной компоненты.
Большое значение играет место крепления стержня к ножкам. Если оно жёсткое, то амплитуда вибраций на основной частоте в стержне будет меньше, а относительный вклад компоненты удвоенной частоты, наоборот, больше. 4}{64}
4}{64}
Таким образом, для двух одинаковых при виде сбоку камертонов, тот, у которого ножки имеют квадратное сечение, должен быть длинней в 1.14 раз, чтобы их основная частота была одинаковой. Если взять одинаковое максимальное напряжение на изгиб для двух камертонов, тот, у которого ножки квадратного сечения, будет иметь амплитуду поперечных смещений в 1.142 больше, чем камертон с ножками круглого сечения, из-за более высокой способности выдерживать нагрузку. Кроме того, если размер стержня не изменяется, то общая масса камертона будет тем легче, чем длиннее будут ножки. Если сложить вклад всех этих случаев, то увеличение амплитуды вертикальной вибрации стержня увеличится примерно на 70% при переходе от круглого сечения ножки к квадратному.
Кроме того, у камертонов круглого сечения соединение между стержнем и ножками обычно более гибкое, что приводит к более высокому уровню вибраций на основной частоте.
Вывод из всего сказанного в том, что эффект удвоения частоты у камертона с квадратным сечением скорее всего будет более явно выражен.
Слышим ли мы удвоенную частоту?
В большинстве случаев ответ «нет». Основная частота всё так же существует, даже если она будет иметь более низкую амплитуду, чем удвоенная частота. Наши органы чувств работают таким образом, что мы будем слышать основную частоту, хоть и с другим тембром. Очень трудно, но не невозможно ударить по камертону таким образом, чтобы уровень звука двойной частоты был выше.
Заключение
Удвоение частоты происходит из-за нелинейного эффекта, когда стержень камертона должен двигаться вверх, чтобы компенсировать небольшое понижение центра масс ножек в момент, когда их амплитуда изгиба максимальна.
Обратите внимание, что стол не влияет на явление удвоения частоты. В данном случае стол выступает резонирующей поверхностью, которая усиливает аксиальные вибрации стержня. Если держать камертон в руке, то будет преобладать звук от вибраций изгибающихся ножек. В обоих случаях движение будет одинаковым, если мы не учитываем импеданс стола. Фактически, можно получить двойную частоту, просто держа камертон в руке, однако она будет на 30 dB ниже основной частоты (по амплитуде).
Фактически, можно получить двойную частоту, просто держа камертон в руке, однако она будет на 30 dB ниже основной частоты (по амплитуде).
Дальнейшие шаги
- Советуем посмотреть оригинальные видео на YouTube-канале standupmaths:
- Советуем более подробно узнать об основах моделирования камертонов в COMSOL:
Презентация и конспект урока физики «Частота и период обращения» — К уроку — Физика и астрономия
Урок по физике 8
класс.
«Период и частота
обращения»
Урок изучения
нового материала с применением
мультимедийной презентации
Разработала:
учитель математики Бузецкая Татьяна
Валерьевна
ГБОУ школа 523
Санкт-Петербурга
«Период и частота
обращения»
Цель урока:
Ввести и
изучить новые характеристики вращательного
движения, в частности движения по
окружности
Задачи урока:
Повторить понятие
скорости при движении по окружности,
центростремительного ускорения, формулы
для вычисления длины окружности,
числовым значением числа пи.
Познакомить с
понятием частота обращения и период
обращения
Рассмотреть
обозначение и единицы измерения этих
величин
Познакомиться с
формулами для вычисления этих величин,
рассмотреть вывод формулы для частоты
обращения
Провести первичное
закрепление на задачах
Развивать внимание,
логику, наблюдательность.
Оборудование:
мультимедийный
проектор,
компьютер,
интерактивная доска, презентация
PowerPoint,
учебник «Физика 8 класс» Громов С.В.,
Родина Н.А.
Этап | Деятельность | Деятельность | Результат | Слайд |
1. | Приветствие | Приветствие | ||
2.Введение | Формулирует | Обсуждают, | Постановка | Слайд |
3.Устный | 1). 2).Что 3).От 4).Приведите | Вспоминают | Вывод | Слайд |
4. | Озвучивает | Решают | Решают | Слайд |
4.Изучение | Знакомит | Слушают, Единицы Единицы Единицы Формула Чему | Знакомство | Слайд |
5. | Организует | Решают | Умение | Слайд |
8. | Знакомит | Записывают | Слайд | |
9.Итог (рефлексия) | Предлагает | Анализируют | Оценка | Слайд |
Частота и длина волны объясняются простым языком с примерами и иллюстрациями.
« Назад к Глоссарию Индекс
Частота и длина волны являются свойствами волн. Они тесно связаны между собой, поэтому в этой статье они обсуждаются вместе.
Частота — это количество повторяющихся движений за период времени. Эти движения могут быть вверх и вниз, как молоток, или вперед и назад, взмахивая рукой. Или какое-то другое повторяющееся движение, может быть, раскачивание маятника. Повторяющиеся движения называются «колебаниями» или «циклами».Итак, частота — это количество циклов в единицу времени, часто измеряемое в секундах.
Эти движения могут быть вверх и вниз, как молоток, или вперед и назад, взмахивая рукой. Или какое-то другое повторяющееся движение, может быть, раскачивание маятника. Повторяющиеся движения называются «колебаниями» или «циклами».Итак, частота — это количество циклов в единицу времени, часто измеряемое в секундах.
Циклы можно изобразить на бумаге, как показано на прилагаемом изображении. В случае движения молотка вверх и вниз по вертикальной оси будет высота, а по горизонтальной оси будет время. Когда молот находится на самой высокой высоте, это гребень. Когда это самая низкая высота, это желоб. Затем со временем молот снова поднимается вверх до гребня и так далее.
Основные свойства волны: период, частота (количество гребней в секунду) и амплитуда.Горизонтальная ось — время. [Источник изображения: модификация Kraaiennest — CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=4038226. Проверено 21 сентября 2017 г.] На этом изображении частота — это количество циклов от вершины к вершине, выполненных за секунду. Или количество движений, от корыта к корыту — то же самое. Чем больше циклов в секунду, тем выше частота.
Или количество движений, от корыта к корыту — то же самое. Чем больше циклов в секунду, тем выше частота.
Частота обозначается либо древнегреческой буквой v (произносится как nu ), либо обозначается просто f для частоты.Символ v обычно используется для обозначения частоты электромагнитных волн; тогда как символ f обычно используется для частоты обычных волн, которые требуют материальной среды, такой как звуковые и водяные волны.
Период волны – это промежуток времени между гребнями (или между впадинами). Чем выше частота, тем короче период. Чем ниже частота, тем больше период. Частота и период обратно пропорциональны.
Свойства волны: длина волны и амплитуда. [Источник изображения: Kraaiennest — CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=4038226. Проверено 21 сентября 2017 г.] Длина волны — это расстояние в пространстве от гребня до гребня. Или от корыта до корыта — такое же расстояние. Длина волны символизируется древнегреческой буквой 𝛌, называемой «лямбда». Как частота и период, частота и длина волны обратно пропорциональны. Чем выше частота, тем короче длина волны. Чем ниже частота, тем больше длина волны.
Или от корыта до корыта — такое же расстояние. Длина волны символизируется древнегреческой буквой 𝛌, называемой «лямбда». Как частота и период, частота и длина волны обратно пропорциональны. Чем выше частота, тем короче длина волны. Чем ниже частота, тем больше длина волны.
Если вы уже разбираетесь в волнах, но хотите узнать больше о частоте и длине волны, вы можете сразу перейти к разделу «Волновые движения возникают циклически.Если вы хотите узнать больше о волнах, читайте дальше.
Что такое волна?
Волна – это движение, распространяющееся в среде. Сопутствующая анимация демонстрирует движение, распространяющееся через толпу на стадионе. Движение рябит вдоль скамеек.
Волна в толпе стадиона, метафора физической волны. [Источник изображения: Hughesdarren, https://en.wikipedia.org/wiki/Wave_(audience), получено 18 февраля 2018 г.] такое же сиденье.Но что-то движется по стадиону — движение — то вверх, то вниз.
В отличие от физики, люди не заставляют друг друга стоять физически — это мысленная связь. Каждый человек решил, что когда мой сосед встанет, а потом начнет сидеть, я встану. Итак, это не волна в физическом определении, но хорошая метафора для нее.
В физической волне определенное движение, колебание передается от одного бита к следующему биту некоторой среды. Он включает в себя физический толчок или притяжение соседней частицы.Затем соседняя частица толкает или притягивает следующую и так далее.
В физике волна — это передача движения от одного конца среды к другому без переноса материи. Движение — это направленная энергия, поэтому волна — это тип передачи энергии через среду. Для получения дополнительной информации см. запись для «волны».
Звуковые волны — пример частоты и длины волны
Звуковая волна представляет собой серию сжатий и разрежений (истончений) молекул воздуха.Эти сжатия и разрежения подталкивают соседние молекулы, так что соседние физически воздействуют на повторение того же движения. Это создает распространяющуюся волну, которая ритмично распространяется по воздуху, создавая цикл низкого атмосферного давления, а затем высокого атмосферного давления, а затем снова низкого по мере своего движения.
Это создает распространяющуюся волну, которая ритмично распространяется по воздуху, создавая цикл низкого атмосферного давления, а затем высокого атмосферного давления, а затем снова низкого по мере своего движения.
Нажмите на картинку, чтобы посмотреть видео о звуковых волнах. Минуты с 1:30 до 4:20 являются наиболее важными.
Частота звуковой волны определяет ее высоту. Например, частота ноты, на которую настраивают свои инструменты многие оркестровые инструменты, на фортепиано выше среднего C.Его частота составляет 440 циклов в секунду. Частота 220 циклов в секунду — это та же нота Ля, но на октаву ниже.
В прилагаемом видео показано, как работают звуковые волны. Участок в минутах с 1:30 до 4:20 наиболее актуален, хотя все видео представляет собой превосходную презентацию звуковых волн.
Частоты световых волн — еще один пример частоты и длины волны
Частота видимого света определяет его цвет. Свет состоит из электромагнитных волн.Когда силы электрических и магнитных полей возрастают и уменьшаются, то есть когда они колеблются, они создают частоту. Цикл от одного гребня к другому происходит определенное количество раз в секунду.
Свет состоит из электромагнитных волн.Когда силы электрических и магнитных полей возрастают и уменьшаются, то есть когда они колеблются, они создают частоту. Цикл от одного гребня к другому происходит определенное количество раз в секунду.
Электромагнитная волна движется вправо. [Источник изображения: https://blog.oureducation.in/some-concepts-of-electromagic-field/ получено 31 марта 2018 г.] Частота видимого света измеряется в терагерцах. «Тера» происходит от греческого слова «чудовище». А один терагерц поистине чудовищен по размеру: один триллион циклов в секунду.Как показано на прилагаемом изображении, частота видимого света колеблется от 400 терагерц (красный свет) до 789 терагерц (фиолетовый свет).
Частота света определяет не только его цвет, но и его энергию. Чем выше частота, тем выше энергия. Фиолетовый свет, частота которого примерно в 1,7 раза превышает частоту красного света, также имеет примерно в 1,6 раза большую энергию. Хотя связь между частотой и энергией не является взаимно однозначной, она пропорциональна. В прилагаемой таблице показаны уровни энергии каждой частоты видимого света.
В прилагаемой таблице показаны уровни энергии каждой частоты видимого света.
Спектр электромагнитных волн. [Источник изображения: Inductiveload, NASA — самодельный, информация NASA, CC BY-SA 3.0; https://en.wikipedia.org/wiki/Electromagnetic_spectrum, получено 31 марта 2018 г.] На частотах ниже красного видимого света природа электромагнетизма меняется. Эти более низкие частоты представляют собой инфракрасные, микроволновые и радиоволны. Взаимодействие видимого света с материей позволяет нам видеть их. Напротив, взаимодействие инфракрасных, микроволновых и радиоволн с веществом вызывает его нагрев.
Выше ультрафиолета электромагнетизм становится рентгеновским излучением, а на еще более высоких частотах — гамма-лучами.
Спектр видимого света — частота, длина волны и энергия. Измерения: Длина волны-нанометры; Частота-Терагерц; Энергия-электрон-вольт. [Источник изображения: адаптировано из Гринджера — собственная работа, общественное достояние, https://en. wikipedia.org/wiki/Visible_spectrum, получено 5 мая 2018 г.] Рентгеновские и гамма-лучи, будучи более высокочастотными, также несут более высокие энергии.Их высокие энергии позволяют им проникать в материю, а также разрывать атомы и молекулы материи. Рентгеновские и гамма-лучи могут повредить наш организм. На самом деле гамма-лучи являются одними из самых разрушительных форм излучения, испускаемого атомными бомбами.
wikipedia.org/wiki/Visible_spectrum, получено 5 мая 2018 г.] Рентгеновские и гамма-лучи, будучи более высокочастотными, также несут более высокие энергии.Их высокие энергии позволяют им проникать в материю, а также разрывать атомы и молекулы материи. Рентгеновские и гамма-лучи могут повредить наш организм. На самом деле гамма-лучи являются одними из самых разрушительных форм излучения, испускаемого атомными бомбами.
Связь между частотой и энергией электромагнитных волн математически выражается как E = hf , где: E = энергия; ч = постоянная Планка, крайне малое число; и f = частота.Другими словами, умножать частоту волны крошечным числом, ч , и вы найдете энергию волны.
Взаимосвязь частоты, длины волны и скорости
частоты не то же самое, что и скорость волны. Скорость водяной волны, например, является расстоянием гребня волны проходит в определенном промежутке времени. Давайте предположим, что мы наблюдаем на гребень волны, идущей к док-станции, что мы сидим на. Он может путешествовать по 10 миль в час по отношению к нам.Но скорость зависит от среды. Замените воду патокой, и волна будет двигаться намного медленнее. Среда решает все. Частота и длина волны не играют никакой роли в определении скорости волн на воде и других волн, которым требуется материальная среда.
Давайте предположим, что мы наблюдаем на гребень волны, идущей к док-станции, что мы сидим на. Он может путешествовать по 10 миль в час по отношению к нам.Но скорость зависит от среды. Замените воду патокой, и волна будет двигаться намного медленнее. Среда решает все. Частота и длина волны не играют никакой роли в определении скорости волн на воде и других волн, которым требуется материальная среда.
Скорость электромагнитной волны также зависит от среды. Но ситуация сложнее, чем это простое утверждение. Электромагнитные волны, в отличие от большинства волн, не требуют материальной среды. Когда электромагнитная волна распространяется в вакууме, а не в материальной среде, она всегда распространяется со скоростью 186 282 мили в секунду.Физики называют все формы электромагнетизма, «свет»; 186,282 миль в секунду скорость света.
При падении электромагнитной волны проходит через вакуум, частоты и длины волны связаны с скоростью. В частности, частота раз длина волны равна скорости. Скорость волны также иногда называют «скорость». Зависимость между частотой, длиной волны, и скорость выражена математически · F Х = v . В этом уравнении, F по частоте; λ является лямбда, греческая буква используется, чтобы символизировать длины волны; и v является скорость.
Скорость волны также иногда называют «скорость». Зависимость между частотой, длиной волны, и скорость выражена математически · F Х = v . В этом уравнении, F по частоте; λ является лямбда, греческая буква используется, чтобы символизировать длины волны; и v является скорость.
Призма разбивает белый свет на частоты. Нажмите на изображение для анимации. [Источник изображения: Лукас В. Барбоза — собственная работа, общественное достояние; https://en.wikipedia.org/wiki/Призма; Проверено 16 мая 2018] Так как скорость света в вакууме всегда одни и те же, как частота может быть связана с скоростью, когда различные электромагнитные волны имеют разные частоты? Вот красивая часть — частота и длина волны компенсируют друг друга, потому что они прямо пропорциональны друг другу.При умножении они всегда дают постоянную скорость, скорость света.
Электромагнитные волны также могут распространяться через материальные среды, например стекло. Когда видимый свет проходит через стекло, волны не проходят прямо сквозь него, не подвергаясь воздействию. Они взаимодействуют со стеклом. Частицы света, фотоны, поглощаются атомами в стекле и снова излучаются. После испускания они возобновляют свой путь через стекло. Всякий раз, когда они путешествуют, они мчатся со скоростью света.Но характер их движения «стоп-старт» замедляет их в среднем до скорости, меньшей скорости света.
Когда видимый свет проходит через стекло, волны не проходят прямо сквозь него, не подвергаясь воздействию. Они взаимодействуют со стеклом. Частицы света, фотоны, поглощаются атомами в стекле и снова излучаются. После испускания они возобновляют свой путь через стекло. Всякий раз, когда они путешествуют, они мчатся со скоростью света.Но характер их движения «стоп-старт» замедляет их в среднем до скорости, меньшей скорости света.
Предположим, что свет, проходящий через стекло, является белым светом — смесью всех различных цветов, то есть частот. Частота влияет на то, насколько свет замедляется при взаимодействии с атомами стекла. Таким образом, разные частоты вызывают разные ощущения при путешествии через стекло. Если стекло окажется призмой, оно будет разделять частоты света в соответствии с их скоростями.Вот почему мы видим белый свет ввести призму и различные цвета светового выхода призмы.
Частота — Период — Физика Видео по Brightstorm
Хорошо. Поговорим о частоте и периоде волны. Частота и период является свойством периодических волн, своего рода, почему они называются периодические волнами, и поэтому частоты числа волн, проходящих через данную точку в определенном промежутке времени. Как вы помните, периодическая волна представляет собой волну, хиты снова и снова и снова несколько раз, и поэтому частота характеризует, сколько раз делает это нападение среда в заданный промежуток времени.
Поговорим о частоте и периоде волны. Частота и период является свойством периодических волн, своего рода, почему они называются периодические волнами, и поэтому частоты числа волн, проходящих через данную точку в определенном промежутке времени. Как вы помните, периодическая волна представляет собой волну, хиты снова и снова и снова несколько раз, и поэтому частота характеризует, сколько раз делает это нападение среда в заданный промежуток времени.
Точка в каком-то смысле противоположна этому. Это то, сколько времени требуется одной волне, чтобы атаковать среду. Хорошо. Итак, у нас есть очень простой способ думать о периоде. Итак, представьте, что вы находитесь в океане. Итак, вы в лодке в океане и подошли к гребню волны. Период — это то, сколько времени вам потребуется, чтобы спуститься и вернуться к следующему гребню. Так что это действительно простой способ понять, что означает период.
Хорошо. Итак, давайте продолжим и просто сделаем пример с частотой.Предположим, что частота составляет 3 волны в секунду. И, конечно, это имеет смысл, если частота показывает, сколько волн приходит за заданный промежуток времени, тогда 3 волны в секунду означают, что за одну секунду приходят 3 волны. Хорошо. Мы обычно не используем волны в секунду в качестве единицы измерения, вместо этого мы используем единицу измерения герц, названную в честь нашего физика, который на самом деле был первым парнем, представившим электромагнитные волны в 1887 году. Хорошо.
И, конечно, это имеет смысл, если частота показывает, сколько волн приходит за заданный промежуток времени, тогда 3 волны в секунду означают, что за одну секунду приходят 3 волны. Хорошо. Мы обычно не используем волны в секунду в качестве единицы измерения, вместо этого мы используем единицу измерения герц, названную в честь нашего физика, который на самом деле был первым парнем, представившим электромагнитные волны в 1887 году. Хорошо.
Таким образом, мы могли бы сказать, что частота составляет 3 герца. Так какой период? Что ж, посмотрим.Если каждую секунду приходят 3 волны, то сколько времени длится каждая волна? Ну, 3 волны в секунду, каждая займет треть секунды. Так что это дает нам на самом деле очень-очень общее соотношение между частотой и периодом. Частота равна единице за период. Это всегда верно. Это следует непосредственно из определений этих величин, и это всегда приятно, потому что это означает, что я всегда могу записать это, и оно никогда не будет неправильным. Хорошо.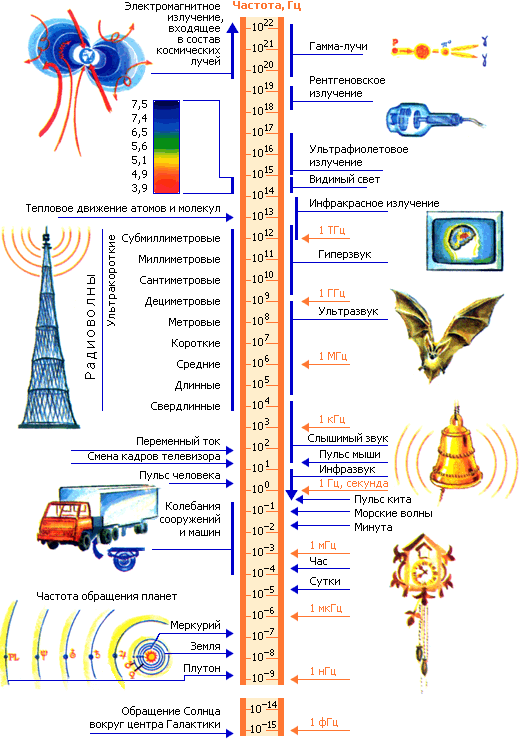
Итак, давайте продолжим и посмотрим на некоторые свойства, связанные с этой реальностью.Частота умноженная на период равна единице. Это означает, что если я увеличу частоту, ну, господи, это число станет больше, но результат останется прежним, поэтому период должен уменьшиться. Таким образом, большая частота, меньший период. И наоборот, чем меньше частота, тем больше период. Хорошо? Еще одна вещь, которую я видел во многих тестах, спрашивают, если я удвою частоту, что произойдет с периодом? Что ж, это очень просто, потому что у меня здесь 2, удваивая частоту, но мне нужно, чтобы продукт оставался прежним.Так что я должен поставить одну половину там. Так что, если я удваивать частоту, я сократил период пополам. И наоборот, если я сократить частоту пополам я дважды период. Реальный реальный реальный простой, но иногда студенты не замечают, как это происходит, и как легко, пока они не видели пример.
Хорошо. Еще одно важное свойство о частоте и период, который придет много позже, в более поздних исследованиях периодических волн является то, что период и frequncy не может измениться.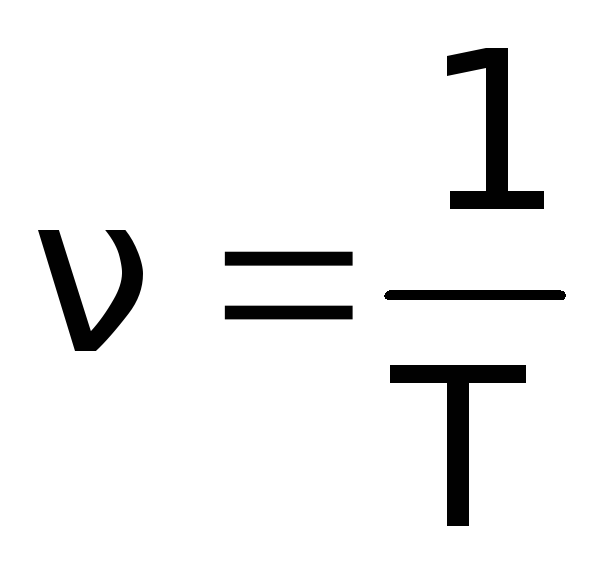 И это на самом деле замечательная вещь о периоде и частоте.Потому что другие свойства волны изменятся. Если я поступлю так, как если бы ко мне проник свет и он попал на кусок стекла, многие его свойства изменились бы, но его частота и период не изменились бы. Почему? Ну, это очень просто. Если у вас есть 3 волны, приходящие в секунду, у вас должно быть 3 волны, уходящие в секунду. Потому что иначе волны соберутся на границе, а граница этого не выдержит. Таким образом, частоту и период можно использовать для характеристики волны, когда она проходит через то, через что она собирается пройти.Что бы с ним ни случилось, частота и период остаются неизменными. И это частота и период.
И это на самом деле замечательная вещь о периоде и частоте.Потому что другие свойства волны изменятся. Если я поступлю так, как если бы ко мне проник свет и он попал на кусок стекла, многие его свойства изменились бы, но его частота и период не изменились бы. Почему? Ну, это очень просто. Если у вас есть 3 волны, приходящие в секунду, у вас должно быть 3 волны, уходящие в секунду. Потому что иначе волны соберутся на границе, а граница этого не выдержит. Таким образом, частоту и период можно использовать для характеристики волны, когда она проходит через то, через что она собирается пройти.Что бы с ним ни случилось, частота и период остаются неизменными. И это частота и период.
Урок 44: Частота, длина волны и амплитуда
Теперь, когда вы знаете что-то о свойствах двух основных типов волн (Урок 43), мы должны убедиться, что вы можете посмотреть на индивидуальных характеристиках, что волны могут иметь.
- Не все волны созданы равные!
- Вы должны уметь видеть конкретные «лица», которые может иметь каждая волна, на основе трех важных характеристик: частоты, длины волны и амплитуды.

Частота
Когда мы впервые начали рассматривать SHM , мы определили период как количество времени, которое требуется для завершения одного цикла… секунд на цикл
- Частота — та же идея, за исключением того, что мы просто поменяем местами.
- Частота — это измерение того, сколько циклов может произойти за определенный промежуток времени… циклов в секунду.
- Если двигатель работает так, что совершает 50 оборотов за одну секунду, я бы сказал, что его частота составляет 50 Гц.
- Герц — это единица частоты, и она просто означает, сколько циклов в секунду.
- Сокращенно Гц .
- Он назван в честь Генриха Герца, одного из членов семьи Герц, который внес важный вклад в физику.
- Частота в формулах обозначается буквой «f».
Поскольку частота и период являются точными обратными значениями друг друга, существует пара очень простых формул, которые можно использовать для вычисления одной, если вы знаете другую…
Очень легко производить эти расчеты на калькуляторах с помощью кнопки x -1 .
Пример 1: Период маятника равен 4,5 с. Определите частоту этого маятника.
Период означает, что маятнику потребуется 4,5 секунды, чтобы один раз качнуться вперед и назад. Итак, я ожидаю, что моя частота будет десятичной, поскольку она будет совершать долю колебания в секунду.
Длина волны
Длина волны — это свойство волны, которое большинство людей (если они знают, что искать) могут быстро и легко определить и использовать для различения волн.Посмотрите на следующую схему…
Рисунок 1
- Любые части волны, которые направлены вверх, как горы, называются гребнями. Любая часть, которая наклонена вниз, как долина, является желобом.
- Длина волны определяется как расстояние от определенной высоты волны до следующего места на волне, где она находится на той же высоте и движется в том же направлении.
- Обычно измеряется в метрах, как и любая длина.
- Нет особой точки, с которой нужно начать на волне, чтобы измерить длину волны, просто убедитесь, что вы вернулись на ту же высоту и двигаетесь в том же направлении.
 Большинству людей нравится измерять от одного гребня до следующего гребня (или от впадины до впадины) просто потому, что их легко заметить.
Большинству людей нравится измерять от одного гребня до следующего гребня (или от впадины до впадины) просто потому, что их легко заметить.
Рисунок 2
Длина волны продольной волны измеряется как расстояние между серединами двух сжатий или серединами двух расширений.
Рисунок 3
Это приводит нас к одной из самых важных формул, которые вы будете использовать при изучении волн.
- Частота говорит нам, сколько волн проходит через точку в секунду, обратное времени .
- Длина волны сообщает нам длину этих волн в метрах, почти как смещение .
- Если мы умножим эти два числа вместе, мы на самом деле умножим 1/с и м… что даст нам м/с, скорость волны!
v = скорость волны (м/с)
f = частота (Гц)
λ = длина волны (м)
Пример 2: Измеренная волна имеет частоту 60 Гц. Если его длина волны равна 24 см, определяет , как быстро он движется.
Пример 3: Скорость света всегда равна 3.00e8 м/с. Определить частоту красного света, имеющего длину волны 700 нм.
Будьте осторожны при переводе 700 нм в метры. Некоторые люди действительно увлекаются преобразованием его в обычную научную запись только с одной цифрой перед десятичным числом. Зачем беспокоиться? Он используется только в расчетах. Вы, вероятно, сделаете ошибку, изменив степень 10, поэтому просто замените префикс на степень и оставьте все остальное в покое… 700 нм = 700 x 10 -9 м, так как «нано» равно 10 -9 .
Амплитуда
Амплитуда — это мера размера волны.
- Представьте волну в океане. Это может быть небольшая рябь или гигантское цунами.
- На самом деле вы видите волны с разной амплитудой.
- Они могут иметь одинаковую частоту и длину волны, но амплитуды волн могут сильно различаться.
Амплитуда волны измеряется как:
- высота от точки равновесия до высшей точки гребня или
- глубина от точки равновесия до нижней точки желоба
Рисунок 4
Когда вы измеряете амплитуду волны, вы действительно смотрите на энергию волны.
- Для создания волны большей амплитуды требуется больше энергии.
- В любое время, когда вам нужно вспомнить об этом, просто подумайте об усилителе домашней стереосистемы… он увеличивает амплитуду волн, используя больше электроэнергии.
единиц частоты и длины волны Рона Куртуса
SfC Home > Физика > Волновое движение >
Рон Куртус
Характеристика сигнала состоит в том, что он имеет амплитуду, длину волны, частоту и скорость.Амплитуда – это высота волны или ее интенсивность. Длина волны – это расстояние между максимумами амплитуды. Частота — это то, как часто максимумы или гребни перемещаются за заданную точку. И, наконец, скорость — или скорость движения волны — это произведение
частоты, умноженной на длину волны ( v = fλ ).
единицы измерения частоты выражены в герцах (Гц) или кратных им единицах. единиц длины волны выражены в метрах, кратных или долях метра. По мере увеличения частоты длина волны уменьшается при условии, что скорость остается постоянной. Например, волны чрезвычайно высоких частот имеют очень короткие длины волн.
По мере увеличения частоты длина волны уменьшается при условии, что скорость остается постоянной. Например, волны чрезвычайно высоких частот имеют очень короткие длины волн.
Экспоненциальные степени 10 используются, когда частоты или длины волн становятся очень большими. Очень короткие длины волн обозначаются как отрицательные экспоненты.
Возможные вопросы:
- Что такое экспоненциальное представление числа 10?
- Что такое частотные термины?
- Что такое условия длины волны?
Этот урок ответит на эти вопросы.Полезный инструмент: Преобразование единиц измерения
Степени числа 10
Удобным способом выражения больших и малых чисел является использование показателей или степеней 10 , кратных 10 .
Большие числа
Вы можете указать большое число, такое как 1 000 000 , как степень или степень 10 , подсчитав количество нулей и записав число как 10 6 или 1*10 6 8 и 3E8 .
Мелкие числа
Следуя тому же методу для небольшого числа 1/100,000 = 1/10 5 , так как 100,000 имеет 5 нулей. Это можно записать как 10 −5 . Обратите внимание, что десятичная версия 1/100,000 равна 0,00001 ,
который имеет только 4 нуля после запятой. Это то, о чем нужно знать. Некоторые другие примеры:
3/10 000 000 = 0.0000003 = 3*10 −7
0,00252 = 2,52*10 −4
0,000000004026 округляется до 4,03*10 −9
Частоты
Частоты измеряются в герцах (Гц), что означает количество циклов или гребней волны в секунду. Вы можете записать частоту с версиями символа, как большое число или как показатель степени.
| Символ | Номер | Экспонента |
|---|---|---|
| 1 Гц (герц) | 1 Гц | 1 Гц |
| 1 кГц (килогерц) | 1000 Гц | 1*10 3 Гц |
| 1 МГц (мегагерц) | 1 000 000 Гц | 1*10 6 Гц |
| 1 ГГц (гигагерц) | 1 000 000 000 Гц | 1*10 9 Гц |
Частота некоторых волновых форм, таких как водная волна цунами, может меняться очень медленно. В таком случае частота может быть указана в циклах в минуту или час. 1/3600 Гц — это 1 цикл в час.
В таком случае частота может быть указана в циклах в минуту или час. 1/3600 Гц — это 1 цикл в час.
Длина волны
Длины волн обычно выражаются в метрической системе или системе СИ, поскольку более удобно иметь число, кратное 10. Длины волн могут варьироваться от многих километров до чрезвычайно коротких длин или долей метра.
| Имя | метров | Экспонента |
|---|---|---|
| 1 км (километр) | 1000 м (метров) | 1*10 3 м |
| 1 м | 1 м | 1 м |
| 1 см (сантиметр) | 0.01 м | 1*10 −2 м |
| 1 мм (миллиметр) | 0,001 м | 1*10 −3 м |
| 1 мкм (микрометр или микрон) | 0,000001 м | 1*10 −6 м |
| 1 нм (нанометр) | 0,000000001 м | 1*10 −9 м |
| 1 Å (ангстрем) | 0,1 нм | 1*10 −10 м |
Резюме
Связь между частотой и длиной волны заключается в том, что — при заданной скорости — по мере увеличения частоты длина волны уменьшается. На очень высоких частотах у вас могут быть очень короткие волны.
На очень высоких частотах у вас могут быть очень короткие волны.
Поскольку числа частот становятся очень большими, они обозначаются фразами, такими как «мега» и «гига», или степенями 10. Очень короткая длина волны обозначается как отрицательная экспонента.
Всегда делай все возможное
Ресурсы и ссылки
Полномочия Рона Куртуса
веб-сайтов
Ресурсы Wave Motion
Книги
(Примечание: Школа чемпионов может получать комиссионные за покупку книг)
Книги с самым высоким рейтингом по Wave Motion
Поделиться этой страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
wave_units.htm
Разместите его в качестве ссылки на своем веб-сайте или в качестве ссылки в своем отчете, документе или диссертации.
Copyright © Ограничения
Где ты сейчас?
Школа Чемпионов
Темы физики
Единицы измерения частоты и длины волны
Частота и период времени — Особенности волн — GCSE Physics (Single Science) Revision
Частоту волны можно рассчитать с помощью следующего уравнения:
\[частота = \frac{1}{time~period}\]
\[f=\frac{1}{T}
\]
где:
f — количество волн, производимых источником в секунду, измеряется в герцах (Гц).
0.0.0.1:0.1.0.$0.$1.$5.$0″> T – время, необходимое для одного полного колебания, измеряется в секундах.
Все волны, включая звуковые волны и электромагнитные волны, следуют этому уравнению. Например, волна с периодом времени 2 секунды имеет частоту 1 ÷ 2 = 0,5 Гц.
- Вопрос
Период времени звуковой волны составляет 0,0001 секунды. Какова его частота?
- Показать ответ
f = 1 ÷ T
3.$1″> f = 1 ÷ 0.0001 сf = 10 000 Гц
- Вопрос
Радиоволна имеет период времени 0,0000000333333 Какова его частота?
- Открыть ответ
= 1 ÷ T
2a8fuulb1n0.0.0.0.1:0.1.0.$0.$1.$8.3.$1.$0″> F = 1 ÷ 0.00000033333333 S
F = F = 3 000 000 Гц
Природа звука — физика HypertextBook
введение
Звук представляет собой продольную механическую волну.
Звук может проходить через любую среду, но не может проходить через вакуум. В космосе нет звука.
Звук — это изменение давления. Область повышенного давления на звуковую волну называется сжатием (или сгущением). Область пониженного давления на звуковую волну называется разрежением (или расширением).
svg»> Увеличить
Источники звука
- вибрирующие твердые тела
- быстрое расширение или сжатие (взрывы и имплозии)
- Плавное (ламинарное) обтекание тупых препятствий воздушным потоком может привести к образованию вихрей (множественное число от вихря), которые отрываются или сбрасываются с характерной частотой.Этот процесс называется вихреобразованием и является еще одним средством формирования звуковых волн. Так звучит свисток или флейта. Также эффект эоловой арфы от поющих линий электропередач и развевающихся жалюзи.
Каковы различные характеристики волны? Что можно измерить о волнах? Амплитуда, частота (и период), длина волны, скорость и, возможно, фаза. Разберитесь с каждым в таком порядке.
амплитуда, интенсивность, громкость, громкость
Амплитуда связана с интенсивностью, громкостью или громкостью.Это основная идея. Подробности в отдельном разделе.
[ИСО 226:2003]
- В отличие от наших ушей и гидрофонов, рыбьи уши не обнаруживают звукового давления, то есть сжатия молекул.
 Вместо этого они воспринимают нечто, называемое движением частиц, крошечные возвратно-поступательные движения частиц в ответ на звуковые волны.
Вместо этого они воспринимают нечто, называемое движением частиц, крошечные возвратно-поступательные движения частиц в ответ на звуковые волны.
скорость звука
Скорость звука зависит от типа среды и ее состояния. Обычно на него влияют две вещи: эластичность и инерция.Это уравнение Ньютона-Лапласа. Лаплас добавил поправочный коэффициент γ (гамма) для идеальных газов.
твердые вещества
| E = | Модуль Юнга |
| ρ = | плотность |
жидкости
| К = | объемный модуль |
| ρ = | плотность |
идеальные газы
| v = √ | К | = √ | γ Р | = √ | γ РТ | = √ | γ кт |
| р | р | М | м |
| К = | объемный модуль |
| γ = | c P / c В удельная теплоемкость |
| P = | абсолютное давление |
| ρ = | плотность |
| Т = | абсолютная температура |
| Ч = | газовая постоянная |
| М = | молярная масса |
| к = | Постоянная Больцмана |
| м = | молекулярная масса |
Акустическая термометрия климата океана (ATOC)
- в воде звуки ниже 1 кГц распространяются намного дальше, чем более высокие частоты
- «шум от транспортировки наиболее громкий в диапазоне от 30 до 200 Гц [от самой низкой ноты фортепиано до середины виолончели]»
- «Синий и финвал — самый громкий звук в диапазоне от 17 до 30 Гц»
- «В доиндустриальные времена низкочастотный диапазон от 15 до 300 Гц, в котором поет большинство усатых китов, был самой тихой частью звукового спектра, расположенной между дозвуковым бормотанием землетрясений и более высоким грохотом ветра, волн.
 и дождь.Боб Холмс. «Noises Off». New Scientist. 1 марта 1997 г .: 30–33.
и дождь.Боб Холмс. «Noises Off». New Scientist. 1 марта 1997 г .: 30–33.
эхо
отходы
- Как и в случае любой волны, скорость звука зависит от среды, в которой он распространяется.
- Звук обычно распространяется быстрее в твердых телах и жидкостях, чем в газах.
- Скорость звука выше в материалах с некоторой жесткостью, таких как сталь, и ниже в более мягких материалах, таких как резина.
- Факторы, влияющие на скорость звука в воздухе.
- Скорость звука в воздухе составляет примерно 345 м/с (около 1 250 км/ч, 770 миль/ч, 1 100 фут/с).
- Скорость звука в воздухе почти одинакова для всех частот и амплитуд.
- Повышается с температурой.
- Определение расстояния до молнии: звуковым волнам требуется примерно 5 секунд, чтобы пройти 1 милю. Используя эту информацию, можно измерить расстояние от молнии. Начните считать сразу после того, как увидите вспышку. Каждые пять отсчитываемых секунд примерно эквивалентны одной миле расстояния.

Скорость звука в различных материалах
| твердые вещества | v (м/с) |
|---|---|
| алюминий | 6 420 |
| бериллий | 12 890 |
| латунь | 4 700 |
| кирпич | 3 650 |
| медь | 4 760 |
| пробка | 500 |
| стекло, заводная головка | 5 100 |
| стекло, кремень | 3 980 |
| стекло, пирекс | 5 640 |
| золото | 3 240 |
| гранит | 5 950 |
| железо | 5 950 |
| свинец | 2 160 |
| люцит | 2 680 |
| мрамор | 3 810 |
| каучук, бутил | 1 830 |
| каучук, вулканизированный | 54 |
| серебро | 3 650 |
| сталь, мягкая | 5 960 |
| сталь, нержавеющая сталь | 5 790 |
| титан | 6 070 |
| дерево, ясень | 4 670 |
| дерево, вяз | 4 120 |
| дерево, клен | 4 110 |
| дерево, дуб | 3 850 |
| жидкости | v (м/с) |
|---|---|
| спирт этиловый | 1 207 |
| спирт метиловый | 1 103 |
| ртуть | 1 450 |
| вода дистиллированная | 1 497 |
| вода, море | 1 531 |
| газы (СТП) | v (м/с) |
|---|---|
| воздух, 000 °C | 331 |
| воздух, 020 °C | 343 |
| аргон | 319 |
| двуокись углерода | 259 |
| гелий | 965 |
| водород (H 2 ) | 1 284 |
| неон | 435 |
| азот | 334 |
| закись азота | 263 |
| кислород (O 2 ) | 316 |
| водяной пар, 134 °C | 494 |
| биологические материалы | v (м/с) |
|---|---|
| мягкие ткани | 1 540 |
Источник: вероятно старая версия CRC
частота, высота тона, тон
Частота звуковой волны называется высотой . Говорят, что высокочастотные звуки «высокие» или просто «высокие»; низкочастотные звуки называются «низкими» или просто «низкими».
Говорят, что высокочастотные звуки «высокие» или просто «высокие»; низкочастотные звуки называются «низкими» или просто «низкими».
| f (Гц) | устройство, событие, явление, процесс |
|---|---|
| 0,1–2,0 × 10 12 | SASER (звуковой лазер) |
| 01–20 × 10 6 | медицинское УЗИ |
| 25–80 × 10 3 | сонар летучей мыши щелкает |
| 40–50 × 10 3 | ультразвуковая очистка |
| 32.768 × 10 3 | кварцевый резонатор, C 11 научная шкала (2 15 Гц) |
| 18–20 × 10 3 | верхний предел человеческого слуха |
| 4–5 × 10 3 | полевой сверчок ( Teleogryllus oceanicus ) |
| 2,2–2,8 × 10 3 | аплодисменты |
| 2–5 × 10 3 | максимальная чувствительность человеческого слуха |
| 4 186 | самая высокая нота современного фортепиано (C 8 ) |
| 0,300–3,000 | частота голоса (VF), важна для понимания речи |
| 2 048 | C 7 научная гамма, высшая нота певицы-сопрано |
| 440 | A 4 стандартная частота настройки (ISO 16), тон тестового шаблона ТВ |
| 435 | A 4 международный тон (нормальный диапазон) |
| 422 | A 4 классический шаг |
| 256 | C 4 научная шкала (2 8 Гц), типичная основная частота для женских голосовых связок |
| 128 | C 3 научная шкала (2 7 Гц), типичная основная частота мужских голосовых связок |
| 64 | C 2 научная гамма (2 6 Гц), самая низкая нота бас-певца |
| 90 | красногорлый колибри в полете |
| 60 | фон переменного тока (США и Япония) |
| 50 | генератор переменного тока (Европа) |
27.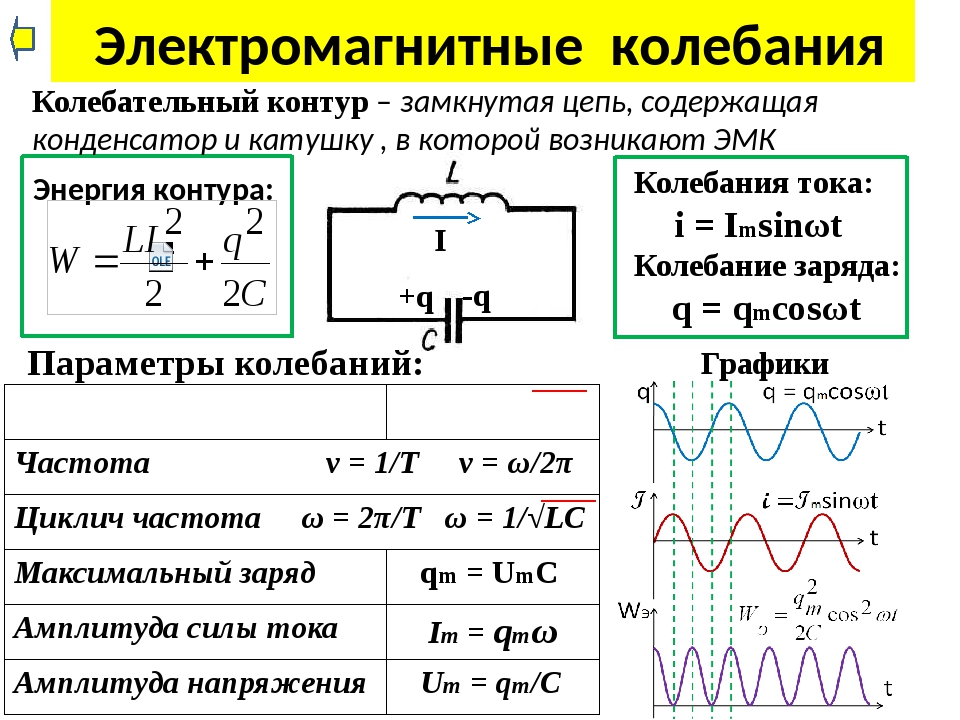 5 5 | самая низкая нота современного фортепиано (A 0 ) |
| 17–30 | синий и финвал — самые громкие морские звуки в этом диапазоне |
| 08–20 | нижний предел человеческого слуха |
| 1–5 | торнадо |
| 2 | C −3 научная шкала (2 1 Гц) |
| 1 | C −4 научная шкала (2 0 Гц) |
человеческий слух и речь
Люди обычно способны слышать звуки частотой от 20 Гц до 20 кГц (хотя я не слышу звуки выше 13 кГц).Звуки с частотами выше диапазона человеческого слуха называются ультразвук . Звуки с частотами ниже диапазона человеческого слуха называются инфразвуком .
- Типичные звуки, издаваемые человеческой речью, имеют частоты порядка 100–1000 Гц.
- Пиковая чувствительность человеческого слуха составляет около 4000 Гц.

- поиск источника звука
- Межушная разница во времени (ITD)
- Интерауральная разность фаз (IPD) Разность фаз — это один из способов локализации звуков.Эффективен только для длин волн, превышающих 2 диаметра головы (расстояние от уха до уха).
- Интерауральная разность уровней (ILD) Звуковые волны легко дифрагируют на длинах волн, превышающих диаметр головы человека (длина волны около 500 Гц равна 69 см). На более высоких частотах голова отбрасывает «тень». Звуки в одном ухе будут громче, чем в другом.
- Человеческое ухо может различить некоторые…
- три (четыре?) голосовых регистра
- (регистр свистков?)
- фальцет
- модальный — обычный разговорный регистр
- вокальный фрай — самый низкий из трех вокальных регистров
Подробнее в следующем разделе.
инфразвук
- лавины: местонахождение, глубина, продолжительность
- метеоров: высота, направление, тип, размер, местоположение
- океанские волны: штормы на море, магнитуда, спектры
- суровая погода: местоположение, интенсивность
- торнадо: обнаружение, местоположение, предупреждение, радиус ядра, форма воронки, предвестники
- турбулентность: уклонение от самолета, высота, сила, протяженность
- землетрясений: предвестники, сейсмоакустическая связь
- вулканов: расположение, интенсивность
- Слоны, киты, бегемоты, носороги, жирафы, окапи и аллигаторы — вот лишь несколько примеров животных, создающих инфразвук.

- Некоторые перелетные птицы способны слышать инфразвуковые звуки, издаваемые океанскими волнами. Это позволяет им ориентироваться по береговой линии.
- Слон способен слышать звуковые волны намного ниже человеческого слуха (приблизительно 30 Гц). Как правило, многочисленные урчания слона имеют частоту от 14 до 35 герц. Далеко идущее использование инфразвука высокого давления открывает пространственное восприятие слона далеко за пределы наших ограниченных возможностей.
- Тихий гром, Кэти Пейн
УЗИ
- эхолокация животных
- microchiropterans также известные как летучие мыши: плотоядные летучие мыши ( не фруктовые летучие мыши или летучие лисицы)
- китообразные : дельфины, морские свиньи, косатки, киты
- два вида птиц: стрижи и масленки
- некоторые слабовидящие люди изучили эту технику
- сонар (аббревиатура от , и , , , , , старение), включая
- батиметрия
- эхолот
- эхолоты
- медицинское ультразвуковое исследование (генерируемые изображения называются сонограммами ).

| частота (МГц) | мощность (Вт) | интенсивность (Вт/см 2 ) | импульс продолжительность | |
|---|---|---|---|---|
| визуализация, эхо | 1–20 | 0,05 | 1,75 | 0,2–1 мкс |
| визуализация, допплер | 1–20 | 0.15 | 15,7 | 0,3–10 мкс |
| физиотерапия | 0,5–3 | <3 | 2,5 | непрерывный |
| Хирургия | 0,5–10 | ~200 | 1 500 | 1–16 с |
Диапазон частот слышимости для выбранных животных (60 дБ)
| рыба | – | актиноптеригии | диапазон частот (Гц) | ||
|---|---|---|---|---|---|
| сельдь американская | – | Алоза сапидиссима | 200 | – | 180 000 м |
| золотая рыбка | – | Carassius auratus | 5 | – | 2000 м |
| атлантическая треска | – | Гадус морхуа | 2 | – | 500 м |
| тунец | – | Туннус … | 50 | – | 1 100 1 |
| сом | – | … … | 50 | – | 4000 1 |
| земноводные | – | амфибия | диапазон частот (Гц) | ||
|---|---|---|---|---|---|
| древесная лягушка | – | … … | 50 | – | 4000 1 |
| лягушка-бык | – | Lithobates catesbeianus | 100 | – | 2 500 2 |
| пещерная саламандра | – | Ангиновый протей | 10 | – | 10 000 и |
| рептилии | – | рептилии, зауропсиды | диапазон частот (Гц) | ||
|---|---|---|---|---|---|
| красноухий ползунок | – | Trachemys scripta elegans | 68 | – | 840 2 |
| очковый кайман | – | Каймановый крокодил | 20 | – | 6000 и |
| птицы | – | пр.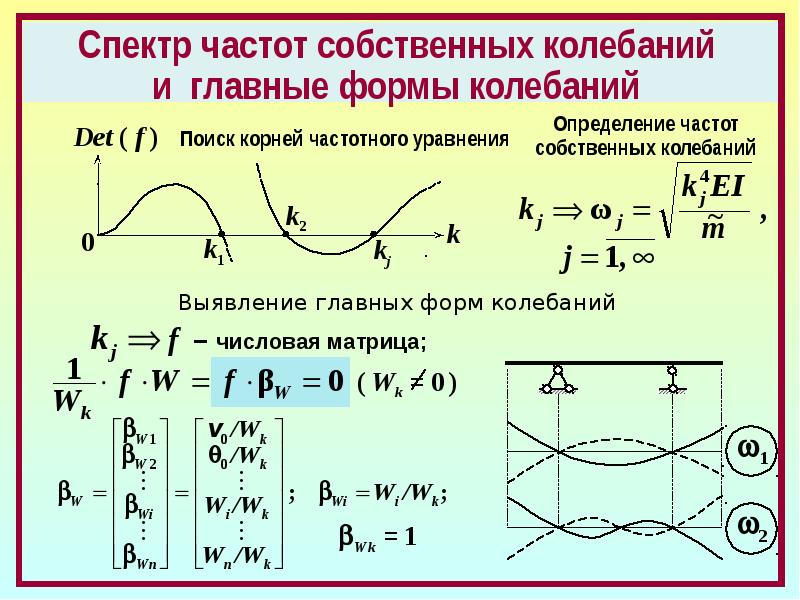 | диапазон частот (Гц) | ||
|---|---|---|---|---|---|
| кряква | – | Анус платиринхус | 300 | – | 8000 б |
| голубь | – | Колумба Ливия | ? | – | 5 800 2 |
| курица | – | Галлус Галлус | 125 | – | 2000 1 |
| канарейка | – | Serinus canaria | 250 | – | 8000 1 |
| корелла | – | Нимфикус голландский | 250 | – | 8000 1 |
| попугай | – | Мелопситакус волнистый | 200 | – | 8 500 1 |
| пингвин | – | Сфениск прикопанный | 100 | – | 15 000 с |
| сова | – | … … | 200 | – | 12 000 1 |
| млекопитающие | – | млекопитающие | диапазон частот (Гц) | ||
|---|---|---|---|---|---|
| крупный рогатый скот | – | Бос Телец | 23 | – | 35 000 1, к |
| овцы | – | Овис Овен | 100 | – | 30 000 1 |
| свинья | – | Sus scrofa domestica | 45 | – | 45 000 2 |
| собака | – | Знакомая волчанка | 67 | – | 45 000 1, 2 |
| кот | – | Felis silvestris catus | 45 | – | 64 000 1, 4 |
| хорек | – | Мустела путориус фуро | 16 | – | 44 000 1 |
| енот | – | Процион Лотор | 100 | – | 40 000 1 |
| синий кит | – | Balaenoptera musculus | 5 | – | 12 000 г |
| горбатый кит | – | Megaptera novaeangliae | 30 | – | 28 000 4 |
| Дельфин Риссо | – | Серый дедушка | 8000 | – | 100 000 й |
| белуха | – | Дельфинаптерус левкас | 1000 | – | 123 000 1 |
| Атлантический афалин | – | Tursiops truncatus | 75 | – | 150 000 1, 4 |
| большая подковоносая летучая мышь | – | Rhinolophus ferrumequinum | 2000 | – | 110 000 1, 4 |
| Ямайская фруктовая летучая мышь | – | Артибеус ямайский | 2 800 | – | 131 000 и |
| северный кволл | – | Dasyurus галлюкатус | 500 | – | 40 000 ф |
| опоссум | – | … … | 500 | – | 64 000 1 |
| ёжик | – | … … | 250 | – | 45 000 1 |
| кролик | – | … … | 360 | – | 42 000 1 |
| лошадь | – | Лошадь Кабаллюс | 55 | – | 33 500 1, к, л |
| Филиппинский долгопят | – | Tarsius syrichta | ? | – | 91 000 или |
| Японский макак | – | Макака кустарная | 28 | – | 34 500 2 |
| обезьяны Старого Света | – | … … | 60 | – | 40 000 г |
| человек | – | Человек разумный | 31 | – | 17 600 2 |
| Азиатский слон | – | Большой слон | 16 | – | 12 000 1 |
| морская свинка | – | Cavia porcellus | 54 | – | 50 000 1, 2 |
| шиншилла | – | Шиншилла ланигера | 90 | – | 22 800 1 |
| хомяк | – | Mesocricetus auratus | 80 | – | 45 000 2 |
| крыса | – | Раттус … | 500 | – | 64 000 2 |
| мышь | – | Мус … | 2 300 | – | 85 500 2 |
| песчанка | – | Meriones unguiculatus | 100 | – | 60 000 1 |
| ламантин | – | Trichechus manatus latirostris | 400 | – | 46 000 ч |
| насекомые | – | насекомое | диапазон частот (Гц) | ||
|---|---|---|---|---|---|
| совки | – | … … | 1000 | – | 240 000 3 |
| кузнечик | – | … … | 100 | – | 50 000 3 |
| моллюски | – | моллюск | диапазон частот (Гц) | ||
|---|---|---|---|---|---|
| Тихоокеанская устрица | – | Магаллана гигас | 10 | – | 1000 нет |
Частоты музыкальных нот, A4 = 440 Гц
Частоты музыкальных нот, A4 = 440 Гц
Частоты равнотемперированного строя, A
4 = 440 Гц
Другие варианты настройки, A 4 =
Скорость звука = 345 м/с = 1130 футов/с = 770 миль/ч (см)
 35
35 18
18 31
31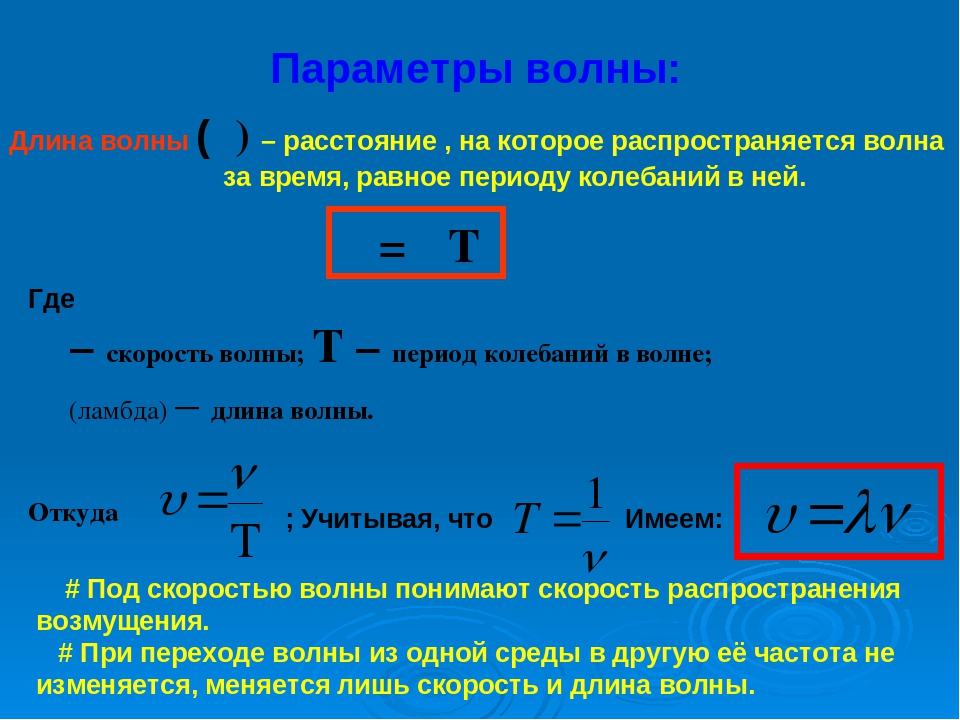 78
78 59
59 02
02 01
01 99
99 51
51 46
46 25
25 88
88(Чтобы преобразовать длину в см в дюймы, разделите на 2,54)
Дополнительная информация о равнотемперированной шкале
Уравнения, используемые для этой таблицы
Вопросы/комментарии по адресу:suits@mtu.образование
На этих страницах нет всплывающих окон или рекламы любого рода.
Если вы их видите, значит, их добавляет третий
стороной без согласия автора.
To Physics of Music Notes
To MTU Physics Home
Информация об авторских правах
.

 1)
1) е. начальными условиями.
е. начальными условиями.

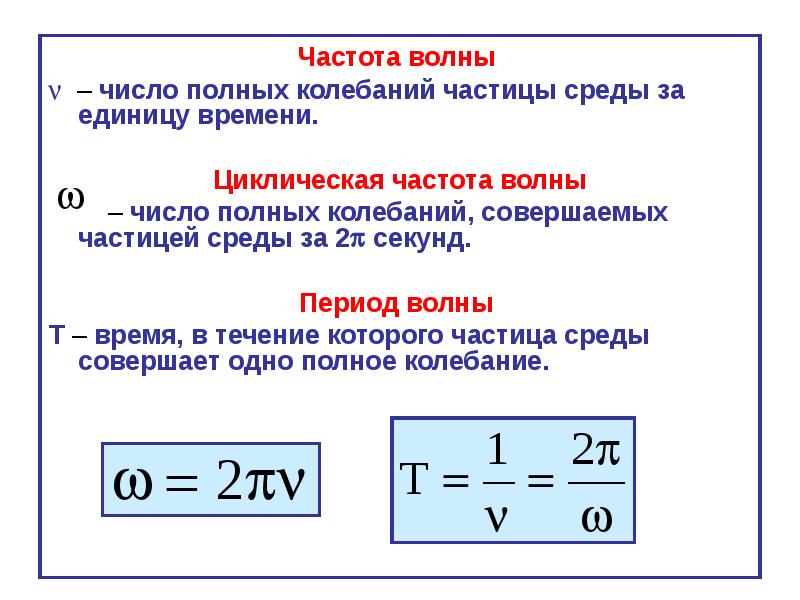
 Организаци-онный
Организаци-онный
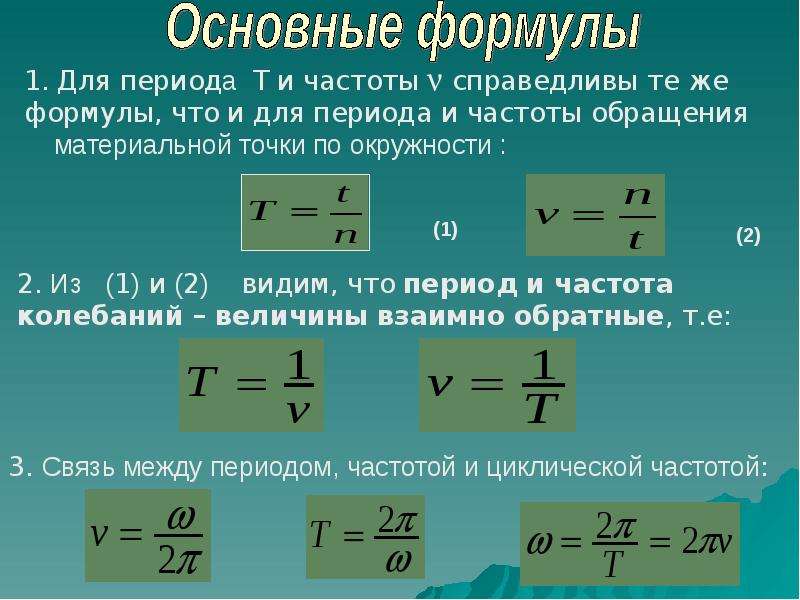
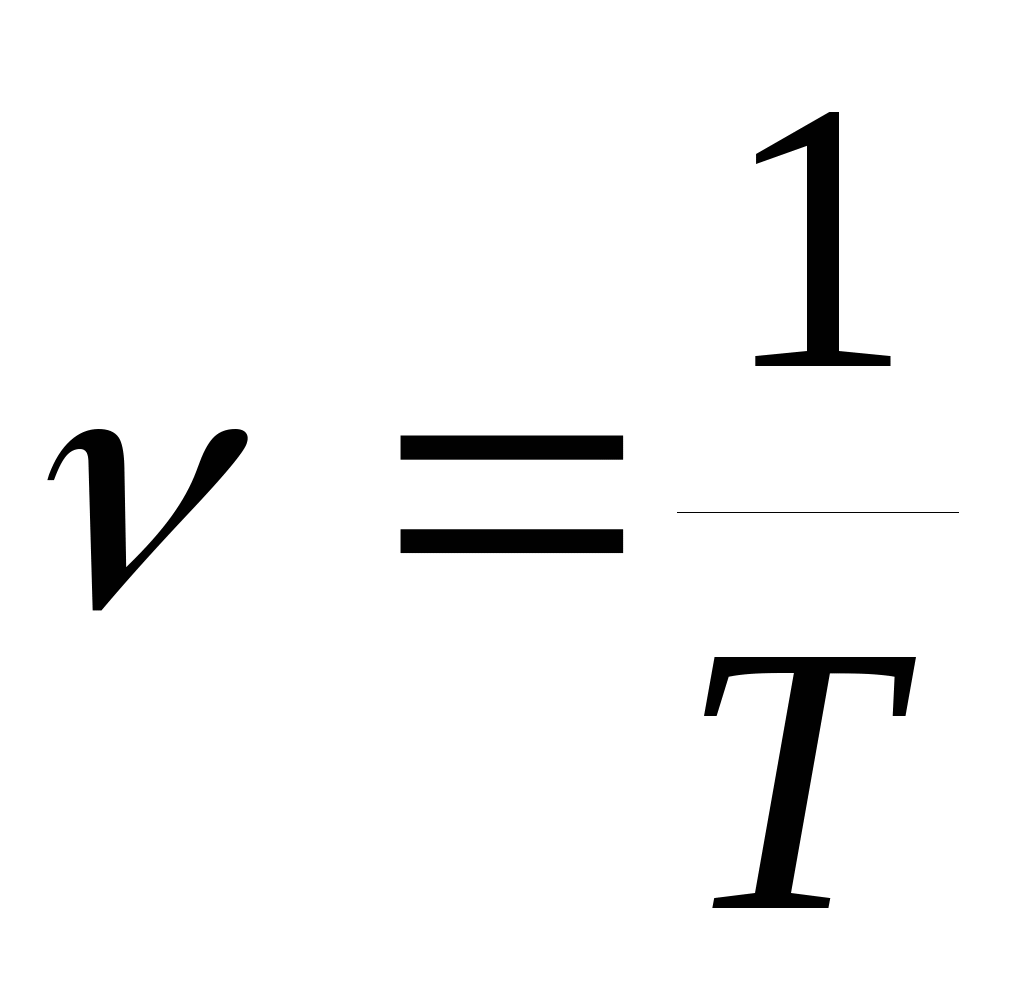
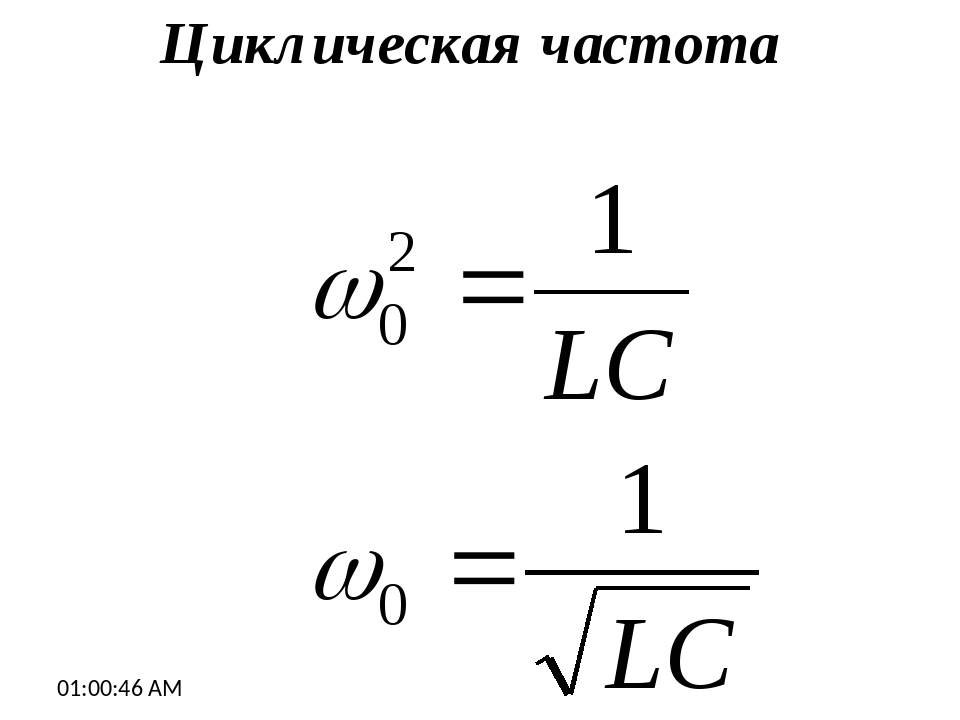
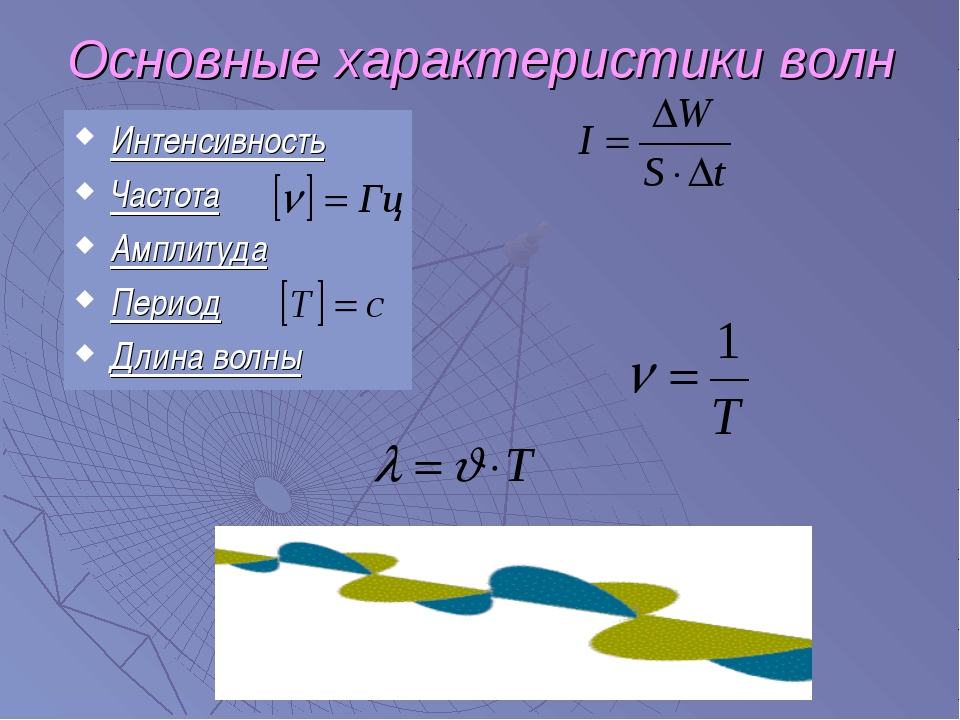 Большинству людей нравится измерять от одного гребня до следующего гребня (или от впадины до впадины) просто потому, что их легко заметить.
Большинству людей нравится измерять от одного гребня до следующего гребня (или от впадины до впадины) просто потому, что их легко заметить.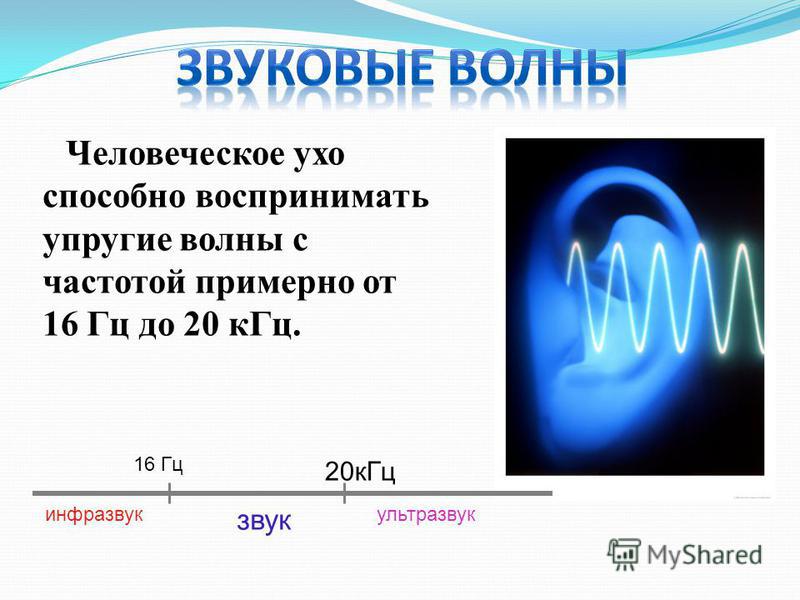 Вместо этого они воспринимают нечто, называемое движением частиц, крошечные возвратно-поступательные движения частиц в ответ на звуковые волны.
Вместо этого они воспринимают нечто, называемое движением частиц, крошечные возвратно-поступательные движения частиц в ответ на звуковые волны. и дождь.Боб Холмс. «Noises Off». New Scientist. 1 марта 1997 г .: 30–33.
и дождь.Боб Холмс. «Noises Off». New Scientist. 1 марта 1997 г .: 30–33.