Мощность (физика) — это… Что такое Мощность (физика)?
Мощность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
Эффективная мощность, мощность двигателя, отдаваемая рабочей машине непосредственно или через силовую передачу. Различают полезную, полную и номинальную Э. м. двигателя. Полезной называют Э. м. двигателя за вычетом затрат мощности на приведение в действие вспомогательных агрегатов или механизмов, необходимых для его работы, но имеющих отдельный привод (не от двигателя непосредственно). Полная Э. м. — мощность двигателя без вычета указанных затрат. Номинальная Э. м., или просто номинальная мощность, — Э. м., гарантированная заводом-изготовителем для определённых условий работы. В зависимости от типа и назначения двигателя устанавливаются Э. м., регламентируемые стандартами или техническими условиями (например, наибольшая мощность судового реверсивного двигателя при определённой частоте вращения коленчатого вала в случае заднего хода судна — так называемая мощность заднего хода, наибольшая мощность авиационного двигателя при минимальном удельном расходе топлива — так называемая крейсерская мощность и т. п.). Э. м. зависит от форсирования (интенсификации) рабочего процесса, размеров и механического кпд двигателя.[1]
п.). Э. м. зависит от форсирования (интенсификации) рабочего процесса, размеров и механического кпд двигателя.[1]
| — средняя мощность |
| — мгновенная мощность |
Так как работа является мерой изменения энергии, мощность можно определить также как скорость изменения энергии системы.
Единицы измерения
В системе СИ единицей измерения мощности является ватт, равный одному джоулю, делённому на секунду.
Другой распространённой единицей измерения мощности является лошадиная сила.
| Единицы | Вт | кВт | МВт | кгс·м/с | эрг/с | л. с. |
|---|---|---|---|---|---|---|
| 1 ватт | 1 | 10-3 | 10-6 | 0,102 | 107 | 1,36·10-3 |
| 1 киловатт | 103 | 1 | 10-3 | 102 | 1010 | 1,36 |
| 1 мегаватт | 106 | 103 | 1 | 102·103 | 1013 | 1,36·103 |
| 1 килограмм-сила-метр в секунду | 9,81 | 9,81·10-3 | 9,81·10-6 | 1 | 9,81·107 | 1,33·10-2 |
| 1 эрг в секунду | 10-7 | 10-10 | 10-13 | 1,02·10-8 | 1 | 1,36·10-10 |
| 1 лошадиная сила[2] | 735,5 | 735,5·10-3 | 735,5·10-6 | 75 | 7,355·109 | 1 |
Мощность в механике
Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:
Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:
F — сила, v — скорость, α — угол между вектором скорости и силы.
Частный случай мощности при вращательном движении:
M — момент, — угловая скорость, — число пи, n — частота вращения (об/мин).
Электрическая мощность
Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.
S=P+jQ
S — Полная мощность, ВА
P — Активная мощность, Вт
Q — Реактивная мощность, ВАр
Приборы для измерения мощности
Примечания
- ↑ Большая Советская энциклопедия
- ↑ «метрическая лошадиная сила»
См. также
Ссылки
Wikimedia Foundation.
2010.
Мощность (физика) — это.
 .. Что такое Мощность (физика)?
.. Что такое Мощность (физика)?
Мощность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
Эффективная мощность, мощность двигателя, отдаваемая рабочей машине непосредственно или через силовую передачу. Различают полезную, полную и номинальную Э. м. двигателя. Полезной называют Э. м. двигателя за вычетом затрат мощности на приведение в действие вспомогательных агрегатов или механизмов, необходимых для его работы, но имеющих отдельный привод (не от двигателя непосредственно). Полная Э. м. — мощность двигателя без вычета указанных затрат. Номинальная Э. м., или просто номинальная мощность, — Э. м., гарантированная заводом-изготовителем для определённых условий работы. В зависимости от типа и назначения двигателя устанавливаются Э. м., регламентируемые стандартами или техническими условиями (например, наибольшая мощность судового реверсивного двигателя при определённой частоте вращения коленчатого вала в случае заднего хода судна — так называемая мощность заднего хода, наибольшая мощность авиационного двигателя при минимальном удельном расходе топлива — так называемая крейсерская мощность и т. п.). Э. м. зависит от форсирования (интенсификации) рабочего процесса, размеров и механического кпд двигателя.[1]
п.). Э. м. зависит от форсирования (интенсификации) рабочего процесса, размеров и механического кпд двигателя.[1]
| — средняя мощность |
| — мгновенная мощность |
Так как работа является мерой изменения энергии, мощность можно определить также как скорость изменения энергии системы.
Единицы измерения
В системе СИ единицей измерения мощности является ватт, равный одному джоулю, делённому на секунду.
Другой распространённой единицей измерения мощности является лошадиная сила.
| Единицы | Вт | кВт | МВт | кгс·м/с | эрг/с | л. с. |
|---|---|---|---|---|---|---|
| 1 ватт | 1 | 10-3 | 10-6 | 0,102 | 107 | 1,36·10-3 |
| 1 киловатт | 103 | 1 | 10-3 | 102 | 1010 | 1,36 |
| 1 мегаватт | 106 | 103 | 1 | 102·103 | 1013 | 1,36·103 |
| 1 килограмм-сила-метр в секунду | 9,81 | 9,81·10-3 | 9,81·10-6 | 1 | 9,81·107 | 1,33·10-2 |
| 1 эрг в секунду | 10-7 | 10-10 | 10-13 | 1,02·10-8 | 1 | 1,36·10-10 |
| 1 лошадиная сила[2] | 735,5 | 735,5·10-3 | 735,5·10-6 | 75 | 7,355·109 | 1 |
Мощность в механике
Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:
Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:
F — сила, v — скорость, α — угол между вектором скорости и силы.
Частный случай мощности при вращательном движении:
M — момент, — угловая скорость, — число пи, n — частота вращения (об/мин).
Электрическая мощность
Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.
S=P+jQ
S — Полная мощность, ВА
P — Активная мощность, Вт
Q — Реактивная мощность, ВАр
Приборы для измерения мощности
Примечания
- ↑ Большая Советская энциклопедия
- ↑ «метрическая лошадиная сила»
См. также
Ссылки
Wikimedia Foundation.
2010.
Мощность (физика) — это.
 .. Что такое Мощность (физика)?
.. Что такое Мощность (физика)?
Мощность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
Эффективная мощность, мощность двигателя, отдаваемая рабочей машине непосредственно или через силовую передачу. Различают полезную, полную и номинальную Э. м. двигателя. Полезной называют Э. м. двигателя за вычетом затрат мощности на приведение в действие вспомогательных агрегатов или механизмов, необходимых для его работы, но имеющих отдельный привод (не от двигателя непосредственно). Полная Э. м. — мощность двигателя без вычета указанных затрат. Номинальная Э. м., или просто номинальная мощность, — Э. м., гарантированная заводом-изготовителем для определённых условий работы. В зависимости от типа и назначения двигателя устанавливаются Э. м., регламентируемые стандартами или техническими условиями (например, наибольшая мощность судового реверсивного двигателя при определённой частоте вращения коленчатого вала в случае заднего хода судна — так называемая мощность заднего хода, наибольшая мощность авиационного двигателя при минимальном удельном расходе топлива — так называемая крейсерская мощность и т. п.). Э. м. зависит от форсирования (интенсификации) рабочего процесса, размеров и механического кпд двигателя.[1]
п.). Э. м. зависит от форсирования (интенсификации) рабочего процесса, размеров и механического кпд двигателя.[1]
| — средняя мощность |
| — мгновенная мощность |
Так как работа является мерой изменения энергии, мощность можно определить также как скорость изменения энергии системы.
Единицы измерения
В системе СИ единицей измерения мощности является ватт, равный одному джоулю, делённому на секунду.
Другой распространённой единицей измерения мощности является лошадиная сила.
| Единицы | Вт | кВт | МВт | кгс·м/с | эрг/с | л. с. |
|---|---|---|---|---|---|---|
| 1 ватт | 1 | 10-3 | 10-6 | 0,102 | 107 | 1,36·10-3 |
| 1 киловатт | 103 | 1 | 10-3 | 102 | 1010 | 1,36 |
| 1 мегаватт | 106 | 103 | 1 | 102·103 | 1013 | 1,36·103 |
| 1 килограмм-сила-метр в секунду | 9,81 | 9,81·10-3 | 9,81·10-6 | 1 | 9,81·107 | 1,33·10-2 |
| 1 эрг в секунду | 10-7 | 10-10 | 10-13 | 1,02·10-8 | 1 | 1,36·10-10 |
| 1 лошадиная сила[2] | 735,5 | 735,5·10-3 | 735,5·10-6 | 75 | 7,355·109 | 1 |
Мощность в механике
Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:
Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:
F — сила, v — скорость, α — угол между вектором скорости и силы.
Частный случай мощности при вращательном движении:
M — момент, — угловая скорость, — число пи, n — частота вращения (об/мин).
Электрическая мощность
Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.
S=P+jQ
S — Полная мощность, ВА
P — Активная мощность, Вт
Q — Реактивная мощность, ВАр
Приборы для измерения мощности
Примечания
- ↑ Большая Советская энциклопедия
- ↑ «метрическая лошадиная сила»
См. также
Ссылки
Wikimedia Foundation.
2010.
Формула мощности в физике
Содержание:
Определение и формулы мощности
Определение
Мощностью некоторой силы является скалярная физическая величина, которая характеризует скорость произведения работы данной силой. Мощность часто обозначают буквами: N, P.
Мощность часто обозначают буквами: N, P.
$$P=\frac{\Delta A}{\Delta t}(1)$$
В том случае, если за равные малые промежутки времени выполняется разная работа, то мощность является переменной во времени.
Тогда вводят мгновенное значение мощности:
$$P=\lim _{\Delta t \rightarrow 0} \frac{\delta A}{\Delta t}=\frac{d A}{d t}$$
где $\delta A$ – элементарная работа, которую выполняет сила,
$\Delta t$ – отрезок времени в течение, которого данная работа была выполнена.
Если мгновенная мощность не является постоянной величиной, то выражение (1) определяет среднюю мощностьза время
$\Delta t$.
Мощность силы можно определить как скалярное произведение силы на скорость, с которой движется точка приложения рассматриваемой силы:
$$P=\bar{F} \bar{v}=F_{\tau} v$$
где $F_{\tau}$ – проекция силы
$\bar{F}$ на направление вектора скорости (
$\bar{v}$).
При поступательном движении некоторого тела, имеющего массу m под воздействием силы
$\bar{F}$ мощность можно вычислить, применяя формулу:
$$P=m v \dot{v}(4)$$
В общем случае произвольного перемещения твердого тела суммарная мощность есть алгебраическая сумма мощностей всех сил,
которые действуют на тело:
$$P=\sum_{i=1}^{k} \bar{F}_{i} \cdot \bar{v}_{i}(5)$$
где $\bar{v}_{i}$ – скорость перемещения точки, к которой приложена сила
$\bar{F}_{i}$.
В случае поступательного движения твердого тела со скоростью $\bar{v}$ мощность можно определить при помощи формулы:
$$P=\overline{F v}(6)$$
где $\bar{F}$ – главный вектор внешних сил.
Если твердое тело совершает вращение вокруг точки О или вокруг неподвижной оси, которая проходит через точку О, то формулой для счет мощности можно считать выражение:
$$P=\bar{M} \bar{\omega}(7)$$
где $\bar{M}$ – главный момент внешних сил по отношению к точке О,
$\bar{omega}$ – мгновенная угловая скорость вращения тела.
Единицы измерения мощности
Основной единицей измерения мощности силы в системе СИ является: [P]=вт (ватт)
В СГС: [P]=эрг/с.
1 вт=107 эрг/( с).
Примеры решения задач
Пример
Задание. Какова мощность (P(t)), развиваемая силой, если она действует на тело, которое имеет массу m и
под воздействием приложенной силы движется поступательно. Сила описывается законом:
$F(t)=2 t \cdot \bar{i}+3 t^{2} \bar{j}$
Решение. {5}\right)$
{5}\right)$
Слишком сложно?
Формула мощности не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Какова мгновенная мощность силы тяжести на высоте h/2. если камень массы m падает с высоты h. Сопротивление воздуха не учитывать.
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для мгновенной мощности вида:
$$P=\bar{F} \cdot \bar{v}(2.1)$$
Сила, действующая на тело – сила тяжести. Она направлена по оси Y, выражение для ее проекции на ось Y запишем как:
$$F=m g(2.2)$$
В начальный момент времени тело имело скорость равную нулю, тогда скорость тела в проекции на ось Y можно вычислить, используя выражение:
$$v=v_{0}+g t=g t(2.3)$$
где v0=0.
Найдем момент времени, в который тело окажется на половине высоты (y=h/2), применим уравнение, которое описывает равноускоренное
движение (из начальных условий y0=0, v0=0):
$$y=y_{0}+v_{0} t+\frac{g t^{2}}{2}=\frac{g t^{2}}{2}=\frac{h}{2} \rightarrow t=\sqrt{\frac{h}{g}}(2. {3} h}$
{3} h}$
Читать дальше: Формула плотности вещества.
Работа, мощность, энергия — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Механическая работа
К оглавлению…
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы. Работой, совершаемой постоянной силой F, называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла между векторами силы F и перемещения S:
Работа является скалярной величиной. Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 ньютон на перемещении 1 метр в направлении действия силы.
Если же сила изменяется с течением времени, то для нахождения работы строят график зависимости силы от перемещения и находят площадь фигуры под графиком – это и есть работа:
Примером силы, модуль которой зависит от координаты (перемещения), может служить сила упругости пружины, подчиняющаяся закону Гука (Fупр = kx).
Мощность
К оглавлению…
Работа силы, совершаемая в единицу времени, называется мощностью. Мощность P (иногда обозначают буквой N) – физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:
По этой формуле рассчитывается средняя мощность, т.е. мощность обобщенно характеризующая процесс. Итак, работу можно выражать и через мощность: A = Pt (если конечно известна мощность и время совершения работы). Единица мощности называется ватт (Вт) или 1 джоуль за 1 секунду. Если движение равномерное, то:
По этой формуле мы можем рассчитать мгновенную мощность (мощность в данный момент времени), если вместо скорости подставим в формулу значение мгновенной скорости. Как узнать, какую мощность считать? Если в задаче спрашивают мощность в момент времени или в какой-то точке пространства, то считается мгновенная.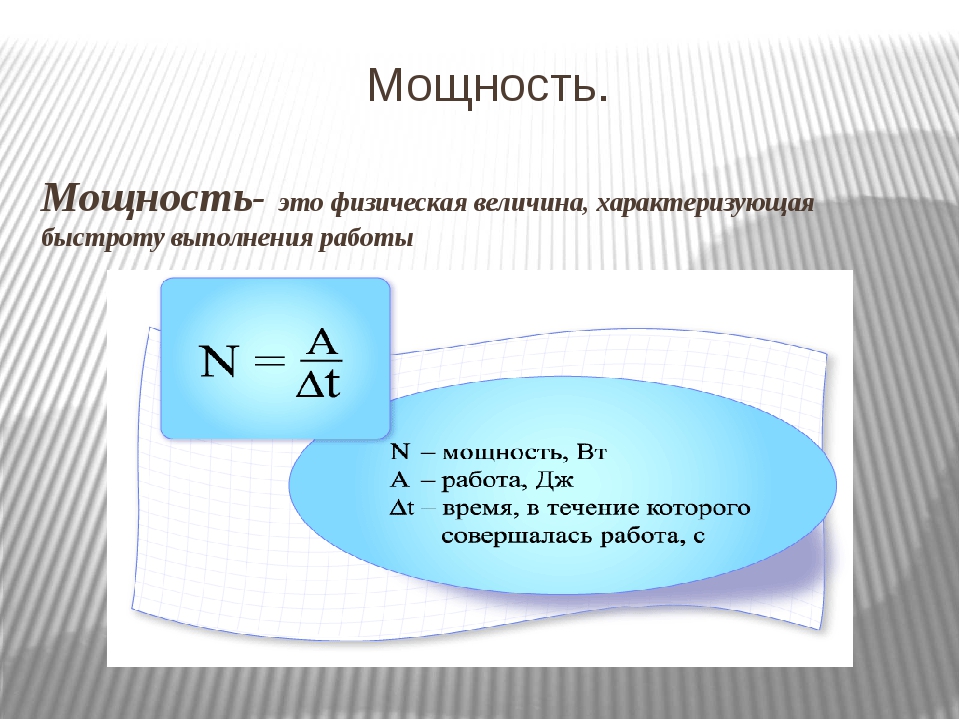 Если спрашивают про мощность за какой-то промежуток времени или участок пути, то ищите среднюю мощность.
Если спрашивают про мощность за какой-то промежуток времени или участок пути, то ищите среднюю мощность.
КПД – коэффициент полезного действия, равен отношению полезной работы к затраченной, либо же полезной мощности к затраченной:
Какая работа полезная, а какая затраченная определяется из условия конкретной задачи путем логического рассуждения. К примеру, если подъемный кран совершает работу по подъему груза на некоторую высоту, то полезной будет работа по поднятию груза (так как именно ради нее создан кран), а затраченной – работа, совершенная электродвигателем крана.
Итак, полезная и затраченная мощность не имеют строгого определения, и находятся логическим рассуждением. В каждой задаче мы сами должны определить, что в этой задаче было целью совершения работы (полезная работа или мощность), а что было механизмом или способом совершения всей работы (затраченная мощность или работа).
В общем случае КПД показывает, как эффективно механизм преобразует один вид энергии в другой. Если мощность со временем изменяется, то работу находят как площадь фигуры под графиком зависимости мощности от времени:
Если мощность со временем изменяется, то работу находят как площадь фигуры под графиком зависимости мощности от времени:
Кинетическая энергия
К оглавлению…
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела (энергией движения):
То есть если автомобиль массой 2000 кг движется со скоростью 10 м/с, то он обладает кинетической энергией равной Ек = 100 кДж и способен совершить работу в 100 кДж. Эта энергия может превратиться в тепловую (при торможении автомобиля нагревается резина колес, дорога и тормозные диски) или может быть потрачена на деформацию автомобиля и тела, с которым автомобиль столкнулся (при аварии). При вычислении кинетической энергии не имеет значения куда движется автомобиль, так как энергия, как и работа, величина скалярная.
Тело обладает энергией, если способно совершить работу. Например, движущееся тело обладает кинетической энергией, т.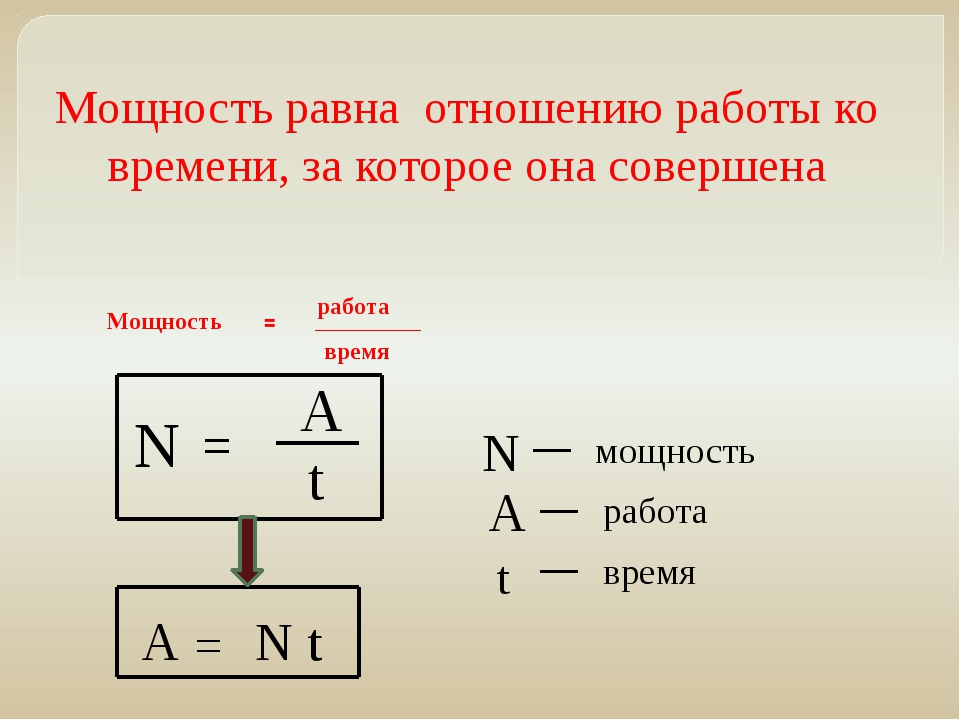 е. энергией движения, и способно совершать работу по деформации тел или придания ускорения телам, с которыми произойдёт столкновение.
е. энергией движения, и способно совершать работу по деформации тел или придания ускорения телам, с которыми произойдёт столкновение.
Физический смысл кинетической энергии: для того чтобы покоящееся тело массой m стало двигаться со скоростью v необходимо совершить работу равную полученному значению кинетической энергии. Если тело массой m движется со скоростью v, то для его остановки необходимо совершить работу равную его первоначальной кинетической энергии. При торможении кинетическая энергия в основном (кроме случаев соударения, когда энергия идет на деформации) «забирается» силой трения.
Теорема о кинетической энергии: работа равнодействующей силы равна изменению кинетической энергии тела:
Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения. Применять данную теорему удобно в задачах на разгон и торможение тела.
Потенциальная энергия
К оглавлению…
Наряду с кинетической энергией или энергией движения в физике важную роль играет понятие потенциальной энергии или энергии взаимодействия тел.
Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями (так называемые консервативные силы). Работа таких сил на замкнутой траектории равна нулю. Таким свойством обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.
Потенциальная энергия тела в поле силы тяжести Земли рассчитывается по формуле:
Физический смысл потенциальной энергии тела: потенциальная энергия равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень (h – расстояние от центра тяжести тела до нулевого уровня). Если тело обладает потенциальной энергией, значит оно способно совершить работу при падении этого тела с высоты h до нулевого уровня. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:
Если тело обладает потенциальной энергией, значит оно способно совершить работу при падении этого тела с высоты h до нулевого уровня. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:
Часто в задачах на энергию приходится находить работу по поднятию (переворачиванию, доставанию из ямы) тела. Во всех этих случаях нужно рассматривать перемещение не самого тела, а только его центра тяжести.
Потенциальная энергия Ep зависит от выбора нулевого уровня, то есть от выбора начала координат оси OY. В каждой задаче нулевой уровень выбирается из соображения удобства. Физический смысл имеет не сама потенциальная энергия, а ее изменение при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.
Потенциальная энергия растянутой пружины рассчитывается по формуле:
где: k – жесткость пружины. Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, то есть сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Растяжение или сжатие х надо рассчитывать от недеформированного состояния тела.
Следовательно, такая пружина обладает запасом энергии. Растяжение или сжатие х надо рассчитывать от недеформированного состояния тела.
Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией. Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x1, тогда при переходе в новое состояние с удлинением x2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком (так как сила упругости всегда направлена против деформации тела):
Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости.
Работа силы трения зависит от пройденного пути (такой вид сил, чья работа зависит от траектории и пройденного пути называется: диссипативные силы). Понятие потенциальной энергии для силы трения вводить нельзя.
Коэффициент полезного действия
К оглавлению…
Коэффициент полезного действия (КПД) – характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Он определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой (формула уже приведена выше).
КПД можно рассчитывать как через работу, так и через мощность. Полезная и затраченная работа (мощность) всегда определяются путем простых логических рассуждений.
В электрических двигателях КПД – отношение совершаемой (полезной) механической работы к электрической энергии, получаемой от источника. В тепловых двигателях – отношение полезной механической работы к затрачиваемому количеству теплоты. В электрических трансформаторах – отношение электромагнитной энергии, получаемой во вторичной обмотке, к энергии, потребляемой первичной обмоткой.
В силу своей общности понятие КПД позволяет сравнивать и оценивать с единой точки зрения такие различные системы, как атомные реакторы, электрические генераторы и двигатели, теплоэнергетические установки, полупроводниковые приборы, биологические объекты и т. д.
д.
Из–за неизбежных потерь энергии на трение, на нагревание окружающих тел и т.п. КПД всегда меньше единицы. Соответственно этому КПД выражается в долях затрачиваемой энергии, то есть в виде правильной дроби или в процентах, и является безразмерной величиной. КПД характеризует как эффективно работает машина или механизм. КПД тепловых электростанций достигает 35–40%, двигателей внутреннего сгорания с наддувом и предварительным охлаждением – 40–50%, динамомашин и генераторов большой мощности – 95%, трансформаторов – 98%.
Задачу, в которой нужно найти КПД или он известен, надо начать с логического рассуждения – какая работа является полезной, а какая затраченной.
Закон сохранения механической энергии
К оглавлению…
Полной механической энергией называется сумма кинетической энергии (т.е. энергии движения) и потенциальной (т.е. энергии взаимодействия тел силами тяготения и упругости):
Если механическая энергия не переходит в другие формы, например, во внутреннюю (тепловую) энергию, то сумма кинетической и потенциальной энергии остаётся неизменной. Если же механическая энергия переходит в тепловую, то изменение механической энергии равно работе силы трения или потерям энергии, или количеству выделившегося тепла и так далее, другими словами изменение полной механической энергии равно работе внешних сил:
Если же механическая энергия переходит в тепловую, то изменение механической энергии равно работе силы трения или потерям энергии, или количеству выделившегося тепла и так далее, другими словами изменение полной механической энергии равно работе внешних сил:
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему (т.е. такую в которой не действует внешних сил, и их работа соответственно равна нолю) и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной:
Это утверждение выражает закон сохранения энергии (ЗСЭ) в механических процессах. Он является следствием законов Ньютона. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой силами упругости и тяготения. Во всех задачах на закон сохранения энергии всегда будет как минимум два состояния системы тел. Закон гласит, что суммарная энергия первого состояния будет равна суммарной энергии второго состояния.
Алгоритм решения задач на закон сохранения энергии:
- Найти точки начального и конечного положения тела.
- Записать какой или какими энергиями обладает тело в данных точках.
- Приравнять начальную и конечную энергию тела.
- Добавить другие необходимые уравнения из предыдущих тем по физике.
- Решить полученное уравнение или систему уравнений математическими методами.
Важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач.
В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими силами действуют силы трения или силы сопротивления среды. Работа силы трения зависит от длины пути.
Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание). Таким образом энергия в целом (т.е. не только механическая) в любом случае сохраняется.
При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.
Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии.
Разные задачи на работу
К оглавлению…
Если в задаче требуется найти механическую работу, то сначала выберите способ её нахождения:
- Работу можно найти по формуле: A = FS∙cosα. Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения.
- Работу внешней силы можно найти, как разность механической энергии в конечной и начальной ситуациях. Механическая энергия равна сумме кинетической и потенциальной энергий тела.
- Работу по подъёму тела с постоянной скоростью можно найти по формуле: A = mgh, где h – высота, на которую поднимается центр тяжести тела.
- Работу можно найти как произведение мощности на время, т.е. по формуле: A = Pt.
- Работу можно найти, как площадь фигуры под графиком зависимости силы от перемещения или мощности от времени.
Закон сохранения энергии и динамика вращательного движения
К оглавлению…
Задачи этой темы являются достаточно сложными математически, но при знании подхода решаются по совершенно стандартному алгоритму. Во всех задачах Вам придется рассматривать вращение тела в вертикальной плоскости. Решение будет сводиться к следующей последовательности действий:
- Надо определить интересующую Вас точку (ту точку, в которой необходимо определить скорость тела, силу натяжения нити, вес и так далее).
- Записать в этой точке второй закон Ньютона, учитывая, что тело вращается, то есть у него есть центростремительное ускорение.
- Записать закон сохранения механической энергии так, чтобы в нем присутствовала скорость тела в той самой интересной точке, а также характеристики состояния тела в каком-нибудь состоянии про которое что-то известно.
- В зависимости от условия выразить скорость в квадрате из одного уравнения и подставить в другое.
- Провести остальные необходимые математические операции для получения окончательного результата.
При решении задач надо помнить, что:
- Условие прохождения верхней точки при вращении на нити с минимальной скоростью – сила реакции опоры N в верхней точке равна 0. Такое же условие выполняется при прохождении верхней точки мертвой петли.
- При вращении на стержне условие прохождения всей окружности: минимальная скорость в верхней точке равна 0.
- Условие отрыва тела от поверхности сферы – сила реакции опоры в точке отрыва равна нулю.
Неупругие соударения
К оглавлению…
Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда неизвестны действующие силы. Примером такого рода задач является ударное взаимодействие тел.
Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц). В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание). Для описания любых ударов Вам нужно записать и закон сохранения импульса, и закон сохранения механической энергии с учетом выделяющейся теплоты (предварительно крайне желательно сделать рисунок).
Абсолютно упругий удар
К оглавлению…
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел. Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара. При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии. Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя.
Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров. Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения. Центральный удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой.
Частным случаем нецентрального упругого удара может служить соударения двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров. В этом случае векторы скоростей шаров после упругого соударения всегда направлены перпендикулярно друг к другу.
Законы сохранения. Сложные задачи
К оглавлению…
Несколько тел
В некоторых задачах на закон сохранения энергии тросы с помощью которых перемещаются некие объекты могут иметь массу (т.е. не быть невесомыми, как Вы могли уже привыкнуть). В этом случае работу по перемещению таких тросов (а именно их центров тяжести) также нужно учитывать.
Если два тела, соединённые невесомым стержнем, вращаются в вертикальной плоскости, то:
- выбирают нулевой уровень для расчёта потенциальной энергии, например на уровне оси вращения или на уровне самой нижней точки нахождения одного из грузов и обязательно делают чертёж;
- записывают закон сохранения механической энергии, в котором в левой части записывают сумму кинетической и потенциальной энергии обоих тел в начальной ситуации, а в правой части записывают сумму кинетической и потенциальной энергии обоих тел в конечной ситуации;
- учитывают, что угловые скорости тел одинаковы, тогда линейные скорости тел пропорциональны радиусам вращения;
- при необходимости записывают второй закон Ньютона для каждого из тел в отдельности.
Разрыв снаряда
В случае разрыва снаряда выделяется энергия взрывчатых веществ. Чтобы найти эту энергию надо от суммы механических энергий осколков после взрыва отнять механическую энергию снаряда до взрыва. Также будем использовать закон сохранения импульса, записанный, в виде теоремы косинусов (векторный метод) или в виде проекций на выбранные оси.
Столкновения с тяжёлой плитой
Пусть навстречу тяжёлой плите, которая движется со скоростью v, движется лёгкий шарик массой m со скоростью uн. Так как импульс шарика много меньше импульса плиты, то после удара скорость плиты не изменится, и она будет продолжать движение с той же скоростью и в том же направлении. В результате упругого удара, шарик отлетит от плиты. Здесь важно понять, что не поменяется скорость шарика относительно плиты. В таком случае, для конечной скорости шарика получим:
Таким образом, скорость шарика после удара увеличивается на удвоенную скорость стены. Аналогичное рассуждение для случая, когда до удара шарик и плита двигались в одном направлении, приводит к результату согласно которому скорость шарика уменьшается на удвоенную скорость стены:
Задачи о максимальных и минимальных значениях энергии сталкивающихся шаров
В задачах такого типа главное понять, что потенциальная энергия упругой деформации шаров максимальна, если кинетическая энергия их движения минимальна – это следует из закона сохранения механической энергии. Сумма кинетических энергий шаров минимальна в тот момент, когда скорости шаров будут одинаковы по величине и направлены в одном направлении. В этот момент относительная скорость шаров равна нулю, а деформация и связанная с ней потенциальная энергия максимальна.
Мощность | Физика
Как вы уже знаете, система тел, обладающая механической энергией, может совершить работу над внешними телами. В этом случае говорят, что тела этой системы являются источниками силы.
Одна и та же работа разными источниками силы может быть совершена за разное время. Например, человек может поднять сотню кирпичей на верхний этаж строящегося дома за несколько часов. Эти же кирпичи на тот же этаж подъемным краном можно поднять за несколько минут. То есть подъемный кран может выполнить работу по подъему кирпичей во много раз быстрее человека. Быстроту совершения работы характеризуют мощностью.
Мощность – физическая величина, характеризующая быстроту совершения работы.
Чтобы определить мощность источника силы, надо работу A силы этого источника разделить на время Δt, за которое была совершена работа:
N = A / Δt
Если за любые равные промежутки времени источник силы совершает одинаковую работу A, то указанное отношение называют мгновенной мощностью (или просто мощностью) этого источника.
В других случаях указанное отношение называют средней мощностью за заданный промежуток времени.
В СИ единицу мощности называют ваттом (Вт):
1 Вт = 1 Дж / 1 с
Единица мощности названа в честь английского физика Джеймса Уатта 1873 г. Сам Уатт использовал в качестве единицы мощности лошадиную илу. Это работа, совершаемая за 1 секунду лошадью, которая работает целый день.
1 л. с. = 735 Вт.
Для примера отметим, что средняя мощность, развиваемая сердцем человека, примерно равна 2 Вт. При интенсивной работе в течение нескольких минут человек может развивать мощность около 1 кВт, а при отдельных движениях (прыжок с места, рывок при поднятии тяжести) мощность может достигать 4-5 кВт. Двигатели различных технических устройств, используемых в быту, имеют мощности от долей милливатта (электронно-механические часы) до сотен ватт (двигатели стиральной машины, электрического точила). Мощность же двигателей ракеты космического корабля «Энергия» достигает величины 1,2 · 1011 Вт.
Мощность источника силы F можно вычислить, зная силу и скорость v точечного тела, на которое она действует. Как вы помните, скорость точки – это отношение перемещения точки к промежутку времени, в течение которого движение точки было практически равномерным и прямолинейным. Следовательно, за такой промежуток времени Δt перемещение точки Δx = v · Δt. В течение этого промежутка времени ускорение точки можно считать равным нулю. Следовательно, сумма действующих на точку сил согласно второму закону Ньютона должна быть равна нулю, а каждую из действующих сил можно считать постоянной. Поэтому работа силы, направление которой совпадает с направлением скорости точки, будет равна A = F · v · Δt. Следовательно, мощность источника силы, которая совпадает по направлению со скоростью, равна
N = F · v
Таким образом, если направления скорости и силы совпадают, то мощность источника силы положительна (значения F и v имеют одинаковые знаки).
Напротив, если скорость тела и действующая на него сила направлены в противоположные стороны, то мощность источника силы отрицательна (значения F и v имеют разные знаки).
Из полученной формулы следует, что, когда мощность двигателя постоянна, сила, которая приложена к движущемуся телу, благодаря работе двигателя увеличивается при уменьшении скорости. Именно поэтому водитель автомобиля, преодолевая участок, на котором сила сопротивления движению автомобиля велика, включает пониженную передачу. Уменьшая скорость автомобиля, он увеличивает силу, вращающую колеса.
Рассмотрим теперь, как можно вычислить мощность источника силы, на примере решения следующих задач.
Задача 1
Спортсмен поднялся по вертикальному канату за время Δt = 16 с на высоту h = 10 м. Какую среднюю мощность развивал этот спортсмен? Масса спортсмена M = 80 кг. Модуль ускорения свободного падения считайте равным g = 10 м/с2.
Решение. При подъеме по канату спортсмен совершил работу против силы тяжести, равную A = M · g · h = 80 кг · 10 м/с2 · 10 м = 8000 Дж. Следовательно, средняя мощность которую развивал спортсмен, равна
N = A / Δt = 8000 Дж / 16 с = 500 Вт.
Ответ: средняя мощность равна 500 Вт.
Задача 2
Определите массу груза, который может поднимать кран с постоянной скоростью v = 90 м/мин. Мощность двигателя крана N = 15 кВт. Модуль ускорения свободного падения считайте равным g = 10 м/с2.
Решение. Из формулы N = F · v найдем модуль силы, с которой кран действует на равномерно поднимаемый груз: F = N/v. При равномерном подъеме эта сила должна уравновешивать действующую на груз силу тяжести F = m · g. Следовательно,
Итоги
Мощность – физическая величина, характеризующая быстроту совершения работы.
Чтобы определить мощность источника силы, надо работу A силы этого источника разделить на время Δt, за которое была совершена работа:
N = A / Δt
Вопросы
- Что такое мощность?
- Как называют единицу мощности в СИ?
- Может ли мощность источника силы быть отрицательной? Приведите примеры источника силы с отрицательной мощностью.
Упражнения
- Какую работу совершили за год генераторы электростанции, если их средняя мощность за год была равна N = 2,5 МВт? Ответ выразите в джоулях.
- Определите среднюю мощность человека при быстрой ходьбе, если за Δt = 0,5 ч он делает 2500 шагов. Известно, что, делая один шаг, человек совершает работу A = 36 Дж.
- Оцените вашу мощность при ходьбе. Для этого подсчитайте, сколько шагов вы делаете в минуту, в час при равномерном движении. Как изменится мощность, если вы будете идти тот же час с вдвое меньшей скоростью, с вдвое большей скоростью?
- Проанализируйте решение задачи 1 из параграфа. Уменьшится ли время подъема на ту же высоту другого спортсмена, если он будет развивать ту же мощность, а его масса равна 60 кг? Найдите время подъема более легкого спортсмена.
- Самолет летит прямолинейно горизонтально с постоянной скоростью 1000 км/ч. Вычислите силу сопротивления движению самолета, если его двигатели развивают мощность 1,8 МВт.
- Автомобиль массой m = 2т движется прямолинейно по горизонтальной дороге со скоростью v = 72 км/ч, преодолевая силу сопротивления, равную 0,05 его веса. Какую мощность развивает двигатель автомобиля?
Физика. Механика
Представим снова элементарную работу в виде
Удельная величина, равная отношению работы совершенной за время dt к этому времени, называется мощностью:
Другими словами, мощность, развиваемая некоторой силой, равна скорости, с которой эта сила производит работу. Можно сказать и так: средняя за единицу времени мощность численно равна работе совершенной за единицу времени. Если мощность за выбранную единицу времени практически не меняется, то слово «средняя» можно опустить: мощность численно равна работе за единицу времени.
Как видно из определения, мощность равна скалярному произведению силы на скорость перемещения её точки приложения, поэтому работа силы за время от t1 до t2 может быть вычислена следующим образом:
Средняя мощность за этот же промежуток времени равна
За единицу мощности принимается такая мощность, при которой в единицу времени совершается единица работы.
В системе СИ единицей измерения мощности является ватт (Вт):
Внесистемная единица мощности — лошадиная сила (л.с.) — равна 736 Вт. В быту часто используют единицу энергии — 1 кВт•ч = 103 Вт•3600 с=3.6 МДж.
Пример. Вертолет массой m = 3 m висит в воздухе. Определить мощность, развиваемую мотором вертолета, если диаметр ротора равен d = 8 м. При расчете принять, что ротор отбрасывает вниз цилиндрическую струю воздуха диаметром, равным диаметру ротора. Плотность воздуха 1.29 кг/м3.
При решении этой задачи надо применить все известные нам законы динамики. Поскольку это — не одно- и не двухходовая задача, попробуем сначала найти вид окончательного выражения, пользуясь анализом размерности (см. тему 1.3). Искомая мощность зависит от: 1) веса вертолета mg; 2) диаметра винта d, 3) плотности воздуха , то есть искомая формула должна иметь вид
Размерность мощности будет [N] = [ML2T–3]. Составляем равенство размерностей в обеих частях искомой формулы:
Решая систему уравнений
находим
то есть искомая мощность двигателя вертолета будет
где C — некий числовой коэффициент.
Решим теперь эту же задачу точно. Пусть — скорость струи воздуха, отбрасываемой винтом. За время частицы воздуха проходят расстояние . Иными словами, за время винт вертолета придает скорость всем частицам воздуха, находящимся в цилиндре с площадью основания и высотой . Масса воздуха в этом объеме равна
а его кинетическая энергия дается выражением
Поскольку мотор передает воздуху кинетическую энергию , то такова и совершаемая им работа. Поэтому развиваемая мотором мощность (без учета потерь мощности во всех трансмиссиях на пути от двигателя до винта) равна
В этом выражении нам надо еще найти скорость струи воздуха, отбрасываемой винтом. Импульс , передаваемый частицам воздуха за время , равен
Из второго закона Ньютона следует, что средняя сила, действующая на отбрасываемый вниз воздух равна . По третьему закону Ньютона такая же сила действует на вертолет со стороны воздуха. Эта сила компенсирует вес вертолета:
Отсюда получаем уравнение
позволяющее найти скорость струи воздуха:
Подставляя найденную скорость в выражение для мощности двигателя вертолета, получаем окончательный результат:
Мы видим, что выражение для мощности действительно оказалось таким, каким ожидалось на основе анализа размерностей. Подставляя числовые данные, находим
Рис.4.5. Мощность в природе и технике
Мощность
Количественная работа связана с силой, вызывающей смещение. Работа не имеет ничего общего с количеством времени, в течение которого эта сила вызывает смещение. Иногда работа выполняется очень быстро, а иногда — довольно медленно. Например, альпинистке требуется необычно много времени, чтобы поднять свое тело на несколько метров вдоль скалы. С другой стороны, турист (который выберет более легкий путь в гору) может поднять свое тело на несколько метров за короткий промежуток времени.Эти два человека могут выполнять одинаковый объем работы, но путешественник выполняет ее значительно быстрее, чем скалолаз. Величина, связанная со скоростью выполнения определенного объема работы, называется мощностью. У туриста номинальная мощность выше, чем у скалолаза.
Мощность — это скорость выполнения работы. Это соотношение работы / времени. Математически это вычисляется с использованием следующего уравнения.
Мощность = Работа / время
или
P = Вт / т
Стандартная метрическая единица измерения мощности — Вт .Как следует из уравнения мощности, единица мощности эквивалентна единице работы, деленной на единицу времени. Таким образом, ватт эквивалентен джоулям в секунду. По историческим причинам, лошадиных сил иногда используется для описания мощности, выдаваемой машиной. Одна лошадиная сила эквивалентна примерно 750 Вт.
Большинство машин спроектировано и построено для работы с объектами. Все машины обычно характеризуются номинальной мощностью.Номинальная мощность указывает скорость, с которой эта машина может работать с другими объектами. Таким образом, мощность машины — это соотношение работы / времени для этой конкретной машины. Автомобильный двигатель — это пример машины, которой задана номинальная мощность. Номинальная мощность относится к тому, насколько быстро автомобиль может разгонять автомобиль. Предположим, что двигатель мощностью 40 лошадиных сил может разогнать автомобиль от 0 миль / час до 60 миль / час за 16 секунд. Если бы это было так, то автомобиль с четырехкратной мощностью в лошадиных силах мог бы выполнять такой же объем работы за четверть времени.То есть 160-сильный двигатель мог разогнать тот же автомобиль с 0 миль / час до 60 миль / час за 4 секунды. Дело в том, что при одинаковом объеме работы мощность и время обратно пропорциональны. Уравнение мощности предполагает, что более мощный двигатель может выполнять такой же объем работы за меньшее время.
Человек — это также машина с номинальной мощностью . Некоторые люди более властны, чем другие. То есть некоторые люди способны выполнять тот же объем работы за меньшее время или больше за то же время.Обычная физическая лаборатория включает в себя быстрый подъем по лестнице и использование информации о массе, росте и времени для определения личных возможностей ученика. Несмотря на диагональное движение по лестнице, часто предполагается, что горизонтальное движение является постоянным, и вся сила от ступенек используется для подъема ученика вверх с постоянной скоростью. Таким образом, вес ученика равен силе, которая воздействует на ученика, а высота лестницы — это смещение вверх. Предположим, что Бен Пумпинирон поднимает свое 80-килограммовое тело на 2.0-метровый подъезд за 1,8 секунды. Если бы это было так, то мы могли бы вычислить номинальную мощность Бена . Можно предположить, что Бен должен приложить к лестнице нисходящую силу 800 Ньютон, чтобы поднять свое тело. Поступая таким образом, лестница толкала тело Бена вверх с достаточной силой, чтобы поднять его тело вверх по лестнице. Также можно предположить, что угол между силой лестницы на Бена и смещением Бена равен 0 градусов. Используя эти два приближения, можно определить номинальную мощность Бена, как показано ниже.
Номинальная мощность Бена — 871 Вт. Он вполне себе лошадка .
Другая формула мощности
Выражение для мощности — работа / время. А поскольку выражение для работы — это сила * смещение, выражение для мощности можно переписать как (сила * смещение) / время. Поскольку выражение для скорости — это смещение / время, выражение для мощности можно еще раз переписать как «сила * скорость».Это показано ниже.
Это новое уравнение мощности показывает, что мощная машина одновременно сильна (большая сила) и быстра (большая скорость). Мощный автомобильный двигатель — сильный и быстрый. Мощная сельскохозяйственная техника — прочная и быстрая. Сильный тяжелоатлет силен и быстр. Сильный лайнмен в футбольной команде силен и быстр. Машина , достаточно сильная, чтобы приложить большую силу, чтобы вызвать смещение за небольшой промежуток времени (т.е., большая скорость) — машина мощная.
Проверьте свое понимание
Используйте свое понимание работы и власти, чтобы ответить на следующие вопросы. По завершении нажмите кнопку, чтобы просмотреть ответы.
1. Два студента-физика, Уилл Н. Эндейбл и Бен Пумпинирон, в зале для тяжелой атлетики. Уилл поднимает 100-фунтовую штангу над головой 10 раз за одну минуту; Бен поднимает 100-фунтовую штангу над головой 10 раз за 10 секунд.Какой студент больше всего работает? ______________ Какой ученик дает больше всего энергии? ______________ Объясните свои ответы.
2. В физической лаборатории Джек и Джилл взбежали на холм. Джек вдвое массивнее Джилл; тем не менее, Джилл преодолевает то же расстояние за половину времени. Кто работал больше всего? ______________ Кто доставил больше всего энергии? ______________ Объясните свои ответы.
3. Уставшая белка (масса около 1 кг) отжимается, прикладывая силу, поднимающую ее центр масс на 5 см, чтобы выполнить работу всего на 0,50 Дж. Если уставшая белка проделает всю эту работу за 2 секунды, то определите ее мощность.
4. При выполнении подтягивания студентка-физик поднимает ее 42.0-кг тело на дистанцию 0,25 метра за 2 секунды. Какую силу развивают бицепсы ученика?
5. Ежемесячный счет за электроэнергию в вашей семье часто выражается в киловатт-часах. Один киловатт-час — это количество энергии, доставленное потоком 1 киловатт электроэнергии за один час. Используйте коэффициенты преобразования, чтобы показать, сколько джоулей энергии вы получаете, покупая 1 киловатт-час электроэнергии.
6. Эскалатор используется для перемещения 20 пассажиров каждую минуту с первого этажа универмага на второй. Второй этаж находится на высоте 5,20 метра над первым этажом. Средняя масса пассажира — 54,9 кг. Определите требуемую мощность эскалатора, чтобы переместить это количество пассажиров за это время.
Power — The Physics Hypertextbook
Обсуждение
Введение
Мощность — это скорость выполнения работы или скорость, с которой энергия передается из одного места в другое или преобразуется из одного типа в другой.
| P = Fv cos θ | P = F · v |
| мощность (Вт) | устройство, событие, явление, процесс |
|---|---|
| гамма-всплеск | |
| 3.6 × 10 39 | типичный квазар |
| 3,6 × 10 26 | Солнце |
| 1,25 × 10 15 | Самый мощный лазер, 1999 (Петаватт) |
| 1,07 × 10 15 | Самый мощный лазер, 2017 г. (LFEX) |
| 1,3 × 10 13 | общее потребление человеком, мировое |
| 3.2 × 10 12 | общее потребление человеком, США |
| 1,2 × 10 10 | космический челнок при запуске |
| 10 9 ~ 10 10 | крупная коммерческая электростанция |
| 4,700,000 | самый мощный тепловоз (GE AC6000 CW) |
| 2 610 000 | Самый мощный грузовик (Komatsu 980E-4) |
| 1,800,000 | Самый мощный радиопередатчик (VLF Cutler, Maine) |
| 1,550,000 | Самый мощный автомобиль (Араш АФ10) |
| 10 000 | Паровая машина Ватта 1778 г. |
| 746 | 1 л.с. |
| 100 | человек, в среднем |
| 1 | 1 ватт |
| 0.293 | 1 БТЕ / ч |
| 10 −5 | человек, звуки, издаваемые при нормальной речи |
шт.
Исходя из основного определения…
любые единицы работы (или энергии) и время могут быть использованы для выработки единицы мощности. В Международной системе для этого используются джоули [Дж] и секунды [с] соответственно.
| ⎡ ⎢ ⎣ | Вт = | Дж | ⎤ ⎥ ⎦ |
| с |
Джоуль в секунду называется Вт [Вт] в честь шотландского инженера-механика Джеймса Ватта.Ватт наиболее известен тем, что изобрел улучшенный паровой двигатель примерно в 1770 году, и немного менее известен тем, что вскоре после этого изобрел концепцию мощности. Мощность была новым способом сравнить его двигатели с машинами, которые они должны были заменить — лошадьми. (Подробнее об этом позже.)
Вт не думали бы о мощности так же, как мы сегодня. Концепция энергии была изобретена только после его смерти. Для него сила была продуктом силы и скорости.
P = Fv
Единицы измерения, конечно же, работают точно так же в системе СИ.Напомним, что джоуль — это произведение ньютона на метр.
| ⎡ ⎢ ⎣ | Вт = | Дж | = | Н м | = Н м / с | ⎤ ⎥ ⎦ |
| с | с |
Но, конечно, Ватт не использовал систему СИ или даже ее предшественницу, метрическую систему. До 1795 года не было килограммов. Ньютон не становился единицей до 1948 года.Когда Ватт был жив, в мире единиц джоулей не было, потому что, по сути, в мире людей не было джоулей. (Джеймсу Джоулю было восемь месяцев, когда умер Джеймс Ватт.)
Джеймс Ватт использовал фунты для силы и различные английские единицы для скорости — дюймы в секунду, футы в минуту, мили в час и т. Д.
- Киловатт-час — это единица энергии, используемая электроэнергетическими предприятиями.
- Британские тепловые единицы в час (часто ошибочно сокращаются до британских тепловых единиц) — это единица измерения мощности, используемая в сфере отопления, вентиляции и охлаждения (HVAC).
- Лошадиная сила — это единица мощности, достаточная для подъема 33000 фунтов на 1 фут каждую 1 минуту (550 фунтов, 1 фут, 1 секунду), что эквивалентно примерно 745,70 Вт
- https://www.google.com/search?q=33000+lbf*1+foot/1+minute
лошадиных сил и
лошадиных сил
Джеймс Ватт был шотландским инженером-механиком, наиболее известным своими усовершенствованиями в конструкции паровых двигателей. Хотя считается, что Томас Ньюкомен изобрел паровой двигатель примерно в 1698 году, усовершенствованная конструкция Ватта, запатентованная в 1769 году, стала отраслевым стандартом, приведшим в действие Промышленную революцию в Великобритании и других странах.
Один из первых коммерческих двигателей, построенных Уаттом, был продан медному руднику в Корнуолле, регионе Англии, где уголь был дорогим. Ватт руководил строительством специально построенных паровых двигателей на шахтах, а затем взимал лицензионный сбор, равный доле денег, сэкономленных за счет перехода на его улучшенную конструкцию.
Двигатели
Newcomen и Watt являются примерами поршневых двигателей . То же самое с двигателями большинства легковых и грузовых автомобилей. Пар нагнетается в вертикальный цилиндр, приводя поршень вверх.Пар конденсируется, и атмосферное давление опускает поршень. В двигателе с более чем одним цилиндром, когда один из поршней движется вверх, другой движется вниз. Движение одного возвратно-поступательно движением другого. (Как ни странно, двигатель с поршневым приводом даже с одним цилиндром до сих пор называют поршневым двигателем.) Поршни Ватта изначально были прикреплены к качающейся балке, которая идеально подходила для привода подъемного насоса. Это классический старинный насос с ручкой, который наверняка видел каждый — по крайней мере на фотографиях, если не лично.Более поздние механические дополнения позволили Ватту преобразовать возвратно-поступательное движение балки во вращательное движение оси. Это открыло для паровой машины новые возможности.
Самым сильным конкурентом паровой машины на момент ее изобретения была лошадь. Одним из наиболее изобретательных способов использования силы лошади была конная мельница (также известная как конский джин) — конструкция с большими спицами и осью, похожая на колесо телеги без обода, которое можно было вращать в горизонтальном направлении.Лошадей пристегивали к концам спиц (от четырех до шести за раз, для больших применений) и заставляли ходить по кругу вокруг центрального приводного вала в течение нескольких часов. Эквивалент конной мельницы с приводом от человека называется беговой дорожкой. Беговые дорожки 18-го века совсем не походили на тренажеры, впервые продаваемые в 20-м веке. Конные мельницы и беговые дорожки были доиндустриальными машинами для выполнения работы — не абстрактной математической работой силы, умноженной на смещение, а подлинным каторжным трудом.
| Гравировка конной мельницы (1624) | Гравюра конной мельницы (1851 г.) |
Чтобы Ватт взимал лицензионный сбор за свои «вращающиеся» паровые двигатели, ему требовался экономический эквивалент — то, с чем он мог бы их сравнить. Лошади были естественным выбором, но сколько работы делает лошадь? Работа даже не подходящая концепция. Одна лошадь может сделать столько работы, но две лошади сделают это в два раза быстрее. Важен не объем работы, которую выполняет лошадь, а скорость, с которой она ее выполняет.
Ватт идентифицировал пивоварню Whitbread в Лондоне как потенциального клиента. По оценкам, крупные лондонские пивоварни, такие как Whitbread’s, использовали в среднем 20 лошадей одновременно. Лошадей Уитбреда привязали к мельнице по шесть ремней и заставили ходить по кругу диаметром 24 фута 144 раза в час, измельчая солодовый ячмень в порошок с силой 180 фунтов. Полученное число было округлено до двух значащих цифр для удобства.
| п. = | Fv |
| п. = | F ∆ s / ∆ t = F ( n 2π r / t ) |
| п. = | (180 фунтов) (144 × 2π × 12 футов) / (60 мин) |
| п. = | 32 572.03263… фунт-фут / мин |
| п. = | 33000 фунт · фут / мин |
До того, как мистер Ватт применил паровую машину для создания вращательного движения, на крупных мануфактурах королевства мельницы приводились в движение с помощью воды, ветра или лошадей; а последние в течение многих лет почти исключительно работали на пивоварнях и ликероводочных заводах мегаполиса. Поэтому для того, кто хотел заменить мощность лошадей мощностью пара, было естественно указать число последних, которому новая мощность при данных условиях будет эквивалентна; и вполне вероятно, что Боултон и Ватт считали, что такой способ сравнения будет более понятным для обычных опасений, чем более точная и научная формула.Это дало мощность двигателя, выраженную в числах, из которых , обычная сила лошади — это единица ….
Бултон и Ватт, однако, не оставили вопрос в состоянии, которое в любом случае можно было бы считать неправильным, но придали ему всю точность, которая может потребоваться, когда по результатам экспериментов, проведенных с использованием сильных лошадей. лондонские пивовары приняли за стандарт лошадиных сил, силу, способную поднять 33000 либов.один фут в минуту ; и это, без сомнения, должно было включать допуск мощности, достаточно достаточный, чтобы покрыть обычные вариации силы лошадей, а также другие обстоятельства, которые могут повлиять на точность результата.
Олинтус Грегори, 1809
физиология
| мощность (Вт) | активность |
|---|---|
| 800 | играет в баскетбол |
| 700 | на велосипеде (21 км / ч) |
| 685 | подъем по лестнице (116 ступенек / мин) |
| 545 | коньки (15 км / ч) |
| 475 | плавание (1.6 км / ч) |
| 440 | играет в теннис |
| 400 | на велосипеде (15 км / ч) |
| 265 | ходьба (5 км / ч) |
| 210 | сидит с сосредоточенным вниманием |
| 125 | стоя в состоянии покоя |
| 120 | сидя в состоянии покоя |
| 83 | спящий |
| орган | Масса (кг) | мощность (Вт) | Плотность мощности (Вт / кг) | % от общего количества |
|---|---|---|---|---|
| печень и селезенка | 23 | 27 | ||
| мозг | 1.40 | 16 | 11 | 19 |
| скелетные мышцы | 28,00 | 15 | 0,55 | 18 |
| почки | 0,30 | 9,1 | 30 | 10 |
| сердце | 0,32 | 5,6 | 17 | 7 |
| остаток | 16 | 19 | ||
| всего | 65 | 85 | 100 |
Определение силы в физике
Мощность — это скорость выполнения работы или передачи энергии за единицу времени.Мощность увеличивается, если работа выполняется быстрее или энергия передается за меньшее время.
Расчетная мощность
Уравнение для мощности P = W / t
- P означает мощность (в ваттах)
- Вт — это количество проделанной работы (в Джоулях) или затраченной энергии (в Джоулях)
- t — количество времени (в секундах)
С точки зрения математики, мощность — это производная работы по времени. Если работа выполняется быстрее, мощность выше.Если работа выполняется медленнее, мощность меньше.
Поскольку работа — это сила, умноженная на смещение (W = F * d), а скорость — это смещение во времени (v = d / t), мощность равна силе, умноженной на скорость: P = F * v. Большая мощность видна, когда система является одновременно мощной и быстрой по скорости.
Ед. Мощности
Мощность измеряется в энергии (джоулях), деленной на время. Единица измерения мощности в системе СИ — ватт (Вт) или джоуль в секунду (Дж / с). Мощность — это скалярная величина, у нее нет направления.
Лошадиная сила часто используется для описания мощности, выдаваемой машиной.Лошадиная сила — это единица мощности в британской системе измерения. Это мощность, необходимая для подъема 550 фунтов на один фут за одну секунду, и составляет около 746 Вт.
Ватт часто используется по отношению к лампочкам. В этом номинальном значении мощности это скорость, с которой лампа преобразует электрическую энергию в свет и тепло. Лампа с большей мощностью потребляет больше электроэнергии в единицу времени.
Если вы знаете мощность системы, вы можете найти объем работы, который будет произведен, как W = Pt.Если лампа имеет номинальную мощность 50 Вт, она будет производить 50 джоулей в секунду. За час (3600 секунд) он произведет 180 000 джоулей.
Работа и власть
Когда вы проходите милю, ваша движущая сила перемещает ваше тело, что измеряется по мере выполнения работы. Когда вы пробегаете одну и ту же милю, вы выполняете такой же объем работы, но за меньшее время. Бегун имеет более высокую номинальную мощность, чем ходок, вырабатывая больше ватт. Автомобиль мощностью 80 лошадиных сил может развивать более быстрое ускорение, чем автомобиль мощностью 40 лошадиных сил.В конце концов, обе машины разгоняются до 60 миль в час, но двигатель мощностью 80 л.с. может развивать эту скорость быстрее.
В гонке между черепахой и зайцем заяц обладал большей мощностью и ускорялся быстрее, но черепаха выполняла ту же работу и преодолевала то же расстояние за гораздо большее время. Черепаха показала меньшую мощь.
Средняя мощность
Обсуждая мощность, люди обычно имеют в виду среднюю мощность, P avg . Это объем работы, выполненной за период времени (ΔW / Δt), или количество энергии, переданной за период времени (ΔE / Δt).
Мгновенная мощность
Какая мощность в конкретное время? Когда единица времени приближается к нулю, для получения ответа требуется расчет, но он приближается к силе, умноженной на скорость.
7.7: Power — Physics LibreTexts
Что такое мощность?
Power — это слово вызывает в воображении множество образов: профессиональный футболист, отталкивающий своего противника, драгстер, ревущий от стартовой линии, вулкан, выбрасывающий лаву в атмосферу, или взрывающаяся ракета, как на рисунке.
Рисунок \ (\ PageIndex {1} \): Эта мощная ракета космического корабля «Индевор» работала и потребляла энергию с очень высокой скоростью. (кредит: НАСА)
Эти образы силы объединяет быстрое выполнение работы, что соответствует научному определению мощности \ (P \) как скорости выполнения работы.
Мощность
Мощность — это скорость выполнения работы.
\ [P = \ dfrac {W} {t} \]
В системе СИ единица измерения мощности — ватт \ (Вт \), где 1 ватт равен 1 джоуль в секунду \ ((1 \, W = 1 \, J / s) \).
Поскольку работа — это передача энергии, мощность — это также скорость, с которой энергия расходуется. Например, лампочка мощностью 60 Вт потребляет 60 Дж энергии в секунду. Большая мощность означает большой объем работы или энергии, выработанный за короткое время. Например, когда мощный автомобиль быстро разгоняется, он выполняет большой объем работы и потребляет большое количество топлива за короткое время.
Расчет мощности по энергии
Пример \ (\ PageIndex {1} \): расчет мощности для подъема по лестнице
Какая выходная мощность у 60.Женщина весом 0 кг, которая поднимается по лестнице высотой 3,00 м за 3,50 с, начиная с состояния покоя, но имея конечную скорость 2,00 м / с? (См. Рисунок.)
Рисунок \ (\ PageIndex {2} \): Когда эта женщина бежит наверх из состояния покоя, она преобразует химическую энергию, исходную из пищи, в кинетическую энергию и гравитационную потенциальную энергию. Ее выходная мощность зависит от того, как быстро она это делает.
Стратегия и концепция
Работа, переходящая в механическую энергию, равна \ (W = KE + PE \). 2 + mgh, \), где \ (h \) — высота лестницы по вертикали.2) (3,00 \, м)} {3,50 \, s} \]
\ [= \ dfrac {120 \, J + 1764 \, J} {3.50 \, s} \]
\ [= 538 \, W. \]
Обсуждение
Женщина выполняет 1764 Дж работы, чтобы подняться по лестнице, по сравнению со всего лишь 120 Дж, чтобы увеличить свою кинетическую энергию; таким образом, большая часть ее мощности требуется для подъема, а не для ускорения.
Впечатляет, что полезная выходная мощность этой женщины чуть меньше 1 лошадиных сил \ ((1 \, л.с. = 746 \, Вт) \). Люди могут генерировать более лошадиные силы с помощью мышц ног в течение коротких периодов времени, быстро превращая доступный в крови сахар и кислород в объем работы.(Лошадь может выдавать 1 л.с. в течение нескольких часов подряд.) Как только кислород истощается, выходная мощность снижается, и человек начинает быстро дышать, чтобы получить кислород для метаболизма большего количества пищи — это известно как этап аэробных упражнений . Если бы женщина поднималась по лестнице медленно, то ее выходная мощность была бы намного меньше, хотя объем выполняемой работы был бы таким же.
Установление связей: расследование на вынос
— Измерьте свой рейтинг мощности
- Определите собственную номинальную мощность, измерив время, необходимое вам, чтобы подняться по лестнице.2 \) Крошечная часть этого удерживается Землей в течение длительного времени. Наш уровень потребления ископаемого топлива намного превышает скорость его хранения, поэтому они неизбежно будут исчерпаны. Сила означает, что энергия передается, возможно, меняя форму. Невозможно полностью преобразовать одну форму в другую, не потеряв часть ее в виде тепловой энергии. Например, лампа накаливания мощностью 60 Вт преобразует в свет всего 5 Вт электроэнергии, а 55 Вт рассеивается в тепловую энергию.6 \) электроэнергии. Но электростанция потребляет химическую энергию в размере около 2500 МВт, создавая передачу тепла в окружающую среду в размере 1500 МВт. (См. Рисунок.)
Рисунок \ (\ PageIndex {3} \): Огромное количество электроэнергии вырабатывается угольными электростанциями, такими как эта в Китае, но еще большее количество энергии идет на передачу тепла в окружающую среду. Здесь большие градирни необходимы для быстрой передачи тепла по мере его производства. Передача тепла характерна не только для угольных электростанций, но является неизбежным следствием выработки электроэнергии из любого топлива — ядерного, угля, нефти, природного газа и т.п.3 \)
Человек в состоянии покоя (вся теплопередача) \ (100 \) Типичная лампа накаливания (общая полезная и теплопередающая) \ (60 \) Сердце, человек в состоянии покоя (общая полезная и теплоотдача) \ (8 \) Часы электрические \ (3 \) Карманный калькулятор \ (10 ^ {- 3} \) Мощность и энергопотребление
Обычно нам приходится платить за энергию, которую мы используем.Стоимость энергии для электроприбора интересно и легко оценить, если известны его потребляемая мощность и затраченное время. Чем выше уровень энергопотребления и чем дольше прибор используется, тем выше его стоимость. Уровень потребляемой мощности равен \ (P = \ frac {W} {t} = \ frac {E} {t} \), где \ (E \) — энергия, поставляемая электроэнергетической компанией. Таким образом, энергия, потребляемая за время \ (t \), составляет
\ [E = Pt. \]
В счетах за электроэнергию указывается использованная энергия в киловатт-часах \ ((кВт \ cdot h) \), которая является произведением мощности в киловаттах и времени в часах.Этот блок удобен тем, что потребление электроэнергии на уровне киловатт в течение нескольких часов является типичным.
Пример \ (\ PageIndex {2} \): расчет затрат на энергию
Какова стоимость эксплуатации компьютера мощностью 0,200 кВт, 6,00 ч в день в течение 30,0 дней, если стоимость электроэнергии составляет 0,120 долл. США за \ (кВт \ cdot ч \)?
Стратегия
Стоимость основана на потребленной энергии; таким образом, мы должны найти \ (E \) из \ (E = Pt \), а затем рассчитать стоимость.Поскольку электрическая энергия выражается в \ (кВт \ cdot h \) в начале такой задачи, удобно преобразовать единицы в \ (кВт \) и часы.
Решение
Энергия, потребляемая в \ (кВт \ cdot ч \), составляет
\ [E = Pt = (0.200 \, кВт) (6.00 \, ч / сут) (30.0 \, d) \]
\ [= 36,0 \, кВт \ cdot ч, \]
, а стоимость просто равна
.
\ [стоимость = (36,0 \, кВт \ cdot ч) (0,120 $ \, за \, кВт \ cdot ч) = 4,32 $ \, за \, месяц.\]
Обсуждение
Стоимость использования компьютера в этом примере не является ни чрезмерной, ни незначительной. Понятно, что стоимость — это сочетание силы и времени. Когда и то и другое высокое, например, кондиционер летом, стоимость высока.
Мотивация к экономии энергии стала более убедительной из-за ее постоянно растущей цены. Вооружившись знанием того, что потребляемая энергия является продуктом мощности и времени, вы можете оценить затраты для себя и сделать необходимые оценочные суждения о том, где экономить энергию.Нужно уменьшить либо мощность, либо время. Наиболее экономически выгодно ограничить использование мощных устройств, которые обычно работают в течение длительного времени, таких как водонагреватели и кондиционеры. Сюда не входят устройства с относительно высокой мощностью, такие как тостеры, потому что они работают всего несколько минут в день. Он также не будет включать электрические часы, несмотря на то, что они используются круглосуточно, потому что они являются устройствами с очень низким энергопотреблением. Иногда можно использовать устройства с большей эффективностью, то есть устройства, потребляющие меньше энергии, для выполнения той же задачи.Одним из примеров является компактная люминесцентная лампа, которая дает в четыре раза больше света на ватт потребляемой мощности, чем ее собрат с лампами накаливания.
Современная цивилизация зависит от энергии, но нынешние уровни потребления и производства энергии не являются устойчивыми. Вероятность связи между глобальным потеплением и использованием ископаемого топлива (с сопутствующим образованием углекислого газа) привела к сокращению использования энергии, а также к переходу на неископаемые виды топлива. Несмотря на то, что энергия в изолированной системе является сохраняемой величиной, конечным результатом большинства преобразований энергии является перенос тепла в окружающую среду, которое больше не используется для выполнения работы.Как мы обсудим более подробно в Термодинамике, способность энергии производить полезную работу «деградировала» при преобразовании энергии.
Сводка
- Мощность — это скорость выполнения работы или в форме уравнения для средней мощности \ (P \) для работы \ (W \), выполненной за время \ (t \), \ (P = W / t \).
- Единицей измерения мощности в системе СИ является ватт (Вт), где \ (1 \, W = 1 \, J / s \).
- Мощность многих устройств, таких как электродвигатели, также часто выражается в лошадиных силах (л.с.), где \ (1 \ space hp = 746 \, W.\)
Глоссарий
- мощность
- скорость выполнения работ
- Вт
- (Вт) Единица мощности в системе СИ, при \ (1 Вт = 1 Дж / с \)
- л.с.
- старая единица мощности вне системы СИ, с \ (1 л.с. = 746 Вт \)
- киловатт-час
- (\ (кВт⋅ч \)) единица, используемая в основном для выработки электроэнергии, поставляемой электроэнергетическими компаниями
Авторы и авторство
Пол Питер Урон (почетный профессор Калифорнийского государственного университета, Сакраменто) и Роджер Хинрикс (Государственный университет Нью-Йорка, колледж в Освего) с авторами: Ким Диркс (Оклендский университет) и Манджула Шарма (Сиднейский университет).Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Power — Высшая школа физики
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105Или заполните форму ниже:
Power — Видео по физике от Brightstorm
Мощность — это скорость выполнения работы. Это связано с энергией, которая является количеством, используемым для измерения работы. Мощность можно рассчитать по соотношению мощность = работа / время и обычно измеряется в ваттах (1 ватт = 1 джоуль в секунду).
Вы, наверное, знаете, что такое сила, и когда мы изучаем физику, когда мы говорим о мощности, мы говорим о работе, проделанной с течением времени. Так что помните, что единица измерения работы — джоули, единица измерения времени — секунда, так что теперь у нас есть мощность, а единица измерения мощности — ватты, имя Джеймса Ватта, парня, который изобрел локомотивный двигатель, большая мощность в паровом двигателе, ладно , поэтому единица измерения — ватты, и часто, когда мы генерируем электроэнергию, мы генерируем много энергии, как электростанция чего-то.Итак, у нас есть несколько довольно распространенных единиц, и одна из них — если у нас есть тысяча ватт, хорошо, и, чтобы упростить, мы можем просто назвать это киловаттом, хорошо, или иногда мы просто сокращаем это маленькое k большое W. Но давайте предположим, что мы генерируя даже гораздо больше энергии, чем этот колодец, если у нас может быть не тысяча, но давайте перейдем к следующей единице, которая представляет собой миллион, который также равен 10 от 6 или 1 с 6 нулями, хорошо.
Что ж, единица измерения, которую мы используем для такой мощности, — это мегаватт, и иногда мы будем сокращать эту большую M, большую W.Итак, это все единицы мощности, мегаватты, киловатты или просто обычный ватт, хорошо. Давайте рассмотрим несколько примеров, которые вас могут попросить решить, связанных с властью и ее отношением к рабочему времени, хорошо? Скажем, например, вы крутите педали на велосипеде и хотите знать, сколько мощности требуется, чтобы приложить 100 джоулей работы на педали велосипеда в течение 5 секунд, хорошо. Итак, формула опять же: мощность равна работе во времени, так что это довольно простая задача, которую мы собираемся решить, наша работа — 100 джоулей, наше время — 5 секунд, или я просто сокращу это нормально, и поэтому наша сила здесь 100, разделенное на 5, будет равно 20, в данном случае 20 Вт.Итак, для приложения этой силы требуется 20 Вт мощности, извините, что поработайте на педали в течение такого количества секунд.
Давайте посмотрим на другой пример, где вам дана единица мощности, и вам нужно выяснить, сколько работы требуется для этого. Опять же, давайте скажем, сколько работы требуется, чтобы запитать лампочку мощностью 40 Вт в течение 1 минуты? Хорошо, здесь нам дали блок питания мощностью 40 Вт, но я хочу знать, сколько работы требуется для его питания в течение 1 минуты. Теперь помните, что здесь единица измерения — это минуты, а единица измерения мощности, о которой мы говорили, — это работа в секунду.Итак, давайте помнить, что на самом деле это 60 секунд. И тогда нам просто нужно настроить нашу проблему. У нас есть 40 ватт, равных работе x за секунды, что составляет 60 секунд, и снова, чтобы решить для x, я собираюсь сказать, что x равно это число, умноженное на это число, число в знаменателе, умноженное на это число, которое будет равно 240. В данном случае единица измерения — ватты, извините, ватт на секунды даст нам наше число в джоулях. Итак, это 2 типа уравнений, которые обычно просят решить, в которых учитывается мощность и ее связь с работой.
Power (Физика): Определение, Формула, Единицы, Как найти (с примерами)
Обновлено 28 декабря 2020 г.
Автор: Эми Дусто
Бодибилдер и пятиклассник могли унести все книги с полки вверх лестничный пролет, но вряд ли они справятся с задачей за то же время. Бодибилдер, вероятно, будет быстрее, потому что у нее рейтинг мощности выше, чем у пятиклассника.
Точно так же гоночный автомобиль с высокой мощностью лошадиных сил сможет проехать дальше намного быстрее, чем лошадь.
TL; DR (слишком долго; не читал)
Мощность — это мера того, сколько работы выполнено за временной интервал.
Краткое замечание о лошадиных силах: этот термин предназначен для сравнения мощности парового двигателя с мощностью лошади, поскольку двигатель мощностью 700 лошадиных сил может выполнять примерно в 700 раз больше работы, чем одна лошадь. Это восходит к тому времени, когда паровые двигатели были новыми, и один из самых выдающихся изобретателей, работавших над повышением их эффективности, Джеймс Ватт, придумал этот термин как способ убедить среднего человека в их ценности.
Формулы для мощности
Есть два способа рассчитать мощность в зависимости от того, какая информация доступна. Кроме того, есть две единицы мощности, которые одинаково действительны.
1. Мощность в терминах работы и времени:
P = \ frac {W} {t}
Где работа Вт измеряется в Ньютон-метрах (Нм), а время t измеряется в секундах (с).
2. Мощность в единицах силы и скорости:
P = Fv
, где сила F выражается в Ньютонах (Н), а скорость v выражается в метрах в секунду (м / с). .
Эти уравнения не эквивалентны случайным образом. Второе уравнение может быть получено из первого следующим образом:
Обратите внимание, что работа совпадает с сила, умноженная на смещение:
W = Fd
Подставьте это в первое уравнение мощности:
Затем, поскольку смещение в любую единицу времени равно скорости (v = d / t), перепишите члены в конце как v , чтобы получить второе уравнение мощности.
Единицы мощности
Единица мощности p в системе СИ обычно представлена как Вт (Вт) , названная в честь того же Джеймса Ватта, который проектировал двигатели и сравнивал их с лошадьми.На бирках лампочек и других бытовых приборов этот блок обычно указывается.
Однако рассмотрение второй формулы для мощности приводит к другой единице. Сила, умноженная на скорость, дает измерение в единицах ньютон-метров в секунду (Нм / с). Затем, поскольку единица энергии джоуль также определяется как один ньютон-метр (Н · м), первую часть этой величины можно переписать как джоуль, в результате чего получится вторая единица мощности в системе СИ: джоулей в секунду (Дж / с).
Как стать могущественным
Рассмотрение определения силы и двух способов ее нахождения дает несколько способов увеличить силу чего-либо : увеличить его силу (использовать больше силы ) или получить та же работа выполняется быстрее (уменьшите t или увеличьте v ).Мощная машина — это сильная и быстрая , а слабая — ни то, ни другое. легче и быстрее может работать , более мощный — объект, выполняющий работу.
Это также означает, что очень сильная машина, скажем, очень мускулистый бодибилдер, может все еще испытывать недостаток мощности . Человек, который может поднять очень тяжелый груз, но только очень медленно, менее силен, чем тот, кто может поднять его быстро.
Точно так же очень быстрая машина или человек, который мало что делает, кто-то быстро крутится на месте, но ни к чему не стремится, на самом деле не является мощным.
Пример расчета мощности
1. Усэйн Болт выработал мощность около 25 Вт в своем рекордном спринте на 100 м, который занял 9,58 секунды. Сколько работы он проделал?
Поскольку даны P и t , а W неизвестно, используйте первое уравнение:
P = \ frac {W} {t} \ подразумевает 25 = \ frac { W} {9.58} \ подразумевает W = 239.5 \ text {Nm}
2. С какой средней силой он давил на землю во время бега?
Так как работа в Нм уже известна, как смещение в метрах, деление на длину гонки даст силы (другими словами, работа совпадает с усилием на смещение: W = F × d):
\ frac {239.5} {100} = 2.395 \ text {N}
3. Какую мощность вырабатывает человек весом 48 кг, который тратит 6 секунд на подъем по 3-метровой лестнице?
В этой задаче указаны смещение и время, что позволяет быстро вычислить скорость:
v = \ frac {d} {t} = \ frac {3} {6} = 0,5 \ text {м / с}
Второе уравнение мощности учитывает скорость, но также включает силу. Человек, поднимающийся по лестнице, пытается противостоять силе тяжести. Итак, силу в этом случае можно найти, используя их массу и ускорение свободного падения, которое на Земле всегда равно 9.8 м / с 2 .
F_ {grav} = mg = 48 \ times 9,8 = 470,4 \ text {N}
Теперь сила и скорость укладываются во вторую формулу мощности:
= Fv = 470,4 \ times 0,5 = 235,2 \ text {J / s}
Обратите внимание, что решение оставить здесь единицы измерения Дж / с, а не ватты, является произвольным. Столь же приемлемый ответ — 235,2 Вт.
4. Одна лошадиная сила в единицах СИ составляет около 746 Вт, что основано на нагрузке, которую подходящая лошадь могла бы выдержать в течение одной минуты. Сколько работы проделала лошадь-пример за это время?
Единственный шаг перед включением значений мощности и времени в первое уравнение — убедиться, что время указано в правильных единицах СИ — секундах, переписав одну минуту как 60 секунд.Тогда:
P = \ frac {W} {t} \ подразумевает 746 = \ frac {W} {60} \ implies W = 44,670 \ text {Nm}
Киловатт и электричество
Многие коммунальные предприятия взимают плату с клиентов. плата, основанная на их киловатт-часах использования. Чтобы понять значение этой общей единицы электроэнергии, начните с разбивки единиц.
Префикс килограмм означает 1000, поэтому киловатт (кВт) равен 1000 ватт. Таким образом, киловатт-час (кВтч) — это количество киловатт, используемое за один час времени.
Для подсчета киловатт-часов умножьте количество киловатт на использованные часы. Таким образом, если кто-то использует 100-ваттную лампочку в течение 10 часов, он в общей сложности израсходует 1000 ватт-часов или 1 кВт-ч электроэнергии.
Пример проблемы киловатт-часов
1. Электроэнергетика взимает 0,12 доллара за киловатт-час. Очень мощный вакуум 3000 Вт используется в течение 30 минут. Сколько стоит это количество энергии домовладельцам?
3 \ text {кВт} \ times 0.5 \ text {h} = 1,5 \ text {кВтч} \ text {и} 1,5 \ text {кВтч} \ times 0,12 \ text {долларов / кВтч} = \ 0,18 долл. США
2. Та же коммунальная компания кредитует домашнему хозяйству 10 долл. США на каждые 4 кВтч электроэнергии возвращается в сеть. Солнце дает около 1000 Вт мощности на квадратный метр. Если солнечный элемент площадью два квадратных метра в доме собирает энергию в течение 8 часов, сколько денег он приносит?
Учитывая информацию в задаче, солнечный элемент должен быть способен собирать 2 000 Вт от Солнца или 2 кВт.
