Формула действующее значение напряжения: Действующие значения тока — Знаешь как

Действующие значения тока — Знаешь как

Расчет цепей переменного тока упрощается, если пользоваться понятием действующего (эффективного) значения переменного тока.

Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период переменного тока то же количество тепла.

Согласно ГОСТ действующие значения обозначаются прописными буквами, т. е ток I, напряжение U.

На шкалах измерительных приборов всегда наносятся действующие значения тока или напряжения.

Если ток изменяется по синусоидальному закону, то действующее значение его составляет 0,707 амплитудного значения тока, т. е.

I = (I_м : √2) = I_м: 1,41 = 0,707I_м

То же соотношение имеет место и для синусоидального напряжения, т. е.

U = (U_м : √2) = 0,707U_м

Докажем правильность приведенных соотношений. Количество тепла, выделенного постоянным током I в сопротивлении r за период переменного тока Т:

Q’ = I²rT

Количество тепла, выделенного переменным током в том же сопротивлении за период Т, может быть выражено через среднее значение мощности Р переменного тока

Q» = PT

Если Q’= Q», то

 I²rT=РТ.

В последнем выражении согласно данному выше определению значение эквивалентного постоянного тока I равно действующему значению переменного тока. Таким образом, действующее значение тока

I = √ (P : r)

Мгновенная мощность при синусоидальном токе  p = i²r = I²_мr sin²ωt

или, приняв во внимание, что sin² α = (11 : 2) — (1 : 2) cos 2α, получим:

p = (I²_мr : 2) — (I²_мr : 2) cos 2ωt

Мгновенная мощность при синусоидальном токе может быть представлена суммой двух слагаемых постоянной ½ I²_мr и переменной, изменяющейся по периодическому синусоидальному закону.

Среднее значение мощности синусоидального тока будет равно постоянной слагаемой

P = ½I²_мr

так как среднее значение за пер и синусоидальной слагаемой ½I²_мr cos 2ωt равно нулю.

Действующее значение переменного синусоидального тока

I = √(P : r) = √ (½I²_мr : r) = I_м : √2 = 0,707I_м

Так как действующие значения синусоидальных токов и

напряжений в √2 раз меньше амплитудных значений, то вектор, выражающий в одном масштабе амплитудное значение, в другом масштабе представляет действующее значение той же величины. В дальнейшем выбор масштабов векторов будет производиться, исходя из действующих значений.

Пример 5-4. Вольтметр,, включенный в сеть, показал напряжение 380 в.

Определить амплитуду напряжения сети:

U_M = √2 U = 1,41 • 380=536 в.

ОБЩИЕ ЗАМЕЧАНИЯ О ЦЕПЯХ ПЕРЕМЕННОГО ТОКА

Любая электрическая цепь обладает параметрами: .сопротивлением r, индуктивностью L и емкостью С,

В цепи постоянного тока при неизменном напряжении будут неизмененными: ток, мощность и запас энергии в электрическом и магнитном полях.

При переменном напряжении на зажимах цепи в ней будет проходить переменный ток, будет изменяться и энергия электрического и магнитного полей. В технике встречаются цели, физические явления в которых определяются наличием одного из параметров r, L или С, тогда как другие параметры выявлены слабо и влиянием их можно пренебречь.

Например, лампу накаливания, нагревательный прибор, реостат можно рассматривать как цепь с сопротивлением r, влиянием емкости и индуктивности которой можно пренебречь.

Цепь ненагруженного трансформатора можно рассматривать как индуктивность, пренебрегая влиянием сопротивления и емкости этой цепи.

Наконец, кабель, работающий вхолостую, можно рассматривать как емкость, так как влияние индуктивности и сопротивления этой цепи незначительны.

Статья на тему Действующие значения тока

Среднеквадратичное (действующее, эффективное) значение

Что же из себя представляет среднеквадратичное значение напряжения и как его замерить? Давайте разберем значение этого термина. Поможет нам в этих делах наш осциллограф OWON SDS6062 , Блок питания, а также ЛАТР (Лабораторный автотрансформатор). Для того, чтобы разобраться в этом, мы проведем простейший опыт.

Лампочка и постоянное напряжение

Для опытов нам также понадобится простая автомобильная лампа накаливания на напряжение 12 Вольт

Вот ее характеристики:  рабочее напряжение U=12 Вольт, мощность Р = 21 Ватт.

Следовательно, зная мощность и напряжение лампы, можно узнать, какую силу тока будет потреблять лампочка. Из формулы P=IU, где I – сила тока,  можно найти I. Значит  I=P/U=21/12=1,75 Ампер.

Ладно, с лампочкой разобрались. Давайте ее зажжем. Для этого на нашем блоке питания выставляем рабочее напряжение для нашей лампы

Подаем напряжение с блока питания на лампу и вуаля!

Замеряем напряжение на  клеммах-крокодилах блока питания с помощью мультиметра . Ровнехонько 12 Вольт, как и предполагалось.

К этим же клеммах цепляем и наш осциллограф

Смотрим осциллограмму:

Видите прямую линию? Это и есть осциллограмма постоянного напряжения. В течение времени  у нас напряжение остается  таким, каким и было и не меняется. Если посчитать, то можно вычислить, чему равняется напряжение. Так как одна клеточка у нас 5 Вольт (на фото внизу слева), то  значит, наше напряжение 12 Вольт. Я также вывел это значение на дисплей осциллографа в самом нижнем левом углу: 12,03 Вольт. Все верно.

Замеряем  силу тока. Как правильно замерить силу тока в цепи, можно узнать, прочитав статью как измерить ток и напряжение мультиметром?.

Получили 1,72 Ампер. А как вы помните, наше расчетное значение было 1,75 Ампер. Думаю, вину можно переложить  на погрешность прибора  или на лампочку 😉

Лампочка и переменное напряжение

Теперь начинается самое интересное. Берем наш ЛАТР

Ставим прибор на измерение переменного напряжения и выставляем с помощью  крутилки ЛАТРа напряжение в 12 Вольт. Обратите внимание, что крутилка на мультиметре  находится в диапазоне измерения переменного напряжения. Забегая вперед, скажу, что мультиметр измеряет среднеквадратичное напряжение.

Цепляем осциллограф к клеммах ЛАТРа, не забывая на осциллографе выставить замеры переменного напряжения и смотрим получившуюся осциллограмму:

Смотрим, сколько  силы тока кушает наша лампочка. Все как положено, 1,71 Ампер.

Среднеквадратичное значение напряжения

Итак, что же у нас получилось? Как и постоянное напряжение, так и переменное напряжение  зажигали одну и ту же лампочку, которая кушала одну и ту же мощность.  Значит эта осциллограмма

и вот эта осциллограмма

Чем то похожи? Но чем??? 

Среднеквадратичное значение напряжения – это такое  значение переменного напряжения, при котором нагрузка потребляет столько же силы тока, как и при постоянном напряжении.  То есть лампочка у нас потребляла 1,71 Ампер и при постоянном токе и при переменном.  То есть, в двух этих случаях, мощность, которую потребляла лампочка, была одинакова.

Также среднеквадратичное напряжение еще называют действующим или эффективным значением напряжения. С помощью несложных умозаключений, инженеры-электрики пришли к выводу действующее (оно же среднеквадратичное) напряжение синусоидального сигнала  любой частоты равняется максимальной его амплитуде, поделенной  на корень из двух

Стоп! Мы ведь не разобрали, что такое максимальная амплитуда! На осциллограмме максимальная амплитуда выглядит примерно вот так:

Если даже посчитать по клеточкам и посмотреть, чему равняется одна клеточка по вертикали (смотрим внизу слева, она равняется 5 Вольт), то U_max = 17 Вольт. Делим это значение на корень из двух. Я беру это значение как 1,41. Получаем, что среднеквадратичное значение равняется 17/1,41=12,06 Вольт. Ну что, все верно 😉

Значит, когда нам говорят, что напряжение в розетке равняется 220 Вольт, то мы то знаем, что на самом деле это среднеквадратичное напряжение.  Максимальная амплитуда этих  220 Вольт равняется 220х1,41=310 Вольт.

Где же  среднеквадратичное напряжение и максимальная амплитуда сигнала прячутся на табличке измерений? Да вот  же они!

Vk – это и есть среднеквадратичное напряжение этого сигнала.

Ma – это  и есть Umax.

Конечно, 16,6/1,41=11,8  Вольт, а он пишет 12,08 Вольт.

Переменное напряжение и его параметры

Всем доброго времени суток! В прошлой статье я рассказал, как рассчитать индуктивность катушки выполненной на разомкнутом сердечнике (например, ферритовой антенны, контурных катушек радиоприёмников, катушек с построечными сердечниками и т. д.). Сегодняшняя статья посвящена переменному напряжению и параметрам, которые его характеризуют.

Что такое переменное напряжение?

Как известно электрическим током называется упорядоченное движение заряженных частиц, которое возникает под действием разности потенциалов или напряжения. Одной из основных характеристик любого типа напряжения является его зависимость от времени. В зависимости от данной характеристики различают постоянной напряжение, значение которого с течением времени практически не изменяется и переменное напряжение, изменяющееся во времени.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Переменное напряжение в свою очередь бывает периодическим и непериодическим. Периодическим называется такое напряжение, значения которого повторяются через равные промежутки времени. Непериодическое напряжение может изменять своё значение в любой период времени. Данная статья посвящена периодическому переменному напряжению.

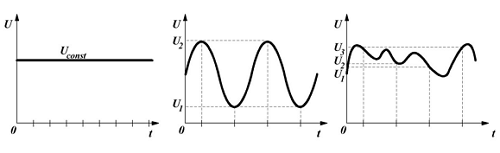
Постоянное (слева), периодическое (в центре) и непериодическое (справа) переменное напряжение.

Минимальное время, за которое значение переменного напряжения повторяется, называется периодом. Любое периодическое переменное напряжение можно описать какой-либо функциональной зависимостью. Если время обозначить через t, то такая зависимость будет иметь вид F(t), тогда в любой период времени зависимость будет иметь вид

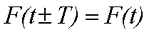
где Т – период.

Величина обратная периоду Т, называется частотой f. Единицей измерения частоты является Герц, а единицей измерения периода является Секунда

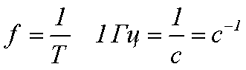
Наиболее часто встречающаяся функциональная зависимость периодического переменного напряжения является синусоидальная зависимость, график которой представлен ниже

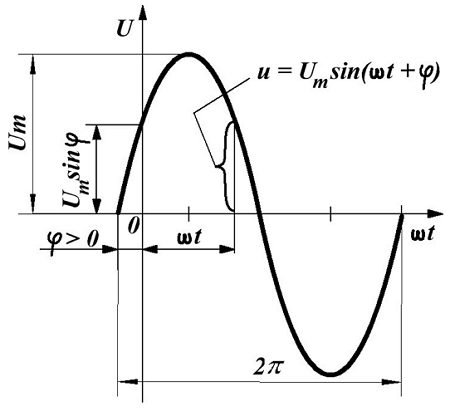Синусоидальное переменное напряжение.

Из математики известно, что синусоида является простейшей периодической функцией, и все другие периодические функции, возможно, представить в виде некоторого количества таких синусоид, имеющих кратные частоты. Поэтому необходимо изначально рассмотреть особенности синусоидального напряжения.

Таким образом, синусоидальное напряжение в любой момент времени, мгновенное напряжение, описывается следующим выражением

где U_m – максимальное значение напряжения или амплитуда,

ω –угловая частота, скорость изменения аргумента (угла),

φ – начальная фаза, определяемая смещением синусоиды относительно начала координат, определяется точкой перехода отрицательной полуволны в положительную полуволну.

Величина (ωt + φ) называется фазой, характеризующая значение напряжения в данный момент времени.

Таким образом, амплитуда U_m, угловая частота ω и начальная фаза φ являются основными параметрами переменного напряжения и определяют его значение в каждый момент времени.

Обычно, при рассмотрении синусоидального напряжения считают, что начальная фаза равна нулю, тогда

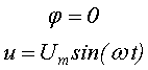
В практической деятельности, довольно часто, используют ещё ряд параметров переменного напряжения, такие как, действующее напряжение, среднее напряжение и коэффициент формы, которые мы рассмотрим ниже.

Что такое действующее напряжение переменного тока?

Как я писал выше, одним из основных параметров переменного напряжения является амплитуда U_m, однако использовать в расчётах данную величину не удобно, так как временной интервал в течение, которого значение напряжения u равно амплитудному U_m ничтожно мал, по сравнению с периодом Т напряжения. Использовать мгновенное значение напряжения u, также не очень удобно, вследствие больших объёмов расчётов. Тогда возникает вопрос, какое значение переменного напряжения использовать при расчётах?

Для решения данного вопроса необходимо обратиться к энергии, которая выделяется под воздействием переменного напряжения, и сравнить её с энергией, которая выделяется под воздействием постоянного напряжения. Для решения данного вопроса обратимся к закону Джоуля – Ленца для постоянного напряжения

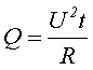
Для переменного напряжения мгновенное значение выделяемой энергии составит

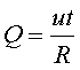
где u – мгновенное значение напряжения

Тогда количество энергии за полный период от t₀ = 0 до t₁ = T составит

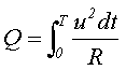
Приравняв выражения для количества энергии при переменном напряжении и постоянном напряжении и выразив полученное выражение через постоянное напряжение, получим действующее значение переменного напряжения

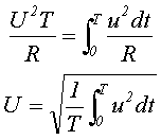
Получившееся выражение, позволяет вычислить действующее значение напряжение U для периодического переменного напряжения любой формы. Из выше изложенного можно сделать вывод, что действующее значение переменного напряжения называется такое постоянное напряжение, которое за такое же время и на таком же сопротивлении выделяет такую же энергию, которая выделяется данным переменным напряжением.

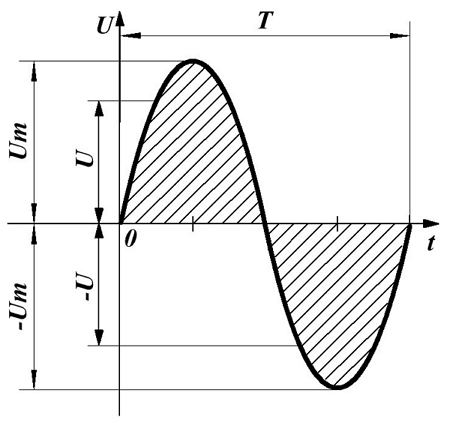
Действующее значение синусоидального напряжения.

Вычислим действующее значение синусоидального напряжения

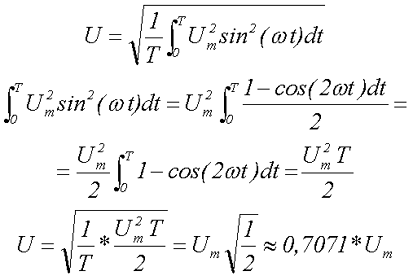
Стоит отметить, все напряжения электротехнических устройств определяются, как правило, действующим значением напряжения.

Для определения амплитудного значения синусоидального напряжения необходимо преобразовать полученное выражение

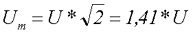
Таким образом если в розетке у нас U = 230 В, следовательно, амплитудное значение данного напряжения

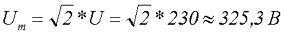
Действующее напряжение также имеет название эффективного напряжения и среднеквадратичного напряжения.

С действующим напряжением разобрались, теперь рассмотрим среднее значение напряжение.

Что такое среднее значение переменного напряжения?

Ещё одним параметром переменного напряжения, который его характеризует, является средним значением переменного напряжения. В отличие от действующего значения переменного напряжения, которое характеризует работу переменного напряжения, среднее значение напряжения характеризует количество электричества, которое перемещается из одной точки цепи в другую, под действием переменного напряжения. Среднее значение напряжения за период определяется следующим выражением

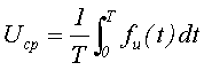
где Т – период переменного напряжения,

f_u(t) – функциональная зависимость напряжения от времени.

Таким образом, среднее значение переменного напряжения численно будет равно высоте прямоугольника с основанием T, площадь которого равна площади, ограниченной функцией f_u(t) и осью Ox за период Т.

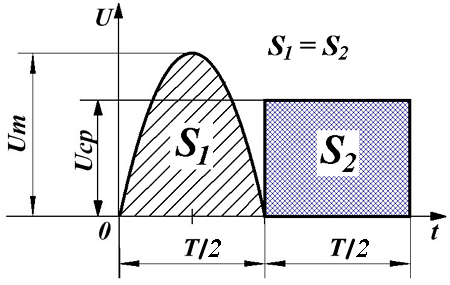
Среднее значение переменного напряжения.

В случае синусоидальной функции, можно говорить только о среднем значении за полупериод, так как в течение всего периода положительная полуволна компенсируется отрицательной полуволной, и тогда среднее за период напряжение будет равно нулю.

Таким образом, среднее за полупериод Т/2 значение переменного напряжения синусоидальной формы будет равно

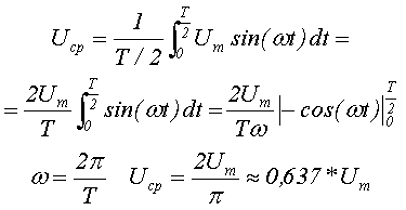
где U_m – максимальное значение напряжения или амплитуда,

ω –угловая частота, скорость изменения аргумента (угла).

Какие коэффициенты, характеризуют переменное напряжение?

Иногда возникает необходимость охарактеризовать форму переменного напряжения. Для этой цели существует ряд параметров данного переменного напряжения:

1. Коэффициент формы переменного напряжения k_ф – показывает как относится действующее значение переменного напряжения U к его среднему значению U_cp.

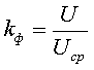
Так для синусоидального напряжения коэффициент формы составит

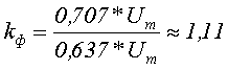
2. Коэффициент амплитуды переменного напряжения k_а – показывает как относится амплитудное значение переменного напряжения U_m к его действующему значению U

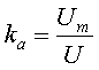
Так для синусоидального напряжения коэффициент амплитуды составит

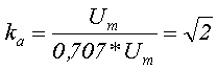
На сегодня всё, в следующей статье я рассмотрю прохождение переменного напряжения через сопротивление, индуктивность и емкость.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

2.9. Действующее и среднее значения переменного тока и напряжения

Действующим значением переменного тока или напряжения называют корень квадратный от интеграла квадрата мгновенных значений тока или напряжения на периоде повторения.

Пользуясь определением, найдем действующее значение синусоидального тока:

После аналогичных вычислений для напряжения получим:

Таким образом, действующие значения переменного тока и напряжения меньше их амплитудных значений в раз.

Действующее значение переменного тока в одной и той же нагрузке r способствует выделению такой тепловой энергии, которая выделилась бы, если по нагрузке пропустить постоянный ток той же величины.

В комплексном виде действующие значения напряжения и тока имеют вид:

;

Средним по модулю значением напряжения или тока, называют интеграл от модуля мгновенного значения тока или напряжения на периоде повторения.

Найдем среднее значение переменного напряжения:

Средние значения напряжения и тока меньше их амплитудных значений в раз. То есть для действующего значения тока: I = 0,707 I_m, а для среднего значения

тока: I_cp = 0,637 I_m .

Активное сопротивление. Действующие значения силы тока и напряжения

Активное сопротивление. Действующие значения силы тока и напряжения

Подробности

Просмотров: 401

«Физика — 11 класс»

Активное сопротивление

Сила тока в цепи с резистором

Есть цепь, состоящая из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R.

Сопротивление R называется активным сопротивлением, т.к. при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора.

Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.

Напряжение на зажимах цепи меняется по гармоническому закону:

u = U_m cos ωt

Мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения.

По закону Ома мгновенное значение силы тока:

В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряжения, а амплитуда силы тока определяется равенством

Мощность в цепи с резистором

В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение меняются.

При прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет меняться во времени.

Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой

Р = I²R

Мгновенная мощность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой

Р = i²R

Cреднее значение мощности за период (используем формулу для мгновенного значения силы тока и выражение ):

График зависимости мгновенной мощности от времени (рис.а):

Согласно графику (рис.б) среднее за период значение cos 2ωt равно нулю, а значит равно нулю второе слагаемое в формуле для среднего значения мощности за период.

Тогда средняя мощность равна:

Действующие значения силы тока и напряжения.

Среднее за период значение квадрата силы тока:

Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы переменного тока.

Действующее значение силы переменного тока обозначается через I:

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.

Действующее значение переменного напряжения определяется аналогично:

Закон Ома для участка цепи переменного тока с резистором в действующих значениях:

В случае электрических колебаний важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность.

Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.

Действующие значения непосредственно определяют среднее значение мощности Р переменного тока:

р = I²R = UI.

Итак:

Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Электромагнитные колебания. Физика, учебник для 11 класса — Класс!ная физика

Свободные и вынужденные электромагнитные колебания. Колебательный контур. Превращение энергии при электромагнитных колебаниях —
Аналогия между механическими и электромагнитными колебаниями —
Уравнение, описывающее процессы в колебательном контуре. Период свободных электрических колебаний —
Переменный электрический ток —
Активное сопротивление. Действующие значения силы тока и напряжения —
Конденсатор в цепи переменного тока —
Катушка индуктивности в цепи переменного тока —
Резонанс в электрической цепи —
Генератор на транзисторе. Автоколебания —
Краткие итоги главы

Эффективные значения тока и напряжения

Задание: Как связана мощность переменного тока на сопротивлении $R$ и эффективные значения тока и напряжения?

Решение:

Среднее значение мощности переменного тока в цепи равно

\[\left\langle P\right\rangle =\frac{A_T}{T}=\frac{U_mI_mcos\varphi }{2}\left(2.1\right),\]

где $cos\varphi $- коэффициент мощности, который показывает эффективность передачи мощности от источника тока к потребителю. С другой стороны средние мощности тока на отдельных элементах цепи $\left\langle P_{tC}\right\rangle =0,\left\langle P_{tL}\right\rangle =0,\left\langle P_{tR}\right\rangle =\frac{1}{2}{I^2}_mR,$ а результирующая мощность может быть найдена как сумма мощностей:

\[\left\langle P\right\rangle =\left\langle P_{tC}\right\rangle +\left\langle P_{tL}\right\rangle +\left\langle P_{tR}\right\rangle \left(2.2\right).\]

Следовательно, можно записать, что:

\[\left\langle P\right\rangle =P_{tR}=\frac{1}{2}{I^2}_mR=\frac{U_mI_mcos \varphi}{2}\left(2.3\right),\]

где $I_m\ $- амплитуда силы тока, $U_m$ — амплитуда внешнего напряжения, $\varphi$ — разность фаз между силой тока и напряжением.

У постоянного тока мгновенная мощность совпадает со средней. Для $I_{ef}$=const можно положить $cos\varphi =1,\ $значит формулу (2.3) можно записать как:

\[P=I_{ef}U\ \left(2.4\right),\]

если вместо амплитудных значений ($U_m\ и\ I_m$) использовать их эффективные (действующие) значения:

\[I_{ef}=\frac{I_m}{\sqrt{2}},\ U_{ef}=\frac{U_m}{\sqrt{2}}\left(2.5\right).\]

Следовательно, мощность тока можно записать как:

\[P_{tR}=U_{ef}I_{ef}cos \varphi \left(2.6\right),\]

где $cos \varphi$ — коэффициент мощности. В технике этот коэффициент делают как можно большим. При малом $cos\varphi $ для того, чтобы в цепи выделялась необходимая мощность нужно пропускать большой ток, что ведет к росту потерь в подводящих проводах.

Такую же мощность (как в выражении (2.3)) развивает постоянный ток, сила которого представлена в формуле (2.5).

Ответ: $P_{tR}=U_{ef}I_{ef}cos\varphi .$

Среднее и действующее значения синусоидально изменяющейся величины

Среднее значение

Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за полпериода.

Среднее значение тока:

т. е. среднее значение синусоидального тока составляет 2/π = 0,638 от амплитудного. Аналогично, Eср = 2Ем/π ; Ucp = 2Uм/π.

Действующее значение

Широко применяют понятие действующего значения синусоидально изменяющейся величины (его называют также эффективным или среднеквадратичным).

Действующее значение тока:

Следовательно, действующее значение синусоидального тока равно 0,707 от амплитудного. Аналогично 

Можно сопоставить тепловое действие синусоидального тока с тепловым действием постоянного тока, текущего то же время по тому же сопротивлению.

Количество теплоты, выделенное за один период синусоидальным током,

Выделенная за то же время постоянным током теплота равна RI^2_пост Т. Приравняем их:

Таким образом, действующее значение синусоидального тока I численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.

Большинство измерительных приборов показывает действующее значение измеряемой величины.

Калькулятор напряжения

RMS — Дюймовый калькулятор

Рассчитайте среднеквадратичное значение напряжения с учетом пика или размаха напряжения с помощью калькулятора ниже.

Преобразование пикового напряжения в среднеквадратичное значение

Преобразование размаха напряжения в напряжение RMS

Вы хотите рассчитать пиковое напряжение или размах напряжения?

Как рассчитать действующее значение напряжения

Среднеквадратичное значение напряжения или среднеквадратичное значение напряжения — это квадратный корень из среднего квадратов напряжений в форме волны переменного тока.Например, если в форме сигнала выбрано 100 значений напряжения, среднеквадратичное значение будет равно квадратному корню из всех напряжений, возведенных в квадрат, сложенных вместе и разделенных на 100.

Следующая формула показывает, как найти среднеквадратичное значение напряжения по выборке напряжений.

V _RMS = √ V ₁ ² + V ₂ ² +… + V _n ² n

Вы также можете найти среднеквадратичное значение напряжения, если знаете пиковое напряжение или размах напряжения.

Диаграмма, показывающая пиковое напряжение, размах напряжения и среднеквадратичное значение напряжения на осциллограмме переменного тока.

Формула между пиковым напряжением и среднеквадратичным напряжением

Учитывая пиковое напряжение, среднеквадратичное напряжение можно рассчитать по этой формуле, где V _P — пиковое напряжение.

В _СКЗ = 1√2 × В _P

Другими словами, действующее значение напряжения равно единице, деленной на квадратный корень из двух значений пикового напряжения.

Например, найдите среднеквадратичное напряжение, используя пиковое напряжение 120 В.

В _СКЗ = 1√2 × 120 В
В _СКЗ = 0,7071 × 120 В
В _СКЗ = 84,8528 В

Формула между размахом и среднеквадратичным напряжением

Среднеквадратичное напряжение также можно найти, если известно размах напряжения, используя эту формулу, где V _P-P — это размах напряжения.

V _RMS = 12 × √2 × V _P-P

Таким образом, среднеквадратичное значение напряжения равно единице, деленной на двукратный корень квадратный из двух, умноженный на пиковое напряжение.

Например, давайте найдем среднеквадратичное значение напряжения, используя размах напряжения 24 В.

В _СКЗ = 12 × √2 × 24 В
В _СКЗ = 0,3536 × 24 В
В _СКЗ = 8,4853 В

.Калькулятор среднеквадратичного напряжения

Этот калькулятор среднеквадратичного напряжения помогает найти значение среднеквадратичного напряжения из известных значений пикового напряжения, размаха напряжения или среднего напряжения. Он вычисляет среднеквадратичное значение напряжения на основе заданных уравнений.

Как рассчитать действующее значение напряжения?

RMS (среднеквадратичное значение) Напряжение (В _rms )

Среднеквадратичное значение каждого сигнала является эквивалентным напряжению постоянного тока.Давайте возьмем пример, если среднеквадратичное значение синусоидального сигнала составляет 10 вольт, это означает, что вы можете подавать такое же количество энергии через источник постоянного тока 10 вольт. Не путайте среднее напряжение и среднеквадратичное напряжение, поскольку они не равны.

Пиковое напряжение (В _p )

A Пиковое напряжение синусоидальной волны измеряется от горизонтальной оси (которая берется из контрольной точки 0) до пика (который является верхним или максимальным уровнем напряжения) формы волны. Пиковое напряжение показывает амплитуду сигнала .

Vp = √2 * Vrms 

По этой формуле мы можем получить значение V _rms относительно пикового напряжения.

V  rms  = 0,7071 * V  p  

Пиковое напряжение (В _pp )

Разница между максимальным пиковым напряжением и минимальным пиковым напряжением, или сумма положительной и отрицательной амплитуды пиков, известна как межпиковое напряжение .

V  pp  = 2√2 * V  rms  

По этой формуле мы можем получить значение V _rms по отношению к размаху напряжения.

V  rms  = 0,35355 * V  pp  

Среднее напряжение (В _ср. )

Среднее значение синусоидальной волны равно нулю, потому что область, покрытая положительным полупериодом, аналогична области отрицательного полупериода, поэтому эти значения компенсируют друг друга, когда берется среднее значение.Тогда среднее значение измеряется только за полупериод, обычно мы берем для измерения положительную часть полупериода.

Среднее напряжение, определяемое как «отношение площади под формой сигнала к времени».

В  ср.  = 2√2 / π * В  среднеквадр.  

По этой формуле мы можем получить значение V _rms по отношению к размаху напряжения.

V  rms  = 1.1107 * V  в среднем  

.

Среднее и среднеквадратичное напряжение — Electronics-Lab.com

Введение

В режиме постоянного тока возможно только одно определение значения напряжения, это значение является однозначным и определяется разницей между опорным значением 0 В и плоской линией сигнала постоянного тока.

Однако в режиме переменного тока может возникнуть путаница, если будет указано только одно значение напряжения. Из простого синусоидального сигнала мы можем по крайней мере перечислить четыре различных определения напряжения:

рис.1: Изображение пикового, среднего и среднеквадратичного значений

Пиковое значение соответствует разнице между опорным значением (которое является значением, в котором колеблется сигнал переменного тока) и максимальным значением сигнала.Пиковое значение — это пиковое значение, умноженное на коэффициент 2, оно соответствует общей вертикальной ширине сигнала.

На рис. 1 мы также выделили красным цветом значения Среднее и RMS , на которых мы сосредоточимся в дальнейшем в этом руководстве.

В двух разделах, разработанных в этой статье, будут отдельно представлены значения Average и RMS , мы увидим, как они определяются, как их определять, и, наконец, мы увидим, что особенного в среднеквадратичном значении.

Среднее напряжение

Для элементарного симметричного синусоидального, треугольного, квадратного или пилообразного сигнала (см. , рис. 2, и учебное пособие по форме сигнала переменного тока) неясно говорить о среднем значении напряжения, которое мы отметим A ниже. Действительно, эти типы сигналов в течение половины своего периода являются положительными, а в другой — отрицательными. Другими словами, сигналы 50% времени находятся выше горизонтальной оси и 50% ниже нее.

Из этого наблюдения легко понять, что если мы рассмотрим среднее значение любого из этих сигналов за полный период, оно будет равно 0 , независимо от пикового значения, и, следовательно, не имеет значения.

рис. 2: Элементарные синусоидальные, треугольные, квадратные и пилообразные формы сигналов

Мы можем продемонстрировать этот результат, объяснив, как вычислить среднее значение. Для конечного набора значений процесс усреднения состоит из суммирования всех значений (V ₁ , V ₂ , V ₃ …) и их деления на кардинальное число N набора (сколько значений имеется в комплекте):

Однако для аналогового сигнала невозможно суммировать все мгновенные значения, также называемые средними ординатами, которые принимает сигнал в течение периода, просто потому, что существует бесконечность.Вместо суммирования используем операцию интегрирования:

уравнение 1: Среднее значение сигнала переменного тока V (t) за полный период

Уравнение 1 представляет собой среднее значение сигнала V (t), взятого между моментами времени 0 и T, то есть за полный период. Член ∫V (t) dt дает значение площади между кривой V (t) и опорным значением 0 В. Поскольку операция интегрирования является линейной, этот член можно разделить на две части:

Для элементарной формы волны, такой как представлена ​​на Рис. 1 , мы можем видеть, что первый и второй члены этой формулы равны, но имеют противоположные знаки, поэтому среднее значение равно 0.

Для того, чтобы среднее значение таких сигналов имело смысл, мы предпочитаем рассматривать отдельно половину положительного и отрицательного периодов, некоторые их значения соответственно выделены красным и зеленым цветом на следующем рисунке. Рисунок 3 :

рис. 3: Некоторые мгновенные значения для положительного полупериода (красным) и отрицательного полупериода (зеленым) синусоидального сигнала

Аналогично уравнению 1 , мы можем определить отдельно средние значения для положительного полупериода (A ₊ ) и отрицательного полупериода (A _—):

уравнение 3: Средние значения переменного сигнала V (t), взятые для положительного (+) и отрицательного (-) полупериодов

Значение A ₊ и A _— зависит от сигнала, с которым мы имеем дело, и их соответствующие пиковые значения (V _p ) _. Мы перечисляем ниже абсолютное значение | A | A + и A _— для наиболее распространенных элементарных и симметричных сигналов переменного тока :

• Форма синусоидального сигнала: | A | = 0,637 × V _p
• Треугольник: | A | = 0
• Прямоугольная форма сигнала: | A | = V _p
• Форма пилообразного сигнала: | A | = 0,5 × V _p

Мы можем завершить этот раздел, сказав, что когда мы хотим усреднить сигнал, нам нужно указать точность, если процесс выполняется на полном периоде или меньшем значении.Для элементарных и симметричных сигналов переменного тока усреднение по всему периоду всегда дает результат 0 В независимо от частоты, пикового значения или периода. По этой причине более целесообразно усреднять эти сигналы в течение их полупериодов.

Действующее значение напряжения

RMS обозначает среднеквадратическое значение, это операция, аналогичная приведенной ранее усредненной величине, но вместо этого мгновенные значения возводятся в квадрат, а общая дробь определяется корнем:

По тем же причинам, что указывалось ранее, мы используем операцию интегрирования для определения V _RMS для аналогового сигнала:

уравнение 4: Среднеквадратичное значение сигнала переменного тока V (t) периода T

В отличие от среднего значения, среднеквадратичное значение всегда определяется для полного периода сигнала, действительно нет никакой путаницы при определении этого значения.

В качестве примера давайте определим среднеквадратичное значение синусоидального сигнала с пиковым значением V _p и угловой пульсацией ω V (t) = V _p × sin (ωt) . Отметим f частоту, которая удовлетворяет f = ω / 2π и T = 1 / f периоду.

Прежде всего, мы вычисляем интегральный член, который мы отмечаем I:

Мы используем тригонометрическую идентичность sin ² (x) = (1-cos (2x)) / 2 , чтобы продолжить:

Вычисление члена скобки между 0 и T дает 2π / ω = T .Следовательно, член интегрирования в итоге равен (πV _p ² ) / ω . Из уравнения (4) видно, что нам все еще нужно умножить на 1 / T, что приводит к [(πV _p ² ) / ω] × [ω / (2π)] = V _p ² /2 на срок под корень.

Наконец, после извлечения корня окончательное выражение для среднеквадратичного значения синусоидального сигнала дается следующим образом:

Мы перечисляем ниже среднеквадратичные значения, которые можно вычислить тем же методом, что и в приведенном выше примере синуса для элементарных и симметричных сигналов, указанных в предыдущем разделе:

• Форма синусоидального сигнала: V _RMS = V _p / √2
• Треугольник и пилообразный сигнал: V _RMS = V _p / √3
• Прямоугольная форма сигнала: В _RMS = В _P

Важно отметить, что V _RMS > | A |, значение RMS всегда больше, чем абсолютное значение среднего.

Что важно для понимания значения RMS, так это то, что оно создает связь между режимами постоянного и переменного тока в соответствии со следующим Рисунок 4 :

рис. 4: Сходство между режимами переменного и постоянного тока

Среднеквадратичные значения напряжения и тока представляют собой значения, которые развивают ту же мощность на сопротивлении в режиме постоянного тока.

Заключение

Средние и среднеквадратичные значения можно легко измерить современными вольтметрами или осциллографами и предоставить информацию о сигнале переменного тока.

Численный подход к усреднению состоит в суммировании всех значений сигнала и делении суммы на количество значений. Для реальных сигналов мы предпочитаем использовать операцию интегрирования, которая является расширением суммы для бесконечного набора значений.

Для среднего значения возможны два определения, в зависимости от того, выполняется ли среднее за полный период или за полупериод. Симметричные сигналы характеризуются средним значением 0 за полный цикл . Среднее значение за полный цикл отличается от 0 только в том случае, если в сигнале присутствует составляющая постоянного тока или если сигнал не является симметричным относительно горизонтального эталона.Усреднение по полупериоду также может быть выполнено для характеристики различных симметричных сигналов.

Среднеквадратичное значение определяется аналогично среднему значению, но вместо этого каждое значение суммы возводится в квадрат, и окончательный результат коренится. Среднеквадратичное значение всегда выше, чем абсолютное значение среднего, и устанавливает связь между режимами переменного и постоянного тока, поэтому его особенно используют инженеры.

.Калькулятор среднеквадратичного напряжения

— от среднего значения, пикового и пикового значения к пиковому значению

Калькулятор среднеквадратичного значения напряжения

Этот калькулятор можно использовать для расчета среднеквадратичного значения напряжения ( _RMS В) синусоидальной волны из различных связанных значений например, среднее значение (V _AV ), пиковое или максимальное значение (V _P или V _MAX ) и значение от пика до пика (V _PP ).

Как рассчитать действующее значение напряжения?

Как уже говорилось ранее о среднеквадратичном (RMS) или V _RMS напряжении, это эквивалентное постоянное напряжение синусоидальной волны i.е. если среднеквадратичное значение напряжения составляет 230 В _{переменного тока} , генерирующего 60 Вт тепла при подключении к нагревательному элементу, например резистору, такое же количество тепла может генерироваться через источник постоянного напряжения 230 В _DC при подключении к тому же нагревательному элементу, что и ранее в цепи переменного тока.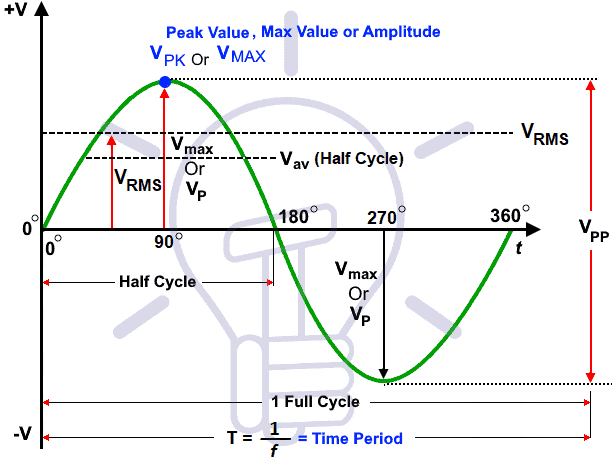

Мы покажем различные уравнения для расчета среднеквадратичного напряжения с примененными формулами и решенными примерами, как показано ниже.

Связанный калькулятор: 3, 4, 5 и 6-полосный калькулятор значений резисторов

Уравнения для калькулятора среднеквадратичных значений

Поскольку калькулятор среднеквадратичного напряжения связан со средним значением (В _AV ), пиковым или максимальным значением (VP или V) _MAX ) и от пика до пика (V _PP ), следующие соответствующие уравнения для калькулятора RMS напряжения показаны на рис.2.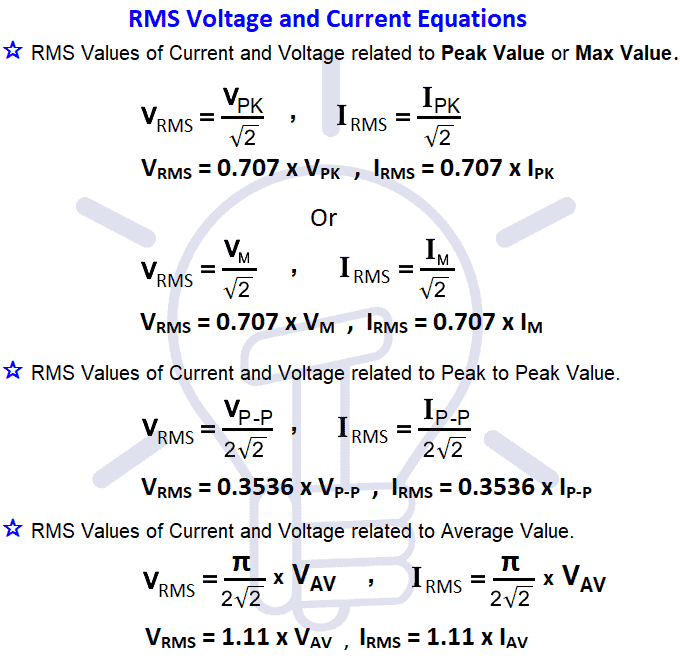

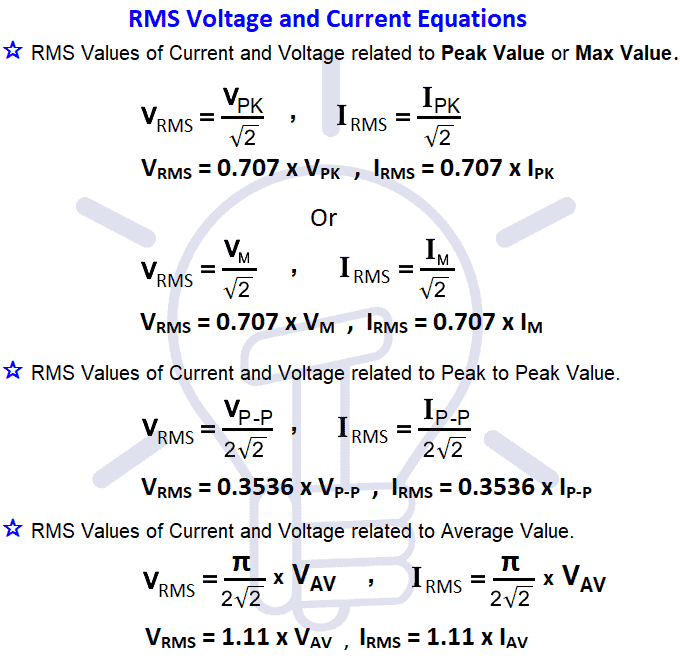
Пиковое значение: V _P или V _MAX

Максимальное положительное или отрицательное значение переменной величины (например, напряжения или тока) известно как ее амплитуда формы волны, максимальное значение или пиковое значение. Обозначается V _P , I _P или E _MAX и I _MAX .

В _P = √2 x V _RMS

Используя приведенную выше формулу, мы можем найти значение RMS напряжения следующим образом:

V _RMS = 0.7071 x В _P

Пример:

Предположим, что значение пикового напряжения составляет 325 В переменного тока, значение RMS напряжения будет:

В _RMS = 0,7071 x 350 В = 229,80 В _RMS

От пика до пика Значение (V _PP )

Сумма положительных и отрицательных пиковых значений в синусоиде называется величиной от пика до пика. Выражается как I _PP или V _PP .

В _PP = 2√2 x V _RMS

Используя приведенную выше формулу, мы можем найти значение RMS напряжения следующим образом:

V _RMS = 0,35355 x V _PP

Пример:

Предположим, что значение пик-пикового напряжения равно 340 В переменного тока, значение RMS напряжения будет:

В _RMS = 0,35355 x 340 В = 120,2 В _RMS

Связанные калькуляторы:

Среднее напряжение Значение (В _AV )

Если мы преобразуем синусоидальную волну переменного тока в волну постоянного тока (DC) через выпрямители, то преобразованное значение в постоянное будет известное как среднее значение этой синусоидальной волны переменного тока.

Имейте в виду, что среднее значение напряжения полной синусоидальной волны переменного тока равно нулю, потому что площадь, покрытая положительными полупериодами, равна площади, покрытой отрицательными полупериодами, которые компенсируют друг друга. Вот почему мы не можем использовать переменный ток для хранения батарей.

Мы используем только полуволны для измерения среднего значения напряжения или тока переменного тока.

В _AV = (2√2) / π x V _RMS

Используя приведенную выше формулу, мы можем найти значение RMS напряжения следующим образом:

V _RMS = 1.11 x V _AV

Пример:

Предположим, что среднее значение напряжения равно 200VAC, значение RMS Voltage будет:

V _RMS = 1,11 x 200V = 222 V _RMS

Связанное сообщение:

.