Формула закона электромагнитной индукции. Формула эдс индукции

Формула ЭДС индукции, E

Закон Фарадея – Максвелла для электромагнитной индукции

Основной формулой, которая определяет ЭДС индукции, является закон Фарадея – Максвелла, больше известный как основной закон электромагнитной индукции (или закон Фарадея). Этот закон утверждает, что ЭДС индукции в контуре, находящемся в переменном магнитном поле, равна по величине и противоположна по знаку скорости изменения магнитного потока () через поверхность, которую ограничивает данный контур:

   

где – скорость изменения магнитного потока. Полная производная в законе (1) охватывает весь спектр причин изменения магнитного потока через поверхность контура. Знак минус в формуле (1) соответствует правилу Ленца. Формула (1) для ЭДС индукции записана для системы СИ.

В случае равномерного изменения магнитного потока формулу ЭДС индукции можно записать как:

   

Частные случаи формул ЭДС индукции

Если контур содержит N витков, которые соединяются последовательно, то ЭДС индукции вычисляют как:

   

где – потокосцепление.

При движении прямолинейного проводника в однородном магнитном поле в нем возникает ЭДС индукции, которая равна:

   

где v – скорость движения проводника; l – длина проводника; B – модуль вектора магнитной индукции поля; .

При вращении с постоянной скоростью в однородном магнитном поле плоского контура вокруг оси, которая лежит в плоскости контура в нем возникает ЭДС индукции, равная:

   

где S – площадь, которую ограничивает виток; – поток самоиндукции витка; — угловая скорость; () – угол поворота контура. Следует учесть, что формула (5) справедлива, если ось вращения составляет прямой угол с направлением вектора внешнего поля .

Если во вращающейся рамке имеется N витков и самоиндукцией рассматриваемой системы можно пренебречь, то:

   

В стационарном проводнике, который находится в переменном магнитном поле, ЭДС индукции находят по формуле:

   

Примеры решения задач по теме «ЭДС индукции»

ru.solverbook.com

ЭДС индукции в движущихся проводниках формула

ЭДС индукции и сила Лоренца

Появление электродвижущей силы (ЭДС) в телах, перемещающихся в магнитном поле легко объяснить, если вспомнить о существовании силы Лоренца. Пусть стержень движется в однородном магнитном поле с индукцией рис.1. Пусть направление скорости движения стержня () и перпендикулярны друг другу.

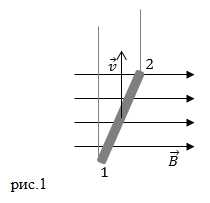
Между точками 1 и 2 стержня индуцируется ЭДС, которая направлена от точки 1 к точке 2. Движение стержня – это перемещение положительных и отрицательных зарядов, которые входят в состав молекул этого тела. Заряды вместе с телом перемещаются в сторону движения стержня. Магнитное поле оказывает воздействие на заряды при помощи силы Лоренца, пытаясь переместить положительные заряды в сторону точки 2, а отрицательные заряды к противоположному концу стержня. Так, действие силы Лоренца порождает ЭДС индукции.

Если в магнитном поле движется металлический стержень, то положительные ионы, находясь в узлах кристаллической решетки, не могут двигаться вдоль стержня. При этом подвижные электроны скапливаются в избытке на конце стержня около точки 1. Противоположный конец стержня будет испытывать недостаток электронов. Появившееся напряжение определяет собой ЭДС индукции.

В том случае, если движущийся стержень сделан из диэлектрика, разделение зарядов при воздействии силы Лоренца, приводит к его поляризации.

ЭДС индукции будет равна нулю, если проводник перемещается параллельно направлению вектора (то есть угол между и равен нулю).

ЭДС индукции в прямом проводнике, движущемся в магнитном поле

Получим формулу для вычисления ЭДС индукции, которая возникает в прямолинейном проводнике, имеющем длину l, движущемся параллельно самому себе в магнитном поле (рис.2). Пусть v – мгновенная скорость проводника, тогда за время он опишет площадь равную:

   

При этом проводник пересечет все линии магнитной индукции, которые проходят через площадку . Получим, что изменение магнитного потока () сквозь контур в который входит перемещающийся проводник:

   

где – составляющая магнитной индукции, перпендикулярная к площадке . Подставим выражение для (2) в основной закон электромагнитной индукции:

   

получим:

   

При этом направление тока индукции определено законом Ленца. То есть индукционный ток имеет такое направление, что механическая сила, которая действует на проводник, замедляет перемещение проводника.

ЭДС индукции в плоском витке, вращающемся в магнитном поле

Если плоский виток вращается в однородном магнитном поле, угловая скорость его вращения равна , ось вращения находится в плоскости витка и , тогда ЭДС индукции можно найти как:

   

где S – площадь, которую ограничивает виток; – поток самоиндукции витка; – угловая скорость; () – угол поворота контура. Необходимо заметить, что выражение (5) справедливо, тогда, когда ось вращения составляет прямой угол с направлением вектора внешнего поля .

Если вращающаяся рамка имеет N витков и ее самоиндукцией можно пренебречь, то:

   

Примеры решения задач

ru.solverbook.com

ЭДС индукции в движущихся проводниках

ЭДС – это аббревиатура трех слов: электродвижущая сила. ЭДС индукции () появляется в проводящем теле, которое находится в переменном магнитном поле. Если проводящим телом является, например, замкнутый контур, то в нем течет электрический ток, который называют током индукции.

Закон Фарадея для электромагнитной индукции

Основным законом, который используют при расчетах, связанных с электромагнитной индукцией является закон Фарадея. Он говорит о том, что электродвижущая сила электромагнитной индукции в контуре равна по величине и противоположна по знаку скорости изменения магнитного потока () сквозь поверхность, которую ограничивает рассматриваемый контур:

   

Закон Фарадея (1) записан для системы СИ. Надо учитывать, что из конца вектора нормали к контуру обход контура должен проходить против часовой стрелки. Если изменение потока происходит равномерно, то ЭДС индукции находят как:

   

Магнитный поток, который охватывает проводящий контур, может изменяться в связи с разными причинами. Это может быть и изменяющееся во времени магнитное поле и деформация самого контура, и перемещение контура в поле. Полная производная от магнитного потока по времени учитывает действие всех причин.

ЭДС индукции в движущемся проводнике

Допустим, что проводящий контур перемещается в постоянном магнитном поле. ЭДС индукции возникает во всех частях контура, которые пересекают силовые линии магнитного поля. При этом, результирующая ЭДС, появляющаяся в контуре будет равна алгебраической сумме ЭДС каждого участка. Возникновение ЭДС в рассматриваемом случае объясняют тем, что на любой свободный заряд, который движется вместе с проводником в магнитном поле, будет действовать сила Лоренца. При воздействии сил Лоренца заряды движутся и образуют в замкнутом проводнике ток индукции.

Рассмотри случай, когда в однородном магнитном поле находится прямоугольная проводящая рамка (рис.1). Одна сторона рамки может двигаться. Длина этой стороны равна l. Это и будет наш движущийся проводник. Определим, как можно вычислить ЭДС индукции, в нашем проводнике, если он перемещается со скоростью v. Величина индукции магнитного поля равна B. Плоскость рамки перпендикулярна вектору магнитной индукции. Выполняется условие .

ЭДС индукции в рассматриваемом нами контуре будет равна ЭДС, которая возникает только в подвижной его части. В стационарных частях контура в постоянном магнитном поле индукции нет.

Для нахождения ЭДС индукции в рамке воспользуемся основным законом (1). Но для начала определимся с магнитным потоком. По определению поток магнитной индукции равен:

   

где , так как по условию плоскость рамки перпендикулярна направлению вектора индукции поля, следовательно, нормаль к рамке и вектор индукции параллельны. Площадь, которую ограничивает рамка, выразим следующим образом:

   

где – расстояние, на которое перемещается движущийся проводник. Подставим выражение (2), с учетом (3) в закон Фарадея, получим:

   

где v – скорость движения подвижной стороны рамки по оси X.

Если угол между направлением вектора магнитной индукции () и вектором скорости движения проводника () составляет угол , то модуль ЭДС в проводнике можно вычислить при помощи формулы:

   

Примеры решения задач

ru.solverbook.com

Формулы электромагнитной индукции

Если проводник замкнут, то есть является контуром, то в нем появляется ток индукции. Явление было открыто в 1831 г. М. Фарадеем.

Основной закон электромагнитной индукции

Основной формулой, при помощи которой определяют ЭДС индукции (), является закон Фарадея – Максвелла, больше известный как основной закон электромагнитной индукции (или закон Фарадея). В соответствии с данным законом, электродвижущая сила индукции в контуре, находящемся в переменном магнитном поле, равна по модулю и противоположна по знаку скорости изменения магнитного потока () через поверхность, которую ограничивает рассматриваемый контур:

   

где – скорость изменения магнитного потока. Полная производная присутствующая в формуле (1) охватывает весь спектр причин изменения магнитного потока через поверхность контура. Знак минус в формуле (1) отвечает правилу Ленца. В виде (1) формула ЭДС записана для международной системы единиц (СИ), в других системах вид закона может отличаться.

При равномерном изменении магнитного потока основной закон электромагнитной индукции записывают как:

   

Формулы ЭДС индукции для частных случаев

ЭДС индукции для контура имеющего N витков, находящегося в переменном магнитном поле можно найти как:

   

где – потокосцепление.

Если прямолинейный проводник движется в однородном магнитном поле, то в нем появляется ЭДС индукции, равная:

   

где v – скорость движения проводника; l – длина проводника; B – модуль вектора магнитной индукции поля; .

Разность потенциалов (U) на концах прямого проводника, движущегося в однородном магнитном поле с постоянной скоростью будет равна:

   

где – угол между направлениями векторов и .

При вращении плоского контура с постоянной скоростью в однородном магнитном поле вокруг оси, которая лежит в плоскости контура в нем появляется ЭДС индукции, которую можно вычислить как:

   

где S – площадь, которую ограничивает виток; – поток самоиндукции витка; — угловая скорость; () – угол поворота контура. Необходимо заметить, что формула (5) применима, в случае, если ось вращения составляет прямой угол с направлением вектора внешнего магнитного поля .

Если вращающаяся рамка обладает N витками, при этом самоиндукцией рассматриваемой системы можно пренебречь, то:

   

Если проводник неподвижен в переменном магнитном поле, то ЭДС индукции можно найти как:

   

Примеры решения задач по теме «Электромагнитная индукция»

ru.solverbook.com

Способы определения ЭДС индукции в движущихся проводниках

 

Нахождение ЭДС индукции через силу Лоренца

Магнитный поток через контур может изменяться по следующим причинам:

В обоих этих случаях будет выполняться закон электромагнитной индукции. При этом происхождение электродвижущей силы в этих случаях различное. Рассмотрим подробнее второй из этих случаев

В данном случае проводник движется в магнитном поле. Вместе с проводником совершают движение и все заряды, которые находятся внутри проводника. На каждый из таких зарядов со стороны магнитного поля будет действовать сила Лоренца. Она и будет способствовать перемещению зарядов внутри проводника.

• ЭДС индукции в данном случае будет иметь магнитное происхождение.

Рассмотрим следующий опыт: магнитный контур, у которого одна сторона подвижная, помещают в однородное магнитное поле. Подвижная сторона длиной l начинает скользить вдоль сторон MD и NC с постоянной скоростью V. При этом она постоянно остаётся параллельной стороне СD. Вектор магнитной индукции поля будет перпендикулярен проводнику и составлять угол а с направлением его скорости. На следующем рисунке представлена лабораторная установка для этого опыта:

Сила Лоренца, действующая на движущуюся частицу, вычисляется по следующей формуле:

Fл = |q|*V*B*sin(a).

Сила Лоренца будет направлена вдоль отрезка MN. Рассчитаем работу силы Лоренца:

A = Fл*l = |q|*V*B*l*sin(a).

ЭДС индукции - это отношение работы, совершаемой силой при перемещении единичного положительного заряда, к величине этого заряда. Следовательно, имеем:

Ei = A/|q| = V*B*l*sin(a).

Эта формула будет справедлива для любого проводника, движущегося в с постоянной скоростью в магнитном поле. ЭДС индукции будет только в этом проводнике, так как остальные проводники контура остаются неподвижными. Очевидно, что ЭДС индукции во всем контуре будет равняться ЭДС индукции в подвижном проводнике.

ЭДС из закона электромагнитной индукции 

Магнитный поток через тот же контур, что и в примере выше, будет равняться: 

Ф = B*S*cos(90-a) = B*S*sin(a).

Здесь угол (90-а) = угол между вектором магнитной индукции и нормалью к поверхности контура. За некоторое время ∆t площадь контура будет изменяться на ∆S = -l*V*∆t. Знак «минус» показывает, что площадь уменьшается. При этом за это время магнитный поток изменится:

∆Ф = -B*l*V*sin(a).

Тогда ЭДС индукции равна:

Ei = -∆Ф/∆t = B*l*V*sin(a).

Если весь контур будет двигаться внутри однородного магнитного поля с постоянной скоростью, то ЭДС индукции будет равняться нулю, так как будет отсутствовать изменение магнитного потока.

• ЭДС индукции будет возникать и при повороте рамки внутри магнитного поля.

Нужна помощь в учебе?

Предыдущая тема: Закон электромагнитной индукции:магнитный поток и электродвижущая сила Следующая тема:&nbsp&nbsp&nbspЭлектродинамический микрофон: самоиндукция

Все неприличные комментарии будут удаляться.

www.nado5.ru

ЭДС индукции, теория и примеры задач

Если контур является замкнутым, то в нем течет электрический ток, который называют током индукции.

Закон электромагнитной индукции Фарадея

Электродвижущая сила электромагнитной индукции в контуре равна по величине и противоположна по знаку скорости изменения магнитного потока () сквозь поверхность, которую ограничивает рассматриваемый контур:

   

Закон Фарадея (1) записан для системы СИ. Надо учитывать, что из конца вектора нормали к контуру обход контура должен проходить против часовой стрелки.

Закон для ЭДС индукции в том случае, когда контур состоит из N витков, соединенных последовательно, записывают в виде:

   

Знак минус в законе индукции отражает правило Ленца.

Магнитный поток, который охватывает проводящий контур, может изменяться в связи с разными причинами. Это может быть и изменяющееся во времени магнитное поле и деформация самого контура, и перемещение контура в поле. Полная производная от магнитного потока по времени учитывает действие всех причин.

Допустим, что проводящий контур перемещается в постоянном магнитном поле. ЭДС индукции возникает во всех частях контура, которые пересекают силовые линии магнитного поля. При этом, суммарная ЭДС, появляющаяся в контуре равна алгебраической сумме ЭДС каждого участка. Возникновение ЭДС в рассматриваемом случае объясняют тем, что на любой свободный заряд, который движется вместе с проводником в магнитном поле, будет действовать сила Лоренца:

   

где – скорость движения проводника; — скорость движения заряда по отношению к проводнику. При воздействии сил Лоренца заряды движутся и образуют в замкнутом проводнике ток индукции.

Некоторые примеры ЭДС индукции

ЭДС индукции в прямолинейном проводнике длины l, перемещающемся в магнитном поле и пересекающем линии магнитной индукции, если скорость его движения () перпендикулярна вектору магнитной индукции (), равна:

   

В плоском контуре, который вращается в однородном магнитном поле со скоростью , причем ось вращения находится в плоскости витка и составляет угол в 90o с направлением вектора внешнего магнитного поля, возникает ЭДС индукции равная:

   

где S – площадь, которую ограничивает виток; – поток самоиндукции витка.

ЭДС индукции в проводнике, которые не движется, а изменяется магнитное поле, находят как:

   

Если изменение потока происходит равномерно, то ЭДС индукции находят как:

   

Примеры решения задач

ru.solverbook.com

Формула закона электромагнитной индукции

Это основной закон, который используют при вычислениях, которые связаны с электромагнитной индукцией.

Формула данного закона выглядит следующим образом:

   

где – электродвижущая сила (ЭДС) индукции, которая возникает в проводнике, если он находится в переменном магнитном поле. Если проводящим телом является, например, замкнутый контур, то в нем течет электрический ток, который называют током индукции. – магнитный поток, через поверхность, ограниченную этим контуром. Формула (1) означает то, что ЭДС индукции равна по модулю и противоположна по знаку скорости изменения магнитного потока через некоторую поверхность.

Магнитный поток, который пронизывает контур, может изменяться из-за разных причин, например, перемещения контура, его деформации, изменения самого магнитного поля. Полная производная в формуле закона электромагнитной индукции охватывает весь спектр действия этих причин.

Следует учесть, что из конца вектора нормали к контуру обход контура должен проходить против часовой стрелки.

Знак минус в законе индукции отражает правило Ленца.

В виде (1), закон электромагнитной индукции записывается в международной системе единиц (СИ).

Если изменение магнитного потока происходит равномерно, то формулу закона электромагнитной индукции можно записать как:

   

Формулу закона для электромагнитной индукции, если контур состоит из N витков, соединенных последовательно, записывают в виде:

   

где – потокосцепление.

Результаты применения основного закона электромагнитной индукции

Формулы ЭДС индукции для частных случаев

ЭДС индукции в прямом проводнике, имеющем длину l, движущемся в магнитном поле и пересекающем линии магнитной индукции, если скорость его движения () перпендикулярна вектору магнитной индукции (), равна:

   

Разность потенциалов (U), возникающая на концах проводника длиной l, движущегося в однородном магнитном поле со скоростью v равна:

   

где – угол между направлением вектора скорости и направлением вектора магнитной индукции.

Если в однородном магнитном поле вращается плоский контур со скоростью , при этом ось вращения находится в плоскости витка и составляет угол в 900 с направлением вектора внешнего магнитного поля, то в контуре появляется ЭДС индукции равная:

   

где S – площадь, которую ограничивает виток; – мгновенное значение угла между и вектором нормали к плоскости рамки; – поток самоиндукции витка.

Если в рамке, вращающейся со скоростью в однородном магнитном поле, имеется N витков, то

   

в формуле (6) самоиндукцией витков пренебрегли.

Пусть проводник находится в покое, при этом изменяется во времени само магнитное поле, тогда ЭДС индукции можно найти как:

   

Примеры решения задач по теме «Закон электромагнитной индукции»

ru.solverbook.com

---

• 
  Авария на чернобыльской атомной станции
• 
  Какой определен порядок установки переносных заземлений
• 
  Переменное электромагнитное поле
• 
  Как разобрать реле
• 
  Лучшие производители бп для пк
• 
  При утечке бытового газа нельзя
• 
  Схема ктп однолинейная
• 
  В какой среде излучение
• 
  Узел электрической цепи
• 
  Как оформить тсж в многоквартирном доме
• 
  Автоматический выключатель из чего состоит