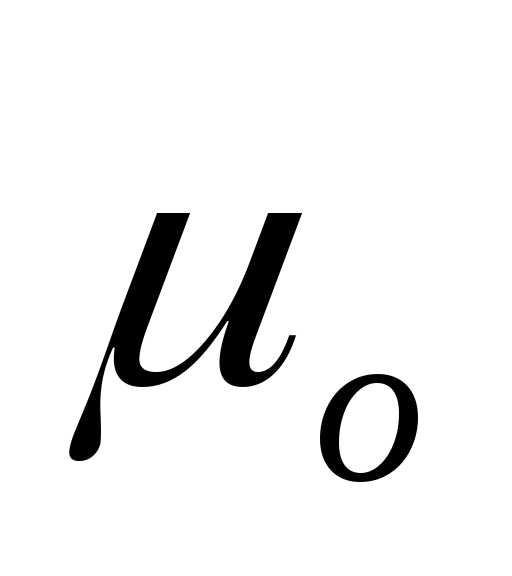5 Переменное электромагнитное поле. Переменное электромагнитное поле

5 Переменное электромагнитное поле

5.1 Рабочая программа

Определение переменного электромагнитного поля. Основные уравнения (уравнение Максвелла) переменного электромагнитного поля. Уравнение непрерывности. Уравнение максвелла в комплексной форме записи. Теорема Умова-Пойнтинга для мгновенных значений и в комплексной форме записи. Переменное электромагнитное поле в однородной и изотропной проводящей среде. Уравнение Максвелла для проводящей среды. Магнитный поверхностный эффект. Электрический поверхностный эффект.

5.2 Основные положения и соотношения

1. Переменное электромагнитное поле (ПЭМП) – совокупность изменяющихся во времени и взаимно связанных и обуславливающих друг друга электрического и магнитного полей. Оно определяется двумя векторными величинами – напряженностью электрического поля и напряженностью магнитного поля.

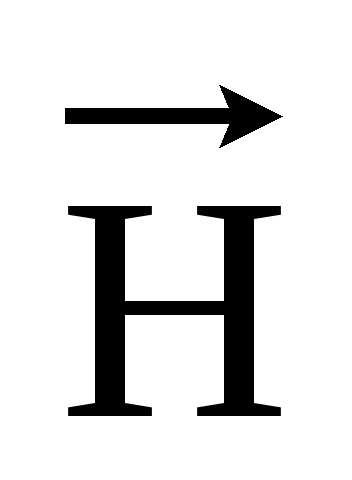2. Уравнения Максвелла. Исследование процессов ПЭМП осуществляют с помощью уравнения Максвелла. Систему уравнений Максвелла образуют четыре уравнения:

Первое уравнение Максвелла выражает связь между ротором напряженности магнитного поля и плотностью тока в той же точке поля. Для мгновенных значений первое уравнение Максвелла записывается следующим образом:

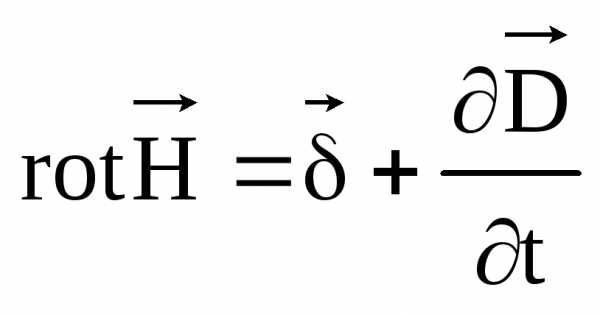В первой части уравнения имеются две плотности тока: плотность тока проводимости и плотность тока смещения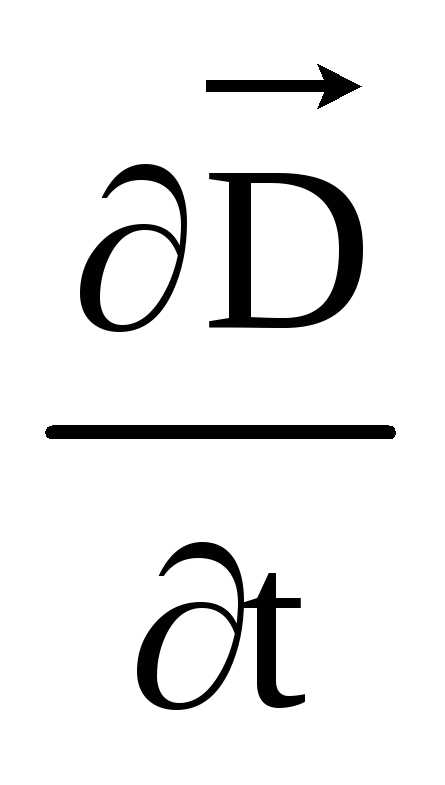. Ток смещения возбуждает магнитное поле так же, как и ток проводимости.

При изменении Е и Н во времени по синусоидальному закону можно воспользоваться символическим методом и записать первое уравнение Максвелла в комплексной форме записи

Второе уравнение Максвелла определяет связь между ротором напряженностью электрического поля и скоростью изменения магнитного поля в той же точке поля. Для мгновенных значений оно записывается следующим образом:

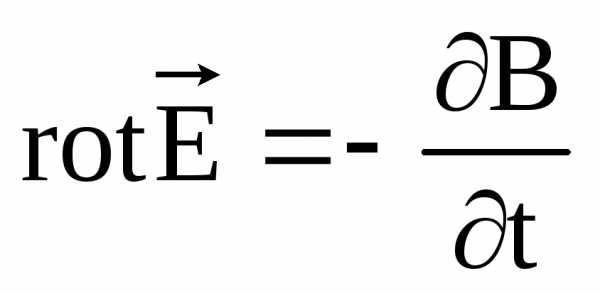т.е. всякое изменение магнитного поля во времени 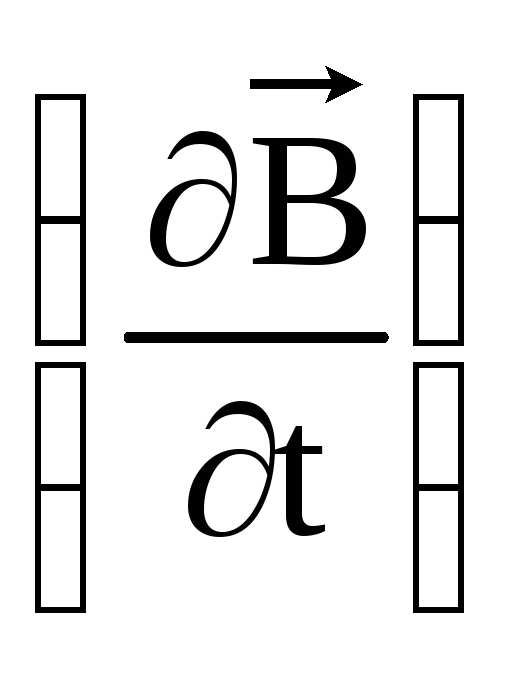в какой-либо точке поля возбуждает вихрь электрического поля в той же точке поля.

В комплексной форме записи второе уравнение Максвелла имеет вид

Уравнение 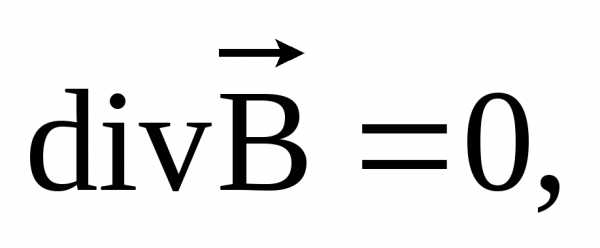выражающее принцип непрерывности магнитного поля.
Уравнение 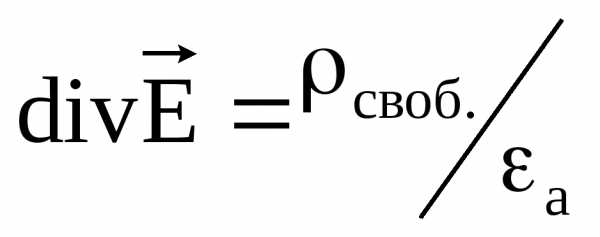выражает связь между истоком напряженности электрического поля и плотностью свободных зарядов в той же точке поля.

3.Уравнение непрерывности. Линии полного тока 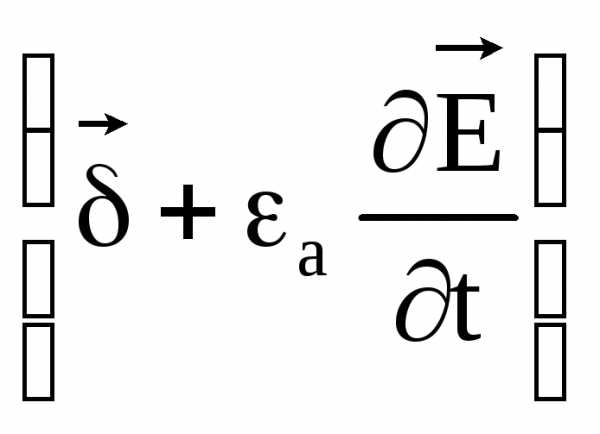являются непрерывны, т.е. на границе проводящей среды и диэлектрика ток проводимости переходит в ток смещения. Уравнение непрерывности записывается следующим образом:

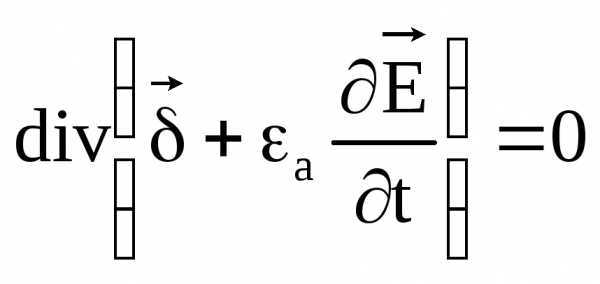Это уравнение можно записывать иначе

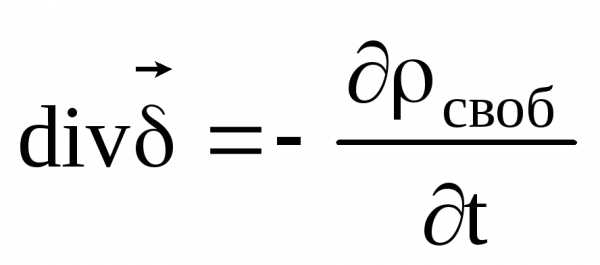Это уравнение также называют законом сохранения заряда. Этот закон означает, что электрический заряд неуничтожим, он может только перемещаться из одного места в другое.

4. Теорема Умова-Пойнтинга.

Теорема Умова-Пойнтинга описывает энергетические соотношения в поле. Она имеет две формы записи: первая – для мгновенных значений, вторая – комплексная фора – для синусоидально изменяющихся величин.

Теорема Умова-Пойнтинга для мгновенных значений записывается следующим образом:

Левая часть уравнения есть поток вектора Пойнтинга 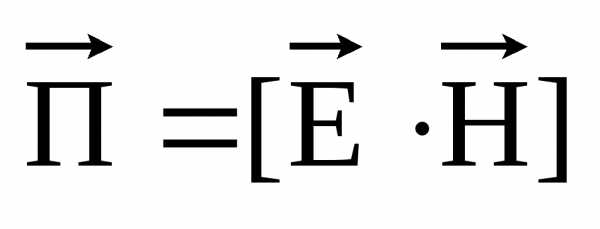(направленный внутрь объема) сквозь любую замкнутую поверхностьS, ограничивающую некоторый объемV. Размерность вектора Пойнтинга равна произведению размерности Е и Н, т.е.

Правая часть уравнения есть энергия 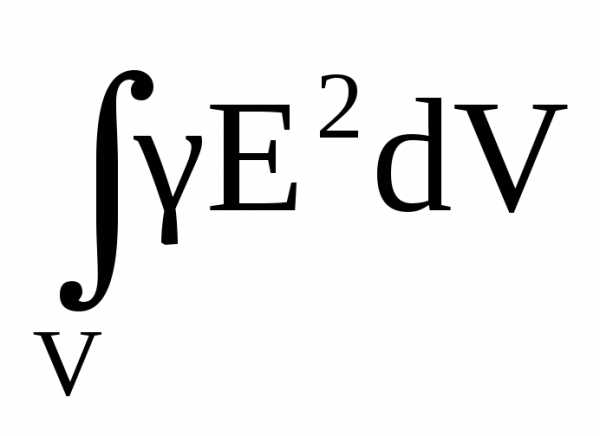, выделяющаяся в виде теплоты в единицу времени в объемеV; иесть скорость изменения запаса электромагнитной энергии в данном объеме.

Теорема Умова-Пойнтинга в комплексной форме записи имеет вид:

Первое слагаемое правой части – активная мощность, второе – реактивная. Следовательно, теорему Умова-Пойнтинга можно записать следующим образом:

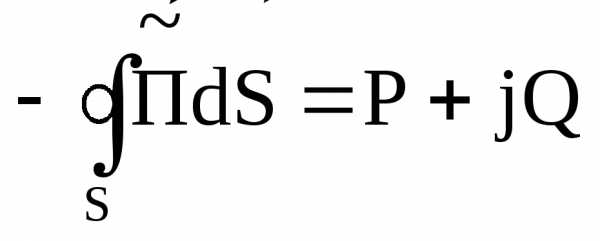В последних выражениях 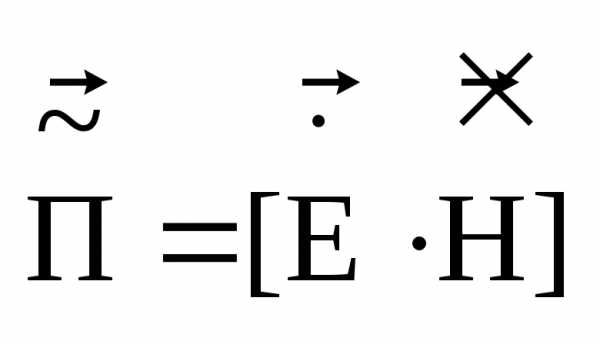– комплексный вектор Пойнтинга.

5. Уравнения Максвелла для проводящей среды.

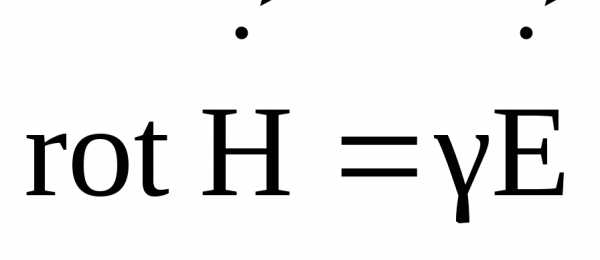6. Плоская электромагнитная волна.

Под плоской электромагнитной волной понимают волну, векторы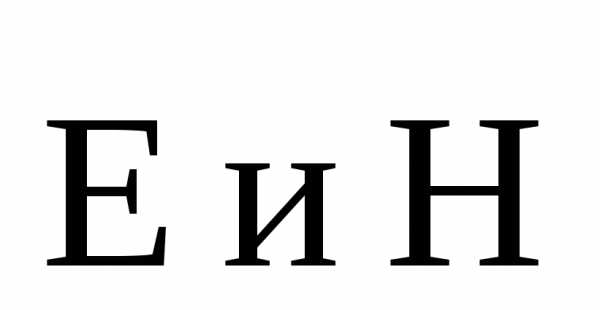которой расположены в плоскостиxoy, перпендикулярной направлению распространения волны (осьz) и изменяющиеся только в функции координатыzи времениt.

Напряженность магнитного поля определяется:

где 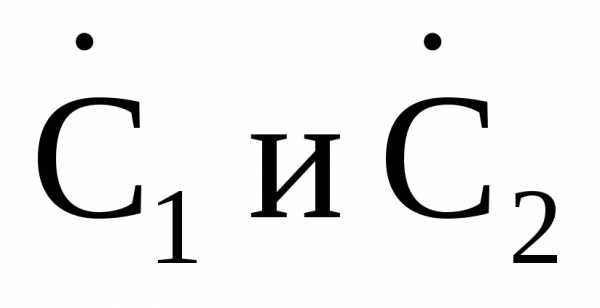– постоянные интегрирования, которые определяются из граничных условий:.

Напряженность электрического поля равна:

где 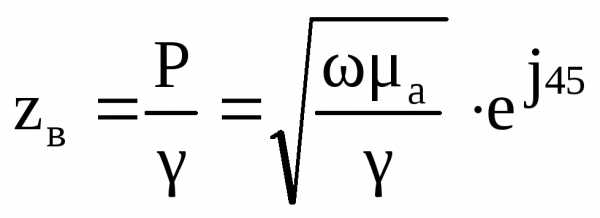– волновое сопротивление.

7. Глубина проникновения и длина волны.

Под глубиной проникновения ∆ понимают расстояние вдоль направления распространения волны (вдоль оси z), на котором амплитуда падающей волны Е (или Н) уменьшится в е = 2,71 раз. Учитывая, что е-К∆ = е-1, получим

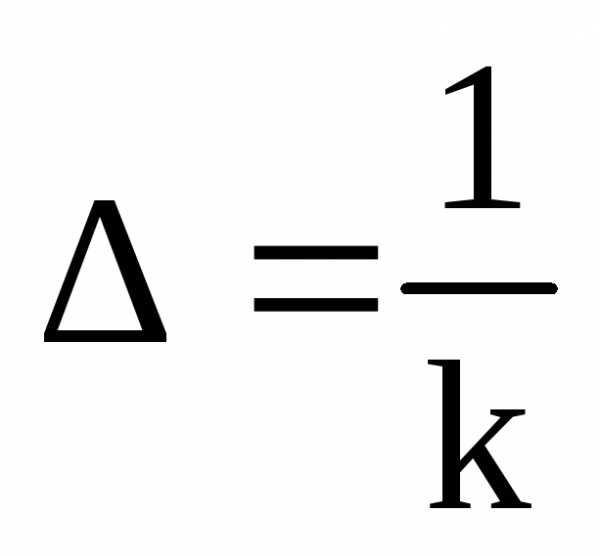Под длиной волны λ в проводящей среде понимают расстояние вдоль направления распространения волны (вдоль оси z), на котором фаза колебания изменяется на 2π. Учитывая, что λ · κ = 2π, получим

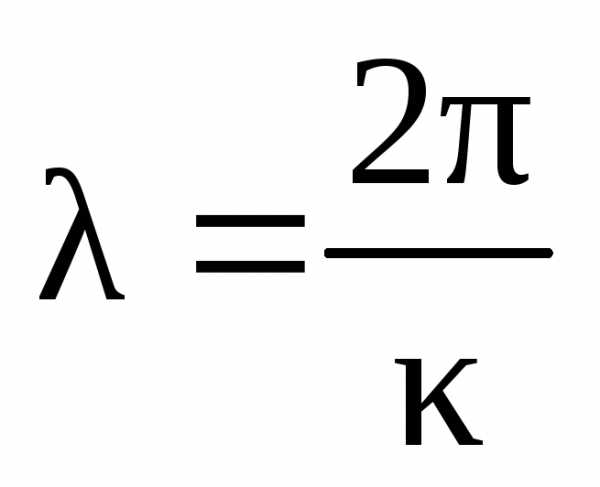Под фазовой скоростью понимают скорость, с которой надо было бы перемещаться вдоль оси z, чтобы колебание имело одну и ту же фазу:

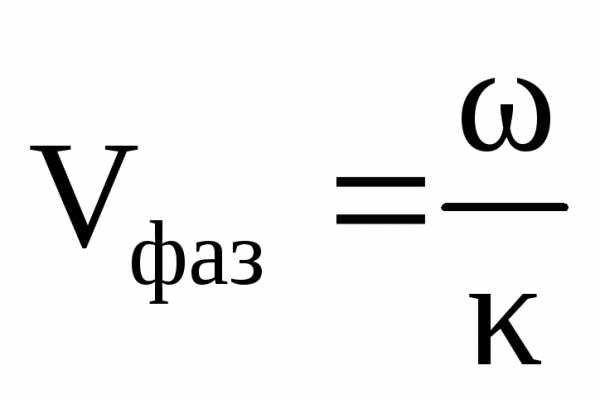8. Магнитный поверхностный эффект.

Явление неравномерного распределения поля по сечению проводящего тепла, вызванное затуханием электромагнитной волны при ее распространении в проводящую среду, при условии, что вдоль листа направлен магнитный поток, называют поверхностным магнитным эффектом. В этом случае:

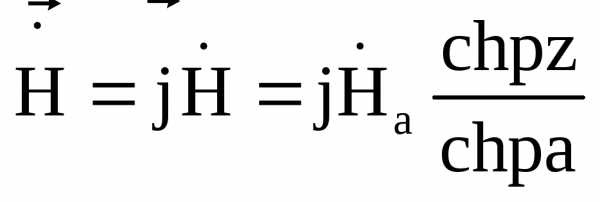Если считать 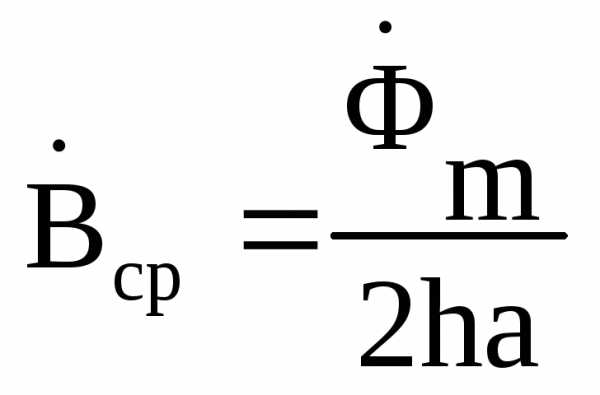, то напряженность поля на поверхности листа можно определить

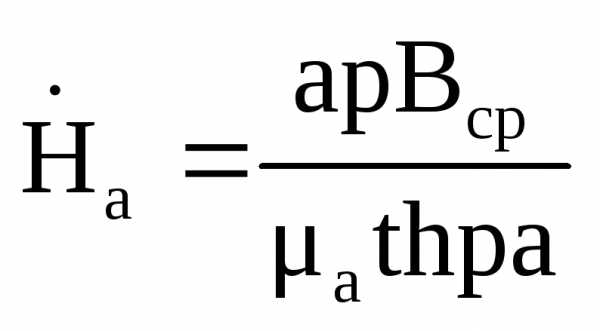9. При электрическом поверхностном эффекте вдоль пластины (шины) направлен синусоидальный ток частоты ω. в этом случае поле внутри пластины определяется по формулам:

,,.

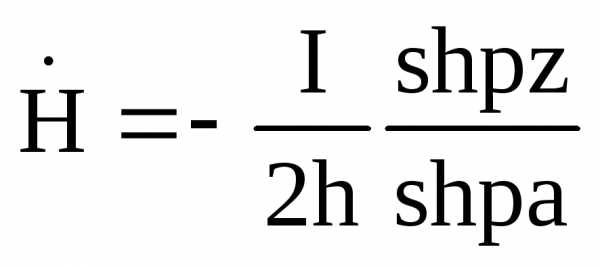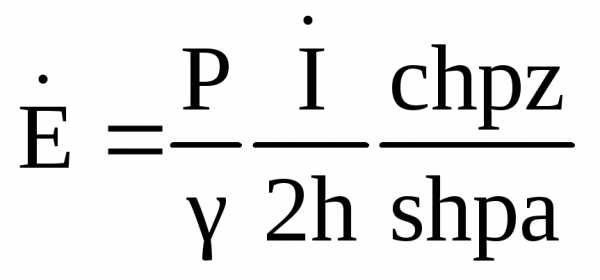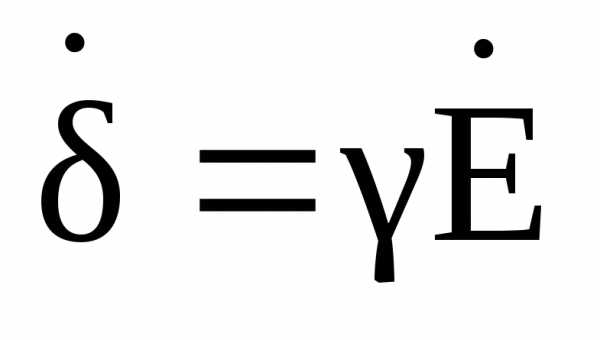studfiles.net

Переменное электромагнитное поле — Мегаобучалка

Рассмотренные уравнения электромагнитного поля обобщают соотношения для постоянных полей: электрического и магнитного. Они же могут использоваться для описания переменного электромагнитного поля. Первое уравнение Максвелла распространяет закон полного тока на токи всех видов: проводимости, смещения и переноса:

где – плотность тока проводимости или переноса.

Второе уравнение Максвелла распространяет закон электромагнитной индукции с проводящего контура на любую среду:

Эти уравнения указывают на неразрывную связь электрического и магнитного полей и их взаимоопределяющее влияние.

Распространение теоремы Гаусса и принципа непрерывности магнитного потока на переменные поля не меняет форму уравнений, полученных для постоянных полей:

Максвелл сформулировал эти обобщения в виде постулатов при создании теории электромагнитного поля. Система уравнений электромагнитного поля также включает соотношения:

;

связывающие величины, входящие в основные уравнения поля.

Систему уравнений дополняют выражения для энергии поля. Максвелл постулировал энергию электромагнитного поля как сумму энергий электрического и магнитного полей, определенных по соотношениям для постоянного поля:

Тепловые потери в электромагнитном поле задаются законом Джоуля - Ленца в дифференциальной форме:

Полная система уравнений электромагнитного поля:

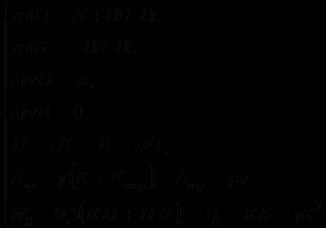(10.36)

На границе проводящей и диэлектрической сред ток проводимости переходит в ток смещения, поэтому систему уравнений поля дополняет уравнение непрерывности линий полного тока:

из которого следует

или

. (10.37)

Уравнение (10.37) представляет собой закон сохранения заряда: ток, выходящий из объема, уменьшает заряд, заключенный внутри него.

Тепловые потери и изменение энергии электромагнитного поля объединены теоремой Умова - Пойнтинга: мощность потока электромагнитной энергии, входящей в объем V, ограниченный поверхностью S, равна тепловой мощности, получаемой объемом V за счет электромагнитной волны, и изменению запаса электромагнитной энергии в данном объеме:

, (10.38)

где – вектор Пойнтинга [ВА/м2].

Теорема Умова - Пойнтинга получена для однородной среды в отсутствие отражений и источников энергии внутри объема V и выражает энергетический баланс: мощность, доставляемая потоком вектора Пойнтинга внутрь объема V, равна расходуемой внутри него мощности.

Энергия передается по диэлектрику, провода линии передачи служат каналами тока, организующими структуру поля в диэлектрике. Провода потребляют энергию из диэлектрика на покрытие тепловых потерь, по проводам энергия не передается.

Поверхностный эффект

В отличие от постоянного переменный ток i распределен неравномерно по сечению провода: плотность тока минимальна на оси провода и максимальна у его поверхности. Магнитный поток Ф распределен аналогично. Неравномерность распределения тока i и потока Ф по сечению провода обусловлена поверхностным эффектом. Поверхностный эффект вызван затуханием электромагнитной волны по мере ее проникновения вглубь проводника и состоит в неравномерном распределении электромагнитного поля в проводящей среде, которое и приводит к неравномерности распределения тока и магнитного потока по сечению.

В большинстве случаев поверхностный эффект вреден, так как уменьшает используемое сечение провода и увеличивает тепловые потери в нем. В установках поверхностного нагрева и закалки поверхностный эффект, наоборот, широко используется.

Зависимости кратности плотности тока в рассматриваемой точке по отношению к току на оси провода и фазового сдвига между векторами плотностей тока и от безразмерной величины , учитывающей радиус r провода, частоту ω переменного тока, магнитную проницаемость μ и электропроводность γ материала провода, приведены на рис. 10.2.

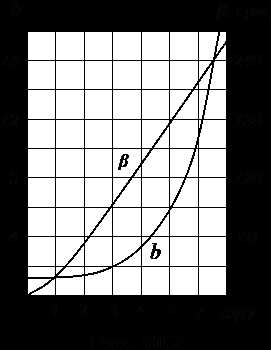Плотность тока на оси провода может быть очень малой по сравнению с ее величиной у поверхности, но всегда отличной от нуля: . Фазовый сдвиг между векторами и может быть любым, в том числе и 180˚, что означает существование в проводе зон, в которых направления токов противоположны друг другу.

Эффект близости

В случае нескольких близко расположенных проводников с переменными токами неравномерность распределения тока в каждом из них определяется не только собственным полем, но и полями остальных проводников. Это явление называют эффектом близости. Эффект близости используют в индукционном поверхностном нагреве перед ковкой и штамповкой, для поверхностной закалки, наплавки и реставрации инструментов, сушки древесины.

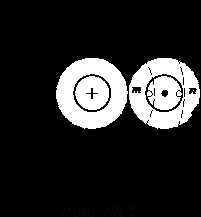
Пусть два провода расположены близко, так что поле одного из них различным образом сцеплено с элементами другого (рис. 10.3).

Элемент m провода, расположенный у его внутренней поверхности, охвачен бóльшим магнитным потоком, создаваемым током соседнего провода, чем элемент n, расположенный у внешней поверхности провода. В результате ЭДС взаимоиндукции eMm элемента m больше ЭДС eMn элемента n. ЭДС индукции зависит от направления магнитных потоков, созданных токами собственного и соседнего проводов, и приводит к неравномерности распределения тока по сечению, дополняющей поверхностный эффект.

При встречном направлении токов в проводах ЭДС индукции равна разности ЭДС само- и взаимоиндукции:

e = eL – eM.

При этом ЭДС, наведенная во внутреннем элементе m,и вызванное ею индуктивное сопротивление элемента m окажутся меньше ЭДС и сопротивления внешнего элемента n, что увеличит плотность тока у внутренней поверхности обоих проводов относительно тока у их внешней поверхности.

При одном направлении токов ЭДС индукции равна сумме ЭДС само- и взаимоиндукции: е = eL + eM.

ЭДС, наведенная во внутреннем элементе m,и индуктивное сопротивление элемента m окажутся больше ЭДС и сопротивления внешнего элемента n, что уменьшит плотность тока у внутренней поверхности проводов относительно тока у внешней поверхности.

megaobuchalka.ru

Переменное электромагнитное поле - Большая Энциклопедия Нефти и Газа, статья, страница 1

Переменное электромагнитное поле

Cтраница 1

Переменное электромагнитное поле является одним из видов материи. Любые возмущения поля в диэлектрике с огромной скоростью, для вакуума равной примерно 3 - 108 м / с. [1]

Переменное электромагнитное поле нельзя в общем случае описать с помощью только электрического и магнитного скалярных потенциалов, так как при этом имеем Е - grad Ua, H - grad Uu и, следовательно, rot E rot H0, что неверно. [2]

Переменное электромагнитное поле с энергией hv приложенное в направлении, перпендикулярном направлению постоянного магнитного поля, индуцирует переориентацию электронов, т.е. переход между зеемановскими уровнями. [4]

Переменное электромагнитное поле может быть использовано для возбуждения колебаний мембраны из мягкого железа. Созданные по этому принципу преобразователи просты по устройству и в эксплуатации. [6]

Переменное электромагнитное поле является одним из видов материи. Оно обладает энергией, массой и количеством движения и может превращаться в другие виды материи. [7]

Переменное электромагнитное поле создается токами и зарядами, зависящими не только от координат, но и от времени. Рассмотрим, каким уравнениям подчиняется векторный потенциал А и скалярный потенциал ф в переменном электромагнитном поле. [8]

Переменное электромагнитное поле отражается от поверхности металла. Если оно меняется во времени не слишком быстро, то под его влиянием электроны на поверхности металла перемещаются так, что напряженность электрического поля внутри металла оказывается равной нулю. Из закона сохранения энергии следует, что энергия падающего на металл поля излучения не может исчезнуть. Часть энергии излучения ( обычно малая) переходит в джоулево тепло, которое выделяется токами, вызванными на поверхности металла полем излучения. Ббльшая же часть энергии излучения покидает поверхность металла с отраженным излучением. [9]

Переменное электромагнитное поле с характерной частотой и создается на границе слабопроводящей диэлектрической среды с параметрами е, / /, А С EQUJ. [10]

Переменное электромагнитное поле распространяется в пространстве со скоростью, равной скорости света. [11]

Переменное электромагнитное поле отражается от поверхности металла. Если оно меняется во времени не слишком быстро, то под его влиянием электроны на поверхности металла перемещаются так, что напряженность электрического поля внутри металла оказывается равной нулю. Из закона сохранения энергии следует, что энергия падающего на металл поля излучения не может исчезнуть. Часть энергии излучения ( обычно малая) переходит в джоулево тепло, которое выделяется токами, вызванными на поверхности металла полем излучения. Большая же часть энергии излучения покидает поверхность металла с отраженным излучением. [12]

Переменное электромагнитное поле, как и постоянное магнитное, проникает только в очень узкий поверхностный слон сверхпроводника, возбуждая в нем переменный ток. В отличие от нулевого сопротивления постоянному току, сопротивление сверхпроводника по отношению к переменному току отлично от нуля и в сверхпроводнике происходит поглощение электромагнитной энергии. [13]

Переменное электромагнитное поле, проникая в вещество, взаимодействует с его частицами ( электронами, ядрами) и вызывает их колебания. Заряженные частицы при этом создают вторичное излучение. Совокупность таких микроскопических процессов приводит к поглощению поля в веществе - различному при разных частотах. Однако она достаточна для понимания качественной стороны процессов. [14]

Переменное электромагнитное поле является одним из видов материи / Оно обладает энергией, массой и количеством движения и может превращаться в другие виды материи. Любые возмущения поля в диэлектрике с огромной скоростью, равной примерно 3 - Ю8 м / сеК, передаются на большие расстояния. [15]

Страницы: 1 2 3 4

www.ngpedia.ru

Переменные электромагнитные поля.

К естесственным переменным электромагнитным полям относят региональные квазигармонические низкочастотные поля космической (их называют магнитотеллурическими) и атмосферной природы.

Магнитотеллурические поля.

Происхождение магнитотеллурических полей объясняют непостоянством солнечной радиации – воздействием на ионосферу Земли потока заряженных частиц (солнечного ветра), посылаемых Солнцем. Этот поток, ориентированный геомагнитным полем, нарушает магнитное равновесие ионосферы. От удара солнечных корпускул по ионосфере образуются ударные волны, которые взаимодействуют с токовыми поверхностями ионосферы. В результате ионосферные источники начинают излучать электромагнитные волны, которые проникают и в геологическую среду. Периодические (одиннадцатилетние, годовые, суточные) вариации геомагнитного поля и магнитные бури вызывают соответствующие изменения этого излучения – магнитотеллурического поля. В целом это поле инфранизкой частоты (от 10-5 до 10 Гц), а на таких частотах затухание поля (скин-эффект) проявляется слабо и потому магнитотеллурические поля проникают в Землю до глубин в десятки и даже первые сотни километров.

В магнитотеллурическом поле выделяют электрическую компоненту Е, связанную с теллурическими (земными) токами и магнитную компоненту Н, связанную с вариациями магнитного поля. Регистрация электрической составляющей осуществляется через пару заземленных электродов или диполей М и N, разнесенных на несколько десятков или сотен метров. К электродам через усилитель подключается электроразведочный осциллограф (регистрация) и производится автоматически направленная запись изменения естественных потенциалов в течение нескольких суток, называемая теллурограммой. Магнитную компоненту записывают с помощью чувствительного магнитометра.

Анализ теллурограмм заключается в выявлении колебаний повторяющейся формы с периодами Т от долей секунды до нескольких минут и даже часов (бухты).

Измеряемыми параметрами магнитотеллурического поля являются электрические Ех (регистрация вдоль линии профиля зондирования) и Еy (перпендикулярно профилю) и магнитные (Нх и Нy) компоненты поля и периоды выявленных вариаций.

Значения параметров зависят, с одной стороны, от интенсивности вариаций теллурического и геомагнитного полей, а с другой стороны – от удельного электрического сопротивления пород разреза. По измеренным взаимно перпендикулярным электрическим и магнитным составляющим (электрическая и магнитная составляющие единого электромагнитного поля сдвинуты по фазе на 90º) можно рассчитать сопротивление однородного полупространства (нормальное поле) с помощью специальной формулы, полученной в теории электроразведки

Здесь – Т период колебаний, - волновое сопротивление (или входной импеданс) среды Z, а – коэффициент пропорциональности, равный 0.2, если Т измерено в секундах, Ех – в мВ/км, Нy – в нТл. Таким образом, можно вычислить и удельное сопротивление ρт и построить кривую МТЗ – зависимость ρтот периода вариаций (или частоты),выявляемых по теллурограммам. Поскольку период определяет глубину проникновения поля в Землю, по такой кривой можно будет оценить строение геоэлектрического разреза, выделив в нем комплексы высокого и низкого сопротивления, соотносимые при наличии соответствующей геолого-геофизической информации (данные бурения, ГИС, сейсморазведка) с терригенными, карбонатными, кристаллическими и иными образованиями. Так как короткопериодные вариации характеризуют верхние горизонты разреза, а длиннопериодные проникают на большие глубины, данными МТЗ можно охарактеризовать всю толщу Земной коры и даже подкоровую верхнемантийную толщу.

Другой модификацией магнито-теллурического метода является магнито-теллурическое профилирование. При профилировании строится зависимость ρтот х (вдоль профиля наблюдений) для выбранной вариации с фиксированным периодом Т. Тем самым удается выявить вертикальные или круто наклоненные неоднородности разреза в определенном интервале глубин. Более подробно на методике профилирований мы остановимся позднее.

Поля грозовой природы.

Происхождение естественных переменных полей атмосферной природы связано с грозовой активностью. Под воздействием гроз в Земле существует слабое грозовое поле, называемое шумовым. Оно представлено периодически повторяющимися импульсами (дугами) синусоидальной формы с преобладающими частотами от 10 Гц до 10 кГц и напряженностью электрической составляющей до долей милливольт на метр.

Измеряемыми параметрами атмосферных токов являются различные составляющие Еср и Нср, которые используются в методах переменного естественного электрического и магнитного поля (ПЕЭП и ПЕМП).

Лекция 8. Методы искусственно создаваемых электрических полей.

Постоянный ток.

Искусственные электрические поля постоянного тока создают с помощью батарей (аккумуляторов, генераторов), которые подключают соединительным проводом к электродам - заземлителям и пропускают через них ток силой I. Эти электроды называют питающими, или токовыми. Пара других электродов – заземлителей М и N (измерительных или приемных) служит для измерения разности потенциалов Δ U с помощью потенциометра (милливольтметра).

Свойства возбуждаемого поля характеризуется через потенциал U, который не зависит от времени t и является только функцией координат x, y, z, то есть рассматриваемое поле является стационарным (смысл потенциала уже обсуждался выше). Скалярная функция U связана с напряженностью поля Е соотношением Е = , причем r – это расстояние от начала координат до точки, где определяется U, напряженность – вектор, его компоненты по координатным осям обозначаются Ex , Ey , Ez.

Основной закон, определяющий величину тока, протекающего через проводник (горную породу) – закон Ома

J = , где U1 и U2 значения потенциала на концах проводника, а R – его сопротивление R=ρ и, соответственно, ΔU = JR= Jρ

Здесь l – длина проводника в м, S – площадь его поперечного сечения в м2, а ρ – удельное сопротивление, измеряемое в Омах, умноженных на метр (Ом·м). Величина, обратная ρ называется удельной электрической проводимостью и измеряется в Сименсах

Наряду с силой тока, одной из характеристик поля является плотность тока j

Это так называемая дифференциальная форма записи закона Ома, устанавливающая пропорциональность плотности тока в проводнике напряженности поля. Эта форма записи может быть применена к проводникам любой формы и к переменным электромагнитным полям. Поле постоянного электрического тока в однородном полупространстве (ρ = const) называют нормальным электрическим полем постоянного тока.

Рассмотрим нормальное поле точечного источника. Получить такое поле, пропуская ток через пару электродов А и В можно, относя второй электрод в бесконечность и анализируя ситуацию в окрестности А. В однородной среде ток от точечного источника стекает во все стороны равномерно. Эквипотенциальные поверхности (поверхности равного потенциала) перпендикулярны к радиальным токовым линиям и имеют форму полусфер с центром в точке А ( рис.22 )

Рис.22.Нормальное поле одного (а) и двух разнополярных (б) точечных электродов

1 – токовые линии; 2 – эквипотенциальные поверхности.

Определим значение потенциала Uм в точке М.

Вначале оценим величину разности потенциалов между двумя близкими эквипотенциальными поверхностями радиусов r и r+dr. Начало координат поместим в точку А. Согласно закону Ома

Здесь dr – длина проводника - в данном случае расстояние между соседними полусферами, S - это поверхность полусферы, то есть 2πr2, где r – радиус полусферы. Поскольку рассматриваются две полусферы, отстоящие друг от друга на dr – правильнее всего выбрать радиус равным r + dr/2 – то есть выбрать некий «средний» радиус близких полусфер

Тогда dV=

Приближенное равенство основано на том, что бесконечно малая dr и при возведении в квадрат и при умножении на конечную величину r дает в результате столь малые «добавки» к r2 , что ими вполне можно пренебречь.

Для нахождения Uм придется просуммировать согласно определению потенциала все dV от бесконечности до r, то есть проинтегрировать приведенное выражение, сложив тем самым приращения потенциала dV всех подобных рассмотренному тонких слоев, вынеся постоянные – силу тока в источнике, удельное сопротивление среды и 2π – за знак интеграла

Исходя из этого, напряженность поля в М

А плотность тока

Получив основные характеристики нормального поля точечного электрода обратимся к рассмотрению реальной ситуации, когда поле создано с помощью пары электродов АВ (рис.22б), а регистрация осуществляется парой МN. Тогда разность потенциалов

Обозначив расстояние АМ через r1 и AN через r2 можем, учитывая симметрию четырехэлектродной установки AMNB относительно центра 0, записать

Учитывая, что r2 – r1равно расстоянию MN

, обозначив π через k,

откуда , а .

k – это коэффициент, характеризующий геометрию расстановки.

Вполне понятно, что если среда однородная, то есть ρ = const, мы будем получать одно и то же значение ρ при любых k, то есть при любых расстояниях АМ и AN.

Однако, в неоднородной среде ρ будет существенно зависеть от k. Эта зависимость обусловлено тем, что плотность тока определяется величиной «разноса» питающих электродов АВ и с увеличением АВ эта относительная плотность с глубиной возрастает, поскольку возрастает и глубина проникновения поля в Землю. Сказанное хорошо видно из рассмотрения такого примера ( рис.23 ).

Пусть мы имеем толщу слоев с разным сопротивлением.

Рис.23.Зависимость глубины проникновения электрического поля в слоистую среду от величины разноса питающих электродов АВ.

При малом разносе АВ токовые линии практически целиком размещаются в слое с сопротивлением ρ1. При большем разносе А1В1 поле сосредоточено большей частью в слое ρ2, здесь плотность тока, отображаемая густотой силовых линий будет наибольшей. С увеличением А1В1 до А2В2 вычисляемое по приведенной формуле ρ будет уже ближе всего к ρ3 и т.п.

В теории электроразведки показано, что отношение тока на глубине h к плотности на поверхности зависит от расстояния между электродами L и при увеличении L эта относительная плотность с глубиной h возрастает по закону

Все сказанное позволяет уяснить идею зондирования среды постоянным током, состоящую в том, что осуществляя серию измерений ΔVMN с разными все возрастающими АВ, мы получаем последовательность значений ρ, характеризующих электрическое сопротивление все более глубоких интервалов геоэлектрического разреза. Такое зондирование называют вертикальным электрическим зондированием ВЭЗ.Помимо ВЭЗ используют другие модификации рассматриваемого метода сопротивлений – ДЭЗ (дипольное электрическое зондирование), ЭП (электропрофилирование) и другие. Во всех этих модификациях основная задача – определение электрической характеристики среды – удельного электрического сопротивления ρ. Однако, что это за ρ? Это в общем случае не ρ1, не ρ2 и не ρ3, а некое ρк – кажущееся сопротивление, зависящее от k (то есть от геометрии 4хэлектродной установки ABMN - от расстояний АВ и MN.), помимо зависимости от этих реальных ρ1 , ρ2 и от толщин слоев геоэлектрического разреза. Таким образом, ρк можно определить как удельное электрическое сопротивление такой воображаемой однородной среды, в которой при тех же АВ и MN и при той же силе питающего тока в цепи АВ регистрируется та же разность потенциалов ΔVMN , что и в среде неоднородной. То есть ρк это сложная функция, зависящая от характеристик реального геоэлектрического разреза и от геометрии расстановки

Самое замечательное состоит в том, что в ряде случаев ρк может оказаться как угодно близким к истинным значениям ρ1 , ρ2 и т.д. Но это будет показано несколько позже. А пока остановимся на рассмотрении упомянутых модификаций и сделаем это несколько подробнее, чем по ранее представленным методам электроразведки. Но прежде одно замечание, которое должно прояснить читателю, почему и теория методов сопротивлений на постоянном токе и практика их применения разъясняются гораздо обстоятельней, чем это делалось ранее в разделах, посвященных МТЗ и пр.. Дело в том, что эти методы занимают особое место среди других методов электроразведки и геофизики в целом. Во-первых, с методики ВЭЗ и каротажа КС (кажущихся сопротивлений) началась в первой трети двадцатого столетия разведочная геофизика как таковая. Во-вторых, эти методики используются в современной геофизике чаще, чем какой-либо другой метод практически во всех разновидностях полевой геофизики (инженерная, рудная, гидрогеологическая, техническая, археологическая и пр.), за исключением нефтегазовой, хотя история нефтегазовой геофизики тоже ведет свой отсчет именно с этих методик.

Наиболее популярны две разновидности метода сопротивлений: ВЭЗ и электропрофилирование. Для электроразведочных методов вообще характерно такое подразделение - зондирование и профилирование. Зондирования предназначены, главным образом, для исследования горизонтально-слоистых сред, представляющих, в основном, осадочные толщи, а профилирование – для выявления вертикальных или крутонаклоненных неоднородностей, свойственных разрезам с блоковой тектоникой. Сочетание зондирований с профилированием позволяет получить всестороннее объемное представление о строении объектов самой разной природы.

Электропрофилирование.

Сущность электропрофилирования заключается в следующем. С учетом эмпирического соотношения глубины h проникновения тока в среду (она зависит от проводимости пород разреза) с величиной питающего разноса АВ: h = ÷ АВ -подбирается такая величина разноса, которая гарантирует достижение необходимой глубины исследования.

Выбранный разнос АВ сохраняется неизменным и эта расстановка АMNВ перемещается вдоль профиля наблюдений. Измерения производятся через определенный интервал, который мотивируется масштабом съемки и геологической задачей. Обработка результатов наблюдений состоит в вычислении ρк в каждой точке наблюдений и в построении графика зависимости ρк(х). Примеры геологической результативности электропрофилирования покажем на моделях 1 и 2 ( рис.24 ).

Рис.24. Кривые электрического профилирования ρк (х).

Модель 1. представляет ситуацию, в которой требуется определить плановое положение скрытого под наносами вертикального контакта пород низкого сопротивления ρ1 (осадочная толща) и высокого сопротивления ρ2 (массив кристаллических пород, прорывающих осадочные).

Пусть ρ1 ≈ 20 Ом·м; ρ2 = 80 Ом·м; О1, О2 и т.д. - точки, в которых располагаются последовательно центры четырехэлектродной установки AMNВ, с чьей помощью проводятся наблюдения (рис.24а )

Пусть толщина наносов, скрывающая положение контакта, составляет 30м. Тогда, выбрав АВ = 80м и размещая последовательно центры электроразведочной установки в точках О1, О2 и т.д. с шагом 50-100 м , мы получим кривую ρк , примерный вид которой показан на рис.23. Вполне понятно, что пока установка находится далеко слева от зоны контакта, значения ρк. будут близки к ρ1 , напротив, если установка размещена в области больших пикетов О ( О7 и далее) ρк станет как угодно близкой к ρ2. В самой приконтактной зоне залегания ρк будет резко изменяться, пока не приблизится к ρ2 .

Модель 2 иллюстрирует ситуацию с вертикальными дайками пород высокого сопротивления (рис.24б). Характер полученной кривой можно объяснить, рассуждая таким же образом, как в примере с моделью 1.

Нередко возникают такие геологические ситуации, которые требуют контроля за электрической неоднородностью двух или нескольких уровней разреза. Тогда используют так называемые комбинированные установки, например АА'МNB'B . С такой установкой для каждой точки наблюдений О используют два различных разноса питающих электродов АВ и А1В1. При этом вычисляются значения ρк, характеризующие два разных интервала глубин. Примером может послужить ситуация, изображенная на модели 3(рис.24в ).

Здесь показан разрез с высокоамплитудными антиклинальной и синклинальной складками, сложенными известняками относительно высокого сопротивления (~150 Ом·м) и терригенной толщей небольшого сопротивления (<50 Ом·м). Видно, что использование больших разносов приведет к пропуску приповерхностной синклинальной формы при правильном воспроизведении особенностей конфигурации глубинного известнякового пласта. В то же время, установка с малым разносом А1В1 позволяет выявить пропущенный объект, но не дает адекватного представления о структуре погруженного известнякового пласта.

Если вертикальные неоднородности высокого сопротивления выявляются методикой электропрофилирования достаточно контрастно, то наоборот, проводящие тела небольшого размера отмечаются на кривых ρк довольно слабыми пологими минимумами. Поэтому для их выявления используют так называемое комбинированное профилирование. Рассмотрим пример его применения на модели 4, где изображено проводящее вертикальное тело, перекрытое толщей наносов (рис.25).

Схема AMNB реализуется через удаленный электрод С и идет поочередно по схеме AMNC и BMNC так, что на каждой расстановке получают два значения ρк : ρкА , когда ток пропускают через А и С и ρкВ (через В и С) – рис.25а

Вдали от проводящего тела над однородной средой ρк будут одинаковыми и для установки AMN∞ (ρкА) и для BMN∞(ρкВ). Однако, когда установка приближается к проводящему телу, равенство нарушается. Когда установка находится слева, ток стремится к С через тело и плотность тока I возрастает в области MN при пропускании его через А1 и уменьшается при пропускании его через В1. Когда установка находится справа – ситуация обратная (рис.25б). Чем больше плотность тока, тем больше ΔV и, следовательно, ρк.

Таким образом, слева от тела появится максимум на кривой ρкА, а справа - на кривой ρкВ. Наличие проводящего тела будет отмечено точкой пересечения кривых ρк с выраженными особыми точками - максимумами и минимумами, тогда как при обычном симметричном профилировании отмечается только слабый минимум (рис. 25в).

Рис.25.Комбинированное профилирование.

На участках сложного геоэлектрического разреза с неоднородными условиями заземления электродов используют еще одну модификацию электропрофилирования – метод срединных градиентов с малыми базами MN. Приемная установка MN при этом перемещается вдоль АВ в центральной части, равной 1/3 АВ. Об этой методике и других вариациях профилирования можно прочитать в учебниках по электроразведке, приведенных в списке литературы. Сходны с электропрофилированием по методу сопротивлений на постоянном токе методики магнитотеллурического профилирования и профилирования с использованием искусственно возбуждаемых переменных электрических полей. Там также строятся зависимости ρк (Х) при выбранном неизменном значении параметра, контролирующего глубину проникновения поля в Землю – периода вариации, частоты, времени становления и т.п. Однако, все эти профилирования не дублируют друг друга – каждое имеет свое предназначение, решает разные задачи, исследует разные интервалы глубин.

Методика ВЭЗ.

Это наиболее важная и востребованная модификации метода сопротивлений, ориентированная, как уже говорилось, на изучение горизонтально-слоистых сред.

Сущность ВЭЗ заключается в том, что центр установки О остается на месте, тогда как разнос АВ меняется, то есть меняется глубина зондирования разреза постоянным током и освещается не один-два интервала глубин, а весь разрез. Максимальное расстояние АВ называется величиной зондирования. Начинается оно с малых разносов. Далее разнос увеличивают, но не равномерно, а с все более возрастающими интервалами, например в такой последовательности (в метрах):

2; 5; 10;20; 50;100; 500 и т.д.

Условия успешного применения метода:

угол наклона границ раздела не должен превышать 10-15º;

залегание слоев – согласное;

в разрезе имеется толща слоев, сильно отличающихся по сопротивлению от перекрывающих пород, называемая опорным горизонтом.

Опорный горизонт должен характеризоваться повсеместным распространением, отображать основные структурные особенности разреза и иметь достаточную мощность для того, чтобы его можно было уверенно выявить по кривой ρк (кривой ВЭЗ). Если зондирование проводится на большую глубину, то местность должна быть подходящей для больших разносов.

По вычисленным для каждого разноса АВ значениям ρк строят кривую ВЭЗ на специальных билогарифмических бланках с масштабным модулем М=6,25 см. Вообще электроразведочные построения обычно осуществляют в логарифмическом масштабе, поскольку диапазон изменения ρк для горных пород (от нуля до бесконечности) в линейном масштабе отобразить практически невозможно. Для вычисления ρк используется уже приводившаяся формула

Измерение силы тока и разности потенциалов могут проводиться с помощью простых приборов, с которыми студент сможет ознакомиться при прохождении учебной геофизической практики.

Кривые ВЭЗ

Рассмотрим, как выглядят кривые ВЭЗ для различных моделей слоистых сред. Кривые изображают в горизонтальной или вертикальной композиции. Воспользуемся последним способом. Так легче провести аналогию с геологическим разрезом.

Двухслойная модель.

Представим себе, что скважина вскрыла такой разрез: терригенная толща 1 имеет мощность h2и сопротивление ρ1 . остальную часть нижнего полупространства занимает карбонатная толща 2 с сопротивлением ρ2 , причем ρ2»ρ1 . ρ и h здесь являются параметрами геоэлектрического разреза, который для рассматриваемых моделей будем представлять в виде пачки плоскопараллельных слоев-пластин, каждая из которых характеризуется своими ρi и hi при горизонтальном залегании.

Кривая строится в системе координат ρк = , так как это вероятная глубина проникновения тока в Землю. Горизонтальная пунктирная линия на графике ρк = соответствует глубине залегания границы раздела сред 1 и 2, а вертикальные прямые отвечают истинным значениям ρ1 и ρ2 соответственно. Задача построения кривой ВЭЗ - при заданных параметрах разреза это, как мы уже знаем, прямая задача и по существу речь в настоящем разделе идет о решении прямой задачи электроразведки методом ВЭЗ. Для уяснения вопроса о том, какой должна быть форма кривой ВЭЗ над модельным разрезом, воспользуемся таким же способом рассуждения, который применяли, обсуждая методику электропрофилирования.

При небольших разносах АВ и, следовательно, концентрации поля в верхних горизонтах разреза значения ρк будут практически неотличимы от ρ1 . Напротив, при очень больших АВ величина ρк вплотную приблизится к ρ2 . Когда разносы окажутся такими, что наибольшей плотностью тока будут характеризоваться приграничные интервалы разреза, значения ρк будут наиболее значимо меняться, возрастая от ρ1 к ρ2 и кривая примет вид, показанный на рис.26а, причем точка перегиба кривой будет проектироваться как раз на границы между двумя контактирующими толщами.

Рассмотрим, как будет меняться кривая ВЭЗ при изменении параметров геоэлектрического разреза ρ и h. Если увеличивать ρ2 , оставляя неизменными ρ1 и h2, можно наблюдать изменение формы кривой при сохранении местоположения точки перегиба. Изменение формы будет определяться тем, что выход ρк на асимптоту ρ2 будет постоянно сдвигаться в сторону больших значений, то есть вправо. Так будет продолжаться до тех пор, пока значения ρк не приблизятся к практической бесконечности, то есть не превысят n·1000 Ом·м. По достижении таких величин кривая ВЭЗ вырождается в прямую, идущую под углом 45º. Такое вырождение является знаковым показателем ограничения глубинности исследований разреза: постоянный ток не проходит в высокоомный горизонт и точка перегиба кривой диагностирует таким образом гипсометрию опорного горизонта.

Рис.26.Двухслойные кривые ВЭЗ.

При обратном соотношении ρ1 и ρ2 (ρ1>ρ2) будет наблюдаться и обратный рисунок кривых ВЭЗ, но выхода кривой на прямолинейную асимптоту здесь уже не будет, так как не может быть бесконечно уменьшена величина ρ2, которая никак не может оказаться меньше нуля (рис.26 б). Поскольку в рассматриваемом случае радикального изменения формы кривой (то есть вырождения ее в прямую) не наблюдается, можно говорить о том, что высокоомные опорные горизонты на кривых ВЭЗ выделяются контрастнее низкоомных. Если изменить местоположение границы h, оставляя неизменным соотношение сопротивлений ρ1 и ρ2 ,будет наблюдаться иная картина: форма кривой ВЭЗ меняться не будет, но местоположение точки перегиба кривой ВЭЗ будет перемещаться вслед за перемещением границы h раздела пластов – кривая как бы сдвигается параллельно самой себе (рис.26в). Таким образом, можно констатировать, что кривая ВЭЗ «откликается» на любое изменение параметров геоэлектрического разреза ρ и h либо изменением своей формы, либо перемещением точки перегиба кривой.

Рис.27.Палетка двухслойных кривых ВЭЗ.

Существуют специальные палетки таких теоретических кривых, рассчитанных для различных соотношений h и ρ, которые используются в последующей интерпретации результатов ВЭЗ (рис27).

Посмотрим далее, как выглядят трехслойные кривые ВЭЗ (рис.28). Для трехслойной модели можно предусмотреть четыре различных сочетания значений ρ.

ρ1>ρ2<ρ3 (H)

ρ1<ρ2<ρ3 (A)

ρ1>ρ2>ρ3 (Q)

ρ1<ρ2>ρ3 (K)

Каждое из этих сочетаний определяет тип получаемой кривой ВЭЗ. Этот тип помечается буквенным индексом, показанным в скобках.

Начнем с кривых H и A, где последняя толща характеризуется высоким сопротивлением. Трехслойную кривую будем как бы составлять из двух двухслойных, соединяя их общей огибающей. В итоге получается кривая, на которой промежуточная толща отмечается минимумом. По аналогии с уже рассмотренными вариациями параметров геоэлектрического разреза получим выходы кривой на прямолинейную асимптоту при стремлении ρ3→∞. Для трехслойной модели так же можно показать другие преобразования формы кривой при изменении ρ1 и ρ2. Не трудно, например, увидеть, что промежуточный пласт будет тем лучше выделяться на кривой, чем больше его мощность и может вообще «выпасть» (исчезнет минимум), если толщина его окажется слишком малой. Учитывая, что кривая строится в логарифмическом масштабе, можно понять, что чем «глубже» кривая, тем эта толщина должна быть больше для того, чтобы минимум появился: для верхних (до 10м) горизонтов разреза это единицы метров, в интервале от 10 до 100 – десятки, за сто – сотни метров и т.д.

На кривой типа А промежуточного минимума быть не может, так как сопротивление горизонтов с глубиной нарастает монотонно. Здесь второй пласт будет выделяться зонами градиентных переходов( Рис.28 )

Рис.28.Трехслойные кривые ВЭЗ.

Эти переходы тем контрастнее, чем больше разница сопротивлений контактирующих сред и чем значительнее толщина промежуточного слоя. Высокоомный опорный горизонт так же, как и в предыдущем случае, будет отмечен вырождением кривой в прямую с ростом ρ3. Кривые K и Q обнаруживают обратный рассмотренным характер (рис.28б) и в отношении контрастности их выделения можно сделать те же самые выводы. Ясно, что значение ρк промежуточного пласта будет тем ближе к истинному значению ρк, чем больше его толщина. На рассмотренных примерах вновь можно убедиться в том, что любое изменение параметров геоэлектрического разреза контролируется формой кривой ВЭЗ и местоположением точек перегиба. Для трехслойных моделей также рассчитаны теоретические кривые применительно к разным сочетаниям h и ρ , обозначенные в альбоме палеток. Для моделей с большей слойностью нетрудно построить свои кривые, используя разные композиции двух и трехслойных кривых.

Интерпретация кривых затруднена сильным проявлением эквивалентности. Она заключается в том, что по кривым для промежуточного пласта могут быть определены не ρ и h в отдельности, а только так называемая продольная проводимость Si = hi/ρiдля кривых Н и А (поскольку для таких сред ток «отжимается» непроводящей толщей ρ3 и течет вдоль ее поверхности) или поперечное сопротивление Ti = hiρi для моделей K и Q (поскольку в этом случае ток течет поперек напластования, стремясь попасть в проводящую толщу ρ3). Отсюда следует, что при определенном сочетании hi и ρi, когда S или Т не меняется, форма кривой также остается неизменной.

Прежде чем перейти к рассмотрению вопросов интерпретации кривых ВЭЗ, приведем пример многослойной кривой (рис.29).

Рис.29.Пятислойная кривая ВЭЗ.

То, что по этой кривой можно выделить в разрезе 5 геоэлектрических слоев различного состава и толщины, не означает, к сожалению, что этот разрез и на самом деле таков. Если нашу установку AMNB поставить вертикально и опустить в скважину с тем, чтобы провести в реальном масштабе глубин регистрацию ρk с определенным интервалом наблюдения, то на такой скважинной (каротажной) кривой можно будет выделить в зависимости от выбранного разноса десятки различных слоев. То есть разрешающая способность полевого ВЭЗ, определяемая и сложным характером зависимости ρk от соотношения сопротивлений и мощностей множества пластов, и использованием логарифмического масштаба изображений, несопоставима с возможностями скважинных исследований. Тем не менее, наиболее существенные крупные комплексы проводящих и непроводящих пород глубинного разреза и достаточно тонкие слои верхней его части выделяются на кривых ВЭЗ достаточно уверенно. Таким образом, становится понятным как определить геологическую природу отмеченных особенностей рельефа кривых. Определить геологическую природу аномалий – максимумов, минимумов и участков, ограниченных резкими градиентными изгибами кривой – это значит поставить им в соответствие тот или иной комплекс пород разреза. Это можно сделать с достаточной надежностью, если в распоряжении исследователя есть результаты бурения или, в худшем случае, сейсморазведки. И, конечно, тогда, когда интерпретатор имеет достаточно четкое представление об электрических свойствах горных пород. Как уже отмечалось выше, важнейшим таким свойством является удельное электрическое сопротивление (или обратная ему величина-проводимость). Сопротивление пород изменяется в очень широких пределах: от 10-5 до 1015 Ом·м, то есть практически от 0 до ∞. Зависит величина сопротивления от минерального состава, физико-механических и водных свойств пород, а также от температуры, глубин залегания, степени метаморфизма и пр.

infopedia.su

Переменное электромагнитное поле — Мегаобучалка

Постоянное электрическое поле

1. Закон Кулона. Напряженность электростатического поля , создаваемого точечными зарядами, диполем. Применение электростатической теоремы Гаусса (вычисление потока напряженности электростатического поля через замкнутую поверхность, напряженности электростатического поля при симметричном распределении зарядов).

2. Потенциал электростатического поля. Потенциал точечного заряда. Потенциал равномерно заряженной сферы . Связь работы по переносу электрического заряда в электростатическом поле с разностью потенциалов. Связь потенциала φ с напряженностью электрического поля . Электростатическое поле системы бесконечных, равномерно заряженных плоскостей и их потенциалы.

3. Расчет конденсаторных цепей.

Постоянный ток. Постоянное магнитное поле

1. Плотность тока. Постоянный ток. Когда возникает объемная плотность заряда при протекании постоянного тока? Какие заряды создают электрическое поле внутри однородного проводника при протекании постоянного тока? Какому условию должна удовлетворять плотность постоянного тока, протекающего в однородном проводнике?

2. Расчет цепей постоянного тока (применение закона Ома для участка цепи, правил Кирхгофа). Закон Джоуля-Ленца.

3. Классическая теория проводимости в металлах. Удельная электропроводность

4. Сила Ампера. Ее величина и направление. Сила Лоренца.

Закон Био-Савара-Лапласа. Принцип суперпозиции магнитных полей. Магнитная индукция, создаваемая прямолинейными токами и токами, текущими по дуге окружности. Закон полного тока и его применение для вычисления напряженности магнитного поля (магнитной индукции) при симметричном распределении токов.

Электромагнитное поле в веществе

1. Типы диэлектриков, их диэлектрическая восприимчивость и проницаемость. Граничные условия для и (граница раздела: диэлектрик – вакуум). Вычисление связанных, сторонних объемных

зарядов , диэлектрической проницаемости при заданной зависимости от декартовых координат поляризованности и напряженности электрического поля в диэлектрике. Энергия электрического поля в диэлектрике.

2. Типы магнетиков. Магнитное поле в магнетиках. Намагниченность . Теорема о циркуляции намагниченности. Напряженность магнитного поля. Магнитная восприимчивость и магнитная проницаемость. Закон полного тока для магнетиков. Энергия магнитного поля неферромагнитного вещества.

Переменное электромагнитное поле

1. Электромагнитная индукция. Правило Ленца. Магнитный поток и индуктивность проводящего контура, соленоида.

2. Гармонический ток. Комплексные сопротивления . Расчет цепей гармонического тока с помощью комплексного представления электрических величин, векторных диаграмм. Колебательный контур (энергия, заряд, ток).

3. Ток смещения. Уравнения Максвелла. Частные случаи. Вектор Пойтинга. Плоские монохроматические электромагнитные волны и их характеристики.

megaobuchalka.ru

Раздел 5. Переменное электромагнитное поле.

Поиск Лекций

Вопросы к итоговой аттестации по ТОЭ

(часть III ― ЗФО)

Раздел 1. Уравнения электромагнитного поля

1. Векторные величины, характеризующие электромагнитное поле.

2. Закон полного тока в интегральной и дифференциальной формах.

3. Закон электромагнитной индукции в интегральной и дифференциальной формах.

4. Принципы непрерывности магнитного потока и непрерывности электрического тока в интегральной и дифференциальной формах.

5. Постулат Максвелла в интегральной и дифференциальной формах.

6. Полная система уравнений электромагнитного поля.

7. Энергия электромагнитного поля. Теорема Умова-Пойтинга.

Раздел 2. Электростатическое поле

1. Электростатическое поле. Уравнения электростатического поля в интегральной и дифференциальной форме. Потенциал. Градиент потенциала.

2. Электростатическое поле заданного распределения зарядов. Поле точечного заряда. Поле линейного заряда.

3. Уравнения Лапласа и Пуассона для потенциала. Граничные условия на границе раздела сред.

4. Энергия электростатического поля.

5. Поле и емкость цилиндрического конденсатора.

6. Поле и емкость плоского конденсатора.

7. Электростатическое поле провода кругового сечения.

8. Метод наложения. Электрическое поле и емкость двухпроводной линии передачи (провода тонкие).

9. Электрическое поле и емкость параллельных несоосных цилиндров.

10. Проводящее тело во внешнем электростатическом поле. Электростатическое экранирование.

11. Метод зеркальных изображений расчета электростатических полей. Поле заряженной оси, расположенной над проводящей плоскостью.

12. Потенциальные коэффициенты. Коэффициенты электростатической индукции. Частичные емкости в системе проводящих тел.

13. Поле и емкость двухпроводной линии с учетом влияния земли.

14. Электрическое поле и емкость трехфазной линии.

15. Графический метод построения картины электростатического поля. Определение емкости по картине поля.

Раздел 3. Стационарное электрическое поле

1. Электрическое поле в диэлектрике, окружающем проводники с постоянным током. Уравнения. Граничные условия.

2. Электрическое поле коаксиального кабеля.

3. Электрическое поле и поле вектора плотности постоянного тока проводящей среде. Уравнения. Потенциал. Граничные условия.

4. Подобие электрического поля в проводящей среде с электростатическим полем. Метод электростатической аналогии.

Расчет тока утечки между двумя жилами коаксиального кабеля

6. Расчет электрического поля сферического заземлителя. Шаговое напряжение. Сопротивление сферического заземлителя.

Раздел 4. Стационарное магнитное поле

1. Уравнения магнитного поля постоянных токов. Граничные условия на границе раздела сред.

2. Векторный магнитный потенциал. Уравнение для векторного магнитного потенциала.

3. Магнитный поток. Энергия магнитного поля. Выражение для магнитного потока и энергии магнитного поля через векторный магнитный потенциал.

4. Скалярный магнитный потенциал. Уравнение для скалярного магнитного потенциала.

5. Магнитное поле и внутренняя индуктивность прямолинейного цилиндрического проводника кругового сечения (ток постоянный во времени).

6. Магнитное поле коаксиального кабеля.

7. Магнитное поле линейных проводов. Принцип соответствия плоскопараллельных электрических и магнитных полей.

8. Магнитное поле и индуктивность двухпроводной линии передачи.

9. Магнитное поле и индуктивность трехфазной линии.

10. Передача энергии вдоль коаксиального кабеля. Передача энергии вдоль двухпроводной линии.

11. Поле токов вблизи плоских поверхностей ферромагнитных тел. Метод зеркальных изображений.

12. Магнитное экранирование.

13. Графический метод построения картины магнитного поля. Определение магнитной проводимости по картине поля.

Раздел 5. Переменное электромагнитное поле.

1. Переменное электромагнитное поле при синусоидальных процессах Уравнения Максвелла в комплексной форме. Теорема Умова-Пойнтинга в комплексной форме.

2. Плоская электромагнитная волна в неограниченном диэлектрическом пространстве при синусоидальном изменении векторов поля во времени. Длина волны. Скорость распространения. Волновое сопротивление.

3. Плоская электромагнитная волна в неограниченном проводящем полупространстве при гармоническом изменении величин векторов поля во времени. Глубина проникновения. Волновое сопротивление. Фазовая скорость.

4. Магнитный поверхностный эффект в стальном листе.

5. Электрический поверхностный эффект в плоской шине. Комплексное сопротивление шины.

6. Эффект близости. Комплексное сопротивление системы двух шин.

7. Распределение переменного тока в цилиндрическом проводнике круглого сечения.

8. Активное и внутреннее индуктивное сопротивление цилиндрических проводов круглого сечения (ток синусоидальный).

9. Электромагнитное экранирование.

Литература

1. Теоретические основы электротехники: В 3-х т. Учебник для вузов. Том 3. – 4-е изд. / К.С. Демирчян, Л.Р. Нейман, Н.В. Коровкин, В.Л. Чечурин. – СПб.6 Питер, 2003.

2. Л.А. Бессонов. Теоретические основы электротехники. Электромагнитное поле: Учебник. (Год изд. - любой).

3. И.И. Бандурин, Н.И.Солнышкин. Теоретические основы электротехники. Расчет электромагнитных полей. Методические указания к расчетно-графическим работам по курсу «Теоретические основы электротехники ч.3». ППИ Псков, 2010.

4. Н. И. Солнышкин, И.И. Бандурин. Моделирование электромагнитных полей. –Псков: Издательство ПсковГУ, 2016.

poisk-ru.ru

Переменное электромагнитное поле - Большая Энциклопедия Нефти и Газа, статья, страница 3

Переменное электромагнитное поле

Cтраница 3

Обычно переменное электромагнитное поле не может проникнуть в глубину металла или другой проводящей среды и локализуется в тонком скин-слое вблизи ее поверхности. Авторы открытия обнаружили, что при определенных условиях переменное электромагнитное поле проникает в маталл на глубину порядка длины свободного пробега электронов, которая может быть в сотни и тысячи раз больше, чем глубина скин-слоя. Перенос электромагнитного поля в глубь металла осуществляется отдельными группами электронов проводимости, каждый из которых, двигаясь в постоянном магнитном поле, излучает поглощенную в скин-слое электромагнитную энергию на тех участках своей траектории в глубине металла, где он движется параллельно его поверхности. [31]

Переменное электромагнитное поле индуктора - индуцирует в расплаве вихревые токи; при этом электрическая энергия превращается в тепло. [32]

Переменное электромагнитное поле индуктора индуцирует в расплаве вихревые токи; при этом электрическая энергия превращается в тепло. [33]

Переменное электромагнитное поле антенны распространяется от антенны в пространстве во все стороны, унося в себе полученную от антенны энергию. Это явление называется излучением электромагнитного поля. [35]

Переменное электромагнитное поле вибратора, длина которого сравнима с длиной излучаемой волны, может существенно отличаться по конфигурации от поля вибратора Герца. [36]

Переменное электромагнитное поле вибратора, длина которого сравнима с длиной излучаемой волны, может существенно отличаться по конфигурации от поля вибратора Герца. Но их общей характерной чертой является то, что, начиная с расстояния в несколько длин волн, от вибратора в любом направлении напряженности электрического и магнитного полей убывают обратно пропорционально расстоянию от вибратора. Вследствие этого через всякую окружающую вибратор сферу, радиус которой превышает несколько длин волн, протекает одно и то же количество электромагнитной энергии, которое не возвращается к вибратору. [37]

Переменное электромагнитное поле вибратора, длина которого сравнима с длиной излучаемой волны, может существенно отличаться по конфигурации от поля вибратора Герца. Но их общей характерной чертой является то, что, начиная с расстояния в несколько длин волн, от вибратора в любом направлении напряженности электрического и малнитно-го полей убывают обратно пропорционально расстоянию от вибратора. Вследствие этого через всякую окружающую вибратор сферу, радиус которой превышает несколько длин волн, протекает одно и то же количество электромагнитной энергии, которое не воз - в. [38]

Рассмотрим теперь переменное электромагнитное поле. [39]

Такое медленно переменное электромагнитное поле внутри данной области называется квазистационарным. [40]

Взаимодействие переменного электромагнитного поля с ферромагнитным металлом вызывает в датчике два эффекта: увеличение индуктивности из-за уменьшения рассеяния магнитного поля, зависящего от величины магнитной проницаемости и магнитного сопротивления, и уменьшение индуктивности и рост потерь, что - вызвано действием вихревых токов. При ярко выраженном скин-эффекте на частотах в десятки и сотни килогерц превалируют вихревые токи. На низких частотах ( до 100 - 200 гц) влияние вихревых токов значительно меньше. [41]

Расчет переменного электромагнитного поля в случае однородной изотропной среды ( г const, ц const) также упрощается, если seera так называемые электродинамические потен-и а л ы, зависящие не только от координат, но и от времени. [42]

Под переменным электромагнитным полем понимают совокупность изменяющихся во, времени и взаимно связанных друг с другом электрического и магнитного полей. [43]

Под переменным электромагнитным полем понимают совокупность изменяющихся во времени и взаимно связанных друг с другом электрического и магнитного полей. [44]

В переменном электромагнитном поле поляризация диэлектрика меняется с частотой поля, причем изменение поляризации происходит с трением частиц. На преодоление трения расходуется энергия, вызывающая нагрев диэлектрика. [45]

Страницы: 1 2 3 4

5 Переменное электромагнитное поле. Переменное электромагнитное поле