Ёмкость плоского конденсатора | Все Формулы
![Rendered by QuickLaTeX.com \[ \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9b26b31cc88858c6b01bc73f6d36171f_l3.png)
Ёмкость плоского конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд.
![Rendered by QuickLaTeX.com \[\Large C=\frac{q}{U}=\frac{q}{\varphi_1-\varphi _2} =\varepsilon \varepsilon _0\frac{S}{d}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-09d765c50887987e2330b40f79a68e3e_l3.png)
Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками
![Rendered by QuickLaTeX.com \[\Large C=\frac{q}{U}=\frac{q}{\varphi_1-\varphi _2}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-25394e74f3d757cdf9d8353c32d600aa_l3.png)
При небольших размерах конденсатор отличается значительной емкостью, не зависящей от наличия вблизи него других зарядов или проводников. Обкладкам конденсатора сообщают одинаковые по модулю, но противоположные по знаку заряды, что способствует накоплению зарядов, так как разноименные заряды притягиваются и поэтому располагаются на внутренних поверхностях пластин.
Под зарядом конденсатора понимают заряд одной пластины.
Так же есть:
Энергия конденсатора:
![Rendered by QuickLaTeX.com \[\large W_p=\frac{U q}{2}=\frac{q^2}{2C}=\frac{CU^2}{2}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-c48185fd72204f7932e94ce28f23e7c3_l3.png)
Ёмкость конденсатора :
![Rendered by QuickLaTeX.com \[\large C=\frac{q}{U}=\frac{q}{\varphi_1-\varphi _2} =\varepsilon \varepsilon _0\frac{S}{d}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-65907405fbd131bc9587b0b2750da723_l3.png)
Ёмкость цилиндрического конденсатора :
![Rendered by QuickLaTeX.com \[\large C=2\pi \varepsilon \varepsilon _0\frac{l}{ln(\frac{R_2}{R_1})} \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-53c9846a6d69f2a5b024b7b42f38ecc7_l3.png)
Емкость сферического конденсатора :
![Rendered by QuickLaTeX.com \[\large C=4\pi \varepsilon \varepsilon _0(\frac{1}{R_1} - \frac{1}{R_2})^{-1} \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-8000dcae1c6bc4a3b16bcb4bd7933302_l3.png)
В формуле мы использовали :
C — Электрическая ёмкость (ёмкость конденсатора)
![Rendered by QuickLaTeX.com \[\varepsilon\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-bb5ae93f2a2e84cf68e4653cb1b294fe_l3.png)
— Относительная диэлектрическая проницаемость
![Rendered by QuickLaTeX.com \[\varepsilon _0 = 8.854185\times 10^{-12}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-6904ff3687cf7fd22eff67df52e5007f_l3.png)
— Электрическая постоянная
S — Площадь одной обкладки
d — Расстояние между обкладками
U — Напряжение на обкладках
q — Заряд конденсатора
Емкость плоского конденсатора — Студопедия
Напряженность эл. поля внутри плоского конденсатора
.
— поверхностная плотность заряда, — заряд на одной пластине, — площадь пластины.
— расстояние между обкладками. Т.к. , то , или
= .
= .
Емкость плоского конденсатора
.
—————————————————————
Конденсатор не пропускает постоянный ток (разрывает цепь). Пропускает переменный ток (оказывает емкостное сопротивление ).
Последовательноеи параллельное соединение конденсаторов.
Послед Параллельн
При последовательном соединении напряжение на батарее конденсаторов равно сумме напряжений на каждом конденсаторе :
(7)
Заряды на конденсаторах одинаковы и равны заряду на батарее:
Так как , то из (7):
, или
. . (8)
При параллельном соединении заряд на батарее равен сумме зарядов на каждом конденсаторе:
Напряжение на всех конденсаторах одинаково и равно напряжению на батарее:
.
Т.к. , то
,
или
, . (9)
Энергия электрического поля
Если конденсатор включить по схеме рисунка 1, то при положении I ключа конденсатор заряжается (лампа не светится). При положении II ключа лампа вспыхивает (конденсатор разряжается).
Электрическое поле в конденсаторе обладает энергией , которая выделяется при разрядке конденсатора. Энергия поля в конденсаторе
, (10)
-электроемкость, — напряжение на обкладках конденсатора.
Т.к. емкость плоского конденсатора , то из (1):
.
— объем поля внутри конденсатора.
Тогда
. (11)
Связь напряженности с напряжением :
.
Из (11):
. (12)
— энергия электрического поля, — объем пространства, в котором находится поле,
— электрическая постоянная, — диэлектрическая проницаемость материала, в котором находится поле, — напряженность поля.
Объемная плотность энергии — энергия, заключенная в единице объема,
.
Объемная плотность энергии электрического поля
. (13)
Диэлектрики в электрическом поле
Диэлектрики (изоляторы) разделяют на три группы:
· неполярные диэлектрики
· полярные диэлектрики
· ионные кристаллы.
Электрические заряды в диэлектрике не могут свободно двигаться по его объему.
В молекулах и атомах положительные заряды имеют ядра атомов, а отрицательные – электронные оболочки атомов.
В неполярных диэлектриках центры положительных и отрицательных зарядов совпадают (Рисунок 3, а). Под действием электрического поля происходит смещение зарядов: положительные смещаются в направлении поля, а отрицательные – противоположно.
В результате на поверхности диэлектрика образуются «связанные» заряды. Связанные заряды создают собственное поле , направленное противоположно внешнему (Рисунок 3, б).
Напряженность результирующего поля,
.
Т. о., диэлектрики ослабляют внешнее эл поле. Диэлектрическая проницаемость показывает, во сколько раз диэлектрик уменьшает поле в вакууме:
.
В полярных диэлектриках положительные и отрицательные заряды атомов смещены относительно друг друга. В отсутствии внешнего поля они расположены беспорядочно и не создают внутреннего поля (Рисунок 4, а).
Под действием внешнего поля атомы ориентируются вдоль него, создавая связанные заряды (Рисунок 4, б).
В ионных кристаллах (Рисунок 5, а) связанные заряды появляются на поверхности диэлектрика за счет смещения ионов, расположенных в узлах кристаллической решетки вещества (Рисунок 5, б).
Смещение зарядов в диэлектрике под действием электрического поля называется поляризацией диэлектрика.
Пьезоэлектрики
На поверхности некоторых веществ электрические заряды образуются вследствие механических деформаций (растяжения, сжатия и изгиба). Эти вещества (кварц, турмалин, сегнетова соль и т.д) называются пьезоэлектриками.
Пьезоэлектрики используют для электрической регистрации механических деформаций.
На противоположные стороны пластинки из пьезоэлектрика, которая подвергается, например, сжатию, накладываются электроды, фиксирующие разность потенциалов. По разности потенциалов регистрируют величину деформации.
Ёмкость конденсатора | Все Формулы
![Rendered by QuickLaTeX.com \[ \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9b26b31cc88858c6b01bc73f6d36171f_l3.png)
Электрическая ёмкость — характеристика проводника (конденсатора), мера его способности накапливать электрический заряд.
![Rendered by QuickLaTeX.com \[\Large C=\frac{q}{U}=\frac{q}{\varphi_1-\varphi _2} =\varepsilon \varepsilon _0\frac{S}{d}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-09d765c50887987e2330b40f79a68e3e_l3.png)
Конденсатор состоит из двух проводников (обкладок), которые разделены диэлектриком. На емкость конденсатора не должны влиять окружающие тела, поэтому проводникам придают такую форму, чтобы поле, которое создается накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) две концентрические сферы; 3) два коаксиальных цилиндра. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, сферические и цилиндрические.
Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками
![Rendered by QuickLaTeX.com \[\Large C=\frac{q}{U}=\frac{q}{\varphi_1-\varphi _2}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-25394e74f3d757cdf9d8353c32d600aa_l3.png)
Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.
Конденсаторы можно классифицировать по следующим признакам и свойствам:
1) по назначению — конденсаторы постоянной и переменной емкости;
2) по форме обкладок различают конденсаторы плоские, сферические, цилиндрические и др.;
3) по типу диэлектрика — воздушные, бумажные, слюдяные, керамические, электролитические и т.д.
Так же есть:
Энергия конденсатора:
![Rendered by QuickLaTeX.com \[\large W_p=\frac{U q}{2}=\frac{q^2}{2C}=\frac{CU^2}{2}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-c48185fd72204f7932e94ce28f23e7c3_l3.png)
Ёмкость цилиндрического конденсатора :
![Rendered by QuickLaTeX.com \[\large C=2\pi \varepsilon \varepsilon _0\frac{l}{ln(\frac{R_2}{R_1})}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-115172d250610c4dc7b3f42da106b07a_l3.png)
Ёмкость плоского конденсатора :
![Rendered by QuickLaTeX.com \[\large C=\varepsilon \varepsilon _0\frac{S}{d} = \frac{q}{U}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-48bd8eac0f29d42fe03ae9cb607237a7_l3.png)
Емкость сферического конденсатора :
![Rendered by QuickLaTeX.com \[\large C=4\pi \varepsilon \varepsilon _0(\frac{1}{R_1} - \frac{1}{R_2})^{-1} \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-8000dcae1c6bc4a3b16bcb4bd7933302_l3.png)
В формуле мы использовали :
C — Электрическая ёмкость (ёмкость конденсатора)
q — Заряд
U — Потенциал проводника (Напряжение)
![Rendered by QuickLaTeX.com \[ \varphi\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-8a660c07df44b196dfc18a90ed9de437_l3.png)
— Потенциал
![Rendered by QuickLaTeX.com \[\varepsilon\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-bb5ae93f2a2e84cf68e4653cb1b294fe_l3.png)
— Относительная диэлектрическая проницаемость
![Rendered by QuickLaTeX.com \[ \varepsilon _0 = 8.854185\times 10^{-12}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-380ba968da8291bc8d0b0977ed36fa7d_l3.png)
— Электрическая постоянная
S — Площадь одной обкладки
d — Расстояние между обкладками
Емкость плоского и других конденсаторов
Конфигурация конденсатора такова, что поле, которое создается зарядами, локализовано между обкладками. В общем случае электроемкость конденсатора равна:
\[C=\frac{q}{{\varphi }_1-{\varphi }_2}=\frac{q}{U}\left(1\right),\]
где ${\varphi }_1-{\varphi }_2=U$ — разность потенциалов обкладок, которую называют напряжением и обозначают $U$. Емкость по определению считается положительной величиной. Она зависит только от геометрии обкладок конденсатора их взаиморасположения и диэлектрика. Форму обкладок и их расположение подбирают так, чтобы внешние поля минимально влияли на внутреннее поле конденсатора. Силовые линии поля конденсатора начинались на проводнике с положительным зарядом и заканчивались на проводнике с отрицательным зарядом. Конденсатор может быть проводником, который помещен в полость, окруженную замкнутой оболочкой.
В соответствии с конфигураций конденсаторов можно выделить три большие группы: плоские, сферические и цилиндрические (по форме обкладок). Вычисление емкости конденсатора сводится к определению $напряжения$ конденсатора при известном заряде на его обкладках.
Плоский конденсатор
Плоский конденсатор (рис.1) — это две разноименно заряженные пластины, разделенные тонким слоем диэлектрика. Формула для расчета емкости такого конденсатора представляет собой выражение:
\[С=\frac{\varepsilon {\varepsilon }_0S}{d}\left(2\right),\]
где $S$ — площадь обкладки, $d$ — расстояние между обкладками, $\varepsilon $ — диэлектрическая проницаемость вещества. Чем меньше $d$, тем больше совпадает расчётная емкость конденсатора (2), с реальной емкостью.

Рис. 1
Электроемкость плоского конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равна $d_i$, диэлектрическая проницаемость этого слоя ${\varepsilon }_i$ вычисляется по формуле:
\[C=\frac{{\varepsilon }_0S}{\frac{d_1}{{\varepsilon }_1}+\frac{d_2}{{\varepsilon }_2}+\dots +\frac{d_N}{{\varepsilon }_N}}\ \left(3\right).\]
Сферический конденсатор
В том случае, если внутренний проводник шар или сфера, внешняя замкнутая оболочка — концентрическая ему сфера, то конденсатор является сферическим. Сферический конденсатор (рис.2) состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком. Емкость его можно рассчитать по формуле:
\[C=4\pi \varepsilon {\varepsilon }_0\frac{R_1R_2}{R_2-R_1}\ \left(4\right),\]
где $R_1{\ и\ R}_2$ — радиусы обкладок.

Рис. 2
Цилиндрический конденсатор
Емкость цилиндрического конденсатора равна:
\[C=\frac{2\pi \varepsilon {\varepsilon }_0l}{{ln \left({R_2}/{R_1}\right)\ }}\left(5\right),\]
где $l$ — высота цилиндров, $R_1$ и $R_2$ — радиусы обкладок. Этот вид конденсаторов представляет собой две коаксиальных (соосных) проводящих цилиндрических поверхности (рис.3).

Рис. 3
Еще одной, но не маловажной характеристикой всех конденсаторов является пробивное напряжение ($U_{max}$)— это напряжение, при котором происходит электрический разряд через слой диэлектрика. $U_{max}$ зависит от толщины слоя и свойств диэлектрика, конфигурации конденсатора.
Помимо одиночных конденсаторов применяют их соединения. Для того чтобы увеличить емкость используют параллельное соединение конденсаторов (соединение одноименными обкладками). В этом случае результирующая емкость такого соединения может быть найдена как сумма${\ С}_i$ где $С_i$ — емкость конденсатора с номером i:
\[C=\sum\limits^N_{i=1}{С_i}\ \left(6\right).\]
Если конденсаторы соединить последовательно (обкладками с разными знаками заряда), то суммарная емкость соединения будет всегда меньше, чем минимальная емкость любого конденсатора, который входит в систему. В этом случаем для того чтобы рассчитать результирующую емкость складывают величины, обратные к емкостям отдельных конденсаторов:
\[\frac{1}{C}=\sum\limits^N_{i=1}{{\frac{1}{C_i}}_i}\left(7\right).\]
Пример 2
Задание: Какова напряженность электростатического поля сферического конденсатора на расстоянии x=1 см=${10}^{-2}м$ от поверхности внутренней обкладки, если внутренний радиус обкладки конденсатора $R_1=$1 см${=10}^{-2}м$, внешний $R_2=$ 3 см=${3\cdot 10}^{-2}м$. Напряжение на обкладках равно ${10}^3В$.
Решение:
Напряженность поля, которое создается проводящей заряженной сферой, вычисляется в соответствии с формулой:
\[E=\frac{1}{4\pi \varepsilon {\varepsilon }_0}\frac{q}{r^2}\ \left(2.1\right),\]
где $q$ — заряд внутренней сферы (обкладки конденсатора), $r=R_1+x$ —расстояние от центра сферы.
Заряд сферы найдем из определения емкости конденсатора (С):
\[q=CU\ \left(2.2\right).\]
Емкость сферического конденсатора определяется как:
\[C=4\pi \varepsilon {\varepsilon }_0\frac{R_1R_2}{R_2-R_1}\ \left(2.3\right),\]
где $R_1{\ и\ R}_2$ — радиусы обкладок конденсатора.
Подставим выражения (2.2) и (2.3) в (2.1), получим искомую напряженность:
\[E=\frac{1}{4\pi \varepsilon {\varepsilon }_0}\frac{U}{{(x+R_1)}^2}4\pi \varepsilon {\varepsilon }_0\frac{R_1R_2}{R_2-R_1}=\frac{U}{{(x+R_1)}^2}\frac{R_1R_2}{R_2-R_1}.\]
Так как все данные в задаче уже переведены в систему СИ, проведем вычисления:
\[E=\frac{{10}^3}{{{(1+1)}^2\cdot 10}^{-4}}\cdot \frac{{{10}^{-2}\cdot 3\cdot 10}^{-2}}{{3\cdot 10}^{-2}-{10}^{-2}}=\frac{3\cdot {10}^{-1}}{8\cdot 10^{-6}}=3,75\cdot {10}^4\left(\frac{В}{м}\right).\]
Ответ: $E=3,75\cdot {10}^4\frac{В}{м}.$
Плоский конденсатор. Заряд и емкость конденсатора.
Наряду с резисторами одними из наиболее часто используемых электронных компонентов являются конденсаторы. И в этой статье мы разберемся, из чего они состоят, как работают и для чего применяются! Давайте, в первую очередь, рассмотрим устройство и принцип работы конденсаторов. А затем плавно перейдем к основным свойствам и характеристикам – заряду, энергии и, конечно же, емкости конденсатора. Как видите, нам сегодня предстоит изучить много интересных моментов 🙂
Плоский конденсатор.
Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин:
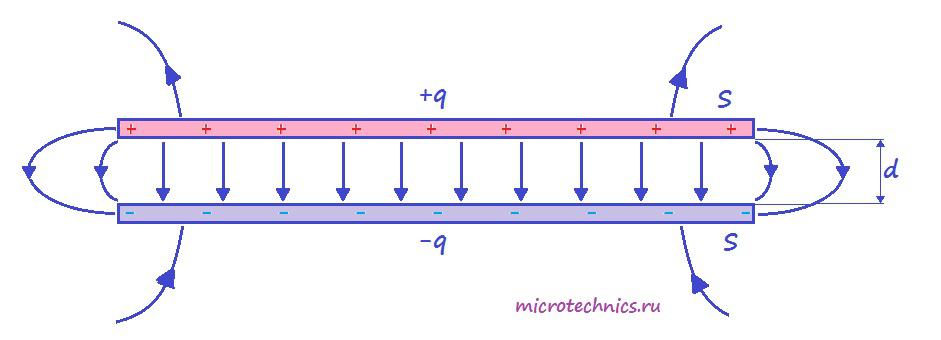
Такое устройство называется плоским конденсатором, а пластины – обкладками конденсатора. Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).
А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит.
Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:
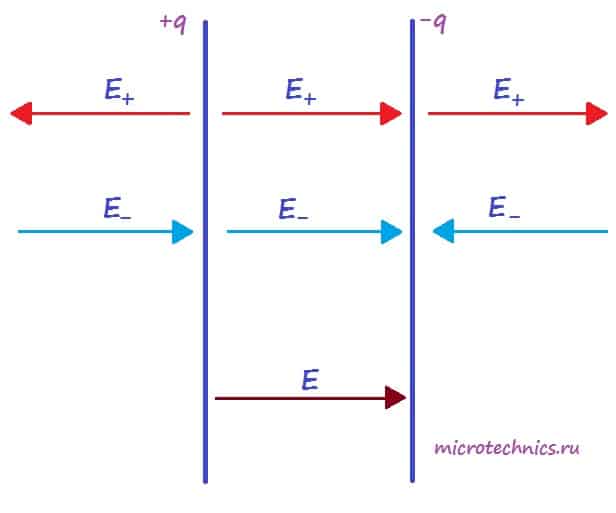
Каждая из обкладок конденсатора в отдельности создает электрическое поле:
- положительно заряженная пластина (+q) создает поле, напряженность которого равна E_{+}
- отрицательно заряженная пластина (-q) создает поле, напряженность которого равна E_{-}
Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:
E = \frac{\sigma}{2\varepsilon_0\thinspace\varepsilon}
Здесь \sigma– это поверхностная плотность заряда: \sigma = \frac{q}{S}, а \varepsilon – диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:
E_+ = E_- = \frac{q}{2\varepsilon_0\thinspace\varepsilon S}
Но направления векторов разные – внутри конденсатора вектора направлены в одну сторону, а вне – в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом:
E = E_+ + E_- = \frac{q}{2\varepsilon_0\thinspace\varepsilon S} + \frac{q}{2\varepsilon_0\thinspace\varepsilon S} = \frac{q}{\varepsilon_0\thinspace\varepsilon S}
А какая же будет величина напряженности вне конденсатора? А все просто – слева и справа от обкладок поля пластин компенсируют друг друга и результирующая напряженность равна 0 🙂
Процессы зарядки и разрядки конденсаторов.
С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:
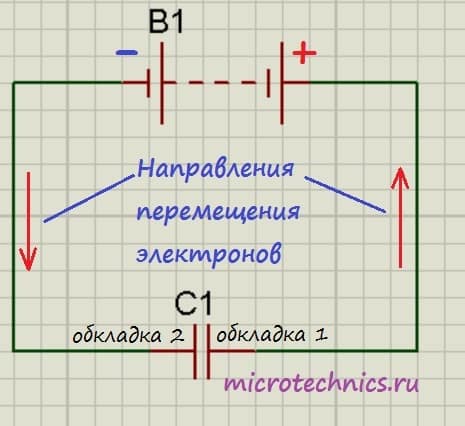
Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?
Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника. Из-за этого на обкладке возникнет недостаток отрицательно заряженных частиц, и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора. В результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока. После этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.
При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:
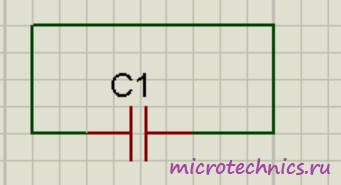
В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.
Как видите, здесь нет ничего сложного 🙂
Емкость и энергия конденсатора.
Важнейшей характеристикой является электрическая емкость конденсатора. Это физическая величина, которая определяется как отношение заряда конденсатора q одного из проводников к разности потенциалов между проводниками:
C = \frac{q}{\Delta\varphi} = \frac{q}{U}
Емкость конденсатора изменяется в Фарадах, но величина 1 Ф является довольно большой, поэтому чаще всего емкость измерятся в микрофарадах (мкФ), нанофарадах (нФ) и пикофарадах (пФ). А поскольку мы уже вывели формулу для расчета напряженности, то давайте выразим напряжение на конденсаторе следующим образом:
U = Ed = \frac{qd}{\varepsilon_0\thinspace\varepsilon S}
Здесь у нас d – это расстояние между пластинами конденсатора, а q – заряд конденсатора. Подставим эту формулу в выражение для емкости:
C = \frac{q\varepsilon_0\thinspace\varepsilon S}{qd} = \frac{\varepsilon_0\thinspace\varepsilon S}{d}
Если в качестве диэлектрика у нас выступает воздух, то во всех формулах можно подставить \varepsilon = 1.
Для запасенной энергии конденсатора справедливы следующие выражения:
W = \frac{CU^2}{2} = \frac{qU}{2} = \frac{q^2}{2C}
Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом. Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение. Это такая величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет.
Итак, мы сегодня рассмотрели основные свойства конденсаторов, их устройство и характеристики! Так что на этом заканчиваем статью, а в следующей мы будем обсуждать различные варианты соединений и маркировку. Не пропустите!
Конденсатор. Энергия электрического поля — материалы для подготовки к ЕГЭ по Физике
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.
Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом — диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах — конденсаторах.
Но прежде введём понятие электрической ёмкости.
Ёмкость уединённого проводника
Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым.
Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду. Коэффициент пропорциональности принято обозначать , так что
Величина называется электрической ёмкостью проводника и равна отношению заряда проводника к его потенциалу:
(1)
Например, потенциал уединённого шара в вакууме равен:
где — заряд шара, — его радиус. Отсюда ёмкость шара:
(2)
Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в раз:
Соответственно, ёмкость шара в раз увеличивается:
(3)
Увеличение ёмкости при наличии диэлектрика — важнейший факт. Мы ещё встретимся с ним при рассмотрении конденсаторов.
Из формул (2) и (3) мы видим, что ёмкость шара зависит только от его радиуса и диэлектрической проницаемости окружающей среды. То же самое будет и в общем случае: ёмкость уединённого проводника не зависит от его заряда; она определяется лишь размерами и формой проводника, а также диэлектрической проницаемостью среды, окружающей проводник. От вещества проводника ёмкость также не зависит.
В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на В. Чем больше ёмкость — тем, соответственно, больший заряд требуется поместить для этого на проводник.
Единицей измерения ёмкости служит фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В.
Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным км.
мкФ.
Как видите, Ф — это очень большая ёмкость.
Единица измерения ёмкости полезна ещё и тем, что позволяет сильно сэкономить на обозначении размерности диэлектрической постоянной . В самом деле, выразим из формулы (2):
Следовательно, диэлектрическая постоянная может измеряться в Ф/м:
Ф.
Так легче запомнить, не правда ли?
Ёмкость плоского конденсатора
Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.
Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников.
Наиболее простым и важным примером такой системы является плоский конденсатор. Он состоит из двух параллельных металлических пластин (называемых обкладками), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.
Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух
Пусть заряды обкладок равны и . Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина — заряд положительной обкладки — называется зарядом конденсатора.
Пусть — площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.
Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:
Здесь — напряжённость поля положительной обкладки, — напряженность поля отрицательной обкладки, — поверхностная плотность зарядов на обкладке:
На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.

Рис. 1. Электрическое поле плоского конденсатора
Согласно принципу суперпозиции, для результирующего поля имеем:
Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):
Внутри конденсатора поле удваивается:
или
(4)
Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:
Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4). Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.
Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты: поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.
Пусть расстояние между обкладками конденсатора равно . Поскольку поле внутри конденсатора является однородным, разность потенциалов между обкладками равна произведению на (вспомните связь напряжения и напряжённости в однородном поле!):
(5)
Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:
(6)
Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на В. Формула (6), таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.
Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора:
(7)
Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними.
Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Как изменится ёмкость конденсатора?
Напряжённость поля внутри конденсатора уменьшится в раз, так что вместо формулы (4) теперь имеем:
(8)
Соответственно, напряжение на конденсаторе:
(9)
Отсюда ёмкость плоского конденсатора с диэлектриком:
(10)
Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.
Важное следствие формулы (10): заполнение конденсатора диэлектриком увеличивает его ёмкость.
Энергия заряженного конденсатора
Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится.
Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке. Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора — ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу.
Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора.
Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора , площадь обкладок .
Возьмём на второй обкладке настолько маленькую площадку, что заряд этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой
где — напряжённость поля первой обкладки:
Следовательно,
Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).
Результирующая сила притяжения второй обкладки к первой складывается из всех этих сил , с которыми притягиваются к первой обкладке всевозможные маленькие заряды второй обкладки. При этом суммировании постоянный множитель вынесется за скобку, а в скобке просуммируются все и дадут . В результате получим:
(11)
Предположим теперь, что расстояние между обкладками изменилось от начальной величины до конечной величины . Сила притяжения пластин совершает при этом работу:
Знак правильный: если пластины сближаются , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины , то работа силы притяжения получается отрицательной, как и должно быть.
С учётом формул (11) и (7) имеем:
где
Это можно переписать следующим образом:
где
(12)
Работа потенциальной силы притяжения обкладок оказалась равна изменению со знаком минус величины . Это как раз и означает, что — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора.
Используя соотношение , из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):
(13)
(14)
Особенно полезными являются формулы (12) и (14).
Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью . Сила притяжения обкладок уменьшится в раз, и вместо (11) получим:
При вычислении работы силы , как нетрудно видеть, величина войдёт в ёмкость , и формулы (12) — (14) останутся неизменными. Ёмкость конденсатора в них теперь будет выражаться по формуле (10).
Итак, формулы (12) — (14) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.
Энергия электрического поля
Мы обещали, что после вычисления энергии конденсатора дадим более глубокое истолкование происхождения этой энергии. Что ж, приступим.
Рассмотрим воздушный конденсатор и преобразуем формулу (14) для его энергии:
Но — объём конденсатора. Получаем:
(15)
Посмотрите внимательно на эту формулу. Она уже не содержит ничего, что являлось бы специфическим для конденсатора! Мы видим энергию электрического поля , сосредоточенного в некотором объёме .
Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.
Итак, электрическое поле само по себе обладает энергией. Ничего удивительного для нас тут нет. Радиоволны, солнечный свет — это примеры распространения энергии, переносимой в пространстве электромагнитными волнами.
Величина — энергия единицы объёма поля — называется объёмной плотностью энергии. Из формулы (15) получим:
(16)
В этой формуле не осталось вообще никаких геометрических величин. Она даёт максимально чистую связь энергии электрического поля и его напряжённости.
Если конденсатор заполнен диэлектриком, то его ёмкость увеличивается в раз, и вместо формул (15) и (16) будем иметь:
(17)
(18)
Как видим, энергия электрического поля зависит ещё и от диэлектрической проницаемости среды, в которой поле находится.
Замечательно, что полученные формулы для энергии и плотности энергии выходят далеко за пределы электростатики: они справедливы не только для электростатического поля, но и для электрических полей, меняющихся во времени.
Электрическая емкость. Конденсаторы. | |
Емкость уединенного проводника. Уединенным будем называть проводник, размеры которого много меньше расстояний до окружающих тел. Пусть это будет шар радиусом r. Если потенциал на бесконечности принять за 0, то потенциал заряженного уединенного шара равен: эта величина не зависит ни от заряда, ни от потенциала и определяется только размерами шара (радиусом) и диэлектрической проницаемостью среды. Этот вывод справедлив для проводника любой формы. |
|
Электрической емкостью проводника наз. отношение заряда проводника к его потенциалу: |
|
Емкость определяется геометрической формой, размерами проводника и свойствами среды (от материала проводника не зависит). Чем больше емкость проводника, тем меньше меняется потенциал при изменении заряда. | Емкость шара в СИ:
|
Единицы емкости. Емкостью 1Ф (фарад) обладает такой проводник, у которого потенциал возрастает на 1 В при сообщении ему заряда в 1 Кл. Емкостью 1Ф обладал бы уединенный шар, радиус которого был бы равен 13 радиусам Солнца. Емкость Земли 700 мкФ Если проводник не уединенный, то потенциалы складываются по правилу суперпозиции и емкость проводника меняется. | 1 мкФ=10-6Ф 1нФ=10-9Ф 1пФ=10-12Ф |
Конденсаторы (condensare — сгущение) . Можно создать систему проводников, емкость которой не зависит от окружающих тел. Первые конденсаторы — лейденская банка (Мушенбрук, сер. XVII в.). |
|
Конденсатор представляет собой систему из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Проводники наз. обкладками конденсатора. Если заряды пластин конденсатора одинаковы по модулю и противоположны по знаку, то под зарядом конденсатора понимают абсолютное значение заряда одной из его обкладок. |
|
На рисунке — плоский и сферический конденсаторы. Поле плоского конденсатора почти все сосредоточено внутри (у идеального — все). Усферического — все поле сосредоточено между обкладками. |
|
Электроемкостью конденсатора называют отношение заряда конденсатора к разности потенциалов между обкладками: |
|
При подключении конденсатора к батарее аккумуляторов происходит поляризация диэлектрика внутри конденсатора и на обкладках появляютсязаряды — конденсатор заряжается. Электрические поля окружающих тел почти не проникают через металлические обкладки и не влияют на разность потенциалов между ними. |
|
Емкость плоского конденсатора.
|
|
Емкость сферического конденсатора . Если зазор между обкладками мал по сравнению с радиусами, то формула переходит в формулу емкости плоского конденсатора. |
|
Виды конденсаторов | |
При подключении электролитического конденсатора необходимо соблюдать полярность. |
|
Назначение конденсаторов
|
|
Емкость конденсатора Формула
 Емкость конденсатора — это способность конденсатора накапливать электрический заряд на единицу напряжения на своих пластинах конденсатора. Емкость определяется делением электрического заряда на напряжение по формуле C = Q / V. Его единица — Фарад.
Емкость конденсатора — это способность конденсатора накапливать электрический заряд на единицу напряжения на своих пластинах конденсатора. Емкость определяется делением электрического заряда на напряжение по формуле C = Q / V. Его единица — Фарад.
Формула
Формула имеет следующий вид:
C = Q / V
Где C — емкость, Q — напряжение, а V — напряжение. Мы также можем найти заряд Q и напряжение V, переставив приведенную выше формулу как:
Q = CV
V = Q / C
Фарад — единица измерения емкости.Один фарад — это величина емкости, когда один кулон заряда хранится с одним вольт на пластинах.
Большинство конденсаторов, используемых в электронике, имеют значения емкости, указанные в микрофарадах (мкФ) и пикофарадах (пФ). Микрофарад — это одна миллионная фарада, а пикофарад — одна триллионная фарада.
Какие факторы влияют на емкость конденсатора?
Это зависит от следующих факторов:
Площадь пластин

Емкость прямо пропорциональна физическому размеру пластин, определяемому площадью пластины A.Большая площадь пластины дает большую емкость и меньшую емкость. На рисунке (а) показано, что площадь пластины конденсатора с параллельными пластинами равна площади одной из пластин. Если пластины перемещаются относительно друг друга, как показано на рис. (B), площадь перекрытия определяет эффективную площадь пластины. Это изменение эффективной площади пластины является основным для определенного типа переменного конденсатора.
Разделение пластин

`Емкость обратно пропорциональна расстоянию между пластинами.Разделение пластин обозначено d, как показано на рис. (А). Чем больше разделение пластин, тем меньше емкость, как показано на рис. (B). Как обсуждалось ранее, напряжение пробоя прямо пропорционально расстоянию между пластинами. Чем дальше разделены пластины, тем больше напряжение пробоя .
Диэлектрическая проницаемость материала
Как известно, изоляционный материал между пластинами конденсатора называется диэлектриком. Диэлектрические материалы имеют тенденцию уменьшать напряжение между пластинами при заданном заряде и, таким образом, увеличивать емкость.Если напряжение фиксировано, из-за наличия диэлектрика может храниться больше заряда, чем может храниться без диэлектрика. Мера способности материала создавать электрическое поле называется диэлектрической постоянной или относительной диэлектрической проницаемостью и обозначается как? r .
Емкость прямо пропорциональна диэлектрической проницаемости. Диэлектрическая проницаемость вакуума определяется как 1, а диэлектрическая проницаемость воздуха очень близка к 1. Эти значения используются в качестве эталона, а для всех других материалов значения ∈r указаны по сравнению с вакуумом или воздухом.Например, материал с εr = 8 может привести к емкости в восемь раз большей, чем у воздуха, при прочих равных условиях.
Диэлектрическая проницаемость ∈r безразмерна, поскольку является относительной мерой. Это отношение абсолютной диэлектрической проницаемости материала, ∈r, к абсолютной диэлектрической проницаемости вакуума, ∈ 0 , выраженное следующей формулой:
∈ r = ∈ / ∈ 0
Ниже приведены некоторые распространенные диэлектрические материалы и типичные диэлектрические постоянные для каждого из них.Значения могут варьироваться, поскольку зависят от конкретного состава материала.
Материал Типичные значения ∈r
- Воздух 1,0
- Тефлон 2,0
- Бумага 2,5
- Масло 4,0
- Слюда 5,0
- Стекло 7,5
- Керамика 1200
Диэлектрическая проницаемость ∈r безразмерна, поскольку относительная мера.Это отношение абсолютной диэлектрической проницаемости материала, ∈r, к абсолютной диэлектрической проницаемости вакуума, ∈0, которое выражается следующей формулой:
∈r = ∈ / ∈0
Значение ∈0 равно 8,85 × 10-12 Ф / м.
Формула емкости в терминах физических параметров
Вы видели, как емкость напрямую связана с площадью пластины, A, и диэлектрической постоянной, ∈r, и обратно пропорциональна расстоянию между пластинами, d. Точная формула для расчета емкости по этим трем величинам:
C = A ∈ r ∈ / d
, где ∈ = ∈ r ∈ 0 = ∈r (8.85 × 10-12Ф / м)
Емкость конденсатора с параллельными пластинами
Рассмотрим конденсатор с параллельными пластинами. Размер пластины большой, а расстояние между пластинами очень мало, поэтому электрическое поле между пластинами однородно.

Электрическое поле E между конденсатором с параллельными пластинами составляет:

Емкость цилиндрических конденсаторов физика
Рассмотрим цилиндрический конденсатор длиной L, образованный двумя коаксиальными цилиндрами радиусов ‘a’ и ‘ б ‘.Предположим, что L >> b, такое, что на концах цилиндров нет окаймляющего поля.

Пусть «q» — это заряд конденсатора, а «V» — разность потенциалов между пластинами. Внутренний цилиндр заряжен положительно, а внешний цилиндр — отрицательно. Мы хотим узнать выражение емкости цилиндрического конденсатора. Для этого мы рассматриваем цилиндрическую гауссову поверхность радиуса «r», такую что a << b.
Если E — напряженность электрического поля в любой точке цилиндрической гауссовой поверхности, то по закону Гаусса:
Если V — разность потенциалов между пластинами, то

Это соотношение для емкость цилиндрического конденсатора.
Емкость сферического конденсатора

Емкость изолированного сферического конденсатора

Внешний источник
https://en.wikipedia.org/wiki/Capacitance
.Конденсаторы
и формулы для расчета емкости
 Конденсаторы — используемые пассивные устройства
Конденсаторы — используемые пассивные устройства
в электронных схемах для хранения энергии в виде электрического поля. Они комплимент
индукторы, хранящие энергию в виде магнитного поля. Идеальный конденсатор
является эквивалентом разомкнутой цепи (бесконечное сопротивление) для постоянного тока (DC) и представляет сопротивление (реактивное сопротивление) к
переменные токи (AC), зависящие от частоты тока (или напряжения).Реактивное сопротивление (сопротивление току
расход) конденсатора обратно пропорционален частоте сигнала, воздействующего на него. Конденсаторы изначально были
называемые «конденсаторами» по причине, восходящей к временам Лейденской банки, когда считалось, что электрические заряды
накапливаться на пластинах в результате конденсации.
Свойство емкости, которая препятствует изменению напряжения, используется для передачи сигналов с
компонент с более высокой частотой, предотвращая прохождение сигналов компонентов с более низкой частотой.Обычное применение
конденсатор в РЧ (радиочастотной) цепи — это место, где есть напряжение смещения постоянного тока, которое необходимо заблокировать от присутствия
в цепи, позволяя РЧ-сигналу проходить. Источники питания постоянного тока используют большие значения емкости параллельно с выходом
клеммы для сглаживания низкочастотных пульсаций из-за выпрямления и / или переключения сигналов.


При использовании последовательно (левый рисунок) или параллельно (правый рисунок) с его
комплемент схемы, индуктор, комбинация индуктор-конденсатор образует контур, который резонирует на определенной частоте
это зависит от значений каждого компонента.В последовательной цепи сопротивление протеканию тока на резонансной частоте
равен нулю с идеальными компонентами. В параллельной цепи (справа) сопротивление току бесконечно с идеальными компонентами.
Реальные конденсаторы, состоящие из физических компонентов, демонстрируют больше, чем просто емкость, когда
 присутствует в цепи переменного тока.
присутствует в цепи переменного тока.
Слева показана модель симулятора общей схемы. Он включает в себя собственно идеальный конденсатор с параллельным резистивным
компонент («Утечка»), реагирующий на переменный ток.Эквивалентный резистивный компонент постоянного тока
(‘ESR’) последовательно с идеальным конденсатором и эквивалентной последовательной индуктивной составляющей
(«ESL») присутствует из-за металлических выводов (если они есть) и характеристик поверхностей пластин.
Эта индуктивность в сочетании с емкостью создает резонансную частоту, на которой конденсатор выглядит как
чистое сопротивление.
Когда рабочая частота увеличивается за пределы резонанса (он же саморезонансная частота или SRF),
схема ведет себя как индуктивность, а не как емкость.Следовательно, требуется тщательное рассмотрение SRF, когда
выбор конденсаторов. В симуляторах типа SPICE используется эта или даже более сложная модель для облегчения более точных расчетов.
в широком диапазоне частот.
Уравнения для последовательного и параллельного объединения конденсаторов приведены ниже. Дополнительные уравнения приведены для конденсаторов
различной конфигурации. Как показывают эти цифры и формулы, емкость — это мера способности двух поверхностей
для хранения электрического заряда.Разделенный и изолированный диэлектриком (изолятором), чистый положительный заряд накапливается на
одна поверхность и чистый отрицательный заряд хранится на другой поверхности. В идеальном конденсаторе заряд будет храниться бесконечно;
однако реальные конденсаторы постепенно теряют свой заряд из-за токов утечки через неидеальный диэлектрик.
|
|
Связанные страницы на RF Cafe
— Конденсаторы и
Расчет емкости
—
Конденсатор
Цветовой код
— Преобразование емкости
—
Конденсатор Диэлектрики
—
Стандартные значения конденсатора
—
Поставщики конденсаторов
—
Благородное искусство разъединения
.
Формулы и калькуляторы емкости
На этой странице представлены формулы и калькуляторы емкостей
конденсаторы различной формы или типа. Это также полезно, если вы
собираетесь использовать свой конденсатор в
Танк LC резонансный
цепь.
Емкость конденсаторов с параллельными пластинами
Конденсатор с параллельными пластинами состоит из двух плоских параллельных пластин, которые
— электроды, разделенные
диэлектрик
или изолятор.Для формулы и калькулятора здесь пластины могут быть
любой формы, если они плоские, параллельны и вы знаете площадь
пластины или что-то еще, что нужно, чтобы найти этот район.
|
|
Формула для определения емкости конденсатора с параллельными пластинами:

Где:
- ε r = относительная диэлектрическая проницаемость диэлектрика
(реже К, диэлектрическая проницаемость) - ε 0 = 8.854×10 -12 Ф / м (фарад / метр) =
диэлектрическая проницаемость вакуума или диэлектрическая проницаемость свободного пространства
На схемах показаны конденсаторы с параллельными пластинами различной формы.
пластины, одна прямоугольная и одна круглая. Формула для расчета
площадь прямоугольника:

а формула для вычисления площади круга:

Где π — это число пи, равное 3,14159.
Емкость цилиндрических конденсаторов
Цилиндрический конденсатор состоит из двух цилиндров, также называемых
пластины, которые являются электродами, разделены
диэлектрик
или изолятор.
|
Формула емкости цилиндрического конденсатора:

Где:
- ε r = относительная диэлектрическая проницаемость диэлектрика
(реже К, диэлектрическая проницаемость) - ε 0 = 8,854×10 -12 Ф / м (фарад / метр) =
диэлектрическая проницаемость вакуума или диэлектрическая проницаемость свободного пространства
.Конденсаторы серии
| Калькулятор формул
— в некоторых случаях конденсаторы могут появляться последовательно, и необходимо иметь возможность рассчитать значение.
Емкостное руководство В комплект входит:
Емкость
Формулы конденсатора
Емкостное реактивное сопротивление
Параллельные конденсаторы
Последовательные конденсаторы
Диэлектрическая проницаемость и относительная диэлектрическая проницаемость
Коэффициент рассеяния, тангенс угла потерь, ESR
Таблица преобразования конденсаторов
В некоторых случаях может потребоваться последовательное подключение конденсаторов.В некоторых схемах это происходит естественным образом, например в некоторых генераторах может быть конденсаторный делитель напряжения переменного тока. В других случаях конденсаторы могут быть включены последовательно по разным причинам, некоторые примеры приведены ниже.
Хотя наиболее распространенная комбинация состоит в том, чтобы видеть два конденсатора последовательно, можно разместить три или более последовательно.
Формула конденсаторов серии
Если конденсаторы размещены параллельно, это немного похоже на увеличение размера пластин конденсатора, и, следовательно, значения конденсаторов, подключенных параллельно, можно просто сложить.Если конденсаторы включены последовательно, их нельзя просто добавить.
Конденсаторы, подключенные последовательно
Теоретически нет ограничений на количество конденсаторов, которые могут быть добавлены последовательно. Очевидно, что могут быть практические ограничения в зависимости от области применения, места и других физических ограничений.
Когда конденсаторы соединены последовательно, общую емкость можно определить, взяв величину, обратную емкости каждого конденсатора, и сложив их вместе, чтобы получить величину, обратную общей емкости.
1Cotal = 1C1 + 1C2 + 1C3. . . . .
Два конденсатора последовательно
При вычислении общего значения общей емкости для серии конденсаторов, включенных последовательно, вычисление может быть немного длинным, если выполняется вручную. Как и в большинстве сетей, только два конденсатора устанавливаются последовательно, что позволяет значительно упростить формулу. Это значительно упрощает ручные вычисления.
Два конденсатора соединены последовательно
Конденсаторы в последовательном калькуляторе
Калькулятор ниже показывает общую емкость для двух последовательно соединенных конденсаторов.Емкость может быть введена в фарадах, мкфарадах, нанофарадах или пикофарадах при условии, что для обоих конденсаторов используются одинаковые единицы. Ответ предоставляется в тех же единицах, что и введенные.
Вычислитель конденсаторов серии
Меры предосторожности при использовании конденсаторов серии
Хотя конденсаторы действительно появляются последовательно в ряде конфигураций схем, таких как генераторы и т.п., конденсаторы могут использоваться последовательно для увеличения рабочего напряжения.
Когда два конденсатора используются последовательно, проблема часто заключается в том, что два конденсатора не распределяют напряжение поровну. Различия в токе утечки возникают между конденсаторами, особенно для конденсаторов, таких как электролитические версии, и это означает, что напряжения на двух конденсаторах могут сильно различаться, и в результате один может подвергаться условиям перенапряжения, что может привести к разрушению одного. или оба конденсатора. Это может произойти, если два конденсатора были включены последовательно, чтобы обеспечить увеличение рабочего напряжения.
Разница в токе утечки может легко возникнуть из-за незначительных различий в производстве или даже из-за разницы в скорости старения двух конденсаторов — ток утечки в электролитических конденсаторах увеличивается со временем, особенно если они не используются.
Два конденсатора, соединенных последовательно с резистивным делителем напряжения
Для помощи в равномерном распределении напряжения между двумя конденсаторами, вокруг конденсаторов размещены резисторы с высокой номинальной стоимостью в качестве делителя потенциала. Значения могут быть порядка 100 кОм или, возможно, даже немного выше, но этого достаточно, чтобы напряжения могли надежно делиться на обоих конденсаторах.
По сути, номиналы двух резисторов должны быть такими, чтобы ток, протекающий через них, был как минимум в десять раз выше, чем ток утечки. Таким образом, напряжение будет более равномерно распределяться между последовательно включенными конденсаторами. Даже при таком подходе хорошо оставлять хороший запас по рабочему напряжению, особенно при использовании электролитических конденсаторов.
Последовательное соединение конденсаторов происходит во многих цепях. Очень полезно знать, как рассчитать общую стоимость, даже если это приблизительный расчет в вашей голове.Если требуется более точное значение, то онлайн-калькулятор последовательного конденсатора может оказаться очень полезным.
Дополнительные основные понятия:
Напряжение
ток
Сопротивление
Емкость
Мощность
Трансформеры
RF шум
Децибел, дБ
Q, добротность
Вернуться в меню основных концепций. . .
.

 , где e — диэлектрическая проницаемость окружающей среды. Следовательно:
, где e — диэлектрическая проницаемость окружающей среды. Следовательно: 
 .
. —
—

 .
.
 , т.о. емкость плоского конденсатора зависит только от его размеров, формы и диэлектрической проницаемости. Для создания конденсатора большой емкости необходимо увеличить площадь пластин и уменьшить толщину слоя диэлектрика.
, т.о. емкость плоского конденсатора зависит только от его размеров, формы и диэлектрической проницаемости. Для создания конденсатора большой емкости необходимо увеличить площадь пластин и уменьшить толщину слоя диэлектрика.
















 Коэффициент рассеяния (DF), также известный как тангенс потерь (tan δ), взаимозаменяемо определяется как
Коэффициент рассеяния (DF), также известный как тангенс потерь (tan δ), взаимозаменяемо определяется как

 означает, что длина дана в дюймах, а индуктивность — в единицах Генри.
означает, что длина дана в дюймах, а индуктивность — в единицах Генри.






