Формула индуктивное сопротивление трансформатора: Расчетные сопротивления трансформаторов — КиберПедия

Реактивное сопротивление трансформатора: формулы расчета

Мы привыкли считать, что все магнитные потоки в трансформаторе пронизывают обе обмотки и магнитопровод. Если бы существовал идеальный трансформатор, то это действительно так бы и происходило. К сожалению, в реальности часть магнитного потока преодолевает изоляционное пространство, выходит за пределы обмоток и замыкается в них (см. рис. 1). В результате возникает реактивное сопротивление трансформатора. Такое явление ещё называют рассеиванием магнитных потоков.

Рис. 1. Схема, иллюстрирующая рассеивание магнитных потоков

В катушках существуют и другие сопротивления, являющиеся причинами потерь мощности. Таковыми являются: внутреннее сопротивление материалов обмоток, и рассеивания, вызванные индуктивными сопротивлениями. Совокупность рассеиваний магнитных потоков называют внутренним сопротивлением или импедансом трансформатора.

Потери реактивных мощностей

Вспомним, как работает идеальный двухобмоточный трансформатор (см. рис. 2). Когда первичная обмотка окажется под переменным напряжением (например, от электрической сети), возникнет магнитный поток, который пронизывает вторичную катушку индуктивности. Под действием магнитных полей происходит возбуждение вторичных обмоток, в витках которых возникает ЭДС. При подключении активной мощности к прибору во вторичной цепи начинает протекать переменный ток с частотой входного тока.

Рис. 2. Устройство трансформатора

В идеальном трансформаторе образуется прямо пропорциональная связь между напряжениями в обмотках. Их соотношение определяется соотношением числа витков каждой из катушек. Если U₁ и U₂ – напряжения в первой и второй обмотке соответственно, а w₁ и w₂ – количество витков обмоток, то справедлива формула: U₁ / U₂ = w₁ / w₂.

Другими словами: напряжение в рабочей обмотке во столько раз больше (меньше), во сколько раз количество мотков второй катушки увеличено (уменьшено) по отношению к числу витков, образующих первичную обмотку.

Величину w₁ / w₂ = k принято называть коэффициентом трансформации. Заметим, что формула, приведённая выше, применима также для автотрансформаторов.

В реальном трансформаторе часть энергии теряется из-за рассеяния магнитных потоков (см. рис. 1). Зоны, где происходит концентрация потоков рассеяния обозначены пунктирными линиями. На рисунке видно, что индуктивность рассеяния охватывает  магнитопровод и выходит за пределы обмоток.

Наличие реактивных сопротивлений в совокупности с активным сопротивлением обмоток приводят к нагреванию конструкции. То есть, при расчётах КПД необходимо учитывать импеданс трансформатора.

Обозначим активное сопротивление обмоток символами R₁ и R₂ соответственно, а реактивное – буквами X₁ и X₂. Тогда импеданс первичной обмотки можно записать в виде: Z₁= R₁+jX₁. Для рабочей катушки соответственно будем иметь: Z₂= R₂+jX₂, где j – коэффициент, зависящий от типа сердечника.

Реактивное сопротивление можно представить в виде разницы индукционного и ёмкостного показателя: X = R_L – R_C. Учитывая, что R_L =  ωL, а R_C = 1/ωC, где ω – частота тока, получаем формулу для вычисления реактивного сопротивления: X = ωL – 1/ωC.

Не прибегая к цепочке преобразований, приведём готовую формулу для расчёта полного сопротивления, то есть, для определения импеданса трансформатора:

Суммарное сопротивление трансформатора необходимо знать для определения его КПД. Величины потерь в основном зависят от материала обмоток и конструктивных особенностей трансформаторного железа. Вихревые потоки в монолитных стальных сердечниках значительно больше, чем многосекционных конструкциях магнитопроводов. Поэтому на практике сердечники изготавливаются из тонких пластин трансформаторной стали. С целью повышения удельного сопротивления материала, в железо добавляют кремний, а сами пластины покрывают изоляционным лаком.

Для определения параметров трансформаторов важно найти активное и реактивное сопротивление, провести расчёты потерь холостого хода. Приведённая выше формула не практична для вычисления импеданса по причине сложности измерений величин индукционного и ёмкостного сопротивлений. Поэтому на практике пользуются другими методами для расчёта, основанными на особенностях режимов работы силовых трансформаторов.

Режимы работы

Двухобмоточный трансформатор способен работать в одном из трёх режимов:

• вхолостую;
• в режиме нагрузки;
• в состоянии короткого замыкания.

Для проведения расчётов режимов электрических цепей проводимости заменяют нагрузкой, величина которой равна потерям при работе в режиме холостого хода. Вычисления параметров схемы замещения проводят опытным путём, переводя трансформатор в один из возможных режимов: холостого хода, либо в состояние короткого замыкания. Таким способом можно определить:

• уровень потерь активной мощности при работе на холостом ходу;
• величины потерь активной мощности в короткозамкнутом приборе;
• напряжение короткого замыкания;
• силу тока холостого хода;
• активное и реактивное сопротивление в короткозамкнутом трансформаторе.

Параметры режима холостого хода

Для перехода в работу на холостом ходу необходимо убрать отсутствует нагрузку на вторичной обмотке, то есть – разомкнуть электрическую цепь. В разомкнутой катушке напряжение отсутствует. Главной составляющей тока в первичной цепи является ток, возникающий на реактивных сопротивлениях. С помощью измерительных приборов довольно просто найти основные параметры переменного тока намагничивания, используя которые можно вычислить потери мощности, умножив силу тока на подаваемое напряжение.

Схема измерений на холостом ходу показана на рисунке 3. На схеме показаны точки для подключения измерительных приборов.

Рис. 3. Схема режима холостого хода

Формула, применяемая для  расчётов параметров реактивной проводимости, выглядит так: В_т = I_х%*S_ном  / 100* U_{в ном}²  Умножитель 100 в знаменателе применён потому, что величина тока холостого хода I_х обычно выражается в процентах.

Режим короткого замыкания

Для перевода трансформатора на работу в режиме короткого замыкания закорачивают обмотку низшего напряжения. На вторую катушку подают такое напряжение, при котором в каждой обмотке циркулирует номинальный ток. Поскольку подаваемое напряжение существенно ниже номинальных напряжений, то потери активной мощности в проводимости настолько малы, что ими можно пренебречь.

Таким образом, у нас остаются активные мощности в трансформаторе, которые расходуются на нагрев обмоток: ΔP_k = 3* I_1ном * R_т. Выразив ток I_{1 ном} через напряжение U_ка и сопротивление R_т, умножив выражение на 100, получим формулу для вычисления падения напряжения в зонах активного сопротивления (в процентах):

Активное сопротивление двухобмоточного силового трансформатора вычисляем по формуле:

Подставив значение R_т в предыдущую формулу, получим:

Вывод: в короткозамкнутом трансформаторе падение напряжения в зоне активного сопротивления (выраженная в %) прямо пропорционально размеру потерь активной мощности.

Формула для вычисления падения напряжения в зонах реактивных сопротивлений имеет вид:

Отсюда находим:

Величины реактивных сопротивлений в современных трансформаторах гораздо меньше активного. Поэтому можно считать что падение напряжения в зоне реактивного сопротивления U_{к р} ≈ U_к, поэтому для практических расчётов можно пользоваться формулой: X_T = U_k*U_{в ном}² / 100*S_ном

Рассуждения, приведённые выше, справедливы также для многообмоточных, в том числе и для трёхфазных трансформаторов. Однако вычисления проводятся по каждой обмотке в отдельности, а задача сводится к решению систем уравнений.

Знание коэффициентов мощности, сопротивления рассеивания и других параметров магнитных цепей позволяет делать расчёты для определения величин номинальных нагрузок. Это, в свою очередь, обеспечивает работу трансформатора в промежутке номинальных мощностей.

Список использованной литературы

• Сивухин Д. В. «Общий курс физики» 1975
• Н.А. Костин, О.Г.Шейкина «Теоретические основы электротехники» 2007
• Нейман Л.Р., Демирчян К.С. «Теоретические основы электротехники» 1981
• Бартош А.И. «Электрика для любознательных» 2019

Сопротивление элементов схемы замещения в сети 0,4 кВ

Содержание

Для того чтобы рассчитать токи КЗ в сети до 1000 В, следует первоначально составить схему замещения, которая состоит из всех сопротивлений цепи КЗ. Активные и индуктивные сопротивления всех элементов схемы замещения выражают в миллиомах (мОм).

Как определять сопротивления отдельных элементов схемы замещения, об этом вы и узнаете в этой статье.

Активные и индуктивные сопротивления питающей энергосистемы рассчитывают на стороне ВН понижающего трансформатора и приводят к стороне НН по формуле 2-6 [Л3. с. 28].

На практике можно не учитывать активное сопротивление энергосистемы, а значение индуктивного сопротивления приравнивать как к полному сопротивлению энергосистемы (на точность расчетов это никак не скажется). В этом случае значение (в Омах) индуктивное (полное) сопротивление энергосистемы определяется по формуле 2-7 [Л3. с. 28].

После того как определили индуктивное сопротивление системы по формуле 2-7 [Л3. с. 28], данное сопротивление нужно привести к стороне НН по формуле 2-6 [Л3. с. 28].

Индуктивное сопротивление системы, также можно определить по формулам представленных в ГОСТ 28249-93:

Как мы видим формула 1 из ГОСТ 28249-93 соответствует формулам 2-6, 2-7 из [Л3. с. 28].

Пример

Определить сопротивление энергосистемы, учитывая, что ток КЗ со стороны энергосистемы на зажимах ВН трансформатора 6/0,4 кВ составляет в максимальном режиме – 19 кА, в минимальном – 13 кА.

Решение

Определяем индуктивное сопротивление энергосистемы по формулам 2-6, 2-7.

Сопротивление энергосистемы в максимальном режиме, приведенное к напряжению 0,4 кВ:

Сопротивление энергосистемы в минимальном режиме, приведенное к напряжению 0,4 кВ:

Значения (в мОм) полного (zт), активного (rт) и индуктивного (хт) сопротивления понижающего трансформатора приведенных к стороне НН определяются по формулам: 2-8, 2-9, 2-10 [Л3. с. 28].

На большинстве трансформаторов 10(6)/0,4 кВ имеется возможность регулирования напряжения путем переключения без возбуждения (ПБВ) при отключенном от сети трансформаторе как со стороны высшего так и низшего напряжения. Напряжение регулируется со стороны высшего напряжения на величину ±2х2,5% от номинального значения.

Для трансформаторов с пределом регулирования ПБВ ±2х2,5%, полное сопротивление будет изменятся в пределах:

Значения индуктивного и активного сопротивления трансформатора по ГОСТ 28249-93 определяются по формулам:

Как видно, формулы из ГОСТ 28249-93 совпадают с формулами приведенными в [Л3. с. 28].

Для упрощения расчета активного и индуктивного сопротивления тр-ра, можно использовать таблицу 2-4 [Л3. с. 29] для схем соединения обмоток трансформатора Y/Yo и ∆/Yo. Причем для схем соединения обмоток трансформатора ∆/Yo, значения активного (r0) и индуктивного (х0) сопротивления нулевой последовательности равны значениям активного и индуктивного сопротивления прямой последовательности: r0 = rт и х0 = хт.

Пример

Определить сопротивление трансформатора ТМ 50/6 со схемой соединения обмоток ∆/Yо.

Решение

По справочным данным определяем технические данные трансформатора: Sном. = 50 кВА, Uном.ВН = 6,3 кВ, Uном.НН = 0,4 кВ, Uкз = 4%, ∆Ркз=1,1 кВт.

Определяем полное сопротивление трансформатора для стороны 0,4 кВ по формуле 2-8:

Определяем активное сопротивление трансформатора для стороны 0,4 кВ по формуле 2-9:

Определяем индуктивное сопротивление трансформатора для стороны 0,4 кВ по формуле 2-10:

Значения активного и индуктивного сопротивления кабелей определяются по формуле 2-11 [Л3. с. 29].

Сопротивление шин и шинопроводов длиной 5м и меньше, можно не рассчитывать, так как они не влияют на значение токов КЗ.

Значения активного и индуктивного сопротивления шин и шинопроводов определяется аналогично кабелям.

Зная расстояние между прямоугольными шинами, можно приближенно определить индуктивное сопротивление (мОм/м) по формуле 2-12 [Л3. с. 29].

Пример

Определить активное и индуктивное сопротивление алюминиевых шин сечением 60х8 мм2 от трансформатора ТМ-630/6 до распределительного щита 0,4 кВ, общая длина проложенных от трансформатора до РП-0,4 кВ составляет 10 м. В данном примере определим сопротивление шин, когда шины находятся как в горизонтальном положении, так и в вертикальном.

Решение

4.1 Определим активное и индуктивное сопротивление шин при горизонтальном расположении.

По таблице 2.6 определяем погонное активное сопротивление r_уд. = 0,074 мОм/м, индуктивное сопротивление определяем по формуле 2-12 [Л3. с. 29].

где: расстояние между шинами первой и второй фазы а₁₂ = 200 мм, между второй и третью а₂₃ = 200 мм, между первой и третью а₁₃ = 200 + 60 + 200 = 460 мм, а среднегеометрическое расстояние:

Сопротивление шин от тр-ра до РП-0,4 кВ:

4.2 Определим активное и индуктивное сопротивление шин при вертикальном расположении

При вертикальном расположении шин, активное сопротивление не изменяется, а индуктивное сопротивление составляет:

где: расстояние между шинами первой и второй фазы а₁₂ = 200 мм, между второй и третью а₂₃ = 200 мм, между первой и третью а₁₃ = 200 + 8 + 200 = 408 мм, а среднегеометрическое расстояние:

Сопротивление шин от тр-ра до РП-0,4 кВ:

Активное и индуктивное сопротивления линий определяется по той же формуле 2-11 [Л3. с. 29], что и кабели.

Значение индуктивного сопротивления для проводов из цветных металлов можно приближенно принимать равным 0,3 мОм/м, активного по табл. 2.8.

Для стальных проводов активное и индуктивное сопротивление определяется исходя из конструкции провода и значения протекающего по нему тока. Зависимость эта сложная и математическому расчету не поддается, из-за большого количества переменных (сечение провода, температура окружающего воздуха, которая постоянно меняется в течении года, времени суток; нагревом провода током КЗ), которые влияют на значение сопротивление стальных проводов.

Поэтому учесть все эти зависимости практически не возможно и на практике активное сопротивление условно принимают при температуре 20°С и определяют по кривым зависимости стальных проводов от проходящего по ним токам, представленных в приложениях П23-П27 [Л4. с. 80-82].

Активное и индуктивное сопротивление для проводов самонесущих изолированных (СИП) определяют по таблицам Б.1, Б.2 [Л5. с. 23-26].

Номинальные параметры реактора уже заданы в обозначении самого реактора типа РТТ и РТСТ. Например у реактора типа РТТ-0,38-100-0,15:

• 0,38 – номинальное напряжение 380 В;
• 100 – номинальный ток 100 А;
• 0,15 – индуктивное сопротивление при частоте 50 Гц равно 150 мОм.

Активное сопротивление для исполнения У3 (алюминиевая обмотка) — 17 мОм, для исполнения Т3 (медная обмотка) – 16 мОм.

Значения активных и индуктивных сопротивлений трансформаторов тока принимаются по приложению 5 таблица 20 ГОСТ 28249-93. Активным и индуктивным сопротивлением одновитковых трансформаторов (на токи более 500 А) при расчетах токов КЗ можно пренебречь.

Согласно [Л3. с. 32] для упрощения расчетов, сопротивления трансформаторов тока не учитывают ввиду почти незаметного влияния на токи КЗ.

Приближенные значения сопротивлений разъемных контактов коммутационных аппаратов напряжением до 1 кВ определяются по приложению 4 таблица 19 ГОСТ 28249-93. При приближенном учете сопротивление коммутационных аппаратов принимают — 1 мОм.

Значения сопротивления контактных соединений кабелей и шинопроводов определяют по приложению 4 таблицы 17,18 ГОСТ 28249-93. Для упрощения расчетов, данными сопротивлениями можно пренебречь. При приближенном учете сопротивлений контактов принимают:
• rк = 0,1 мОм — для контактных соединений кабелей;
• rк = 0,01 мОм — для шинопроводов.

1. Рекомендации по расчету сопротивления цепи «фаза-нуль». Главэлектромонтаж. 1986 г.
2. ГОСТ 28249-93 – Методы расчета в электроустановках переменного тока напряжением до 1 кВ.
3. Беляев А.В. Выбор аппаратуры, защит и кабелей в сети 0,4 кВ. Учебное пособие. 2008 г.
4. Голубев М.Л. Расчет токов короткого замыкания в электросетях 0,4 — 35 кВ. 2-e изд. 1980 г.
5. ТУ 16-705.500-2006. Провода самонесущие изолированные и защищенные для воздушных линий электропередач.

что это, как рассчитать, формулы и примеры

Трансформатор, как элемент радиотехники и электротехники, работает на основе электромагнитной индукции. Говоря об индуктивности трансформатора, имеют в виду индуктивность обмоток и взаимоиндукцию между ними.

Каждая из обмоток представляет некоторое количество витков провода, намотанных на ферромагнитный сердечник, то есть обыкновенную катушку индуктивности.

Трудность в определении параметров катушки заключается в том, что они изменяются в зависимости от нескольких параметров и их сочетания:

• токи в обмотках;
• уровень намагниченности магнитопровода;
• магнитные характеристики сердечника;
• взаимодействие между соседними обмотками;
• наличия постоянной составляющей тока.

Конструкция и принцип действия силового трансформатора

В основе конструкции любого трансформатора находятся следующие элементы:

1. Сердечник из ферромагнитного материала.
2. Первичная и вторичные обмотки. В случае автотрансформатора одна обмотка выполняет обе функции.

В сетях переменного тока промышленной частоты (50 или 60Гц) в качестве ферромагнитного материала используется сталь, обработанная по специальной технологии. На высоких частотах часто делаются трансформаторы без сердечника, поскольку для нормальной работы достаточно взаимосвязи межу катушками.

Принцип работы:

• в первичной обмотке, подключенной в цепь питания, создается переменное электрическое поле;
• под действием поля первичной катушки в сердечнике создается переменное магнитное поле;
• в силу электромагнитной индукции во всех обмотках наблюдается ЭДС индукции.

ЭДС индукции в первичной обмотке направлена противоположно поданному напряжению, поэтому они взаимно компенсируются. В результате, при отсутствии нагрузки через первичную обмотку протекает сравнительно небольшой ток холостого хода.

Наличие тока вторичной цепи аналогично вызывает дополнительный магнитный поток, а он – ЭДС самоиндукции в первичное катушке. В результате компенсация первичного напряжения снижается и растет ток в первичной цепи.

Физическое понятие индуктивности обмоток

Индуктивность представляет собой коэффициент пропорциональности между током, создаваемым замкнутым электрическим контуром, и магнитным потоком, который создается этим контуром.

Более понятной формулировкой будет та, которая говорит о величине ЭДС самоиндукции в замкнутом контуре, которая возникает при изменении силы тока за единицу времени. То есть, понятие индуктивности справедливо для изменяющегося тока.

При постоянном токе говорить об индуктивности бессмысленно.

В идеальном трансформаторе все электромагнитное поле, создаваемое обмотками, замкнуто в магнитном сердечнике. В реальных конструкциях существует поле рассеяния, величина которого зависит от способа выполнения катушки и конструктивных особенностей сердечника. Чем больше толщина намотки, тем большая часть электромагнитного поля замыкается вне магнитопровода.

Этому способствует также качество сборки магнитопровода. Зазоры между пластинами способствуют резкому увеличению рассеивания. В связи с этим наилучшими свойствами обладают О-образные сердечники.

Формулы и измерение

Формулы для расчета индуктивности катушек довольно сложны и имеет различный вид для различных типов исполнения обмоток:

• линейный проводник;
• одновитковая катушка;
• плоская катушка;
• соленоидальная обмотка;
• тороидальная форма.

Наибольшие сложности возникают при расчетах многовитковых многослойных катушек, то есть тех, которые составляют обмотку трансформаторов.

В подавляющем большинстве случаев точный расчет невозможен, поэтому приходится использовать примерные данные и уточнять их после проведения измерений.

Формулы  для расчета индуктивности трансформатора основаны на расчетах соленоида:

L=µ_{µN²S/l, где}

µ0 – магнитная постоянная;

µ – магнитная проницаемость сердечника;

N – количество витков;

S – площадь одного витка;

l – длина обмотки.

Для измерения индуктивности существует несколько методик и приборов, созданных на их основе. В большинстве случаев измерение производится путем вычислений индуктивного сопротивления катушки при подаче образцового напряжения заданной частоты и измеренного значения тока через обмотку.

В специализированных приборах вычисления производятся автоматически, и пользователь только считывает показания шкалы прибора, выраженные в единицах индуктивности – Гн, мГн или мкГн.

Как измерить в домашних условиях

Приборы для непосредственного измерения индуктивности имеют высокую стоимость и редко используются в домашних условиях. С приемлемой точностью результаты можно получить, используя обычные приборы для измерения переменного тока: амперметр и вольтметр. Также необходим омметр.

Порядок действий следующий:

1. При помощи омметра определяют активное сопротивление обмотки R.
2. Подключают трансформатор последовательно с амперметром в сеть.
3. Параллельно обмотке подключают вольтметр.
4. По показаниям приборов определяют полное сопротивление трансформатора: Z=U/I
5. Индуктивное сопротивление находят, вычитая из полного сопротивления активное: X_L=Z-R
6. Индуктивность определяется по формуле: L=X_L/(2πf), где π – число пи 3.14, f – частота измерений.

Как правило, активное сопротивление намотки значительно (на несколько порядков) меньше индуктивного, поэтому можно его не учитывать. Именно поэтому, включение трансформатора в цепь постоянного напряжения вызывает короткое  замыкание. Ток обмотки при этом будет ограничиваться только активным сопротивлением.

Пример расчета

К примеру, требуется рассчитать индуктивность первичной обмотки трансформатора питания. Путем измерений определено:

1. Сопротивление обмотки 3 Ом.
2. Напряжение сети 220 В.
3. Частота питающего напряжения 50 Гц.
4. Ток холостого хода 05 А.

Полное сопротивление:

Z=U/I=220/0.05=4400 Ом

Активное сопротивление меньше полного в 10000 раз и его можно не учитывать.

Определяем индуктивность:

L=X_L/(2πf) =4400/ (2∙3.14∙50) =14 Гн.

Определяем активное и индуктивное сопротивление трансформатора — Мегаобучалка

                                                 (1)

                                (1)

где — мощность потерь короткого замыкания, кВт;

— базовое напряжение, В;

— мощность трансформатора, Ква

Сопротивление токовой катушки автоматического выключателя на цех

— активное сопротивление токовой катушки;

— реактивное сопротивление токовой катушки;

— переходное сопротивление контактов.

Сопротивление шин до щита 0,4 (кВ)

                                                       (1)

                                                      (1)

где — активное сопротивление шины;

— реактивное сопротивление шины;

— длина шин от трансформатора до щита 0,4(кВ).

Определяем сопротивление магистрального шинопровода

                                           (1)

                                                   (1)

где — активное сопротивление на фазу;

-реактивное сопротивление на фазу;

— длина магистрального шинопровода

Сопротивление токовой катушки автоматического выключателя на ШР1

— активное сопротивление токовой катушки;

— реактивное сопротивление токовой катушки;

— переходное сопротивление контактов

Определяем сопротивление распределительного шинопровода

                                                      (1)

                                                     (1)

где — активное сопротивление на фазу;

-реактивное сопротивление на фазу;

— длина распределительного шинопровода

Определяем результирующее сопротивление

                          (1)

                            (1)

где — активное сопротивление трансформатора, мОм;

— активное сопротивление токовой катушки, мОм;

— переходное сопротивление контактов, мОм;

— сопротивление шины до щита 0,4 (кВ), мОм;

— активное сопротивление магистрального шинопровода, мОм;

— активное сопротивление распределительного шинопровода, мОм;

— реактивное сопротивление трансформатора, мОм;

— реактивное сопротивление токовой катушки, мОм;

— реактивное сопротивление шины до щита 0,4 (кВ), мОм;

— реактивное сопротивление магистрального шинопровода, мОм;

— реактивное сопротивление распределительного шинопровода, мОм.

Определяем ток КЗ от источника:

                                        (1)

Определяем ударный ток системы:

                                             (1)

где — ударный коэффициент, определяется по графику

,

следовательно выбираем

Определяем апериодическую составляющую:

                     (1)

где — ток первого двигателя, кА

— мощность первого двигателя, кВт;

— номинальное напряжение первого двигателя, В;

— коэффициент мощности первого двигателя;

— КПД первого двигателя.

Определяем ударный ток от электродвигателей:

                                                   (1)

Определяем токи КЗ в точке короткого замыкания:

                                                 (1)

                                            (1)

где — ток КЗ от источника;

— апериодическая составляющая;

— ударный ток системы;

— ударный ток от электродвигателей.

Заключение

В данном курсовом проекте по дисциплине Электрическое снабжение отрасли на тему «Расчет электрической сети электромонтажного цеха» сделан и обоснован выбор типов двигателей по условию технологического задания. Выписаны их паспортные данные, произведено определение расчетных нагрузок исходя из мощности и числа механизмов с учетом Ки и Км. Так же осуществлен выбор проводников и шинопроводов.

Произведен выбор компенсирующего устройства, рассчитаны потери напряжения. Произведен расчет мощности силового трансформатора, а так же трансформатора тока для всего цеха и компенсирующего устройства.

Выполнена графическая часть курсового проекта.

Мною были приобретены навыки со справочной и нормативно-технической литературой.

Список литературы

1 Л.Л Коновалов Л.Д Рожкова «Электроснобжение промышленых предприятий и установок» Москва энергоатомиздат 1989г.

2 В.П Шеховцов «Расчет и проиктирование схем электроснобжения.Методическое пособие для курсового проектирования.» Москва ФОРУМ-ИНФРА-М 2005г.

3 Липкин Б.Ю. Электроснабжение промышленных предприятий и установок. М. Высшая школа, 1990 г.

3.2. Сопротивления и проводимости трансформаторов и автотрансформаторов

При
расчете передачи с трансформаторами
сопротивления, напряжения и токи ли­ний
и трансформаторов приводятся к какому-то
одному напряжению. Чаще всего приведение
делается к входной стороне, т. е. при
понижающем трансформаторе к стороне
высшего напряжения.

Здесь
и в дальнейшем напряжение, к которому
производится приведение (в данном случае

)
будет обозначаться через
.

3. 3.2.1.
   Активные и индуктивные сопротивления
   трансформатора

Для
двухобмоточных трансформаторов активное
сопротивление:

(3.7)

Потери
короткого замыкания
даются в паспортных данных. Для
трехобмоточных трансформаторов заводами
да­ются потери короткого замыканиядля худшего случая, которым является
протекание тока по двум обмот­кам при
третьей разомкнутой. Сопротивление
трансформатора определяется как:

. (3.8)

Для
автотрансформаторов заводами даются
потери короткого замыкания для каждой
пары обмоток
,и.
Чтобы определить сопротивление каждого
луча, можно ориенти­ровочно принять:

,
(3.9)

. (3.10)

Аналогично
находятся и потери
.
Тогда:

,
,. (3.11)

Индуктивное
сопротивление для двухобмоточного
трансформатора:

, (3.12)

где
— напряжение короткого замыкания в
процентах от номи­нального.

Для
трехобмоточных трансформаторов и
автотрансформаторов напряжения
ко­роткого замыкания даются заводами
для каждой пары обмоток в процентах от
номинального, поэтому индуктивное
сопротивление каждого луча, %, аналогично
(3.14) и (3.15):

. (3.13)

Откуда:

. (3.14)

Аналогично
рассчитываются
и.

Индуктивные
сопротивления мощных трансформаторов
и авто­трансформаторов в противоположность
кабельным линиям во много раз больше
активных.

3.2.2.
Активные и реактивные проводимости
трансформаторов

Активные
проводимости обусловлены перемагничиванием
и вихревыми токами и могут быть определены
как:

, (3.15)

где
— потери холостого хода, Вт.

Реактивные
проводимости обусловлены намагничивающей
мощностью, имеют индуктивный характер,
противоположный реактивной проводимости
линий и определя­ются как:

, (3.16)

где
— ток холостого хода в процентах от
номинального.

Полная проводимость
трансформатора:

. (3.17)

3.3.
Эквивалентное сопротивление элементов
системы

Чтобы определить
обобщенные постоянные всей линии
передачи, четырехполюсники соединяются
после­довательно, параллельно или
последовательно и параллельно в
зависимости от характера передачи (рис.
3). Для получения эквивалентного
сопротивления двухполюсников при
последовательном их соединении
складывают­ся сопротивления, а при
парал­лельном — проводимости. При
одинаковых параллельно соеди­ненных
четырехполюсни­ках сопротивления
делятся по­полам, а проводимости
умножа­ются на два.

Схема
четырехполюсников в общем виде может
быть представлена, как показано на рис.
4, а. Тогда обобщенные по­стоянные

параллельно включенных одинаковых
элементов (линий или трансформаторов)
запишутся как:

;
;

;

, (3.18)

где


— постоянные одного элемента.

Схема
принимает вид, показанный на рис. 4, б.
Два четы­рехполюсника этой схемы
можно соединить последовательно.
Окончательные значения обобщенных
постоянных

(рис. 4, в) можно представить в виде:

;

; (3.19)

;

.

Система относительных единиц при расчетах КЗ — Студопедия

Выражение электрических величин в относительных единицах широко применяется в теории электрических машин. Это обусловлено тем, что представление любой величины не в именованных, а относительных единицах существенно упрощает теоретические выкладки и придает результатам расчета большую наглядность. Достоинства системы относительных единиц:

1) не нужно следить за обозначениями;

2) позволяет выбрать удобные для расчета числа;

3) основа теории подобия позволяет связать задачи поля с задачами расчета цепей:

;; ; , где ,

Тогда: ; ; .

Под относительным значением какой-либо величины следует понимать ее отношение к другой одноименной величине, принятой за базисную:

. (4.10)

Следовательно, перед тем как представить какие-либо величины в относительных единицах, надо выбрать базисные единицы.

За базисный ток и базисное линейное напряжение принимаются произвольные величины I_б, U_б. Тогда базисная мощность трехфазной цепи будет определяться формулой:

, (4.11)

а базисное сопротивление:

. (4.12)

Отсюда вытекает, что только две базисные величины могут быть выбраны произвольно, а остальные являются связанными. Обычно выбирается и U_б . Причем выбранные базисные величины должны быть едиными для всей расчетной схемы и применяться как к полным величинам, так и к их отдельным составляющим. Следовательно, параметры электрической системы в относительных

единицах при выбранных базисных условиях будут вычисляться по формулам:

; ; ; (4.13)

; ; ; (4.14)

. (4.15)

Здесь U, I, S, Z − параметры в именованных единицах. При расчетах токов КЗ приняты размерности расчетных параметров кВ, кА, МВ·А, МВт, Мвар, Ом. При этом все формулы не требуют дополнительных согласующих коэффициентов.

При задании паспортных данных оборудования в относительных единицах их параметры относят к номинальным параметрам элементов:

; ; ; ; . (4.16)

Так, относительное сопротивление при номинальных условиях показывает относительное падение напряжения на элементе при протекании номинального тока, что придает физическую наглядность параметру:

.

При расчетах в системе относительных единиц исходные параметры обычно задаются либо в именованных единицах (и.е.) либо в относительных единицах (о.е.) при номинальных условиях элемента. При построении расчетных схем замещения требуется их перевод в относительные единицы при базисных условиях с обязательным приведением параметров на основную ступень.

При этом для построения расчетных формул требуется решение двух задач:

1) заданы параметры в и.е. − требуется их перевод в о.е. при базисных условиях с приведением на основную ступень;

2) заданы параметры в о.е. при номинальных условиях − требуется их перевод в о.е. при базисных условиях с приведением на основную ступень.

Рассмотрим порядок построения расчетных формул на примере сопротивлений и ЭДС.

1) Заданы , .

(4.17)

Здесь: − базисное напряжение, приведенное на расчетную ступень.

(4.18)

Формулы (4.17) и (4.18) являются формулами точного приведения. При приближенном приведении

; (4.19)

, (4.20)

где − номинальное напряжение ступени, где установлен элемент.

При обычно используемом условии формулы принимают вид:

; . (4.21)

2) Заданы , .

(4.22)

. (4.23)

Здесь − номинальное паспортное напряжение элемента.

Формулы (4.22) и (4.23) являются формулами точного приведения. При приближенном приведении

(4.24)

(4.25)

При обычно используемых условиях и формулы принимают вид:

. (4.26)

В дальнейшем индекс приведения будет опускаться.

4.4. Определение сопротивления элементов электрических систем
и их схемы замещения

Формулы определения сопротивлений приведены в относительных единицах при приближенном приведении к базисным условиям.

Генераторы. У генераторов практически никогда не учитывается активное сопротивление, так как оно пренебрежительно мало по сравнению с индуктивным. Номинальное сопротивление генератора в относительных единицах может быть определено из паспортных данных:

− , − синхронные сопротивления по продольной и поперечной оси, которые характеризуют установившийся режим.

− и , и − переходные и сверхпереходные сопротивления в момент времени t = 0.

− ,− сопротивления обратной и нулевой последовательностей.

Номинальное сопротивление генератора в относительных единицах при базисных условиях определяется формулой: .

Двигатели. Параметры синхронных электродвигателей определяются ана­ло­ги­ч­но генераторам.

Реакторы. Токоограничивающие реакторы могут иметь различное устройство и конструктивное исполнение, а также технические и технико-экономические характеристики и параметры.

Линейные реакторы, включаемые последовательно в соответствующую линию, ограничивают ток КЗ и поддерживают относительно высокий уровень остаточного напряжения. Сопротивление линейного реактора можно определить по формуле:

, где лежит в пределах 0,1…0,4 Ом.

Сдвоенный реактор обладает лучшими характеристиками. Между ветвями реактора существует магнитная связь, которая в сквозном режиме позволяет уменьшить потери напряжения в реакторе. Коэффициент магнитной связи идентичных ветвей обмотки реактора равен:

.

Сдвоенный реактор имеет 3 режима работы (рис. 4.11)

Одноцепный режим (рис. 4.11а). В одноцепном режиме общее сопротивление реактора определятся как сопротивление одной его ветви:

а) б) в)

Рис. 4.11. Режимы работы сдвоенного реактора

Двухцепный (сквозной) режим (рис. 4.11б). Двухцепный режим – это нормальный режим работы реактора. В таком режиме магнитные потокиветвейнаправлены встречно, что вызывает уменьшение индуктивного сопротивления одной ветви.

Индуктивное сопротивление одной ветви: .

Общее индуктивное сопротивление: .

Продольный режим (рис. 4.11в). В продольном режиме магнитные потоки ветвейнаправлены согласно и индуктивность ветви увеличивается.

.

Каждый режим работы реактора может быть представлен своей схемой замещения. Активное сопротивление обычно не учитывается, но оно может быть найдено по потерям активной мощности в реакторе. На рисунке 3 приведена общая схема замещения сдвоенного реактора.

Рис. 4.12. Обозначение сдвоенного реактора и его схема замещения

Рассмотрим пример. Используя схему замещения (рис. 4.12), определим сопротивление реактора в одноцепном, сквозном и продольном режимах. Коэффициент связи равен 0,5.

В режиме КЗ (одноцепном):

.

В нормальном (сквозном) режиме:

.

В продольном режиме:

.

Трансформаторы

Двухобмоточный трансформатор. Схема замещения двухобмоточного тра­н­с­форматора приведена на рисунке 4.13.

Рис. 4.13. Условное обозначение и схема замещения двухобмоточного трансформатора

Параметры схемы замещения производятся по данным опытов холостого хода и короткого замыкания.

Опыт холостого хода (рис. 4.14) позволяет определить ток холостого хода , потери в ветви намагничивания и сопротивление холостого хода.

Потери холостого хода:

Сопротивление холостого хода:

; .

Рис. 4.14. Опыт холостого хода

Опыт короткого замыкания (рис. 4.15) позволяет определить напряжение короткого замыкания и потери короткого замыкания:

, следовательно, индуктивное сопротивление рассеивания определяется как .

Напряжение короткого замыкания .

Рис. 4.15. Опыт короткого замыкания

Потери короткого замыкания:

Активное сопротивление трансформатора:

Пренебрегая ветвью намагничивания , получим упрощенную схему замещения (рис. 4.16):

Рис. 4.16. Схема замещения

Активное сопротивление трансформатора в относительных единицах, приведенное к базисным условиям:

,

где − номинальное активное сопротивление в относительных единицах.

Трехобмоточный трансформатор

Рис. 4.17. Условное обозначение и схема замещения трёхобмоточного трансформатора

В относительных единицах напряжения короткого замыкания обмоток будут равняться их сопротивлениям рассеивания и их значения для обмоток высшего, среднего и низшего напряжений трехобмоточного трансформатора могут быть определены по формулам:

,где ;

Данные формулы справедливы и для автотрансформатора,обычно в расчеты не вводится.

Трансформатор с расщепленной обмоткой. На электростанциях и подстанциях применяются силовые трансформаторы и автотрансформаторы с расщепленной обмоткой низшего напряжения, так как это позволяет существенно снизить ток КЗ в сетях низшего напряжения. Повышающие трансформаторы и автотрансформаторы с расщепленной обмоткой используются для формирования укрупненных блоков электростанций, особенно на ГЭС.

а) б)

Рис. 4.18 Условное обозначение трансформатора с расщепленной обмоткой:

а) обмотка низшего напряжения расщеплена на 2 части;

б) обмотки низшего напряжения расщеплена на 3 части

Сопротивление трансформатора с расщепленной обмоткой характеризуется следующими параметрами:

− сопротивление расщепления , равное сопротивлению между выводами двух произвольных частей расщепленной обмотки;

− сквозное сопротивление , равное сопротивлению между выводами обмотки высшего напряжения и объединенными выводами частей расщепленной обмотки низшего напряжения;

− коэффициент расщепления , равный отношению сопротивления расщепления к сквозному сопротивлению:

При расщеплении обмотки на две части (рис. 4.18а), а при расщеплении на три части (рис. 4.18б). Коэффициент расщепления также зависит от исполнения трансформатора, например, для трансформатора броневого исполнения (рис. 4.18а) при отсутствии других данных следует принимать . Для группы однофазных трансформаторов .

а) б) в) г)

Рис. 4.19 Схемы замещения трансформатора с расщепленной обмоткой

Сопротивление рассеивания обмоток трансформатора:

При расщеплении низшей обмотки на 2 части (рис. 4.19а) сопротивление обмоток низшего напряжения:

Сопротивление обмотки высшего напряжения:

Для трансформатора стрежневого типа и схемы замещения для активных и индуктивных сопротивлений приведены на рис. 4.19б, в.

При расщеплении низшей обмотки на 3 части (рис. 4.19г) сопротивление обмотки высшего напряжения: .

Сопротивление обмоток низшего напряжения:

Пример. Автотрансформатор с расщепленной обмоткой низшего напряжения на 2 части (рис. 4.20).

Сопротивление расщепленных обмоток низшего напряжения:

Сопротивления обмоток высшего, среднего и низшего напряжений:

Рис. 4.20. Автотрансформатор с расщепленной обмоткой и его схема замещения

Практическое руководство к практическим работам по курсу «Устойчивость электрических систем», страница 2

          В практических расчетах активное сопротивление
воздушных линий электропередачи при передаче средней и большой мощности может
не учитываться.

1.3.
Трансформаторы и автотрансформаторы

          Двухобмоточные
трансформаторы в схемах замещения представляются индуктивным сопротивлением .

          Сопротивление
двухобмоточного трансформатора в относительных единицах при приближенном
приведении определяется по формуле:

          , о.е., (1.9)

где –
номинальная мощность трансформатора, МВА;

            – напряжение
короткого замыкания трансформатора, %.

          Сопротивления
трехобмоточного трансформатора или автотрансформатора в относительных единицах
при приближенном приведении определяются по формулам:

          , о.е., (1.10)

          , о.е., (1.11)

          , о.е., (1.12)

где –
напряжение короткого замыкания трансформатора между обмотками высшего и
среднего напряжения, %;

      – напряжение
короткого замыкания трансформатора между обмотками высшего и низшего
напряжения, %;

      –
напряжение короткого замыкания трансформатора между обмотками среднего и
низшего напряжения, %.

1.4.
Токоограничивающие и шунтирующие реакторы

          Токоограничивающие и
шунтирующие реакторы в схемах замещения представляются индуктивным
сопротивлением .

          Сопротивление
токоограничивающего реактора в относительных единицах при приближенном
приведении определяется по формуле:

          , о.е., (1.13)

где –
номинальное или средненоминальное напряжение в месте установки реактора, кВ;

      –
номинальное сопротивление реактора, Ом.

          Сопротивление
шунтирующего реактора в относительных единицах при приближенном приведении
определяется по формуле:

          , о.е., (1.14)

где –
номинальная мощность реактора, МВА.

1.5. Асинхронные
двигатели

          Асинхронные двигатели в схемах замещения в
зависимости от вида расчета могут представляться:

—
полной Т-образной схемой;

—
Т-образной схемой без учета активного сопротивления статора;

—
Г-образной схемой без учета активного сопротивления статора;

—
Г-образной схемой без учета активных сопротивлений;

—
активным и реактивным сопротивлениями;

—
реактивным сопротивлением.

          При расчете пуска асинхронного двигателя его
сопротивление определяется по формуле:

          , о.е., (1.15)

где –
номинальная полная мощность двигателя, определяется по формуле:

          , МВА, (1.16)

где – номинальная мощность двигателя,
МВт;

      – номинальная
коэффициент мощности двигателя, о.е.;

       – кратность пускового
тока двигателя, о.е;

       – номинальный КПД
двигателя, о.е.

          При нормальной работе
асинхронного двигателя со скольжением  потребляемая
активная мощность определяется по формуле:

          , о.е., (1.17)

где    – реактивное
сопротивление двигателя, о.е.;

         – активное
сопротивление ротора двигателя, о.е.;

       – номинальный КПД
двигателя, о.е.

          Реактивное сопротивление
двигателя  определяется по формуле:

          , о.е. (1.18)

          Активное сопротивление двигателя  определяется, подставляя в формулу (1.17)
значения номинального режима , ,  и решая
квадратное уравнение.

1.6. Синхронные
двигатели

          Синхронные двигатели в
схемах замещения представляются такими же сопротивлениями как и синхронные
генераторы. Имеются различия – синхронные двигатели могут длительно работать
как в режиме недовозбуждения (ток возбуждения меньше номинального), так и
перевозбуждения (ток возбуждения больше номинального значения).

          ЭДС недовозбужденного
двигателя  меньше подведенного напряжения и он
потребляет реактивную мощность. ЭДС перевозбужденного двигателя  больше подведенного напряжения и любое
снижение напряжения приводит к  увеличению реактивного тока.

          ЭДС двигателя рассчитывается
по формуле:

          , о.е., (1.19)

где ,  –
активный и реактивный токи синхронного двигателя, о.е.

          В формуле (1.19) знак «+» соответствует режиму
перевозбуждению, знак «–» – недовозбуждению.

Сопротивление обмотки трансформатора — формула и объяснение

Идеальный трансформатор не имеет сопротивления, но в реальном трансформаторе всегда присутствует некоторое сопротивление первичной и вторичной обмоток. Для упрощения расчетов сопротивление трансформатора можно перенести в любую сторону. Сопротивление передается с одной стороны на другую таким образом, что процент падения напряжения остается неизменным, когда он представлен с обеих сторон. Эти сопротивления показаны снаружи обмоток на рисунке ниже.

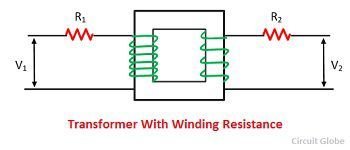
Пусть сопротивление первичной обмотки R ₁ будет перенесено на вторичную сторону, и новое значение этого сопротивления будет R ’ ₁ . R ’ ₁ называется эквивалентным сопротивлением первичной обмотки относительно вторичной стороны, как показано на рисунке ниже. I ₁ и I ₂ — это первичный и вторичный ток полной нагрузки соответственно.

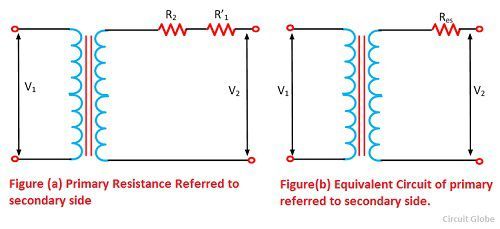
Затем,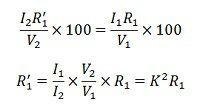

Суммарное эквивалентное сопротивление относительно вторичной обмотки,

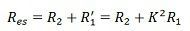
Теперь рассмотрим сопротивление R ₂ , когда оно передается в первичную обмотку, значение нового сопротивления будет R ’ ₂ .R ’ ₂ называется эквивалентным сопротивлением вторичной обмотки, называемой первичной, как показано на рисунке ниже.

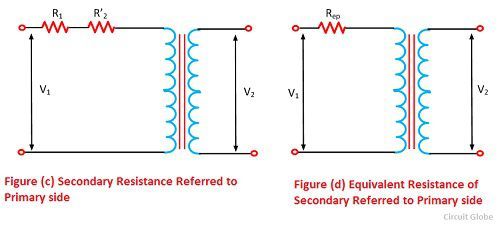
Затем,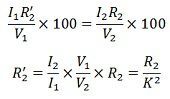

Общее эквивалентное сопротивление относительно первичной обмотки,

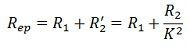Если обмотка трансформатора соединена звездой, то их сопротивление будет измеряться между нейтралью и линией.

.Формула сопротивления

и решенные примеры

• • БЕСПЛАТНАЯ ЗАПИСЬ КЛАСС
  • КОНКУРСНЫЕ ЭКЗАМЕНА
    • BNAT
    • Классы
      • Класс 1-3
      • Класс 4-5
      • Класс 6-10
      • Класс 110003 CBSE
        • Книги NCERT
          • Книги NCERT для класса 5
          • Книги NCERT, класс 6
          • Книги NCERT для класса 7
          • Книги NCERT для класса 8
          • Книги NCERT для класса 9
          • Книги NCERT для класса 10
          • NCERT Книги для класса 11
          • NCERT Книги для класса 12
        • NCERT Exemplar
          • NCERT Exemplar Class 8
          • NCERT Exemplar Class 9
          • NCERT Exemplar Class 10
          • NCERT Exemplar Class 11

          9plar

          • RS Aggarwal
            • RS Aggarwal Решения класса 12
            • RS Aggarwal Class 11 Solutions
            • RS Aggarwal Решения класса 10
            • Решения RS Aggarwal класса 9
            • Решения RS Aggarwal класса 8
            • Решения RS Aggarwal класса 7
            • Решения RS Aggarwal класса 6
          • RD Sharma
            • RD Sharma Class 6 Решения
            • RD Sharma Class 7 Решения
            • Решения RD Sharma Class 8
            • Решения RD Sharma Class 9
            • Решения RD Sharma Class 10
            • Решения RD Sharma Class 11
            • Решения RD Sharma Class 12
          • PHYSICS
            • Механика
            • Оптика
            • Термодинамика
            • Электромагнетизм
          • ХИМИЯ
            • Органическая химия
            • Неорганическая химия
            • Периодическая таблица
          • MATHS
            • Статистика
            • 9000 Pro Числа
            • Числа
            • 9000 Pro Числа Тр Игонометрические функции
            • Взаимосвязи и функции
            • Последовательности и серии
            • Таблицы умножения
            • Детерминанты и матрицы
            • Прибыль и убытки
            • Полиномиальные уравнения
            • Деление фракций
          • Microology
            0003000
          • FORMULAS
            • Математические формулы
            • Алгебраные формулы
            • Тригонометрические формулы
            • Геометрические формулы
          • КАЛЬКУЛЯТОРЫ
            • Математические калькуляторы

            0003000

            • 000 CALCULATORS
            • 000
            • 000 Калькуляторы по химии 900 Образцы документов для класса 6
            • Образцы документов CBSE для класса 7
            • Образцы документов CBSE для класса 8
            • Образцы документов CBSE для класса 9
            • Образцы документов CBSE для класса 10
            • Образцы документов CBSE для класса 1 1
            • Образцы документов CBSE для класса 12
          • Вопросники предыдущего года CBSE
            • Вопросники предыдущего года CBSE, класс 10
            • Вопросники предыдущего года CBSE, класс 12
          • HC Verma Solutions
            • HC Verma Solutions Класс 11 Физика
            • HC Verma Solutions Класс 12 Физика
          • Решения Лакмира Сингха
            • Решения Лахмира Сингха класса 9
            • Решения Лахмира Сингха класса 10
            • Решения Лакмира Сингха класса 8

          9000 Класс

          9000BSE 9000 Примечания3 2 6 Примечания CBSE

        • Примечания CBSE класса 7

        Примечания

        • Примечания CBSE класса 8
        • Примечания CBSE класса 9
        • Примечания CBSE класса 10
        • Примечания CBSE класса 11
        • Примечания 12 CBSE
      • Примечания к редакции 9000 CBSE 9000 Примечания к редакции класса 9
      • CBSE Примечания к редакции класса 10
      • CBSE Примечания к редакции класса 11
      • Примечания к редакции класса 12 CBSE
    • Дополнительные вопросы CBSE
      • Дополнительные вопросы по математике класса 8 CBSE
      • Дополнительные вопросы по науке 8 класса CBSE
      • Дополнительные вопросы по математике класса 9 CBSE
      • Дополнительные вопросы по математике класса 9 CBSE Вопросы
      • CBSE Class 10 Дополнительные вопросы по математике
      • CBSE Class 10 Science Extra questions
    • CBSE Class
      • Class 3
      • Class 4
      • Class 5
      • Class 6
      • Class 7
      • Class 8 Класс 9
      • Класс 10
      • Класс 11
      • Класс 12
    • Учебные решения
  • Решения NCERT
    • Решения NCERT для класса 11
      • Решения NCERT для класса 11 по физике
      • Решения NCERT для класса 11 Химия
      • Решения NCERT для биологии класса 11
      • Решение NCERT s Для класса 11 по математике
      • NCERT Solutions Class 11 Accountancy
      • NCERT Solutions Class 11 Business Studies
      • NCERT Solutions Class 11 Economics
      • NCERT Solutions Class 11 Statistics
      • NCERT Solutions Class 11 Commerce
    • NCERT Solutions for Class 12
      • Решения NCERT для физики класса 12
      • Решения NCERT для химии класса 12
      • Решения NCERT для биологии класса 12
      • Решения NCERT для математики класса 12
      • Решения NCERT, класс 12, бухгалтерский учет
      • Решения NCERT, класс 12, бизнес-исследования
      • NCERT Solutions Class 12 Economics
      • NCERT Solutions Class 12 Accountancy Part 1
      • NCERT Solutions Class 12 Accountancy Part 2
      • NCERT Solutions Class 12 Micro-Economics
      • NCERT Solutions Class 12 Commerce
      • NCERT Solutions Class 12 Macro-Economics
    • NCERT Solut Ионы Для класса 4
      • Решения NCERT для математики класса 4
      • Решения NCERT для класса 4 EVS
    • Решения NCERT для класса 5
      • Решения NCERT для математики класса 5
      • Решения NCERT для класса 5 EVS
    • Решения NCERT для класса 6
      • Решения NCERT для математики класса 6
      • Решения NCERT для науки класса 6
      • Решения NCERT для класса 6 по социальным наукам
      • Решения NCERT для класса 6 Английский язык
    • Решения NCERT для класса 7
      • Решения NCERT для математики класса 7
      • Решения NCERT для науки класса 7
      • Решения NCERT для социальных наук класса 7
      • Решения NCERT для класса 7 Английский язык
    • Решения NCERT для класса 8
      • Решения NCERT для математики класса 8
      • Решения NCERT для науки 8 класса
      • Решения NCERT для социальных наук 8 класса ce
      • Решения NCERT для класса 8 Английский
    • Решения NCERT для класса 9
      • Решения NCERT для класса 9 по социальным наукам
    • Решения NCERT для математики класса 9
      • Решения NCERT для математики класса 9 Глава 1
      • Решения NCERT для математики класса 9, глава 2

      Решения NCERT

      • для математики класса 9, глава 3
      • Решения NCERT для математики класса 9, глава 4
      • Решения NCERT для математики класса 9, глава 5

      Решения NCERT

      • для математики класса 9, глава 6
      • Решения NCERT для математики класса 9, глава 7

      Решения NCERT

      • для математики класса 9, глава 8
      • Решения NCERT для математики класса 9, глава 9
      • Решения NCERT для математики класса 9, глава 10

      Решения NCERT

      • для математики класса 9, глава 11

      Решения

      • NCERT для математики класса 9 Глава 12

      Решения NCERT

      • для математики класса 9 Глава 13
      • NCER Решения T для математики класса 9 Глава 14
      • Решения NCERT для математики класса 9 Глава 15
    • Решения NCERT для науки класса 9
      • Решения NCERT для науки класса 9 Глава 1
      • Решения NCERT для науки класса 9 Глава 2
      • Решения NCERT для науки класса 9 Глава 3
      • Решения NCERT для науки класса 9 Глава 4
      • Решения NCERT для науки класса 9 Глава 5
      • Решения NCERT для науки класса 9 Глава 6
      • Решения NCERT для науки класса 9 Глава 7
      • Решения NCERT для науки класса 9 Глава 8
      • Решения NCERT для науки класса 9 Глава 9
      • Решения NCERT для науки класса 9 Глава 10
      • Решения NCERT для науки класса 9 Глава 12
      • Решения NCERT для науки класса 9 Глава 11
      • Решения NCERT для науки класса 9 Глава 13

      Решения NCERT

      • для науки класса 9 Глава 14
      • Решения NCERT для класса 9 по науке Глава 15
    • Решения NCERT для класса 10
      • Решения NCERT для класса 10 по социальным наукам
    • Решения NCERT для математики класса 10
      • Решения NCERT для математики класса 10 Глава 1
      • Решения NCERT для математики класса 10, глава 2
      • Решения NCERT для математики класса 10, глава 3
      • Решения NCERT для математики класса 10, глава 4
      • Решения NCERT для математики класса 10, глава 5

      Решения NCERT для математики класса 10, глава 6

.

Что такое реактивное сопротивление и импеданс

• • БЕСПЛАТНАЯ ЗАПИСЬ КЛАСС
  • КОНКУРСНЫЕ ЭКЗАМЕНА
    • BNAT
    • Классы
      • Класс 1-3
      • Класс 4-5
      • Класс 6-10
      • Класс 110003 CBSE
        • Книги NCERT
          • Книги NCERT для класса 5
          • Книги NCERT, класс 6
          • Книги NCERT для класса 7
          • Книги NCERT для класса 8
          • Книги NCERT для класса 9
          • Книги NCERT для класса 10
          • NCERT Книги для класса 11
          • NCERT Книги для класса 12
        • NCERT Exemplar
          • NCERT Exemplar Class 8
          • NCERT Exemplar Class 9
          • NCERT Exemplar Class 10
          • NCERT Exemplar Class 11

          9plar

          • RS Aggarwal
            • RS Aggarwal Решения класса 12
            • RS Aggarwal Class 11 Solutions
            • RS Aggarwal Решения класса 10
            • Решения RS Aggarwal класса 9
            • Решения RS Aggarwal класса 8
            • Решения RS Aggarwal класса 7
            • Решения RS Aggarwal класса 6
          • RD Sharma
            • RD Sharma Class 6 Решения
            • RD Sharma Class 7 Решения
            • Решения RD Sharma Class 8
            • Решения RD Sharma Class 9
            • Решения RD Sharma Class 10
            • Решения RD Sharma Class 11
            • Решения RD Sharma Class 12
          • PHYSICS
            • Механика
            • Оптика
            • Термодинамика
            • Электромагнетизм
          • ХИМИЯ
            • Органическая химия
            • Неорганическая химия
            • Периодическая таблица
          • MATHS
            • Статистика
            • 9000 Pro Числа
            • Числа
            • 9000 Pro Числа Тр Игонометрические функции
            • Взаимосвязи и функции
            • Последовательности и серии
            • Таблицы умножения
            • Детерминанты и матрицы
            • Прибыль и убытки
            • Полиномиальные уравнения
            • Деление фракций
          • Microology
            0003000
          • FORMULAS
            • Математические формулы
            • Алгебраные формулы
            • Тригонометрические формулы
            • Геометрические формулы
          • КАЛЬКУЛЯТОРЫ
            • Математические калькуляторы

            0003000

            • 000 CALCULATORS
            • 000
            • 000 Калькуляторы по химии 900 Образцы документов для класса 6
            • Образцы документов CBSE для класса 7
            • Образцы документов CBSE для класса 8
            • Образцы документов CBSE для класса 9
            • Образцы документов CBSE для класса 10
            • Образцы документов CBSE для класса 1 1
            • Образцы документов CBSE для класса 12
          • Вопросники предыдущего года CBSE
            • Вопросники предыдущего года CBSE, класс 10
            • Вопросники предыдущего года CBSE, класс 12
          • HC Verma Solutions
            • HC Verma Solutions Класс 11 Физика
            • HC Verma Solutions Класс 12 Физика
          • Решения Лакмира Сингха
            • Решения Лахмира Сингха класса 9
            • Решения Лахмира Сингха класса 10
            • Решения Лакмира Сингха класса 8

          9000 Класс

          9000BSE 9000 Примечания3 2 6 Примечания CBSE

        • Примечания CBSE класса 7

        Примечания

        • Примечания CBSE класса 8
        • Примечания CBSE класса 9
        • Примечания CBSE класса 10
        • Примечания CBSE класса 11
        • Примечания 12 CBSE
      • Примечания к редакции 9000 CBSE 9000 Примечания к редакции класса 9
      • CBSE Примечания к редакции класса 10
      • CBSE Примечания к редакции класса 11
      • Примечания к редакции класса 12 CBSE
    • Дополнительные вопросы CBSE
      • Дополнительные вопросы по математике класса 8 CBSE
      • Дополнительные вопросы по науке 8 класса CBSE
      • Дополнительные вопросы по математике класса 9 CBSE
      • Дополнительные вопросы по математике класса 9 CBSE Вопросы
      • CBSE Class 10 Дополнительные вопросы по математике
      • CBSE Class 10 Science Extra questions
    • CBSE Class
      • Class 3
      • Class 4
      • Class 5
      • Class 6
      • Class 7
      • Class 8 Класс 9
      • Класс 10
      • Класс 11
      • Класс 12
    • Учебные решения
  • Решения NCERT
    • Решения NCERT для класса 11
      • Решения NCERT для класса 11 по физике
      • Решения NCERT для класса 11 Химия
      • Решения NCERT для биологии класса 11
      • Решение NCERT s Для класса 11 по математике
      • NCERT Solutions Class 11 Accountancy
      • NCERT Solutions Class 11 Business Studies
      • NCERT Solutions Class 11 Economics
      • NCERT Solutions Class 11 Statistics
      • NCERT Solutions Class 11 Commerce
    • NCERT Solutions for Class 12
      • Решения NCERT для физики класса 12
      • Решения NCERT для химии класса 12
      • Решения NCERT для биологии класса 12
      • Решения NCERT для математики класса 12
      • Решения NCERT, класс 12, бухгалтерский учет
      • Решения NCERT, класс 12, бизнес-исследования
      • NCERT Solutions Class 12 Economics
      • NCERT Solutions Class 12 Accountancy Part 1
      • NCERT Solutions Class 12 Accountancy Part 2
      • NCERT Solutions Class 12 Micro-Economics
      • NCERT Solutions Class 12 Commerce
      • NCERT Solutions Class 12 Macro-Economics
    • NCERT Solut Ионы Для класса 4
      • Решения NCERT для математики класса 4
      • Решения NCERT для класса 4 EVS
    • Решения NCERT для класса 5
      • Решения NCERT для математики класса 5
      • Решения NCERT для класса 5 EVS
    • Решения NCERT для класса 6
      • Решения NCERT для математики класса 6
      • Решения NCERT для науки класса 6
      • Решения NCERT для класса 6 по социальным наукам
      • Решения NCERT для класса 6 Английский язык
    • Решения NCERT для класса 7
      • Решения NCERT для математики класса 7
      • Решения NCERT для науки класса 7
      • Решения NCERT для социальных наук класса 7
      • Решения NCERT для класса 7 Английский язык
    • Решения NCERT для класса 8
      • Решения NCERT для математики класса 8
      • Решения NCERT для науки 8 класса
      • Решения NCERT для социальных наук 8 класса ce
      • Решения NCERT для класса 8 Английский
    • Решения NCERT для класса 9
      • Решения NCERT для класса 9 по социальным наукам
    • Решения NCERT для математики класса 9
      • Решения NCERT для математики класса 9 Глава 1
      • Решения NCERT для математики класса 9, глава 2

      Решения NCERT

      • для математики класса 9, глава 3
      • Решения NCERT для математики класса 9, глава 4
      • Решения NCERT для математики класса 9, глава 5

      Решения NCERT

      • для математики класса 9, глава 6
      • Решения NCERT для математики класса 9, глава 7

      Решения NCERT

      • для математики класса 9, глава 8
      • Решения NCERT для математики класса 9, глава 9
      • Решения NCERT для математики класса 9, глава 10

      Решения NCERT

      • для математики класса 9, глава 11

      Решения

      • NCERT для математики класса 9 Глава 12

      Решения NCERT

      • для математики класса 9 Глава 13
      • NCER Решения T для математики класса 9 Глава 14
      • Решения NCERT для математики класса 9 Глава 15
    • Решения NCERT для науки класса 9
      • Решения NCERT для науки класса 9 Глава 1
      • Решения NCERT для науки класса 9 Глава 2
      • Решения NCERT для науки класса 9 Глава 3
      • Решения NCERT для науки класса 9 Глава 4
      • Решения NCERT для науки класса 9 Глава 5
      • Решения NCERT для науки класса 9 Глава 6
      • Решения NCERT для науки класса 9 Глава 7
      • Решения NCERT для науки класса 9 Глава 8
      • Решения NCERT для науки класса 9 Глава 9
      • Решения NCERT для науки класса 9 Глава 10
      • NCER

.Формула эквивалентного сопротивления

— Формула эквивалентного сопротивления для последовательного и параллельного сопротивления, решенные примеры

• • БЕСПЛАТНАЯ ЗАПИСЬ КЛАСС
  • КОНКУРСНЫЕ ЭКЗАМЕНА
    • BNAT
    • Классы
      • Класс 1-3
      • Класс 4-5
      • Класс 6-10
      • Класс 110003 CBSE
        • Книги NCERT
          • Книги NCERT для класса 5
          • Книги NCERT, класс 6
          • Книги NCERT для класса 7
          • Книги NCERT для класса 8
          • Книги NCERT для класса 9
          • Книги NCERT для класса 10
          • NCERT Книги для класса 11
          • NCERT Книги для класса 12
        • NCERT Exemplar
          • NCERT Exemplar Class 8
          • NCERT Exemplar Class 9
          • NCERT Exemplar Class 10
          • NCERT Exemplar Class 11

          9plar

          • RS Aggarwal
            • RS Aggarwal Решения класса 12
            • RS Aggarwal Class 11 Solutions
            • RS Aggarwal Решения класса 10
            • Решения RS Aggarwal класса 9
            • Решения RS Aggarwal класса 8
            • Решения RS Aggarwal класса 7
            • Решения RS Aggarwal класса 6
          • RD Sharma
            • RD Sharma Class 6 Решения
            • RD Sharma Class 7 Решения
            • Решения RD Sharma Class 8
            • Решения RD Sharma Class 9
            • Решения RD Sharma Class 10
            • Решения RD Sharma Class 11
            • Решения RD Sharma Class 12
          • PHYSICS
            • Механика
            • Оптика
            • Термодинамика
            • Электромагнетизм
          • ХИМИЯ
            • Органическая химия
            • Неорганическая химия
            • Периодическая таблица
          • MATHS
            • Статистика
            • 9000 Pro Числа
            • Числа
            • 9000 Pro Числа Тр Игонометрические функции
            • Взаимосвязи и функции
            • Последовательности и серии
            • Таблицы умножения
            • Детерминанты и матрицы
            • Прибыль и убытки
            • Полиномиальные уравнения
            • Деление фракций
          • Microology
            0003000
          • FORMULAS
            • Математические формулы
            • Алгебраные формулы
            • Тригонометрические формулы
            • Геометрические формулы
          • КАЛЬКУЛЯТОРЫ
            • Математические калькуляторы

            0003000

            • 000 CALCULATORS
            • 000
            • 000 Калькуляторы по химии 900 Образцы документов для класса 6
            • Образцы документов CBSE для класса 7
            • Образцы документов CBSE для класса 8
            • Образцы документов CBSE для класса 9
            • Образцы документов CBSE для класса 10
            • Образцы документов CBSE для класса 1 1
            • Образцы документов CBSE для класса 12
          • Вопросники предыдущего года CBSE
            • Вопросники предыдущего года CBSE, класс 10
            • Вопросники предыдущего года CBSE, класс 12
          • HC Verma Solutions
            • HC Verma Solutions Класс 11 Физика
            • HC Verma Solutions Класс 12 Физика
          • Решения Лакмира Сингха
            • Решения Лахмира Сингха класса 9
            • Решения Лахмира Сингха класса 10
            • Решения Лакмира Сингха класса 8

          9000 Класс

          9000BSE 9000 Примечания3 2 6 Примечания CBSE

        • Примечания CBSE класса 7

        Примечания

        • Примечания CBSE класса 8
        • Примечания CBSE класса 9
        • Примечания CBSE класса 10
        • Примечания CBSE класса 11
        • Примечания 12 CBSE
      • Примечания к редакции 9000 CBSE 9000 Примечания к редакции класса 9
      • CBSE Примечания к редакции класса 10
      • CBSE Примечания к редакции класса 11
      • Примечания к редакции класса 12 CBSE
    • Дополнительные вопросы CBSE
      • Дополнительные вопросы по математике класса 8 CBSE
      • Дополнительные вопросы по науке 8 класса CBSE
      • Дополнительные вопросы по математике класса 9 CBSE
      • Дополнительные вопросы по математике класса 9 CBSE Вопросы
      • CBSE Class 10 Дополнительные вопросы по математике
      • CBSE Class 10 Science Extra questions
    • CBSE Class
      • Class 3
      • Class 4
      • Class 5
      • Class 6
      • Class 7
      • Class 8 Класс 9
      • Класс 10
      • Класс 11
      • Класс 12
    • Учебные решения
  • Решения NCERT
    • Решения NCERT для класса 11
      • Решения NCERT для класса 11 по физике
      • Решения NCERT для класса 11 Химия
      • Решения NCERT для биологии класса 11
      • Решение NCERT s Для класса 11 по математике
      • NCERT Solutions Class 11 Accountancy
      • NCERT Solutions Class 11 Business Studies
      • NCERT Solutions Class 11 Economics
      • NCERT Solutions Class 11 Statistics
      • NCERT Solutions Class 11 Commerce
    • NCERT Solutions for Class 12
      • Решения NCERT для физики класса 12
      • Решения NCERT для химии класса 12
      • Решения NCERT для биологии класса 12
      • Решения NCERT для математики класса 12
      • Решения NCERT, класс 12, бухгалтерский учет
      • Решения NCERT, класс 12, бизнес-исследования
      • NCERT Solutions Class 12 Economics
      • NCERT Solutions Class 12 Accountancy Part 1
      • NCERT Solutions Class 12 Accountancy Part 2
      • NCERT Solutions Class 12 Micro-Economics
      • NCERT Solutions Class 12 Commerce
      • NCERT Solutions Class 12 Macro-Economics
    • NCERT Solut Ионы Для класса 4
      • Решения NCERT для математики класса 4
      • Решения NCERT для класса 4 EVS
    • Решения NCERT для класса 5
      • Решения NCERT для математики класса 5
      • Решения NCERT для класса 5 EVS
    • Решения NCERT для класса 6
      • Решения NCERT для математики класса 6
      • Решения NCERT для науки класса 6
      • Решения NCERT для класса 6 по социальным наукам
      • Решения NCERT для класса 6 Английский язык
    • Решения NCERT для класса 7
      • Решения NCERT для математики класса 7
      • Решения NCERT для науки класса 7
      • Решения NCERT для социальных наук класса 7
      • Решения NCERT для класса 7 Английский язык
    • Решения NCERT для класса 8
      • Решения NCERT для математики класса 8
      • Решения NCERT для науки 8 класса
      • Решения NCERT для социальных наук 8 класса ce
      • Решения NCERT для класса 8 Английский
    • Решения NCERT для класса 9
      • Решения NCERT для класса 9 по социальным наукам
    • Решения NCERT для математики класса 9
      • Решения NCERT для математики класса 9 Глава 1
      • Решения NCERT для математики класса 9, глава 2

      Решения NCERT

      • для математики класса 9, глава 3
      • Решения NCERT для математики класса 9, глава 4
      • Решения NCERT для математики класса 9, глава 5

      Решения NCERT

      • для математики класса 9, глава 6
      • Решения NCERT для математики класса 9, глава 7

      Решения NCERT

      • для математики класса 9, глава 8
      • Решения NCERT для математики класса 9, глава 9
      • Решения NCERT для математики класса 9, глава 10

      Решения NCERT

      • для математики класса 9, глава 11

      Решения

      • NCERT для математики класса 9 Глава 12

      Решения NCERT

      • для математики класса 9 Глава 13
      • NCER Решения T для математики класса 9 Глава 14
      • Решения NCERT для математики класса 9 Глава 15
    • Решения NCERT для науки класса 9
      • Решения NCERT для науки класса 9 Глава 1
      • Решения NCERT для науки класса 9 Глава 2
      • Решения NCERT для науки класса 9 Глава 3
      • Решения NCERT для науки класса 9 Глава 4
      • Решения NCERT для науки класса 9 Глава 5
      • Решения NCERT для науки класса 9 Глава 6
      • Решения NCERT для науки класса 9 Глава 7

.