Формула мощность ток: Мощность электрического тока

Содержание

Формула мощности тока в физике

Электрический ток, на каком угодно участке цепи совершает некоторую работу (А). Допустим, что у нас есть произвольный участок
цепи (рис.1) между концами которого имеется напряжение U.

Работа, которая выполняется при перемещении заряда равного 1 Кл между точками A и B (рис.1) будет равна
U. В том случае, если через проводник протекает ток силой I за время равное
по указанному выше участку пройдет заряд (q) равный:

Следовательно, работа, которую совершает электрический ток на данном участке, равна:

Надо отметить, что выражение (2) является справедливым при I=const для любого участка цепи
(в таком участке могут содержаться проводники 1–го и 2–го рода).

Определение и формула мощности тока

Определение

Мощность тока – есть работа тока в единицу времени:

Формулой для вычисления мощности можно считать выражение:

В том случае, если участок цепи содержит источник тока, то формулу мощности можно представить в виде:

где – разность потенциалов,
– ЭДС источника, который включен в цепь.

Выражение (5) является интегральной записью. Это выражение можно представить в дифференциальной форме, если использовать понятие
удельной мощности ( – мощность, развиваемая током в
единице объема проводника):

где j – плотность тока, – удельное сопротивление.

Единицы измерения мощности тока

Основной единицей измерения мощности тока (как и мощности вообще) в системе СИ является: [P]=Вт=Дж/с.

В СГС: [P]=эрг/с.

1 Вт=10⁷ эрг/( с).

Выражение (4) применяют в системе СИ для того, чтобы дать определение единицы напряжения.
Так, единицей напряжения (U) является вольт (В), который равен: 1 В= (1 Вт)/(1 А).

Вольтом называют электрическое напряжение, которое порождает в электроцепи постоянный ток силы 1 А при мощности 1 Вт.

Примеры решения задач

Пример

Задание. Какой должна быть сила тока, которая течет через обмотку электрического мотора для того,
чтобы полезная мощность двигателя (P_A) стала максимальной?Какова максимальная полезная мощность?
Если двигатель постоянного тока подключен к напряжению U, сопротивление обмотки якоря – R.

Решение. Мощность, которую потребляет электроприбор, идет на нагревание (P_Q) и совершение
работы (P_A):

Мощность, идущую на нагревание можно рассчитать как:

Потребляемую мощность найдем как:

Выразим P_A из (1.1) и используем (1.2) и (1.3):

Для нахождения экстремума функции, которая представлена в выражении (1.4) найдем производную
и приравняем ее к нулю:

Найдем максимальную полезную мощность,используя выражение (1.4) и I_max:

Ответ.

Пример

Задание. Электрические лампочкис мощностями
P₁ и P₂ номинальным напряжением U₁=U₂ соединяют последовательно
(рис.2) и включают в сеть с постоянным напряжением U. Какова мощность, потребляемая первой лампочкой P₁^*).

Решение. Лампочки по условию задачи соединены последовательно, значит сила тока, текущая через лампочки
одинакова, а падение напряжения на каждой из лампочек зависит от их сопротивлений. Искомую мощность можно найти как:

Сопротивления лампочек можно найти из данных в условиях номинальных мощностей:

Силу тока можно найти по закону Ома, учитывая, что лампочки соединены последовательно:

Электрическая мощность — Википедия

Материал из Википедии — свободной энциклопедии

Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии. Единицей измерения в Международной системе единиц (СИ) является ватт (русское обозначение: Вт, международное: W).

Мгновенная электрическая мощность

Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.

По определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки A{\displaystyle A} в точку B{\displaystyle B}, к величине пробного заряда. То есть можно сказать, что электрическое напряжение равно работе по переносу единичного заряда из точки A{\displaystyle A} в точку B{\displaystyle B}. Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу, численно равную электрическому напряжению, действующему на участке цепи. Умножив работу на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца. Мощность, по определению, — это работа в единицу времени. Введём обозначения:

U{\displaystyle U} — напряжение на участке A−B{\displaystyle A-B} (принимаем его постоянным на интервале Δt{\displaystyle \Delta t}),

Q{\displaystyle Q} — количество зарядов, прошедших от A{\displaystyle A} к B{\displaystyle B} за время Δt{\displaystyle \Delta t},

A{\displaystyle A} — работа, совершённая зарядом Q{\displaystyle Q} при движении по участку A−B{\displaystyle A-B},

P{\displaystyle P} — мощность.

Записывая вышеприведённые рассуждения, получаем:

PA−B=AΔt{\displaystyle P_{A-B}={\frac {A}{\Delta t}}}

Для единичного заряда на участке A−B{\displaystyle A-B}:

Pe(A−B)=UΔt{\displaystyle P_{e(A-B)}={\frac {U}{\Delta t}}}

Для всех зарядов:

PA−B=UΔt⋅Q=U⋅QΔt{\displaystyle P_{A-B}={\frac {U}{\Delta t}}\cdot {Q}={U}\cdot {\frac {Q}{\Delta t}}}

Поскольку ток есть электрический заряд, протекающий по проводнику в единицу времени, то есть I=QΔt{\displaystyle I={\frac {Q}{\Delta t}}} по определению, в результате получаем:

PA−B=U⋅I{\displaystyle P_{A-B}=U\cdot I}.

Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности:

мгновенная электрическая мощность p(t){\displaystyle p(t)}, выделяющаяся на участке электрической цепи, есть произведение мгновенных значений напряжения u(t){\displaystyle u(t)} и силы тока i(t){\displaystyle i(t)} на этом участке:

p(t)=u(t)⋅i(t).

{2}}{R}}}.

Дифференциальные выражения для электрической мощности

Мощность, выделяемая в единице объёма, равна:

w=dPdV=E⋅j{\displaystyle w={\frac {dP}{dV}}=\mathbf {E} \cdot \mathbf {j} },

где E{\displaystyl

инструкция с формулой, таблицей и онлайн формой

Иногда можно услышать такой простой вопрос: «какая мощность в розетке?». Ответ, как ни странно, чаще всего такой: 10 ампер. Или – 220 вольт. Понятно, что вопрос – дурацкий. Но и объяснение не лучше – «А на розетке так написано».

Оглавление статьи:

Мощность и ток

Если правильно отвечать на поставленный вопрос, то для читателей, прогуливающих в детстве уроки физики, можно сказать, что мощность электричества зависит от двух величин:

величины напряжения;
силы тока.

В общем, эти две величины определяют величину мощности как переменного, так и постоянного тока. Память может подсказать что-то типа: для участка цепи, для полной цепи.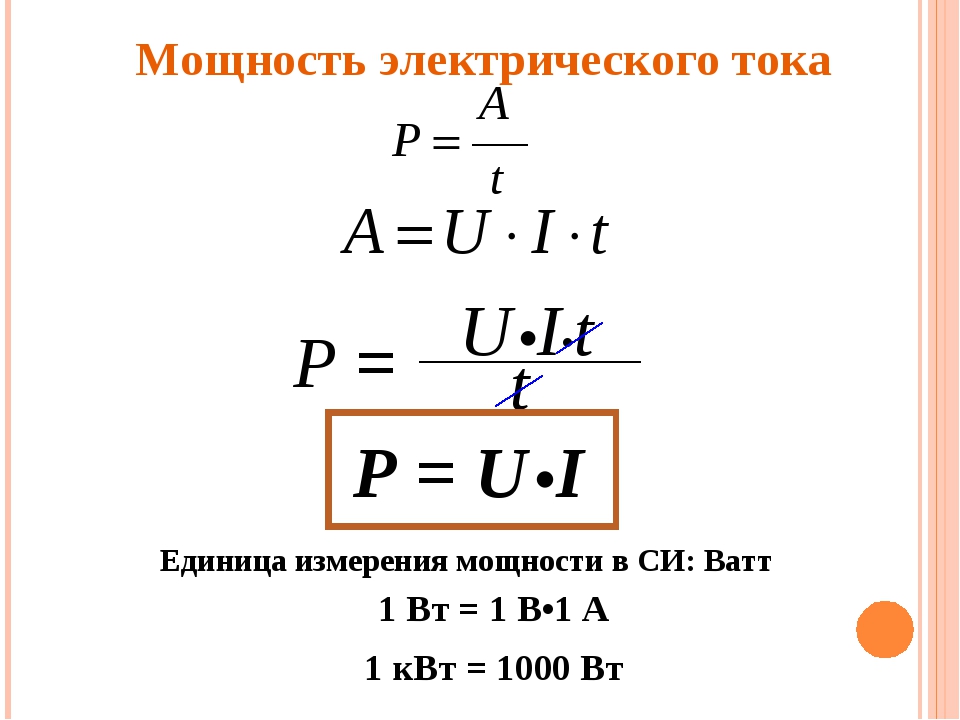 Это отголоски того же школьного учебника физики, где говорится о законе Ома.

Рекомендуем портал опытных и начинающих электриков: https://electrikexpert.ru

Да, этот знаменитый закон и позволяет рассчитать мощность электрического тока. Конечно, школьная программа представляла этот закон для цепей постоянного тока, но суть от этого не меняется. Формула вечная и неизменная: P = U х I.

Перефразируя закон ома в простой язык, получаем простой ответ на вопрос о мощности в розетке: сила тока зависит от нагрузки.

Сила тока и приложенная нагрузка

Тривиальное понятие этого тезиса позволит не производить элементарных действий, постоянно совершаемых нами, или окружающими нас людьми:

включать один электрический удлинитель в другой, втыкая в оба все доступные вилки от разных, иногда достаточно мощных, потребителей электроэнергии;
подключать к севшему аккумулятору автомобиля другой, соединяя их проводами от старой электропроводки;
наращивать провода от электрического чайника кабелем с витой парой;
устанавливать в гараже нагреватель, мощностью 5 квт, подключая его к обыкновенной розетке.

Аналогичные примеры неграмотных действий можно приводить до бесконечности. Человеческая беспечность не знает границ. Чтобы больше не допускать подобных ошибок, давайте разберем как правильно производить расчет электрической мощности.

Чайник и электрическая мощность

Не забивая головы простейшими формулами (есть дела и поважнее этого), запомним простое соотношение, достаточное для применения его в быту. Точность его не соответствует формуле расчета, но позволяет помнить, что: 1 квт электроэнергии – это приблизительно 5 ампер тока в сети 220 вольт.

Таким образом, становится понятно, что электрический чайник, включенный в кухонную розетку, потребляет около 5 ампер тока. А лампа накаливания, мощностью 100 Вт – в десять раз меньше: 0,5 ампера. Конечно, такие примитивные знания нужны для домохозяек, расчет мощности электрического тока производится по формулам.

Необходимость расчетов мощности

Человек мало сталкивается с необходимостью проведения расчетов (мощностей постоянного электрического тока) в быту. Чаще всего такая необходимость возникает при ремонте автомобиля, где источником тока служит аккумулятор. Или какой-то продвинутый пользователь начинает подбирать новый кулер для своего процессора в компьютере.

Чаще возникает необходимость провести элементарные расчеты при ремонтных работах в квартире, при подборе сгоревшего блока питания и пр.

Расчет мощности электрического тока по формулам

Существует формула расчета электрического тока для однофазной и трехфазной сети. Вряд ли кто-то захочет и сможет ими воспользоваться – разбираться что такое cosφ при замене электрической проводки в доме или квартире нецелесообразно.

Реально можно произвести все необходимые расчеты в режиме онлайн. Интернет набит разными таблицами, соответствующими графиками и калькуляторами. Для очень нуждающихся читателей можно добавить, что сечение кабеля для осветительной сети — 1,5 кв. мм. А для электропитания розеток применяется кабель сечением 2,5 кв. мм.

Остальные расчеты, требующиеся при производстве электромонтажных работ в различных областях деятельности – лучше доверить специалистам, которые в своей работе используют различные приборы: амперметры, вольтметры, индикаторы фазы, измерители сопротивления изоляции, измерители сопротивления заземления и пр.

Ремонт и строительство домов и квартир, особенности расчетов

Чтобы произвести расчет электропроводки в квартире недостаточно произвести подбор сечения электрических проводов. В электрическом щите устанавливаются и электрические автоматы, и защитные устройства и электрический счетчик. Эти установочные изделия также подбираются и рассчитываются при разработке проекта электропитания, в котором производится также расчет количества и параметров устройств защитного заземления.

Для расчетов и подбора видов электропроводки, использующейся при изготовлении удлинителей, организации временных схем электропитания, необходимо понимать, что силовые кабели для однофазной и трехфазной цепи различны по количеству жил, условиям прокладки, токовым нагрузкам и прочим параметрам.

При использовании кабелей и проводов необходимо учитывать и материал изготовления токопроводящих жил.

Наличие в загородном доме, даче трехфазных потребителей электроэнергии, таких как скважинный насос, электродвигатели, сварочное оборудование, требует при подборе кабелей электропроводки учитывать их пусковые токи. А при выборе электрического счетчика электроэнергии – активную и реактивную составляющую в потребляемой мощности, если предполагается постоянная работа трехфазного оборудования.

Удачи!

Фото

Мощность в цепи постоянного тока

Здравствуйте! Эту статью можно считать началом знакомства с электричеством. Напряжение, ток, сопротивление – это три главные величины, на которых построены основные законы электротехники и эти величины связаны между собой еще одной – мощностью. А чтобы было проще знакомиться с электротехникой, мы будем рассматривать мощность в цепи постоянного тока. Дело в том, что при расчетах в цепях переменного тока появляется довольно много условий. Впрочем, обо всём по порядку и вы сейчас сами с этим разберётесь.

Для удобства я сразу напишу международные обозначения этих четырёх величин:

U – напряжение (В, вольт)

I – ток (А, ампер)

R – сопротивление (Ом, ом)

P – мощность (Вт, ватт – не надо путать с вольтом, который обозначается только одной буквой В)

Для начала абстрактный пример, чтобы проще было понимать термины, которые я сейчас буду использовать. Допустим, есть магазин товаров (условно это можно представить, как напряжение), есть деньги (условно это будет ток), есть совесть, которая не позволяет вам тратить много или наоборот, шепчет, чтобы вы крупно потратились (это можно считать сопротивлением) и есть купленные товары или продукты, которые вы несёте домой (это мощность). Собственно, на этом примере можно объяснить многие законы, связанные с электрическим током. Все обозначенные величины связаны между собой законом Ома, который гласит, что сила тока в цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению цепи, а именно:

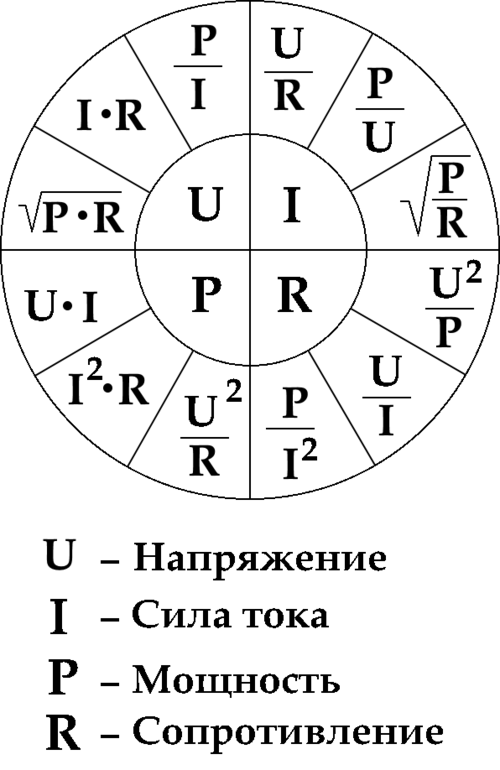
В абстрактном примере – чем больше магазин (напряжение) и чем меньше вам шепчет совесть (сопротивление), тем больше вы тратите денег (сила тока), а когда вы несёте купленный товар домой, вы совершаете работу (мощность). Мощность в цепи постоянного тока это и есть работа, совершаемая электричеством. Мощность это произведение тока на напряжение, а если вместо тока или напряжения подставить соответствующие значения, то можно получить мнемоническую табличку:

Как видите, мощность в цепи постоянного тока это довольно простое понятие, если немного вдуматься в материал. По сути, это всего две формулы с заменой значений. Как это выглядит:

Если теперь в формуле мощности подставить место значения тока формулу тока, то получим следующее:

Именно таким образом и получилось 12 формул на основе закона Ома, которые вы видите в мнемонической табличке. Что такое мощность в цепях постоянного тока мы более или менее разобрались, но есть ещё один момент.

Баланс мощностей в цепи постоянного тока.

Собственно, это просто проверка правильности расчетов электрической цепи. Возвращаясь к нашему абстрактному примеру это выглядит так: вы купили товары, забрали их на кассе, отошли от кассы и вам показалось, что ваши пакеты должны быть больше или меньше, чем получились. Тогда вы берёте чек и начинаете сравнивать товар в чеке и товар в наличии. Если товары в чеке и товары в руках совпали, значит всё в порядке. Если мы обратимся к определению, то баланс мощностей – сумма мощностей потребляемых приемниками, равна сумме мощностей отдаваемых источниками.

Как это использовать на практике? Допустим, у нас есть задача, которую нужно решить:

Поскольку решение задачи не является целью этой статьи, я дам уже готовые ответы.

Теперь надо проверить правильно ли были посчитаны токи в задаче. Ток в цепи равен току , следовательно, мощность источника питания (Е1хI1) должна быть равна сумме мощностей сопротивлений

Что мы и получаем с учетом потерь при округлениях.

Таким образом, баланс мощностей в электрической цепи постоянного тока — это ничто иное, как проверка самого себя, своих расчётов.

Как видите, мощность в цепи постоянного тока посчитать довольно легко. Гораздо больше сложностей возникнет, если ток будет переменный. Другими словами, на примере магазина это выглядит так:

Постоянный ток – от входа до выхода прямая линия и вы спокойно идете от начала и до конца без каких-либо приключений.

Переменный ток – магазин представляет из себя зигзаг и вам приходится делать лишние движения.

Поэтому в переменном токе мощность считать немного сложнее, но это уже тема совсем другой статьи.

Поделиться ссылкой:

Похожее

Мощность в цепях переменного тока — Студопедия

В цепях переменного тока различают три вида мощностей: активную Р, реактивную Q и полную S.

Активная мощность вычисляется по формуле:

(2.20)

Активную мощность потребляет резистивный элемент. Единица измерения активной мощности называется Ватт (Вт), производная единица – килоВатт (кВт), равная 10³ Вт.

Реактивная мощность вычисляется по формуле:

(2.21)

Реактивная мощность потребляется идеальным индуктивным и

емкостным элементами. Единица измерения реактивной мощности называется Вольт-Ампер реактивный (Вар), производная единица – килоВАр (кВАр), равная 10³ ВАр.

Полная мощность потребляется полным сопротивлением и обозначается буквой S:

S= (2.22)

Единица измерения полной мощности называется ВА (Вольт-Ампер), производная единица – килоВольт-Ампер (кВА), равная 10³ ВА.

По сути, размерность у всех выше перечисленных единиц измерения одинакова – . Разные название этих единиц нужны, чтобы различать эти виды мощности.

Проявляются различные виды мощности по-разному. Активная мощность необратимо преобразуется в другие виды мощности (например, тепловую, механическую). Реактивная мощность обратимо циркулирует в электрических цепях: энергия электрического поля конденсатора преобразуется в энергию магнитного поля, и наоборот. «Извлечь» реактивную мощность с «пользой для дела» невозможно.

Из формул (2.19) – (2.21) следует, что между активной, реактивной и полной мощностью имеет место соотношение:

(2.23)

Соотношение между P, Q и S можно интерпретировать как соотношение сторон прямоугольного треугольника (вспомните треугольник сопротивлений, треугольник напряжений – все эти треугольники подобны).

Рис. 2.10

Из рис. 2.10 видно, что cosφ = (2.24)

Отсюда вытекает определение одной из основных характеристик цепей переменного тока – коэффициента мощности. Специального обозначения он не получил.

Коэффициент мощности показывает, какую долю полной мощности составляет активная мощность.

Желательно, чтобы коэффициент мощности цепи был как можно больше, т.е. приближался к 1. Реально предприятия электрических сетей устанавливают такое ограничение для промышленных предприятий : соs φ = (0,92-0,95). Достигать значений соs φ >0,95 рискованно, так как разность фаз φ при этом может скачком перейти от положительных значений к отрицательным, что вредно для электрооборудования. Если соsφ < 0,92, предприятия подвергаются штрафу.

Если коэффициент мощности оказывается мал, его необходимо повышать. График функции соs φ имеет вид монотонно убывающей функции в интервале от 0⁰ до 90⁰. Следовательно, увеличить соsφ – значит уменьшить разность фаз , то есть уменьшить (Х_L-Х_С).

Если влиять на (Х_L-Х_С), меняя С и L, то это приведет к увеличению тока в последовательной цепи и изменению режима работы оборудования, поэтому такой способ практически не применяется. В следующем разделе рассмотрен другой способ повышения коэффициента мощности.

Цепь переменного тока с параллельным соединением ветвей.

Рассмотрим электрическую цепь с двумя параллельными ветвями (рис. 2.11). Полученные выводы распространим на цепь с любым количеством ветвей. К цепи, содержащей две параллельные ветви, включающие активные, индуктивные и емкостные элементы (R₁, L₁, C₁и R₂, L₂, C₂cоответственно), подводится переменное напряжение U частоты f.

Прямая задача: Заданы все Обратная задача: Заданы свойства входящие в цепь элементы. цепи. Найти неизвестные элементы Найти все токи и разности цепи (эта задача решена в лаборафаз. торной работе Ц-5)

Решим прямую задачу, то есть найдем токи I_1,I₂ и общий ток I .

Рис. 2.11. Электрическая цепь с двумя параллельными ветвями

Из второго закона Кирхгофа следует, что напряжения на параллельных участках цепи одинаковы:

U₁ = U₂ = U (2.25)

На основании закона Ома найдем токи I₁и I₂ :

; (2.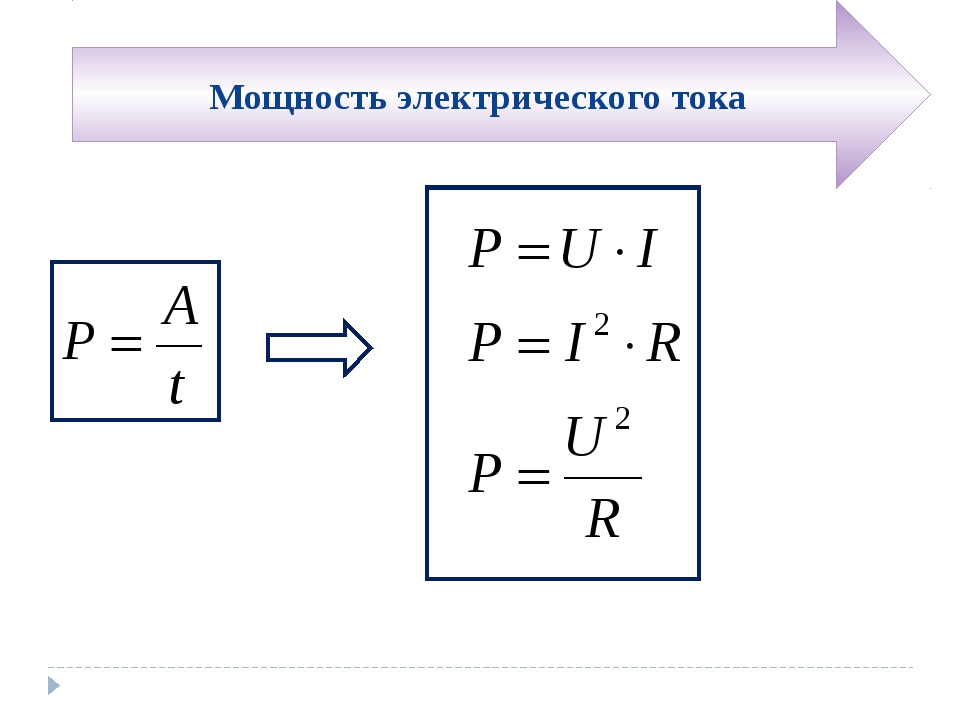 26)

Найдем также разности фаз тока и напряжения для каждой ветви:

(2.27)

На основании первого закона Кирхгофа применительно к узлу А можно записать:

_{= +}(2.28)

Таким образом, для определения тока I необходимо векторно сложить токи I₁ и I₂. В качестве опорного вектора удобно выбрать вектор напряжения .

Предположим, что при расчете разностей фаз тока и напряжения в ветвях цепи оказалось, что φ₁>0, а φ₂ под углом φ₁к вектору , и вектор под углом φ₂к вектору . Графически складываем эти векторы (см. рис.2.12). Величина тока определяется длиной полученного вектора с учетом выбранного масштаба. Разность фаз неразветвленного участка цепи определяется углом между векторами и

Рис. 2.12

Формула электрического тока с решенными примерами

- БЕСПЛАТНАЯ ЗАПИСЬ КЛАСС
- КОНКУРСНЫЕ ЭКЗАМЕНА
  BNAT
  Классы
  Класс 1-3
  Класс 4-5
  Класс 6-10
  Класс 110003 CBSE
  Книги NCERT
  Книги NCERT для класса 5
  Книги NCERT, класс 6
  Книги NCERT для класса 7
  Книги NCERT для класса 8
  Книги NCERT для класса 9
  Книги NCERT для класса 10
  NCERT Книги для класса 11
  NCERT Книги для класса 12
  NCERT Exemplar
  NCERT Exemplar Class 8
  NCERT Exemplar Class 9
  NCERT Exemplar Class 10
  NCERT Exemplar Class 11
  9plar
  RS Aggarwal
  RS Aggarwal Решения класса 12
  RS Aggarwal Class 11 Solutions
  RS Aggarwal Решения класса 10
  Решения RS Aggarwal класса 9
  Решения RS Aggarwal класса 8
  Решения RS Aggarwal класса 7
  Решения RS Aggarwal класса 6
  RD Sharma
  RD Sharma Class 6 Решения
  RD Sharma Class 7 Решения
  Решения RD Sharma класса 8
  Решения RD Sharma класса 9
  Решения RD Sharma класса 10
  Решения RD Sharma класса 11
  Решения RD Sharma Class 12
  PHYSICS
  Механика
  Оптика
  Термодинамика
  Электромагнетизм
  ХИМИЯ
  Органическая химия
  Неорганическая химия
  Периодическая таблица
  MATHS
  Статистика
  Числа
  Числа Пифагора Тр Игонометрические функции
  Взаимосвязи и функции
  Последовательности и серии
  Таблицы умножения
  Детерминанты и матрицы
  Прибыль и убыток
  Полиномиальные уравнения
  Разделение фракций
  Microology
  FORMULAS
  Математические формулы
  Алгебраные формулы
  Тригонометрические формулы
  Геометрические формулы
  КАЛЬКУЛЯТОРЫ
  Математические калькуляторы
  0003000
  000
  000 Калькуляторы по химии
  000
  000
  000 Образцы документов для класса 6
  Образцы документов CBSE для класса 7
  Образцы документов CBSE для класса 8
  Образцы документов CBSE для класса 9
  Образцы документов CBSE для класса 10
  Образцы документов CBSE для класса 1 1
  Образцы документов CBSE для класса 12
  Вопросники предыдущего года CBSE
  Вопросники предыдущего года CBSE, класс 10
  Вопросники предыдущего года CBSE, класс 12
  HC Verma Solutions
  HC Verma Solutions Класс 11 Физика
  HC Verma Solutions Класс 12 Физика
  Решения Лакмира Сингха
  Решения Лакмира Сингха класса 9
  Решения Лакмира Сингха класса 10
  Решения Лакмира Сингха класса 8
  9000BSE 9000 Класс
  2 6 Примечания CBSE
  Примечания CBSE класса 7
  Примечания
  Примечания CBSE класса 8
  Примечания CBSE класса 9
  Примечания CBSE класса 10
  Примечания CBSE класса 11
  Примечания 12 CBSE
  Примечания к редакции 9000 CBSE 9000 Примечания к редакции класса 9
  CBSE Примечания к редакции класса 10
  CBSE Примечания к редакции класса 11
  Примечания к редакции класса 12 CBSE
- Дополнительные вопросы CBSE
  Дополнительные вопросы по математике для класса 8 CBSE
  Дополнительные вопросы по науке для класса 8 CBSE
  Дополнительные вопросы по математике класса 9 CBSE
  Вопросы
  CBSE Class 10 Дополнительные вопросы по математике
  CBSE Class 10 Science Extra questions
- CBSE Class
  Class 3
  Class 4
  Class 5
  Class 6
  Class 7
  Class 8 Класс 9
  Класс 10
  Класс 11
  Класс 12
- Учебные решения
Решения NCERT
Решения NCERT для класса 11
Решения NCERT для класса 11 по физике
Решения NCERT для класса 11 Химия
Решения NCERT для биологии класса 11
Решение NCERT s Для класса 11 по математике
NCERT Solutions Class 11 Accountancy
NCERT Solutions Class 11 Business Studies
NCERT Solutions Class 11 Economics
NCERT Solutions Class 11 Statistics
NCERT Solutions Class 11 Commerce
NCERT Solutions for Class 12
Решения NCERT для физики класса 12
Решения NCERT для химии класса 12
Решения NCERT для биологии класса 12
Решения NCERT для математики класса 12
Решения NCERT, класс 12, бухгалтерия
Решения NCERT, класс 12, бизнес-исследования
NCERT Solutions Class 12 Economics
NCERT Solutions Class 12 Accountancy Part 1
NCERT Solutions Class 12 Accountancy Part 2
NCERT Solutions Class 12 Micro-Economics
NCERT Solutions Class 12 Commerce
NCERT Solutions Class 12 Macro-Economics
NCERT Solut Ионы Для класса 4
Решения NCERT для математики класса 4
Решения NCERT для класса 4 EVS
Решения NCERT для класса 5
Решения NCERT для математики класса 5
Решения NCERT для класса 5 EVS
Решения NCERT для класса 6
Решения NCERT для математики класса 6
Решения NCERT для науки класса 6
Решения NCERT для класса 6 по социальным наукам
Решения NCERT для класса 6 Английский язык
Решения NCERT для класса 7
Решения NCERT для математики класса 7
Решения NCERT для науки класса 7
Решения NCERT для социальных наук класса 7
Решения NCERT для класса 7 Английский язык
Решения NCERT для класса 8
Решения NCERT для математики класса 8
Решения NCERT для науки 8 класса
Решения NCERT для социальных наук 8 класса ce
Решения NCERT для класса 8 Английский
Решения NCERT для класса 9
Решения NCERT для класса 9 по социальным наукам
Решения NCERT для математики класса 9
Решения NCERT для математики класса 9 Глава 1
Решения NCERT для математики класса 9, глава 2
Решения NCERT
для математики класса 9, глава 3
Решения NCERT для математики класса 9, глава 4
Решения NCERT для математики класса 9, глава 5
Решения NCERT
для математики класса 9, глава 6
Решения NCERT для математики класса 9 Глава 7
Решения NCERT
для математики класса 9 Глава 8
Решения NCERT для математики класса 9 Глава 9
Решения NCERT для математики класса 9 Глава 10
Решения NCERT
для математики класса 9 Глава 11
Решения
NCERT для математики класса 9 Глава 12
Решения NCERT
для математики класса 9 Глава 13
NCER Решения T для математики класса 9 Глава 14
Решения NCERT для математики класса 9 Глава 15
Решения NCERT для науки класса 9
Решения NCERT для науки класса 9 Глава 1
Решения NCERT для науки класса 9 Глава 2
Решения NCERT для науки класса 9 Глава 3
Решения NCERT для науки класса 9 Глава 4
Решения NCERT для науки класса 9 Глава 5
Решения NCERT для науки класса 9 Глава 6
Решения NCERT для науки класса 9 Глава 7
Решения NCERT для науки класса 9 Глава 8
Решения NCERT для науки класса 9 Глава 9
Решения NCERT для науки класса 9 Глава 10
Решения NCERT для науки класса 9 Глава 12
Решения NCERT для науки класса 9 Глава 11
Решения NCERT для науки класса 9 Глава 13
Решения NCERT
для науки класса 9 Глава 14

Формула мощности — уравнения с примерами

Вы знаете, что такое сила? Что ж, сила — это энергия, необходимая для выполнения чего-либо за единицу времени. Все мы знаем, что способность выполнять работу называется энергией. Энергия, потребляемая при выполнении любой работы, называется Силой.

Предположим, что двое мужчин собирают кирпичи на четвертый этаж (при условии, что они оба несут одинаковое количество кирпичей), теперь человеку А требуется 5 минут, чтобы добраться до этих кирпичей до места назначения, а второму человеку, то есть B, требуется 10 минут. минут, что вдвое превышает время, затрачиваемое А. Итак, здесь человек А имеет больше силы, чем В. Если мы запишем это выражение в форме уравнения мощности, то получится:

P = Fv = Force X Velocity = Сила x смещение / время = работа / время или W / T

или P = E / T = W / T, формула требуемой мощности

Здесь W = работа,

T = время, а E — потребляемая энергия делать работу.{-2}]} {[T]} \] = [ML²T⁻³], а его единица измерения — ватт.

У нас также есть разные формулы мощности; Давайте посмотрим на них:

Формула электрической мощности

Мощность, потребляемая электроприбором, может быть вычислена с помощью двух формул. {2}} {R} \].Единица мощности — ватт.

Где

В = напряжение, приложенное к концам,

R = сопротивление и

I = ток, протекающий по цепи.

Теперь мы увидим несколько решенных примеров, основанных на формуле расчета мощности:

Что такое коэффициент мощности (Cosθ)? Cos fi или P.f Определения и формулы

Определения и формулы коэффициента мощности

В электротехнике коэффициент мощности относится только и только к цепям переменного тока i.е. в цепях постоянного тока отсутствует коэффициент мощности (P.f) из-за нулевой частоты и разности фаз (Φ) между током и напряжением.

Что такое коэффициент мощности?

Коэффициент мощности может быть определен тремя следующими определениями и формами.

1). Косинус угла между током и напряжением называется коэффициентом мощности.

Где:

P = мощность в ваттах
V = напряжение в вольтах
I = ток в амперах
W = активная мощность в ваттах
VA = полная мощность в вольт-амперах или ваттах
Cosθ = коэффициент мощности

2).Соотношение между сопротивлением и импедансом в цепи переменного тока известно как коэффициент мощности.

Cosθ = R / Z

Где:

R = Сопротивление в Ом (Ом)
Z = Импеданс (Сопротивление в цепях переменного тока, т.е. X _L , X

C R , известное как Индуктивное реактивное сопротивление , емкостное реактивное сопротивление и сопротивление соответственно) в Ом (Ом)

Cosθ = Коэффициент мощности

Импеданс «Z» — это полное сопротивление цепи переменного тока i.е.

Z = √ [R ² + (XL + XC) ²]

Где:

X _L = 2π f L… L — индуктивность в Генри
X _C = 1 / 2π f C… C — это емкость в фарадах

Связанное сообщение: Разница между активной и реактивной мощностью

3). Отношение активной мощности к полной мощности в вольтах-амперах называется коэффициентом мощности.

Cosθ = Активная мощность / Полная Мощность
Cosθ = P / S
Cosθ = кВт / кВА

Где

—

Реальная мощность Вт
кВА = Полная мощность в киловольт-амперах или ваттах
Cosθ = Коэффициент мощности

Формула коэффициента мощности в трехфазных цепях переменного тока

Коэффициент мощности Cosθ = P / √3 В _L x I _L

Треугольник коэффициента мощности и примеры

Пивная аналогия активной или истинной мощности , реактивной мощности, полной мощности и коэффициента мощности.

Аналогия мешка для чипов истинной или активной мощности , реактивной мощности, полной мощности и коэффициента мощности.

Полезно знать:

В чисто резистивной цепи коэффициент мощности равен 1 из-за нулевой разности фаз (Φ) между током и напряжением.

В чисто емкостной цепи коэффициент мощности является опережающим из-за запаздывающих VAR. Т.е. напряжение отстает на 90 ° от тока. Другими словами, ток опережает напряжение на 90 ° (ток и напряжение на 90 ° не совпадают по фазе друг с другом, при этом ток идет впереди, а напряжение отстает).

В чисто индуктивной цепи коэффициент мощности отстает из-за опережающих VAR, то есть напряжение опережает на 90 ° от тока. Другими словами, ток отстает на 90 ° от напряжения (ток и напряжение не совпадают по фазе на 90 ° друг с другом, другие — где напряжение впереди, а ток отстает).

Калькулятор закона Ома — Дюймовый калькулятор

Используйте закон Ома для расчета напряжения, тока, сопротивления или мощности в электрической цепи. Введите любые два известных значения, чтобы найти два других.Например, введите напряжение и мощность, чтобы найти ток и сопротивление.

Как использовать закон Ома для расчета напряжения, тока, сопротивления или мощности

Закон Ома определяет соотношение между электрическим током, сопротивлением и напряжением. В частности, закон Ома гласит, что ток через элемент схемы прямо пропорционален приложенной к нему разности потенциалов и обратно пропорционален сопротивлению . ^[1]

Закон Ома позволяет найти напряжение, ток, мощность и сопротивление, если известны как минимум два значения.

Например, если известны напряжение и сопротивление, калькулятор найдет мощность и ток. В качестве альтернативы мощность и сопротивление можно решить, если известны напряжение и ток.

Что такое формула закона Ома?

Формула закона Ома: I = E / R, где I — ток через проводник, измеренный в амперах, E — разность потенциалов на проводнике, измеренная в вольтах, а R — измеренное сопротивление проводника. в ом.^[2]

I = ER

Таким образом, формула закона Ома утверждает, что ток I равен напряжению E , деленному на сопротивление R .

Треугольник закона Ома, где E представляет напряжение, I представляет ток, а R представляет сопротивление.

Треугольник закона Ома показывает, как найти вольт, ампер или ом. Чтобы использовать его, накройте единицу, которую вы хотите вычислить, чтобы открыть формулу для ее решения.

Например, чтобы найти вольты, прикройте E большим пальцем, что показывает, что напряжение равно I × R.

Что означают буквы E, I и R в формуле закона Ома?

В формуле закона Ома E представляет электродвижущую силу или напряжение, I представляет силу или ток, а R представляет сопротивление.

Георг Симон Ом создал закон Ома в статье, опубликованной в 1827 году, ^[3] задолго до того, как были определены единицы измерения напряжения, тока и сопротивления.

Только в 1881 году были определены вольт, ампер и ом, то есть более чем через 50 лет после публикации закона Ома.Это объясняет, почему буквы не относятся к современным единицам, используемым в формуле.

Закон Ватта и формула мощности

Закон Ватта гласит, что электрическая мощность, измеряемая в ваттах, равна току в цепи, умноженному на напряжение. Эта формула очень похожа на закон Ома и может помочь определить мощность / мощность.

Мы часто используем формулу мощности в сочетании с законом Ома для определения электрических свойств, когда мощность цепи известна.

P = I × E

Таким образом, формула мощности утверждает, что мощность P равна I , умноженному на напряжение E .^[4]

Формула мощности, где P представляет мощность, I представляет ток, а E представляет напряжение.

Треугольник мощности иллюстрирует формулу для определения ватт, вольт или ампер. Так же, как треугольник закона Ома, накройте единицу, которую вы хотите найти, чтобы найти формулу для ее решения.

Например, чтобы найти усилители, прикройте I большим пальцем, чтобы увидеть, что ток равен P / E.

Наш калькулятор ватт в ампер использует эту формулу, например, для преобразования мощности в ток в электрических цепях.

Колесо формул закона Ома

Закон Ома используется для определения вольт, ватт, ампер или ом, если известны как минимум два измерения. Формула закона Ома позволяет нам вывести уравнения для расчета любого измерения с учетом двух других известных значений.

Колесо закона Ома показывает все формулы, которые можно использовать для определения вольт, ватт, ампер или ом. Вы также можете увидеть формулы ниже.

Колесо формул закона Ома со всеми формулами, которые можно использовать для решения вольт, ампер, ом или ватт.

Формулы для расчета напряжения

Найдите напряжение по формулам:

Напряжение = ток × сопротивление

Напряжение = мощность ÷ ток

Напряжение = мощность × сопротивление

Формулы для расчета ватт

Найдите мощность по этим формулам:

Мощность = Напряжение × Ток

Мощность = Напряжение ² ÷ Сопротивление

Мощность = ток ² × сопротивление

Формулы для расчета силы тока

Найдите ток, используя следующие формулы:

Ток = Напряжение ÷ Сопротивление

Ток = Мощность ÷ Напряжение

Ток = мощность ÷ сопротивление

Формулы для расчета сопротивления

Найдите сопротивление, используя следующие формулы:

Сопротивление = Напряжение ÷ Ток

Сопротивление = Напряжение ² ÷ Мощность

Сопротивление = мощность ÷ ток ²

Мы используем закон Ома для многих вещей, таких как определение максимального размера микроволн или максимального количества осветительных приборов, с которыми цепь может безопасно обращаться, не создавая опасности возгорания.

Наш калькулятор затрат на освещение может помочь определить потребление энергии на освещение, а наш калькулятор затрат на электроэнергию поможет определить затраты на питание электрических устройств.

Используйте закон Ома, чтобы определить размер электрической цепи или выяснить, какой размер нагревателя можно безопасно использовать в обычной розетке. Вы также можете найти наш калькулятор падения напряжения, чтобы определить падение напряжения, необходимый минимальный размер провода и максимальную длину провода для вашего следующего электрического проекта.

Электрическая мощность — номиналы, формулы и расчеты

Введение

В этом уроке мы рассмотрим разницу между мощностью и энергией.Мы увидим, как рассчитать электрическую мощность и как понять номинальную мощность, которую вы видите на электрических устройствах.

Основное представление о мощности

Power сообщает нам, как быстро преобразуется энергия.

Анимация, объясняющая идею мощности как скорости преобразования энергии.

Некоторые лампы могут быть ярче других, даже если они питаются от батареи того же типа. Более яркая лампа будет более мощной, потому что она преобразует электрическую энергию в световую энергию быстрее, чем более тусклая.

Игра Вам предстоит стрелять правильным ответом на вопросы о понятиях силы и энергии.

Как наша анимация показывает электрическую мощность

В наших анимациях мощность показана скоростью расширяющегося красного энергетического круга вокруг лампочки. Чем быстрее движется круг, тем выше мощность, которую мы показываем.

Задание по пересмотру того, как наша визуализация схемы используется для связи яркости, мощности и тока.

Вы можете использовать анимацию, чтобы увидеть, что когда три лампочки подключены к одному и тому же напряжению, самая мощная лампочка будет самой яркой и через нее будет проходить самый большой ток.Когда заряды перемещаются быстро, энергия должна быстро передаваться в лампочку.

Простой расчет мощности

Единица измерения мощности — ватт, названный в честь изобретателя паровой машины, шотландца 18 века Джеймса Ватта.

1 ватт означает, что вы передаете энергию со скоростью 1 джоуль в секунду. 2 Вт означает, что вы передаете энергию со скоростью 2 джоуля в секунду и так далее.

Анимация проведет вас через простой расчет мощности с использованием энергии и времени.

Почему мощность зависит как от тока, так и от напряжения

Должен иметь смысл, что энергия передается быстро (мощность высокая), если к компоненту каждую секунду поступает много зарядов (т.е. большой ток), и каждый заряд передает много энергии (т.е. большой p.d.).

Энергия передается медленно (низкая мощность), если каждую секунду поступает только несколько зарядов (т.е. небольшой ток), и каждый заряд передает только небольшое количество энергии (т.е. малый p.d.).

Вот почему мощность зависит как от тока, так и от напряжения.

Игра Правда или ложь с утверждениями о власти. Вы должны нацелить заявление на тележку для покупок или мусорный бак.

Использование P = I V

Анимация, объясняющая, почему мощность зависит от напряжения и тока.

Специальная формула для электрической мощности —

мощность = ток x напряжение

Например, если лампа с током 2 А и п.д. 6 В через него будет иметь мощность 12 Вт.

Анимация проведет вас через простой расчет мощности с использованием напряжения и тока.Игра Используйте напряжение и ток, чтобы вычислить мощность. Проведите космический вездеход над черной дырой, используя только квадраты мощностью ровно 6 Вт.

Номинальные мощности электрооборудования

Если вы посмотрите на лампочку, вы можете увидеть что-то вроде 240 В, 100 Вт. Это не означает, что на лампе всегда будет напряжение 240 В или что она всегда будет преобразовывать энергию со скоростью 100 Вт.

Это означает: «Если вы случайно подключите к этой лампе 240 В, то она преобразует энергию со скоростью 100 Вт.’

Анимация, показывающая, где найти номинальную мощность лампочки и что это значит.

Если вы подключите его к более низкому напряжению, его мощность будет меньше 100 Вт, и он будет тусклее. Если вы подключите его к более высокому напряжению, его мощность будет более 100 Вт, и он станет ярче.

Анимация, объясняющая, что произойдет, если вы не подключите лампочку к ее рабочему напряжению, а что-то другое.

Если вы подключите его к сети, намного превышающей 240 В, то нить накаливания, вероятно, перегорит, и лампа не будет работать.Так 240 В называется рабочим напряжением. Это напряжение, на которое рассчитана лампа.

График, показывающий, как яркость связана с номиналом лампы для разных рабочих напряжений.

Анимация, объясняющая некоторые распространенные заблуждения о номинальных характеристиках ламп.

Изменение количества батареек, изменение количества лампочек

Распространенная ошибка — думать, что если вы удвоите количество батарей, вы примерно удвоите яркость лампы. Аналогичная ошибка — думать, что две последовательно соединенные лампочки примерно вдвое меньше яркости одной лампочки.

Важно помнить, что яркость зависит как от тока, так и от напряжения.

Если вы удвоите количество батарей, вы удвоите напряжение и, таким образом, вы также примерно (потому что сопротивление лампочки изменяется в зависимости от тока) удвоите ток. Это означает, что удвоение количества батареек примерно в четыре раза увеличивает яркость.

Точно так же, если у вас есть две последовательно соединенные лампочки, каждая из них примерно на четверть ярче одной лампочки.Это связано с тем, что примерно удвоение сопротивления примерно вдвое уменьшает ток через каждую лампочку, но каждая лампочка также получает только половину напряжения.

P = I ² R и P = V ² / R

Вы можете объединить P = IV с V = IR, чтобы получить два полезных уравнения.

Анимация, демонстрирующая происхождение и последствия P = I2R и P = V2 / R.

Если мы исключим V, мы получим P = I ² R.

Это означает, что если вы удвоите ток, вы увеличите мощность в четыре раза.На первый взгляд может показаться, что это уравнение предполагает, что если вы поддерживаете постоянный ток, то увеличение сопротивления увеличивает мощность. Но если вы увеличите сопротивление, вы сможете поддерживать постоянным ток только за счет увеличения напряжения, так что это никогда не будет честным сравнением.

Лампы с низким сопротивлением обычно ярче, чем лампы с высоким сопротивлением, если они подключены к одному и тому же напряжению, потому что ток через них больше.

Если исключить I, получим P = V ² / R.

Это означает, что если вы удвоите напряжение, вы увеличите мощность в четыре раза. Это имеет больше смысла, потому что удвоение напряжения также удваивает ток (примерно). В уравнении также говорится, что если вы поддерживаете постоянное напряжение и уменьшаете сопротивление, вы увеличиваете мощность. Это потому, что, уменьшая сопротивление, вы увеличиваете ток и, таким образом, увеличиваете мощность.

Возврат к краткой информации об электричестве

Функции, сигналы и перечисления — Power Apps

17.07.2020
5 минут на чтение

В этой статье

Формулы объединяют множество элементов.Ниже перечислены:

Функции принимают параметры, выполняют операцию и возвращают значение. Например, Sqrt (25) возвращает 5 . Функции моделируются по образцу функций Microsoft Excel. Некоторые функции имеют побочные эффекты, например SubmitForm , которые подходят только в формуле поведения, например Button.OnSelect .
Сигналы возвращают информацию об окружающей среде. Например, Location возвращает текущие координаты GPS устройства.Сигналы не принимают параметров и не имеют побочных эффектов.
Перечисления возвращают предварительно определенное постоянное значение. Например, Color — это перечисление, которое имеет предварительно определенные значения для Color.Red , Color.Blue и так далее. Сюда включены общие перечисления; Перечисления, специфичные для функции, описываются с помощью функции.
Именованные операторы , такие как ThisItem и Self , обеспечивают доступ к информации из контейнера.

Другие элементы включают:

А

Abs — Абсолютное значение числа.

Acceleration — Считывает показания датчика ускорения вашего устройства.

Acos — возвращает арккосинус числа в радианах.

Acot — возвращает арккотангенс числа в радианах.

AddColumns — возвращает таблицу с добавленными столбцами.

, и — логическая логика И.Возвращает true , если все аргументы true . Вы также можете использовать оператор && .

Приложение — Предоставляет информацию о текущем запущенном приложении и контролирует его поведение.

Asin — возвращает арксинус числа в радианах.

Утвердить — Оценивает истинность или ложь в тесте.

As — Называет текущую запись в галерее, форме и функциях области записи, например ForAll , With и Sum .

AsType — обрабатывает ссылку на запись как конкретный тип объекта.

Atan — возвращает арктангенс числа в радианах.

Atan2 — возвращает арктангенс на основе координаты ( x , y ) в радианах.

Среднее значение — Вычисляет среднее значение табличного выражения или набора аргументов.

B

Назад — Отображение предыдущего экрана.

Пусто — возвращает пустое значение , которое можно использовать для вставки значения NULL в источник данных.

С

Календарь — Получает информацию о календаре для текущего языкового стандарта.

Char — переводит код символа в строку.

Choices — Возвращает таблицу возможных значений для столбца подстановки.

Очистить — Удаляет все данные из коллекции.

ClearCollect — Удаляет все данные из коллекции, а затем добавляет набор записей.

Часы — Получает информацию о часах для текущего языкового стандарта.

Coalesce — заменяет пустых значений , оставляя не пустыми значениями без изменений.

Собрать — Создает коллекцию или добавляет данные в источник данных.

Цвет — Устанавливает свойство на встроенное значение цвета.

ColorFade — Уменьшает значение цвета.

ColorValue — преобразует имя цвета CSS или шестнадцатеричный код в значение цвета.

Компас — возвращает направление по компасу.

Concat — объединяет строки в источнике данных.

Concatenate — объединяет строки.

Параллельно — Оценивает несколько формул одновременно друг с другом.

Подключение — Возвращает информацию о вашем сетевом подключении.

Счетчик — Подсчитывает записи таблицы, содержащие числа.

Cos — возвращает косинус угла, указанного в радианах.

Cot — возвращает котангенс угла, указанного в радианах.

CountA — подсчитывает непустые записи таблицы.

CountIf — подсчитывает записи таблицы, удовлетворяющие условию.

CountRows — Подсчет записей таблицы.

D

DataSourceInfo — Предоставляет информацию об источнике данных.

Дата — возвращает значение даты / времени на основе значений года , месяца и дня .

DateAdd — Добавляет дни, месяцы, кварталы или годы к значению даты / времени.

DateDiff — вычитает два значения даты и показывает результат в днях, месяцах, кварталах или годах.

DateTimeValue — Преобразует строку даты и времени в значение даты / времени.

DateValue — Преобразует строку, содержащую только дату, в значение даты / времени.

День — извлекает дневную часть значения даты / времени.

По умолчанию — Возвращает значения по умолчанию для источника данных.

Градусы — Преобразует радианы в градусы.

Отключить — Отключает сигнал, например Местоположение для чтения GPS.

Distinct — Суммирует записи таблицы, удаляя дубликаты.

Загрузить — загружает файл из Интернета на локальное устройство.

DropColumns — возвращает таблицу с удаленным одним или несколькими столбцами.

E

EditForm — Сбрасывает элемент управления формы для редактирования элемента.

Включить — Включает сигнал, например Местоположение , для чтения GPS.

EncodeUrl — кодирует специальные символы с использованием кодировки URL.

EndsWith — Проверяет, заканчивается ли текстовая строка другой текстовой строкой.

Ошибки — Предоставляет информацию об ошибках для предыдущих изменений источника данных.

exactin — Проверяет, содержится ли текстовая строка в другой текстовой строке или таблице, в зависимости от регистра. Также используется для проверки наличия записи в таблице.

Выход — Выход из текущего запущенного приложения и, при необходимости, выход из системы текущего пользователя.

Exp — возвращает e в степени.

F

Фильтр — возвращает отфильтрованную таблицу на основе одного или нескольких критериев.

Найти — Проверяет, появляется ли одна строка в другой, и возвращает местоположение.

Первая — возвращает первую запись таблицы.

FirstN — возвращает первый набор записей (N записей) таблицы.

ForAll — вычисляет значения и выполняет действия для всех записей таблицы.

G

GroupBy — возвращает таблицу с сгруппированными вместе записями.

GUID — преобразует строку GUID в значение GUID или создает новое значение GUID.

H

HashTags — Извлекает хэштеги (#strings) из строки.

Час — Возвращает часовую часть значения даты / времени.

I

Если — возвращает одно значение, если условие верно, и другое значение, если нет.

IfError — обнаруживает ошибки и предоставляет альтернативное значение или принимает меры.

in — Проверяет, содержится ли текстовая строка в другой текстовой строке или таблице, независимо от регистра. Также используется для проверки наличия записи в таблице.

IsBlank — Проверяет наличие пустого значения.

IsEmpty — Проверяет наличие пустой таблицы.

IsError — Проверяет наличие ошибки.

IsMatch — Проверяет строку по шаблону.Можно использовать регулярные выражения.

IsNumeric — Проверяет числовое значение.

IsToday — Проверяет, соответствует ли значение даты / времени сегодняшнему дню.

IsType — Проверяет, относится ли ссылка на запись к определенному типу сущности.

Дж

JSON — Создает текстовую строку JSON для таблицы, записи или значения.

L

Язык — возвращает языковой тег текущего пользователя.

Последняя — возвращает последнюю запись таблицы.

LastN — возвращает последний набор записей (N записей) таблицы.

Запуск — запускает веб-страницу или приложение холста.

Left — возвращает крайнюю левую часть строки.

Len — Возвращает длину строки.

Ln — возвращает натуральный логарифм.

LoadData — Загружает коллекцию из хранилища локального устройства.

Местоположение — Возвращает ваше местоположение в виде координат карты с использованием глобальной системы позиционирования (GPS) и другой информации.

LookUp — выполняет поиск отдельной записи в таблице на основе одного или нескольких критериев.

Нижний регистр — Преобразует буквы в строке текста во все строчные.

M

Match — извлекает подстроку на основе шаблона. Можно использовать регулярные выражения.

MatchAll — извлекает несколько подстрок на основе шаблона.Можно использовать регулярные выражения.

Макс. — максимальное значение табличного выражения или набора аргументов.

Mid — возвращает среднюю часть строки.

Мин. — Минимальное значение табличного выражения или набора аргументов.

Минуты — извлекает минутную часть значения даты / времени.

Mod — возвращает остаток после деления дивиденда на делитель.

Месяц — извлекает часть месяца из значения даты / времени.

N

Navigate — Изменяет отображаемый экран.

NewForm — Сбрасывает элемент управления формы для создания элемента.

Not — Логическая логика НЕ. Возвращает true , если его аргумент равен false , и возвращает false , если его аргумент true . Вы также можете использовать ! Оператор .

Уведомить — Отображает баннерное сообщение для пользователя.

Сейчас — Возвращает текущее значение даты / времени.

O

или — логическая логика ИЛИ. Возвращает true , если какой-либо из его аргументов true . Вы также можете использовать || Оператор .

-П

Param — параметры доступа, передаваемые приложению холста при запуске.

Родительский — Предоставляет доступ к свойствам элемента управления контейнера.

Патч — изменяет или создает запись в источнике данных или объединяет записи вне источника данных.Оператор .

Правильный — Преобразует первую букву каждого слова в строке в верхний регистр и преобразует остальные в нижний регистр.

R

Радианы — Преобразует градусы в радианы.

Rand — возвращает псевдослучайное число.

Обновить — обновляет записи источника данных.

Связать — связывает записи двух сущностей посредством отношения «один ко многим» или «многие ко многим».

Удалить — Удаляет одну или несколько определенных записей из источника данных.

RemoveIf — Удаляет записи из источника данных на основе условия.

RenameColumns — переименовывает столбцы таблицы.

Заменить — Заменяет часть строки другой строкой по начальной позиции строки.

ЗапросСкрыть — скрывает форму SharePoint.

Reset — Сбрасывает элемент управления вводом до значения по умолчанию, отменяя любые изменения, сделанные пользователем.

ResetForm — Сбрасывает элемент управления формы для редактирования существующего элемента.

Отменить — повторно загружает и удаляет ошибки для записей источника данных.

RGBA — возвращает значение цвета для набора красного, зеленого, синего и альфа-компонентов.

Справа — возвращает крайнюю правую часть строки.

Round — Округление до ближайшего числа.

RoundDown — округляет до наибольшего предыдущего числа.

RoundUp — Округление до наименьшего следующего числа.

S

SaveData — сохраняет коллекцию в хранилище локального устройства.

Поиск — Находит записи в таблице, которые содержат строку в одном из своих столбцов.

Second — извлекает вторую часть значения даты / времени.

Select — имитирует действие выбора элемента управления, в результате чего вычисляется формула OnSelect .

Self — Предоставляет доступ к свойствам текущего элемента управления.

Sequence — создание таблицы последовательных чисел, полезно при итерации с ForAll .

Установить — Устанавливает значение глобальной переменной.

SetFocus — перемещает фокус ввода на конкретный элемент управления.

SetProperty — имитирует взаимодействие с элементами управления вводом.

ShowColumns — возвращает таблицу только с выбранными столбцами.

Shuffle — Произвольно переупорядочивает записи таблицы.

Sin — возвращает синус угла, указанного в радианах.

Сортировка — возвращает отсортированную таблицу на основе формулы.

SortByColumns — возвращает отсортированную таблицу на основе одного или нескольких столбцов.

Разделить — Разбивает текстовую строку на таблицу подстрок.

Sqrt — возвращает квадратный корень числа.

StartsWith — Проверяет, начинается ли текстовая строка с другой текстовой строки.

StdevP — возвращает стандартное отклонение своих аргументов.

Замена — заменяет часть строки другой строкой путем сопоставления строк.

SubmitForm — Сохраняет элемент в элементе управления формы в источнике данных.

Sum — Вычисляет сумму табличного выражения или набора аргументов.

Switch — соответствует набору значений, а затем вычисляет соответствующую формулу.

Т

Таблица — Создает временную таблицу.

Tan — возвращает тангенс угла, указанного в радианах.

Текст — Преобразует любое значение и форматирует число или значение даты / времени в строку текста.

ThisItem — возвращает запись для текущего элемента в галерее или элементе управления формы.

ThisRecord — Возвращает запись для текущего элемента в функции области записи, например ForAll , With и Sum .

Время — Возвращает значение даты / времени на основе значений часов , минут и секунд .

TimeValue — Преобразует строку, содержащую только время, в значение даты / времени.

TimeZoneOffset — Возвращает разницу между временем в формате UTC и местным временем пользователя в минутах.

Сегодня — возвращает текущее значение даты / времени.

Trace — Предоставьте дополнительную информацию в результатах теста.

Обрезать — Удаляет лишние пробелы с концов и внутри строки текста.

TrimEnds — Удаляет лишние пробелы только с концов строки текста.

U

Разгруппировать — Удаляет группировку.

Несвязать — Разъединяет записи двух сущностей из отношения «один ко многим» или «многие ко многим».

Обновление — заменяет запись в источнике данных.

UpdateContext — Устанавливает значение одной или нескольких переменных контекста текущего экрана.

UpdateIf — изменяет набор записей в источнике данных на основе условия.