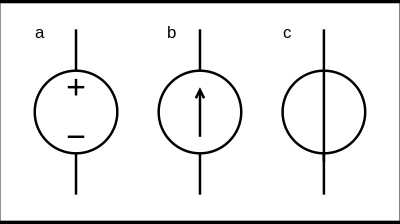
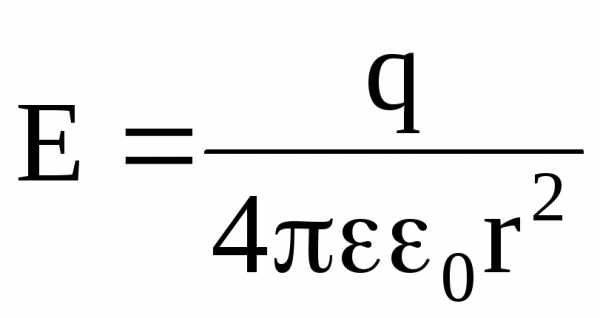Фазные токи формула. Трёхфазный переменный ток. Формула тока в трехфазной цепи переменного тока

Основные законы и формулы, описывающие цепи трёхфазного переменного тока

Приведём важнейшие законы из теории общей электротехники, касающиеся принципов работы электрооборудования на трёхфазном переменном токе.

Синусоидальные токи и напряжения можно представлять как в виде мгновенных величин, так и в виде действующих.

Мгновенные токи и напряжения описывают изменение физической величины в каждый момент времени и обозначаются малыми буквами i, u.

Синусоидальный ток зависит от времени t по формуле:

i(t) = imaxsin(ωt + φi),

где imax – амплитуда синусоиды тока;

ω – угловая частота;

φi – начальная фаза.

Угловая частота определяется по формуле:

ω = 2π f,

где f – частота переменного тока.

Если принять f = 50 Гц, то ω = 314 рад/с.

Аналогично определяется мгновенное напряжение:

u(t) = umaxsin(ωt + φu),

Тепловое действие тока, а также механическая сила взаимодействия двух проводников, по которым проходит один и тот же ток, пропорциональны квадрату тока. Поэтому о величине тока можно судить по его среднеквадратичному значению за период, то есть по действующему значению. В этом случае применяют большую букву I. Действующее значение синусоидального тока численно равно такому постоянному току, который за период выделяет такое же количество тепла, что и синусоидальный ток. Аналогично вводится понятие действующего напряжения U. Действующее значение в раз меньше амплитудного.

Для удобства математического обращения с синусоидальными величинами токов и напряжений, их представляют в виде вращающихся векторов на комплексной плоскости. Так, например, симметричная трёхфазная система токов может быть представлена графически в виде тройки векторов, имеющих одинаковые длины и рассоложенных под углами 120° друг относительно друга – рис. 1.2.

 

Рис. 1.2. Изображение симметричной трёхфазной системы токов в виде векторов на плоскости

 

Такое представление позволяет графически складывать и вычитать токи и напряжения, анализировать сдвиг фаз между ними.

Для трёхфазной системы напряжений вводятся понятия фазного и линейного напряжения. Фазное напряжение Uф – это разность потенциалов между фазой и «землёй» (то есть точкой нулевого потенциала). Линейное напряжение Uл – это разность потенциалов между двумя фазами. На рис. 1.3 показано графическое отображение фазных и линейных напряжений. Пользуясь тригонометрией, несложно доказать, что линейное напряжение в раз больше фазного. Так, например, для сетей жилых зданий линейное напряжение составляет 380 В, а фазное 380/корень3 ≈ 220 В.

 

Рис. 1.3. К понятию фазного и линейного напряжения

 

Закон Ома связывает напряжение U, ток I и полное сопротивление цепи Z:

U = I ∙ Z.

Полное сопротивление цепи состоит из активной R и реактивной Х составляющих:

Z = .

Геометрически данное выражение можно представить в виде треугольника сопротивлений на рис. 1.4. Угол φ между активной и полной составляющей определяет разность фаз между синусоидами тока и напряжения. Косинус этого угла называется коэффициентом мощности и имеет очень важное значение для экономичности работы сети. При φ = 0 сопротивление цепи имеет число активный характер, а ток и напряжение совпадают по фазе.

 

Рис. 1.4. Треугольник сопротивлений

 

Активное сопротивление определяется удельным сопротивлением проводника ρ, его длиной l и площадью поперечного сечения s по формуле:

R = ρ∙ l / s.

Реактивное сопротивление Х может быть индуктивным (положительным) и емкостным (отрицательным).

Индуктивное сопротивление катушки с индуктивностью L зависит от угловой частоты тока ω прямо пропорционально:

ХL = ω L.

Если сопротивление цепи чисто индуктивное, то синусоида тока отстаёт от синусоиды напряжения по фазе на 90° (φ = + 90°).

Емкостное сопротивление конденсатора с ёмкостью С зависит от угловой частоты тока ω обратно пропорционально:

ХС = 1 / ω С.

Если сопротивление цепи чисто емкостное, то синусоида тока опережает синусоиду напряжения по фазе на 90° (φ = – 90°).

Суммарное реактивное сопротивление складывается из сопротивлений ХL и ХС с учётом их знаков:

Х = ХL – ХС.

Закон электромагнитной индукции Фарадея описывает возникновение ЭДС в рамке при изменении магнитного потока. Фактически данный закон описывает принцип действия простейшего генератора переменного тока. Закон гласит: если внутри рамки изменять магнитный поток Ф, то на концах рамки возникнет ЭДС индукции εi, прямо пропорциональная скорости изменения магнитного потока dФ/dt и числу витков рамки N:

εi = – N dФ/dt,

где знак минус описывается правилом Ленца: индукционный ток, возникающий при изменении внешнего магнитного потока, имеет такое направление, что его собственный магнитный поток компенсирует изменение внешнего магнитного потока, вызвавшего этот ток.

Важное значение в электротехнике имеет закон, описывающий взаимодействие проводника с током и магнитного поля. При помещении проводника длиной l с током I в магнитное поле с индукцией В, на данный проводник действует сила Ампера:

FА = В∙I∙l∙sinα,

где α – угол между векторами тока и магнитной индукции.

Направление силы Ампера определяется по правилу левой руки: линии магнитного поля входят в ладонь, четыре пальца указывают направление тока, отставленный большой палец указывает направление силы Ампера. Данный закон описывает принцип действия любого электродвигателя.

Закон Джоуля-Ленца оговаривает тепловое действие тока. Если через проводник сопротивлением R в течение времени t пропускать ток I, то в данном проводнике будет выделяться теплота количеством:

Q = I2∙R∙t.

Квадратичный характер тепловых потерь вынуждает при одной и той же мощности снижать ток за счёт увеличения напряжения, что активно используется в современной энергетике.

pdnr.ru

7.1. Основные определения    Трехфазная  цепь  является совокупностью трех электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты, сдвинутые относительно друг друга по фазе на 120o, создаваемые общим источником. Участок трехфазной системы, по которому протекает одинаковый ток, называется фазой.    Трехфазная цепь состоит из трехфазного генератора, соединительных проводов и приемников или нагрузки, которые могут быть однофазными или трехфазными.      Трехфазный генератор представляет собой синхронную машину. На статоре генератора размещена обмотка, состоящая из трех частей или фаз, пространственно смещенных относительно друг друга на 120o. В фазах генератора индуктируется симметричная трехфазная система ЭДС, в которой электродвижущие силы одинаковы по амплитуде и различаются по фазе на 120o. Запишем мгновенные значения и комплексы действующих значений ЭДС.      Сумма электродвижущих сил симметричной трехфазной системы в любой момент времени равна нулю.        Соответственно                      На схемах трехфазных цепей начала фаз обозначают первыми буквами латинского алфавита ( А, В, С ), а концы - последними буквами ( X, Y, Z ). Направления ЭДС указывают от конца фазы обмотки генератора к ее началу.      Каждая фаза нагрузки соединяется с фазой генератора двумя проводами: прямым и обратным. Получается несвязанная трехфазная система, в которой имеется шесть соединительных проводов. Чтобы уменьшить количество соединительных проводов, используют трехфазные цепи, соединенные звездой или треугольником. 7.2. Соединение в звезду. Схема, определения      Если концы всех фаз генератора соединить в общий узел, а начала фаз соединить с нагрузкой, образующей трехлучевую звезду сопротивлений, получится трехфазная цепь, соединенная звездой. При этом три обратных провода сливаются в один, называемый нулевым или нейтральным. Трехфазная цепь, соединенная звездой, изображена на рис. 7. 1. Рис. 7.1      Провода, идущие от источника к нагрузке называют линейными проводами, провод, соединяющий нейтральные точки источника Nи приемника N' называют нейтральным (нулевым) проводом.     Напряжения  между началами фаз  или между линейными проводами называют линейными напряжениями. Напряжения между началом и концом фазы или между линейным и нейтральным проводами называются фазными напряжениями.       Токи в фазах приемника или источника называют фазными токами, токи в линейных проводах - линейными токами. Так как линейные провода соединены последовательно с фазами источника и приемника, линейные токи при соединении звездой являются одновременно фазными токами. Iл = Iф. ZN - сопротивление нейтрального провода.      Линейные напряжения равны геометрическим разностям соответствующих фазных напряжений      (7.1)      На рис. 7.2 изображена векторная диаграмма фазных и линейных напряжений симметричного источника. Рис. 7.2        Из векторной диаграммы видно, что        При симметричной системе ЭДС источника линейное напряжение больше фазного в √3 раз. Uл = √3 Uф 7.3. Соединение в треугольник. Схема, определения        Если конец каждой фазы обмотки генератора соединить с началом следующей фазы, образуется соединение в треугольник. К точкам соединений обмоток подключают три линейных провода, ведущие к нагрузке.         На рис. 7.3 изображена трехфазная цепь, соединенная треугольником. Как видно из рис. 7.3, в трехфазной цепи, соединенной треугольником, фазные и линейные напряжения одинаковы. Uл = Uф        IA, IB, IC - линейные токи;        Iab, Ibc, Ica- фазные токи.        Линейные и фазные токи нагрузки связаны между собой первым законом Кирхгофа для узлов а, b, с. Рис. 7.3        Линейный ток равен геометрической разности соответствующих фазных токов.     На рис. 7.4  изображена  векторная  диаграмма трехфазной цепи, соединенной треугольником при симметричной нагрузке. Нагрузка является симметричной, если сопротивления фаз одинаковы. Векторы фазных токов совпадают по направлению с векторами соответствующих фазных напряжений, так как нагрузка состоит из активных сопротивлений. Рис. 7.4        Из векторной диаграммы видно, что , Iл = √3 Iф при симметричной нагрузке.      Трехфазные цепи, соединенные звездой, получили большее распространение, чем трехфазные цепи, соединенные треугольником. Это объясняется тем, что, во-первых, в цепи, соединенной звездой, можно получить два напряжения: линейное и фазное. Во-вторых, если фазы обмотки электрической машины, соединенной треугольником, находятся в неодинаковых условиях, в обмотке появляются дополнительные токи, нагружающие ее. Такие токи отсутствуют в фазах электрической машины, соединенных по схеме "звезда". Поэтому на практике избегают соединять обмотки трехфазных электрических машин в треугольник. 7.4. Расчет трехфазной цепи, соединенной звездой        Трехфазную цепь,   соединенную звездой, удобнее всего рассчитать методом двух узлов.        На рис. 7.5 изображена трехфазная цепь при соединении звездой. В общем случае сопротивления фаз нагрузки неодинаковы (ZA ≠ ZB ≠ ZC )        Нейтральный провод имеет конечное сопротивление ZN .        В схеме между нейтральными точками источника и нагрузки возникает узловое напряжение или напряжение смещения нейтрали.        Это напряжение определяется по формуле (7.2).                 Рис.7.5      (7.2)        Фазные токи определяются по формулам (в соответствии с законом Ома для активной ветви):      (7.3)        Ток в нейтральном проводе                  (7.4)        Частные случаи.     1. Симметричная нагрузка.   Сопротивления фаз нагрузки   одинаковы и равны некоторому активному сопротивлению ZA = ZB = ZC = R.        Узловое напряжение , потому что трехфазная система ЭДС симметрична,     .         Напряжения фаз нагрузки и генератора одинаковы:      Фазные токи  одинаковы по  величине и совпадают по фазе со своими фазными напряжениями. Ток в нейтральном проводе отсутствует        В трехфазной системе, соединенной звездой, при симметричной нагрузке нейтральный провод не нужен.       На рис. 7.6 изображена векторная диаграмма трехфазной цепи для симметричной нагрузки.        2. Нагрузка несимметричная,   RAB = RC, но сопротивление нейтрального провода равно нулю:  ZN = 0. Напряжение смещения нейтрали рис. 7.6        Фазные напряжения нагрузки и генератора одинаковы        Фазные токи определяются по формулам       Вектор тока в нейтральном проводе равен геометрической сумме векторов фазных токов.        На  рис.  7.7  приведена  векторная  диаграмма    трехфазной    цепи,    соединенной    звездой,    с нейтральным    проводом,    имеющим     нулевое     сопротивление,    нагрузкой   которой      являются   неодинаковые   по    величине    активные  сопротивления.                     Рис. 7.7        3. Нагрузка несимметричная, RAB = RC, нейтральный провод отсутствует,        В схеме появляется напряжение смещения нейтрали, вычисляемое по формуле:       Система фазных напряжений генератора остается симметричной. Это объясняется тем, что источник трехфазных ЭДС имеет практически бесконечно большую мощность. Несимметрия нагрузки не влияет на систему напряжений генератора.     Из-за напряжения  смещения нейтрали фазные  напряжения нагрузки становятся неодинаковыми.       Фазные напряжения генератора и нагрузки отличаются друг от друга. При отсутствии нейтрального провода геометрическая сумма фазных токов равна нулю.        На рис. 7.8 изображена векторная диаграмма трехфазной цепи с несимметричной нагрузкой и оборванным нейтральным проводом. Векторы фазных токов совпадают по направлению с векторами соответствующих фазных напряжений нагрузки. Нейтральный провод с нулевым сопротивлением в схеме с несимметричной нагрузкой выравнивает несимметрию фазных напряжений нагрузки, т.е. с включением данного нейтрального провода фазные напряжения нагрузки становятся одинаковыми.                 Рис. 7.8 7.5. Мощность в трехфазных цепях      Трехфазная цепь является обычной цепью синусоидального тока с несколькими источниками.         Активная мощность трехфазной цепи равна сумме активных мощностей фаз    (7.5)        Формула (7.5) используется для расчета активной мощности в трехфазной цепи при несимметричной нагрузке.         При симметричной нагрузке:         При соединении в треугольник симметричной нагрузки        При соединении в звезду .        В обоих случаях .

nwpi-fsap.narod.ru

Фазные токи формула. Трёхфазный переменный ток

Токи в фазах генератора и приемника называются фазными токами, а токив линейных проводах - линейными.

При симметричном режиме трехфазной цепи и соединении обмоток генератора звездой положительные направления токов в линейных проводах выбирают от генератора к приемнику, а тока – в нейтральном проводе в обратном направлении. У симметричного трехфазного приемника или у трех одинаковых приемников, соединенных звездой, сопротивления фаз равны по модулю , из чего следует, что линейные и фазные токи численно равны.

, (3.11)

где – полное сопротивление фазы.

Линейные или фазные токи сдвинуты по фазе относительно друг друга на равные углы, равные 120°. Сумма векторов трех токов, образующих симметричную тройку, равна нулю, как и трех векторов фазных напряжений. Поэтому тока в нейтральном проводе нет: , и от нейтрального провода можно отказаться. Такую четырехпроводную систему можно заменить трехпроводной (рис. 3.4).

Рис. 3.4. Схема трехфазной трехпроводной цепи

При симметричном режиме трехфазной цепи и соединении обмоток генератора треугольником положительное направление линейных токов, как и при соединении звездой, выбираются от генератора к приемникам. За положительное направление фазных токов в приемниках принимаются направления от а к b , от b к с , от с к а , что указывается порядком букв в индексах. Например, – это ток в фазе bc , направленный от узла b к узлу c .

Ток в каждом линейном проводе равен разности токов двух фаз, которые соединены в один узел с этим проводом.

При симметричной системе напряжений и одинаковых сопротивлениях фаз приемника фазные токи образуют симметричную систему. Действующие значения токов одинаковы, а по фазе токи сдвинуты относительно друг друга на углы 120°. Линейные токи равны разностям соответствующих фазных токов, их действующие значения одинаковые, сдвиги по фазе между ними, как и между фазными токами, равны 120°. Векторы фазных токов смежных фаз вместе с вектором соответствующего линейного тока образуют равнобедренный треугольник с углами при основании 30° и углом при вершине 120°. Основание треугольника определяет линейный ток.

Из треугольника получается, что:

Линейный ток больше фазного в раз при симметричном режиме трехфазной цепи и соединении треугольником. Каждый линейный ток отстает по фазе от соответствующего фазного тока на угол 30°.

Пример 3.2. Фазные напряжения генератора U Ф =240 В, сопротивления фаз приемника za = ra =20 Ом, zb = rb =8 Ом, zc = rc =50 Ом. Сопротивлением линейных

realapex.ru

---

• 
  Вода из крана то горячая то холодная вода
• 
  Чем источник эдс отличается от источника тока
• 
  Класс напряжения что это
• 
  Формула емкости цилиндрического конденсатора
• 
  Передать показания гук жилфонд
• 
  Устройство ветряной электростанции
• 
  Тт защитные свойства
• 
  Первая помощь при ударе током на производстве
• 
  Когда возникает режим короткого замыкания в цепи
• 
  Птэ и птб электроустановок потребителей
• 
  Можно ли на отопление поставить счетчик