Формулы давления в физике: Недопустимое название — Викиверситет

Формула давления в физике

Содержание:

Определение и формула давления

Определение

Давление – это физическая величина,характеризующая состояние сплошной среды. Оно равно пределу отношения нормальной составляющей силы,
которая действует на участок поверхности тела площади
$\Delta S$ к размеру данной площади при
$\Delta S \rightarrow 0$ . Обозначается давление буквой p. Тогда математической
записью определения давления станет формула:

$$p=\lim _{\Delta S \rightarrow 0} \frac{\Delta F_{n}}{\Delta S}=\frac{d F_{n}}{d S}$$

Выражение (1) определяет давление в точке.

Среднее давление

Средним давлением на поверхность называют величину:

$$\langle p\rangle=\frac{F_{n}}{S}(2)$$

где F_n – нормальная составляющая силы, которая действует на рассматриваемую поверхность, S – площадь этой поверхности.

Давление идеального газа

Давление идеального газа вычисляют, используя основное уравнение молекулярно – кинетической теории:

$$p=n k T(3)$$

где $n=\frac{N}{V}$– концентрация молекул газа
(N – число частиц), k=1,38•10^-23 Дж/К – постоянная Больцмана, T – абсолютная температура газа. {*}$ –поверхностное натяжение жидкости,p₀^* – давление под не искривлённым слоем жидкости,
H — средняя кривизна поверхности жидкости, вычисляемая по закону Лапласа:

$$H=\frac{1}{2}\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}\right)$$

R₁, R₂ – главные радиусы кривизны.

Единицы измерения давления

Основной единицей измерения давления в системе СИ является: [p]=Па (паскаль)

Внесистемные единицы давления: [p]=мм рт.ст.(миллиметр ртутного столба),мм в.ст (мм водяного столба),атмосфера,бар.

Па= Н/м² и 1 бар=10⁵ Па.

Техническая атмосфера ~1 бар. Физическая атмосфера 1,01 бар=760 мм рт.ст.. 1 мм рт.ст.=133 Па.

Примеры решения задач

Пример

Задание. Каково давление в море на глубине h=8,5 м, если атмосферное давление равно
p₀=10⁵ Па, плотность морской воды равна
$\rho$=1,03•10³ кг/м³

Решение. {5}$ (Па)

Слишком сложно?

Формула давления не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. Каково давление струи на неподвижную плоскость, если струя воды ударяет ее под углом
$\alpha$ к нормали
плоскости, и упруго отскакивает от нее без изменения скорости? Скорость струи v.

Решение. Сделаем рисунок.

За время $\Delta t$ о стенку ударяется масса воды равная:

$$m=l S \rho=v \Delta t S \rho$$

где S — поперечное сечение струи, $\rho$ – плотность воды. В соответствии с законом сохранения импульса имеем:

$$F \Delta t=m \Delta v \rightarrow F=\frac{m \Delta v}{\Delta t}(2.2)$$

где F – сила, с которой вода действует на стенку.

Примем за положительное направление нормали внешней к опоре и учитывая, что струя отскакивает от стены без потери скорости, получаем:

$$\Delta v=v_{2} \cos \alpha-\left(-v_{1} \cos \alpha\right)=v_{2} \cos \alpha+v_{1} \cos \alpha=2 v \cos \alpha(2. {2}$

Читать дальше: Формула закона Ома.

просто и понятно о том, как определяется давление

Определение

Давление – очень важная физическая величина, играющая огромную роль, как в окружающей природе, так и жизни человека. Внешне незаметное человеческому глазу давление может очень хорошо ощущаться каждым из нас. Особенно хорошо это усвоили люди в возрасте, часто страдающие от повышенного давления (или наоборот от пониженного). Но в нашей статье мы больше поговорим именно о давлении в физике, о том, как оно измеряется и рассчитывается, какие есть формулы для расчетов давления разных субстанций: воздуха, жидкости или твердого тела.

Определение

Под давлением в физике понимается термодинамическая величина, выраженная соотношением перпендикулярной силы давления на площадь поверхности, на которую она воздействует.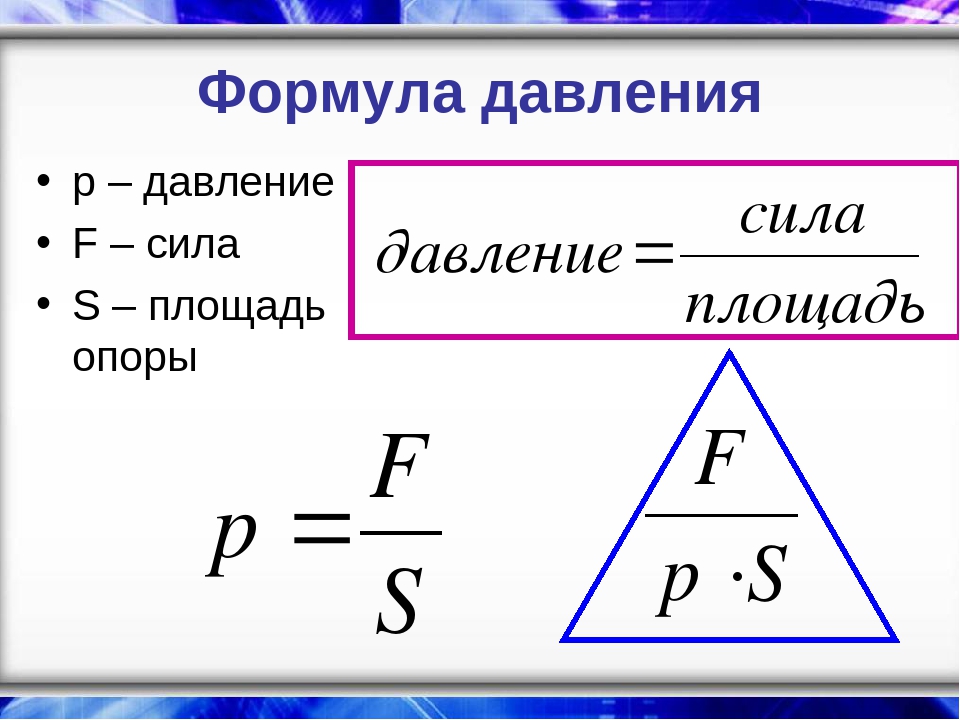 При этом согласно закону Паскаля если система находится в состоянии равновесия, то давление на нее будет одинаковым для всех точек системы.

В физике, как впрочем и химии, давление обозначают большой буквой Р, идущей от латинского слова «pressura» – давление. (В английском языке давление так и осталось почти без изменения – pressure).

Общая формула

Из классического определения того, что такое давление можно вывести общую формулу для его расчета. Выглядеть она будет таким образом:

P = F/S

Где F – это сила давления, а S – площадь поверхности на которую она действует. То есть иными словами формула нахождения давления – это сила, воздействующая на определенную поверхность, разделенная на площадь этой самой поверхности.

Как видно из формулы, при расчете давления всегда действует следующий принцип: чем меньше пространство, на которое влияет сила, тем большее количество давящей силы на него приходится и наоборот.

Это можно проиллюстрировать простым жизненным примером: хлеб легче всего порезать острым ножом, потому что у острого ножа заточенное лезвие, то есть площадь поверхности S из формулы у него минимальна, а значит, давление ножа на хлеб будет максимально равно приложенной силе F того кто держит нож. А вот тупым ножом порезать хлеб уже сложнее, так как у его лезвия большая площадь поверхности S, и давление ножа на хлеб будет меньшим, и значит, чтобы отрезать себе кусок хлеба нужно приложить большее количество силы F.

Общая формула давления, по сути, отлично описывает формулу давления твердого тела.

Единицы измерения

Согласно стандартам Международной метрической системы давление измеряется в паскалях. Один паскаль из классической формулы равен одному Ньютону (Как мы знаем, Ньютон у нас единица измерения силы) разделенному на один квадратный метр.

Но увы на практике паскаль оказывается очень маленькой единицей и использовать его для измерения давления не всегда удобно, поэтому часто для измерения давления применяют другие единицы:

• Бары – один бар равен 105 паскалей
• Миллиметры водяного столпа
• Метры водяного столпа
• Технические и физические атмосферы

Формула гидростатического давления

Как мы знаем, разные агрегатные состояния вещества, имеют разные физические свойства. Жидкости своими свойствами отличаются от твердых тел, а газы в свою очередь отличаются от них всех. Поэтому вполне логично, что способы определения давления для жидкостей, твердых тел и газов также будут разными. Так, например, формула давления воды (или гидростатического давления) будет иметь следующий вид:

P = p*g*h

Где маленькая p – плотность вещества, g – ускорение свободного падения, h – высота.

В частности эта формула объясняет, почему при погружении водолазов (или батискафа или подводной лодки) на глубину все больше возрастает давление окружающей воды. Также из этой формулы понятно, почему на предмет, погруженный в какой-нибудь кисель, будет воздействовать большее давление, чем на предмет, погруженный просто в воду, так как плотность киселя (p) выше, чем у воды, а чем выше плотность жидкости, тем выше ее гидростатическое давление.

Приведенная нами формула гидростатического давления справедлива не только для жидкостей, но и для газов. Поэтому поднимаясь высоко в горы (где воздух более разрежен, а значит меньшее давление), как и спускаясь в подводные глубины, человек, водолаз или альпинист должен пройти специальную адаптацию, привыкнуть к тому, что на него будет воздействовать другое давление.

Резкая смена давления может привести к кессоной болезни (в случае с водолазами) или к «горной» болезни (в случае с альпинистами). И «кесонка» и «горняшка», как их сленгово называют водолазы и альпинисты, вызвана резкой сменной давления окружающей среды. То есть, если не подготовленный человек начнет вдруг подниматься на Эверест, то он быстро словит «горняшку», а если этот же человек начнет опускаться на дно Мариинской впадины, то гарантировано получит «кесонку». В первом случае причиной будет не адаптация организма к пониженному давлению, а во втором – к повышенному.

Американские водолазы в декомпрессионой камере, призванной подготовить их к глубоководным погружениям и адаптировать организм к высокому давлению океанских глубин.

Парциальное давление и его формула

Хотя формула гидростатического давления применима для газов, но давления для них удобнее вычислять по другой формуле, формуле парциального давления.

Дело в том, что в природе редко встречаются абсолютно чистые вещества, причем это касается как жидкостей, так и газов. Обычно на практике в окружающем мире преобладают различные смеси, и логично, что каждый из компонентов такой смеси может оказывать разное давление, такое разное давление и называют парциальным. Определить парциальное давление просто – оно равно суме давлений каждого компонента рассматриваемой смеси. Отсюда формула парциального давления будет иметь следующий вид:

P = P₁+P₂+P₃

Где P₁, P₂ и P₃ – давления каждого из компонентов газовой смеси, так званный «идеальный газ».

К примеру, чтобы определить давления воздуха обычной формулы гидростатического давления проделанной только с кислородом недостаточно, так как воздух в реальности представляет собой смесь разных газов, где помимо основного компонента кислорода, которым мы все дышим, есть и другие: азот, аргон и т. д.

Такие расчеты нужно проделывать при помощи формулы парциального давления.

Формула давления идеального газа

Также стоит заметить, что давление идеального газа, то есть каждого отдельного из компонентов газовой смеси удобно посчитать по формуле молекулярно-кинетической теории.

P = n*k*T

Где n – концентрация молекул газа, T – абсолютная температура газа, k – постоянная Больцмана (указывает на взаимосвязь между кинетической энергией частицы газа и ее абсолютной температурой), она равна 1,38*10^-23 Дж/К.

Приборы для измерения давления

Разумеется, человечество изобрело многие приборы, позволяющие быстро и удобно измерять уровень давления. Для измерения давления окружающей среды, оно же атмосферное давление используют такой прибор как манометр или барометр.

Так выглядит классический барометр для измерения атмосферного давления.

Чтобы узнать артериальное давление у человека, часто служащее причиной недомоганий используется прибор известный большинству под названием неинвазивный тонометр. Таких приборов существует множество разновидностей.

Также биологи в своих исследованиях занимаются расчетами осмотического давления – это давление внутри и снаружи клетки. А метеорологи, в частности по перепадам давления в окружающей среде предсказывают нам погоду.

Рекомендованная литература и полезные ссылки

• Кузнецов В. Н. Давление. Большая Российская Энциклопедия. Дата обращения 27 августа 2016.
• E.R. Cohen et al, «Quantities, Units and Symbols in Physical Chemistry», IUPAC Green Book, 3rd Edition, 2nd Printing, IUPAC & RSC Publishing, Cambridge (2008). — p. 14.

Видео

Автор: Павел Чайка, главный редактор журнала Познавайка

При написании статьи старался сделать ее максимально интересной, полезной и качественной. Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту [email protected] или в Фейсбук, с уважением автор.

в физике, в чем измеряется, какой буквой обозначается, формула

Подготовили для вас краткую статью о том, что такое давление, чтобы помочь разобраться и структурировать свои знания по этой теме. 2} ).\)

Внесистемными единицами измерения данной величины являются мм рт.ст. (миллиметр ртутного столба), мм.в.ст. (миллиметр водяного столба), атмосфера, бар.

Общая формула 

Значение давления находится по формуле:

\(p=\frac{F}{S} ,\)

где \(F\) — сила, которая действует на поверхность, \(S\) — площадь этой поверхности.

Основываясь на формуле, можно сделать вывод о том, что чем больше площадь опоры, тем меньше давление, которое воздействует одной и той же силой на эту опору. Это отлично демонстрируется, когда человек на лыжах меньше проваливается в снег, чем тот, который передвигается без них.

Давление, которое производится на жидкость или газ, передается на любую точку равнонаправленно, то есть одинаково в каждом из направлений. Данное утверждение получило название закона Паскаля.

Формула гидростатического давления

Гидростатическое давление — это воздействие столба жидкости в состоянии равновесия на дно, а также стенки сосуда.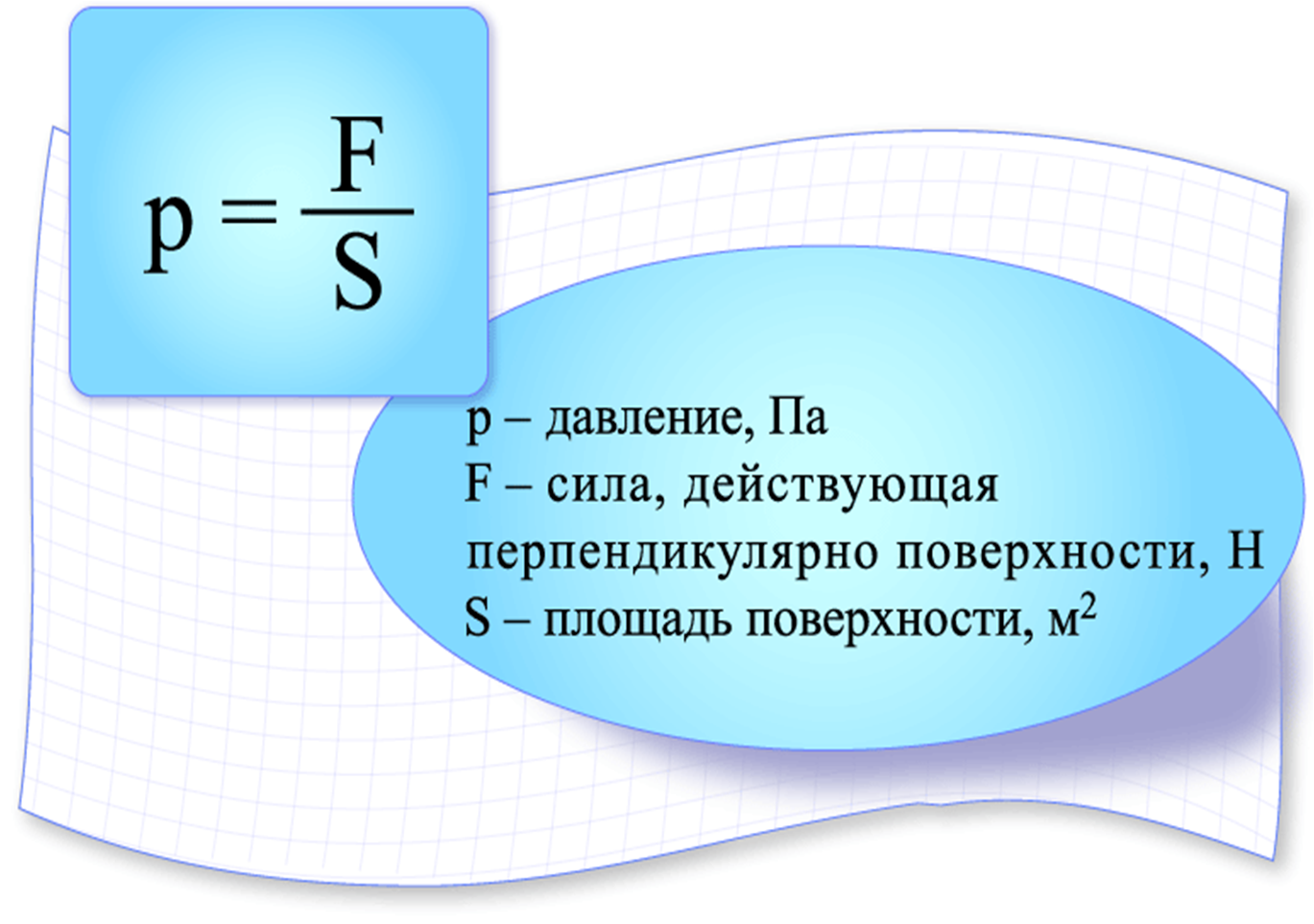

Важно понимать:

• давление внутри жидкости на определенном уровне одинаково во всех направлениях. При увеличении глубины давление увеличивается;
• давление столба жидкости не зависит от формы сосуда.

Давление жидкости на дно сосуда обуславливается плотностью жидкости, а также ее высотой столба. Измерить можно по формуле:

\(p = gρh\)

При данном расчете плотность \(ρ\) следует считать в килограммах на кубический метр, а высоту столба жидкости \(h\) — в метрах, \(g = 9,8 \frac{Н}{кг}\), тогда итог будет выражен в паскалях.

Парциальное давление и его формула

Парциальное давление — то, которое имел бы газ, который входит в состав газовой смеси, если бы он один занимал весь объем, который занимает объем смеси при той же температуре.

Давление отдельного газа из смеси находится по формуле:

\(p1 = x1p,\)

где \(p1\) — парциональное давление конкретного газа в газовой смеси, \(x1\) — мольная доля этого газа, а \(p\) — общее давление газовой смеси.

Также его можно найти следующим образом:

\(p1=\frac{h2RT}{V}\)

Здесь \(V\) — объем смеси, \(T\) — температура смеси.

Общее давление газовой смеси равно сумме парциальных давлений каждого газа в смеси.

\(p = p1 + p2 + p3 … + p4\)

Формула давления идеального газа

Давление газа на стенки сосуда, а также на помещенное в него тело, возникает благодаря ударам молекул.

Для установления связи между объемом, давлением и температурой существует уравнение Клапейрона-Менделеева. Оно имеет вид:

\(pV=nRT\)

Здесь \(V\) — объем, \(R\) — газовая постоянная, равная \(8,31431 \frac{Дж}{моль\cdotК}\) , \(T\) — температура, \(n\) — количество молей газа.

Выводы на основе данного уравнения:

• при уменьшении объема газа его давление увеличивается, а при увеличении объема — уменьшается при условии того, что масса и температура газа остаются неизменными;
• давление газа в закрытом сосуде увеличивается при увеличении температуры газа.

Основное уравнение молекулярно-кинетической теории имеет вид:

\(p=\frac{2}{3}nEk\)

Сложно? Обращайтесь за помощью к нашим авторам. Для ФениксХелп нет ничего невозможного.

Давление в физике — виды, формулы и определения с примерами

Содержание:

Давление:

Вы уже знаете, что тело, находящееся на горизонтальной опоре, действует на опору силой давления. Она приложена к опоре и направлена перпендикулярно к ней. Опора деформируется. А от чего зависит степень ее деформации?

Проделаем такой опыт. Поместим столик вверх ножками в ящик с песком, на столик поставим гирю (рис. 166, а). Столик с гирей лишь незначительно погрузится в песок. А теперь перевернем столик ножками вниз и поставим ту же гирю (рис. 166, б). Ножки погрузятся в песок. Результат действия одной и той же силы давления (веса столика с гирей) оказался разным. Почему? Потому, что сила давления действовала на разную площадь поверхности опоры. В первом случае ее действие распределилось на площадь поверхности песка под крышкой, во втором — на площадь поверхности песка под ножками столика. Ясно, что площадь под ножками значительно меньше площади под крышкой столика. А если убрать гирю, т. е. уменьшить силу давления, не меняя площади поверхности, на которую она действует (рис. 166, в)? Ножки погрузятся в песок, но не так сильно.

Результат действия силы давления на поверхность можно определить с помощью физической величины — давления. Обозначим давление буквой р. Из опыта следует, что давление тем больше, чем больше сила давления и чем меньше площадь поверхности, на которую она действует.

Что такое давление

Давление — это физическая величина, равная отношению силы давления, действующей перпендикулярно поверхности, к площади поверхности.

Математически это можно выразить так:

В СИ единицей давления является  Ее называют паскалем (Па) в честь французского ученого Блеза Паскаля, изучавшего давление в жидкостях и газах.

1 паскаль — это давление на поверхность площадью производимое силой 1 Н, действующей перпендикулярно.

Применяют кратные единицы давления: гектопаскаль (гПа), килопаскаль (кПа) и мегапаскаль (МПа). Обратите внимание:

Позлее вы познакомитесь и с другими единицами давления.

Силой давления может быть не только вес тела, но и любая сила, перпендикулярная поверхности, на которую она действует.

Простой пример: вы загоняете канцелярскую кнопку в вертикальную доску (рис. 167). Силой давления на кнопку является сила действия руки, направленная горизонтально (перпендикулярно доске). Пружины дивана оказывают давление на сидящего на нем человека. Сила давления (сила упругости пружин) при этом направлена вертикально вверх.

Для практических целей иногда необходимо уменьшить давление, а в ряде случаев, наоборот, — увеличить. Как изменить давление?

Обратимся к формуле  Совершенно ясно: чтобы уменьшить давление, нужно уменьшить силу давления или увеличить площадь поверхности.

Например, чтобы увеличить проходимость тяжелых машин (трактора, танка), их снабжают гусеницами (рис. 168). Площадь поверхности, на которую действует сила давления, увеличивается, а давление — уменьшается. Широкие шины у автомобилей, лыжи у человека (рис. 169), довольно большие по площади стопы у слона (рис. 170) играют ту же роль, что и гусеницы у трактора. Приведите сами подобные примеры.

А как увеличить давление? Из формулы давления следует: надо увеличить силу давления или уменьшить площадь поверхности, на которую действует сила. Затачивая лезвия ножей, ножниц (рис. 171), кос, острия игл, зубцы пил и др., мы стараемся уменьшить площадь поверхности. Тем самым, действуя малой силой, можно создать большое давление.

Животному миру природа сама обеспечила возможность создавать большое давление небольшим усилием, вооружив его представителей иглами, клювами и когтями (рис. 172), зубами, клыками, жалами и т. д.

Главные выводы:

1. Давление — это физическая величина, равная отношению силы давления к площади поверхности.
2. Чем больше действующая на поверхность сила давления, чем меньше площадь поверхности, на которую действует сила давления, тем больше давление.
3. В СИ единицей давления является 1 Па.

Для любознательных:

Человек при ходьбе создает давление до 300—400 кПа (определите давление, которое создаете вы, стоя на полу; сравните полу ценные результаты с приведенным значением и объясните причину расхождения этих значений). Гусеничный трактор создает давление на почву в 40—60 кПа, а колеса вагона поезда па рельсы — около 50 МПа.

Пример решения задачи:

Семиклассник массой m = 50 кг стоит на полу. Определите давление, которое он производит на пол, если площадь соприкосновения подошвы его ботинка с полом Коэффициент 

Дано:

m = 50 кг

Решение:

Давление, которое производит семиклассник на пол:

Сила давления F равна весу P семиклассника. Вес  Тогда:

Ответ: p = 50 кПа.

Давление газа

Газы, как и твердые тела, тоже производят давление. Но твердые тела передают давление в том направлении, в котором действует сила давления. Кнопка (см. рис. 167) передает давление перпендикулярно доске, лопата (рис. 174) — в направлении силы давления ноги и т. д.

А вот газы передают давление во все стороны. Чем обусловлена такая особенность газов? От чего зависит давление газа?

Вам уже известно, что газы, как жидкости и твердые тела, состоят из частиц (атомов, молекул). Но расстояния между частицами у газов больше, чем у жидкостей и твердых тел. Поэтому силы взаимодействия между частицами у газов практически отсутствуют (кроме процессов столкновения). Двигаясь хаотически, они сталкиваются между собой и со стенками сосуда. Так как число частиц газа в сосуде чрезвычайно велико (например, в их примерно ), то стенка воспринимает удары частиц как действие вполне ощутимой силы давления.

В газах среднее число ударов хаотически движущихся частиц и средняя сила ударов на единицу площади поверхности стенки по всем направлениям одинаковы.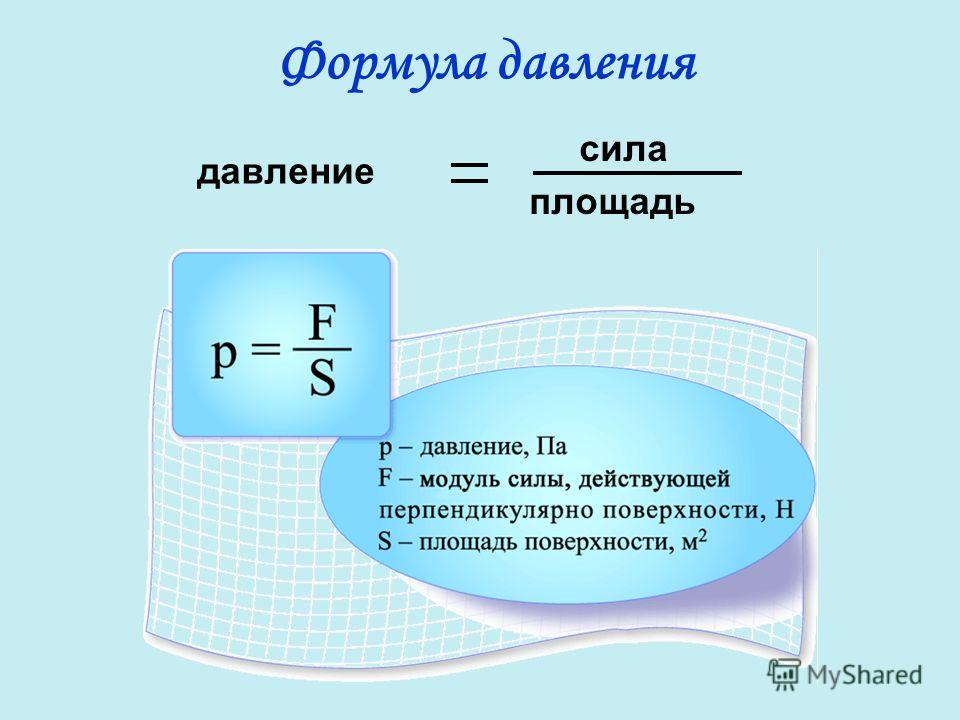 Значит, и среднее давление по всем направлениям одинаково.

Подтвердим это опытом. Под стеклянный колокол поместим завязанную оболочку резинового шара, внутри которой находится газ (рис. 175). Будем откачивать воздух из-под колокола. Объем шара по мере откачки воздуха увеличивается. Это связано с тем, что давление газа под колоколом становится меньше, чем внутри шара.

Форма оболочки в виде шара — доказательство того, что давление газа по всем направлениям одинаково.

Каким образом можно изменить давление газа? Поскольку давление обусловлено числом ударов частиц и силой удара каждой частицы о стенку, то есть два пути его изменения. Первый из них — изменить число частиц в единице объема.

Подтвердим сказанное опытом. В пробковом пистолете между пробкой и поршнем находится воздух (рис. 176, а), который оказывает давление по всем направлениям. Если будем поршнем сжимать газ, не меняя его температуры, то пробка вылетит из пистолета (рис. 176, б). Почему?

Уменьшая объем газа, мы увеличиваем число частиц в единице объема. Это приводит к увеличению числа ударов о стенки. Давление газа возрастает. А с увеличением давления растет сила давления газа на пробку, и она вылетает из пистолета. Если увеличивать объем газа при постоянной температуре, то давление будет уменьшаться.

Итак, при уменьшении объема (сжатии) газа при постоянной температуре его давление увеличивается, а при увеличении объема (расширении) газа давление уменьшается.

Второй путь изменить (например, увеличить) давление газа — это изменить силу удара частиц о стенки. Для этого газ нужно нагреть. Тогда скорость хаотического движения частиц увеличится, и, следовательно, увеличится и сила ударов их о стенки.

Зависимость давления от температуры можно подтвердить опытом. Если объем газа в пробковом пистолете (рис. 177, а) сохранять постоянным, но повышать температуру газа, подогревая его на спиртовке (рис. 177, б), то пробка вылетит вследствие увеличения давления. Значит, чем выше температура газа, тем больше его давление; чем ниже температура, тем меньше давление.

Главные выводы:

1. Давление газа есть результат ударов частиц о стенки сосуда, в котором он находится.
2. Давление газа можно увеличить, если уменьшать его объем при постоянной температуре или, сохраняя объем газа, увеличивать его температуру.
3. Давление газа можно уменьшить, если увеличивать (расширять) его объем при постоянной температуре или охлаждать газ, сохраняя его объем.

Для любознательных:

Возрастание давления газа при его нагревании вызвано не только увеличением силы отдельных ударов. В холодном и горячем газе будет неодинаковым и среднее число ударов частиц о стенки сосуда за единицу времени (т. е. частота ударов). Подумайте, как влияет этот фактор на давление газа.

На баллоне с лаком для волос написано: «Предохранять от воздействия прямых солнечных лучей и нагревания выше +50 °С!» Объясните необходимость таких мер предосторожности с точки зрения физики.

Передача давления газами и жидкостями. Закон Паскаля

Вы уже знаете, что частицы твердых тел (атомы, молекулы) жестко связаны между собой и могут совершать лишь хаотические колебательные движения около положений равновесия. У газов частицы движутся по всему объему хаотически поступательно. У жидкостей они совершают и хаотическое колебательное, и хаотическое поступательное движение. Значит, у газов и жидкостей подвижность частиц значительно выше, чем у твердых тел. Поэтому жидкости и газы не сохраняют своей формы, а принимают форму сосуда, в котором находятся (рис. 178).

Кроме того, некоторые законы для жидкостей и газов одинаковы. Рассмотрим один из них. Проведем опыт. Шар с отверстиями заполним дымом и присоединим к трубке с поршнем. Дым с имеющимся в шаре воздухом займет весь объем шара. Будем перемещать поршень вниз. Мы заметим, что из всех отверстий начнут вытекать струйки дыма (рис. 179). Как объяснить это явление?

Подвижность частиц дыма и молекул воздуха приводит к тому, что они распределяются равномерно по всему объему. Сталкиваясь со стенками шара, молекулы и частицы дыма действуют на стенки, создавая давление. Сжимая газ (воздух с дымом), мы уменьшаем объем и тем самым увеличиваем вначале давление непосредственно под поршнем. Благодаря подвижности молекул давление передается газом во все точки шара, и газ вытекает из отверстий во всех направлениях. Такой же эффект достигается в случае, когда в шаре будет только воздух (без дыма). Дым лишь делает видимыми вытекающие струйки.

Аналогичный опыт можно провести с жидкостью, например с водой. При нажатии на поршень струйки воды через отверстия шара будут вытекать но всем направлениям.

Проведем еще опыт. Через пробку в банку с водой вставим четыре трубки (рис. 180). Через трубку 1 будем накачивать в банку воздух, увеличивая там его давление. Увеличение внешнего давления (давления воздуха) на поверхность воды передается водой от слоя к слою по всем направлениям. В результате вода во всех трубках поднимается, причем на одну и ту же высоту.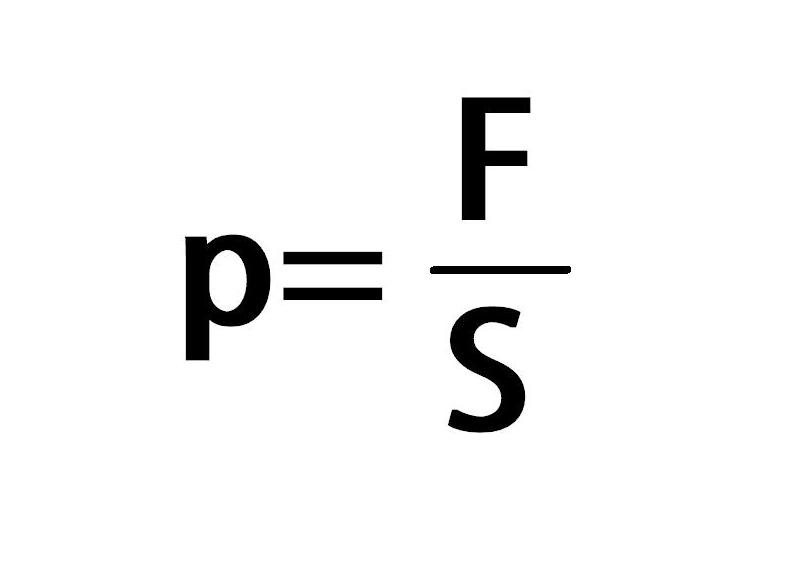 Значит, давление в воде сбоку (трубка 2), снизу (трубка 3), сверху (трубка 4) на одной глубине одинаково.

А вспомните, как с одинаковым напором вытекают струйки воды из всех дыр, появившихся в шланге для полива огорода (рис. 181). Давление, производимое внешней силой на жидкость (газ), находящуюся в сосуде, передается жидкостью (газом) во все точки жидкости (газа) без изменения. К такому выводу еще в XVII в. пришел французский ученый Блез Паскаль. Этот вывод называют законом Паскаля.

В твердых телах подвижность частиц ограничена, и эти тела не подчиняются закону Паскаля. Если вы поставите на стол тяжелый предмет, например гирю, то вес гири создаст давление лишь на площадь поверхности стола под гирей, т. е. только в направлении действия силы.

Главные выводы:

1. Частицы жидкости и газа обладают подвижностью.
2. Благодаря подвижности частиц жидкости и газы передают производимое на них давление во все точки без изменения.
3. Твердые тела передают давление только в направлении действия силы давления.

Давление жидкости, обусловленное ее весом

Благодаря подвижности частиц (атомов, молекул) жидкость принимает форму того сосуда, в который она налита. Если на жидкость действует внешняя сила давления, то жидкость передает созданное этой силой давление во все точки. Но жидкость создает давление и за счет своего веса, причем не только на дно сосуда, но и на стенки.

В том, что жидкость давит на стенки и дно сосуда, можно убедиться, используя эластичный полиэтиленовый пакет или трубку, нижний конец которой закрыт резиновой пленкой. Постепенно наливая подкрашенную воду в сосуд, мы обнаружим увеличивающийся прогиб пленки (рис. 182).

Причиной увеличения прогиба является рост давления воды на пленку. Притягиваясь к Земле, жидкость давит своим весом на пленку подобно тому, как давит на стол стопка книг. Давление неподвижной жидкости, обусловленное ее весом, называют гидростатическим (от лат. hydros — вода, station — неподвижный).

Гидростатическое давление можно рассчитать. Так, давление столба жидкости высотой h на дно сосуда с вертикальными стенками и площадью дна S (рис. 183) равно Силой давления F является вес жидкости. Для неподвижной жидкости ее вес численно равен силе тяжести: 

Запишем массу m жидкости через плотность  и объем V. Масса: Объем  тогда  Подставим в формулу давления, получим:

Итак, давление жидкости на дно сосуда зависит от ее плотности и высоты столба жидкости.

Выведенная формула справедлива для сосуда любой формы, даже если таким «сосудом» является пруд или океан. Чтобы подтвердить формулу, к сосуду с эластичным дном присоединим измерительную систему (рис. 184). При замене цилиндрического сосуда (а) на конические (б и в) (сосуды имеют одинаковую площадь дна и равные высоты столбов жидкости) прибор показывает равные силы давления. Значит, давления жидкости на дно всех сосудов равны, хотя масса жидкости в сосудах разная.

Формула позволяет найти давление не только на дно, но и на боковые стенки. Действительно, давление на стенку на данной глубине, как и на дно, зависит от высоты столба жидкости. Подтвердим это опытом. Нальем в пластиковую бутылку с проколотыми в стенке отверстиями подкрашенную воду (рис. 185). Наблюдения за вытекающими струями показывают, что гидростатическое давление действует и на стенку бутылки. Его величина возрастает по мере увеличения высоты столба воды в бутылке над отверстием, поэтому струя III падает дальше, чем струя I. Чтобы объяснить это явление, разделим мысленно жидкость на слои /, 2> 3, 4. На каждый нижний слой жидкости действует вес верхних ее слоев. Сила тяжести, действующая на слой /, прижимает его к слою 2. Слой 2 передает производимое на него давление слоя 1 по всем направлениям. На слой 3 действует вес слоев 2, 2. Следовательно, давление в слое 3 больше, чем в слое 2. Наибольшим оно будет на дно и стенку у дна сосуда.

Главные выводы:

1. Гидростатическое давление обусловлено весом покоящейся жидкости.
2. Гидростатическое давление на данной глубине зависит от плотности жидкости и высоты столба жидкости.
3. Гидростатическое давление на боковую стенку сосуда и на поверхность находящегося в жидкости тела на глубине h равно

Для любознательных:

Гидростатическое давление — главное препятствие для проникновения людей в глубины Мирового океана. Уже на глубине 2,5 м нетренированный ныряльщик испытывает боль в ушах из-за давления воды на барабанные перепонки. Корпуса подводных лодок, изготовленные из прочнейших сталей, на глубине в несколько сотен метров находятся на грани превышения допустимой прочности. Тогда почему рыбы на большой глубине чувствуют себя комфортно? Оказывается, вода давит на рыб не только извне, но и изнутри, т. е. происходит компенсация сил давления.

Пример №1

Определите глубину водоема, на которой давление воды р = 100 кПа. Какая сила давления воды действует на ракушку с площадью поверхности лежащую на дне? Коэффициент  примите равным

Дано:

Давление воды на глубине h равно:

 откуда  где  (плотность воды).

Сила давления:

Ответ: 

Сообщающиеся сосуды

Действие на жидкость силы тяжести и подвижность ее молекул приводят к тому, что в широких сосудах поверхность жидкости устанавливается горизонтально. Это легко проверить с помощью прямоугольного треугольника (рис. 187). Горизонтальной будет поверхность жидкости и в сосудах, соединенных между собой, независимо от их формы.

Возьмем несколько соединенных между собой открытых сосудов. Их называют сообщающимися. Будем наливать в один из них воду. Вода перетечет в остальные сосуды и установится во всех сосудах на одном уровне (рис. 188) (если сосуды не очень узкие). Почему это происходит?

Рассмотрим самые простые сообщающиеся сосуды (рис. 189). Выделим внутри тонкий слой жидкости  Как и вся жидкость, он неподвижен. Значит, слева и справа на него действуют силы с равными модулями, но противоположные по направлению. Это силы давления столбов жидкости Но чтобы модули этих сил были равны, необходимо, чтобы были одинаковыми давления, создаваемые левым и правым столбами жидкости, т. е.

После сокращения получим:

В открытых сообщающихся сосудах поверхности однородной жидкости устанавливаются на одинаковом уровне.

С сообщающимися сосудами вы встречаетесь постоянно: это чайники, лейки для полива (рис. 190, а), водомерные трубки в больших емкостях с водой или топливом (рис. 190, б). На принципе действия сообщающихся сосудов работает, к примеру, безнасосный фонтан (рис. 191).

Сложную систему сообщающихся сосудов используют в дачных поселках и деревнях в башенном водопроводе. Схема простейшего водопровода представлена на рисунке 192. Вода из артезианского источника насосом (1) подается в бак водонапорной башни (2). От бака идут трубы с ответвлениями, вводимыми в дома на все этажи. Концы ответвлений труб закрываются кранами. Давление воды в кране определяется высотой столба воды в башне над уровнем крана. Поэтому чем выше этаж, тем давление воды в кране меньше. Чтобы вода смогла достигать всех этажей, башни строят высокими.

А если вам потребуется строго горизонтально установить поверхность стола или стиральной машины? Как в этом случае вам смогут помочь сообщающиеся сосуды? Приведите еще примеры использования сообщающихся сосудов.

Все полученные в этом параграфе закономерности справедливы для широких сосудов, в которых поверхности жидкости плоские. В очень узких сосудах поверхности жидкости искривляются (рис. 193) и данные закономерности не выполняются.

Главные выводы:

1. В широких неподвижных сосудах поверхность жидкости всегда горизонтальна.
2. Уровень поверхностей однородной жидкости в открытых сообщающихся сосудах одинаков и не зависит от формы сосудов.

Для любознательных:

Что мы будем наблюдать, если в сообщающиеся сосуды налиты разные жидкости, например ртуть и вода (см. рис.)? В таком случае для равновесия тонкого слоя  нужно, чтобы давление, создаваемое левым (ртутным) столбом высотой было равно давлению правого столба воды и ртути высотой , т. е. откуда Используя свойства пропорции, запишем окончательно:

Посмотрите в таблицу плотностей жидкостей. Плотность ртути в 13,6 раза больше плотности воды. Значит,  будет в 13,6 раза меньше

В открытых сообщающихся сосудах высоты столбов несмешивающихся жидкостей над уровнем их раздела обратно пропорциональны плотностям жидкостей.

Пример №2

Поверхность воды в водонапорной башне находится на h = 40 м выше кухонного водопроводного крана. Определите давление воды в кране. Коэффициент  примите равным 

Дано:

Решение:

Давление в кране создается столбом воды высотой ;  где  — плотность воды; 

Ответ: 

Газы и их вес

То, что жидкость имеет вес, никого не удивляет. Каждый из вас ощущал вес, держа в руке ведро воды (рис. 197), бутылку растительного масла или напитка. Однако мы не чувствуем изменения веса футбольного мяча при его накачивании воздухом.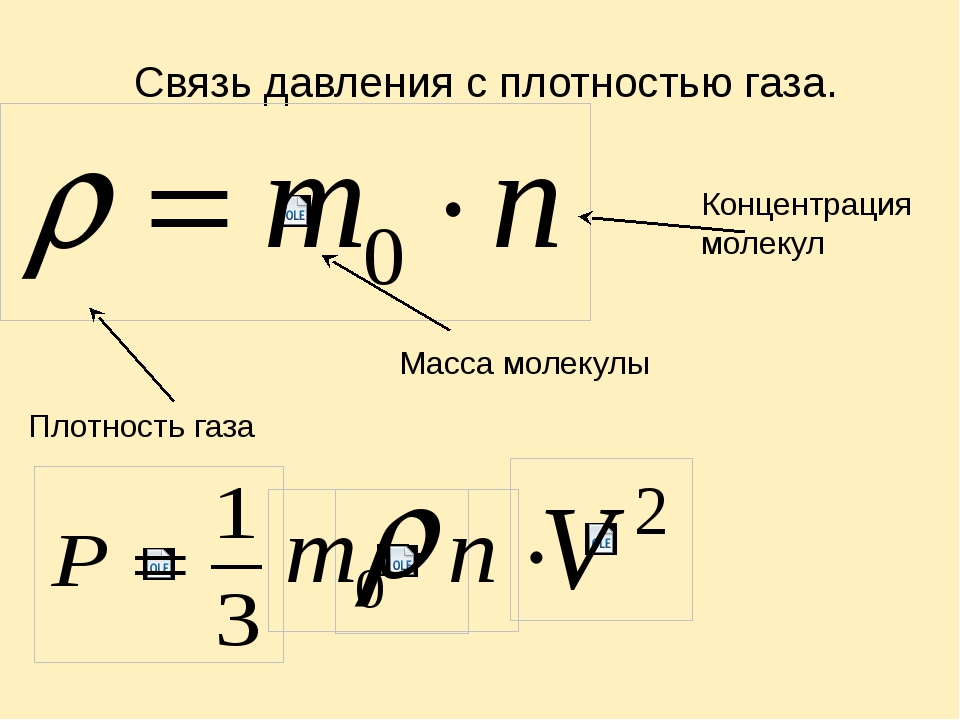 Почему?

Посмотрите в таблицу плотностей и сравните плотность воздуха и воды. Плотность воздуха почти в 800 раз меньше плотности воды.

Расчеты показывают, что, например, в сильно накачанном мяче вес воздуха находится в пределах 0,1 Н, а его масса около 10 г.

Покажем на опыте наличие у воздуха массы, а следовательно, веса. Уравновесим на весах стеклянный сосуд, заполненный воздухом. Откачаем насосом воздух и взвесим сосуд повторно. Он стал легче (рис. 198). Добавляя на чашку с сосудом разновес, можно узнать массу откачанного воздуха и его вес.

Воздушный слой, окружающий нашу Землю (земная атмосфера), тоже имеет вес. На каждую молекулу этого слоя действует Земля силой тяжести. Молекулы земной атмосферы, если бы на них не действовала сила тяжести, двигаясь хаотично, давно бы покинули нашу планету. Но тяготение Земли стремится расположить их у поверхности, что приводит к неоднородности атмосферы. Ее плотность заметно убывает с высотой. Так, на высоте км плотность воздуха уже в 2 раза меньше, чем у поверхности Земли.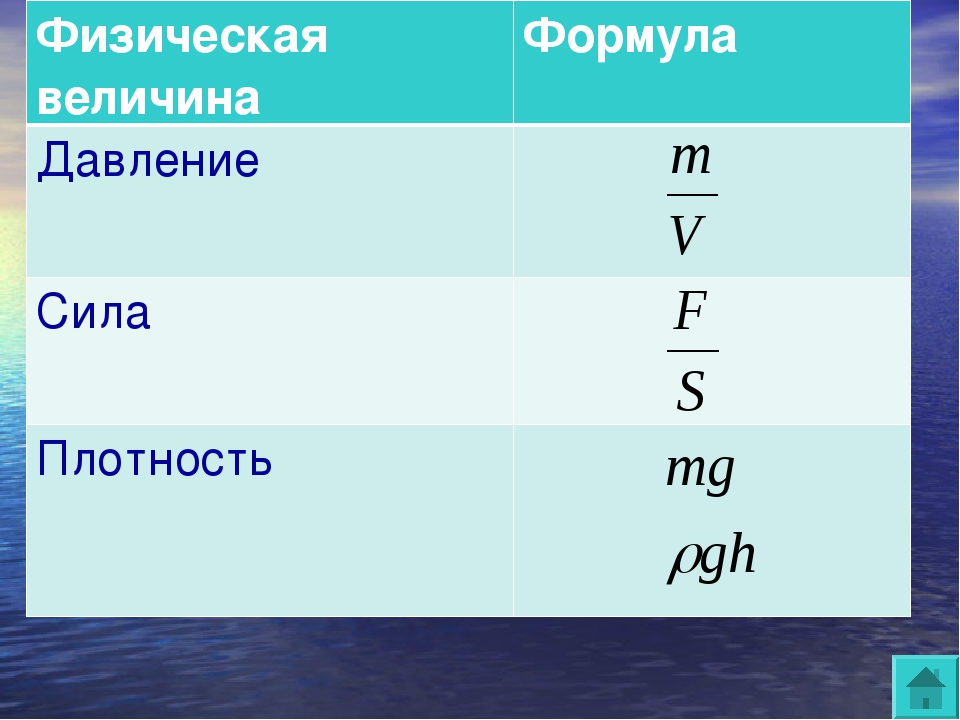 На высоте км плотность  а на высоте 400 км, где летают спутники, об атмосфере можно говорить лишь условно, так как ее плотность 

Главные выводы:

1. Газы обладают массой и весом.
2. Земная атмосфера обладает весом вследствие действия на нее притяжения Земли.
3. Действие силы тяжести и хаотичное движение молекул приводят к неодинаковой плотности земной атмосферы.

Для любознательных:

Обратите внимание, что приведенные в таблице 3 плотности газов указаны при нормальных условиях, т. е. при строго определенной температуре и давлении. При сжатии газов (и обычного воздуха) их плотности могут возрастать во много раз. Такие сильно сжатые газы, во-первых, очень удобны при транспортировке, например в баллонах с кислородом для сварки или в баллонах аквалангистов. Во-вторых, сжатые до высокого давления газы удобно использовать при работе отбойного молотка и пневматических (от греч. pneuma — дуновение, дыхание) тормозов, которые устанавливаются на мощных автомобилях, в том числе на автомобилях МАЗ и БелАЗ. Устройства для сжатия различных газов называют компрессорами.

Атмосферное давление

Вы знаете, что атмосфера Земли — газовая оболочка, в состав которой входят азот, кислород, углекислый газ, водяные пары и другие газы (рис. 199).

Всякий газ, если он находится в сосуде, производит давление на стенки сосуда, так как молекулы газа непрерывно бомбардируют эти стенки. А производит ли давление атмосфера Земли? Чем обусловлено это давление?

Атмосфера Земли удерживается силой тяжести, действующей со стороны Земли. В результате действия этой силы верхние слои атмосферы давят на нижние. Поэтому нижний слой оказывается наиболее сжатым. Давление одного слоя атмосферы на другой по закону Паскаля передается по всем направлениям и действует на любое тело: на здания, на растения, на людей. Это давление называют атмосферным. Атмосферное давление по мере удаления от поверхности Земли уменьшается. Уменьшается толщина слоя воздуха, создающего давление, и его плотность.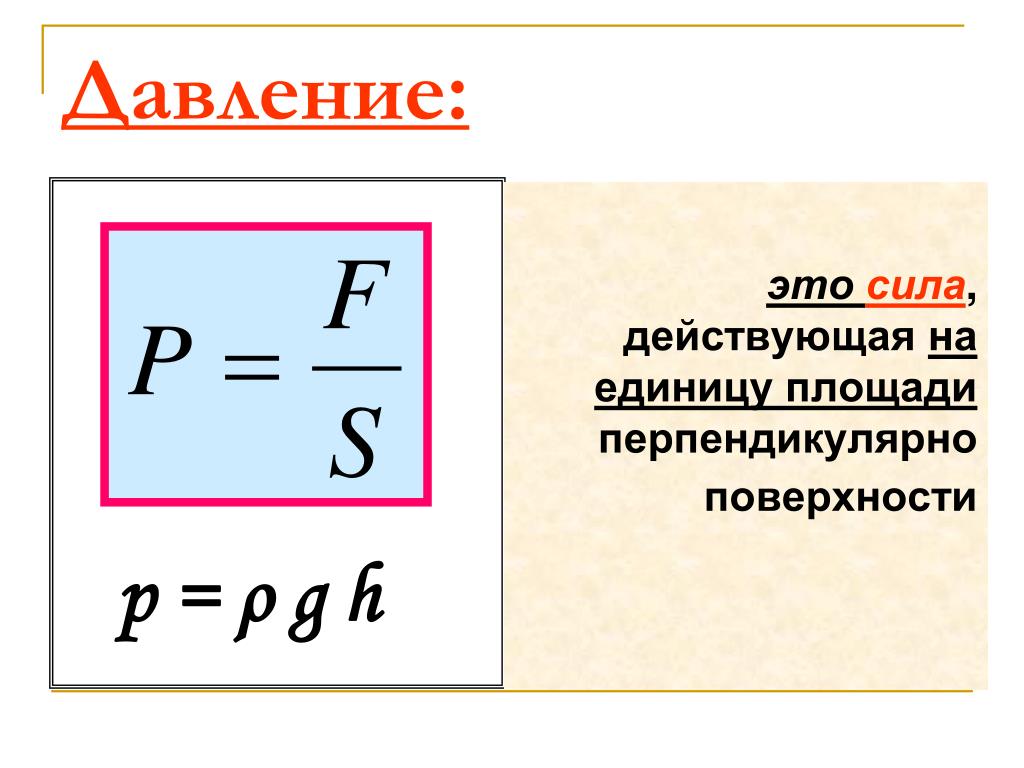

Атмосферное давление можно рассчитать. Результаты этих расчетов не могут не удивлять. Атмосферное давление равно примерно  Значит, на каждый квадратный сантиметр нашего тела действует сила 10 Н, а на всю площадь поверхности тела (примем ее за ) — сила 100 000 Н. Это равно весу десятитонного МАЗа! Как же мы живем под таким гигантским давлением?

Вспомним глубоководных рыб. Подобно им, мы просто не замечаем этой огромной сжимающей силы, так как она компенсируется равной расширяющей силой, создаваемой давлением воздуха внутри нас (он растворен даже в нашей крови).

Так что же, атмосферное давление вообще нельзя обнаружить? Для ответа на этот вопрос обратимся к опыту. Возьмем стакан с водой, накроем его листом бумаги, перевернем, придерживая рукой лист, а затем уберем руку (см. рис. 200). Мы видим, что вода из стакана не выливается, лист не отрывается. Сила атмосферного давления, приложенная к листу бумаги, компенсирует действие веса налитой воды и разреженного воздуха в стакане.

Опустите иглу шприца в подкрашенную воду и поднимайте поршень вверх. Вы увидите, что жидкость поднимается вслед за поршнем (рис. 201) противоположно направлению действия силы тяжести. Сила атмосферного давления заставляет сок подниматься вверх по трубочке (рис. 202). Опытов, в которых проявляется действие атмосферного давления, много.

Как измерить атмосферное давление? Рассмотрим наиболее важный из опытов, проведенный в 1643 г. по предложению итальянского физика и математика Эванджелисты Торричелли.

В этом опыте запаянная с одной стороны метровая стеклянная трубка (рис. 203, а) заполнялась ртутью. Верхний конец трубки закрывался, трубка переворачивалась и опускалась в широкий сосуд со ртутью, после чего отверстие открывалось. Часть ртути вытекала из трубки в сосуд. В трубке оставался столб ртути высотой Н около 76 см (760 мм) (рис. 203, б).

Что же удерживало от вытекания оставшуюся в трубке ртуть? Широкий сосуд и трубка — это, по сути, уже известные вам сообщающиеся сосуды. Над ртутью в трубке воздуха нет. На ртуть в широком сосуде действует атмосферное давление, которое жидкая ртуть передает по всем направлениям, в том числе вверх. Сила этого давления и поддерживает ртутный столб.

Рассмотрим условия равновесия тонкого слоя ртути (на рисунке 203, б он обозначен желтым цветом). Это условие требует, чтобы сила атмосферного давления снизу и сила гидростатического давления столба ртути сверху были равны. А это значит, что Таким образом, измерив высоту столба ртути Н, мы можем рассчитать его давление по формуле и тем самым определить величину атмосферного давления.

Поскольку атмосферное давление определяется высотой столба ртути, то понятно, почему очень часто его измеряют не в международных единицах (паскалях), а в миллиметрах ртутного столба.

Выразим в паскалях внесистемную единицу давления 1 миллиметр ртутного столба (сокращенно 1 мм рт. ст.):

По договоренности атмосферное давление считают нормальным, если оно равно давлению столба ртути высотой h = 760 мм при температуре t = 20 °С. Такое давление называют одной нормальной, или физической, атмосферой (сокращенно 1 атм):

В большинстве случаев мы будем использовать округленное значение: 

Атмосферное давление играет важную роль во многих бытовых и технических устройствах. Оно не только позволяет пользоваться пипеткой или шприцом для набора лекарств, но и дает возможность простого, недорогого способа подъема воды. Знакомые многим резиновые присоски (рис. 204) используются как в быту, так и на заводах для переноса сложнейших узлов электроники, прикосновение к которым (даже в перчатках) совершенно недопустимо. 

Главные выводы:

1. Удерживаемая земным притяжением атмосфера Земли производит давление.
2. Человек не ощущает атмосферного давления, так как оно действует как снаружи, так и изнутри него.
3. За нормальное атмосферное давление принято давление столба ртути высотой 760 мм.

Для любознательных:

В середине XVII в. в немецком городе Магдебурге ученым Отто фон Герике был проведен опыт-спектакль. Из пространства между двумя одинаковыми медными полушариями был выкачан воздух. Для разрыва полушарий, т. е. для преодоления сил атмосферного давления, потребовалось 8 пар самых сильных лошадей. Разрыв сопровождался сильным хлопком, подобным звуку выстрела.

Измерение атмосферного давления. Барометры и манометры

Ежедневно мы получаем информацию о величине атмосферного давления и его изменении. Почему оно не является постоянным? Почему на разных территориях Земли давление разное? Как давление зависит от высоты?

Атмосферное давление зависит от состава воздуха. Так, например, при поступлении влажного воздуха, насыщенного водяными парами, давление уменьшается, поскольку масса молекул воды заметно меньше массы других молекул атмосферы — азота и кислорода. Наиболее сжатыми, а значит, более плотными являются прилегающие к поверхности Земли слои атмосферы. Следовательно, значение атмосферного давления зависит от высоты места над уровнем моря. На вершине самой высокой (h = 8848 м) горы Эверест (рис. 208) давление почти в 3 раза меньше, чем у ее подножия.

Вода, как и другие жидкости, практически несжимаема. Поэтому давление жидкости от высоты столба зависит прямо пропорционально Зависимость же атмосферного давления от высоты описывается гораздо более сложной формулой. Однако для расчетов, не требующих большой точности (при не очень больших высотах), можно считать, что при подъеме на каждые 12 м давление убывает на 1 мм рт. ст. Зависимость давления от высоты можно использовать для измерения высоты подъема (альпинистов, летательных аппаратов).

Так, если при подъеме давление уменьшилось на 20 мм рт. ст., то это значит, что высота подъема:

Приборы, измеряющие высоту по такому принципу, называют альтиметрами (от лат. altius — выше и metron — мера) (рис. 209).

Атмосферное давление измеряют барометра ми (от греч. baros — тяжесть и metron — мера). Простейшим барометром является сосуд со ртутью и трубка, используемые в опыте Торричелли (см. рис. 203). Однако ртутные барометры не находят широкого применения, хотя имеют высокую точность. Пары ртути вредны для человека. На практике в основном пользуются металлическим барометром — анероидом. Хотя он менее точен, чем ртутный, но совершенно безопасен.

Внешний вид и внутреннее устройство барометра-анероида представлены на рисунке 210, а, б. Главной частью анероида является металлическая коробочка с волнистой (гофрированной) верхней и нижней поверхностями. Воздух из коробочки частично откачан.

При увеличении атмосферного давления увеличивается сила давления на коробочку. Коробочка сжимается и растягивает пружину, прикрепленную к ней. Пружина связана со стрелкой, которая перемещается по шкале в сторону больших значений давления.

Если давление снижается, сила давления на коробочку уменьшается, силы упругости распрямляют коробочку, и стрелка перемешается по шкале в противоположную сторону.

Шкалу анероида предварительно градуируют, т. е. наносят деления по показаниям ртутного барометра. Значения давления на шкале выражены в миллиметрах ртутного столба и в гектопаскалях (гПа).

Для измерения разности давления в сосуде и атмосферного давления служат манометры. Простейший манометр — жидкостный. Он представляет собой рассмотренную нами ранее U-образную трубку с жидкостью (см. рис. 189). Одно колено трубки (рис. 211) присоединяется к сосуду, давление в котором необходимо измерить. Другое колено открыто. Если уровень поверхности жидкости в колене, соединенном с сосудом, ниже, чем в открытом, значит, давление газа  в сосуде больше атмосферного  на величину давления столба жидкости высотой h, т. е.

А если давление газа в несколько раз больше атмосферного? Для измерения высоких давлений применяют металлический манометр (рис. 212). Его основным элементом является полая тонкостенная металлическая трубка (/), согнутая в дугу. Один конец трубки (3) закрыт, другой (2) присоединяется к сосуду с газом. Закрытый конец (3) через зубчатый механизм соединен со стрелкой, движущейся относительно шкалы. Чем больше давление в трубке (а значит, в сосуде), тем больше распрямляется трубка и тем больше отклоняется стрелка. Нуль на шкале соответствует атмосферному давлению. Значит, если стрелка стоит на цифре «8», давление в сосуде в 9 раз больше атмосферного. Именно так устроен манометр для контроля давления в автомобильных шинах (рис. 213).

Главные выводы:

1. Атмосферное давление зависит от высоты местности и метеоусловий.
2. Зависимость атмосферного давления от высоты и метеоусловий можно использовать для измерения высоты и для прогноза погоды.
3. Атмосферное давление измеряют барометрами, а давление газов в сосудах — манометрами.

Для любознательных:

Жидкостными манометрами можно измерять давление, отличающееся от атмосферного лишь незначительно. Так, если в примере на с. 127—128 давление в сосуде будет в 2 раза больше атмосферного, т. е. то, согласно формуле имеем:

откуда

При использовании в манометре воды

Только представьте размеры такого прибора! При использовании ртути размеры уменьшаются в 13,6 раза, но возникают новые проблемы — пары ртути ядовиты.

Пример №3

У подножия горы барометр показывает давление мм рт. ст., а на ее вершине — мм рт. ст. Определите высоту данной горы.

Дано: 

Решение:

Разность давлений у подножия горы и на ее вершине:

Учтем, что на 1 мм рт. ст. давление уменьшается при подъеме примерно на высоту Тогда высота горы:

Ответ: H = 120 м.

Давление твердых тел — формулы, определение, формулировка

Давление твердого тела

Идущий по рыхлому снегу человек будет в него постоянно проваливаться. Но, надев лыжи, он может передвигаться по снегу спокойно. Казалось бы, сила и масса человека не меняется — он воздействует на снег с одинаковой силой и на лыжах, и без них.

Дело в том, что «проваливание» в снег характеризуется не только силой — оно также зависит от площади, на которую эта сила воздействует. Площадь поверхности лыжи в 20 раз больше площади поверхности подошвы, поэтому человек, стоя на лыжах, действует на каждый квадратный сантиметр с силой в 20 раз меньшей, чем без них.

Или, например, если втыкать кнопки в пробковую доску, и действовать на них с одинаковой силой — легче войдет та кнопка, у которой более заостренный конец, так как у него площадь меньше.

А теперь подтвердим этот вывод опытами, как настоящие физики.

Резюмируем

Результат действия силы зависит не только от ее модуля, направления и точки приложения, но и от площади поверхности, к которой эта сила приложена.

А теперь подтвердим этот вывод опытами, как настоящие физики

Возьмем небольшую доску и вобьем гвозди в ее углы. 2]

Как уменьшить или увеличить давление

Тяжелый гусеничный трактор производит давление на почву, равное 40 — 50 кПа. Мальчик массой 45 кг производит давление всего лишь в 3 раза меньше, чем такой трактор. Это связано как раз с тем, что площадь гусениц больше.

В зависимости от того, какое давление хотят получить, площадь опор уменьшают или увеличивают. Например, чтобы уменьшить давление здания на грунт, в процессе строительства увеличивают площадь нижней части фундамента.

Шины грузовых автомобилей делают значительно шире легковых автомобилей (обратите внимание на колеса какой-нибудь большой фуры). Самые широкие шины можно увидеть на автомобилях, предназначенных для передвижения в пустыне. Тот же самый «лайфхак» используется в шасси самолетов.

Обратная зависимость тоже используется, например, при создании лезвий колющих и режущих инструментов. Острое лезвие имеет малую площадь, поэтому даже при небольшом нажатии создается большое давление.

Задачка раз

Книга лежит на столе. Масса книги равна 0,6 кг. Площадь ее соприкосновения со столом равна 0,08 м2. Определите давление книги на стол.

Решение:

На стол будет давить сила, равная весу книги. Так как она покоится, ее вес будет равен силе тяжести. Следовательно:

p = mg/S = 0,6*10/0,08 = 75 Па

Ответ: давление книги на стол будет равно 75 Па

Задачка два

Гусеничный трактор ДТ-75М массой 6610 кг имеет опорную площадь обеих гусениц 1,4 м2. Определите давление этого трактора на почву.

Решение:

Возьмем небольшую доску и вобьем гвозди в ее углы. Также возьмем емкость с песком и поставим конструкцию из доски и гвоздей в эту емкость. Сначала расположим конструкцию так, как показано на рисунке — «шляпками» вниз — и поставим на нее гирю. Конструкция не потонет в песке, а только чуть-чуть углубится.

p=m⋅g/S = 6610⋅10/1,4 = 47 214Па = 47,2 кПа.

Ответ: давление трактора на почву составляет 47,2 кПа

Задачка три

Человек массой 80 кг с сумкой весом 100 Н стоит неподвижно на полу. Сила давления подошв его ботинок на пол равномерно распределена по площади 600 см2. Какое давление человек оказывает на пол?

Решение:

Масса человека: m = 80 кг.

Вес сумки, которую держит человек: Pc = 100 Н.

Площадь соприкосновения подошвы ботинок с полом: S = 600 кв. см.

600 кв. см = 600/10000 кв. м = 0,06 кв. м

Давление — это отношение силы к площади, на которую она действует. В данном случае на площадь действует сила, равная сумме силы тяжести человека и веса сумки:

F = mg + Pc

Поэтому давление, оказываемое человеком с сумкой на пол, равно

p = (mg + Pc)/S = (80*10 + 100)/0,06 = 15 000 Па = 15 кПа

Ответ: давление человека, держащего сумку, на пол равно 15 кПа

Еще больше задачек — на онлайн-курсах по физике для 9 класса в школе Skysmart.

Гидростатика — Физика — Теория, тесты, формулы и задачи

Оглавление:

Основные теоретические сведения

Давление. Закон Паскаля. Гидростатическое давление

К оглавлению…

Основным отличием жидкостей от твердых (упругих) тел является способность легко изменять свою форму. Части жидкости могут свободно сдвигаться, перемещаясь друг относительно друга. Поэтому жидкость принимает форму сосуда, в который она налита. В жидкость, как и в газообразную среду, можно погружать твердые тела. В отличие от газов жидкости практически несжимаемы. На тело, погруженное в жидкость или газ, действуют силы, распределенные по поверхности тела. Для описания таких распределенных сил в гидростатике вводится новая физическая величина – давление.

Давление определяется как отношение модуля силы F, действующей перпендикулярно поверхности, к площади S этой поверхности:

Если же сила направлена под некоторым углом к перпендикуляру к площадке, то создаваемое этой силой давление находится по формуле:

В системе СИ давление измеряется в паскалях (Па): 1 Па = 1 Н/м2. Часто используются внесистемные единицы: нормальное атмосферное давление (атм) и давление одного миллиметра ртутного столба (мм.рт.ст.):

1 атм = 101325 Па = 760 мм.рт.ст.

Закон Паскаля: давление, оказываемое на жидкость (или, к слову, газ), передается в любую точку этой жидкости без изменений и во всех направлениях.

Давление жидкости на дно или боковые стенки сосуда зависит от высоты столба жидкости над той точкой в которой измеряется давление. Гидростатическое давление столба жидкости рассчитывается по формуле:

Обратите внимание, что оказываемое давление никоим образом не зависит от формы сосуда, а зависит только от рода жидкости (т.е. её плотности) и от высоты столба этой жидкости. Такое же давление на глубине h в соответствии с законом Паскаля жидкость оказывает и на боковые стенки сосуда.

Итак, если в задаче по гидростатике идет речь о давлении столба жидкости на боковую грань в некоторой конкретной точке, то такое давление находится по предыдущей формуле, где h – расстояние от этой точки до поверхности жидкости. Но иногда в задачах по гидростатике необходимо рассчитать среднее давление на всю боковую поверхность сосуда. В таком случае применим формулу:

В этом случае, h – это общая высота столба жидкости в сосуде.

Если жидкость находится в цилиндре под поршнем, то действуя на поршень некоторой внешней силой F, можно создавать в жидкости дополнительное давление p₀ = F/S, где: S – площадь поршня. Таким образом, полное давление в жидкости на глубине h можно записать в виде:

Если поршень убрать, то давление на поверхность жидкости будет равно атмосферному давлению. Если мы погружаемся в воду, то давление на некоторой глубине тоже будет состоять из двух давлений – давления атмосферы и давления столба воды (которое определяется глубиной погружения).

Сообщающиеся сосуды

К оглавлению…

Сообщающимися называют сосуды, имеющие между собой канал, заполненный жидкостью. Наблюдения показывают, что в сообщающихся сосудах любой формы однородная жидкость всегда устанавливается на одном уровне. задачи на сообщающиеся сосуды очень распространены в гидростатике.

Иначе ведут себя разнородные жидкости даже в одинаковых по форме и размерам сообщающихся сосудах. Дело в том, что в сообщающихся сосудах должно устанавливаться одинаковое давление на одной и той же высоте во всех частях сосуда. Но если жидкости различные, то и высота столбов этих жидкостей должна быть различной, чтобы создать одинаковое давление. Поэтому, разнородные жидкости в сообщающихся сосудах могут и не устанавливаться на одном уровне.

Алгоритм решения задач по гидростатике на сообщающиеся сосуды:

1. Сделать рисунок.
2. Выбрать горизонтальный уровень, ниже которого во всех сосудах находится одинаковая жидкость. Если такого уровня нет, то, естественно, за нулевой уровень выбираем дно сосудов.
3. Записать давления относительно этого уровня во всех сосудах и приравнять.
4. При необходимости использовать свойство несжимаемости жидкости (объем жидкости, вытекающей из одного сосуда, равен объему жидкости, втекающей в другой сосуд).
5. Решить математически полученную систему уравнений.

Гидравлический пресс

К оглавлению…

Если оба вертикально расположенных цилиндра сообщающихся сосудов закрыть поршнями, то с помощью внешних сил, приложенных к поршням, в жидкости можно создать большое давление p, во много раз превышающее гидростатическое давление ρgh в любой точке системы. Тогда можно считать, что во всей системе устанавливается одинаковое давление p (согласно закону Паскаля). Если поршни имеют разные площади S₁ и S₂, то на них со стороны жидкости действуют разные силы F₁ = pS₁ и F₂ = pS₂. Такие же по модулю, но противоположно направленные внешние силы должны быть приложены к поршням для удержания системы в равновесии. Таким образом, для гидравлического пресса имеем формулу:

Это соотношение вытекает из равенства давлений и выполняется только в идеальном гидравлическом прессе, т.е. таком в котором нет трения. Если S₂ >> S₁, то и F₂ >> F₁. Устройства в которых выполняются эти условия называют гидравлическими прессами (машинами, домкратами). Они позволяют получить значительный выигрыш в силе. Если поршень в узком цилиндре переместить вниз под действием внешней силы F₁ на расстояние h₁, то поршень в широком цилиндре переместится на расстояние h₂, которое может быть найдено из соотношения:

Данное соотношение вытекает из равенства объемов и выполняется в любом гидравлическом прессе. Это выражение получается потому, что при перемещении поршня перемещаются одинаковые объемы жидкости, то есть сколько жидкости ушло из одного цилиндра столько же пришло во второй, или V₁ = V₂. Таким образом, выигрыш в силе обязательно сопровождается таким же проигрышем в расстоянии. При этом произведение силы на расстояние остается неизменным:

Последняя формула вытекает из равенства работ и выполняется только для идеальных машин, в которых не действуют силы трения. Таким образом, в гидравлическом прессе всё происходит в полном соответствии с «золотым правилом механики»: во сколько раз мы выигрываем в силе, во столько же раз мы проигрываем в расстоянии. При этом ни одна машина не может дать выигрыша в работе.

Так как гидравлический пресс является механизмом, то его работу можно характеризовать КПД (коэффициентом полезного действия). КПД гидравлического пресса в задачах по гидростатике рассчитывается по следующей формуле:

где: А_пол = F₂h₂ – полезная работа (работа по подъему груза), А_затр = F₁h₁ – затраченная работа. В большинстве задач КПД гидравлического пресса принимают за 100%. КПД рассчитывается в том случае, если речь идет о неидеальном гидравлическом прессе.

Еще раз подчеркнем, что для неидеального гидравлического пресса выполняется только соотношение, вытекающее из равенства объемов вытесненной жидкости, а также для таких прессов рассчитывается КПД. Остальные соотношения из этого раздела выполняются только для идеального гидравлического пресса.

Закон Архимеда. Вес тела в жидкости

К оглавлению…

Из–за разности давлений в жидкости на разных уровнях возникает выталкивающая или Архимедова сила, которая вычисляется по формуле:

где: V – объем вытесненной телом жидкости, или же объем погружённой в жидкость части тела, ρ – плотность жидкости в которую погружено тело, и следовательно, ρV – масса вытесненной жидкости.

Архимедова сила, действующая на погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом.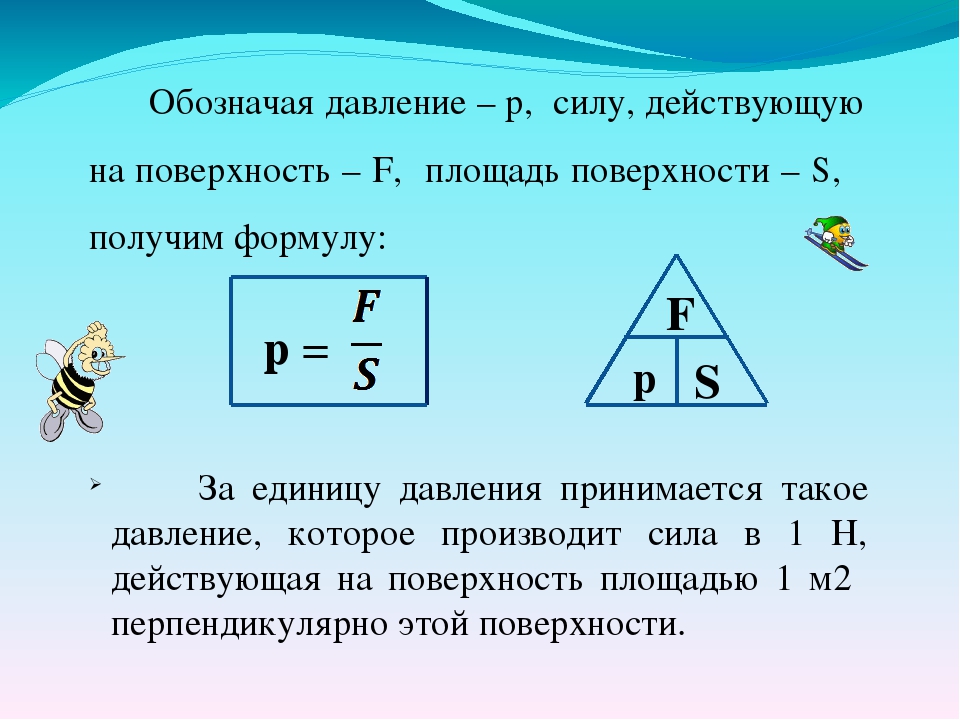 Это утверждение, называемое законом Архимеда, справедливо для тел любой формы.

При этом вес тела (т.е. сила с которой тело действует на опору или подвес) погруженного в жидкость уменьшается. Если принять, что вес покоящегося тела в воздухе равен mg, а именно так мы и будем поступать в большинстве задач (хотя вообще говоря на тело в воздухе также действует очень маленькая сила Архимеда со стороны атмосферы, ведь тело погружено в газ из атмосферы), то для веса тела в жидкости можно легко вывести следующую важную формулу:

Эта формула может быть использована при решении большого количества задач. Ее можно запомнить. При помощи закона Архимеда осуществляется не только мореплавание, но и воздухоплавание. Из закона Архимеда вытекает, что если средняя плотность тела ρ_т больше плотности жидкости (или газа) ρ (или по–другому mg > F_A), тело будет опускаться на дно. Если же ρ_т < ρ (или по–другому mg < F_A), тело будет плавать на поверхности жидкости.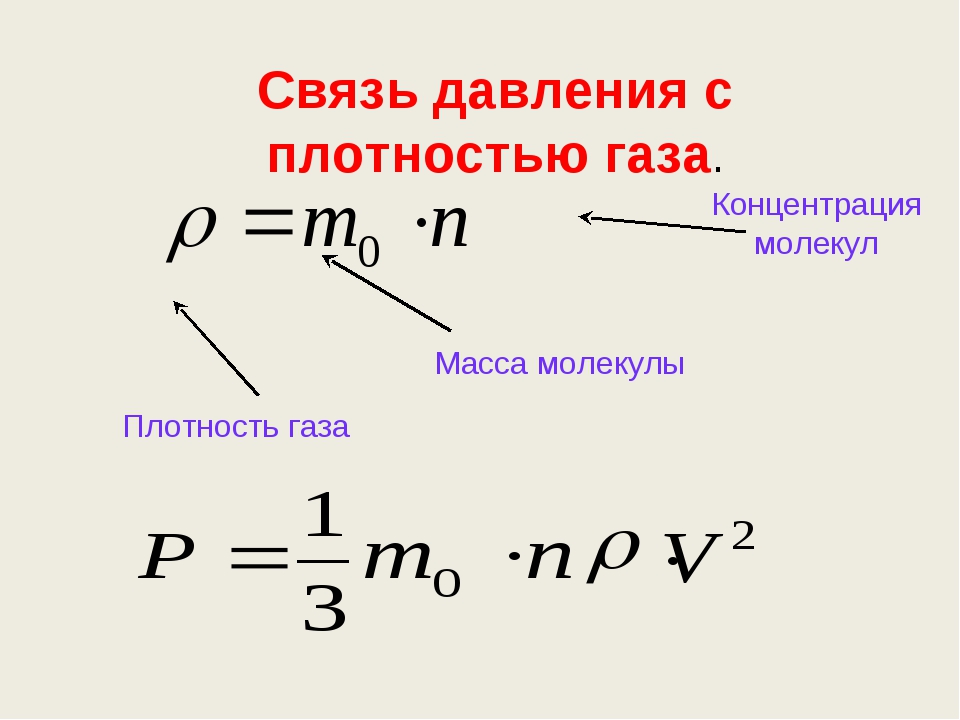 Объем погруженной части тела будет таков, что вес вытесненной жидкости равен весу тела. Для подъема воздушного шара в воздухе его вес должен быть меньше веса вытесненного воздуха. Поэтому воздушные шары заполняют легкими газами (водородом, гелием) или нагретым воздухом.

Плавание тел

К оглавлению…

Если тело находится на поверхности жидкости (плавает), то на него действует всего две силы (Архимеда вверх и тяжести вниз), которые уравновешивают друг друга. Если тело погружено только в одну жидкость, то записав второй закон Ньютона для такого случая и выполнив простые математические операции можем получить следующее выражение связывающее объемы и плотности:

где: V_погр – объем погруженной части тела, V – полный объем тела. При помощи этого соотношения легко решается большинство задач на плавание тел.

Типы давления: абсолютное давление, избыточное давление, дифференциальное давление

Наравне с температурой давление является одним из наиболее важных параметров, описывающих физическое состояние среды. Давление определяется как сила (F_N), постоянно действующая на заданную площадь поверхности (A). Типы давления отличаются друг от друга только по отношению к выбранному эталонному давлению.

Абсолютное давление

Наиболее приемлемым эталонным давлением является нулевое, которое существует в безвоздушном космическом пространстве. Любое давление относительно данного известно как абсолютное давление. Абсолютное давление обозначается как “ abs”, что является сокращением от латинского слова “absolutus”, означающего отдельный, независимый.

Атмосферное давление

Наверное наиболее важным типом давления для жизни на земле является атмосферное давление, p_amb (amb = ambiens = окружающий). Это давление образовано массой атмосферы, окружающей землю на высоте примерно до 500 км. До этой высоты, на которой абсолютное давление p_abs = 0, его величина постоянно уменьшается. Тем не менее, атмосферное давление подвержено погодным колебаниям, что хорошо нам известно из ежедневного прогноза погоды. На уровне моря p_amb в среднем составляет 1013,25 гектопаскаля (ГПа), что соответствует 1013,25 миллибара (мбар). Благодаря “циклонам” и “антициклонам” атмосферное давление может колебаться в пределах, примерно, 5 %.

Дифференциальное давление

Разница между двумя величинами давления p₁ и p₂ известна как перепад давления Δp = p₁ — p₂. В случаях, когда разница между двумя значениями представляет собой измеренное значение переменной процесса, говорят о дифференциальном давлении p_1,2.

Избыточное (манометрическое) давление

К наиболее часто встречающемуся типу измеряемого давления на технологических объектах относится перепад атмосферного давления, P_e (e = excedens = превышение). Оно представляет собой разницу между абсолютным давлением P_abs и относительным (абсолютным) атмосферным давлением (p_e = p_abs – p_amb), более известное как избыточное или манометрическое давление.

Понятие положительного избыточного давления используют, когда абсолютное давление превышает атмосферное. В противном случае говорят об отрицательном избыточном давлении.

Сокращения в формулах “abs”, “amb” и “e” однозначно указывают на тип измеряемого давления. Эти сокращения относятся в формулах к букве Р, но не к единицам измерения.

Неважно какое давление — абсолютное, избыточное или дифференциальное. С помощью WIKA вы подберете необходимый измерительный прибор для любого типа давления:

Свяжитесь с нами

Вам нужна дополнительная информация? Напишите нам:

14.3: Жидкости, плотность и давление (Часть 2)

Изменение давления с глубиной в жидкости постоянной плотности

Давление определено для всех состояний вещества, но особенно важно при обсуждении жидкостей. Важной характеристикой жидкостей является отсутствие значительного сопротивления компоненту силы, приложенной параллельно поверхности жидкости.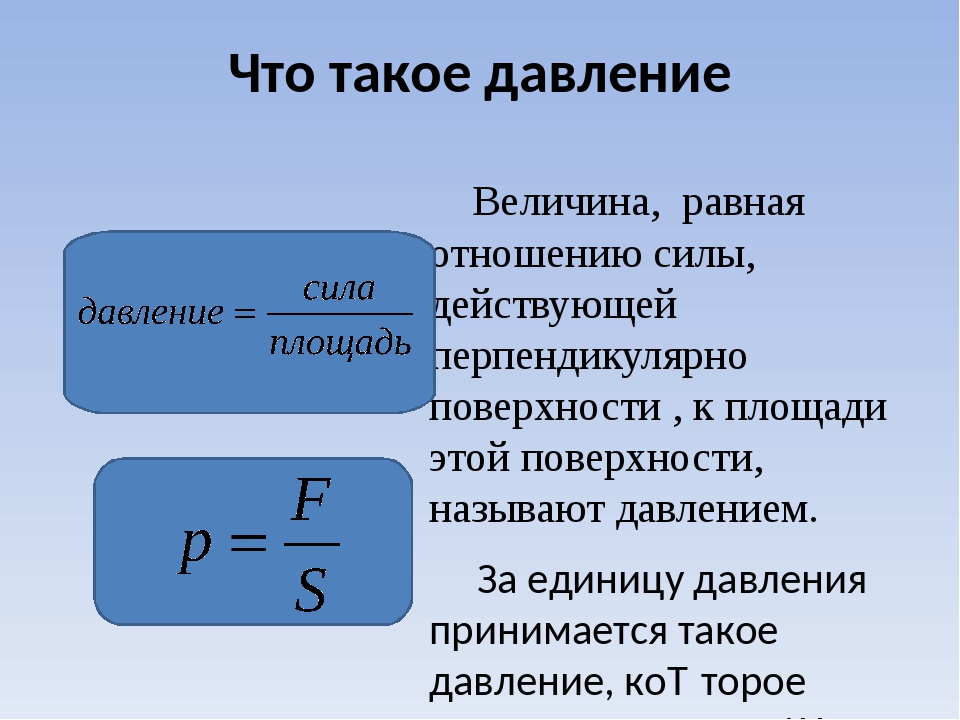 Молекулы жидкости просто текут, чтобы приспособиться к горизонтальной силе. Сила, приложенная перпендикулярно к поверхности, сжимает или расширяет жидкость.Если вы попытаетесь сжать жидкость, вы обнаружите, что сила реакции развивается в каждой точке внутри жидкости во внешнем направлении, уравновешивая силу, приложенную к молекулам на границе.

Рассмотрим жидкость постоянной плотности, как показано на рисунке \ (\ PageIndex {1} \). Давление в нижней части емкости возникает из-за давления атмосферы (p ₀ ) плюс давление из-за веса жидкости. Давление, создаваемое жидкостью, равно весу жидкости, деленному на площадь.Вес жидкости равен ее массе, умноженной на ускорение свободного падения.

Рисунок \ (\ PageIndex {1} \): Дно этого контейнера поддерживает весь вес находящейся в нем жидкости. Вертикальные стороны не могут оказывать на жидкость восходящую силу (так как она не может выдерживать силу сдвига), поэтому дно должно поддерживать все это.

Поскольку плотность постоянна, вес можно рассчитать, используя плотность:

\ [w = mg = \ rho Vg = \ rho Ahg \ ldotp \]

Следовательно, давление на дне контейнера равно атмосферному давлению, добавленному к весу жидкости, разделенному на площадь:

\ [p = p_ {0} + \ frac {\ rho Ahg} {A} = p_ {0} + \ rho hg \ ldotp \]

Это уравнение применимо только для давления на глубине для жидкости постоянной плотности

Давление на глубине для жидкости постоянной плотности

Давление на глубине в жидкости постоянной плотности равно давлению атмосферы плюс давление, обусловленное весом жидкости, или

\ [p = p_ {0} + \ rho hg, \ label {14. 4} \]

Где p — давление на определенной глубине, p ₀ — давление атмосферы, \ (\ rho \) — плотность жидкости, g — ускорение свободного падения, а h — глубина.

Рисунок \ (\ PageIndex {2} \): Плотина «Три ущелья», возведенная на реке Янцзы в центральном Китае в 2008 году, создала огромный водохранилище, в результате которого было перемещено более миллиона человек. (Источник: «Le Grand Portage» / Flickr)

Пример 14.1: Какую силу должна выдержать плотина?

Рассмотрим давление и силу, действующие на плотину, удерживающую резервуар с водой (Рисунок \ (\ PageIndex {2} \)).Предположим, что плотина имеет ширину 500 м, а глубина воды у плотины составляет 80,0 м, как показано ниже. а) Каково среднее давление воды на плотину? (b) Рассчитайте силу, действующую на плотину.

Среднее давление p из-за веса воды — это давление на средней глубине h, равной 40,0 м, поскольку давление увеличивается линейно с глубиной. Сила, оказываемая водой на плотину, равна среднему давлению, умноженному на площадь контакта, F = pA.

Решение

1. Среднее давление, обусловленное весом жидкости, составляет $$ p = h \ rho g \ ldotp \ label {14.{10} \; M \ ldotp \ end {split} $$

Значение

Хотя эта сила кажется большой, она мала по сравнению с весом воды в резервуаре 1,96 x 10 ¹³ Н. На самом деле это всего 0,0800% от веса.

Упражнение 14.1

Если водохранилище в примере \ (\ PageIndex {1} \) покрывает вдвое большую площадь, но сохраняется на той же глубине, потребуется ли перепроектировать плотину?

Давление в статической жидкости в однородном гравитационном поле

Статическая жидкость — это жидкость, которая не движется.В любой точке статической жидкости давление со всех сторон должно быть одинаковым, иначе жидкость в этой точке отреагирует на результирующую силу и ускорится.

Давление в любой точке статической жидкости зависит только от глубины в этой точке.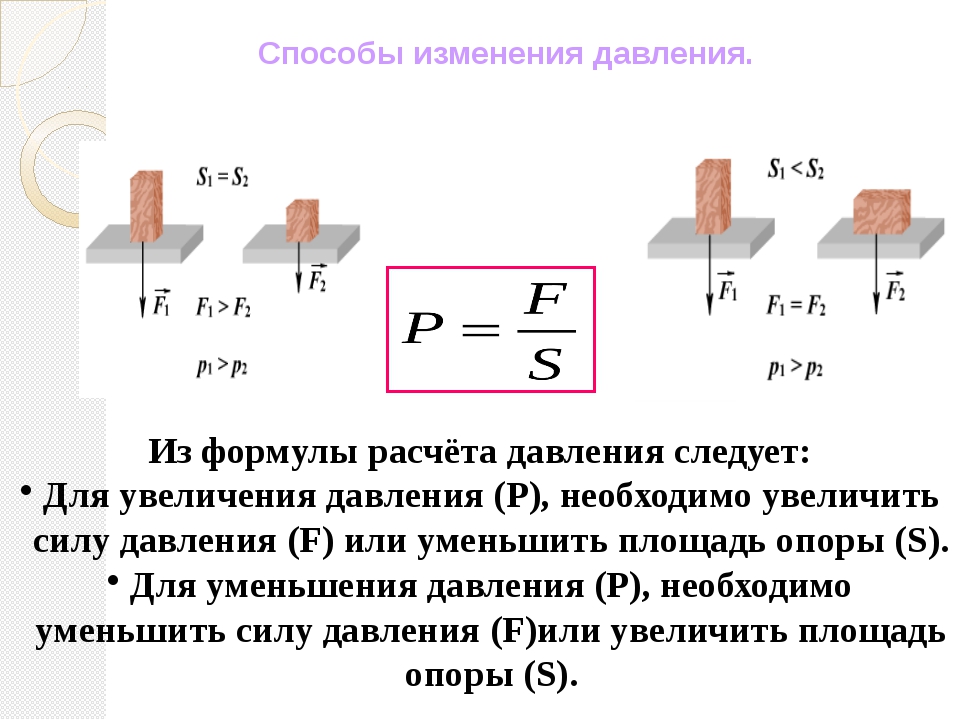 Как уже говорилось, давление в жидкости около Земли изменяется с глубиной из-за веса жидкости над определенным уровнем. В приведенных выше примерах мы предполагали, что плотность постоянна, а средняя плотность жидкости является хорошим представлением плотности.Это разумное приближение для жидкостей, таких как вода, где для сжатия жидкости или изменения объема требуются большие силы. Например, в плавательном бассейне плотность примерно постоянна, и вода внизу очень слабо сжимается под весом воды наверху. Однако путешествие вверх в атмосфере — это совсем другая ситуация. Плотность воздуха начинает значительно меняться буквально на небольшом расстоянии от поверхности Земли.

Чтобы вывести формулу для изменения давления с глубиной в резервуаре, содержащем жидкость с плотностью \ (\ rho \) на поверхности Земли, мы должны начать с предположения, что плотность жидкости непостоянна.Жидкость, расположенная на более глубоких уровнях, подвергается большей силе, чем жидкость, находящаяся ближе к поверхности, из-за веса жидкости над ней. Следовательно, давление, рассчитанное на заданной глубине, отличается от давления, рассчитанного с использованием постоянной плотности.

Представьте себе тонкий элемент жидкости на глубине h, как показано на рисунке \ (\ PageIndex {3} \). Пусть элемент имеет площадь поперечного сечения A и высоту \ (\ Delta \) y. Силы, действующие на элемент, возникают из-за давлений p (y) сверху и p (y + \ (\ Delta \) y) под ним.Вес самого элемента также показан на диаграмме свободного тела.

Рисунок \ (\ PageIndex {3} \): Силы, действующие на элемент массы внутри жидкости. Вес самого элемента показан на диаграмме свободного тела.

Поскольку элемент жидкости между y и y + \ (\ Delta \) y не ускоряется, силы уравновешены. Используя декартову ось y, ориентированную вверх, мы находим следующее уравнение для y-компоненты:

\ [p (y + \ Delta y) A — p (y) A — g \ Delta m = 0 (\ Delta y <0) \ ldotp \ label {14.6} \]

Обратите внимание, что если бы элемент имел ненулевую y-компоненту ускорения, правая часть не была бы равна нулю, а вместо этого была бы массой, умноженной на y-ускорение. Массу элемента можно записать через плотность жидкости и объем элементов:

\ [\ Delta m = | \ rho A \ Delta y | = — \ rho A \ Delta y \ quad (\ Delta y <0) \ ldotp \]

Подставляя это выражение для \ (\ Delta \) m в уравнение \ ref {14.6}, а затем разделив обе части на A \ (\ Delta \) y, находим

\ [\ frac {p (y + \ Delta y) — p (y)} {\ Delta y} = — \ rho g \ ldotp \ label {14.7} \]

Переходя к пределу бесконечно тонкого элемента \ (\ Delta \) y → 0, мы получаем следующее дифференциальное уравнение, которое дает изменение давления в жидкости:

\ [\ frac {dp} {dy} = — \ rho g \ ldotp \ label {14.8} \]

Это уравнение говорит нам, что скорость изменения давления в жидкости пропорциональна плотности жидкости. Решение этого уравнения зависит от того, постоянна ли плотность \ (\ rho \) или изменяется с глубиной; то есть функция \ (\ rho \) (y).

Если диапазон анализируемой глубины не слишком велик, мы можем считать плотность постоянной. Но если диапазон глубин достаточно велик для того, чтобы плотность могла заметно варьироваться, например, в случае атмосферы, плотность меняется с глубиной. В этом случае мы не можем использовать приближение постоянной плотности.

Давление в жидкости с постоянной плотностью

Давайте воспользуемся уравнением \ ref {14.9}, чтобы найти формулу для давления на глубине h от поверхности в резервуаре с жидкостью, такой как вода, где плотность жидкости можно считать постоянной.{-h} \ rho gdy \\ p — p_ {0} & = \ rho gh \\ p & = p_ {0} + \ rho gh \ ldotp \ end {split} \ label {14.9} \]

Следовательно, давление на глубине жидкости на поверхности Земли равно атмосферному давлению плюс \ (\ rho \) gh, если плотность жидкости постоянна по высоте, как мы обнаружили ранее.

Обратите внимание, что давление в жидкости зависит только от глубины от поверхности, а не от формы емкости. Таким образом, в контейнере, где жидкость может свободно перемещаться в различных частях, жидкость остается на одном уровне во всех частях, независимо от формы, как показано на рисунке \ (\ PageIndex {4} \).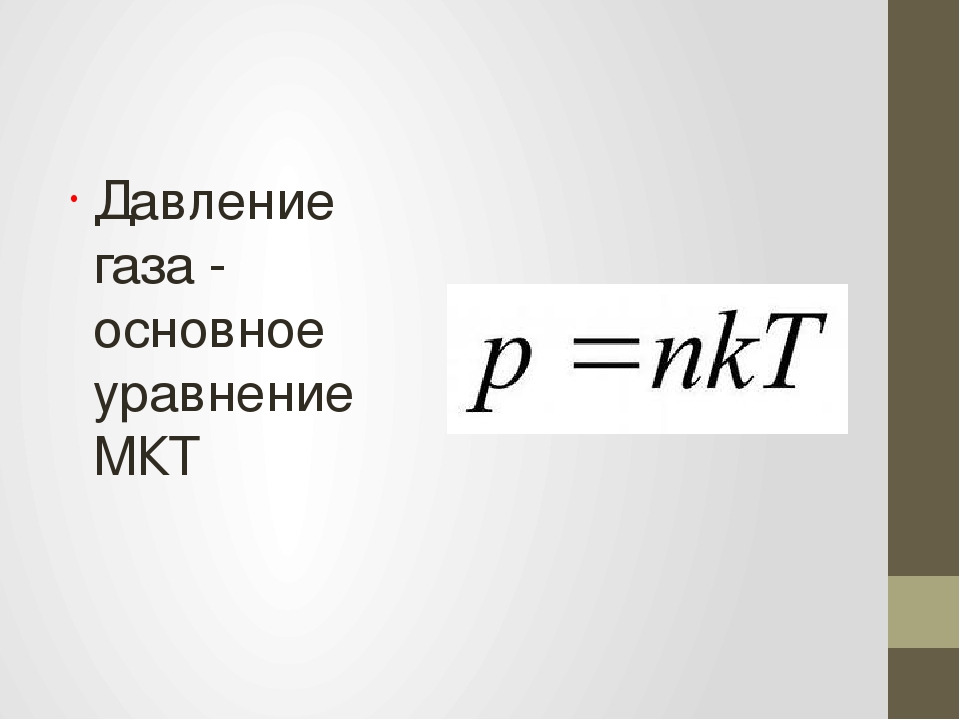

Рисунок \ (\ PageIndex {4} \): Если жидкость может свободно течь между частями контейнера, она поднимается на одинаковую высоту в каждой части. В изображенном контейнере давление внизу каждой колонки одинаковое; если бы это было не так, жидкость текла бы до тех пор, пока давления не сравнялись бы.

Изменение атмосферного давления с высотой

Особый интерес представляет изменение атмосферного давления с высотой. Предполагая, что температура воздуха постоянна и что закон термодинамики идеального газа описывает атмосферу в хорошем приближении, мы можем найти изменение атмосферного давления с высотой, когда температура постоянна.(Мы обсудим закон идеального газа в следующей главе, но мы предполагаем, что вы знакомы с ним из средней школы и химии.) Пусть p (y) будет атмосферным давлением на высоте y. Плотность \ (\ rho \) в точке y, температура T по шкале Кельвина (K) и масса m молекулы воздуха связаны с абсолютным давлением по закону идеального газа в виде

\ [p = \ rho \ frac {k_ {B} T} {m} \; (атмосфера), \ label {14.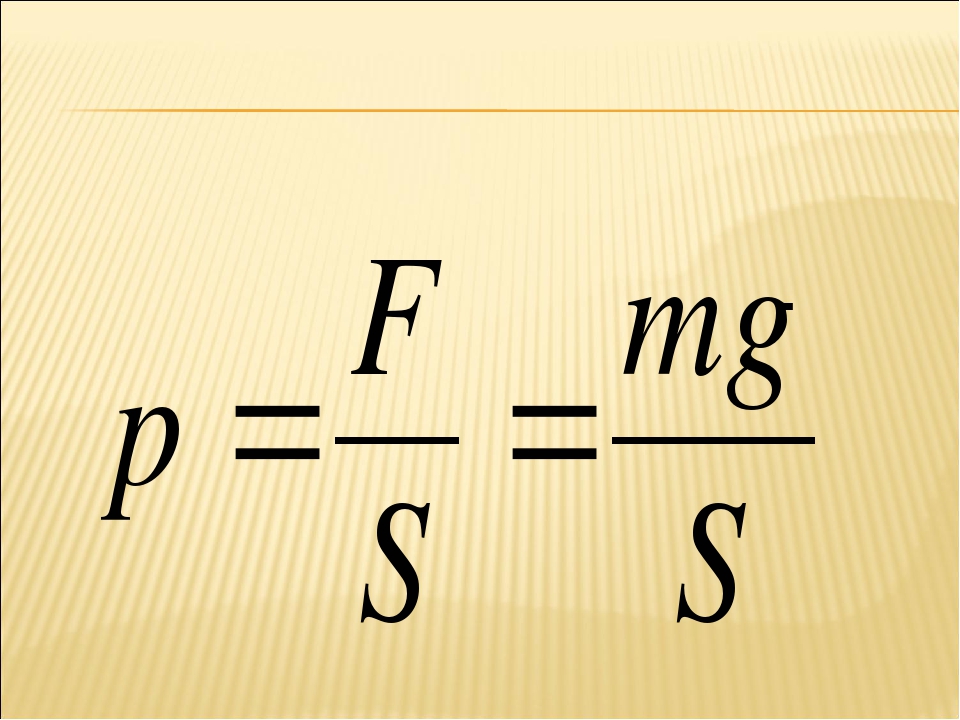 10} \]

, где k _B — постоянная Больцмана, которая имеет значение 1.38 x 10 ⁻²³ Дж / К.

Вы, возможно, встречали закон идеального газа в форме pV = nRT, где n — число молей, а R — газовая постоянная. Здесь тот же закон был записан в другой форме, с использованием плотности \ (\ rho \) вместо объема V. Следовательно, если давление p изменяется с высотой, то же самое происходит и с плотностью \ (\ rho \). Используя плотность из закона идеального газа, скорость изменения давления с высотой определяется как

.

\ [\ frac {dp} {dy} = -p \ left (\ dfrac {mg} {k_ {B} T} \ right), \]

, где в скобках указаны постоянные количества.{- \ alpha y} \ ldotp \]

Таким образом, атмосферное давление экспоненциально падает с высотой, поскольку ось y направлена ​​вверх от земли, а y имеет положительные значения в атмосфере над уровнем моря. Давление падает в \ (\ frac {1} {e} \) раз, когда высота равна \ (\ frac {1} {\ alpha} \), что дает нам физическую интерпретацию для \ (\ alpha \) : Константа \ (\ frac {1} {\ alpha} \) представляет собой шкалу длины, которая характеризует, как давление изменяется с высотой, и часто называется высотой шкалы давления. {-23} \; Дж / К) \ раз (300 \; К)} = \ гидроразрыва {1} {8800 \; m} \ ldotp \]

Следовательно, на каждые 8800 метров давление воздуха падает в 1 / е, или примерно на одну треть от своего значения. Это дает нам лишь приблизительную оценку реальной ситуации, поскольку мы предположили и постоянную температуру, и постоянный g на таких больших расстояниях от Земли, что в действительности не является правильным.

Направление давления в жидкости

Давление жидкости не имеет направления, будучи скалярной величиной, тогда как силы, возникающие из-за давления, имеют четко определенные направления: они всегда действуют перпендикулярно любой поверхности.Причина в том, что жидкости не могут противостоять усилиям сдвига или проявлять их. Таким образом, в статической жидкости, заключенной в резервуар, сила, действующая на стенки резервуара, действует перпендикулярно внутренней поверхности. Точно так же давление действует перпендикулярно к поверхностям любого объекта в жидкости. На рисунке \ (\ PageIndex {5} \) показано давление воздуха на стенки шины и давление воды на тело пловца.

Рисунок \ (\ PageIndex {5} \): (a) Давление внутри этой шины оказывает силы, перпендикулярные всем поверхностям, с которыми она контактирует.Стрелки показывают направления и величины сил, действующих в различных точках. (b) Давление оказывается перпендикулярно всем сторонам этого пловца, так как вода текла бы в пространство, которое он занимает, если бы его там не было. Стрелками показаны направления и величины сил, действующих на пловца в различных точках. Обратите внимание, что силы внизу больше из-за большей глубины, что дает чистую восходящую или выталкивающую силу. Чистая вертикальная сила, действующая на пловца, равна сумме выталкивающей силы и веса пловца.

Авторы и авторство

• Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4. 0).

Сила давления — обзор

7.2 Происхождение радиационных сил

Несмотря на то, что силы радиационного давления проистекают непосредственно из решений уравнения Максвелла для электрических полей (Максвелл, 1873), много лет спустя целенаправленная попытка их обработки и применения о силах материи сообщил Ашкин (1970).В частности, манипулирование частицами и их захват с помощью сил светового излучения впервые было предложено Ашкином (1970). С тех пор в этой области была проделана значительная работа по развитию концепции организации материи с помощью оптических инструментов (Ашкин 1978, 1992; Ашкин и др. ., 1986; Динеровиц и др. ., 2008; Йонас и др. Земанек, 2008).

Рассмотрим луч, распространяющийся в прозрачной среде. Как только луч встречает «препятствие», например, полимерную мицеллу или металлическую наночастицу в растворе, он рассеивается и меняет направление (рис.7.1). Такое изменение вызывает передачу импульса от пучка к препятствию. Рассматривая фотонное приближение для светового луча, очевидно, что каждый импульс фотона передается объекту. Согласно второму закону Ньютона получаем:

7.1. Схематическое изображение оптических сил, действующих в прозрачной среде за счет рефракции.

[7.1] F = ΔpΔt

то есть скорость изменения импульса, связанная с изменением потока импульса пучка. Однако понятно, что если частица не находится на оси распространения луча, то есть она сходится или расходится, поток импульса будет уменьшаться.

В зависимости от относительного размера частицы по сравнению с длиной волны взаимодействия это взаимодействие света и вещества можно рассматривать в двух режимах. Во-первых, в режиме Рэлея размер частиц намного меньше длины волны падающего света. В этом случае частица действует как простой точечный диполь, и радиационная сила может быть разделена на две составляющие: (а) сила рассеяния , связанная с изменением импульса электромагнитной волны из-за рассеяния на диполе, и (b) градиентная сила , связанная с силой Лоренца, действующей на диполь.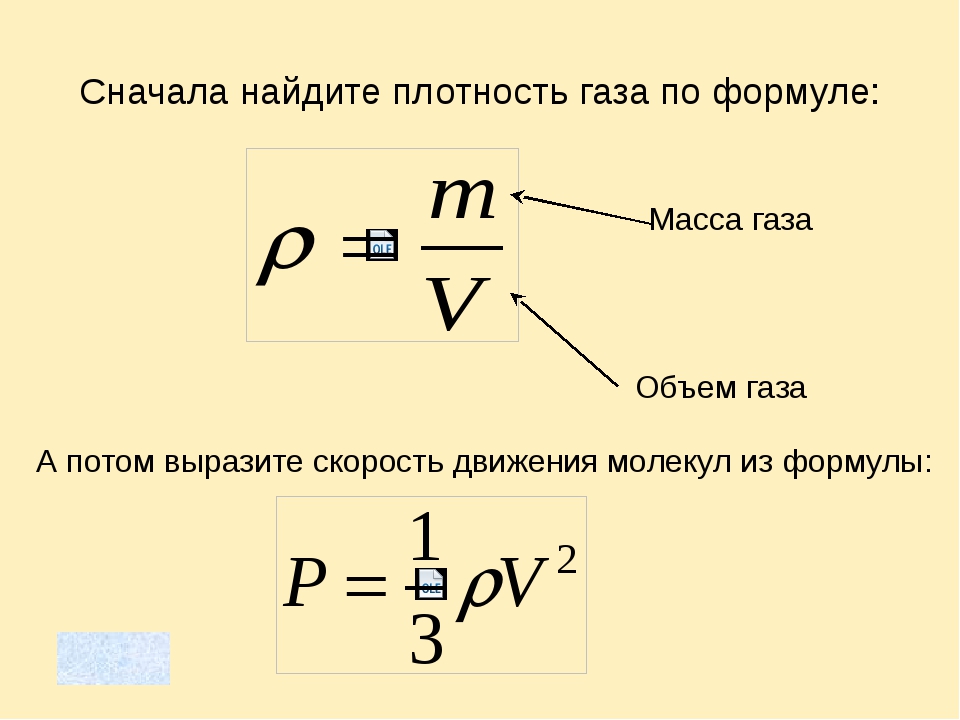 Второй — это режим Лоренца-Ми, в котором размер частицы намного превышает длину волны лазера (Cizmar et al ., 2010).

Рассмотрим частицу в растворе, находящемся в режиме Рэлея. В этом приближении легко разделяются компоненты рассеивающей и градиентной сил. Как электрическое поле колеблется гармонично, так и электрический диполь, излучающий вторичные волны во всех направлениях. Таким образом, потоки энергии и индуцированная сила рассеяния действуют на диполь вдоль оси распространения света.Результирующая сила рассеяния имеет вид (Harada and Asakura, 1996; Nieminen et al ., 2007):

[7.2] Fsc≈a | E | 2

, где α — поляризуемость частицы.

Чтобы оценить как силы рассеяния, так и градиентные силы, необходимо определить поляризуемость диэлектрической частицы. Поляризуемость можно определить как отношение дипольного момента к приложенному полю. В случае диэлектрических частиц, как и в нашем случае, локальная поляризуемость возникает в основном из-за связанных электронов.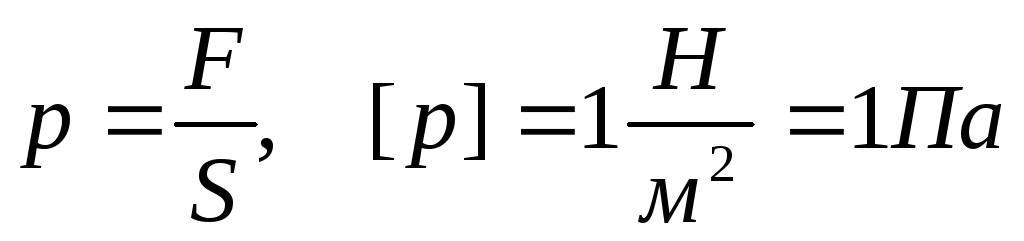 С помощью процедуры Клаузиуса-Моссотти можно показать (Harada and Asakura, 1996), что:

[7.3] a = 8πnsolk4rsph6c (m2−1m2 + 2)

, где n _sol — раствор / средний показатель преломления. , n _sph — показатель преломления микросферы, r _sph — радиус микросферы и m — относительный показатель преломления m = nsphnsol.

Градиентная сила возникает из-за силы Лоренца электромагнитного поля, действующей на диполь (Draine, 1988).Это заставляет частицу притягиваться частями поля высокой интенсивности, то есть в фокальной области, которая зависит от градиента интенсивности падающего луча и действует в направлении пространственного градиента поля. Градиентная сила, пропорциональная поляризуемости частицы и градиенту оптической интенсивности, может быть выражена (Harada and Asakura, 1996; Nieminen et al ., 2007) как:

[7.4] Fgrad ~ a ∙ ∇ | E | 2

При попытке исследовать влияние радиационного давления на частицу, окруженную средой, например раствором, необходимо учитывать тепловые силы. Облучающий луч вызывает температурный градиент в среде, окружающей частицу, из-за поглощения. Это, в свою очередь, вызывает тепловую силу и движение частицы, называемое фотофорезом. Подробности по этому поводу можно найти в другом месте (Greene et al ., 1985). Чтобы минимизировать или даже устранить такие эффекты, среда и частицы должны быть прозрачными для падающего света. Таков настоящий случай с использованием прозрачных полимерных растворов.

На практике, однако, частицы свободно перемещаются случайным образом внутри раствора из-за тепловых флуктуаций и броуновского движения.Тепловая энергия определяется по формуле k _B T . Градиентная сила — это градиент так называемого потенциала захвата, который определяется формулой (Nieminen et al ., 2007):

[7,5] U≈ − a ∙ | E | 2

Если потенциал захвата превышает тепловая кинетическая энергия, частицы регулируются исключительно градиентной силой. В этих условиях радиационная сила лазерного луча влияет на движение частиц, втягивая их в область более высокой интенсивности луча, в то время как силы рассеяния толкают их вдоль направления распространения луча.

В случае облучения относительно большой сферы, имеющей радиус порядка микрон, ее оптическое поведение становится более сложным и уже не может быть описано простой дипольной моделью, но требует обобщения, которое включает мультипольные эффекты. Это достигается в рамках теории рассеяния Лоренца – Ми (Metzger et al ., 2006), применяемой соответствующим образом для получения более точных и в целом достоверных результатов.

Давление жидкости — видео по физике от Brightstorm

Хорошо, давайте поговорим о давлении жидкости.Раньше мы говорили о давлении, которое представляет собой просто силу воздействия на площадь, но оказывается, что когда вы спускаетесь в жидкость, вниз в жидкость, давление становится все больше и больше. Ну почему это? Что ж, вы должны выдерживать вес всей жидкости, которая на вас сверху. Так вот откуда исходит давление жидкости. Итак, давайте просто посмотрим, допустим, что мы находимся на высоте h метров ниже поверхности воды, это может быть другая жидкость, но давайте пока просто представим, что это вода, и мы хотим посмотреть, какое давление оказывается из-за вес всей этой воды над нами. Ну давление равно силе над площадью, ну что я поддерживаю? Я поддерживаю вес воды. Вес воды всегда равен массе воды надо мной, умноженной на ускорение свободного падения. Затем мы делим по площади, и теперь мы собираемся сделать что-то немного хитрое, о чем вы даже не думали.

Масса всей этой воды над нами — это просто плотность воды, умноженная на объем этого цилиндра. Но объем этого цилиндра равен площади поперечного сечения, умноженной на высоту, а это означает, что у нас есть плотность, умноженная на объем, умноженная на ускорение свободного падения, разделенное на площадь.Но мы сказали, что объем — это площадь поперечного сечения, умноженная на высоту, поэтому площадь поперечного сечения сокращается, и это дает нам следующее выражение для давления жидкости. Плотность жидкости в нашем случае вода, но она так же хорошо работает с другими жидкостями, умноженными на ускорение из-за силы тяжести, умноженное на то, насколько глубоко вы находитесь в жидкости. Хорошо, давайте разберемся с этим на примере задачи, просто чтобы посмотреть, как все идет, эти проблемы на самом деле не так уж и сложны.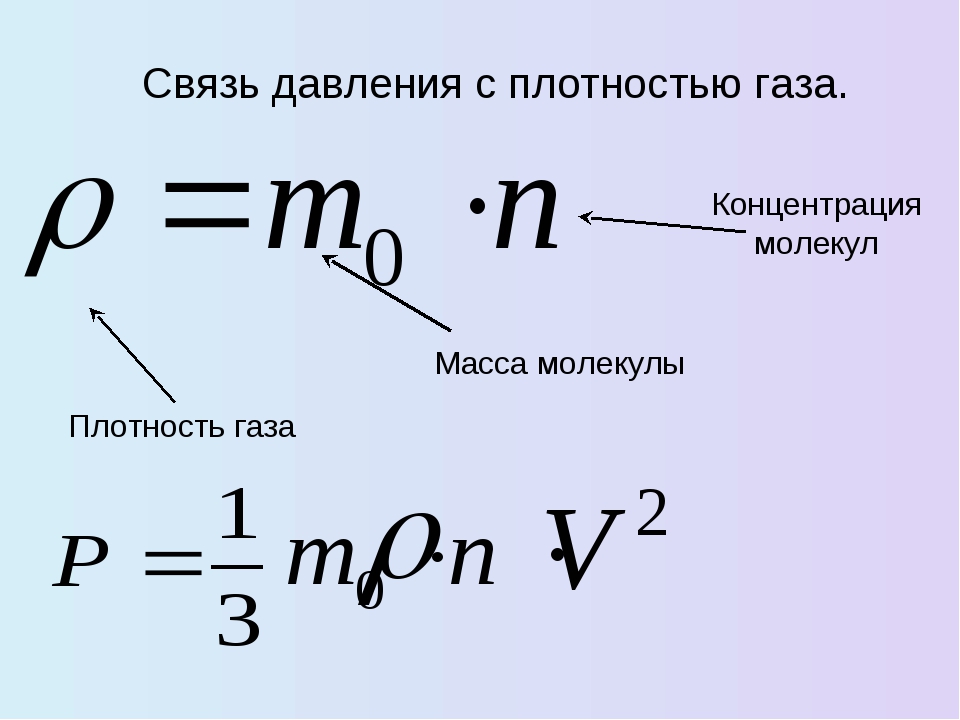 Итак, какое давление оказывает вода глубиной 4 км? И затем у меня есть второй вопрос по этому поводу: насколько плотнее вода на дне этого бассейна, я [думаю, на самом деле этого] океана, чем на его поверхности.

Хорошо, первый вопрос сделать несложно, у нас давление равно rho, g, h. Теперь плотность воды, если это не морская вода, морская вода немного больше, но давайте просто проигнорируем это, чтобы числа были хорошими. Плотность чистой воды — 1000 килограммов на кубический метр, ускорение свободного падения — 9,8 метра в секунду в квадрате. Но знаете что, давайте сделаем числа хорошими, мне все равно, давайте просто назовем это 10, это всего 2% от правильного, так что у нас будет 10 метров в секунду в квадрате, а затем какова высота, ну это 4 километра, это не нормально.Вы не можете сказать мне километры, вы должны сказать мне в единицах СИ, иначе цифры будут неправильными. Итак, мне нужно 4 умножить на 10 в 3, а затем мы просто умножим эти числа, и эти числа легко умножить вместе, потому что посмотрите на все десятки. Итак, у нас будет 4, а затем сколько десятков я получил 3, 4, 7.

Хорошо, а что это за единица? Посмотрите на все эти единицы, плавающие вокруг, я не хочу всего этого, но подождите минутку, мы были осторожны, чтобы всегда работать в единицах СИ. А это значит, что нам не нужно об этом думать.Это давление. Какая единица давления в системе СИ? Паскаля, все сделано правильно, хорошо, так что я надеюсь, что этот прошел довольно хорошо. Я имею в виду, что вы просто берете плотность, нагрузку от силы тяжести, высоту. Если у вас есть разница в высоте, если вы хотите узнать разницу в давлении между двумя разными глубинами в океане, вы просто используете разницу в высоте, а не всю высоту, достаточно просто. Что ж, если я хочу знать, насколько плотнее эта вода. Я имею в виду, посмотрите на это, это довольно большое давление, 40 миллионов Паскаля, верно?

Итак, с обоими модулями мы видели, что когда вы оказываете такое давление на воду, оно уменьшается, становится меньше.Он будет увеличивать свою плотность или уменьшать объем.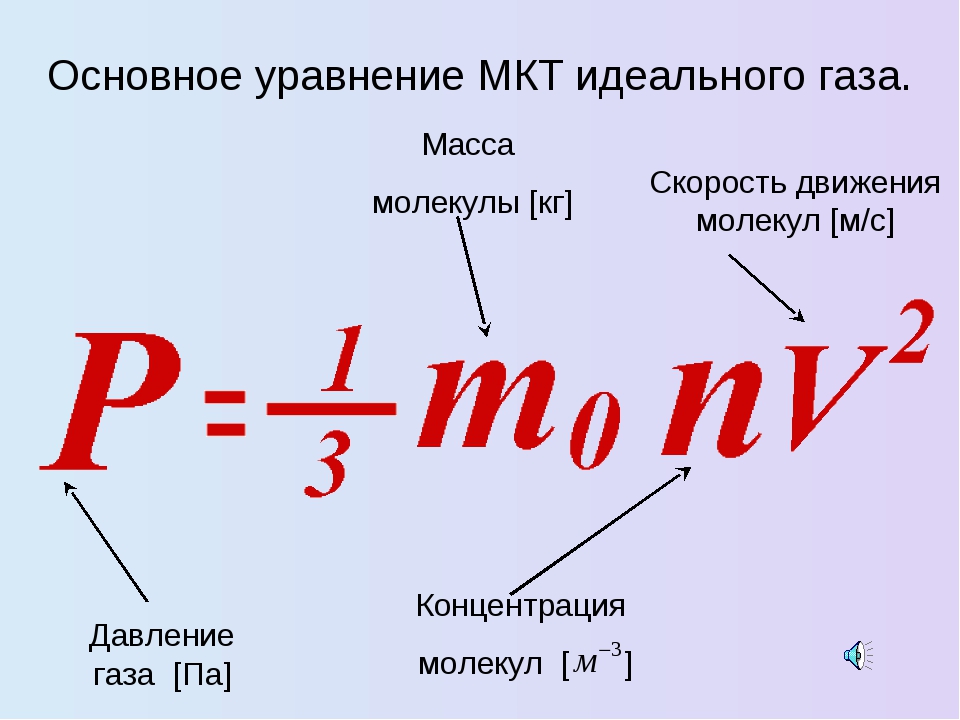 Так что, конечно, это вызовет у нас небольшую проблему. Потому что это означает, что если плотность, которую мы использовали здесь, 1000 килограммов на кубический метр, на самом деле не подходит для всего, она будет немного плотнее внизу. Так что давление на самом деле будет немного больше. Но насколько это влияет? Что ж, давайте посмотрим, это давление, которое мы прилагаем, чтобы узнать, насколько оно сжимает воду, мы смотрим на соотношение.Что это делится на объемный модуль? Ну, это будет 4 умножить на 10 на 7 Паскаля, разделенное на объемный модуль, который мы можем найти 2,2 умножить на 10 на 9 Паскаля, и если мы введем это в калькулятор, то получим 1,9 умножить на 10 на минус 2, хорошо ?

Теперь помните, если бы это было равно, то это означало бы 100% уменьшение плотности, извините, увеличение плотности. Поскольку это 1,9 умноженное на 10 к минус 2, это увеличение плотности на 2%. Это небольшое увеличение, поэтому можно сказать, что это довольно точный ответ.Вот и все давление жидкости.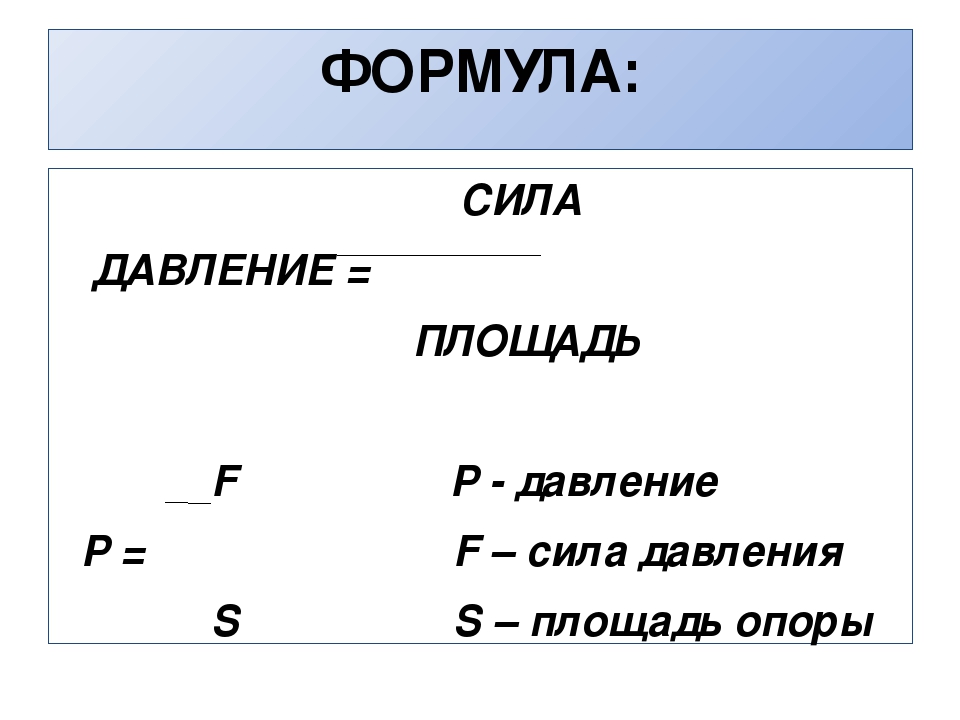

Давление жидкости — формула, условия и принцип Паскаля

Что такое давление и что такое давление жидкости?

Давление — это скалярная величина, которая определяется как сила на единицу площади, где сила действует в направлении, перпендикулярном поверхности. Давление — важная физическая величина, она играет важную роль в самых разных областях, от термодинамики до механики твердого тела и жидкости. В зависимости от контекста использования существует ряд единиц, в которых может быть выражено давление.

Давление жидкости можно определить как измерение силы на единицу площади, действующей на данный объект на поверхности закрытого контейнера или в жидкости. Факторы, вызывающие это давление, — это сила тяжести, ускорение или силы вне закрытого контейнера.

Формула давления жидкости

[Изображение будет загружено в ближайшее время]

Следующее соотношение можно использовать для расчета давления в жидкости.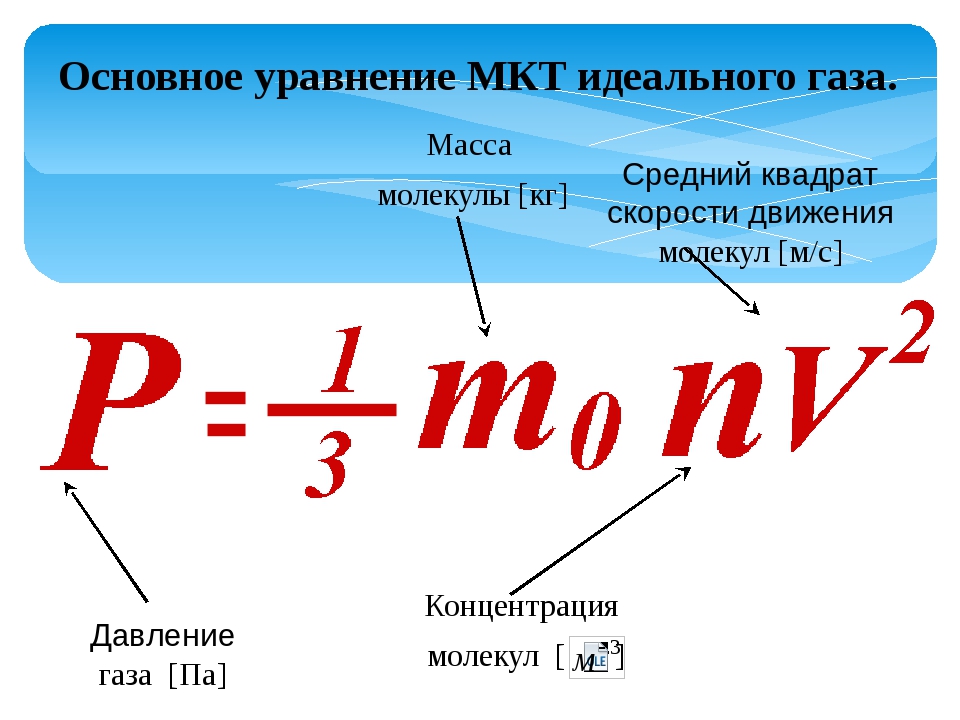

Pfluid = P + ρgh

Где,

P = Давление в контрольной точке

Pfluid = Давление в точке, измеренной в жидкости

Ρ = Плотность жидкости

г = Ускорение под действием силы тяжести (с учетом земли г = 9.8 м / с)

h = высота от опорной точки

Разделив массу жидкости с учетом объема жидкости, можно рассчитать плотность жидкости:

ρ = м / об

Где

m = масса жидкости

v = объем рассматриваемой жидкости

Общее давление в системе определяется следующим образом, если жидкость подвергается атмосферному давлению:

Pfluid = Po + ρgh

Где,

Po = атмосферное давление

Условия учета давления жидкости:

1. В открытом состоянии или потоке в открытом канале

2. В закрытом состоянии или закрытом трубопроводе

Давление в любой точке статической жидкости

Внутри статической жидкости в данной точке пространства сумма действующих сил должна быть равна нулю. В противном случае условие статического равновесия не было бы выполнено. Рассмотрим прямоугольную область в жидкой среде с плотностью ρL (такой же, как у жидкой среды), шириной w, длиной l и высотой h для анализа такой простой системы. Затем в среде учитываются силы, действующие в этой области. Во-первых, сила тяжести, действующая вниз (ее вес) в области, равна его плотности объекта (ρ), умноженному на его объем объекта (v), умноженному на ускорение свободного падения (g).Из-за жидкости над областью, направленная вниз сила, действующая на эту область, равна давлению, умноженному на площадь контакта. Аналогичным образом, из-за жидкости под областью, на эту область действует направленная вверх сила, которая равна давлению, умноженному на площадь контакта. Сумма этих сил должна быть равна нулю для достижения статического равновесия. Давление текучей среды ниже области должно быть больше давления текучей среды выше на вес области для любой области внутри текучей среды, чтобы достичь статического равновесия.

Принцип Паскаля

Принцип Паскаля (также известный как закон Паскаля) применяется к статическим жидкостям, а в статических жидкостях используется зависимость давления от высоты. Принцип Паскаля можно использовать для использования давления статической жидкости в качестве меры энергии на единицу объема для выполнения заданной работы, например, в гидравлических прессах.

Принцип Паскаля качественно утверждает, что в замкнутой статической жидкости передается неизменное давление.Количественно закон Паскаля в жидкости может быть получен из выражения, которое определяет давление на заданной высоте (или глубине) и определяется принципом Паскаля:

p2 = p1 + Δp

Δp = ρgΔh

Где

p1 = внешнее давление

ρ = плотность жидкости

Δh = разница в высоте статической жидкости

g = ускорение свободного падения

Знаете ли вы?

Давление также отвечает за дыхательный механизм и играет важную роль в дыхательной системе. Вдыхание — это результат разницы давлений между легкими и атмосферой, которая создает возможность попадания воздуха в легкие. Механизм, приводящий к вдоху, происходит из-за опускания диафрагмы, что увеличивает объем грудной полости, окружающей легкие, тем самым снижая ее давление, как определено законом идеального газа. Снижение давления в грудной полости, которая обычно имеет отрицательное манометрическое давление, таким образом поддерживая легкие раздутыми, втягивает воздух в легкие, раздувая альвеолы ​​и приводя к транспорту кислорода, необходимому для дыхания.Когда диафрагма восстанавливается и движется вверх, давление в грудной полости увеличивается, что приводит к выдоху. Цикл повторяется, приводя к дыханию, которое, как уже говорилось, механически связано с изменениями давления. Основные функции, такие как кровообращение и дыхание, были бы невозможны без давления в теле и соответствующего потенциала для динамических процессов в организме.

Давление — это сила на единицу площади, Рон Куртус

SfC Home> Физика> Сила>

от Рона Куртуса

Давление — это сила , действующая на объект, которая распространяется на площадь поверхности .

Уравнение давления — это сила, деленная на площадь приложения силы. Хотя это измерение является простым, когда твердое тело толкает твердое тело, в случае твердого тела, толкающего жидкость или газ, необходимо, чтобы жидкость была заключена в контейнер.

Сила также может создаваться весом объекта.

Вопросы, которые могут у вас возникнуть:

• Какое давление возникает, когда твердое тело давит на другое твердое тело?
• Что происходит, когда твердое тело сталкивается с замкнутой жидкостью?
• Что происходит, когда сила гравитации?

Этот урок ответит на эти вопросы.Полезный инструмент: Конвертация единиц

Давление твердого тела на твердое

Когда вы прикладываете силу к твердому объекту, давление определяется как приложенная сила, разделенная на область приложения. Уравнение для давления:

P = F / A

где

• P давление
• F — приложенная сила
• A — это площадь поверхности, на которую прикладывается сила
• F / A — это F , разделенное на A

Например, если вы давите на объект рукой с силой 20 фунтов, а площадь вашей руки составляет 10 квадратных дюймов, то давление, которое вы оказываете, составит 20/10 = 2 фунта на квадратный дюйм.

Давление равно Силе, разделенной на площадь

Вы можете видеть, что для данной силы, если площадь поверхности меньше, давление будет больше. Если вы используете большую площадь, вы распределяете силу, и давление (или сила на единицу площади) становится меньше.

Твердое прессование в замкнутой жидкости

Когда жидкость или газ заключены в контейнер или цилиндр, вы можете создать давление, приложив силу с помощью твердого поршня. Давление, создаваемое в цилиндре, равно приложенной силе, разделенной на площадь поршня: P = F / A .

В замкнутой жидкости — если пренебречь влиянием силы тяжести на жидкость — давление одинаково во всем контейнере, одинаково давя на все стенки. В случае велосипедного насоса давление, создаваемое внутри насоса, будет передаваться через шланг в велосипедную шину. Но воздух все еще закрыт.

Давление в жидкости во всех направлениях

Увеличение силы увеличивает давление внутри цилиндра.

Вызвано гравитацией

Поскольку вес объекта является силой, вызванной гравитацией, мы можем подставить вес в уравнение давления.Таким образом, давление ( P ), вызванное весом ( W ) объекта, представляет собой этот вес, деленный на площадь ( A ), на которую действует груз.

P = W / A

Если вы кладете твердый предмет на пол, давление на пол в зоне контакта определяется массой объекта, деленной на площадь на полу.

Давление равно весу, разделенному на площадь

Пример с обувью

Хороший пример того, как сила на небольшой площади может привести к очень высокому давлению, — это женская обувь на высоком каблуке с шипами.Эти типы обуви могут повредить некоторые полы из-за очень высокого давления на пол в области пятки.

Средняя обувь распределяет вес человека на 20 квадратных дюймов. Таким образом, человек весом 100 фунтов наносит на пол 100/20 = 5 фунтов на квадратный дюйм.

Поскольку размер каблука-шипа составляет всего 0,25 квадратных дюйма, человек весом 100 фунтов будет наносить 100 / 0,25 = 400 фунтов на квадратный дюйм на пол в области пятки! В некоторых случаях этого достаточно, чтобы повредить пол.

Масса жидкости

Если вы поместите жидкость в контейнер, вес этой жидкости будет давить на дно контейнера так же, как вес твердого предмета. Давление на дно контейнера будет таким же, как если бы вес был твердым:

P = W / A .

Единственная разница в том, что давление в жидкости распространяется во всех направлениях. Таким образом, давление по бокам внизу будет таким же.

Газы и жидкости испытывают давление из-за своего веса в каждой точке жидкости.

Сводка

Давление — это сила, действующая на объект, которая распространяется по площади поверхности. Уравнение для давления: P = F / A . Давление можно измерить для твердого тела, давящего на твердое тело, но в случае, когда твердое тело толкает жидкость или газ, необходимо, чтобы жидкость была заключена в контейнер.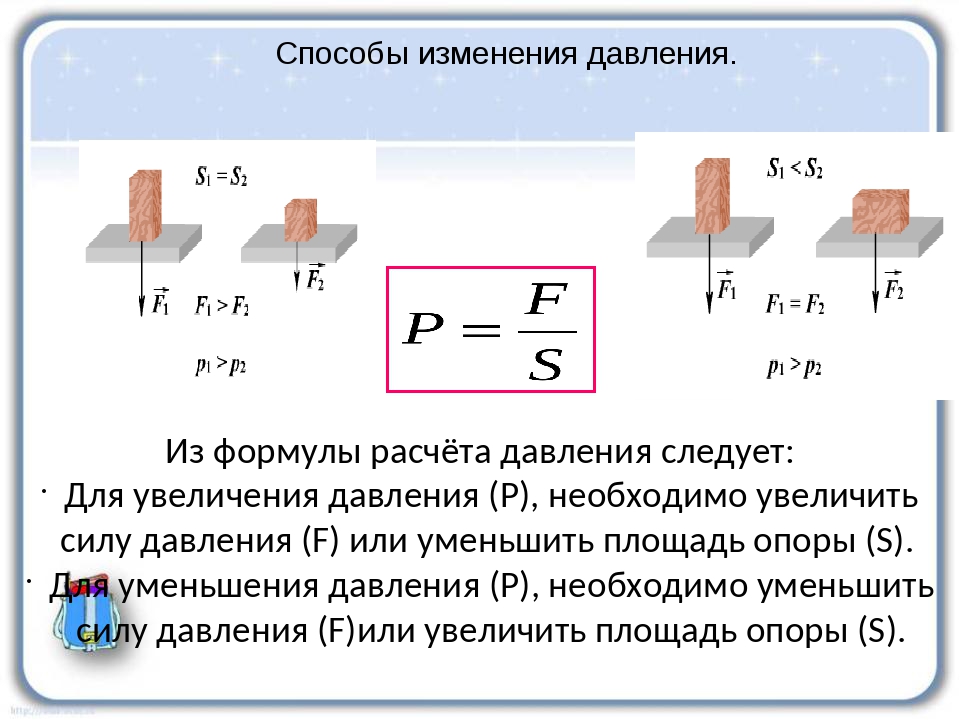 Сила также может создаваться весом объекта.

Давай на себя, чтобы преуспеть

Ресурсы и ссылки

Полномочия Рона Куртуса

Сайты

Физические ресурсы

Книги

(Примечание: Школа чемпионов может получать комиссионные от покупки книг)

Книги по физике силы с самым высоким рейтингом

Поделиться страницей

Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:

Студенты и исследователи

Веб-адрес этой страницы:
www.school-for-champions.com/science/
давление.htm

Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или диссертации.

Авторские права © Ограничения

Где ты сейчас?

Школа чемпионов

По физике

Давление — это сила на единицу площади

Давление на поверхности — Давление — KS3 Physics Revision

1ygjhqajq2m.0.0.0.1:0.1.0.$0.$1.$0″> Возможно, вас предупреждали о том, что вы должны раскачиваться на одной ножке стула.Помимо риска повредить стул или пораниться, ножка стула может повредить пол. Это потому, что он слишком сильно давит на пол.

Расчет давления

Чтобы рассчитать давление, вам нужно знать две вещи:

• прилагаемую силу или вес
• площадь поверхности, на которую распространяется сила или вес

Давление рассчитывается с использованием этого уравнения:

Пример

Сила 20 Н действует на площади 4 м ^{1ygjhqajq2m.0.0.0.1:0.1.0.$0.$2.$6.$1″> 2} .Рассчитайте давление.

давление = сила ÷ площадь

= 20 Н ÷ 4 м ² = 5 Н / м ²

Обратите внимание, что единицей давления здесь является Н / м ² (ньютонов на квадратный метр). Иногда вы увидите, что используется другой блок. Это называется паскаль и обозначается символом Па.

1 Па = 1 Н / м ² , поэтому в приведенном выше примере давление составляет 5 Па.

Использование давления

1ygjhqajq2m.0.0.0.1:0.1.0.$0.$3.$1″> Если вы идете по снегу, вы обычно погрузиться в нее.Это потому, что у вашей обуви небольшая площадь поверхности. Ваш вес распределяется только по небольшой площади, поэтому давление на снег велико. Однако на лыжах так далеко в снег не утонешь. Это связано с тем, что ваш вес распределяется по большей площади, поэтому давление на снег невелико.

Штифты для рисования хорошо используют разные давления при одинаковой силе

Штифты для рисования имеют большой круглый конец, на который можно нажимать большим пальцем. Круглый конец имеет большую площадь, поэтому он оказывает небольшое давление на большой палец.У острого конца очень маленькая площадь. Та же толкающая сила создает там высокое давление, поэтому оно вдавливается в доску объявлений.

Если вы качаетесь на одной ножке стула, вы оказываете в четыре раза большее давление на одну точку пола, чем если бы вы сидели правильно. Это потому, что четыре ножки стула распределяют давление по площади в четыре раза больше, чем одна ножка стула.

Давление — AP Physics 2

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects. org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

.