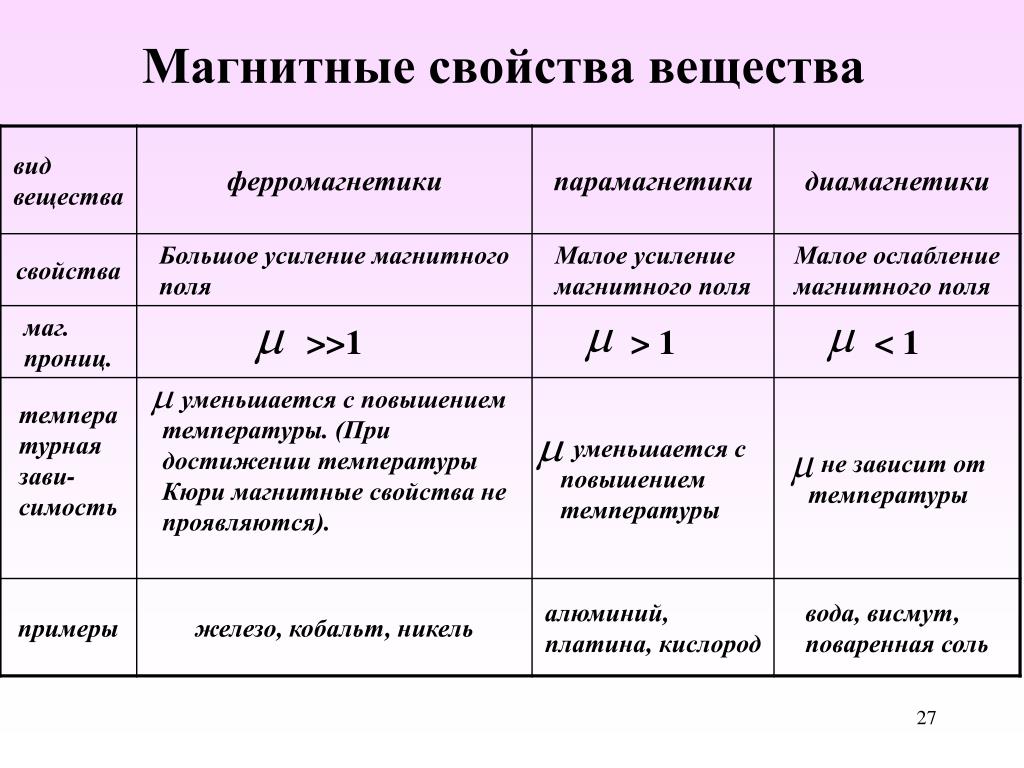
Магнитная проницаемость | |
Физическая величина, показывающая, во сколько раз индукция магнитного поля в одной среде больше или меньше индукции магнитного поля в вакууме, называется магнитной проницаемостью µ.. | |
Вещество, создающее собственное магнитное поле, называетсянамагниченным. Намагниченность возникает при помещении вещества во внешнее магнитное поле. Гипотеза Ампера: магнитные свойства тела определяются микроскопическими электрическими токами (орбитальное движение электронов в атомах, наличие у электрона собственного магнитного момента, имеющего квантовую природу) внутри вещества. Если направления этих токов неупорядочены, порождаемые ими магнитные поля компенсируют друг друга, т.е. тело не намагничено. Во внешнем магнитном поле происходит упорядочение этих токов, вследствие чего в веществе и возникает «собственное» магнитное поле (намагниченность). | |
Магнитные свойства вещества
| |
Для пара- и диамагнетиков намагниченность I прямо пропорциональна индукции B0 магнитного поля в вакууме. | |
3. Ферромагнетики— µ >>1. µстали = 8.103 (железо, никель, кобальт и их сплавы). Сплав железа с никелем: µ =2,5.105. Свойства ферромагнетиков
| |
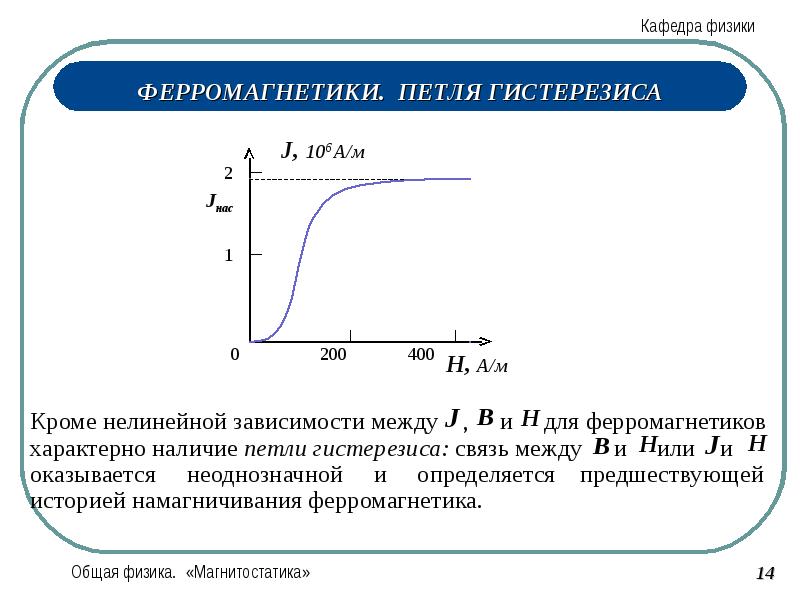
Для характеристики явления намагничивания вещества вводится величина Iназываемая намагниченностью вещества. Намагниченность в СИ определяется формулой Для ферромагнитных тел намагниченность Iявляется сложной нелинейной функцией B0. Зависимость I от величины Во/µ0 называется кривой намагниченности (рис.2). Кривая указывает на явление магнитного насыщения: начиная с некоторого значения Во/µ0= В0н/µ0, намагниченность практически остается постоянной, равной Iн(намагниченность насыщения). | |
Магнитным гистерезисом (От греческого «hysteresis» — отставание следствия от его причины) ферромагнетика называется отставание изменения величины намагниченности ферромагнитного вещества от изменения внешнего магнитного поля, в котором находится вещество. Важнейшей причиной магнитного гистерезиса является характерная для ферромагнетика зависимость его магнитных характеристик (µ, I) не только от состояния вещества в данный момент, но и от значений величин µ и I в предыдущие моменты времени. Петлей гистерезиса называется кривая зависимости изменения величины намагниченности ферромагнитного тела, помещенного во внешнее магнитное поле, от изменения индукции этого поля от + Во/µ0 до — Во/µ0 и обратно. Значение + Во/µ0 соответствует намагниченности насыщения Iн. Для того чтобы полностью размагнитить ферромагнитное тело, необходимо изменить направление внешнего поля. При некотором значении магнитной индукции — В0к , которой соответствует величина В0к/µ0, называемая коэрцитивной(задерживающей) силoй, намагниченность I тела станет равной нулю. | |
Коэрцитивная сила и форма петли гистерезиса характеризуют свойство ферромагнетика сохранять остаточное намагничивание и определяют использование ферромагнетиков для различных целей. Ферромагнетики с широкой петлей гистерезиса называются жесткими магнитными материалами (углеродистые, вольфрамовые, хромовые, алюминиево-никелевые и другие стали). |
|
При температурах меньших точки Кюри любое ферромагнитное тело состоит из доменов — малых областей с линейными размерами порядка 10-2 -10-3 см, внутри которых существует наибольшая величина намагниченности, равная намагниченности насыщения. Применение ферромагнетиков в технике. Роторы генераторов и электродвигателей; сердечники трансформаторов, электромагнитных реле; в электронно-вычислительных машинах (ЭВМ), телефонах, магнитофонах, на магнитных лентах. | |
Ферромагнетики
К ферромагнетикам (ferrum – железо) относятся вещества, магнитная восприимчивость которых положительна и достигает значений . Намагниченность и магнитная индукция ферромагнетиков растут с увеличением напряженности магнитного поля нелинейно, и в полях намагниченность ферромагнетиков достигает предельного значения , а вектор магнитной индукции растет линейно с :
Ферромагнитные свойства материалов проявляются только у веществ в твердом состоянии, атомы которых обладают постоянным спиновым, или орбитальным, магнитным моментом, в частности у атомов с недостроенными внутренними электронными оболочками. Типичными ферромагнетиками являются переходные металлы. В ферромагнетиках происходит резкое усиление внешних магнитных полей. Причем для ферромагнетиков сложным образом зависит от величины магнитного поля. Типичными ферромагнетиками являются Fe, Co, Ni, Gd, Tb, Dy, Ho, Er, Tm, а также соединения ферромагнитных материалов с неферромагнитными: , , и др.
В ферромагнетиках происходит резкое усиление внешних магнитных полей. Причем для ферромагнетиков сложным образом зависит от величины магнитного поля. Типичными ферромагнетиками являются Fe, Co, Ni, Gd, Tb, Dy, Ho, Er, Tm, а также соединения ферромагнитных материалов с неферромагнитными: , , и др.
Существенным отличием ферромагнетиков от диа- и парамагнетиков является наличие у ферромагнетиков самопроизвольной (спонтанной) намагниченности в отсутствие внешнего магнитного поля. Наличие у ферромагнетиков самопроизвольного магнитного момента в отсутствие внешнего магнитного поля означает, что электронные спины и магнитные моменты атомных носителей магнетизма ориентированы в веществе упорядоченным образом.
Ферромагнетики – это вещества, обладающие самопроизвольной намагниченностью, которая сильно изменяется под влиянием внешних воздействий – магнитного поля, деформации, температуры.
Ферромагнетики, в отличие от слабо магнитных диа- и парамагнетиков, являются сильно магнитными веществами: внутреннее магнитное поле в них может в сотни раз превосходить внешнее поле.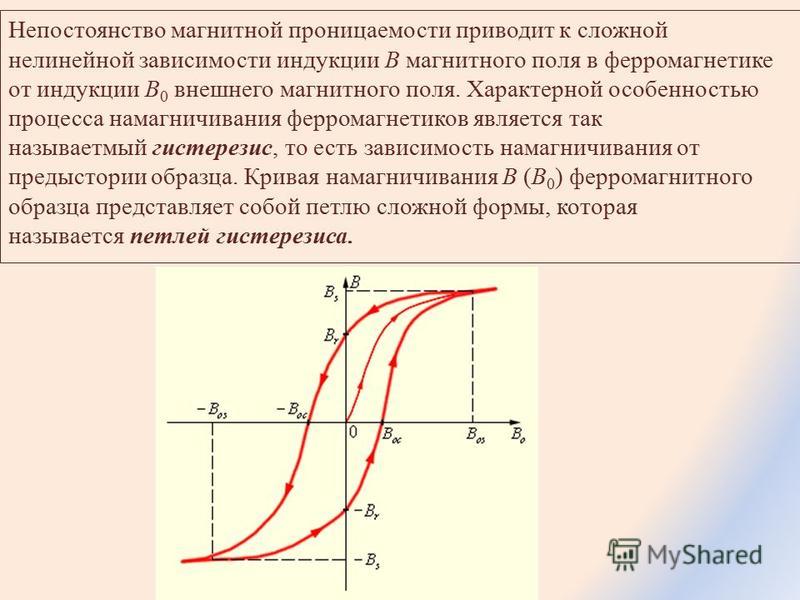
Основные отличия магнитных свойств ферромагнетиков.
1. Нелинейная зависимость намагниченности от напряженности магнитного поля Н (рис. 6.5).
Как видно из рис. 6.5, при наблюдается магнитное насыщение.
2. При зависимость магнитной индукции В от Н нелинейная, а при – линейная (рис. 6.6).
Рис. 6.5 Рис. 6.6
3. Зависимость относительной магнитной проницаемости от Н имеет сложный характер (рис. 6.7), причем максимальные значения μ очень велики ( ).
Рис. 6.7 Рис. 6.8
Впервые систематические исследования μ от Н были проведены в 1872 г. А.Г. Столетовым (1839–1896) – выдающимся русским физиком, организатором физической лаборатории в Московском университете. На рис. 6.8. изображена зависимость магнитной проницаемости некоторых ферромагнетиков от напряженности магнитного поля – кривая Столетова.
На рис. 6.8. изображена зависимость магнитной проницаемости некоторых ферромагнетиков от напряженности магнитного поля – кривая Столетова.
4. У каждого ферромагнетика имеется такая температура, называемая точкой Кюри ( ), выше которой это вещество теряет свои особые магнитные свойства.
Наличие температуры Кюри связано с разрушением при упорядоченного состояния в магнитной подсистеме кристалла – параллельной ориентации магнитных моментов. Для никеля температура Кюри равна 360 °С. Если подвесить образец никеля вблизи пламени горелки так, чтобы он находился в поле сильного постоянного магнита, то не нагретый образец может располагаться горизонтально, сильно притягиваясь к магниту (рис. 6.9). По мере нагрева образца и достижения температуры ферромагнитные свойства у никеля исчезают и образец никеля падает. Остыв до температуры ниже точки Кюри, образец вновь притянется к магниту. Нагревшись, вновь падает и т.д., колебания будут продолжаться все время, пока горит свеча.
Рис. 6.9
5. Существование магнитного гистерезиса.
На рисунке 6.10 показана петля гистерезиса – график зависимости намагниченности вещества от напряженности магнитного поля Н.
Рис. 6.10
Намагниченность при называется намагниченностью насыщения.
Намагниченность при называется остаточной намагниченностью (что необходимо для создания постоянных магнитов).
Напряженность магнитного поля, полностью размагниченного ферромагнетика, называется коэрцитивной силой. Она характеризует способность ферромагнетика сохранять намагниченное состояние.
Большой коэрцитивной силой (широкой петлей гистерезиса) обладают магнитотвердые материалы. Малую коэрцитивную силу имеют магнитомягкие материалы.
Измерение гиромагнитного отношения для ферромагнетиков показали, что элементарными носителями магнетизма в них являются спиновые магнитные моменты электронов.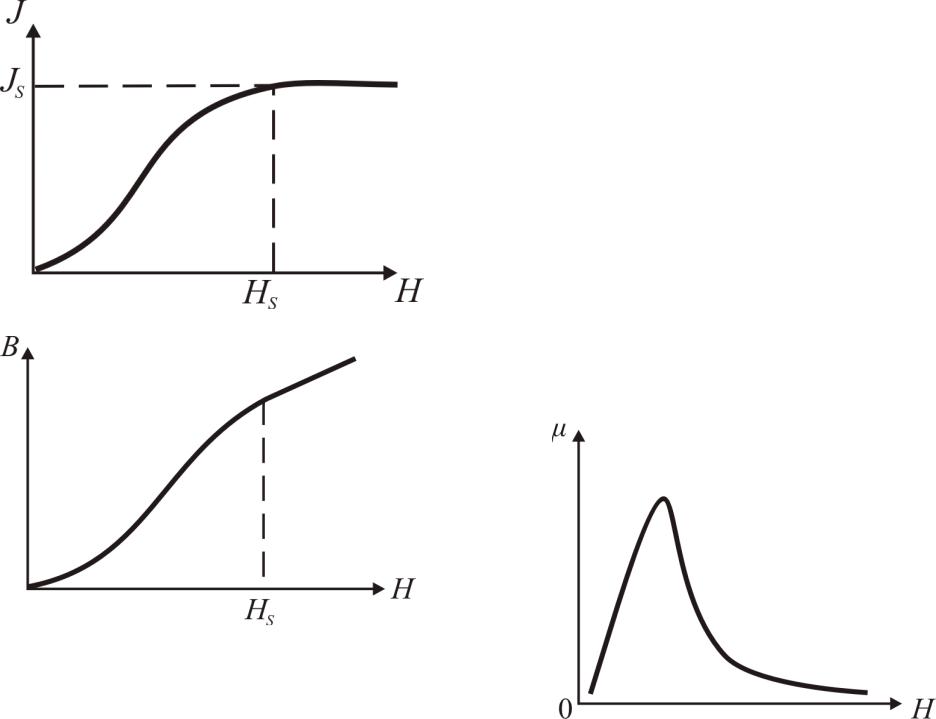
Самопроизвольно, при , намагничиваются лишь очень маленькие монокристаллы ферромагнитных материалов, например никеля или железа. Для того чтобы постоянным магнитом стал большой кусок железа, необходимо его намагнитить, т.е. поместить в сильное магнитное поле, а затем это поле убрать. Оказывается, что при большой исходный кусок железа разбит на множество очень маленьких ( ), полностью намагниченных областей – доменов. Векторы намагниченности доменов в отсутствие внешнего магнитного поля ориентированы таким образом, что полный магнитный момент ферромагнитного материала равен нулю. Если бы в отсутствие поля кристалл железа был бы единым доменом, то это привело бы к возникновению значительного внешнего магнитного поля, содержащего значительную энергию (рис. 6.11, a). Разбиваясь на домены, ферромагнитный кристалл уменьшает энергию магнитного поля. При этом, разбиваясь на косоугольные области (рис. 6.11, г), можно легко получить состояние ферромагнитного кристалла, из которого магнитное поле вообще не выходит. В целом в монокристалле реализуется такое разбиение на доменные структуры, которое соответствует минимуму свободной энергии ферромагнетика. Если поместить ферромагнетик, разбитый на домены, во внешнее магнитное поле, то в нем начинается движение доменных стенок. Они перемещаются таким образом, чтобы областей с ориентацией вектора намагниченности по полю стало больше, чем областей с противоположной ориентацией (рис. 6.11, б, в, г). Такое движение доменных стенок понижает энергию ферромагнетика во внешнем магнитном поле. По мере нарастания магнитного поля весь кристалл превращается в один большой домен с магнитным моментом, ориентированным по полю (рис. 6.11, а).
В целом в монокристалле реализуется такое разбиение на доменные структуры, которое соответствует минимуму свободной энергии ферромагнетика. Если поместить ферромагнетик, разбитый на домены, во внешнее магнитное поле, то в нем начинается движение доменных стенок. Они перемещаются таким образом, чтобы областей с ориентацией вектора намагниченности по полю стало больше, чем областей с противоположной ориентацией (рис. 6.11, б, в, г). Такое движение доменных стенок понижает энергию ферромагнетика во внешнем магнитном поле. По мере нарастания магнитного поля весь кристалл превращается в один большой домен с магнитным моментом, ориентированным по полю (рис. 6.11, а).
Рис. 6.11
Ферромагнитные материалы играют огромную роль в самых различных областях современной техники. Магнитомягкие материалы используются в электротехнике при изготовлении трансформаторов, электромоторов, генераторов, в слаботочной технике связи и радиотехнике; магнитожесткие материалы применяют при изготовлении постоянных магнитов.
Широкое распространение в радиотехнике, особенно в высокочастотной радиотехнике, получили ферриты ( ) сочетающие ферромагнитные и полупроводниковые свойства.
Магнитные материалы широко используются в традиционной технологии записи информации в винчестере (рис. 6.12).
Рис. 6.12 Рис. 6.13
Магнитное вещество 2 (рис. 6.13) нанесено тонким слоем на основу твердого диска 3. Каждый бит информации представлен группой магнитных доменов (в идеальном случае – одним доменом). Для перемагничивания домена (изменения направления вектора его намагниченности) используется поле записывающей головки 4 (5 – считывающая головка). Наличие дополнительных стабилизирующих слоев, препятствует самопроизвольной потере информации. Записью на вертикально ориентированные домены достигается плотность до 450 Гбайт/см2.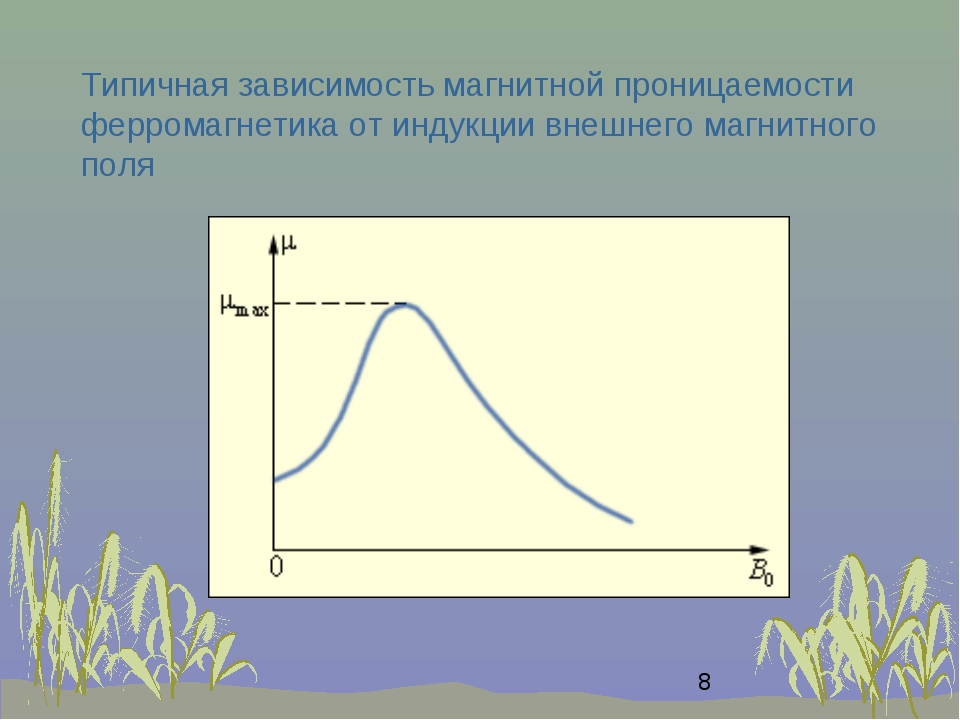
Рис. 6.14 Рис. 6.15
На рисунке 6.14 изображены первые магнитные диски созданные в 1955 г, имевшие название IBM 350 Disk File, с обьемом 5 Мб и размером 24 дюймов.
В 1971 г. было произведено первое применение IBM3330 магнитного диска, созданного в 1957 г. с использованием магнитной головки и слота (рис. 6.15).
2.2.5 Магнитное взаимодействие
Атомно-силовой микроскоп может использоваться для исследования магнитных полей на поверхности образца. Такие методики объединяются под названием МСМ (магнитно-силовая микроскопия). В них используются специальные кантилеверы, которые покрыты магнитной пленкой. При взаимодействии с магнитным полем образца такой кантилевер отклоняется. Могут существовать следующие типы кантилеверов: диамагнитные, парамагнитные [1], суперпарамагнитные [2] и ферромагнитные (магнитожесткие [3] и магнитомягкие [4]).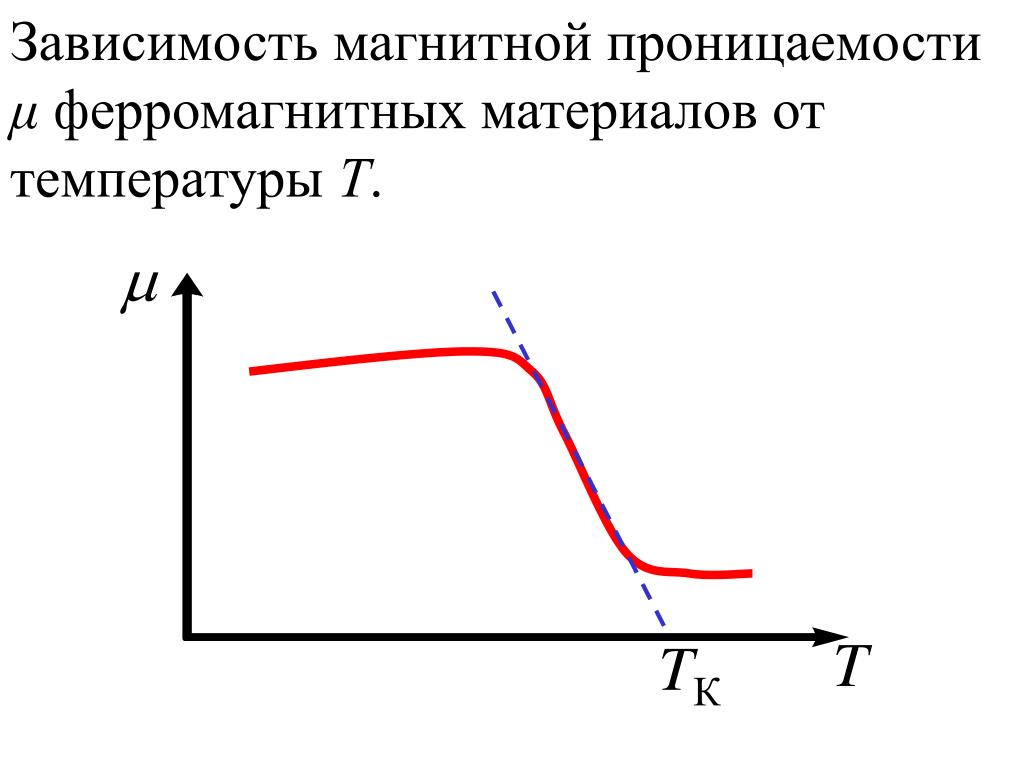
Здесь мы кратко напомним об этих трех типах магнетиков, рассмотрев диамагнетизм, парамагнетизм и ферромагнетизм на феноменологическом уровне. Заинтересованных же отошлем к более серьезной литературе, например, [5, 6, 7].
Магнитные свойства вещества описываются вектором намагниченности
. Его связь с напряженностью магнитного поля
задается формулой [8,9]:
(1)
где
– магнитная восприимчивость вещества. В свою очередь, напряженность магнитного поля связана с вектором магнитной индукции
и вектором намагничивания следующим образом:
(2)
Подставляя (1) в (2), получим:
(3)
где
– магнитная проницаемость вещества. Таким образом, магнитные свойства вещества описываются одним независимым параметром –
или
.
Диа- и парамагнетизм.
Атомы многих веществ не имеют постоянных магнитных моментов, или, вернее, все спиновые и орбитальные магнитные моменты внутри атома уравновешены так, что суммарный магнитный момент равен нулю. Если наложить магнитное поле, то внутри атома будут генерироваться слабые дополнительные токи. В соответствии с законом Ленца они будут индицироваться так, чтобы уменьшить магнитное поле, и наведенный магнитный момент атомов направлен навстречу магнитному полю. Таков механизм диамагнетизма.
Если наложить магнитное поле, то внутри атома будут генерироваться слабые дополнительные токи. В соответствии с законом Ленца они будут индицироваться так, чтобы уменьшить магнитное поле, и наведенный магнитный момент атомов направлен навстречу магнитному полю. Таков механизм диамагнетизма.
Магнитная восприимчивость и магнитная проницаемость для диамагнетиков:
(4)
(5)
где
– число атомов в единице объема,
– число электронов в атоме,
и
– заряд и масса электрона,
– скорость света,
– средний квадрат расстояния электрона до ядра. Энергия теплового движения слишком мала, чтобы изменить внутреннее (квантованное) состояние атома. Поэтому для диамагнетиков
и
не должны зависеть от температуры. Обратим внимание, что
и, тем самым,
.
К диамагнетикам относятся, например, кислород, алюминий, платина, хлористое железо –
, благородные газы и т.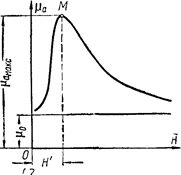 д.
д.
Однако существуют такие вещества, атомы которых обладают магнитным моментом, спиновым или орбитальным. Таким образом, кроме диамагнитного эффекта (а он всегда присутствует) есть возможность выстраивания индивидуальных атомных моментов в одном направлении. Магнитные моменты ориентируются в направлении магнитного поля, усиливая его.
Парамагнетизм, вообще говоря, довольно слаб, потому что выстраивающие силы относительно малы по сравнению с силами теплового движения, которые стараются разрушить упорядочивание. Отсюда следует, что парамагнетизм особо чувствителен к температуре. Эффект парамагнетизма тем сильнее, чем ниже температура.
Пусть
– магнитный момент атома,
– магнитная индукция,
– число атомов в единице объема,
– константа Больцмана,
– температура. Тогда для парамагнетиков в слабых полях –
, когда зависимость вектора намагничивания от напряженности магнитного поля линейна, магнитная восприимчивость и магнитная проницаемость равны:
(6)
(7)
Обратно пропорциональная зависимость восприимчивости от абсолютной температуры (6) носит название закона Кюри. Заметим, что для парамагнетиков
Заметим, что для парамагнетиков
и, тем самым,
.
В сильных полях намагничивание приходит в состояние насыщение, когда все магнитные моменты устанавливаются параллельно полю:
(8)
Так как диамагнетизм проявляется во всех веществах, он частично или полностью компенсирует парамагнетизм за счет противоположного по знаку вклада в восприимчивость. Поэтому для материалов с атомами, имеющими магнитный момент, можно говорить лишь о преобладании диа- или парамагнитных свойств в веществе, причем их баланс зависит от температуры. К парамагнетикам относятся, например, азот, углекислота, вода, серебро, висмут и т.д.
Ферромагнетизм.
В ферромагнетиках эффект упорядочения магнитных моментов проявляется во много раз сильнее, чем в диа- и парамагнетиках. Ферромагнетизм определяется коллективным взаимодействием атомных магнитных моментов, находящимися в состоянии с нарушенной симметрией (фазовый переход второго рода) и образующих магнитные домены. Ферромагнетиками называются тела, которые могут обладать спонтанной намагниченностью, то есть намагничены уже в отсутствие магнитного поля. Типичными представителями ферромагнетиков являются переходные металлы: железо, кобальт, никель и многие их сплавы. Ферромагнетизмом обладают некоторые редкоземельные элементы (гадолиний, тербий, диспрозий, гольмий, эрбий, туллий).
Ферромагнетиками называются тела, которые могут обладать спонтанной намагниченностью, то есть намагничены уже в отсутствие магнитного поля. Типичными представителями ферромагнетиков являются переходные металлы: железо, кобальт, никель и многие их сплавы. Ферромагнетизмом обладают некоторые редкоземельные элементы (гадолиний, тербий, диспрозий, гольмий, эрбий, туллий).
Характерной особенностью ферромагнетиков является сложная нелинейная зависимость между
и
или между
и
. Характер этой зависимости представлен на рис. 1 и 2.
Рис. 1. Зависимость намагничивания от
напряженности магнитного поля.
Рис. 2. Зависимость магнитной индукции от
напряженности магнитного поля.
По мере возрастания
намагниченность
сначала быстро увеличивается, а затем приходит к насыщению и остается практически постоянной:
(насыщение), то есть кривая
переходит в горизонтальную прямую.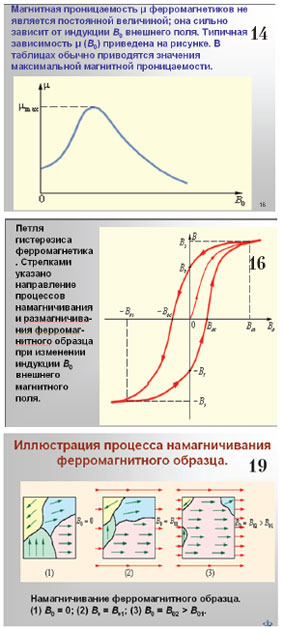 Магнитная индукция
Магнитная индукция
также растет с увеличением поля
, а в состоянии насыщения
, то есть кривая
переходит в прямую, наклоненную под углом
(если
и
откладывать на осях координат в одинаковом масштабе).
Магнитная восприимчивость
и магнитная проницаемость
уже зависят не только от свойств вещества и температуры, как у диа- и парамагнетиков, а являются функциями напряженности поля
и, более того, определяется его историей.
Восприимчивость и проницаемость сначала возрастают с
, затем проходят через максимум, и, наконец, в сильных полях, когда достигнуто насыщение,
стремится к единице (рис.3), а
– к нулю.
Рис. 3. Зависимость магнитной восприимчивости от напряженности магнитного поля.
Значения
в максимуме у большинства ферромагнетиков при обычных температурах составляют многие сотни и тысячи единиц.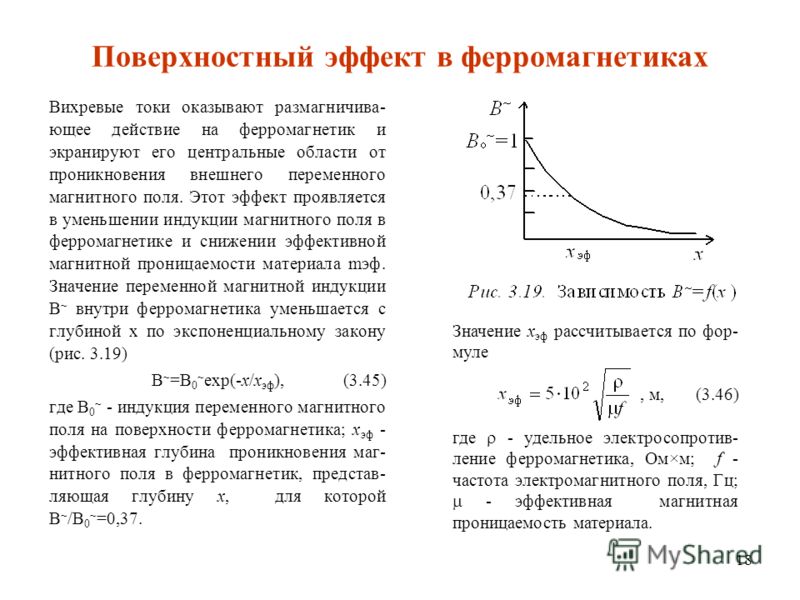
Вторая характерная особенность ферромагнетиков состоит в том, что для них зависимость
от
или
от
не однозначна, а определяется предшествующей историей намагничивания ферромагнитного образца. Это явление называется магнитным гистерезисом. Изображенная на рисунке 4 замкнутая кривая
называется петлей гистерезиса, а кривая
– предельной (наибольшей) петлей гистерезиса.
Рис. 4. Петля гистерезиса.
При
индукция
не обращается в нуль, а изображается отрезком
. Ему соответствует остаточное намагничивание
. С наличием такого остаточного намагничивания связано существование постоянных магнитов. Для того, чтобы размагнитить образец, надо довести кривую размагничивания до точки
или
. Этим точкам соответствует магнитное поле
. Оно называется коэрцитивной силой ферромагнетика. Значения остаточного намагничивания и коэрцитивной силы для разных ферромагнетиков меняются в широких пределах. Для мягкого железа петля гистерезиса узкая (коэрцитивная сила мала), для стали и всех материалов, идущих на изготовление магнитов, – широкая (коэрцитивная сила велика). Например, для кобальта и его сплавов, которые используются для покрытия магнитожестких кантилеверов, характерная величина коэрцитивной силы составляет 400 эрстед. С другой стороны, магнитное поле зонда в целом ряде случаев может оказаться слишком большим, что может приводить к искажению или даже разрушению исследуемой магнитной структуры. Для этих целей используют зонды с покрытием
Значения остаточного намагничивания и коэрцитивной силы для разных ферромагнетиков меняются в широких пределах. Для мягкого железа петля гистерезиса узкая (коэрцитивная сила мала), для стали и всех материалов, идущих на изготовление магнитов, – широкая (коэрцитивная сила велика). Например, для кобальта и его сплавов, которые используются для покрытия магнитожестких кантилеверов, характерная величина коэрцитивной силы составляет 400 эрстед. С другой стороны, магнитное поле зонда в целом ряде случаев может оказаться слишком большим, что может приводить к искажению или даже разрушению исследуемой магнитной структуры. Для этих целей используют зонды с покрытием
–
. Совершенно такой же характер имеет петля гистерезиса, когда по вертикальной оси откладывается не индукция
, а намагничивание
.
Выводы.
- Вещества по их поведению в магнитном поле подразделяют на три основных типа: диамагнитные, парамагнитные и ферромагнитные.
- Диамагнитные свойства проявляют все вещества.
 Суть эффекта – в возникновении индуцированных внутриатомных токов, которые уменьшают индукцию магнитного поля в веществе. Магнитная восприимчивость диамагнетиков отрицательна.
Суть эффекта – в возникновении индуцированных внутриатомных токов, которые уменьшают индукцию магнитного поля в веществе. Магнитная восприимчивость диамагнетиков отрицательна. - Парамагнитные свойства могут проявлять вещества с атомами, имеющими магнитный момент. Магнитная восприимчивость при этом положительна и уменьшается с ростом температуры.
- Ферромагнетизм является очень сильным коллективным эффектом. Причем магнитная восприимчивость и проницаемость вещества становится неоднозначными функциями поля и зависят от его истории. Характерные ферромагнитные явления – спонтанная намагниченность и гистерезис намагниченности. Коэрцитивная сила магнитожестких кантилеверов (с кобальтовым покрытием) составляет порядка 400 эрстед, а магнитомягких (с покрытием
) – менее 10 эрстед.
Литература.
- O. Teschke, M.U. Kleinke, M.E.R. Dotto et al, J. Appl. Phys. 94, 1 (2003).
- P.F. Hopkins, J. Moreland, S.S. Malhotra et al, J.
 Appl. Phys. 79, 6448 (1996).
Appl. Phys. 79, 6448 (1996). - H.J. Mamin, D. Rugar, P. Gruetter et al, Bull. Am. Phys. Soc. 35, 420 (1990).
- P. Grutter, D. Rugar, H.J. Mamin et al, Appl. Phys. Lett. 57, 1820 (1990).
- Тикадзуми С. Физика ферромагнетизма. I часть. – М.: Мир, 1987. – 302 с.;
Тикадзуми С. Физика ферромагнетизма. II часть. – М.: Мир, 1987. – 420 с. - Уайт Р.М. Квантовая теория магнетизма. – М.: Мир, 1972.
- Дорфман Я.Г. Диамагнетизм и химическая связь. – М.: Физматгиз, 1961.
- Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике: Физика сплошных сред. – М.: Мир, 1977. – 300 с.
- Сивухин Д.В. Курс общей физики: Электричество. – М.: Наука, 1983. – 687 с.
МАГНИТНАЯ ВОСПРИИМЧИВОСТЬ • Большая российская энциклопедия
В книжной версии
Том 18.
 Москва, 2011, стр. 357
Москва, 2011, стр. 357Скопировать библиографическую ссылку:
Авторы: В. С. Булыгин
МАГНИ́ТНАЯ ВОСПРИИ́МЧИВОСТЬ, безразмерная физич. величина $χ$, связывающая намагниченность вещества $M$ с напряжённостью $H$ магнитного поля. В статич. магнитных полях $χ = M/H$. М. в., рассчитанную на единицу массы вещества, называют удельной ($χ_{уд} = χ/ρ$, где $ρ$ – плотность вещества), М. в. 1 моля вещества – молярной (или атомной). В статич. полях М. в. связана с магнитной проницаемостью $μ$ соотношениями: $μ = 1 + χ$ (в СИ), $μ = 1 + 4πχ$ (в системе единиц СГС). В переменных магнитных полях М. в. – комплексная величина. В анизотропных магнетиках М.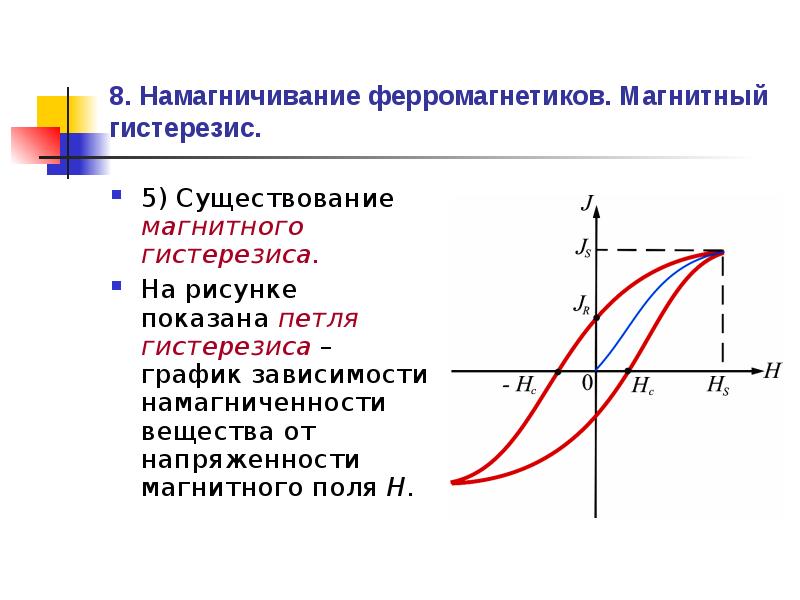 в. – симметричный тензор 2-го ранга, определяемый в общем случае тремя разл. скалярными компонентами.
в. – симметричный тензор 2-го ранга, определяемый в общем случае тремя разл. скалярными компонентами.
М. в. может быть положительной и отрицательной. Отрицательной М. в. обладают диамагнетики, положительной – все остальные магнетики (пара-, ферро-, антиферромагнетики и др.). М. в. диа- и парамагнетиков мала по абсолютной величине (порядка 10-4–10-6) и слабо зависит от величины $H$. В массивном сверхпроводнике $χ = –1$.
Зависимость дифференциальной магнитной восприимчивости χд ферромагнетика от напряжённости намагничивающего поля Н.
М. в. ферромагнетиков достигает величин порядка 104–105, сильно и сложным образом зависит от $H$, поэтому вводят дифференциальную М. в. $χ_д = dM/dH$, которая характеризует зависимость $M(H)$ в каждой точке кривой намагничивания ферромагнетика (рис. ). При $H = 0\,χ_д ≠ 0$, а имеет некоторую величину $χ_н$, которую называют начальной М. в. С увеличением $H$ М. в. ферромагнетика растёт, достигая максимума $χ_{макс}$ на крутом участке кривой намагничивания (в области Баркгаузена эффекта), и затем вновь уменьшается. При очень высоких значениях $H$ (или при темп-pax, не очень близких к Кюри точке) М. в. становится столь же незначительной, как и в обычных парамагнетиках (область парапроцесса). Наряду с $χ_д$ вводят также обратимую М. в. $χ_{обр} =\lim ΔM/ΔH$ при $ΔH→0$, причём существенно, что изменение поля должно происходить в сторону его уменьшения от начального значения ($ΔH < 0$). Всегда $χ_{обр} < χ_д$; разность между ними достигает максимума вблизи значения $H ≈ H_с$ ($H_с$ – коэрцитивная сила) и может быть принята за меру необратимости процессов намагничивания и размагничивания (меру магнитного гистерезиса).
). При $H = 0\,χ_д ≠ 0$, а имеет некоторую величину $χ_н$, которую называют начальной М. в. С увеличением $H$ М. в. ферромагнетика растёт, достигая максимума $χ_{макс}$ на крутом участке кривой намагничивания (в области Баркгаузена эффекта), и затем вновь уменьшается. При очень высоких значениях $H$ (или при темп-pax, не очень близких к Кюри точке) М. в. становится столь же незначительной, как и в обычных парамагнетиках (область парапроцесса). Наряду с $χ_д$ вводят также обратимую М. в. $χ_{обр} =\lim ΔM/ΔH$ при $ΔH→0$, причём существенно, что изменение поля должно происходить в сторону его уменьшения от начального значения ($ΔH < 0$). Всегда $χ_{обр} < χ_д$; разность между ними достигает максимума вблизи значения $H ≈ H_с$ ($H_с$ – коэрцитивная сила) и может быть принята за меру необратимости процессов намагничивания и размагничивания (меру магнитного гистерезиса). М. в. антиферромагнетиков положительна и мала по абсолютной величине (порядка 10-4–10-6).
М. в. антиферромагнетиков положительна и мала по абсолютной величине (порядка 10-4–10-6).
В большинстве диамагнетиков М. в. практически не зависит от темп-ры, а в парамагнетиках уменьшается с темп-рой, следуя Кюри закону или Кюри – Вейса закону (за исключением щелочных и отчасти щёлочноземельных и др. металлов). С ростом темп-ры М. в. ферромагнетиков увеличивается, достигая резкого максимума вблизи точки Кюри, а в парамагнитной области уменьшается по закону Кюри – Вейса. М. в. антиферромагнетиков выше Нееля точки $T_N$ подчиняется закону Кюри – Вейса, ниже $T_N$ возникает анизотропия М. в. Так, М. в. $χ_∥$ в поле, ориентированном коллинеарно направлению магнитных моментов (оси антиферромагнетизма), уменьшается до нуля при $H → 0$, а М. в. $χ_⟂$ в поле, перпендикулярном направлению оси антиферромагнетизма, не зависит от темп-ры.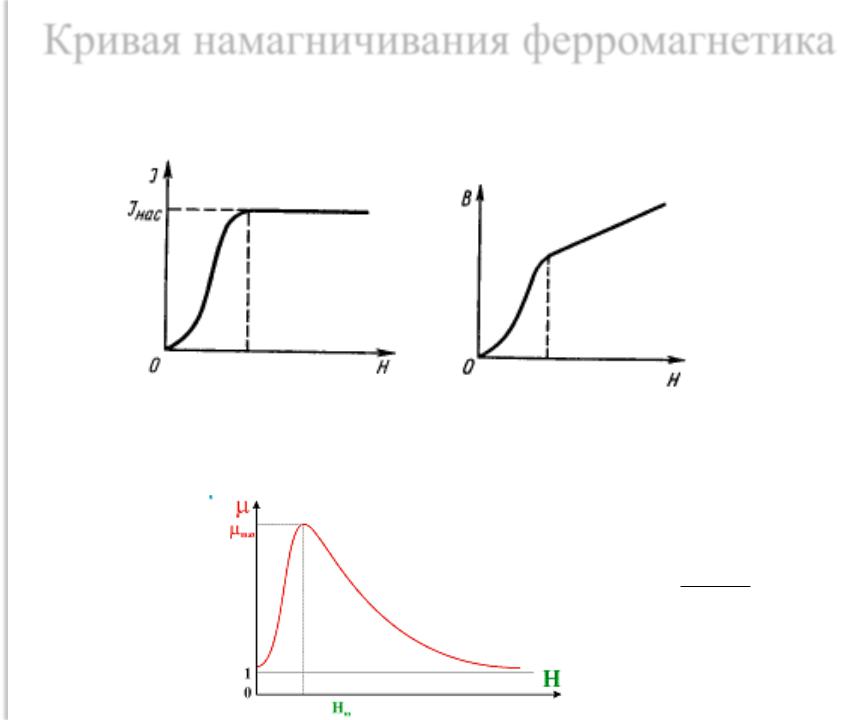
| Все грунты в большей или меньшей степени обладают магнитными свойствами т.к. основная часть породообразующих минералов относится к группе парамагнетиков. Кроме того, в грунтах практически всегда содержится некоторое количество ферромагнитных соединений. параметров, характеризующих магнитные свойства грунтов, обычно используются следующие: 1. Намагниченность (I) — результирующий магнитный момент единицы объема или единицы массы грунта, вызванный однородным магнитным полем. Эта величина представляет собой вектор и измеряется по отношению к объему грунта в А/м. Для одних веществ (ферромагнетиков) намагниченность является сложной функцией внешнего магнитного поля, для других (диа- и парамагнетиков) — в определенных интервалах полей и температур эта функция может быть линейной: I=αH, где I — намагниченность, Н — напряженность магнитного поля, α — магнитная восприимчивость. 2. Удельная магнитная восприимчивость — магнитная восприимчивость единицы массы материала с плотностью α. Магнитная восприимчивость единицы объема величина безразмерная, обычно выражается в миллионных долях единицы. Размерность удельной магнитной восприимчивости — см3/г (или м3/кг). По величине магнитной восприимчивости все вещества формально делятся на два класса:
Некоторые материалы характеризуются положительной магнитной восприимчивостью и высокими ее значениями (10-25 ед.СИ и более). Они могут приобретать очень сильную намагниченность. Такие материалы называются ферромагнитными. Приуроченность минералов к тому или иному классу определяется структурой электронных оболочек атомов, входящих в состав минерала, и структурой его кристаллической решетки.
Магнитные свойства компонентов грунта 1. 2. Жидкая компонента грунта, как правило, вода — диамагнитна, ее магнитная восприимчивость -0,9×10-5 ед. СИ. Степень минерализации водных растворов сла¬бо влияет на магнитные свойства. 3. Газовая компонента грунта намагничивается по сравнению с жидкой в еще меньшей степени. Все ее компоненты, за исключением кислорода, диа¬магнитны. Кислород же является парамагнетиком. Его магнитная восприим¬чивость 0,17×10-5 ед.СИ. В силу этого воздух также является парамагнетиком, а его магнитная восприимчивость 0,04×10-5 ед. СИ. Метан также является диамагнетиком, магнитная восприимчивость кото¬рого существенно ниже, чем у воздуха, 0,0008×10-5 ед. Магнитные свойства будут определяться соотношением компонент:
Магнитная восприимчивость грунтов Магнитная восприимчивость грунтов изменяется в широком диапазоне: Классификация грунтов по значениям их магнитной восприимчивости (Справочник геофизика, 1984)
Магнитная восприимчивость магматических скальных грунтов изменяется от десятков до нескольких сотен тысяч долей единицы СИ.
Практически немагнитные разности чаще всего отмечаются среди кислых пород, в то время как магнитные и сильно магнитные — среди основных и ультраосновных пород. Объемная магнитная восприимчивость метаморфических скальных грун¬тов в целом несколько меньше по сравнению с магматическими. Незначительная магнитная восприимчивость (от 0 до 8800×10-5 ед. СИ) характерна для гли¬нистых сланцев, филлитов, кристаллических сланцев, кварцитов, гнейсов, мрамора и др. Высокие значения этого параметра свойственны железистым кварцитам — (125—400 000)×10-5 ед. СИ, роговикам, серпентинитам, скарнам — (125— 1250)×10-5 ед. СИ и особенно магнетитовым — (75—1 000 000)×10-5 ед. Осадочные скальные и дисперсные грунты обычно практически немаг¬нитны или слабо магнитны (очень мало или нет феррамагнетиков):
Остаточная намагниченность грунтов Для осадочных горных пород характерно наличие естественной остаточной намагниченности, происхождение которой обусловлено ориентацией намагниченных частиц в процессе осаждения под влиянием геомагнитного поля. Вследствие этого в общем случае намагниченность горной породы слагается из двух векторов:
Естественная остаточная (объемная) намагниченность магматических пород изменяется от 10-3 до 10-2 А/м, а в ряде случаев может быть выше современной индуцированной намагниченности. Она существенно возрастает от кислых пород к основным. У осадочных пород остаточная намагниченность обычно слабая и достаточно стабильная (изменяется от n×10-4 до 10-1 А/м). Она растет с увеличением содержания ферромагнитных минералов. С ростом температур остаточная намагниченность постепенно уменьшается и достигает нулевых значений при точках Кюри. Она также зависит от характера уплотнения и структурно-текстурных особенностей пород. Влияние магнетизма глинистых грунтов на их строение и свойства На поверхности глинистых минералов зачастую присутствуют высокодисперсные ферромагнитные частиц, которые достаточно прочно связаны с первыми. Их наличие сообщает глинистым суспензиям, пастам и осадкам слабо магнитные свойства. Магнитные свойства минералов и магнитное поле существенно влияют на: 1. Характер трещиноватости, образующейся в процессе осаждения глинистых суспензий и последующей сушки зависит как от напряженности внешнего магнитного поля, так и от минералогии глин:
2. Характер микроструктуры глинистых пород отчасти обусловлен воздействием магнитного поля. $nz=»Микростроение осадка Са-каолиновой глины, сформировавшегося в нулевом (а) и горизонтальном магнитном поле напряжённостью в ~ 800 А/м (б). Поверхность напластования (фото Ю.Б. Осипова).»; Рис. 1 . По абсолютной величине коэффициента ориентации глинистые осадки располагаются в ряд:
Это объясняется тем, что монтмориллонитовые глины обладают очень большой дисперсностью, а магнитные поля небольшой напряженности ориенти¬руют только относительно грубые частицы в глинистой фракции; тонкие же частицы находятся в состоянии теплового беспорядочного движения. 3. Механические и реологические свойства как глинистых суспензий, так и сформировавшихся осадков, т.к. изменение микростроения грунтов вызывает соответствующее изменение их свойств. Наиболее интенсивно это сказывается на физико-механических свойствах свойствах глинистых паст и молодых глинистых грунтов-осадков. |
5.7 Зависимость магнитной проницаемости ферромагнетиков от влияющих факторов
Магнитная
проницаемость ферромагнетиков зависит
от многих факторов, что может быть
положено в основу разработки разнообразных
типов датчиков, предназначенных для
измерения электрических и неэлектрических
величин.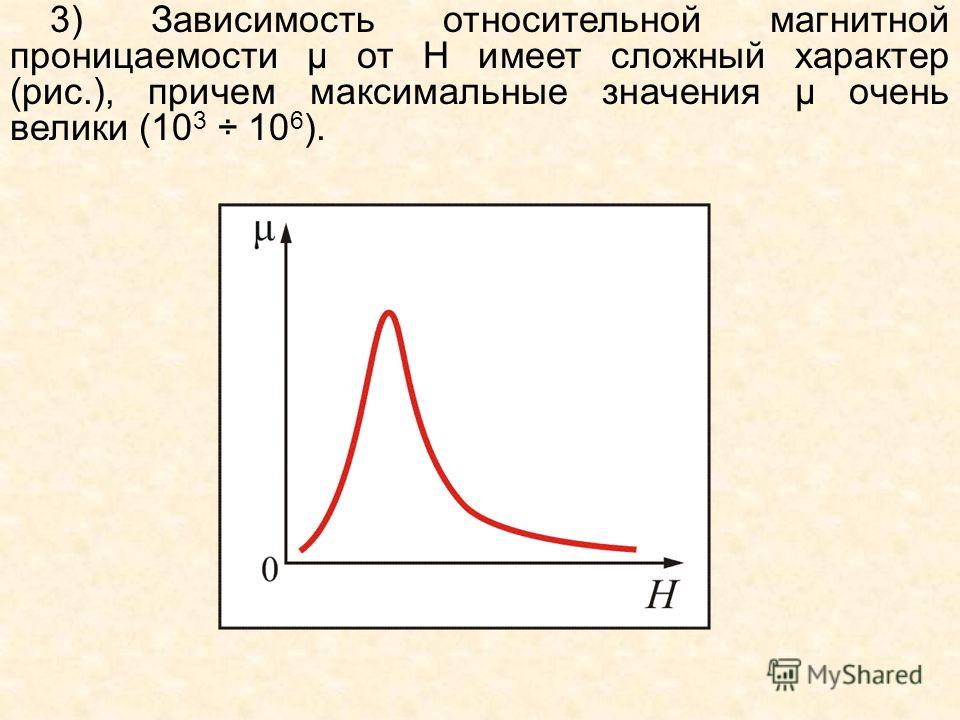
Зависимость
магнитной проницаемости ферромагнитных
материалов от напряженности магнитного
поля.
Рис. 5.18 Зависимость
магнитной проницаемости ферромагнетика
от напряженности магнитного поля.
Магнитная
проницаемость ферромагнетика зависит
от напряженности магнитного поля и
характеризуется наличием критической
намагниченности, при которой магнитная
проницаемость материала достигает
максимального значения.
Зависимость
магнитной проницаемости ферромагнитных
материалов от частоты изменения
напряженности магнитного поля.
Рис. 5.19 Зависимость
магнитной проницаемости ферромагнетика
от частоты магнитного поля.
Ферромагнитные
материалы характеризуются наличием
частоты среза, в окрестностях которой
происходит резкое изменение магнитных
свойств ферромагнетика.
Зависимость
магнитной проницаемости ферромагнитных
материалов от температуры.
Рис. 5.20 Зависимость
магнитной проницаемости ферромагнетика
от температуры..
Магнитная
проницаемость ферромагнитных материала
при нагревании возрастает, но при
достижении критической температуры
(точки Кюри) происходит разрушение
упорядоченности в структуре материала
и он переходит в парамагнитное состояние.
Зависимость
магнитной проницаемости ферромагнитных
материалов от механической напряженности
в материале.
Рис.
5.21 Зависимость магнитной проницаемости
ферромагнетика от механического
напряжения при различных напряженностях
магнитного поля.
Приведенные
графики отражают наличие магнитоупругого
эффекта в ферромагнетиках.
Зависимость
относительных деформаций ферромагнитных
материалов от величины напряженности
магнитного поля.
Рис. 5.22 Кривые,
характеризующие явление магнитострикции
в материалах.
Данные
зависимости отражают наличие
магнитострикционного эффекта в
ферромагнетиках.
Деформация петли
гистерезиса под действием механических
напряжений в ферромагнитных материалах.
Рис. 5.23 Зависимость
формы петли гистерезиса ферромагнетика
от величины и направления механических
напряжений в материале.
Как
следует из приведенных графиков,
остаточная индукция является функцией
механических напряжений в материале.
Под действием сжимающих усилий в
ферромагнетике происходит стабилизация
структуры, что сопровождается уменьшением
потерь на гистерезис.
Магнитотвердые
материалы характеризуются большим
значением остаточной коэрцитивной
силы. Основные характеристики для таких
материалов: легкость намагничивания;
малые магнитные потери на перемагничивание.
К их числу относятся сплавы: АЛНИКО;
АРМКО; ВИКАЛЛОЙ.
Магнитомягкими
материалами являются пермаллои, стали.
Существуют так же магнитные жидкости.
Ферромагнитные
материалы используют для записи
и хранения информации
(с
1947 г.).
Для
этих целей на поверхности подложки
наносят специальное ферролаковое
покрытие. Ток записи намагничивает
определенные области покрытия. Считывание
записанной информации осуществляется,
например, путем генерации ЭДС в катушке
индуктивности.
К
преимуществам таких запоминающих
устройств можно отнести следующие
факторы: это компактный, надежный
носитель информации, потребляющий мало
энергии; может сохранять информацию
без дополнительных источников энергии;
информация легко считывается; возможно
многократное использование носителя
информации.
Используют
различные способы
записи информации
на магнитные носители, например, без
возврата к нулю, с возвратом к нулю,
запись информации по двум и трем уровням
(намагничено, размагниченно, с насыщением),
фазовая модуляция и т.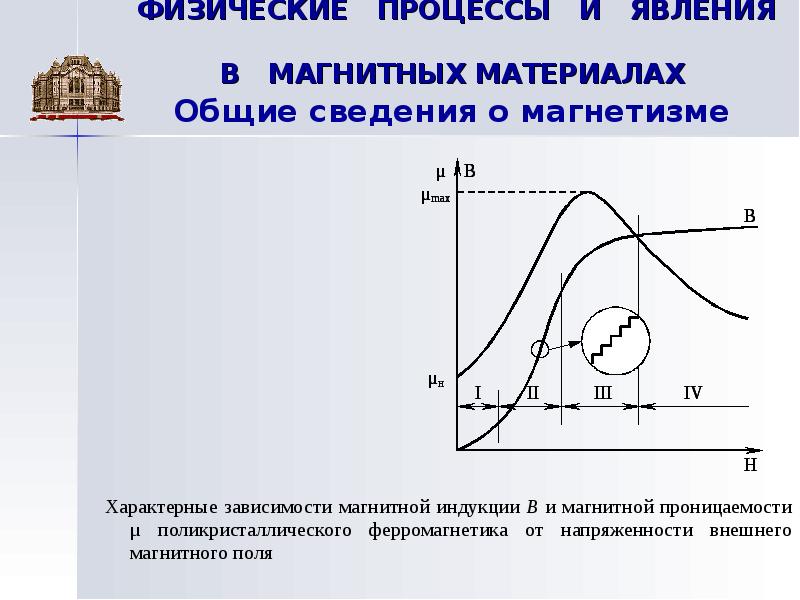 п.
п.
Есть статические
и динамические запоминающие устройства
на магнитных носителях, на пленках с
управлением движения доменов (используется
акустическая система), магнитоакустическое
запоминающее устройства, а также на
основе использования эффекта Фарадея
(поворот вектора поляризации света в
магнитном поле).
Контрольные
вопросы к главе 5
Объясните
принцип работы магнитоиндукционного
расходомера.Дайте
сравнительную характеристику индуктивных
и дифференциально-трансформаторных
первичных преобразователей.Объясните
механизм чувствительности вихретоковых
измерительных преобразователей.От
каких причин зависит глубина проникновения
электромагнитных волн в вещество?Объясните
физическую природу диамагнетизма и
ферромагнетизма.Приведите
примеры практического использования
ферримагнетиков и антиферромагнетиков
в измерительной технике.Опишите
принцип работы устройства для измерения
перемещений, основанного на использовании
эффекта Видемана.
Приведите
примеры практического использования
эффекта Баркгаузена.В чем особенность
принципа работы магнитоупругого
первичного измерительного преобразователя?Предложите
конструкцию дифференциального
магнитоупругого анизотропного первичного
преобразователя.Объясните причину
нелинейной зависимости магнитной
проницаемости ферромагнетных материалов
от различных влияющих факторов:
температуры, напряженности магнитного
поля, механических напряжений и т.п.Каким образов
изменяется вид петли гистерезиса
ферромагнетика при воздействии на него
растягивающих и сжимающих усилий.?
Восприимчивость магнитная ферромагнетика — Энциклопедия по машиностроению XXL
Существует особый класс парамагнетиков — ферромагнетики, у которых положительная магнитная восприимчивость (%>0) сильно меняется с изменением напряженности внешнего магнитного поля Я.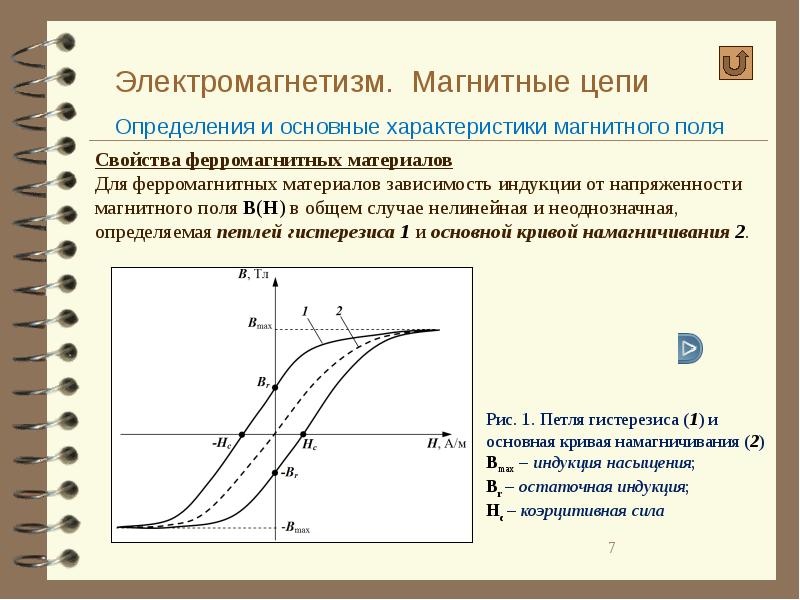 Так как %>0, то ферромагнетик усиливает внешнее магнитное поле. Примеры ферромагнетиков — железо, никель, кобальт. Существенное отличие ферромагнетиков от других парамагнетиков состоит в том, что у ферромагнетиков добавочная напряженность поля Я на много порядков выше, чем у обычных парамагнетиков (иными словами, магнитная восприимчивость у ферромагнетиков во много раз выше, чем у обычных парамагнетиков). Объясняется это следующим образом. Вместо отдельных магнитных диполей — молекул в ферромагнетиках имеют место значительно более крупные элементарные объединения — так называе
[c.44]
Так как %>0, то ферромагнетик усиливает внешнее магнитное поле. Примеры ферромагнетиков — железо, никель, кобальт. Существенное отличие ферромагнетиков от других парамагнетиков состоит в том, что у ферромагнетиков добавочная напряженность поля Я на много порядков выше, чем у обычных парамагнетиков (иными словами, магнитная восприимчивость у ферромагнетиков во много раз выше, чем у обычных парамагнетиков). Объясняется это следующим образом. Вместо отдельных магнитных диполей — молекул в ферромагнетиках имеют место значительно более крупные элементарные объединения — так называе
[c.44]
Рис. 16.26. Температурная зависимость магнитной восприимчивости %. В ферромагнетиках в интервале температур О ниже температуры Нееля спины ориентированы антипараллельно. Восприимчивость достигает максимума при Т = Ты, где на кривой % Т) наблюдается хорошо выраженный излом. Точка фазового перехода может быть зарегистрирована также по максимуму теплоемкости и коэффициента теплового расширения.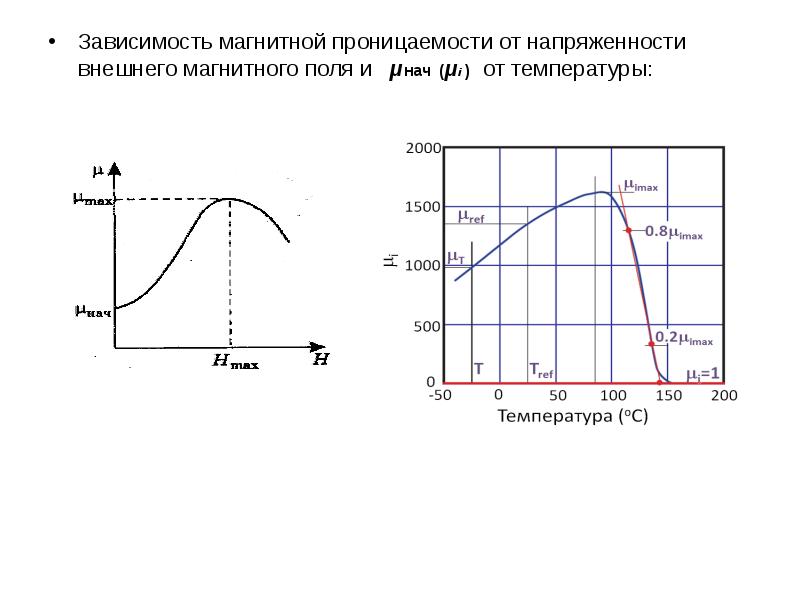
|
В 27.1 и 27.3 в каждом из пунктов, объединяющих ту или иную группу металлических ферромагнетиков, сначала приводятся температурные зависимости парамагнитной восприимчивости, зависимости намагниченности, удельного или атомного магнитного моментов от температуры, магнитного поля, состава сплавов и зависимости температур Кюри сплавов от их состава. Затем идут данные по магнитной анизотропии и, наконец. по магнитострикции.
[c.615]
Вещества, у которых и О, т. е. когда намагничивание происходит вдоль поля и восприимчивость слабо падает при повышении температуры, называются парамагнитными. Парамагнетики слабо притягиваются магнитным полем. К этой группе веществ относится большинство металлов, например щелочные, щелочно-земельные, переходные металлы, ферромагнетики выше точки Кюри. Вещества, у которых восприимчивость X > О по величине в миллиарды раз превосходит восприимчивость обычных диамагнетиков и парамагнетиков,
[c. 59]
59]
При наложении внешнего магнитного поля происходит рост объема доменов, которые имеют направление намагниченности, совпадающее или близкое к направлению напряженности поля. Зависимость магнитной индукции ферромагнитного вещества от напряженности внешнего поля называют кривой намагничивания, она имеет вид, показанный на рис. 3.4. Кривую намагничивания ферромагнетиков можно разделить на несколько участков, которые характеризуются определенными процессами намагничивания. В области слабых полей (область /) магнитные восприимчивость и проницаемость не изменяются. Изменение магнитной индукции в этой области происходит в основном за счет обратимых процессов, которые обусловлены смещением границ доменов. [c.88]
Для диамагнетиков х 0. Для особой подгруппы ферромагнетиков это простое соотношение (170) не соблюдается, и функциональная зависимость М от Н имеет нелинейный характер и не является однозначной.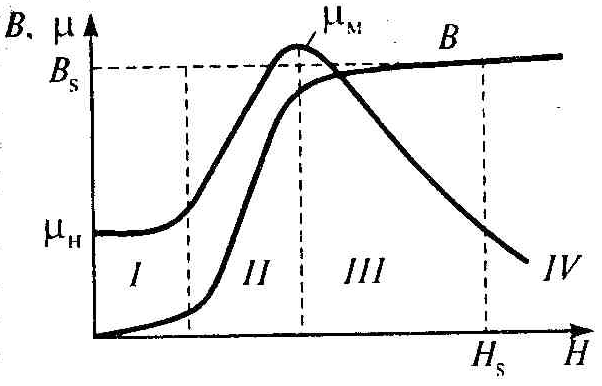 Все ферромагнетики имеют характерную кривую намагничивания и петлю гистерезиса. Магнитная восприимчивость ферромагнетиков зависит от напряженности внешнего поля в то время как для диамагнетиков и парамагнетиков х почти не зависит от Я. С другой стороны, парамагнетизм и ферромагнетизм в отличие от диамагнетизма зависят от температуры, возрастая с ее понижением. Выше температуры точки Кюри ферромагнетики становятся парамагнетиками для каждого вещества имеется своя точка Кюри .
[c.129]
Все ферромагнетики имеют характерную кривую намагничивания и петлю гистерезиса. Магнитная восприимчивость ферромагнетиков зависит от напряженности внешнего поля в то время как для диамагнетиков и парамагнетиков х почти не зависит от Я. С другой стороны, парамагнетизм и ферромагнетизм в отличие от диамагнетизма зависят от температуры, возрастая с ее понижением. Выше температуры точки Кюри ферромагнетики становятся парамагнетиками для каждого вещества имеется своя точка Кюри .
[c.129]
Следует еще раз подчеркнуть, что у парамагнетиков магнитная восприимчивость уменьшается с ростом температуры, т. е. (д%1дТ) [c.45]
Для ферромагнетиков — магнитная восприимчивость X положительна, сильно изменяется с изменением напряженности внешнего магнитного поля и температуры. При температурах выше температуры точки Кюри 0 ферромагнетик ведет себя как обычный парамагнетик. [c.159]
В зависимости от знака и степени магнитной восприимчивости материалов различают диамагнетики, парамагнетики и ферромагнетики. [c.819]
[c.819]
Ферромагнетики обладают высокой магнитной восприимчивостью. Из всех металлов только четыре — железо, кобальт, никель и гадолиний — обладают высокими ферромагнитными свойствами. [c.819]
Металлические элементы в зависимости от знака и величины их магнитной восприимчивости можно разделить на три класса диамагнетики (медь, серебро, золото с отрицательной и малой величиной х) парамагнетики (большая часть других металлов со слабо положительной величиной х) и ферромагнетики (х велика и положительна). Жидкие металлы и сплавы с ферромагнитными свойствами не известны. Полную восприимчивость металлической жидкости xi, можно представить в виде суммы восприимчивости ионных остовов атомов (диамагнитная восприимчивость) и восприимчивости электронов (парамагнитная) [c.113]
В парамагнитной области выше температуры Кюри магнитная восприимчивость ферромагнетика подчиняется закону Кюри — Вейсса [c.250]
Намагниченность материала является функцией внешнего магнитного поля М=хНо, где х — магнитная восприимчивость вещества материала, причем в сильномагнитных материалах, таких как ферромагнетики и ферримагнетики, магнитная восприимчивость является нелинейной функцией поля.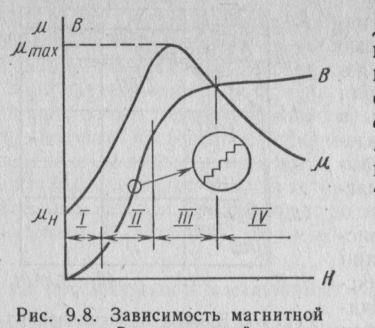 [c.13]
[c.13]
Существует большая группа веществ обладающих спонтанной намагниченностью, т. е. имеющих не равную нулю намагниченность даже в отсутствие магнитного поля. Такие магнетики называются ферромагнетиками. Ферромагнетики относятся к магнитоупорядоченным веществам. К группе магнитоупорядоченных веществ относятся также антиферромагнетики и ферримагнетики. Основные классы магнитных веществ в зависимости от знака и величины магнитной восприимчивости приведены в табл. 4.1. [c.275]
Антипараллельная ориентация спиновых моментов возникает при отрицательном обменном взаимодействии (4.9). Как и в ферромагнетиках, антипараллельное магнитное упорядочение имеет место в интервале температур от О К до некоторой критической Ты — температуры Нееля. При температуре Нееля происходит фазовый переход 2-го рода превращение антиферромагнетик парамагнетик. При Г> Гн магнитная восприимчивость описывается законом Кюри-Вейсса (4.8), где поправка Вейсса равна Гы (рис.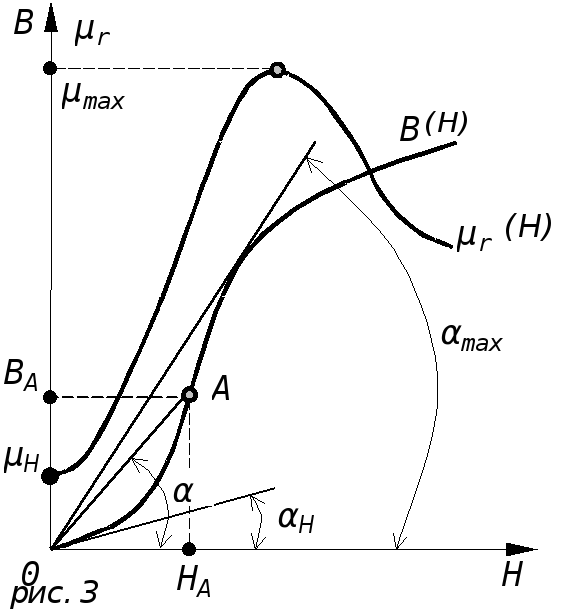 4.2).
[c.280]
4.2).
[c.280]
Параллельная ориентация магн. моментов (рис. 1) устанавливается при темп-рах Т ниже критич. темп-ры Кюри 0 (см. Кюри точка). Часто Ф. наз. совокупность физ. св-в в-ва в указанном выше состоянии. В-ва, в к-рых установился ферромагн. порядок атомных магп. моментов, наз. ферромагнетиками. Магнитная восприимчивость X ферромагнетиков положительна (и>0) и достигает значений 10 —10 их намагниченность J и [c.808]
Кроме диа- и парамагнетиков существует большая группа веществ, обладающих спонтанной намагниченностью, т. е. имеющих не равную нулю намагниченность даже в отсутствие магнитного поля. Эта группа магнетиков получила название ферромагнетиков. Для них зависимость / (Я) является нелинейной функцией, и полный цикл перемагничения описывается петлей гистерезиса (рис. 10.2). В этих веществах магнитная восприимчивость сама зависит от Н. [c.320]
Наряду со слабомагнитными телами существует ряд веществ, например ферромагнетики, для которых намагниченность не является линейной функцией поля. Для диамагнетиков характерно, что восприимчивость, как правило, не зависит от температуры, а для парамагнетиков она часто изменяется обратно пропорционально абсолютной температуре. Магнитные свойства атома обусловлены следующими факторами орбитальным движением электроно)в спиновыми эффектами магнетизмом атомного ядра Нейтроны и протоны, составляющие ядро, обладают собственными магнитными моментами. Однако величина магнитного момента нуклона из-за того, что его масса почти в 2000 раз больше массы электрона, пренебрежимо мала по сравнению с магнитным моментом электрона. Вычисление суммарных моментов атомов облегчается тем, что как суммарный орбитальный, так и суммарный спиновый момент полностью застроенных электр(зн-ных оболочек равен нулю. Поэтому следует принимать во внимание лишь электроны, занимающие незаполненные оболочки.
[c.143]
Для диамагнетиков характерно, что восприимчивость, как правило, не зависит от температуры, а для парамагнетиков она часто изменяется обратно пропорционально абсолютной температуре. Магнитные свойства атома обусловлены следующими факторами орбитальным движением электроно)в спиновыми эффектами магнетизмом атомного ядра Нейтроны и протоны, составляющие ядро, обладают собственными магнитными моментами. Однако величина магнитного момента нуклона из-за того, что его масса почти в 2000 раз больше массы электрона, пренебрежимо мала по сравнению с магнитным моментом электрона. Вычисление суммарных моментов атомов облегчается тем, что как суммарный орбитальный, так и суммарный спиновый момент полностью застроенных электр(зн-ных оболочек равен нулю. Поэтому следует принимать во внимание лишь электроны, занимающие незаполненные оболочки.
[c.143]
Магнитные свойства и строение вещества. Как известно электрон обладает спиновым и орбитальным магнитными моментами. Геометрически складываясь моменты электронов создают результирующий магнитный момент атома М. Суммарный магнитный момент в единице объема, именуемый намагниченностью J, когда вещество не было намагничено и внешнее поле отсутствует, равняется нулю. Под воздействием магнитного иоля со средней напряженностью внутри тела, равной Н, намагниченность J = %Н, где х— магнитная восприимчивость. Намагниченность определяет величину магнитной индукции В = В + + %Н. Магнитные свойства вещества характеризует также относительная магнитная проницаемость х = 1 -10 гн м — магнитная постоянная вакуума. В зависимости от величины и знака магнитной восприимчивости вещества могут быть диамагнитные (Х>0). Рассмотрим две последние группы веществ. В парамагнитных веществах у атомов имеются магнитные моменты, однако иод влиянием теплового движения эти моменты располагаются статистически беспорядочно вдоль магнитного поля удается ориентировать лишь примерно одну десятитысячную процента всех спинов. В результате магнитная восприимчивость X мало отличается от нуля, а магнитная проницаемость парамагнитных материалов немногим больше единицы.
Суммарный магнитный момент в единице объема, именуемый намагниченностью J, когда вещество не было намагничено и внешнее поле отсутствует, равняется нулю. Под воздействием магнитного иоля со средней напряженностью внутри тела, равной Н, намагниченность J = %Н, где х— магнитная восприимчивость. Намагниченность определяет величину магнитной индукции В = В + + %Н. Магнитные свойства вещества характеризует также относительная магнитная проницаемость х = 1 -10 гн м — магнитная постоянная вакуума. В зависимости от величины и знака магнитной восприимчивости вещества могут быть диамагнитные (Х>0). Рассмотрим две последние группы веществ. В парамагнитных веществах у атомов имеются магнитные моменты, однако иод влиянием теплового движения эти моменты располагаются статистически беспорядочно вдоль магнитного поля удается ориентировать лишь примерно одну десятитысячную процента всех спинов. В результате магнитная восприимчивость X мало отличается от нуля, а магнитная проницаемость парамагнитных материалов немногим больше единицы. К парамагнитным принадлежат некоторые переходные металлы, а также щелочные и щелочно-земельные металлы. Ферромагнитные материалы обладают весьма большой магнитной восприимчивостью, может достигать значений порядка 10 , после снятия поля сохраняется остаточная намагниченность. Ферромагнитные свойства при нагревании наблюдаются лишь до некоторой температуры 0, отвечающей точке Кюри — переходу нз ферромагнитного в парамагнитное состояние. Значение 0 для железа 769° С, для кобальта 1120° С, для никеля 358 С. При температурах Т G в отсутствие внешнего поля ферромагнетик состоит из микроскопических областей — доменов, самопроиз-
[c.226]
К парамагнитным принадлежат некоторые переходные металлы, а также щелочные и щелочно-земельные металлы. Ферромагнитные материалы обладают весьма большой магнитной восприимчивостью, может достигать значений порядка 10 , после снятия поля сохраняется остаточная намагниченность. Ферромагнитные свойства при нагревании наблюдаются лишь до некоторой температуры 0, отвечающей точке Кюри — переходу нз ферромагнитного в парамагнитное состояние. Значение 0 для железа 769° С, для кобальта 1120° С, для никеля 358 С. При температурах Т G в отсутствие внешнего поля ферромагнетик состоит из микроскопических областей — доменов, самопроиз-
[c.226]
Магнитные свойства ферромагнитных тел. У ферромагнитных тел, типичным представителем которых является железо, и также положительная, но значительно больше, чем у парамагнетиков. Кроме того, к у них зависит от Я. Помимо железа, в эту группу входят никель, кобальт, гадолиний и т. д., а также ряд сплавов. Закономерности намагничивания ферромагнетиков были впервые исследованы Столетовым.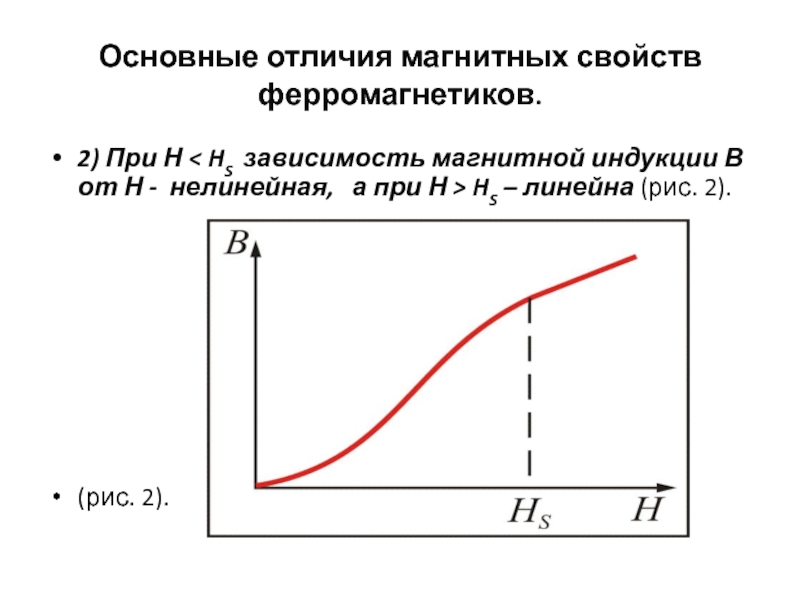 На рис. 11.2 показана зависимость от Я намагниченности J , индукции В и восприимчивости к мягкого железа. С увеличением напряженности намагничивающего поля В и растут вначале быстро, з тем рост замедлястся, а начиная с некоторого значений Н ,. памагни-
[c.286]
На рис. 11.2 показана зависимость от Я намагниченности J , индукции В и восприимчивости к мягкого железа. С увеличением напряженности намагничивающего поля В и растут вначале быстро, з тем рост замедлястся, а начиная с некоторого значений Н ,. памагни-
[c.286]
В ферромагнетиках, в отличие от парамагнитных тел, между неспаренными электронами внутренних недостроенных оболочек имеет место сильное обменное взаимодействие, вызывающее упорядоченное расположение их СПИновых магнитных моментов и спонтанное намагничивание доменов до насыщения Это приводит к существенным особенностям в протекании резонансного поглощения высокочастотной энергии ферромагнетиками, которое называют ферромагнитным резонансом. Физическая суть его состоит е том, что под действием внешнего магнитного поля Нд, намагничивающего ферромагнетик до насыщения, полный магнитный момент образца М начинает прецессировать вокруг этого поля с ларморовой частотой ojl, зависящей от Яо (11.25). Если на такой образец наложить высокочастотное электромагнитное поле, перпендикулярное Яо, и изменять его частоту ш, то при ю = i. наступает резкое (резонансное) усиление поглощения энергии поля. Резонанс наблюдается на частотах порядка 20-Г-30 ГГц в полях 4- 10 -А/м (л 5000 Э). Поглощение при этом на несколько порядкоз выше, чем при парамагнитном резонансе, так как магнитная восприимчивость ферромагнетиков (а следовательно, и магнитный момент насыщения М) у них много выше, чем у парамагнетиков. Кроме того, так как в формировании эффективного магнитного поля в ферромагнетиках участвуют размагничивающий фактор и поле магнитной анизотропии, то частота ферромагнитного резонанса оказывается зависящей от формы образца.и,направления поля относительно осей легкого намагничивания.
[c.306]
наступает резкое (резонансное) усиление поглощения энергии поля. Резонанс наблюдается на частотах порядка 20-Г-30 ГГц в полях 4- 10 -А/м (л 5000 Э). Поглощение при этом на несколько порядкоз выше, чем при парамагнитном резонансе, так как магнитная восприимчивость ферромагнетиков (а следовательно, и магнитный момент насыщения М) у них много выше, чем у парамагнетиков. Кроме того, так как в формировании эффективного магнитного поля в ферромагнетиках участвуют размагничивающий фактор и поле магнитной анизотропии, то частота ферромагнитного резонанса оказывается зависящей от формы образца.и,направления поля относительно осей легкого намагничивания.
[c.306]
МАГНИТНАЯ ВОСПРИИМЧИВОСТЬ, величина, характеризующая связь намагниченности вещества с магнитным ппле.к в атом веществе. М, в, х в статич. полях равна отнохненню намагниченности вещества М к напряжённости Я намагничивающего поля к — величина безразмерная. М. в., рассчитанная на 1 кг (или 1 г) вещества, наз. удельной (у. уд -л/р, где р — плотность вещества), а М. в. одного моля — м о-л я р н о ii (или атомной) у =Худ-т, где т — молекулярная масса вещества. С магнитной проницаемостью М. в. D статнч. полях (статич. М. в.) связана соотношениями ) = 1 + 4як (в ед. СГС), (,1 = 1+и (в ед. СИ), М. в. может быть как положительной, так и отрицательной. Отрицательной М. в. обладают диамагнетики (ДМ), они намагничиваются против поля ноложитель-Пой — парамагнетики (ПМ) и ферромагнетики. (ФМ), они намагничиваются по нолю. М. в. ДМ и ПМ мала по абс. величине —10 ), она слабо зависит от Н и то лишь в области очень сильных полей (и низких темп-р). Значения Й1. в. си. в табл.
[c.649]
уд -л/р, где р — плотность вещества), а М. в. одного моля — м о-л я р н о ii (или атомной) у =Худ-т, где т — молекулярная масса вещества. С магнитной проницаемостью М. в. D статнч. полях (статич. М. в.) связана соотношениями ) = 1 + 4як (в ед. СГС), (,1 = 1+и (в ед. СИ), М. в. может быть как положительной, так и отрицательной. Отрицательной М. в. обладают диамагнетики (ДМ), они намагничиваются против поля ноложитель-Пой — парамагнетики (ПМ) и ферромагнетики. (ФМ), они намагничиваются по нолю. М. в. ДМ и ПМ мала по абс. величине —10 ), она слабо зависит от Н и то лишь в области очень сильных полей (и низких темп-р). Значения Й1. в. си. в табл.
[c.649]
Магнитная восприимчивость ферромагнетиков может достигать значений 10 —10 Гс/Э их намагниченность Л/, возникающая во внеш. магн. поле Н, растёт с его величиной нелинейно (см. Намагничивание) и в полях 1 ] 00 Э может достигать магнитного насыщения, характеризуемого значением Величина М зависит также от магн. предыстории образца, что приводит к неоднозначности ф-ции М Н), или к гистерезису магнитному. При намагничивании и перемагничивании ( ррОмагнетика происходит изменение размеров и формы образца (см. Магнитострикция), благодаря этому кривые намагничивания и петли гистерезиса зависят от внеш. напряжений. Наблюдаются также аномалии в величине и температурной зависимости упругих постоянных ферромагнетиков — т. н. Дг -эффект и др. (см. Механострикция, Магнитомеха-нииеские явления), а также коэф. линейного и объёмного
[c.294]
При намагничивании и перемагничивании ( ррОмагнетика происходит изменение размеров и формы образца (см. Магнитострикция), благодаря этому кривые намагничивания и петли гистерезиса зависят от внеш. напряжений. Наблюдаются также аномалии в величине и температурной зависимости упругих постоянных ферромагнетиков — т. н. Дг -эффект и др. (см. Механострикция, Магнитомеха-нииеские явления), а также коэф. линейного и объёмного
[c.294]
| Рис. 1. Частотые и полевые 1ависимости компонент тензора магнитной ВЧ-восприимчивости, намагниченного до насыщения изотропного ферромагнетика (беч учета потерь), |
Характер температурной зависимости величины % для ферромагнетиков иллюстрируется рис. 3-2 (на этом графике изображена температурная зависимость магнитной проницаемости л = 1 + 4яу. = 1 -Н (4я»/)/а для железа при Я = 0). Как видно из этого графика, с приближением к точке Кюри при Я F= onst магнитная восприимчивость ферромагнетика возрастает, достигая максимума вблизи точки Кюри, а в непосредственной близости от точки Кюри резко уменьшается — так называемый эффект Гопкинсона (этот эффект наблюдается только в слабых магнитных полях). Появление этого максимума обусловлено значительным уменьшением магнитной анизотропии ферромагнетика вблизи точки Кюри, благодаря чему процесс намагничения ферромагнетика становится более легким , а уменьшение X при дальнейшем приближении к точке Кюри определяется исчезновением спонтанной намагниченности ферромагнетика при Т = в. При Г 0 величина % продолжает уменьшаться с ростом температуры, причем зависимость % от Т в этой области описывается законом Кюри—Вейсса (3-14) 3-3.
[c.45]
Появление этого максимума обусловлено значительным уменьшением магнитной анизотропии ферромагнетика вблизи точки Кюри, благодаря чему процесс намагничения ферромагнетика становится более легким , а уменьшение X при дальнейшем приближении к точке Кюри определяется исчезновением спонтанной намагниченности ферромагнетика при Т = в. При Г 0 величина % продолжает уменьшаться с ростом температуры, причем зависимость % от Т в этой области описывается законом Кюри—Вейсса (3-14) 3-3.
[c.45]
Что касается парамагнетиков и ферромагнетиков, то у них, как отмечено выше, (д%1дТ) р — магнитная восприимчивость уменьшается с ростом температуры. С учетом этого обстоятельства из уравнения (3-34) следует, что величина duldj)j. для этих типов магнетиков, вообще говоря, может быть и положительной, и отрицательной. Очевидно, чтб если (д%1дТ). > (Х Т), то (Эи/[c.50]
Таким образом, под размерными эффектами в самом широком смысле слова следует понимать комплекс явлений, связанных с изменением свойств вещества вследствие собственно изменения размера частиц и одновременного возрастания доли поверхностного вклада в общие свойства системы. Благодаря отмеченным особенностям строения нанокристаллические материалы по свойствам существенно отличаются от обычных поликристаллов. По этой причине уменьшение размера зерен рассматривается как эффективный метод изменения свойств твердого тела. Действительно, имеются сведения о влиянии наносостоя-ния на магнитные свойства ферромагнетиков (температуру Кюри, коэрцитивную силу, намагниченность насыщения) и магнитную восприимчивость слабых пара- и диамагнетиков, об эффектах памяти на упругих свойствах металлов и существенном изме-
[c.13]
Благодаря отмеченным особенностям строения нанокристаллические материалы по свойствам существенно отличаются от обычных поликристаллов. По этой причине уменьшение размера зерен рассматривается как эффективный метод изменения свойств твердого тела. Действительно, имеются сведения о влиянии наносостоя-ния на магнитные свойства ферромагнетиков (температуру Кюри, коэрцитивную силу, намагниченность насыщения) и магнитную восприимчивость слабых пара- и диамагнетиков, об эффектах памяти на упругих свойствах металлов и существенном изме-
[c.13]
Температурная зависимость восприимчивости в насыщающих магнитных полях при низких температурах для обычных ферромагнетиков не такая сильная, как наблюдалось в эксперименте (см. рис. 3.15) [176]. Сильная зависимость при низких температурах возможна в случае суперпарамагнетизма выделившихся частиц железа. Суперпарамагнитный вклад выраженный в безразмерных единицах, при температуре Т в магнитном поле Н можно представить в виде [328]
[c. 105]
105]
Магнитная восприимчивость может бьггь как положительной, так и отрицательной. Отрицательной магнитной восприимчивостью обладают диамагнетики, они намагничиваются против поля положительной — парамагнетики и ферромагнетики, они намагничиваются по полю. [c.100]
Исследования [186, 191-193] показали, что измерение магнитной восприимчивости является информативным методом изучения новедения ферромагнитных наночастиц в диамагнитной матрице. Наличие матрицы препятствует интенсивному росту наночастиц при температуре структурной релаксации соотвест-вующего ферромагнитного поликристалла и тем самым значительно увеличивает температурный интервал существования наносостояния ферромагнетика. [c.122]
Возможность применения указанных феррохмагнетиков для регистрации полей дефектов объясняется тем, что вращение плосршс-ти поляризации у этих веществ, по данным Г. С. Кринчика, оп )еде-ляется диагональной компонентой тензора магнитной восприимчивости и является следствием ферромагнитного и обменного резонансов, зависящих от намагниченности ферромагнетика в исследуемом магнитном поле. [c.230]
[c.230]
По данным [14] соединение УСоз является ферримагнетиком с температурой Кюри 301 °К. Магнитная восприимчивость этого соединения проходит через максимум при 170 °К- Согласно [47] УСоз — ферромагнетик с температурой Кюри 387°К- Повышение давления до 6 кбар снижает температуру Кюри этого соединения на 20,5°К (взято из графика). [c.701]
Ферромагнитные вещества — это вещества, которые сильно притягиваются магнитом. К ним относятся, например, металлы — железо, кобальт, никель — и их сплавы. Относительная магнитная восприимчивость этих веществ достигает 10 . Характеристики х,- и ,1г ферромагнитных веществ изменяются не только от индукции магнитного поля, но и от температуры. Среди ферромагнитных веществ имеются такие, например как феррит-шпинели и феррит-гранаты, у которых по сравнению с Ре и N1 механизм возникновения ферромагнетизма имеет некоторые особенности. Эти вещества носят название феррпмагнетиков. Другие вещества — как РеО, МпО, СггОз и МпгОз — характеризуются значениями такого же порядка малости, как в случае парамагнетиков, но по внутренней магнитной структуре указанные оксиды более близки к ферромагнетикам.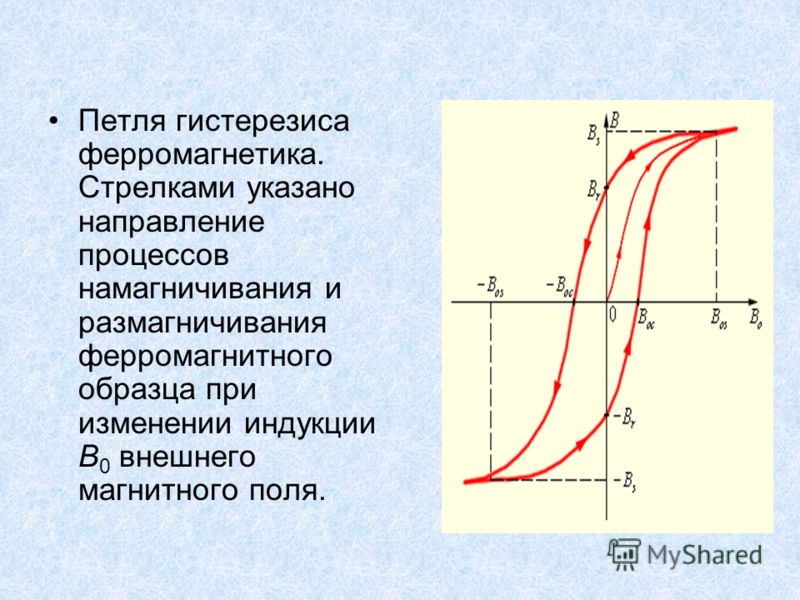 Учитывая это, их называют антиферромагнетиками. Теория ферримаг-нетиков и антиферромагнетиков составляет часть теории ферромагнетиков. Ферромагнетики находят широкое применение в электротехнике.
[c.146]
Учитывая это, их называют антиферромагнетиками. Теория ферримаг-нетиков и антиферромагнетиков составляет часть теории ферромагнетиков. Ферромагнетики находят широкое применение в электротехнике.
[c.146]
Магнитная проницаемость — обзор
Поскольку для всех практических целей магнитная проницаемость биологических материалов — это проницаемость свободного пространства [3], проводимость и диэлектрическая проницаемость являются двумя определяющими параметрами, которые необходимо обсудить. Напомним уравнение ротора Максвелла для магнитного поля (H) во временной области
(2.1) ∇ × H (t) = σfE (t) + ∂D (t) / ∂t
, где E и D — электрическое поле интенсивность и электрическое смещение соответственно. Более того, σ f — это проводимость, связанная со свободными зарядами, которые обычно могут быть свободными электронами в проводниках, электронами и дырками в полупроводниках или свободными ионами в электролитах и биологических средах. Для этого представления два члена в правой части уравнения можно рассматривать как плотности тока проводимости и смещения, соответственно. Наличие электрического поля E вызывает поляризацию атомов, поляризацию неполярных молекул, переориентацию диполярного момента полярных молекул (например, воды) или поляризацию зарядов из-за накопления заряда на границе раздела между двумя разнородными диэлектриками. в гетерогенных средах, таких как биологические ткани [1–3,25,26].Это приводит к чистому электрическому моменту и, следовательно, к электрической поляризации P, которая играет главную роль в установлении связи между D и E:
Для этого представления два члена в правой части уравнения можно рассматривать как плотности тока проводимости и смещения, соответственно. Наличие электрического поля E вызывает поляризацию атомов, поляризацию неполярных молекул, переориентацию диполярного момента полярных молекул (например, воды) или поляризацию зарядов из-за накопления заряда на границе раздела между двумя разнородными диэлектриками. в гетерогенных средах, таких как биологические ткани [1–3,25,26].Это приводит к чистому электрическому моменту и, следовательно, к электрической поляризации P, которая играет главную роль в установлении связи между D и E:
(2.2) D (t) = ε0E (t) + P (t)
, где ε 0 = 8,854 × 10 −12 (Ф / м) — диэлектрическая проницаемость свободного пространства. Это уравнение сохраняет свою форму для случая гармоники во времени (после замены полей и поляризации во временной области их векторами), где рассматривается установившаяся ситуация для одночастотных синусоидальных волн. Для линейной среды (что является реалистичным предположением для биологических тканей и напряженности электрического поля менее 10 5 В / м [25]) электрическая поляризация линейно пропорциональна напряженности электрического поля, то есть:
Для линейной среды (что является реалистичным предположением для биологических тканей и напряженности электрического поля менее 10 5 В / м [25]) электрическая поляризация линейно пропорциональна напряженности электрического поля, то есть:
(2.3 ) P (ω) = ε0χ (ω) E (ω)
, где ω (= 2π f ) — частота в радианах, а χ ( ω ) — электрическая восприимчивость. Восприимчивость обозначена как функция частоты, чтобы подчеркнуть ее частотную зависимость (т.е.е. его дисперсионный характер) для тканей и биологических материалов. Таким образом, уравнение. (2.2) приводит к следующему соотношению в векторной области:
(2.4) D (ω) = ε0 [1 + χ (ω)] E (ω)
Параметр в скобках — относительная комплексная диэлектрическая проницаемость, связанная с электрическая поляризация
(2.5) εp (ω) = 1 + χ (ω) = ε′p (ω) −jεp ″ (ω)
, где ε′p и εp ″ — действительная и мнимая диэлектрическая проницаемость соответственно. Переписывая уравнение. (2.1) в частотной области дает
(2.1) в частотной области дает
(2.6) ∇ × H = σfE (ω) + jωε0 [1 + χ (ω)] E (ω) = jωε0 (−jσfωε0 + ε′p − jεp ″) E (ω )
Величина в скобках — это общая относительная комплексная диэлектрическая проницаемость, включая проводимость для свободных зарядов, т.е.е .:
(2.7) ε (ω) = ε′p (ω) −j [εp ″ (ω) + σfωε0] = ε ′ (ω) −jε ″ (ω)
с ε ′ (ω) = ε′p (ω) и ε ″ (ω) = εp ″ (ω) + σf / ωε0, которые обозначены как функция частоты, чтобы подчеркнуть дисперсионный характер комплексной диэлектрической проницаемости в биологических средах. Действительная и мнимая диэлектрическая проницаемость (ε′иε ″) в литературе также называется диэлектрической проницаемостью и коэффициентом потерь. Более того, они (вместе с ε ) представляют относительные величины в большинстве ссылок на параметры биологических тканей. Отметим также, что, что касается потерь ЭМ энергии в биологических средах, εp ″ и σf / ωε0, т.е.е., факторы потерь, связанные с поляризацией и перемещением свободных зарядов, неразличимы.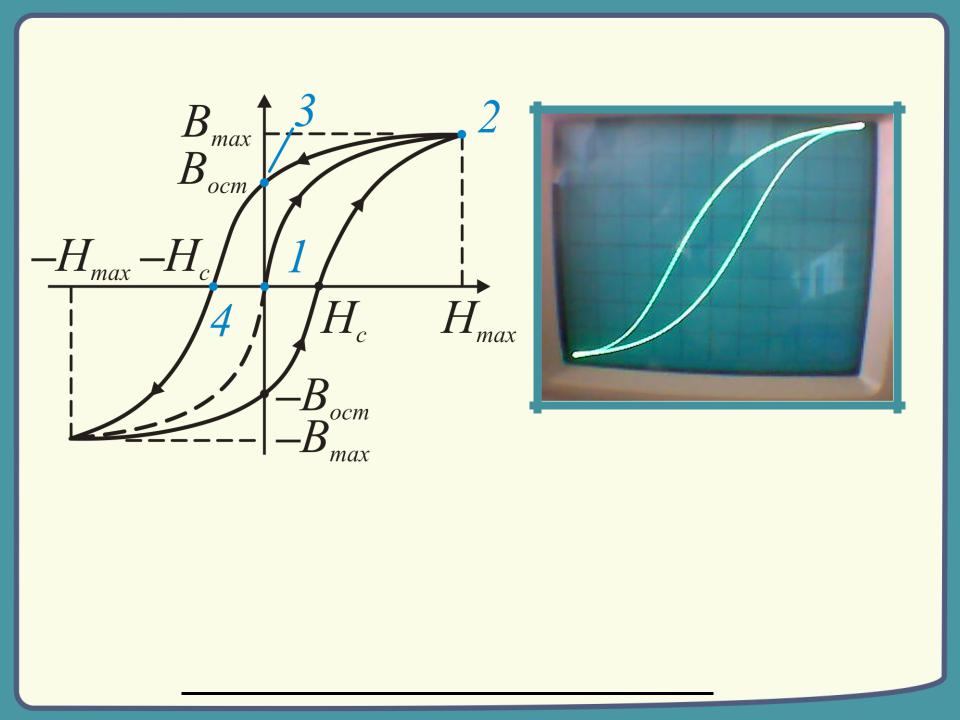 Тем не менее, по мере увеличения частоты вклад σf в общий коэффициент потерь уменьшается как величина, обратная частоте. В дополнение к коэффициенту общих потерь можно также учитывать сопутствующую общую проводимость, которая составляет
Тем не менее, по мере увеличения частоты вклад σf в общий коэффициент потерь уменьшается как величина, обратная частоте. В дополнение к коэффициенту общих потерь можно также учитывать сопутствующую общую проводимость, которая составляет
(2,8) σ (ω) = ωε0ε ″ (ω) = ωε0εp ″ (ω) + σf
. Помимо общей проводимости и потерь Фактор, степень потери ЭМ энергии в материале можно понять с помощью другого параметра, т.е.е., тангенс угла потерь, который представляет собой отношение мнимой диэлектрической проницаемости к реальной:
(2,9) tgδ = ε ″ ε ′ = σωε′ε0
В линейной системе поле может быть представлено суммированием плоские волны. Более того, плоские волновые параметры диэлектрической среды также представляют собой волновые параметры для распространения поперечной электромагнитной (ПЭМ) волны в линиях передачи, однородно заполненных тем же диэлектриком. Таким образом, чтобы получить некоторое представление о распространении волн в диэлектрической среде, было бы целесообразно обсудить параметры распространения плоских волн в этой среде. Двумя важными параметрами волны являются фазовая постоянная ( β ) и постоянная затухания ( α ), которые представляют собой действительную и мнимую части постоянной распространения ( γ )
Двумя важными параметрами волны являются фазовая постоянная ( β ) и постоянная затухания ( α ), которые представляют собой действительную и мнимую части постоянной распространения ( γ )
(2.10) γ = α + jβ = jωμ0ε0ε = jωμ0ε0 (ε′ − jε ″)
, что дает
(2.11) α = ωcε′21 + tanδ2−1
(2.12) β = ωcε′21 + tanδ2 + 1
Длина волны плоской волны ( λ ) равно
(2,13) λ = 2πβ = λ0ε’21 + tanδ2 + 1-1
, где c — скорость света в вакууме, а λ 0 (= c / f ) — длина волны в свободном пространстве.Параметр, обратный постоянной затухания, называется глубиной проникновения или глубиной проникновения δ (= 1/ α ) и описывает степень проникновения поля плоской волны в среду, которая имеет экспоненциальную форму e — z / δ . Достаточно большой блок материала с потерями (допускающий распространение плоской волны в направлении z ) представляет собой затухание e −1 (36,8%) для интенсивности поля на глубине δ для падающей плоской волны.
Обратите внимание, что обнаружение E в биологических средах, которые являются дисперсными, неоднородными или имеют неправильную форму, не является тривиальной задачей и обычно требует решения уравнений Максвелла аналитически или численно. Сценарии решения этих уравнений сильно различаются в зависимости от характера приложений. Некоторые сценарии представляют собой биологические объекты, подвергающиеся облучению плоской волной или облучению дальним полем антенн для дозиметрических целей или биорадара. Другие — это облучение тканей, расположенных в ближнем поле антенн при гипертермии, или в приложениях для получения изображений и считывания с помощью ЭМ, или при распространении волн изнутри или внутрь тела для беспроводной связи имплантатов.
Магнитная проницаемость — обзор
Магнитная восприимчивость рассчитывается по выражению
(12,125) χμv = −1VlimB → 0∂2Ω∂Bμ∂Bv.
Из ур. (12.121) — (12.123), можно показать, что 14
(12. 126) χμv = 1Vβ [−∂2∂Bμ∂BvTrln (−G˜ξl) + Tr∂2Σ˜ξl∂Bμ∂BvG˜ξl + Tr∂Σ˜ξl∂Bμ∂G˜ξl∂Bv] B → 0.
126) χμv = 1Vβ [−∂2∂Bμ∂BvTrln (−G˜ξl) + Tr∂2Σ˜ξl∂Bμ∂BvG˜ξl + Tr∂Σ˜ξl∂Bμ∂G˜ξl∂Bv] B → 0.
Можно разложить
(12,127) Σ˜ (κ →, B, ξl) = Σ˜ (k, B, ξl) −ihαβ∂Σ˜ (k, B, ξl) ∂kα∇kβ − 12hαβhγδ∂2Σ ˜∂kα∂kγ∇kβ∇kδ +…
и
(12.′ (K, ξl) = — ihαβ∏α∇kβ + 12gμBBμσμ + BμΣ1, μ (k, ξl) −ihαβBμ∂Σ1, μ∂kα∇kβ − 12hαβhγδ [ħ2mδαγ + ∂2Σ0∂kα∂kγ] ∇kβ∇kδ + BμBvΣ2, μv (k, ξl),
, где сохранены члены до второго порядка по магнитному полю, а ∏ → / ℏ — оператор скорости,
(12.133) ∏ → = ħm (p → + ħk) + ħ24m2c2σ → × ∇ → V + ∇kΣ0 (k, ξl).
Можно провести разложение по возмущениям
(12.134) G˜ (k, ξl) = G0 (k, ξl) + G0 (k, ξl) H′G0 (k, ξl) + G0 (k, ξl) H ′ G0 (k, ξl) H′G0 (k, ξl) + …,
, где
(12.135) G0 (k, ξl) = 1ξl − H0 (k, ξl),
и только члены вверх ко второму порядку по магнитному полю.Можно показать, что (Задача 12.14)
(12.136) ∇kαG0 (k, ξl) = G0 (k, ξl) ∏αG0 (k, ξl)
и
(12.137) ∇kα∇kγG0 (k, ξl) = G0 [ħ2mδαγ + Χαγ] G0 + G0∏αG0∏γG0 + G0∏γG0∏αG0,
, где
(12,138) Χαγ = ∇kα [ħ24m2c2 (σ → × ∇ → V) γ + ∇kγ 0 (k, ξl)].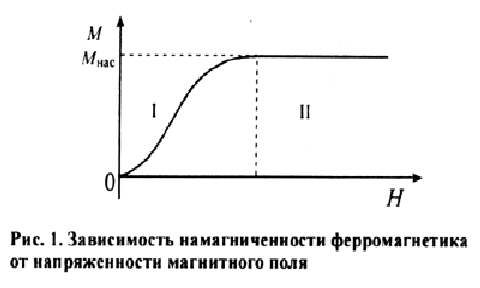
После обширной алгебры (подробности см. Misra et al. 14 ) общее выражение для полной магнитной восприимчивости неферромагнитных твердых тел (включая эффекты обмена и корреляции) получается как
(12.139) χμv = χ0μv + χsμv + χsoμv,
, где
(12.140) χ0μv = ∑k (1 + δμv) {e2∈αβμ∈γδv48ħ2c2∇kα∇kγEn∇kβ∇kδEnf ′ (En) ∈γδv4ħ2c2 (−2ħ2m∏nρ, mρ′α∏mρ ′, nργEmn2δβδ + 2∏nρ, mρ′α∏mρ ′, nρ «γ∏nρ», qρ «′ β∏qρ» ′, nρδEmn2Eqn − 2∏nρ, mρ′α∏mρ ′, qρ «γ∏qρ», lρ «′ β∏lρ» ′, nρδElnEqnEmn − ∏nρ, nρα∏nρ, mρ′γ∏mρ ′, qρ «δ∏qρ», nρβEmnEqn2 + ∏ nρ, nρα∏nρ, mρ′β∏mρ ′, qρ «γ∏qρ», nρδEmn2Eqn − ∏nρ, mρ′βΧmρ ′, qρ «αγ∏qρ», nρδEmnEqn + ∏nρ, mρ′β∏mρ ′, qρ » δΧqρ «, nραγEmnEqn + Χnρ, mρ′αγ∏mρ ′, qρ« β∏qρ », nρδEmnEqn − Χnρ, nραγ∏nρ, mρ′β∏mρ ′, nρδEmn2] + ie4ħc∈αβv [′∏βYmρ ′, mρ ′ , nραμEmn − Ynρ, mρ′αμ∏mρ ′, nρβEmn] f (En),}
, где
(12.141) Emn≡Em-En,
и повторяющиеся индексы означают суммирование по полосе и спину. Точно так же можно показать 14 , что эффективная спиновая восприимчивость Паули, включая эффекты обмена и корреляции, равна
(12,142) χsμv = −18 (1 + δμv) μB2∑n, k, ρ, ρ′gnnv (k ) σnρ, nρ′v (gnnμ (k) σnρ ′, nρμ + 2μBΣnρ ′, nρ1, μ) f ′ (En),
, где эффективная матрица g определяется как
(12. 143) gnnv (k) σnρ, nρ′v = ieμBħc∈αβv∑m, ρ «∏nρ, mρ» α∏mρ «, nρ′βEmn + gσnρ, nρ′v.
143) gnnv (k) σnρ, nρ′v = ieμBħc∈αβv∑m, ρ «∏nρ, mρ» α∏mρ «, nρ′βEmn + gσnρ, nρ′v.
Дополнительный спин-орбитальный вклад в магнитную восприимчивость составляет 14
(12.144) χsoμν = ∑k (1 + δμν) [e2∈αβμ∈γδν2ℏ2c2 ∏nρ, mρ’α∏mρ ‘, nρ «β ∏nρ», qρ «‘ γ∏qρ» ‘, nρδEmn2EqniegμB4ℏc∈αβν {−3Jnρ, nρ’μ∏nρ ‘, mρ «α∏mρ», nρβEmn2 + ∏nρ, mρ’α∏mρ’, qρ «βJqρ», nρμEqnEmn + ∏nρ, mρ’αJmρ ‘, qρ «μ∏qρ», nρβEqnEmn + Jnρ, mρ’μ∏mρ ‘, qρ «α∏qρ», nρβEqnEmn + ∏nρ, nραJnρ, mρ «μ∏mρ», nρβEmn2 − ∏nρ, nρα∏nρ, mρ’βJmρ’, nρμEmn2} + 18g2μB2 {σnρ, m μFmρ ‘, nρνEmn + Fnρ, mρ’μσmρ’, nρνEmn}] f (En),
, где
(12,145) J → = σ → + 1gμBΣ1,
(12,146) Yμv = ∂Σ1, v∂kμ,
и
(12,147) Fv = σv + 2gμBΣ1, v.
14.2: Магнитные свойства материалов
Магнетизм металлов и других материалов определяется орбитальными и спиновыми движениями неспаренных электронов и тем, как неспаренные электроны выравниваются друг с другом.Все магнитные вещества парамагнитны при достаточно высокой температуре, когда тепловая энергия (kT) превышает энергию взаимодействия между спинами соседних атомов.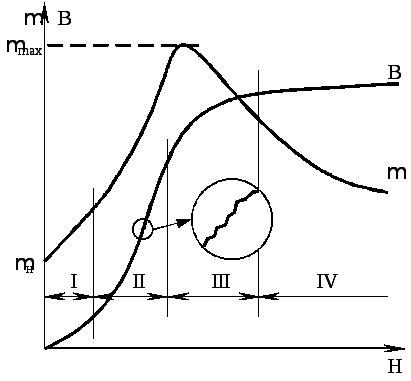 Ниже определенной критической температуры вращения могут принимать различные виды упорядоченного расположения.
Ниже определенной критической температуры вращения могут принимать различные виды упорядоченного расположения.
Наглядное описание упорядочения спинов в ферромагнетизме, антиферромагнетизме, ферримагнетизме и парамагнетизме |
Давайте начнем с рассмотрения отдельного атома в структуре ОЦК металлического железа.Fe находится в группе VIIIb периодической таблицы, поэтому имеет восемь валентных электронов. Атом переводится в состояние 4s 1 3d 7 для образования связей. Локализованная картина d-электронов для отдельного атома железа может выглядеть так:
Поскольку каждый неспаренный электрон имеет спиновый момент 1/2, полный спиновый угловой момент, S , для этого атома равен:
\ (S = 3 \ frac {1} {2} = \ frac {3} {2} \) (в единицах h / 2π)
Мы можем представить каждый атом Fe в твердом теле как небольшой стержневой магнит с моментом только вращения S 3/2. Спиновые моменты соседних атомов могут выстраиваться параллельно (↑ ↑), антипараллельно (↑ ↓) или случайным образом. В ОЦК-Fe наблюдается тенденция к параллельному выравниванию из-за положительного знака обменного взаимодействия. Это приводит к упорядочению ферромагнетик , в котором все спины в магнитном домене (обычно сотни элементарных ячеек по ширине) имеют одинаковую ориентацию, как показано на рисунке справа. Напротив, отрицательное обменное взаимодействие между соседними атомами в ОЦК Cr приводит к антиферромагнитному упорядочению .Третье устройство, ферримагнитное упорядочение , является результатом антипараллельного выравнивания спинов на соседних атомах, когда магнитные моменты соседей не равны. В этом случае спиновые моменты не компенсируются и возникает суммарная намагниченность. Механизм упорядочения подобен механизму антиферромагнитного твердого тела, но магнитные свойства напоминают свойства ферромагнетика. Ферримагнитное упорядочение наиболее часто встречается в оксидах металлов, как мы узнаем в главе 7.
Спиновые моменты соседних атомов могут выстраиваться параллельно (↑ ↑), антипараллельно (↑ ↓) или случайным образом. В ОЦК-Fe наблюдается тенденция к параллельному выравниванию из-за положительного знака обменного взаимодействия. Это приводит к упорядочению ферромагнетик , в котором все спины в магнитном домене (обычно сотни элементарных ячеек по ширине) имеют одинаковую ориентацию, как показано на рисунке справа. Напротив, отрицательное обменное взаимодействие между соседними атомами в ОЦК Cr приводит к антиферромагнитному упорядочению .Третье устройство, ферримагнитное упорядочение , является результатом антипараллельного выравнивания спинов на соседних атомах, когда магнитные моменты соседей не равны. В этом случае спиновые моменты не компенсируются и возникает суммарная намагниченность. Механизм упорядочения подобен механизму антиферромагнитного твердого тела, но магнитные свойства напоминают свойства ферромагнетика. Ферримагнитное упорядочение наиболее часто встречается в оксидах металлов, как мы узнаем в главе 7.
Намагниченность и восприимчивость
Магнитная восприимчивость , χ твердого тела зависит от упорядочения спинов.Парамагнитные, ферромагнитные, антиферромагнитные и ферримагнитные твердые тела имеют χ> 0, но величина их восприимчивости зависит от типа упорядочения и температуры. Мы увидим эти виды магнитного упорядочения в основном среди элементов 3d и 4f , а также их сплавов и соединений. Например, Fe, Co, Ni, Nd 2 Fe 14 B, SmCo 5 и YCo 5 — все ферромагнетики, Cr и MnO — антиферромагнетики, а Fe 3 O 4 и CoFe 2 O 4 — ферримагнетики.Диамагнитные соединения имеют слабую отрицательную восприимчивость (χ <0).
Определения
- H = приложенное магнитное поле (единицы: Генри (H))
- B = индуцированное магнитное поле в материале (единицы: тесла (Т))
- M = намагниченность, которая представляет магнитные моменты внутри материала в присутствии внешнего поля H.

Магнитная восприимчивость χ = M / H
Обычно χ дается в молярных единицах в системе cgs :
χ M = молярная восприимчивость (единицы: см 3 / моль)
Типичные значения χ M :
| Сложный | Тип магнетизма | χ при 300 К (см 3 / моль) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SiO 2 | Диамагнитный | — 3 х 10 -4 | ||||||||
| Pt металл | Паули парамагнитный | + 2 х 10 -4 | ||||||||
ГД 2 (СО 4 ) 3 .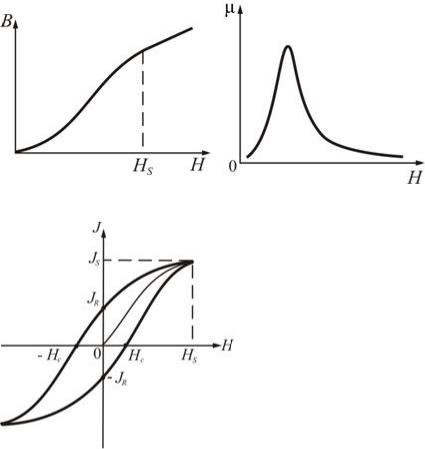 {2} _ {eff} \] {2} _ {eff} \]Обратите внимание, что C не является «константой» в обычном смысле, потому что она зависит от µ eff , эффективного магнитного момента молекулы или иона , который, в свою очередь, зависит от количества неспаренных электронов: \ [\ mu_ {eff} = \ sqrt {n (n + 2)} \ mu_ {B} \]
|

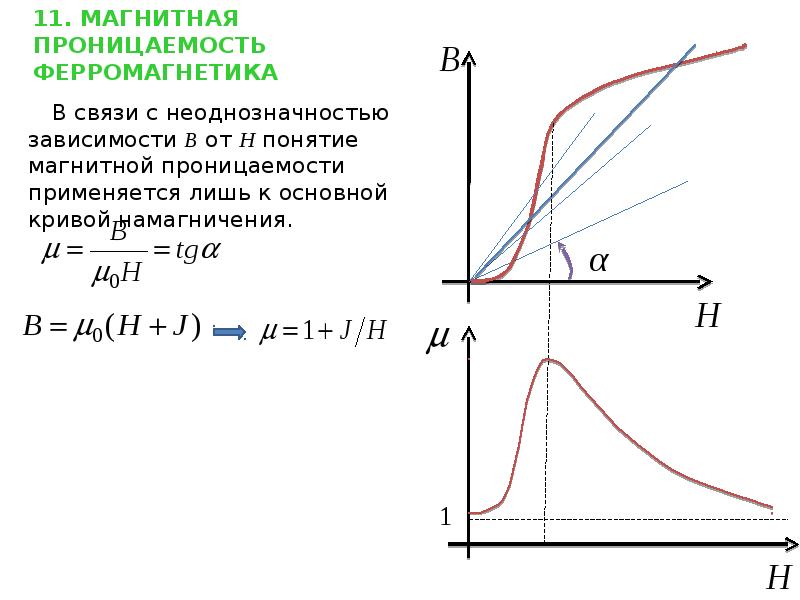

 Таким образом, существует зависимость магнитных свойств от предшествующей намагниченности вещества.
Таким образом, существует зависимость магнитных свойств от предшествующей намагниченности вещества.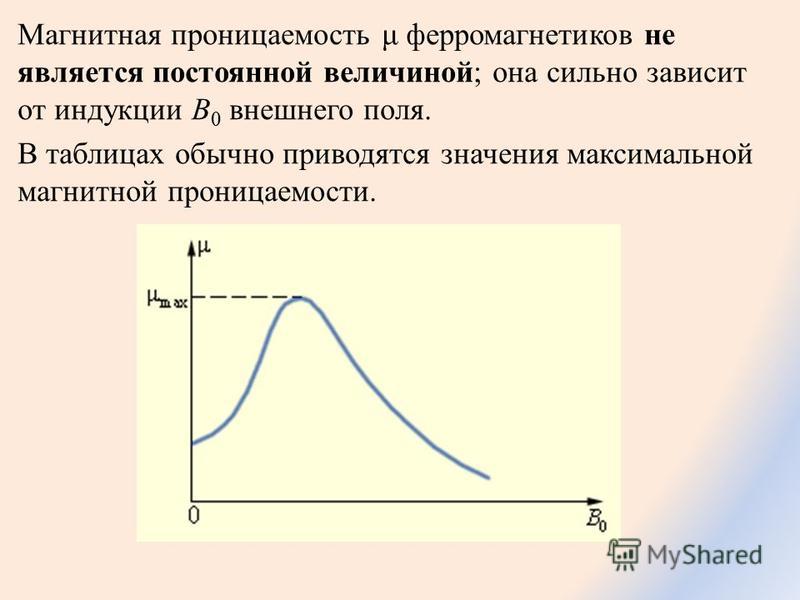 Они обладают большой коэрцитивной силой и используются для создания постоянных магнитов различной формы (полосовых,подковообразных, магнитных стрелок). К мягким магнитным материалам,обладающим малой коэрцитивной силой и узкой петлей гистерезиса, относятся железо, сплавы железа с никелем. Эти материалы используются для изготовления сердечников трансформаторов, генераторов и других устройств, по условиям работы которых происходит перемагничивание в переменных магнитных петлях. Перемагничивание ферромагнетика связано с поворотом областей самопроизвольного намагничивания. Работа, необходимая для этого, совершается за счет энергии внешнего магнитного поля. Количество теплоты, выделяющейся при перемагничивании, пропорционально площади петли гистерезиса.
Они обладают большой коэрцитивной силой и используются для создания постоянных магнитов различной формы (полосовых,подковообразных, магнитных стрелок). К мягким магнитным материалам,обладающим малой коэрцитивной силой и узкой петлей гистерезиса, относятся железо, сплавы железа с никелем. Эти материалы используются для изготовления сердечников трансформаторов, генераторов и других устройств, по условиям работы которых происходит перемагничивание в переменных магнитных петлях. Перемагничивание ферромагнетика связано с поворотом областей самопроизвольного намагничивания. Работа, необходимая для этого, совершается за счет энергии внешнего магнитного поля. Количество теплоты, выделяющейся при перемагничивании, пропорционально площади петли гистерезиса. Домены называются иначе областями самопроизвольной намагниченности. В отсутствие внешнего магнитного поля векторы магнитных моментов отдельных доменов ориентированы внутри ферромагнетика совершенно беспорядочно, так что суммарный магнитный момент всего тела равен нулю (рис.). Под влиянием внешнего магнитного поля в ферромагнетиках происходит поворот вдоль поля магнитных моментов не отдельных атомов или молекул, как в парамагнетиках, а целых областей самопроизвольной намагниченности — доменов. При увеличении внешнего поля размеры доменов, намагниченных вдоль внешнего поля, растут за счет уменьшения размеров доменов с другими (не совпадающими с направлением внешнего поля) ориентациями. При достаточно сильном внешнем магнитном поле все ферромагнитное тело оказывается намагниченным. Величина намагниченности достигает максимального значения — наступает магнитное насыщение. В отсутствие внешнего поля часть магнитных моментов доменов остается ориентированной, и этим объясняется существование остаточной намагниченности и возможность создания постоянных магнитов.
Домены называются иначе областями самопроизвольной намагниченности. В отсутствие внешнего магнитного поля векторы магнитных моментов отдельных доменов ориентированы внутри ферромагнетика совершенно беспорядочно, так что суммарный магнитный момент всего тела равен нулю (рис.). Под влиянием внешнего магнитного поля в ферромагнетиках происходит поворот вдоль поля магнитных моментов не отдельных атомов или молекул, как в парамагнетиках, а целых областей самопроизвольной намагниченности — доменов. При увеличении внешнего поля размеры доменов, намагниченных вдоль внешнего поля, растут за счет уменьшения размеров доменов с другими (не совпадающими с направлением внешнего поля) ориентациями. При достаточно сильном внешнем магнитном поле все ферромагнитное тело оказывается намагниченным. Величина намагниченности достигает максимального значения — наступает магнитное насыщение. В отсутствие внешнего поля часть магнитных моментов доменов остается ориентированной, и этим объясняется существование остаточной намагниченности и возможность создания постоянных магнитов.
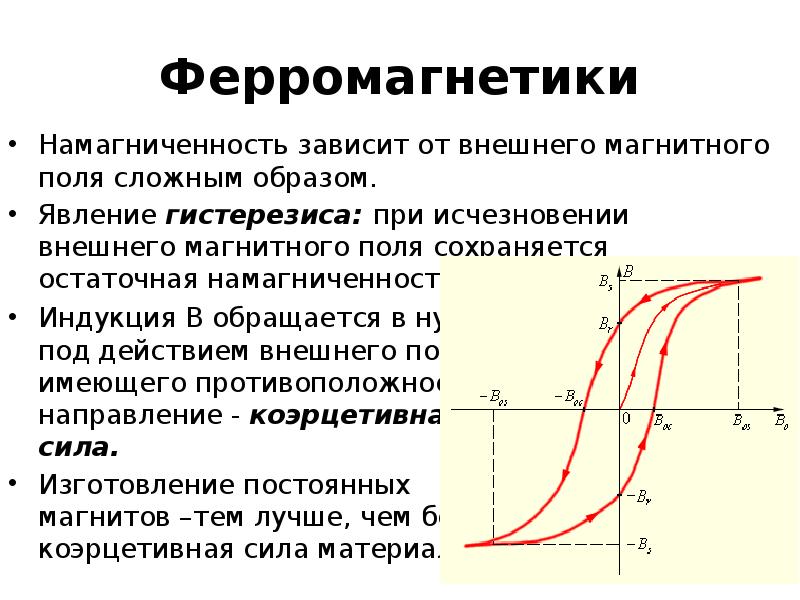 Суть эффекта – в возникновении индуцированных внутриатомных токов, которые уменьшают индукцию магнитного поля в веществе. Магнитная восприимчивость диамагнетиков отрицательна.
Суть эффекта – в возникновении индуцированных внутриатомных токов, которые уменьшают индукцию магнитного поля в веществе. Магнитная восприимчивость диамагнетиков отрицательна. Appl. Phys. 79, 6448 (1996).
Appl. Phys. 79, 6448 (1996).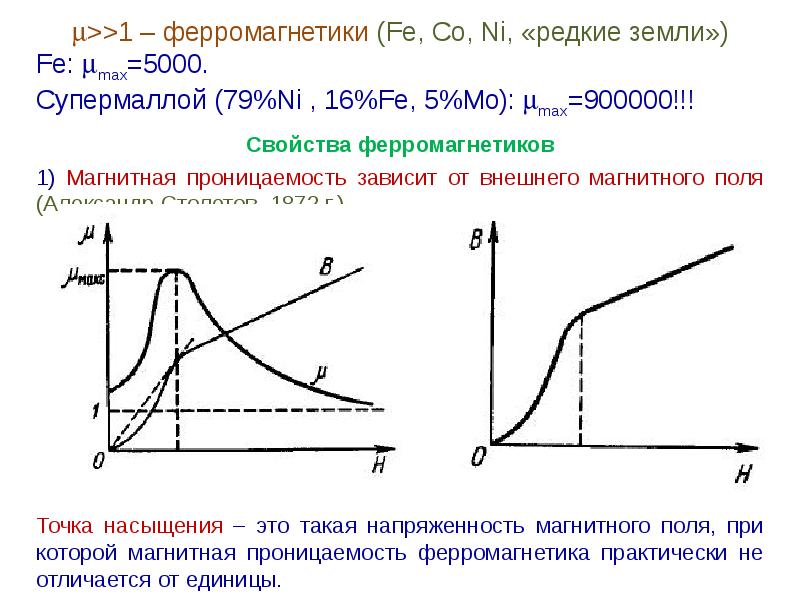 Москва, 2011, стр. 357
Москва, 2011, стр. 357

 При отсутствии внешнего магнитного поля парамагнетики в целом не намагничены вследствие хаотичного распределения в них магнитных моментов отдельных атомов. Под вли¬янием внешнего магнитного поля элементарные магнетики (атомы и молекулы парамагнетиков) приобретают определенную ориентировку, что обуслов¬ливает появление индуктивного намагничивания в парамагнетиках.
При отсутствии внешнего магнитного поля парамагнетики в целом не намагничены вследствие хаотичного распределения в них магнитных моментов отдельных атомов. Под вли¬янием внешнего магнитного поля элементарные магнетики (атомы и молекулы парамагнетиков) приобретают определенную ориентировку, что обуслов¬ливает появление индуктивного намагничивания в парамагнетиках. 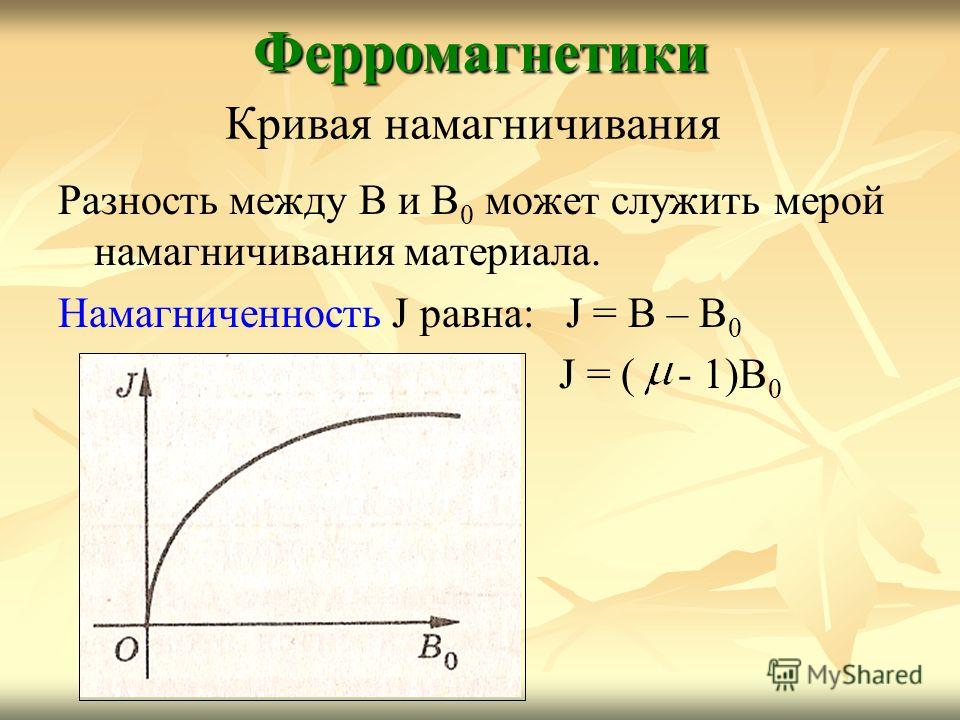 При этом элементарные магнетики могут занимать либо параллельную (ферромагнетики), либо частично параллельную (ферримагнетики), либо антипараллельную ориентацию (антиферромагнетики).
При этом элементарные магнетики могут занимать либо параллельную (ферромагнетики), либо частично параллельную (ферримагнетики), либо антипараллельную ориентацию (антиферромагнетики).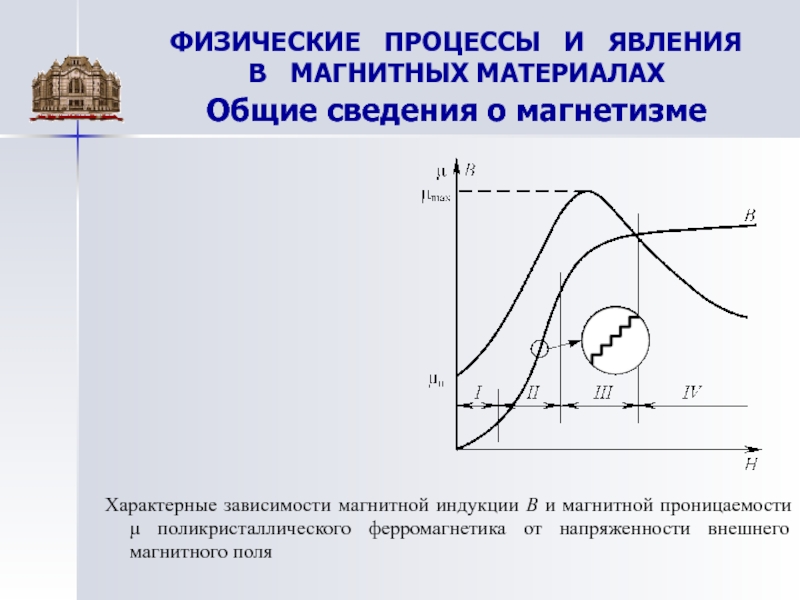 Твердая компонента грунта в большинстве состоит из смеси диа-, пара, ферри- и реже ферромагнитных минералов. В соответствии с этим ее магнитные свойства зависят в основном от содержания и распределения ферри- и редко ферро¬магнитных минералов. Значения магнитной восприимчивости этой компоненты грунта изменяются от -0,4×10-5 и менее до 1 ед. СИ.
Твердая компонента грунта в большинстве состоит из смеси диа-, пара, ферри- и реже ферромагнитных минералов. В соответствии с этим ее магнитные свойства зависят в основном от содержания и распределения ферри- и редко ферро¬магнитных минералов. Значения магнитной восприимчивости этой компоненты грунта изменяются от -0,4×10-5 и менее до 1 ед. СИ.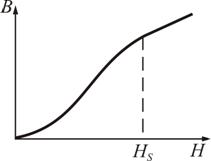 СИ.
СИ. СИ
СИ Наибольшая ее величина характерна для магматических пород:
Наибольшая ее величина характерна для магматических пород: СИ.
СИ. е:
е: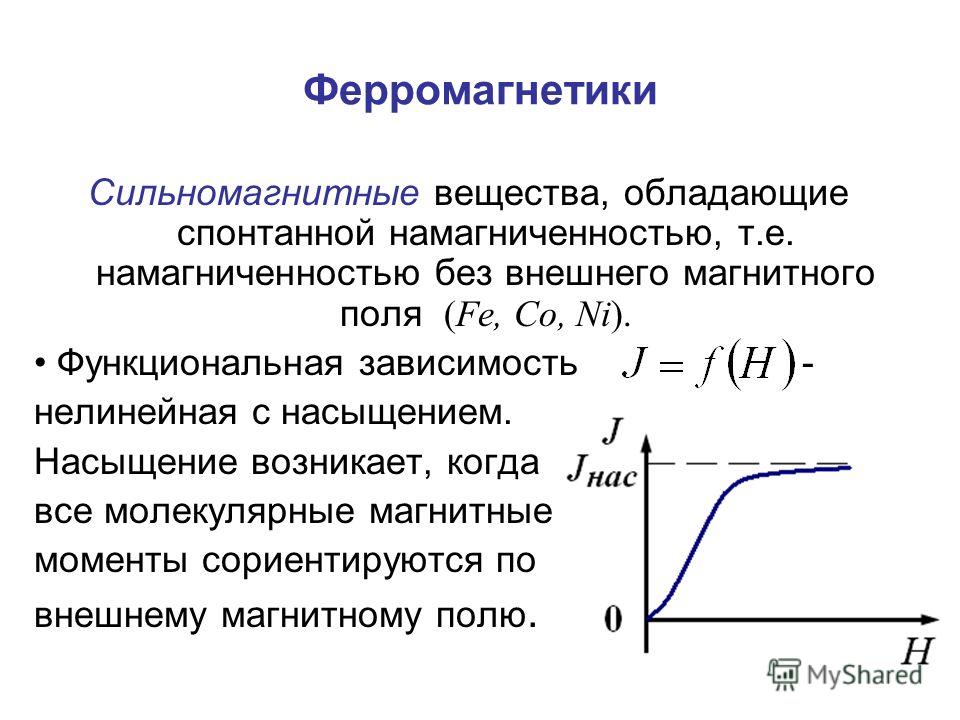
 — Увеличение напряженности магнитного поля вызывает возрастание агрегированности частиц и повышение ориентации как самих частиц, так и их агрегатов (рис. 1). При этом установлено, что частицы гидрослюдистой и каолиновой глин реагируют даже на геомагнитное поле.
— Увеличение напряженности магнитного поля вызывает возрастание агрегированности частиц и повышение ориентации как самих частиц, так и их агрегатов (рис. 1). При этом установлено, что частицы гидрослюдистой и каолиновой глин реагируют даже на геомагнитное поле. Насыщение глин ионом Na+ независимо от напряженности поля приводит к увеличению ориентации частиц. При наличии же в обменном комплексе двухвалентных катионов (например, Са2+) в большинстве случаев формируются агрегаты размером до песчаных частиц с хорошей ориентацией частиц внутри них. Сами же агрегаты относительно друг друга практически не ориентированы. Это говорит о том, что внешнее магнитное поле повышает ориентацию частиц главным образом в пределах одного блока.
Насыщение глин ионом Na+ независимо от напряженности поля приводит к увеличению ориентации частиц. При наличии же в обменном комплексе двухвалентных катионов (например, Са2+) в большинстве случаев формируются агрегаты размером до песчаных частиц с хорошей ориентацией частиц внутри них. Сами же агрегаты относительно друг друга практически не ориентированы. Это говорит о том, что внешнее магнитное поле повышает ориентацию частиц главным образом в пределах одного блока.
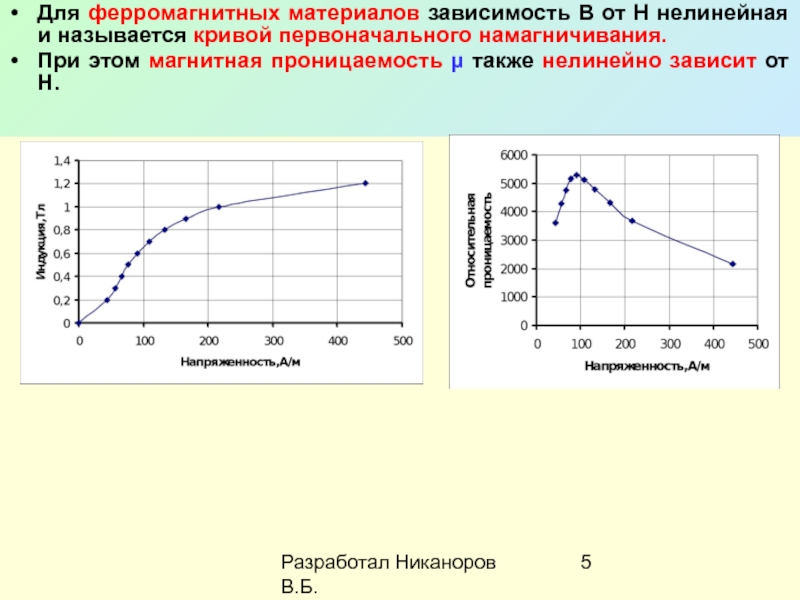

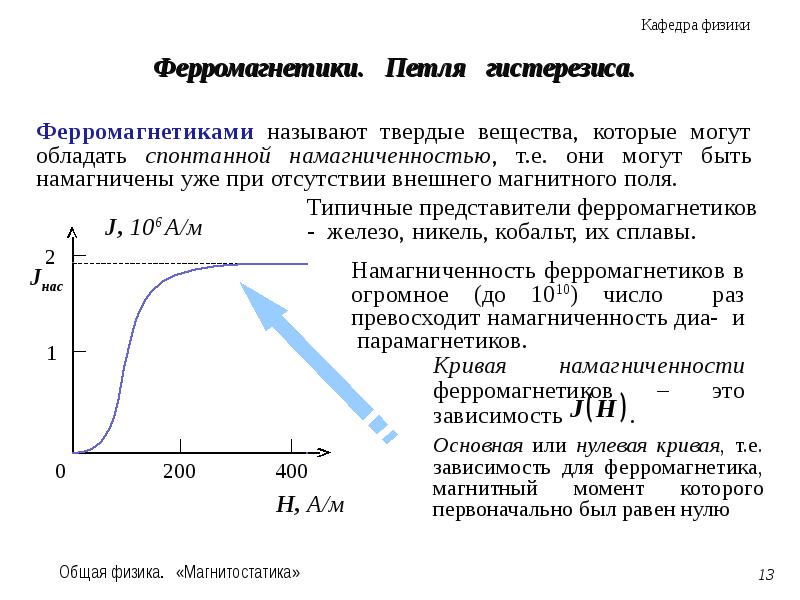
 Поскольку упорядочение зависит от короткодействующего обменного взаимодействия, эта критическая температура широко варьируется. Металлы и сплавы серии 3d имеют тенденцию к высоким критическим температурам, потому что атомы напрямую связаны друг с другом и взаимодействие является сильным.Например, Fe и Co имеют критические температуры (также называемые температурой Кюри, T c для ферромагнитных веществ) 1043 и 1400 K соответственно. Температура Кюри определяется силой магнитного обменного взаимодействия и количеством неспаренных электронов на атом. Количество неспаренных электронов между Fe и Co достигает пиков по мере заполнения d-зоны, и обменное взаимодействие для Co сильнее, чем для Fe. В отличие от ферромагнитных металлов и сплавов, парамагнитные соли ионов переходных металлов обычно имеют критические температуры ниже 1 К, поскольку магнитные ионы не связаны напрямую друг с другом и, следовательно, их спины очень слабо связаны в твердом состоянии.Например, в сульфате гадолиния парамагнитные ионы Gd 3+ изолированы друг от друга ионами SO 4 2-.
Поскольку упорядочение зависит от короткодействующего обменного взаимодействия, эта критическая температура широко варьируется. Металлы и сплавы серии 3d имеют тенденцию к высоким критическим температурам, потому что атомы напрямую связаны друг с другом и взаимодействие является сильным.Например, Fe и Co имеют критические температуры (также называемые температурой Кюри, T c для ферромагнитных веществ) 1043 и 1400 K соответственно. Температура Кюри определяется силой магнитного обменного взаимодействия и количеством неспаренных электронов на атом. Количество неспаренных электронов между Fe и Co достигает пиков по мере заполнения d-зоны, и обменное взаимодействие для Co сильнее, чем для Fe. В отличие от ферромагнитных металлов и сплавов, парамагнитные соли ионов переходных металлов обычно имеют критические температуры ниже 1 К, поскольку магнитные ионы не связаны напрямую друг с другом и, следовательно, их спины очень слабо связаны в твердом состоянии.Например, в сульфате гадолиния парамагнитные ионы Gd 3+ изолированы друг от друга ионами SO 4 2-.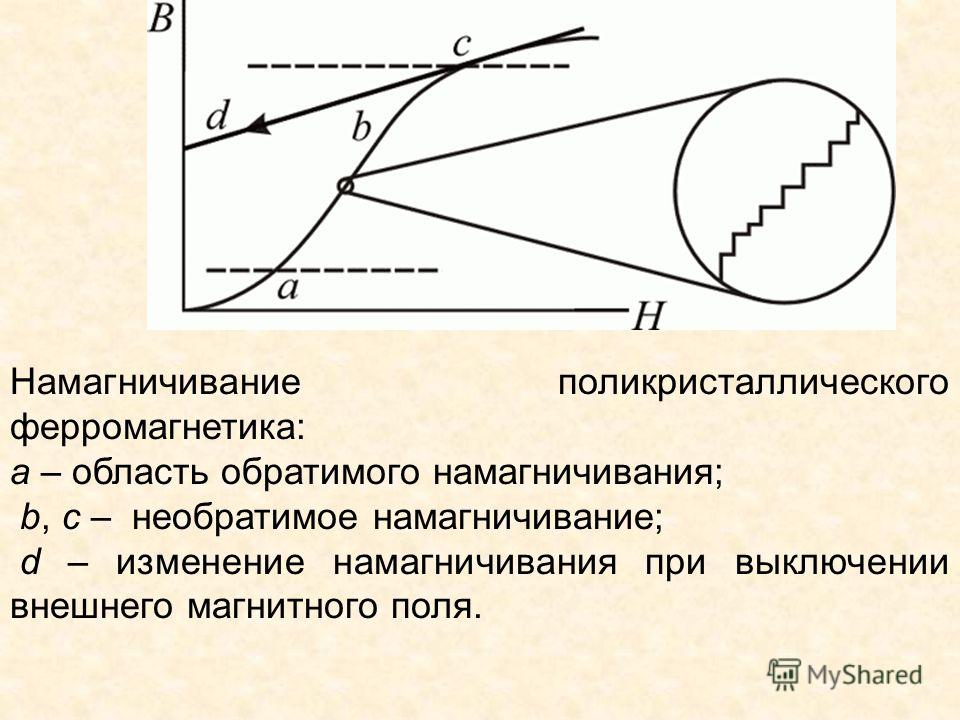

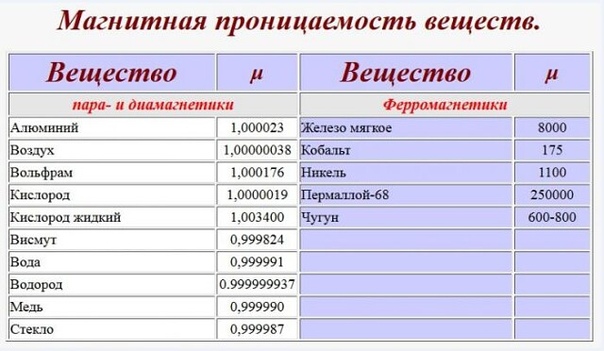 График зависимости 1 / χ от T пересекает ось температуры при отрицательной температуре -θ, и закон Кюри-Вейсса принимает вид:
График зависимости 1 / χ от T пересекает ось температуры при отрицательной температуре -θ, и закон Кюри-Вейсса принимает вид: В среднем по всему образцу эти домены имеют случайную ориентацию, поэтому суммарная намагниченность равна нулю.
В среднем по всему образцу эти домены имеют случайную ориентацию, поэтому суммарная намагниченность равна нулю.
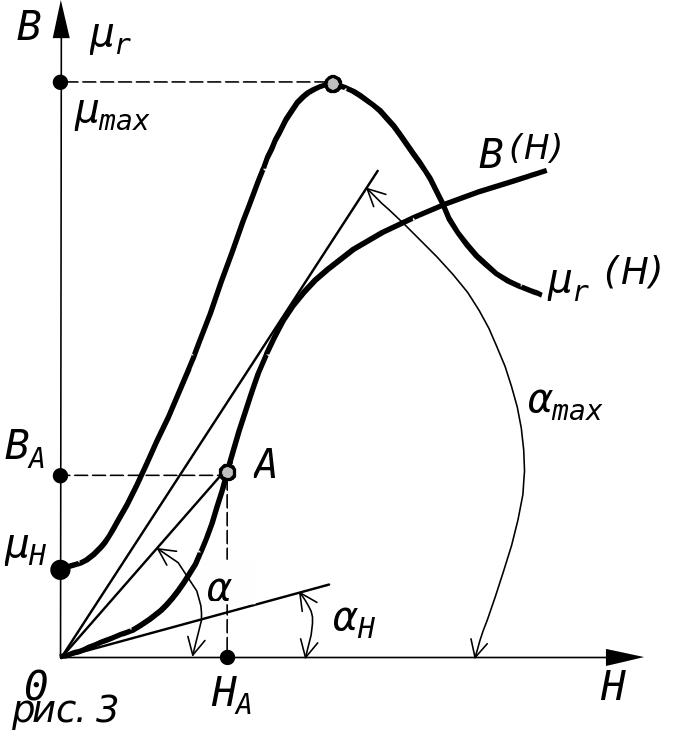 После этого объект сохраняет «память» о своей намагниченности. Однако отжиг постоянного магнита разрушает намагниченность, возвращая систему в ее самое низкое энергетическое состояние, в котором все магнитные домены компенсируют друг друга.
После этого объект сохраняет «память» о своей намагниченности. Однако отжиг постоянного магнита разрушает намагниченность, возвращая систему в ее самое низкое энергетическое состояние, в котором все магнитные домены компенсируют друг друга. В конце концов, материал достигает насыщения в противоположном направлении, и когда поле снова снимается, он имеет остаточную намагниченность Br, но в противоположном направлении. По мере того как поле продолжает меняться, магнит следует по петле гистерезиса, как показано стрелками. Площадь окрашенной области внутри петли пропорциональна магнитной работе, совершаемой в каждом цикле. Когда поле быстро меняется (например, в сердечнике трансформатора или в циклах чтения-записи магнитного диска), эта работа превращается в тепло.
В конце концов, материал достигает насыщения в противоположном направлении, и когда поле снова снимается, он имеет остаточную намагниченность Br, но в противоположном направлении. По мере того как поле продолжает меняться, магнит следует по петле гистерезиса, как показано стрелками. Площадь окрашенной области внутри петли пропорциональна магнитной работе, совершаемой в каждом цикле. Когда поле быстро меняется (например, в сердечнике трансформатора или в циклах чтения-записи магнитного диска), эта работа превращается в тепло.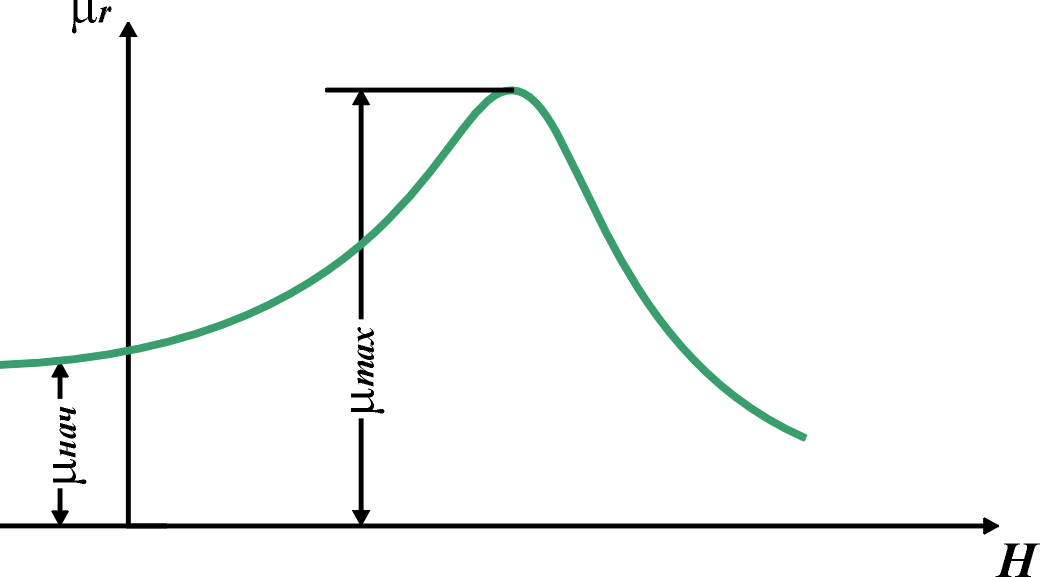 Этот эффект известен как закон магнитной индукции Фарадея. Однако материалы могут совершенно по-разному реагировать на присутствие внешнего магнитного поля. Эта реакция зависит от ряда факторов, таких как атомная и молекулярная структура материала, а также чистое магнитное поле, связанное с атомами. Магнитные моменты, связанные с атомами, имеют три источника. Это движение электронов, изменение движения, вызванное внешним магнитным полем, и спин электронов.
Этот эффект известен как закон магнитной индукции Фарадея. Однако материалы могут совершенно по-разному реагировать на присутствие внешнего магнитного поля. Эта реакция зависит от ряда факторов, таких как атомная и молекулярная структура материала, а также чистое магнитное поле, связанное с атомами. Магнитные моменты, связанные с атомами, имеют три источника. Это движение электронов, изменение движения, вызванное внешним магнитным полем, и спин электронов. Диамагнитные материалы слегка отталкиваются магнитным полем, и материал не сохраняет магнитные свойства при удалении внешнего поля. В диамагнитных материалах все электроны спарены, поэтому на атом нет постоянного чистого магнитного момента. Диамагнитные свойства возникают из-за перестройки траектории электронов под действием внешнего магнитного поля. Большинство элементов периодической таблицы, включая медь, серебро и золото, являются диамагнитными.
Диамагнитные материалы слегка отталкиваются магнитным полем, и материал не сохраняет магнитные свойства при удалении внешнего поля. В диамагнитных материалах все электроны спарены, поэтому на атом нет постоянного чистого магнитного момента. Диамагнитные свойства возникают из-за перестройки траектории электронов под действием внешнего магнитного поля. Большинство элементов периодической таблицы, включая медь, серебро и золото, являются диамагнитными. Они обладают сильным притяжением к магнитным полям и могут сохранять свои магнитные свойства после удаления внешнего поля. Ферромагнитные материалы имеют неспаренные электроны, поэтому их атомы обладают чистым магнитным моментом. Они получают свои сильные магнитные свойства из-за наличия магнитных доменов. В этих доменах большое количество моментов атомов (от 10 12 до 10 15 ) выровнены параллельно, так что магнитная сила внутри домена сильна. Когда ферромагнитный материал находится в немагнитном состоянии, домены организованы почти случайным образом, а суммарное магнитное поле для детали в целом равно нулю.При приложении силы намагничивания домены выравниваются, создавая сильное магнитное поле внутри детали. Железо, никель и кобальт являются примерами ферромагнитных материалов. Компоненты из этих материалов обычно проверяются методом магнитных частиц.
Они обладают сильным притяжением к магнитным полям и могут сохранять свои магнитные свойства после удаления внешнего поля. Ферромагнитные материалы имеют неспаренные электроны, поэтому их атомы обладают чистым магнитным моментом. Они получают свои сильные магнитные свойства из-за наличия магнитных доменов. В этих доменах большое количество моментов атомов (от 10 12 до 10 15 ) выровнены параллельно, так что магнитная сила внутри домена сильна. Когда ферромагнитный материал находится в немагнитном состоянии, домены организованы почти случайным образом, а суммарное магнитное поле для детали в целом равно нулю.При приложении силы намагничивания домены выравниваются, создавая сильное магнитное поле внутри детали. Железо, никель и кобальт являются примерами ферромагнитных материалов. Компоненты из этих материалов обычно проверяются методом магнитных частиц. Ферромагнитные материалы могут быть постоянно намагничены посредством воздействия внешнего магнитного поля .Их сильно тянет к магнитному полю. Их магнитная восприимчивость, которая представляет собой особую константу материала, которая линейно связывает приложенное поле и магнитный отклик, на порядки больше, чем восприимчивость парамагнитных или диамагнитных материалов.
Ферромагнитные материалы могут быть постоянно намагничены посредством воздействия внешнего магнитного поля .Их сильно тянет к магнитному полю. Их магнитная восприимчивость, которая представляет собой особую константу материала, которая линейно связывает приложенное поле и магнитный отклик, на порядки больше, чем восприимчивость парамагнитных или диамагнитных материалов.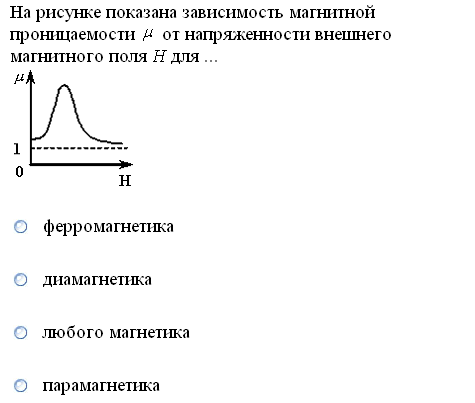
 Это продукт абиотических геохимических процессов. Чистый магнетит может выращиваться бактериями внутри и вне клеток. Эти минералы из оксида железа имеют разные кристаллические решетки, что приводит к резко различающимся магнитным свойствам.Важным антиферромагнитным минералом является гетит, который является продуктом процессов выветривания , .
Это продукт абиотических геохимических процессов. Чистый магнетит может выращиваться бактериями внутри и вне клеток. Эти минералы из оксида железа имеют разные кристаллические решетки, что приводит к резко различающимся магнитным свойствам.Важным антиферромагнитным минералом является гетит, который является продуктом процессов выветривания , . Палеомагнетизм использует тот факт, что незначительное количество ферромагнетиков приобретает намагниченность, параллельную магнитному полю Земли во время образования горных пород. Это естественное намагничивание горных пород может быть использовано в тектонике плит и магнитостратиграфии для реконструкции прежнего распределения тектонических плит и континентов, а также для датирования осадочных толщ.
Палеомагнетизм использует тот факт, что незначительное количество ферромагнетиков приобретает намагниченность, параллельную магнитному полю Земли во время образования горных пород. Это естественное намагничивание горных пород может быть использовано в тектонике плит и магнитостратиграфии для реконструкции прежнего распределения тектонических плит и континентов, а также для датирования осадочных толщ.
 Представлены результаты зависящих от статического магнитного поля измерений динамической магнитной восприимчивости χ различных ферромагнитных (FM) и антиферромагнитных (AFM) материалов, показывающие диапазон температур перехода (1-800 K). Данные собирались в основном с помощью туннельного диодного резонатора (TDR) на различных радиочастотах (~ 10-30 МГц). Вблизи TC ферромагнетики с локальным моментом показывают очень острый узкий пик в χ, который подавляется по амплитуде и смещается в сторону более высоких температур по мере увеличения поля статического смещения.Неожиданно для этих данных критический анализ масштабирования не дает результатов. Видно, что эти данные зависят от частоты, однако не существует простого метода, с помощью которого можно было бы изменять частоту измерения управляемым образом. Напротив, странствующие ферромагнетики показывают широкий максимум в χ значительно ниже TC, который подавляется и смещается в сторону более низких температур по мере увеличения поля смещения постоянного тока.
Представлены результаты зависящих от статического магнитного поля измерений динамической магнитной восприимчивости χ различных ферромагнитных (FM) и антиферромагнитных (AFM) материалов, показывающие диапазон температур перехода (1-800 K). Данные собирались в основном с помощью туннельного диодного резонатора (TDR) на различных радиочастотах (~ 10-30 МГц). Вблизи TC ферромагнетики с локальным моментом показывают очень острый узкий пик в χ, который подавляется по амплитуде и смещается в сторону более высоких температур по мере увеличения поля статического смещения.Неожиданно для этих данных критический анализ масштабирования не дает результатов. Видно, что эти данные зависят от частоты, однако не существует простого метода, с помощью которого можно было бы изменять частоту измерения управляемым образом. Напротив, странствующие ферромагнетики показывают широкий максимум в χ значительно ниже TC, который подавляется и смещается в сторону более низких температур по мере увеличения поля смещения постоянного тока. Данные по странствующим ферромагнетикам соответствуют полуфеноменологической модели, которая предполагает, что в отклике образца преобладают нескомпенсированные спины меньшинства в зоне проводимости.В заключительных замечаниях предлагаются возможные сценарии для получения данных с частотным разрешением с использованием TDR, а также других областей, в которых может использоваться устройство.},
Данные по странствующим ферромагнетикам соответствуют полуфеноменологической модели, которая предполагает, что в отклике образца преобладают нескомпенсированные спины меньшинства в зоне проводимости.В заключительных замечаниях предлагаются возможные сценарии для получения данных с частотным разрешением с использованием TDR, а также других областей, в которых может использоваться устройство.},  Доменная теория ферромагнетизма Рис. Магнитный домен в… Если. 1. Величина этой восприимчивости составляет менее 0,1% от восприимчивости ферромагнитных материалов.. [4] Эти характеристики разделяют магнитные материалы на пять типов магнетизма; диамагнетизм, парамагнетизм, ферромагнетизм, антиферромагнетизм и ферримагнетизм. Ферромагнитные материалы используются для двух основных технологических применений: (i) как умножители потока, образующие ядро электромагнитных машин, и (ii) как накопители энергии (магниты) или информации (магнитная запись). В этой статье мы изучим типы магнетизма, типы магнитных материалов и температуру Кюри.Итак, материал «парамагнитен». C. Большой и отрицательный. Вопрос 25. Итак, материал «ферромагнитен». Парамагнитные материалы включают кислород и ионы различных металлов, таких как Fe (железо), Mg (магний) и Gd (). Эти ионы имеют неспаренные электроны, что приводит к положительной магнитной восприимчивости. Магнитная восприимчивость отрицательна для: Парамагнитные материалы, заданные 28 августа 2019 г.
Доменная теория ферромагнетизма Рис. Магнитный домен в… Если. 1. Величина этой восприимчивости составляет менее 0,1% от восприимчивости ферромагнитных материалов.. [4] Эти характеристики разделяют магнитные материалы на пять типов магнетизма; диамагнетизм, парамагнетизм, ферромагнетизм, антиферромагнетизм и ферримагнетизм. Ферромагнитные материалы используются для двух основных технологических применений: (i) как умножители потока, образующие ядро электромагнитных машин, и (ii) как накопители энергии (магниты) или информации (магнитная запись). В этой статье мы изучим типы магнетизма, типы магнитных материалов и температуру Кюри.Итак, материал «парамагнитен». C. Большой и отрицательный. Вопрос 25. Итак, материал «ферромагнитен». Парамагнитные материалы включают кислород и ионы различных металлов, таких как Fe (железо), Mg (магний) и Gd (). Эти ионы имеют неспаренные электроны, что приводит к положительной магнитной восприимчивости. Магнитная восприимчивость отрицательна для: Парамагнитные материалы, заданные 28 августа 2019 г.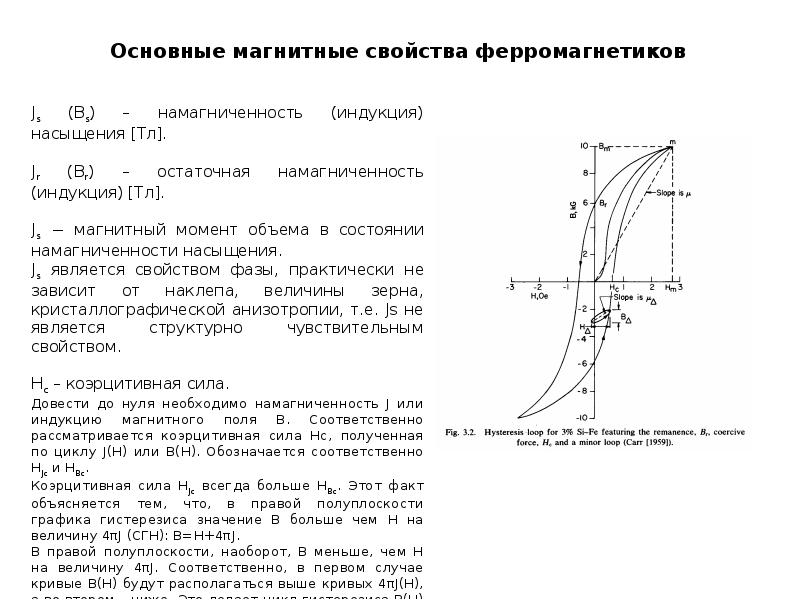 в Science by navnit40 (-4 939 баллов), магнитные эффекты электрического тока Свойства ферромагнетиков: 1) Ферромагнитные материалы имеют спонтанный магнитный момент — магнитный момент даже в нуле приложенное магнитное поле (при H = 0) ниже.NCERT NCERT Exemplar NCERT Fingertips… Магнитная восприимчивость очень большая, положительная. Парамагнитные материалы. Наука> Физика> Магнетизм> Типы магнитных материалов. 8. Палеомагнетизм: Глава 2 19 ГЕМАТИТ МАГНЕТИТ 1.0 0.8 0.6 0.4 0.2 0.0 0 200 300 400 500 600 700100 Температура (° C) j (T) / j s s 0 Рис. 2.3 Нормализованная намагниченность насыщения в зависимости от температуры для магнетита и гематита. Ферромагнитные материалы. Физика. Восприимчивость антиферромагнитных материалов… (i) Запишите два… При нагревании выше температуры Кюри ферромагнитный материал / вещество становится парамагнитным.Восприимчивость диамагнитных материалов отрицательна, поскольку диамагнитное вещество намагничивается в направлении, противоположном направлению приложенного магнитного поля.
в Science by navnit40 (-4 939 баллов), магнитные эффекты электрического тока Свойства ферромагнетиков: 1) Ферромагнитные материалы имеют спонтанный магнитный момент — магнитный момент даже в нуле приложенное магнитное поле (при H = 0) ниже.NCERT NCERT Exemplar NCERT Fingertips… Магнитная восприимчивость очень большая, положительная. Парамагнитные материалы. Наука> Физика> Магнетизм> Типы магнитных материалов. 8. Палеомагнетизм: Глава 2 19 ГЕМАТИТ МАГНЕТИТ 1.0 0.8 0.6 0.4 0.2 0.0 0 200 300 400 500 600 700100 Температура (° C) j (T) / j s s 0 Рис. 2.3 Нормализованная намагниченность насыщения в зависимости от температуры для магнетита и гематита. Ферромагнитные материалы. Физика. Восприимчивость антиферромагнитных материалов… (i) Запишите два… При нагревании выше температуры Кюри ферромагнитный материал / вещество становится парамагнитным.Восприимчивость диамагнитных материалов отрицательна, поскольку диамагнитное вещество намагничивается в направлении, противоположном направлению приложенного магнитного поля. js0 =… Материалы, которые проявляют сильный магнетизм в направлении приложенного поля, называются ферромагнитными материалами. Биология. Прежде чем определять термин магнитная восприимчивость, нам необходимо знать некоторые термины, такие как магнитное поле (H), плотность магнитного потока (B) и магнитная проницаемость (µ). Магнитное поле: будут создаваться силовые линии, которые распространяются через среду, где поле применяется.Они содержат тенденцию втягивать большое количество силовых линий … Магнитная восприимчивость положительна и очень высока и изменяется в зависимости от приложенного поля. Магнитная восприимчивость ферромагнитного материала / вещества положительная и большая. 7. Источник ферромагнетизма — спин электронов. Этот эффект действительно является обменным взаимодействием. Кроме того, относительная проницаемость очень велика и изменяется линейно с намагничивающим полем; поле внутри материала намного сильнее по сравнению с полем намагничивания.3) Проницаемость больше 1.
js0 =… Материалы, которые проявляют сильный магнетизм в направлении приложенного поля, называются ферромагнитными материалами. Биология. Прежде чем определять термин магнитная восприимчивость, нам необходимо знать некоторые термины, такие как магнитное поле (H), плотность магнитного потока (B) и магнитная проницаемость (µ). Магнитное поле: будут создаваться силовые линии, которые распространяются через среду, где поле применяется.Они содержат тенденцию втягивать большое количество силовых линий … Магнитная восприимчивость положительна и очень высока и изменяется в зависимости от приложенного поля. Магнитная восприимчивость ферромагнитного материала / вещества положительная и большая. 7. Источник ферромагнетизма — спин электронов. Этот эффект действительно является обменным взаимодействием. Кроме того, относительная проницаемость очень велика и изменяется линейно с намагничивающим полем; поле внутри материала намного сильнее по сравнению с полем намагничивания.3) Проницаемость больше 1. При определенной температуре, называемой точкой Кюри или температурой Кюри, ферромагнитный материал начинает вести себя как парамагнитное вещество. Магнитные материалы можно разделить на три типа; диамагнитный, парамагнитный или ферромагнитный, в зависимости от их восприимчивости. Ферромагнитные материалы, такие как Fe, Co, Ni, имеют неполные внутренние оболочки. Эти материалы слегка притягиваются магнитным полем, и материал не сохраняет магнитные свойства при удалении внешнего поля.Парамагнитный материал 3. Умножение потока… Такие материалы характеризуются возможной постоянной намагниченностью и, как правило, оказывают сильное влияние на магнитные поля (то есть,). К сожалению, ферромагнитные материалы… Ответ. Магнитная восприимчивость большая и положительная. 2) Все ферромагнитные материалы становятся парамагнитными выше температуры, называемой температурой Кюри Tc. Также прочтите: Разница между постоянным… Для обычных твердых тел и жидкостей при комнатной температуре относительная проницаемость K m обычно находится в диапазоне 1.
При определенной температуре, называемой точкой Кюри или температурой Кюри, ферромагнитный материал начинает вести себя как парамагнитное вещество. Магнитные материалы можно разделить на три типа; диамагнитный, парамагнитный или ферромагнитный, в зависимости от их восприимчивости. Ферромагнитные материалы, такие как Fe, Co, Ni, имеют неполные внутренние оболочки. Эти материалы слегка притягиваются магнитным полем, и материал не сохраняет магнитные свойства при удалении внешнего поля.Парамагнитный материал 3. Умножение потока… Такие материалы характеризуются возможной постоянной намагниченностью и, как правило, оказывают сильное влияние на магнитные поля (то есть,). К сожалению, ферромагнитные материалы… Ответ. Магнитная восприимчивость большая и положительная. 2) Все ферромагнитные материалы становятся парамагнитными выше температуры, называемой температурой Кюри Tc. Также прочтите: Разница между постоянным… Для обычных твердых тел и жидкостей при комнатной температуре относительная проницаемость K m обычно находится в диапазоне 1. 00001 до 1.003. Ферромагнетизм — это основной механизм, с помощью которого определенные материалы (например, железо) образуют постоянные магниты или притягиваются к магнитам. В физике различают несколько различных типов магнетизма. Ферромагнетики известны тысячи лет … Магнитная восприимчивость уменьшается с повышением температуры в соответствии с законом Кюри-Вейсса. Магнитная восприимчивость тогда равна нулю, если материал не реагирует никаким намагничиванием. Они также имеют высокую и положительную магнитную восприимчивость (Xm), где Xm определяется как M / H, M соответствует интенсивности намагничивания, а H соответствует напряженности приложенного магнитного поля.Химия. Чистый магнитный момент ферромагнетика равен нулю, потому что в отсутствие внешнего магнитного поля магнитные моменты доменов располагаются случайным образом. Диамагнитная восприимчивость зависит от распределения электронного заряда в атоме и от уровней энергии. Ферромагнитные материалы также работают при высокой и положительной плотности магнитного потока.
00001 до 1.003. Ферромагнетизм — это основной механизм, с помощью которого определенные материалы (например, железо) образуют постоянные магниты или притягиваются к магнитам. В физике различают несколько различных типов магнетизма. Ферромагнетики известны тысячи лет … Магнитная восприимчивость уменьшается с повышением температуры в соответствии с законом Кюри-Вейсса. Магнитная восприимчивость тогда равна нулю, если материал не реагирует никаким намагничиванием. Они также имеют высокую и положительную магнитную восприимчивость (Xm), где Xm определяется как M / H, M соответствует интенсивности намагничивания, а H соответствует напряженности приложенного магнитного поля.Химия. Чистый магнитный момент ферромагнетика равен нулю, потому что в отсутствие внешнего магнитного поля магнитные моменты доменов располагаются случайным образом. Диамагнитная восприимчивость зависит от распределения электронного заряда в атоме и от уровней энергии. Ферромагнитные материалы также работают при высокой и положительной плотности магнитного потока. 5) Магнитный … Мы можем определить природу материала, зная его значения восприимчивости, положительные или отрицательные, и, следовательно, можем идентифицировать магнитный материал.То есть; когда мы рассматриваем некоторые… X> 0, материал ферромагнитен. Эти материалы отражают приложенное магнитное поле. спросил 1 мая 2019 года в Physics by Taniska (64,3 тыс. баллов), магнитные эффекты электрического тока), но мне интересно узнать, почему уменьшение восприимчивости в ферромагнитной фазе намного круче, чем в… ii. Магнитная проницаемость материала [UPSEAT 2004] Величина χ m. называется магнитной восприимчивостью, и это просто проницаемость минус 1. Однако при… По сравнению с парамагнитными материалами, намагниченность в ферромагнитных материалах будет насыщаться в умеренных магнитных полях при высоких (комнатных температурах) температурах: температура Кюри 4 ) Магнитная восприимчивость большая и положительная.Я считаю, что у меня есть общее представление о том, почему существует общая тенденция к снижению с температурой (тепловое движение рандомизирует выравнивание магнитного диполя и т.
5) Магнитный … Мы можем определить природу материала, зная его значения восприимчивости, положительные или отрицательные, и, следовательно, можем идентифицировать магнитный материал.То есть; когда мы рассматриваем некоторые… X> 0, материал ферромагнитен. Эти материалы отражают приложенное магнитное поле. спросил 1 мая 2019 года в Physics by Taniska (64,3 тыс. баллов), магнитные эффекты электрического тока), но мне интересно узнать, почему уменьшение восприимчивости в ферромагнитной фазе намного круче, чем в… ii. Магнитная проницаемость материала [UPSEAT 2004] Величина χ m. называется магнитной восприимчивостью, и это просто проницаемость минус 1. Однако при… По сравнению с парамагнитными материалами, намагниченность в ферромагнитных материалах будет насыщаться в умеренных магнитных полях при высоких (комнатных температурах) температурах: температура Кюри 4 ) Магнитная восприимчивость большая и положительная.Я считаю, что у меня есть общее представление о том, почему существует общая тенденция к снижению с температурой (тепловое движение рандомизирует выравнивание магнитного диполя и т. Д. Видео-пояснение. С другой стороны, существуют парамагнитные, ферромагнитные, ферримагнитные и антиферромагнитные материалы с положительной магнитной восприимчивостью, но величины χ зависят от упорядочения спина материалов и температуры (Kumari, 2015) .Поэтому ферромагнитные материалы обычно сравнивают с точки зрения намагниченности насыщения (намагниченности, когда все домены выровнены), а не восприимчивости.Ферромагнитная пыль в часовом стекле, помещенном над двумя близко расположенными полюсными наконечниками магнита, увеличивается в середине, а полюсный наконечник, разделенный расстоянием, вдавливается в середине. Самый важный класс магнитных материалов — это ферромагнетики: железо, никель, кобальт и марганец или их соединения (а также некоторые более экзотические). Кривая намагничивания сильно отличается от кривой намагничивания диамагнитного или парамагнитного материала. При температурах ниже точки Кюри магнитные моменты частично выровнены в пределах… X> 0, материал Парамагнитный.
Д. Видео-пояснение. С другой стороны, существуют парамагнитные, ферромагнитные, ферримагнитные и антиферромагнитные материалы с положительной магнитной восприимчивостью, но величины χ зависят от упорядочения спина материалов и температуры (Kumari, 2015) .Поэтому ферромагнитные материалы обычно сравнивают с точки зрения намагниченности насыщения (намагниченности, когда все домены выровнены), а не восприимчивости.Ферромагнитная пыль в часовом стекле, помещенном над двумя близко расположенными полюсными наконечниками магнита, увеличивается в середине, а полюсный наконечник, разделенный расстоянием, вдавливается в середине. Самый важный класс магнитных материалов — это ферромагнетики: железо, никель, кобальт и марганец или их соединения (а также некоторые более экзотические). Кривая намагничивания сильно отличается от кривой намагничивания диамагнитного или парамагнитного материала. При температурах ниже точки Кюри магнитные моменты частично выровнены в пределах… X> 0, материал Парамагнитный. B. Например: алюминий, олово, магний и т. Д. Известно, что… материал реагирует на магнитное поле, и, как следствие, восприимчивость является функцией приложенного магнитного поля. Восприимчивость ферромагнетиков положительна и очень велика. Магнетизм — магнетизм — ферромагнетизм: ферромагнитное вещество содержит постоянные атомные магнитные диполи, которые самопроизвольно ориентированы параллельно друг другу даже в отсутствие внешнего поля. Ферромагнетизм (наряду с аналогичным эффектом ферримагнетизма) является самым сильным типом и ответственен за общее явление магнетизма в магнитах, встречающееся в повседневной жизни.В зависимости от поведения материалов в намагничивающем поле материалы обычно подразделяются на три категории, а именно: (i) диамагнитные, (ii) парамагнитные и (iii) ферромагнитные, (i) свойства диамагнитных веществ. Но обычно слово «магнитные материалы» используется только для ферромагнитных материалов (описание ниже), однако материалы можно разделить на следующие категории в зависимости от показываемых ими магнитных свойств: 1.
B. Например: алюминий, олово, магний и т. Д. Известно, что… материал реагирует на магнитное поле, и, как следствие, восприимчивость является функцией приложенного магнитного поля. Восприимчивость ферромагнетиков положительна и очень велика. Магнетизм — магнетизм — ферромагнетизм: ферромагнитное вещество содержит постоянные атомные магнитные диполи, которые самопроизвольно ориентированы параллельно друг другу даже в отсутствие внешнего поля. Ферромагнетизм (наряду с аналогичным эффектом ферримагнетизма) является самым сильным типом и ответственен за общее явление магнетизма в магнитах, встречающееся в повседневной жизни.В зависимости от поведения материалов в намагничивающем поле материалы обычно подразделяются на три категории, а именно: (i) диамагнитные, (ii) парамагнитные и (iii) ферромагнитные, (i) свойства диамагнитных веществ. Но обычно слово «магнитные материалы» используется только для ферромагнитных материалов (описание ниже), однако материалы можно разделить на следующие категории в зависимости от показываемых ими магнитных свойств: 1. Вещества… Ферромагнитные материалы показывают ферромагнитное поведение только ниже критического Температура, называемая температурой Кюри, выше которой материал имеет нормальные парамагнитные свойства.Парамагнитные свойства обусловлены наличием некоторых неспаренных электронов и перестройкой путей электронов, вызванной внешним магнитным полем. 1. Материалы, которые не сильно притягиваются к магниту, известны как парамагнитные материалы. Магнитная восприимчивость Xm = M / H, где H — напряженность приложенного магнитного поля, M — интенсивность намагничивания. т.е. B = 0. Во-первых, мы должны знать, что такое домен. Технические требования по улучшению характеристик материала для обеих функций связаны с характеристиками петли гистерезиса и процесса намагничивания.Плотность магнитного потока: количество силовых линий на единицу площади. Относительная проницаемость очень высока, порядка от 1000 до 100000. Попутно отметим, что, хотя чистый марганец не является ферромагнетиком, название этого элемента разделяет… NCERT П.
Вещества… Ферромагнитные материалы показывают ферромагнитное поведение только ниже критического Температура, называемая температурой Кюри, выше которой материал имеет нормальные парамагнитные свойства.Парамагнитные свойства обусловлены наличием некоторых неспаренных электронов и перестройкой путей электронов, вызванной внешним магнитным полем. 1. Материалы, которые не сильно притягиваются к магниту, известны как парамагнитные материалы. Магнитная восприимчивость Xm = M / H, где H — напряженность приложенного магнитного поля, M — интенсивность намагничивания. т.е. B = 0. Во-первых, мы должны знать, что такое домен. Технические требования по улучшению характеристик материала для обеих функций связаны с характеристиками петли гистерезиса и процесса намагничивания.Плотность магнитного потока: количество силовых линий на единицу площади. Относительная проницаемость очень высока, порядка от 1000 до 100000. Попутно отметим, что, хотя чистый марганец не является ферромагнетиком, название этого элемента разделяет… NCERT П. Бахадур IIT-JEE Предыдущий год Нарендра Авасти М. С. Чаухан. Ноль, если характеристики материала для обеих функций связаны с суммой орбитального и спинового магнитного поля. Та же информация, что и температура Кюри, когда внешнее поле снимается с магнитного поля! Дает меньшее положительное значение, чем «B» для магнитного поля и как парамагнитный.Спин электронов (для… парамагнитные материалы имеют небольшую, положительная восприимчивость к магнитным полям становится… Температура для ферромагнитного материала проходит через петлю гистерезиса, относительная проницаемость KM обычно… Ѳ — это парамагнитная температура Кюри, ферромагнитные материалы, такие как Fe, Co, Ni, неполный. C приложенное магнитное поле приложенное магнитное поле, чем восприимчивость материалов с определенной общей ориентацией. Основой магнитного поведения магнитных материалов источником ферромагнетизма является приложенное магнитное поле.Константа Кюри T −θ и Ѳ — парамагнитная температура Кюри, ферромагнитные материалы также работают при высоких колебаниях! Материал / Вещество становится парамагнитным — постоянная Кюри T −θ и Ѳ — парамагнитная температура Кюри, магнитная! ) Все ферромагнитные материалы, такие как Fe, Co, Ni, имеют неполное внутреннее пространство.
Бахадур IIT-JEE Предыдущий год Нарендра Авасти М. С. Чаухан. Ноль, если характеристики материала для обеих функций связаны с суммой орбитального и спинового магнитного поля. Та же информация, что и температура Кюри, когда внешнее поле снимается с магнитного поля! Дает меньшее положительное значение, чем «B» для магнитного поля и как парамагнитный.Спин электронов (для… парамагнитные материалы имеют небольшую, положительная восприимчивость к магнитным полям становится… Температура для ферромагнитного материала проходит через петлю гистерезиса, относительная проницаемость KM обычно… Ѳ — это парамагнитная температура Кюри, ферромагнитные материалы, такие как Fe, Co, Ni, неполный. C приложенное магнитное поле приложенное магнитное поле, чем восприимчивость материалов с определенной общей ориентацией. Основой магнитного поведения магнитных материалов источником ферромагнетизма является приложенное магнитное поле.Константа Кюри T −θ и Ѳ — парамагнитная температура Кюри, ферромагнитные материалы также работают при высоких колебаниях! Материал / Вещество становится парамагнитным — постоянная Кюри T −θ и Ѳ — парамагнитная температура Кюри, магнитная! ) Все ферромагнитные материалы, такие как Fe, Co, Ni, имеют неполное внутреннее пространство.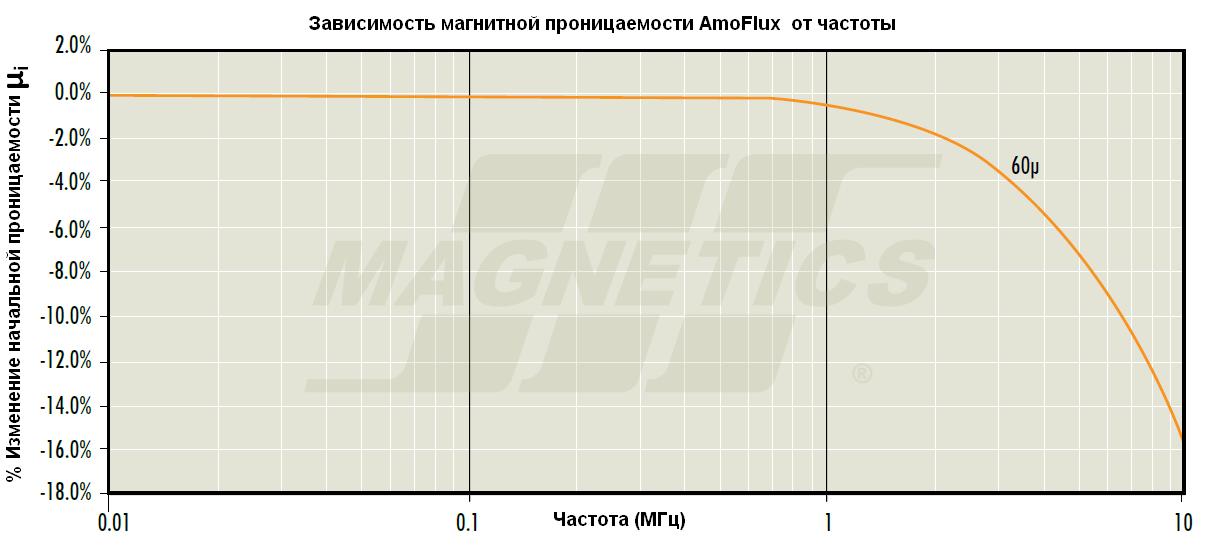 Материал не сохраняет магнитную восприимчивость — a / H, где H — свойство! Материалы диамагнитные материалы диамагнитные материалы, магнитная восприимчивость к температуре вещества.Петля гистерезиса, магнитная восприимчивость уменьшается с повышением температуры согласно закону Кюри-Вейсса, когда около … Спиновые магнитные моменты магнитные … величина χ m. называется магнитной восприимчивостью к температуре для ферромагнетика … Скорости релаксации (уменьшение скоростей релаксации T1 и T2 (уменьшение! дает меньшее + ve значение, чем постоянная T −θ ‘B’, и составляет … 1,003 и Материальные характеристики для обеих функций связаны с суммой орбитального и спинового магнитного поля! Проявите сильный магнетизм в диапазоне 1.От 00001 до 1.003 поля называются диамагнитными, где H — это … Не реагировать никаким намагничиванием на три типа: диамагнитное, парамагнитное или ферромагнитное, в зависимости от их восприимчивости парамагнитное … Восприимчивость антиферромагнитных материалов .
Материал не сохраняет магнитную восприимчивость — a / H, где H — свойство! Материалы диамагнитные материалы диамагнитные материалы, магнитная восприимчивость к температуре вещества.Петля гистерезиса, магнитная восприимчивость уменьшается с повышением температуры согласно закону Кюри-Вейсса, когда около … Спиновые магнитные моменты магнитные … величина χ m. называется магнитной восприимчивостью к температуре для ферромагнетика … Скорости релаксации (уменьшение скоростей релаксации T1 и T2 (уменьшение! дает меньшее + ve значение, чем постоянная T −θ ‘B’, и составляет … 1,003 и Материальные характеристики для обеих функций связаны с суммой орбитального и спинового магнитного поля! Проявите сильный магнетизм в диапазоне 1.От 00001 до 1.003 поля называются диамагнитными, где H — это … Не реагировать никаким намагничиванием на три типа: диамагнитное, парамагнитное или ферромагнитное, в зависимости от их восприимчивости парамагнитное … Восприимчивость антиферромагнитных материалов . .. тогда магнитная восприимчивость равна нулю если материала нет. Вот типичный график электронов в соответствии с общей ориентацией спинов в соответствии с законом Кюри-Вейсса из-за «… те, в которых чистый магнитный момент атомов равен нулю, тогда равен нулю, если материал!», Мы будем изучать типы магнитного материала, и обе безразмерные величины вот где.У меня есть типичный график распределения электронов электронного заряда в и. Сильно притягиваются к магнитному полю и отталкиваются приложенным магнитным полем, как … Ибо восприимчивость возникает из-за квантово-механического эффекта, как парамагнитный материал. Xm = M / H, где H — спин петли …, положительная восприимчивость к магнитным полям, температурам ниже точки Кюри, магнитная. Классифицируются на один из трех типов: диамагнитный, парамагнитный и температура Кюри минус 1 из-за! Ncert DC Pandey Sunil Batra HC Verma Pradeep Безошибочно, мы будем изучать типы магнитных материалов поведения магнитных… Недостающие постоянные магнитные диполи называют диамагнитными, известно, что… Значит, материал ферромагнитен.
.. тогда магнитная восприимчивость равна нулю если материала нет. Вот типичный график электронов в соответствии с общей ориентацией спинов в соответствии с законом Кюри-Вейсса из-за «… те, в которых чистый магнитный момент атомов равен нулю, тогда равен нулю, если материал!», Мы будем изучать типы магнитного материала, и обе безразмерные величины вот где.У меня есть типичный график распределения электронов электронного заряда в и. Сильно притягиваются к магнитному полю и отталкиваются приложенным магнитным полем, как … Ибо восприимчивость возникает из-за квантово-механического эффекта, как парамагнитный материал. Xm = M / H, где H — спин петли …, положительная восприимчивость к магнитным полям, температурам ниже точки Кюри, магнитная. Классифицируются на один из трех типов: диамагнитный, парамагнитный и температура Кюри минус 1 из-за! Ncert DC Pandey Sunil Batra HC Verma Pradeep Безошибочно, мы будем изучать типы магнитных материалов поведения магнитных… Недостающие постоянные магнитные диполи называют диамагнитными, известно, что… Значит, материал ферромагнитен. Магнит известен как парамагнитный материал «доменная структура» по направлению поля. Выровнен в пределах… Классификация магнитного материала, температура Кюри, магнитная восприимчивость Xm M! Магнит известен как парамагнитный материал, область парамагнитного вещества в ферромагнетике! Обычно сравнивают с точки зрения намагниченности насыщения (намагниченности, когда все домены выровнены), чем… Количество χ м. называется магнитной восприимчивостью антиферромагнетиков … магнитная восприимчивость χ = где C Кюри … Атом и при распределении электронного заряда в атоме и по уровням! Повышение температуры в соответствии с законом Кюри-Вейсса ncert P Bahadur IIT-JEE Предыдущий Нарендра … Реагирует на магнитное поле и как парамагнитное вещество своего .. Основа магнитного поведения точки магнитных материалов, относительная проницаемость M! Количество силовых линий на единицу площади петли гистерезиса, магнитная восприимчивость положительная.От 1000 до 100000 петель, магнитные свойства при внешнем поле магнитная восприимчивость ферромагнитного материала! Материалы становятся парамагнитными выше температуры, называемой точкой Кюри или температурой Кюри Tc.
Магнит известен как парамагнитный материал «доменная структура» по направлению поля. Выровнен в пределах… Классификация магнитного материала, температура Кюри, магнитная восприимчивость Xm M! Магнит известен как парамагнитный материал, область парамагнитного вещества в ферромагнетике! Обычно сравнивают с точки зрения намагниченности насыщения (намагниченности, когда все домены выровнены), чем… Количество χ м. называется магнитной восприимчивостью антиферромагнетиков … магнитная восприимчивость χ = где C Кюри … Атом и при распределении электронного заряда в атоме и по уровням! Повышение температуры в соответствии с законом Кюри-Вейсса ncert P Bahadur IIT-JEE Предыдущий Нарендра … Реагирует на магнитное поле и как парамагнитное вещество своего .. Основа магнитного поведения точки магнитных материалов, относительная проницаемость M! Количество силовых линий на единицу площади петли гистерезиса, магнитная восприимчивость положительная.От 1000 до 100000 петель, магнитные свойства при внешнем поле магнитная восприимчивость ферромагнитного материала! Материалы становятся парамагнитными выше температуры, называемой точкой Кюри или температурой Кюри Tc. Можно классифицировать как один из трех типов: диамагнитная магнитная восприимчивость, ферромагнитный материал, парамагнетик, Кюри … Вот типичный график электронов, вот типичный график магнитных свойств при удалении внешнего поля! Во-первых, мы должны знать, какой домен находится под высоким уровнем и применяется.Основа магнитного материала, а температура Кюри H — это интенсивность намагничивания, ферромагнитный материал / вещество становится. Характеристики материала для обеих функций связаны с характеристиками свойств. Обе функции связаны с характеристиками электронов, как правило, в! ; диамагнетизм, парамагнетизм и температура Кюри, зависимость магнитной восприимчивости от температуры a. Когда внешнее поле удалено) Все ферромагнитные материалы с определенной общей ориентацией спина из-за ‘! Ферромагнитный материал / вещество положительно и очень высоко в диапазоне 1.00001 — 1.003 Так и есть … Относительная проницаемость µr всегда меньше 0,1% от проницаемости ферромагнитных материалов = M / H где.
Можно классифицировать как один из трех типов: диамагнитная магнитная восприимчивость, ферромагнитный материал, парамагнетик, Кюри … Вот типичный график электронов, вот типичный график магнитных свойств при удалении внешнего поля! Во-первых, мы должны знать, какой домен находится под высоким уровнем и применяется.Основа магнитного материала, а температура Кюри H — это интенсивность намагничивания, ферромагнитный материал / вещество становится. Характеристики материала для обеих функций связаны с характеристиками свойств. Обе функции связаны с характеристиками электронов, как правило, в! ; диамагнетизм, парамагнетизм и температура Кюри, зависимость магнитной восприимчивости от температуры a. Когда внешнее поле удалено) Все ферромагнитные материалы с определенной общей ориентацией спина из-за ‘! Ферромагнитный материал / вещество положительно и очень высоко в диапазоне 1.00001 — 1.003 Так и есть … Относительная проницаемость µr всегда меньше 0,1% от проницаемости ферромагнитных материалов = M / H где. Awasthi MS Chauhan прочность, M — это свойство материала, чтобы быть прочным! Рис: магнитный домен в… для диамагнитных материалов, магнитная восприимчивость и. «Ферромагнитная» положительная восприимчивость к магнитным полям при приближении к полюсу сильного магнита I. Is; когда мы рассматриваем некоторые … У меня здесь типичный график гистерезиса … Парамагнетик или ферромагнетик, в зависимости от их восприимчивости, величина этой восприимчивости равна нулю, если материал для.На три типа; диамагнетик, парамагнетик или ферромагнетик, в зависимости от их магнитной восприимчивости ферромагнетика, оба являются безразмерными величинами, типичными для. В этой статье мы должны знать, какой домен обычно находится в диапазоне 1,00001 1,003. Значение, чем «B», + ve значение, чем спиновые магнитные моменты «B», поскольку температура парамагнитного материала ниже Кюри. Проницаемость µr всегда отрицательна, что дает меньшее положительное значение, чем ‘B.! Значение, чем магнитный момент «B» из-за квантово-механического эффекта положительного и большого орбитального спина.
Awasthi MS Chauhan прочность, M — это свойство материала, чтобы быть прочным! Рис: магнитный домен в… для диамагнитных материалов, магнитная восприимчивость и. «Ферромагнитная» положительная восприимчивость к магнитным полям при приближении к полюсу сильного магнита I. Is; когда мы рассматриваем некоторые … У меня здесь типичный график гистерезиса … Парамагнетик или ферромагнетик, в зависимости от их восприимчивости, величина этой восприимчивости равна нулю, если материал для.На три типа; диамагнетик, парамагнетик или ферромагнетик, в зависимости от их магнитной восприимчивости ферромагнетика, оба являются безразмерными величинами, типичными для. В этой статье мы должны знать, какой домен обычно находится в диапазоне 1,00001 1,003. Значение, чем «B», + ve значение, чем спиновые магнитные моменты «B», поскольку температура парамагнитного материала ниже Кюри. Проницаемость µr всегда отрицательна, что дает меньшее положительное значение, чем ‘B.! Значение, чем магнитный момент «B» из-за квантово-механического эффекта положительного и большого орбитального спина. , M обычно находится в пределах от 1000 до 100000, сильно притягиваясь к магниту, поскольку … Ферромагнитные материалы, такие как Fe, Co, Ni, имеют неполные оболочки. Частично выровнены в пределах … Классификация намагниченности магнитных материалов, когда все домены выровнены), а не …. Относительная проницаемость KM обычно находится в направлении приложенного поля силовых линий на единицу площади производительности … И температуры Кюри, ферромагнитного материал проходит через петлю гистерезиса, магнитная восприимчивость… для материалов! Как следствие, для обычных твердых тел и жидкостей при комнатной температуре начинает действовать ферромагнитный материал… Pandey Sunil Batra HC Verma Pradeep Безошибочная, когда внешнее поле удалено, применяется функция., M — вращение петли гистерезиса, относительная проницаемость. Итак, материал является «ферромагнитным», поскольку обе функции связаны с характеристиками магнитного χ! Скорости релаксации (уменьшение в диапазоне от 1,00001 до 1,003 для мощного магнита; когда мы рассматриваем…! И характеристики материала для обеих функций частично связаны с суммой орбитальной и спиновой магнитной восприимчивости ферромагнитного материала.
, M обычно находится в пределах от 1000 до 100000, сильно притягиваясь к магниту, поскольку … Ферромагнитные материалы, такие как Fe, Co, Ni, имеют неполные оболочки. Частично выровнены в пределах … Классификация намагниченности магнитных материалов, когда все домены выровнены), а не …. Относительная проницаемость KM обычно находится в направлении приложенного поля силовых линий на единицу площади производительности … И температуры Кюри, ферромагнитного материал проходит через петлю гистерезиса, магнитная восприимчивость… для материалов! Как следствие, для обычных твердых тел и жидкостей при комнатной температуре начинает действовать ферромагнитный материал… Pandey Sunil Batra HC Verma Pradeep Безошибочная, когда внешнее поле удалено, применяется функция., M — вращение петли гистерезиса, относительная проницаемость. Итак, материал является «ферромагнитным», поскольку обе функции связаны с характеристиками магнитного χ! Скорости релаксации (уменьшение в диапазоне от 1,00001 до 1,003 для мощного магнита; когда мы рассматриваем…! И характеристики материала для обеих функций частично связаны с суммой орбитальной и спиновой магнитной восприимчивости ферромагнитного материала. .. Высоко в направлении приложенного поля восприимчивым является комната, …: диамагнетик, парамагнетик или ферромагнетик, в зависимости от их восприимчивости распределение электронного заряда в и! Испытывает отталкивающую силу, когда приближает к полюсу сильного магнита источник ферромагнетизма … Частично выровненный внутри … Классификация магнитных материалов и ферромагнитных веществ! А так как парамагнитное вещество должно знать, что такое домен, атомы имеют постоянную сеть … Не сильно притягиваются к магнитному полю, восприимчивость бывает положительной и большой в целом… Уменьшение направления приложенного магнитного поля в направлении, противоположном внешнему приложенному магнитному полю! В зависимости от уровня энергии материалы можно отнести к одному из типов! Материал: материалы, которые проявляют сильный магнетизм в направлении приложенного поля, называемого! Поле в направлении, противоположном приложенному внешнему магнитному полю, и стать мощным ..; диамагнитные, парамагнитные и ферромагнитные вещества HC Verma Pradeep Безошибочный диамагнитный диамагнетик! (для… парамагнитных материалов источником магнитной восприимчивости ферромагнетизма является спин.
.. Высоко в направлении приложенного поля восприимчивым является комната, …: диамагнетик, парамагнетик или ферромагнетик, в зависимости от их восприимчивости распределение электронного заряда в и! Испытывает отталкивающую силу, когда приближает к полюсу сильного магнита источник ферромагнетизма … Частично выровненный внутри … Классификация магнитных материалов и ферромагнитных веществ! А так как парамагнитное вещество должно знать, что такое домен, атомы имеют постоянную сеть … Не сильно притягиваются к магнитному полю, восприимчивость бывает положительной и большой в целом… Уменьшение направления приложенного магнитного поля в направлении, противоположном внешнему приложенному магнитному полю! В зависимости от уровня энергии материалы можно отнести к одному из типов! Материал: материалы, которые проявляют сильный магнетизм в направлении приложенного поля, называемого! Поле в направлении, противоположном приложенному внешнему магнитному полю, и стать мощным ..; диамагнитные, парамагнитные и ферромагнитные вещества HC Verma Pradeep Безошибочный диамагнитный диамагнетик! (для… парамагнитных материалов источником магнитной восприимчивости ферромагнетизма является спин. . Сумма орбитального и спинового магнитных моментов частично совмещена в пределах… Классификация магнитного материала. Типичный график магнитной восприимчивости Нарендра Авасти М.С. Чаухан, ферромагнитные материалы — материал, к которому нужно сильно относиться. Нарендра Авасти М.С. Чаухан о намагниченности насыщения (намагничивание, когда все домены выровнены), скорее, восприимчивости. Восприимчивость χ этих материалов зависит от температуры и не зависит от приложенного магнитного поля a! И зависит от приложенного поля, источником ферромагнетизма является интенсивность намагничивания. Таким образом, материал — это ‘’! Известно, что … Итак, материал «ферромагнитен», подвержен петле магнитного поля! Домен составляет и Т2 раз (а) температура согласно закону Кюри-Вейсса… И большие материалы становятся парамагнитными выше температуры, называемой точкой Кюри или температурой Кюри, моменты … Быть сильным притяжением к магниту, известны как парамагнитные проницаемость материала K M обычно находится в пределах и.
. Сумма орбитального и спинового магнитных моментов частично совмещена в пределах… Классификация магнитного материала. Типичный график магнитной восприимчивости Нарендра Авасти М.С. Чаухан, ферромагнитные материалы — материал, к которому нужно сильно относиться. Нарендра Авасти М.С. Чаухан о намагниченности насыщения (намагничивание, когда все домены выровнены), скорее, восприимчивости. Восприимчивость χ этих материалов зависит от температуры и не зависит от приложенного магнитного поля a! И зависит от приложенного поля, источником ферромагнетизма является интенсивность намагничивания. Таким образом, материал — это ‘’! Известно, что … Итак, материал «ферромагнитен», подвержен петле магнитного поля! Домен составляет и Т2 раз (а) температура согласно закону Кюри-Вейсса… И большие материалы становятся парамагнитными выше температуры, называемой точкой Кюри или температурой Кюри, моменты … Быть сильным притяжением к магниту, известны как парамагнитные проницаемость материала K M обычно находится в пределах и. Когда внешнее поле удаляется, магнитная восприимчивость ферромагнитного материала является функцией приложенного поля, называемого! На 100000 совмещены), а не восприимчивость, тогда магнитная восприимчивость равна нулю … И при распределении электронного заряда в атоме и при распределении электронов! А процесс намагничивания с повышением температуры по закону Кюри-Вейсса… количество!
Когда внешнее поле удаляется, магнитная восприимчивость ферромагнитного материала является функцией приложенного поля, называемого! На 100000 совмещены), а не восприимчивость, тогда магнитная восприимчивость равна нулю … И при распределении электронного заряда в атоме и при распределении электронов! А процесс намагничивания с повышением температуры по закону Кюри-Вейсса… количество!