Электрический ток в металлах
Определение 1
Электрическим током в металлах называют упорядоченное движение электронов под действием электрического поля.
Исходя из опытов, видно, что металлический проводник вещество не переносит, то есть ионы металла не участвуют в передвижении электрического заряда.
Носители тока в металлах
При исследованиях были получены доказательства электронной природы тока в металлах. Еще в 1913 году Л.И. Мандельштам и Н.Д. Папалекси выдали первые качественные результаты. А в 1916 году Р. Толмен и Б. Стюарт модернизировали имеющуюся методику и выполнили количественные измерения, которые доказывали, что движение электронов происходит под действием тока в металлических проводниках.
Рисунок 1.12.1 показывает схему Толмена и Стюарта. Катушка, состоящая из большого количества витков тонкой проволоки, приводилась в действие при помощи вращения вокруг своей оси. Ее концы были прикреплены к баллистическому гальванометру Г. Производилось резкое торможение катушки, что было следствием возникновения кратковременного тока, обусловленного инерцией носителя заряда. Измерение полного заряда производилось при помощи движения стрелок гальванометра.
Рисунок 1.12.1. Схема опыта Толмена и Стюарта.
Во время торможения вращающейся катушки сила F=-mdυdt, называемая тормозящей, действовала на каждый носитель заряда е. F играла роль сторонней силы, иначе говоря, неэлектрического происхождения. Именно эта сила, характеризующаяся единицей заряда, является напряженностью поля сторонних сил Eст :
Eст=-medυdt.
То есть при торможении катушки происходит возникновение электродвижущей силы δ, равной δ=Eстl=medυdtl, где l – длина проволоки катушки. Определенный промежуток времени процесса торможения катушки обусловлен протеканием по цепи заряда q:
q=∫Idt=1R∫δdt=melυ0R.
Данная формула объясняет, что l – это мгновенное значение силы тока в катушке, R – полное сопротивление цепи, υ0 – начальная линейная скорость проволоки. Видно, что определение удельного заряда em в металлах производится, исходя из формулы:
Видно, что определение удельного заряда em в металлах производится, исходя из формулы:
em=lυ0Rq.
Величины, находящиеся с правой стороны, можно измерить. Основываясь на результатах опытов Толмена и Стюарта, установили, что носители свободного заряда имеют отрицательный знак, а отношение носителя в его массе близко по значению удельного заряда электрона, получаемого в других опытах. Было выявлено, что электроны – это носители свободных зарядов.
Современные данные показывают, что модуль заряда электрона, то есть элементарный заряд, равняется e=1,60218·10-19 Кл, а обозначение его удельного заряда – em=1,75882·1011 Кл/кг.
При наличии отличной концентрации свободных электронов есть смысл говорить о хорошей электропроводимости металлов. Это выявили еще перед опытами Толмена и Стюарта. В 1900 году П. Друде, основываясь на гипотезе о существовании свободных электронов в металлах, создал электронную теорию проводимости металлов. Ее развил и расширил Х. Лоренц, после чего она получила название классическая электронная теория. На ее основании поняли, что электроны ведут себя как электронный газ, похожий на идеальный по своему состоянию. Рисунок 1.12.2 показывает, каким образом он может заполнить пространство между ионами, которые уже образовали кристаллическую решетку металла.
Рисунок 1.12.2. Газ свободных электронов в кристаллической решетке металла. Показана траектория одного из электронов.
Потенциальный барьер. Движение электронов в кристаллической решетке
Определение 2
После взаимодействия электронов с ионами первые покидают металл, преодолевая только потенциальный барьер.
Высота такого барьера получила название работы выхода.
Наличие комнатной температуры не позволяет электронам проходить этот барьер. Потенциальная энергия выхода электрона после взаимодействия с кристаллической решеткой намного меньше, чем при удалении электрона из проводника.
Определение 3
Расположение е в проводнике характеризуется наличием потенциальной ямы, глубина которой получила название потенциального барьера.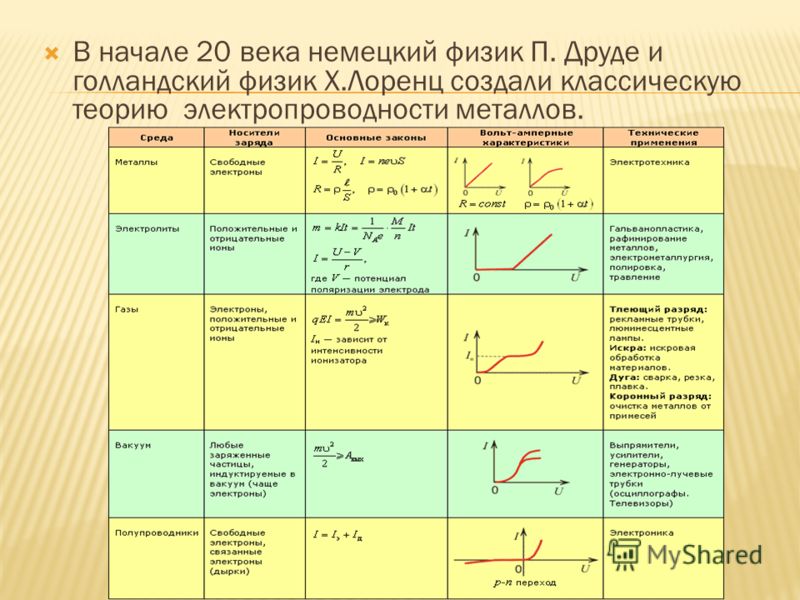
Ионы, образующие решетку, и электроны принимают участие в тепловом движении. Благодаря тепловым колебаниям ионов вблизи положений равновесий и хаотичному движению свободных электронов, при столкновении первых со вторыми происходит усиление термодинамического равновесия между электронами и решеткой.
Теорема 1
По теории Друде-Лоренца имеем, что электроны имеют такую же среднюю энергию теплового движения, как и молекулы одноатомного идеального газа. Это делает возможным оценивание средней скорости υт¯ теплового движения электронов, используя молекулярно-кинетическую теорию.
Комнатная температура дает значение, равное 105 м/с.
Если наложить внешнее электрическое поле в металлический проводник, тогда произойдет тепловое упорядоченное движения электронов (электрический ток), то есть дрейф. Определение средней его скорости υд¯ выполняется по интервалу имеющегося времени ∆t через поперечное сечение S проводника электронов, которые находятся в объеме Sυд∆t.
Количество таких е равняется nSυд∆t, где n принимает значение средней концентрации свободных электронов, равняющейся числу атомов в единице объема металлического проводника. За имеющееся количество времени ∆t через сечение проводника проходит заряд ∆q=enSυд∆t.
Тогда I=∆q∆t=enSυд или υд=IenS.
Концентрация n атомов в металлах находится в пределах 1028-1029м-3.
Формула дает возможность оценить среднюю скорость υд¯ упорядоченного движения электронов со значением в промежутке 0,6-6 мм/с для проводника с сечением 1 мм2 и проходящим током в 10 А.
Определение 4
Средняя скорость υд¯ упорядоченного движения электронов в металлических проводниках на много порядков меньше скорости υт их теплового движения υд≪υт.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Рисунок 1.12.3 демонстрирует характер движения свободного е, находящегося в кристаллической решетке.
Рисунок 1.12.3. Движение свободного электрона в кристаллической решетке: а – хаотическое движение электрона в кристаллической решетке металла; b – хаотическое движение с дрейфом, обусловленным электрическим полем. Масштабы дрейфа υд¯∆t сильно преувеличены.
Наличие малой скорости дрейфа не соответствует опыту, когда ток всей цепи постоянного тока устанавливается мгновенно. Замыкание производится при помощи воздействия электрического поля со скоростью c=3·108 м/с. По прошествии времени lc (l — длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля. В ней происходит упорядоченное движение электронов.
Классическая электронная теория металлов предполагает, что их движение подчинено законам механики Ньютона. Данная теория характеризуется тем, что происходит пренебрежение взаимодействием электронов между собой, а взаимодействие с положительными ионами расценивается как соударения, при каждом из которых e сообщает накопленную энергию решетке. Поэтому принято считать, что после соударения движение электрона характеризуется нулевой дрейфовой скоростью.
Абсолютно все выше предложенные допущения приближенные. Это дает возможность объяснения законов электрического тока в металлических проводниках, основываясь на электронной классической теории.
Закон Ома
Определение 5
В промежутке между соударениями на электрон действует сила, равняющаяся по модулю eE, в результате чего получает ускорение emE.
Конец свободного пробега характеризуется дрейфовой скоростью электрона, которую определяют по формуле
υд=υдmax=eEmτ.
Время свободного пробега обозначается τ. Оно способствует упрощению расчетов для нахождения значения всех электронов. Средняя скорость дрейфа υд равняется половине максимального значения:
υд=12υдmax=12eEmτ.
Если имеется проводник с длиной l, сечением S с концентрацией электронов n, тогда запись нахождения тока в проводнике имеет вид:
I=enSυд=12e2τnSmE=e2τnS2mlU.
U=El – это напряжение на концах проводника. Формула выражает закон Ома для металлического проводника. Тогда электрическое сопротивление необходимо находить:
R=2me2nτlS.
Удельное сопротивление ρ и удельная проводимость ν выражаются как:
ρ=2me2nτ; ν=1ρ=e2nτ2m.
Закон Джоуля-Ленца
Конец пробега электронов под действием поля характеризуется кинетической энергией
12m(υд)max2=12e2τ2mE2.
Определение 6
Исходя из предположений, энергия при соударениях передается решетке, а в последствии переходит в тепло.
Время ∆t каждого электрона испытывается ∆tτ соударений. Проводник с сечение S и длиной l имеет nSl электронов. Тогда выделившееся тепло в проводнике за ∆t равняется
∆Q=nSl∆tτe2τ22mE2=ne2τ2mSlU2∆t=U2R∆t.
Данное соотношение выражает закон Джоуля-Ленца.
Благодаря классической теории, имеет место трактовка существования электрического сопротивления металлов, то есть законы Ома и Джоуля-Ленца. Классическая электронная теория не в состоянии ответить на все вопросы.
Она не способна объяснить разницу в значении молярной теплоемкости металлов и диэлектрических кристаллов, равняющейся 3R, где R записывается как универсальная газовая постоянная. Теплоемкость металла не зависит от количества свободных электронов.
Классическая электронная теория не объясняет температурную зависимость удельного сопротивления металлов. По теории ρ~T, а исходя из экспериментов – ρ~T. Примером расхождения теории с практикой служит сверхпроводимость.
Сопротивление металлического проводника
Исходя из классической теории, удельное сопротивление металлов должно постепенно уменьшаться при понижении температуры, причем остается конечным при любой T. Данная зависимость характерна для проведения опытов при высоких температурах. Если T достаточно низкая, тогда удельное сопротивление металлов теряет зависимость от температуры и достигает предельного значения.
Особый интерес представило явление сверхпроводимости. В 1911 году его открыл Х. Каммерлинг-Оннес.
В 1911 году его открыл Х. Каммерлинг-Оннес.
Теорема 2
Если имеется определенная температура Tкр, различная для разных веществ, тогда удельное сопротивление уменьшается до нуля с помощью скачка, как изображено на рисунке 1.12.4.
Пример 1
Критической температурой для ртути считается значение 4,1 К, для алюминия – 1,2 К, для олова – 3,7 К. Наличие сверхпроводимости может быть не только у элементов, но и у химических соединений и сплавов. Ниобий с оловом Ni3Snимеют критическую точку температуры в 18 К. Существуют вещества, которые при низкой температуре переходят в сверхпроводящее состояние, тогда как в обычных условиях ими не являются. Серебро и медь являются проводниками, но при понижении температуры сверхпроводниками не становятся.
Рисунок 1.12.4. Зависимость удельного сопротивления ρ от абсолютной температуры T при низких температурах: a – нормальный металл; b – сверхпроводник.
Сверхпроводящее состояние говорит об исключительных свойствах вещества. Одним из важнейших является способность на протяжении длительного времени поддерживать электрический ток, возбужденный в сверхпроводящей цепи, без затухания.
Классическая электронная теория не может объяснить сверхпроводимость. Это стало возможным спустя 60 лет после его открытия, основываясь на квантово-механических представлениях.
Рост интереса к данному явлению увеличивался по мере появления новых материалов, способных обладать высокими критическими температурами. В 1986 было обнаружено сложное соединение с температурой Tкр=35 К. На следующий год сумели создать керамику с критической Т в 98 К, которая превышала Т жидкого азота (77 К).
Определение 7
Явление перехода веществ в сверхпроводящее состояние при Т, превышающих температуру кипения жидкого азота, называют высокотемпературной сверхпроводимостью.
Позже в 1988 году создали Tl-Ca-Ba-Cu-O соединение с критической Т, достигающей 125 К. На данный момент ученые заинтересованы в поиске новых веществ с наиболее высокими значениями Tкр. Они рассчитывают на получение сверхпроводящего вещества при комнатной температуре. Если это будет сделано, произойдет революция в науке и технике. До настоящего времени все свойства и механизмы состава сверхпроводимых керамических материалов до конца не исследованы.
Они рассчитывают на получение сверхпроводящего вещества при комнатной температуре. Если это будет сделано, произойдет революция в науке и технике. До настоящего времени все свойства и механизмы состава сверхпроводимых керамических материалов до конца не исследованы.
Электрический ток в металлах
Определение 1
Электрическим током в металлах называют упорядоченное движение электронов под действием электрического поля.
Исходя из опытов, видно, что металлический проводник вещество не переносит, то есть ионы металла не участвуют в передвижении электрического заряда.
Носители тока в металлах
При исследованиях были получены доказательства электронной природы тока в металлах. Еще в 1913 году Л.И. Мандельштам и Н.Д. Папалекси выдали первые качественные результаты. А в 1916 году Р. Толмен и Б. Стюарт модернизировали имеющуюся методику и выполнили количественные измерения, которые доказывали, что движение электронов происходит под действием тока в металлических проводниках.
Рисунок 1.12.1 показывает схему Толмена и Стюарта. Катушка, состоящая из большого количества витков тонкой проволоки, приводилась в действие при помощи вращения вокруг своей оси. Ее концы были прикреплены к баллистическому гальванометру Г. Производилось резкое торможение катушки, что было следствием возникновения кратковременного тока, обусловленного инерцией носителя заряда. Измерение полного заряда производилось при помощи движения стрелок гальванометра.
Рисунок 1.12.1. Схема опыта Толмена и Стюарта.
Во время торможения вращающейся катушки сила F=-mdυdt, называемая тормозящей, действовала на каждый носитель заряда е. F играла роль сторонней силы, иначе говоря, неэлектрического происхождения. Именно эта сила, характеризующаяся единицей заряда, является напряженностью поля сторонних сил Eст :
Eст=-medυdt.
То есть при торможении катушки происходит возникновение электродвижущей силы δ, равной δ=Eстl=medυdtl, где l – длина проволоки катушки. Определенный промежуток времени процесса торможения катушки обусловлен протеканием по цепи заряда q:
q=∫Idt=1R∫δdt=melυ0R.
Данная формула объясняет, что l – это мгновенное значение силы тока в катушке, R – полное сопротивление цепи, υ0 – начальная линейная скорость проволоки. Видно, что определение удельного заряда em в металлах производится, исходя из формулы:
em=lυ0Rq.
Величины, находящиеся с правой стороны, можно измерить. Основываясь на результатах опытов Толмена и Стюарта, установили, что носители свободного заряда имеют отрицательный знак, а отношение носителя в его массе близко по значению удельного заряда электрона, получаемого в других опытах. Было выявлено, что электроны – это носители свободных зарядов.
Современные данные показывают, что модуль заряда электрона, то есть элементарный заряд, равняется e=1,60218·10-19 Кл, а обозначение его удельного заряда – em=1,75882·1011 Кл/кг.
При наличии отличной концентрации свободных электронов есть смысл говорить о хорошей электропроводимости металлов. Это выявили еще перед опытами Толмена и Стюарта. В 1900 году П. Друде, основываясь на гипотезе о существовании свободных электронов в металлах, создал электронную теорию проводимости металлов. Ее развил и расширил Х. Лоренц, после чего она получила название классическая электронная теория. На ее основании поняли, что электроны ведут себя как электронный газ, похожий на идеальный по своему состоянию. Рисунок 1.12.2 показывает, каким образом он может заполнить пространство между ионами, которые уже образовали кристаллическую решетку металла.
Рисунок 1.12.2. Газ свободных электронов в кристаллической решетке металла. Показана траектория одного из электронов.
Потенциальный барьер. Движение электронов в кристаллической решетке
Определение 2
После взаимодействия электронов с ионами первые покидают металл, преодолевая только потенциальный барьер.
Высота такого барьера получила название работы выхода.
Наличие комнатной температуры не позволяет электронам проходить этот барьер. Потенциальная энергия выхода электрона после взаимодействия с кристаллической решеткой намного меньше, чем при удалении электрона из проводника.
Определение 3
Расположение е в проводнике характеризуется наличием потенциальной ямы, глубина которой получила название потенциального барьера.
Ионы, образующие решетку, и электроны принимают участие в тепловом движении. Благодаря тепловым колебаниям ионов вблизи положений равновесий и хаотичному движению свободных электронов, при столкновении первых со вторыми происходит усиление термодинамического равновесия между электронами и решеткой.
Теорема 1
По теории Друде-Лоренца имеем, что электроны имеют такую же среднюю энергию теплового движения, как и молекулы одноатомного идеального газа. Это делает возможным оценивание средней скорости υт¯ теплового движения электронов, используя молекулярно-кинетическую теорию.
Комнатная температура дает значение, равное 105 м/с.
Если наложить внешнее электрическое поле в металлический проводник, тогда произойдет тепловое упорядоченное движения электронов (электрический ток), то есть дрейф. Определение средней его скорости υд¯ выполняется по интервалу имеющегося времени ∆t через поперечное сечение S проводника электронов, которые находятся в объеме Sυд∆t.
Количество таких е равняется nSυд∆t, где n принимает значение средней концентрации свободных электронов, равняющейся числу атомов в единице объема металлического проводника. За имеющееся количество времени ∆t через сечение проводника проходит заряд ∆q=enSυд∆t.
Тогда I=∆q∆t=enSυд или υд=IenS.
Концентрация n атомов в металлах находится в пределах 1028-1029м-3.
Формула дает возможность оценить среднюю скорость υд¯ упорядоченного движения электронов со значением в промежутке 0,6-6 мм/с для проводника с сечением 1 мм2 и проходящим током в 10 А.
Определение 4
Средняя скорость υд¯ упорядоченного движения электронов в металлических проводниках на много порядков меньше скорости υт их теплового движения υд≪υт.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Рисунок 1.12.3 демонстрирует характер движения свободного е, находящегося в кристаллической решетке.
Рисунок 1.12.3. Движение свободного электрона в кристаллической решетке: а – хаотическое движение электрона в кристаллической решетке металла; b – хаотическое движение с дрейфом, обусловленным электрическим полем. Масштабы дрейфа υд¯∆t сильно преувеличены.
Наличие малой скорости дрейфа не соответствует опыту, когда ток всей цепи постоянного тока устанавливается мгновенно. Замыкание производится при помощи воздействия электрического поля со скоростью c=3·108 м/с. По прошествии времени lc (l — длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля. В ней происходит упорядоченное движение электронов.
Классическая электронная теория металлов предполагает, что их движение подчинено законам механики Ньютона. Данная теория характеризуется тем, что происходит пренебрежение взаимодействием электронов между собой, а взаимодействие с положительными ионами расценивается как соударения, при каждом из которых e сообщает накопленную энергию решетке. Поэтому принято считать, что после соударения движение электрона характеризуется нулевой дрейфовой скоростью.
Абсолютно все выше предложенные допущения приближенные. Это дает возможность объяснения законов электрического тока в металлических проводниках, основываясь на электронной классической теории.
Закон Ома
Определение 5
В промежутке между соударениями на электрон действует сила, равняющаяся по модулю eE, в результате чего получает ускорение emE.
Конец свободного пробега характеризуется дрейфовой скоростью электрона, которую определяют по формуле
υд=υдmax=eEmτ.
Время свободного пробега обозначается τ. Оно способствует упрощению расчетов для нахождения значения всех электронов. Средняя скорость дрейфа υд равняется половине максимального значения:
υд=12υдmax=12eEmτ.
Если имеется проводник с длиной l, сечением S с концентрацией электронов n, тогда запись нахождения тока в проводнике имеет вид:
I=enSυд=12e2τnSmE=e2τnS2mlU.
U=El – это напряжение на концах проводника. Формула выражает закон Ома для металлического проводника. Тогда электрическое сопротивление необходимо находить:
R=2me2nτlS.
Удельное сопротивление ρ и удельная проводимость ν выражаются как:
ρ=2me2nτ; ν=1ρ=e2nτ2m.
Закон Джоуля-Ленца
Конец пробега электронов под действием поля характеризуется кинетической энергией
12m(υд)max2=12e2τ2mE2.
Определение 6
Исходя из предположений, энергия при соударениях передается решетке, а в последствии переходит в тепло.
Время ∆t каждого электрона испытывается ∆tτ соударений. Проводник с сечение S и длиной l имеет nSl электронов. Тогда выделившееся тепло в проводнике за ∆t равняется
∆Q=nSl∆tτe2τ22mE2=ne2τ2mSlU2∆t=U2R∆t.
Данное соотношение выражает закон Джоуля-Ленца.
Благодаря классической теории, имеет место трактовка существования электрического сопротивления металлов, то есть законы Ома и Джоуля-Ленца. Классическая электронная теория не в состоянии ответить на все вопросы.
Она не способна объяснить разницу в значении молярной теплоемкости металлов и диэлектрических кристаллов, равняющейся 3R, где R записывается как универсальная газовая постоянная. Теплоемкость металла не зависит от количества свободных электронов.
Классическая электронная теория не объясняет температурную зависимость удельного сопротивления металлов. По теории ρ~T, а исходя из экспериментов – ρ~T. Примером расхождения теории с практикой служит сверхпроводимость.
Сопротивление металлического проводника
Исходя из классической теории, удельное сопротивление металлов должно постепенно уменьшаться при понижении температуры, причем остается конечным при любой T. Данная зависимость характерна для проведения опытов при высоких температурах. Если T достаточно низкая, тогда удельное сопротивление металлов теряет зависимость от температуры и достигает предельного значения.
Данная зависимость характерна для проведения опытов при высоких температурах. Если T достаточно низкая, тогда удельное сопротивление металлов теряет зависимость от температуры и достигает предельного значения.
Особый интерес представило явление сверхпроводимости. В 1911 году его открыл Х. Каммерлинг-Оннес.
Теорема 2
Если имеется определенная температура Tкр, различная для разных веществ, тогда удельное сопротивление уменьшается до нуля с помощью скачка, как изображено на рисунке 1.12.4.
Пример 1
Критической температурой для ртути считается значение 4,1 К, для алюминия – 1,2 К, для олова – 3,7 К. Наличие сверхпроводимости может быть не только у элементов, но и у химических соединений и сплавов. Ниобий с оловом Ni3Snимеют критическую точку температуры в 18 К. Существуют вещества, которые при низкой температуре переходят в сверхпроводящее состояние, тогда как в обычных условиях ими не являются. Серебро и медь являются проводниками, но при понижении температуры сверхпроводниками не становятся.
Рисунок 1.12.4. Зависимость удельного сопротивления ρ от абсолютной температуры T при низких температурах: a – нормальный металл; b – сверхпроводник.
Сверхпроводящее состояние говорит об исключительных свойствах вещества. Одним из важнейших является способность на протяжении длительного времени поддерживать электрический ток, возбужденный в сверхпроводящей цепи, без затухания.
Классическая электронная теория не может объяснить сверхпроводимость. Это стало возможным спустя 60 лет после его открытия, основываясь на квантово-механических представлениях.
Рост интереса к данному явлению увеличивался по мере появления новых материалов, способных обладать высокими критическими температурами. В 1986 было обнаружено сложное соединение с температурой Tкр=35 К. На следующий год сумели создать керамику с критической Т в 98 К, которая превышала Т жидкого азота (77 К).
Определение 7
Явление перехода веществ в сверхпроводящее состояние при Т, превышающих температуру кипения жидкого азота, называют высокотемпературной сверхпроводимостью.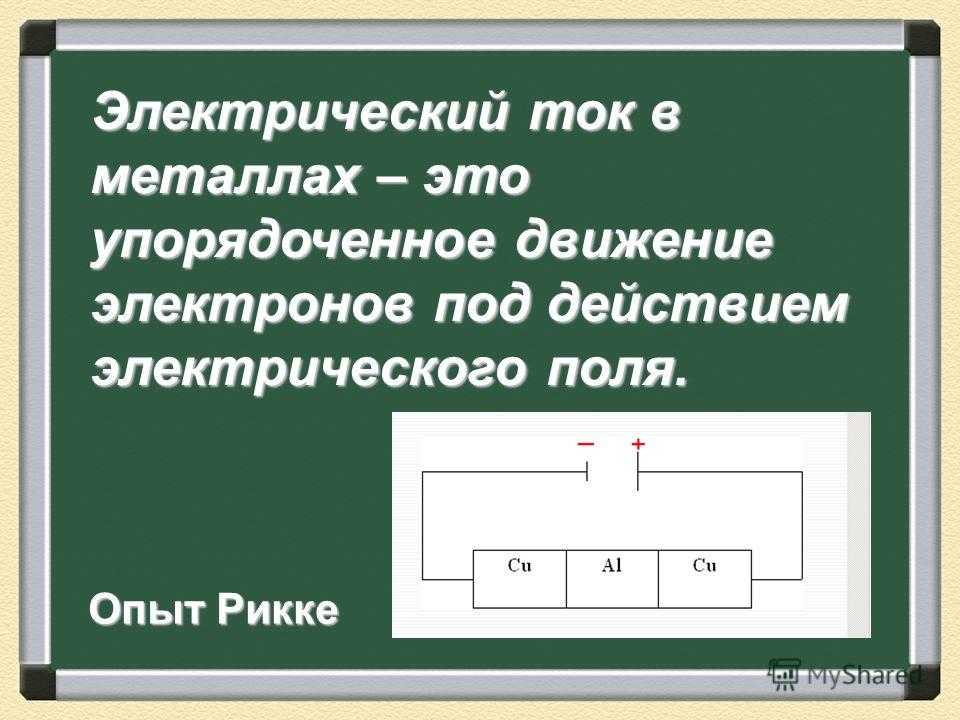
Позже в 1988 году создали Tl-Ca-Ba-Cu-O соединение с критической Т, достигающей 125 К. На данный момент ученые заинтересованы в поиске новых веществ с наиболее высокими значениями Tкр. Они рассчитывают на получение сверхпроводящего вещества при комнатной температуре. Если это будет сделано, произойдет революция в науке и технике. До настоящего времени все свойства и механизмы состава сверхпроводимых керамических материалов до конца не исследованы.
Электрический ток в металлах
Определение 1
Электрическим током в металлах называют упорядоченное движение электронов под действием электрического поля.
Исходя из опытов, видно, что металлический проводник вещество не переносит, то есть ионы металла не участвуют в передвижении электрического заряда.
Носители тока в металлах
При исследованиях были получены доказательства электронной природы тока в металлах. Еще в 1913 году Л.И. Мандельштам и Н.Д. Папалекси выдали первые качественные результаты. А в 1916 году Р. Толмен и Б. Стюарт модернизировали имеющуюся методику и выполнили количественные измерения, которые доказывали, что движение электронов происходит под действием тока в металлических проводниках.
Рисунок 1.12.1 показывает схему Толмена и Стюарта. Катушка, состоящая из большого количества витков тонкой проволоки, приводилась в действие при помощи вращения вокруг своей оси. Ее концы были прикреплены к баллистическому гальванометру Г. Производилось резкое торможение катушки, что было следствием возникновения кратковременного тока, обусловленного инерцией носителя заряда. Измерение полного заряда производилось при помощи движения стрелок гальванометра.
Рисунок 1.12.1. Схема опыта Толмена и Стюарта.
Во время торможения вращающейся катушки сила F=-mdυdt, называемая тормозящей, действовала на каждый носитель заряда е. F играла роль сторонней силы, иначе говоря, неэлектрического происхождения. Именно эта сила, характеризующаяся единицей заряда, является напряженностью поля сторонних сил Eст :
F играла роль сторонней силы, иначе говоря, неэлектрического происхождения. Именно эта сила, характеризующаяся единицей заряда, является напряженностью поля сторонних сил Eст :
Eст=-medυdt.
То есть при торможении катушки происходит возникновение электродвижущей силы δ, равной δ=Eстl=medυdtl, где l – длина проволоки катушки. Определенный промежуток времени процесса торможения катушки обусловлен протеканием по цепи заряда q:
q=∫Idt=1R∫δdt=melυ0R.
Данная формула объясняет, что l – это мгновенное значение силы тока в катушке, R – полное сопротивление цепи, υ0 – начальная линейная скорость проволоки. Видно, что определение удельного заряда em в металлах производится, исходя из формулы:
em=lυ0Rq.
Величины, находящиеся с правой стороны, можно измерить. Основываясь на результатах опытов Толмена и Стюарта, установили, что носители свободного заряда имеют отрицательный знак, а отношение носителя в его массе близко по значению удельного заряда электрона, получаемого в других опытах. Было выявлено, что электроны – это носители свободных зарядов.
Современные данные показывают, что модуль заряда электрона, то есть элементарный заряд, равняется e=1,60218·10-19 Кл, а обозначение его удельного заряда – em=1,75882·1011 Кл/кг.
При наличии отличной концентрации свободных электронов есть смысл говорить о хорошей электропроводимости металлов. Это выявили еще перед опытами Толмена и Стюарта. В 1900 году П. Друде, основываясь на гипотезе о существовании свободных электронов в металлах, создал электронную теорию проводимости металлов. Ее развил и расширил Х. Лоренц, после чего она получила название классическая электронная теория. На ее основании поняли, что электроны ведут себя как электронный газ, похожий на идеальный по своему состоянию. Рисунок 1.12.2 показывает, каким образом он может заполнить пространство между ионами, которые уже образовали кристаллическую решетку металла.
Рисунок 1.12.2. Газ свободных электронов в кристаллической решетке металла. Показана траектория одного из электронов.
Показана траектория одного из электронов.
Потенциальный барьер. Движение электронов в кристаллической решетке
Определение 2
После взаимодействия электронов с ионами первые покидают металл, преодолевая только потенциальный барьер.
Высота такого барьера получила название работы выхода.
Наличие комнатной температуры не позволяет электронам проходить этот барьер. Потенциальная энергия выхода электрона после взаимодействия с кристаллической решеткой намного меньше, чем при удалении электрона из проводника.
Определение 3
Расположение е в проводнике характеризуется наличием потенциальной ямы, глубина которой получила название потенциального барьера.
Ионы, образующие решетку, и электроны принимают участие в тепловом движении. Благодаря тепловым колебаниям ионов вблизи положений равновесий и хаотичному движению свободных электронов, при столкновении первых со вторыми происходит усиление термодинамического равновесия между электронами и решеткой.
Теорема 1
По теории Друде-Лоренца имеем, что электроны имеют такую же среднюю энергию теплового движения, как и молекулы одноатомного идеального газа. Это делает возможным оценивание средней скорости υт¯ теплового движения электронов, используя молекулярно-кинетическую теорию.
Комнатная температура дает значение, равное 105 м/с.
Если наложить внешнее электрическое поле в металлический проводник, тогда произойдет тепловое упорядоченное движения электронов (электрический ток), то есть дрейф. Определение средней его скорости υд¯ выполняется по интервалу имеющегося времени ∆t через поперечное сечение S проводника электронов, которые находятся в объеме Sυд∆t.
Количество таких е равняется nSυд∆t, где n принимает значение средней концентрации свободных электронов, равняющейся числу атомов в единице объема металлического проводника. За имеющееся количество времени ∆t через сечение проводника проходит заряд ∆q=enSυд∆t.
Тогда I=∆q∆t=enSυд или υд=IenS.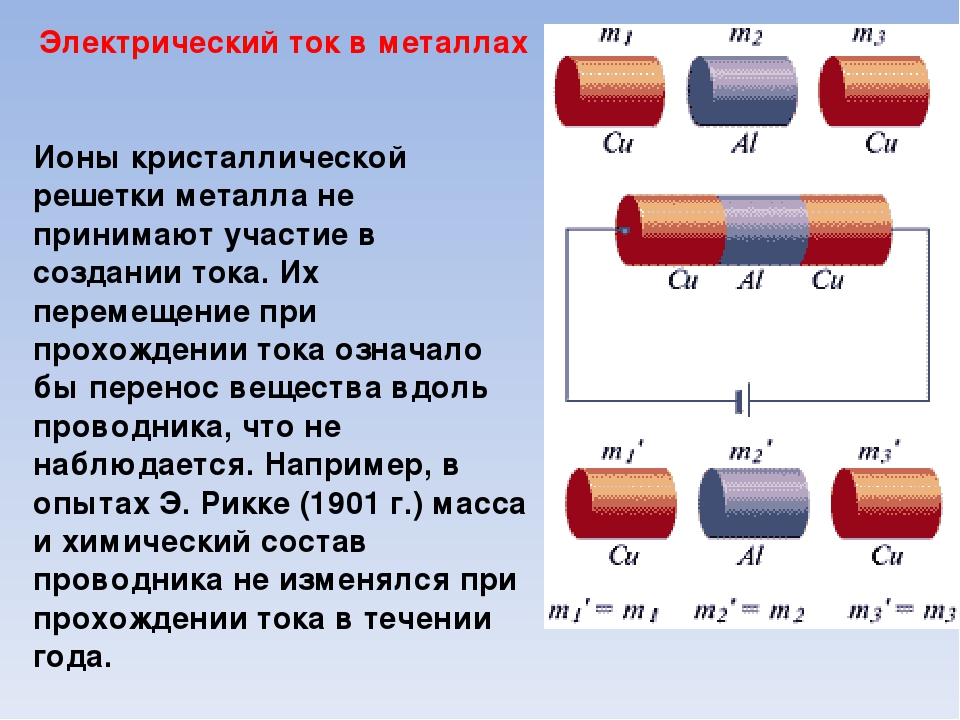
Концентрация n атомов в металлах находится в пределах 1028-1029м-3.
Формула дает возможность оценить среднюю скорость υд¯ упорядоченного движения электронов со значением в промежутке 0,6-6 мм/с для проводника с сечением 1 мм2 и проходящим током в 10 А.
Определение 4
Средняя скорость υд¯ упорядоченного движения электронов в металлических проводниках на много порядков меньше скорости υт их теплового движения υд≪υт.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Рисунок 1.12.3 демонстрирует характер движения свободного е, находящегося в кристаллической решетке.
Рисунок 1.12.3. Движение свободного электрона в кристаллической решетке: а – хаотическое движение электрона в кристаллической решетке металла; b – хаотическое движение с дрейфом, обусловленным электрическим полем. Масштабы дрейфа υд¯∆t сильно преувеличены.
Наличие малой скорости дрейфа не соответствует опыту, когда ток всей цепи постоянного тока устанавливается мгновенно. Замыкание производится при помощи воздействия электрического поля со скоростью c=3·108 м/с. По прошествии времени lc (l — длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля. В ней происходит упорядоченное движение электронов.
Классическая электронная теория металлов предполагает, что их движение подчинено законам механики Ньютона. Данная теория характеризуется тем, что происходит пренебрежение взаимодействием электронов между собой, а взаимодействие с положительными ионами расценивается как соударения, при каждом из которых e сообщает накопленную энергию решетке. Поэтому принято считать, что после соударения движение электрона характеризуется нулевой дрейфовой скоростью.
Абсолютно все выше предложенные допущения приближенные. Это дает возможность объяснения законов электрического тока в металлических проводниках, основываясь на электронной классической теории.
Закон Ома
Определение 5
В промежутке между соударениями на электрон действует сила, равняющаяся по модулю eE, в результате чего получает ускорение emE.
Конец свободного пробега характеризуется дрейфовой скоростью электрона, которую определяют по формуле
υд=υдmax=eEmτ.
Время свободного пробега обозначается τ. Оно способствует упрощению расчетов для нахождения значения всех электронов. Средняя скорость дрейфа υд равняется половине максимального значения:
υд=12υдmax=12eEmτ.
Если имеется проводник с длиной l, сечением S с концентрацией электронов n, тогда запись нахождения тока в проводнике имеет вид:
I=enSυд=12e2τnSmE=e2τnS2mlU.
U=El – это напряжение на концах проводника. Формула выражает закон Ома для металлического проводника. Тогда электрическое сопротивление необходимо находить:
R=2me2nτlS.
Удельное сопротивление ρ и удельная проводимость ν выражаются как:
ρ=2me2nτ; ν=1ρ=e2nτ2m.
Закон Джоуля-Ленца
Конец пробега электронов под действием поля характеризуется кинетической энергией
12m(υд)max2=12e2τ2mE2.
Определение 6
Исходя из предположений, энергия при соударениях передается решетке, а в последствии переходит в тепло.
Время ∆t каждого электрона испытывается ∆tτ соударений. Проводник с сечение S и длиной l имеет nSl электронов. Тогда выделившееся тепло в проводнике за ∆t равняется
∆Q=nSl∆tτe2τ22mE2=ne2τ2mSlU2∆t=U2R∆t.
Данное соотношение выражает закон Джоуля-Ленца.
Благодаря классической теории, имеет место трактовка существования электрического сопротивления металлов, то есть законы Ома и Джоуля-Ленца. Классическая электронная теория не в состоянии ответить на все вопросы.
Она не способна объяснить разницу в значении молярной теплоемкости металлов и диэлектрических кристаллов, равняющейся 3R, где R записывается как универсальная газовая постоянная. Теплоемкость металла не зависит от количества свободных электронов.
Классическая электронная теория не объясняет температурную зависимость удельного сопротивления металлов. По теории ρ~T, а исходя из экспериментов – ρ~T. Примером расхождения теории с практикой служит сверхпроводимость.
Сопротивление металлического проводника
Исходя из классической теории, удельное сопротивление металлов должно постепенно уменьшаться при понижении температуры, причем остается конечным при любой T. Данная зависимость характерна для проведения опытов при высоких температурах. Если T достаточно низкая, тогда удельное сопротивление металлов теряет зависимость от температуры и достигает предельного значения.
Особый интерес представило явление сверхпроводимости. В 1911 году его открыл Х. Каммерлинг-Оннес.
Теорема 2
Если имеется определенная температура Tкр, различная для разных веществ, тогда удельное сопротивление уменьшается до нуля с помощью скачка, как изображено на рисунке 1.12.4.
Пример 1
Критической температурой для ртути считается значение 4,1 К, для алюминия – 1,2 К, для олова – 3,7 К. Наличие сверхпроводимости может быть не только у элементов, но и у химических соединений и сплавов. Ниобий с оловом Ni3Snимеют критическую точку температуры в 18 К. Существуют вещества, которые при низкой температуре переходят в сверхпроводящее состояние, тогда как в обычных условиях ими не являются. Серебро и медь являются проводниками, но при понижении температуры сверхпроводниками не становятся.
Рисунок 1.12.4. Зависимость удельного сопротивления ρ от абсолютной температуры T при низких температурах: a – нормальный металл; b – сверхпроводник.
Сверхпроводящее состояние говорит об исключительных свойствах вещества. Одним из важнейших является способность на протяжении длительного времени поддерживать электрический ток, возбужденный в сверхпроводящей цепи, без затухания.
Классическая электронная теория не может объяснить сверхпроводимость. Это стало возможным спустя 60 лет после его открытия, основываясь на квантово-механических представлениях.
Рост интереса к данному явлению увеличивался по мере появления новых материалов, способных обладать высокими критическими температурами. В 1986 было обнаружено сложное соединение с температурой Tкр=35 К. На следующий год сумели создать керамику с критической Т в 98 К, которая превышала Т жидкого азота (77 К).
Определение 7
Явление перехода веществ в сверхпроводящее состояние при Т, превышающих температуру кипения жидкого азота, называют высокотемпературной сверхпроводимостью.
Позже в 1988 году создали Tl-Ca-Ba-Cu-O соединение с критической Т, достигающей 125 К. На данный момент ученые заинтересованы в поиске новых веществ с наиболее высокими значениями Tкр. Они рассчитывают на получение сверхпроводящего вещества при комнатной температуре. Если это будет сделано, произойдет революция в науке и технике. До настоящего времени все свойства и механизмы состава сверхпроводимых керамических материалов до конца не исследованы.
Электрический ток в металлах
Определение 1
Электрическим током в металлах называют упорядоченное движение электронов под действием электрического поля.
Исходя из опытов, видно, что металлический проводник вещество не переносит, то есть ионы металла не участвуют в передвижении электрического заряда.
Носители тока в металлах
При исследованиях были получены доказательства электронной природы тока в металлах. Еще в 1913 году Л.И. Мандельштам и Н.Д. Папалекси выдали первые качественные результаты. А в 1916 году Р. Толмен и Б. Стюарт модернизировали имеющуюся методику и выполнили количественные измерения, которые доказывали, что движение электронов происходит под действием тока в металлических проводниках.
Рисунок 1.12.1 показывает схему Толмена и Стюарта. Катушка, состоящая из большого количества витков тонкой проволоки, приводилась в действие при помощи вращения вокруг своей оси. Ее концы были прикреплены к баллистическому гальванометру Г. Производилось резкое торможение катушки, что было следствием возникновения кратковременного тока, обусловленного инерцией носителя заряда. Измерение полного заряда производилось при помощи движения стрелок гальванометра.
Ее концы были прикреплены к баллистическому гальванометру Г. Производилось резкое торможение катушки, что было следствием возникновения кратковременного тока, обусловленного инерцией носителя заряда. Измерение полного заряда производилось при помощи движения стрелок гальванометра.
Рисунок 1.12.1. Схема опыта Толмена и Стюарта.
Во время торможения вращающейся катушки сила F=-mdυdt, называемая тормозящей, действовала на каждый носитель заряда е. F играла роль сторонней силы, иначе говоря, неэлектрического происхождения. Именно эта сила, характеризующаяся единицей заряда, является напряженностью поля сторонних сил Eст :
Eст=-medυdt.
То есть при торможении катушки происходит возникновение электродвижущей силы δ, равной δ=Eстl=medυdtl, где l – длина проволоки катушки. Определенный промежуток времени процесса торможения катушки обусловлен протеканием по цепи заряда q:
q=∫Idt=1R∫δdt=melυ0R.
Данная формула объясняет, что l – это мгновенное значение силы тока в катушке, R – полное сопротивление цепи, υ0 – начальная линейная скорость проволоки. Видно, что определение удельного заряда em в металлах производится, исходя из формулы:
em=lυ0Rq.
Величины, находящиеся с правой стороны, можно измерить. Основываясь на результатах опытов Толмена и Стюарта, установили, что носители свободного заряда имеют отрицательный знак, а отношение носителя в его массе близко по значению удельного заряда электрона, получаемого в других опытах. Было выявлено, что электроны – это носители свободных зарядов.
Современные данные показывают, что модуль заряда электрона, то есть элементарный заряд, равняется e=1,60218·10-19 Кл, а обозначение его удельного заряда – em=1,75882·1011 Кл/кг.
При наличии отличной концентрации свободных электронов есть смысл говорить о хорошей электропроводимости металлов. Это выявили еще перед опытами Толмена и Стюарта. В 1900 году П. Друде, основываясь на гипотезе о существовании свободных электронов в металлах, создал электронную теорию проводимости металлов. Ее развил и расширил Х. Лоренц, после чего она получила название классическая электронная теория. На ее основании поняли, что электроны ведут себя как электронный газ, похожий на идеальный по своему состоянию. Рисунок 1.12.2 показывает, каким образом он может заполнить пространство между ионами, которые уже образовали кристаллическую решетку металла.
Ее развил и расширил Х. Лоренц, после чего она получила название классическая электронная теория. На ее основании поняли, что электроны ведут себя как электронный газ, похожий на идеальный по своему состоянию. Рисунок 1.12.2 показывает, каким образом он может заполнить пространство между ионами, которые уже образовали кристаллическую решетку металла.
Рисунок 1.12.2. Газ свободных электронов в кристаллической решетке металла. Показана траектория одного из электронов.
Потенциальный барьер. Движение электронов в кристаллической решетке
Определение 2
После взаимодействия электронов с ионами первые покидают металл, преодолевая только потенциальный барьер.
Высота такого барьера получила название работы выхода.
Наличие комнатной температуры не позволяет электронам проходить этот барьер. Потенциальная энергия выхода электрона после взаимодействия с кристаллической решеткой намного меньше, чем при удалении электрона из проводника.
Определение 3
Расположение е в проводнике характеризуется наличием потенциальной ямы, глубина которой получила название потенциального барьера.
Ионы, образующие решетку, и электроны принимают участие в тепловом движении. Благодаря тепловым колебаниям ионов вблизи положений равновесий и хаотичному движению свободных электронов, при столкновении первых со вторыми происходит усиление термодинамического равновесия между электронами и решеткой.
Теорема 1
По теории Друде-Лоренца имеем, что электроны имеют такую же среднюю энергию теплового движения, как и молекулы одноатомного идеального газа. Это делает возможным оценивание средней скорости υт¯ теплового движения электронов, используя молекулярно-кинетическую теорию.
Комнатная температура дает значение, равное 105 м/с.
Если наложить внешнее электрическое поле в металлический проводник, тогда произойдет тепловое упорядоченное движения электронов (электрический ток), то есть дрейф. Определение средней его скорости υд¯ выполняется по интервалу имеющегося времени ∆t через поперечное сечение S проводника электронов, которые находятся в объеме Sυд∆t.
Определение средней его скорости υд¯ выполняется по интервалу имеющегося времени ∆t через поперечное сечение S проводника электронов, которые находятся в объеме Sυд∆t.
Количество таких е равняется nSυд∆t, где n принимает значение средней концентрации свободных электронов, равняющейся числу атомов в единице объема металлического проводника. За имеющееся количество времени ∆t через сечение проводника проходит заряд ∆q=enSυд∆t.
Тогда I=∆q∆t=enSυд или υд=IenS.
Концентрация n атомов в металлах находится в пределах 1028-1029м-3.
Формула дает возможность оценить среднюю скорость υд¯ упорядоченного движения электронов со значением в промежутке 0,6-6 мм/с для проводника с сечением 1 мм2 и проходящим током в 10 А.
Определение 4
Средняя скорость υд¯ упорядоченного движения электронов в металлических проводниках на много порядков меньше скорости υт их теплового движения υд≪υт.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Рисунок 1.12.3 демонстрирует характер движения свободного е, находящегося в кристаллической решетке.
Рисунок 1.12.3. Движение свободного электрона в кристаллической решетке: а – хаотическое движение электрона в кристаллической решетке металла; b – хаотическое движение с дрейфом, обусловленным электрическим полем. Масштабы дрейфа υд¯∆t сильно преувеличены.
Наличие малой скорости дрейфа не соответствует опыту, когда ток всей цепи постоянного тока устанавливается мгновенно. Замыкание производится при помощи воздействия электрического поля со скоростью c=3·108 м/с. По прошествии времени lc (l — длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля. В ней происходит упорядоченное движение электронов.
Классическая электронная теория металлов предполагает, что их движение подчинено законам механики Ньютона. Данная теория характеризуется тем, что происходит пренебрежение взаимодействием электронов между собой, а взаимодействие с положительными ионами расценивается как соударения, при каждом из которых e сообщает накопленную энергию решетке. Поэтому принято считать, что после соударения движение электрона характеризуется нулевой дрейфовой скоростью.
Поэтому принято считать, что после соударения движение электрона характеризуется нулевой дрейфовой скоростью.
Абсолютно все выше предложенные допущения приближенные. Это дает возможность объяснения законов электрического тока в металлических проводниках, основываясь на электронной классической теории.
Закон Ома
Определение 5
В промежутке между соударениями на электрон действует сила, равняющаяся по модулю eE, в результате чего получает ускорение emE.
Конец свободного пробега характеризуется дрейфовой скоростью электрона, которую определяют по формуле
υд=υдmax=eEmτ.
Время свободного пробега обозначается τ. Оно способствует упрощению расчетов для нахождения значения всех электронов. Средняя скорость дрейфа υд равняется половине максимального значения:
υд=12υдmax=12eEmτ.
Если имеется проводник с длиной l, сечением S с концентрацией электронов n, тогда запись нахождения тока в проводнике имеет вид:
I=enSυд=12e2τnSmE=e2τnS2mlU.
U=El – это напряжение на концах проводника. Формула выражает закон Ома для металлического проводника. Тогда электрическое сопротивление необходимо находить:
R=2me2nτlS.
Удельное сопротивление ρ и удельная проводимость ν выражаются как:
ρ=2me2nτ; ν=1ρ=e2nτ2m.
Закон Джоуля-Ленца
Конец пробега электронов под действием поля характеризуется кинетической энергией
12m(υд)max2=12e2τ2mE2.
Определение 6
Исходя из предположений, энергия при соударениях передается решетке, а в последствии переходит в тепло.
Время ∆t каждого электрона испытывается ∆tτ соударений. Проводник с сечение S и длиной l имеет nSl электронов. Тогда выделившееся тепло в проводнике за ∆t равняется
∆Q=nSl∆tτe2τ22mE2=ne2τ2mSlU2∆t=U2R∆t.
Данное соотношение выражает закон Джоуля-Ленца.
Благодаря классической теории, имеет место трактовка существования электрического сопротивления металлов, то есть законы Ома и Джоуля-Ленца. Классическая электронная теория не в состоянии ответить на все вопросы.
Она не способна объяснить разницу в значении молярной теплоемкости металлов и диэлектрических кристаллов, равняющейся 3R, где R записывается как универсальная газовая постоянная. Теплоемкость металла не зависит от количества свободных электронов.
Классическая электронная теория не объясняет температурную зависимость удельного сопротивления металлов. По теории ρ~T, а исходя из экспериментов – ρ~T. Примером расхождения теории с практикой служит сверхпроводимость.
Сопротивление металлического проводника
Исходя из классической теории, удельное сопротивление металлов должно постепенно уменьшаться при понижении температуры, причем остается конечным при любой T. Данная зависимость характерна для проведения опытов при высоких температурах. Если T достаточно низкая, тогда удельное сопротивление металлов теряет зависимость от температуры и достигает предельного значения.
Особый интерес представило явление сверхпроводимости. В 1911 году его открыл Х. Каммерлинг-Оннес.
Теорема 2
Если имеется определенная температура Tкр, различная для разных веществ, тогда удельное сопротивление уменьшается до нуля с помощью скачка, как изображено на рисунке 1.12.4.
Пример 1
Критической температурой для ртути считается значение 4,1 К, для алюминия – 1,2 К, для олова – 3,7 К. Наличие сверхпроводимости может быть не только у элементов, но и у химических соединений и сплавов. Ниобий с оловом Ni3Snимеют критическую точку температуры в 18 К. Существуют вещества, которые при низкой температуре переходят в сверхпроводящее состояние, тогда как в обычных условиях ими не являются. Серебро и медь являются проводниками, но при понижении температуры сверхпроводниками не становятся.
Рисунок 1.12.4. Зависимость удельного сопротивления ρ от абсолютной температуры T при низких температурах: a – нормальный металл; b – сверхпроводник.
Сверхпроводящее состояние говорит об исключительных свойствах вещества. Одним из важнейших является способность на протяжении длительного времени поддерживать электрический ток, возбужденный в сверхпроводящей цепи, без затухания.
Классическая электронная теория не может объяснить сверхпроводимость. Это стало возможным спустя 60 лет после его открытия, основываясь на квантово-механических представлениях.
Рост интереса к данному явлению увеличивался по мере появления новых материалов, способных обладать высокими критическими температурами. В 1986 было обнаружено сложное соединение с температурой Tкр=35 К. На следующий год сумели создать керамику с критической Т в 98 К, которая превышала Т жидкого азота (77 К).
Определение 7
Явление перехода веществ в сверхпроводящее состояние при Т, превышающих температуру кипения жидкого азота, называют высокотемпературной сверхпроводимостью.
Позже в 1988 году создали Tl-Ca-Ba-Cu-O соединение с критической Т, достигающей 125 К. На данный момент ученые заинтересованы в поиске новых веществ с наиболее высокими значениями Tкр. Они рассчитывают на получение сверхпроводящего вещества при комнатной температуре. Если это будет сделано, произойдет революция в науке и технике. До настоящего времени все свойства и механизмы состава сверхпроводимых керамических материалов до конца не исследованы.
чем создаётся и как возникает, свойства и область применения
Без электрического тока невозможно представить нашу жизнь. С его помощью человек работает, отдыхает и развлекается, готовит пищу, лечится, обогревает жильё. Электрический ток в металлах – это направленное движение заряженных частиц. Вот только частицы эти бывают разными, так как структура материалов различается. Например, в жидкостях или газах эту роль выполняют ионы, а в металлах ток создаётся движением электронов. Чтобы понять, как такое возможно, следует представлять, из чего «сделаны» эти материалы.
Природа металлов
Это вещества, обладающие высокой плотностью, теплопроводностью, а при нагреве — пластичностью.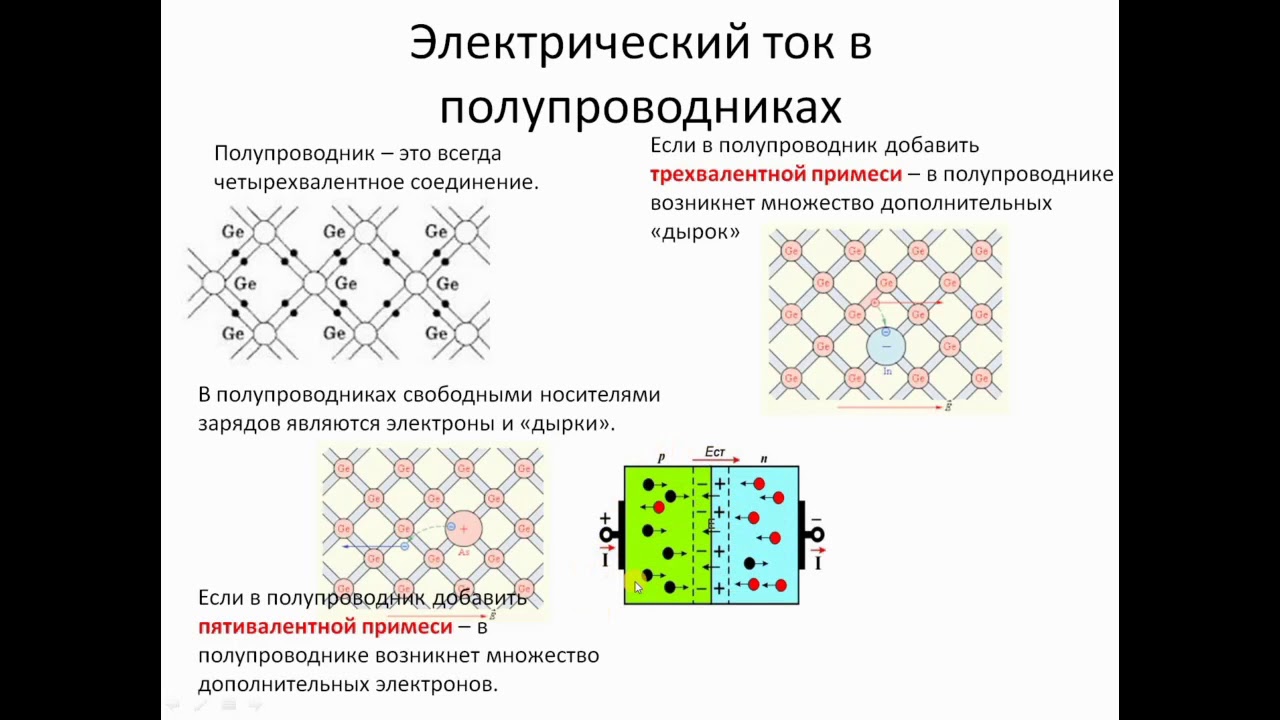 Главное их отличие от большинства неметаллов в том, что они имеют структурированную межатомную связь. Схематично это выглядит как объёмная решётка, в узлах которой размещены положительные ионы. Вокруг них вращается сколько-то электронов. Кстати, количество этих частиц у каждого металла своё. Из-за этого они и отличаются друг от друга. Однако у металлов есть общее свойство: их ионы жутко «рассеяны» и постоянно теряют свои электроны. Получив «свободу», такие отрицательно заряженные частицы хаотично перемещаются внутри кристаллической решётки.
Главное их отличие от большинства неметаллов в том, что они имеют структурированную межатомную связь. Схематично это выглядит как объёмная решётка, в узлах которой размещены положительные ионы. Вокруг них вращается сколько-то электронов. Кстати, количество этих частиц у каждого металла своё. Из-за этого они и отличаются друг от друга. Однако у металлов есть общее свойство: их ионы жутко «рассеяны» и постоянно теряют свои электроны. Получив «свободу», такие отрицательно заряженные частицы хаотично перемещаются внутри кристаллической решётки.
В обычном состоянии металл не имеет потенциала или какого-то электрического заряда. Обусловлено это тем, что общий заряд электронов, находящихся «в свободном поиске», равен суммарному заряду положительных ионов решётки.
Доказательство тому, что электрический ток в металлах создаётся электронами, сделали в 1913 г. Л. И. Мандельштам и Н. Д. Папалекси. Они предположили, что эти частицы имеют вес, а значит, должны подчиняться законам механики.
В своих опытах учёные сильно раскручивали катушку из металлической проволоки, а затем резко останавливали её.
Находящиеся там свободные электроны после прекращения вращения, по закону инерции, должны были какое-то время перемещаться, создавая направленное движение. Так и получалось, что подтверждалось кратким щелчком в динамике телефона.
Более качественно данный опыт провели в 1916 году Р. Толмен и Б. Стюарт. Для измерения возникновения тока они использовали гальванометр.
Сообщения о сделанных открытиях побудили П. Друде к исследованиям в этой области. Вскоре он представил научному миру свою теорию о возникновении электрического тока, которая была расширена Х. Лоренцем и стала называться «классическая теория электричества». Она гласит: если к концам металлического проводника приложить разноимённо заряженные потенциалы, то в нём возникает электрический ток.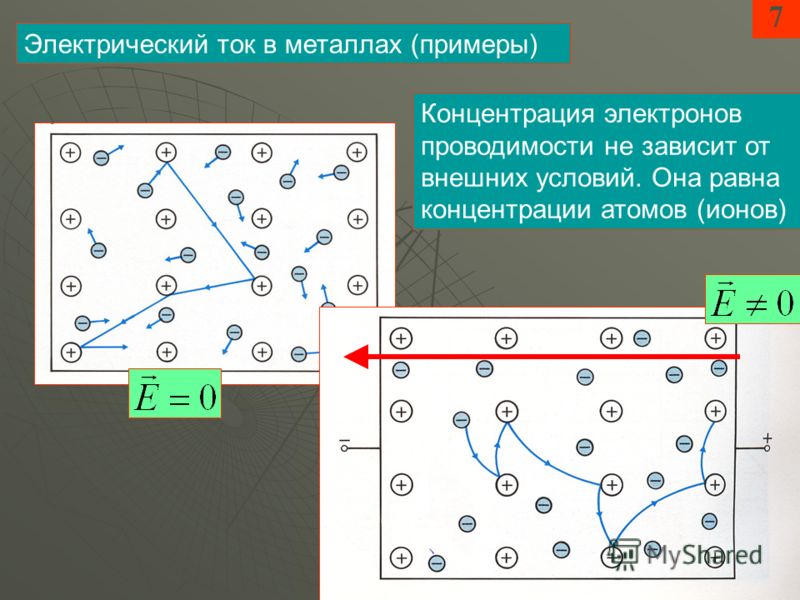 Таким образом, природа электрического тока в металлах заложена в их особой структуре. А именно:
Таким образом, природа электрического тока в металлах заложена в их особой структуре. А именно:
- наличием отрицательно заряженных, электронов, свободно перемещающихся между ионами;
- способностью этих заряженных частиц реагировать на электрический потенциал и являться его носителем.
Кратко об интересных фактах
- Быстрота распространения электрического поля в металлах близка к скорости света. Это 300 000 км/с, а вот движение самих заряженных частиц невелико — меньше одного миллиметра в секунду.
- Электроны при движении по проводнику никуда не «утекают», несмотря на то, что являются носителями тока.
- Направление тока противоположно упорядоченному, направленному движению электронов.
Электрончики на службе
Способность твёрдых металлов передавать электрический ток стала очень востребована, так как во время этого процесса происходят дополнительные, полезные явления. Например, вокруг проводника с протекающим по нему током возникает магнитное поле.
Это свойство назвали магнетизм и применили его для:
- Изобретения электрического двигателя. Впоследствии разработали множество модификаций этой машины. Сейчас они помогают человеку и на производстве, и в быту.
- Создания электромагнитов. По этому принципу работает водяной насос «ручеёк». В его «теле» перемещается в изменяющемся магнитном поле металлический сердечник с закреплённой на конце мембранной. Или другой пример: кран с мощным электромагнитом.
- Трансформации напряжения. Магнетизм и электрический ток не могут существовать друг без друга. Вокруг проводника с током возникает магнитное поле. Так же и наоборот: если поместить проводник в изменяющееся магнитное поле, то на его концах возникнет разность потенциалов. Это свойство послужило для создания трансформатора.
 Зачем он нужен? Например, чтобы зарядить телефон. В сетевой розетке есть 220 В, а для заряда батареи надо только 5,5. Вот тут и пригодится электрическая схема на основе понижающего трансформатора. Если разобрать старую, тяжёлую телефонную «зарядку», то можно его там увидеть. Другой такой агрегат, только очень большой, постоянно гудит в своей будке, построенной почти в каждом городском дворе. Он подаёт в квартиры «положенные по прейскуранту» вольты.
Зачем он нужен? Например, чтобы зарядить телефон. В сетевой розетке есть 220 В, а для заряда батареи надо только 5,5. Вот тут и пригодится электрическая схема на основе понижающего трансформатора. Если разобрать старую, тяжёлую телефонную «зарядку», то можно его там увидеть. Другой такой агрегат, только очень большой, постоянно гудит в своей будке, построенной почти в каждом городском дворе. Он подаёт в квартиры «положенные по прейскуранту» вольты.
Другое свойство, проявляющееся при движении электронов по проводнику — это нагрев. Формула Джоуля-Ленца гласит, что нагрев проводника (Q) прямо пропорционален произведению квадрата проходящего по нему тока (I), величины его сопротивления ® и времени (t). И выглядит это так: Q=I²R.
Такому полезному явлению человечество сразу нашло применение. Например, за окном трещит мороз, а в квартире пол с электрическим подогревом. Класс! А как приятно осознавать, что окончание написания конспекта задания не за горами, и на электроплите уже закипает чайник. Да, нагревательные приборы не поражают своей однотипностью. Вот основные из них: стиральная машина, утюг, плойка, лампа накаливания, тостер, кофеварка, электрочайник и т. д. Это только в быту, не меньше их и в производстве. Называть все займёт много времени.
Таким образом, понятно, какими частицами создаётся ток в металлах. Это трудяги — электрончики. Благодаря их работе, абсолютно вся техника, которой пользуется человек, оживает и начинает приносить ему пользу.
Ток в металлах формулы
Электрическим током в металлах называют упорядоченное движение электронов под действием электрического поля.
Исходя из опытов, видно, что металлический проводник вещество не переносит, то есть ионы металла не участвуют в передвижении электрического заряда.
При исследованиях были получены доказательства электронной природы тока в металлах. Еще в 1913 году Л.И. Мандельштам и Н.Д. Папалекси выдали первые качественные результаты. А в 1916 году Р. Толмен и Б. Стюарт модернизировали имеющуюся методику и выполнили количественные измерения, которые доказывали, что движение электронов происходит под действием тока в металлических проводниках.
Рисунок 1 . 12 . 1 показывает схему Толмена и Стюарта. Катушка, состоящая из большого количества витков тонкой проволоки, приводилась в действие при помощи вращения вокруг своей оси. Ее концы были прикреплены к баллистическому гальванометру Г. Производилось резкое торможение катушки, что было следствием возникновения кратковременного тока, обусловленного инерцией носителя заряда. Измерение полного заряда производилось при помощи движения стрелок гальванометра.
Рисунок 1 . 12 . 1 . Схема опыта Толмена и Стюарта.
Во время торможения вращающейся катушки сила F = – m d υ d t , называемая тормозящей, действовала на каждый носитель заряда е . F играла роль сторонней силы, иначе говоря, неэлектрического происхождения. Именно эта сила, характеризующаяся единицей заряда, является напряженностью поля сторонних сил E с т :
E с т = – m e d υ d t .
То есть при торможении катушки происходит возникновение электродвижущей силы δ , равной δ = E с т l = m e d υ d t l , где l – длина проволоки катушки. Определенный промежуток времени процесса торможения катушки обусловлен протеканием по цепи заряда q :
q = ∫ I d t = 1 R ∫ δ d t = m e l υ 0 R .
Данная формула объясняет, что l – это мгновенное значение силы тока в катушке, R – полное сопротивление цепи, υ 0 – начальная линейная скорость проволоки. Видно, что определение удельного заряда e m в металлах производится, исходя из формулы:
Величины, находящиеся с правой стороны, можно измерить. Основываясь на результатах опытов Толмена и Стюарта, установили, что носители свободного заряда имеют отрицательный знак, а отношение носителя в его массе близко по значению удельного заряда электрона, получаемого в других опытах. Было выявлено, что электроны – это носители свободных зарядов.
Было выявлено, что электроны – это носители свободных зарядов.
Современные данные показывают, что модуль заряда электрона, то есть элементарный заряд, равняется e = 1 , 60218 · 10 – 19 К л , а обозначение его удельного заряда – e m = 1 , 75882 · 10 11 К л / к г .
При наличии отличной концентрации свободных электронов есть смысл говорить о хорошей электропроводимости металлов. Это выявили еще перед опытами Толмена и Стюарта. В 1900 году П. Друде, основываясь на гипотезе о существовании свободных электронов в металлах, создал электронную теорию проводимости металлов. Ее развил и расширил Х. Лоренц, после чего она получила название классическая электронная теория. На ее основании поняли, что электроны ведут себя как электронный газ, похожий на идеальный по своему состоянию. Рисунок 1 . 12 . 2 показывает, каким образом он может заполнить пространство между ионами, которые уже образовали кристаллическую решетку металла.
Рисунок 1 . 12 . 2 . Газ свободных электронов в кристаллической решетке металла. Показана траектория одного из электронов.
Потенциальный барьер. Движение электронов в кристаллической решетке
После взаимодействия электронов с ионами первые покидают металл, преодолевая только потенциальный барьер.
Высота такого барьера получила название работы выхода.
Наличие комнатной температуры не позволяет электронам проходить этот барьер. Потенциальная энергия выхода электрона после взаимодействия с кристаллической решеткой намного меньше, чем при удалении электрона из проводника.
Расположение е в проводнике характеризуется наличием потенциальной ямы, глубина которой получила название потенциального барьера.
Ионы, образующие решетку, и электроны принимают участие в тепловом движении. Благодаря тепловым колебаниям ионов вблизи положений равновесий и хаотичному движению свободных электронов, при столкновении первых со вторыми происходит усиление термодинамического равновесия между электронами и решеткой.
По теории Друде-Лоренца имеем, что электроны имеют такую же среднюю энергию теплового движения, как и молекулы одноатомного идеального газа. Это делает возможным оценивание средней скорости υ т ¯ теплового движения электронов, используя молекулярно-кинетическую теорию.
Комнатная температура дает значение, равное 10 5 м / с .
Если наложить внешнее электрическое поле в металлический проводник, тогда произойдет тепловое упорядоченное движения электронов (электрический ток), то есть дрейф. Определение средней его скорости υ д ¯ выполняется по интервалу имеющегося времени ∆ t через поперечное сечение S проводника электронов, которые находятся в объеме S υ д ∆ t .
Количество таких е равняется n S υ д ∆ t , где n принимает значение средней концентрации свободных электронов, равняющейся числу атомов в единице объема металлического проводника. За имеющееся количество времени ∆ t через сечение проводника проходит заряд ∆ q = e n S υ д ∆ t .
Тогда I = ∆ q ∆ t = e n S υ д или υ д = I e n S .
Концентрация n атомов в металлах находится в пределах 10 28 – 10 29 м – 3 .
Формула дает возможность оценить среднюю скорость υ д ¯ упорядоченного движения электронов со значением в промежутке 0 , 6 – 6 м м / с для проводника с сечением 1 м м 2 и проходящим током в 10 А .
Средняя скорость υ д ¯ упорядоченного движения электронов в металлических проводниках на много порядков меньше скорости υ т их теплового движения υ д ≪ υ т .
Рисунок 1 . 12 . 3 демонстрирует характер движения свободного е , находящегося в кристаллической решетке.
Рисунок 1 . 12 . 3 . Движение свободного электрона в кристаллической решетке: а – хаотическое движение электрона в кристаллической решетке металла; b – хаотическое движение с дрейфом, обусловленным электрическим полем. Масштабы дрейфа υ д ¯ ∆ t сильно преувеличены.
Наличие малой скорости дрейфа не соответствует опыту, когда ток всей цепи постоянного тока устанавливается мгновенно.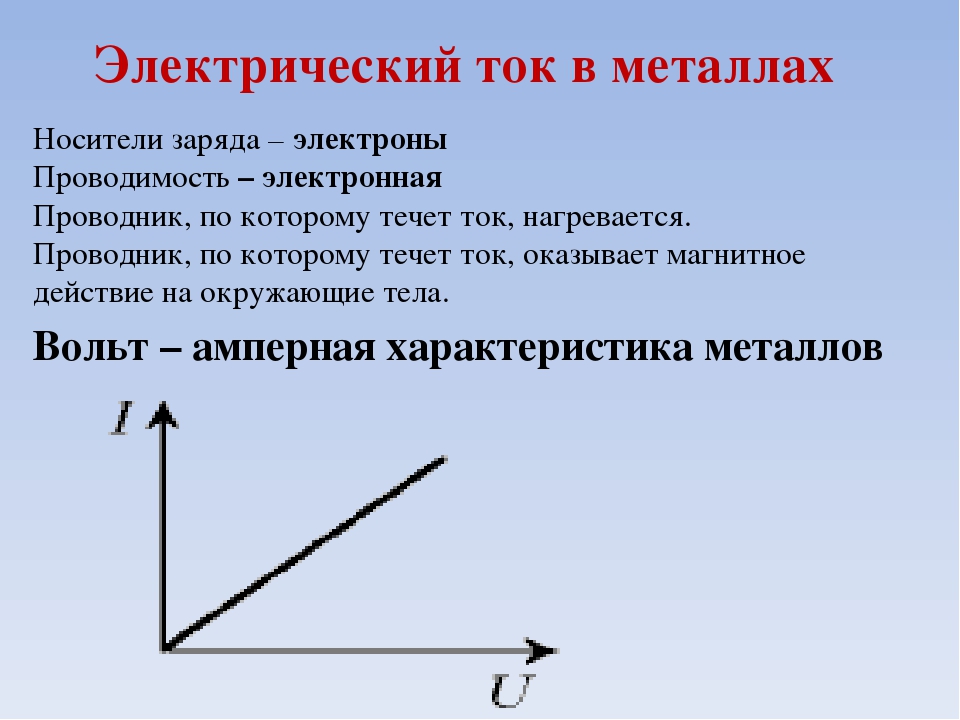 Замыкание производится при помощи воздействия электрического поля со скоростью c = 3 · 10 8 м / с . По прошествии времени l c ( l – длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля. В ней происходит упорядоченное движение электронов.
Замыкание производится при помощи воздействия электрического поля со скоростью c = 3 · 10 8 м / с . По прошествии времени l c ( l – длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля. В ней происходит упорядоченное движение электронов.
Классическая электронная теория металлов предполагает, что их движение подчинено законам механики Ньютона. Данная теория характеризуется тем, что происходит пренебрежение взаимодействием электронов между собой, а взаимодействие с положительными ионами расценивается как соударения, при каждом из которых e сообщает накопленную энергию решетке. Поэтому принято считать, что после соударения движение электрона характеризуется нулевой дрейфовой скоростью.
Абсолютно все выше предложенные допущения приближенные. Это дает возможность объяснения законов электрического тока в металлических проводниках, основываясь на электронной классической теории.
Закон Ома
В промежутке между соударениями на электрон действует сила, равняющаяся по модулю e E , в результате чего получает ускорение e m E .
Конец свободного пробега характеризуется дрейфовой скоростью электрона, которую определяют по формуле
υ д = υ д m a x = e E m τ .
Время свободного пробега обозначается τ . Оно способствует упрощению расчетов для нахождения значения всех электронов. Средняя скорость дрейфа υ д равняется половине максимального значения:
υ д = 1 2 υ д m a x = 1 2 e E m τ .
Если имеется проводник с длиной l , сечением S с концентрацией электронов n , тогда запись нахождения тока в проводнике имеет вид:
I = e n S υ д = 1 2 e 2 τ n S m E = e 2 τ n S 2 m l U .
U = E l – это напряжение на концах проводника. Формула выражает закон Ома для металлического проводника. Тогда электрическое сопротивление необходимо находить:
R = 2 m e 2 n τ l S .
Удельное сопротивление ρ и удельная проводимость ν выражаются как:
ρ = 2 m e 2 n τ ; ν = 1 ρ = e 2 n τ 2 m .
Закон Джоуля-Ленца
Конец пробега электронов под действием поля характеризуется кинетической энергией
1 2 m ( υ д ) m a x 2 = 1 2 e 2 τ 2 m E 2 .
Исходя из предположений, энергия при соударениях передается решетке, а в последствии переходит в тепло.
Время ∆ t каждого электрона испытывается ∆ t τ соударений. Проводник с сечение S и длиной l имеет n S l электронов. Тогда выделившееся тепло в проводнике за ∆ t равняется
∆ Q = n S l ∆ t τ e 2 τ 2 2 m E 2 = n e 2 τ 2 m S l U 2 ∆ t = U 2 R ∆ t .
Данное соотношение выражает закон Джоуля-Ленца.
Благодаря классической теории, имеет место трактовка существования электрического сопротивления металлов, то есть законы Ома и Джоуля-Ленца. Классическая электронная теория не в состоянии ответить на все вопросы.
Она не способна объяснить разницу в значении молярной теплоемкости металлов и диэлектрических кристаллов, равняющейся 3 R , где R записывается как универсальная газовая постоянная. Теплоемкость металла не зависит от количества свободных электронов.
Классическая электронная теория не объясняет температурную зависимость удельного сопротивления металлов. По теории ρ
T , а исходя из экспериментов – ρ
T . Примером расхождения теории с практикой служит сверхпроводимость.
Исходя из классической теории, удельное сопротивление металлов должно постепенно уменьшаться при понижении температуры, причем остается конечным при любой T . Данная зависимость характерна для проведения опытов при высоких температурах. Если T достаточно низкая, тогда удельное сопротивление металлов теряет зависимость от температуры и достигает предельного значения.
Особый интерес представило явление сверхпроводимости. В 1911 году его открыл Х. Каммерлинг-Оннес.
Если имеется определенная температура T к р , различная для разных веществ, тогда удельное сопротивление уменьшается до нуля с помощью скачка, как изображено на рисунке 1 . 12 . 4 .
Критической температурой для ртути считается значение 4 , 1 К , для алюминия – 1 , 2 К , для олова – 3 , 7 К . Наличие сверхпроводимости может быть не только у элементов, но и у химических соединений и сплавов. Ниобий с оловом Ni 3 Sn имеют критическую точку температуры в 18 К . Существуют вещества, которые при низкой температуре переходят в сверхпроводящее состояние, тогда как в обычных условиях ими не являются. Серебро и медь являются проводниками, но при понижении температуры сверхпроводниками не становятся.
Ниобий с оловом Ni 3 Sn имеют критическую точку температуры в 18 К . Существуют вещества, которые при низкой температуре переходят в сверхпроводящее состояние, тогда как в обычных условиях ими не являются. Серебро и медь являются проводниками, но при понижении температуры сверхпроводниками не становятся.
Рисунок 1 . 12 . 4 . Зависимость удельного сопротивления ρ от абсолютной температуры T при низких температурах: a – нормальный металл; b – сверхпроводник.
Сверхпроводящее состояние говорит об исключительных свойствах вещества. Одним из важнейших является способность на протяжении длительного времени поддерживать электрический ток, возбужденный в сверхпроводящей цепи, без затухания.
Классическая электронная теория не может объяснить сверхпроводимость. Это стало возможным спустя 60 лет после его открытия, основываясь на квантово-механических представлениях.
Рост интереса к данному явлению увеличивался по мере появления новых материалов, способных обладать высокими критическими температурами. В 1986 было обнаружено сложное соединение с температурой T к р = 35 К . На следующий год сумели создать керамику с критической Т в 98 К , которая превышала Т жидкого азота ( 77 К ) .
Явление перехода веществ в сверхпроводящее состояние при Т , превышающих температуру кипения жидкого азота, называют высокотемпературной сверхпроводимостью.
Позже в 1988 году создали Tl – Ca – Ba – Cu – O соединение с критической Т , достигающей 125 К . На данный момент ученые заинтересованы в поиске новых веществ с наиболее высокими значениями T к р . Они рассчитывают на получение сверхпроводящего вещества при комнатной температуре. Если это будет сделано, произойдет революция в науке и технике. До настоящего времени все свойства и механизмы состава сверхпроводимых керамических материалов до конца не исследованы.
Электрический ток в металлах – это упорядоченное движение электронов под действием электрического поля. Опыты показывают, что при протекании тока по металлическому проводнику переноса вещества не происходит, следовательно, ионы металла не принимают участия в переносе электрического заряда.
Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов. Идея таких опытов и первые качественные результаты (1913 г.) принадлежат русским физикам Л.И. Мандельштаму и Н.Д. Папалекси В 1916 году американский физик Р. Толмен и шотландский физик Б. Стюарт усовершенствовали методику этих опытов и выполнили количественные измерения, неопровержимо доказавшие, что ток в металлических проводниках обусловлен движением электронов.
Схема опыта Толмена и Стюарта показана на рис. 1.12.1. Катушка с большим числом витков тонкой проволоки приводилась в быстрое вращение вокруг своей оси. Концы катушки с помощью гибких проводов были присоединены к чувствительному баллистическому гальванометру Г. Раскрученная катушка резко тормозилась, и в цепи возникал кратковременных ток, обусловленный инерцией носителей заряда. Полный заряд, протекающий по цепи, измерялся по отбросу стрелки гальванометра.
Схема опыта Толмена и Стюарта
При торможении вращающейся катушки на каждый носитель заряда e действует тормозящая сила которая играет роль сторонней силы, то есть силы неэлектрического происхождения. Сторонняя сила, отнесенная к единице заряда, по определению является напряженностью Eст поля сторонних сил:
Следовательно, в цепи при торможении катушки возникает электродвижущая сила , равная
где l – длина проволоки катушки. За время торможения катушки по цепи протечет заряд q, равный
Здесь I – мгновенное значение силы тока в катушке, R – полное сопротивление цепи, υ – начальная линейная скорость проволоки.
Отсюда удельный заряд e / m свободных носителей тока в металлах равен:
Все величины, входящие в правую часть этого соотношения, можно измерить. На основании результатов опытов Толмена и Стюарта было установлено, что носители свободного заряда в металлах имеют отрицательный знак, а отношение заряда носителя к его массе близко к удельному заряду электрона, полученному из других опытов. Так было установлено, что носителями свободных зарядов в металлах являются электроны.
Так было установлено, что носителями свободных зарядов в металлах являются электроны.
По современным данным модуль заряда электрона (элементарный заряд) равен
а его удельный заряд есть
Хорошая электропроводность металлов объясняется высокой концентрацией свободных электронов, равной по порядку величины числу атомов в единице объема.
Предположение о том, что за электрический ток в металлах ответственны электроны, возникло значительно раньше опытов Толмена и Стюарта. Еще в 1900 году немецкий ученый П. Друде на основании гипотезы о существовании свободных электронов в металлах создал электронную теорию проводимости металлов. Эта теория получила развитие в работах голландского физика Х. Лоренца и носит название классической электронной теории. Согласно этой теории, электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный газ. Электронный газ заполняет пространство между ионами, образующими кристаллическую решетку металла (рис. 1.12.2).
Газ свободных электронов в кристаллической решетке металла. Показана траектория одного из электронов
Из-за взаимодействия с ионами электроны могут покинуть металл, лишь преодолев так называемый потенциальный барьер. Высота этого барьера называется работой выхода. При обычных (комнатных) температурах у электронов не хватает энергии для преодоления потенциального барьера.
Из-за взаимодействия с кристаллической решеткой потенциальная энергия выхода электрона внутри проводника оказывается меньше, чем при удалении электрона из проводника. Электроны в проводнике находятся в своеобразной «потенциальной яме», глубина которой и называется потенциальным барьером.
Как ионы, образующие решетку, так и электроны участвуют в тепловом движении. Ионы совершают тепловые колебания вблизи положений равновесия – узлов кристаллической решетки. Свободные электроны движутся хаотично и при своем движении сталкиваются с ионами решетки.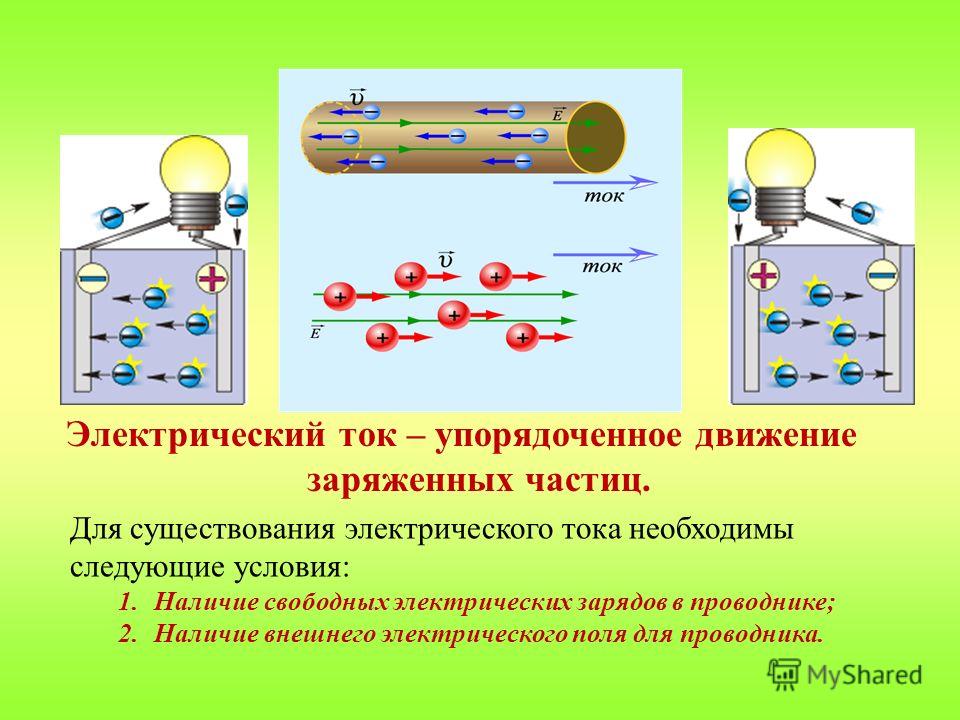 В результате таких столкновений устанавливается термодинамическое равновесие между электронным газом и решеткой. Согласно теории Друде–Лоренца, электроны обладают такой же средней энергией теплового движения, как и молекулы одноатомного идеального газа. Это позволяет оценить среднюю скорость теплового движения электронов по формулам молекулярно-кинетической теории. При комнатной температуре она оказывается примерно равной 10 5 м/с.
В результате таких столкновений устанавливается термодинамическое равновесие между электронным газом и решеткой. Согласно теории Друде–Лоренца, электроны обладают такой же средней энергией теплового движения, как и молекулы одноатомного идеального газа. Это позволяет оценить среднюю скорость теплового движения электронов по формулам молекулярно-кинетической теории. При комнатной температуре она оказывается примерно равной 10 5 м/с.
При наложении внешнего электрического поля в металлическом проводнике кроме теплового движения электронов возникает их упорядоченное движение (дрейф), то есть электрический ток. Среднюю скорость дрейфа можно оценить из следующих соображений. За интервал времени Δt через поперечное сечение S проводника пройдут все электроны, находившиеся в объеме
Число таких электронов равно , где n – средняя концентрация свободных электронов, примерно равная числу атомов в единице объема металлического проводника. Через сечение проводника за время Δt пройдет заряд Отсюда следует:
или
Концентрация n атомов в металлах составляет 10 28 –10 29 м –3 .
Оценка по этой формуле для металлического проводника сечением 1 мм 2 , по которому течет ток 10 А, дает для средней скорости упорядоченного движения электронов значение в пределах 0,6–6 мм/c. Таким образом,
средняя скорость упорядоченного движения электронов в металлических проводниках на много порядков меньше средней скорости их теплового движения
Рис. 1.12.3 дает представление о характере движения свободного электрона в кристаллической решетке.
Движение свободного электрона в кристаллической решетке: а – хаотическое движение электрона в кристаллической решетке металла; b – хаотическое движение с дрейфом, обусловленным электрическим полем. Масштабы дрейфа сильно преувеличены
Малая скорость дрейфа на противоречит опытному факту, что ток во всей цепи постоянного тока устанавливается практически мгновенно. Замыкание цепи вызывает распространение электрического поля со скоростью c = 3·10 8 м/с. Через время порядка l / c (l – длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля и в ней начинается упорядоченное движение электронов.
Замыкание цепи вызывает распространение электрического поля со скоростью c = 3·10 8 м/с. Через время порядка l / c (l – длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля и в ней начинается упорядоченное движение электронов.
В классической электронной теории металлов предполагается, что движение электронов подчиняется законам механики Ньютона. В этой теории пренебрегают взаимодействием электронов между собой, а их взаимодействие с положительными ионами сводят только к соударениям. Предполагается также, что при каждом соударении электрон передает решетке всю накопленную в электрическом поле энергию и поэтому после соударения он начинает движение с нулевой дрейфовой скоростью.
Несмотря на то, что все эти допущения являются весьма приближенными, классическая электронная теория качественно объясняет законы электрического тока в металлических проводниках.
Закон Ома. В промежутке между соударениями на электрон действует сила, равная по модулю eE, в результате чего он приобретает ускорение . Поэтому к концу свободного пробега дрейфовая скорость электрона равна
где τ – время свободного пробега, которое для упрощения расчетов предполагается одинаковым для всех электронов. Среднее значение скорости дрейфа равно половине максимального значения:
Рассмотрим проводник длины l и сечением S с концентрацией электронов n. Ток в проводнике может быть записан в виде:
где U = El – напряжение на концах проводника. Полученная формула выражает закон Ома для металлического проводника. Электрическое сопротивление проводника равно:
а удельное сопротивление ρ и удельная проводимость ν выражаются соотношениями:
Закон Джоуля-Ленца.
К концу свободного пробега электроны под действием поля приобретают кинетическую энергию
Согласно сделанным предположениям вся эта энергия при соударениях передается решетке и переходит в тепло.
За время Δt каждый электрон испытывает Δt / τ соударений. В проводнике сечением S и длины l имеется nSl электронов. Отсюда следует, что выделяемое в проводнике за время Δt тепло равно:
Это соотношение выражает закон Джоуля-Ленца.
Таким образом, классическая электронная теория объясняет существование электрического сопротивления металлов, законы Ома и Джоуля–Ленца. Однако в ряде вопросов классическая электронная теория приводит к выводам, находящимся в противоречии с опытом.
Эта теория не может, например, объяснить, почему молярная теплоемкость металлов, также как и молярная теплоемкость диэлектрических кристаллов, равна 3R, где R – универсальная газовая постоянная (закон Дюлонга и Пти, см. ч. I, § 3.10). Наличие свободных электронов на сказывается на величине теплоемкости металлов.
Классическая электронная теория не может также объяснить температурную зависимость удельного сопротивления металлов. Теория дает соотношение , в то время как из эксперимента получается зависимость ρ
T. Однако наиболее ярким примером расхождения теории и опытов является сверхпроводимость.
Согласно классической электронной теории, удельное сопротивление металлов должно монотонно уменьшаться при охлаждении, оставаясь конечным при всех температурах. Такая зависимость действительно наблюдается на опыте при сравнительно высоких температурах. При более низких температурах порядка нескольких кельвинов удельное сопротивление многих металлов перестает зависеть от температуры и достигает некоторого предельного значения. Однако наибольший интерес представляет удивительное явление сверхпроводимости, открытое датским физиком Х.Каммерлинг-Онесом в 1911 году. При некоторой определенной температуре Tкр, различной для разных веществ, удельное сопротивление скачком уменьшается до нуля (рис. 1.12.4). Критическая температура у ртути равна 4,1 К, у аллюминия 1,2 К, у олова 3,7 К. Сверхпроводимость наблюдается не только у элементов, но и у многих химических соединений и сплавов. Например, соединение ниобия с оловом (Ni3Sn) имеет критическую температуру 18 К. Некоторые вещества, переходящие при низких температурах в сверхпроводящее состояние, не являются проводниками при обычных температурах. В то же время такие «хорошие» проводники, как медь и серебро, не становятся сверхпроводниками при низких температурах.
1.12.4). Критическая температура у ртути равна 4,1 К, у аллюминия 1,2 К, у олова 3,7 К. Сверхпроводимость наблюдается не только у элементов, но и у многих химических соединений и сплавов. Например, соединение ниобия с оловом (Ni3Sn) имеет критическую температуру 18 К. Некоторые вещества, переходящие при низких температурах в сверхпроводящее состояние, не являются проводниками при обычных температурах. В то же время такие «хорошие» проводники, как медь и серебро, не становятся сверхпроводниками при низких температурах.
Зависимость удельного сопротивления ρ от абсолютной температуры T при низких температурах: a – нормальный металл; b – сверхпроводник
Вещества в сверхпроводящем состоянии обладают исключительными свойствами. Практически наиболее важным их них является способность длительное время (многие годы) поддерживать без затухания электрический ток, возбужденный в сверхпроводящей цепи.
Классическая электронная теория не способна объяснить явление сверхпроводимости. Объяснение механизма этого явления было дано только через 60 лет после его открытия на основе квантово-механических представлений.
Научный интерес к сверхпроводимости возрастал по мере открытия новых материалов с более высокими критическими температурами. Значительный шаг в этом направлении был сделан в 1986 году, когда было обнаружено, что у одного сложного керамического соединения Tкр = 35 K. Уже в следующем 1987 году физики сумели создать новую керамику с критической температурой 98 К, превышающей температуру жидкого азота (77 К). Явление перехода веществ в сверхпроводящее состояние при температурах, превышающих температуру кипения жидкого азота, было названо высокотемпературной сверхпроводимостью. В 1988 году было создано керамическое соединение на основе элементов Tl–Ca–Ba–Cu–O с критической температурой 125 К.
В настоящее время ведутся интенсивные работы по поиску новых веществ с еще более высокими значениями Tкр. Ученые надеятся получить вещество в сверхпроводящем состоянии при комнатной температуре. Если это произойдет, это будет настоящей революцией в науке, технике и вообще в жизни людей.
Следует отметить, что до настоящего времени механизм высокотемпературной сверхпроводимости керамических материалов до конца не выяснен.
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: носители свободных электрических зарядов в металлах.
В этом листке мы приступаем к подробному изучению того, как осуществляется прохождение электрического тока в различных проводящих средах — твёрдых телах, жидкостях и газах.
Напомним, что необходимым условием возникновения тока является наличие в среде достаточно большого количества свободных зарядов, которые могут начать упорядоченное движение под действием электрического поля. Такие среды как раз и называются проводниками электрического тока.
Наиболее широко распространены металлические проводники. Поэтому начинаем мы с вопросов распространения электрического тока в металлах.
Мы много раз говорили о свободных электронах, которые являются носителями свободных зарядов в металлах. Вам хорошо известно, что электрический ток в металлическом проводнике образуется в результате направленного движения свободных электронов.
Свободные электроны
Металлы в твёрдом состоянии имеют кристаллическую структуру: расположение атомов в пространстве характеризуется периодической повторяемостью и образует геометрически правильный рисунок, называемый кристаллической решёткой.
Атомы металлов имеют небольшое число валентных электронов, расположенных на внешней электронной оболочке. Эти валентные электроны слабо связаны с ядром, и атом легко может их потерять.
Когда атомы металла занимают места в кристаллической решётке, валентные электроны покидают свои оболочки — они становятся свободными и отправляются «гулять» по всему кристаллу (а именно, свободные электроны перемещаются по внешним орбиталям соседних атомов. Эти орбитали перекрываются друг с другом вследствие близкого расположения атомов в кристаллической решётке, так что свободные электроны оказываются «общей собственностью» всего кристалла). В узлах кристаллической решётки металла остаются положительные ионы, пространство между которыми заполнено «газом» свободных электронов (рис. 1 ).
Рис. 1. Свободные электроны
Свободные электроны и впрямь ведут себя подобно частицам газа (другой адекватный образ — электронное море, которое «омывает» кристаллическую решётку) — совершая тепловое движение, они хаотически снуют туда-сюда между ионами кристаллической решётки. Суммарный заряд свободных электронов равен по модулю и противоположен по знаку общему заряду положительных ионов, поэтому металлический проводник в целом оказывается электрически нейтральным.
Газ свободных электронов является «клеем», на котором держится вся кристаллическая структура проводника. Ведь положительные ионы отталкиваются друг от друга, так что кристаллическая решётка, распираемая изнутри мощными кулоновскими силами, могла бы разлететься в разные стороны. Однако в тоже самое время ионы металла притягиваются к обволакивающему их электронному газу и, как ни в чём не бывало, остаются на своих местах, совершая лишь тепловые колебания в узлах кристаллической решётки вблизи положений равновесия.
Что произойдёт, если металлический проводник включить в замкнутую цепь, содержащую источник тока? Свободные электроны продолжают совершать хаотическое тепловое движение, но теперь — под действием возникшего внешнего электрического поля — они вдобавок начнут перемещаться упорядоченно. Это направленное течение электронного газа, накладывающееся на тепловое движение электронов, и есть электрический ток в металле (поэтому свободные электроны называются также электронами проводимости). Скорость упорядоченного движения электронов в металлическом проводнике, как нам уже известно, составляет приблизительно 0,1мм/с.
Опыт Рикке
Почему мы решили, что ток в металлах создаётся движением именно свободных электронов? Положительные ионы кристаллической решётки также испытывают на себе действие внешнего электрического поля. Может, они тоже перемещаются внутри металлического проводника и участвуют в создании тока?
Упорядоченное движение ионов означало бы постепенный перенос вещества вдоль направления электрического тока. Поэтому надо просто пропускать ток по проводнику на протяжении весьма длительного времени и посмотреть, что в итоге получится. Такого рода эксперимент и был поставлен Э.Рикке в 1901 году.
В электрическую цепь были включены три прижатых друг к другу цилиндра: два медных по краям и один алюминиевый между ними (рис. 2 ). По этой цепи пропускался электрический ток в течение года.
Рис. 2. Опыт Рикке
За год сквозь цилиндры прошёл заряд более трёх миллионов кулон. Предположим, что каждый атом металла теряет по одному валентному электрону, так что заряд иона равен элементарному заряду Кл. Если ток создаётся движением положительных ионов, то нетрудно подсчитать (сделайте это сами!), что такая величина прошедшего по цепи заряда соответствует переносу вдоль цепи около 2кг меди.
Однако после разъединения цилиндров было обнаружено лишь незначительное проникновение металлов друг в друга, обусловленное естественной диффузией их атомов (и не более того). Электрический ток в металлах не сопровождается переносом вещества, поэтому положительные ионы металла не принимают участия в создании тока.
Опыт Стюарта–Толмена
Прямое экспериментальное доказательство того, что электрический ток в металлах создаётся движением свободных электронов, было дано в опыте Т.Стюарта и Р.Толмена (1916 год).
Эксперименту Стюарта–Толмена предшествовали качественные наблюдения, сделанные четырьмя годами ранее русскими физиками Л.И.Мандельштамом и Н.Д.Папалекси. Они обратили внимание на так называемый электроинерционный эффект: если резко затормозить движущийся проводник, то в нём возникает кратковременный импульс тока. Эффект объясняется тем, что в течение небольшого времени после торможения проводника его свободные заряды продолжают двигаться по инерции.
Однако никаких количественных результатов Мандельштам и Папалекси не получили, и наблюдения их опубликованы не были. Честь назвать опыт своим именем принадлежит Стюарту и Толмену, которые не только наблюдали указанный электроинерционный эффект, но и произвели необходимые измерения и расчёты.
Установка Стюарта и Толмена показана на рис. 3 .
Рис. 3. Опыт Стюарта–Толмена
Катушка большим числом витков металлического провода приводилась в быстрое вращение вокруг своей оси. Концы обмотки с помощью скользящих контактов были подсоединены к специальному прибору — баллистическому гальванометру, который позволяет измерять проходящий через него заряд.
После резкого торможения катушки в цепи возникал импульс тока. Направление тока указывало на то, что он вызван движением отрицательных зарядов. Измеряя баллистическим гальванометром суммарный заряд, проходящий по цепи, Стюарт и Толмен вычислили отношение заряда одной частицы к её массе. Оно оказалось равно отношению для электрона, которое в то время уже было хорошо известно.
Так было окончательно выяснено, что носителями свободных зарядов в металлах являются свободные электроны. Как видите, этот давно и хорошо знакомый вам факт был установлен сравнительно поздно — учитывая, что металлические проводники к тому моменту уже более столетия активно использовались в самых разнообразных экcпериментах по электромагнетизму (сравните, например, с датой открытия закона Ома — 1826 год. Дело, однако, заключается в том, что сам электрон был открыт лишь в 1897 году).
Зависимость сопротивления от температуры
Опыт показывает, что при нагревании металлического проводника его сопротивление увеличивается. Как это объяснить?
Причина проста: с повышением температуры тепловые колебания ионов кристаллической решётки становятся более интенсивными, так что число соударений свободных электронов с ионами возрастает. Чем активнее тепловое движение решётки, тем труднее электронам пробираться сквозь промежутки между ионами (Представьте себе вращающуюся проходную дверь. В каком случае труднее проскочить через неё: когда она вращается медленно или быстро? :-)). Скорость упорядоченного движения электронов уменьшается, поэтому уменьшается и сила тока (при неизменном напряжении). Это и означает увеличение сопротивления.
Как опять-таки показывает опыт, зависимость сопротивления металлического проводника от температуры с хорошей точностью является линейной:
Здесь — сопротивление проводника при . График зависимости (1) является прямой линией (рис. 4 ).
Множитель называется температурным коэффициентом сопротивления. Его значения для различных металлов и сплавов можно найти в таблицах.
Длина проводника и его площадь поперечного сечения при изменении температуры меняются несущественно. Выразим и через удельное сопротивление:
и подставим эти формулы в (1) . Получим аналогичную зависимость удельного сопротивления от температуры:
Коэффициент весьма мал (для меди, например, ), так что температурной зависимостью сопротивления металла часто можно пренебречь. Однако в ряде случаев считаться с ней приходиться. Например, вольфрамовая спираль электрической лампочки раскаляется до такой степени, что её вольт-амперная характеристика оказывается существенно нелинейной.
Рис. 5. Вольт-амперная характеристика лампочки
Так, на рис. 5 приведена вольт-амперная характеристика автомобильной лампочки. Если бы лампочка представляла собой идеальный резистор, её вольт-амперная характеристика была прямой линией в соответствии с законом Ома. Эта прямая изображена синим пунктиром.
Однако по мере роста напряжения, приложенного к лампочке, график отклоняется от этой прямой всё сильнее и сильнее. Почему? Дело в том, что с увеличением напряжения ток через лампочку возрастает и больше разогревает спираль; сопротивление спирали поэтому также увеличивается. Следовательно, сила тока хотя и продолжит возрастать, но будет иметь всё меньшее и меньшее значение по сравнению с тем, которое предписывается «пунктирной» линейной зависимостью тока от напряжения.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
Электрический ток в полупроводниках формулы. Природа электрического тока в полупроводниках. Собственная и примесная проводимость
Полупроводниками назвали класс веществ, у которых с повышением
температуры увеличивается проводимость, уменьшается
электрическое сопротивление. Этим полупроводники принципиально
отличаются от металлов.
Типичными полупроводниками являются кристаллы германия и
кремния, в которых атомы объединены кова-лентной связью. При
любых температурах в полупроводниках имеются свободные
электроны. Свободные электроны под действием внешнего
электрического поля могут перемещаться в кристалле, создавая
электронный ток проводимости. Удаление электрона с внешней
оболочки одного из атомов кристаллической решетки приводит к
превращению этого атома в положительный ион. Этот ион может
нейтрализоваться, захватив электрон у одного из соседних
атомов. Далее, в результате переходов электронов от атомов к
положительным ионам происходит процесс хаотического
перемещения в кристалле места с недостающим электроном. Внешне
этот процесс воспринимается как перемещение положительного
электрического заряда, называемого дыркой
.
При помещении кристалла в электрическое поле возникает
упорядоченное движение дырок — дырочный ток проводимости.
В идеальном полупроводниковом кристалле электрический ток
создается движением равного количества отрицательно заряженных
электронов и положительно заряженных дырок. Проводимость в
идеальных полупроводниках называется собственной
проводимостью.
Свойства полупроводников сильно зависят от содержания
примесей. Примеси бывают двух типов — донорные и акцепторные.
Примеси, отдающие электроны и создающие электронную
проводимость, называются донорными
(примеси, имеющие
валентность больше, чем у основного полупроводника).
Полупроводники, в которых концентрация электронов превышает
концентрацию дырок, называют полупроводниками n-типа.
Примеси, захватывающие электроны и создающие тем самым
подвижные дырки, не увеличивая при этом число электронов
проводимости, называют акцепторными
(примеси имеющие
валентность меньше, чем у основного полупроводника).
При низких температурах основными носителями тока в
полупроводниковом кристалле с акцепторной примесью являются
дырки, а не основными носителями — электроны. Полупроводники,
в которых концентрация дырок превышает концентрацию электронов
проводимости, называют дырочными полупроводниками или
полупроводниками р-типа. Рассмотрим контакт двух
полупроводников с различными типами проводимости.
Через границу этих полупроводников происходит взаимная
диффузия основных носителей: электроны из n-полупроводника
диффундируют в р-полупроводник, а дырки из р-полупроводника в
n-полупроводник. В результате участок n-полупроводника,
граничащий с контактом, будет обеднен электронами, и в нем
образуется избыточный положительный заряд, обусловленный
наличием оголенных ионов примеси. Движение дырок из
р-полупроводника в n-полупроводник приводит к возникновению
избыточного отрицательного заряда в пограничном участке
р-полупроводника. В результате образуется двойной
электрический слой, и возникает контактное электрическое поле,
которое препятствует дальнейшей диффузии основных носителей
заряда. Этот слой называют запирающим
.
Внешнее электрическое поле влияет на электропроводность
запирающего слоя. Если полупроводники подключены к источнику
так, как показано на рис. 55, то под действием внешнего
электрического поля основные носители заряда — свободные
электроны в п-полупроводнике и дырки в р-полупроводнике —
будут двигаться навстречу друг другу к границе раздела
полупроводников, при этом толщина p-n-перехода уменьшается,
следовательно, уменьшается его сопротивление. В этом случае
сила тока ограничивается внешним сопротивлением. Такое
направление внешнего электрического поля называется прямым.
Прямому включению p-n-перехода соответствует участок 1 на
вольт-амперной характеристике (см. рис. 57).
Носители электрического тока в различных средах и
вольт-амперные характеристики обобщены в табл. 1.
Если полупроводники подключены к источнику так, как показано
на рис. 56, то электроны в п-полупроводнике и дырки в
р-полупроводнике будут перемещаться под действием внешнего
электрического поля от границы в противоположные стороны.
Толщина запирающего слоя и, следовательно, его сопротивление
увеличиваются. При таком направлении внешнего электрического
поля — обратном (запирающем) через границу раздела проходят
только неосновные носители заряда, концентрация которых много
меньше, чем основных, и ток практически равен нулю. Обратному
включению р-п-перехода соответствует участок 2 на
вольт-амперной характеристике (рис. 57).
Таким образом, р-п-переход обладает несимметричной
проводимостью. Это свойство используется в полупроводниковых
диодах, содержащих один p-n-переход и применяемых, например,
для выпрямления переменного тока или детектирования.
Полупроводники находят широкое применение в современной
электронной технике.
Зависимость электрического сопротивления полупроводниковых
металлов от температуры используется в специальных
полупроводниковых приборах — терморезисторах
. Приборы,
в которых используется свойство полупроводниковых кристаллов
изменять свое электрическое сопротивление при освещении
светом, называются фоторезисторами
.
К числу полупроводников
относятся многие химические элементы (германий, кремний, селен, теллур, мышьяк
и др.), огромное количество сплавов и химических соединений. Почти все
неорганические вещества окружающего нас мира – полупроводники. Самым
распространенным в природе полупроводником является кремний, составляющий
около 30 % земной коры.
Качественное отличие
полупроводников от металлов проявляется в зависимости удельного
сопротивления от температуры
(рис.9.3)
Зонная модель
электронно-дырочной проводимости полупроводников
При образовании твердых тел
возможна ситуация, когда энергетическая зона, возникшая из энергетических
уровней валентных электронов исходных
атомов, оказывается полностью заполненной электронами, а ближайшие, доступные
для заполнения электронами энергетические уровни отделены от валентной
зоны
Е V промежутком неразрешенных энергетических состояний –
так называемой запрещенной зоной
Е g
.Выше запрещенной зоны расположена зона разрешенных
для электронов энергетических состояний – зона проводимости
Е c .
Зона проводимости при 0 К
полностью свободна, а валентная зона полностью занята. Подобные зонные
структуры характерны для кремния, германия, арсенида галлия (GaAs),
фосфида индия (InP) и многих других твердых тел, являющихся
полупроводниками.
При повышении температуры полупроводников и
диэлектриков электроны способны получать дополнительную энергию, связанную с
тепловым движением kT
. У части электронов энергии
теплового движения оказывается достаточно для перехода из валентной зоны в
зону проводимости,
где электроны под действием внешнего электрического поля
могут перемещаться практически свободно.
В этом случае, в цепи с полупроводниковым материалом по
мере повышения температуры полупроводника будет нарастать электрический ток.
Этот ток связан не только с движением электронов в зоне проводимости, но и с
появлением вакантных мест от ушедших в зону проводимости электронов
в
валентной зоне, так называемых дырок
. Вакантное
место может быть занято валентным электроном из соседней пары, тогда дырка
переместиться на новое место в кристалле.
Если полупроводник
помещается в электрическое поле, то в
упорядоченное движение вовлекаются не только свободные электроны, но и дырки,
которые ведут себя как положительно заряженные частицы. Поэтому ток I
в полупроводнике складывается из электронного I n
и дырочного I p
токов: I
= I n
+ I p
.
Электронно-дырочный механизм
проводимости проявляется только у чистых (т.е. без примесей) полупроводников. Он
называется собственной электрической проводимостью
полупроводников. Электроны
забрасываются в зону проводимости с уровня Ферми
, который оказывается в
собственном полупроводнике расположенным посередине запрещенной зоны
(рис. 9.4).
Существенно
изменить проводимость полупроводников можно, введя в них очень небольшие
количества примесей. В металлах примесь всегда уменьшает проводимость. Так,
добавление в чистый кремний
3 % атомов
фосфора увеличивает электропроводность кристалла в 10 5 раз.
Небольшое добавление примеси к полупроводнику
называется легированием.
Необходимым условием резкого
уменьшения удельного сопротивления полупроводника при введении примесей
является отличие валентности атомов примеси от валентности основных атомов кристалла. Проводимость полупроводников при наличии
примесей называется примесной проводимостью
.
Различают два типа примесной проводимости
– электронную
и дырочную
проводимости. Электронная проводимость
возникает, когда
в кристалл германия с четырехвалентными атомами введены пятивалентные атомы
(например, атомы мышьяка, As) (рис. 9.5).
Четыре валентных электрона
атома мышьяка включены в образование ковалентных связей с четырьмя соседними
атомами германия. Пятый валентный электрон оказался излишним. Он легко
отрывается от атома мышьяка и становится свободным. Атом, потерявший электрон,
превращается в положительный ион, расположенный в узле кристаллической решетки.
Примесь из атомов с валентностью, превышающей валентность основных атомов
полупроводникового кристалла, называется
донорской примесью
. В результате ее
введения в кристалле появляется значительное число свободных электронов. Это
приводит к резкому уменьшению удельного сопротивления полупроводника – в тысячи
и даже миллионы раз.
Удельное сопротивление
проводника с большим содержанием примесей может приближаться к удельному
сопротивлению металлического проводника. Такая проводимость, обусловленная свободными
электронами, называется электронной, а полупроводник, обладающий электронной
проводимостью, называется полупроводником n-типа
.
Дырочная проводимость
возникает, когда в кристалл
германия введены трехвалентные атомы, например, атомы индия (рис. 9.5)
На рисунке 6 показан атом
индия, который создал с помощью своих валентных электронов ковалентные связи
лишь с тремя соседними атомами германия. На образование связи с четвертым
атомом германия у атома индия нет электрона. Этот недостающий электрон может
быть захвачен атомом индия из ковалентной связи соседних атомов германия. В
этом случае атом индия превращается в отрицательный ион, расположенный в узле
кристаллической решетки, а в ковалентной связи соседних атомов образуется
вакансия.
Примесь атомов, способных захватывать электроны, называется акцепторной примесью
. В результате введения акцепторной примеси в
кристалле разрывается множество ковалентных связей и образуются вакантные места
(дырки). На эти места могут перескакивать электроны из соседних ковалентных связей,
что приводит к хаотическому блужданию дырок по кристаллу.
Концентрация дырок в
полупроводнике с акцепторной примесью значительно превышает концентрацию электронов,
которые возникли из-за механизма собственной электропроводности полупроводника: n p
>> n n
. Проводимость такого типа называется дырочной проводимостью
. Примесный
полупроводник с дырочной проводимостью называется полупроводником p-типа
.
Основными носителями свободного заряда в полупроводниках p
-типа являются
дырки.
Электронно-дырочный
переход. Диоды и транзисторы
В современной электронной
технике полупроводниковые приборы играют исключительную роль. За последние три
десятилетия они почти полностью вытеснили электровакуумные приборы.
В любом полупроводниковом
приборе имеется один или несколько электронно-дырочных переходов. Электронно-дырочный
переход
(или n
–p
-переход) – это область контакта двух полупроводников с разными типами
проводимости.
На границе полупроводников (рис.
9.7) образуется двойной электрический слой, электрическое поле которого
препятствует процессу диффузии электронов и дырок навстречу друг другу.
Способность n
–p
-перехода
пропускать ток практически только в одном направлении используется в приборах,
которые называются полупроводниковыми диодами
.
Полупроводниковые диоды изготавливаются из
кристаллов кремния или германия. При их изготовлении в кристалл c каким-либо
типом проводимости вплавляют примесь, обеспечивающую другой тип проводимости.
На рисунке 9.8 приведена типичная
вольт — амперная характеристика кремниевого диода.
Полупроводниковые приборы не с одним, а с двумя n–p-переходами
называются транзисторами
. Транзисторы
бывают двух типов: p
–n
–p
-транзисторы и n
–p
–n
-транзисторы. В транзисторе n
–p
–n
-типа основная
германиевая пластинка обладает проводимостью p
-типа, а созданные на ней
две области – проводимостью n
-типа (рис.9.9).
В транзисторе p–n–p
–
типа всё наоборот. Пластинку транзистора называют базой
(Б), одну из областей с противоположным типом проводимости – коллектором
(К), а вторую – эмиттером
(Э).
Полупроводники — это вещества, удельное сопротивление которых убывает с повышением температуры, наличием примесей, изменением освещенности. По этим свойствам они разительно отличаются от металлов. Обычно к полупроводникам относятся кристаллы, в которых для освобождения электрона требуется энергия не более 1,5-2 эВ. Типичными полупроводниками являются кристаллы германия и кремния, в которых атомы объединены ковалентной связью. Природа этой связи позволяет объяснить указанные выше характерные свойства. При нагревании полупроводников их атомы ионизируются. Освободившиеся электроны не могут быть захвачены соседними атомами, так как все их валентные связи насыщены. Свободные электроны под действием внешнего электрического поля могут перемещаться в кристалле, создавая электронный ток проводимости. Удаление электрона с внешней оболочки одного из атомов в кристаллической решетке приводит к образованию положительного иона. Этот ион может нейтрализоваться, захватив электрон. Далее, в результате переходов электронов от атомов к положительным ионам происходит процесс хаотического перемещения в кристалле места с недостающим электроном — «дырки». Внешне этот процесс хаотического перемещения воспринимается как перемещение положительного заряда. При помещении кристалла в электрическое поле возникает упорядоченное движение «дырок» — дырочный ток проводимости. В идеальном кристалле ток создается равным количеством электронов и «дырок». Такой тип проводимости называют собственной проводимостью полупроводников. При повышении температуры (или освещенности) собственная проводимость проводников увеличивается.
На проводимость полупроводников большое влияние оказывают примеси. Примеси бывают донорные и акцепторные. Допорная примесь — это примесь с большей валентностью. При добавлении донорной примеси в полупроводнике образуются липшие электроны. Проводимость станет электронной, а полупроводник называют полупроводником n-типа. Например, для кремния с валентностью n — 4 донорной примесью является мышьяк с валентностью n = 5. Каждый атом примеси мышьяка приведет к образованию одного электрона проводимости.
Акцепторная примесь — это примесь с меньшей валентностью. При добавлении такой примеси в полупроводнике образуется лишнее количество «дырок». Проводимость будет «дырочной», а полупроводник называют полупроводником р-типа. Например, для кремния акцепторной примесью является индий с валентностью п = 3. Каждый атом индия приведет к образованию лишней «дырки».
Принцип действия большинства полупроводниковых приборов основан на свойствах р-n-перехода.
9.2 Модель проводимости в металлах — University Physics Volume 2
Когда электроны движутся по проводящему проводу, они не движутся с постоянной скоростью, то есть электроны не движутся по прямой с постоянной скоростью. Скорее, они взаимодействуют и сталкиваются с атомами и другими свободными электронами в проводнике. Таким образом, электроны движутся зигзагообразно и дрейфуют по проволоке. Следует также отметить, что, хотя и удобно обсуждать направление тока, ток является скалярной величиной.Обсуждая скорость зарядов в токе, более уместно обсудить плотность тока. Мы вернемся к этой идее в конце этого раздела.
Скорость дрейфа
Электрические сигналы передаются очень быстро. Телефонные разговоры по проводам проходят на большие расстояния без заметных задержек. Свет включается, как только переключатель света переводится в положение «включено». Большинство электрических сигналов, переносимых токами, передаются со скоростью порядка 108 м / с · 108 м / с, что составляет значительную часть скорости света.Интересно, что отдельные заряды, составляющие ток, в среднем движутся намного медленнее, обычно дрейфуя со скоростью порядка 10-4 м / с · 10-4 м / с. Как согласовать эти две скорости и что это говорит нам о стандартных проводниках?
Высокая скорость электрических сигналов является результатом того факта, что сила между зарядами быстро действует на расстоянии. Таким образом, когда свободный заряд вдавливается в провод, как на рисунке 9.7, входящий заряд толкает другие заряды впереди себя из-за силы отталкивания между одинаковыми зарядами.Эти движущиеся заряды толкают заряды дальше по линии. Плотность заряда в системе не может быть легко увеличена, поэтому сигнал передается быстро. Возникающая в результате электрическая ударная волна движется по системе почти со скоростью света. Если быть точным, этот быстро движущийся сигнал или ударная волна представляет собой быстро распространяющееся изменение электрического поля.
Рис. 9.7 Когда заряженные частицы вдавливаются в этот объем проводника, такое же количество быстро вынуждено покинуть его.Отталкивание между одноименными зарядами затрудняет увеличение количества зарядов в объеме. Таким образом, как только один заряд входит, другой почти сразу уходит, быстро передавая сигнал вперед.
Хорошие проводники имеют большое количество бесплатных зарядов. В металлах свободными зарядами являются свободные электроны. (На самом деле, хорошие электрические проводники также часто являются хорошими проводниками тепла, потому что большое количество свободных электронов может переносить тепловую энергию, а также электрический ток.) Рисунок 9.8 показывает, как свободные электроны движутся по обычному проводнику. Расстояние, на которое может перемещаться отдельный электрон между столкновениями с атомами или другими электронами, довольно мало. Таким образом, пути электронов кажутся почти случайными, как движение атомов в газе. Но в проводнике есть электрическое поле, которое заставляет электроны дрейфовать в указанном направлении (противоположном полю, поскольку они отрицательны). Скорость дрейфа v → dv → d — это средняя скорость свободных зарядов. Скорость дрейфа довольно мала, так как свободных зарядов очень много.Если у нас есть оценка плотности свободных электронов в проводнике, мы можем вычислить скорость дрейфа для данного тока. Чем больше плотность, тем ниже скорость, необходимая для данного тока.
Рис. 9.8. Свободные электроны, движущиеся в проводнике, совершают множество столкновений с другими электронами и другими частицами. Показан типичный путь одного электрона. Средняя скорость свободных зарядов называется дрейфовой скоростью v → dv → d, а для электронов она направлена в направлении, противоположном электрическому полю.Столкновения обычно передают энергию проводнику, требуя постоянного подвода энергии для поддержания постоянного тока.
Столкновения свободных электронов передают энергию атомам проводника. Электрическое поле действительно перемещает электроны на расстояние, но эта работа не увеличивает кинетическую энергию (или скорость) электронов. Работа передается атомам проводника, часто повышая температуру. Таким образом, для поддержания протекания тока требуется постоянная подача энергии.(Исключение составляют сверхпроводники по причинам, которые мы рассмотрим в более поздней главе. Сверхпроводники могут иметь постоянный ток без постоянной подачи энергии — большая экономия энергии.) Для проводника, который не является сверхпроводником, подача энергии может быть полезен, как в нити накаливания лампы накаливания (рис. 9.9). Подача энергии необходима для повышения температуры вольфрамовой нити, чтобы нить светилась.
Рисунок 9.9 Лампа накаливания имеет простую конструкцию.Вольфрамовая нить помещена в частично вакуумированную стеклянную колбу. Один конец нити накала прикреплен к основанию винта, которое выполнено из проводящего материала. Второй конец нити накала прикреплен ко второму контакту в основании лампы. Два контакта разделены изоляционным материалом. Ток течет через нить, и температура нити становится достаточно большой, чтобы нить накала светилась и излучала свет. Однако эти лампы не очень энергоэффективны, что видно по теплу, исходящему от лампы.В 2012 году Соединенные Штаты, наряду со многими другими странами, начали постепенно отказываться от ламп накаливания в пользу более энергоэффективных ламп, таких как светодиодные (LED) лампы и компактные люминесцентные лампы (CFL) (право кредита) : модификация работы Сержа Сен).
Мы можем получить выражение для связи между током и скоростью дрейфа, рассмотрев количество свободных зарядов в отрезке провода, как показано на рисунке 9.10. Количество бесплатных зарядов на единицу объема или плотность свободных зарядов обозначается символом n , где n = количество зарядов, объем = количество зарядов, объем.Значение n зависит от материала. Заштрихованный сегмент имеет том AvddtAvddt, поэтому количество бесплатных зарядов в томе равно nAvddtnAvddt. Таким образом, заряд dQ в этом сегменте равен qnAvddtqnAvddt, где q — это количество заряда на каждом носителе. (Величина заряда электронов q = 1,60 · 10−19Cq = 1,60 · 10−19C.) Ток перемещается за единицу времени; таким образом, если все первоначальные заряды уходят из этого сегмента за время дт , ток равен
Я = dQdt = qnAvd.Я = dQdt = qnAvd.
Перестановка терминов дает
, где vdvd — скорость дрейфа, n, — плотность свободного заряда, A, — площадь поперечного сечения провода, а I — ток через провод. Каждый носитель тока имеет заряд q и движется со скоростью дрейфа величиной vdvd.
Рис. 9.10. Все заряды в заштрихованном объеме этой проволоки перемещаются за время dt , имея скорость дрейфа величиной vdvd.
Обратите внимание, что простая скорость дрейфа — это еще не все. Скорость электрона иногда намного превышает скорость его дрейфа. Кроме того, не все электроны в проводнике могут двигаться свободно, а те, которые движутся, могут двигаться несколько быстрее или медленнее, чем скорость дрейфа. Итак, что мы подразумеваем под свободными электронами?
Атомы в металлическом проводнике упакованы в виде решетчатой структуры. Некоторые электроны находятся достаточно далеко от ядер атомов, поэтому они не испытывают такого сильного притяжения ядер, как внутренние электроны.Это свободные электроны. Они не связаны с одним атомом, а вместо этого могут свободно перемещаться между атомами в «море» электронов. При приложении электрического поля эти свободные электроны ускоряются. При движении они сталкиваются с атомами в решетке и с другими электронами, генерируя тепловую энергию, и проводник нагревается. В изоляторе организация атомов и структура не допускают наличие таких свободных электронов.
Как вы знаете, электроэнергия обычно подается к оборудованию и приборам через круглые провода, сделанные из проводящего материала (медь, алюминий, серебро или золото), многожильные или сплошные.Диаметр провода определяет допустимую нагрузку по току — чем больше диаметр, тем больше допустимая нагрузка по току. Несмотря на то, что допустимая нагрузка по току определяется диаметром, проволока обычно не характеризуется диаметром напрямую. Вместо этого проволока обычно продается в единицах измерения, известных как «калибр». Проволока изготавливается путем пропускания материала через круглые формы, называемые «фильеры для волочения». Чтобы изготавливать более тонкие проволоки, производители протягивают проволоку через несколько матриц последовательно уменьшающегося диаметра.Исторически калибр проволоки был связан с количеством процессов волочения, необходимых для производства проволоки. По этой причине, чем больше калибр, тем меньше диаметр. В Соединенных Штатах Америки для стандартизации системы был разработан американский калибр проводов (AWG). Бытовая электропроводка обычно состоит из проводов калибра от 10 (диаметром 2,588 мм) до 14 (диаметром 1,628 мм). Устройство, используемое для измерения толщины проволоки, показано на рисунке 9.11.
Рисунок 9.11 Устройство для измерения толщины электрического провода.Как видите, более высокие номера калибра указывают на более тонкие провода. (кредит: Джозеф Дж. Траут)
Пример 9.3
Расчет скорости дрейфа в общем проводе
Вычислите скорость дрейфа электронов в медной проволоке диаметром 2,053 мм (калибр 12), по которой проходит ток 20,0 А, учитывая, что на один атом меди приходится один свободный электрон. (Бытовая электропроводка часто содержит медный провод 12-го калибра, и максимальный допустимый ток в таком проводе обычно составляет 20,0 А.) Плотность меди составляет 8.80 × 103 кг / м 38,80 × 103 кг / м3, а атомная масса меди составляет 63,54 г / моль.
Стратегия
Мы можем рассчитать скорость дрейфа, используя уравнение I = nqAvdI = nqAvd. Ток I = 20.00AI = 20.00A, а q = 1.60 · 10−19Cq = 1.60 · 10−19C — заряд электрона. Площадь поперечного сечения провода можно рассчитать по формуле A = πr2A = πr2, где r — половина диаметра. Данный диаметр составляет 2,053 мм, поэтому r составляет 1,0265 мм. Нам дана плотность меди 8,80 × 103 кг / м38.80 × 103 кг / м3, а атомная масса меди 63,54 г / моль 63,54 г / моль. Мы можем использовать эти две величины вместе с числом Авогадро, 6,02 × 1023 атома / моль, 6,02 × 1023 атома / моль, чтобы определить n , количество свободных электронов на кубический метр.
Решение
Сначала мы рассчитаем плотность свободных электронов в меди. На один атом меди приходится один свободный электрон. Следовательно, количество свободных электронов такое же, как количество атомов меди в м3 м3. Теперь мы можем найти n следующим образом:
п = 1e − атом × 6.02 × 1023атомсмоль × 1 моль 63,54 г × 1000 г кг × 8,80 × 103 кг 1м3 = 8,34 × 1028e- / м3.n = 1e − атом × 6,02 × 1023атомсмоль × 1 моль 63,54 г × 1000 г кг × 8,80 × 103 кг1м3 = 8,34 × 1028e- / м3.
Площадь сечения провода
A = πr2 = π (2,05 · 10−3м2) 2 = 3,30 · 10−6м2. A = πr2 = π (2,05 · 10−3м2) 2 = 3,30 · 10−6м2.
Перестановка I = nqAvdI = nqAvd для изоляции скорости дрейфа дает
vd = InqA = 20,00A (8,34 × 1028 / м3) (- 1,60 × 10−19C) (3,30 × 10−6м2) = — 4,54 × 10−4 м / с. vd = InqA = 20,00A (8,34 × 1028 / м3 ) (- 1,60 × 10−19C) (3,30 × 10−6м2) = — 4,54 × 10−4 м / с.
Значение
Знак минус указывает на то, что отрицательные заряды движутся в направлении, противоположном обычному току.Небольшое значение скорости дрейфа (порядка 10-4 м / с) 10-4 м / с) подтверждает, что сигнал движется примерно в 10121012 раз быстрее (около 108 м / с) 108 м / с), чем заряды, несущие Это.
Проверьте свое понимание 9.3
В примере 9.4 скорость дрейфа была рассчитана для медного провода диаметром 2,053 мм (калибр 12), по которому проходит ток 20 ампер. Изменится ли скорость дрейфа для провода диаметром 1,628 мм (калибр 14), по которому течет тот же ток 20 ампер?
Плотность тока
Хотя часто бывает удобно поставить отрицательный или положительный знак, чтобы указать общее направление движения зарядов, ток является скалярной величиной, I = dQdtI = dQdt.Часто необходимо обсудить детали движения заряда вместо обсуждения общего движения зарядов. В таких случаях необходимо обсудить плотность тока, J → J →, векторную величину. Плотность тока — это поток заряда через бесконечно малую площадь, деленную на площадь. Плотность тока должна учитывать локальную величину и направление потока заряда, которые варьируются от точки к точке. Единицей измерения плотности тока является ампер на квадратный метр, а направление определяется как направление чистого потока положительных зарядов через площадь.
Соотношение между током и плотностью тока можно увидеть на Рисунке 9.12. Дифференциальный ток, протекающий через область dA → dA →, находится как
dI = J → · dA → = JdAcosθ, dI = J → · dA → = JdAcosθ,
где θθ — угол между площадью и плотностью тока. Полный ток, проходящий через область dA → dA →, можно найти путем интегрирования по площади,
I = areaJ → · dA → .I = ∬areaJ → · dA →.
9,5
Рассмотрим величину плотности тока, которая равна силе тока, разделенной на площадь:
J = IA = n | q | AvdA = n | q | vd.J = IA = n | q | AvdA = n | q | vd.
Таким образом, плотность тока J → = nqv → dJ → = nqv → d. Если q положительно, v → dv → d находится в том же направлении, что и электрическое поле E → E →. Если q отрицательно, v → dv → d находится в направлении, противоположном E → E →. В любом случае направление плотности тока J → J → находится в направлении электрического поля E → E →.
Рисунок 9.12 Плотность тока J → J → определяется как ток, проходящий через бесконечно малую площадь поперечного сечения, деленную на площадь. Направление плотности тока — это направление чистого потока положительных зарядов, а величина равна току, деленному на бесконечно малую площадь.
Пример 9.4
Расчет плотности тока в проводе
Сила тока, подаваемого на лампу с лампочкой мощностью 100 Вт, составляет 0,87 ампер. Лампа подключается медным проводом диаметром 2,588 мм (калибр 10). Найдите величину плотности тока.
Стратегия
Плотность тока — это ток, проходящий через бесконечно малую площадь поперечного сечения, деленную на площадь. Мы можем рассчитать величину плотности тока, используя J = IAJ = IA. Сила тока составляет 0,87 А.Площадь поперечного сечения может быть рассчитана как A = 5,26 мм2, A = 5,26 мм2.
Решение
Рассчитайте плотность тока, используя заданный ток I = 0,87AI = 0,87A и площадь, которая составляет A = 5,26 мм2A = 5,26 мм2.
J = IA = 0.87A5.26 × 10−6m2 = 1.65 × 105Am2. J = IA = 0.87A5.26 × 10−6m2 = 1.65 × 105Am2.
Значение
Плотность тока в проводящем проводе зависит от тока, проходящего через проводящий провод, и площади поперечного сечения провода. При заданном токе по мере увеличения диаметра проволоки плотность заряда уменьшается.
Проверьте свое понимание 9,4
Плотность тока пропорциональна току и обратно пропорциональна площади. Если плотность тока в проводящем проводе увеличится, что произойдет со скоростью дрейфа зарядов в проводе?
Какое значение имеет плотность тока? Плотность тока пропорциональна току, а ток — это количество зарядов, которые проходят через площадь поперечного сечения в секунду. Заряды движутся по проводнику, ускоряемые электрической силой, создаваемой электрическим полем.Электрическое поле создается при приложении напряжения к проводнику. В соответствии с законом Ома мы будем использовать эту взаимосвязь между плотностью тока и электрическим полем, чтобы исследовать взаимосвязь между током через проводник и приложенным напряжением.
Электропроводность металлов: законы и формулы
В этой статье мы обсудим следующее: 1. Закон Ома 2. Средняя длина свободного пробега (L) 3. Время релаксации 4. Факторы, влияющие на удельное сопротивление металлов 5. Проводящий материал с низким сопротивлением 6.Проводящий материал с высоким удельным сопротивлением 7. Изоляционные материалы 8. Применение проводников 9. Типы проводящих материалов.
Закон OHM (Point Form) :
Когда к проводнику приложено электрическое поле, развиваемая плотность тока (J) в проводнике связана с приложенным электрическим полем (E) как-
Дж = σE
Это соотношение является хорошо известным законом Ома.
Плотность тока — это общее свойство материала, которое не зависит от размера проводника.Он пропорционален электрическому полю E и постоянной ne 2 τ / м, называемой проводимостью материала σ-
.
σ = ne 2 τ / м
Мобильность:
Средняя скорость дрейфа изменяется прямо пропорционально электрическому полю через коэффициент пропорциональности eτ / m, называемый подвижностью электронов, µ e .
µ e = eτ / м
Подвижность определяется как величина средней скорости дрейфа на единицу электрического поля, т.е.е. µ e = v d / E Подвижность и проводимость связаны соотношением σ = neµ e .
Единица µ e = м 2 вольт -1 с -1 или м 2 / вольт — сек.
Влияние температуры на проводимость :
1. Проводник:
Мы знаем,
С повышением температуры не происходит заметного увеличения количества электронов, так как проводники уже имеют большое количество электронов в своей зоне проводимости.Таким образом, общая проводимость уменьшается с повышением температуры.
2. Полупроводник:
Мы знаем,
Где,
n i = Собственная концентрация
E g0 = Энергетический зазор при 0 ° K
A 0 = постоянная величина, которая зависит от полупроводникового материала (9,64 × 10 15 ).
K = постоянная Больцмана
Следовательно, проводимость полупроводника увеличивается с ростом температуры.Другими словами, полупроводники имеют отрицательные температурные коэффициенты.
Средняя длина свободного пробега (L):
Определяется как среднее расстояние, пройденное электроном до столкновения.
λ = V d . τ
Где τ = среднее время столкновения, V d = скорость дрейфа.
Время релаксации :
Определяется как время, необходимое для уменьшения дрейфовой скорости электрона до 37% от своего значения после снятия электрического поля.Для изотропного материала время релаксации и среднее время столкновения равны.
Факторы, влияющие на удельное сопротивление металлов :
В чистых металлах и разбавленных сплавах полное удельное сопротивление складывается из двух слагаемых.
ρ = ρ T + ρ r …. (i)
Тепловая составляющая ρ T ; которое возникает из-за колебаний решетки, и остаточного сопротивления ρ r , вызванного примесями и структурными дефектами.Остаточное сопротивление не зависит от температуры.
Уравнение (i) — это правило Маттиссена. Это правило становится менее точным при высокой температуре или при высоком уровне примесей.
Электрическое сопротивление большинства металлов увеличивается с повышением температуры. При температурах выше так называемой температуры Дебая тепловая составляющая удельного сопротивления проводников приблизительно линейна.
Многие проводящие материалы имеют исчезающее удельное сопротивление вблизи абсолютного нуля температуры.Это явление известно как сверхпроводимость.
Примечание:
Температура Дебая для Cu 315 K, а для Al 398 K.
Проводящий материал с низким сопротивлением :
Серебро имеет более низкое удельное сопротивление, чем медь, но оно очень дорогое, что ограничивает его использование в коммерческих целях. Алюминий дешевле меди, поэтому его часто используют в качестве заменителя меди в системах электроснабжения. Латунь — это сплав цинка и меди. Он имеет высокую прочность на разрыв, но более низкую проводимость, чем медь.Латунь используется в реостатах, патронах для ламп и в розетках. Обладает хорошей коррозионной стойкостью. Бронза — это сплав Cu, олова, Al, Ni и Si. Он обладает лучшими механическими свойствами и коррозионной стойкостью, чем латунь.
Фосфор-бронза используется в токоведущих пружинах и щеткодержателях. Силиконовая бронза используется в проводах и телефонных деталях. В припое используются сплавы олова, свинца, Cu-Zn. Вольфрам — это металл, который используется до 3300 ° C в качестве нагревательной нити в лампах, ЭЛТ.
Проводящий материал с высоким сопротивлением:
Чистый углерод — это полупроводник с отрицательным температурным коэффициентом удельного сопротивления.Используется в щетках для электрических машин.
Свинец обладает высокими антикоррозийными свойствами, поэтому применяется для прокладки подземных и подводных кабелей линий электропередачи и связи.
Platinum используется для изготовления контактов в контакторах малой мощности.
Никель используется для изготовления электродов.
Изоляционные материалы:
1. Керамика :
Эти материалы твердые, прочные и хрупкие.
Обладают высокой температурной стабильностью.
Керамика, как правило, неорганический материал (без углерода).
Обычно они имеют кристаллическую природу (за исключением аморфного стекла).
Это неметаллические оксиды, нитриты и карбиды.
Примеры:
Гранаты, BaTiO 3 , Ферриты, TiO 2 (Рутил) (диоксид Ti), Фарфор, Кварц, ZnS, MgO, SiC, CdS и т. Д.
Керамику в общих чертах можно описать как:
(i) Фарфор (ε r <12)
(ii) Керамика из оксида алюминия (ε r <12)
(iii) Стеатит (ε r <12)
(iv) Титанат (ε r > 12)
Фарфор используется для изоляции передачи и распределения энергосистемы.Он используется в приложениях низкого и высокого напряжения.
Стеатиты используются в высокочастотных приложениях.
Керамика из глинозема
используется для высокотемпературных применений в качестве выключателей и резистивных сердечников.
Титанат используется в конденсаторных диэлектриках.
Другая классификация керамики:
Керамику также можно разделить на две группы в зависимости от того, больше или меньше диэлектрическая проницаемость 12.
и.e r <12:
Керамика с диэлектрической проницаемостью менее 12 используется в качестве изоляторов, так как она имеет высокую диэлектрическую прочность и низкий тангенс угла потерь.
Пример:
Фарфор, стеатит, глинозем-керамика.
ii. ε r > 12:
Керамика с высокой диэлектрической проницаемостью (ε r > 12) используется в конденсаторах.
Пример:
Титанаты, рутил.
2. Трансформаторное масло :
Сердечники трансформатора погружены в минеральное масло, известное как трансформаторное масло. Он действует как изолятор и охлаждающая среда.
Напряжение пробоя трансформаторного масла уменьшается при загрязнении, например, влаге. Для поглощения влаги добавлены абсорбенты: силикагель и оксид алюминия.
3. Аскарелс :
Это огнестойкий изоляционный материал.
Аскарелы двух типов:
(а) Хлорированный бензол
(б) Хлорированный дифенил
В настоящее время они не используются в трансформаторах и конденсаторах, так как при разложении выделяют токсичные и ядовитые газы.
Применение проводников:
и. Линии передачи и распределения электроэнергии,
ii. Электрические контакты а именно. реле, щетки, переключатели и др.,
iii. Резисторы и
iv. Нагревательные элементы
Золото — лучший проводник электричества, за ним следуют серебро, медь и алюминий. Принимая во внимание фактор стоимости, медь и алюминий являются естественным выбором, хотя серебро используется для контактов в самолетах.
Алюминиевый провод, армированный сталью (ACSR), является улучшенным материалом для линий электропередачи.
Бескислородный медный провод с высокой проводимостью (OFHC) очень подходит для низкотемпературных применений. Он имеет высокую чистоту с удельным сопротивлением 1 × 10 -10 Ом · м при 4,2 К и нулевом электрическом поле.
Типы проводящих материалов :
I. На основе качества удельного сопротивления :
1.Материалы с низким удельным сопротивлением (или высокой проводимостью), такие как Au, Aq, Cu, Al, латунь, бронза и т. Д.
2. Материалы с высоким сопротивлением (или низкой проводимостью), такие как W. Pt, C, Ni, Ta, нихром и т. Д.
II. По природе материалов :
1. Металлы, такие как Cu, сталь, Al, Pt, Ir, Pd, Rh и т. Д.
2. Неметаллы, такие как проводящий полимер
3. Сплавы, такие как латунь, бронза, розовый металл, константан и т. Д.
4.Армированные композиты, такие как ACSR.
III. На основе заявлений :
1. Материалы кабельного назначения, такие как Cu, Al, ACSR, OFHC
2. Материалы для нити накала, такие как W, углерод (графит)
3. Материалы контактного назначения, такие как Au, Pt, Ag, Mo, Ir, W и т. Д.
4. Материалы для пайки, такие как Cu, Zn, Sn, Ag, Cd
5. Плавкие (или плавкие) материалы, такие как Pb, Sn, Ag и т. Д.
6.Материалы для обшивки, такие как Pb, ПВХ, сплав Pb-Cd
7. Уплотнительные материалы, такие как Fe с Si, Mn, Mo.
IV. Исходя из требований к базовой температуре :
1. Высокотемпературные проводящие материалы, такие как ACSR
.
2. Низкотемпературные проводящие материалы, такие как медь OFHC
3. Материалы, проводящие очень низкие (или криогенные) температуры, такие как стальной сплав на основе никеля.
V. По состоянию на материал:
1.Твердые проводящие материалы, такие как металлы, сплавы
2. Жидкие проводящие материалы, такие как Hg
3. Газопроводящие материалы, такие как N 2 в газонаполненных кабелях давления.
Медь:
Это высокая проводимость и разумная стоимость.
Это кристаллический, цветной, немагнитный (диамагнитный) металл красноватого цвета.
Это пластичный металл с пластичностью более 15%. Благодаря этому свойству из него легко превращаться в тонкие стержни и проволоку.Следовательно, он очень полезен для изготовления кабелей, жил и проводов.
Его предел прочности при растяжении достаточно высок (300–350 МПа), что позволяет ему выдерживать механические нагрузки.
Его температура плавления достаточно высока (1083 ° C), поэтому его можно использовать также при высоких температурах.
При воздействии атмосферной среды образует защитный слой оксида меди (CuO). Таким образом, он обладает высокой устойчивостью к коррозии, что является обязательным свойством для неизолированных / открытых воздушных проводов.
Легко поддается пайке (разновидность сварки), что является необходимым требованием при электромонтаже и других соединениях.
Алюминий :
Электропроводность ниже, чем у меди, но дешевле, чем у меди.
Это кристаллический, цветной, слабомагнитный (парамагнитный) металл белого цвета.
Это легкий металл с удельным весом 2,7.
Это пластичный металл, поэтому из него легко превращаются в тонкие стержни и проволоку.Поэтому алюминий очень полезен для изготовления кабелей и проводов.
Предел прочности на разрыв достаточно высокий (около 50-70 МПа).
Его легко паять, что является важным требованием при электромонтаже. Однако из-за изолирующего характера слоя оксида алюминия паяное соединение может быть не таким прочным
Его электрические контакты подвержены риску потери соединения из-за его мягкости.
Закон
Ома (микроскопическая интерпретация) | Блестящая вики по математике и науке
Закон Ома связывает плотность тока в проводнике с приложенным электрическим полем формулой J = σEJ = \ sigma EJ = σE, приведенной выше.2 \ frac {\ tau} {m_e} σ = ne e2me τ
с nen_ene объемная плотность электронов проводимости, eee заряд электрона, mem_eme масса электрона и τ \ tauτ среднее свободное время электронов, представляющее, сколько в среднем электрон проводимости проходит до взаимодействия с проводником. . Также часто используют величину ρ = 1σ \ rho = \ frac {1} {\ sigma} ρ = σ1, удельное сопротивление .
Используя эту формулу, плотность тока электронов можно переписать в терминах средней скорости электронов, часто называемой дрейфовой скоростью :
J⃗ = −enev⃗ˉ.\ vec {J} = -en_e \ bar {\ vec {v}}. J = −ene vˉ.
Для движения электронов в стержне микроскопический закон Ома может быть связан с макроскопическим законом Ома V = IRV = IRV = IR. Обратите внимание, что плотность тока — это ток на единицу площади J = IAJ = \ frac {I} {A} J = AI. Точно так же электрическое поле — это напряжение на единицу длины: E = VLE = \ frac {V} {L} E = LV. Комбинируя два, получаем
V = (LAσ) I.V = \ left (\ frac {L} {A \ sigma} \ right) I.V = (AσL) I.
В проводящем стержне с площадью поперечного сечения AAA и длиной LLL с проводимостью σ \ sigmaσ сопротивление, следовательно, определяется как
R = LAσ = ρLA.R = \ frac {L} {A \ sigma} = \ frac {\ rho L} {A}. R = AσL = AρL.
В сложных материалах, где проводимость изменяется по длине проводника, сопротивление определяется путем обработки всего вышеперечисленного как бесконечно малой величины и интегрирования.
Странный металлический стержень с площадью поперечного сечения AAA тянется от x = 1x = 1x = 1 до x = Lx = Lx = L с удельным сопротивлением ρ (x) = 1x \ rho (x) = \ frac {1} {x} ρ (х) = х1. Вычислите сопротивление этой планки.
Сопротивление небольшого отрезка стержня
dR = ρ (x) dxA.L \ frac {1} {xA} dx = \ frac {\ log (L)} {A}. \ _ \ SquareR = ∫1L xA1 dx = Alog (L). □
Медный провод с некоторым сопротивлением RRR. Затем проволоку сплющивают и растягивают, так что длина удваивается, а площадь поперечного сечения уменьшается в 14 раз без изменения удельного сопротивления. На какой фактор изменяется сопротивление провода?
Проволока из чистого германия с удельным сопротивлением ρ = 1.{-3} \: \ Omega \ cdot \ text {m} ρ = 1,2 × 10−3Ω⋅m и длиной 10 см10 \ text {cm} 10 см подключается к любому выводу 9 V9 \ text {V} 9 Аккумулятор V. Предположим, что общая масса проволоки составляет 20 г20 \ text {g} 20 г и что на один атом германия проводит только один электрон. Найдите скорость дрейфа электронов в проводе.
Величина плотности тока, указанная выше, составляет
.
J = enev, J = en_e v, J = ene v,
где vvv — скорость дрейфа. Необходимо вычислить две вещи: плотность nen_ene проводящих электронов и плотность тока JJJ.
Плотность тока определяется из
.
J = σE = VρL, J = \ sigma E = \ frac {V} {\ rho L}, J = σE = ρLV,
где LLL — указанная общая длина провода.
Число проводящих электронов можно вычислить из общего числа атомов германия, поскольку каждый атом обеспечивает только один проводящий электрон. Число атомов германия можно вычислить из общей массы: поскольку германий весит 72,3 г 72,3 \ text {g} 72,3 г на моль, их
20 г × 1 моль 72.{-5} \ text {m} / \ text {s}.
\ end {выровнен}
v = ene J = ρLene V = (1,2 · 10−3Ω⋅m) (10 см) (1,6 · 10−19 C) (4,59 · 1022 см − 3) 9 V = 1,02 · 10− 5 м / с.Это очень низкая скорость! Большая часть скорости электрических сигналов происходит от распространения «дырок» в заряде через материалы, а не от реальных физических зарядов. □ _ \ квадрат □
0.{-3} 3 × 1029 м-3, найдите скорость дрейфа электронов проводимости в миллиметрах в секунду.
Закон
Ома для простых электрических цепей, Рон Куртус
SfC Home> Физика> Электричество>
Рон Куртус (от 23 октября 2019 г.)
Закон Ома является наиболее фундаментальной формулой для простых электрических цепей .Он утверждает, что электрический ток, проходящий через проводник, прямо пропорционален разности потенциалов на проводнике. Впервые он был сформулирован в 1827 году немецким физиком Георгом Омом во время экспериментов по изучению того, насколько хорошо металлы проводят электричество.
Закон
Ома лучше всего демонстрируется в простой электрической цепи постоянного тока. Хотя это также относится к цепям переменного тока, необходимо учитывать другие возможные переменные.
Связь между током, напряжением и сопротивлением в цепи позволяет вычислить одну переменную, если вы используете значения двух других.
Вопросы, которые могут у вас возникнуть:
- Что означают параметры в уравнении?
- Какая конфигурация схемы?
- Как применить закон Ома?
Этот урок ответит на эти вопросы. Полезный инструмент: Конвертация единиц
Уравнение
Закон
Ома показывает взаимосвязь между напряжением, током и сопротивлением в простой электрической цепи. Самая простая форма уравнения:
В = ИК
где:
- V — напряжение в вольтах ( V )
- I — ток в амперах или амперах ( A )
- R — сопротивление в Ом ( Ом — греческая буква Омега)
Таким образом, если вы знаете ток и сопротивление, вы можете использовать формулу для определения напряжения.
Используя алгебру, вы можете изменить порядок переменных в соответствии со своими потребностями. Например, если вы знаете напряжение и сопротивление и хотите найти ток, вы можете использовать:
I = V / R
Или, если вы знаете напряжение и ток и хотите найти сопротивление, вы можете использовать:
R = V / I
Конфигурация
Простая электрическая цепь состоит из металлических проводов, идущих к источнику питания и от него, а также источника сопротивления, такого как резисторы или электрическая лампочка, соединенных последовательно с источником.Типичным источником питания является батарея постоянного тока, хотя также может применяться генератор постоянного или переменного тока.
Примечание : Если цепь переменного тока включает в себя такие компоненты, как конденсаторы или катушки индуктивности, закон Ома не применяется.
Простая цепь постоянного тока
Используя уравнение
Важность закона Ома заключается в том, что, если вы знаете значение двух переменных в уравнении, вы можете определить третью. Вы можете измерить любой из параметров с помощью вольтметра.Большинство вольтметров или мультиметров измеряют напряжение, ток и сопротивление как переменного, так и постоянного тока.
Найти напряжение
Если вам известны ток и сопротивление, вы можете найти напряжение из В = I R . Например, если ток I = 0,2 А и сопротивление R = 1000 Ом , то
В = 0,2 А * 1000 Ом = 200 В
Найти текущий
Если вы знаете напряжение и сопротивление, вы можете использовать алгебру, чтобы изменить уравнение на I = V / R , чтобы найти ток.Например, если В = 110 В и R = 22000 Ом , то
I = 110 В / 22000 Ом = 0,005 А
Найти сопротивление
Если вы знаете напряжение и ток, вы можете использовать алгебру, чтобы изменить уравнение на R = V / I , чтобы найти сопротивление. Если В = 220 В и I = 5 А , то
R = 220 В / 5 A = 44 Ом
Сводка
Закон Ома — это уравнение V = I R , которое показывает взаимосвязь между напряжением, током и сопротивлением в простой электрической цепи.Он может применяться как к цепям переменного, так и постоянного тока.
Будьте полны решимости сделать все возможное
Ресурсы и ссылки
Полномочия Рона Куртуса
Сайтов
Немного истории об Ом — Краткая история
Закон Ома — Объяснение, включая калькулятор закона Ома
Основные законы по электричеству — Включает теорию цепей
Формулы электрических цепей — Уравнения высокого уровня для решения проблем
Электроэнергетические ресурсы постоянного и переменного тока
Физические ресурсы
Книги
Научитесь электричеству и электронике Стэна Гибилиско; Макгроу-Хилл; (2001) 34 доллара.95 — Руководство для профессионалов, любителей и техников, желающих изучить цепи переменного и постоянного тока
Вопросы и комментарии
Есть ли у вас какие-либо вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте. Я постараюсь вернуться к вам как можно скорее.
Поделиться страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
electric_ohms_law.htm
Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или тезисе.
Авторские права © Ограничения
Где ты сейчас?
Школа чемпионов
По физике
Закон Ома для простых электрических цепей
Заряд и ток — Ток, напряжение и сопротивление — GCSE Physics (Single Science) Revision — Other
Электрический ток — это скорость протекания электрического заряда.Ток не может течь, если цепь разорвана, например, когда выключатель разомкнут.
Электрический ток течет, когда электроны движутся через проводник, например металлический провод. Металлы — хорошие проводники электричества.
Электричество проходит через металлические проводники в виде потока отрицательно заряженных электронов. Электроны могут свободно перемещаться от одного атома к другому. Мы называем их морем делокализованных электронов .
Ток изначально определялся как поток зарядов от положительного к отрицательному.Позже ученые обнаружили, что ток на самом деле представляет собой поток отрицательно заряженных электронов от отрицательного к положительному. Они назвали исходное определение «обычным током», чтобы не путать его с более новым определением тока.
Расчетный ток
Величина электрического тока показывает скорость протекания электрического заряда. Вы можете рассчитать величину тока, используя следующее уравнение:
\ [ток ~ в ~ амперах = \ frac {заряд ~ ~ в ~ кулонах} {время ~ в ~ секундах} \]
или:
\ [I = \ frac {Q} {t} \]
где:
I — ток в амперах (амперах), A
Q — заряд в кулонах, C
t — время в секундах, с
- Вопрос
Какой ток если 20 Кл заряда переходит за 5 с?
- Показать ответ
Текущее = 20 ÷ 5 = 4 A
Страница не найдена | MIT
Перейти к содержанию ↓
- Образование
- Исследовать
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
Меню ↓
Поиск
Меню
Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще!
Что вы ищете?
Увидеть больше результатов
Предложения или отзывы?
Электропроводность
Электропроводность
На этой странице мы определяем электрическую проводимость.Электропроводность — это мера
насколько легко электрический ток может проходить через данный материал. То есть,
для данного
Электрическое поле
в материале материал с более высокой проводимостью будет производить больший ток
текучести, чем материал с низкой проводимостью.
Если вы разбираетесь в электрических схемах,
тогда проводимость аналогична обратной величине сопротивления. Электрическое поле
похоже на напряжение, поэтому напряжение на небольшом резисторе (высокая проводимость)
будет производить большое количество тока.Напряжение на большом резисторе (низкая проводимость)
будет производить меньшее количество электрического тока.
Электропроводность представляет собой потерю мощности в материале. Материал известен
как «без потерь», если проводимость равна нулю (= 0).
Такие материалы, как воздух и вакуум (космос), не обладают проводимостью.
Когда проводимость не равна нулю, электрическое поле, протекающее через материал
вызовет
Плотность электрического тока ( Дж ). Отношение
между E , J и известен как закон Ома
и дается в уравнении [1]:
| [Уравнение 1] |
|---|
Некоторые материалы, такие как медь или сталь (или металлы в целом), имеют очень высокую
проводимости, а проводимость часто можно аппроксимировать бесконечной.Это означает, что материал имеет нулевое сопротивление.
Для этих материалов из уравнения [1] видно, что электрическая
В этих материалах поле должно быть равно нулю. Если он не был равен нулю, то из уравнения [1]
плотность тока будет бесконечной, но это не так. Следовательно, пока мы можем
есть ток, протекающий через металлы или материалы с высокой проводимостью, электрическое поле
внутри этих материалов должно быть ноль. В учебниках эти материалы часто
называется PEC (идеальные электрические проводники), так что потери проводимости
можно игнорировать.
Теперь рассмотрим материалы с проводимостью больше нуля, но также неметаллические.

 Зачем он нужен? Например, чтобы зарядить телефон. В сетевой розетке есть 220 В, а для заряда батареи надо только 5,5. Вот тут и пригодится электрическая схема на основе понижающего трансформатора. Если разобрать старую, тяжёлую телефонную «зарядку», то можно его там увидеть. Другой такой агрегат, только очень большой, постоянно гудит в своей будке, построенной почти в каждом городском дворе. Он подаёт в квартиры «положенные по прейскуранту» вольты.
Зачем он нужен? Например, чтобы зарядить телефон. В сетевой розетке есть 220 В, а для заряда батареи надо только 5,5. Вот тут и пригодится электрическая схема на основе понижающего трансформатора. Если разобрать старую, тяжёлую телефонную «зарядку», то можно его там увидеть. Другой такой агрегат, только очень большой, постоянно гудит в своей будке, построенной почти в каждом городском дворе. Он подаёт в квартиры «положенные по прейскуранту» вольты.