Базовые логические элементы И, ИЛИ, НЕ. И или логические

Базовые логические элементы И, ИЛИ, НЕ

ВОПРОС 1) Логические элементы ЭВМ и их основные характеристики.

Алгебра логики– это математический аппарат, с помощью которого записывают, вычисляют, упрощают и преобразовывают логические высказывания.

 

Создателем алгебры логики является английский математик Джордж Буль (19 век), в честь которого она названа булевой алгеброй высказываний.

Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.

 

Логический элемент компьютера — это часть электронной логической схемы, которая реализует элементарную логическую функцию.

 

Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и др. (называемые также вентилями), а также триггер.

С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера.

Работу логических элементов описывают с помощью таблиц истинности.

 

Базовые логические элементы И, ИЛИ, НЕ

 

Схема Иреализует конъюнкцию (логическое умножение) двух или более логических значений.

Таблица истинности

х y х и у

0 0 0

0 1 0

1 0 0

1 1 1

 

 

Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет нуль, на выходе также будет нуль.

Связь между выходом z этой схемы и входами х и у описывается соотношением z = х ^ у (читается как «х и у»).

Операция конъюнкции на функциональных схемах обозначается знаком & (читается как «амперсэнд»), являющимся сокращенной записью английского слова and.

 

Схема ИЛИ реализует дизъюнкцию (логическое сложение) двух или более логических значений.

 

Таблица истинности

х y х или у

0 0 0

0 1 1

1 0 10

1 1 1

 

 

Когда хотя бы на одном входе схемы ИЛИ будет единица, на ее выходе также будет единица.

Знак «1» на схеме — от устаревшего обозначения дизъюнкции как «>=!» (т.е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1). Связь между выходом z этой схемы и входами х и у описывается соотношением z = х или у.

 

Схема НЕ (инвертор) реализует операцию отрицания.

Таблица истинности

х не х

0 1

1 0

 

 

Связь между входом х этой схемы и выходом z можно записать соотношением Z =не х , где х читается как «не х» или «инверсия.

Если на входе схемы 0, то на выходе 1. Когда на входе 1 на выходе 0.

ВОПРОС 2) Узлы как элементы ЭВМ, их типы.

Узлы ЭВМ классифицируются на :

1. комбинационные - это узлы, выходные сигналы которых определяются только сигналом на входе, действующим в настоящий момент времени (дешифратор). Выходной сигнал дешифратора зависит только от двоичного кода, поданного на вход в настоящий момент времени. Комбинационные узлы называют также автоматами без памяти.

2. последовательностные (автоматы с памятью) - это узлы, выходной сигнал которых зависит не только от комбинации входных. сигналов, действующих в настоящий момент времени, но и от предыдущего состояния узла (счетчик).

3. программируемыеузлы функционируют в зависимости от того, какая программа в них записана. Например, программируемая логическая матрица (ПЛМ), которая в зависимости от прожженной в ней программы может выполнять функции сумматора, дешифратора, ПЗУ.

studopedya.ru

Логическое ИЛИ - Википедия

Материал из Википедии — свободной энциклопедии

Дизъю́нкция (лат. disjunctio — разобщение), логи́ческое сложе́ние, логи́ческое ИЛИ, включа́ющее ИЛИ; иногда просто ИЛИ — логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу»[1].

Дизъюнкция может быть бинарной операцией (иметь два операнда), тернарной операцией (иметь три операнда) или n{\displaystyle n}-арной операцией (иметь n{\displaystyle n} операндов).

Запись может быть префиксной — знак операции стоит перед операндами (польская запись), инфиксной — знак операции стоит между операндами или постфиксной — знак операции стоит после операндов. При числе операндов более 2-х префиксная и постфиксная записи экономичнее.

Обозначения[ | ]

Наиболее часто встречаются следующие обозначения для операции дизъюнкции:

a∨b,a{\displaystyle a\lor b,\;a} || b,a{\displaystyle b,\;a} | b,a ORb{\displaystyle b,\;a~{\mbox{OR}}\,\,b},max(a,b).{\displaystyle ,\;\max(a,b).}

При этом обозначение a∨b{\displaystyle a\lor b}

encyclopaedia.bid

Логическая операция. Основные логические операции

Информатика как наука о методиках сбора, упорядочивания и обработки различных данных начинает своё развитие в середине ХХ столетия. Хотя некоторые историки считают, что начало формированию информатики было положено ещё в 17 веке, с изобретением первого механического калькулятора, большинство ассоциирует ее с эпохой более продвинутой вычислительной техники. В 40-е годы 20 века, с появлением первых компьютеров, информатика получила новый толчок в развитии.

Предмет изучения информатики

Именно с появлением первых вычислительных машин появилась необходимость в разработке новых методов систематизации, вычисления и обработки больших массивов данных, а также в разработке алгоритмов, которые позволили бы использовать весь потенциал новых компьютеров. Информатика получила статус самостоятельной научной дисциплины и перешла из плоскости математических вычислений к изучению вычисления в целом.

Вся современная компьютерная наука базируется на логических операциях. Их можно назвать основополагающей составляющей. В программировании вычислительных систем понятие логической операции – это некое действие, после выполнения которого порождается новое понятие или значение, формирующееся на базе уже имеющихся понятий. Набор подобных действий может варьироваться в зависимости от процессорного элемента, который должен выполнять команды. Однако существуют некоторые операции, которые являются общими практически для всех существующих систем. Это операции, которые работают с содержанием самих значений, например отрицание, или те, которые изменяют количественную характеристику понятия, – сложение, вычитание, умножение, деление.

Типы операндов логических операций

Поскольку алгебра логики подразумевает работу над абстрактными понятиями, то и в качестве операндов всех логических операций выступают обобщённые типы данных. Классическими элементами, с которыми работает алгебра высказываний, являются высказывания, ложные или истинные. В электронике и программировании для описания этих терминов используют булевские переменные true и false или же целочисленные значения 1 (истина) и 0 (ложь). На комбинации этих значений, как бы невероятно это ни звучало, завязана работа самых сложных и масштабных систем. Весь программный код, который выполняется в компьютере или любом цифровом устройстве, динамически переводится в последовательность единиц и нулей – универсальный код, который может быть обработан любым процессором.

Виды логических операций

Как было уже сказано ранее, в классической булевой алгебре существует 2 типа функций. Основные логические операции над двоичными типами данных – это действия, влияющие на само высказывание (унарная, или одноместная, операция). Сюда же относят и операции, порождающие новые высказывания на основании существующих значений (бинарные операции, или двуместные). Порядок логических операций такой же, как и при выполнении любых математических вычислений: слева направо, с учётом скобок.

Наиболее простой и одной из самых известных функций булевой логики является функция отрицания. Эта простейшая логическая операция представляет собой противоположное значение входного операнда. В электронике это действие ещё иногда называется инверсией. К примеру, если проинвертировать суждение «истина», то результатом будет «ложь». И наоборот – отрицание значения «ложь» даст в результате значение «истина». Такая логическая операция в программировании очень часто используется для ветвления алгоритмов и реализации «выбора» последующего набора команд на основании уже имеющихся результатов или изменившихся условий.

Бинарные операции

В программировании и информатике используется ограниченный набор двоичных (бинарных) операций. Они получили своё название от латинского слова bi, означающего «два», и являются видом функций, которые принимают на входе два аргумента и в результате возвращают одно новое значение. Для описания всех функций булевой алгебры используются таблицы истинности.

Для чего они нужны

Данная система составляется для определённого количества входных операндов и описывает все результирующие значения, которые может вернуть заданная логическая операция при указанном наборе входных параметров.

Наиболее часто используемыми функциями в информатике и вычислительной технике являются операции логического сложения (дизъюнкция) и логического умножения (конъюнкция).

Конъюнкция

Логическая операция «И» - это функция по выбору наименьшего из двух или n входных операндов. На входе эта функция может иметь два (бинарная функция), три значения (тернарная) или же неограниченное количество операндов (n-арная операция). При вычислении результата функции им станет наименьшее из предоставленных входных значений.

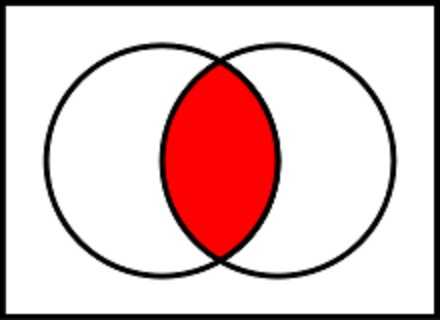
Аналогом в обычной алгебре является функция умножения. Поэтому операция конъюнкции часто называется логическим умножением. При записи функции знаком выступает либо знак умножения (точка) либо амперсант. Если составить таблицу истинности для этой функции, то станет видно, что функция принимает значение «истина», или 1, только при истинности всех входных операндов. Если же хотя бы один из входных параметров будет равен нулю, или значению «ложь», то результатом функции также будет «ложь».

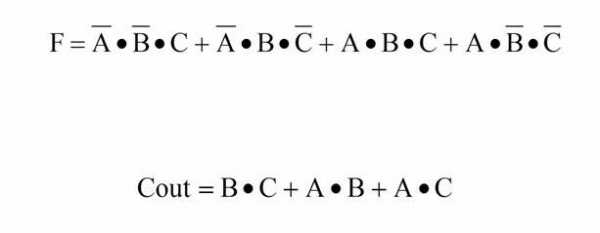
Это отражает аналогию с арифметическим умножением: умножение любого числа и набора чисел на 0 в результате вернёт всегда 0. Эта логическая операция коммутативна: порядок, в котором она получает входные параметры, никак не повлияет на конечный результат вычисления.

Другим свойством этой функции является ассоциативность, или сочетательность. Это свойство позволяет при вычислении последовательности бинарных операций не учитывать порядок вычисления. Поэтому для 3 и более последовательных операций логического умножения нет необходимости учитывать скобки. В программировании эта функция используется зачастую для того, чтобы убедиться в том, что специфические команды выполнятся только при выполнении совокупности определённых условий.

Дизъюнкция

Логическая операция «ИЛИ» - вид булевой функции, который является аналогом алгебраического сложения. Другие названия этой функции – логическое сложение, дизъюнкция. Точно так же, как и операция логического умножения, дизъюнкция может быть бинарной (вычислять значение на основе двух аргументов), тернарной или n-арной.

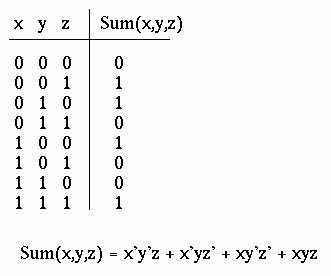
Таблица истинности для данной логической операции является своего рода альтернативой конъюнкции. Логическая операция «ИЛИ» вычисляет максимальный результат среди предоставленных аргументов. Дизъюнкция принимает на выходе значение «ложь», или 0, только если все входные параметры поступают со значениями 0 («ложь»). В любом другом случае на выходе будет получено значение «истина», или 1. Для записи этой функции чаще всего используется математический знак сложения («плюс») или две вертикальные полосы. Второй вариант распространён в большинстве языков программирования и предпочтительнее, потому что позволяет чётко отделить логическую операцию от арифметической.

Общие свойства логических операций

Основные логические операции, будь то унарные, бинарные, тернарные или другие функции, подчинены определённым правилам и свойствам, которые описывают их поведение. Одним из таких фундаментальных свойств, которыми обладают описанные выше логические функции, является коммутативность.

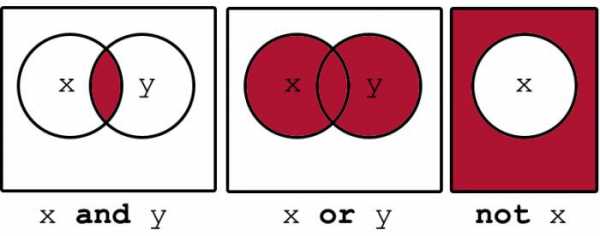
Это свойство гарантирует, что от перестановки мест операндов значение функции не изменится. Не все операции имеют это свойство. В отличие от конъюнкции и дизъюнкции, которые удовлетворяют требованиям коммутативности, функция умножения матриц таковой не является, и перестановка множителей в этой операции повлечёт изменение результата, так же как и возведение в степень.

Дополнительный аспект

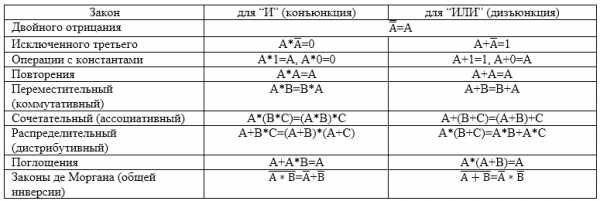
Другим важным свойством, которое часто применяется в электронике и схемотехнике, является подчиненность пар логических операций законам де Моргана.

Эти законы связывают пары логических операций с помощью функции логического отрицания, то есть позволяют выразить одну логическую операцию с помощью другой. К примеру, функцию отрицания конъюнкции можно выразить с помощью дизъюнкции отрицаний отдельных операндов. С помощью этих законов логические операции "И", "ИЛИ" могут быть взаимовыражены и реализованы с минимальными аппаратными затратами. Это свойство крайне полезно в схемотехнике, так как позволяет экономить ресурсы при расчёте и формировании микросхем.

fb.ru

---

• 
  Мини электростанция для дома своими руками
• 
  Ксо камеры
• 
  Рп 6 кв
• 
  Паяное соединение
• 
  0 логики
• 
  Услуги вц в квитанции что это
• 
  Технические характеристики ап50б 2мт
• 
  Из холодного крана течет горячая вода куда жаловаться
• 
  Правило ленца правило правой руки
• 
  Из чего состоит кабель
• 
  Реле что это такое