Индуктивность характеризует: Индуктивность — это… Что такое Индуктивность?

Содержание

Индуктивность | Страница 3 из 3 | Electronov.net

Основные параметры индуктивностей:

Номинальная индуктивность:

Заводское значение индуктивности конкретного прибора, измеряется это значение в Генри (производные наноГенри (нГн), микроГенри (мкГн) и т.д). Номинальные значения индуктивностей выбираются из специальных номинальных рядов Е6, Е12, Е24 и т.д.

Допуск (точность):

Допустимое отклонение величины реальной индуктивности от номинальной. Указывается в процентах от номинального значения индуктивности. Допуск может достигать 20%.

Ток насыщения:

Величина тока, при достижении которой, происходит интенсивное рассеяние магнитного потока вне сердечника, что вызывает наведение токов индукции в близко расположенных проводниках. При периодическом насыщении возникают всплески помех, частоты которых распространяются и на звуковых частотах, и в радиочастотном диапазоне. Также насыщение сердечника приводит к его перегреву, вплоть до физического разрушения.

Температурный коэффициент индуктивности:

$TCI=\frac{\Delta L}{L\cdot \Delta T}\text{.}$

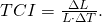
Параметр, характеризующий зависимость индуктивности катушки от температуры. Температурная нестабильность индуктивности обусловлена целым рядом факторов: при нагреве увеличивается длина и диаметр провода обмотки, увеличивается длина и диаметр каркаса, в результате чего изменяются шаг и диаметр витков; кроме того при изменении температуры изменяются диэлектрическая проницаемость материала каркаса, что ведёт к изменению собственной ёмкости катушки. Очень существенно влияние температуры на магнитную проницаемость ферромагнетика сердечника.

Маркировка индуктивностей:

Кодовая маркировка:

Применяется 2 варианта кодовой маркировки:

1 Вариант: XYZ обозначает XY•10^Z мкГн, причем для индуктивностей менее 10 мкГн десятичным разделителем является буква «R», менее 1 мкГн – буква «N», и в этом случае значение индуктивности в нГн.

Иначе говоря, первые 2 цифры определяют число (мантиссу), а последняя цифра определяет количество нулей (десятичная степень).

2 Вариант: значение номинальной индуктивности непосредственно указано числом в мкГн.

После цифрового кода указывается буквенный код допуска, в случае его отсутствия – допуск 20%.

Например: 102 — это 10•10² мкГн = 1000 мкГн = 1 мГн, допуск — 20%; 6R8J – 6.8 мкГн, допуск — 5%; R68K – 0.68 мкГн, допуск — 10%; 22N – 22 нГн, допуск — 20%; 2N2D – 2.2 нГн, допуск — ±0,3 нГн.

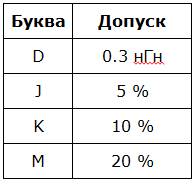Таблица 1 — Кодирование допуска индуктивности.

Цветовая маркировка:

Наиболее часто применяется кодировка 4 или 3 цветными кольцами или точками.

Первые две метки указывают на значение номинальной индуктивности (мантисса) в микрогенри (мкГн, uН), третья метка — множитель (десятичная степень), четвертая — допуск. В случае кодирования 3 метками подразумевается допуск 20%. Цветное кольцо, обозначающее первую цифру номинала, может быть шире, чем все остальные.

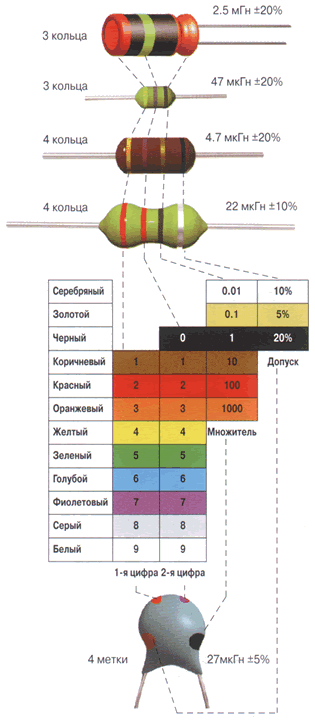Рисунок 2 — Цветовое кодирование индуктивности.

Условное обозначение индуктивностей на схемах:

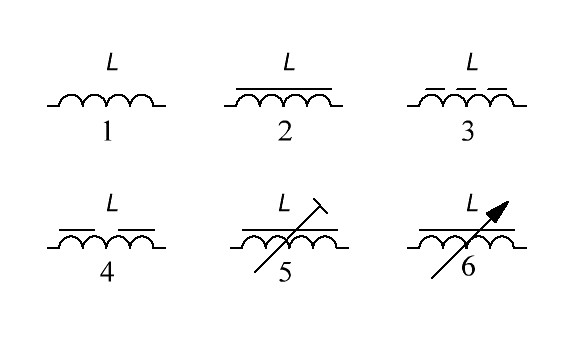Рисунок 3 — УГО индуктивности.

– бескаркасная индуктивность;
– индуктивность с ферритовым сердечником;
– индуктивность с сердечником из магнитодиэлектрика, т.е. диэлектрического магнитного материала;
– индуктивность с ферритовым сердечником с зазором;
– индуктивность с возможностью регулировки положения ферритового сердечника;
– переменная индуктивность (вариометр).

Рядом с условным обозначением указывается тип элемента (L) и порядковый номер, также рядом с условным обозначением может указываться (не является обязательным требованием) номинал элемента.

На электрических принципиальных схемах номинальная индуктивность обычно указывается в микрогенри (1 мкГн = 1·10³ нГн = 1·10⁻⁶ Гн).

Внешний вид катушек индуктивности:

Рисунок 4 — Внешний вид индуктивностей.

Индуктивность | Страница 2 из 3 | Electronov.net

Свойства индуктивности:

Индуктивность обладает комплексным импедансом (сопротивлением):

${{\dot{Z}}_{L}}=j\omega L=j2\pi fL\text{,}$

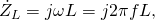
где:

j — мнимая единица;

ω — циклическая частота (рад/с) протекающего синусоидального тока;

f — частота в Гц;

L — индуктивность катушки (Генри).

Комплексный импеданс в общем случае записывается как сумма активного и реактивного сопротивлений:

${{\dot{Z}}_{c}}=R+j\cdot {{X}_{c}}=j\omega L.$

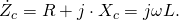
Отсюда следует, что активное сопротивление идеальной индуктивности равно нулю, а реактивное сопротивление равно: Для постоянного тока частота равна нулю, следовательно, реактивное сопротивление равно нулю. Индуктивность по определению численно равна отношению создаваемого током потока магнитного поля, пронизывающего катушку, к силе протекающего тока. Отсюда следует, что применять катушки индуктивности имеет смысл только в цепях переменного тока.

Если Вы не привыкли слепо доверять формулам, то следующий абзац для Вас:

Спойлер

Чтобы разобраться, почему с ростом частоты тока у индуктивности растет реактивное сопротивление, необходимо вспомнить явление самоиндукции, которое можно сформулировать в 2 эквивалентных вариантах:

Возникновение магнитного потока самоиндукции при протекании по цепи тока;
Возникновение ЭДС индукции в том контуре, по которому протекает переменный ток.

По Закону электромагнитной индукции Фарадея, ЭДС индукции можно записать как:

${{\varepsilon }_{i}}=-\frac{d\Phi }{dt}\text{,}$

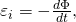
где:

ε_i — величина ЭДС индукции;

Φ — величина магнитного потока.

В случае контура, содержащего N витков, используется понятие потокосцепления Ψ_s самоиндукции (Ψ_s = NΦ_s).

${{\psi }_{s}}=LI\text{,}$

$L=\frac{{{\psi }_{s}}}{I}\text{.}$

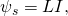
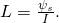
С учетом данных формул, можно записать ЭДС и ток самоиндукции:

${{I}_{s}}=\frac{{{\varepsilon }_{s}}}{R}=-\frac{L}{R}\frac{dI}{dt}\text{.}$

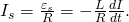
Знак минуса показывает, что направление тока самоиндукции противоположно направлению основного тока.

Из этих формул следует, что любые изменения тока в цепи тормозятся, и тем сильнее, чем больше индуктивность цепи и меньше ее сопротивление.

Если сформулировать по научному:

Правило Ленца для явления самоиндукции – ток самоиндукции препятствует любым изменениям основного тока, текущего по цепи.

Можно также сказать, что индуктивность цепи является мерой ее электрической инертности, подобно тому, как масса в механике является мерой инертности тела при его поступательном движении.

И как Вы уже наверняка догадались, природа реактивного сопротивления индуктивности заключена в явлении ЭДС и тока самоиндукции, а скорость изменения величины тока – это его частота.

Схема замещения не идеальной (реальной) индуктивности:

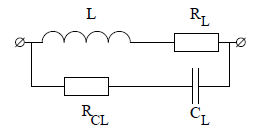Рисунок 1 — Схема замещения неидеальной (реальной) индуктивности.

Сопротивление потерь:

В катушках индуктивности помимо основного эффекта взаимодействия тока и магнитного поля, наблюдаются паразитные эффекты, вследствие которых импеданс катушки не является чисто реактивным. Наличие паразитных эффектов ведет к появлению потерь в катушке, оцениваемых сопротивлением потерь:

${{R}_{lose}}={{R}_{CL}}+{{R}_{L}}\text{,}$

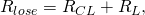
где:

R_CL – диэлектрические потери;

R_L – индуктивные потери.

Диэлектрические потери вызваны магнитными свойствами диэлектрика, а также паразитной емкости, которая образуется между витками, вследствие наличия изоляции обмоточного провода, и соответственно появляются межвитковые утечки и прочие потери, характерные для диэлектриков конденсаторов. Однако для современных катушек общего применения эти потери пренебрежимо малы.

Индуктивные потери складываются из следующих составляющих:

Потери в проводах:

В свою очередь, потери в проводах вызваны тремя причинами:

Провода обмотки обладают омическим (активным) сопротивлением.
Сопротивление провода обмотки возрастает с ростом частоты, что обусловлено поверхностным эффектом (скин-эффектом). Суть эффекта состоит в вытеснении тока в поверхностные слои провода. Как следствие, уменьшается полезное сечение проводника и растет сопротивление. Подробнее о поверхностном эффекте можно прочитать [гиперссылка]здесь[/гиперссылка].
В проводах обмотки, свитой в спираль, проявляется эффект близости (англ. proximity effect), суть которого состоит в вытеснении тока под воздействием вихревых токов и магнитного поля, которые появляются из-за явления взаимной индуктивности, к периферии намотки. В результате сечение, по которому протекает ток, принимает серповидную форму, что ведет к дополнительному возрастанию сопротивления провода. Подробнее о эффекте близости можно прочитать [гиперссылка]здесь[/гиперссылка].

Потери на перемагничивание ферромагнитного сердечника:

Данные потери связаны с эффектом гистерезиса в ферромагнетиках.

Потери на вихревые токи (токи Фуко):

Переменное магнитное поле индуцирует вихревые ЭДС в окружающих проводниках, т.е. витках и сердечнике. При этом возникают вихревые (т.е. замкнутые в кольце) токи — токи Фуко, которые по физической природе ничем не отличаются от индукционных токов, возникающих в линейных проводах. Помимо электрических потерь, вихревые токи также разогревают каркас и обмотку катушки.

Резонансная частота индуктивности:

${{f}_{p}}=\frac{1}{2\pi \sqrt{L{{C}_{L}}}}.$

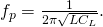
При f > f_р катушка индуктивности в цепи переменного тока ведет себя как конденсатор. Следовательно, индуктивность целесообразно использовать лишь на частотах f < f_p, на которых ее сопротивление носит индуктивный характер. Обычно максимальная рабочая частота индуктивности примерно в 2—3 раза ниже резонансной.

Добротность:

Добротность катушки индуктивности определяется отношением между ее реактивным и активным сопротивлениями:

Повышение добротности достигается оптимальным выбором диаметра провода, увеличением размеров катушки индуктивности и применением сердечников с высокой магнитной проницаемостью и малыми потерями, намоткой вида «универсаль», применением посеребренного провода, применением многожильного провода вида «литцендрат» для снижения потерь, вызванных скин-эффектом. Подробнее о проводе вида «литцендрат» можно прочитать [гиперссылка]здесь[/гиперссылка].

Что такое индуктивность и какие она имеет свойства

Электрический ток, проходя по проводу, создает вокруг него магнитное поле. В то же время магнитное поле, пересекая провода, создает в них (индуктирует) э. д. с. (электродвижущую силу).

Магнитное поле может пересекать провода, когда они движутся в поле или когда движется само поле в месте расположения проводов. Последнее явление происходит, в частности, при возникновении магнитного поля (при включении тока) и при его исчезновении, (при выключении тока), а также при всевозможных изменениях величины поля, вызванных изменениями величины тока. Во всех этих случаях в проводах, находящихся в поле, в том числе и в проводах, по которым проходит вызвавший изменения поля ток, возникает (индуктируете) э. д. с.

Электродвижущая сила, индуктированная в проводе (катушке) под влиянием изменения ее собственного магнитного потока, называется электродвижущей силой самоиндукции.

Согласно закону Ленца электродвижущая сила самоиндукции всегда противодействует вызвавшей ее причине. Если ток в проводе возрастает, то э. д. с. самоиндукции стремится задержать, замедлить нарастание тока. Если ток в цепи уменьшается, э. д. с. самоиндукции препятствует быстрому спаданию тока.

При питании цепи постоянным током э. д. с. самоиндукции появляется и оказывает влияние на изменение тока только в моменты замыкания или размыкания цепи. Когда цепь замкнута и в ней уже установился постоянный ток, а следовательно, и создаваемое током магнитное поле постоянно, э. д. с. самоиндукции не возникает.

Прямолинейный проводник имеет довольно слабое магнитное поле, и поэтому возникающая э. д. с. самоиндукции невелика. Она заметно сказывается только в очень длинных проводниках. Значительная э. д. с. возникает в проводниках, смотанных в катушку.

Если же в катушку ввести еще стальной сердечник, а тем более сделать его замкнутым, то магнитное поле катушки усилится во много раз и э. д. с. самоиндукции будет достигать очень большой величины по сравнению с э. д. с. самоиндукции прямого провода.

Различные катушки обладают различной способностью индуктировать э. д. с. самоиндукции, что зависит от числа витков, формы и конструкции катушек. Эту способность катушек называют индуктивностью.

Индуктивность катушек характеризуют величиной э. д. с. самоиндукции возникающей в катушке при изменении величины тока на 1 а в секунду.

Единицей измерения индуктивности является генри (гн).

Катушка индуктивности с замкнутым стальным сердечником.

Катушка обладает индуктивностью а один генри, если в ней при изменении величины тока на един ампер в одну секунду индуктируется э. д. с. самондукции в один вольт.

Генри — единица относительно большая. Практически чаще употребляются более мелкие единицы —доли генри: одна тысячная — миллигенри (мгн) и одгіа миллионная — микрогенри (мкгн).

Катушки, у которых для тех или иных целей используется их индуктивность, в отличие от катушек с другим назначением носят название катушек индуктивности.

Если в цепи постоянного тока индуктивность катушек и индуктированная э. д. с. самоиндукции сказываются только при включении и выключении тока, то совсем иначе обстоит дело, когда по катушке протекает переменный ток.

Переменный ток создает и переменное магнитное поле. Переменное же поле непрерывно индуктирует в катушке э. д. с. самоиндукции, направленную навстречу напряжению питающего катушку генератора переменного тока и тем большую, чем больше частота переменного тока.

Появление э. д. с. самоиндукции приводит к тому, что при одном и том же напряжении источника электрической энергии величина переменного тока, протекающего через катушку, получается меньше величины постоянного тока.

Исходя из закона Ома, можно сделать вывод, что сопротивление одной и той же катушки переменному току больше, чем постоянному, так как при одинаковых напряжениях постоянный ток имеет большую величину, чем переменный.

Если бы удалось сделать такую катушку, которая совсем не оказывала бы сопротивления постоянному току, то при включении ее в цепь переменного тока она все равно оказывала бы этому току сопротивление, называемое индуктивным сопротивлением.

Индуктивное сопротивление катушки зависит от величины индуктивности катушки и пропорционально частоте переменного тока. Поэтому там, где необходимо возможно большее сопротивление переменному току, применяют катушки со стальными замкнутыми сердечниками.

Способность катушек оказывать переменному току значительно большее сопротивление, чем постоянному, позволяет использовать их в тех случаях, когда требуется отделить переменный ток от постоянного. В радиотехнике катушки, используемые для этой цели, носят название дросселей.

Казалось бы, что идея применения стальных сердечников для увеличения индуктивности катушек исключительно заманчива. Ведь можно получить необходимую индуктивность в сравнительно небольших катушках с малым количеством витков. Но, оказывается, применение стали связано с рядом неудобств.

Из них прежде всего следует отметить большие потери энергии в стальном сердечнике. Эти потери резко возрастают с увеличением частоты переменного тока. Поэтому сердечники из обычной мягкой стали можно применять только в цепях с относительно низкой частотой (не выше нескольких десятков тысяч герц).

Одна из причин потерь в сердечнике — появление в нем самом совершенно бесполезных вихревых токов (поскольку сердечник тоже находится в переменном магнитном поле, в нем индуктируется э. д. с., вызывающая появление этих токов).

Чтобы уменьшить величины .вихревых токов, сердечники катушек делают из тонких изолированных один от другого стальных листов. Но на высоких частотах и эта мера предосторожности не помогает, поэтому стали делать катушки либо вовсе без сердечников, либо изготовлять их из железного порошка, скрепленного особой изолирующей массой.

В таких веществах каждая мельчайшая пылинка железа изолирована от других, и поэтому в них не могут образоваться вихревые токи большой величины, а следовательно, и потери будут незначительны. К таким веществам относятся магнетит, альсифер, ферриты.

Другая причина потерь в стали — необходимость затраты энергии на перемагничивание стали. Полностью устранить потери на перемагничивание невозможно, и поэтому стремятся применять для сердечников катушек такие сорта стали, в которых эти потери были бы наименьшими.

Источник: Бурлянд В.А., Жеребцов И.П. Хрестоматия радиолюбителя. 1963 г.

Что такое индуктивность

Что такое индуктивность — это физическая величина, которая рассказывает нам о магнитных свойствах электрической цепи. Индуктивность измеряют в Гн (Генри).

Если вы вообще не понимаете о чём речь, то советую ознакомиться сначала с вот с этой статьей.

В электрических схемах например, нам встречаются какие-то непонятные катушки, дроссели и многие даже не знают их функциональную роль. В этой статье я постараюсь доступным языком рассказать, что такое индуктивность и как это явление применить на своей любимой работе.

Давайте посмотрим на рисунок

Давайте начнём движение проводника в магнитном поле таким образом, чтобы он пересек силовые линии постоянного магнита. Если это условие выполняется, то тогда в нашем проводнике появляется электродвижущая сила (ЭДС). Или наоборот проводник остаётся на месте, а магнит передвигают таким образом, чтобы силовые линии магнита пересекали проводник. Сейчас был пример электромагнитной индукции. Значение индуцированной электродвижущей силы в проводнике прямо пропорциональна магнитной индукции поля, скорости перемещения и длине проводника

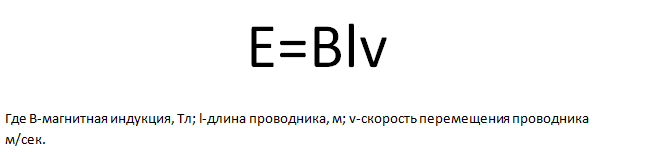
Направление возникшей электродвижущей силы в проводнике
определяют через правило правой руки.

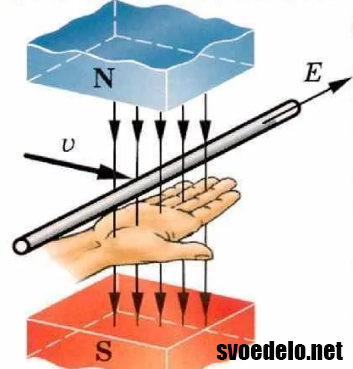
Правая рука находится в таком положении чтобы силовые линии
магнита заходили в ладонь. Следовательно, большой палец показывает нам направление
перемещения проводника, а остальные пальцы покажут нам направление возникшей
электродвижущей силы.

Для усиления электродвижущей силы индукции применяют электрические
катушки

А если подать напряжение на катушку, то по её виткам потечёт ток, который создаёт своё магнитное поле.

Закон Ленца

Закон Ленца говорит нам, что индуцированный ток направлен
так, чтобы препятствовать той причине, которая его вызвала. Например, подаём мы
на катушку напряжение. В катушке образуется магнитное поле которое в момент
включения пересекает витки катушки и наводит там электродвижущую силу
самоиндукции. По закону Ленца индуцированная ЭДС самоиндукции будет направлена
навстречу току который её вызвал.

Если подавать (а) и снимать (б) напряжение с катушки, то произойдёт следующее. Магнитное поле будет то появляться, то исчезать. В результате изменяющееся магнитное поле будет пересекать витки катушки и индуцировать в ней ЭДС.

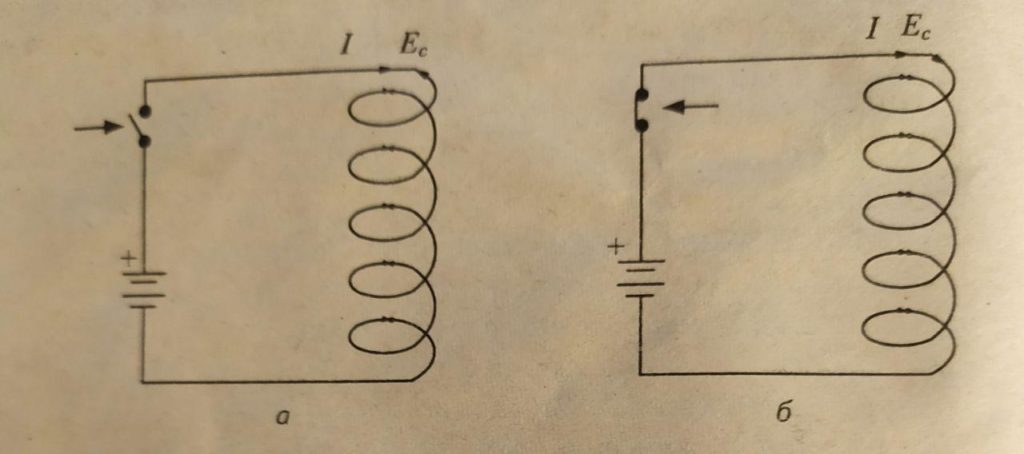
Новое понятие ЭДС самоиндукции. Давайте рассмотрим её поподробнее.

ЭДС самоиндукции

Если подавать и снимать напряжение с электрической катушки,
то магнитное поле будет появляться, исчезать, появляться, исчезать… В итоге
получаем магнитное поле, которое
постоянно меняется. Проходя через витки
катушки магнитное поле будет индуцировать в ней электродвижущую силу, которая
называется ЭДС самоиндукции.

Коэффициент самоиндукции – это величина ЭДС самоиндукции,
возникающей при изменении тока в единицу времени. Коэффициент самоиндукции
измеряется в Генри (Гн).

Индуктивностью в 1 Генри обладает катушка. В которой при
изменении тока на 1 Ампер в 1 секунду возникает ЭДС самоиндукции в 1 Вольт.

Давайте напряжение цепи катушки обозначим через U, результирующее напряжение Uр, а ЭДС самоиндукции Ес, тогда
получим следующие формулы:

В момент замыкания цепи результирующее напряжение будет следующим:

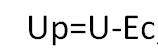
А в момент размыкания цепи:

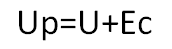
Величина ЭДС самоиндукции может многократно превышать напряжение источника тока. Поэтому при размыкании цепей с большой индуктивностью появляется дуга, и соответственно обгорают контакты.

Что такое дроссель

Дроссель — это вид катушки индуктивности, которая оказывает высокое сопротивление переменному току и малое постоянному.

Применяется дроссель в следующих случаях:

Защита устройств от резких скачков напряжения;
Для уменьшения скорости увеличения тока короткого замыкания ;
Уменьшения импульсных помех;

И это только перечислена маленькая часть того где применяются
дроссели.

Пример:

Давайте представим, что у нас стоит дроссель перед электродвигателем. И в какой-то момент происходит скачок тока, что происходит: Мы знаем, что в момент пропускания тока через дроссель, формируется электромагнитное поле вокруг катушки. А для формирования поля нам нужна энергия, поэтому в самом начале протекания тока он тратится на формирование электромагнитного поля. По закону Ленца, мы знаем, что ток в катушке не может измениться мгновенно. А явление самоиндукции при изменении тока, направлено навстречу основному току. Таким образом дроссель просто скушает скачок тока в сети.

Подводим ИТОГИ:

Возникший индуктированный ток всегда направлен так, чтобы препятствовать той причине, которая его вызвала;
При изменении тока в цепи, у нас изменяется магнитный поток. А согласно закону электромагнитной индукции, в цепи возникает индуцированная ЭДС. Это и есть – самоиндукция;
Величина ЭДС самоиндукции может многократно превышать напряжение источника;
Дроссель- это вид катушки индуктивности, которая оказывает высокое сопротивление переменному току и малое постоянному.

Физическая природа индуктивности

Источник — Свободный взгляд

Физическая природа индуктивности.

Катушки индуктивности обладают свойством оказывать реактивное
сопротивление переменному току при незначительном сопротивлении
постоянному току. Совместно с конденсаторами они используются для
создания фильтров, осуществляющих частотную селекцию электрических
сигналов, а так же для создания элементов задержки сигналов и
запоминающих элементов, осуществления связи между цепями через
магнитный поток и т.д. В отличие от резисторов и конденсаторов они
не являются стандартизованными изделиями, а изготавливаются для
конкретных целей и имеют такие параметры, которые необходимы для
осуществления тех или иных преобразований электрических сигналов,
токов и напряжений.

Функционирование катушек индуктивности основано на взаимодействии
тока и магнитного потока. Известно, что при изменении магнитного
потока Ф в проводнике, находящемся в магнитном поле,
возникает ЭДС, определяемая скоростью изменения магнитного
потока

(2.25)

Поэтому при подключении к проводнику источника постоянного
напряжения ток в нем устанавливается не сразу, так как в момент
включения изменяется магнитный поток и в проводе индуцируется ЭДС,
препятствующая нарастанию тока, а спустя некоторое время, когда
магнитный поток перестает изменяться. Если же к проводнику подключен
источник переменного напряжения, то ток и магнитный поток будут
изменяться непрерывно и наводимая в проводнике ЭДС будет
препятствовать протеканию переменного тока, что эквивалентно
увеличению сопротивления проводника. Чем выше частота изменения
напряжения, приложенного к проводнику,, тем больше величина ЭДС,
наводимая в нем, следовательно, тем больше сопротивление,
оказываемое проводником протекающему току. Это сопротивление
X_L не связано с потерями энергии, поэтому является
реактивным. При изменении тока по синусоидальному закону наводимая
ЭДС будет равна

(2.26)

Она пропорциональна частоте w, а
коэффициентом пропорциональности является индуктивность L.
Следовательно, индуктивность характеризует способность проводника
оказывать сопротивление переменному току. Величина этого
сопротивления Х_L=wL

Индуктивность короткого проводника (мкГн) определяется его
размерами:

(2.26)

где l -длина провода в см, d — диаметр провода в
см.

Если провод намотан на каркас, то образуется катушка
индуктивности. В этом случае магнитный поток концентрируется и
величина индуктивности возрастает.

2.3.2.Конструкции катушек индуктивности.

Конструкционной основой катушки индуктивности является
диэлектрический каркас, на который наматывается провод в виде
спирали. Обмотка может быть как однослойной (рис.2.21,а), так и
многослойной (рис.2.21,6). В некоторых случаях многослойная обмотка
делается секционированной (рис.2.21,в). В интегральных схемах
применяются плоские спиральные катушки индуктивности
(рис.2.21,г).

Для увеличения индуктивности применяют магнитные сердечники.
Помещенный внутрь катушки сердечник концентрирует магнитное поле и
тем самым увеличивает ее индуктивность. Перемещением сердечника
внутри каркаса можно изменяп, индуктивность. На рис.2.22
представлены три разнидности цилиндрических сердечников: С —
стержневой, Т — трубчатый и ПР — подстроечный резьбовой и две
разновидности броневых. Броневые сердечники состоят из двух чашек 2,
изготовленных из карбонильного железа или ферритаов.

Они могут иметь либо замкнутый магнитопровод (тип СБ — а), либо
разомкнутый (тип С Б — б). Для изменения индуктивности служит
подстроечный цилиндрический сердечник 1. Помимо цилиндрических и
броневых сердечников применяют торроидальные (кольцевые) сердечники.
На высоких частотах (десятки-сотни МГц) применяют подстроечные
цилиндрические сердечники из диамагнетиков (латунь, медь). При
введении этих сердечников внутрь катушки индуктивность
уменьшается.

В катушках индуктивности, работающих на низких в качестве
сердечников используют пермаллои. При этом рается из тонких пластин
толщиной 0,002-0,1мм.

Для уменьшения влияния электромагнитного поля катушки на другие
элементы схемы, а также для уменьшения влияния внешних полей на
катушку индуктивности, ее располагают внутри металлического экрана,
как это показано на рис.2.23 (1 — заглушка, 2 — экран, 3 — корпус, 4
— обмотка, 5 — каркас, 6 -подстроечный стержень, 7 — чашка
сердечника, 8 — основание, 9 — заливка).

2.3.3. Индуктивность и собственная емкость катушек
индуктивности.

Индуктивность является основным параметром катушки индуктивности.
Ее величина (мкТн) определяется соотношением

где W — число витков, D — диаметр катушки в см,
L₀ — коэффициент, зависящий от отношения длины
катушки / к ее диаметру О.

Для однослойных катушек величина L₀ определяется
соотношением

(2.29)

Оптимальными в этом случае являются отношение а
диаметр катушки в пределах от 1 до 2 см. При расчете диаметр катушки
D принимается равным диаметру каркаса D₀

Для многослойных катушек величина
L₀зависит не только от величины
1/D , но и от отношения толщины намотки t к
диаметру катушки D. Она определяется по графикам (рис.2.24). В этом
случае внешний диаметр катушки D=D₀+ 2t

При расчете катушки индуктивности предварительно задаются
геометрическими размерами катушки и определяют коэффициент
L₀, а затем по заданной величине индуктивности L
находят число витков:

(2.30)

где I, — в мкГн , D — в см.

Для намотки катушки обычно применяют провод оптимального
диаметра, который рассчитывается с помощью эмпирических формул и
графиков. Для этого по графику S=f(t/D;l/D) (рис.2.25)
находят вспомогательный коэффициент S. Затем рассчитывают
коэффициент

(2.31)

где f -в мкГц , D — в см. Затем рассчитывают
коэффициент a₁

где f — частота в Гц. После чего по графику b₁=f(a₁)
(рис. 2.26) находят вспомогательный
коэффициент b_1S и расчитывают
оптимальный диаметр провода (мм)

(2.32)

Полученное значение округляется до ближайшего
стандартного значения (табл.2.6) и выбирается марка провода с
диаметром d_из

Таблица 2.6

Основные параметры обмоточных проводов

d, мм

Sn, мм~

Максимальный диаметр в изоляции , мм

ПЭВТЛК

ПЭМ-1

ПЭВ-1

ПЭВ-2,ПЭТВ
ПЭМ-2

0,063

0,0028

0.11

0,09

0,085

0,09

0,071

0,0038

0,12

0,09

0,095

0,1

0,08

0,005

0,13

0,1

0,105

0,11

0,09

0,0064

0,14

0,11

0,115

0,12

0,1

0,0079

0,15

0,12

0,125

0,13

0,112

0,0095

0,16

0,14

0,135

0,14

0,125

0,0113

0,17

0,15

0,155

0,14

0,0154

0,185

0,16

0,165

0,17

0,16

0,02

0,2

0,19

0,2

0,18

0,0254

0,23

0,21

0,22

0,2

0,0314

0,25

0,23

0,24

0,224

0,0415

0,27

0,25

0,26

0,27

0,25

0,0491

0,3

0,29

0,3

0,28

0,0615

0,34

0,32

0,33

0,315

0,0755

0,37

0,35

0,355

0,365

0,355

0,0962

0,405

0,39

0,395

0,415

0,4

0,126

0,47

0,44

0,46

0,45

0,158

—

0,49

0,51

0,5

0,193

—

0,55

0,57

0,56

0,246

—

0,61

0,63

0,311

—

0,68

0,7

0,71

0,39

—

0,76

0,79

0,75

0.435

—

0,81

0,84

0,8

0,503

—

0,86

0,89

0,85

0,567

—

0,91

0,94

0,9

0,636

—

0,96

0,99

0,95

0,71

—

1,01

1,04

0,785

—

1,08

1,07

1, 11

После выбора оптимального диаметра провода проверяют возможность
размещения обмотки в заданных размерах l и t.
Для однослойных катушек рассчитывают шаг намотки

(2.33)

Если t>d_из; то обмотка размещается. В
противном случае задаются большей величиной l и
повторяют расчет.

Для многослойных катушек рассчитывают толщину обмотки

(2.34)

где а — коэффициент неплотности обмотки ( a = 1,05…1,3), и находят фактическое значение
наружного диаметра катушки D=D₀+2t. Если эта
величина отличается от выбранной в начале расчета более чем на 10%,
то задаю тся новыми значениями l и t и расчет
повторяют. При помещении катушки в экран индуктивность катушки
уменьшается

(2.35)

где h — коэффициент, зависящий от
отношения l/D (рис.2.27),

D — диаметр катушки,

D_эк-диаметр экрана.

Индуктивность уменьшается тем больше, чем меньше диаметр экрана.
В большинстве случаев D_эк/D >1,6ё1,8.При этом индуктивность уменьшается не
более чем на 20%.

Многослойные катушки обычно выполняют с сердечниками броневого
типа, при использовании которых большая часть силовых линий
магнитного поля катушки замыкается через сердечник, а меньшая-через
воздух, вследствие чего влияние экрана на индуктивность катушки
значительно ослабляется.

Применение сердечников из магнитных материалов позволяет
уменьшить число витков катушки индуктивности и соответственно ее
габариты. Основным параметром сердечника является магнитная
проницаемость m_с При его наличии индуктивность катушки становится
равной

Поскольку в расчетные формулы входят эмпирические коэффициенты,
то индуктивность изготовленной катушки отличается от расчетной.
Применение подстроечных магнитных сердечников позволяет получить
требуемое значение индуктивности.

Собственная емкость является паразитным параметром катушки
индуктивности, ограничивающим возможности ее применения. Ее
возникновение обусловлено конструкцией катушки индуктивности:
емкость существует между отдельными витками катушки, между витками и
сердечником, витками и экраном, витками и другими элементами
конструкции. Все эти распределенные емкости можно объединить в одну,
называемую собственной емкостью катушки C_L

Наименьшей собственной емкостью обладают однослойные катушки
индуктивности Приближенно она рассчитывается по формуле (пФ)

С_L >(0,5ё1.0)D,

(2.37)

где D — диаметр катушки в см. Обычно она не превышает
1-2пФ.

Собственная емкость многослойных катушек значительно больше. При
многослойной рядовой намотке она достигает ЗОпФ; при намотке
«внавал» она несколько меньше. Существенное уменьшение емкости
многослойных катушек достигается при использовании универсальной
обмотки, при выполнении которой провод укладывается под некоторым
углом к образующей цилиндрического каркаса. Схема такой намотки
показана на рис.2.28. Как только провод доходит до края катушки,
направление укладки меняется. Цикл универсальной обмотки выбирается
таким, что, совершив один оборот вокруг каркаса, провод возвращается
к положение, отличающееся от исходного на угол b. Этот угол выбирается таким, чтобы каждый
последующий виток находился рядом с предыдущим.

Очевидно, что

(2.38)

Угол j ,
под которым осуществляется укладка провода, находится из
соотношения

(2.39)

где l-осевая длина катушки,

D — диаметр витка.

Наименьшее значение угла j
получается для витков, имеющих наименьший диаметр, равный диаметру
каркаса D_0.

Обычно при использовании универсальной обмотки длину катушки
принимают в пределах от 2 до 10мм. Количество циклов намотки связано
с рачетнным числом витков W соотношением

(2.40)

Величина собственной емкости катушек с универсальной обмоткой
составляет от 3 до 8пФ. Дополнительное снижение емкости достигается
серкцонированием обмотки, как показано на рис.2.21,в.

Совместное действие индуктивности и емкости можно учесть
введением понятия об эквивалентной индуктивности катушки,
определяемой из уравнения

откуда

(2.41)

где -собственная резонансная частота катушки
индуктивности.

Если рабочая частота много ниже собственной резонансной частоты
w_L, то приближенно можно считать
L_э=L.

В процессе работы на катушку действуют различные
внешние факторы:температура, влага и другие, влияющие на ее
индуктивность.Наиболее существенным является влияние температуры,
которое оценивают температурным коэффициентом .

Температурная нестабильность индуктивности обусловлена целым
рядом факторов: при нагреве увеличивается длина и диаметр провода
обмотки, увеличивается длина и диаметр каркаса, в результате чего
изменяются шаг и диаметр витков; кроме того при изменении
температуры изменяются диэлектрическая проницаемость материала
каркаса, что ведет к изменению собственной емкости катушки.

Для повышения температурной стабильности применяют каркасы из
материала с малым значением коэффициента линейного расширения. Этим
требованиям в наибольшей степени удовлетворяет керамика. Повышению
температурной стабильности катушек способствует прочное сцепление
обмотки с каркасом. С этой целью обмотку выполняют методом вжигания
серебра в керамический каркас. В этом случае изменение размеров
токопроводящего слоя определяется только линейным расширением
каркаса. Такие катушки индуктивности имеют TKL >(5-100)^.10^-6Стабильность
многослойных катушек существенно хуже, так как в них невозможно
избежать изменения линейных размеров провода обмотки. Многослойные
катушки имеют TKL>
(50-100)^.10^-6

2.3.4. Потери в катушках индуктивности.

В катушках индуктивности помимо основного эффекта взаимодействия
тока и магнитного поля наблюдаются паразитные эффекты, вследствие
которых сопротивление катушки не является чисто реактивным и равным
Х_L. Наличие паразитных эффектов ведет к появлению
потерь в катушке, оцениваемых сопротивлением потерь R_П
, которое определяет добротность катушки индуктивности

(2.42)

Потери складываются из потерь в проводах, диэлектрике, сердечнике
и экране.

Потери в проводах вызваны тремя причинами.

Во-первых, провода обмотки обладают омическим
сопротивлением

(2.43)

где l -длина провода обмотки, d- диаметр провода,
р- удельное сопротивление.

Это сопротивление (Ом) можно выразить через число витков W
и средний диаметр катушки D_СР

(2.44)

где -диаметр провода в см.

Во-вторых, сопротивление провода обмотки переменному току
возрастает с ростом частоты, что обусловлено поверхностным эффектом,
суть которого состоит в том, что ток протекает не по всему сечению
проводника, а по кольцевой части поперечного сечения (рис.2.29),
ширина (мм) которой равна

(2.45)

где f— частота в МГц,

r— удельное сопротивление в
мкOм^{· м.}

Вследствие этого провод длиной l имеет сопротивление
переменному току равное

(2.46)

где S_ЭФ — площадь кольца, которая равна

(2.47)

где

После преобразования получаем

(2.48)

В третьих, в проводах обмотки, свитой в спираль, проявляется
эффект близости (рис.2.30), суть которого состоит в вытеснении тока
под воздействием вихревых токов и магнитного поля к периферии
провода, прилегающей к каркасу, в результате чего сечение, по
которому протекает ток, принимает серповидный характер, что ведет к
дополнительному возрастанию сопротивления провода.

Сопротивление r_Б, обусловленное эффектом
близости, прямо пропорционально диаметру провода, а сопротивление
r_П, обусловленное эфектом, обратно пропорционально
диаметру провода ( рис.2.31).

Существует оптимальный диаметр провода d_опт,
при котором сопротивление

провода току высокой частоты r_f= r_Б +
r_Показывается минимальным. Для однослойных катушек
d_опт= 0,2-0,6мм, для многослойных
d_опт =0,08-0,2мм. Существенно уменьшить потери в
проводах можно применяя провод «литцендрат», состоящий из большего
числа жилок, скрученных в жгут. При небольшом диаметре тонких жилок
ослабляется поверхностный эффект, а скручивание жилок в жгут
ослабляет эффект близости.

Существует методика расчета сопротивления r_f,
по которой предварительно рассчитывается вспомогательный
коэффициент

(2.49)

где f — частота в Гц,

d- диаметр провода в см.

Затем по таблице находятся коэффициенты F(z) и G(z).

F(z)

G(z)

0,5

0,001

0,6

0,002

0,7

0,004

0,8

0,006

0,9

0,01

1,01

0,015

1,5

1,03

0,07

1,08

0,17

2,5

1,18

0,3

1,3

0,4

1,7

0,6

0,8

7-.5

2,9

1,2

3,8

1,6

7,3

3,4

9,1

4,3

8,2

100

После этого по графику (рис.2.32) определяется вспомогательный
коэффициент К_з, зависящий от геометрии
катушки.

По (2.50) рассчитывается сопротивление провода катушки току
высокой частоты

(2.50)

где D— наружный диаметр катушки в см,

d -диаметр провода в см.

Если однослойная катушка намотана проводом оптимального диаметра
и параметр z >5, то сопротивление r_f можно
определить по формуле

(2.51)

где D — в см, d — в см, f‘- в
МГц.

Потери в диэлектрике обусловлены тем, что между соседними
витками катушки существует емкость, имеющая две составляющих-емкость
через воздух С_ови емкость через диэлектрик
С_од (рис.2.33).

Потери в диэлектрике учитываются величиной tgd, зная которую можно рассчитать
сопротивление потерь

r_Д=
0,25С_одtg dL²f ^{3 .}
10^-3

(2.52)

где С_од— в пф, L — в мкГн,
f — в МГц.

Потери в сердечнике складываются из потерь на вихревые
токи d_в, потерь на
гистерезис d_г и начальных
потерь d_пи учитываются как
тангенс угла потерь в сердечнике

tg d_с= d_вf +
d_гН + d_п

(2.53)

В справочниках приводятся значения. tg d_сдля различных типов
сердечников. Сопротивление потерь определяется по формуле

Потери в экране обусловлены тем, что ток, протекающий по
катушке, индуцирует ток в экране. Потери, вносимые экраном,
определяются по формуле

(2.55)

где D_э— диаметр экрана в см,

l_э — длина экрана в см,

f — частота в МГц.

Величина h =
f(l/D) определяется по графику
(рис.2.27).

Таким образом суммарное сопротивление потерь в катушке
индуктивности, определяющее ее добротность, равно

R_п = r_f+
r_д +r_c+ r_э

(2.56)

Практически величина добротности лежит в пределах от 30 до 200.
Повышение добротности достигается оптимальным выбором диаметра
провода, увеличением размеров катушки индуктивности и применением
сердечников с высокой магнитной проницаемостью и малыми потерями. С
учетом потерь и паразитной емкости катушку индуктивности можно
представить в виде эквивалент-

ной схемы (рис.2.34,а), где R_п =
r_f+ r_д +r_c+
r_э. эта схема может быть приведена к более
удобному виду (рис.2.34,б), где L_э -эквивалентная
индуктивность, учитывающая собственную емкость. Величины.
L_э и R_п, а следовательно, добротность
Q = wL/R_п
зависят от температуры. Зависимость Q от температуры
определяется температурным коэффициентом добротности
ТКД=DQ/QDТ

2.3.5.Разновидности катушек индуктивности.

Контурные катушки индуктивности. Эти катушки используются
совместно с конденсаторами для получения резонансных контуров. Они
должны иметь высокую стабильность, точность и добротность. В
диапазоне длинных и средних волн эти катушки многослойные, как
правило, с намоткой типа «универсаль». Для повышения добротности
применяют многожильные провода типа «литцендрат». Для изменения
индуктивности применяют цилиндрические сердечники из альсифера или
карбонильного железа.

В диапазоне коротких и ультракоротких волн используются
однослойные катушки с индуктивностью порядка единиц микрогенри и
добротностью порядка 50 — 100. Число витков таких катушек не
превышает одного-двух десятков, диаметр каркаса 10 — 20 мм. В
качестве каркасов используют керамику, полиэтилен и полистирол. Для
уменьшения собственной емкости применяют ребристые каркасы. Обмотка
выполняется одножильным медным проводом диаметром около 1 мм. На УКВ
применяют бескаркасные катушки из неизолированного провода.

Катушки связи. Эти катушки применяются для обеспечения
индуктивной связи между отдельными цепями и каскадами. Такая связь
позволяет разделить по постоянному току цепи базы и коллектора и
т.д.

К таким катушкам не предъявляются жесткие требования на
добротность и точность, поэтому они выполняются из тонкого провода в
виде двух обмоток небольших габаритов. Основными параметрами этих
катушек являются индуктивность и коэффициент связи

где L₁и L₂— индуктивность связанных
катушек,

М — взаимная индуктивность между ними. Величина
коэффициента связи зависит от расстояния между катушками, чем оно
меньше, тем больше k.

Вариометры. Это такие катушки, в которых
предусмотрена возможность изменения индуктивности в процессе
эксплуатации для перестройки колебательных контуров.

Они состоят из двух катушек, соединенных последовательно. Одна из
катушек неподвижная (статор), другая располагается внутри первой и
вращается (ротор). При изменении положения ротора относительно
статора изменяется величина взаимоиндукции, а следовательно,
индуктивность вариометра

Такая система позволяет изменять индуктивность в 4 — 5 раз.

Дроссели. Это катушки индуктивности, обладающие высоким
сопротивлением переменному току и малым сопротивлением постоянному .
Обычно включаются в цепях питания усилительных устройств.
Предназначены для защиты источников питания от попадания в них
высокочастотных сигналов. На низких частотах они используются в
фильтрах цепей питания и обычно имеют металлические сердечники.

Катушки индуктивности для ГИС. На частотах порядка 10 —
100 МГц находят применение тонкопленочные спиральные катушки. На
площади в 1 кв.см, располагается не более 10 витков. Добротность
таких катушек не превышает 20-30. Поэтому они находят ограниченное
применение. В ГИС предпочтительны миниатюрные торроидальные катушки
на ферритовых сердечниках, индуктивность которых достигает десятков
тысяч микрогенри.

В последнее время наметилась тенденция замены катушек
специальными схемами на транзисторах (гираторы) и
электромеханическими, пьезоэлектрическими и акустоэлектронными
фильтрами, основанными на принципе механических упругих колебаний и
механического резонанса. Скорость распространения упругих колебаний
в твердом теле примерно в 100 тысяч раз меньше скорости
распространения электромагнитных волн, что позволяет создавать очень
компактные механические резонаторы с распределенными параметрами,
обладающие добротностью порядка 10³. Развитие
микроэлектроники привело к появлению фильтров на приборах с
зарядовой связью и фильтров на поверхностных акустических волнах.
Кроме того, в ИМС широкое применение находят активные RC — фильтры,
в которых используются операционные усилители с глубокой
частотно-зависимой обратной связью.

Источник — Свободный
взгляд

ТОЭ Лекции — №20 Самоиндукция. Индуктивность. Ток в индуктивности

Если в катушке, изображенной на рис. 20.1, магнитное поле создается собственным
током i, то магнитный поток называется потоком самоиндукции и обозначается ФL, а индуцируемая в катушке
ЭДС еL – ЭДС самоиндукции. В соответствии с формулой (20.1) она равна:

где ψ – потокосцепление самоиндукции, величина, пропорциональная протекающему по
катушке току: ψ = Li.

Коэффициент пропорциональности L между потокосцеплением и током называется
собственной индуктивностью или просто индуктивностью катушки (контура). Она зависит от формы и размеров
катушки, а также от магнитной проницаемости сердечника. Ее размерность В x с/А=Ом x с. Эта единица
измерения называется генри (Гн).

Подставляя последнее выражение в (2.15) и полагая L = const, получаем следующую
формулу, определяющую ЭДС самоиндукции:

На рис. 2.18 показано изображение индуктивности на электрической схеме; uL –
напряжение на зажимах катушки, обусловленное электродвижущей силой самоиндукции, или другими словами,
напряжение, наведенное в катушке собственным переменным магнитным полем.

Все три стрелки на схеме (i, eL, uL) принято направлять в одну сторону. Раньше мы
видели, что при одинаковых направлениях стрелок напряжения и ЭДС они имеют разные знаки. Поэтому:

Знак минус в правой части формулы (2.16) обусловлен принципом Ленца, определяющим
направление индуцированной ЭДС. В рассматриваемом случае он может быть сформулирован следующим
образом:

ЭДС самоиндукции направлена так, что своим действием препятствует причине,
вызвавшей ее появление.

Причина появления ЭДС самоиндукции – изменение тока. Поэтому при возрастании тока
она направлена ему навстречу, при уменьшении тока – в одну с ним сторону.

Препятствуя изменению тока, ЭДС самоиндукции оказывает ему сопротивление, которое
называется индуктивным и обозначается хL. В соответствии с формулой (2.16) его величина определяется
индуктивностью и скоростью изменения тока, т.е. частотой. Формула, определяющая индуктивное
сопротивление, имеет вид:

В цепях постоянного тока такого понятия мы не встречали, так как при постоянных
магнитных полях ЭДС самоиндукции не возникает. Пусть ток, протекающий по индуктивности, определяется
выражением (2.13). Тогда напряжение на ее зажимах, в соответствии с формулой (2.17), равно:

Это – мгновенное значение напряжения. Его амплитуда равна:

Аналогичное выражение получается (после деления на √2) и для действующих
значений:

откуда

где Bl — индуктивная проводимость.

Запишем соответствующие формулы в символической форме:

Так как

Реактивное сопротивление | электроника | Britannica

Реактивность , в электричестве, мера сопротивления, которое цепь или часть цепи представляет электрическому току, поскольку ток переменный или переменный. Постоянные электрические токи, протекающие по проводникам в одном направлении, испытывают сопротивление, называемое электрическим сопротивлением, но не реактивным. Реактивность присутствует в дополнение к сопротивлению, когда по проводникам протекает переменный ток. Реактивность также возникает в течение коротких промежутков времени, когда постоянный ток изменяется по мере приближения к установившемуся потоку или отклонения от него, например, когда переключатели замкнуты или разомкнуты.

Британская викторина

Гаджеты и технологии: факт или вымысел?

Голограммы сделаны фотоаппаратами.

Реактивное сопротивление бывает двух типов: индуктивное и емкостное. Индуктивное реактивное сопротивление связано с магнитным полем, окружающим провод или катушку, по которой проходит ток.Переменный ток в таком проводнике или индукторе создает переменное магнитное поле, которое, в свою очередь, влияет на ток и напряжение (разность потенциалов) в этой части цепи. Катушка индуктивности по существу противодействует изменениям тока, заставляя изменения тока отставать от изменений напряжения. Ток нарастает по мере того, как управляющее напряжение уже уменьшается, имеет тенденцию к продолжению на максимальном значении, когда напряжение меняет свое направление, падает до нуля, когда напряжение увеличивается до максимума в противоположном направлении, и меняет свое направление и нарастает в в том же направлении, что и напряжение, даже когда напряжение снова падает.Индуктивное реактивное сопротивление, мера этого противодействия току, пропорционально как частоте f переменного тока, так и свойству индуктора, называемому индуктивностью (обозначено L и, в свою очередь, зависит от размеров индуктора, расположения, и окружающая среда). Индуктивное реактивное сопротивление X _L равно 2π умноженному на произведение частоты тока и индуктивности проводника, просто X _L = 2π f L. Индуктивное реактивное сопротивление выражается в омах. (Единица измерения частоты — герцы, индуктивности — генри.)

Емкостное реактивное сопротивление, с другой стороны, связано с изменяющимся электрическим полем между двумя проводящими поверхностями (пластинами), отделенными друг от друга изолирующей средой. Такой набор проводников, конденсатор, по существу противодействует изменениям напряжения или разности потенциалов на своих пластинах. Конденсатор в цепи замедляет прохождение тока, заставляя переменное напряжение отставать от переменного тока, в отличие от отношения, вызванного индуктором.Емкостное реактивное сопротивление, мера этого противостояния, обратно пропорционально частоте f переменного тока и свойству конденсатора, называемому емкостью (обозначается C и зависит от размеров конденсатора, его расположения и изоляционной среды. ). Емкостное реактивное сопротивление X _C равно произведению 2π, частоты тока и емкости этой части цепи, просто X _C = 1 / (2 π f C ).Емкостное реактивное сопротивление измеряется в омах. (Единица измерения емкости — фарады.)

Поскольку индуктивное реактивное сопротивление X _L заставляет напряжение опережать ток, а емкостное реактивное сопротивление X _C вызывает отставание напряжения от тока, всего реактивное сопротивление X является их разницей, то есть X = X _L — X _C. Величина, обратная реактивному сопротивлению, 1/ X , называется восприимчивостью и выражается в единицах обратного сопротивления, называемых mho ( Ом записано наоборот).

Получите эксклюзивный доступ к контенту из нашего первого издания 1768 с вашей подпиской.
Подпишитесь сегодня

Основные характеристические параметры индуктивности

18 апреля 2019 г.

Основные характеристические параметры индуктивности

Следующие данные предоставлены производителем функционального генератора .

Индуктивность L

Индуктивность L представляет собственные характеристики самой катушки,
не зависит от тока.За исключением специальной катушки индуктивности (цветовой код
индуктивность), величина индуктивности обычно специально не указывается на
катушка, но помеченная конкретным названием.

Индуктивность XL

Сопротивление катушки индуктивности переменному току называется индуктивным XL в
Ом. Это связано с индуктивностью L и частотой переменного тока f как XL = 2 PI.
fL.

Коэффициент качества Q

Коэффициент качества Q — это физическая величина, представляющая качество катушки, Q —
отношение индуктивности XL к эквивалентному ей сопротивлению, то есть Q = XL / R.В
чем выше значение добротности катушки, тем меньше потери в контуре. Значение Q
катушка связана с сопротивлением провода постоянному току, диэлектрик
потеря каркаса, потеря, вызванная экраном или сердечником, и эффект
высокочастотный скин-эффект. Значение добротности катушки обычно составляет от десятков до сотен.
Значение добротности катушки можно улучшить, используя катушку с магнитным сердечником и несколько
толстые катушки.

Страница не найдена | MIT

Перейти к содержанию ↓

Образование
Исследование
Инновации
Прием + помощь
Студенческая жизнь
Новости
Выпускников
О MIT
Подробнее ↓
Прием + помощь
Студенческая жизнь
Новости
Выпускников
О MIT

Меню ↓

Поиск

Меню

Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще!

Что вы ищете?

Увидеть больше результатов

Предложения или отзывы?

расчетов емкости / индуктивности

расчетов емкости / индуктивности
простой расчет электрических характеристик

Наиболее часто используемые электрические характеристики провода и кабеля следующие.Сопротивление, емкость, индуктивность и проводимость называются первичными.
параметры и используются для низкочастотных приложений. Характеристика
импеданс, соотношение скоростей (фазовая постоянная) и затухание называются
вторичные параметры и используются для высокочастотных приложений.

сопротивление: Сопротивление кабеля сильно зависит от частоты из-за
скин-эффект и эффект близости проводника.
(используйте «расчет калибра провода» для сопротивления постоянному току.)
емкость: Емкость кабеля зависит от геометрической конструкции и
диэлектрическая проницаемость изоляционного материала.Диэлектрик
константа зависит от частоты и температуры, но для
полиэтилен, полипропилен и тетрафуруолоэтилен,
он почти не зависит от частоты и температуры. В
диэлектрическая проницаемость ПВХ сильно зависит от температуры,
частота и конструкция соединения.
индуктивность: Индуктивность кабеля зависит от геометрической конструкции и допустимости
проводника и изоляционного материала. Но его ценность для кабеля
очень маленький, как и другие электрические детали, для большинства
случаи.
проводимость: Проводимость кабеля зависит от сопротивления изоляции при постоянном токе,
но это зависит от диэлектрических потерь на высокой частоте.
характеристическое сопротивление: Характеристический импеданс сильно зависит от частоты при низких значениях.
Диапазон частот. Но почти постоянно в высокочастотном диапазоне.
порядка нескольких МГц и выше.
передаточное число: Коэффициент скорости кабеля зависит от диэлектрической проницаемости кабеля.
изоляционный материал.
затухание: Константа затухания кабеля зависит от сопротивления проводника
и диэлектрические потери изоляции. В нижнем частотном диапазоне как
ниже 1 ГГц диэлектрические потери незначительны.

Эти характеристики поддаются аналитическому вычислению только на очень простых
конструкции. Мы должны использовать численный метод для сложной структуры.
Но значения этих базовых конструкций полезны для приближения
во многих случаях.
Индуктивность

— Wikipédia

Эта статья посвящена индукции и концепции телосложения.Налейте композит, voir Bobine (électricité).

Selon le théorème d’Ampère, tout courant parcourant un circuit crée un champ magnétique à travers la section qu’il entoure, c’est le phénomène d’induction électromagnétique. L ‘ индуктивность в цепи — это коэффициент магнитного потока, равный силе тока, проходящего через цепь ^[1] ^, ^[2] ^, ^[3]. L’unité SI de l’inductance est le henry (H), nom donné en l’honneur du Physicien Joseph Henry ^[4].En toute rigueur ce terme n’a d’intérêt que pour les conditions dans lesquelles le flux est — ou peut être considéré related au courant.

Par synecdoque, по заявке на индуктивность tout composant electronique destiné par sa construction àvoir une suree valeur d’inductance (великолепное телосложение) ^[1] (все соответствует заявке сопротивлений для компонентов) . Ces dipôles sont généralement des bobines , сувенирные апелляции self ^[5] ^, ^[6].

Термин «индуктивность» задан Оливером Хевисайдом в 1886 г. ^[7]. Символ L используется в почетном звене физика Генриха Ленца для работы в области электромагнетизма ^[8] ^, ^[9] ^, ^[10].

Примечание: «коэффициент самоиндукции», quelquefois Employé est un anglicisme ^[5].

Lignes de champ magnétique autour d’un élément de longueur d’un fil parcouru par un courant électrique.

Champ magnétique Induit [модификатор | модификатор кода файла]

On se place dans le cas d’un circuit electrique formé d’une seule maille (au sens des lois de Kirchhoff). Эта цепь является не парком, а электрическая линия I , постоянно действующей на протяжении всей цепи (mais que l’expérience peut évidemment faire varier, à condition que ce soit lentement, et on ne se preoccupe pas directement des petits effets transitoires dus à ces вариации).

Comme le montre l’expérience d’Ørsted, dont les resultats sont formisés par la loi d’Ørsted ^[11], la présence d’un courant electrique crée alors un champ magnétique dans l’espace, dont la configuration exacte peut être complexe, fonction du tracé du circuit lui-même потенциэлементный комплекс.{3}}} \ right)}}}

На сайте donc que le champ magnétique est là présent partout dans l’espace, mais dans le cas général, il n’y a généralement aucun moyen pratique permettant d’en calculer Sa valeur en un point déterminé. Mais indépendamment de sa complexité dans l’espace, ce champ Indit est (en première аппроксимация — dans le vide) пропорционально в tout point au courant électrique qui l’a créé, et c’est ce point qui est fondamental pour la suite.

Энергия создания великих чемпионов [модификатор | модификатор кода файла]

La Creation d’un Champ magnétique demande nécessairement le transfert d’une suree energie électromagnétique par unité de volume.Dans le cas d’un circuit créant un champ magnétique, l’énergie globale ainsi transférée (somitation sur tout l’espace de l’électromagnétique créée en chaque point) résulte nécessairement d’un travail du courant électricontrement renquelle оппозиция. Compte tenu du circuit, cette оппозиция ne peut se manifestester que sous la forme d’une force contre-électromotrice E Induite (c’est-à-dire, quelque выбрал qui aurait le même effet qu’une напряжен. d’une manière ou d’une autre serait immanent à l’ensemble du circuit), apparaissant dans le circuit en пропорционально вариации куранта, et traduisant implicitement la mise en place du Champ magnétique par ce courant électrique.

Le travail d W effectué par le courant à un Instant t pendant un interval de temps d t соответствует électrique eelectrique associée electromotrice E . Cependant, toutes choses égales par ailleurs, le travail n’existe que dans la mesure où le champ magnétique varie, et il est d’autant plus grand pendant un interval de temps d t qu’est rapide la change de courant qui la génère. Globalement, le travail doit donc être пропорционально à la fois au courant I et al. D I / d t , que multiplie un factor L caractérisant la géométrie du circuit et la manière un champ magnétique, коэффициент d’autant плюс grand que le champ magnétique cré est important pour unetensité donnée:

dW = E.{2} \ over 2} \ right)}

Коэффициент автоиндукции [модификатор | модификатор кода файла]

Неиндуктивность sous form de composant.

Независимость от сложных интеграций, материализация и константа номинального коэффициента связи L , on voit donc que (1) le champ magnétique est ratio au courant, (2) la force contre-électromotrice E est de la form E = −L. (DI / dt) {\ displaystyle \ scriptstyle E = -L. (\ Mathrm {d} I / \ mathrm {d} t)}, et (3) l’énergie de education du champ magnétique est W = -12L.{2}}.

Номинальное определение, коэффициент сцепления L — это имя по названию « коэффициент автоматической индукции » рассматриваемой электрической цепи.

En réalité, ce коэффициент автоиндукции является généralement faible dans un circuit usuel, il ne prend des valeurs importantes (и индукция сил, управляющих важными электродвигателями) que lorsque la forme du circuit est spécialement Diséee pour qu’un courant электрический сравнительный анализ важен.Dans ce, но, за счет использования возможностей Boucle de Courant à Créer un moment magnétique unitaire (пропорция à l’intensité électrique et à la surface de la boucle), чтобы множитель le nombre de boucles накладывал на электрическую схему и некомпозиционно местный , qui prend la forme d’une bobine ou d’un solénoïde.

Sous une telle form, коэффициент автоиндукции цепи является важным элементом из-за вопроса о составном компоненте. По определению, это значение имеет индуктивность и соответствует элементу , не учитывающему фактический вклад в восстановление цепи.

L’inductance d’un composant est celle du circuit lorsque ce composant est seul, mais si une autre bobine est montée sur le même circuit ou sur un circuit séparé, les interférences entre les deux seront souvent complex et l’inductance de l ‘сложный ансамбль с определением с точностью до тела. Dans le cas simple où les bobines appartiennent au même circuit et sont à near l’une de l’autre et enfilées sur une même tige ferromagnétique, l’inductance globale sera (sensiblement) для некоторых индуктивностей для компонентов.

Индукционные взаимные цепи [модификатор | модификатор кода файла]

Si l’on se place à présent au niveau d’un élément de longueur du circuit, la force contre-électromotrice d’ensemble ne peut être que le résultat d’une intégrale de chemin d’un champ électrique élémentaire le long du circuit ; et la seule выбрали видимое место действия, par cet élément de longueur est la вариация locale du champ magnétique. En reprenant la présentation du phénomène ci-dessus, et abstraction faite des considérations énergétiques, on voit que l’on peut décomposer l’auto-индуктивность en deux phénomènes indépendants: d’une part la création d’un champ magnffet sous l’e d’un courant électrique dans un определенной цепи; et d’autre part l’apparition d’une force contre-electromotrice dans un определенной цепи, последовательной в соответствии с вариацией de ce champ.Le point important est qu’il n’y aucune raison que les deux circuit soient les mêmes: du moment qu’un circuit est экспонируется в различных вариациях великих чемпионов, верра l’apparition d’une force contre-électromagnétique, независимость de savoir si ce champ a été créé par un courant traversant ce même circuit — même s’il a été créé par un courant, puisqu’il peut autant l’être par un aimant.

Dans le cas d’un circuit (en maille unique) quelconque, la force contre-électromotrice Indite varie suivant la loi de Lenz-Faraday, qui relie cette force contre-électromotrice à la вариация магнетизма потока, flux du champ magnétique traversant le circuit considéré.Можно получить выражение этой силы, управляющей электродвигателем, с партией потенциального вектора величайшего чемпиона A → {\ displaystyle \ scriptstyle {\ vec {A}}}, la «примитивное пространство» магнита B → {\ displaystyle \ scriptstyle {\ vec {B}}} тел. очередь B → = ∇ → ∧A → {\ displaystyle \ scriptstyle {\ overrightarrow {B}} = {\ overrightarrow {\ nabla}} \ wedge {\ overrightarrow {A}}}.
Par rapport à ce потенциальный вектор, la loi de Lenz-Faraday indique que la force contre-électromotrice d’une longueur élémentaire du circuit is liée à la вариация temporelle du Potentiel Vecteur en ce point:

E → ⋅dℓ → = −∂∂tA → ⋅dℓ → {\ displaystyle {\ vec {E}} \ cdot {\ vec {d \ ell}} = — {\ partial \ over \ partial t} {\ vec {A}} \ centerdot {\ vec {d \ ell}}}

L’intégrale de cette force contre-electromotrice le long de la boucle du circuit, électrique fournit donc la force total.

La Creation d’un tel Champ индуктивный дон (dans un circuit electrique formé d’une seule maille, éventuellement différent) усилие, препятствующее электромеханической обработке в цепи приемника. Ici encore le calc du коэффициент индукции mutuelle entre deux circuit peut être complexe, cette complexité est résumée par ce «ratio» qu’il est possible determiner expérimentalement.

Электромоторная сила и магнитный поток [модификатор | модификатор кода файла]

Analytiquement, l’expression de la force contre-electromotrice sur l’ensemble du circuit is donc donnée par l’intégrale de chemin, où A → {\ displaystyle \ scriptstyle {\ vec {A}}} est la «примитивное пространство» великолепный чемпион B → {\ displaystyle \ scriptstyle {\ vec {B}}} tel que B → = ∇ → ∧A → {\ displaystyle \ scriptstyle {\ overrightarrow {B}} = {\ overrightarrow {\ nabla}} \ клин {\ overrightarrow {A}}}.:

E = ∮E → ⋅dℓ → = −∮∂∂tA → ⋅dℓ → {\ displaystyle E = \ oint {\ vec {E}} \ cdot {\ vec {d \ ell}} = — \ oint { \ partial \ over \ partial t} {\ vec {A}} \ centerdot {\ vec {d \ ell}}}

Теория вращения, не имеющая отношения к обращению в этой «примитивной» среде вектор A → {\ displaystyle \ scriptstyle {\ vec {A}}} sur une boucle fermée est égale au flux de ce même champ vectoriel sur une surface s’appuyant sur cette boucle:

∮CA → ⋅dℓ → = ∬S∇ → ∧A → ⋅dS → = ∬SB → ⋅dS → {\ displaystyle \ oint _ {C} {\ vec {A}} \ cdot {\ overrightarrow {\ mathrm {d} \ ell}} = \ iint _ {S} {\ vec {\ nabla}} \ wedge {\ vec {A}} \ cdot {\ overrightarrow {\ mathrm {d} S}} = \ iint _ { S} {\ vec {B}} \ cdot {\ overrightarrow {\ mathrm {d} S}}}

La forme de la boucle fermée que constitue le circuit étant (sensiblement) constante dans le temps, «l’intégrale временная вариация »ветеринарного потенциала на сете букле, являющаяся игрой в« временную вариацию l’intégrale ».Par conséquent, la force contre-électromotrice is gale à la вариация магнитного потока, пересекающая цепь:

E = −∮∂∂tA → ⋅dℓ → = −∂∂t (∮A → ⋅dℓ →) = — ∂∂t (∬SB → ⋅dS →) {\ displaystyle E = — \ oint {\ partial \ over \ partial t} {\ vec {A}} \ centerdot {\ vec {d \ ell}} = — {\ partial \ over \ partial t} \ left (\ oint {\ vec {A}} \ centerdot { \ vec {d \ ell}} \ right) = — {\ partial \ over \ partial t} \ left (\ iint _ {S} {\ vec {B}} \ cdot {\ overrightarrow {\ mathrm {d} S }} \ right)}

Сила, управляющая электродвигателем, E , форма E = −L.(dI / dt) {\ displaystyle \ scriptstyle E = -L. (\ mathrm {d} I / \ mathrm {d} t)}, номинальное значение индуктивности L , на voit que cette dernière est reliée au магнитный поток номиналом L = Φ / I {\ displaystyle L = {\ Phi} / {I}}.

Великолепная электромагнетизм и единица [модификатор | модификатор кода файла]

Коэффициент автоиндукции (ou plus redument, d’induction mutuelle) s’exprime suivant une grandeur body dénommée l ’ индуктивности . Сын единицы в международной системе единиц есть Генри.Comme présenté ci-dessus, l’inductance se caractérise par E = −L. (DI / dt) {\ displaystyle \ scriptstyle E = -L. (\ Mathrm {d} I / \ mathrm {d} t)}. L’inductance d’un circuit is donc de 1 henry si un courant parcourant ce circuit, en option uniform à raison de 1 ampère par second (T ^{{\ displaystyle \,} — 1} · I), produit à ses Возникла электрическая сила 1 вольт (M · L ^{{\ displaystyle \,} 2} · T ^{{\ displaystyle \,} — 3} · I ^{{\ displaystyle \,} — 1}).Par conséquent, индуктивность — это размерность M · L ^{{\ displaystyle \,} 2} · T ^{{\ displaystyle \,} — 2} · I ^{{\ displaystyle \,} — 2}, soit en unités de базовый SI:

1 H = 1 V A ⁻¹ с = 1 м ² кг с ⁻² A ⁻² = 1 м ² кг C ⁻² .

C’est une grandeur scalaire. C’est une grandeur обширный, dans le sens où elle caractérise un système body dans son ensemble, et non pas localement.Par rapport à son caractère extended, сын caractère «additif» зависит от экспериментальных условий, и не чувствует, что si les deux индуктивностей, которые не имеют места в геометрической конфигурации. En cas de superposition de deux индуктивности, dans le cas général, la valeur de l’inductance global depend très fortement de la géométrie du système. L’inductance deux nappes de boucles de courant superposées en un même bobinage et alignées sur un même noyau ferromagnétique является эффективным для сомме индуктивности де ces nappes (on est alors dans un cas de «toutes choses égales par ailleurs»); mais dès que les bobinages s’éloignent les uns des autres, on Entre dans le domaine du coeffect d’induction mutuelle, et l’additivité (ou pas) devient très dependante des conditions géométriques.

La définition la plus courante d’inductance propre est la suivante:

Поверхность циркулярного контура по схеме électrique parcouru par un courant I est traversée par le

Индуктивность | Страница 3 из 3 | Electronov.net

Основные параметры индуктивностей:

Маркировка индуктивностей:

Кодовая маркировка:

Цветовая маркировка:

Условное обозначение индуктивностей на схемах:

Внешний вид катушек индуктивности:

Индуктивность | Страница 2 из 3 | Electronov.net

Свойства индуктивности:

Индуктивность обладает комплексным импедансом (сопротивлением):

Схема замещения не идеальной (реальной) индуктивности:

Сопротивление потерь:

Резонансная частота индуктивности:

Добротность:

Что такое индуктивность и какие она имеет свойства

Что такое индуктивность

Что такое индуктивность

Закон Ленца

ЭДС самоиндукции

Что такое дроссель

Подводим ИТОГИ:

Физическая природа индуктивности

Физическая природа индуктивности.

2.3.2.Конструкции катушек индуктивности.

2.3.3. Индуктивность и собственная емкость катушек индуктивности.

2.3.4. Потери в катушках индуктивности.

2.3.5.Разновидности катушек индуктивности.

ТОЭ Лекции — №20 Самоиндукция. Индуктивность. Ток в индуктивности

Реактивное сопротивление | электроника | Britannica

Основные характеристические параметры индуктивности

расчетов емкости / индуктивности

сопротивление

емкость