Исключающее или: Логический элемент Исключающее ИЛИ | HomeElectronics

Логический элемент Исключающее ИЛИ | HomeElectronics

Всем доброго времени суток! Сегодня мы рассмотрим последние два элемента, которые выполняют простейшие логические функции. Такими элементами являются Исключающее ИЛИ (Exclusive-OR, XOR) и Исключающее ИЛИ-НЕ (None Exclusive-OR, NXOR). Предыдущие статьи смотрите здесь, здесь, здесь и здесь.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Логический элемент Исключающее ИЛИ, как и ранее рассмотренные логические элементы имеет несколько равноправных входов и один выход, но не один из входных выводов не может заблокировать другие входы, установив выходной сигнал к уровню единицы или нуля. Исходя из сказанного, можно установить логику работы элемента Исключающее ИЛИ: высокий логический уровень на выходе появляется только тогда, когда только на одном из входов есть высокий уровень, а если на всех входах одновременно присутствуют сигналы логического нуля или логической единицы, то на выходе буде низкий уровень напряжения. Так же как и все остальные логические элементы элемент Исключающее ИЛИ может иметь инверсию на выходе, такой элемент называют Исключающее ИЛИ-НЕ. Логика работы такого элемента следующая: высокий уровень на выходе логического элемента Исключающее ИЛИ-НЕ появиться только в том случае, когда на всех входах одновременно присутствует сигналы лог. 0 или лог. 1. Таким образом таблица истинности логических элементов Исключающее ИЛИ и Исключающее ИЛИ-НЕ будет иметь следующий вид:

Элементы Исключающее ИЛИ из-за своего специфического функционала не имеют широкого применения, поэтому отдельных суффиксов в их обозначении не присутствует, они в основном входят в серию ЛП (например, К555ЛП5, КР1533ЛП12, К561ЛП2), в составе которой микросхемы с различным функционалом. Логические элементы Исключающее ИЛИ имеют своё графическое обозначение, которое приведено ниже.

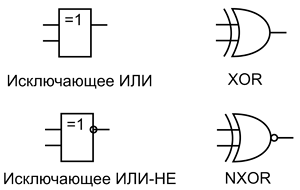
Условное графическое обозначение элементов Исключающее ИЛИ: DIN (слева) и ANSI (справа).

Применение элемента Исключающее ИЛИ

С точки зрения математики, элемент Исключающее ИЛИ выполняет операцию суммирования по модулю 2. Поэтому эти элементы иногда называют сумматорами по модулю два. Основное предназначение элементов Исключающее ИЛИ состоит в сравнении двух входных сигналов (когда на входы приходят два высоких или два низких логических уровня на выходе формируется лог. 0), очень часто данный элемент применяют для формирования задержки сигнала или формирования коротких импульсов.

Управляемый инвертор

Важное применение элементов Исключающее ИЛИ – управляемый инвертор. Опишем его работу. Один из входов используется как управляющий, а на другой поступает сигнал. Если на управляющем входе высокий логический уровень, то сигнал инвертируется, а если низкий, то не инвертируется. Чаще всего управляющий сигнал задаётся постоянным уровнем, определяя режим работы элемента, а информационный сигнал является импульсным. То есть элемент Исключающее ИЛИ может изменять полярность входного сигнала или фронта, а может и не изменять в зависимости от управляющего сигнала.

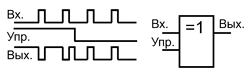
Элемент Исключающее ИЛИ в качестве управляемого инвертора.

Смешивание сигналов

В случае, когда имеется два сигнала и исключается их одновременный приход на элемент Исключающее ИЛИ, то он может быть использован для смешивания сигналов. Такое применение данного элемента может быть использовано в тех случаюх, когда остаются неиспользованными некоторые элементы Исключающее ИЛИ.

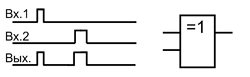
Применение элемента Исключающее ИЛИ для смешивания двух неодновременных сигналов.

Формирование коротких импульсов

Второе важное применение данного элемента – выделение фронта и среза входного импульса, которое традиционно делали с помощью дифференцирующего RC-звена, с последующим усилением и формированием сигнала. Микросхема с элементами Исключающее ИЛИ упрощает данную задачу.

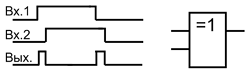
Выделения фронта и среза импульса.

Ниже представлена схема для выделения среза и фронта входящего импульса. Входной сигнал задерживается цепочкой элементов, а затем исходный сигнал и его задержаная копия поступают на входы элемента Исключающее ИЛИ. В результате такого преобразования можно говорить об удвоении частоты входного сигнала, так как выходные импульсы следуют вдвое чаще, чем входные.

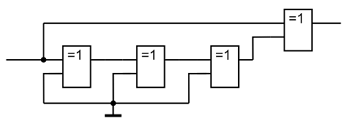
Схема реализующая выделение фронта и среза импульса.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Исключающее ИЛИ — это… Что такое Исключающее ИЛИ?

Сложе́ние по модулю 2 (исключа́ющее «ИЛИ», XOR, «сумма по модулю 2») — ло­ги­чес­кая опе­ра­ция, по сво­ему при­ме­не­нию мак­си­маль­но при­бли­жен­ная к грам­ма­ти­чес­кой кон­струк­ции «либо … либо …».

Это бинарная инфиксная опе­ра­ция, то есть она имеет два опе­ранда и ста­вит­ся между ними. Чаще всего встре­ча­ют­ся сле­ду­ю­щие ва­ри­анты за­пи­си:
^ .

Булева алгебра

В булевой алгебре сложение по модулю 2 — это функция двух переменных (они же — операнды операции). Переменные могут принимать значения из множества . Результат также принадлежит множеству . Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений может использоваться любая другая пара подходящих символов, например или или «ложь», «истина».

Правило: результат равен , если оба операнда равны; во всех остальных случаях результат равен .

Таблица истинности:

Программирование

В языках C/C++ (а также Java, C#, Ruby, PHP, JavaScript и т. д.) эта операция обозначается символом «^», в языках Паскаль, Delphi, Ada — зарезервированным словом XOR, в языке ассемблера — одноименной логической командой. Сложение по модулю 2 выполняется для всех битов левого и правого операнда попарно. Например,

если
a =
b =
то
a ^ b =

Выполнение операции XOR для значений логического типа (true, false) производится в разных языках программирования по-разному. Например в Delphi используется встроенный оператор XOR (пример: condition1 xor condition2). В языке C, начиная со стандарта С++ оператор «^» для логического типа bool возвращает результат согласно описанным правилам, для остальных же типов проихводится его побитовое применение. Перегрузка для стандартных типов невозможна, но операцию XOR над ними можно реализовать, исходя из принципа «исключающего ИЛИ». Выглядит это так:

(condition1 || condition2) && (condition1 != condition2)

(при этом нет разницы, применяются ли побитовые операторы & и |, или же логические && и ||)

Связь с естественным языком

Часто указывают на сходство между сложением по модулю 2 и конструкцией «либо … либо …» в естественном языке. Составное утверждение «либо A, либо B» считается истинным, когда истинно либо A, либо B, но не оба сразу; в противном случае составное утверждение ложно. Это в точности соответствует определению операции в булевой алгебре, если «истину» обозначать как 1, а «ложь» как 0.

Эту операцию нередко сравнивают с дизъюнкцией потому, что они очень похожи по свойствам, и обе имеют сходство с союзом «или» в повседневной речи. Сравните правила для этих операций:

1. истинно, если истинно или , или оба сразу.
2. истинно, если истинно или , но не оба сразу.

Операция исключает последний вариант («оба сразу») и по этой причине называется исключающим «ИЛИ». Операция включает последний вариант («оба сразу») и по этой причине иногда называется включающим «ИЛИ». Неоднозначность естественного языка заключается в том, что союз «или» может применяться в обоих случаях.

См. также

Wikimedia Foundation.
2010.

Исключающее или — это… Что такое Исключающее или?

Сложе́ние по модулю 2 (исключа́ющее «ИЛИ», XOR, «сумма по модулю 2») — ло­ги­чес­кая опе­ра­ция, по сво­ему при­ме­не­нию мак­си­маль­но при­бли­жен­ная к грам­ма­ти­чес­кой кон­струк­ции «либо … либо …».

Это бинарная инфиксная опе­ра­ция, то есть она имеет два опе­ранда и ста­вит­ся между ними. Чаще всего встре­ча­ют­ся сле­ду­ю­щие ва­ри­анты за­пи­си:
^ .

Булева алгебра

В булевой алгебре сложение по модулю 2 — это функция двух переменных (они же — операнды операции). Переменные могут принимать значения из множества . Результат также принадлежит множеству . Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений может использоваться любая другая пара подходящих символов, например или или «ложь», «истина».

Правило: результат равен , если оба операнда равны; во всех остальных случаях результат равен .

Таблица истинности:

Программирование

В языках C/C++ (а также Java, C#, Ruby, PHP, JavaScript и т. д.) эта операция обозначается символом «^», в языках Паскаль, Delphi, Ada — зарезервированным словом XOR, в языке ассемблера — одноименной логической командой. Сложение по модулю 2 выполняется для всех битов левого и правого операнда попарно. Например,

если
a =
b =
то
a ^ b =

Выполнение операции XOR для значений логического типа (true, false) производится в разных языках программирования по-разному. Например в Delphi используется встроенный оператор XOR (пример: condition1 xor condition2). В языке C, начиная со стандарта С++ оператор «^» для логического типа bool возвращает результат согласно описанным правилам, для остальных же типов проихводится его побитовое применение. Перегрузка для стандартных типов невозможна, но операцию XOR над ними можно реализовать, исходя из принципа «исключающего ИЛИ». Выглядит это так:

(condition1 || condition2) && (condition1 != condition2)

(при этом нет разницы, применяются ли побитовые операторы & и |, или же логические && и ||)

Связь с естественным языком

Часто указывают на сходство между сложением по модулю 2 и конструкцией «либо … либо …» в естественном языке. Составное утверждение «либо A, либо B» считается истинным, когда истинно либо A, либо B, но не оба сразу; в противном случае составное утверждение ложно. Это в точности соответствует определению операции в булевой алгебре, если «истину» обозначать как 1, а «ложь» как 0.

Эту операцию нередко сравнивают с дизъюнкцией потому, что они очень похожи по свойствам, и обе имеют сходство с союзом «или» в повседневной речи. Сравните правила для этих операций:

1. истинно, если истинно или , или оба сразу.
2. истинно, если истинно или , но не оба сразу.

Операция исключает последний вариант («оба сразу») и по этой причине называется исключающим «ИЛИ». Операция включает последний вариант («оба сразу») и по этой причине иногда называется включающим «ИЛИ». Неоднозначность естественного языка заключается в том, что союз «или» может применяться в обоих случаях.

См. также

Wikimedia Foundation.
2010.

Исключающее «или» — это… Что такое Исключающее «или»?

Сложе́ние по модулю 2 (исключа́ющее «ИЛИ», XOR, «сумма по модулю 2») — ло­ги­чес­кая опе­ра­ция, по сво­ему при­ме­не­нию мак­си­маль­но при­бли­жен­ная к грам­ма­ти­чес­кой кон­струк­ции «либо … либо …».

Это бинарная инфиксная опе­ра­ция, то есть она имеет два опе­ранда и ста­вит­ся между ними. Чаще всего встре­ча­ют­ся сле­ду­ю­щие ва­ри­анты за­пи­си:
^ .

Булева алгебра

В булевой алгебре сложение по модулю 2 — это функция двух переменных (они же — операнды операции). Переменные могут принимать значения из множества . Результат также принадлежит множеству . Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений может использоваться любая другая пара подходящих символов, например или или «ложь», «истина».

Правило: результат равен , если оба операнда равны; во всех остальных случаях результат равен .

Таблица истинности:

Программирование

В языках C/C++ (а также Java, C#, Ruby, PHP, JavaScript и т. д.) эта операция обозначается символом «^», в языках Паскаль, Delphi, Ada — зарезервированным словом XOR, в языке ассемблера — одноименной логической командой. Сложение по модулю 2 выполняется для всех битов левого и правого операнда попарно. Например,

если
a =
b =
то
a ^ b =

Выполнение операции XOR для значений логического типа (true, false) производится в разных языках программирования по-разному. Например в Delphi используется встроенный оператор XOR (пример: condition1 xor condition2). В языке C, начиная со стандарта С++ оператор «^» для логического типа bool возвращает результат согласно описанным правилам, для остальных же типов проихводится его побитовое применение. Перегрузка для стандартных типов невозможна, но операцию XOR над ними можно реализовать, исходя из принципа «исключающего ИЛИ». Выглядит это так:

(condition1 || condition2) && (condition1 != condition2)

(при этом нет разницы, применяются ли побитовые операторы & и |, или же логические && и ||)

Связь с естественным языком

Часто указывают на сходство между сложением по модулю 2 и конструкцией «либо … либо …» в естественном языке. Составное утверждение «либо A, либо B» считается истинным, когда истинно либо A, либо B, но не оба сразу; в противном случае составное утверждение ложно. Это в точности соответствует определению операции в булевой алгебре, если «истину» обозначать как 1, а «ложь» как 0.

Эту операцию нередко сравнивают с дизъюнкцией потому, что они очень похожи по свойствам, и обе имеют сходство с союзом «или» в повседневной речи. Сравните правила для этих операций:

1. истинно, если истинно или , или оба сразу.
2. истинно, если истинно или , но не оба сразу.

Операция исключает последний вариант («оба сразу») и по этой причине называется исключающим «ИЛИ». Операция включает последний вариант («оба сразу») и по этой причине иногда называется включающим «ИЛИ». Неоднозначность естественного языка заключается в том, что союз «или» может применяться в обоих случаях.

См. также

Wikimedia Foundation.
2010.

Сложение по модулю 2 — Википедия

Рис. 1 График побитового исключающего «или»

Сложе́ние по мо́дулю 2 (логи́ческая неравнозна́чность, исключа́ющее «ИЛИ», строгая дизъюнкция, XOR, поразрядное дополнение, побитовый комплемент, жегалкинское сложение, логическое вычитание) — булева функция, а также логическая и битовая операция. В случае двух переменных результат выполнения операции истинен тогда и только тогда, когда один из аргументов истинен, а второй — ложен. Для функции трёх и более переменных результат выполнения операции будет истинным только тогда, когда количество аргументов, равных 1, составляющих текущий набор, — нечётное. Такая операция естественным образом возникает в кольце вычетов по модулю 2, откуда и происходит название операции.

Сложение по модулю 2 следует отличать от простого сложения, которое соответствует обыкновенному неисключающему «или» (логической дизъюнкции).

В теории множеств сложению по модулю 2 соответствует операция симметричной разности двух множеств.

в префиксной записи

max(a,b)−min(a,b){\displaystyle max(a,b)-min(a,b)}.

Обозначения

Запись может быть префиксной («польская запись») — знак операции ставится перед операндами, инфиксной — знак операции ставится между операндами и постфиксной — знак операции ставится после операндов. При числе операндов более 2 префиксная и постфиксная записи экономичнее инфиксной записи. Чаще всего встречаются следующие варианты записи:
⊕2(a,b), a{\displaystyle \oplus _{2}(a,b),~a} ^ b, a⊕b,a⊕2b,a+2b,{\displaystyle b,~a\oplus b,a\oplus _{2}b,a+_{2}b,} a ≠ b, a≠b,(a,b)⊕2,a XOR b{\displaystyle a\neq b,(a,b)\oplus _{2},a~XOR~b}

В таблице символов Юникод есть символы для сложения по модулю 2: XOR — U+22BB (⊻), CIRCLED PLUS — U+2295 (⊕) и PLUS SIGN WITH SUCSCRIPT TWO — U+2A27 (⨧), а также символ для суммы по модулю 2: MODULO TWO SUM — U+2A0A (⨊).

Свойства

Булева алгебра

В булевой алгебре сложение по модулю 2 — это функция двух, трёх и более переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества {0,1}{\displaystyle \{0,1\}}. Результат также принадлежит множеству {0,1}{\displaystyle \{0,1\}}. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений 0,1{\displaystyle 0,1} может использоваться любая другая пара подходящих символов, например false,true{\displaystyle false,true} или F,T{\displaystyle F,T} или «ложь», «истина», но при этом необходимо доопределять старшинство, например, true>false{\displaystyle true>false}.

Таблицы истинности:

Правило: результат равен 0{\displaystyle 0}, если оба операнда равны; во всех остальных случаях результат равен 1{\displaystyle 1}.

Правило: результат равен 0{\displaystyle 0}, если нет операндов, равных 1{\displaystyle 1}, либо их чётное количество.

Программирование

В языках C/C++, Java, C#, Ruby, PHP, JavaScript, Python и т. д. битовая операция поразрядного дополнения обозначается символом «^», в языках Паскаль, Delphi, Ada, Visual Basic — зарезервированным словом xor, в языке ассемблера — одноимённой логической командой. При этом сложение по модулю 2 выполняется для всех битов левого и правого операнда попарно. Например,

если

a=011001012{\displaystyle a=01100101_{2}}

b=001010012{\displaystyle b=00101001_{2}}

то

a ^b=010011002{\displaystyle a{\hat {\ }}b=01001100_{2}}

Выполнение операции исключающее «или» для значений логического типа (true, false) производится в разных языках программирования по-разному. Например, в Delphi используется встроенный оператор XOR (пример: условие1 xor условие2). В языке C, начиная со стандарта C99, оператор «^» над операндами логического типа возвращает результат применения логической операции XOR. В С++ оператор «^» для логического типа bool возвращает результат согласно описанным правилам, для остальных же типов производится его побитовое применение.

Связь с естественным языком

В естественном языке операция «сложение по модулю» эквивалентна двум выражениям:

1. «результат истинен (равен 1), если A не равно B (A≠B)»;
2. «если A не равно B (A≠B), то истина (1)».

Часто указывают на сходство между сложением по модулю 2 и конструкцией «либо … либо …» в естественном языке. Составное утверждение «либо A, либо B» считается истинным, когда истинно либо A, либо B, но не оба сразу; в противном случае составное утверждение ложно. Это в точности соответствует определению операции в булевой алгебре, если «истину» обозначать как 1{\displaystyle 1}, а «ложь» как 0{\displaystyle 0}.

Эту операцию нередко сравнивают с дизъюнкцией потому, что они очень похожи по свойствам, и обе имеют сходство с союзом «или» в повседневной речи. Сравните правила для этих операций:

1. A∨B{\displaystyle A\lor B} истинно, если истинно A{\displaystyle A} или B{\displaystyle B}, или оба сразу («хотя бы один из двух»).
2. A⊕B{\displaystyle A\oplus B} истинно, если истинно A{\displaystyle A} или B{\displaystyle B}, но не оба сразу («только один из двух»).

Операция ⊕{\displaystyle \oplus } исключает последний вариант («оба сразу») и по этой причине называется исключающим «ИЛИ».
Операция ∨{\displaystyle \lor } включает последний вариант («оба сразу») и по этой причине иногда называется включающим «ИЛИ».
Неоднозначность естественного языка заключается в том, что союз «или» может применяться в обоих случаях.

В квантовых компьютерах аналог операции сложения по модулю 2 — вентиль CNOT.

Ссылки

Побитовые операторы в C++: И, ИЛИ, НЕ и исключающее ИЛИ | Уроки С++

  Обновл. 11 Сен 2020  | 

Побитовые операторы манипулируют отдельными битами в пределах переменной.

Примечание: Для некоторых этот материал может показаться сложным. Если вы застряли или что-то не понятно — пропустите этот урок (и следующий), в будущем сможете вернуться и разобраться детально. Он не столь важен для прогресса в изучении языка C++, как другие уроки, и изложен здесь в большей мере для общего развития.

Зачем нужны побитовые операторы?

В далеком прошлом компьютерной памяти было очень мало и ею сильно дорожили. Это было стимулом максимально разумно использовать каждый доступный бит. Например, в логическом типе данных bool есть всего лишь два возможных значения (true и false), которые могут быть представлены одним битом, но по факту занимают целый байт памяти! А это, в свою очередь, из-за того, что переменные используют уникальные адреса памяти, а они выделяются только в байтах. Переменная bool занимает 1 бит, а другие 7 бит — тратятся впустую.

Используя побитовые операторы, можно создавать функции, которые позволят уместить 8 значений типа bool в переменную размером 1 байт, что значительно сэкономит потребление памяти. В прошлом такой трюк был очень популярен. Но сегодня, по крайней мере, в прикладном программировании, это не так.

Теперь памяти стало существенно больше и программисты обнаружили, что лучше писать код так, чтобы было проще и понятнее его поддерживать, нежели усложнять его ради незначительной экономии памяти. Поэтому спрос на использование побитовых операторов несколько уменьшился, за исключением случаев, когда необходима уж максимальная оптимизация (например, научные программы, которые используют огромное количество данных; игры, где манипуляции с битами могут быть использованы для дополнительной скорости; встроенные программы, где память по-прежнему ограничена).

В языке С++ есть 6 побитовых операторов:

В побитовых операциях следует использовать только целочисленные типы данных unsigned, так как C++ не всегда гарантирует корректную работу побитовых операторов с целочисленными типами signed.

Правило: При работе с побитовыми операторами используйте целочисленные типы данных unsigned.

Побитовый сдвиг влево (<<) и побитовый сдвиг вправо (>>)

В языке C++ количество используемых бит основывается на размере типа данных (в 1 байте находятся 8 бит). Оператор побитового сдвига влево (<<) сдвигает биты влево. Левый операнд является выражением, в котором они сдвигаются, а правый — количество мест, на которые нужно сдвинуть. Поэтому в выражении 3 << 1 мы имеем в виду «сдвинуть биты влево в литерале 3 на одно место».

Примечание: В следующих примерах мы будем работать с 4-битными двоичными значениями.

Рассмотрим число 3, которое в двоичной системе равно 0011:

3 = 0011
3 << 1 = 0110 = 6
3 << 2 = 1100 = 12
3 << 3 = 1000 = 8

В последнем третьем случае один бит перемещается за пределы самого литерала! Биты, сдвинутые за пределы двоичного числа, теряются навсегда.

Оператор побитового сдвига вправо (>>) сдвигает биты вправо. Например:

12 = 1100
12 >> 1 = 0110 = 6
12 >> 2 = 0011 = 3
12 >> 3 = 0001 = 1

В третьем случае мы снова переместили бит за пределы литерала. Он также потерялся навсегда.

Хотя в примерах, приведенных выше, мы смещаем биты только в литералах, мы также можем смещать биты и в переменных:

unsigned int x = 4;
x = x << 1; // x должен стать равным 8

Следует помнить, что результаты операций с побитовыми сдвигами в разных компиляторах могут отличаться.

Что!? Разве операторы << и >> используются не для вывода и ввода данных?

И для этого тоже.

Сейчас польза от использования побитовых операторов не так велика, как это было раньше. Сейчас в большинстве случаев оператор побитового сдвига влево используется для вывода данных. Например, рассмотрим следующую программу:

#include <iostream>

int main()
{
unsigned int x = 4;
x = x << 1; // оператор << используется для побитового сдвига влево
std::cout << x; // оператор << используется для вывода данных в консоль

return 0;
}

Результат выполнения программы:

8

А как компилятор понимает, когда нужно применить оператор побитового сдвига влево, а когда выводить данные? Всё очень просто. std::cout переопределяет значение оператора << по умолчанию на новое (вывод данных в консоль). Когда компилятор видит, что левым операндом оператора << является std::cout, то он понимает, что должен произойти вывод данных. Если левым операндом является переменная целочисленного типа данных, то компилятор понимает, что должен произойти побитовый сдвиг влево (операция по умолчанию).

Побитовый оператор НЕ

Побитовый оператор НЕ (~), пожалуй, самый простой для объяснения и понимания. Он просто меняет каждый бит на противоположный, например, с 0 на 1 или с 1 на 0. Обратите внимание, результаты побитового НЕ зависят от размера типа данных!

Предположим, что размер типа данных составляет 4 бита:

4 = 0100
~ 4 = 1011 (двоичное) = 11 (десятичное)

Предположим, что размер типа данных составляет 8 бит:

4 = 0000 0100
~ 4 = 1111 1011 (двоичное) = 251 (десятичное)

Побитовые операторы И, ИЛИ и исключающее ИЛИ (XOR)

Побитовые операторы И (&) и ИЛИ (|) работают аналогично логическим операторам И и ИЛИ. Однако, побитовые операторы применяются к каждому биту отдельно! Например, рассмотрим выражение 5 | 6. В двоичной системе это 0101 | 0110. В любой побитовой операции операнды лучше всего размещать следующим образом:

0 1 0 1 // 5
0 1 1 0 // 6

А затем применять операцию к каждому столбцу с битами по отдельности. Как вы помните, логическое ИЛИ возвращает true (1), если один из двух или оба операнды истинны (1). Аналогичным образом работает и побитовое ИЛИ. Выражение 5 | 6 обрабатывается следующим образом:

0 1 0 1 // 5
0 1 1 0 // 6
-------
0 1 1 1 // 7

Результат:

0111 (двоичное) = 7 (десятичное)

Также можно обрабатывать и комплексные выражения ИЛИ, например, 1 | 4 | 6. Если хоть один бит в столбце равен 1, то результат целого столбца — 1. Например:

0 0 0 1 // 1
0 1 0 0 // 4
0 1 1 0 // 6
--------
0 1 1 1 // 7

Результатом 1 | 4 | 6 является десятичное 7.

Побитовое И работает аналогично логическому И — возвращается true, только если оба бита в столбце равны 1. Рассмотрим выражение 5 & 6:

0 1 0 1 // 5
0 1 1 0 // 6
--------
0 1 0 0 // 4

Также можно решать и комплексные выражения И, например, 1 & 3 & 7. Только при условии, что все биты в столбце равны 1, результатом столбца будет 1.

0 0 0 1 // 1
0 0 1 1 // 3
0 1 1 1 // 7
--------
0 0 0 1 // 1

Последний оператор — побитовое исключающее ИЛИ (^) (сокр. «XOR» от англ. «eXclusive OR«). При обработке двух операндов, исключающее ИЛИ возвращает true (1), только если один и только один из операндов является истинным (1). Если таких нет или все операнды равны 1, то результатом будет false (0). Рассмотрим выражение 6 ^ 3:

0 1 1 0 // 6
0 0 1 1 // 3
-------
0 1 0 1 // 5

Также можно решать и комплексные выражения XOR, например, 1 ^ 3 ^ 7. Если единиц в столбце чётное количество, то результатом будет 0, если же нечётное количество, то результат — 1. Например:

0 0 0 1 // 1
0 0 1 1 // 3
0 1 1 1 // 7
--------
0 1 0 1 // 5

Побитовые операторы присваивания

Как и в случае с арифметическими операторами присваивания, язык C++ предоставляет побитовые операторы присваивания для облегчения внесения изменений в переменные.

Например, вместо х = х << 1; мы можем написать х <<= 1;.

Заключение

При работе с побитовыми операторами (используя метод столбца) не забывайте о том, что:

   При вычислении побитового ИЛИ, если хоть один из битов в столбце равен 1, то результат целого столбца равен 1.

   При вычислении побитового И, если все биты в столбце равны 1, то результат целого столбца равен 1.

   При вычислении побитового исключающего ИЛИ (XOR), если единиц в столбце нечётное количество, то результат равен 1.

Тест

Задание №1

Какой результат 0110 >> 2 в двоичной системе счисления?

Задание №2

Какой результат 5 | 12 в десятичной системе счисления?

Задание №3

Какой результат 5 & 12 в десятичной системе счисления?

Задание №4

Какой результат 5 ^ 12 в десятичной системе счисления?

Ответы

Ответ №1

Результатом 0110 >> 2 является двоичное число 0001.

Ответ №2

Выражение 5 | 12:

0 1 0 1
1 1 0 0
--------
1 1 0 1 // 13 (десятичное)

Ответ №3

Выражение 5 & 12:

0 1 0 1
1 1 0 0
--------
0 1 0 0 // 4 (десятичное)

Ответ №4

Выражение 5 ^ 12:

0 1 0 1
1 1 0 0
--------
1 0 0 1 // 9 (десятичное)

Оценить статью:

Загрузка…

Поделиться в социальных сетях:

C++ — ^ — побитовое XOR (исключающее ИЛИ)

пример

int a = 5;     // 0101b  (0x05)
int b = 9;     // 1001b  (0x09)
int c = a ^ b; // 1100b  (0x0C)

std::cout << "a = " << a << ", b = " << b << ", c = " << c << std::endl;

Выход

a = 5, b = 9, c = 12

Зачем

Немного мудрый XOR (эксклюзивный или) работает на уровне бит и использует следующую логическую таблицу истинности:

true OR true = false
true OR false = true
false OR false = false

Обратите внимание, что при операции XOR true OR true = false где, как и при действии true AND/OR true = true , следовательно, исключительный характер операции XOR.

Используя это, когда двоичное значение для ( a 0101 ) и бинарное значение b ( 1001 ) являются XOR — е изд «вместе мы получим двоичное значение 1100 :

int a = 0 1 0 1
int b = 1 0 0 1 ^
        ---------
int c = 1 1 0 0

Бит мудрый XOR не изменяет значения исходных значений, если специально не назначено использование битового оператора присваивания соединения ^= :

int a = 5;  // 0101b  (0x05)
a ^= 9;    // a = 0101b ^ 1001b

Бит мудрый XOR может использоваться многими способами и часто используется в операциях бит-маски для шифрования и сжатия.

Примечание . Следующий пример часто показан в качестве примера приятного трюка. Но не следует использовать в производственном коде (для достижения такого же результата лучше использовать std::swap() ).

Вы также можете использовать операцию XOR для замены двух переменных без временного:

int a = 42;
int b = 64;

// XOR swap
a ^= b;
b ^= a;
a ^= b;

std::cout << "a = " << a << ", b = " << b << "\n";

Чтобы произвести это, вам нужно добавить чек, чтобы убедиться, что он может быть использован.

void doXORSwap(int& a, int& b)
{
    // Need to add a check to make sure you are not swapping the same
    // variable with itself. Otherwise it will zero the value.
    if (&a != &b)
    {
        // XOR swap
        a ^= b;
        b ^= a;
        a ^= b;
    }
}

Таким образом, хотя это выглядит как хороший трюк в изоляции, он не полезен в реальном коде. xor не является базовой логической операцией, а комбинацией других: a ^ c = ~ (a & c) & (a | c)

также в 2015 году переменные компиляторов могут быть назначены как двоичные:

int cn=0b0111;

Исключающая или

Логическая операция Исключительная дизъюнкция , также называемая исключающая или (обозначенная XOR или EOR ), является типом логической дизъюнкции двух операндов, которая приводит к значению «истина», если и только если «ровно один из операндов имеет значение« истина ». [ См. «Стэнфордскую энциклопедию философии», статья «[ http://plato.stanford.edu/entries/disjunction/ Disjunction ]» ]

Другими словами, исключительная дизъюнкция — логическая операция над два логических значения, обычно значения двух предложений, которые дают значение «истина» только в тех случаях, когда значения истинности операндов различаются.

Таблица истинности

Таблица истинности p, mathrm {XOR}, q (также записывается как p oplus q или p
уравнение q) выглядит следующим образом:

Обратите внимание на трехстороннюю симметрию результатов: идентификаторы p, q и oplus в этой таблице могут быть произвольно переназначены, и таблица все равно будет правильной.

Диаграмма Венна

Диаграмма Венна A oplus B (красная часть соответствует действительности)

Эквивалентности, исключение и введение

Следующие эквиваленты могут быть затем выведены, записаны с помощью логических операторов, в математике и инженерии обозначение :: egin {матрица} p oplus q & = & (p land lnot q) & lor & (lnot p land q) = poverline {q} + overline {p} q \\ & = & (p lor q) & земля & (lnot p lor lnot q) = (p + q) (overline {p} + overline {q}) \\ & = & (p lor q) & land & lnot (p land q) = (p + q ) (overline {pq}) end {matrix}

Обобщенный или n-арный XOR выполняется, когда количество 1-бит нечетно.

Исключительная дизъюнкция p oplus q может быть выражена в терминах логической конъюнкции (land), дизъюнкции (lor) и отрицания (lnot) следующим образом: egin {matrix} p oplus q & = & (p land lnot q) lor (lnot p land q) end {matrix}

Исключительная дизъюнкция p oplus q также может быть выражена следующим образом: egin {matrix} p oplus q & = & lnot (p land q) land ( p lor q) end {matrix}

Это представление XOR может оказаться полезным при построении схемы или сети, поскольку оно имеет только одну операцию lnot и небольшое количество операций land и lor.Доказательство этого тождества приводится ниже: egin {matrix} p oplus q & = & (p land lnot q) & lor & (lnot p land q) \ & = & ((p land lnot q) lor lnot p) & и & ((p land lnot q) lor q) \ & = & ((p lor lnot p) land (lnot q lor lnot p)) & land & ((p lor q) land (lnot q lor q)) \ & = & (lnot p lor lnot q) & land & (p lor q) \ & = & lnot (p land q) & land & (p lor q) end {matrix}

Иногда полезно написать p oplus q следующим образом :: egin {matrix} p oplus q & = & lnot ((p land q) lor (lnot p land lnot q)) end {matrix}

Эту эквивалентность можно установить, применяя законы Де Моргана дважды до четвертой строки приведенного выше доказательства.

Исключающее или также эквивалентно отрицанию логического биконусловия по правилам материальной импликации (материальное условие эквивалентно дизъюнкции отрицания его антецедента и его следствия) и материальной эквивалентности.

Связь с современной алгеброй

Хотя операторы land (конъюнкция) и lor (дизъюнкция) очень полезны в логических системах, они не дают более обобщаемой структуры следующим образом:

Системы ({T, F} , land) и ({T, F}, lor) — моноиды.К сожалению, это препятствует объединению этих двух систем в более крупные структуры, такие как математическое кольцо.

Однако система, использующая исключающее ИЛИ ({T, F}, oplus) , является абелевой группой. Комбинация операторов land и oplus над элементами {T, F} дает хорошо известное поле F_2. Это поле может представлять любую логику, доступную с помощью системы (земля, лор), и имеет дополнительное преимущество в виде арсенала инструментов алгебраического анализа для полей.

Исключительное «или» на естественном языке

Оксфордский словарь английского языка объясняет «либо… или» следующим образом: «Основная функция любого и т. Д., состоит в том, чтобы подчеркнуть безразличие двух (или более) вещей или направлений… но второстепенная функция — подчеркнуть взаимную исключительность, = одного из двух, но не обоих ».

Следуя такой интуиции здравого смысла относительно «Или», иногда утверждают, что во многих естественных языках, включая английский, слово «или» имеет «исключительный» смысл. Исключительная дизъюнкция пары предложений, («p», «q»), должно означать, что «p» истинно или «q» истинно, но не то и другое одновременно.Например, утверждается, что обычное намерение такого утверждения, как «Вы можете выпить кофе или вы можете выпить чай», состоит в том, чтобы оговорить, что точно одно из условий может быть истинным. Конечно, при многих обстоятельствах предложение, подобное этому примеру, следует воспринимать как запрещающее возможность принятия обоих вариантов. Тем не менее, есть веские основания полагать, что предложения такого рода вовсе не дизъюнктивны. Если все, что мы знаем о некоторой дизъюнкции, — это то, что она верна в целом, мы не можем быть уверены, что любой из ее дизъюнкций истинен.Например, если женщине сказали, что ее друг находится в закусочной или на теннисном корте, она не может сделать достоверный вывод, что он находится на теннисном корте. Но если официант говорит ей, что она может пить кофе или чай, она может сделать обоснованный вывод, что она может пить чай. Этим свойством не обладает ничто, что в классическом понимании считается дизъюнкцией. Это настолько даже при условии, что она могла бы разумно посчитать своего официанта отказом ей в возможности пить и кофе, и чай.

Есть также веские общие причины полагать, что ни одно слово на любом естественном языке не может быть адекватно представлено двоичным исключающим «или» формальной логики.Во-первых, любое двоичное или другое n-арное исключающее «или» истинно тогда и только тогда, когда оно имеет нечетное количество истинных входов. Но кажется, что ни одно слово на любом естественном языке, которое может объединить список из двух или более вариантов, не обладает этим общим свойством. Во-вторых, как указали Барретт и Стеннер в статье 1971 года «Миф об исключительном« ИЛИ »» (Mind, 80 (317), 116–121), ни один автор не привел пример английского или-предложения, которое появляется быть ложным, потому что оба его входа истинны. Конечно, есть много or-предложений, таких как «Лампочка горит или выключена», в которых очевидно, что оба дизъюнкта не могут быть истинными.Но не очевидно, что это связано с природой слова «или», а не с конкретными фактами о мире.

Альтернативные символы

Символ, используемый для исключительной дизъюнкции, меняется от одной области приложения к другой и даже зависит от свойств, которые подчеркиваются в данном контексте обсуждения. В дополнение к аббревиатуре «XOR» также может отображаться любой из следующих символов:
* Знак плюс (+). Это имеет смысл математически, потому что исключительная дизъюнкция соответствует модулю сложения 2, который имеет следующую таблицу сложения, явно изоморфную приведенной выше:

* Использование знака плюс имеет дополнительное преимущество, заключающееся в том, что все обычные алгебраические свойства математических колец и поля можно использовать без лишних слов.Однако знак плюс также используется для инклюзивной дизъюнкции в некоторых системах счисления.
* Знак плюс, который каким-то образом изменен, например, обведен кружком (oplus). Это использование сталкивается с возражением, что этот же символ уже используется в математике для «прямой суммы» алгебраических структур.
* Инклюзивный символ дизъюнкции (lor), который каким-либо образом изменен, например, подчеркнут (подчеркивание) или точкой сверху (dotvee).
* В нескольких языках программирования, таких как C, C ++, C #, Java, Perl и Python, знак вставки ( ^ ) используется для обозначения побитового оператора XOR.Это не используется вне контекста программирования, потому что его слишком легко спутать с другими вариантами использования каретки.
* Символ.
* В символах МЭК исключительное или помечено «= 1».

Свойства

В этом разделе используются следующие символы: egin {matrix} 0 & = & mbox {false} \ 1 & = & mbox {true} \ lnot p & = & mbox {not} p \ p + q & = & p mbox {xor} q \ p land q & = & p mbox {and} q \ p lor q & = & p mbox {or} qend {matrix}

Следующие уравнения следуют из логических аксиом: egin {матрица} p + 0 & = & p \ p + 1 & = & lnot p \ p + p & = & 0 \ p + lnot p & = & 1 \\ p + q & = & q + p \ p + q + p & = & q \ p + (q + r) & = & (p + q) + r \ p + q & = & lnot p + lnot q \ lnot (p + q) & = & lnot p + q & = & p + lnot q \\ p + (lnot p land q) & = & p lor q \ p + (p land lnot q) & = & p land q \ p + (p lor q) & = & lnot p land q \ lnot p + (p lor lnot q) & = & p lor q \ p land (p + lnot q) & = & p land q \ p lor (p + q) & = & p lor qend {matrix}

Ассоциативность и коммутативность

Ввиду изоморфизма между сложением по модулю 2 и исключительной дизъюнкцией, ясно, что XOR является одновременно ассоциативным и коммутативным оператором. эрация.Таким образом, круглые скобки можно опускать в последовательных операциях, а порядок терминов не влияет на результат. Например, у нас есть следующие уравнения :: egin {matrix} p + q & = & q + p \\ (p + q) + r & = & p + (q + r) & = & p + q + rend {matrix}

Другие свойства

* сохранение ложности : Интерпретация, при которой всем переменным присваивается значение истинности «ложь», дает значение истинности «ложь» в результате исключительной дизъюнкции.
* linear

Информатика

Побитовая операция

Исключительная дизъюнкция часто используется для побитовых операций. Примеры:
* 1 xor 1 = 0
* 1 xor 0 = 1
* 1110 xor 1001 = 0111 (это эквивалентно сложению без переноса)

Как отмечалось выше, поскольку исключительная дизъюнкция идентична сложению по модулю 2, побитовое исключительная дизъюнкция двух «n» -битных строк идентична стандартному вектору сложения в векторном пространстве (/ 2) ^ n.

В информатике исключительная дизъюнкция имеет несколько применений:
* Он сообщает, неравны ли два бита.
* Это дополнительный переворот битов (решающий вход выбирает, инвертировать ли входные данные).
* Он сообщает, существует ли нечетное количество 1 бит (A oplus B oplus C oplus D oplus E истинно, если истинно нечетное число переменных).

В логических схемах можно сделать простой сумматор с логическим элементом XOR для сложения чисел и серией логических элементов AND, OR и NOT для создания вывода переноса.

На некоторых компьютерных архитектурах более эффективно хранить ноль в регистре, исключающим регистр с самим собой (биты, исключаемые с самим собой, всегда равны нулю) вместо загрузки и сохранения нулевого значения.

В простых нейронных сетях, активируемых порогом, для моделирования функции «xor» требуется второй уровень, поскольку «xor» не является линейно разделяемой функцией.

Exclusive-or иногда используется как простая функция смешивания в криптографии, например, с одноразовым блокнотом или сетевыми системами Фейстеля.

XOR используется в RAID 3–6 для создания информации о четности. Например, RAID может «выполнить резервное копирование» байтов 10011100 и 01101100 с двух (или более) жестких дисков с помощью операции XOR ( 11110000 ) и записи на другой диск. Согласно этому методу, если один из трех жестких дисков потерян, потерянный байт может быть воссоздан путем операции XOR с байтами оставшихся дисков. Если диск, содержащий 01101100 , потерян, 10011100 и 11110000 можно выполнить XOR для восстановления потерянного байта.

XOR также используется для обнаружения переполнения в результате двоичной арифметической операции со знаком. Если крайний левый оставшийся бит результата не совпадает с бесконечным числом цифр слева, это означает, что произошло переполнение. Выполнение операции XOR для этих двух битов даст «единицу», если произойдет переполнение.

XOR может использоваться для обмена двумя числовыми переменными в компьютерах с использованием алгоритма обмена XOR; однако это считается скорее любопытством и на практике не поощряется.

В компьютерной графике методы рисования на основе XOR часто используются для управления такими элементами, как ограничивающие прямоугольники и курсоры в системах без альфа-каналов или плоскостей наложения.

ee также

* Подтверждение дизъюнкции
* Ampheck
* Булева алгебра (логика)
* Список тем булевой алгебры
* Логическая область
* Логическая функция
* Логическая функция
* Управляемый вентиль НЕ
* Дизъюнктивный силлогизм
* Логика первого порядка
* Инклюзивное или
* Инволюция
* Логический граф
* Логическое значение
* Оператор минимального отрицания
* Многоступенчатый оператор
* Операция
* Параметрический оператор
* Бит четности
* Исчисление высказываний
* Симметричное разница
* Связанный список XOR
* Шлюз XOR
* Шифр ​​XOR

Примечания

Внешние ссылки

* [ http: // www.xor.me/ Интернет-шифрование XOR ]

Фонд Викимедиа.
2010.

.`использование?

Переполнение стека

1. Около

2. Продукты

3. Для команд

1. Переполнение стека
   Общественные вопросы и ответы

2. Переполнение стека для команд
   Где разработчики и технологи делятся частными знаниями с коллегами

3. Вакансии
   Программирование и связанные с ним технические возможности карьерного роста

4. Талант
   Нанимайте технических специалистов и создавайте свой бренд работодателя

5. Реклама
   Обратитесь к разработчикам и технологам со всего мира

6. О компании

Загрузка…

2. Авторизоваться
   зарегистрироваться

3. текущее сообщество
   

.

эксклюзивное ИЛИ — это … Что такое эксклюзивное ИЛИ?

.

AND, OR, XOR, Shift и дополнение (с примером)

• Home

• Testing

  • • Back
    • Agile Testing
    • BugZilla
    • Cucumber
    • 9000 Testing 9000 Database Testing
    • JIRA
    • Назад
    • JUnit
    • LoadRunner
    • Ручное тестирование
    • Мобильное тестирование
    • Mantis
    • Почтальон
    • QTP
  • SAP Центр тестирования качества SAP
  • Selenium
  • SoapUI
  • Управление тестированием
  • TestLink