Мощность в физике — обозначение, формулы и примеры
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение мощности
Допустим, нам необходимо убрать урожай пшеницы с поля площадью 100 га. Это можно сделать вручную или с помощью комбайна. Очевидно, что пока человек обработает 1 га площади, комбайн успеет сделать намного больше. В данном случае разница между человеком и техникой — именно то, что называют мощностью. Отсюда вытекает первое определение.
Мощность в физике — это количество работы, которая совершается за единицу времени. |
Рассмотрим другой пример: между точкой А и точкой Б расстояние 15 км, которое человек проходит за 3 часа, а автомобиль может проехать всего за 10 минут. Понятно, что одно и то же количество работы они сделают за разное время. Что показывает мощность в данном случае? Как быстро или с какой скоростью выполняется некая работа.
Что показывает мощность в данном случае? Как быстро или с какой скоростью выполняется некая работа.
В электромеханике данная величина тоже связана со скоростью, а конкретно — с тем, как быстро передается ток по участку цепи. Исходя из этого, мы можем рассмотреть еще одно определение.
Мощность — это скалярная физическая величина, которая характеризует скорость передачи энергии от системы к системе или скорость преобразования, изменения, потребления энергии. |
Напомним, что скалярными величинами называются те, значение которых выражается только числом (без вектора направления).
Мощность человека в зависимости от деятельности
Вид деятельности | Мощность, Вт |
|---|---|
Неспешная ходьба | 60–65 |
Бег со скоростью 9 км/ч | 750 |
Плавание со скоростью 50 м/мин | 850 |
Игра в футбол | 930 |
Как обозначается мощность: единицы измерения
В таблице выше вы увидели обозначение в ваттах, и читая инструкции к бытовой технике, можно заметить, что среди характеристик прибора обязательно указано количество ватт. Это единица измерения механической мощности, используемая в международной системе СИ. Она обозначается буквой W или Вт.
Это единица измерения механической мощности, используемая в международной системе СИ. Она обозначается буквой W или Вт.
Измерение мощности в ваттах было принято в честь шотландского ученого Джеймса Уатта — изобретателя паровой машины. Он стал одним из родоначальников английской промышленной революции.
В физике принято следующее обозначение мощности: 1 Вт = 1 Дж / 1с.
Это значит, что за 1 ватт принята мощность, необходимая для совершения работы в 1 джоуль за 1 секунду.
В каких единицах еще измеряется мощность? Ученые-астрофизики измеряют ее в эргах в секунду (эрг/сек), а в автомобилестроении до сих пор можно услышать о лошадиных силах.
Интересно, что автором этой последней единицы измерения стал все тот же шотландец Джеймс Уатт. На одной из пивоварен, где он проводил свои исследования, хозяин накачивал воду для производства с помощью лошадей. И Уатт выяснил, что 1 лошадь за секунду поднимает около 75 кг воды на высоту 1 метр.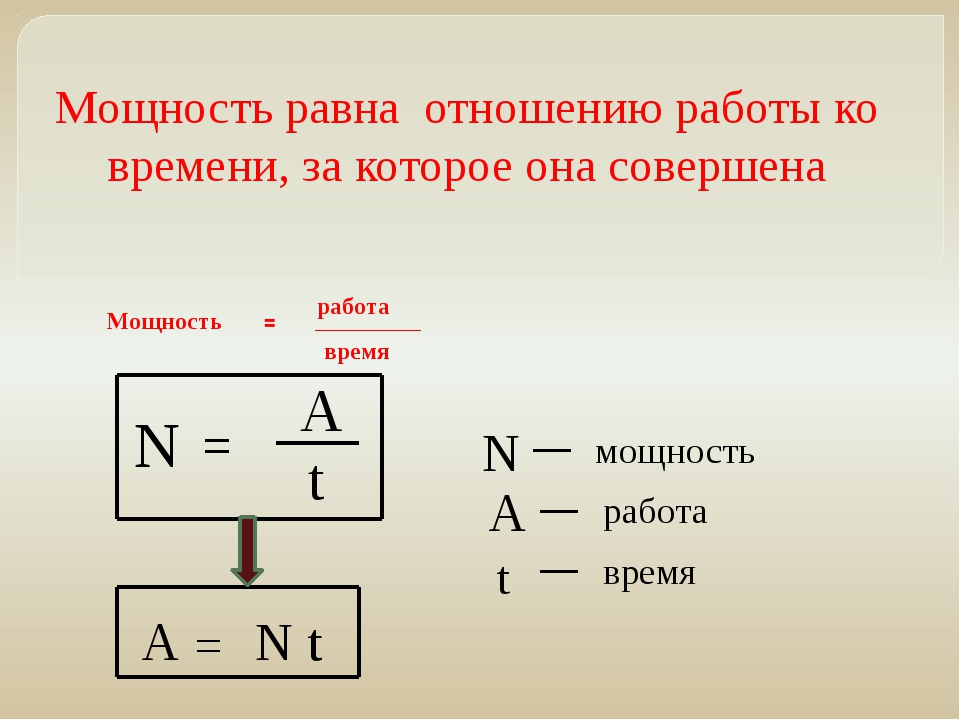 Вот так и появилось измерение в лошадиных силах. Правда, сегодня такое обозначение мощности в физике считается устаревшим.
Вот так и появилось измерение в лошадиных силах. Правда, сегодня такое обозначение мощности в физике считается устаревшим.
Одна лошадиная сила — это мощность, необходимая для поднятия груза в 75 кг за 1 секунду на 1 метр. 🐴
Единицы измерения | Вт |
|---|---|
1 ватт | 1 |
1 киловатт | 103 |
1 мегаватт | 106 |
1 эрг в секунду | 10-7 |
1 метрическая лошадиная сила | 735,5 |
Подготовка к ОГЭ по физике онлайн поможет снять стресс перед экзаменом и получить высокий балл.
Все формулы мощности
Зная определения, несложно понять формулы мощности, используемые в разных разделах физики — в механике и электротехнике.
В механике
Механическая мощность (N) равна отношению работы ко времени, за которое она была выполнена.
Основная формула:
N = A / t, где A — работа, t — время ее выполнения.
Если вспомнить, что работой называется произведение модуля силы, модуля перемещения и косинуса угла между ними, мы получим формулу измерения работы.
Если направления модуля приложения силы и модуля перемещения объекта совпадают, угол будет равен 0 градусов, а его косинус равен 1. В таком случае формулу можно упростить:
A = F × S
Используем эту формулу для вычисления мощности:
N = A / t = F × S / t = F × V
В последнем выражении мы исходим из того, что скорость (V) равна отношению перемещения объекта на время, за которое это перемещение произошло.
В электротехнике
В общем случае электрическая мощность (P) говорит о скорости передачи энергии. Она равна произведению напряжения на участке цепи на величину тока, проходящего по этому участку.
Она равна произведению напряжения на участке цепи на величину тока, проходящего по этому участку.
P = I × U, где I — напряжение, U — сила тока.
В электротехнике существует несколько видов мощности: активная, реактивная, полная, пиковая и т. д. Но это тема отдельного материала, сейчас же мы потренируемся решать задачи на основе общего понимания этой величины. Посмотрим, как найти мощность, используя вышеуказанные формулы по физике.
Задача 1
Допустим, человек поднимает ведро воды из колодца, прикладывая силу 60 Н. Глубина колодца составляет 10 м, а время, необходимое для поднятия — 30 сек. Какова будет мощность в этом случае?
Решение:
Найдем вначале величину работы, используя тот факт, что мы знаем расстояние перемещения (глубину колодца 10 м) и приложенную силу 60 Н.
A = F × S = 60 Н × 10 м = 600 Дж
Когда известно значение работы и времени, найти мощность несложно:
N = A / t = 600 Дж / 30 сек = 20 Вт
Ответ: человек развивает мощность 20 ватт.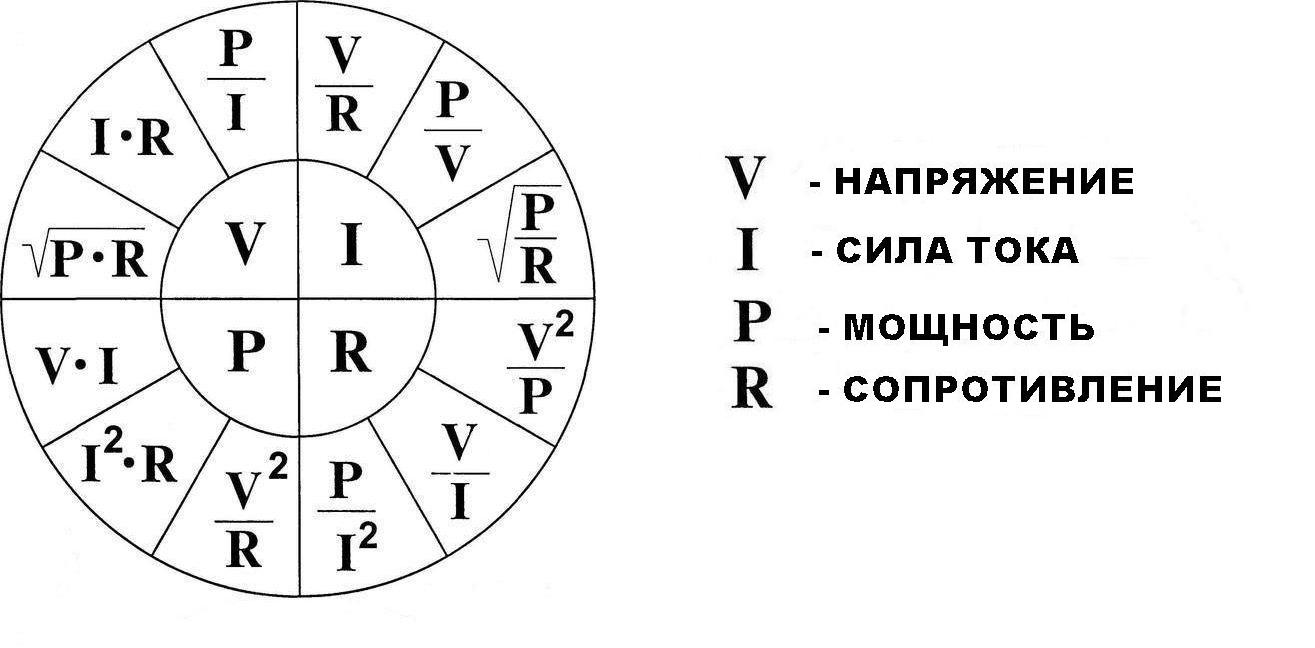
Задача 2
В комнате включена лампа мощностью 100 Вт. Напряжение домашней электросети — 220 В. Какая сила тока пройдет через эту лампу?
Решение:
Мы знаем, что Р = 100 Вт, а U = 220 В.
Поскольку P = I × U, следовательно I = P / U.
I = 100 / 220 = 0,45 А.
Ответ: через лампу пройдет сила тока 0,45 А.
Вопросы для самопроверки
Что характеризует механическая мощность?
Какие существуют единицы измерения мощности в физике?
Какая из единиц измерения считается устаревшей?
Мощность можно назвать скалярной величиной? Что это означает?
Как из формулы нахождения мощности получить работу?
Какой буквой обозначается мощность в механике, а какой — в электротехнике?
Какую работу производит за 30 минут устройство мощностью 600 Вт?
Как узнать напряжение в сети, если мы знаем мощность подключенного к ней прибора и силу тока, проходящую через прибор?
Если в течение 1 часа автомобиль №1 едет со скоростью 60 км/ч, а автомобиль №2 — со скоростью 90 км/ч, одинаковую ли мощность они развивают в это время?
Допустим, автобус отвез пассажиров из города А в город В за 1 час.
 Если он планирует вернуться в город А пустым по той же трассе и потратить на это 1 час, ему понадобится развить такую же мощность или меньшую?
Если он планирует вернуться в город А пустым по той же трассе и потратить на это 1 час, ему понадобится развить такую же мощность или меньшую?
Мощность электрического тока — Основы электроники
Обычно электрический ток сравнивают с течением жидкости по трубке, а напряжение или разность потенциалов — с разностью уровней жидкости.
В этом случае поток воды, падающий сверху вниз, несет с собой определенное количество энергии. В условиях свободного падения эта энергия растрачивается бесполезно для человека. Если же направить падающий поток воды на лопасти турбины, то последняя начнет вращаться и сможет производить полезную работу.
Работа, производимая потоком воды в течение определенного промежутка времени, например, в течение одной секунды, будет тем больше, чем с большей высоты падает поток и чем больше масса падающей воды.
Точно так же и электрический ток, протекая по цепи от высшего потенциала к низшему, совершает работу. В каждую данную секунду времени будет совершаться тем больше работы, чем больше разность потенциалов и чем большее количество электричества ежесекундно проходит через поперечное сечение цепи.
В каждую данную секунду времени будет совершаться тем больше работы, чем больше разность потенциалов и чем большее количество электричества ежесекундно проходит через поперечное сечение цепи.
Мощность электрического тока это количество работы, совершаемой за одну секунду времени, или скорость совершения работы.
Количество электричества, проходящего через поперечное сечение цепи в течение одной секунды, есть не что иное, как сила тока в цепи. Следовательно, мощность электрического тока будет прямо пропорциональна разности потенциалов (напряжению) и силе тока в цепи.
Для измерения мощности электрического тока принята единица, называемая ватт (Вт).
Мощностью в 1 Вт обладает ток силой в 1 А при разности потенциалов, равной 1 В.
Для вычисления мощности постоянного тока в ваттах нужно силу тока в амперах умножить на напряжение в вольтах.
Если обозначить мощность электрического тока буквой P, то приведенное выше правило можно записать в виде формулы
P = I*U. (1)
(1)
Воспользуемся этой формулой для решения числового примера. Требуется определить, какая мощность электрического тока необходима для накала нити радиолампы, если напряжение накала равно 4 в, а ток накала 75 мА
Определим мощность электрического тока, поглощаемую нитью лампы:
Р= 0,075 А*4 В = 0,3 Вт.
Мощность электрического тока можно вычислить и другим путем. Предположим, что нам известны сила тока в цепи и сопротивление цепи, а напряжение неизвестно.
В этом случае мы воспользуемся знакомым нам соотношением из закона Ома:
U=IR
и подставим правую часть этого равенства (IR) в формулу (1) вместо напряжения U.
Тогда формула (1) примет вид:
P = I*U =I*IR
или
Р = I2*R. (2)
Например, требуется узнать, какая мощность теряется в реостате сопротивлением в 5 Ом, если через него проходит ток, силой 0,5 А. Пользуясь формулой (2), найдем:
P= I2*R = (0,5)2*5 =0,25*5 = 1,25 Вт.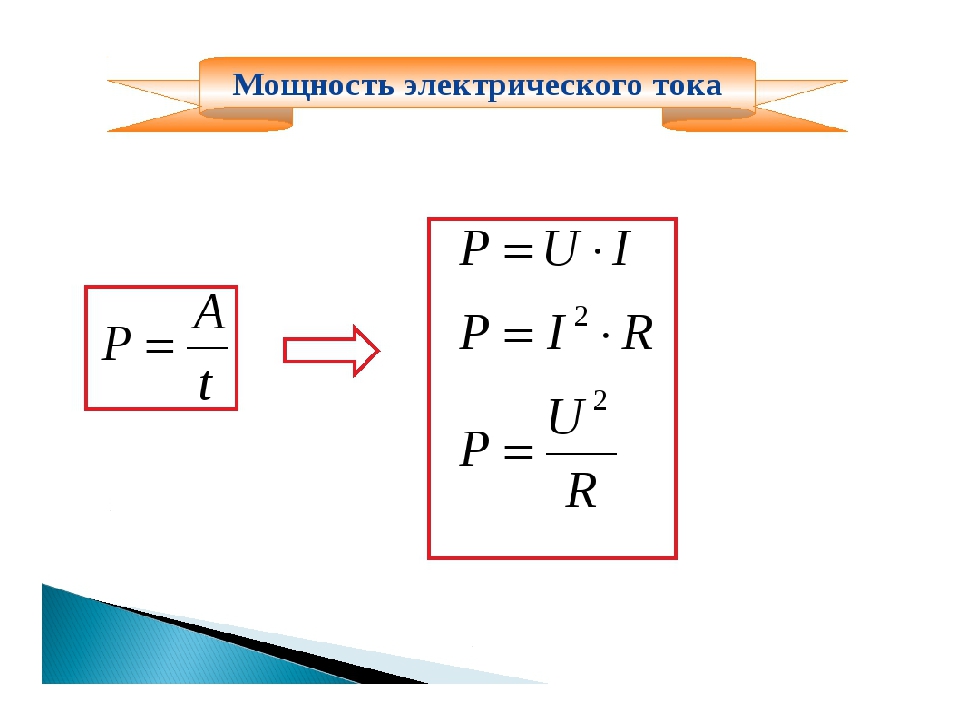
Наконец, мощность электрического тока может быть вычислена и в том случае, когда известны напряжение и сопротивление, а сила тока неизвестна. Для этого вместо силы тока I в формулу (1) подставляется известное из закона Ома отношение U/R и тогда формула (1) приобретает следующий вид:
Р = I*U=U2/R (3)
Например, при 2,5 В падения напряжения на реостате сопротивлением в 5 Ом поглощаемая реостатом мощность будет равна:
Р = U2/R=(2,5)2/5=1,25 Вт
Таким образом, для вычисления мощности требуется знать любые две из величин, входящих в формулу закона Ома.
Мощность электрического тока равна работе электрического тока, производимой в течение одной секунды.
P = A/t
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Формула мощности в физике
Содержание:
Определение и формулы мощности
Определение
Мощностью некоторой силы является скалярная физическая величина, которая характеризует скорость произведения работы данной силой. Мощность часто обозначают буквами: N, P.
Мощность часто обозначают буквами: N, P.
$$P=\frac{\Delta A}{\Delta t}(1)$$
В том случае, если за равные малые промежутки времени выполняется разная работа, то мощность является переменной во времени.
Тогда вводят мгновенное значение мощности:
$$P=\lim _{\Delta t \rightarrow 0} \frac{\delta A}{\Delta t}=\frac{d A}{d t}$$
где $\delta A$ – элементарная работа, которую выполняет сила,
$\Delta t$ – отрезок времени в течение, которого данная работа была выполнена.
Если мгновенная мощность не является постоянной величиной, то выражение (1) определяет среднюю мощностьза время
$\Delta t$.
Мощность силы можно определить как скалярное произведение силы на скорость, с которой движется точка приложения рассматриваемой силы:
$$P=\bar{F} \bar{v}=F_{\tau} v$$
где $F_{\tau}$ – проекция силы
$\bar{F}$ на направление вектора скорости (
$\bar{v}$).
При поступательном движении некоторого тела, имеющего массу m под воздействием силы
$\bar{F}$ мощность можно вычислить, применяя формулу:
$$P=m v \dot{v}(4)$$
В общем случае произвольного перемещения твердого тела суммарная мощность есть алгебраическая сумма мощностей всех сил,
которые действуют на тело:
$$P=\sum_{i=1}^{k} \bar{F}_{i} \cdot \bar{v}_{i}(5)$$
где $\bar{v}_{i}$ – скорость перемещения точки, к которой приложена сила
$\bar{F}_{i}$.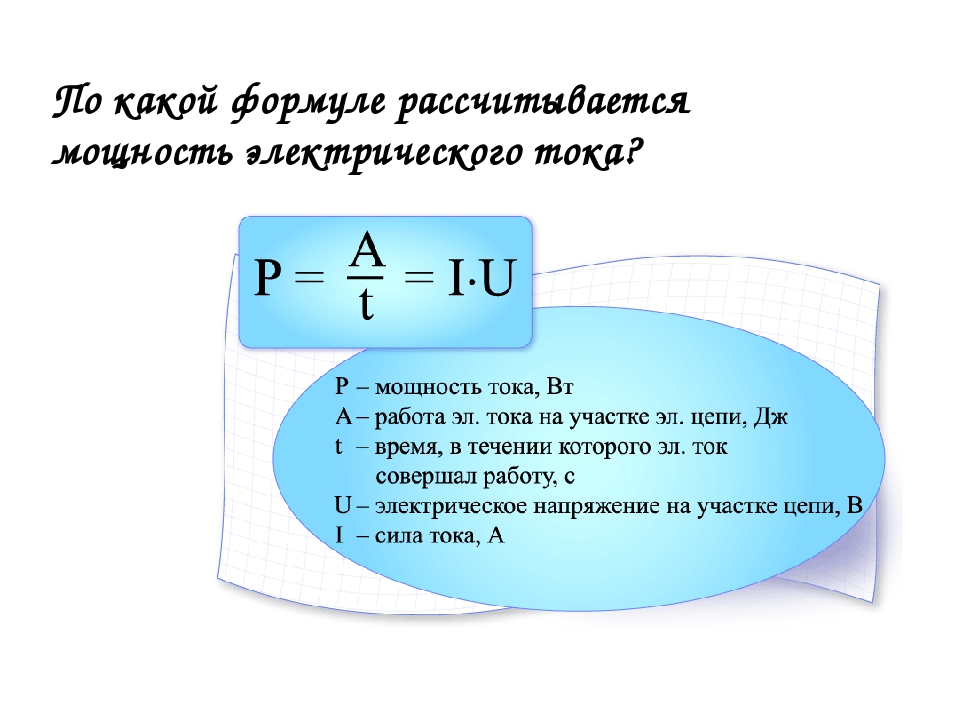
В случае поступательного движения твердого тела со скоростью $\bar{v}$ мощность можно определить при помощи формулы:
$$P=\overline{F v}(6)$$
где $\bar{F}$ – главный вектор внешних сил.
Если твердое тело совершает вращение вокруг точки О или вокруг неподвижной оси, которая проходит через точку О, то формулой для счет мощности можно считать выражение:
$$P=\bar{M} \bar{\omega}(7)$$
где $\bar{M}$ – главный момент внешних сил по отношению к точке О,
$\bar{omega}$ – мгновенная угловая скорость вращения тела.
Единицы измерения мощности
Основной единицей измерения мощности силы в системе СИ является: [P]=вт (ватт)
В СГС: [P]=эрг/с.
1 вт=107 эрг/( с).
Примеры решения задач
Пример
Задание. Какова мощность (P(t)), развиваемая силой, если она действует на тело, которое имеет массу m и
под воздействием приложенной силы движется поступательно. Сила описывается законом:
$F(t)=2 t \cdot \bar{i}+3 t^{2} \bar{j}$
Решение. {5}\right)$
{5}\right)$
Слишком сложно?
Формула мощности не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Какова мгновенная мощность силы тяжести на высоте h/2. если камень массы m падает с высоты h. Сопротивление воздуха не учитывать.
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для мгновенной мощности вида:
$$P=\bar{F} \cdot \bar{v}(2.1)$$
Сила, действующая на тело – сила тяжести. Она направлена по оси Y, выражение для ее проекции на ось Y запишем как:
$$F=m g(2.2)$$
В начальный момент времени тело имело скорость равную нулю, тогда скорость тела в проекции на ось Y можно вычислить, используя выражение:
$$v=v_{0}+g t=g t(2.3)$$
где v0=0.
Найдем момент времени, в который тело окажется на половине высоты (y=h/2), применим уравнение, которое описывает равноускоренное
движение (из начальных условий y0=0, v0=0):
$$y=y_{0}+v_{0} t+\frac{g t^{2}}{2}=\frac{g t^{2}}{2}=\frac{h}{2} \rightarrow t=\sqrt{\frac{h}{g}}(2. {3} h}$
{3} h}$
Читать дальше: Формула плотности вещества.
Формула мощности электрического тока. Как узнать, найти, вычислить, рассчитать мощность.
Электрическая мощность является одной из наиболее важных и значимых характеристик, которая показывает величину, силу той электротехники, систем, цепей, что работают, выполняя ту или иную функцию. Естественно, как и любая другая физическая величина электрическая мощность должна иметь свою меру, благодаря которой появляется возможность ее рассчитывать, делая заведомо точные, экономичные, эффективные устройства, системы и т.д. Для расчетов существуют определенные формулы, по которым и находятся нужные значения мощности.
Формула мощности тока (электрического) достаточно проста и выражается как произведение напряжения на силу тока. То есть, чтобы найти электрическую мощность достаточно просто напряжение умножить на ток. Если воспользоваться законом ома, то ее можно найти и через сопротивление. В этом случае электрическая мощность будет равна силе тока в квадрате умноженный на сопротивление или же напряжение в квадрате деленное на сопротивление.
Напомню, что при использовании формул подразумевается применение основных единиц измерения физических величин. В нашем случае основными единицами будут:
Электрическая мощность — Ватт;
Сила тока — Ампер;
Напряжение — Вольт;
Сопротивление — Ом.
Исходя из этого формула мощности электрического тока будет звучать так — 1 Ватт равен 1 Вольт умноженный на 1 Ампер. Думаю вы смысл поняли. Меньшими единицами измерения мощности является милливатты (1000 мВт = 1 Вт), большими единицами являются киловатты и мегаватты (1 кВт = 1000 Вт, 1 МВт = 1000 000 Вт). Милливатты это достаточно маленькая мощность, ее используют в электронике, радиотехнике. К примеру мощность слухового аппарата измеряется именно в милливаттах. Мощность в ваттах можно встретить в звуковых усилителях, у небольших блоках питания, мини электродвигателях. Киловатты это мощность, которая часто встречается в бытовых и технических устройствах (электрочайники, электродвигатели, обогреватели и т.д.). Мегаватты это уже достаточно большая мощность, ее можно встретить на электроподстанциях, электростанциях, у потребителях электроэнергии размером с город и т.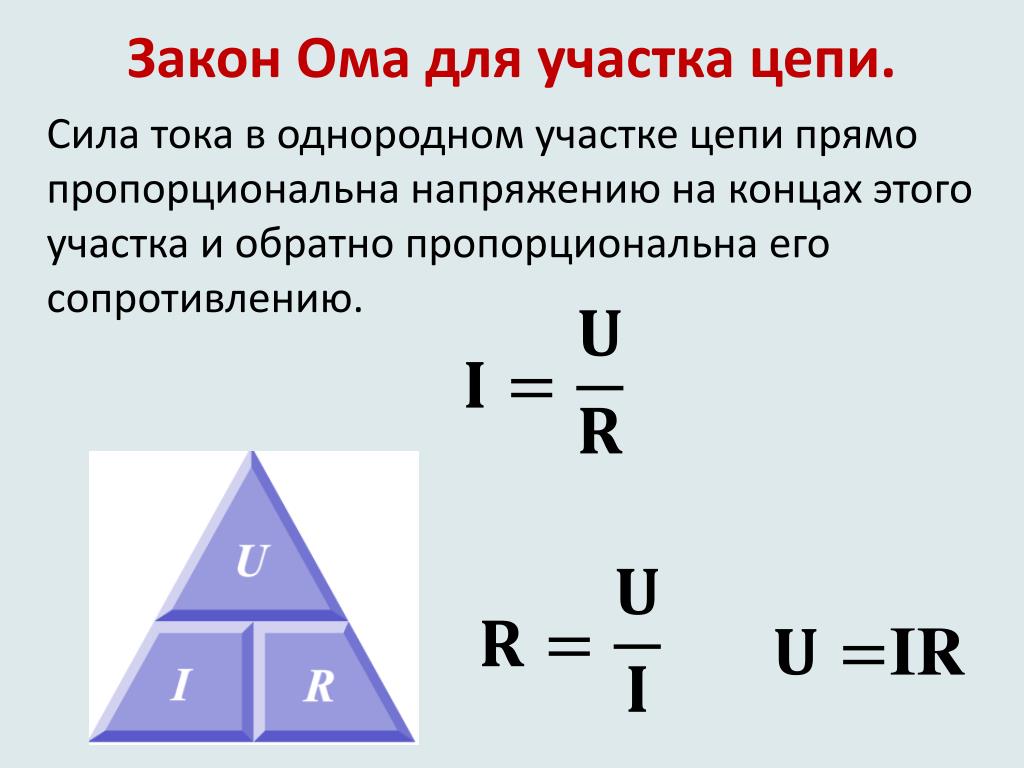 д.
д.
Если говорить о формуле более научной, которая электрическую мощность тока выражает через работу и время, то она будет звучать так — электрическая мощность равна отношению работы тока на участке цепи ко времени, в течении которого совершается эта работа.
То есть, работа деленная на время будет определять мощность. Кроме этого часто путают такие величины как ватты и ватт-час. В ваттах измеряется электрическая мощность — скорость изменения энергии (передачи, преобразования, потребления). А ватт-час являются единицей измерения самой энергии (работы). В ватт-часах выражается энергия, произведенная (переданная, преобразованная, потребленной) за определенное время.
Мощность также разделяется на активную и реактивную. Активная мощность — часть полной мощности, что удалось передать в нагрузку за период переменного тока. Она равна произведению действующих значений напряжения и тока на cosφ (косинус угла сдвига фаз между ними). Электрическая мощность, что не была передана в нагрузку, а привела к некоторым потерям (на излучение, нагрев) называется реактивной мощностью. Она равна произведению действующих значений напряжения и тока на sinφ (синус угла сдвига фаз между ними).
Она равна произведению действующих значений напряжения и тока на sinφ (синус угла сдвига фаз между ними).
P.S. Электрическая мощность является одной из главных величин и характеристик, используемые в электротехнике. Именно ее мы узнаем при покупки того или иного электрического устройства. Ведь она определяет силу, с которой электротехника может работать. К примеру электродрель. Если мы купим дрель недостаточной мощности, то она просто не сможет обеспечить нам нормальную работу при сверлении. Хотя гнаться за слишком большой мощностью также не следует, ведь это ведет к излишней трате электроэнергии, за которую вы будете платить. Так что у всего должна быть своя мера и мощность.
Физика. Механика
Представим снова элементарную работу в виде
Удельная величина, равная отношению работы совершенной за время dt к этому времени, называется мощностью:
Другими словами, мощность, развиваемая некоторой силой, равна скорости, с которой эта сила производит работу. Можно сказать и так: средняя за единицу времени мощность численно равна работе совершенной за единицу времени. Если мощность за выбранную единицу времени практически не меняется, то слово «средняя» можно опустить: мощность численно равна работе за единицу времени.
Можно сказать и так: средняя за единицу времени мощность численно равна работе совершенной за единицу времени. Если мощность за выбранную единицу времени практически не меняется, то слово «средняя» можно опустить: мощность численно равна работе за единицу времени.
Как видно из определения, мощность равна скалярному произведению силы на скорость перемещения её точки приложения, поэтому работа силы за время от t1 до t2 может быть вычислена следующим образом:
Средняя мощность за этот же промежуток времени равна
За единицу мощности принимается такая мощность, при которой в единицу времени совершается единица работы.
В системе СИ единицей измерения мощности является ватт (Вт):
Внесистемная единица мощности — лошадиная сила (л.с.) — равна 736 Вт. В быту часто используют единицу энергии — 1 кВт•ч = 103 Вт•3600 с=3.6 МДж.
Пример. Вертолет массой m = 3 m висит в воздухе. Определить мощность, развиваемую мотором вертолета, если диаметр ротора равен d = 8 м. При расчете принять, что ротор отбрасывает вниз цилиндрическую струю воздуха диаметром, равным диаметру ротора. Плотность воздуха 1.29 кг/м3.
Вертолет массой m = 3 m висит в воздухе. Определить мощность, развиваемую мотором вертолета, если диаметр ротора равен d = 8 м. При расчете принять, что ротор отбрасывает вниз цилиндрическую струю воздуха диаметром, равным диаметру ротора. Плотность воздуха 1.29 кг/м3.
При решении этой задачи надо применить все известные нам законы динамики. Поскольку это — не одно- и не двухходовая задача, попробуем сначала найти вид окончательного выражения, пользуясь анализом размерности (см. тему 1.3). Искомая мощность зависит от: 1) веса вертолета mg; 2) диаметра винта d, 3) плотности воздуха , то есть искомая формула должна иметь вид
Размерность мощности будет [N] = [ML2T–3]. Составляем равенство размерностей в обеих частях искомой формулы:
Решая систему уравнений
находим
то есть искомая мощность двигателя вертолета будет
где C — некий числовой коэффициент.
Решим теперь эту же задачу точно. Пусть — скорость струи воздуха, отбрасываемой винтом. За время частицы воздуха проходят расстояние . Иными словами, за время винт вертолета придает скорость всем частицам воздуха, находящимся в цилиндре с площадью основания и высотой . Масса воздуха в этом объеме равна
а его кинетическая энергия дается выражением
Поскольку мотор передает воздуху кинетическую энергию , то такова и совершаемая им работа. Поэтому развиваемая мотором мощность (без учета потерь мощности во всех трансмиссиях на пути от двигателя до винта) равна
В этом выражении нам надо еще найти скорость струи воздуха, отбрасываемой винтом. Импульс , передаваемый частицам воздуха за время , равен
Из второго закона Ньютона следует, что средняя сила, действующая на отбрасываемый вниз воздух равна . По третьему закону Ньютона такая же сила действует на вертолет со стороны воздуха. Эта сила компенсирует вес вертолета:
Эта сила компенсирует вес вертолета:
Отсюда получаем уравнение
позволяющее найти скорость струи воздуха:
Подставляя найденную скорость в выражение для мощности двигателя вертолета, получаем окончательный результат:
Мы видим, что выражение для мощности действительно оказалось таким, каким ожидалось на основе анализа размерностей. Подставляя числовые данные, находим
Рис.4.5. Мощность в природе и технике
как вычислить мощность тока формулой, как рассчитать ампераж
Чтобы электропроводка и все электрическое оборудование, которое имеется в доме, работало исправно и правильно, необходимо правильно сделать вычисление мощности по току и электронапряжению, поскольку при неправильно подобранных показателях может возникнуть короткое замыкание или возгорание. Как сделать расчёт потребляемой мощности по току и напряжению, как вычисляется сила тока, формула через мощность и напряжение и другое, далее.
Как узнать силу тока, зная мощность и напряжения
Чтобы ответить на вопрос, как определить ток, необходимо поделить электронапряжение на общее число ватт. При этом сделать все необходимые вычисления можно самостоятельно, а можно прибегнуть к специальному онлайн-калькулятору.
Расчет мощностного показателя по амперам и ваттам
Узнать потребление электроэнергии по токовой силе резистора можно умножением первой на сопротивление, выражаемое в Омах. В итоге, получится значение, представленное в вольтах, перемноженных на ом. Получится ампер.
Обратите внимание! Если нет сопротивления, нужно поделить ваттный показатель на токовую энергию, то есть следует поделить ватты на амперы и получится значение электроэнергии в вольтах. Понять мощностное показание через величину электричества с электронапряжением, можно умножив соответствующие показания с устройства.
Расчет электроэнергии через электромощность и электронапряжение
Формулы для расчета тока в трехфазной сети
Подсчитать токовую энергию в трехфазной сети сложно, поскольку вместе одной фазы есть три. К тому же, сложность заключается в использовании нескольких схем соединения. Трудность состоит в симметрии или ее отсутствии во время распределения нагрузки по фазам.
К тому же, сложность заключается в использовании нескольких схем соединения. Трудность состоит в симметрии или ее отсутствии во время распределения нагрузки по фазам.
Для определения силы тока в трехфазной сети, нужно общее число ватт поделить на показатель 1,73, перемноженный на напряжение и косинус мощностного коэффициента, который отражает активную и реактивную составляющую сопротивления нагрузки. Что касается однофазной сети, то из выражения для подсчета убирается показатель 1,73. Остается формула I = P/(U*cos φ).
Формула подсчета электротока в трехфазной сети
Как рассчитать ампераж
Ампераж является значением электротока, которое выражена в амперах. Рассчитать ампераж можно так: I=P/U.
Подсчет ампеража
Расчет потребляемой мощности
Электромощность является величиной, которая отвечает за факт скорости изменения или передачи электрической энергии. Есть полная и активная мощностная нагрузка, а также активная и реактивная. Полная вычисляется так: S = √ (P2 + Q2), где P является активной частью, а Q реактивной. Для нахождения потребляемого мощностного показателя необходимо знать число электротока, которое потребляется нагрузкой, а также питательное напряжение, которое выдается при помощи источника.
Для нахождения потребляемого мощностного показателя необходимо знать число электротока, которое потребляется нагрузкой, а также питательное напряжение, которое выдается при помощи источника.
Что касается бытового определения потребляемой электрической энергии, необходимо вычислить общее количество ватт питания электрических приборов и паспортные данные номинальной силы электротока котла. Как правило, все электрические приборы работают с переменным током и напряжением в 220 вольт. Для вычисления тока проще всего воспользоваться амперметром. Зная первый и второй параметры, реально узнать величину потребляемой энергии.
Стоит указать, что измерить мощность через напряжение или сделать расчет мощности по сопротивлению и напряжению возможно не только формулой, но и прибором. Для этого можно воспользоваться мультиметром с токоизмерительными клещами или специализированным измерителем — ваттметром.
Обратите внимание! Оба работают по одному и тому же принципу, указанному в руководстве по их эксплуатации.
Подсчет потребляемой мощности
Мощность, ток и напряжение — три составляющие расчета проводки в доме. Узнать все необходимые параметры в любой сети просто при помощи формул, представленных выше. От этих значений будет зависеть исправность работы всей домашней электрики и безопасность ее владельца.
НЕ ЗАБЫВАЕМ: Законы Кирхгофа они же Правила Кирхгофа для тока и напряжения.
Цепь переменного синусоидального тока c частотой ω.
Применимость формул: пренебрегаем зависимостью сопротивлений от силы тока и частоты.
Напомним, что любой сигнал, может быть с любой точностью разложен в ряд Фурье, т.е. в предположении, что параметры сети
Закон Ома для цепей переменного тока:
|
Расчет электроэнергии | Закон Ома
Изучите формулу силы
Мы видели формулу для определения мощности в электрической цепи: умножая напряжение в «вольтах» на силу тока в «амперах», мы получаем ответ в «ваттах». Давайте применим это к примеру схемы:
Как использовать закон Ома для определения силы тока
В приведенной выше схеме мы знаем, что у нас есть напряжение батареи 18 вольт и сопротивление лампы 3 Ом.Используя закон Ома для определения тока, получаем:
Теперь, когда мы знаем ток, мы можем взять это значение и умножить его на напряжение, чтобы определить мощность:
Это говорит нам о том, что лампа рассеивает (высвобождает) 108 ватт мощности, скорее всего, в виде света и тепла.
Увеличение напряжения батареи
Давайте попробуем взять ту же схему и увеличить напряжение батареи, чтобы посмотреть, что произойдет. Интуиция должна подсказывать нам, что ток цепи будет увеличиваться по мере увеличения напряжения, а сопротивление лампы останется прежним. Точно так же увеличится и мощность:
Интуиция должна подсказывать нам, что ток цепи будет увеличиваться по мере увеличения напряжения, а сопротивление лампы останется прежним. Точно так же увеличится и мощность:
Теперь напряжение аккумулятора составляет 36 вольт вместо 18 вольт. Лампа по-прежнему обеспечивает электрическое сопротивление 3 Ом потоку тока. Текущий сейчас:
Это понятно: если I = E/R, и мы удваиваем E, а R остается прежним, ток должен удвоиться.Действительно, имеет: у нас теперь 12 ампер тока вместо 6. А что с мощностью?
Что влияет на питание повышение напряжения батареи?
Обратите внимание, что мощность увеличилась, как мы и подозревали, но она увеличилась немного больше, чем ток. Почему это? Поскольку мощность является функцией напряжения, умноженного на ток, а и , и напряжение, и ток удвоены по сравнению с их предыдущими значениями, мощность увеличится в 2 x 2 или 4 раза.
Вы можете проверить это, разделив 432 ватта на 108 ватт и увидев, что соотношение между ними действительно равно 4. Снова используя алгебру для манипулирования формулой, мы можем взять нашу исходную формулу мощности и изменить ее для приложений, где мы не знаем оба напряжение и ток: если мы знаем только напряжение (E) и сопротивление (R):
Если мы знаем только ток (I) и сопротивление (R):
Закон Джоуля против.Закон Ома
Историческая справка: именно Джеймс Прескотт Джоуль, а не Георг Саймон Ом, первым обнаружил математическую связь между рассеиваемой мощностью и током через сопротивление. Это открытие, опубликованное в 1841 году, соответствовало форме последнего уравнения (P = I 2 R) и известно как закон Джоуля.
Однако эти уравнения мощности так часто ассоциируются с уравнениями закона Ома, связывающими напряжение, ток и сопротивление (E=IR ; I=E/R ; и R=E/I), что их часто приписывают Ому.
ОБЗОР:
- Мощность измеряется в Вт , обозначается буквой «Вт».
- Закон Джоуля: P = I 2 R ; Р = ИЭ; Р = Е 2 /Р
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Попробуйте наш калькулятор закона Ома в разделе «Инструменты».
Как найти степень числа — видео и расшифровка урока
Сила числа
Есть супергерой, который может сделать число огромным.Его сила — это сила числа! Это работает так: вы выбираете любое число. Возьмем 10: 10 + 2 = 12; мы все это знаем. Но это только дополнение.
Как насчет 10 х 2 = 20? Хорошо, мы это тоже знаем.
А как насчет 102? Вот это настоящая сила. Это означает 10 x 10, что равно 100. Это намного больше, чем 12 или 20!
Степень числа имеет специальное название: показатель степени . Итак, мы показываем степень числа с помощью показателя степени, а когда мы показываем число с показателем степени, мы говорим, что число возведено в степень — степень показателя степени! Этот показатель говорит нам, сколько раз мы собираемся умножить базовое число само на себя.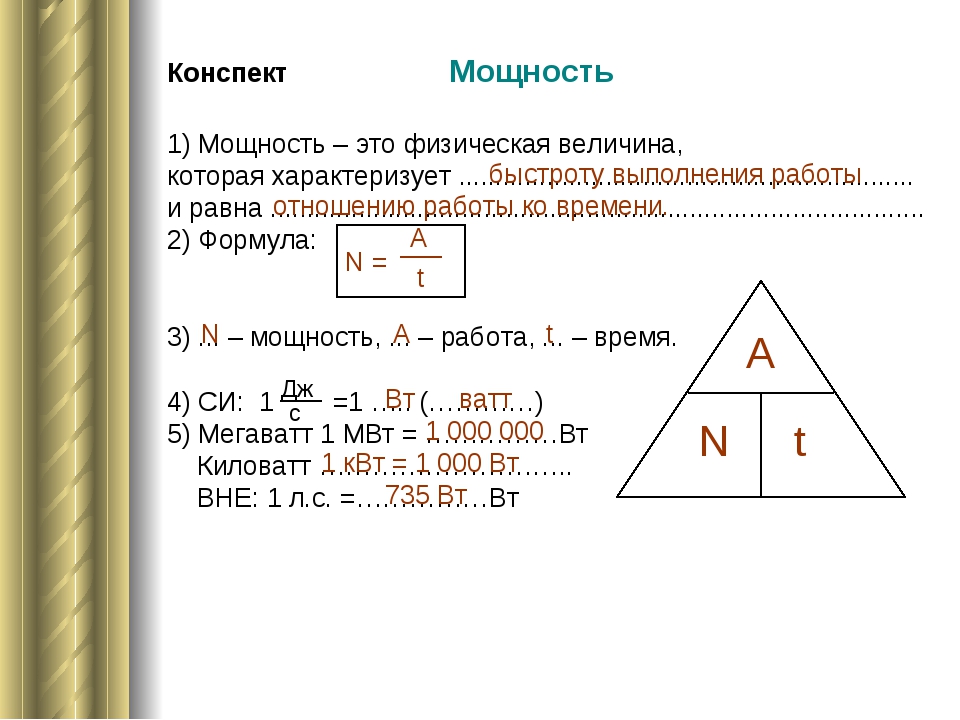 5) будет сделано следующим образом:
5) будет сделано следующим образом:
7 x 7 = 49
49 x 7 = 343
343 x 7 = 2401
2401 x 7 = 16 807
.Показатель степени 5 говорит нам, сколько раз мы собираемся умножать основание само на себя. Мы используем экспоненты, потому что они могут сэкономить время. Чтобы записать 75, нам пришлось бы написать 7 х 7 х 7 х 7 х 7 — это много.
Давайте посмотрим еще парочку. Воспользуйтесь калькулятором, если он у вас есть. Давайте попробуем 5 x 5 x 5 x 5. Во-первых, запишите это, используя степень числа (что означает показать его в форме степени): 54. Мы назвали бы это пятью в четвертой степени или пятью в степени четыре. Давайте посмотрим, насколько велико это число. «в кубе», когда показатель степени равен 3).Давайте попробуем: 2 x 2 x 2 = 8. Видите ли, 2 x 2 = 4. Теперь умножьте это само на себя в третий раз: 4 x 2 = 8.
Краткое содержание урока
Степень числа выражается экспонента. Показатель степени указывает, сколько раз базовое число будет умножено само на себя. Любое число, возведенное в степень, будет расти очень быстро!
Любое число, возведенное в степень, будет расти очень быстро!
Электроэнергия — Learn.sparkfun.com
Избранное
Любимый
50
Расчетная мощность
Электроэнергия — это скорость передачи энергии.Измеряется в джоулях в секунду (Дж/с) — ватт (Вт). Учитывая несколько основных терминов электричества, которые мы знаем, как мы можем рассчитать мощность в цепи? Что ж, у нас есть очень стандартное измерение, включающее потенциальную энергию — вольты (В), которые определяются в джоулях на единицу заряда (кулон) (Дж/Кл). Ток, еще один из наших любимых терминов в области электричества, измеряет ток заряда во времени в амперах (А) — кулонах в секунду (Кл/с). Соединяем вместе и что мы получаем?! Сила!
Чтобы рассчитать мощность любого конкретного компонента в цепи, умножьте падение напряжения на нем на ток, протекающий через него.
Например,
Ниже приведена простая (хотя и не очень функциональная) схема: батарея 9 В, подключенная к 10-омному проводу. резистор.
резистор.
Как рассчитать мощность на резисторе? Сначала мы должны найти ток, протекающий через него. Достаточно просто… Закон Ома!
Хорошо, 900 мА (0,9 А) проходит через резистор и 9 В через него. Какая мощность подается на резистор?
Резистор преобразует электрическую энергию в тепло.Таким образом, эта схема каждую секунду преобразует 8,1 Дж электрической энергии в тепло.
Расчет мощности в резистивных цепях
Когда дело доходит до расчета мощности в чисто резистивной цепи, достаточно знать два из трех значений (напряжение, ток и/или сопротивление).
Подключив закон Ома (V=IR или I=V/R) к нашему традиционному уравнению мощности, мы можем создать два новых уравнения. Первый, чисто по напряжению и сопротивлению:
Итак, в нашем предыдущем примере 9В 2 /10Ом; (V 2 /R) равно 8.1 Вт, и нам никогда не придется рассчитывать ток, протекающий через резистор.
Второе уравнение мощности можно составить только через ток и сопротивление:
Какое нам дело до мощности, падающей на резистор? Или любой другой компонент в этом отношении.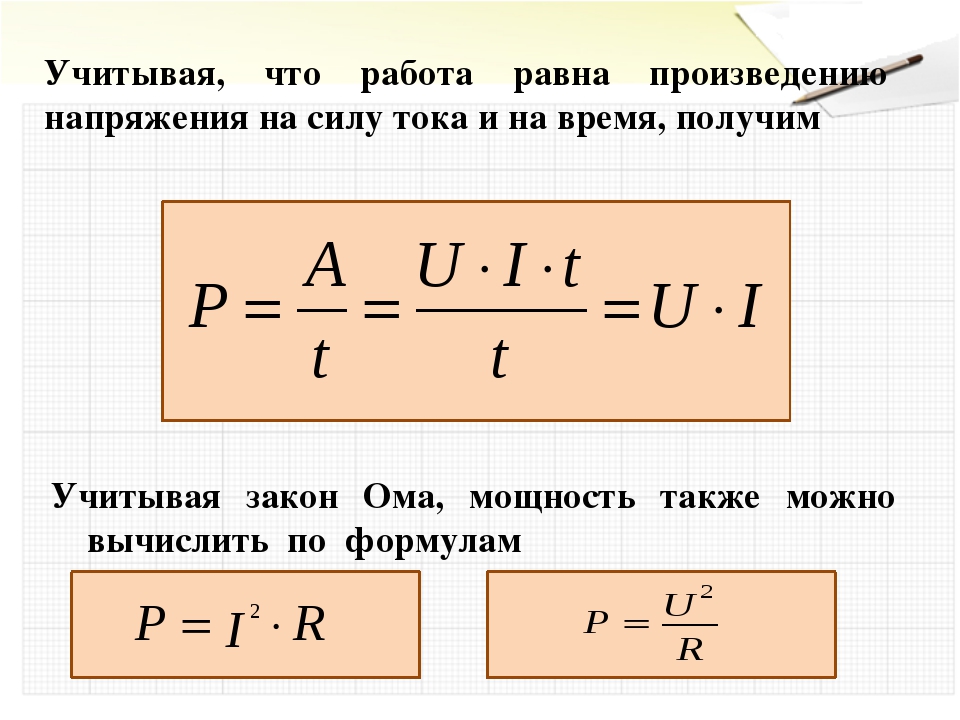 Помните, что мощность – это передача энергии из одного вида в другой. Когда эта электрическая энергия, вытекающая из источника питания, попадает на резистор, энергия превращается в тепло. Возможно, больше тепла, чем может выдержать резистор.Что приводит нас к… номинальной мощности.
Помните, что мощность – это передача энергии из одного вида в другой. Когда эта электрическая энергия, вытекающая из источника питания, попадает на резистор, энергия превращается в тепло. Возможно, больше тепла, чем может выдержать резистор.Что приводит нас к… номинальной мощности.
Определение мощности и размера выборки
Определение мощности и размера выборки
Определение мощности и объема выборки
Автор:
Лиза Салливан, доктор философии
Профессор биосатистики
Школа общественного здравоохранения Бостонского университета
Критически важным аспектом любого исследования является определение соответствующего размера выборки для ответа на вопрос исследования.Этот модуль будет посвящен формулам, которые можно использовать для оценки размера выборки, необходимой для получения оценки доверительного интервала с заданным пределом погрешности (точности) или для обеспечения того, чтобы проверка гипотезы имела высокую вероятность обнаружения значимой разницы в параметр.
Исследования должны быть разработаны таким образом, чтобы в них участвовало достаточное количество участников, чтобы адекватно ответить на вопрос исследования. Исследования с недостаточным или чрезмерно большим числом участников являются расточительными с точки зрения времени участников и исследователей, ресурсов для проведения оценок, аналитических усилий и так далее.Эти ситуации также можно рассматривать как неэтичные, поскольку участники могли подвергаться риску в рамках исследования, которое не смогло ответить на важный вопрос. Исследования, которые намного больше, чем они должны быть, чтобы ответить на вопросы исследования, также являются расточительными.
Представленные здесь формулы позволяют оценить необходимый размер выборки на основе статистических критериев. Однако во многих исследованиях размер выборки определяется финансовыми или логистическими ограничениями. Например, предположим, что предлагается провести исследование для оценки нового скринингового теста на синдром Дауна. Предположим, что скрининговый тест основан на анализе образца крови, взятого у женщин на ранних сроках беременности. Для оценки свойств скринингового теста (например, чувствительности и специфичности) каждой беременной женщине будет предложено сдать образец крови и дополнительно пройти амниоцентез. Амниоцентез включен в качестве золотого стандарта, и планируется сравнить результаты скринингового теста с результатами амниоцентеза. Предположим, что сбор и обработка образца крови стоит 250 долларов на участника, а амниоцентез — 900 долларов на участника.Одни только эти финансовые ограничения могут существенно ограничить число женщин, которые могут быть зачислены. Точно так же, как важно учитывать как статистическую, так и клиническую значимость при интерпретации результатов статистического анализа, также важно взвешивать как статистические, так и логистические аспекты при определении размера выборки для исследования.
Предположим, что скрининговый тест основан на анализе образца крови, взятого у женщин на ранних сроках беременности. Для оценки свойств скринингового теста (например, чувствительности и специфичности) каждой беременной женщине будет предложено сдать образец крови и дополнительно пройти амниоцентез. Амниоцентез включен в качестве золотого стандарта, и планируется сравнить результаты скринингового теста с результатами амниоцентеза. Предположим, что сбор и обработка образца крови стоит 250 долларов на участника, а амниоцентез — 900 долларов на участника.Одни только эти финансовые ограничения могут существенно ограничить число женщин, которые могут быть зачислены. Точно так же, как важно учитывать как статистическую, так и клиническую значимость при интерпретации результатов статистического анализа, также важно взвешивать как статистические, так и логистические аспекты при определении размера выборки для исследования.
После завершения этого модуля студент сможет:
- Приведите примеры, демонстрирующие, как предел погрешности, размер эффекта и изменчивость результата влияют на расчет размера выборки.

- Вычислите размер выборки, необходимый для точной оценки параметров генеральной совокупности.
- Интерпретация статистической мощности при проверке гипотез.
- Вычислите размер выборки, необходимый для обеспечения высокой мощности при проверке гипотез.
В модуле по доверительным интервалам представлены методы оценки доверительных интервалов для различных параметров (например, μ , p, ( μ 1 — μ 2 ), μ d , (p 1 -p 2 ). )).Доверительные интервалы для каждого параметра имеют следующий общий вид:
Оценка точки + Погрешность
В модуле по доверительным интервалам мы вывели формулу доверительного интервала для μ как
На практике мы используем стандартное отклонение выборки для оценки стандартного отклонения генеральной совокупности. Обратите внимание, что существует альтернативная формула для оценки среднего значения непрерывного результата в одной популяции, и она используется, когда размер выборки мал (n<30). Он включает значение из t-распределения, а не из стандартного нормального распределения, чтобы отразить желаемый уровень достоверности. При расчете размера выборки мы используем приведенную здесь формулу для большой выборки. [Примечание: результирующий размер выборки может быть небольшим, и на этапе анализа необходимо использовать соответствующую формулу доверительного интервала.]
Он включает значение из t-распределения, а не из стандартного нормального распределения, чтобы отразить желаемый уровень достоверности. При расчете размера выборки мы используем приведенную здесь формулу для большой выборки. [Примечание: результирующий размер выборки может быть небольшим, и на этапе анализа необходимо использовать соответствующую формулу доверительного интервала.]
Точечная оценка среднего значения генеральной совокупности является средним значением выборки, а предел погрешности равен
.
При планировании исследований мы хотим определить размер выборки, необходимый для обеспечения того, чтобы погрешность была достаточно малой, чтобы быть информативной.Например, предположим, что мы хотим оценить средний вес студенток колледжа. Мы проводим исследование и получаем 95% доверительный интервал следующим образом: 125 90 255 + 90 256 40 фунтов, или от 85 до 165 фунтов. Погрешность настолько широка, что доверительный интервал неинформативен. Чтобы быть информативным, исследователь может захотеть, чтобы предел погрешности не превышал 5 или 10 фунтов (это означает, что 95% доверительный интервал будет иметь ширину (от нижнего предела до верхнего предела) 10 или 20 фунтов). Чтобы определить необходимый размер выборки, исследователь должен указать желаемую погрешность .Важно отметить, что это не статистический вопрос, а клинический или практический. Например, предположим, что мы хотим оценить средний вес при рождении младенцев, рожденных матерями, которые курили сигареты во время беременности. Вес при рождении младенцев явно имеет гораздо более ограниченный диапазон, чем вес студенток колледжа. Следовательно, мы, вероятно, хотели бы создать доверительный интервал для среднего веса при рождении, который имеет погрешность, не превышающую 1 или 2 фунта.
Чтобы определить необходимый размер выборки, исследователь должен указать желаемую погрешность .Важно отметить, что это не статистический вопрос, а клинический или практический. Например, предположим, что мы хотим оценить средний вес при рождении младенцев, рожденных матерями, которые курили сигареты во время беременности. Вес при рождении младенцев явно имеет гораздо более ограниченный диапазон, чем вес студенток колледжа. Следовательно, мы, вероятно, хотели бы создать доверительный интервал для среднего веса при рождении, который имеет погрешность, не превышающую 1 или 2 фунта.
Допустимая погрешность в доверительном интервале одной выборки для μ может быть записана следующим образом:
.
Наша цель — определить размер выборки n, который гарантирует, что погрешность « E » не превышает заданного значения. Мы можем взять приведенную выше формулу и с помощью некоторой алгебры найти n :
.
Сначала умножьте обе части уравнения на квадратный корень из n . Затем вычеркните квадратный корень из n из числителя и знаменателя в правой части уравнения (поскольку любое число, деленное само на себя, равно 1). Это оставляет:
Затем вычеркните квадратный корень из n из числителя и знаменателя в правой части уравнения (поскольку любое число, деленное само на себя, равно 1). Это оставляет:
Теперь разделите обе части на «Е» и вычеркните «Е» из числителя и знаменателя в левой части.Это оставляет:
Наконец, возведите в квадрат обе части уравнения, чтобы получить:
Эта формула генерирует размер выборки n , необходимый для того, чтобы погрешность E не превышала заданного значения. Чтобы найти n , мы должны ввести « Z », « σ», и « E ».
- Z — значение из таблицы вероятностей стандартного нормального распределения для желаемого уровня достоверности (т.г., Z = 1,96 для достоверности 95%)
- E — предел погрешности, который исследователь определяет как важный с клинической или практической точки зрения.

- σ — стандартное отклонение интересующего результата.
Иногда трудно оценить σ . Когда мы используем приведенную выше формулу размера выборки (или одну из других формул, которые мы представим в следующих разделах), мы планируем исследование для оценки неизвестного среднего значения конкретной переменной результата в популяции.Маловероятно, что мы узнаем стандартное отклонение этой переменной. При расчете размера выборки исследователи часто используют значение стандартного отклонения из предыдущего исследования или исследования, проведенного в другой, но сопоставимой популяции. Вычисление размера выборки не является применением статистического вывода, и поэтому разумно использовать соответствующую оценку стандартного отклонения. Оценка может быть получена из другого исследования, о котором сообщалось в литературе; некоторые исследователи проводят небольшое пилотное исследование для оценки стандартного отклонения. Пилотное исследование обычно включает небольшое количество участников (например, n = 10), которые отбираются по принципу удобства, а не методом случайной выборки. Данные участников пилотного исследования можно использовать для расчета стандартного отклонения выборки, которое служит хорошей оценкой σ в формуле размера выборки. Независимо от того, как получена оценка изменчивости исхода, она всегда должна быть консервативной (т. е. настолько большой, насколько это разумно), чтобы результирующий размер выборки не был слишком мал.
Пилотное исследование обычно включает небольшое количество участников (например, n = 10), которые отбираются по принципу удобства, а не методом случайной выборки. Данные участников пилотного исследования можно использовать для расчета стандартного отклонения выборки, которое служит хорошей оценкой σ в формуле размера выборки. Независимо от того, как получена оценка изменчивости исхода, она всегда должна быть консервативной (т. е. настолько большой, насколько это разумно), чтобы результирующий размер выборки не был слишком мал.
Формула дает минимальный размер выборки, чтобы гарантировать, что погрешность доверительного интервала не превысит E . При планировании исследований исследователи также должны учитывать отсев или выбывание из-под наблюдения. Приведенная выше формула дает количество участников, необходимых для полных данных, чтобы гарантировать, что погрешность в доверительном интервале не превышает E . В следующих разделах мы проиллюстрируем, как проблема истощения решается в исследованиях по планированию, на примерах.
В исследованиях, в которых планируется оценить среднее значение непрерывной переменной результата в отдельной популяции, формула для определения размера выборки приведена ниже:
, где Z — значение стандартного нормального распределения, отражающее уровень достоверности, который будет использоваться (например, Z = 1,96 для 95%), σ — стандартное отклонение переменной результата, а E — желаемое значение. допустимая погрешность.Вышеприведенная формула генерирует минимальное количество испытуемых, необходимое для того, чтобы погрешность доверительного интервала для μ не превышала E .
Пример 1:
Исследователь хочет оценить среднее систолическое артериальное давление у детей с врожденными пороками сердца в возрасте от 3 до 5 лет. Сколько детей должно быть включено в исследование? Исследователь планирует использовать 95% доверительный интервал (т.е. Z=1,96) и хочет погрешность в 5 единиц. Стандартное отклонение систолического артериального давления неизвестно, но исследователи провели поиск литературы и обнаружили, что стандартное отклонение систолического артериального давления у детей с другими пороками сердца составляет от 15 до 20. Чтобы оценить размер выборки, мы рассматриваем больший стандарт. отклонение для получения наиболее консервативного (наибольшего) размера выборки.
Стандартное отклонение систолического артериального давления неизвестно, но исследователи провели поиск литературы и обнаружили, что стандартное отклонение систолического артериального давления у детей с другими пороками сердца составляет от 15 до 20. Чтобы оценить размер выборки, мы рассматриваем больший стандарт. отклонение для получения наиболее консервативного (наибольшего) размера выборки.
Чтобы гарантировать, что 95% доверительный интервал оценки среднего систолического артериального давления у детей в возрасте от 3 до 5 лет с врожденным пороком сердца находится в пределах 5 единиц от истинного среднего значения, необходима выборка размером 62.[ Примечание : Мы всегда округляем; формулы размера выборки всегда генерируют минимальное количество субъектов, необходимое для обеспечения заданной точности.] Если бы мы предположили, что стандартное отклонение равно 15, размер выборки был бы n=35. Поскольку оценки стандартного отклонения были получены в результате исследований детей с другими пороками сердца, было бы целесообразно использовать большее стандартное отклонение и запланировать исследование с участием 62 детей. Выбор меньшего размера выборки потенциально может дать оценку доверительного интервала с большей погрешностью.
Выбор меньшего размера выборки потенциально может дать оценку доверительного интервала с большей погрешностью.
Исследователь хочет оценить средний вес детей при рождении в срок (примерно 40 недель беременности) у матерей в возрасте 19 лет и младше. Средняя масса тела при рождении доношенных детей от матерей в возрасте 20 лет и старше составляет 3510 граммов при стандартном отклонении 385 граммов. Сколько женщин в возрасте 19 лет и младше должно быть включено в исследование, чтобы гарантировать, что оценка среднего веса при рождении их детей с доверительным интервалом 95% имеет погрешность, не превышающую 100 граммов? Попробуйте проработать расчет, прежде чем смотреть на ответ.
Ответ
В исследованиях, план которых заключается в оценке доли успехов в дихотомической переменной исхода (да/нет) в одной популяции, формула для определения размера выборки:
, где Z — значение из стандартного нормального распределения, отражающее уровень достоверности, который будет использоваться (например, Z = 1,96 для 95%), а E — желаемая погрешность. p — доля успехов в популяции.Здесь мы планируем исследование для создания 95% доверительного интервала для неизвестной доли населения, p . Уравнение для определения размера выборки для определения p, кажется, требует знания p, но очевидно, что это круговой аргумент, потому что если бы мы знали долю успехов в популяции, то исследование было бы не нужно! Что нам действительно нужно, так это приблизительное значение p или ожидаемое значение. Диапазон p составляет от 0 до 1, и, следовательно, диапазон p(1-p) составляет от 0 до 1.Значение p, которое максимизирует p(1-p), равно p=0,5. Следовательно, если нет доступной информации для аппроксимации p, то можно использовать p = 0,5 для получения наиболее консервативного или наибольшего размера выборки.
p — доля успехов в популяции.Здесь мы планируем исследование для создания 95% доверительного интервала для неизвестной доли населения, p . Уравнение для определения размера выборки для определения p, кажется, требует знания p, но очевидно, что это круговой аргумент, потому что если бы мы знали долю успехов в популяции, то исследование было бы не нужно! Что нам действительно нужно, так это приблизительное значение p или ожидаемое значение. Диапазон p составляет от 0 до 1, и, следовательно, диапазон p(1-p) составляет от 0 до 1.Значение p, которое максимизирует p(1-p), равно p=0,5. Следовательно, если нет доступной информации для аппроксимации p, то можно использовать p = 0,5 для получения наиболее консервативного или наибольшего размера выборки.
Пример 2:
Исследователь хочет оценить долю первокурсников своего университета, которые в настоящее время курят сигареты (т. е. распространенность курения). Сколько первокурсников должно быть вовлечено в исследование, чтобы гарантировать, что оценка 95% доверительного интервала доли курящих первокурсников находится в пределах 5% от истинной доли?
Поскольку у нас нет информации о доле курящих первокурсников, мы используем 0. 5, чтобы оценить размер выборки следующим образом:
5, чтобы оценить размер выборки следующим образом:
Чтобы гарантировать, что оценка 95% доверительного интервала доли курящих первокурсников находится в пределах 5% от истинной доли, необходима выборка размером 385.
Предположим, что аналогичное исследование было проведено 2 года назад и обнаружило, что распространенность курения среди первокурсников составила 27%. Если исследователь считает, что это разумная оценка распространенности спустя 2 года, ее можно использовать для планирования следующего исследования.Используя эту оценку p, какой размер выборки необходим (при условии, что снова будет использоваться 95% доверительный интервал, и мы хотим такой же уровень точности)?
Ответ
Пример 3:
Исследователь хочет оценить распространенность рака молочной железы среди женщин в возрасте от 40 до 45 лет, проживающих в Бостоне. Сколько женщин должно быть вовлечено в исследование, чтобы оценка была точной? Национальные данные показывают, что у 1 из 235 женщин диагностируют рак молочной железы к 40 годам. Это соответствует доле 0,0043 (0,43%) или распространенности 43 на 10 000 женщин. Предположим, исследователь хочет, чтобы оценка была в пределах 10 на 10 000 женщин с достоверностью 95%. Размер выборки рассчитывается следующим образом:
Это соответствует доле 0,0043 (0,43%) или распространенности 43 на 10 000 женщин. Предположим, исследователь хочет, чтобы оценка была в пределах 10 на 10 000 женщин с достоверностью 95%. Размер выборки рассчитывается следующим образом:
Выборка размером n = 16 448 гарантирует, что оценка 95% доверительного интервала распространенности рака молочной железы находится в пределах 0,10 (или в пределах 10 женщин на 10 000) от его истинного значения. Это ситуация, когда исследователи могут решить, что выборка такого размера невозможна.Предположим, что исследователи сочли, что выборка размером 5000 будет разумной с практической точки зрения. Как точно мы можем оценить распространенность при размере выборки n=5000? Напомним, что формула доверительного интервала для оценки распространенности:
.
Предполагая, что распространенность рака молочной железы в выборке будет близка к таковой, основанной на национальных данных, мы ожидаем, что предел погрешности будет примерно равен следующему:
Таким образом, при n=5000 женщин можно ожидать, что 95% доверительный интервал будет иметь погрешность 0. 0018 (или 18 на 10 000). Исследователи должны решить, будет ли это достаточно точным, чтобы ответить на исследовательский вопрос. Обратите внимание, что вышеизложенное основано на предположении, что распространенность рака молочной железы в Бостоне аналогична общенациональной. Это может быть или не быть разумным предположением. Фактически, целью настоящего исследования является оценка распространенности в Бостоне. Исследовательская группа при участии клинических исследователей и специалистов по биостатистике должна тщательно оценить последствия выбора размера выборки n = 5000, n = 16 448 или любого промежуточного размера.
0018 (или 18 на 10 000). Исследователи должны решить, будет ли это достаточно точным, чтобы ответить на исследовательский вопрос. Обратите внимание, что вышеизложенное основано на предположении, что распространенность рака молочной железы в Бостоне аналогична общенациональной. Это может быть или не быть разумным предположением. Фактически, целью настоящего исследования является оценка распространенности в Бостоне. Исследовательская группа при участии клинических исследователей и специалистов по биостатистике должна тщательно оценить последствия выбора размера выборки n = 5000, n = 16 448 или любого промежуточного размера.
В исследованиях, в которых планируется оценить разницу в средних значениях между двумя независимыми совокупностями, ниже приводится формула для определения размера выборки в каждой группе сравнения:
, где n i — размер выборки, требуемый в каждой группе (i = 1,2), Z — значение стандартного нормального распределения, отражающее уровень достоверности, который будет использоваться, а E — желаемая погрешность. σ снова отражает стандартное отклонение переменной результата.Напомним из модуля о доверительных интервалах, что, когда мы генерировали оценку доверительного интервала для разницы в средних, мы использовали Sp, объединенную оценку общего стандартного отклонения, в качестве меры изменчивости результата (на основе объединения данных). , где Sp вычисляется следующим образом:
σ снова отражает стандартное отклонение переменной результата.Напомним из модуля о доверительных интервалах, что, когда мы генерировали оценку доверительного интервала для разницы в средних, мы использовали Sp, объединенную оценку общего стандартного отклонения, в качестве меры изменчивости результата (на основе объединения данных). , где Sp вычисляется следующим образом:
Если имеются данные о вариабельности исхода в каждой группе сравнения, можно рассчитать Sp и использовать его в формуле размера выборки. Однако чаще бывает так, что данные о вариабельности исхода доступны только для одной группы, часто не получавшей лечения (например,g., плацебо-контроль) или неэкспонированная группа. При планировании клинического испытания нового препарата или процедуры часто доступны данные других испытаний, в которых участвовало плацебо или активная контрольная группа (т. е. стандартное лекарство или лечение, назначенное для изучаемого состояния). Стандартное отклонение переменной исхода, измеренное у пациентов, отнесенных к группе плацебо, контрольной группе или группе, не подвергавшейся воздействию, можно использовать для планирования будущих испытаний, как показано ниже.
Обратите внимание, что формула для размера выборки генерирует оценки размера выборки для выборок одинакового размера.Если планируется исследование, в котором будет назначено разное количество пациентов или разное количество пациентов будет составлять группы сравнения, то можно использовать альтернативные формулы.
Пример 4:
Исследователь хочет запланировать клиническое испытание для оценки эффективности нового препарата, предназначенного для повышения уровня холестерина ЛПВП («хорошего» холестерина). План состоит в том, чтобы зарегистрировать участников и случайным образом назначить им либо новый препарат, либо плацебо. Холестерин ЛПВП будет измеряться у каждого участника через 12 недель назначенного лечения.Основываясь на предыдущем опыте подобных испытаний, исследователь ожидает, что 10% всех участников будут потеряны для последующего наблюдения или выпадут из исследования в течение 12 недель. Будет рассчитан 95% доверительный интервал для количественной оценки разницы средних уровней ЛПВП между пациентами, принимающими новый препарат, по сравнению с плацебо. Исследователь хотел бы, чтобы погрешность была не более 3 единиц. Сколько пациентов следует набрать в исследование?
Исследователь хотел бы, чтобы погрешность была не более 3 единиц. Сколько пациентов следует набрать в исследование?
Размер выборки рассчитывается следующим образом:
Основная проблема заключается в определении вариабельности интересующего исхода (σ), в данном случае стандартного отклонения холестерина ЛПВП.Чтобы спланировать это исследование, мы можем использовать данные Framingham Heart Study. У участников, присутствовавших на седьмом обследовании в рамках исследования «Потомство» и не получавших лечения от высокого уровня холестерина, стандартное отклонение холестерина ЛПВП составляет 17,1. Мы будем использовать это значение и другие входные данные для вычисления размера выборки следующим образом:
Образцы размером n 1 = 250 и n 2 = 250 гарантируют, что 95% доверительный интервал для разницы средних уровней ЛПВП будет иметь погрешность не более 3 единиц.Опять же, эти размеры выборки относятся к количеству участников с полными данными. Исследователи предположили, что коэффициент отсева (или отсева) составляет 10% (в обеих группах). Чтобы гарантировать, что общий размер выборки в 500 человек будет доступен через 12 недель, исследователь должен набрать больше участников, чтобы учесть отсев.
Исследователи предположили, что коэффициент отсева (или отсева) составляет 10% (в обеих группах). Чтобы гарантировать, что общий размер выборки в 500 человек будет доступен через 12 недель, исследователь должен набрать больше участников, чтобы учесть отсев.
N (число для регистрации) * (% оставшихся) = желаемый размер выборки
Следовательно, N (число для регистрации) = желаемый размер выборки/(% оставшихся)
Н = 500/0.90 = 556
Если они ожидают 10% отсева, исследователи должны зарегистрировать 556 участников. Это обеспечит N = 500 с полными данными в конце испытания.
Пример 5:
Исследователь хочет сравнить две программы диеты для детей, страдающих ожирением. Одна диета — это диета с низким содержанием жиров, а другая — диета с низким содержанием углеводов. План состоит в том, чтобы зачислить детей и взвесить их в начале исследования. Затем каждому ребенку будет случайным образом назначена либо диета с низким содержанием жиров, либо диета с низким содержанием углеводов. Каждый ребенок будет соблюдать назначенную диету в течение 8 недель, после чего его снова взвесят. Количество потерянных килограммов будет подсчитано для каждого ребенка. Основываясь на данных, полученных в ходе испытаний диеты у взрослых, исследователь ожидает, что 20% всех детей не завершат исследование. Будет рассчитан 95% доверительный интервал для количественной оценки разницы в весе, потерянном между двумя диетами, и исследователь хотел бы, чтобы погрешность не превышала 3 фунтов. Сколько детей должно быть привлечено к исследованию?
Каждый ребенок будет соблюдать назначенную диету в течение 8 недель, после чего его снова взвесят. Количество потерянных килограммов будет подсчитано для каждого ребенка. Основываясь на данных, полученных в ходе испытаний диеты у взрослых, исследователь ожидает, что 20% всех детей не завершат исследование. Будет рассчитан 95% доверительный интервал для количественной оценки разницы в весе, потерянном между двумя диетами, и исследователь хотел бы, чтобы погрешность не превышала 3 фунтов. Сколько детей должно быть привлечено к исследованию?
Размер выборки рассчитывается следующим образом:
Опять же проблема заключается в определении вариабельности интересующего результата (σ), здесь стандартное отклонение в фунтах, потерянных за 8 недель.Чтобы спланировать это исследование, исследователи используют данные опубликованного исследования у взрослых. Предположим, в одном таком исследовании сравнивались одни и те же диеты у взрослых, и в каждой диетической группе участвовало 100 человек. В исследовании сообщалось о стандартном отклонении веса, потерянного за 8 недель на диете с низким содержанием жиров, на 8,4 фунта, и стандартном отклонении веса, потерянного за 8 недель на диете с низким содержанием углеводов, на 7,7 фунта. Эти данные можно использовать для оценки общего стандартного отклонения потери веса следующим образом:
В исследовании сообщалось о стандартном отклонении веса, потерянного за 8 недель на диете с низким содержанием жиров, на 8,4 фунта, и стандартном отклонении веса, потерянного за 8 недель на диете с низким содержанием углеводов, на 7,7 фунта. Эти данные можно использовать для оценки общего стандартного отклонения потери веса следующим образом:
Теперь мы используем это значение и другие входные данные для вычисления размеров выборки:
Образцы размером n 1 = 56 и n 2 = 56 гарантируют, что 95% доверительный интервал для разницы в весе, потерянном между диетами, будет иметь погрешность не более 3 фунтов.Опять же, эти размеры выборки относятся к количеству детей с полными данными. Следователи ожидают 20% отсева. Чтобы гарантировать, что общий размер выборки 112 будет доступен через 8 недель, исследователь должен набрать больше участников, чтобы учесть отсев.
N (число для регистрации) * (% оставшихся) = желаемый размер выборки
Следовательно, N (число для регистрации) = желаемый размер выборки/(% оставшихся)
Н = 112/0,80 = 140
В исследованиях, в которых планируется оценить среднюю разницу непрерывного результата на основе сопоставленных данных, формула для определения размера выборки приведена ниже:
, где Z — значение стандартного нормального распределения, отражающее уровень достоверности, который будет использоваться (т. g., Z = 1,96 для 95%), E — желаемая погрешность, а σ d — стандартное отклонение разностных оценок. Чрезвычайно важно, чтобы стандартное отклонение разности баллов (например, разница, основанная на измерениях во времени или разница между совпадающими парами) использовалась здесь для надлежащей оценки размера выборки.
g., Z = 1,96 для 95%), E — желаемая погрешность, а σ d — стандартное отклонение разностных оценок. Чрезвычайно важно, чтобы стандартное отклонение разности баллов (например, разница, основанная на измерениях во времени или разница между совпадающими парами) использовалась здесь для надлежащей оценки размера выборки.
В исследованиях, целью которых является оценка разницы в пропорциях между двумя независимыми популяциями (т.т. е., для оценки разницы рисков), формула для определения размера выборки, необходимой в каждой группе сравнения:
, где n i — размер выборки, требуемый в каждой группе (i = 1,2), Z — значение из стандартного нормального распределения, отражающее уровень достоверности, который будет использоваться (например, Z = 1,96 для 95%), и E — желаемая погрешность. p 1 и p 2 — доли успехов в каждой группе сравнения. Опять же, здесь мы планируем исследование для получения 95% доверительного интервала для разницы в неизвестных пропорциях, и формула для оценки необходимых размеров выборки требует p 1 и p 2 . Чтобы оценить размер выборки, нам нужны приблизительные значения p 1 и p 2 . Значения p 1 и p 2 , которые максимизируют размер выборки, составляют p 1 = p 2 = 0,5. Таким образом, если нет доступной информации для аппроксимации p 1 и p 2 , то можно использовать 0,5 для получения наиболее консервативных или самых больших размеров выборки.
Чтобы оценить размер выборки, нам нужны приблизительные значения p 1 и p 2 . Значения p 1 и p 2 , которые максимизируют размер выборки, составляют p 1 = p 2 = 0,5. Таким образом, если нет доступной информации для аппроксимации p 1 и p 2 , то можно использовать 0,5 для получения наиболее консервативных или самых больших размеров выборки.
Подобно ситуации с двумя независимыми выборками и непрерывным результатом в верхней части этой страницы, может случиться так, что будут доступны данные о доле успешных результатов в одной группе, обычно не получавшей лечения (например,g., плацебо-контроль) или неэкспонированная группа. Если это так, то известную пропорцию можно использовать как для p 1 , так и для p 2 в формуле, показанной выше. Формула, показанная выше, генерирует оценки размера выборки для выборок одинакового размера. Если планируется исследование, в котором будет назначено разное количество пациентов или разное количество пациентов будет составлять группы сравнения, то можно использовать альтернативные формулы. Заинтересованные читатели могут увидеть Fleiss для более подробной информации. 4
Заинтересованные читатели могут увидеть Fleiss для более подробной информации. 4
Пример 6:
Исследователь хочет оценить влияние курения во время беременности на преждевременные роды.Нормальная беременность длится примерно 40 недель, а преждевременные роды происходят до 37 недель. В отчете Национальной статистики естественного движения населения за 2005 год указано, что примерно 12% младенцев в Соединенных Штатах рождаются преждевременно. 5 Исследователь планирует собрать данные посредством просмотра медицинской документации и создать 95% доверительный интервал для разницы в доле младенцев, родившихся недоношенными у женщин, которые курили во время беременности, по сравнению с теми, кто не курил. Сколько женщин должно быть включено в исследование, чтобы гарантировать, что 95% доверительный интервал для разницы в пропорциях имеет погрешность не более 4%?
Размер выборки (т.т. е. число женщин, куривших и не куривших во время беременности), можно рассчитать по приведенной выше формуле. Национальные данные свидетельствуют о том, что 12% младенцев рождаются недоношенными. Мы будем использовать эту оценку для обеих групп при расчете размера выборки.
Национальные данные свидетельствуют о том, что 12% младенцев рождаются недоношенными. Мы будем использовать эту оценку для обеих групп при расчете размера выборки.
Выборки размером n 1 = 508 женщин, которые курили во время беременности, и n 2 = 508 женщин, которые не курили во время беременности, гарантируют, что 95%-й доверительный интервал для разницы в доле преждевременных родов будет иметь запас погрешность не более 4%.
Является ли здесь проблемой истощение?
Ответ
В модуле по проверке гипотез для средних и пропорций мы представили методы для средних, пропорций, различий в средних и различиях в пропорциях. В то время как каждый тест включал детали, которые были специфичны для интересующего результата (например, непрерывный или дихотомический) и количества групп сравнения (одна, две, более двух), в каждом тесте были общие элементы.Например, в каждой проверке гипотезы могут быть допущены две ошибки. Первая называется ошибкой типа I и относится к ситуации, когда мы ошибочно отвергаем H 0 , хотя на самом деле это правда. На первом этапе любой проверки гипотезы мы выбираем уровень значимости α и α = P (ошибка типа I) = P (отклонение H 0 | H 0 верно). Поскольку мы намеренно выбираем малое значение для α, мы контролируем вероятность совершения ошибки первого рода. Второй тип ошибки называется ошибкой типа II и определяется как вероятность того, что мы не отклоним H 0 , когда она ложна.Вероятность ошибки типа II обозначается β, и β = P (ошибка типа II) = P (не отклонять H 0 | H 0 — ложь). При проверке гипотез мы обычно ориентируемся на мощность, которая определяется как вероятность того, что мы отклоним H 0 , когда она ложна, т. е. мощность = 1-β = P(Reject H 0 | H 0 ложна). ). Мощность — это вероятность того, что тест правильно отвергнет ложную нулевую гипотезу. Хороший тест — это тест с низкой вероятностью совершения ошибки первого рода (т.
Первая называется ошибкой типа I и относится к ситуации, когда мы ошибочно отвергаем H 0 , хотя на самом деле это правда. На первом этапе любой проверки гипотезы мы выбираем уровень значимости α и α = P (ошибка типа I) = P (отклонение H 0 | H 0 верно). Поскольку мы намеренно выбираем малое значение для α, мы контролируем вероятность совершения ошибки первого рода. Второй тип ошибки называется ошибкой типа II и определяется как вероятность того, что мы не отклоним H 0 , когда она ложна.Вероятность ошибки типа II обозначается β, и β = P (ошибка типа II) = P (не отклонять H 0 | H 0 — ложь). При проверке гипотез мы обычно ориентируемся на мощность, которая определяется как вероятность того, что мы отклоним H 0 , когда она ложна, т. е. мощность = 1-β = P(Reject H 0 | H 0 ложна). ). Мощность — это вероятность того, что тест правильно отвергнет ложную нулевую гипотезу. Хороший тест — это тест с низкой вероятностью совершения ошибки первого рода (т. т. е., малое α) и большой мощности (т. е. малое β, большая мощность).
т. е., малое α) и большой мощности (т. е. малое β, большая мощность).
Здесь мы представляем формулы для определения размера выборки, необходимой для обеспечения высокой мощности теста. Вычисления размера выборки зависят от уровня значимости, aα, желаемой мощности теста (эквивалентной 1-β), изменчивости результата и размера эффекта. Величина эффекта представляет собой разницу в интересующем параметре, которая представляет собой клинически значимую разницу. Подобно погрешности в приложениях доверительного интервала, размер эффекта определяется на основе клинических или практических критериев, а не статистических критериев.
Понятие статистической мощности может быть трудно понять. Прежде чем представить формулы для определения размеров выборки, необходимых для обеспечения высокой мощности в тесте, мы сначала обсудим мощность с концептуальной точки зрения.
Предположим, мы хотим проверить следующие гипотезы при aα = 0,05: H 0 : μ = 90 по сравнению с H 1 : μ ≠ 90. Предположим, что для проверки гипотез мы выбираем выборку размером n = 100. Для этого примера предположим, что стандартное отклонение результата равно σ=20.Мы вычисляем среднее значение выборки, а затем должны решить, предоставляет ли среднее значение выборки свидетельство в поддержку альтернативной гипотезы или нет. Это делается путем вычисления тестовой статистики и сравнения тестовой статистики с соответствующим критическим значением. Если нулевая гипотеза верна (μ = 90), то мы, вероятно, выберем выборку, среднее значение которой близко к 90. Однако также можно выбрать выборку, среднее значение которой намного больше или намного меньше 90. Напомним из Центральной предельной теоремы (см. стр. 11 в модуле о вероятности), что для больших n (здесь n=100 достаточно велико) распределение выборочных средних приблизительно нормально со средним значением
Предположим, что для проверки гипотез мы выбираем выборку размером n = 100. Для этого примера предположим, что стандартное отклонение результата равно σ=20.Мы вычисляем среднее значение выборки, а затем должны решить, предоставляет ли среднее значение выборки свидетельство в поддержку альтернативной гипотезы или нет. Это делается путем вычисления тестовой статистики и сравнения тестовой статистики с соответствующим критическим значением. Если нулевая гипотеза верна (μ = 90), то мы, вероятно, выберем выборку, среднее значение которой близко к 90. Однако также можно выбрать выборку, среднее значение которой намного больше или намного меньше 90. Напомним из Центральной предельной теоремы (см. стр. 11 в модуле о вероятности), что для больших n (здесь n=100 достаточно велико) распределение выборочных средних приблизительно нормально со средним значением
и
Если нулевая гипотеза верна, можно наблюдать любое среднее значение выборки, показанное на рисунке ниже; все возможно при H 0 : μ = 90.
Когда мы устанавливаем решающее правило для нашей проверки гипотезы, мы определяем критические значения на основе α = 0,05 и двустороннего теста. Когда мы проводим проверки гипотез, мы обычно стандартизируем данные (например, преобразуем в Z или t), а критические значения являются соответствующими значениями из распределения вероятностей, используемого в тесте. Чтобы облегчить интерпретацию, мы продолжим это обсуждение с в отличие от Z. Критические значения для двустороннего теста с α = 0,05 равны 86.06 и 93,92 (эти значения соответствуют -1,96 и 1,96 соответственно по шкале Z), поэтому правило принятия решения следующее: Отклонить H 0 , если < 86,06 или если > 93,92. Область отторжения показана в конце рисунка ниже.
Область отклонения для теста H 0 : μ = 90 по сравнению с H 1 : μ ≠ 90 при α = 0,05
.
Площади на двух концах кривой представляют вероятность ошибки первого рода, α = 0. 05. Эта концепция обсуждалась в модуле «Проверка гипотез».
05. Эта концепция обсуждалась в модуле «Проверка гипотез».
Теперь предположим, что альтернативная гипотеза H 1 верна (т. е. μ ≠ 90) и что истинное среднее на самом деле равно 94. На рисунке ниже показано распределение среднего значения выборки при нулевой и альтернативной гипотезах. значения выборочного среднего показаны по горизонтальной оси.
Распределение Under H 0 : μ = 90 и Under H 1 : μ = 94
Если истинное среднее значение равно 94, то альтернативная гипотеза верна.В нашем тесте мы выбрали α = 0,05 и отклонили H 0 , если наблюдаемое среднее значение выборки превышает 93,92 (сейчас сосредоточив внимание на верхнем хвосте области отклонения). Критическое значение (93,92) указано вертикальной линией. Вероятность ошибки II рода обозначается β, и β = P(Не отвергать H 0 | H 0 ложно), т. е. вероятность не отвергнуть нулевую гипотезу, если нулевая гипотеза верна. β показан на рисунке выше как площадь под самой правой кривой (H 1 ) слева от вертикальной линии (где мы не отбрасываем H 0 ). Мощность определяется как 1- β = P(Отклонить H 0 | H 0 неверно) и показана на рисунке как площадь под самой правой кривой (H 1 ) справа от вертикальной линии ( где мы отбрасываем H 0 ).
Мощность определяется как 1- β = P(Отклонить H 0 | H 0 неверно) и показана на рисунке как площадь под самой правой кривой (H 1 ) справа от вертикальной линии ( где мы отбрасываем H 0 ).
Обратите внимание, что β и мощность связаны с α, изменчивостью результата и величиной эффекта. Из рисунка выше видно, что произойдет с β и мощностью, если мы увеличим α. Предположим, например, что мы увеличиваем α до α=0,10. Верхнее критическое значение будет равно 92.56 вместо 93,92. Вертикальная линия сдвинется влево, увеличивая α, уменьшая β и увеличивая мощность. Хотя лучшим тестом является тест с более высокой мощностью, не рекомендуется увеличивать α как средство увеличения мощности. Тем не менее, существует прямая связь между α и мощностью (с увеличением α увеличивается и мощность).
β и мощность также связаны с изменчивостью исхода и величиной эффекта. Величина эффекта — это разница в интересующем параметре (например, μ), которая представляет собой клинически значимую разницу. На приведенном выше рисунке графически показаны α, β и мощность, когда разница среднего значения при нулевой гипотезе по сравнению с альтернативной гипотезой составляет 4 единицы (т. Е. 90 против 94). На рисунке ниже показаны те же компоненты для ситуации, когда среднее значение по альтернативной гипотезе равно 98.
На приведенном выше рисунке графически показаны α, β и мощность, когда разница среднего значения при нулевой гипотезе по сравнению с альтернативной гипотезой составляет 4 единицы (т. Е. 90 против 94). На рисунке ниже показаны те же компоненты для ситуации, когда среднее значение по альтернативной гипотезе равно 98.
Рисунок — Распределение Under H 0 : μ = 90 и Under H 1 : μ = 98.
Обратите внимание, что мощность намного выше, когда существует большая разница между средним значением H 0 по сравнению с H 1 (т.э., 90 против 98). Статистический тест с гораздо большей вероятностью отклонит нулевую гипотезу в пользу альтернативной, если истинное среднее значение равно 98, чем если истинное среднее значение равно 94. В этом случае также обратите внимание на то, что распределения нулевой и альтернативной гипотез мало перекрываются. . Если наблюдается выборочное среднее значение 97 или выше, очень маловероятно, что оно получено из распределения, среднее значение которого равно 90. На предыдущем рисунке для H 0 : µ = 90 и H 1 : µ = 94, если мы наблюдали выборочное среднее значение 93, например, было бы не так ясно, произошло ли оно из распределения, среднее значение которого равно 90, или из распределения, среднее значение которого равно 94.
На предыдущем рисунке для H 0 : µ = 90 и H 1 : µ = 94, если мы наблюдали выборочное среднее значение 93, например, было бы не так ясно, произошло ли оно из распределения, среднее значение которого равно 90, или из распределения, среднее значение которого равно 94.
При планировании исследований большинство людей принимают во внимание мощность 80 % или 90 % (точно так же, как мы обычно используем 95 % в качестве доверительного уровня для оценок доверительного интервала). Входные данные для формул размера выборки включают желаемую мощность, уровень значимости и размер эффекта. Величина эффекта выбирается для представления клинически значимого или практически важного различия в интересующем параметре, как мы проиллюстрируем.
Формулы, которые мы приводим ниже, дают минимальный размер выборки, чтобы гарантировать, что проверка гипотезы будет иметь заданную вероятность отклонения нулевой гипотезы, когда она ложна (т.д., указанная мощность). При планировании исследований исследователи снова должны учитывать отсев или выпадение из-под наблюдения. Формулы, показанные ниже, позволяют получить необходимое количество участников с полными данными, и мы проиллюстрируем, как решается проблема отсева в исследованиях по планированию.
При планировании исследований исследователи снова должны учитывать отсев или выпадение из-под наблюдения. Формулы, показанные ниже, позволяют получить необходимое количество участников с полными данными, и мы проиллюстрируем, как решается проблема отсева в исследованиях по планированию.
В исследованиях, в которых планируется выполнить проверку гипотезы, сравнивая среднее значение непрерывной переменной исхода в отдельной популяции с известным средним значением, представляют интерес следующие гипотезы:
H 0 : μ = μ 0 и H 1 : μ ≠ μ 0 , где μ 0 — известное среднее значение (т.г., исторический контроль). Формула для определения размера выборки, чтобы гарантировать, что тест имеет заданную мощность, приведена ниже:
, где α — выбранный уровень значимости, а Z 1-α/2 — значение стандартного нормального распределения, ниже которого находится 1-α/2. Например, если α=0,05, то 1-α/2 = 0,975 и Z=1,960. 1-β — выбранная мощность, а Z 1-β — значение из стандартного нормального распределения, на 1-β ниже которого. Оценки размера выборки для проверки гипотез часто основаны на достижении 80% или 90% мощности.Значения Z 1-β для этих популярных сценариев приведены ниже:
1-β — выбранная мощность, а Z 1-β — значение из стандартного нормального распределения, на 1-β ниже которого. Оценки размера выборки для проверки гипотез часто основаны на достижении 80% или 90% мощности.Значения Z 1-β для этих популярных сценариев приведены ниже:
- Для мощности 80 % Z 0,80 = 0,84
- Для 90% мощности Z 0,90 =1,282
ES — это размер эффекта , определяемый следующим образом:
, где μ 0 — среднее значение по H 0 , μ 1 — среднее значение по H 1 , а σ — стандартное отклонение интересующего результата.Числитель размера эффекта, абсолютное значение разницы средних | μ 1 — μ 0 | представляет то, что считается клинически значимым или практически важным различием в средних значениях. Подобно проблеме, с которой мы столкнулись при планировании исследований для оценки доверительных интервалов, иногда бывает сложно оценить стандартное отклонение. При расчете размера выборки исследователи часто используют значение стандартного отклонения из предыдущего исследования или исследования, проведенного в другой, но сопоставимой популяции.Независимо от того, как получена оценка изменчивости исхода, она всегда должна быть консервативной (т. е. настолько большой, насколько это разумно), чтобы результирующий размер выборки не был слишком мал.
При расчете размера выборки исследователи часто используют значение стандартного отклонения из предыдущего исследования или исследования, проведенного в другой, но сопоставимой популяции.Независимо от того, как получена оценка изменчивости исхода, она всегда должна быть консервативной (т. е. настолько большой, насколько это разумно), чтобы результирующий размер выборки не был слишком мал.
Пример 7:
Исследователь предполагает, что у людей без диабета уровень глюкозы в крови натощак, фактор риска ишемической болезни сердца, выше у тех, кто выпивает не менее 2 чашек кофе в день. Планируется поперечное исследование для оценки среднего уровня глюкозы в крови натощак у людей, выпивающих не менее двух чашек кофе в день.Средний уровень глюкозы в крови натощак у людей без диабета составляет 95,0 мг/дл со стандартным отклонением 9,8 мг/дл. 7 Если средний уровень глюкозы в крови у людей, выпивающих не менее 2 чашек кофе в день, составляет 100 мг/дл, это может иметь клиническое значение. Сколько пациентов должно быть включено в исследование, чтобы гарантировать, что мощность теста составляет 80% для обнаружения этой разницы? Будет использован двусторонний тест с уровнем значимости 5%.
Сколько пациентов должно быть включено в исследование, чтобы гарантировать, что мощность теста составляет 80% для обнаружения этой разницы? Будет использован двусторонний тест с уровнем значимости 5%.
Размер эффекта рассчитывается как:
.
Величина эффекта представляет собой значимую разницу в среднем для генеральной совокупности — здесь 95 против 100, или разница в 0,51 единицы стандартного отклонения. Теперь мы подставляем размер эффекта и соответствующие значения Z для выбранных α и мощности, чтобы вычислить размер выборки.
Таким образом, размер выборки n=31 гарантирует, что двусторонний тест с α =0,05 имеет мощность 80% для обнаружения разницы в 5 мг/дл в среднем уровне глюкозы в крови натощак.
В запланированном исследовании участников попросят голодать в течение ночи и сдать образец крови для анализа уровня глюкозы.Основываясь на предыдущем опыте, исследователи предполагают, что 10% участников не будут голодать или откажутся следовать протоколу исследования. Таким образом, в исследование будет включено в общей сложности 35 участников, чтобы гарантировать, что 31 человек будет доступен для анализа (см. ниже).
Таким образом, в исследование будет включено в общей сложности 35 участников, чтобы гарантировать, что 31 человек будет доступен для анализа (см. ниже).
N (число для регистрации) * (% следования протоколу) = желаемый размер выборки
Следовательно, N (число для регистрации) = желаемый размер выборки/(% оставшихся)
Н = 31/0,90 = 35.
В исследованиях, в которых планируется провести проверку гипотезы, сравнивая пропорцию успешных результатов в дихотомической исходной переменной в одной популяции с известной пропорцией, представляют интерес следующие гипотезы:
против
, где p 0 — известная пропорция (т.г., исторический контроль). Формула для определения размера выборки для обеспечения заданной мощности теста приведена ниже:
, где α — выбранный уровень значимости, а Z 1-α/2 — значение стандартного нормального распределения, ниже которого находится 1-α/2. 1-β — выбранная мощность, Z 1-β – значение из стандартного нормального распределения, в котором 1-β находится ниже него, а ES – величина эффекта, определяемая следующим образом:
, где p 0 — пропорция по H 0 , а p 1 — пропорция по H 1 . Числитель величины эффекта, абсолютное значение разницы в пропорциях |p 1 -p 0 |, снова представляет то, что считается клинически значимым или практически важным различием в пропорциях.
Числитель величины эффекта, абсолютное значение разницы в пропорциях |p 1 -p 0 |, снова представляет то, что считается клинически значимым или практически важным различием в пропорциях.
Пример 8:
Недавний отчет Framingham Heart Study показал, что 26% людей без сердечно-сосудистых заболеваний имели повышенный уровень холестерина ЛПНП, определяемый как ЛПНП > 159 мг/дл. 9 Исследователь предполагает, что более высокая доля пациентов с сердечно-сосудистыми заболеваниями в анамнезе будет иметь повышенный уровень холестерина ЛПНП.Сколько пациентов необходимо обследовать, чтобы убедиться, что мощность теста составляет 90 % для выявления 5 % разницы в пропорции с повышенным холестерином ЛПНП? Будет использован двусторонний тест с уровнем значимости 5%.
Сначала мы вычисляем размер эффекта:
Теперь мы подставляем размер эффекта и соответствующие значения Z для выбранных α и мощности, чтобы вычислить размер выборки.
Выборка размера n=869 обеспечит выполнение двустороннего теста с α =0.05 имеет 90-процентную мощность для выявления 5-процентной разницы в доле пациентов с сердечно-сосудистыми заболеваниями в анамнезе, у которых повышен уровень холестерина ЛПНП.
Производитель медицинского оборудования производит имплантируемые стенты. В процессе производства примерно 10% стентов признаются бракованными. Производитель хочет проверить, превышает ли доля дефектных стентов 10%. Если в процессе получается более 15% дефектных стентов, необходимо предпринять корректирующие действия.Поэтому производитель хочет, чтобы тест имел мощность 90% для обнаружения разницы в пропорциях этой величины. Сколько стентов необходимо оценить? Для своих расчетов используйте двусторонний тест с уровнем значимости 5%. (Проведите вычисления самостоятельно, прежде чем смотреть ответ.)
Ответ
В исследованиях, в которых планируется выполнить проверку гипотезы, сравнивая средние значения непрерывной переменной результата в двух независимых выборках, представляют интерес следующие гипотезы:
против
, где μ 1 и μ 2 — средние значения в двух сравниваемых популяциях. Формула для определения размера выборки, чтобы убедиться, что тест имеет заданную мощность:
Формула для определения размера выборки, чтобы убедиться, что тест имеет заданную мощность:
, где n i — размер выборки, требуемый в каждой группе (i = 1,2), α — выбранный уровень значимости, а Z 1-α /2 — значение из стандартного нормального распределения, содержащего 1-α /2 ниже него, а 1-β — это выбранная степень, а Z 1-β — это значение из стандартного нормального распределения, содержащее 1-β ниже него. ES — размер эффекта, определяемый как:
где | мк 1 — мк 2 | является абсолютным значением разницы в средних значениях между двумя группами, ожидаемой согласно альтернативной гипотезе, H 1 .σ — стандартное отклонение интересующего результата. Вспомните из модуля «Проверка гипотез», что, когда мы проводили проверку гипотез, сравнивая средние значения двух независимых групп, мы использовали Sp, объединенную оценку общего стандартного отклонения, как меру изменчивости результата.
Sp вычисляется следующим образом:
Если имеются данные о вариабельности исхода в каждой группе сравнения, можно рассчитать Sp и использовать его для создания размеров выборки.Однако чаще бывает так, что данные о вариабельности исхода доступны только для одной группы, обычно не получавшей лечения (например, плацебо-контроль) или не подвергавшейся воздействию. При планировании клинического испытания нового препарата или процедуры часто доступны данные из других испытаний, в которых могло участвовать плацебо или активная контрольная группа (т. е. стандартное лекарство или лечение, назначенное для изучаемого состояния). Стандартное отклонение переменной исхода, измеренное у пациентов, отнесенных к группе плацебо, контрольной группе или группе, не подвергавшейся воздействию, можно использовать для планирования будущих испытаний, как показано на рисунке.
Также обратите внимание, что приведенная выше формула позволяет получить оценки размера выборки для выборок одинакового размера. Если планируется исследование, в котором будет назначено разное количество пациентов или разное количество пациентов будет составлять группы сравнения, то можно использовать альтернативные формулы (см. Howell 3 для получения более подробной информации).
Если планируется исследование, в котором будет назначено разное количество пациентов или разное количество пациентов будет составлять группы сравнения, то можно использовать альтернативные формулы (см. Howell 3 для получения более подробной информации).
Пример 9:
Исследователь планирует клиническое испытание для оценки эффективности нового препарата, предназначенного для снижения систолического артериального давления.План состоит в том, чтобы зарегистрировать участников и случайным образом назначить им либо новый препарат, либо плацебо. Систолическое артериальное давление будет измеряться у каждого участника через 12 недель назначенного лечения. Основываясь на предыдущем опыте проведения подобных испытаний, исследователь ожидает, что 10% всех участников будут потеряны для последующего наблюдения или выпадут из исследования. Если новый препарат показывает снижение среднего систолического артериального давления на 5 единиц, это будет клинически значимым снижением. Сколько пациентов должно быть включено в исследование, чтобы гарантировать, что мощность теста составляет 80% для обнаружения этой разницы? Будет использован двусторонний тест с уровнем значимости 5%.
Сколько пациентов должно быть включено в исследование, чтобы гарантировать, что мощность теста составляет 80% для обнаружения этой разницы? Будет использован двусторонний тест с уровнем значимости 5%.
Для расчета размера эффекта необходима оценка вариабельности систолического артериального давления. Анализ данных Framingham Heart Study показал, что стандартное отклонение систолического артериального давления составило 19,0. Это значение можно использовать для планирования испытания.
Размер эффекта:
Теперь мы подставляем размер эффекта и соответствующие значения Z для выбранных α и мощности, чтобы вычислить размер выборки.
Выборки размером n 1 = 232 и n 2 = 232 гарантируют, что проверка гипотезы будет иметь 80%-ную мощность для обнаружения разницы в 5 единиц среднего систолического артериального давления у пациентов, получающих новый препарат, по сравнению с пациентами. прием плацебо.Однако исследователи предположили, что уровень отсева составляет 10% (в обеих группах), и чтобы обеспечить общий размер выборки в 232 человека, им необходимо учесть отсев.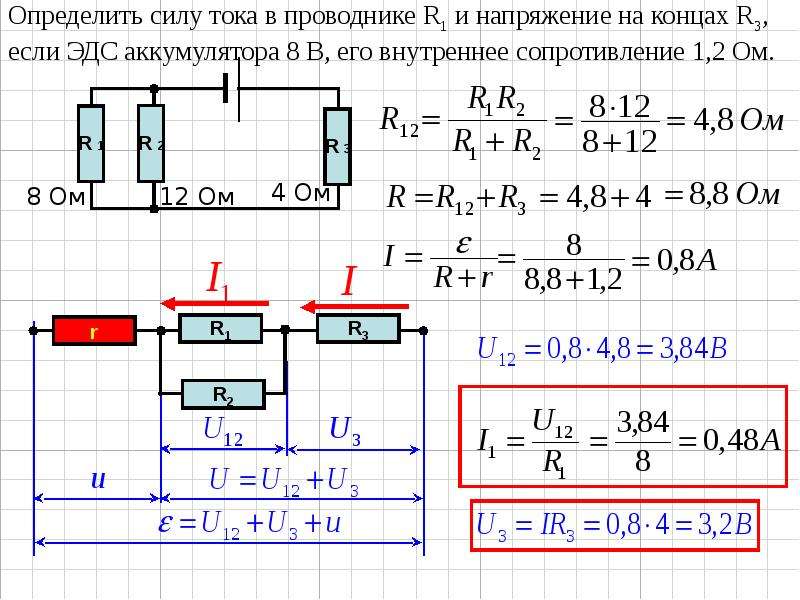
N (число для регистрации) * (% оставшихся) = желаемый размер выборки
Следовательно, N (число для регистрации) = желаемый размер выборки/(% оставшихся)
N = 232/0,90 = 258.
Исследователь должен зарегистрировать 258 участников, которым случайным образом будет назначено либо новое лекарство, либо плацебо.
Исследователь планирует исследование для оценки связи между потреблением алкоголя и средним баллом среди выпускников колледжей.План состоит в том, чтобы классифицировать учащихся как сильно пьющих или не употребляющих 5 или более порций алкоголя в обычный день употребления алкоголя в качестве критерия злоупотребления алкоголем. Средние средние баллы будут сравниваться между учащимися, классифицированными как сильно пьющие, и учащимися, не использующими двух независимых выборок для проверки материального положения. Предполагается, что стандартное отклонение среднего балла составляет 0,42, а значимая разница в среднем балле (по отношению к употреблению алкоголя) составляет 0,25 единицы. Сколько выпускников колледжей должно быть зачислено в исследование, чтобы гарантировать, что мощность теста составляет 80% для обнаружения 0.25 единиц разницы в среднем балле? Используйте двусторонний тест с уровнем значимости 5%.
Сколько выпускников колледжей должно быть зачислено в исследование, чтобы гарантировать, что мощность теста составляет 80% для обнаружения 0.25 единиц разницы в среднем балле? Используйте двусторонний тест с уровнем значимости 5%.
Ответ
В исследованиях, где планируется выполнить проверку гипотезы о средней разнице в непрерывной переменной результата на основе сопоставленных данных, представляют интерес следующие гипотезы:
против
, где μ d — средняя разница в популяции. Формула для определения размера выборки для обеспечения заданной мощности теста приведена ниже:
, где α — выбранный уровень значимости, а Z 1-α/2 — значение из стандартного нормального распределения, содержащее 1-α/2 ниже него, 1-β — выбранная степень, а Z 1-β — значение из стандартного нормального распределения, содержащее 1-β ниже него, а ES представляет собой величину эффекта, определяемую следующим образом:
, где μ d — средняя разница, ожидаемая при альтернативной гипотезе, H 1 , а σ d — стандартное отклонение разницы в результате (т. г., разница, основанная на измерениях во времени, или разница между подобранными парами).
г., разница, основанная на измерениях во времени, или разница между подобранными парами).
Пример 10:
Исследователь хочет оценить эффективность лечения иглоукалыванием для уменьшения боли у пациентов с хроническими мигренозными головными болями. План состоит в том, чтобы зарегистрировать пациентов, которые страдают от мигрени. Каждому будет предложено оценить тяжесть боли, которую он испытывает при следующей мигрени, прежде чем будет назначено какое-либо лечение.Боль будет регистрироваться по шкале от 1 до 100, где более высокие баллы указывают на более сильную боль. Затем каждый пациент проходит курс лечения иглоукалыванием. При следующей мигрени (после лечения) каждого пациента снова попросят оценить тяжесть боли. Разница в боли будет рассчитана для каждого пациента. Будет проведена двусторонняя проверка гипотезы при α = 0,05, чтобы оценить, существует ли статистически значимая разница в показателях боли до и после лечения. Сколько пациентов должно быть вовлечено в исследование, чтобы гарантировать, что тест имеет мощность 80% для обнаружения разницы в 10 единиц по шкале боли? Предположим, что стандартное отклонение в оценках различий составляет приблизительно 20 единиц.
Сначала вычислите размер эффекта:
Затем подставьте размер эффекта и соответствующие значения Z для выбранных α и мощности, чтобы вычислить размер выборки.
Выборка размером n = 32 пациента с мигренью гарантирует, что двусторонний тест с α = 0,05 имеет мощность 80% для определения средней разницы в 10 баллов в боли до и после лечения, при условии, что все 32 пациента завершили лечение. .
В исследованиях, в которых планируется провести проверку гипотез, сравнивая доли успешных результатов в двух независимых выборках, представляют интерес следующие гипотезы:
H 0 : p 1 = p 2 по сравнению с H 1 : p 1 ≠ p 2
, где p 1 и p 2 — пропорции в двух сравниваемых популяциях.Формула для определения размеров выборки для обеспечения заданной мощности теста приведена ниже:
, где n i — размер выборки, необходимый в каждой группе (i = 1,2), α — выбранный уровень значимости, а Z 1-α/2 — значение из стандартного нормального распределения, содержащего 1-α /2 ниже него, а 1-β — это выбранная степень, а Z 1-β — это значение из стандартного нормального распределения, содержащее 1-β ниже него. ES – размер эффекта, определяемый следующим образом:
ES – размер эффекта, определяемый следующим образом:
,
где |p 1 — p 2 | — абсолютное значение разницы в пропорциях между двумя группами, ожидаемое при альтернативной гипотезе, H 1 , а p — общая пропорция, основанная на объединении данных из двух сравниваемых групп (p можно вычислить, взяв среднее пропорций в двух сравниваемых группах, предполагая, что группы будут примерно одинакового размера).
Пример 11:
Исследователь выдвинул гипотезу о том, что заболеваемость гриппом среди учащихся, которые регулярно посещают спортивные сооружения, выше, чем среди их сверстников, которые этого не делают. Исследование будет проводиться весной. Каждого учащегося спросят, регулярно ли он посещал спортивный комплекс в течение последних 6 месяцев и болел ли он гриппом. Будет проведена проверка гипотезы для сравнения доли учащихся, которые регулярно посещали спортивные сооружения и заболели гриппом, с долей учащихся, которые не посещали спортивные сооружения и заболели гриппом. В течение обычного года примерно 35% учащихся болеют гриппом. Исследователи считают, что увеличение заболеваемости гриппом на 30% среди тех, кто регулярно посещал спортивные сооружения, было бы клинически значимым. Сколько студентов должно быть зачислено в исследование, чтобы мощность теста составила 80% для обнаружения этой разницы в пропорциях? Будет использован двусторонний тест с уровнем значимости 5%.
В течение обычного года примерно 35% учащихся болеют гриппом. Исследователи считают, что увеличение заболеваемости гриппом на 30% среди тех, кто регулярно посещал спортивные сооружения, было бы клинически значимым. Сколько студентов должно быть зачислено в исследование, чтобы мощность теста составила 80% для обнаружения этой разницы в пропорциях? Будет использован двусторонний тест с уровнем значимости 5%.
Сначала мы вычисляем размер эффекта, подставляя доли учащихся в каждой группе, у которых ожидается развитие гриппа, p 1 =0.46 (т.е. 0,35*1,30=0,46) и p 2 =0,35 и общая пропорция p=0,41 (т.е. (0,46+0,35)/2):
Теперь мы подставляем размер эффекта и соответствующие значения Z для выбранных α и мощности, чтобы вычислить размер выборки.
Выборки размером n 1 = 324 и n 2 = 324 гарантируют, что проверка гипотезы будет иметь 80-процентную мощность для выявления 30-процентной разницы в доле учащихся, заболевших гриппом, между теми, кто заболел, и теми, кто не заболел регулярно пользоваться спортивными сооружениями.
Донорский кал? Действительно? Clostridium difficile (также называемый «C. difficile» или «C. diff.») представляет собой вид бактерий, который можно обнаружить в толстой кишке человека, хотя его численность контролируется другой нормальной флорой толстой кишки. Терапия антибиотиками иногда уменьшает нормальную флору в толстой кишке до такой степени, что C. difficile процветает и вызывает инфекцию с симптомами, варьирующимися от диареи до опасного для жизни воспаления толстой кишки. Болезнь от С.difficile чаще всего поражает пожилых людей в больницах или учреждениях длительного ухода и обычно возникает после применения антибиотиков. В последние годы инфекции, вызванные C. difficile, стали более частыми, более тяжелыми и труднее поддающимися лечению. По иронии судьбы C. difficile сначала лечат путем прекращения приема антибиотиков, если они все еще назначаются. Если это не помогло, инфекцию лечили переходом на другой антибиотик. Однако лечение другим антибиотиком часто не приводит к излечению C. тяжелая инфекция. Имеются спорадические сообщения об успешном лечении путем введения фекалий здоровых доноров в двенадцатиперстную кишку пациентов, страдающих C. difficile. (Юк!) Это восстанавливает нормальную микробиоту в толстой кишке и противодействует чрезмерному росту C. diff. Эффективность этого подхода была проверена в рандомизированном клиническом исследовании, опубликованном в New England Journal of Medicine (январь 2013 г.). Исследователи планировали случайным образом назначать пациентов с рецидивирующей инфекцией C. difficile либо на антибактериальную терапию, либо на дуоденальное введение донорских фекалий.Чтобы оценить размер необходимой выборки, исследователи предположили, что вливание фекалий будет успешным в 90% случаев, а терапия антибиотиками будет успешной в 60% случаев. Сколько испытуемых потребуется в каждой группе, чтобы мощность исследования составила 80 % при уровне значимости α = 0,05?
тяжелая инфекция. Имеются спорадические сообщения об успешном лечении путем введения фекалий здоровых доноров в двенадцатиперстную кишку пациентов, страдающих C. difficile. (Юк!) Это восстанавливает нормальную микробиоту в толстой кишке и противодействует чрезмерному росту C. diff. Эффективность этого подхода была проверена в рандомизированном клиническом исследовании, опубликованном в New England Journal of Medicine (январь 2013 г.). Исследователи планировали случайным образом назначать пациентов с рецидивирующей инфекцией C. difficile либо на антибактериальную терапию, либо на дуоденальное введение донорских фекалий.Чтобы оценить размер необходимой выборки, исследователи предположили, что вливание фекалий будет успешным в 90% случаев, а терапия антибиотиками будет успешной в 60% случаев. Сколько испытуемых потребуется в каждой группе, чтобы мощность исследования составила 80 % при уровне значимости α = 0,05?
Ответ
Определение надлежащего дизайна исследования важнее, чем статистический анализ; плохо спланированное исследование никогда нельзя спасти, в то время как плохо проанализированное исследование можно проанализировать повторно. Важнейшим компонентом дизайна исследования является определение соответствующего размера выборки. Размер выборки должен быть достаточно большим, чтобы адекватно ответить на вопрос исследования, но не слишком большим, чтобы охватить слишком много пациентов, когда было бы достаточно меньшего числа. Определение соответствующего размера выборки включает в себя статистические критерии, а также клинические или практические соображения. Определение размера выборки требует командной работы; специалисты по биостатистике должны тесно сотрудничать с исследователями-клиницистами, чтобы определить размер выборки, которая позволит решить интересующий вопрос исследования с достаточной точностью или мощностью для получения клинически значимых результатов.
Важнейшим компонентом дизайна исследования является определение соответствующего размера выборки. Размер выборки должен быть достаточно большим, чтобы адекватно ответить на вопрос исследования, но не слишком большим, чтобы охватить слишком много пациентов, когда было бы достаточно меньшего числа. Определение соответствующего размера выборки включает в себя статистические критерии, а также клинические или практические соображения. Определение размера выборки требует командной работы; специалисты по биостатистике должны тесно сотрудничать с исследователями-клиницистами, чтобы определить размер выборки, которая позволит решить интересующий вопрос исследования с достаточной точностью или мощностью для получения клинически значимых результатов.
В следующей таблице приведены формулы размера выборки для каждого описанного здесь сценария. Формулы организованы по предлагаемому анализу, оценке доверительного интервала или проверке гипотезы.
Ситуация | Размер образца до Оценка доверительного интервала | Размер выборки для проверки гипотезы |
|---|---|---|
Непрерывный результат, Один образец: CI для µ, H 0 : µ = µ 0 | ||
Непрерывный результат, Два независимых образца: CI для ( μ 1 — μ 2 ), H 0 : μ 1 = μ 2 | ||
Непрерывный результат, Два совпадающих образца: ДИ для μ d , H 0 : μ d = 0 | ||
Дихотомический исход, Один образец: CI для p , H 0 : p = p 0 | ||
Дихотомический исход, Два независимых образца: CI для (p 1 -p 2 ) , H 0 : p 1 = p 2 |
- Бушман Н.
 А., Фостер Г., Викерс П.Девочки-подростки и их дети: достижение оптимального веса при рождении. Прибавка массы тела во время беременности и исход беременности с точки зрения срока беременности при родах и массы тела при рождении: сравнение между подростками до 16 лет и взрослыми женщинами. Ребенок: уход, здоровье и развитие. 2001 г.; 27(2):163-171.
А., Фостер Г., Викерс П.Девочки-подростки и их дети: достижение оптимального веса при рождении. Прибавка массы тела во время беременности и исход беременности с точки зрения срока беременности при родах и массы тела при рождении: сравнение между подростками до 16 лет и взрослыми женщинами. Ребенок: уход, здоровье и развитие. 2001 г.; 27(2):163-171. - Фойер Э.Дж., Вун Л.М. ДЕВКАН: вероятность развития или смерти от рака. Версия 4.0. Bethesda, MD: Национальный институт рака, 1999.
- Хауэлл, округ Колумбия. Статистические методы в психологии.Бостон, Массачусетс: Duxbury Press, 1982.
- Флейсс Дж.Л. Статистические методы для ставок и пропорций. Нью-Йорк, штат Нью-Йорк: John Wiley and Sons, Inc., 1981.
- Национальный центр статистики здравоохранения. Health, Соединенные Штаты, 2005 г., с картой тенденций в области здоровья американцев. Хаятсвилл, Мэриленд: Типография правительства США; 2005.
- Plaskon LA, Penson DF, Vaughan TL, Stanford JL.
 Курение сигарет и риск рака предстательной железы у мужчин среднего возраста. Эпидемиология рака, биомаркеры и профилактика.2003 г.; 12: 604-609.
Курение сигарет и риск рака предстательной железы у мужчин среднего возраста. Эпидемиология рака, биомаркеры и профилактика.2003 г.; 12: 604-609. - Руттер М.К., Мейгс Дж.Б., Салливан Л.М., Д’Агостино Р.Б., Уилсон П.В. С-реактивный белок, метаболический синдром и прогнозирование сердечно-сосудистых событий в исследовании Framingham Offspring. Тираж. 2004; 110: 380-385.
- Рамачандран В., Салливан Л.М., Уилсон П.В., Семпос К.Т., Сандстром Дж., Каннел В.Б., Леви Д., Д’Агостино Р.Б. Относительная значимость пограничных и повышенных уровней факторов риска ишемической болезни сердца. Анналы внутренней медицины. 2005 г.; 142: 393-402.
- Векслер Х., Ли Дж. Э., Куо М., Ли Х. Пьянство в колледже в 1990-х годах: продолжающаяся проблема. Результаты Гарвардской школы общественного здравоохранения, 1999 г. Колледж здравоохранения, 2000 г.; 48: 199-210.
.
Ответ на вопрос о массе тела при рождении — стр. 3
Исследователь хочет оценить средний вес детей при рождении в срок (примерно 40 недель беременности) у матерей в возрасте 19 лет и младше. Средняя масса тела при рождении доношенных детей от матерей в возрасте 20 лет и старше составляет 3510 граммов при стандартном отклонении 385 граммов.Сколько женщин в возрасте 19 лет и младше должно быть включено в исследование, чтобы гарантировать, что оценка среднего веса при рождении их детей с доверительным интервалом 95% имеет погрешность, не превышающую 100 граммов?
Средняя масса тела при рождении доношенных детей от матерей в возрасте 20 лет и старше составляет 3510 граммов при стандартном отклонении 385 граммов.Сколько женщин в возрасте 19 лет и младше должно быть включено в исследование, чтобы гарантировать, что оценка среднего веса при рождении их детей с доверительным интервалом 95% имеет погрешность, не превышающую 100 граммов?
Чтобы гарантировать, что оценка 95% доверительного интервала среднего веса при рождении находится в пределах 100 граммов от истинного среднего значения, необходима выборка размера 57. При планировании исследования исследователь должен учитывать тот факт, что у некоторых женщин возможны преждевременные роды.Если женщины включаются в исследование во время беременности, то необходимо будет включить более 57 женщин, чтобы после исключения преждевременно родивших 57 женщин с информацией о результатах были доступны для анализа. Например, если ожидается преждевременные роды у 5% женщин (т. е. 95% родят в срок), то необходимо включить 60 женщин, чтобы гарантировать, что 57 родят в срок. Количество женщин, которые должны быть зачислены, N, рассчитывается следующим образом:
95% родят в срок), то необходимо включить 60 женщин, чтобы гарантировать, что 57 родят в срок. Количество женщин, которые должны быть зачислены, N, рассчитывается следующим образом:
N (количество участников) * (% оставшихся) = желаемый размер выборки
N (0.95) = 57
N = 57/0,95 = 60.
Ответ первокурсников курит — Страница 4
Предположим, что аналогичное исследование было проведено 2 года назад и обнаружило, что распространенность курения среди первокурсников составила 27%. Если исследователь считает, что это разумная оценка распространенности спустя 2 года, ее можно использовать для планирования следующего исследования. Используя эту оценку p, какой размер выборки необходим (при условии, что снова будет использоваться 95% доверительный интервал, и мы хотим такой же уровень точности)?
Чтобы гарантировать, что оценка 95% доверительного интервала доли курящих первокурсников находится в пределах 5% от истинной доли, необходима выборка размером 303. Обратите внимание, что этот размер выборки существенно меньше, чем оцененный выше. Наличие некоторой информации о величине доли в совокупности всегда будет давать размер выборки, меньший или равный размеру, основанному на доле в совокупности, равной 0,5. Однако оценка должна быть реалистичной.
Обратите внимание, что этот размер выборки существенно меньше, чем оцененный выше. Наличие некоторой информации о величине доли в совокупности всегда будет давать размер выборки, меньший или равный размеру, основанному на доле в совокупности, равной 0,5. Однако оценка должна быть реалистичной.
Ответ на проблему с медицинским устройством — стр. 7
Производитель медицинского оборудования производит имплантируемые стенты. В процессе производства примерно 10% стентов признаются бракованными.Производитель хочет проверить, превышает ли доля дефектных стентов 10%. Если в процессе получается более 15% дефектных стентов, необходимо предпринять корректирующие действия. Поэтому производитель хочет, чтобы тест имел мощность 90% для обнаружения разницы в пропорциях этой величины. Сколько стентов необходимо оценить? Для своих расчетов используйте двусторонний тест с уровнем значимости 5%.
Затем подставьте размер эффекта и соответствующие значения z для выбранной альфы и мощности, чтобы вычислить размер выборки.
Размер выборки из 364 стентов гарантирует, что двусторонний тест с α = 0,05 имеет мощность 90% для обнаружения разницы в 0,05 или 5% в доле произведенных дефектных стентов.
Ответ на алкоголь и средний балл — Страница 8
Исследователь планирует исследование для оценки связи между потреблением алкоголя и средним баллом среди выпускников колледжей. План состоит в том, чтобы классифицировать учащихся как сильно пьющих или не употребляющих 5 или более порций алкоголя в обычный день употребления алкоголя в качестве критерия злоупотребления алкоголем.Средние средние баллы будут сравниваться между учащимися, классифицированными как сильно пьющие, и учащимися, не использующими двух независимых выборок для проверки материального положения. Предполагается, что стандартное отклонение среднего балла составляет 0,42, а значимая разница в среднем балле (по отношению к употреблению алкоголя) составляет 0,25 единицы. Сколько выпускников колледжей должно быть зачислено в исследование, чтобы гарантировать, что мощность теста составляет 80%, чтобы обнаружить разницу в 0,25 единицы в средних баллах? Используйте двусторонний тест с уровнем значимости 5%.
Сначала вычислите размер эффекта.
Теперь подставьте размер эффекта и соответствующие значения z для альфы и мощности, чтобы вычислить размер выборки.
Размеры выборки из n i = 44 сильно пьющих и 44 тех, кто выпивает менее пяти порций в обычный день употребления алкоголя, гарантируют, что проверка гипотезы имеет 80%-ную мощность для обнаружения разницы в 0,25 единицы в среднем среднем балле.
Ответ на донорский кал — Страница 8
Сначала мы вычисляем размер эффекта, подставляя доли пациентов, которые, как ожидается, будут излечены при каждом лечении, p 1 =0.6 и р 2 =0,9, а общая пропорция, р=0,75:
Теперь мы подставляем размер эффекта и соответствующие значения Z для выбранных a и мощности, чтобы вычислить размер выборки.
Выборки размером n 1 = 33 и n 2 = 33 гарантируют, что проверка гипотезы будет иметь 80% мощности для обнаружения этой разницы в доле пациентов, излеченных от C. diff. инфузией фекалий по сравнению с антибактериальной терапией.
diff. инфузией фекалий по сравнению с антибактериальной терапией.
Фактически, исследователи зачислили по 38 человек в каждую группу, чтобы учесть отсев. Тем не менее, исследование было остановлено после промежуточного анализа. Из 16 пациентов в группе инфузии у 13 (81%) диарея, связанная с C. difficile, разрешилась после первой инфузии. Остальным 3 пациентам была проведена повторная инфузия фекалий от другого донора с разрешением у 2 пациентов. Разрешение инфекции C. difficile произошло только у 4 из 13 пациентов (31%), получавших антибиотик ванкомицин.
экспонентов
показатель степени числа говорит сколько раз использовать число при умножении.
В 8 2 «2» говорит о том, что при умножении дважды используется 8,
, поэтому 8 2 = 8 × 8 = 64
Прописью: 8 2 можно было бы назвать «8 в степени 2» или «8 во второй степени», или
просто «8 в квадрате»
Экспоненты также называются степенями или индексами.
Еще несколько примеров:
Пример:
5 3 = 5 × 5 × 5 = 125
- Прописью: 5 3 можно назвать «5 в третьей степени», «5 в степени 3» или просто
«5 кубов»
Пример:
2 4 = 2 × 2 × 2 × 2 = 16
- Прописью: 2 4 можно было бы назвать «2 в четвертой степени» или «2 в степени 4» или просто
«2 к 4-му»
Экспоненты упрощают запись и использование многих операций умножения
Пример: 9 6 легче писать и читать, чем 9 × 9 × 9 × 9 × 9 × 9
Вы можете умножать любое число само по себе столько раз , сколько хотите, используя показатели степени.4 = 2 × 2 × 2 × 2 = 16
Отрицательные показатели
Отрицательный? Что может быть противоположным умножению? Разделение!
Итак, мы каждый раз делим на число, что равносильно умножению на 1 число
Пример: 8 -1 = 1 8 = 0,125
Мы можем продолжить так:
Пример: 5 -3 = 1 5 × 1 5 × 1 5 = 0. 008
008
Но часто проще сделать так:
5 -3 также можно рассчитать как:
1 5 × 5 × 5 = 1 5 3 = 1 125 = 0,008
Отрицательный? Переверни позитив!
Последний пример показал более простой способ обработки отрицательных показателей:
|
Другие примеры:
| Отрицательная экспонента | Обратная величина Положительная экспонента | Ответить | ||
|---|---|---|---|---|
| 4 -2 | = | 1 / 4 2 | = | 1/16 = 0. 0625 0625 |
| 10 -3 | = | 1 / 10 3 | = | 1/1000 = 0,001 |
| (-2) -3 | = | 1 / (-2) 3 | = | 1/(-8) = -0,125 |
Что делать, если показатель степени равен 1 или 0?
| 1 | Если показатель степени равен 1, то у вас есть только само число (пример 9 1 = 9 ) | |
| 0 | Если показатель степени равен 0, то вы получаете 1 (пример 9 0 = 1 ) | |
А как насчет 0 0 ? Это может быть либо 1, либо 0, поэтому люди говорят, что это «неопределенное» . |
Все имеет смысл
Если вы посмотрите на эту таблицу, вы увидите, что положительный, нулевой или
отрицательные показатели на самом деле являются частью одного и того же (довольно простого) шаблона:
| Пример: Степени числа 5 | |||
|---|---|---|---|
| .. и т.д.. | |||
| 5 2 | 5 × 5 | 25 | |
| 5 1 | 5 | 5 | |
| 5 0 | 1 | 1 | |
| 5 -1 | 1 5 | 0.2 | |
| 5 -2 | 1 5 × 1 5 | 0,04 | |
. . и т.д.. . и т.д.. | |||
Будьте осторожны с группировкой
Во избежание путаницы используйте круглые скобки () в таких случаях:
| С () : | (−2) 2 = (−2) × (−2) = 4 |
| Без () : | -2 2 = -(2 2 ) = -(2 × 2) = -4 |
| С () : | (аб) 2 = аб × аб |
| Без () : | ab 2 = a × (b) 2 = a × b × b |
305, 1679, 306, 1680, 1077, 1681, 1078, 1079, 3863, 3864
Калькулятор мощности насоса
Мощность гидравлического насоса
Идеальная гидравлическая мощность для привода насоса зависит от
- массового расхода
- плотности жидкости
- перепада высоты
5 от одной высоты до другой или общий компонент потери напора в системе — и может быть рассчитан как
P ч(кВт) = q ρ gh / (3.
6 10 6 ) 6 )
= QP / (3.6 10 6 ) (1)
где
P H (кВт) = Гидравлическая мощность (кВт)
Q = поток (M 3 / H)
9 ρ = плотность жидкости (кг / м 3 )
9 г = ускорение тяжести (9,81 м / с 2 )
H = дифференциальная головка (м)
p = дифференцированное давление (N / M 2 , PA)
Гидравлическая мощность лошади может быть рассчитана как:
P ч(л.с.) = P ч(кВт) / 0.746 (2)
P
3 H (HP) = Гидравлические лошадиных сил (HP)
или — альтернативно
P H (HP) = Q GPM = Q FT H FT SG / (3960 η ) (2b)
, где
Q GPM = flow (GPM)
H FT = Дифференциальная головка (FT)
SG = Удельный вес (1 для воды)
η = насос КПД
Пример — перекачка воды насосом
1 м 3 /ч ред головка 10 м . Теоретическая мощность насоса может быть рассчитана как
Теоретическая мощность насоса может быть рассчитана как
P ч(кВт) = ( 1 м 3 /ч ) (1000 кг/м 3 ) (9,81 м/с 2
2 ) ( м) / (3,6 10 6 )
= 0,027 кВт
Мощность насоса на валу
из насоса и можно рассчитать как
P
3 S (кВт) = P
3 H (KW) / η ( 3)
Откуда
P S (кВт) = вал мощности (кВт)
η = эффективность насоса
онлайн Калькулятор насоса — единицы СИ
Приведенный ниже калькулятор можно использовать для расчета гидравлической мощности и мощности на валу насоса:
Онлайн-калькулятор насоса — британские единицы
Приведенный ниже калькулятор можно использовать для расчета гидравлической мощности и мощности на валу насоса с помощью Имперские единицы:
Связанные мобильные приложения от The Engineering ToolBox
— бесплатные приложения для автономного использования на мобильных устройствах.
Функция поиска в Power Apps — Power Apps
- Статья
- 2 минуты на чтение
Полезна ли эта страница?
Пожалуйста, оцените свой опыт
да
Нет
Любая дополнительная обратная связь?
Отзыв будет отправлен в Microsoft: при нажатии кнопки отправки ваш отзыв будет использован для улучшения продуктов и услуг Microsoft.Политика конфиденциальности.
Представлять на рассмотрение
Спасибо.
В этой статье
Находит текстовую строку, если она существует, в другой строке.
Описание
Функция Find ищет строку в другой строке и чувствительна к регистру.

 Если он планирует вернуться в город А пустым по той же трассе и потратить на это 1 час, ему понадобится развить такую же мощность или меньшую?
Если он планирует вернуться в город А пустым по той же трассе и потратить на это 1 час, ему понадобится развить такую же мощность или меньшую?
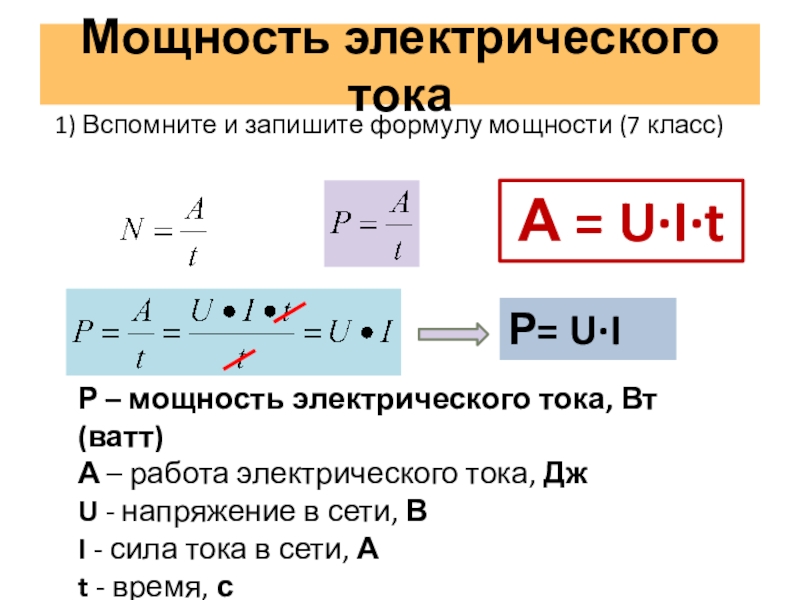
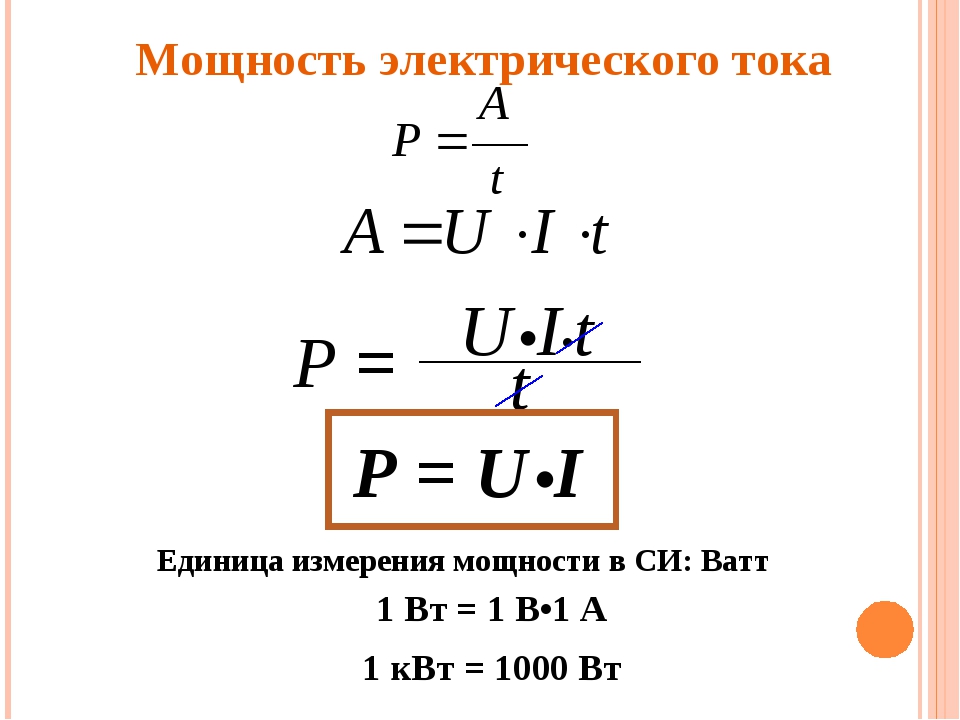

 А., Фостер Г., Викерс П.Девочки-подростки и их дети: достижение оптимального веса при рождении. Прибавка массы тела во время беременности и исход беременности с точки зрения срока беременности при родах и массы тела при рождении: сравнение между подростками до 16 лет и взрослыми женщинами. Ребенок: уход, здоровье и развитие. 2001 г.; 27(2):163-171.
А., Фостер Г., Викерс П.Девочки-подростки и их дети: достижение оптимального веса при рождении. Прибавка массы тела во время беременности и исход беременности с точки зрения срока беременности при родах и массы тела при рождении: сравнение между подростками до 16 лет и взрослыми женщинами. Ребенок: уход, здоровье и развитие. 2001 г.; 27(2):163-171. Курение сигарет и риск рака предстательной железы у мужчин среднего возраста. Эпидемиология рака, биомаркеры и профилактика.2003 г.; 12: 604-609.
Курение сигарет и риск рака предстательной железы у мужчин среднего возраста. Эпидемиология рака, биомаркеры и профилактика.2003 г.; 12: 604-609. 6 10 6 ) 6 )
6 10 6 ) 6 )