Как найти период через частоту: Колебания: частота, период

Содержание

Колебания: частота, период

Прежде, чем начинать решать “серьезные” задачи, нужно хорошо освоить терминологию, основу. Поэтому вводная статья посвящена определению периода, частоты, циклической частоты колебаний, амплитуды и общей записи закона колебаний.

Колебания

Задача 1. Грузик на пружине за t=6 с совершил n=18 колебаний. Найти период и частоту колебаний.

Период – время одного полного колебания:

$T=\frac{t}{n}=\frac{6}{18}=\frac{1}{3}$

Частота колебаний

$\nu=\frac{1}{T}=3$

Ответ: $T=\frac{1}{3}$ c, $\nu=3$ Гц.

Задача 2. Груз на пружине за t=1 мин совершает n=86 колебаний. Определить период колебаний и циклическую частоту.

Период – время одного полного колебания:

$T=\frac{t}{n}=\frac{60}{86}=0,7$

Циклическая частота (угловая частота) равна:

$\omega=2\pi \nu=\frac{2\pi}{T}=\frac{2\pi}{0,7}=8,98$

Ответ: T=0,7 c, $\omega =9$ рад/с.

Задача 3. За 1 с комар совершает 600 взмахов крыльями, а период колебаний крыльев шмеля 5 мс. Какое из насекомых и на сколько сделает в полете большее количество взмахов за 1 мин?

Частота колебаний крыльев комара – 600 Гц. Частота колебаний крыльев шмеля равна:

$\nu=\frac{1}{T}=\frac{1}{0,005}=200$

Следовательно, комар делает на 400 взмахов за 1 с больше, чем шмель, а за 1 минуту – на 24000 взмахов.

Ответ: комар, на 24000.

Задача 4. Крылья пчелы колеблются с частотой f= 240 Гц. Сколько взмахов крыльями сделает пчела, пока долетит до цветочного поля, расположенного на расстоянии в 500 м, если она летит со скоростью $\upsilon = 4$ м/с?

Если скорость полета пчелы известна и известно расстояние, определим время полета:

$t=\frac{S}{t}$

Тогда количество взмахов за это время равно:

$n=f \cdot \frac{S}{\upsilon}=240 \cdot \frac{500}{4}=30000$

Ответ: 30 000.

Задача 5. Найти амплитуду, период и частоту колебаний, если закон колебаний материальной точки имеет вид $x =5 \cos 6,28 t$ (см).

Амплитуда – первое число в законе колебаний, то есть A=5 . Циклическая частота – множитель при , $\omega=6,28$ . Тогда период

$T=\frac{2\pi}{\omega}=1$

А частота:

$\nu=\frac{1}{T}=1$

Ответ: T=1 с, $\nu=1$ Гц.

Движение по окружности, период обращения и частота.

1. Равномерное движение по окружности

Внимание следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения.

Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу.

Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня.

Таким образом,

Во время движения по кругу скорость в любой точке траектории направлена по касательной к окружности в этой точке.

Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время меняется.

2. Период вращения и вращающаяся частота

Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения.

Период обращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот.

Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток.

При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле:

$T = \frac{t}{N}.$

Если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности: 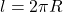$l = 2 \pi R$ . Итак,

$\nu = \frac{l}{T} = \frac{2 \pi R}{T}.$

Движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой:

частота вращения равна количеству полных оборотов за одну секунду.

Частота вращения и период обращения связаны следующим соотношением:

$\nu=\frac{1}{T}$

Частоту в СИ измеряют в

$\frac{1}{c}(c^{-1})$

3. Вращательное движение

В природе довольно распространенный вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. Д.

Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусов.

Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу крупнейшего радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.

ПРОВЕРЬТЕ СЕБЯ

Приведите два-три примера криволинейного движения.
Приведите два-три примера равномерного движения по кругу.
Что такое вращательное движение? Приведите примеры такого движения.
Как направлена мгновенная скорость при движении по кругу Приведите два-три примера.

1.Равномерное движение по кругу. Внимание учащихся следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения. Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу. Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня. Таким образом, • Во время движения по кругу скорость в любой точке траектории направлена по касательной к окружности в этой точке. Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время изменяется.

2. Период вращения и частота вращения. Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения. • Период вращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот. Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток. При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле: если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности:. Итак, движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой: • вращающаяся частота равна количеству полных оборотов в одну секунду. Частота вращения и период обращения связаны следующим соотношением: 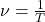$\nu=\frac{1}{T}$ Частоту в СИ измеряют в обратных секундах.

3. Вращательного движения. В природе довольно распространенно вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. д.Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусив. Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу самого большого радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.

Период и частота

Физика > Период и частота

Как найти период и частоту – определение и формула. Читайте, что такое угловая частота, цикл, частоты синусоидальных волн, единицы измерения, уравнения.

Период – продолжительность цикла повторяющегося события, а частота – количество циклов за временной промежуток.

Задача обучения

Преобразование между частотой и периодом.

Основные пункты

Регулярно повторяющееся движение – периодическое. Одно полное повторение – цикл.
Продолжительность цикла – период.
Частота отображает число циклов, осуществленное за определенный временной промежуток. Это обратная величина периода и определяется формулой f = 1/T.
Некоторые перемещения лучше всего характеризовать угловой частотой (ω). Она относится к угловому смещению за временной промежуток. Вычисляется по формуле: ω = 2πf.

Термины

Угловая частота – угловое смещение за временной промежуток.
Период – длительность одного цикла в повторяющемся событии.
Частота – соотношение количества раз (n) периодического явления за временную единицу (t): f = n/t.

Пример

Когда-то существовал викторианский трюк. Человеку нужно было вслушаться в звук мухи, воспроизвести музыкальную ноту на пианино и сказать, сколько раз летучая мышь ударила крыльями за секунду. Если это 200 раз в секунду, то частота движения – f = 200/1 с = 200 Гц. Период составляет 1/200-ю секунду: T = 1/f = (1/200) с = 0.005 с.

Период и частота

Эти термины используют для выражения повторного движения. Период – время, которое тратится на одно повторение. Один полноценный проход – цикл. Частота – количество циклов за конкретный временной промежуток (f).

Синусоидальные волны разных частот. Нижние обладают более высокими частотами, а горизонтальная ось отображает время.

Понятия выражаются в формуле: F = 1/T.

Допустим, частота сердца новорожденного составляет 120 раз в минуту, а период – половина секунды. Если вы отточите интуицию на ожидание сопряженности больших частот с короткими периодами (и наоборот), то избежите ошибок.

Единицы

Чаще всего частота рассчитывается в герцах (Гц). 1 Гц указывает на то, что событие происходит раз в секунду. Традиционная единица, применимая во вращающихся механических приборах, – обороты в минуту (об/мин). Единица периода – секунда.

Угловая частота

Частота периодического движения лучше всего передается через угловую частоту – ω. Она относится к угловому смещению на единицу времени или скорости перемены состояния синусоидальной формы волны. В виде формулы:

Колеса совершают вращение с частотой f циклов в секунду, что можно описать как ω радиан в секунду. Механическая связь позволяет линейным колебаниям поршней парового двигателя руководить колесами

у (t) = sin(θ(т)) = sin(ωt) = sin(2πft)

ω = 2πf

Угловая частота часто отображается в радианах на секунду.

Период обращения | Все Формулы

\[ \]

Период обращения — Время, за которое тело совершает один оборот, т.е. поворачивается на угол 2 пи, называется периодом обращения

$\LARGE T=\frac{2\pi }{\omega }=\frac{1}{n }$

Сидерические периоды обращения планет Солнечной системы:

Период обращения (меркурий, венера, солнце, земля)

Найдем период обращения:

Если, например, за время t = 4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой Т и определяется по формуле

$\Large T=\frac{1}{n }$

Найдем частоту обращения:

Если, например, за время t = 4 с тело совершило n = 20 оборотов,то за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой V (читается: ню) и определяется по формуле:

$\Large \omega =\frac{n}{T}$

За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с-1 (читается: секунда в минус первой степени).

В формуле мы использовали :

T — Период обращения

$\omega$

— Частота обращения

n — Число оборотов

ФИЗИКА: Задачи на Механические колебания — Ответы и решения

Задачи на Механические колебания с решениями

Формулы, используемые на уроках «Задачи на Механические колебания».

Название величины	Обозначение	Единица измерения	Формула
*Амплитуда колебаний*	A	м
*Период колебаний*	T	с	T = 1 / v ; T = t / N
*Частота колебаний*	v	Гц	*v = 1 / T ;* *v = N / t*
*Число колебаний за какое-то время*	N		*N = t /T ;* *N = vt*
*Время*	t	с	t = NT ; t = N / v
*Циклическая частота колебаний*	ω	Гц
*Период колебаний пружинного маятника*	T	c
*Период колебаний математического маятника*	T	c
*Уравнение гармонических колебаний*			x(t) = Asin(ωt+φ₀)

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
Шарик на нити совершил 60 колебаний за 2 мин. Определите период и частоту колебаний шарика.

Задача № 2.
На рисунке изображен график зависимости координаты от времени колеблющегося тела.

По графику определите: 1) амплитуду колебаний; 2) период колебаний; 3) частоту колебаний; 4) запишите уравнение координаты.

Задача № 3.
Амплитуда незатухающих колебаний точки струны 2 мм, частота колебаний 1 кГц. Какой путь пройдет точка струны за 0,4 с? Какое перемещение совершит эта точка за один период колебаний?

Задача № 4.
Пользуясь графиком изменения координаты колеблющегося тела от времени, определить амплитуду, период и частоту колебаний. Записать уравнение зависимости x(t) и найти координату тела через 0,1 и 0,2 с после начала отсчета времени.

Задача № 5.
Какова длина математического маятника, совершающего гармонические колебания с частотой 0,5 Гц на поверхности Луны? Ускорение свободного падения на поверхности Луны 1,6 м/с².

Задача № 6.
Груз массой 400 г совершает колебания на пружине с жесткостью 250 Н/м. Амплитуда колебаний 15 см. Найти полную механическую энергию колебаний и наибольшую скорость движения груза.

Задача № 7.
Частота колебаний крыльев вороны в полете равна в среднем 3 Гц. Сколько взмахов крыльями сделает ворона, пролетев путь 650 м со скоростью 13 м/с?

Задача № 8.
Гармоническое колебание описывается уравнением
Чему равны циклическая частота колебаний, линейная частота колебаний, начальная фаза колебаний?

Задача № 9.
Математический маятник длиной 0,99 м совершает 50 полных колебаний за 1 мин 40 с. Чему равно ускорение свободного падения в данном месте на поверхности Земли? (Можно принять π² = 9,87.)

Задача № 10.
ОГЭ
Как и во сколько раз изменится период колебаний пружинного маятника, если шарик на пружине заменить другим шариком, радиус которого вдвое меньше, а плотность — в два раза больше?

Задача № 11.
ЕГЭ
Два математических маятника за одно и то же время совершают — первый N₁ = 30, а второй — N₂ = 40 колебаний. Какова длина каждого из них, если разность их длин Δl = 7 см?

Краткая теория для решения Задачи на Механические колебания.

Это конспект по теме «ЗАДАЧИ на Механические колебания». Выберите дальнейшие действия:

Перевод длины волны в частоту для всего диапазона электромагнитных колебаний

Онлайн калькулятор перевода длины волны в частоту для широкого диапазона частот, включая радиоволны, микроволны, инфракрасное излучение,
видимый свет, ультрафи- олетовое излучение, рентгеновские и гамма лучи.

Электромагнитные колебания — это взаимосвязанные колебания электрического и магнитного полей, проявляющиеся в периодическом изменении
напряжённости (E) и индукции (B) поля в электроцепи или пространстве. Эти поля перпендикулярны друг другу в направлении движения волны
(Рис.1) и, в зависимости от частоты, представляют собой: радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое
излучение, рентгеновские либо гамма-лучи.

Рис.1

Длина волны, обозначаемая буквой λ и измеряемая в метрах —
это расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе.
Другими словами, это расстояние, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π.

Время, за которое волна успевает преодолеть это расстояние (λ), т. е. интервал времени, за который периодический колебательный процесс
повторяется, называется периодом колебаний, обозначается буквой ፐ (тау) или Т и измеряется в метрах.

Частота электромагнитных колебаний связана с периодом простейшим соотношением:
f (Гц) = 1 / T (сек).

Скорость распространения электромагнитных волн в вакууме (v) равна скорости
света и составляет величину:
v = С = 299792458 м/сек.

В среде эта скорость уменьшается: v = С / n, где
n > 1 — это показатель преломления среды.

Абсолютный показатель преломления любого газа (в том числе воздуха) при обычных условиях мало чем отличается от единицы, поэтому
с достаточной точностью его можно не учитывать в условиях распространения электромагнитных волн в воздушном пространстве.

Соотношение, связывающее длину волны со скоростью распространения в общем случае, выглядит следующим образом:
λ (м) = v (м/сек) *Т (сек) = v (м/сек) / f (Гц).

И окончательно для воздушной среды:

λ (м) = 299792458 *Т (сек) = 299792458 / f (Гц).

Прежде чем перейти к калькуляторам, давайте рассмотрим шкалу частот и длин волн непрерывного диапазона электромагнитных волн,
которая традиционно разбита на ряд поддиапазонов. Соседние диапазоны могут немного перекрываться.

Диапазон	Полоса частот	Длина волны
Сверхдлинные радиоволны	3…30 кГц	100000…10000 м
Длинные радиоволны	30…300 кГц	10000…1000 м
Средние радиоволны	300…3000 кГц	1000…100 м
Короткие радиоволны	3…30 МГц	100…10 м
Метровый радиодиапазон	30…300 МГц	10…1 м
Дециметровый радиодиапазон	300…3000 МГц	1…0,1 м
Сантиметровый СВЧ диапазон	3…30 ГГц	10…1 см
Микроволновый СВЧ диапазон	30…300 ГГц	1…0,1 см
Инфракрасное излучение	0,3…405 ТГц	1000…0,74 мкм
Красный цвет	405…480 ТГц	740…625 нм
Оранжевый цвет	480…510 ТГц	625…590 нм
Жёлтый цвет	510…530 ТГц	590…565 нм
Зелёный цвет	530…600 ТГц	565…500 нм
Голубой цвет	600…620 ТГц	500…485 нм
Синий цвет	620…680 ТГц	485…440 нм
Фиолетовый цвет	680…790 ТГц	440…380 нм
Ультрафиолетовое излучение	480…30000 ТГц	400…10 нм
Рентгеновское излучение	30000…3000000 ТГц	10…0,1 нм
Гамма излучение	3000000…30000000 ТГц	0,1…0,01 нм

А теперь можно переходить к калькуляторам.

КАЛЬКУЛЯТОР РАСЧЁТА ДЛИНЫ ВОЛНЫ ПО ЧАСТОТЕ

КАЛЬКУЛЯТОР РАСЧЁТА ЧАСТОТЫ ПО ДЛИНЕ ВОЛНЫ

В радиочастотной практике имеет распространение величина Kp, называемая коэффициентом укорочения. Однако здесь
существует некоторая путаница. Одни источники интерпретируют эту величину, как отношение длины волны в среде к длине волны в вакууме,
т. е. численно равной Kp = 1/n, где n — это, как мы помним, показатель преломления среды.
Другие, наоборот — как отношение длины волны в вакууме к длине волны в среде, т. е. Kp = n.

Поэтому надо иметь в виду — если Kp > 1, то значение показателя преломления среды, которое следует подставлять в калькулятор n = Kp, а
если Kp

Как вы рассчитываете период и частоту?

Тригонометрия

Наука

Анатомия и физиология
Астрономия
Астрофизика
Биология
Химия
наука о планете Земля
Наука об окружающей среде
Органическая химия
Физика

Математика

Алгебра
Исчисление
Геометрия

matlab — Как найти период периодической функции с помощью БПФ?

Переполнение стека

Около
Продукты
Для команд

Переполнение стека
Общественные вопросы и ответы
Переполнение стека для команд
Где разработчики и технологи делятся частными знаниями с коллегами
Вакансии
Программирование и связанные с ним технические возможности карьерного роста
Талант
Нанимайте технических специалистов и создавайте свой бренд работодателя
Реклама
Обратитесь к разработчикам и технологам со всего мира
О компании

Как рассчитать угловую частоту массы на пружине

Образование
Наука
Физика
Как рассчитать угловую частоту массы на пружине

Стивен Хольцнер

По физике, вы можете применить закон Гука вместе с концепцией простого гармонического движения, чтобы найти угловую частоту массы на пружине. А поскольку вы можете связать угловую частоту и массу пружины, вы можете найти смещение, скорость и ускорение массы.

Закон Гука гласит, что

F = — kx

, где F — сила, прилагаемая пружиной, k — жесткость пружины, а x — смещение от равновесия. Благодаря Исааку Ньютону вы знаете, что сила также равна массе, умноженной на ускорение:

F = ма

Эти уравнения сил даны в терминах смещения и ускорения, которые вы видите в простом гармоническом движении в следующих формах:

Подставив эти два уравнения в уравнения сил, вы получите следующее:

Теперь вы можете найти угловую частоту (угловую скорость) массы на пружине, поскольку она связана с жесткостью пружины и массой.Вы также можете связать угловую частоту с частотой и периодом колебаний, используя следующее уравнение:

С помощью этого уравнения и формулы угловой частоты можно записать формулы для частоты и периода в терминах k и m:

Предположим, что пружина на рисунке имеет жесткость пружины k, , равную 15 ньютонам на метр, и что вы прикрепляете к пружине 45-граммовый шарик.

Направление усилия пружины.

Какой период колебания? После преобразования граммов в килограммы все, что вам нужно сделать, это ввести числа:

Период колебания 0,34 секунды. Сколько отказов вы получите в секунду? Количество отказов представляет частоту, которую вы найдете следующим образом:

Вы получаете почти 3 колебания в секунду.

Поскольку вы можете связать угловую частоту,

на жесткость пружины и массу на конце пружины, вы можете предсказать смещение, скорость и ускорение массы, используя следующие уравнения для простого гармонического движения:

Используя пример пружины на рисунке — с жесткостью пружины 15 ньютонов на метр и прикрепленным шариком весом 45 грамм — вы знаете, что угловая частота следующая:

Вы можете проверить, как работают единицы.Помните, что

, поэтому единицы, которые вы получаете из уравнения для угловой скорости, составляют

Скажем, например, что вы тянете мяч на 10,0 сантиметра перед тем, как отпустить его (делая амплитуду 10,0 сантиметра). В этом случае вы обнаружите, что

Об авторе книги

Стивен Хольцнер, доктор философии, работал редактором журнала PC Magazine и работал на факультете Массачусетского технологического института и Корнельского университета.Он написал Physics II For Dummies , Physics Essentials For Dummies и Quantum Physics for Dummies .

Колебания: частота, период

Движение по окружности, период обращения и частота.

Период и частота

Задача обучения

Основные пункты

Термины

Пример

Период и частота

Единицы

Угловая частота

Период обращения | Все Формулы

ФИЗИКА: Задачи на Механические колебания — Ответы и решения

Задачи на Механические колебания с решениями

Название величины

Обозначение

Единица измерения

Формула

Амплитуда колебаний

A

м

Период колебаний

T

с

T = 1 / v ;

T = t / N

Частота колебаний

v

Гц

v = 1 / T ;

v = N / t

Число колебаний за какое-то время

N

N = t /T ;

N = vt

Время

t

с

t = NT ;

t = N / v

Циклическая частота колебаний

ω

Гц

<img decoding="async" src="/800/600/https/uchitel.pro/wp-content/uploads/2018/12/2018-12-11_19-48-01.jpg" alt="" />

Период колебаний пружинного маятника

T

c

<img decoding="async" src="/800/600/https/uchitel.pro/wp-content/uploads/2018/12/2018-12-11_19-50-53.jpg" alt="" />

Период колебаний математического маятника

T

c

<img decoding="async" src="/800/600/https/uchitel.pro/wp-content/uploads/2018/12/2018-12-11_19-51-08.jpg" alt="" />

Уравнение гармонических колебаний

x(t) = Asin(ωt+φ0)

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Краткая теория для решения Задачи на Механические колебания.

Перевод длины волны в частоту для всего диапазона электромагнитных колебаний

Как вы рассчитываете период и частоту?

Наука

Математика

matlab — Как найти период периодической функции с помощью БПФ?

Как рассчитать угловую частоту массы на пружине

Об авторе книги

alexxlab

Вам также может понравиться

Обозначение выключателей на схемах: Обозначение розеток и выключателей на строительных чертежах и электрических схемах.

Какие бывают припои: Виды припоя (ПОС30, ПОС40 и ПОС61) | Баббит | Олово | Припой | Купорос | Никель

Реле времени с выдержкой времени: Модульные реле времени (таймеры) Schneider Electric RE17

Добавить комментарий Отменить ответ

x(t) = Asin(ωt+φ₀)