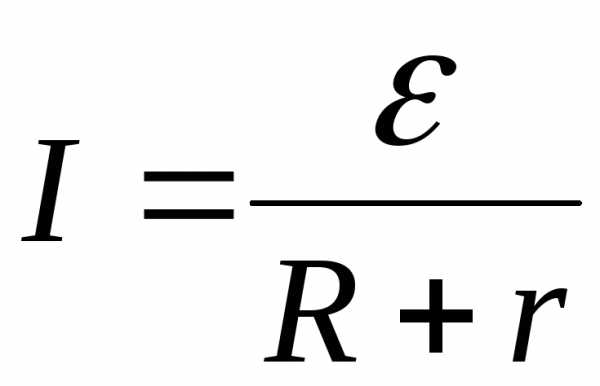3.1.Сопротивление параллельного контура при резонансе. Как найти сопротивление контура

3.1.Сопротивление параллельного контура при резонансе

Сопротивление параллельного контура при резонансе чисто активное; напряжение на контуре и ток в неразветвленной части цепи совпадают по фазе. Реальный контур отбирает от питающего генератора некоторое количество энергии, которое превращается в тепло на активном сопротивлении R (сопротивлении потерь) контура. На основании закона сохранения энергии мощность, отдаваемая генератором, и мощность, расходуемая на тепло в активном сопротивлении контура, равны.

Мощность, отдаваемая генератором, определяется выражением

где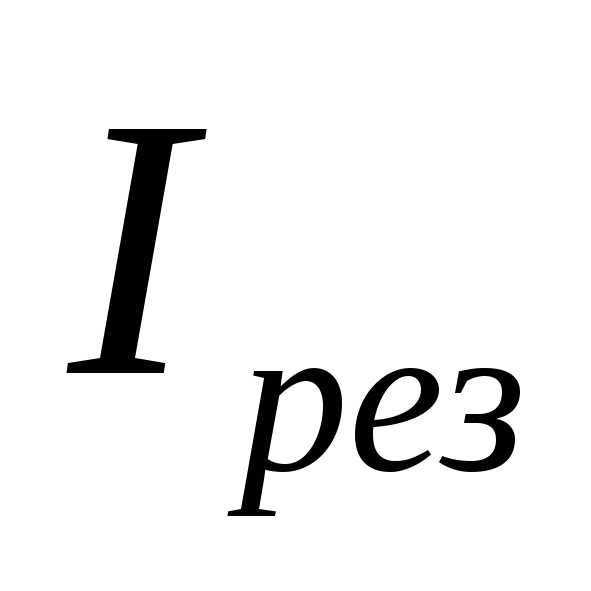–ток в неразветвленной части цепи при резонансе;

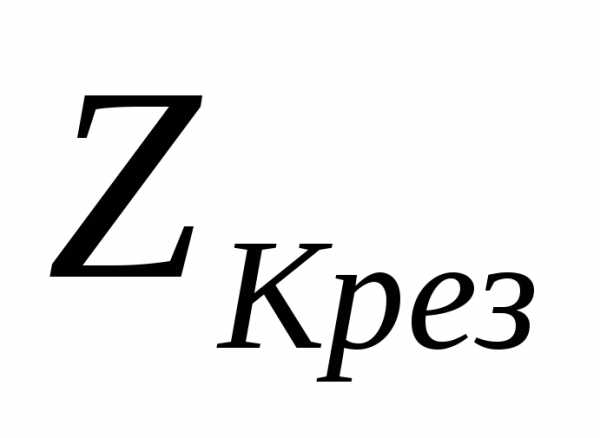–сопротивление контура при резонансе.

Мощность, расходуемая в активном сопротивлении R, равна

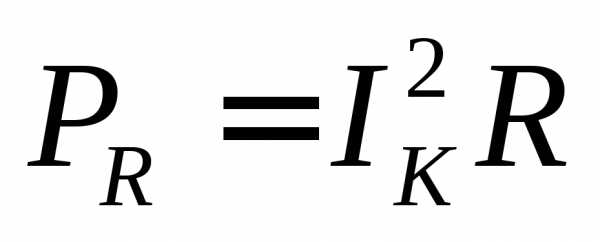где 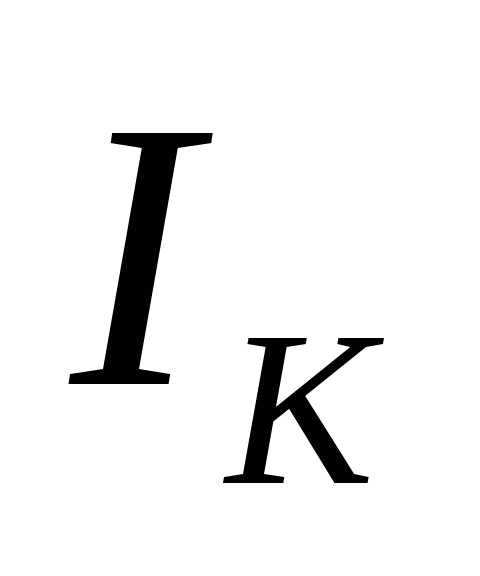–ток внутри контура при резонансе ().

R –активное сопротивление, учитывающее потери энергии вкатушке.

Если напряжение на зажимах генератора 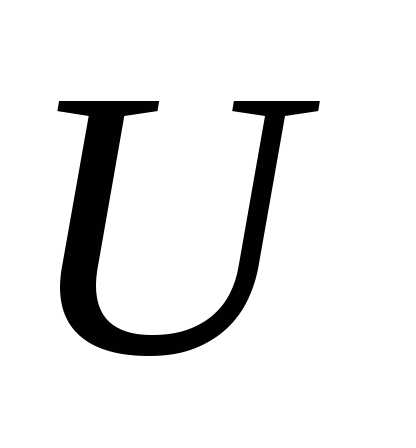, то

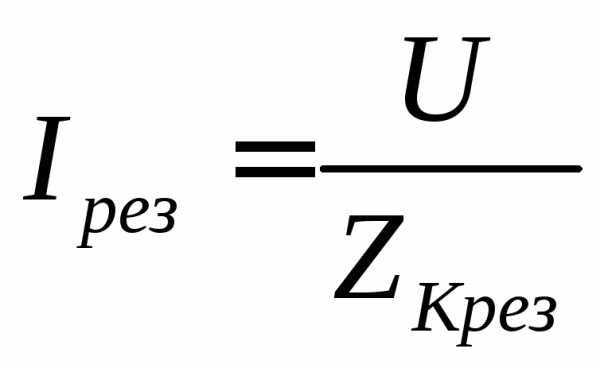
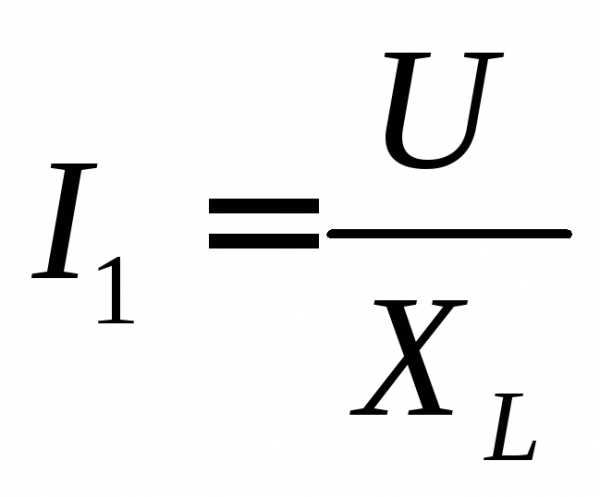Имея в виду последние два выражения, приравняем мощности и: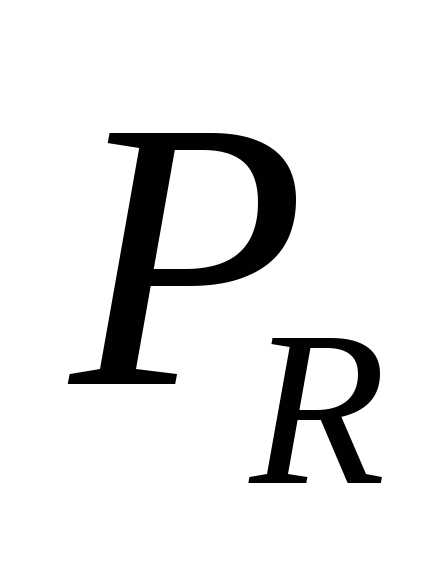

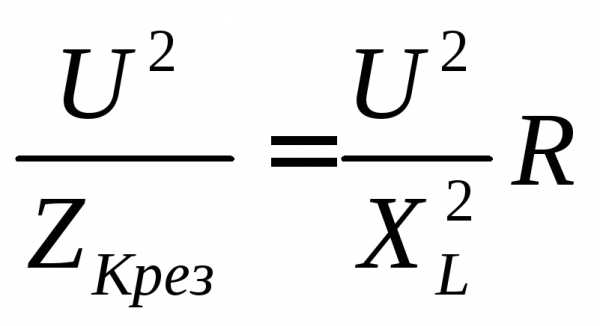Отсюда

или

Так как , то,

где 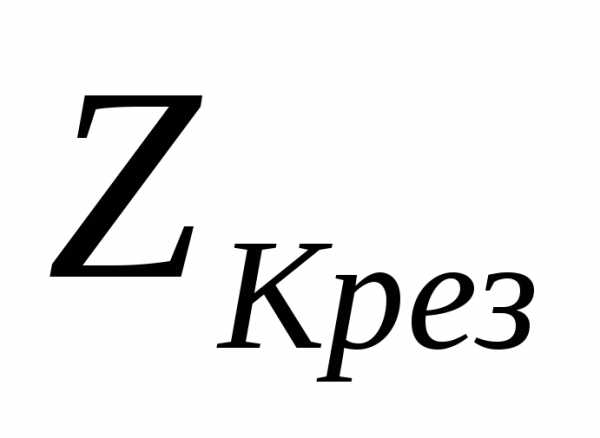– резонансное сопротивление контура в омах;

L –индуктивность контура в генри;

С –емкость контура в фарадах;

R – активное сопротивление в омах.

Резонансное сопротивление параллельного контура зависит от величины активного сопротивления потерь R и от соотношения величин L и С, т. е. от волнового сопротивления контура. Чем больше R, тем больше энергии расходуется в нем на тепло и тем больше энергии (большая мощность) поступает от генератора в контур. Следовательно, чем больше сопротивление потерь R, тем больше ток 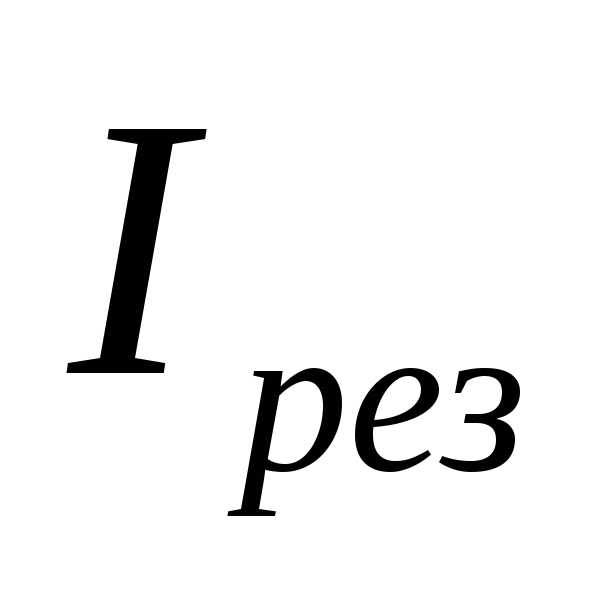в общей части цепи. Но по величине тока можно судить о величине сопротивления контура: чем больше ток, тем меньше сопротивление. Поэтому чем больше сопротивление потерь, тем меньше сопротивление параллельного контура при резонансе. В отсутствиеR .

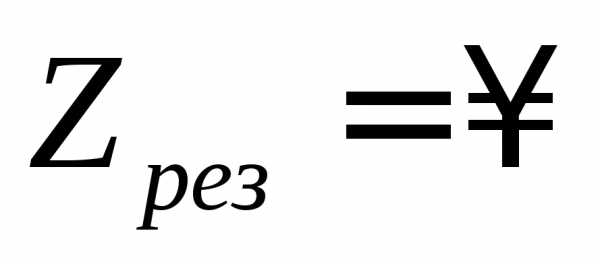3.2. Зависимость сопротивления параллельного контура от частоты

Пусть частота генератора, питающего параллельный контур, изменяется в широких пределах. При повышении частоты генератора емкостное сопротивление конденсатора уменьшается:

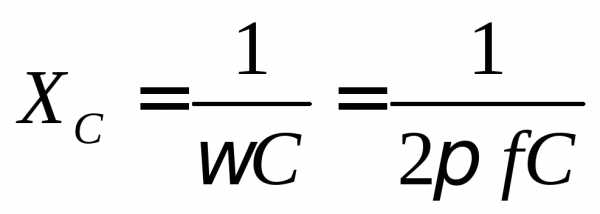а индуктивное сопротивление увеличивается:

При этом ток в емкостной ветви увеличивается, а в индуктивной уменьшается. При частоте ниже резонансной в общей цепи преобладает индуктивный ток и контур ведет себя как индуктивное сопротивление. При частоте генератора, равной собственной частоте контура , емкостной и индуктивный токи равны по величине и реактивный ток в общей части цепи равен нулю (состояние резонанса). Сопротивление контура имеет чисто активный характер и значительную величину, определяемую формулой

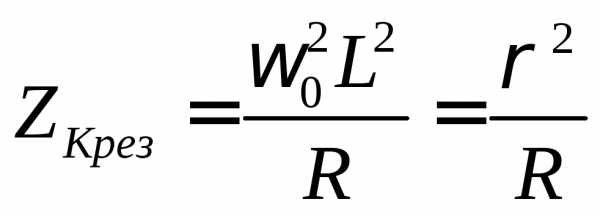При частоте выше резонансной в общей цепи преобладает емкостной ток и контур ведет себя как емкостное сопротивление.

Чем больше частота генератора отличается от собственной (резонансной) частоты контура, тем больше различаются ток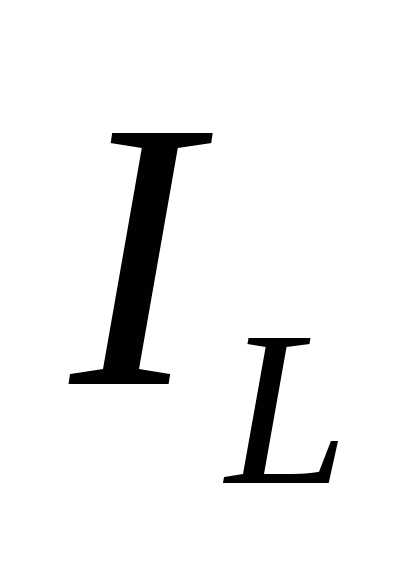ии, тем больше реактивный ток в общей части цепи и меньше реактивное сопротивление контура. Исходя из этих рассуждений, можно показать зависимость сопротивления параллельного контура от частоты питающего генератора (рис.14).

Рис.14. Зависимость сопротивления параллельного контура от частоты генератора

При изменении частоты генератора изменяется фазовый сдвиг между напряжением генератора и током 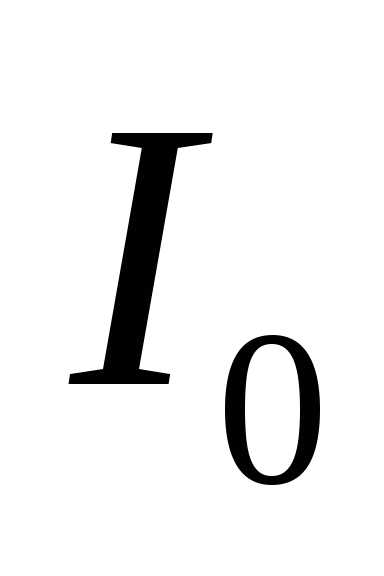, идущим через контур. Если частота генератора значительно ниже собственной (резонансной) частоты контура, то сопротивление контура можно считать чисто индуктивным, т.к. реактивный ток в общей цепи во много раз больше активного. Угол фазового сдвига между напряжением генератора и током 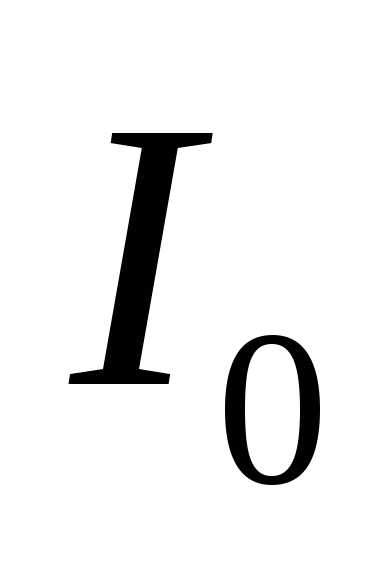при этом близок к. По мере повышения частоты генератора реактивная составляющая тока в общей цепи и фазовый угол уменьшаются. При резонансе сопротивление контура является чисто активным и фазовый сдвиг между напряжением генератора и током 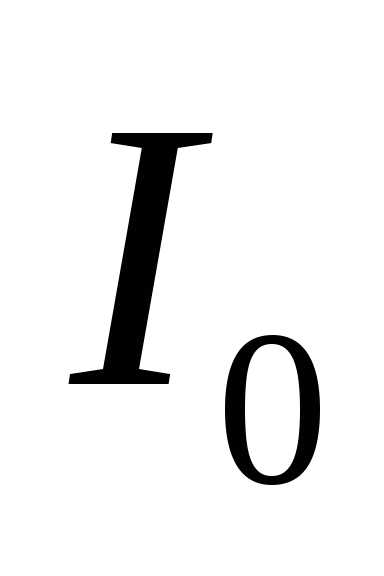равен нулю. Если частота генератора превышает резонансную частоту контура, то сопротивление контура состоит из активной и емкостной составляющих. По мере повышения частоты генератора соотношение между активной и реактивной составляющими изменяется и угол фазового сдвига между напряжением генератора и током 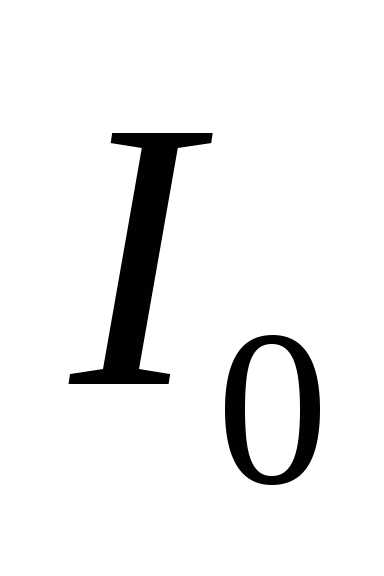приближается к.

Кривая, показывающая зависимость угла фазового сдвига между напряжением генератора и током через контур, называется фазо-частотной характеристикой параллельногоконтура(рис.15).

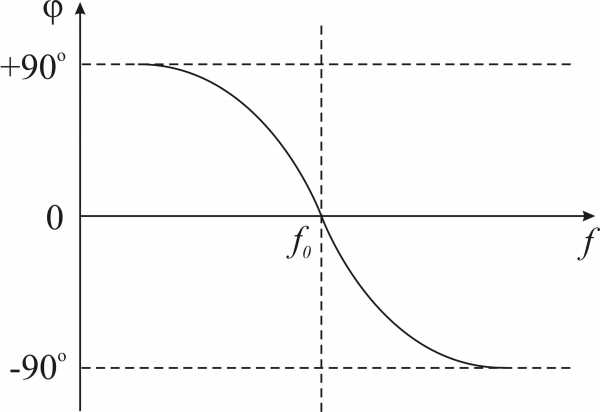
Рис.15. Фазо-частотная характеристика параллельного контура

studfiles.net

Электротехника: Резонансная частота.

Параллельный колебательный контур (рисунок 1) или последовательный колебательный контур (рисунок 2) могут использоваться в генераторах синусоидальных колебаний. Если в одной из этих схем зарядить конденсатор то он будет разряжаться заряжая катушку индуктивности, катушка разряжаясь будет заряжать конденсатор, этот процесс будет повторяться с определённым периодом T. Период это время одного колебания. Частота колебаний это величина обратная периоду. Разделив единицу на численное значение периода получим численное значение частоты. Рисунок 1 - Параллельный колебательный контур

Рисунок 2 - Последовательный колебательный контур

Частота возникших колебаний называется собственной частотой колебаний контура для контуров изображённых на рисунках выше эта частота равна резонансной частоте этих контуров. Резонансная частота контура зависит от индуктивности L и ёмкости C её элементов, для колебательного контура (последовательного или параллельного) её можно найти по формуле: Где L-индуктивность катушки контура, C-ёмкость конденсатора контура. Если на параллельный или последовательный колебательный контур подавать переменное синусоидальное напряжение и изменять его частоту то будут меняться реактивные сопротивления элементов контура, если частота увеличивается то сопротивление конденсатора уменьшается а сопротивление катушки увеличивается и наоборот: если частота уменьшается то сопротивление конденсатора увеличивается а сопротивление катушки уменьшается, очевидно что есть такая частота при которой сопротивление катушки и конденсатора равны эта частота и есть резонансная. Сопротивление параллельного колебательного контура при этой частоте будет наибольшим (по сравнению с сопротивлениями этого контура при других частотах) а сопротивление последовательного колебательного контура при такой частоте будет наименьшим. Эти свойства контуров используют для построения фильтров например в полосно-пропускающем фильтре последовательно с нагрузкой ставиться последовательный контур и при подаче на это соединение (нагрузки и контура) переменного напряжения с резонансной частотой ток в нагрузке будет максимальным при других частотах ток будет меньше. Резонанс в параллельном контуре называют - резонансом токов, резонанс в последовательном контуре - резонансом напряжений. Можно простым способом определить каким будет сопротивление контура при резонансной частоте: например допустим что на параллельный колебательный контур подаётся постоянный ток, постоянный ток можно считать частным случаем переменного короче говоря постоянный ток это переменный с наименьшей возможной частотой, известно что при постоянном токе катушка действует как перемычка следовательно сопротивление контура будет равно нулю если резонансная частота не бесконечно мала (т.е. не постоянный ток) и сопротивление есть то оно больше нуля (т.е. сопротивления при постоянном токе) следовательно сопротивление параллельного колебательного контура на резонансной частоте максимальное а у последовательного контура наоборот. Зная то что конденсатор постоянный ток не пропускает, можно аналогично определить каким д.б. сопротивление последовательного контура на резонансной частоте. Выведем формулу для расчёта резонансной частоты зная то что при резонансе реактивные сопротивления элементов (катушки и конденсатора) контура равны:

Для расчёта резонансной частоты и периода колебаний колебательного контура с катушкой и конденсатором можно воспользоваться программой:

electe.blogspot.com

Параллельный колебательный контур и его свойства

Обратная связь

ПОЗНАВАТЕЛЬНОЕ

Сила воли ведет к действию, а позитивные действия формируют позитивное отношение

Как определить диапазон голоса - ваш вокал

Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими

Целительная привычка

Как самому избавиться от обидчивости

Противоречивые взгляды на качества, присущие мужчинам

Тренинг уверенности в себе

Вкуснейший "Салат из свеклы с чесноком"

Натюрморт и его изобразительные возможности

Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.

Как научиться брать на себя ответственность

Зачем нужны границы в отношениях с детьми?

Световозвращающие элементы на детской одежде

Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия

Как слышать голос Бога

Классификация ожирения по ИМТ (ВОЗ)

Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Параллельным колебательным контуром называется двухполюсная электрическая цепь, подключенная к источнику гармонического сигнала и содержащая в своем составе резистор, конденсатор и индуктивность, соединенные параллельно (рис. 3.11).

Резистор в контур может специально не включаться, но в контуре он всегда будет присутствовать, отражая потери, имеющие место в реальных реактивных элементах.

Комплексная проводимость параллельного контура определяется следующими соотношениями

(3.33)

Изобразим для параллельного колебательного контура график зависимости реактивной проводимости Y от частоты (рис. 3.12), учитывая, что

(3.34)

Рис. 3.11. Параллельный колебательный контур

Анализ графика показывает, что на частоте ω0реактивная проводимость контура становиться равной нулю. Это свидетельствует о том, что сопротивление цепи становиться чисто резистивным (активным) и сдвиг фаз между напряжением и током в контуре равен нулю. Следовательно, в параллельном контуре также имеет место явление электрического резонанса.

Резонансная частота параллельного контура определяется той же формулой что и резонансная частотота последовательного контура

(3.35)

В диапазоне частот, когда частота источника сигнала меньше резонансной частоты f<f0 , преобладает реактивное сопротивление индуктивности, сопротивление контура имеет активно - индуктивный характер и фазовый сдвиг между напряжением и током есть величина положительная.

Рис. 3.12. График зависимости реактивной проводимости параллельного контура от частты

В области частот f>f0 преобладает реактивное сопротивление конденсатора, сопротивление контура активно – емкостное, ток источника опережает по фазе напряжение на выводах.

Если рассмотреть, что происходит в параллельном контуре с энергией, то можно установить, что и при параллельном соединении реактивных элементов на резонансной частоте происходит непрерывный периодический процесс обмена энергиями между электрическим полем конденсатора и магнитным полем индуктивности, который сопровождается необратимыми потерями части энергии на резисторе. Энергия, поступающая от источника электрической энергии в контур, компенсирует тепловые потери на сопротивлении контура.

Контур оценивается добротностью, показывающей отношение (с учетом 2π) величин энергий, накапливаемых на резонансной частоте в реактивных элементах параллельного контура к энергии, расходуемой в цепи в виде необратимых потерь, за период. Добротность параллельного контура определяется формулой

(3.36)

Следует иметь в виду, что, величины R, входящие в формулу добротности в параллельном (3.36) и последовательном (3.27, 3.28) контуре, существенно различны. Если не включать в контур дополнительный резистор, а учитывать только потери реактивных элементов, величины R в формулах добротности последовательного и параллельного контуров будут различаться на несколько порядков. При последовательном соединении L и C величина R = r, определяясь сопротивлением провода катушки r, будет составлять несколько десятков Ом. В параллельном контуре потери на тепловыделение за счет нагревания провода пересчитывают по формуле R =ρ2 /r, поэтому его величина десятки кОм.

Отметим, что величина добротности параллельных контуров в зависимости от качества конденсатора и катушки индуктивности составляет Q =50 – 120.

Поскольку реактивные проводимости на резонансной частоте равны и на них одно и тоже напряжение, то амплитуды токов на реактивных элементах контура равны ImL = ImC . К тому же,

(3.37)

(3.38)

Следовательно, на резонансной частоте амплитуды токов на реактивных элементах в Q раз превышают амплитуду тока, поданного на контур от источника.

Комплексное сопротивление параллельного контура, если его выразить через добротность, равно

(3.39)

Тогда полное сопротивление цепи равно

(3.40)

График зависимости полного сопротивления параллельного контура от частоты показан на рис.3.13.

Рис. 3.13. График зависимости полного сопротивления параллельного контура от частоты

Полное сопротивление контура на резонансной частоте максимально и равно сопротивлению R. С отклонением от резонансной частоты (с увеличением расстройки относительно резонансной частоты) полное сопротивление контура уменьшается.

Если параллельный контур подключить к реальному источнику гармонического тока, то можно утверждать, что параллельный контур «выделяет» напряжение резонансной частоты, а также сигналы, частоты которых находятся в полосе (диапазоне) частот примыкающей к резонансной частоте. Этот диапазон частот называют полосой пропускания контура. Границы полосы пропускания определяют частоты f1 и f2. Полоса пропускания контура определяется формулой

(3.41)

Резюмируя сказанное отметим, что параллельный колебательный контур обладает следующими свойствами.

1. В контуре наблюдается явление электрического резонанса. Поскольку ток на реактивных элементах увеличиваются в Q раз по сравнению с током источника, то правильнее говорить, что в контуре имеет место явление электрического резонанса токов.

2. В случае высокой добротности контура явление резонанса характеризуется тем, что контур мало энергии потребляет от источника, а внутри него идет непрерывно периодический процесс обмена энергиями реактивных элементов. Контур как бы становиться генератором гармонической ЭДС.

3. Ток на реактивных элементах может почти в 100 раз (точнее в Q раз) превышать ток источника.

4. Если источник гармонического тока вырабатывает сигналы с несколькими частотами, то параллельный контур выделяет сигналы, частоты которых лежат в его полосе пропускания. Выделение сигналов будет тем лучше, чем больше величина добротности контура. Это свойство можно использовать для выделения полезных сигналов, например в радиовещательном приемнике.

5. Сопротивление параллельного контура на резонансной частоте максимально. Для обеспечения передачи энергии от источника в нагрузку параллельный контур, при работе на резонансной частоте, должен подключаться к реальному источнику тока, обладающему большим внутренним сопротивлением. При малых величинах внутренних сопротивлений источника добротность контура существенно уменьшается.

megapredmet.ru

Активное сопротивление - колебательный контур

Cтраница 1

Активное сопротивление колебательного контура г равно сумме сопротивлений TL катушки и те конденсатора. Сопротивление г зависит от частоты. Это объясняется главным образом явлением поверхностного эффекта. [2]

Если, активное сопротивление R колебательного контура равно нулю, то общая величина энергии контура остается неизменной, и свободные электромагнитные колебания называются незатухающими. [3]

В большинстве случаев активное сопротивление колебательного контура определяется, главным образом, активным сопротивлением включенной в контур катушки индуктивности. С увеличением частоты индуктивное сопротивление катушки растет, но вследствие поверхностного эффекта растет и ее активное сопротивление. [4]

В большинстве случаев активное сопротивление колебательного контура определяется главным образом актизным сопротивлением входящей в контур катушки. С увеличением частоты индуктивное сопротивление катушки растет, но вследствие поверхностного эффекта ( см.) растет и ее активное сопротивление. [5]

В большинстве случаев активное сопротивление колебательного контура определяется главным образом активным сопротивлением входящей в контур катушки. С увеличением частоты индуктивное сопротивление катушки растет, но вследствие поверхностного эффекта ( см.) растет и ее активное сопротивление. [6]

Множитель при I2 представляет собой активное сопротивление колебательного контура, характеризующее его способность к излучению. Его называют сопротивлением излучения. [7]

Множитель при / 2 представляет собой активное сопротивление колебательного контура, характеризующего его способность к излучению. Его называют сопротивлением излучения. [8]

Множитель при / 2 представляет собой активное сопротивление колебательного контура, характеризующее его способность к излучению. Его называют сопротивлением, излучения. [9]

Множитель при / а представляет собою активное сопротивление колебательного контура, характеризующее его способность излучать энергию. Его называют сопротивлением излучения. [10]

Множитель при / 2 представляет собой активное сопротивление колебательного контура, характеризующее его способность к излучению. Его называют сопротивлением излучения. [11]

Этот метод служит для определения активного сопротивления колебательного контура. Другим вариантом является следующий. Нек-рый колебательный контур настраивают в резонанс с частотой лампового генератора. [12]

Резонансным методом можно также измерять величину активного сопротивления колебательного контура, однако эти измерения значительно сложнее, и рассмотрение их выходит за рамки данной книги. Измерение добротности также обычно производят резонансным методом. [14]

Определяют логарифмические декременты для различных емкостей и активных сопротивлений колебательного контура. Строят графики зависимости логарифмического декремента от емкости и сопротивления контура. [15]

Страницы: 1 2

www.ngpedia.ru

Колебательные контуры - RadioRadar

Документация

Главная Справочник Документация

"Документация" - техническая информация по применению электронных компонентов, особенностях построения различных радиотехнических и электронных схем, а также документация по особенностям работы с инженерным программным обеспечением и нормативные документы (ГОСТ).

Последовательный колебательный контур

Как известно, простейшими резонансными (или колебательными) цепями являются последовательный и параллельный колебательные контуры. Рассмотрим цепь, состоящую из последовательно включенных катушки индуктивности и конденсатора (рис. 1). При воздействии на такую цепь переменного (в простейшем случае гармонического) напряжения, через катушку и конденсатор будет протекать переменный ток, величина (амплитуда) которого может быть вычислена согласно закону Ома: I = U/|ХΣ| , где |ХΣ| -модуль суммы реактивных сопротивлений последовательно включенных катушки и конденсатора. На рис. 2 приведены зависимости реактивных сопротивлений катушки XL и конденсатора ХC от круговой частоты ω, а также график зависимости от частоты ω их алгебраической суммы ХΣ Последний график, по сути, показывает зависимость от частоты общего реактивного сопротивления цепи, изображенной на рис. 1. Из этого графика видно, что на некоторой частоте ω=ωр , на которой реактивные сопротивления катушки и конденсатора равны по модулю, общее сопротивление цепи обращается в ноль. На этой частоте в цепи наблюдается максимум тока, который ограничен только омическими потерями в катушке индуктивности (т.е. сопротивлением провода обмотки катушки) и внутренним сопротивлением источника тока (генератора). Такую частоту, при которой наблюдается рассмотренное явление, называемое в физике резонансом, называют резонансной частотой или собственной частотой колебаний цепи, а саму цепь, изображенную на рис. 1, принято называть последовательным колебательным контуром. Также из рис. 2 видно, что на частотах ниже частоты резонанса реактивное сопротивление последовательного колебательного контура носит емкостной характер, а на более высоких частотах - индуктивный. Что касается самой резонансной частоты, то она может оыть вычислена при помощи известной формулы Томсона: ωр = 1/√(LC).

Рис. 1Последовательный колебательный контур

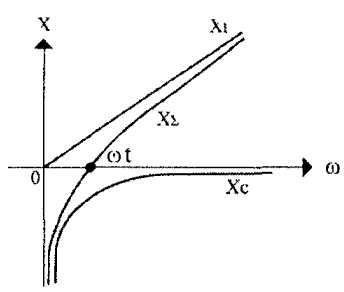
Рис. 2Зависимости реактивных сопротивлений катушки XL и конденсатора ХC от круговой частоты ω

На рис.3 изображена эквивалентная схема последовательного резонансного контура с учетом омических потерь r, подключенного к идеальному генератору гармонического напряжения с амплитудой U. Модуль полного сопротивления (импеданса) такой цепи определяется следующим образом: |z| = √(r2+|XΣ|2), где |XΣ| = ωL-1/ωC. Очевидно, что на резонансной частоте, когда величины реактивных сопротивлений катушки XL = jωL и конденсатора ХC= -j/ωС равны по модулю, величина |XΣ| обращается в нуль (следовательно, сопротивление цепи чисто активное), а ток в цепи определятся отношением амплитуды напряжения генератора к сопротивлению омических потерь: I= U/r. При этом на катушке и на конденсаторе, в которых запасена реактивная электрическая энергия, падает одинаковое напряжение UL=UC=I|XL|=I|XC|. На любой другой частоте, отличной от резонансной, напряжения на катушке и конденсаторе неодинаковы - они определяются амплитудой тока в цепи и величинами модулей реактивных сопротивлений |XL| и |XC| .Поэтому резонанс в последовательном колебательном контуре принято называть резонансом напряжений. С учетом приведенной записи для импеданса цепи можно привести часто встречающееся определение резонансной частоты: резонансной частотой контура называют такую частоту, на которой сопротивление контура имеет чисто активный (резистивный) характер.

Рис. 3Эквивалентная схема последовательного резонансного контура

Одними из наиболее важных параметров колебательного контура (кроме, разумеется, резонансной частоты) являются его характеристическое сопротивление ρ и добротность Q. Характеристическим сопротивлением контура ρ называется величина модуля реактивного сопротивления емкости и индуктивности контура на резонансной частоте: ρ = |ХL| =|ХC| при ω =ωр . В общем случае характеристическое сопротивление может быть вычислено следующим образом: ρ = √(LC). Характеристическое сопротивление ρ является количественной мерой оценки энергии, запасенной реактивными элементами контура - катушкой (энергия магнитного поля) WL= (LI2)/2 и конденсатором (энергия электрического поля) WC=(CU2)/2. Отношение энергии, запасенной реактивными элементами контура, к энергии омических (резистивных) потерь за период принято называть добротностью Q контура, что в буквальном переводе с английского языка обозначает "качество". Величину, обратную добротности d=1/Q называют затуханием контура. Для определения добротности обычно пользуются формулой Q=ρ/r, где r-сопротивление омических потерь контура, характеризующее мощность резистивных (активных потерь) контура Р=I2r. Добротность реальных колебательных контуров, выполненных на дискретных катушках индуктивности и конденсаторах, составляет от нескольких единиц до сотни и более. Добротность различных колебательных систем, построенных на принципе пьезоэлектрических и других эффектов (например, кварцевые резонаторы) может достигать нескольких тысяч и более.

Рис.4 а

Рис.4 б


Рис. 5 а	Рис. 5 б

Частотные свойства различных цепей в технике принято оценивать с помощью амплитудно-частотных характеристик (АЧХ). На рис. 4а и рис. 4б представлены два простейших четырехполюсника, содержащих последовательный колебательный контур. АЧХ этих цепей приведены (показаны сплошными линями) на рис. 5а и рис. 5б соответственно. По вертикальной оси отложена величина коэффициента передачи цепи по напряжению К, показывающая отношение выходного напряжения цепи к входному. Для пассивных цепей (не т.е. содержащих усилительных элементов и источников энергии), величина К никогда не превышает единицу. Очевидно, что сопротивление цепи на рис. 4а переменному току будет минимально при частоте воздействия, равной резонансной частоте контура. В этом случае коэффициент передачи цепи близок к единице (определяется омическими потерями в контуре). На частотах, сильно отличающихся от резонансной, сопротивление контура переменному току достаточно велико, а следовательно, и коэффициент передачи цепи будет падать практически до нуля. При резонансе в цепи, изображенной на рис. 4б, источник входного сигнала оказывается фактически замкнутым накоротко малым сопротивлением контура, благодаря чему коэффициент передачи такой цепи на резонансной частоте падает практически до нуля (опять-таки в силу наличия конечного сопротивления потерь). Наоборот, при частотах входного воздействия, значительно отстоящих от резонансной, коэффициент передачи цепи оказывается близким к единице. Свойство колебательного контура в значительной степени изменять коэффициент передачи на частотах, близких к резонансной, широко используется на практике, когда требуется выделить сигнал с конкретной частотой из множества ненужных сигналов, расположенных на других частотах. Так, в любом радиоприемнике при помощи колебательных цепей обеспечивается настройка на частоту нужной радиостанции. Свойство колебательного контура выделять из множества частот одну принято называть селективностью или избирательностью. При этом интенсивность изменения коэффициента передачи цепи при отстройке частоты воздействия от резонанса принято оценивать при помощи параметра, называемого полосой пропускания. Чаще всего за полосу пропускания принимается диапазон частот, в пределах которого уменьшение (или увеличение - в зависимости от вида цепи) коэффициента передачи относительного его значения на резонансной частоте, не превышает величины 0,707 (3дБ).

Пунктирными линиями на рис. 5а и рис. 5б показаны АЧХ точно таких же цепей, как на рис. 4а и рис. 4б соответственно, колебательные контуры которых имеют такие же резонансные частоты, как и для случая рассмотренного выше, но обладающие меньшей добротностью (например, катушка индуктивности намотана проводом, обладающим большим сопротивлением постоянному току). Как видно из рис. 5а и рис. 5б, при этом расширяется полоса пропускания цепи и ухудшаются ее селективные (избирательные) свойства. Исходя из этого, при расчете и конструировании колебательных контуров нужно стремиться к повышению их добротности. Однако, в ряде случаев, добротность контура, наоборот, приходится занижать (например, включая последовательно с катушкой индуктивности резистор небольшой величины сопротивления), что позволяет избежать искажений широкополосных сигналов. Хотя, если на практике требуется выделить достаточно широкополосный сигнал, селективные цепи, как правило, строятся не на одиночных колебательных контурах, а на более сложных связанных (многоконтурных) колебательных системах, в т.ч. многозвенных фильтрах.

Параллельный колебательный контур

В различных радиотехнических устройствах наряду с последовательными колебательными контурами часто (даже чаще, чем последовательные) применяют параллельные колебательные контуры На рис. 6 приведена принципиальная схема параллельного колебательного контура Здесь параллельно включены два реактивных элемента с разным характером реактивности Как известно, при параллельном включении элементов складывать их сопротивления нельзя - можно лишь складывать проводимости На рис. 7 приведены графические зависимости реактивных проводимостей катушки индуктивности BL = j/ωL, конденсатора ВC = -jωC, а также суммарной проводимости ВΣ, этих двух элементов, являющаяся реактивной проводимостью параллельного колебательного контура. Аналогично, как и для последовательного колебательного контура, имеется некоторая частота, называемая резонансной, на которой реактивные сопротивления (а значит и проводимости) катушки и конденсатора одинаковы. На этой частоте суммарная проводимость параллельного колебательного контура без потерь обращается в нуль. Это значит, что на этой частоте колебательный контур обладает бесконечно большим сопротивлением переменному току. Действительно, если построить зависимость реактивного сопротивления контура от частоты XΣ=1/BΣ, эта кривая (рис. 8) в точке ω = ωр будет иметь разрыв второго рода. Сопротивление реального параллельного колебательного контура (т.е с потерями), разумеется, не равно бесконечности - оно тем меньше, чем больше омическое сопротивление потерь в контуре, т.е уменьшается прямо пропорционально уменьшению добротности контура. В целом, физический смысл понятий добротности, характеристического сопротивления и резонансной частоты колебательного контура, а также их расчетные формулы, справедливы как для последовательного, так и для параллельного колебательного контура.

Рис. 6Параллельный колебательный контур

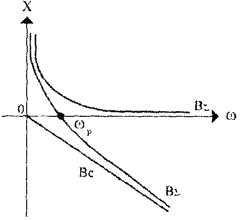
Рис. 7Зависимости реактивных поводимостей катушки и конденсатора и суммарная проводимость этих двух элементов

Рис. 8Зависимость реактивного сопротивления контура от частоты

Рассмотрим цепь, состоящую из генератора гармонических колебаний и параллельного колебательного контура. В случае, когда частота колебаний генератора совпадает с резонансной частотой контура его индуктивная и емкостная ветви оказывают равное сопротивление переменному току, в следствие чего токи в ветвях контура будут одинаковыми. В этом случае говорят, что в цепи имеет место резонанс токов. Как и в случае последовательного колебательного контура, реактивности катушки и конденсатора компенсируют друг друга, и сопротивление контура протекающему через него току становится чисто активным (резистивным). Величина этого сопротивления, часто называемого в технике эквивалентным, определяется произведением добротности контура на его характеристическое сопротивление Rэкв=Q·ρ. На частотах, отличных от резонансной, сопротивление контура уменьшается и приобретает реактивный характер (рис. 8) на более низких частотах - индуктивный (поскольку реактивное сопротивление индуктивности падает при уменьшении частоты), а на более высоких - наоборот, емкостной (т к реактивное сопротивление емкости падает с ростом частоты). В процессе работы контура, дважды за период колебаний, происходит энергетический обмен между катушкой и конденсатором (рис. 9). Энергия поочередно накапливается то в виде энеогии электрического поля заряженного конденсатора, то в виде энергии магнитного поля катушки индуктивности. При этом в контуре протекает собственный контурный ток Iк, превосходящий по величине ток во внешней цепи I в Q раз. В случае идеального контура (без потерь), добротность которого теоретически бесконечна, величина контурного тока также будет бесконечно большой.

Рис. 9Процесс работы контура


Рис. 10 а	Рис. 10 б

Рассмотрим, как изменяются коэффициенты передачи четырехполюсников, аналогичных приведенным на рис. 4а и рис. 4б, от частоты, при включении в них не последовательных колебательных контуров, а параллельных. Четырехполюсник, изображенный на рис. 10а, на резонансной частоте контура представляет собой огромное сопротивление току, поэтому при ω=ωр его коэффициент передачи будет близок к нулю (с учетом омических потерь). На частотах, отличных от резонансной, сопротивление контура будет уменьшатся, а коэффициент передачи четырехполюсника - возрастать. Этот случай соответствует графику АЧХ, приведенному на рассмотренном ранее рис. 5б. Для четырехполюсника, приведенного на рис. 10б, ситуация будет противоположной - на резонансной частоте контур будет представлять собой очень большое сопротивление и практически все входное напряжение поступит на выходные клеммы (т.е коэффициент передачи будет максимален и близок к единице). При значительном отличии частоты входного воздействия от резонансной частоты контура, источник сигнала, подключаемый к входным клеммам четырехполюсника, окажется практически закороченном накоротко, а коэффициент передачи будет близок к нулю. АЧХ такого четырехполюсника соответствует изображенной на рис. 5а.

В заключении настоящего экскурса отметим тот факт, что достаточно часто в реальной радиоэлектронной аппаратуре приходится сталкиваться с необходимостью перестройки колебательных контуров - например, в приемнике, для обеспечения возможности приема радиостанций, работающих на разных частотах В этом случае емкостные элементы контуров выполняются в виде конденсаторов переменной емкости, либо специальных диодов - варикапов, обладающих большой барьерной емкостью, зависящей от приложенного к ней запирающего напряжения В ряде случаев применяют и перестраиваемый катушки индуктивности - вариометры.

Дата публикации: 09.09.2003

Павел / 12.01.2017 - 09:20Спасибо!
Поиск / 14.01.2016 - 21:21подскажите как вычислить частоту контура, если включить катушку параллельно последовательному контуру?
Кирилл / 18.02.2014 - 22:22Мужики дайте схему подключения аудиомодуляции к первичке тесла? Хочу переделать Ионофон под поющий транс тесла. Или подскажите где такие схемы найти если они есть? Пожалуйста и заранее спасибо!
николай / 21.10.2013 - 07:32подскажите как вычислить частоту контура, если включить конденсатор параллельно последовательному контуру
sad / 10.07.2013 - 13:22Ыыыы!!!
Денис / 20.06.2013 - 09:43Как изменится период колебаний контура, если пластины конденсатора, включенного в контур сблизить между собой: а) уменьшится ; б) увеличится Дать математически обоснованный ответ. Помогите я в физике дуб дубом.. :( Зарание спасибо
витя / 19.04.2013 - 11:51спасибо за информацию
Влад... / 23.11.2012 - 17:41Спасибо, очень доходчиво написано.
ааааааа / 04.10.2012 - 10:24ааааааа
Света / 18.09.2012 - 15:06колебательній контур состоит из конденсатора емкостью 2 Пф и катушки с индуктивностью 0,50 мкГн,какова частота колебаний в контуре
серегей / 15.09.2012 - 11:51помогите пожалуста .как отличается зависимость полного сопротивления от частоты для последовательного и параллельного контуров?
Срез умоляю помогите / 05.06.2012 - 05:57колебательный контур излучает в воздухе электромагнитные войны длиной 150м. Какая емкость включена в контур, если его индуктивноть равна 0,25 мГн? Активным сопротивлением пренебречь
Денис / 13.05.2012 - 19:09ребят, подскажите плиз) эт вопрос на билет к экзамену( не могу нигде найти( Реальный колебательный контур.Свободные колебание в контуре с потерями. Характеристики оценивающие реальный колебательный контур.
Денис / 13.05.2012 - 19:00ребят, подскажите плиз) эт вопрос на билет к экзамену( не могу нигде найти( Реальный колебательный контур.Свободные колебание в контуре с потерями. Характеристики оценивающие реальный колебательный контур.
Ann / 11.05.2012 - 15:31как изменится форма резонансной кривой,если в колебательный контур включить резистор?
Ann / 11.05.2012 - 15:29как изменится форма резонансной кривой,если в колебательный контур включить резистор?
василий / 16.04.2012 - 10:11обьясните пожалуста как рабтает колебательный контур ?
Сергей,Ужгород / 10.02.2012 - 13:33Спасибо автору. Простое и понятное объяснение без заумной теории и формул. Кому надо более глубокий анализ - изучайте курс ЛРТУ (линейные радиотехнические устройства). А всякие придирки типа "Скажите, где вы видите контур на рис.1. Лично я вижу там двухполюсник" - чепуха, игра слов. Все изожено просто и понятно.
Саша / 19.12.2011 - 09:35Ну что,могу сказать только одно,отличный сайт!Очень познавательный,вот только если б кто подкрепил теорию вечного двигателя основанного на резонансе,практикой,и выложил бы материалы на сайт,я думаю было бы ещё интересней.должен же кто нибудь когда нибудь до этого дойти.Я поддерживаю идею этого,по сути простейшего,вечного двигателя.И Теслу уважаю,он был прав на счет всего о чем сейчас ведутся разговоры.Его ещё вспомнят!Я считаю,что от наших разговоров о резонансе и получении на выходе мощности больше чем на входе,закон сохранения энергии уже канул в лето,вопреки всему,свободная энергия существует!!!:)как сказал один ... :"и всё таки она вертится!",только в нашем случае:"и всё таки она существует!!!"
Алекс / 16.09.2011 - 12:16Здравствуйте. Характеристическое сопротивление равно корень квадратный из отношения L/С (а не произведения LC)

1 2345 Вперед

Вы можете оставить свой комментарий, мнение или вопрос по приведенному вышематериалу:

www.radioradar.net

Активное и реактивное сопротивление в цепи переменного тока

В электрической цепи переменного тока существует два вида сопротивлений: активное и реактивное. Это является существенным отличием от цепей постоянного тока.

Активное сопротивление

При прохождении тока через элементы, имеющие активное сопротивление, потери выделяющейся мощности необратимы. Примером может служить резистор, выделяющееся на нем тепло, обратно в электрическую энергию не превращается. Кроме резистора активным сопротивлением может обладать линии электропередач, соединительные провода, обмотки трансформатора или электродвигателя.

Отличительной чертой элементов имеющих чисто активное сопротивление – это совпадение по фазе тока и напряжения, поэтому вычислить его можно по формуле

Активное сопротивление зависит от физических параметров проводника, таких как материал, площадь сечения, длина, температура.

Реактивное сопротивление

При прохождении переменного тока через реактивные элементы возникает реактивное сопротивление. Оно обусловлено в первую очередь ёмкостями и индуктивностями.

Индуктивностью в цепи переменного тока обладает катушка индуктивности, причём в идеальном случае, активным сопротивлением её обмотки пренебрегают. Реактивное сопротивление катушки переменному току создаётся благодаря её ЭДС самоиндукции. Причем с ростом частоты тока, сопротивление также растёт.

Реактивное сопротивление катушки зависит от частоты тока и индуктивности катушки

Конденсатор обладает реактивным сопротивлением благодаря своей ёмкости. Его сопротивление с увеличением частоты тока уменьшается, что позволяет его активно использовать в электронике в качестве шунта переменной составляющей тока.

Сопротивление конденсатора можно рассчитать по формуле

Треугольник сопротивлений

Цепи переменного тока обладают полным сопротивлением. Полное сопротивление цепи определяется как сумма квадратов активного и реактивного сопротивлений

Графическим изображением этого выражения служит треугольник сопротивлений, который можно получить в результате расчёта последовательной RLC-цепи. Выглядит он следующим образом:

На треугольнике видно, что катетами являются активное и реактивное сопротивление, а полной сопротивление гипотенуза.

electroandi.ru

3.1.Сопротивление параллельного контура при резонансе. Как найти сопротивление контура