Модуль магнитной индукции — FizikaKlass.ru
Количественной характеристикой магнитного поля может служить величина силы, действующей в этом поле на проводник с током: чем сильнее поле, тем больше эта сила.
Опыт показывает, однако, что эта сила зависит не только от поля, но и от величин, характеризующих проводник с током: силы тока  в проводнике, длины проводника
в проводнике, длины проводника  и угла
и угла  между проводником и вектором магнитной индукции
между проводником и вектором магнитной индукции 
При заданных силе тока и длине проводника сила  действующая со стороны магнитного поля на проводник с током, максимальна, когда проводник расположен перпендикулярно вектору магнитной индукции.
действующая со стороны магнитного поля на проводник с током, максимальна, когда проводник расположен перпендикулярно вектору магнитной индукции.
Поэтому именно такое расположение проводника с током удобно выбрать для определения модуля магнитной индукции.
Согласно опытам, сила, действующая в магнитном поле на проводник с током, прямо пропорциональна произведению силы тока на длину проводника, то есть выражению 
Значит, отношение  не зависит ни от силы тока в проводнике, ни от длины этого проводника и, следовательно, характеризует само магнитное поле. Поэтому это отношение выбрали для определения модуля магнитной индукции.
не зависит ни от силы тока в проводнике, ни от длины этого проводника и, следовательно, характеризует само магнитное поле. Поэтому это отношение выбрали для определения модуля магнитной индукции.
Итак,
модуль магнитной индукции равен отношению силы, действующей на проводник с током, расположенный перпендикулярно вектору магнитной индукции, к произведению силы тока в проводнике и длины проводника: 
Статьи энциклопедии
Урок 3. магнитная индукция. действие магнитного поля на проводник с током и движущуюся заряженную частицу — Физика — 11 класс
Физика, 11 класс
Урок 3. Магнитная индукция. Действие магнитного поля на проводник и движущуюся заряжённую частицу
Перечень вопросов, рассматриваемых на уроке:
1) магнитное поле;
2) вектор магнитной индукции, линии магнитной индукции;
3) сила Ампера, сила Лоренца;
4) правило буравчика, правило левой руки.
Глоссарий по теме
Магнитная индукция – векторная величина, характеризующая величину и направление магнитного поля.
Сила Ампера – сила, действующая со стороны магнитного поля на проводник с током.
Сила Лоренца – сила, действующая со стороны магнитного поля на движущую частицу с зарядом.
Правило «буравчика» — правило для определения направления магнитного поля проводника с током.
Правило левой руки – правило для определения направления силы Ампера и силы Лоренца.
Соленоид – проволочная катушка.
Рамка с током – небольшой длины катушка с двумя выводами из скрученного гибкого проводника с током, способная поворачиваться вокруг оси, проходящей через диаметр катушки.
Основная и дополнительная литература по теме урока
Мякишев Г.Я., Буховцев Б.Б.,. Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций. М.: Просвещение, 2014. – С. 3 – 20
2. А.П. Рымкевич. Сборник задач по физике. 10-11 классы. — М: Дрофа, 2009. – С.109 — 112
Основное содержание урока
Магнитное поле – особый вид материи, которая создаётся электрическим током или постоянными магнитами. Для демонстрации действия и доказательства существования магнитного поля служат магнитная стрелка, способная вращаться на оси, или небольшая рамка (или катушка) с током, подвешенная на тонких скрученных гибких проводах.
Рамка с током и магнитная стрелка под действием магнитного поля поворачиваются так, что северный полюс (синяя часть) стрелки и положительная нормаль рамки указывают направление магнитного поля.
Магнитное поле, созданное постоянным магнитом или проводником с током, занимает всё пространство в окрестности этих тел. Магнитное поле принято (удобно) изображать в виде линий, которые называются линиями магнитного поля. Магнитные линии имеют вихревой характер, т.е. линии не имеют ни начала, ни конца, т.е. замкнуты. Направление касательной в каждой точке линии совпадает с направлением вектора магнитной индукции. Поля с замкнутыми линиями называются вихревыми.
Магнитное поле характеризуется векторной величиной, называемой магнитной индукцией. Магнитная индукция характеризует «силу» и направление магнитного поля – это количественная характеристика магнитного поля.
Она обозначается символом  За направление вектора магнитной индукции принимают направление от южного полюса к северному магнитной стрелки, свободно установившейся в магнитном поле.
За направление вектора магнитной индукции принимают направление от южного полюса к северному магнитной стрелки, свободно установившейся в магнитном поле.
Направление магнитного поля устанавливают с помощью вектора магнитной индукции.
Направление вектора магнитной индукции прямого провода с током определяют по правилу буравчика (или правого винта).
Правило буравчика звучит следующим образом:
если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитного поля тока.
Направление магнитного поля внутри соленоида определяют по правилу правой руки.
Определим модуль вектора магнитной индукции.
Наблюдения показывают, что максимальное значение силы, действующей на проводник, прямо пропорционально силе тока, длине проводника, находящегося в магнитном поле.
F_max ~ I; F ~ Δl.
Тогда, зависимость силы от этих двух величин выглядит следующим образом

Отношение  зависит только от магнитного поля и может быть принята за характеристику магнитного поля в данной точке.
зависит только от магнитного поля и может быть принята за характеристику магнитного поля в данной точке.
Величина, численно равная отношению максимальной силы, действующей на проводник с током, на произведение силы тока и длины проводника, называется модулем вектора магнитной индукции:

Единицей измерения магнитной индукции является 1 тесла (Тл).
1Тл = 1Н/(1А∙1м).
Закон Ампера:
Сила, действующая на проводник с током в магнитном поле, равна произведению модуля магнитной индукции, силы тока, длины проводника и синуса угла между вектором магнитной индукции и направлением тока:

где α – угол между вектором B и направлением тока.
Направление силы Ампера определяется правилом левой руки:
Если ладонь левой руки развернуть так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 900 большой палец покажет направление силы Ампера.
Сила Ампера — сила, действующая на проводник с током со стороны магнитного поля.
Сила Лоренца – сила, действующая на движущуюся заряженную частицу со стороны магнитного поля. Её численное значение равно произведению заряда частицы на модули скорости и магнитной индукции и синус угла меду векторами скорости и магнитной индукции:

 – заряд частицы;
– заряд частицы;
 – скорость частицы;
– скорость частицы;
B – модуль магнитной индукции;
 – угол между векторами скорости частицы и магнитной индукции.
– угол между векторами скорости частицы и магнитной индукции.
Направление силы Лоренца также определяют по правилу левой руки:
Если четыре вытянутых пальца левой руки направлены вдоль вектора скорости заряженной частицы, а вектор магнитной индукции направлен в ладонь, то отведённый на 900 большой палец покажет направление силы Лоренца. Если частица имеет заряд отрицательного знака, то направление силы Лоренца противоположно тому направлению, которое имела бы положительная частица.
Получим формулы для радиуса окружности и периода вращения частицы, которая влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции, применяя формулы второго закона Ньютона и центростремительного ускорения.




Согласно 2-му закону Ньютона

Отсюда

Время, за которое частица делает полный оборот (период обращения), равно:

Многим юным бывает досадно, что они не родились в старые времена, когда делались открытия. Им кажется, что теперь всё известно и никаких открытий на их долю не осталось.
Одной из нераскрытых тайн является механизм земного магнитного поля. Как же и чем вызывается магнитное поле Земли? Подумайте и может быть…
Одна из возможных гипотез.
Как известно, ядро Земли имеет высокую температуру
и высокую плотность. Судя по исследованиям, в самом центре содержится твёрдое ядро. При вращении Земли вокруг своей оси центр тяжести не совпадает с геометрическим центром из-за притяжения Солнца. В результате сместившееся из центра ядро вращаясь относительно оболочки Земли вызывает такое же движение жидкой расплавленной массы мантии, как чайная ложка, перемешивающая воду в стакане. Получается не что иное, как направленное движение зарядов. Есть электрический ток, а он, в свою очередь, создаёт магнитное поле.
Разбор тренировочных заданий
1. На рисунке изображён проводник с током, помещённый в магнитное поле. Стрелка указывает направление тока в проводнике. Вектор магнитной индукции направлен перпендикулярно плоскости рисунка к нам. Как направлена сила, действующая на проводник с током?

Варианты ответов:
1. вправо →;
2. влево ←;
3. вниз ↓;
4. вверх ↑.
 — точка означает, что магнитная индукция направлена на нас из глубины плоскости рисунка.
— точка означает, что магнитная индукция направлена на нас из глубины плоскости рисунка.
Используя правило левой руки, определяем направление силы Ампера:
Левую руку располагаем так, чтобы линии магнитной индукции входили в ладонь, 4 пальца направим вниз по направлению тока, тогда отогнутый на 900 большой палец покажет направление силы Ампера, т. е. она направлена влево.
Правильный вариант:
2. влево ←.
2. По проводнику длиной 40 см протекает ток силой 10 А. Чему равна индукция магнитного поля, в которое помещён проводник, если на проводник действует сила 8 мН?
(Ответ выразите в мТл).
3. Определите модуль силы, действующей на проводник длиной 50 см при силе тока 10 А в магнитном поле с индукцией 0,15 Тл. (Ответ выразите в мН).
4. Протон в магнитном поле с индукцией 0,01 Тл описал окружность радиусом 10 см. Найдите скорость протона. (Ответ выразите в км/с, округлив до десятков)
5. С какой скоростью влетает электрон в однородное магнитное поле (индукция 1,8 Тл) перпендикулярно к линиям индукции, если магнитное поле действует на него с силой 3,6∙10—¹² Н? Ответ выразите в км/с.
6. Электрон движется в однородном магнитном поле с индукцией 3,14мТл. Чему равен период обращения электрона? (Ответ выразите в наносекундах, округлив до целых)
2. Дано:
l = 40cм = 0,4 м,
I = 10 A,
F =8 мН = 0,008 Н.
Найти: B
Решение:
Запишем формулу модуля магнитной индукции:

Делаем расчёт:
B = 0,008 Н / ( 0,4м·10 A) = 0,002 Tл = 2 мTл.
Ответ: 2 мTл.
3. Дано:
l = 50 cм = 0,5 м,
I = 10 A,
B = 0,l5 Tл.
Найти: F
Решение:
Запишем формулу силы Ампера:

Делаем расчёт:
F = 0,l5 Tл· 10 A· 0,5 м = 0,75 Н = 750 мН
Ответ: 750 мН.
4. Дано:
B = 0,0l Tл,
r = l0 cм = 0,l м.
Найти: v
Решение:
Заряд протона равен: q₀ = l,6·l0⁻ˡ⁹ Кл,
масса протона: m = l,67·l0⁻²⁷ кг.
Согласно 2-му закону Ньютона:

Отсюда следует:

Делаем расчёт:
v = ( l,6·l0⁻ˡ⁹ Кл·0,l м·0,0l Tл) / l,67·l0⁻²⁷ кг ≈ 0,00096·l0⁸ м/с ≈ l00 км/с.
Ответ: v ≈ l00 км/с.
5. Дано:
B = l,8 Tл,
F = 3,6·l0⁻¹² Н,
α = 90°.
Найти: 
Решение:
Заряд электрона равен: q₀ = l,6·l0⁻ˡ⁹ Кл.
Используем формулу силы Лоренца:
 .
.
Выразим из формулы силы скорость, учитывая, что sin90°=l,

Делаем расчёт:
v = 3,6·l0⁻¹² Н / (l,6·l0⁻ˡ⁹ Кл· l,8 Tл) = l,25·l0⁷м/с = l2500 км/с.
Ответ: v = l2500 км/с.
6. Дано:
B = 3,l4 мТл = 3,l4·l0⁻³ Tл,
q₀ = l,6·l0⁻ˡ⁹ Кл,
Найти: Т
Решение:
Масса электрона равна: m = 9,l·l0⁻³¹ кг.
Время, за которое частица делает полный оборот (период обращения), равно:

Делаем расчёт:
T = 2·3,l4·9,l·l0⁻³¹ кг/( l,6·l0⁻ˡ⁹ Кл·3,l4·l0⁻³ Tл) = ll,375·l0⁻⁹ с ≈ ll нс.
Ответ: T ≈ ll нс.
Магнитная индукция в вакууме | HomeElectronics
Всем доброго времени суток. В прошлой статье я рассказал о магнитном поле и немного остановился на его параметрах. Данная статья продолжает тему магнитного поля и посвящена такому параметру как магнитная индукция. Для упрощения темы я буду рассказывать о магнитном поле в вакууме, так как различные вещества имеют разные магнитные свойства, и как следствие необходимо учитывать их свойства.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Закон Био – Савара – Лапласа
В результате исследования магнитных полей создаваемых электрическим током, исследователи пришли к таким выводам:
- магнитная индукция, создаваемая электрическим током пропорциональна силе тока;
- магнитная индукция имеет зависимость от формы и размеров проводника, по которому протекает электрический ток;
- магнитная индукция в любой точке магнитного поля зависит от расположения данной точки по отношению к проводнику с током.
Французские учёные Био и Савар, которые пришли к таким выводам обратились к великому математику П. Лапласу для обобщения и вывода основного закона магнитной индукции. Он высказал гипотезу, что индукция в любой точке магнитного поля, создаваемое проводником с током можно представить в виде суммы магнитных индукций элементарных магнитных полей, которые создаются элементарным участком проводника с током. Данная гипотеза и стала законом магнитной индукции, называемого законом Био – Савара – Лапласа. Для рассмотрения данного закона изобразим проводник с током и создаваемую им магнитную индукцию
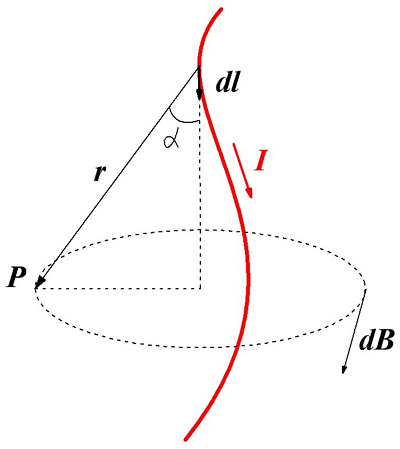
Магнитная индукция dB, создаваемая элементарным участком проводника dl.
Тогда магнитная индукция dB элементарного магнитного поля, которое создается участком проводника dl, с током I в произвольной точке Р будет определяться следующим выражением
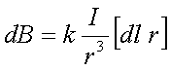
где I – сила тока, протекающая по проводнику,
r – радиус-вектор, проведённый от элемента проводника к точке магнитного поля,
dl – минимальный элемент проводника, который создает индукцию dB,
k – коэффициент пропорциональности, зависящий от системы отсчёта, в СИ k = μ0/(4π)
Так как [dl r] является векторным произведением, тогда итоговое выражение для элементарной магнитной индукции будет выглядеть следующим образом
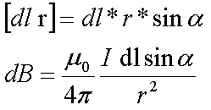
Таким образом, данное выражение позволяет найти магнитную индукцию магнитного поля, которое создается проводником с током произвольной формы и размеров при помощи интегрирования правой части выражения
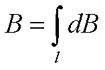
где символ l обозначает, что интегрирование происходит по всей длине проводника.
Магнитная индукция прямолинейного проводника
Как известно простейшее магнитное поле создает прямолинейный проводник, по которому протекает электрический ток. Как я уже говорил в предыдущей статье, силовые линии данного магнитного поля представляют собой концентрические окружности расположенные вокруг проводника.
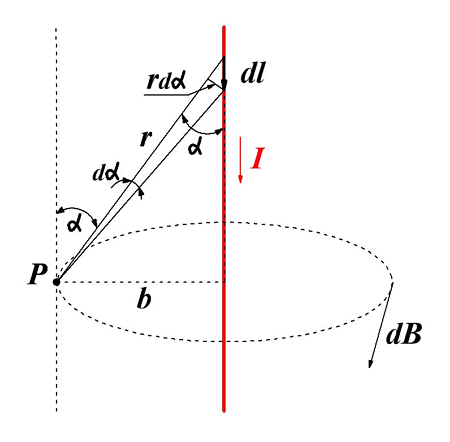
Магнитная индукция магнитного поля создаваемого прямолинейным проводником с током.
Для определения магнитной индукции В прямого провода в точке Р введем некоторые обозначения. Так как точка Р находится на расстоянии b от провода, то расстояние от любой точки провода до точки Р определяется как r = b/sinα. Тогда наименьшую длину проводника dl можно вычислить из следующего выражения
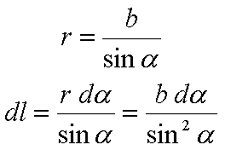
В итоге закон Био – Савара – Лапласа для прямолинейного провода бесконечной длины будет иметь вид
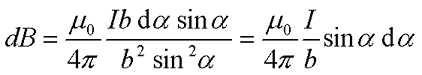
где I – ток, протекающий по проводу,
b – расстояние от центра провода до точки, в которой рассчитывается магнитная индукция.
Теперь просто проинтегрируем получившееся выражение по dα в пределах от 0 до π.
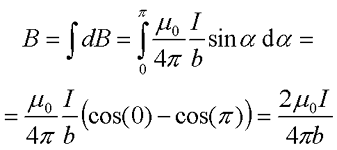
Таким образом, итоговое выражение для магнитной индукции прямолинейного провода бесконечной длины будет иметь вид
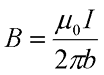
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м,
I – ток, протекающий по проводу,
b – расстояние от центра проводника до точки, в которой измеряется индукция.
Магнитная индукция кольца
Индукция прямого провода имеет небольшое значение и уменьшается при удалении от проводника, поэтому в практических устройствах практически не применяется. Наиболее широко используются магнитные поля созданные проводом, намотанным на какой либо каркас. Поэтому такие поля называются магнитными полями кругового тока. Простейшим таким магнитным поле обладает электрический ток, протекающий по проводнику, который имеет форму окружности радиуса R.
В данном случае практический интерес представляет два случая: магнитное поле в центре окружности и магнитное поле в точке Р, которое лежит на оси окружности. Рассмотрим первый случай.
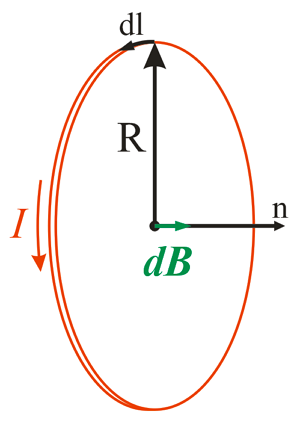
Магнитная индукция в центре кругового тока.
В данном случае каждый элемент тока dl создаёт в центре окружности элементарную магнитную индукцию dB, которая перпендикулярна к плоскости контура, тогда закон Био-Савара-Лапласа будет иметь вид
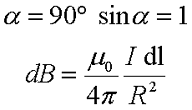
Остается только проинтегрировать полученное выражение по всей длине окружности
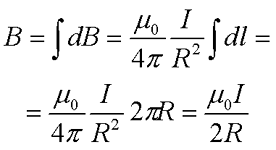
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м,
I – сила тока в проводнике,
R – радиус окружности, в которое свернут проводник.
Рассмотрим второй случай, когда точка, в которой вычисляется магнитная индукция, лежит на прямой х, которая перпендикулярна плоскости ограниченной круговым током.
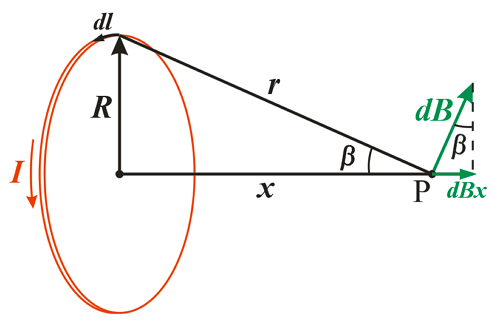
Магнитная индукция в точке, лежащей на оси окружности.
В данном случае индукция в точке Р будет представлять собой сумму элементарных индукций dBX, которые в свою очередь представляет собой проекцию на ось х элементарной индукции dB
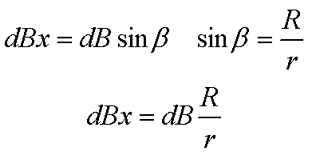
Применив закон Био-Савара-Лапласа вычислим величину магнитной индукции
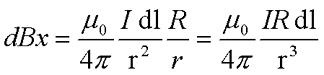
Теперь проинтегрируем данное выражение по всей длине окружности
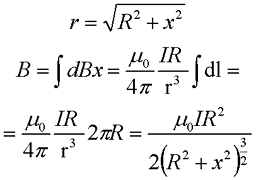
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м,
I – сила тока в проводнике,
R – радиус окружности, в которое свернут проводник,
х – расстояние от точки, в которой вычисляется магнитная индукция, до центра окружности.
Как видно из формулы при х = 0, получившееся выражение переходит в формулу для магнитной индукции в центре кругового тока.
Циркуляция вектора магнитной индукции
Для расчёта магнитной индукции простых магнитных полей достаточно закона Био-Савара-Лапласа. Однако при более сложных магнитных полях, например, магнитное поле соленоида или тороида, количество расчётов и громоздкость формул значительно увеличится. Для упрощения расчётов вводится понятие циркуляции вектора магнитной индукции.
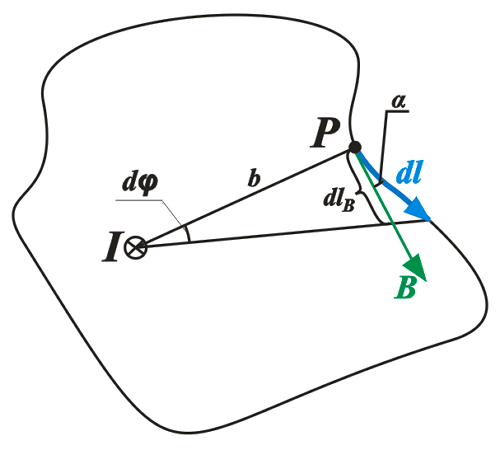
Циркуляция вектора магнитной индукции по произвольному контуру.
Представим некоторый контур l, который перпендикулярный току I. В любой точке Р данного контура, магнитная индукция В направлена по касательной к данному контуру. Тогда произведение векторов dl и В описывается следующим выражением
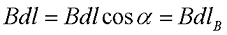
Так как угол dφ достаточно мал, то векторов dlВ определяется, как длина дуги
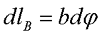
Таким образом, зная магнитную индукцию прямолинейного проводника в данной точке, можно вывести выражение для циркуляции вектора магнитной индукции
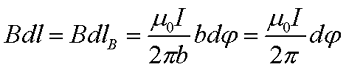
Теперь остаётся проинтегрировать получившееся выражение по всей длине контура
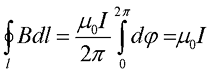
В нашем случае вектор магнитной индукции циркулирует вокруг одного тока, в случае же нескольких токов выражение циркуляции магнитной индукции переходит в закон полного тока, который гласит:
Циркуляция вектора магнитной индукции по замкнутому контуру пропорциональна алгебраической сумме токов, которые охватывает данный контур.
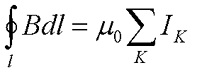
Магнитное поле соленоида и тороида
С помощью закона полного тока и циркуляции вектора магнитной индукции достаточно легко определить магнитную индукцию таких сложных магнитных полей как у соленоида и тороида.
Соленоидом называется цилиндрическая катушка, которая состоит из множества витков проводника, намотанных виток к витку на цилиндрический каркас. Магнитное поле соленоида фактически состоит из множества магнитных полей кругового тока с общей осью, перпендикулярной к плоскости каждого кругового тока.
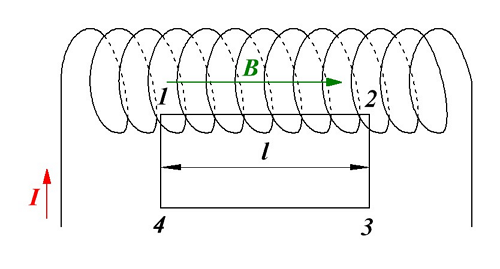
Магнитная индукция соленоида.
Воспользуемся циркуляцией вектора магнитной индукции и представим циркуляцию по прямоугольному контуру 1-2-3-4. Тогда циркуляция вектора магнитной индукции для данного контура будет иметь вид
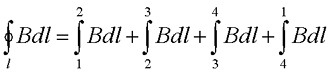
Так как на участках 2-3 и 4-1 вектор магнитной индукции перпендикулярен к контуру, то циркуляция равна нулю. На участке 3-4, который значительно удалён от соленоида, то его так же можно не учитывать. Тогда с учётом закона полного тока магнитная индукция в соленоиде достаточно большой длины будет иметь вид
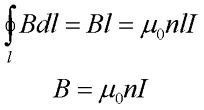
где n – число витков проводника соленоида, которое приходится на единицу длины,
I – ток, протекающий по соленоиду.
Тороид образуется путём намотки проводника на кольцевой каркас. Данная конструкция эквивалентна системе из множества одинаковых круговых токов, центры которых расположены на окружности.
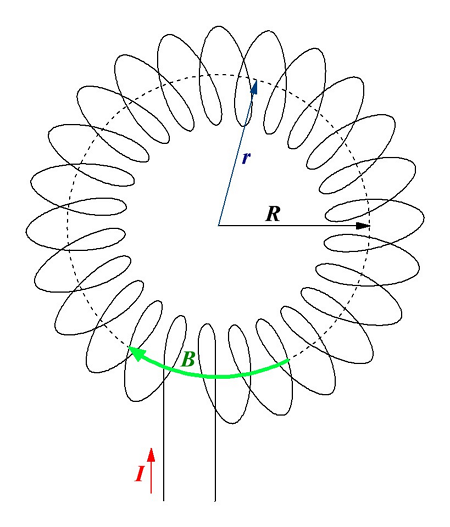
Магнитная индукция тороида.
В качестве примера рассмотрим тороид радиуса R, на который намотано N витков провода. Вокруг каждого витка провода возьмём контур радиуса r, центр данного контура совпадает в центром тороида. Так как вектор магнитной индукции B направлен по касательной к контуру в каждой точке контура, то циркуляция вектора магнитной индукции будет иметь вид
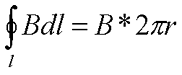
где r – радиус контура магнитной индукции.
Контур проходя внутри тороида охватывает N витков провода с током I, тогда закон полного тока для тороида будет иметь вид
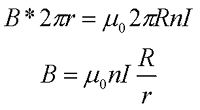
где n – число витков проводника, которое приходится на единицу длины,
r – радиус контура магнитной индукции,
R – радиус тороида.
Таким образом, используя закон полного тока и циркуляцию вектора магнитной индукции можно рассчитать сколь угодно сложное магнитное поле. Однако закон полного тока дает правильные результаты только лишь в вакууме. В случае расчёта магнитной индукции в веществе необходимо учитывать так называемые молекулярные токи. Об этом пойдёт речь в следующей статье.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Модуль магнитной индукции | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Вращающий момент, действующий на виток в магнитном поле, пропорционален силе тока в нем:
Mmax ~ Iвит,
а максимальный вращающий момент, который действует на виток в магнитном поле, пропорционален его площади:
Mmax ~ Sвит.
Отношение пропорциональных величин всегда является постоянной величиной. Поэтому
Mmax / (Iвит • Sвит) = B.
B является модулем магнитной индукции. Он определяет силовое действие магнитного поля на виток и не зависит от характеристик измерителя (витка).
Модуль магнитной индукции равен отношению максимального вращающего момента, который действует в магнитном поле на виток с током, к произведению силы тока в витке на его площадь.
На практике часто используют прямоугольную рамку с током. Это не изменяет результатов измерения.
Для измерения магнитной индукции используется единица, которая носит название тесла (Тл). Эта единица названа в честь известного сербского ученого и изобретателя Николы Тесла.
Никола Тесла (1856—1943), уроженец Сербии, изобретатель в области электротехники и радиотехники. Работая инженером на предприятиях Венгрии, Франции, США, дал четкое научное определение вращающего магнитного поля; создал многофазные электродвигатели переменного тока и многофазные системы передачи электроэнергии; разработал системы радиоуправляемых аппаратов: изобрел электросчетчик, частотомер; предложил принцип действия устройства для радиообнаружения подводных лодок.
Исходя из определения магнитной индукции, можно записать:
1 Тл = 1 Н•м / 1 А•м2 = 1 Н/(А•м).
На практике применяются и меньшие единицы:
1 милитесла = 1 мТл = 10-3 Тл.
1 микротесла = 1 мкТл = 10‑6 Тл.
| Рис. 6.9. Лабораторный магнитометр для школьных опытов |
На практике значения магнитной индукции измеряют приборами, которые называются индикаторами магнитной индукции, или магнитометрами (рис. 6.9). Принцип их действия основан на различных проявлениях действия магнитного поля на проводник с током или на вещество. Дополненные специальными электронными устройствами, эти приборы позволяют проводить измерения очень малых значений магнитной индукции.
Во многих случаях вместо измерений пользуются формулами, которые связывают характеристики магнитного поля с характеристиками проводника. Таким примером может быть расчет модуля магнитной индукции прямого проводника с током. Экспериментальные исследования показывают, что магнитная индукция поля прямого проводника пропорциональна силе тока в нем и обратно пропорциональна расстоянию от проводника до исследуемой точки поля:
B = k • I / r. Материал с сайта http://worldofschool.ru
Магнитная индукция прямого проводника с током пропорциональна силе тока в нем и обратно пропорциональна расстоянию от проводника до точки наблюдения.
Коэффициент пропорциональности зависит от выбора системы единиц измерения. В Международной системе единиц (СИ) он имеет значение
k = μ0 / 2π,
где μ0 — магнитная постоянная, значение которой 12,56 • 10-7 Н/А2.
Тогда окончательно для расчетов модуля магнитной индукции поля прямого проводника получим формулу
B = μ0I / 2πr,
где I — сила тока в проводнике; r — расстояние от данной точки поля до проводника; μ0 — магнитная постоянная.
На этой странице материал по темам:
Решение задач по теме » магнитног
Электродинамические величины
Определение модуля магнитной индукции
Вопросы по этому материалу:
Почему для определения модуля магнитной индукции применяют отношение Mmax / IS?
Какие единицы измерения магнитной индукции?
Как называются приборы для измерения магнитной индукции?
От чего зависит магнитная индукция поля прямого проводника с током?
Вектор магнитной индукции — Студопедия
Вектор магнитной индукции (В) — это основная силовая характеристика магнитного поля (обозначается В). Пробный контур, помещенный в магнитное поле, испытывает со стороны магнитного поля действие вращающего момента сил М.
Бесконечно длинный ток величины I создает на расстоянии r от себя магнитное поле:
где Мо — магнитная постоянная, R — расстояние, I — сила тока в проводнике.
Магнитная индукция — это векторная физическая величина, являющаяся силовой характеристикой в данной точке магнитного поля.
Единица магнитной индукции — тесла (Тл).
Магнитная индукция — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .
В вакууме B = μ0H.
Более конкретно, — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля на заряд , движущийся со скоростью , равна
где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика).
Вектор магнитной индукции (В) – аналог напряженности электрического поля. Основной силовой характеристикой магнитного поля является вектор магнитной индукции.
Опытным путем было установлено, что для одной и той же точки магнитного поля максимальный вращающий момент М (момент сил) пропорционален произведению силы тока I в контуре на его площадь S. Величину IS называют магнитным моментом контура Pm.
| Рисунок– Электрический ток (I), проходя по проводнику, создаёт магнитное поле (B) вокруг проводника. | Рисунок – Правило буравчика |
Правило буравчика (винта): Если направление поступательного движения буравчика (винта) совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции поля, создаваемого этим током.
На практике удобно пользоваться следующим правилом: Если обхватить соленоид (катушку) правой рукой так, что бы четыре пальца были направлены по току, то отогнутый большой палец покажет направление магнитного поля внутри соленоида.
А) Б)
Рисунок 3.2 – А) Образование магнитного потока в соленоиде
Б) Схема полей в соленоиде при протекании по обмотке переменного тока
Единица измерения В в СИ — тесла (Тл). Единица названа в честь сербского электротехника Н. Тесла.
ЭДС индукции. Примеры решения задач по физике. 10-11 класс
ЭДС индукции. Примеры решения задач по физике. 10-11 класс
- Подробности
- Просмотров: 1127
Задачи по физике — это просто!
Не забываем, что решать задачи надо всегда в системе СИ!
А теперь к задачам!
Элементарные задачи из курса школьной физики на вычисление ЭДС индукции.
Задача 1
За время 5 мс в соленоиде, содержащем 500 витков провода, магнитный поток равномерно убывает от 7 мВб до 3 мВб.
Найдите ЭДС индукции в соленоиде.
Задача 2
Какой магнитный поток пронизывает каждый виток катушки, имеющей 1000 витков, если при равномерном исчезновении магнитного поля в течение 0,1 с в катушке индуцируется ЭДС равная 10 В ?
Задача 3
Виток проводника площадью 2 см2 расположен перпендикулярно вектору магнитной индукции.
Чему равна ЭДС индукции в витке, если за время 0,05 секунд магнитная индукция равномерно убывает с 0,5 Тл до 0,1 Тл?
Задача 4
В однородном
магнитном поле перпендикулярно к направлению вектора индукции , модуль которого 0,1 Тл, движется провод длиной 2 метра со скоростью 5 м/с, перпендикулярной проводнику.
Какая ЭДС индуцируется в этом проводнике?
Задача 5
Перпендикулярно вектору магнитной индукции перемещается проводник длиной 1,8 метра со скоростью 6 м/c. ЭДС индукции равна 1,44 В.
Найти магнитную индукцию магнитного поля.
Задача 6
Самолет имеет размах крыльев 15 метров. Горизонтальная скорость полета равна720 км/час.
Определить разность потенциалов, возникающих между концами крыльев. Вертикальная составляющая магнитной индукции (перпендикулярно поверхности Земли) равна 50 мкТл.
Задача 7
Магнитный поток через контур проводника сопротивлением 0,03 Ом за 2 секунды изменился на 0,012 Вб.
Найдите силу тока в проводнике если изменение потока происходило равномерно.
Задача 8
В однородном магнитном поле находится плоский виток площадью 10 см2, расположенный перпендикулярно вектору магнитной индукции.
Какой ток течет по витку, если поле будет убывать с постоянной скоростью 0,5 Тл/с?
Задача 9
Сопротивление замкнутого контура равно 0,5 Ом. При перемещении кольца в магнитном поле магнитный поток через кольцо изменился на 5×10-3 Вб.
Какой за это время прошел заряд через поперечное сечение проводника?
Магнитная индукция — статья энциклопедии
.
В физике и, в частности, в теории электромагнетизма, магнитная индукция (также известная как плотность магнитного потока ) описывает магнитное поле (вектор) в каждой точке пространства. Магнитная индукция обычно обозначается B ( r , t ) и является векторным полем, то есть зависит от положения r и времени t . В нерелятивистской физике пространство, в котором определяется B , является трехмерным евклидовым пространством  — бесконечным миром, в котором мы живем.Поле B тесно связано с магнитным полем H , часто называемым магнитным полем напряженности , а иногда просто полем H . Фактически, некоторые авторы называют B магнитным полем, а H — вспомогательным полем.
— бесконечным миром, в котором мы живем.Поле B тесно связано с магнитным полем H , часто называемым магнитным полем напряженности , а иногда просто полем H . Фактически, некоторые авторы называют B магнитным полем, а H — вспомогательным полем.
Физический источник поля B может быть
или комбинации этих трех. Вблизи этих источников существует магнитное поле. В общем, сила магнитного поля уменьшается как малая мощность 1/ R , обратная расстоянию R до источника.
Магнитная сила может воздействовать на
- постоянный магнит (который представляет собой магнитный диполь или, примерно, два магнитных монополя),
- намагничивающийся (ферромагнитный) материал, такой как железо,
- движущиеся электрические заряды (за счет силы Лоренца)
- элементарных частиц из-за их собственного спина, который связан с их собственными магнитными свойствами через их гиромагнитные отношения.
Термин плотность магнитного потока относится к тому факту, что B — это магнитный поток.
на единицу поверхности.Это соотношение основано на законе магнитной индукции Фарадея.
Единицей измерения силы B в системе СИ является Т (тесла = Вебер / м 2 ), а единицей Гаусса B является G (гаусс = максвелл / см 2 ). Одна тесла — это 10 000 гаусс.
Для обозначения величин: магнитное поле (или лучше: магнитная индукция) Земли составляет около 0,5 Гс (50 мкТл). Магнит подковы составляет около 100 Гс. Медицинский диагностический аппарат МРТ обычно поддерживает поле до 2 Тл (20 кГс).В настоящее время самые сильные магниты в лабораториях имеют мощность около 30 Т (300 кГ).
Примечание к номенклатуре
В большинстве учебников по электричеству и магнетизму различают магнитное поле H и магнитную индукцию B . Однако на практике физики и химики почти всегда называют B магнитным полем , потому что термин «индукция» предполагает индуцированный магнитный момент. Поскольку индуцированный момент обычно не проявляется, термин индукция может сбивать с толку.Среди ученых распространены такие фразы, как: «Этот спектр ЭПР был измерен при магнитном поле 3400 гаусс» и «Наш магнит может создавать магнитные поля величиной до 20 тесла». То есть большинство ученых используют термин «поле» с единицами тесла или гаусса, в то время как, строго говоря, гаусс и тесла — это единицы B . Некоторые авторы идут еще дальше и резервируют название «магнитное поле» для B и называют H «вспомогательным магнитным полем».
Связь между B и H
В вакууме (также известном как микроскопический случай, см. Уравнения Максвелла), в отсутствие намагничивающейся среды поля B и H связаны следующим образом:
где μ 0 — магнитная постоянная (равная 4π⋅10 −7 Н / Д 2 ).Обратите внимание, что в гауссовых единицах размеры H (Oer) и B (G = гаусс) равны, 1 Oer = 1 G, хотя единицы имеют другое определение (Oer основано на поле соленоида , G — магнитный поток на поверхность). При отсутствии намагничивающейся среды нет необходимости вводить и B , и H , потому что они различаются точным и постоянным коэффициентом (единица для гауссовых единиц и μ 0 для единиц СИ).
На микроскопическом уровне магнитный поток B и электрическое поле E определяют поведение зарядов.Например, один движущийся заряд подчиняется закону силы Лоренца, который в единицах СИ равен:
Однако рассматривать все заряды в системе на микроскопическом уровне непрактично, поэтому вводятся приближения. Некоторые части системы рассматриваются под микроскопом, а некоторые рассматриваются как «материалы», в частности, диэлектрики и магнитные материалы. Отклик магнитного материала на магнитный поток вводится через намагниченность материала , другое векторное поле M ( r , t ).
В присутствии намагничивающейся среды соотношение между B и H включает намагниченность M среды,
Чтобы фактически определить поведение системы, намагниченность M должна быть определена в терминах B или H , чтобы реакция системы зависела только от одной переменной поля. Это определение M может быть очень сложным. Например, это может включать введение квантовой механики и статистической механики, изучаемой в области физики конденсированного состояния.Однако во многих неферромагнитных средах намагниченность M линейна в H ,
Для магнитно-изотропной среды тензор магнитной восприимчивости χ является константой, умноженной на единичную матрицу 3 × 3, χ = χ м 1 . Для изотропной среды соотношение между B и H выражается в единицах СИ и гауссовых единицах соответственно,
Постоянная материала μ, которая выражает «легкость» намагничивания среды, представляет собой магнитную проницаемость среды.В большинстве неферромагнитных материалов χ м << 1 и, следовательно, B ≈ μ 0 H (SI) или B ≈ H (гауссовский). Для ферромагнитных материалов магнитная проницаемость μ может быть значительной (χ м >> 1). В этом случае намагниченность среды сильно увеличивает магнитное поле.
Два макроскопических уравнения Максвелла, которые содержат заряды и токи, являются уравнениями для H и электрического смещения D .Это является следствием того факта, что плотности тока Дж и электрические поля E (из-за зарядов) модифицируются намагниченностью M и поляризацией P среды. В единицах СИ уравнение Максвелла для магнитного поля имеет следующий вид:
Микроскопическая (без среды) форма этого уравнения получается путем исключения D и H через
D = ε 0 E и H = B / μ 0 ( P = 0 и M = 0).
Два уравнения Максвелла, которые не содержат токов и зарядов, дают отношения между основными полями E и B , а не между вспомогательными полями H и D . Например, закон индукции Фарадея в единицах СИ:
Это уравнение верно как микроскопически (вакуум), так и макроскопически (в присутствии среды). Но, конечно, в микроскопическом случае появляются подробные микроскопические токи и заряды, обусловленные элементарными источниками, тогда как в макроскопическом случае некоторые из этих микроскопических токов и зарядов учитываются в свойствах материала, например, в различных диэлектрических и магнитных проницаемости.Таким образом, поля E и B в этих двух ситуациях различаются, при этом макроскопические поля усредняются, чтобы удалить некоторые микроскопические детали.
.
Что такое электромагнитная индукция? — Определение, принцип, приложение
- БЕСПЛАТНАЯ ЗАПИСЬ КЛАСС
- КОНКУРСНЫЕ ЭКЗАМЕНА
- BNAT
- Классы
- Класс 1-3
- Класс 4-5
- Класс 6-10
- Класс 110003 CBSE
- Книги NCERT
- Книги NCERT для класса 5
- Книги NCERT, класс 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- NCERT Книги для класса 11
- NCERT Книги для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
9plar
- Книги NCERT
- RS Aggarwal
- RS Aggarwal Решения класса 12
- RS Aggarwal Class 11 Solutions
- RS Aggarwal Решения класса 10
- Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- RD Sharma
- RD Sharma Class 6 Решения
- RD Sharma Class 7 Решения
- Решения RD Sharma класса 8
- Решения RD Sharma класса 9
- Решения RD Sharma класса 10
- Решения RD Sharma класса 11
- Решения RD Sharma Class 12
- PHYSICS
- Механика
- Оптика
- Термодинамика
- Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- MATHS
- Статистика
- 9000 Pro Числа
- Числа
- 9000 Pro Числа Тр Игонометрические функции
- Взаимосвязи и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убытки
- Полиномиальные уравнения
- Деление фракций
- Microology
- 0003000
- FORMULAS
- Математические формулы
- Алгебраные формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- 000 CALCULATORS
- 000
- 000 Калькуляторы по химии Образцы документов для класса 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 1 1
- Образцы документов CBSE для класса 12
0003000
- Вопросники предыдущего года CBSE
- Вопросники предыдущего года CBSE, класс 10
- Вопросники предыдущего года CBSE, класс 12
- HC Verma Solutions
- HC Verma Solutions Класс 11 Физика
- HC Verma Solutions Класс 12 Физика
- Решения Лакмира Сингха
- Решения Лахмира Сингха класса 9
- Решения Лахмира Сингха класса 10
- Решения Лакмира Сингха класса 8
9000 Класс
9000BSE 9000 Примечания3 2 6 Примечания CBSE
Примечания
- Дополнительные вопросы по математике класса 8 CBSE
- Дополнительные вопросы по науке 8 класса CBSE
- Дополнительные вопросы по математике класса 9 CBSE
- Дополнительные вопросы по математике класса 9 CBSE Вопросы
- CBSE Class 10 Дополнительные вопросы по математике
- CBSE Class 10 Science Extra questions
- Class 3
- Class 4
- Class 5
- Class 6
- Class 7
- Class 8 Класс 9
- Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для класса 11 по физике
- Решения NCERT для класса 11 Химия
- Решения NCERT для биологии класса 11
- Решение NCERT s Для класса 11 по математике
- NCERT Solutions Class 11 Accountancy
- NCERT Solutions Class 11 Business Studies
- NCERT Solutions Class 11 Economics
- NCERT Solutions Class 11 Statistics
- NCERT Solutions Class 11 Commerce
- NCERT Solutions for Class 12
- Решения NCERT для физики класса 12
- Решения NCERT для химии класса 12
- Решения NCERT для биологии класса 12
- Решения NCERT для математики класса 12
- Решения NCERT, класс 12, бухгалтерский учет
- Решения NCERT, класс 12, бизнес-исследования
- NCERT Solutions Class 12 Economics
- NCERT Solutions Class 12 Accountancy Part 1
- NCERT Solutions Class 12 Accountancy Part 2
- NCERT Solutions Class 12 Micro-Economics
- NCERT Solutions Class 12 Commerce
- NCERT Solutions Class 12 Macro-Economics
- NCERT Solut Ионы Для класса 4
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для класса 5
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для класса 6
- Решения NCERT для математики класса 6
- Решения NCERT для науки класса 6
- Решения NCERT для класса 6 по социальным наукам
- Решения NCERT для класса 6 Английский язык
- Решения NCERT для класса 7
- Решения NCERT для математики класса 7
- Решения NCERT для науки класса 7
- Решения NCERT для социальных наук класса 7
- Решения NCERT для класса 7 Английский язык
- Решения NCERT для класса 8
- Решения NCERT для математики класса 8
- Решения NCERT для науки 8 класса
- Решения NCERT для социальных наук 8 класса ce
- Решения NCERT для класса 8 Английский
- Решения NCERT для класса 9
- Решения NCERT для класса 9 по социальным наукам
- Решения NCERT для математики класса 9
- Решения NCERT для математики класса 9 Глава 1
- Решения NCERT для математики класса 9, глава 2
- для математики класса 9, глава 3
- Решения NCERT для математики класса 9, глава 4
- Решения NCERT для математики класса 9, глава 5
- для математики класса 9, глава 6
- Решения NCERT для математики класса 9 Глава 7
- для математики класса 9 Глава 8
- Решения NCERT для математики класса 9 Глава 9
- Решения NCERT для математики класса 9 Глава 10
- для математики класса 9 Глава 11
- NCERT для математики класса 9 Глава 12
- для математики класса 9 Глава 13
- NCER Решения T для математики класса 9 Глава 14
- Решения NCERT для математики класса 9 Глава 15
Решения NCERT
Решения NCERT
Решения NCERT
Решения NCERT
Решения
Решения NCERT
- Решения NCERT для науки класса 9
- Решения NCERT для науки класса 9 Глава 1
- Решения NCERT для науки класса 9 Глава 2
- Решения NCERT для науки класса 9 Глава 3
- Решения NCERT для науки класса 9 Глава 4
- Решения NCERT для науки класса 9 Глава 5
- Решения NCERT для науки класса 9 Глава 6
- Решения NCERT для науки класса 9 Глава 7
- Решения NCERT для науки класса 9 Глава 8
- Решения NCERT для науки класса 9 Глава 9
- Решения NCERT для науки класса 9 Глава 10
- Решения NCERT для науки класса 9 Глава 12
- Решения NCERT для науки класса 9 Глава 11
- Решения NCERT для науки класса 9 Глава 13
- для науки класса 9 Глава 14
- Решения NCERT для класса 9 по науке Глава 15
Решения NCERT
- Решения NCERT для класса 10
- Решения NCERT для класса 10 по социальным наукам
- Решения NCERT для математики класса 10
- Решения NCERT для класса 10 по математике Глава 1
- Решения NCERT для математики класса 10, глава 2
- Решения NCERT для математики класса 10, глава 3
- Решения NCERT для математики класса 10, глава 4
- Решения NCERT для математики класса 10, глава 5
- Решения NCERT для математики класса 10, глава 6
- Решения NCERT для математики класса 10, глава 7
- Решения NCERT для математики класса 10, глава 8
- Решения NCERT для математики класса 10, глава 9
- Решения NCERT для математики класса 10, глава 10
- Решения NCERT для математики класса 10 Глава 11
- Решения NCERT для математики класса 10 Глава 12
- Решения NCERT для математики класса 10 Глава ter 13
- Решения NCERT для математики класса 10 Глава 14
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки класса 10
- Решения NCERT для класса 10 науки Глава 1
- Решения NCERT для класса 10 Наука, глава 2
- Решения NCERT для класса 10, глава 3
- Решения NCERT для класса 10, глава 4
- Решения NCERT для класса 10, глава 5
- Решения NCERT для класса 10, глава 6
- Решения NCERT для класса 10 Наука, глава 7
- Решения NCERT для класса 10, глава 8,
- Решения NCERT для класса 10, глава 9
- Решения NCERT для класса 10, глава 10
- Решения NCERT для класса 10, глава 11
- Решения NCERT для класса 10 Наука Глава 12
- Решения NCERT для класса 10 Наука Глава 13
- NCERT S Решения для класса 10 по науке Глава 14
- Решения NCERT для класса 10 по науке Глава 15
- Решения NCERT для класса 10 по науке Глава 16
- Программа NCERT
- NCERT
- Class 11 Commerce Syllabus
- Учебный план класса 11
- Учебный план класса 11
- Учебный план экономического факультета 11
- Учебный план по коммерции класса 12
- Учебный план класса 12
- Учебный план класса 12
- Учебный план
- Класс 12 Образцы документов для торговли
- Образцы документов для предприятий класса 11
- Образцы документов для коммерческих предприятий класса 12
- TS Grewal Solutions
- TS Grewal Solutions Class 12 Accountancy
- TS Grewal Solutions Class 11 Accountancy
- Отчет о движении денежных средств 9 0004
- Что такое предпринимательство
- Защита потребителей
- Что такое основные средства
- Что такое баланс
- Что такое фискальный дефицит
- Что такое акции
- Разница между продажами и маркетингом
9100003
- Образцы документов ICSE
- Вопросы ICSE
- ML Aggarwal Solutions
- ML Aggarwal Solutions Class 10 Maths
- ML Aggarwal Solutions Class 9 Maths
- ML Aggarwal Solutions Class 8 Maths
- ML Aggarwal Solutions Class 7 Maths Решения Математика класса 6
- Решения Селины
- Решения Селины для класса 8
- Решения Селины для класса 10
- Решение Селины для класса 9
- Решения Фрэнка
- Решения Фрэнка для математики класса 10
- Франк Решения для математики 9 класса
9000 4
- ICSE Class
- ICSE Class 6
- ICSE Class 7
- ICSE Class 8
- ICSE Class 9
- ICSE Class 10
- ISC Class 11
- ISC Class 12
- 900 Экзамен IAS
- Пробный тест IAS 2019 1
- Пробный тест IAS4
2
- Экзамен KPSC KAS
- Экзамен UPPSC PCS
- Экзамен MPSC
- Экзамен RPSC RAS
- TNPSC Group 1
- APPSC Group 1
- Экзамен BPSC
- Экзамен WPSC
- Экзамен GPSC
- Ответный ключ UPSC 2019
- Коучинг IAS Бангалор
- Коучинг IAS Дели
- Коучинг IAS Ченнаи
- Коучинг IAS Хайдарабад
- Коучинг IAS Мумбаи
9000 JEE 9000 JEE 9000 Advanced
- Программа BYJU NEET
- NEET 2020
- NEET Eligibility
- NEET Eligibility
- NEET Eligibility 2020 Подготовка
- NEET Syllabus
- Support
- Разрешение жалоб
- Служба поддержки
- Центр поддержки
- GSEB
- GSEB Syllabus
GSEB
Образец статьи
003 GSEB Books
- MSBSHSE Syllabus
- MSBSHSE Учебники
- MSBSHSE Образцы статей
- MSBSHSE Вопросники
- 9000 AP Board
- AP 2 Year Syllabus
- 9000
- MP Board Syllabus
- MP Board Образцы документов
- MP Board Учебники
- Assam Board Syllabus
- Assam Board
- Assam Board
- Assam Board Документы
- Bihar Board Syllabus
- Bihar Board Учебники
- Bihar Board Question Papers
- Bihar Board Model Papers
- Odisha Board
- Odisha Board
- Odisha Board 9000
- ПСЕБ 9 0002
- PSEB Syllabus
- PSEB Учебники
- PSE
.
Что такое электромагнитная индукция?
Что такое электромагнитная индукция?
Индуцированный E.M.F. и наведенный ток
- На рисунке показана индукционная плита. Во время варки нагревается только сковорода. Поверхность плиты не нагревается. Как это стало возможным?
- В индукционной плите используется магнитное поле от до , которое создает вихревые токи в металлической сковороде с помощью процесса, известного как электромагнитная индукция .Вихревые токи в сковороде выделяют тепло.
- На рисунке медный стержень выпущен так, что он попадает в магнитное поле между парой магнитов. Обнаружено, что стрелка центрального нулевого гальванометра показывает отклонение при перемещении стержня между магнитами. Затем указатель вернется в исходное нулевое положение.
- Это показывает, что электромагнитная сила (ЭДС) индуцируется поперек медного стержня, когда он движется поперек магнитного поля. вызвал e.м.ф. вызывает протекание тока в медном стержне .
- Приведенная ниже блок-схема суммирует три этапа создания наведенного тока.
Люди тоже спрашивают
Что такое закон Фарадея?
Величина индуцированного тока: закон Фарадея
- Закон Фарадея гласит, что величина индуцированной ЭДС. прямо пропорциональна скорости изменения магнитного потока или скорости сокращения магнитного потока.
- Для прямого провода наведенная ЭДС. может быть увеличен за счет:
(a) увеличения скорости движения
(b) увеличения напряженности магнитного поля - Для соленоида наведенная э.д.с. может быть увеличен за счет:
(a) увеличения скорости относительного движения
(b) увеличения числа витков
(c) использования более сильного магнитного поля - Величина индуцированного тока зависит от:
(a) величина наведенной ЭДС
(b) Сопротивление цепи
Взаимосвязь между наведенным током и влияющими на него факторами сведена в Таблицу.Управляемая переменная Ответная переменная Фиксированные переменные Скорость магнита увеличена Увеличивается индуцированный ток Количество витков, сила магнита, сопротивление цепи Увеличено количество витков Увеличивается наведенный ток Скорость магнита, сила магнита, сопротивление цепи Увеличивается сила магнита Увеличивается индуцированный ток Скорость магнита, количество витков, сопротивление цепь Сопротивление цепи увеличивается Индуцированный ток уменьшается Скорость магнита, количество витков, сила магнита
Индуцированная E.М.Ф. и наведенный ток в прямом проводнике
- Когда провод движется и разрезает силовые линии магнитного поля (или магнитный поток ), э.д.с. индуцируется по проводу.
- Электромагнитная индукция Производится э.д.с. поперек проводника, когда он отсекает магнитный поток.
- Если провод замкнут, то наведет э.д.с. вызовет протекание индуцированного тока .
- На рисунке показано направление движения провода, в котором возникает индуцированный ток.
- Направление индуцированного тока может быть определено с помощью правила правой руки Флеминга .
- Используются следующие шаги, как показано на рисунке (а).
(a) Укажите указательным пальцем правой руки по направлению магнитного поля от северного полюса к южному полюсу.
(b) Вращайте правой рукой, пока большой палец не укажет в направлении движения.
(c) Второй палец покажет направление индуцированного тока. - Еще одно правило, которое можно использовать, — это правило удара правой рукой, как показано на рисунке (b).
(a) Укажите четырьмя пальцами правой руки в направлении поля.
(b) Вращайте рукой, пока большой палец не укажет в направлении движения.
(c) Нанесите пощечину. Направление удара — это направление индуцированного тока. - На рисунке показано изменение направления индуцированного тока при изменении направления движения.
Что такое закон электромагнитной индукции Ленца?
Индуцированная E.М.Ф. и наведенный ток в соленоиде:
- Когда стержневой магнит перемещается к соленоиду, магнитный поток перемещается вместе с магнитом и разрезает обмотки соленоида.
- Э.д.с. индуцируется в соленоиде, как показано на рисунке.
- Электромагнитная индукция также может быть определена как создание ЭДС. через соленоид, когда обмотки соленоида перерезаются магнитным потоком.
- Если концы соленоида подключены к чувствительному гальванометру с центром в ноль, отклонение указателя покажет, что в соленоиде течет индуцированный ток, как показано на рисунке.
- Закон Ленца используется для определения полярности концов соленоида, обращенных к магниту. Затем используется правило правого захвата для определения направления индуцированного тока в соленоиде.
- Закон Ленца гласит, что направление индуцированного тока таково, что вызывающее его движение будет противоположным . Использование закона Ленца показано на рисунке.
- Закон Ленца для соленоидов представлен в таблице.
Относительное движение между магнитом и соленоидом Полярность на конце соленоида, обращенном к магниту Сила между соленоидом и магнитом По направлению друг к другу Такая же полярность, как у магнита Отталкивание Вдали друг от друга Противоположная полярность, как у магнита Притяжение - Закон Ленца является примером принципа сохранения энергии.Когда магнит или соленоид перемещаются против противодействующей силы, работа выполняется. Следовательно, механическая энергия преобразуется в электрическую.
Примеры электромагнитной индукции
- На рисунке показано направление индуцированного тока в проводе.
В каком направлении двигался провод, создавая наведенный ток?
Решение:
Используя правило правой руки Флеминга или правило правой руки, направление движения проволоки — D. - На рисунке показан стержневой магнит, падающий на соленоид.
Какова полярность в точке X и направление тока в точке Y?
Решение:
Магнит движется к соленоиду. Согласно закону Ленца, магнит и соленоид должны отталкивать друг друга. Следовательно, X — северный полюс. Ток на конце X идет против часовой стрелки. Следовательно, ток в точке Y находится слева.
Факторы, влияющие на величину индуцированного тока Эксперимент
Цель: Изучить факторы, влияющие на величину индуцированного тока.
Материалы: Два соленоида с 600 и 1200 витками соответственно, два стержневых магнита, соединительные провода, резиновые ленты
Аппаратура: Чувствительный гальванометр с центром и нулем
Метод:
- Устройство установлено, как показано на рисунке .
- Стержневой магнит медленно вставляется в соленоид на 600 оборотов. Регистрируется максимальное показание гальванометра.
- Стержневой магнит быстро вставляется в соленоид на 600 оборотов. Регистрируется максимальное показание гальванометра.
- Барный магнит медленно вдвигается в соленоид на 1200 оборотов. Регистрируется максимальное показание гальванометра.
- Резиновые ленты используются для связывания двух стержневых магнитов вместе с одинаковыми полюсами рядом.
- Два магнита медленно вставляются в соленоид на 600 оборотов. Регистрируется максимальное показание гальванометра.
Наблюдения:
| Шаг | Количество стержневых магнитов | Скорость магнита | Количество оборотов соленоида | Максимальное показание гальванометра |
| Шаг 2 | 1 | Медленный | 600 | 16 |
| Шаг 3 | 1 | Быстрый | 600 | 30 |
| Шаг 4 | 1 | Медленный | 1200 | 32 |
| Шаг 6 | 2 | Медленный | 600 | 28 |
Обсуждение:
- Показания гальванометра пропорциональны наведенному току.
- Путем сравнения наблюдений на этапах 2 и 3, величина индуцированного тока увеличивается при увеличении скорости магнита.
- Путем сравнения наблюдений на шагах 2 и 4, величина индуцированного тока увеличивается при увеличении количества витков соленоида.
- Два стержневых магнита с одинаковыми полюсами, расположенные рядом, создают более сильное магнитное поле. Сравнивая наблюдения на этапах 2 и 6, можно увидеть, что величина индуцированного тока увеличивается с увеличением напряженности магнитного поля.
Вывод:
Величина индуцированного тока в соленоиде увеличивается с увеличением скорости магнита, количества витков соленоида или напряженности магнитного поля.
Приложения электромагнитной индукции
Приложения электромагнитной индукции:
- Генератор постоянного тока и генератор переменного тока используют электромагнитную индукцию для создания выходного напряжения.
- Катушка вращается под действием внешней силы и отсекает магнитный поток.
- Переменная ЭДС. индуцируется в катушке.
- В генераторе постоянного тока постоянный ток на выходе получается с помощью коммутатора с разъемным кольцом. В генераторе переменного тока два контактных кольца используются для получения переменного тока на выходе.
На рисунке и в таблице сравниваются генератор постоянного тока и генератор переменного тока.
| Генератор постоянного тока | Генератор переменного тока |
| Катушка, состоящая из многих витков, вращаемая внешней силой в магнитном поле, создаваемом постоянными магнитами. | |
| Использует электромагнитную индукцию для создания ЭДС. в катушке. | |
| Концы катушки подключены к коммутатору с разъемным кольцом. | Концы катушки соединены с двумя контактными кольцами. |
| Две половины коммутатора с разрезным кольцом обмениваются контактом с угольными щетками каждые полоборота. | Каждое контактное кольцо всегда контактирует с одной и той же угольной щеткой. |
Выходной ток течет в одном направлении через сопротивление нагрузки R. | Выходной ток через нагрузку течет туда-сюда в противоположных направлениях j сопротивление, R. |
| |
Эксперимент с электромагнитной индукцией
Цель: Наблюдать за электромагнитной индукцией в диапазоне
A. прямой провод B. соленоид
A. Электромагнитная индукция в прямом проводе
Материалы: Медный стержень с оголенными концами
Аппаратура: магниты Magnadur , соединительные провода с зажимами типа «крокодил», чувствительный центр -нулевой гальванометр
Метод:
- Устройство установлено, как показано на рисунке.
- Медный стержень неподвижно удерживается между полюсами магнита. Наблюдается показание гальванометра.
- Стержень быстро перемещается в направлении 1, как показано на рисунке. Наблюдается показание стрелки гальванометра.
- Шаг 3 повторяется для направлений 2, 3, 4, 5 и 6.
Наблюдения:
Обсуждение:
- Линии магнитного поля представляют собой горизонтальные линии от северного полюса до южного полюса.
- Направления 3, 4, 5 и 6 — это направления движения, при которых медный стержень движется вдоль силовых линий магнитного поля и не пересекает их.
- Направления 1 и 2 — это направления движения, в которых медный стержень пересекает силовые линии магнитного поля.
- Гальванометр обнаруживает электрический ток, когда его стрелка показывает отклонение.
- В медном стержне возникает ток, когда его перемещают, чтобы пересечь силовые линии магнитного поля.
B. Электромагнитная индукция в соленоиде
Материалы: Соленоид на 600 витков
Аппаратура: Прутковый магнит, соединительные провода, чувствительный гальванометр с центром в нуле
Метод:
- Аппарат настроен вверх, как показано на рисунке.
- Соленоид остается неподвижным. Показания гальванометра наблюдаются для каждого из следующих действий:
(a) стержневой магнит вдавливается в соленоид
(b) стержневой магнит удерживается неподвижно в соленоиде
(c) стержневой магнит вытаскивается из соленоид - Магнит стержня удерживается неподвижно. Показания гальванометра наблюдаются при каждом из следующих действий:
(a) Соленоид подталкивается к стержневому магниту
(b) Соленоид отводится от стержневого магнита
Наблюдения:
Обсуждение :
- Постоянный магнит создает магнитное поле в области вокруг себя.Когда магнит перемещается, магнитное поле движется вместе с ним.
- Когда магнит перемещается к соленоиду и внутрь, силовые линии магнитного поля разрезают соленоид.
- Гальванометр показал положительное значение, когда магнит и соленоид приближаются друг к другу. Это показывает, что в соленоиде в определенном направлении возник ток.
- Когда магнит перемещается из соленоида и от него, силовые линии магнитного поля снова режут соленоид.
- Гальванометр показал отрицательное значение, когда магнит и соленоид перемещались дальше друг от друга. В соленоиде протекал ток в обратном направлении.
- В соленоиде возникает ток, когда между соленоидом и магнитом происходит относительное движение.
Заключение:
Ток индуцируется в прямом проводнике, когда он движется и разрезает силовые линии магнитного поля. Ток индуцируется в соленоиде при относительном движении между соленоидом и магнитом.
.







