Векторная диаграмма параллельной RLC-цепи
Главная
→
Теория электрических цепей
→
Векторная диаграмма параллельной RLC-цепи
Векторная диаграмма параллельной RLC-цепи
Векторная диаграмма параллельной RLC-цепи (рис. 2) соответствует комплексной схеме замещения и правилам качественного построения векторных диаграмм.
Векторная диаграмма параллельной RLC-цепи
Изображены два варианта ВД: в центре рисунка ВД построена с использованием суммирования векторов по правилу треугольника (на ВД указаны комплексные амплитуды), а справа – по правилу параллелограмма (на ВД указаны комплексные действующие значения).
ВД позволяет рассчитать установившийся синусоидальный режим в цепи на основании очевидных из геометрии ВД формул
I=IR2+(IL−IC)2; φ=αu−αi=arctgIL−ICIR.
Очевидно, при ZL = ZC имеем IL = IC, то есть участок LC ≡ ХХ, в цепи простейший резонанс токов, когда iR = i, а синусоиды токов iL(t), iC(t), имея одинаковые амплитуды, находятся в противофазе и поэтому полностью компенсируются.
При резонансе ток в цепи совпадает по фазе с напряжением, приложенным к цепи, а характер нагрузки чисто активный.
Если ZL > ZC, имеем IL = U/ZL < IC = U/ZC, φ < 0, αi > αu, и цепь имеет емкостный характер.
Если ZLZC, имеем IL > IC, φ > 0, αiαu, то есть напряжение опережает ток и цепь имеет индуктивный характер.
Векторная диаграмма,
параллельная RLC-цепь
15.10.2015, 23492 просмотра.
Какой закон реализует векторная диаграмма последовательной цепи — MOREREMONTA
Допустим, имеется цепь с последовательно соединенными элементами r, L, C (рис. 3.11) по которой протекает синусоидальный ток:
Согласно второму закону Кирхгофа:
.
Соотношения между величинами действующих значений напряжений на элементах цепи, можно оценить с помощью векторной диаграммы (рис. 3. 12).
Порядок построения векторной диаграммы следующий.
1. Откладываем вектор тока I в произвольном направлении.
2. Откладываем падение напряжения на всех элементах:
2.1. Напряжение на резистивном элементе совпадает по направление с током .
2.2. Напряжение на индуктивном элементе опережает по направлению ток на 90 0 .
2.3. Напряжение на емкостном элементе отстает по направлению от тока на 90 0 .
3. Вектор напряжения на зажимах цепи, получаем путем векторного сложения , , (начало вектора соединяем с концом вектора ).
Из векторной диаграммы следует:
где –полное сопротивление цепи.
Выражение называют законом Ома для цепи синусоидального тока.
Угол jпоказывает сдвиг по фазе между напряжением и током на зажимах.
В приведенном примере напряжение опережает ток на j, т.к. xL > xCи режим работы цепи активно-индуктивный.
1. Определяем омические сопротивления реактивных элементов:
(Ом),
(Ом),
(Ом).
2. Определяем полное сопротивление ветви.
2.1. Эквивалентное активное сопротивление
(Ом).
2.2. Эквивалентное индуктивное сопротивление
(Ом).
2.3. Эквивалентное емкостное сопротивление
(Ом).
2.4. Полное сопротивление
(Ом).
3. Определяем ток в цепи (А).
4. Определяем напряжения на каждом элементе цепи
(В),
(В),
(В),
(В),
(В),
(В).
5. Напряжение на участке цепи 3-6 равно
(В).
6. Векторная диаграмма рассматриваемой цепи приведена на рисун- ке 3.18.
Дата добавления: 2015-04-21 ; просмотров: 1906 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
в цепи с активным сопротивлением ток и напряжение совпадают по фазе j=0;
в цепи с индуктивностью ток отстает от напряжения на угол 90°;
в цепи с емкостью ток опережает напряжение на 90°.
Для соответствующих участков электрической цепи векторные диаграммы токов и напряжений будут выглядеть следующим образом.
Треугольник сопротивлений и треугольник мощностей.
Если разделить стороны треугольника напряжений на ток (в цепи с последовательным соединением элементов ток одинаков во всех участках), то (в соответствии с законом Ома) получим треугольник сопротивлений.
Здесь х=xL— xC — реактивное сопротивление цепи, а Z — полное сопротивление цепи:
.
Полученное уравнение устанавливает связь межу различными сопротивлениями цепи.
Если умножить стороны треугольника напряжений на ток, то получим треугольник мощностей:
Здесь Р=URI — активная мощность, которая выделяется на активных сопротивлениях цепи. Она связана с необратимыми преобразованиями электрической энергии, то есть с совершением работы (полезной) в электроустановке. Активная мощность измеряется в ваттах [Вт].
Активная мощность измеряется в ваттах [Вт].
Q=UxI — реактивная мощность. Связана в электроустановках с совершением обратимых преобразований энергии, полезной работы она не совершает. В электроустановках затрачивается на создание электрических (С) и магнитных (L) полей. Реактивная мощность измеряется вольт амперах реактивных [вар].
Реактивная мощность оказывает существенное влияние на режим работы электрической цепи. Циркулируя по проводам трансформаторов, генераторов, двигателей, линий электропередач, она нагревает их. Поэтому расчет проводов и других элементов устройств переменного тока производят из полной мощности, которая учитывает активную и реактивную мощности.
S=UI — полная мощность, измеряется в вольт амперах [В*А]. Из треугольника мощностей определим:
.
Параллельное соединение идеальных элементов R, L и C в цепи переменного тока. Метод проводимостей. Векторная диаграмма для токов в цепи. Активная, реактивная и полная проводимости цепи. Треугольник проводимостей и треугольник мощностей.
Векторная диаграмма для токов в цепи. Активная, реактивная и полная проводимости цепи. Треугольник проводимостей и треугольник мощностей.
Цепь с параллельным соединением элементов состоит из ряда параллельных ветвей, включенных между двумя узлами.
По первому закону Кирхгофа для токов можно записать:
.
Действующие значения токов в отдельных ветвях будут определяться:
, , .
Построение векторных диаграмм для параллельного соединения элементов цепи начинают с вектора U (т.к. оно одинаково для всех участков цепи).
Цепь в зависимости от соотношения сопротивлений xL и xC также может иметь индуктивный, емкостный или чисто активный характер.
На построенных диаграммах можно выделить треугольник токов.
IA — активная составляющая тока;
IP — реактивная составляющая тока.
Связь между полным током и его составляющими выражается:
.
Метод проводимостей: При этом ток каждой ветви рассматривают состоящим из двух составляющих: активной и реактивной .
,
где — активная проводимость ветви
, где
,
где — реактивная проводимость ветви
, где
где
— полная активная проводимость цепи;
— полная реактивная проводимость цепи.
, где
— полная проводимость цепи.
.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
ПОСЛЕДОВАТЕЛЬНОЙ ЦЕПИ СИНУСОИДАЛЬНОГО ПЕРЕМЕННОГО ТОКА
Дана последовательная цепь из R, L и C (рис. 6.1). Цепь такого вида часто называют последовательным колебательным контуром. В этой цепи заданы: приложенное напряжение U , частота f и числовые значения параметров R, L ,C . Требуется найти ток и напряжение на элементах.
Решение этой задачи выполняем на основе построения векторной диаграммы. В последовательной цепи общим для всех элементов является протекающий по ним ток. Поэтому именно с него начинаем построение векторной диаграммы последовательной электрической цепи.
На рис.6.2 изображаем вектор тока, например, горизонтально, хотя его направление можно выбирать произвольно. Выбор горизонтального направления диктуется соображениями удобства. Далее строятся векторы напряжений на всех элементах. В соответствии со вторым законом Кирхгофа можно получить вектор входного напряжения:
Рис. 6.1. Последовательная цепь
Рис. 6.2. Векторная диаграмма
последовательной цепи переменного тока
Сложение векторов удобнее выполнять по правилу многоугольника, когда каждый последующий вектор пристраивается к концу предыдущего. Известно, что напряжение на активном сопротивлении R совпадает по фазе с
Известно, что напряжение на активном сопротивлении R совпадает по фазе с
током, поэтому вектор UR направлен по вектору тока I . К его концу пристраиваем вектор UL и направляем его вверх под углом 90°, так как напряжение на индуктивности UL опережает ток на 90°. Напряжение на ёмкости UC находится в противофазе с U L , т. е. отстаёт от тока на 90°, поэтому вектор UC , пристроенный к концу вектора UL, направлен вниз. Сумма векторов UR + UL + UC даёт вектор напряжения U .
Величины напряжений на отдельных элементах цепи известны согласно закону Ома
Векторная диаграмма на рис. 6.2 построена для случая, когда UL > UC . Это имеет место при X L > XC , когда в цепи преобладает индуктивность и цепь носит
активно-индуктивный характер. В этом случае общий ток I отстаёт по фазе от
входного напряжения на угол ϕ. Возможны также режимы, когда UL резонансом напряжения . Это означает, что входное реактивное сопротивление в цепи равно нулю:
В этом случае UL = UC и цепь носит чисто активный характер, т.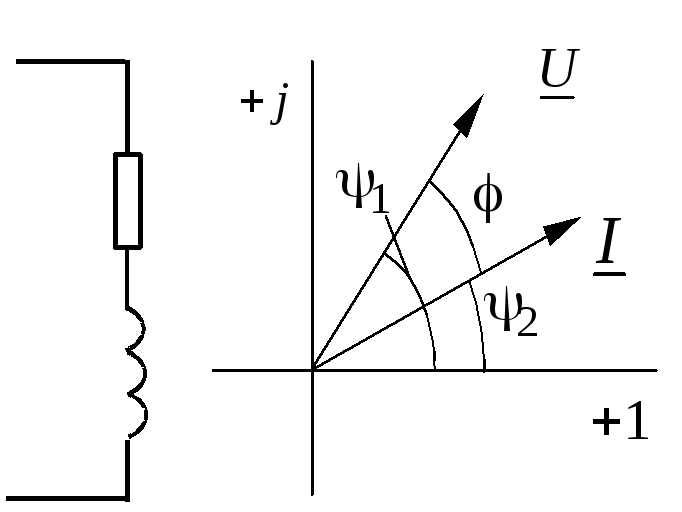 е. Z = R и сдвиг фаз отсутствует (ϕ = 0 ).
е. Z = R и сдвиг фаз отсутствует (ϕ = 0 ).
Рассмотрим более подробно резонанс напряжений. Так как при резонансе , то соответственно
Напряжения на индуктивности и ёмкости в этом режиме равны по величине и, находясь в противофазе, компенсируют друг друга. Всё приложенное к цепи напряжение приходится на её активное сопротивление. Это видно из векторной диаграммы, представленной на рис. 6.4.
Рис. 6.4. Векторная диаграмма при резонансе напряжения Напряжение на индуктивности и ёмкости может значительно превышать
напряжение на входе цепи. Их отношение, называемое добротностью контура Q , определяется величинами индуктивного (или ёмкостного) и активного сопротивлений
Добротность показывает, во сколько раз напряжения на индуктивности и ёмкости при резонансе превышают напряжение, приложенное к цепи. В радиотехнических цепях она может достигать несколько сотен единиц.
Из условия (8.1) следует, что резонанса можно достичь, изменяя любой из параметров – частоту, индуктивность, ёмкость. При этом меняются реактивное и полное сопротивления цепи, а вследствие этого – ток, напряжение на элементах и сдвиг фаз.
При этом меняются реактивное и полное сопротивления цепи, а вследствие этого – ток, напряжение на элементах и сдвиг фаз.
Ёмкость С0 , при которой наступает резонанс, можно определить из формулы
Например, если индуктивность контура L= 0,2 Гн, то при частоте f = 50 Гц резонанс наступит при ёмкости
. Решив это уравнение относительно
где f0 – собственная частота колебания контура.
Таким образом, при резонансе напряжений частота f источника напряжения равна собственной частоте f0 колебания контура.
При резонансе напряжения
Величину называют волновым сопротивлением контура . Тогда добротность Q равна
При резонансе напряжений можно построить зависимость (частотную характеристику) действующего значения тока в контуре от частоты источника напряжения при неизменной собственной частоте контура (рис.6 5).
Резонансная кривая характеризует способность колебательного контура выделять ток резонансной частоты и ослаблять токи других частот.
На рис. 6.6 показана зависимость реактивного сопротивления X , индуктивного X L и ёмкостного XC сопротивлений от частоты f источника напряжения.
Рис. 6.5. Резонансная кривая
Рис. 6.6. Зависимости Х, ХL и XC
последовательного контура из R , L , C.
Резонанс напряжений широко используется в радиотехнике для выделения
сигналов заданной частоты.
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ R, L, C И МЕТОДЫ РЕШЕНИЯ ПАРАЛЛЕЛЬНЫХ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ПЕРЕМЕННОГО ТОКА
Дана схема, состоящая из параллельно соединённых активного R и реактивных L , C элементов (рис. 7.1). Такую цепь называют параллельным колебательным контуром.
В этой цепи заданы: приложенное напряжение U , частота f и числовые значения параметров R, L и C . Требуется найти токи на элементах цепи. Решение этой задачи выполняем на основе метода векторных диаграмм.
Рис. 7.1. Параллельная цепь переменного тока
Находим токи ветвей:
Для определения общего тока I необходимо построить векторную диаграмму (рис.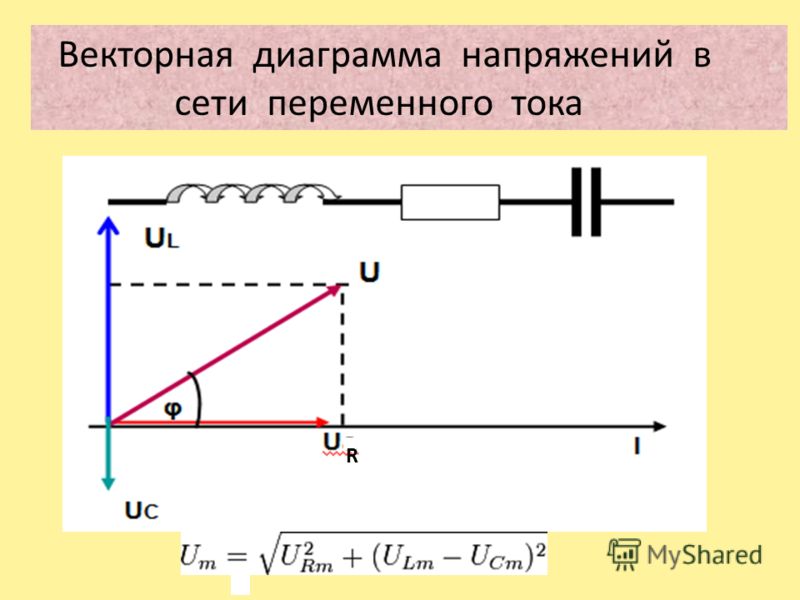 7.2). Построение начинаем с вектора напряжения, так как оно является общим для всех ветвей схемы.
7.2). Построение начинаем с вектора напряжения, так как оно является общим для всех ветвей схемы.
Рис. 7.2. Векторная диаграмма параллельной цепи переменного тока
Из векторной диаграммы имеем где Y – полная проводимость цепи
B – общая реактивная проводимость
Векторы токов на диаграмме образуют треугольник токов (рис. 7.3, а). При этом вектор Ia – активная составляющая тока, Ia = U G ; I p – реактивная составляющая тока, которая определяется как разность длин векторов
Рис. 7.3. Треугольники токов (а) и проводимостей (б)
Разделив все стороны треугольника токов на U , получим треугольник проводимостей (рис. 7.3, б).
Стороны треугольника проводимостей связаны следующими соотношениями:
Угол сдвига фаз φ между напряжением U и током I определяется из треугольника токов (рис.7.3, а) или треугольника проводимостей (рис. 7.3, б), используя соотношения (7.2).
Векторная диаграмма на рис. 7.2 построена для случая, когда IL > IC . Это имеет место при ВL > ВC , когда в цепи преобладает индуктивность и цепь носит активно-индуктивный характер. В этом случае общий ток I отстаёт по фазе от входного напряжения на угол ϕ. Возможны также режимы, когда IL резонансом тока . Это означает, что входная реактивная проводимость в цепи равно нулю:
Это имеет место при ВL > ВC , когда в цепи преобладает индуктивность и цепь носит активно-индуктивный характер. В этом случае общий ток I отстаёт по фазе от входного напряжения на угол ϕ. Возможны также режимы, когда IL резонансом тока . Это означает, что входная реактивная проводимость в цепи равно нулю:
В этом случае IL = IC и цепь носит чисто активный характер, т.е. Y = G и сдвиг фаз отсутствует (ϕ = 0 ).
Рассмотрим более подробно резонанс токов. Для того чтобы ток I в неразветвлённой части цепи совпадал по фазе с напряжением источника, реактивный ток индуктивной ветви I L должен быть равен реактивному току ёмкостной ветви IC , т.е. IL = IC .
Ничего не найдено для Book Uploads %d0%a2%d0%95%d0%a5%d0%9D%d0%98%d0%9A%d0%90 Osnovu_Teorii_Cepey Veprincev Pdf
МЕНЮ
Закрыть
- ГЛАВНАЯ
- СПЕЦПРЕДЛОЖЕНИЯ!
ПРОДУКЦИЯ
- Каталог станков
Деревообрабатывающие
- Деревообрабатывающие
- CNC micro
- CNC mini
- CNC Wood Router
- SUPER Wood Router
- Весь чугунный ЧПУ 707
- CNC 10-mini
- CNC 777
- CNC-3030/4040/6060
- CNC-6060/6090/6012
- CNC-1212/1218/1224
- ЧПУ SM Lite
- 5-шп SM-1313×5+A с автосменой
- ЧПУ SM
- ЧПУ SM PRO
- ЧПУ 10+4
- Круглофрезерные 4-х коорд.
 704
704 - 2-х шп. круглофрезерные 724
- ЧПУ CNC BALUSTER
- Проф. фрезерные 6-коорд. 17+6
- SM-1777 5-и осевой
Металлообработка
- Металлообработка
- Чугунный станок МО-002
Вакуумное оборудование
- Вакуумное оборудование
- Вакуум-формовочный пресс
Обработка камня
- Обработка камня
- CNC-1212/1218/1224/1515
- CNC-1313/1315/1325/1530
- Проф станки серии 17
- Круглофрез дерево/камень 737
- Балясинный дерево/камень 757
- 5-и коорд.
 SM-1325+5
SM-1325+5 - Обрабатывающий центр «Ракета»
- Станок «Камнерез» камень/гранит/мрамор
- Фрезер 5-и осевой «Илья Муромец»
- Фрезерно-мостовые ЧПУ
- 2-х шп CNC-1325-2H+4
Чугунные станки
- Чугунные станки
- ЧПУ по металлу OPTIMUMAX
- ЧПУ по металлу токарные
Многошпиндельные
- Многошпиндельные
- 5-коорд.
 8-12 шп для колонн 108
8-12 шп для колонн 108 - 8-шп. SM-2525×8+4 c 4-й осью
Лазерные станки
- Лазерные станки
- Лазерные граверы СО2 Эконом
- Лазерные граверы с подкатным столом СО2+Т
- Лазерные ЧПУ-Лазер
- Лазерная резка металла
Плазменные станки
- Плазменные станки
- Проф. плазморезы серия 40
- Проф.
 плазморезы серия 47
плазморезы серия 47 - Проф. плазморезы серия 30
- Плазморез для резки труб 30+4
- 5-6 корд. плазморез Extra
- Плазморез для резки труб ЧПУ-6000Р
Ювелирные станки
- Ювелирные станки
- Ювелир-4-ПРО
- Ювелир-5-ПРО
- 4-х коорд. Jeweller Mini
- 5-и коорд. Jeweller Ultra
- 5-и коорд. Jeweller Maxi
Обработка пенопласта
- Обработка пенопласта
- Станок ЧПУ Пенорез Ультра
- Станок по пенопласту CNC STYROFOAM
- ЧПУ по пенопласту и поролону (Поролонорезы)
- Пенорезы ЧПУ с абразивной струной
- 5-коорд.
 обработка пенопласта
обработка пенопласта
Расчет параллельных цепей переменного тока — Мегаобучалка
Методика (с примером) решения задач на тему: Электрические цепи с параллельным соединением активного, емкостного и индуктивного сопротивлений
Цель. Рассчитать напряжения, токи на элементах цепи. Построить диаграмму напряжений и токов.
Теория к работе.
Для такой цепи характерно, что электроприемники, соединенные параллельно, находятся под одинаковым (общим) напряжением. (При отсутствии на параллельных цепях какого-либо элемента вместо них в формулах будет стоять, естественно, нуль!).
Ток каждой ветви определяется по закону Ома:
I1 = U/Z1, где Z1 = , I2 = U/Z2, где Z2 =
Углы сдвига фазφ1иφ2между током и напряжением каждой ветви определяются с помощью тригонометрических функций:
cos φ1= R1 / Z1и sin φ1= XL1/ Z1, cos φ2= R2 / Z2и sin φ2= — XC2/ Z2
Угол сдвига фаз обязательно следует проверять по синусу во избежание потери знака угла(cos является четной функцией), но находить его тоже нужно. Он потребуется в дальнейшем расчете цепи.
Он потребуется в дальнейшем расчете цепи.
Общий ток цепи следует из I закона Кирхгофа, он равен векторной сумме токов ветвей: I = I1 + I2
Векторная диаграмма этих токов:
Общий суммарный или результирующий ток можно найти не только графически (диаграмма строится в масштабе), но и математически, на основании теоремы Пифагора:
I = ,
где Iа – проекция вектора общего тока на вектор напряжений, она называется активной составляющей общего тока.
Iр – проекция вектора общего тока на линию, перепндикулярную линии напряжения, она называется реактивной составляющей общего тока. Из диаграммы видно, что Iа = Iа1 + Iа2 , Iр = IL1 Iс2
В этих формулах: Iа1 и Iа2— активные составляющие токов первой и второй ветви.
IL1— реактивные составляющие тока первой ветви. Носит индуктивный характер − взята знаком “плюс”.
Iс2— реактивные составляющие тока второй ветви. Носит емкостной характер −взята знаком “минус”.
Введем в формулу общего тока его составляющие, тогда I =
Значения составляющих токов ветвей можно определять по формулам:
Iа1 = I1cos φ1; Iа2= I2 cos φ2; IL1 = I1sin φ1; IC2 = I2sin φ2 ;
Активная мощность цепи равна арифметической сумме активных мощностей ветвей:
Р = Р1 + Р2,гдеР1 = U I1cos φ1; Р1 = I12R1; Р2 = U I2cos φ2; Р2 = I22R2
Реактивная мщность цепи равна алгебраической сумме реактивных мощностей ветвей:
Q =QL1–QC2 , где
QL1= U I1 sin φ1; QL1=I12 Х L1; Q C2= U I2 sin φ2;QС2=I22 Х С2
Активнуюи реактивную мощность можно найти и так: Р = U I cos φ или Q= U I sin φ где
cos φ = ; sin φ=
cos φ и sin φ используют также для определения угла сдвига фаз между общим током и напряжением.
Полная мощность цепи: S =U I или S =
Угол сдвига фаз между общим токомм и напряжением можно определять и из выражений:
cos φ = Р / S, sin φ = Q/ S
Закон сложения векторов параллелограмма
Утверждение закона параллелограмма
Если два вектора, действующих одновременно в точке, могут быть представлены как по величине, так и по направлению соседними сторонами параллелограмма, проведенного из точки, то результирующий вектор представляется как по величине, так и по направлению диагональю параллелограмма, проходящего через эту точку. .
Вывод закона
Примечание. Все буквы, выделенные жирным шрифтом, обозначают векторы, а нормальные буквы обозначают только величину.
Пусть P и Q будут двумя векторами, действующими одновременно в точке и представленными как по величине, так и по направлению двумя соседними сторонами OA и OD параллелограмма OABD, как показано на рисунке.
Пусть θ будет углом между P и Q и R будет результирующим вектором. Тогда, согласно закону параллелограмма сложения векторов, диагональ OB представляет собой результат P и Q .
Итак, имеем
R = P + Q
Теперь разверните A до C и проведите BC перпендикулярно OC.
От треугольника OCB,
В треугольнике ABC,
Также,
Величина результирующей:
Подставляя значения AC и BC в (i), получаем
— величина результирующего.
Направление результирующего: Пусть ø будет углом, образованным результирующим R и P . Затем
От треугольника OBC,
— направление результирующего.
Числовая задача
Две силы величиной 6 Н и 10 Н наклонены друг к другу под углом 60 °. Вычислите величину равнодействующей и угол, образованный равнодействующей силой 6 Н.
Вычислите величину равнодействующей и угол, образованный равнодействующей силой 6 Н.
Решение:
Пусть P и Q представляют собой две силы с величиной 6 Н и 10 Н соответственно, а θ — угол между ними. Пусть R будет равнодействующей силой.
Итак, P = 6N, Q = 10N и θ = 60 °
У нас,
, что является необходимой величиной
.
Пусть ø будет углом между P и R .Затем
, что является требуемым углом.
PPT — Презентация PowerPoint по параллельным и последовательным схемам, бесплатная загрузка
1 Параллельные и последовательные схемы 1
2 Определения • Напряжение (В) • электрический потенциал, измеренный в вольтах (В) • электрический ток ( I) • мера скорости, с которой протекают электрические заряды, измеряется в амперах (A) • сопротивление (R) • способность препятствовать потоку электронов в проводниках, измеряется в омах (Вт)
Электрическое сопротивление & Закон Ома • Разница потенциалов: потеря электрического потенциала, вызванная сопротивлением при протекании электрического тока через проводник (также называемое падением напряжения). • Закон Ома: разность потенциалов между двумя точками на проводнике напрямую связана с протекающим электрическим током. через проводник • Формула: V = I x R • Закон Ома применяется только к электрическим нагрузкам, сопротивление которых не изменяется при изменении температуры
• Закон Ома: разность потенциалов между двумя точками на проводнике напрямую связана с протекающим электрическим током. через проводник • Формула: V = I x R • Закон Ома применяется только к электрическим нагрузкам, сопротивление которых не изменяется при изменении температуры
3 Серия Cir cuit • Последовательная цепь • электрическая цепь, в которой электрические нагрузки подключены друг к другу по единому пути • Гирлянда рождественских огней является примером последовательной цепи; когда один сгорает, цепь разрывается, и ни одна из лампочек не работает.
0,5 A 1,0 A 9 Вт 9 В 9 Вт 9 В 9 Вт 1,0 A 0,5 A Последовательная цепь с несколькими нагрузками • Если сопротивление в последовательной цепи увеличивается, то по закону Ома ток будет уменьшаться. • Пример:
Характеристики последовательной цепи • Общее сопротивление в последовательной цепи увеличивается при добавлении каждой нагрузки • Электрический ток одинаков во всех частях последовательной цепи • Ток в последовательной цепи перестанет течь, если путь тока прерывается в любой точке
4 Параллельная цепь • Параллельная цепь • электрическая цепь, в которой каждая электрическая нагрузка подключена к источнику энергии своим собственным отдельным путем или ответвленной цепью • Ответвленная цепь • отдельная цепь, по которой ток проходит к каждой нагрузке в параллельной цепи
3. 0 A 2,0 A 1 A 9 W 1 A 1,0 A 1 A 1 A 9 W 9 V 9 W 9 V 9 V 9 W 1 A 9 W 9 W 3,0 A 1,0 A 2,0 A Параллельная цепь с несколькими нагрузками • Добавление ответвления цепь в параллельную серию позволяет одинаковому количеству тока проходить через каждый путь • Падение напряжения одинаково для каждой ответвленной цепи, поэтому ток будет увеличиваться с каждой нагрузкой • Пример:
0 A 2,0 A 1 A 9 W 1 A 1,0 A 1 A 1 A 9 W 9 V 9 W 9 V 9 V 9 W 1 A 9 W 9 W 3,0 A 1,0 A 2,0 A Параллельная цепь с несколькими нагрузками • Добавление ответвления цепь в параллельную серию позволяет одинаковому количеству тока проходить через каждый путь • Падение напряжения одинаково для каждой ответвленной цепи, поэтому ток будет увеличиваться с каждой нагрузкой • Пример:
Характеристики параллельной цепи • общий ток, протекающий от источника электроэнергии, равен сумме разветвленных цепей • Добавление еще одной нагрузки приведет к увеличению общего тока • Можно использовать отдельные ответвленные цепи, не влияя на другие (пример: использование тостера, но не кофеварка)
Комбинация последовательных и параллельных цепей • В электрических цепях часто используются параллельные и последовательные цепи, соединенные вместе • Пример: • Когда вы включаете набор из трех лампочек, вы используете два переключателя: один — выключатель безопасности на м в электрическом пульте управления, а второй — выключатель на стене. Это параллельные цепи. Последовательная схема представляет собой набор из трех лампочек.
Это параллельные цепи. Последовательная схема представляет собой набор из трех лампочек.
Источники • Изображения: Получено 3 февраля 2003 г. из … • 1: whyfiles. larc.nasa.gov/…/electricity/circuits2.html • 2: http://www.edugateway.com/sites/tkids/ • 3 и 4: www.nscdiscovery.org/…/ParallelCircuits.htm • Текст: • Пламб, Дональд и др. al. Наука 9. Скарборо, ОН: Нельсон, 1999. (Глава 10).
Параллельные вселенные: теории и доказательства
Уникальна ли наша Вселенная? От научной фантастики до научных фактов существует концепция, которая предполагает, что могут существовать и другие вселенные, помимо нашей, где все выборы, которые вы сделали в этой жизни, разыгрывались в альтернативных реальностях.Эта концепция известна как «параллельная вселенная» и является одним из аспектов астрономической теории мультивселенной.
Эта идея широко используется в комиксах, видеоиграх, телевидении и фильмах. Во многих франшизах от «Баффи — истребительница вампиров» до «Звездного пути» и «Доктора Кто» и «Дигемона» идея используется для расширения сюжетных линий. (Более полный список параллельных вселенных в художественной литературе находится в конце статьи.)
(Более полный список параллельных вселенных в художественной литературе находится в конце статьи.)
На самом деле существует довольно много свидетельств существования мультивселенной. Во-первых, полезно понять, как предположительно возникла наша Вселенная.
Споры в пользу мультивселенной
Около 13,7 миллиарда лет назад, попросту говоря, все, что мы знаем о космосе, было бесконечно малой сингулярностью. Затем, согласно теории Большого взрыва, какой-то неизвестный триггер заставил его расширяться и раздуваться в трехмерном пространстве. Когда огромная энергия этого начального расширения остыла, свет начал просвечивать. В конце концов, маленькие частицы начали формироваться в более крупные куски материи, которые мы знаем сегодня, такие как галактики, звезды и планеты.
Один большой вопрос в этой теории: единственная ли Вселенная существует? С нашей нынешней технологией мы ограничены наблюдениями внутри этой Вселенной, потому что Вселенная изогнута, и мы находимся внутри аквариума, не имея возможности видеть его внешнюю сторону (если есть снаружи).
Есть по крайней мере пять теорий, почему мультивселенная возможна, как объяснялось в статье на Space.com в 2012 году:
1. Бесконечные вселенные . Мы не знаем точно, какова форма пространства-времени.Одна известная теория гласит, что он плоский и продолжается вечно. Это представит возможность существования многих вселенных. Но, имея в виду эту тему, вполне возможно, что вселенные начнут повторяться. Причина в том, что частицы можно соединить разными способами. Подробнее об этом чуть позже.
2. Вселенные пузырей . Другая теория множественности вселенных исходит из «вечной инфляции». Основываясь на исследовании космолога из Университета Тафтса Александра Виленкина, если смотреть на пространство-время в целом, некоторые области космоса перестают раздуваться, как Большой взрыв раздул нашу собственную вселенную.Другие, однако, будут расти. Итак, если мы представим нашу собственную вселенную в виде пузыря, то это будет сеть пузырьковых вселенных пространства. Что интересно в этой теории, так это то, что законы физики других вселенных могут сильно отличаться от нашей, поскольку они не связаны между собой.
Что интересно в этой теории, так это то, что законы физики других вселенных могут сильно отличаться от нашей, поскольку они не связаны между собой.
3. Дочерние вселенные . Или, возможно, несколько вселенных могут следовать теории квантовой механики (как ведут себя субатомные частицы) как часть теории «дочерней вселенной». Если вы следуете законам вероятности, это предполагает, что для каждого исхода, который может возникнуть в результате одного из ваших решений, будет ряд вселенных, каждая из которых видела один исход.Итак, в одной вселенной вы взяли эту работу в Китай. В другом случае, возможно, вы были в пути, и ваш самолет приземлился в другом месте, и вы решили остаться. И так далее.
4. Математические вселенные . Другой возможный путь — изучение математических вселенных, которые, проще говоря, объясняют, что структура математики может меняться в зависимости от того, в какой вселенной вы живете. «Математическая структура — это то, что вы можете описать способом, полностью независимым от человеческого багажа», — сказал автор теории Макс Тегмарк из Массачусетского технологического института, как цитируется в статье 2012 года. 122 различных возможности, если быть точным. Таким образом, с бесконечным количеством космических пятен расположение частиц внутри них должно повторяться — бесконечно много раз. Это означает, что существует бесконечно много «параллельных вселенных»: космические участки, точно такие же, как наша (содержащие кого-то точно такого же, как вы), а также участки, которые отличаются только положением одной частицы, участки, которые отличаются положением двух частиц, и т. Д. вплоть до патчей, которые полностью отличаются от наших.
122 различных возможности, если быть точным. Таким образом, с бесконечным количеством космических пятен расположение частиц внутри них должно повторяться — бесконечно много раз. Это означает, что существует бесконечно много «параллельных вселенных»: космические участки, точно такие же, как наша (содержащие кого-то точно такого же, как вы), а также участки, которые отличаются только положением одной частицы, участки, которые отличаются положением двух частиц, и т. Д. вплоть до патчей, которые полностью отличаются от наших.
Известно, что последняя работа физика Стивена Хокинга перед его смертью также касалась мультивселенной.Газета была опубликована в мае 2018 года, всего через несколько месяцев после кончины Хокинга. Что касается теории, он сказал Кембриджскому университету в интервью, опубликованном в The Washington Post: «Мы не сводимся к единой уникальной вселенной, но наши открытия подразумевают значительное сокращение мультивселенной до гораздо меньшего диапазона возможных вселенных».
Споры против параллельной вселенной
Теории параллельных вселенных предполагают, что это бесконечная Земля, лишь немного отличающаяся от нашей.(Изображение предоставлено Виктором Хаббиком / Shutterstock)
Однако не все согласны с теорией параллельной вселенной. В статье о Medium 2015 года астрофизика Итана Сигала соглашается, что пространство-время теоретически может существовать вечно, но говорится, что у этой идеи есть некоторые ограничения.
Ключевая проблема в том, что Вселенной чуть меньше 14 миллиардов лет. Итак, возраст нашей Вселенной, очевидно, не бесконечен, а конечен. Это (проще говоря) ограничит количество возможностей для перегруппировки частиц и, к сожалению, сделает менее вероятным, что ваше альтернативное «я» все-таки попадет на этот самолет, чтобы увидеть Китай.
Кроме того, расширение в начале Вселенной происходило по экспоненте, потому что было так много «энергии, присущей самому пространству», сказал он. Но со временем эта инфляция, очевидно, замедлилась — частицы вещества, образовавшиеся в результате Большого взрыва, не продолжают расширяться, отметил он. Среди его выводов: это означает, что у мультивселенных будут разные темпы инфляции и разное время (больше или меньше) инфляции. Это уменьшает возможности вселенных, подобных нашей.
Среди его выводов: это означает, что у мультивселенных будут разные темпы инфляции и разное время (больше или меньше) инфляции. Это уменьшает возможности вселенных, подобных нашей.
«Даже если оставить в стороне вопросы о том, что может существовать бесконечное количество возможных значений фундаментальных констант, частиц и взаимодействий, и даже отложив в сторону вопросы интерпретации, например, действительно ли многомировая интерпретация описывает нашу физическую реальность», — сказал Сигал, «Дело в том, что количество возможных результатов растет так быстро — намного быстрее, чем просто экспоненциально — что, если инфляция не происходит действительно бесконечное количество времени, не существует параллельных вселенных, идентичных этой.
Но вместо того, чтобы рассматривать это отсутствие других вселенных как ограничение, Сигал вместо этого использует философию, которая показывает, как важно праздновать уникальность. Он советует делать выбор, который работает для вас, который «не оставляет вас без сожалеет. «Это потому, что нет других реальностей, в которых выбор вашего снобличия разыгрывается; следовательно, вы единственный человек, который может сделать этот выбор.
«Это потому, что нет других реальностей, в которых выбор вашего снобличия разыгрывается; следовательно, вы единственный человек, который может сделать этот выбор.
Параллельные вселенные в научной фантастике
Вот некоторые из большего видное использование параллельных вселенных в научной фантастике.(Это ни в коем случае не полный список, а лишь некоторые из наиболее цитируемых примеров.)
- Комиксы Marvel и DC Comics рассказывают истории, происходящие в параллельных вселенных, которые являются частью мультивселенной.
- Во многих аниме-сериалах, таких как «Дигимон», «Жемчуг дракона» и «Еж Соник», представлены альтернативные версии их персонажей из других вселенных.
- Параллельные вселенные появляются в таких играх, как «Dungeons & Dragons», «BioShock Infinite», франшиза «Final Fantasy», «Half-Life», «League of Legends», «Mortal Kombat» и «The Legend of Zelda».»
- » Флатландия: Многогранный роман «(1884) Эдвина А. Эбботта — это рассказ о двухмерном мире, который включает в себя живые геометрические фигуры, такие как круги, треугольники и квадраты. Роман также включает другие вселенные таких как Lineland, Spaceland и Pointland. Эта книга была адаптирована в художественный фильм в 2007 году.
- «Люди, подобные богам» (1923), роман Герберта Уэллса, включал машину «паратайм» и исследовал мультивселенную. Хроники Нарнии »(1950-56), C.В серии книг С. Льюиса рассказывается о нескольких детях, которые перемещаются между нашим миром и миром Нарнии, где есть говорящие животные. Некоторые из этих книг были выпущены в качестве художественных фильмов в начале 2000-х годов.
- В эпизоде «Звездного пути» была представлена «зеркальная вселенная», в которой персонажи были более безжалостными и воинственными. Эта концепция повторялась почти в каждом последующем сериале «Звездный путь». В 2009 году вселенная «Звездного пути» была перезагружена в фильме, в котором персонажи оригинального сериала 1960-х годов оказались в альтернативной вселенной.В фильме снимались Крис Пайн и Закари Куинто, и он положил начало серии других фильмов «Звездного пути».
- В «Темной башне», сериале Стивена Кинга, который начался в 1982 году, путешественники проходят через порталы на разные уровни титульной башни (другими словами, на параллельные Земли). Часть этого сериала была адаптирована в художественный фильм в 2017 году.
- Сериал фильмов «Назад в будущее» (который начался в 1985 году) рассказывает о приключениях семьи МакФлай, включая посещения 1885, 1955 и 2015 годов. Второй фильм В частности, показаны недостатки альтернативной реальности, когда один персонаж использует ее, чтобы разбогатеть гнусными способами.В сериале снялся Майкл Дж. Фокс.
- В серии «Его темные материалы» Филипа Пулмана дети перемещаются между несколькими мирами. По первой книге «Золотой компас» в 2007 году был экранизирован фильм.
- «Раздвижные двери» (1998) — это фильм, в котором показаны две параллельные вселенные в зависимости от того, поймал ли главный герой поезд или нет. В нем снимались Гвинет Пэлтроу и Джон Ханна.
- «Беги, Лола, беги» (1998) — фильм с Франкой Потенте в главной роли. В фильме показано несколько вариантов, поскольку женщина пытается получить 100 000 немецких марок всего за 20 минут, чтобы спасти жизнь своего парня.
- «Хронология» (1999) Майкла Крайтона рассказывает об историках, восходящих к средневековью. (Хотя эта книга в основном представляет собой книгу о путешествиях во времени, в ней также используется мультивселенная.) В 2003 году был выпущен фильм, основанный на книге.
- «Донни Дарко» (2001) — это фильм, в котором учащийся средней школы сталкивается с видениями и пытается понять их значение. В нем снялся Джейк Джилленхол.
- Серия книг Терри Пратчетта и Стивена Бакстера «Длинная Земля» обсуждает параллельные вселенные, которые могут быть почти такими же, как Земля.
- «Очень странные дела» (с 2016 г. по настоящее время) — научно-фантастический сериал ужасов, который начинается с расследования исчезновения мальчика в небольшом городке. Серия включает обсуждение альтернативного измерения, называемого «вверх ногами».
Разница между скалярной и векторной величинами (со сравнительной таблицей)
Скалярная величина относится к количеству, которое имеет только величину и не имеет направления. С другой стороны, векторная величина подразумевает физическую величину, которая включает как величину, так и направление.
Физика — это наука, основанная на математике. Изучая физику, мы проходим ряд концепций и понятий, которые опираются на математику. Математические величины, объясняющие движение тела, делятся на две группы: скалярные величины и векторные величины.
Для непрофессионала эти два термина одинаковы, но в мире физики существует огромная разница между скалярной и векторной величиной. Итак, взгляните на предоставленную вам статью для лучшего понимания.
Содержимое: скалярное количество по сравнению с векторным количеством
- Сравнительная таблица
- Определение
- Ключевые отличия
- Заключение
Сравнительная таблица
| Основа для сравнения | Скалярная величина | Векторная величина |
|---|---|---|
| Значение | Любая физическая величина, которая не включает направление, называется скалярной величиной. | Векторная величина — это величина, которая имеет как величину, так и направление. |
| Количества | Одномерные величины | Многомерные величины |
| Изменение | Оно меняется с изменением их величины. | Он изменяется с изменением направления или величины, либо того и другого вместе. |
| Операции | Следуйте обычным правилам алгебры. | Следуйте правилам векторной алгебры. |
| Сравнение двух величин | Простое | Сложное |
| Деление | Скаляр может разделить другой скаляр. | Два вектора никогда не могут делиться. |
Определение скалярной величины
Термин «скалярная величина» определяется как величина, которая имеет только один элемент числового поля, прикрепленный к единице измерения, такой как градусы или метры. Это величина, которая показывает только величину или размер, то есть определяется числовым значением вместе с единицей измерения. Например, скорость автомобиля, температура тела, расстояние между двумя точками и т. Д.
Правила обычной алгебры могут применяться для комбинирования скалярных величин, так что скаляры можно складывать, вычитать или умножать так же, как числа. Однако операция скаляра возможна только для величин с той же единицей измерения.
Определение величины вектора
Математическая величина, для полного описания которой необходимы две независимые характеристики, то есть величина и направление. Здесь величина представляет размер величины, которая также является ее абсолютным значением, а направление представляет собой сторону, т.е.е. восток, запад, север, юг и т. д. Например, смещение между двумя точками, скорость и ускорение движущегося тела, сила, вес и т. д.
Векторная величина подчиняется закону сложения треугольника. Стрелка используется для обозначения количества вектора, помещенного над или рядом с символом, обозначающим вектор.
Ключевые различия между скалярными и векторными величинами
Что касается разницы между скалярной и векторной величиной, то следует отметить следующие моменты:
- .Скалярная величина описывается как величина, имеющая только одну характеристику, то есть величину. Векторная величина — это физическая величина, для определения которой нужны как величина, так и направление.
- Скалярные величины объясняют одномерные величины. С другой стороны, многомерные величины объясняются векторной величиной.
- Скалярные величины изменяются только при изменении их величины. В отличие от этого, векторная величина изменяется с изменением их величины, направления или того и другого.
- Обычные правила алгебры сопровождаются скалярными величинами для выполнения таких операций, как сложение, вычитание и умножение, тогда как для выполнения операций векторные величины подчиняются правилам векторной алгебры.
- При сравнении двух скалярных величин вы должны учитывать только величину, тогда как при сравнении двух векторных величин следует учитывать как величину, так и направление. Таким образом, с векторными величинами работать немного сложнее, чем со скалярными величинами.
- И последнее, но не менее важное: скалярная величина может делить другой скаляр, но этого нельзя сделать в случае векторной величины.
Заключение
Короче говоря, скалярная величина дает вам представление о том, сколько существует объекта, но векторная величина дает вам представление о том, сколько существует объекта и в каком направлении. Итак, основное различие между этими двумя величинами связано с направлением, т.е. скаляры не имеют направления, а векторы имеют.
Векторов
Это вектор:
Вектор имеет величину звездной величины (размер) и направление :
Длина линии показывает ее величину, а стрелка указывает направление.
Мы можем сложить два вектора, соединив их голова к хвосту:
И неважно, в каком порядке мы их добавляем, результат будет тот же:
Пример: самолет летит на север, но ветер дует с северо-запада.
Два вектора (скорость, создаваемая гребным винтом, и скорость ветра) приводят к немного более низкой путевой скорости при движении немного восточнее севера.
Если бы вы смотрели на самолет с земли, казалось бы, он немного поскользнулся.
Вы когда-нибудь видели такое? Возможно, вы видели птиц, борющихся с сильным ветром, которые, кажется, летят боком. Векторы помогают это объяснить.
Скорость, ускорение, сила и многое другое — векторы.
Вычитание
Мы также можем вычесть один вектор из другого:
- сначала мы меняем направление вектора, который мы хотим вычесть,
- , затем добавьте их как обычно:
а — б
Обозначение
Вектор часто пишется полужирным шрифтом , например a или b .
| Вектор также может быть записан как буквы его головы и хвоста со стрелкой над ним, например: |
Расчеты
Сейчас… как мы делаем расчеты?
Самый распространенный способ — сначала разбить векторы на части x и y, например:
Вектор a разбит на
два вектора a x и a y
(Позже мы увидим, как это сделать.)
Добавление векторов
Затем мы можем сложить векторы, добавив части x и добавив части y :
Сумма вектора (8, 13) и вектора (26, 7) дает вектор (34, 20)
Пример: складываем векторы a = (8, 13) и b = (26, 7)
c = a + b
с = (8, 13) + (26, 7) = (8 + 26, 13 + 7) = (34, 20)
Когда мы разбиваем такой вектор, каждая часть называется компонентом :
Вычитание векторов
Для вычитания сначала переверните вектор, который мы хотим вычесть, а затем сложите.
Пример: вычесть k = (4, 5) из v = (12, 2)
a = v + — k
a = (12, 2) + — (4, 5) = (12, 2) + (−4, −5) = (12−4, 2−5) = (8, −3)
Величина вектора
Величина вектора показана двумя вертикальными полосами по обе стороны от вектора:
| a |
ИЛИ можно написать с двойной вертикальной чертой (чтобы не путать с абсолютным значением):
|| a ||
Мы используем теорему Пифагора для его вычисления:
| a | = √ (х 2 + у 2 )
Пример: какова величина вектора b = (6, 8)?
| b | = √ (6 2 + 8 2 ) = √ (36 + 64) = √100 = 10
Вектор с величиной 1 называется единичным вектором.
Вектор против скалярного
Скаляр имеет звездную величину (размер) только .
Скаляр: просто число (например, 7 или -0,32) … определенно не вектор.
Вектор имеет величину и направление и часто выделяется полужирным шрифтом , поэтому мы знаем, что это не скаляр:
- , поэтому c — вектор, он имеет величину и направление
- , но c — это просто значение, например 3 или 12.4
Пример: k b на самом деле является скаляром, умноженным на k, вектор b .
Умножение вектора на скаляр
Когда мы умножаем вектор на скаляр, это называется «масштабированием» вектора, потому что мы изменяем размер вектора.
Пример: умножить вектор m = (7, 3) на скаляр 3
| a = 3 м = (3 × 7, 3 × 3) = (21, 9) |
По-прежнему указывает в том же направлении, но в 3 раза длиннее
(И теперь вы знаете, почему числа называются «скалярами», потому что они «масштабируют» вектор вверх или вниз.)
Умножение вектора на вектор (скалярное произведение и кросс-произведение)
Как нам перемножить два вектора вместе? Есть несколько способов! (Подробности см. На этих страницах.) |
Более двух размеров
Векторы также отлично работают в трех и более измерениях:
Вектор (1, 4, 5)
Пример: складываем векторы a = (3, 7, 4) и b = (2, 9, 11)
c = a + b
с = (3, 7, 4) + (2, 9, 11) = (3 + 2, 7 + 9, 4 + 11) = (5, 16, 15)
Пример: какова величина вектора w = (1, −2, 3)?
| w | = √ (1 2 + (−2) 2 + 3 2 ) = √ (1 + 4 + 9) = √14
Вот пример с 4-мя измерениями (но его сложно нарисовать!):
Пример: вычесть (1, 2, 3, 4) из (3, 3, 3, 3)
(3, 3, 3, 3) + — (1, 2, 3, 4)
= (3, 3, 3, 3) + (−1, −2, −3, −4)
= (3 −1, 3−2, 3−3, 3−4)
= (2, 1, 0, −1)
Звездная величина и направление
Мы можем знать величину и направление вектора, но нам нужны его длины по x и y (или наоборот):
| <=> | ||
| Вектор a в полярных координатах Координаты | Вектор a в декартовой системе координат Координаты |
Вы можете прочитать, как преобразовать их в полярные и декартовы координаты, но вот краткое описание:
| От полярных координат (r, θ ) до декартовых координат (x, y) | От декартовых координат (x, y) до полярных координат (r, θ) | |
|---|---|---|
|
|
Пример
Сэм и Алекс тянут ящик.
- Сэм тянет с силой 200 Ньютонов при 60 °
- Алекс тянет с силой 120 Ньютонов под углом 45 °, как показано на рисунке
Что такое объединенная сила и ее направление?
Давайте сложим два вектора голова к хвосту:
Первое преобразование из полярной системы в декартовую (до 2 десятичных знаков):
Вектор Сэма:
- x = r × cos ( θ ) = 200 × cos (60 °) = 200 × 0,5 = 100
- y = r × sin ( θ ) = 200 × sin (60 °) = 200 × 0.8660 = 173,21
Вектор Алекса:
- x = r × cos ( θ ) = 120 × cos (-45 °) = 120 × 0,7071 = 84,85
- y = r × sin ( θ ) = 120 × sin (-45 °) = 120 × -0,7071 = -84,85
Теперь у нас:
Добавьте их:
(100, 173,21) + (84,85, -84,85) = (184,85, 88,36)
Этот ответ действителен, но давайте вернемся к полярному, поскольку вопрос был в полярном:
- r = √ (x 2 + y 2 ) = √ (184.85 2 + 88,36 2 ) = 204,88
- θ = tan -1 (y / x) = tan -1 (88,36 / 184,85) = 25,5 °
И у нас есть результат (округленный):
А для Сэма и Алекса это выглядит так:
Они могли бы получить лучший результат, если бы располагались плечом к плечу.
Как определить, является ли вектор линейной комбинацией других векторов
Идея линейной комбинации векторов очень важна для изучения линейной алгебры.Мы можем использовать линейные комбинации, чтобы понять покрывающие множества, пространство столбцов матрицы и большое количество других тем. Один из самых полезных навыков при работе с линейными комбинациями — это определение того, когда один вектор является линейной комбинацией заданного набора векторов.
реклама
Предположим, что у нас есть вектор \ (\ vec {v} \), и мы хотим знать ответ на вопрос: «является ли \ (\ vec {v} \) линейной комбинацией векторов \ (\ vec {a} _ {1} \), \ (\ vec {a} _ {2} \) и \ (\ vec {a} _ {3} \)? ».n \) для некоторого \ (n \), то на этот вопрос можно ответить, используя эквивалентную расширенную матрицу:
\ (\ left [\ begin {array} {ccc | c} \ vec {a} _1 & \ vec {a} _2 & \ vec {a} _3 & \ vec {v} \\ \ end {array} \ right ] \)
Если эта матрица представляет собой непротиворечивую систему уравнений, то мы можем сказать, что \ (\ vec {v} \) является линейной комбинацией других векторов.
Пример
Определите, является ли вектор \ (\ begin {bmatrix} 5 \\ 3 \\ 0 \\ \ end {bmatrix} \) линейной комбинацией векторов:
\ (\ begin {bmatrix} 2 \\ 0 \\ 1 \\ \ end {bmatrix} \), \ (\ begin {bmatrix} 1 \\ 4 \\ 3 \\ \ end {bmatrix} \), \ (\ begin {bmatrix} 8 \\ 1 \\ 1 \\ \ end {bmatrix} \) и \ (\ begin {bmatrix} -4 \\ 6 \\ 1 \\ \ end {bmatrix} \)
Решение
Помните, что это означает, что мы хотим найти константы \ (x_ {1} \), \ (x_ {2} \), \ (x_ {3} \) и \ (x_ {4} \) такие, что:
\ (\ begin {bmatrix} 5 \\ 3 \\ 0 \\ \ end {bmatrix} = x_ {1} \ begin {bmatrix} 2 \\ 0 \\ 1 \\ \ end {bmatrix} + x_ {2} \ begin {bmatrix} 1 \\ 4 \\ 3 \\ \ end {bmatrix} + x_ {3} \ begin {bmatrix} 8 \\ 1 \\ 1 \\ \ end {bmatrix} + x_ {4} \ begin {bmatrix} -4 \\ 6 \\ 1 \\ \ end {bmatrix} \)
Это векторное уравнение эквивалентно расширенной матрице.Настроив эту матрицу и уменьшив строку, мы находим, что:
\ (\ left [\ begin {array} {cccc | c} 2 & 1 & 8 & -4 & 5 \\
0 & 4 & 1 & 6 & 3 \\
1 & 3 & 1 & 1 & 0 \ \
\ end {array} \ right]
\)
эквивалентно:
\ (\ left [\ begin {array} {cccc | c} 1 & 0 & 0 & — \ dfrac {103} {29} & — \ dfrac {74} {29} \\
0 & 1 & 0 & \ dfrac {42} {29} & \ dfrac {13} {29} \\
0 & 0 & 1 & \ dfrac {6} {29} & \ dfrac {35} {29} \\
\ end {array} \верно]\)
Хотя это не красиво, но эта матрица НЕ содержит такую строку, как \ (\ begin {bmatrix} 0 & 0 & 0 & 0 & c \\ \ end {bmatrix} \), где \ (c \ neq 0 \ ), что указывает на непоследовательность базовой системы.Следовательно, базовая система согласована (имеет решение), что означает, что векторное уравнение также согласовано.
Итак, мы можем сказать, что \ (\ begin {bmatrix} 5 \\ 3 \\ 0 \\ \ end {bmatrix} \) является линейной комбинацией других векторов.
Пошаговый процесс
В общем, если вы хотите определить, является ли вектор \ (\ vec {u} \) линейной комбинацией векторов \ (\ vec {v} _ {1} \), \ (\ vec {v} _ { 2} \),…, \ (\ vec {v} _ {p} \) (для любого целого числа \ (p> 2 \)) вы сделаете следующее.
Шаг 1
Настроить расширенную матрицу
\ (\ left [\ begin {array} {cccc | c} \ vec {v} _1 & \ vec {v} _2 & \ cdots & \ vec {v} _p & \ vec {u} \\ \ end {массив } \ right] \)
и ряд уменьшить.
Шаг 2
Используйте сокращенную форму матрицы, чтобы определить, представляет ли расширенная матрица непротиворечивую систему уравнений. Если это так, то \ (\ vec {u} \) является линейной комбинацией остальных. В противном случае это не так.
На втором этапе важно помнить, что система уравнений непротиворечива, если существует одно решение ИЛИ много решений.Количество решений не имеет значения — важно только то, что существует хотя бы одно решение. Это означает, что существует по крайней мере один способ записать данный вектор как линейную комбинацию других.
Запись вектора как линейной комбинации других векторов
Иногда вас могут попросить записать вектор как линейную комбинацию других векторов. Это требует той же работы, что и выше, с еще одним шагом. Вам нужно использовать решение векторного уравнения, чтобы записать, как векторы объединяются для создания нового вектора.
Давайте начнем с более простого случая, чем тот, который мы делали раньше, а затем вернемся к нему, поскольку он немного сложен.
Пример
Запишите вектор \ (\ vec {v} = \ begin {bmatrix} 2 \\ 4 \\ 2 \\ \ end {bmatrix} \) как линейную комбинацию векторов:
\ (\ begin {bmatrix} 2 \ \ 0 \\ 1 \\ \ end {bmatrix} \), \ (\ begin {bmatrix} 0 \\ 1 \\ 0 \\ \ end {bmatrix} \) и \ (\ begin {bmatrix} -2 \ \ 0 \\ 0 \\ \ end {bmatrix} \)
Решение
Шаг 1
Мы настраиваем нашу расширенную матрицу и сокращаем ее по строкам.
\ (
\ left [\ begin {array} {ccc | c} 2 & 0 & -2 & 2 \\
0 & 1 & 0 & 4 \\
1 & 0 & 0 & 2 \\
\ end { array} \ right]
\)
эквивалентно
\ (
\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & 2 \\
0 & 1 & 0 & 4 \\
0 & 0 & 1 & 1 \\
\ end {массив } \ right]
\)
Шаг 2
Мы определяем, представляет ли матрица непротиворечивую систему уравнений.
Исходя из сокращенной матрицы, базовая система согласована. Опять же, это связано с тем, что в части коэффициентов матрицы нет строк со всеми нулями, а в дополнении нет единственного ненулевого значения. (в качестве аргумента можно также использовать количество точек поворота.)
В отличие от предыдущего, мы хотим не только проверять наличие линейной комбинации. Мы хотим показать саму линейную комбинацию. Значит, нам нужно реальное решение. В данном случае только один:
\ (x_1 = 2 \), \ (x_2 = 4 \), \ (x_3 = 1 \)
Используя эти значения, мы можем записать \ (\ vec {v} \) как:
\ (\ vec {v} = \ begin {bmatrix} 2 \\ 4 \\ 2 \\ \ end {bmatrix} = (2) \ begin {bmatrix} 2 \\ 0 \\ 1 \\ \ end {bmatrix} + (4) \ begin {bmatrix} 0 \\ 1 \\ 0 \\ \ end {bmatrix} + (1) \ begin {bmatrix} -2 \\ 0 \\ 0 \\ \ end {bmatrix} \)
Теперь вернемся к нашему первому примеру (с сумасшедшими дробями), но немного изменим инструкции.
Пример
Запишите вектор \ (\ vec {v} = \ begin {bmatrix} 5 \\ 3 \\ 0 \\ \ end {bmatrix} \) как линейную комбинацию векторов:
\ (\ begin {bmatrix} 2 \ \ 0 \\ 1 \\ \ end {bmatrix} \), \ (\ begin {bmatrix} 1 \\ 4 \\ 3 \\ \ end {bmatrix} \), \ (\ begin {bmatrix} 8 \\ 1 \\ 1 \\ \ end {bmatrix} \) и \ (\ begin {bmatrix} -4 \\ 6 \\ 1 \\ \ end {bmatrix} \)
Когда мы сделали шаг 1, у нас была следующая работа. Это показало, что эквивалентное векторное уравнение было непротиворечивым, и подтвердило, что \ (\ vec {v} \) было линейной комбинацией других векторов.
\ (\ left [\ begin {array} {cccc | c} 2 & 1 & 8 & -4 & 5 \\
0 & 4 & 1 & 6 & 3 \\
1 & 3 & 1 & 1 & 0 \ \
\ end {array} \ right]
\)
эквивалентно:
\ (\ left [\ begin {array} {cccc | c} 1 & 0 & 0 & — \ dfrac {103} {29} & — \ dfrac {74} {29} \\
0 & 1 & 0 & \ dfrac {42} {29} & \ dfrac {13} {29} \\
0 & 0 & 1 & \ dfrac {6} {29} & \ dfrac {35} {29} \\
\ end {array} \верно]\)
Что, если бы мы хотели записать линейную комбинацию.Это отличается от предыдущего примера тем, что существует бесконечно много решений векторного уравнения.
При более внимательном рассмотрении этой расширенной матрицы мы видим, что есть одна свободная переменная \ (x_ {4} \). Если мы выпишем уравнения, у нас будет:
\ (x_1 — \ left (\ dfrac {103} {29} \ right) x_4 = — \ dfrac {74} {29} \)
\ (x_2 + \ left (\ dfrac {42} {29} \ right) x_4 = \ dfrac {13} {29} \)
\ (x_3 + \ left (\ dfrac {6} {29} \ right) x_4 = \ dfrac {35} {29} \)
Поскольку \ (x_ {4} \) — свободная переменная, мы можем дать ей любое значение и найти решение этой системы уравнений.Действительно «хорошее» значение будет равно нулю. Если \ (x_4 = 0 \), то:
\ (x_1 — \ dfrac {103} {29} (0) = — \ dfrac {74} {29} \)
\ (x_2 + \ dfrac {42} {29} (0) = \ dfrac {13} {29} \)
\ (x_3 + \ dfrac {6} {29} (0) = \ dfrac {35} {29} \)
Используя это решение, мы можем записать \ (\ vec {v} \) как линейную комбинацию других векторов.
\ (\ vec {v} = \ begin {bmatrix} 5 \\ 3 \\ 0 \\ \ end {bmatrix} = \ left (- \ dfrac {72} {29} \ right) \ begin {bmatrix} 2 \ \ 0 \\ 1 \\ \ end {bmatrix} + \ left (\ dfrac {13} {29} \ right) \ begin {bmatrix} 1 \\ 4 \\ 3 \\ \ end {bmatrix} + \ left ( \ dfrac {35} {29} \ right) \ begin {bmatrix} 8 \\ 1 \\ 1 \\ \ end {bmatrix} + (0) \ begin {bmatrix} -4 \\ 6 \\ 1 \\ \ конец {bmatrix} \)
Это было бы одно решение, но поскольку \ (x_4 \) бесплатно, их бесконечно много.Для каждого возможного значения \ (x_4 \) у вас есть другой правильный способ записать \ (\ vec {v} \) как линейную комбинацию других векторов. Например, если \ (x_4 = 1 \):
\ (\ begin {align} x_1 & = — \ dfrac {74} {29} + \ dfrac {103} {29} \\ & = \ dfrac {29} {29} \\ & = 1 \ end {align} \)
\ (\ begin {align} x_2 & = \ dfrac {13} {29} — \ dfrac {42} {29} \\ & = — \ dfrac {29} {29} \\ & = -1 \ end {align } \)
\ (\ begin {align} x_3 & = \ dfrac {35} {29} — \ dfrac {6} {29} \\ & = \ dfrac {29} {29} \\ & = 1 \ end {align} \ )
Используя это, мы также можем написать:
\ (\ vec {v} = \ begin {bmatrix} 5 \\ 3 \\ 0 \\ \ end {bmatrix} = (1) \ begin {bmatrix} 2 \\ 0 \\ 1 \\ \ end {bmatrix} + (-1) \ begin {bmatrix} 1 \\ 4 \\ 3 \\ \ end {bmatrix} + (1) \ begin {bmatrix} 8 \\ 1 \\ 1 \\ \ end {bmatrix} + (1 ) \ begin {bmatrix} -4 \\ 6 \\ 1 \\ \ end {bmatrix} \)
Как это хорошо? (примечание: обычно мы не записываем 1 в уравнении, показывающем линейную комбинацию.Я оставил его там, чтобы вы могли видеть, где заканчивается каждое число из решения).
Опять же, у такой проблемы есть бесконечно много ответов. Все, что вам нужно сделать, это выбрать значение для свободных переменных, и у вас будет одно конкретное решение, которое вы можете использовать при написании линейной комбинации.
Когда вектор НЕ является линейной комбинацией других
Стоит увидеть один пример, где вектор не является линейной комбинацией некоторых заданных векторов. Когда это произойдет, мы получим расширенную матрицу, указывающую на противоречивую систему уравнений.
Пример
Определите, является ли вектор \ (\ begin {bmatrix} 1 \\ 2 \\ 1 \\ \ end {bmatrix} \) линейной комбинацией векторов:
\ (\ begin {bmatrix} 1 \\ 1 \\ 0 \\ \ end {bmatrix} \), \ (\ begin {bmatrix} 0 \\ 1 \\ -1 \\ \ end {bmatrix} \) и \ (\ begin {bmatrix} 1 \\ 2 \\ — 1 \\ \ end {bmatrix} \).
Решение
Шаг 1
Мы настраиваем нашу расширенную матрицу и сокращаем ее по строкам.
\ (
\ left [\ begin {array} {ccc | c} 1 & 0 & 1 & 1 \\
1 & 1 & 2 & 2 \\
0 & -1 & -1 & 1 \\
\ end {array} \ right]
\)
эквивалентно:
\ (
\ left [\ begin {array} {ccc | c} 1 & 0 & 1 & 0 \\
0 & 1 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\ end {массив } \ right]
\)
Шаг 2
Мы определяем, представляет ли матрица непротиворечивую систему уравнений.
Учитывая форму последней строки, эта матрица представляет противоречивую систему уравнений. Это означает, что нельзя записать этот вектор как линейную комбинацию других векторов. Вот и все — больше нечего сказать! Это будет нашим выводом каждый раз, когда сокращение строки приводит к появлению строки с нулями и ненулевым значением при увеличении.
Учебное пособие — линейные комбинации и пролет
Вам нужно больше практики с линейными комбинациями и диапазоном? Это 40-страничное учебное пособие поможет! Он включает объяснения, примеры, практические задачи и полные пошаговые решения.
Получить учебное пособие
Подпишитесь на нашу рассылку!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.
Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!
Связанные
.

 704
704 SM-1325+5
SM-1325+5 8-12 шп для колонн 108
8-12 шп для колонн 108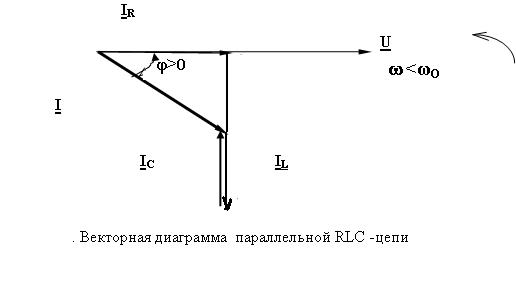 плазморезы серия 47
плазморезы серия 47 обработка пенопласта
обработка пенопласта