Класс точности амперметра как определить: Определить класс точности амперметра

Содержание

Как рассчитать класс точности прибора

ПОГРЕШНОСТИ И КЛАССЫ ТОЧНОСТИ ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ

Измеренная прибором величина всегда отличается от истинного значения на некоторое число, называемое погрешностью прибора. Погрешности измерительных приборов определяют поверкой, т. е. сравнением показаний поверяемого прибора с показаниями более точного, образцового прибора при измерении ими одной и той же величины. Значение измеряемой величины, определенное по образцовому прибору, принято считать действительным. Однако действительное значение отличается от истинного на погрешность, присущую данному образцовому прибору. Различают абсолютную, относительную и приведенную погрешности измерения.

Абсолютной погрешностью измерительного прибора называют разность между его показанием и действительным значением измеряемой величины.

Относительной погрешностью называют отношение абсолютной погрешности к действительному значению измеряемой величины, выраженное в относительных единицах или в процентах.

Приведенная погрешность – это отношение наибольшей абсолютной погрешности к верхнему пределу измерений прибора.

По значению приведенной погрешности измерительные приборы делят на группы по классу точности. Класс точности – обобщенная характеристика измерительного прибора, определяющая пределы допустимых погрешностей. Для электроизмерительных приборов класс точности указывается в вида числа, равного максимальной допустимой приведенной погрешности (в %). Согласно ГОСТ 1845-59, электроизмерительные приборы делят на 8 классов по точности: 0,05; 0,1; 0,2 – образцовые приборы; 0,5; 1,0 – лабораторные; 1,5; 2,5; 4,0 – технические приборы. Образцовые приборы считаются более высокого класса точности по отношению к лабораторным и техническим приборам, а лабораторные – по отношению к техническим.

Определим по классу точности прибора его погрешности. Если прибор (например, вольтметр с верхним пределом измерений 150 В) имеет класс точности 1,0, то основная приведенная погрешность не превышает 1 %. Максимальная абсолютную погрешность, которую может иметь прибор в любой точке шкалы не будет превышать Относительная же погрешность при этом зависит от измеряемого напряжения.

Если этим вольтметром можно измерять напряжение 10 В, то относительная погрешность может составить . Если же измерять напряжение 100 В, то относительная погрешность может составить

Из этого примера видно, что для повышения точности измерения прибор надо выбирать так, чтобы, во-первых, он имел более высокий класс точности, и чтобы, во-вторых, предел измерения был близок к значению измеряемой величины. Это означает, что для получения возможно меньших относительных ошибок, надо добиваться достаточно большого отклонения стрелки (желательно, чтобы использовалась последняя треть шкалы).

С другой стороны, для того чтобы добиться большой точности при измерении прибором более низкого класса, необходимо выбрать прибор с наименьшим возможным диапазоном измерений.

Следует правильно формулировать предложение, в котором дана количественная оценка погрешности. Например: «Измерение тока с абсолютной погрешностью до 1 мА», «Измерение тока с относительной погрешностью до 1 %. (Выражение «Измерение тока с точностью до 1 мА» неправильно).

Источник: kursak.net

Классы точности приборов

По приведенной погрешности (по классу точности) приборы делятся на восемь классов: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0.

Приборы класса точности 0,05; 0,1; 0,2; 0,5 применяются для точных лабораторных измерений и называются прецизионными (от англ. precision – точность). В технике применяются приборы классов 1,0; 1,5: 2,5 и 4,0 (технические).

Класс точности прибора указывается на шкале прибора. Если на шкале такого обозначения нет, то данный прибор внеклассный, то есть его приведенная погрешность превышает 4%.Производитель, выпускающий прибор, гарантирует относительную погрешность измерения данным прибором, равную классу точности (приведенной погрешности) прибора при измерении величины, дающей отброс указателя на всю шкалу. Определив по шкале прибора класс точности и предельное значение, легко рассчитать его абсолютную погрешность ΔX = ± гX_пр / 100%, которую принимают одинаковой на всей шкале прибора. Знаки «+» и «–» означают, что по-грешность может быть допущена как в сторону увеличения, так и в сторону уменьшения от действительного значения измеряемой величины.

При использовании приборов для конкретных измерений редко бывает так, чтобы измеряемая величина давала отброс стрелки прибора на всю его шкалу. Как правило, измеряемая величина меньше. Это увеличивает относительную погрешность измерения. Для оптимального использования приборов их подбирают так, чтобы значения измеряемой величины приходились на конец шкалы прибора, это уменьшит относительную погрешность измерения и приблизит ее к классу точности прибора. В тех случаях, когда на приборе класс точности не указан, абсолютная погрешность принимается равной половине цены наименьшего деления.

Источник: fevt.ru

Класс точности прибора 24651

Класс точности определяет гарантированные границы, за пределы которых не выходит погрешность прибора в установленном для него диапазоне измерений.

Класс точности К_Т электромеханических стрелочных измерительных приборов нормируют в виде процентного отношения предела Х_макс (гарантированных границ) абсолютной погрешности прибора, к нормирующему значению Х_норм его шкалы:

(2)

где нормирующим значением Х_норм для приборов с равномерной шкалой служит верхний предел измеряемой прибором величины, а для приборов с неравномерной шкалой — длина её рабочей части, т.е. длина участка между отметками шкалы, соответствующими диапазону измерений прибора.

Для электромеханических стрелочных измерительных приборов установлены следующие цифры классов точности: 0,05; 0,1; 0,2; 0,5 (для лабораторных приборов) и 1;.1,5; 2,5; 4 (для технических приборов).

Цифра класса точности прибора указывается на его шкале. Для приборов с равномерной шкалой эта цифра указывается без каких-либо знаков (кружков, квадратов, звёздочек), например, 2,5. Для приборов с неравномерной шкалой цифра класса точности подчеркивается ломаной линией, например, 2,5.

По формуле (2) класса точности прибора проводят оценку предельно допустимого значения его абсолютной погрешности. Такая оценка необходима для определения погрешности результата измерения, выполняемого прибором, а также для выбора прибора, обеспечивающего требуемую точность измерений.

Расчет предела абсолютной погрешности прибора с равномерной шкалой проводится непосредственно по формуле (2) класса точности, а для приборов с неравномерной шкалой по формуле (2) сначала определяется погрешность прибора в единицах длины (мм) шкалы, а затем по ней и чувствительности прибора рассчитывается абсолютная погрешность в единицах измеряемой величины.

Пример 1. Определить предел DI_макс абсолютной погрешности амперметра, который имеет равномерную шкалу, верхний предел измеряемого тока I_макс = 5А и класс точности К_Т =1.

Решение.1. Прибор имеет равномерную шкалу, следовательно, нормирующим значением в формуле (2) его класса точности является верхний предел измеряемого тока 1_макс = 5 А.

2. Предел абсолютной погрешности амперметра находится непосредственно из формулы (2):

Пример 2. Определить предел DR_макс абсолютной погрешности омметра с неравномерной шкалой в трёх её точках (начале, середине и конце), если диапазон измерений прибора лежит в пределах от 3 до 300 кОм, длина рабочего участка шкалы (т.е. между отметками 3 и 300) составляет L_p = 60мм, класс точности К_т=2,5, чувствительность прибора в начале, середине к конце рабочего участка шкалы соответственно равна S_н = 10 мм/нОм , S_с =1 мм/ нОм к S_к = 0,1 мм/кОм.

Решение.1. Прибор имеет неравномерную шкалу, следовательно, нормирующим значением в формуле (2) его класса точности является длина рабочего участка L_p = 60 мм.

2. По формуле (2) класса точности омметра определяется предел DL_макс его абсолютной погрешности, выраженный в единицах длины шкалы:

мм

3. Предел DR_макс абсолютной погрешности омметра в единицах измеряемой величины (т.е.

кОм;

кОм.

Пример 3. Определить пределы абсолютной DI_макс и относительной d_макс погрешностей результата измерения тока амперметром, у которого верхний предел измерения I_макс = 5А, класс точности К_Т =1, шкала равномерная. Показание амперметра при измерении равно I_изм = 3А.

Решение. 1. Предел DI_макс абсолютной погрешности результата измерения определяется пределом абсолютной погрешности прибора, который находится по классу точности прибора:

2. Предел относительной погрешности результата измерения

Примечание. Как следует из примера, предел относительной погрешности результата измерения будет возрастать с уменьшением уровня измеряемой величины. Следовательно, относительная погрешность получаемых результатов измерения будет близка к наименьшему своему возможному значению, равному цифре класса точности прибора, только в случае, если измеряемая величина близка к верхнему пределу измерения прибора.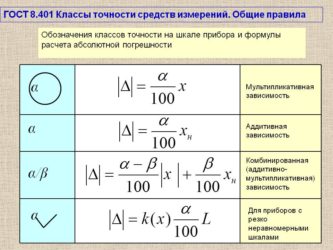

2.7.Выбор приборов для измерений

Основными метрологическими характеристиками прибора, определяющими погрешность результата измерения, являются верхний предел измерения и класс точности.

Верхний предел измерения прибора влияет, как видно из примера 3, на относительную погрешность получаемого результата измерения. Эта погрешность возрастает с уменьшением уровня измеряемой величины. Следовательно, приборы необходимо подбирать таким образом, чтобы их верхний предел измерения был как можно ближе к уровню измеряемой величины. В этом случае относительная погрешность получаемого результата измерения будет близка к наименьшему своему значению, равному цифре класса точности прибора.

Класс точности определяет способность прибора «улавливать» флуктуации измеряемой величины. К таким флуктуациям, например, относится технологический разброс параметров технических изделий, т.е. неповторимость параметров отдельных изделий одного вида. (Этот разброс обусловлен несовершенством технологии изготовления изделий. )

Флуктуации измеряемой величины и погрешность отдельного прибора носят случайный характер и между собой не коррелированы (не взаимосвязаны).

(3)

Точность «улавливания» флуктуации DX_ф измеряемой величины повышается с уменьшением погрешности DХ_п прибора. Однако, следует иметь в виду, что приборы с меньшей погрешностью имеют более высокую стоимость. Поэтому выбор приборов с меньшей погрешностью целесообразен до тех пор, пока уменьшение погрешности DХ_п оказывает существенное влияние на величину DХ_и. Отмеченное обстоятельство иллюстрируется графиком (рис.3) зависимости (3), представленной в виде

где составляющие DХ_и и DХ_п выражены относительно флуктуации DX_ф, которая является независимой величиной. Из графика видно, что в зоне DХ_п/DX_ф = 0,3 ¸ 0,5 отношение DХ_и/DХ_ф практически не изменяется. Следовательно, при выборе прибора по классу точности целесообразно использовать условие

Рис. 3 — Зависимость погрешности результата измерения

от погрешности прибора

Пример 4. Выбрать вольтметр, обеспечивавший удовлетворительную точность результата измерения выходного напряжения U_вых= 20 В блока питания, которое из-за технологического разброса параметров составных элементов блока может изменяться на ±1 % от указанного значения.

Решение.1. Выбор вольтметра заключается в определении его верхнего предела измерения и класса точности.

2. Верхний предел измерения вольтметра выбирается, как было отмечено в разд. 2.7, наиболее близким к уровню измеряемой величины.

У стандартных электромеханических вольтметров наиболее близким к уровню измеряемого напряжения U_вых= 20 является верхний предел измерения U_v_макс = 30 В.

3. В рассматриваемом примере технологический разброс DU_вых выходного напряжения блока питания составляет ±1 % от среднего значения 20 В:

4. Согласно указанному в разделе 2.7 правилу, предел U_v_макс = 30 В абсолютной погрешности вольтметра должен удовлетворять условию

5. Класс точности К_Т выбираемого вольтметра, определяется по формуле (2):

Среди стандартных электромеханических вольтметров указанному условию удовлетворяет прибор с классом точности 0,2.

6. Заключение: для измерения выходного, напряжения блока питания выбираем вольтметр с верхним пределом измерения U_v_макс = 30В и классом точности К_Т = 0,2.

Источник: studepedia.org

Определение класса точности прибора

Класс точности измерительного прибора — это обобщенная характеристика, определяемая пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами, влияющими на точность, значения которых установлены в стандартах на отдельные виды средств измерений. Класс точности средств измерений характеризует их свойства в отношении точности, но не является непосредственным показателем точности измерений, выполняемых при помощи этих средств.

Для того чтобы заранее оценить погрешность, которую внесет данное средство измерений в результат, пользуются нормированными значениями погрешности. Под ними понимают предельные для данного типа средства измерений погрешности.

Погрешности отдельных измерительных приборов данного типа могут быть различными, иметь отличающиеся друг от друга систематические и случайные составляющие, но в целом погрешность данного измерительного прибора не должна превосходить нормированного значения. Границы основной погрешности и коэффициентов влияния заносят в паспорт каждого измерительного прибора.

Основные способы нормирования допускаемых погрешностей и обозначения классов точности средств измерений установлены ГОСТ.

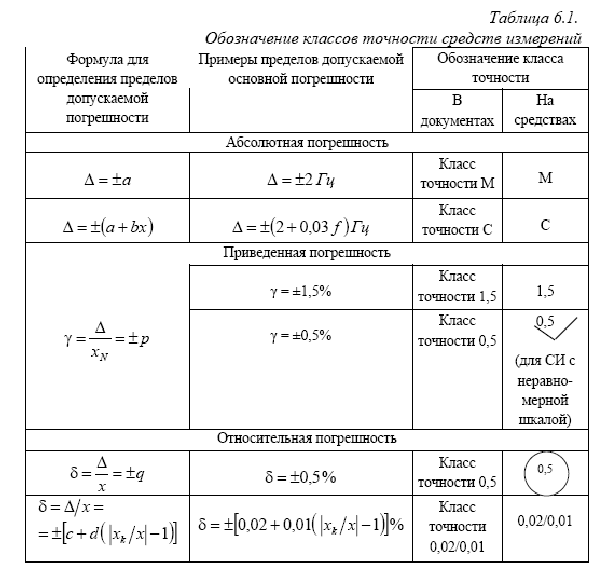
На шкале измерительного прибора маркируют значение класса точности измерительного прибора в виде числа, указывающего нормированное значение погрешности. Выраженное в процентах, оно может иметь значения 6; 4; 2,5; 1,5; 1,0; 0,5; 0,2; 0,1; 0,05; 0,02; 0,01; 0,005; 0,002; 0,001 и т. д.

Если обозначаемое на шкале значение класса точности обведено кружком, например 1,5, это означает, что погрешность чувствительности δs = 1,5%. Так нормируют погрешности масштабных преобразователей (делителей напряжения, измерительных шунтов, измерительных трансформаторов тока и напряжения и т. п.).

Это означает, что для данного измерительного прибора погрешность чувствительности δs = dx/x — постоянная величина при любом значении х. Граница относительной погрешности δ(х) постоянна и при любом значении х просто равна значению δs, а абсолютная погрешность результата измерений определяется как dx = δsx

Для таких измерительных приборов всегда указывают границы рабочего диапазона, в которых такая оценка справедлива.

Если на шкале измерительного прибора цифра класса точности не подчеркнута, например 0,5, это означает, что прибор нормируется приведенной погрешностью нуля δо = 0,5 %. У таких приборов для любых значений х граница абсолютной погрешности нуля dx = dо = const, а δо = dо/хн.

При равномерной или степенной шкале измерительного прибора и нулевой отметке на краю шкалы или вне ее за хн принимают верхний предел диапазона измерений. Если нулевая отметка находится посредине шкалы, то хн равно протяженности диапазона измерений, например для миллиамперметра со шкалой от -3 до +3 мА, хн= 3 — (-3)=6 А.

Однако будет грубейшей ошибкой полагать, что амперметр класса точности 0,5 обеспечивает во всем диапазоне измерений погрешность результатов измерений ±0,5 %. Значение погрешности δо увеличивается обратно пропорционально х, то есть относительная погрешность δ(х) равна классу точности измерительного прибора лишь на последней отметке шкалы (при х = хк). При х = 0,1хк она в 10 раз больше класса точности. При приближении х к нулю δ(х) стремится к бесконечности, то есть такими приборами делать измерения в начальной части шкалы недопустимо.

На измерительных приборах с резко неравномерной шкалой (например на омметрах) класс точности указывают в долях от длины шкалы и обозначают как 1,5 с обозначением ниже цифр знака «угол».

Если обозначение класса точности на шкале измерительного прибора дано в виде дроби (например 0,02/0,01), это указывает на то, что приведенная погрешность в конце диапазона измерений δпрк = ±0,02 %, а в нуле диапазона δпрк = -0,01 %. К таким измерительным приборам относятся высокоточные цифровые вольтметры, потенциометры постоянного тока и другие высокоточные приборы.

В этом случае δ(х) = δк + δн (хк/х — 1), где хк — верхний предел измерений (конечное значение шкалы прибора), х — измеряемое значение.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Сдача сессии и защита диплома — страшная бессонница, которая потом кажется страшным сном. 8738 — | 7137 — или читать все.

188.64.173.93 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Источник: studopedia. ru

Как определить класс точности манометра

Манометр — измерительный прибор, который позволяет установить значение избыточного давления, действующего в трубопроводе или в рабочих частях различных видов оборудования. Такие приборы широко применяются в системах отопления, водоснабжения, газоснабжения, других инженерных сетях коммунального и промышленного назначения. В зависимости от условий эксплуатации измерителя существуют определенные ограничения по допустимому пределу его погрешности. Поэтому важно знать, как определить класс точности манометра.

Что такое класс точности манометра, и как его определить

Класс точности манометра является одной из основных величин, характеризующих прибор. Это процентное выражение максимально допустимая погрешность измерителя, приведенная к его диапазону измерений. Абсолютная погрешность представляет собой величину, которая характеризует отклонение показаний измерительного прибора от действительного значения давления. Также выделяют основную допустимую погрешность, которая представляет собой процентное выражение абсолютного допустимого значения отклонения от номинального значения. Именно с этой величиной связан класс точности.

Существует два типа измерителей давления — рабочие и образцовые. Рабочие применяются для практического измерения давления в трубопроводах и оборудовании. Образцовые — специальные измерители, которые служат для поверки показаний рабочих приборов и позволяют оценить степень их отклонения. Соответственно, образцовые манометры имеют минимальный класс точности.

Классы точности современных манометров регламентируются в соответствии с ГОСТ 2405-88 Они могут принимать следующие значения:

Таким образом, этот показатель имеет прямую зависимость с погрешностью. Чем он ниже, тем ниже максимальное отклонение, которое может давать измеритель давления, и наоборот. Соответственно, от этого параметра зависит, насколько точными являются показания измерителя. Высокое значение указывает на меньшую точность измерений, а низкое соответствует повышенной точности. Чем ниже значение класса точности, тем более высокой является цена устройства.

Узнать этот параметр достаточно просто. Он указан на шкале в виде числового значения, перед которым размещаются литеры KL или CL. Значение указывается ниже последнего деления шкалы.

Указанная на приборе величина является номинальной. Чтобы определить фактический класс точности, нужно выполнить поверку и рассчитать его. Для этого проводят несколько измерений давления образцовым и рабочим манометром. После этого необходимо сравнить показания обоих измерителей, выявить максимальное фактическое отклонение. Затем остается только посчитать процент отклонения от диапазона измерений прибора.

Определение погрешности

Владельцев измерительных приборов интересует, прежде всего, величина максимальной погрешности, характерной для манометра. Она зависит не только от класса точности, но и от диапазона измерений. Таким образом, чтобы получить значение погрешности, нужно произвести некоторые вычисления.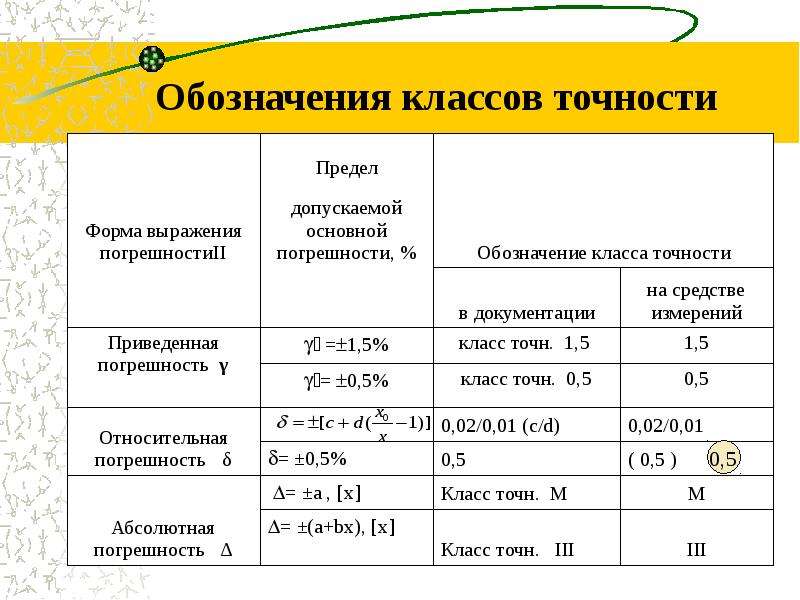 Например, для манометра с диапазоном измерений, равным 6 МПа, и классом точности 1,5 погрешность будет рассчитываться по формуле 6*1,5/100=0,09 МПа.

Необходимо отметить, что таким способом можно посчитать только основную погрешность. Ее величина определяется идеальными условиями эксплуатации. На нее оказывают влияние только конструктивные характеристики, а также особенности сборки прибора, например, точность градуировки делений на шкале, сила трения в измерительном механизме. Однако эта величина может отличаться от фактической, поскольку существует также дополнительная погрешность, определяемая условиями, в которых эксплуатируется манометр. На нее может влиять вибрация трубопровода или оборудования, температура, уровень влажности и другие параметры.

Также точность измерения давления зависит от еще одной характеристики манометра — величины его вариации, которую определяют в ходе поверки. Это максимальная разница показаний измерителя, выявленная по результатам нескольких измерений. Величина вариации в значительной мере зависит от конструкции манометра, а именно от способа уравновешивания, которое может быть жидкостным (давлением столба жидкости) или механическим (пружиной). Механические манометры имеют более выраженную вариацию, что часто обусловлено дополнительным трением при плохой смазке или износе деталей, потере упругости пружины и другими факторами.

Источник: grom.ru

Амперметр — класс — точность

Cтраница 1

Амперметр класса точности 2 5 с пределом измерения 15 А и внутренним сопротивлением 0 018 Ом включен параллельно шунту, расширяющему предел измерения в десять раз.
[1]

Амперметр класса точности 1 с пределом измерения 5 А и внутренним сопротивлением 0 09 Ом включен параллельно шунту, расширяющему пределы измерения до 50 А.
[2]

Амперметр класса точности 1 5 имеет 100 делений.
[3]

Амперметр класса точности 1 5 с пределом измерения 100 А имеет наружный шунт сопротивлением гт0 001 Ом.
[4]

Амперметр класса точности 1 5 с пределом измерения 0 3 А имеет внутреннее сопротивление 0 08 Ом.
[5]

Амперметр класса точности 2 5 с пределом измерения 15 А и внутренним сопротивлением 0 018 Ом включен параллельно шунту, расширяющему предел измерения в десять раз.
[6]

Амперметр класса точности 1 с пределом измерения 5 А и внутренним сопротивлением 0 09 Ом включен параллельно шунту, расширяющему пределы измерения до 50 А.
[7]

Амперметр класса точности 1 5 с пределом измерения 0 3 А имеет внутреннее сопротивление 0 08 Ом.
[8]

Амперметр класса точности 1 5 имеет 100 делений.
[9]

Амперметр класса точности 1 5 с пределом измерения 100 А имеет наружный шунт сопротивлением гш — 0 001 Ом.
[10]

Чему равны относительные погрешности измерений, если пятиамперным амперметром класса точности 0 5 в первый раз измерили ток 2 А, а во второй — 4 А. Какой нужно сделать вывод.
[11]

В подготовку схемы для комплексных испытаний входит подключение контрольных амперметров класса точности не ниже 0 5 во все фазы токовых цепей для измерения тока в обмотках статора генератора и контроля всех вторичных токовых цепей, включение контрольных вольтметров в цепи напряжения класса точности не ниже 0 5 для измерения напряжения всех фаз обмоток генератора, включение контрольного шунта в цепь ротора с милливольтметром, включение приборов постоянного тока класса точности не ниже 0 5, необходимых для снятия характеристик возбудителя и контроля системы возбуждения.
[12]

Какая погрешность определяет класс точности прибора

Во время лабораторных измерений требуется знать точность измерительных средств, которые в свою очередь обладают определенными характеристиками и различаются по устройству. Каждое из средств измерения (СИ) имеют определенные неточности, которые делится на основные и дополнительные. Зачастую возникают ситуации, когда нет возможности или просто не требуется производить подробный расчет. Каждому средству измерения присвоен определенный класс точности, зная который, можно выяснить его диапазон отклонений.

Вовремя выяснить ошибки измерительного средства помогут нормированные величины погрешностей. Под этим определением стоит понимать предельные, для измерительного средства показатели. Они могут быть разными по величине и зависеть от разных условий, но пренебрегать ими не стоит ни в коем случае, ведь это может привести к серьезной ошибке в дальнейшем. Нормированные значения должны быть меньше чем покажет прибор. Границы допустимых величин ошибок и необходимые коэффициенты вносятся в паспорт каждого замеряющего размеры устройства. Узнать подробные значения нормирования для любого прибора можно воспользовавшись соответствующим ГОСТом.

Класс точности измерительного прибора

Обобщающая характеристика, которая определяется пределами погрешностей (как основных, так и дополнительных), а также другими влияющими на точные замеры свойствами и показатели которых стандартизированы, называется класс точности измерительного аппарата. Класс точности средств измерений дает информацию о возможной ошибке, но одновременно с этим не является показателем точности данного СИ.

Средство измерения – это такое устройство, которое имеет нормированные метрологические характеристики и позволяет делать замеры определенных величин. По своему назначению они бывают примерные и рабочие. Первые используются для контроля вторых или примерных, имеющих меньший ранг квалификации. Рабочие используются в различных отраслях. К ним относятся измерительные:

приборы;
преобразователи;
установки;
системы;
принадлежности;
меры.

На каждом средстве для измерений имеется шкала, на которой указываются классы точности этих средств измерений. Они указываются в виде чисел и обозначают процент погрешности. Для тех, кто не знает, как определить класс точности, следует знать, что они давно стандартизованы и есть определенный ряд значений. Например, на устройстве может быть одна из следующих цифр: 6; 4; 2,5; 1,5; 1,0; 0,5; 0,2; 0,1; 0,05; 0,02; 0,01; 0,005; 0,002; 0,001. Если это число находится в круге, то это погрешность чувствительности. Обычно ее указывают для масштабных преобразователей, таких как:

делители напряжения;
трансформаторы тока и напряжения;
шунты.

Обозначение класса точности

Обязательно указывается граница диапазона работы этого прибора, в пределах которой значение класса точности будет верно.

Те измерительные устройства, которые имеют рядом со шкалой цифры: 0,05; 0,1; 0,2; 0,5, именуются как прецизионные. Сфера их применения – это точные и особо точные замеры в лабораторных условиях. Приборы с маркировкой 1,0; 1,5; 2,5 или 4,0 называются технические и исходя из названия применяются в технических устройствах, станках, установках.

Возможен вариант, что на шкале такого аппарата не будет маркировки. В такой ситуации погрешность приведенную принято считать более 4%.

Если значение класса точности устройства не подчеркнуто снизу прямой линией, то это говорит о том, что такой прибор нормируется приведенной погрешностью нуля.

Грузопоршневой манометр, класс точности 0,05

Если шкала отображает положительные и отрицательные величины и отметка нуля находится посередине такой шкалы, то не стоит думать, что погрешность во всем диапазоне будет неизменной. Она будет меняться в зависимости от величины, которую измеряет устройство.

Если замеряющий агрегат имеет шкалу, на которой деления отображены неравномерно, то класс точности для такого устройства указывают в долях от длины шкалы.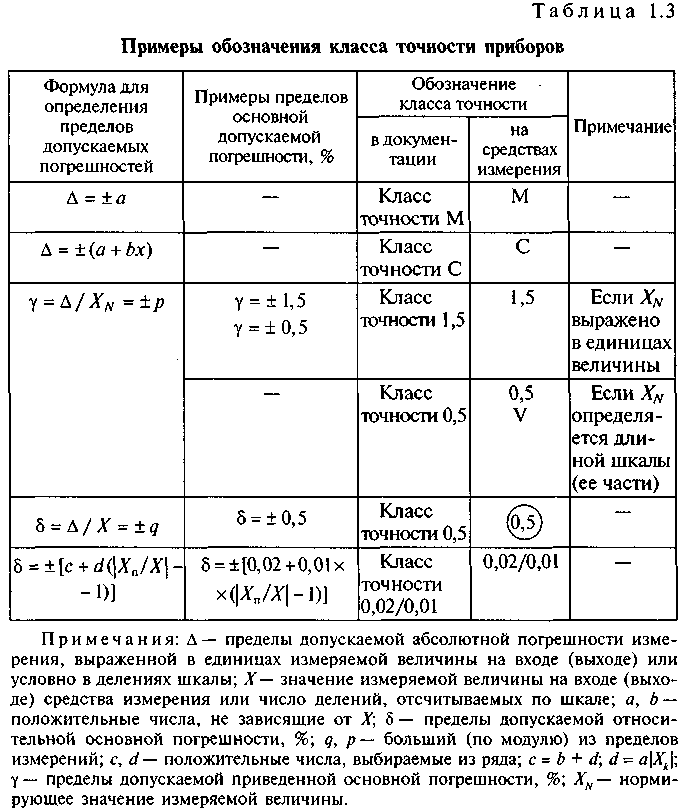

Возможны варианты измерительных аппаратов со значениями шкалы в виде дробей. Числитель такой дроби укажет величину в конце шкалы, а число в знаменателе при нуле.

Нормирование

Классы точности средств измерений сообщают нам информацию о точности таких средств, но одновременно с этим он не показывает точность измерения, выполненного с помощью этого измерительного устройства. Для того, чтобы выявить заблаговременно ошибку показаний прибора, которую он укажет при измерении люди нормируют погрешности. Для этого пользуются уже известными нормированными значениями.й

Нормирование осуществляется по:

Формулы расчета абсолютной погрешности по ГОСТ 8.401

Каждый прибор из конкретной группы приспособлений для замера размеров имеет определенное значение неточностей. Оно может незначительно отличаться от установленного нормированного показателя, но не превышать общие показатели. Каждый такой агрегат имеет паспорт, в который записываются минимальные и максимальные величины ошибок, а также коэффициенты, оказывающие влияние в определенных ситуациях.

Все способы нормирования СИ и обозначения их классов точности устанавливаются в соответствующих ГОСТах.

Виды маркирования

Классы точности абсолютно всех измерительных приборов подлежат маркировке на шкале этих самых приборов в виде числа. Используются арабские цифры, которые обозначают процент нормированной погрешности. Обозначение класса точности в круге, например число 1,0, говорит о том, что ошибочность показаний стрелки аппарата будет равна 1%.

Если в обозначении используется кроме цифры еще и галочка, то это значит, что длина шкалы применяется в роли нормирующего значения.

Латинские буквы для обозначения применяются если он определяется пределами абсолютной погрешности.

Существуют аппараты, на шкалах которых нет информации о классе точности. В таких случаях абсолютную следует приравнивать к одной второй наименьшего деления.

Пределы

Как уже говорилось раньше, измерительный прибор, благодаря нормированию уже содержит случайную и систематические ошибки. Но стоит помнить, что они зависят от метода измерения, условий и других факторов. Чтобы значение величины, подлежащей замеру, было на 99% точным, средство измерения должно иметь минимальную неточность. Относительная должна быть примерно на треть или четверть меньше погрешности измерений.

Базовый способ определения погрешности

При установке класса точности в первую очередь нормированию подлежат пределы допустимой основной погрешности, а пределы допускаемой дополнительной погрешности имеют кратное значение от основной. Их пределы выражают в форме абсолютной, относительной и приведенной.

Приведенная погрешность средства измерения – это относительная, выраженная отношением предельно-допустимой абсолютной погрешности к нормирующему показателю. Абсолютная может быть выражена в виде числа или двучлена.

Если класс точности СИ будет определяться через абсолютную, то его обозначают римскими цифрами или буквами латиницы. Чем ближе буква будет к началу алфавита, тем меньше допускаемая абсолютная погрешность такого аппарата.

Класс точности 2,5

Благодаря относительной погрешности можно назначить класс точности двумя способами. В первом случае на шкале будет изображена арабская цифра в кружке, во втором случае дробью, числитель и знаменатель которой сообщают диапазон неточностей.

Основная погрешность может быть только в идеальных лабораторных условиях. В жизни приходится умножать данные на ряд специальных коэффициентов.

Дополнительная случается в результате изменений величин, которые каким-либо образом влияют на измерения (например температура или влажность). Выход за установленные пределы можно выявить, если сложить все дополнительные погрешности.

Случайные ошибки имеют непредсказуемые значения в результате того, что факторы, оказывающие на них влияние постоянно меняются во времени. Для их учета пользуются теорией вероятности из высшей математики и ведут записи происходивших раньше случаев.

Пример расчета погрешности

Статистическая измерительного средства учитывается при измерении какой-либо константы или же редко подверженной изменениям величины.

Динамическая учитывается при замерах величин, которые часто меняют свои значения за небольшой отрезок времени.

Классы точности болтов

Болты и другие крепежные изделия изготавливают нескольких классов:

Каждый из них имеет свои допуски измеряемой величины, отличные от остальных и применяется в различных сферах.

Крепеж С используют в отверстиях с диаметром немногим больше диаметра болта (до 3мм). Болты без труда устанавливаются, не отнимая много времени на работу. Из минусов стоит отметить то, что при физическом воздействии на такой крепеж, болтовое соединение может сместиться на несколько миллиметров.

Крепеж В подразумевает использование болтов, диаметр которых меньше отверстия в пределах 1-1,5 мм. Это позволяет конструкции меньше подвергаться смещениям и деформациям, но повышаются требования к изготовлению отверстий в креплениях.

Гайки шестигранные класса точности В

Крепеж А создается по проекту. Диаметр болта такого типа, меньше диаметра отверстия максимум на 0,3 мм и имеет допуск только со знаком минус. Это делает крепеж неподвижным, не позволяет происходить смещению узлов. Изготовление болтов А-класса стоит дороже и не всегда используется в производстве.

Класс точности присутствует в описании всех измерительных приборов и является одной из самых важных характеристик. Чем выше его значение, тем более дорогостоящий будет прибор, но в то же время он сможет предоставить более точную информацию. Выбор стоить делать исходя из сложившейся ситуации и целей в которых будет использоваться такое средство. Важно понимать, что в некоторых ситуациях экономически выгодно будет приобрести дорогостоящее сверхточное оборудование, чтобы в дальнейшем сберечь деньги.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Класс точности измерительного прибора — это обобщенная характеристика, определяемая пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами, влияющими на точность, значения которых установлены в стандартах на отдельные виды средств измерений. Класс точности средств измерений характеризует их свойства в отношении точности, но не является непосредственным показателем точности измерений, выполняемых при помощи этих средств.

Класс точности магнитоэлектрического миллиамперметра с конечным

1. Ток резистора, сопротивление которого 8 Ом, равен 2,4 А. При измерении напряжения на этом резисторе вольтметр показал напряжение 19,3 В. Определить абсолютную и относительную погрешности измерения сопротивления в данном случае.

Решение:

2. Определить класс точности амперметра с пределом измерения 10 А, если точкам шкалы 2, 4, 6, 8, 10 А соответствуют значения токов 2,041; 3,973; 6,015; 8,026; 9,976 А.

Решение:

3. При пятикратном измерении одного и того же напряжения с помощью вольтметра были получены следующие результаты: 6,35; 6,4; 6,3; 6,45; 6,25 В. Считая среднее арифметическое значение измеряемого напряжения действительным его значением, определить границы абсолютной и относительной погрешности.

Решение:

4. Определить класс точности магнитоэлектрического миллиамперметра с пределом измерения шкалы I_Н = 0,5 мА для измерения тока 0,1 ¸ 0,5 мА, если относительная погрешность измерения тока не превышает 1 %.

Решение:

5. При поверке милливольтметра класса точности 1,0 с пределом измерения 300 мВ максимальные погрешности измерения напряжения от 50 до 300 мВ с шагом 50 мВ составили 1,5; 1,0; 0,5; 3,0; 2,5 мВ. Соответствует ли милливольтметр своему классу точности?

Решение:

6. При изменении измеряемого тока от 5 до 10 мА указатель одного миллиамперметра переместился на четыре деления, а другого — на десять делений. Определить соотношения между чувствительностями и постоянными шкал приборов.

Решение:

7. Миллиамперметр рассчитан на ток 200 мА и имеет чувствительность 0,5 дел/мА. Чему равны число делений шкалы, цена деления и измеренный ток, если указатель миллиамперметра отклонился на 30 делений?

Решение:

8. Определить относительную погрешность косвенного измерения тока I, если этот ток равен: а) сумме токов I₁ = 4 А и I₂ = 3 А; б) разности токов I₁ = 4 А и I₂ = 3 А. Измерение производилось амперметрами класса точности 1,0 с номинальным током 5 А.

Решение:

9. После ремонта щитового амперметра с классом точности 1,5 и пределом измерения 5 А произвели поверку его основной приведенной погрешности. Наибольшая абсолютная погрешность прибора составляла 30 мА. Сохранил ли амперметр свой класс точности после ремонта?

Решение:

10. Вольтметр с пределом измерения 7,5 В и максимальным числом делений 150 имеет наибольшую абсолютную погрешность 36 мВ. Определить класс точности прибора и относительную погрешность в точках 40, 80, 90, 100 и 120 делений.

Решение:


Деления	Показания, В	Относительная погрешность d, %
4,5

11. Амперметр класса точности 1,5 имеет 100 делений. Цена каждого деления 0,5 А. Определить предел измерения прибора, наибольшую абсолютную погрешность и относительную погрешность в точках 10, 30, 60, 70 и 90 делений.

Решение:


Деления	Показания, А	Относительная погрешность, %

12. При поверке амперметра с пределом измерения 10 А класса точности 0,5 относительная погрешность на отметке 2 А составила 4,5%. Определить, соответствует ли прибор указанному классу точности, если абсолютная погрешность в этой точке имеет наибольшее значение.

Решение:

13. Определить класс точности микроамперметра с двусторонней шкалой и пределом измерения 100 мкА, если наибольшее значение абсолютной погрешности получено на отметке 40 мкА и равно 1,7 мкА. Определить относительную погрешность прибора для этого значения.

Решение:

14. Основная приведенная погрешность показаний магнитоэлектрического прибора составляет 0,5%. Какая наибольшая возможная относительная погрешность измерения при отклонении стрелки на 75; 50; 25 % его шкалы?

Решение:

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась – это был конец пары: «Что-то тут концом пахнет». 8428 – | 8040 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Задача 1. 1

Результат измерения тока содержит случайную погрешность, распределенную по нормальному закону. Среднее квадратическое отклонение σ=4мА, систематическая погрешность ∆с= 0.

Определить вероятность того, что погрешность превысит по абсолютному значению 12 мА [СП, раздел 3.4, задача 3.4.5].

Задача 1. 2

Погрешность измерения напряжения ∆U распределена по нормальному закону, причем систематическая погрешность ∆с = 0, среднее квадратическое отклонение σ = 60 мВ.

Определить вероятность того, что результат измерения отличается от истинного значения не более чем на 144 мВ [СП, раздел 3.4, задача 3.4.5].

Задача 1.3

Результат измерения мощности содержит случайную погрешность, распределенную по нормальному закону, σ = 100 мВт и ∆с = 50 мВт. Определить вероятность того, что неисправленный результат измерения превысит истинное значение мощности [СП, раздел 3.4, задача 3.4.6].

Задача 1.4

Погрешность результата измерения напряжения распределена по закону Симпсона в интервале от -1 до +3 мВ.

Определить систематическую погрешность и среднее квадратическое отклонение результата измерения;вероятность того, что исправленный результат измерения отличается от истинного значения измеряемого напряжения не более чем на 1 мВ [СП, раздел 3.4, задача 3.4.7].

Ответ: 1 мВ; 0.58 мВ; 0.75 мВ.

Задача 1.5

Оценить вероятность того, что сопротивление отличается от своего математического ожидания не более чем на 1 Ом. Закон распределения погрешности неизвестен, среднее квадратическое отклонение σ = 0,4 Ом [СП, раздел 3.4, задача 3.4.8].

Задача 1.6

Сопротивление R составлено из параллельно включенных сопротивления R1 и R2, математические ожидания и средние квадратические отклонения которых известны: m₁= 24 Ом; m₂ = 30 Ом; σ₁ = 1 Ом; σ₂ = 0,5 Ом.

Определить математическое ожидание m и среднее квадратическое отклонение σ сопротивления R [СП, раздел 3.4, задача 3.4.10].

Задача 1.7

В результате измерений сопротивлений получены следующие значения: R0 = 200 Ом; R1 = 100 Ом; R2 = 600 Ом; R3 = 500 Ом. Средние квадратические отклонения измеренных сопротивлений соответственно равны: 0.3: 0.2; 0.6; 0.3 Ом.

Определить среднее квадратическое отклонение сопротивления Rx, если

Задача 1.8

Определить оценки емкостей конденсаторов С1 и С2 и их дисперсии, если по результатам совокупных измерений получены следующие данные: емкости каждого из них в отдельности, а так же при параллельном и последовательном их соединении равны С1 = 0.2071 мкФ; С2 = 0.2056 мкФ; С1С2/(С1 + С2) = 0.1035мкФ; С1 + С2 = 0.4111 мкФ [СП, раздел 3.4, задача 3.4.10].

Ответ: 0.20661 мкФ; 0.20512 мкФ; 6.3*10 4 мкФ.

Задача 1.9

Микроамперметр с входным сопротивлением 600 Ом включен последовательно нагрузке сопротивлением 1200 ОМ.

Вычислить погрешность влияния при данном измерении [СП, раздел 3.4, задача 3.4.10].

Задача 1.10

Определить по составному критерию, отвечает ли нормальному закону

распределения 13 равноточных результатов измерений напряжения. Результаты измерений следующие: 100.08; 100.09; 100.07; 100.10; 100.05; 100.06; 100.04; 100.06; 99.95; 99.92; 100.02; 99.98; 99.97.

Рассчитать среднеарифметическое значение напряжения,

среднеквадратическое отклонение, доверительный интервал при доверительной вероятности Р = 0,98 и записать результат измерений по стандарту [СП, раздел 3.4, задача 3.4.9].

Задача 1.11

Оценить вероятность того, что сопротивление отличается от своего математического ожидания не более чем на 1 Ом. Закон распределения погрешности неизвестен, среднее квадратическое отклонение s = 0,4 Ом [СП, раздел 3.4, задача 3.4.8].

Задача 1.12

Определить погрешность, с которой выполнено измерение индуктивности катушки L = 85 мГн и сопротивления резистора R = 2,83 Ом. Основная погрешность моста задана в виде двух составляющих: аддитивной и мультипликативной:

где L – индуктивность мкГн;

Задача 2.1

Определить класс точности магнитоэлектрического прибора с конечным значением шкалы Iк = 0,5 мА для измерения тока I = (0.1. 0.5) мА так, чтобы относительная погрешность измерения тока не превышала 1 % [СП, раздел 3.4, задача 3.4.1].

Задача 2.2

Определить класс точности магнитоэлектрического прибора с конечным значением шкалы Uк= 10В для измерения напряжения U =(1. 10)В так, чтобы относительная погрешность измерения не превышала 1 % [СП, раздел 3.4, задача 3.4.1].

Задача 2.3

Определить показания двух последовательно включенных магнитоэлектрических миллиамперметров с конечным значением шкалы Iк = 100 мА (шкала имеет 100 делений) и классами точности 1.0 и 0.5. Действительное значение тока при измерении равно 50 мА.

Определить наибольшую разницу в показаниях двух миллиамперметров [СП, раздел 3.4, задача 3.4.2].

Задача 2.4

Определить показания двух последовательно включенных магнитоэлектрических вольтметров с конечным значением шкалы U_K = 150В (шкала имеет 150 делений) и классами точности 1.0 и 0.5. Действительное значение напряжения при измерении равно 75 В. Определить наибольшую разницу в показаниях двух вольтметров [СП, раздел 3.4, задача 3.4.2].

Задача 2.5

Определить класс точности магнитоэлектрического миллиамперметра с конечным значением диапазона измерений тока Iк =0.5 мА, если предельное значение абсолютной погрешности измерений постоянно и равно 0.0015 мА [СП, раздел 3.4, задача 3.4.4].

Задача 2.6

Определить класс точности магнитоэлектрического вольтметра с конечным значением диапазона измерений Uk= 300В, если предельное значение абсолютной погрешности измерений постоянно и равно 1.5В [СП, раздел 3.4, задача 3.4.4].

Задача 2.7

Многопредельный электронный вольтметр переменного тока имеет 11 поддиапазонов с верхними пределами: 1, 3, 10, 30,…. 100000 мВ.

Максимальная приведенная погрешность прибора составляет ±1.5% на всех поддиапазонах. Прибор имеет две шкалы: область значений первой ограничена числами 3 и 10, а второй – числами 10 и 30.

Определить динамический диапазон прибора [раздел 1.5.2, формула 1.3] и наибольшее значение относительной погрешности на каждом из поддиапазонов [раздел 3.5, формула 3.4, СП].

Задача 2.8

Цена деления шкалы вольтметра составляет один вольт, класс точности равен 1.5. При каком максимальном верхнем значении данный вольтметр будет относиться к заданному классу точности [раздел 3.5, формулы (3.2 – 3.3), СП].

Задача 2.9

Записать обозначение класса точности аналогового прибора, если при измерении максимального значения погрешность составляла 1% , а при измерении максимума пополам составляла 1.5% [раздел 1.7, формула 1.12].

Задача 2.10

Класс точности первого вольтметра равен (1/0.5), а второго – (1.5/0.25). Диапазон измерений (0 – 10)В.Определить при каких значениях измеряемого напряжения выгоднее использовать первый прибор [раздел 1.7, формула 1.11].

Задача 3.1

Задача 3.2

Задача 3.3

Выполнить коррекцию высокоомного делителя на частоте 2 МГц. Для чего выбрать переменную емкость, аппаратуру для контроля процесса настройки и рассчитать величину погрешности на высокой частоте. Данные для решения взять из задач 4.1 и 4.2 [КП, раздел 3.5].

Задача 3.4

Рассчитать сопротивление шунта Rш для расширения пределов измерения миллиамперметра до 10А с током полного отклонения Iп =50 мкА, внутренним сопротивлением Rвh = 1500 Ом [СП, раздел 3.4, задача 3.4.15].

Ответ: 7.5*10 -3 Ом.

Задача 3.5

Определить внутреннее сопротивление комбинированного аналогового прибора, имеющего ток полного отклонения рамки 50 мкА, падение напряжение на рамке 15 мВ при измерении постоянного тока на пределах 50 мкА; 10 мА; 100мА; 1А [СП, раздел 3.4, задача 3.4.16].

Ответ: 1.5 кОм; 1.5 Ом; 0.75 Ом; 0.075 Ом;

Задача 3.6

Задача 3.7

Рисунок 4.1- Пиковый детектор

Задача 3.8

Задача 3.9

Задача 3.10

Ток полного отклонения в рамке измерительного механизма милливольтметра, имеющего предел измерения 15 мВ, равен I_{=0,12 мА. Определите сопротивления шунта R₁ и R₂для пределов измерения 5 и 0,15 мА, если сопротивление цепи рамки измерительного механизма R_{=125 Ом [СП, раздел 3.4, задача 3.4.15].}}

Задача 3.11

Для электромагнитного вольтметра, имеющего ток полного отклонения 3 мА и внутреннее сопротивление 30 кОм, определите верхний предел измерения и сопротивление добавочного резистора, необходимого для расширения верхнего предела измерения до 600В[СП, раздел 3.4, задача 3.4.16].

Задача 3.12

Определите возможные пределы первичного тока, если показание в нормальных условиях амперметра класса 1.5, включенного во вторичную обмотку трансформатора тока с K_I =100/5, равно I₂ =4 А. Амперметр имеет верхний предел измерения I_в=5 А, а погрешность тока трансформатора тока составляет f_I=-0,5 % [СП, раздел 3.4, задача 3.4.17].

Задача 3.13

Верхний предел измерения микроамперметра 100 мкА, внутреннее сопротивление 15 Ом. Чему должно быть равно сопротивление шунта, чтобы верхний предел измерения увеличился в 10 раз [СП, раздел 3.4, задача 3.4.16]

Задача 3.14

Определите, какое нужно иметь сопротивление добавочного резистора к электродинамическому вольтметру с верхним пределом измерения 100В и внутренним сопротивлением 4 кОм, чтобы расширить его верхний предел измерения в 3 раза [СП, раздел 3.4, задача 3.4.16].

Задача 3.15

К вольтметру, сопротивление которого R_в=30 кОм, подключен резистор с сопротивлением R_д = 90 кОм, При этом верхний предел измерения прибора составляет 600 В. Определите, какое напряжение можно измерять прибором без добавочного резистора R_д[СП, раздел 3.4, задача 3.4.16].

Задача 4.1

Определить, какими могут быть показания ваттметра электродинамической системы, подключенного в цепь постоянного тока к нагрузке, которая находится под напряжением 120В и в ней протекает ток 1А, если ваттметр имеет класс точности 0.5, выбраны пределы катушки токов 2.5А и катушки напряжения 150В [СП, раздел 3.4, задача 3.4.18].

Задача 4.2

Определить, какими могут быть показания ваттметра электродинамической системы, подключенного в цепь переменного тока к нагрузке, которая находится под напряжением 220В и в ней протекает ток 1А, если

ваттметр имеет класс точности 0.5, выбраны пределы катушки токов 2.5А, а

катушки напряжения 300В.

Известно, что между током и напряжением существует сдвиг по фазе

Задача 4.3

Размеры рамки механизма магнитоэлектрического милливольтметра на 75 мВ обозначены на рисунке 5.1.

Определите коэффициент успокоения Р и время успокоения t_yподвижной части механизма, если индукция в воздушном зазоре B=0,145 Тл, число витков рамки до ω=13,5, момент инерции подвижной части J=0,87*10 -7 кг*м 2 , удельный противодействующий момент W=65*10 -7 Н*м/рад, погрешность установки v=0,02, удельное электрическое сопротивление материала каркаса ρ = 0,03 Ом*мм 3 /м, активная площадь обмотки рамки s=3,2 см 2 , полное сопротивление цепи рамки Rcx=R0+Rbh=5 Ом. Размеры каркаса рамки: ширина с =4 мм; толщина

δ = 0,2 мм; средний периметр l=76 мм [СП, раздел 3.4, задача 3.4.11].

Задача 4.4

Определите коэффициент успокоения Р, степень успокоения β и время успокоения t_yмеханизма магнитоэлектрического милливольтметра на 5 мВ, если индукция в воздушном зазоре В =0,232 Тл, число витков рамки ω= 1200,5, момент инерции подвижной части J=0,05*10 -7 кг*м 2 , удельный противодействующий момент W=4,58*10 Н*м/рад, активная площадь обмотки рамки s=4 см 2 , погрешность установки v=0,02, полное сопротивление цепи рамки R_сх=10 5 Ом [СП, раздел 3.4, задача 3.4.11].

Ответ: 1,24*10-7 Н*м*с/рад; 1,3; 0,3 с.

Задача 4.5

Механизм магнитоэлектрического стрелочного гальванометра характеризуется следующими конструктивными параметрами: индукция в зазоре постоянного магнита В=0.25 Тл, активная площадь рамки s=1.66 см 2 , удельный противодействующий момент W=5.5*10 -7 Н*м/рад, число витков ω=1500.5, средняя длина витка рамки l=5.4 см, диаметр провода марки ПЭЛ 0.03 мм, момент инерции подвижной части J=0.45*10 -7 кг*м 2 , угол полного отклонения α_н=13°, что соответствует отклонению по шкале 20 делений; сопротивление одного метра провода, равно R’=24,6 Ом/м.

Определите: чувствительность механизма по току S_i в рад/А, дел/А, град/А; ток полного отклонения I_н; сопротивление обмотки рамки механизма; критическое сопротивление R_кр; постоянную по напряжению Си; период собственных колебаний подвижной части T_{[ СП, раздел 3.4, задача 3.4.12].}

Задача 4.6

Вычислите баллистическую постоянную механизма гальванометра М25/3 для значений β = 0,6; 1,0; 1,5; при разомкнутой цепи (T_{=7 с, С₁=0,85*10 -11 А*мм/м, ω_{=2π/T_{=0,89 рад/с.) [СП, раздел 3.4, задача 3.4.13].}}}

Задача 4.7

Оцените амплитуду колебаний стрелки механизма магнитоэлектрического миллиамперметра с пределом измерения 30 мА, шкала которого имеет 150 делений (а_н=150 дел.), при пропускании через его обмотку переменного тока частотой f=50 Гц, амплитудное значение которого равно I_m=30 мА. Известно, что момент инерции подвижной части механизма равен J=4,48*10 -7 кг*м 2 , а удельный противодействующий момент W=203*10 -7 Н*м/рад [СП, раздел 3.4, задача 3.4.14].

Задача 5.1

Вычислить время, в течение которого световой луч опишет фигуру Лиссажу – квадрат и вернется в исходное положение. Частота напряжения, подведенного к горизонтальным пластинам ЭЛТ, равна 1000 Гц [СП, раздел 3.5, формула 3.5].

Задача 5.2

Вычислить неизвестную частоту, поданную на вход Y, при которой световой луч опишет фигуру Лиссажу – наклонный отрезок прямой. Частота напряжения, подведенного к входу X равна 100 Гц [СП, раздел 3.5, формула 3.5].

Задача 5.3

Отрезок в одно деление по горизонтали в центре экрана переместили на край экрана, и отрезок уменьшился до величины, равной 0.9. Найти нелинейность амплитудной характеристики горизонтального канала [раздел 4.1.1, формула 4.2].

Задача 5.4

Описать устройство и принцип действия генератора:

Задача 5.5

Амплитудному значению исследуемого напряжения соответствует на экране осциллографа отрезок длиной 45мм. Для калибровки на вход Y осциллографа подано синусоидальное напряжение 10В.

Чему равна амплитуда исследуемого напряжения, если двойной амплитуде калибровочного напряжения соответствует отрезок длиной 50мм? [СП, раздел 3.5, формула 3.6].

Задача 5.6

Какова должна быть скорость развертки универсального моноблочного осциллографа для наблюдения прямоугольного импульса длительностью tи = 10нс и частотой следования f = 100 кГц по всей длине рабочей части экрана 36*60 мм [раздел 4.1.1, формула 4.14].

Задача 5.7

Какова скорость развертки осциллографа, если диапазон длительности развертки изменяется от 50 мс/дел до 0.2 мкс/дел (1 деление соответствует 6 мм) [раздел 4.1.1, формула 4.14].

Ответ: 0.12 м/с и 30 км/с

Задача 5.8

Описать устройство, принцип действия универсального моноблочного электронного осциллографа и методы измерения с его помощью [раздел 4.1.3, рисунок 4.3].

Задача 6.1

С помощью анализатора спектра исследуется тракт радиоприемника с полосой пропускания 10 кГц на частоте 7 МГц. Скорость изменения частоты характериографа выбрали равной 100 МГц/с ( = 0,64). Избирательная система содержит четыре слабо связанных контура. Вычислить погрешности измерений [СП, раздел 3.5, таблица 18].

Задача 6.2

Решить предыдущую задачу, если избирательная система состоит из двух критически связанных контуров. Расчетные соотношения можно взять из справочника [СП, раздел 3.5, таблица 18].

Задача 6.3

Используя теоретический материал [раздел 4.2, формулы (4.19 – 4.21)], вычислить разрешающую способность анализатора последовательного типа при добротности контура, равного номеру варианта. Полоса пропускания 10 кГц, частота 5 МГц, скорость изменения частоты характериографа считать очень медленной.

Задача 1. 1

Определить вероятность того, что погрешность превысит по абсолютному значению 12 мА [СП, раздел 3.4, задача 3.4.5].

Задача 1. 2

Задача 1.3

Задача 1.4

Погрешность результата измерения напряжения распределена по закону Симпсона в интервале от -1 до +3 мВ.

Ответ: 1 мВ; 0.58 мВ; 0.75 мВ.

Задача 1.5

Задача 1.6

Задача 1.7

Определить среднее квадратическое отклонение сопротивления Rx, если

Задача 1.8

Ответ: 0.20661 мкФ; 0.20512 мкФ; 6.3*10 4 мкФ.

Задача 1.9

Микроамперметр с входным сопротивлением 600 Ом включен последовательно нагрузке сопротивлением 1200 ОМ.

Вычислить погрешность влияния при данном измерении [СП, раздел 3.4, задача 3.4.10].

Задача 1.10

Определить по составному критерию, отвечает ли нормальному закону

Рассчитать среднеарифметическое значение напряжения,

Задача 1.11

Оценить вероятность того, что сопротивление отличается от своего математического ожидания не более чем на 1 Ом. Закон распределения погрешности неизвестен, среднее квадратическое отклонение s = 0,4 Ом [СП, раздел 3.4, задача 3.4.8].

Задача 1.12

где L – индуктивность мкГн;

Задача 2.1

Задача 2.2

Задача 2.3

Определить наибольшую разницу в показаниях двух миллиамперметров [СП, раздел 3.4, задача 3.4.2].

Задача 2.4

Задача 2.5

Задача 2.6

Задача 2.7

Задача 2.8

Задача 2.9

Задача 2.10

Задача 3.1

Задача 3.2

Задача 3.3

Задача 3.4

Ответ: 7.5*10 -3 Ом.

Задача 3.5

Ответ: 1.5 кОм; 1.5 Ом; 0.75 Ом; 0.075 Ом;

Задача 3.6

Задача 3.7

Рисунок 4.1- Пиковый детектор

Задача 3.8

Задача 3.9

Задача 3.10

Задача 3.11

Задача 3.12

Задача 3.13

Задача 3.14

Задача 3.15

Задача 4.1

Задача 4.2

ваттметр имеет класс точности 0.5, выбраны пределы катушки токов 2.5А, а

катушки напряжения 300В.

Известно, что между током и напряжением существует сдвиг по фазе

Задача 4.3

Размеры рамки механизма магнитоэлектрического милливольтметра на 75 мВ обозначены на рисунке 5.1.

δ = 0,2 мм; средний периметр l=76 мм [СП, раздел 3.4, задача 3.4.11].

Задача 4.4

Ответ: 1,24*10-7 Н*м*с/рад; 1,3; 0,3 с.

Задача 4.5

Задача 4.6

Задача 4.7

Задача 5.1

Задача 5.2

Задача 5.3

Задача 5.4

Описать устройство и принцип действия генератора:

Задача 5.5

Задача 5.6

Задача 5.7

Ответ: 0.12 м/с и 30 км/с

Задача 5.8

Задача 6.1

Задача 6.2

Задача 6.3

Как определить класс точности манометра

Что такое класс точности манометра, и как его определить

0,15;

0,25;

0,4;

0,6;

1,0;

1,5;

2,5;

4,0.

Определение погрешности

Классы точности для водомеров и теплосчетчиков

Выбирая приборы учета, потребитель должен обращать внимание не только на внешний вид устройства, его цену, размеры, но в первую очередь и на технические параметры счетчика, а также его совместимость с системой, с которой планируется его эксплуатация. Из многих технических параметров класс точности привлекает внимание покупателя, наверное, в последнюю очередь, что и логично, так как приборы с более высокой точностью имеют и более высокую цену. А в этом случае фактор цены играет существенную роль, так как от него зависит и период окупаемости счетчика. Но между тем, выбрав неправильно прибор учета по классу точности, потребитель может «наказать» как поставщика, так и самого себя, что малоприятно.

Что такое класс точности прибора учета

Любые счетчики, в том числе предназначенные для учета расхода теплоносителя, горячей и холодной воды относятся к сложным техническим устройствам. Их основная функция – это учет количества потребления ресурса за счет фиксирования и отображения его расхода. Также, в зависимости от модели, приборы учета позволяют архивировать и сохранять данные за определенный период времени.

Однако не все счетчики, предназначенные как для бытового (квартирного) учета, так и для коммунального, показывают одинаковую точность во время измерений, что позволяет легко классифицировать приборы по этому параметру и в соответствие с ним определять требования к устройствам, в зависимости от места их установки и способа эксплуатации. Как правило, для индивидуального учета допускается использовать приборы более низкого класса, а на промышленных или коммунальных объектах к этому критерию прибора требования строже.

Связано это с тем, что точность прибора учета определяется как максимально допустимая погрешность при измерениях и, соответственно, чем больше потребление, тем больше и будет искажение, если, например, устанавливается счетчик низшего класса. А в квартирном учете такая точность не столь принципиальна, так как водопотребление и расход теплоносителя можно считать незначительными.

Классы точности счетчиков воды

Разделение водомеров на классы точности определяется в соответствии с ГОСТ 50193.1-98. И в соответствии с ним существует 4 класса точности для водомеров: «A», «B», «C», «D», при этом повышение по классу идет от класса «A» вверх. Однако для бытовых приборов последний класс не используется (к приборам с наивысшей точностью относятся только промышленные устройства), так как для учета потребления, измеряемого в кубических метрах (м³) высокая точность не требуется.

У приборов, предназначенных для квартирного учета, имеющаяся погрешность вполне вписывается в допустимый диапазон. Поэтому у индивидуальных потребителей наибольшим спросом пользуются счетчики воды двух первых классов: «A» и «B». Приборы класса «C» также могут устанавливаться в квартирах для организации индивидуального учета, но в силу их более высокой цены, малопривлекательны для потребителя.

Но следует отметить, что перед установкой водомера требуется консультация с водопоставляющей организацией по вопросу требований к классу точности монтируемого прибора. Также следует учитывать, что некоторые из наиболее популярных моделей водосчетчиков класса точности «B» могут устанавливаться двумя способами: горизонтально и вертикально. Но в этом случае, при вертикальном монтаже прибор в один момент понижается в классе, то есть вместо точности класса «В» счетчик воды получает класс «А». О такой особенности и правилах монтажа производитель уведомляет потребителя и об этом всегда есть информация в инструкции к изделию. Такие метаморфозы происходят из-за того, что счетчики воды, как правило, рассчитаны на установку считывающим устройством вверх. А если меняется положение прибора с горизонтального на вертикальное (или угловое), то для работы устройства создаются определенные препятствия и сложности, что автоматически приводит к снижению (впрочем, незначительному) точности получаемых данных.

ЗАКАЗАТЬ УСЛУГУ У АККРЕДИТОВАННЫХ КОМПАНИЙ

Преимущества и недостатки счетчиков разных классов

Счетчики воды класса «С» являются наиболее точными приборами, однако, несмотря на это, не нашли широкого применения и практически не представлены бытовыми устройствами. Многие производители просто не занимаются изготовлением данной продукции. Причина банальна – более высокая стоимость изделий, что сказывается на окупаемости приборов и целесообразности их эксплуатации. Поэтому потребители и отдают предпочтение менее точным, но отлично справляющимся с квартирным учетом устройствам классов «A» и «B» с помощью которых можно легко определить расход в кубических метрах, а именно в них и определяется потребление воды в коммунальной сфере. Кроме того, следует обращать внимание и на другой фактор, а именно, на межповерочный период. Часто он совпадает у приборов разных классов. Поэтому нет смысла покупать и устанавливать более дорогой прибор, стоимость которого будет окупаться в течение значительно более продолжительного периода, для того чтобы через 4 года (максимум 6 лет) прийти к начальной точке. Справедливости следует отметить, что и между классами водомеров «A» и «B» тоже имеется своеобразная конкуренция и вторые выигрывают с заметным перевесом.

Более высокая цена на счетчики воды класса «C», в принципе, обоснованна, так как:

при их производстве используются различные инновационные решения как при конструировании самого прибора, так и при разработках принципа их работы;

использование новейших, более качественных материалов, что позволяет заложить больший запас прочности и надежности;

применение более эффективных мер для защиты прибора от магнитного воздействия, которое, как известно, способно искажать получаемые данные и т.д.

Для водопоставляющих компаний выгодно, если потребитель выбирает счетчик класса «C», так как такие приборы позволяют регистрировать даже незначительные расходы, что, естественно, сказывается на общем потреблении. Порог чувствительности у счетчиков класса «C» превышает аналогичный параметр приборов класса «B» в 10-15 раз (в зависимости от модели).

Как определяются классы точности счетчиков воды

Класс точности водомера измеряется пределом погрешности измерений, для определения которых важны следующие параметры устройства:

стартовый расход, обозначающий минимальное потребление воды, при котором происходит срабатывание счетчика или по-другому – это порог чувствительности прибора;

величина Q1, составляющая минимальный расход, при котором погрешность измерений колеблется в диапазоне от +/- 5%;

переходной расход, обозначаемый как Q2 и представляющий потребление воды, при котором погрешность находится в пределах от +/- 2%;

номинальный расход (Q3) с допускаемой погрешностью +/- 2%;

максимальный расход (Q4) – в этом случае погрешность не может превышать +/- 2%.

Также важен и параметр динамического диапазона, обозначаемого как «R», и представляющего собой соотношение между номинальным и минимальным расходом. Важно обратить внимание на то, что для каждого класса существуют свои предельные нормативы.

Имеет значение и Ду (диаметр условного прохода), особенно для объектов с повышенным водопотреблением. Если, например, в городской квартире расход небольшой, то в загородном доме с садом и газоном, которые требуют регулярного полива, а также с бассейном, баней и другими объектами, отличающимися высоким водопотреблением, расход будет иной. В этом случае устанавливается прибор учета с Ду от 25 мм и выше. При этом следует помнить, что порог чувствительности счетчика класса «C» с Ду 50 мм соответствует аналогичному параметру прибора класса «B», но с Ду 25 мм.

Классы точности счетчиков тепла

Теплосчетчики, как и другие приборы учета, также разделены на классы по критерию точности, но в отличие от водомеров, для них используется иная шкала. Классы счетчиков тепла обозначаются цифрами от 1 до 3, при этом высший класс точности – это первый. Критерием деления на классы для этих приборов выступает дифференцирование по наименьшей разности температур в трубах: подающей и обратной. Соответственно, самые высокие требования к счетчикам тепла, относящимся к классу «1» и минимальные – к приборам класса «3». Однако, при выборе счетчика для индивидуального учета требования весьма лояльны: устанавливать приборы первого класса нужно, если потребление теплоносителя от 100 м³/час.

Важно отметить, что деление теплосчетчиков на классы происходит в соответствии с нормами ГОСТ Р 51649-2014. В нем четко указываются максимально допустимые значения относительной погрешности для каждого из классов точности:

для класса «1» это показатель составляет ±1%, но не более, чем ±3,5%;

для класса «2» – ±2%, но не более, чем ±5%;

для класса «3» – ±3%, но не более, чем ±5%.

Требования к точности счетчиков тепла, устанавливаемых для квартирного и домового учета

Довольно высокие тарифы на теплоснабжение, а также тенденция к их постоянному росту заставляет как предприятия, генерирующие энергию, так и конечного потребителя обратить внимание на вопрос, связанный с организацией точного учета потребления этого ресурса. А справиться с такой задачей можно только с помощью приборов учета. Но и в этом случае имеются проблемы, связанные с выбором устройства. И вопрос здесь не только в цене или конкретной модели, существует также много технических требований, начиная от особенностей систем отопления и заканчивая классом точности прибора. Именно последний фактор важен во время введения счетчика в эксплуатацию, так как, установив прибор несоответствующего класса, поставщик ресурса имеет право не признавать его данные, определяя их как недостоверные.

Нормы ГОСТ «Теплосчетчики для водяных систем отопления» Р 51649-2014 были введены в 2015 году, в сентябре. В этом документе были учтены все правила и требования для учета тепловой энергии в коммерческих целях. Также приняты во внимание и международные нормы и рекомендации, в частности, MP 75:2002. В 2017 году начинают действовать и новые технические требования, предъявляемые к точности расходомеров.

В соответствии с этими нормами класс теплосчетчика определяется классом расходомера, но это правило актуально только для классов «1» и «2». При этом для жильцов, желающих установить в своей квартире прибор учета тепловой энергии, этот критерий классификации важен, так как именно устройства двух первых классов и рекомендованы для эксплуатации в квартирных условиях. Приборы третьего класса практически не устанавливаются, поэтому и фактически нет предложений от производителей.

При этом, выбирая прибор учета тепла, следует знать, что счетчики класса «1» устанавливаются на объектах с расходом теплоносителя от 100 м³/ч, а если этот показатель ниже, то вполне оптимальным решением станет монтаж устройства класса «2». Но нужно отметить, что потребление от 100 м³/ч в городской квартире является скорее исключением, чем нормой, поэтому для квартирного учета вполне подойдет прибор с точностью класса «2». А счетчики класса «1» могут использоваться в больших офисных центрах, небольших гостиницах и на других объектах социальной и общественной сфер, хотя, в основном, они предназначены для коммерческого учета на предприятиях, генерирующих тепловую энергию.

Точность и прецизионность | София Обучение

Ошибка относится к отсутствию точности, точности или того и другого. Систематические и грубые ошибки поддаются контролю, случайные ошибки — нет. Знание типа ошибки может привести к решению.

Систематическая ошибка возникает из-за плана эксперимента и влияет на результат в одном направлении, вверх или вниз.

Грубая ошибка возникает из-за необнаруженной ошибки, из-за которой результат измерения сильно отличается от среднего.Это измерение называется выбросом. Если это обнаруживается, это называется ошибкой или несчастным случаем, и эксперимент повторяется.

Случайная ошибка возникает от природы и влияет на результат в двух направлениях: вверх и вниз.

Давайте посмотрим, как они выглядят в ваших наборах данных.

Случайная ошибка

Эти результаты показывают разброс данных над и под линией. Поскольку данные расположены «повсюду» (низкая точность) или выше и ниже линии, они классифицируются как случайные.У ученых нет способа исправить случайную ошибку, поэтому мы говорим об этом как есть и сообщаем со стандартными отклонениями и значениями R ², которые взяты из стандартных отклонений. Точность снижается, но точность сохраняется.

Систематическая ошибка

На этом графике синей линией показана систематическая ошибка. Он постоянно находится над красной линией, указывая на то, что что-то не так. Когда эксперимент дает результат, который значительно выше или ниже измерения (низкая точность, высокая точность), требуется проверка на систематическую ошибку.Точность повреждена, точность нет.

Общая ошибка

Иногда в науке вы ошибаетесь. Такое случается. В большинстве случаев ученые замечают это, пожимают плечами и повторяют эксперимент. Иногда они не замечают, это называется грубейшей ошибкой. Похоже на этот график, если он всего один. Хорошие регулярные, несколько линейные данные, а затем исчезнет та единственная точка, которую вы хотите.

Если вы не заметили, что что-то пошло не так, было бы нечестно не записывать выброс.Объявить точку выбросом статистически сложно. Это должно быть 3 стандартных отклонения от того, что должно быть, и это высокая планка. Иногда ученые решают это, повторяя эту часть эксперимента и заменяя данные. Иногда они просто избавляются от этого. Эти повреждают точность и аккуратность.

Итак, может произойти три типа ошибок.

Систематический — все немного вверх или немного вниз

Случайно — все немного вверх и немного вниз

Gross — одна часть очень сильно вверх или очень сильно вниз.

Физика 9702 Сомнения | Страница справки 4

Вопрос 22:
[Радиоактивность]

(a) Образец радиоактивного изотопа содержит ядра N в момент времени t. Вовремя
(t + Δt), он содержит (N — ΔN) ядер изотопа. Для периода Δt, состояние, в
члены N, ΔN и Δt,

(i) Средняя активность образца

(ii) Вероятность распада ядра

(b) Источник кобальта-60 с периодом полураспада 5.27 лет откалибровано и
обнаружена активность 3,50 × 10 ⁵ Бк. Неопределенность калибровки
составляет ± 2%. Рассчитайте продолжительность времени в днях после калибровки для
заявленная активность 3,50 × 10 ⁵ Бк с максимально возможной погрешностью
10%.

Ссылка: Отчет о прошедшем экзамене — Отчет за июнь 2009 г., 9 квартал

Решение 22:

(а)

(i)

{Активность — это скорость
распад ИЛИ количество ядер, распадающихся за единицу времени}

Средняя активность образца = ΔN / Δt

(ii)

Вероятность распада ядра = ΔN
/ N

б)

{Калибровка
начальная активность A _o содержит погрешность 2%.

[Активность — это скорость
распад ИЛИ количество ядер, распадающихся в единицу времени] Активность
уменьшается со временем по мере распада источника. Итак, изменение активности с
время говорит нам о количестве ядер, распавшихся за это время .

Калибровка для деятельности
A в момент времени t содержит погрешность 10%. Итак, изменение активности ΔA (= A _o — A) соответствует увеличению погрешности на 10 —
2 = 8%. Как указывалось ранее, этот процент также говорит нам о количестве
распавшиеся ядра.Итак, источник должен быть разрушен на 8%}

Источник должен распасться на 8%

{Активность, A в момент времени t = A _o exp (-λt) и константа распада, λ = ln2 / T _½
где T _½ — период полураспада.}

Активность, A = A _o exp (-
(ln2) т / т _½) или
A / A _o = 1 / (2 ^{т / т})

{Для случая OR, описанного выше, —
(ln2) т / т _½ = ln 2 ^{-т / т ½}. Итак, exp (ln 2 ^{-t / T½}) =
2 ^{-т / T½} = 1 / (2 ^{-т / T½}).

Источник распался на
8%. Начальная активность (которая представляет собой начальное количество ядер в
источник) соответствует 100%. Следовательно, действие A (которое представляет
количество ядер в момент времени t), в момент времени t, соответствует 92%. A / A _o =
92/100 = 0,92}

0,92 = exp (- (ln2) t / 5,27) или 0,92 = 1 / (2 ^{t / 5,27})

Время, t = 0,634 года = 230 дней

Вопрос 23: [Электромагнетизм
> Закон Ленца]

Вам предоставлен моток проволоки,
стержневой магнит и чувствительный амперметр.Схема эксперимента по проверке закона Ленца.

Ссылка: Отчет о прошедшем экзамене — Отчет за июнь 2009 г. 4 Q7

Решение 23:

Катушка соединена последовательно с
измеритель [чувствительный амперметр — гальванометр] (не допускать включения ячейки). Известный полюс (магнита)
вставлен в катушку. Текущее направление
(не читает) наблюдается. (Индуцированное) поле / поле от катушки отталкивает
магнит.

ЛИБО сформулируйте правило для определения
направление магнитной катушки {Правая ручка
правило — скрученные пальцы указывают направление течения и большого пальца,
перпендикулярно согнутому пальцу показывает направление поля}
ИЛИ Изменение направления магнита приводит к противоположному отклонению счетчика.

(Закон Ленца 🙂 Направление
индуцированный ток (вызывает эффекты) такой, чтобы противодействовать изменению
производя это.

(Схема взята из
Интернет.Кредит принадлежит его первоначальному владельцу.)

Вопрос 24:
[Радиоактивный распад> Импульс]

Франций-208 радиоактивен и
испускает α-частицы с кинетической энергией 1,07 × 10 ^–12 Дж с образованием
ядра астата, как показано.

(а) Природа α-частицы:

(b) Покажите, что начальная скорость α-частицы после распада франция
ядро примерно 1,8 × 107 мс ^–1:

(в)

(i) Государственный принцип сохранения
количества движения:

(ii) Ядро франция-208 стационарно
до распада.Оценить скорость ядра астата сразу после распада:

(d) Тщательное изучение распада ядра франция показывает, что
Ядро астата и α-частица не выбрасываются точно в противоположных направлениях.
Предложите объяснение этому наблюдению:

Ссылка: Отчет о прошедшем экзамене — Отчет за 3 квартал 2006 г., ноябрь 2006 г.

Решение 24:

(а)

Α-частица — это ядро гелия ИЛИ
содержит 2 протона и 2 нейтрона

б)

{Масса α-частицы = 4 ед.1u = 1,66×10 ^-27 кг}

Кинетическая энергия α-частицы = ½ мв ²

½ [4 (1.66×10 ^-27)] v ²
= 1.07×10 ^-12

Начальная скорость α-частицы, v = 1.8×10 ⁷ мс ^-1

(в)

(i)

Принцип сохранения
линейный импульс утверждает, что сумма импульсов (в любом направлении) постоянна /
общий импульс постоянен в замкнутой системе / отсутствие внешней силы

(ii)

{Перед распадом
Ядро франция-209 неподвижно — скорость = 0 и, следовательно, импульс (= mv) = 0}

Импульс франция (= 0) =
импульс α-частицы + импульс астата

{импульс астата =
(-) импульс α-частицы}

204 (v) = 4 (1.8х10 ⁷)

Скорость ядра астата, v =
3,5×10 ⁵ мс ^-1

(г)

{Они не выбрасываются
точно в противоположных направлениях — это означает, что сумма импульсов не равна
постоянный. Итак, должна быть еще одна частица / фотон, которая будет учитывать
недостающий импульс}

Испускается другая частица / фотон
{одновременно} под углом к направлению
α-частица

Вопрос 25: [Волны
> Интерференция> Двойные щели]

(a) Укажите три условия, необходимые для формирования максимумов в
интерференционная картина, создаваемая двумя источниками микроволн.

(b) СВЧ-источник M излучает микроволны с частотой 12 ГГц. Покажи это
длина волны микроволн 0,025 м.

(c) Две прорези S ₁ и S ₂ расположены перед
микроволновый источник M описан в (b), как показано. Расстояния S ₁ O и S ₂ O
равны. СВЧ-детектор перенесен с О на П.

Расстояние S ₁ P составляет 0,75 м
а расстояние S ₂ P составляет 0,90 м. СВЧ-детектор дает максимальное считывание
у О.Изменение показаний микроволнового детектора при его медленном перемещении
по линии от О до П.

(d) Источник СВЧ M заменен на источник когерентного света. состояние
два изменения, которые необходимо внести в прорези на рис. 5.1, чтобы наблюдать интерференцию
шаблон.

Ссылка: Отчет о прошедшем экзамене — Отчет за июнь 2013 г., 5 квартал

Решение 25:

(а)

Выбирайте любой 3:

Волны должны перекрываться / встречаться /
наложить

Волны должны быть когерентными /
постоянная разность фаз (не постоянная λ или частота)

Разность хода = 0, λ, 2 λ ИЛИ разность фаз = 0, 2π, 4π

Y должен иметь то же направление
поляризации / неполяризованный

б)

Длина волны, λ = v / f

Частота, f = 12×10 ⁹ Гц

Длина волны, λ = (3×10 ⁸) / (12×10 ⁹) =
0.025м

(в)

{Максимумы образуются, когда
разность хода = n λ, где n = 0, 1, 2, 3,… В точке O максимумы соответствуют
n = 0. Разность хода между S ₁ P и S ₂ P = 0,90 —
0,75 = 0,15 м. Это соответствует n = 0,15 / 0,025 = 6. Следовательно, включая
максимумов в O, всего 7 максимумов от O до P [исключая максимумы в O
и P, между O и P есть 5 максимумов].

Минимумы находятся, когда путь
разница = 0.5λ,
1,5λ, 2,5λ,… то есть на полпути между 2
максимумы. Таким образом, между двумя последовательными максимумами существует минимум. Поскольку есть
всего 7 максимумов, найдено 6 минимумов между O и P.}

Есть максимум на P и несколько
минимумы или максимумы между O и P. Есть 5 максимумов / 6 минимумов между O и P
ИЛИ 7 максимумов / 6 минимумов, включая O и P.

(г)

Источник СВЧ M заменен на
источник когерентного света. Укажите два изменения, которые необходимо внести в прорези на рис.5.1 для наблюдения интерференционной картины:

Прорези необходимо сделать уже

Прорези необходимо закрыть
вместе

Вопрос 26:
[Электрическое поле> Напряженность электрического поля]

Две заряженные точки A и B являются
разделены расстоянием 6,0 см, как показано.

Вариация с расстоянием d от A
показана напряженность электрического поля E вдоль линии AB.

Электрон испускается с незначительной
скорость от A и едет по AB.

(a) Зависимость напряженности электрического поля E от потенциала V.

(b) Область под линией графика на фиг.8 представляет разность потенциалов.
между A и B. Используйте рис, чтобы определить разность потенциалов между A и B.

(c) Используйте ответ на (b), чтобы вычислить скорость электрона, когда он достигнет
пункт Б.

(г)

(i) Используйте рис, чтобы определить значение d
при котором электрон имеет максимальное ускорение.

(ii) Без дальнейшего
расчет, опишите изменение ускорения электрона с расстоянием d.

Ссылка: Отчет о прошедшем экзамене — Отчет за июнь 2007 г., 3 квартал

Решение 26:

(а)

Напряженность электрического поля равна
к отрицательному градиенту потенциала

{E = — V / d}

б)

Площадь под линией графика = 21.2
см ² ± 0,4 см ²

{По оси абсцисс (
ось положения), 10 квадратов представляют 2 см величины d. Но если мы измерим
с линейкой 1 см на миллиметровой бумаге соответствует 5 квадратам. Итак, 1 см (
длина, измеренная линейкой) по оси x представляет собой [(2/10) x 5 =] 1,0 см
количество d. В метре это 1,0 × 10 ^–2 м количества d.

Точно так же по оси Y
10 квадратов представляют 5кВм ^-1 величины E. Опять же, если мы измеряем
с линейкой 1 см на миллиметровой бумаге соответствует 5 квадратам.Итак, 1 см (
длина, измеренная линейкой) по оси ординат представляет [(5/10) x 5 =] 2,5 кВм ^-1
количества E.}

Из графика, 1,0 см ²
представляет ([1,0 × 10 ^–2] × [2,5 × 10 ³] =) 25 В

Лучший класс точности амперметра — отличные предложения по классу точности амперметра от глобальных продавцов класса точности амперметра

Отличные новости !!! Вы попали в нужное место по классу точности амперметра.К настоящему времени вы уже знаете, что что бы вы ни искали, вы обязательно найдете это на AliExpress. У нас буквально тысячи отличных продуктов во всех товарных категориях. Ищете ли вы товары высокого класса или дешевые и недорогие оптовые закупки, мы гарантируем, что он есть на AliExpress.

Вы найдете официальные магазины торговых марок наряду с небольшими независимыми продавцами со скидками, каждый из которых предлагает быструю доставку и надежные, а также удобные и безопасные способы оплаты, независимо от того, сколько вы решите потратить.

AliExpress никогда не уступит по выбору, качеству и цене. Каждый день вы будете находить новые онлайн-предложения, скидки в магазинах и возможность сэкономить еще больше, собирая купоны. Но вам, возможно, придется действовать быстро, поскольку этот высший класс точности амперметра вскоре станет одним из самых востребованных бестселлеров. Подумайте, как вам будут завидовать друзья, когда вы скажете им, что получили свой класс точности амперметра на AliExpress.Благодаря самым низким ценам в Интернете, дешевым тарифам на доставку и возможности получения на месте вы можете еще больше сэкономить.

Если вы все еще не уверены в классе точности амперметра и думаете о выборе аналогичного продукта, AliExpress — отличное место для сравнения цен и продавцов. Мы поможем вам решить, стоит ли доплачивать за высококлассную версию или вы получаете столь же выгодную сделку, приобретая более дешевую вещь.А если вы просто хотите побаловать себя и потратиться на самую дорогую версию, AliExpress всегда позаботится о том, чтобы вы могли получить лучшую цену за свои деньги, даже сообщая вам, когда вам будет лучше дождаться начала рекламной акции. и ожидаемая экономия.AliExpress гордится тем, что у вас всегда есть осознанный выбор при покупке в одном из сотен магазинов и продавцов на нашей платформе. Реальные покупатели оценивают качество обслуживания, цену и качество каждого магазина и продавца.Кроме того, вы можете узнать рейтинги магазина или отдельных продавцов, а также сравнить цены, доставку и скидки на один и тот же продукт, прочитав комментарии и отзывы, оставленные пользователями. Каждая покупка имеет звездный рейтинг и часто имеет комментарии, оставленные предыдущими клиентами, описывающими их опыт транзакций, поэтому вы можете покупать с уверенностью каждый раз. Короче говоря, вам не нужно верить нам на слово — просто слушайте миллионы наших довольных клиентов.

А если вы новичок на AliExpress, мы откроем вам секрет.Непосредственно перед тем, как вы нажмете «купить сейчас» в процессе транзакции, найдите время, чтобы проверить купоны — и вы сэкономите еще больше. Вы можете найти купоны магазина, купоны AliExpress или собирать купоны каждый день, играя в игры в приложении AliExpress. Вместе с бесплатной доставкой, которую предлагают большинство продавцов на нашем сайте, вы сможете приобрести амперметр класса точности по самой выгодной цене.

У нас всегда есть новейшие технологии, новейшие тенденции и самые обсуждаемые лейблы.На AliExpress отличное качество, цена и сервис всегда в стандартной комплектации. Начните самый лучший шоппинг прямо здесь.

Точность и точность

Они означают несколько разные вещи!

Точность

Точность — это насколько близко измеренное значение к фактическому (истинному) значению .

точность

Точность — это насколько близки измеренные значения друг к другу .

Примеры

Вот пример нескольких значений в числовой строке:

И пример на Target:


Высокая точность Низкая точность	Низкая точность Высокая точность	Высокая точность Высокая точность

Пример: попадание в столб

Если вы играете в футбол и всегда попадаете в правильную стойку ворот, вместо того, чтобы забивать, тогда ваша точность , а не , но , точность !

Как помнить?

a C curate is C orrect (яблочко).
p R ecise R epeating (попадание в ту же точку, но, возможно, не в правильную)

Смещение (не позволяйте точности вводить вас в заблуждение!)

Когда мы что-то измеряем несколько раз и все значения близки, они могут быть ошибочными, если есть « Bias »

Смещение — это систематическая (встроенная) ошибка, из-за которой все измерения ошибочны на определенную величину.

Примеры смещения

Когда на весах ничего нет, на весах «1 кг»
Вы всегда измеряете свой рост в обуви на толстой подошве.
Секундомер, который останавливается за полсекунды при нажатии

В каждом случае все измерения ошибочны на одинаковую величину. Это предвзятость.

Степень точности

Степень точности зависит от прибора, которым мы измеряем. Но как правило:

Степень точности составляет половинной единицы с каждой стороны единицы измерения.

Примеры:

Когда прибор измеряет в «1» с , любое значение между 6½ и 7½ измеряется как «7»
Когда прибор измеряет за «2» с , любое значение от 7 до 9 измеряется как «8»

(Обратите внимание, что стрелка указывает на одно и то же место, но измеренные значения отличаются!
Подробнее см. Ошибки измерения.)

Мы должны показать окончательные значения, которые соответствуют точности наших наименьших используемых точных значений.

Пример: Нам сказали, что собака ростом около 2 футов.

Мы можем преобразовать это в 609,6 мм, но это предполагает, что мы знаем высоту с точностью до 0,1 мм!

Итак, мы должны использовать 600 мм

Как определить степени ненасыщенности молекулы

Образование
Наука
Химия
Как определить степени ненасыщенности молекулы

Число степеней ненасыщенности по Артуру Винтер

в молекуле полезно, потому что это число связано с тем, сколько кратных связей или колец присутствует в неизвестном соединении.(Этот кусочек информации становится очень полезным, когда вы хотите определить структуру неизвестного соединения.)

Степени ненасыщенности в молекуле являются аддитивными — молекула с одной двойной связью имеет одну степень ненасыщенности, молекула с двумя двойными связями имеет две степени ненасыщенности и так далее. Так же, как образование двойной связи вызывает потерю двух атомов водорода, образование кольца также приводит к потере двух атомов водорода, поэтому каждое кольцо в молекуле также добавляет одну степень ненасыщенности.Для каждой тройной связи к молекуле добавляются две степени ненасыщенности, потому что молекула должна потерять четыре атома водорода, чтобы образовалась тройная связь. Здесь показаны некоторые примеры трехуглеродных молекул с различным числом степеней ненасыщенности.

Степени ненасыщенности трехуглеродных молекул.

Чтобы определить количество степеней ненасыщенности для любой произвольной структуры, вы суммируете все отдельные элементы ненасыщенности в молекуле. На следующем рисунке показана молекула, состоящая из одного кольца, одной двойной связи и одной тройной связи.Таким образом, эта молекула имеет четыре степени ненасыщенности, потому что двойная связь и кольцо добавляют по одной степени ненасыщенности, а тройная связь добавляет две степени, всего четыре.

Молекула с четырьмя степенями ненасыщенности.

Более важным, чем определение количества степеней ненасыщенности по молекулярной структуре, является возможность определить количество степеней ненасыщенности по молекулярной формуле. Число степеней ненасыщенности можно определить по молекулярной формуле с использованием следующего уравнения.

С помощью этого уравнения можно определить количество степеней ненасыщенности для любого углеводорода, молекулярная формула которого известна. (Для соединений, структура и формула которых неизвестны, химики используют инструментальный метод, называемый масс-спектрометрией , , чтобы определить молекулярную формулу соединения.)

Но как насчет молекул, содержащих атомы, отличные от водорода и углерода? В таких случаях вам необходимо преобразовать эти многоатомные молекулярные формулы в эквивалентные формулы, содержащие только углерод и водород, чтобы их можно было вставить в предыдущее уравнение.Для этого используются следующие коэффициенты пересчета:

Галогены (F, Cl, Br, I): Добавьте один водород в молекулярную формулу для каждого присутствующего галогена.
Азот: Вычтите один водород для каждого присутствующего азота.
Кислород или сера: Игнорировать.

Например, чтобы определить количество степеней ненасыщенности в формуле C ₈ H ₆ F ₃ NO ₂, вы сначала сделаете правильные замены для всех атомов, которые не являются водородом и углеродом.Фтор — это галоген, поэтому вы добавляете три атома водорода к молекулярной формуле (по одному на каждый F). Молекула содержит один азот, поэтому вы вычитаете один водород из молекулярной формулы. Два атома кислорода в молекуле, которые вы игнорируете. Это дает сокращенное уравнение C ₈ H _{6 + 3–1} = C ₈ H ₈. Другими словами, обе формулы C ₈ H ₆ F ₃ NO ₂ и формула C ₈ H ₈ имеют одинаковое количество степеней ненасыщенности.Подстановка этой сокращенной формулы в предыдущее уравнение дает пять степеней ненасыщенности для молекулярной формулы C ₈ H ₆ F ₃ NO ₂.

Как измерить точность цветопередачи и использовать измерения Delta-E

Подавляющее большинство людей чрезвычайно чувствительно к различиям и несоответствиям в цвете. Интуитивно мы можем чувствовать, когда цвет «выключен». Однако когда дело доходит до научного оборудования и цветных датчиков, таких как Nix Pro и Nix Mini, возникает необходимость определять точность математическими терминами.

Цвет «Координаты»

Цвет можно точно описать в нескольких различных системах координат, таких как XYZ, RGB, CYMK или L * a * b *. В этих системах переменным, таким как L *, a * и b *, присваиваются разные значения.

Источник: w-enter.com

В частности, систему L * a * b * можно представить в виде сферы, содержащей сотни тысяч различных цветов. У каждого цвета есть своя уникальная точка в сфере.

Измерение «Дельта-Е»

Чтобы вычислить разницу между двумя цветами в системе L * a * b *, все, что вам нужно сделать, это вычислить расстояние между их соответствующими точками на сфере.С математической точки зрения, это по сути тригонометрия (вот статья в Википедии для ботаников).

Источник: https://pengantar-warna.blogspot.ca/

Расстояние между двумя цветами известно как Delta-E и является отраслевым стандартом, за которым наблюдает Международная комиссия по освещению. С практической точки зрения, средний человеческий глаз не может обнаружить какие-либо цветовые различия со значением Delta-E 3 или меньше , а исключительно тренированный и чувствительный человеческий глаз сможет воспринимать цветовые различия только с Delta-E, равным 1. или выше.

Как это на самом деле выглядит?

Чтобы дать вам представление о том, как разные значения Delta-E на самом деле проявляются в реальной жизни, мы создали следующие наборы цветовых образцов. Обратите внимание, что качество вашего монитора или смартфона может повлиять на вашу способность правильно воспринимать эти цвета.

Дельта-E: 12,78

На Delta-E такого большого размера два цвета явно отличаются друг от друга.

Дельта-E: 5,65

Даже при относительно большом Delta-E, равном 5.65, эти два образца цвета не сильно отличаются друг от друга.

Дельта-E: 3,31

Значение Delta-E, равное примерно 3, представляет собой предел восприятия большинства людей. Возможно, потребуется второй взгляд, чтобы понять, что это два разных цвета.

Дельта-E: 1.06

Обычному человеку эти два цвета кажутся одинаковыми. Только несколько человек, читающих это, смогут заметить разницу.

Определение цвета с помощью устройств Nix

Датчик цвета Nix Pro может сравнивать образцы цветов для определения разницы Delta-E двух цветов.Его можно использовать для подтверждения выбора или вывода цвета, пробных отпечатков и промышленных процессов, чтобы обеспечить точность цветопередачи быстро, дешево и эффективно.

С датчиком цвета Nix QC вы получите доступ ко всем инструментам, необходимым для оптимизации контроля качества цвета и уверенного достижения согласованности цвета во всех аспектах вашего бизнеса.