Коэффициент мощности как найти: Формула расчета коэффициента использования производственных мощностей

Формула расчета коэффициента использования производственных мощностей

Одним из ведущих показателей, характеризующих работу предприятия, является коэффициент использования производственной мощности. Лицам, участвующим в организации трудового процесса, необходимо знать, что описывает этот параметр, и как определяется его значение.

Коэффициент предоставляет информацию, полезную для оптимизации производственного процесса

Определение коэффициента

Данный коэффициент показывает то, насколько производственное оборудование используется на практике, по сравнению с показателем, достигаемым при максимально возможной нагрузке на линии. Он является одним из индикаторов производительности фирмы и дает возможность оценить эффективность используемых технологий и методов работы, выявить проблемы с рациональной эксплуатацией машин. Это поспособствует лучшему выстраиванию производственного процесса и оптимизации использования оборудования.

Важно! Коэффициент может использоваться не только для оценки работы фабрики, участка цеха или иного промышленного предприятия, но и для фирмы, занимающейся торговлей или оказывающей услуги населению. Так определяют, насколько производительны коллектив и используемые технические средства.

Метод сбора информации

Первое время данные для расчета реальной и потенциальной мощностных величин собираются ручным методом и заносятся в специально подготовленную отчетность. Когда значение второй из упомянутых величин будет установлено, последующие вычисления можно автоматизировать, базируясь на имеющихся данных и трендах.

Формула расчета

Основная формула, применяемая для вычисления коэффициента, имеет такой вид:

К = Vфакт/Мср,

где:

• Vфакт – объем изготовленной за определенное время продукции,
• Мср – средняя производственная мощность за тот же временной период.

Формула нахождения коэффициента использования мощности

Формула производственной мощности, используемая в вычислениях, рассчитывается с применением прироста и выбытия на балансе предприятия за прошедший период (как правило, годовых). Мощность определенного вида оборудования может вычисляться двумя способами: с использованием трудоемкости единицы производимой продукции или производительности одного экземпляра техники.

Формулы производственной мощности

Целевые значения

В качестве ориентира можно использовать значение 80% – средний показатель для фирм Соединенных Штатов. В Европе он несколько выше – 82%.

Особенности измерения

Данные, используемые для будущих вычислений, собираются каждый рабочий день ручным способом. При наличии возможности организуется автоматическая фиксация данных – это поможет тратить меньше временных и трудовых ресурсов для нахождения реального показателя загруженности. Потенциальный показатель считают для определенного временного периода и затем подставляют в формулу.

Важно! Итоговый коэффициент можно определить как для единичной машины или линии, так и для цехового помещения или предприятия в целом. Так что для разных масштабов данные фиксируются с разной периодичностью: статистику по отдельному станку собирают несколько раз в день (например, раз в час), а для всей фирмы ее высчитывают за более длинный период: месячный, сезонный или годовой.

Норматив и толкование значения

Рассматриваемый показатель не имеет четких фиксированных нормативных рамок. Для разных категорий фирм границы целевого диапазона будут различны, особенно в применении к человеческим ресурсам. Тем не менее, получившаяся цифра может указывать следующее:

1. Если результат ниже 0,7, технологические процессы организованы нерационально, и есть необходимость в изменении стратегий работы (опционально также в добавочных производственных мощностях).
2. При более высоком значении эффективность работы можно повысить внутренними силами предприятия.
3. Если коэффициент равен единице (стопроцентная загруженность), принадлежащие фирме ресурсы используются максимально. Если есть цель производить еще больше продукции, потребуется приобретение дополнительных единиц техники. Превышать показатель в 100% коэффициент не может.

Важно! На итоговую цифру может оказывать влияние ряд сторонних факторов: внезапное изменение ситуации на фирме или в ее окружении, компании-конкуренты, изменение спроса.

Пример расчета

Составить представление о методике можно, например, на основе показателей работы завода, производящего пеллеты. Для каждого из используемых типов оборудования (мельницы разного назначения, барабан для сушки, аппарат для формирования гранул и т.д.) фиксируют планируемый и реальный объем перерабатываемого сырья в кубических метрах и на их основе считают коэффициент. Можно разделить месяц на три декады и сформировать статистику за каждую из них и за месяц в целом.

К примеру, наиболее производительной из используемых машин оказался барабан. Тогда значение коэффициента у него будет выше всего. Если требуется повысить производительность других типов станков, их нужно нагружать интенсивнее. Чем больше коэффициент у конкретного станка, тем большую нагрузку относительно своего потенциала он несет. 80-85% является хорошим показателем, но даже в этом случае допускается стремление к повышению ввиду наличия 15-20% запасной мощности.

Практическое применение КИМ

Вычисление показателя для единичного станка или машины дает возможность узнать следующие данные:

• есть ли эпизоды простаивания в рабочем процессе, и чем они обусловлены;
• насколько востребован данный экземпляр оборудования, и как часто он используется;
• за какую часть приносимой прибыли ответственен станок;
• можно ли эксплуатировать единицу техники более эффективно, стоит ли ее модернизировать.

Определение коэффициента для организации в целом сможет показать:

• насколько можно увеличить объем производимой продукции или оказываемых услуг;
• эффективно ли эксплуатируется установленное оборудование;
• насколько загружены производственные линии;
• в каких границах может расти себестоимость продуктов (при низком коэффициенте возможен рост объема продукции, сопряженный с увеличением себестоимости единичного экземпляра).

Чтобы определить потенциал увеличения объема производства, нужно узнать значение разрыва (обозначим его Р) между возможным и реальным количеством производимой продукции. Оно вычисляется по формуле:

Р = (РОП-ПОП)/ПОП * 100%,

где РОП – реальный объем производства, а ПОП – потенциальный.

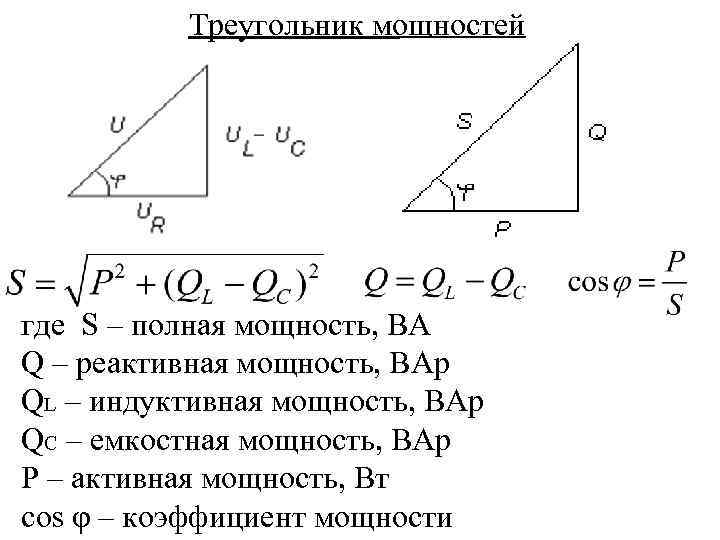
Коэффициент использования мощности

Коэффициент, обозначаемый как cos φ, показывает долю наибольшей возможной мощности, обеспечиваемую переменным электротоком вследствие задерживания напряжения. Он равен косинусу угла смещения этих двух величин. Диапазон возможных значений показателя находится между нулем и единицей. У полностью емкостных (конденсаторные элементы) или индуктивных (трансформаторы и другие устройства с катушками) контуров рассматриваемый угол будет прямым, соответственно, его косинус равен 0. При этом для элементов первого типа ток опережает напряжение, для второго – наоборот. У абсолютно резистивных цепочек электроток идет в фазе с прилагаемым напряжением, угол равен 0, а его косинус – 1. При фиксированном мощностном показателе и не меняющемся напряжении токовая сила будет уменьшаться с увеличением cos φ.

Проблемы низкого cos φ

Важность данного показателя обусловлена его ответственностью за поддержание индуктивной нагруженности. Когда коэффициент слишком низок, проблема может корениться в искажении формы электротока или большой разнице фаз между ним и напряжением на нагрузочных зажимах. Идеальным является значение коэффициента, равное единице, определенно недостаточным – ниже 0,8. При низких значениях соответствующий процент мощности (для 0,8 это 20%) сохраняется в системе, что может нанести вред генератору или двигателю (в частности, подшипниковым элементам). Также это накладывает дополнительную нагрузку на провода, от них требуется большая толщина. Необходимость выдерживать больший ток приводит к снижению общей эффективности из-за увеличения потерь тепла.

Решение проблемы низкого cos φ

Чаще всего для этой цели применяется установка коммутируемой группы конденсаторных элементов параллельно электроцепи. Можно задать автоматическое включение и выключение блока с опорой на значения разных показателей системы. Чаще конденсаторы ставят в первичной электросети силовой подстанции.

Коррекция низкого коэффициента осуществляется через использование конденсаторов

Планирование потребности в производственных мощностях (CRP)

Использование данных систем преследует цель повысить эффективность работы оборудования, команд сотрудников, конвейерных линий.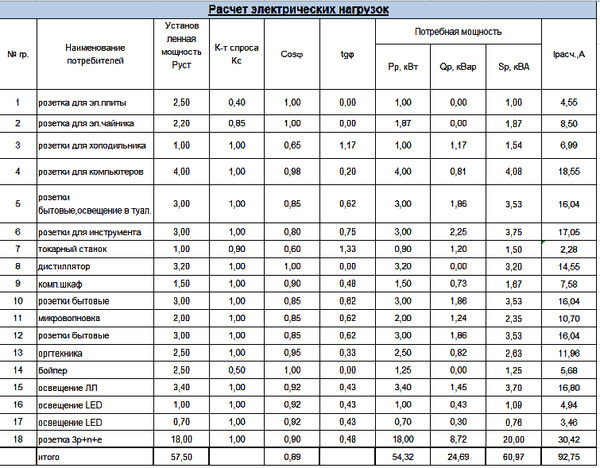 Суть состоит в планировании и нахождении баланса загруженности для реализации плана по выпуску конечного продукта. Планировать необходимые объемы мощностей нужно для каждого типа производимой продукции с учетом структуры технологического процесса. Система генерирует отчет о расхождениях между необходимой загрузкой и представленными в наличии мощностями.

Планирование потребности в производственных мощностях

Коэффициент использования мощности – важный параметр, помогающий определить, какими возможностями для повышения эффективности обладает предприятие, отдельная производственная линия или единица оборудования. Проведение расчетов с его использованием поможет оптимизировать производство, выявить, какие оборудование и технологические процессы нуждаются в модернизации или замене.

Видео

Коэффициент мощности

Коэффициент мощности (Power Factor) – комплексный показатель, характеризующий потери энергии в электросети,
обусловленные фазовыми и нелинейными искажениями тока и напряжения в нагрузке,
численно равный отношению активной мощности P нагрузки к её полной мощности S.

Реактивная составляющая

Наиболее значимую часть потерь в сети создают реактивные элементы
по причине своей физической способности накапливать и возвращать неиспользованную энергию обратно в источник.
Реактивная составляющая тока нагрузок не осуществляет полезной работы,
но остаётся в виде падения напряжения на активном сопротивлении всех участков сети энергосистемы,
попросту разогревая провода ЛЭП, кабели и трансформаторы подстанций.

В этом случае, если не рассматривать другие потери,
коэффициент мощности будет равен косинусу угла сдвига фаз между током и напряжением в нагрузке.

PF = P/S = cosφ

PF — Power Factor — Коэффициент Мощности (КМ).
P — Потребляемая (полезная, активная) мощность. P=UIcosφ.
S — Полная мощность. S = UI.
φ — Угол сдвига фаз между током и напряжением, созданный реактивными элементами нагрузок (обмотки электродвигателей,
трансформаторов, электромагнитов . ..)
Подробнее об этом на страничке реактивная мощность.

В целях устранения реактивных потерь на производственных предприятиях используют специальные конденсаторные установки,
компенсируя положительный сдвиг фаз, созданный индуктивными нагрузками.
На начальном этапе компенсация фазового сдвига, внесённого суммарно всеми потребителями сети, осуществляется на электростанциях путём контроля подмагничивания роторных обмоток генераторов.

Гармонические искажения

В настоящее время большая часть бытовой техники является для электросети нелинейной нагрузкой.
Телевизоры, компьютеры, мониторы, муз. центры, адаптеры, зарядные устройства, энергосберегающие лампочки и многие другие бытовые приборы
имеют выпрямитель или импульсный блок питания, искажающий форму тока.
В результате, дополнительно к основной частоте 50 гц, в сети появляются высшие кратные гармоники — 100 гц, 150 гц, 200 гц, 250 гц и.т.д…
Высшие гармоники тока на активной нагрузке выделяют активную мощность, но энергетически не связаны с источником (генератором)
и являются потерями для энергосистемы.
Мощность высших гармоник, как и реактивная, будет рассеиваться на активном сопротивлении проводов, кабелей,
трансформаторов и линий электропередач в виде тепла и других негативных явлений в силовых установках сети (паразитный резонанс, вихревые токи и.т.д…).
Коэффициент мощности для нелинейных нагрузок определится из коэффициента гармоник соотношением:

DPF (Distortion Power Factor) — это тот же PF, но только для гармонических искажений, без учёта сдвига фаз.

THD (Total Harmonic Distortion) — коэффициент гармоник,
равный отношению суммы квадратов тока или напряжения высших гармоник к квадрату тока (напряжения) основной гармоники.

В этом случае коэффициент мощности можно выразить, как отношение действующего значения тока основной гармоники
к действующему значению тока в нагрузке.

Многие бытовые потребители снабжены симисторным регулятором мощности,
который не только вносит гармонические искажения тока, но и сдвигает фазу основной гармоники тока, что приводит к дополнительным (фазовым) потерям.
То есть, в таких случаях, коэффициент мощности определится не только коэффициентом искажений, но и сдвигом фазы основной гармоники.

Здесь cosφ₁ — косинус угла сдвига фазы тока основной (первой) гармоники относительно напряжения сети.

Современные пылесосы и стиральные машины с симисторными регуляторами оборотов вносят весь комплекс искажений тока по причине наличия электродвигателя,
как реактивной составляющей в нагрузке.
Тогда угол сдвига фаз для основной гармоники в расчётах увеличится с учётом общего сдвига тока индуктивностями обмоток двигателя.

Более существенные гармонические искажения в электросети возникают при использовании мощных сварочных преобразователей — инверторов,
которые могут искажать не только форму тока, но и напряжения в сети.
А это внесёт дополнительные потери мощности для всех других потребителей этой сети.

В общем случае для любых нагрузок, независимо от степени искажений и угла сдвига фаз, коэффициент мощности PF можно определить, как соотношение P/S,
вычислив активную P и полную S мощности интегрированием тока и напряжения во времени,
которое способны произвести современные цифровые измерительные приборы на основе микроконтроллеров.

Потребляемая (активная) мощность P — это среднее значение мощности в нагрузке за период,
т.е среднеарифметическое всех мгновенных значений UI.
Полная мощность — это произведение среднеквадратичных значений напряжения сети и тока нагрузки.
Тогда коэффициент мощности вычисляется следующим образом:

В целях компенсации гармонических искажений, в электрические потребители, содержащие нелинейные элементы в силовых цепях,
устанавливают специальные Корректоры Коэффициента Мощности (ККМ) — Power Factor Correction (PFC),
которые могут быть как пассивными (фильтры L или LC), так и активными.
Активные PFC — это преобразователи, способные приблизить форму тока в нагрузке к синусоидальной,
тем самым устранив (по возможности) высшие гармоники из общего спектра колебаний тока.

В качестве ознакомления можно посмотреть пример использования вышеописанных расчётных формул для варианта с симисторным управлением активной нагрузкой
по ссылке ограничение мощности симистором.

Другие полезные статьи:
Закон Ома.
Дизель-генератор.

Замечания и предложения принимаются и приветствуются!

Формула коэффициента мощности: косинус фи для потребителей, единица измерения

Мощность в цепи переменного тока и коэффициент мощности (косинус φ) В профессиональном лексиконе электрика наиболее популярны слова: фаза, ток, напряжение и словосочетание «косинус-фи». Этот «косинус-фи» всегда головная боль заводского энергетика.

Попробуем популярно объяснить причину такого уважения электриков к тригонометрической функции cos φ. «Косинус-фи» в электроэнергетике еще называют коэффициентом мощности.

Коэффициент мощности характеризует потребителя электрической энергии с точки зрения наличия в нагрузке реактивной составляющей, при которой переменный ток и напряжение не совпадают по фазе.

Коэффициент мощности показывает, насколько переменный ток в нагрузке сдвигается по фазе относительно напряжения на ней (отстает или опережает). Численно коэффициент мощности равен косинусу этого фазового сдвига.

В электроэнергетике для коэффициента мощности принято обозначение cos φ (где φ — угол сдвига по фазе между током и напряжением). При наличии в нагрузке реактивной составляющей наряду со значением коэффициента мощности часто указывают и характер нагрузки: активно-ёмкостная или активно-индуктивная. Тогда коэффициент мощности называют соответственно опережающим или отстающим.

Мощность в цепи переменного тока

Для начала следует подробно рассмотреть вопрос электрической мощности. В электрической цепи постоянного тока все просто и достаточно понятно. В такой цепи зная напряжение на зажимах потребителя и протекающий ток можем легко определить потребляемую мощность, умножив величину тока на напряжение: В цепи переменного тока формулы для расчета мощности и само понятие мощности несколько сложнее. В общем случае в электрической цепи синусоидального переменного тока изменение напряжения и тока во времени не совпадают. Или другими словами напряжение и ток не совпадают по фазе. Ток отстает по фазе от напряжения при индуктивной нагрузке, и опережает напряжение при емкостной нагрузке. Только в частном случае, когда нагрузка чисто активная, ток и напряжение совпадает по фазе. В сети переменного тока различают полную, активную и реактивную мощность. Отметим, что само понятие реактивной мощности актуально только для электротехнических устройств переменного тока. Оно никогда не применяется к потребителям постоянного тока в силу малости (мизерности) соответствующих эффектов, проявляющихся кратковременно только при переходных процессах (включении/выключении, регулирование, изменение нагрузки). Полная мощность в цепи переменного тока (для однофазной нагрузки) равна произведению действующего значения тока на действующее значение напряжения (измеряется в ВА , кВА – вольт-амперах, кило вольт-амперах) Полная мощность представляет практический интерес, как величина, определяющая фактические электрические нагрузки на обмотки, провода, кабели, аппаратуру распределительных щитов, силовые трансформаторы, линии электропередач. Собственно поэтому номинальная мощность генераторов и трансформаторов, нагрузки аппаратов распределительных щитов и пропускная способность линий электропередач указывается в вольт-амперах, а не в ваттах. Полная мощность состоит из двух составляющих – активной Р, и реактивной Q мощности. Активная мощность это та часть электрической энергии выработанной генератором, которая безвозвратно преобразуется в тепловую (лампы накаливания, электроплиты, электропечи сопротивления, потери в трансформаторах и линиях электропередачи) или в механическую (электрические двигатели) энергию. Активная мощность измеряется в Вт, кВт (ватт, киловатт). Активную мощность можно определить по следующей формуле (для однофазной нагрузки): Вот здесь и появляется знаменитый cos φ Если ток совпадает по фазе с приложенным напряжением то угол φ = 0, и соответственно cos φ =1. Для электрической сети это оптимальный вариант. В этом случае полная мощность равна активной мощности и вся электрическая энергия в нагрузке превращается в другие виды энергии. Например, в электрочайнике – в тепловую энергию. Чаще потребители электрической энергии имеют обмотки и магнитопроводы (электрические двигатели, трансформаторы, дроссели газорязрядных ламп, пускатели и реле) необходимые для их нормальной работы. В общем случае такая нагрузка называется индуктивной. При чисто индуктивной нагрузке ток отстает от напряжения на угол φ = 90О , при котором cos φ = 0 и активная мощность также P = 0. Для характеристики таких потребителей в электротехнике введено понятие реактивной мощности: Реактивная мощность измеряется в Вар, кВАр (вольт-амперах реактивных, кило вольт-амперах реактивных). Кстати, реактивную мощность можно измерить с помощью счетчика реактивной энергии, также как и активную счетчиком активной энергии. Названа мощность реактивной совсем не по аналогии с «ракетой»!!. Мы помним, что в физике термин «реактивный» обычно употребляется как связанный с возникновением движения под действием силы отдачи струи пара, газа и т. п., вытекающей с большой скоростью в противоположную силе отдачи сторону. В электротехнике это элемент электрической цепи, обладающий индуктивностью и/или электрической ёмкостью, и термин реактивный употребляется для характеристики элемента электрической цепи, обладающего этими свойствами. Источниками реактивной мощности в сети переменного тока являются катушки индуктивности и конденсаторы. Физически реактивная мощность, это мощность, которая накапливается в электрических и магнитных полях. При наличии в сети индуктивности и, например, статического конденсатора электромагнитная энергия в один полупериод изменения тока накапливается в электромагнитном поле катушки индуктивности, в следующий полупериод возвращается конденсатору, где накапливается в его электрическом поле, а затем возвращается обратно к индуктивности. Следует понимать, что реактивная мощность не расходуется на выполнение работы электротехнического устройства (нагрев, выполнение механической работы) но она необходима для его нормальной работы. Так в трансформаторе электрическая энергия передается с первичной обмотки во вторичную цепь посредством электромагнитного поля, для создания которого и необходима реактивная мощность. Преобразование электрической энергии в асинхронном электродвигателе осуществляется с помощь того же электромагнитного поля, и снова для его создания также требуется источник реактивной мощности. На генерацию активной мощности расходуются первичные энергоресурсы – газ, мазут, уголь, энергия ветра или падающей воды. Поскольку каждые полпериода переменного тока накопленная в магнитном поле реактивная энергия отдается обратно в источник (синхронный генератор, конденсатор) то в идеале на генерацию реактивной мощности не требуется расход первичного энергоносителя. Однако при более глубоком рассмотрении оказывается, что реактивная энергия не такая уж безобидная. На генерацию реактивной мощности все- таки требуется расходовать некоторое количество первичного энергоносителя для покрытия механических и электрических потерь в генераторах, диэлектрических потерь в конденсаторах. Кроме того при передаче реактивной энергии в линиях и трансформаторах возникают потери на нагрев. Еще одна неприятность состоит в том, что генерация и передача реактивной энергии требует увеличения установленной мощности генераторов, увели

Коэффициент мощности — Википедия. {\circ }} (cos⁡φ=0,71{\displaystyle \cos \varphi =0{,}71}) — нагрузка имеет и активную, и реактивную составляющие. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны из переменного напряжения и тока с коэффициентом мощности, равным 0,71. Расположение синей линии (графика мгновенной мощности) под осью абсцисс показывает, что некоторая часть подводимой мощности всё же возвращается в сеть в течение части цикла, отмеченного φ.

Коэффицие́нт мо́щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.

Численно коэффициент мощности равен косинусу этого фазового сдвига.

Можно показать, что если к источнику синусоидального тока (например, розетка ~230 В, 50 Гц) подключить нагрузку, в которой ток опережает или отстаёт по фазе на некоторый угол от напряжения, то на внутреннем активном сопротивлении источника выделяется повышенная мощность. На практике это означает, что при работе на нагрузку со сдвинутыми напряжением и током от электростанции требуется больше отвода тепла, чем при работе на активную нагрузку; избыток передаваемой энергии выделяется в виде тепла в проводах и может быть довольно значительным.

Коэффициент мощности равен отношению потребляемой электроприёмником активной мощности к полной мощности. Активная мощность расходуется на совершение работы. Полная мощность — геометрическая сумма активной и реактивной мощностей (в случае синусоидальных тока и напряжения). В общем случае полную мощность можно определить как произведение действующих (среднеквадратических) значений тока и напряжения в цепи. Полная мощность равна корню квадратному из суммы квадратов активной и реактивной мощностей. В качестве единицы измерения полной мощности принято использовать вольт-ампер (В∙А) вместо ватта (Вт).

Согласно неравенству Коши—Буняковского, активная мощность, равная среднему значению произведения тока и напряжения, всегда не превышает произведение соответствующих среднеквадратических значений. Поэтому коэффициент мощности принимает значения от нуля до единицы (то есть от 0 до 100 %).

Коэффициент мощности математически можно интерпретировать как косинус угла между векторами тока и напряжения. Поэтому в случае синусоидальных напряжения и тока величина коэффициента мощности совпадает с косинусом угла, на который отстают соответствующие фазы.

В электроэнергетике для коэффициента мощности приняты обозначения cos⁡φ{\displaystyle \operatorname {cos} \varphi } (где φ{\displaystyle \varphi } — сдвиг фаз между силой тока и напряжением) либо λ. Когда для обозначения коэффициента мощности используется λ{\displaystyle \lambda }, его величину обычно выражают в процентах.

При наличии реактивной составляющей в нагрузке кроме значения коэффициента мощности иногда также указывают характер нагрузки: активно-ёмкостный или активно-индуктивный. В этом случае коэффициент мощности соответственно называют опережающим или отстающим.

В случае синусоидального напряжения, но несинусоидального тока, если нагрузка не имеет реактивной составляющей, коэффициент мощности равен доле мощности первой гармоники тока в полной мощности, потребляемой нагрузкой.

коэффициент мощности — это… Что такое коэффициент мощности?



коэффициент мощности

1.3.24 коэффициент мощности (power factor): Отношение активной мощности и очевидной мощности конденсатора.

Смотри также родственные термины:

253 коэффициент мощности (двухполюсника)

Скалярная величина, равная отношению активной мощности двухполюсника к полной мощности

3.41 коэффициент мощности брутто (gross output factor) GOF, %: Рассчитывается по формуле

35 коэффициент мощности источника электропитания РЭА: Скалярная величина, равная отношению активной мощности источника электропитания радиоэлектронной аппаратуры к полной мощности.

<2>

3.65 коэффициент мощности нетто (net output factor) NOF, %: Рассчитывается по формуле

3. 12 коэффициент мощности цепи: Отношение измеренной потребляемой активной мощности к произведению среднеквадратических значений питающего напряжения и потребляемого тока.

3.14 коэффициент мощности цепи; (circuit power factor; λ):Коэффициент мощности комплекта устройств управления лампами и ламп, для которых предназначено устройство управления лампами.

3.2 коэффициент мощности цепи; A, (circuit power factor; X): Отношение значения измеренной мощности цепи к произведению действующих значений напряжения и тока сети.

Словарь-справочник терминов нормативно-технической документации.
academic.ru.
2015.

• коэффициент морозного пучения
• коэффициент мощности (двухполюсника)

Смотреть что такое «коэффициент мощности» в других словарях:

• коэффициент мощности — Скалярная величина, равная отношению активной мощности двухполюсника к полной мощности. [ГОСТ Р 52002 2003] коэффициент мощности (цепи) Отношение активного сопротивления к полному сопротивлению при промышленной частоте в эквивалентной цепи,… …   Справочник технического переводчика

• КОЭФФИЦИЕНТ МОЩНОСТИ — (косинус фи) отношение активной мощности к полной. В случае синусоидального тока равен косинусу угла сдвига фаз ? между напряжением и током; отпределяется отношением активного сопротивления цепи (r) к полному (Z): cos ? = r/Z …   Большой Энциклопедический словарь

• Коэффициент мощности — Синусоидальное напряжение (красная линия) и ток (зелёная линия) синфазны между ними нет фазового сдвига ( …   Википедия

• коэффициент мощности — отношение активной мощности к полной. В случае синусоидального тока равен косинусу угла сдвига фаз φ между напряжением и током; определяется отношением активного сопротивления цепи (r) к полному (Z): cosφ = r/Z. * * * КОЭФФИЦИЕНТ МОЩНОСТИ… …   Энциклопедический словарь

• коэффициент мощности — galios koeficientas statusas T sritis automatika atitikmenys: angl. power factor vok. Leistungsfaktor, m rus. коэффициент мощности, m pranc. facteur de puissance, m …   Automatikos terminų žodynas

• коэффициент мощности — galios faktorius statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, lygus aktyviosios ir pilnutinės galios dalmeniui. atitikmenys: angl. power factor vok. Leistungsfaktor, m; Wirkfaktor, m rus. коэффициент мощности, m pranc.… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• коэффициент мощности — galios faktorius statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, skaitine verte lygus kintamosios elektros srovės elektros energijos imtuvo aktyviosios galios ir pilnutinės galios dalmeniui. atitikmenys: angl. power factor vok …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• коэффициент мощности — Коэффициент пропорциональности A в уравнении подобия N = An3D5, связывающем мощность N на ведущем валу гидропередачи, число его оборотов n и активный диаметр D …   Политехнический терминологический толковый словарь

• КОЭФФИЦИЕНТ МОЩНОСТИ — отношение активной мощности к полной. В случае синусоидального тока равен косинусу угла сдвига фаз ф между напряжением и током; определяется отношением активного сопротивления цепи (r) к полному (Z): cosф = r/Z …   Естествознание. Энциклопедический словарь

• Коэффициент мощности — English: Powers factor Отношение активной мощности к полной (по ГОСТ 19880 74) Источник: Термины и определения в электроэнергетике. Справочник …   Строительный словарь

Коэффициент мощности — Руководство по устройству электроустановок

Определение коэффициента мощности

Коэффициент мощности (cos φ) есть отношение кВт к кВА. Чем ближе коэффициент мощности приближается к своему максимальному значению 1, тем больше польза для потребителя и поставщика. PF = P (кВт)/S (кВА), где: P = активная мощность; S = полная мощность.

Коэффициент мощности нагрузки, которая может являться электроприемником (ЭП) или совокупностью таких ЭП (например, вся система), задается отношением P/S, т. е. число кВт, деленное на число кВА в заданный момент времени.

Значение коэффициента мощности изменяется в диапазоне 0-1.

Если токи и напряжения являются идеальными синусоидальными сигналами, коэффициент мощности равен cos φ.

Коэффициент мощности около единицы означает, что реактивная мощность мала в сравнении с активной, а низкое значение коэффициента указывает на противоположное.

Векторная диаграмма мощности

• Активная мощность P (кВт):

  —  однофазная (1 фаза и нейтраль): P = V х I х cos φ;
  —  однофазная (фаза-фаза): P = U х I х cos φ;
  —  трехфазная (3 провода или 3 провода + нейтраль): P = 3{\displaystyle {\sqrt {3}}}х U х I cos φ.

• Реактивная мощность Q (квар):

  —  однофазная (1 фаза и нейтраль): Q = V х I х sin φ;
  —  однофазная (фаза-фаза): Q = U х I х sin φ;
  —  трехфазная (3 провода или 3 провода + нейтраль): Q = 3{\displaystyle {\sqrt {3}}} х U х I sin φ.

• Полная мощность S (кВА):

  —  однофазная (1 фаза и нейтраль): S = V х I;
  —  однофазная (фаза-фаза): S = U х I;
  —  трехфазная (3 провода или 3 провода + нейтраль): S = 3{\displaystyle {\sqrt {3}}} х U х I,
где:
V — линейное напряжение;
U — фазное напряжение;
 I —  ток;
φ — угол между векторами напряжения и тока;
 —  для симметричных или почти симметричных нагрузок четырехпроводных систем.

Векторы тока и напряжения и вывод векторной диаграммы мощности

Векторная диаграмма мощности – полезный инструмент, выводимый непосредственно из истинной диаграммы вращающихся векторов токов и напряжений следующим образом:

Напряжения энергосистемы принимаются в качестве исходных величин, и рассматривается только одна фаза, исходя из предположения о симметричной трехфазной нагрузке.

Исходное напряжение фазы (V) совпадает с горизонтальной осью, а ток (I) этой фазы сдвинут (отстает) (практически для всех нагрузок энергосистемы) относительно напряжения на угол φ.

Составляющая тока I, совпадающая по фазе с напряжением V, является реактивной составляющей тока I и равна I·cos φ, значение V·I cos φ равно активной мощности (кВт) в цепи, если V выражается в кВ.

Составляющая тока I с отставанием 90 градусов от напряжения V является безваттной составляющей тока I и равна I·sin φ, а значение V·I·sin φ равно реактивной мощности (квар), если напряжение V выражается в кВ.

Результат умножения I на V в кВ (V·I) равен полной мощности (кВА) для цепи.

Получается простая формула S² = P² + Q²

Следовательно, умноженные на 3, указанные выше значения кВт, квар и кВА на фазу могут удобно представлять взаимосвязь кВА, кВт, квар и коэффициента мощности для общей трехфазной нагрузки, как показано на рис. L3.

Рис. L3 : Диаграмма мощности

Пример расчета мощности

(см. рис. L4)

Тип цепи		Полная мощность S (кВА)	Актив. мощность P (кВт)	Реакт. мощность Q (квар)
Однофазная (фаза и нейтраль)		S = VI	P = VI cos φ	Q = VI sin φ
Однофазная (фаза-фаза)		S = UI	P = UI cos φ	Q = UI sin φ
Пример:	5 кВт нагрузки	10 кВA	5 кВт	8,7 квар
	cos φ = 0. 5
Трехфазная (3 провода или 3 провода + нейтраль)		S = 3{\displaystyle \definecolor {bggrey}{rgb}{0.9176470588235294,0.9176470588235294,0.9176470588235294}\pagecolor {bggrey}{\sqrt {3}}} UI	P = 3{\displaystyle \definecolor {bggrey}{rgb}{0.9176470588235294,0.9176470588235294,0.9176470588235294}\pagecolor {bggrey}{\sqrt {3}}} UI cos φ	Q = 3{\displaystyle \definecolor {bggrey}{rgb}{0.9176470588235294,0.9176470588235294,0.9176470588235294}\pagecolor {bggrey}{\sqrt {3}}} UI sin φ
Пример:	Двигатель Pn = 51 кВт	65 кВА	56 кВт	33 квар
	cos φ = 0,86
	ρ= 0,91 (КПД двигателя)

Рис. L4 : Пример расчета активной и реактивной мощностиzh:功率因数

Что такое коэффициент мощности

Коэффициент мощности (PF) по определению представляет собой соотношение между рабочей мощностью P (ватты) и полной мощностью S (вольт-амперы): PF = P / S = Вт / Vrms × Irms Это величина, которая сообщает нам, насколько эффективно ваше устройство использует электричество. Чтобы легко объяснить физический смысл PF, рассмотрим простой пример. Предположим, вы подключаете идеальный конденсатор «C» к линии переменного тока. Поскольку напряжение переменного тока постоянно меняет свою полярность, половину времени этот конденсатор будет заряжаться от входа, а половину времени он будет возвращать накопленную энергию обратно к источнику (см. Анимационное видео ниже). Ваш браузер не поддерживает видео тег. Пожалуйста, обновите браузер. Предоставлено Джо Вулфом из Physclips Project в UNSW. В результате в линии будет постоянно циркулировать переменный ток, но передачи полезной энергии не будет. Итак, у нас будут и вольты, и амперы, но не полезная мощность. Произведение «ВА» называется кажущейся мощностью , потому что это просто математическая величина, не имеющая реального физического значения. Выше приведен пример нагрузки с PF = 0.Точно так же один идеальный индуктор приведет к PF = 0, за исключением того, что его ток будет отставать от напряжения. Теперь рассмотрим противоположный крайний случай резистивной нагрузки. В таком случае вся электрическая энергия, поступающая в нагрузку, потребляется и преобразуется в другие формы энергии, такие как тепло. Это пример PF = 1. Все реальные схемы работают где-то между этими двумя крайностями. При анализе цепей синусоидальный сигнал может быть представлен комплексным числом (называемым вектором ), модуль которого пропорционален величине сигнала, а угол равен его фазе относительно некоторого эталона.В линейных цепях PF = cosφ , где φ — угол между векторами напряжения и тока. Эти и соответствующие векторы для активной и реактивной составляющих мощности можно представить в виде треугольника (см. Диаграмму ниже). Конечно, напряжение — это электрическое поле, а ток — это поток электронов, поэтому так называемый угол между их векторами — не более чем еще одна математическая величина. По соглашению, индуктивная нагрузка создает положительную реактивную мощность (ВАХ). Это связано с так называемым «запаздывающим» коэффициентом мощности, потому что ток отстает от напряжения.

Точно так же емкостная нагрузка создает отрицательные значения VAR и «опережающий» коэффициент мощности. Катушки индуктивности и колпачки — не единственные причины низкого коэффициента мощности. За исключением идеальных R, L и C, все практические электрические цепи являются нелинейными , особенно из-за наличия активных компонентов, таких как выпрямители. В таких схемах ток I (t) не пропорционален напряжению V (t), т.е. даже если V (t) является чистой синусоидой, I (t) будет периодическим, но несинусоидальным. Согласно теореме Фурье, любая периодическая функция представляет собой сумму синусоидальных волн с частотами, целыми кратными исходной.Эти волны называются гармониками. Можно показать, что они не способствуют передаче чистой энергии, но увеличивают Irms и уменьшают PF. Когда напряжение синусоидально, только первая гармоника I 1 среднеквадратичное значение может обеспечить реальную мощность. Однако его величина зависит от фазового сдвига между I 1 rms и V. Эти факты отражены общей формулой для PF: PF = (I 1 rms / I rms ) × cosφ Первый член в этом уравнении представляет искажения, второй — реактивные сопротивления.Если вы хотите увидеть, как выводится эта формула, ознакомьтесь с математическим анализом мощности переменного тока.

Коррекция коэффициента мощности | Обороты

Вы платите

Коэффициент мощности

Штраф?

Сэкономьте тысячи долларов на ежемесячных счетах за электроэнергию, изменив коэффициент мощности.

Что такое

Коэффициент мощности?

Коэффициент мощности — это показатель того, насколько эффективно вы используете электроэнергию.Он определяется как отношение рабочей мощности (кВт) к общей мощности (кВА).

Коэффициент мощности = рабочая мощность (кВт) / общая мощность (кВА)

Коэффициент мощности 0,7 означает, что 70% электроэнергии, подаваемой на объект, используется эффективно, а 30% расходуется впустую — эти потери часто приводят к увеличению счета за коммунальные услуги

com/wp-content/uploads/2016/07/RPM-Blue-slide-100×50.jpg» data-rotate=»0″ data-saveperformance=»off» data-title=»Cause of…» data-param1=»» data-param2=»» data-param3=»» data-param4=»» data-param5=»» data-param6=»» data-param7=»» data-param8=»» data-param9=»» data-param10=»» data-description=»»>

Причины низкого

Коэффициент мощности?

Низкий коэффициент мощности вызван индуктивными нагрузками, такими как блоки HVAC, двигатели переменного тока, конвейеры чиллеров и другое электрическое оборудование на вашем предприятии

Помимо уменьшения счета за коммунальные услуги, коррекция коэффициента мощности может уменьшить преждевременный отказ двигателя и повысить напряжение.

com/wp-content/uploads/2016/07/RPM-Blue-slide-100×50.jpg» data-rotate=»0″ data-saveperformance=»off» data-title=»Why Improve..» data-param1=»» data-param2=»» data-param3=»» data-param4=»» data-param5=»» data-param6=»» data-param7=»» data-param8=»» data-param9=»» data-param10=»» data-description=»»>

Зачем нужно улучшать свой

Коэффициент мощности?

Штрафы за коэффициент мощности часто трудно найти в счетах за коммунальные услуги. Определение штрафа за коэффициент мощности и его корректировка может сэкономить вам тысячи долларов в месяц.

Ваш счет за коммунальные услуги может быть меньше — значительно меньше!

jpg» data-rotate=»0″ data-saveperformance=»off» data-title=»Are You Paying…» data-param1=»» data-param2=»» data-param3=»» data-param4=»» data-param5=»» data-param6=»» data-param7=»» data-param8=»» data-param9=»» data-param10=»» data-description=»»>

Вы платите

Коэффициент мощности

Штраф?

Нажмите, чтобы узнать, сможете ли вы сэкономить

Что такое

Решение?

Наиболее распространенным и экономичным решением для исправления низкого коэффициента мощности является установка конденсаторов в системе распределения электроэнергии вашего предприятия.

С 2002 года Rapid Power Management устанавливает готовые решения с конденсаторами, чтобы помочь коммерческим, промышленным и институциональным пользователям устранить штрафы за коэффициент мощности.

Коэффициент мощности — определение коэффициента мощности по The Free Dictionary

Некоторые из мер, которые могут быть предприняты для улучшения качества электроэнергии, включают развертывание устройств автоматического регулирования напряжения, устройств активной коррекции коэффициента мощности, балансировщиков источника и нагрузки и цифровых подстанций; контроль и управление пиковой мощностью; и эффективное управление реактивной мощностью.Дата выпуска — 18062019 — Diodes Incorporated (Nasdaq: DIOD) сегодня объявила о выпуске светодиодного подавителя пульсаций тока AL5822, который обеспечивает высокий уровень подавления пульсаций при сохранении высокого коэффициента мощности для коммерческого и промышленного освещения. Они могут даже состоять из секций синусоидальной волны [7], чтобы максимизировать коэффициент мощности (PF) водителя.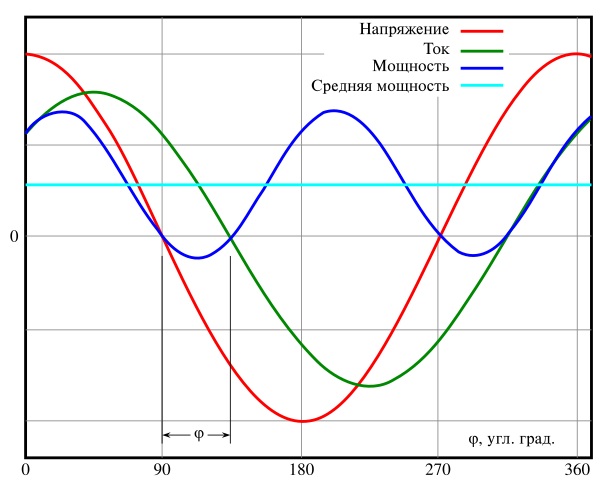 Не углубляясь в это слишком глубоко, коэффициент мощности настраивается таким образом, чтобы стрелки не могли «обмануть», используя маломощные боеприпасы, которые дали бы у них преимущество, потому что они могут делать попадания быстрее из-за меньшей отдачи и меньшего подъема дула.Простая запись коэффициента мощности на ежемесячной основе (см. Совет месяца по энергосбережению # 82) быстро покажет, соответствует ли оборудование PFC и работает ли оно правильно. 3.5 Форма волны моделирования для коррекции коэффициента мощности в предлагаемой системе: Мисс Годселл продолжает: «Просто установив коррекцию коэффициента мощности или оптимизацию напряжения, мы можем сэкономить до 40% на энергопотреблении предприятия за счет управления напряжением и током. Двигатели для этих систем имели постоянную скорость, и единственными критериями выбора могли быть КПД и коэффициент мощности последствия эксплуатации этих двигателей на более низких уровнях крутящего момента из-за снижения нагрузки.* Активная коррекция коэффициента мощности согласно EN 61000-3-2 D. Разность фаз (или косинус угла) между формой волны тока и формой волны напряжения надлежащим образом называется коэффициентом мощности смещения и обычно связана с не- резистивные (или «нелинейные») электрические нагрузки, которые могут быть индуктивными (форма волны тока отстает от формы напряжения) или емкостными (форма волны тока опережает форму волны напряжения). Стандартные функции включают фильтрацию в соответствии с EN 55022, класс B, коэффициент активной мощности поправка на EN 61000-3-2 D, пиковая выходная мощность до 900 Вт и изоляция входа / выхода 3000 В переменного тока.Коэффициент мощности — это отношение энергии, передаваемой нагрузке, к максимальной энергии.

Калькулятор размера выборки — уровень достоверности, доверительный интервал, размер выборки, размер совокупности, соответствующая совокупность

Этот калькулятор размера выборки представлен как общедоступная услуга программного обеспечения для проведения опросов Creative Research Systems.
Вы можете использовать его, чтобы определить, сколько людей вам нужно проинтервьюировать, чтобы получить результаты, отражающие целевую совокупность настолько точно, насколько это необходимо.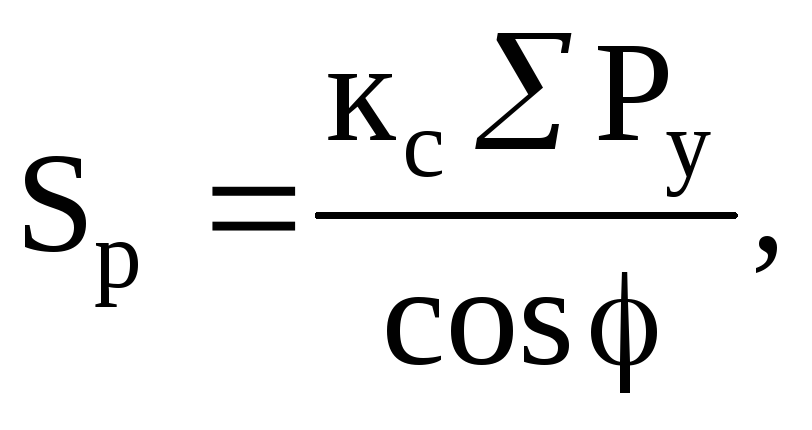 Вы также можете найти уровень точности, который у вас есть в существующем образце.

Прежде чем использовать калькулятор размера выборки, вам необходимо знать два термина. Это: доверительный интервал и доверительный интервал . Если вы не знакомы с этими условиями, щелкните здесь. Чтобы узнать больше о факторах, влияющих на размер доверительных интервалов, щелкните здесь.

Введите свой выбор в калькулятор ниже, чтобы найти необходимый размер выборки или доверительный интервал.
у тебя есть. Оставьте поле Население пустым, если популяция очень большая или неизвестна.

Термины калькулятора размера выборки: доверительный интервал и доверительный уровень

Доверительный интервал (также называемый пределом погрешности) — это положительное или отрицательное значение, обычно указываемое в результатах газетных или телевизионных опросов. Например, если вы используете доверительный интервал 4 и 47% процентов вашей выборки выбирают ответ, вы можете быть «уверены», что если бы вы задали вопрос всей соответствующей совокупности, от 43% (47-4) до 51% (47 + 4) выбрали бы этот ответ.

Уровень достоверности говорит вам, насколько вы можете быть уверены. Он выражается в процентах и ​​показывает, как часто истинный процент населения, которое выберет ответ, находится в пределах доверительного интервала. Уровень достоверности 95% означает, что вы можете быть уверены на 95%; Уровень достоверности 99% означает, что вы можете быть уверены на 99%. Большинство исследователей используют уровень достоверности 95%.

Если сложить доверительный интервал и доверительный интервал, можно сказать, что вы на 95% уверены, что истинный процент населения составляет от 43% до 51%.Чем шире доверительный интервал, который вы готовы принять, тем больше у вас будет уверенности в том, что ответы всего населения будут в пределах этого диапазона.

Например, если вы спросили выборку из 1000 человек в городе, бренд c

Факторизация — Математика GCSE Revision

Факторизация — Расширяющиеся скобки

В этом разделе показано, как разложить на множители, и включены примеры, примеры вопросов и видео.

Скобки следует раскрывать следующим образом:
Для выражения формы a (b + c) расширенная версия — ab + ac, i.е., умножьте член вне скобки на все, что находится внутри скобки (например, 2 x ( x + 3) = 2x² + 6x [помните, что x x x равно x²]).
Для выражения формы (a + b) (c + d) расширенная версия имеет вид ac + ad + bc + bd, другими словами, все в первой скобке должно быть умножено на все во второй.

Пример

Развернуть (2x + 3) (x — 1):
(2x + 3) (x — 1)
= 2x² — 2x + 3x — 3
= 2x² + x — 3

Факторизация

Факторизация — это противоположность раскрывающихся скобок, так что, например, 2x² + x — 3 помещаются в форму (2x + 3) (x — 1).Это важный способ решения квадратных уравнений.
Первый шаг факторизации выражения — «исключить» все общие множители, которые есть в терминах. Итак, если вас попросят разложить на множители x² + x, поскольку x входит в оба члена, вы должны написать x (x + 1).

Факторизация квадратичных расчетов

В этом видео показано, как решить квадратное уравнение с помощью факторизации.

Простого метода разложения квадратичного выражения на множители не существует, но после небольшой практики он становится проще.Однако есть один систематический метод:

Пример

Разложите на множители 12y² — 20y + 3
= 12y² — 18y — 2y + 3 [здесь 20y было разделено на два числа, кратное 36. 36 было выбрано, потому что это произведение 12 и 3, двух других чисел] .
Первые два члена, 12y² и -18y, оба делятся на 6y, поэтому «уберите» этот множитель 6y.
6y (2y — 3) — 2y + 3 [мы можем это сделать, потому что 6y (2y — 3) совпадает с 12y² — 18y]
Теперь сделайте последние два выражения похожими на выражение в скобках:
6y ( 2y — 3) -1 (2y — 3)
Ответ: (2y — 3) (6y — 1)

Пример

Разложить на множители x² + 2x — 8
Нам нужно разделить 2x на два числа, которые умножаются, чтобы получить -8. Это должно быть 4 и -2.
x² + 4x — 2x — 8
x (x + 4) — 2x — 8
x (x + 4) — 2 (x + 4)
(x + 4) (x — 2)

Когда вы поймете, что происходит, этот метод упрощает факторизацию любого выражения. Стоит изучить эти примеры дальше, если вы не понимаете, что происходит. К сожалению, единственный другой метод факторизации — это метод проб и ошибок.

Разница двух квадратов

Если вас попросят факторизовать выражение, состоящее из одного квадрата за вычетом другого, вы можете немедленно разложить его на множители.Это потому, что a² — b² = (a + b) (a — b).

Пример

Разложите на множители 25 — x²
= (5 + x) (5 — x) [представьте, что a = 5 и b = x]

Щелкните здесь, чтобы получить дополнительную информацию о квадратных уравнениях.

.