Колебания резонанс: Резонанс — друг и враг

Резонанс — друг и враг

Резонанс — это явление резкого возрастания амплитуды вынужденных колебаний системы, которое наступает при приближении частоты внешнего воздействия к определенным значениям (резонансных частот), обусловленным свойствами системы. Таким образом, причиной резонанса является совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы.

Резонанс встречается в механике, электронике, оптике, акустике, астрофизике.

Явление резонанса лежит в основе проектирования музыкальных инструментов: рояля, скрипки, флейты …

Используется явление резонанса и в электронике. Колебательный контур, состоящий из емкости и индуктивности, используется в элементах настройки и электрических фильтрах. Однако резонанс может быть и вредным, если он вызывает искажение сигнала или паразитные шумы.

Наблюдается резонанс и в космосе, когда два небесных тела, которые имеют периоды обращения, относящихся друг с другом как небольшие целые числа, делают регулярное гравитационное воздействие друг на друга, которое может стабилизировать их орбиты (орбитальный резонанс в небесной механике).

Однако наиболее часто резонанс бывает в классической и строительной механике, а также гидро- и аэромеханике. И, к ​​сожалению, во многих случаях именно тогда, когда он совершенно нежелателен.

… Известно, что военным подразделениям при прохождении мостов приписывается «сбивать ногу» и идти не строевым, а свободным шагом. Горький опыт некоторых катастроф научил военнослужащих в подобных ситуациях отходить от многовековых традиций.

Так, 12 апреля 1831 разрушился Бротонский подвесной мост через реку Ирвелл в Англии, когда по нему шел военный отряд. Частота шагов воинов, шагавших в ногу, совпала с частотой собственных колебаний моста, через которые амплитуда резко возросла, цепи оборвались, и мост рухнул в реку. Именно этот случай, в результате которого два десятка человек были травмированы, способствовал принятию в британской армии правила «идти не в ногу» при прохождении войсками мостов. По той же причине в 1850 году неподалеку от французского города Анже был разрушен подвесной цепной мост над рекой Мин длиной более ста метров, что привело к многочисленным жертвам. Также существует версия, что 1905 году в результате прохождения кавалерийского эскадрона через резонанс разрушился и Египетский мост через реку Фонтанку в Петербурге. Однако эта версия, скорее всего, безосновательна, поскольку не существует методов дрессировки значительного количества лошадей для их движения «в ногу».

Причиной разрушения мостов из-за резонанса могут стать не только пешеходы, но и железнодорожные поезда. Для исключения резонанса моста поезд может двигаться или медленно, или на максимальной скорости (вспомните, как замедляют ход поезда метрополитена во время их движения через мост Метро в Киеве). Это обычно делается для исключения совпадения частоты ударов колес по стыкам рельсов с собственной частотой колебаний моста (по этой же причине участок рельсов на мосту часто выполняют сплошной, т.е. без стыков).

Катастрофические последствия для мостов могут послужить также и от воздействия ветра. Так, 7 ноября 1940 через игнорирование действия ветровой нагрузки на мост при его проектировании и вследствие возникновения резонанса разрушился Такомский подвесной мост общей длиной 1800 м и длиной центрального пролета 850 м (США).

С резонансом можно столкнуться не только на суше, но и на море и в воздухе. Так, при некоторых частотах вращения гребного вала в резонанс входили даже корабли. А на заре развития авиации некоторые авиационные двигатели вызывали столь сильные резонансные колебания элементов самолета, что он полностью разрушался в воздухе.

Причиной резонанса элементов летательных аппаратов и их разрушение может стать и флаттер — сочетание самовозбуждающиеся незатухающих изгибающих и крутильных автоколебаний элементов конструкции (главным образом крыла самолета или несущего винта вертолета). Одним из путей борьбы с этим явлением является использование так называемых протифлатерных грузов.

Интересно, что крепления двигателей на пилонах крыльев самолетов — это не прихоть конструкторов и дизайнеров, а насущная необходимость, поскольку двигатели демпфирующие колебания крыла в полете воздушного судна, будучи при этом своеобразным протифлатерним грузом.

Также известны случаи, когда во время выступлений знаменитого русского певца Федора Ивановича Шаляпина часто лопались плафоны в люстрах. И происходило это опять же через резонанс, когда частота собственных колебаний стекла совпадала с частотой акустических волн, воспроизводимых певцом.

Еще более интересным фактом является то, что во время Великой Отечественной войны все тот же резонанс едва не поставил под угрозу существование единой ниточки, проходившей по льду Ладожского озера и связывала блокадный Ленинград с «большой землей».

… Во время наведения участка Дороги жизни по Ладожскому озеру защитники Ленинграда неожиданно столкнулись с необычным явлением, когда после нормального прохождения по льду тяжелого грузовика, легкая машина, которая шла по тому же пути, нередко проваливалась под лед.

Перед учеными была поставлена ​​задача срочно разобраться с ситуацией, сложившейся и предоставить рекомендации по преодоления автомобилями ледяного покрова. В южной части Ладожского озера, под артиллерийским и минометным огнем врага гидрограф и гидротехники проводили эксперименты по определению предельных нагрузок на лед. Все выводы ученых поступали в Ледовую службу Морской обсерватории. Было изучено деформационную устойчивость льда под статической нагрузкой и данные про упругие деформации льда при распространении по льду взрывной волны. При проведении автоколонн по Ладоге наблюдались и неизвестные ранее колебания ледяного покрова: водяной волна, образовавшаяся под льдом проседала, двигалась с постоянной для определенной толщины льда и глубины водоема скоростью. Она могла опережать приложенную нагрузку или отставать от нее, но опасным было совпадения этих скоростей — тогда вода прекращала поддержку ледяного покрова, и поддержка обеспечивалась только упругими свойствами льда. При этом наступал резонанс, что приводило к разрушению льда. Это проявление резонанса было названо изгибно-гравитационной волной.

По результатам исследований для автомобилей, которые двигались по льду, были установлены определенные скорости и дистанции. Ежедневно по ледяному покрову в обе стороны перевозилось около 6 тыс. Тонн грузов, а общее количество доставленных в Ленинград по Дороге жизни грузов за весь период ее существования составила более 1 млн 615 тыс. Тонн. Также за это же время с осажденного города было эвакуировано около 1 млн 376 тыс. Его жителей.

С учетом приобретенного опыта позже был разработан резонансный метод разрушения льда, энергоемкость которого в несколько раз меньше энергоемкости традиционного разрушения ледяного покрова с помощью ледоколов и ледокольного навесного оборудования.

Как видим, резонанс может быть достаточно коварным, но укротить его и вернуть на пользу человеку вполне по силам!

явление резкого возрастания амплитуды вынужденных колебаний — Офтоп на TJ

Он наступает при совпадении частоты собственных колебаний с частотой колебаний вынуждающей силы.

Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с некоторой другой частотой, определяемой из параметров колебательной системы, таких как внутренняя (собственная) частота, коэффициент вязкости и т. п. Обычно резонансная частота не сильно отличается от собственной нормальной, но далеко не во всех случаях можно говорить об их совпадении.

Слева: диаграмма распространения звуковых волн в винном бокале. Справа: треснувший из-за резонанса винный бокал

В результате резонанса при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротностью. При помощи резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.

График резонанса

Явление резонанса впервые было описано Галилео Галилеем в 1602 г. в работах, посвященных исследованию маятников и музыкальных струн.

Галилео Галилей

23 635

просмотров

{
«author_name»: «Даниил Здоров»,
«author_type»: «self»,
«tags»: [],
«comments»: 34,
«likes»: 94,
«favorites»: 4,
«is_advertisement»: false,
«subsite_label»: «flood»,
«id»: 23268,
«is_wide»: true,
«is_ugc»: true,
«date»: «Wed, 17 Feb 2016 17:51:23 +0300»,
«is_special»: false }

{«id»:6058,»url»:»https:\/\/tjournal. ru\/u\/6058-daniil-zdorov»,»name»:»\u0414\u0430\u043d\u0438\u0438\u043b \u0417\u0434\u043e\u0440\u043e\u0432″,»avatar»:»5ee32af0-122c-427b-7231-507123d57a68″,»karma»:23099,»description»:»»,»isMe»:false,»isPlus»:false,»isVerified»:false,»isSubscribed»:false,»isNotificationsEnabled»:false,»isShowMessengerButton»:false}

{«url»:»https:\/\/booster.osnova.io\/a\/relevant?site=tj»,»place»:»entry»,»site»:»tj»,»settings»:{«modes»:{«externalLink»:{«buttonLabels»:[«\u0423\u0437\u043d\u0430\u0442\u044c»,»\u0427\u0438\u0442\u0430\u0442\u044c»,»\u041d\u0430\u0447\u0430\u0442\u044c»,»\u0417\u0430\u043a\u0430\u0437\u0430\u0442\u044c»,»\u041a\u0443\u043f\u0438\u0442\u044c»,»\u041f\u043e\u043b\u0443\u0447\u0438\u0442\u044c»,»\u0421\u043a\u0430\u0447\u0430\u0442\u044c»,»\u041f\u0435\u0440\u0435\u0439\u0442\u0438″]}},»deviceList»:{«desktop»:»\u0414\u0435\u0441\u043a\u0442\u043e\u043f»,»smartphone»:»\u0421\u043c\u0430\u0440\u0442\u0444\u043e\u043d\u044b»,»tablet»:»\u041f\u043b\u0430\u043d\u0448\u0435\u0442\u044b»}},»isModerator»:false}

Еженедельная рассылка

Одно письмо с лучшим за неделю

Проверьте почту

Отправили письмо для подтверждения

Резонанс — урок.

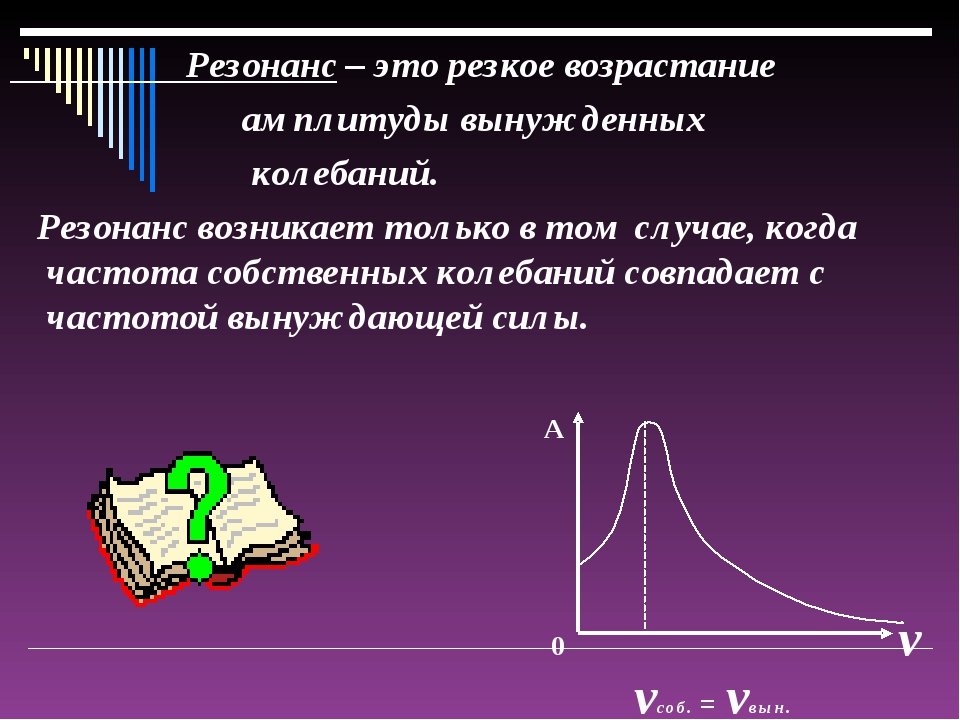Физика, 9 класс.

если вам случалось путешествовать на поезде, то наверняка вы обратили внимание на заметное, сильное раскачивание железнодорожного вагона при случайном совпадении его собственной частоты колебаний на рессорах с частотой ударов колёс на стыках рельсов.

Ещё один очень яркий пример проявления явления резонанса — это несколько случаев обрушения мостов, когда по ним строевым шагом проходила рота солдат.

Чеканный шаг солдатских сапог совпал с собственной частотой колебаний моста. Мост стал колебаться с такой амплитудой, на которую его прочность не была рассчитана и… развалился. Тогда и родилась новая воинская команда «…не в ногу». Она звучит, когда пешая или конная рота солдат проходит по мосту.

Однако самый яркий пример разрушительного действия резонанса — это рухнувший \(7\) ноября \(1940\) года почти двухкилометровый Такомский подвесной мост в США (штат Вашингтон).

Данный случай и видео волнообразного раскачивания конструкции даже рекомендованы к просмотру на факультетах физики некоторых университетов как самый хрестоматийный пример такого явления резонанса.

Разрушение подвесного моста под действием ветра — это иллюстрация того, как относительно постоянная сила вызывает резонанс. При этом происходит следующее:

1. порыв ветра отклоняет часть конструкции в сторону движения ветра — внешняя сила способствует возникновению колебаний;

2. при обратном движении конструкции сопротивления воздуха недостаточно, чтобы погасить колебание или значительно снизить его амплитуду;

3. вследствие упругости системы начинается новое движение по ветру, которое он (ветер) и усиливает, продолжая дуть в одном направлении.

Это пример поведения комплексного объекта, где резонанс развивается на фоне высокой добротности и значительной упругости под действием постоянного воздействия силы в одном направлении. К сожалению, Такомский мост — это не единственный пример обрушения конструкций. Случаи, аналогичные описанному, наблюдались и наблюдаются по всему миру, в том числе и в России.

Вынужденные колебания.

Автоколебания. Резонанс. | Объединение учителей Санкт-Петербурга

2.

3.3 Колебания при наличии внешней вынуждающей периодической силы

Идеальный случай.

Пусть на шарик в пружинном маятнике действует периодическая внешняя сила

(1)

В этом случае для смещения шарика вблизи положения равновесия вместо уравнения (1) пункта 2.3.1 получаем

(2)

где .

Нетрудно проверить, что решение уравнения (1) в случае
имеет вид [1-3]:

(3)

где

Первое слагаемое в (3) описывает свободные колебания, а второе – так называемые вынужденные колебания с амплитудой
. Таким образом, амплитуда и начальная фаза колебаний при действии вынуждающей силы зависят не только от начальных условий, но и от параметров силы.

В предельном случае точного совпадения частот
и
система уже не может совершать периодические колебания. Зависимость координаты
от времени будет выражаться формулой

(4)

Такое движение можно рассматривать как колебания с линейно нарастающей со временем амплитудой. Явление раскачки колебаний под действием периодической внешней силы называется резонансом.

Следует подчеркнуть, что неограниченный резонансный рост амплитуды вынужденных колебаний есть идеализация системы. Во-первых, когда амплитуда колебаний становится достаточно большой, осциллятор, как правило, перестаёт быть линейным. Во-вторых, при записи уравнения (12) не учитывались силы трения, приводящие к затуханию колебаний. Рассмотрим роль последнего фактора более подробно.

Вынужденные колебания при наличии трения.

Если на осциллятор с трением действует внешняя сила (1), то уравнение таких колебаний имеет вид

(5)

где
– коэффициент затухания, определённый в пункте 2.3.2.

Общее решение (5) имеет вид [1–3]

(6)

где
– решение уравнения (5) в отсутствие внешней силы (собственные колебания осциллятора (3) – (5) пункта 2. 3.2.

Благодаря трению
, собственные колебания затухают:
при
. Поэтому через время
колебательная система будет совершать только вынужденные колебания, описываемые вторым слагаемым в (6). Важно отметить, что параметры вынужденных колебаний не зависят от начальных условий. Эти колебания происходят с частотой внешней силы
, характеризуются амплитудой
и фазовым сдвигом

(7)

(8)

Как следствие из формулы (8), коэффициент
связан с производной функции
следующим образом:

(9)

Важным отличием от случая вынужденных колебаний осциллятора без трения является наличие сдвига фазы
между колебаниями вынуждающей силы и колебаниями осциллятора. При точном совпадении частот,
, вне зависимости от величины затухания, сдвиг фазы составляет
.

Другим существенным следствием наличия затухания является качественное изменение вида резонансной кривой.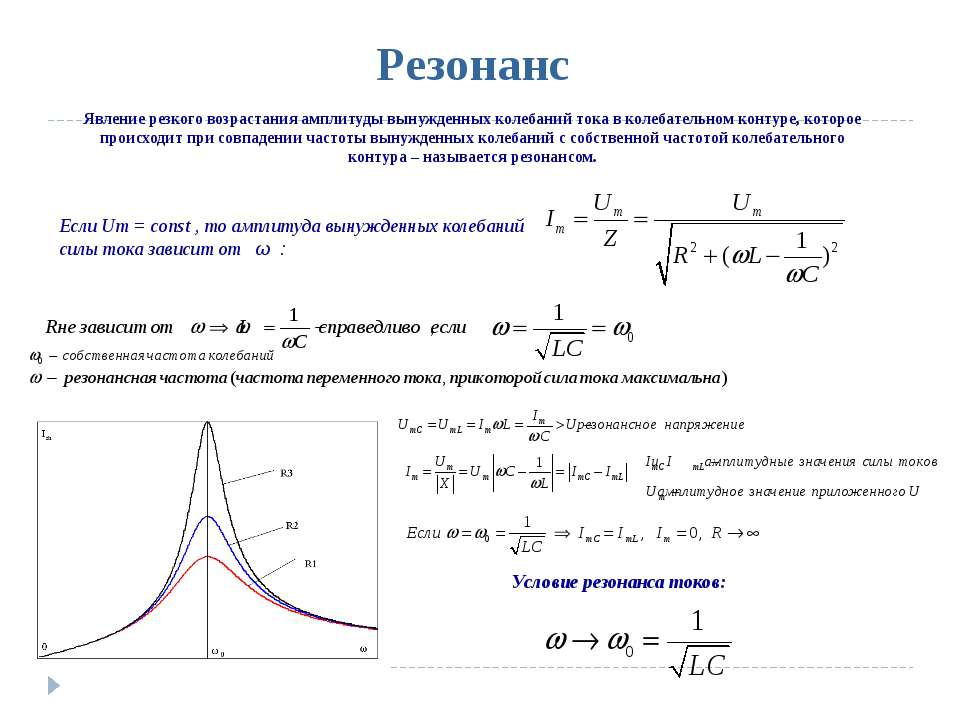 На рис. 1 приведена зависимость
и
для некоторых характерных значений
.

Рис. 1б.  Зависимость сдвига фаз
(ФЧХ) между колебаниями вынуждающей силы и осциллятора.

Максимальное значение амплитуды вынужденных колебаний (7), определяется формулой

(10)

Этому максимуму соответствует резонансная частота

(11)

при условии, что
. Если затухание мало
() то максимум резонансной кривой приблизительно совпадает с собственной частотой осциллятора
. По мере роста
этот максимум смещается в сторону меньших частот (рис. 1а). При
максимум амплитуды вынужденных колебаний
приходится на частоту
. TПо существу это означает исчезновение резонанса. Ранее указывалось, что режим апериодического затухания свободных колебаний возникает лишь при
. Следовательно, в интервале
вынужденные колебания уже не имеют резонансного характера, а собственные движения осциллятора ещё сохраняют колебательный характер.

Как видно из формулы (7), при слабом затухании
амплитуда вынужденных колебаний быстро убывает по мере удаления от резонансной частоты. В частности, она уменьшается в
раза при значениях
, равных

,  

(12)

Величину
принято называть шириной резонанса. При малых
эта величина составляет
. Тогда добротность, определяемая формулой (8) пункта 2.3.2, связана с шириной резонансной кривой соотношением

(13)

Таким образом, ширина резонансной кривой определяется добротностью и собственной частотой. Чем больше добротность колебательной системы, тем меньше ширина резонансного пика. Как видно из формулы (13), добротность колебательной системы можно оценить из экспериментальных АЧХ осциллятора и соответственно определить коэффициент затухания.

Выводы.

Литература.

1. С.Э. Хайкин. Механика. – М.: ОГИЗ, 1947. – 574 с.
2. Д. В. Сивухин. Механика. – М.: Наука, 1989. – 576. с.
3. Карлов Н.В., Кириченко Н.А. Колебания, волны, структуры. – М.: ФИЗМАТЛИТ, 2003. – 496 с.

Вынужденные колебания. Резонанс. Автоколебания

Если колебания совершаются под воздействием внешней силы, они называются вынужденными. Работа внешней силы, которая обеспечивает колебательную систему энергией, при этом является положительной. Благодаря ей колебания не затухают и могут противодействовать силам трения.

Внешняя сила не обязательно должна быть постоянной. С течением времени она может изменяться по разным законам. Особый случай – воздействие на колебательную систему внешней силы, которая изменяется по гармоническому закону с частотой, равной ω, в то время как сама система совершает собственные колебания с той же самой частотой.

Определение 1

Установившиеся вынужденные колебания всегда происходят с частотой внешней силы. Частоту свободных колебаний определяют параметры системы.

Когда внешняя сила начинает воздействовать на колебательную систему, должно пройти некоторое время Δt , прежде чем вынужденные колебания установятся. Это время будет равно тому времени τ, за которое затухают свободные колебания в данной системе.

В момент начала воздействия в системе начинают происходить два процесса одновременно – свободные колебания с собственной частотой ω0 и вынужденные с частотой ω. Однако из-за сил трения свободные колебания в определенный момент затухают, поэтому по прошествии времени в системе сохраняются лишь стационарные колебания с той частотой, которая соответствует внешней (вынуждающей) силе.

Пример 1

Разберем пример. У нас есть тело на пружине, совершающее вынужденные колебания (см. иллюстрацию ниже). Приложим внешнюю силу, обозначенную F→вн, к свободному концу пружины, после чего этот конец начнет перемещаться по закону, выражаемому формулой:

y=ymcos ωt.

Здесь буквой ω обозначена круговая частота, а ym – амплитуда колебаний.

Перемещения такого рода обеспечиваются шатунным механизмом, который преобразует круговые движения в возвратно-поступательные.

Рисунок 2.5.1. Груз на пружине, совершающий вынужденные колебания. Перемещение свободного конца выражено формулой y=ym cos ωt, где l означает длину недеформированной пружины, а k –ее жесткость.

При смещении левого конца пружины на некоторое расстояние y и правого – на x по сравнению с первоначальным положением недеформированной пружины будет происходить ее удлинение. Найти величину этого удлинения можно по следующей формуле:

∆l=x-y=x-ymcos ωt.

В таком случае мы можем переформулировать второй закон Ньютона для этого случая следующим образом:

ma=-k(x-y)=-kx+kymcos ωt.

Здесь сила, которая действует на тело, показана как сумма двух слагаемых, первым из которых является упругость, стремящаяся к равновесию тела, а вторым – внешнее воздействие, совершающееся с определенными интервалами. Внешнюю силу также называют вынуждающей.

Теперь выразим эту зависимость в строгой математической формуле, учитывающей связь между координатой тела a=x¨  и его ускорением. У нас получится следующее:

x¨+ω02x=A cos ωt.

Эта зависимость называется уравнением внешних колебаний. Здесь ω0=km является собственной круговой частотой свободного колебания, а ω – циклической частотой внешней (вынуждающей) силы.

Чтобы найти величину A для вынужденного колебания груза на пружине, нужно воспользоваться следующей формулой:

A=kmym-ω02ym.

То уравнение, что мы записали перед этим, не учитывает, что на тело действуют также и силы трения. В уравнении вынужденных колебаний, в отличие от уравнения свободных, учитываются сразу обе частоты – частота вынуждающей силы и частота свободных колебаний.

Вынужденные колебания груза на пружине, которые устанавливаются со временем, имеют частоту внешнего воздействия. Это определяется следующим законом:

x(t)=xmcos (ωt+θ).

Здесь xm обозначает амплитуду вынужденного колебания, а буква θ – его начальную фазу. Значения обоих этих показателей будут зависеть от амплитуды внешней силы и соотношения частот.

Если частоты очень низкие, т.е. ω≪ω0, то тело, прикрепленное к правому концу пружины, движется точно так же, как и левый конец этой пружины. Тогда получается, что x(t)=y(t). Сама пружина при этом практически не деформируется, а модуль внешней силы F→вн, приложенной к ее левому концу, стремится к нулю. Работа при этом не совершается.

Слишком сложно?

Не парься, мы поможем разобраться и подарим скидку 10% на любую работу

Опиши задание

Понятие резонанса

Определение 2

Резонанс – это резкое возрастание амплитуды вынужденных колебаний при сближении частоты внешней силы с собственной частотой колебания тела.

С помощью резонансной кривой (резонансной характеристики) можно описать зависимость, существующую между амплитудой внешних колебаний xm и частотой вынуждающей силы ω.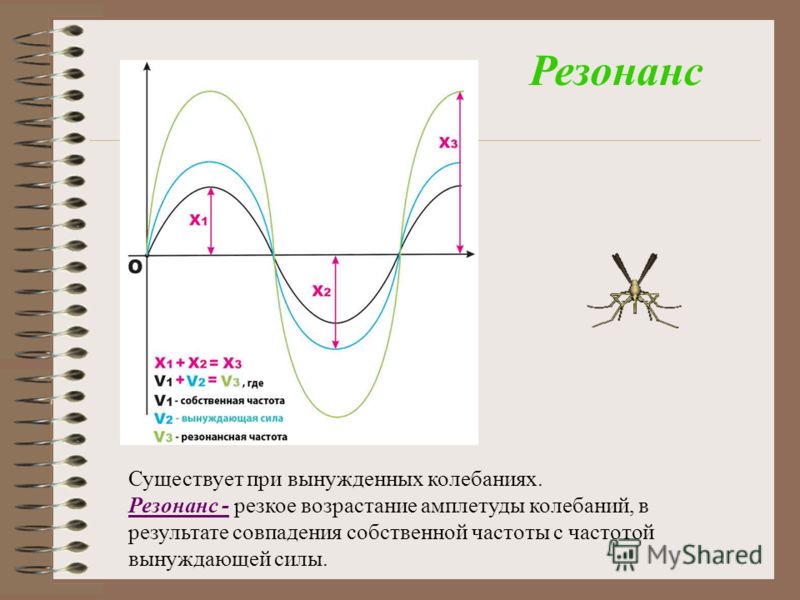

Когда происходит резонанс, амплитуда xm может оказаться значительно больше, чем амплитуда колебаний левого (свободного) конца пружины.. Если мы не будем учитывать силы трения, то получится, что при резонансной частоте амплитуда вынужденных колебаний будет возрастать неограниченно. В реальности она будет зависеть от следующего условия: работа внешней силы в течение всего времени колебаний должна совпадать с потерями механической энергии, происходящими из-за трения. При уменьшении трения (и, соответственно, повышении добротности Q колебательной системы) амплитуда вынужденных колебаний при резонансе возрастет.

Рисунок 2.5.2. Моделирование вынужденных колебаний.

Если добротность колебательной системы невысока (менее 10), то частота резонанса будет находиться ближе к низким частотам. Это показано на иллюстрации 2.5.2.

Явление резонанса имеет большое практическое значение. Именно из-за него зачастую разрушаются здания, мосты и другие сооружения. Это происходит в тот момент, когда их собственные частоты совпадают с частотой внешней силы, например, колебаниями мотора.

Рисунок 2.5.3. Изображение затухания различных колебаний при помощи резонансных кривых: 1 — условная система без учета трения (бесконечное возрастание амплитуды вынужденных колебаний), 2,3,4 – резонансные колебания в реальных условиях, происходящих в системах разной степени добротности (Q2>Q3>Q4). Если частоты низкие, то (ω≪ω0) xm≈ym, а если высокие, то (ω≫ω0) xm→0.

Вынужденные колебания являются незатухающими. При трении неизбежно теряется часть энергии, однако воздействие внешних периодически действующих сил компенсирует ее.

Что такое автоколебательные системы

Определение 3

Автоколебательные системы – это системы, в которых могут возникать незатухающие колебания безотносительно внешнего воздействия, а лишь за счет способности самостоятельно регулировать подвод энергии от внешнего источника. Процесс колебаний в таких системах называют автоколебаниями.

Внутри этой системы можно выделить три составляющих – саму систему, источник внешней постоянной энергии и обратную связь между ними. Первым элементом выступает любая механическая система, которая может совершать затухающие колебания, например, часовой маятник. В качестве источника можно использовать потенциальную энергию груза в поле тяжести или энергию деформации пружины. Система обратной связи – это, как правило, особый механизм, функцией которого является регулирование поступлений энергии. На иллюстрации показано, как эти компоненты взаимодействуют между собой.

Рисунок 2.5.4. Автоколебательная система со всеми основными составляющими.

Какие можно привести примеры таких систем? Ярким примером является часовой механизм с так называемым анкерным ходом. В нем есть ходовое колесо с косыми зубчиками, прочно сцепленное с зубчатым барабаном, через который перекинута цепочка с грузом. В верхней части маятника закреплен якорек (анкер), состоящий из двух твердых пластинок, дугообразно изогнутых по окружности с центром на основной оси. В механизме ручных часов вместо гири используется пружина, а вместо маятника – маховичок-балансир, соединенный со спиральной пружиной, который совершает круговые колебания вокруг своей оси. В качестве источника внешней энергии выступает заведенная пружина или поднятая гиря. Обратная связь осуществляется с помощью анкера: он позволяет ходовому колесу совершать поворот только на один зубец за полупериод. Когда анкер взаимодействует с ходовым колесом, происходит передача энергии. Когда маятник колеблется, зубец ходового колеса передает анкерной вилке энергию по направлению движения маятника, и именно этим компенсируются силы трения. Таким образом, энергия поднятой гири или заведенной пружины поступает маленькими порциями к маятнику.

Существует также много других автоколебательных систем, которые широко применяются в технике. Автоколебания происходят внутри двигателей внутреннего сгорания, паровых машин, электрических звонков, музыкальных инструментов, голосовых связок и т.д.

Рисунок 2. 5.5. Схема маятникового часового механизма.

Оптика и волны

В случае вынужденных колебаний система колеблется под действием периодической внешней (вынуждающей) силы. За счет работы этой силы компенсируются потери энергии системы. Частота вынужденных колебаний зависит от частоты изменения внешней силы (для краткости мы будем называть её «вынуждающей частотой»). Практически наиболее интересным является случай, когда вынуждающая сила изменяется по гармоническому закону:

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Это явление называется резонансом.

Видео 1.21 Резонансное взаимодействие маятников

Видео 1.22 Камертоны: резонансное поглощение энергии волны

Видео 1.23 Резонанс доски с мотором

Явление резонанса используется для усиления колебаний, например электрических. Однако при конструировании машин и сооружений необходимо учитывать явление резонанса, чтобы предотвратить чаще всего нежелательные, а иногда и разрушительные последствия резонансного увеличения амплитуды вынужденных колебаний.

Для пружинного маятника уравнение вынужденного колебательного движения имеет вид:

или

где

и    — вынуждающая частота.

Если рассматривать электрический колебательный контур, то компенсировать потери энергии в контуре можно с помощью подводимой извне периодически изменяющейся по гармоническому закону ЭДС или переменного напряжения

Рис. 1.25. Вынужденные колебания в электромагнитном контуре

Уравнение колебаний в контуре (рис. 1.25) можно записать, используя закон Ома для замкнутой цепи

или, с учетом, что

где

— собственная частота контура,

— коэффициент затухания, a

Таким образом, вынужденные колебания в электрическом контуре описываются тем же самым линейным неоднородным дифференциальным уравнением второго порядка, что и в случае колебаний пружинного маятника. Предположим, что нам известно хотя бы одно решение этого уравнения — некое частное решение . Тогда разность любого другого решения q(t) и этого частного решения  будет удовлетворять однородному уравнению (с нулем в правой части), которое мы подробно изучили в предыдущем разделе. Поэтому общее решение уравнения (1.87) может быть записано как

где

— частота свободных затухающих колебаний.

С течением времени из-за экспоненциального множителя  роль второго слагаемого уменьшается (оно важно на начальной стадии установления колебаний). По прошествии достаточно большого времени, а именно, при

,

им можно пренебречь, сохраняя лишь первое слагаемое. Таким образом, задача исследования установившихся вынужденных колебаний сводится к нахождению хотя бы одного частного решения уравнения (1.87).

Частное решение неоднородного уравнения будем искать в виде гармонической функции, частота изменения которой совпадает с частотой вынуждающей силы:

Подставим  в виде (1.89) в уравнение (1.87):

Так как функции синуса и косинуса линейно независимы, коэффициенты при них в левой части (1.90) должны быть равны нулю:

Решение этой системы имеет вид:

Решение (1.89) с коэффициентами (1.92) можно записать в стандартном виде:

где

и

При знаке минус в фазе косинуса в выражении (1.93) начальная фаза  имеет простой физический смысл: это отставание по фазе установившегося вынужденного колебания от гармонической вынуждающей «силы» (1.85).

Видео 1.24 Резонансный язычковый частотомер

Видео 1.25 Спектр модулированного колебания

Рассмотрим отклик системы на изменение частоты внешней силы. Под квадратным корнем в выражении для амплитуды стоит квадратичная функция частоты

Эта функция имеет минимум (а значит, амплитуда имеет максимум).

Для нахождения точки минимума дифференцируем функцию  по  и приравниваем производную нулю. В итоге получаем следующие выражения для резонансной частоты

и амплитуды установившихся вынужденных колебаний при резонансе

Следует отметить, что при  значение резонансной частоты   практически совпадает с собственной частотой  колебательной системы. Поскольку   стоит в знаменателе выражения для , резонансная амплитуда колебаний растет с уменьшением затухания. На графике 1.26 видно, что чем меньше затухание, тем выше и правее лежит максимум резонансной кривой.

Рис. 1.26. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы

При увеличении частоты внешнего воздействия амплитуда стремится к нулю:

Физически это понятно: система обладает некой инерционностью и не успевает следовать за быстрыми изменениями внешнего воздействия. В другом предельном случае малой внешней частоты

мы имеем дело со статическим случаем — действием постоянной внешней силы F₀ на пружинный маятник, или подсоединением контура к источнику с постоянным напряжением U_m. В этом случае предельное значение амплитуды вынужденных колебаний равно

и не зависит от затухания. Последнее вполне естественно, так как затухание обусловлено действием силы сопротивления, которая пропорциональна скорости и проявляется только при движении системы, а не в статическом пределе. В случае механических колебаний

что равно удлинению пружины под действием постоянной силы F₀.

В случае электромагнитных колебаний в контуре

что равно заряду на конденсаторе при подсоединении его к источнику постоянного напряжения U_m.

Найдем отношение резонансной амплитуды к статической при малом затухании, когда :

Иными словами, добротность Q характеризует также резонансные свойства колебательной системы: чем больше добротность, тем выше и относительно уже резонансный пик (см. рис. 1.26).

Автоколебательные системы. Параметрический резонанс.

Видео 1.26 Анкерный механизм механических часов

Видео 1.27 Колебания линейки под струёй воды

Видео 1.28 Спираль Роже

Видео 1.29 Параметрический резонанс

Дополнительная информация

http://class-fizika.spb.ru/index.php/slaid/193-kol – Много интересных анимаций, видео, слайд-шоу по колебаниям и волнам.

http://www.fxyz.ru/формулы_по_физике/колебания_и_волны – Основные формулы по колебаниям и волнам (см. Также раздел «подтемы» справа вверху)

http://physics-lectures.ru/category/mexanicheski-kolebaniya-i-volny/ – Лекции по колебаниям и волнам

http://www.alleng.ru/d/phys/phys105.htm – Д.В. Сивухин. Электричество, колебания и волны. Учебник.

http://www.ph5s.ru/book_ph_koleb.html  – Ссылки на книги по колебаниям и волнам. Сайт бывшего преподавателя МИФИ А.Н. Варгина.

http://fmclass. ru/math.php?id=485a8e5cc78f8 – Статьи по колебаниям и оптике из журнала «Квант»

http://www.physel.ru/mainmenu-48.html – Полезные материалы по колебаниям и волнам.

http://koi.tspu.ru/waves/index.htm – А.Г.  Парфенов, Электронный мультимедиа-учебник по колебаниям и волнам

http://www.alleng.ru/d/phys/phys126.htm – Савельев, Курс общей физики. Т.1 – Механика, колебания и волны, молекулярная физика.

http://www.alleng.ru/d/phys/phys260.htm – А.Я. Исаков , В.В. Исакова.  Колебательные и волновые процессы, руководство по самостоятельной работе.

http://lib.mexmat.ru/books/6452 – Г.С. Ландсберг.  Элементарный учебник физики. Колебания и волны. Оптика. Атомная и ядерная физика.

http://elkniga.ucoz.ru/ – Г.Я. Мякишев, А.З. Синяков. Учебник по колебаниям и волнам для углубленного изучения в 11-м классе.

http://repetitor.mathematic.of.by/spravka_fizika.htm#M2 – Основные формулы по механике, в том числе – по колебаниям.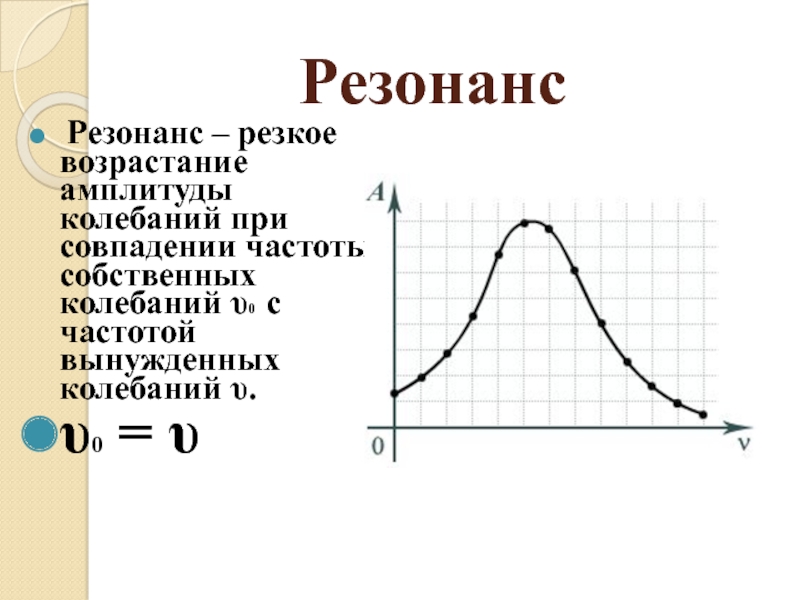

 http://www.alleng.ru/d/phys/phys194.htm – Л.Н. Коршунова. Колебания и волны. Пособия по решению задач.

 http://fizportal.ru/fluctuation-b – Банк задач по колебаниям и волнам с решениями.

http://www.alleng.ru/d/phys/phys127.htm – Савельев, Курс общей физики. Т.2 — Электричество и магнетизм. Волны. Оптика.

http://ligis.ru/effects/science/238/index.htm – Эффект механического резонанса.

http://schools.keldysh.ru/sch2216/students/spr_resh_zad/wob_wave/wob_wave1.htm – Задачи по колебаниям и волнам с решениями.

http://sgtnd.narod.ru/papers/TASKS.pdf – А.П. Кузнецов, А.Г. Рожнев, Д.И. Трубецков. Линейные колебания и волны. Сборник задач.

http://www.phys.kemsu.ru/viewpage.php?page_id=178 – Задачи по колебаниям и волнам повышенной сложности для старшеклассников.

http://physbook.ru/index.php/PPT._Маятник_Фуко – Маятник Фуко. История, модели.

Что такое резонанс вибрации?

Резонанс вибрации возникает, когда оборудование или продукт подвергаются внешней вынужденной вибрации, возникающей на одной или нескольких собственных частотах. Возникающая в результате вибрация продукта усиливается и может быть огромной! Вибрационные резонансы могут серьезно повредить изделия и значительно сократить срок их службы. Примеры вибрационных резонансов можно увидеть ниже и на нашей странице видео.

Собственная частота — это частота, с которой система будет колебаться после того, как внешняя сила будет приложена и затем удалена.Все объекты имеют собственную частоту вибрации. Большинство продуктов имеют много собственных частот.

Во время вибрационных испытаний с использованием вибрационных шейкеров для изучения резонансов в продуктах используется сканирование резонанса синусоидальной вибрации или поиск резонанса. При выполнении резонансного сканирования вибростол подвергает продукт управляемым вынужденным колебаниям в диапазоне частот, чтобы изучить ответные колебания продукта. Уровни вынужденной вибрации низкие (обычно ½ G) и считаются не повреждающими.Ускорение реакции продукта сравнивается с контролируемым ускорением стола. Любое усиление, равное или превышающее 2: 1, обычно считается резонансным. Частота, при которой это происходит, называется резонансной частотой . DES видел очень серьезные резонансные пики, превышающие 20 к 1! Типичный график резонансного сканирования показан ниже. Например, ускорение отклика продукта (DUT) составляет 2,288 G при 688,1 Гц. Ускорение стола (Control) составляет ½ G при 688.1 Гц. Таким образом, 688,1 Гц считается резонансной частотой, потому что отношение ускорения продукта к столу составляет 2,288G / 0,5G = 4,576, что больше 2: 1.

Некоторые спецификации испытаний на случайную вибрацию, такие как RTCA DO-160 (Условия окружающей среды и процедуры испытаний для бортового оборудования), требуют сканирования резонанса синусоидальной вибрации до и после испытания вдоль каждой оси. Любое существенное изменение результатов резонансного сканирования может быть признаком повреждения или поломки продукта.

Самым известным провалом, вызванным резонансом, было катастрофическое обрушение моста Tacoma Narrows Bridge, как видно из статьи нашего блога «Вибрационная реакция продукции». Когда изделия подвергаются вибрациям, близким к их собственным частотам, могут возникать усталостные разрушения из-за вибрационного резонанса. Компрессоры и двигатели — это примеры оборудования, которое может создавать значительные вибрации. Продукты, установленные рядом с таким оборудованием, не должны иметь собственных частот, близких к их рабочей скорости.

Чтобы предотвратить ранние отказы вашего продукта из-за усталости, DES может тестировать и анализировать вибрационный отклик вашего продукта, используя свои обширные знания и программное обеспечение для анализа вибрации.

Эта запись была размещена в рубрике Вибрационные и ударные испытания и помечена как Sinusoidal Vibration Testing, Vibration Testing, автор: DES. Добавьте в закладки постоянную ссылку.

Resonance | вибрация | Britannica

Resonance , в физике, относительно большой избирательный отклик объекта или системы, которые колеблются пошагово или по фазе, с приложенной извне колебательной силой. Впервые резонанс исследовали в акустических системах, таких как музыкальные инструменты и человеческий голос.Примером акустического резонанса является вибрация, возникающая в струне скрипки или фортепиано заданной высоты звука, когда рядом поется или играет музыкальная нота той же высоты.

Подробнее по этой теме

электричество: резонанс

Наиболее интересное состояние, известное как резонанс, возникает, когда фазовый угол равен нулю в уравнении (31), или, что эквивалентно, когда угловой …

Понятие резонанса было расширено по аналогии на некоторые механические и электрические явления. Известно, что механический резонанс, создаваемый в мостах ветром или марширующими солдатами, достиг размеров, достаточно больших, чтобы быть разрушительными, как в случае разрушения моста Tacoma Narrows Bridge ( qv ) в 1940 году. Космические аппараты, самолеты и надводные аппараты должны быть спроектированы таким образом, чтобы вибрации, вызываемые их двигателями или их движением по воздуху, были сведены к безопасному минимуму.

Резонанс в электрических системах имеет несколько иную природу. Его появление в частотно-чувствительных цепях (переменного тока) позволяет устройствам связи, оборудованным такими цепями, принимать сигналы одних частот и отклонять другие. В телевизионном приемнике, например, резонанс возникает, когда частота одного из входящих сигналов, достигающих цепи, близка к собственной частоте цепи, которая затем реагирует поглощением максимальной энергии из сигнала, когда ток в цепи возвращается назад и вперед в ногу с очень слабым током в антенне.

В ядерном масштабе была обнаружена форма резонанса, отчасти аналогичная определенному виду механического резонанса. Это явление, называемое магнитным резонансом, возникает, когда атомы или их ядра реагируют на приложение различных магнитных полей, испуская или поглощая электромагнитное излучение радио- и микроволнового диапазона. См. Также магнитный резонанс .

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас

Хиппи были правы: все дело в вибрации, дружище!

Почему одни вещи осознаются, а другие — нет? Крыса в сознании? Летучая мышь? Таракан? Бактерия? Электрон?

Все эти вопросы являются аспектами древней «проблемы разума и тела», которая в течение тысяч лет сопротивлялась в целом удовлетворительному выводу.

Проблема разума и тела претерпела серьезный ребрендинг за последние два десятилетия, и теперь она широко известна как «трудная проблема» сознания (обычно с большой буквы), после того как философ Нью-Йоркского университета Дэвид Чалмерс ввел этот термин в ставшее уже классическим слово 1995 года. paper и его книге 1996 года The Conscious Mind : In Search of a Fundamental Theory .

Перенесемся в настоящую эпоху, и теперь мы можем спросить себя: действительно ли хиппи решили эту проблему? Мой коллега Джонатан Шулер из Калифорнийского университета в Санта-Барбаре и я думаю, что они действительно это сделали, с радикальной интуицией, что все дело в вибрациях… человек. За последнее десятилетие мы разработали «резонансную теорию сознания», которая предполагает, что резонанс — другое слово для обозначения синхронизированных вибраций — лежит в основе не только человеческого сознания, но и физической реальности в целом.

Так как же были правы хиппи? Что ж, мы согласны с тем, что вибрации, резонанс, являются ключевым механизмом человеческого сознания, а также сознания животных в целом. И, как я расскажу ниже, они являются основным механизмом всех физических взаимодействий.

Все вещи в нашей вселенной постоянно находятся в движении, вибрируют. Даже объекты, которые кажутся неподвижными, на самом деле колеблются, колеблются, резонируют на различных частотах. Резонанс — это тип движения, характеризующийся колебаниями между двумя состояниями. И в конечном итоге вся материя — это просто колебания различных нижележащих полей.

Интересное явление возникает, когда различные вибрирующие предметы / процессы приближаются друг к другу: через некоторое время они часто начинают вибрировать вместе с одинаковой частотой. Они «синхронизируются», иногда это может показаться загадочным. Сегодня это называют феноменом спонтанной самоорганизации.

Изучение этого явления ведет к потенциально глубокому пониманию природы сознания и вселенной в целом.

ВСЕ ОБЪЯВЛЯЮТСЯ НА ОПРЕДЕЛЕННЫХ ЧАСТОТАХ

Стивен Строгац приводит различные примеры из физики, биологии, химии и нейробиологии, чтобы проиллюстрировать то, что он называет «синхронизацией» в своей книге 2003 года, также называемой Sync , в том числе:

• Светлячки определенных видов начинают синхронно мигать своими маленькими огнями в больших скоплениях светлячков, что может быть трудно объяснить с помощью традиционных подходов.
• Крупномасштабное возбуждение нейронов может происходить в мозгу человека на определенных частотах, при этом сознание млекопитающих, как считается, обычно связано с различными видами нейрональной синхронности.
• Лазеры образуются, когда фотоны одинаковой мощности и частоты испускаются вместе.
• Вращение Луны точно синхронизировано с ее орбитой вокруг Земли, поэтому мы всегда видим одно и то же лицо.

Резонанс — действительно универсальное явление, лежащее в основе того, что иногда может показаться загадочной тенденцией к самоорганизации.

Паскаль Фрис, немецкий нейрофизиолог из Института Эрнста Штрюнгмана, в течение последних двух десятилетий исследовал в своей широко цитируемой работе, как различные электрические паттерны, в частности, гамма-, тета- и бета-волны, работают вместе в мозге, чтобы произвести различные типы человеческого сознания.

Эти названия относятся к скорости электрических колебаний в различных областях мозга, которые измеряются электродами, размещенными на внешней стороне черепа. Гамма-волны обычно определяются как от 30 до 90 циклов в секунду (герц), тета — как ритм от 4 до 7 Гц, а бета — как 12.От 5 до 30 Гц. Это не жесткие ограничения — это практические правила — и они несколько различаются у разных видов.

Итак, тета и бета значительно медленнее гамма-волн. Но все три работают вместе, чтобы создавать или, по крайней мере, способствовать (точная взаимосвязь между электрическими моделями мозга и сознанием все еще остается предметом споров) различных типов человеческого сознания.

Фрис называет свою концепцию «коммуникацией через согласованность» или СТС. Для Фрайса все дело в нейронной синхронизации.Синхронизация с точки зрения общих частот электрических колебаний обеспечивает плавную связь между нейронами и группами нейронов. Без согласованности (синхронизации) входные данные поступают в случайные фазы цикла возбудимости нейрона и неэффективны или, по крайней мере, гораздо менее эффективны в общении.

Наша резонансная теория сознания основана на работах Фрайса и многих других в более широком подходе, который может помочь объяснить не только сознание человека и млекопитающих, но и сознание в более широком смысле.Мы также рассуждаем метафизически о природе сознания как более общего явления всей материи.

ВСЕ ВЕЩИ хотя бы немного сознательны?

Основываясь на наблюдаемом поведении окружающих нас сущностей, от электронов до атомов и молекул до бактерий, парамеций и мышей, летучих мышей, крыс и т. Д., Все вещи можно рассматривать как по крайней мере немного сознательные. На первый взгляд это звучит странно, но «панпсихизм» — точка зрения о том, что вся материя имеет некоторое связанное с ней сознание — становится все более принятой позицией в отношении природы сознания.

Панпсихист утверждает, что сознание (субъективность) не возникло; скорее, он всегда связан с материей, и наоборот (это две стороны одной медали), но разум, связанный с большей частью материи в нашей Вселенной, обычно очень прост. Электрон или атом, например, обладают лишь крошечной долей сознания. Но как материя «усложняется», так и ум усложняется, и наоборот.

Биологические организмы используют более быстрый обмен информацией с помощью различных биофизических путей, включая электрические и электрохимические пути. Эти более быстрые информационные потоки обеспечивают большее количество макромасштабных уровней сознания, чем это могло бы происходить в структурах аналогичного масштаба, таких как валуны или куча песка, просто потому, что в биологических структурах значительно больше взаимосвязей и, следовательно, больше «происходит», чем в валуне. или куча песка. У валунов и кучи песка есть только тепловые пути с очень ограниченной пропускной способностью.

Валуны и груды песка — это «простые агрегаты» или просто скопления более рудиментарных сознательных сущностей (вероятно, только на атомарном или молекулярном уровне), а не комбинации микросознательных сущностей, которые объединяются в макросознательную сущность более высокого уровня, которая это признак биологической жизни.

Соответственно, связь типа между резонирующими структурами является ключом к расширению сознания за пределы рудиментарного типа сознания, который, как мы ожидаем, может возникнуть в более основных физических структурах.

Центральный тезис нашего подхода заключается в следующем: особые связи, которые позволяют возникать макросознанию, являются результатом общего резонанса между многими составляющими микросознания. Скорость присутствующих резонансных волн является ограничивающим фактором, определяющим размер каждой сознательной сущности.

По мере того, как общий резонанс распространяется на все больше и больше составляющих, конкретная сознательная сущность становится больше и сложнее. Таким образом, общий резонанс в человеческом мозгу, который, например, достигает гамма-синхронизации, включает гораздо большее количество нейронов и нейронных связей, чем в случае одних только бета- или тета-ритмов.

Это резонирующие структуры вниз и вверх.

Наша резонансная теория сознания пытается предоставить единую основу, которая включает нейробиологию и изучение человеческого сознания, а также более фундаментальные вопросы нейробиологии и биофизики.Это касается сути различий, которые имеют значение, когда дело доходит до сознания и эволюции физических систем.

Это все о вибрациях, но это также о типах вибраций и, что наиболее важно, об общих вибрациях.

Вставьте это в трубку и выкурите… чувак.

Как определить и исправить состояние резонанса

Многие специалисты, работающие в области анализа вибрации, согласятся, что резонанс — очень частая причина чрезмерной вибрации оборудования.

Резонанс — это результат воздействия внешней силы, вибрирующей с той же частотой, что и собственная частота системы. Собственная частота характерна для каждой машины, конструкции и даже животных.

Часто резонанс можно спутать с собственной частотой или критической частотой. Если оборудование работает в состоянии резонанса, уровни вибрации значительно возрастут, что может вызвать отказ оборудования и простои завода. Поэтому важно, чтобы скорость работы оборудования была вне диапазона резонанса.

Как определить резонансную частоту

Многие методы могут использоваться для идентификации и / или подтверждения высокого уровня вибрации, вызванного резонансной частотой. Очень важно подтвердить явление резонанса по крайней мере двумя различными типами тестов, прежде чем пытаться его исправить. Мы рассмотрим несколько методов, обычно используемых в отрасли.

Методы подтверждения резонанса

Испытание на удар: Один из наиболее часто используемых методов измерения собственной частоты системы — это удар массой и измерение отклика.

Этот метод эффективен, поскольку при ударе в оборудование передается небольшая сила в большом диапазоне частот.

При выполнении этой техники важно попытаться воздействовать на разные места конструкции, поскольку все резонансные частоты конструкции всегда можно измерить, воздействуя в одном месте и измеряя в одном и том же месте.

При попытке определить резонансы машины следует проводить измерения как точки привода, так и точки передачи.

Этот тип теста должен выполняться при выключенном оборудовании. Таким образом можно легко определить собственные частоты оборудования (см. Рисунок 1).

Рис. 1. Испытание на удар, оборудование выключено

Испытание на удар с использованием молотка с инструментами: Это испытание в основном такое же, как и обычное испытание на удар, за исключением того, что для возбуждения системы используется молоток с инструментами. Этот молоток, оснащенный акселерометром на одном конце, используется в тандеме с датчиком, используемым для измерения вибрации.

Необходим двухканальный виброанализатор, в котором один канал подключен к оборудованному молотку, а другой — к датчику вибрации.

Используя этот метод, вы можете эффективно измерить силу, создаваемую системой отбойным молотком, и отклик на разных частотах. Когда фаза сдвигается на 90 градусов, частота, на которой это происходит, является собственной частотой (рисунок 2).

Преимущество использования этого метода заключается в том, что он позволяет контролировать фазовые сдвиги и согласованность. С помощью этой информации вы можете создавать рабочие формы отклонения для визуализации вибрирующего тела.

Рис. 2. Испытание на удар силовым молотком

Удержание пикового значения по инерции: Другой используемый метод — мониторинг уровня вибрации с помощью функции удержания пика при выключении оборудования, как обычно.

Уровень вибрации должен снижаться с постоянной скоростью. Если уровни вибрации начинают расти в любой момент, когда оборудование выключается, скорость, с которой возрастают амплитуды, является возможной собственной частотой (Рисунок 3).

Рис. 3. Удержание пика накатом вниз

Пиковая фаза выбега: Подобно удержанию пика выбега, этот тест должен проводиться во время отключения оборудования. Установив фотоприхватку и кусок световозвращающей ленты на вращающийся вал оборудования, вы сможете контролировать вибрацию и ее фазу.

Это позволит вам увидеть амплитуду и фазовый сдвиг на всех скоростях работы оборудования.Если нет резонанса, вызываемого скоростью поворота, уровни вибрации должны падать с постоянной скоростью.

Если вибрация достигает пика при определенной скорости, а фаза сдвигается на 180 градусов, это указывает на собственную частоту оборудования или конструкции. Фактическая собственная частота — это частота, расположенная в середине фазового сдвига (90 градусов) (Рисунок 4).

Рис. 4. Фаза пика выбега вниз

Формула для собственной частоты

Собственная частота — это частота свободных колебаний системы, при которой система вибрирует для рассеивания своей энергии.Собственная частота (ω n ) оборудования, выраженная в радианах в секунду, является функцией его жесткости (k) и его массы (m), как показано в следующем уравнении:

Если изменить любой из этих двух параметров, собственная частота изменится.

Как изменить собственную частоту?

Если мы хотим изменить собственную частоту тела, нам нужно изменить жесткость или массу. Увеличение массы или снижение жесткости приведет к снижению собственной частоты, в то время как уменьшение массы или увеличение жесткости приведет к увеличению собственной частоты.

Как мы можем управлять критически важным оборудованием, если мы не можем изменить собственную частоту?

Если мы не можем изменить жесткость или массу оборудования, нам предлагаются два возможных варианта. Одно из простых решений — изменить рабочую скорость оборудования на 20–30 процентов, но обычно это не вариант.

Другое решение — установить на оборудование динамический амортизатор, чтобы значительно снизить уровень вибрации оборудования.Динамический поглотитель представляет собой систему пружины и массы, которая устанавливается последовательно с резонансной системой для создания противофазной возбуждающей силы для эффективного противодействия начальной возбуждающей силе.

Резонанс, вероятно, является одной из пяти распространенных причин чрезмерной вибрации машины. Эффективное определение резонансной частоты может быть сложной задачей.

Нам необходимо точно определить собственную частоту, выполнив по крайней мере два различных теста, таких как испытание на удар, удержание пика выбегом, фазу пика выбега или испытание на удар с помощью отбойного молотка.

После подтверждения резонанса измените массу или жесткость оборудования, чтобы изменить его собственную частоту. Если это невозможно, попробуйте изменить скорость работы оборудования. Если это не удается, подумайте об установке динамического поглотителя, чтобы противодействовать начальной возбуждающей силе.

Номер ссылки

Фокс, Рэнди. «Динамические поглотители для решения резонансных задач».

Об авторе:
Ален Пеллегрино (Alain Pellegrino) — специалист по профилактическому обслуживанию в Laurentide Controls Ltd. Laurentide Controls, местный деловой партнер Emerson Process Management, является крупнейшим поставщиком решений для автоматизации в восточной части Канады. Для получения дополнительной информации посетите www.laurentide.com.

Как диагностировать и предотвратить резонанс

7 июня 2016 г.

Автор: Грант Слингер — инженер-механик II

Как консультантов по вибрации в Pioneer Engineering нас часто вызывают для исследования оборудования, которое демонстрирует чрезмерную вибрацию.Часто предполагается, что простая балансировка ротора решит проблему вибрации. Однако при дальнейшем исследовании нередко обнаруживается, что структурный резонанс является основной причиной чрезмерной вибрации, а балансировка не является жизнеспособным или долгосрочным решением проблемы. Это особенно часто встречается в оборудовании с регулируемой скоростью или оборудовании, скорость движения которого недавно изменилась. Но что такое резонанс и как правильно диагностировать и устранять проблему?

Что такое резонанс?

Есть два типа вибрации, которые необходимо учитывать при исследовании проблемы потенциального резонанса; вынужденная вибрация и свободная вибрация.Вынужденная вибрация возникает, когда объект вынужден вибрировать с определенной частотой под действием колебательного входа или силы (например, силы дисбаланса). Свободная вибрация возникает, когда объекту придают начальное смещение, а затем позволяют «звенеть» без внешней силы, которая удерживает его в движении. Частота, на которой естественно возникает эта свободная вибрация, известна как собственная частота. Если объект заставляют вибрировать на собственной частоте, возникает резонанс. Это то, что вызывает большие амплитуды вибрации, когда скорость движения машины равна или близка к собственной частоте, даже если входные силы низкие.

Как определить резонанс

Можно выполнить несколько различных полевых испытаний, чтобы убедиться, что резонанс действительно является причиной чрезмерной вибрации в системе. Двумя наиболее распространенными испытаниями являются испытание на удар в модальном режиме и сбор данных при запуске или выбеге.

Анализ запуска и останова

Данные о вибрации, собранные во время запуска или остановки машины, предоставляют обширную информацию, недоступную из данных установившегося состояния. Что наиболее важно, он дает возможность сравнивать амплитуду и фазу вибрации во всем диапазоне рабочих скоростей.Различные источники вибрации по-разному ведут себя при изменении скорости. Например, дисбаланс обычно вызывает амплитуду вибрации, которая экспоненциально увеличивается с увеличением скорости. Несоосность обычно вызывает вибрацию, которая линейно увеличивается с увеличением скорости. Однако резонанс характеризуется большим увеличением вибрации на резонансной частоте, но обычно более низкими амплитудами на всех других скоростях. На приведенном ниже каскадном графике показан пример типичной вибрации, проявляющейся во время запуска машины с собственной частотой конструкции в ее рабочем диапазоне скоростей.

Испытание на ударную вязкость

Часто известный как испытание на удар или модальный анализ, это метод, который позволяет нам экспериментально определить собственные частоты, формы колебаний и демпфирование испытательной конструкции. Если любая из вычисленных собственных частот находится в пределах или около диапазона рабочих скоростей машины, существует вероятность возникновения резонансного состояния. Обычно полевые модальные испытания проводятся с откалиброванным модальным ударным молотком. В наконечнике молотка имеется датчик нагрузки, который обеспечивает прямое измерение силы удара, приложенной к системе.Акселерометры размещены по всей испытательной конструкции для измерения отклика системы на удар молота. Спектр этого сигнала вызова может быть использован для определения собственных частот системы. Этот тест обычно выполняется при выключенной машине, однако расширенная обработка сигналов также может использоваться для усреднения вибрации в условиях работы и определения только свободной вибрации.

Как избежать резонанса

Как мы видели, резонанс возникает, когда собственная частота системы совпадает с ожидаемыми частотами вынужденной вибрации (например, дисбалансом), что может привести к серьезным уровням вибрации.Если установлено, что резонанс на самом деле является причиной чрезмерной вибрации, что можно сделать, чтобы остановить или минимизировать эффект резонансного состояния?

Собственная частота системы зависит от двух основных факторов; жесткость и масса. Если собственная частота равна w, w = sqrt (k / m).

Где k — жесткость, m — масса. Следовательно, чтобы изменить собственную частоту, нам нужно изменить либо k, либо m, либо оба. Обычно цель состоит в том, чтобы увеличить собственную частоту так, чтобы она была выше любых ожидаемых частот вибрации.Если собственная частота выше или значительно дальше от ожидаемых частот вибрации, резонанс, скорее всего, не будет возбужден. Эта теория лежит в основе любых структурных изменений, проводимых во избежание резонанса.

На практике следующие правила могут использоваться для сдвига собственной частоты и минимизации вибрационной характеристики системы;

1. Добавление жесткости увеличивает собственную частоту
2. Добавление массы уменьшает собственную частоту
3. Увеличение демпфирования снижает пиковый отклик, но расширяет диапазон отклика
4. Уменьшение демпфирования увеличивает пиковый отклик, но сужает диапазон отклика
5. Уменьшение амплитуды воздействия снижает резонансную реакцию

Если изменение собственной частоты признано лучшим решением, важно полностью охарактеризовать систему, прежде чем предпринимать какие-либо изменения конструкции.Недавно мы провели анализ вибрации при запуске небольшого здания, примыкающего к энергетической турбине, работающей на природном газе мощностью 200 МВт. При запуске было отмечено значительное увеличение вибрации в здании, когда турбина вышла из диапазона 700 об / мин. Модальные испытания здания на удар показали, что собственная частота равна той же частоте 700 циклов в минуту, что подтверждает наличие резонансного состояния. Можно легко предположить, просто добавив жесткость несущей конструкции здания позволит снизить амплитуды колебаний.Однако было известно, что первый критический вал ротора был около 1500 циклов в минуту. Если к конструкции вслепую добавить жесткость, она легко сместит собственную частоту в диапазон 1500 циклов в минуту, что значительно ухудшит вибрацию. В этом случае может быть лучше добавить к системе массу и сместить собственную частоту вниз до частоты, при которой силы ниже.

В Pioneer Engineering мы рекомендуем использовать проверенную модель анализа методом конечных элементов (FEA) для определения оптимальных изменений конструкции, чтобы исправить и избежать резонансных условий.Это позволяет нам сначала протестировать различные возможные изменения конструкции в компьютерном моделировании, прежде чем рекомендовать какие-либо структурные изменения. Просмотрите канал Pioneer для следующей статьи, озаглавленной «Важность проверки моделей FEA», чтобы получить дополнительную информацию о том, как Pioneer Engineering проверяет и тестирует конструктивные изменения, чтобы избежать резонанса.

Pioneer Engineering имеет обширный опыт проведения модального анализа для диагностики проблем резонанса, а также создания теоретических компьютерных моделей FEA для рекомендации проверенных структурных изменений.Для получения дополнительной информации о том, как модальный анализ и FEA могут быть реализованы на вашем предприятии, свяжитесь с нами по телефону 970-266-9005 или здесь.

Учебное пособие по физике: Резонанс

Цель урока 11 учебного курса по физике — развить понимание природы, свойств, поведения и математики звука и применить это понимание к анализу музыки и музыкальных инструментов. До сих пор в этом модуле были применены принципы звуковых волн к обсуждению ударов, музыкальных интервалов, акустики концертного зала, различий между шумом и музыкой, а также воспроизведения звука музыкальными инструментами.В Уроке 5 основное внимание будет уделено применению математических соотношений и концепций стоячей волны к музыкальным инструментам. Будут исследованы три основные категории инструментов: инструменты с вибрирующими струнами (которые будут включать струны гитары, струны скрипки и струны фортепиано), инструменты с открытой воздушной колонной (которые будут включать медные инструменты, такие как тромбон, и деревянные духовые инструменты, такие как флейта и блок-флейта), а также инструменты с воздушной колонной закрытого типа (которые будут включать в себя органную трубу и флаконы поп-бутылочного оркестра ). Четвертая категория — вибрационные механические системы (в которую входят все ударные инструменты) — обсуждаться не будет. Эти категории инструментов могут быть необычными для некоторых; они основаны на общности их моделей стоячих волн и математических соотношениях между частотами, производимыми инструментами.

Резонанс

Как было упомянуто в Уроке 4, музыкальные инструменты приводятся в колебательное движение с их естественной частотой, когда человек ударяет, ударяет, звенит, щиплет или как-то мешает объекту.Каждая собственная частота объекта связана с одним из множества паттернов стоячих волн, с помощью которых объект может вибрировать. Собственные частоты музыкального инструмента иногда называют гармониками инструмента. Инструмент можно заставить вибрировать на одной из своих гармоник (с одной из его моделей стоячих волн), если другой взаимосвязанный объект толкает его с одной из этих частот. Это известно как резонанс — когда один объект вибрирует с той же собственной частотой, что и второй объект, заставляет этот второй объект совершать колебательные движения.

Слово «резонанс» происходит от латинского и означает «резонировать» — звучать вместе с громким звуком. Резонанс — частая причина звукоизвлечения музыкальных инструментов. Одна из наших лучших моделей резонанса в музыкальном инструменте — резонансная трубка (полая цилиндрическая трубка), частично заполненная водой и вызываемая вибрацией с помощью камертона. Камертон — это объект, который заставил воздух внутри резонансной трубки войти в резонанс. Поскольку зубцы камертона вибрируют на своей собственной частоте, они создают звуковые волны, которые сталкиваются с отверстием резонансной трубки.Эти падающие звуковые волны, создаваемые камертоном, заставляют воздух внутри резонансной трубки вибрировать с той же частотой. Тем не менее, в отсутствие резонанса звук этих вибраций недостаточно громкий, чтобы его можно было различить. Резонанс возникает только тогда, когда первый объект вибрирует с собственной частотой второго объекта. Таким образом, если частота, на которой вибрирует камертон, не идентична одной из собственных частот воздушного столба внутри резонансной трубки, резонанса не произойдет, и два объекта не будут издавать звук вместе с громким звуком. Но положение уровня воды можно изменить, поднимая и опуская резервуар с водой, тем самым уменьшая или увеличивая длину столба воздуха. Как мы узнали ранее, увеличение длины колебательной системы (здесь воздух в трубке) увеличивает длину волны и уменьшает собственную частоту этой системы. И наоборот, уменьшение длины колебательной системы уменьшает длину волны и увеличивает собственную частоту. Таким образом, повышая и понижая уровень воды, собственная частота воздуха в трубке может быть согласована с частотой, с которой вибрирует камертон.Когда согласование достигается, камертон заставляет столб воздуха внутри резонансной трубки вибрировать с собственной частотой, и достигается резонанс. Результатом резонанса всегда является сильная вибрация, то есть громкий звук.

Еще одна распространенная физическая демонстрация, которая служит прекрасной моделью резонанса, — это знаменитая демонстрация «поющего жезла». В центре держится длинный полый алюминиевый стержень. Как опытный музыкант, учитель достает канифольный пакет, чтобы подготовиться к мероприятию.Затем с большим энтузиазмом он / она медленно проводит рукой по длине алюминиевого стержня, заставляя его звучать громко. Это пример резонанса. Когда рука скользит по поверхности алюминиевого стержня, трение между рукой и стержнем вызывает колебания алюминия. Колебания алюминия заставляют воздушный столб внутри стержня колебаться с собственной частотой. Сопоставление колебаний столба воздуха и одной из собственных частот поющего стержня вызывает резонанс.Результатом резонанса всегда является сильная вибрация, то есть громкий звук.

Знакомый шум моря , который слышится, когда морская ракушка подносится к уху, также объясняется резонансом. Даже в явно тихой комнате есть звуковые волны с разными частотами. Эти звуки в основном неслышны из-за их низкой интенсивности. Этот так называемый фоновый шум заполняет морскую ракушку, вызывая колебания внутри морской раковины. Но у морской раковины есть набор собственных частот, на которых она будет вибрировать. Если одна из частот в комнате заставляет воздух внутри ракушки вибрировать с собственной частотой, возникает резонансная ситуация. И всегда результатом резонанса является сильная вибрация, то есть громкий звук. На самом деле звук достаточно громкий, чтобы его можно было услышать. Поэтому в следующий раз, когда вы услышите звук моря в морской раковине, помните, что все, что вы слышите, — это усиление одной из множества фоновых частот в комнате.

Резонансные и музыкальные инструменты

Музыкальные инструменты воспроизводят выбранные звуки таким же образом. Медные инструменты обычно состоят из мундштука, прикрепленного к длинной трубке, наполненной воздухом. Трубку часто изгибают, чтобы уменьшить размер инструмента. Металлическая трубка служит просто контейнером для столба воздуха. Именно вибрации этой колонны производят звуки, которые мы слышим. Длину вибрирующего столба воздуха внутри трубки можно регулировать, сдвигая трубку для увеличения и уменьшения ее длины, или открывая и закрывая отверстия, расположенные вдоль трубки, чтобы контролировать, где воздух входит и выходит из трубки. Медные духовые инструменты включают в себя вдувание воздуха в мундштук. Вибрации губ относительно мундштука создают диапазон частот. Одна из частот в диапазоне частот соответствует одной из собственных частот столба воздуха внутри медного инструмента.Это вызывает резонансные колебания воздуха внутри колонны. Результатом резонанса всегда является сильная вибрация, то есть громкий звук.

Деревянные духовые инструменты работают аналогичным образом. Только источником вибраций являются не губы музыканта, соприкасающиеся с мундштуком, а вибрация трости или деревянной полоски. Работа деревянных духовых инструментов часто моделируется на уроках физики с помощью пластиковой соломинки. Концы соломки обрезаются ножницами, образуя конический язычок . Когда воздух проходит через трость, трость вибрирует, создавая турбулентность с диапазоном частот колебаний. Когда частота колебаний язычка совпадает с частотой колебаний столба воздуха в соломе, возникает резонанс. И еще раз, результатом резонанса является сильная вибрация — язычок и столб воздуха издаются вместе, создавая громкий звук. Как будто этого было недостаточно, длину соломинки обычно сокращают, отрезая небольшие кусочки от противоположного конца. По мере того, как соломинка (и столб воздуха, который в ней содержится) укорачивается, длина волны уменьшается, а частота увеличивается.По мере укорачивания соломы наблюдаются все более высокие шаги. Деревянные духовые инструменты издают звуки, похожие на соломенную демонстрацию. Вибрирующий язычок заставляет столб воздуха колебаться на одной из собственных частот. Только для духовых инструментов длина столба воздуха регулируется путем открытия и закрытия отверстий в металлической трубке (поскольку трубки немного трудно разрезать и их слишком дорого заменять каждый раз, когда их разрезают).

Резонанс — причина образования звука в музыкальных инструментах.В оставшейся части Урока 5 математика стоячих волн будет применена для понимания того, как резонирующие струны и воздушные колонны создают свои определенные частоты.

Учебное пособие по физике: Принудительная вибрация

Музыкальные инструменты и другие предметы приводят в действие вибрацию с их естественной частотой, когда человек ударяет, ударяет, звенит, щиплет или каким-либо образом трогает предмет.Например, струна гитары играет или щиплет; при нажатии на педаль по струне фортепьяно бьют молотком; а зубцы камертона ударяются резиновым молотком. В любом случае человек или вещь вкладывают энергию в инструмент путем прямого контакта с ним. Эта подводимая энергия возмущает частицы и заставляет объект совершать колебательные движения — с его собственной частотой.

Если вы возьмете гитарную струну и натянете ее до заданной длины и заданной плотности и попросите друга дернуть ее, вы услышите шум; но шум даже не был бы близок по сравнению с громкостью, производимой акустической гитарой. С другой стороны, если струна прикреплена к звуковой коробке гитары, вибрирующая струна способна заставить звуковую коробку вибрировать с той же собственной частотой. Звуковая коробка, в свою очередь, заставляет частицы воздуха внутри коробки совершать колебательные движения с той же собственной частотой, что и струна. Вся система (струна, гитара и замкнутый воздух) начинает вибрировать и заставляет окружающие частицы воздуха совершать колебательные движения. Стремление одного объекта заставить другой объект , примыкающий к или взаимосвязанному объекту , совершать колебательное движение, называется принудительной вибрацией .В случае гитарной струны, установленной на звуковой коробке, тот факт, что площадь поверхности звуковой коробки больше, чем площадь поверхности струны, означает, что большее количество окружающих частиц воздуха будет вынуждено вибрировать. Это вызывает увеличение амплитуды и, следовательно, громкости звука.

Тот же принцип принудительной вибрации часто демонстрируется в классе физики с помощью камертона. Если вы держите камертон в руке и ударяете резиновым молотком, раздается звук, когда зубцы камертона приводят окружающие частицы воздуха в колебательное движение.Звук, производимый камертоном, едва слышен студентам из задних рядов комнаты. Однако, если камертон установлен на панель белой доски или стеклянную панель диапроектора, панель начинает вибрировать с той же собственной частотой камертона. Камертон заставляет окружающие частицы стекла (или винила) совершать колебательные движения. Вибрирующая доска или панель диапроектора, в свою очередь, заставляет окружающие частицы воздуха совершать колебательные движения, в результате чего увеличивается амплитуда и, следовательно, громкость звука.Этот принцип принудительной вибрации объясняет, почему демонстрационные камертоны установлены на звуковой коробке, почему коммерческий механизм музыкальной шкатулки установлен на деке, почему в гитаре используется звуковая коробка и почему струна фортепиано прикреплена к деке. Более громкий звук всегда производится, когда сопутствующий объект с большей площадью поверхности вынужден вибрировать с той же собственной частотой.

Резонанс

Теперь рассмотрим похожую ситуацию, которая напоминает другую обычную демонстрацию физики.Предположим, что камертон установлен на звуковом ящике и установлен на столе; и предположим, что вторая система камертона / звукового ящика, имеющая ту же собственную частоту (скажем, 256 Гц), размещена на столе рядом с первой системой. Ни один из камертонов не вибрирует. Предположим, что первый камертон ударяется резиновым молотком, и зубцы начинают вибрировать с собственной частотой — 256 Гц. Эти колебания заставляют его звуковую коробку и воздух внутри звуковой коробки вибрировать с одинаковой собственной частотой 256 Гц.Частицы окружающего воздуха приводятся в колебательное движение с той же собственной частотой 256 Гц, и каждый ученик в классе слышит звук. Затем захватывают зубцы камертона, чтобы предотвратить их вибрацию, и примечательно, что звук с частотой 256 Гц все еще слышен. Только теперь звук издает второй камертон — тот, по которому не ударили молотком. Удивительный!! Демонстрация часто повторяется, чтобы убедиться, что наблюдаются такие же удивительные результаты. Они есть! Что случилось?

В этой демонстрации один камертон заставляет другой камертон совершать колебательные движения с той же собственной частотой.Две вилки соединены частицами окружающего воздуха. Когда частицы воздуха, окружающие первую вилку (и подсоединенную к ней звуковую коробку), начинают вибрировать, создаваемые ею волны давления начинают с периодической и регулярной частотой 256 Гц воздействовать на второй камертон (и подключенный к нему звуковой ящик). Энергия, переносимая этой звуковой волной по воздуху, настроена на на частоту второго камертона. Поскольку входящие звуковые волны имеют ту же собственную частоту, что и второй камертон, камертон легко начинает вибрировать на своей собственной частоте.Это пример резонанса — когда один объект вибрирует с той же собственной частотой, что и второй объект, заставляет этот второй объект совершать колебательные движения.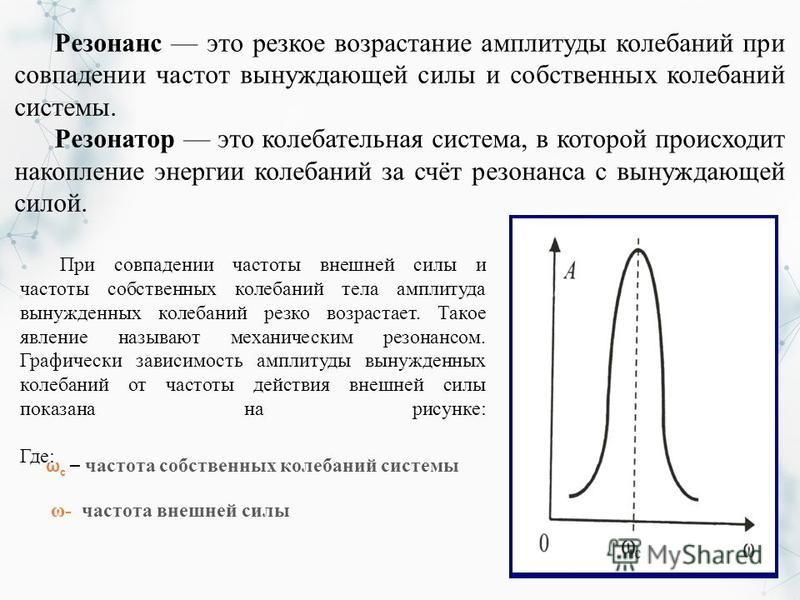

Результатом резонанса всегда является сильная вибрация. Независимо от вибрирующей системы, если возникает резонанс, возникает сильная вибрация. Это часто демонстрируется на уроках физики со странной механической системой, напоминающей перевернутый маятник. Аппарат состоит из трех наборов из двух одинаковых пластиковых бобин, установленных на очень эластичной металлической стойке, которые, в свою очередь, прикреплены к металлической планке.Каждый металлический стержень и прикрепленный к нему боб имеют разную длину, что придает ему разную собственную частоту колебаний. Бобы часто имеют цветовую маркировку, чтобы различать их; они окрашены в красный, синий и зеленый цвета (набор из трех цветов, который будет важен позже в Учебнике по физике). Красные бобышки установлены на более длинных стойках, и у них самая низкая собственная частота колебаний. Синие бобы устанавливаются на более короткие стойки и имеют самую высокую собственную частоту колебаний.(Обратите внимание на соотношение длины волны и частоты, которое обсуждалось ранее. ) Когда красный боб нарушен, он начинает вибрировать с собственной частотой. Это, в свою очередь, заставляет прикрепленную планку вибрировать с той же частотой; и это заставляет другой прикрепленный красный боб вибрировать с той же собственной частотой. Это резонанс — один боб, колеблющийся с заданной частотой, заставляет второй объект с той же собственной частотой колебаться. В то время как зеленый и синий бобы нарушались вибрациями, передаваемыми через металлический стержень, резонировать мог только красный боб.Это потому, что частота первого красного боба настроена на частоту второго красного боба; они имеют одинаковую собственную частоту. В результате второй красный боб начинает вибрировать с огромной амплитудой.

Смотри!

Другая распространенная демонстрация резонанса в классе — это пластиковая трубка, содержащая столб воздуха. Длина столба воздуха регулировалась подъемом и опусканием резервуара с водой (окрашенного в красный цвет).Подъем и опускание резервуара регулируют высоту воды в трубе открытого воздуха и, таким образом, регулируют длину столба воздуха внутри трубы. По мере уменьшения длины столба воздуха собственная частота столба воздуха увеличивается. (Снова обратите внимание на соотношение длины волны и частоты, которое обсуждалось ранее.) При регулировке высоты жидкости в трубке вибрирующая вилка удерживается над воздушным столбом трубки. Когда собственная частота столба воздуха настроена на на частоту вибрирующего камертона, возникает резонанс и возникает громкий звук.Удивительно, но вибрирующий камертон заставляет частицы воздуха в столбе воздуха совершать колебательные движения. Еще раз в этой резонансной ситуации камертон и столб воздуха имеют одинаковую частоту колебаний.

В заключение, резонанс возникает, когда два взаимосвязанных объекта имеют одинаковую частоту колебаний.