Радиотехника в аэрологии. Колебания резонанс

Вынужденные колебания и резонанс

Вынужденные колебания и резонанс

Возбудить колебания маятника или иной колебательной системы можно и не так, как было показано на рис. 21, а с помощью посторонних колебаний, имеющих частоту, близкую или равную частоте свободных колебаний этой системы.

Если кратким и легким дуновением воздуха вывести маятник из положения покоя и затем подвергать- его таким же повторным воздействиям в моменты, когда он удаляется, раскачать его можно очень сильно. Равным образом, подводя к контуру слабые переменные напряжения частоты, равной частоте свободных колебаний контура, можно получить значительно увеличенные напряжения возникающих при этом в контуре вынужденных электрических колебаний.

Возбуждение усиленных колебаний в колебательных системах с помощью слабых приходящих колебаний определенной частоты называется резонансом.

В радиотехнике резонанс имеет огромное значение, причем используются два вида резонансных колебательных контуров: контура резонанса напряжений, или последовательного резонанса, и контура резонанса токов, или параллельного резонанса.

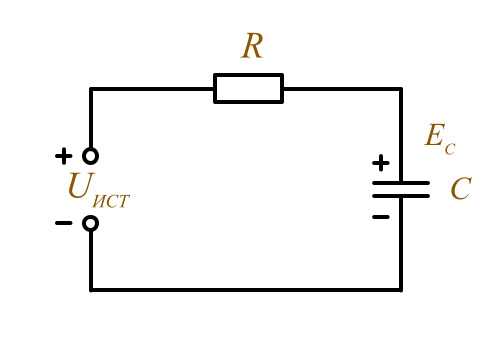
На рис. 22 а изображен контур последовательного резонанса, питаемый от источника переменной э. д. с. изменяющейся частоты. Рассмотрим, как будут изменяться емкостное сопротивление конденсатора и индуктивное сопротивление катушки в зависимости от частоты питающего тока. Для этого обратимся к графику на рис. 22 б. По оси абсцисс откладываются частоты f, по оси ординат — значения Хl и Хс.

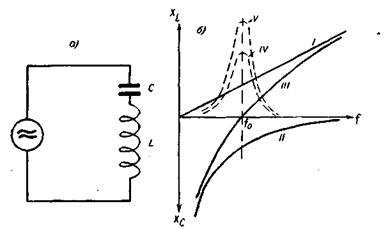
Рис. 22. Контур последовательного резонанса (я) и графики реактивных сопротивлений (б).

Из формулы полного сопротивления последовательной цепи переменному току (импеданца)

следует, что емкостные сопротивления должны быть представлены на графике в виде отрицательных величин.

Суммируя ординаты кривых XL (I) и Хс (II), получим кривую III изменения реактивного сопротивления контура, пересекающую ось частот в точке f0. При частоте f0,  являющейся резонансной, реактивные элементы контура XL и Хс компенсируют друг друга, и проходящий через контур ток будет иметь максимальное значение, ограничиваемое лишь величиной R внутреннего сопротивления источника Е.

Подобные друг другу пунктирные кривые IV а V иллюстрируют изменения тока и напряжения в контуре при изменениях частоты. Они называются резонансными кривыми. Чем меньше R, тем отчетливее появляется резонанс, тем острее кривые резонанса. Значение f0 легко выразить через L и С из условия XL — Хс = 0, приняв, что

Как можно теперь видеть, резонансная частота выражается  через данные контура точно так же, как частота собственных колебаний. Сделав параметры контура L или С произвольно изменяемыми, его можно настраивать на ту или иную частоту резонанса.

В системе последовательно соединенных L и С мгновенные значения тока одинаковы для каждого участка цепи. Поскольку напряжение на катушке опережает ток на 90°, а напряжение на конденсаторе отстает от тока на 90°, суммарный сдвиг фаз между напряжениями катушки и конденсатора оказывается равным 180° (или π). Вследствие указанного на конденсаторе и на катушке вблизи области настройки в резонанс с питающим напряжением Е возникают напряжения Ес и EL, в несколько раз превосходящие Е, что создает для конденсатора, опасность пробоя.

Колебательные контуры из последовательно включенных. L и С называют контурами последовательного резонанса, а резонанс в них — резонансом напряжений.

Во всех реальных случаях последовательно с L и С включено не только внутреннее сопротивление источника э.д.с. R, но и неизбежные сопротивления потерь в соединительных, проводах и в катушке. На частоту резонанса последовательного контура вся эта сумма омических сопротивлений влияния не оказывает.

При параллельном соединении L и С также образуется электрический колебательный контур с резонансными свойствами, проявляющимися при его питании токами различных частот. На рис. 23 изображена схема такого контура, питаемого от генератора э.д.с. изменяемых частот, и график, помогающий, правильно истолковать происходящие с изменениями частоты изменения свойств контура. В отличие от рис. 22 здесь рассматриваются не сопротивления, а проводимости индуктивной и емкостной ветвей, причем мгновенные значения Е для них одинаковы и по абсолютной величине, и по фазе, а токи сдвинуты по фазе на 180° (в емкостной — опережение на 90°,. в индуктивной — отставание на 90°).

Полученная после суммирования (кривая I) и ώС (кривая II) суммарная кривая III общей реактивной проводимости параллельного соединения L и С пересекает ось абсцисс в точке f0, где абсолютные значения  равны между собой:

откуда

Этот результат следует понимать так, что и в контуре из шараллельно соединенных L и С резонанс наступает лишь в том случае, если частота питающего напряжения равна собственной частоте контура, причем в момент резонанса колебательный контур обладает по отношению к источнику питающей его э.д.с. максимальным сопротивлением. Из графика рис. 23 следует, что это сопротивление равно бесконечности, но в действительности так никогда не бывает, потому что из-за наличия омического сопротивления у соединительных проводов и у катушки, а также из-за потерь в конденсаторе, в питающей цепи и при резонансе остается какой-то ток, принимающий лишь свое минимальное значение.

Рис. 23. Контур параллельного резонанса (а) и графики реактивных проводимостей (б).

Ток в самом контуре в момент резонанса максимален. В зависимости от суммарной величины потерь он может во много раз превосходить ток в питающей цепи, вследствие чего случай параллельного резонанса называют также резонансом токов. Резонансные кривые для контуров параллельного резонанса имеют вид, вполне подобный кривым последовательного резонанса.

Омическое сопротивление, неизбежно присутствующее в контуре, при параллельном резонансе ограничивает величину резонансных контурных токов и, кроме того, в отличие от случая последовательного резонанса, оказывает некоторое влияние на резонансную частоту, уменьшая ее с возрастанием R. Точный учет указанного влияния можно произвести по формуле

В большинстве случаев практики вычитаемое под знаком радикала является величиной, весьма малой в сравнении с 1/LC поэтому в приблизительных расчетах влиянием R на  f0 можно пренебрегать.

Колебательные контуры, возбуждаясь при резонансе, создают на своих элементах — конденсаторах и катушках — напряжения, во много раз превосходящие величину возбуждающих напряжений. Накапливая колебательную энергию за счет явления резонанса, контуры „усиливают" подводимые к ним слабые напряжения, причем усиление тем больше, чем меньше потерь в катушках.

Количественный учет „усилительной способности" контуров производится оценкой добротности Q их контурных катушек. Если индуктивность катушки L, а омическое сопротивление при частоте f0 R, то

Добротность обычных катушек самоиндукции, применяемых в контурах радиоприемников, имеет значения от 50 до 500. Если Q превышает 100, — это уже хорошая катушка. У плохих катушек Q≤20.

Добротность Q называют иногда „множителем вольтажа", потому что выражающее ее число показывает, во сколько раз напряжение на катушке превысит возбуждающее напряжение при резонансе.

Пример. Катушка контура простейшего радиоприемника обладает добротностью Q = 120. Какое напряжение Еk возникнет на колебательном контуре приемника при настройке на радиостанцию, создающую возбуждающее напряжение Е в 5 мв?

Решение.

Смотрите также

aerologiya.ru

Резонанс - Наука и образование

Рассматривая колебания маятника, мы установили, что возможны два типа колебаний: 1) собственные колебания, частота которых определяется свойствами самого колеблющегося тела, и 2) вынужденные колебания, частота которых равна частоте изменений внешней силы, действующей на тело,

Случай, когда частота собственных колебаний тела совпадает с частотой вынужденных колебаний, особенно важен. Рассмотрим его на опыте.

На рисунке изображена установка, позволяющая наблюдать вынужденные колебания. К верёвочной растяжке подвешены маятники А и В. Длину маятника А можно изменять, подтягивая рукой, свободный конец нити, на которой он висит.

Когда маятник А находится в положении, обозначенном на рисунке цифрой I, приведём его в колебание. Мы заметим, что и маятник В придёт в колебание. Будем теперь изменять длину маятника А и наблюдать за маятником В. Отмечая при разных длинах маятника А амплитуду маятника В, можно обнаружить, что с изменением длину маятника А меняемся амплитуда колебаний маятника В. Наибольшего значения амплитуда колебания маятника В достигнет тогда, когда длины обоих маятников будут одинаковы.

Это явление находит очень простое объяснение. Всем хорошо известно, что при раскачивании какого-нибудь подвешенного на верёвке тела (например, качелей) необходимо подталкивать его извне, хотя и с небольшой силой, но действующей на тело в такт с его собственными колебаниями. Любой же несогласованный толчок (против хода) вызовет уменьшение амплитуды.

Точно так же протекает явление и в нашем опыте с маятниками. Изменяя длину маятника А, мы тем самым изменяем частоту изменений вынуждающей силы, действующей на маятник В. Причиной, вынуждающей колебания маятника В, являются периодические колебания растяжки с частотой колебания маятника А. Чем ближе частота изменений вынуждающей силы подходит к собственной частоте колебаний маятника В, тем большее число импульсов силы будет способствовать увеличению амплитуды маятника В. Вынужденное колебание маятника В будет иметь наибольшую амплитуду тогда, когда собственная его частота будет равна частоте изменений вынуждающей силы, в данном случае частоте колебаний маятника А (положение II на рисунке). В этом случае говорят о резонансе.

Резонансом называется явление резкого возрастания амплитуды вынужденных колебаний тела, когда частота изменений вынуждающей силы равна частоте собственных колебаний тела.

Если частота вынуждающих колебаний, т. е. частота колебаний маятника А, будет возрастать И. далее, то амплитуда вынужденных колебаний маятника В снова будет уменьшаться и при очень большой частоте вынуждающих колебаний станет близкой к нулю.

На рисунке показан график зависимости амплитуды вынужденных колебаний от частоты изменений вынуждающей периодической силы. На этом рисунке по горизонтальной оси (оси абсцисс) отложены частоты вынужденных колебаний, а на вертикальной оси (оси ординат) – соответствующие им амплитуды колебаний тела. Когда частота вынужденных колебаний (fвын) становится равной частоте собственных колебаний тела (fсобств), амплитуда колебаний достигает наибольшей величины. На рисунке такая амплитуда изображена ординатой точки К. Частоту fвын = fсобств называют резонансной частотой. При отклонении частоты периодически изменяющейся вынуждающей силы от резонансной частоты (влево или вправо от неё) амплитуда колебаний уменьшается.

Явление резонанса наглядно можно продемонстрировать на следующем простом опыте. Подвесим к стойке массивный маятник А и рядом с ним несколько других маятников разной длины.

Выведем маятник А из положения равновесия. Колебания этого маятника передадутся стойке, а последняя будет действовать с частотой, равной частоте маятника А, на другие маятники. Мы увидим, что только маятник С, длина которого равна длине маятника А, сильно раскачается. Этот маятник находится в резонансе с маятником А. Маятники же D и Е будут колебаться с очень малой амплитудой, а самый короткий маятник В почти совсем не будет колебаться; его частота далека от частоты колебаний маятника А.

Значение резонанса в технике. Явление резонанса приходится учитывать в технике. Рассмотрим некоторые примеры.

Резонанс в технике

Вследствие неравномерности хода всякая машина совершает небольшие колебания, частота которых равна числу оборотов вала машины в секунду. Если эта частота совпадёт с собственной частотой упругих колебаний, которые могут совершать различные части машины или опора, на которой установлена машина, то наступит резонанс. Амплитуды этих вынужденных колебаний могут оказаться столь большими, что произойдёт катастрофа – разрушится машина или опора.

Случалось, что вследствие резонанса разваливался на части самолёт в воздухе, а под действием периодических толчков колёс поезда на стыках рельсов обрушивался железнодорожный мост.

Разительный случай резонанса имел место в 1907 году, когда в зале заседания Государственной думы в Таврическом дворце (в Петербурге) обвалилась вся штукатурка с потолка. Виновником этой катастрофы оказался небольшой мотор, установленный под потолком и служивший для вентиляции.

Можно привести много примеров поломок коленчатых валов машин, гребных винтов у судов, воздушных винтов у самолётов, которые вызывались явлением резонанса. Во всех таких случаях с резонансом приходится бороться.

Однако резонанс играет в технике и положительную роль. Явление резонанса, как мы увидим дальше, используется в устройстве многих приборов.

scibio.ru

Вынужденные колебания и резонанс

Если на тело с массой m действуют упругая сила Fу = -kX, сила трения и внешняя периодическая сила , то оно совершает вынужденные колебания. В этом случае дифференциальное уравнение движения имеет вид

, или, (33)

где,- коэффициент затухания,- собственная частота свободных незатухающих колебаний тела,F0 – амплитуда, ω – частота периодической силы.

В начальный момент времени работа внешней силы превосходит энергию, которая расходуется на трение (рис. 6). Энергия и амплитуда колебаний тела будет возрастать до тех

пор, пока вся сообщаемая внешней силой энергия не будет целиком расходоваться на преодоление трения, которое пропорционально скорости. Поэтому устанавливается равновесие, при котором сумма кинетической и потенциальной энергии оказывается постоянной. Это условие характеризует стационарное состояние системы.

В таком состоянии движение тела будет гармоническим с частотой, равной частоте внешнего возбуждения, но вследствие инерции тела его колебания будут сдвинуты по фазе по отношению к мгновенному значению внешней периодической силы:

X = AСos(ωt + φ). (34)

В отличие от свободных колебаний амплитуда А и фаза  вынужденных колебаний

зависят не от начальных условий движения, а будут определяться только свойствами колеблющейся системы, амплитудой и частотой вынуждающей силы:

, (35)

. (36)

Видно, что амплитуда и сдвиг по фазе зависят от частоты вынуждающей силы (рис.7 и 8).

Характерной особенностью вынужденных колебаний является наличие резонанса. Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте свободных незатухающих колебаний тела ω0носит название механического резонанса. Амплитуда колебаний тела при резонансной частотедостигает максимального значения:

(37)

По поводу резонансных кривых (см. рис. 7) сделаем следующие замечания. Если ω→ 0, то все кривые (см. также (35)) приходят к одному и тому же, отличному от нуля, предельному значению , так называемому статистическому отклонению. Если ω→ ∞, то все кривые асимптотически стремятся к нулю.

При условии малого затухания (β2 ‹‹ω02) резонансная амплитуда (см.(37))

(37а)

При этом условии возьмем отношение резонансного смещения к статическому отклонению.

,

из которого видно, что относительное увеличение амплитуды колебаний при резонансе определяется добротностью колебательной системы. Здесь добротность является по сути коэффициентом усиления отклика системы и при малом затухании может достигать больших значений.

Это обстоятельство обусловливает огромное значение явления резонанса в физике и технике. Его используют, если хотят усилить колебания, например, в акустике – для усиления звучания музыкальных инструментов, в радиотехнике – для выделения нужного сигнала из множества других, отличающихся по частоте. Если резонанс можетпривести к нежелательному росту колебаний, пользуются системой с малой добротностью.

СВЯЗАННЫЕКОЛЕБАНИЯ

Источником внешней периодической силы может служить вторая колебательная система, упруго связанная с первой. Обе колебательные системы могут действовать одна на другую. Так, например, случай двух связанных маятников (рис. 9).

Система может совершать как синфазные (рис. 9б), так и противофазные (рис. 9с) колебания. Такие колебания называются нормальным типом или нормальной модой колебаний и характеризуются своей собственной нормальной частотой. При синфазных колебаниях смещения маятников во все моменты времени Х1 = Х2, а частота ω1 точно такая же, как частота отдельно взятого маятника . Это объясняется тем, что легкая пружина находится в свободном состоянии и не оказывает никакого влияния на движение. При противофазных колебаниях во все моменты времени – Х1 = Х2. Частота таких колебаний больше и равна , так как пружина, обладающая жесткостьюk и осуществляющая связь, все время находится то в растянутом, то в сжатом состоянии.

Любое состояние нашей связанной системы, в том числе и начальное смещение Х (рис. 9а), можно представить в виде суперпозиции двух нормальных мод:

и.

Если привести систему в движение из начального состояния Х1 = 0, , Х2 = 2А, ,

то смещения маятников будут описываться выражениями:

,

(38)

На рис. 10 представлено изменение смещения отдельных маятников во времени.

Частота колебаний маятников равна средней частоте двух нормальных мод

(39)

а их амплитуда изменяется по закону синуса или конуса с меньшей частотой, равной половине разности частоты нормальных мод

. (40)

Медленное изменение амплитуды с частотой, равной половине разности частот нормальных мод, называется “биениями” двух колебаний с почти одинаковыми частотами. Частота “биений” равна разности ω1 –ω2 частот, (а не половине этой разности), поскольку максимум амплитуды 2А достигается дважды за период, соответствующий частоте

Отсюда период биений оказывается равным

(41)

При биениях между маятниками происходит обмен энергией. Однако полный обмен энергией возможен только тогда, когда обе массы одинаковы и отношение (ω1+ω2 / ω1-ω2) равно целому числу. Необходимо отметить один важный момент: хотя отдельные маятники могут обмениваться энергией, обмен энергией между нормальными модами отсутствует.

Наличие таких колеблющихся систем, которые взаимодействуют между собой и способны передавать друг другу свою энергию, составляют основу волнового движения.

ВОЛНЫ

Колеблющееся материальное тело, помещенное в упругую среду, увлекает за собой и приводит в колебательное движение прилегающие к нему частицы среды. Благодаря наличию упругих связей между частицами колебания распространяются с характерной для данной среды скоростью по всей среде.

Процесс распространения колебаний в упругой среде называется волной. Различают два основных типа волн: продольные и поперечные. В продольных волнах частицы среды колеблются вдоль направления распространения волны, а в поперечных – перпендикулярно к направлению распространения волны. Не во всякой упругой среде возможно распространение поперечной волны. Поперечная упругая волна возможна лишь в таких средах, в которых имеет место упругая деформация сдвига. Например, в газах и жидкостях распространяются только продольные упругие волны (звук).

Геометрическое место точек среды, до которых к данному моменту времени дошло колебание, называется фронтом волны. Фронт волны отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникали. В зависимости от формы фронта различают волны плоские, сферические, цилиндрические и т.д.

Уравнение плоской волны, распространяющейся без потерь в однородной среде, имеет вид

, (42)

где ξ(Х,t) – смещение частиц среды с координатой Х от положения равновесия в момент времени t, А – амплитуда, - фаза волны,- круговая частота колебания частиц среды,v – скорость распространения волны.

Длиной волны λ называется расстояние между точками, колеблющимися с разностью фаз 2π, другими словами, длиной волны называется путь, проходимый любой фазой волны за один период колебаний:

λ = vT, (43)

фазовая скорость, т.е. скорость распространения данной фазы:

λ / Т (44)

Волновое число – число длин волн, укладывающихся на длине 2π единиц:

k = ω / v = 2π / λ. (45)

Подставляя эти обозначения в (42), уравнение плоской бегущей монохроматической волны можно представить в виде

(46)

Отметим, что уравнение волны (46) обнаруживает двойную периодичность по координате и времени. Действительно, фазы колебаний совпадают при изменении координаты на λ и при

изменении времени на Т (период). Поэтому изобразить графически волну на плоскости нельзя. Часто фиксируют время t и на графике представляют зависимость смещения ξ от координаты Х, т.е. мгновенное распределение смещений частиц среды вдоль направления распространения волны (рис.11). Разность фаз Δφ колебаний точек среды зависит от расстояния ΔХ =Х2 – Х1 между этими точками

(47)

Если волна распространяется противоположно направлению Х, то уравнение обратной волны запишется в виде:

ξ (Х,t) = АСos(ωt + kX). (48)

СТОЯЧИЕ ВОЛНЫ – это результат особого вида интерференции волн. Они образуются при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами.

Уравнения двух плоских волн, распространяющихся вдоль оси Х в противоположных направлениях, имеют вид:

ξ1 =АСos(ωt – kX)

ξ2 = AСos(ωt + kX). (49)

Складывая эти уравнения по формуле суммы косинусов и учитывая, что k = 2π / λ, получим уравнение стоячей волны

. (50)

Множитель Сos ωt показывает, что в точках среды возникает колебание той же частоты ω с амплитудой , зависящей от координаты Х рассматриваемой точки. В точках среды, где

, (51)

амплитуда колебаний достигает максимального значения, равного 2А. Эти точки называются пучностями. Из выражения (51) можно найти координаты пучностей:

(52)

В точках, где , (53)

амплитуда колебаний обращается в нуль. Эти точки называются узлами. Координаты узлов

. (54)

Расстояния между соседними пучностями и соседними узлами одинаковы и равны λ/2. Расстояние между узлом и соседней пучностью равно λ / 4. При переходе через узел множительменяет знак, поэтому фазы колебаний по разные стороны от узла отличаются на π, т.е. точки, лежащие по разные стороны от узла, колеблются в противофазе. Точки, заключенные между двумя соседними узлами, колеблются с разными амплитудами, но с одинаковыми фазами.

Распределение узлов и пучностей в стоячей волне зависит от условий, имеющих место на границе раздела двух сред, от которой происходит отражение. Если отражение волны происходит от среды более плотной, то фаза колебаний в месте отражения волны меняется на противоположную или, как говорят, теряется половина волны. Поэтому, в результате сложения колебаний противоположных направлений смещение на границе равно нулю, т.е. имеет место узел (рис. 12).При отражении волны от границы менее плотной среды фаза колебаний в месте отражения остается без изменения и у границы складываются колебания с одинаковыми фазами – получается пучность.

В стоячей волне нет перемещения фаз, нет распространения волны, нет переноса энергии, с чем и связано название такого типа волн.

studfiles.net

• 
  Что такое осциллятор
• 
  Монтаж асинхронного двухсекционного двигателя
• 
  Шаговое напряжение это напряжение
• 
  Маркировка выпрямительных диодов
• 
  Схемы с узо
• 
  Будет ли проходить в цепи постоянный ток если вместо источника эдс включить заряженный конденсатор
• 
  Договор между управляющей организацией и ресурсоснабжающей организацией
• 
  Ток утечки как найти
• 
  Сварочный аппарат постоянка
• 
  Принцип работы однофазного двигателя асинхронного
• 
  Принцип работы контакторы