Конденсаторы параллельное и последовательное соединение конденсаторов: Параллельное и последовательное соединение конденсаторов: ёмкость и сопротивление

Параллельное и последовательное соединение конденсаторов: ёмкость и сопротивление

Практически все электрические цепи включают в себя емкостные элементы. Соединение конденсаторов между собой выполняют по схемам. Их необходимо знать как при расчетах, так и при выполнении монтажа.

Последовательное соединение

Конденсатор, а в просторечии — «ёмкость», та деталь, без которой не обходится ни одна электрическая или электронная плата. Даже в современных гаджетах он присутствует, правда, уже в измененном виде.

Вспомним, что представляет собой этот радиотехнический элемент. Это накопитель электрических зарядов и энергии, 2 проводящие пластины, между которыми расположен диэлектрик. При прикладывании к пластинам источника постоянного тока через устройство кратковременно потечет ток, и оно зарядится до напряжения источника. Его емкость используют для решения технических задач.

Само это слово произошло задолго до того, как придумали устройство. Термин появился ещё тогда, когда люди считали, что электричество — это что-то типа жидкости, и ею можно наполнить какой-нибудь сосуд. Применительно к конденсатору — он неудачен, т.к. подразумевает, что прибор может вместить только конечное количество электричества. Хотя это и не так, но термин остался неизменным.

Чем больше пластины, и меньше расстояние между ними, тем больше ёмкость конденсатора. Если его обкладки соединить с каким-либо проводником, то через этот проводник произойдет быстрый разряд.

В координатных телефонных станциях с помощью этой особенности происходит обмен сигналами между приборами. Длина импульсов, необходимых для команд, таких как: «соединение линии», «ответ абонента», «отбой», регулируется величиной ёмкости установленных в цепь конденсаторов.

Единица измерения ёмкости — 1 Фарад. Т.к. это большая величина, то пользуются микрофарадами, пикофарадами и нанофарадами, (мкФ, пФ, нФ).

На практике, выполнив последовательное соединение, можно добиться увеличения прикладываемого напряжения. В этом случае поданное напряжение получают 2 внешние обкладки собранной системы, а обкладки, находящиеся внутри, заряжаются с помощью распределения зарядов.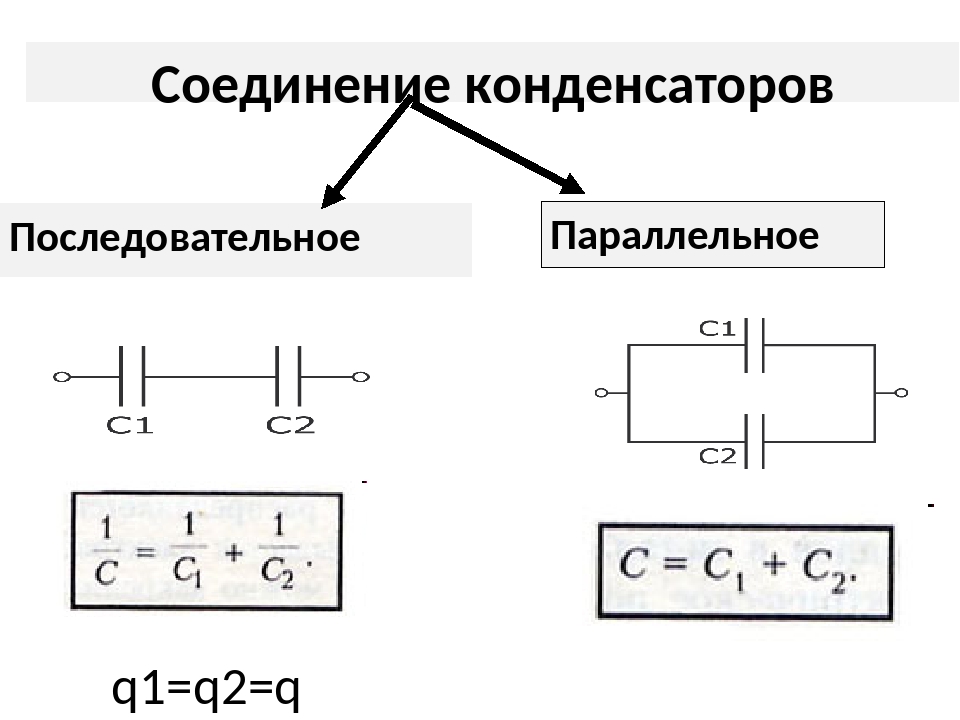 К таким приемам прибегают, когда под рукой не оказывается нужных элементов, зато есть детали других номиналов по напряжению.

К участку, имеющему 2 последовательно соединенных конденсатора, рассчитанных на напряжение 125 В, можно подключить питание 250 В.

Если для постоянного тока, конденсатор является препятствием за счет своего диэлектрического промежутка, то с переменным — все иначе. Для токов разных частот, подобно катушкам и резисторам, сопротивление конденсатора будет меняться. Токи высокой частоты он пропускает хорошо, а для их собратьев низкой частоты создает барьер.

У радиолюбителей есть способ — через емкость 220-500 пФ к радиоприемнику подключают вместо антенны сеть освещения напряжением 220 В. Ток с частотой 50 Гц он отфильтрует, а токи высокой частоты пропустит. Это сопротивление конденсаторов легко рассчитать по формуле для емкостного сопротивления:RC =1/6*f*C.

Где:

• Rc — емкостное сопротивление, Ом;
• f — частота тока, Гц;
• C — емкость данного конденсатора, Ф;
• 6 — округленное до целой части число 2π.

Но не только прикладываемое напряжение к цепи можно изменить, пользуясь подобной схемой включения. Так добиваются изменений емкостей при последовательных соединениях. Для легкости запоминания придумали подсказку, что общее значение емкости, полученное при выборе подобной схемы, получается всегда меньше меньшей из двух, включенных в цепочку.

Если так соединить 2 детали одинаковой ёмкости, то их общее значение будет вдвое меньше каждой из них. Расчеты последовательных соединений конденсатора можно выполнить по приведенной ниже формуле:

Собщ = С1*С2/С1+С2,

Пусть С1=110 пФ, а С2=220 пФ, тогда Собщ = 110×220/110+220 = 73 пФ.

Не стоит забывать про простоту и удобство монтажа, а также обеспечение качественной работы собранного устройства или оборудования. В последовательных соединениях у емкостей должен быть 1 производитель. А если детали всей цепочки будут одной партии выпуска, то проблем с эксплуатацией созданной цепи не будет.

Параллельное соединение

Накопители электрического заряда постоянной емкости, различают:

• керамические;
• бумажные;
• слюдяные;
• металлобумажные;
• электролитические конденсаторы.

Их делят на 2 группы: низковольтные и высоковольтные. Применяют их в фильтрах выпрямителей, для связи между низкочастотными участками цепей, в блоках питания различных устройств и т.д.

Конденсаторы переменной ёмкости тоже существуют. Они нашли свое предназначение в настраиваемых колебательных контурах теле- и радиоприемников. Емкость регулируется за счет изменения положения пластин относительно друг друга.

Рассмотрим соединение конденсаторов, когда их выводы соединятся попарно. Подобное включение подходит для 2 или более элементов, рассчитанных на одно и то же напряжение. Номинальное напряжение, которое указано на корпусе детали, превышать нельзя. В противном случае произойдет пробой диэлектрика, и элемент выйдет из строя. Но в цепь, где присутствует напряжение меньше номинального, конденсатор включать можно.

Параллельным включением конденсаторов можно добиться увеличения общей ёмкости. В некоторых устройствах необходимо обеспечить большое накопление электрического заряда.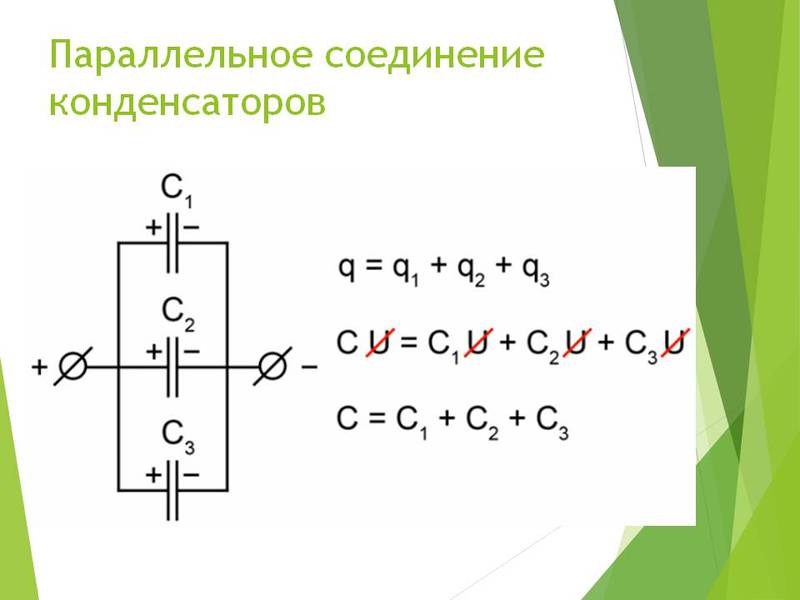 Существующих номиналов не хватает, приходится выполнять параллели и использовать то, что есть под рукой. Определить общую величину полученного соединения просто. Для этого нужно просто сложить величины всех используемых элементов.

Для вычисления емкостей конденсаторов формула имеет вид:

Собщ = С1+С2, где С1 и С2 — емкость соответствующих элементов.

Если С1=20 пФ, а С2=30 пФ, то Собщ = 50 пФ. Деталей в в параллели может быть n-ое количество.

На практике такое соединение находит применение в специальных устройствах, используемых в энергетических системах, и на подстанциях. Их монтируют, зная, как соединить конденсаторы для увеличения емкости, в целые блоки из батарей.

Для того чтобы поддерживать равновесие реактивной мощности как в энергоснабжающих установках, так и в установках энергопотребителей, существует необходимость включать в работу компенсирующие устройства реактивной мощности (УКРМ). Для снижения потерь и регулировки напряжения в сетях при расчетах устройства необходимо знать величины реактивных сопротивлений конденсаторов, используемых в установке.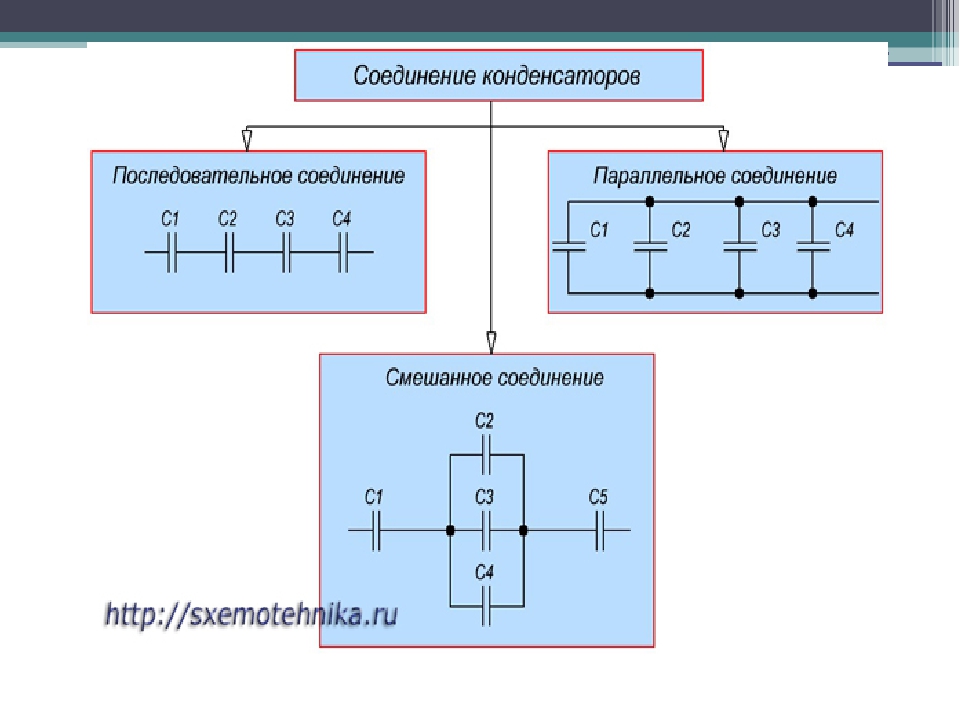

Случается, что возникает необходимость вычислить по формуле напряжение на конденсаторах. В этом случае будем исходить из того, что С=q/U, т.е. отношение заряда к напряжению. И если величина заряда — q, а ёмкость — C, можем получим искомое число, подставляя значения. Она имеет вид:

U=q/C.

Смешанное соединение

При расчете цепи, представляющей собой совокупность рассмотренных выше комбинаций, поступают так. Сначала ищем в сложной цепи конденсаторы, которые соединены между собой либо параллельно, либо последовательно. Заменив их эквивалентным элементом, получим более простую схему. Потом в новой схеме с участками цепи проводим те же манипуляции. Упрощаем до тех пор, пока не останется только параллельное или последовательное соединение. Их рассчитывать мы уже научились в этой статье.

Параллельно-последовательное соединение применимо для увеличения емкости, батареи или для того, чтобы приложенное напряжение не превышало рабочего напряжения конденсатора.

При последовательном соединении конденсаторов их суммарная емкость — советы электрика

Комбинации конденсаторов: последовательные и параллельные

Физика > Комбинации конденсаторов: последовательные и параллельные

Изучите соединения конденсаторов – последовательные и параллельные. Как выглядят последовательно и параллельно соединенные конденсаторы, емкость, схемы.

Конденсаторы можно использовать в последовательных или параллельных цепях.

Задача обучения

• Вывести общую емкость конденсаторов в разных типах соединения.

Основные пункты

 – последовательное соединение.

• Собщая = С1 + С2 + … + Сn – параллельное соединение.
• Если конденсаторы пребывают в последовательном или параллельном подключении, то лучше упростить схему и решить по частям.

Термины

• Конденсатор – электронная составляющая, способная сберегать электрический заряд.
• Схема – маршрут электрического тока, представленный отдельными электронными составляющими, вроде резисторов, транзисторов, конденсаторов, катушек индуктивности и т.д.
• Конденсаторы можно применить в различных комбинациях цепей. Они могут быть последовательными (несколько конденсаторов расположены на одном пути) и параллельными (на разных путях).

Последовательные конденсаторы

Посмотрим на схему, где конденсаторы соединены последовательно. Обратная общая емкость достигает суммы обратных значений емкости каждого отдельного конденсатора:

Здесь показаны последовательные конденсаторы С1, С2, С3 и до Сn

Последовательно соединенные конденсаторы можно также выразить:

Параллельные конденсаторы

Суммарная емкость в параллельном соединении конденсаторов находится при обычном добавлении отдельных емкостей каждого конденсатора.

Здесь показаны параллельные конденсаторы С1, С2, С3 и до Сn

Собщая = С1 + С2 + … + Сn.

Последовательные и параллельные конденсаторы

Бывает так, что схема вмещает сразу два типа соединения (параллельное и последовательное соединение конденсаторов). Чтобы отыскать общую емкость, нужно разделить цепочку на отдельные сегменты.

Задачу можно сделать проще, если сначала решить проблему с последовательным соединением, а потом заняться параллельным

В (а) расположены последовательные конденсаторы, выступающие параллельными C3. Если найти емкость для последовательных, то можно потом заняться вычислением для одного конденсатора. Оно будет равняться примерно 0.83 мкФ.

Обратите внимание

В одновременном выводе двух оставшихся конденсаторов, можно приплюсовать их емкости и получим общую – 8.83 мкФ.

(1

Источник: https://v-kosmose.com/fizika/kombinatsii-kondensatorov-posledovatelnyie-i-parallelnyie/

Последовательное и параллельное соединение конденсаторов

На практике часто используются тела, обладающие малыми (и очень малыми) размерами, которые могут накопить большой заряд, при этом имея небольшой потенциал. Такие объекты называют конденсаторами. Одна из основных характеристик конденсатора – это его емкость.

Имея в резерве набор конденсаторов, обладающих разными параметрами, можно расширить спектр величин емкостей и диапазон рабочих напряжений, если применять их соединения.

Различают три типа соединений конденсаторов: последовательное, параллельное и смешанное (параллельное и последовательное).

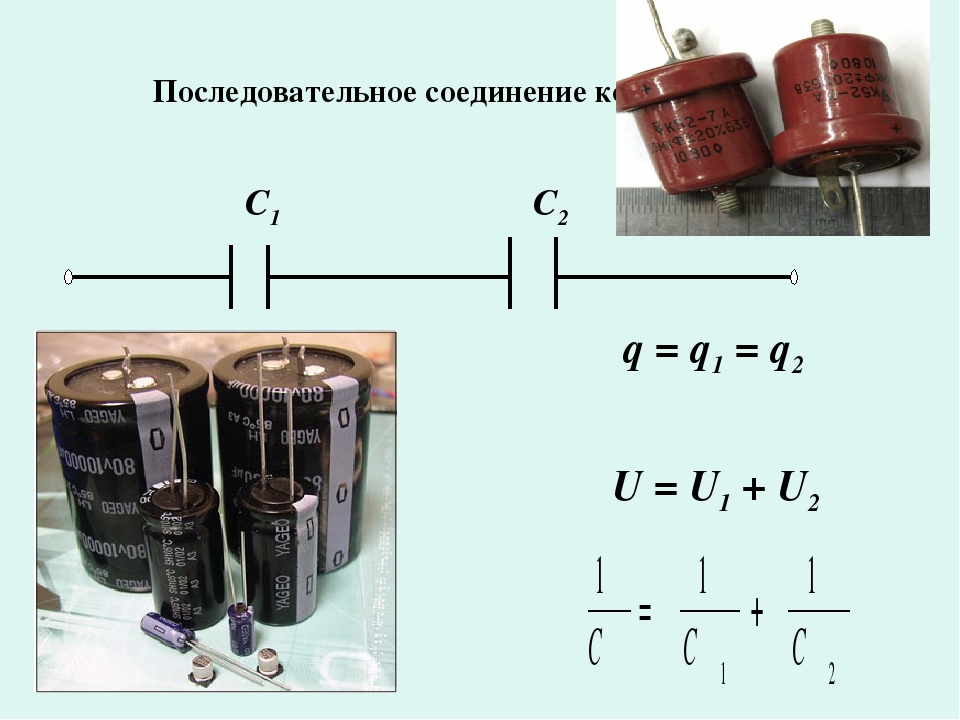
Последовательное соединение конденсаторов

Последовательное соединение изконденсаторов изображено на рис. 1

Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды. Электрическая емкость последовательного соединения конденсаторов вычисляется по формуле:

где– электрическая емкость i-го конденсатора.

Если емкости конденсаторов при последовательном соединении равны, то емкость последовательного их соединения составляет:

где N – количество последовательно соединенных конденсаторов. При этом предельное напряжение (U), которое выдержит подобная батарея конденсаторов составит:

где– предельное напряжение каждого конденсатора соединения. При последовательном соединении конденсаторов следует следить за тем, чтобы ни на один из конденсаторов батареи не падало напряжение, превышающее его максимальное рабочее напряжение.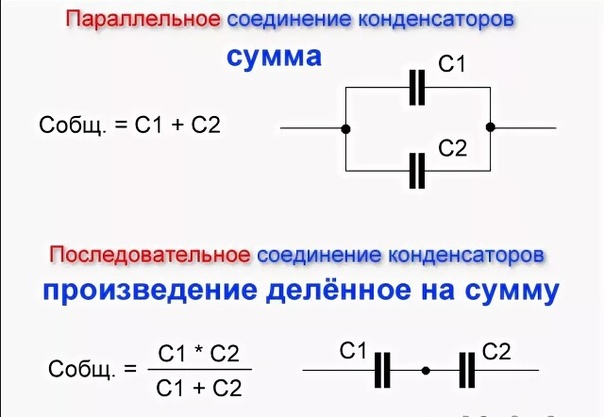

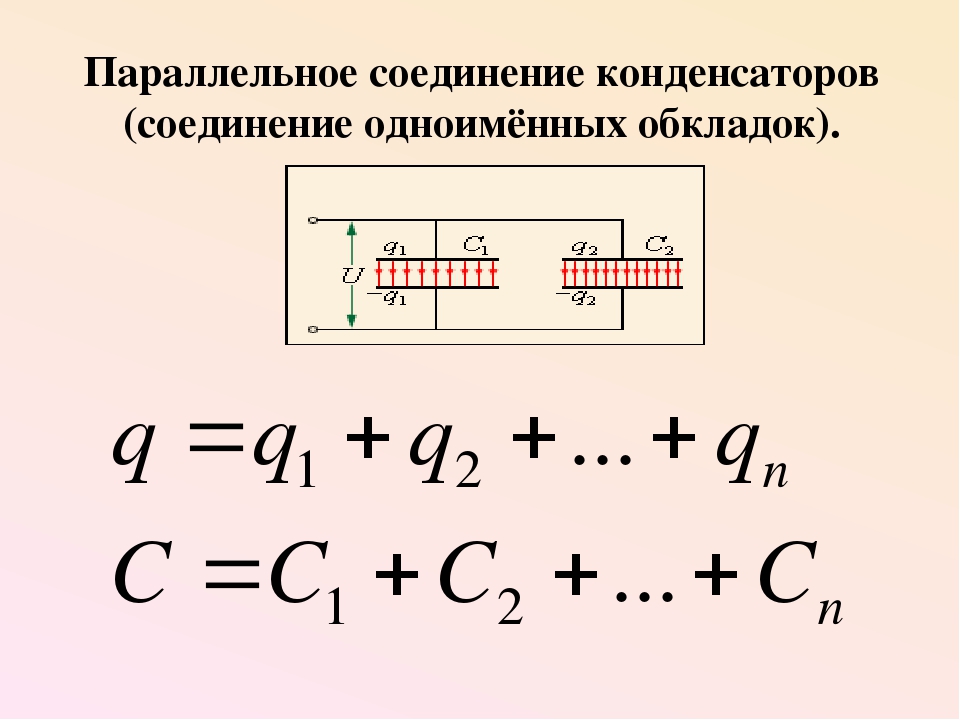
Параллельное соединение конденсаторов

Параллельное соединение N конденсаторов изображено на рис. 2.

При параллельном соединении конденсаторов соединяют обкладки, обладающие зарядами одного знака (плюс с плюсом; минус с минусом). В результате такого соединения одна обкладка каждого конденсатора имеет одинаковый потенциал, например,, а другая. Разности потенциалов на обкладках всех конденсаторов при их параллельном соединении равны.

При параллельном соединении конденсаторов суммарная емкость соединения рассчитывается как сумма емкостей отдельных конденсаторов:

При параллельном соединении конденсаторов напряжение равно самой наименьшей величине рабочего напряжения конденсатора из состава рассматриваемого соединения.

Примеры решения задач

Источник: http://ru. solverbook.com/spravochnik/fizika/posledovatelnoe-i-parallelnoe-soedinenie-kondensatorov/

Маркировка конденсаторов. Параллельное и последовательное соединение

Продолжаем обсуждение и изучение электронных компонентов под названием конденсаторы (ссылка). Основные аспекты устройства и принципа работы конденсаторов мы обсудили в предыдущей статье, а сегодня мы обсудим цифровую маркировку, а также разные варианты соединения конденсаторов. Сначала разберем теорию, а затем рассмотрим несколько практических примеров. Собственно, приступим к делу

Источник: https://microtechnics.ru/markirovka-kondensatorov-parallelnoe-i-posledovatelnoe-soedinenie/

Соединение конденсаторов Как правильно соединять конденсаторы?

 У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”

 Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим необходимый конденсатор.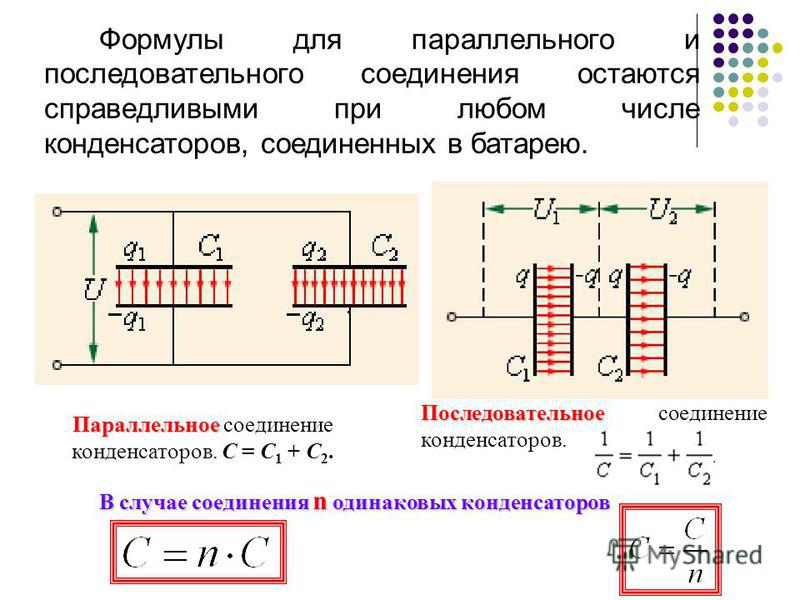 Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!

Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь 2 – 3 конденсатора на 470 микрофарад. Ставить конденсатор на 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров за одним конденсатором?

Важно

Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.

В реальности это выглядит так:

Параллельное соединение

Принципиальная схема параллельного соединения

Последовательное соединение

Принципиальная схема последовательного соединения

Также можно комбинировать параллельное и последовательное соединение конденсаторов. На практике вам вряд ли это пригодиться.

Как рассчитать общую ёмкость соединённых конденсаторов?

Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.

Общая ёмкость параллельно соединённых конденсаторов:

С1 – ёмкость первого конденсатора;

С2 – ёмкость второго конденсатора;

С3 – ёмкость третьего конденсатора;

СN – ёмкость N-ого конденсатора;

Cобщ – суммарная ёмкость составного конденсатора.

Как видим, при параллельном соединении ёмкости конденсаторов нужно всего-навсего сложить!

Внимание! Все расчёты необходимо производить в одних единицах. Если рассчитываем ёмкости в микрофарадах, то нужно указывать ёмкость C1, C2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!

Чтобы не допустить ошибку при переводе микрофарад в пикофарады или нанофарады можно воспользоваться специальной таблицей. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно пересчитать значения величин. 

Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:

Внимание! Данная формула справедлива только для двух конденсаторов! Для большего количества последовательно включенных конденсаторов потребуется другая формула. Она более запутанная, да и не всегда пригождается .

Или то же самое, но более понятно:

Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении конденсаторов их результирующая ёмкость будет всегда меньше наименьшей ёмкости, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсатор ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость составного конденсатора будет меньше 5.

Совет

В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула упрощается и принимает вид:

Здесь, вместо буквы M ставиться количество конденсаторов, а C1 – ёмкость конденсатора.

Стоит также запомнить простое правило:

При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из конденсаторов.

Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате ёмкость составного конденсатора составит 5 нанофарад.

Проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул для расчёта

Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.), другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ с функцией измерения ёмкости конденсаторов и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).

Замер ёмкости последовательно соединённых конденсаторов

Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)

А теперь проделаем то же самое, но для параллельного соединения конденсаторов. Проверим результат с помощью тестера (см. фото).

Измерение ёмкости параллельно соединённых конденсаторов

Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).

Во-первых, не стоит забывать, что кроме ёмкости у конденсаторов есть ещё один немаловажный параметр, как номинальное напряжение.

При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально ёмкостям этих конденсаторов. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое должно быть у конденсатора взамен которого мы ставим составной конденсатор.

Если же используются конденсаторы одинаковой ёмкости, то напряжение между ними разделится поровну.

Для электролитических конденсаторов.

При соединении электролитических конденсаторов строго соблюдайте полярность! При параллельном соединении электролитических конденсаторов всегда соединяйте минусовой вывод одного конденсатора с минусовым выводом другого. Плюсовой вывод с плюсовым.

Параллельное соединение электролитических конденсаторов

Схема параллельного соединения

Обратите внимание

В последовательном соединении электролитических конденсаторов ситуация обратная. Необходимо соединять плюсовой вывод с минусовым. Получается что-то вроде последовательного соединения батареек.

Последовательное соединение электролитических конденсаторов

Схема последовательного соединения конденсаторов

Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор.

То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт.

Если хоть один из этих конденсаторов будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.

Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше будет, если они взяты из одной партии.

Конечно, возможно и смешанное (комбинированное) соединение конденсаторов, но в практике оно не применяется (я не видел ). Расчёт ёмкости смешанного соединения конденсаторов обычно достаётся тем, кто решает задачи по физике и сдаёт экзамены 🙂

Источник: http://radiodvor.com/news/fashion/soedinenie-kondensatorov-kak-pravilno-so.html

Последовательное соединение конденсаторов: формула :

Под последовательным соединением подразумевают случаи, когда два или больше элемента имеют вид цепи, при этом каждый из них соединяется с другим только в одной точке. Зачем конденсаторы так размещаются? Как это правильно сделать? Что необходимо знать? Какие особенности последовательное соединение конденсаторов имеет на практике? Какая формула результата?

Что необходимо знать для правильного соединения?

Увы, но здесь не всё так легко сделать, как может показаться. Многие новички думают, что если на схематическом рисунке написано, что необходим элемент на 49 микрофарад, то достаточно его просто взять и установить (или заменить равнозначным).

Но необходимые параметры подобрать сложно даже в профессиональной мастерской. И что делать, если нет нужных элементов? Допустим, есть такая ситуация: необходим конденсатор на 100 микрофарад, а есть несколько штук на 47. Поставить его не всегда можно.

Важно

Ехать на радиорынок за одним конденсатором? Не обязательно. Достаточно будет соединить пару элементов. Существует два основных способа: последовательное и параллельное соединение конденсаторов. Вот о первом мы и поговорим.

Но если говорить про последовательное соединение катушки и конденсатора, то тут особых проблем нет.

Зачем так делают?

Когда с ними проводятся такие манипуляции, то электрические заряды на обкладках отдельных элементов будут равны: КЕ=К1=К2=К3. КЕ – конечная емкость, К – пропускаемое значение конденсатора.

Почему так? Когда заряды поступают от источника питания на внешние обкладки, то на внутренних может быть осуществлен перенос величины, которая является значением элемента с наименьшими параметрами.

То есть если взять конденсатор на 3 мкФ, а после него подсоединить на 1 мкФ – то конечный результат будет 1 мкФ. Конечно, на первом можно будет наблюдать значение в 3 мкФ.

Но второй элемент не сможет столько пропустить, и он будет срезать всё, что больше необходимого значения, оставляя большую емкость на первоначальном конденсаторе. Давайте рассмотрим, что нужно рассчитать, когда делается последовательное соединение конденсаторов. Формула:

Н=КЕ/ОЕК

• ОЕ – общая емкость;
• Н – напряжение;
• КЕ – конечная емкость.

Что ещё необходимо знать, чтобы правильно соединить конденсаторы?

Для начала не забывайте, что кроме ёмкости они ещё обладают номинальным напряжением. Почему? Когда осуществляется последовательное соединение, то напряжение распределяется обратно пропорционально их ёмкостям между ними самими.

Поэтому использовать такой подход имеет смысл только в тех случаях, когда любой конденсатор сможет предоставить минимально необходимые параметры работы. Если используются элементы, у которых одинаковая емкость, то напряжение между ними будет разделяться поровну.

Также небольшое предостережение относительно электролитических конденсаторов: при работе с ними всегда внимательно контролируйте их полярность. Ибо при игнорировании этого фактора последовательное соединение конденсаторов может дать ряд нежелательных эффектов. И хорошо, если всё ограничится только пробоем данных элементов.

Помните, что конденсаторы копят ток, и если что-то пойдёт не так, в зависимости от схемы может случиться прецедент, в результате которого из строя выйдут другие составляющие схемы.

Ток при последовательном соединении

Из-за того, что у него существует только один возможный путь протекания, он будет иметь одно значение для всех конденсаторов. При этом количество накопленного заряда везде обладает одинаковым значением. От емкости это не зависит.

Посмотрите на любую схему последовательного соединения конденсаторов. Правая обкладка первого соединена с левой второго и так далее. Если используется больше 1 элемента, то часть из них будет изолированной от общей цепи.

Таким образом, эффективная площадь обкладок становится меньшей и равняется параметрам самого маленького конденсатора. Какое физическое явление лежит в основе этого процесса? Дело в том, что как только конденсатор наполняется электрическим зарядом, то он перестаёт пропускать ток.

И он тогда не может протекать по всей цепи. Остальные конденсаторы в таком случае тоже не смогут заряжаться.

Падение напряженности и общая емкость

Каждый элемент понемногу рассеивает напряжение. Учитывая, что емкость ему обратно пропорциональна, то чем она меньше, тем большим будет падение.

Как уже упоминалось ранее, последовательно соединённые конденсаторы обладают одинаковым электрическим зарядом. Поэтому при делении всех выражений на общее значение можно получить уравнение, которое покажет всю емкость.

В этом последовательное и параллельное соединение конденсаторов сильно разнятся.

Пример № 1

Давайте воспользуемся представленными в статье формулами и рассчитаем несколько практических задач. Итак, у нас есть три конденсатора. Их емкость составляет: С1 = 25 мкФ, С2 = 30 мкФ и С3 = 20 мкФ. Они соединены последовательно.

Необходимо найти их общую емкость. Используем соответствующее уравнение 1/С: 1/С1 + 1/С2 + 1/С3 = 1/25 + 1/30 + 1/20 = 37/300.

Переводим в микрофарады, и общая емкость конденсатора при последовательном соединении (а группа в данном случае считается как один элемент) составляет примерно 8,11 мкФ.

Пример № 2

Давайте, чтобы закрепить наработки, решим ещё одну задачу. Имеется 100 конденсаторов. Емкость каждого элемента составляет 2 мкФ. Необходимо определить их общую емкость. Нужно их количество умножить на характеристику: 100*2=200 мкФ. Итак, общая емкость конденсатора при последовательном соединении составляет 200 микрофарад. Как видите, ничего сложного.

Заключение

Итак, мы проработали теоретические аспекты, разобрали формулы и особенности правильного соединения конденсаторов (последовательно) и даже решили несколько задачек. Хочется напомнить, чтобы читатели не упускали из внимания влияние номинального напряжения. Также желательно, чтобы подбирались элементы одного типа (слюдяные, керамические, металлобумажные, плёночные). Тогда последовательное соединение конденсаторов сможет дать нам наибольший полезный эффект.

Источник: https://www.syl.ru/article/237511/new_posledovatelnoe-soedinenie-kondensatorov-formula

Параллельное и последовательное соединение конденсаторов: способы, правила, формулы

Не всегда удаётся подобрать конденсатор нужного номинала

Очень часто начинающие домашние мастера, обнаружив поломку прибора, стараются самостоятельно обнаружить причину. Увидев сгоревшую деталь, они стараются найти подобную, а если это не удаётся, несут прибор в ремонт.

На самом деле, не обязательно, чтобы показатели совпадали. Можно использовать конденсаторы меньшего номинала, соединив их в цепь. Главное – сделать это правильно. При этом достигается сразу 3 цели – поломка устранена, приобретён опыт, сэкономлены средства семейного бюджета.

Попробуем разобраться, какие способы соединения существуют и на какие задачи рассчитаны последовательное и параллельное соединение конденсаторов.

Часто без соединения конденсаторов в батарею не обойтись. Главное – сделать это правильно

Соединение конденсаторов в батарею: способы выполнения

Существует 3 способа соединения, каждый из которых преследует свою определённую цель:

1. Параллельное – выполняется в случае необходимости увеличить ёмкость, оставив напряжение на прежнем уровне.
2. Последовательное – обратный эффект. Напряжение увеличивается, ёмкость уменьшается.
3. Смешанное – увеличивается как ёмкость, так и напряжение.

Теперь рассмотрим каждый из способов более подробно.

Параллельное соединение: схемы, правила

На самом деле всё довольно просто. При параллельном соединении расчёт общей ёмкости можно вычислить путём простейшего сложения всех конденсаторов. Итоговая формула будет выглядеть следующим образом: Собщ= С₁ + С₂ + С₃ + … + Сn. При этом напряжение на каждом их элементов будет оставаться неизменным: Vобщ= V₁ = V₂ = V₃ = … = Vn.

Соединение при таком подключении будет иметь следующий вид:

Получается, что подобный монтаж подразумевает подключение всех пластин конденсаторов к точкам питания. Такой способ встречается наиболее часто. Но может произойти ситуация, когда важно увеличить напряжение. Разберёмся, каким образом это сделать.

Последовательное соединение: способ, используемый реже

При использовании способа последовательного подключения конденсаторов напряжение в цепи возрастает.

Оно складывается из напряжения всех элементов и выглядит так: Vобщ= V₁ + V₂ + V₃ +…+ Vn.

При этом ёмкость изменяется в обратной пропорции: 1/Собщ= 1/С₁ + 1/С₂ + 1/С₃ + … + 1/Сn. Рассмотрим изменения ёмкости и напряжения при последовательном включении на примере.

Дано: 3 конденсатора с напряжением 150 В и ёмкостью 300 мкф. Подключив их последовательно, получим:

• напряжение: 150 + 150 + 150 = 450 В;
• ёмкость: 1/300 + 1/300 + 1/300 = 1/С = 299 мкф.

Внешне подобное подключение обкладок (пластин) будет выглядеть так:

Выполняют такое соединение в том случае, если есть опасность пробоя диэлектрика конденсатора при подаче напряжения в цепь. Но ведь существует и ещё один способ монтажа.

Полезно знать! Применяют также последовательное и параллельное соединение резисторов и конденсаторов. Это делается с целью снижения подаваемого на конденсатор напряжения и исключения его пробоя. Однако следует учитывать, что напряжения должно быть достаточно для работы самого прибора.

Смешанное соединение конденсаторов: схема, причины необходимости применения

Такое подключение (его ещё называют последовательно-параллельным) применяют в случае необходимости увеличения, как ёмкости, так и напряжения. Здесь вычисление общих параметров немного сложнее, но не настолько, чтобы нельзя было разобраться начинающему радиолюбителю. Для начала посмотрим, как выглядит такая схема.

Составим алгоритм вычислений.

• всю схему нужно разбить на отдельные части, высчитать параметры которых просто;
• высчитываем номиналы;
• вычисляем общие показатели, как при последовательном включении.

Выглядит подобный алгоритм следующим образом:

Преимущество смешанного включения конденсаторов в цепь по сравнению с последовательным или параллельным

Смешанное соединение конденсаторов решает задачи, которые не под силу параллельным и последовательным схемам. Его можно использовать при подключении электродвигателей либо иного оборудования, его монтаж возможен отдельными участками. Монтаж его намного проще за счёт возможности выполнения отдельными частями.

Интересно знать! Многие радиолюбители считают этот способ более простым и приемлемым, чем два предыдущих. На самом деле, так и есть, если полностью понять алгоритм действий и научиться пользоваться им правильно.

Смешанное, параллельное и последовательное соединение конденсаторов: на что обратить внимание при его выполнении

Соединяя конденсаторы, в особенности электролитические, обратите внимание на строгое соблюдение полярности. Параллельное присоединение подразумевает подключение «минус/минус», а последовательное – «плюс/минус». Все элементы должны быть однотипны –плёночные, керамические, слюдяные либо металлобумажные.

А вот что умеют делать всем известные китайские «изобретатели» – такой конденсатор явно долго не протянетПолезно знать! Выход из строя конденсаторов часто происходит по вине производителя, экономящего на деталях (чаще это приборы китайского производства). Поэтому правильно рассчитанные и собранные в схему элементы будут работать намного дольше. Конечно, при условии отсутствия замыкания в цепи, при котором работа конденсаторов невозможна в принципе.

Калькулятор расчёта ёмкости при последовательном соединении конденсаторов

А что делать, если необходимая ёмкость неизвестна? Не каждому хочется самостоятельно рассчитывать необходимую ёмкость конденсаторов вручную, а у кого-то на это просто нет времени. Для удобства производства подобных действий редакция Seti.

guru предлагает нашему уважаемому читателю воспользоваться онлайн-калькулятором расчёта конденсаторов при последовательном соединении или вычисления ёмкости. В работе он необычайно прост. Пользователю необходимо лишь ввести в поля необходимые данные, после чего нажать кнопку «Рассчитать».

Программы, в которые заложены все алгоритмы и формулы последовательного соединения конденсаторов, а также вычислений необходимой ёмкости, моментально выдаст необходимый результат.

Как рассчитать энергию заряженного конденсатора: выводим окончательную формулу

Первое, что для этого необходимо сделать – рассчитать, с какой силой притягиваются обкладки друг к другу. Это можно сделать по формуле F = q₀ × E, где q₀ является показателем величины заряда, а E – напряжённостью обкладок.

Далее нам необходим показатель напряжённости обкладок, который можно вычислить по формуле E = q / (2ε₀S), где q – заряд, ε₀ – постоянная величина, S – площадь обкладок.

В этом случае получим общую формулу для расчёта силы притяжения двух обкладок: F = q₂ / (2ε₀S).

Совет

Итогом наших умозаключений станет вывод выражения энергии заряженного конденсатора, как W = A = Fd. Однако это не окончательная формула, которая нам необходима.

Следуем далее: учитывая предыдущую информацию, мы имеем: W = dq₂ / (2ε₀S). При ёмкости конденсатора, выражаемой как C = d / (ε₀S) получаем результат W = q₂ / (2С).

Применив формулу q = СU, получим итог: W = CU² /2.

Редакция Seti.guru советует сохранить эту памятку

Конечно, для начинающего радиолюбителя все эти расчёты могут показаться сложными и непонятными, но при желании и некоторой усидчивости с ними можно разобраться. Вникнув в смысл, он поразится, насколько просто производятся все эти расчёты.

Для чего нужно знать показатель энергии конденсатора

По сути, расчёт энергии применяется редко, однако есть области, в которых это знать необходимо. К примеру, фотовспышка камеры – здесь вычисление показателя энергии очень важно. Она накапливается за определённое время (несколько секунд), а вот выдаётся мгновенно. Получается, что конденсатор сравним с аккумулятором – разница лишь в ёмкости.

Ни одна фотовспышка не сможет работать без накопителя энергии, такого, как конденсатор

Подводя итог

Порой без соединения конденсаторов не обойтись, ведь не всегда можно подобрать подходящие по номиналам.

Поэтому знание того как это сделать может выручить при поломке бытовой техники или электроники, что позволит значительно сэкономить на оплате труда специалиста по ремонту.

Как наверняка уже понял Уважаемый читатель, сделать это несложно и под силу даже начинающим домашним мастерам. А значит стоит потратить немного своего драгоценного времени и разобраться в алгоритме действий и правилах их выполнения.

Правильность соединения конденсаторов гарантирует их долгую бесперебойную работу

Надеемся, что информация, изложенная в сегодняшней статье, была полезна нашим читателям. Возможно, у Вас остались какие-либо вопросы? В этом случае их можно изложить в обсуждении ниже. Редакция Seti.guru с удовольствием на них ответит в максимально короткие сроки.

Если же Вы имеете опыт самостоятельного соединения конденсаторов (неважно, положительный он или отрицательный), убедительная просьба поделиться им с другими читателями. Это поможет начинающим мастерам более полно понять алгоритм действий и избежать ошибок. Пишите, делитесь, спрашивайте.

А напоследок мы предлагаем посмотреть короткий, но довольно информативный видеоролик по сегодняшней теме.

Источник: https://seti.guru/parallelnoe-i-posledovatelnoe-soedinenie-kondensatorov

Лекция № 3 Соединение конденсаторов

 Последовательное, параллельное и смешанное соединение конденсаторов

1. В электрических цепях применяются различные способы соединения конденсаторов. 

Соединение конденсаторов может производиться:

• последовательно, 
• параллельно и 
• последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов).

Существующие виды соединения конденсаторов показаны на рисунке 1.

Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).

Рисунок 2. Параллельное соединение конденсаторов.

При заряде группы конденсаторов, соединенных параллельно, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока. Общее же количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор.

Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.

Обозначим суммарную емкость соединенных в батарею конденсаторов буквой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:

Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и вообще при любом числе конденсаторов.

Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).

Рисунок 2. Последовательное соединение конденсаторов.

При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются через влияние. При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.

Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.

Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.

Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.

Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.

Для вычисления общей емкости при последовательном соединении конденсаторов удобнее всего пользоваться следующей формулой:

Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:

Последовательно-параллельным соединением конденса-торов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.

На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.

Рисунок 4. Последовательно-параллельное соединение конденсаторов.

При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов.

Алгоритм расчета :

1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.

2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.

3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.

4. Рассчитывают емкость полученной схемы.

Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.

Рисунок 5. Пример расчета последовательно-параллельного соединения конденсаторов.

Вопросы для самопроверки:

1. Перечислить способы соединения конденсаторов применяются в электрических цепях.

2. Обьяснить, какой способ соединения конденсаторов  наз. параллельным?

3. Определить, чему равна суммарная емкость конденсаторов при параллельном соединении.

4. Обьяснить, какой способ соединения конденсаторов  наз. последо-вательным?

5. Определить, чему равна суммарная емкость конденсаторов при последовательном соединении.

Маркировка конденсаторов

Соединение конденсаторов: последовательное, параллельное и смешанное

Схемы в электротехнике состоят из электрических элементов, в которых способы соединения конденсаторов могут быть разными. Надо понимать, как правильно подключить конденсатор. Отдельные участки цепи с подключенными конденсаторами можно заменить одним эквивалентным элементом.

Он заменит ряд конденсаторов, но должно выполняться обязательное условие: когда напряжение, подводимое к обкладкам эквивалентного конденсатора, равняется напряжению на входе и выходе группы заменяющихся конденсаторов, тогда заряд емкости будет такой же, как и на группе емкостей.

Для понимания вопроса, как подключить конденсатор в любой схеме, рассмотрим виды его включения.

Параллельное включение конденсаторов в цепь

Параллельное соединение конденсаторов — это когда все пластины подключаются к точкам включения цепи, образовывая батарею емкостей.

Параллельное соединение конденсаторов:

Параллельное соединение конденсаторов

Разность потенциалов на пластинах накопителей емкости будет одинаковая, так как они все заряжаются от одного источника тока. В этом случае каждый заряжающийся конденсатор имеет собственный заряд при одинаковой величине, подводимой к ним энергии.

Параллельные конденсаторы, общий параметр количества заряда полученной батареи накопителей, рассчитывается, как сумма всех зарядов, помещающихся на каждой емкости, потому что каждый заряд емкости не зависит от заряда другой емкости, входящей в группу конденсаторов, параллельно включенных в схему.

При параллельном соединении конденсаторов емкость равняется:

Формула и расшифровка

Из представленной формулы можно сделать вывод, что всю группу накопителей можно рассматривать как один равноценный им конденсатор.

Конденсаторы, соединенные параллельно, имеют напряжение:

Формула

Последовательное включение конденсаторов в цепь

Когда в схеме выполнено последовательное соединение конденсаторов, оно выглядит как цепочка емкостных накопителей, где пластина первого и последнего накопителя емкости (конденсатора) подключены к источнику тока.

Последовательное соединение конденсатора:

Формула

При последовательном соединении конденсаторов все устройства этого участка берут одинаковое количество электроэнергии, потому что в процессе участвует первая и последняя пластинка накопителей, а пластины 2, 3 и другие до N проходят зарядку посредством влияния.

По этой причине заряд пластины 2 накопителя емкости равняется по значению заряду 1 пластины, но имеет обратный знак.

Заряд пластины накопителя 3 равняется значению заряда пластины 2, но так же с обратным знаком, все последующие накопители имеет аналогичную систему заряда.

Формула нахождения заряда на конденсаторе, схема подключения конденсатора:

Последовательное соединение конденсаторов

Когда выполняется последовательное соединение конденсаторов, напряжение на каждом накопители емкости будет различное, так как в зарядке одинаковым количеством электрической энергии участвуют разные емкости.

Зависимость емкости от напряжения такова: чем она меньше, тем большее напряжение необходимо подать на пластины накопителя для его зарядки. И обратная величина: чем выше емкость накопителя, тем меньше требуется напряжения для его зарядки.

Можно сделать вывод, что емкость последовательно соединенных накопителей имеет значение для величины напряжения на пластинах — чем она меньше, тем больше напряжения требуется, а также накопители большой емкости требуют меньшего напряжения.

Основное отличие схемы последовательного соединения накопителей емкости в том, что электроэнергия протекает только в одном направлении, а это означает, что в каждом накопителе емкости составленной батареи ток будет одинаковым. В этом виде соединений конденсаторов обеспечивается равномерное накопление энергии независимо от емкости накопителей.

Группу накопителей емкости можно также на схеме рассматривать как эквивалентный накопитель, на пластины которого подается напряжение, определяемое формулой:

Основные моменты

Заряд общего (эквивалентного) накопителя группы емкостных накопителей последовательного соединения равен:

Формула

Общему значению емкости последовательно соединенных конденсаторов соответствует выражение:

Формула

Смешанное включение емкостных накопителей в схему

Параллельное и последовательное соединение конденсаторов на одном из участков цепи схемы называется специалистами смешанным соединением.

Участок цепи подсоединенных смешанным включением накопителей емкости:

Схема подключения конденсаторов

Смешанное соединение конденсаторов в схеме рассчитывается в определенном порядке, который можно представить следующим образом:

• разбивается схема на простые для вычисления участки, это последовательное и параллельное соединение конденсаторов;
• вычисляем эквивалентную емкость для группы конденсаторов, последовательно включенных на участке параллельного соединения;
• проводим нахождение эквивалентной емкости на параллельном участке;
• когда эквивалентные емкости накопителей определены, схему рекомендуется перерисовать;
• рассчитывается емкость получившейся после последовательного включения эквивалентных накопителей электрической энергии.

Последовательное, параллельное и смешанное соединение конденсаторов

Накопители емкостей (двухполюсники) включены разными способами в цепь, это дает несколько преимуществ в решении электротехнических задач по сравнению с традиционными способами включения конденсаторов:

1. Использование для подключения электрических двигателей и другого оборудования в цехах, в радиотехнических устройствах.
2. Упрощение вычисления величин электросхемы. Монтаж выполняется отдельными участками.
3. Технические свойства всех элементов не меняются, когда изменяется сила тока и магнитное поле, это применяется для включения разных накопителей. Характеризуется постоянной величиной емкости и напряжения, а заряд пропорционален потенциалу.

Вывод

Разного вида включения конденсаторов в цепь применяются для решения электротехнических задач, в частности, для получения полярных накопителей из нескольких неполярных двухполюсников.

В этом случае решением будет соединение группы однополюсных накопителей емкости по встречно-параллельному способу (треугольником). В этой схеме минус соединяется с минусом, а плюс — с плюсом.

Происходит увеличение емкости накопителя, и меняется работа двухполюсника.

Не отображаются имеющиеся вхождения: последовательное параллельное и смешанное соединение конденсаторов, последовательное и параллельное соединение конденсаторов, при параллельном соединении конденсаторов емкость.

Источник: https://domelectrik.ru/baza/komponenty/soedinenie-kondensatorov

Соединение конденсаторов

Радиоэлектроника для начинающих

У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”

Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!

Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?

Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.

• В реальности это выглядит так:
• Параллельное соединение
• Принципиальная схема параллельного соединения
• Последовательное соединение
• Принципиальная схема последовательного соединения

Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.

Как рассчитать общую ёмкость соединённых конденсаторов?

Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.

Общая ёмкость параллельно соединённых конденсаторов:

1. С1 – ёмкость первого;
2. С2 – ёмкость второго;
3. С3 – ёмкость третьего;
4. СN – ёмкость N-ого конденсатора;
5. Cобщ – суммарная ёмкость составного конденсатора.
6. Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!

Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C1, C2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!

Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте здесь.

Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:

Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается .

Или то же самое, но более понятно:

Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.

• В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:
• Здесь, вместо буквы M ставиться количество конденсаторов, а C1 – его ёмкость.
• Стоит также запомнить простое правило:

При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.

Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.

Не будем пускать слов по ветру, а проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.

Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).

Замер ёмкости при последовательном соединении

Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)

А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).

Измерение ёмкости при параллельном соединении

Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).

Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.

При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.

Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.

Для электролитических конденсаторов

При соединении электролитических конденсаторов (электролитов) строго соблюдайте полярность! При параллельном соединении всегда подключайте минусовой вывод одного конденсатора к минусовому выводу другого,а плюсовой вывод с плюсовым.

Параллельное соединение электролитов

Схема параллельного соединения

В последовательном соединении электролитов ситуация обратная. Необходимо подключать плюсовой вывод к минусовому. Получается что-то вроде последовательного соединения батареек.

Последовательное соединение электролитов

Схема последовательного соединения

Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор.

То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт.

Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.

Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.

1. Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены 🙂
2. Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!
3. Главная » Радиоэлектроника для начинающих » Текущая страница
4. Также Вам будет интересно узнать:

Источник: https://go-radio.ru/connection-of-capacitors.html

Последовательное и параллельное соединение конденсаторов

Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.

Последовательное соединение конденсаторов

При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику ЭДС/тока одной из своих пластин.

Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга.

При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.

Напряжение на данном участке цепи соотносятся следующим образом:

Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:

Сократив выражение на Q, получим знакомую формулу:

Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:

Параллельное соединение конденсаторов

При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.

Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:

• Так как заряд конденсатора
• А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов

1. Пример 1
2. Какова результирующая емкость 4 конденсаторов включенных последовательно и параллельно, если известно что С1 = 10 мкФ, C2 = 2 мкФ, C3 = 5 мкФ, а C4 = 1 мкФ?
3. При последовательном соединении общая емкость равна:

• При параллельном соединении общая емкость равна:
• Пример 2
• Определить результирующую емкость группы конденсаторов подключенных последовательно-параллельно, если известно, что С1 = 7 мкФ, С2 = 2 мкФ, С3 = 1 мкФ.
• Сначала найдем общую емкость параллельного участка цепи:
• Затем найдем общую емкость для всей цепи:
• По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.
• Советуем прочесть — Заряд и разряд конденсатора

1 1 1 1 1 1 1 1 1 1 3.31 (8 Голоса)

Источник: https://electroandi.ru/elektronika/posledovatelnoe-i-parallelnoe-soedinenie-kondensatorov.html

Последовательное и параллельное соединение конденсаторов

Все наверняка уже знают, что собой представляют последовательное и параллельное соединения.
Соединение, при котором конец одного устройства соединен с началом следующего, называется последовательным.

• Последовательное соединение конденсаторов
• При последовательном соединении конденсаторов, получаемая цепь выглядит следующим образом:
• Эта схема состоит из следующих элементов:                                                                                          трех конденсаторов C1, C2, С3 и источника электрической энергии E.

Мы видим, что конденсаторы подключены по всем правилам последовательного соединения, то есть вывод конденсатора C1 соединён с началом конденсатора C2, ну а конец конденсатора C2 соединен с началом третьего конденсатора C3.
Стоит обратить внимание на то, как распределяются ёмкости каждого.

При таком соединении, все ёмкостя следующим образом.

Дело в том, что общая емкость всех включенных конденсаторов не будит превышать емкости любого из конденсаторов. Проще говоря, если в данной группе конденсаторов, будит конденсатор с наименьшей емкостью, например, в 100 миро фарад, то общая емкость трех конденсаторов не будит превышать этих ста микрофарад.
Общую емкость можно рассчитать по следующей формуле:

Если в цепи имеются всего лишь два последовательно соединенных конденсатора, то общая емкость определяется по формуле:

1. Параллельное соединение конденсаторов
2. При параллельном соединении, начала всех конденсаторов соединяются в одну точку, а концы в другую, как показано на рисунке ниже:

• Это как два пишем один в уме, только в данном случаи один рисуем, а три в уме.
• Смешанное соединение конденсаторов
• Смешанное соединение конденсаторов выглядит следующим образом:

То есть, емкость каждого конденсатора, включенного параллельно суммируется и получается одна большая емкость, которую можно на схеме представить одним конденсатором.

И представляет с собой различные сочетания параллельного и последовательного соединений.
Для вычисления общей емкости таких соединений, применяют метод замещения: все конденсаторы делят на последовательно и параллельно соединенные группы, рассчитывают ёмкость каждой группы в отдельности, так что в конце выйдет две параллельных или последовательных емкостей, которые можно без труда посчитать.

Например, дана следующая схема и следующие данные:

C1=0.4Ф
C2=0.8Ф
C3=0,73Ф
Необходимо найти общую емкость всех трех конденсаторов.
Как мы видим конденсаторы C1 и C2 соединены последовательно, а конденсатор C3 по отношению к первым двум параллельно.
Посчитав общую емкость последовательно соединенных конденсаторов C1 и C2, их можно представить, как один конденсатор C1,2.

Теперь нам не составит труда посчитать емкость двух параллельно соединенных конденсаторов, просто сложив их ёмкости.

Применения параллельного и последовательного соединений конденсаторов нашло свое применение в тех случаях, когда необходимо получить ту или иную величину емкости. Допустим у вас нет подходящего конденсатора, но есть куча других. Выполнив несколько не хитрых расчетов можно подобрать необходимую емкость.

Источник: https://white-santa.ru/soedinenie_kondensatorov/

Формулы при параллельном соединении конденсаторов. Параллельное,последовательное и смешанное соединение конденсаторов

Электрические конденсаторы широко используются в радиоэлектронной аппаратуре. Они лидируют по количеству применения в блоках аппаратуры и по некоторым критериям уступают лишь резисторам.

Конденсаторы присутствуют в любом электронном устройстве и их потребность в современной электронике постоянно растет.

Наряду с имеющейся широкой номенклатурой, продолжаются разработки новых типов, которые имеют улучшенные электрические и эксплуатационные характеристики.

Что такое конденсатор?

Конденсатором называется элемент электрической цепи, который состоит из проводящих электродов, изолированных друг от друга диэлектриком.

Конденсаторы отличают по емкости, а именно по отношению заряда к разности потенциалов, который передается этим зарядом.

В международной системе СИ за единицу емкости принимают емкость конденсатора
с возрастанием потенциала на один вольт при сообщении заряда в один кулон. Эта единица называется фарадой. Она слишком велика для применения в практических целях. Поэтому принято использовать более мелкие единицы измерения, такие как пикофарад (пФ), нанофарад (нФ) и микрофарад (мкФ).

Группы по виду диэлектрика

Диэлектрики применяют для изоляции пластин друг от друга. Они изготавливаются из органических и неорганических материалов. Нередко, в качестве диэлектрика, применяют оксидные пленки металлов.

По виду диэлектрика элементы делят на группы:

• органические;
• неорганические;
• газообразные;
• оксидные.

Элементы с органическим диэлектриком изготавливают путем намотки тонких лент специальной бумаги или пленки. Также применяют комбинированный диэлектрик
с фольговыми или металлизированными электродами. Такие элементы могут быть как высоковольтные (свыше 1600 В), так и низковольтные (до 1600 В).

В изделиях с неорганическим диэлектриком используют керамику, слюду, стекло и стеклокерамику, стеклоэмаль. Их обкладки состоят из тонкого слоя металла, который нанесен на диэлектрик путем металлизации. Бывают высоковольтные, низковольтные и помехоподавляющие.

В качестве газообразного диэлектрика используют сжатый газ (фреон, азот, элегаз), воздух или вакуум. По характеру изменения емкости и выполняемой функции такие элементы бывают постоянными и переменными.

Наибольшее распространение получили элементы с вакуумным диэлектриком. Они имеют большие удельные емкости (по сравнению с газообразным диэлектриком) и более высокую электрическую прочность. Элементы с вакуумным диэлектриком обладают стабильностью параметров
при температурных изменениях окружающей среды.

Область применения – передающие устройства, работающие на коротких, средних и длинных волнах диапазонов с частотой до 30-80 МГц.

Элементы с оксидным диэлектриком бывают:

• общего назначения;
• пусковые;
• импульсные;
• неполярные;
• высокочастотные;
• помехоподавляющие.

Диэлектриком является оксидный слой, который наносится на анод электрохимическим путем.

Условные обозначения

При сокращенной системе наносятся буквы и цифры
, где буквой обозначается подкласс, цифрой — группа в зависимости от применяемого диэлектрика. Третий элемент указывает регистрационный номер типа изделия.

При полном условном обозначении указываются параметры и характеристики в следующей последовательности:

• условное обозначение конструктивного исполнения изделия;
• номинальное напряжение изделия;
• номинальная емкость изделия;
• допустимое отклонение емкости;
• температурная стабильность емкости изделия;
• номинальная реактивная мощность изделия.

Подбор номинала

Конденсаторы могут соединяться друг с другом различными способами.

На практике нередко возникают ситуации, когда при монтаже схемы или замене неисправного элемента, приходится использовать ограниченное количество радиодеталей. Не всегда удается подобрать элементы нужного номинала.

В этом случае приходится применять последовательное и параллельное соединение конденсаторов.

При параллельной схеме соединения, их суммарная величина составит сумму емкостей
отдельных элементов. При этой схеме подключения все обкладки элементов соединяются по группам. Один из выводов каждого элемента соединяется в одну группу, а другой вывод в другую группу.

При этом напряжение на всех обкладках будет одинаково
, потому что все группы подключены к одному источнику питания. Фактически получается одна емкость, суммарной величины всех емкостей в данной цепи.

Чтобы получить большую емкость, применяют параллельное соединение конденсатора.

Например, необходимо подключить двигатель с тремя фазами к однофазной сети 220 В. Для рабочего режима двигателя необходима емкость величиной в 135 мкФ. Ее найти очень трудно, но можно получить, применив параллельное соединение элементов на 5, 30 и 100 мкФ. В результате сложения получаем необходимую единицу в 135 мкФ.

Последовательно соединение конденсаторов

При последовательном соединении конденсаторов каждый его вывод соединяется с одним выводом другого элемента. Получается некая цепочка из последовательно соединенных конденсаторов, где крайние выводы подключаются к источнику питания.

Емкость общей батареи всегда меньше минимальной емкости элементов, входящих в нее. То есть, половина от емкости каждой из этих емкостей.

• При последовательном соединении конденсаторов увеличивается расстояние между обкладками элементов.
• Например, при последовательном соединении двух элементов напряжением 200 В можно смело включать в схему напряжением до 1000 В.
• Данный метод соединения используется гораздо реже
  , потому что емкости такой величины и рабочего напряжения можно приобрести в магазинах.
• Таким образом, зная принцип общего расчета параллельного и последовательного соединения конденсаторов, всегда можно выйти из затруднительного положения, имея под рукой ограниченное количество номиналов.

Источник: https://offlink.ru/configuring-wi-fi/formuly-pri-parallelnom-soedinenii-kondensatorov-parallelnoe-posledovatelnoe-i-smeshannoe-soedine/

Соединение конденсаторов Параллельное соединение конденсаторов

1. При параллельном соединении конденсаторов к каждому кон­денсатору приложено одинаковое напряжениеU, а величина за­ряда на обкладках каждого конденсатора Qпропорциональна его емкости (рис. 2).

Рис.2 U=U1=U2=U3

1. Общий заряд Qвсех конденсаторов

1. Общая емкость С, или емкость батареи, параллельно включенных конденсаторов равна сумме емкостей этих конденсаторов.

Параллельное
подключение конденсатора к группе
других включенных конденсаторов
увеличивает общую емкость батареи этих
конденсаторов. Следовательно, параллельное
соединение конденсаторов при­меняется
для увеличения емкости.

4)Если
параллельно включены т
одинаковых
конденсаторов ем­костью С´ каждый,
то общая (эквивалентная) емкость батареи
этих конденсаторов может быть определена
выражением

Последовательное соединение конденсаторов

Рис.3

1. На обкладках последовательно соединенных конденсаторов, подключенных к источнику постоянного тока с напряжением U, появятся заряды одинаковые по величине с противоположными знаками.

Q=Q1=Q2=Q3

1. Напряжение на конденсаторах распределяется обратно пропорционально емкостям конденса­торов:

1. Обратная величина общей емкости последовательно соединенных конденсаторов равна сумме обратных величин емкостей этих кон­денсаторов.

При последовательном
включении двух конденсаторов их об­щая
емкость определяется следующим
выражением:

Если
в цепь включены последовательно п
одинаковых
конден­саторов емкостью С
каждый,
то общая емкость этих конденса­торов:

Из
(14) видно, что, чем больше конденсаторов
п
соединено
последовательно, тем меньше будет их
общая емкость С,
т.
е. по­следовательное включение
конденсаторов приводит к уменьше­нию
общей емкости батареи конденсаторов.

На
практике может оказаться , что допустимое
ра­бочее напряжение Upконденсатора
меньше напряжения, на кото­рое
необходимо подключить конденсатор.
Если этот конденсатор подключить на
такое напряжение, то он выйдет из строя,
так как будет пробит диэлектрик.

Если
же последовательно включить не­сколько
конденсаторов, то напряжение распределится
между ними и на каждом конденсаторе
напряжение окажется мень­ше его
допустимого рабочего Up.

Следовательно,
последовательное
соединение конденсаторов применяют
для того, чтобы напряжение на каждом
конденсаторе не превышало его рабочего
напряжения Up.

Смешанное соединение конденсаторов

• Смешанное соединение
  (последовательно-параллельное)
  кон­денсаторов применяют тогда, когда
  необходимо увеличить ем­кость и
  рабочее напряжение батареи конденсаторов.
• Рассмотрим смешанное
  соединение конденсаторов на ниже­приведенных
  примерах.
• Энергия
  конденсаторов
• где Q—
  заряд конденсатора или конденсаторов,
  к которым при­ложено напряжение U;
  С —
  электрическая емкость конденсатора
  или батареи соединенных конденсаторов,
  к которой приложено напряжение U.
• Таким образом,
  конденсаторы служат для накопления и
  сохра­нения электрического поля и
  его энергии.

15.Дайте
определение
понятиям
трех лучевая звезда и треугольник
сопротивлений. Запишите формулы для преобразования трех лучевой звезды
сопротивлений в треугольник сопротивлений
и наоборот. Преобразуйте схему к двум
узлам (Рисунок 5)

Рисунок 5- Схема
электрическая

6.СХЕМЫ ЗАМЕЩЕНИЯ

Для облегчения расчета составляется
схема замещения электрической цепи, т.
е. схема, отображающая свойства цепи
при определенных условиях.

На схеме замещения изображают все
элементы, влиянием которых на результат
расчета нельзя пренебречь, и указывают
также электрические соединения между
ними, которые имеются в цепи.

1.Схемы замещения элементов электрических цепей

На расчетных схемах источник энергии
можно представить ЭДС без внутреннего
сопротивления, если это сопротивление
мало по сравнению с сопротивлением
приемника (рис. 3.13,6).

Приr= 0 внутреннее падение напряженияUо
= 0, поэтому

1. напряжение на зажимах источника при любом токе равно
2. ЭДС: U=E=const.

В некоторых случаях источник электрической
энергии на расчетной схеме заменяют
другой (эквивалентной) схемой (рис. 3.14,
а), где вместо ЭДСЕ источник
характеризуется его током короткого
замыканияIK,
а вместо внутреннего со­противления
в расчет вводится внутренняя проводимостьg=1/r.

• Возможность такой замены можно доказать,
  разделив равенство (3.1) на r:
• U/r
  = E/r—I,
• где U/r
  = Io—некоторый ток,
  равный отношению напряжения на зажимах
  источника к внутреннему сопротивлению;E/r
  = IK— ток короткого замыкания источника;

Вводя новые обозначения, получим
равенство IK
= Io + I,
которому удовлетворяет эквивалентная
схема рис. 3.14,а.

В этом случае при любой величине
напряжения на зажимах; источника его
ток остается равным току короткого
замыкания (рис. 3.14,6):

1. I=Iк=const.
2. Источник с неизменным током, не зависящим
   от внешнего сопротивления, называют
   источником тока.
3. Один и тот же источник электрической
   энергии может быть заменен в расчетной
   схеме источником ЭДС или источником
   тока.

Источник: https://studfile.net/preview/4293202/page:7/

Последовательное соединение конденсаторов

Конденсаторы, наряду с резисторами и диодами, входят в тройку наиболее распространённых электронных компонентов. Различные их соединения встречаются в подавляющем большинстве электробытовых приборов. Их можно встретить в персональных компьютерах, пылесосах, лампочках и даже смартфонах.

Как правильно соединять конденсаторы

Чтобы узнать, как подключить конденсатор правильно, нужно разобраться, к какому именно типу он относится. Данных электронных приборов существует огромное множество. Все конденсаторы подразделяются на две группы:

• полярные (электролитические) – подключая их, необходимо учитывать, где у детали плюсовой, а где минусовой контакт;
• неполярные (все остальные) – эти конденсаторы способны работать от переменного тока, у них не бывает положительных и отрицательных клемм.

Затем нужно учесть конструкцию электронного компонента. С этой точки зрения конденсаторы могут быть:

• Выводными. Подключаются к плате с помощью тонких медных ножек, покрытых (лужёных) для защиты слоем припоя.
• Для поверхностного монтажа (SMD). В основном применяются в компактной электронике. Очень миниатюрны, часто в поперечнике не превышают 1 мм.

Также важно принять во внимание рабочее напряжение конденсатора. Это особенно принципиально для электролитических приборов данного типа, ведь при превышении их номинального вольтажа они, вероятнее всего, взорвутся, разбрызгивая во все стороны кипящий электролит.

Важно! На крышке электролитического конденсатора имеются две насечки. Эти слабые места служат для мгновенной разгерметизации изделия в случае избыточного внутреннего давления. При ремонте и наладке оборудования следует избегать направленности насечек на лицо или одежду. При внештатной ситуации с их стороны может брызнуть горячий электролит.

Не менее критичен порог максимального напряжения и для прочих видов конденсаторов, особенно имеющих мелкие габариты и не способных длительно выдерживать перегрузки.

Последний, но не наименее важный фактор, который следует учесть при соединении конденсаторов, – это их ёмкость. Она измеряется в микрофарадах (в честь Майкла Фарадея).

Это их главная характеристика, поэтому конденсаторы часто называют электрическими ёмкостями. В некоторых электронных устройствах этот параметр может существенно отклоняться как в меньшую, так и в большую сторону.

В других – недопустимо погрешность и на 1 %.

Схема последовательного соединения

Последовательное и параллельное соединение аккумуляторов

Последовательное соединение конденсаторов подразумевает, что правая ножка каждой предстоящей ёмкости будет подключена к левому выводу последующей. Иными словами, детали объединяются в цепь, в которой они идут друг за другом, как люди в длинной очереди в магазине.

Если подключаются электролитические конденсаторы, то плюс одной детали соединяется с минусом другой, по тому же принципу, как и батарейки в различных портативных гаджетах.

Последовательное включение ёмкостей

В случае с распаянными на плате SMD деталями у каждой детали есть своё место, подключаются они тонкими медными проводниками – дорожками при помощи паяльника (редко) или термофена.

При последовательном соединении двух и более ёмкостей их рабочее напряжение суммируется. Нередко такой подход используется радиолюбителями, когда у них нет детали на нужный вольтаж. Формула для вычисления рабочего напряжения линейки из n конденсаторов выглядит следующим образом:

Uобщ.посл = U1 + U2 + … + Un.

Здесь U1, U2… – максимальный вольтаж каждого отдельно взятого конденсатора.

С ёмкостью линейки последовательно включенных деталей всё обстоит иначе. Она наоборот снижается. Объясняется это конструктивными особенностями этих приборов, а именно виртуальным увеличением расстояния между их обкладками. При последовательном соединении общая ёмкость определяется следующим выражением:

1/Cобщ.посл = (1/С1) + (1/С2) + … + (1/Сn).

Здесь C1, C2… – ёмкости отдельных конденсаторов.

Имеется более простой расчет этого параметра, но он пригоден только в том случае, если подключены два конденсатора, не более:

Cобщ.посл = С1*С2/(С1 + С2).

Параллельное и комбинированное соединение

Выделяются другие способы соединения, а именно комбинированное и параллельное подключение конденсаторов. Для них справедливы иные физические законы.

Параллельные конденсаторы

Напряжение всей группы при параллельном соединёнии конденсаторов равно вольтажу самого наименьшего из них. Т.е., если имеется цепь из трёх конденсаторов на 16, 25 и 50 В, то максимум, который на них можно подать, это 16 В. В такой схеме к каждой отдельной ёмкости будет приложено полное напряжение источника питания.

Ёмкость такой батареи складывается. Вызвано это виртуальным сложением площадей обкладок всех отдельных конденсаторов. На языке физики это выглядит так:

Cобщ.пар = С1 + С2 + … + Сn.

Зачем нужно такое соединение? Оно используется для увеличения ёмкости конденсаторов, например, в высоковольтной части сварочных инверторов и многих мощных блоках питания.

Дополнительная информация. Параллельное соединение позволяет снизить общее внутреннее сопротивление сборки, следовательно, и её нагрев. Тем самым можно увеличить срок службы ёмкости.

Комбинированное (смешанное) соединение наиболее сложное. В нём встречаются как последовательные, так и параллельные элементы. Расчёт параметров таких схем даётся с опытом. Для простоты его принято изучать по треугольнику, разбивая на более простые части.

Из схемы очевидно, что конденсаторы C1 и C2 включены последовательно. Их общую ёмкость можно рассчитать по вышеописанной формуле – Cобщ.посл. Далее схема упрощается. Здесь уже имеются два параллельных конденсатора Cобщ.посл и C3.

Вычисляется по вышестоящей формуле Cобщ.пар. В итоге сложный для восприятия элемент цепи превращается в один эквивалентный конденсатор.

Данная методика описывает алгоритм упрощения, с помощью которого можно рассчитывать гораздо более сложные конденсаторные фигуры (квадрат, куб и т.п.).

Ток при последовательном соединении конденсаторов

Электрический ток бывает двух видов: постоянным и переменным. Для работы ёмкостей это имеет большое значение.

Конденсатор и постоянный ток

Маркировка танталовых smd конденсаторов

Постоянный ток через конденсатор не проходит вообще. Справедливо это и для линейки из последовательно соединённых ёмкостей. Объясняется такой эффект опять же конструкцией самого электронного прибора. Конденсатор имеет две металлические обкладки. В простых электролитических приборах они сделаны из алюминиевой фольги.

Между ними расположен тонкий слой диэлектрика (оксид алюминия). Если приложить к обкладкам разность потенциалов (напряжение), то ток потечёт, но только очень короткое время, пока конденсатор полностью ни зарядится. Далее движение носителей заряда прекратится, т.к. они не смогут пройти через диэлектрик.

В этот момент можно сказать, что электрический ток равен нулю, и конденсатор его не пропускает.

Конденсатор и переменный ток

При переменном токе носители заряда периодически меняют своё направление. В случае с бытовой сетью изменение происходит 50 раз в секунду. Поэтому говорят, что частота тока в розетке равна 50 Гц.

Важно! Конденсаторы способны накапливать и длительно удерживать заряд. При работе с ёмкостями, заряженными от сети 220 В, их всегда следует разряжать сопротивлением в 100-1000 ом. Несоблюдение правила однажды приведёт к неприятному удару током.

Конденсатор определённо пропустит переменный ток, но не факт, что весь. Количество носителей заряда, которые смогут пройти через этот электронный прибор, зависит от ёмкости конденсатора, приложенного к нему напряжения и частоты смены направления зарядов. Математически это выражается так:

I = 2pfCU.

Здесь I – это электрический ток с частотой f, проходящий через конденсатор ёмкостью C, если к его обкладкам приложить напряжение U. 2 – просто число, а p = 3.14.

Такая способность конденсаторов ограничивать переменный ток широко применяется в аудиотехнике для построения различных звуковых фильтров. Изменяя ёмкость, можно влиять на частоту сигнала, которую она пропускает.

Падение напряженности и общая емкость

• Ёмкость конденсатора – это величина, определяющая количество заряда, который он способен в себе сохранить. Выражение имеет следующий вид:
• C = q/U.
• Здесь q – заряд, накопленный между обкладками конденсатора, U – напряжение к ним приложенное.
• Вышеописанная формула представляет общий случай. На практике при расчете ёмкости конденсатора следует учитывать ряд других переменных:
• C = E0ES/d,
• где:

• E0 – электрическая постоянная, равная 8,85*10-12 Ф/м,
• E – диэлектрическая проницаемость среды, в которой располагаются обкладки конденсатора,
• S – их площадь пересечения,
• d – расстояние между обкладками.

Стандартная модель конденсатора имеет следующий вид.

Обкладки чаще всего изготовлены из тонкого листового алюминия и скручены в рулон. Делается это для увеличения их площади, ведь так ёмкость конденсатора становится существенно больше.

От выбора диэлектрика, устанавливаемого производителем между обкладками конденсатора, зависит номинальное и максимальное напряжение прибора. Это, в свою очередь, определяет его сферу применения.

Если к обкладкам приложить чрезмерную разность потенциалов, то напряжённость поля между ними превысит допустимый уровень, и произойдёт пробой диэлектрика. Подобная ситуация особенно пагубно влияет на электролитические конденсаторы и ионисторы.

В случае их пробоя прибор частично или полностью теряет способность накапливать заряд и в дальнейшем становится непригодным для работы.

При последовательном и параллельном включении разных конденсаторов существенно изменяются их характеристики. Данное свойство этих деталей активно используется инженерами-электронщиками и радиолюбителями. Знание принципов подключения позволяет им более продуктивно разрабатывать новые устройства.

Видео

Источник: https://amperof.ru/teoriya/posledovatelnoe-soedinenie-kondensatorov.html

Соединение конденсаторов

Конденсаторы, как и резисторы, можно соединять последовательно и параллельно. Рассмотрим соединение конденсаторов: для чего применяются каждая из схем, и их итоговые характеристики.

Параллельное соединение конденсаторов

Параллельное соединение конденсаторов

Эта схема – самая распространенная. В ней обкладки конденсаторов соединяются между собой, образуя эквивалентную емкость, равную сумме соединяемых емкостей.

При параллельном соединении электролитических конденсаторов необходимо, чтобы между собой соединялись выводы одной полярности.

Особенность такого соединения – одинаковое напряжение на всех соединяемых конденсаторах. Номинальное напряжение группы параллельно соединенных конденсаторов равно рабочему напряжению конденсатора группы, у которого оно минимально.

Токи через конденсаторы группы протекают разные: через конденсатор с большей емкостью потечет больший ток.

На практике параллельное соединение применяется для получения емкости нужной величины, когда она выходит за границы диапазона, выпускаемого промышленностью, или не укладываются в стандартный ряд емкостей. В системах регулирования коэффициента мощности (cos ϕ) изменение емкости происходит за счет автоматического подключения или отключения конденсаторов в параллель.

Последовательное соединение конденсаторов

Последовательное соединение конденсаторов

При последовательном соединении обкладки конденсатором соединяются друг к другу, образуя цепочку. Крайние обкладки подключаются к источнику, а ток по всем конденсаторам группы потечет одинаковый.

Эквивалентная емкость последовательно соединенных конденсаторов ограничена самой маленькой емкостью в группе. Объясняется это тем, что как только она полностью зарядится, ток прекратится. Подсчитать общую емкость двух последовательно соединенных конденсаторов можно по формуле

а трех –

Но применение последовательного соединения для получения нестандартных номиналов емкостей не так распространено, как параллельного.

При последовательном соединении напряжение источника питания распределяется между конденсаторами группы. Это позволяет получить батарею конденсаторов, рассчитанную на большее напряжение, чем номинальное напряжение входящих в нее компонентов. Так из дешевых и небольших по размерам конденсаторов изготавливаются блоки, выдерживающие высокие напряжения.

Еще одна область применения последовательного соединения конденсаторов связана с перераспределением напряжений между ними. Если емкости одинаковы, напряжение делится пополам, если нет – на конденсаторе большей емкости напряжение получается большим. Устройство, работающее на этом принципе, называют емкостным делителем напряжения.

Смешанное соединение конденсаторов

Пример смешанного соединения конденсаторов

Такие схемы существуют, но в устройствах специального назначения, требующие высокой точности получения величины емкости, а также для их точной настройки.

Оцените качество статьи:

Как соединить конденсаторы? Последовательное и параллельное соединение

Вопрос о том, как соединить конденсаторы может возникнуть у любого человека, интересующегося электроникой и пайкой. Чаще всего, необходимость в этом возникает в случаях отсутствия под рукой устройства подходящего номинала при сборке или ремонте какого-либо прибора.

К примеру, человеку нужно отремонтировать устройство, заменив в нем электролитический конденсатор ёмкостью 1000 микрофарад или больше, на руках подходящие по номиналу детали отсутствуют, но есть несколько изделий с меньшими параметрами. В этом случае есть три варианта выхода из сложившейся ситуации:

1. Поставить вместо конденсатора на 1000 микрофарад устройство с меньшим номиналом.
2. Поехать в ближайший магазин или радио-рынок для покупки подходящего варианта.
3. Соединить несколько элементов вместе для получения необходимой ёмкости.

От установки радиоэлемента меньшего номинала лучше отказаться, так как подобные эксперименты не всегда заканчиваются успешно. Можно съездить на рынок или в магазин, но это требует немало времени. Потому в сложившейся ситуации чаще соединяют несколько конденсаторов и получают необходимую емкость.

Параллельное соединение конденсаторов

Параллельная схема подключения конденсаторов предполагает соединение в две группы всех обкладок приборов. В одну группу соединяются первые выводы, а в другую группу – вторые выводы. На рисунке ниже представлен пример.

Конденсаторы, соединенные параллельно между собой, подключаются к одному источнику напряжения, поэтому на них существует две точки напряжения или разности потенциалов. Следует учитывать, что на всех выводах подключенных параллельно конденсаторов напряжение будет иметь одинаковую величину.

Параллельная схема образует из элементов единую ёмкость, величина которой равняется сумме ёмкостей всех подключенных в группу конденсаторов. При этом через конденсаторы в процессе работы устройства будет протекать ток разной величины. Параметры проходящего через изделия тока зависят от индивидуальной ёмкости устройства. Чем выше ёмкость, тем больший по величине ток пройдет через него. Формула, характеризующее параллельное соединение, имеет следующий вид:

Параллельная схема чаще всего используется в быту, она позволяет собрать необходимую ёмкость из любого числа отдельных, различных по номиналу элементов.

Последовательное соединение конденсаторов

Схема последовательного подключения представляет собой цепочку, в которой первая обкладка конденсатора соединяется со второй обкладкой предыдущего устройства, а вторая обкладка – с первой обкладкой следующего прибора. Первый вывод первого конденсатора и второй вывод последней детали в цепи соединяются с источником электрического тока, благодаря чему между ними осуществляется перераспределение электрических зарядов. Все промежуточные обкладки имеют одинаковые по величине заряды, чередующиеся по знаку.

На рисунке ниже представлен пример последовательного подключения.

Через соединенные в группу конденсаторы протекает ток одинаковой величины. Общая мощность ограничивается площадью обкладок устройства с наименьшим номиналом, так как после зарядки наименьшего по ёмкости устройства, вся цепь перестанет пропускать ток.

Несмотря на явные недостатки, данный способ обеспечивает увеличение изоляции между отдельными обкладками до суммы расстояний между выводами на всех последовательно соединенных конденсаторах. То есть, при последовательном соединении двух элементов с рабочим напряжением 200 В, изоляция между их выводами сможет выдерживать напряжение до 1000 В. Ёмкость по формуле:

Данный способ позволяет получить эквивалент меньшего по ёмкости конденсатора в группе, способной работать при высоких напряжениях. Всего этого можно достичь путем покупки одного единственного элемента подходящего номинала, потому на практике последовательные соединения практически не встречаются.

Эта формула актуальна для расчета общей ёмкости цепи последовательно соединенных двух конденсаторов. Для определения общей ёмкости цепи с большим числом приборов необходимо воспользоваться формулой:

Смешанная схема

Пример смешанной схемы подключения представлен ниже.

Чтобы определить общую ёмкость нескольких устройств, всю схему необходимо разделить на имеющиеся группы последовательного и параллельного соединения и рассчитать параметры ёмкости для каждой из них.

На практике данный способ встречаются на различных платах, с которыми приходиться работать радиолюбителям.

8.3: Последовательные и параллельные конденсаторы

Несколько конденсаторов могут быть соединены вместе для использования в различных приложениях. Несколько подключений конденсаторов ведут себя как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения. Конденсаторы могут быть организованы в два простых и распространенных типа соединений, известных как серии и параллельно , для которых мы можем легко вычислить общую емкость.Эти две основные комбинации, последовательная и параллельная, также могут использоваться как часть более сложных соединений.

Серия конденсаторов

На рисунке \ (\ PageIndex {1} \) показано последовательное сочетание трех конденсаторов, расположенных в ряд внутри схемы. Как и в случае любого конденсатора, емкость комбинации связана как с зарядом, так и с напряжением:

\ [C = \ dfrac {Q} {V}. \]

Когда эта последовательная комбинация подключена к батарее с напряжением В , каждый из конденсаторов получает одинаковый заряд Q .Чтобы объяснить, сначала обратите внимание, что заряд на пластине, подключенной к положительной клемме батареи, равен \ (+ Q \), а заряд на пластине, подключенной к отрицательной клемме, равен \ (- Q \). Затем на других пластинах индуцируются заряды, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю. Однако падение потенциала \ (V_1 = Q / C_1 \) на одном конденсаторе может отличаться от падения потенциала \ (V_2 = Q / C_2 \) на другом конденсаторе, потому что, как правило, конденсаторы могут иметь разные емкости.Последовательная комбинация двух или трех конденсаторов напоминает один конденсатор с меньшей емкостью. Как правило, любое количество последовательно соединенных конденсаторов эквивалентно одному конденсатору, емкость которого (называемая эквивалентной емкостью ) меньше наименьшей из емкостей в последовательной комбинации. Заряд этого эквивалентного конденсатора такой же, как заряд любого конденсатора в последовательной комбинации: то есть все конденсаторы последовательной комбинации имеют одинаковый заряд .Это происходит из-за сохранения заряда в цепи. Когда заряд Q в последовательной цепи удаляется с пластины первого конденсатора (который мы обозначаем как \ (- Q \)), он должен быть помещен на пластину второго конденсатора (который мы обозначаем как \ ( + Q \)) и т. Д.

Рисунок \ (\ PageIndex {1} \): (a) Три конденсатора соединены последовательно. Величина заряда на каждой пластине равна Q. (b) Сеть конденсаторов на (a) эквивалентна одному конденсатору, который имеет меньшую емкость, чем любая из отдельных емкостей на (a), а заряд на его пластинах равен В.

Мы можем найти выражение для полной (эквивалентной) емкости, рассматривая напряжения на отдельных конденсаторах. Потенциалы на конденсаторах 1, 2 и 3 равны, соответственно, \ (V_1 = Q / C_1 \), \ (V_2 = Q / C_2 \) и \ (V_3 = Q / C_3 \). Эти потенциалы должны суммироваться с напряжением батареи, давая следующий баланс потенциалов:

\ [V = V_1 + V_2 + V_3. \]

Потенциал \ (V \) измеряется на эквивалентном конденсаторе, который держит заряд \ (Q \) и имеет эквивалентную емкость \ (C_S \).Вводя выражения для \ (V_1 \), \ (V_2 \) и \ (V_3 \), получаем

\ [\ dfrac {Q} {C_S} = \ dfrac {Q} {C_1} + \ dfrac {Q} {C_2} + \ dfrac {Q} {C_3}. \]

Отменяя заряд Q , мы получаем выражение, содержащее эквивалентную емкость \ (C_S \) трех последовательно соединенных конденсаторов:

\ [\ dfrac {1} {C_S} = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3}. \]

Это выражение можно обобщить на любое количество конденсаторов в последовательной сети.

Комбинация серии

Для конденсаторов, соединенных последовательно, эквивалентная емкость равна сумме обратных величин индивидуальных емкостей:

\ [\ dfrac {1} {C_S} = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3} + \ dots \ label {capseries} \]

Пример \ (\ PageIndex {1} \): эквивалентная емкость последовательной сети

Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их индивидуальные емкости равны \ (1.000 мкФ \), \ (5.000 мкФ \) и \ (8.000 мкФ \).

Стратегия

Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение \ ref {capseries} с тремя членами.

Решение

Вводим указанные емкости в уравнение \ ref {capseries}:

\ [\ begin {align *} \ dfrac {1} {C_S} & = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3} \\ [4pt] & = \ dfrac {1} {1.000 \ mu F} + \ dfrac {1} {5.000 \ mu F} + \ dfrac {1} {8.000 \ mu F} \\ [4pt] & = \ dfrac {1.325} {\ mu F}. \ End {align *} \]

Теперь инвертируем этот результат и получаем

\ [\ begin {align *} C_S & = \ dfrac {\ mu F} {1.325} \\ [4pt] & = 0.755 \ mu F. \ end {align *} \ nonumber \]

Значение

Обратите внимание, что в последовательной сети конденсаторов эквивалентная емкость всегда меньше наименьшей отдельной емкости в сети.

Параллельная комбинация конденсаторов

Параллельная комбинация трех конденсаторов, одна пластина каждого конденсатора подключена к одной стороне цепи, а другая пластина подключена к другой стороне, показана на рисунке \ (\ PageIndex {2a} \).Поскольку конденсаторы соединены параллельно, все они имеют одинаковое напряжение V на пластинах . Однако каждый конденсатор в параллельной сети может сохранять свой заряд. Чтобы найти эквивалентную емкость \ (C_p \) параллельной сети, отметим, что общий заряд Q , хранящийся в сети, является суммой всех отдельных зарядов:

\ [Q = Q_1 + Q_2 + Q_3. \]

В левой части этого уравнения мы используем соотношение \ (Q = C_pV \), которое выполняется для всей сети.В правой части уравнения мы используем соотношения \ (Q_1 = C_1 V \), \ (Q_2 = C_2V \) и \ (Q_3 = C_3V \) для трех конденсаторов в сети. Таким образом получаем

\ [C_pV = C_1V + C_2V + C_3V. \]

Это уравнение в упрощенном виде представляет собой выражение для эквивалентной емкости параллельной сети из трех конденсаторов:

\ [C_p = C_1 + C_2 + C_3. \]

Это выражение легко обобщается на любое количество конденсаторов, включенных параллельно в сеть.

Параллельная комбинация

Для конденсаторов, соединенных параллельно, эквивалентная (полезная) емкость представляет собой сумму всех индивидуальных емкостей в сети,

\ [C_p = C_1 + C_2 + C_3 + … \ label {capparallel} \]

Рисунок \ (\ PageIndex {2} \): (a) Три конденсатора подключены параллельно. Каждый конденсатор подключен непосредственно к батарее. (b) Заряд эквивалентного конденсатора представляет собой сумму зарядов отдельных конденсаторов.

Пример \ (\ PageIndex {2} \): эквивалентная емкость параллельной сети

Найдите полезную емкость для трех конденсаторов, соединенных параллельно, учитывая, что их отдельные емкости равны \ (1.0 \ mu F \), \ (5.0 \ mu F \) и \ (8.0 \ mu F \).

Стратегия

Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение \ ref {capparallel} с тремя членами.

Решение

Ввод заданных емкостей в уравнение \ ref {capparallel} дает

\ [\ begin {align *} C_p & = C_1 + C_2 + C_3 \\ [4pt] & = 1.0 \ mu F + 5.0 \ mu F + 8.0 \ mu F \\ [4pt] & = 14.0 \ mu F.\ end {align *} \]

Значение

Обратите внимание, что в параллельной сети конденсаторов эквивалентная емкость всегда больше, чем любая из отдельных емкостей в сети.

Конденсаторные сети обычно представляют собой комбинацию последовательных и параллельных соединений, как показано на Рисунке \ (\ PageIndex {3} \). Чтобы найти чистую емкость таких комбинаций, мы определяем части, которые содержат только последовательные или только параллельные соединения, и находим их эквивалентные емкости.Мы повторяем этот процесс, пока не сможем определить эквивалентную емкость всей сети. Следующий пример иллюстрирует этот процесс.

Рисунок \ (\ PageIndex {3} \): (a) Эта схема содержит как последовательные, так и параллельные соединения конденсаторов. (b) \ (C_1 \) и \ (C_2 \) идут последовательно; их эквивалентная емкость \ (C_S \) c) Эквивалентная емкость \ (C_S \) подключена параллельно с \ (C_3 \). Таким образом, эквивалентная емкость всей сети является суммой \ (C_S \) и \ (C_3 \).

Пример \ (\ PageIndex {3} \): эквивалентная емкость сети

Найдите общую емкость комбинации конденсаторов, показанной на рисунке \ (\ PageIndex {3} \). Предположим, что емкости известны с точностью до трех десятичных знаков (\ (C_1 = 1.000 мкФ, C_2 = 5.000 мкФ, C_3 = 8.000 мкФ \)). Округлите ответ до трех знаков после запятой.

Стратегия

Сначала мы определяем, какие конденсаторы включены последовательно, а какие — параллельно. Конденсаторы \ (C_1 \) и \ (C_2 \) включены последовательно.Их комбинация, помеченная \ (C_S \), параллельна \ (C_3 \).

Решение

Поскольку \ (C_1 \) и \ (C_2 \) включены последовательно, их эквивалентная емкость \ (C_S \) получается с помощью уравнения \ ref {capseries}:

\ [\ begin {align *} \ dfrac {1} {C_S} & = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} \\ [4pt] & = \ dfrac {1} {1.000 \ mu F} + \ dfrac {1} {5.000 \ mu F} \\ [4pt] & = \ dfrac {1.200} {\ mu F} \ end {align *} \]

Для этого

\ [C_S = 0,833 \ mu F. \ nonumber \]

Емкость \ (C_S \) соединена параллельно с третьей емкостью \ (C_3 \), поэтому мы используем уравнение \ ref {capparallel}, чтобы найти эквивалентную емкость C всей сети:

\ [\ begin {align *} C & = C_S + C_3 \\ [4pt] & = 0.833 \ mu F + 8.000 \ mu F \\ [4pt] & = 8.833 \ mu F. \ end {align *} \]

Сеть конденсаторов

Определите чистую емкость C комбинации конденсаторов, показанной на рисунке \ (\ PageIndex {4} \), когда емкости равны \ (C_1 = 12,0 мкФ, C_2 = 2,0 мкФ \) и \ (C_3 = 4,0 мкФ \). Когда на комбинации поддерживается разность потенциалов 12,0 В, найдите заряд и напряжение на каждом конденсаторе.

Рисунок \ (\ PageIndex {4} \): (a) Комбинация конденсаторов.(b) Эквивалентная комбинация из двух конденсаторов. Стратегия

Сначала мы вычисляем чистую емкость \ (C_ {23} \) параллельного соединения \ (C_2 \) и \ (C_3 \). Тогда C — это чистая емкость последовательного соединения \ (C_1 \) и \ (C_ {23} \). Мы используем соотношение \ (C = Q / V \), чтобы найти заряды \ (Q_1, Q_2 \) и \ (Q_3 \), а также напряжения \ (V_1, V_2 \) и \ (V_3 \) на конденсаторы 1, 2 и 3 соответственно.

Решение Эквивалентная емкость для \ (C_2 \) и \ (C_3 \) составляет

\ [C_ {23} = C_2 + C_3 = 2.0 мк F + 4,0 мк F = 6,0 мк F. \]

Вся комбинация из трех конденсаторов эквивалентна двум последовательно включенным конденсаторам,

\ [\ dfrac {1} {C} = \ dfrac {1} {12.0 \ mu F} + \ dfrac {1} {6.0 \ mu F} = \ dfrac {1} {4.0 \ mu F} \ Rightarrow C = 4,0 мкм F. \]

Рассмотрим эквивалентную комбинацию из двух конденсаторов на рисунке \ (\ PageIndex {2b} \). Поскольку конденсаторы включены последовательно, они имеют одинаковый заряд, \ (Q_1 = Q_ {23} \). Кроме того, конденсаторы имеют общую разность потенциалов 12,0 В, поэтому

\ [12.0 V = V_1 + V_ {23} = \ dfrac {Q_1} {C_1} + \ dfrac {Q_ {23}} {C_ {23}} = \ dfrac {Q_1} {12.0 \ mu F} + \ dfrac {Q_1 } {6.0 \ mu F} \ Rightarrow Q_1 = 48.0 \ mu C. \]

Теперь разность потенциалов на конденсаторе 1 равна

.

\ [V_1 = \ dfrac {Q_1} {C_1} = \ dfrac {48.0 \ mu C} {12.0 \ mu F} = 4.0 V. \]

Поскольку конденсаторы 2 и 3 подключены параллельно, они имеют одинаковую разность потенциалов:

\ [V_2 = V_3 = 12,0 В — 4,0 В = 8,0 В. \]

Следовательно, заряды на этих двух конденсаторах равны, соответственно,

\ [Q_2 = C_2V_2 = (2.0 мкФ) (8,0 В) = 16,0 мкФ, \]

\ [Q_3 = C_3V_3 = (4,0 мкФ) (8,0 В) = 32,0 мкФ \]

Значение Как и ожидалось, чистая плата за параллельную комбинацию \ (C_2 \) и \ (C_3 \) составляет \ (Q_ {23} = Q_2 + Q_3 = 48,0 \ mu C. \)

Упражнение \ (\ PageIndex {1} \)

Определите чистую емкость C каждой сети конденсаторов, показанной ниже. Предположим, что \ (C_1 = 1,0 пФ, C_2 = 2,0 пФ, C_3 = 4,0 пФ \) и \ (C_4 = 5,0 пФ \). Найдите заряд каждого конденсатора, предполагая, что разность потенциалов равна 12.0 В в каждой сети.

Ответьте на

\ (C = 0,86 пФ, Q_1 = 10 пКл, Q_2 = 3,4 пКл, Q_3 = 6,8 пКл \)

Ответ b

\ (C = 2,3 пФ, Q_1 = 12 пКл, Q_2 = Q_3 = 16 пКл \)

Ответ c

\ (C = 2,3 пФ, Q_1 = 9,0 пКл, Q_2 = 18 пКл, Q_3 = 12 пКл, Q_4 = 15 пКл \)

конденсаторов последовательно и параллельно с примерами

Последовательные и параллельные конденсаторы

Системы с более чем одним конденсатором имеют эквивалентную емкость.Конденсаторы можно соединять между собой двумя способами. Их можно подключать последовательно и параллельно. Сначала мы увидим конденсаторы, включенные параллельно.

В этой цепи конденсаторы включены параллельно.

Потому что левые стороны конденсаторов подключены к потенциалу a, а правые стороны конденсаторов подключены к потенциалу b.Другими словами, мы можем сказать, что каждый конденсатор имеет одинаковую разность потенциалов. Находим заряд каждого конденсатора как;

Q ₁ = C ₁ .V

Q ₂ = C ₂ .V

Q ₃ = C ₃ .V

Общий заряд системы определяется сложением каждого заряда.

Q _всего = C _экв .V

Q _итого = Q ₁ + Q ₂ + Q ₃ = C ₁ .V + C ₂ .V + C ₃ .V = V. (C ₁ + C ₂ + C ₃ ) = C _экв.

C _экв = C ₁ + C ₂ + C ₃

Как видите, мы нашли эквивалентную емкость системы как C ₁ + C ₂ + C ₃

Теперь посмотрим последовательно включенные конденсаторы;

В конденсаторах, подключенных последовательно, каждый конденсатор имеет одинаковый поток заряда от батареи.В этой схеме заряд + Q течет от положительной части батареи к левой пластине первого конденсатора и притягивает заряд –Q на правой пластине, с той же идеей заряд -Q течет от батареи к правой пластине. третьего конденсатора и притягивает + Q на левой пластине. Таким же образом заряжаются и другие конденсаторы. Подводя итог, можно сказать, что каждый конденсатор имеет одинаковый заряд с батареей.

C ₁ .V ₁ = Q

С ₂ .V ₂ = Q, V = V ₁ + V ₂ + V ₃ и Q = C _экв .V

C ₃ .V ₃ = Q

Пример: вычислить эквивалентную емкость между точками a и b.

Пример: В приведенной ниже схеме C1 = 60 мкФ, C2 = 20 мкФ, C3 = 9 мкФ и C4 = 12 мкФ.Если разность потенциалов между точками a an b Vab = 120V, найдите заряд второго конденсатора.

Емкостное реактивное сопротивление — Как найти последовательные и параллельные конденсаторы

Найдите емкостное реактивное сопротивление цепи с последовательными или параллельными конденсаторами, используя этот простой двухэтапный процесс.

Шаг 1: Найдите общую емкость цепи

Предположим, у нас есть три конденсатора, 12 Ф, 20 Ф и 30 Ф, подключенных к источнику с частотой 60 Гц.Каково полное емкостное реактивное сопротивление (X _C ) при последовательном или параллельном подключении?

1А. Для конденсаторов серии

Когда конденсаторы соединены последовательно, общая емкость меньше, чем любая из отдельных емкостей последовательных конденсаторов. Если два или более конденсатора соединены последовательно, общий эффект будет таким, как у одиночного (эквивалентного) конденсатора, имеющего суммарное расстояние между пластинами отдельных конденсаторов.

Конденсаторы серии

Пример:

1/12 = 0,083, 1/20 = 0,050, 1/30 = 0,033

0,083 + 0,050 + 0,033 = 0,166

1 / 0,163 = 6,02 мкФ

Примечание: математические расчеты упрощены для целей иллюстрации. Для более точных чисел воспользуйтесь калькулятором.

1Б. Для параллельных конденсаторов

При параллельном подключении конденсаторов общая емкость представляет собой сумму емкостей отдельных конденсаторов.Если два или более конденсатора подключены параллельно, общий эффект будет таким, как у одного эквивалентного конденсатора, имеющего сумму площадей пластин отдельных конденсаторов.

Параллельные конденсаторы Пример:

12 + 20 + 30 = 62 мкФ

Шаг 2: Определите емкостное сопротивление

Как и сопротивление, реактивное сопротивление измеряется в Ом, но ему присваивается символ X, чтобы отличать его от чисто резистивного значения R, и, поскольку рассматриваемый компонент является конденсатором, реактивное сопротивление конденсатора называется емкостным реактивным сопротивлением (X _C ) который измеряется в Ом.

Поскольку конденсаторы заряжаются и разряжаются пропорционально скорости изменения напряжения на них, чем быстрее изменяется напряжение, тем больше тока протекает. Точно так же, чем медленнее изменяется напряжение, тем меньше будет протекать ток. Это означает, что реактивное сопротивление конденсатора переменного тока «обратно пропорционально» частоте источника питания.

X _C — емкостное реактивное сопротивление в Ом, f — частота в герцах и C — емкость переменного тока в фарадах. Очень важно преобразовать наш пример из микрофарад в фарады, чтобы получить правильный результат!

1 мкФ = 0,000001 F

Серия 60 Гц Пример:

6,02 мкФ = 0,000006 Ф (упрощенно)
2 х 3,14 х 60 х 0,000006 = 0,0022608
1 / 0,0022608 = 442,32 Ом

Параллельный 60 Гц Пример:

62 мкФ = 0,000062 F
2 х 3.14 х 60 х 0,000062 = 0,0233616
1 / 0,0233616 = 42,805 Ом

Теперь посмотрим, что произойдет при изменении частоты на 400 Гц :

Серия 400 Гц Пример:

2 х 3,14 х 400 х 0,000006 = 0,015072
1 / 0,015072 = 66,34 Ом

Параллельный 400 Гц Пример:

2 х 3,14 х 400 х 0,000062 = 0,155744
1 / 0,155744 = 6,42 Ом

Полезные ссылки

Параллельно резисторов и конденсаторов

Введение

В этом последнем разделе мы исследуем частотную характеристику цепей, содержащих резисторы и конденсаторы в параллельных комбинациях.Как и в предыдущем разделе, мы можем использовать анализ постоянного тока параллельных цепей резисторов в качестве отправной точки, а затем учесть фазовое соотношение между током, протекающим через резистор и компоненты конденсатора.

Анализ параллельных цепей RC

Как мы видели ранее, в параллельной цепи у тока есть несколько альтернативных путей, и выбранный маршрут зависит от относительного «сопротивления» каждой ветви. На рисунке ниже показано параллельное сочетание одного резистора и конденсатора между точками A и B .

Для расчета полного импеданса (сопротивления) этой цепи мы снова используем емкостное реактивное сопротивление Xc как эквивалентное сопротивление конденсатора. Затем мы используем те же правила, что и для последовательного суммирования резисторов, помня, что теперь мы имеем дело с векторными величинами. Вы помните, что правило для параллельного суммирования резисторов дает

.

, рассматривая R2 выше как емкостное реактивное сопротивление и небольшую часть алгебры комплексных чисел, мы можем показать, что величина импеданса и фазовый угол задаются следующим образом

Теперь мы рассмотрим реакцию схемы, как указано выше, с емкостным сопротивлением 50 Ом и сопротивлением 100 Ом

и угол составляет -63,4 °. Частотная характеристика схемы этого типа показана ниже в виде вектора и боде.

Видно, что фазовый угол изменяется от 0 ° на низких частотах, где ток почти полностью проходит через плечо резистора, до -90 ° на высоких частотах, когда ток протекает через ветвь, содержащую конденсатор.

Что такое серийная компенсация? Преимущества и расположение последовательных конденсаторов

Определение: Последовательная компенсация — это метод повышения напряжения системы путем последовательного подключения конденсатора к линии передачи.Другими словами, при последовательной компенсации реактивная мощность вводится последовательно с линией передачи для улучшения импеданса системы. Это улучшает способность линии передавать мощность. Он в основном используется в линиях сверхвысокого и сверхвысокого напряжения.

Преимущества серийной компенсации

Компенсация серии

имеет несколько преимуществ, таких как увеличение пропускной способности, улучшение стабильности системы, регулирование управляющего напряжения и обеспечение правильного распределения нагрузки между параллельными фидерами.Эти преимущества обсуждаются ниже.

• Увеличение мощности передачи — Передача мощности по линии задается параметром

, где P ₁ — мощность, передаваемая на фазу (Вт)
В _с — фазное напряжение на передающем конце (В)
В _r — фазовое напряжение на приемном конце
X _L — последовательное индуктивное реактивное сопротивление линия
δ — фазовый угол между V _s и V _r

Если конденсатор с емкостным реактивным сопротивлением X _c включен последовательно с линией, реактивное сопротивление линии уменьшается с X _L до (X _L — X _c ).Передача мощности дана

где, Коэффициент k известен как степень компенсации или коэффициент компенсации. Таким образом, на единицу компенсации дается уравнение, процентное вознаграждение дается уравнением

Где X _L = полное последовательное индуктивное сопротивление линии на фазу
X _C = емкостное реактивное сопротивление конденсаторной группы на фазу
На практике k находится в пределах от 0,4 до 0,7. Для k = 0,5

Таким образом, передача мощности удваивается с компенсацией 50%.

• Повышение стабильности системы — Для одинаковой передачи мощности и для одного и того же значения конечного напряжения передачи и приема, фазовый угол δ в случае последовательной линии полного сопротивления меньше, чем для некомпенсированной линии. Уменьшенное значение δ дает более высокую стабильность.
• Разделение нагрузки между параллельными линиями — Конденсаторы серии используются в системах передачи для улучшения разделения нагрузки между параллельными линиями. Когда новая линия с большой способностью передачи мощности работает параллельно с уже существующей линией, тогда трудно загрузить новую линию без перегрузки старой линии.В таком случае последовательная компенсация снижает последовательное реактивное сопротивление, и правильное разделение нагрузки между параллельными цепями может быть легко выполнено. Разделение нагрузки увеличивает способность системы передавать мощность и снижает потери.
• Контроль напряжения — В последовательном конденсаторе происходит автоматическое изменение Var (реактивной мощности) при изменении тока нагрузки. Таким образом, падение уровня напряжения из-за внезапных изменений нагрузки исправляется мгновенно.

Расположение последовательного конденсатора

Расположение последовательного конденсатора зависит от экономических и технических соображений линии.Последовательный конденсатор может быть расположен на передающем конце, приемном конце или в центре линии. Иногда они располагаются в двух или более точках на линии.

Степень компенсации и характеристика линии определяют расположение конденсаторов. Их установка на клеммах обеспечивает возможность технического обслуживания, но перенапряжение, возникающее на клеммах конденсаторов в условиях неисправности, приведет к перенапряжению конденсатора.

Конденсаторы устанавливаются в промежуточной коммутационной станции сравнительно протяженных линий.Расположение в центре линии также снизило номинальные характеристики конденсатора. Номинал последовательного конденсатора равен

.

где I — линейный ток. Конденсаторные батареи состоят из небольших блоков, соединенных последовательно, параллельно или и тем, и другим для получения желаемого напряжения и номинальной мощности.

Схемы защиты последовательного конденсатора

При возникновении неисправности или перегрузки через последовательный конденсатор линии протекает большой ток. Таким образом, на линии передачи возникает чрезмерное падение напряжения.Для защиты конденсаторов от таких аномальных напряжений к клеммам конденсатора подключены искровые разрядники и устройство защиты от перенапряжения. Параллельно с ним также подключается автоматический выключатель. Некоторые из методов последовательного конденсатора показаны ниже.

Проблема, связанная с последовательным конденсатором

Некоторые проблемы, связанные с применением последовательного конденсатора, подробно описаны ниже.

• Линия с последовательной компенсацией создает последовательный резонанс на частотах ниже, чем рабочие частоты.Это называется субсинхронным резонансом. Подсинхронный резонанс вызывает механическое напряжение, из-за которого в валу ротора возникает высокое скручивающее напряжение. Проблема подсинхронного резонанса чаще всего возникает во время неисправностей или переключения. Проблема субсинхронности с линиями с последовательной компенсацией решается следующими способами.
  • С помощью фильтра.
  • Путем включения последовательной батареи конденсаторов в условиях резонанса.
  • Отключение генератора в условиях резонанса.

Конденсаторы серии

• создавали высокое восстанавливающееся напряжение на контакте выключателя.
• Если степень компенсации и расположение конденсаторов неправильные, дистанционные реле, используемые для защиты линии, могут работать неправильно.
• Включение ненагруженного трансформатора в конце последовательной компенсации линии может вызвать нелинейный резонанс или феррорезонанс. Это может привести к непрерывным колебаниям. Частота колебаний может быть снижена путем использования шунтирующих реакторов между конденсаторами или временного короткого замыкания конденсаторов.
• Малонагруженные синхронные двигатели имеют склонность к «охоте».

Конденсатор серии

вызывает большее повышение сетевого напряжения, из-за чего происходит большее падение напряжения.

Hc Verma II для класса 12 Science Physics Chapter 31

Страница № 163:

Ответ:

Дано:
Заряд на положительной плоскости = + Q ₁
Заряд на отрицательной пластине = — Q ₂

Для расчета: Заряд на конденсаторе

Пусть ABCD будет гауссовой поверхностью такие, что грани AD и BC лежат внутри пластин X и Y соответственно.
Пусть q будет зарядом, появляющимся на поверхности II. Тогда распределение зарядов на гранях I, III и IV будет в соответствии с рисунком.

Пусть площадь пластин будет A , а диэлектрическая проницаемость свободного пространства будет∈0.

Теперь, чтобы определить q в терминах Q ₁ и Q ₂ , нам нужно применить закон Гаусса для расчета электрического поля, создаваемого всеми четырьмя гранями конденсатора в точке P.Также мы знаем, что электрическое поле внутри конденсатора равно нулю.

Электрическое поле от грани I в точке P, E ₁ = Q1-q2∈0A
Электрическое поле от грани II в точке P, E ₂ = + q2∈0A
Электрическое поле из-за к грани III в точке P, E ₃ = -q2∈0A
Электрическое поле от грани IV в точке P, E ₄ = —Q2 + q2∈0A (Отрицательный знак используется как точка P лежит на левой стороне грани IV.)
Поскольку точка P находится внутри проводника,
E ₁ + E ₂ + E ₃ + E ₄ = 0

∴ Q ₁ — q + q — q — (- Q ₂ + q ) = 0
q3 9044⇒ = Q1 + Q22
Таким образом, заряд конденсатора равен Q1 + Q22, который является зарядом на гранях II и III.

Страница № 163:

Ответ:

Нет. Поскольку емкость является константой пропорциональности, она не зависит ни от заряда на пластинах, ни от потенциала. Это зависит только от размера и формы конденсатора, а также от диэлектрика, используемого между пластинами.
Формула, показывающая его зависимость от размера и формы конденсатора, выглядит следующим образом:
C = ∈0Ad
Здесь A — площадь пластин конденсатора, а d — расстояние между пластинами. пластины конденсатора.

Страница № 163:

Ответ:

Потенциал металлической сферы прямо пропорционален передаваемому ей заряду q и обратно пропорционален ее радиусу r.
, то есть V = q4π∈0r
Поскольку обе сферы являются проводниками с одинаковым радиусом и зарядом, данный им заряд появляется на поверхности равномерно. Таким образом, потенциал на поверхности или внутри сферы будет одинаковым, независимо от того, является ли сфера полой или твердой.

Страница № 163:

Ответ:

Принято, что обкладки конденсатора имеют одинаковые заряды. Другими словами, они имеют одинаковый потенциал, поэтому разность потенциалов между ними равна нулю.

Предположим, что заряд на грани II равен q , так что индуцированный заряд на грани III равен — q и распределение соответствует рисунку.
Теперь, если мы рассмотрим гауссову поверхность ABCD, грани которой лежат внутри двух пластин, и вычислим поле в точке P из-за всех четырех поверхностей, оно будет
E ₁ = Q-q2∈0A
E ₂ = q2∈0A
E ₃ = _q2∈0A
E ₄ = _ Q + q2∈0A (Это -ve, потому что точка P находится на левой стороне грани IV. )
Теперь, когда точка P лежит внутри проводника, полное поле должно быть равно нулю.
∴ E ₁ + E ₂ + E ₃ + E _{4 902 9045 или 9045 Q64 или 9045 Q64} + q — q + Q + q = 0
∴ q = 0
Следовательно, на гранях II и III заряд равен нулю; а на гранях I и IV — Q .
Таким образом, кажется, что весь данный заряд перемещается к внешним поверхностям с нулевым зарядом на обращенных поверхностях.

Страница № 163:

Ответ:

Нет. Этой информации недостаточно. Поскольку заряд пропорционален разности потенциалов на конденсаторе, нам необходимо знать разность потенциалов, приложенную к конденсатору.

q ∝ V ⇒ q = CV

Здесь q — это заряд, V — приложенная разность потенциалов и C — константа пропорциональности, т.е.е. емкость.

Страница № 163:

Ответ:

Величину поляризации можно понять как степень идеального выравнивания молекул диэлектрика с внешним электрическим полем. Чем больше молекулы выровнены по отношению к внешнему магнитному полю, тем больше поляризация и тем выше будет диэлектрическая проницаемость.
Но с повышением температуры тепловое возбуждение молекул или хаотичность их совмещения с полем увеличивается.
Таким образом, мы можем сказать, что повышение температуры приводит к уменьшению поляризации и диэлектрической проницаемости.

Страница № 163:

Ответ:

По мере уменьшения энергии системы изменение энергии отрицательное.
Сила определяется как отрицательная скорость изменения энергии по отношению к расстоянию.
F = -∂U∂x
Итак, по мере уменьшения энергии сила электрического поля конденсатора увеличивается, когда диэлектрик втягивается в конденсатор.

Страница № 164:

Ответ:

(d) ноль

Так как чистый заряд, заключенный в гауссовой поверхности, равен нулю, полный поток электрического поля через замкнутую гауссову поверхность, окружающую конденсатор, равен нулю.

Φ = ∯E.ds = q∈0 = 0
Здесь
Φ = электрический поток
q = общий заряд, заключенный на гауссовой поверхности.

Страница № 164:

Ответ:

(d) C /2 и 2 В

Поскольку при последовательном соединении конденсаторов напряжение складывается, напряжение комбинации составляет 2 В .
Кроме того, емкость последовательной комбинации задается как
1Cnet = 1C1 + 1C2
Здесь
C _net = Чистая емкость комбинации
C ₁ = C ₂ = C
∴ C _{нетто = C2}

Страница № 164:

Ответ:

(c) 2 C и V

При параллельной комбинации конденсаторов разность потенциалов на конденсаторах остается той же самой, как и на правой и левой пластинах обоих конденсаторы подключаются к этим же выводам АКБ.Следовательно, потенциал остается прежним, то есть В .

Для параллельной комбинации конденсаторов емкость определяется как
C _экв = C ₁ + C ₂
Здесь
C ₁ 4 = C 2 = C
∴ C _экв = 2 C

Страница № 164:

Ответ:

(b) 2 C

Поскольку потенциал в точке A равен потенциалу в точке B, ток не будет течь по плечу AB.Следовательно, конденсатор на плече AB не будет вносить вклад в схему. Кроме того, поскольку оставшиеся два конденсатора подключены параллельно, полезная емкость цепи определяется как
C _экв = C + C = 2 C

Страница № 164:

Ответ:

(c) остается неизменным

Сила между пластинами задается соотношением
F = q22∈0A
Поскольку конденсатор изолирован, заряд на пластинах остается постоянным.
Мы знаем, что заряд сохраняется в изолированной системе.
Таким образом, сила, действующая между пластинами, остается неизменной.

Страница № 164:

Ответ:

(d) 1r4

Плотность энергии U определяется как

U = 12∈0E2 … (1)

Электрическое поле, создаваемое точечным зарядом на расстоянии r , определяется как
E = q4π∈0r2

При помещении вышеуказанной формы E в ур.1, получаем

U = 12∈0q4π∈0r22

Таким образом, U прямо пропорционально 1r4.

Страница № 164:

Ответ:

(b) Q + = Q-

Заряд, индуцированный на пластинах конденсатора, не зависит от их площади.
∴ Q + = Q-

Страница № 164:

Ответ:

(d) ∞

Тонкая металлическая пластина, вставленная между пластинами конденсатора с параллельными пластинами емкости C , соединяет две пластины конденсатора; следовательно, расстояние d между пластинами конденсатора уменьшается до нуля.Можно заметить, что заряды на пластинах начинают перекрывать друг друга через металлическую пластину и, следовательно, начинают непрерывно проводить.

Математически
C = ∈0Ad
В данном случае d = 0.
∴ C = ∞

Страница № 164:

Ответ:

(c) C ₁ < C ₂

Область AB показывает разность потенциалов на конденсаторе C ₁ , а область CD показывает разность потенциалов на конденсаторе C ₂ .Теперь мы можем видеть из графика, что область AB больше, чем область CD. Следовательно, разность потенциалов на конденсаторе C ₁ больше, чем на конденсаторе C ₂ .
∵ Емкость, C = QV
∴ C ₁ 2 ( Q остается неизменным при последовательном соединении.)

Страница № 164:

Ответ:

(а) увеличить

Масло между пластинами конденсатора действует как диэлектрик.Мы знаем, что электрическое поле уменьшается в 1К от исходного поля, когда мы вставляем диэлектрик между пластинами конденсатора ( К, — диэлектрическая проницаемость диэлектрика). Таким образом, если масло откачивается, электрическое поле между пластинами будет увеличиваться, поскольку диэлектрик удален.

Страница № 164:

Ответ:

(b) Q1Q2 = C1C2

Когда сферы соединены, между ними течет заряд, пока они не приобретут одинаковый общий потенциал В .
Окончательные заряды сфер даются по формуле
Q ₁ = C ₁ V и Q ₂ = C ₂ V

∴Q1Q2 = C1VC2V = C1C2

C1C2V

Страница № 164:

Ответ:

(d) 2 мкФ, 18 мкФ

Минимальную емкость можно получить, подключив все конденсаторы последовательно.Его можно рассчитать следующим образом:
1C = 16 + 16 + 16 = 12
⇒ C = 2 мкФ

Максимальную емкость можно получить, подключив все конденсаторы параллельно. Его можно рассчитать следующим образом:
C = 6 + 6 + 6 = 18 мкФ

Страница № 164:

Ответ:

(c) заряды на пластинах

Емкость конденсатора определяется как

C = ∈0Ad

Здесь A — площадь пластин конденсатора, а d — расстояние между пластинами.
Итак, мы можем ясно видеть, что емкость конденсатора действительно зависит от размера и формы пластин и расстояния между пластинами; это не зависит от зарядов на пластинах.

Страница № 164:

Ответ:

(b) Заряд на конденсаторе

Когда мы вставляем диэлектрик между пластинами конденсатора, на поверхности диэлектрика появляются индуцированные заряды противоположной полярности.Они создают внутри диэлектрика электрическое поле, направленное противоположно исходному полю конденсатора.
Таким образом, результирующий эффект — уменьшенное электрическое поле.
Кроме того, поскольку потенциал пропорционален полю, потенциал уменьшается, как и запасенная энергия U , которая задается формулой
U = qV2
Таким образом, только заряд на конденсаторе остается неизменным, так как заряд сохраняется в изолированной системе.

Стр. № 165:

Ответ:

(d) Q ‘должно быть меньше Q .

Связь между наведенным зарядом Q ‘и зарядом на конденсаторе Q определяется как
Q ‘ = Q1-1K
Здесь K — диэлектрическая проницаемость, которая всегда больше или равна to 1.
Итак, мы видим, что для K > 1, Q ‘всегда будет меньше Q .

Стр. № 165:

Ответ:

(a) лицевые поверхности конденсатора имеют равные и противоположные заряды
(b) две пластины конденсатора имеют одинаковые и противоположные заряды
(d) внешние поверхности пластин имеют одинаковые заряды

H.C Верма ответ: (a), (c), (d). Но, по нашему мнению, ответ должен быть следующим: (a), (b), (d) все эти параметры являются свойствами конденсатора, а вариант (c) неверен, потому что аккумулятор является источником энергии, а не заряжается. Более того, если пластины конденсатора имеют одинаковый заряд снаружи и одинаковый заряд внутри, то можно подумать, что заряд на пластинах также должен быть одинаковым, поэтому вариант (b) не может быть неверным.

Стр. № 165:

Ответ:

(b) Разность потенциалов на конденсаторе
(c) Энергия конденсатора.

Поскольку заряд всегда сохраняется в изолированной системе, он остается неизменным.
Теперь
V = Qd∈0A
Здесь Q , A и d — это заряд, площадь и расстояние между пластинами соответственно.
Таким образом, по мере увеличения d , V увеличивается.
Энергия равна
E = qV2
Таким образом, она также будет увеличиваться.
Плотность энергии u , то есть энергия, запасенная на единицу объема в электрическом поле, задается как
u = 12∈0E2
Таким образом, u останется постоянным с увеличением расстояния между пластинами.

Стр. № 165:

Ответ:

(d) Равные и противоположные заряды появятся на двух сторонах металлической пластины.

Емкость конденсатора, в котором диэлектрическая пластина с диэлектрической постоянной K , площадью A и толщиной t вставлена ​​между пластинами конденсатора площадью A и разнесена на расстояние d , составляет дается по формуле

C = ∈0Ad-t + t / K

Поскольку дано, что толщина листа пренебрежимо мала, приведенная выше формула сводится к C = ∈0Ad.Другими словами, не будет никаких изменений в электрическом поле, потенциале или заряде.

Только одинаковые и противоположные заряды будут появляться на двух сторонах металлической пластины из-за индукции из-за наличия зарядов на пластинах конденсатора.

Стр. № 165:

Ответ:

(b) Заряд, появляющийся на конденсаторе, больше после действия XWY , чем после действия XYZ.
(c) Электрическая энергия, запасенная в конденсаторе, больше после действия WXY , чем после действия XYW .
(d) Электрическое поле в конденсаторе после воздействия XW такое же, как после WX .

Обоснование варианта (b)

Если потенциал остается постоянным, то есть батарея остается подключенной к цепи, то заряд конденсатора увеличивается в К при введении диэлектрика с диэлектрической проницаемостью К между обкладками конденсатора.

Математически
q = Kq ₀
Здесь q ₀ и q — заряды без диэлектрика и с диэлектриком соответственно.
Количество накопленного заряда не зависит от полярности пластин.
Таким образом, заряд, появляющийся на конденсаторе, больше после действия XWY , чем после действия XYZ.

Обоснование варианта (c)

Поскольку аккумулятор отключается перед вставкой диэлектрика, величина заряда остается постоянной, то есть q = q ₀ , потому что после отключения аккумулятора конденсатор не получает источника для хранения заряда.Другими словами, конденсатор теперь представляет собой изолированную систему, в которой сохраняется количество заряда, равно как и энергия U как 12q ε . Следовательно, установка диэлектрика после отключения батареи не приведет к изменению количества заряда, хранящегося в конденсаторе. Таким образом, энергия, запасенная в конденсаторе, также не изменится после действия XYW .
Однако во время действия WXY, количество заряда, которое будет храниться в конденсаторе, будет увеличиваться в К, , поскольку батарея отключается после вставки диэлектрика между пластинами конденсатора и энергии сохраненный также будет умножен на коэффициент К.
Таким образом, электрическая энергия, запасенная в конденсаторе, больше после действия WXY , чем после действия XYW.

Обоснование варианта (d)

Электрическое поле между пластинами E зависит от потенциала на конденсаторе и расстояния d между пластинами конденсатора.
Математически
E = εd
В любом случае, то есть во время действий XW и WX, потенциал остается прежним, то есть ε.Таким образом, электрическое поле E остается прежним.

Отказ от опции (a)

Во время действия XYZ аккумулятор должен выполнить дополнительную работу, эквивалентную 12 CV ² , чтобы изменить полярность пластин конденсатора. Другими словами, общий объем работы, который должен выполнить аккумулятор, составит 12 CV ² + 12 CV ² . Эта дополнительная проделанная работа будет рассеиваться в виде тепловой энергии. Таким образом вырабатывается тепловая энергия.Однако накопленная электрическая энергия остается неизменной, то есть 12 CV ² .

Стр. № 165:

Ответ:

Поскольку 1,0 × 10 ¹² электронов передаются от одного проводника к другому, проводник, к которому переносятся электроны, становится отрицательно заряженным, а другой проводник становится заряженным положительно.
Итак,
Величина чистого заряда на каждом проводнике, Q = (1.0 × 10 ¹² ) × (1,6 × 10 ^-19 ) C = 1,6 × 10 ^-7 C
Величина разности потенциалов между проводниками, В = 10 В

Емкость C представляет собой отношение величины заряда на любом проводнике к величине разности потенциалов между проводниками.
C = QV
⇒ C = 1,6 × 10-710 = 1,6 × 10-8 F

Следовательно, значение емкости данных двухпроводных систем составляет 1,6 × 10 ^-8 F.

Стр. № 165:

Ответ:

Емкость конденсатора с параллельными пластинами определяется как
C = ∈0 Ad
Здесь
A = Площадь пластины
d = Расстояние между параллельными пластинами
Дано:
A = πr2 = π × 5 × 10-22d = 1,0 × 10-3 m∈0 = 8,85 × 10-12 Ф / м∴C = ∈0 Ad = 8,85 × 10-12 × 3,14 × 25 × 10-410-3 = 6,95 × 10- 5 мкФ

Стр. № 165:

Ответ:

Емкость конденсатора с параллельными пластинами определяется как
C = ∈0 Ad
Здесь
A = Площадь пластины
d = Расстояние между параллельными пластинами
Теперь
Пусть радиус диска быть р.
∴C = ∈0Ad = ∈0πr2d⇒r = Cd∈0π⇒r = 1 × (1 × 10-3) 8,85 × 10-12 × 3,14 = 35,98 × 106 м⇒r≈36 × 106 м = 6 × 103 м = 6 км

Таким образом, радиус пластин конденсатора для данной конфигурации составляет 6 км.

Стр. № 165:

Ответ:

Емкость конденсатора с параллельными пластинами определяется как
C = ∈0 Ad
Здесь
A = Площадь пластины
d = Расстояние между параллельными пластинами
Дано:
A = 25 см ² = 25 × 10 ^-4 м ²
d = 1.00 мм = 1 × 10 ^-3 м
Итак,

C = ∈0 Ad = 8,85 × 10-12 × 25 × 10-41 × 10-3 = 2,21 × 10-11 F

Когда батарея Напряжение 6 В подключено к конденсатору, заряд ( Q ), который течет от батареи, равен количеству заряда, который может удерживать данный конденсатор.
⇒ Q = CV
⇒Q = 2,21 × 10-11 × 6,0 = 1,33 × 10-10 C

Работа, выполняемая аккумулятором при зарядке конденсатора, рассчитывается как произведение величины передаваемый заряд и напряжение аккумулятора.
Таким образом, получаем
W = QV = 1,33 × 10-10 × 6,0 = 8,0 × 10-10 Дж

Таким образом, заряд, прошедший через аккумулятор, равен 1,33 × 10 ^-10 Кл и работа, выполняемая аккумулятором составляет 8,0 × 10 ^-10 Дж.

Стр. № 165:

Ответ:

Дано:
Площадь пластины, A = 25 см ² = 25 × 10 ^-4 м ²
Расстояние между пластинами, d = 2 мм = 2 × 10 ^-3 м
Разница потенциалов между пластинами, В = 12 В
Емкость данного конденсатора определяется как
C = ∈0 Ad
= (8.85 × 10-12) × (25 × 10-4) (2 × 10-3) = 11,06 × 10-12 F

(a) Заряд конденсатора равен
Q = CV
= 11,06 × 10-12 × 12 = 1,33 × 10-10 C

(b) Когда расстояние между пластинами уменьшается до 1 мм, емкость C ‘может быть рассчитана как:
C’ = ∈0 Ad = (8,85 × 10 -12) × (25 × 10-4) 1 × 10-3 = 22,12 × 10-12 F

Заряд на конденсаторе равен
Q ‘= C’V
= 22,12 × 10-12 × 12 = 2,65 × 10-10 C Дополнительный заряд = 2,65 × 10-10-1,32 × 10-10 C = 1.33 × 10-10 С

Стр. № 165:

Ответ:

Емкости трех конденсаторов равны C ₁ = 2 мкФ, C ₂ = 4 мкФ и C ₃ = 6 мкФ, а напряжение батареи ( В, ) составляет 12 В. .
Поскольку конденсаторы соединены параллельно, эквивалентная емкость определяется как
C _экв = C ₁ + C ₂ + _C
= (2 + 4 + 6) мкФ = 12 мкФ = 12 × 10 ^-6 F

Из-за параллельного подключения разность потенциалов на каждом конденсаторе одинакова и равна 12 В.

Следовательно, заряд на каждом конденсаторе может быть рассчитан следующим образом:
Заряд на конденсаторе емкости C ₁ = 2 мкФ определяется как

Q _{1 = C 1 В = (2 × 10 ^-6 ) × 12 C = 24 × 10 ^-6 C = 24 мкКл}

Точно так же заряды на двух других конденсаторах даются по формуле
Q ₂ = C ₂ V = (4 × 10 ^-6 ) × 12 C = 48 × 10 ^-6 C = 48 мкКл
и
Q _{3 = C 3 V = (6 × 10 ^-6 ) × 12 C = 72 × 10 ^-6 C = 72 мкКл}

Стр. № 165:

Ответ:

Когда конденсаторы соединены последовательно, эквивалентная емкость определяется как

1ceq = 1c1 + 1c2 + 1c31ceq = 120 + 130 + 140 × 110-6⇒ ceq = 9.23 мкФ

Поскольку конденсаторы соединены последовательно, одинаковый заряд будет идти на каждый из них, и он равен общему заряду аккумулятора.
Теперь,
Пусть заряд на каждом конденсаторе равен Ом.
∴q = CV = (9,23 × 10-6) × 12 q = 110,76 мкКл

Работа, выполняемая аккумулятором ( Вт, ), определяется как

W = qV⇒W = 12 × 110,76 × 10- 6⇒W = 1,33 × 10-3 Дж

Стр. № 165:

Ответ:

Давайте сначала найдем эквивалентную емкость.Из принципиальной схемы видно, что конденсаторы B и C включены параллельно и последовательно с конденсатором A.

Эквивалентная емкость может быть рассчитана следующим образом:
1Ceq = 1CA + 1CB + CC1Ceq = 18 + 14 + 4 = 18 + 18⇒1Ceq = 28⇒Ceq = 4 мкФ

Конденсаторы B и C параллельны и включены последовательно с конденсатором A. Эквивалентная емкость конденсаторов B и C равна
(4 + 4) мкФ = 8 мкФ
Это такая же емкость, как у конденсатора A. Следовательно, на конденсаторе A и системе конденсаторов B и C.
Теперь,
Разность потенциалов на конденсаторе A = 6 В
Таким образом,
Заряд конденсатора A = (8 мкФ) × (6 В) = 48 мкКл
А,
Разность потенциалов на конденсаторах B и C = 6 В
Таким образом,
Заряд конденсатора B = (4 мкФ) × (6 В) = 24 мкФ
Заряд конденсатора C = (4 мкФ) × (6 В) = 24 мкФ

Стр. № 165:

Ответ:

(a)

Для комбинации конденсаторов, показанной на рисунке (a), пары конденсаторов C _{1 и C 2 соединены параллельно.
Эквивалентная емкость каждой параллельной комбинации конденсаторов определяется по формуле
C 1 + C 2 = 4 + 6 = 10 мкФ
Эквивалентную схему можно нарисовать как:}

Эквивалент Емкость для вышеуказанной последовательной цепи равна
1Ceq = 1C1 + C2 + 1C1 + C2 = 110 + 110 = 210⇒Ceq = 5 мкФ

(b)

Для комбинации конденсаторов, показанной на рисунке (b), пары конденсаторов C _{1 и C 2 включены параллельно.
Эквивалентная емкость каждой параллельной комбинации конденсаторов определяется по формуле:
C 1 + C 2 = 4 + 6 = 10 мкФ}

Эквивалентную схему можно представить как:

На приведенной выше схеме можно увидеть, что C _A и C _B находятся последовательно и параллельны последовательной комбинации C _C и C _B .

Эквивалентная емкость для последовательной комбинации C _A и C _B определяется как
1Ceq = 1CA + 1CB = 1C1 + C2 + 1C1 + C2 = 110 + 110 = 15⇒Ceq = 5 мкФ
Аналогичным образом эквивалентная емкость последовательной комбинации C _C и C _D составляет 5 мкФ.

∴ Эквивалентная емкость нетто = 5 + 5 = 10 мкФ

Страница № 166:

Ответ:

Эквивалентная схема для данного случая может быть представлена ​​как:

. Можно заметить, что конденсаторы C _{1 и C 2 подключены параллельно.
Следовательно, эквивалентная емкость определяется выражением
C eq = C 1 + C 2
= 5 + 6 = 11 мкФ
Теперь
Заряд, обеспечиваемый батареей = ( C экв ) (В) = (11 мкФ) × (10 В) = 110 мкКл}

Страница № 166:

Ответ:

Предусмотрено, что внешние цилиндры находятся в контакте, а внутренние цилиндры соединены проводом.Таким образом, эквивалентная схема может быть представлена ​​как:

Левая пластина конденсаторов (A и B), показанных на рисунке, представляет собой внутренние пластины цилиндрических конденсаторов.

Поскольку конденсаторы подключены параллельно, разность потенциалов на них одинакова.
∴ Величина заряда на каждом конденсаторе = CV = (2,2 мкФ) × (10 В) = 22 мкКл
Поскольку пластины A и B подключены к положительному выводу батареи, заряд на каждой из них составляет +22 мкКл.
∴ Чистый заряд на внутренних пластинах = 22 мкКл + 22 мкКл = +44 мкКл

Страница № 166:

Ответ:

Нам нужно рассчитать емкость изолированного заряженного шара.
Предположим, что заряд на сфере равен Q , а его радиус равен R .

Емкость заряженной сферы можно определить, представив концентрическую сферу бесконечного радиуса, состоящую из заряда −Q.
Разность потенциалов между сферами = 14π∈0QR — 0 = 14π∈0QR

Емкость — это отношение величины заряда на каждом проводнике к разности потенциалов между ними.
C = Q14π∈0QR = 4π∈0R
Следовательно, емкости сфер радиусом R ₁ и R ₂ равны C ₁ и C ₂ соответственно. Они задаются формулой

C1 = 4π∈0 R1C2 = 4π∈0 R2

Если сферы соединены металлической проволокой, заряд будет перетекать от одной сферы к другой, пока их потенциалы не станут одинаковыми.
Когда потенциалы становятся одинаковыми, разность потенциалов между проводниками обоих конденсаторов также становится одинаковой.Таким образом, можно сделать вывод, что конденсаторы подключены параллельно.

Таким образом, емкость комбинации определяется выражением
Ceq = C ₁ + C ₂

= 4π∈0 R1 + R2

Страница № 166:

Ответ:

В данной системе три ряда конденсаторов соединены параллельно. В каждом ряду последовательно включены по три конденсатора емкостью 2 мкФ.

Для каждой строки эквивалентная емкость определяется как
1Cr = 12 + 12 + 12⇒Cr = 23 мкФ
Поскольку три строки соединены параллельно, их эквивалентная емкость определяется как
C _{eq = C r + C r + C r = 23 + 23 + 23 = 2 мкФ}

Напряжение в каждой строке одинаковое и равно 60 В.
Как и все конденсаторы одинаковой емкости в каждом ряду, разность потенциалов на их пластинах одинакова.

∴ Разность потенциалов на каждом конденсаторе = 20 В

Страница № 166:

Ответ:

Пусть количество конденсаторов последовательно (соединенных в ряд) будет x .
Максимальное напряжение, которое могут выдерживать конденсаторы, составляет 50 В.
Напряжение на каждой строке должно быть равно 200 В.
Следовательно,
x × 50 = 200
Таким образом,
x = 4 конденсатора
Теперь,
Пусть таких строк у .
Таким образом, эквивалентная емкость комбинации будет xy.
⇒ xy = 10
⇒ y = 10 x = 4 конденсатора
Таким образом, чтобы получить требуемый результат, комбинация 4 рядов, каждый из 4 конденсаторов с емкостью 10 мкФ и напряжением пробоя 50 В, требуется.

Страница № 166:

Ответ:

(a)
Емкость двух параллельно соединенных строк задается формулой
C1 = 4 × 84 + 8 = 83 мкФ и C2 = 3 × 63 + 6 = 189 мкФ = 2 мкФ

Поскольку две строки параллельно, разность потенциалов в каждом ряду одинакова и равна 50 В.
Заряд на ответвлении ACB с емкостью 83 мкФ определяется как
Q = 83 мкФ × (50 В) = 4003 мкКл

Заряд на ответвлении ADB с емкостью 2 мкФ определяется как

Q = C × VQ = 2 мкФ × 50 = 100 мкКл

Потенциал в точке D определяется как

VD = qC1 = 100 мкКл 6 мкФВД = 503 В

Аналогично, потенциал в точке C определяется как

VC = 503 В

(b) Поскольку разность потенциалов между точками C и D равна нулю, мост остается сбалансированным и заряд не течет от C к D.Если конденсатор подключен между точками C и D, то изменение конденсатора будет нулевым.

Страница № 166:

Ответ:

Конденсаторы C _{1 и C 2 сверху и снизу ab подключены последовательно и параллельно с C 3 .
Таким образом, эквивалентный конденсатор между a и b определяется как}

Ceq = C1C2C1 + C2 + C3 + C1C2C1 + C2⇒Ceq = C3 + 2C1C2 C1 + C2

Страница № 166:

Ответ:

Общая площадь плоской пластины A .Ширина каждой ступеньки одинакова. Следовательно, площадь поверхности каждой ступени, обращенной к плоской пластине, одинакова, то есть A3.

Из рисунка видно, что конденсаторная сборка состоит из трех конденсаторов. Три конденсатора подключены параллельно.
Для конденсатора C ₁ площадь пластин составляет A3, а расстояние между пластинами составляет d .
Для конденсатора C ₂ , площадь пластин A3, а расстояние между пластинами ( d + b ).
Для конденсатора C ₃ , площадь пластин A3, а расстояние между пластинами ( d + 2 b ).
Следовательно,

C1 = ∈0 A3d C2 = ∈0 A3d + bC3 = ∈0 A3d + 2b

Поскольку три конденсатора соединены параллельно,

C = C1 + C2 + C3⇒C = ∈0 A3d + ∈ 0 A3d + b + ∈0 A3d + 2b⇒C = ∈0 A33d2 + 6bd + 2b2dd + bd + 2b

Страница № 166:

Ответ:

(a) Емкость цилиндрического конденсатора определяется как

C = 2π∈0 llnR2R1⇒C = 2 × 3.14 × 8,85 × 10-12 × 0,10ln 2 ⇒C = 8 пФ ∵ln 2 = 0,693

(б) Если взять конденсатор такой же высоты с цилиндрами радиусом 4 мм и 8 мм, его емкость составит 8 pF, то же самое, что и выше, потому что соотношение радиусов такое же.

Страница № 166:

Ответ:

Дано:
C1 = 100 пФ V = 24 В
Заряд данного конденсатора, q = C1V = 24 × 100 пКл

Емкость незаряженного конденсатора, C2 = 20 пФ
Когда заряженный конденсатор соединен с незаряженным конденсатором , чистый заряд системы конденсаторов становится
q1 + q2 = 24 × 100 qC… (i)

Разность потенциалов на пластинах конденсаторов будет такой же.
Таким образом,
q1C1 = q2C2⇒q1100 = q220⇒q1 = 5q2 … (ii)

Из ур. (i) и (ii) получаем
q1 + q15 = 24 × 100 pC⇒6q1 = 5 × 24 × 100 pC⇒q1 = 5 × 24 × 1006 pCNow, V1 = q1C1 = 5 × 24 × 100 pC6 × 100 пФ = 20 В

Страница № 166:

Ответ:

Первоначально, когда переключатель S разомкнут, эквивалентная емкость определяется как
Ceq = 2C × C3C⇒Ceq = 23C = 23 × 5.0 мкФ

Заряд, обеспечиваемый батареей, определяется выражением
Q = Ceq × V⇒Q = 23 × (5,0 мкФ) × (50 В) ⇒Q = 5003 мкКл
Когда переключатель S замкнут, заряд не происходит. конденсатор подключен параллельно переключателю.
Таким образом, эквивалентная емкость определяется как

Ceq = 2C = 2 × 5,0 = 10 мкФ
Заряд, обеспечиваемый батареей, определяется как
Q = 10 мкФ × 50 = 500 мкКл
Начальный заряд, накопленный в закороченном конденсаторе начинает разряжаться »?
Следовательно, заряд, который течет от A к B, определяется как
Qnet = 500 мкКл-5003 мкКл⇒Qnet = 3.3 × 10-4 С

Страница № 166:

Ответ:

Частица уравновешивается, когда электрическая сила, действующая на нее, уравновешивается ее весом.
Таким образом,
mg = qE mg = q × V’d … (i)
Здесь
d = расстояние между пластинами конденсатора
V ‘ = разность потенциалов на конденсаторе, содержащем частицу

Мы знаем, что емкость конденсатора определяется как
C = ∈0Ad⇒d = ∈0AC
Таким образом, уравнение.