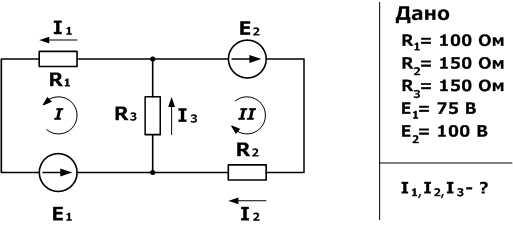
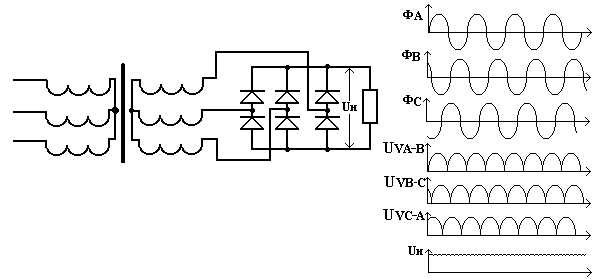
Логические схемы. Переход от логического выражения к логической схеме и наоборот. Логическая схема это любая схема

Информатика и ИКТ. Профильный курс.

Уроки №8-11

Логические схемы

Основные понятия:

Логические схемы нужны для того чтобы в наглядной графической форме отобразить последовательность выполнения операций при вычислении логических формул.

Входящие слева линии и цифры около них обозначают значения операндов, линия справа и соответствующая цифра - результат операции (значение на выходе логических элементов). 1 - это логическая единица (истина), 0 - логический ноль (ложь).

Таблицы истинности в форме логических схем будут выглядеть т.о.

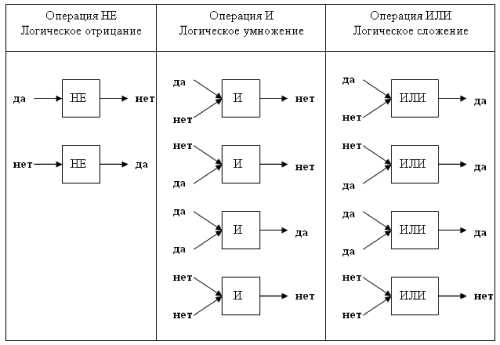
Пример 1. Нарисовать схему для логического выражения: 1 ИЛИ 0 и 1.

Читать эту схему надо слева направо. Первой выполняется операция И (что наглядно видно на схеме), затем ИЛИ. 

Теперь в порядке слева направо припишем к выходящим линиям результаты операций:

В результате получилась 1, т.е. "истина".

Пример 2. Представить в виде логической схемы логическую формулу: НЕ (А И (В ИЛИ С) И D)

Логическая схема будет выглядеть так:

Теперь с помощью схемы рассчитаем значение формулы при А=С=D=1, B=0

В результате получится логический ноль, т.е. "ложно".

FLASH "Логические элементы" с задачами.(Интерактивная логика)

FLASH "Логические схемы" с заданиями (Интерактивная логика)

FLASH "Переключательные схемы" с заданиями (Интерактивная логика)

Игра-тренажер "Логика"

Он-лайн тест "Упрощение логических выражений" (К.Поляков)

 Компьютерный практикум:

doc. Реализация логических схем с помощью электронных таблиц. (Метод.рекомендации. И.Г. Семакин)

Задание

1. Пусть а, b, c - логические переменные, которые имеют следующие значения: а=истина, b=ложь, с=истина. Используя логические схемы, определить результаты вычисления следующих логических формул для этих значений:

1) а и b

2) а или b

3) не а или b

4) а и b или с

5)а или b и с

6) не а или b и с

7)(а или b) и (с или b)

8) не (а или b) и (с или b)

9) не (а и b и с)

 Самостоятельная работа

1.Значения А=1; В=0; С=1. Найти не (А или В и (А или С) или не (В или не С)) и построить логическую схему.

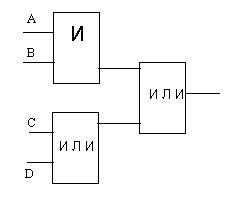
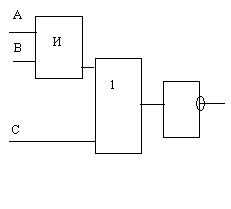
2. Запишите формулы, соответствующие логическим схемам. Постройте таблицы истинности для формул:

а)                                                             

 

Дополнительные источники:

Вычисление логических выражений ppt

doma10.ucoz.ru

Виды задач на логические элементы. Построение логической схемы по заданной логической функции; Запись логической функции по заданной логической схеме; Определение сигнала на выходе логической схемы по заданным значениям сигналов на всех входах этой схемы; Построение таблицы истинности для заданной логической схемы; Познакомимся с ними поочередно. Построение логической схемы по заданной логической функции. Задача: Дана логическая функция: Составить логическую схему для неё. Решение: Расставим порядок выполнения логических операций, руководствуясь правилами: отрицание умножение сложение Не забываем про приоритет скобок. Получаем: Строим схему по указанному порядку. Посмотреть. Запись логической функции по заданной логической схеме. Задача: Дана логическая схема: Составить логическую функцию по ней. Решение: Рассматриваем схему с конца и записываем соответствующие логические операции, учитывая, что в записываемой функции три операнда А, В, С Посмотреть. Можно сначала подписать на схеме промежуточные функции, получаемые на выходе каждого блока, а потом сцепить их логическими операциями. Посмотреть. Определение сигнала на выходе логической схемы по заданным значениям сигналов на всех входах этой схемы. Задача: Дана логическая схема и значения сигналов на всех входах: Определить значение функции F на выходе схемы. Решение: Пользуясь таблицами истинности для соответствующих логических элементов схемы, расставляем значения сигналов на выходах и соответственно на входах каждого логического элемента пока не доберёмся до конца схемы. Получаем: Ответ: Значение функции F на выходе схемы = 1. Построение таблицы истинности для заданной логической схемы. Задача: Дана логическая схема: Построить для неё таблицу истинности. Решение: Проверяем количество входов на схеме. Количество комбинаций сигналов на 2 входах равно 4, для 3 входов равно 8, для 4 входов равно 16 и т. д. Составляем таблицу истинности, в которой первые столбцы - это входы схемы, обозначенные буквами, следущие столбцы - функции, полученные на выходах каждого элемента схемы, а строки - отражают разные комбинации сигналов на входах. Количество строк совпадает с количеством комбинаций сигналов. Пользуясь таблицами истинности для соответствующих логических элементов схемы, расставляем значения сигналов на выходах каждого логического элемента, т. е. по каждому столбцу пока не доберёмся до конца схемы. Получаем: Ответ:

uchlogic.narod.ru

Лаб_6_Построение логических схем

Лабораторная работа №4.

Схемотехническая реализация логических элементов. Построение логических схем.

Теоретическая часть.

В основе обработки компьютером информации лежит алгебра логики, разработанная Дж. Булем. Было доказано, что все электронные схемы ЭВМ могут быть реализованы с помощью логических элементов И, ИЛИ, НЕ.

Элемент НЕ

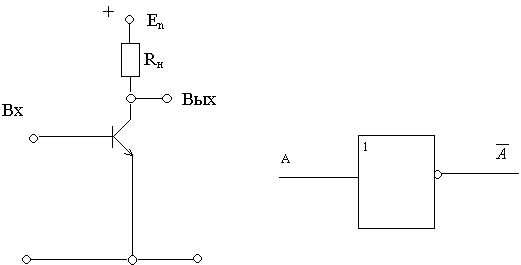
A
0	1
1	0

При подаче на вход схемы сигнала низкого уровня (0) транзистор будет заперт, т.е. ток через него проходить не будет, и на выходе будет сигнал высокого уровня (1). Если же на вход схемы подать сигнал высокого уровня (1), то транзистор “откроется”, начнет пропускать электрический ток. На выходе за счет падения напряжения установится напряжение низкого уровня. Таким образом, схема преобразует сигналы одного уровня в другой, выполняя логическую функцию.

Элемент ИЛИ

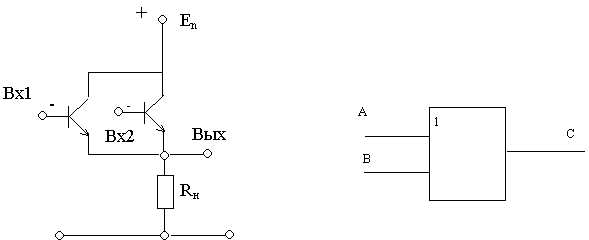
А	В	С
0	0	0
0	1	1
1	0	1
1	1	1

Функция “ИЛИ” - логическое сложение (дизъюнкция), ее результат равен 1, если хотя бы 1 из аргументов равен 1. Здесь транзисторы включены параллельно друг другу. Если оба закрыты, то их общее сопротивление велико и на выходе будет сигнал низкого уровня (логический “0”). Достаточно подать сигнал высокого уровня (“1”) на один из транзисторов, как схема начнет пропускать ток, и на сопротивлении нагрузки установится также сигнал высокого уровня (логическая “1”).

Элемент И

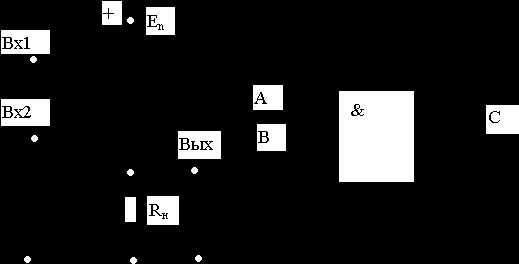
A	B	C
0	0	0
0	1	0
1	0	0
1	1	1

Если на входы Вх1 и Вх2 поданы сигналы низкого уровня (логические “0”), то оба транзистора закрыты, ток через них не проходит, выходное напряжение на Rн близко к нулю. Пусть на один из входов подано высокое напряжение (“1”). Тогда соответствующий транзистор откроется, однако другой останется закрытым, и ток через транзисторы и сопротивление проходить не будет. Следовательно, при подаче напряжения высокого уровня лишь на один из транзисторов, схема не переключается и на выходе остается напряжение низкого уровня. И лишь при одновременной подаче на входы сигналов высокого уровня (“1”) на выходе мы также получим сигнал высокого уровня.

Таким образом, каждой базовой логической функции – «И», «ИЛИ», «НЕ» - соответствует особым образом сконструированная схема, называемая логическим элементом. Комбинируя сигналы, обозначающие логические переменные, и выходы, соответствующие логическим функциям, с помощью логических элементов, пользуясь таблицей истинности или представлением логической функции в виде КНФ и ДНФ, можно составить структурную или функциональную схему (см. примеры ниже), являющуюся основой для аппаратной реализации схемы.

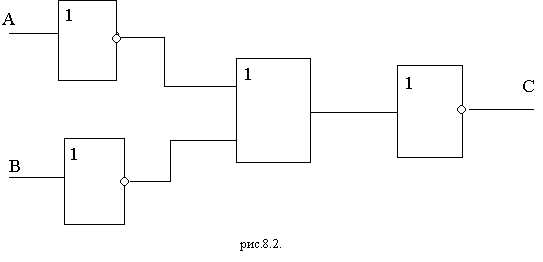
Анализируя функциональную схему, можно понять, как работает логическое устройство, т.е. дать ответ на вопрос: какую функцию она выполняет. Не менее важной формой описания логических устройств является структурная формула. Покажем на примере как выписывают формулу по заданной функциональной схеме (1 схема). Ясно, что элемент “И” осуществляет логическое умножение значений и В. Над результатом в элементе “НЕ” осуществляется операция отрицания, т.е. вычисляется значение выражения:Формулаи есть структурная формула логического устройства.

Итак, основные логические функции обозначаются

Инверсия
Конъюнкция
Дизъюнкция

Пример:дана логическая схема:

A E I Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 0 1 1 1 0

Она построена на основании булева выражения - Y = Ē /\ I \/ Ē /\ A \/ Ā /\ E

Практическая часть.

Задание 1. Для каждой из функциональных схем выписать соответствующую структурную формулу.

 

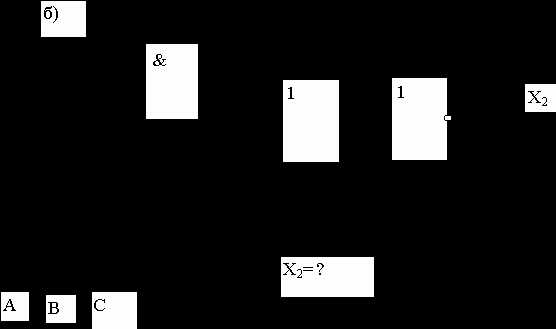
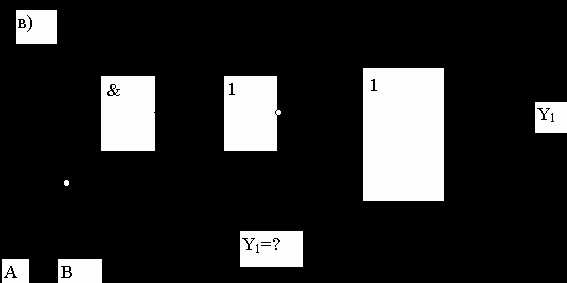
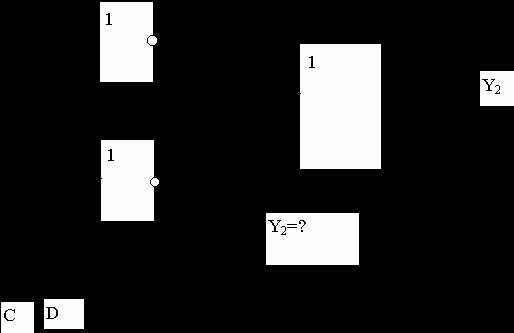
2) Для КНФ и ДНФ из лабораторной работы 5 построить функциональные схемы.

studfiles.net

ЛОГИЧЕСКАЯ СХЕМА - это... Что такое ЛОГИЧЕСКАЯ СХЕМА?

 ЛОГИЧЕСКАЯ СХЕМА

ЛОГИЧЕСКАЯ СХЕМА, электрическая цепь проводников, состоящая из модулей (например, усилителей) и других компонентов (транзисторов, диодов, резисторов и конденсаторов), используемая для распределения и обработки электронных сигналов (например, напряжения) в соответствии с правилами символической логики и БУЛЕВОЙ АЛГЕБРЫ. В вычислительной и формальной математике логическая схема - это цепь связанных логических решений и операций, называемых ЛОГИЧЕСКИМИ ЭЛЕМЕНТАМИ.

Научно-технический энциклопедический словарь.

• ЛОГАРИФМИЧЕСКИЕ ФУНКЦИИ
• ЛОГИЧЕСКИЙ ЭЛЕМЕНТ

Смотреть что такое "ЛОГИЧЕСКАЯ СХЕМА" в других словарях:

• логическая схема — [Интент] логическая блок схема логическая схема — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Рис. Schneider Electric Тематики Булева алгебра, элементы… …   Справочник технического переводчика

• логическая схема — loginė grandinė statusas T sritis automatika atitikmenys: angl. logic circuit vok. logische Schaltung, f; logischer Schaltkreis, m rus. логическая схема, f pranc. circuit logique, m …   Automatikos terminų žodynas

• логическая схема — loginė schema statusas T sritis automatika atitikmenys: angl. logic diagram vok. logisches Diagramm, n; logisches Schema, n rus. логическая схема, f pranc. schéma logique, m …   Automatikos terminų žodynas

• логическая схема И — loginis IR grandynas statusas T sritis radioelektronika atitikmenys: angl. AND circuit vok. logische UND Schaltung, f rus. логическая схема И, f pranc. circuit ET, m …   Radioelektronikos terminų žodynas

• логическая схема И-НЕ — loginis IR NE grandynas statusas T sritis radioelektronika atitikmenys: angl. NAND circuit; NOT AND circuit vok. logische NAND Schaltung, f rus. логическая схема И НЕ, f pranc. circuit ET NON, m …   Radioelektronikos terminų žodynas

• логическая схема НЕ — loginis NE grandynas statusas T sritis radioelektronika atitikmenys: angl. NOT circuit vok. logische NICHT Schaltung, f rus. логическая схема НЕ, f pranc. circuit NON, m …   Radioelektronikos terminų žodynas

• логическая схема — loginė grandinė statusas T sritis fizika atitikmenys: angl. logic circuit; logical circuit vok. logische Schaltung, f; logischer Schaltkreis, m rus. логическая схема, f pranc. circuit logique, m …   Fizikos terminų žodynas

• логическая схема устройства управления фазовращателем ФАР — логическая схема Часть устройства управления фазовращателем ФАР, обеспечивающая логическую обработку и преобразование команд, поступающих к каналу управления СУЛ. [ГОСТ 23066 78] Тематики антенны Обобщающие термины канал управления СУЛ Синонимы… …   Справочник технического переводчика

• Логическая схема (модель данных) — Логическая схема модель данных специфической области вопросов, выраженная в понятиях технологии управления данными. Не будучи продуктом исключительно теории управления базами данных, она оперирует терминами и понятиями или реляционных таблиц и… …   Википедия

• логическая схема - вентиль «ИЛИ» — Схема, дающая выход, когда совпадает несколько входных импульсов [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN OR gate …   Справочник технического переводчика

Книги

• Теория и практика социальной работы, Ю. В. Манько, К. М. Оганян. В пособии рассматриваются основные проблемы теории и практики социальной работы как теории и профессиональной деятельности. Особое внимание уделено анализу объекта, предмета, принципов,… Подробнее  Купить за 441 руб
• Условная оптимизация: методы и задачи, Софиева Ю.Н.. Настоящая книга написана на базе курса лекций по методам оптимизации и оптимального управления для студентов, специализирующихся по прикладной математике и управлению технологическими… Подробнее  Купить за 378 руб
• Условная оптимизация. Методы и задачи, Ю. Н. Софиева, А. М. Цирлин. Настоящая книга написана на базе курса лекций по методам оптимизации и оптимального управления для студентов, специализирующихся по прикладной математике и управлению технологическими… Подробнее  Купить за 378 руб

Другие книги по запросу «ЛОГИЧЕСКАЯ СХЕМА» >>

dic.academic.ru

14. Электронная логическая схема операции не.

Логическая операция «НЕ» основана на отрицании и исключении условия в ответе логической операции. В противопоставлении условия и ответа. «ДА» — «НЕТ». Одно условие и один результат. И результат противоположен условию.

0 – 1 и 1- 0, вот сегодняшняя математическая интерпретация такого противопоставления. Мы задаем условие и получаем его, вроде бы, противоположность. Как результат действия условия. Если «не черное», то – «белое»?

Не совсем так. «Не черное» — оно и есть, не черное. Какое угодно, только — не черное.

В математике логики есть только две цифры: 0 и 1.

Это привело к слиянию нескольких смыслов операции «НЕ» -,противоположности, противопоставления и исключения условия из результата. Вот и осталось одно противопоставление в виде противоположности. Да уж, иная простота – хуже воровства…

Далее математика определила свое дополнение: Нет условия и – нет результата.

Очень жесткое дополнение. И ограничение. Получается, что ответ в задаче есть, только пока мы решаем эту задачу. Решили, и — ответ пропал.

А мы так к нему стремились …

Но мы все же запишем ответ. И пусть все условия задачи пропадут, и уйдут из памяти, ответ, вот он – остался. Как результат операции. Это против математического ограничения, но соответствует философской концепции логики. Ответ в задаче должен быть. И если мы его нашли, то он должен остаться. Даже если задача уже не актуальна. Может быть, она для нас уже и не задача, мы же знаем ответ, но для следующих пытливых умов она снова встанет на пути. Знание ответа поможет им пойти дальше, чем довелось нам.

Вот на этом и остановимся. Математическое выражение противопоставления, это решаемая нами задача. И у задачи должен быть ответ, как результат её решения. Отдельно от выражения. Сам по себе. Уже, как событие для следующей задачи.

Рис.50. Счетное «НЕ».

В качестве элемента счетного «противоположного НЕ» можно использовать RS триггер. Только входы поменять местами, как на рис.50. Теперь подача импульса на вход приведет к появлению единичного состояния на выходе -Q. А на выходе Q появится состояние 0.

Что соответствует противоположности и противопоставлению логической функции НЕ:

А не А

(79)

Результат в виде потенциала на выходе триггера останется и при прекращении действия условий на его входе. Это зафиксированный ответ логической задачи противопоставления.

Для изменения результата надо изменить условие на входе. В данном случае, подать импульс на другой вход — «Установка». И элемент снова готов к работе.

А как же смысл «НЕ» — исключение условия из результата операции?

Рис.51. Триггеры на логических элементах.

Вот пример (рис.51. б) триггера на 3 устойчивых состояния. Он взят из публикаций А.П. Стахова [17 ].

Его работа соответствует смыслу «исключающего НЕ — ИЛИ» с фиксацией результата. Условие исключено, а на каком, из оставшихся выходов будет 1 – безразлично.

15. Электронная логическая схема операции или

Логическая операция «ИЛИ» изначально, также имела другой смысл. Она означала, что любое решение задачи – правильное. Любое. Но, одно. Или это, или то, или вот это…

Одно начальное условие и множественность ответа.

Математика перекроила эту логическую посылку. И установила обратное ее понимание. Теперь наоборот, множественность возможных условий приводит к единственности ответа. И уже на этом основании ввела математическую интерпретацию. Логическое сложение.

1+1=1 мы же это помним.

Из задачи с множеством выходов нас привели к задаче с множеством входов. И закрепили это в логических электронных схемах.

Может быть, вернуться к начальному пониманию «ИЛИ»?

Управление выходами по входу. Ну, это совсем просто. Этой функции соответствует, например, триггер со счетным входом на рис.48.

Рис. 48. Счетное «ИЛИ» выхода.

Любой новый импульс на счетном входе приведет к изменению состояния на выходах триггера. Уж, куда-нибудь он переключится…

Большее количество вариантов выбора, это увеличение количества выходов при единственности входа. Это уже управляемая коммутация.

Рис.49. Счетное «ИЛИ» входа.

Функциональная схема счетного «ИЛИ» по входу приведена на рис.49. Она отличается от принятой логической схемы фиксацией единичного состояния входа. Если счетный импульс пришел на любой вход, то на выходе схемы он уже не пропадет. До переустановки схемы в исходное состояние.

16.Электронная логическая схема операции И.

«ЖӘНЕ» функциясы: f6= Х1Х1

16. Электронная логическая схема операции И-НЕ.

Сандық техниканық логикалық негізін Буль алгебрасының негізінде көрсетуге болады.

«Емес» функциясы: f1=

«Қайталау» функциясы: f2=X

«0-ге айналдыру» функциясы: f3=0

«1-ге айналдыру» функциясы: f4=1

Х

«НЕМЕСЕ» функциясы: f5= Х1Х2

Х1

«Пирс» функциясы (НЕМЕСЕ-ЕМЕС): f7= Х1Х1

Х1

studfiles.net

Логические схемы. Переход от логического выражения к логической схеме и наоборот

Разделы: Информатика

Цели:

1. Образовательные

• Основные логические операции.
• Построение таблиц истинности сложных высказываний.
• Логические схемы и логические выражения.

2. Развивающие

• Развитие исследовательской и познавательной деятельности.
• Лаконично, полно и содержательно отвечать и делать обобщающие выводы.

3. Воспитательные

• Формирование аккуратности при работе с компьютером.
• Понимание связей между другими учащимися, культурой поведения.

Тип урока: комбинированный

Методы организации учебной деятельности:

• фронтальная
• индивидуальная
• ученик-компьютер

Программно-дидактическое обеспечение: ПК, презентация, задание для практической работы, раздаточный материал, Electronics Workbench (EWB512), PowerPoint.

ХОД УРОКА

I. Организационный момент.

II. Актуализация ранее изученного материала и проверка домашнего задания.

Задания для выполнения в тетради и у доски.

№1. Составьте таблицы истинности для следующих логических выражений:

№3. Нарисовать на доске логические элементы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ.

III. Новый материал.

Над возможностями применения логики в технике ученые и инженеры задумывались уже давно. Например, голландский физик Пауль Эренфест (1880 - 1933), еще в 1910 году писал: "...Пусть имеется проект схемы проводов автоматической телефонной станции. Надо определить:

1) будет ли она правильно функционировать при любой комбинации, могущей встретиться в ходе деятельности станции; 2) не содержит ли она излишних усложнений.

Каждая такая комбинация является посылкой, каждый маленький коммутатор есть логическое "или-или", воплощенное в эбоните и латуни; все вместе - система чисто качественных... "посылок", ничего не оставляющая желать в отношении сложности и запутанности... правда ли, что, несмотря на существование алгебры логики, своего рода "алгебра распределительных схем" должна считаться утопией?".

Созданная позднее М.А. Гавриловым (1903 - 1979) теория релейно-контактных схем показала, что это вовсе не утопия.

Посмотрим на микросхему. На первый взгляд ничего того, что нас бы удивило, мы не видим! Но если рассматривать ее при сильном увеличении, она поразит нас своей стройной архитектурой. Чтобы понять, как она работает, вспомним, что компьютер работает на электричестве, то есть любая информация представлена в компьютере в виде электрических импульсов.

Почему необходимо уметь строить логические схемы?

Дело в том, что из вентилей составляют более сложные схемы, которые позволяют выполнять арифметические операции и хранить информацию. Причем схему, выполняющую определенные функции, можно построить из различных по сочетанию и количеству вентилей. Поэтому значение формального представления логической схемы чрезвычайно велико. Оно необходимо для того, чтобы разработчик имел возможность выбрать наиболее подходящий ему вариант построения схемы из вентилей. Процесс разработки общей логической схемы устройства (в том числе и компьютера в целом), становится иерархическим, причем на каждом следующем уровне в качестве "кирпичиков" используются логические схемы, созданные на предыдущем этапе. Алгебра логики дала в руки конструкторам мощное средство разработки, анализа и совершенствования логических схем. В самом деле, гораздо проще, быстрее и дешевле изучать свойства и доказывать правильность работы схемы с помощью выражающей ее формулы, чем создавать реальное техническое устройство. Именно в этом состоит смысл любого математического моделирования.

Логические схемы необходимо строить из минимально возможного количества элементов, что в свою очередь, обеспечивает большую скорость работы и увеличивает надежность устройства.

Правило построения логических схем:

1) Определить число логических переменных. 2) Определить количество базовых логических операций и их порядок. 3) Изобразить для каждой логической операции соответствующий ей вентиль и соединить вентили в порядке выполнения логических операций.

Рассмотрение двух примеров перехода от выражения к схеме. (Презентация)

Рассмотрение двух примеров перехода от схемы к выражению. (Презентация)

Чаще в жизни возникает ситуация, когда известен результат и для его реализации необходимо построить устройство.

Рассмотрим следующую задачу: (Презентация)

Задача 1. В двухэтажном доме лестница освещается одной лампой Х. На первом этаже установлен один выключатель А, на втором этаже - выключатель В. Если включают А, то лампа загорается. При поднятии на второй этаж и включении В лампа гаснет. Если кто-то выходит и нажмет В, то лампа включается, при спуске на первый этаж и нажатии А лампа должна погаснуть.

Алгоритм решения:

• Составить таблицу истинности.
• Определить логическую функцию.
• Построить логическую схему.

 

A	B	X
0	0	0
1	0	1
1	1	0
0	1	1
0	0	0

Чтобы создать логическую функцию по таблице истинности, надо записывать значения выходной переменной.

Между строками таблицы будет стоять знак логического сложения, а между столбцами - знак логического умножения .

Задача 2. (Презентация)

IV. Закрепление изученного материала.

Работа у доски и в тетради по карточкам.

№1. По логическому выражению построить логическую схему:

№2. По логической схеме составьте логическое выражение:

V. Компьютерный практикум.

Практическая работа с использованием электронной лаборатории Electronics Workbench (EWB512).

Вариант 1

1. Упростите логическое выражение

2. Проверьте свою работу, используя программу Electronics Workbench:

- Запишите исходное выражение в Logic Converter; - Составьте таблицу истинности - Упростите выражение используя - Постройте упрощенную логическую схему .

3. Проверьте правильность выполненных упрощений.

VI. Домашнее задание:

а) упростите логическое выражение, постройте логическую схему и таблицу истинности б) по таблице истинности (00001011) составьте выражение, упростите его, нарисуйте схему.

xn--i1abbnckbmcl9fb.xn--p1ai

7.2. Логические элементы

Логические операции реализуются с использованием электрических схем, которые называются логическими элементами. Они изготавливаются в виде интегральных микросхем в большинстве своем на базе диодов и транзисторов, либо только транзисторов. В связи с этим различают два типа логических элементов: ДТЛ (диодно-транзисторная логика) и ТТЛ (транзисторно-транзисторная логика). На рис. 7.2 представлены схемные обозначения элементов, выполняющих простейшие логические операции. При этом элементы “ИЛИ” и “И” – двухвходовые, т.е. выполняющие операции с двумя входными переменными. Однако промышленностью выпускаются логические элементы “ИЛИ” и “И” с большим числом входных клемм.

Рисунок 7.2. Схемное обозначение логических элементов

На рис. 7.3 приведена схема на диодах, с помощью которой реализуется операция логического сложения. Действительно, при отсутствии на входах этой схемы сигналов (x = 0, гдеi = 1, 2, … n)все диоды будут находиться в закрытом состоянии и на резисторе падение напряжения равно нулю(F = 0).При подаче хотя бы на один вход схемы сигнала положительной полярности диод, установленный на этом входе, перейдет в открытое состояние. Через него и последовательно включенный с ним резисторRбудет протекать ток, падение напряжения на резисторе будет отличаться от нуля.F = 1.

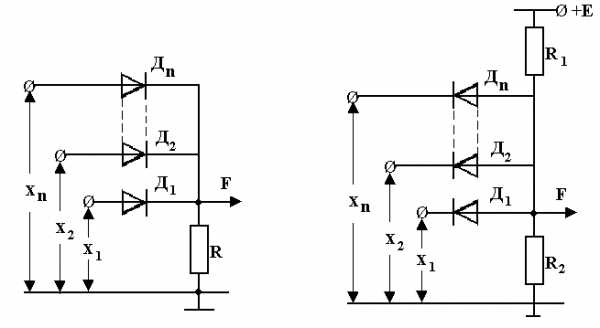
Рисунок 7.3. Реализация Рисунок 7.4. Реализация логической логической операции операции «И» на диодах

«ИЛИ» на диодах

Нетрудно также показать, что схема на рис. 7.4 обеспечивает выполнение операции “И”. Через резистор Rбудет протекать ток, и с этого резистора будет сниматься напряжение, равноеUвых = ER/(R + R), т.е. F = 1, когда катоды всех диодов будут под положительным потенциалом, превышающим величинуUвых (x = 1), а, следовательно, все диоды будут закрыты. Если хотя бы на одном входе схемы сигнал отсутствует, соответствующий диод будет открыт, и через него будет протекать ток в обход резистораR, поскольку его сопротивление выбирается много больше сопротивления открытого диода. Падение напряжения на резистореRв данном случае будет равно нулю.F = 0.

Операция “НЕ” может быть реализована на биполярном транзисторе типа n-p-n, включенного по параллельному варианту построения ключевой схемы (рис. 4.2.а). Как было показано в разделе 4.1, при подаче на вход схемы сигнала положительной полярности определенного уровня(x = 1) транзистор будет находиться в открытом состоянии, т.е. в точке “б” на рис. 4.4,б. Этому режиму транзистора соответствует очень малая величина напряжения коллектор-эмиттер, ΔUКЭ ОТК, которая является выходом схемы, F = 0. При отсутствии на входе сигнала(x = 0)транзистор будет закрыт (точка «а» на рис. 4.4,в), и с выхода схемы снимается напряжение, практически равное+Е, т.е. F = 1.

Следует отметить, что напряжение на выходе схем рис.7.3 и 7.4, равное нулю, обеспечиваются лишь при идеальном шунтировании резистора, с которого снимается выходное напряжение открытыми диодами. При реализации логической операции «НЕ» из-за наличия остаточного напряжения на открытом транзисторе выходное напряжение также отличается от нуля. Таким образом, в реальных логических элементах логическим нулем, фактически, является не нулевое, а малая величина напряжения. В связи с этим в справочных данных обычно вместо «0» указывается «н» (низкий уровень напряжения) и соответственно вместо «1» указывается «в» (высокий уровень напряжения).

Логические элементы выпускаются промышленностью в виде серий. Элементы каждой серии, выполняющие различные операции, могут сопрягаться в сложную схему логического устройства. Элементы серии создаются на базе основного элемента, который обычно выполняет операции “ИЛИ-НЕ” или “И-НЕ”. Математическая форма представления этих операций имеет вид:

F = иF = .

Схемы, реализующие операции “ИЛИ-НЕ” и “И-НЕ”, могут быть получены при последовательном соединении двух схем, выполняющих операции соответственно “ИЛИ”-“НЕ” и “И”-“НЕ”, что показано на рис. 7.5,а и 7.6,а для случая двухвходовых элементов. Схемные обозначения элементов “ИЛИ-НЕ” и “И-НЕ” представлены на рис. 7.5,б и 7.6,б, а таблицы истинности – в табл. 7.4 и 7.5.

Рисунок 7.5. Логическая операция «ИЛИ-НЕ»:

а – принцип реализации операции,

б - схемное обозначение логического элемента

Рисунок 7.6. Логическая операция «И-НЕ»:

а – принцип реализации операции,

б - схемное обозначение логического элемента

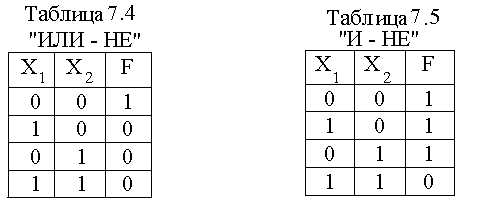
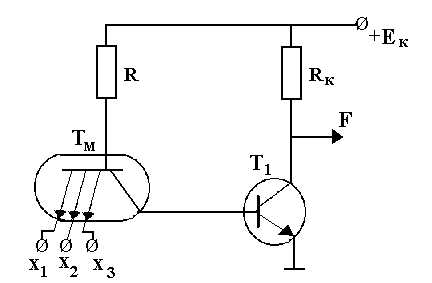
Рисунок 7.7. Реализация логической операции «И-НЕ»

на транзисторах

На рис. 7.7 представлена схема на транзисторах, реализующая логическую операцию “И-НЕ”. Особенностью этой схемы является использование многоэмиттерного транзистора Т, которым заменяется диодная часть элемента “И-НЕ”, выполняющего операцию “И”. В многоэмиттерном транзисторе эмиттерный слой состоит из нескольких областей при общих базовом и коллекторном слоях. Принцип работы схемы рис. 7.7 следующий. Если на все эмиттерные входы транзистораТбудет подано положительное напряжение, равноеЕ(т.е. всеx = 1), все эмиттерные переходы транзистора будут закрыты, а его ток базы будет протекать через открытый коллекторный переход, обусловливая протекание коллекторного тока, который одновременно является базовым током транзистораТ. ТранзисторТ, который выполняет операцию логического отрицания, в этом случае будет находиться в открытом состоянии, и на его выходе напряжение будет практически отсутствовать(F = 0). При отсутствии хотя бы на одном эмиттерном входе транзистораТсигнала положительной полярности, ток, протекающий через резисторRи через соответствующий открытый эмиттерный переход, будет замыкаться по цепи этого эмиттерного входа. Базовый ток транзистораТ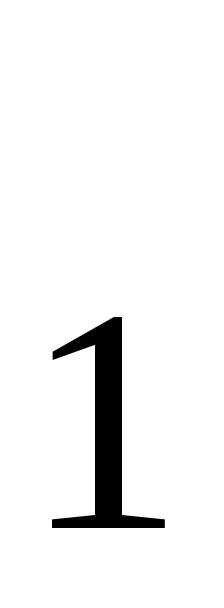будет равен нулю, поскольку суммарное сопротивление коллекторного перехода транзистораТи базового слоя транзистораТ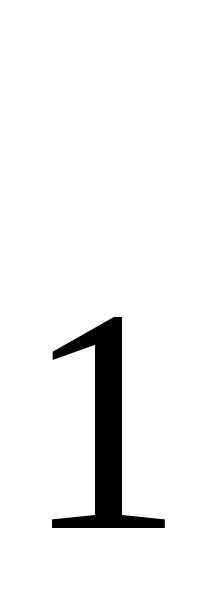оказывается довольно большим по сравнению с сопротивлением открытого эмиттерного перехода транзистораТ. ТранзисторТ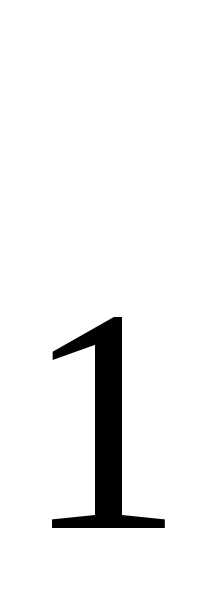поэтому будет находиться в закрытом состоянии, и на его выходе напряжение будет близко к величине+Е, т.е.F = 1.

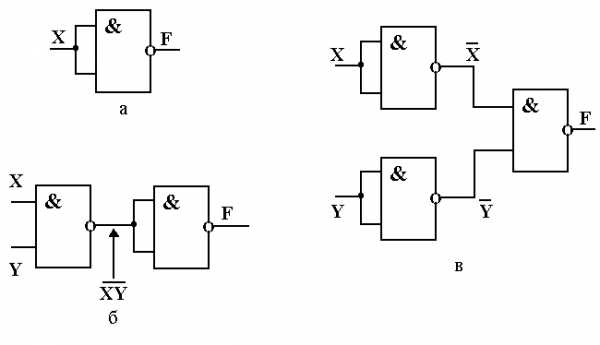
Рисунок 7.8. Схемы реализации логических операций на элементах «И-НЕ»

а – операции «НЕ», б – операции «И», в - операции «ИЛИ»

Логические элементы «ИЛИ-НЕ» и «И-НЕ» называют базовыми, поскольку схемы, составленные только из этих элементов одного типа, позволяют реализовывать простейшие логические операции. Это нетрудно доказать с использованием формул алгебры логики, например, на схемах, составленных из элементов «И-НЕ», которые приведены на рис. 7.8.

На вход элемента схемы рис. 7.8,а подаются две одинаковых переменных x. Поэтому согласно тождествам (7.11) и (7.1)

F = = + = .

Таким образом, схема рис. 7.8,а выполняет операцию “НЕ”.

В качестве выходного каскада схемы рис. 7.8,б используется элемент “И-НЕ”, включенный по схеме рис. 7.8,а. Он инвертирует информацию, поступающую с входа первого элемента. Если учесть тождество (7.9), то

F = =xy.

Следовательно, схема рис. 7.8,б выполняет операцию “И”.

Информация, поступающая на каждый входной элемент схемы рис. 7.8,в, инвертируется, т.е. и . Тогда последовательное использование тождеств (7.11) и (7.9) позволяет показать, что эта схема реализует операцию логического сложения “ИЛИ”

F = 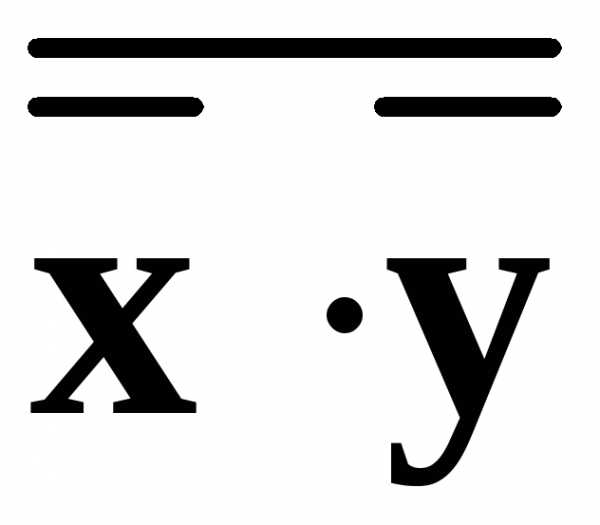=+= x + y.

К основным показателям логических элементов, в первую очередь, относят быстродействие, потребляемую мощность и помехоустойчивость. Быстродействие характеризуется временем задержки реакции выходного сигнала при изменении сигнала на входе элемента. Время задержки логических элементов обычно составляет 0,01 – 0,3 мкс. Их потребляемая мощность обычно находится в пределах от 1 мкВт до 250 мВт и связана с быстродействием: потребляющие большую мощность элементы имеют более высокое быстродействие. При работе логических элементов в составе аппаратуры возможны случаи ложного срабатывания под действием напряжений помех, попадающих на вход микросхемы. Мерой невосприимчивости элементов к помехам является помехоустойчивость, которая зависит от структуры микросхемы, режима работы в ней транзисторов, величины питающего напряжения.

studfiles.net

---

• 
  Как крепить люстру на натяжной потолок
• 
  Санпин по освещенности рабочих мест
• 
  Схема подключения тт к счетчику
• 
  Законы кирхгофа примеры
• 
  Диаметр от сечения провода
• 
  Передача электроэнергии по воздуху
• 
  Правила замены электросчетчика в многоквартирном доме
• 
  Выпрямитель в схеме
• 
  Теплоноситель и тепловая энергия чем отличаются
• 
  Теплогенераторы для воздушного отопления
• 
  Суммарная максимальная мощность энергопринимающих устройств