Индукция магнитного поля соленоида. Магнитная индукция соленоида
Магнитное поле соленоида
Соленоидом называется совокупность N одинаковых витков изолированного проводящего провода, равномерно намотанных на общий каркас или сердечник. По виткам проходит одинаковый ток. Магнитные поля, созданные каждым витком в отдельности, складываются по принципу суперпозиции. Индукция магнитного поля внутри соленоида велика, а вне его - мала. Для бесконечно длинного соленоида индукция магнитного поля вне соленоида стремится к нулю. Если длина соленоида во много раз больше диаметра его витков, то соленоид можно практически считать бесконечно длинным. Магнитное поле такого соленоида целиком сосредоточено внутри него и является однородным (рис.6).
Величину индукции магнитного поля внутри бесконечно длинного соленоида можно определить, используя теорему о циркуляции вектора  :циркуляция вектора
:циркуляция вектора  по произвольному замкнутому контуру равна алгебраической сумме токов, охватываемых контуром, умноженной на магнитную постоянную μо:
по произвольному замкнутому контуру равна алгебраической сумме токов, охватываемых контуром, умноженной на магнитную постоянную μо:
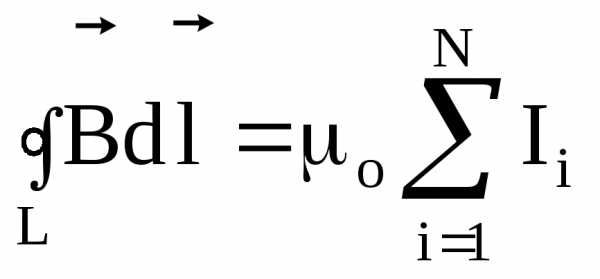 , (20)
, (20)
где μ0 = 4π 10-7 Гн/м.
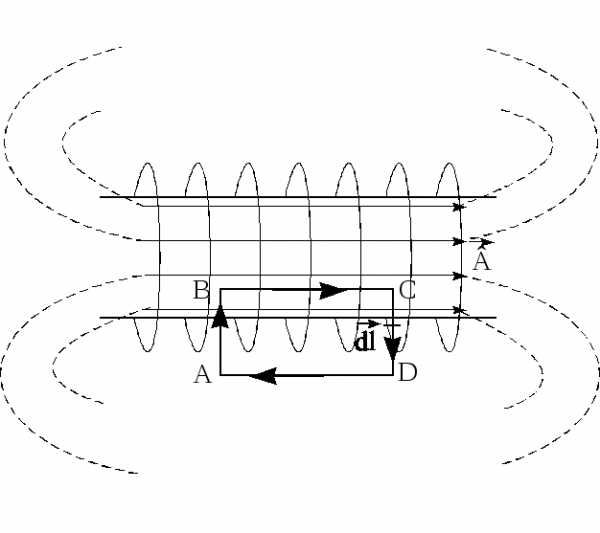
Рис.6. Магнитное поле соленоида
Для определения величины магнитной индукции В внутри соленоида выберем замкнутый контур ABCD прямоугольной формы, где 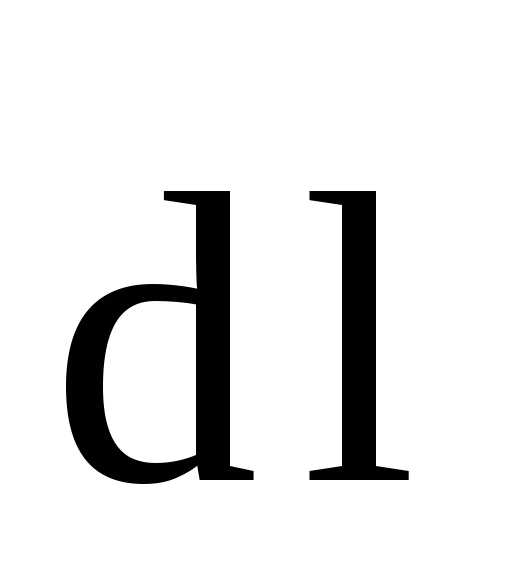 - элемент длины контура, задающий направление обхода (рис.6). При этом длиныAB и CD будем считать бесконечно малыми.
- элемент длины контура, задающий направление обхода (рис.6). При этом длиныAB и CD будем считать бесконечно малыми.
Тогда циркуляция вектора  по замкнутому контуруABCD, охватывающему N витков, равна:
по замкнутому контуруABCD, охватывающему N витков, равна:
(21)
На участках AB и CD произведение 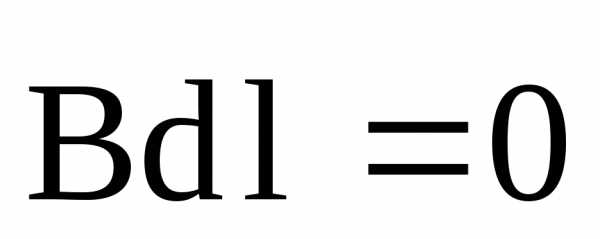 , так как вектора
, так как вектора и
и взаимно перпендикулярны. Поэтому
взаимно перпендикулярны. Поэтому
. (22)
На участке DA вне соленоида интеграл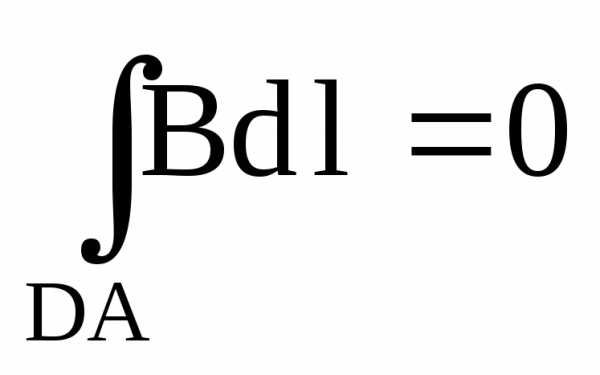 , так как магнитное поле вне контура равно нулю.
, так как магнитное поле вне контура равно нулю.
Тогда формула (21) примет вид:
, (23)
где l – длина участка BC. Сумма токов, охватываемых контуром, равна
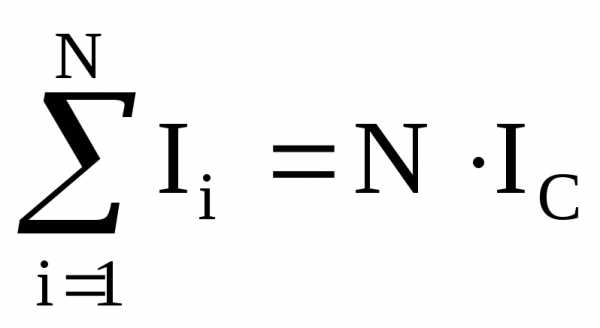 , (24)
, (24)
где Ic – сила тока соленоида; N – число витков, охватываемых контуром ABCD.
Подставив (23) и (24) в (20), получим:
. (25)
Из (25) получим выражение для индукции магнитного поля бесконечно длинного соленоида:
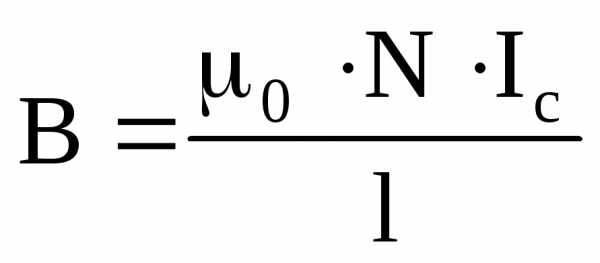 . (26)
. (26)
Так как число витков на единицу длину соленоида n равно:
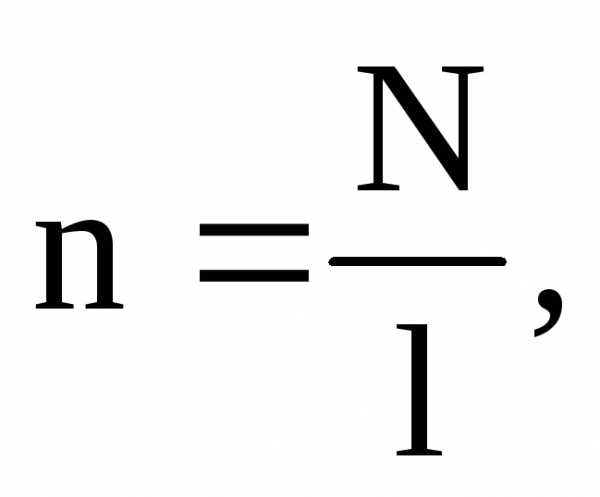 (27)
(27)
то окончательно получим:
. (28)
Если внутрь соленоида помещен сердечник, то формула (28) для В примет вид:
. (29),
где - магнитная проницаемость материала сердечника.
Таким образом, индукция В магнитного поля соленоида определяется током соленоида Ic, числом витком n на единицу длины соленоида и магнитной проницаемостью материала сердечника.
Цилиндрический магнетрон
Магнетроном называется двухэлектродная электронная лампа (диод), содержащая накаливаемый катод и холодный анод и помещенная во внешнее магнитное поле.
Анод диода имеет форму цилиндра радиусом 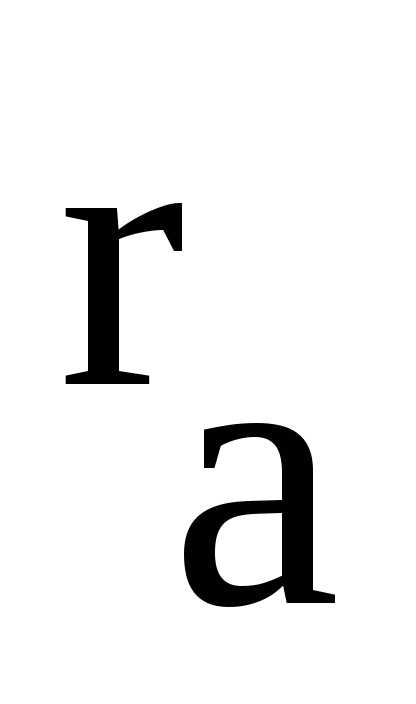 . Катод представляет собой полый цилиндр радиусом
. Катод представляет собой полый цилиндр радиусом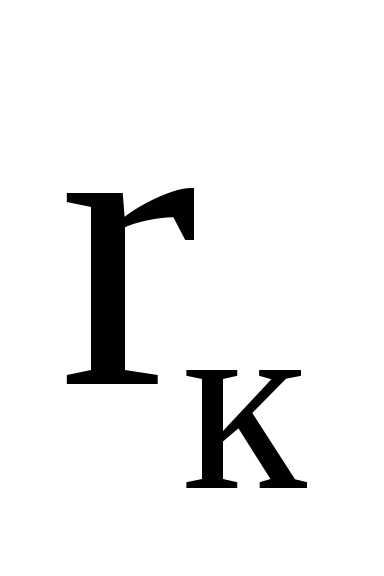 , вдоль оси которого расположена нить накала, как правило, изготавливаемая из вольфрама (рис.7).
, вдоль оси которого расположена нить накала, как правило, изготавливаемая из вольфрама (рис.7).
Раскалённый катод в результате явления термоэлектронной эмиссии испускает термоэлектроны, которые образуют вокруг катода электронное облако. При подаче анодного напряжения  (рис.8), электроны начинают перемещаться от катода к аноду вдоль радиусов, что приводит к возникновению анодного тока
(рис.8), электроны начинают перемещаться от катода к аноду вдоль радиусов, что приводит к возникновению анодного тока . Анодный ток регистрируется миллиамперметром.
. Анодный ток регистрируется миллиамперметром.
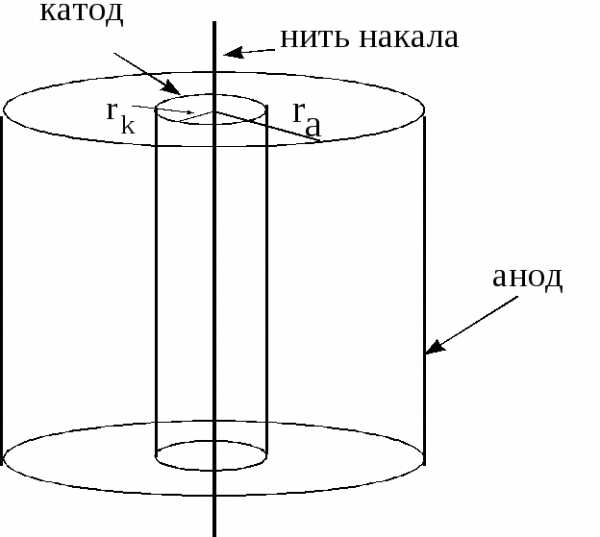
Рис.7. Схема диода
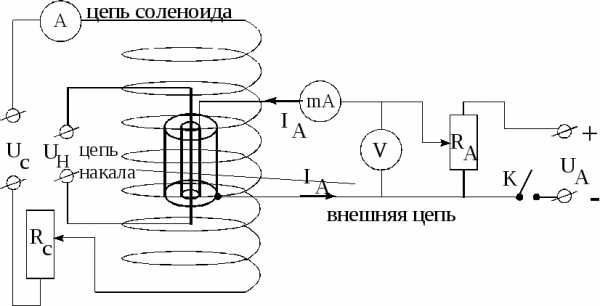 Рис.8. Электрическая схема цепи
Рис.8. Электрическая схема цепи
Величина анодного напряжения регулируется потенциометром RA. Чем больше анодное напряжение, тем большее количество электронов за единицу времени достигает анода, следовательно, тем больше анодный ток.
Напряжённость электрического поля Е между катодом и анодом такая же, как и в цилиндрическом конденсаторе:
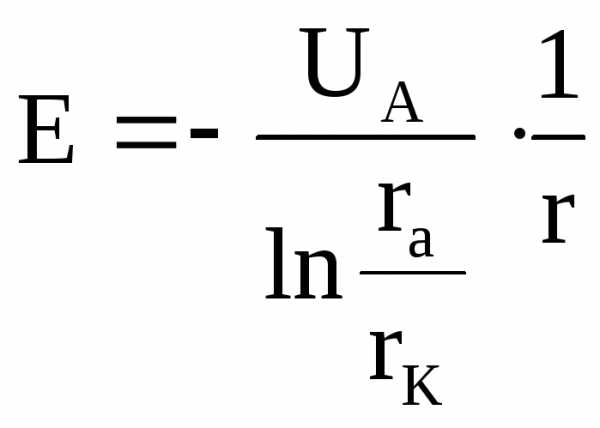 , (30)
, (30)
где r – расстояние от оси катода до данной точки пространства между катодом и анодом.
Из формулы (30) следует, что напряжённость поля Е обратно пропорциональна расстоянию r до оси катода. Следовательно, напряженность поля максимальна у катода.
Так как
rк <<ra, (31)
то значение логарифма ln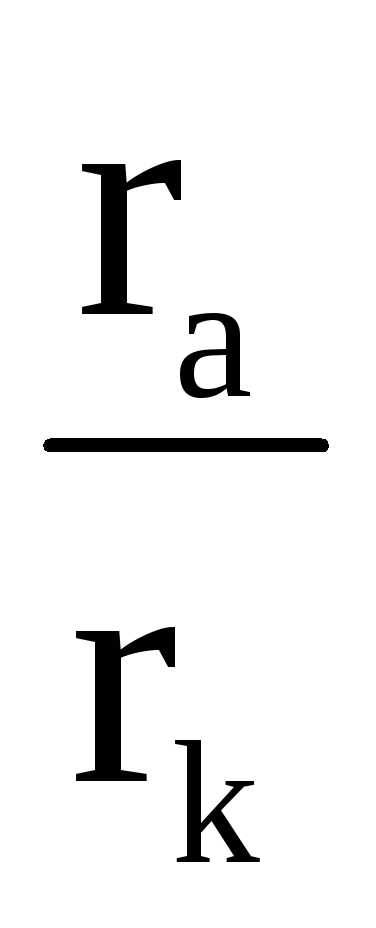 стремится к большой величине. Тогда с увеличением расстояния r напряженность электрического поля между катодом и анодом снижается до нуля. Поэтому, можно считать, что электроны приобретают скорость под действием поля только вблизи катода, и дальнейшее их движение к аноду происходит с постоянной по величине скоростью.
стремится к большой величине. Тогда с увеличением расстояния r напряженность электрического поля между катодом и анодом снижается до нуля. Поэтому, можно считать, что электроны приобретают скорость под действием поля только вблизи катода, и дальнейшее их движение к аноду происходит с постоянной по величине скоростью.
Внешнее магнитное поле, в которое помещён диод, создаётся соленоидом (рис.8). Длина соленоида l много больше диаметра его витков, поэтому поле внутри соленоида можно считать однородным. Ток в цепи соленоида изменяется с помощью потенциометра RC (рис.8) и регистрируется амперметром.
Характер движения электронов в зависимости от величины поля соленоида показан на рис.9. Если ток в цепи соленоида отсутствует, то индукция магнитного поля В = 0. Тогда электроны движутся от катода к аноду практически по радиусам.
Увеличение тока в цепи соленоида приводит к возрастанию величины В. При этом, траектории движения электронов начинают искривляться, однако все электроны достигают анода. В анодной цепи будет течь ток такой же, как и в отсутствии магнитного поля.
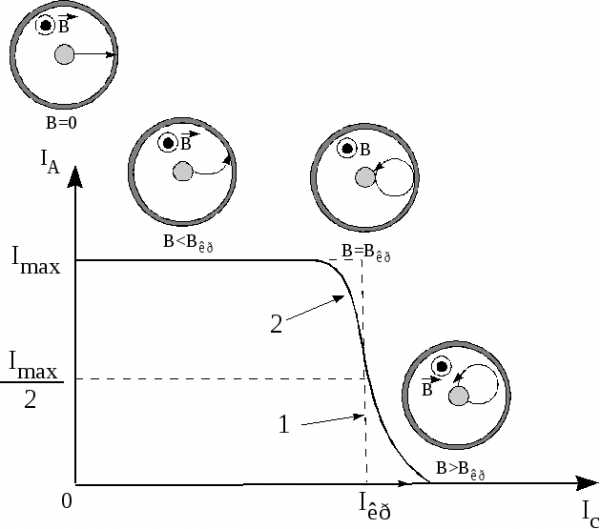
Рис.9. Зависимость анодного тока IA от величины тока соленоида Ic в идеальном (1) и реальном (2) случаях, а также характер движения электронов в зависимости от величины поля соленоида.
При некотором значении тока в соленоиде радиус окружности, по которой движется электрон, становится равным половине расстояния между катодом и анодом:
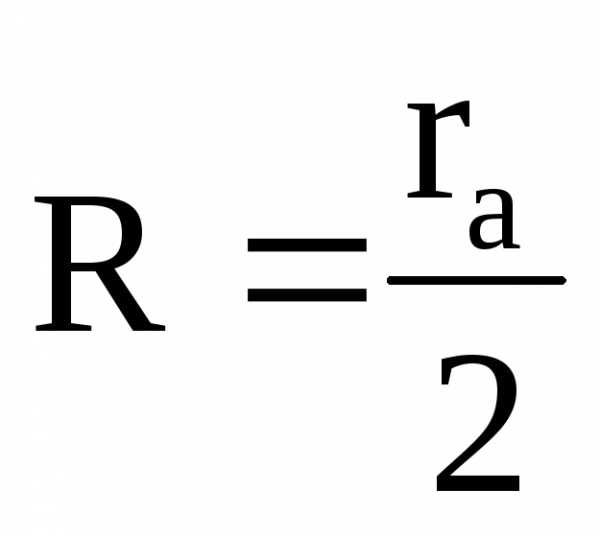 .. (32)
.. (32)
Электроны в этом случае касаются анода и уходят к катоду (рис.9). Такой режим работы диода называется критическим. При этом по соленоиду течёт критический ток Iкр, которому соответствует критическое значение индукции магнитного поля В = Вкр.
При В = Вкр анодный ток в идеальном случае должен скачком уменьшиться до нуля. При В > Вкр электроны не попадают на анод (рис.9), и анодный ток также будет равен нулю (рис.9, кривая 1).
Однако на практике, вследствие некоторого разброса скоростей электронов и нарушения соосности катода и соленоида, анодный ток уменьшается не скачком, а плавно (рис.9, кривая 2). При этом значение силы тока соленоида, соответствующее точке перегиба на кривой 2, считается критическим Iкр. Критическому значению тока соленоида соответствует анодный ток, равный:
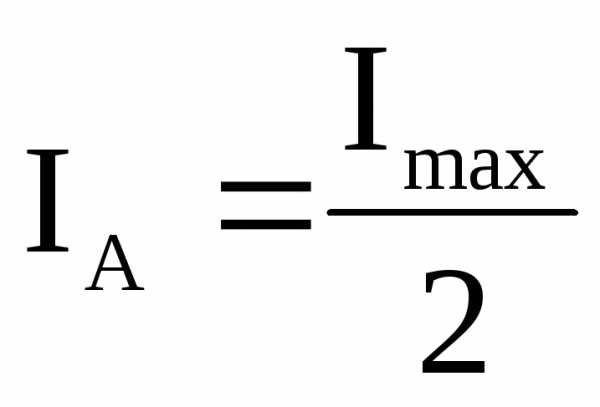 , (33)
, (33)
где 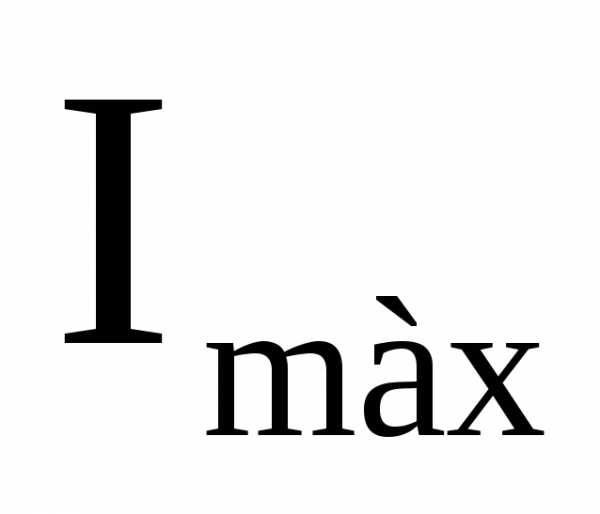 – максимальное значение анодного тока при В = 0.
– максимальное значение анодного тока при В = 0.
Зависимость анодного тока IA от величины индукции магнитного поля В (или от тока в соленоиде) при постоянном анодном напряжении и постоянном накале называется сбросовой характеристикой магнетрона.
studfiles.net
Магнитное поле соленоида
Применим теорему о циркуляции вектора для вычисления простейшего магнитного поля – бесконечно длинного соленоида, представляющего собой тонкий провод, намотанный плотно виток к витку на цилиндрический каркас (рис. 2.11).
Рис. 2.11
Соленоид можно представить в виде системы одинаковых круговых токов с общей прямой осью.
Бесконечно длинный соленоид симметричен любой, перпендикулярной к его оси плоскости. Взятые попарно (рис. 2.12), симметричные относительно такой плоскости витки создают поле, в котором вектор перпендикулярен плоскости витка, т.е. линии магнитной индукции имеют направление параллельное оси соленоида внутри и вне его.
Рис. 2.12
Из параллельности вектора оси соленоида вытекает, что поле как внутри, так и вне соленоида должно быть однородным.
Возьмём воображаемый прямоугольный контур 1–2–3–4–1 и разместим его в соленоиде, как показано на рисунке 2.13.
Рис. 2.13
Второй и четвёртый интегралы равны нулю, т.к. вектор перпендикулярен направлению обхода, т.е .
Возьмём участок 3–4 – на большом расстоянии от соленоида, где поле стремится к нулю; и пренебрежём третьим интегралом, тогда
где – магнитная индукция на участке 1–2 – внутри соленоида, – магнитная проницаемость вещества.
Если отрезок 1–2 внутри соленоида, контур охватывает ток:
где n – число витков на единицу длины, I – ток в соленоиде (в проводнике).
Тогда магнитная индукция внутри соленоида:
| , | (2.7.1) |
Вне соленоида:
и , т.е. .
Бесконечно длинный соленоид аналогичен плоскому конденсатору – и тут, и там поле однородно и сосредоточено внутри.
Произведение nI – называется число ампер витков на метр.
У конца полубесконечного соленоида, на его оси магнитная индукция равна:
| , | (2.7.2) |
Практически, если длина соленоида много больше, чем его диаметр, формула (2.7.1) справедлива для точек вблизи середины, формула (2.7.2) для точек около конца.
Если же катушка короткая, что обычно и бывает на практике, то магнитная индукция в любой точке А, лежащей на оси соленоида, направлена вдоль оси (по правилу буравчика) и численно равна алгебраической сумме индукций магнитных полей создаваемых в точке А всеми витками. В этом случае имеем:
· В точке, лежащей на середине оси соленоида магнитное поле будет максимальным:
| , | (2.7.3) |
где L – длина соленоида, R – радиус витков.
· В произвольной точке конечного соленоида (рис. 2.14) магнитную индукцию можно найти по формуле
| , | (2.7.4) |
Рис. 2.14
На рисунке 2.15 изображены силовые линии магнитного поля : а) металлического стержня; б) соленоида; в) железные опилки, рассыпанные на листе бумаги, помещенной над магнитом, стремятся вытянуться вдоль силовых линий; г) магнитные полюсы соленоида.
Рис. 2.15
ens.tpu.ru
Индукция магнитного поля соленоида
Для создания магнитного поля в технике используется соленоид – цилиндрическая катушка, состоящая из большого числа витков, равномерно намотанных на общий сердечник (рис. 4.5).
Рассмотрим соленоид длиной L, имеющий N витков, по которому течет ток I. Длину соленоида считаем во много раз большей диаметров его витков. Магнитное поле такого соленоида целиком сосредоточено внутри него и однородно. Снаружи соленоида поле мало и его практически можно считать равным нулю.
Величину индукции магнитного поля соленоида можно найти, складывая магнитные индукции полей, создаваемых каждым витком соленоида. Так как витки соленоида намотаны вплотную друг к другу, на длине dx сосредоточено витков. Суммарный ток, протекающий по кольцу, толщиной dx, равен . В точке, находящейся на оси соленоида каждое такое кольцо создает магнитное поле, согласно (4.7), равное:
.
Суммарное поле:
(4.9)
При интегрировании соленоид считаем бесконечным. Как видно из (4.9) магнитное поле соленоида зависит от плотности намотки – числа витков на единицу длины соленоида .
Магнитный поток
Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, равная:
dФ = ВndS = Bcos α × dS, (4.10)
где Вn – проекция вектора В на направление, перпендикулярное к площадке dS; α – угол между вектором нормали nи вектором В.
Положительное направление нормали связано правилом правого винта с током, текущим по контуру, ограничивающему площадку dS. Магнитный поток Ф через произвольную поверхность S можно представить в виде:
. (4.11)
Действие магнитного поля на заряды
На электрический заряд q, движущийся в магнитном поле с индукцией В со скоростью V, действует сила Лоренца:
. (4.12)
Абсолютная величина магнитной силы:
F = qvB Sin α ,
где α – угол между векторами V и В.
По правилу векторного произведения магнитная сила Fперпендикулярна плоскости, в которой лежат вектора Vи B.
Если q>0, магнитная сила Fсовпадает с направлением векторного произведения [V,B], если q<0, то противоположно.
Для положительного заряда, движущегося в магнитном поле, как показано на рисунке 4.6, сила F направлена вдоль отрицательного направления оси Z. Продольная компонента скорости Vll под действием магнитного поля изменяться не будет и движение заряженной частицы вдоль оси Х – равномерное. Результирующее движение частицы – по винтовой линии (рис.4.6). Спираль может быть как правой, так и левой в зависимости от знака заряда q.
Радиус спирали R найдем из условия, что при равномерном движении частицы по окружности сила Fявляется центростремительной силой:
,
где m – масса заряженной частицы. Отсюда:
.
Время, за которое частица совершит полный оборот (период):
. (4.13)
Из формулы (4.13) следует, что период обращения частицы не зависит от ее скорости. Однако надо помнить, что этот вывод справедлив только при условии V<<c, где: с – скорость света.
Если движение частицы происходит как в магнитном поле с индукцией B, так и в электрическом поле с напряженностью Е, то на нее действует обобщенная сила Лоренца:
. (4.14)
Электромагнитная индукция
Если поток магнитной индукции сквозь контур изменяется со временем, то, согласно закону электромагнитной индукции Фарадея, в контуре возникает ЭДС индукции:
E= – , (4.15)
где
Знак (–) означает: индукционный ток всегда имеет такое направление, что создаваемое им магнитное поле стремиться скомпенсировать то изменение магнитного потока, которым вызван данный индукционный ток (правило Ленца).
Ток в замкнутом контуре создает в окружающем пространстве магнитное поле, индукция которого пропорциональна току: В ~I. Поэтому сцепленный с контуром магнитный поток пропорционален силе тока в контуре I:
Ф = LI,
гдеL–коэффициент пропорциональности называют коэффициентом самоиндукции или индуктивностью контура.
 Если по контуру протекает изменяющийся со временем ток I(t), то изменяется магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции:
Если по контуру протекает изменяющийся со временем ток I(t), то изменяется магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции:
(4.16)
Индуктивность контура L в общем случае зависит от геометрии контура и магнитной проницаемости среды µ. Если эти величины не изменяются, то L = const. Т.е., если контур жесткий и поблизости нет ферромагнетиков, то L = const.
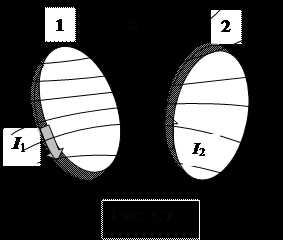
Рассмотрим два контура 1 и 2, расположенных на некотором расстоянии друг от друга (рис. 4.7). Если по контуру 1 пропустить ток I1, то он создает поток магнитной индукции через контур 2:
Ф21= L21I1. (4.17)
Коэффициент пропорциональности L21 называют коэффициентом взаимной индукции контуров (взаимная индуктивность контуров). Он зависит от формы и взаимного расположения контуров 1 и 2, а также от магнитных свойств окружающей среды.
При изменении силы тока в первом контуре магнитный поток сквозь второй контур изменяется; следовательно, в нем наводится ЭДС взаимной индукции:
. (4.18)
Формула справедлива в отсутствие ферромагнетиков.
Если поменять местами контуры 1 и 2 и повторить все предыдущие рассуждения, то получим:
. (4.19)
Коэффициенты взаимной индукции равны:
L21 = L12 .
pdnr.ru
Магнитное поле соленоида — Мегаобучалка
Соленоид представляет собой тонкий провод, навитый плотно (виток к витку) на цилиндрический каркас. На рис. 21 представлено схематическое изображение бесконечно длинного соленоида диаметром D. Будем считать, что намотка выполнена плотно, соседние витки прилегают друг к другу и по соленоиду течет ток силой I.
Выясним, как направлен вектор в различных точках магнитного поля соленоида. Для этого рассмотрим два любых элемента тока и , равных по величине и расположенных симметрично относительно плоскости сечения АА, перпендикулярной к оси соленоида (рис. 22). Элементы и перпендикулярны плоскости рисунка.
По закону Био–Савара–Лапласа рассматриваемые элементы тока создадут в каждой точке сечения АА магнитные поля, индукции которых и равны по величине, а их результирующий вектор параллелен оси соленоида.
Этот вывод справедлив для любой пары одинаковых элементов тока соленоида, расположенных симметрично относительно плоскости сечения АА. Из принципа суперпозиции следует, что линии индукции магнитного поля бесконечно длинного соленоида, если оно отлично от нуля, должны быть параллельны оси соленоида как внутри, так и вне соленоида.
Теперь докажем, что в точках, находящихся на расстоянии, много большем диаметра соленоида с плотной намоткой витков, магнитное поле равно нулю. Для этого рассмотрим два равных по модулю элемента тока и , расположенных симметрично относительно оси соленоида (рис. 23).
В точках, достаточно удале 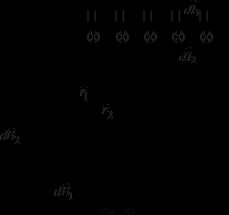 нных от соленоида, для которых , по закону Био–Савара–Лапласа магнитные индукции и будут равны и противоположны по направлению с хорошей степенью точности. Этот вывод справедлив для любой пары одинаковых элементов тока соленоида, расположенных симметрично относительно оси соленоида. Из принципа суперпозиции следует, что в достаточно удаленных от соленоида точках магнитное поле отсутствует.
нных от соленоида, для которых , по закону Био–Савара–Лапласа магнитные индукции и будут равны и противоположны по направлению с хорошей степенью точности. Этот вывод справедлив для любой пары одинаковых элементов тока соленоида, расположенных симметрично относительно оси соленоида. Из принципа суперпозиции следует, что в достаточно удаленных от соленоида точках магнитное поле отсутствует.
Для вычисления величины индукции магнитного поля соленоида применим теорему о циркуляции вектора по замкнутому контуру. Выберем контур прямоугольной формы, две стороны которого параллельны, а другие две стороны перпендикулярны оси соленоида (рис. 24, а, б).
Пусть участок контура находится от соленоида на расстоянии, много большем его диаметра, а участок , параллельный оси соленоида, расположен в первом случае внутри соленоида (рис. 24, а) и во втором случае вне соленоида (рис. 24, б).
Циркуляция вектора на контуре 1–2–3–4 равна сумме линейных интегралов:
.
Из соображений симметрии и так как линии магнитной индукции должны быть параллельны оси соленоида, как было показано выше, во всех точках участка . На участках контура и перпендикулярен элементарному перемещению. Следовательно, во всех точках участков и . Точки участка находятся на расстоянии, много большем диаметра соленоида, и в них, как отмечалось ранее, можно считать с хорошей степенью точности.
Таким образом,
, (1.17)
где – длина участка .
Согласно теореме о циркуляции в случае, когда контур охватывает ток (рис. 24, а),
, (1.18)
где n – плотность намотки (число витков на единицу длины соленоида), а n – число витков на длине . Если контур не охватывает ток (рис. 24, б), то
. (1.19)
Из сравнения (1.17) с (1.18) и (1.19) следует, что магнитное поле внутри бесконечно длинного соленоида однородно. Магнитная индукция поля равна
. (1.20)
Поле вне соленоида отсутствует.
megaobuchalka.ru
12.7. Магнитное поле соленоида
С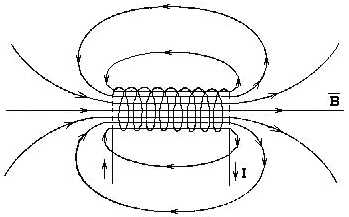 оленоид представляет собой провод, навитый равномерно в виде спирали на общий цилиндрический каркас (см. рис. 12.14). Произведение (IN) числа витков однослойной намотки соленоида на силу тока, обтекающего витки, называется числом ампер-витков.
оленоид представляет собой провод, навитый равномерно в виде спирали на общий цилиндрический каркас (см. рис. 12.14). Произведение (IN) числа витков однослойной намотки соленоида на силу тока, обтекающего витки, называется числом ампер-витков.
Рис. 12.14
Соленоиды предназначены для создания в небольшом объеме пространства достаточно сильного магнитного поля. При плотной намотке витков поле соленоида эквивалентно полю системы круговых параллельных токов с общей осью. Если диаметр d витков соленоида во много раз меньше его длины (d l), то соленоид считается бесконечно длинным (или тонким). Магнитное поле такого соленоида практически целиком сосредоточено внутри, причем вектор магнитной индукции  внутри направлен вдоль оси соленоида и связан с направлением тока правилом правого винта.
внутри направлен вдоль оси соленоида и связан с направлением тока правилом правого винта.
Р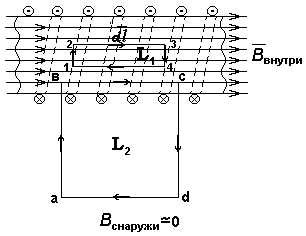 ис. 12.15
ис. 12.15
Рассмотрим воображаемый замкнутый контур 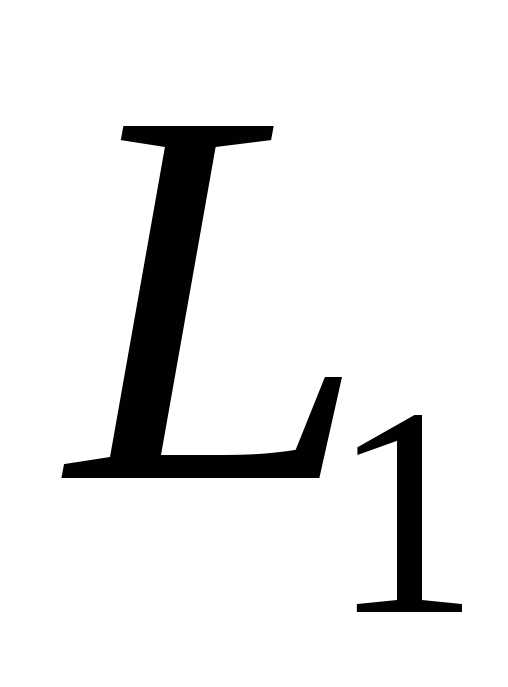 внутри соленоида (рис. 12.15). Этот контур не охватывает токов, поэтому по теореме о циркуляции
внутри соленоида (рис. 12.15). Этот контур не охватывает токов, поэтому по теореме о циркуляции
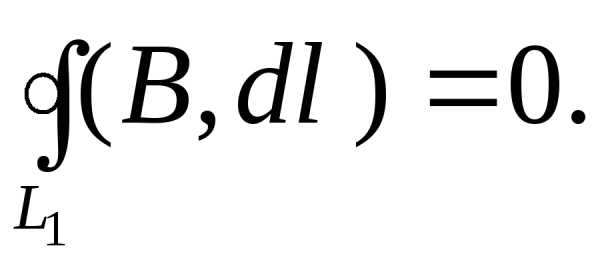
Разобьем этот круговой интеграл на четыре интеграла (по сторонам контура) и учтем, что на отрезках (1-2) и (3-4) вектор  перпендикулярен
перпендикулярен , поэтому скалярное произведение (
, поэтому скалярное произведение ( ,
, ) здесь обращается в ноль. Индукция поля во всех точках отрезка (2-3) одинакова и равна
) здесь обращается в ноль. Индукция поля во всех точках отрезка (2-3) одинакова и равна 23, а на отрезке (4-1)
23, а на отрезке (4-1)  41, причем l23 = l41 = l.
41, причем l23 = l41 = l.
Таким образом, обойдя контур по часовой стрелке, получим
Так как l 0, то В23 = В41 = В внутри.
Поскольку контур внутри соленоида был выбран произвольно, то полученный результат справедлив для любых внутренних точек соленоида, то есть поле внутри соленоида однородное:
 внутри = const.
внутри = const.
Чтобы найти величину индукции этого поля, рассмотрим контур L2 (а –b –c –d –а ), охватывающий N витков с током (рис. 12.15). Согласно теореме о циркуляции (и на основании предыдущих рассуждений), получим соотношение
Поле снаружи бесконечно длинного соленоида очень слабое ( снаружи =0), им можно пренебречь, следовательно,
снаружи =0), им можно пренебречь, следовательно,
(12.35)
где n=N/l - число витков, приходящихся на единицу
длины соленоида.
Таким образом, индукция магнитного поля внутри бесконечно длинного соленоида одинакова по величине и направлению и пропорциональна числу ампер-витков, приходящихся на единицу длины соленоида.
Симметрично расположенные витки вносят одинаковый вклад в магнитную индукцию на оси соленоида, поэтому у конца полубесконечного соленоида на его оси магнитная индукция равна половине того значения, которое дает формула (12.35), т.е.
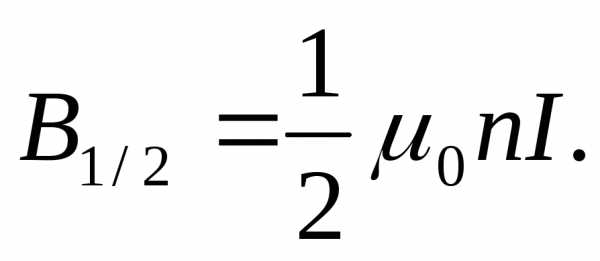 (12.36)
(12.36)
Практически, если (l d), то формула (12.35) справедлива для точек в средней части соленоида, а формула (12.36) – для точек на оси вблизи его концов.
Применяя закон Био-Савара-Лапласа, можно найти магнитную индукцию поля соленоида конечной длины (рис. 12.16) в произвольной точке А на его оси:
(12.37)
где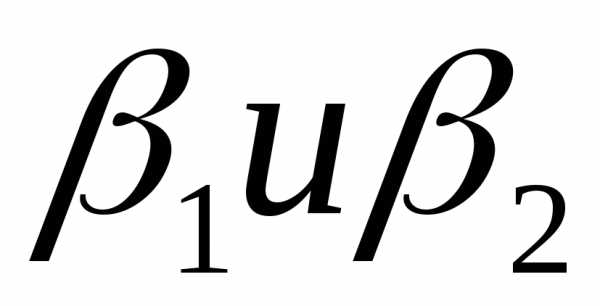 - углы между осью соленоида и радиус- вектором, проведенным из рассматриваемой точки к концам соленоида.
- углы между осью соленоида и радиус- вектором, проведенным из рассматриваемой точки к концам соленоида.
Рис. 12.16
Поле такого соленоида неоднородное, величина индукции зависит от положения точки А и длины соленоида. Для бесконечно длинного соленоида 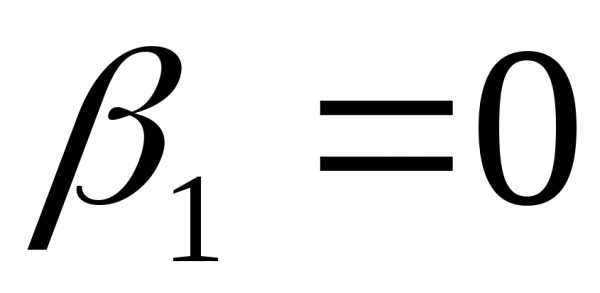 ,
,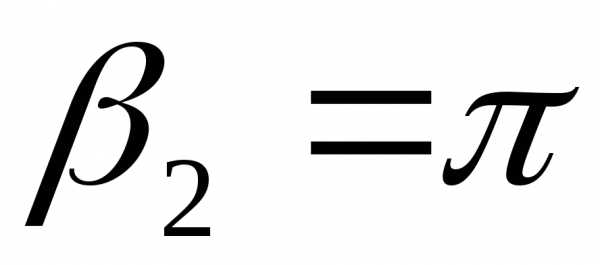 , и формула (12.37) переходит в формулу (12.35).
, и формула (12.37) переходит в формулу (12.35).
studfiles.net
Магнитное поле соленоида
Используя теорему о циркуляции, найдем МП соленоида (цилиндрической катушки) длиной . Для простоты расчета полагаем, что поле соленоида конечной длины совпадает с полем бесконечно длинного соленоида. Это позволит применить теорему о циркуляции, вследствие высокой симметрии задачи. Из эксперимента известно, что магнитное поле внутри такого соленоида однородное. Вне соленоида оно практически рано нулю. Конечно, такая замена вносит некоторую ошибку в определение МП из-за граничных эффектов. Чем длиннее соленоид (, где- диаметр катушки), тем меньше влияние граничных эффектов.
Выберем контур интегрирования (на рисунке 1234). Обход контура согласован с направлением тока в обмотках соленоида и направлением МП. Распишем контурный интеграл:
.
На участках ивекторперпендикулярен вектору элемента контура. Участокрасположен внутри контура, параллелен оси симметрии катушки и в силу однородности полепостоянное в любой точке этой прямой. Участокнаходится вне соленоида, где МП равно нулю. Считаем, что длина прямойравна длине соленоида. Согласно теореме полного тока, данный контур охватывает ток равный, где- число витков катушки. Поставим значения интеграла и тока в Ур. (1).
или.
Это выражение определят величину МП в соленоиде. Краевыми эффектами пренебрегли.
Поток магнитной индукции.
Введем важную величину – поток магнитной индукции. Она используется для описания многих физических характеристик систем. Определим поток вектора магнитной индукции (магнитный поток) через элемент поверхности:
(1)
Полный поток магнитного поля через поверхность равен
. (2)
Для однородного поля и плоской поверхности:, где- площадь поперечного сечения. Ток, текущий по замкнутому контуру, создает магнитное поле с индукцией. Это магнитное поле пронизывает контур, создавая положительный магнитный поток. Магнитный поток через замкнутую поверхность
(3)
Он равен нулю и отражает тот факт, что нет магнитных зарядов, и что линии магнитного поля являются замкнутыми. Это теорема Гаусса для магнитного поля. Рассмотрим поток магнитного поля сквозь соленоид. Внутри катушки магнитное поле является однородным. Пусть внутри соленоида имеется сердечник с магнитной проницаемостью. Тогда величина магнитного поля
.
Магнитный поток через один виток соленоида, площадью , равен. Длявитков магнитный поток, сцепленный со всеми витками соленоида
.
Эта величина называется потокосцеплением.
Проводник с током в магнитном поле.
Согласно закону Ампера на проводник с током в магнитном поле действует сила. Поэтому при перемещении проводника с током в магнитном поле будет совершаться работа. Пусть имеется: однородное магнитное поле ; проводник с током, который может свободно перемещается без трения по параллельным проводникам с расстоянием между ними. Направление тока показано на рисунке. Согласно закону Ампера на проводник с током действует сила. Под действием силы проводник переместится на расстояние.
Элементарная работа силы равна
.
Где .
Элементарная работа по перемещению проводника с током равна произведению силы тока на величину магнитного потока через площадь поверхности, которая определяется движущимся проводником. Аналогичное выражение получается при перемещении произвольного контура с током в магнитном поле. В случае конечного перемещения работа равна:
.
Работа совершается силами Ампера для замкнутого контура. - изменение магнитного потока, сцепленного с контуром. Форма контура произвольная. Изменение магнитного потока может быть вызвано либо движущимся проводником в постоянном МП, либо переменным магнитным полем, которое пронизывает неподвижный контур.
Единицы измерения – тесла..
Единица измерения - вебер.
studfiles.net
Магнитное поле соленоида. Электромагниты
Без сомнения, всем в детстве нравилось играться с магнитом. Раздобыть постоянный магнит было очень просто: для этого нужно было найти старую колонку, извлечь из нее звуковоспроизводящий динамик и, после несложных «вандальных действий», достать из нее кольцевой магнит. Неудивительно, что многие проводили опыт с металлическим опилками и листом бумаги. Опилки располагались полосами – вдоль линий напряженности поля.
В электротехнике намного большее распространение получили не постоянные, а электромагниты. Из курса физики известно, что при протекании электрического тока по проводнику, вокруг последнего создается магнитное поле, величина которого непосредственно связана с действующим значением тока.
Сомневающиеся могут повторить простейший опыт Эрстеда, когда рядом с прямолинейным проводником с током размещается компас. При этом стрелка будет отклоняться от географического северного полюса планеты (перпендикулярно проводу). Направление отклонения можно определить при помощи правила правой руки: размещаем правую руку параллельно проводнику ладонью вниз. 4 пальца должны указывать направление тока. Тогда отогнутый на 90 градусов большой палец укажет сторону отклонения стрелки. Вокруг прямого провода магнитное поле имеет вид цилиндра с проводом посередине. А вот линии напряженности образуют кольца.
В электротехнике указанные магнитные поля используются, прежде всего, в катушках. Часто можно услышать выражение «магнитное поле соленоида». Представим себе обыкновенный гвоздь и тонкий провод в изоляции. Равномерно наматывая провод на гвоздь, получаем соленоид. В данном случае гвоздь влияет на магнитное поле соленоида, но это тема совершенно другой статьи. Важно понять, что именно понимают под термином. Если теперь подключить катушку к источнику тока, то вокруг нее возникнет магнитное поле.
Энергия магнитного поля соленоида прямопропорциональна значению индуктивности и квадрату проходящего по виткам тока. В свою очередь, индуктивность зависит от квадрата числа витков. При этом нужно учитывать конструкцию обмотки: это может быть простой случай с одним слоем витков, а также многослойная структура, где направление тока в витках оказывает корректирующее действие на суммарную энергию. Соленоиды используются в схемах трамваев, режущих механизмов, контакторов и пр.
Магнитное поле соленоида представляет собой кольца, выходящие из одного конца обмотки и входящие в другой. Внутри катушки силовые линии не прерываются, а распространяются в диэлектрической среде или по проводящему сердечнику. Следствие: поле соленоида полярно. Линии выходят из магнитного северного полюса, а возвращаются в южный. Нетрудно догадаться, что магнитное поле соленоида зависит от полярности источника тока, подключенного к концам провода. Магнитные свойства соленоида практически совпадают с постоянным магнитом. Это позволяет использовать соленоид в качестве электромагнита. На производстве можно увидеть краны, у которых вместо крюка размещен диск электромагнита. Это «большой брат» соленоида – обмотка на сердечнике. Особенность всех электромагнитов в том, что магнитные свойства существуют лишь при протекании тока по виткам.
Кроме соленоидов часто используются тороиды. Это те же самые витки провода, но намотанные на магнитопроводе круглой формы. Соответственно, магнитное поле соленоида и тороида различны. Главная особенность в том, что силовые линии напряженности магнитного поля распространяются по основе-магнитопроводу внутри самой катушки, а не вне ее, как в случае соленоида. Все это свидетельствует о более высоком КПД катушек на кольцевом магнитопроводящем материале. Следствие: тороидальные трансформаторы надежны и обладают меньшими потерями, чем их привычные собратья.
fb.ru
Видеоматериалы
Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше
Подробнее...С начала года из ветхого и аварийного жилья в республике были переселены десятки семей
Подробнее...Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе
Подробнее...Актуальные темы
ОТЧЕТ о деятельности министерства энергетики, ЖКХ и тарифной политики Кабардино-Балкарской Республики в сфере государственного регулирования и контроля цен и тарифов в 2012 году и об основных задачах на 2013 год
Подробнее...Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год
Подробнее...
КОНТАКТЫ
360051, КБР, г. Нальчик
ул. Горького, 4
тел: 8 (8662) 40-93-82
факс: 8 (8662) 47-31-81
e-mail:
Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.