5. Работа и мощность в цепи переменного тока. Работа переменного тока

5. Работа и мощность в цепи переменного тока

Мгновенное значение мощности р(t) переменного тока равно произведению мгновенных значений напряжения u(t) =U0cosωtи силы токаi(t) = I0cos(ωt– φ):

р(t) = U0cosωtI0 cos(ωt – 900) = I0U0 cosωt cos(ωt – 900).()

Воспользовавшись формулой получим:.

Практический интерес представляет среднее по времени значение мощности Р. Т.к. среднее значение cos(2ωt- φ) равно нулю, то

. ()

Из векторной диаграммы рис. 7б следует, что U0 cosφ= RI0. Поэтому. Такую же мощность развивает постоянный ток, силой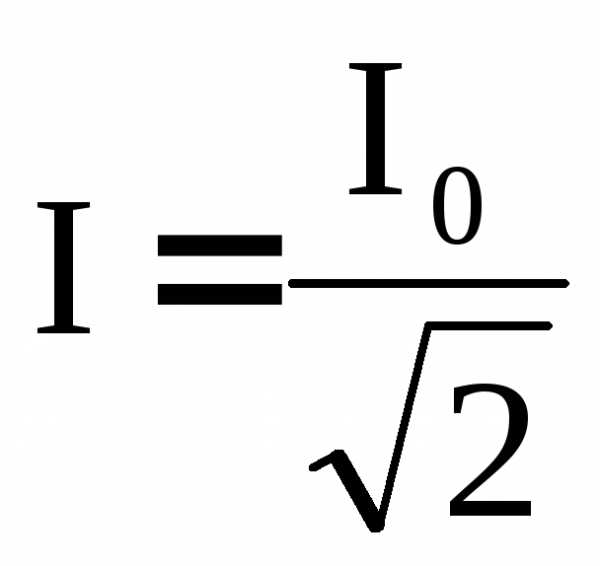. Это значение называется действующим (или эффективным) значением силы переменного тока. Аналогично величинаназывается действующим (или эффективным) значением напряжения. С использованием действующих (или эффективных) значений тока и напряжения Р =U0 I0cosφ.Множительcosφназывается коэффициентом мощности. Как видно из диаграммы рис. 7б, при равенстве реактивных значений сопротивлений ХC= ХLмножительcosφ= 1 (φ = 0) Р =U0 I0, т.е. выделяющаяся в цепи мощность имеет максимальное значение. При чисто реактивном сопротивлении цепи (R= 0) мощность, выделяемая в цепи, равна нулю. По этой причине на практике электрическую цепь переменного тока стремятся сбалансировать так чтобы значения реактивных сопротивлений ХCи ХLбыли как можно ближе. Для промышленных установок наименьшее допустимое значениеcosφ= 0,85.

или. (48)

Работа за период T:. (49)

Средняя мощность переменного тока 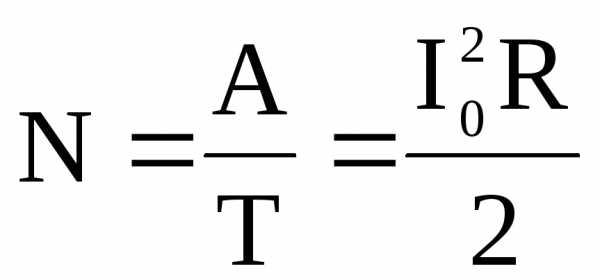. (50)

Обозначим 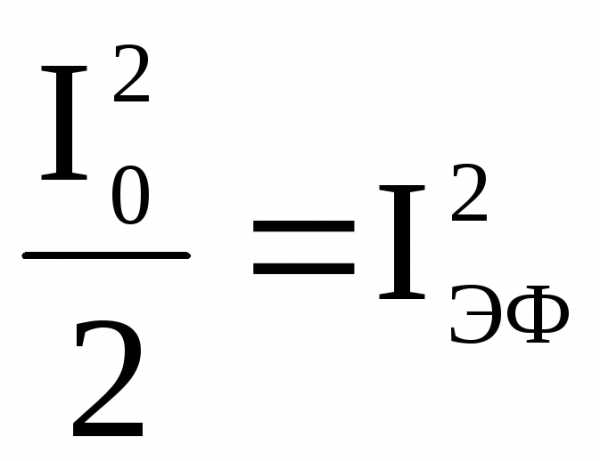, откуда эффективный (действующий) ток -. (51)

Тогда 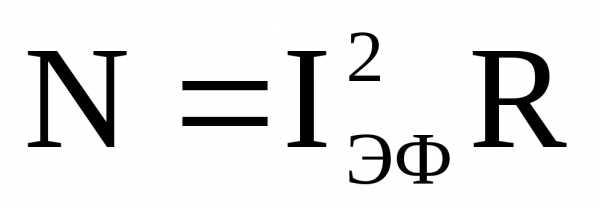. (52)

Из сравнения соотношений (47) и (52) следует, что эффективная сила переменного равна силе такого постоянного тока, который имеет ту же мощность, что и данный переменный ток.

Если в цепи переменного тока имеются реактивные сопротивления, то мощность:

(53)

(на основании тригонометрического тождества: ).

Среднее значение мощности NСза период Т, а, следовательно, и за любой промежуток времениt>>T, равно разности средних значений. Но первый член есть постоянная величина, не зависящая от времени, а второй – периодическая функция, среднее значение которой за периодTравна нулю. Таким образом,(54)

или (55)

Множитель 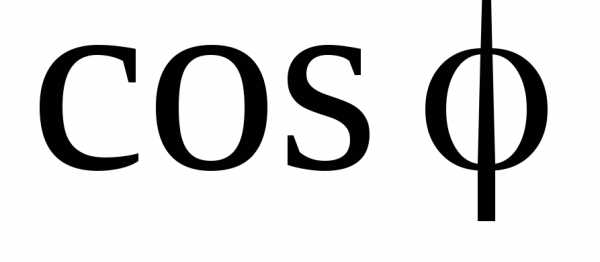называется коэффициентом мощности электрической цепи. ЕслиR=0, то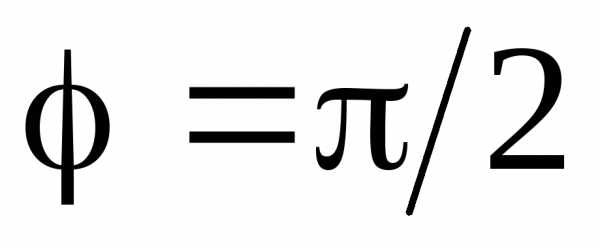иNC=0. Энергия, которая поступает в цепь от источника за T/2, возвращается источнику в течение следующей половины периода. Следовательно, для повышения мощности, отдаваемой переменным током в цепь, необходимо добиться повышения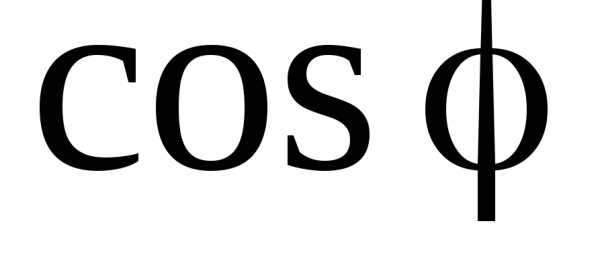путём включения в цепь такихRLиRCнагрузок, которые соответствуют условию резонанса (45).

6. Природа емкостных свойств тканей организма

ИМПЕДАНС БИОЛОГИЧЕСКИХ ТКАНЕЙ

Метод электропроводности в медицине

Как показывает опыт, электропроводность растворов не зависит от частоты переменного тока. При изучении электропроводности биологических объектов обнаружили, что их сопротивление на высоких частотах (~107 Гц) гораздо меньше, чем на низких. На рис.9 (кривая 1) представлена зависимость сопротивления мышечной ткани от частоты (кривая дисперсии). Дисперсия электропроводности обычно наблюдается в интервале частот 102 ÷ 108 Гц. Наличие дисперсии импеданса для живых тканей обусловлено тем, что при низких частотах (как и для постоянного тока) на величину электропроводности значительное влияние оказывает макроструктурная поляризация в тканях. По мере увеличения частоты поляризационные явления сказываются всё меньше и меньше.

Отмирание ткани ведёт к росту проницаемости мембран, при этом крутизна дисперсии уменьшается (рис.9, кривая 2). Для мёртвой ткани поляризация на границах раздела практически полностью исчезает и явление дисперсии импеданса больше не наблюдается (рис.9, кривая 3). Т.о. крутизна графика зависимости Z = f(ω) позволяет судить о жизнеспособности той или иной ткани.

Наличие дисперсии электропроводности говорит о том, что в биологических объектах наряду со структурами, которые оказывают переменному току активное сопротивление, есть и такие, которые обладают реактивным сопротивлением. Как оказалось, структуры с индуктивным сопротивлением (подобные катушкам) в биологических организмах отсутствуют.

Клеточные мембраны, омываемые с одной стороны тканевой жидкостью, а с другой цитоплазмой, представляют собой системы подобные конденсатору. В тканях имеются так же макроскопические образования, состоящие из различных непроводящих соединительных оболочек и перегородок, по обе стороны которых находятся ткани, хорошо проводящие электрический ток. Это так же придаёт тканям емкостные свойства.

В целом, сопротивление биологических тканей будет определяться суммой омического и емкостного сопротивления:

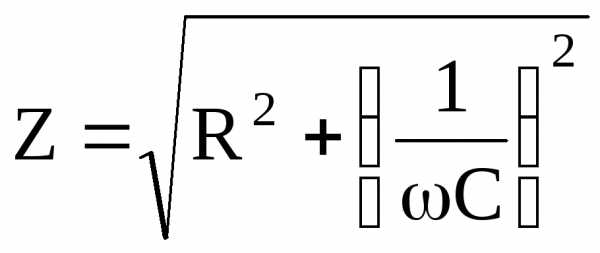. (12)

Присутствие в биологических организмах структур с ёмкостным сопротивлением подтверждается также наличием сдвига фаз между током и напряжением. Для биологических систем характерна большая величина этого угла, например, на частоте 1000 Гц: кожа человека – φ = 550, мышца кролика – φ = 650, нерв лягушки – φ = 640. Это показывает, что доля емкостного сопротивления в импедансе тканей велика.

При моделировании электропроводности живых клеток и тканей прибегают к эквивалентным схемам, т.е. к таким комбинациям омического сопротивления и ёмкости, которые в некотором приближении могут отражать характер течения тока и значения электрических параметров клетки и тканей. Простейшими из таких моделей являются схемы с последовательным и с параллельным соединением R и C – (рис.10а и 11а). Но эти простейшие схемы не отражают истинного положения дел, т.к. графики зависимости Z от ω противоречат данным по живым тканям (сравните рис.10б, 11б и рис.6, кривая1).

Наиболее удачной моделью является схема, представленная на рис.12а. На этой схеме Rк,1 и Rк,2 – активные сопротивления кожи на входе и выходе тока; Rт – общее омическое сопротивление подкожных тканей; C1, C2 и C3 – конденсаторы, моделирующие биологические структуры, обладающие ёмкостным сопротивлением. Стрелками показан маршрут переменного тока, т.е. показаны структуры, через которые проходит ток на каждом из участков биологического организма между электродами за один полупериод. Зависимость сопротивления этой эквивалентной схемы от частоты хорошо согласуется с кривой дисперсии импеданса для биотканей (рис.12б) Существуют и другие эквивалентные схемы, однако ниодна из них в точности не может воспроизвести закономерности течения переменного тока, присущие биологическим системам.

Измерение электропроводности биологических тканей для переменного тока широко используется в диагностике, а так же в биологических и медицинских исследованиях. Например, значительное возрастанию импеданса ткани на низких частотах позволяет обнаружить воспаление уже на первых стадиях. Некоторые заболевания щитовидной железы диагностируются по изменению угла сдвига фаз между током и напряжением. Для характеристики физиологического состояния тканей используют также величину крутизны кривой дисперсии. Этот критерий применяют, например, при оценке жизнеспособности ткани, предназначенной для трансплантации.

Импеданс тканей существенным образом зависит от кровенаполнения сосудов. Кровь имеет меньшее сопротивление, чем стенки сосудов или клетки, поэтому во время систолы полное сопротивление ткани уменьшается, а при диастоле – увеличивается. Диагностический метод, основанный на регистрации импеданса тканей в процессе сердечной деятельности, называется реографией (импеданс – плетизмографией). С помощью этого метода получают реограммы головного мозга (реоэнцефалограмма), сердца (реокардиограмма), лёгких, печени, сосудов, конечностей. Измерения обычно проводят на частоте 30 кГц.

studfiles.net

Работа и мощность переменного тока

Мгновенная мощность в цепи переменного тока (частный случай)

Допустим, что цепь имеет только активное сопротивление. Пусть напряжение на концах цепи изменяется по гармоническому закону:

Мы помним, что сдвига фаз между током и напряжением в нашей цепи (только $R$) не будет, следовательно, запишем, что:

Если рассмотреть маленький промежуток времени, то переменный ток можно рассмотреть как постоянный, значит мгновенная мощность переменного тока ($P_{tR}$) равна:

Работа в цепи переменного тока (частный случай)

Работа переменного тока на маленький промежуток времени $dt$ равна (${dA}_t$):

Следовательно, работа за один период полного колебания ($A_T$) может быть определена как:

Рассмотрим общий случай цепи переменного напряжения, когда она содержит и активное и реактивное сопротивление. Теперь между током и напряжением существует разность фаз. Работа, совершенная во внешней цепи за время $dt$, равна:

Напряжение $U$, можно разложить на две составляющие: активную ($U_a$) и реактивную ($U_r$).

Активная составляющая совершает колебания в одной фазе с током, она равна:

Реактивная составляющая смещена по фазе относительно тока на $\pm \frac{\pi }{2}$ и имеет вид:

При вычислении работы за период, получится два слагаемых. Учитывая, что реактивная составляющая за полный период равна нулю, следовательно, полная работа определена только активной составляющей напряжения:

Средняя мощность

Чаще, чем понятием мгновенная мощность, оперируют понятием среднее значение мощности. Причем рассматривают большой промежуток времени, который включает множество периодов колебаний. Так как мы рассматривает периодический процесс, то нам будет достаточно найти среднее значение мощности на один полный период.

Ее легко найти как:

где $cos\varphi $- коэффициент мощности. Формула (10) показывает, что в общем случае выделяемая в цепи мощность зависит не только от силы тока и напряжения, но и от сдвига фаз между ними.

Замечание

Зависимость мощности от коэффициента мощности учитывают при проектировании линий электропередачи для переменного тока. Если нагрузки вцепи имеют большое реактивное сопротивление, то $\varphi \ne 0$ и $cos\varphi $ может быть заметно меньше единицы. В таких случаях для передачи нужной мощности необходимо учесть силу тока, что ведет к возрастанию выделения тепла Джоуля -- Ленца или требует увеличения сечения проводов, что увеличивает стоимость линии электропередач. На практике всегда стремятся распределить нагрузки так, чтобы $cos\varphi \ $был как можно ближе к единице.

Средняя мощность при наличии в цепи только активного сопротивления, равна:

Пример 1

Задание: Пусть сила тока изменяется в соответствии с законом: $I=I_m{sin \left(\omega t\right)\ }.$ Запишите выражения для мгновенных мощностей, развиваемых током на разных элементах цепи ($C,L$).

Решение:

Используя соотношение:

\[U=\frac{q}{C}(1.1)\]

и выражение:

\[I=\frac{dq}{dt}\to q=\int{Idt}=-\frac{I_m}{\omega }{cos \left(\omega t\right)\ }+q_0=-\frac{I_m}{\omega }{cos \left(\omega t\right)\ }\left(1.2\right),\]

где мы можем положить $q_0=0,$ так как эта постоянная интегрирования с колебаниями тока не связана, запишем уравнение для колебания напряжения на конденсаторе:

\[U_C=-\frac{I_m}{C\omega }{cos \left(\omega t\right)\ }=\frac{I_m}{C\omega }{sin \left(\omega t-\frac{\pi }{2}\right)\ }\left(1.3\right).\]

Мгновенная мощность на конденсаторе равна:

\[P_{tC}=U_CI=\frac{I_m}{C\omega }{sin \left(\omega t-\frac{\pi }{2}\right)\ }\ I_m{sin \left(\omega t\right)\ }=-\frac{I^2}{C\omega }{sin \left(\omega t\right){cos \left(\omega t\right)\ }\ }.\]

Изменение напряжения на индуктивности выразим как:

\[U_L=L\frac{dI}{dt}=LI_m\omega {cos \left(\omega t\right)\left(1.5\right).\ }\]

Мгновенная мощность тока на индуктивности:

\[P_{tL}=U_LI=L{I^2}_m\omega {cos \left(\omega t\right){sin \left(\omega t\right)\ }.\ }\]

Мгновенные мощности на емкости и индуктивности меняют знак. Часть времени ток совершает положительную работу, то есть передает энергию на элементы, другая часть времени работа отрицательна, то есть энергия этих элементов возвращается к источнику сторонних ЭДС. Происходит обмен энергиями между индуктивностями, емкостями и источниками ЭДС в процессе которого емкости и индуктивности выполнят роль источников ЭДС.

Ответ: $P_{tC}=-\frac{I^2}{C\omega }{sin \left(\omega t\right){cos \left(\omega t\right)\ }\ },$ $P_{tL}=L{I^2}_m\omega {cos \left(\omega t\right){sin \left(\omega t\right)\ }.\ }$

Пример 2

Задание: Чему равна средняя мощность на сопротивлении, емкости и индуктивности?

Решение:

Для того чтобы получить средние мощности тока за период колебаний необходимо усреднить выражения:

\[P_{tC}=-\frac{I^2}{C\omega }{sin \left(\omega t\right){cos \left(\omega t\right)(2.1)\ }\ },\] \[P_{tR}={I^2}_mR{sin}^2\left(\omega t\right)\left(2.2\right),\] \[P_{tL}=L{I^2}_m\omega {cos \left(\omega t\right){sin \left(\omega t\right)(2.3)\ }.\ }\]

Учтем, что за период колебаний выполняются соотношения:

\[\left\langle {cos \left(\omega t\right){sin \left(\omega t\right)\ }\ }\right\rangle =0\ \left(2.4\right).\] \[\left\langle {s{in}^2 \left(\omega t\right)\ }\right\rangle =\frac{1}{2}\left(2.5\right).\]

Используя (2.5) и (2.4) из (2.1) -- (2.2) получим:

\[\left\langle P_{tC}\right\rangle =0,\] \[\left\langle P_{tL}\right\rangle =0,\] \[\left\langle P_{tR}\right\rangle =\frac{1}{2}{I^2}_mR.\]

Ответ: $\left\langle P_{tC}\right\rangle =0,\left\langle P_{tL}\right\rangle =0,\left\langle P_{tR}\right\rangle =\frac{1}{2}{I^2}_mR.$

spravochnick.ru

Работа и мощность переменного тока — Мегаобучалка

Энергия, поставляемая источником электродвижущей силы во внешнюю цепь, испытывает превращения в другие виды энергии. Если в цепи имеется только активное сопротивление, то вся энергия превращается в тепло, выделяемое на сопротивлении . Между током и напряжением сдвиг фаз отсутствует. Кроме того, в течение малого промежутка времени переменный ток можно рассматривать как постоянный. Поэтому мгновенная мощность, развиваемая переменным током на сопротивлении:

.

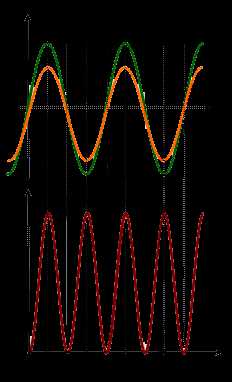
Хотя ток и напряжение бывают как положительными, так и отрицательными, мощность, равная их произведению, всегда положительна. Однако она пульсирует, изменяясь от нуля до максимального значения с частотой, равной удвоенной частоте переменного тока. На рис. 7.12 показана временная зависимость тока, напряжения и мощности переменного тока, выделяемой на активном сопротивлении. Ясно, что средняя передаваемая мощность меньше максимальной и равна половине максимальной мощности. Среднее значение и за период равно . Это можно объяснить следующим образом: , а за полный цикл среднее значение равно среднему значению . Поэтому среднее значение мощности будет равно

.

В общем случае, когда цепь содержит не только активное сопротивление, но и индуктивность и емкость, между током и напряжением существует сдвиг фаз, и это сказывается на величине мощности. В цепи с индуктивностью энергия источника переходит в энергию магнитного поля, равную , изменяющуюся с течением времени. Мощность, которая требуется для создания магнитного поля в катушке индуктивности, равна произведению силы тока и разности потенциалов на катушке:

.

Из последней формулы видно, что в том интервале времени, когда , мощность положительна. Это означает, что источник передает энергию во внешнюю цепь, она идет на увеличение энергии магнитного поля. Когда же , мощность отрицательна, в эти промежутки времени энергия, запасенная в магнитном поле, возвращается из внешней цепи в источник. Таким образом, в цепи, содержащей индуктивность, знак мощности периодически изменяется. Так же будет и в случае, когда внешняя цепь содержит конденсатор емкостью . Однако в этом случае происходит переход энергии источника в энергию электрического поля конденсатора, равную . Развиваемая мощность также меняет знак в зависимости от знака .

В катушке индуктивности с нулевым активным сопротивлением или в конденсаторе напряжение сдвинуто по фазе на относительно тока, и поэтому энергия вообще не поглощается. Например, как видно из рис. 7.13, мгновенная мощность в чисто емкостном сопротивлении колеблется между положительными и отрицательными значениями, что соответствует поглощению мощности и затем возвращению ее к источнику. В результате средняя мощность за период равна нулю.

В общем случае полная мощность, развиваемая источником сторонних сил, равна . Эту величину называют мощностью тока, а величины , , – мощностями тока на сопротивлении, индуктивности и емкости соответственно. При силе тока падение напряжения на активном сопротивлении равно , падение напряжения на индуктивности – , падение напряжения на емкости – . Мгновенные значения мощностей соответственно равны

Интерес представляет среднее значение мощности за период. Так как синус и косинус сдвинуты относительно друг друга по фазе на , то среднее значение их произведения равно нулю: . Средние значения квадратов синуса и косинуса . Поэтому , , . Таким образом, отлична от нуля только средняя мощность на активном сопротивлении R, поэтому его и называют активным сопротивлением. На индуктивности и емкости средние мощности равны нулю. Эти элементы в среднем энергетически нейтральны, их называют реактивными сопротивлениями.

megaobuchalka.ru

Работа переменного тока - Великие физики

Конец XIX  века можно однозначно назвать началом электрической эры. Именно тогда было сделано множество изобретений, которые можно считать прототипами современных устройств и приборов. Начало электрической эры Из курса физики известно, что работа, которая совершается в электрической цепи, если в ней протекает переменный электрический ток, полностью превращается в тепло, если цепь имеет только активное сопротивление. Этот принцип лежит в основе работы всем известной электрической лампочки, запатентованной Томасом Эдисоном в 1879 году. В конце XIX века начали проводиться первые попытки внедрения электричества в повседневную жизнь: совершенствовались электрические генераторы, строились первые линии электропередач. Использовать электрический ток первоначально предполагалось для освещения в качестве альтернативы свечам, керосиновым лампам и газовым фонарям. "Война токов" и ее победители Наличие в арсенале потребителей электрического тока только устройств для освещения заметно сужало массовость их применения. Постепенно назревала необходимость в надежном устройстве, способном преобразовывать электрическую энергию в механическую. Этот период теперь характеризуют как «Война токов». Дело в том, что первоначально распространение получил постоянный электрический ток. Именно он использовался в построенной Эдисоном схеме производства и потребления электроэнергии, которая была рассчитана на целый городской район и соединяла нужным образом электролампы, провода, электрогенераторы, розетки, вилки и т.п. В противоположность Эдисону известный хорватский ученый Никола Тесла был по сути создателем переменного электрического тока и долгое время работал над созданием устройств его генерирующих и потребляющих. Какое-то время он даже работал в производственной компании Эдисона, но будучи сторонником идей, не признаваемых своим руководителем, вскоре был вынужден сменить место работы. В результате долгих теоретических изысканий и экспериментов ему удалось создать трансформатор, в котором переменный ток трансформировался до более высокого напряжения при сравнительно малой силе тока. В таком виде его можно было передавать на большие расстояния без существенных потерь. Для потребителей ток вновь понижался трансформатором до определенных значений. Таким образом, была заложена основа всех современных централизованных систем электроснабжения. Такое преобразование возможно только в цепях переменного тока. В случае использования постоянного тока построение эффективной системы электроснабжения невозможно. Поэтому в электрических схемах Эдисона, использовавших постоянный ток, планировалось строительство электростанций в каждом городском районе во избежание больших потерь. Кроме того, Тесла открыл вращающееся магнитное поле и стал применять несколько электрических фаз. Эти открытия легли в основу созданного Никола Тесла в 1884 году асинхронного двигателя, который достаточно широко распространен в наше время и является одним из самых основных потребителей переменного электрического тока.Таким образом «Война токов» была, бесспорно, выиграна Никола Тесла, а вместе с ним выиграли и все мы, получив возможность пользоваться многочисленными удобствами, основой многих из которых стали изобретения великого ученого.

www.phisiki.com

Работа - переменный ток - Большая Энциклопедия Нефти и Газа, статья, страница 1

Работа - переменный ток

Cтраница 1

Работа переменного тока за период, переходящая, например, в тепло в сопротивлении, величина которого равна единице, может быть наглядно представлена графически. На рис. 8 - 10 приведены графики i ( t) синусоидального ( а) и несинусоидального ( б) токов, имеющих одинаковые максимальные значения. Затем построены графики i2 ( t) и заштрихованные прямоугольники, площади которых равны площадям, ограниченным горизонтальной осью и линиями соответствующих графиков t2 ( t) на протяжении одного периода.  [2]

Работа реле переменного тока имеет ряд особенностей, обусловивших его конструкцию.  [3]

Однако работа реле переменного тока имеет ряд особенностей, определяющих его конструкцию.  [4]

Поэтому принцип работы реле переменного тока не отличается от принципа работы реле постоянного тока, которое также может быть использовано в цеди переменного тока.  [6]

Третья особенность работы реле переменного тока состоит в вибрации якоря.  [8]

Однако в работе реле переменного тока имеются некоторые особенности, связанные с изменением тока во времени.  [10]

Если интересоваться работой переменного тока за промежуток времени, сравнимый с периодом Т 2л / ш, то в выражении ( 15) для мощности следует учитывать оба слагаемых. При вычислении работы, совершаемой током за промежуток времени, значительно превышающий период, вклад второго слагаемого будет пренебрежимо малым.  [11]

Таким образом, работа переменного тока за период равна произведению средней мощности и продолжительности периода.  [12]

Таким образом, работа переменного тока за период рав на произведению средней мощности и продолжительност.  [13]

Реактивная энергия как работа переменного тока не существует. Реактивная составляющая тока нагрузки обусловливается лишь колебаниями энергии между источником и магнитным полем приемника. Для краткости в дальнейшем слова так называемая опущены.  [14]

Пульсация силы отрицательно сказывается на работе ЭМ переменного тока, вызывая шум и вибрацию электромеханической системы. Под действием этой ЭДС в витке протекает ток / к, который совпадает с ней по фазе и создает магнитный поток Фк, совпадающий по фазе с током. Результирующие потоки Ф ] и Ф2 изменяются по величине, сдвигаются по фазе на угол ф и создают силы притяжения, сдвинутые во времени. В результате постоянная составляющая; силы увеличивается, а пульсирующая уменьшается. Установлено, что лучшие результаты получаются, когда виток охватывает две трети полюса.  [15]

Страницы:      1    2

www.ngpedia.ru

Работа и мощность переменного тока. Действующее значение тока и напряжения.

Найдем мощность, выделяемую в цепи переменного тока. Мгно­венное значение мощности равно произведению мгновенных значе­ний напряжения и силы тока:

***Воспользуемся формулой :

 

Выражению *** можно придать вид:

**

 

Практический интерес представляет среднее по времени значе­ние Р(t), которое мы обозначим просто Р. Так как среднее значе­ние равно нулю,

*

 

Из * *следует , что мгновенная мощность колеблется около среднего значения с частотой, в 2 раза превышающую частоту тока.

 

Подставив это значение в формулу * и учтя, что , получим

 

 

Такую же мощность развивает постоянный ток, сила которого равна - действующее значение силы тока. - действующее значение напряжения.

Выражение средней мощности через действующие значения силы тока и напряжения имеет вид

- коэффициент мощности. В технике стремятся сделать как можно больше. При малом для выделеия в цепи необходимой мощности нужно пропускать ток большей силы, что приводит к возрастанию потерь в подводящих проводах.

 

Электрический заряд. Дискретность заряда. Закон сохранения электрического заряда. Взаимодействие зарядов. Закон Кулона.

Напряженность электростатического поля. Принцип суперпозиции. Расчет напряженности поля тон­кого заряженного стержня.

Электрический диполь и его поле.

Силовые линии электростатического поля. Поток вектора. Электростатическая теорема Гаусса и ее применение для расчета полей.

Работа электростатического поля. Теорема о циркуляции напряженности электростатического поля. Потенциал. Эквипотенциальная поверхность. Связь потенциала с напряженностью.

Проводники в электростатическом поле. Распределение заряда в проводнике. Электростатическое по­ле в полости.

Поверхностная плотность заряда. Граничные условия на границе проводника с вакуумом.

Дифференциальная форма теоремы Гаусса. Уравнение Пуассона. Общая задача электростатики.

Емкость уединенного проводника. Конденсатор. Емкость конденсаторов различной конфигурации. Соединение конденсаторов.

Энергия конденсатора. Плотность энергии электростатического поля.

Поляризация диэлектриков. Связанные заряды. Вектор поляризации. Диэлектрическая проницае­мость.

Теорема Гаусса для электростатических полей в веществе. Электрическое смещение. Граничные условия на границе раздела диэлектриков.

Электрический ток и его характеристики. Условия существования тока. Законы Ома и Джоуля- Ленца в дифференциальной форме.

Сторонние силы. ЭДС. Закон Ома для участка цепи с источником ЭДС. Закон Джоуля-Ленца в ин­тегральной форме.

Правила Кирхгофа и расчет электрических цепей.

Магнитное поле. Сила Лоренца и сила Ампера. Вектор магнитной индукции.

Закон Био-Савара. Принцип суперпозиции. Магнитное поле прямолинейного тока и кругового тока.

Виток с током в магнитном поле. Момент сил, действующих на виток с током в магнитном поле.

Теорема Гаусса для магнитного поля. Закон полного тока. Магнитное поле соленоида.

Магнитная энергия тока. Плотность энергии магнитного поля.

Движение заряженных частиц в электрическом и магнитном полях.

Масс-спектрометр. Принцип работы и применение.

Эффект Холла. Постоянная Холла.

Явление электромагнитной индукции. ЭДС индукции, возникающая в движущихся проводниках. Закон электромагнитной индукции. Правило Ленца.

Явление самоиндукции. Индуктивность. Индуктивность длинного соленоида.

Магнитное поле в веществе. Молекулярные токи. Намагниченность. Магнитная проницаемость.

Пара- и диамагнетики и их свойства. Элементарная теория диамагнетизма.

Ферромагнетики и их свойства.

Максвелловская трактовка закона электромагнитной индукции. Обобщение теоремы о циркуляции

электростатического поля на случай переменных полей.

Ток смещения. Обобщение закона полного тока на случай переменных полей.

Система уравнений Максвелла в интегральной форме. Материальные уравнения. Скорость распро­странения электромагнитных возмущений.

Скин-эффект и его элементарная теория.

Генератор переменного тока. Емкость, индуктивность и активное сопротивление в цепи переменно­го тока. Закон Ома для переменных токов.

Затухающие колебания в колебательном контуре. Коэффициент затухания и логарифмический дек­ремент затухания колебаний.

Вынужденные колебания в колебательном контуре. Резонанс.

Работа и мощность переменного тока. Действующее значение тока и напряжения.

 



infopedia.su

Вынужденные электромагнитные колебания. Работа и устройство генератора переменного тока. Активное сопротивление в цепи переменного тока.

Вынужденные электромагнитные колебания.  Переменный ток.
Вынужденными электромагнитными колебаниями наз. незатухающие колебания заряда, напряжения, силы тока, вызванные периодически изменяющейся синусоидальной эдс.
Синусоидальная эдс возникает при вращении рамки с угловой скоростью ω в стационарном магнитном поле с индукцией B. Согласно закону электромагнитной индукции
Т.о., если цепь замкнута, то возникает индукционный ток, который непрерывно меняется по модулю, а каждые полпериода – по направлению. В России промышленная частота переменного тока – 50 Гц.		ν = 50 Гц
Работа и устройство генератора переменного тока.
Работа основана на явлении электромагнитной индукции.
Устройство Обмотка статора с большим числом витков, размещенных в его пазах. В ней наводится ЭДС. Станина, внутри которой размещены статор и ротор. Ротор (вращающаяся часть генератора) создает магнитное поле от электромашины постоянного тока. Может иметь n пар полюсов. Статор состоит из отдельных пластин для уменьшения нагрева от вихревых токов. Пластины — изэлектротехнической стали. Клеммный щиток на корпусе станины для снятия напряжения. При равномерном вращении ротора в обмотках статора наводится ЭДС: , где N - число витков обмотки статора. Частота ЭДС равна: ν=np, где р - число пар полюсов, а n - число оборотов ротора в секунду.  На гидроэлектростанциях в генераторе число пар полюсов равно 40 - 50, а на тепловых - 10 -16. Вырабатываемое напряжение в промышленных генераторах 103 - 104В.
Активное сопротивление в цепи переменного тока.
Активное сопротивление Электрические устройства, преобразующие электрическую энергию во внутреннюю, называютсяактивными сопротивлениями. Активное сопротивление  , где ρ - удельное сопротивление.
Высокоомные провода, спирали нагревательных приборов, резисторы — активные сопротивления. Мгновенное значение напряжения меняется по гармоническому закону . Мгновенное значение силы, тока пропорционально мгновенному значению напряжения и совпадает по фазе: Колебания тока и напряжения в цепи с активной нагрузкой совпадают по фазе.
Об электрическом токе мы можем судить по его действиям. Одним из основных действий тока является тепловое. Мгновенное значение тепловой мощности равно: Среднее значение мощности за период в цепи переменного тока равно:  , следовательно, .
Величина, равная квадратному корню из среднего значения квадрата мгновенного тока, называется действующим значением силы переменного тока: .   Действующее значение переменного тока равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за то же время.
Действующее значение переменного напряжения опреде­лятся аналогично действующему значению силы тока: . Например, в осветительной сети Uд=220В.		Uд=220В. Umax ≈ 311 В
Закон Ома для цепи с активным сопротивлением выполняется.

www.eduspb.com

---

• 
  Припои и флюсы для разных металлов и температура их плавления
• 
  1 класс электрозащиты
• 
  Сколько стоит ночь
• 
  Опн что это такое
• 
  Дифференциальная защита линии
• 
  Виды воздействия электрического тока
• 
  Какие схемы бывают
• 
  Передать показания счетчика за воду по нижегородской области центр сбк
• 
  Мостовой метод измерения сопротивления
• 
  Тип помещения это
• 
  Что такое гэсв