Метрология, измерения, средства измерений.
Метрология, измерения, средства измерений.
Метрология – наука изучающая общепринятые основы измерений, методы и средства измерений, единицы физических величин, методы точности измерений, принципы обеспечения единства измерений и единообразия средств измерений. В метрологии очень плотно рассматриваются такие понятия как: эталоны и образцовые средства измерений, применение образцовых средств измерений к средствам измерений применяемых в производстве.
Главными задачами и целями метрологии являются – изучение всех аспектов измерений физических величин. А также международное содействие в области метрологии и законодательные элементы.
Современная метрология разделяется на такие направления как:
· теоретическая метрология – раздел метрологии, изучающий общие теоретические проблемы измерений;
· законодательная метрология – это один из разделов метрологии, совмещающий комплексы общепринятых правил, норм , требований и других вопросов, требующих контроля и регламентации со стороны государства. Изучение этих аспектов направлено на метрологическое обеспечение единства измерений и однообразия средств измерений;
Изучение этих аспектов направлено на метрологическое обеспечение единства измерений и однообразия средств измерений;
· прикладная метрология – раздел метрологии, рассматривающий вопросы применения метрологических методов и средств измерений на практике;
· историческая метрология;
Единство измерений – комплекс принятых мер, при которых результаты измерений выражены в общепринятых узаконенных единицах величин и погрешности измерений не превышают установленных стандартов с учитываемой вероятностью;
Средство измерений – устройство, предназначенное для проведения измерений.
Метрологическая служба – субъект управления, контроля и регламентирования видов работ, направленных на обеспечение единства и единообразия измерений.
Поверка средства измерений – комплекс мер, исполняемых объектами государственной метрологической службы с целью подтверждения соответствия СИ установленным ГОСТ техническим требованиям.
Калибровка средства измерений – комплекс принятых мер, исполняемых для подтверждения и определения действующих значений метрологических характеристик и(или) годности к использованию СИ, не подлежащего обязательному государственному контролю и метрологическому надзору.

Метрология – это самая точная наука и наука о самой точности.
Все права сайта Метрология защищены авторскими правами. Метрология — 2008-2012 год.
это средство измерения, предназначенное для воспроизведения физической величины заданного размера.
Метод измерений — совокупность приемов использования принципов и средств измерений.
Приемы использования мер:
Сравнение с мерой.Измеряемую величину сравнивают с величиной, воспроизводимой мерой (по шкале измерительного прибора прямого действия). Например, измерение массы на рычажных весах в количестве меньше килограмма или на весах с одной чашкой; измерение массы в пределах больше килограмма на рычажных весах. Гиря позволяет измерить массу, измерительный резистор — электрическое сопротивление, кварцевый генератор — частоту электрических колебаний, мерная колба — известный объем.
Противопоставление с мерой.Сравнение с мерой, при котором измеряемая величина и мера одновременно воздействуют на измерительный прибор. Например, груз и гири на равноплечих весах.
Разностное сравнение с мерой. Сравнение с мерой, при котором на измерительный прибор воздействуют разность измеряемой величины и известной величины, воспроизводимой мерой.
Выход на нулевой уровень. Сравнение с мерой, при котором эффект воздействия величин на прибор доводят до нуля. Например, измерение электрического сопротивления мостом.
Замещение мерой.Сравнение с мерой, при котором измеряемую величину замещают известной величиной, воспроизводимой мерой. Например, взвешивание с поочередным помещением измеряемой массы и гирь на одну и ту же чашку весов.
Совпадение с мерой. Сравнение с мерой, при котором разность между измеряемой и воспроизводимой мерой величинами измеряют, используя совпадения отметок шкал или периодических сигналов. Например, измерение длины с помощью штангенциркуля или частоты вращения стробоскопом.
Например, измерение длины с помощью штангенциркуля или частоты вращения стробоскопом.
Измерения должны осуществляться в соответствии с аттестованными в установленном порядке методиками.
МЕТОДИКА ИЗМЕРЕНИЯ– описание оптимальной и однозначной последовательности операций с реактивами, оборудованием, стандартами, определенным классом специалистов для выполнения измерений с заданной точностью.
Средства и методы измерений — online presentation
1. Тема 1. Основы метрологии Занятие 1.3. Средства и методы измерений
ОП. 08. «Стандартизация, метрология и подтверждение
соответствия»
Преподаватель: Юрченко Е.А.
2. Средства измерений (СИ)
Средство измерений (СИ) представляет собой техническое
устройство, предназначенное для измерений и имеющее
нормированные метрологические характеристики.
3. К СИ относятся:
Меры
Измерительные приборы
Измерительные преобразователи
Измерительные установки
Измерительные системы
4.
 Мера — это средство измерения, предназначенное для воспроизведения физической величины заданного размера
Мера — это средство измерения, предназначенное для воспроизведения физической величины заданного размера
Мера — это средство измерения, предназначенное для
воспроизведения физической величины заданного размера. К
мерам относят гири, концевые меры длины, нормальные
элементы (меры ЭДС).
5. Меры
Однозначные меры
(воспроизводят величину
одного размера)
• гиря
• концевые меры длины
Многозначные меры
(воспроизводят ряд
однородных величин)
• линейка с мм
делениями
6. Погрешность меры
Широкое применение находят наборы и магазины мер. Указанное
на мере (или приписанное мере) значение величины является
номинальным значением меры.
Разность между номинальным и действительным значениями
меры называется погрешностью меры, которая является
метрологической характеристикой мер.
7. Стандартный образец
Стандартный образец — средство измерений в виде вещества
(материала), состав и свойства которого установлены при
метрологической аттестации.
В последние годы стандартные образцы нашли широкое
применение в метрологической деятельности и в практике
измерений.
8. Измерительный прибор
Измерительный прибор — средство измерения, предназначенное для
выработки сигнала измерительной информации в форме доступной для
непосредственного восприятия наблюдателем.
Измерительные приборы по способу получения результата измерений
подразделяют на показывающие (аналоговые и цифровые) и
регистрирующие (самопишущие и печатающие).
Для измерительных приборов обязательно должны быть нормированы:
цена деления шкалы, пределы шкал аналоговых приборов; выходной
код, число его разрядов, номинальная цена единицы наименьшего
разряда кода для цифровых приборов.
Кроме этих характеристик нормируются и другие, оказывающие
влияние на результат измерения.
9. Измерительный преобразователь
Измерительный преобразователь — средство измерения
предназначенное для выработки сигнала измерительной
информации в форме, удобной для передачи, дальнейшего
преобразования, обработки или хранения.
В отличие от измерительного прибора сигнал на выходе
измерительного преобразователя не может восприниматься
наблюдателем.
10. Измерительная установка
Измерительная установка — совокупность функционально
объединенных средств измерений (мер, измерительных приборов
измерительных преобразователей) и вспомогательных устройств
предназначенных для выработки сигналов измерительной
информации в форме, которая удобна для непосредственного
восприятия наблюдателем, и расположенных в одном месте.
11. Измерительная система
Погрешности измерений и средств измерений. Методы их оценки
из «Справочник конструктора »
Под методом измерения понимают совокупность приемов использования принципов и средств измерений. Для прямых измерений можно выделить несколько основных методов непосредственной оценки, сравнения с мерой, дифференциальный, нулевой и совпадения.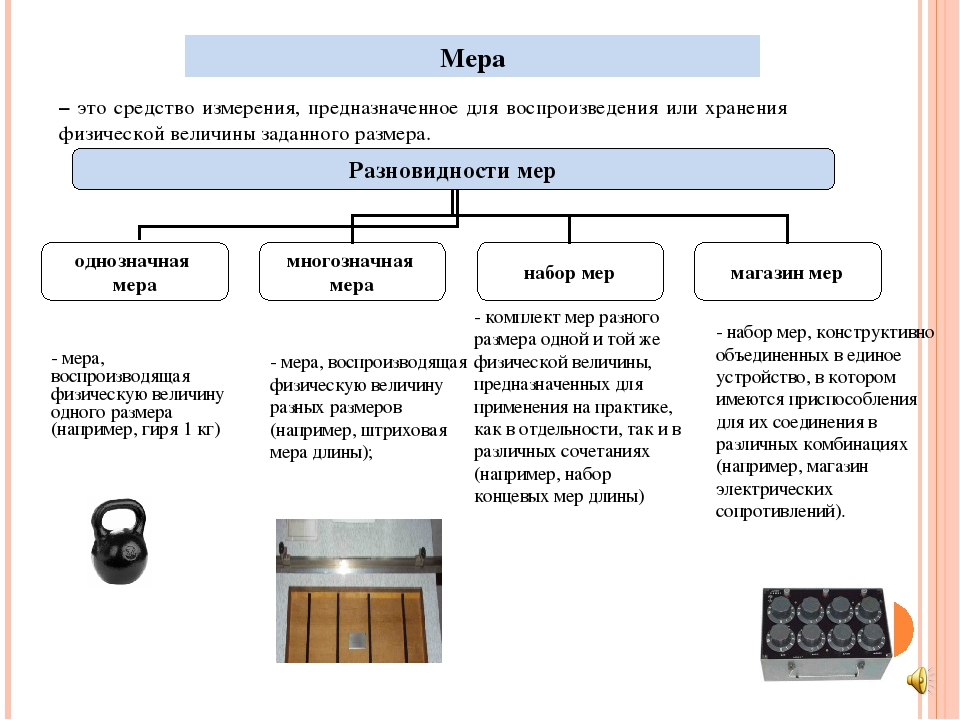 При косвенных измерениях широко применяется преобразование измеряемой величины в процессе измерений.
[c.903]
При косвенных измерениях широко применяется преобразование измеряемой величины в процессе измерений.
[c.903]
Средство измерения — это техническое средство, используемое при измерениях и имеющее нормированные метрологические свойства. К средствам измерений относят меры, измерительные приборы, преобразователи, установки и системы. От средств измерений зависит правильное определение значения измеряемой величины в процессе измерения.
[c.903]
Мера — это средство измерений, предназначенное для воспроизведения физической величины заданного размера. К мерам относятся также стандартные образцы и образцовые вещества.
[c.903]
ИЛИ более точных образцовых средств рабочим средствам. Образцовыми средствами измерений являются меры, измерительные приборы и устройства, прошедшие метрологическую аттестацию и утвержденные органами государственной или ведомственной метрологических служб в качестве образцовых. [c.904]
[c.904]
Эталон — это средство измерений (или комплекс средств измерений), обес-печиваюп1,ее воспроизведение и хранение единицы с целью передачи ее размера нижестояш им по поверочной схеме средствам измерений, выполненное по особой спецификации и официально утвержденное в установленном порядке.
[c.904]
Измерительный прибор представляет собой средство измерений, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем.
[c.904]
По способу образования показаний приборы подразделяются на показыва-юш ие и регистрирующие. Показывающие приборы, в свою очередь, подразделяются на аналоговые и цифровые.
[c.904]
Аналоговые приборы — это, как правило, стрелочные приборы с отсчетными устройствами, состоящими из двух элементов — шкалы и указателя, связанного с подвижной частью прибора. Показания таких приборов являются непрерывной функцией измеряемой величины. [c.904]
[c.904]
Цифровые измерительные приборы автоматически вырабатывают дискретные сигналы измерительной информации, которые представляют в цифровой форме в виде набора десятичных цифр.
[c.904]
Цифровые приборы по сравнению со стрелочными имеют ряд достоинств процесс измерения автоматизирован, что исключает возникновение погрешностей, обусловленных ошибками оператора время измерения очень мало результат измерений, выдаваемый в цифровой форме, легко фиксируется цифропечатающим устройством и удобен для ввода в электронно-вычислительную машину.
[c.904]
Измерительный преобразователь (ИП) — средство измерений, служащее для выработки измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки и хранения, но не поддающейся непосредственному восприятию наблюдателем.
[c.904]
Преобразуемая физическая величина называется входной, а результат преобразования — выходной величиной. Связь между выходной и входной величинами преобразователя устанавливается функцией процессов.
[c.904]
Связь между выходной и входной величинами преобразователя устанавливается функцией процессов.
[c.904]
Основное требование к измерительным преобразователям — точная передача информации, т. е. минимальные потери информации, иначе говоря, минимальные погрешности. Измерительное преобразование — это отражение размера одной физической величины размером другой физической величины, функционально с ней связанной. Измерительный преобразователь, к которому подведена измеряемая величина, называется первичным преобразователем.
[c.904]
Совокупность нескольких измерительных преобразователей также является измерительным преобразователем. Конструктивно объединенная совокупность измерительных преобразователей и вспомогательных элементов, предназначенная для восприятия измеряемой величины и преобразования ее в форму, удобную для дальнейшей обработки и передачи, и расположенная на объекте, называется датчиком. Остальные элементы измерительного средства, расположенные вне объекта, называются вторичным прибором. Датчик и вторичный прибор связаны между собой линией (каналом) связи.
[c.904]
Датчик и вторичный прибор связаны между собой линией (каналом) связи.
[c.904]
Измерительная установка — это совокупность функционально объединенных средств измерений (мер, измерительных приборов, измерительных преобразователей) и вспомогательных устройств, предназначенных для выработки сигналов измерительной информации в форме, удобной для непосредственного восприятия наблюдателем, и расположенных в одном месте.
[c.905]
Измерительные системы предназначены для выработки сигналов измерительной информации в форме, удобной для автоматической обработки, передачи и использования в автоматических системах управления. Их главная цель — автоматизация процесса измерений и использования результатов измерения для автоматического управления различными процессами производства.
[c.905]
Измерительные системы представляют собой разновидность более широкого класса систем, получившего общее название информационных систем. Информационные системы решают круг задач, связанных со сбором, переработкой, передачей, хранением, поиском и выдачей разнообразной информации человеку. Те из информационных систем, которые предназначаются для получения и обработки измерительной информации, получили название измерительных информационных систем (ИИС).
[c.905]
Информационные системы решают круг задач, связанных со сбором, переработкой, передачей, хранением, поиском и выдачей разнообразной информации человеку. Те из информационных систем, которые предназначаются для получения и обработки измерительной информации, получили название измерительных информационных систем (ИИС).
[c.905]
Информационно-измерительная система — это совокупность функционально объединенных измерительных, вычислительных и других вспомогательных технических средств для получения измерительной информации, ее преобразования, обработки с целью представления потребителю в требуемом виде либо автоматического осуществления функции контроля, диагностики, идентификации.
[c.905]
Существует несколько разновидностей ИИС.
[c.905]
Системы автоматического контроля — их функция состоит в установлении соответствия между состоянием объекта и заданной нормой и в выработке суждений о данном или (и) о будущем состоянии объекта. С помощью таких систем измеряются физические величины, характеризующие состояние объекта, и результаты измерений сравниваются со значениями, принятыми в качестве нормы. Для выработки суждения о будущем состоянии объекта система контроля должна выполнять прогнозирование на основе сведений о предыдущих состояниях объекта, полученных в ходе измерений, а также на основе его динамических характеристик, известных благодаря проведенным ранее исследованиям.
[c.905]
С помощью таких систем измеряются физические величины, характеризующие состояние объекта, и результаты измерений сравниваются со значениями, принятыми в качестве нормы. Для выработки суждения о будущем состоянии объекта система контроля должна выполнять прогнозирование на основе сведений о предыдущих состояниях объекта, полученных в ходе измерений, а также на основе его динамических характеристик, известных благодаря проведенным ранее исследованиям.
[c.905]
Вернуться к основной статье
Мера Определение и примеры — Биологический онлайн-словарь
Мера
1. Провести измерение или измерения.
2. Привести, или получить, по измерению; так как зерно хорошо измеряется; части измеряются неравномерно.
3. Иметь определенный размер или количество, или иметь определенную длину, ширину или толщину, или определенную емкость в соответствии со стандартной мерой; например, ткань измеряет три четверти ярда; дерево измеряет три фута в диаметре.
1. Эталон размера; фиксированная единица количества или степени; степень или количество, выраженное в долях или кратных единицах, из которых что-либо оценивается и указывается; следовательно, правило, по которому что-либо регулируется или оценивается.
2. Инструмент, с помощью которого измеряется размер или количество, такой как градуированная линейка, стержень, сосуд и т.п. Все ложные оценки и меры должны быть уничтожены. (Р. Глостер)
3. Размеры или вместимость чего-либо, рассчитанные по какому-либо стандарту; размер или протяженность, определенные и заявленные; предполагаемая степень; например, снять мерку для пальто. Мера его длиннее земли и шире моря. (работа xi. 9)
4. Содержимое сосуда, которым измеряется количество; количество, определенное стандартом; установленное или ограниченное количество или сумма. Это как закваска, которую женщина взяла и спрятала в три меры муки. (Лк. XIII. 21)
5. Объем или степень не чрезмерны и не выходят за пределы; Умеренность; должная сдержанность; особенно. В фразах, в меру; с мерой; без меры или сверх меры. Преисподняя расширилась и безмерно разверзла пасть свою. (Ис. В. 14)
В фразах, в меру; с мерой; без меры или сверх меры. Преисподняя расширилась и безмерно разверзла пасть свою. (Ис. В. 14)
6. Определенная протяженность, не превышающая; лимит; выделенная доля действия, влияния, способности и т.п.; должная пропорция. Господи, скажи мне конец мой и меру дней моих. (Пс. Xxxix. 4)
7. Количество, определяемое измерением, особенно при купле-продаже; как, чтобы дать хорошую или полную меру.
8. Количество неопределенное; степень; степень. При исповеди следует проявлять большую осмотрительность. (Джер. Тейлор)
9. (Наука: медицина) Регулируемое членение движения: Способ упорядочивания и сочетания величин или долгих и кратких слогов; метр; ритм; следовательно, ступня; как, стихотворение в размере ямба.
10.(Наука: математика) Число, которое входит в данное число определенное количество раз без остатка; как во фразах, общая мера, наибольшая общая мера и т. д. двух или более чисел.
11. Шаг или определенная часть прогрессивного курса или политики; средство для достижения цели; действие, направленное на достижение цели; как, политические меры; разумные меры; малоэффективная мера. Его величество понял, какие неправильные меры он принял при оказании этого доверия, и посетовал на свою ошибку. (Кларендон)
Его величество понял, какие неправильные меры он принял при оказании этого доверия, и посетовал на свою ошибку. (Кларендон)
12. Акт обмера; измерение.
13. (Науки: геология) пласты или пласты; как, уголь меры; опережающие меры. Линейная, или длинная, мера, мера длины; мера линий или расстояний. Жидкостная мера, мера жидкостей. Квадратная мера, мера площади поверхности в квадратных единицах, таких как дюймы, футы, мили и т. Д. Иметь жесткую меру, подвергать суровому обращению с одним; подвергаться жестокому или жестокому обращению. Принимать меры, готовиться; предоставить средства.Снять мерку, снять мерку, как с одежды; следовательно, составить мнение о своем расположении, характере, способностях и т. д. Выступить в меру, танцевать в так называемом стиле. См. 9 . Скажи ей, мы отмерили много верст, Чтоб отмерить с нею меру на этой траве. (Шак)
Происхождение: др.-англ. Mesure, F. Mesure, L. Mensura, фр. Metiri, mensus, измерять; сродни метру поэтическому размеру, гр, е. метр. См. Огромный, Измерение, Mete для измерения.
метр. См. Огромный, Измерение, Mete для измерения.
Что такое измерение? — Определение, факты и примеры
Измерение
- Сколько тебе лет?
- Сколько ты весишь?
- Какой у тебя рост?
- Сколько воды можно наполнить в бутылку с водой?
- Как жарко сегодня?
Чтобы ответить на вышеуказанные вопросы; что нам нужно, так это измерить.
- Чтобы узнать, сколько вам лет, нужно измерить время.
- Чтобы узнать, сколько вы весите, вы должны взвеситься.
- Чтобы узнать, какой у вас рост, вам нужно измерить свой рост (длину тела)
- Чтобы узнать, сколько воды вы можете налить в бутылку с водой, вам нужно измерить вместимость вашей бутылки.
- Чтобы узнать, насколько сегодня жарко, нужно измерить температуру.
Итак, что такое «измерение»?
Измерение — это процесс нахождения числа, которое показывает количество чего-либо.
Время
Текущая последовательность событий — это время. Мы можем измерять время в секундах, минутах, часах, днях, неделях, месяцах и годах.
Часы и календарь помогают нам измерять время.
Масса
Количество материи, из которой состоит вещь, называется ее весом. Измерение веса означает измерение тяжести вещи.
Вес можно измерять в граммах, килограммах и фунтах.
Длина
Количество чего-либо, измеренное от одного конца до другого по самой длинной стороне, называется его длиной.
Длина измеряется в сантиметрах, метрах, километрах, футах и милях
Емкость
Вместимость — это мера того, какое количество вещей может вместить вещь.
Емкость измеряется в литрах и галлонах
Температура
Температура предмета — это мера того, насколько он горячий или холодный.
Температура измеряется в градусах Цельсия, Фаренгейта и Кельвина.
Мы можем конвертировать из одной единицы измерения в другую.
Есть две системы измерения: 438834709
Метрическая система:
Эта система основана на использовании метра, литра и грамма как единиц длины (расстояния), емкости (объема) и веса (массы) соответственно.
Стандартные единицы США:
Эта система использует дюймы, футы, ярды и мили для измерения длины или расстояния.
Вместимость или объем измеряется в жидких унциях, чашках, пинтах, квартах или галлонах.
Вес или масса измеряется в унциях, фунтах и тоннах.
Интересные факты:
|
Что такое единицы измерения? — Определение, факты и примеры
Единицы измерения
Измерение заключается в том, чтобы найти число, которое показывает количество чего-либо. Единица измерения — это стандартная величина, используемая для выражения физической величины. Давайте узнаем о физических величинах и некоторых стандартных единицах, используемых для их измерения.
Длина
Длина описывает длину объекта от одного конца до другого.
| Метрическая единица измерения | Стандартная единица измерения США (английская или общепринятая единица измерения) |
Миллиметры (мм) Используется для измерения очень коротких длин или толщин. Пример, длина кончика карандаша.
Сантиметр (см): Используется для измерения небольших длин. Пример: Длина карандаша.
Метр (м): Используется для измерения больших длин. Пример: Длина классной комнаты.
Километр (км): Используется для измерения очень больших длин или расстояний. Пример: Расстояние между двумя точками. | Дюймы (дюймы): Используется для измерения длины небольших объектов. Пример: Длина кровати.
Футы (футы): Используется для измерения коротких расстояний и высот. Пример: Высота зданий.
Ярдов (ярдов): Это больше, чем фут. Пример: Длина футбольного поля.
Миля (миль): Используется для измерения больших расстояний. Пример: Расстояние между двумя точками. |
Вес
Количество материи, из которой состоит вещь, является ее весом.
| Метрическая единица измерения | Стандартная единица измерения США (английская или общепринятая единица измерения) |
Миллиграмм (мг): Используется для измерения очень легких предметов. Пример: Лекарства
Грамм (г): Используется для измерения мелких предметов. Пример: Картофель
Килограмм (кг): Используется для измерения тяжелых предметов. Пример: Масса тела | Унция (oz): Используется для измерения небольших количеств. Пример: Хлеб.
Фунт (фунт): Используется для измерения массы тела и т. д.
Тонны: Используется для измерения более тяжелых предметов. Пример: Грузовые автомобили |
Емкость (объем)
Вместимость — это количество, которое может вместить контейнер.
| Метрическая единица измерения | Стандартная единица измерения США (английская или общепринятая единица измерения) |
Миллилитр (мл): Используется для измерения очень малых количеств. Пример: Лекарства.
Литр (л): Используется для измерения жидкостей. Пример: сок, молоко | Стакан Пинта Кварта Галлон |
Время
Текущая последовательность событий — это время.
Метрические единицы и стандартные единицы США на данный момент одинаковы | |
Секунда (с) Минута (мин) Час (час) День Неделя Месяц Год | |
Забавный факт
|
единиц измерения
Меры измерения
Словарь единиц измерения
Для получения информации о конкретном блоке нажмите на первый
буква названия:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Комментарии и пояснения
- Международная система единиц (СИ)
- Международная система единиц
- Базовые и производные единицы измерения; другие единицы включены (и некоторые, которые не включены).
- Определение базовых единиц
- Текущие определения секунд, метров, килограммов, ампер, молей, кельвинов и кандел, в том числе пересмотренные в ноябре 2018 г.
- Единицы, производные от системы СИ и совместимые с системой СИ
- 22 производные единицы, которые входят в СИ, и еще 10, которые не входят.
- Метрические префиксы и префиксы единиц СИ
- От йотта- (септиллион) до йокто- (септиллион).

- Использование чисел и символов единиц измерения в измерениях
- Правила SI для чисел (десятичные маркеры, группировка цифр и т.д.) и правила SI для обработки символов единиц.
- Долгая дорога к СИ
- Английский Обычный
Веса и меры - Краткий рассказ о долгой (но увлекательной) истории.
- Метрическая система
- Новая идея, которой уже более 200 лет.
- КГС и МКС
Единицы - Две противоборствующие когерентные системы юнитов. Спойлер: MKS побеждает.
- Метрическая система
в США - Неправда, что У.С. не смог принять метрическую систему. Что правда?
- Прочие вопросы, представляющие интерес
- Роман и «арабский»
Цифры - Как работают римские цифры и как мы получили нашу текущую систему счисления.
- Наименования больших
Номера - Непрекращающийся спор: сколько составляет миллиард?
- Правописание
Метрические единицы - Метр? метр? метр? метро? Зависит от вашего языка, но SI это не волнует.

Ссылки на таблицы и весы
Введение в словарь
Американцы, вероятно, используют большее разнообразие единиц измерения
чем кто-либо еще в мире. Пойманный в медленном переходе
от привычных к метрическим единицам, мы используем увлекательный и иногда
досадное смешение единиц в разговорах об одном и том же. Мы
измерять длину пробега в метрах, а длину длинной
событие прыжка в футах и дюймах. Мы говорим о мощности двигателя в
лошадиных сил и его рабочий объем в литрах.В этом же депеше мы
описать скорость ветра урагана в узлах и его центральное давление
в миллибарах.
Иногда говорят, что Соединенные Штаты — одна из двух-трех стран, не принявших метрическую систему. Это грубое искажение истории. С 1875 года США подписались на
Международная система весов и
Меры, официальная версия метрической системы. Конгресс повторял это обязательство несколько раз, но он не заставлял широкую общественность использовать метрические единицы на всех этапах повседневной жизни. Таким образом, американцы приняли метрическую систему, они просто не используют ее во многих параметрах.
Таким образом, американцы приняли метрическую систему, они просто не используют ее во многих параметрах.
Метрические единицы образуют так называемую связную систему; это означает, что они точно соответствуют друг другу, и их легко преобразовать из одной метрической единицы в другую или объединить единицы для создания новых единиц для различных явлений. Английские общепринятые единицы
не образуют целостной системы. Отражая их разнообразные корни в
Кельтская, римская, саксонская и скандинавская культуры часто путают
и противоречиво.Существуют две системы измерения земли (одна
на основе двора, а другой на стержне) и третья система для
расстояния на море. Есть две системы (avoirdupois и troy) для
малые грузы и еще два (в расчете на длинную и короткую тонны) для
большие веса. Американцы используют две системы для объемов (одна для сухих
товары и один для жидкостей), а британцы используют третий (британский
Имперская мера).
Этот словарь включает:
- все подразделения Международной системы
единиц (СИ); - многие другие единицы метрической системы, используемые в быту или в науке в настоящее время или недавно;
- различные неметрические научные единицы, такие как астрономические
единица, электронвольт и парсек; - все единицы традиционной английской системы, с которыми я сталкивался и которые можно определить с достаточной точностью;
- избранные традиционные единицы из культур, отличных от английского;
и - определенные термины измерения и обозначения, не являющиеся «единицами измерения»
измерения» в строгом смысле, но которые часто используются
как если бы они были.
Определение каждой единицы измерения включает коэффициенты пересчета, которые вы можете
используйте для преобразования этой единицы в другие единицы, измеряющие ту же концепцию. Тем не менее, предостережение в порядке.
В случае традиционных единиц помните, что во многих случаях
«точное» определение более старой единицы (например,
лига или бочка) не было создано до девятнадцатого
век. Неразумно слишком полагаться на эти относительно современные определения, когда
чтение старых произведений. Кроме того, многие единицы, имеющие точное значение
теперь, такие как баррель и галлон, прежде имели множество
особого значения применительно к конкретным товарам; там
нет места в словаре для всех этих значений.
Надеюсь, словарь окажется для вас полезным и информативным. Предложения (и исправления, если вы обнаружите ошибки) всегда приветствуются и могут быть отправлены в rowlett по адресу электронной почты.unc.edu.
Формальности
Автор:
Расс Роулетт
Профессор педагогики на пенсии и адъюнкт-профессор математики
Университет Северной Каролины в
Чапел-Хилл.
Все материалы в этой папке защищены авторскими правами 2018 г. Расса Роулетта и
Университет Северной Каролины в Чапел-Хилл.Разрешение предоставляется для личных
использования и для использования отдельными учителями при проведении своих собственных занятий. Все
другие права защищены. Вы можете размещать ссылки на эту или любую другую страницу
словарь. Пожалуйста, не копируйте содержимое любой страницы словаря
на другой сайт. Материал на этом сайте часто обновляется как новый
информация добавляется, поэтому ссылка на сайт, а не его копирование находится в
наилучшие интересы каждого.
Информация, содержащаяся в словаре, является настолько точной, насколько я могу это сделать;
пожалуйста, сообщите мне, если вы найдете какие-либо
ошибки. Ни автор, ни Университет Северной Каролины не предполагают
любую ответственность за использование информации, представленной на этом веб-сайте.
словарь не предназначен для продвижения какой-либо системы измерения.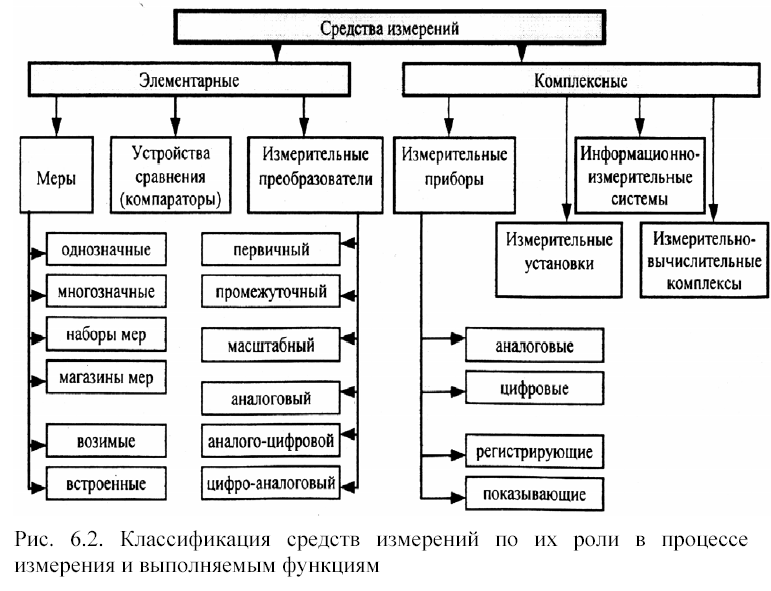 Это только
Это только
цель состоит в том, чтобы представить информацию, полезную для всех, кто интересуется предметом.
24 апреля 2018 г.
Измерение в науке (Стэнфордская философская энциклопедия)
Современные философские дискуссии об измерении, охватывающие
с конца девятнадцатого века до наших дней — можно разделить
на несколько направлений науки.Эти нити отражают разные
точки зрения на характер измерения и условия, которые делают
измерение возможно и надежно. Основные направления математические.
теории измерения, операционализм, конвенционализм, реализм,
теоретико-информационные счета и счета, основанные на моделях. Эти нити
науки не являются, по большей части, непосредственно
конкурирующие взгляды. Вместо этого их лучше всего понимать как выделение
различные и взаимодополняющие аспекты измерения. Ниже приводится
очень грубый обзор этих перспектив:
- Математические теории
измерение представление измерения как отображение качественного
эмпирические отношения к отношениям между числами (или другим математическим
сущности).
- Операционалисты и конвенционалисты вид
измерение как совокупность операций, формирующих смысл и/или
регулируют использование количественного термина. - Реалисты рассматривают измерение как оценку
независимые от разума свойства и/или отношения. - Информационно-теоретические счета представление измерений
как сбор и интерпретация информации о
система. - Счета на основе модели представление измерения как
согласованное присвоение значений параметрам в теоретическом и/или
статистическая модель процесса.
Эти взгляды в принципе согласуются друг с другом. Пока
математические теории измерения имеют дело с математическими
основы шкал измерения, операционализм и конвенционализм
в первую очередь связаны с семантикой количественных терминов, реализмом
занимается метафизическим статусом измеримых величин,
а теоретико-информационные и основанные на моделях расчеты касаются
эпистемологические аспекты измерения. Тем не менее, предмет
Тем не менее, предмет
домен не так четко разделен, как предполагает приведенный выше список.Проблемы
относительно метафизики, эпистемологии, семантики и математики
основы измерения взаимосвязаны и часто опираются на одно
Другая. Отсюда, например, операционалисты и конвенционалисты
часто придерживались антиреалистических взглядов и сторонников модельного
отчеты выступают против преобладающей эмпиристской интерпретации
математических теорий измерения. Эти тонкости станут
ясно в следующем обсуждении.
Список направлений стипендий не является ни исключительным, ни
исчерпывающий.Он отражает историческую траекторию философского
дискуссия до сих пор, а не какое-либо принципиальное различие между
различные уровни анализа измерений. Некоторые философские работы
по измерению принадлежат более чем одной нити, в то время как многие другие работы
тоже точно не подходят. Это особенно актуально, поскольку
начале 2000-х, когда измерения вернулись на первый план
философская дискуссия после нескольких десятилетий относительного забвения.
Эту недавнюю группу ученых иногда называют
эпистемология измерения» и включает в себя богатый массив работ
которые еще не могут быть классифицированы в отдельные школы мысли.То
Последний раздел этой статьи будет посвящен обзору некоторых
эти разработки.
Хотя философия измерения сформировалась как отдельная область
исследования только во второй половине XIX в.
основные понятия измерения, такие как величина и количество
обсуждались с древности. Согласно Евклиду
Элементы , величина — например, линия, поверхность или
твердый — измеряет другой, когда последний является целым кратным
прежний (Книга V, опр.1 и 2). Две величины имеют общее
меры, когда они оба являются целыми кратными некоторой величины, и
в противном случае несоизмеримы (Книга X, опр. 1). Открытие
несоизмеримые величины позволили Евклиду и его современникам
развить понятие отношения величин. Соотношения могут быть
либо рационально, либо иррационально, и поэтому понятие отношения
более общий, чем мера (Michell 2003, 2004a;
Граттан-Гиннесс 1996).
Аристотель различал количество и качество.Примеры
количества – это числа, линии, поверхности, тела, время и место,
тогда как примерами качеств являются справедливость, здоровье, горячность и
бледность ( Категории §6 и §8). В соответствии с
Аристотель, количества допускают равенство и неравенство, но не
градусов, так как «одна вещь не более четырех футов, чем другая»
(там же 6.6a19). Качества, наоборот, не допускают равенства или
неравенство, но допускают степени, «ибо одно называется
бледнее или менее бледнее другого» (там же, 8.10b26).Аристотель
не указал четко, являются ли степени таких качеств, как бледность
соответствуют различным качествам, или одно и то же качество,
бледность, была способна различной интенсивности. Эта тема была на
центр продолжающихся дебатов в тринадцатом и четырнадцатом веках
(Юнг 2011). Дунс Скот поддерживал «теорию сложения».
согласно которому изменение степени качества может быть
объясняется сложением или вычитанием меньших степеней этого
качество (2011: 553). Позже эта теория была уточнена Николь Орем.
Позже эта теория была уточнена Николь Орем.
которые использовали геометрические фигуры для представления изменений интенсивности
такие качества, как скорость (Clagett 1968; Sylla 1971).Орем
геометрические представления установили подмножество качеств, которые
поддавались количественной обработке, тем самым бросая вызов
строгая аристотелевская дихотомия количества и качества. Эти
развития сделали возможным формулирование количественных законов
движения в шестнадцатом и семнадцатом веках (Грант
1996).
Концепция качественной интенсивности получила дальнейшее развитие у Лейбница.
и Кант. Лейбниц сформулировал «принцип непрерывности».
что все естественные изменения производятся постепенно.Лейбниц утверждал, что
этот принцип применим не только к изменениям протяженных величин, таких как
как длина и продолжительность, но и интенсивность репрезентативного
состояния сознания, такие как звуки (Jorgensen 2009; Diehl 2012).
Считается, что Кант опирался на принцип Лейбница.
преемственность, чтобы сформулировать свое различие между экстенсивным и
интенсивные величины. По Канту, экстенсивные величины
По Канту, экстенсивные величины
те, «в которых изображение частей делает возможным
представление целого» (1787: A162/B203).Пример
длина: линия может быть мысленно представлена только последовательным
синтез, при котором части линии соединяются в единое целое. Для Канта
возможность такого синтеза обосновывалась в формах
интуиция, а именно пространство и время. Интенсивные величины, такие как тепло или
цвета, также приходят в непрерывных степенях, но их понимание занимает
место в одно мгновение, а не посредством последовательного синтеза
части. Степени интенсивных величин «могут быть только
представлен через приближение к отрицанию» (1787: A
168/B210), то есть воображая их постепенное уменьшение до тех пор, пока
полное отсутствие.
Научные разработки XIX века поставили под сомнение
Различие между экстенсивными и интенсивными величинами. Термодинамика
и волновая оптика показали, что различия в температуре и оттенке
соответствовали различиям в пространственно-временных величинах, таких как
скорость и длина волны. Электрические величины, такие как сопротивление и
Электрические величины, такие как сопротивление и
было показано, что проводимость способна к сложению и делению, несмотря на
не являющиеся экстенсивными в кантианском смысле, т. е. не синтезируемыми из
пространственные или временные части.Кроме того, первые эксперименты в
психофизика предположила, что интенсивность ощущений, таких как
яркость и громкость можно представить как сумму «просто
заметные различия» среди стимулов, и поэтому может быть
считать состоящим из частей (см.
Раздел 3.3).
Эти выводы, наряду с достижениями в аксиоматизации ветвей
математики, мотивировало некоторых ведущих ученых позднего
девятнадцатого века, чтобы попытаться прояснить математические основы
измерений (Максвелл 1873; фон Крис 1882; Гельмгольц 1887; Мах
1896 г.; Пуанкаре 1898; Гельдер 1901; для исторических обзоров
см. Darrigol 2003; Мичелл 1993, 2003; Канту и Шлаудт, 2013 г.;
Бьяджоли 2016: гл.4, 2018). Эти работы сегодня рассматриваются как
предшественники научной группы, известной как «измерение
теория».
Математические теории измерения (часто называемые собирательно
как «теория измерений») касаются условий
какие отношения между числами (и другими математическими объектами) могут быть
используется для выражения отношений между
объекты. [2]
Чтобы понять необходимость математических теорий
измерения, учтите тот факт, что отношения, демонстрируемые
числа, такие как равенство, сумма, разность и отношение, не
всегда соответствуют отношениям между объектами, измеряемыми теми
числа.Например, 60 дважды равно 30, но можно ошибиться, если
думая, что объект, измеренный при температуре 60 градусов по Цельсию, в два раза горячее
как объект при 30 градусах Цельсия. Это связано с тем, что нулевая точка
шкала Цельсия произвольна и не соответствует отсутствию
из
температура. [3]
Точно так же числовые интервалы не всегда несут эмпирическую
Информация. Когда испытуемых просят оценить по шкале от 1 до 7
насколько сильно они согласны с данным утверждением, нет прима
facie причина думать, что интервалы между 5 и 6 и
от 6 до 7 соответствуют равным приращениям силы мнения. Чтобы предоставить третий пример, равенство между числами является транзитивным [если
Чтобы предоставить третий пример, равенство между числами является транзитивным [если
(a=b & b=c), затем a=c], но эмпирические сравнения между физическими
величины обнаруживают лишь приблизительное равенство, которое не является транзитивным
связь. Эти примеры показывают, что не все математические
отношения между числами, используемыми в измерении, устанавливаются эмпирически
значительным, и что различные виды шкал измерения передают
различные виды эмпирически значимой информации.
Изучение шкал измерений и эмпирической информации, которую они
передача является основной задачей математических теорий измерения.В
его основополагающее эссе 1887 года «Счет и измерение» Германа
фон Гельмгольц сформулировал ключевой вопрос теории измерения как
следует:
[Что] является объективным значением выражения через наименования
нумерует отношения реальных предметов как величины, и под каким
условия мы можем это сделать? (1887: 4)
В широком смысле теория измерения ставит своей целью (i) идентифицировать
предположения, лежащие в основе использования различных математических структур для
описания аспектов эмпирического мира и (ii) извлечения уроков о
адекватность и пределы использования этих математических структур для
описание аспектов эмпирического мира. Вслед за Отто Гёльдером
Вслед за Отто Гёльдером
(1901), теоретики измерения часто решают эти задачи с помощью формальных
доказательства, при этом предположения в (i) служат аксиомами, а уроки
в (ii) следующие как теоремы. Ключевым моментом теории измерения является
что эмпирически значимые аспекты данного математического
структурой являются те, которые отражают соответствующие отношения между
измеряемые объекты. Например, отношение «больше
чем» среди чисел является эмпирически значимым для измерения
длина, поскольку она отражает отношение «длиннее, чем»
среди объектов.Это отражение или отображение отношений между
объекты и математические объекты составляют шкалу измерений. В виде
будет пояснено ниже, шкалы измерений обычно понимаются как
изоморфизмы или гомоморфизмы между объектами и математическими
сущности.
Помимо этих широких целей и утверждений, теория измерения представляет собой
весьма неоднородный корпус ученых. В него входят произведения, охватывающие
с конца девятнадцатого века до наших дней и поддерживают широкий
множество взглядов на онтологию, эпистемологию и семантику
измерение. Два основных различия между математическими теориями
Два основных различия между математическими теориями
измерения, заслуживают особого упоминания. Первый касается
природа relata , или «объектов», чьи
числа отношений должны отражать. Эти реляты могут быть
понимается по крайней мере четырьмя различными способами: как конкретное индивидуальное
объекты, как качественные наблюдения за конкретными отдельными объектами,
как абстрактные представления отдельных объектов или как универсальные
свойства предметов. Какая интерпретация будет принята, зависит от
большая часть на метафизическом и эпистемологическом
обязательства.Этот вопрос будет особенно актуален для обсуждения
реалистичных подходов к измерению
(Раздел 5).
Во-вторых, разные теоретики измерения занимают разные позиции.
о том, какие эмпирические данные необходимы для установления
сопоставления между предметами и числами. В результате измерение
теоретики пришли к разногласиям по поводу необходимых условий для
установление измеримости атрибутов и, в частности, о
поддаются ли измерению психологические атрибуты. Споры о
Споры о
измеримости оказались очень плодотворными для развития
теории измерений, а в следующих подразделах будут представлены некоторые
этих дискуссий и основных концепций, разработанных в них.
3.1 Основные и производные измерения
В конце девятнадцатого и начале двадцатого века несколько
были предприняты попытки дать универсальное определение измерения.
Хотя подходы к измерениям различались, все согласны с тем, что
измерение — это метод присвоения чисел величинам .
Например, Гельмгольц (1887: 17) определял измерение как процедуру
по которому находят номинальное число, выражающее стоимость
величина, где «номинальное число» — это число
вместе с единицей, т.е.г., 5 метров, а величина есть качество
объекты, которые поддаются упорядочению от меньшего к большему, например,
длина. Точно так же Бертран Рассел заявил, что измерение равно
.
любой метод, с помощью которого достигается однозначное и взаимное соответствие
устанавливается между всеми или некоторыми величинами вида и всеми или
некоторые из чисел, целые, рациональные или действительные.(1903: 176)
Норман Кэмпбелл определял измерение просто как «процесс
присвоение чисел для представления качеств», где качество — это
свойство, которое допускает непроизвольный порядок (1920: 267).
Определение измерения как числового присвоения поднимает вопрос:
какие задания адекватны и при каких условиях? Рано
теоретики измерения, такие как Гельмгольц (1887 г.), Гельдер (1901 г.) и
Кэмпбелл (1920) утверждал, что чисел достаточно для выражения
величин, поскольку алгебраические операции над числами отражают
эмпирические отношения между величинами. Например, качественный
отношение «длиннее, чем» между жесткими стержнями равно (примерно)
переходный и асимметричный, и в этом отношении имеет общие структурные
функции с отношением «больше чем» между числами.Более того, сквозное сцепление жестких стержней имеет общие структурные
особенности, такие как ассоциативность и коммутативность, с
математическая операция сложения. Аналогичная ситуация имеет место для
измерение веса с помощью равноплечих весов. Здесь отклонение от
Здесь отклонение от
оружие обеспечивает упорядочение гирь и нагромождение гирь на
одна панорама представляет собой конкатенацию.
Ранние теоретики измерения сформулировали аксиомы, описывающие эти
качественные эмпирические структуры и использовал эти аксиомы для доказательства
теоремы об адекватности присвоения чисел величинам, которые
демонстрируют такие структуры.В частности, они доказали, что упорядочение и
конкатенации вместе достаточно для построения
дополнение числовое представление соответствующих величин.
Аддитивное представление — это представление, в котором сложение производится эмпирически.
осмысленное, а значит, и умножение, деление и т. д. Кэмпбелл
называются измерительными процедурами, удовлетворяющими условиям
аддитивность «фундаментальная», потому что они не включают
измерение любой другой величины (1920: 277). Виды величин
для которых была разработана основная процедура измерения
найдены, такие как длина, площадь, объем, продолжительность, вес и
электрическое сопротивление — Кэмпбелл назвал «фундаментальным
величины».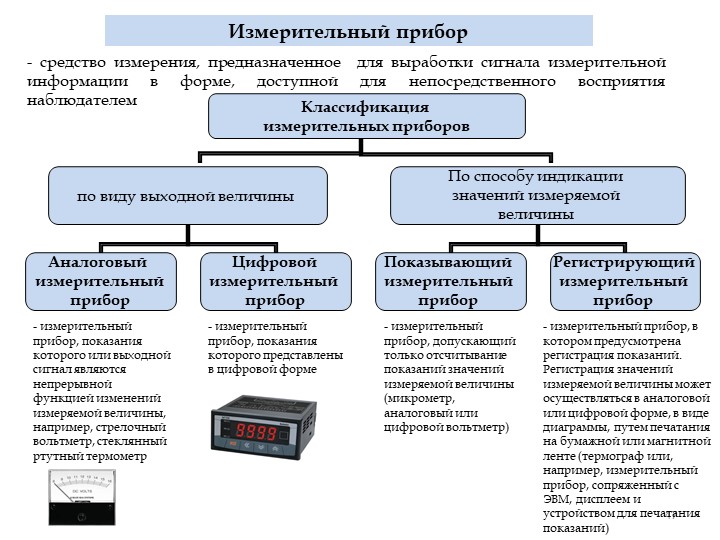 Отличительной чертой таких масштабов является то, что они
Отличительной чертой таких масштабов является то, что они
их можно сгенерировать, объединив стандартную последовательность
равные единицы, как в примере с рядом равноотстоящих меток на
правитель.
Хотя они считали аддитивность отличительной чертой измерения, большинство
первые теоретики измерения признавали, что аддитивность не
необходимо для измерения. Существуют и другие величины, допускающие упорядочение
от меньшего к большему, но отношения и/или различия которых не могут
в настоящее время определяются, кроме как через их отношения к другим,
принципиально измеримые величины.Примерами являются температура, которая
можно измерить, определив объем ртутного столба, и
плотность, которую можно измерить как отношение массы к объему. Такой
косвенное определение стало называться «производным».
измерение и соответствующие величины, «полученные
величин» (Campbell 1920: 275–277).
На первый взгляд различие между фундаментальным и производным
измерение может показаться напоминающим различие между экстенсивным
и интенсивные величины, и действительно фундаментальное измерение
иногда называют «обширным». Тем не менее важно
Тем не менее важно
отметить, что эти два различия основаны на существенно различающихся
критерии измеримости. Как обсуждалось в
Раздел 2,
экстенсивно-интенсивное различие сосредоточено на внутреннем
структура рассматриваемой величины, т. е. является ли она
состоит из пространственно-временных частей. Фундаментальное производное
различие, напротив, фокусируется на свойствах измерения
операций . Принципиально измеримая величина – это величина,
найдена фундаментальная операция измерения.Следовательно, фундаментальность не является внутренним свойством
величина: производная величина может стать фундаментальной с
открытие новых операций для его измерения. Более того, в
фундаментальное измерение числовое присвоение не обязательно должно отражать
структура пространственно-временных частей. Электрическое сопротивление, для
Например, можно принципиально измерить, подключив резисторы в
серия (Campbell 1920: 293). Это считается фундаментальным
операция измерения, потому что она имеет общую структуру с числовыми
Кроме того, даже несмотря на то, что объекты с одинаковым сопротивлением обычно не
равны по размеру.
Различие между фундаментальным и производным измерением было
переработаны последующими авторами. Брайан Эллис (1966: главы 5–8)
различают три типа измерений: фундаментальные,
ассоциативный и производный. Фундаментальное измерение требует упорядочения и
операции конкатенации, удовлетворяющие тем же условиям, указанным
Кэмпбелл. Ассоциативные процедуры измерения основаны на
корреляция двух упорядоченных отношений, например, корреляция
между объемом ртутного столбика и его температурой.Полученный
процедуры измерения заключаются в определении значения
постоянным в физическом законе. Константа может быть локальной, как в
определение удельной плотности воды по массе и объему,
или универсальным, как в определении ньютоновского гравитационного
постоянной от силы, массы и расстояния. Генри Кибург (1984: гл.
5–7) предложил несколько иное тройственное различие между
прямое, косвенное и систематическое измерение, которое не полностью
пересекаются с тем, что
Эллис. [4]
Более радикальный пересмотр различия между фундаментальными и
производное измерение было предложено Р. Дунканом Люсом и Джоном Тьюки.
Дунканом Люсом и Джоном Тьюки.
(1964) в их работе по совместному измерению, которая будет обсуждаться
в
Раздел 3.4.
3.2 Классификация весов
В предыдущем подразделе обсуждалась аксиоматизация эмпирических
структуры, направление исследований, которое восходит к ранним дням
теория измерений. Дополнительная линия исследования в рамках измерения
теория касается классификации шкал измерений.То
психофизик С. С. Стивенс (1946, 1951) выделял среди четырех
виды шкал: номинальная, порядковая, интервальная и пропорциональная. Номинальные весы
представлять объекты как принадлежащие к классам, не имеющим определенного
порядок, например, мужской и женский. Порядковые шкалы представляют порядок, но не
дальнейшая алгебраическая структура. Например, шкала Мооса минералов.
твердость представляет собой минералы с номерами от 1 (самый мягкий) до
10 (самый сложный), но нет никакого эмпирического значения в равенстве между
интервалы или отношения этих
числа. [5]
Цельсия и Фаренгейта являются примерами интервальных шкал: они
представляют равенство или неравенство между интервалами температуры, но
не отношения температур, потому что их нулевые точки произвольны.
Шкала Кельвина, напротив, представляет собой шкалу отношений, как и привычные
шкалы, представляющие массу в килограммах, длину в метрах и продолжительность
в секундах. Позднее Стивенс усовершенствовал эту классификацию и
различают линейную и логарифмическую шкалы интервалов (1959:
31–34) и между шкалами отношений с натуральной единицей и без нее.
(1959: 34).Шкалы отношений с натуральными единицами, такие как те, которые используются для
для подсчета дискретных объектов и для представления вероятностей, были
называются «абсолютными» весами.
Как отмечает Стивенс, типы шкал индивидуализируются семействами
преобразования, которые они могут претерпевать без потери эмпирической
Информация. Эмпирические отношения, представленные на шкалах отношений, для
например, инвариантны относительно умножения на положительное число,
например, умножение на 2,54 преобразует дюймы в сантиметры.
Линейные шкалы интервалов допускают умножение на положительное число
и постоянный сдвиг, т.е.г., преобразование из градусов Цельсия в градусы Фаренгейта
по формуле °С × 9/5 + 32 = °F.
Порядковые шкалы допускают любую функцию преобразования, если она
монотонная и возрастающая, а номинальные шкалы допускают любые взаимно-однозначные
замена. Абсолютные шкалы не допускают никаких преобразований, кроме
личность. Классификация чешуи Стивенса была позже
обобщены Louis Narens (1981, 1985: Ch. 2) и Luce et al. (1990:
Ч. 20) с точки зрения однородности и уникальности соответствующих
группы трансформации.
В то время как классификация весов Стивенса встречалась с общими
одобрение в научных и философских кругах, его более широкое
последствия для теории измерения стали темой значительного
дебаты. Особенно спорными были два вопроса. Первый был ли
операции классификации и упорядочения заслуживают того, чтобы их называли
операции «измерения» и, соответственно,
представление величин в номинальной и порядковой шкалах должно
считать измерением. Несколько физиков, в том числе Кэмпбелл, утверждали,
что операции классификации и упорядочивания не обеспечивают
достаточно богатая структура, чтобы оправдать использование чисел, и, следовательно,
не должны считаться операциями измерения. Второй спорный вопрос
Второй спорный вопрос
нужно ли было найти операцию конкатенации для величины
до того, как его можно было фундаментально измерить по шкале отношений. Дебаты
стал особенно накален, когда он снова разжег более длительную полемику
вокруг измеримости интенсивности ощущений. Это для
этот спор мы сейчас перейдем.
3.3 Измеримость ощущения
Один из главных катализаторов развития математических теорий
измерения были постоянными дебатами вокруг измеримости в
психология.Споры часто восходят к Густаву Фехнеру.
(1860) Элементы психофизики , в которой он описал
Метод измерения интенсивности ощущений. метод Фехнера
был основан на записи «просто заметных
различия» между ощущениями, связанными с парами
раздражители, например, два звука разной интенсивности. Эти различия
считались равными приращениями интенсивности ощущения. В виде
Фехнер показал, что при этом предположении устойчивая линейная зависимость имеет вид
между интенсивностью ощущения и логарифмом
интенсивность раздражителя, отношение, которое стало известно как
«Закон Фехнера» (Heidelberger 1993a: 203; Luce and
Суппес 2004: 11–2). Этот закон, в свою очередь, обеспечивает метод
Этот закон, в свою очередь, обеспечивает метод
косвенно измеряя интенсивность ощущений, измеряя
интенсивность стимула и, следовательно, Фехнер утверждал, обеспечивает
обоснование измерения интенсивности ощущений на реальном
числа.
Утверждения Фехнера об измеримости ощущения
стал предметом ряда дебатов, длившихся почти столетие.
и оказался чрезвычайно плодотворным для философии измерения,
с участием ключевых фигур, таких как Мах, Гельмгольц, Кэмпбелл и Стивенс
(Гейдельбергер 1993а: гл.6 и 1993b; Мичелл 1999: гл. 6). Те
возражая против измеримости ощущения, такие как Кэмпбелл,
подчеркнул необходимость эмпирической операции конкатенации для
фундаментальное измерение. Поскольку интенсивность ощущений не может быть
соединены друг с другом способом, обеспечиваемым длинами и
веса, не может быть фундаментального измерения ощущения
интенсивность. Более того, Кэмпбелл утверждал, что ни одно из психофизических
открытые к настоящему времени закономерности достаточно универсальны, чтобы считать
как законы в смысле, необходимом для производных измерений (Кэмпбелл в
Фергюсон и др. 1940: 347). Все, что показали психофизики,
1940: 347). Все, что показали психофизики,
что интенсивность ощущений можно последовательно упорядочить, но упорядочить
само по себе еще не гарантирует использование числовых отношений, таких как
суммы и соотношения для выражения эмпирических результатов.
Центральным оппонентом Кэмпбелла в этих дебатах был Стивенс, чей
Различие между типами шкал измерения обсуждалось выше.
Стивенс определял измерение как «присвоение цифр
объектов или событий в соответствии с правилами» (1951: 1) и утверждал, что
любое последовательное и неслучайное назначение считается измерением в
широкий смысл (1975: 47).В полезных случаях научных исследований Стивенс
заявленное, измерение может быть истолковано несколько более узко как
числовое присвоение, основанное на результатах сопоставления с
операции, такие как привязка температуры к объему ртути или
соответствие ощущений друг другу. Стивенс выступал против
считают, что отношения между числами должны отражать качественные эмпирические
структур, утверждая вместо этого, что шкалы измерения должны быть
рассматриваются как произвольные формальные схемы и принимаются в соответствии с
их полезность для описания эмпирических данных.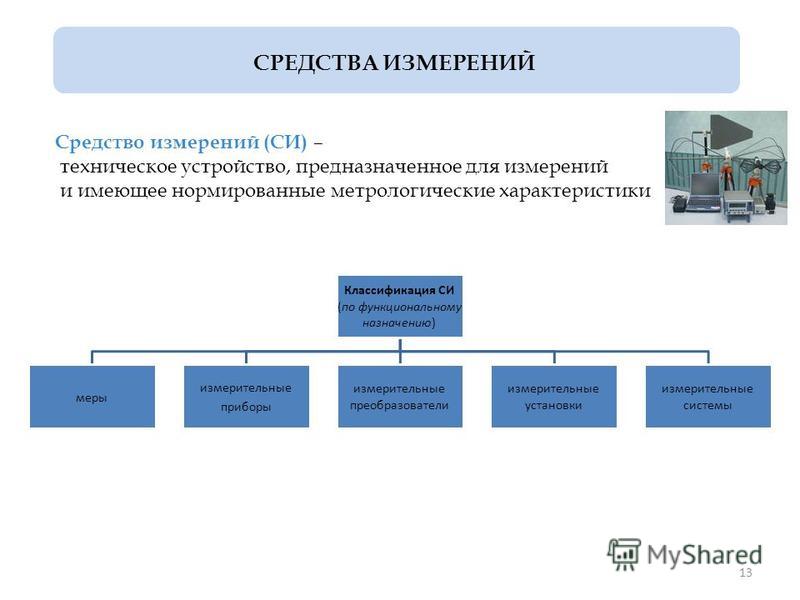 Например, принятие
Например, принятие
шкала отношений для измерения ощущений громкости, громкости и
плотность звуков приводит к формулировке простого линейного соотношения
среди отчетов подопытных: громкость = громкость ×
плотность (1975: 57–8). Такое присвоение цифр ощущениям
считается измерением, потому что оно последовательно и неслучайно, потому что
он основан на операциях сопоставления, выполняемых экспериментальными
испытуемых, а также потому, что он фиксирует закономерности в экспериментальных
Результаты. По словам Стивенса, эти условия вместе
достаточно, чтобы оправдать использование шкалы отношений для измерения
ощущения, несмотря на то, что «ощущения не могут быть
разделены на составные части или уложены встык, как измерительные
палочки» (1975: 38; см. также Hempel 1952: 68–69).
3.4 Репрезентативная теория измерений
В середине двадцатого века два основных направления исследований в
теории измерения, посвященной эмпирическим условиям
количественная оценка и классификация весов,
сошлись в работах Патрика Суппеса (1951; Скотт и Суппес, 1958;
исторические обзоры см. в Savage and Ehrlich 1992; Диез, 1997а,б).
в Savage and Ehrlich 1992; Диез, 1997а,б).
Работа Зюппеса заложила основу репрезентативной теории
Измерение (RTM), которое остается самым влиятельным математическим
теории измерения на сегодняшний день (Krantz et al.1971 год; Суппес и др. 1989 год;
Люс и др. 1990). RTM определяет измерение как построение
отображения эмпирических реляционных структур в числовые
реляционные структуры (Кранц и др. 1971: 9). Эмпирическое отношение
структура состоит из набора эмпирических объектов (например, жестких стержней)
наряду с определенными качественными отношениями между ними (например, упорядоченность,
конкатенация), в то время как числовая реляционная структура состоит из
набор чисел (например, действительных чисел) и конкретных математических
отношения между ними (т.г., «равно или больше»,
добавление). Проще говоря, шкала измерения – это отношение «многие к одному».
отображение — гомоморфизм — от эмпирического к числовому
реляционная структура, а измерение есть построение
напольные весы. [6]
RTM уделяет большое внимание разъяснению предположений, лежащих в основе
построение различных типов измерительных шкал. Каждый тип
Каждый тип
масштаба связано с набором предположений о качественном
отношения, возникающие между объектами, представленными на шкале этого типа.Из этих предположений или аксиом авторы RTM выводят
репрезентативной адекватности каждого масштабного типа, а также семейства
допустимые преобразования, делающие этот тип шкалы уникальным. В этом
способ, которым RTM обеспечивает концептуальную связь между эмпирической основой
измерение и типология
напольные весы. [7]
Что касается измеримости, репрезентативная теория занимает
средний путь между либеральным подходом, принятым Стивенсом, и
строгий акцент на операциях конкатенации, поддерживаемых Кэмпбеллом.Нравится
Кэмпбелл, RTM признает, что правила количественного определения должны быть основаны на
известных эмпирических структур и не должны выбираться произвольно, чтобы соответствовать
данные. Однако RTM отвергает идею о том, что аддитивные шкалы
подходит только тогда, когда доступны операции конкатенации (Luce и
Суппес 2004: 15). Вместо этого RTM утверждает существование фундаментальных
Вместо этого RTM утверждает существование фундаментальных
операции измерения, не связанные с конкатенацией. Центральный
Пример такого типа операции известен как «аддитивный конджойнт».
измерения» (Luce and Tukey 1964; Krantz et al.1971:
17–21 и гл. 6–7). Здесь измерения двух или более
различные типы атрибутов, такие как температура и давление
газа, получают путем наблюдения за их совместным действием, например
объем газа. Люс и Тьюки показали, что, устанавливая определенные
качественные отношения между объемами при изменении температуры
и давления можно построить аддитивные представления
температуры и давления, не прибегая к каким-либо предшествующим методам
измерение объема. Такого рода процедура применима к любому
соответственно связанная тройка атрибутов, таких как громкость,
интенсивность и частота чистых тонов или предпочтение вознаграждения,
его размер и задержка с его получением (Luce and Suppes 2004: 17).То
открытие аддитивного совместного измерения привело авторов RTM к
разделить фундаментальные измерения на два вида: традиционные измерения
процедуры, основанные на операциях конкатенации, которые они назвали
«обширное измерение» и совместное или
«неэкстенсивное» фундаментальное измерение. Под этим новым
Под этим новым
концепция фундаментальности, все традиционные физические атрибуты
могут быть измерены фундаментально, как и многие психологические
атрибуты (Кранц и др. 1971: 502–503).
Выше мы видели, что математические теории измерения в первую очередь
связанные с математическими свойствами шкал измерения и
условия их применения.Связанная, но отдельная нить
наука касается значения и использования количественных терминов. Научный
теории и модели обычно выражаются в терминах количественных
отношения между параметрами, носящие имена, такие как
«продолжительность», «уровень безработицы» и
«интроверсия». Реалист в отношении одного из этих терминов
утверждают, что это относится к набору свойств или отношений, которые существуют
независимо от измерения. Операционалист или конвенционалист
утверждал бы, что то, как такие количественные термины применяются к конкретным
детали зависят от нетривиального выбора, сделанного людьми, и
особенно на выбор, который имеет отношение к тому, как соответствующие
измеряется количество. Обратите внимание, что в рамках этой широкой интерпретации реализм
Обратите внимание, что в рамках этой широкой интерпретации реализм
совместим с операционализмом и конвенционализмом. То есть это
возможно, что выбор метода измерения регулирует использование
количество-термин и что при правильном выборе этот термин
удается сослаться на независимое от разума свойство или отношение.
Тем не менее, многие операционалисты и конвенционалисты приняли
более сильные взгляды, согласно которым нет никаких фактов по делу, как
какая из нескольких и нетривиально различных операций верна
для применения заданного количественного термина.Эти более сильные варианты
несовместимы с реализмом в отношении измерения. Этот раздел будет
посвященный операционализму и конвенционализму, а рядом
реализм в измерении.
Операционализм (или «операционализм») в отношении измерения
точка зрения, согласно которой значение количественных понятий определяется
набор операций, используемых для их измерения. Самое сильное выражение
операционализма появляется в ранних работах Перси Бриджмена (1927),
кто утверждал, что
мы подразумеваем под любым понятием не что иное, как совокупность операций; в
понятие является синонимом соответствующего набора операций.(1927:
5)
Длина, например, будет определена как результат операции
соединения жестких стержней. Согласно этой крайней версии
операционализм, разные операции измеряют разные величины.
Длина измеряется линейкой и синхронизацией электромагнитных импульсов.
следует, строго говоря, разделить на два различных
количественные понятия, помеченные как «длина-1» и
«длина-2» соответственно. Этот вывод привел Бриджмена к
утверждают, что принятые в настоящее время концепции количества
«суставы», где различные операции перекрываются в их
область применения.Он предостерег от догматической веры в единство
количественных понятий в этих «стыках», призывая вместо этого
чтобы единство проверялось опытами всякий раз, когда применяется
понятие количества должно быть расширено в новую область. Тем не менее,
Бриджмен признал, что до тех пор, пока результаты различных операций
согласен в пределах ошибки эксперимента, прагматически оправдано маркировать
соответствующие одноименные величины (1927:
16). [8]
[8]
Операционализм стал влиятельным в психологии, где он
хорошо принят такими бихевиористами, как Эдвин Боринг (1945) и Б.Ф.
Скиннер (1945). Действительно, Скиннер утверждал, что бихевиоризм
«не более чем тщательный оперативный анализ
традиционные менталистические концепции» (1945: 271). Стивенс, который был
Ученик Боринга, был ключевым пропагандистом операционализма в
психологии, и утверждал, что психологические понятия имеют эмпирические
значение только в том случае, если они означают определенные и конкретные операции (1935:
517; см. также Исаак 2017). Представление о том, что понятия определяются
операции измерения согласуются с либеральными взглядами Стивенса
по измеримости, которые обсуждались выше
(Раздел 3.3).
Пока присвоение номеров объектам выполняется в
в соответствии с конкретными и последовательными правилами, Стивенс утверждал, что
такое присвоение имеет эмпирический смысл и не требует выполнения каких-либо
дополнительные ограничения. Тем не менее, Стивенс, вероятно, не принял
антиреалистический взгляд на психологические атрибуты. Вместо этого там
Вместо этого там
есть веские основания полагать, что он понимал операционализм как
методологическая установка, которая была ценна в той мере, в какой
позволили психологам обосновать выводы, которые они сделали из
эксперименты (Фест, 2005).Например, Стивенс не лечил
операционные определения как априори , но как поддающиеся
улучшение в свете эмпирических открытий, подразумевая, что он принял
психологические атрибуты, чтобы существовать независимо от таких определений
(Стивенс 1935: 527). Это говорит о том, что операционализм Стивенса
был более умеренным разнообразием, чем то, что можно найти в ранних произведениях.
из
Бриджмен. [9]
Поначалу операционализм был встречен с энтузиазмом логическими позитивистами.
рассматривал его как родственное верификационизму.Тем не менее, вскоре
показало, что любая попытка построить теорию значения на
операционалистские принципы были пронизаны проблемами. Среди таких
проблемы заключались в автоматическом операционализме надежности, присущем
измерительные операции, двусмысленность, связанная с понятием
операция, чрезмерно ограничительный операционный критерий
осмысленность, а также тот факт, что многие полезные теоретические концепции
не имеют четких операционных определений (Chang
2009). [10]
[10]
В частности, Карл Хемпель (1956, 1966) критиковал операционалистов.
за неспособность определить диспозиционные термины, такие как
«растворимость в воде», и для умножения числа
научных концепций таким образом, который противоречит необходимости
систематические и простые теории.Соответственно, большинство писателей на
семантика количественных терминов избегала поддержки операционного
анализ. [11]
Более широко пропагандируемый подход допускал наличие традиционного элемента в
использование количественных терминов, сопротивляясь попыткам уменьшить
значение количественных терминов для операций измерения. Эти аккаунты
классифицируются под общим заголовком
«конвенционализм», хотя они различаются в конкретных
аспекты измерения, которые они считают общепринятыми, и в степени
произвол они приписывают таким
соглашения. [12]
Первым предшественником конвенционализма был Эрнст Мах, исследовавший
понятие равенства температурных интервалов (1896: 52). Маха
Маха
отметил, что различные типы термометрической жидкости расширяются в разное время.
(и нелинейно связанные) скорости при нагреве, что ставит вопрос:
Какая жидкость наиболее равномерно расширяется при изменении температуры? В соответствии с
Мах, нет никакой разницы, какая жидкость расширяется больше
равномерно, поскольку само понятие равенства температур
интервалы не имеют определенного применения до обычного
выбор стандартной термометрической жидкости.Мах ввел термин
«принцип координации» для такого рода
условно выбранный принцип применения величины
концепция. Понятия единообразия времени и пространства получили схожие
обработки Анри Пуанкаре (1898, 1902: Часть 2).
Пуанкаре утверждал, что процедуры, используемые для определения равенства
среди продолжительностей проистекают из бессознательного предпочтения ученых
описательной простоты, а не от каких-либо фактов о природе.
Точно так же выбор ученых представлять пространство либо
Евклидова или неевклидова геометрия не определяется опытом
а из соображений удобства.
Конвенционализм в отношении измерения достиг своего наибольшего
изощренное выражение в логическом позитивизме. Логические позитивисты
как Ганс Райхенбах и Рудольф Карнап предложили «координационную
определения» или «правила соответствия» в качестве
семантическая связь между теоретическими и наблюдательными терминами. Эти а
Priori , формулировки, подобные определениям, предназначались для регулирования
использование теоретических терминов, связывая их с эмпирическими процедурами
(Reichenbach 1927: 14–19; Carnap 1966: Ch.24). Пример
координационным определением является утверждение: «измерительная рейка
сохраняет свою длину при транспортировке». Согласно Рейхенбаху,
это утверждение не может быть проверено эмпирически, потому что универсальное и
может существовать экспериментально необнаружимая сила, которая в равной степени искажает
длина каждого объекта при его транспортировке. В соответствии с
верификационизм, утверждения, которые не поддаются проверке, не являются ни истинными, ни
ложный. Наоборот, Рейхенбах воспринял это заявление как выражение
Наоборот, Рейхенбах воспринял это заявление как выражение
произвольное правило регулирования использования понятия равенства
длина, а именно, для определения того, являются ли конкретные экземпляры длины
равны (Reichenbach 1927: 16).В то же время координационный
определения рассматривались не как замена, а как необходимость
дополнения к привычному виду теоретических определений понятий
с точки зрения других понятий (1927: 14). Под конвенционалистом
точки зрения, то спецификация операций измерения не
исчерпывают смысл таких понятий, как длина или равенство длины,
тем самым избегая многих проблем, связанных с
операционализм. [13]
Реалисты в отношении измерения утверждают, что измерение лучше всего
понимается как эмпирическая оценка объективного свойства или
связь.Необходимо сделать несколько поясняющих замечаний в отношении
это характеристика измерения. Во-первых, термин
«объективный» не означает исключения ментальных свойств или
отношения, являющиеся объектами психологического измерения. Скорее,
Скорее,
измеримые свойства или отношения считаются объективными, поскольку
поскольку они независимы от верований и условностей людей
проведения измерения и методов, используемых для измерения. За
например, реалист утверждал бы, что отношение длины данного
сплошной стержень к эталонному метру имеет объективное значение независимо от
измеряется ли и как.Во-вторых, термин
«оценка» используется реалистами, чтобы подчеркнуть факт
что результаты измерений являются всего лишь приближениями истинных
ценностей (Trout 1998: 46). В-третьих, по мнению реалистов, измерение
направлена на получение знаний о свойствах и отношениях, а не
чем при присвоении значений непосредственно отдельным объектам. Это
важно, потому что наблюдаемые объекты (например, рычаги, химические
решения, люди) часто создают экземпляры измеримых свойств и
отношения, не наблюдаемые непосредственно (т.г., количество механических
работа, более кислая, чем интеллект). Знание утверждает о таких
свойства и отношения должны предполагать некоторую фоновую теорию. От
От
перенос акцента с объектов на свойства и отношения,
реалисты подчеркивают теоретический характер измерений.
Реализм в отношении измерения не следует путать с реализмом в отношении
объекты (например, электроны). И не реализм в измерении
обязательно влекут за собой реализм в отношении свойств (например, температуры), поскольку
в принципе можно было принять только реальность отношений (т.г.,
отношения между количествами), не принимая во внимание реальность лежащих в основе
характеристики. Тем не менее, большинство философов, защищавших реализм
об измерении сделали это, выступив за некую форму реализма
о свойствах (Байерли и Лазара, 1973; Суойер, 1987; Манди, 1987;
Форель 1998, 2000). Эти реалисты утверждают, что по крайней мере некоторые измеримые
свойства существуют независимо от верований и условностей
людей, которые их измеряют, и что существование и структура этих
properties обеспечивает лучшее объяснение ключевых особенностей
измерения, включая полезность чисел для выражения
результаты измерений и надежность средств измерений.
Например, типичный реалист об измерении длины сказал бы:
что эмпирические закономерности, проявляемые отдельными объектами
длины, когда они упорядочены и соединены, лучше всего объясняются
предполагая, что длина является объективным свойством, имеющим обширную
структура (Swoyer 1987: 271–274). То есть отношения между длинами
такие как «длиннее, чем» и «сумма» существуют
независимо от того, являются ли какие-либо объекты упорядоченными и
соединены людьми, и действительно независимо от того, являются ли объекты
некоторая конкретная длина вообще существует.Существование
экстенсивная структура свойств означает, что длины разделяют большую часть своих
структура с положительными действительными числами, и это объясняет
полезность положительных вещественных чисел в представлении длин. Более того, если
измеримые свойства анализируются в терминах диспозиции, становится
легко объяснить, почему некоторые измерительные приборы надежны. За
Например, если предположить, что определенное количество электрического тока в
провод влечет за собой склонность отклонять стрелку амперметра на определенную
угла, следует, что показания амперметра
контрфактически зависят от количества электрического тока в проводе,
и, следовательно, амперметр надежен (Trout 1998: 65).
Другой аргумент в пользу реализма в отношении измерения принадлежит Джоэлу.
Мичелл (1994, 2005), который предлагает реалистическую теорию чисел, основанную на
Евклидово понятие соотношения. По словам Мичелла, цифры
отношения между величинами и, следовательно, существуют в пространстве и времени.
В частности, действительных чисел являются отношениями между парами
бесконечные стандартные последовательности, например последовательность длин обычно
обозначаются «1 метр», «2 метра» и т. д., а
последовательность целых кратных длины, которую мы пытаемся измерить.Измерение – это обнаружение и оценка таких соотношений. Ан
интересным следствием этого эмпирического реализма в отношении чисел является
что измерение является не репрезентативной деятельностью, а скорее
деятельность по приближению чисел, не зависящих от разума (Michell 1994:
400).
Реалистические подходы к измерению в значительной степени сформулированы в оппозиции
к сильным версиям операционализма и конвенционализма, которые
доминировал в философских дискуссиях об измерениях с 1930-х годов.
до 1960-х годов.Помимо недостатков операционализма
уже обсуждалось в предыдущем разделе, реалисты отмечают, что
антиреализм в отношении измеримых величин не имеет смысла
научная практика. Если бы величины не имели действительных значений независимо от
выбор процедуры измерения, было бы трудно
объяснить, что ученые подразумевают под «точностью измерения» и
«погрешность измерения», и почему пытаются повысить точность
и уменьшить ошибку. Напротив, реалисты могут легко понять
представления о точности и погрешности с точки зрения расстояния между реальными
и измеренные значения (Byerly and Lazara 1973: 17–8; Swoyer 1987:
239; Траут 1998: 57).Тесно связанным моментом является тот факт, что более новые
процедуры измерения, как правило, улучшают точность старых.
Если бы выбор процедуры измерения был просто условным, это было бы
трудно понять смысл такого прогресса. Кроме того, реализм
обеспечивает интуитивно понятное объяснение того, почему различные измерения
процедуры часто дают аналогичные результаты, а именно потому, что они
чувствительны к одним и тем же фактам (Swoyer 1987: 239; Trout 1998: 56).
Наконец, реалисты отмечают, что конструкция измерительной аппаратуры
и при анализе результатов измерений руководствуются теоретическими
предположения о причинно-следственных связях между величинами.То
способность таких причинно-следственных предположений направлять измерения предполагает, что
количества онтологически предшествуют процедурам измерения
их. [14]
Хотя их позиция в отношении операционализма и конвенционализма
в значительной степени критичны, реалисты более снисходительны в своих оценках
математические теории измерения. Брент Манди (1987) и Крис
Swoyer (1987) оба принимают аксиоматическую трактовку измерения.
шкалы, но возражают против эмпирической интерпретации, данной
аксиомы выдающихся теоретиков измерения, таких как Кэмпбелл (1920) и
Эрнест Нагель (1931; Коэн и Нагель, 1934: гл.15). Скорее, чем
интерпретируя аксиомы как относящиеся к конкретным объектам или к
наблюдаемые отношения между такими объектами Манди и Свойер интерпретируют по-новому.
аксиомы, относящиеся к универсальным величинам, например, к
универсальное свойство быть длиной 5 метров, а не бетоном
экземпляры этого свойства. Эта конструкция сохраняет
Эта конструкция сохраняет
интуитивно понятно, что такие утверждения, как «размер x в два раза
размер y ”в первую очередь около двух
размеры , и только производные от объектов х и
и самих себя (Mundy 1987:
34). [15]
Манди и Свойер утверждают, что их интерпретация носит более общий характер.
потому что оно логически влечет за собой все следствия первого порядка
эмпирическая интерпретация вместе с дополнительными утверждениями второго порядка
о вселенских величинах. Более того, в их интерпретации
теория измерения становится подлинно научной теорией,
объясняющие гипотезы и проверяемые предсказания. Опираясь на это
работа, Джо Вольф (2020a) недавно предложил новый реалистический взгляд на
величин, которая опирается на репрезентативную теорию
Измерение.Согласно структуралистской теории Вольфа
количество, количественные признаки являются реляционными структурами.
В частности, атрибут является количественным, если его структура
переводы, образующие архимедову упорядоченную группу. Вольфа
Вольфа
сосредоточиться на переводах, а не на конкретных отношениях, таких как
конкатенация и упорядочение означает, что количественность может быть
реализуется несколькими способами и не ограничивается экстенсивным
структуры. Это также означает, что количество не имеет ничего
специально для работы с числами, как числовыми, так и нечисловыми
структуры могут быть количественными.
Информационно-теоретические подходы к измерению основаны на аналогии
между измерительными системами и системами связи. В простом
системы связи, сообщение (вход) кодируется в сигнал на
стороне передатчика, отправленной стороне получателя, и
затем декодируется обратно (выход). Точность передачи зависит
на особенности системы связи, а также на особенности
окружающей среды, т. е. уровень фонового шума. Аналогично, измерение
инструменты можно рассматривать как «информационные машины».
(Финкельштейн 1977), которые взаимодействуют с объектом в заданном состоянии.
(вход), закодировать это состояние во внутренний сигнал и преобразовать его
сигнал в показания (выход). Точность измерения
Точность измерения
аналогично зависит от инструмента, а также от уровня шума
в его среде. Задуманный как особый вид информации
передачи, измерение становится доступным для анализа с точки зрения
концептуальный аппарат теории информации (Хартли, 1928; Шеннон
1948 год; Шеннон и Уивер, 1949). Например, информация о том, что
чтение \(y_i\) сообщает о возникновении состояния \(x_k\)
объект можно количественно определить как \(\log \left[\frac{p(x_k \mid
y_i)}{p(x_k)}\right]\), а именно как функцию уменьшения
неопределенность состояния объекта (Финкельштейн 1975: 222; для
альтернативные формулировки см. Brillouin 1962: Ch.15; Кирпатовский
1974 год; и Мари 1999: 185).
Людвик Финкельштейн (1975, 1977) и Лука Мари (1999) предложили
возможность синтеза теории информации Шеннона-Уивера
и теория измерения. Как они утверждают, обе теории
к идее отображения: теория информации занимается отображением
между символами во входных и выходных сообщениях, а измерение
теория касается отображения между объектами и числами. Если
Если
измерение считается аналогичным манипулированию символами, тогда
Теория Шеннона-Уивера могла бы обеспечить формализацию синтаксиса
измерение, в то время как теория измерения могла бы обеспечить формализацию
его семантика.Тем не менее Мари (1999: 185) также предупреждает, что
аналогия между системами связи и измерения ограничена.
Принимая во внимание, что сообщение отправителя может быть известно с произвольной точностью
независимо от его передачи состояние объекта не может быть
известен с произвольной точностью независимо от его измерения.
Информационно-теоретические подходы к измерению изначально
разработан метрологами — специалистами в области физических измерений и
стандартизация — при небольшом участии философов.Независимо от достижений в области метрологии Бас ван Фраассен (2008 г.:
141–185) недавно предложил концепцию измерения в
какая информация играет ключевую роль. Он рассматривает измерение как составленное
двух уровней: на физическом уровне измерительная аппаратура
взаимодействует с объектом и производит чтение, например, указатель
должность. [16]
[16]
На абстрактном уровне теория фона представляет собой
возможные состояния объекта в пространстве параметров. Измерение
находит объект в подобласти этого абстрактного пространства параметров,
тем самым уменьшая диапазон возможных состояний (2008: 164 и 172).Это сокращение возможностей сводится к сбору
информацию об измеряемом объекте. Анализ Ван Фраассена
измерения отличается от теоретико-информационного счета, разработанного
в метрологии в ее явной апелляции к фоновой теории и в
тот факт, что он не обращается к символической концепции информации
разработан Шенноном и Уивером.
С начала 2000-х годов началась новая волна философских исследований.
появился, который подчеркивает взаимосвязь между измерением и
теоретическое и статистическое моделирование (Morgan 2001; Boumans 2005a,
2015 г.; Мари 2005b; Мари и Джордани, 2013 г.; Таль 2016, 2017; Паркер 2017;
Мияке 2017).Согласно модельным счетам, измерение состоит
двух уровней: (i) конкретный процесс взаимодействия между
интересующий объект, инструмент и окружающая среда; и (ii)
теоретическая и/или статистическая модель того процесса, где
«модель» обозначает абстрактное и локальное представление
строится из упрощающих предположений. Центральная цель
Центральная цель
измерение в соответствии с этим представлением состоит в том, чтобы присвоить значения одному или нескольким
интересующие параметры модели таким образом, который удовлетворяет определенным
эпистемологические требования, в частности когерентность и последовательность.
Счета на основе моделей были разработаны путем изучения измерения
практики в науках, и особенно в метрологии. Метрология,
официально определяется как «наука об измерениях и их
применение» (JCGM 2012: 2.2), является областью исследования, касающейся
с проектированием, обслуживанием и усовершенствованием средств измерений
в области естественных и технических наук. Метрологи обычно работают
в бюро стандартизации или в специализированных лабораториях,
ответственный за калибровку измерительного оборудования,
сравнение стандартов и оценка измерений
неопределенности, среди других задач.Вот только недавно
философы начали заниматься богатыми концептуальными проблемами
лежащей в основе метрологической практики, и особенно с выводами
участие в оценке и повышении точности измерений
стандарты (Chang 2004; Boumans 2005a: Глава 5, 2005b, 2007a; Frigerio
и другие. 2010 г.; Теллер 2013, 2018; Риордан 2015; Шлаудт и Хубер, 2015 г.;
2010 г.; Теллер 2013, 2018; Риордан 2015; Шлаудт и Хубер, 2015 г.;
Таль 2016а, 2018; Митчелл и др. 2017; Мёсснер и Нордманн
2017; де Куртенэ и др. 2019).
Центральным мотивом для разработки счетов на основе моделей является
попытка прояснить эпистемологические принципы, лежащие в основе
аспекты измерительной практики.Например, метрологи используют
различные методы калибровки средств измерений,
стандартизация и отслеживание единиц и оценка
неопределенности (обсуждение метрологии см. в предыдущем
раздел). Традиционные философские объяснения, такие как математические
теории измерения не уточняют допущения, выводы
моделей, доказательных оснований или критериев успеха, связанных с такими
методы. Как Фриджерио и др. (2010) утверждают, что теория измерения
плохо подходит для разъяснения этих аспектов измерения, потому что
абстрагируется от процесса измерения и фокусируется исключительно на
математические свойства весов.Напротив, основанный на модели
учетные записи считают построение масштаба просто одной из нескольких задач
участвуют в измерении, наряду с определением измеряемого
параметры, конструкция прибора и калибровка, отбор проб объекта и
подготовка, обнаружение ошибок и оценка неопределенности, среди прочего
(2010: 145–147).
7.1 Роль моделей в измерении
Согласно основанным на модели счетам, измерение включает взаимодействие
между объектом интереса («системой под
измерение»), прибор («измерительный
система») и окружение, включающее измерительную
предметы.Другие, вторичные взаимодействия также могут иметь значение для
определение результата измерения, такого как взаимодействие
между измерительным прибором и эталонами, используемыми для
его калибровка и цепочка сравнений, которые отслеживают эталон
вернуться к первичным стандартам измерений (Mari 2003: 25).
Измерение происходит путем представления этих взаимодействий набором
параметры и присвоение значений подмножеству этих параметров
(известные как «измеряемые величины») на основе результатов
взаимодействия.Когда измеряемые параметры являются числовыми, они называются
«количества». Хотя измеряемые величины не обязательно должны быть количествами,
предполагается количественный сценарий измерения, в котором
следует.
Два вида выходных данных измерений различаются на основе модели.
счета [JCGM 2012: 2.9 и 4.1; Джордани и Мари 2012: 2146; Таль
2013]:
- Показания приборов (или
«показания»): это свойства измерительного
прибор в своем конечном состоянии после процесса измерения
полный.Примерами являются цифры на дисплее, метки на множественном выборе.
анкеты и биты, хранящиеся в памяти устройства. Показания
могут быть представлены числами, но такие числа описывают состояния
инструмент, и его не следует путать с результатами измерений, которые
касаются состояний измеряемого объекта. - Результаты измерения (или «результаты»):
это утверждения о знаниях о значениях одной или нескольких величин
относятся к измеряемому объекту и обычно сопровождаются
указанием единицы измерения и масштаба и оценкой
неопределенности измерения.Например, результатом измерения может быть
выражается предложением «масса объекта a равна
20±1 грамм с вероятностью 68%».
Как подчеркивают сторонники основанных на моделях счетов, выводы из
показания прибора к результатам измерений нетривиальны и
зависит от множества теоретических и статистических предположений о
измеряемый объект, прибор, окружающая среда и
процесс калибровки. Результаты измерения часто получаются с помощью
Результаты измерения часто получаются с помощью
статистический анализ нескольких показаний, тем самым вовлекая
предположения о форме распределения показаний и
случайность эффектов окружающей среды (Боген и Вудворд, 1988:
307–310).Результаты измерений также включают поправки на
систематические эффекты, и такие поправки основаны на теоретических
предположения относительно работы прибора и его
взаимодействия с объектом и окружающей средой. Например, длина
измерения должны быть скорректированы для изменения измерения
длина стержня в зависимости от температуры, поправка, которая выводится
из теоретического уравнения теплового расширения. Систематический
поправки включают в себя собственные неопределенности, например, в
определение значений констант, и эти неопределенности
оценивается с помощью вторичных экспериментов, включающих дальнейшие теоретические
и статистические предположения.Кроме того, неопределенность, связанная с
результат измерения зависит от методов, используемых для
калибровка прибора. Калибровка требует дополнительных
Калибровка требует дополнительных
предположения о приборе, калибровочном аппарате,
измеряемая величина и свойства эталонов
(Rothbart and Slayden 1994; Franklin 1997; Baird 2004: Ch. 4; Soler et al.
др. 2013). Другой компонент неопределенности возникает из-за неопределенности
в определении измеряемой величины и называется
«дефиниционная неопределенность» (Mari and Giordani, 2013;
Грежис 2015).Наконец, измерение включает в себя фон
предположения о типе шкалы и используемой системе единиц, и эти
предположения часто связаны с более широкими теоретическими и технологическими
соображения, касающиеся определения и реализации масштабов
и единицы.
Эти различные теоретические и статистические предположения составляют основу
для построения одной или нескольких моделей процесса измерения.
В отличие от математических теорий измерения, где термин
«модель» означает теоретико-множественную структуру, которая
интерпретирует формальный язык, здесь термин «модель»
обозначает абстрактное и локальное представление целевой системы, которое
построен на упрощении
предположения. [17]
[17]
Соответствующей целевой системой в данном случае является процесс измерения,
то есть система, состоящая из измерительного прибора, объектов или
измеряемые события, окружающая среда (включая людей-операторов),
вторичные инструменты и эталоны, эволюция во времени
эти компоненты и их различные взаимодействия друг с другом.
Измерение рассматривается как набор процедур, целью которых является
последовательно присваивать значения параметрам модели на основе инструмента
показания. Таким образом, модели рассматриваются как необходимые предварительные условия для
возможность вывода результатов измерения из прибора
показаний, и как решающее значение для определения содержания измерения
результаты.Как подчеркивают сторонники модельных счетов,
показания, полученные в результате одного и того же процесса измерения, могут использоваться для
установить различные результаты измерения в зависимости от того, как
процесс измерения моделируется, например, в зависимости от того, какая среда
влияния учитываются, какие статистические допущения
используется для анализа шума, и какие приближения используются при применении
фоновая теория. Как говорит Лука Мари,
Как говорит Лука Мари,
любой результат измерения сообщает информацию, которая имеет смысл только в
в контексте метрологической модели, такая модель должна
включать спецификацию для всех объектов, которые явно или
неявно появляются в выражении результата измерения.(2003:
25)
Точно так же говорят, что модели обеспечивают необходимый контекст для
оценка различных аспектов качества результатов измерения,
включая точность, прецизионность, ошибку и неопределенность (Боуманс, 2006 г.,
2007а, 2009, 2012б; Мари 2005b).
Представления, основанные на моделях, расходятся с эмпирическими интерпретациями
теории измерения в том, что они не требуют соотношений между
результаты измерения должны быть изоморфны или гомоморфны наблюдаемым
отношения между измеряемыми предметами (Mari 2000).Верно,
по модельным счетам отношения между измеряемыми объектами
вовсе не обязательно наблюдать до их измерения (Frigerio et
др. 2010: 125). Вместо этого ключевым нормативным требованием модельного
учетных записей заключается в том, что значения параметров модели присваиваются в согласованной
способ. Критерий согласованности можно рассматривать как совокупность двух
Критерий согласованности можно рассматривать как совокупность двух
подкритерии: (i) согласованность допущений модели с соответствующими
фоновые теории или другие существенные предположения о
измеряемое количество; и (ii) объективность, т.е.д., взаимное
непротиворечивость результатов измерений при различных измерениях
инструменты, среда и
модели [18]
(Фриджерио и др., 2010; Таль, 2017а; Теллер, 2018). Первое
Подкритерий предназначен для обеспечения того, чтобы предполагаемое количество
измеряется, а второй подкритерий предназначен для обеспечения
что результаты измерения могут быть обоснованно отнесены к измеряемому
объект , а не какой-то артефакт измерения
инструмент, среда или модель.В совокупности эти два
требования гарантируют, что результаты измерений остаются в силе
независимо от конкретных предположений, связанных с их
производства, и, следовательно, зависимость измерения от контекста
результаты не угрожают их общей применимости.
7.
 2 Модели и измерения в экономике
2 Модели и измерения в экономике
Помимо их применимости к физическим измерениям, основанные на моделях
Анализы также проливают свет на измерения в экономике. Как физическое
количества, значения экономических переменных часто невозможно наблюдать
непосредственно и должно быть выведено из наблюдений, основанных на абстрактных и
идеализированные модели.Экономист девятнадцатого века Уильям Джевонс, для
Например, измеряли изменения стоимости золота, постулируя определенные
причинно-следственная связь между стоимостью золота, предложением золота и
общий уровень цен (Hoover and Dowell 2001: 155–159;
Морган 2001: 239). Как показывает Джулиан Рейсс (2001), Джевонс
измерения стали возможными благодаря использованию двух моделей:
каузально-теоретическая модель экономики, в основе которой лежит
предположение, что количество золота способно увеличить или
низкие цены; и статистическая модель данных, основанная на
предположение о том, что местные колебания цен взаимно
независимы и, следовательно, компенсируют друг друга при усреднении.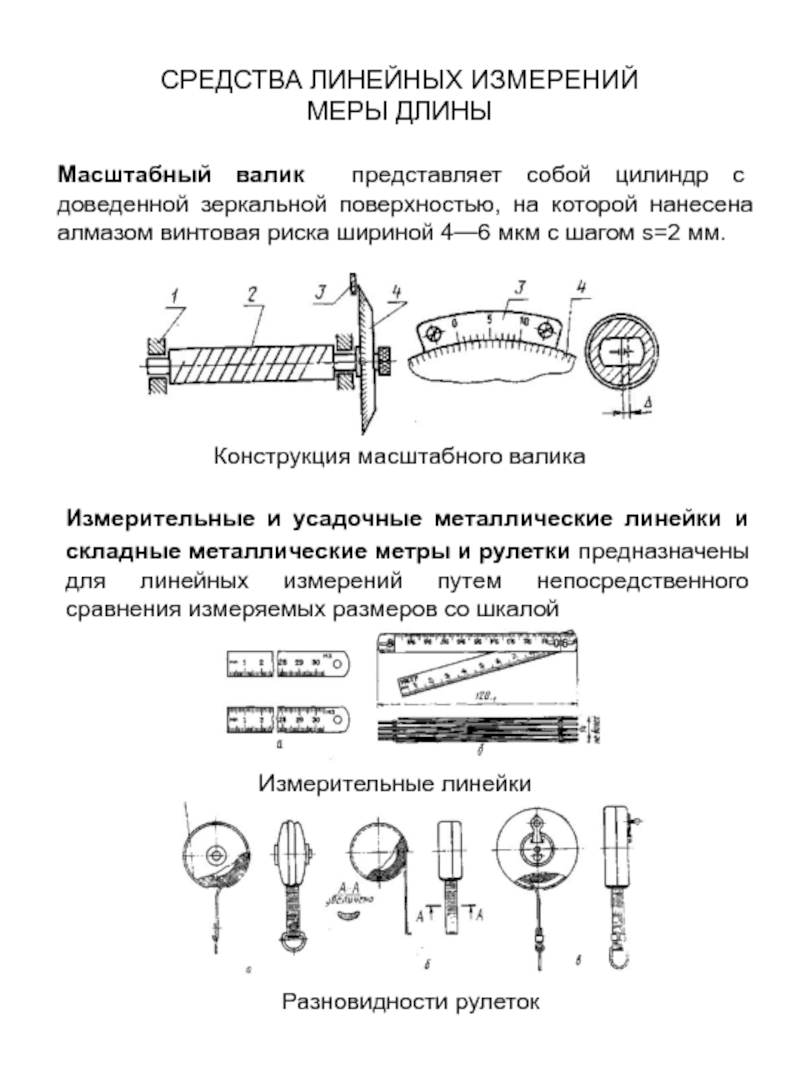 Взятый
Взятый
вместе эти модели позволили Джевонсу сделать вывод об изменении значения
золота из данных об исторических ценах различных
товары. [19]
Способы, которыми модели функционируют в экономических измерениях, привели
некоторые философы считают определенные экономические модели мерой
инструменты сами по себе, по аналогии с линейками и весами
(Боуманс, 1999, 2005с, 2006, 2007а, 2009, 2012а, 2015; Морган, 2001).
Марсель Буманс объясняет, как макроэкономисты могут изолировать
интересующая переменная от внешних воздействий путем настройки параметров в
модель макроэкономической системы.Этот метод освобождает экономистов
от невыполнимой задачи управления реальной системой. Как Боуманс
утверждает, что макроэкономические модели функционируют как измерительные инструменты в той мере, в какой
поскольку они производят инвариантные отношения между входами (показаниями) и
выходы (исходы), и поскольку эта инвариантность может быть проверена
калибровка по известным и устойчивым фактам. Когда такая модель на основе
Когда такая модель на основе
процедуры сочетаются с экспертным заключением, они могут дать
надежные измерения экономических явлений даже вне контролируемых
лабораторных условиях (Боуманс 2015: гл.5).
7.3 Психометрические модели и конструктная валидность
Еще одна область, в которой модели играют центральную роль в измерении, — это
психология. Измерение большинства психологических характеристик, таких как
интеллекта, тревоги и депрессии, не опирается на гомоморфные
отображения, поддерживаемые репрезентативной теорией
Измерение (Уилсон 2013: 3766). Вместо этого психометрическая теория опирается
преимущественно на разработке абстрактных моделей, предназначенных для
прогнозировать эффективность испытуемых в определенных задачах.Эти модели
построены из содержательных и статистических предположений о
измеряемый психологический атрибут и его отношение к каждому
задача измерения. Например, популярная теория отклика на предмет.
подход к психологическим измерениям, использует различные модели для
оценить надежность и валидность анкет. Рассмотрим
Рассмотрим
анкета, предназначенная для оценки понимания английского языка
(«способность»), предъявляя испытуемым ряд
вопросы «да/нет» («пункты»).Одна из самых простых моделей
для калибровки таких вопросников используется модель Раша (Rasch, 1960).
Эта модель предполагает прямое алгебраическое соотношение — известное
как «логарифм шансов» — между вероятностью
того, что испытуемый ответит на заданный вопрос правильно, сложность
этот конкретный предмет и способность субъекта. Новый
анкеты калибруются путем проверки соответствия между их
показания и предсказания модели Раша и назначение
уровни сложности для каждого элемента соответственно.Затем модель используется в
в сочетании с анкетой для определения уровня владения английским языком
понимание (результаты) из необработанных баллов анкеты (показания)
(Уилсон, 2013; Мари и Уилсон, 2014).
Вид статистической калибровки (или «масштабирования»)
модели Раша дают повторяемые результаты, но часто
только первый шаг к полноценному психологическому измерению.
Психологов обычно интересуют результаты измерения, а не
ради самого себя, а ради оценки некоторых основополагающих и
скрытый психологический признак, e.г., понимание английского языка.
Хорошее соответствие между ответами на вопросы и статистической моделью еще не
определить, что измеряет анкета. Процесс
установление того, что процедура измеряет предполагаемое психологическое
атрибут известен как «валидация». Один из способов проверки
психометрический инструмент предназначен для проверки различных процедур, которые
предназначены для измерения одного и того же скрытого атрибута, обеспечивают согласованное
Результаты. Такое тестирование относится к семейству методов проверки
известная как «проверка конструкции».Конструкция – это
абстрактное представление скрытого атрибута, предназначенного для
измерено, и
отражает гипотезу […] о том, что разнообразие поведения будет
коррелируют друг с другом в исследованиях индивидуальных различий и/или
будут аналогичным образом затронуты экспериментальными манипуляциями.(обычно
и Бернстайн 1994: 85)
Конструкции обозначаются переменными в модели, которая предсказывает, какие
будут наблюдаться корреляции между показаниями различных
меры, если они действительно являются мерами одного и того же атрибута.Такой
модели включают существенные предположения об атрибуте, в том числе
его внутреннюю структуру и его отношения с другими атрибутами, а также
статистические предположения о корреляции между различными показателями
(Campbell & Fiske 1959; Nunnally & Bernstein 1994: Ch. 3;
Ангнер 2008).
В последние годы философы науки все чаще
интересуется психометрией и концепцией валидности. Одна дискуссия
касается онтологического статуса латентных психологических атрибутов.Денни Борсбум выступал против операционализма в отношении латентных
атрибутов и в пользу определения валидности таким образом, чтобы
охватывает реализм: «тест действителен для измерения атрибута, если
и только если а) атрибут существует и б) вариации в
атрибут причинно порождает вариации результатов
процедура измерения» (2005: 150; см. также Hood 2009, 2013;
также Hood 2009, 2013;
Праздник 2020). Элина Вессонен защитила умеренную форму
операционализм о психологических атрибутах, и утверждал, что
умеренный операционализм совместим с осторожным типом реализма
(2019).Другая недавняя дискуссия посвящена обоснованию
построить процедуры проверки. По словам Анны Александровой,
конструктивная валидация в принципе является оправданной методологией, поскольку
поскольку он устанавливает согласованность с теоретическими предположениями и
фоновые знания о скрытом атрибуте. Тем не менее, Александрова
отмечает, что на практике психометристы, намеревающиеся измерить
счастье и благополучие часто избегают теоретизировать об этих
конструкты, а вместо этого апеллируют к народным верованиям респондентов.Это противоречит цели валидации конструкции и превращает ее в
узкотехническое упражнение (Александрова и Хайброн 2016; Александрова
2017; см. также McClimans et al. 2017).
Более фундаментальная критика психометрии заключается в том, что она
догматически предполагает, что психологические атрибуты могут быть
количественно. Мичелл (2000, 2004b) утверждает, что психометрия
Мичелл (2000, 2004b) утверждает, что психометрия
не предприняли серьезных попыток проверить, являются ли атрибуты, на которые они претендуют,
для измерения имеют количественную структуру, и вместо этого приняли чрезмерно
расплывчатое представление об измерении, скрывающее это пренебрежение.В
ответ, Борсбум и Мелленберг (2004) утверждают, что ответ на предмет
Теория обеспечивает вероятностные тесты количественной оценки
атрибуты. Психометристы, которые строят статистическую модель
сначала предположить, что атрибут является количественным, а затем
подвергнуть модель эмпирическим испытаниям. В случае успеха такие испытания
обеспечить косвенное подтверждение исходной гипотезы, т.е. от
показывая, что атрибут имеет аддитивную совместную структуру (см.
также Вессонен 2020).
Несколько ученых указали на сходство между моделями способов
используются для стандартизации измеримых величин в естественных и
социальные науки.Например, Марк Уилсон (2013) утверждает, что
психометрические модели можно рассматривать как инструменты для построения
эталоны измерений в том же смысле, что и «измерительные
стандарт», используемый метрологами. Другие выразили сомнения в
Другие выразили сомнения в
целесообразность и желательность брать пример
естественных наук при стандартизации конструкций в социальных науках.
Нэнси Картрайт и Роза Ранхардт (2014) обсуждают
Концепции Ballung, термин, который они заимствовали у Отто Нейрата.
для обозначения понятий с нечеткой и контекстно-зависимой областью применения.Примеры
концепций Баллунга являются раса, бедность, социальная изоляция и
качество докторских программ. Такие понятия слишком многогранны, чтобы
измеряется одной метрикой без потери смысла и должен
представлены либо матрицей индексов, либо несколькими различными
меры в зависимости от того, какие цели и ценности играют роль (см. также
Брэдберн, Картрайт и Фуллер, 2016 г., другие интернет-ресурсы).
Александрова (2008) отмечает, что этические соображения
вопросы об обоснованности мер благосостояния не менее
соображения воспроизводимости.Такие этические соображения
зависит от контекста и может применяться только частично. В подобном
вене, Лия Макклиманс (2010) утверждает, что единообразие не всегда
подходящая цель для разработки вопросников, так как открытость
вопросов часто и неизбежны, и желательны для получения
актуальная информация от
предметы. [20]
[20]
Переплетение этических и эпистемологических соображений
особенно ясно, когда психометрические опросники используются в медицинских
условия для оценки самочувствия и психического здоровья пациентов.В таком
случаи, небольшие изменения в дизайне анкеты или анализа
его результатов может причинить значительный вред или пользу пациентам
(Макклиманс, 2017; Стегенга, 2018, глава 8). Эти выводы подчеркивают
ценностный и контекстуальный характер измерения умственных и
социальные явления.
Разработка счетов на основе моделей обсуждалась в предыдущем
раздел является частью более крупного «эпистемического поворота» в
философия измерения, возникшая в начале 2000-х гг.Скорее
чем подчеркивание математических основ, метафизики или
семантика измерения, философская работа в последние годы тяготеет к
сосредоточить внимание на предпосылках и логических выводах, вовлеченных в
конкретные практики измерения, а также исторические, социальные и
материальные размеры измерения. Философское изучение этих
тематика получила название «эпистемология
измерения» (Mari 2003, 2005a; Leplège 2003; Tal 2017a).
В самом широком смысле эпистемология измерения — это изучение
отношения между измерением и знанием.Центральные темы
которые подпадают под сферу эпистемологии измерения, включают
условия, при которых измерение производит знание; в
содержание, объем, обоснование и пределы таких знаний; в
причины, по которым конкретные методологии измерения и
стандартизация преуспела или потерпела неудачу в поддержке конкретных знаний
претензии, а также взаимосвязь между измерением и другими
познавательная деятельность, такая как наблюдение, теоретизирование,
экспериментирование, моделирование и расчет.Преследуя эти
целей, философы опираются на работы историков и
социологи науки, которые исследовали измерение
практики в течение более длительного периода (Wise and Smith 1986; Latour 1987: Ch.
6; Шаффер 1992; Портер 1995, 2007; Мудрый 1995; Ольха 2002; Галисон
2003 г.; Добрый день, 2004 г.; Crease 2011), а также по истории и
философия научных экспериментов (Harré 1981; Hacking
1983 год; Франклин 1986; Картрайт 1999). Следующие подразделы
Следующие подразделы
рассмотреть некоторые из тем, обсуждаемых в этой растущей группе
литература.
8.1 Стандартизация и научный прогресс
Тема, которая привлекла значительное внимание философов в
последние годы является выбор и совершенствование измерения
стандарты. Вообще говоря, стандартизировать понятие количества означает
предписывают определенный способ применения этого понятия к
конкретный
подробности. [21]
Стандартизировать измерительный прибор означает оценить, насколько хорошо
результаты измерения этим прибором соответствуют заданному режиму
применение соответствующей концепции. [22]
Соответственно термин «эталон» имеет по крайней мере
два значения: с одной стороны, оно обычно используется для обозначения
абстрактные правила и определения, регулирующие использование количества
понятия, такие как определение метра. С другой стороны,
Термин «стандарт измерения» также обычно используется для обозначения
к конкретным артефактам и процедурам, которые считаются образцовыми
применение концепции количества, такой как металлический стержень, который
служил эталоном до 1960 года. Эта двойственность смысла
Эта двойственность смысла
отражает двойственную природу стандартизации, которая включает в себя как
абстрактный и конкретный аспекты.
В
Раздел 4
было отмечено, что стандартизация предполагает выбор среди нетривиальных
альтернативы, такие как выбор среди различных термометрических жидкостей
или среди различных способов маркировки равной продолжительности. Эти варианты
нетривиальны в том смысле, что они влияют на то,
температурные (или временные) интервалы считаются равными и, следовательно, влияют на
независимо от того, содержат ли утверждения естественного права термин
«температура» (или «время») получаются верными.Обращение к теории, чтобы решить, какой стандарт является более точным, было бы
круговой, так как теория не может быть однозначно применена к
сведения до выбора эталона. Этот
циркулярность по-разному называли «проблемой
координация» (van Fraassen 2008: Ch. 5) и «проблема
номического измерения» (Chang 2004: Ch. 2). Как уже упоминалось,
конвенционалисты попытались избежать цикличности, постулировав a
априорных утверждений , известных как «координационные
определения», которые должны были связать количественные термины с
специальные измерительные операции. Недостатком этого решения является то, что
Недостатком этого решения является то, что
предполагается, что выбор эталона измерения произволен и
статичны, тогда как в реальной практике стандарты измерения, как правило,
выбираются на основе эмпирических соображений и в конечном итоге улучшаются
или заменены стандартами, которые считаются более точными.
Новое направление в литературе по проблеме координации появилось в
последние годы, в первую очередь из работ Хасок Чанга
(2001, 2004, 2007; Барвич и Чанг, 2015) и Бас ван Фраассен (2008:
Ч.5; 2009, 2012; см. также Падовани 2015, 2017; Мишель 2019). Эти
работы используют историко-когерентистский подход к проблеме.
Вместо того, чтобы пытаться полностью избежать проблемы цикличности,
как и их предшественники, они намеревались показать, что циркулярность
не порочный. Чанг утверждает, что построение концепции количества и
стандартизация его измерения являются взаимозависимыми и повторяющимися задачами.
Каждая «эпистемическая итерация» в истории
стандартизация уважает существующие традиции и в то же время
исправляя их (Chang 2004: Ch. 5). Донаучная концепция
5). Донаучная концепция
температура, например, была связана с грубым и неоднозначным
способы упорядочения объектов от горячего к холодному. Термоскопы и
в конечном итоге термометры, помогли изменить первоначальную концепцию и сделали
это точнее. С каждой такой итерацией понятие количества было
пересогласованы с более стабильным набором стандартов, который, в свою очередь,
позволили более точно проверить теоретические предсказания,
облегчение последующего развития теории и построения
более стабильных стандартов и так далее.
Как этот процесс позволяет избежать порочного круга, становится ясно, если мы посмотрим
на него либо «сверху», т. е. задним числом, учитывая наши
современные научные знания, или «изнутри», глядя
на исторические события в их первоначальном контексте (ван Фраассен
2008: 122). С любой точки зрения координация успешна, потому что
это увеличивает согласованность между элементами теории и инструментами.
Вопросы «что считать измерением количества
х ? и «что такое количество X ?»,
хотя и неразрешимы независимо друг от друга, адресуются
вместе в процессе взаимного совершенствования. Только когда человек принимает
Только когда человек принимает
фундаменталистский взгляд и попытки найти отправную точку для
координация, свободная от предположения, что этот исторический процесс
ошибочно кажется, что ему не хватает эпистемологического обоснования (2008: 137).
Новая литература по координации смещает акцент
обсуждение от определений количественных терминов до
реализаций этих определений. Говоря метрологическим жаргоном,
«реализация» — это физический инструмент или процедура,
приблизительно удовлетворяет данному определению (см.JCGM 2012: 5.1).
Примерами метрологических реализаций являются официальные прототипы
килограмм и цезиевые фонтанные часы, используемые для стандартизации
второй. Недавние исследования показывают, что методы, используемые для проектирования,
поддерживать и сравнивать реализации имеют прямое отношение к
практическое применение понятий количества, единицы и масштаба, не менее
чем определения этих понятий (Riordan 2015; Tal 2016). То
связь между определением и реализациями единицы становится
особенно сложно, когда определение сформулировано в теоретических терминах. Некоторые из основных единиц Международной системы (СИ) —
Некоторые из основных единиц Международной системы (СИ) —
в том числе метр, килограмм, ампер, кельвин и моль — не
больше определяется ссылкой на любой конкретный тип физической системы,
а зафиксировав числовое значение фундаментальной физической константы.
Например, в 2019 году килограмм был переопределен как единица массы.
так что численное значение постоянной Планка точно
6,62607015 × 10 -34 кг м 2 с -1
(BIPM 2019:131). Понимание килограмма в соответствии с этим определением является
сильно теоретизированная задача.Изучение практической реализации
такие единицы пролили новый свет на развивающиеся отношения между
измерение и теория (Таль, 2018; де Куртенэ и др., 2019; Вольф
2020б).
8.2 Теоретическая нагрузка измерения
Как уже говорилось выше (разделы
7
и
8.1),
теория и измерение взаимозависимы как исторически, так и
концептуально. С исторической стороны развитие теории и
измерение происходит посредством итеративных и взаимных уточнений. На
На
концептуальная сторона, спецификация форм процедур измерения
эмпирическое содержание теоретических понятий, а теория дает
систематическая интерпретация показаний измерения
инструменты.Эта взаимозависимость измерения и теории может показаться
как угроза доказательной роли, которую измерение должно
играть в научном предприятии. В конце концов, результаты измерений
считается способным проверять теоретические гипотезы, и это, кажется,
требуют некоторой степени независимости измерения от теории. Этот
угроза особенно очевидна, когда теоретическая гипотеза
уже предполагается как часть модели измерения
инструмент. Чтобы привести пример из работы Франклина и соавт.(1989: 230):
На первый взгляд может показаться, что существует порочный цикл, если
использовать ртутный термометр для измерения температуры
объекты как часть эксперимента, чтобы проверить, расширяются ли объекты
по мере повышения их температуры.
Тем не менее, Франклин и др. сделать вывод, что цикличность не
беспощадный. Ртутный термометр может быть откалиброван по другому
Ртутный термометр может быть откалиброван по другому
термометр, принцип действия которого не предполагает закона
теплового расширения, например газовый термометр постоянного объема,
тем самым установив надежность ртутного термометра на
независимые основания.Говоря более широко, в контексте
локальной проверки гипотез угроза циркулярности обычно может быть
избегать, обращаясь к другим видам инструментов и другим частям
теория.
Другой вид беспокойства по поводу доказательной функции измерения
возникает в глобальном масштабе, когда проверка целых теорий
обеспокоенный. Как утверждает Томас Кун (1961), научные теории
обычно принимаются задолго до появления количественных методов их проверки
становятся доступными. Надежность вновь введенного измерения
методы обычно проверяются на соответствие предсказаниям теории
а не наоборот.По словам Куна, «…
Дорога от научного закона к научному измерению редко бывает
путешествовал в обратном направлении» (1961: 189). Например,
Закон Дальтона, который гласит, что веса элементов в
химические соединения связаны друг с другом целыми числами
пропорции, изначально противоречащие некоторым из наиболее известных
измерения таких пропорций. Это только если предположить
Это только если предположить
Закон Дальтона, который последующие химики-экспериментаторы смогли
исправить и улучшить свои методы измерения (1961: 173).Следовательно,
Куна, функция измерения в физических науках
не проверять теорию, а применять ее во все возрастающей степени и
точность и, в конечном счете, позволить устойчивым аномалиям всплыть на поверхность
это ускорит следующий кризис и научную революцию. Примечание
что Кун не утверждает, что измерение не имеет доказательной роли для
играть в науку. Вместо этого он утверждает, что измерения не могут проверить
теория изолированно, а только в сравнении с какой-либо альтернативной теорией
это предлагается в попытке объяснить обнаруженные аномалии
за счет все более точных измерений (для наглядного обсуждения
тезиса Куна см. Hacking 1983: 243–245).
Традиционные рассуждения о перегруженности теорией, как у Куна, были
на фоне логических позитивистов
Различие между теоретическим и наблюдательным языком. То
Теоретичность измерений была правильно воспринята как угроза
возможность четкого разграничения между двумя языками.
Современных дискуссий, напротив, больше нет.
перегруженность теорией как эпистемологическая угроза, но принимать как должное
что некоторый уровень теоретической нагрузки является предпосылкой для измерений
иметь какую-либо доказательную силу.Без какого-то минимального основного
предположения об измеряемой величине, такие как ее аменабельность
манипулированию и его отношениям к другим величинам, было бы
невозможно интерпретировать показания измерительных приборов и
следовательно, невозможно установить доказательную значимость тех
показания. На это уже обращал внимание Пьер Дюэм (1906:
153–6; см. также Carrier 1994: 9–19). Кроме того,
современные авторы подчеркивают, что теоретические предположения играют
решающую роль в исправлении ошибок измерения и оценке
неопределенности измерения.Действительно, процедуры физических измерений
становятся на точнее на , когда модель, лежащая в их основе,
деидеализированный, процесс, который включает в себя увеличение теоретического
богатство модели (Tal 2011).
Признание того, что теория имеет решающее значение для гарантии
доказательная надежность измерения обращает внимание на
«задача наблюдательного заземления», которая является обратной
вызов традиционной угрозе перегруженности теорией (Tal 2016b).
Задача состоит в том, чтобы указать, какую роль наблюдение играет в
измерение, и в частности, какая связь с наблюдением
необходимо и/или достаточно, чтобы измерения могли играть
доказательную роль в науках.Эта проблема особенно очевидна, когда
одна попытка объяснить растущее использование вычислительных
методы выполнения задач, которые традиционно выполнялись
измерительные приборы. В роли Маргарет Моррисон (2009) и Венди Паркер
(2017) утверждают, что есть случаи, когда надежная количественная информация
собирается о целевой системе с помощью компьютера
симуляции, но таким образом, который удовлетворяет некоторым основным
требования к измерению, такие как эмпирическое обоснование и
взгляд назад (см. также Lusk 2016).Такая информация не зависит
по сигналам, передаваемым от интересующего объекта к
инструмента, а на использовании теоретических и статистических моделей для
обрабатывать эмпирические данные о связанных объектах. Например, данные
Например, данные
методы ассимиляции обычно используются для оценки прошлых атмосферных
температуры в регионах, где недоступны показания термометров.
Некоторые методы делают это путем подгонки вычислительной модели
поведение атмосферы в сочетании с доступными данными из
близлежащие регионы и модельный прогноз условий на момент
наблюдение (Паркер, 2017).Затем эти оценки используются в различных
способами, в том числе в качестве данных для оценки перспективных климатических моделей.
Независимо от того, называют ли эти оценки
«измерения», они бросают вызов идее о том, что производство
требуется надежное количественное свидетельство о состоянии объекта
наблюдая за этим объектом, как бы широко ни понимали термин
«наблюдение». [23]
8.3 Точность и прецизионность
Два ключевых аспекта надежности результатов измерения:
тщательность и точность.Рассмотрим серию повторных взвешиваний
измерения, выполненные на конкретном объекте равноплечим
остаток средств. С реалистической точки зрения, основанной на ошибках,
результаты этих измерений точны если они близки
истинному значению измеряемой величины — в нашем случае
истинное отношение веса объекта к выбранному
единица — и точное , если они близки друг к другу. Ан
Ан
аналогия, часто цитируемая для пояснения основанного на ошибках различия, заключается в том, что
стрелы, выпущенные в цель, с точностью, аналогичной близости
попадания в яблочко и точность, аналогичную герметичности
распространения попаданий (см.JCGM 2012: 2.13 и 2.15, Теллер 2013: 192).
Хотя и интуитивно понятный, основанный на ошибках способ провести различие
вызывает эпистемологическую трудность. Принято считать, что
точные истинные значения большинства величин, представляющих интерес для науки,
непознаваемы, по крайней мере, когда эти величины измеряются на непрерывном
напольные весы. Если это предположение принимается, то точность, с которой
измеряемые величины не могут быть известны с точностью, а только
оцениваются путем сравнения неточных измерений друг с другом.И все еще
неясно, почему сходимость среди неточных измерений должна быть
воспринимается как указание на истину. Ведь измерения могут быть
страдают от общего предубеждения, которое предотвращает их индивидуальные неточности
от компенсации друг друга при усреднении. В отсутствие
В отсутствие
когнитивный доступ к истинным ценностям, как оценивается измерение
точность возможна?
Отвечая на этот вопрос, философы извлекли пользу из изучения
различных смыслах термина «точность измерения».
используется практикующими учеными.По крайней мере, пять различных органов чувств
выделяют: метафизический, эпистемологический, операциональный, сравнительный и
прагматичный (Tal 2011: 1084–1085). В частности, эпистемологический или
«основанный на неопределенности» смысл термина метафизически
нейтральна и не предполагает существования истинных ценностей. Вместо,
точность результата измерения принимается за близость
согласие между значениями, разумно приписываемыми данной величине
имеющиеся эмпирические данные и фоновые знания (ср. JCGM 2012: 2.13
Заметка 3; Джордани и Мари, 2012 г .; де Куртенэ и Грежи
2017).Таким образом, точность измерения можно оценить по
установление устойчивости среди последствий моделей, представляющих
различные процессы измерения (Бассо, 2017; Таль, 2017б; Бокулич, 2020;
Стейли 2020).
Согласно концепции, основанной на неопределенности, неточность представляет собой особый вид
неточности. Например, погрешность измерения веса
широта разброса значений, обоснованно приписываемых
вес предмета с учетом показаний весов и
имеющиеся базовые знания о том, как работают весы и
используются стандартные веса.Неточность этих измерений
компонент погрешности, возникающий из-за неконтролируемых изменений в
показания баланса по повторным испытаниям. Другие источники
неточность помимо неточности включает несовершенные поправки к
систематические ошибки, неточно известные физические константы и расплывчатые
определения измеряемых величин, среди прочего (см.
Раздел 7.1).
Пол Теллер (2018) выдвигает другое возражение против основанного на ошибках
понятие точности измерений. Он возражает против предположения, что
называет «реализмом точности измерений», согласно которому
измеряемые величины имеют в действительности определенные значения.Теллер утверждает
что это предположение неверно, поскольку оно касается величин
обычно измеряется в физике, потому что всякое указание определенного
значений (или диапазонов значений) для таких величин предполагает идеализацию и
следовательно, не может относиться ни к чему в действительности. Например, концепция
Например, концепция
обычно понимают под фразой «скорость звука в
воздух» включает в себя множество неявных идеализаций, касающихся
однородность химического состава воздуха, температуры и
давление, а также стабильность единиц измерения.Удаление
эти идеализации полностью потребовали бы добавления бесконечного количества
подробно к каждой спецификации. Как утверждает Теллер, точность измерения
следует понимать как полезную идеализацию, а именно как
концепция, которая позволяет ученым оценивать согласованность и согласованность
среди результатов измерения как будто языковое выражение
эти результаты цеплялись за что угодно в мире. Точность
также идеализированная концепция, основанная на открытом и
неопределенная спецификация того, что считается повторением измерения
при «тех же» обстоятельствах (Teller 2013: 194).
Измерение — Энциклопедия Нового Света
Детская бутылочка, которая измеряет объем в трех распространенных системах измерения: имперской (Великобритания), обычной в США и метрической.
Измерение — это оценка величины некоторого атрибута объекта, такого как его длина или вес, относительно стандартной единицы измерения. Измерение обычно включает использование измерительного инструмента, такого как линейка или весы, которые откалиброваны для сравнения объекта с некоторым эталоном, таким как метр или килограмм.
Метрология – это научное исследование измерений. В теории измерений измерение — это наблюдение, которое уменьшает неопределенность, выраженную в виде количества. В качестве глагола измерение делает такие наблюдения. [1] Включает оценку физической величины, такой как расстояние, энергия, температура или время. Это может также включать такие вещи, как оценка взглядов, ценностей и восприятия в ходе опросов или проверка способностей отдельных лиц.
Для измерения часто требуется инструмент, разработанный и откалиброванный для этой цели, такой как термометр, спидометр, весы или вольтметр.Опросы и тесты также называются «инструментами измерения» в таких областях, как академическое тестирование, тестирование способностей и опросы избирателей.
Измерение имеет фундаментальное значение в науке; это одна из вещей, которая отличает науку от лженауки. Легко придумать теорию о природе, трудно придумать научную теорию, предсказывающую измерения с большой точностью. Измерение также необходимо в промышленности, торговле, машиностроении, строительстве, производстве, фармацевтическом производстве и электронике.
История
Слово «измерение» происходит от греческого «метрон», означающего ограниченную пропорцию. Это также имеет общий корень со словами «луна» и «месяц», возможно, поскольку луна и другие астрономические объекты были одними из первых методов измерения времени.
История измерений является темой истории науки и техники. Метр (или метр) был стандартизирован как единица длины после Французской революции и с тех пор принят во всем мире.
Когда вы можете измерить то, о чем говорите, и выразить это в цифрах, вы кое-что об этом знаете; но когда вы не можете выразить это числом, ваши знания скудны и неудовлетворительны; это может быть началом знания, но вы едва ли продвинулись в своих мыслях к состоянию науки.
Лорд Кельвин
Точность и неопределенность измерения
Измерения всегда содержат ошибки и, следовательно, погрешности.На самом деле уменьшение — не обязательно устранение — неопределенности занимает центральное место в концепции измерения. Часто предполагается, что ошибки измерения нормально распределены относительно истинного значения измеряемой величины. Согласно этому предположению, каждое измерение состоит из трех компонентов: оценка, граница ошибки и вероятность того, что фактическая величина находится в пределах границы ошибки оценки. Например, измерение длины доски может дать результат 2,53 метра плюс-минус 0.01 метр, с вероятностью 99 процентов.
Исходное состояние неопределенности перед любыми наблюдениями необходимо оценить при использовании статистических методов, основанных на априорных знаниях (байесовские методы). Это можно сделать с помощью калиброванной оценки вероятности.
В науке, где решающее значение имеет точное измерение, измерение понимается как состоящее из трех частей: во-первых, само измерение, во-вторых, предел погрешности и, в-третьих, уровень достоверности, т. е. вероятность того, что фактическое свойство физический объект находится в пределах погрешности.Например, мы можем измерить длину объекта как 2,34 метра плюс-минус 0,01 метра с уровнем достоверности 95 процентов.
е. вероятность того, что фактическое свойство физический объект находится в пределах погрешности.Например, мы можем измерить длину объекта как 2,34 метра плюс-минус 0,01 метра с уровнем достоверности 95 процентов.
Стандарты
Законы, регулирующие измерения, изначально были разработаны для предотвращения мошенничества. Однако единицы измерения в настоящее время обычно определяются на научной основе и устанавливаются международными договорами. В Соединенных Штатах Национальный институт стандартов и технологий (NIST), подразделение Министерства торговли США, регулирует коммерческие измерения.
Агрегаты и системы
Определение или спецификация точных эталонов измерения включает в себя две ключевые особенности, которые очевидны в Международной системе единиц (СИ). В частности, в этой системе определение каждой из базовых единиц относится к конкретным эмпирическим условиям и, за исключением килограмма, также к другим количественным признакам. Каждая производная единица СИ , производная от , определяется исключительно с точки зрения отношения, включающего ее и другие единицы; например, единица скорости измеряется через длину: 1 м/с (метр в секунду). Поскольку производные единицы относятся к базовым единицам, спецификация эмпирических условий является подразумеваемым компонентом определения всех единиц.
Поскольку производные единицы относятся к базовым единицам, спецификация эмпирических условий является подразумеваемым компонентом определения всех единиц.
Имперская система
До того, как единицы СИ получили широкое распространение во всем мире, британская система английских единиц, а затем имперские единицы использовались в Великобритании, Содружестве и Соединенных Штатах. Эта система стала известна как обычные единицы измерения США в Соединенных Штатах и до сих пор используется там и в нескольких странах Карибского бассейна.Эти различные системы измерения иногда назывались системами фут-фунт-секунда после имперских единиц измерения расстояния, веса и времени. Многие имперские единицы по-прежнему используются в Великобритании, несмотря на то, что она официально перешла на систему СИ. Дорожные знаки по-прежнему указываются в милях, ярдах, милях в час и так далее, люди склонны измерять свой рост в футах и дюймах, а молоко продается в пинтах, и это лишь несколько примеров.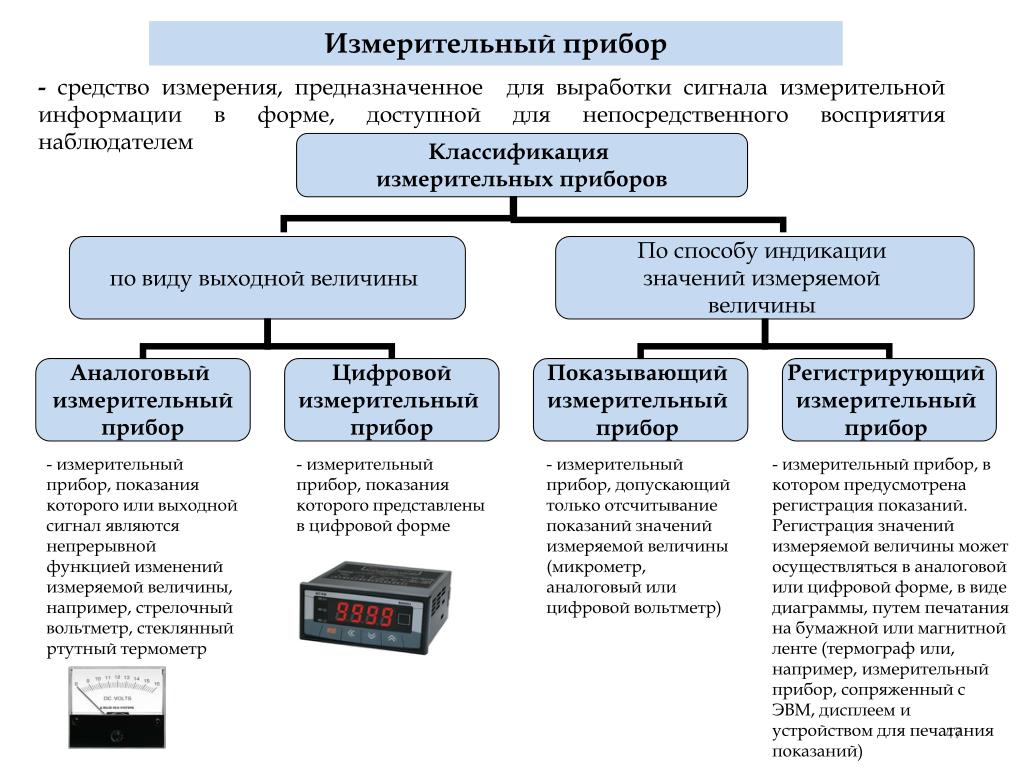 Имперские единицы используются во многих других местах, например, во многих странах Содружества, которые считаются метрическими, площадь земли измеряется в акрах, а площадь пола в квадратных футах, особенно для коммерческих операций (а не для государственной статистики).Точно так же имперские галлоны используются во многих странах, которые считаются метрическими на заправочных станциях, например, в Объединенных Арабских Эмиратах.
Имперские единицы используются во многих других местах, например, во многих странах Содружества, которые считаются метрическими, площадь земли измеряется в акрах, а площадь пола в квадратных футах, особенно для коммерческих операций (а не для государственной статистики).Точно так же имперские галлоны используются во многих странах, которые считаются метрическими на заправочных станциях, например, в Объединенных Арабских Эмиратах.
Метрическая система
Метрическая система представляет собой десятичную систему измерения, основанную на метре и грамме. Он существует в нескольких вариантах с различным выбором базовых единиц, хотя это не влияет на его повседневное использование. С 1960-х годов Международная система единиц (СИ), поясняемая ниже, является международно признанной стандартной метрической системой.Метрические единицы массы, длины и электричества широко используются во всем мире как в повседневных, так и в научных целях.
Основным преимуществом метрической системы является то, что она имеет единую базовую единицу для каждой физической величины. Все остальные единицы представляют собой степени десяти или кратные десяти этой базовой единицы. Преобразование единиц измерения всегда просто, потому что они будут в соотношении десять, сто, тысяча и т. д. Все длины и расстояния, например, измеряются в метрах, или тысячных долях метра (миллиметрах), или тысячах метров ( км) и так далее.Нет большого количества различных единиц с разными коэффициентами преобразования, как в имперской системе (например, дюймы, футы, ярды, сажени, стержни). Кратные и дольные связаны с основной единицей коэффициентами степени десяти, так что можно преобразовать, просто переместив десятичный знак: 1,234 метра составляет 1234 миллиметра или 0,001234 километра. Использование дробей, таких как две пятых (2/5) метра, не запрещено, но редко.
Все остальные единицы представляют собой степени десяти или кратные десяти этой базовой единицы. Преобразование единиц измерения всегда просто, потому что они будут в соотношении десять, сто, тысяча и т. д. Все длины и расстояния, например, измеряются в метрах, или тысячных долях метра (миллиметрах), или тысячах метров ( км) и так далее.Нет большого количества различных единиц с разными коэффициентами преобразования, как в имперской системе (например, дюймы, футы, ярды, сажени, стержни). Кратные и дольные связаны с основной единицей коэффициентами степени десяти, так что можно преобразовать, просто переместив десятичный знак: 1,234 метра составляет 1234 миллиметра или 0,001234 километра. Использование дробей, таких как две пятых (2/5) метра, не запрещено, но редко.
СИ
Международная система единиц (сокращенно SI от названия французского языка Système International d’Unités ) является современной, пересмотренной формой метрической системы. Это наиболее широко используемая в мире система единиц как в повседневной торговле, так и в науке. СИ была разработана в 1960 году на основе системы метр-килограмм-секунда (МКС), а не системы сантиметр-грамм-секунда (СГС), которая, в свою очередь, имела множество вариантов. При своем развитии СИ также ввела несколько единиц с новыми названиями, которые ранее не входили в метрическую систему.
Это наиболее широко используемая в мире система единиц как в повседневной торговле, так и в науке. СИ была разработана в 1960 году на основе системы метр-килограмм-секунда (МКС), а не системы сантиметр-грамм-секунда (СГС), которая, в свою очередь, имела множество вариантов. При своем развитии СИ также ввела несколько единиц с новыми названиями, которые ранее не входили в метрическую систему.
Существует два типа единиц СИ: базовые и производные. Базовыми единицами являются простые измерения времени, длины, массы, температуры, количества вещества, электрического тока и силы света.Производные единицы состоят из основных единиц, например, плотность составляет кг/м 3 .
Преобразование префиксов
Система SI позволяет легко производить умножение при переключении между единицами, имеющими одинаковую основу, но разные префиксы. Например, (dec, deci = 10) (Cent, centi = 100) (kilo = 1000) Для перевода из метров в сантиметры необходимо только количество метров умножить на 100, так как в метре 100 сантиметров. И наоборот, чтобы перейти от сантиметров к метрам, число сантиметров умножается на .01.
И наоборот, чтобы перейти от сантиметров к метрам, число сантиметров умножается на .01.
Расстояние
2-х метровая столярная линейка.
Линейка или линейка — это инструмент, используемый, например, в геометрии, техническом черчении, машиностроении и плотницком деле для измерения расстояний или проведения прямых линий. Строго говоря, линейка — это инструмент, используемый для построения прямых линий линейки , а калиброванный инструмент, используемый для определения длины, называется мерой , , однако в обычном использовании оба инструмента называются линейками , а используется специальное название линейка . для непомеченного правила.Использование слова мера, в смысле измерительного инструмента , сохранилось во фразе рулетка, инструмент, который можно использовать для измерения, но нельзя использовать для проведения прямых линий. Как видно на фотографиях на этой странице, двухметровую плотничную линейку можно сложить до длины всего 20 сантиметров, чтобы она легко поместилась в кармане, а пятиметровая рулетка легко убирается, чтобы поместиться в кармане. маленькое жилье.
маленькое жилье.
Время
Наиболее распространенными устройствами для измерения течения времени являются часы.Хронометр — это прибор для измерения времени, достаточно точный, чтобы его можно было использовать в качестве переносного эталона времени. Исторически изобретение хронометров было большим достижением в определении долготы и помощи в астрономической навигации. Самым точным прибором для измерения времени являются атомные часы.
До изобретения часов люди измеряли время с помощью песочных, солнечных и водяных часов.
Масса
Масса относится к внутреннему свойству всех материальных объектов сопротивляться изменениям их импульса. Вес, , с другой стороны, относится к направленной вниз силе, возникающей, когда масса находится в гравитационном поле. В свободном падении объекты теряют вес, но сохраняют свою массу. Имперские единицы массы включают унцию, фунт и тонну. Метрические единицы грамм и килограмм являются единицами массы.
Единица измерения веса или массы называется весами или, чаще, просто весами . Пружинные весы измеряют силу, но не массу; весы сравнивают одну массу с другой, но для работы требуется гравитационное поле.Наиболее точным инструментом для измерения веса или массы являются цифровые весы, которые также требуют гравитационного поля и не будут работать при свободном падении.
Экономика
Меры, используемые в экономике, представляют собой физические меры, меры стоимости в номинальной цене и меры стоимости в фиксированной цене. Эти меры отличаются друг от друга переменными, которые они измеряют, и переменными, исключенными из измерений. Измеряемыми переменными в экономике являются количество, качество и распределение.Исключение переменных из измерения позволяет лучше сфокусировать измерение на данной переменной, однако это означает более узкий подход.
Трудности
Поскольку точные измерения необходимы во многих областях и поскольку все измерения обязательно являются приблизительными, необходимо приложить немало усилий, чтобы сделать измерения как можно более точными. Например, рассмотрим задачу измерения времени, за которое объект падает с высоты одного метра (39 дюймов).Используя физику, можно показать, что в гравитационном поле Земли любому объекту требуется около 0,45 секунды, чтобы упасть на один метр. Однако ниже приведены лишь некоторые из источников возникающих ошибок. Во-первых, в этом расчете использовалось ускорение свободного падения 9,8 метра в секунду за секунду (32,2 фута/с²). Но это измерение не точное, а только с точностью до двух значащих цифр. Также гравитационное поле Земли незначительно меняется в зависимости от высоты над уровнем моря и других факторов.Затем вычисление 0,45 секунды включало извлечение квадратного корня, математическую операцию, которая требовала округления до некоторого количества значащих цифр, в данном случае до двух значащих цифр.
Например, рассмотрим задачу измерения времени, за которое объект падает с высоты одного метра (39 дюймов).Используя физику, можно показать, что в гравитационном поле Земли любому объекту требуется около 0,45 секунды, чтобы упасть на один метр. Однако ниже приведены лишь некоторые из источников возникающих ошибок. Во-первых, в этом расчете использовалось ускорение свободного падения 9,8 метра в секунду за секунду (32,2 фута/с²). Но это измерение не точное, а только с точностью до двух значащих цифр. Также гравитационное поле Земли незначительно меняется в зависимости от высоты над уровнем моря и других факторов.Затем вычисление 0,45 секунды включало извлечение квадратного корня, математическую операцию, которая требовала округления до некоторого количества значащих цифр, в данном случае до двух значащих цифр.
До сих пор мы рассматривали только научные источники ошибок. На практике, сбрасывая предмет с высоты метровой палки и используя секундомер для определения времени его падения, мы имеем другие источники ошибок. Первая и самая распространенная — это простая небрежность. Затем возникает проблема определения точного времени, когда объект высвобождается, и точного времени, когда он падает на землю.Существует также проблема, заключающаяся в том, что и измерение высоты, и измерение времени содержат некоторую погрешность. Наконец, существует проблема сопротивления воздуха.
Первая и самая распространенная — это простая небрежность. Затем возникает проблема определения точного времени, когда объект высвобождается, и точного времени, когда он падает на землю.Существует также проблема, заключающаяся в том, что и измерение высоты, и измерение времени содержат некоторую погрешность. Наконец, существует проблема сопротивления воздуха.
Научные измерения должны выполняться с большой осторожностью, чтобы устранить как можно больше ошибок и сохранить реалистичность оценок ошибок.
Определения и теории
Классическое разрешение
В классическом определении, которое является стандартным для всех физических наук, измерение есть определение или оценка отношений величин.Количество и измерение взаимно определены: количественные признаки — это те, которые возможно измерить, по крайней мере в принципе. Классическая концепция количества восходит к Джону Уоллису и Исааку Ньютону и была предвосхищена в «Элементах» Евклида. [2]
Теория представлений
В репрезентативной теории измерение определяется как «соотношение чисел с сущностями, не являющимися числами». Самая сильная форма репрезентативной теории также известна как аддитивное совместное измерение.В этой форме репрезентативной теории числа присваиваются на основе соответствий или сходств между структурой числовых систем и структурой качественных систем. Свойство является количественным, если такое структурное сходство может быть установлено. В более слабых формах репрезентативной теории, таких как те, которые имплицитно представлены в работах Стэнли Смита Стивенса, числа нужно присваивать только в соответствии с правилом.
Самая сильная форма репрезентативной теории также известна как аддитивное совместное измерение.В этой форме репрезентативной теории числа присваиваются на основе соответствий или сходств между структурой числовых систем и структурой качественных систем. Свойство является количественным, если такое структурное сходство может быть установлено. В более слабых формах репрезентативной теории, таких как те, которые имплицитно представлены в работах Стэнли Смита Стивенса, числа нужно присваивать только в соответствии с правилом.
Концепция измерения часто ошибочно понимается как простое присвоение значения, но можно присвоить значение способом, который не является измерением с точки зрения требований аддитивного совместного измерения.Можно присвоить значение росту человека, но до тех пор, пока не будет установлено, что существует корреляция между измерениями роста и эмпирическими отношениями, это не измерение в соответствии с теорией аддитивных совместных измерений. Точно так же вычисление и присвоение произвольных значений, таких как «балансовая стоимость» актива в бухгалтерском учете, не является измерением, поскольку оно не удовлетворяет необходимым критериям.
Разное
Измерение отношений между физическими величинами является важным разделом физики.
Некоторые важные физические величины включают:
- Скорость света
- постоянная Планка
- Гравитационная постоянная
- Элементарный заряд (электрический заряд электронов, протонов и других частиц)
- Постоянная тонкой структуры
- Количество
См. также
Примечания
- ↑ Дуглас В. Хаббард. 2007. Как измерить что-либо: поиск ценности «нематериальных активов» в бизнесе. (Хобокен, Нью-Джерси: John Wiley & Sons.ISBN 978-0470110126.)
- ↑ Евклид, Томас Литтл Хит и Дана Денсмор. 2002. Элементы Евклида: все тринадцать книг в одном томе: перевод Томаса Л. Хита. (Санта-Фе, Нью-Мексико: Green Lion Press. ISBN 1888009195.)
Ссылки
Ссылки ISBN поддерживают NWE за счет реферальных сборов
- Адамс, Дэни Спенсер. 2003.
 Лабораторная математика: Справочник по измерениям, расчетам и другим количественным навыкам для использования на стенде. Колд-Спринг-Харбор, Нью-Йорк: Издательство лаборатории Колд-Спринг-Харбор. ISBN 978-0879696344.
Лабораторная математика: Справочник по измерениям, расчетам и другим количественным навыкам для использования на стенде. Колд-Спринг-Харбор, Нью-Йорк: Издательство лаборатории Колд-Спринг-Харбор. ISBN 978-0879696344.
- Bucher, Jay L. 2004. Справочник по метрологии. Милуоки, Висконсин: ASQ Quality Press. ISBN 978-0873896207.
- Кертис, Марк А. и Фрэнсис Т. Фараго. 2007. Справочник по габаритным измерениям, , 4-е изд. Нью-Йорк: Промышленная пресса. ISBN 978-0831132620.
- Кимоти, Шри Кришна. 2002. Неопределенность измерений: физико-химическая метрология: влияние и анализ. Милуоки, Висконсин: ASQ Press. ISBN 0873895355 .
- Миллс, Ян. 1993. Количества, единицы и символы в физической химии. Международный союз теоретической и прикладной химии. Оксфорд: Научные публикации Блэквелла. ISBN 0632035838 .
- Педхазур, Элазар Дж. и Лиора Педхазур Шмелкин. 1991. Измерение, проектирование и анализ: комплексный подход.
 Хиллсдейл, Нью-Джерси: Lawrence Erlbaum Associates. ISBN 0805810633.
Хиллсдейл, Нью-Джерси: Lawrence Erlbaum Associates. ISBN 0805810633.
Внешние ссылки
Все ссылки получены 11 сентября 2018 г.
| |||||||||||||||||||||
Кредиты
New World Encyclopedia писатели и редакторы переписали и дополнили статью Wikipedia
в соответствии со стандартами New World Encyclopedia . Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с надлежащим указанием авторства. Упоминание должно осуществляться в соответствии с условиями этой лицензии, которая может ссылаться как на авторов New World Encyclopedia , так и на самоотверженных добровольных участников Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:
Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с надлежащим указанием авторства. Упоминание должно осуществляться в соответствии с условиями этой лицензии, которая может ссылаться как на авторов New World Encyclopedia , так и на самоотверженных добровольных участников Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:
История этой статьи с момента ее импорта в New World Encyclopedia :
Примечание. На использование отдельных изображений, лицензированных отдельно, могут распространяться некоторые ограничения.
1. Основные понятия измерения
Глава 1. Основные понятия измерения
Прежде чем использовать статистику для анализа проблемы, необходимо преобразовать информацию о
проблема в данные. То есть вы должны установить или принять систему
То есть вы должны установить или принять систему
присвоение значений, чаще всего чисел, объектам или понятиям, которые
занимает центральное место в рассматриваемой проблеме. Это не эзотерический процесс, а
то, что люди делают каждый день. Например, когда вы покупаете что-то в
магазине цена, которую вы платите, является измерением: она присваивает номер, означающий
сумма денег, которую вы должны заплатить, чтобы купить товар.Точно так же, когда вы
наступите утром на весы в ванной, и вы увидите цифру
измерение массы тела. В зависимости от того, где вы живете, этот номер
может выражаться как в фунтах, так и в килограммах, но принцип
присвоение числа физической величине (весу) верно как в
кейс.
Данные не обязательно должны быть числовыми по своей сути, чтобы их можно было использовать в анализе. За
например, категории мужчины и
женский широко используются как в науке, так и в быту.
жизни для классификации людей, и в них нет ничего числового по своей сути.
две категории.Точно так же мы часто говорим о цветах предметов в широком смысле.
такие классы, как красный и синий , и
в этих категориях также нет ничего числового по своей сути. (Несмотря на то что
вы могли бы привести аргумент о разных длинах волн света, это не
необходимо иметь эти знания для классификации предметов по цвету.)
Такой способ мышления категориями является совершенно обычным, бытовым
опыта, и нас редко беспокоит тот факт, что разные категории
могут применяться в разных ситуациях.Например, художник может
различать цвета, такие как кармин ,
малиновый и гранатовый , тогда как
непрофессионал был бы удовлетворен, называя их всех
красный . Точно так же социолог может быть заинтересован
при сборе информации о семейном положении человека в таких терминах, как
холост — никогда не был женат , холост — разведен , и
холостой — овдовевший , тогда как кому-то другому, человеку в
любая из этих трех категорий может быть просто рассмотрена
одиночный . Дело в том, что уровень детализации, используемый в
Дело в том, что уровень детализации, используемый в
система классификации должна быть соответствующей, основанной на причинах
классификация и использование информации
ставить.
Измерение — это процесс систематического присвоения номеров объектам и их
свойства для облегчения использования математики в изучении и описании
объекты и их отношения. Некоторые виды измерений достаточно
конкретные: например, измерение веса человека в фунтах или килограммах
или его рост в футах и дюймах или в метрах.Обратите внимание, что конкретный
используемая система измерения не так важна, как тот факт, что мы применяем
последовательный набор правил: мы можем легко преобразовать вес, выраженный в
килограммов к эквивалентному весу в фунтах, например. Хотя любой
система единиц может показаться произвольной (попробуйте защитить футы и дюймы, чтобы
кто-то, кто вырос с метрической системой!), пока система имеет
последовательной связи с измеряемым свойством, мы можем использовать
результаты расчетов.
Измерение не ограничивается физическими качествами, такими как рост и
масса. Тесты для измерения абстрактных конструктов, таких как интеллект или
схоластические способности обычно используются в образовании и психологии, а
Область психометрии в значительной степени связана с развитием и
совершенствование методов исследования этих типов конструкций. Создание
то, что конкретное измерение является точным и значимым, сложнее
когда его нельзя наблюдать непосредственно. Хотя можно проверить точность
по одной шкале путем сравнения результатов с результатами, полученными по другой шкале
известна своей точностью, и вы можете видеть очевидную пользу от знания
вес предмета, ситуация сложнее, если вас интересует
при измерении такого конструкта, как интеллект.В этом случае не только
не существует общепринятых мер интеллекта, против которых вы
можно сравнить новую меру, нет даже общего согласия о том, что
значит «интеллект». Иными словами, трудно сказать,
уверенность в том, каков чей-либо реальный интеллект, потому что нет
определенным способом измерить его, и на самом деле может даже не быть общего
соглашение о том, что это такое. Эти вопросы особенно актуальны для
Эти вопросы особенно актуальны для
социальные науки и образование, где большое количество исследований сосредоточено на
просто такие абстрактные понятия.
Статистики обычно различают четыре типа или уровня
измерения, и одни и те же термины могут относиться к данным, измеренным на каждом уровне.
Уровни измерения различаются как с точки зрения смысла
числа, используемые в системе измерения и в типах статистических
процедуры, которые могут быть надлежащим образом применены к данным, измеренным в каждом
уровень.
При номинальных данных , как следует из названия, числа функционируют как
имя или метка и не имеют числового значения.За
Например, вы можете создать переменную для пола, которая принимает значение
1, если человек мужчина, и 0, если человек женщина. 0 и 1 имеют
не имеют числового значения, а функционируют просто как метки так же, как
вы можете записать значения как M или F. Однако исследователи часто предпочитают
системы числового кодирования по нескольким причинам. Во-первых, это может упростить
Во-первых, это может упростить
анализ данных, потому что некоторые статистические пакеты не принимают
нечисловые значения для использования в определенных процедурах.(Следовательно, любые данные, закодированные
нечисловые значения должны быть перекодированы перед анализом.) Во-вторых, кодирование
с числами обходит некоторые проблемы при вводе данных, такие как конфликт
между прописными и строчными буквами (к компьютеру,
M отличается от m ,
но человек, выполняющий ввод данных, может рассматривать эти два символа как
эквивалент).
Номинальные данные не ограничиваются двумя категориями. Например, если
вы изучали взаимосвязь между многолетним опытом и
зарплаты у бейсболистов, вы можете классифицировать игроков по
их основное положение, используя традиционную систему, в которой 1
назначены питчерам, 2 — кэтчерам, 3 — игрокам первой базы и т. д.
на.
Если вы не можете решить, номинальные у вас данные или какие-то другие
уровне измерения, задайте себе этот вопрос: сделать цифры
присвоенные этим данным представляют некоторое качество, такое, что более высокое значение
указывает, что объект имеет больше этого качества, чем более низкое значение?
Рассмотрим пример кодирования пола, так что 0 означает женский пол, а 1
означает мужчина. Есть ли какое-то свойство гендерности, которым обладают мужчины?
Есть ли какое-то свойство гендерности, которым обладают мужчины?
больше, чем женщины? Явно нет, и схема кодирования тоже сработает.
если бы женщины были закодированы как 1, а мужчины как 0.Тот же принцип применяется в
пример с бейсболом: бейсбольного качества не бывает
аутфилдеры имеют больше, чем кувшины. Цифры просто для удобства
способ обозначить предметы в исследовании, и самый важный момент заключается в том, что
каждой позиции присваивается отдельное значение. Другое название номинального
данные категориальные данные, ссылаясь на факт
что измерения помещают объекты в категории (мужские или женские,
ловец или игрок с первой базы), а не измерять какое-то внутреннее качество
в них.Глава 5
обсуждает методы анализа, подходящие для этого типа данных, и
некоторые из методов, описанных в главе 13 по непараметрической статистике,
также подходит для категорийных данных.
Когда данные могут принимать только два значения, как в примере мужчина/женщина, их также можно
называется двоичными данными .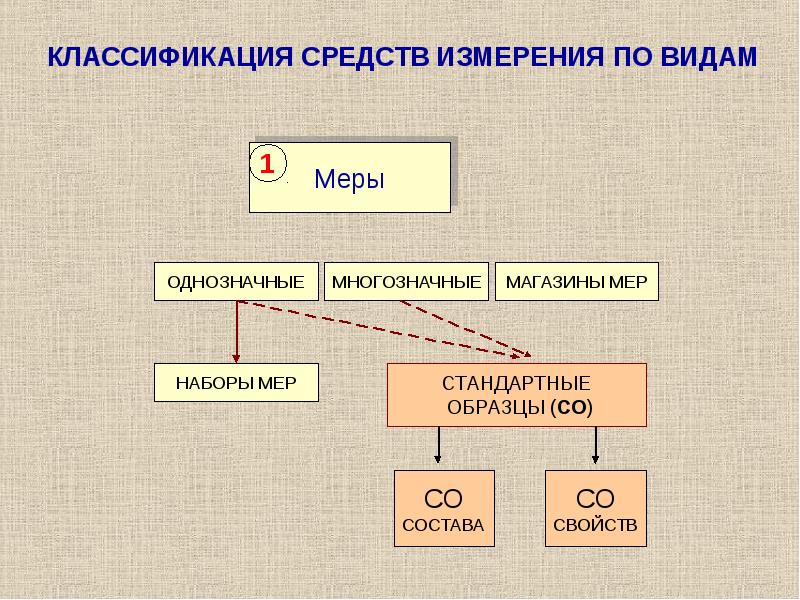 Этот тип данных настолько распространен
Этот тип данных настолько распространен
что для его изучения разработаны специальные методики, в том числе
логистическая регрессия (обсуждается в главе 11), которая
применения во многих областях.Многие медицинские статистические данные, такие как шансы
коэффициент и коэффициент риска (обсуждается в главе 15), были разработаны
для описания взаимосвязи между двумя бинарными переменными, потому что бинарные
переменные так часто встречаются в медицинских исследованиях.
Порядковые данные относятся к данным, которые имеют некоторый значимый порядок , поэтому
что более высокие значения представляют больше некоторых характеристик, чем более низкие
ценности. Например, в медицинской практике обычно описывают ожоги.
по их степени, которая характеризует величину повреждения тканей, вызванного
ожог.Ожог первой степени характеризуется покраснением кожи,
незначительная боль и повреждение только эпидермиса (внешнего слоя кожи).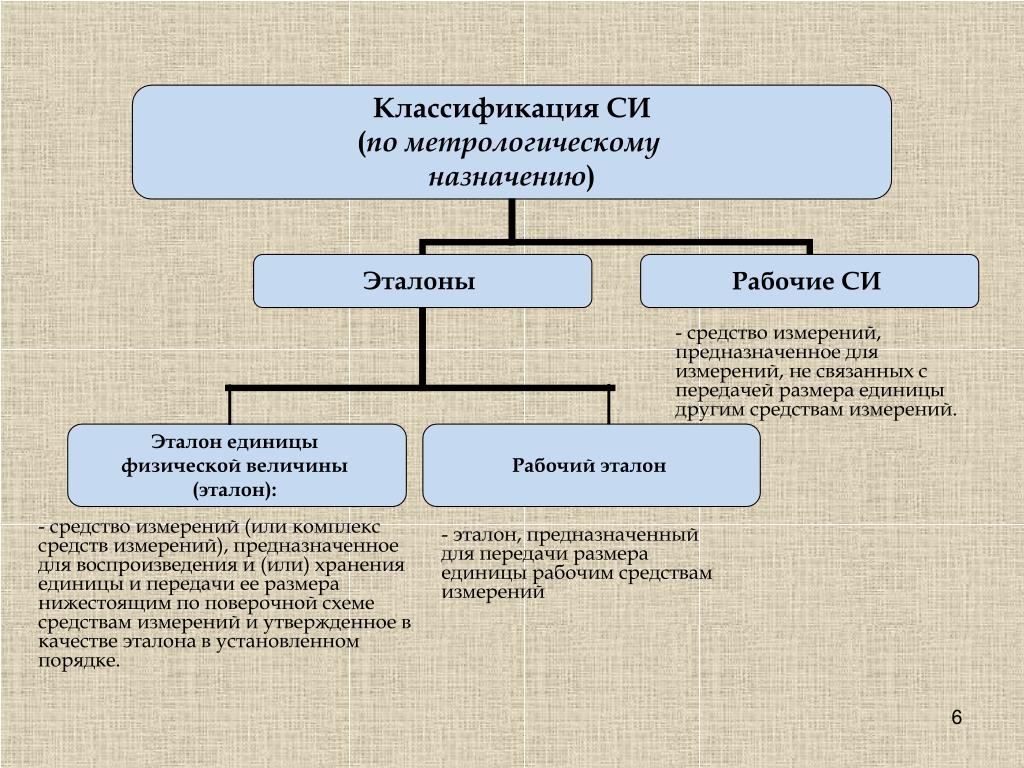 А
А
ожог второй степени включает образование пузырей и затрагивает поверхностные
слой дермы (слой кожи между эпидермисом и
подкожные ткани), а ожог третьей степени распространяется через
дермы и характеризуется обугливанием кожи и, возможно,
разрушение нервных окончаний. Эти категории могут быть ранжированы в
логический порядок: ожоги первой степени наименее серьезны с точки зрения
повреждение тканей, ожоги второй степени более серьезные и ожоги третьей степени
самый серьезный.Однако там
не является метрикой, аналогичной линейке или шкале для количественной оценки того, насколько велико
расстояние между категориями равно, и невозможно определить,
разница между ожогами первой и второй степени такая же, как и у
Разница между ожогами второй и третьей степени.
Многие порядковые шкалы включают ранги. Например, кандидаты
прием на работу может ранжироваться отделом кадров в порядке
желательность в качестве нового сотрудника. Этот рейтинг говорит вам, кто является предпочтительным
Этот рейтинг говорит вам, кто является предпочтительным
кандидат, второй по предпочтениям и так далее, но не говорит вам
действительно ли первый и второй кандидаты очень похожи друг на друга
другой или первый кандидат намного предпочтительнее, чем
второй.Вы также можете ранжировать страны мира в порядке их
населения, создавая осмысленный порядок, ничего не говоря о
была ли, скажем, разница между 30-й и 31-й странами
аналогично тому, что между 31-й и 32-й странами. Используемые числа
для измерения с порядковыми данными имеют большее значение, чем те, которые используются в
номинальные данные, и многие статистические методы были разработаны для
в полной мере использовать информацию, содержащуюся в заказе, в то же время не
предполагая любые другие свойства весов.Например, это
подходит для вычисления медианы (центрального значения) порядковых данных, но
не среднее, потому что предполагает равные промежутки и требует деления,
который требует данных на уровне отношений.
Интервал данных имеет значимый порядок и качество равно
интервалы между измерениями, представляющие равные изменения в
количество того, что измеряется. Самый распространенный пример
интервальный уровень измерения – температурная шкала Фаренгейта.Если вы описываете температуру по шкале Фаренгейта, разница
от 10 градусов до 25 градусов (разница в 15 градусов)
представляет такое же количество изменения температуры, как разница
от 60 до 75 градусов. Сложение и вычитание подходят для
интервальные шкалы, потому что разница в 10 градусов представляет один и тот же
величина изменения температуры по всей шкале. Тем не менее
Шкала Фаренгейта не имеет естественной нулевой точки, потому что 0 на шкале Фаренгейта
масштаб не представляет отсутствие температуры, а просто местоположение
относительно других температур.Умножение и деление не
подходит для интервальных данных: нет математического смысла в
утверждение, что 80 градусов в два раза горячее, чем 40 градусов, например
(хотя справедливо сказать, что 80 градусов на 40 градусов горячее, чем
40 градусов). Интервальные шкалы — редкость, и думать трудно
Интервальные шкалы — редкость, и думать трудно
общего примера, отличного от шкалы Фаренгейта. По этой причине,
термин «интервальные данные» иногда используется для описания как интервальных, так и
данные отношения (обсуждается в следующем разделе).
Отношение Данные обладают всеми качествами интервальных данных (значащий порядок, равенство
интервалы) и естественный нуль. Многие физические измерения
данные соотношения: например, рост, вес и возраст соответствуют требованиям. Так же
доход: вы, безусловно, можете заработать 0 долларов в год или иметь 0 долларов в
ваш банковский счет, а это означает отсутствие денег. С участием
данные на уровне отношения, уместно умножать и делить, а также
складывать и вычитать; имеет смысл сказать, что кто-то со 100 долларами имеет дважды
столько же денег, сколько у человека с 50 долларами или у человека в возрасте 30 лет.
в 3 раза старше человека, которому 10 лет.
Следует отметить, что хотя многие физические измерения
на уровне отношения большинство психологических измерений являются порядковыми. Это
Это
особенно верно в отношении мер стоимости или предпочтения, которые часто
измеряется по шкале Лайкерта. Например, человек может быть представлен
заявлением (например, «Федеральное правительство должно увеличить помощь
образование») и попросили выбрать из упорядоченного набора ответов (например,
полностью согласен, согласен, нет мнения, не согласен, категорически не согласен).Эти
вариантам выбора иногда присваиваются номера (например, 1 — полностью согласен, 2 — согласен,
д.), и это иногда создает у людей впечатление, что это
подходит для применения методов интервала или отношения (например, вычисление
означает, что включает в себя деление и, следовательно, является методом отношения) к
такие данные. Это правильно? Не с точки зрения А.
статистик, но иногда приходится идти на поводу у босса
а не то, что вы считаете истинным в абсолютном выражении.
Непрерывные и дискретные данные
Другое важное различие состоит в том, что между непрерывными и
дискретных данных. Непрерывные данные могут принимать любое значение
Непрерывные данные могут принимать любое значение
или любое значение в диапазоне. Большинство данных, измеренных по интервалу и отношению
шкалы, отличные от основанных на счете, непрерывны: например,
вес, рост, расстояние и доход непрерывны.
В ходе анализа данных и построения моделей исследователи
иногда перекодируйте непрерывные данные в категории или более крупные блоки.За
Например, вес может быть указан в фунтах, но анализироваться в 10-фунтовых единицах.
приращения или возраст, записанный в годах, но проанализированный с точки зрения
категории 0–17 , 18–65 и
старше 65 . Со статистической точки зрения существует
нет абсолютной точки, в которой данные становятся непрерывными или дискретными для
целей использования конкретных аналитических методов (и это стоит
помня о том, что если вы записываете возраст в годах, вы все равно производите впечатление
дискретные категории непрерывной переменной). Различные эмпирические правила
Различные эмпирические правила
Были предложены. Например, некоторые исследователи говорят, что когда
переменная имеет 10 или более категорий (или, альтернативно, 16 или более категорий).
категории), его можно смело анализировать как непрерывное. это решение
должно быть сделано на основе контекста, информированного обычными стандартами и
практики вашей конкретной дисциплины и типа анализа
предложенный.
Дискретные переменные могут принимать только определенные значения, и
являются четкими границами между этими значениями.Как говорится в старой шутке, вы можете
иметь 2 детей или 3 детей, но не 2,37 детей, поэтому «количество
детей» является дискретной переменной. В самом деле, любая переменная, основанная на
подсчет является дискретным, независимо от того, считаете ли вы количество книг
купленных в течение года, или количество посещений дородового ухода, совершенных в течение года.
беременность. Данные, измеренные на номинальной шкале, всегда дискретны, т. к.
к.
двоичные и ранговые данные.
Люди, только начинающие изучать какую-либо область, часто думают, что трудности
исследования покоятся в первую очередь на статистическом анализе, поэтому они сосредотачивают свои
усилия по изучению математических формул и компьютерного программирования
методы проведения статистических расчетов.Однако одна серьезная проблема
в исследованиях имеет очень мало общего ни с математикой, ни со статистикой
и все, что связано со знанием вашей области обучения и мышления
тщательно через практические проблемы измерения. Это проблема
операционализация , что означает процесс
указание того, как понятие будет определяться и измеряться.
Операционализация всегда необходима, когда интересующее качество
нельзя измерить напрямую.Яркий пример — интеллект. Там
невозможно измерить интеллект напрямую, поэтому вместо такого
прямое измерение, мы принимаем то, что можем измерить, например
оценка на тесте IQ. Точно так же нет прямого способа измерить
Точно так же нет прямого способа измерить
«готовность к стихийным бедствиям» для города, но мы можем
концепции путем создания контрольного списка задач, которые должны быть выполнены и
присвоение каждому городу оценки готовности к стихийным бедствиям на основе количества
выполненных задач и качества или тщательности выполнения.Для
В третьем примере предположим, что вы хотите измерить количество физических
деятельность, выполняемая отдельными субъектами в исследовании. Если у вас нет
возможность напрямую отслеживать их поведение во время упражнений, вы можете
ввести в действие «количество физической активности» как количество, указанное на
заполняется анкетой или записывается в дневник.
Поскольку многие качества, изучаемые в социальных науках,
абстрактно, операционализация является общей темой обсуждения в тех
поля.Однако он применим и во многих других областях. За
Например, конечные цели медицинской профессии включают сокращение
смертность (смерть) и уменьшение бремени болезней и страданий.
Смертность легко поддается проверке и количественной оценке, но часто слишком прямолинейна.
инструмент, чтобы быть полезным, поскольку это, к счастью, редкий результат для
большинство болезней. «Бремя болезни» и «страдание», с другой стороны,
концепции, которые можно использовать для определения соответствующих результатов для многих
исследования, но которые не имеют прямых средств измерения и поэтому должны
быть введена в действие.Примеры операционализации бремени болезни
включать измерение уровня вируса в кровотоке у пациентов с
СПИД и измерение размера опухоли у больных раком. Уменьшился
уровни страданий или улучшение качества жизни могут быть операционализированы
как более высокая самооценка здоровья
государство, более высокий балл по инструменту опроса, предназначенному для измерения качества
жизни, улучшение настроения, измеряемое личным
интервью или снижение количества морфина, запрашиваемого для обезболивания
рельеф.
Некоторые утверждают, что измерение даже таких физических величин, как
длина требует операционализации, потому что существуют разные способы
измерять даже конкретные свойства, такие как длина. (Правитель может быть
соответствующий инструмент в одних случаях, микрометр в других.)
Даже если вы согласитесь с этим, кажется ясным, что проблема
операционализации гораздо больше в гуманитарных науках, когда
объекты или качества, представляющие интерес, часто не могут быть измерены
напрямую.
Термин косвенное измерение относится к процессу замены одного измерения на
Другая. Хотя решение о косвенных измерениях можно рассматривать как
подкласс операционализации, в этой книге он будет рассматриваться как отдельный
тема. Наиболее распространенное использование прокси-измерения заключается в замене
измерение, которое является недорогим и легко доступным для другого
измерение, которое было бы более сложным или дорогостоящим, если не невозможным,
собирать. Другой пример — сбор информации об одном человеке.
Другой пример — сбор информации об одном человеке.
попросив другого, например, попросив родителя оценить
состояние настроения.
В качестве простого примера прокси-измерения рассмотрим некоторые
Методы, используемые сотрудниками полиции для оценки трезвости лиц
пока в поле. Не имея портативной медицинской лаборатории, офицер не может
измерить содержание алкоголя в крови водителя непосредственно, чтобы определить,
водитель находится в состоянии алкогольного опьянения. Вместо этого офицер может полагаться на
наблюдаемые признаки, связанные с пьянством, простые полевые тесты, которые
хорошо коррелируют с содержанием алкоголя в крови, выдыхаемым
тест на алкоголь, или все это.Наблюдательные признаки алкоголя
интоксикация включает запах алкоголя изо рта, невнятную речь и
покрасневшая кожа. Полевые тесты, используемые для быстрой оценки алкогольного опьянения
обычно требуют, чтобы субъекты выполняли такие задачи, как стояние на одном
ногу или слежение за движущимся объектом глазами. Алкотестер тест
Алкотестер тест
измеряет количество алкоголя в выдыхаемом воздухе. Ни одна из этих оценок
методы обеспечивают прямую проверку количества алкоголя в крови,
но они принимаются как разумные приближения, быстрые и
легко управлять в полевых условиях.
Чтобы посмотреть на другое распространенное использование прокси-измерения, рассмотрим
различные методы, используемые в Соединенных Штатах для оценки качества
медицинское обслуживание, предоставляемое больницами и врачами. Это сложно для
подумайте о прямом способе измерения качества медицинской помощи, за исключением, возможно,
непосредственно наблюдая за оказываемой помощью и оценивая ее в отношении
общепринятые стандарты (хотя вы также можете утверждать, что измерение
участие в таком процессе оценки все равно будет
операционализация абстрактного понятия «качество медицинской помощи»).Внедрение такого метода оценки было бы непомерно дорогим,
будет полагаться на подготовку большой группы оценщиков и на их
согласованности и было бы нарушением права пациентов на неприкосновенность частной жизни. А
А
вместо этого принятое решение состоит в измерении процессов, которые
Предполагается, что это отражает более высокое качество медицинской помощи: например,
антитабачное консультирование было надлежащим образом предоставлено во время визита в офис или
были ли назначены соответствующие лекарства сразу после
больной был госпитализирован.
Прокси-измерения наиболее полезны, если помимо
относительно легко получить, они являются хорошим индикатором истинной направленности
интерес. Например, при правильном выполнении предписанных процессов
медицинская помощь при конкретном лечении тесно связана с хорошим
результаты пациента для этого состояния, и если они плохие или отсутствуют
выполнение этих процессов тесно связано с плохим состоянием пациента.
результаты, то выполнение этих процессов может быть полезным прокси для
качество.Если этой тесной связи не существует, то полезность
прокси-измерений менее надежен. Никакой математический тест не
Никакой математический тест не
сказать вам, является ли один показатель хорошим показателем для другого, хотя
вычислительная статистика, такая как корреляции или хи-квадраты между
меры могут помочь оценить этот вопрос. Кроме того, прокси-измерения
могут создавать свои трудности. Возьмем пример оценки
медицинской помощи с точки зрения проводимых процедур, этот метод предполагает, что
можно определить, не зная отдельных случаев, что
представляет собой надлежащее лечение, и что имеются записи,
содержать информацию, необходимую для определения того, какие процедуры были
выполненный.Как и многие другие проблемы измерения, выбор хорошего прокси
измерения является предметом суждения, основанного на знании
предметная область, обычная практика в рассматриваемой области и общие
смысл.
Мы можем с уверенностью предположить, что очень немногие измерения, если таковые имеются, абсолютно точны. Это
верно не только потому, что измерения производятся и записываются людьми
но также и потому, что процесс измерения часто включает присвоение
дискретные числа в непрерывный мир. Одна проблема теории измерения
Одна проблема теории измерения
представляет собой концептуализацию и количественную оценку степени ошибки, присутствующей в
определенный набор измерений и оценка источников и последствий
этой ошибки.
Классическая теория измерения рассматривает любое измерение или
наблюдаемая оценка, состоящая из двух частей: истинная оценка
( T ) и ошибка ( E ). Это
выражается следующей формулой:
X = T +
E
, где X — наблюдаемое измерение,
T — истинная оценка, а E —
Ошибка. Например, весы в ванной могут измерять чей-то вес.
как 120 фунтов, когда истинный вес этого человека составляет 118 фунтов, а ошибка
2 фунта из-за неточности весов.Это было бы
выражается с помощью предыдущей формулы как:
120 = 118 + 2
, что представляет собой просто математическое равенство, выражающее отношение
среди трех компонентов. Однако и T и
E — гипотетические конструкции. В реальном мире мы
В реальном мире мы
редко знают точное значение истинной оценки и поэтому не могут знать
точное значение оценки ошибки. Большая часть процесса
измерение включает в себя оценку обеих величин и максимизацию истинного
компонента при минимизации ошибок.Например, если вы взяли несколько
измерения массы тела одного человека за короткий период (чтобы его
можно предположить, что истинный вес оставался постоянным), используя недавно
калиброванная шкала, вы можете принять среднее значение всех этих измерений
в качестве хорошей оценки истинного веса этого человека. Вы могли бы тогда
рассмотрите разницу между этим средним значением и каждым отдельным измерением
как ошибка из-за процесса измерения, например, небольшая неисправность
в весах или неточность техника в чтении и записи
Результаты.
Случайная и систематическая ошибка
Поскольку мы живем в реальном мире, а не в платоновской вселенной, мы предполагаем
что все измерения содержат некоторую погрешность. Однако не все ошибки
созданы равными, и мы можем научиться жить с случайными
ошибка , делая все возможное, чтобы избежать
систематическая ошибка . Случайная ошибка — это ошибка из-за
шанс: у него нет определенного шаблона, и предполагается, что он компенсирует себя
при повторных измерениях.Например, ошибка оценивается числом
Предполагается, что измерения одного и того же объекта имеют нулевое среднее значение.
Следовательно, если кого-то взвешивают 10 раз подряд на одном и том же
шкале, вы можете заметить небольшие различия в возвращаемом вам числе:
некоторые будут выше, чем истинное значение, а некоторые будут ниже.
Предполагая, что истинный вес составляет 120 фунтов, возможно, первое измерение
вернет наблюдаемый вес 119 фунтов (включая ошибку -1
фунт), второй наблюдаемый вес 122 фунта (для ошибки +2
фунтов), третий наблюдаемый вес 118.5 фунтов (ошибка −1,5
фунтов) и так далее. Если весы точны и единственная ошибка
случайно, средняя ошибка по многим испытаниям будет равна 0, а средняя
наблюдаемый вес будет 120 фунтов. Вы можете стремиться уменьшить сумму
случайной ошибки, используя более точные инструменты, тренируя
техников, чтобы использовать их правильно, и так далее, но вы не можете ожидать,
полностью исключить случайную ошибку.
Предполагается, что к случайной ошибке применяются два других условия:
не связанный с истинной оценкой, и компонент ошибки одного измерения
не связан с компонентом ошибки любого другого измерения.Первое
условие означает, что значение составляющей ошибки любого измерения
не связано со значением истинной оценки для этого измерения. За
Например, если вы измерите вес ряда людей, чьи
истинные веса различаются, вы не ожидаете, что компонент ошибки каждого
измерения, чтобы иметь какое-либо отношение к истинному весу каждого человека.
Это означает, что, например, компонент ошибки не должен
систематически быть больше, когда истинная оценка (фактическая
вес) больше.Второе условие означает, что составляющая ошибки
каждой оценки независима и не связана с компонентом ошибки для
любой другой балл. Например, в серии измерений закономерность
размер компонента ошибки не должен увеличиваться со временем, поэтому
что более поздние измерения имеют большие ошибки или ошибки в последовательном
направлении относительно предыдущих измерений. Первое требование
иногда выражается, говоря, что соотношение истинного и ошибочного
баллов равно 0, тогда как второй иногда выражается, говоря, что
корреляция компонентов ошибки равна 0 (корреляция обсуждается
более подробно в главе 7).
Напротив, систематическая ошибка имеет наблюдаемую закономерность, а не
случайно, и часто имеет причину или причины, которые могут быть идентифицированы
и исправлено. Например, весы могут быть неправильно откалиброваны.
показать результат, который на 5 фунтов больше истинного веса, поэтому среднее значение
несколько измерений человека, чей истинный вес составляет 120 фунтов,
быть 125 фунтов, а не 120. Систематическая ошибка также может быть связана с человеческим фактором.
факторы: возможно, техник считывает показания весов с
под таким углом, чтобы она видела, что игла регистрируется выше, чем на самом деле
указание.Если закономерность обнаружена с систематической ошибкой, для
Например, измерения дрейфуют со временем все выше (поэтому ошибка
компоненты случайны в начале эксперимента, но позже
постоянно высоки), это полезная информация, потому что мы можем
вмешаться и перекалибровать весы. Было приложено много усилий
потрачены на выявление источников систематических ошибок и разработку методов для
выявлять и устранять их: это обсуждается далее в следующем
раздел Смещение измерения.
Существует много способов присвоить данным номера или категории, и не все из них
одинаково полезно. Два стандарта, которые мы обычно используем для оценки методов
измерения (например, опрос или тест)
надежность и достоверность .
В идеале мы хотели бы, чтобы каждый метод, который мы используем, был надежным и действительным.
На самом деле эти качества не абсолютны, а зависят от степени
и часто зависят от обстоятельств. Например, опрос, который очень
надежный при использовании с демографическими группами может быть ненадежным при использовании
с другой группой.По этой причине вместо обсуждения
надежность и валидность как абсолюты, часто полезнее оценивать
насколько действителен и надежен метод измерения для конкретной цели
и приемлемы ли определенные уровни надежности и валидности
в конкретном контексте. Надежность и валидность также обсуждаются в
Глава 18 в контексте дизайна исследования и
в главе 16 в
контекст педагогического и психологического тестирования.
Надежность относится к тому, насколько последовательными или воспроизводимыми являются измерения.Например, если мы дадим
один и тот же человек дважды сдавал один и тот же тест, будут ли баллы
одинаково в обоих случаях? Если мы обучим трех человек пользоваться рейтингом
шкала, предназначенная для измерения качества социального взаимодействия между
отдельных лиц, затем показать каждому из них один и тот же фильм о группе людей
взаимодействия и попросите их оценить продемонстрированное социальное взаимодействие,
будут ли их рейтинги одинаковыми? Если у нас техник весит одинаково
часть 10 раз с использованием одного и того же прибора, будут ли измерения
каждый раз похожи? В каждом случае, если ответ да, мы можем сказать,
тест, шкала или оценщик надежны.
Большая часть теории надежности была разработана в области
педагогической психологии, и по этой причине меры надежности
часто описывается с точки зрения оценки надежности тестов.
Однако соображения надежности не ограничиваются образовательными
тестирование; те же концепции применимы ко многим другим типам измерений,
включая опросы, опросы и поведенческие рейтинги.
Обсуждение в этой главе останется на базовом уровне.Информация о расчете конкретных показателей надежности
более подробно обсуждается в главе 16 в контексте
теория теста. Многие меры надежности опираются на
коэффициент корреляции (также называемый просто
корреляция ), которая подробно обсуждается в главе 7, поэтому начиная
статистики, возможно, захотят сосредоточиться на логике надежности и
достоверность и оставить детали их оценки до тех пор, пока они не будут
освоил понятие коэффициента корреляции.
Существует три основных подхода к измерению надежности, каждый из которых
полезны в определенных контекстах, и каждый из них имеет определенные преимущества и
недостатки:
Многократная надежность
Многократная надежность
Внутренняя согласованность надежность
иногда называется тест-ретест надежности ,
относится к тому, насколько одинаково тест или шкала работает при повторении
администрация.По этой причине его иногда называют индексом.
временная стабильность , что означает стабильность во времени.
Например, вы можете попросить одного и того же человека провести два психологических эксперимента.
оценка состояния пациента на основе видеозаписи интервью с
оценки, проведенные с интервалом в две недели, и сравните результаты. Для этого
тип надежности, чтобы иметь смысл, вы должны предположить, что количество
измеряемый объект не изменился, отсюда и использование той же видеозаписи.
интервью, а не отдельные живые интервью с пациентом, чей
психологическое состояние могло измениться за двухнедельный период.Многократная надежность не является подходящей мерой для изменчивых
качества, такие как состояние настроения, или если качество или количество
измеренное могло измениться за время между двумя измерениями
(например, знание студентом предмета, которым он активно занимается)
изучение). Распространенный метод оценки множественных случаев
надежность заключается в вычислении коэффициента корреляции между оценками
от каждого случая тестирования; это называется коэффициент
стабильности .Несколько форм —
надежность (также называется
параллельный — формирует надежность )
относится к тому, насколько разные версии теста или анкеты
выполнить при измерении одного и того же объекта. Распространенный тип множественных форм
надежность половинная надежность , в которой
создается пул предметов, считающихся однородными, затем половина предметов
распределяются на форму А и половину на форму В. Если две (или более) формы
испытания проводятся одним и тем же людям в одно и то же время,
корреляция между баллами, полученными по каждой форме, является оценкой
множественной надежности.Эту корреляцию иногда называют
коэффициент эквивалентности . Множественные формы
надежность особенно важна для стандартизированных тестов, которые существуют
в нескольких версиях. Например, различные формы SAT
(Тест на академические способности, используемый для измерения академических способностей среди
студенты, поступающие в американские колледжи и университеты) калибруются
поэтому полученные баллы эквивалентны независимо от того, какая форма
студент берет.Надежность внутренней согласованности
относится к тому, насколько хорошо элементы, из которых состоит инструмент (для
Например, тест или опрос) отражают один и тот же конструкт.Чтобы сказать это
с другой стороны, надежность внутренней согласованности измеряет, насколько
предметы на инструменте измеряют одно и то же. в отличие
надежность в нескольких формах и в нескольких случаях, внутренняя непротиворечивость
надежность можно оценить, применяя один инструмент на
единственный случай. Надежность внутренней непротиворечивости является более сложной
количество для измерения, чем несколько случаев или параллельные формы
надежность, и для ее оценки разработано несколько методов;
они более подробно обсуждаются в главе 16.Однако все
эти методы зависят, прежде всего, от межпредметной корреляции, которая
то есть соотношение каждого пункта шкалы или теста друг с другом
пункт. Если такие корреляции высоки, это интерпретируется как свидетельство
что элементы измеряют одно и то же, а различные статистические данные
используемые для измерения надежности внутренней согласованности, будут высокими. Если
межпредметные корреляции низкие или непоследовательные, внутренние
статистика достоверности непротиворечивости будет ниже, и это
интерпретируется как свидетельство того, что предметы не измеряются одинаково
вещь.Две простые меры внутренней согласованности наиболее полезны для тестов, состоящих из нескольких
предметы, охватывающие одну и ту же тему, одинаковой сложности, и это будет
оценивается как совокупность: 90 008 средних межпредметных
корреляция и средний элемент-сумма
корреляция . Чтобы рассчитать среднюю корреляцию между элементами,
вы находите корреляцию между каждой парой элементов и берете среднее
всех этих соотношений. Для расчета средней суммы товара
корреляции, вы создаете общий балл, складывая баллы по каждому
отдельный элемент на шкале, а затем вычислить корреляцию каждого
пункт с итогом.Средняя корреляция элементов и суммы — это среднее значение
этих корреляций между отдельными пунктами и общим количеством.Надежность с разделением пополам, описанная ранее, является еще одним методом
определение внутренней согласованности. Этот метод имеет недостаток, т.
если элементы не являются действительно однородными, будут созданы различные разделения
формы разной сложности, а коэффициент надежности составит
разные для каждой пары форм. Метод, преодолевающий это
сложность альфа Кронбаха (также называемая
коэффициент альфа ), что эквивалентно
среднее значение всех возможных разделенных половинных оценок.Чтобы узнать больше о Кронбахе
альфа, включая демонстрацию того, как его вычислить, см. главу 16.Валидность относится к тому, насколько хорошо тест или рейтинговая шкала измеряют то, что они должны
мера. Некоторые исследователи описывают валидацию как процесс
сбор доказательств в поддержку типов выводов, которые должны быть
взятые из рассматриваемых измерений. Исследователи расходятся во мнениях относительно того, как
существует много типов валидности, и научный консенсус менялся
на протяжении многих лет, поскольку различные типы действительности подпадают под
единая позиция в течение одного года, а затем отделяется и рассматривается как отдельная
следующий.Для простоты эта книга будет придерживаться общепринятого
принятая категоризация валидности, которая признает четыре типа: содержание
валидность, конструктивная валидность, параллельная валидность и прогностическая
срок действия. Внешняя действительность, которая тесно связана с содержанием
достоверность, также будет обсуждаться. Эти типы валидности обсуждаются
далее в контексте дизайна исследования в главе 18.Валидность содержания относится к тому, насколько хорошо процесс измерения отражает
важное содержание интересующей области и вызывает особую озабоченность
когда цель измерения состоит в том, чтобы сделать выводы о большем
область интересов.Например, потенциальные сотрудники, ищущие работу в качестве
программистов могут попросить сдать экзамен, который
требует, чтобы они писали или интерпретировали программы на языках, на которых они
использовать на работе, если наняли. Из-за ограничений по времени, только ограниченный контент
и навыки программирования могут быть включены в такой экзамен,
по сравнению с тем, что на самом деле может потребоваться профессионалу
работа по программированию. Однако, если подмножество контента и компетенций
хорошо выбраны, баллы на таком экзамене могут быть хорошим показателем
индивидуальные способности во всех важных типах программирования, необходимых
по работе.Если это так, то можно сказать, что экзамен имеет содержание.
срок действия.Тесно связанная концепция достоверности содержания известна как лицевая достоверность .
Появляется мера с хорошей лицевой валидностью (члену общего
общественность или типичное лицо, которое может быть оценено мерой) быть
справедливая оценка изучаемых качеств. Например, если высокий
школьный тест по геометрии оценивают родители учащихся, сдающих
чтобы быть честным тестом по алгебре, тест имеет хорошую лицевую валидность.Лицо
валидность важна для установления достоверности; если вы утверждаете, что
измерение геометрии учащихся
достижение, но родители ваших учеников не согласны, они могут быть
склонны игнорировать ваши заявления об уровне развития их детей.
достижения в этом предмете. Кроме того, если учащимся говорят, что они
пройти тест по геометрии, который кажется им чем-то другим
полностью, они могут быть не мотивированы сотрудничать и выдвигать свои
все усилия, поэтому их ответы могут не отражать их истинное
способности.Параллельная валидность относится к тому, насколько хорошо можно использовать выводы, сделанные на основе измерения.
чтобы предсказать какое-либо другое поведение или производительность, которая измеряется в
примерно в то же время. Например, если результат теста достижений
тесно связана с текущей школьной успеваемостью или с оценками по
аналогичные тесты, он имеет высокую параллельную валидность. Предиктивный
действительность аналогична, но касается возможности рисовать
выводы о каком-то событии в будущем.Чтобы продолжить предыдущий
например, если оценка на тесте успеваемости тесно связана со школой
производительность в следующем году или к успеху на работе, предпринятой в
будущее, он имеет высокую прогностическую достоверность.Поскольку каждая система измерения имеет свои недостатки, исследователи часто используют несколько подходов.
измерять одно и то же. Например, американские университеты часто используют
несколько типов информации для оценки старшеклассников
способности к учебе и вероятность того, что они преуспеют в
университетские исследования.Измерения, используемые для этой цели, могут включать
баллы на стандартных экзаменах, таких как SAT, оценки в средней школе,
личное заявление или эссе, а также рекомендации от учителей. В
Подобным образом решения о найме в компании обычно принимаются после
рассмотрение нескольких видов информации, включая оценку
опыта работы каждого соискателя, его образования, впечатления, которое он
делает во время собеседования и, возможно, образец работы и один или несколько
компетентностные или личностные тесты.Этот процесс объединения информации из нескольких источников в
прийти к истинному или, по крайней мере, более точному значению называется
триангуляция , свободная аналогия процесса в
геометрия определения местоположения точки с точки зрения ее
связь с двумя другими известными точками. Ключевая идея, стоящая за
триангуляции заключается в том, что хотя единичное измерение понятия может
содержать слишком много ошибок (как известных, так и неизвестных типов), чтобы быть либо
надежен или действителен сам по себе, путем объединения информации из нескольких типов
измерений, хотя бы некоторые из характеристик которых уже
известно, мы можем прийти к приемлемому измерению неизвестного
количество.Мы ожидаем, что каждое измерение содержит ошибку, но мы надеемся, что это
не включает ошибку того же типа , так что
с помощью нескольких типов измерений мы можем получить разумную оценку
интересующего количества или качества.Создание метода триангуляции — дело непростое. Одна историческая попытка сделать это
это матрица мультипризнаков, мультиметодов (MTMM), разработанная Кэмпбеллом и
Фиске (1959). Их особая забота заключалась в том, чтобы отделить часть
измерение из-за интереса к качеству этой части из-за
используемый метод измерения.Хотя используется их специфическая методология.
меньше сегодня, и полное обсуждение техники MTMM выходит за рамки
начального текста, концепция остается полезной как пример одного из способов
думать об ошибке измерения и достоверности.MTMM представляет собой матрицу корреляций между показателями нескольких
концепции (черты), каждая из которых измеряется несколькими способами (методами).
В идеале для каждого признака будут использоваться одни и те же несколько методов. В пределах
в этой матрице мы ожидаем, что различные измерения одной и той же черты будут очень
Связанный; например, показатели интеллекта, измеряемые несколькими
такие методы, как карандашно-бумажный тест, решение практических задач и
структурированное интервью, все должно быть сильно коррелировано.Тем же
логика, баллы, отражающие различные конструкты, которые измеряются в
же путь не должен быть сильно связан; например, баллы на
интеллект, поведение и общительность, измеряемые
анкеты, написанные карандашом и бумагой, не должны быть слишком
коррелированный.Рассмотрение смещения измерения является
важно практически во всех областях, но особую озабоченность вызывает
наук о человеке. Было выявлено множество конкретных типов предубеждений,
определенный.Не все они будут названы здесь, но несколько общих типов будут
обсуждалось. В большинстве учебников по дизайну исследований систематическая ошибка измерения трактуется очень серьезно.
подробно и с ними можно ознакомиться для дальнейшего обсуждения этой темы. Большинство
важным моментом является то, что исследователь должен всегда быть начеку
возможность предвзятости из-за неспособности рассмотреть и решить проблемы
связанные с предвзятостью, могут сделать недействительными результаты образцового в других отношениях
учиться.Предвзятость может поступать в исследования двумя основными способами: во время отбора и
сохранение предметов изучения или способов сбора информации
о предметах.В любом случае определяющей чертой смещения является то, что
это источник систематических , а не
случайная ошибка . Результат предвзятости состоит в том, что данные
анализируемый в исследовании систематически неверен, что может привести к
к ложным выводам, несмотря на применение правильных статистических
процедуры и техники. В следующих двух разделах обсуждаются некоторые из наиболее
распространенные типы систематической ошибки, разделенные на две основные категории: систематическая ошибка в выборке
выбор и удержание и предвзятость в результате сбора информации и
запись.Систематическая ошибка при отборе и хранении образцов
Большинство исследований проводится на выборках субъектов, будь то пациенты
с лейкемией или штучками, произведенными на фабрике, потому что это было бы
непомерно дорого, если не совсем невозможно изучить весь
интересующее нас население. Образец должен хорошо отражать
исследуемая популяция (популяция, для которой предназначены результаты
применить) для того, чтобы исследователю было удобно использовать результаты
выборка для описания населения.Если выборка необъективна, то есть
не является репрезентативным для исследуемой популяции, выводы, сделанные на основании
выборка исследования может не относиться к изучаемой популяции.Предвзятость отбора существует, если некоторые потенциальные испытуемые с большей вероятностью, чем другие
отобраны для выборки исследования. Этот термин обычно зарезервирован для предвзятости
это происходит из-за процесса выборки. Например, телефон
опросы, проводимые с использованием номеров из опубликованных справочников по дизайну
удалить из пула потенциальных респондентов людей с неопубликованными
номеров или тех, кто изменил номера телефонов с тех пор, как справочник был
опубликовано.Методы случайного набора цифр (RDD) решают эти проблемы.
но по-прежнему не включает людей, живущих в домохозяйствах без телефонов
или у кого есть только сотовый (мобильный) телефон. Это задача для исследования
исследование, потому что если исключенные люди систематически различаются по
характеристика интереса (а это очень частое явление),
результаты опроса будут необъективными. Например, люди, живущие в
домохозяйства без телефонной связи, как правило, беднее, чем те,
имеют телефон, и люди, у которых есть только сотовый телефон (т.д., без земли
линия), как правило, моложе тех, у кого есть телефонная связь по месту жительства.
Если бедность или молодость связаны с изучаемым предметом, за исключением
эти лица из выборки внесут необъективность в
учиться.Предвзятость добровольцев относится к тому факту, что люди
которые добровольно участвуют в исследованиях, обычно не являются представителями
населения в целом. По этой причине результаты полностью добровольных
образцы, такие как телефонные опросы, показанные на некоторых
программы, бесполезны для научных целей (если, конечно,
население, представляющее интерес, — это люди, которые добровольно участвуют в таких
опросы).В этом случае может работать несколько слоев неслучайного выбора.
пример. Например, чтобы ответить, человек должен смотреть на
рассматриваемая телевизионная программа. Это означает, что она, вероятно, дома;
следовательно, ответы на опросы, проводимые в течение обычного рабочего дня, могут привлечь
аудитория в основном пенсионеров, домохозяек и безработных.
Для ответа человеку также необходимо иметь свободный доступ к телефону и
иметь какие-либо черты личности, которые могли бы повлиять на его выбор
телефон и позвонить по номеру, который он видит на экране телевизора.То
проблемы с телефонными опросами уже обсуждались, и
Вероятность того, что черты личности связаны с другими качествами
изучено слишком высоко, чтобы его игнорировать.Систематическая ошибка, связанная с отсутствием ответов относится к другой стороне систематической ошибки добровольцев. Так же, как люди, которые
добровольно принять участие в исследовании, вероятно, систематически различаются
от тех, кто этого не делает, поэтому люди, которые отказываются от участия в исследовании
когда их приглашают сделать это, очень вероятно, отличаются от тех, кто соглашается на это.
принимать участие.Вы, наверное, знаете людей, которые отказываются участвовать в каких-либо
вид телефонного опроса. (Я сам такой человек.) Кажется, они
случайный выбор из общей массы? Возможно нет; за
например, Совместная Канада/США. Обследование здоровья выявило не только
различные показатели ответов для канадцев по сравнению с американцами, но обнаружено
систематическая ошибка, связанная с неполучением ответов, почти по всем основным показателям состояния здоровья и медико-санитарной помощи
меры доступа [результаты приведены здесь].Информационная цензура может создать предвзятость
в любом лонгитюдном исследовании (исследование, в котором испытуемые
следовали через определенный промежуток времени).Потеря субъектов в течение длительного
учеба — обычное дело, но настоящая проблема возникает, когда испытуемые
выбывают не случайно, а по причинам, связанным с исследованием
цель. Предположим, мы сравниваем два метода лечения хронического
заболевания путем проведения клинического испытания, в котором испытуемые случайным образом
отнесены к одной из нескольких групп лечения и наблюдались в течение пяти лет.
чтобы увидеть, как прогрессирует их болезнь. Благодаря нашему использованию рандомизированного
дизайн, мы начинаем с идеально сбалансированного набора предметов.Тем не мение,
со временем субъекты, для которых назначенное лечение не
эффективен, с большей вероятностью выпадут из исследования, возможно, в поисках
лечения в другом месте, что приводит к предвзятости. Если окончательную выборку испытуемых мы
Анализ состоит только из тех, кто остается в процессе до его
заключение, и если те, кто выбывает из исследования, не являются случайными
отбор тех, кто ее начал, анализируемой нами выборки уже не будет
хорошо рандомизированная выборка, с которой мы начали.Вместо этого, если отсев был
связанных с неэффективностью лечения, окончательный пул субъектов будет
предвзято относились к тем, кто эффективно реагировал на возложенные на них
лечение.Даже если идеальная выборка выбрана и сохранена, систематическая ошибка может войти в исследование из-за методов
используется для сбора и записи данных. Этот тип смещения часто называют
предвзятость информации потому что она влияет на достоверность
информацию, на которой основано исследование, что, в свою очередь, может
признать недействительными результаты исследования.Когда данные собираются с помощью личных или телефонных интервью,
существуют социальные отношения между интервьюером и испытуемым
ходе интервью. Эта связь может негативно сказаться на
качество собранных данных. Когда систематическая ошибка вносится в собранные данные, потому что
отношения или поведения интервьюера, это известно как
предвзятость интервьюера . Этот тип смещения может быть
создается непреднамеренно, когда интервьюер знает цель
исследование или статус опрашиваемых лиц.Например,
интервьюеры могут задавать более наводящие вопросы, чтобы подбодрить тему
вспомнить химические воздействия, если они знают, что субъект страдает от
редкий тип рака, связанный с химическим воздействием. Предвзятость интервьюера
также может быть создано, если интервьюер демонстрирует личное отношение или
мнения, которые сигнализируют субъекту, что он не одобряет
изучаемое поведение, такое как беспорядочные половые связи или употребление наркотиков, что делает
субъект с меньшей вероятностью будет сообщать о таком поведении.Ошибка припоминания относится к тому факту, что люди с таким жизненным опытом, как страдание
от серьезной болезни или травмы, с большей вероятностью помнят события, которые
они считают, что связаны с этим опытом. Например, женщины, которые
перенесла выкидыш, вероятно, провела много времени
исследуя свои воспоминания на предмет разоблачений или инцидентов, в которые они верят
могло стать причиной выкидыша. Женщины, у которых были нормальные роды, могут иметь
имели подобные воздействия, но не уделяли им должного внимания и, таким образом,
не вспомнит их, когда их спросят в опросе.Систематическая ошибка обнаружения относится к тому факту, что определенные характеристики могут с большей вероятностью
обнаруживаться или сообщаться у одних людей, чем у других. Например,
спортсмены в некоторых видах спорта подлежат регулярному тестированию на
препараты, улучшающие работоспособность, и результаты тестов публикуются.
Пловцы мирового уровня регулярно проверяются на анаболические стероиды.
Например, положительные тесты официально регистрируются и часто публикуются.
также в средствах массовой информации.Спортсмены, соревнующиеся на более низком уровне или в
другие виды спорта могут использовать те же препараты, но потому что они не проверены
как регулярно, или потому что результаты испытаний не сообщаются публично,
нет никаких записей об их употреблении наркотиков. Было бы неверно предполагать,
например, поскольку сообщил о анаболических
использование стероидов выше в плавании, чем в бейсболе,
фактическая скорость использования стероидов выше при плавании
чем в бейсболе. Наблюдаемая разница в использовании стероидов может быть связана с
более агрессивное тестирование со стороны официальных лиц по плаванию и многое другое
публичное оглашение результатов испытаний.









 (1903: 176)
(1903: 176) (1927:
(1927: (обычно
(обычно
 Лабораторная математика: Справочник по измерениям, расчетам и другим количественным навыкам для использования на стенде. Колд-Спринг-Харбор, Нью-Йорк: Издательство лаборатории Колд-Спринг-Харбор. ISBN 978-0879696344.
Лабораторная математика: Справочник по измерениям, расчетам и другим количественным навыкам для использования на стенде. Колд-Спринг-Харбор, Нью-Йорк: Издательство лаборатории Колд-Спринг-Харбор. ISBN 978-0879696344. Хиллсдейл, Нью-Джерси: Lawrence Erlbaum Associates. ISBN 0805810633.
Хиллсдейл, Нью-Джерси: Lawrence Erlbaum Associates. ISBN 0805810633.