Электротехника. Метод контурных токов — Botva-Project
Сегодня мы разберем еще один важный (и по секрету, наш любимый) метод определения токов в цепи постоянного тока. Это метод контурных токов. На наш взгляд он проще, чем уравнения Кирхгофа, хотя бы потому, что уравнений в системе, которую придется решать, ровно в два раза меньше. Итак, рассмотрим ту же электрическую цепь постоянного тока, которую мы рассчитывали по методу Кирхгофа. Напомним, как выглядит схема
В данной схеме нас интересует количество независимых контуров, выбираем их так же, как мы делали это в прошлый раз. Здесь три независимых контура.
В каждой ветви цепи наносим стрелками направления неизвестных токов, так же, как мы делали ранее (если вы уже рассчитали цепь любым другим способом, то направления и нумерацию токов имеет смысл сохранить, чтобы была возможность сравнить результаты расчета двумя методами). В методе Кирхгофа мы это делали так, повторим.
И последний штрих — в каждом контуре выбираем направление обхода и рисуем контурный ток. Мы любим брать те же направления, что и в методе Кирхгофа, как минимум для того, чтобы не рисовать два раза одно и тоже. Контурные токи обозначают большой буквой I, с нижним индексом 11, 22, 33.
Мы любим брать те же направления, что и в методе Кирхгофа, как минимум для того, чтобы не рисовать два раза одно и тоже. Контурные токи обозначают большой буквой I, с нижним индексом 11, 22, 33.
Подготовительная часть работы завершена, переходим непосредственно к определению токов. Записывается три уравнения (по числу контурных токов). По сути каждое уравнение представляет собой что-то, похожее на второй закон Кирхгофа, только для контурного тока.
В общем виде система уравнений для трех контуров имеет вид
Контурные токи, само собой, неизвестны, их надо определить. Сопротивления R11, R22, R33 — это полные сопротивления каждого контура, взятые со знаком «плюс». То есть обходим по кругу каждый контур и суммируем все сопротивления, которые в него входят.
Для контура 1 — это резисторы 1 и 2, для контура 2 — резистор 4, для контура 3 — резистор 5.
Сопротивления типа Rij — это сопротивления ветвей, общих для i и j контуров. То есть, если мы хотим определить R12, мы находим ветвь, общую для контуров 1 и 2, и записываем ее сопротивление.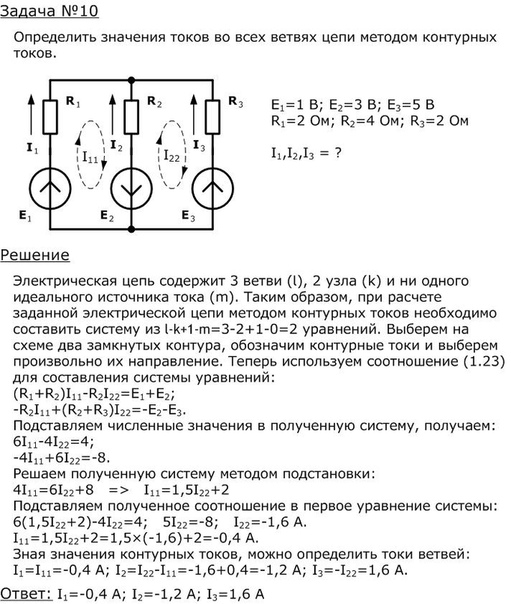 Знак при этом определяется направлением контурных токов: если токи в двух контурах направлены одинаково, то сопротивление ветви берется в «плюсом»; если токи направлены в разные стороны, то берется с «минусом». На примере сопротивления R12: общая для контуров 1 и 2 ветвь — это ветвь между узлами 2 и 4 (ветвь №2 согласно нумерации токов). Резисторов на ней нет, так что сопротивление R12=0. Знак, конечно, в таком случае значения не имеет, но токи I11 и I22 в данной ветви направлены противоположно, так что если бы сопротивление было, то мы бы записали его в систему со знаком «минус». Сопротивления с индексами ij и ji, разумеется, равны.
Знак при этом определяется направлением контурных токов: если токи в двух контурах направлены одинаково, то сопротивление ветви берется в «плюсом»; если токи направлены в разные стороны, то берется с «минусом». На примере сопротивления R12: общая для контуров 1 и 2 ветвь — это ветвь между узлами 2 и 4 (ветвь №2 согласно нумерации токов). Резисторов на ней нет, так что сопротивление R12=0. Знак, конечно, в таком случае значения не имеет, но токи I11 и I22 в данной ветви направлены противоположно, так что если бы сопротивление было, то мы бы записали его в систему со знаком «минус». Сопротивления с индексами ij и ji, разумеется, равны.
Для всех ветвей системы получается более чем просто:
В правых частях уравнения идут суммы ЭДС источников напряжения. Принцип тот же, что и во втором законе Кирхгофа: суммируем ЭДС, учитывая знаки. Если направление ЭДС совпадает с направлением контурного тока, то берем его с плюсом, если не совпадает — то с минусом.
На примере контура 1: в контуре 1 только один источник напряжения E1, направление которого противоположно направлению контурного тока. Значит,
Значит,
Для всех контуров получаем
Теперь мы готовы записать и решить полную систему уравнений для трех контурных токов. Получается так:
Упрощая и сокращая то, что упрощается и сокращается, получим несложную систему уравнений с тремя неизвестными, из которой однозначно определяются контурные токи.
Определив контурные токи, мы должны еще определить токи в ветвях. Это делается совсем несложно. Идем по порядку по ветвям нашей цепи и смотрим, как из контурных токов суммируются токи в ветвях. В образовании тока ветви 1 принимает участие только один контурный ток I11, причем он направлен в другую сторону. Значит
В ветви 2 ток I2 складывается из контурных токов I11 и I22, причем I22 берется с «плюсом» (направление тока I2 и I22 совпадают), а I11 — с «минусом» (направления I2 и I11 противоположны)
Для всех ветвей
Вот и все, задача решена. Остается только сравнить результаты с ответами, полученными другим методом, и убедиться, что все сделано правильно.
Всегда ваша, Botva-Project
12.Метод контурных токов.
Метод контурных
токов является одним из основных методов
расчета сложных электрических цепей,
которым широко пользуются на практике.
При расчете методом
контурных токов полагают, что в каждом
независимом контуре течет свой контурный
ток. Уравнения составляют относительно
контурных токов, после чего определяют
токи ветвей через контурные токи.
Таким образом, метод
контурных токов можно определить как
метод расчета, в котором за искомые
принимают контурные токи. Число
неизвестных в этом методе равно числу
уравнений, которые необходимо было бы
составить для схемы по II
закону Кирхгофа, т.е.
.
Следовательно, этот метод более экономичен
при вычислениях, чем метод уравнений
Кирхгофа.
Разработаем алгоритм
расчета цепей методом контурных токов
на примере приведенной на рис. 2.3. схемы,
2.3. схемы,
в которой три независимых контура.
Предположим, что в каждом контуре
протекает свой контурный ток в указанном
направлении. Для каждого из контуров
составим уравнения по II
закону Кирхгофа. При этом учтем, что по
смежной ветви для контурных токов
и
(ветвь
bd,
содержащая сопротивление
)
протекает ток
,
по смежной ветви для контурных токов
и
(ветвь
dс,
содержащая сопротивление
)
протекает ток
,
по смежной ветви для контурных токов
и
(ветвь
аd,
содержащая сопротивление
)
протекает ток
.
Тогда уравнения
по II
закону Кирхгофа для каждого контура
принимают следующий вид:
Сгруппируем
слагаемые при одноименных токах:
(2.5)
Введем обозначения:
В окончательном
виде система уравнений для контурных
токов приобретает следующий вид:
(2. 6)
6)
в матричной форме
(2.7)
Собственное
сопротивление контура (Rii)
представляет собой арифметическую
сумму сопротивлений всех потребителей,
находящихся в i-ом
контуре.
Общее сопротивление
контура (Rij
= Rji)
представляет собой алгебраическую
сумму сопротивлений потребителей ветви
(нескольких ветвей), одновременно
принадлежащих i-ому
и j-ому
контурам. В эту сумму сопротивление
входит со знаком «+», если контурные
токи протекают через данное сопротивление
в одном направлении (согласно), и знак
«–», если они протекают встречно.
Контурные ЭДС
представляют
собой алгебраическую сумму ЭДС источников,
входящих в контур. Со знаком «+» в эту
сумму входят ЭДС источников, действующих
согласно с обходом контура, со знаком
«–» входят ЭДС источников, действующих
встречно.
Решение полученной
системы удобно выполнить методом Крамера
,
(2.8)
где ,
1,
2,
3,
– соответственно определители матриц:
(2.9)
По найденным контурным
токам при помощи I
закона Кирхгофа определяются токи
ветвей.
Таким образом,
методика расчета цепи постоянного тока
методом контурных токов следующая:
1. Обозначить
все токи ветвей и их положительное
направление.
2. Произвольно
выбрать совокупность p
независимых контуров, нанести на
схему положительное направление
контурных токов, протекающих в выбранных
контурах.
3. Определить
собственные, общие сопротивления и
контурные ЭДС и подставить их в систему
уравнений вида (2.3).
4. Разрешить
полученную систему уравнений относительно
контурных токов, используя метод Крамера.
5. Определить
токи ветвей через контурные токи по I
закону Кирхгофа.
6. В случае
необходимости, с помощью обобщенного
закона Ома определить потенциалы узлов.
7. Проверить
правильность расчетов при помощи баланса
мощности.
Если в цепи содержится
q
источников
тока, количество
совместно рассматриваемых уравнений
сокращается на q
и становится равным р
– q,
поскольку токи в таких ветвях известны
(для контуров с Iii = J
уравнение
можно не записывать). В этом случае
следует выбирать такую совокупность
независимых контурных токов, чтобы
часть из них стала известными. Для этого
необходимо, чтобы каждый источник тока
входил только в один контур. Напряжения
UJ
источников
войдут в качестве неизвестных в правые
части уравнений, т.е. в состав контурных
ЭДС.
13. Метод узловых
Метод узловых
потенциалов.
Ток в любой ветви
схемы можно найти по обобщенному закону
Ома. Для того, чтобы можно было применить
закон Ома, необходимо знать значение
потенциалов узлов схемы. Метод расчета
электрических цепей, в котором за
неизвестные принимают потенциалы узлов
схемы, называют методом узловых
потенциалов. Число неизвестных в методе
узловых потенциалов равно числу
уравнений, которые необходимо составить
для схемы по I
закону Кирхгофа. Метод узловых потенциалов,
как и метод контурных токов, – один из
основных расчетных методов. В том случае,
когда п-1
< p
(n
– количество
узлов, p – количество
независимых контуров), данный метод
более экономичен, чем метод контурных
токов.
Проиллюстрируем на
простом примере получение методики
расчета электрической цепи методом
узловых потенциалов:
1. Записываем
Записываем
(n
– 1) уравнение
по I
закону Кирхгофа (при выбранном опорном
узле 4,
потенциал которого условно принимаем
равным нулю)
узел
1: – I1
+ I4
— I6
= 0
узел
2: I1
– I2
+
J3
= 0
узел 3:
I2
– I4
+ I5
= 0
2. Для каждого из
m
токов записываем выражение по обобщенному
закону Ома через потенциалы узлов с
учетом, что потенциал 4
=
0:
3. Полученные в п. 2
выражения подставляем в уравнения,
составленные по I
закону Кирхгофа
Приведем подобные
слагаемые при различных потенциалах и
получим каноническую систему уравнений:
(2. 10)
10)
Введем обозначения:
В окончательном
виде система уравнений для контурных
токов приобретает следующий вид:
(2.11)
в матричной форме
(2.12)
Собственная
проводимость узла (Gii)
представляет собой арифметическую
сумму проводимостей всех ветвей,
соединенных в i-ом
узле.
Общая проводимость
i-ого
и j-ого
узлов (Gij
= Gji)
представляет собой взятую со знаком
«–» сумму проводимостей ветвей,
присоединенных одновременно к i—ому
и j—ому
узлам.
Проводимости
ветвей с источниками тока полагаются
равными нулю и в собственные и общие
проводимости не входят!
Узловой ток
(Jii)
состоит из двух алгебраических сумм:
первая содержит токи источников тока,
содержащиеся в ветвях, соединенных в i
—ом узле; вторая
представляет собой произведение ЭДС
источников напряжения на проводимости
соответствующих ветвей, соединенных в
i
—ом узле. Со
Со
знаком «+» в эту сумму входят E
и J
источников,
действие которых направлено к узлу, со
знаком «–» остальные.
Решение системы
уравнений по методу узловых потенциалов
в общем случае выполняется методом
Крамера при помощи определителей:
Тогда неизвестные
потенциалы могут вычислены следующим
образом:
(2.14)
Нетрудно, показать,
что аналогичную систему уравнений можно
построить для случая n
узлов в цепи.
Тогда необходимо составить для (n—1)
узлов
соответствующие уравнения, полагая
потенциал n-ого
узла, равным нулю.
Таким образом,
методика расчета цепи постоянного тока
методом узловых потенциалов следующая:
1. Обозначить
все токи ветвей и их положительное
направление.
2. Произвольно
выбрать опорный узел (n)и
пронумеровать все остальные (n—1)—e
узлы.
3. Определить
собственные и общие проводимости узлов,
а также узловые токи, т.е. рассчитать
коэффициенты в системе уравнений.
4. Записать
систему уравнений в виде
Метод контурных токов для чайников
В каждой электрической цепи имеются так называемые Р — ребра (они же ветви, звенья, участки) и У – узлы. Для ее описания существует система уравнений, в которых используются два правила Кирхгофа. В них, в качестве независимых переменных, выступают токи ребер. Поэтому количество независимых переменных будет равно количеству уравнений, что дает возможность нормального разрешения данной системы.
На практике используются определенные методики, направленные на сокращение числа уравнений. Среди них очень часто используется метод контурных токов, позволяющий выполнять сложные расчеты и получать довольно точные результаты.
Суть метода контурных токов
Основные принципы данного метода основываются на том факте, что протекающие в ребрах цепи токи, не все считаются независимыми. Присутствующие в системе У-1 уравнения для узлов, четко показывают зависимость от них У-1 токов. При выделении в электрической цепи независимого тока Р-У+1, вся система может быть сокращена до уравнений Р-У+1. Таким образом, метод контурных токов представляет собой очень простое и удобное выделение в цепи независимых токов Р-У+1.
Присутствующие в системе У-1 уравнения для узлов, четко показывают зависимость от них У-1 токов. При выделении в электрической цепи независимого тока Р-У+1, вся система может быть сокращена до уравнений Р-У+1. Таким образом, метод контурных токов представляет собой очень простое и удобное выделение в цепи независимых токов Р-У+1.
Использование данного способа расчетов допускает, что в каждом независимом контуре Р-У+1 осуществляется циркуляция определенного виртуального контурного тока. Если какое-либо ребро относится лишь к одному конкретному контуру, то значение протекающего в нем реального тока будет равно контурному. В том случае, когда ребро входит в состав сразу нескольких контуров, ток, протекающий в нем, будет представлять собой сумму, включающую в себя соответствующие контурные токи. В этом случае обязательно учитывается направление обхода контуров. Независимыми контурами перекрывается практически вся схема, поэтому ток, протекающий в каком угодно ребре может быть выражен путем контурных токов, составляющих полную систему всех токов.
Для того чтобы построить систему независимых контуров, используется простой и наглядный метод создания планарных графов. На данной схеме ветви и узлы цепи размещаются на плоскости таким образом, что взаимное пересечение ребер полностью исключается. С помощью этого метода плоскость разбивается на области, ограниченные замкнутыми цепочками ребер. Именно они и составляют систему независимых контуров. Данный метод более всего подходит для ручных расчетов схем. Однако его применение может стать затруднительным или вовсе невозможным, если рассматриваемая схема не укладывается в рамки планарного графа.
Другим способом расчетов служит метод выделения максимального дерева. Само дерево представлено в виде подмножества звеньев электрической цепи и является односвязным графом, в котором отсутствуют замкнутые контуры. Для того чтобы оно появилось, из цепи постепенно исключаются некоторые звенья. Дерево становится максимальным, когда к нему добавляется любое исключенное звено, в результате чего образуется контур.
Применение метода выделения максимального дерева представляет собой последовательное исключение из цепи заранее установленных звеньев в соответствии с определенными правилами. Каждый шаг в цепи предполагает произвольное исключение одного звена. Если такое исключение нарушает односвязность графа, разбивая его на две отдельные части, в этом случае звено может возвратиться обратно в цепь. Если граф остается односвязным, то и звено остается исключенным. В конечном итоге, количество звеньев, исключенных из цепи, оказывается равным количеству независимых контуров, расположенных в схеме. Получение каждого нового независимого контура связано с присоединением к электрической цепи конкретного исключенного звена.
Применение метода контурных токов для расчета цепи
В соответствии с этой методикой, неизвестными величинами являются расчетные или контурные токи, предположительно протекающие во всех независимых контурах. В связи с этим, все неизвестные токи и уравнения в системе, равны количеству независимых контуров электрической цепи.
Токи ветвей в соответствии с данным методом рассчитываются следующим образом:
- В первую очередь вычерчивается схема цепи с обозначением всех ее элементов.
- Далее определяется расположение всех независимых контуров.
- Направления протекания контурных токов задаются произвольно по часовой или против часовой стрелки в каждом независимом контуре. Они обозначаются с использованием цифровых или комбинированных символов.
- В соответствии со вторым законом Кирхгофа, затрагивающего контурные токи, составляются уравнения для всех независимых контуров. В записанном равенстве направления обхода контура и контурного тока этого же контура совпадают. Необходимо учитывать и то обстоятельство, что в ветвях, расположенных рядом, протекают собственные контурные токи. Падение напряжения потребителей берется отдельно от каждого тока.
- Следующим этапом является решение полученной системы любым удобным методом, и окончательное определение контурных токов.
- Нужно задать направление реальных токов во всех ветвях и обозначить их отдельной маркировкой, чтобы не перепутать с контурными.

- Далее нужно от контурных токов перейти к реальным, исходя из того, что значение реального тока конкретной ветви составляет алгебраическую сумму контурных токов, протекающих по этой ветви.
Если направление контурного тока совпадает с направлением реального тока, то при выполнении алгебраического суммирования математический знак не меняется. В противном случае значение контурного тока нужно умножить на -1.
Метод контурных токов очень часто применяется для расчетов сложных цепей. В качестве примера для приведенной схемы нужно задать следующие параметры: Е1 = 24В, Е2 = 12В, r1 = r2 = 4 Ом, r3 = 1 Ом, r4 = 3 Ом.
Для решения этой сложной задачи составляются два уравнения, соответствующие двум независимым контурам. Направление контурных токов будет по часовой стрелке и обозначается I11 и I22. На основании второго закона Кирхгофа составляются следующие уравнения:
После решения системы получаются контурные токи со значением I11 = I22 = 3 А. Далее произвольно обозначается направление реальных токов, как I1, I2, I3. Все они имеют одинаковое направление – вверх по вертикали. После этого выполняется переход от контурных к реальным. В первой ветви имеется течение только одного контурного тока т I11. Его направление совпадает с реальным током, поэтому I1 + I11 = 3 А.
Далее произвольно обозначается направление реальных токов, как I1, I2, I3. Все они имеют одинаковое направление – вверх по вертикали. После этого выполняется переход от контурных к реальным. В первой ветви имеется течение только одного контурного тока т I11. Его направление совпадает с реальным током, поэтому I1 + I11 = 3 А.
Формирование реального тока во второй ветке осуществляется за счет двух контурных токов I11 и I22. Направление тока I22 совпадает с реальным, а направление I11 будет строго противоположно реальному. Таким образом, I2 = I22 — I11 = 3 — 3 = 0 А. В третьей ветке I3 наблюдается течение лишь контурного тока I22. Его направление будет противоположным направлению реального тока, поэтому в данном случае расчеты выглядят следующим образом: I3 = -I22 = -3А.
Основным положительным качеством метода контурных токов по сравнению с вычислениями по законам Кирхгофа, является значительно меньшее количество уравнений, используемых для вычислений.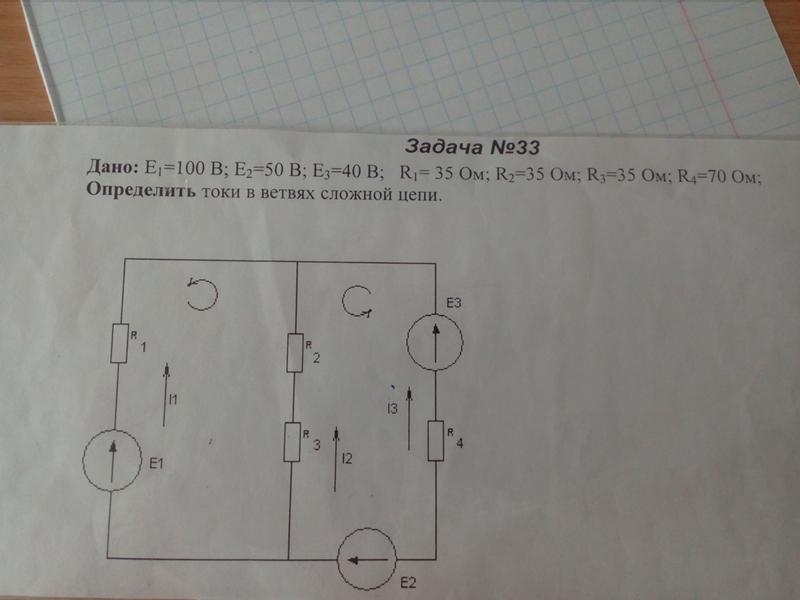 Тем не менее, здесь присутствуют определенные сложности. Например, реальные токи ветвей не всегда удается определить быстро и с высокой точностью.
Тем не менее, здесь присутствуют определенные сложности. Например, реальные токи ветвей не всегда удается определить быстро и с высокой точностью.
Один из методов анализа электрической цепи является метод контурных токов. Основой для него служит второй закон Кирхгофа. Главное его преимущество это уменьшение количества уравнений до m – n +1, напоминаем что m — количество ветвей, а n — количество узлов в цепи. На практике такое уменьшение существенно упрощает расчет.
Основные понятия
Контурный ток — это величина, которая одинакова во всех ветвях данного контура. Обычно в расчетах они обозначаются двойными индексами, например I11, I22 и тд.
Действительный ток в определенной ветви определяется алгебраической суммой контурных токов, в которую эта ветвь входит. Нахождение действительных токов и есть первоочередная задача метода контурных токов.
Контурная ЭДС — это сумма всех ЭДС входящих в этот контур.
Собственным сопротивлением контура называется сумма сопротивлений всех ветвей, которые в него входят.
Общим сопротивлением контура называется сопротивление ветви, смежное двум контурам.
Общий план составления уравнений
1 – Выбор направления действительных токов.
2 – Выбор независимых контуров и направления контурных токов в них.
3 – Определение собственных и общих сопротивлений контуров
4 – Составление уравнений и нахождение контурных токов
5 – Нахождение действительных токов
Итак, после ознакомления с теорией предлагаем приступить к практике! Рассмотрим пример.
Выполняем все поэтапно.
1. Произвольно выбираем направления действительных токов I1-I6.
2. Выделяем три контура, а затем указываем направление контурных токов I11,I22,I33. Мы выберем направление по часовой стрелке.
3. Определяем собственные сопротивления контуров. Для этого складываем сопротивления в каждом контуре.
Определяем собственные сопротивления контуров. Для этого складываем сопротивления в каждом контуре.
Затем определяем общие сопротивления, общие сопротивления легко обнаружить, они принадлежат сразу нескольким контурам, например сопротивление R4 принадлежит контуру 1 и контуру 2. Поэтому для удобства обозначим такие сопротивления номерами контуров к которым они принадлежат.
4. Приступаем к основному этапу – составлению системы уравнений контурных токов. В левой части уравнений входят падения напряжений в контуре, а в правой ЭДС источников данного контура.
Так как контура у нас три, следовательно, система будет состоять из трех уравнений. Для первого контура уравнение будет выглядеть следующим образом:
Ток первого контура I11, умножаем на собственное сопротивление R11 этого же контура, а затем вычитаем ток I22, помноженный на общее сопротивление первого и второго контуров R21 и ток I33, помноженный на общее сопротивление первого и третьего контура R31.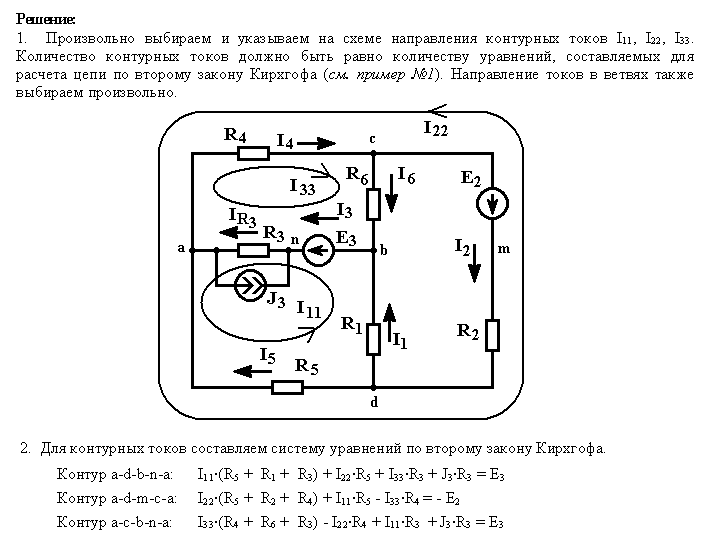 Данное выражение будет равняться ЭДС E1 этого контура. Значение ЭДС берем со знаком плюс, так как направление обхода (по часовой стрелке) совпадает с направление ЭДС, в противном случае нужно было бы брать со знаком минус.
Данное выражение будет равняться ЭДС E1 этого контура. Значение ЭДС берем со знаком плюс, так как направление обхода (по часовой стрелке) совпадает с направление ЭДС, в противном случае нужно было бы брать со знаком минус.
Те же действия проделываем с двумя другими контурами и в итоге получаем систему:
В полученную систему подставляем уже известные значения сопротивлений и решаем её любым известным способом.
5. Последним этапом находим действительные токи, для этого нужно записать для них выражения.
Контурный ток равен действительному току, который принадлежит только этому контуру. То есть другими словами, если ток протекает только в одном контуре, то он равен контурному.
Но, нужно учитывать направление обхода, например, в нашем случае ток I2 не совпадает с направлением, поэтому берем его со знаком минус.
Токи, протекающие через общие сопротивления определяем как алгебраическую сумму контурных, учитывая направление обхода.
Например, через резистор R4 протекает ток I4, его направление совпадает с направлением обхода первого контура и противоположно направлению второго контура. Значит, для него выражение будет выглядеть
А для остальных
Так решаются задачи методом контурных токов. Надеемся что вам пригодится данный материал, удачи!
Один из методов анализа электрической цепи является метод контурных токов. Основой для него служит второй закон Кирхгофа. Главное его преимущество это уменьшение количества уравнений до m – n +1, напоминаем что m — количество ветвей, а n — количество узлов в цепи. На практике такое уменьшение существенно упрощает расчет.
Основные понятия
Контурный ток — это величина, которая одинакова во всех ветвях данного контура. Обычно в расчетах они обозначаются двойными индексами, например I11, I22 и тд.
Действительный ток в определенной ветви определяется алгебраической суммой контурных токов, в которую эта ветвь входит. Нахождение действительных токов и есть первоочередная задача метода контурных токов.
Нахождение действительных токов и есть первоочередная задача метода контурных токов.
Контурная ЭДС — это сумма всех ЭДС входящих в этот контур.
Собственным сопротивлением контура называется сумма сопротивлений всех ветвей, которые в него входят.
Общим сопротивлением контура называется сопротивление ветви, смежное двум контурам.
Общий план составления уравнений
1 – Выбор направления действительных токов.
2 – Выбор независимых контуров и направления контурных токов в них.
3 – Определение собственных и общих сопротивлений контуров
4 – Составление уравнений и нахождение контурных токов
5 – Нахождение действительных токов
Итак, после ознакомления с теорией предлагаем приступить к практике! Рассмотрим пример.
Выполняем все поэтапно.
1. Произвольно выбираем направления действительных токов I1-I6.
2. Выделяем три контура, а затем указываем направление контурных токов I11,I22,I33. Мы выберем направление по часовой стрелке.
Мы выберем направление по часовой стрелке.
3. Определяем собственные сопротивления контуров. Для этого складываем сопротивления в каждом контуре.
Затем определяем общие сопротивления, общие сопротивления легко обнаружить, они принадлежат сразу нескольким контурам, например сопротивление R4 принадлежит контуру 1 и контуру 2. Поэтому для удобства обозначим такие сопротивления номерами контуров к которым они принадлежат.
4. Приступаем к основному этапу – составлению системы уравнений контурных токов. В левой части уравнений входят падения напряжений в контуре, а в правой ЭДС источников данного контура.
Так как контура у нас три, следовательно, система будет состоять из трех уравнений. Для первого контура уравнение будет выглядеть следующим образом:
Ток первого контура I11, умножаем на собственное сопротивление R11 этого же контура, а затем вычитаем ток I22, помноженный на общее сопротивление первого и второго контуров R21 и ток I33, помноженный на общее сопротивление первого и третьего контура R31. Данное выражение будет равняться ЭДС E1 этого контура. Значение ЭДС берем со знаком плюс, так как направление обхода (по часовой стрелке) совпадает с направление ЭДС, в противном случае нужно было бы брать со знаком минус.
Данное выражение будет равняться ЭДС E1 этого контура. Значение ЭДС берем со знаком плюс, так как направление обхода (по часовой стрелке) совпадает с направление ЭДС, в противном случае нужно было бы брать со знаком минус.
Те же действия проделываем с двумя другими контурами и в итоге получаем систему:
В полученную систему подставляем уже известные значения сопротивлений и решаем её любым известным способом.
5. Последним этапом находим действительные токи, для этого нужно записать для них выражения.
Контурный ток равен действительному току, который принадлежит только этому контуру. То есть другими словами, если ток протекает только в одном контуре, то он равен контурному.
Но, нужно учитывать направление обхода, например, в нашем случае ток I2 не совпадает с направлением, поэтому берем его со знаком минус.
Токи, протекающие через общие сопротивления определяем как алгебраическую сумму контурных, учитывая направление обхода.
Например, через резистор R4 протекает ток I4, его направление совпадает с направлением обхода первого контура и противоположно направлению второго контура. Значит, для него выражение будет выглядеть
А для остальных
Так решаются задачи методом контурных токов. Надеемся что вам пригодится данный материал, удачи!
Метод узловых потенциалов. Теория в примерахt
Важным вопросом этого раздела является расчет распределения токов в сложных линейных цепях с несколькимим источниками. Классическим методом расчета таких цепей являетя непосредственное применение законов Кирхгофа. Все остальные методы расчета исходят из этих фундаметнальных законовв электротехники.
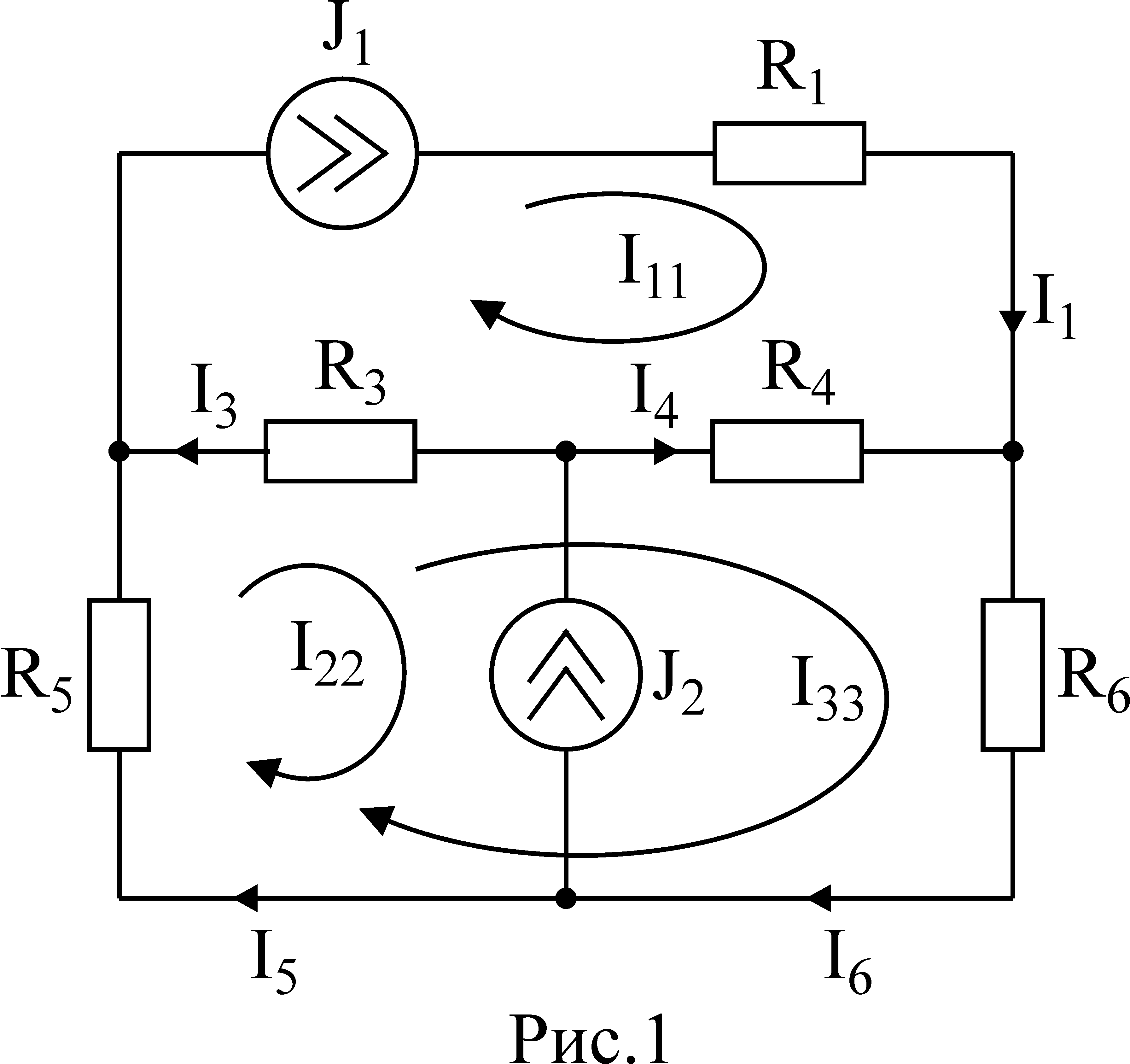
Рассмотрим сложную электрическую цепь (рисунок 1), которая содержит шесть ветвей. Если будут заданы значения всех ЭДС и споротивлений резисторов, а по условию задачи требуется определить токи в ветвях, то имеем задачу с шестью неизвестными. Такие задачи решаются с помощью законов Кирхгофа. В этом случае должно быть составлено столько уравнений, сколько неизвестных токов
В этом случае должно быть составлено столько уравнений, сколько неизвестных токов
Порядок расчета следующий:
- Если цепь содержит последовательные и параллельные соединения, то ее упрощают, заменяя эти соединения эквивалентными.
- Произвольно указывают направления токов во всех ветвях. Если принятое направление тока не совпадает с действительным, то при расчете такие токи получаются со знаками минус.
- Составляют (n-1) уравнений по первому закону Кирхгофа (n – число узлов).
- Недостающие уравнения в количестве m-(n-1), где m – число ветвей, составляют по второму закону Кирхгофа, при этом обход контура можно производить как по часовой стрелке, так и против нее. За положительные ЭДС и токи принимаются такие, направление которых совпадает с направлением обхода контура. Направление действия ЭДС внутри источника всегда принимают от минуса к плюсу (рисунок 1).
Рисунок 1.
- Полученную систему уравнений решают относительно неизвестных токов.
 Составим расчетные уравнения для электрической цепи, изображенной на рисунке 1. Выбрав произвольно напрвление токов в ветвях цепи, составляем уравнение по первому закону Кирхгофа для a, b, c :
Составим расчетные уравнения для электрической цепи, изображенной на рисунке 1. Выбрав произвольно напрвление токов в ветвях цепи, составляем уравнение по первому закону Кирхгофа для a, b, c :
I1 + I2 + I3 = 0
I5 — I1 — I4 = 0
I4 — I2 — I6 = 0,
Получившуюся систему линейных уравнений обозначим (1).
Приняв направление обхода контуров по часовой стрелке, составляем уравнения по второму закону Кирхгофа для трех произвольно выбранных контуров:
для контуров:
- (adkba) E1 = R1*I1 – R3*I3 + R01*I5; (2)
- (baclkb) E1 – E2 = R1*I1 – R2*I2 + R01*I5+R02*I6; (3)
- (bmncab) 0 = — R1*I1 + R2*I2 + R4*I4; (4)
Решая совместно уравнения (1), (2), (3) и (4), определяем токи в ветвях электрической цепи.
Легко заметить, что решение полученной системф из шести уравнений является весьма трудоемкой операцией. Поэтому при анализе электрических цепей с несколькими источниками целесообразно применять метод контурных токов (метод ячеек), позволяющий уменьшить число совместно решаемых уравнений, составляемых по методу контурных токов, равно (m – n + 1) .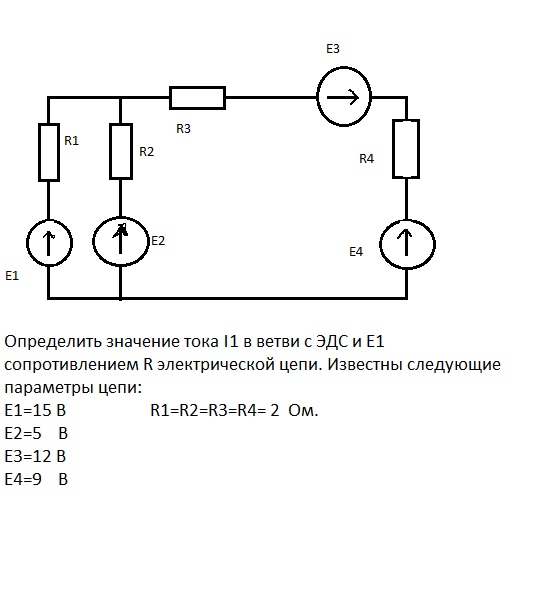 При решении этим методом количество уравнений определяется числом ячеек. Ячейкой называют такой контур, внутри которого отсутсвую ветви. В данном случае таких контуров-ячеек три: badkb, aclda, mncabm.
При решении этим методом количество уравнений определяется числом ячеек. Ячейкой называют такой контур, внутри которого отсутсвую ветви. В данном случае таких контуров-ячеек три: badkb, aclda, mncabm.
Расчет сложных электрических цепей методом контурных токов ведется следующим образом:
- Вводя понятие «контурный ток» , произвольно задаемся направлением этих токов в ячейках. Удобнее все токи указать в одном направлении, например, по часовой стрелке (рисунок 2)
- Составляем для каждого конутра-ячейки уравнение по второму закону Кирхгофа. Обход контуров производим по часовой стрелке:
- первый контур:
E1 = (R01 + R1 +R3) * I_k1 – R3*I_k2 – R1*I_k3 ; - второй контур
— E2 = – R3*I_k1 + (R02 + R2 +R3) * I_k2 – R2*I_k3 ; - третий контур
0 = – R1*I_k1 – R2*I_k2 + (R1 + R2 +R4) * I_k3 . - Решая совместно уравнение (5), (6), (7), определяем контурные токи.
 В том случае, когда контурный ток получается со знаком минус, это означает, что его направление противоположно выбранному на схеме (примечание: изменять его не нужно, ответ так и записываем с минусом)
В том случае, когда контурный ток получается со знаком минус, это означает, что его направление противоположно выбранному на схеме (примечание: изменять его не нужно, ответ так и записываем с минусом) - Токи во внутренних ветвях схемы поределяются как сумма или разность соотвествующих контурных токов. В том случае, когда контурные токи в ветви совпадают, берут сумму, а когда направлены на встречу — из большего тока вычитают меньший (примечание: тут для меня, например, не совсем понятно это выражение. Я просто беру алгебраическую сумму токов (во всех случаях). Если направление токов совпадает с обходом, оба берутся со знаком плюс, если же одно из направлений токов не совпадает с обходом, то он (ток) берется со знаком минус)
- Токи во внешних ветвях схемы по значению равны соотвествующим контурным токам (предыдущее примечание справедливо и в этом случае. Только ток один)
Рисунок 2.
Расчет электрической цепи методом контурных токов – образцы и примеры
Содержание:
- Метод расчета электрической цепи с применением контурных токов
- Алгоритм расчета электрической цепи методом контурных токов
- Пример задачи с решением 1
- Пример задачи с решением 1.
 1.1
1.1 - Пример задачи с решением 1.1.2
Метод расчета электрической цепи с применением контурных токов
Для расчета электрической цепи методом контурных токов выбирается система независимых контуров, по которым протекают контурные токи, направление которых выбирается произвольно. Если ветвь включена только в одну цепь, ток в этой ветви равен току в цепи. Если ветвь включена в более чем одну цепь, ток в этой ветви равен сумме токов цепи, проходящих через эту ветвь, с учетом знака и выбранного направления. Контурные токи находят, решая систему уравнений, составленную по второму закону Кирхгофа для каждого контура. По найденным контурным токам определяют токи ветвей схемы.
По этой ссылке вы найдёте полный курс лекций по теоретическим основам электротехники (ТОЭ):
Алгоритм расчета электрической цепи методом контурных токов
1. Вычерчиваем принципиальную схему цепи и обозначаем все элементы, задаем направления токов ветвей.
2. Определяем все независимые контуры.
Определяем все независимые контуры.
3. Произвольно задаемся направлением протекания контурных токов в каждом из независимых контуров (по часовой стрелке или против). Обозначаем эти токи. Для нумерации контурных токов можно использовать арабские сдвоенные цифры или римские цифры.
4. По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независимых контуров. При записи уравнений учитывайте, что направление обхода цепи, из которого создаются уравнения, совпадает с направлением тока цепи в этой цепи. Необходимо учитывать тот факт, что в соседних ветвях, принадлежащих к двум цепям, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях надо брать от каждого тока в отдельности.
5. Решаем любым методом полученную систему относительно контурных токов и определяем их.
6. Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские цифры .
Для нумерации реальных токов можно использовать одиночные арабские цифры .
7. Переходим от контурных токов к реальным, считая, что реальный ток ветви равен алгебраической сумме контурных токов, протекающих по данной ветви.
При алгебраическом суммировании без изменения знака берется контурный ток, направление которого совпадает с принятым направлением реального тока ветви. В противном случае контурный ток умножается на минус единицу.
Возможно вам будут полезны данные страницы:
Пример задачи с решением 1
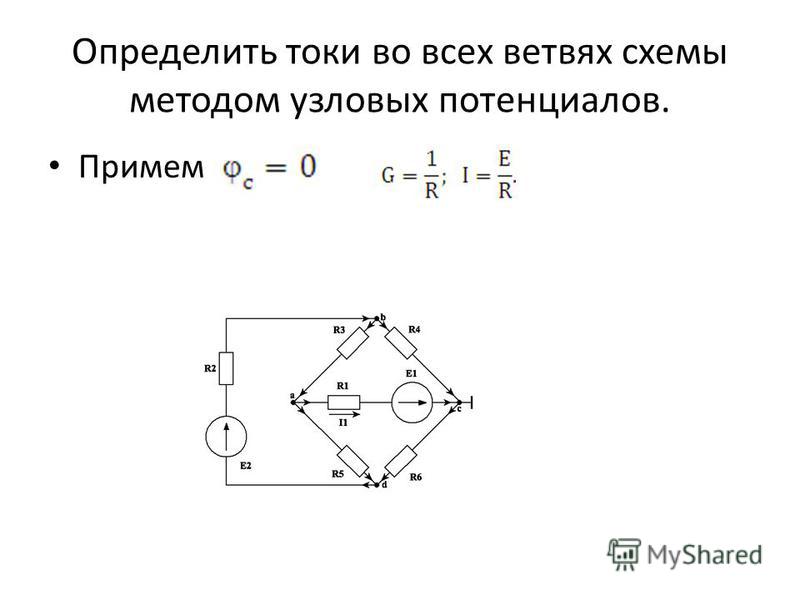
Определить токи в ветвях схемы рис. 4 методом контурных токов. Правильность решения проверить по балансу мощностей.
Решение
1. В соответствии с алгоритмом, зададимся направлением токов ветвей и обозначим их на схеме рис. 4
2. Определяем независимые контура и выбираем направления контурных токов
3. Поскольку в схеме имеется ветвь, содержащая источник тока J, контурный ток , а для контурных токов запишем систему уравнений метода контурных токов:
или
Подставив значения сопротивлений, получаем численную систему уравнений метода контурных токов с двумя неизвестными контурными токами:
откуда
4. Определяем токи в ветвях схемы по,ие/иоду контурных токов:
Определяем токи в ветвях схемы по,ие/иоду контурных токов:
Хотя все токи в ветвях можно определить методом контурных токов , токи определим по первому закону Кирхгофа. Составим уравнения по первому закону Кирхгофа:
для узла
откуда
для узла
откуда
5. Правильность решения проверяем по балансу мощностей. Предварительно находим напряжение па зажимах источника тока:
Тогда
Пример задачи с решением 1.1.1
Методом контурных токов определить токи в ветвях схемы (рисунок 1) если ,
Решение:
Определяем количество уравнений системы:
Выбираем контуры и записываем для каждого уравнения по второму закону Кирхгофа:
Решив систему одним из численных методов, получим значения контурных токов:
Затем выражаем токи ветвей из контурных токов:
Составляем баланс мощностей:
Что такое теоретические основы электротехники (ТОЭ) вы узнаете по этой ссылке:
Пример задачи с решением 1.1.2
Методом контурных токов определить токи в ветвях схемы (рисунок 2), если
Решение:
Определяем количество уравнений системы:
Первый независимый контур выбираем так, чтобы он был образован ветвью с идеальным источником тока .7, и контурный ток данного контура считаем равным току источника тока остальные контуры выбираем так, чтобы ветвь с источником тока не являлась образующей (рисунок 2).
Запишем систему уравнений:
Так как ток первого контура известен, то его произведение на взаимное сопротивление контуров можно перенести в правую часть уравнения, и система уравнений будет иметь следующий вид:
Решив систему уравнений, получим значения контурных токов:
Методом наложения определяем токи в ветвях схемы:
Составляем уравнение баланса мощностей:
где — напряжение на зажимах источника тока.
Для схемы рисунка 2 напряжение выразим из уравнения, записанного по II закону Кирхгофа для контура 1-2-4-1:
откуда
Тогда
Метод контурных токов (MKT) пример с решением
Обоснование последовательности расчета
На рисунке 3.45. представлена сложная электрическая цепь, в которой заданы величины всех ЭДС
источников тока и резисторов . Необходимо выполнить расчет величин токов в ветвях электрической цепи.
На первом этапе необходимо проставить произвольное направление токов в ветвях и упростить электрическую цепь, по известным методам, пронумеровав узлы. На рисунке 3.46. представлена упрощенная цепь, где
Положительные направления результирующих ЭДС в ветвях выбираются произвольно и в данном примере выбраны совпадающими с электрической цепью на рисунке 3.39.
Воспользуемся для обоснования метода MKT методом непосредственного применения законов Кирхгофа и составим по первому закону Кирхгофа (к — 1) уравнений (т. е. 4 — 1 = 3) для узлов 1,2,3 и по второму закону Кирхгофа для контуров, I, II, III:
Ветви 4, 5 и 6 — ветви дерева (рисунок 3.40.), а ветви 1, 2 и 3 — ветви соединения. Токи ветвей соединения называют контурными токами и обозначают
Выразим токи ветвей дерева через контурные токи из уравнений (3.38):
Исключаем токи смежных ветвей (дерева) из системы уравнений (3.39), для чего выражения для токов (3.40) — (3.42) подставим в уравнения (3.39):
Выполним группировку коэффициентов при контурных токах уравнений системы (3.43) и получим стандартную форму системы уравнений по MKT:
Анализ системы уравнений (3.44) позволяет прийти к следующим выводам:
- коэффициент при контурном токе, номер которого совпадает с номером контура, для которого составлено уравнение, равняется арифметической сумме сопротивлений этого контура, ее мы будем называть собственным сопротивлением контура :
- коэффициенты при контурных токах, номера которых не совпадают с номером контура, для которого составляется уравнение, являются сопротивлениями ветвей, которые принадлежат одновременно двум контурам; знак этих коэффициентов зависит от того, одинаково или противоположно направлены токи в этих ветвях, и мы будем называть их взаимными сопротивлениями контуров
Левые части уравнений (3.44) являются алгебраическими суммами источников ЭДС по второму закону Кирхгофа и мы будем называть их контурными
Группировка коэффициентов в правых частях уравнений (3.44) приведет к системе уравнений (3.48):
Система уравнений может быть решена с помощью определителей:
где
— алгебраические дополнения формул.
Система уравнений (3.48) является стандартной формой записи уравнений по методу контурных токов для любой электрической цени с
тремя независимыми контурами. Учитывая, что
можно рассчитать остальные токи по формулам (3.40) — (3.42).
Можно сформулировать правило:
Ток в любой ветви равен алгебраической сумме контурных токов в этой ветви, при этом положительный знак выбирают при совпадении направления контурного тока с направлением тока ветви, и отрицательный — наоборот. Расчет остальных токов выполним по схеме (рисунок 3.45).
Для узла 5 по первому закону Кирхгофа
. Аналогично для узла 1 ; для узла 9 ; для узла 8 .
Если количество независимых контуров
, система уравнений по методу контурных токов будет иметь вид:
В матричной форме систему (3.52) можно записать в полном виде:
где
— квадратичная матрица собственных и взаимных сопротивлений контуров или кратко — матрица сопротивлений; — матрица-столбец контурных ЭДС; — соответственно номера рядка и столбца элементов матриц.
Матрица сопротивлений симметричная, так как
. На главной диагонали этой матрицы расположены собственные сопротивлении контуров . Решение матричных уравнений (3.53) и (3.54) относительно неизвестной матрицы контурных токов имеет вид:
где
— обратная матрица сопротивлений.
Последовательность расчёта по методу контурных токов
Расчет цепей по методу контурных токов рекомендуется вести в следующей последовательности.
- Упростить исходную цепь, заменив реальные источники тока на реальные источники напряжения.
- Выбрать независимые контуры, направление контурных токов в них и направления токов в ветвях, входящих только в один контур должны совпадать с направлением контурного тока.
- Записать и решить стандартную систему уравнений по методу контурных токов.
- По найденным контурным токам найти по первому закону Кирхгофа токи в остальных ветвях схемы.
- Выполнить проверку результатов расчёта.
Если в схеме идеальные источники тока и их не преобразовали в модели с источниками ЭДС, расчет имеет ряд особенностей. Чтобы выбрать независимые контуры, необходимо использовать дерево графа так, чтобы в идеальные источники тока входили в ветви соединения. В этом случае токи источников тока приравниваем к известным контурным токам, а уравления составляют и решают только для контуров с неизвестными контурными токами. При этом в уравнения включаются слагаемые, которые приравняли токам идеальных источников тока.
Задача 3.9.
Для электрической цепи, схема которой изображена на рисунке 3.47. выполнить расчёт токов в ветвях электрической цепи, если параметры элементов имеют следующие значения:
Решение:
На первом этапе упростим схему рисунка 3.47, заменив модели источников энергии с источниками тока на модели с источниками ЭДС. Так заменяем:
и на эквивалентные источники ЭДС
и на эквивалентный источник
и на
На втором этапе выбираем положительные направления токов в ветвях схемы с неизвестными контурными токами и произвольно выбираем положительные их направления (рисунок 3.48).
На третьем этапе составляем стандартную систему уравнений по MKT для трёх неизвестных контурных токов
:
Здесь:
Подставляем полученные значения коэффициентов в уравнения системы (3.56) получаем:
Решаем полученную систему уравнений с помощью определителей:
Правила вычисления определителей при раскрытии по первому столбцу:
На четвёртом этапе вычисляем токи ветвей:
Ток
, вычисляем для узла 1 по первому закону Кирхгофа:
Аналогично величины токов:
На пятом этапе выполняем проверку вычислений подстановкой величин токов в уравнения, составленные по второму закону Кирхгофа для исходной схемы рисунка 3.47:
Подставляем заданные параметры элементов электрической цепи и величины токов в систему уравнений (3.63):
Система уравнений (3.63) превратилась в верное равенство.
Эта страница взята со страницы задач по электротехнике:
Задачи по электротехнике: теория и практика
Возможно эти страницы вам будут полезны:
Практическая работа Расчет электрических цепей методом контурных токов
Практическое занятие №14
Тема: Расчет электрических цепей методом контурных токов
Цель работы: научиться рассчитывать сложные электрические схемы постоянного тока методом контурных токов (МКТ)
Задание
— Записать название работы, тему и цель работы
— рассмотреть и записать в конспект приведенный пример
— решить индивидуальное задание
Краткие теоретические сведения
Решение задачи требует знания закона Ома, формул мощности, законов Кирхгофа, свойств последовательного и параллельного, соединения резисторов.
В электрической цепи за положительное направление ЭДС Е принимается направление, совпадающее с силой, действующей на положительный заряд, т.е. от «–» источника к «+» источника питания.
За положительное направление напряжения U принято направление, совпадающее с направлением действия электрического поля, т.е. от «+» к «–» источника.
За положительное направление тока I принято направление, совпадающее с перемещением положительных зарядов, т.е. от «+» к «–» источника.
Электродвижущая сила источника в электрической цепи может иметь одинаковое и противоположное направление с током. В первом случае источник ЭДС работает в режиме генератора, т.е. является источником электрической энергии. При этом ЭДС оказывается больше напряжения на его зажимах (Е >U). При направлении ЭДС в цепи противоположно току источник становится потребителем электрической энергии, и ЭДС оказывается меньше напряжения U на зажимах источника (Е <U) на величину внутреннего падения напряжения IR0, где R0 – внутреннее сопротивление источника.
При расчетах электрических цепей реальные источники электрической энергии заменяются схемами замещения. Схема замещения источника ЭДС содержит ЭДС и внутреннее сопротивление R0 источника, которое много меньше сопротивления Rн потребителя электроэнергии (R0<<Rн). При расчетах часто приходится внутреннее сопротивление источника ЭДС приравнивать нулю.
В идеализированном источнике ЭДС падение напряжения на внутреннем сопротивлении IR0 = 0, при этом напряжение на зажимах источника U = const не зависит от тока I и равно ЭДС источника (U = E). В этом случае источник электроэнергии работает в режиме, близком к режиму холостого хода.
В источниках тока внутреннее сопротивление во много раз превосходит сопротивление потребителя электроэнергии (R0>>Rн), при этом в источнике тока ток является величиной практически постоянной, не зависящей от нагрузки (j = const).
Реальный источник электрической энергии можно представить в схеме замещения последовательным соединением идеального источника ЭДС и внутреннего сопротивления R0.
Для участка цепи, не содержащего источник энергии (например, для схемы пассивного участка на рис. 1), связь между током I и напряжением U12 определяется законом Ома для участка цепи
где φ1 и φ2 – потенциалы точек 1 и 2 цепи соответственно; U12 = φ1 — φ2 – напряжение (разность потенциалов) между точками 1 и 2 цепи; ΣR – арифметическая сумма сопротивлений на участке цепи; R1 и R2 – сопротивления участков цепи.
Рисунок 1 — Электрическая схема пассивного участка
Для участка цепи, содержащего источники ЭДС (рис. 2), т.е. для активного участка цепи, связь между током I, напряжением U12 и ЭДС источников определяется обобщенным законом Ома
где ΣE – алгебраическая сумма всех ЭДС участка цепи, причем со знаком «+» в нее входят ЭДС, совпадающие с направлением тока и со знаком «-» в нее входят ЭДС, не совпадающие с направлением тока.
Рисунок 2 — Электрическая схема участка цепи, содержащего источники ЭДС
На основании закона сохранения энергии мощность, развиваемая источниками электрической энергии, должна быть равна мощности преобразования в цепи электрической энергии в другие виды энергии
ΣEI=Σ(I2·R),
где ΣEI – сумма мощностей, развиваемых источниками;
Σ(I2·R)– сумма мощностей всех приемников и необратимых преобразований энергии внутри источников (потери мощности на внутренних сопротивлениях).
Приведенное равенство называется балансом мощностей электрической цепи.
Если положительное направление тока совпадает с направлением ЭДС и в результате расчета получено положительное значение тока, то источник вырабатывает (генерирует) электрическую энергию, т.е. работает в режиме генератора. Если же получено отрицательное значение тока, то произведение EI отрицательно, т.е. источник работает в режиме потребителя и является приемником электрической энергии (например, электродвигатель, аккумулятор в режиме зарядки).
В любой электрической цепи в соответствии с первым законом Кирхгофа алгебраическая сумма токов, направленных к узлу разветвления, равна нулю:
0
где Ik – ток в k-й ветви.
В соответствии со вторым законом Кирхгофа алгебраическая сумма ЭДСв любом замкнутом контуре электрической цепи равна алгебраической сумме напряжений и алгебраической сумме падений напряжений в этом контуре
,
где Rk– сопротивление участка цепи рассматриваемого контура;
Ik – ток в сопротивлении Rk.
При расчете электрических цепей любым методом выбирают условно положительные направления токов, ЭДС и напряжений на участках цепи, которые обозначают стрелками на схеме, затем выбирают замкнутые контуры и задаются положительным направлением обхода контуров. При этом для удобства расчетов направление обхода для всех контуров рекомендуется выбирать одинаковым (например, по часовой стрелке).
Задача предусматривает расчет сложной электрической цепи. Сложные цепи имеют несколько замкнутых контуров, электрически связанных друг с другом. В ветвях контуров, где находятся источники Э.Д.С. и резисторы, протекают разные по величине токи.
Методика расчета сложной цепи методом контурных токов
Метод контурных токов используется для расчета резистивных линейных цепей с постоянными токами и для расчета комплексных схем замещения линейных цепей с гармоническими токами. При этом в расчет вводятся контурные токи – это фиктивные токи, которые замыкаются в независимых замкнутых контурах, отличающихся друг от друга наличием хотя бы одной новой ветви.
Контурный ток — это величина, которая одинакова во всех ветвях данного контура. Обычно в расчетах они обозначаются двойными индексами, например I11, I22 и т.д.
Действительный ток в определенной ветви определяется алгебраической суммой контурных токов, в которую эта ветвь входит. Нахождение действительных токов и есть первоочередная задача метода контурных токов.
Контурная ЭДС — это сумма всех ЭДС входящих в этот контур, причем, со знаком «плюс» записываются ЭДС, действующие в направлении контурного тока, со знаком «минус» — направленные против контурного тока.
Собственным сопротивлением контура называется сумма сопротивлений всех ветвей, которые в него входят.
Общим сопротивлением контура называется сопротивление ветви, смежное (принадлежащее) двум контурам.
В методе контурных токов за неизвестные величины принимаются расчетные (контурные) токи, которые якобы протекают в каждом из независимых контуров. Таким образом, количество неизвестных токов и уравнений в системе равно числу независимых контуров цепи.
Расчет токов ветвей по методу контурных токов выполняют в следующем порядке:
1 Вычерчиваем принципиальную схему цепи и обозначаем все элементы.
2 Определяем все независимые контуры.
3 Произвольно задаемся направлением протекания контурных токов в каждом из независимых контуров (например, по часовой стрелке). Обозначаем эти токи. Для нумерации контурных токов можно использовать арабские сдвоенные цифры (I11, I22, I33 и т. д.) или римские цифры.
4 По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независимых контуров. При записи равенства считать, что направление обхода контура, для которого составляется уравнение, совпадает с направлением контурного тока данного контура. Следует учитывать и тот факт, что в смежных ветвях, принадлежащих двум контурам, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях надо брать от каждого тока в отдельности.
5 Решаем любым методом полученную систему относительно контурных токов и определяем их.
6 Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские цифры (I1, I2, I3 и т. д.).
7 Переходим от контурных токов к реальным, считая, что реальный ток ветви равен алгебраической сумме контурных токов, протекающих по данной ветви.
При алгебраическом суммировании без изменения знака берется контурный ток, направление которого совпадает с принятым направлением реального тока ветви. В противном случае контурный ток умножается на минус единицу.
Пример
Определить токи во всех ветвях цепи (рисунок 3), если Э.Д.С. источников энергии Е1 = 150В, Е2 = 80В, их внутренние сопротивления R01 = 1 Ом, R02=0.5 Ом; сопротивления резисторов R1=9 Ом, R2=19,5 Ом, R3 = 25 Ом. Задачу решить методом контурных токов. Составить уравнение баланса мощностей.
Рисунок 3 — Электрическая схема
Решение
На схеме произвольно показываем направление токов ветвей.
Намечаем два независимых контура и указываем направление контурных токов (по часовой стрелке)
Рисунок 4 — Электрическая схема
Определяем Э.Д.С. каждого контура
Важно!!! Со знаком «плюс» записываются ЭДС, действующие в направлении контурного тока, со знаком «минус» — направленные против контурного тока.
Е I= Е1 – Е2 = 150 -80 = 70 В
Е II = Е2 = 80 В
4. Определяем собственные и общие сопротивления контуров:
— собственные сопротивления (входящие в один контур)
R11 = R1 + R01 + R02 + R2 = 9 + 1 + 0,5 + 19,5 = 30 Ом
R22 = R2 + R02 + R3 = 19,5 + 0,5 + 25 = 45 Ом
— общие сопротивления (принадлежащие двум соседним контарам)
R12 = R21 = R2 + R02 = 19,5 + 0.5 = 20 Ом
Составляем уравнения:
I I R11 – I II R12 = E I (1)
– I I R21+ I II R22 = E II (2)
Подставляем данные, полученные в пунктах 3, 4 и решаем систему уравнений методом подстановки или любым другим методом.
I I 30 – I II 20 = 70 (1) (× 2)
— I I 20 + I II 45 = 80 (2) (× 3)
60 I I– 40 I II = 140 (3)
+
— 60 I I + 135 I II = 240 (4)
95 III = 380
III = 4 A
7. Подставляем значениеIII в формулу (1) и определяем ток II.
30 I I – 4 · 20 = 70
I I = 150 / 30
I I = 5 A
Определяем действительные токи в ветвях, исходя из условия, что действительный ток, совпадающий по направлению с контурным током берется со знаком «+», и наоборот, ток в ветви не совпадающий с контурным током берется со знаком «-».
I1 = I I = 5 A
I2 = I II– I I = 4 – 5 = -1 A
I3= III =4A
Индивидуальные задания для практической работы №14
Задача На рисунке 5 изображена схема сложной электрической цепи: Е1, Е2 – Э.Д.С. источников энергии; R01, R02 – их внутренние сопротивления; R1, R2, R3 – сопротивления резисторов.
Числовые значения этих параметров указаны в таблице 1
Начертить схему цепи; показать направление токов в ветвях. Определить токи ветвей I1, I2, I3 методом контурных токов.
Составить уравнение баланса мощностей
Указание:
Перед решением задачи изучите методические указания к решению задачи и решение типового примера.
В задаче обязательно вычертить электрическую схему, соответствующую условию задачи, и показать на ней заданные и искомые величины, а также направление токов. Привести данные своего варианта.
Решение задачи сопровождается краткими пояснениями.
Текст, формулы, числовые выкладки должны быть четкими без помарок. Цифровая подстановка в уравнении должна даваться один раз без промежуточных сокращений и расчетов. Численное значение каждого символа должно обязательно занимать то же место в формуле, что и сам символ. Все расчеты необходимо вести в системе СИ. Буквенные обозначения единиц измерения ставятся только возле окончательного результата и в скобки не заключаются, например, 120 В, 13 А, 100 Вт.
Рисунок 5 — Электрическая схема
Таблица 1 — Исходные данные к задаче
вар
Е1, В
Е2, В
R01, Ом
R02, Ом
R1, Ом
R2, Ом
R3,
Ом
Метод расчета
1, 5, 9, 13, 17, 21, 25
85
200
0,3
2,0
12,0
1,7
12,0
Метод контурных токов
2, 6, 10, 14, 18, 22, 26
55
120
0,2
0,5
6,0
15,0
6,0
3, 7, 11, 15, 19, 23
105
146
2,0
2,0
50,0
4,5
50,0
4, 8, 12, 16, 20, 24
80
34
0,5
0,3
20,0
19,0
20,0
Метод и анализ тока
Mesh | Анализ сети постоянного тока
Метод Mesh-Current Method , также известный как Loop Current Method , очень похож на метод тока ответвления в том, что он использует одновременные уравнения, закон напряжения Кирхгофа и закон Ома для определения неизвестных токов в сети. Он отличается от метода Branch Current тем, что , а не , использует закон тока Кирхгофа, и обычно он может решить схему с меньшим количеством неизвестных переменных и меньшим количеством одновременных уравнений, что особенно удобно, если вы вынуждены решать без калькулятор.
Mesh Current, традиционный метод
Давайте посмотрим, как этот метод работает на той же задаче:
Определить петли
Первым шагом в методе Mesh Current является определение «петель» в цепи, охватывающей все компоненты. В нашей примерной схеме цикл, образованный B 1 , R 1 и R 2 , будет первым, а цикл, образованный B 2 , R 2 и R 3 , будет второй.Самая странная часть метода Mesh Current представляет собой циркулирующие токи в каждой из петель. Фактически, этот метод получил свое название от идеи объединения этих токов между петлями, как набор вращающихся шестерен:
Выбор направления каждого тока совершенно произвольный, как и в методе Branch Current, но полученные уравнения легче решить, если токи идут в одном направлении через пересекающиеся компоненты (обратите внимание, как токи I 1 и I 2 оба идут «вверх» через резистор R 2 , где они «сцепляются» или пересекаются).Если предполагаемое направление тока сетки неверно, ответ для этого тока будет иметь отрицательное значение.
Обозначьте полярность падения напряжения
Следующим шагом является маркировка всех полярностей падения напряжения на резисторах в соответствии с предполагаемыми направлениями токов сетки. Помните, что «входной» конец резистора всегда будет отрицательным, а «выходной» конец резистора положительным по отношению друг к другу, поскольку электроны заряжены отрицательно. Полярность батарей, конечно, определяется ориентацией их символов на схеме и может или не может «совпадать» с полярностью резистора (предполагаемое направление тока):
Используя закон напряжения Кирхгофа, мы можем теперь обойти каждую из этих петель, создавая уравнения, представляющие падения напряжения и полярности компонентов.Как и в случае метода Branch Current, мы будем обозначать падение напряжения на резисторе как произведение сопротивления (в омах) и соответствующего ему тока сетки (эта величина пока неизвестна). Если два тока соединяются вместе, мы запишем этот член в уравнении с током резистора, равным сумме двух токов зацепления.
Отслеживание левого контура цепи с помощью уравнений
Отслеживание левого контура цепи, начиная с левого верхнего угла и двигаясь против часовой стрелки (выбор начальных точек и направлений в конечном итоге не имеет значения), считая полярность, как если бы у нас в руке был вольтметр, красный провод на точке впереди и черное преимущество на точке позади, получаем следующее уравнение:
Обратите внимание, что средний член уравнения использует сумму токов сетки I 1 и I 2 как ток через резистор R 2 .Это связано с тем, что токи I 1 и I 2 проходят в одном направлении через R 2 и, таким образом, дополняют друг друга. Распределяя коэффициент 2 на члены I 1 и I 2 , а затем объединяя члены I 1 в уравнении, мы можем упростить как таковое:
На данный момент у нас есть одно уравнение с двумя неизвестными. Чтобы иметь возможность найти два неизвестных тока сетки, мы должны иметь два уравнения. Если мы проследим другой контур цепи, мы сможем получить другое уравнение KVL и получить достаточно данных для решения двух токов.Я — создание по привычке, я начну с левого верхнего угла правой петли и начну с трассировки против часовой стрелки:
Упрощая уравнение, как и раньше, получаем:
Решение неизвестного
Теперь, имея два уравнения, мы можем использовать один из нескольких методов для математического решения неизвестных токов I 1 и I 2 :
Схема перерисовки
Зная, что эти решения являются значениями для ячеек токов, а не ветвей токов, мы должны вернуться к нашей диаграмме, чтобы увидеть, как они сочетаются друг с другом, чтобы дать токи через все компоненты:
Решение -1 ампер для I 2 означает, что мы изначально предположили, что направление тока было неправильным.На самом деле, I 2 течет против часовой стрелки при значении (положительном) 1 А:
Это изменение направления тока от того, что предполагалось изначально, изменит полярность падений напряжения на R 2 и R 3 из-за тока I 2 . Отсюда можно сказать, что ток через R 1 составляет 5 ампер, при этом падение напряжения на R 1 является произведением тока и сопротивления (E = IR), 20 вольт (положительное слева и отрицательное на право).
Также можно смело сказать, что ток через R 3 составляет 1 ампер, при падении напряжения 1 вольт (E = IR), положительный слева и отрицательный справа. Но что происходит на R 2 ?
Ток в ячейке I 1 идет «вниз» через R 2 , а ток в ячейке I 2 «вверх» через R 2 . Чтобы определить фактический ток через R 2 , мы должны увидеть, как взаимодействуют токи сетки I 1 и I 2 (в данном случае они противоположны), и алгебраически сложить их, чтобы получить окончательное значение.Так как I 1 идет «вниз» при 5 А, а I 2 «растет» на 1 А, реальный ток через R 2 должен иметь значение 4 А, «вниз» :
Ток 4 А через сопротивление 2 Ом R 2 дает нам падение напряжения 8 В (E = IR), положительное вверху и отрицательное внизу.
Преимущества анализа тока в сетке
Основное преимущество анализа Mesh Current заключается в том, что он обычно позволяет решать большую сеть с меньшим количеством неизвестных значений и меньшим количеством одновременных уравнений.В нашем примере задачи потребовалось три уравнения для решения метода Branch Current и только два уравнения с использованием метода Mesh Current. Это преимущество тем больше, чем больше сложность сетей:
Чтобы решить эту сеть с использованием токов ответвления, нам нужно было бы установить пять переменных для учета каждого уникального тока в цепи (с I 1 по I 5 ). Для этого потребуется пять уравнений для решения в форме двух уравнений KCL и трех уравнений KVL (два уравнения для KCL в узлах и три уравнения для KVL в каждом цикле):
Я полагаю, если у вас нет ничего лучше, чем использовать свое время, как решить пять неизвестных переменных с помощью пяти уравнений, вы можете не возражать против использования метода анализа тока ветви для этой схемы.Для тех из нас, у кого есть лучших способа распорядиться своим временем, метод Mesh Current намного проще, требуя для решения только трех неизвестных и трех уравнений:
Меньшее количество уравнений для работы является решающим преимуществом, особенно при выполнении одновременного решения уравнений вручную (без калькулятора).
Несбалансированный мост Уитстона
Другой тип схемы, которая хорошо подходит для Mesh Current, — это несбалансированный мост Уитстона.Возьмем, например, эту схему:
Поскольку отношения R 1 / R 4 и R 2 / R 5 не равны, мы знаем, что будет напряжение на резисторе R 3 и некоторое количество тока через него. Как обсуждалось в начале этой главы, этот тип схемы не подлежит сокращению с помощью обычного последовательно-параллельного анализа и может быть проанализирован только каким-либо другим методом.
Мы могли бы применить метод тока ответвления к этой схеме, но для этого потребуется шесть токов (от I 1 до I 6 ), что приведет к очень большому набору одновременных уравнений для решения.Однако, используя метод Mesh Current, мы можем решить для всех токов и напряжений с гораздо меньшим количеством переменных.
Нарисовать сетку
Первым шагом в методе Mesh Current является рисование тока сетки, достаточного для учета всех компонентов в цепи. Глядя на нашу мостовую схему, должно быть очевидно, где разместить два из этих токов:
Направления этих сеточных токов, конечно, произвольны. Однако двух токов сетки в этой схеме недостаточно, потому что ни I 1 , ни I 2 не проходят через батарею.Итак, мы должны добавить третий ток сетки, I 3 :
Здесь я выбрал I 3 , чтобы выполнить петлю от нижней стороны батареи, через R 4 , через R 1 и обратно к верхней стороне батареи. Это не единственный путь, который я мог бы выбрать для I 3 , но он кажется самым простым.
Обозначьте полярность падения напряжения на резисторе
Теперь мы должны обозначить полярность падения напряжения на резисторе, следуя каждому из предполагаемых направлений тока:
Обратите внимание на кое-что очень важное: на резисторе R 4 полярности для соответствующих токов сетки не совпадают.Это потому, что эти сеточные токи (I 2 и I 3 ) проходят через R 4 в разных направлениях. Это не исключает использования метода анализа Mesh Current, но немного его усложняет. Но позже мы покажем, как избежать нынешнего столкновения R 4 . (См. Пример ниже)
Использование KVL
Создание уравнения KVL для верхней петли моста, начиная с верхнего узла и отслеживая по часовой стрелке:
В этом уравнении мы представляем общие направления токов их суммой через общие резисторы.Например, на резисторе R 3 со значением 100 Ом падение напряжения представлено в приведенном выше уравнении KVL выражением 100 (I 1 + I 2 ), поскольку оба тока I 1 и I 2 пройду через R 3 справа налево. То же самое можно сказать и о резисторе R 1 с выражением падения напряжения, показанным как 150 (I 1 + I 3 ), поскольку оба I 1 и I 3 проходят через него снизу вверх. резистор, и, таким образом, сработайте вместе с , чтобы создать на нем падение напряжения.
Сгенерировать уравнение КВЛ для нижнего контура моста будет не так просто, поскольку у нас есть два тока, идущие друг против друга через резистор R 4 . Вот как я это делаю (начиная с правого узла и отслеживая против часовой стрелки):
Обратите внимание, что второй член в исходной форме уравнения имеет значение резистора R 4 , равное 300 Ом, умноженное на разность между I 2 и I 3 (I 2 — I 3 ) .Вот как мы представляем комбинированный эффект двух токов сетки, проходящих в противоположных направлениях через один и тот же компонент. Здесь очень важен выбор подходящих математических знаков: 300 (I 2 — I 3 ) не означает то же самое, что 300 (I 3 — I 2 ). Я решил написать 300 (I 2 — I 3 ), потому что сначала я думал об эффекте I 2 (создание положительного падения напряжения, измерение с помощью воображаемого вольтметра на R 4 , красный провод на нижний и черный провод вверху), и во вторую очередь эффекта I 3 (создание отрицательного падения напряжения, красный провод внизу и черный провод вверху).Если бы я думал в терминах эффекта I 3 в первую очередь и во вторую очередь эффекта I 2 , удерживая мои воображаемые выводы вольтметра в одних и тех же положениях (красный внизу и черный вверху), выражение было бы следующим: -300 (I 3 — I 2 ). Обратите внимание, что это выражение математически эквивалентно первому: +300 (I 2 — I 3 ).
Ну, это касается двух уравнений, но мне все еще нужно третье уравнение, чтобы завершить мой одновременный набор уравнений из трех переменных, трех уравнений.Это третье уравнение также должно включать в себя напряжение батареи, которое до этого момента не фигурировало ни в одном из двух предыдущих уравнений KVL. Чтобы сгенерировать это уравнение, я снова прослежу цикл своим воображаемым вольтметром, начиная с нижнего (отрицательного) вывода батареи, шагая по часовой стрелке (опять же, направление, в котором я шагаю, произвольно и не обязательно должно совпадать с направлением тока сетки в этом контуре):
Решение токов
Решение для I 1 , I 2 и I 3 с использованием любого метода одновременных уравнений, который мы предпочитаем:
Пример: Используйте Octave, чтобы найти решение для I 1 , I 2 и I 3 из упрощенной выше формы уравнений.
Решение: В Octave, клоне Matlab® с открытым исходным кодом, введите коэффициенты в матрицу A в квадратных скобках с элементами столбцов, разделенными запятыми, и строками, разделенными точкой с запятой. Введите напряжения в вектор-столбец: b. Неизвестные токи: I 1 , 2 и I 3 вычисляются командой: x = A \ b. Они содержатся в векторе-столбце x.
октава: 1> A = [300,100,150; 100,650, -300; -150,300, -450]
А =
300 100 150
100 650 -300
-150 300-450
октава: 2> b = [0; 0; -24]
b =
0
0
-24
октава: 3> x = A \ b
х =
-0.093793
0,077241
0,136092
Отрицательное значение, полученное для I 1 , говорит нам, что предполагаемое направление для этого тока сетки было неправильным. Таким образом, фактические значения тока через каждый резистор равны
.
Расчет падений напряжения на каждом резисторе:
Моделирование SPICE подтверждает точность наших расчетов напряжения:
несбалансированный мост Уитстона v1 1 0 г1 1 2 150 г2 1 3 50 г3 2 3 100 г4 2 0 300 г5 3 0250 .постоянного тока v1 24 24 1 .print dc v (1,2) v (1,3) v (3,2) v (2,0) v (3,0) .конец v1 v (1,2) v (1,3) v (3,2) v (2) v (3) 2.400E + 01 6.345E + 00 4.690E + 00 1.655E + 00 1.766E + 01 1.931E + 01
Пример:
(a) Найдите новый путь для тока I 3 , который не создает противоречивой полярности ни на одном резисторе по сравнению с I 1 или I 2 . R 4 был проблемным компонентом. (b) Найдите значения для I 1 , I 2 и I 3 .(c) Найдите пять токов резистора и сравните их с предыдущими значениями.
Решение:
(a) Маршрут I 3 через R 5 , R 3, и R 1 , как показано:
Обратите внимание, что конфликт полярности на R 4 был удален. Более того, ни один из других резисторов не имеет противоречивой полярности.
(b) Octave, бесплатный клон Matlab с открытым исходным кодом, выдает вектор тока сетки в «x»:
октава: 1> A = [300,100,250; 100,650,350; -250, -350, -500]
А =
300 100 250
100 650 350
-250-350-500
октава: 2> b = [0; 0; -24]
b =
0
0
-24
октава: 3> x = A \ b
х =
-0.093793
-0,058851
0,136092
Не все токи I 1 , I 2 и I 3 совпадают (I 2 ) с предыдущим мостом из-за различных цепей контура. Однако токи резистора сравниваются с предыдущими значениями:
IR1 = I1 + I3 = -93,793 мА + 136,092 мА = 42,299 мА
IR2 = I1 = -93,793 мА
IR3 = I1 + I2 + I3 = -93,793 мА -58,851 мА + 136,092 мА = -16,552 мА
IR4 = I2 = -58,851 мА
IR5 = I2 + I3 = -58.851 ма + 136,092 ма = 77,241 ма
Поскольку токи резистора такие же, как и предыдущие значения, напряжения резисторов будут идентичными и не нужно рассчитывать заново.
ОБЗОР:
- Шаги, которые необходимо выполнить для метода анализа «Mesh Current»:
- (1) Нарисуйте сеточные токи в контурах цепи, достаточные для учета всех компонентов.
- (2) Обозначьте полярность падения напряжения на резисторе в зависимости от предполагаемого направления токов сетки.
- (3) Напишите уравнения KVL для каждого контура цепи, подставляя произведение IR вместо E в каждом члене резистора в уравнении. Если два тока сетки пересекаются через компонент, выразите ток как алгебраическую сумму этих двух токов сетки (то есть I 1 + I 2 ), если токи проходят в одном направлении через этот компонент. Если нет, выразите силу тока как разность (т.е. I 1 — I 2 ).
- (4) Найдите неизвестные сеточные токи (системы уравнений).
- (5) Если какое-либо решение отрицательное, то предполагаемое направление тока неверно!
- (6) Алгебраически сложите токи сетки, чтобы найти компоненты тока, разделяющие несколько токов сетки.
- (7) Найдите падение напряжения на всех резисторах (E = IR).
Ток сетки при осмотре
Мы еще раз посмотрим на «метод сеточного тока», когда все токи идут по часовой стрелке (cw). Мотивация состоит в том, чтобы упростить запись уравнений сетки, игнорируя полярность падения напряжения на резисторе.Однако следует обратить внимание на полярность источников напряжения относительно предполагаемого направления тока. Знак падения напряжения на резисторе будет фиксированным.
Если мы напишем набор обычных уравнений сеточного тока для схемы ниже, где мы обратим внимание на признаки падения напряжения на резисторах, мы можем переставить коэффициенты в фиксированную структуру:
После перестановки мы можем писать уравнения путем проверки. Знаки коэффициентов следуют фиксированному шаблону в паре выше или в наборе из трех в правилах ниже.
Mesh Текущие правила:
- Этот метод предполагает использование обычных источников напряжения тока. Замените любой источник тока, подключенный параллельно, с резистором, на эквивалентный источник напряжения, подключенный последовательно с эквивалентным сопротивлением.
- Игнорируя направление тока или полярность напряжения на резисторах, нарисуйте токовые петли против часовой стрелки, проходящие через все компоненты. Избегайте вложенных циклов.
- Напишите уравнения закона напряжения в терминах неизвестных токов: I 1 , I 2 и I 3 .Коэффициент 1 по уравнению 1, коэффициент 2 по уравнению 2 и коэффициент 3 по уравнению 3 представляют собой положительные суммы резисторов вокруг соответствующих контуров.
- Все остальные коэффициенты отрицательны и представляют сопротивление, общее для пары шлейфов. Коэффициент 2 уравнения 1 — это резистор, общий для контуров 1 и 2, коэффициент 3 — резистор, общий для контуров 1 и 3. Повторите для других уравнений и коэффициентов.
- + (сумма петли R 1) I1 — (общая петля R 1-2) I2 — (общая петля R 1-3) I3 = E1
— (общая петля R 1-2) I1 + (сумма петли 2 R ) I2 — (общий контур R 2-3) I3 = E2
— (общий контур R 1-3) I1 — (общий контур R 2-3) I2 + (сумма петли R 3) I3 = E3 - Правая часть уравнений равна источнику напряжения электронного тока.Повышение напряжения по сравнению с предполагаемым током против часовой стрелки является положительным и 0 для отсутствия источника напряжения.
- Решите уравнения для токов в сетке: I 1 , I 2 и I3. Найдите токи через отдельные резисторы с помощью KCL. Решите для напряжений с Законом Ома и KVL.
Хотя приведенные выше правила специфичны для трехуровневой схемы, правила могут быть расширены на более мелкие или большие сетки. На рисунке ниже показано применение правил. Все три тока тянутся в одном направлении по часовой стрелке.Для каждого из трех контуров записывается одно уравнение КВЛ. Обратите внимание, что на резисторах отсутствует полярность. Нам это не нужно для определения знаков коэффициентов. Хотя нам нужно обратить внимание на полярность источника напряжения по отношению к направлению тока. Ток I 3 по часовой стрелке течет от положительной клеммы (+) источника l24 В, а затем возвращается к клемме (-). Это повышение напряжения при обычном протекании тока. Следовательно, правая часть третьего уравнения равна -24V.
В Octave введите коэффициенты в матрицу A с элементами столбцов, разделенными запятыми, и строками, разделенными точкой с запятой. Введите напряжения в вектор-столбец b. Найдите неизвестные токи: I 1 , I 2 и I 3 с помощью команды: x = A \ b. Эти токи содержатся в векторе-столбце x. Положительные значения показывают, что все три тока сетки текут в предполагаемом направлении по часовой стрелке.
октава: 2> A = [300, -100, -150; -100,650, -300; -150, -300,450]
А =
300-100 -150
-100 650 -300
-150 -300 450
октава: 3> b = [0; 0; 24]
b =
0
0
24
октава: 4> x = A \ b
х =
0.093793
0,077241
0,136092
Токи сетки соответствуют предыдущему решению за счет другого метода тока сетки. Расчет напряжений и токов резисторов будет идентичен предыдущему решению. Здесь нет необходимости повторяться.
Обратите внимание, что тексты по электротехнике основаны на обычном потоке тока. В этих текстах методы петлевого тока и тока сетки будут использовать предполагаемые токи сетки по часовой стрелке . Обычный ток течет через клемму (+) батареи через цепь, возвращаясь к клемме (-).Обычное повышение ток-напряжения соответствует отслеживанию предполагаемого тока от (-) до (+) через любые источники напряжения.
Ниже приводится еще один пример предыдущей схемы. Сопротивление вокруг контура 1 составляет 6 Ом, вокруг контура 2: 3 Ом. Общее сопротивление обоих контуров составляет 2 Ом. Обратите внимание на коэффициенты I 1 и I 2 в паре уравнений. Отслеживание предполагаемого тока петли 1 по часовой стрелке через B 1 от (+) до (-) соответствует увеличению напряжения потока электронного тока.
Таким образом, знак 28 В положительный. Контур 2 против часовой стрелки предположил, что ток идет от (-) до (+) через B 2 , то есть падение напряжения. Таким образом, знак B 2 отрицательный, -7 во втором уравнении сетки. Опять же, на резисторах нет маркировки полярности. Они также не фигурируют в уравнениях.
Оба тока I 1 = 5 A и I 2 = 1 A являются положительными. Оба они текут в направлении петель по часовой стрелке.Это сравнивается с предыдущими результатами.
Резюме:
- Модифицированный метод определения тока сетки позволяет избежать необходимости определять знаки коэффициентов уравнения путем рисования всех токов сетки по часовой стрелке для обычного протекания тока.
- Однако нам необходимо определить знак любых источников напряжения в контуре. Источник напряжения является положительным, если предполагаемый непрерывный ток протекает с батареей (источником). Знак отрицательный, если предполагаемый непрерывный ток течет по батарее.
- Подробнее см. В правилах выше.
СВЯЗАННЫЙ ТАБЛИЦА:
Метод тока отделения | Анализ сети постоянного тока
Первый и наиболее простой метод сетевого анализа называется Branch Current Method . В этом методе мы предполагаем направления токов в сети, а затем записываем уравнения, описывающие их отношения друг к другу с помощью законов Кирхгофа и Ома. Если у нас есть одно уравнение для каждого неизвестного тока, мы можем решить одновременные уравнения и определить все токи и, следовательно, все падения напряжения в сети.
Решение с использованием метода тока ветви
Давайте использовать эту схему, чтобы проиллюстрировать метод:
Выбор узла
Первый шаг — выбрать узел (соединение проводов) в цепи, чтобы использовать его как точку отсчета для наших неизвестных токов. Я выберу узел, соединяющий правую часть R 1 , верхнюю часть R 2 и левую часть R 3 .
В этом узле угадайте, в каком направлении идут токи трех проводов, обозначив три тока как I 1 , I 2 и I 3 соответственно.Имейте в виду, что эти направления тока на данный момент являются спекулятивными. К счастью, если окажется, что какое-либо из наших предположений было ошибочным, мы узнаем это, когда математически решим токи (любые «неправильные» направления тока будут отображаться в нашем решении как отрицательные числа).
Применить действующий закон Кирхгофа (KCL)
Закон Кирхгофа (KCL) говорит нам, что алгебраическая сумма токов, входящих и выходящих из узла, должна равняться нулю, поэтому мы можем связать эти три тока (I 1 , I 2 и I 3 ) с каждым из них. другое в одном уравнении.Ради условности я буду обозначать любой текущий , входящий в узел, как положительный по знаку, а любой текущий , выходящий из узла, как отрицательный по знаку:
Обозначьте все падения напряжения
Следующим шагом является маркировка всех полярностей падения напряжения на резисторах в соответствии с предполагаемыми направлениями токов. Полярность положительная, когда ток входит в резистор, и отрицательная, когда он выходит из резистора:
Полярность батареи, конечно же, остается прежней в соответствии с их символикой (короткий конец отрицательный, длинный конец положительный).Это нормально, если полярность падения напряжения на резисторе не совпадает с полярностью ближайшей батареи, при условии, что полярность напряжения резистора правильно основана на предполагаемом направлении тока через него. В некоторых случаях мы можем обнаружить, что ток будет принудительно вытеснен обратно через батарею, вызывая именно этот эффект. Здесь важно помнить, что все полярности резисторов и последующие вычисления должны основываться на изначально предполагаемых направлениях тока. Как было сказано ранее, если ваше предположение окажется неверным, это станет очевидным после того, как уравнения будут решены (с помощью отрицательного решения).Однако масштаб решения все равно будет правильным.
Применить закон Кирхгофа о напряжении (KVL)
Закон Кирхгофа по напряжению (KVL) говорит нам, что алгебраическая сумма всех напряжений в контуре должна быть равна нулю, поэтому мы можем создать больше уравнений с текущими членами (I 1 , I 2 и I 3 ) для наши системы уравнений. Чтобы получить уравнение КВЛ, мы должны подсчитать падения напряжения в контуре цепи, как если бы мы измеряли с помощью настоящего вольтметра.Я выберу сначала обвести левую петлю этой схемы, начиная с верхнего левого угла и двигаясь против часовой стрелки (выбор начальных точек и направлений произвольный). Результат будет выглядеть так:
Завершив нашу трассировку левого контура, мы складываем эти показания напряжения вместе для получения нулевой суммы:
Конечно, мы еще не знаем, какое напряжение на R 1 или R 2 , поэтому мы не можем вставить эти значения в уравнение в виде числовых значений на данном этапе.Однако мы с по знаем, что все три напряжения должны алгебраически складываться с нулем, поэтому уравнение верно. Мы можем пойти дальше и выразить неизвестные напряжения как произведение соответствующих неизвестных токов (I 1 и I 2 ) и их соответствующих резисторов, следуя закону Ома (E = IR), а также исключить 0 термины:
Поскольку мы знаем значения всех резисторов в омах, мы можем просто подставить эти цифры в уравнение, чтобы немного упростить задачу:
Вам может быть интересно, почему мы взяли на себя все усилия по манипулированию этим уравнением из его первоначальной формы (-28 + E R2 + E R1 ).В конце концов, последние два члена до сих пор неизвестны, поэтому какая польза от выражения их в терминах неизвестных напряжений или неизвестных токов (умноженных на сопротивления)? Цель этого состоит в том, чтобы получить уравнение KVL, выраженное с использованием тех же неизвестных переменных , что и уравнение KCL, поскольку это является необходимым требованием для любого метода решения одновременного уравнения. Чтобы найти три неизвестных тока (I 1 , I 2 и I 3 ), мы должны иметь три уравнения, связывающих эти три тока (а не напряжений !) Вместе.
Применяя те же шаги к правому контуру схемы (начиная с выбранного узла и двигаясь против часовой стрелки), мы получаем другое уравнение KVL:
Теперь, зная, что напряжение на каждом резисторе может быть и должно быть равно , выраженному как произведение соответствующего тока и (известного) сопротивления каждого резистора, мы можем переписать уравнение как таковое:
Поиск неизвестного
Теперь у нас есть математическая система из трех уравнений (одно уравнение KCL и два уравнения KVL) и трех неизвестных:
Для некоторых методов решения (особенно для любого метода с использованием калькулятора) полезно выражать каждый неизвестный член в каждом уравнении любым постоянным значением справа от знака равенства и любыми членами «единицы», выраженными явным коэффициент 1.Переписывая уравнения еще раз, получаем:
Используя любые доступные нам методы решения, мы должны прийти к решению для трех неизвестных значений тока:
Итак, я 1 — это 5 ампер, я 2 — 4 ампер, а я 3 — отрицательный 1 ампер. Но что означает «отрицательный» ток? В этом случае это означает, что наше предполагало направление для I 3 было противоположным его действительному направлению .Возвращаясь к нашей исходной схеме, мы можем перерисовать стрелку тока для I 3 (и перерисовать полярность падения напряжения R 3 , чтобы она соответствовала):
Перерисуйте схему
Обратите внимание, как ток проталкивается назад через батарею 2 (электроны текут «вверх») из-за более высокого напряжения батареи 1 (ток которой направлен «вниз», как обычно)! Несмотря на то, что полярность батареи B2 пытается вытолкнуть электроны вниз в этой ветви цепи, электроны вытесняются обратно через нее из-за более высокого напряжения батареи B1.Означает ли это, что более сильная батарея всегда будет «выигрывать», а более слабая батарея всегда будет пропускать ток в обратном направлении? Нет! На самом деле это зависит от относительных напряжений и батарей и номиналов резисторов в цепи. Единственный надежный способ определить, что происходит, — это потратить время на математический анализ сети.
Расчет падения напряжения на всех резисторах
Теперь, когда мы знаем величину всех токов в этой цепи, мы можем рассчитать падение напряжения на всех резисторах по закону Ома (E = IR):
Анализируйте сеть с помощью SPICE
Давайте теперь проанализируем эту сеть с помощью SPICE, чтобы проверить наши значения напряжения.Мы могли бы анализировать ток также с помощью SPICE, но поскольку для этого требуется установка дополнительных компонентов в схему, и поскольку мы знаем, что если все напряжения одинаковы и все сопротивления одинаковы, то токи должны быть то же самое, я выберу менее сложный анализ. Вот повторный чертеж нашей схемы с номерами узлов для SPICE:
пример сетевого анализа v1 1 0 v2 3 0 постоянного тока 7 г1 1 2 4 г2 2 0 2 г3 2 3 1 .постоянного тока v1 28 28 1 .print dc v (1,2) v (2,0) v (2,3) .конец v1 v (1,2) v (2) v (2,3) 2.800E + 01 2.000E + 01 8.000E + 00 1.000E + 00
Разумеется, все значения напряжения оказываются одинаковыми: 20 В на R 1 (узлы 1 и 2), 8 В на R 2 (узлы 2 и 0) и 1 В на R 3 (узлы 2 и 3). Обратите внимание на знаки всех этих значений напряжения: все они положительные! SPICE основывает свои полярности на порядке, в котором перечислены узлы: первый узел является положительным, а второй — отрицательным.Например, число положительных (+) 20 вольт между узлами 1 и 2 означает, что узел 1 является положительным по отношению к узлу 2. Если бы значение было отрицательным в анализе SPICE, мы бы знали, что наша фактическая полярность была «Назад» (узел 1 отрицателен по отношению к узлу 2). Проверяя порядок узлов в списке SPICE, мы видим, что все полярности соответствуют тому, что мы определили с помощью метода анализа Branch Current.
ОБЗОР:
- Шаги, которые необходимо выполнить для метода анализа «Branch Current»:
- Выберите узел и предположите направления токов.
- Напишите уравнение KCL, связывающее токи в узле.
- Обозначьте полярность падения напряжения на резисторе с учетом предполагаемых токов.
- Напишите уравнения KVL для каждого контура цепи, подставляя произведение IR вместо E в каждом члене резистора в уравнениях.
- Найдите неизвестные токи ответвления (системы уравнений).
- Если какое-либо решение отрицательное, то предполагаемое направление тока для этого решения неверно!
- Найдите падение напряжения на всех резисторах (E = IR).
СВЯЗАННЫЙ ТАБЛИЦА:
Метод тока ответвления
В методе тока ответвления законы напряжения и тока Кирхгофа используются для определения тока в каждой ветви цепи. Как только токи ответвления известны, можно определить напряжения.
ШАГОВ
Ниже приведены общие шаги, используемые при применении метода тока ветви.
Шаг 1: Назначьте ток в каждой цепи, в каком направлении она разветвляется.
Шаг 2: Покажите полярность напряжений резистора в соответствии с назначенным направлением тока ветви.
Шаг 3: Примените закон Кирхгофа для каждого замкнутого контура (сумма напряжений равна нулю).
Шаг 4: Примените закон Кирхгофа к минимальному количеству узлов, чтобы были учтены все токи ответвления (сумма токов в узле равна нулю).
Шаг 5: Решите уравнения, полученные на шагах 3 и 4 для значений тока ветви.
ЦЕПЬ ДЕМОНСТРАЦИИ АНАЛИЗА ТОКА ОТРАСЛИ
| Первая | Ток ответвления I 1 , I 2 и I 3 присваиваются в направлении, показанном на рисунке-1. На данном этапе не беспокойтесь о текущих направлениях. |
| Второй | Полярности падений напряжения на R 1 , R 2 и R 3 показаны на рисунке 1 в соответствии с направлениями тока. |
| Третий | Закон Кирхгофа по напряжению, примененный к двум контурам, дает следующие уравнения. Уравнение 1: R 1 I 1 + R 2 I 2 —- V S1 = 0 для контура 1 Уравнение 2: R 2 I 2 + R 3 I 3 —— V S2 = 0 для контура 2 |
| Четвертый | Закон Кирхгофа применяется к узлу A, включая все токи ответвления, следующим образом. Уравнение 3: I 1 — I 2 + I 3 = 0 отрицательный знак указывает на то, что я 2 находится вне стыка. |
| Пятая | Три уравнения должны быть решены для трех неизвестных токов: I 1 , I 2 и I 3 . |
Три уравнения на вышеуказанных шагах называются одновременными уравнениями и могут быть решены путем подстановки.
ПРИМЕР МЕТОДА ТЕКУЩЕГО РАЗВИТИЯ
Определение тока в каждой ветви с использованием метода тока ветви.
| Шаг 1: | Назначьте ток ответвления имейте в виду, что вы можете принять любое направление тока в этой точке и что окончательное решение будет иметь отрицательный знак, если фактический ток противоположен назначенному току. |
| Шаг 2: | Отметьте полярность падения напряжения на резисторе, как показано на рисунке. |
| Шаг 3: | Применение закона Кирхгофа по напряжению вокруг левого контура дает 47I 1 + 22I 2 — 10 = 0 Вокруг правой петли дает 22I 2 + 68I 3 — 5 = 0 |
| Шаг 4: | В узле A текущее уравнение — Я 1 — Я 2 + Я 3 = 0 |
| Шаг 5: | Уравнение решается подстановкой следующим образом.Сначала найдите I в терминах I 2 и I 3 Я 1 = Я 2 — Я 3 Теперь замените I 2 — I 3 на I 1 в уравнении левого цикла. 47 (I 2 — I 3 ) + 22I 2 = 10 47I 2 — 47I 3 + 22I 2 = 10 69I 2 — 47I 3 = 10 Затем возьмите уравнение правой петли и решите для I 2 через I 3 22I 2 = 5 — 68I 3 I 2 = (5 — 68I 3 ) / 22 Подставляя это выражение для I2 в 69I 2 — 47I 3 = 10 вы получите 69 (5-68I 3 /22) — 47I 3 = 10 (345 — 4692I 3 ) / 22 — 47I 3 = 10 -260.27I 3 = -5,68 I 3 = 5,68 / 260,27 = 0,0218 A = 21,8 мА Теперь подставьте это значение I 3 в уравнение правой петли. 22I 2 + 68 (0,0218) = 5 Решить для I 2 I 2 = (5-68 (0,0218)) / 22 = 3,52 / 22 = 0,16 A = 160 мА Подставив значения I 2 и I 3 в текущее уравнение в узле A, вы получите Я 1 — 0.16 + 0,0218 = 0 I 1 = 0,16 — 0,0218 = 0,138 A = 138 мА |
Метод токовой петли
Метод токовой петли
Далее: Эквивалентные схемы
Up: Законы Кирхгофа
Предыдущая: Метод тока ветви
Этот метод также называется методом петли сетки.
В качестве независимых переменных тока принимаем циркулирующие
ток в каждом из внутренних шлейфов.
- Обозначьте токи внутреннего контура на диаграмме.
- Получите выражения для изменения напряжения вокруг каждого интерьера
петля. - Решите систему алгебраических уравнений.
В зависимости от проблемы в конечном итоге может потребоваться
алгебраически суммируйте токи двух контуров, чтобы получить необходимое
ток внутренней ветви для окончательного ответа.
Давайте рассмотрим пример схемы моста Уитстона, показанной на
рисунок 1.6.
Мы хотим рассчитать токи вокруг контуров.
Три тока обозначаются как: ток по часовой стрелке
вокруг большой внутренней петли, которая включает ЭДС,
по часовой стрелке ток вокруг верхнего равностороннего треугольника, а
по часовой стрелке ток вокруг нижнего равностороннего треугольника.Выражения петли напряжения для трех петель тока:
Рисунок 1.6:
Петлевой метод для схемы моста Уитстона.
Сбор терминов, содержащих одинаковый ток, дает
Если используются значения параметров, показанные на диаграмме,
текущие значения можно найти, решив набор одновременных
уравнения, чтобы дать
Более того, если пронумеровать отдельные токи через каждый резистор
используя ту же схему, что и для каждого компонента (ток через
есть, есть и т. д.) и идентифицировать как
ток из батареи, затем
Это те же токи, которые можно было бы найти, используя только ток Кирхгофа.
уравнения; однако здесь нам пришлось обрабатывать только три одновременных
уравнения вместо шести.
Пример:
Используйте метод тока контура для определения напряжения, развиваемого на
клеммы AB в схеме, показанной на рисунке 1.7.Рисунок 1.7: Пример схемы для анализа с использованием
метод токовой петли.Рассмотрим токовую петлю по часовой стрелке через два
резисторы и два потенциала.
Аналогичным образом рассмотрим ток по часовой стрелке вокруг другого
внутренний контур, состоящий из трех резисторов и.
Закон Кирхгофа даетРешение двух вышеупомянутых уравнений относительно неизвестных токов в контуре
и даетНапряжение на AB определяется просто
Далее: Эквивалентные схемы
Up: Законы Кирхгофа
Предыдущая: Метод тока ветви
Вт 13 июля 16:55:15 EDT 1999
Анализ цепей
— Как узнать о существовании петлевых токов?
Я постараюсь дать вам ответ, основанный на том, как я это представляю — то, что я пытаюсь сделать, когда алгебраический ответ кажется неудовлетворительным.Это настолько неформально, насколько это возможно, но я думаю, что это помогает понять, как получилось (и правильно) уменьшить такое количество токов ответвления до гораздо меньшего количества токов сетки.
Представьте себе узел, из которого выходят 4 ветви. Каждая ветвь несет «настоящий» ток \ $ i_ {k} \ $. Теперь визуализируйте его в 3D, поместив каждую ветвь на высоту, равную ее текущей:
Для удобства из узла выходят положительные токи (высоты). Поскольку сумма токов равна нулю, то сумма высот также равна нулю.
С другой стороны, токи сетки будут подобны зданиям / блокам, потому что это один и тот же компонент тока вокруг каждого внутреннего цикла / панели:
Так как каждая «панель» имеет одну общую сторону со своим соседом, тогда вертикальное расстояние между зданиями должно быть равно «реальному» току ветви. Поэтому они здания «привязаны» друг к другу по вертикали, а разница в высоте и есть ответвление тока.
Если смотреть на группу зданий вокруг узла сверху:
И каждый из них «привязан» друг к другу по вертикали, вы можете пройти условия блокировки: 1 >> 2 >> 3 >> 4, и результирующая высота панели 4 должна волшебным образом совпадать с альтернативным путем 1 >> 4.
Магия исходит из предустановленного факта, что сумма токов (или «высот») ветвей, выходящих из центрального узла, равна нулю. Какая бы высота ни была достигнута на пути, она должна быть возвращена в конце. Строения петель, эквивалентные исходным токам, будут следующими:
Таким образом, замки по высоте являются самосогласованными, но общая высота на этом этапе может иметь любое значение, если разница равна токам ответвлений (вы можете подтолкнуть вверх или вниз группу зданий в целом и все еще будьте последовательны).
Единственное решение достигается благодаря крайним краям цепи, где нет соседей, а ток сетки равен току ветви.
Вы также можете считать, что самый внешний сосед, лежащий за пределами границы схемы, имеет известную нулевую высоту. Это граничное условие делает решение уникальным.
Итак, я в основном говорю, что ПОТОМУ ЧТО токи от узла в сумме равны нулю, можно назначить эквивалентные токи сетки. Если вы нарушите это и назначите какой-либо ток какой-либо ветви, тогда невозможно будет использовать токи сетки для представления одной и той же системы.
Вы также можете прийти к такому же выводу, представив большую плоскую схему и предположив, что ее можно выразить как сеточные токи. Вы начинаете с внешнего края, поскольку токи сетки равны токам ответвления. Все соседи согласованы из-за простого соотношения токов на краю. Затем вы продвигаетесь внутрь, причем каждый ток сетки представляет собой разницу между током ветви и уже назначенным током внешней соседней сетки. Все работает до последнего цикла.
Определение тока, протекающего в цепи
Следующие пункты выделяют две теоремы, используемые для определения тока, протекающего в цепи. Вот теоремы: 1. Теорема Максвелла о циркулирующем токе 2. Теорема об узловом напряжении.
1. Теорема Максвелла о циркулирующем токе:
Если сеть с несколькими источниками имеет более двух узлов, ток в ней можно определить по теореме Максвелла о циркулирующем токе. Это один из самых универсальных методов решения сетей.
В ряде случаев сеть может рассматриваться как состоящая из набора смежных петель, каждая из которых образует многоугольник, состоящий из нескольких ветвей сети (без каких-либо диагоналей). Некоторые ветви сети являются общими для двух соседних петель, в то время как другие образуют внешнюю цепь, где каждая ветвь встречается только в одной петле.
Эта теорема включает представление тока, который, как предполагается, циркулирует по замкнутому контуру, изогнутой стрелкой и пометку стрелки с ее идентифицирующим символом тока I нижним индексом.
По этой теореме ток, протекающий через ветвь, общую для двух сеток, будет равен алгебраической сумме двух токов контура, протекающих через нее. Направление любого тока контура может быть принято как по часовой стрелке, так и против часовой стрелки, но для систематического решения предполагается, что направления всех токов контура одинаковы (скажем, по часовой стрелке).
Затем второй закон Кирхгофа применяется к каждой сетке и получаются алгебраические уравнения. Общее количество независимых уравнений равно количеству ячеек (т.е.е. уравнений меньше, чем в чисто кирхгофском решении). Следовательно, они могут быть решены как одновременные уравнения, чтобы определить циркулирующие токи, а затем токи ответвления. Таким образом, этот метод избавляет от большого количества утомительных расчетов, связанных с методом тока ветви.
Применение теоремы Максвелла о циркулирующем токе будет более ясно из следующих иллюстраций:
Пример 1:
Решите сеть, показанную на рис.2,65 методом тока сетки.
Решение:
Сеть перерисовывается, как показано на рис. 2.66. Есть две независимые петли. Токи контура сняты по часовой стрелке, как указано на принципиальной схеме. Отдельные токи ответвления вместе с их направлениями потока также показаны на принципиальной схеме.
Применяя закон Кирхгофа к сеткам I и II, получаем:
2.Теорема о напряжении узла:
Для применения теоремы о напряжении узла один из узлов берется как опорный или нулевой потенциал или опорный узел, а разность потенциалов между каждым из других узлов и опорным узлом выражается в терминах неизвестного напряжения (обозначено как V 1 , V 2 или V A , V B или V x , V y и т. Д.), И в каждом узле применяется первый (или текущий) закон Кирхгофа, предполагающий возможные направления токов ответвления.
Это предположение не меняет постановки задачи, так как токи ответвлений определяются разностью потенциалов между соответствующими узлами, а не абсолютными значениями узловых потенциалов.
Подобно теореме Максвелла о циркулирующем токе, теорема об узловом напряжении сокращает количество уравнений, которые необходимо решить для определения неизвестных величин. Если имеется n узлов, должно быть (n — 1) количество узловых уравнений в терминах (n — 1) числа неизвестных переменных узловых напряжений.Решая эти уравнения, известно, что узловые напряжения вычисляют токи ответвления.
Когда число узлов минус один меньше числа независимых ячеек в сети, это фактически более выгодно. Кроме того, он особенно подходит для сетей, имеющих много параллельных цепей с общим заземленным узлом, например, в электронных цепях.
Пример 2:
Рассмотрим, например, двухузловую сеть, как показано на рис.2.72.
Узел C был взят как опорный узел. Пусть соответственно относительно узла C. Пусть распределение тока будет таким, как показано на принципиальной схеме (рис. 2.72) произвольно. Теперь давайте получим независимые уравнения для этих двух узлов.
Узел A представляет собой соединение резисторов R 1 , R 2 и R 4 . Итак, текущее уравнение для узла A:
Узел B — это место соединения резисторов R 2 , R 3 и R 5 .Итак, текущее уравнение для узла B:
Уравнения. Теперь можно решить (2.34) и (2.35), чтобы получить значения V A и V B , а затем значения токов I 1 , I 2 , I 3 , I 4 и I 5 можно легко вычислить.
Пример 3:
Две батареи A и B подключены параллельно к нагрузке 10 Ом. Батарея A имеет ЭДС 12 В и внутреннее сопротивление 2 Ом, а батарея B имеет ЭДС 10 В и внутреннее сопротивление 1 Ом.Используя узловой анализ, определите токи, подаваемые каждой батареей, и ток нагрузки.
Решение:
принимая узел С в качестве опорного узла и потенциалы узлов А и В V и V B , соответственно, и распределение тока, как показано на рис. 2.73 произвольно.
Из принципиальной схемы, представленной на рис. 2.73.
правил Кирхгофа | Физика
Найдите токи, протекающие в цепи на Рисунке 5.
Рисунок 5. Эта схема аналогична схеме на рисунке 1, но указаны сопротивления и ЭДС. (Каждая ЭДС обозначена буквой E.) Токи в каждой ветви отмечены и предполагается, что они движутся в показанных направлениях. В этом примере для поиска токов используются правила Кирхгофа.
Стратегия
Эта схема достаточно сложна, поэтому токи нельзя найти с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа.Токи обозначены на рисунке I 1 , I 2 и I 3 , и сделаны предположения относительно их направлений. Места на диаграмме обозначены буквами от a до h. В решении мы применим правила перехода и петли, ища три независимых уравнения, которые позволят нам решить три неизвестных тока.
Решение
Начнем с применения правила Кирхгофа первого или перекрестка в точке а.Это дает
I 1 = I 2 + I 3 ,
с I 1 течет в стык, а I 2 и I 3 вытекает. Применение правила соединения в e дает точно такое же уравнение, так что новая информация не получается. Это одно уравнение с тремя неизвестными — необходимы три независимых уравнения, поэтому необходимо применять правило цикла.Теперь рассмотрим цикл abcdea. Двигаясь от a к b, мы проходим R 2 в том же (предполагаемом) направлении текущего I 2 , поэтому изменение потенциала составляет — I 2 R 2 . Затем, переходя от b к c, мы переходим от — к +, так что изменение потенциала составляет + ЭДС 1 . Прохождение внутреннего сопротивления r 1 от c до d дает — I 2 r 1 .Завершение цикла путем перехода от d к a снова проходит через резистор в том же направлении, что и его ток, давая изменение потенциала — I 1 R 1 . Правило цикла гласит, что сумма изменений потенциала равна нулю. Таким образом,
— I 2 R 2 + ЭДС 1 — I 2 r 1 — I 1 R 1 = — I 2 ( R 2 + R 1 ) + ЭДС 1 — I 1 R 1 = 0.
Подстановка значений из принципиальной схемы для сопротивлений и ЭДС и удаление единиц ампер дает
−3 I 2 + 18-6 I 1 = 0.
Теперь, применяя правило цикла к aefgha (мы могли бы также выбрать abcdefgha) аналогичным образом дает
+ I 1 R 1 + I 3 R 3 + I 3 r 2 — ЭДС 2 = + I 1 R 1 + I 3 ( R 3 + r 2 ) — ЭДС 2 = 0.
Обратите внимание, что знаки меняются местами по сравнению с другим циклом, потому что элементы перемещаются в противоположном направлении. С введенными значениями это становится
+6 I 1 + 2 I 3 — 45 = 0.
Этих трех уравнений достаточно для решения трех неизвестных токов. Сначала решите второе уравнение относительно I 2 :
I 2 = 6 — 2 I 1 .
Теперь решите третье уравнение относительно I 3 :
I 3 = 22,5 — 3 I 1 .
Подстановка этих двух новых уравнений в первое позволяет нам найти значение для I 1 :
I 1 = I 2 + I 3 = (6−2 I 1 ) + (22,5− 3 I 1 ) = 28,5 — 5 Я 1 .
Объединение терминов дает
6 I 1 = 28,5 и
I 1 = 4,75 А.
Подставляя это значение вместо I 1 обратно в четвертое уравнение, получаем
I 2 = 6 — 2 I 1 = 6 — 9,50
I 2 = −3,50 A.
Знак минус означает, что I 2 течет в направлении, противоположном предполагаемому на рисунке 5.Наконец, подстановка значения I 1 в пятое уравнение дает
I 3 = 22,5 — 3 I 1 = 22,5 — 14.

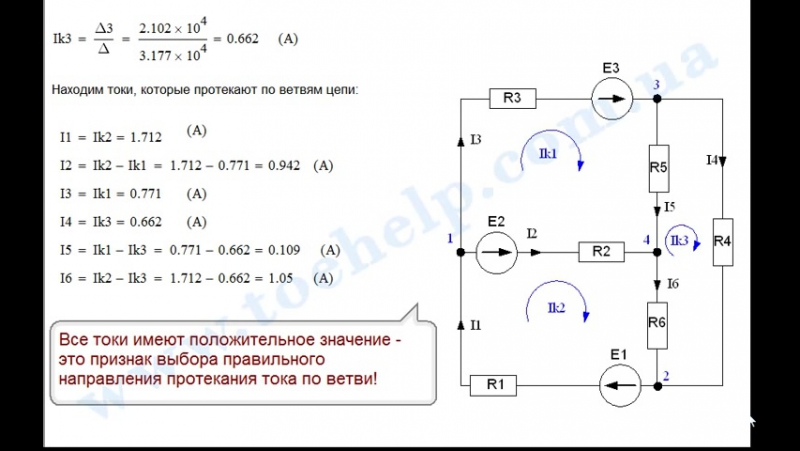
 Составим расчетные уравнения для электрической цепи, изображенной на рисунке 1. Выбрав произвольно напрвление токов в ветвях цепи, составляем уравнение по первому закону Кирхгофа для a, b, c :
Составим расчетные уравнения для электрической цепи, изображенной на рисунке 1. Выбрав произвольно напрвление токов в ветвях цепи, составляем уравнение по первому закону Кирхгофа для a, b, c : В том случае, когда контурный ток получается со знаком минус, это означает, что его направление противоположно выбранному на схеме (примечание: изменять его не нужно, ответ так и записываем с минусом)
В том случае, когда контурный ток получается со знаком минус, это означает, что его направление противоположно выбранному на схеме (примечание: изменять его не нужно, ответ так и записываем с минусом) 1.1
1.1