Параметры нелинейных элементов и некоторые схемы их замещения — Студопедия
Классификация нелинейных элементов
Нелинейные электрические цепи
РАЗДЕЛ II. НЕЛИНЕЙНЫЕ ЦЕПИ
Нелинейные цепи — это цепи, в которых есть хотя бы один нелинейный элемент, Нелинейный элемент — это элемент, для которого связь тока и напряжения задают нелинейным уравнением.
В нелинейных цепях не выполняется принцип наложения, и поэтому нет общих методов расчёта. Это вызывает необходимость разработки специальных методов расчета для каждого типа нелинейных элементов и режима их работы.
Нелинейные элементы классифицируют:
1) по физической природе: проводниковые, полупроводниковые, диэлектрические, электронные, ионные и т.д.;
2) по характеру делят на резистивные, емкостные и индуктивные;
ВАХ КВХ ВАХ
3) по виду характеристик все элементы делят
— на симметричные и несимметричные. Симметричные – это такие, у которых характеристика симметрична относительно начала координат. Для не симметричных элементов раз и навсегда выбирают положительное направление напряжения или тока и для них в справочниках приводится ВАХ. Только такое направление можно использовать при решении задач с использованием этих ВАХ.
Симметричные – это такие, у которых характеристика симметрична относительно начала координат. Для не симметричных элементов раз и навсегда выбирают положительное направление напряжения или тока и для них в справочниках приводится ВАХ. Только такое направление можно использовать при решении задач с использованием этих ВАХ.
— на однозначные и неоднозначные. Неоднозначные, когда одному значению тока или напряжения на ВАХ соответствуют несколько точек;
4) инерционные и безынерционные элементы. Инерционными элементами называют такие элементы, у которых нелинейность обусловлена нагревом тела при прохождении тока. Т. к. температура не может изменяться сколь угодно быстро, то при прохождении по такому элементу переменного тока с достаточно высокой частотой и неизменным действующим значением, температура элемента остается практически постоянной в течение всего периода изменения тока. Поэтому для мгновенных значений элемент оказывается линейным и характеризуется какой-то постоянной величиной R (I,U). Если же изменится действующее значение тока, то изменится температура и получится другое сопротивление, т. е. для действующих значений элемент станет нелинейным.
Если же изменится действующее значение тока, то изменится температура и получится другое сопротивление, т. е. для действующих значений элемент станет нелинейным.
5) управляемые и неуправляемые элементы. Выше мы говорили о неуправляемых элементах. К управляемым элементам относят элементы с тремя и более выводами, у которых, изменяя ток или напряжение на одном выводе, можно менять ВАХ относительно других выводов.
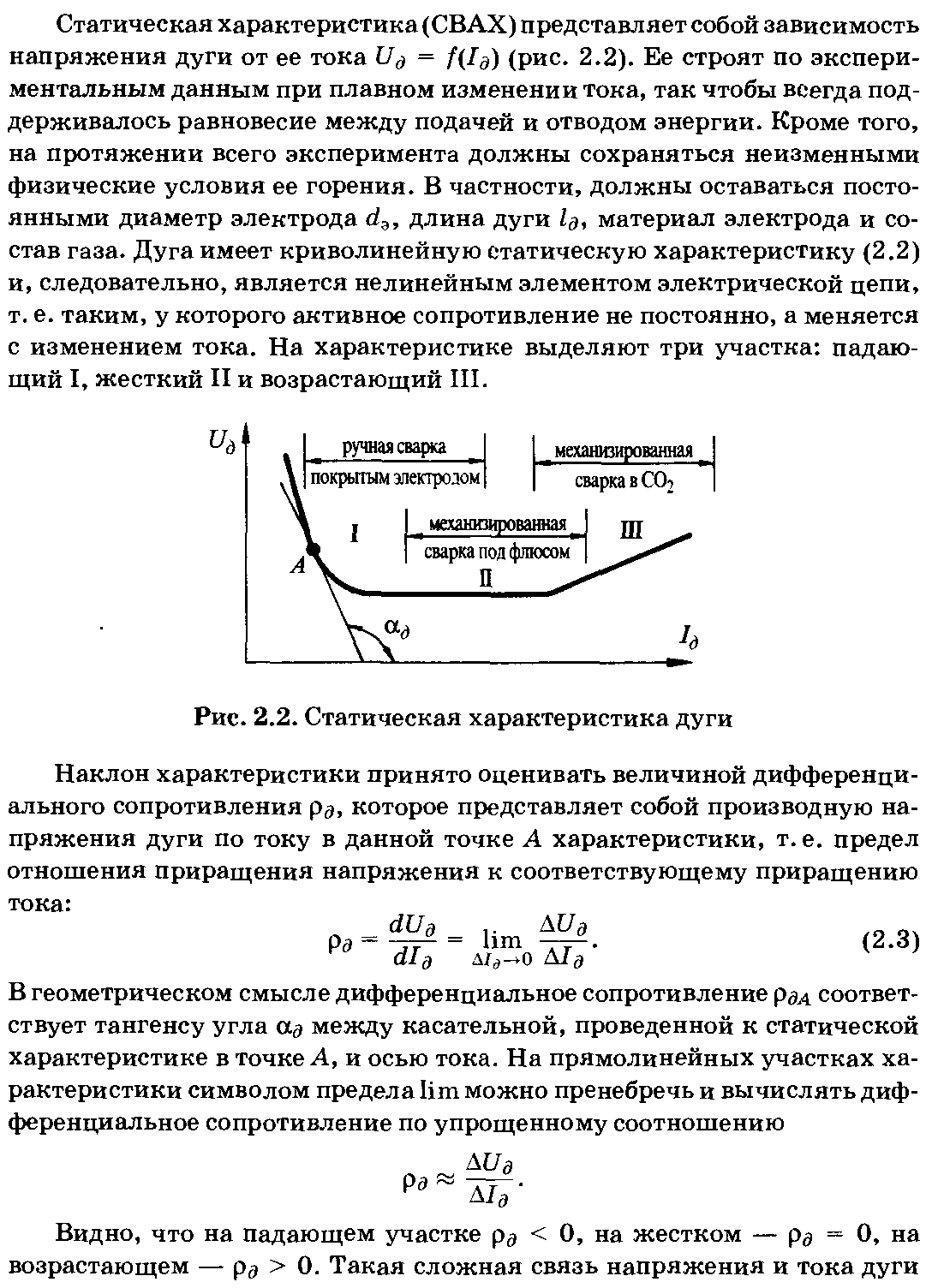
В зависимости от конкретной задачи удобно применять те или иные параметры элементов и общее число их велико, но чаще всего используют статические и дифференциальные параметры. Для резистивного двухполюсного элемента это будут статическое и дифференциальное сопротивления.
— в заданной точке ВАХ
— в заданной рабочей точке ВАХ
Это сопротивление RД можно посчитать двумя способами:
1. Дают небольшое приращение напряжения. Находят по ВАХ, вызванное этим приращением, приращение тока и берут их отношение. Недостатком этого способа является то, что для повышения точности расчета нужно уменьшать DU и DI, но при этом трудно работать с графиком.
Недостатком этого способа является то, что для повышения точности расчета нужно уменьшать DU и DI, но при этом трудно работать с графиком.
2. К заданной точке кривой проводят касательную и тогда по геометрическому определению производной, получают
Где приращения берут на этой касательной и могут быть сколь угодно большими.
Если известен режим работы нелинейного элемента, то в этой точке известно его статическое сопротивление, а также напряжение и ток, поэтому его можно заменить одним из 3-х способов.
Если известно, что во время работы цепи ток и напряжение меняются в пределах «более-менее прямолинейного участка ВАХ», то этот участок описывают линейным уравнением и ставят ему в соответствие такую эквивалентную схему.
Линеаризуют этот участок уравнением вида U=a+ib.Получают для него коэффициенты уравнения.
При i=0 и U=U0=а,
— усреднённое значение на этом участке.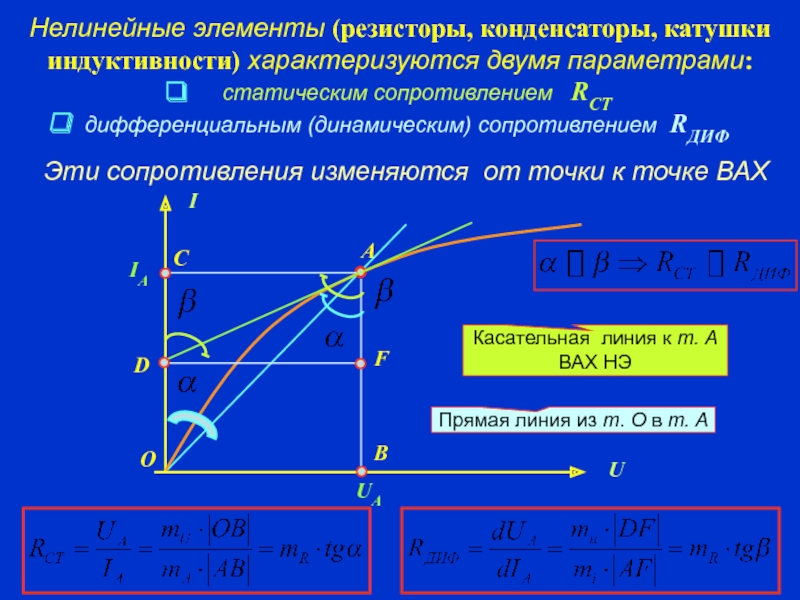
Тогда , что соответствует следующей схеме замещения:
Эта схема будет справедлива для участка, ограниченного волнистой линией.
Тоже самое выражение можно записать по другому:
Поэтому в некоторых задачах, где заранее известно, что токи и напряжения нелинейного элемента представляют в виде суммы постоянной составляющей Uрт, Iрт и переменной составляющей u~, i~ c амплитудой << чем величина постоянной составляющей, отдельно рассчитывают режим на постоянном токе (напряжении) и отдельно для переменной составляющей. Из записей видно, что двухполюсный элемент для малой переменной составляющей можно заменить просто дифференциальным сопротивлением в рабочей точке.
Этот же подход применяют и в схемах с многополюсными элементами, но там не удаётся ввести только одно сопротивление, т.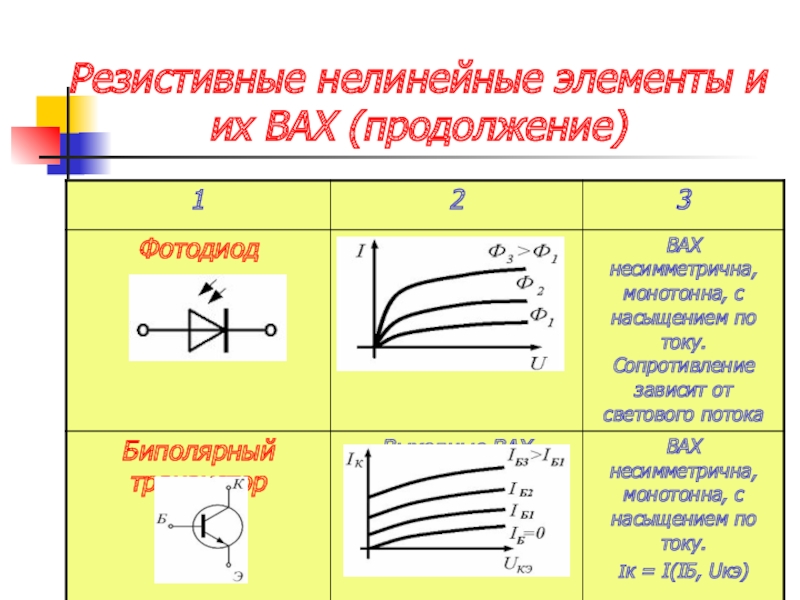 к. Ч. П. характеризуются четырьмя коэффициентами уравнений. Но можно найти эти коэффициенты для малых переменных составляющих токов и напряжений.
к. Ч. П. характеризуются четырьмя коэффициентами уравнений. Но можно найти эти коэффициенты для малых переменных составляющих токов и напряжений.
Пример: Биполярный транзистор (схема с общим эмиттером).
Пусть известно, что uj=Upτ+ukj , ij=Ipτ+ikj
Схема замещения:
Применим дифференцирующие параметры и получим в форме «И».
uбк=h21iб+h12uкэ
iкэ=h21iб+h22uкэ
Uбэ=H11Iб+H21Uкэ
Эти уравнения пишут для переменных составляющих, потому что изменяется процедура расчета элементов.
H11=Uбэ/Iб при Iб=0, т.е. iб=Iбр.т.
H12=Uбэ/Uкэ при Iб=0
H21=Iк/Iб при Uкэ=0
H22=Iк/Uкэ при Iб=0, т.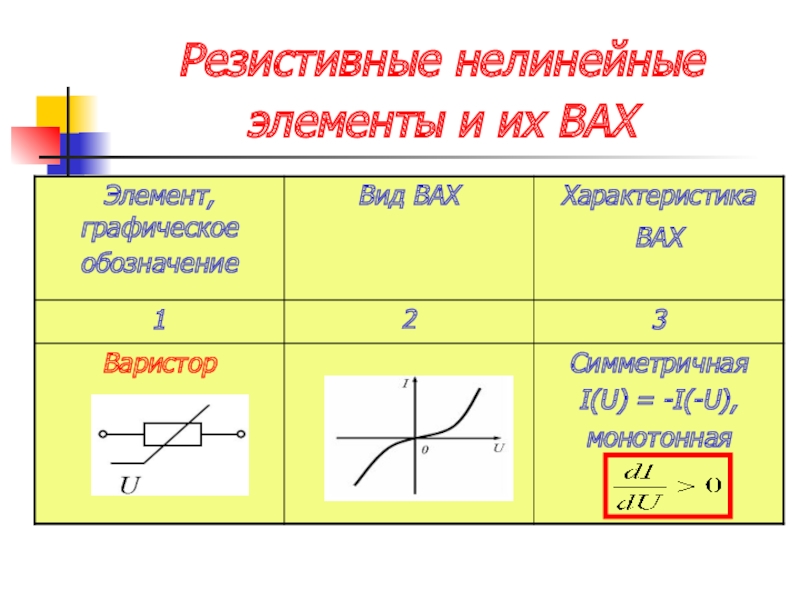 е. iб=Iбр.т.
е. iб=Iбр.т.
h12=ΔUбэ/ΔUкэ h21=Δiк/Δiб h22=Δiк/Δuкэ,
где I, U есть приращения токов и напряжений в окрестности рабочей точки.
Вольтамперные характеристики данного нелинейного элемента.
Методы расчёта нелинейных цепей постоянного тока
Различают: численные, аналитические и графические методы.
1) Численные – это методы численного решения нелинейных уравнений. Обычно используют ЭВМ. Они позволяют решить широкий круг задач, но ответ получается в виде числа.
2) Аналитические – это методы в основе которых лежит аппроксимация ВАХ какой-нибудь подходящей функции. Если эта функция нелинейная, то получается нелинейная система уравнений. Чтобы она могла быть решена, приходиться очень аккуратно выбирать аппроксимирующую функцию.
Аналитический метод расчета нелинейных электрических цепей
Для аналитического расчета электрических цепей с нелинейными элементами участки вольт-амперных характеристик заменяют прямыми участками. За счет этого нелинейный элемент электрической цепи заменяется эквивалентным линейным элементом. Расчет эквивалентной схемы с линейными элементами осуществляется одним из известных методов, применяемых при расчетах линейных электрических цепей.
За счет этого нелинейный элемент электрической цепи заменяется эквивалентным линейным элементом. Расчет эквивалентной схемы с линейными элементами осуществляется одним из известных методов, применяемых при расчетах линейных электрических цепей.
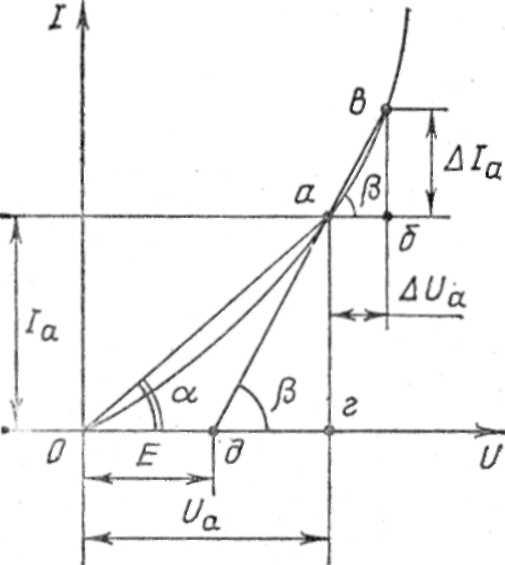
Рисунок 1 — Вольт-амперная характеристика нелинейного элемента, сопротивление которого уменьшается с увеличением напряжения.
На рис. 1 дана ВАХ нелинейного элемента по оси абсцисс (x) в масштабе mU [В/см] отложено напряжение, а по оси ординат (y) в масштабе mI [А/см] ток. Часть нелинейного участка вольт-амперной характеристики между точками ав заменена прямым отрезком.
Статическое сопротивление
Нелинейный элемент на любом участке ВАХ будет характеризоваться статическим сопротивлением, определяемым отношением напряжения к току, соответствующим рассматриваемой точке вольт-амперной характеристики. Для точки a статическое сопротивление будет равно:
То есть статическое сопротивление будет пропорционально котангенсу угла а; mr = mU/mI [Ом]
Статическое сопротивление нелинейного элемента, ВАХ которого представлена на рисунке 1, с ростом напряжения уменьшается.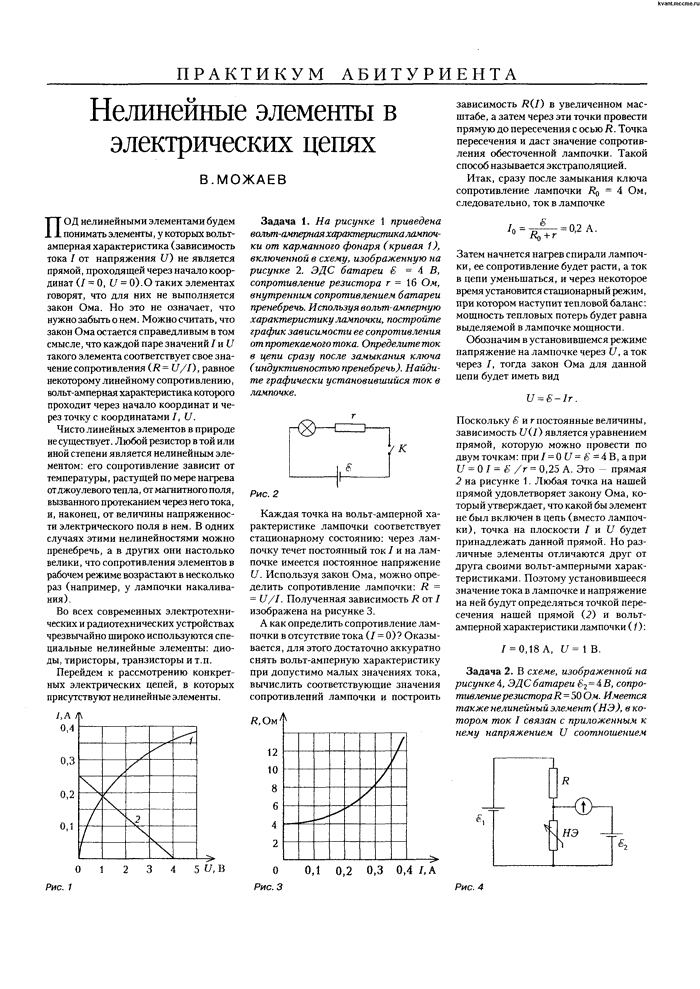
Дифференциальное сопротивление
Второй характеристикой нелинейного элемента выступает дифференциальное сопротивление, которое определяется отношением бесконечно малого приращения напряжения к соответствующему приращению тока. Для точки a дифференциальное сопротивление будет равно:
где β — угол наклона касательной, проведенной через точку а.
У линейного элемента статическое сопротивление равно дифференциальному. Схема замещения нелинейного элемента.
Проведем через точку а и в прямую.
Рисунок 2 — Вольт-амперная характеристика нелинейного элемента, сопротивление которого увеличивается с увеличением напряжения.
В общем случае эта прямая не проходит через начало координат рисунок 1-2. Поэтому нелинейный элемент в близи точки а невозможно заменить только резистором с сопротивлением rдиф. Необходимо в схему замещения включить дополнительные источник ЭДС E, значение которого определяется точкой пересечения с осью х (точка д). Если точка пересечения д находится на отрицательной части оси х (рисунок 2), то эдс в схеме замещения направлена в противоположную сторону (рисунок 3 б)
Если точка пересечения д находится на отрицательной части оси х (рисунок 2), то эдс в схеме замещения направлена в противоположную сторону (рисунок 3 б)
Рисунок 3, а — схема замещения нелинейного элемента, сопротивление которого возрастает с увеличением напряжения (ВАХ рисунок 1). б — схема замещения для нелинейного элемента, статическое сопротивление которого увеличивается с ростом напряжения на выводах (ВАХ рисунок 2).
Данные схемы замещения верны только при значениях напряжения и тока, близких к расчетной точке а, для которой найдено дифференциальное сопротивление. В других рабочих точках необходимо найти новые значение rдиф и E.
При известном значении напряжения U ток I определяется по обобщенному закону Ома. Для схемы замещения рисунок 3 а:
Для схемы замещения рисунок 3 б:
Графический расчет нелинейных электрических цепей
Расчет электрических цепей, содержащих нелинейные элементы, может проводиться аналитическим или графическим методом расчета.
Рассмотрим расчет неразветвленной нелинейной электрической цепи графическим методом (рисунок 1).
Рисунок 1 – Неразветвленная электрическая цепь с нелинейными элементами
Для определения параметров нелинейной электрической цепи необходимо построить вольт-амперные характеристики нелинейных элементов в одном масштабе по оси абсцисс и ординат (рисунок 2).
Рисунок 2 — Построение вольт-амперной характеристики неразветвленной цепи
При последовательном соединении элементов в электрической цепи сумма напряжений на каждом элементе равна прикладываемому к цепи напряжению источника напряжения. Для построения вольт-амперной характеристики цепи необходимо для одного и того же значения тока по оси произвести сложение координат абсцисс точек вольт-амперных характеристик нелинейных элементов (О’А= О’А’ + О’А’ ‘).
Вольт-амперная характеристика I1(U1) соответствует для нелинейного элемента НЭ1, характеристика I2(U2) — для НЭ2.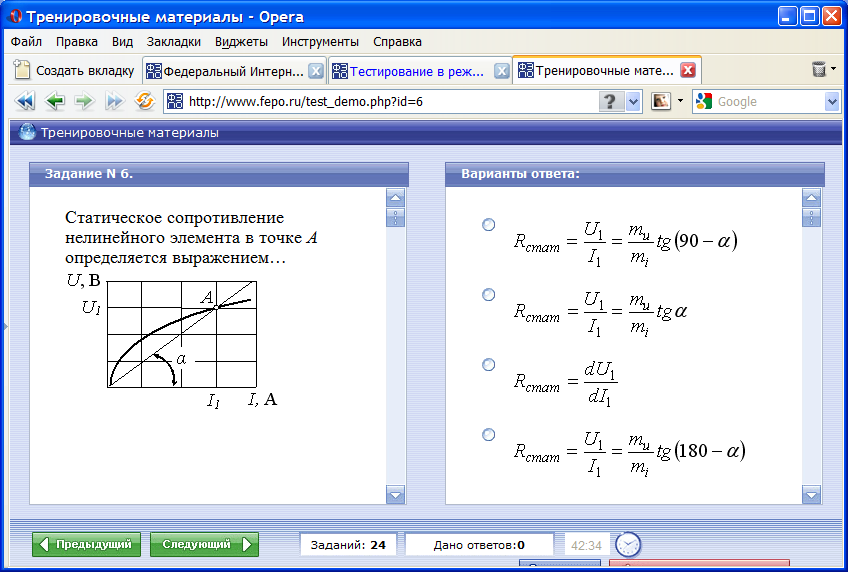 ВАХ I (U) — является «суммой» двух первых характеристик.
ВАХ I (U) — является «суммой» двух первых характеристик.
Полученная ВАХ I(U) дает возможность по заданному напряжению найти ток в цепи н напряжения на нелинейных элементах и, наоборот, при заданном токе определить общее напряжение и напряжения на нелинейных элементах.
Например при заданном токе I’ напряжение на НЭ1 будет равно U’2, на НЭ2 — U’1
Рассмотрим графический метод расчета для параллельно соединенных элементов.
Рисунок 3 — Электрическая цепь с параллельно соединенными нелинейными элементами.
При расчете нелинейной электрической цепи с параллельно включенными элементами необходимо определить по вольт-амперным характеристикам токи в ветвях I1 и I2, т.к. напряжения на этих элементах равны.
Рисунок 4 — График для определения токов при параллельном соединении двух нелинейных элементов.
Отложив на оси абсцисс заданное напряжение источника питания (отрезок 0А) и восстановив перпендикуляр из точки А, найдем отрезки AA1 и АА2, выражающие токи I1 и I2.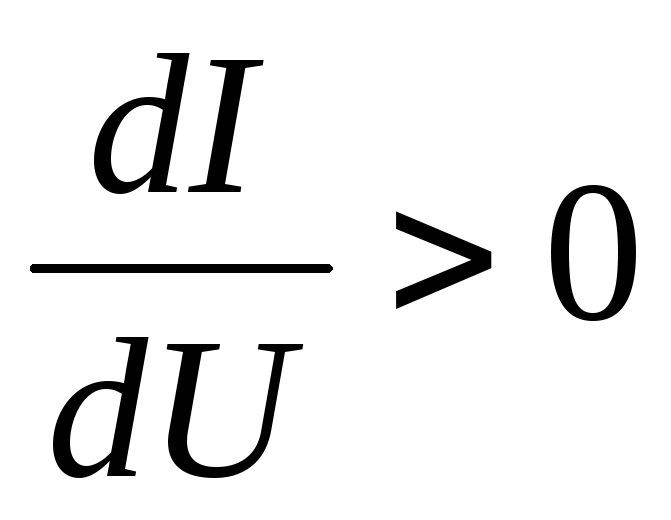 Ток в неразветвленной части цепи равен сумме токов в ветвях.
Ток в неразветвленной части цепи равен сумме токов в ветвях.
Если требуется найти токи по заданному току в неразветвленной части цепи, то необходимо построить общую ВАХ I(U), складывая ординаты ВАХ параллельных ветвей, соответствующие одним и тем же значениям напряжения (рис. 4).
Графический метод расчета цепей со смешанным соединением нелинейных элементов заключается в построении общих вольт-амперных характеристик для разветвленных участков цепи и для последовательно соединенных участков. Полученная таким образом общая ВАХ цепи дает возможность определить токи и напряжения yа всех участках цепи.
Calculus II — серия Power
Онлайн-заметки Павла
Примечания
Быстрая навигация
Скачать
- Перейти к
- Примечания
Проблемы с практикой
Проблемы с назначением
- Показать / Скрыть «> Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Оценка стоимости серии
- Силовая серия и функции
- Разделы
- Параметрические уравнения и полярные координаты
- Векторы
- Классы
Алгебра
Исчисление I
- Исчисление II
Исчисление III
Дифференциальные уравнения
- Дополнительно
Алгебра и триггерный обзор
Распространенные математические ошибки
Праймер для комплексных чисел
Как изучать математику
Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои студенты
- Заметки Загрузки
- Полная книга
- Текущая глава
Как легко рассчитать удельную мощность — Даже в голове!
Если вы всегда хотели узнать простой способ расчета удельной мощности — даже без использования нашего калькулятора, даже в уме, это идеальный пост для вас. 2
2
Этот расчет может быть немного утомительным и трудоемким, особенно для технических специалистов и полевых инженеров, которые хотят сделать расчет как можно быстрее и проще.
Как я могу вам помочь?
Рад, что вы спросили!
Используя следующую формулу, можно напрямую найти плотность мощности лазерного луча, используя диаметр луча в миллиметрах:
Вот как выводится это уравнение: мы можем записать выражение для плотности мощности пучка диаметром 1 мм, которое выглядит просто:
Делительное выражение плотности мощности пучка 1 мм — Power / π (0. 2 :
Примечание. Эта формула предполагает, что луч представляет собой луч с плоским верхом, плотность мощности которого одинакова.
Для гауссова луча с заданной перетяжкой луча в мм умножьте эту формулу на два, чтобы получить формулу, приведенную выше (коэффициент умножения обусловлен тем, что для гауссова луча пиковая мощность в центре вдвое больше средней мощности Плотность пучка.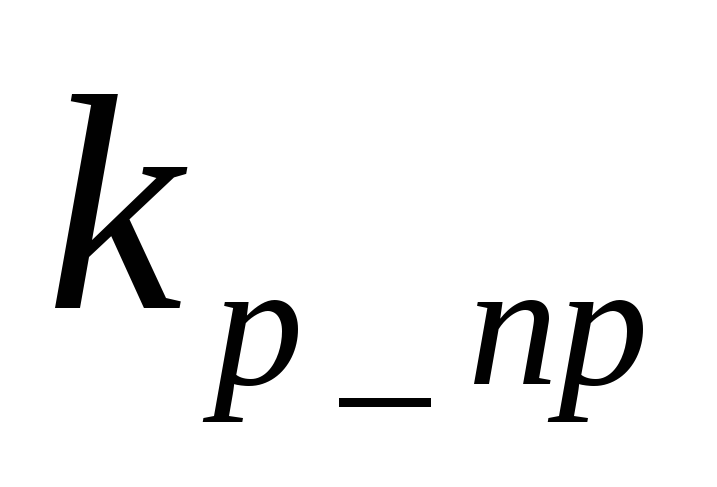 Значение на самом деле ближе к 255, а не к 250, но эта разница незначительна и вносит только ~ 2% ошибки.Расширитель формулы n используется для описания выражения для данного n-го значения формулы. Биномиальная теорема применяется здесь для расширения формулы. Любое алгебраическое выражение, состоящее всего из двух членов, называется биномиальным выражением. Его разложение по степеням n известно как биномиальное разложение. Формула, с помощью которой любая степень биномиального выражения может быть разложена в виде ряда, известна как биномиальная теорема.
Значение на самом деле ближе к 255, а не к 250, но эта разница незначительна и вносит только ~ 2% ошибки.Расширитель формулы n используется для описания выражения для данного n-го значения формулы. Биномиальная теорема применяется здесь для расширения формулы. Любое алгебраическое выражение, состоящее всего из двух членов, называется биномиальным выражением. Его разложение по степеням n известно как биномиальное разложение. Формула, с помощью которой любая степень биномиального выражения может быть разложена в виде ряда, известна как биномиальная теорема.
Согласно теореме, можно расширить степень (a + b) n и (a — b) n , используя ключевую точку Треугольника Паскаля.Где n называется индексом бинома. Значения биномиальных коэффициентов располагаются симметрично относительно среднего значения, если индекс n четный, и около двух средних значений, если индекс нечетный. Таким образом, тот же метод используется в этом (A + B) и (A-B) калькуляторе формул n-й степени, чтобы расширить любую степень бинома (A + B) и (A-B).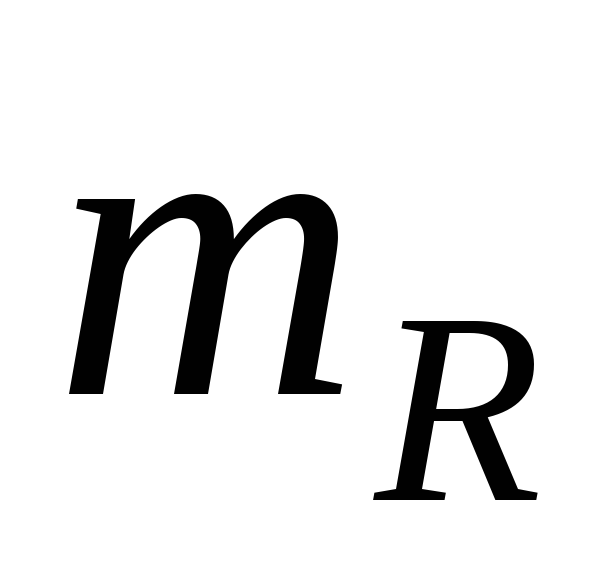 В приведенной ниже таблице приведены примеры ввода и вывода калькулятора (A + B) n и (A-B) n .
В приведенной ниже таблице приведены примеры ввода и вывода калькулятора (A + B) n и (A-B) n .
| (A + B) n | в словах | Формула |
|---|---|---|
| (A + B) 2 | A + B весь квадрат | A 2 + 2AB + B 2 |
| (A + B) 3 | A + B весь куб | A 3 + 3A 2 B + 3AB 2 + B 3 |
| ( A + B) 4 | A + B полная мощность 4 | A 4 + 4A 3 B + 6A 2 B 2 + 4AB 3 + B 4 |
| (A + B) 5 | A + B полная мощность 5 | A 5 + 5A 4 B + 10A 3 B 2 + 10A 2 B 3 + 5AB 4 + B 5 |
| (A + B) 6 | A + B полная мощность 6 | A 6 + 6A 5 B + 15A 90 093 4 B 2 + 20A 3 B 3 + 15A 2 B 4 + 6AB 5 + B 6 |
| (AB) n | в словах | Формула |
|---|---|---|
| (AB) 2 | AB весь квадрат | A 2 — 2AB + B 2 |
| (AB) 3 | весь куб | A 3 — 3A 2 B + 3AB 2 — B 3 |
| (AB) 4 | AB полная мощность 4 | A 4 — 4A 3 B + 6A 2 B 2 — 4AB 3 + B 4 |
| (AB) 5 | AB вся мощность 5 | A 5 — 5A 4 B + 10A 3 B 2 — 10A 2 B 3 + 5AB 9 0093 4 — B 5 |
| (AB) 6 | AB вся мощность 6 | A 6 — 6A 5 B + 15A 4 B 2 — 20A 3 B 3 + 15A 2 B 4 — 6AB 5 + B 6 |
Формулы движения — линейное и круговое
Формулы линейного движения
Средняя скорость / скорость a движущийся объект можно рассчитать как
v = s / t (1a)
где
v = скорость или скорость (м / с, фут / с)
s = пройденное расстояние (м, футы)
t = время (с)
- расстояние — это длина пути, по которому тело движется из одной точки в другую — смещение — это расстояние по прямой линии между начальным и конечным положениями из body
- мы используем взаимозаменяемые скорость и скорость — но имейте в виду, что скорость — это мера того, насколько быстро или медленно преодолевается расстояние, скорость, с которой преодолевается расстояние — скорость — это вектор, определяющий, насколько быстро или медленно проходит расстояние покрыты и направление
Если ускорение постоянное, то скорость может быть выражена как:
v = v 0 + a t (1b)
где
v 0 = начальное линейная скорость (м / с, фут / с)
a = ускорение (м / с 2 , фут / с 2 )
Линейное расстояние может быть выражено следующим образом (если ускорение постоянное):
s = v 0 t + 1/2 a t 2 (1c)
Объединение 1b и 1c для выражения конечной скорости ity
v = (v 0 2 + 2 as) 1/2 (1d)
Скорость может быть выражена как (скорость переменная)
v = ds / dt (1f)
где
ds = изменение расстояния (м, фут)
dt = изменение во времени (с)
Ускорение можно выразить как
a = dv / dt (1g)
где
dv = изменение скорости (м / с, фут / с)
Пример — марафонский бег
Если марафон — 42195 м — выполняется за потрясающие 2:03:23 (7403 секунды) (Уилсон Кипсанг, Кения — Берлинский марафон 29 сентября 2013 г.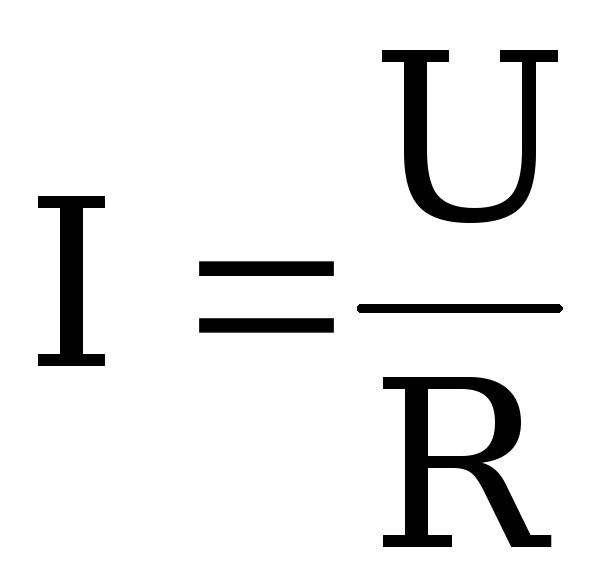 ) — средняя скорость может быть рассчитана
) — средняя скорость может быть рассчитана
v = (42195 м) / (7403 с)
= 5.7 м / с
= 20,5 км / ч
Пример — ускорение автомобиля
Автомобиль ускоряется с 0 км / ч до 100 км / ч за 10 секунд . Ускорение можно рассчитать, преобразовав (1b) в
a = (v — v 0 ) / t
= ((100 км / ч) (1000 м / км) / (3600 с / ч) — (0 км / ч) ( 1000 м / км) / (3600 с / ч)) / (10 с)
= 2.78 (м / с 2 )
Калькуляторы линейного движения
Средняя скорость
с — расстояние (м, км, футы, мили)
t — затраченное время (с, ч)
Расстояние
v 0 — начальная скорость (м / с, фут / с)
a — ускорение (м / с 2 , фут / с 2 )
t — используемое время (с, ч)
Final Velocity
v 0 — начальная скорость (м / с, фут / с)
a — ускорение (м / с 2 , фут / с 2 )
с — расстояние (м, фут)
Ускорение
v — конечная скорость (м / с, фут / с)
v 0 — начальная скорость (м / с, фут / с)
t — используемое время (с)
Круговое движение — вращение
Угловая скорость
Угловая скорость может быть выражена как (угловая скорость = постоянная):
ω = θ / t (2)
где
ω = угловая скорость (рад / с)
θ = угловое расстояние (рад)
t = время (с)
Угловая скорость и об / мин:
ω = 2 π n / 60 (2a)
где
n = оборотов в минуту (об / мин)
π = 3. 14 …
14 …
Тангенциальная скорость точки в угловой скорости — в метрических или британских единицах, таких как м / с или фут / с — может быть рассчитана как
v = ω r (2b )
где
v = тангенциальная скорость (м / с, фут / с, дюйм / с)
r = расстояние от центра до точки (м, фут, дюйм)
Пример — тангенциальная скорость велосипедной шины
Велосипедное колесо 26 дюймов вращается с угловой скоростью π радиан / с (0.5 оборотов в секунду) . Тангенциальная скорость шины может быть рассчитана как
v = ( π радиан / с ) ((26 дюймов) / 2)
= 40,8 дюйма / с
Угловая скорость и ускорение
Угловая скорость также может быть выражена как (угловое ускорение = константа):
ω = ω o + α t (2c)
где
ω o = угловая скорость в нулевой момент времени (рад / с)
α = угловое ускорение или замедление (рад / с 2 )
Угловое смещение
Угловое расстояние можно выразить как (угловое ускорение постоянно):
θ = ω o t + 1/2 α t 2 (2d)
Объединение 2a и 2c:
ω = (ω 904 92 o 2 + 2 α θ) 1/2
Угловое ускорение
Угловое ускорение можно выразить как:
α = dω / dt = d 2 θ / dt 2 (2e)
, где
dθ = изменение углового расстояния (рад)
dt = изменение во времени (с)
Пример — замедление маховика
By Geni (Фото автора Пользователь: geni) [GFDL или CC-BY-SA-3.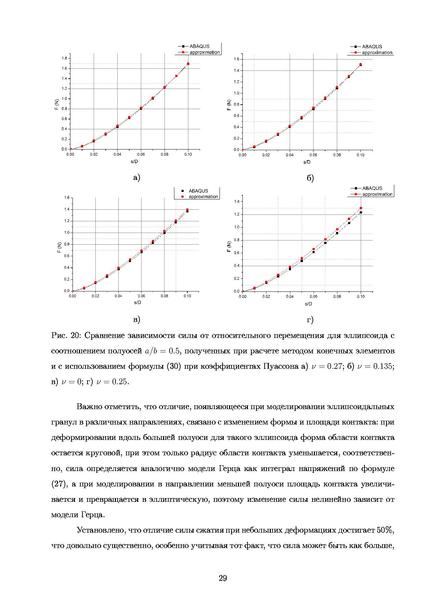 0-2,5-2,0-1,0], через Wikimedia Commons
0-2,5-2,0-1,0], через Wikimedia Commons
Маховик замедляется с 2000 об / мин ( оборотов, об / мин) до 1800 об / мин за 10 с . Замедление маховика можно рассчитать как
α = ((2000 об / мин ) — (1800 об / мин )) (0,01667 мин / с) (2 π рад / об. ) / (10 с)
= 2,1 рад / с 2
= (2.1 рад / с 2 ) (360 / (2 π) градусов / рад)
= 120 градусов / с 2
Угловой момент — или крутящий момент
Угловой момент или крутящий момент могут быть выражены как:
T = α I (2f)
где
T = угловой момент или крутящий момент (Н · м)
I = момент инерции (фунт м фут 2 , кг м 2 )
Анализ расхода энергии | IntechOpen
1. Формулировка проблемы
Формулировка проблемы
Анализ потока мощности — фундаментальное исследование, обсуждаемое в любом учебнике по анализу энергосистем, например [1, 2, 3, 4, 5, 6]. Цель исследования потока мощности — вычислить напряжения (величину и угол) для данной нагрузки, генерации и состояния сети. Когда известны напряжения для всех шин, можно рассчитать линейные потоки и потери. Отправной точкой решения проблем потока мощности является определение известных и неизвестных переменных в системе. На основе этих переменных автобусы подразделяются на три типа: резервные, генерирующие и загруженные, как показано в таблице 1.
| Тип шины | Напряжение (| Vi | ∠δi) | Реальная мощность | Реактивная мощность | |||||
|---|---|---|---|---|---|---|---|---|
| Величина | Угол | Угол Нетто (Pi) | Поколение | Нагрузка | Нетто (Q i) | |||
| Slack / Swing | Указано | Указано | Неизвестно | Указано | 16 Неизвестно | |||
| Генератор / Регулируемый / PV | Указано | Неизвестно | Указано | Указано | Указано | Неизвестно | Указано | Неизвестно | Неизвестно | Нагрузка / PQ2 | указано | указано | указано | Определено | Определено |
Таблица 1.
Тип шин в задаче перетока.
Резервная шина требуется для обеспечения несоответствия запланированной генерации общей нагрузке системы, включая потери, и общей генерации. Слабина шина обычно считаются в качестве опорной шины, поскольку оба величина напряжения и углы указаны; поэтому ее называют поворотной шиной. Остальные генераторные шины называются регулируемыми или фотоэлектрическими шинами, поскольку указана полезная реальная мощность и регулируется величина напряжения. Большинство автобусов в практических энергосистемах являются грузовыми автобусами.Шины нагрузки называются шинами PQ, потому что указаны нагрузки как чистой реальной, так и реактивной мощности.
Для шин PQ неизвестны как величины напряжения, так и углы, тогда как для шин PV неизвестен только угол напряжения. Поскольку для шины Slack указаны как величины напряжения, так и углы, нет переменных, для которых необходимо вычислить. В системе с шинами n и генераторами g имеется 2 ( n-1) — (g-1) неизвестных. Для решения этих неизвестных используются уравнения баланса активной и реактивной мощности.Чтобы написать эти уравнения, сеть передачи моделируется с использованием матрицы проводимости (Y-bus).
Для решения этих неизвестных используются уравнения баланса активной и реактивной мощности.Чтобы написать эти уравнения, сеть передачи моделируется с использованием матрицы проводимости (Y-bus).
2. Матрица полной проводимости и уравнение потока мощности
Матрица полной проводимости энергосистемы представляет собой абстрактную математическую модель системы. Он состоит из значений пропускной способности как линий, так и автобусов. Y-шина представляет собой квадратную матрицу с размерами, равными количеству шин. Эта матрица симметрична по диагонали.
Y = Y11 ⋯ Y1n ⋮ ⋱ ⋮ Yn1 ⋯ YnnE1
Значения диагональных элементов (Yii) равны сумме проводов, подключенных к шине и .Недиагональные элементы (Yij) равны отрицательной проводимости, соединяющей две шины i и j . Стоит отметить, что в больших системах Y-bus представляет собой разреженную матрицу.
Yii = ∑j = 0j ≠ inyijE2
Yij = Yji = −yijE3
Чистая введенная мощность на любой шине может быть рассчитана с использованием напряжения на шине (Vi), напряжений соседних шин (Vj) и допусков между шиной и соседние шины (yij), как показано на рисунке 1.
Ii = Viyi0 + Vi − V1yi1 + Vi − V2yi2 +… + Vi − Vjyij
Рисунок 1.
Чистая введенная мощность.
Переставляя элементы в зависимости от напряжений, текущее уравнение принимает следующий вид:
Ii = Viyi0 + yi1 + yi2 + .. + yij − V1yi1 − V2yi2−… −Vjyij
Ii = Vi∑j = 0j ≠ iyij −∑j = 1j ≠ iyijVj = ViYii + ∑j = 1j ≠ iYijVj
Уравнение мощности на любой шине можно записать следующим образом:
Si = Pi + jQ i = ViIi ∗
Или
Si ∗ = Pi− jQ i = Vi ∗ Ii
Подстановка выражения для тока в уравнение Si ∗ приводит к следующей формуле:
Si ∗ = Vi ∗ Vi∑j = 0j ≠ iyij − ∑j = 1j ≠ iyijVj = Vi ∗ ViYii + ∑ j = 1j ≠ iYijVj
Реальную и реактивную мощность можно рассчитать по следующим уравнениям:
Pi = ReVi ∗ Vi∑j = 0j ≠ iyij − ∑j = 1j ≠ iyijVj = ReVi ∗ ViYii + ∑j = 1j ≠ iYijVj
Q i = −ImVi ∗ Vi∑j = 0j ≠ iyij − ∑j = 1j ≠ iyijVj = −ImVi ∗ ViYii + ∑j = 1j ≠ iYijVj
Или
Pi = ∑j = 1nViVjYijcosθij −
+ δjE2 i = −∑j = 1nViVjYijsinθij − δi + δjE5
И ток ( Ii ) можно записать как функцию мощности следующим образом:
Pi − jQ i Vi ∗ = Vi∑j = 0j ≠ iyij − ∑j = 1j ≠ iyijVj = ViYii + ∑j = 1j ≠ iYijVjE6
Пример 1: Формирование матрицы пропускной способности.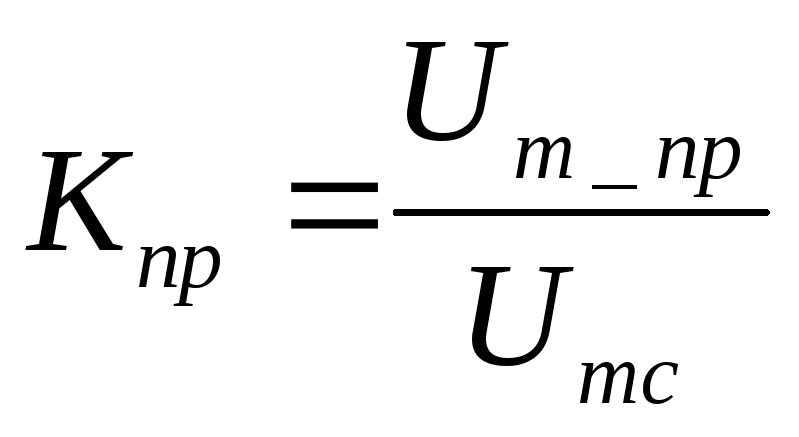
Для нижеприведенной системы с 4 шинами на рисунке 2 матрица проводимости строится путем преобразования всех импедансов в системе в проводимости, как показано на рисунке 3. Затем диагональные и недиагональные элементы рассчитываются с использованием формул. (2) и (3).
Y = −j7.5j4j2.50j4 − j7.750j2.5j2.50 − j4.5j20j2.5j2 − j4.5 = 7,5∠ − 90 ° 4∠90 ° 2,5∠90 ° 04∠90 ° 7,75∠ − 90 ° 02,5∠90 ° 2,5∠90 ° 04,5∠ − 90 ° 2∠90 ° 02,5∠90 ° 2∠90 ° 4,5∠ − 90 °
Рис. 2.
Диаграмма импеданса.
Рисунок 3.
График пропускной способности.
3. Метод Гаусса-Зейделя
Метод Гаусса-Зейделя (GS), также известный как метод последовательного смещения, представляет собой простейший итерационный метод, используемый для решения задач потока мощности. В общем, метод GS следует следующим итерационным шагам, чтобы найти решение для функции fx = 0:
Преобразуйте функцию в форму x = gx, чтобы вычислить неизвестную переменную.
Рассчитайте значение gx0 на основе первоначальных оценок x0.

Рассчитайте улучшенное значение x1 = gx0.
Продолжайте решение для улучшенных значений, пока решение не будет в допустимых пределах xk + 1 − xk≤ϵ.
Скорость сходимости можно улучшить с помощью коэффициентов ускорения, изменив размер шага α.
xk + 1 = xk + αgxk + 1 − xkE7
В контексте проблемы потока мощности неизвестные переменные — это напряжения на всех шинах, но резерв. И величины напряжения, и углы неизвестны для шин нагрузки, тогда как углы напряжения неизвестны для шин с регулируемой нагрузкой / генерацией.
Напряжение на шине Viat может быть рассчитано с использованием любого уравнения:
Vi = 1∑j = 1j ≠ iyijPisch − jQ ischVi ∗ + ∑jyijVjE8
Vi = 1YiiPisch − jQ ischVi ∗ −∑j = 1j ≠ iY0003
, где yij — это пропускная способность между шинами i и j, Yij — это элемент Y-шины, Pisch — запланированная вводимая реальная мощность, Q isch — чистая запланированная вводимая реактивная мощность, а Vi ∗ — это величина, сопряженная с Vi.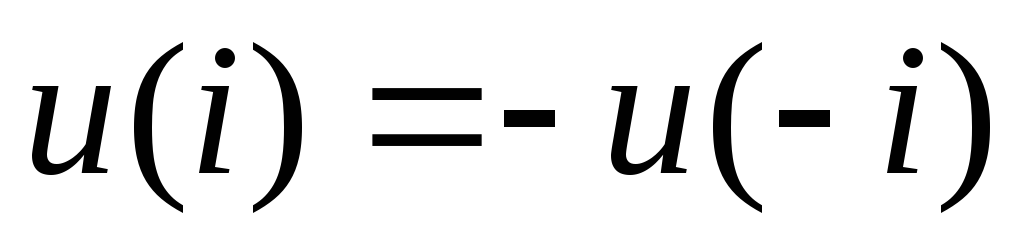 Впрыскиваемые чистые количества — это сумма выработки за вычетом нагрузки. Обычно начальные оценки Vi = 1∠0 °.
Впрыскиваемые чистые количества — это сумма выработки за вычетом нагрузки. Обычно начальные оценки Vi = 1∠0 °.
Итерационное уравнение напряжения выглядит следующим образом:
Vik + 1 = 1YiiPisch − jQ ischVi ∗ k − ∑j ≠ iYijVjkork + 1E10
Или
Vik + 1 = 1∑j = 0yijPisch − jQ ischVi ∗ + ∑j ≠ iyijVjkork + 1E11
Как реальная, так и реактивная мощности запланированы для шин нагрузки, и уравнение. 6 используется для определения как величин напряжения, так и углов (Vi∠δ) для каждой итерации (Vik + 1).
Для регулируемых автобусов запланирована только реальная мощность. Следовательно, чистая введенная реактивная мощность рассчитывается на основе итерационных напряжений (Vik + 1) с использованием любого из уравнений:
Q ik + 1 = −ImVi ∗ kVik∑j = 0nyij − ∑j = 1j ≠ inyijVjkork + 1E12
Q ik + 1 = −∑j = 1nVikVjkork + 1Yijsinθij − δik + δjkE13
, где Vi и Vj — значения напряжения на шинах i и j, соответственно.δi и δj — соответствующие углы.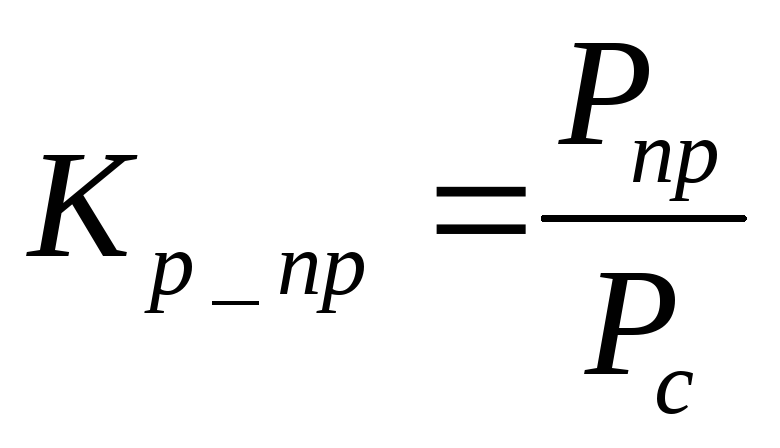 yij — это проход между автобусами i и j. Yij — величина элемента Y-шины между двумя автобусами; и θij — соответствующий угол.
yij — это проход между автобусами i и j. Yij — величина элемента Y-шины между двумя автобусами; и θij — соответствующий угол.
Так как величина напряжения (Vi) указывается на регулируемых / фотоэлектрических шинах, уравнения. (8) или (9) будут использоваться только для определения углов напряжения. Для этого можно использовать два варианта:
При использовании полярной формы (Vi∠δi) отбросьте итеративную величину напряжения и сохраните итерационный угол.
При использовании прямоугольной формы (Rei + jImi) отбросьте действительную часть (Re
Нелинейные задачи — A FEniCS Tutorial 1.0 документация
Теперь мы рассмотрим, как решать нелинейные уравнения в частных производных в FEniCS. Наши
Образец УЧП для реализации взят как нелинейное уравнение Пуассона:
Коэффициент делает уравнение нелинейным (если только
постоянна в).
Чтобы легко проверить нашу реализацию,
выбираем область « и границу
такие условия, что у нас есть
простое и точное решение.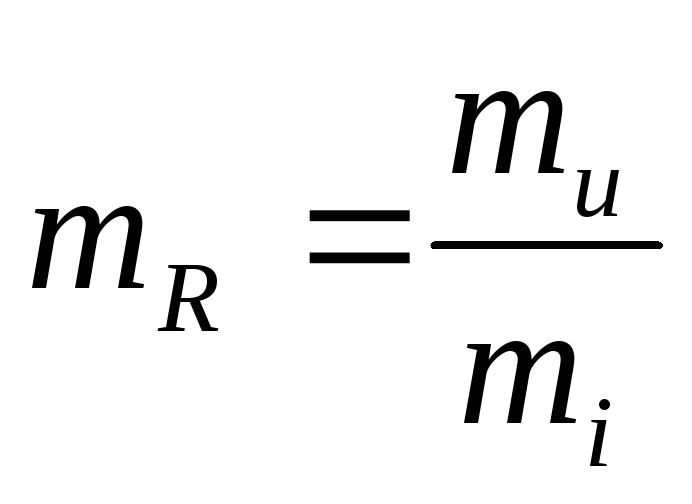 Позволять
Позволять
быть единичным гиперкубом
в габаритах« для,
для и на всех других границах
а также , .Координаты теперь представлены
символы. Тогда точное решение —
.
Мы обращаемся к разделу Параметризация размеров пространства для получения подробной информации о формулировании PDE.
проблема в космических габаритах.
Вариационная формулировка нашей модельной задачи гласит:
Найдите такое, что
(1)
где
(2)
и
Дискретная проблема возникает, как обычно, при ограничении и до
пара дискретных пространств.Как обычно, мы опускаем индексы на дискретных
пространства и просто сказать и выбираются конечномерными
по некоторой сетке с некоторым типом элемента.
Аналогично, мы принимаем дискретное решение и используем для
точное решение, если возникнет необходимость провести различие между ними.
Тогда дискретная нелинейная задача записывается как: найти такое, что
(3)
с. Поскольку — нелинейная функция
вариационной постановки порождает систему
нелинейные алгебраические уравнения. [[[
[[[
FEniCS может использоваться альтернативными способами для решения нелинейного уравнения в частных производных.
проблема. В следующих подразделах мы рассмотрим четыре
стратегии решения:
- простая итерация типа Пикара,
- Метод Ньютона на алгебраическом уровне,
- метод Ньютона на уровне PDE и
- автоматический подход, в котором FEniCS атакует нелинейные вариационные
проблема напрямую.
Стратегия «черного ящика» 4 определенно является самой простой из
точки зрения программиста, но другие дают больше ручного управления
процесс решения нелинейных уравнений (который также имеет некоторые
педагогические преимущества, особенно для новичков в нелинейной конечной
элемент проблемы).
Итерация Пикарда
Итерация Пикара — это простой способ обработки нелинейных уравнений в частных производных: мы просто
использовать известное предыдущее решение в нелинейных терминах, чтобы эти
условия становятся линейными в неизвестном. Стратегия также известна как
Стратегия также известна как
метод последовательных замен.
Для нашей конкретной проблемы
мы используем известное предыдущее решение в коэффициенте.
Точнее, получив решение от итерации, мы ищем
новое (надеюсь, улучшенное) решение в итерации, такое
который решает линейную задачу ,
(4)
Итерации требуют первоначального предположения.Надеюсь, что как и что
достаточно близко к точному
решение дискретной задачи всего за несколько итераций.
Легко сформулировать вариационную задачу для от
последнее уравнение.
Эквивалентно, мы можем аппроксимировать в
для получения той же линейной вариационной задачи.
В обоих случаях проблема состоит в поиске
так что
(5)
с
(6)
Поскольку это линейная задача в неизвестном, мы можем эквивалентным образом
используйте формулировку
с
Итерации можно остановить, когда, скажем, есть небольшой допуск, или
когда количество итераций превышает некоторый критический предел. Последний
Последний
случай подберет расхождение в методе или недопустимо медленное
конвергенция.
В алгоритме решения нам нужно сохранить только и,
называется u_k и u в приведенном ниже коде.
Тогда алгоритм может быть выражен следующим образом:
def q (u):
возврат (1 + u) ** м
# Определить вариационную задачу для итерации Пикара
u = Пробная функция (V)
v = TestFunction (V)
u_k = interpolate (Constant (0.0), V) # предыдущий (известный) u
a = внутренний (q (u_k) * grad (u), grad (v)) * dx
f = Константа (0,0)
L = f * v * dx
# Итерации Пикарда
u = Function (V) # новая неизвестная функция
eps = 1.0 # мера погрешности || u-u_k ||
tol = 1.0E-5 # допуск
iter = 0 # счетчик итераций
maxiter = 25 # максимально допустимое количество итераций
в то время как eps> tol и iter Нам нужно определить предыдущее решение в итерациях, u_k,
как функция конечных элементов, так что u_k может быть обновлен с помощью
u в конце цикла.Мы можем создать начальную
Функция u_k
путем интерполяции
выражение или константа
в то же векторное пространство, что и u живет в (V).
В приведенном выше коде мы демонстрируем, как использовать
numpy функциональность для вычисления нормы
разница между двумя последними решениями. Здесь мы применяем
максимальная норма (норма) на разности векторов решений
(ord = 1 и ord = 2 задают вектор и
нормы — для массивов numpy возможны другие нормы,
см. pydoc numpy.linalg.norm).
Файл picard_np.py содержит полный код для
это нелинейная проблема Пуассона.
Реализация габаритная, с сеткой
построение и установка условий Дирихле, как описано в
раздел Параметризация количества пространственных измерений .
Для сетки с нам нужно 9 итераций для сходимости
когда толерантность есть.
Метод Ньютона на алгебраическом уровне
После дискретизации нашей нелинейной задачи в частных производных мы можем
использовать метод Ньютона для решения системы нелинейных алгебраических уравнений.Из непрерывной вариационной задачи
дискретная версия приводит к
система уравнений для неизвестных параметров
(7)
Метод Ньютона для системы,
можно сформулировать как
где — параметр релаксации, а —
индекс итерации. Первоначальное предположение должно
быть предоставлено для запуска алгоритма.
Оригинальный метод Ньютона имеет, но в задачах, где он
трудно добиться сходимости,
так называемая недостаточная релаксация может помочь.Это означает, что
делается шаг меньший, чем предполагает метод Ньютона.
Нам нужно в программе вычислить якобиан
матрица
и вектор правой части.
Наша настоящая проблема изложена выше.
Производная становится
.
(8)
Для получения предыдущего уравнения были использованы следующие результаты:
Мы можем переформулировать матрицу Якоби
введя короткое
обозначение:
Чтобы заставить FEniCS вычислить эту матрицу, нам необходимо сформулировать
соответствующая вариационная задача. Глядя на
Глядя на
линейная система уравнений по методу Ньютона,
мы можем ввести в качестве общей тестовой функции, заменяющей,
и мы можем идентифицировать неизвестное
. Из линейной системы
теперь мы можем пойти «назад», чтобы построить соответствующий линейный
дискретная слабая форма, которая должна быть решена на каждой итерации Ньютона:
(9)
Эта вариационная форма соответствует стандартным обозначениям
с
Обратите внимание на важную особенность метода Ньютона.
что
предыдущее решение заменяет
в формулах при вычислении матрицы
и вектор для линейной системы в
каждую итерацию Ньютона.
Теперь перейдем к реализации.
Чтобы получить хорошее начальное предположение, мы можем решить упрощенную линейную
проблема, как правило, с, что приводит к стандартному лапласовскому
уравнение. Рецепт решения этой проблемы
содержится в разделах Вариационная формулировка ,
Реализация (1) и Объединение условий Дирихле и Неймана .
Код для вычисления становится следующим:
тол = 1Э-14
def left_boundary (x, on_boundary):
return on_boundary и abs (x [0]) Здесь u_k обозначает функцию решения для предыдущего
итерация, так что решение
после каждой итерации Ньютона u = u_k + omega * du.Изначально u_k - это начальное предположение, которое мы вызываем в математике.
Граничные условия Дирихле для, в
проблема, которую нужно решить в каждом Ньютоне
итерация несколько отличаются от условий для.
Предполагая, что выполняется
Условия Дирихле для, должны быть равны нулю на границах
где применяются условия Дирихле, чтобы выполнить
правильные граничные значения. Поэтому мы определяем дополнительный список
Объекты граничных условий Дирихле для:
Gamma_0_du = DirichletBC (V, Константа (0), left_boundary)
Gamma_1_du = DirichletBC (V, Константа (0), правая_граница)
bcs_du = [Gamma_0_du, Gamma_1_du]
Необходимо определить нелинейный коэффициент и его производную.
до кодирования слабой формы системы Ньютона:
def q (u):
возврат (1 + u) ** м
def Dq (u):
return m * (1 + u) ** (m-1)
du = Пробная функция (V) # u = u_k + omega * du
a = внутренний (q (u_k) * grad (du), grad (v)) * dx + \
внутренний (Dq (u_k) * du * grad (u_k), grad (v)) * dx
L = -внутренняя (q (u_k) * grad (u_k), grad (v)) * dx
Итерационный цикл Ньютона очень похож на итерационный цикл Пикара.
в разделе Picard Iteration :
du = Функция (V)
u = Функция (V) # u = u_k + omega * du
омега = 1. 0 # параметр релаксации
eps = 1.0
tol = 1.0E-5
iter = 0
maxiter = 25
в то время как eps> tol и iter
0 # параметр релаксации
eps = 1.0
tol = 1.0E-5
iter = 0
maxiter = 25
в то время как eps> tol и iter Есть и другие способы реализации
также обновление решения:
u.assign (u_k) # u = u_k
u.vector (). axpy (омега, ду.вектор())
# или
u.vector () [:] + = omega * du.vector ()
Операция axpy (a, y) добавляет скаляр, умноженный на вектор.
y в объект Vector. Обычно это быстрая операция
вызов оптимизированной процедуры BLAS для расчета.
Построение сетки для $ d $ -мерной задачи произвольной степени
элементы Лагранжа могут быть выполнены как
объяснено в разделе Параметризация количества пространств .
Полная программа появляется в файле alg_newton_np.py.
Метод Ньютона на уровне PDE
Хотя метод Ньютона в задачах УЧП обычно формулируется
уровень линейной алгебры, т. е. как метод решения систем нелинейных
е. как метод решения систем нелинейных
алгебраических уравнений, мы также можем сформулировать метод на уровне PDE.
Этот подход приводит к линеаризации УЧП перед их дискретизацией.
Пользователи FEniCS, вероятно, сочтут этот метод более простым в применении, чем
более стандартный метод в разделе Метод Ньютона на алгебраическом уровне .
Учитывая приближение к полю решения, ищем
возмущение так, что
выполняет нелинейное уравнение в частных производных.
Однако проблема для все еще является нелинейной, и нет ничего
получил. Поэтому идея состоит в том, чтобы предположить, что достаточно
маленький, так что мы можем линеаризовать задачу относительно.
Вставляя в PDE,
линеаризация члена как
и отбрасывая нелинейные члены в,
получаем
Мы можем собрать термины с неизвестным слева,
Слабая форма этого PDE получается умножением на тестовую функцию
и интегрируя, интегрируя как обычно
производные второго порядка по частям:
Вариационная задача гласит: найти такое, что
для всех, где
Функциональные пространства и, будучи непрерывными или дискретными,
как в
линейная задача Пуассона из раздела Вариационная постановка .
Мы должны дать некоторое начальное предположение, например, решение
PDE с. Соответствующая слабая форма
имеет
После этого мы вводим цикл и решаем
для и вычислить новое приближение
. Обратите внимание, что это исправление, поэтому, если
удовлетворяет предписанному
Условия Дирихле на некоторой части границы,
мы должны требовать.
Глядя на только что выведенные уравнения,
мы видим, что вариационная форма такая же, как и для метода Ньютона
на алгебраическом уровне в разделе Метод Ньютона на алгебраическом уровне .Поскольку метод Ньютона в
алгебраический уровень потребовал некоторой «обратной» конструкции
лежащие в основе слабых форм, пользователи FEniCS могут предпочесть метод Ньютона в
Уровень PDE, который автор считает более простым, хотя и не очень
обычно описывается в литературе по численным методам для PDE.
По-видимому, нет необходимости в дифференцировании для вывода якобиана.
матрица, но математически эквивалентный вывод выполняется, когда
нелинейные члены линеаризуются с использованием первых двух членов ряда Тейлора
и когда пренебрегают продуктами в возмущении.
Реализация идентична той, что в
раздел Метод Ньютона на алгебраическом уровне и находится в
файл pde_newton_np.py. Читателю предлагается пойти
через этот код, чтобы убедиться, что настоящий метод на самом деле
заканчивается той же программой, что и для метода Ньютона на
уровень линейной алгебры в разделе Метод Ньютона на алгебраическом уровне .
Непосредственное решение нелинейной вариационной задачи
Предыдущие ручные расчеты и ручное выполнение
Методы Пикара или Ньютона можно автоматизировать с помощью инструментов FEniCS.В двух словах можно написать
проблема = нелинейная вариационная задача (F, u, bcs, J)
solver = NonlinearVariationalSolver (проблема)
solver.solve ()
где F соответствует нелинейной форме,
u - неизвестный объект Function, bcs
представляет собой существенные граничные условия (в общем, список
DirichletBC) и
J - вариационная форма якобиана F.
Давайте подробно объясним, как использовать встроенные инструменты для
нелинейные вариационные задачи и их решение. Соответствующая форма F
Соответствующая форма F
прямо определяется следующим образом, предполагая, что q (u) равно
закодирована как функция Python:
u_ = Function (V) # последнее вычисленное решение
v = TestFunction (V)
F = внутренний (q (u _) * grad (u_), grad (v)) * dx
Обратите внимание, что u_ - это функция (а не TrialFunction).
Альтернативная и, возможно, более интуитивная формула для
определять прямо с точки зрения
пробная функция для и тестовая функция для, а затем
создать правильную букву F на
u = пробная функция (V)
v = TestFunction (V)
F = внутренний (q (u) * grad (u), grad (v)) * dx
u_ = Function (V) # последнее вычисленное решение
F = действие (F, u_)
Последний оператор эквивалентен, где -
существующая функция конечных элементов, представляющая последний
вычисленное приближение к решению.(Обратите внимание, что и в предыдущих обозначениях
соответствуют и в настоящее время
обозначение. Мы изменили обозначения, чтобы лучше согласовать математику с
соответствующий код UFL. )
)
Производная (J) функции (F) формально является
Производная Гато
из в в направлении.
Технически эта производная Гато получается путем вычисления
(10)
Теперь пробная функция и предыдущая
приближение к решению.
Начнем с
и получаем
, что приводит к
как.Это последнее выражение является производным от Гато. Мы можем использовать или
для этой производной, последняя имеет преимущество
что мы легко распознаем выражение как билинейную форму. Однако в
в следующих примерах кода J используется как имя переменной для
якобиан.
Спецификация J
выглядит следующим образом, если du - TrialFunction:
du = Пробная функция (V)
v = TestFunction (V)
u_ = Function (V) # последнее вычисленное решение
F = внутренний (q (u _) * grad (u_), grad (v)) * dx
J = внутренний (q (u _) * grad (du), grad (v)) * dx + \
внутренний (Dq (u _) * du * grad (u_), grad (v)) * dx
Альтернативная спецификация F, где u как
TrialFunction, ведет к
u = пробная функция (V)
v = TestFunction (V)
u_ = Function (V) # последнее вычисленное решение
F = внутренний (q (u) * grad (u), grad (v)) * dx
F = действие (F, u_)
J = внутренний (q (u _) * grad (u), grad (v)) * dx + \
внутренний (Dq (u _) * u * grad (u_), grad (v)) * dx
Язык UFL, используемый для определения слабых форм, поддерживает дифференциацию
форм. Эта функция облегчает автоматическое вычисление символьного значения
Эта функция облегчает автоматическое вычисление символьного значения
Якобиан J, называя производную функции с F, наиболее
недавно вычисленное решение (функция) и неизвестное
(TrialFunction) в качестве параметров:
du = Пробная функция (V)
v = TestFunction (V)
u_ = Function (V) # последнее вычисленное решение
F = внутренний (q (u _) * grad (u_), grad (v)) * dx
J = производная (F, u_, du) # Производная Гато в реж. дю
или
u = пробная функция (V)
v = TestFunction (V)
u_ = Function (V) # последнее вычисленное решение
F = внутренний (q (u) * grad (u), grad (v)) * dx
F = действие (F, u_)
J = производная (F, u_, u) # Производная Гато в реж.из вас
Очевидно, что производная функция
очень удобно в задачах, где дифференцировать F вручную
подразумевает длительные вычисления.
Предпочтительная реализация F и J, в зависимости от того,
du или u - объект TrialFunction,
это дело личного вкуса. Вывод производной Гато
вручную, как показано выше, наиболее естественно соответствует
реализация, где du - это TrialFunction, а
использование автоматического символьного дифференцирования с помощью производной
функция наиболее естественно соответствует реализации, в которой
u - пробная функция. Мы реализовали оба подхода в двух файлах:
Мы реализовали оба подхода в двух файлах:
vp1_np.py с
u как TrialFunction и
vp2_np.py с du в качестве TrialFunction.
Каталог
static / nonlinear_poisson содержит оба файла.
Первый аргумент командной строки определяет, должен ли якобиан
автоматически выводиться или вычисляться по формуле, выведенной вручную.
Следующий код определяет нелинейную вариационную задачу и
связанный решатель, основанный на методе Ньютона. Здесь мы демонстрируем
как ключевые параметры в
Может быть установлен метод Ньютона, а также выбор
решатель и прекондиционер, а также связанные параметры для
линейная система, возникающая в итерации Ньютона.
проблема = нелинейная вариационная задача (F, u_, bcs, J)
solver = NonlinearVariationalSolver (проблема)prm = solver.parameters
prm ['newton_solver'] ['absolute_tolerance'] = 1E-8
prm ['newton_solver'] ['relative_tolerance'] = 1E-7
prm ['newton_solver'] ['maximum_iterations'] = 25
prm ['newton_solver'] ['relax_parameter'] = 1.0
если iterative_solver:
prm ['linear_solver'] = 'gmres'
prm ['preconditioner'] = 'ilu'
prm ['krylov_solver'] ['absolute_tolerance'] = 1E-9
prm ['krylov_solver'] ['relative_tolerance'] = 1E-7
prm ['krylov_solver'] ['maximum_iterations'] = 1000
prm ['krylov_solver'] ['gmres'] ['restart'] = 40
prm ['krylov_solver'] ['preconditioner'] ['ilu'] ['fill_level'] = 0
set_log_level (ПРОГРЕСС)
решатель.

 Формулировка проблемы
Формулировка проблемы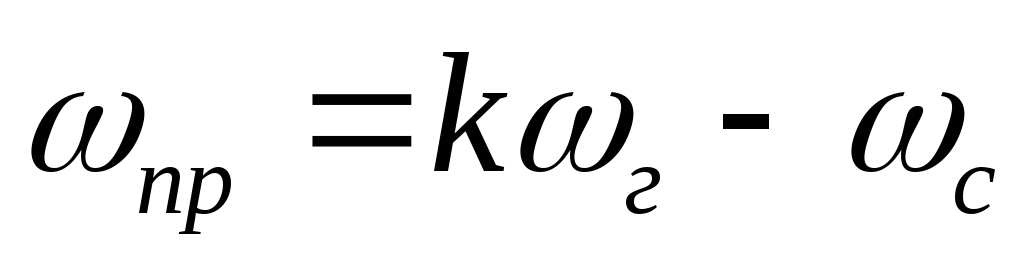
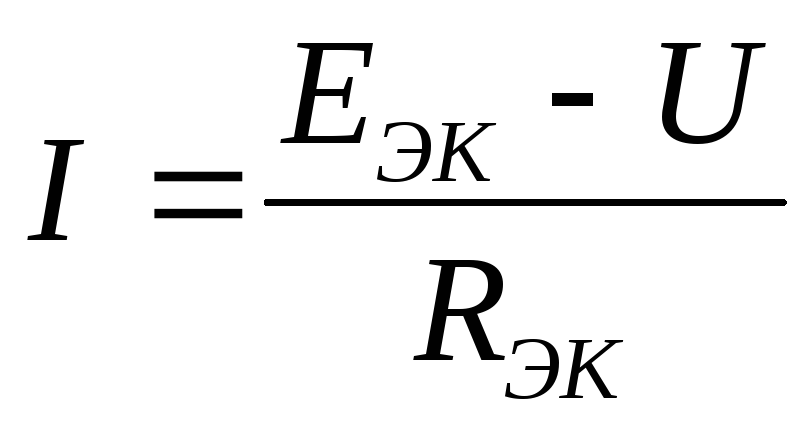 0 # параметр релаксации
eps = 1.0
tol = 1.0E-5
iter = 0
maxiter = 25
в то время как eps> tol и iter
0 # параметр релаксации
eps = 1.0
tol = 1.0E-5
iter = 0
maxiter = 25
в то время как eps> tol и iter  е. как метод решения систем нелинейных
е. как метод решения систем нелинейных
 Соответствующая форма F
Соответствующая форма F )
) Эта функция облегчает автоматическое вычисление символьного значения
Эта функция облегчает автоматическое вычисление символьного значения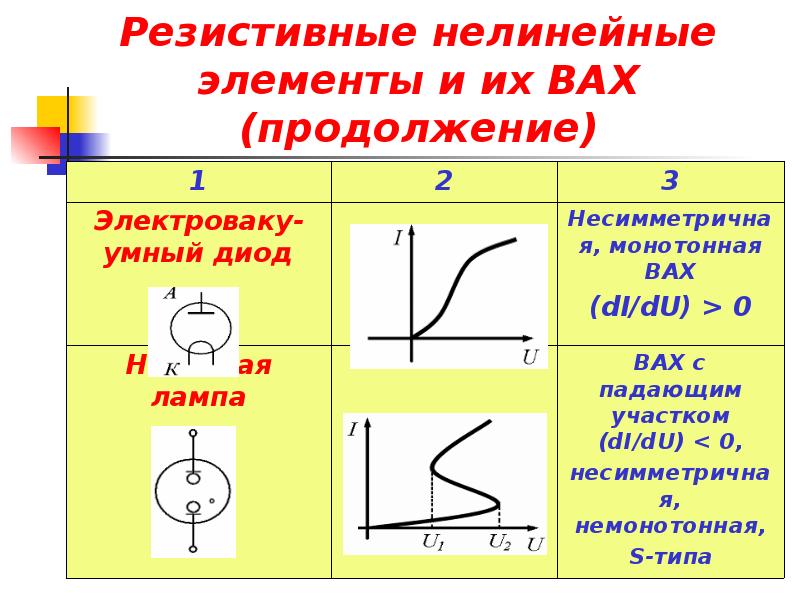 Мы реализовали оба подхода в двух файлах:
Мы реализовали оба подхода в двух файлах: