5. Мостовые измерительные схемы
5.3. Мост Максвелла – Вина
Быстро и просто измерить неизвестную индуктивность можно с помощью моста Максвелла – Вина
(рис.5.5).
Для этой конфигурации моста имеем:
(Rх + jωLx ) |
|
| 1 | = R4R1 | (5.16) | ||||||
1 | + jωC2 | ||||||||||
|
|
|
|
|
|
|
| ||||
или |
|
|
|
|
| R2 |
|
|
| ||
|
|
|
|
|
|
|
|
| |||
|
|
|
| R4R1 + jωC |
|
| |||||
R | х | + jω L | x | = | R R . | (5.17) | |||||
|
|
|
| R2 | 2 | 4 1 |
| ||||
|
|
|
|
|
|
|
|
| |||
Приравняв порознь действительные и мнимые части уравнения (5.17), для неизвестных Rx и Lx получим уравнения:
| L | R | x | = R4R1 , | (5.18а) | |
| x |
| R2 |
| ||
Rx | R1 |
|
|
| ||
Lx | = R4R1C2 . | (5.18б) | ||||
| (R3) | |||||
|
|
|
|
| ||
| Uм | Если использовать для R1 и R4 | постоянные сопротивле- | |||
| ния, а переменными | сделать С2 и | R2, как это показано на | |||
| С2 | рис.5.5, легко определить индуктивность Lx и величину потерь | ||||
R4 |
| Rx. Обычно для грубого уравновешивания применяют R1 и R4, | ||||
| изменяемые ступенчато. В качестве нуль — индикатора можно | |||||
| R2 | |||||
| использовать телефонный капсюль, с помощью которого легко | |||||
|
| |||||
|
| установить минимум. |
|
|
| |
Рис. 5.5. Мост Маквелла-Вина для |
|
|
|
| ||
измерения индуктивности |
|
|
|
| ||
5.4. Мост Грютцмахера
Если не имеется ни образцовой индуктивности, ни образцовой ёмкости, для измерения кажущегося сопротивления неизвестных ёмкости и индуктивности можно применить мост Грютцмахера. Для измерения кажущегося сопротивления – его модуля и фазы – в этом мосте нужны только омические сопротивления. Особым преимуществом этого моста по сравнению с другими является возможность измерения этих параметров в рабочем режиме измеряемого элемента. Это необходимо, например, при измерении параметров дросселей, трансформаторов, снабжённых ферромагнитными сердечниками, индуктивность которых нелинейно зависит от рабочего тока.
Измерение модуля. Измерение модуля основывается на простом сравнении напряжений (рис.5.6). Переменное напряжение питания моста UМ прикладывается к мосту, и электронным вольтмет-
ром V измеряется падение напряжения на Zx и Rобр. Вольтметр последовательно переключают в пози-
ции 1 и 2 и Rобр изменяют до тех пор, пока падения напряжения на Zx и Rобр не сравняются между собой. Тогда получим:
Zx = Rобр .
Измерение фазового сдвига. Схема измерения показана на рис.5.7, где величина Rобр = Zx , что
получено из предыдущего измерения. Резистор R3 включён как делитель напряжения. Его изменяют до тех пор, пока напряжения между точками b и a сравняются с напряжениями между точками b и d, т.е. Uba = Ubd. Для этого электронный вольтметр переключают то в положение 3, то в положение 4. Кроме того, должно быть выбрано
R3 = R2,
Следовательно,
Ubf = Ueb .
Мостовые измерительные схемы. — Студопедия
МДК 01.01
В мостовых измерительных схемах устраняется главный недостаток большинства измерительных цепей с делителями напряжения — наличие ненулевого выходного сигнала 1/ВЬ1х0 при ? = 0. Например, в простой потенциометрической схеме 1/вых0 = 0,5 Е. Схемы с симметричным питанием и тем более схемы, работающие на переменном токе, лишены этого недостатка, однако они значительно сложнее схем на постоянном токе. Более того, многие датчики не работают на переменном токе, и их нельзя включать в измерительные схемы переменного тока.
Мостовая измерительная схема (рис. 1.20) имеет два плеча — измерительное, в которое включен параметрический датчик 1?х, и опорное с резисторами Д3, Д,. При запитке моста напряжением (рис. 1.20, а) на одну диагональ моста подается напряжение Е, ас другой, на сопротивлении нагрузки Дн — снимается выходной сигнал.
Рис. 1.20. Простой мост (мост Уитстона):а— при запитке напряжением;б— при запитке током
Если мост сбалансирован, то 1/вых = НАВ = 0. Любая разбалансировка моста вызывает появление АПвых = ДНАВ, что эквивалентно маленькому приращению выходного сигнала на фоне нулевого синфазного сигнала. Если к такой схеме применить методы анализа электрических цепей, например, метод контурных токов, метод узловых потенциалов, метод эквивалентного генератора и т. д., то можно показать, что
При запитке мостовой схемы от источника тока /0 (рис. 1.20, б)
В режиме холостого хода (XX), когда Дн Ду, выражение (1.2) упрощается:
Выражения (1.3) являются основными при расчете мостовых схем, запитанных напряжением, что наиболее часто встречается на практике. При этом по умолчанию полагают, что условие XX (Дн ;» Ду) выполняется, поскольку при современном уровне развития аналоговой схемотехники выполнить его не представляет особого труда.
Рис. 1.21. Полумостовая схема
Существуют разные виды мостов. В рассмотренном «простом» мосте (мост Уитстона) датчик «Д» включен только в одно плечо (см. рис. 1.20). В полумосте (рис. 1.21) в смежные плечи моста включается дифференциальный датчик, а в полном мосте (рис. 1.22, а) в оба плеча моста включаются два дифференциальных датчика, например два круговых потенциометра. Условное представление полного моста приведено на рис. 1.22, б.
Заметим, что если сигнал в диагонали моста равен нулю, то такой мост называется сбалансированным. Условие балансировки моста может быть получено из выражения (1.3а)
Это условие на практике может выполняться в нескольких случаях. Во-первых, когда
где Д0 — номинальное значение, что соответствует полной симметрии моста (поэтому такой мост называется симметричным).
Во-вторых, это условие выполняется при
что соответствует несимметричному мосту. Момент баланса регистрируется нуль-органом, включаемым в измерительную диагональ
Рис. 1.22. Полная мостовая схема:а— схема на двух круговых потенциометрах;б— условное обозначение
моста. Важным обстоятельством является то, что условие балансировки не зависит ни от внутреннего сопротивления источника питания, ни от сопротивления нагрузки. Из условий балансировки (1.4) следует, что сопротивление датчика можно определить как
Формула (1.5) называется рабочей формулой моста и широко используется для точного измерения сопротивлений. В этом случае опорное плечо фиксировано (резисторы Д3 и заранее известны), а
Я2 подбирается из магазина сопротивлений таким образом, чтобы сбалансировать мост. Относительная погрешность измерения сопротивления, как следует из (1.5), составляет
и может приближаться к сотым и тысячным долям процента.
При автоматической балансировке мостов достигается более высокая точность, так как исключается субъективный фактор при настройке моста. Обычно современные сбалансированные автоматические мосты применяются с использованием операционных усилителей. Одна из возможных схем автоматической балансировки моста Уитстона приведена на рис. 1.23, где ОУ включен в диагональ моста, а датчик — в цепь обратной связи ОУ.
Рис. 1.23. Мостовая схема с автобалансировкой
В такой схеме автоматически поддерживается ?7АВ =0, так как дифференциальная разность ?/д —> 0. При этом
где К+ и К_ — коэффициенты усиления ОУ по неинвертирующему и инвертирующему входу ОУ соответственно. Заметим, что в данной схеме никаких требований к величине Дн не выставляется. Более того, чувствительность схемы удвоена, а выходной сигнал схемы не содержит синфазной составляющей, что позволяет подавать его в последующем на недифференциальный вход измерительной схемы.
В рассмотренной схеме (см. рис. 1.23) датчик включен в цепь ОС ОУ и является «плавающим», т. е. изолирован от земли. При использовании заземленного датчика часто применяют схему, изображенную на рис. 1.24.
Рис. 1.24. Схема моста с автобалансировкой и заземленным датчиком
Для точки В условие баланса запишется в виде
С учетом того, что
получим I
Подставляя (1.7) в (1.6) и решая относительно Пвых с учетом Их = 7?0(1 + е), получим
-Е —
п
1 + 2п 1 + ?
При ?<1 передаточная характеристика измерительного моста линейна и
Для режима XX в нагрузке выходное напряжение в диагонали моста определяется очевидным соотношением
Воспользуемся основной формулой теории чувствительности для оценки влияния АЛ, на выходное напряжение:
Вычисляя частные производные (функции чувствительности), находим
Подставляя найденные значения в формулу (1.8), получим
Как следует из формулы (1.9), если разбалансировать только одно плечо, например, положить = Е0 (1 + е), что соответствует мосту Уитстона, то
В инженерной практике с точностью до величин второго порядка малости в расчетах для моста Уитстона принимают
Таким образом, передаточная характеристика моста Уитстона в общем случае нелинейна, а в ограниченном диапазоне, где в <§С 1, ее можно полагать передаточную характеристику квазилинейной, т. е.
Нормированные передаточные характеристики моста Уитстона при различных аппроксимациях и соответствующие им отклонения от линейности Л2 и Д2 приведены на рис. 1.25. Из анализа этих характеристик можно сделать вывод, что мост Уитстона имеет удовлетворительную линейность, когда | е | < 0,1. Аналогично из формулы (1.9) можно вычислить зависимости для выходного напряжения полумоста (7?! = Д (1 + е), Я2 = Д> (1 — в), Я3 = Д = Д0) и полного моста
(Д = Д*= Д)(1 + е)> Д>= Дз = До (1 — Е))-
Рис. 1.25. Нормированные передаточные характеристики моста Уитстона(С/х, С/г) и соответствующие им погрешности нелинейности(Дх, Дг)
Приведем сводку инженерных соотношений, которые используются при анализе и расчете мостов (предполагается, что Д, 3> Д,). Напомним, что измерительные мосты могут запитываться как током, так и напряжением (так называемые мосты тока и мосты напряжения) и передаточные характеристики у них могут несколько отличаться.
1. Простой мост. При запитке моста напряжением (Е)
где е— относительное изменение сопротивления.
Вывод: в простом мосте связь между ?/вых и гнелинейна. Абсолютная Д и относительная 8 нелинейности моста определяются выражениями
Например, при в <0,1 имеем 181 < 0,05. Если мост запитывается источником тока (/), то нелинейность уменьшается:
2. В полумосте при запитке напряжением (Е) и током (/) соответственно
3. В полном мосте аналогично:
Как видим, и в полумосте и в полном мосте передаточная характеристика линейна при е <С1. Кроме того, чувствительность схем возрастает. Например, полный мост в 4 раза чувствительней простого моста и в 2 раза чувствительней полумоста.
Заметим, что в окрестностях точки баланса, когда Я^ « Я0, из формулы (1.36) получим соотношение
из которого следует, что идентичные (коррелированные) изменения номиналов в смежных плечах моста не приводят к разбалансу. Выражение (1.11) используется для построения схем компенсации влияния соединительных проводов в высокоточных низкоомных датчиках (см. разд. 1.3.4).
В случае, если условие Дн » Rj не выполняется, приведенные соотношения должны корректироваться. Фактическое выходное напряжение и’вых на нагрузке может быть найдено из соотношения
гДеДэкв = Я2||Я3 +-^1|Я4.
Например, в полумосте при запитке напряжением
Из последнего выражения следует, что отклонение от линейности является величиной второго порядка малости относительно е.
Очевидно, что баланс может быть достигнут как в симметричном. (равноплечем), так и в несимметричном неравноплечем мосте. При этом изменяется чувствительность и нелинейность схемы. Чтобы убедиться в этом, достаточно в формуле (1.3) положить Я±/Я2 = М и АЯ1 = е Я. Тогда для простого моста при Яа 3> Я •
где а = М/{М + I)2 — чувствительность моста.
Хотя нелинейность при М > 1 и будет уменьшаться, одновременно будет уменьшаться и чувствительность а. Из графика нормированной чувствительности неравноплечего моста (рис. 1.26) видно, что если мост неравноплечий (например Я1 <С Я2 или Я1 :» Я2), то чувствительность моста при балансе существенно уменьшается. Для получения высокой чувствительности импедансы плеч измерительного моста должны быть соизмеримы.
Как правило, мост Уитстона используется для измерения резисторов в диапазоне (1-Ч08) Ом. Нижний предел ограничивается влиянием сопротивления соединительных проводов, контактов и паразитными термоЭДС. Верхний предел определяется токами утечки высокоомных цепей, к которым для повышения чувствительности приходится подводить большое напряжение запитки.
Точность определения номиналов резисторов с помощью мостовых схем зависит от чувствительности нуль-органа, фиксирующего момент баланса, стабильности и точности образцовых резисторов,
Рис. 1.26. Нормированная чувствительность неравноплечего моста
а в ряде случаев — от сопротивления соединительных проводов, контактов и от паразитных термоЭДС.
В промышленных мостах магазины сопротивлений изготавливают из высокостабильного манганина (ТКС < 10_3% “С»1, временной дрейф < 10 ‘3% /год), а сопротивления устанавливаются, например, с помощью декадных переключателей в диапазонах от 1 Ом до 10 кОм. В этом случае можно перекрыть диапазон измерения в девять порядков. Для устранения влияния паразитной термоЭДС на результат измерения Ях вычисляют по двум замерам с разной полярностью источника питания. В последующих разделах рассматриваются и вопросы компенсации сопротивления соединительных проводов.
Мост Уитстона трудно использовать для измерения малых сопротивлений (менее 1 Ом), так как по крайней мере два сопротивления моста будут низкоимпедансными и значительные погрешности могут возникнуть из-за сопротивлений соединительных проводов.
Эти трудности преодолеваются в двойном мосте, или мосте Томсона (рис. 1.27), где в стандартный мост включено дополнительное плечо Д5-Т?6. Плечи /?3-Д4 и Д5-Д6 являются высокоомными, а плечо jR4-r-.fi2 — низкоомным. Распределенное сопротивление соединительного проводника представлено резистором г, — измеряемое сопротивление, Л2 — образцовое сопротивление такого же порядка, что и Ях.
Для обеспечения необходимой чувствительности источник питания с помощью значительного тока /0 должен создавать падение напряжения Е порядка единиц вольт. Таким образом в схеме
Рис. 1.27. Двойной мост Томсона
иА / ив, а потенциалы в узлах С и Б измерительной диагонали определяются выражениями
Полагая, что (Д5 +Ив)г, (#з + ^4) (Лх + г + Д2)> можно записать
Приравнивая потенциалы в точках С и Б с учетом последних выражений, получим
Если в процессе балансировки моста выдерживать условие
(ДзД6= ^4-^5)’то
Следовательно, двойной мост позволяет компенсировать сопротивление соединительного провода г, не прибегая к использованию слишком низкоомных резисторов в плечах моста. Точность двойного моста составляет около 0,05% в диапазоне от 10 4 Ом до 1 Ом. Очевидно, что мост Томсона обладает определенной универсальностью, поскольку с его помощью можно измерять сопротивление резисторов большего номинала.
Рис. 1.28. Модифицированная схема моста Уитстона
Особенно эффективны мостовые измерительные схемы с использованием ОУ. На рисунке 1.28 приведена модифицированная схема моста Уитстона, в которой измерительное плечо моста (Кх — К2) с датчиком 1?! включено в цепь отрицательной обратной связи ОУ Ог. Измерительное плечо запитывается стабильным током /0 = ?7оп//?5, следовательно, напряжение запитки моста составит
Подставляя значение питания Е в основную формулу моста (1.36) и учетывая, что 111 = Я0 (1 + е), й2= Д3 = Д4 = Д0, получим
Как видим, схема имеет удвоенную чувствительность и линейную передаточную характеристику во всем диапазоне изменения.
Задание:
1.Прочитать внимательно текст.
2.Составить кластер.
3.Зарисовать схемы и формулы. 4.Составить вопросы которые вам не понятны.
Исследование работы мостовой измерительной схемы
Цель работы
Исследовать принцип действия мостовой измерительной схемы, научиться измерять сопротивление с помощью мостовой измерительной схемы и рассчитывать параметры термометрического датчика, включённого в схему.
Краткие теоретические сведения
В основе многих контрольно-измерительных приборов лежит мостовая схема для измерения сопротивления (мост Уитсона) на постоянном токе, разработанная в 1843 году и часто используемая до сих пор. Мостовые измерительные схемы применяются для определённого включения датчиков (параметрических) с целью измерения контролируемых величин и преобразования полученного сигнала в удобный для дальнейшего использования (изменение напряжения).
Мостовые измерительные схемы (мост) – это электрические схемы, имеющие четыре плеча, к одной диагонали которых подводится питающее напряжение, а с другой диагонали снимается выходное напряжение.
Конструкция мостовой измерительной схемы представлена в соответствии с рисунком 8.
Рисунок 8 – Конструкция мостовой измерительной схемы
Нулевым условием для моста является равенство падений напряжения на резисторах U1=U3, U2=U4 и тогда Uвых равно нолю. Основной метод определения величины сопротивления одного резистора основан на расчёте по известным величинам сопротивлений остальных резисторов. Например, если резистор с неизвестным сопротивлением подсоединён вместо резистора R4, величины сопротивлений резисторов R1 и R3 известны, а резистор R2 представляет собой проградуированный в Омах потенциометр. Выполнив нулевое условие (Uвых=0) при помощи потенциометра, и считав значение сопротивления потенциометра, можно вычислить величину сопротивления резистора R4 из соотношения R1/R2=R3/R4.
Современные мосты создаются на основе цифровых процессоров. Микропроцессорное ядро позволяет автоматизировать процедуру измерения (расчёты выполняются аппаратурой), обеспечить многофункциональность устройства (многие мосты интегрированы с многофункциональными измерительными приборами), устранить помехи (посторонние постоянные и переменные напряжения почти всегда присутствуют на жилах кабелей), организовать дальнейшую обработку накопленных результатов измерений (хранение, обмен с компьютером) и др.
Применяются два основных типа мостовой измерительной схемы:
— неравновесная (небалансная) – это мостовая схема, предусматривающая измерения методом непосредственного отсчёта по измерительному прибору, включённому в диагональ моста;
— равновесная (балансная) – это мостовая схема, предусматривающая нулевой метод измерения.
Первый тип часто применяют для измерения неэлектрических величин электрическими методами.
Второй тип применяют в тех случаях, когда задачей мостовой схемы является не измерение, а управление каким-либо процессом. Схема используется как устройство сравнения, а выходное напряжение пропорционально сигналу рассогласования δ=R2-R1∙R4/R3.
Задание
Снять значение сопротивления потенциометра при равновесии мостовой измерительной схемы.
Определить сопротивление термометрического датчика, включённого в измерительную мостовую схему; определить чувствительность (коэффициент передачи) датчика и измеренную температуру; построить статическую характеристику датчика R=f(t0).
Проанализировать проделанную работу.
Экспериментальная схема представлена в соответствии с рисунком 9.
Рисунок 9 — Экспериментальная схема
Четыре плеча измерительной схемы содержат два резистора с постоянными сопротивлениями R1, R3, один проградуированный в Омах потенциометр R2 и одно переменное сопротивление – термометрический датчик R4. К диагонали ab подключён источник постоянного тока, а с другой диагонали cd снимается выходное напряжение с помощью вольтметра PV. Ток, проходящий через нагревательный элемент НЭ, регулируется с помощью потенциометра R от источника переменного тока.
Исходные данные для расчёта, выбираются в соответствии с последней цифрой в порядковом номере по списку, в таблице 3.
Таблица 3 — Исходные данные для расчёта по вариантам
| Вариант | Технические характеристики терморезистора | Мостовая схема | |||||||
| Сопротивление при t0,
R0, Ом | Начальная температура,
t0, 0С | Предел измерения температура,
t, 0С | Значение постоянных коэффициентов для ТРП | Температурный коэффициент удельного сопротивления для ТРМ,
α, 0С | Сопротивление,
R1, Ом | Сопротивление,
R3, Ом | Потенциометр,
R2, Ом | ||
| А,
∙ 10-3 | В,
∙ 10-6 | ||||||||
| - | - | 0,0043 | |||||||
| 3,9083 | -5,775 | - | |||||||
Порядок выполнения расчёта
Собрать экспериментальную схему, представленную в соответствии с рисунком 9.
При равенстве падений напряжений на резисторах R1/R2=R3/R4 вольтметр PV покажет ноль. При перемещении движка потенциометра R (от положения 1 к положению n) изменяется ток, проходящий через нагревательный элемент НЭ (увеличивается), и изменяется температура нагревательного элемента НЭ (увеличивается). При изменении температуры (увеличении) изменяется сопротивление (увеличится) термометрического датчика R4 и равновесие моста нарушается. Вольтметр PV покажет некоторое значение напряжение выхода. Перемещая движок проградуированного потенциометра R2, и выполнив нулевое условие (стрелка вольтметра показывает ноль), шкала потенциометра R2 покажет значение его сопротивление.
Результаты измерений записать в таблицу технических и экспериментальных данных.
По значению этого сопротивления можно определить температуру, измеряемую термометрическим датчиком, параметры и характеристики датчика.
Для определения сопротивления термометрического датчика необходимо воспользоваться условием равновесия мостовой схемы, которое определяется соотношением
(13)
где R1, R2, R3, R4 – сопротивления в плечах мостовой схемы.
Из этого соотношения можно выразить неизвестное сопротивление термометрического датчика R4, Ом
Для определения температуры, при которой наступит равновесие мостовой схемы, необходимо вычислить динамическую чувствительность (коэффициент передачи) датчика s, Ом/0С, определяется по формуле
(14)
где R – сопротивление датчика при температуре t, Ом;
t – предел измерения датчика, 0С;
R0 – сопротивление датчика при температуре t0;
t0 – начальная температура, 0С.
Сопротивление медного терморезистора (ТРМ) R, Ом, определяется по формуле
(15)
где α – температурный коэффициент удельного сопротивления, 0С-1.
Сопротивление платинового терморезистора (ТРП) R, Ом, определяется по формуле
(16)
где А, В – постоянные коэффициенты.
Чувствительность (коэффициент передачи) для данного датчика величина постоянная, поэтому можно использовать туже формулу для определения измеряемой температуры s, Ом/0С
где R4 – сопротивление при измеряемой температуре t4, Ом;
t4 – измеряемая температура датчика, 0С.
Измеряемая температура датчика t4, 0С
Пример выполнения расчёта
Исходные данные для расчёта:
— сопротивление терморезистора при начальной температуре R0 = 50 Ом;
— начальная температура терморезистора t0 = 0 0С;
— предел измерения терморезистора t = 200 0С;
— температурный коэффициент удельного сопротивления терморезистора α = 0,0043 0С-1;
— сопротивление плеч мостовой схемы R1 = 50 Ом, R3 = 40 Ом, R2 = 75 Ом.
Экспериментальная схема представлена в соответствии с рисунком 9.
Неизвестное сопротивление термометрического датчика
Сопротивление медного терморезистора при пределе измеряемой температуры
Динамическая чувствительность (коэффициент передачи) датчика
Измеряемая температура датчика
Статическая характеристика термометрического датчика R=f(t0) представлена в соответствии с рисунком 10.
Рисунок 10 — Статическая характеристика
термометрического датчика R=f(t0)
В ходе практической работы были изучены конструкция, принцип действия и методы измерения сопротивлений с помощью мостовой измерительной схемы. Рассчитаны параметры термометрического датчика, включённого в схему: сопротивление 60 Ом, чувствительность 0,22 Ом/0С, измеряемая температура 46,51 0С. По полученным входным и выходным данным построена статическая характеристика термометрического датчика R=f(t0) которая имеет линейный вид.
Контрольные вопросы
1) Для чего применяют мостовые измерительные схемы?
2) Что представляет собой мостовая измерительная схема?
3) Что такое нулевое условие мостовой измерительной схемы?
4) Как производят измерения сопротивления с помощью мостовой измерительной схемы?
5) Каким образом мостовая измерительная схема применяется как устройство сравнения?
Практическая работа №4
2. Мостовая измерительная схема постоянного тока
Принципиальная
схема одинарного моста постоянного
тока (рис. 2) состоит из четырех резисторов
с активными сопротивлениями R1,
R2,
R3
и R4,
которые соединены в замкнутый
четырехугольник АБВГ.
Входящие
в схему резисторы R1—
R4
называют плечами или ветвями моста.
Плечи можно обозначать и буквами,
например плечо АБ.
В
четырехугольнике АБВГ
можно
выделить две диагонали:
АВ и
БГ.
В
диагональ БГ
моста
включен измерительный прибор, имеющий
активное сопротивление Rпр.
В диагональ АВ
включен
источник питания с ЭДС Е
и
внутренним сопротивлением RE.

Рис. 2. Мостовая
измерительная схема
Можно
подобрать сопротивления плеч моста
так, чтобы потенциалы точек Б
и
Г, между
которыми включен измерительный прибор,
были одинаковы. В этом случае ток в цепи
прибора Inp
отсутствует (Inp
= 0). Процесс подбора таких сопротивлений,
обеспечивающих Inp
= 0, называется уравновешиванием или
балансировкой моста. Условие равновесия
моста может быть получено на основании
законов Кирхгофа, записанных для токов
в плечах моста с учетом принятых на рис.
2 направлений токов:
 ;
;

откуда

(3)

(4)
Разделив (3) на (4),
получим

(5)
Так
как в уравновешенном мосте ток в цепи
прибора Inp
= 0, то I1
= I2,
I3
= I4
и равенство (5) имеет вид

или

(6)
т. е.
условие равновесия
моста можно сформулировать так:
произведения сопротивлений противолежащих
плеч должны быть равны.
С
помощью мостовой схемы можно измерить
неизвестное сопротивление Rx,
включив его в одно из плеч моста, например
в плечо ВГ
вместо
резистора R4.
При трех известных сопротивлениях R1,
R2,
R3
неизвестное сопротивление  .
.
Уравновешивание моста может быть
достигнуто изменением либо одного
сопротивления (R2),
либо
отношения двух сопротивлений ( ).
).
В уравновешенных мостах измерительный
прибор должен быть очень чувствительным,
он должен реагировать на малые токи.
Именно по показаниям
этого прибора и фиксируется равновесие
моста. Поэтому в уравновешенных мостах
в качестве измерительного прибора
используется обычно гальванометр.
Кроме
уравновешенных
существуют так называемые неуравновешенные
(или небалансные) мосты, в которых Inp
≠ 0и измеряемое
сопротивление Rx
определяется именно
по отклонению стрелки прибора, т. е. по
величине Inp,
поскольку Inp
= f(Rx).
В качестве
измерительного прибора в неуравновешенных
мостах используются амперметры (так
как токи невелики, то обычно мили- или
микроамперметры). Уравновешенные мосты
требуют ручной или автоматической
балансировки, в то время как неуравновешенные
мосты не требуют регулировки при каждом
измерении. Поэтому неуравновешенные
мосты проще, их чаще используют для
электрических измерений неэлектрических
величин.
На
основании законов Кирхгофа могут быть
получены выражения для тока в диагонали
моста, содержащей измерительный прибор,
через напряжение питания U:

(7)
через
ток питания I:

(8)
где 
(9)

(10)
Кстати,
из (7) или (8), приравнивая Inp
нулю, можно вывести уже полученное нами
условие равновесия моста (6).
Сложное
соединение сопротивлений R1—
R4,
Rпр
в мостовой схеме можно преобразовать
в эквивалентное сопротивление RM
— входное сопротивление
моста по диагонали питания АВ.
Эквивалентная схема
моста показана на рис. 3. В зависимости
от соотношения RM
и RE
различают низкоомные
и высокоомные мостовые измерительные
схемы.

Рис.
3. Эквивалентная схема моста
Если
RM<<RE,
то мост называется
низкоомным. В таких мостах изменение
сопротивления плеч почти не влияет на
ток питания I,
т. е. можно считать, что I
≈ const.
При расчете низкоомных мостов обычно
используют уравнение (8).
Если
RM>>RE,
то мост называется высокоомным. В этом
случае постоянной величиной
можно считать напряжение на зажимах
моста U
=E—I
RE
≈
const.
При расчете высокоомных мостов обычно
используют уравнение (7).
Разделив (7) на (8),
получим выражение для входного
сопротивления моста

(11)
Линейно-инверсный мост и мост модулированного тока
Для измерения параметров RLC-элементов традиционно используют мостовые измерительные схемы — мост Уитстона (рис. 30.1). В зависимости от используемой разновидности мостовой схемы шкалы приборов имеют линейный либо нелинейный характер (с растянутой частью шкалы). Общий недостаток линейных мостовых схем — узкий диапазон измерений.
Мостовая схема, сочетающая возможность измерения параметров RLC как в схеме линейного, так и в схеме инверсного моста (рис. 30.1 — 30.3), позволяет заметно расширить диапазоны измеряемых значений [Рл 3/01-30].
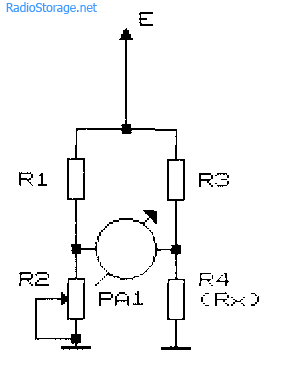
Рис. 30.1. Схема линейного моста
На рис. 30.1 и 30.2 показаны, соответственно, схемы линейного и инверсного мостов, в таблице 30.1 — основные соотношения элементов мостов и расчетные формулы для определения искомого значения (на примере определения Rx). Множитель диапазона К кратен десяти. В качестве элемента балансировки моста должен быть использован специальный потенциометр. Это может быть многооборотный (десятиоборотный) потенциометр со счетчиком оборотов и линейной зависимостью изменения сопротивления от угла поворота, либо однооборотный проволочный потенциометр с редуктором, либо магазин сопротивлений (двух, трехдекадный набор последовательно включаемых эталонных сопротивлений). Шкала градуируется от 0 до 1,00 с дискретностью отсчета не хуже 0,01 ед. Для решения учебно-исследовательских задач в качестве такого потенциометра допустимо использовать однооборотный потенциометр с линейной зависимостью изменения сопротивления от угла поворота.
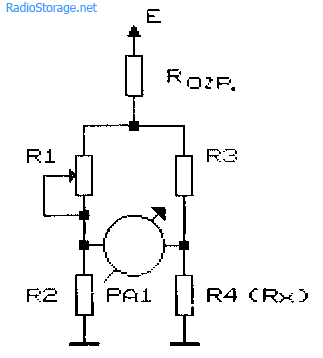
Рис. 30.2. Схема инверсного моста
Для повышения точности отсчета при создании прибора для измерений с повышенной точностью желательно использовать но-ниусную шкалу (как на микрометрах или штангенциркулях).
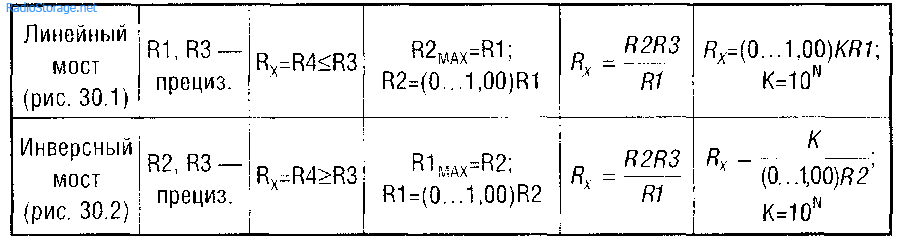
Таблица 30.1
На рис. 30.3 приведен фрагмент практической блок-схемы линейно-инверсного моста. Переключатель SA1 выполняет одновременно несколько функций: позволяет отключать источник питания, а также переключать измерительный мост на питание от внешнего источника постоянного или переменного тока, внутреннего генератора переменного тока или источника постоянного тока. Резистор Rorp (рис. 30.2, 30.3) служит для ограничения тока короткого замыкания при измерении малых сопротивлений. Переключатель SA2 предназначен для изменения режима работы моста с линейного на инверсный. Для измерения параметров L и С (рис. 30.3) эталонный и неизвестный элементы включают вместо элементов R3 и R4 моста. В качестве нуль-индикатора РА1 может быть использован внешний измерительный прибор — милливольтметр переменного тока.
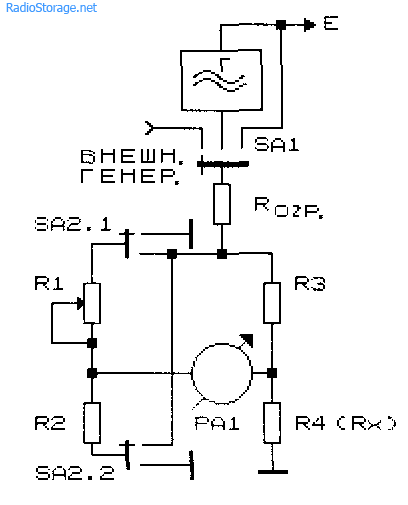
Рис. 30.3
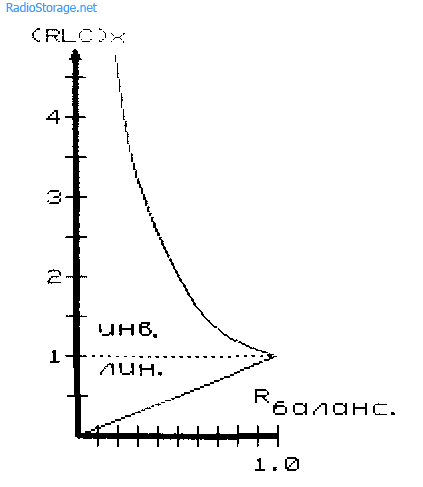
Рис. 30.4
На рис. 30.4 показаны возможные пределы измерения мостовой схемы в зависимости от угла поворота оси (в долях или процентах) балансировочного потенциометра в линейном и инверсном включении моста. Использование инверсного включения моста позволяет расширить диапазон измерений параметров RLC на один, два порядка в сторону больших значений при сохранении возможности измерения меньших значений относительно эталонного значения в режиме линейного моста. Это позволяет заметно упростить конструкцию моста и сократить вдвое количество дорогостоящих дефицитных прецизионных (имеющих малое отклонение от номинала) элементов.
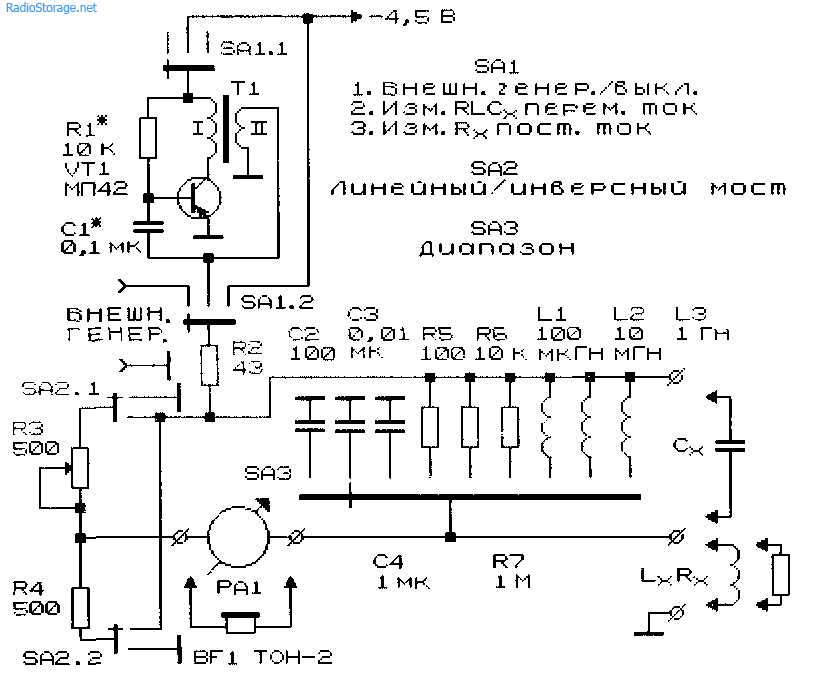
Рис. 30.5
На рис. 30.5 приведена практическая схема линейно-инверсного моста, способного работать как на переменном, так и на постоянном токе от внутреннего или внешнего источника (генератора). В качестве внутреннего генератора звукового диапазона используется блокинг-генератор на транзисторе VT1. В генераторе может быть использован кремниевый транзистор типа КТ361. В случае отсутствия генерации выводы одной из обмоток трансформатора следует поменять местами. Частота генерации блокинг-генератора определяется свойствами трансформатора и постоянной времени R1C1, поэтому желателен подбор этих элементов.
Переключатель (выключатель) SA1 позволяет подавать питание на мост от внешнего генератора (источника постоянного или переменного тока), от внутренних звукового генератора или источника постоянного тока напряжением 4,5 В.
Переключатель SA2 переводит устройство в режим линейного или инверсного моста. В устройстве использовано минимальное количество прецизионных RLC-элементов. Эти элементы могут быть отобраны или составлены из обычных резисторов или конденсаторов с контролем полученной величины по цифровому измерительному прибору.
Диапазоны измерений линейного-инверсного моста составляют: от 1 Ом до 100 МОм, от 1 пФ до 100 мкФ, от 1 мкГн до 100 Гч.
В качестве индицирующего прибора при измерении на переменном токе желательно использовать высокоомные головные телефоны ТОН-1/ТОН-2; на постоянном токе — высокоомные измерительные приборы магнитоэлектрической системы. Кроме того, в качестве нуль-индикаторов можно подключить внешние измерительные приборы, например, милливольтметр переменного тока.
В качестве трансформатора Т1 можно использовать выходной или согласующий трансформатор от портативного радиоприемника.
На рис. 30.6 показана мостовая измерительная схема — мост модулированного тока. Питание моста осуществляется модулированным постоянным током, что позволяет использовать в качестве нуль-индикаторов измерительные и индикаторные приборы, чувствительные как к переменному, так и к постоянному току.
Рис. 30.7. Схема моста переменного тока Максвелла транзисторе VT1. Переключатель SA1 одновременно является выключателем устройства.
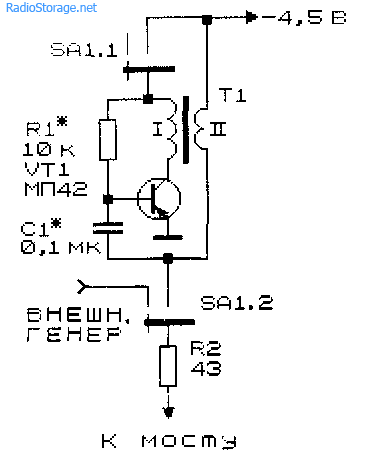
Рис. 30.6
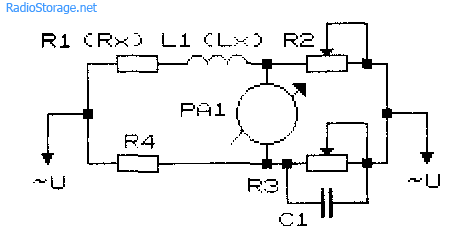
Рис. 30.7. Схема моста переменного тока Максвелла
Мост Уитстона, рис. 30.1, является далеко не единственной мостовой схемой, предназначенной для измерения сопротивлений, индуктивностей или емкостей. Для сопоставления на рис. 30.7 — 30.10 приведены мостовые схемы Максвелла (рис. 30.7), Хэя (рис. 30.8), Соти (рис. 30.9), Вина (рис. 30.10), названные так в честь предложивших их исследователей. При помощи этих приборов можно получить также сведения о тангенсе угла диэлектрических потерь конденсаторов, измерить величину добротности катушек индуктивности. Обозначения элементов моста условны. Для выполнения условия балансировки моста (нулевые показания индикатора) должно выполняться равенство соотношения элементов плеч моста.
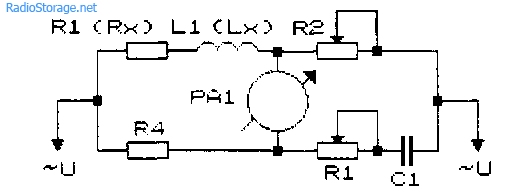
Рис. 30.8. Схема моста переменного тока Хея
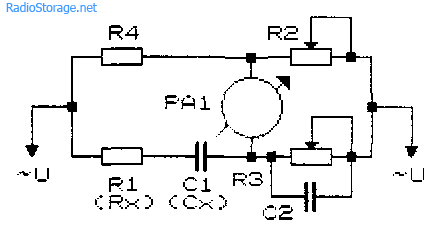
Рис. 30.9. Схема моста переменного тока Соти
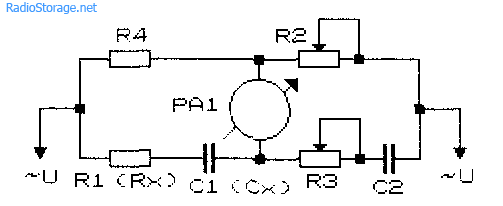
Рис. 30.10. Схема моста переменного тока Вина
Общий принцип действия мостов переменного тока — подача питающего переменного напряжения и последующая балансировка моста при помощи регулируемых элементов. Стрелка измерительного прибора, милливольтметра переменного тока, при балансировке должна быть на нуле. Если в качестве индикатора баланса используются головные телефоны, в телефонах не должен прослушиваться звуковой сигнал.
Для нахождения неизвестного (определяемого) значения емкости, индуктивности, сопротивления регулируемые элементы мостов — потенциометры R2 и R3, либо заменяющие их наборы переключаемых эталонных резисторов, должны быть откалибро-ваны. Калибровочные значения могут быть нанесены на лимбы ручек регулирующих элементов.
Мостовые схемы, процесс их балансировки, а также принципы, заложенные в этом методе измерения, широко используют в радиоэлектронике: например, в балансных модуляторах, в измерительных приборах и преобразователях. В этой связи рекомендуется подробно изучить различные варианты мостовых схем, оценить перспективы их использования в своих последующих самостоятельных конструкциях.
Литература: Шустов М.А. Практическая схемотехника (Книга 1), 2003 год
Мостовой метод — Студопедия
Мостовой метод положен в основу работы измерительных мостов (Е7), которые являются универсальными приборами. С их помощью можно измерять сопротивление резисторов, емкость конденсаторов, индуктивность катушек, добротность и тангенс потерь.
Название «мост» прибор получил потому, что между двумя параллельными ветвями (Żl, Ż2 и Ż3, Ż4) индикаторная диагональ образует как бы мост.
Ветви, в которые включены комплексные сопротивления Żl, Ż2, Ż3 и Ż4, называют плечами моста. В одну диагональ моста включен генератор Г питающего напряжения, в другую — индикатор И равновесия (баланса) моста.
Схемы четырехплечного моста показаны на рис. 4.6.
Рис. 4.6. Схемы четырехплечного моста в общем виде (а) и для измерения сопротивления резисторов (6)
Измерение сопротивления резисторов выполняют в цепях постоянного и переменного тока. Во все плечи моста включены чисто активные сопротивления.
Условием равновесия моста является равенство произведений сопротивлений двух противоположных плеч:
Откуда
(4.8)
Признак равновесия моста — отсутствие показаний на индикаторе.
Если поменять местами индикаторную диагональ и диагональ питания, то равновесие моста не нарушится.
Процесс уравновешивания моста постоянного тока достигается изменением (подбором) отношения R2 / R1переключателя «Множитель» и плавным изменением сопротивления потенциометра R3 — регулировки «Отсчет», что позволяет значительно расширить диапазон измерения. Уравновешивание моста считается законченным при полностью использованном значении напряжения питания (регулировка «Чувствительность») генератора.
Результат измерения представляет собой произведение от умножения показания регулировки «Отсчет» на показание переключателя «Множитель».
Чувствительность моста зависит от чувствительности используемого индикатора и значения напряжения источника питания. Поэтому в качестве индикатора в аналоговых мостах используется прибор магнитоэлектрической системы с двухсторонней шкалой (с нулем посередине).
Измерение емкости конденсаторов выполняется мостом только переменного тока. Сопротивление четырехплечного моста в общем виде носит комплексный характер, поэтому условия равновесия моста переменного тока будут определяться двумя условиями: по модулю и по фазе.
Мосты переменного тока чаще всего питаются от внутреннего генератора со звуковой частотой 100 или 1000 Гц (если на лицевой панели \ моста частота не указана, то это всегда 1000 Гц). Возможно питание от внешнего генератора, для чего предусмотрены гнезда (обычно на задней панели). При питании напряжением звуковой частоты еще мало сказывается влияние паразитных емкостей и индуктивностей на погрешность измерения.
В качестве индикатора равновесия моста служат электромеханический индикатор выпрямительной системы или электронный вольтметр типа У—Д, в точных мостах — электронный осциллограф (в момент равновесия моста на экране ЭЛТ будет только горизонтальная линия развертки).
Конденсаторы различаются не только значением емкости и рабочим напряжением, но и активными потерями в диэлектрике, которые характеризуются тангенсом угла потерь tg δ. Эквивалентные схемы конденсатора без потерь (идеального конденсатора), с малыми и большими потерями представлены на рис. 4.7.
Рис. 4.7. Эквивалентные схемы конденсаторов без потерь (а),
с малыми (б) и с большими потерями (в)
Отечественная промышленность и зарубежные фирмы выпускают множество разнообразных конденсаторов с малыми и большими потерями. Рассмотрим функциональную схему моста для измерения емкости конденсаторов с малыми потерями (рис. 4.8, а).
Рис. 4.8. Функциональные схемы мостов для измерения емкости конденсаторов с малыми (а) и с большими потерями (б)
Условие равновесия моста в комплексном виде выражается как:
Раскрыв скобки и приравняв отдельно вещественные и мнимые части, получим:
откуда
(по фазе) (4.9)
откуда
(по модулю) (4.10)
С помощью рассматриваемой схемы моста можно измерять tgδ. Электрическая цепь левого верхнего плеча моста показана на рис. 4.9, а.
Рис. 4.9. Электрическая цепь левого верхнего плеча моста (а) и векторная диаграмма тока и напряжений в плече (б)
В векторной диаграмме (рис. 4.9, б) угол φ — фазовый сдвиг между током и напряжением в левом плече, угол δ — угол потерь в диэлектрике:
(4.11)
Определим tgδ через известные (образцовые) параметры элементов цепи. Для этого перемножим уравнение (4.9) и (4.10), умножив левую и правую части на ω:
ωCxRx = ωC0R0 = tgδ (4.12)
Из выражения (4.12) следует, что при ω = const и C0 = const сопротивление образцовой цепи R0можно градуировать непосредственно в значениях tgδ .
Рассмотрим функциональную схему моста для измерения емкости конденсаторов с большими потерями (см. рис. 4.8,6).
Условие равновесия моста в комплексном виде выражается формулой
откуда
(по модулю) (4.13)
(по фазе) (4.14)
Тангенс угла потерь конденсатора находим по формуле
(4.15)
Условие равновесия моста зависит от частоты, поэтому мостовые схемы измерения предназначены для работы на одной (реже — на двух) фиксированной частоте.
Измерение индуктивности катушеквыполняется мостом только переменного тока. Измерение возможно путем сравнения с индуктивностью L0 образцовой катушки или с емкостью С0 образцового конденсатора. Образцовые катушки переменной индуктивности изготовить трудно, и надежность их невысока, поэтому на практике используют схемы сравнения с образцовыми конденсаторами. Функциональная схема моста для измерения индуктивности катушки приведена на рис. 4.10.
Рис. 4.10. Функциональная схема моста для измерения индуктивности катушек
Условие равновесия моста:
R1 · R2 = Ż0 · Żx ; Żx = Rx + jωLx ; Ż0 = R0 / 1 + jωC0R0
где Rx— сопротивление потерь в измеряемой катушке;
откуда
(4.16)
откуда
Lx = C0 R1 R2 (4.17)
С помощью рассматриваемого моста можно измерять также добротность Q катушек. Известно, что Q = ωL / R. Разделив уравнение (4.17) на уравнение (4.16) и умножив их левые и правые части на ω, получим
(4.18)
Таким образом, мостовая схема для измерения параметров R, L, С, Q, tgδ применяется в так называемых универсальных мостах, представляющих собой сочетание мостов постоянного и переменного тока.
Источниками погрешности при измерении параметров элементов цепей мостовым методом являются неточность уравновешивания моста, нестабильность значения напряжения и частоты источника питания моста, погрешность значений образцовых элементов.
К достоинствам мостового метода относятся универсальность мостов при измерении параметров; к недостаткам — большая погрешность (до 3%) аналоговых мостов, невозможность измерения параметров на рабочих частотах, трудоемкость измерений. Меньшую погрешность (0,2%) и возможность автоматизации измерений обеспечивают цифровые мосты.
4. Мостовая схема переменного тока
В
плечи мостовой схемы переменного тока
(рис. 6) включены полные сопротивления,
состоящие из активной и реактивной
составляющих. Будем пользоваться
комплексной формой записи полных
сопротивлений
 .
.
В
диагональ АВ
моста
включен источник переменного
синусоидального напряжения
 ,
,
а в диагональБГ
—
измерительный прибор переменного тока.
Направления токов в плечах моста могут
быть выбраны произвольно. Ток измерительной
диагонали

(22)
где
 (23)
(23)
 (24)
(24)
 ,
,

—
комплексные выражения, аналогичные
выражениям в уравнениях (9) и (10) для моста
постоянного тока.
Условия
равновесия моста переменного тока
получим, приравнивая (22) нулю:
 (25)
(25)
где
 ;
; ;
;
 ;
;

Рис. 6. Мостовая
измерительная схема на переменном токе
Напомним,
что при показательной форме записи
комплексной величины модуль
 ,
,
а аргумент
В соответствии с
условием равновесия моста подставим в
(25) значения полных сопротивлений

Представим левую
и правую части в виде действительной и
мнимой составляющих:

Две комплексные
величины равны только в том случае, если
равны порознь их действительные и мнимые
части:
 (26)
(26)
 (27)
(27)
Таким
образом, получаем два независимых
условия равновесия, которые должны
выполняться одновременно. Если в мостах
постоянного тока имеется одно условие
равновесия и уравновешивание достигается
регулировкой одного сопротивления, то
в мостах переменного тока для
уравновешивания необходима регулировка
не менее двух параметров схемы. Трудность
уравновешивания моста переменного тока
состоит в том, что в процессе обеспечения
одного условия (например, равенства
произведений модулей сопротивлений в
противолежащих плечах:
 )
)
нарушается другое соотношение — между
фазовыми сдвигами: .
.
Обычно такие мосты регулируются вручную
методом последовательных приближений.
В некоторых частных
случаях уравновешивание моста
обеспечивается выполнением одного из
трех условий.
Если
R1
=
R2
=
R3
— R4
= 0,
т. е. плечи моста имеют только ре активные
сопротивления, то условие равновесия

Если
 ,
,
т. е. плечи моста имеют только активные
сопротивления, условие равновесия
Если
два соседних плеча имеют только
реактивные сопротивления, а два других
—только активные (любая пара соседних
плеч), например
 ,
,
то условие равновесия
Следует иметь в
виду, что катушки индуктивности всегда
кроме индуктивного сопротивления имеют
активное сопротивление, которое в
некоторых случаях настолько мало, что
им можно пренебречь.
Расчет
чувствительности моста переменного
тока можно провести в соответствии с
(12), Считывая, что вместо R4
следует подставить
комплексное сопротивление. Чувствительность
моста по току

(28)
чувствительность
по напряжению

(29)
Уравновешивание
моста переменного тока может осуществляться
автоматически при соотношениях
сопротивлений плеч, рассмотренных для
частных случаев 1—3.
Автоматическое
уравновешивание мостов переменного и
постоянного тока выполняется по схеме,
показанной на рис. 7. Напряжение разбаланса
ΔU
снимается с измерительной диагонали
моста и подается на исполнительный
микроэлектродвигатель (ЭД)
через усилитель (У).
Двигатель через редуктор (Р)
перемещает движок
переменного резистора R
до тех пор, пока не
будет обеспечено условие равновесия и
напряжение разбаланса ΔU
не станет равным нулю. Одновременно
будет перемещаться и стрелка по шкале,
которая может быть проградуирована в
единицах сопротивления датчика или в
соответствующих этому сопротивлению
единицах измеряемой неэлектрической
величины.

Рис. 7. Схема
автоматического уравновешивания моста
Что такое мост Шеринга? — Высоковольтный мост Шеринга и измерение относительной проницаемости
Мост Шеринга используется для измерения емкости конденсатора, коэффициента рассеяния, свойств изолятора, вводов конденсатора, изоляционного масла и других изоляционных материалов. Это один из наиболее часто используемых мостов переменного тока. Мост Шеринга работает по принципу балансировки нагрузки на плечо.
Пусть, C 1 — конденсатор, емкость которого подлежит определению,
r 1 — последовательное сопротивление, представляющее потери конденсатора C 1 .
C 2 — стандартный конденсатор (термин стандартный конденсатор означает, что конденсатор не имеет потерь)
R 3 — безиндуктивное сопротивление
C 4 — конденсатор переменной емкости.
R 4 — переменное безиндуктивное сопротивление, параллельное переменному конденсатору C 4 .
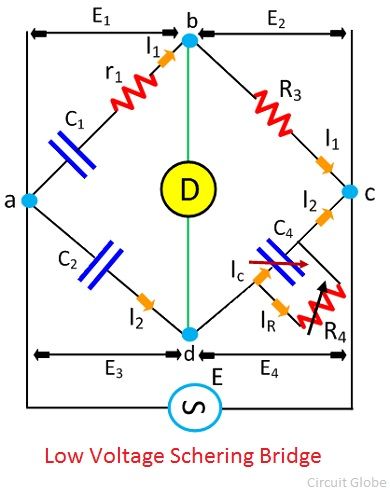 Когда мост находится в сбалансированном состоянии, нулевой ток проходит через детектор, что показывает, что потенциал на детекторе равен нулю. В состоянии баланса
Когда мост находится в сбалансированном состоянии, нулевой ток проходит через детектор, что показывает, что потенциал на детекторе равен нулю. В состоянии баланса
Z 1 / Z 2 = Z 3 / Z 4
Z 1 Z 4 = Z 2 Z 3
Итак, 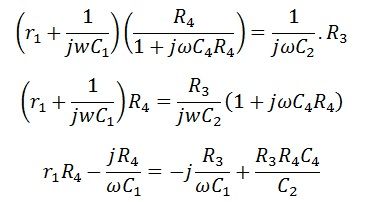 Приравнивая действительное и мнимое уравнения, мы получаем
Приравнивая действительное и мнимое уравнения, мы получаем 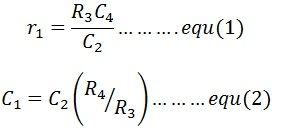 Уравнения (1) и (2) являются сбалансированными уравнениями, и они не зависят от частоты.
Уравнения (1) и (2) являются сбалансированными уравнениями, и они не зависят от частоты.
Коэффициент рассеяния определяется с помощью векторной диаграммы. Коэффициент рассеяния определяет скорость потери энергии, которая происходит из-за колебаний электрического и механического инструмента.
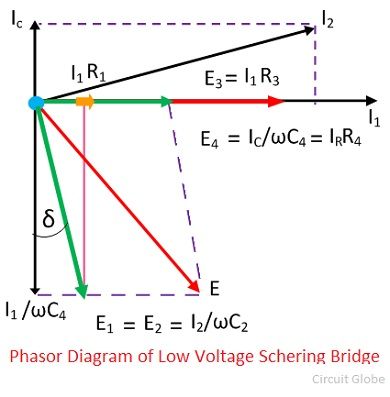
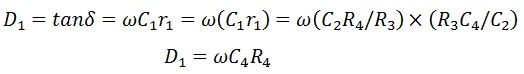 С помощью приведенного выше уравнения мы можем вычислить значение tanδ, которое является коэффициентом рассеяния моста Шеринга.
С помощью приведенного выше уравнения мы можем вычислить значение tanδ, которое является коэффициентом рассеяния моста Шеринга.
Преимущества моста Шеринга
Ниже приведены преимущества моста Шеринга.
- Уравнения баланса свободны от частоты.
- Устройство моста менее затратно по сравнению с другими мостами.
Высокое напряжение Schering Voltage
Низковольтный мост Шеринга имеет несколько недостатков, и по этой причине для измерения малой емкости требуется высокое напряжение и высокая частота. Принципиальная схема моста Шеринга показана на рисунке ниже.
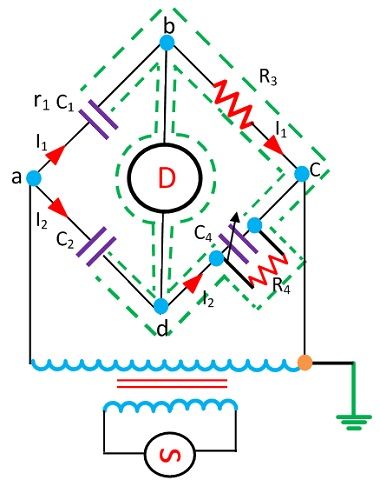 Ниже перечислены особенности моста Шеринга.
Ниже перечислены особенности моста Шеринга.
- Высокое напряжение поступает от операционного усилителя. Вибрационный гальванометр используют в качестве датчика для моста.
- Высоковольтные рабочие конденсаторы размещены в плечах ab и ad. Импеданс рычага ab и ad очень высок по сравнению с рычагом bc и cd. Термин «импеданс» означает сопротивление цепи протеканию тока. Точка c заземлена.
- Импеданс плеч ab и ad поддерживается на высоком уровне, так что высокое напряжение не влияет на потенциал на плечах bc и cd .Потенциал на детекторе также остается низким.
- Искровой разрядник устанавливает места на каждом плече для предотвращения опасного высокого напряжения, которое возникает на плечах bc и dc из-за пробоя высоковольтных конденсаторов.
- Потеря мощности очень мала в плечах ab и ad из-за высокого импеданса плеч ab и ad.
Измерение относительной проницаемости с помощью моста Шеринга
Мост Шеринга используется для измерения низкой проницаемости диэлектрического материала.Относительная проницаемость показывает способность материала создавать магнитное поле. Он рассчитывается с помощью емкости и размеров электродов.
Относительная проницаемость системы параллельных пластин выражается как
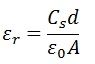 C s — измеренное значение емкости при рассмотрении образца как диэлектрика.
C s — измеренное значение емкости при рассмотрении образца как диэлектрика.
d — Расстояние между электродами
A — Эффективная площадь электродов.
ε 0 — диэлектрическая проницаемость свободного пространства
Другой метод расчета относительной диэлектрической проницаемости образца объясняется ниже.
Относительная диэлектрическая проницаемость образца зависит от толщины образца и расстояния между ними и электродом.
Пусть, C — емкость между электродом и образцом
A — площадь электродов
d — толщина образца
t — зазор между образцом и электродом.
x — уменьшение расстояния между образцом и электродом. 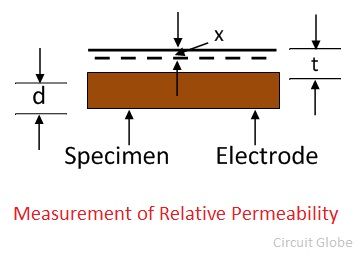 C с — емкость образца.
C с — емкость образца.
C 0 — Емкость между пространством из-за образца и электрода.
C — эффективная емкость C с и C 0 .
Емкость между образцом и электродом выражается как
.
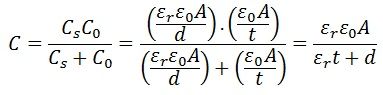 Когда мы уменьшаем образец и расстояние снова регулируется для получения того же значения емкости, выражение для уменьшения образца будет.
Когда мы уменьшаем образец и расстояние снова регулируется для получения того же значения емкости, выражение для уменьшения образца будет.
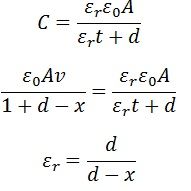 Изоляционные свойства электрических кабелей и оборудования также можно измерить с помощью моста Шеринга.
Изоляционные свойства электрических кабелей и оборудования также можно измерить с помощью моста Шеринга.
.
Тензодатчики и мостовые схемы
Соединения для тензодатчиков и мостовые схемы
Способ подключения тензодатчика зависит от типа инструмента. В таблице ниже представлены комбинации метода измерения и мостовой схемы.
| Пример режима измерения | Мостовая схема | Подключение проводов к распределительной коробке | Подключение проводов к мостовой коробке | Выход моста |
|---|---|---|---|---|
Квартальный мост | | | | E: Входное напряжение e: Выходное напряжение ⊿e: Выходное напряжение из-за деформации e 0 : Выходное напряжение до возникновения деформации R 0 : Сопротивление до возникновения деформации R: Изменение сопротивления из-за деформации ε: величина деформации K: коэффициент тензодатчика e = e 0 + ⊿e R 1 = R 0 + ⊿R R = R 0 |
Четвертьмост, 3-проводный | | | | |
Четвертьмостовая 3-проводная ширина с двумя датчиками, соединенными последовательно на одной руке, что исключает деформацию изгиба | |
.
Что такое мост Уитстона и другие схемы тензодатчиков
Измерительные схемы

Чтобы измерить деформацию с помощью тензодатчика сопротивления, он должен быть подключен к электрической цепи, способной измерять мельчайшие изменения сопротивления, соответствующие деформации. В тензодатчиках обычно используются четыре элемента тензодатчика, электрически соединенные для образования мостовой схемы Уитстона (рис. 2-6).
Мост Уитстона — это разделенная мостовая схема, используемая для измерения статического или динамического электрического сопротивления.Выходное напряжение схемы моста Уитстона выражается в выходных милливольтах на входной вольт. Схема Уитстона также хорошо подходит для температурной компенсации.
Уравнение моста Уитстона: если R1, R2, R3 и R4 равны, а напряжение VIN приложено между точками A и C, то выходной сигнал между точками B и D не будет показывать разность потенциалов. Однако, если R4 изменить на какое-то значение, не равное R1, R2 и R3, мост станет несимметричным, и на выходных клеммах появится напряжение.В так называемой конфигурации G-моста датчик переменной деформации имеет сопротивление Rg, а другие плечи являются резисторами фиксированного значения.
Однако датчик может занимать одно, два или четыре плеча моста Уитстона, в зависимости от области применения. Общая деформация или выходное напряжение цепи (VOUT) эквивалентно разнице между падением напряжения на R1 и R4, или Rg. Это также можно записать как:

Подробнее см. Рисунок 2-6.Мост считается сбалансированным, если R1 / R2 = Rg / R3 и, следовательно, VOUT равен нулю.
Любое небольшое изменение сопротивления тензодатчика приведет к нарушению баланса моста, что сделает его пригодным для определения деформации. Когда мост настроен так, что Rg является единственным активным тензодатчиком, небольшое изменение Rg приведет к выходному напряжению с моста. Если коэффициент измерения равен GF, измерение деформации связано с изменением Rg следующим образом:

Количество активных тензодатчиков, которые должны быть подключены к мосту, зависит от области применения.Например, может быть полезно соединить датчики, которые находятся на противоположных сторонах балки, один при сжатии, а другой при растяжении. В такой конфигурации можно эффективно удвоить мощность моста при той же деформации. В установках, где все рычаги подсоединены к тензодатчикам, температурная компенсация тензодатчиков выполняется автоматически, поскольку изменение сопротивления из-за колебаний температуры будет одинаковым для всех плеч моста Уитстона.
В четырехэлементном мосту Уитстона обычно два датчика соединены при сжатии и два при растяжении.Например, если R1 и R3 находятся в состоянии растяжения (положительное), а R2 и R4 — в состоянии сжатия (отрицательное), то выходной сигнал будет пропорционален сумме всех деформаций, измеренных отдельно. Для датчиков, расположенных на соседних опорах, мост становится неуравновешенным пропорционально разнице в деформации. Для манометров на противоположных опорах мост балансируется пропорционально сумме деформаций. Независимо от того, измеряется ли деформация изгиба, осевая деформация, деформация сдвига или деформация кручения, устройство тензодатчика будет определять взаимосвязь между выходным сигналом и типом измеряемой деформации.Как показано на рис. 2-6, если положительная деформация растяжения возникает на датчиках R2 и R3, а отрицательная деформация испытывается на датчиках R1 и R4, общий выходной сигнал, VOUT, будет в четыре раза превышать сопротивление одного датчика. В этой конфигурации компенсируются температурные изменения измерителя пятна.

Шевронный мост показан на Рисунке 2-7. Это многоканальная схема, которая служит для компенсации изменений сопротивлений перемычек путем их периодического переключения.Здесь четыре позиции каналов используются для переключения цифрового вольтметра (DVM) между конфигурациями G-моста (один активный датчик) и H-моста (два активных датчика). Измерительный прибор DVM всегда использует источник питания и внутренний H-мост. Эта конструкция наиболее популярна для измерения деформации вращающихся машин, где она может уменьшить количество требуемых контактных колец.
Хотя схема моста Уитстона является одним из самых популярных методов измерения электрического сопротивления, можно использовать и другие методы.Основное преимущество четырехпроводной омной схемы состоит в том, что подводящие провода не влияют на измерение, поскольку напряжение регистрируется непосредственно на элементе тензодатчика.

Установка четырехпроводной омической схемы может состоять из вольтметра, источника тока и четырех выводных резисторов R1, соединенных последовательно с измерительным резистором Rg (рисунок 2-8). Вольтметр подключается к клеммам измерения сопротивления цифрового вольтметра, а источник тока подключается к клеммам источника сопротивления цифрового вольтметра.Для измерения величины деформации в цепь подается слабый ток (обычно один миллиампер). В то время как вольтметр измеряет падение напряжения на Rg, абсолютное значение сопротивления вычисляется мультиметром на основе значений тока и напряжения.
Измерение обычно выполняется, сначала измеряя значение сопротивления датчика в ненапряженном состоянии, а затем выполняя второе измерение с приложенной деформацией. Разница в измеренных сопротивлениях датчика, деленная на сопротивление без деформации, дает дробное значение деформации.Это значение используется с калибровочным коэффициентом (GF) для расчета деформации.
Четырехпроводная схема также подходит для автоматической компенсации смещения напряжения. Напряжение сначала измеряется при отсутствии тока. Это измеренное значение затем вычитается из показания напряжения при протекании тока. Полученная разность напряжений затем используется для вычисления сопротивления датчика. Из-за своей чувствительности четырехпроводные тензодатчики обычно используются для измерения низкочастотных динамических деформаций.При измерении деформаций более высоких частот необходимо усилить выходной сигнал моста. Эту же схему можно использовать с полупроводниковым тензометрическим датчиком и высокоскоростным цифровым вольтметром. Если чувствительность ДВМ составляет 100 микровольт, источник тока — 0,44 миллиампера, сопротивление тензометрического элемента — 350 Ом и его коэффициент измерения — 100, то разрешающая способность измерения составит 6 микродеформаций.

Сопротивление можно измерить, возбуждая мост постоянным напряжением или источником постоянного тока.Поскольку R = V / I, если либо V, либо I остается постоянным, другой будет изменяться в зависимости от сопротивления. Можно использовать оба метода.
Хотя нет теоретических преимуществ использования источника постоянного тока (рис. 2-9) по сравнению с постоянным напряжением, в некоторых случаях выход моста будет более линейным в системе постоянного тока. Кроме того, если используется источник постоянного тока, отпадает необходимость в измерении напряжения на мосту; поэтому к тензодатчику необходимо подключить только два провода.
Цепь постоянного тока наиболее эффективна при измерении динамической деформации. Это связано с тем, что, если динамическая сила вызывает изменение сопротивления тензодатчика (Rg), можно измерить изменяющуюся во времени составляющую выходного сигнала (VOUT), в то время как медленно меняющиеся эффекты, такие как изменение сопротивления выводов из-за температуры варианты будут отклонены. При использовании этой конфигурации температурные дрейфы становятся практически незначительными.
Выходной сигнал схемы тензодатчика представляет собой сигнал напряжения очень низкого уровня, требующий чувствительности 100 микровольт или выше.Низкий уровень сигнала делает его особенно восприимчивым к нежелательным шумам от других электрических устройств. Емкостная связь, вызванная слишком близким расположением выводных проводов к силовым кабелям переменного тока или токами заземления, является потенциальным источником ошибок при измерении деформации. Другие источники ошибок могут включать в себя магнитно-индуцированные напряжения, когда выводные провода проходят через переменные магнитные поля, паразитные (нежелательные) контактные сопротивления выводных проводов, нарушение изоляции и эффекты термопары на стыке разнородных металлов.Сумма таких помех может привести к значительному ухудшению качества сигнала.
Большинство проблем с электрическими помехами и шумом можно решить с помощью экранирования и защиты. Экран вокруг проводов измерительных выводов улавливает помехи, а также может уменьшить любые ошибки, вызванные ухудшением изоляции. Экранирование также защитит измерение от емкостной связи. Если измерительные провода проложены рядом с источниками электромагнитных помех, такими как трансформаторы, скручивание проводов минимизирует ухудшение сигнала из-за магнитной индукции.Скручивая провод, индуцированный магнитным потоком ток инвертируется, и области, которые пересекает магнитный поток, компенсируются. В промышленных процессах практически без исключения используются скрученные и экранированные подводящие провода.
Защита самой аппаратуры так же важна, как и защита проводов. Ограждение представляет собой коробку из листового металла, окружающую аналоговую схему и соединенную с экраном. Если токи заземления протекают через тензометрический элемент или его подводящие провода, схема моста Уитстона не может отличить их от потока, создаваемого источником тока.Защита гарантирует, что клеммы электрических компонентов имеют одинаковый потенциал, что предотвращает протекание постороннего тока.
Подключение защитного провода между испытуемым образцом и отрицательной клеммой источника питания обеспечивает дополнительный путь тока вокруг измерительной цепи. Если разместить защитный проводник на пути тока, вызывающего ошибку, все задействованные элементы (т.е. плавающий источник питания, тензодатчик, все другое измерительное оборудование) будут иметь тот же потенциал, что и испытательный образец.Используя скрученные и экранированные подводящие провода и интегрируя цифровые видеомагнитофоны с защитой, можно практически исключить ошибку синфазного шума.

Тензодатчики иногда устанавливают на расстоянии от измерительного оборудования. Это увеличивает вероятность ошибок из-за колебаний температуры, снижения чувствительности свинца и изменений сопротивления провода. В двухпроводной установке (рисунок 2-10A) два провода соединены последовательно с тензодатчиком, и любое изменение сопротивления подводящего провода (R1) будет неотличимо от изменений сопротивления тензодатчика. (Rg).
Чтобы скорректировать влияние проводов, можно ввести дополнительный третий вывод к верхнему плечу моста, как показано на Рисунке 2-10B. В этой конфигурации провод C действует как измерительный провод, в котором не течет ток, а провода A и B находятся на противоположных сторонах моста. Это минимально приемлемый метод подключения тензодатчиков к мосту, чтобы хотя бы частично устранить влияние ошибок удлинительного провода. Теоретически, если подводящие провода к датчику имеют одинаковое номинальное сопротивление, одинаковый температурный коэффициент и поддерживаются при одинаковой температуре, достигается полная компенсация.На самом деле провода изготавливаются с допуском около 10%, а трехпроводная установка не исключает полностью двухпроводных ошибок, но снижает их на порядок. Если желательно дальнейшее улучшение, следует рассмотреть вариант установки с четырехпроводным подключением и компенсацией смещения (рисунки 2-10C и 2-10D).
В двухпроводных установках погрешность, связанная с сопротивлением выводного провода, является функцией отношения сопротивлений R1 / Rg. Ошибка вывода обычно не имеет значения, если сопротивление выводного провода (R1) мало по сравнению с сопротивлением датчика (Rg), но если сопротивление выводного провода превышает 0.1% от номинального сопротивления датчика, этот источник погрешности становится значительным. Поэтому в промышленных приложениях длину подводящих проводов следует минимизировать или исключить, располагая преобразователь непосредственно у сенсора.

Чувствительные к деформации материалы, такие как медь, изменяют свою внутреннюю структуру при высоких температурах. Температура может изменить не только свойства элемента тензодатчика, но также может изменить свойства основного материала, к которому прикреплен тензодатчик.Различия в коэффициентах расширения материала датчика и основного материала могут вызвать изменение размеров чувствительного элемента. Следовательно, потребуется схема температурной компенсации.
Расширение или сжатие тензометрического элемента и / или основного материала приводит к ошибкам, которые трудно исправить. Например, изменение удельного сопротивления или температурного коэффициента сопротивления тензометрического элемента изменяет нулевую точку отсчета, используемую для калибровки устройства.
Измерительный фактор — это чувствительность датчика к деформации.Производитель всегда должен предоставлять данные о температурной чувствительности манометрического коэффициента. На рис. 2-11 показано изменение коэффициентов измерения для различных материалов тензодатчиков в зависимости от рабочей температуры. Медно-никелевые сплавы, такие как Advance, имеют калибровочные коэффициенты, которые относительно чувствительны к колебаниям рабочей температуры, что делает их наиболее популярным выбором для материалов для датчиков деформации.
.
Что такое Венский мост? — Объяснение и принципиальная схема
Использование моста Вина в цепях переменного тока для определения значения неизвестной частоты . Мост измеряет частоты от 100 Гц до 100 кГц. Точность мостов составляет от 0,1 до 0,5 процента. Мост используется для различных других приложений, таких как измерение емкости, анализатор гармонических искажений и генератор ВЧ-частоты.
Мост Вина чувствителен к частоте. Таким образом, получить в нем точку равновесия сложно.Входное напряжение питания не является чисто синусоидальным, и в них есть некоторые гармоники. Гармоники питающего напряжения нарушают балансное состояние моста. Для решения этой проблемы в мосте используется фильтр. Фильтр подключается последовательно с детектором нуля. 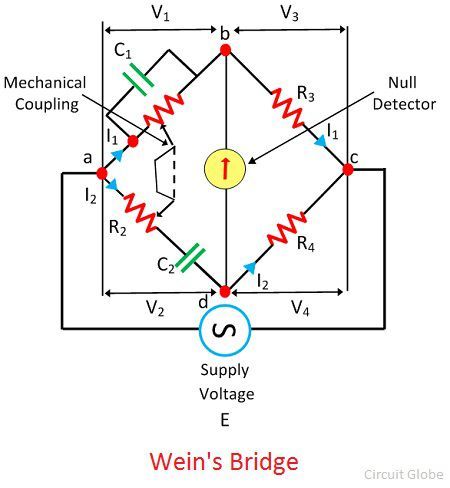
Когда мост находится в сбалансированном состоянии, потенциал узлов B и C равны, то есть V 1 = V 2 и V 3 = V 4 Фаза и величина V 3 = I 1 R 3 и V 4 = I 2 R 4 равны, и они перекрывают друг друга.Ток I 1 , протекающий через плечо BD, и ток I 2 , протекающий через R 4 , также находятся в фазе вместе с I 1 R 3 и I 2 R 4 .
Полное падение напряжения на плече переменного тока равно сумме падения напряжения I 2 R 2 на сопротивлении R 2 и падения емкости I 2 / wC 2 на емкости C 2 . Когда мост находится в уравновешенном состоянии, напряжения V 1 и V 2 равны по величине и фазе.
Фаза напряжения V 1 и падение напряжения I R R 1 на плечах R 1 также одинаковы. Сопротивление R 1 находится в той же фазе, что и напряжение V 1 . Сумма векторов V 1 и V 3 или V 2 и V 4 даст результирующее напряжение питания.
В состоянии баланса, 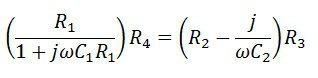
При равенстве действительной части,
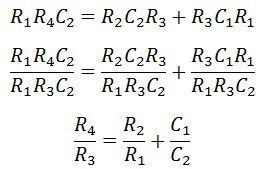
При сравнении мнимой части,
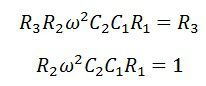
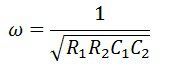
Подставив значение ω = 2πf,
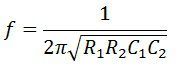
Ползунок сопротивления R 1 и R 2 механически соединяются между собой.Таким образом, получаем R 1 = R 2 .
.


 ,
,
 ,
,









