простое объяснение для чайников с формулой и понятиями
Говорят: «не знаешь закон Ома – сиди дома». Так давайте же узнаем (вспомним), что это за закон, и смело пойдем гулять.
Основные понятия закона Ома
Как понять закон Ома? Нужно просто разобраться в том, что есть что в его определении. И начать следует с определения силы тока, напряжения и сопротивления.
Сила тока I
Пусть в каком-то проводнике течет ток. То есть, происходит направленное движение заряженных частиц – допустим, это электроны. Каждый электрон обладает элементарным электрическим зарядом (e= -1,60217662 × 10-19 Кулона). В таком случае через некоторую поверхность за определенный промежуток времени пройдет конкретный электрический заряд, равный сумме всех зарядов протекших электронов.
Отношение заряда к времени и называется силой тока. Чем больший заряд проходит через проводник за определенное время, тем больше сила тока. Сила тока измеряется в Амперах.
Сила тока измеряется в Амперах.
Напряжение U, или разность потенциалов
Это как раз та штука, которая заставляет электроны двигаться. Электрический потенциал характеризует способность поля совершать работу по переносу заряда из одной точки в другую. Так, между двумя точками проводника существует разность потенциалов, и электрическое поле совершает работу по переносу заряда.
Физическая величина, равная работе эффективного электрического поля при переносе электрического заряда, и называется напряжением. Измеряется в Вольтах. Один Вольт – это напряжение, которое при перемещении заряда в 1 Кл совершает работу, равную 1 Джоуль.
Сопротивление R
Ток, как известно, течет в проводнике. Пусть это будет какой-нибудь провод. Двигаясь по проводу под действием поля, электроны сталкиваются с атомами провода, проводник греется, атомы в кристаллической решетке начинают колебаться, создавая электронам еще больше проблем для передвижения. Именно это явление и называется сопротивлением. Оно зависит от температуры, материала, сечения проводника и измеряется в Омах.
Именно это явление и называется сопротивлением. Оно зависит от температуры, материала, сечения проводника и измеряется в Омах.
Памятник Георгу Симону Ому
Формулировка и объяснение закона Ома
Закон немецкого учителя Георга Ома очень прост. Он гласит:
Сила тока на участке цепи прямо пропорционально напряжению и обратно пропорциональна сопротивлению.
Георг Ом вывел этот закон экспериментально (эмпирически) в 1826 году. Естественно, чем больше сопротивление участка цепи, тем меньше будет сила тока. Соответственно, чем больше напряжение, тем и ток будет больше.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Данная формулировка закона Ома – самая простая и подходит для участка цепи. Говоря «участок цепи» мы подразумеваем, что это однородный участок, на котором нет источников тока с ЭДС. Говоря проще, этот участок содержит какое-то сопротивление, но на нем нет батарейки, обеспечивающей сам ток.
Если рассматривать закон Ома для полной цепи, формулировка его будет немного иной.
Пусть у нас есть цепь, в ней есть источник тока, создающий напряжение, и какое-то сопротивление.
Закон запишется в следующем виде:
Объяснение закона Ома для полой цепи принципиально не отличается от объяснения для участка цепи. Как видим, сопротивление складывается из собственно сопротивления и внутреннего сопротивления источника тока, а вместо напряжения в формуле фигурирует электродвижущая сила источника.
Кстати, о том, что такое что такое ЭДС, читайте в нашей отдельной статье.
Как понять закон Ома?
Чтобы интуитивно понять закон Ома, обратимся к аналогии представления тока в виде жидкости. Именно так думал Георг Ом, когда проводил опыты, благодаря которым был открыт закон, названный его именем.
Представим, что ток – это не движение частиц-носителей заряда в проводнике, а движение потока воды в трубе. Сначала воду насосом поднимают на водокачку, а оттуда, под действием потенциальной энергии, она стремиться вниз и течет по трубе. Причем, чем выше насос закачает воду, тем быстрее она потечет в трубе.
Причем, чем выше насос закачает воду, тем быстрее она потечет в трубе.
Отсюда следует вывод, что скорость потока воды (сила тока в проводе) будет тем больше, чем больше потенциальная энергия воды (разность потенциалов)
Сила тока прямо пропорциональна напряжению.
Теперь обратимся к сопротивлению. Гидравлическое сопротивление – это сопротивление трубы, обусловленное ее диаметром и шероховатостью стенок. Логично предположить, что чем больше диаметр, тем меньше сопротивление трубы, и тем большее количество воды (больший ток) протечет через ее сечение.
Сила тока обратно пропорциональна сопротивлению.
Такую аналогию можно проводить лишь для принципиального понимания закона Ома, так как его первозданный вид – на самом деле довольно грубое приближение, которое, тем не менее, находит отличное применение на практике.
В действительности, сопротивление вещества обусловлено колебанием атомов кристаллической решетки, а ток – движением свободных носителей заряда. В металлах свободными носителями являются электроны, сорвавшиеся с атомных орбит.
В металлах свободными носителями являются электроны, сорвавшиеся с атомных орбит.
Ток в проводнике
В данной статье мы постарались дать простое объяснение закона Ома. Знание этих на первый взгляд простых вещей может сослужить Вам неплохую службу на экзамене. Конечно, мы привели его простейшую формулировку закона Ома и не будем сейчас лезть в дебри высшей физики, разбираясь с активным и реактивным сопротивлениями и прочими тонкостями.
Если у Вас возникнет такая необходимость, Вам с удовольствием помогут сотрудники нашего студенческого сервиса. А напоследок предлагаем Вам посмотреть интересное видео про закон Ома. Это действительно познавательно!
Закон Ома для участка цепи, пример расчета.
21 Января 2017
4292
Всем привет.
В предыдущей статье мы собрали простую замкнутую цепь, состоящий из источника питания, проводников по которым протекает ток и нагрузки. Выяснили, что такое сопротивление проводника и сопротивление нагрузки. Так же рассмотрели взаимосвязь между напряжением тока, силой тока и сопротивлением на разных участках цепи (проводника и нагрузки). Все эти отношения установлены в основном законе электротехники – в законе Ома.
В этой статье, мы рассмотрим Закон Ома для участка цепи.
Закон Ома для участка цепи
Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.
Давайте рассмотрим этот закон на примере. Соберем следующую схему:
Так как сопротивление проводников близко к нулю, будем считать, что они равны нулю. В нашу электрическую цепь, кроме нагрузки, мы еще добавили два прибора.
Амперметр – прибор для измерения силы тока, или другими словами измеряет сколько потребляет нагрузка, так легче запомнить. Соединяется последовательно с нагрузкой.
Соединяется последовательно с нагрузкой.
Вольтметр – прибор для измерения напряжения тока, при подключении к нагрузке, показывает сколько падает напряжение на нагрузку. Соединятся параллельно с нагрузкой.
Давайте нагрузку поставим сопротивлением равной 100 Ом, с источника питания пустим напряжение 5 В (вольт). Снимем показания с приборов. Нас интересует показатель амперметра. Амперметр показывает — 0,05 А (ампер) для удобства можно перевести в миллиамперы – 50 мА (миллиампер).
наведите или кликните мышкой, для анимации
Теперь поменяем напряжение тока, вместо 5 В установим 10 В. Снимем показатель амперметра. Амперметр показывает — 0,1 А переводим в миллиамперы – 100 мА. Сразу отметим для себя — с увеличением напряжения увеличилась сила тока.
В законе ома: «сила тока в участке цепи прямо пропорциональна напряжению … ».
наведите или кликните мышкой, для анимации
Теперь вернемся к первому опыту, то есть установим напряжение обратно на значение 5 В. Попробуем изменить сопротивление нагрузки.
Попробуем изменить сопротивление нагрузки.
Поменяем нагрузку со значение сопротивления 200 Ом. Снимем показатели с амперметра и сравним с показателями первого опыта. Амперметр показывает — 0,025 А переводим в миллиамперы – 25 мА. Таким образом увеличение сопротивления нагрузки, уменьшило силу тока.
В законе ома: «сила тока в участке цепи … обратно пропорциональна электрическому сопротивлению».
наведите или кликните мышкой, для анимации
Закон Ома для участка цепи записывается следующей формулой:
I = U/R
Как нам уже известно:
I = сила тока
U = напряжение тока
R = сопротивление (сопротивление нагрузки)
Так же эту формулу можно преобразовывать для определения напряжения тока или сопротивления нагрузки. Что бы легче запомнить формулы, надо запомнить треугольник Ома, который изображен выше. Закрывая искомую величину пальцем, можно увидеть формулу для нее.
Закрывая искомую величину пальцем, можно увидеть формулу для нее.
Формула для определения напряжения:
Формула для определения сопротивления:
Рассмотрим простой пример расчета используя закон Ома для участка цепи. Если в примере выше, мы бы не использовали амперметр, зная напряжение тока 5 В (U) и сопротивление нагрузки 100 Ом (R). Использую следующую формулу I = U/R, мы бы получили результат: 5/100 = 0,05. Ответ 0,05 А = 50 мА.
Мы разобрали закон Ома для участка цепи, ознакомились с формулами для определения силы тока, напряжение тока и сопротивления. Так же хочу добавить, при расчетах, необходимо переводить единицы измерения в систему СИ. В примерах выше для демонстраций замкнутой цепи, я использовал программу — Electronics Workbench. Программа предназначена для моделирования и анализа электронных схем.
Закон Ома для участка цепи: формулировка и формула, применение
От силы тока в цепи зависит величина воздействия, которое ток может оказывать на проводник, будь то тепловое, химическое или магнитное действие тока. То есть, регулируя силу тока, можно управлять его воздействием. Электрический ток, в свою очередь – это упорядоченное движение частиц под действием электрического поля.
То есть, регулируя силу тока, можно управлять его воздействием. Электрический ток, в свою очередь – это упорядоченное движение частиц под действием электрического поля.
Зависимость силы тока и напряжения
Очевидно, что чем сильнее поле действует на частицы, тем больше будет сила тока в цепи. Электрическое поле характеризуется величиной, называемой напряжением. Следовательно, мы приходит к выводу, что сила тока зависит от напряжения.
И действительно, опытным путем удалось установить, что сила тока связана с напряжением прямо пропорционально. В случаях, когда изменяли величину напряжения в цепи, не меняя всех остальных параметров, сила тока возрастала или уменьшалась во столько же раз, во сколько меняли напряжение.
Связь с сопротивлением
Однако любая цепь или участок цепи характеризуются еще одной немаловажной величиной, называемой сопротивлением электрическому току. Сопротивление связано с силой тока обратно пропорционально. Если на каком-либо участке цепи изменить величину сопротивления, не меняя напряжения на концах этого участка, сила тока также изменится. Причем если мы уменьшим величину сопротивления, то сила тока возрастет во столько же раз. И, наоборот, при увеличении сопротивления сила тока пропорционально уменьшается.
Причем если мы уменьшим величину сопротивления, то сила тока возрастет во столько же раз. И, наоборот, при увеличении сопротивления сила тока пропорционально уменьшается.
Формула закона Ома для участка цепи
Сопоставив две эти зависимости, можно прийти к такому же выводу, к которому пришел немецкий ученый Георг Ом в 1827 г. Он связал воедино три вышеуказанные физические величины и вывел закон, который назвали его именем. Закон Ома для участка цепи гласит:
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
I=U/R,
где I – сила тока,
U – напряжение,
R – сопротивление.
Применение закона Ома
Закон Ома – один из основополагающих законов физики. Открытие его в свое время позволило сделать огромный скачок в науке. В настоящее время невозможно себе представить любой самый элементарный расчет основных электрических величин для любой цепи без использования закона Ома. Представление об этом законе – это не удел исключительно инженеров-электронщиков, а необходимая часть базовых знаний любого мало-мальски образованного человека. Недаром есть поговорка: «Не знаешь закон Ома – сиди дома».
Представление об этом законе – это не удел исключительно инженеров-электронщиков, а необходимая часть базовых знаний любого мало-мальски образованного человека. Недаром есть поговорка: «Не знаешь закон Ома – сиди дома».
Из формулы для закона Ома можно рассчитать также величины напряжения и сопротивления участка цепи:
U=IR и R=U/I
Правда, следует понимать, что в собранной цепи величина сопротивления некоторого участка цепи есть величина постоянная, поэтому при изменении силы тока будет изменяться только напряжение и наоборот. Для изменения сопротивления участка цепи следует собрать цепь заново. Расчет же требуемой величины сопротивления при проектировании и сборке цепи можно произвести по закону Ома, исходя из предполагаемых значений силы тока и напряжения, которые будут пропущены через данный участок цепи.
Нужна помощь в учебе?
Предыдущая тема: Сопротивление тока: притяжение ядер, проводники и непроводники
Следующая тема:   Расчёт сопротивления проводников и реостаты: формулы
Закон Ома | Физика
В предыдущих параграфах были рассмотрены три величины, характеризующие протекание электрического тока в цепи,— сила тока I, напряжение U и сопротивление R. Между этими величинами существует определенная связь. Закон, выражающий эту связь, был установлен в 1827 г. немецким ученым Г. Омом и поэтому носит его имя.
Между этими величинами существует определенная связь. Закон, выражающий эту связь, был установлен в 1827 г. немецким ученым Г. Омом и поэтому носит его имя.
Выделим в произвольной электрической цепи участок, обладающий сопротивлением R и находящийся под напряжением U (рис. 37). Согласно закону Ома:
Сила тока на участке цепи равна отношению напряжения на этом участке к его сопротивлению.
Математически закон Ома записывается в виде следующей формулы:
I = U/R (14.1)
Закон Ома позволяет установить, что будет происходить с силой тока на участке цепи при изменении его сопротивления или напряжения.
1. При неизменном сопротивлении сила тока прямо пропорциональна напряжению: чем больше напряжение U на концах участка цепи, тем больше сила тока I на этом участке. Увеличив (или уменьшив) напряжение в несколько раз, мы во столько же раз увеличим (или уменьшим) силу тока.
Проиллюстрируем эту закономерность на опыте. Соберем электрическую цепь из источника тока, лампы, амперметра и ключа (рис. 38, а). В качестве источника тока будем использовать устройство, позволяющее регулировать выходное напряжение от 4 до 12 В. Измеряя силу тока в цепи при разных напряжениях, можно убедиться в том, что она действительно пропорциональна напряжению.
Соберем электрическую цепь из источника тока, лампы, амперметра и ключа (рис. 38, а). В качестве источника тока будем использовать устройство, позволяющее регулировать выходное напряжение от 4 до 12 В. Измеряя силу тока в цепи при разных напряжениях, можно убедиться в том, что она действительно пропорциональна напряжению.
2. При неизменном напряжении сила тока обратно пропорциональна сопротивлению: чем больше сопротивление R участка цепи, тем меньше сила тока I в нем.
Для проверки этой закономерности заменим в используемой цепи лампу на магазин сопротивлений (рис. 38, б). Измеряя силу тока при разных сопротивлениях, мы увидим, что сила тока I и сопротивление R действительно находятся в обратно пропорциональной зависимости.
При уменьшении сопротивления сила тока возрастает. Если сила тока превысит допустимое для данной цепи значение, включенные в нее приборы могут выйти из строя; провода при этом могут раскалиться и стать причиной пожара. Именно такая ситуация возникает при коротком замыкании. Так называют соединение двух точек электрической цепи, находящихся под некоторым напряжением, коротким проводником, обладающим очень малым сопротивлением.
Так называют соединение двух точек электрической цепи, находящихся под некоторым напряжением, коротким проводником, обладающим очень малым сопротивлением.
Короткое замыкание может возникнуть при соприкосновении оголенных проводов, при небрежном ремонте проводки под током, при большом скоплении пыли на монтажных платах и даже при случайном попадании какого-нибудь насекомого внутрь прибора.
На законе Ома основан экспериментальный способ определения сопротивления. Из формулы (14.1) следует, что
R = U/I (14.2)
Поэтому для нахождения сопротивления R участка цепи надо измерить на нем напряжение U, затем силу тока I, после чего разделить первую из этих величин на вторую. Соответствующая этому схема цепи изображена на рисунке 39.
Если, наоборот, известны сопротивление R и сила тока I на участке цепи, то закон Ома позволяет рассчитать напряжение U на его концах. Из формулы (14.1) получаем
U = IR (14.3)
Чтобы найти напряжение U на концах участка цепи, надо силу тока I на этом участке умножить на его сопротивление R.
Опубликовав книгу, в которой излагался открытый им закон «Теоретические исследования электрических цепей», Георг Ом написал, что «рекомендует ее добрым людям с теплым чувством отца, не ослепленного обезьяньей любовью к детям, но довольствующегося указанием на открытый взгляд, с которым его дитя смотрит на злой мир». Мир действительно оказался для него злым, и уже через год после выхода его книги в одном из журналов появилась статья, в которой работы Ома были подвергнуты уничтожающей критике. «Тот, кто благоговейными глазами взирает на вселенную,— говорилось в статье,— должен отвернуться от этой книги, являющейся плодом неисправимых заблуждений, преследующих единственную цель — умалить величие природы».
Злобные и безосновательные нападки на Ома не прошли бесследно. Теорию Ома не приняли. И вместо продолжения научных исследований он должен был тратить время и энергию на полемику со своими оппонентами. В одном из своих писем Ом написал: «Рождение «Электрических цепей» принесло мне невыразимые страдания, и я готов проклясть час их зарождения».
Но это были временные трудности. Постепенно, сначала в России, а затем и в других странах, теория Ома получила полное признание. Закон Ома внес такую ясность в правила расчета токов и напряжений в электрических цепях, что американский ученый Дж. Генри, узнав об открытиях Ома, не удержался от восклицания: «Когда я первый раз прочел теорию Ома, то она мне показалась молнией, вдруг осветившей комнату, погруженную во мрак».
??? 1. Сформулируйте закон Ома. 2. Как изменится сила тока на участке цепи, если при неизменном сопротивлении увеличить напряжение на его концах? 3. Как изменится сила тока, если при неизменном напряжении увеличить сопротивление участка цепи? 4. Как с помощью вольтметра и амперметра можно измерить сопротивление проводника? 5. По какой формуле находится напряжение, если известны сила тока и сопротивление данного участка? 6. Что называют коротким замыканием? Почему при этом увеличивается сила тока? 7. Объясните причину короткого замыкания в ситуациях, изображенных на рисунке 40.
Закон Ома кратко и понятно для чайников
Закон Ома является одним из фундаментальных законов электродинамики, который определяет взаимосвязь между напряжением, сопротивлением и силой тока. Его важно знать и понимать. Понятное объяснение вы найдёте в статье.
Закон Ома официально и абсолютно оправдано можно отнести к ряду основополагающих в физике по нескольким признакам. Данный закон объясняют в школе на базовом уровне, а после, более углубленно, в учреждениях, специализирующихся на изучении технических аспектов технологий.
Закон Ома – определение
Впервые данный закон был официально зафиксирован и сформулирован в восемнадцатом веке, благодаря сделанному сейчас уже широко известным всем Георгом Симоном Омом открытию. Благодаря данному закону получило грамотное и исчерпывающее объяснение наличие количественной связи между тремя фигурирующими в определении параметрами. Зависимость рассматривается как пропорциональная. Когда данное явление только было выявлено, закон несколько раз формулировали. В итоге сейчас всем известно данное определение: «величина тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку, и обратно пропорциональна его сопротивлению».
В итоге сейчас всем известно данное определение: «величина тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку, и обратно пропорциональна его сопротивлению».
Для лучшего понимания разделим определение на две части и разберём отдельно более понятным языком смысл каждой.
- Первая часть определения указывает на то, что если на определенной отрезке цепи происходит количественный скачок напряжения, то величина тока также увеличивается на данном участке. Важно упомянуть, что становится больше и величина тока на заданном участке цепи.
- Концовка определения расшифровывается также просто. Выше напряжение – меньше сила тока.
Закон Ома – формула
Иллюстрация связи сопротивления
Рисунок наглядно демонстрирует связь фигурирующих в понятии «участников». Таким образом, вытекают простые выводы:
1. При данных условиях: на конкретном отрезке увеличивается напряжение, но при том сопротивление остаётся прежним, ток резко возрастает;
2. Иная ситуация: наоборот, изменяется сопротивление, а точнее возрастает, при том что уровень напряжения не меняется вовсе, тока становится меньше.
Иная ситуация: наоборот, изменяется сопротивление, а точнее возрастает, при том что уровень напряжения не меняется вовсе, тока становится меньше.
В итоге в законе Ома участвуют всего три величины.
Готовая формула выглядит так:
I = U/R
Фигурируют и другие две переменные, их также можно вычислить, при условии, что другие два значения известны. Видоизменив формулу, получим:
| Формула сопротивления | R = U/I |
| Формула напряжения | U = I × R |
| Формула силы тока | I = U/R |
Важно!
Шпаргалка для закона Ома
На начальном этапе, когда составлять формулы ещё сложно, можно воспользоваться небольшой шпаргалкой.
На треугольнике просто нужно закрыть то значение, которое необходимо найти.
Закон Ома для участка цепи
Итоговая формула не видоизменяется вовсе. Обычно сопротивление в данном законе является явной характеристикой проводника, потому что это значение не постоянная величина: в зависимости от материала и других параметров число может увеличиваться или уменьшаться. Закон применим как при расчёте с использованием металлов, так и растворов электролитов, однако существует важный нюанс: в цепи не должно быть реального источника тока, или же источник должен быть идеальным, то есть он не должен создавать дополнительное сопротивление.
Закон применим как при расчёте с использованием металлов, так и растворов электролитов, однако существует важный нюанс: в цепи не должно быть реального источника тока, или же источник должен быть идеальным, то есть он не должен создавать дополнительное сопротивление.
Шпаргалка для использования закона Ома
С ЭДС
Обобщённый закон Ома формулируется так:
I = (Uab+E)/R
Также формулу можно выразить через проводимость:
I = (Uab + E) × G, как понятно, G – проводимость участка электрической цепи. Эти формулы можно использовать, если сохраняются условия, зафиксированные на рисунке.
Участок цепи с ЭДС
Без ЭДС
Для начала определим, что положительное направление – это то, что слева направо. Только в этом случае напряжение на участке будет равняться разности потенциалов.
Разность потенциалов
Если сохраняется условие и потенциал конечный меньше потенциала начального, то напряжение будет больше нуля. Значит, как и полагается, направление линий напряженности в проводнике будет от начала к концу, следовательно, направление тока будет идентичным. Именно такое направление тока принято считать положительным, I > O. Данный вариант самый простой для расчётов. Формула действительна с любыми числами.
Именно такое направление тока принято считать положительным, I > O. Данный вариант самый простой для расчётов. Формула действительна с любыми числами.
Закон Ома для полной (замкнутой) цепи
При данной вариации закона выявляется значение тока при реальных условиях, то есть в настоящей полной цепи. Важно учитывать то, что получившееся в результате расчетов число зависит от нескольких параметров, а не только от сопротивления нагрузки.
Сопротивление нагрузки – внешнее сопротивление, а сопротивление самого источника тока – внутреннее сопротивление (обозначается маленькой r).
Вывод формулы закона Ома для замкнутой цепи
Если к цепи подключено напряжение и в цепи замечено напряжение (ток), то, чтобы поддержать его во внешней цепи, необходимо создать условия, при которых между её концами возникнет разность потенциалов. Это число будет равняться I × R. Однако важно помнить о том, что вышеупомянутый ток будет и во внутренней цепи и его также необходимо поддерживать, поэтому нужно создать разность потенциалов между концами сопротивления r. Эта разность равняется I × r.
Эта разность равняется I × r.
Чтобы поддержать ток в цепи, электродвижущая сила (ЭДС) аккумулятора должна иметь величину:
E = I × r + I × R
Эта формула показывает, что электродвижущая сила в цепи равна сумме внешнего и внутреннего падений напряжения. Вынося I за скобки, получим:
E = I(r + R)
или
I = E / (r + R)
Две последние формулы выражают закона Ома для полной цепи.
Закон Ома в дифференциальной форме
Дифференциальная форма закона Ома
Закон можно представить таким образом, чтобы он не был привязан к размерам проводника. Для этого выделим участок проводника Δl, на концах которой расположены ф1 и ф2. Среднюю площадь проводника обозначают ΔS , а плотность тока j, при таких условиях сила тока будет равняться:
I = jΔS = (ф1- ф2) / R = -(((ф1 — ф2)ΔS) / pΔl , отсюда следует, что j = -y × (Δф/Δl)
При условии, что Δl будет равен 0, то, взяв предел отношения:
lim (-(Δф/Δl)) = -(dф/dl) = Е,
окончательное выражение будет выглядеть так:
j = yE
Данное выражение закона находит силу тока в произвольной точке проводника в зависимости от его свойств и электрического состояния.
Закон Ома в интегральной форме
В данной интерпретации закона не содержится в условиях ЭДС, то есть формула выглядит так:
I = U/R
Чтобы найти значение для однородного линейного проводника, выразим R через p и получим:
R = p (l/S), где за р принимаем удельное объёмное сопротивление.
Линией тока принято называть кривую, в каждой точке которой вектор плотности тока направлен по касательной к этой кривой. При таких условиях вектор плотности находится из отношения J = jt, где t – это единичный вектор касательной к линии тока.
Для лучшего понимания предположим, что удельное сопротивление, а также напряженность поля движущих сил на поперечном сечении проводника однородны. При таком условии Е однородна, а значит, и j также однородная величина. Примем произвольное значение поперечного сечения цепи S, тогда pl/s = E. Получившееся равенство умножим на dl. Тогда Edl = (Е эл.ст.+Е стор.) dl = Е эл.ст. dl + Е стор. dl = -dф + dE. Отсюда получим (pI/S) dl = -dф + dE. Возьмём в учёт, что p/s dl = dR и запишем закон Ома в интегральной форме:
Тогда Edl = (Е эл.ст.+Е стор.) dl = Е эл.ст. dl + Е стор. dl = -dф + dE. Отсюда получим (pI/S) dl = -dф + dE. Возьмём в учёт, что p/s dl = dR и запишем закон Ома в интегральной форме:
IdR = -dф + dE.
Закон Ома в комплексной форме
Чтобы провести анализ электрических цепей синусоидального тока, комфортнее использовать закон Ома в комплексной форме. Для лучшего понимания введем основное понятие, фигурирующее в данной интерпретации закона: синусоидальный ток – это линейные цепи с установившимся режимом работы, после того, как переходные процессы в них завершены, уровень напряжения резко уменьшается на конкретной дистанции, токи в ветвях и ЭДС источников являются синусоидальными функциями времени. В противном случае, когда данные параметры не соблюдаются, закон не может быть применим. Чем отличается эта форма от обычной? Ответ прост: токи, сопротивление и ЭДС фиксируются как комплексные числа. Это обусловлено тем, что существуют как активные так и реактивные значения напряжений, токов и сопротивлений, а в результате этого требуется внесение определенных коррективов.
Вместо активного сопротивления используется полное, то есть комплексное сопротивление цепи Z. Падение напряжения, ток и ЭДС тоже превращаются в комплексные величины. При реальных расчетах лучше и удобнее применять действующие значения. Итак, закон в комплексной форме выглядит так:
i = U/Z, i = UY
В данной формуле Z – комплексное сопротивление, Y – комплексная проводимость.
Чтобы выявить эти величины, выведены формулы. Пропустим шаги их создания и приведем готовые формулы:
Z = ze = z cosф + jz sinф = r + jx
Y = 1/ ze = ye = y cos ф — jy sin ф = g + jb
Закон Ома для переменного тока
После того как Фарадей открыл электромагнитную индукцию, стали активно использовать генераторы сперва постоянного, а после и переменного тока.
Используется уже известная формула:
I = U/Z
Полное сопротивление тока – это совокупность активного, а также индуктивного и емкостного сопротивлений. 2
2
Цепь
В такой цепи колебания тока и напряжения разные по фазе, а разность фаз зависит от индуктивности катушки и ёмкости конденсатора:
U = Um sin (ωt)
I = Im sin (ωt + ф)
Закон Ома для постоянного тока
В данном случае частота будет равняться нулевому значению, поэтому остальные показатели также будут нулевыми соответственно, в то время как значение ёмкости достигнет бесконечности. Цепь разорвётся. Поэтому отсюда вытекает логичный вывод: реактивное сопротивление элементов в цепях постоянного напряжения отсутствует.
Закон Ома для однородного участка цепи
Формула выглядит уже известным образом:
I = U/R
В данном случае главной характеристикой проводника остаётся сопротивление. От того, как выглядит проводник, зависит количество узлов кристаллической решётки и атомов примесей. Поэтому электроны могут замедляться или ускоряться.
Сопротивление будет зависеть от вида проводника, а именно от его сечения, материала и длины:
R = p (L/S)
Закон Ома для неоднородного участка цепи
При решении задачи становится понятным, что для того, чтобы поддерживался стабильный ток в замкнутой цепи, нужны силы совершенной другой природы, а не кулоновские. В этом случае можно заметить такую закономерность: заряды, которые никак не соприкасаются друг с другом, выступают в двух ролях одновременно, то есть они являются силами электрического поля и силами иного вида – сторонними в это же время. Участок, на котором замечена данная закономерность, называется неоднородным.
В этом случае можно заметить такую закономерность: заряды, которые никак не соприкасаются друг с другом, выступают в двух ролях одновременно, то есть они являются силами электрического поля и силами иного вида – сторонними в это же время. Участок, на котором замечена данная закономерность, называется неоднородным.
Неоднородный участок цепи
Формула принимает вид:
E = Eq + Est
Закон Ома в данном подразделе был сформулирован таким образом: сила тока прямо пропорциональна напряжению на данном участке и обратно пропорциональна его полному сопротивлению.
Итак, готовая формула:
I = U12/R, где U12
Закон Ома для магнитной цепи
В каждом электромагните совмещены несколько важных элементов: стальной сердечник и катушка. По последней протекает ток. При совмещении нескольких участков образуется магнитная цепь.
При кольцевом магнитопроводе все поле находится внутри кольца. Тогда поток в магнитопроводе равен:
Ф = Вср S = μHср S
Формула закона для магнитной цепи:
Формула закона ома для магнитной цепи
Задачи с решениями на закон Ома
Задача №1
Нихромовая проволока длиной 120 м и площадью сечения 0,5 мм включена в цепь с напряжением 127 В. Определить силу тока в проволоке.
Определить силу тока в проволоке.
Дано:
- l = 120 м,
- S = 0,5 мм,
- U = 127 В,
- p = 1,1 Ом*мм2 /м.
Найти: I — ?
Решение:
- R = p * l / S,
- R = 1,1 Ом*мм2 /м * 120 м : 0,5 мм = 264 Ом,
- I = 127 В : 264 Ом = 0,48 А.
Ответ: I = 0,48 Ом
Задача №2
Нихромовая проволока длиной 120 м и площадью сечения 0,5 мм включена в цепь с напряжением 220 В. Определить силу тока в проволоке.
Дано:
- l = 120 м,
- S = 0,5 мм,
- U = 220 В,
- p = 1,1 Ом*мм2 /м.
Найти: I — ?
Решение:
- R = p * l / S,
- R = 1,1 Ом*мм2 /м * 120 м : 0,5 мм = 264 Ом,
- I = 220 В : 264 Ом = 0,83 А.
Ответ: I = 0,83 Ом
Задача №3
Дано:
- U = 15 В,
- R1 = 3 Ом,
- R2 = R3 = 4 Ом.

Найти: I — ?
Решение:
- R2 и R3 соединены параллельно R2 = R3, R2.3 = R2 / 2 = 2 Ом, составим эквивалентную схему:
- R = R1 + R2,3
- R = 3 Ом + 2 Ом = 5 Ом
- Найдем силу тока на участке цепи по закону Ома I = U / R
- I = 15 В / 5 Ом = 3 А
Ответ: I = 3 A.
Формула закона Ома в физике
Содержание:
Определение и формула закона Ома
Определение
Закон был получен Омом опытным путем. Построив вольт – амперную характеристику для проводника можно увидеть, что сила тока (I),
текущего через проводник пропорциональна напряжению (U) на нем $(I \sim U)$.
Закон Ома для участка цепи
Если на рассматриваемом участке цепи, содержащей проводник, источников ЭДС нет
$\left(U_{21}=\varphi_{1}-\varphi_{2}\right)$, то формула закона Ома является предельно простой:
$$I=\frac{U}{R}=\frac{\varphi_{1}-\varphi_{2}}{R}(1)$$
где R – сопротивление проводника (совокупности проводников, участка цепи).
Если источник тока в участок цепи включен и характеризуется при помощи ЭДС ($\varepsilon$), то формула закона Ома преобразуется к виду:
$$I=\frac{U}{R}=\frac{\varphi_{1}-\varphi_{2}+\varepsilon}{R}(2)$$
Закон Ома для замкнутой цепи
В том случае, если цепь является замкнутой, закон Ома принимает вид:
$$I=\frac{\varepsilon}{R}(3)$$
где под R=Rvnesh+rist понимают полное сопротивление цепи, которое включает так называемое внешнее
сопротивление (Rvnesh) и сопротивление источника ЭДС (rist).
Формула закона Ома в дифференциальной форме
Все выше приведенные формулы закона Ома были представлены в интегральной форме. Этот закон можно записать в дифференциальной форме,
которая характеризует электрическое состояние в точке.
$$\bar{j}=\sigma \bar{E}(4)$$
где $\sigma=\frac{1}{\rho}$ – удельная проводимость,
$\rho$ – удельное сопротивление,
$\bar{j}$ – вектор плотности тока,
$\bar{E}$ – вектор напряженности электрического поля. {d} \frac{1}{\left(\sigma_{1}+\frac{\sigma_{2}-\sigma_{1}}{d}\right.} r\right) \frac{d r}{S}=\frac{d}{S\left(\sigma_{2}-\sigma_{1}\right)}\left[\ln \left(d \sigma_{2}\right)-\ln \left(d \sigma_{1}\right)\right]= \\
{d} \frac{1}{\left(\sigma_{1}+\frac{\sigma_{2}-\sigma_{1}}{d}\right.} r\right) \frac{d r}{S}=\frac{d}{S\left(\sigma_{2}-\sigma_{1}\right)}\left[\ln \left(d \sigma_{2}\right)-\ln \left(d \sigma_{1}\right)\right]= \\
=\frac{d}{S\left(\sigma_{2}-\sigma_{1}\right)} \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)(1.2)
\end{array}
$$
Подставим найденное в (1.2) сопротивление в (1.1), получим искомую силу тока:
$I=\frac{U}{\frac{d}{S\left(\sigma_{2}-\sigma_{1}\right)} \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)}=\frac{U S\left(\sigma_{2}-\sigma_{1}\right)}{d \cdot \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)}$
Ответ. $I=\frac{U S\left(\sigma_{2}-\sigma_{1}\right)}{d \cdot \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)}$
Слишком сложно?
Формула закона Ома не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Какой будет плотность тока в металлическом проводнике (удельное сопротивление считать равным
$\rho$) постоянного сечения, имеющем длину l, если напряжение,
которое приложено к проводу равно U?
Решение. Плотность тока для проводника, который имеет постоянное сечение S можно найти как:
Плотность тока для проводника, который имеет постоянное сечение S можно найти как:
$$j=\frac{I}{S}(2.1)$$
Силу тока можно вычислить, если использовать формулу Закона Ома для участка цепи не имеющего ЭДС:
$$I=\frac{U}{R}(2.2)$$
Сопротивление провода найдем, применяя формулу:
$$R=\rho \frac{l}{S}(2.3)$$
Подставим, необходимые величины в (2.1), получим:
$$j=\frac{U}{S R}=\frac{U S}{S \rho l}$$
Ответ. $j=\frac{U S}{S \rho l}$
Читать дальше: Формула мощности тока.
Закон Ома для электрической цепи
Электрический ток, как и любой процесс, подчиняется законам физики. Знаменитый немецкий физик Георг Симон Ом, именем которого названа единица измерения сопротивления, в 1826 году эмпирически вывел формулы, связывающие между собой ток, напряжение и сопротивление. Поначалу закон вызвал недоверие и критику в научных кругах. Затем правильность его рассуждений была подтверждена французом Клодом Пулье и труды Ома получили заслуженное признание.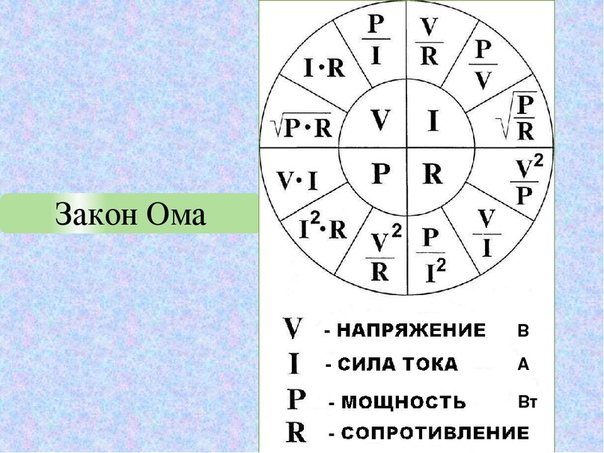
Закон Ома для электрической цепи (полной)
Частный случай – закон Ома для участка цепи:
Обозначение | Единица измерения | Физический смысл |
| I | Ампер | Сила тока в цепи |
| ԑ | Вольт | Электродвижущая сила (э.д.с.) источника питания |
| r | Ом | Внутреннее сопротивление источника питания |
| R | Ом | Сопротивление нагрузки, подключенной и источнику |
| U | Вольт | Падение напряжения на сопротивлении нагрузки |
Поясняющая схема к закону Ома
Добавим к этим формулам еще и электрическую мощность, выделяемую при прохождении тока:
В результате получается ряд формул, которые выводятся математически. Они связывают между собой все перечисленные физические величины.
Они связывают между собой все перечисленные физические величины.
Электродвижущая сила и внутреннее сопротивление
Электродвижущая сила источника напряжения характеризует его способность обеспечивать постоянную разность потенциалов на выводах. Эта сила имеет неэлектрическую природу: химическую у батареек, механическую – у генераторов.
Какова роль внутреннего сопротивления источника питания и что это такое? Допустим, вы замкнули накоротко выводы автомобильного аккумулятора медным проводником небольшого сечения. В физическом смысле вы подключили к источнику постоянного тока сопротивление, близкое к нулю. Если воспользоваться формулой для участка цепи, то через аккумулятор и проволоку должен пойти ток бесконечно большой величины. На деле этого не происходит, но проволока сгорит.
Теперь замкнем этой же проволокой батарейку. Ток через нее пойдет меньший. Это объясняется большим, чем у аккумулятора, значением внутреннего сопротивления. При малом сопротивлении нагрузки формула закона для полной цепи превращается в
При малом сопротивлении нагрузки формула закона для полной цепи превращается в
В итоге ток через замкнутую накоротко батарейку будет иметь конечное значение, а мощность приведет к нагреву батарейки. Если бы мы замкнули аккумулятор более толстым проводом, выдержавшим ток короткого замыкания, то он ощутимо нагрел бы источник изнутри.
Э.Д.С. источника можно с некоторой точностью измерить вольтметром с высоким входным сопротивлением. Внутреннее же сопротивление источника нельзя измерить напрямую, а только рассчитать.
Закон Ома для переменного тока
На переменном токе в формуле закона Ома используется не активное, а полное сопротивление (Z).
Эта величина учитывает и активное, и реактивное сопротивление нагрузки, которое в свою очередь имеет индуктивную
и емкостную
составляющие.
Общее реактивное сопротивление цепи:
Знак (-) означает, что индуктивный и емкостной токи находятся в противофазе и друг друга компенсируют.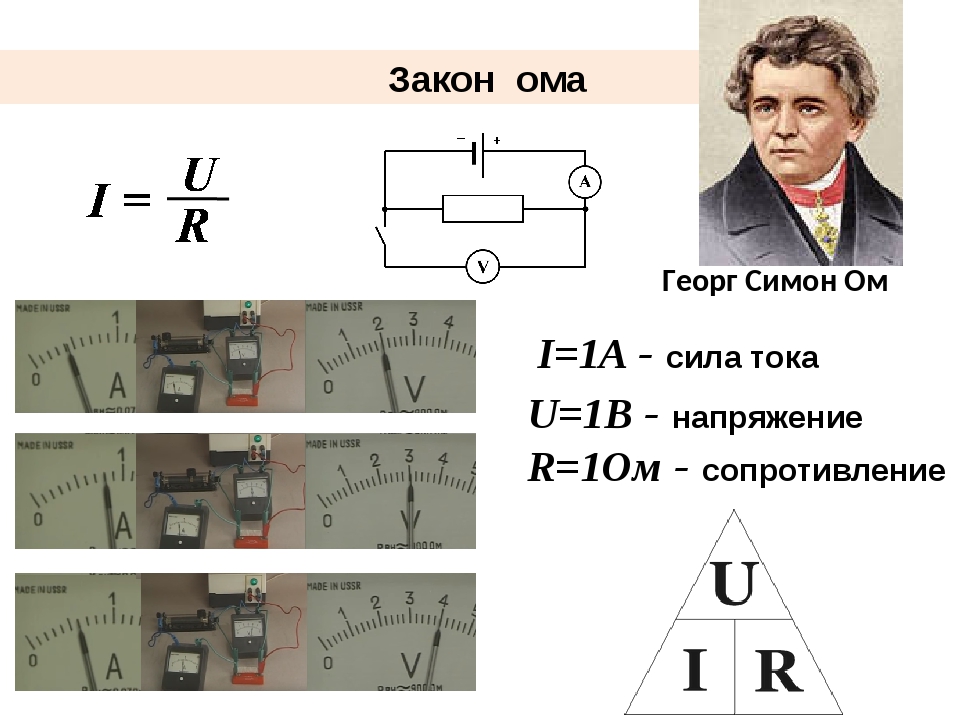
Оцените качество статьи:
Закон
Ома — Как соотносятся напряжение, ток и сопротивление | Закон Ома
Первая и, возможно, самая важная взаимосвязь между током, напряжением и сопротивлением называется законом Ома, открытым Георгом Симоном Омом и опубликованным в его статье 1827 года «Гальваническая цепь, исследованная математически».
Напряжение, ток и сопротивление
Электрическая цепь образуется, когда создается проводящий путь, позволяющий электрическому заряду непрерывно перемещаться. Это непрерывное движение электрического заряда через проводники цепи называется током , и его часто называют «потоком», как поток жидкости через полую трубу.
Сила, побуждающая носители заряда «течь» в цепи, называется напряжением . Напряжение — это особая мера потенциальной энергии, которая всегда относительна между двумя точками.
Когда мы говорим об определенном количестве напряжения, присутствующем в цепи, мы имеем в виду измерение того, сколько потенциальной энергии существует для перемещения носителей заряда из одной конкретной точки в этой цепи в другую конкретную точку.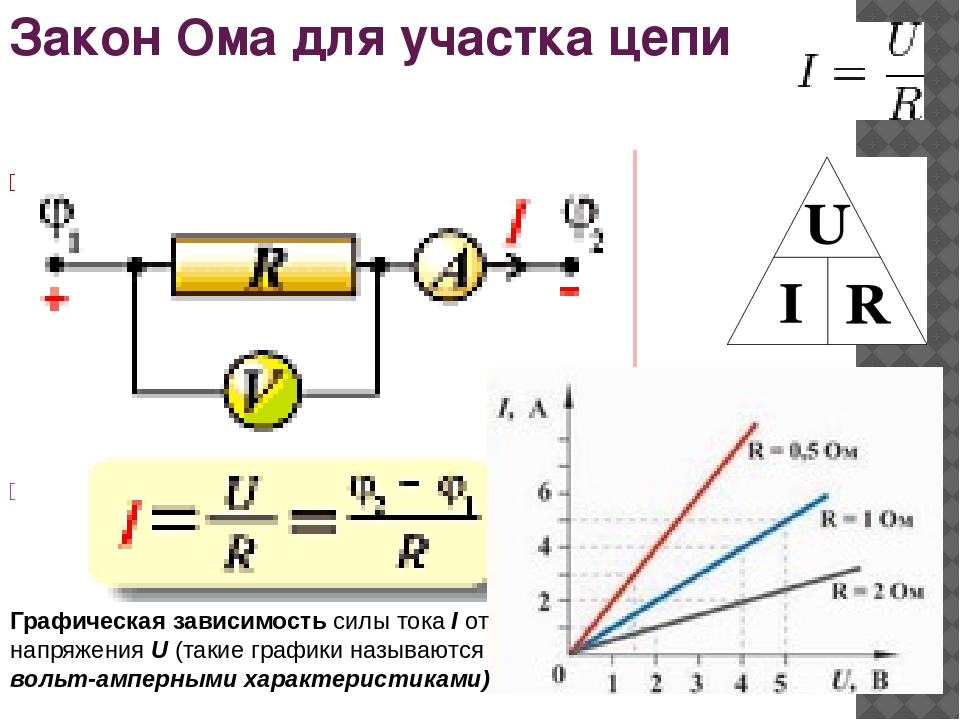 Без ссылки на две конкретные точки термин «напряжение» не имеет значения.
Без ссылки на две конкретные точки термин «напряжение» не имеет значения.
Ток имеет тенденцию проходить через проводники с некоторой степенью трения или сопротивления движению. Это противодействие движению более правильно называть сопротивлением . Сила тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующей прохождению тока.
Как и напряжение, сопротивление — это величина, относительная между двумя точками. По этой причине величины напряжения и сопротивления часто указываются как «между» или «поперек» двух точек в цепи.
Единицы измерения: вольт, ампер и ом
Чтобы иметь возможность делать осмысленные утверждения об этих величинах в цепях, нам нужно уметь описывать их количества так же, как мы могли бы количественно определить массу, температуру, объем, длину или любой другой вид физической величины. Для массы мы можем использовать единицы «килограмм» или «грамм».
Для температуры мы можем использовать градусы Фаренгейта или градусы Цельсия. Вот стандартные единицы измерения электрического тока, напряжения и сопротивления:
Вот стандартные единицы измерения электрического тока, напряжения и сопротивления:
«Символ», присвоенный каждой величине, представляет собой стандартную буквенную букву, используемую для представления этой величины в алгебраическом уравнении.Подобные стандартизированные буквы распространены в физических и технических дисциплинах и признаны во всем мире.
«Аббревиатура единицы» для каждой величины представляет собой алфавитный символ, используемый в качестве сокращенного обозначения для конкретной единицы измерения. И да, этот странно выглядящий символ «подкова» — это заглавная греческая буква Ω, просто символ иностранного алфавита (извинения перед читателями-греками).
Каждая единица измерения названа в честь известного экспериментатора в области электричества: amp в честь француза Андре М.Ампер, вольт после итальянского Алессандро Вольта и Ом после немца Георга Симона Ома.
Математический символ для каждой величины также имеет значение. «R» для сопротивления и «V» для напряжения говорят сами за себя, тогда как «I» для тока кажется немного странным. Считается, что буква «I» должна представлять «интенсивность» (потока заряда), а другой символ напряжения, «E», означает «электродвижущую силу». Судя по исследованиям, которые мне удалось провести, по поводу значения слова «я», похоже, есть споры.”
«R» для сопротивления и «V» для напряжения говорят сами за себя, тогда как «I» для тока кажется немного странным. Считается, что буква «I» должна представлять «интенсивность» (потока заряда), а другой символ напряжения, «E», означает «электродвижущую силу». Судя по исследованиям, которые мне удалось провести, по поводу значения слова «я», похоже, есть споры.”
Символы «E» и «V» по большей части взаимозаменяемы, хотя в некоторых текстах зарезервировано «E» для обозначения напряжения на источнике (таком как батарея или генератор) и «V» для обозначения напряжения на чем-либо еще.
Все эти символы выражаются заглавными буквами, за исключением случаев, когда величина (особенно напряжение или ток) описывается в терминах короткого периода времени (называемого «мгновенным» значением). Например, напряжение батареи, которое стабильно в течение длительного периода времени, будет обозначаться заглавной буквой «E», в то время как пик напряжения удара молнии в тот самый момент, когда он попадает в линию электропередачи, скорее всего, будет обозначается строчной буквой «е» (или строчной буквой «v»), чтобы обозначить это значение как имеющееся в один момент времени.
То же самое соглашение о нижнем регистре справедливо и для тока, строчная буква «i» представляет ток в некоторый момент времени. Однако большинство измерений постоянного тока (DC), которые стабильны во времени, будут обозначены заглавными буквами.
Кулон и электрический заряд
Одна из основополагающих единиц измерения электрического тока, которую часто преподают в начале курсов электроники, но нечасто используют впоследствии, — это единица кулонов , которая является мерой электрического заряда, пропорциональной количеству электронов в несбалансированном состоянии.Один кулон заряда равен 6 250 000 000 000 000 000 электронов.
Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается заглавной буквой «C». Бывает, что единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этих терминах ток — это скорость движения электрического заряда по проводнику.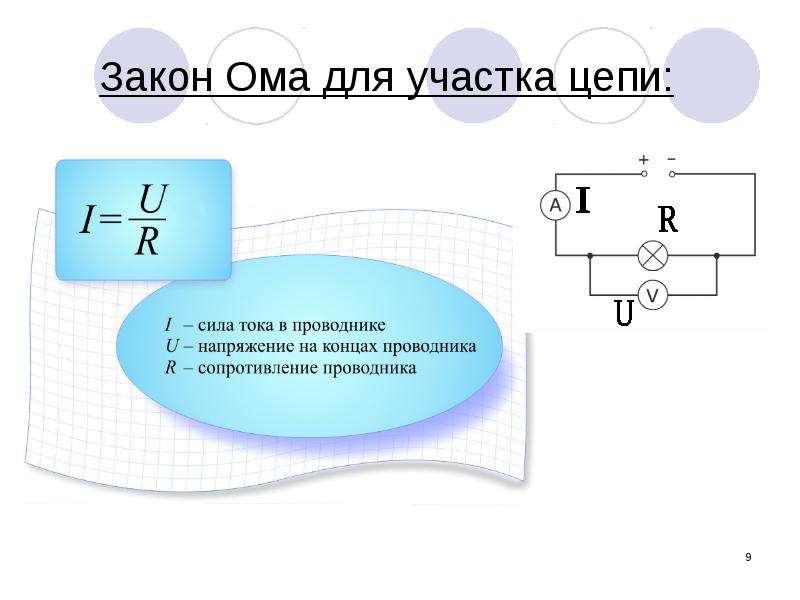
Как указывалось ранее, напряжение является мерой потенциальной энергии на единицу заряда , доступной для стимулирования прохождения тока из одной точки в другую.Прежде чем мы сможем точно определить, что такое «вольт», мы должны понять, как измерить эту величину, которую мы называем «потенциальной энергией». Общая метрическая единица для энергии любого вида — джоулей , равная количеству работы, совершаемой силой в 1 ньютон при движении на 1 метр (в том же направлении).
В британских подразделениях это чуть меньше 3/4 фунта силы, приложенной на расстоянии 1 фута. Проще говоря, требуется около 1 джоуля энергии, чтобы поднять гирю весом 3/4 фунта на 1 фут от земли или перетащить что-то на расстояние 1 фут, используя параллельную тянущую силу 3/4 фунта.В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленный на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.
Эти единицы и символы электрических величин станут очень важны, когда мы начнем исследовать взаимосвязи между ними в цепях.
Уравнение закона Ома
Основное открытие
Ома заключалось в том, что величина электрического тока, протекающего через металлический проводник в цепи, прямо пропорциональна напряжению, приложенному к нему, для любой заданной температуры.Ом выразил свое открытие в виде простого уравнения, описывающего взаимосвязь напряжения, тока и сопротивления:
В этом алгебраическом выражении напряжение (E) равно току (I), умноженному на сопротивление (R). Используя методы алгебры, мы можем преобразовать это уравнение в два варианта, решая для I и R соответственно:
Анализ простых схем с помощью закона Ома
Давайте посмотрим, как эти уравнения могут работать, чтобы помочь нам анализировать простые схемы:
В приведенной выше схеме есть только один источник напряжения (батарея слева) и только один источник сопротивления току (лампа справа). Это позволяет очень легко применять закон Ома. Если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой цепи, мы можем использовать закон Ома для определения третьей.
Это позволяет очень легко применять закон Ома. Если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой цепи, мы можем использовать закон Ома для определения третьей.
В этом первом примере мы вычислим величину тока (I) в цепи, учитывая значения напряжения (E) и сопротивления (R):
Какой ток (I) в этой цепи?
В этом втором примере мы рассчитаем величину сопротивления (R) в цепи, учитывая значения напряжения (E) и тока (I):
Какое сопротивление (R) дает лампа?
В последнем примере мы вычислим величину напряжения, подаваемого батареей, учитывая значения тока (I) и сопротивления (R):
Какое напряжение обеспечивает аккумулятор?
Техника треугольника закона Ома
Закон Ома — очень простой и полезный инструмент для анализа электрических цепей. Он так часто используется при изучении электричества и электроники, что серьезный студент должен запомнить его. Для тех, кто еще не знаком с алгеброй, есть уловка, позволяющая запомнить, как найти любое количество, учитывая два других.
Он так часто используется при изучении электричества и электроники, что серьезный студент должен запомнить его. Для тех, кто еще не знаком с алгеброй, есть уловка, позволяющая запомнить, как найти любое количество, учитывая два других.
Сначала расположите буквы E, I и R в виде треугольника:
Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:
Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:
Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:
В конце концов, вам придется быть знакомым с алгеброй, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений.Если вы хорошо разбираетесь в алгебре, все, что вам нужно сделать, это зафиксировать E = IR в памяти и вывести из нее две другие формулы, когда они вам понадобятся!
ОБЗОР:
- Напряжение измеряется в вольт , обозначается буквами «E» или «V».

- Ток измеряется в ампер , обозначается буквой «I».
- Сопротивление измеряется в Ом. обозначается буквой «R».
- Закон Ома: E = IR; I = E / R; R = E / I
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Попробуйте наш калькулятор закона Ома в разделе «Инструменты».
Закон Ома для начинающих и новичков
Закон Ома для начинающих и новичков
Основной закон Ома
HTML от: http://www.btinternet.com/~dtemicrosystems/beginner.htm
ЧТО ЭТО. КАК И ГДЕ ПРИМЕНЯТЬ
Хотя закон Ома применим не только к резисторам — как мы увидим позже — кажется,
логично включить его сейчас, так как он обеспечит хорошую точку отсчета для резистора
подробности приведены выше.
ЧТО ТАКОЕ ЗАКОН ОМС? :
Используя диаграмму слева, закон Ома определяется как; «При условии, что температура
остается постоянным, отношение разности потенциалов (p.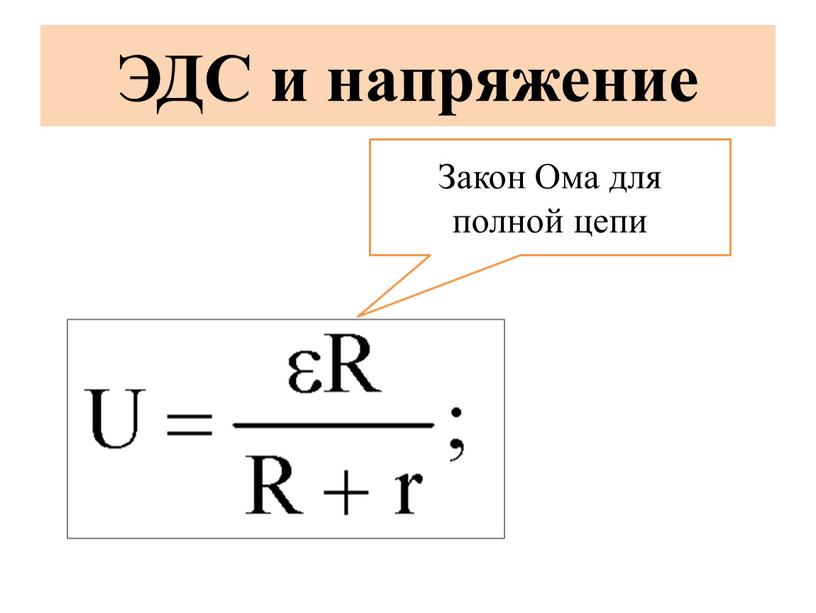 d.) на концах проводника
d.) на концах проводника
(R) к току (I), протекающему в этом проводнике, также будет постоянным ». Здесь заканчивается
проповедь!
Из этого мы заключаем, что; Ток равен напряжению, разделенному на сопротивление (I = V / R),
Сопротивление равно напряжению, разделенному на ток (R = V / I), а напряжение равно току, умноженному на
Сопротивление (V = IR).
Важным фактором здесь является температура. Если расчеты по закону Ома должны
давать точные результаты, это должно оставаться постоянным. В «реальном» мире это почти никогда
делает, и с точки зрения новичка вам не нужно беспокоиться об этом.
далее, поскольку схемы, с которыми вы, вероятно, столкнетесь в данный момент, — и около 95%
все те, с которыми вы столкнетесь в будущем — будут работать нормально, даже если они горячие
или холодно!
ЗАКОН ОМС ПРОСТОЙ:
На рисунке 1 слева показан наиболее распространенный треугольник закона Ома.Начиная с любого раздела
треугольник, его можно читать в любом направлении — по часовой стрелке, против часовой стрелки, сверху
вниз или снизу вверх — и он всегда предоставит вам расчет, который вы
требовать.
Если рассматривать (слегка диагональные) горизонтальные линии как знаки разделения, а короткие
вертикальная линия как знак умножения, и всегда начинайте свой расчет с любого количества
вы ищете, т.е. «V =», «I =» или «R =» у вас будет все
возможные формулы, основанные на этом конкретном законе Ома.То есть; V = IxR, I = V / R, R = V / I. Это
должно быть очевидно, что формула работает и в обратном направлении, то есть; IxR = V, RxI = V, V / I = R
и V / R = I.
Эти объяснения могут показаться немного сложными, но их легко применить на практике.
Как правило, для начинающих будет более понятен полезный пример, а не эти
причудливые столы, так что поехали.
ПОЯСНЕНИЕ НА ПРИМЕРЕ:
Допустим, друг просит вас установить красную сигнальную лампу на приборную панель его / ее автомобиля.Как энтузиаст электроники вы решили использовать красный светоизлучающий диод (LED),
поскольку они излучают достаточно чистый красный свет, не выделяют чрезмерного тепла
лампы накаливания, они также дешевы по сравнению и выглядят высокотехнологичными!
С точки зрения принципиальной схемы расположение будет таким, как показано слева.
ОГРАНИЧИТЕЛЬ ТОКА РЕЗИСТОР:
Стандартные светодиоды не могут получать питание напрямую от 12 В без установки ограничения тока
резистор включен последовательно с одним из выводов, но какое значение вы используете? Как общее правило
на практике, вашему среднему светодиоду требуется около 15 мА тока для получения приемлемого света.
выход.Учитывая это, теперь у нас есть две известные величины для использования в наших расчетах:
напряжение и ток. Используя треугольник закона Ома, требуемое сопротивление равно
рассчитывается по формуле «R = V / I», которая дает нам 12 / 0,015 = 800 Ом (см. ниже
для ‘Vf’). Не забывайте, ток измеряется в амперах.
Поначалу это может показаться проблемой, поскольку 800 Ом не является стандартным значением.
доступен в диапазоне E12. Однако в этом типе схемы сопротивление не
критического, и ближайшего предпочтительного значения будет вполне достаточно, а именно 820 Ом.
НЕ ЗАБЫВАЙТЕ ОБ «Vf»:
Все электронные компоненты демонстрируют — в большей или меньшей степени — то, что известно как
‘выбывать’.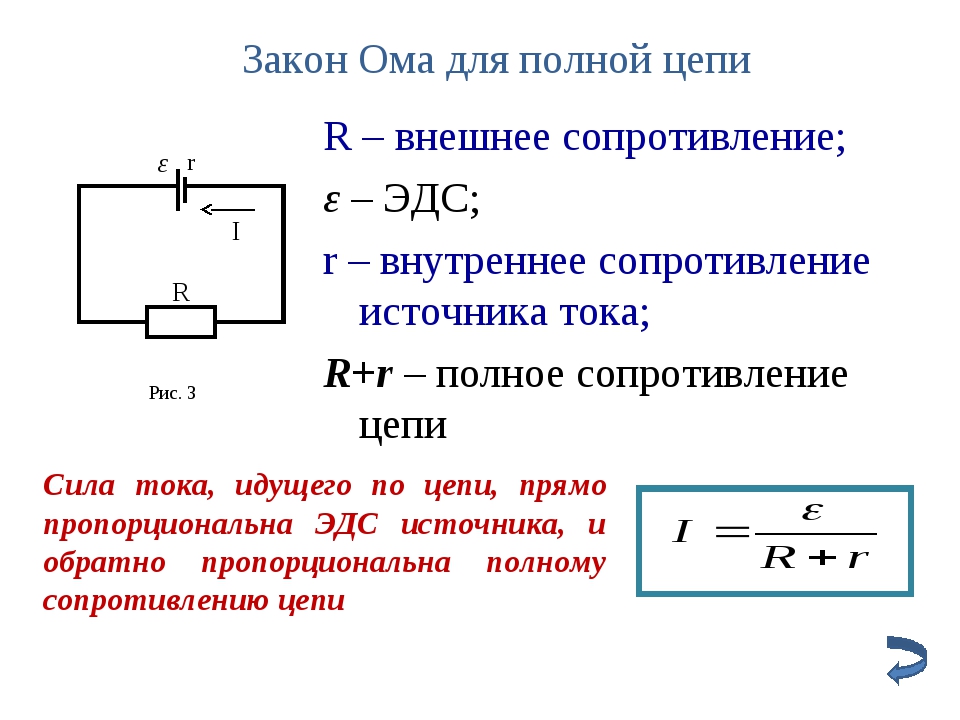 Он имеет различные сокращения в зависимости от типа компонента, к которому он
Он имеет различные сокращения в зависимости от типа компонента, к которому он
ссылается, но обычно они означают одно и то же. На самом деле это количество напряжения, которое
используется компонентом для работы. Для стандартного светодиода это значение составляет
около 1,5 — 3 вольт, и для наших целей мы будем считать, что это 2 В.
Это означает, что из ваших 12 вольт от аккумулятора 2 вольта будут израсходованы светодиодом.
Сама по себе, поэтому ваш расчет закона Ома должен быть основан на 10 вольт.Истинная формула
действительно должно быть; (12-Vf) /0.015=666.66 Ом (повторяется для мастеров математики среди
ты!). Ближайшее значение в диапазоне E12 составляет 680 Ом, поэтому в идеале это должно быть
ценность для использования. В целях безопасности, когда ваши результаты заканчиваются непонятными значениями, такими как
при этом всегда выбирайте ближайшее значение выше, а не следующее ниже.
РЕЗИСТОРЫ ПОСЛЕДОВАТЕЛЬНО И ПАРАЛЛЕЛЬНО
Возможно «изготовление» стандартных и нестандартных номиналов резисторов на
соответствовать вашим потребностям, если требуемое значение отсутствует. Это достигается подключением
Это достигается подключением
два или более из них параллельно, последовательно или их комбинация. Однако вам нужно
заранее знать, как они взаимодействуют друг с другом в этих конфигурациях.
РЕЗИСТОРЫ СЕРИИ:
На рисунке слева показаны три резистора, соединенные последовательно друг с другом. Это
самый простой способ получить «фабричные» значения. Формула прямой для
расчет окончательного значения; «R» = R1 + R2 + R3. Другими словами, независимо от
от количества резисторов или их индивидуальных значений окончательное значение
«R» всегда будет их суммой.Расчет по ноге изображения
работает для любого количества значений, соединенных последовательно, вы просто продолжаете добавлять их в
список других.
ПАРАЛЛЕЛЬНЫЕ РЕЗИСТОРЫ:
Когда резисторы соединены параллельно друг другу, вычисления немного
посложнее. На рисунке слева показаны три резистора, включенных параллельно. Мы будем
не заботиться о трех отдельных ценностях, а сосредоточиться на том, что
окончательное значение «R» будет с использованием примеров значений. Расчет у подножия
Расчет у подножия
изображение работает для любого количества значений, соединенных параллельно, вы просто продолжаете добавлять их в
список других в скобках. Для наших целей предположим, что R1 — 47K, R2 —
150К, а R3 — 820К. Формула прямой линии для окончательного значения: «R» = 1 / (
(1 / R1) + (1 / R2) + (1 / R3)).
В этой формуле содержится много ненужных скобок (скобок),
и вот в чем причина; почти для всех расчетов электроники вам нужно использовать
калькулятор, который отдает приоритет функциям умножения и деления, а также наиболее научным
калькуляторы работают именно так.К сожалению, многие «простые» калькуляторы этого не делают, поэтому
дополнительные скобки были показаны, чтобы компенсировать те, которые вычисляют цифры в
порядок их ввода. С научным калькулятором вы можете использовать упрощенный
формула прямой линии; «R» = 1 / (1 / R1 + 1 / R2 + 1 / R3).
Важно определить значения в скобках, прежде чем применять окончательный
Функция «1 /». Если вы этого не сделаете, то формула станет 1 / R1 + 1 / R2 + 1 / R3 =? если ты
попробуйте это на своем калькуляторе, используя наши примеры значений, вы, вероятно, подумаете, что у вас
неправильный ответ (0. 02916 …), а у вас нет. На самом деле у вас точно есть право
02916 …), а у вас нет. На самом деле у вас точно есть право
ответ, ему просто не хватает последней функции «1 /».
Если в вашем калькуляторе есть «1 / X» (единица, деленная на все, что показано в
display), затем нажмите эту кнопку сейчас. Если эта функция недоступна, поместите
результат в памяти (убедившись, что раньше там ничего не было), очистить дисплей
а затем введите «1 MR =» или другую подобную последовательность. Результат должен быть
34,29 кОм (34 290,29005 Ом), что правильно.Итак, итоговое значение всех трех
резисторы, включенные параллельно — 34,29К.
ДЛЯ ЧЕГО ДРУГОЙ ТРЕУГОЛЬНИК?
На рисунке 2 слева показан второй по величине
часто используемый треугольник закона Ома. К этому можно подойти точно так же, как и к
выше, только на этот раз он используется для расчета мощности, напряжения и тока. В
объяснения здесь таковы; Ток равен мощности, деленной на напряжение (I = P / V), мощность равна
Ток, умноженный на напряжение (P = VxI), и напряжение равно мощности, деленной на ток (V = P / I).
ДЕМОНСТРАЦИЯ НА ПРИМЕРЕ:
Чтобы продемонстрировать использование этого треугольника, мы применим его к обычному электрическому / электронному
компонент — трансформатор. Их характеристики обычно цитируются с точки зрения
их выходное напряжение вторичной обмотки, вместе с мощностью — в ВА —
это напряжение. Термин «VA» означает ватты и происходит от формулы
«Вольт на Ампер» (отсюда — ВА). Это обозначается буквой «P» в
треугольник закона Ома.
КАКОЙ ТРАНСФОРМАТОР ДЕЛАТЬ
НЕОБХОДИМОСТЬ ?
Допустим, у вас есть цепь на 9 В, которая потребляет 1.5 ампер тока. Вы хотите знать, если
трансформатор с номиналом 9 В при 25 ВА будет достаточным для питания вашей цепи. Ты
уже есть две величины от трансформатора — напряжение (В) и мощность (P или
VA), и по ним вы хотите узнать, какой будет доступный ток (I).
Используя формулу «I = P / V» из треугольника, результат: 25/9 = 2,77
усилители. Таким образом, этот трансформатор подойдет для ваших нужд на 1,5 А. В целях безопасности
В целях безопасности
если цепь будет постоянно потреблять определенное количество тока, независимо от
каким может быть этот ток, тогда всегда используйте трансформатор, доступный как минимум на 50%
ток, чем требует ваша схема.Никогда не используйте тот, у которого «ровно столько» тока,
потому что он станет слишком горячим, что приведет к изменению характеристик напряжения и
текущий указан. Эти изменения сложны, и мы не будем их объяснять в этой статье.
раздел для начинающих, но будьте осторожны при выборе трансформаторов.
Закон
Ома | Основы резистора
Что такое закон Ома?
Закон
Ома гласит, что электрический ток через проводник пропорционален разности потенциалов на нем.Кроме того, электрическое сопротивление проводника постоянно. Это приводит к математическому уравнению:
, где I — ток в амперах, V — напряжение в вольтах, R — сопротивление в омах. Для иллюстрации: резистор сопротивлением 1 Ом, на который действует ток 1 А, имеет разность напряжений на выводах 1 В. Уравнение названо в честь Георга Ома. В 1827 году он опубликовал свои выводы, которые легли в основу формулы, которая используется сегодня. Он провел большую серию экспериментов, которые показали связь между приложенным напряжением и током, протекающим через проводник.Следовательно, закон эмпирический. Хотя закон Ома является одной из основ электротехники, на момент публикации он был встречен критикой. Ом принят в качестве официальной единицы измерения электрического сопротивления в системе СИ. Густав Кирхгоф (известный из законов схем Кирхгофа) сделал обобщение, которое больше используется в физике:
Уравнение названо в честь Георга Ома. В 1827 году он опубликовал свои выводы, которые легли в основу формулы, которая используется сегодня. Он провел большую серию экспериментов, которые показали связь между приложенным напряжением и током, протекающим через проводник.Следовательно, закон эмпирический. Хотя закон Ома является одной из основ электротехники, на момент публикации он был встречен критикой. Ом принят в качестве официальной единицы измерения электрического сопротивления в системе СИ. Густав Кирхгоф (известный из законов схем Кирхгофа) сделал обобщение, которое больше используется в физике:
где σ — параметр проводимости (зависит от материала), J — плотность тока в месте расположения этого материала, а E — электрическое поле в этом месте.
Закон Ома и резисторы
Резисторы — это пассивные элементы, которые создают сопротивление прохождению электрического тока в цепи. Резистор, работающий по закону Ома, называется омическим резистором. Когда ток проходит через омический резистор, падение напряжения на выводах пропорционально величине сопротивления. Формула Ома действительна также для цепей с переменным напряжением или током, поэтому ее можно использовать и для цепей переменного тока. Для конденсаторов и катушек индуктивности этот закон, конечно, не может быть использован, поскольку их ВАХ по своей природе не является линейной (не омической).
Формула Ома действительна также для цепей с переменным напряжением или током, поэтому ее можно использовать и для цепей переменного тока. Для конденсаторов и катушек индуктивности этот закон, конечно, не может быть использован, поскольку их ВАХ по своей природе не является линейной (не омической).
Формула
Ома действительна для цепей с несколькими резисторами, которые можно соединить последовательно, параллельно или и то, и другое. Группы резисторов, включенных последовательно или параллельно, можно упростить с помощью эквивалентного сопротивления. В статьях «Резисторы в серии» или «Резисторы в параллели» более подробно описано, как это сделать.
Георг Симон Ом (1789-1854)Георг Симон Ом Немецкий физик Георг Симон Ом опубликовал в 1827 году свою полную теорию электричества под названием «Гальваническая цепь, исследованная математически.Он обнаружил, что падение напряжения в части цепи является произведением проходящего через нее тока и сопротивления этой части. Его коллеги не оценили его выводы, и закон был нелегко принят. Ом был в то время учителем в гимназии в Кельне, и он решил уйти в отставку. Позже он стал профессором экспериментальной физики Мюнхенского университета. Позже он, наконец, получил признание и получил медаль Копли в 1841 году от Королевского общества. |
Уравнения закона Ома
Формула
Ом может использоваться, когда известны две из трех переменных. Связь между сопротивлением, током и напряжением можно записать по-разному. Чтобы запомнить это, может оказаться полезным калькулятор треугольника Ома. Два примера ниже демонстрируют использование калькулятора треугольников.
или
или
Примеры | |
Рассмотрим резистор на 1 Ом в цепи с падением напряжения от 100 В до 10 В на его выводах. Какой ток через резистор? Треугольник напоминает нам, что: Какой ток через резистор? Треугольник напоминает нам, что: | |
| Рассмотрим резистор 10 Ом в цепи, подверженной току 2 Ампера и напряжению 120 В. Какое падение напряжения на резисторе? Использование треугольника показывает нам, что: Таким образом, напряжение на оконечном выводе составляет 120-20 = 100 В. | |
Степенной закон Ома
Резистор рассеивает мощность, когда через него проходит ток.Энергия выделяется в виде тепла. Мощность является функцией тока I и приложенного напряжения V:
, где P — мощность в ваттах. В сочетании с законом Ома степенной закон можно переписать в виде:
или
Идеальные резисторы рассеивают всю энергию и не накапливают электрическую или магнитную энергию. У каждого резистора есть предел мощности, которая может рассеиваться без повреждения. Это называется номинальной мощностью. Окружающие условия могут снизить это значение.Например, корпус вокруг резистора или более высокая температура окружающей среды уменьшат количество энергии, которое резистор может рассеять. Этот эффект называется снижением мощности, и его можно визуализировать с помощью диаграммы снижения мощности. На практике резисторы редко имеют указанную номинальную мощность. Однако большинство резисторов рассчитаны на 1/4 или 1/8 Вт. Круговая диаграмма помогает быстро найти соотношение между электрической мощностью, током, напряжением и сопротивлением. Для каждого из четырех параметров показано, как рассчитать их значение.
Окружающие условия могут снизить это значение.Например, корпус вокруг резистора или более высокая температура окружающей среды уменьшат количество энергии, которое резистор может рассеять. Этот эффект называется снижением мощности, и его можно визуализировать с помощью диаграммы снижения мощности. На практике резисторы редко имеют указанную номинальную мощность. Однако большинство резисторов рассчитаны на 1/4 или 1/8 Вт. Круговая диаграмма помогает быстро найти соотношение между электрической мощностью, током, напряжением и сопротивлением. Для каждого из четырех параметров показано, как рассчитать их значение.
Ниже приведены несколько примеров задач закона Ома. Вы можете попробовать решить проблему самостоятельно, прежде чем читать ответ.
Цветовой код резистора
Значение сопротивления в омах часто обозначается цветовым кодом на резисторе. Комбинация цветов указывает значение, а также допуск резистора. Для получения дополнительной информации по этой теме см. Цветовую кодировку резистора.
Цветовую кодировку резистора.
Закон
Ома | Клуб электроники
Закон Ома | Клуб электроники
Следующая страница: Power and Energy
См. Также: Напряжение и ток | Сопротивление
Закон Ома показывает взаимосвязь между напряжением, током и сопротивлением
Чтобы ток протекал через сопротивление, на этом сопротивлении должно быть напряжение.Закон Ома показывает взаимосвязь между тремя величинами: напряжением, током и сопротивлением.
Закон Ома можно записать в виде словесного уравнения :
| напряжение = ток × сопротивление |
Или используя символы для обозначения величин напряжения (В), тока (I) и сопротивления (R):
На самом деле это можно записать тремя способами, и вы можете выбрать версию, которая лучше всего подходит для ваших целей:
Треугольник ВИР — способ запомнить закон Ома
Вы можете использовать треугольник VIR, чтобы помочь вам запомнить три версии закона Ома.
- Для расчета напряжения, В : поместите палец на V,
это оставляет I R, поэтому уравнение V = I × R - Чтобы рассчитать ток , I : положите палец на I,
это оставляет V над R, поэтому уравнение I = V / R - Чтобы рассчитать сопротивление , R : поместите палец на R,
это оставляет V над I, поэтому уравнение R = V / I
Расчет по закону Ома
Используйте этот метод для проведения расчетов:
- Запишите значения , при необходимости конвертируя единицы.
- Выберите нужное Equation (используйте треугольник VIR).
- Подставьте чисел в уравнение и вычислите ответ.
Должно быть V ery E asy N ow!
См. Примеры ниже:
Пример 3:
Резистор 1,2 кОм пропускает ток 0,2 А, какое напряжение на нем?
Пример 4:
9 В подается на резистор 15 кОм, какой ток?
- V alues: V = 9V, I =?, R = 15k
- E предложение: I = V / R
- N umbers: Ток, I = 9 / 15 = 0.
 6 мА
6 мА
(использование k для сопротивления означает, что расчет дает ток в мА)
Следующая страница: Энергетика | Исследование
Политика конфиденциальности и файлы cookie
Этот сайт не собирает личную информацию.
Если вы отправите электронное письмо, ваш адрес электронной почты и любая личная информация будет
используется только для ответа на ваше сообщение, оно не будет передано никому.
На этом веб-сайте отображается реклама, если вы нажмете на
рекламодатель может знать, что вы пришли с этого сайта, и я могу быть вознагражден.Рекламодателям не передается никакая личная информация.
Этот веб-сайт использует некоторые файлы cookie, которые классифицируются как «строго необходимые», они необходимы для работы веб-сайта и не могут быть отклонены, но они не содержат никакой личной информации.
Этот веб-сайт использует службу Google AdSense, которая использует файлы cookie для показа рекламы на основе использования вами веб-сайтов.
(включая этот), как объяснил Google.
Чтобы узнать, как удалить файлы cookie и управлять ими в своем браузере, пожалуйста
посетите AboutCookies.org.
клуб электроники.инфо © Джон Хьюс 2021
Веб-сайт размещен на Tsohost
Расчет по закону Ома
| В трех таблицах справа вы можете ввести два из трех факторов в (исходном) Законе Ома. Это напряжение (В) или (E), измеренное в вольтах, , ток или сила тока (I), измеренные в ампер, (амперы) и сопротивление (R), измеренное в Ом, . Третий фактор будет рассчитан для вас, когда вы нажмете кнопку «Рассчитать» для этой таблицы. Закон Ома: V = I x R, где V = напряжение, I = ток и R = сопротивление. Один Ом — это значение сопротивления, при котором один вольт будет поддерживать ток в один ампер . Георг Симон Ом был баварским физиком, который определил математический закон электрических токов, называемый законом Ома. Ом, электрическая единица сопротивления, был назван в его честь. В последующие годы мы также приписали коэффициент мощности Ому. Мощность обычно обозначается сокращением (Вт) и измеряется в ваттах. Для расчета по закону Ома с мощностью, нажмите здесь . Чтобы проверить цветовую кодировку резисторов, используйте нашу таблицу цветовых кодов резисторов и калькулятор . Этот преобразователь требует использования браузеров с поддержкой Javascript .
|
Закон Ома — основы
Настройка CQ-Calling All Обзоры продуктов Рекламная информация | Основной закон Ома Здесь мы попытаемся объяснить закон Ома Закон Ома Что такое Ом Закон Ома составлен из Что такое напряжение? An заполненный Что сейчас? По аналогии с , ведущие к крану. Что такое сопротивление? Аналогия Все три из них: напряжение, ток и сопротивление Информация: Закон Ома назван в честь баварцев. Закон Ома может быть I измеряется ток ампер R — это сопротивление в зависимости от размера труб и крана: В = I x R = I = V / R (ток = Зная любые два значения цепи , Например, чтобы найти напряжение в Если в цепи есть ток 2 ампера, и (В = 2 ампера x 1 Ом = 2 Чтобы найти ток в той же цепи выше В этом третьем примере мы знаем ток (2 ампера) и Иногда очень полезно
Колесо вверху Вольт Чтобы использовать, просто Пример: Чтобы найти Вот Вы знаете Просто Вы
В указанном выше Ан Информация: Обычно закон Ома применяется только к Проводной
|
Понимание закона Ома — Pi My Life Up
Закон Ома является одной из основ электроники и невероятно удобен для быстрого расчета тока, напряжения или сопротивления цепи. Вам нужно будет знать как минимум два значения.
Вам нужно будет знать как минимум два значения.
Закон Ома определяет математическое соотношение между током, напряжением и сопротивлением сети.
Этот закон был назван в честь немецкого физика и математика XIX века Георга Ома. Ом обнаружил эту взаимосвязь еще в то время, когда не было возможности легко измерить ток, напряжение или сопротивление.
Несмотря на то, что при первой публикации он был встречен холодно, он стал обязательным для всех, кто интересуется электрическими схемами. Закон Ома стал частью нашего нынешнего понимания электрических схем.
Если вы занимаетесь каким-либо из наших проектов электроники Raspberry Pi, которые связаны со схемами, то этот учебник может оказаться вам полезным.
Что такое закон Ома?
Закон Ома гласит, что ток, проходящий через проводник между двумя точками, прямо пропорционален напряжению в этих двух точках и обратно пропорционален сопротивлению между двумя точками.
Проще говоря, если в цепи удваивается ток, то удваивается и напряжение. Точно так же, если сопротивление в цепи увеличится вдвое, ток упадет вдвое.
Точно так же, если сопротивление в цепи увеличится вдвое, ток упадет вдвое.
Хотя это может показаться немного сложным, фактическая математика, лежащая в основе этой теории, невероятно проста для понимания и запоминания.
Формула закона Ома
К счастью для нас, формула закона Ома невероятно проста для понимания.
Закон Ома можно выразить математической формулой, как показано ниже.
Эта формула говорит, что напряжение ( В ) равно току ( I ), умноженному на сопротивление ( R ).
Во всех формулах закона Ома мы используем следующие переменные.
- В = напряжение, выраженное в вольтах.
- I = ток, выраженный в амперах.
- R = Сопротивление, выраженное в Ом.
Хотя формулу можно использовать для расчета напряжения, ею также можно управлять, чтобы вместо этого вычислить ток или сопротивление в цепи.
Для начала давайте изменим формулу так, чтобы мы могли вычислить ток ( I ) цепи.
Мы также можем изменить базовую формулу закона Ома, чтобы мы могли вычислить сопротивление ( R ) цепи.
Калькулятор закона Ома
Чтобы использовать этот калькулятор закона Ома, сначала выберите, хотите ли вы рассчитать напряжение, ток или сопротивление.
При выбранном режиме все, что вам нужно сделать, это ввести два требуемых значения. Калькулятор автоматически рассчитает правильные значения.
Треугольник закона Ома
Один из самых простых способов запомнить три различных формулы закона Ома — это треугольник.
Средний горизонтальный делитель треугольника представляет деление, то есть всякий раз, когда в формуле участвует напряжение ( В, ), все остальные буквы делятся на него.
Например, если мы хотим вычислить ток ( I ), нам нужно разделить напряжение ( В, ) на сопротивление ( R ).
Обведя кружком « I » в треугольнике, мы увидим, что формула остается в треугольнике с V над R .
Мы также можем использовать этот же треугольник, чтобы разработать формулу для расчета сопротивления ( R ) цепи.
Обведя сопротивление ( R ), мы можем увидеть формулу, которую мы должны использовать: напряжение ( В, ), деленное на ток ( I )
Вертикальная линия в треугольнике представляет умножение.Эта линия используется только при расчете напряжения (В).
Используя снова треугольник закона Ома, мы можем быстро увидеть формулу, которую нам нужно использовать, обведя кружком « V », поскольку это значение, которое мы хотим вычислить.
Из этого мы легко можем видеть, что для расчета напряжения ( В, ) все, что нам нужно сделать, это умножить ток ( I ) на сопротивление ( R ).
Пример закона Ома в действии
Далее мы рассмотрим три различных примера схем.
Эти примеры касаются использования каждого варианта трех различных формул закона Ома.
Пример напряжения
В этом первом примере мы начнем с формулы закона базового сопротивления для расчета напряжения цепи.
Для расчета напряжения нам необходимо знать сопротивление ( R ) и ток ( I ) цепи.
В этой примерной схеме вы можете видеть, что у нас есть сопротивление ( R ) 200 Ом и ток ( I ) 5 А.
Чтобы рассчитать напряжение, нам нужно вставить два наших значения в формулу закона Ома.
После заполнения формулы вы видите, что все, что нам нужно сделать, это умножить 200 на 5 , чтобы рассчитать напряжение.
Умножив сопротивление и ток, мы увидим, что напряжение для схемы в примере равно 1000 вольт .
Пример тока
В этом втором примере мы будем использовать модифицированную версию формулы закона Ома для расчета тока следующей цепи.
Из этой схемы мы знаем, что сопротивление ( R ) составляет 50 Ом, и что напряжение ( В, ) составляет 24 В, .
Нам нужно поместить эти значения в формулу закона Ома, которая была изменена для расчета тока ( I ).
Используя значения сопротивления и напряжения, введенные в формулу, мы видим, что нам нужно разделить 24 на 50 , чтобы вычислить ток.
Используя закон Ома, мы вычисляем ток в цепи как 0.48 Ампер .
Пример сопротивления
В нашем третьем и последнем примере мы будем использовать третью версию формулы закона Ома. В этом случае мы будем использовать формулу для расчета сопротивления цепи.
Для расчета сопротивления цепи нам нужно знать напряжение ( В, ) и ток ( I ) цепи.
Из этой примерной схемы мы можем видеть, что наша примерная схема имеет ток 10 ампер и напряжение 20 вольт .
Нам нужно вставить эти два значения в формулу сопротивления закона Ома.
Отсюда мы можем рассчитать необходимое нам сопротивление, разделив напряжение 20 на 10 ампер .



 Это легло в основу того закона, который мы используем сегодня. Закон — одно из основополагающих соотношений для резисторов.
Это легло в основу того закона, который мы используем сегодня. Закон — одно из основополагающих соотношений для резисторов. 6 мА
6 мА Между 1825 и 1827 годами он разработал теорию или взаимосвязь, и это было ему приписано в конце 1827 года.
Между 1825 и 1827 годами он разработал теорию или взаимосвязь, и это было ему приписано в конце 1827 года. 828 x 10 -6
828 x 10 -6  Мы предположим
Мы предположим Период, термин
Период, термин


