Производительность - это... Формула производительности. Обозначение производительность

Производительность

Продолжаем изучать элементарные задачи по математике. Сегодня мы рассмотрим очень интересную физическую величину — производительность.

Что такое сила?

Сила — это физическое явление, способное изменять форму материальных тел, вызывать их движение, менять направление и скорость движения этих тел или приводить тело в состояние покоя.

Примеры сил:

• ребята слепили снеговика, а хулиганы его разрушили. Получается, что хулиганы приложили к снеговику свою силу, тем самым вызвали изменение формы снеговика;

• на дворе стояла тележка. Прохожий случайно задел её и тележка сдвинулась с места. Получается, что прохожий применил силу к тележке и вызвал её движение;

• далее тот же прохожий остановил тележку, чтобы она далеко не уехала. Получается, что прохожий применил силу, тем самым привел тележку в состояние покоя.

Сила является физической величиной — мерой воздействия на тело других тел. Сила обозначается заглавной латинской буквой F.

Что такое работа?

Работа — это количественная мера действия силы на тело. Работа зависит от количества силы, приложенной на тело и от направления этой силы, а также от перемещения данного тела.

Например, если мы попробуем сдвинуть шкаф с места и он сдвинется, то можно сказать, что мы совершили работу, поскольку сила, которую мы приложили, привела к тому, что шкаф совершил перемещение на некоторое расстояние.

Если же мы, к примеру, попробуем толкнуть стену, то стена с места не сдвинется, а значит и работа не будет совершена, поскольку сила была приложена, но эта сила не вызвала никакого перемещения стены.

Работа обозначается заглавной латинской  буквой A.

Производительность

Производительностью называют работу, выполненную за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда. Производительность обозначается латинской буквой v

Рассмотрим следующий пример. Два пекаря пекли булочки. Первый пекарь испёк 40 булочек за 10 минут, а второй 15 булочек за 5 минут. Как узнать, кто из пекарей работал быстрее, первый или второй?

Работал быстрее тот, кто за одну минуту выпекает больше булочек. Говорят, что у него производительность больше. Для нахождения производительности предусмотрено следующее правило:

Чтобы найти производительность, надо выполненную работу разделить на время работы.

Также, можно воспользоваться формулой:

где v — производительность, A — выполненная работа, t — время работы.

Вернемся к нашей задаче. Зная правило или формулу нахождения производительности, можно определить сколько булочек приходится на одну минуту.

Найдём производительность первого пекаря. Разделим работу, которую он выполнил, на время которое он на нее затратил. Выполненная работа это количество испеченных им булочек, то есть 40, а время — 10 минут

40 : 10 = 4 булочки в минуту

Аналогично найдём производительность второго пекаря. Разделим 15 на 5

15 : 5 = 3 булочки в минуту

4 > 3

Первый пекарь в минуту выпекает больше булочек чем второй, значит его производительность выше. Отсюда делаем вывод, что работает он быстрее второго пекаря.

Также можно воспользоваться формулой нахождения производительности. В этом случае решение принимает следующий вид:

Под буквой v можно делать метки, указывающие для кого/чего мы находим производительность.

Задача 2. Тому нужно за 2 дня прочитать книгу, в которой 100 страниц. В первый день он читал 4 часа со скоростью 12 страниц в час. С какой скоростью ему надо читать оставшуюся часть книги, если у него есть  на это 4 часа?

Узнаем сколько страниц Том прочитал в первый день. Он читал 12 страниц в час. Чтению в первый день он посвятил 4 часа, поэтому для нахождения количества прочитанных страниц в первый день, нужно 12 умножить на 4

12 × 4 = 48 страниц прочитано в первый день

Узнаем сколько страниц осталось прочесть. Вычтем из всех общего количество страниц (100) количество прочитанных страниц (48)

100 − 48 = 52 страницы осталось прочесть

Осталось прочесть 52 страницы. Теперь найдем такую производительность, при которой Том сможет прочесть 52 страницы за 4 часа. Раскидаем 52 страницы на 4 часа поровну

52 : 4 = 13 страниц в час

Ответ: чтобы прочитать оставшуюся часть книги за 4 часа, Том должен читать ее со скоростью 13 страниц в час.

Замечание. В некоторых источниках слово «производительность» может быть заменено на слова «скорость», «эффективность», «продуктивность», «плодотворность» и т.д.

Задача 3. Один насос работал 4 часа, выкачивая 158 ведёр воды в час, а другой — 3 часа, выкачивая 169 вёдер воды в час. Определить какой из насосов выкачал больше вёдер.

Решение

Определим сколько всего вёдер выкачал каждый насос по отдельности. Для этого умножим их производительность на время их работы:

158 в/ч × 4 = 632 вёдер выкачал первый насос

169 в/ч × 3 = 507 вёдер выкачал второй насос

632 > 507

Ответ: первый насос выкачала больше вёдер, чем второй.

Задача 4. За 2 часа насос выкачал 80 литров воды. Определить сколько литров он выкачает за 5 часов.

Решение

Сначала нужно определить сколько литров воды насос выкачивает за час. Для этого 80 литров разделим на 2 часа — получим 40 литров

80 : 2 = 40 литров в час

За один час насос выкачивает 40 литров воды. За 5 часов выкачает в пять раз больше

40 × 5 = 200 литров

Ответ: за 5 часов насос выкачает 200 литров воды.

Если известны производительность и время работы, то можно найти выполненную работу. Выполненная работа равна производительности умноженной на время работы:

A = v × t

Например, если производительность пекаря составляет 50 булочек в час, и он проработал 4 часа, то можно найти всю выполненную работу за эти четыре часа. Для этого производительность (50 бул/ч) нужно умножить на время его работы (4ч)

50 × 4 = 200 булочек

Если известны работа и производительность, то можно найти время работы. Время работы равно отношению выполненной работы к производительности:

Например, если в неделю бригада отстраивает 2 этажа, то можно узнать сколько недель потребуется для отстройки 8 этажей. Чтобы определить время отстройки восьми этажей, нужно выполненную работу (8 этажей) разделить на производительность (2 эт./нед):

8 : 2 = 4 нед.

Либо с помощью формулы, приведенной выше:

Если в неделю строится 2 этажа, то 8 этажей будет отстроено за четыре недели. В данном случае вся работа была равна восьми. Производительность была равна двум, поскольку по определению производительность есть работа, выполненная за единицу времени – в нашем случае два этажа за неделю.

Задача 6. Принтер работает с прозводительностью 70 стр./ч. Сколько страниц он напечатает за 5 часов?

Решение

Если в час принтер печатает 70 страниц, то за 5 часов он напечатает в 5 раз больше:

70 × 5 = 350 страниц

Также, решение можно записать с помощью формулы нахождения работы. В данном случае, количество напечатанных страниц являются выполненной работой:

A = v × t = 70 × 5 = 350 страниц

A = 350 страниц

Задача 7. Принтер напечатал 350 страниц за 5 часов. С какой производительностью он работал?

Решение

Если в течении пяти часов принтер напечатал 350 страниц, то в течении часа он печатал  . То есть, работал с производительностью 70 страниц в час:

350 : 5 = 70 стр./ч.

Либо с помощью формулы нахождения производительности:

Задача 8. Принтер работал с производительностью 70 страниц в час и напечатал 350 страниц. Определить время работы принтера.

Решение

Выражение «работал с производительностью 70 страниц в час» означает, что в каждом часе принтер печатал по 70 страниц. И это продолжалось до тех пор, пока он не напечатал 350 страниц. Очевидно, что разделив 350 страниц по 70, мы определим время работы принтера, то есть узнаем сколько часов он работал

350 : 70 = 5 ч.

Либо с помощью формулы нахождения времени:

Задача 9. Машинистка в первый день напечатала 48 страниц рукописи, а во второй день — на 12 страниц больше, чем в первый. На всю работу в эти 2 дня она затратила 9 часов. Сколько часов работала она в каждый из этих дней, если производительность её не менялась ?

Решение

Определим сколько страниц напечатала машинистка во второй день. В условии сказано, что напечатала она на 12 страниц больше, чем в первый:

48 + 12 = 60 страниц во второй день.

Определим сколько страниц машинистка напечатала за два дня:

48 + 60 = 108 страниц за два дня.

На эту работу машинистка затратила 9 часов. Также сказано, что производительность её не менялась. Если мы разделим выполненную работу (108) на время выполнения (9), то определим производительность машинистки:

108 : 9 = 12 страниц в час.

Теперь мы можем определить сколько часов работала машинистка в каждый из двух дней. Для этого поочередно разделим выполненные работы в каждом из двух дней на производительность:

48 : 12 = 4 часа работала машинистка в первый день

60 : 12 = 5 часов работала машинистка во второй день.

Задача 10. Джон решил 10 примеров за 5 минут. С какой производительностью он решал эти примеры?

10 примеров это выполненная Джоном работа. 5 минут — время работы. Разделим выполненную работу на время работы и определим производительность Джона:

10 : 5 = 2 примера в минуту.

Производительность Джона равна двум примерам в минуту.

Задача 11. Джон решил несколько примеров за 5 минут. С какой производительностью он решил эти примеры?

Это та же самая задача, что и предыдущая, но в ней работа не выражена каким-либо числом. Сказано лишь то, что Джон выполнил эту работу за 5 минут. Поэтому, конкретную производительность в такой задаче узнать нельзя. Но можно воспользоваться дробями. Обозначим выполненную работу через единицу. Тогда производительность работы Джона будет выражаться дробью – частью примеров, решенных за единицу времени. Если вы изучили задачи на дроби, то должны понимать о чем идёт речь.

Итак, обозначим выполненную работу через единицу:

A = 1

Мы знаем, что для нахождения производительности, выполненную работу нужно разделить на время. Время работы у нас равно пяти минутам. Поэтому, единицу делим на пять минут:

Дробь  выражает  часть работы, выполненную Джоном за единицу времени. Если мы вернемся к предыдущей задаче, где выполненная работа была равна десяти примерам и найдем одну пятую от этой работы, то получим 2

Выражать выполненную работу через единицу часто приходиться при решении задач на совместную работу.

Задачи на совместную работу

Задача 1. Первый мастер за 2 часа изготавливает 64 детали, а второй за 3 часа – 72 детали. За сколько часов они изготовят 336 деталей?

В данной задаче речь идет о совместной работе. Необходимо определить производительность обоих мастеров и найти время за которое они изготовят 336 деталей.

Для начала определим производительность первого мастера:

64 : 2 = 32 дет./час

Определим производительность второго мастера:

72 : 3 = 24 дет./час

Определим совместную производительность мастеров. Для этого сложим количество деталей, которые они изготавливают по отдельности за единицу времени. То есть, сложим их производительности:

32 дет./час  + 24 дет./час = 56 дет./час

Вместе за один час мастера изготавливают 56 деталей. Чтобы узнать за сколько часов они изготовят 336 деталей, нужно определить сколько раз 336 содержит по 56

336 : 56 = 6 часов

Задача 2. Первый мастер может покрасить забор за 20 минут, а второй мастер – за 30 минут. За сколько минут, работая вместе, они могут покрасить забор?

Решение

В данной задаче, в отличие от предыдущей, работа не выражена каким-либо числом. Сказано лишь то, что эту работу первый мастер может выполнить за 20 минут, а второй за 30 минут.

В такой ситуации можно воспользоваться дробями. Мы можем обозначить всю работу (покраску забора) через единицу.

Итак, обозначим работу (покраску забора) через единицу:

A = 1

Производительность первого мастера будет выражаться дробью . То есть, за одну минуту он покрасит одну двадцатую часть забора. Единица это вся работа, а двадцать минут это время работы. Запишем производительность первого мастера с помощью формулы нахождения производительности:

А производительность второго мастера будет выражаться дробью . То есть, за одну минуту он покрасит одну тридцатую часть забора:

Определим общую производительность мастеров. Для этого сложим дроби, выражающие производительность первого и второго мастеров:

 это дробь, выражающая общую производительность обоих мастеров. То есть, за одну минуту мастера вместе покрасят  часть забора.

Определим время за которое мастера покрасят забор вместе. Для этого воспользуемся формулой нахождения времени: разделим выполненную работу на общую производительность мастеров. Выполненная работа у нас выражена единицей, а производительность — дробью 

Ответ: работая вместе, мастера покрасят забор за 12 минут.

Задача 3. Первый рабочий может выполнить заказ за 8 часов, а второй за 6 часов. Два часа они работали вместе, а заканчивал работу один второй рабочий. Сколько времени потребовалось для выполнения этого заказа?

Решение

Обозначим всю работу через единицу

A = 1

Тогда первый рабочий за один час может выполнить  часть работы, а второй рабочий  часть работы. А вместе за один час они могут выполнить  часть работы

Рабочие работали вместе два часа, поэтому умножим часть работы, выполняемую ими за один час на 2:

Остальную часть работы, а именно  работы заканчивал один второй рабочий:

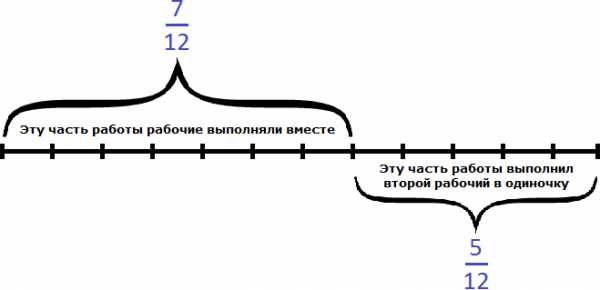
Второй рабочий за один час мог выполнить  часть работы. Чтобы определить время за которое он завершил оставшуюся  часть работы, воспользуемся формулой нахождения времени.

Переменная A теперь равна , переменная v — 

Теперь определим общее время заказа. Первые два часа рабочие работали вместе, остальную часть работы второй рабочий выполнил за два с половиной часа, отсюда имеем 4,5 ч.

2 + 2,5 = 4,5 ч.

Ответ: для выполнения заказа потребовалось 4,5 ч.

Задача 4. Одна труба наполняет бассейн за 6 ч, а другая – за 4 ч. Засколько часов наполняют бассейн обе трубы, работая вместе?

Решение

Обозначим работу (наполнение бассейна) через единицу

A = 1

Тогда первая труба за один час выполнит  часть работы, а вторая труба —  часть работы. Работая вместе за один час они выполнят  часть работы:

Определим время за которое обе трубы наполняют бассейн, работая вместе:

2,4 это два целых часа и четыре десятых часа

2,4 = 2 ч + 0,4 ч

А четыре десятых часа это 24 минуты

60 мин. × 0,4 = 24 мин.

Ответ: работая вместе обе трубы наполнят бассейн за 2 ч 24 мин.

Задачи для самостоятельного решения

Задача 1. Первая бригада может выполнить некоторое задание за 12 часов, вторая – за 4 часа. За сколько часов они выполнят задание, если будут работать вместе?

Решение

Обозначим работу через единицу:

A = 1

Тогда первая бригада за один час выполнит часть работы, а вторая за один час часть работы. Их общая производительность равна сумме дробей и :

Определим время за которое обе бригады выполнят задание, работая вместе:

Ответ: обе бригады выполнят задание за 3 часа.

Задача 2. Лошадь съедает копну сена за 1 сутки, корова может съесть такую же копну за 3 суток, а овца за 6 суток. За какое время съедят эту копну лошадь, корова и овца вместе.

Решение

Работа в данном случае это съедание копны сена. Обозначим её через единицу:

A = 1

Тогда производительность лошади будет выражаться единицей, производительность коровы — дробью , производительность овцы — дробью . Их совместная производительность равна следующей сумме:

Определим время, за которое лошадь, корова и овца съедят 1 копну сена:

Ответ: лошадь, корова и овца съедят 1 копну сена за суток или 16 часов.

Задача 3. Сосуд наполняется шлангом за 12 мин, а полный сосуд опорожняется при открытии крана за 20 мин. За какое время наполнится пустой сосуд, если одновременно открыть кран и вливать в него воду через шланг?

Решение

Работа в данном случае это наполнение сосуда. Обозначим эту работу через единицу:

A = 1

В условии сказано, что сосуд наполняется шлангом за 12 минут. Значит в минуту будет наполняться часть сосуда. При этом сказано, что одновременно открыт кран сосуда и из него вытекает вода, которой наполняется сосуд. Вода, которая вытекает равна части сосуда, поскольку в условии сказано, что полный сосуд опорожняется за 20 минут.

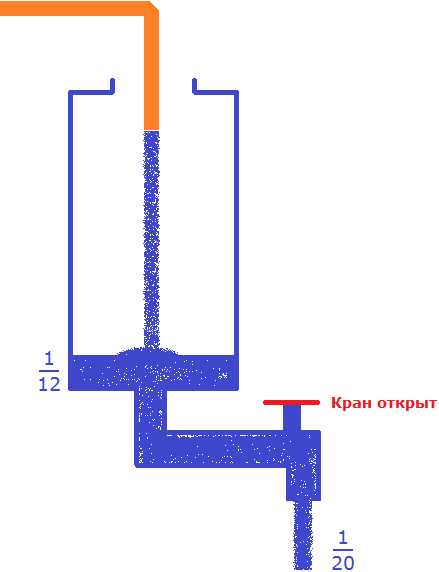
В сосуд поступает воды больше, чем вытекает. Дробь больше, чем .

Несмотря на то, что часть поступающей в сосуд воды будет вытекать, с каждой минутой сосуд будет пополняться на определенную часть. Узнаем, что эта за часть. Для этого из поступающей части вычтем ту часть, которая вытекает:

Каждую минуту сосуд будет наполняться на .

Определим время за которое наполнится пустой сосуд, если одновременно открыть кран и вливать в него воду через шланг:

Ответ: если одновременно открыть кран и вливать в пустой сосуд воду через шланг, то он наполнится за 30 минут.

Задача 4. Через первую трубу бассейн можно заполнить за 20 ч, через вторую за 30 ч. Какая часть бассейна заполниться через обе трубы за 1 ч?

Решение

Работа в данном случае это заполнение бассейна. Обозначим эту работу через единицу:

A = 1

Производительность заполнения бассейна через первую трубу будет выражаться дробью , через вторую трубу — дробью . Совместная производительность будет выражаться дробью

Производительность по определению есть работа, выполненная за единицу времени. Значит дробь является ответом к задаче, поскольку нас интересовало какая часть бассейна заполниться через обе трубы за 1 час. Это можно проверить, воспользовавшись формулой нахождения работы. Переменная v у нас имеет значение , а переменная t равна единице (одному часу). Формула нахождения работы позволит нам определить какая часть работы будет выполнена за 1 час:

Ответ: за один час заполниться часть бассейна.

Задача 5. На прокладку траншеи требуется затратить 10 ч. Экскаватор проработал 8 ч, после чего ему осталось пройти 50 м. Найти общую длину траншеи.

Решение

В задаче подразумевается, что экскаватор работал с одинаковой производительностью на протяжении всей работы. На работу требовалось затратить 10 ч. Проработано было 8 ч. Значит осталось еще 2 часа. На 2 часа приходятся оставшиеся 50 метров траншеи. Если разделить 50 метров на 2, то можно определить сколько метров экскаватор прокладывает за один час:

50 : 2 = 25 м./ч

В час экскаватор прокладывал 25 метров. Работал он 10 часов. Умножим 25 на 10, мы определим общую длину траншеи:

25 × 10 = 250 м

Ответ: общая длина траншеи составляет 250 м.

Задача 6. Ванна заполняется холодной водой за 6 мин 40 с, горячей – за 8 мин. Кроме того, если из полной ванны вынуть пробку, вода вытечет за 13 мин 20 с. Сколько времени понадобится, чтобы наполнить ванну полностью, при условии, что открыты оба крана, но ванна не заткнута пробкой?.

Решение

Для удобства переведем время данное в задаче в секунды

6 мин 40 с = 400 с 8 мин = 480 с 13 мин 20 с = 800 с

Обозначим заполнение ванны через единицу:

A = 1

Производительность первого крана будет выражаться дробью , производительность второго крана — дробью . Совместная производительность обоих кранов равна сумме дробей и

Одновременно с открытыми двумя кранами, вынута пробка из ванны. Поэтому часть поступающей в ванну воды сразу выходит через слив. Эта часть будет выражаться дробью .

С каждой секундой ванна будет пополняться на определенную часть воды. Узнаем какая это часть. Для этого из поступающей части воды вычтем ту часть, которая вытекает через слив.

Определим сколько времени понадобится, чтобы наполнить ванну:

Ванна наполниться за 300 секунд. Поскольку задача завершена, секунды можно обратно перевести в минуты. Триста секунд это пять минут:

300 : 60 = 5 мин

Ответ: ванна заполниться за 5 мин.

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Навигация по записям

spacemath.xyz

Производительность - это... Формула производительности

Производительность – это мера эффективности работы. При этом данный показатель используется как для оценки выполнения поставленных задач персоналом фирмы или предприятия, так и для функционирования станков, персональных компьютеров, их составных частей и отдельного программного обеспечения. Обычно под производительностью понимают количество продукции или объем перерабатываемой информации за час, минуту или секунду. Обратная к ней величина – трудоемкость – отражает время, которое затрачивается на выпуск или же анализ данных.

Основа эффективного бизнеса

Ключевым вопросом на повестке дня любого предприятия является рост производительности труда, т. е. сокращение затрат времени на изготовление продукции и увеличение объема без дополнительных расходов на наем новых рабочих. Поэтому стратегия и основанные на ней цели и задачи должны учитывать основные резервы ее повышения и факторы, стимулирующие персонал работать лучше в качественном и количественном аспекте. Без этого никакие конкурентные преимущества не смогут сделать предприятие лидером в отрасли.

Формула производительности

Экономическая статистика занимается изучением эффективности работы предприятия с помощью целого ряда показателей. Основными являются выработка и трудоемкость. Фактическая производительность – это как раз и есть количество продукции, выпускаемое на предприятии за определенный период времени. Если обозначить Q как выпуск товаров, T – затраты труда в часах, то можно составить формулу. Таким образом, производительность – это произведение Q и T, или P = Q х T.

Полученный результат отражает реальную эффективность работы предприятия. Для прогнозов рассчитывают наличную производительность. Это позволяет менеджерам или руководителю понять, какой максимальный объем продукции может выпускать предприятие на данном этапе развития технологии. Дополнительные издержки и вероятность простоев в этой формуле не учитываются.

Другие способы оценки эффективности

В отраслевой экономике оценка производительности труда (ПТ) осуществляется с помощью двух методов: прямого и факторного. Для первого способа нужны следующие показатели: выпуск продукции в текущем (О1) и базовом (О0) периодах, а также соответствующая им численность персонала (Ч1 и Ч0 соответственно). Таким образом,

ПТ = (О1 х Ч0/О0 х Ч1) х 100-100.

При использовании факторного счета производительность – это показатель, который рассчитывается в несколько этапов. На первом происходит классификация параметров. Факторы распределяются по группам: организационно-технические, объемные и структурные. Первый параметр связан с высвобождением работников и равен соотношению численности персонала в текущем периоде и разницы – по сравнению с предыдущим – в процентах.

Производительность труда по объемному фактору определяется произведением роста объема производства и удельного веса постоянных работников (в общей численности) в процентах, разделенным на 100. Структурная составляющая равна результату умножения трудоемкости на удельный вес этого продукта в общем выпуске. Общая производительность определяется сложением роста по каждому из трех факторов.

Повышение производительности труда

Основа ведения любого бизнеса – это рациональное и эффективное использование имеющихся ресурсов, в том числе и труда. Вполне логично, что менеджмент стремится увеличить объем выпускаемой продукции без дополнительных затрат на наем работников. Эксперты выделяют несколько факторов, которые позволяют улучшить производительность:

1. Управленческий стиль (главная задача руководителя – мотивировать персонал, создать организационную культуру, в которой ценится активность и трудолюбие).
2. Инвестиции в технические инновации (покупка нового оборудования, соответствующего запросам времени, позволяет значительно сократить временные затраты каждого работника).
3. Тренинги и семинары по повышению квалификации (знание специфики производства позволяет персоналу участвовать в совершенствовании производственного процесса).

Резервы эффективности персонала

Как показывает формула производительности, этот показатель не является неизменным, а может корректироваться целым рядом факторов. Среди них основное место занимают технический прогресс и правильная организация труда. Совершенствование технической составляющей производства, комплексная автоматизация функциональных процессов и налаживание коммуникации между отдельными подразделениями позволяют сократить временные затраты на выпуск. С другой стороны, рост производительности труда можно обеспечить за счет применения методов научного менеджмента. Однако важно понимать, что увеличение данного показателя не всегда способствует улучшению эффективности предприятия в целом. Это связано с тем, что, согласно классической экономической теории, факторами производства наряду с трудом является сырье (земля) и капитал.

Национальные особенности

Производство в экономике – это главный объект изучения на международном уровне. Поскольку в большинстве развитых стран мира наблюдается старение населения, то экстенсивный путь его расширения становится невозможным. Поэтому менеджмент обращается к интенсивному повышению эффективности труда. Россия по темпам прироста производительности опережает страны G7, Центральной и Восточной Европы. Этот показатель для РФ в среднем составляет 4%. Однако сейчас темпы стали постепенно замедляться, что связано с не совсем правильно выбранной моделью экономического роста.

В 2003-2008 годах эффективность труда улучшилась на 6%, а в 2014 – только на 0,8%. При этом производительность в различных отраслях возрастает неравномерно, поэтому эксперты предполагают, что высокая безработица может стать фактором выхода из кризиса. Это связано с тем, что увольнение работников в малоприбыльных отраслях приведет к переливу трудовой силы в более эффективные сегменты национального хозяйства.

fb.ru

Обозначения физических величин

Величины
Наименование	Обозначение
Механические величины
Вес	G, P, W
Время	t
Высота	h
Давление	p
Диаметр	d
Длина	l
Длина пути	s
Импульс (количество движения)	p
Количество вещества	ν, n
Коэффициент жесткости (жесткость)	Ʀ
Коэффициент запаса прочности	Ʀ, n
Коэффициент полезного действия	η
Коэффициент трения качения	Ʀ
Коэффициент трения скольжения	μ, f
Масса	m
Масса атома	ma
Масса электрона	me
Механическое напряжение	σ
Модуль упругости (модуль Юнга)	E
Момент силы	M
Мощность	P, N
Объем, вместимость	V, ϑ
Период колебания	T
Плотность	ϱ
Площадь	A, S
Поверхностное натяжение	σ, γ
Постоянная гравитационная	G
Предел прочности	σпч
Работа	W, A, L
Радиус	r, R
Сила, сила тяжести	F, Q, R
Скорость линейная	ϑ
Скорость угловая	ώ
Толщина	d, δ
Ускорение линейное	a
Ускорение свободного падения	g
Частота	ν, f
Частота вращения	n
Ширина	b
Энергия	E, W
Энергия кинетическая	EƦ
Энергия потенциальная	Ep
Акустические величины
Длина волны	λ
Звуковая мощность	P
Звуковая энергия	W
Интенсивность звука	I
Скорость звука	c
Частота	ν, f
Тепловые величины и величины молекулярной физики
Абсолютная влажность	a
Газовая постоянная (молярная)	R
Количество теплоты	Q
Коэффицент полезного действия	η
Относительная влажность	ϕ
Относительная молекулярная масса	Mr
Постоянная (число) Авогадро	NA
Постоянная Больцмана	Ʀ
Постоянная (число) Лошмидта	NL
Температура Кюри	TC
Температура па шкале Цельсия	t, ϴ
Температура термодинамическая (абсолютная температура)	T
Температурный коэффицент линейного расширения	a, ai
Температурный коффицент объемного расширения	β, av
Удельная теплоемкость	c
Удельная теплота парообразования	r
Удельная теплота плавления	λ
Удельная теплота сгорания топлива (сокращенно: теплота сгорания топлива)	q
Число молекул	N
Энергия внутренняя	U
Электрические и магнитные величины
Диэлектрическая проницаемость вакуума (электрическая постоянная)	Ԑo
Индуктивность	L
Коэффицент самоиндукции	L
Коэффицент трансформации	K
Магнитная индукция	B
Магнитная проницаемость вакуума (магнитная постоянная)	μo
Магнитный поток	Ф
Мощность электрической цепи	P
Напряженность магнитного поля	H
Напряженность электрического поля	E
Объемная плотность электрического заряда	ϱ
Относительная диэлектрическая проницаемость	Ԑr
Относительная магнитная проницаемость	μr
Плотность энергии магнитного поля удельная	ωm
Плотность энергии электрического поля удельная	ωэ
Плотность заряда поверхностная	σ
Плотность электрического тока	J
Постоянная (число) Фарадея	F
Проницаемость диэлектрическая	ԑ
Работа выхода электрона	ϕ
Разность потенциалов	U
Сила тока	I
Температурный коэффицент электрического сопротивления	a
Удельная электрическая проводимость	γ
Удельное электрическое сопротивление	ϱ
Частота электрического тока	f, ν
Число виток обмотки	N, ω
Электрическая емкость	C
Электрическая индукция	D
Электрическая проводимость	G
Электрический момент диполя молекулы	p
Электрический заряд (количество электричества)	Q, q
Электрический потенциал	V, ω
Электрическое напряжение	U
Электрическое сопротивление	R, r
Электродвижущая сила	E, Ԑ
Электрохимический эквивалент	Ʀ
Энергия магнитного поля	Wm
Энергия электрического поля	Wэ
Энергия Электромагнитная	W
Оптические величины
Длина волны	λ
Освещенность	E
Период колебания	T
Плотность потока излучения	Ф
Показатель (коэффицент) преломления	n
Световой поток	Ф
Света сила объектива	f
Сила света	I
Скорость света	c
Увеличение линейное	β
Увеличение окуляра, микроскопа, лупы	Ѓ
Угол отражения луча	έ
Угол падения луча	ԑ
Фокусное расстояние	F
Частота колебаний	ν, f
Энергия излучения	Q, W
Энергия световая	Q
Величины атомной физики
Атомная масса относительная	Ar
Время полураспада	T1/2
Дефект массы	Δ
Заряд электрона	e
Масса атома	ma
Масса нейтрона	mn
Масса протона	mp
Масса электрона	me
Постоянная Планка	h, ħ
Радиус электрона	re
Величины ионизирующих излучений
Поглощеная доза излучения (доза излучения)	D
Мощность поглощенной дозы излучения	Ď
Активность нуклида в радиоактивном источнике	A

nanomil.ru

Основные буквенные обозначения нагрузки

с. 1 ОСНОВНЫЕ БУКВЕННЫЕ ОБОЗНАЧЕНИЯ Нагрузки

F — сосредоточенная нагрузка;

G — то же постоянная;

V — временная;

S — снеговая;

W — ветровая;

g — распределенная нагрузка постоянная;

v — то же временная;

s — s снеговая;

w — ветровая.

Усилия от внешних нагрузок и воздействий

N — продольная сила;

Q — поперечная сила;

М — изгибающий момент. Параметры предварительного напряжения элемента

Ро — обобщенное усилие предварительного обжатия;

Р01, Р02 -— усилия обжатия элемента с учетом первых и всех потерь;

Мгр — момент силы Ро относительно ядровой точки;

σsр,σ'sp — предварительные напряжения соответственно в напрягаемой арматуре S и S' до обжатия бетона (при натяжении арматуры на упоры) либо в момент снижения значения предварительного напряжения в бетоне до нуля воздействием на элемент внешних фактических или условных сил;

σsр1, σ'sp1 - то же с учетом первых потерь;

σsр2, σ'sp2 то же с учетом всех потерь;

σbp - сжимающие напряжения в бетоне в стадии предварительного обжатия;

σcon 1, σ'con 1 - контролируемые напряжения в арматуре при натяжении соответственно на упоры и на бетон;

γsp — коэффициент точности натяжения арматуры. Характеристики материалов

Rb, Rb, ser- расчетные сопротивления бетона осевому сжатию для предельных состояний соответственно первой и второй групп;

Rbt, Rbt, serрасчетные сопротивления бетона осевому растяжению для предельных состояний соответственно первой и второй групп;

Rbp — передаточная прочность бетона;

Rs, Rs, ser — расчетные сопротивления арматуры растяжению для предельных состояний соответственно первой и второй групп;

Rsw - расчетное сопротивление поперечной арматуры растяжению;

Rsc - расчетное сопротивление арматуры сжатию для предельных состояний первой группы;

R - расчетное сопротивление каменной кладки и грунта сжатию;

Rt - расчетное сопротивление каменной кладки растяжению;

Rtb - расчетное сопротивление каменной кладки растяжению при изгибе;

Rtw - расчетное сопротивление каменной кладки главным растягивающим напряжениям при изгибе;

Rsc - расчетное сопротивление каменной кладки срезу;

Rtc - расчетное сопротивление дерева поперек волокон сжатию;

R ts - расчетное сопротивление дерева скалыванию;

Rz - расчетное сопротивление грунта слабого подстилающего слоя;

Eb — начальный модуль упругости бетона при сжатии и растяжении;

Es — модуль упругости арматуры;

E — модуль деформации каменной кладки и грунта;

υ — коэффициент Пуассона, коэффициент упругости;

cz— коэффициент жесткости постели.

Расчетные усилия (напряжения) в поперечном сечении элемента

Ncr — условная критическая сила;

Qb, Qw, Qinc — поперечные силы, воспринимаемые бетоном, хомутами {поперечными стержнями) и отгибами;

Мсrс — расчетный изгибающий момент, который может быть воспринят сечением железобетонного элемента перед образованием трещин;

Madm — расчетный изгибающий момент, который может быть воспринят сечением элемента перед разрушением;

σmc, σmt — главные сжимающие и главные растягивающие напряжения;

P min, Pmaх — максимальные и минимальные краевые давления под подошвой фундамента;

Fи — сила предельного сопротивления основания под фундаменты, несущая способность сваи по грунту.

Геометрические характеристики

Ь — ширина сечения элемента или подошвы фундамента;

h — высота сечения элемента;

bf, b' f — ширина полки таврового . и двутаврового сечений соответственно в растянутой и сжатой зонах;

hf, hf ' — высота полки таврового и двутаврового сечений соответственно в растянутой и сжатой зонах;

а, а ' — расстояния от равнодействующей усилий в арматуре соответственно в растянутой и сжатой зонах до ближайшей грани сечения;

h0 — рабочая высота сечения элемента;

х — высота сжатой зоны бетона или координата по длине элемента;

H — высота этажа или сооружения; толщина линейно-деформируемого слоя;

s — расстояние между хомутами в железобетонных элементах и сетками в каменных конструкциях;

е0 — эксцентриситет приложения продольной силы N относительно центра тяжести приведенного сечения;

е0p — эксцентриситет усилия предварительного обжатия Ро относительно центра тяжести приведенного сечения;

l— пролет элемента; длина;

l0 — расчетная длина элемента;

А — площадь сечения элемента, сечения арматуры, подошвы фундамента;

I — момент инерции сечения относительно его центра тяжести,

I — радиус инерция поперечного сечения элемента относительно его центра тяжести;

W — момент сопротивления сечения или подошвы фундамента;

µ — коэффициент армирования.

Индексы при буквенных обозначениях

adm — допустимый;

act — активный;

an — апкеровка;

b — балка, бетон, нижний;

con — контролируемый, контактный;

сr — критический, ригель;

сrс — трещина;

el — упругость;

fl — перекрытие;

inc — наклонная арматура;

h— горизонтальный;

j — шов;

к — шпонка;

l — длительный, пролет;

lin — перемычка;

loc — местный, смятие;

т — середина, среднее значение;

п — нормативный;

р — предварительное напряжение, простенок;

pan — панель;

pas — пассивный;

pl — пластичность, платформенный;

red — приведенный;

s — плита, сталь, грунт;

sup — опора;

ser — эксплуатационный;

sh — краткосрочный, сдвиг, срез, усадка;

t — верхний, время, растяжение;

tot — суммарный;

и — предельный;

υ — вертикальный, нижний;

w — ветер, стена;

wel — сварочный.с. 1

prerek.ru

Что такое мощность алфавита? Как находить мощность алфавита: формула

Современные компьютерные технологии, информатика, мощность алфавита, системы исчисления и многие другие понятия имеют самые непосредственные связи между собой. Очень немногие пользователи сегодня достаточно хорошо разбираются в этих вопросах. Попробуем прояснить, что такое мощность алфавита, как ее вычислять и применять на практике. В дальнейшем это, вне всякого сомнения, может пригодиться на практике.

Как измеряется информация

Прежде чем приступить к изучению вопроса о том, какова мощность алфавита, и вообще, что это такое, следует начать, так сказать, с азов.

Наверняка всем известно, что сегодня существуют специальные системы измерения каких-либо величин, на основе эталонных значений. Например, для расстояний и аналогичных величин это метры, для массы и веса – килограммы, для временных промежутков – секунды и т.д.

Но как же измерить информацию в смысле объема текста? Именно для этого и было введено понятие мощности алфавита.

Что такое мощность алфавита: начальное понятие

Итак, если следовать общепринятому правилу, что конечное значение какой-либо величины представляет собой параметр, определяющий, какое количество раз эталонная единица уложена в измеряемой величине, можно сделать вывод: мощность алфавита есть полное количество символов, использующихся для того или иного языка.

Чтобы было понятнее, оставим пока вопрос о том, как находить мощность алфавита, в стороне, и обратим внимание на сами символы, естественно, с точки зрения информационных технологий. Грубо говоря, полный список используемых символов содержит литеры, цифры, всевозможные скобки, специальные символы, знаки препинания, и т.д. Однако, если подходить к вопросу о том, что такое мощность алфавита именно компьютерным способом, сюда следует включить еще и пробел (единичный разрыв между словами или другими символами).

Возьмем в качестве примера русский язык, вернее, клавиатурную раскладку. Исходя из вышесказанного, полный перечень содержит 33 литеры, 10 цифр и 11 специальных знаков. Таким образом, полная мощность алфавита равна 54.

Информационный вес символов

Однако общее понятие мощности алфавита не определяет сущности вычислений информационных объемов текста, содержащего литеры, цифры и символы. Здесь требуется особый подход.

В принципе, задумайтесь, ну вот каким может быть минимальный набор с точки зрения компьютерной системы, сколько символов он может содержать? Ответ: два. И вот почему. Дело в том, что каждый символ, будь то буква или цифра, имеет свой информационный вес, по которому машина и распознает, что именно перед ней. Но компьютер понимает лишь представление в виде единиц и нулей, на чем, собственно, и основана вся информатика.

Таким образом, любой символ можно представить в виде последовательностей, содержащих цифры 1 и 0, то есть, минимальная последовательность, обозначающая букву, цифру или символ, состоит из двух компонентов.

Сам же информационный вес, принятый за стандартную информационную единицу измерения, называется битом (1 бит). Соответственно, 8 бит составляют 1 байт.

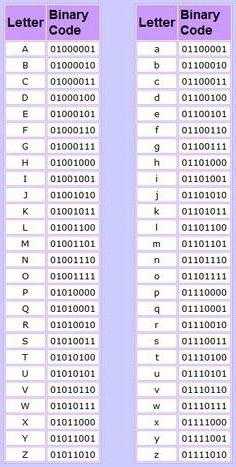
Представление символов в двоичном коде

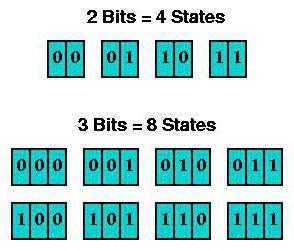
Итак, что такое мощность алфавита, думается, уже немного понятно. Теперь посмотрим на другой аспект, в частности, практическое представление мощности с использованием двоичного кода. В качестве примера для простоты возьмем алфавит, содержащий всего 4 символа.

В двузначном двоичном коде последовательность и их информационное представление можно описать следующим образом:

Порядковый номер	1-ый	2-ой	3-ий	4-ый
Двоичный код	00	01	10	11

Отсюда – простейший вывод: при мощности алфавита N=4 вес единичного символа составляет 2 бита.

Если использовать трехзначный двоичный код для алфавита, например, с 8 символами, количество комбинаций будет следующим:

Порядковый номер	1-ый	2-ой	3-ий	4-ый	5-ый	6-ой	7-ой	8-ой
Двоичный код	000	001	010	011	100	101	110	111

Иными словами, при мощности алфавита N=8 вес одного символа для трехзначного двоичного кода будет равен 3 битам.

Как находить мощность алфавита и использовать ее в компьютерном выражении

Теперь попробуем посмотреть на зависимость, которую выражает количество знаков в коде и мощность алфавита. Формула, где N – алфавитная мощность алфавита, а b – количество знаков в двоичном коде, будет выглядеть так:

N=2b

То есть, 21=2, 22=4, 23=8, 24=16 и т.д. Грубо говоря, искомое количество знаков самого двоичного кода и есть вес символа. В информационном выражении это выглядит так:

Мощность алфавита, N	2	4	8	16
Количество знаков кода, b	1 бит	2 бита	3 бита	4 бита

Измерение информационного объема

Однако это были всего лишь простейшие примеры, так сказать, для начального понимания того, что такое мощность алфавита. Перейдем непосредственно к практике.

На данном этапе развития компьютерной техники для набора текста с учетом заглавных, прописных и строчных букв, кириллических и латинских литер, знаков препинания, скобок, знаков арифметических действий и т.д. используется 256 символов. Исходя из того, что 256 это 28, нетрудно догадаться, что вес каждого символа в таком алфавите равен 8, то есть, 8 битам или 1 байту.

Если исходить из всех известных параметров, можно с легкостью получить нужное нам значение информационного объема любого текста. Например, у нас есть компьютерный текст, содержащий 30 страниц. На одной странице располагается 50 строк по 60 любых знаков или символов, включая и пробелы.

Таким образом, одна страница будет содержать 50 х 60= 3 000 байт информации, а весь текст – 3000 х 50=150000 байт. Как видим даже небольшие тексты измерять в байтах неудобно. А что говорить о целых библиотеках?

В данном случае лучше переводить объем в более мощные величины – килобайты, мегабайты, гигабайты и т.д. Исходя из того, что, например, 1 килобайт равен 1024 байта (210), а мегабайт – 210 килобайт (1024 килобайта), нетрудно посчитать, что объем текста в информационно-математическом выражении для нашего примера составит 150000/1024=146,484375 килобайт или приблизительно 0,14305 мегабайт.

Вместо послеловия

В общем и целом, это вкратце и все, что касается рассмотрения вопроса, что такое мощность алфавита. Остается добавить, что в данном описании был использован чисто математический подход. Само собой разумеется, что смысловая нагрузка текста в данном случае не учитывается.

Но, если подходить к вопросам рассмотрения именно с позиции, которая дает человеку что-то для осмысления, набор бессмысленного сочетания или последовательностей символов в этом плане будет иметь нулевую информационную нагрузку, хотя, с точки зрения понятия информационного объема, результат все равно можно вычислить.

В целом же, знания о мощности алфавита и сопутствующих понятиях не так уж и сложны для понимания и элементарно могут применяться в смысле практических действий. При этом любой пользователь практически каждый день сталкивается с этим. Достаточно привести в пример популярный редактор Word или любой другой такого же уровня, в котором используется такая система. Но не путайте его с обычным «Блокнотом». Здесь мощность алфавита ниже, поскольку при наборе текста не используются, скажем, прописные буквы.

fb.ru

Значение - производительность - Большая Энциклопедия Нефти и Газа, статья, страница 3

Значение - производительность

Cтраница 3

В табл. 46 приведены значения производительности и числа разгрузок для экскаваторов различных типоразмеров при работе в разных группах грунтов.  [31]

В табл. 31.1 приведены значения производительности, характеристики упрочнения поверхностного слоя и среднее арифметическое отклонение микропрофиля обработанной поверхности для различных материалов и методов обработки на оптимальных режимах.  [33]

Следует отметить, что значение производительности существенно зависит от ресурсов памяти УВК, в первую очередь оперативной. В приведенной выше формуле для оценки производительности это положение учитывается. Однако на этапе разработки алгоритма управления и схемы информационных потоков в системе технологический процесс - АСУ ТП важно оценивать такой параметр, как средний объем оперативной памяти за единицу времени.  [35]

На рис. 11 показаны значения производительности винтового питателя и транспортирующего конвейера погрузчика в зависимости от п и VK при перегрузке щебня.  [37]

В табл. 10 приведены значения производительности различных электродегидраторов и соответствующих им линейных скоростей в зоне электродов.  [38]

Суммируют отдельно для каждого значения производительности значения АР различных участков головки.  [39]

В таблице 10 даны значения минимально допустимой производительности ЭЦН, ниже которой их эксплуатация запрещена.  [40]

Сравнение прогнозируемого и фактического значений производительности труда за 1971 - 1974 гг. подтверждает достаточную достоверность прогноза для практических целей.  [41]

Видно, что одному значению производительности соответствует целый ряд значений суточных расходов пара.  [43]

На практике часто пользуются значением производительности катализатора, под которой подразумевают количество данного продукта, образующегося в единицу времени на единице объема катализатора.  [44]

Во всех приведенных примерах указано значение производительности для случая получения продуктов с суммарным содержанием органических примесей не более 0 1 на колонне диаметром 80 мм.  [45]

Страницы:      1    2    3    4    5

www.ngpedia.ru

---

• 
  Устройства автоматизации
• 
  Как сделать сварочный аппарат своими руками
• 
  Что называется изображением протяженного источника света
• 
  Взрыв в чернобыле атомного реактора
• 
  Маркировка твердотельные конденсаторы
• 
  Предохранитель пк 10 расшифровка
• 
  Фланцевый электродвигатель
• 
  Почему вместо горячей воды бежит холодная
• 
  Кабели из сшитого полиэтилена характеристики
• 
  Как сделать сварочный аппарат своими руками
• 
  Документы для заключения договора энергоснабжения для юридических лиц