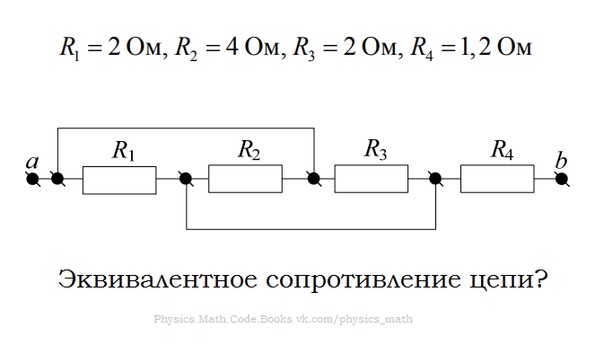
Расчет простой электрической цепи методом эквивалентных сопротивлений.
Решение:
|
1.4. Способы соединения сопротивлений и расчет эквивалентного сопротивления электрической цепи
Сопротивления
в электрических цепях могут быть
соединены последовательно, параллельно,
по смешанной схеме и по схемам «звезда»,
«треугольник».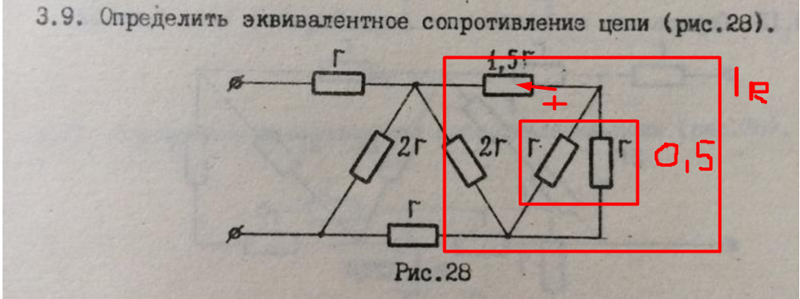 Расчет сложной схемы
Расчет сложной схемы
упрощается, если сопротивления в этой
схеме заменяются одним эквивалентным
сопротивлением Rэкв,
и вся схема представляется в виде схемы
на рис. 1.3, где R=Rэкв,
а расчет токов и напряжений производится
с помощью законов Ома и Кирхгофа.
Электрическая
цепь с последовательным соединением
элементов
Рис. | Рис. |
Последовательным
называют такое соединение элементов
цепи, при котором во всех включенных в
цепь элементах возникает один и тот же
ток I (рис. 1.4).
На
основании второго закона Кирхгофа (1.5)
общее напряжение U всей цепи равно сумме
напряжений на отдельных участках:
U
= U1
+ U2
+ U3 или
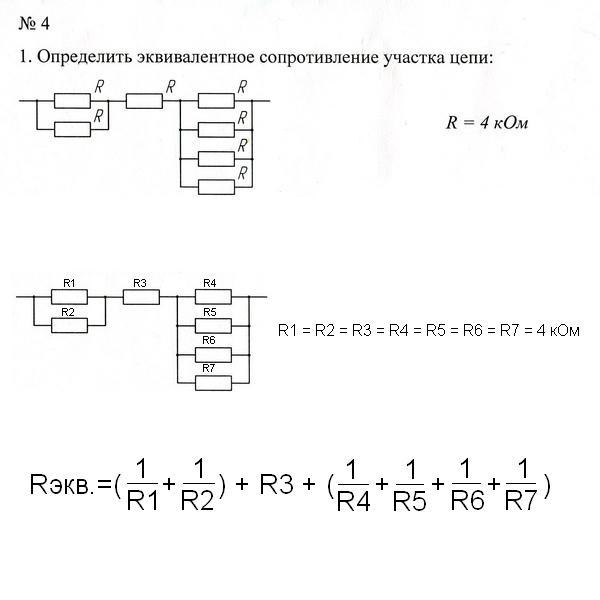
IRэкв
= IR1
+ IR2
+ IR3,
откуда
следует
(1. 5)
5)
Rэкв
= R1
+ R2
+ R3.
Таким
образом, при последовательном соединении
элементов цепи общее эквивалентное
сопротивление цепи равно арифметической
сумме сопротивлений отдельных участков.
Следовательно, цепь с любым числом
последовательно включенных сопротивлений
можно заменить простой цепью с одним
эквивалентным сопротивлением Rэкв
(рис. 1.5). После этого расчет цепи
сводится к определению тока I всей цепи
по закону Ома
,
и
по вышеприведенным формулам рассчитывают
падение напряжений U1,
U2,
U3
на соответствующих участках электрической
цепи (рис. 1.4).
Недостаток
последовательного включения элементов
заключается в том, что при выходе из
строя хотя бы одного элемента, прекращается
работа всех остальных элементов цепи.
Электрическая
цепь с параллельным соединением элементов
Параллельным
называют такое соединение, при котором
все включенные в цепь потребители
электрической энергии, находятся под
одним и тем же напряжением (рис. 1.6).
1.6).
Рис.
1.6
В
этом случае они присоединены к двум
узлам цепи а и b, и на основании первого
закона Кирхгофа (1.3) можно записать, что
общий ток I всей цепи равен алгебраической
сумме токов отдельных ветвей:
I
= I1
+ I2
+ I3,
т.е.
,
откуда
следует, что
(1.6)
.
В
том случае, когда параллельно включены
два сопротивления R1
и R2,
они заменяются одним эквивалентным
сопротивлением
(1.7)
.
Из
соотношения (1.6), следует, что эквивалентная
проводимость цепи равна арифметической
сумме проводимостей отдельных ветвей:
gэкв
= g1
+ g2
+ g3.
По
мере роста числа параллельно включенных
потребителей проводимость цепи gэкв
возрастает, и наоборот, общее сопротивление
Rэкв
уменьшается.
Напряжения
в электрической цепи с параллельно
соединенными сопротивлениями (рис. 1.6)
U
= IRэкв
= I1R1
= I2R2 =
I3R3.
Отсюда
следует, что
,
т.е.
ток в цепи распределяется между
параллельными ветвями обратно
пропорционально их сопротивлениям.
По
параллельно включенной схеме работают
в номинальном режиме потребители любой
мощности, рассчитанные на одно и то же
напряжение. Причем включение или
отключение одного или нескольких
потребителей не отражается на работе
остальных. Поэтому эта схема является
основной схемой подключения потребителей
к источнику электрической энергии.
Электрическая
цепь со смешанным соединением элементов
Смешанным
называется такое соединение, при котором
в цепи имеются группы параллельно и
последовательно включенных сопротивлений.
Рис.
1.7
Для
цепи, представленной на рис. 1.7, расчет
эквивалентного сопротивления начинается
с конца схемы. Для упрощения расчетов
примем, что все сопротивления в этой
схеме являются одинаковыми: R1=R2=R3=R4=R5=R.
Сопротивления R4
и R5
включены параллельно, тогда сопротивление
участка цепи cd равно:
.
В
этом случае исходную схему (рис. 1.7)
можно представить в следующем виде
(рис. 1.8):
Рис.
1.8
На
схеме (рис. 1.8) сопротивление R3
и Rcd
соединены последовательно, и тогда
сопротивление участка цепи ad равно:
.
Тогда
схему (рис. 1.8) можно представить в
сокращенном варианте (рис. 1.9):
Рис.
1.9
На
схеме (рис.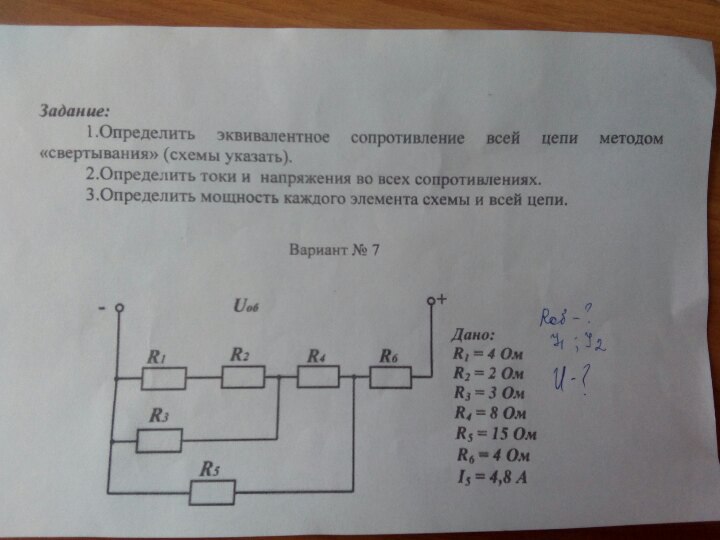 1.9) сопротивление R2
1.9) сопротивление R2
и Rad
соединены параллельно, тогда сопротивление
участка цепи аb равно
.
Схему
(рис. 1.9) можно представить в упрощенном
варианте (рис. 1.10), где сопротивления
R1
и Rab
включены последовательно.
Тогда
эквивалентное сопротивление исходной
схемы (рис. 1.7) будет равно:
.
Рис. | Рис. |
В
результате преобразований исходная
схема (рис. 1.7) представлена в виде
схемы (рис. 1.11) с одним сопротивлением
Rэкв.
Расчет токов и напряжений для всех
элементов схемы можно произвести по
законам Ома и Кирхгофа.
Соединение
элементов электрической цепи по схемам
«звезда» и «треугольник»
В
электротехнических и электронных
устройствах элементы цепи соединяются
по мостовой схеме (рис.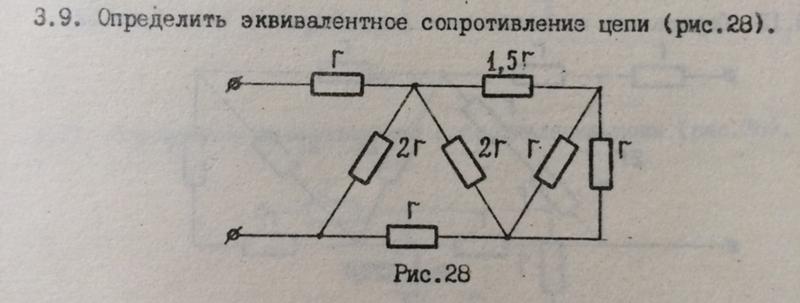 1.12). Сопротивления
1.12). Сопротивления
R12,
R13,
R24,
R34
включены в плечи моста, в диагональ 1–4
включен источник питания с ЭДС Е, другая
диагональ 3–4 называется измерительной
диагональю моста.
Рис. | Рис. |
В
мостовой схеме сопротивления R13,
R12,
R23
и R24,
R34,
R23
соединены по схеме «треугольник».
Эквивалентное сопротивление этой схемы
можно определить только после замены
одного из треугольников, например
треугольника R24
R34
R23
звездой R2
R3
R4
(рис. 1.13). Такая замена будет
эквивалентной, если она не вызовет
изменения токов всех остальных элементов
цепи. Для этого величины сопротивлений
звезды должны рассчитываться по следующим
соотношениям:
(1. 8)
8)
;
;
.
Для
замены схемы «звезда» эквивалентным
треугольником необходимо рассчитать
сопротивления треугольника:
(1.9)
;
;
.
После
проведенных преобразований (рис. 1.13)
можно определить величину эквивалентного
сопротивления мостовой схемы (рис. 1.12)
.
1.1.2 Решение типовых задач
Задача
1.1. Генератор
постоянного тока бортовой сети самолета
при токе 20 А имеет на зажимах напряжение
200 В, а при токе 60 А – 196 В. Определить
внутреннее сопротивление и ЭДС источника
электрической энергии. Построить внешнюю
характеристику.
Решение
Генератор является
реальным источником ЭДС и имеет схему
замещения (рис.1.1.10 а). Основной
характеристикой, связывающей напряжение
на генераторе и ток нагрузки, является
вольтамперная характеристика, называемая
внешней
характеристикой.
Она описывается уравнением U
= E
— R0I
и представляет
собой прямую линию (рис. 1.1.10 ,б).
Рис. 1.1.10
Заданы
два рабочих режима (точки 1 и 2), описываемых
этим уравнением, следовательно можно
составить систему из этих двух уравнений,
путем решения которой определить E
и R0:
Откуда
E
= 202 В, R0
= 0,1 Ом.
Задача
1.2. Заданы
параметры элементов электрической цепи
Е, B,
R1,
Ом:
определить
токи в ветвях;определить
показание вольтметра PV.
Решение
Цепь
имеет один источник ЭДС, поэтому для
определения токов в ветвях необходимо
воспользоваться методом эквивалентных
преобразований, т.е. сложное смешанное
соединение приемников (рис. 1.1.11,а) путем
1.1.11,а) путем
поэтапных преобразований привести к
простейшему виду (рис. 1.1.11,б)
Исходное
направление токов в ветвях выбирают
произвольно. Цепь имеет 5 ветвей и 3 узла.
Вольтметр не создает пути для протекания
тока, так как Rv,
поэтому в расчетную схему его не включают.
1.
Определение эквивалентного сопротивления
Rэ.
Схема
«сворачивается» к источнику ЭДС.
Сопротивления R5
и
R6
соединены
параллельно, их эквивалентное сопротивление
определяется из условия:
или
.
Сопротивление
R4
соединено
последовательно с R56
R456=
R4+
R56=24+6=30
Ом.
Сопротивления
R2
и
R3
соединены
последовательно (представляют собой
одну ветвь)
R23=
R2+
R3=10+20=30
Ом.
В
результате проведенных преобразований
схема имеет вид (рис. 1.3, а).
Сопротивления
R23
и
R456
соединены параллельно, так как имеют
общие узлы а
и с
Сопротивление
R1
соединено
с R23456
последовательно, это и будет эквивалентное
сопротивление (рис. 1.1.12, б)
Rэ=
R1+
R23456=10+15=25
Ом.
2. Определение токов в ветвях.
Ток, протекающий
через источник,
Остальные токи
определяются по I
и II
законам Кирхгофа.
Для
контура, содержащего сопротивления R1,
R2
и
R3,
можно
составить уравнение по II
закону Кирхгофа. Направление обхода
выбирают произвольно, например, против
часовой стрелки
R1
I1+
R2I2+R3I2=E,
.
Ток
I4
определяется по I
закону Кирхгофа, уравнение для узла а
имеет вид: I1
— I2
— I4
= 0; I4
= I1—
I2
= 10 – 5 = 5 А.
Токи
I5
и I6
можно определить аналогично токам I2
и I4
по законам Кирхгофа, или с точки зрения
удобства воспользоваться формулами
разброса
,
.
Эти
формулы получены из условия, что токи
в ветвях обратно – пропорциональны
сопротивлениям рассматриваемых ветвей.
3.Определение
показаний вольтметра pV.
Вольтметр
можно заменить стрелкой напряжения Vвd
произвольного направления (рис. 1.1.12).
Для этого контура напряжений уравнение
по II
закону Кирхгофа имеет вид
отсюда
.
Знак
«минус» показывает, что выбранное
направление напряжения ошибочно,
истинное направление противоположно,
а показание вольтметра pV
составит 70
В.
4. Анализ результатов
– составление баланса мощностей.
Для
проверки правильности выполненного
решения необходимо составить баланс
мощностей – мощность, производимая
источником, равна сумме мощностей,
производимых приемниками
Pист=
EI1
= 25010
=2500 Вт,
Баланс выполняется,
значит токи определены верно.
Задача
1.3. Определить
входное сопротивление цепи Raв.
Решение
Исходную
схему (рис. 1.1.13, а) необходимо преобразовать
к удобному виду. Линии аа
и bb
не имеют собственного сопротивления.
Они соединяют равнопотенциальные точки,
поэтому цепь имеет вид (рис. 1.5, б).
Эквивалентное
сопротивление относительно точек аb
равно:
Задача
1. 4. Определить
4. Определить
входное сопротивление цепи Rab.
Решение
Заземленные
узлы в исходной схеме являются
равнопотенциальными (=0),
поэтому их можно «стянуть» в одну точку
с;
в результате образуется схема (рис.
1.1.14, б), в которой сопротивления R5
и R6
находятся между точками равного
потенциала, ток через них не пойдет,
поэтому они не будут влиять на входное
сопротивление цепи Rab.
Заземленные
узлы в исходной схеме являются
равнопотенциальными (=0),
поэтому их можно «стянуть» в одну точку
с;
в результате образуется схема (рис.
1.1.14, б), в котором сопротивления R5
и R6
находятся между точками равного
потенциала, ток через них не пойдет,
поэтому они не будут влиять на входное
сопротивление цепи Rab.
Эквивалентное
сопротивление
.
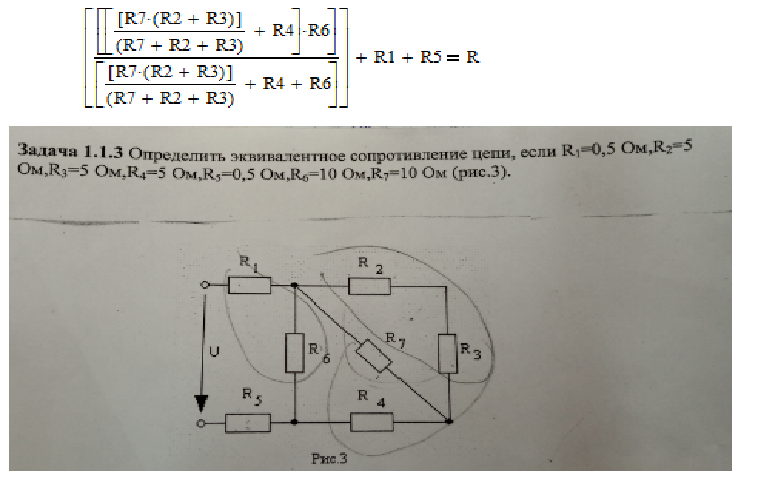
Задача
1. 5.
5.
В схеме измерительного моста заданы
параметры электрической цепи E
[В],
Ri
[Ом]. Определить ток I.
Решение:
В
исходной схеме измерительного моста
(рис. 1.1.15,а) сопротивления R1,
R2,
R3,
R4,
R5
–
соединены
между собой
либо «звездой», либо «треугольником».
Для определения эквивалентного
сопротивления цепи необходимо один из
треугольников преобразовать в звезду
(рис. 1.1.15,б) либо наоборот. Используем
готовые формулы такого преобразования
Сопротивления
R51
и R4,
а также
R25
и R3
оказались соединенными последовательно,
их эквивалентные сопротивления равны:
R514=R51+R4=0,435+1,2=1,635
Ом;
R253=R25+R3=0,696+2=2,696
Ом.
В
результате эквивалентное сопротивление
цепи (рис. 1.1.15, в) составит:
.
Ток,
потребляемый измерительной схемой
Задача 1.6.
Определить показания вольтметра pV
(рис.1.1.16) и
указать, в каких режимах работают
источники ЭДС (Ri,
Ом, Ej,
B).
Как определить величину эквивалентного сопротивления
К выполнению контрольной работы
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Пример методики решения задачи №1. «Расчет цепей постоянного тока»
Для схемы, приведенной на рисунке 1.1, заданы сопротивления резисторов и ток I4 в резисторе R4. Определить:
1.эквивалентное сопротивление цепи RAB,
2. токи в каждом резисторе,
3. напряжение UAB, приложенное к цепи.
Решение.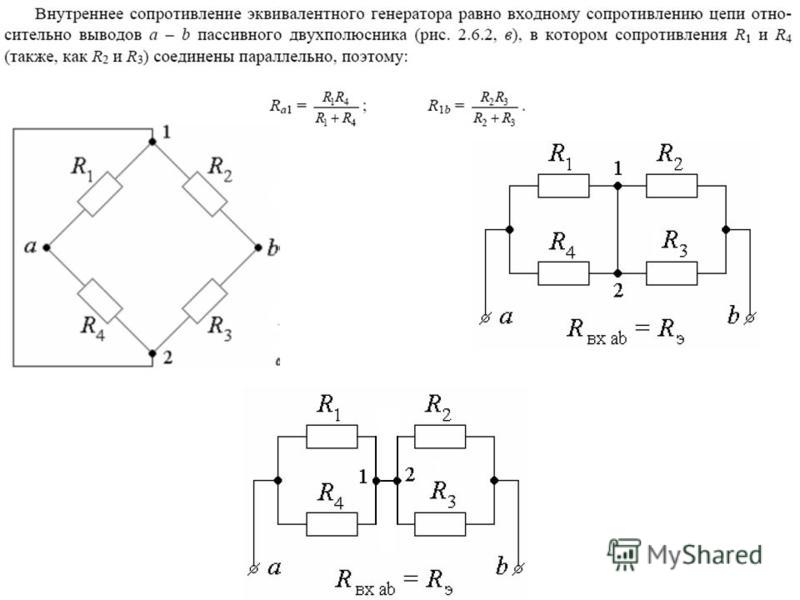 Задача относится к теме «Электрические цепи постоянного тока» После усвоения условия задачи приводим поэтапное решение, предварительно обозначив стрелкой направление тока в каждом резисторе. Индекс тока должен соответствовать номеру резистора, по которому он проходит.
Задача относится к теме «Электрические цепи постоянного тока» После усвоения условия задачи приводим поэтапное решение, предварительно обозначив стрелкой направление тока в каждом резисторе. Индекс тока должен соответствовать номеру резистора, по которому он проходит.
1.1. Определяем общее сопротивление разветвления R2, R3. Резисторы соединены
= Ом
Теперь схема принимает вид, показанный на рисунке 1.2
1.2 Резисторы R2,3 и R5 соединены последовательно, их общее сопротивление
Соответствующая схема приведена на рисунке 1.3
1.2. Резисторы R2,3,5 и R4 соединены параллельно, их общее сопротивление
Ом
Теперь схема цепи имеет вид, приведенный на рисунке 1.4
1.3. Находим эквивалентное сопротивление всей цепи:
2.Определение токов в резисторах
2.1.Зная силу тока I4, находим напряжение на резисторе R4:
Это же напряжение приложено к резисторам R2,3 +R5 (рисунок 1. 2.). Поэтому ток в
2.). Поэтому ток в
2.2 Находим падение напряжения на резисторе R5:
Поэтому напряжение на резисторах R2 и R3:
2.3 Определяем токи в резисторах R2 и R3 :
Применяя закономерности параллельного соединения резисторов, находим ток в резисторе R1:
2.4. Вычисляем падение напряжения на резисторе R1:
3. Находим напряжение UAB, приложенное ко всей цепи:
Задача 1 (Варианты 01 – 30)
Цепь постоянного тока содержит шесть резисторов, соединенных смешанно. Схема цепи и значения резисторов указаны на соответствующем рисунке. Номер рисунка и величина одного из заданных токов или напряжений приведена в таблице 3. Индекс тока или напряжения совпадает с индексом резистора, по которому проходит этот ток или на котором действует указанное напряжение. Например, через резистор R5 проходит ток I5 и на нем действует напряжение U5.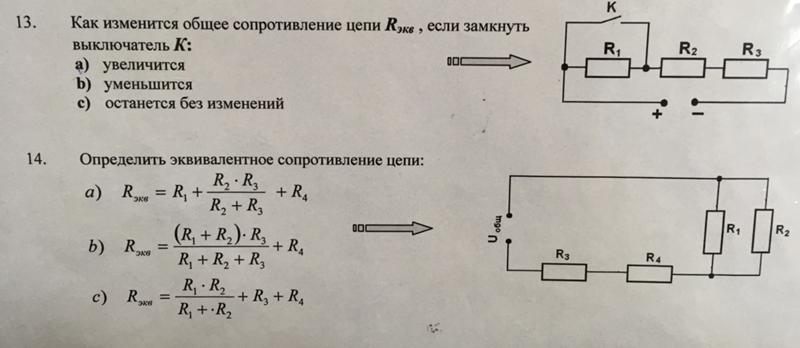 Определить:
Определить:
1) эквивалентное сопротивление цепи относительно вводов АВ;
2) ток в каждом резисторе;
3) напряжение на каждом резисторе;
4) расход электрической энергии цепью за 10 часов.
Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением Rэкв, и вся схема представляется в виде схемы на рис. 1.3, где R=Rэкв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа.
Электрическая цепь с последовательным соединением элементов
Рис. 1.4
Рис. 1.5
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).
На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением Rэкв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома
Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением Rэкв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома
,
и по вышеприведенным формулам рассчитывают падение напряжений U1, U2, U3 на соответствующих участках электрической цепи (рис. 1.4).
Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).
В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:
I = I1 + I2 + I3, т. е. ,
е. ,
откуда следует, что
.
В том случае, когда параллельно включены два сопротивления R1 и R2, они заменяются одним эквивалентным сопротивлением
.
Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:
По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление Rэкв уменьшается.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)
Отсюда следует, что
,
т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.
Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R1=R2=R3=R4=R5=R. Сопротивления R4 и R5 включены параллельно, тогда сопротивление участка цепи cd равно:
.
В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):
На схеме (рис. 1.8) сопротивление R3 и Rcd соединены последовательно, и тогда сопротивление участка цепи ad равно:
.
Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):
На схеме (рис. 1.9) сопротивление R2 и Rad соединены параллельно, тогда сопротивление участка цепи аb равно
.
Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R1 и Rab включены последовательно.
Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:
.
Рис. 1.10
Рис. 1.11
В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением Rэкв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.
Соединение элементов электрической цепи по схемам «звезда» и «треугольник»
В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 1.12). Сопротивления R12, R13, R24, R34 включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.
Рис. 1.12
Рис. 1.13
В мостовой схеме сопротивления R13, R12, R23 и R24, R34, R23 соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника R24 R34 R23 звездой R2 R3 R4 (рис. 1.13). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям:
Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника R24 R34 R23 звездой R2 R3 R4 (рис. 1.13). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям:
; ; .
Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника:
; ; .
После проведенных преобразований (рис. 1.13) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 1.12)
.
Расчёт электрических схем, содержащих несколько сопротивлений (резисторов), при нахождении силы тока в цепи, напряжения или мощности, производится с использованием метода свёртывания. Метод заключается в том, чтобы найти эквивалентное сопротивление выделенных участков цепи. Основная задача – замена резисторов, имеющих различное подключение относительно друг друга, на эквивалент (Rэкв.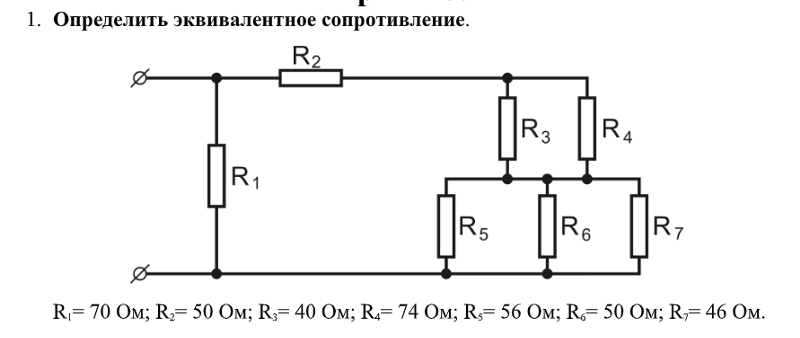 ).
).
Определение эквивалентного сопротивления
При рассмотрении схем любых электрических или электронных устройств можно увидеть, что такие компоненты, как резисторы, имеют разные типы соединений между собой. Чтобы определить эквивалентное соединение, необходимо рассматривать два элемента, включенных в определённом порядке. Несмотря на то, что на чертеже их может быть несколько десятков, и соединены они по-разному, есть только два типа включения их друг с другом: последовательное и параллельное. Остальные конфигурации – это лишь их вариации.
Последовательное соединение элементов
Подобное включение подразумевает комбинацию деталей в прямой последовательности. Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же.
Внимание! Снижение потенциала на каждом резистивном элементе в сумме даст полное напряжение, приложенное к последовательной цепи.
В случае постоянного тока формула закона Ома для отрезка цепи имеет вид:
Сила тока зависит от приложенного напряжения и оказанного ему сопротивления. Если выразить R, его формула:
Параметры последовательной цепи, включающей n соединённых друг с другом элементов, имеют свои особенности.
Проходящий по цепи ток везде одинаковый:
Прикладываемое напряжение является суммой напряжений на каждом резисторе:
Следовательно, рассчитать можно общее:
Rэкв.= U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn.
Важно! Последовательная цепь, имеющая в своём составе N резисторов равного номинала, имеет эквивалентное сопротивление Rэкв. = N*R.
Параллельное соединение
Когда условные выходы деталей имеют общий контакт в одной точке (узле) схемы, а условные входы так же объединены во второй, говорят о параллельном соединении. Узел на чертеже обозначается графической точкой. Это место, где происходят разветвления цепей в схемах. Такой вариант подключения резисторов обеспечивает одинаковое падение напряжения U для всех параллельных элементов. Ток в этой позиции будет равен сумме токов, идущих по каждому компоненту.
Узел на чертеже обозначается графической точкой. Это место, где происходят разветвления цепей в схемах. Такой вариант подключения резисторов обеспечивает одинаковое падение напряжения U для всех параллельных элементов. Ток в этой позиции будет равен сумме токов, идущих по каждому компоненту.
Когда в параллельное подключение входит n резистивных элементов, то разность потенциалов, ток и общее сопротивление будут иметь следующие выражения:
- общий ток: I = I1 + I2 + … + In;
- общее напряжение: U = U1 = U2 = … = Un;
- Rобщ. = Rэкв. = U/I1 + U/I2 + …+ U/In) = 1/R1 + 1/R2 +…+ 1/Rn.
Величину, обратно пропорциональную сопротивлению 1/R, называют проводимостью.
Если n равных по номиналу сопротивлений включить параллельно, то Rэкв. = (R*R)/n*R = R/n. Формула подходит и для индуктивных сопротивлений проволочных катушек и ёмкостных сопротивлений конденсаторов.
Расчёт при смешанном соединении устройств
Произвести расчет сопротивления цепи, когда она разветвлена и наполнена разными видами резистивных соединений, просто не получится. Затрудняет решение задачи множество участков, где детали подключены друг другу в разных комбинациях. В таких обстоятельствах желательно выполнять ряд преобразований, добиваясь упрощения схемы вводом отдельных эквивалентных элементов. Выявляют при этом подходящие контуры последовательных и параллельных присоединений.
Затрудняет решение задачи множество участков, где детали подключены друг другу в разных комбинациях. В таких обстоятельствах желательно выполнять ряд преобразований, добиваясь упрощения схемы вводом отдельных эквивалентных элементов. Выявляют при этом подходящие контуры последовательных и параллельных присоединений.
Например, выискав некоторое количество последовательных подключений резисторов, заменяют их на один эквивалентный компонент. Определив элементы, соединённые последовательно, также рисуют вместо него эквивалент. Вновь начинают искать подобные простые соединения.
Метод называют «методом свёртывания». Схему упрощают до тех пор, пока в ней не останется одно Rэкв.
Важно! Метод эквивалентных преобразований применяется тогда, когда питание рассматриваемого участка цепи осуществляется от одного источника электрического тока, а также при определении Rэкв. в замкнутом контуре с одной ЭДС.
Такой относительный способ определения Rэкв используют и для изучения зависимости токов в некоторой цепи от значения R нагрузки.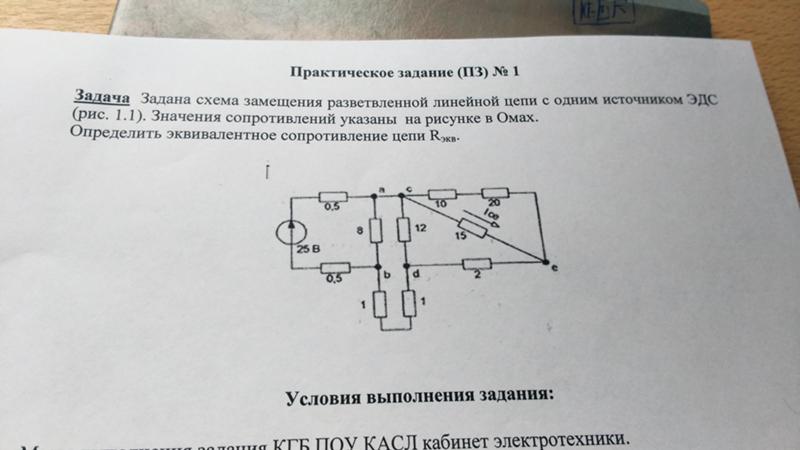 Это метод эквивалентного генератора, при котором сложный двухполюсник, являющийся активным, представляют эквивалентным генератором. При этом считают, что ЭДС его соответствует Uх.х. (холостого хода) на зажимах, R внутреннее соответствует R входному двухполюсника пассивного на тех же зажимах. Для такого определения источники тока разъединяют, а канал ЭДС закорачивают.
Это метод эквивалентного генератора, при котором сложный двухполюсник, являющийся активным, представляют эквивалентным генератором. При этом считают, что ЭДС его соответствует Uх.х. (холостого хода) на зажимах, R внутреннее соответствует R входному двухполюсника пассивного на тех же зажимах. Для такого определения источники тока разъединяют, а канал ЭДС закорачивают.
Физические формулы и примеры вычислений
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.
У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.
Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.
Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:
- R1 = 1 Ом;
- R2 = 2 Ом;
- R3 = 3 Ом;
- R4 = 6 Ом;
- R5 = 9 Ом;
- R6 = 18 Ом;
- R7 = 2Ом;
- R8 = 2Ом;
- R9 = 8 Ом;
- R10 = 4 Ом.
Напряжение, поданное на схему:
Требуется рассчитать токи на всех резистивных элементах.
Для расчётов применяется закон Ома:
I = U/R, подставляя вместо R эквивалентное сопротивление.
Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте.
Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.
На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:
- АВ – участок, имеющий две параллельных ветви;
- ВС – отрезок, вмещающий в себя последовательное сопряжение;
- CD – отрезок схемы с расположением трёх параллельных цепочек.
Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.
Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.
Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:
- Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
- Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
- Rэкв.
 7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.
7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.
Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.
Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:
- Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
- Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
- 1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.
В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.
Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков:
Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.
Далее, используя закон Ома, находят ток в последнем последовательном участке:
I = U/ Rэкв.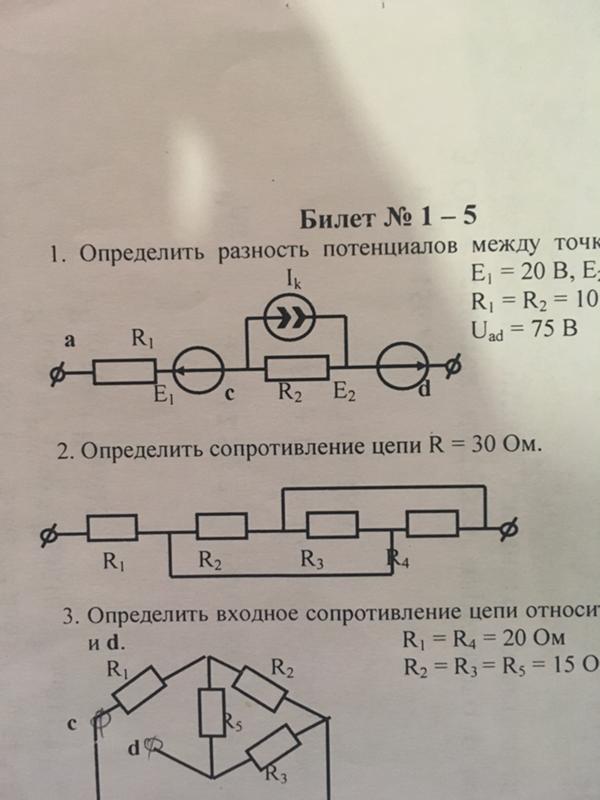 = 24/56,83 = 0,42 А.
= 24/56,83 = 0,42 А.
Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:
- UAB = I* Rэкв.AB= 0,42*0,83 = 0,35 В;
- UBC = I* Rэкв.BC= 0,42*15 = 6,3В;
- UCD = I* Rэкв.CD = 0,42*0,41 = 0,17 В.
Следующим шагом станет определение токов на параллельных отрезках AB и CD:
- I1 = UAB/R1 = 0,35/1 = 0,35 А;
- I2 = UAB/Rэкв.2,3 = 0,35/5 = 0,07 А;
- I3 = UCD/R6 = 0,17/18 = 0,009 А;
- I6 = UCD/Rэкв.7,8,9= 0,17/9 = 0,02 А;
- I7 = UCD/R10 = 0,17/4 = 0,04 А.
Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9.
U9 = R9*I6 = 8*0,02 = 0,16 В.
Теперь напряжение, падающее на Rэкв.7,8, будет разностью между U CD и U9.
U7,8 = UCD – U9= 0,17 – 0,16 = 1 В.
После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:
- I4 = U7,8/R7 = 1/2 = 0,5 A;
- I5 = U7,8/R8 = 1/2 = 0,5 A.
Стоит заметить! Ток, протекающий через R4 и R5, по своему значению равен току на отрезке, не имеющем разветвления.
Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов.
Видео
Сложные цепи. Метод эквивалентного преобразования схемы — Студопедия
Метод эквивалентного преобразования схемы используют при расчете простых электрических цепей. В отдельных случаях имеется возможность применить его и для расчета сложных электрических цепей.
В отдельных случаях имеется возможность применить его и для расчета сложных электрических цепей.
Суть метода эквивалентного преобразования схемы заключается в упрощении схемы, когда два (или несколько) однотипных элемента электрической цепи замещаются одним эквивалентным элементом того же типа. Под термином «эквивалентный элемент» подразумевается такой элемент, замещение на который не меняет значений токов и напряжений в остальной части электрической цепи.
Схематичный пример использования метода эквивалентного преобразования схемы для расчета сложной электрической цепи изображен ниже:
Например, после замены источника тока источником напряжения (рис. 1.3) в обобщенной ветви последняя будет выглядеть так:
| = | ||
| Рис.3.1 | Рис.3.2 |
где . Обратите внимание, направление эквивалентного источника ЭДС совпадает с напряжением источника тока . Ниже будет показано, что данный участок цепи можно упростить, как показано на рис. (3.2), где .
(3.2), где .
3.2. Последовательное соединение резисторов при эквивалентной замене суммируется:
,
где – число последовательно соединенных резисторов. При данном соединении всегда больше большего из сопротивлений. В частном случае, если каждое из сопротивлений равно , то .
Пример. Определить эквивалентное сопротивление цепи на зажимах .
a)
.
| = | ||
| Рис 3.4 | Рис 3.5 |
б)
| . | |
| Рис 3.6 |
Здесь , т.к. разрыв цепи между точками и имеет бесконечно большое сопротивление.
3.3. При параллельном соединении резистора суммируется их проводимость , где — число параллельно соединенных резисторов, и . При параллельном соединении всегда меньше меньшего из сопротивлений. В частном случае, если каждое из сопротивлений равно , то .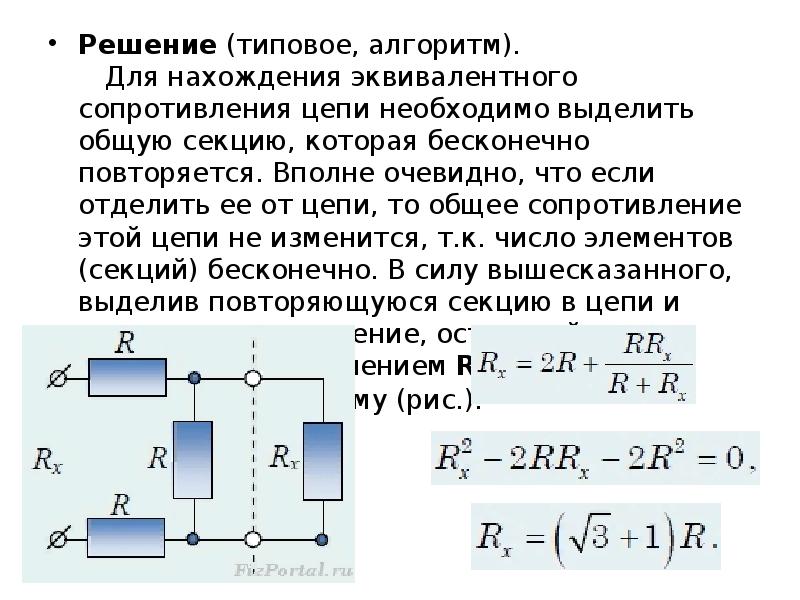 В случае двух параллельно соединенных сопротивлений и :
В случае двух параллельно соединенных сопротивлений и :
Пример. Определить на зажимах .
а)
| = | ||
| Рис 3.9 | Рис 3.10 |
.
б)
| . | |
| Рис 3.10 |
Здесь , т.к. сопротивление закоротки равно нулю.
РАСЧЕТНЫЕ ФОРМУЛЫ
3.4. При смешанном соединении резисторов эквивалентное сопротивление цепи определяет последовательным упрощением схемы и «сворачиванием» ее к одному сопротивлению, равному . При расчете токов в отдельных ветвях ЭЦ «разворачивают» в обратной последовательности.
Пример. Определить относительно зажимов .
а)
| = | = | |||
| Рис 3.11 | Рис 3.12 | Рис 3.12 |
,
.
б)
| = | = | |||
| Рис 3.13 | Рис 3.14 | Рис 3.15 |
, .
| = | ||
| Рис 3.16 | Рис 3.17 | |
| = | ||
| Рис 3.18 | Рис 3.19 |
, где .
В последнем примере сопротивление закорочено, а сопротивления , , имеют только одну общую точку со схемой и поэтому они не учитываются. Сопротивления и включены последовательно и эквивалентное им сопротивление , а и включены параллельно, поэтому:
.
3.5. Преобразование пассивного треугольника сопротивлений в эквивалентную трехлучевую звезду. Схемы будут эквивалентны, если сопротивления между узлами и , и , и в обеих схемах «звезды» и «треугольника» будут одинаковыми:
| = | ||
| Рис. 3.20 | Рис. 3.21 |
, , .
Решая совместно эти уравнения, получим:
, , ,
, , .
Обратное преобразование трехлучевой звезды в треугольник:
, , .
Пример. Определить эквивалентное сопротивление ЭЦ относительно зажимов .
| = | ||
| Рис 3.22 | Рис 3.23 | |
| = | ||
| Рис 3.24 | Рис 3.25 |
Сначала преобразуем треугольник сопротивлений , , в эквивалентную трехлучевую звезду , , ; затем преобразуем последовательно соединенные резисторы , и , , эквивалентные сопротивления которых соединены между собой параллельно и могут быть заменены одним :
.
Резистор включен параллельно резисторам и , соединенным между собой последовательно. Поэтому эквивалентное сопротивление всей ЭЦ относительно зажимов :
.
3.6. Преобразование ветвей, содержащих последовательные и параллельные соединения источников ЭДС и тока.
а)
| = | ||
| Рис 3.26 | Рис 3.27 |
б)
| = | ||
| Рис 3.28 | Рис 3.29 |
в)
| = | или | |||
| Рис 3.30 | Рис 3.31 | Рис 3.32 |
г)
| Если . Два источника тока могут быть соединены последовательно, если они равны и одинаково направлены в противном случае не будет выполняться ЗТК в месте соединения двух источников. |
д)
| . Два источника ЭДС могут быть включены параллельно, если они равны и имеют одинаково включенную полярность. Если эти условия не выполняются, то ЗНК будет нарушен в контуре, содержащем эти источники. |
3.7. Часть схемы, состоящей из параллельных ветвей ЭДС и проводимостями , эквивалентно либо одной ветви с проводимостью и ЭДС :
, ,
либо двум параллельным ветвям с той же проводимостью и источником тока :
.
ПРАВИЛО ЗНАКОВ. Слагаемые , берутся с плюсом при совпадении направления ЭДС и , при несовпадении – с минусом.
Пример. Преобразовать схему с параллельными ветвями, содержащими источники ЭДС, в эквивалентную.
| = | = | |||
| Рис 3.33 | Рис 3.34 | Рис 3.35 |
, , .
Пример.В заданной ЭЦ (рис.2.1) найти токи, используя эквивалентные преобразования.
Для начала преобразуем источник тока в источник напряжения: .
Заменим сопротивления и на эквивалентные и , на .
Элементы , , соединены в трехлучевую звезду, которую можно преобразовать в треугольник с сопротивлениями: , , .
, , .
После преобразований схема приобретает вид:
| Þ | ||
Последовательно упрощаем схему,
где
, , ,
, .
Схему можно заменить на , где
, .
Заменяя и на эквивалентное :
.
Тогда ток, протекающий через элементы , будет равен:
.
Токи, протекающие через , равны: ( ):
, .
Посредством найдем токи на резисторах и ( и ):
1. ,
1. .
Остальные токи можно найти посредством ЗТК для изначальной схемы:
, , .
Практическая работа по дисциплине Электротехника. название Расчёт цепи постоянного тока методом эквивалентного сопротивления.
ПРАКТИЧЕСКАЯ РАБОТА №4
Наименование работы: Расчёт цепи постоянного тока методом эквивалентного сопротивления.
Цель работы: Определить общий ток и токи в ветвях при смешанном соединении приемников электрической энергии. Определить эквивалентное сопротивление. Проверить баланс мощности рассматриваемой цепи.
Пояснения к работе.
Неразветвленная электрическая цепь это последовательное соединение приемников электрической энергии.
R1 R2 R3
I U1 U2 U3
U I
Последовательным называется такое соединение приемников электрической энергии, при котором по всем элементам протекает один и тот же ток.
U = U1 + U2 + U3
Эквивалентное сопротивление цепи равно сумме сопротивлений последовательно включенных резисторов : Rэкв = R1 + R2 + R3
Эквивалентным называется такое сопротивление, которое будучи включенным вместо данных резисторов, не изменяет режима работы электрической цепи.
Закон Ома для всей замкнутой цепи имеет вид:
I = U/ (R1 + R2 + R3) I = U/Rэкв
Р = Р1 + Р2 + Р3 – уравнение баланса мощностей.
Общая мощность равна сумме мощностей последовательно включенных резисторов.
Мощности на последовательно включенных резисторах распределяются прямо пропорционально сопротивлениям резисторов.
Напряжение на последовательно включенных резисторах распределяется прямо пропорционально сопротивлениям резисторов.
Разветвленная электрическая цепь это параллельное соединение приемников электрической энергии.
I1 R1
I I2 R2 I
I3 R3
U
Параллельным называется такое соединение приемников электрической энергии, при котором на зажимах всех элементов имеется одно и то же напряжение.
U = U1 = U2 = U3
Согласно первого закона Кирхгофа: I = I1 + I2 + I3
Обратная величина эквивалентного сопротивления равна сумме обратных величин сопротивлений резисторов, включенных параллельно: 1/Rэкв = 1/R1 + 1/R2 + 1/R3
Величина обратная сопротивлению является проводимостью.
Gэкв = 1/Rэкв Gэкв = G1 + G2 + G3
Эквивалентное сопротивление двух резисторов, включенных параллельно, определяется по формуле: Rэкв = R1•R2 /(R1 + R2)
Смешанное соединение – это такое соединение, при котором в электрической схеме имеются одновременно участки с последовательно и параллельно включенными элементами. К этим участкам применяются формулы последовательного и параллельного соединения приемников электрической энергии, а данный метод называется методом эквивалентного сопротивления или методом «свертывания».
Задание:
1. В практической работе необходимо определить общий ток и токи в ветвях при смешанном соединении приемников электрической энергии. Определить эквивалентное сопротивление. Проверить баланс мощности рассматриваемой цепи.
2. Начертить принципиальную схему своего варианта.
варианты № 4, 8, 12, 16 варианты № 3, 7, 11, 15
R1 R5 R1
R2 R2 R4
R6
U U
R3 R4 R6 R3 R5
варианты № 1, 5, 9, 13 варианты № 2, 6, 10, 14
R1
R2 R3 R1 R3
R5 R5
U U
R4 R6 R6 R2 R4
варианты № 20, 24, 28, 32 варианты № 19, 23, 27, 31
R1 R1
R2 R4 R2 R3 R5
U U
R3 R5 R6 R4 R6
варианты № 17, 21, 25, 29 варианты № 18, 22, 26, 30
R1 R1
R2 R4 R5 R2 R4
R5
U U
R3 R6 R6 R3
3. Переписать из таблицы данные своего варианта.
4. Выполнить расчет, в соответствии с предлагаемым методом, применяя следующие формулы: последовательное соединение — U = U1 + U2 + U3 ; Rэкв = R1 + R2 + R3 ; Р = Р1 + Р2 + Р3 ; I = U/
2 = Коэффициент детерминации уравнения регрессии
Значение коэффициента находится в диапазоне от 0 до 1, где значение 0 указывает, что независимая переменная не объясняет вариацию зависимой переменной, а значение 1 указывает, что независимая переменная прекрасно объясняет вариацию зависимой переменной. переменная.
Примеры
Пример # 1
Попробуем разобраться в формуле коэффициента детерминации на примере. Попробуем выяснить, какова связь между расстоянием, пройденным водителем грузовика, и возрастом водителя грузовика. Кто-то действительно составляет уравнение регрессии, чтобы проверить, подтверждается ли то, что он думает о взаимосвязи между двумя переменными, уравнением регрессии. В этом конкретном примере мы увидим, какая переменная является зависимой переменной, а какая — независимой.
Зависимой переменной в этом уравнении регрессии является расстояние, пройденное водителем грузовика, а независимой переменной — возраст водителя грузовика. Мы можем найти корреляцию с помощью формулы и возвести в квадрат, чтобы получить коэффициент уравнения регрессии. Набор данных и переменные представлены в прилагаемой таблице Excel.
Лаборатория 3 — Цепи постоянного тока и закон Ома
Лаборатория 3 — Цепи постоянного тока и закон Ома
- Содержание>
- Лаборатория 3 — Цепи постоянного тока и закон Ома
Введение
В течение девятнадцатого века было сделано столько успехов в понимании электрической природы материи, что это было названо «веком электричества».«Одно из таких достижений было сделано немецким физиком по имени Георг Симон Ом. Ом интересовался изучением относительной проводимости металлов и исследованием взаимосвязи между электродвижущей силой (разностью потенциалов) и током в проводнике.
Взяв провода, сделанные из разных материалов, но одинаковой толщины, пропустив через эти провода ток и измерив электродвижущую силу, то есть разность потенциалов между концами проводящего провода, он смог экспериментально определить относительную проводимость некоторых металлы, такие как серебро, медь и золото.В другом эксперименте с использованием устройства, которое он построил, Ом исследовал влияние тока в проводнике на падение напряжения на проводнике. Он обнаружил, что для данного проводника падение напряжения прямо пропорционально току в проводе. Когда напряжение отображается в зависимости от тока в данном проводнике, данные могут быть уложены на прямую линию, наклон которой равен сопротивлению проводника. Этот результат был опубликован в 1826 году. В знак признания работы Ома это эмпирическое соотношение носит его имя.
Обсуждение принципов
Закон Ома можно записать алгебраически как Δ V = RI , где Δ V , измеренное в вольтах, представляет падение потенциала или разность потенциалов на проводнике, I — ток в проводнике, измеренный в амперах, и R — сопротивление проводника, измеряемое в единицах, называемых «омами», которые символизируются Ω, греческой омегой в верхнем регистре. Примечание. В некоторых учебниках для разности потенциалов используется значение В , а не Δ В .
Сопротивление и резисторы
Сопротивление — это свойство материалов. Резисторы представляют собой проводящие устройства, изготовленные из материалов, удовлетворяющих закону Ома.
Решения
NCERT для класса 12 по естественной физике Глава 3
Стр. № 127:
Вопрос 3.1:
Аккумуляторная батарея
у автомобиля ЭДС 12 В. Если внутреннее сопротивление аккумулятора
составляет 0,4 Ом, что является максимальным
ток, который можно взять из аккума?
Ответ:
ЭДС батареи, E
= 12 В
Внутреннее сопротивление
аккумулятор, r = 0.4 Ом
Максимальный потребляемый ток
от АКБ = I
По данным Ома
закон,
Максимальный ток
от данной батареи — 30 А.
Стр. № 127:
Вопрос 3.2:
Батарея эдс 10 В
и внутреннее сопротивление 3 Ом равно
подключен к резистору. Если ток в цепи 0,5 А, то какой
такое сопротивление резистора? Какое напряжение на клеммах
аккумулятор при замкнутой цепи?
Ответ:
ЭДС батареи, E
= 10 В
Внутреннее сопротивление
аккумулятор, r = 3 Ом
Ток в цепи,
Я = 0.5 А
Сопротивление
резистор = R
Соотношение для
ток по закону Ома,
Напряжение на клеммах
резистор = В
По данным Ома
закон,
В = ИК
= 0,5 × 17
= 8,5 В
Следовательно,
сопротивление резистора 17 Ом
и напряжение на зажимах
8,5 В.
Стр. № 127:
Вопрос 3.3:
(а) Три резистора 1 Ом,
2 Ом и 3 Ом являются
объединены последовательно. Какое полное сопротивление комбинации?
(б) Если комбинация подключена к аккумулятору ЭДС 12 В
и незначительное внутреннее сопротивление, получите падение потенциала на
каждый резистор.
Ответ:
(а) Три резистора сопротивлением 1 Ом,
2 Ом и 3 Ом являются
объединены последовательно.Общее сопротивление комбинации определяется как
алгебраическая сумма индивидуальных сопротивлений.
Общее сопротивление = 1 + 2 + 3 = 6 Ом
(б) Ток, протекающий по цепи = I
ЭДС
батареи, E = 12 В
Всего
сопротивление цепи, R = 6 Ом
соотношение для тока с использованием закона Ома составляет
Потенциал
падение на резисторе 1 Ом =
В 1
От
По закону Ома значение В 1 можно получить как
В 1
= 2 × 1 = 2 В
… (I)
Потенциал
падение через резистор 2 Ом =
В 2
Опять же,
по закону Ома значение В 2 может быть
получено как
В 2
= 2 × 2 = 4 В
… (Ii)
Потенциал
падение на резисторе 3 Ом =
В 3
Опять же,
по закону Ома значение В 3 может быть
получено как
В 3
= 2 × 3 = 6 В
… (Iii)
Следовательно,
падение потенциала на 1 Ом,
2 Ом и 3 Ом
резисторы на 2 В, 4 В и 6 В соответственно.
Стр. № 127:
Вопрос 3.4:
(а) Три резистора 2 Ом,
4 Ом и
5 Ом являются
combin
Electronics Club — Импеданс и реактивное сопротивление
Electronics Club — Импеданс и реактивное сопротивление — входное сопротивление, выходное сопротивление
Импеданс | Реактивное сопротивление |
Входное сопротивление | Выходное сопротивление |
Импеданс делителя напряжения
Следующая страница: Аналоговые и цифровые
См. Также: Емкость | Сопротивление
Импеданс
Импеданс (символ Z) — это мера полного сопротивления цепи току,
другими словами: насколько цепь препятствует потоку заряда .Это похоже на сопротивление, но также учитывает влияние емкости и индуктивности.
Импеданс измеряется в омах ().
Импеданс сложнее сопротивления из-за влияния емкости и
индуктивность зависит от частоты тока, проходящего через цепь, и
это означает, что полное сопротивление изменяется с частотой .
Эффект сопротивления постоянен независимо от частоты.
В = напряжение в вольтах (В)
I = ток в амперах (А)
Z = полное сопротивление в Ом ()
R = сопротивление в Ом ()
Импеданс в простых цепях
Термин «импеданс» часто используется (совершенно правильно) для простых цепей.
которые не имеют емкости или индуктивности, например, для обозначения их
«входной импеданс» или «выходной импеданс».Сначала это может показаться запутанным, но для этих простых схем вы можете предположить, что это просто другое слово для обозначения сопротивления.
Импеданс можно разделить на две части:
- Сопротивление R (часть, которая постоянна независимо от частоты)
- Реактивное сопротивление X (часть, которая зависит от частоты из-за емкости и индуктивности)
Емкость и индуктивность вызывают сдвиг фазы (см. Примечание) между
ток и напряжение, что означает, что сопротивление и реактивное сопротивление нельзя просто сложить для получения полного сопротивления.Вместо этого они должны быть добавлены как векторы с реактивным сопротивлением, перпендикулярным сопротивлению, как показано на диаграмме.
Четыре электрические величины определяют полное сопротивление (Z) цепи:
сопротивление (R), емкость (C),
индуктивность (L) и частота (f).
В следующем разделе реактивного сопротивления объясняется, как емкость, индуктивность и частота
влияют на импеданс.
Что означает «фазовый сдвиг»?
Фазовый сдвиг означает, что ток и напряжение не совпадают друг с другом.Подумайте о зарядке конденсатора.
Когда напряжение на конденсаторе равно нулю, ток максимален;
когда конденсатор заряжен и напряжение максимальное, ток минимальный.
Зарядка и разрядка происходят постоянно с переменным током, и ток вскоре достигает максимума.
до того, как напряжение достигнет своего максимума: мы говорим, что ток опережает напряжение.
Реактивное сопротивление, X
Реактивное сопротивление (символ X) — это мера противостояния емкости и индуктивности.
к текущему.Реактивное сопротивление зависит от частоты электрического сигнала.
Реактивное сопротивление измеряется в омах ().
Существует два типа реактивного сопротивления: емкостное реактивное сопротивление (Xc) и индуктивное реактивное сопротивление (X L ).
Общее реактивное сопротивление (X) — это разница между двумя:
| Полное реактивное сопротивление, X = X L — Xc |
Емкостное реактивное сопротивление Xc
Емкостное реактивное сопротивление (Xc) велико на низких частотах и мало на высоких.Для постоянного постоянного тока с нулевой частотой (f = 0 Гц) Xc бесконечно (полное противодействие),
Это означает, что конденсаторов пропускают переменный ток, но блокируют постоянный ток .
| Емкостное реактивное сопротивление, Xc = | 1 |
| 2fC |
Xc = реактивное сопротивление в Ом ()
f = частота в герцах (Гц)
C = емкость в фарадах (Ф)
Например: конденсатор 1 мкФ имеет реактивное сопротивление
3.2k для сигнала 50 Гц,
но когда частота выше 10 кГц, его реактивное сопротивление всего 16.
Индуктивное реактивное сопротивление, X L
Индуктивное реактивное сопротивление, X L мало на низких частотах и большое на высоких.
Для постоянного постоянного тока (нулевая частота) X L равно нулю (нет противодействия),
Это означает, что индуктивности пропускают постоянный ток, но блокируют высокочастотный переменный ток .
| Индуктивное реактивное сопротивление, X L = 2fL |
X L = реактивное сопротивление в Ом ()
f = частота в герцах (Гц)
L = индуктивность в Генри (Гн)
Например: индуктор 1 мГн имеет реактивное сопротивление только 0.3 для сигнала 50 Гц,
но когда частота выше 10 кГц, его реактивное сопротивление равно 63.
Входное сопротивление Z IN
Входное сопротивление (Z IN ) — это импеданс, «видимый» всем, что подключено к входу.
схемы или устройства (например, усилителя). Это совокупный эффект всего сопротивления,
емкость и индуктивность, подключенные к входу внутри схемы или устройства.
Термин «входной импеданс» является нормальным даже в простых случаях, когда имеется только сопротивление.
и вместо этого можно использовать термин «входное сопротивление».На самом деле обычно разумно предположить
что входной импеданс — это просто сопротивление, при условии, что входной сигнал имеет низкую частоту (менее 1 кГц).
Влияние емкости и индуктивности зависит от частоты, поэтому, если они присутствуют, входное сопротивление
будет меняться в зависимости от частоты. Влияние емкости и индуктивности обычно наиболее существенно на высоких частотах.
Обычно входной импеданс должен быть высоким , по крайней мере, в десять раз больше выходного сопротивления
схемы (или компонента), подающей сигнал на вход.Это гарантирует, что вход не будет «перегружен».
источник сигнала и значительно уменьшите силу (напряжение) сигнала.
Выходное сопротивление Z OUT
Выход любой схемы или устройства эквивалентен выходному сопротивлению (Z OUT )
последовательно с идеальным источником напряжения (V SOURCE ). Это называется
Схема замещения и представляет собой совокупное влияние всех источников напряжения, сопротивления,
емкость и индуктивность, подключенные к выходу внутри схемы или устройства.Обратите внимание, что V SOURCE обычно , а не , как напряжение питания Vs.
Термин «выходной импеданс» является нормальным даже для простых случаев, когда имеется только сопротивление.
вместо этого можно использовать термин «выходное сопротивление». На самом деле обычно разумно предположить
что выходной импеданс — это просто сопротивление, при условии, что выходной сигнал имеет низкую частоту (менее 1 кГц).
Схема замещения любого выхода
Влияние емкости и индуктивности зависит от частоты, поэтому, если они присутствуют, выходное сопротивление
будет меняться в зависимости от частоты.Влияние емкости и индуктивности обычно наиболее существенно на высоких частотах.
Обычно выходное сопротивление должно быть низким , менее одной десятой полного сопротивления нагрузки
подключен к выходу. Если выходной импеданс слишком высок, он не сможет обеспечить достаточно сильный
сигнал к нагрузке, потому что большая часть напряжения сигнала будет « потеряна » внутри цепи, управляющей током через
выходное сопротивление Z OUT .
Нагрузкой может быть отдельный компонент или входное сопротивление другой цепи.
Низкое выходное сопротивление , Z ВЫХ << Z НАГРУЗКА
Большая часть В ИСТОЧНИК появляется на нагрузке, очень небольшое напряжение «теряется»
управляя выходным током через выходное сопротивление. Обычно это лучшая аранжировка.
Согласованные импедансы , Z ВЫХ = Z НАГРУЗКА
Половина V ИСТОЧНИК появляется в нагрузке, другая половина «теряется»
управляя выходным током через выходное сопротивление.Такое расположение полезно в некоторых
ситуаций (например, усилитель, управляющий громкоговорителем), потому что он обеспечивает максимальной мощности на
нагрузка . Обратите внимание, что равное количество энергии тратится впустую, управляя выходным током через
Z OUT , КПД 50%.
Высокое выходное сопротивление , Z ВЫХ >> Z НАГРУЗКА
Лишь небольшая часть V SOURCE появляется в нагрузке, большая часть «потеряна»
управляя выходным током через выходное сопротивление.Такое расположение неудовлетворительно.
Нагрузка может быть однокомпонентной или
входным сопротивлением другой цепи
Выходное сопротивление делителя напряжения
Делители напряжения
широко используются в электронике,
например, для подключения входного преобразователя, такого как LDR, к входу схемы.
Для успешного использования выходное сопротивление делителя напряжения должно быть намного меньше.
чем входное сопротивление подключенной к нему цепи.
В идеале выходное сопротивление должно быть меньше одной десятой входного сопротивления.
В эквивалентной схеме делителя напряжения выходное сопротивление — это просто сопротивление.
и можно использовать термин «выходное сопротивление». R ВЫХ равно
к двум параллельно подключенным сопротивлениям (R1 и R2):
| Выходное сопротивление, R OUT = | R1 × R2 | |
| R1 + R2 |
Источник напряжения V SOURCE в эквивалентной цепи значение
выходное напряжение Vo, когда к выходу ничего не подключено (и, следовательно, нет выходного тока).Иногда его называют напряжением холостого хода.
| Источник напряжения, В ИСТОЧНИК = | Vs × R2 | |
| R1 + R2 |
Схема замещения делителя напряжения
.

 При необходимости производят дальнейшие замещения, пока схема не примет вид одного сопротивления. Исходными данными являются значения напряжения на зажимах цепи и сопротивления резисторов. В результате расчета необходимо определить ток через каждый резистор. Рассмотрим на примере.
При необходимости производят дальнейшие замещения, пока схема не примет вид одного сопротивления. Исходными данными являются значения напряжения на зажимах цепи и сопротивления резисторов. В результате расчета необходимо определить ток через каждый резистор. Рассмотрим на примере. Новое сопротивление
Новое сопротивление Такой же ток будет и в участках цепи 1-2, 3-4 (рис.1). В ветвях этих участков ток разветвляется и будет равен сумме элементов данного участка. Чтобы узнать ток в каждом элементе участка цепи, нужно сначала найти напряжение на данном участке. Так для участка цепи 3-4 напряжение будет равно:
Такой же ток будет и в участках цепи 1-2, 3-4 (рис.1). В ветвях этих участков ток разветвляется и будет равен сумме элементов данного участка. Чтобы узнать ток в каждом элементе участка цепи, нужно сначала найти напряжение на данном участке. Так для участка цепи 3-4 напряжение будет равно:
 7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.
7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.