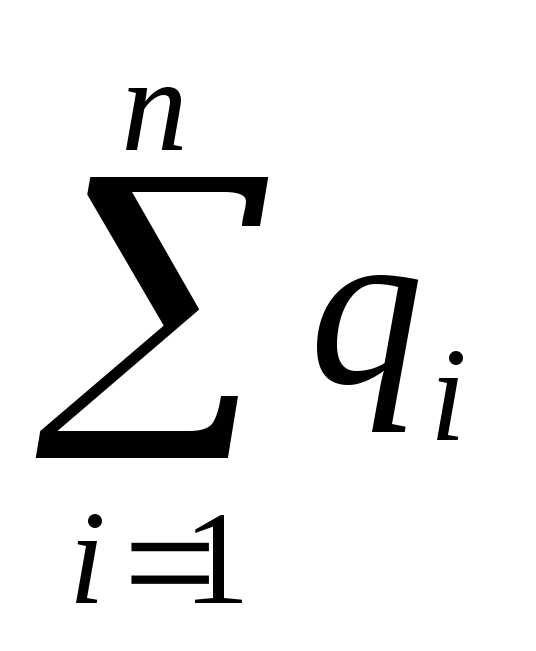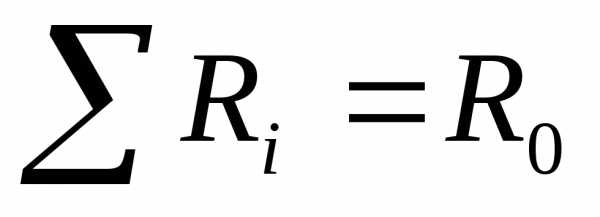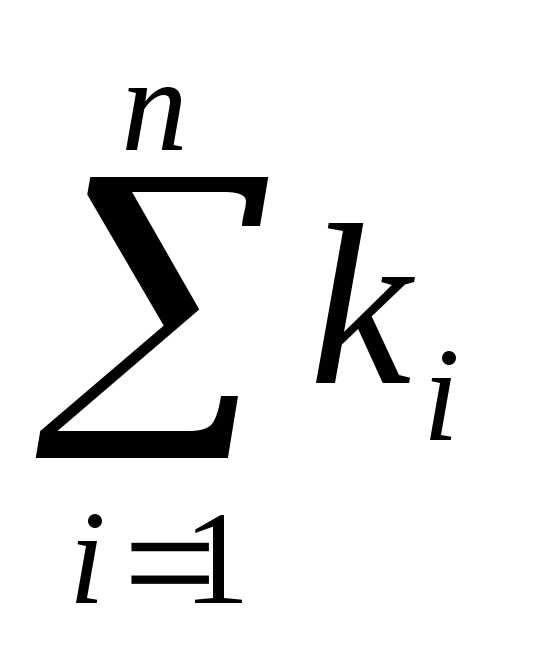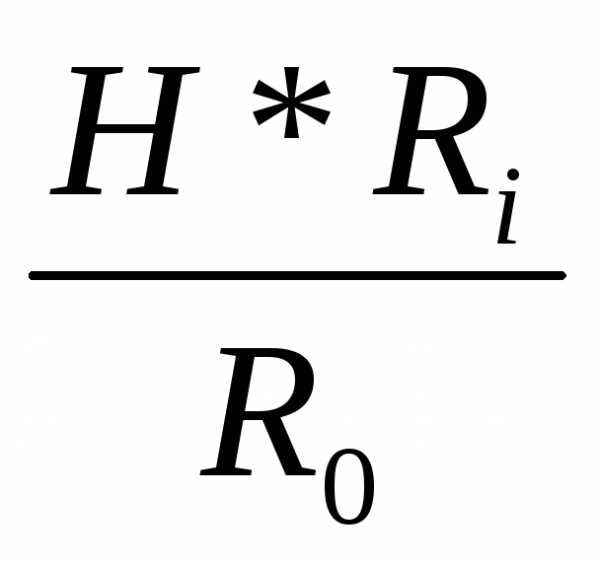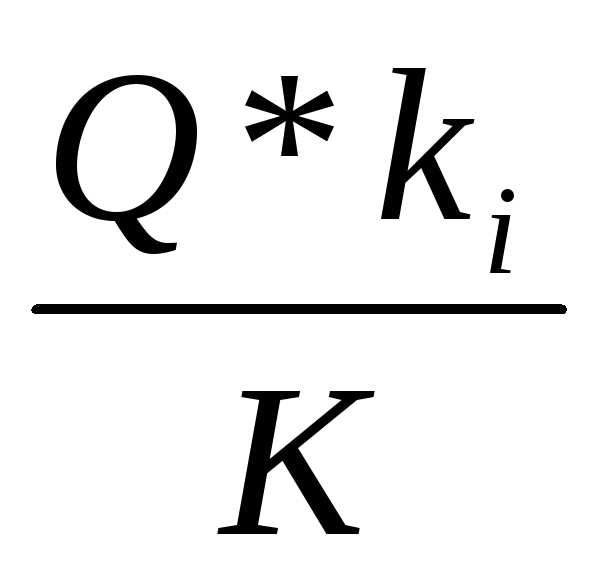Последовательное и параллельное соединение проводников. Определение параллельное соединение
§4. Последовательное и параллельное соединения — Phystech.Academy
Для расчёта цепей особое значение имеют два типа соединений элементов: последовательное и параллельное. В ходе их анализа достаточно изобразить на схеме лишь рассматриваемый участок (а не всю цепь), поэтому возможные подключения других элементов цепи мы будем отмечать на схеме многоточиями .
Два элемента, имеющих по два вывода у каждого, называются соединёнными последовательно, если есть точка соединения одного вывода первого элемента с одним выводом второго элемента и к этой точке больше ничего не подключено, либо если есть третий элемент, который соединён последовательно с каждым из двух рассматриваемых.
Два элемента, имеющих по два вывода у каждого, называются соединёнными параллельно, если есть точка соединения одного вывода первого элемента с одним выводом второго элемента, а также есть точка соединения другого вывода первого элемента с другим выводом второго элемента.
4.1 Основные свойства и примеры соединений
Последовательно соединённые резисторы можно видеть на рис. 4.1 и 4.2, а конденсаторы – на рис. 4.3 и 4.4. Последовательно можно соединить любое количество элементов, причём они могут быть разных типов (рис. 4.5).

Вне зависимости от количества (пусть их будет `n` штук) и типа последовательно соединённых элементов справедливы следующие утверждения:
1. Общая сила тока через последовательно соединённые элементы равна силе тока через любой из них:
`I=I_1=I_2=...=I_n`. (4.1)
2. Общее напряжение на последовательно соединённых элементах равно сумме напряжений на каждом из них:
`U=U_1+U_2+...+U_n`. (4.2)
Параллельно соединённые резисторы можно видеть на рис. 4.6 и 4.7, а конденсаторы – на рис. 4.8 и 4.9. Параллельно можно соединить любое количество элементов, причём они могут быть разных типов (рис. 4.10).
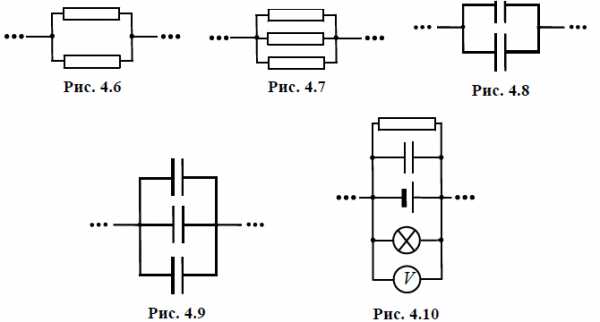
Вне зависимости от количества (пусть их будет `n` штук) и типа параллельно соединённых элементов справедливы следующие утверждения:
1. Общая сила тока через параллельно соединённые элементы равна сумме сил токов через каждый из них:
`I=I_1+I_2+...+I_n`. (4.3)
2. Общее напряжение на параллельно соединённых элементах равно напряжению на любом из них:
`U=U_1=U_2=...=U_n`. (4.4)
При использовании формул (4.2) и (4.3) очень важно помнить, что сумма в них подразумевается алгебраическая (с учётом знака). Если полярность некоторого элемента не соответствует полярности последовательного соединения в целом, то в (4.2) перед напряжением на этом элементе следует ставить минус. Если ток через некоторый элемент направлен против тока через параллельное соединение в целом, то в (4.3) перед силой тока через этот элемент следует ставить минус.
Существует множество схем, элементы которых соединены не последовательно, но и не параллельно. Приведём в качестве примера пару таких схем, которые даже получили собственные названия: «треугольник» (рис. 4.11) и «звезда» (рис. 4.12). Одним из методов упрощения схем является преобразование «треугольника» в «звезду».

Как (последовательно или параллельно) соединены батарейка, лапочка и ключ в карманном фонарике?
Рассмотрим оба соединения: последовательное (рис. 4.13) и параллельное (рис. 4.14). В первой схеме: когда ключ замкнут, лампочка горит; а когда разомкнут, – не горит. Во второй схеме: когда ключ разомкнут, лампочка горит; а когда замкнут, существенная часть создаваемого батарейкой тока пойдёт через ключ (а не через лампочку). Про лампочку в этом случае мы пока (до следующего параграфа) ничего сказать не можем, однако ясно, что во второй схеме ток через батарейку идёт при любом положении ключа, то есть она разряжается всё время (даже при выключенном фонарике). Следовательно, вторая схема нерациональна и на практике не используется. Таким образом, ответ получен – элементы соединены последовательно.
.
Как (последовательно или параллельно) соединены несколько лампочек в обычной люстре?
Без сомнения всем случалось наблюдать люстру, в которой горят не все лампочки (остальные перегорели или выкручены). У перегоревшей лампочки разрывается спираль и она больше не пропускает ток. Если бы лампочки были соединены последовательно, то в силу (4.1) сила тока через все лампочки была бы равна нулю, то есть ни одна лампочка не горела бы. Это противоречит экспериментальным наблюдениям, следовательно, лампочки в люстре соединены параллельно.
Как (последовательно или параллельно) соединены между собой телевизор и холодильник, включённый в сеть в одной комнате?
Напряжение сети (`220` В) одинаково для каждого бытового электроприбора вне зависимости от того, что включено в соседнюю розетку. Это полностью соответствует свойству (4.4). Кроме того, можно непосредственно проследить путь проводов, и тогда от любого прибора мы придём к счётчику электроэнергии. Таким образом, все приборы в одной квартир соединены параллельно. Утверждать то же самое для приборов в разных квартирах нельзя, так как счётчик у них не общий.
4.2. Резисторы
Рассмотрим последовательное (рис. 4.15) и параллельное (рис. 4.16) соединения двух резисторов сопротивлениями `R_1` и `R_2`. В обоих случаях напряжения `U_1` и `U_2` на каждом из резисторов и силы токов `I_1` и `I_2` через них связаны законом Ома, который мы запишем в двух видах:
`U_1=R_1I_1`, `U_2=R_2I_2`, (4.5)
или
`I_1=(U_1)/(R_1)`, `I_2=(U_2)/(R_2)`. (4.6)
А вот общее напряжение `U` на обоих резисторах и общая сила тока `I` через них будут зависеть от способа подключения.
В случае последовательного соединения `U=U_1+U_2`, `I=I_1=I_2`. Используя эти свойства и соотношения (4.5), выразим общее сопротивление участка цепи, состоящего из двух резисторов:
`R=U/I=(U_1+U_2)/I=(R_1I_1+R_2I_2)/I=(R_1I+R_2I)/I=R_1+R_2`.
Это означает, что два последовательно соединённых резистора сопротивлениями `R_1` и `R_2` эквивалентны одному резистору сопротивлением `R=R_1+R_2`.
Аналогичным образом можно доказать более общее утверждение: последовательно соединённые резисторы сопротивлениями `R_1,R_2,...R_n` эквивалентны одному резистору сопротивлением
`R=R_1+R_2+...+R_n`. (4.7)
В случае параллельного соединения `U=U_1=U_2`, `I=I_1+I_2`.
Используя эти свойства и соотношения (4.6), выразим общее сопротивление участка цепи, состоящего из двух резисторов:
`R=U/I=U/(I_1+I_2)=U/(U_1/R_1+U_2/R_2)=U/(U/R_1+U/R_2)=1/(1/R_1+1/R_2)=(R_1R_2)/(R_1+R_2)`.
Это означает, что два параллельно соединённых резистора сопротивлениями `R_1` и `R_2` эквивалентны одному резистору сопротивлением
`R=(R_1R_2)/(R_1+R_2)`. (4.8)
Аналогичным образом можно доказать более общее утверждение: параллельно соединённые резисторы сопротивлениями `R_1,R_2,...,R_n` эквивалентны одному резистору сопротивлением
`R=1/(1/R_1+1/R_2+...+1/R_n)`. (4.9)
Отметим, что выражение (4.8) получено после алгебраического преобразования, пригодного только для случая двух резисторов, поэтому его формальное обобщение приводит к неправильному (даже по размерности!) результату:
R=R1R2·...·RnR1+R2+...+Rn.\xcancel{R=\dfrac{R_1R_2\cdot...\cdot R_n}{R_1+R_2+...+R_n}.}
Найдите сопротивление `R` изображённого на рис. 4.17 участка цепи. Значения отмеченных на рисунке параметров элементов известны.
Резисторы `R_2` и `R_3` соединены параллельно, поэтому их можно заменить одним резистором сопротивлением `R_(23)=R_2R_3//(R_2+R_3)`. После замены резисторы `R_1` и `R_(23)` оказываются соединены последовательно, значит, их можно заменить одним резистором сопротивлением `R_(123)=R_1+R_(23)`. После второй замены остаётся один резистор, следовательно, искомое сопротивление
`R=R_(123)=R_1+R_(23)=R_1+(R_2R_3)/(R_2+R_3)`.
Найдите сопротивление `R` изображённого на рис. 4.18 участка цепи. Значения отмеченных на рисунке параметров элементов известны.
Резисторы `R_1` и `R_2` соединены последовательно, поэтому их можно заменить одним резистором сопротивлением `R_(12)=R_1+R_2`. После замены резисторы `R_(12)` и `R_3` оказываются соединены параллельно, значит, их можно заменить одним резистором сопротивлением `R_(123)=R_(12)R_3//(R_(12)+R_3)`. После второй замены остаётся один резистор, следовательно, искомое сопротивление
`R=R_(123)=(R_(12)R_3)/(R_(12)+R_3)=((R_1+R_2)R_3)/((R_1+R_2)+R_3)`.
Найдите отношение напряжений `U_1` и `U_2` на резисторах `R_1` и `R_2`, а также отношение сил токов `I_3` и `I_4` через резисторы `R_3` и `R_4` (4.19). Значения отмеченных на рисунке параметров элементов известны.
1. В силу свойств последовательного соединения силы токов через резисторы `R_1` и `R_2` одинаковы: `I_1=I_2`. По закону Ома `U_1=R_1I_1` и `U_2=R_2I_2`.
Отсюда искомое отношение `U_1//U_2=R_1//R_2`.
2. В силу свойств параллельного соединения напряжения на резисторах `R_3` и `R_4` одинаковы: `U_3=U_4`. По закону Ома `I_3=U_3//R_3` и `I_4=U_4//R_4`. Отсюда искомое отношение `I_3//I_4=R_4//R_3`.
Обратите внимание, что каждый из ответов не зависит от остальной части схемы. Таким образом, напряжения на последовательно соединённых резисторах пропорциональны их сопротивлениям, а силы тока через параллельно соединённые резисторы обратно пропорциональны их сопротивлениям.
Найдите силу тока `I` через источник постоянного тока, напряжение на котором постоянно и равно `U` (4.19). Значения отмеченных на рисунке параметров элементов известны.
Резисторы `R_3` и `R_4` соединены параллельно, поэтому их можно заменить на один резистор сопротивлением `R_(34)=R_3R_4//(R_3+R_4)`. После замены резисторы `R_1`, `R_2` и `R_(34)` оказываются соединены последовательно (4.20), значит, их можно заменить одним резистором сопротивлением
`R=R_1+R_2+R_(34)=R_1+R_2+(R_3R_4)/(R_3+R_4)`.
В результате в схеме остаются только источник и один резистор (4.21). Их можно рассматривать как соединённые и последовательно, и параллельно. В силу первого сила тока через резистор равна искомой, а в силу второго напряжение на резисторе равно `U`. Тогда по закону Ома
`I=U/R=U/(R_1+R_2+(R_3R_4)/(R_3+R_4))`.
4.3. Конденсаторы
Прежде чем перейти к расчётам цепей с конденсаторами, вспомним их основные свойства, которые были подробно изучены в рамках электростатики.
Конденсатор – это система из двух изолированных друг от друга проводников (называемых обкладками), к которым подведены контакты.
В обычном режиме работы конденсатора заряды обкладок противоположны (равны по модулю и имеют разные знаки). Это условие может быть нарушено, если на одной из обкладок изначально был ненулевой заряд, что можно осуществить только при «изготовлении» конденсатора (но не за счёт каких-либо подключений его к цепи, так как заряд притёкший по проводу на одну обкладку, заставляет такой же по величине заряд покинуть другую обкладку по второму проводу конденсатора). Далее всюду будем предполагать обычный режим, если иное не оговорено особо.
Заряд на конденсаторе – это заряд одной из обкладок, выбор которой является такой же условностью, как и выбор положительного направления тока в определении силы тока.
Следует чётко отличать приведённое выше понятие заряда на конденсаторе, применяемое при расчётах цепей, от полного заряда конденсатора как тела (суммы зарядов всех его частиц), который в обычном режиме равен нулю. Наличие зарядов на обкладках приводит к появлению между ними разности потенциалов, которая называется напряжением на конденсаторе.
Ёмкость конденсатора `C` - это величина, равная отношению заряда `q` на конденсаторе к напряжению `U` на нём: `C=q//U`. Ёмкость измеряется в фарадах (Ф), причём Ф`=`Кл/В.
Рассмотрим последовательное (рис. 4.22) и параллельное (рис.4.23) соединения двух конденсаторов ёмкостями `C_1` и `C_2`. В обоих случаях напряжения `U_1` и `U_2` на каждом из конденсаторов и заряды `q_1` и `q_2` на них можно связать через ёмкости:
`U_1=(q_1)/(C_1)`, `U_2=(q_2)/(C_2)`, (4.10)
или
`q_1=C_1U_1`, `q_2=C_2U_2`. (4.11)
А вот общее напряжение `U` на обоих конденсаторах и общий заряд `q` на конденсаторах в целом (заряд, протёкший через точку `A` в процессе зарядки) будут зависеть от способа подключения.
В случае последовательного соединения `U=U_1+U_2`, а заряд `q`, протёкший через точку `A`, окажется на каждом из конденсаторов, то есть `q=q_1=q_2`. Используя эти свойства и соотношения (4.10), выразим общую ёмкость участка цепи, состоящего из двух конденсаторов:
`C=q/U=q/(U_1+U_2)=q/(q_1/C_1+q_2/C_2)=q/(q/C_1+q/C_2)=1/(1/C_1+1/C_2)=(C_1C_2)/(C_1+C_2)`.
Это означает, что два последовательно соединённых конденсатора ёмкостями `C_1` и `C_2`, заряженных соответственно до напряжений `U_1` и `U_2`, эквивалентны одному конденсатору ёмкостью
`C=(C_1C_2)/(C_1+C_2)`, (4.12)
заряженному до напряжения `U=U_1+U_2` и несущему заряд `q=CU`.
Аналогичным образом можно доказать более общее утверждение: последовательно соединённые конденсаторы ёмкостями `C_1,C_2,...C_n`, заряженные соответственно до напряжений `U_1,U_2,...,U_n`, эквивалентны одному конденсатору ёмкостью `C`, заряженному до напряжения `U` (соответствующего заряду `q=CU`):
`C=1/(1/C_1+1/C_2+...+1/C_n)`, `U=U_1+U_2+...+U_n`. (4.13)
Отметим, что выражение (4.12) получено после алгебраического преобразования, пригодного для случая двух конденсаторов, поэтому его формальное обобщение приводит к неправильному (даже по размеренности!) результату:
C=C1C2·...·CnC1+C2+...+Cn.\xcancel{C=\dfrac{C_1C_2\cdot...\cdot C_n}{C_1+C_2+...+C_n}}.
В случае параллельного соединения `U=U_1=U_2`, а заряд `q`, протёкший через точку `A`, разделится между конденсаторами, то есть `q=q_1+q_2`. Используя эти свойства и соотношения (4.11), выразим общую ёмкость участка цепи, состоящего из двух конденсаторов:
`C=q/U=(q_1+q_2)/U=(C_1U_1+C_2U_2)/U=(C_1U+C_2U)/U=C_1+C_2`.
Это означает, что два параллельно соединённых конденсатора ёмкостями `C_1` и `C_2`, несущие соответственно заряды `q_1` и `q_2`, эквивалентны одному конденсатору ёмкостью `C=C_1+C_2`, несущему заряд `q=q_1+q_2` и заряженному до напряжения `U=q//C`.
Аналогичным образом можно доказать более общее утверждение: параллельно соединённые конденсаторы ёмкостями `C_1,C_2,...,C_n`, несущие соответственно заряды `q_1,q_2,...,q_n`, эквивалентны одному конденсатору ёмкостью `C`, несущему заряд `q` (соответствующий напряжению `U=q//C`):
`C=C_1+C_2+...+C_n`, `q=q_1+q_2+...+q_n`. (4.14)
Суммы напряжений в (4.13) и зарядов в (4.14) подразумеваются алгебраические (с учётом полярности заряженных конденсаторов). А вот в выражениях для общей ёмкости минусов никогда не бывает. Формулы (4.13) и (4.14) справедливы при любых напряжениях на конденсаторах (даже не только для обычного режима), в частности, когда некоторые конденсаторы заряжены, а некоторые – нет. Из понятия эквивалентности следует, что если к системе конденсаторов подключить вольтметр, то он покажет напряжение на эквивалентном конденсаторе, а если систему конденсаторов замкнуть проводом, то по нему протечёт заряд эквивалентного конденсатора.
Три конденсатора ёмкостями `C_1=20` мкФ, `C_2=40` мкФ и `C_3=40` мкФ соединили последовательно с ключом (рис. 4.24). Конденсатор `C_1` изначально был не заряжен, а напряжения на конденсаторах `C_2` и `C_3` были соответственно `U_2=2` B и `U_3=3` B. Найдите заряд `q`, который протечёт через ключ после замыкания цепи.
Искомая величина – это заряд эквивалентного конденсатора. В соответствии с (4.13) сначала найдём его ёмкость
`C=1/(1/C_1+1/C_2+1/C_3)=10` мкФ,
а потом выразим напряжение `U=0+-U_2+-U_3`.
Знаки `+-` означают, что нам неизвестно, в какой полярности конденсаторы соединены друг с другом. В зависимости от выбора знаков мы получим четыре значения для `U:` `5`B, `1`B, `-1`B, `-5`B. Поскольку в итоге нам нужно найти `|q|=C|U|`, то последние два значения `U` дадут тот же результат, что и первые два, поэтому их можно отбросить. Из оставшихся двух выбрать какое-то одно невозможно (не хватает данных). Поэтому задача имеет два ответа: `q_1=50` мкКл и `q_2=10` мкКл.
Цепь собрана из бесконечного числа звеньев, состоящих из двух конденсаторов ёмкостями `C_1` и `C_2` (рис. 4.25). Многоточия на этой схеме обозначают остальные звенья цепи, а не произвольные элементы. Чему эквивалентен участок цепи между точками `A` и `B`?
Любая схема, состоящая только из конденсаторов и имеющая два вывода, эквивалентна одному конденсатору. Нужно лишь найти его ёмкость `C_0`. Заменим исходную цепь на эквивалентный ей конденсатор `C_0` и добавим к схеме ещё одно звено (рис. 4.26). Пользуясь свойствами последовательного и параллельного соединений, рассчитаем ёмкость `C_0^'` участка цепи между точками `A^'` и `B^'`. Конденсаторы `C_2` и`C_0` соединены параллельно, поэтому их можно заменить на один конденсатор ёмкостью `C_(20)=C_2+C_0`. Конденсаторы `C_1` и `C_(20)` соединены последовательно, значит, их общая ёмкость
`C_0^'=(C_1C_(20))/(C_1+C_(20))=(C_1(C_2+C_0))/(C_1+(C_2+C_0))`. (4.15)
Теперь сравним исходную и полученную цепи. Добавление одного звена не меняет факта бесконечности цепи. Поскольку все звенья одинаковы, то цепь с дополнительным звеном эквивалентна исходной, а их ёмкости равны: `C_0^'=C_0`, откуда после подстановки (4.15) получаем `C_0^2+C_2C_0-C_1C_2=0`. Решая полученное квадратное уравнение относительно `C_0` и отбрасывая отрицательный корень, не имеющий физического смысла, находим
`C_0=1/2(sqrt(C_2^2+4C_1C_2)-C_2)`.
Рассмотренная задача является типичным примером целого класса задач – на бесконечные цепочки. В качестве элементов цепочки могут быть также резисторы, источники и т. д. Кроме того, звенья цепи могут быть не одинаковы, например, сопротивление резисторов в каждом следующем звене в два раза больше, чем в предыдущем. Вообще, звенья могут состоять из разнотипных элементов, например, в схеме на 4.25 заменим мысленно все конденсаторы ёмкостью `C_1` на резисторы. В этом случае цепь будет эквивалентна не одному элементу, а участку из нескольких разнотипных элементов.
1) заменяем исходную бесконечную цепочку не эквивалентный ей элемент `X` и добавляем к нему ещё одно звено исходной цепочки;
2) рассчитываем параметры цепи с дополнительным звеном, полагая известными параметры элемента `X`;
3) сравниваем полученную цепь с исходной и определяем соотношение их параметров; 4) поставляем в это соотношение выражение из пункта №2 и решаем уравнение.
phystech.academy
Параллельное соединение и его свойства
Параллельное соединение горных выработок может быть простым (рис.6.8) и сложным (рис.6.9).
Простым параллельным называется такое соединение вентиляционных ветвей, в котором все начала ветвей расходятся в одном узле, а сходятся в другом (рис.6.8).
Сложным параллельным соединением называется такое соединение, когда кроме параллельных ветвей расходящихся в одном узле и сходящимся в другом в этих ветвях имеются дополнительные параллельные ветви (рис.6.9).
Рис.6.9 Сложное параллельное соединение
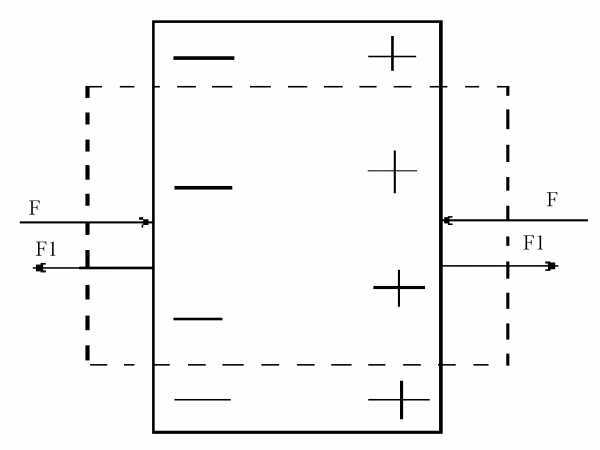
Рассмотрим свойства простого параллельного соединения. Согласно определению депрессии разность давления в узлах 1, 2 определяет как депрессию любой ветви входящей в соединение, так и депрессию всего соединения, тогда можно записать
Р1-Р2=h2=h3= =hi= hn=H (6.25)
То есть в параллельном соединении депрессии всех ветвей одинаковы и равны депрессии всего соединения.
Так как к узлу 1 притекает поток Q , равный общему потоку соединения, а вытекают из него потоки q1, q2 qi qn , а в узле 2 все наоборот, то в соответствии с первым законом сетей можно записать
Q= (6.26)
(6.26)
Общий поток параллельного соединения равен сумме потоков в отдельных ветвях.
Поток воздуха в любой ветви параллельного соединения, а также общий расход воздуха можно вы разить через депрессию и аэродинамическое сопротивление т. е.
Q=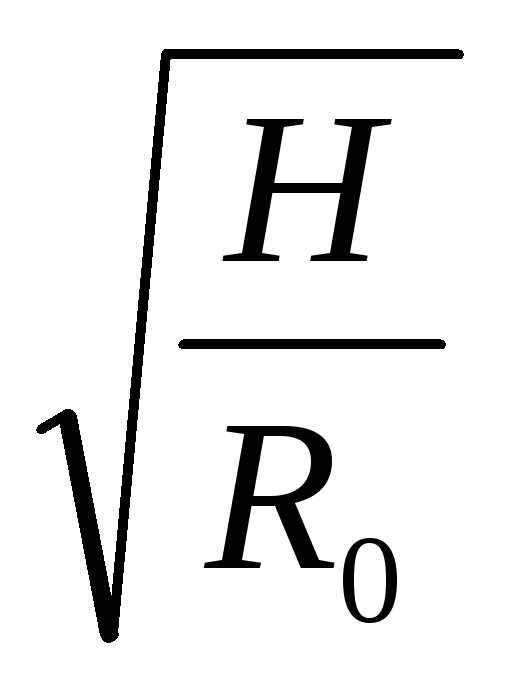 (6.27) qi=
(6.27) qi=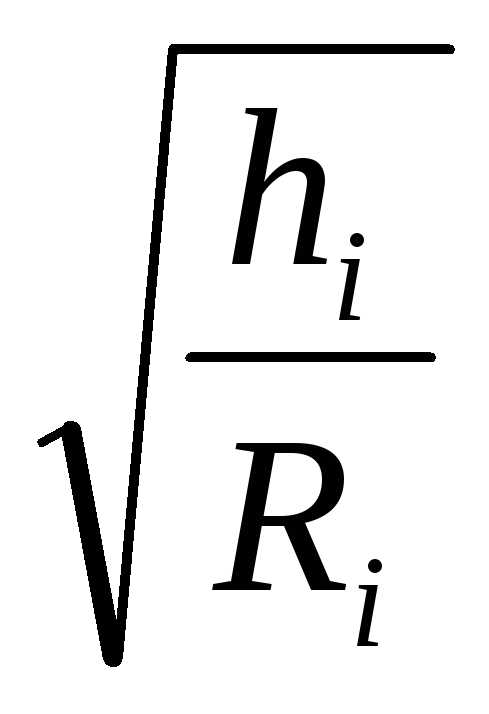 (6.28)
(6.28)
С учетом равенств (6.27), (6.28) равенство (6.26) можно записать в виде
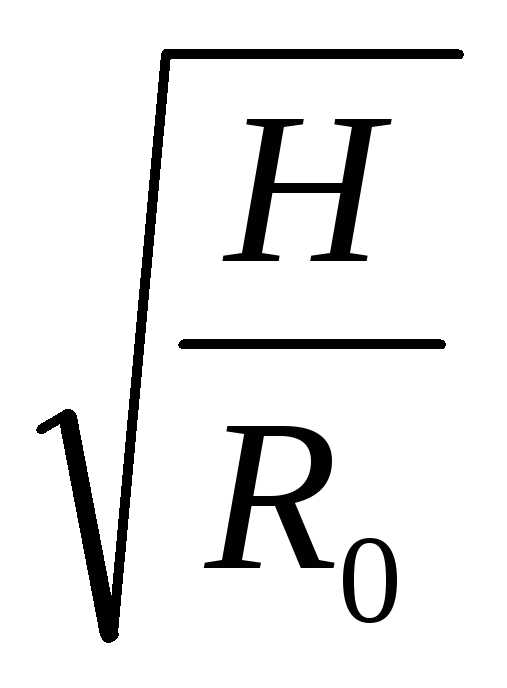 =
=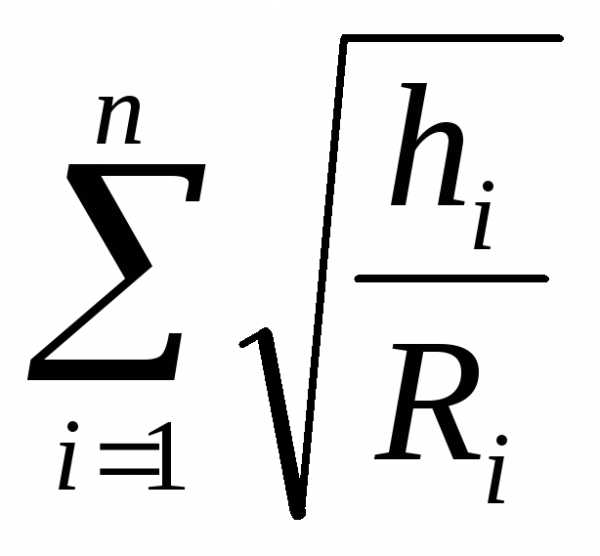 (6.29)
(6.29)
Так как в параллельном соединении Н=hi, то, сократив обе части последнего равенства на 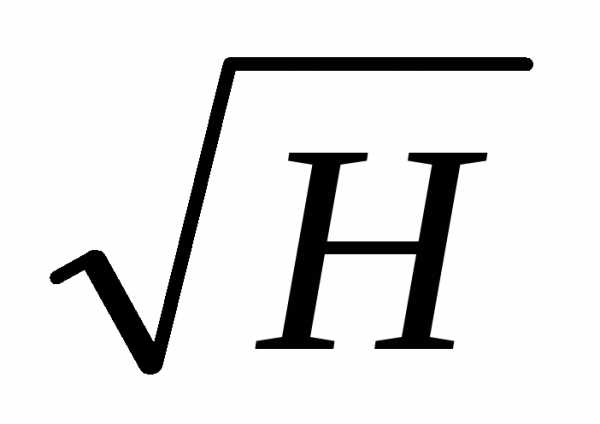 , получим
, получим
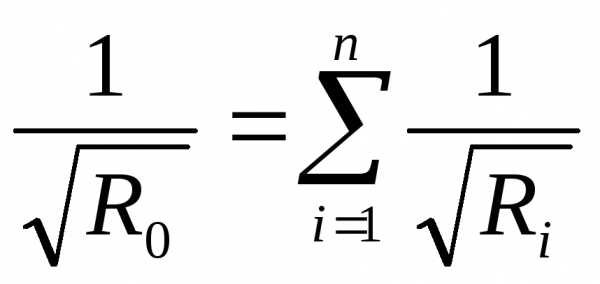 (6.30)
(6.30)
Величина обратная корню квадратному из сопротивления называется пропускной способностью, следовательно
K=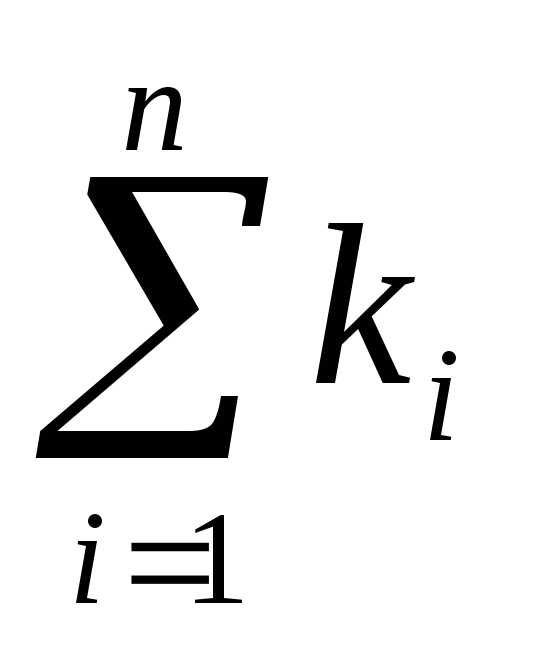 (6.31)
(6.31)
То есть общая пропускная способность параллельного соединения равна сумме пропускных способностей ветвей соединения.
Так как К=1/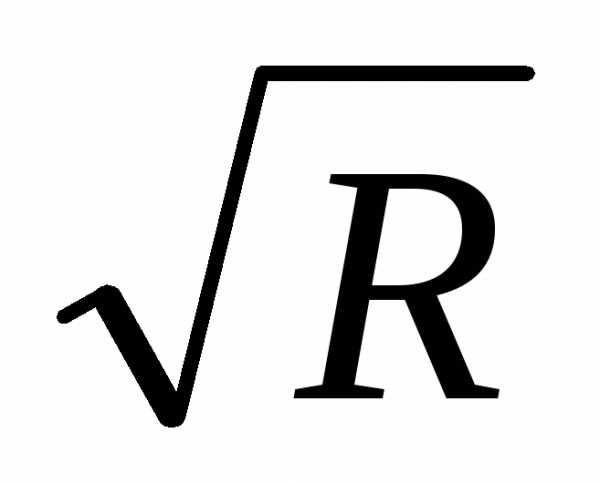 , то равенства (6.27), (6.28) можно переписать в виде
, то равенства (6.27), (6.28) можно переписать в виде
Q=K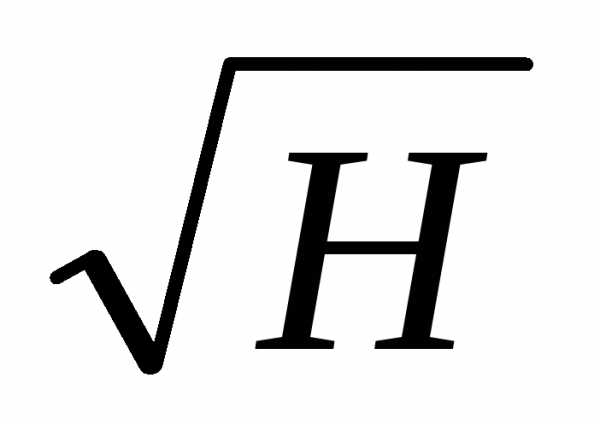 (6.32) qi=ki
(6.32) qi=ki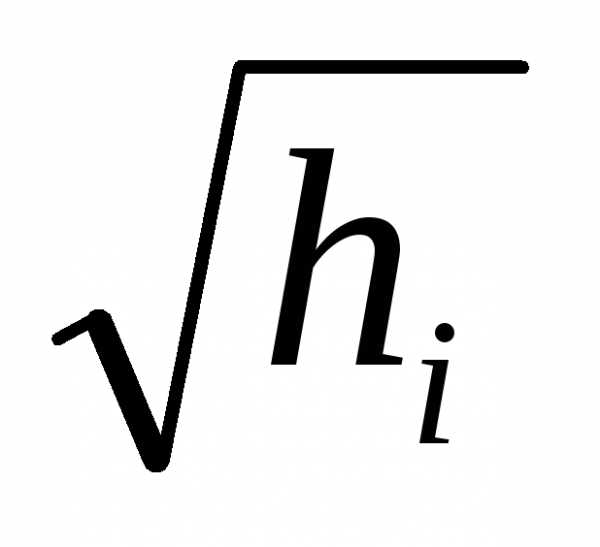 (6.33)
(6.33)
Так как в параллельном соединении H=hi то из равенств (6.32) (6.33) получим,
Qi=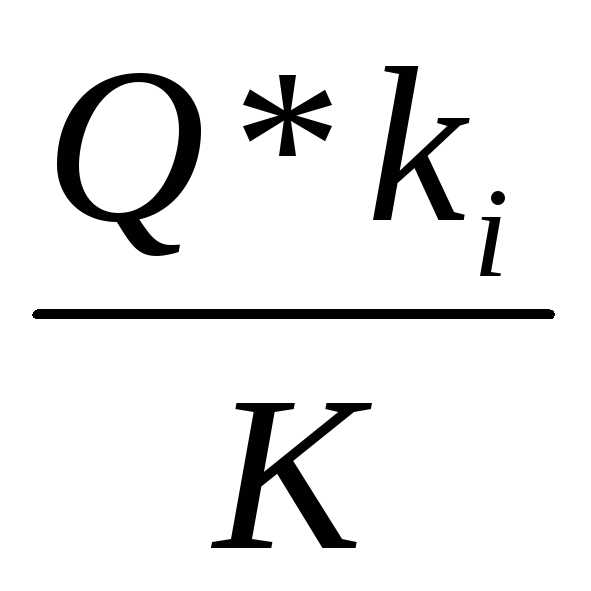 (6.34)
(6.34)
Потоки воздуха в отдельных ветвях параллельного соединения пропорциональны пропускной способности этих ветвей.
Теперь целесообразно выписать основные расчетные формулы последовательного и параллельного соединения и сравнить их.
| Последовательное соединение | Параллельное соединение |
| q1=q2= qi= qn=Q | h2=h3= =hi= hn=H |
|
| Q= |
|
| K= |
| Hi = | Qi= |
В последовательном соединении потоки воздуха во всех ветвях одинаковы, депрессия и сопротивления складываются, а депрессия каждой ветви пропорциональна ее сопротивлению.
В параллельном соединении депрессии всех ветвей одинаковы, потоки воздуха и пропускные способности суммируются, а расходы воздуха в ветвях пропорциональны их пропускной способности.
Полученные зависимости позволяют выполнять расчет сложных последовательно-параллельных соединений. Рассмотрим пример расчета сложного последовательно-параллельного соединения.
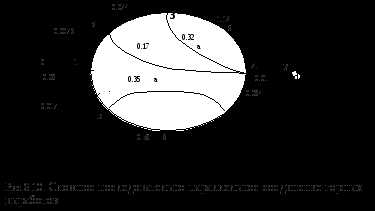
Заданы аэродинамические сопротивления ветвей сложного последовательно-параллельного соединения горных выработок и общая депрессия соединения (Рис.6.10). Рассчитать режим проветривания всех ветвей соединения (q,м3/c, h, даПа). Сопротивления ветвей на схеме заданы в киломюргах (кг*с2/м8) , а депрессия в даПа.
Схема вентиляционных соединений и исходные данные для расчетов.
Н=150 даПа
Решение задачи производится в следующей последовательности:
1. Обозначим узлы и ветви схемы представленной на рис.6.10. Если из одного узла в другой идет одна ветвь она обозначается числами-парами соединяемых узлов. Например, 0-1, 1-2, 6-4 и т. д. Отдельные ветви параллельных разветвлений обозначим номерами узлов и буквами. Например, 3-а-4, 3-б-4 и т. д. Разветвленный участок сети между двумя узлами номерами узлов в скобках. Например, (3-4) (5-6) и т. д.
2. Для определения общего расхода воздуха в сети Q и расхода воздуха в ветвях qi, необходимо определить общее сопротивление сети R0. Расчет величины R0 производим в следующей последовательности:
2.1 Определяем общее сопротивление простого параллельного соединения между узлами .3-4
R (3-4)= K (3-4)=+
K (3-4)=+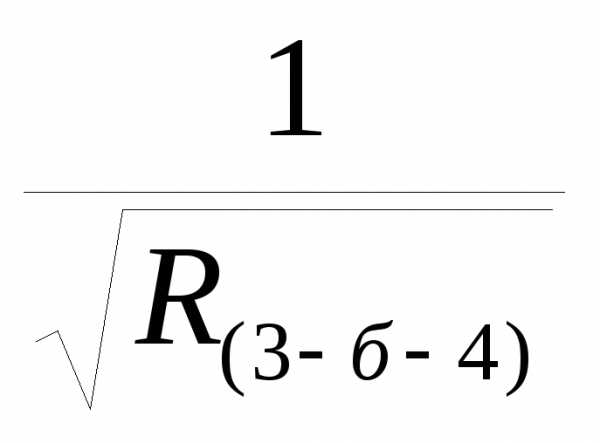
2.2 Определяем общее сопротивление ветвей последовательного соединения
2-3, (3-4)
R2-(3-4)=R2-3+R(3-4)
2.3 Определяем общее сопротивление параллельного соединения между узлами 2-4.
R (2-4)=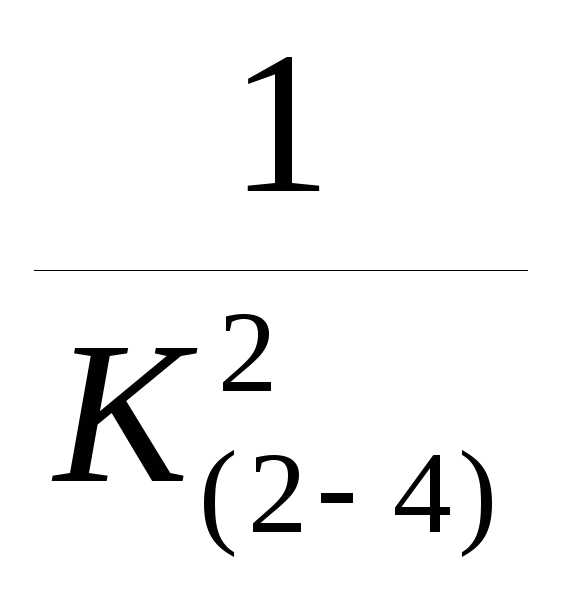 К(2-4)=
К(2-4)=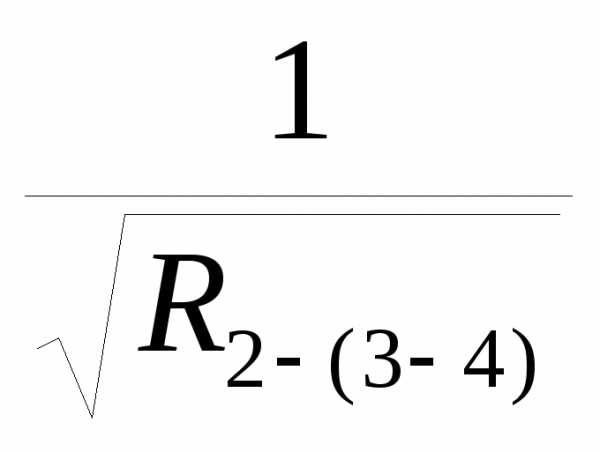 +
+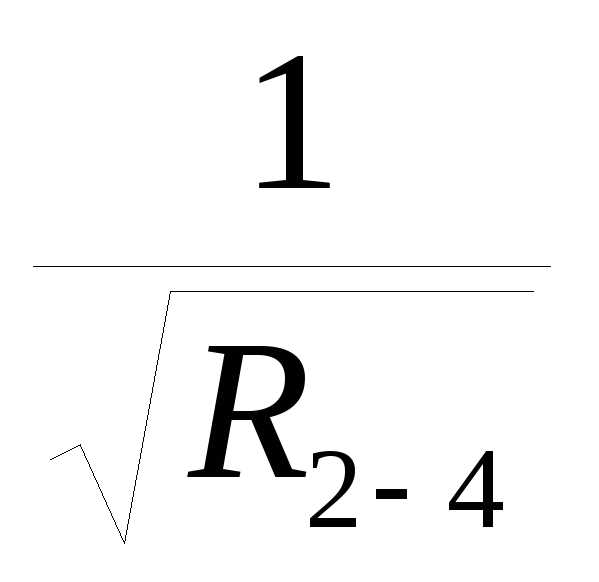
2.4 Определяем общее сопротивление последовательного соединения ветвей 1-2 и (2-4)
R1-(2-4)= R1-2+ R(2-4)
2.5 Определяем общее сопротивление параллельного соединения между узлами 5-6
R (5-6)=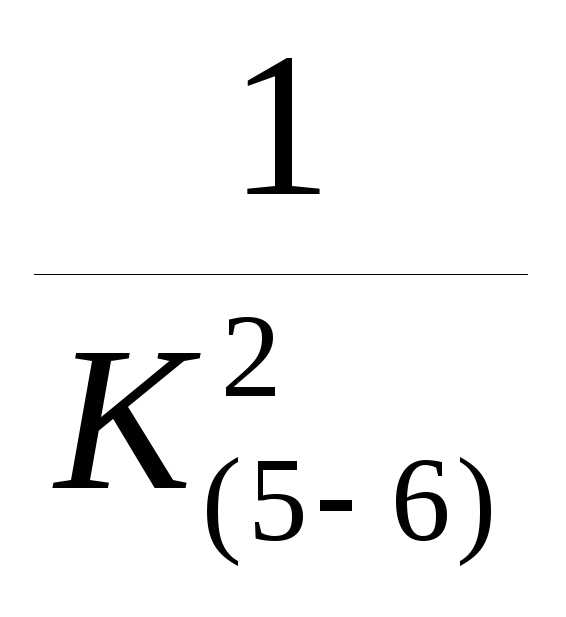 K(5-6)=
K(5-6)=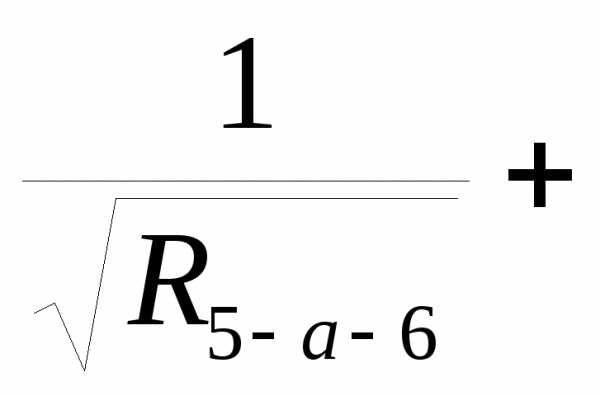
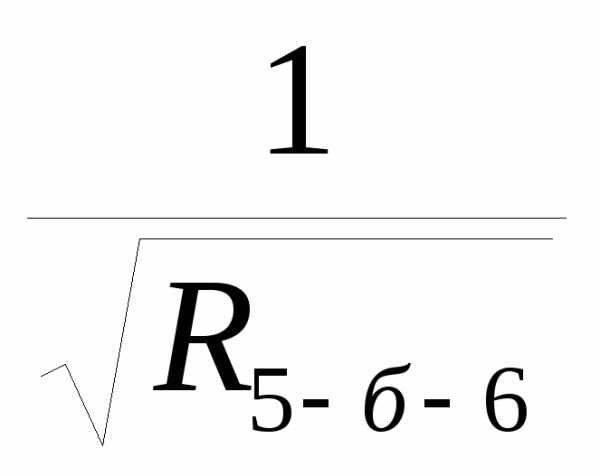
2.6 Определяем общее сопротивление последовательного соединения ветвей 1-5, (5-6) и 6-4
R1-(5-6)-4= R1-5+ R(5-6) + R6-4
2.7 Определяем общее сопротивление параллельного соединения между узлами 1-4
R(1-4)=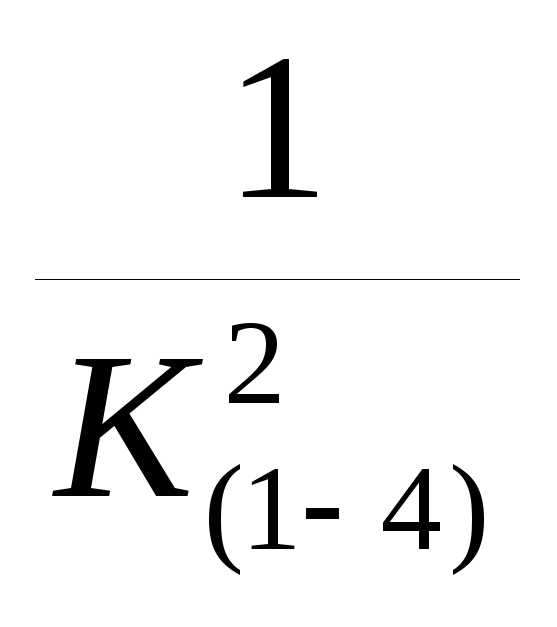 K(1-4)=
K(1-4)=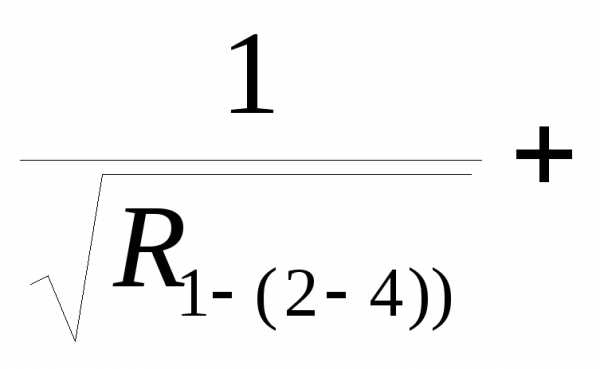
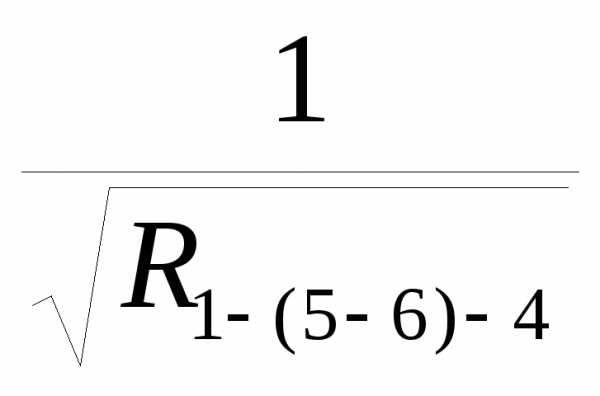
Определяем общее сопротивление вентиляционной сети
R(0-7)= R0-1+ R(1-4) + R4-7
Определяем общий расход воздуха в сети
Q=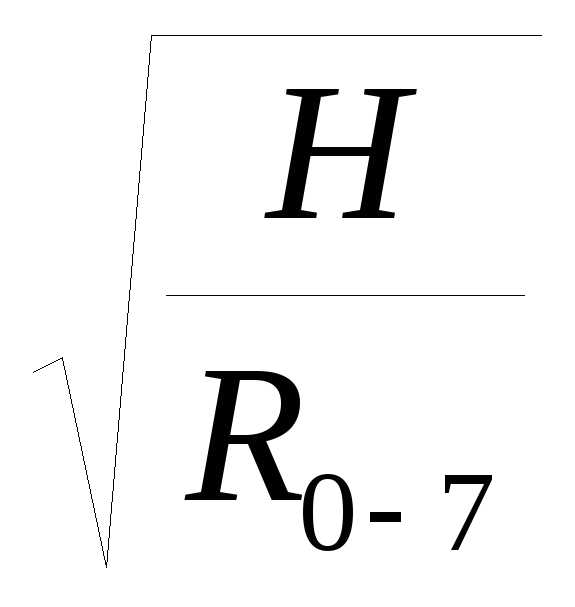
3.1 Определяем расходы воздуха в ветвях параллельного соединения 1-(2-4) и
1-(5-6)-4
q1-(2-4)=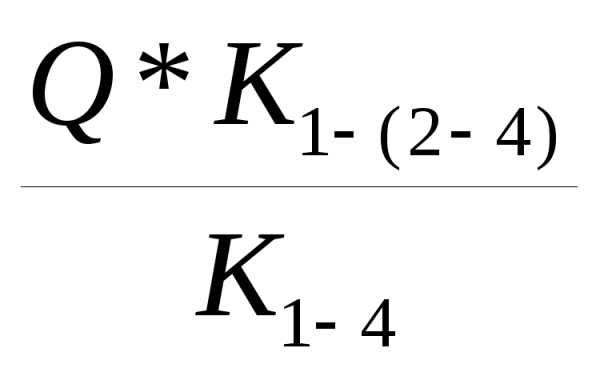 q1-(5-6)-4=
q1-(5-6)-4=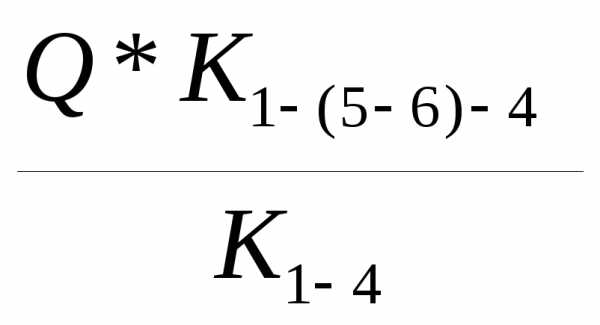
3.2 Определяем расходы воздуха в ветвях параллельного соединения 2-(3-4) и 2-4
q (2-3)-4=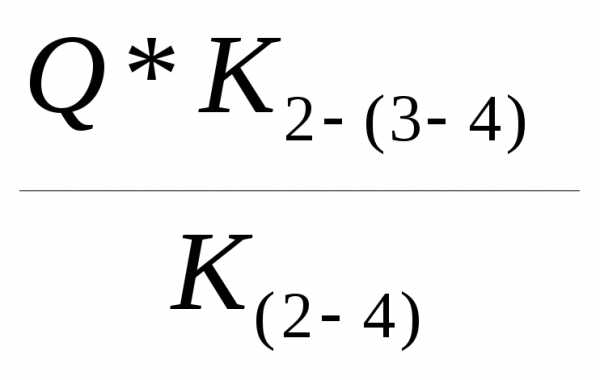 q 2-4=
q 2-4=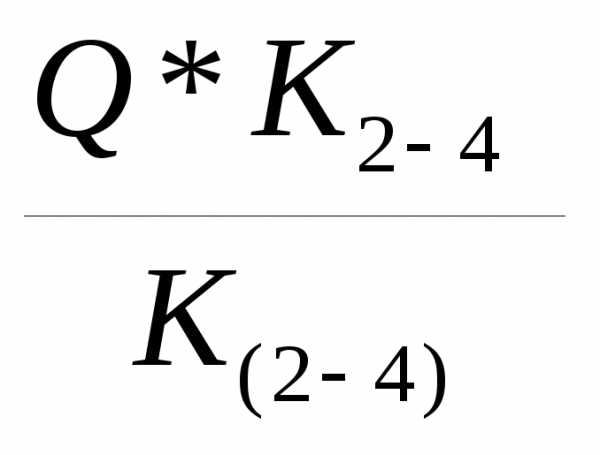
Определяем расходы воздуха в ветвях (3-а-4, и 3-б-4), по формулам
q3-а-4=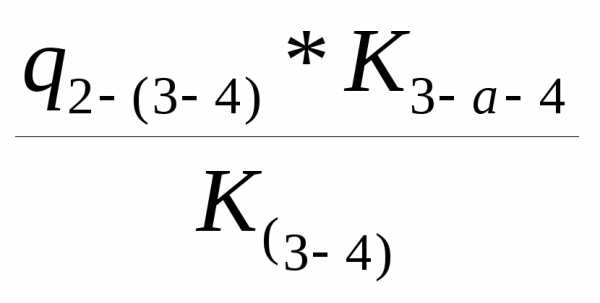 q 3-б-4=
q 3-б-4=
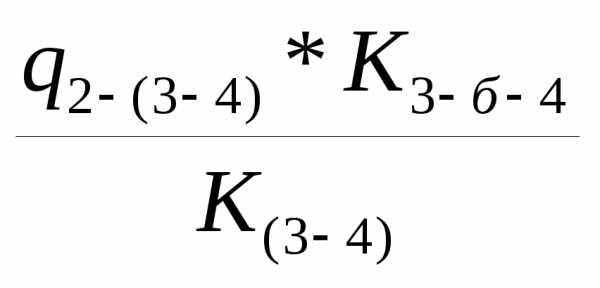
3.3 Определяем расходы воздуха в ветвях 5-а-6, (5-б-6) и (5-в-6), по формулам
q 5-а-6=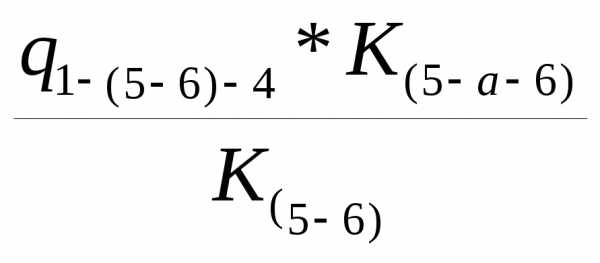 q (5-б-6)=
q (5-б-6)=
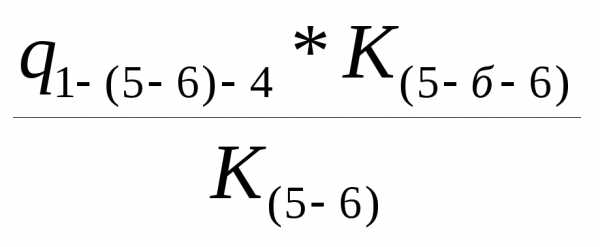
Результаты расчетов сложного последовательно-параллельного соединения, представленного на рис.6.10 по формулам сводим в таблицу.
Таблица
Результаты расчетов воздухораспределения в сложном последовательно параллельном соединении
| Обозначения ветвей схемы | Сопротивление ветвей R , кг*с2/м8 | Пропускная способность К,м3/с | Расход воздуха, q,м3/с | Депрессия ветвей, h, кг/м2 |
| 3-а-4 | 1.12 | 0.94 | 3.96 | 17.6 |
| 3-б-4 | 0.32 | 1.77 | 7.44 | 17.7 |
| (3-4) | 0.136 | 2.71 | 11.4 | 17.7 |
| 2-3 | 0.074 | 11.4 | 9.6 | |
| 2-(3-4) | 0.21 | 2.18 | 11.4 | 27.3 |
| 2-4 | 0.17 | 2.44 | 12.7 | 27.4 |
| (2-4) | 0.047 | 4.62 | 24.1 | 27.4 |
| 1-2 | 0.0076 | 24.1 | 4.4 | |
| 1-(2-4) | 0.0546 | 4.28 | 24.1 | 31.7 |
| 5-а-6 | 0.35 | 1.7 | 6.9 | 16.7 |
| 5-б-6 | 0.58 | 1.3 | 5.3 | 16.3 |
| (5-6) | 0.111 | 3.0 | 12.2 | 16.5 |
| 1-5 | 0.017 | 12.2 | 2.5 | |
| 6-4 | 0.084 | 12.2 | 12.5 | |
| 1-(5-6)-4 | 0.212 | 2.17 | 12.2 | 31.6 |
| (1-4) | 0.024 | 6.45 | 36.3 | 31.6 |
| 0-1 | 0.080 | 36.3 | 105.4 | |
| 4-7 | 0.0098 | 36.3 | 12.9 | |
| (0-7) | 0.1138 | 36.3 | 150 |
studfiles.net
Последовательное и параллельное соединение проводников
Последовательное соединение проводников. Параллельное соединение проводников.Последовательное и параллельное соединения в электротехнике — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию.
При последовательном соединении проводников сила тока во всех проводниках одинакова.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Последовательное соединение
При последовательном соединении проводников сила тока в любых частях цепи одна и та же:
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:
Резисторы
Катушка индуктивности
Электрический конденсатор
.Мемристоры
Параллельное соединение
Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединённых проводниках:
Напряжение на участках цепи АВ и на концах всех параллельно соединённых проводников одно и то же:
Резистор
При параллельном соединении резисторов складываются величины, обратно пропорциональные сопротивлению (то есть общая проводимость складывается из проводимостей каждого резистора )
Если цепь можно разбить на вложенные подблоки, последовательно или параллельно включённые между собой, то сначала считают сопротивление каждого подблока, потом заменяют каждый подблок его эквивалентным сопротивлением, таким образом находится общее(искомое) сопротивление.
Доказательство
Для двух параллельно соединённых резисторов их общее сопротивление равно: .
Если , то общее сопротивление равно:
При параллельном соединении резисторов их общее сопротивление будет меньше наименьшего из сопротивлений.
Катушка индуктивности
Электрический конденсатор
.Мемристоры
См. также
Ссылки
| В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 14 мая 2011. |
med.academic.ru
11.4. Последовательное и параллельное соединения трубопроводов Последовательное соединение
Рассмотрим систему из последовательно соединенных труб различных диаметров и длин. Такое соединение участков трубопровода называется последовательным (рис. 11.5). Очевидно, что расход во всех последовательно соединенных трубах один и тот же, а полные потери напора Н для всего трубопровода равны сумме потерь напора на всех участках, т.е.
Q1=Q2=Q3 =…=Qn =Q, (11.12)
H=h2+h3+ h4+…+ Hn,(11.13)
где h2, h3, h4, …, Hn – потери напора на 1, 2, 3, …, n-м участке.
Учитывая, что для каждого участка последовательного соединения справедлива зависимость (11.6) и имея в виду, что на каждом участке расход одинаковый, запишем (11.9) в виде:
. (11.14)
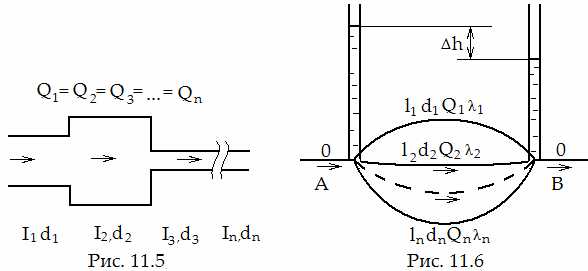
l1,d1l2,d2 l3,d3l4,d4
ln,dnQnλn
Рис. 11.5 Рис. 11.6
Из (11.14) следует, что решение первой и второй задач при последовательном соединении участков трубопровода разного диаметра будет таким же, как для простого трубопровода (трубопровода постоянного диаметра).
Третья же задача, если в ней потребовать определения диаметров для всех участков, становится неопределенной, так как в этом случае уравнение (11.14) содержит n неизвестных. Для решения этой задачи необходимо задать диаметры труб для всех участков, кроме одного, который может быть тогда определен.
Параллельное соединение
При параллельном соединении участков трубопровода жидкость, подходя с расходом Q к точке их разветвления А, распределяется по ответвлениям и далее снова собирается в точке их соединения В (рис. 11.6). При параллельном соединении обычно заданы: 1) Суммарный расход до точки разветвления; 2) Длина, диаметр, величина кэ каждой ветви и все коэффициенты ζi . Основными задачами гидравлического расчета в этом случае являются: 1. Определение расходов Q1, Q2, Q3, …, Qn на отдельных участках, соединенных параллельно. 2.Определение потерь напора Δh между точками А и В на каждом участке.
При решении задачи, прежде всего, учтем очевидное условие: равенство расхода Q сумме всех расходов
Q = Q1 + Q2 + Q3 + … + Qn . (11.15)
Для дальнейшего решения представим, что в точках А и В установлены пьезометры; так как концы всех трубопроводов смыкаются в одних и тех же точках А и В, то потери на всех этих участках одинаковы и равны Δh (Δh - разность показаний пьезометров, установленных в точках А и В). Поэтому справедливы следующие равенства
Δh=Δh2=Δh3=Δh4= …= Δhn . (11.16)
Решая систему уравнений (11.16), можно выразить все расходы через один (например, через Q1) и, подставив затем эти значения расходов в (11.15), найти Q1. После этого с помощью (11.16) определяют последовательно расходы Q2, Q3, ..., Qn , а по любому из уравнений системы (11.16) определяют потери напора Δh.
Задача 11.6. Определить расходы и потери напора в каждой из n параллельно соединенных ветвей, считая, что как местные сопротивления, так и сопротивления по длине - в квадратичной области.
Решение. В общем случае имеем для потерь в каждой ветви
(11.17)
Имеем также Q=Q1+Q2+Q3+…+ Qn. (11.18)
Примем обозначения .
тогда уравнения (11.17) перейдут в такие
. (11.19)
Из последнего уравнения выражаем все расходы через один, например Q1
. (11.20)
Затем из (11.18) получаем
. (11.21)
Решая последнее уравнение относительно Q1, определим его значение, а из (11.21) и все остальные расходы; по любой из зависимостей (4.6) находим hw.
studfiles.net
Параллельное соединение элементов
⇐ ПредыдущаяСтр 2 из 4Следующая ⇒Соединение нескольких элементов называется параллельным, если их выводы объединены в два узла; на каждом элементе цепи имеет место одно и то же напряжение.
Узлом называют соединение трех и более элементов или ветвей. В узле ток разветвляется.
Рис. 1.3. Эквивалентное преобразование параллельного соединения элементов
На рис. 1.3,a показано параллельное соединение резистивных элементов. Его можно заменить эквивалентным, используя одну из формул:
где gk = 1/rk ; g э= 1/rэ – проводимости элементов.
Для параллельного соединения элементов r1 и r2 имеем
Для параллельного соединения индуктивных элементов, емкостных элементов и источников тока на рис. 1.3,б,в,г формулы имеют вид
в последнем соотношении токи суммируются алгебраически.
Параллельное соединение источников напряжения не рассматривается.
В разветвленных электрических цепях можно выделить фрагменты последовательно и параллельно соединенных элементов. Такое соединение называется смешанным. Постепенно, шаг за шагом, заменой отдельных групп элементов на эквивалентные, можно представить все элементы одним эквивалентным, присоединенным к источнику питания. Если такое преобразование осуществляется с резистивными элементами, то конечный результат называется входным сопротивлением цепи со стороны источника питания.
1.1.Определить входное сопротивление для схемы рис. 1.4 со стороны источника питания с напряжением u.
Рис. 1.4. Последовательность упрощения разветвленной цепи
Решение рекомендуем начинать с упрощения удаленных от источника питания элементов. На первом этапе объединяем последовательно соединенные элементы r1 и r2 и параллельно соединенные r3и r4 :
Схема упрощается и на рис. 1.4,б принимает вид последовательного соединения трёх элементов. На втором этапе суммируем r12, r34 и r5 (рис. 1.4,в):
rэ = r12 + r34 + r5.
В результате вся совокупность резистивных элементов сведена к одному эквивалентному, которое и будет входным сопротивлением цепи.
Задача решена.
1.2. Определить входные сопротивления для схем рис. 1.5.
Рис. 1.5
Анализ этих схем показывает, что на рис. 1.5,a-д можно выделить последовательно и параллельно соединенные элементы, но в схеме рис. 1.5,е их нет. Чтобы получить такие группы элементов и на этой схеме, необходимо найти соединение "звездой" или "треугольником" и эквивалентно преобразовать одного в другое.
На рис. 1.6 показаны такие соединения и формулы эквивалентного
перехода.
Рис. 1.6. Преобразование ”Треугольник”Ы ”Звезда”
Варианты упрощения схемы на рис. 1.5,е могут быть следующими.
Рис. 1.7
Так преобразуя "звезду" r4, r5, r6 в "треугольник", получаем схему рис. 1.7,a, где можно выделить параллельно и последовательно соединенные элементы. Аналогично можно, к примеру, преобразовать "треугольник" r1, r4, r5, в "звезду" и также упростить схему (рис. 1.7,б). Возможны и другие преобразования.
1.3. Полагая все значения сопротивлений исходной цепи (рис. 1.5,е) равными 1[Ом], найти ее входное сопротивление, используя схемы на рис. 1.7.
1.4. Заменив в схемах рис. 1.5 все резистивные элементы на индуктивные и, сохранив прежнюю нумерацию элементов, определить эквивалентную индуктивность каждой схемы.
1.5. Заменить в схемах рис. 1.5 все резистивные элементы на емкостные с прежней нумерацией. Определить эквивалентную емкость цепи для каждой схемы.
Рис. 1.8. Последовательность эквивалентного преобразования цепи
с емкостными элементами
Например, для схемы рис. 1.4 после такой замены получим рис. 1.8,а. Объединяя элементы по аналогичным формулам, найдем на первом этапе преобразования (рис.1.8,б)
На втором этапе соответственно получим (рис. 1.8,в):
Задача решена.
Рассмотрены простейшие приемы преобразования пассивных цепей, составленных элементами R, L, C. Эквивалентные индуктивность, емкость и входное сопротивление определялись по отношению к выводам источника питания.
Однако существует необходимость в определении входного сопротивления относительно любой ветви пассивной цепи, получающейся после того, как напряжения источников ЭДС и токи источников тока исходной цепи приняты равными нулю. Например, при расчете тока в ветви методом эквивалентного генератора, при оценке результатов измерения напряжения вольтметром с малым внутренним сопротивлением.
Для определения входного сопротивления в данном случае необходимо выполнить следующее.
1. Разомкнуть ветвь, по отношению к которой требуется определить входное сопротивление. Зажимы разомкнутой ветви как-либо обозначить.
2. Исключить источники энергии, сохранив их внутренние сопротивления: источники напряжения закоротить (ru = 0), а источники тока разомкнуть (rj ® Ґ ).
3. Объединяя последовательно и параллельно соединенные элементы, привести цепь к одному сопротивлению по отношению к обозначенным зажимам. Это сопротивление и будет входным со стороны рассматриваемой ветви.
1.6. Для схемы на рис. 1.9 найти входное сопротивление по отношению к пятой ветви.
Рис. 1.9
На рис. 1.10,a показана схема цепи после исключения всех источников и сохранения их внутренних сопротивлений. В разомкнутой пятой ветви зажимы помечены символами m, n и показано стрелкой, что входное сопротивление Rвх5 определяется относительно именно этих зажимов.
Рис. 1.10
На первом этапе объединяем элементы слева от пятой ветви
схема упрощается до представленной на рис. 1.10,б. Окончательно объединяем параллельно соединенные сопротивления rэ и r6 и добавляем к ним сопротивление пятой ветви r5:
Полученный результат и будет решением поставленной задачи.
Читайте также:
lektsia.com
Видеоматериалы
Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше
Подробнее...С начала года из ветхого и аварийного жилья в республике были переселены десятки семей
Подробнее...Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе
Подробнее...Актуальные темы
ОТЧЕТ о деятельности министерства энергетики, ЖКХ и тарифной политики Кабардино-Балкарской Республики в сфере государственного регулирования и контроля цен и тарифов в 2012 году и об основных задачах на 2013 год
Подробнее...Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год
Подробнее...
КОНТАКТЫ
360051, КБР, г. Нальчик
ул. Горького, 4
тел: 8 (8662) 40-93-82
факс: 8 (8662) 47-31-81
e-mail:
Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.
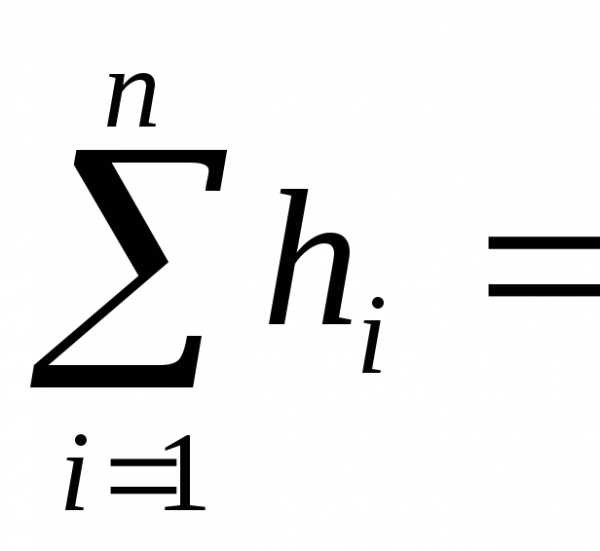 Н
Н