Предназначен для проведения лабораторных занятий по курсам «Электротехника и основы электроники», «Теория электрических цепей и основы электроники», «Электрические машины», «Электрический привод». Состав:
Методическое обеспечение:
Технические характеристики:
Лабораторные работы: Теория электрических цепей и основы электроники 1. Электрический привод |
Как заколебать ток. Конденсаторы и катушки. Параллельное соединение резистора, катушки индуктивности и конденсатора
Дроссель, катушка индуктивности
это спиралевидная, винтовидная либо винтоспиралевидная катушка, сконструированная из свёрнутого, хорошо заизолированного проводника. Данный провод обладает значительными показателями индуктивности при достаточно малой ёмкости и сопротивлении.
И отсюда следует, что при протекании по катушке переменного электрического тока, наблюдается значительная инерционность.
Дроссели в основном применяются: для подавления незначительных помех, для сглаживания относительно небольших пульсаций, а также для ограничения электрического тока и накопления энергии. На схемах катушка индуктивности без магнитопровода обозначена под номером 1
. Под номером 2
Под номером 2
изображена также катушка, но уже с отводами.
№ 3
– Дроссель со скользящими контактами;
№ 4
– Дроссель с ферромагнитным магнитопроводом;
№ 5
– Реактор.
Обычно обозначение №5
применяется в схемах электроснабжения. Реакторы обычно применяются для сглаживания пульсаций выпрямленного тока в цепях тяговых двигателей.
Катушки индуктивности могут иметь не только ферромагнитные магнитопроводы, как у дросселей, но и магнитопроводы со специальными свойствами. Они рассмотрены в статье .
О видах и характеристиках трансформаторов, можете почитать .
Конденсатор
в переводе с латинского языка «condensare
»
— означает «уплотнять», «сгущать». Данный элемент представляет собой — специфический двухполюсник, обладающий как определёнными, так и переменными значениями показателя емкости и относительно малым показателем проводимости. Конденсатор, первым делом, предназначен для накопления электрической энергии и заряда электрического поля.
Конденсатор — пассивный электронный компонент. Самый простой конденсатор – это конструкция, состоящая из двух электродов в виде пластин, которые называются обкладками, разделённых слоем диэлектрика (все вещества, которые не пропускают электрический ток, называются диэлектриками). Толщина этого вещества с размерами самих обкладок довольно мала. Конденсаторы, по своим свойствам, подразделяются на конденсаторы переменной
и постоянной
ёмкости. Как следует из названий, емкость переменных конденсаторов можно изменять вручную, а у постоянных конденсаторов емкость – неизменна.
Постоянный и переменный конденсаторы
На электрических схемах постоянные конденсаторы
обозначаются как на картинках № 6
. Далее на картинках № 7 / 8/ 9
/10
представлены поляризованный, и электролитический поляризованный и неполяризованный конденсаторы соответственно. Обозначение № 9
— уже устарело, и его можно встретить только на старых советских схемах.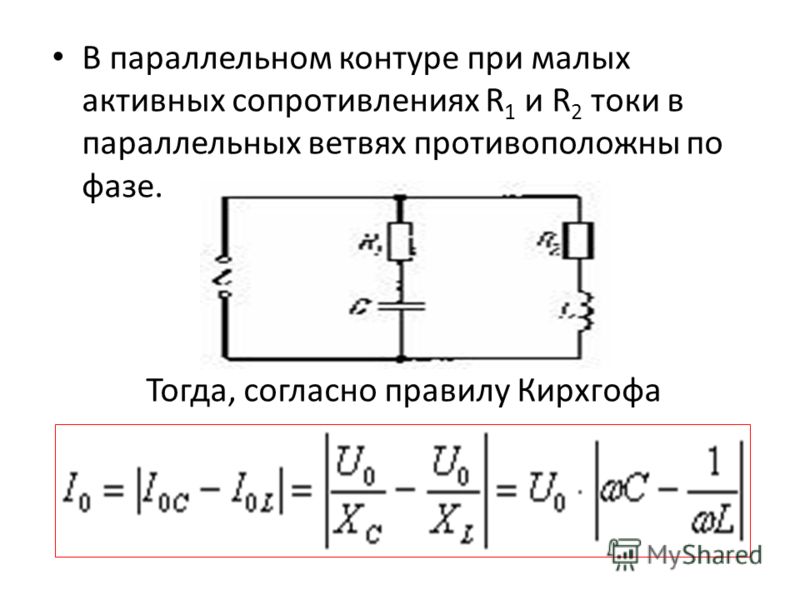
Конденсаторы переменной емкости на электротехнических схемах обозначены рисунками вида: рис. № 11
, № 12
— подстроечный. На рис № 13
проиллюстрирован – конденсатор – с нелинейной зависимостью емкости от напряжения.
Вариконд — конденсатор с нелинейной зависимостью ёмкости от напряжения
Если нужно показать подвижную обкладку конденсатора, то есть его ротор, то ее изображают в виде дуги № 14
. На рис. № 15
приведено старое обозначение, здесь вместо дуги ставили точку.
Положим
теперь, что участок цепи содержит
конденсатор емкости C
,
причем сопротивлением и индуктивностью
участка можно пренебречь, и посмотрим,
по какому закону будет изменяться
напряжение на концах участка в этом
случае. Обозначим напряжение между
точками а
и b
через u
и будем
считать заряд конденсатора q
и силу тока i
положительными, если они соответствуют
рис.4.
Тогда
,
и,
следовательно,
.
,
(1)
то заряд конденсатора
равен
.
Постоянная
интегрирования q
0
здесь обозначает произвольный постоянный
заряд конденсатора, не связанный с
колебаниями тока, и поэтому мы положим
.
Следовательно,
.
(2)
Рис.4. Конденсатор | Рис.5. Зависимости |
Сравнивая
(1) и (2), мы видим, что при синусоидальных
колебаниях тока в цепи напряжение на
конденсаторе изменяется также по закону
косинуса. Однако колебания напряжения
на конденсаторе отстают по фазе от
колебаний тока на /2.
Изменения тока и напряжения во времени
изображены графически на рис.5. Полученный
результат имеет простой физический
смысл. Напряжение на конденсаторе в
какой-либо момент времени определяется
существующим зарядом конденсатора. Но
этот заряд был образован током, протекавшим
предварительно в более ранней стадии
колебаний.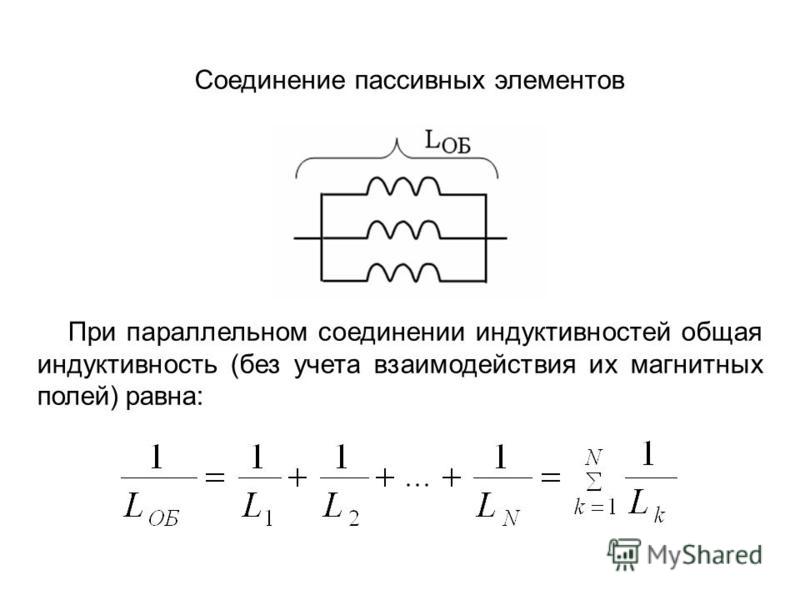 Поэтому и колебания напряжения
Поэтому и колебания напряжения
запаздывают относительно колебаний
тока.
Формула
(2) показывает, что амплитуда напряжения
на конденсаторе равна
.
Сравнивая
это выражение с законом Ома для участка
цепи с постоянным током (
),
мы видим, что величина
играет
роль сопротивления участка цепи, она
получила название емкостного сопротивления.
Емкостное сопротивление зависит от
частоты и
при высоких частотах даже малые емкости
могут представлять совсем небольшое
сопротивление для переменного тока.
Важно отметить,
что емкостное сопротивление определяет
связь между амплитудными, а не мгновенными
значениями тока и напряжения.
меняется
со временем по синусоидальному закону
с удвоенной частотой. В течение времени
от 0 до T
/4
мощность
положительна, а в следующую четверть
периода ток и напряжение имеют
противоположные знаки и мощность
становится отрицательной.
Поскольку
среднее значение за период колебаний
величины
равно нулю, то средняя мощность переменного
тока на конденсаторе
.
Катушка индуктивности в цепи переменного тока
Рассмотрим,
наконец, третий частный случай, когда
участок цепи содержит только индуктивность.
Обозначим по-прежнему через U
напряжение между точками а
и б
и будем считать ток I
положительным, если он направлен от а
к б
(рис.6). При наличии переменного тока в
катушке индуктивности возникнет ЭДС
самоиндукции, и поэтому мы должны
применить закон Ома для участка цепи,
содержащего эту ЭДС:
.
В
нашем случае R
= 0, а ЭДС самоиндукции
.
.
(3)
Если сила тока в
цепи изменяется по закону
,
Рис.6. Катушка переменного | Рис.7. индуктивности |
Видно,
что колебания напряжения на индуктивности
опережают по фазе колебания тока на
/2.
Когда сила тока, возрастая, проходит
через нуль, напряжение уже достигает
максимума, после чего начинает уменьшаться;
когда сила тока становится максимальной,
напряжение проходит через нуль, и т.д.
(рис.7).
Из
(4) следует, что амплитуда напряжения
равна
,
и, следовательно,
величина
играет
ту же роль, что сопротивление участка
цепи. Поэтому
называют индуктивным сопротивлением.
Индуктивное сопротивление пропорционально
частоте переменного тока, и поэтому при
очень больших частотах даже малые
индуктивности могут представлять
значительное сопротивление для переменных
токов.
Мгновенная
мощность переменного тока
также,
как и в случае идеальной емкости, меняется
со временем по синусоидальному закону
с удвоенной частотой. Очевидно, что
средняя за период мощность равна нулю.
Таким
образом, при протекании переменного
тока через идеальные емкость и
индуктивность обнаруживается ряд общих
закономерностей:
Колебания
тока и напряжения происходят в различных
фазах — сдвиг по фазе между этими
колебаниями равен /2.
Амплитуда
переменного напряжения на емкости
(индуктивности) пропорциональна
амплитуде протекающего через этот
элемент переменного тока
где
X
— реактивное (емкостное или индуктивное
сопротивление). Важно иметь в виду, что
это сопротивление связывает между собой
не мгновенные значения тока и напряжения,
а только их максимальные значения.
Реактивное сопротивление отличается
от омического (резистивного) сопротивления
еще и тем, что оно зависит от частоты
переменного тока.
На
реактивном сопротивлении не рассеивается
мощность (в среднем за период колебаний),
это означает, что, например, через
конденсатор может протекать переменный
ток очень большой амплитуды, но
тепловыделение на конденсаторе будет
отсутствовать. Это является следствием
фазового сдвига между колебаниями тока
и напряжения на реактивных элементах
цепи (индуктивности и емкости).
Резистивный
элемент, который описывается в
рассматриваемом частотном диапазоне
законом Ома для мгновенных
токов и напряжений
,
называют омическим
или активным сопротивлением.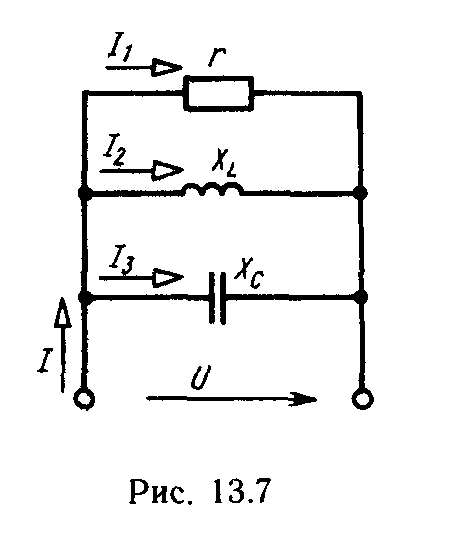 На активных
На активных
сопротивлениях происходит выделение
мощности.
§ 54. Индуктивность в цепи переменного тока
Прохождение электрического тока по проводнику или катушке сопровождается появлением магнитного поля. Рассмотрим электрическую цепь переменного тока (рис. 57, а), в которую включена катушка индуктивности, имеющая небольшое количество витков проволоки сравнительно большого сечения, активное сопротивление которой можно считать практически равным нулю.
Под действием э. д. с. генератора в цепи протекает переменный ток, возбуждающий переменный магнитный поток. Этот поток пересекает «собственные» витки катушки и в ней возникает электродвижущая сила самоиндукции
где L
— индуктивность катушки;
— скорость изменения тока в ней.
Электродвижущая сила самоиндукции, согласно правилу Ленца, всегда противодействует причине, вызывающей ее. Так как э. д. с. самоиндукции всегда противодействует изменениям переменного тока, вызываемым э. д. с. генератора, то она препятствует прохождению переменного тока. При расчетах это учитывается по индуктивному сопротивлению, которое обозначается X L
При расчетах это учитывается по индуктивному сопротивлению, которое обозначается X L
и измеряется в омах.
Таким образом, индуктивное сопротивление катушки X L
, зависит от величины э. д. с. самоиндукции, а следовательно, оно, как и э. д. с. самоиндукции, зависит от скорости изменения тока в катушке (от частоты ω) и от индуктивности катушки L
X L
= ωL
, (58)
где X L
— индуктивное сопротивление, ом
;
ω — угловая частота переменного тока, рад/сек
;
L
— индуктивность катушки, гн
.
Так как угловая частота переменного тока ω = 2πf
, то индуктивное сопротивление
X L
= 2πf L
, (59)
где f
— частота переменного тока, гц
.
Пример.
Катушка, обладающая индуктивностью L
= 0,5 гн
, присоединена к источнику переменного тока, частота которого f
= 50 гц
. Определить:
1) индуктивное сопротивление катушки при частоте f
= 50 гц
;
2) индуктивное сопротивление этой катушки переменному току, частота которого f
= 800 гц
.
Решение
. Индуктивное сопротивление переменному току при f
= 50 гц
X L
= 2πf L
= 2 · 3,14 · 50 · 0,5 = 157 ом
.
При частоте тока f
= 800 гц
X L
= 2πf L
= 2 · 3,14 · 800 · 0,5 = 2512 ом
.
Приведенный пример показывает, что индуктивное сопротивление катушки повышается с увеличением частоты переменного тока, протекающего по ней. По мере уменьшения частоты тока индуктивное сопротивление убывает. Для постоянного тока, когда ток в катушке не изменяется и магнитный поток не пересекает ее витки, э. д. с. самоиндукции не возникает, индуктивное сопротивление катушки X L
равно нуло. Катушка индуктивности для постоянного тока представляет собой лишь сопротивление
Выясним, как изменяется з. д. с. самоиндукции, когда по катушке индуктивности протекает переменный ток.
Известно, что при неизменной индуктивности катушки э. д. с. самоиндукции зависит от скорости изменения силы тока и она всегда направлена навстречу причине, вызвавшей ее.
На графике (рис. 57, в) переменный ток показан в виде синусоиды (сплошная линия). В первую четверть периода сила тока возрастает от нулевого до максимального значения. Электродвижущая сила самоиндукции е
с, согласно правилу Ленца, препятствует увеличению тока в цепи. Поэтому на графике (пунктирной линией) показано, что ес в это время имеет отрицательное значение. Во вторую четверть периода сила тока в катушке убывает до нуля. В это время э. д. с. самоиндукции изменяет свое направление и увеличивается, препятствуя убыванию силы тока. В третью четверть периода ток изменяет свое направление и постепенно увеличивается до максимального значения; э. д. с. самоиндукции имеет положительное значение и далее, когда сила тока убывает, э. д. с. самоиндукции опять меняет свое направление и вновь препятствует уменьшению силы тока в цепи.
Из сказанного следует, что ток в цепи и э. д. с. самоиндукции не совпадают по фазе. Ток опережает э. д. с. самоиндукции по фазе на четверть периода или на угол φ = 90°.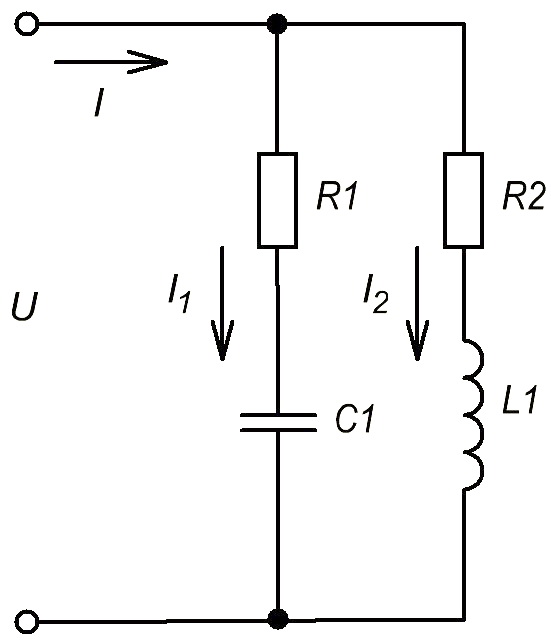 Необходимо также иметь в виду, что в цепи с индуктивностью, не содержащей г, в каждый момент времени электродвижущая сила самоиндукции направлена навстречу напряжению генератора U
Необходимо также иметь в виду, что в цепи с индуктивностью, не содержащей г, в каждый момент времени электродвижущая сила самоиндукции направлена навстречу напряжению генератора U
. В связи с этим напряжение и э. д. с. самоиндукции е
с также сдвинуты по фазе друг относительно друга на 180°.
Из изложенного следует, что в цепи переменного тока, содержащей только индуктивность, ток отстает от напряжения, вырабатываемого генератором, на угол φ = 90° (на четверть периода) и опережает э. д. с. самоиндукции на 90°. Можно также сказать, что в индуктивной цепи напряжение опережает по фазе ток на 90°.
Построим векторную диаграмму тока и напряжения для цепи переменного тока с индуктивным сопротивлением. Для этого отложим вектор тока I
по горизонтали в выбранном нами масштабе (рис. 57, б.)
Чтобы на векторной диаграмме показать, что напряжение опережает по фазе ток на угол φ = 90°, откладываем вектор напряжения U
вверх под углом 90°. Закон Ома для цепи с индуктивностью можно выразить так:
Следует подчеркнуть, что имеется существенное отличие между индуктивным и активным сопротивлением переменному току.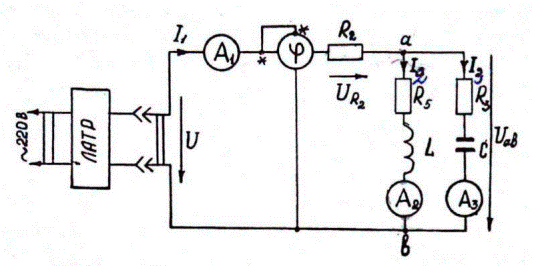
Когда к генератору переменного тока подключена активная нагрузка, то энергия безвозвратно потребляется активным сопротивлением.
Если же к источнику переменного тока присоединено индуктивное сопротивление r
= 0, то его энергия, пока сила тока возрастает, расходуется на возбуждение магнитного поля. Изменение этого поля вызывает возникновение э. д. с. самоиндукции. При уменьшении силы тока энергия, запасенная в магнитном поле, вследствие возникающей при этом э. д. с. самоиндукции возвращается обратно генератору.
В первую четверть периода сила тока в цепи с индуктивностью возрастает и энергия источника тока накапливается в магнитном поле. В это время э. д. с. самоиндукции направлена против напряжения.
Когда сила тока достигнет максимального значения и начинает во второй четверти периода убывать, то э. д. с. самоиндукции, изменив свое направление, стремится поддержать ток в цепи. Под действием э. д. с. самоиндукции энергия магнитного поля возвращается к источнику энергии — генератору. Генератор в это время работает в режиме двигателя, преобразуя электрическую энергию в механическую.
Генератор в это время работает в режиме двигателя, преобразуя электрическую энергию в механическую.
В третью четверть периода сила тока в цепи под действием э. д. с. генератора увеличивается, и при этом ток протекает в противоположном направлении. В это время энергия генератора вновь накапливается в магнитном поле индуктивности.
В четвертую четверть периода сила тока в цепи убывает, а накопленная в магнитном поле энергия при воздействии э. д. с. самоиндукции вновь возвращается генератору.
Таким образом, в первую и третью четверть каждого периода генератор переменного тока расходует свою энергию в цепи с индуктивностью на создание магнитного поля, а во вторую и четвертую четверть каждого периода энергия, запасенная в магнитном поле катушки в результате возникающей э. д. с. самоиндукции, возвращается обратно генератору.
Из этого следует, что индуктивная нагрузка в отличие от активной в среднем не потребляет энергию, которую вырабатывает генератор, а в цепи с индуктивностью происходит «перекачивание» энергии от генератора в индуктивную нагрузку и обратно, т. е. возникают колебания энергии.
е. возникают колебания энергии.
Из сказанного следует, что индуктивное сопротивление является реактивным. В цепи, содержащей реактивное сопротивление, происходят колебания энергии от генератора к нагрузке и обратно.
Конденсаатор — (от лат. condensare — «уплотнять»,
«сгущать» или от лат. condensatio — «накопление») —
двухполюсник с определённым или переменным
значением ёмкости и малой проводимостью; устройство
для накопления заряда и энергии электрического поля.
Конденсатор является пассивным электронным компонентом. В
простейшем варианте конструкция состоит из двух электродов в
форме пластин (называемых обкладками), разделённых
диэлектриком, толщина которого мала по сравнению с размерами
обкладок (см. рис.). Практически применяемые конденсаторы имеют
много слоёв диэлектрика и многослойные электроды, или ленты
чередующихся диэлектрика и электродов, свёрнутые в цилиндр или
параллелепипед со скруглёнными четырьмя рёбрами (из-за намотки).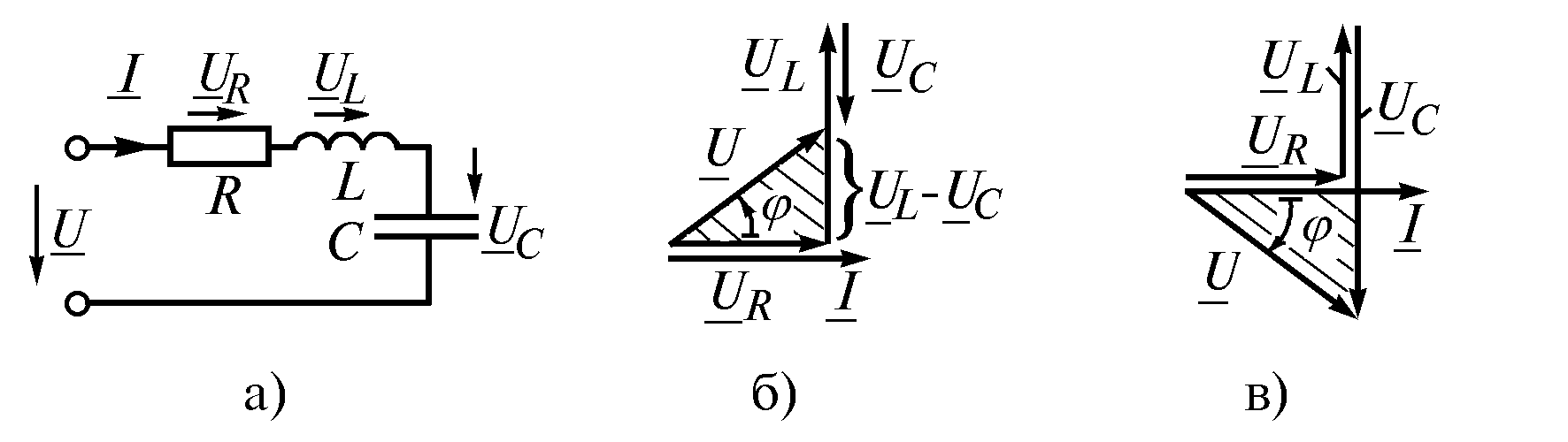
Виды конденсаторов
1.воздушный
2.бумажный
3.керамический
4.слюдяной
5.электролитический
В России условные графические обозначения конденсаторов на схемах должны
соответствовать ГОСТ 2.728-74 либо международному стандарту IEEE 315-1975:
Обозначение
по ГОСТ 2.728-74Описание Конденсатор постоянной ёмкости Поляризованный (полярный)
конденсатор Подстроечный конденсатор переменной ёмкости ВарикапНа
электрических принципиальных схемах номинальная ёмкость конденсаторов обычно
указывается в микрофарадах (1 мкФ = 1·106 пФ = 1·10−6 Ф) и пикофарадах (1 пФ = 1·10−12Ф),
но нередко и в нанофарадах (1 нФ = 1·10−9 Ф). При ёмкости не более 0,01 мкФ, ёмкость
конденсатора указывают в пикофарадах, при этом допустимо не указывать единицу измерения,
то есть постфикс «пФ» опускают. При обозначении номинала ёмкости в других единицах
указывают единицу измерения. Для электролитических конденсаторов, а также для
высоковольтных конденсаторов на схемах, после обозначения номинала ёмкости, указывают их
максимальное рабочее напряжение в вольтах (В) или киловольтах (кВ). Например так: «10 мкФ
Например так: «10 мкФ
x 10 В». Для переменных конденсаторов указывают диапазон изменения ёмкости, например
так: «10 — 180». В настоящее время изготавливаются конденсаторы с номинальными
ёмкостями из десятичнологарифмических рядов значений Е3, Е6, Е12, Е24, то есть на одну
декаду приходится 3, 6, 12, 24 значения, так, чтобы значения с соответствующим допуском
(разбросом) перекрывали всю декаду.
Применение конденсаторов
накапливать на короткое время заряд или энергию
для быстрого изменения потенциала;
радиотехника:колебательный контур,выпрямитель;
вспышка при фотографировании;
клавиатура компьютера;
электротехника;
защита оборудования силовых цепей
электровозов;
Конденсаторы электровозов
КОНДЕНСАТОРЫ КС-0,5-19 Назначение. Конденсаторы КС-0,5-19 (рис. 8.48) предназначены для
работы в цепях вспомогательных машин. Они удовлетворяют
требованиям, предъявляемым к тяговой электроаппаратуре, и
устанавливаются при замене комплекта конденсаторов типа КМ-0,5.
Конструкция.
Конструкция. Конденсаторы состоят из корпуса, крышки с выводами и выемной части. Корпус, сваренный из
листовой стали, имеет скобы для перемещения конденсатора. На крышке, штампованной из листовой стали,
расположены изоляторы с выводами для подключения проводов. Пакет выемной части состоит из секций,
образующих две группы конденсаторов, соединенных параллельно. Группы имеют общий вывод, обозначенный на
крышке знаком 0. Каждая секция снабжена индивидуальным плавким предохранителем, встроенным в конденсатор
и недоступным для замены. При коротком замыкании перегорает предохранитель секции и она отключается. При
этом снижается емкость конденсатора, но он не выводится из работы.
Благодаря
Благодаря применению специальной синтетической пропитывающей жидкости конденсаторы могут работать при
температуре -50 °С.
10. Защита оборудования силовых цепей
Защита от перенапряжений и помехоподавляющее устройство. Защита от атмосферных и
коммутационных перенапряжений осуществляется биполярным разрядником 48-2 типа РМВУ-3,3,
который вместе с регистратором числа срабатываний установлен на крыше 2-й секции и подключен
к главной токоведущей шине.
Для снижении уровня помех в канале поездной радиосвязи, возникающих при работе локомотивного
электрооборудования, на электровозах ВЛЮ до № 1 704 (ТЭВЗ) и до № 1348 (НЭВЗ) установлено
устройство, состоящее из контура индуктивности и емкости. В качестве индуктивности применен
дроссель Д-8Г (схемное обозначение 21-1), который включен в силовую цепь между токоприемником
и быстродействующими выключателями 51-1 и 53-2. В качестве емкости применен конденсатор
(схемное обозначение 156-1), подключенный в силовую цепь между дросселем и
быстродействующим выключателями.
Начиная с электровозов ВЛ10-1704 выпуска ТЭВЗ и ВЛ10-1318 выпуска НЭВЗ, внедрена новая
схема п о м е х о п о д а в л е н и я, которая обеспечивает комплексное подавление помех в канале
поездной радиосвязи как от нарушения токосъема, так и от работы электрооборудования. С этой
целью установлены дроссели 21-1 и 21-2, конденсаторы 156-1, 156-2, блоки разделительного
контура 230-1, 230-2 и конденсатор 219-1.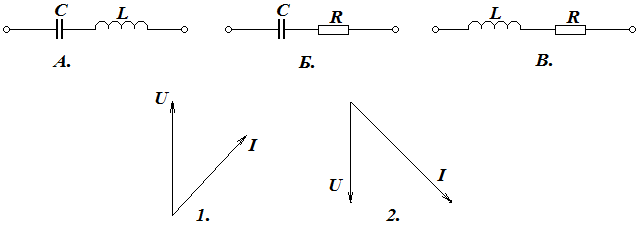
При такой схеме помехоподавляющего устройства снижение уровня помех от токосъема достигается
благодаря образованию резонансного контура, который настраивается на частоту радиостанции.
Настройка контура на частоту 2130 кГц достигается с помощью конденсатора С2 (рис. 216).
От больших токов к. з. силовая цепь защищена быстродействующим автоматическим
выключателем 51-1 (БВ-1). Защита от малых токов к. з., не превышающих тока установки
выключателя БВ-1, осуществляется дифференциальным реле 52-1, которое при срабатывании
своими блок-контактами разрывает цепь удерживающей катушки выключателя 51-1.
Для защиты высоковольтных шин, установленных на крыше электровоза, от помех, создаваемых
электрооборудованием электровоза, служит конденсатор 219-1, включенный у главного ввода. — »~ _
Защита от коротких замыканий.
11. Схема помехоподавляющего устройства
Схема помехоподавляющего устройства
12.
Действие защиты
(ТЭВЗ) и до № 1308 (НЭВЗ) защита осуществляется
переключением двигателей на последовательное возбуждение
быстродействующими контакторами БК-2Б (302-1, 303-1, 302-2,
303-2, рис.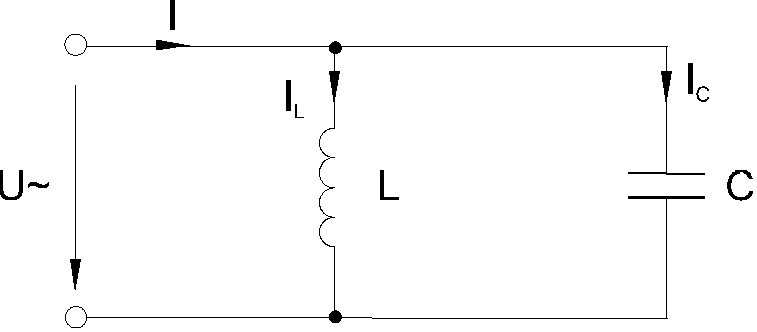 217, ■218, 219), удерживающие катушки которых
217, ■218, 219), удерживающие катушки которых
включены в цепь двигателей вентиляторов.
Для снижения перенапряжений контакты БК шунтированы
разрядными резисторами Р203-Р204, Р207-Р208, Р211-Р212,
Р213-Р214. Этой же цели служат разрядные резисторы Р201-
Р202 и Р209-Р210 генераторов преобразователей.
Действие защиты во время рекуперативного торможения
контактором БК-2Б можно рассмотреть на примере
параллельного соединения обмоток якорей тяговых двигателей
(см. рис. 217). При к. з. напряжение в контактной сети равно нулю,
поэтому ток к. з. будет быстро расти. Возрастание тока к. з. в
обмотках противовозбуждения 112-НИ2 и НЗ-ИНЗ генераторов
преобразователей не может вызвать быстрого уменьшения их
магнитного потока и э. д. с, что объясняется значительным
отставанием магнитного потока от тока. За время к. з. магнитный
поток генераторов преобразователей практически не
уменьшается.
13. Схема действия защиты при к.
 з. в процессе рекуперативного торможения на параллельном соединении обмоток якорей тяговых двигателей элект
з. в процессе рекуперативного торможения на параллельном соединении обмоток якорей тяговых двигателей элект
Схема действия защиты при к. з. в процессе рекуперативного
торможения на параллельном соединении обмоток якорей
тяговых двигателей электровозов с контакторами БК-2Б
14. Техника безопасности:
Заряженный
конденсатор опасен
для жизни!
15.
1.Резистор в цепи переменного
тока
Схема включения
u=U cosωt
~
u i
Umcosωt
m
R
R – активное
сопротивление
Y
T= 2π/ω
Um
Im
O
-Im
-Um
T/2
T
t
Im
Um
O
Напряжение и сила тока в резисторе
совпадают по фазе в любой момент
X
16. 2. Мощность тока в резисторе
P
0.5
t
O
T/4
T/2
Действующее значение силы
переменного тока равно силе
постоянного тока, при котором в
проводнике выделяется такое же
количество теплоты, что и при
3T/4
T
17.

3. Конденсатор в цепи переменного тока
u=Umcosωt
Схема включения
~
u i
Umcosωt
С
Ёмкостное
сопротивление
T= 2π/ω
Um
Im
O
-Im
-Um
T/2
T
t
Im
Um
O
X
Сила тока через конденсатор опережает
напряжение на нем на π/2
18.
4. Мощность тока на конденсаторе
T/2
O
T/4
3T/4
T
t
Среднее значение мощности
переменного тока на конденсаторе за
19.
5. катушка индуктивности в цепи переменного тока
u=Umcosωt
Схема включения
~
u i
Umcosωt
L
Индуктивное
сопротивлени
е
T= 2π/ω
Um
Im
O
-Im
T/2
T
t
O
Im
Um
X
Колебания силы тока в катушке индуктивности
отстают по фазе на π/2 от колебаний напряжения
20.
6. Мощность тока в катушке
T/2
O
T/4
3T/4
T
t
Среднее значение мощности переменного
тока в катушке индуктивности за период Т
21.
Список литературы
1.Мякишев Г.Я.,Буховцев Б.Б., Сотский Н.Н., Физика: учебник для 10 кл.
общеобразовательных учреждений.- М.: Просвещение, 2005.
2.Бородулин Б. М. Новые системы электроснабжения для участков переменного тока. — Электр. и тепловоз. тяга, 1974, № 9, с. 44-45.
3.Быстрицкий X. Я., Дубровский З. М., Ребрик Б. Н. Устройство и работа электровозов переменного тока. 3-е изд., перераб. и доп. М., Транспорт, 1973, 464 с
4.Головатый А. Т., Исаев И. П., Горчаков Е. В. Независимое возбуждение тяговых двигателей электровозов. М., Транспорт, 1976. 150 с.
5.Грузовой электровоз постоянного тока типа ВЛ12 / Б. Р. Бондаренко, Л. Д. Сокут, Б. К. Баранов и др. — Электр. и тепловоз. тяга, 1976, № 3, с. 33-35.
6.Калинин В. К., Михайлов Н. Н., Хлебников В. Н. Электроподвижной состав железных дорог. 3-е изд., перераб. и доп. М., Транспорт, 1972. 536 с.
7.
Каминский Е. А. Техника чтения схем электроустановок. 2-е изд., перераб. и доп. М., Энергия, 1972. 120 с.
120 с.
8.
Сидоров Н. И. Как устроен и работает электровоз. 3-е изд., перераб и доп. М., Транспорт, 1974. 224 с.
2.Тихменев Б. Н., Трахтман Л. М, Подвижной состав электрических железных дорог. Теория работы электрооборудованияя электрические схемы и аппараты. Изд. 3-е, перераб. и доп. М.,
Транспорт, 1969, 408 с.
2.Токоприемники электроподвижного состава/И. А. Беляев, В. Г. Бердзенишвили, В. П. Михеев и др. Под ред. И. А. Беляева. М., Транспорт, 1970. 192 с.
3.Трехсекционный грузовой электровоз ВЛ11 с рекуперативным торможением / Г. И. Чиракадзе, Г. С. Башалеишвили, Б. Н. Болашвили и др. — Электр. и тепловоз. тяга, 1976, № 7, с. 32-33.
4.Устройство и ремонт электровозов постоянного тока / С. И. Осипов, В. Н. Хлебников, Е. В. Горчаков и др. М., Транспорт, 1977, 463 с.
5.Фуфрянский Н. А. Основные направления развития электрической и дизельной тяги. — Электр. и тепловоз. тяга, 1970, № 10, с. 1-15.
6.Электровоз ВЛ80К. Руководство по эксплуатации. М. , Транспорт, 1973, 432 с. В надзаг.: Новочеркасский электровозостроит. з-д.
, Транспорт, 1973, 432 с. В надзаг.: Новочеркасский электровозостроит. з-д.
7.Электровоз ВЛ60к. Руководство по эксплуатации. М., Транспорт, 1976, 352 с. В надзаг.: Новочеркасский электровозостроит. з-д.
8.Электровоз ВЛ10. Руководство по эксплутации / О. А. Кикнадзе, Г. Г. Гудавадзе, Г. И. Ксоврели и др.; Под ред. О. А. Кикнадзе. М., Транспорт, 1975. 520 с. В надзаг: Тбил.
электровозостроит. з-д. нм. В. И. Ленина.
9.Электровоз ВЛ80Т. Руководство по эксплуатации /Н. П. Козельский, М. П. Орлов, А. А. Матлахов и др.; Под ред. Б. Р. Бондаренко М., Транспорт, 1977, 568 с. В надзаг.: Всесоюз. н.-и.
проектно-конструк. и технолог, и-т электровозостроения; Новочерк. электровозостроит. з-д.
10.
Яковлев Д. В. Управление электровозом и его обслуживание. 3-е изд., доп. и перераб. М., Транспорт, 1977. 344 с.
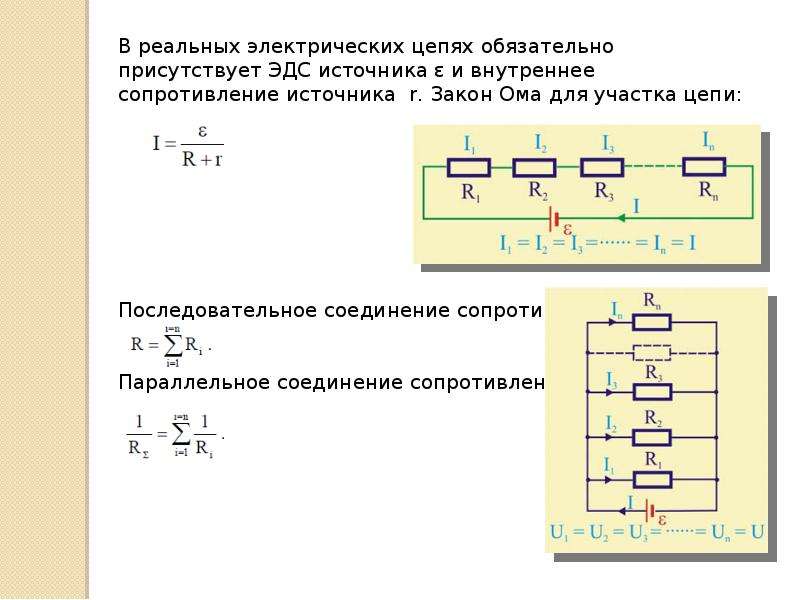
По закону Ома, в замкнутой цепи
постоянного тока
напряжение на зажимах источника меньше
ЭДС
U =
IR; U = E — Ir
Резистор в цепи переменного тока
Рассмотрим
схему, состоящую из источника переменного
тока, резистора и идеальных проводов.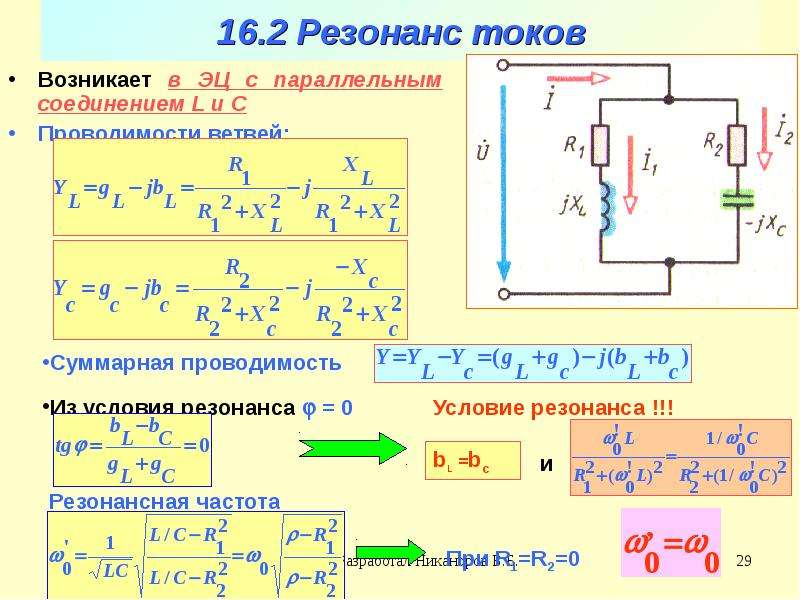
Предположим, что напряжение на резисторе
изменяется по гармоническому закону
U = U
0
cos
ω
t .
Найдем силу тока, протекающего через
резистор.
По закону Ома для участка цепи
I=U/R ==> I = I
0
cos
ω
t
Амплитуда силы тока I
0
=
U
0
/
R
Ток и напряжение изменяются по
одинаковому гармоническому закону
(косинуса), то есть совпадают по фазе.
Это означает,
что, например, в тот
момент времени, когда в цепи максимальна
сила тока, напряжение на резисторе также
максимально.
Конденсатор в цепи переменного тока
Включим конденсатор в цепь постоянного
тока.
Некоторый заряд перетечет от
источника тока на обкладки конденсатора.В цепи возникает кратковременный
импульс зарядного тока. Конденсатор
заряжается до напряжения источника,
после чего ток прекращается. Через
Через
конденсатор постоянный ток течь не
может!
Рассмотрим
процессы, происходящие при включении
конденсатора в цепь переменного тока
зарядный ток
Через диэлектрик, разделяющий обкладки
конденсатора, электрический ток
протекать, как и прежде, не может. Но в
результате периодически повторяющихся
процессов зарядки и разрядки конденсатора
в цепи появится переменный ток.
Если напряжение в цепи изменяется по
гармоническому закону,
U = U
0
cos ωt
то заряд на обкладках конденсатора
изменяется
также по
гармоническому закону
q=Cu = CU
0
cos
ω
t
и силу тока в цепи можно найти как
производную заряда
i = q
/
i= -CU
0
ω
sin
ω
t
= CU
0
ω
cos(ω
t+π/2),
i= I
0
ω
cos(ω
t+π/2)
Амплитуда силы тока I
0
=
CU
0
ω
Из полученной формулы видно, что в любой
момент времени
фаза тока больше фазы напряжения на
π
/2.
В цепи переменного напряжение на
конденсаторе тока отстает по фазе от
тока на
π
/2, или
на четверть периода.
Емкостное сопротивление
Величину
называют емкостным сопротивлением.
Связь между амплитудными значениями
силы тока и напряжения формально
совпадает с законом Ома для участка
цепи
Такое же соотношение выполняется для
действующих значений силы тока и
напряжения
.
Емкостное сопротивление конденсатора
зависит от частоты переменного
напряжения. С увеличением частоты
колебаний напряжения емкостное
сопротивление уменьшается, поэтому
амплитуда силы тока увеличивается прямо
пропорционально частоте
I
0
=
CU
0
ω.
При уменьшении частоты амплитуда силы
тока уменьшается и при ω=0 обращается в
0. Отметим, что нулевая частота колебаний
означает, что в цепи протекает постоянный
ток
.
Катушка индуктивности в цепи переменного тока
Мы предполагаем, что катушка индуктивности
обладает пренебрежимо малым активным
сопротивлением R. Такой
Такой
элемент включать в цепь постоянного
тока нельзя, потому что произойдет
короткое замыкание.
В цепи переменного тока мгновенному
нарастанию силы тока препятствует ЭДС
самоиндукции. При этом для сверхпроводника
e
i
+u=0.
Используя закон Фарадея для самоиндукции
e
i
= -Li
/
,
можно показать, что, если сила тока в
цепи изменяется по гармоническому
закону
Соединение катушек — Основы электроники
Соединение катушек индуктивности при отсутствии взаимного влияния магнитных полей катушек.
Последовательное соединение катушек индуктивности.
Суммарная индуктивность двух или нескольких катушек, соединенных последовательно и расположенных на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой (рисунок 1), равна сумме их индуктивностей.
Рисунок 1. Последовательное соединение катушект индуктивности.
Цепь, изображенная на рисунке 1, обладает общей индуктивностью L, которая выражается так:
где L1, L2 и L3 — индуктивности отдельных катушек.
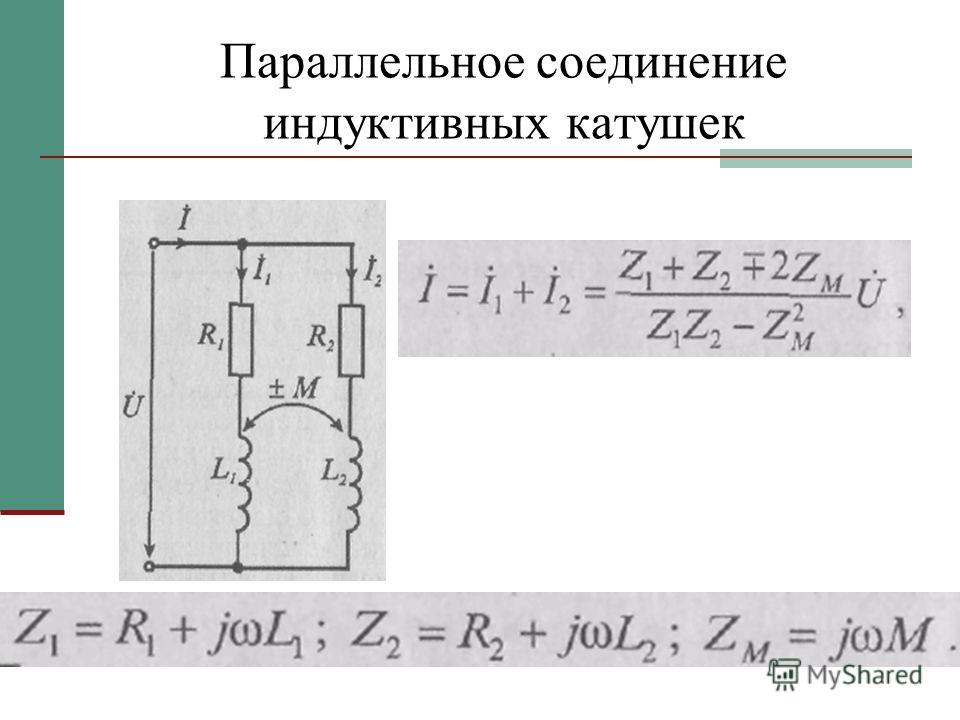
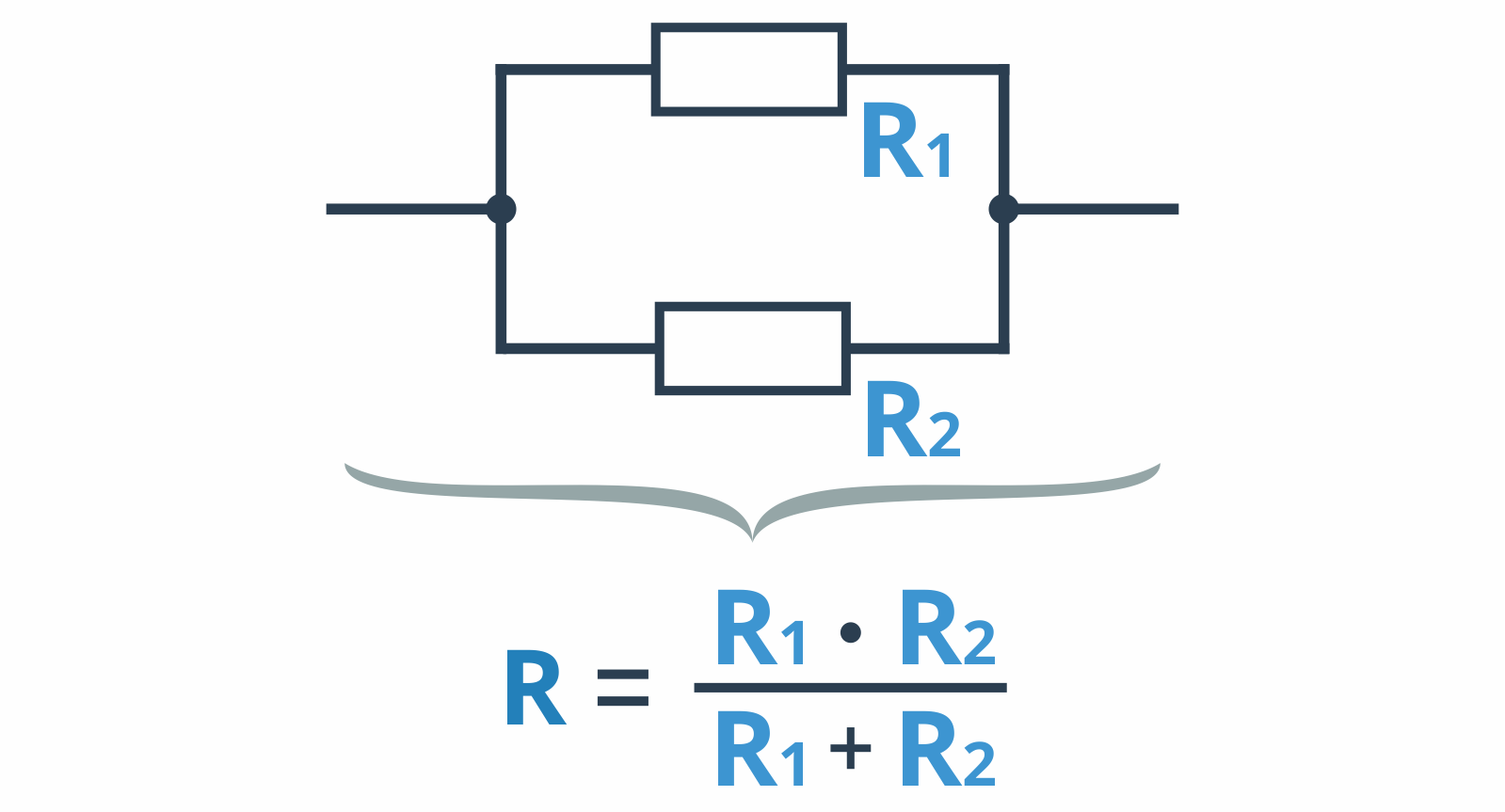
Параллельное соединение катушек индуктивности.
Индуктивность цепи, составленной из тех же катушек при параллельном их соединении (рисунок 2) и при соблюдении того же условия относительно их расположения (отсутствие магнитного взаимодействия), подсчитывается по следующей формуле:
Рисунок 2. Параллельное соединение катушек индуктивности.
Индуктивность двух катушек, соединенных параллельно, определяется по следующей формуле:
Как видим, формулы для подсчета результирующих индуктивностей катушек, соединенных последовательно или параллельно и не взаимодействующих между собой, совершенно тождественны с формулами для подсчета омического сопротивления цепи при последовательном и параллельном соединении резисторов.
Соединение катушек при наличии взаимного влияния их магнитных полей.
Если катушки, включенные в цепь последовательно, расположены близко друг к другу, т. е. так, что часть магнитного потока одной катушки пронизывает витки другой, т. е. между катушками существует индуктивная связь (рисунок 3а), то для определения их общей индуктивности приведенная выше формула будет уже непригодна. При таком расположении катушек могут быть два случая, а именно:
- Магнитные потоки обеих катушек имеют одинаковые направления
- Магнитные потоки обеих катушек направлены навстречу друг другу
Тот или другой случай будет иметь место в зависимости от направления витков обмотки катушек и от направлений токов в них.
Рисунок 3. Соединение катушек индуктивности: а)суммарная индуктивность увеличивается за счет взаимной индукции б)суммарная индуктивность уменьшается за счет взаимной индукции.
Если обе катушки намотаны в одну сторону и токи в них текут в одном направлении, то это будет соответствовать первому случаю; если же токи текут в противоположных направлениях (рисунок 3б), то будет иметь место второй случай.
Разберем первый случай, когда магнитные потоки направлены в одну сторону. Очевидно, при этих условиях витки каждой катушки будут пронизываться своим потоком и частью потока другой катушки, т. е. магнитные потоки в той и в другой катушке будут больше по сравнению с тем случаем, когда между катушками нет индуктивной связи. Увеличение магнитного потока, пронизывающего витки той или иной катушки, равносильно увеличению ее индуктивности. Поэтому общая индуктивность цепи в рассматриваемом случае будет больше суммы индуктивностей отдельных катушек, из которых составлена цепь.
Рассуждая таким же образом, мы придем к выводу, что для второго случая, когда потоки направлены навстречу друг другу, общая индуктивность цепи будет меньше суммы индуктивностей отдельных катушек.
Подсчет величины индуктивности цепи, составленной из двух соединенных последовательно катушек индуктивности L1 и L2 при наличии между ними индуктивной связи, производится по формуле:
В первом случае ставится знак + (плюс), а во втором случае знак — (минус).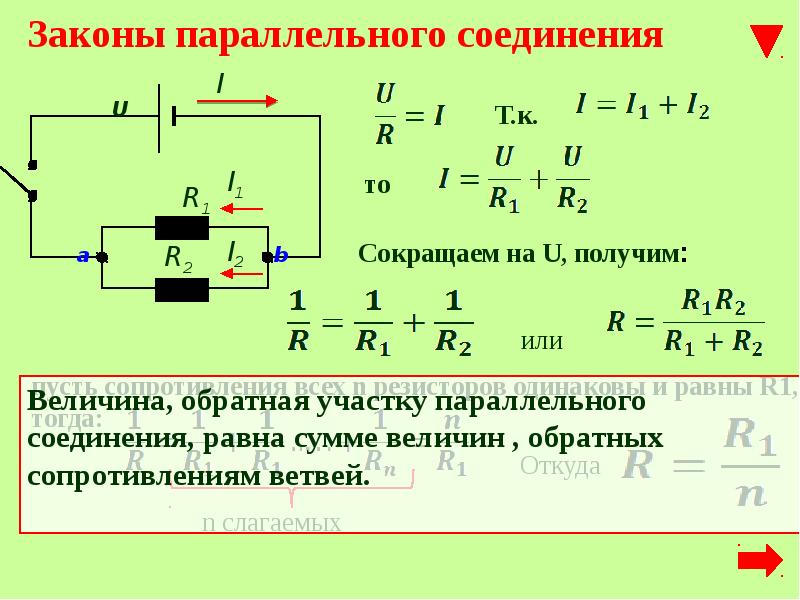
Величина М, называемая коэффициентом взаимной индукции, представляет собой добавочную индуктивность, обусловленную частью магнитного потока, общей для обеих катушек.
На явлении взаимоиндукции основано устройство вариометров. Вариометр состоит из двух катушек, общая индуктивность которых может, по желанию, плавно изменяться в некоторых пределах. В радиотехнике вариометры применяются для настройки колебательных контуров приемников и передатчиков.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Резистор, индуктивная катушка и конденсатор в цепи синусоидального тока
Лекция № 4 Резистор, индуктивная катушка и конденсатор в цепи синусоидального тока.
Термин «сопротивление» для цепей переменного тока, оказывается недостаточно полным, поскольку сопротивление переменному току оказывают не только те элементы цепи, в которых выделяется энергия в виде теплоты (их называют активными сопротивлениями), но и те элементы цепи, в которых энергия периодически запасается в электрическом или магнитном полях.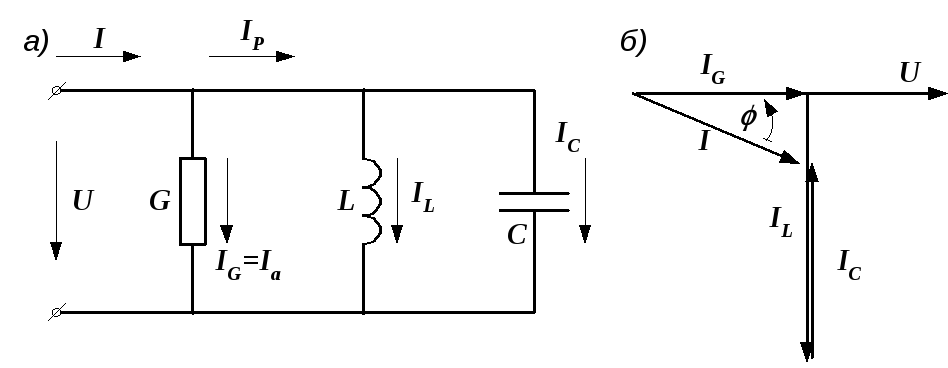 Такие элементы цепи называют реактивными сопротивлениями. Реактивными сопротивлениями обладают индуктивности и емкости.
Такие элементы цепи называют реактивными сопротивлениями. Реактивными сопротивлениями обладают индуктивности и емкости.
Активное сопротивление в цепи синусоидального тока.
Если по активному сопротивлению течет ток тогда
по закону Ома
или
где
Т. е. в активном сопротивлении элемента цепи комплекс тока совпадает с комплексом напряжения
Рис. 4.1 – Графики мгновенных значений
Мгновенная мощность
=
или
т. е. мгновенная мощность имеет постоянную составляющую и переменную составляющую меняющуюся с частотой равной (на рис. 4.1)
Индуктивность в цепи переменного синусоидального тока.
Практически любая обмотка (катушка) обладает некоторой индуктивностью и активным сопротивлением .
Схема замещения катушки может быть представлена в виде последовательного соединения индуктивности и активного сопротивления .
Выделим из схемы одну индуктивность
Рис. 4.2
4.2
Если через индуктивность течет ток , то в катушке наводится ЭДС самоиндукции — .
Для прохождения переменного тока через индуктивность необходимо, чтобы на ее зажимах было напряжение , равное и противоположно направленное .
,
где — индуктивное сопротивление
где — частота, Гц,
— индуктивность, Гн.
Движению переменного тока через индуктивность оказывается сопротивление за счет накопления энергии , это сопротивление называется индуктивным.
Размерность индуктивного сопротивления
.
Значение тока в цепи с индуктивностью опережает ЭДС самоиндукции на 90°, но т. к. вектор напряжения на катушке индуктивности направлен в противоположную сторону ЭДС.
т. е.
т. о. в цепи с индуктивностью вектор тока отстает от вектора напряжения на угол 90°.
Действующее значение тока в цепи с индуктивностью равно действующему значению напряжения, деленному на индуктивное сопротивление.
т. е.
е.
Приведенная формула похожа на закон Ома. Это внешнее сходство позволяет определить ток в цепи с индуктивностью, подобно тому, как в цепи с активным сопротивлением. Но нужно помнить, что индуктивное сопротивление с физической точки зрения с обычным сопротивлением ничего общего не имеет.
Понятие об индуктивном сопротивлении формально введено для облегчения расчета.
Оно заменяет фактическое влияние ЭДС самоиндукции на ток в цепи.
Мгновенная и реактивная мощность
Мгновенное значение мощности или
График изменения мощности представляет собой синусоиду двойной частоты с амплитудой
.
Наибольшее значение мощности в цепи с индуктивностью равно произведению действующих значений напряжения и тока.
В первую четверть периода, когда ток в цепи увеличивается, энергия накапливается в магнитном поле катушки за счет энергии источника. Катушка в это время является приемником энергии: ток направлен против ЭДС самоиндукции.
Во вторую четверть периода, когда ток уменьшается, энергия возвращается в сеть (источнику). Направление ЭДС самоиндукции и тока совпадают. Катушка является источником энергии.
В следующую половину периода процесс повторяется.
Средняя активная мощность за период равна нулю , т. к. в цепи с индуктивностью преобразования электрической энергии в другие виды энергии не происходит.
Цепь с емкостью –
К конденсатору с идеальным диэлектриком, т. е. в нем нет потерь энергии, подведено напряжение
Определим ток и мощность
Ток в цепи.
Заряд конденсатора пропорционален напряжению между его обкладками, поэтому изменение напряжения сопровождается изменением заряда.
Скорость изменения заряда пропорциональна скорости изменения напряжения.
но скорость изменения заряда равна электрическому току
т. к.
то
Сопоставляя:
получаем, что ток через конденсатор по фазе опережает напряжение на конденсаторе на угол 90°. На векторной диаграмме вектор тока опережает вектор напряжения на угол 90°.
На векторной диаграмме вектор тока опережает вектор напряжения на угол 90°.
Амплитуда тока
Действующее значение тока
или
где — реактивное сопротивление конденсатора
Построение графика мгновенной мощности конденсатора выполняют также как и для индуктивной катушки.
т. к.
В первую четверть периода, когда напряжение на конденсаторе возрастает, энергия накапливается в электрическом поле конденсатора за счет работы источника, конденсатор в это время заряжается, т. е. является приемником энергии. Направления тока и напряжения совпадают.
Во вторую четверть периода, когда напряжение уменьшается, энергия в том же количестве возвращается в сеть к источнику. Ток направлен против напряжения сети – конденсатор является источником энергии ( разряжается ) и так в 3й и 4й части периода.
Активная мощность равна нулю, а реактивная
Установившийся режим в простейшей неразветвленной цепи с сосредоточенными параметрами.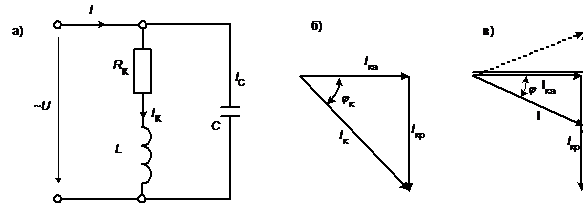
Электрические цепи характеризуются двумя режимами: переходным и установившимся.
Переходные режимы возникают в результате перераспределения энергии электрических и магнитных полей в и при резком изменении параметров электрической цепи.
Простейшая электрическая цепь переменного тока с
Общее сопротивление такой цепи
где — реактивное сопротивление
или
где
Если по цепи протекает ток, то:
или
в комплексной форме
Отсюда или
— закон Ома в комплексной форме
где — комплексное сопротивление
— модуль комплексного сопротивления
Величина обратная комплексному сопротивлению называется комплексной проводимостью.
(сименс)
Умножая на сопряженный комплекс получаем
где — активная проводимость,
— реактивная проводимость.
,
по модулю
Умножив сопротивление на ток получим треугольник U.
Напряжение можно представить в виде двух составляющих
Цепь
Пусть
По второму закону Кирхгофа
где и — синусоидальные напряжения
В комплексной форме
тогда
или
где — комплекс полного сопротивления индуктивной катушки (цепи )
Показательная форма записи
где — модуль комплекса полного сопротивления цепи
— аргумент.
Если , а ,
тогда
где , а
Если ток , то .
— Комплекс тока в цепи с равен комплексу напряжения деленному на комплекс полного сопротивления катушки.
Умножив треугольники на получим:
– полная мощность (ВА)
— реактивная мощность (ВАp)
— активная мощность (Вт)
или
— коэффициент мощности, зависит от соотношения и по его величине судят о том, какую часть полной мощности цепи составляет активная мощность.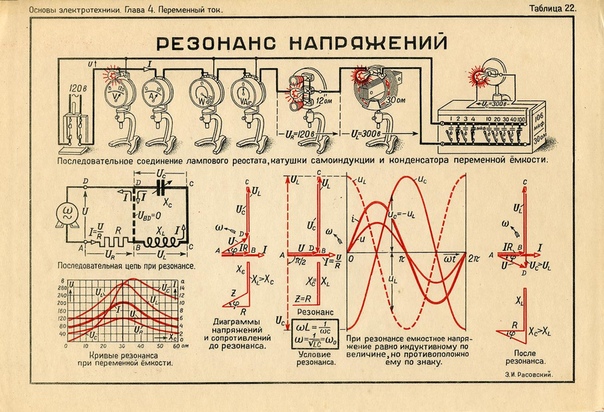
Активную мощность измеряют ваттметром.
Цепь
Пусть .
По второму закону Кирхгофа
, т. к. напряжение отстает от тока
или
– комплекс полного сопротивления
— модуль комплекса
— аргумент
Напряжение на входе цепи отстает от тока на угол сдвига фаз
т. о. , т. к.
Аналогично цепи
или
Сложные цепи, состоящие из последовательных и параллельных участков
Расчет
1. При расчете цепи определяют активные и реактивные проводимости параллельных ветвей
; ; ; .
2. Далее определяют активную и реактивную проводимость разветвления аb
3.Преобразуют схему в эквивалентную
4.Определяют активное и реактивное сопротивление всей цепи
тогда ; ; ; ,
где , а .
Построение векторной диаграммы (по активным и реактивным составляющим).
Лучше построение векторной диаграммы начать с последней ветви и идти к началу цепи, т. е.к общему току и напряжению.
В нашем случае построение начнем с напряжения — откладываем его произвольно в масштабе.
Топографическая диаграмма:
при последовательном соединении напряжений и параллельных токов.
Топографическая диаграмма – такая векторная диаграмма, каждая точка которой соответствует определенной точке электрической цепи.
Резонанс при последовательном и параллельном соединении элементов
Резонанс – такой режим цепи содержащей , индуктивность и емкость, при котором ее входное сопротивление (или проводимость) имеет активный характер.
В зависимости от вида цепи (последовательное или параллельное соединение) существует резонанс напряжений и токов.
1. Последов. соединение R, L,C.
Условие резонанса:
или
т. к. , а , т. о.
, т. е. или
где — резонансная угловая частота.
при резонансе
При последовательном соединении и в резонансном режиме , т. е. имеется резонанс напряжений.
При резонансе значения и могут значительно превышать напряжения на зажимах.
Ток при резонансе
или , т. к. , а
т. о. , делим на , сокращаем
,
где — характеристическое (волновое) сопротивление контура имеет размерность сопротивления.
т. к. ; ; .
Отношение напряжения на индуктивности (или емкости) к напряжению на зажимах цепи при резонансе называется добротностью контура.
.
Величина обратная называется затуханием ()
Параллельное соединение
Условие резонанса: , т. е .
При равенстве реактивных проводимостей ветвей противоположные по фазе реактивные составляющие токов и равны по величине.
Такой режим работы цепи называют резонансом токов.
,
,
тогда
или ,
т. к. , то .
т. е. общий ток носит чисто активный характер (совпадает с ) и может быть меньше и .
е. общий ток носит чисто активный характер (совпадает с ) и может быть меньше и .
Символический метод анализа электрических цепей синусоидального тока.
В режиме синусоидального тока можно перейти от уравнений составленных для мгновенных значений (дифференциальных уравнений) к алгебраическим уравнениям, составленным относительно комплексов тока и ЭДС.
Например ,
Для схемы:
или
,
т. к. амплитуда действующего напряжения на , то знак говорит о том, что опережает на 90°.
Для емкости — напряжение отстает от тока на 90°.
Если – комплексная амплитуда действующей ЭДС, то
и ,
т. о.умножение на равносильно повороту вектора на 90°, а на — на “-90°”.
Три формы записи комплексных чисел:
— алгебраическая форма,
— показательная форма,
— тригонометрическая.
Операции с комплексными числами
Сложение и вычитание комплексных чисел производится в алгебраической форме.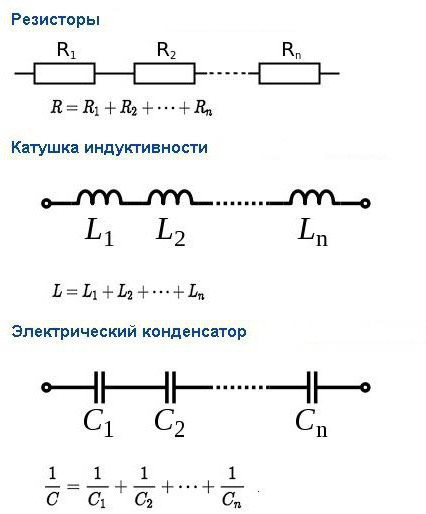
.
Деление и умножение производится в показательной форме:
;.
,
где , а .
Чему равны реактивные сопротивления катушки и конденсатора. Параллельное соединение катушки и конденсатора
При последовательном соединении катушки и конденсатора на расчетной схеме каждый из этих элементов электрической цепи может быть представлен активным и реактивным сопротивлениями или активной и реактивной проводимостями.
Для расчета более простой является схема рис. 14.1, а, где элементы соединены последовательно, а в схеме рис. 14.1, б они соединены смешанно.
Предположим известными параметры катушки R1, L и конденсатора R2, C; ток в цепи i = I m sinωt
.
Требуется определить напряжение на участках цепи и мощность.
Векторная диаграмма и полное сопротивление цели
Мгновенную величину общего напряжения можно представить суммой мгновенных напряжений на отдельных элементах схемы:
u = u 1R + u L + u C + u 2R ,
Имея в виду несовпадение по фазе
активных и реактивных напряжений, общее напряжение получим векторным сложением:
U = U 2R + U L + U C +U 2R
Для построения векторной диаграммы находим:
U 1R = IR 1 ; U 2R = IR 2 ; U L = IX L ; U C = IX C .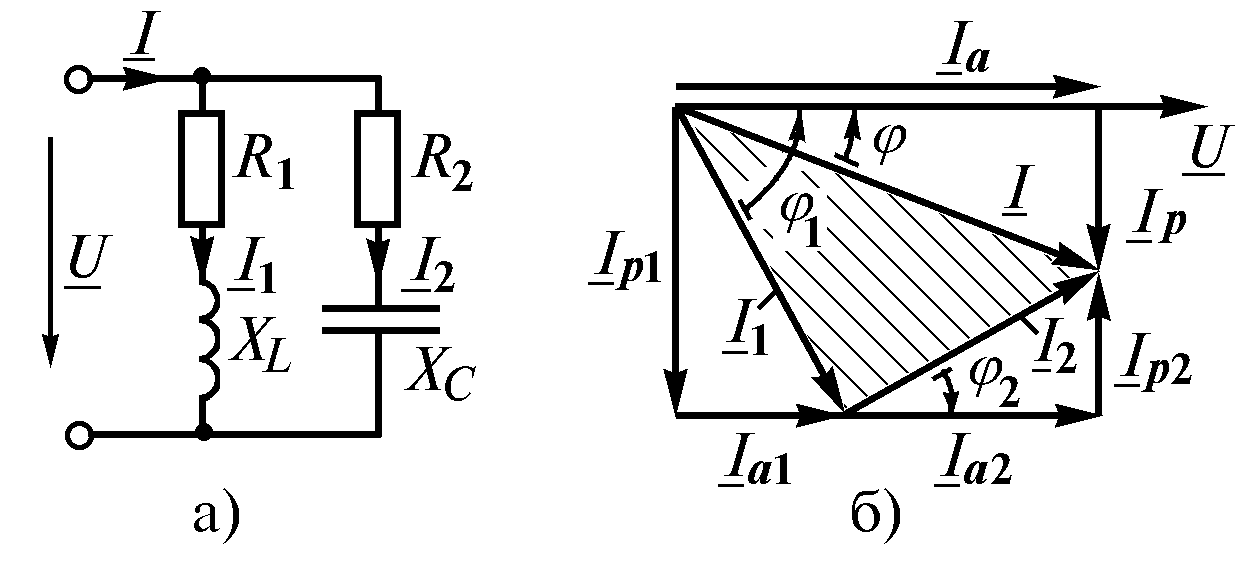
В зависимости от соотношения величин реактивных сопротивлений индуктивности и емкости можно отметить три случая:
1.
Х L >Х C
. Для этого случая векторная диаграмма представлена на рис. 14.2. На диаграмме построены треугольники напряжений для катушки и конденсатора и найдены векторы напряжения U 1 и U 2 на этих элементах.
Векторная сумма напряжений U 1 + U 2 = U
дает общее напряжение в цепи. Вместе с тем вектор U является гипотенузой прямоугольного треугольника напряжений, катеты которого — активное и реактивное напряжения цепи (U а
и U р
). Так как векторы активных составляющих напряжения направлены в одну сторону, их численные значения складываются: U a = U 1R + U 2R.
Векторы реактивных составляющих напряжения направлены по одной прямой в противоположные стороны, поэтому им придают разные знаки: реактивное напряжение индуктивности считают положительным, а напряжение емкости — отрицательным: U р = U L — U C .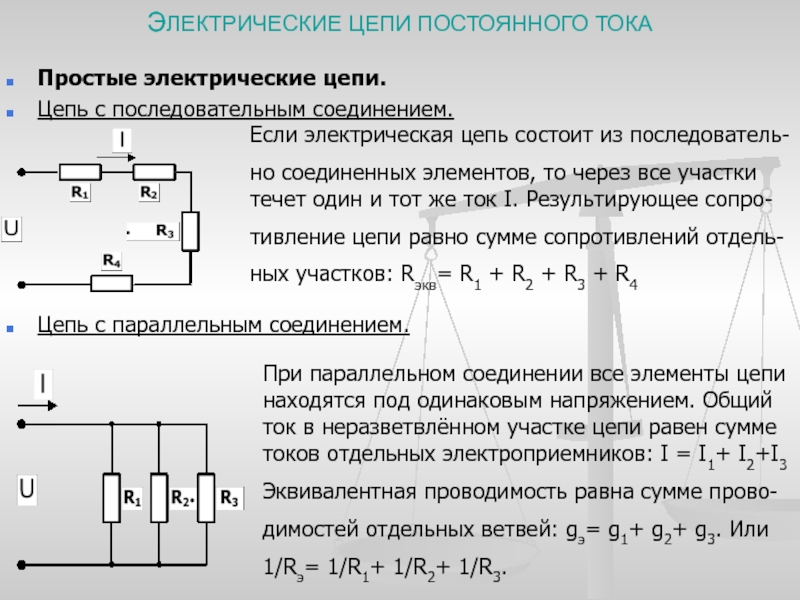
При одинаковом токе во всех элементах цепи U L >U C
. Ток отстает от общего напряжения
по фазе на угол φ
. Из треугольника напряжений следует
где R = R 1 + R 2
и X = X L — X C
общее и активное и реактивное сопротивление цепи. Полное сопротивление цепи — Z.
Эти сопротивления графически можно изобразить сторонами прямоугольного треугольника сопротивлений, который получают уже известным способом из треугольника напряжений.
Полное сопротивление цепи Z
является коэффициентом пропорциональности между действующими величинами тока и общего напряжения цепи:
U = IZ; I = U/Z; Z = U/I.
Из треугольников напряжения и сопротивлений определяют следующие величины:
Угол сдвига по фазе между напряжением и током в цепи положительный (φ
>0) (фазовые токи отсчитываются от вектора тока).
2.
Х L
Векторная диаграмма изображена на рис. 14.3, где U L φ
Р
е
активное сопротивление цепи носит емкостный
характер
.
Расчетные формулы для первого случая остаются без изменения и для второго случая.
3. X L = Х C
. В этом случае реактивные составляющие напряжения катушки и конденсатора равны по величине и взаимно компенсированы: U L = U C
(рис. 14.4). Поэтому реактивная составляющая общего напряжения и общее реактивное сопротивление равны нулю, а полное сопротивление цепи Z = R.
Общее напряжение совпадает по фазе с током и равно по величине активной
составляющей напряжения.
Угол φ сдвига фаз между током и общим напряжением равен нулю.
Ток в цепи и общее напряжение связаны формулой
U = IR, или I = U/R.
В случае X L = Х C в цепи имеет место явление резонанса напряжений.
Энергетический процесс в цепи с последовательном соединении конденсатора и катушки
Из треугольника напряжений легко получить треугольник мощностей из которого следуют уже известные формулы:
Реактивные мощности входят в расчеты также с разными знаками: индуктивная мощность положительна, а емкостная — отрицательна.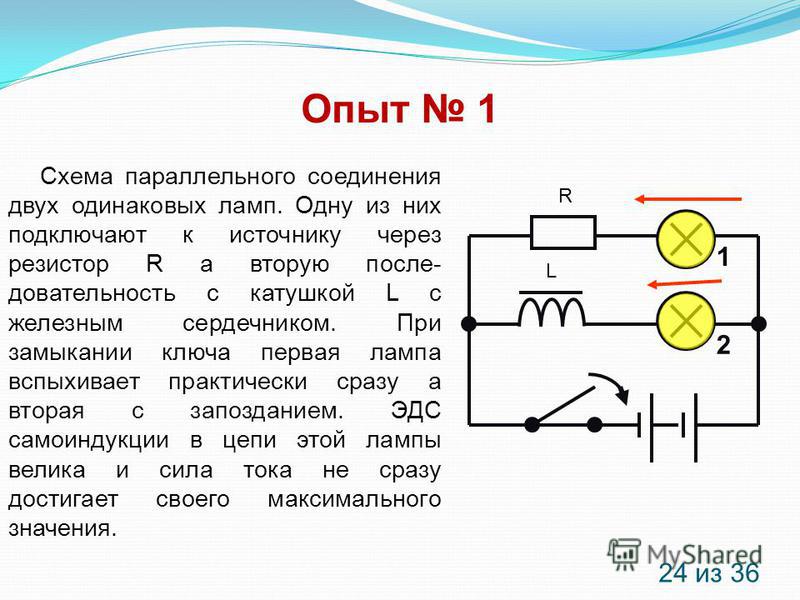
В соответствии с этим знак реактивной мощности всей цепи может быть тем или другим, что следует и из формул (14.2).
При φ>0 Q>0
; при φ
Активная мощность положительна при любом угле, так как cosφ
= cos(-φ
).
Полная мощность также всегда положительна. На основании формул (14.2) можно сделать вывод, что в рассматриваемой цепи совершается преобразование электрической энергии (Р ≠ 0) и обменный процесс между генератором и приемником (Q ≠ 0 при φ
≠ 0).
Энергетические процессы в данном случае сложнее, чем в ранее рассмотренных простых цепях. Усложнение объясняется тем, что наряду с обменом энергией между генератором и приемником совершается обмен энергией внутри приемника, между катушкой и конденсатором.
Особенности энергетического процесса в цепи с последовательным соединением катушки и конденсаторов отражены на рис. 14.5, где показаны графики мгновенной мощности отдельных элементов и цепи в целом при X L = Х С
.
Катушка и конденсатор в течение полупериода накапливают равные количества энергии. Однако в первую четверть периода, когда ток увеличивается, а напряжение на конденсаторе уменьшается, энергия накапливается в магнитном поле катушки и уменьшается в электрическом поле конденсатора, причем скорость изменения энергии (мощность) в любой момент времени одинакова. Это дает основание считать, что обмен энергией происходит только в приемнике между катушками
и конденсатором.
Для преобразования электрической энергии в другой вид приемник получает ее от генератора со средней скоростью (мощностью) Р.
Задачи по теме и пример решения задачи для схемы с последовательным соединением конденсатора и катушки
Рис. 4.12.
Рис. 4.13
если ток, подаваемый в схему, которая содержит катушку, резко увеличить, то ток в схеме будет нарастать плавно до достижения своего максимального значения.
Способность катушки индуктивности препятствовать изменению силы тока, протекающего через нее, носит название индуктивности этой катушки. Индуктивность обозначается буквой L
Индуктивность обозначается буквой L
, единицей ее измерения является генри (Гн).
Постоянная времени RС
-цепи
На рис. 4.13 последовательная цепочка из конденсатора и резистора соединяется через ключ с источником питания. Когда ключ находится в положении 1, конденсатор постепенно заряжается через сопротивление, пока напряжение на нем не достигнет уровня Е
т. е. ЭДС или напряжения источника питания.
Процесс заряда конденсатора показан на рис. 4.14(а) экспоненциальной кривой. Время, за которое напряжение на конденсаторе достигает значения 0,63 от максимума, т. е. в данном случае 0,63Е
, называется постоянной времени контура или цепи.
Вернемся к рис. 4.13. Если ключ установить в положение 2, конденсатор будет сохранять запасенную энергию. При переведении ключа в положение3 конденсатор начинает разряжаться на землю через резистор R, и напряжение на нем постепенно падает до нуля. Процесс разряда конденсаторапоказан на рис. 4. 14(б). В этом случае постоянной времени цепи называется время, за которое напряжение на конденсаторе уменьшается 0,63 от своего максимального значения.
14(б). В этом случае постоянной времени цепи называется время, за которое напряжение на конденсаторе уменьшается 0,63 от своего максимального значения.
Рис. 4.14.
Кривые заряда (а) и разряда (б) конденсатора, где t —
постоянная времени.
Как для случая заряда, так и для случая разряда конденсатора через резистор R постоянная времени цепи выражается формулой
где t —
постоянная времени в секундах, С
— емкость в фарадах, R —
сопротивление, выраженное в омах.
Например, для случая С
= 10мкФ и R
=
10 кОм постоянная времени цепи равна
На рис. 4.15 изображены графики процессов заряда для цепей с малой и с большой постоянной времени.
Рис. 4.15.
Постоянная времени
RL
-цепи
Рассмотрим схему, изображенную на рис. 4.16. Катушка индуктивности L
соединена последовательно с резистором R
, имеющим сопротивление 1 кОм. В момент замыкания ключа S
ток в цепи равен нулю, хотя под действиемЭДС источника он, казалось бы, должен резко увеличиться. Однако катушка индуктивности, как известно, препятствует всякому изменению силы тока, протекающего через нее, поэтому ток в цепи будет возрастать по экспоненциальному закону, как показано на рис. 4.17. Ток будет возрастать до тех пор, пока не достигнет своего максимального значения. После этого увеличение тока прекратится, а падение напряжения на резисторе R
Однако катушка индуктивности, как известно, препятствует всякому изменению силы тока, протекающего через нее, поэтому ток в цепи будет возрастать по экспоненциальному закону, как показано на рис. 4.17. Ток будет возрастать до тех пор, пока не достигнет своего максимального значения. После этого увеличение тока прекратится, а падение напряжения на резисторе R
станет равным приложенному напряжению Е.
Установившееся значение тока равно
E/
R =
20 В/1 кОм = 20 мА.
Скорость изменения тока в цепи зависит от конкретных значений R
и L
. Время, необходимое для того, чтобы сила тока достигла значения, равного 0,63 от его максимальной величины, носит название постоянной времени цепи. Постоянная времени вычисляется по формуле L/
R
где L
выражается в генри, а R —
в омах. В этом случае постоянная времени получается в секундах. Используя значения L
и R
, указанные на рисунке, получаем
Следует заметить, что, чем больше R
, тем меньше L/R
и тем быстрее изменяется ток в цепи.
Рис. 4.16.
Рис. 4.17.
Сопротивление по постоянному току
Катушка индуктивности, включенная в цепь, не препятствует протеканию постоянного тока, если, конечно, но принимать во внимание очень малое сопротивление провода, из которого она сделана. Следовательно, катушка индуктивности имеет нулевое или очень малое сопротивление и может рассматриваться в цепи постоянного тока как цепь короткого замыкания. Конденсатор же в связи с наличием в нем изолирующего диэлектрика имеет бесконечное или очень большое сопротивление и может рассматриваться в цепи постоянного тока как разрыв.
Векторное представление
Сигнал синусоидальной формы может быть представлен в виде вектора ОА, вращающегося против часовой стрелки с угловой скоростью ω
= 2πf
, где f
– частота сигнала (рис. 4.18). По мере того как поворачивается вектор, ордината его конца характеризует показанный на рисунке синусоидальный сигнал. Один полный оборот вектора (360°, или 2π) соответствует одному полному периоду. Половина оборота (180°, или π) соответствует половине периода, и так далее. Таким образом, ось времени, как показано на рисунке, может использоваться для нанесения значений угла, на который повернулся вектор. Максимум сигнала достигается при 90° (1/4 периода), а минимум — при 270° (3/4 периода).
Один полный оборот вектора (360°, или 2π) соответствует одному полному периоду. Половина оборота (180°, или π) соответствует половине периода, и так далее. Таким образом, ось времени, как показано на рисунке, может использоваться для нанесения значений угла, на который повернулся вектор. Максимум сигнала достигается при 90° (1/4 периода), а минимум — при 270° (3/4 периода).
Теперь рассмотрим два синусоидальных сигнала, представленных на рис. 4.19(а) векторами ОА и ОВ соответственно. Если оба сигнала имеют одинаковые частоты, то векторы ОА и ОВ будут вращаться с одинаковой угловой скоростью ω
= 2πf
. Это означает, что угол между этими векторами
Рис. 4.18.
Рис. 4.19.
Разность фаз. Вектор ОА опережает вектор ОВ
(или вектор ОВ отстает от вектора ОА) на угол θ
.
изменяться не будет. Говорят, что вектор ОА опережает вектор ОВ на угол θ
, а вектор ОВ отстает от вектора ОА на угол в.
На рис.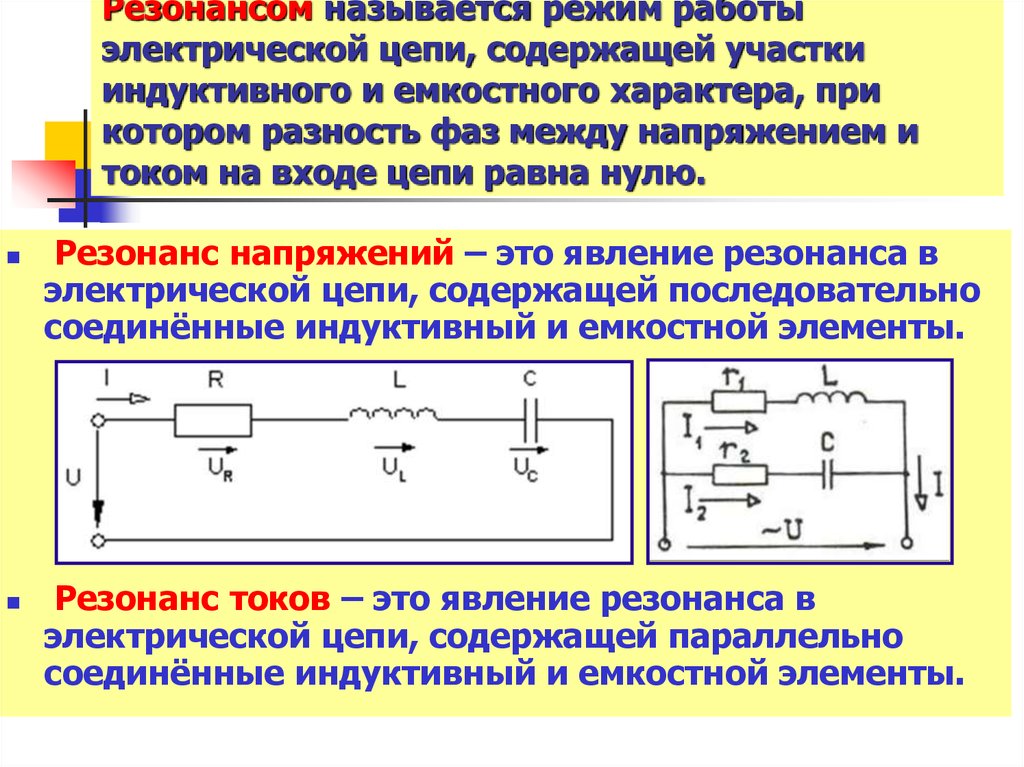 4.19(б) эти сигналы развернуты во времени.
4.19(б) эти сигналы развернуты во времени.
Если оба этих синусоидальных сигнала сложить, то в результате получим другой синусоидальный сигнал, имеющий ту же частоту f
, но другую амплитуду. Результирующий сигнал может быть представлен вектором ОТ, который, как показано на рис. 4.19(в), является векторной суммой векторов ОА и ОВ. Вектор ОТ опережает вектор ОВ на угол α
и отстает от вектора ОА на угол γ. Дальше вы увидите, что векторное представление является весьма удобным приемом при анализе и расчете цепей переменного тока.
В этом видео рассказывается о катушке индуктивности:
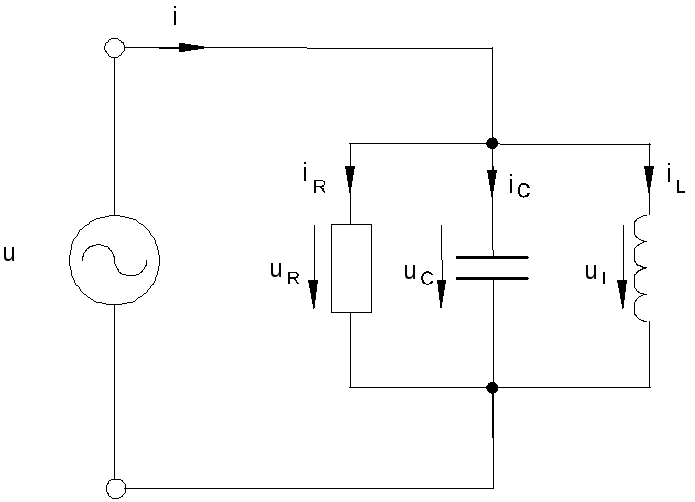
Для рассмотрения параллельного соединения катушки и конденсатора представим их на схеме активными и реактивными проводимостями (рис. 14.11, а).
На схеме рис. 14.1.1, б те же катушки и конденсатор представлены активными и реактивными сопротивлениями. Первая схема имеет некоторое преимущество, так как в ней все элементы соединены параллельно, а в другой они соединены смешанно.
Считая известными параметры катушки G1, BL и конденсатора G2, BC, а также напряжение u = Umsinωt
При последовательном: индуктивность складывается. С емкостью 1/Cобщ=1/С1+1/C2+1/С3
При параллельном: емкости складываются, с индуктивностями, как с конденсаторами при последовательном соединении
Вариант 2. ёмкость при параллельном соединении складывается (напряжение пробоя остается тем же) , при последовательном высчитывается по формуле как параллельные сопротивления, напряжение просто складывается.
а индуктивность при последовательном складывается, а при параллельном как сопротивления параллельные высчитывается.
40.Метод комплексных амплитуд.
Метод комплексных амплитуд состоит в следующем:
1) исходная схема электрической цепи заменяется комплексной схемой замещения, в которой:
а) все пассивные элементы заменяются их комплексными сопротивлениями, как показано на рис. 4.27.
б) все токи и напряжения в схеме заменяются их комплексными амплитудами, т.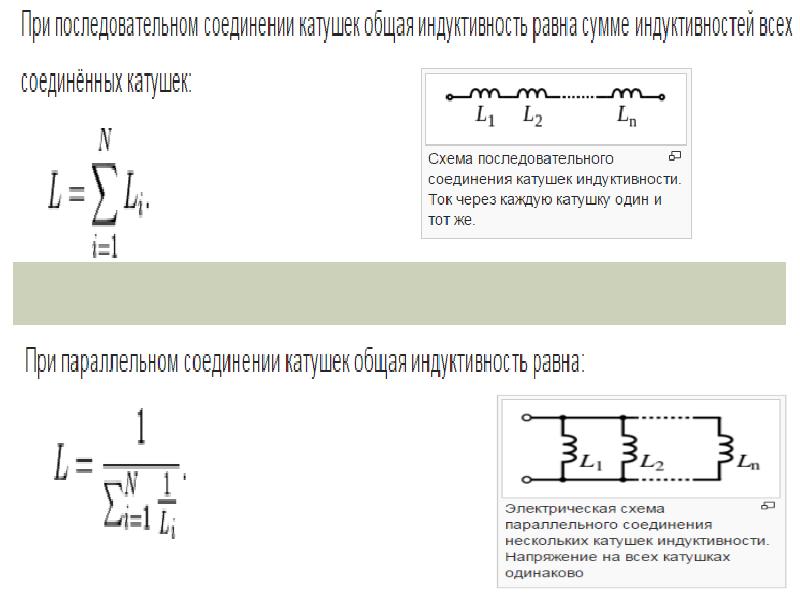 е. х
е. х
(t
) = Xm
cos(w0t –
jx
) ® Xm
= Xm e–j
jx.
Z
L=j
wL
Z
C=
1/(j
wC
)
Z
R=R
Рис. 4.27
2) Расчет электрической цепи сводится к составлению уравнений состояния цепи на основе законов Ома и Кирхгофа в комплексной форме и нахождению комплексных амплитуд токов или напряжений на интересующих нас участках цепи, т.е.Ym = Ym e–j
jy.
3) Запись окончательного решения состоит в замене рассчитанных комплексных амплитуд на гармонические функции времени, т.е.
Ym
=Ym e –j
jy
® y
(t
) = Ym
cos(w0t
– jy
).
Пример 1. Алгоритм метода рассмотрим на примере анализа цепи, схема которой приведена на рис. 4.29.
Рис. 4.29. RLC
-цепь второго порядка
На вход цепи подается синусоидальное воздействие. Параметры воздействия и элементов цепи известны: Um
=1 В, ω =1 с-1 , φ u
=900 , R
=1 Ом, L
=1 Гн, C
=1 Ф. Требуется определить токи и напряжения ветвей, построить векторную диаграмму.
Требуется определить токи и напряжения ветвей, построить векторную диаграмму.
1. Представим воздействие в комплексной форме:
2. Построим схему замещения цепи в частотной области, заменив элементы цепи комплексными двухполюсниками, как это показано на рис. 4.30.
Рис. 4.30. Схема замещения цепи в частотной области
3. Произведем расчет реакций (токов и напряжений) в комплексной области. При этом можно воспользоваться законами Кирхгофа и Ома в комплексной форме, а также известными методами расчета резистивных цепей:
51.41. Элементы R
, L
и С
в цепях переменного тока. Импеданс.
Физическими элементами реальной электрической цепи являются резисторы, катушки индуктивности, конденсаторы, трансформаторы, транзисторы и другие компоненты электроники. При изучении электрических цепей реальные элементы заменят их математическими моделями, которые с нужной точностью воспроизводят свойства и параметры физических элементов.
Рис. 1.1. Условные обозначения резистивного (а), емкостного (б) и индуктивного (в) элементов.
1.1. Условные обозначения резистивного (а), емкостного (б) и индуктивного (в) элементов.
К пассивным элементам относятся резистивные R, индуктивные L, и емкостные C элементы, условные обозначения которых показаны на рис. 1.1.
Резистивным элементом (рис. 1.1,а) называют такой элемент, который обладает только свойством рассеивания энергии. Математическая модель резистивного элементаR определяется законом Ома, который устанавливает зависимость напряжения u от тока i, протекающего через сопротивление R. Такую зависимость называют вольт-амперной характеристикой (ВАХ) резистивного элемента и записывают в следующем виде:
Если в (1.6) u = 1В, i = 1А, то R = 1Ом. Более крупными единицами измерения величины сопротивления являются килоом (1кОм = 103Ом) и мегоом (1мОм = 106Ом). Величина, обратная сопротивлению, называется проводимостью резистора. Она обозначается G и измеряется в сименсах (См). ВАХ для линейного и нелинейного резистивных элементов показаны на рис. 1.2.
Рис. 1.2. ВАХ линейного (а) и нелинейного (б) резистивных элементов.
1.2. ВАХ линейного (а) и нелинейного (б) резистивных элементов.
Согласно уравнению (1.5) мощность, рассеиваемая резистивным элементом в виде тепла, равна:
Источником напряжения (Рис. 1.3,а и б) называют идеализированный двухполюсный элемент, напряжение на зажимах (полюсах) которого не зависит от протекающего через него тока. Часто источник напряжения называют генератором напряжения и в качестве характеристики используют напряжение или электродвижущую силу генератораuг или eг.
Электри?ческий импеда?нс
(комплексное сопротивление
, полное сопротивление
) — комплексное сопротивление двухполюсника для гармонического сигнала.
В отличие от резистора, электрическое сопротивление которого характеризует соотношение напряжения к току на нём, попытка применения термина электрическое сопротивление
к реактивным элементам (катушка индуктивности и конденсатор) приводит к тому, что сопротивление идеальной катушки индуктивности стремится к нулю, а сопротивление идеального конденсатора — к бесконечности.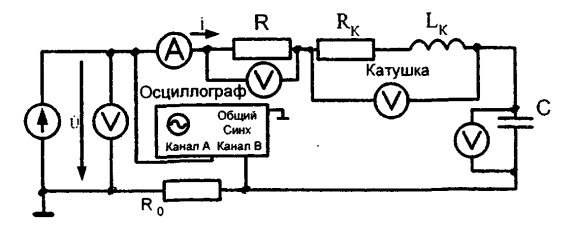
Сопротивление
правильно описывает свойства катушки и конденсатора только на постоянном токе. В случае же переменного тока свойства реактивных элементов существенно иные: напряжение на катушке индуктивности и ток через конденсатор не равны нулю. Такое поведение сопротивлением уже не описывается, поскольку сопротивление предполагает постоянное, не зависящее от времени соотношение тока и напряжения, то есть отсутствие фазовых сдвигов тока и напряжения.
Было бы удобно иметь некоторую характеристику и для реактивных элементов, которая бы при любых условиях связывала ток и напряжение на них подобно сопротивлению. Такую характеристику можно ввести, если рассмотреть свойства реактивных элементов при гармонических воздействиях на них. В этом случае ток и напряжение оказываются связаны некоей стабильной константой (подобной в некотором смысле сопротивлению), которая и получила название электрический импеданс
(или просто импеданс
). При рассмотрении импеданса используется комплексное представление гармонических сигналов, поскольку именно оно позволяет одновременно учитывать и амплитудные, и фазовые характеристики сигналов и систем.
42.Мощность, рассеиваемая элементами R
, L
и С
.
Рассеиваемая (поглощаемая) мощность элемента электрической цепи
– значение мощности рассеиваемой на элементе цепи, которую элемент может поглотить (выдержать) без изменения его номинальных параметров (выхода из строя). Рассеиваемая мощность резисторов обозначается в его названии (например: двух ваттный резистор — ОМЛТ-2, десяти ваттный проволочный резистор – ПЭВ-10). При расчёте принципиальных схем, значение необходимой рассеиваемой мощности элемента цепи рассчитывается по формулам:
Для надёжной работы, определённое по формулам значение рассеиваемой мощности элемента умножается на коэффициент 1,5 , учитывающий то, что должен быть обеспечен запас по мощности.
Так как напряжение u и ток i могут совпадать или не совпадать по направлению, то согласно (1.14) мощность p может быть как положительной, так и отрицательной.
При p > 0 емкостной элемент накапливает энергию, а при p
43. Расчёт цепей переменного тока. Характер импеданса (емкостной и индуктивный).
Расчёт цепей переменного тока. Характер импеданса (емкостной и индуктивный).
// Первую половину вопросов вытащить из методички по первой лабе.
Любой ток изменяющийся по величине является переменным. Но на практике под переменным током понимают такой ток, закон изменения которого во времени есть синусоидальная функция.
Математическое выражение для синусоидального тока можно записать в виде:
где, i — мгновенное значение тока, показывающее величину тока в конкретный момент времени, Im — амплитудное (максимальное) значение тока, выражение в скобках есть фаза, которая определяет значение тока в момент времени t, f — частота переменного тока, это величина, обратная периоду изменения синусоидальной величины Т, ω — угловая частота, ω = 2πf = 2π / T, α — начальная фаза, показывает значение фазы в момент времени t = 0.
Индуктивное сопротивление
() обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи. Изменение тока и, как следствие, изменение его магнитного поля вызывает препятствующее изменению этого тока ЭДС самоиндукции. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока:
Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока:
Ёмкостное сопротивление
(). Величина ёмкостного сопротивления зависит от ёмкости элемента и также частоты протекающего тока:
Здесь — циклическая частота, равная.
44.Четырёхполюсники. Передаточная характеристика и её измерение.
Четырёхпо?люсник
— электрическая цепь, разновидность многополюсника, имеющая четыре точки подключения. Как правило, две точки являются входом, две другие — выходом.
При анализе электрических цепей очень часто бывает удобным выделить фрагмент цепи, имеющий две пары зажимов. Поскольку электрические (электронные) цепи очень часто связаны с передачей энергии или обработкой и преобразованием информации, одну пару зажимов обычно называют «входными», а вторую — «выходными». На входные зажимы подаётся исходный сигнал, с выходных снимается преобразованный.
Такими четырёхполюсниками являются, например, трансформаторы, усилители, фильтры, стабилизаторы напряжения, телефонные линии, линии электропередачи и т. д.
д.
Передаточная характеристика, где Uвых, UВХ – соответственно напряжение на выходе и входе схемы. Характеристика снимается для одного входа (нагрузкой элемента являются аналогичные элементы).
На входах х2, х3 будет уровень напряжения U0ВХ, а на входе х1 – напряжение UВХ. Изменяя напряжение на входе х1 от Uвх U0вх до Uвх U1вх и измеряя напряжение на входе х1 и на выходах схемы у1 и у2, получим передаточную характеристику.
45.Четырёхполюсники. Переходная, импульсная и частотная характеристики.
Четырёхпо́люсник
— электрическая цепь, разновидность многополюсника, имеющая четыре точки подключения . Как правило, две точки являются входом, две другие — выходом.
Симметричный четырёхполюсник
— четырёхполюсник, у которого схема одинакова относительно его входных и выходных зажимов. Тогда для симметричного четырёхполюсника Z11 = Z22. Ещё: если при перемене местами источника и приемника энергии их токи не меняются, то такой четырёхполюсник называется симметричным.
Пассивный четырёхполюсник
— это четырёхполюсник, который не содержит источников энергии, либо содержит скомпенсированные источники энергии.
Активный четырёхполюсник
— это четырёхполюсник, который содержит нескомпенсированные источники энергии.
Обратимый четырёхполюсник
— четырёхполюсник, у которого выполняется теорема обратимости, то есть передаточное сопротивление входных и выходных контуров не зависят от того, какая пара зажимов входная, а какая выходная: U1/I2=U2/I1
Частотные характеристики.
Бывают АЧХ и ФЧХ. Поскольку при подаче на вход линейной системы синусоидального сигнала на выходе также появляется синусоидальный сигнал той же частоты, частотные характеристики связывают амплитуды и фазы этих сигналов. АЧХ – отношение амплитуды выходного сигнала к амплитуде входного сигнала в зависимости от частоты. ФЧХ – сдвиг фаз между входным и выходным сигналами в зависимости от частоты.
Интегрирующая RC-цепь:
— Комплексная частотная характеристика
— АЧХ
— ФЧХ
АЧХ и ФЧХ интегрирующей цепи:
Частотные характеристики показывают как преобразуется синусоидальный сигнал в данной системе.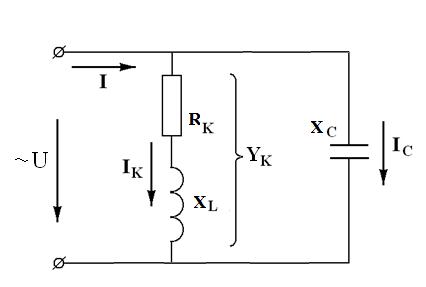 Следовательно, воспользовавшись разложением Фурье для входного сигнала можно получить спектр выходного сигнала. Для этого спектр амплитуд умножают на АЧХ почастотно, а спектр фаз складывают также почастотно.
Следовательно, воспользовавшись разложением Фурье для входного сигнала можно получить спектр выходного сигнала. Для этого спектр амплитуд умножают на АЧХ почастотно, а спектр фаз складывают также почастотно.
Связь между частотными, переходными и импульсными характеристиками.
Импульсная характеристика связана с переходной интегрирования, потому что импульс — это производная от ступеньки. Частотная характеристика связана c импульсной преобразованием Фурье, так как частотная характеристика строится в частотной области, а импульсная — во временной.
Связь между частотной, переходной и импульсной характеристиками:
46.АЧХ и ФЧХ четырёхполюсников.
//обратиться к методичке от первой лабы
47.Основные типы электрических фильтров.
Электрический фильтр — это устройство, предназначенное для выделения или подавления электрических сигналов заданных частот.
По характеру полосы пропускаемых частот фильтры делятся на шесть типов:
1) ФНЧ (фильтр нижних частот) — пропускает сигналы с частотой от 0 до f в (f в =ω в /2π).
2) ФВЧ (фильтр верхних частот) — пропускает сигналы с частотой от f н до ∞
3) ФПП (полосовой фильтр) — пропускает сигналы с частотой от f н до f в.
4) РФ (режекторный фильтр) — не пропускает сигналы заданной частоты или полосы частот
5) ГПФ (гребенчатый фильтр) — фильтр, имеющий несколько полос пропускания.
6) РГФ (режекторный гребенчатый фильтр) — фильтр, имеющий несколько полос подавления.
48.Последовательный колебательный контур, его основные свойства.
Колебательный контур
— осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения).
последовательный колебательный контур, сопротивление которого на резонансной частоте стремится к нулю.
Последовательный колебательный контур является простейшей резонансной (колебательной) цепью. Состоит последовательный колебательный контур, из последовательно включенных катушки индуктивности и конденсатора. При воздействии на такую цепь переменного (гармонического) напряжения, через катушку и конденсатор будет протекать переменный ток, величина которого вычисляется по закону Ома: I = U / Х Σ
При воздействии на такую цепь переменного (гармонического) напряжения, через катушку и конденсатор будет протекать переменный ток, величина которого вычисляется по закону Ома: I = U / Х Σ
, где Х Σ
— сумма реактивных сопротивлений последовательно включенных катушки и конденсатора (используется модуль суммы).
Одними из наиболее важных параметров колебательного контура (кроме, разумеется, резонансной частоты) являются его характеристическое (или волновое) сопротивление ρ
и добротность контура Q
. Характеристическим (волновым) сопротивлением контура ρ
называется величина реактивного сопротивления емкости и индуктивности контура на резонансной частоте: ρ = Х L = Х C
при ω =ω р
. Характеристическое сопротивление может быть вычислено следующим образом: ρ = √(L/C)
. Характеристическое сопротивление ρ
является количественной мерой оценки энергии, запасенной реактивными элементами контура — катушкой (энергия магнитного поля) W L = (LI 2)/2
и конденсатором (энергия электрического поля) W C =(CU 2)/2
. Отношение энергии, запасенной реактивными элементами контура, к энергии омических (резистивных) потерь за период принято называть добротностью Q
Отношение энергии, запасенной реактивными элементами контура, к энергии омических (резистивных) потерь за период принято называть добротностью Q
контура, что в буквальном переводе с английского языка обозначает «качество». Добротность колебательного контура
— характеристика, определяющая амплитуду и ширину АЧХ резонанса и показывающая, во сколько раз запасы энергии в контуре больше, чем потери энергии за один период колебаний. Добротность учитывает наличие активного сопротивления нагрузки R
.
Для последовательного колебательного контура в RLC цепях, в котором все три элемента включены последовательно, добротность вычисляется:
где R
, L
и C
— сопротивление, индуктивность и ёмкость резонансной цепи, соответственно. Величину, обратную добротности d = 1 / Q
называют затуханием контура. Для определения добротности обычно пользуются формулой Q = ρ / R
, где R
-сопротивление омических потерь контура, характеризующее мощность резистивных (активных потерь) контура Р = I 2 R
.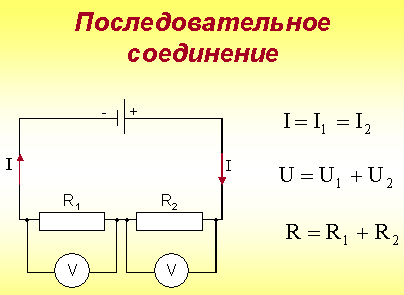 Добротность реальных колебательных контуров, выполненных на дискретных катушках индуктивности и конденсаторах, составляет от нескольких единиц до сотни и более. Добротность различных колебательных систем, построенных на принципе пьезоэлектрических и других эффектов (например, кварцевые резонаторы) может достигать нескольких тысяч и более.
Добротность реальных колебательных контуров, выполненных на дискретных катушках индуктивности и конденсаторах, составляет от нескольких единиц до сотни и более. Добротность различных колебательных систем, построенных на принципе пьезоэлектрических и других эффектов (например, кварцевые резонаторы) может достигать нескольких тысяч и более.
Частотные свойства различных цепей в технике принято оценивать с помощью амплитудно-частотных характеристик (АЧХ), при этом сами цепи рассматривают как четырёхполюсники.
49.Параллельный колебательный контур, его основные свойства.
В различных радиотехнических устройствах наряду с последовательными колебательными контурами часто (даже чаще, чем последовательные) применяют параллельные колебательные контуры На рисунке приведена принципиальная схема параллельного колебательного контура. Здесь параллельно включены два реактивных элемента с разным характером реактивности Как известно, при параллельном включении элементов складывать их сопротивления нельзя — можно лишь складывать проводимости. На рисунке приведены графические зависимости реактивных проводимостей катушки индуктивности B L = 1/ωL
На рисунке приведены графические зависимости реактивных проводимостей катушки индуктивности B L = 1/ωL
, конденсатора В C = -ωC
, а также суммарной проводимости В Σ
, этих двух элементов, являющаяся реактивной проводимостью параллельного колебательного контура. Аналогично, как и для последовательного колебательного контура, имеется некоторая частота, называемая резонансной, на которой реактивные сопротивления (а значит и проводимости) катушки и конденсатора одинаковы. На этой частоте суммарная проводимость параллельного колебательного контура без потерь обращается в нуль. Это значит, что на этой частоте колебательный контур обладает бесконечно большим сопротивлением переменному току.
50.RC
-цепь и её характерное время.
RC-цепь
— электрическая цепь, состоящая из конденсатора и резистора. Её можно рассматривать как делитель напряжения с одним из плеч, обладающих ёмкостным сопротивлением переменному току.
Если соединить резистор и конденсатор, то получится пожалуй одна из самых полезных и универсальных цепей.
Резистор — его задача ограничивать ток. Это статичный элемент, чье сопротивление не меняется, про тепловые погрешности сейчас не говорим — они не слишком велики. Ток через резистор определяется законом ома — I=U/R
, где U напряжение на выводах резистора, R — его сопротивление.
Конденсатор штука поинтересней. У него есть интересное свойство — когда он разряжен то ведет себя почти как короткое замыкание — ток через него течет без ограничений, устремляясь в бесконечность. А напряжение на нем стремится к нулю. Когда же он заряжен, то становится как обрыв и ток через него течь перестает, а напряжение на нем становится равным заряжающему источнику. Получается интересная зависимость — есть ток, нет напряжения, есть напряжение — нет тока.
«В этом случае скорость заряда конденсатора будет зависить от сопротивлений в цепи и емкости кондера, а сам заряд будет идти по экспоненциальному закону.»
и там же, в этой же статье:
«А у этого закона есть пара характерных величин:
Т — постоянная времени, это время при котором величина достигнет 63% от своего максимума.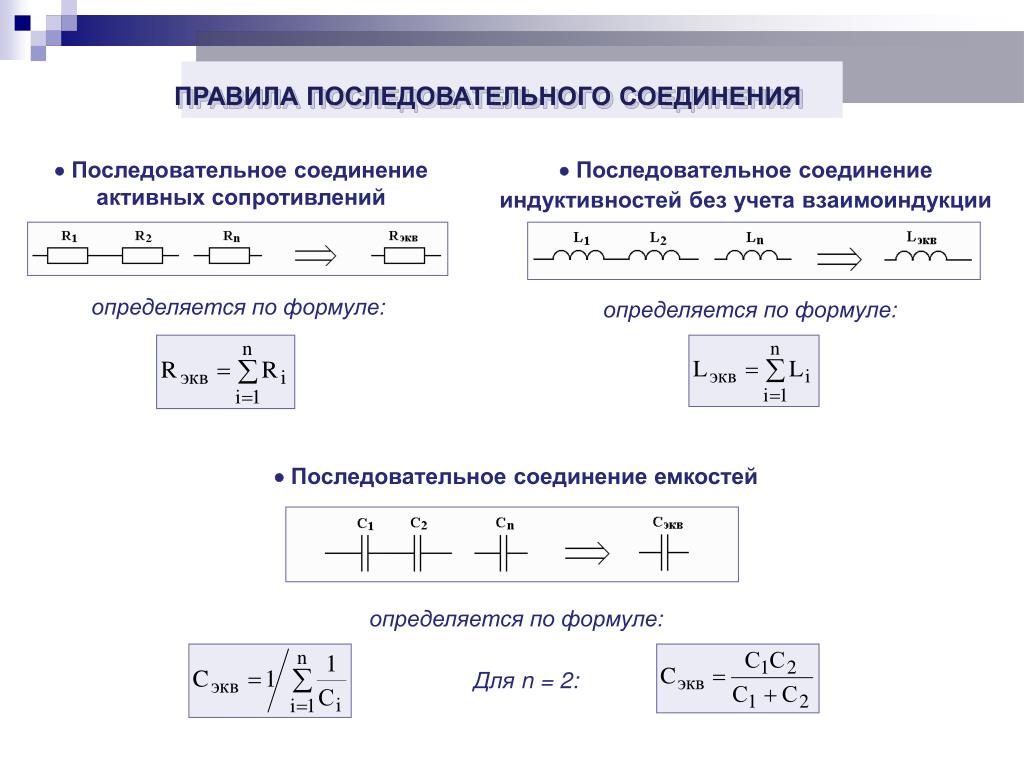 63% тут взялись не случайно, тут прямая завязка на такую формулу VALUET=max–1/e*max.
63% тут взялись не случайно, тут прямая завязка на такую формулу VALUET=max–1/e*max.
3T — а при троекратной постоянной значение достигнет 95% своего максимума.
Постоянная времени для RC цепи Т=R*C.»
51.RL
-цепь и её характерное время.
LR-цепь
— электрическая цепь, состоящая из резистора и индуктивности. Её можно рассматривать как делитель напряжения, в котором одно из плеч представляет собой индуктивное сопротивление переменному току.
Рассмотрим цепь, состоящую из последовательно соединенных резистора R и катушки L, в электротехнике такая цепь часто называетсяпоследовательной RL-цепью
.
В случае RC-цепи напряжение снимается с резистора, а в случае RL-цепи – с индуктивности.
Простейшие
.
В настоящее время большинство дифференцирующих цепей основаны на RC-цепях, поэтому будем рассматривать их, но все основные выкладки соответствуют также и RL-цепям.
52.Дифференцирующие и интегрирующие RLC
-цепи и условия их работы.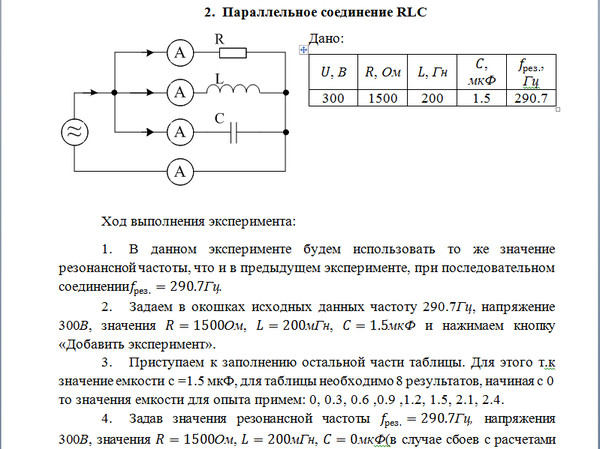
Рассмотрим цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки индуктивности.
LR-цепь дифференцирующего типа является фильтром верхних частот. Фильтр верхних частот
(ФВЧ
) — электронный или любой другой фильтр, пропускающий высокие частоты входного сигнала, при этом подавляя частоты сигнала ниже частоты среза. Степень подавления зависит от конкретного типа фильтра.
Не так давно, мы с вами рассматривали, как ведет себя конденсатор в цепи постоянного и переменного тока . А в этой статье рассмотрим, как ведет себя катушка индуктивности , если на нее подать постоянный и переменный ток. Хочу вам напомнить, что постоянный ток — это ток, который течет всегда в одном направлении, а переменный ток — это ток, который меняет свое направление с какой-то частотой.
Катушка индуктивности в цепи постоянного тока.
Итак, для этого опыта нам понадобится блок питания , который выдает постоянное напряжение, лампочка накаливания и собственно сама катушка индуктивности.
Чтобы сделать катушку индуктивности с хорошей индуктивностью, нам надо взять ферритовый сердечник:
Намотать на него лакированного медного провода и зачистить выводы:
Замеряем индуктивность нашей катушки с помощью LC метра :
132 микроГенри.
Теперь собираем все это вот по такой схеме:
где
L
— катушка индуктивности
La
— лампочка накаливания на напряжение 12 Вольт
Bat
— блок питания, с выставленным напряжением 12 Вольт
Лампочка засветилась!
Как вы помните, конденсатор у нас не пропускал постоянный электрический ток:
Делаем вывод: постоянный электрический ток почти беспрепятственно течет через катушку индуктивности. Сопротивлением обладает только сам провод, из которого сделана катушка.
Катушка индуктивности в цепи переменного тока.
Для того, чтобы узнать, как ведет себя катушка индуктивности в цепи переменного тока, нам понадобится осциллограф , генератор частоты , собственно сама катушка индуктивности и резистор на 100 Ом. Чем больше сопротивление, тем меньше будет проседать напряжение с моего генератора частоты, поэтому я взял резистор на 100 Ом.
Чем больше сопротивление, тем меньше будет проседать напряжение с моего генератора частоты, поэтому я взял резистор на 100 Ом.
Собираем все это дело по такой схеме:
Получилось как то так:
Сразу договоримся, что у нас первый канал будет красным цветом, а второй канал — желтым. Следовательно, красная синусоида — это частота, которую нам выдает генератор частоты, а желтая синусоида — это сигнал, который снимается с резистора.
Мы с вами узнали, что при нулевой частоте (постоянный ток), катушка почти беспрепятственно пропускает через себя электрический ток. В нашем опыте мы будем подавать с генератора частоты синусоидальный сигнал с разной частотой и смотреть, меняется ли напряжение на резисторе.
Кто до сих пор не знает что такое осциллограф, можно прочитать про него . Что такое цифровой
осциллограф, можно прочитать . Про автоматическое измерение параметров с помощью цифрового осцилла, читаем Кто уже читал и все знает, идем дальше.
Для начала подаем сигнал с частотой в 1 КилоГерц.
Давайте разберемся, что есть что. В зеленой рамочке я вывел автоматические замеры, которые делает осциллограф
Красный кружок с цифрой «1» — это замеры «красного»канала. Как мы видим, F
(частота) =1 КилоГерц, а Ма
(амплитуда) = 1,96 Вольт. Ну грубо скажем 2 Вольта. Смотрим на кружочек с цифрой «2». F
=1 КилоГерц, а Ма
=1,96 Вольт. То есть можно сказать, что сигнал на выходе точно такой же, как и на входе.
Увеличиваем частоту до 10 КилоГерц
Амплитуда не уменьшилась. Сигнал какой есть, такой и остался.
Увеличиваем до 100 КилоГерц
Видели да? Амплитуда желтого сигнала стала меньше, да еще и график желтого сигнала сдвигается вправо, то есть запаздывает, или научным языком, появляется сдвиг фаз
. Красный сигнал никуда не сдвигается, запаздывает именно желтый. Это имейте ввиду.
Сдвиг фаз
— это разность между начальными фазами двух измеряемых величин
. В данном случае напряжения. Для того, чтобы произвести замер сдвига фаз, должно быть условие, что у этих сигналов одна и та же частота
В данном случае напряжения. Для того, чтобы произвести замер сдвига фаз, должно быть условие, что у этих сигналов одна и та же частота
. Амплитуда может быть любой. Ниже на рисунке приведен этот самый сдвиг фаз или, как еще его называют, разность фаз
:
Увеличиваем частоту до 200 КилоГерц
На частоте 200 КилоГерц амплитуда упала вдвое, да и разность фаз стала больше.
Увеличиваем частоту до 300 КилоГерц.
Амплитуда желтого сигнала упала уже до 720 миллиВольт. Разность фаз стала еще больше.
Увеличиваем частоту до 500 КилоГерц
Амплитуда уменьшилась до 480 миллиВольт.
Добавляем еще частоту до 1 МегаГерца
Амплитуда желтого канала стала 280 миллиВольт
.
Ну и добавляем частоту до предела, который позволяет выдать генератор частоты: 2 МегаГерца
Амплитуда «желтого» сигнала стала настолько маленькой, что мне пришлось ее даже увеличить на осцилле в 5 раз.
И можно сказать, что сдвиг фаз стал почти 90 градусов или π/2.
Но станет ли сдвиг фаз больше, чем 90 градусов, если подать очень-очень большую частоту? Эксперименты говорят, что нет. Если сказать просто, то при бесконечной частоте сдвиг фаз будет равняться 90 градусов. Если совместить наши графики на бесконечной частоте, то можно увидеть примерно вот такой рисунок:
Так какой вывод можно сделать?
С увеличением частоты сопротивление катушки растет, а также увеличивается сдвиг фаз. И чем больше частота, тем больше будет сдвиг фазы, но не более, чем 90 градусов.
Давайте же уменьшим индуктивность катушки. Прогоним еще раз по тем же самым частотам. Я убрал половину витков и сделал витки на край феррита, тем самым уменьшил индуктивность до 33 микроГенри.
Итак, прогоняем все по тем же значениям частоты
При частоте в 1 КилоГерц у нас значение почти не изменилось.
10 КилоГерц
Здесь тоже ничего не изменилось.
100 КилоГерц
Тоже почти ничего не изменилось, кроме того, что желтый сигнал стал тихонька сдвигаться.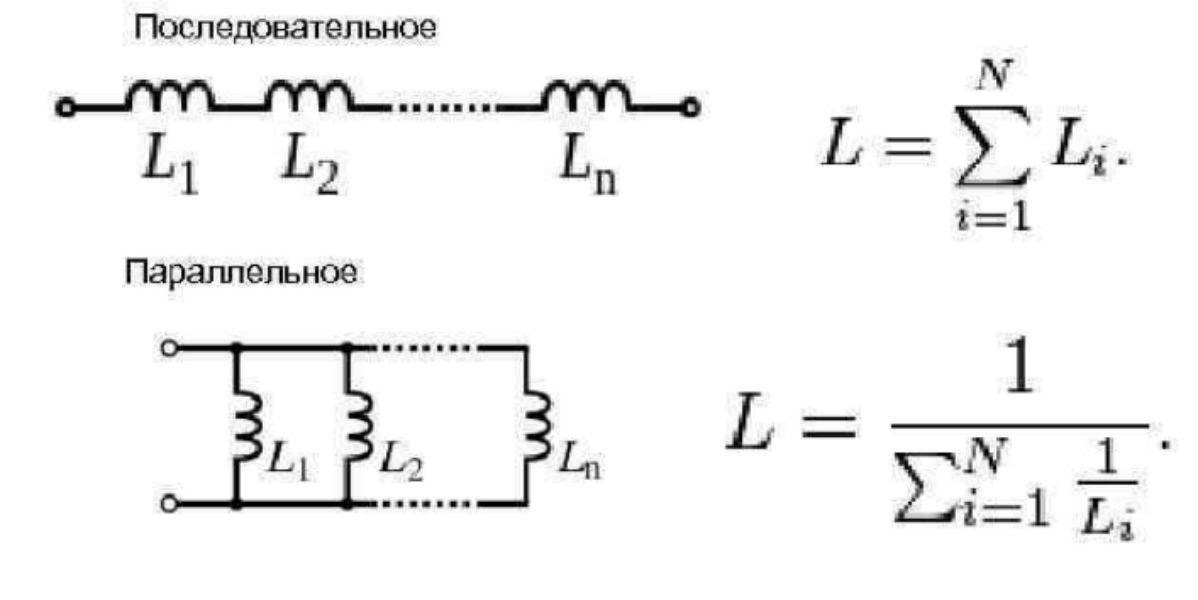
200 КилоГерц
Здесь уже видим, что амплитуда на желтом сигнале начинает проседать и сдвиг фаз наращивает обороты.
300 КилоГерц
Сдвиг фаз стал больше и амплитуда просела еще больше
500 КилоГерц
Сдвиг стал еще больше и амплитуда желтого сигнала тоже просела.
1 МегаГерц
Амплитуда желтого сигнала падает, сдвиг фаз прибавляется. 😉
2 МегаГерца, предел моего генератор частоты
Сдвиг фаз стал почти равен 90 градусов, а амплитуда стала даже меньше, чем пол Вольта.
Обратите внимание на амплитуду в Вольтах на тех же самых частотах. В первом случае у нас индуктивность была больше, чем во втором случае, но амплитуда желтого сигнала во втором случае больше, чем в первом.
Отсюда вывод напрашивается сам собой:
При уменьшении индуктивности, сопротивление катушки индуктивности также уменьшается.
С помощью нехитрых умозаключений, физиками была выведена формула:
где
Х L
— сопротивление катушки, Ом
П
— постоянная и равна приблизительно 3,14
F
— частота, Гц
L
— индуктивность
В данном опыте мы с вами получили фильтр низких частот (ФНЧ). Как вы видели сами, на низких частотах катушка индуктивности почти не оказывает сопротивление напряжению, следовательно амплитуда и мощность на выходе такого фильтра будет почти такой же, как и на входе. Но с увеличением частоты у нас амплитуда гасится. Применив такой фильтр на динамик, можно с уверенностью сказать, что будет усиливаться только бас, то есть низкая частота звука.
Как вы видели сами, на низких частотах катушка индуктивности почти не оказывает сопротивление напряжению, следовательно амплитуда и мощность на выходе такого фильтра будет почти такой же, как и на входе. Но с увеличением частоты у нас амплитуда гасится. Применив такой фильтр на динамик, можно с уверенностью сказать, что будет усиливаться только бас, то есть низкая частота звука.
РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ
ТЕОРИЯ: ПОНЕМНОГУ — ОБО ВСЕМ
1.6. Реактивное сопротивление.
Если через обмотку катушки индуктивности с магнитопроводом
(сердечником) пропустить переменный ток, изменяющийся по синусоидальному
закону simt (см. рис. 3),
возникнет, как мы говорили, магнитный поток, намагничивающий магнитопровод.
Ток и магнитный поток в магнитопроводе будут также переменными и возбудят
в обмотке ЭДС индукции. Она равна напряжению на выводах катушки, и в
то же время пропорциональна скорости изменения магнитного потока. В
В
итоге напряжение будет сдвинуто по фазе на -90° относительно тока. Это
значит, что ток отстает по фазе на 90° от напряжения.
Ток, протекающий через катушку, называется реактивным,
и в отличие от тока через активное сопротивление, он не приводит к расходованию
мощности. Кроме того, напряжение на катушке при фиксированном токе пропорционально
частоте, следовательно, сопротивление катушки возрастает с частотой.
Напряжение на катушке может быть рассчитано по закону Ома, в который
в качестве сопротивления надо подставить индуктивное сопротивление катушки:
XL = jL = j2fL
(индуктивное сопротивление). Перед обозначением реактивного сопротивления
ставят символ j, в математике обозначающий мнимую величину, равную квадратному
корню из -1.
Посмотрим теперь, что получится, если к пластинам
конденсатора приложить переменное напряжение, изменяющееся по синусоидальному
закону simt. Через конденсатор
Через конденсатор
потечет переменный ток, вызванный тем, что пластины конденсатора должны
будут перезаряжаться столько раз в секунду, сколько раз ток изменяет
свое направление. Заряд на пластинах прямо пропорционален приложенному
напряжению (q = CU), а ток пропорционален скорости изменения заряда
(I = dq/dt).
Таким образом, ток через конденсатор также реактивный,
но опережает напряжение на 90°. Ток пропорционален частоте, следовательно,
емкостное сопротивление конденсатора обратно пропорционально частоте:
Хс = 1/jС = -j/С
(емкостное сопротивление).
Зависимости реактивных сопротивлений от частоты
показаны на рис. 6,а. В реальных электрических цепях встречаются как
реактивные, индуктивные и емкостные, так и активные сопротивления. Вместе
они образуют комплексные, или полные сопротивления, обозначаемые буквой
Z и математически представляющие собой комплексные числа, содержащие
действительную R и мнимую X части: Z = R + jX (полное сопротивление).
Рис. 6
Как складываются активные сопротивления при последовательном и параллельном
соединении, мы уже изучали (рис. 2,г), и теперь нам осталось сказать, что и
полные сопротивления складываются точно так же, только не надо забывать про
знак реактивного сопротивления и символ j.
Будет очень полезно, если вы немного потренируетесь и попробуете написать полное
сопротивление цепей, содержащих различным образом включенные катушки индуктивности,
конденсаторы и резисторы (рис. 6, б-д). Очень скоро вы убедитесь, что одно и
то же полное сопротивление на одной, заданной частоте могут иметь цепи, выполненные
по-разному, и это открывает возможность их преобразования.
Например, цепь из последовательно соединенных резистора и конденсатора можно
заменить цепью, где те же элементы включены параллельно, но, разумеется, номиналы
у них будут другими. Также легко убедиться, что при последовательном соединении
двух катушек их индуктивности складываются, а вот емкости складываются при параллельном
соединении конденсаторов. Ну а теперь перейдем к обещанному рассказу о трансформаторах.
Ну а теперь перейдем к обещанному рассказу о трансформаторах.
Радио, 1998
Электрические и магнитные цепи ЭОЭ2М-С-Р
Электрические и магнитные цепи ЭОЭ2М-С-Р
Вы смотрите фотографию с сайта ООО Учебное и лабораторное оборудование —
чтобы вернуться на него перейдите по ссылке uilomsk.ru
1. Электрические цепи постоянного тока.
1.1. Параметры электрической цепи, постоянных напряжения и тока.
1.2. Закон Ома.
1.3. Исследование цепей с резисторами.
1.3.1. Линейные резисторы.
1.3.2. Терморезисторы с отрицательным температурным коэффициентом.
1.3.3. Терморезисторы с положительным температурным коэффициентом.
1.3.4. Варисторы.
1.3.5. Фоторезисторы.
1.3.6. Последовательное соединение резисторов.
1.3.7. Параллельное соединение резисторов.
1.3.8. Последовательно-параллельное соединение резисторов.
1.3.9. Резистивный делитель напряжения.
1.4.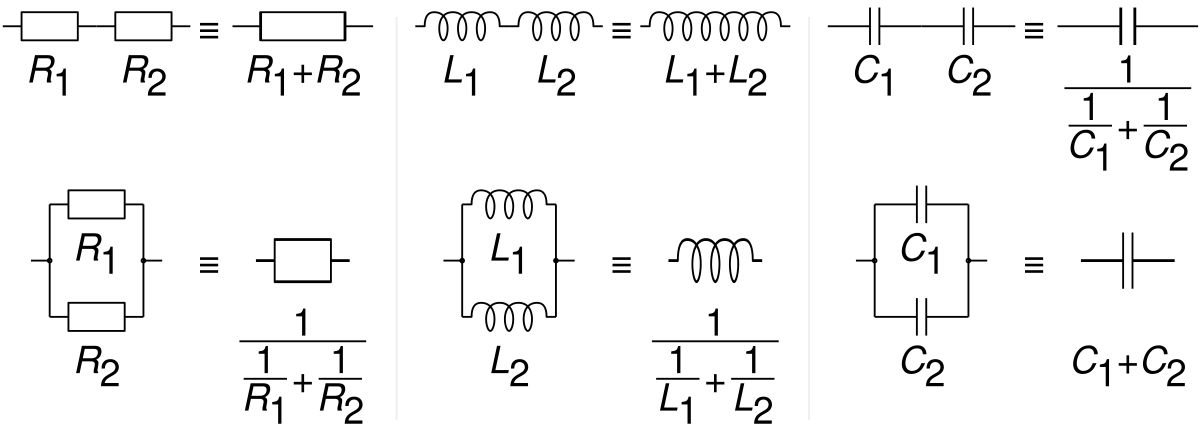 Эквивалентный источник напряжения (ЭДС).
Эквивалентный источник напряжения (ЭДС).
1.5. Последовательное соединение источников напряжения (ЭДС).
1.6. Параллельное соединение источников напряжения (ЭДС).
1.7. Электрическая мощность и работа.
1.8. Коэффициент полезного действия электрической цепи.
1.9. Согласование источника и нагрузки по напряжению, току и мощности.
1.10. Процессы заряда и разряда конденсатора (при наличии осциллографа).
1.11. Процессы при включении под напряжение и коротком замыкании катушки индуктивности (при наличии осциллографа).
2. Электрические цепи переменного тока.
2.1. Параметры синусоидальных напряжения и тока (при наличии осциллографа).
2.2. Цепи синусоидального тока с конденсаторами.
2.2.1. Напряжение и ток конденсатора (при наличии осциллографа).
2.2.2. Реактивное сопротивление конденсатора (при наличии осциллографа).
2.2.3. Последовательное соединение конденсаторов.
2.2.4. Параллельное соединение конденсаторов.
2.2.5. Реактивная мощность конденсатора (при наличии осциллографа).
2.3. Цепи синусоидального тока с катушками индуктивности.
2.3.1. Напряжение и ток катушки индуктивности (при наличии осциллографа).
2.3.2. Реактивное сопротивление катушки индуктивности (при наличии осциллографа).
2.3.3. Последовательное соединение катушек индуктивности.
2.3.4. Параллельное соединение катушек индуктивности.
2.3.5. Реактивная мощность катушки индуктивности (при наличии осциллографа).
2.4. Цепи синусоидального тока с резисторами, конденсаторами и катушками индуктивности.
2.4.1. Последовательное соединение резистора и конденсатора.
2.4.2. Параллельное соединение резистора и конденсатора.
2.4.3. Последовательное соединение резистора и катушки индуктивности.
2.4.4. Параллельное соединение резистора и катушки индуктивности.
2.4.5. Последовательное соединение конденсатора и катушки индуктивности. Понятие о резонансе напряжений.
2.4.6. Последовательное соединение конденсатора и катушки индуктивности. Понятие о резонансе токов.
2.4.7. Частотные характеристики последовательного резонансного контура.
2.4.8. Частотные характеристики параллельного резонансного контура.
2.5. Трехфазные цепи синусоидального тока.
2.5.1. Напряжения и токи в трехфазной цепи (при наличии осциллографа).
2.5.2. Трехфазная нагрузка, соединенная по схеме «звезда».
2.5.3. Трехфазная нагрузка, соединенная по схеме «треугольник».
2.5.4. Аварийные режимы трёхфазной цепи при соединении нагрузки по схеме «звезда».
2.5.5. Аварийные режимы трёхфазной цепи при соединении нагрузки по схеме «треугольник».
2.6. Расчёт и экспериментальное исследование цепи при несинусоидальном приложенном напряжении (при наличии осциллографа).
2.7. Переходные процессы в линейных электрических цепях (при наличии осциллографа).
2.7.1. Переходные процессы в цепи с конденсатором и резисторами.
2. 7.2. Переходные процессы в цепи с катушкой индуктивности.
7.2. Переходные процессы в цепи с катушкой индуктивности.
2.7.3. Переходные процессы в колебательном контуре.
3. Электронные приборы и устройства.
3.1. Выпрямительные диоды.
3.1.1. Характеристики диода.
3.1.2. Однофазный однополупериодный неуправляемый выпрямитель (при наличии осциллографа).
3.1.3. Однофазный мостовой неуправляемый выпрямитель (при наличии осциллографа).
3.1.4. Трехфазный нулевой неуправляемый выпрямитель (при наличии осциллографа).
3.1.5. Трехфазный мостовой неуправляемый выпрямитель (при наличии осциллографа).
3.2. Стабилитроны.
3.2.1. Характеристики стабилитрона.
3.2.2. Исследование параметрического стабилизатора напряжения.
3.2.3. Сглаживание пульсаций выпрямленного напряжения (при наличии осциллографа).
3.3. Диоды с особыми свойствами.
3.3.1. Характеристики светодиода.
3.3.2. Характеристики варикапа.
3.4. Биполярные транзисторы.
3. 4.1. Испытание слоев и исследование выпрямительного действия биполярных транзисторов.
4.1. Испытание слоев и исследование выпрямительного действия биполярных транзисторов.
3.4.2. Исследование распределения тока в транзисторе и управляющего эффекта тока базы транзистора.
3.4.3. Характеристики транзистора.
3.4.4. Установка рабочей точки транзистора и исследование влияния резистора в цепи коллектора на коэффициент усиления по напряжению усилительного каскада с общим эмиттером (при наличии осциллографа).
3.4.5. Усилители на биполярных транзисторах (при наличии осциллографа).
3.4.6. Линейный регулятор напряжения.
3.4.7. Линейный регулятор тока.
3.5. Униполярные (полевые) транзисторы.
3.5.1. Испытание слоев и исследование выпрямительного действия униполярных транзисторов.
3.5.2. Характеристика включения затвора полевого транзистора.
3.5.3. Управляющий эффект затвора полевого транзистора n-типа.
3.5.4. Выходные характеристики полевого транзистора.
3.5.5. Усилители на полевых транзисторах (при наличии осциллографа).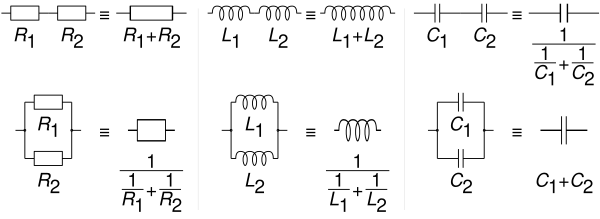
3.6. Тиристоры.
3.6.1. Характеристики диодного тиристора (симистора).
3.6.2. Характеристики триодного тиристора.
3.6.3. Фазовое управление тиристором (при наличии осциллографа).
3.7. Логические элементы.
3.7.1. Логический элемент «И».
3.7.2. Логический элемент «ИЛИ».
3.7.3. Логический элемент «НЕ».
3.7.4. Логический элемент «И-НЕ».
3.7.5. Логический элемент «ИЛИ-НЕ».
3.8. Операционные усилители.
3.8.1. Инвертирующий усилитель.
3.8.2. Неинвертирующий усилитель.
3.8.3. Суммирующий усилитель.
3.8.4. Дифференциальный усилитель.
3.8.5. Исследование операционного усилителя в динамике (при наличии осциллографа).
Электрические машины
1. Трансформаторы.
1.1. Определение коэффициента трансформации двухобмоточного трансформатора.
1.2. Снятие и определение характеристик холостого хода I0=f(U), Р0=f(U),cosφ0= f(U) однофазного трансформатора.
1.3. Снятие и определение характеристик короткого замыкания IК=f(U), РК=f(U), cosφК= f(U) однофазного трансформатора.
1.4. Снятие и определение характеристик холостого хода I0=f(U), Р0=f(U),cosφ0= f(U) трехфазного трансформатора.
1.5. Снятие и определение характеристик короткого замыкания IК=f(U), РК=f(U), cosφК= f(U) трехфазного трансформатора.
1.6. Определение уравнительного тока, вызванного неравенством коэффициентов трансформации параллельно включенных однофазных трансформаторов (при наличии не менее двух комплектов лабораторного оборудования ЭОЭ1-Н-Р).
1.7. Определение группы соединений обмоток трехфазного трансформатора (при наличии осциллографа).
1.8. Подтверждение недопустимости параллельной работы трехфазных трансформаторов с различными группами соединения обмоток (при наличии не менее двух комплектов лабораторного оборудования ЭОЭ1-Н-Р).
2. Генераторы постоянного тока.
2.1. Снятие характеристики холостого хода E0=f(If) генератора постоянного тока с независимым возбуждением.
2.2. Снятие характеристики короткого замыкания IК=f(If) генератора постоянного тока с независимым возбуждением.
2.3. Определение внешней U=f(I), регулировочной If= f(I) и нагрузочной U=f(If) характеристик генератора постоянного тока с независимым / параллельным возбуждением.
3. Двигатели постоянного тока.
3.1. Определение механической характеристики n=f(M) двигателя постоянного тока с независимым / параллельным / последовательным возбуждением.
3.2. Определение рабочих характеристик n=f(P2), M=f(P2), η=f(P2)двигателя постоянного тока с независимым / параллельным / последовательным возбуждением.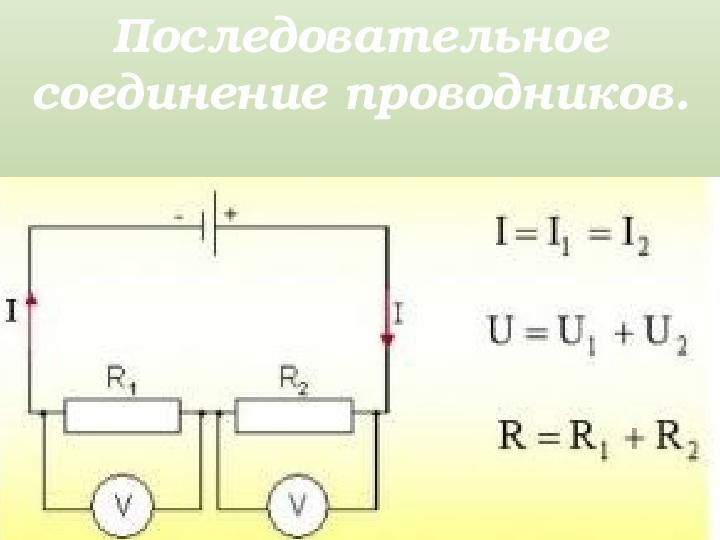
4. Трехфазные асинхронные двигатели.
4.1. Снятие и определение характеристик холостого хода I0=f(U), Р0=f(U), cosφ0=f(U) трехфазного асинхронного двигателя с короткозамкнутым ротором.
4.2. Снятие и определение характеристик короткого замыкания IК=f(U), РК=f(U), cosφК=f(U) трехфазного асинхронного двигателя с короткозамкнутым ротором.
4.3. Определение механической характеристики n=f(M) трехфазного асинхронного двигателя с короткозамкнутым ротором.
4.4. Определение рабочих характеристик I=f(P2), P1=f(P2), s=f(P2), η=f(P2), cosφ=f(P2), M=f(P2) трехфазного асинхронного двигателя с короткозамкнутым ротором.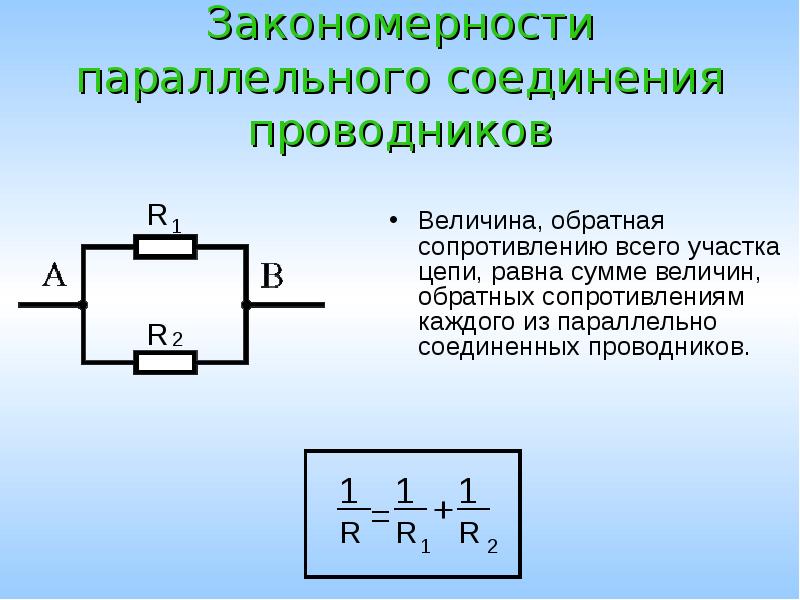
Электрический привод
1. Исследование неавтоматизированных электроприводов постоянного тока в статическом режиме.
1.1. Электропривод системы «Источник ЭДС – двигатель постоянного тока независимого/параллельного/последовательного возбуждения».
1.2. Электропривод системы «Тиристорный преобразователь — двигатель постоянного тока независимого/параллельного/последовательного возбуждения».
1.3. Электропривод системы «Реверсивный тиристорный преобразователь — двигатель постоянного тока независимого возбуждения».
2. Исследование неавтоматизированных электроприводов переменного тока в статическом режиме.
2.1. Электропривод системы «Тиристорный регулятор напряжения промышленной частоты — асинхронный двигатель с короткозамкнутым ротором».
2.2. Электропривод системы «Преобразователь частоты — асинхронный двигатель с короткозамкнутым ротором».
CОСТАВ
СТЕНДА
- Электромашинный агрегат с маховиком (с машиной постоянного тока 101.
 2, асинхронным двигателем 106 и преобразователем углового перемещения) – 1 шт.
2, асинхронным двигателем 106 и преобразователем углового перемещения) – 1 шт. - Однофазный тиристорный преобразователь – 1 шт.
- Блок генераторов напряжений – 1 шт.
- Преобразователь частоты – 1 шт.
- Однофазный источник питания – 2 шт.
- Трехполюсный выключатель – 1 шт.
- Наборная панель – 1 шт.
- Реостат возбуждения машины постоянного тока – 1 шт.
- Линейный реактор – 1 шт.
- Регулируемый автотрансформатор – 1 шт.
- Выпрямитель – 1 шт.
- Реостат – 1 шт.
- Трехфазная трансформаторная группа – 2 шт.
- Модель однородной длинной линии – 1 шт.
- Трехфазный регулируемый автотрансформатор – 1 шт.
- Блок мультиметров (3 мультиметра) – 1 шт.
- Ваттметр – 1 шт.
- Вольтамперметр – 1 шт.

- Многофункциональный электроизмерительный прибор – 1 шт.
- Набор миниблоков «Электрические и электронные компоненты» – 1 шт.
- Набор миниблоков «Трансформаторы» – 1 шт.
- Лабораторный стол с двухсекционным контейнером и двухуровневой рамой – 1 шт.
- Лабораторный стол с двухсекционным контейнером и одноуровневой рамой – 1 шт.
- Лабораторный стол с контейнером для проводников и двухуровневой рамой – 1 шт.
- Набор аксессуаров для комплекта ТЭЦОЭ2-Н-Р – 1 шт.
- Секундомер – 1 шт.
- Блок мультиметров (2 мультиметра) – 1 шт.
- Активная нагрузка – 1 шт.
- Указатель частоты вращения – 1 шт.
- Трехфазный источник питания – 1 шт.
- Набор аксессуаров для комплекта ЭП1М-Н-Р – 1 шт.
- Руководство по выполнению базовых экспериментов «Электрические цепи постоянного тока»
- Руководство по выполнению базовых экспериментов «Электрические цепи переменного тока»
- Руководство по выполнению базовых экспериментов «Электронные приборы и устройства»
- Руководство по выполнению базовых экспериментов «Однородная длинная линия»
- Сборник руководств по эксплуатации компонентов аппаратной части комплекта ТЭЦОЭ2-С-Р
- Руководство по выполнению базовых экспериментов «Электрический привод»
- Сборник руководств по эксплуатации компонентов аппаратной части комплекта ЭМП1М-С-Р
- Руководство по выполнению базовых экспериментов «Электрические машины»
- Компакт-диск с методическим обеспечением комплекта ЭОЭ2М-С-Р
ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
| Потребляемая мощность, В·А, не более | 500 |
| Электропитание:- от трехфазной сети переменного тока с рабочим нулевым и защитным проводниками напряжением, В — и от однофазной сети переменного тока с рабочим нулевым и защитным проводниками напряжением, В — частота, Гц | 380 ± 38 220 ± 2250 ± 0,5 |
| Класс защиты от поражения электрическим током | I |
| Габаритные размеры, мм, не более — длина (по фронту) — ширина (ортогонально фронту) — высота | 2750300800 |
| Масса, кг, не более | 150 |
| Количество человек, которое одновременно и активно может работать на комплекте | 3 |
© ООО Учебное и лабораторное оборудование
RL Параллельная цепь | Электрические4U
В RL параллельная цепь резистор и катушка индуктивности соединены параллельно друг другу, и эта комбинация питается от источника напряжения, В в . Выходное напряжение схемы составляет В из . Поскольку резистор и катушка индуктивности соединены параллельно, входное напряжение равно выходному напряжению, но токи, протекающие через резистор и катушку индуктивности, различны.
Выходное напряжение схемы составляет В из . Поскольку резистор и катушка индуктивности соединены параллельно, входное напряжение равно выходному напряжению, но токи, протекающие через резистор и катушку индуктивности, различны.
Параллельная RL-цепь не используется в качестве фильтра для напряжений, поскольку в этой схеме выходное напряжение равно входному напряжению, и по этой причине она обычно не используется по сравнению с последовательной RL-схемой.
Скажем: I T = общий ток, протекающий от источника напряжения в амперах.
I R = ток, протекающий в ветви резистора, в амперах.
I L = ток, протекающий в ветви индуктора, в амперах.
θ = угол между I R и I T .
Таким образом, общий ток I T ,
В комплексной форме токи записываются как
Полное сопротивление параллельной цепи RL
Пусть, Z = полное сопротивление цепи в омах.
R = сопротивление цепи в омах.
L = индуктор цепи в Генри.
X L = индуктивное сопротивление в омах.
Поскольку сопротивление и катушка индуктивности соединены параллельно, полное сопротивление цепи определяется как
Чтобы удалить «j» из знаменателя, умножьте и разделите числитель и знаменатель на (R – j X L ),
Анализ параллельной RL-цепи
В параллельной RL-цепи известны значения сопротивления, индуктивности, частоты и напряжения питания. Для нахождения других параметров RL-параллельной цепи выполните следующие действия:
Шаг 1. Поскольку значение частоты уже известно, мы можем легко найти значение индуктивного сопротивления X L ,
Шаг 2. Мы знаем, что в параллельной цепи напряжение на катушке индуктивности и резисторе остается одинаковым, поэтому
Шаг 3. Используйте закон Ома, чтобы найти ток, протекающий через индуктор и резистор,
Шаг 4. Теперь рассчитайте полный ток,
Теперь рассчитайте полный ток,
Шаг 5. Определите фазовые углы для резистора и индуктора и для параллельного цепь, это всегда
Шаг 6. Поскольку мы уже рассчитали полный ток, протекающий в цепи, и напряжение V нам также известно, используя закон Ома; мы можем легко вычислить полное сопротивление:
Шаг 7. Теперь вычислите полный фазовый угол для цепи, которая определяется как,
Полный фазовый угол параллельной RL-цепи всегда лежит между 0 o до -90 или . Это 0 o для чисто резистивной цепи и -90 o для чисто индуктивной цепи.
Резистор, конденсатор и катушка индуктивности, включенные последовательно-параллельно
Резистор, конденсатор и катушка индуктивности, соединенные последовательно и параллельно – формулы и уравнения
Следующее основное и полезное уравнение и формулы можно использовать для проектирования, измерения, упрощения и анализа электрических цепей для различных компонентов и электрических элементов, таких как резисторы, конденсаторы и катушки индуктивности, соединенных последовательно и параллельно.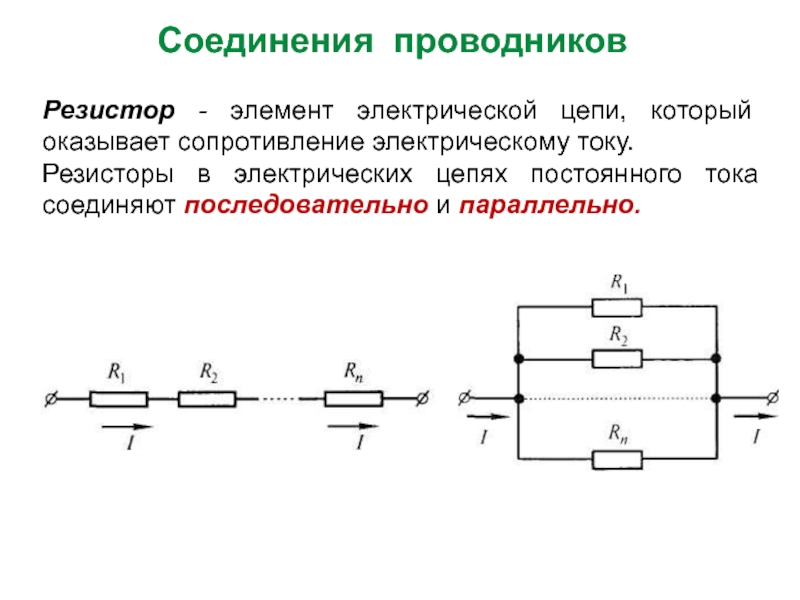
Сопротивление в последовательных и параллельных уравнениях
Сопротивление:
Суммарное эквивалентное сопротивление резисторов, соединенных последовательно или параллельно, определяется по следующей формуле:
Сопротивление Последовательно:
Когда два или более резистора соединены последовательно, как показано на рисунке, их эквивалентное сопротивление рассчитывается по формуле:
R Eq = R 1 + R 2 + R 3 +… R n
Параллельное сопротивление:
, когда резисторы подключены параллельно, эквивалентное сопротивление становится:
Где
- R Eq эквивалентное сопротивление всех резисторов (R 1 , R 2 , R 3 … R n )
Похожие сообщения:
Преобразование треугольника Δ в звезду Y (пи в тройник):
Соединение треугольник (Δ) также называется Соединение Pi и Соединение звездой (Y) также упоминается как Тройник (T) .
От треугольника (Δ) до звезды (Y) Соединение:
Соединение от звезды (Y) до треугольника (Δ)
Для получения более подробной информации и решенных примеров см. Преобразование звезды в дельту и дельты в звезду.
Емкость в последовательных и параллельных уравнениях
Емкость:
Общая емкость конденсатора, подключенного параллельно и последовательно, приведена ниже:
Емкость Последовательно:
Когда конденсаторы соединены последовательно, эквивалентная емкость становится:
Емкость Параллельно:
Емкость суммируется, когда они соединены вместе в параллельной конфигурации
C Eq = C 1 + C 2 + C 3 +… C n
Где
- C Eq является эквивалентной емкостью всех конденсаторов (C 1 , C 2 , C 3 … C n )
Похожие сообщения:
Индуктивность в последовательных и параллельных уравнениях
Индуктивность:
Расчет общей индуктивности катушек индуктивности внутри цепи напоминает резисторы.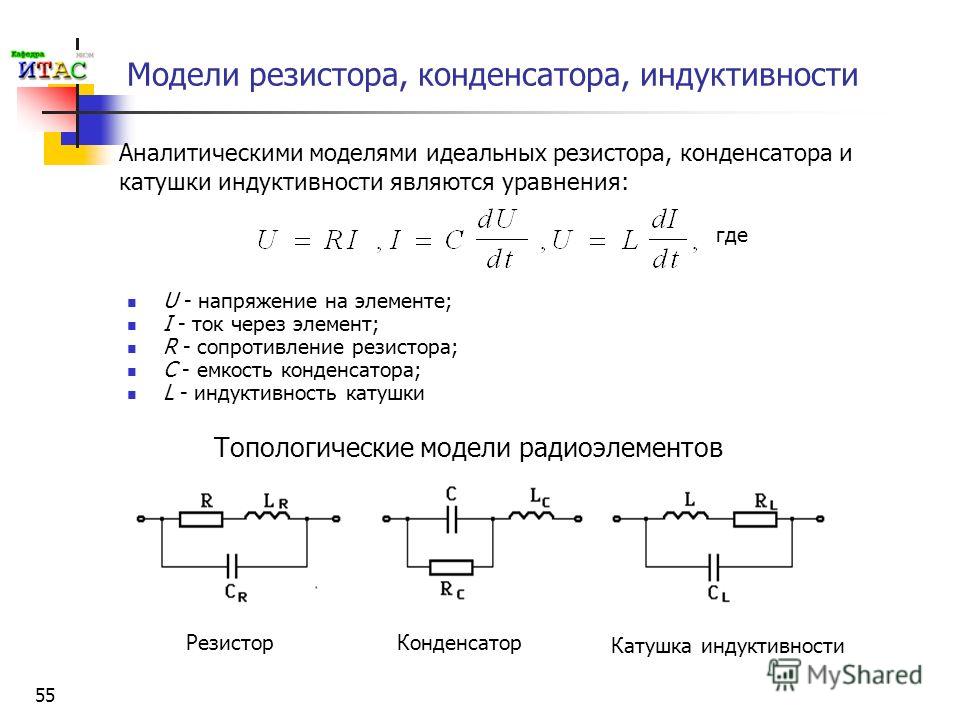
Индуктивность Последовательно:
Когда катушки индуктивности соединены последовательно, как показано на рисунке, их индуктивность суммируется.
L Eq = L 1 + L 2 + L 3 +… L n
Индуктивность Параллельно:
При параллельном соединении эквивалентная индуктивность катушек индуктивности определяется как
.
Где
- L Eq эквивалентная индуктивность всех катушек индуктивности (L 1 , L 2 , L 3 … L n )
Связанные формулы и уравнения Сообщений:
Резистивно-индуктивные параллельные цепи
ЦЕЛИ
• обсудить работу параллельной цепи, содержащей сопротивление и
индуктивность.
• вычислить значения цепи R-L параллельной цепи.
• подключите параллельную цепь R-L и измерьте значения цепи с помощью теста
инструменты.
УСЛОВИЯ ДЛЯ РЕЗИСТИВНО-ИНДУКТИВНОЙ ПАРАЛЛЕЛЬНОЙ ЦЕПИ
- угол тета (θ u) — разность фазового угла между напряжением и током
в цепи, содержащей реактивный компонент, такой как катушка индуктивности или конденсатор - полная мощность (ВА) — значение, полученное путем умножения приложенного
напряжение на общий ток цепи переменного тока.Полная мощность измеряется
в вольт-амперах (ВА) и не следует путать с реальной мощностью, измеренной
в ваттах - ток, протекающий через индуктор (IL) — количество протекающего тока
через индуктор - ток, протекающий через резистор (IR) — количество протекающего тока
через резистор - коэффициент мощности (PF) — отношение активной мощности к кажущейся реактивной мощности.
мощность Вар - полный ток (ИТ) — полный ток, протекающий по электрической цепи;
в параллельной цепи R-L это определяется векторным сложением
резистивный ток и индуктивный ток - полный импеданс (Z) — общее ограничение тока в цепи переменного тока
- истинная мощность (P) — количество преобразуемой электрической энергии.

в какую-либо другую форму энергии, такую как тепловая или кинетическая; также известный
как ватт - ватта — реальная мощность в цепи; указывает количество эл.
энергия, преобразованная в какую-либо другую форму 90 163
—————-
В этом разделе обсуждаются цепи, содержащие сопротивление и индуктивность, соединенные
параллельно друг другу.
Математические расчеты будут использоваться, чтобы показать взаимосвязь текущих
и напряжения на всей цепи, и отношения тока через
разные ветви цепи.
РЕЗИСТИВНО-ИНДУКТИВНЫЕ ПАРАЛЛЕЛЬНЫЕ ЦЕПИ
Цепь, содержащая резистор и катушку индуктивности, соединенные параллельно
показан на фиг. 1.
Поскольку напряжение, подаваемое на любое параллельное устройство, должно быть одинаковым,
напряжение, подаваемое на резистор и катушку индуктивности, должно быть синфазным и иметь
такое же значение.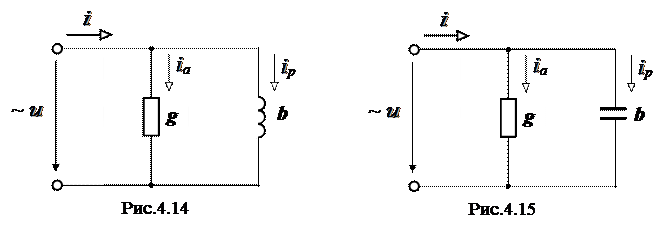 Ток, протекающий через индуктор, будет находиться под углом 90° от
Ток, протекающий через индуктор, будет находиться под углом 90° от
фаза с напряжением, и ток, протекающий через резистор, будет
быть в фазе с напряжением (РИС. 2). Эта конфигурация производит
разность фаз 90° между током, протекающим через чисто индуктивный
нагрузка и чисто резистивная нагрузка (фиг. 3).
РИС. 1 Резистивно-индуктивная параллельная цепь.
РИС. 2 Соотношение напряжения и тока в R-L параллельной цепи.
РИС. 3 Резистивные и индуктивные токи не совпадают по фазе на 90° с
друг друга в R-L параллельной цепи.
Величина фазового сдвига между полным током цепи и
напряжение определяется отношением величины сопротивления к величине
индуктивности. Коэффициент мощности цепи по-прежнему определяется соотношением
кажущейся мощности к истинной мощности.
ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ЦЕПИ
В схеме, показанной на РИС.4, подключено сопротивление 15 Ом
параллельно с индуктивным сопротивлением 20 Ом. Цепь подключена
Цепь подключена
на напряжение 240 В переменного тока и частоту 60 Гц.
В этом примере задачи будут вычислены следующие значения схемы:
IR — протекание тока через резистор
P — ватт (истинная мощность)
IL — протекание тока через дроссель
ВАР — реактивная мощность
IT — общий ток цепи
Z — полное сопротивление цепи
ВА — полная мощность
PF — коэффициент мощности
θ u — угол отклонения напряжения и тока друг от друга по фазе:
РЕЗИСТИВНЫЙ ТОК
В любой параллельной цепи напряжение одинаково на всех компонентах
в цепи.Таким образом, 240 В подается как на резистор, так и на
индуктор.
Поскольку величина напряжения, подаваемого на резистор, известна, величина
тока через резистор (IR) можно рассчитать с помощью
формула:
I Р = Э/Р
I Р = 240/15
I R = 16 А
РИС. 4 Типичная параллельная цепь R-L.
4 Типичная параллельная цепь R-L.
ВАТТ
Истинная мощность (P) или ватты может быть рассчитана с использованием любой из ватт.
формулы и значения чистого сопротивления.
Количество реальной мощности в этой цепи будет вычислено по формуле
P = E R x I R
П = 240 х 16
P = 3840 Вт
ИНДУКТИВНЫЙ ТОК
Поскольку напряжение, подаваемое на индуктор, известно, ток, протекающий
можно найти, разделив напряжение на индуктивное сопротивление. Количество
тока через индуктор (IL) будет вычисляться по формуле
I L = E/X L
I L = 240/20
I L = 12 А
ВАРС
Количество реактивной мощности, ВАр, будет рассчитываться по формуле
ВАр = E L x I L
ВАР = 240 x 12
ВАР = 2880
ИНДУКТИВНОСТЬ
Частота и индуктивное сопротивление известны, поэтому индуктивность
катушки можно найти по формуле
л = Х л 2пФ
Д = 20/377
л = 0. 053H
053H
ОБЩИЙ ТОК
РИС. 5 Соотношение резистивного, индуктивного и полного тока в
R-L параллельная цепь.
РИС. 6 Построение графика полного тока методом параллелограмма.
Полный ток (IT), протекающий по цепи, можно рассчитать, добавив
ток течет через резистор и катушку индуктивности. Поскольку эти два
токи не совпадают по фазе на 90°, сложение векторов будет
использовал.Если бы эти текущие значения были нанесены на график, они образовали бы прямоугольный треугольник.
аналогичный показанному на фиг. 5. Обратите внимание, что ток течет через
резистор и катушка индуктивности образуют стороны прямоугольного треугольника, а сумма
ток это гипотенуза. Следовательно, теорему Пифагора можно использовать
чтобы сложить эти токи вместе.
Метод параллелограмма для построения графика полного тока показан на РИС. 6.
ИМПЕДАНС
Теперь, когда известны общий ток и общее напряжение,
общий импеданс (Z) можно рассчитать, заменив R на Z в омах.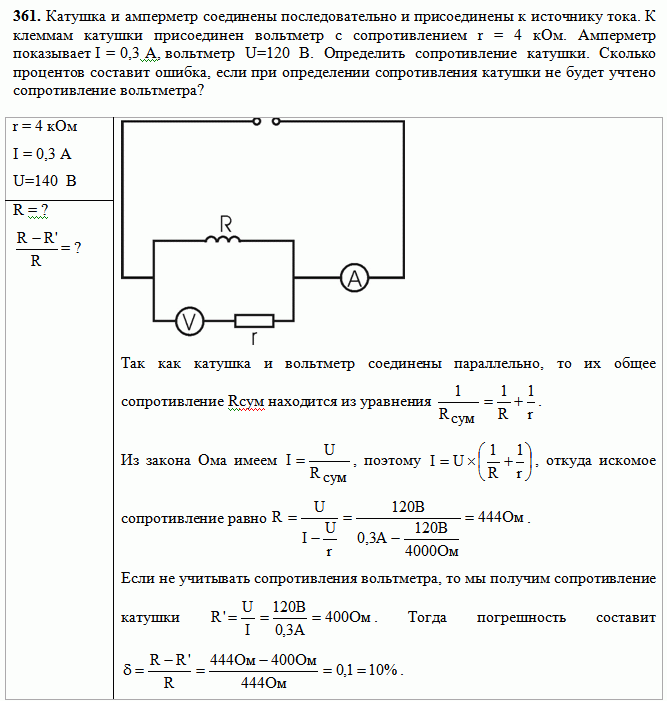
формула закона.
Общее сопротивление цепи можно рассчитать по формуле
Значение импеданса также можно найти, если суммарный ток и напряжение
не известны. В параллельной цепи величина, обратная полному сопротивлению
равно сумме обратных величин каждого резистора. Это же правило
могут быть изменены, чтобы разрешить использование аналогичной формулы в параллели R-L.
схема. Поскольку сопротивление и индуктивное сопротивление сдвинуты по фазе на 90 °
друг с другом, сложение векторов должно использоваться, когда обратные
добавлен.Исходная формула:
Эта формула утверждает, что квадрат обратной величины импеданса
равен сумме квадратов обратных величин сопротивления и
индуктивное реактивное сопротивление. Чтобы удалить квадрат из обратной величины импеданса,
возьми квадратный корень из обеих частей уравнения.
Обратите внимание, что формулу теперь можно использовать для нахождения обратной величины
импеданс, а не импеданс.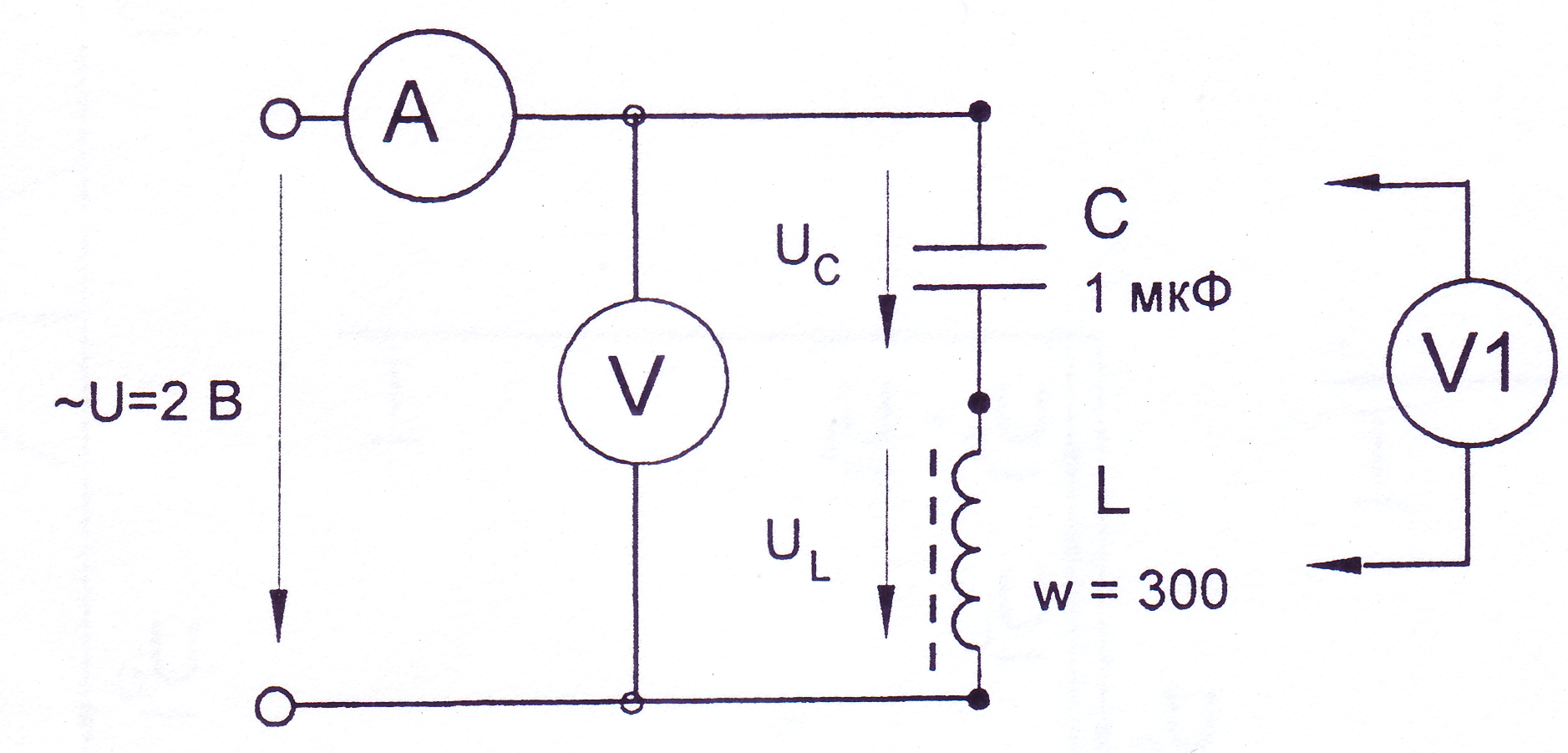 Изменить формулу так, чтобы она была равна
Изменить формулу так, чтобы она была равна
к импедансу, возьмите обратную величину обеих частей уравнения.
Теперь в формулу можно подставлять числовые значения для определения импеданса.
цепи.
Другая формула, которую можно использовать для определения импеданса сопротивления
а индуктивное сопротивление, соединенное параллельно, равно
.
Подстановка одинаковых значений сопротивления и индуктивного сопротивления в
эта формула даст тот же ответ.
ПОЛНАЯ МОЩНОСТЬ
Полная мощность (ВА) может быть рассчитана путем умножения напряжения цепи
по общему течению.Соотношение вольт-ампер, ватт и реактивной мощности
то же самое для параллельной цепи R-L, что и для последовательной цепи R-L,
потому что мощность добавляется в цепи любого типа. Поскольку истинная мощность и реактивная
мощности сдвинуты по фазе на 90° друг к другу, они образуют прямоугольный треугольник
с кажущейся мощностью в качестве гипотенузы (РИС.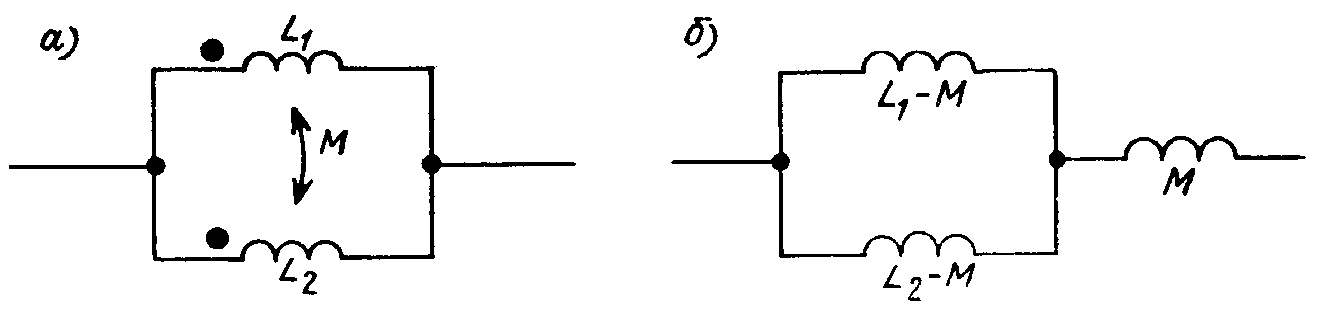 7).
7).
ВА = ET x IT
ВА = 240 х 20
ВА = 4800
КОЭФФИЦИЕНТ МОЩНОСТИ
РИС.7 Соотношение полной мощности (вольт-ампер), истинной мощности (ватт),
и реактивная мощность (вар) в параллельной цепи R-L.
Коэффициент мощности (PF) в параллельной цепи R-L представляет собой отношение кажущейся
мощность до истинной мощности, как это было в цепи серии R-L.
Существуют некоторые различия в формулах, используемых для расчета коэффициента мощности.
в параллельной цепи, как всегда. В цепи серии R-L коэффициент мощности
можно вычислить, разделив падение напряжения на резисторе на
общее или приложенное напряжение.В параллельной цепи напряжение равно
одинаковые, а токи разные. Таким образом, можно рассчитать коэффициент мощности.
путем разделения тока, протекающего через резистивные части цепи
по полному току цепи.
ПФ = ИК/ИТ
Другая формула, которая меняется, включает сопротивление и импеданс. Параллельно
Параллельно
цепи, полное сопротивление цепи будет меньше, чем сопротивление.
Следовательно, если коэффициент мощности должен быть рассчитан с использованием импеданса и сопротивления,
импеданс надо разделить на сопротивление.
ПФ = З/Р
Коэффициент мощности цепи в этом примере будет вычисляться по формуле
УГОЛ ТЕТА
Косинус угла тета (θ u) равен коэффициенту мощности.
COSθ u = 0,80
θ u = 36,87°
Векторная диаграмма с использованием полной мощности, активной мощности и реактивной мощности.
показан на фиг. 8.
Обратите внимание, что угол тета — это угол, создаваемый кажущейся мощностью и
истинная власть.Соотношение тока и напряжения для этой цепи
показан на фиг. 9. Схема со всеми значениями показана на фиг. 10.
РИС. 8 Угол тета.
РИС. 9 Ток не совпадает по фазе с напряжением на 36,87°.
РИС.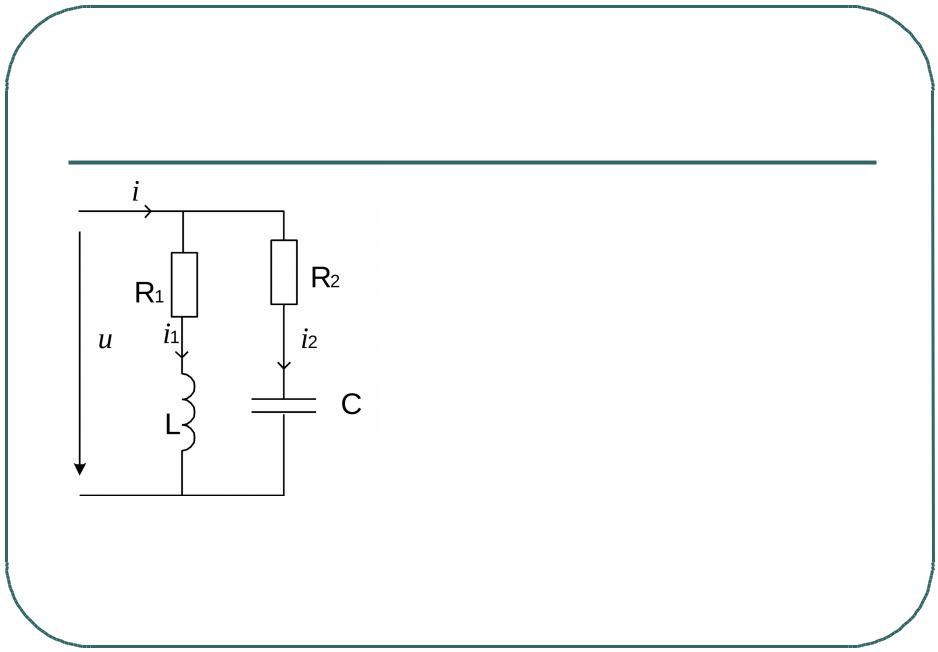 10 Все значения найдены.
10 Все значения найдены.
ОБЗОР
• Напряжение, подаваемое на компоненты в параллельной цепи, должно быть
то же.
• Ток, протекающий через резистивные части цепи, будет в
фаза с напряжением.
• Ток, протекающий через индуктивные части цепи, будет отставать от
напряжение на 90°.
• Общий ток в параллельной цепи равен сумме отдельных
токи. Необходимо использовать сложение векторов, потому что ток через
резистивные части цепи не совпадают по фазе на 90° с текущим током
через индуктивные части.
• Полное сопротивление R-L параллельной цепи можно вычислить с помощью вектора
Кроме того, чтобы добавить обратные величины сопротивления и индуктивного реактивного сопротивления.
• Полная мощность, действительная мощность и реактивная мощность суммируются в цепи любого типа.
Однако необходимо использовать сложение векторов, поскольку истинная мощность и реактивная
мощности не совпадают по фазе на 90° друг с другом.
ВИКТОРИНА
1. Сколько градусов при параллельном соединении катушки индуктивности и резистора
не совпадают по фазе ток, протекающий через резистор, и ток
течь через индуктор?
2. Катушка индуктивности и резистор подключены параллельно к сети 120 В, 60 Гц.
линия.Резистор имеет сопротивление 50 Ом, а катушка индуктивности имеет
индуктивность 0,2 Гн. Каков общий ток, протекающий по цепи?
3. Каков импеданс рассматриваемой цепи 2?
4. Каков коэффициент мощности рассматриваемой цепи 2?
5. На сколько градусов не совпадают по фазе рассматриваемые ток и напряжение
2?
6. В схеме, показанной на фиг. 1, через резистор протекает ток
6,5 А, а через дроссель протекает ток 8 А.Какова общая
ток в этой цепи?
7. Резистор и катушка индуктивности соединены параллельно. Резистор имеет
сопротивление 24 Ом, а индуктивное сопротивление катушки индуктивности
20 Ом.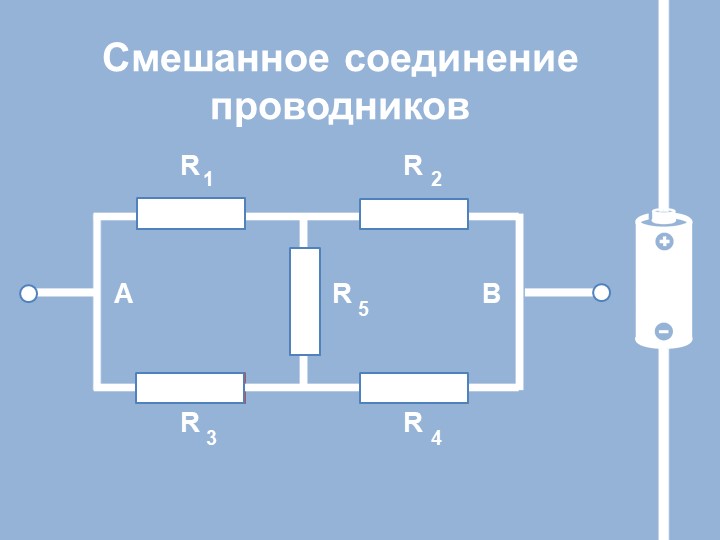 Каково сопротивление этой цепи?
Каково сопротивление этой цепи?
8. Параллельная цепь R-L, показанная на фиг. 1 имеет кажущуюся мощность
325 ВА. Коэффициент мощности схемы составляет 66%. В чем истинная сила этого
схема?
9. Параллельная цепь R-L, показанная на РИС.1 имеет кажущуюся мощность
465 ВА и реальной мощностью 320 Вт. Что такое реактивная мощность?
10. На сколько градусов не совпадают по фазе суммарный ток и напряжение в
вопрос 9?
ПРАКТИЧЕСКИЕ ЗАДАЧИ
См. схему, показанную на РИС. 1.
Используйте формулы переменного тока в резистивно-индуктивной параллели.
Раздел «Схемы» приложения.
1. Предположим, что схема, показанная на РИС.1 подключен к 60-Гц
линия и имеет общий ток 34,553 А. Катушка индуктивности имеет индуктивность
0,02122 Гн, а резистор имеет сопротивление 14 Ом.
ET ER EL IT 34.553 IR IL Z R14 XL VA P VARSL PF θ u L 0,02122
2.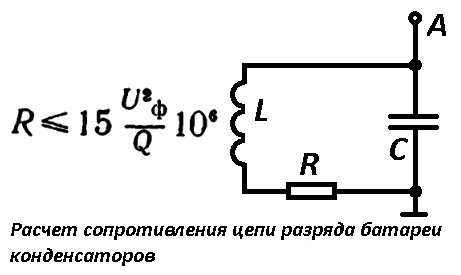 Предположим, что ток, протекающий через резистор IR, равен 15 А; в
Предположим, что ток, протекающий через резистор IR, равен 15 А; в
ток через индуктор IL равен 36 А; и схема имеет
полная мощность 10 803 ВА. Частота переменного напряжения 60 Гц.
ET ER EL IT IR 15 IL 36 Z R XL VA 10,803 P VARSL PF θ u L
3.Предположим, что схема на фиг. 1 имеет кажущуюся мощность 144
ВА и реальная мощность 115,2 Вт. Катушка индуктивности имеет индуктивность 0,15915.
Н, а частота 60 Гц.
ET ER EL IT IR IL Z R XL VA 144 P 115.2 VARSL PF θ u L 0,15915
4. Предположим, что схема на РИС. 1 имеет коэффициент мощности 78%,
полная мощность 374,817 ВА, частота 400 Гц. Индуктор имеет
индуктивность 0,0382 Гн
ET ER EL IT IR IL Z R XL VA 374.817 P VARSL PF 78% θ u L 0,0382
РЕАЛЬНЫЕ ПРИМЕНЕНИЯ
1. Лампы накаливания мощностью 500 Вт подключены параллельно с индуктивным
нагрузка. Токоизмерительные клещи показывают общий ток цепи 7 А.
Чему равна индуктивность нагрузки, подключенной параллельно с лампой накаливания?
огни? Предположим, напряжение 120 В при 60 Гц.
2. Вы работаете над бытовым тепловым насосом. Тепловой насос подключен
к сети 240 В, 60 Гц.Компрессор потребляет ток 34 А, когда
операционная. Компрессор имеет коэффициент мощности 70%. Запасная полоса
тепловая мощность 10кВт. Вам нужно знать сумму общего текущего потребления
это произойдет, если обогрев полосы будет включаться во время работы компрессора.
4.3: Последовательно-параллельный импеданс — Engineering LibreTexts
Правила объединения резисторов, конденсаторов и катушек индуктивности в последовательно-параллельных цепях переменного тока аналогичны правилам, установленным для объединения резисторов в цепях постоянного тока.Очевидно, первым пунктом является определение реактивных сопротивлений конденсаторов и катушек индуктивности. В этот момент можно идентифицировать простые серии и параллельные комбинации. Каждая из этих комбинаций сводится к комплексному импедансу. Как только это будет завершено, сеть снова исследуется, чтобы увидеть, могут ли эти новые комплексные импедансы быть идентифицированы как части новых последовательных или параллельных подсхем и упрощены. Этот процесс повторяется до тех пор, пока не останется один комплексный импеданс. Опять же, полезно помнить, что фазовые углы реактивных компонентов могут иногда приводить к неожиданным результатам, например, когда последовательная подсхема имеет величину импеданса меньше, чем ее наибольший компонент — то, что никогда не произойдет с сетью, состоящей только из резисторы.Важность использования векторных вычислений невозможно переоценить.
Каждая из этих комбинаций сводится к комплексному импедансу. Как только это будет завершено, сеть снова исследуется, чтобы увидеть, могут ли эти новые комплексные импедансы быть идентифицированы как части новых последовательных или параллельных подсхем и упрощены. Этот процесс повторяется до тех пор, пока не останется один комплексный импеданс. Опять же, полезно помнить, что фазовые углы реактивных компонентов могут иногда приводить к неожиданным результатам, например, когда последовательная подсхема имеет величину импеданса меньше, чем ее наибольший компонент — то, что никогда не произойдет с сетью, состоящей только из резисторы.Важность использования векторных вычислений невозможно переоценить.
Начнем с относительно простой последовательно-параллельной сети RLC, где значения реактивного сопротивления уже найдены.
Пример \(\PageIndex{1}\)
Определите эквивалентное сопротивление сети, показанной на рисунке \(\PageIndex{1}\).
Рисунок \(\PageIndex{1}\): Пример сети \(\PageIndex{1}\).
Глядя с левой стороны, мы видим, что катушка индуктивности и резистор 33 кОм\(\Омега\) параллельны, так как они оба связаны с одними и теми же двумя узлами.{\circ} \Omega \nonumber\]
Очевидно, что здесь доминирует индуктор. Параллельный резистор примерно на два порядка больше индуктивного сопротивления и оказывает минимальное влияние на параллельную комбинацию. Кроме того, комплексный импеданс, полученный из комбинации конденсатор/резистор, также значительно больше, и, учитывая, что он имеет отрицательный (емкостной) фазовый угол, он частично компенсирует индуктивное реактивное сопротивление. Это оставляет нам величину немного большую, чем у одного лишь индуктивного реактивного сопротивления, и фазовый угол, сдвинутый в резистивную сторону.
Последовательные и параллельные комбинации могут быть намного сложнее, чем в предыдущей сети. Лестничные сети, например, имеют набор секций, которые загружают другие секции, что приводит к повторяющимся последовательностям, а затем к параллельным упрощениям.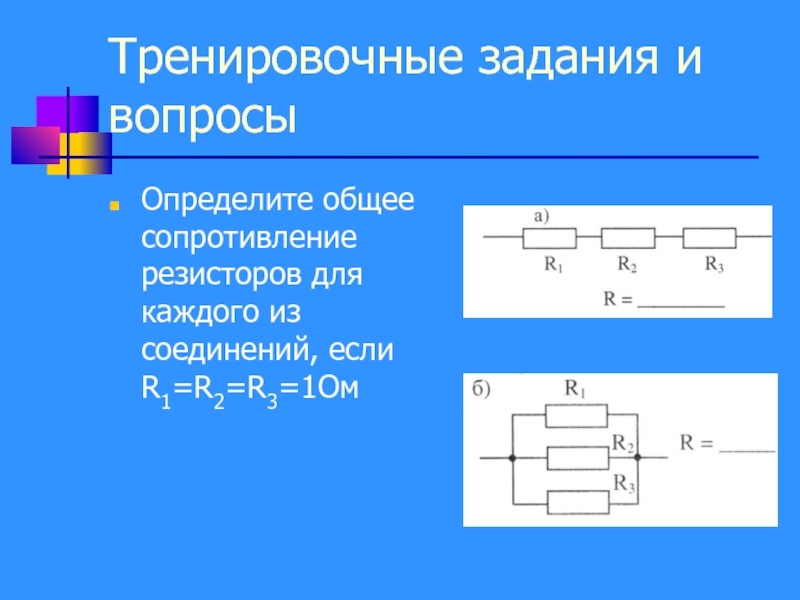 В этой ситуации лучше всего начинать работу с самого дальнего от интересующих узлов конца. Следующий пример проиллюстрирует это в скромном масштабе.
В этой ситуации лучше всего начинать работу с самого дальнего от интересующих узлов конца. Следующий пример проиллюстрирует это в скромном масштабе.
Пример \(\PageIndex{2}\)
Определите эквивалентное сопротивление сети, показанной на рисунке \(\PageIndex{2}\).
Рисунок \(\PageIndex{2}\): Пример сети \(\PageIndex{2}\).
Заглянув с правой стороны, сразу видим резистор 750\(\Омега\). Это последовательно с подсхемой, состоящей из оставшихся пяти компонентов. Эту подсхему можно рассматривать как конденсатор \(-j800 \Omega \) параллельно другой подсхеме, содержащей остальные четыре компонента. Эта четырехкомпонентная подсхема состоит из катушки индуктивности, соединенной последовательно с еще одной подсхемой, состоящей из двух последних резисторов и конденсатора.Эта подсхема из трех элементов состоит из резистора 2,2 кОм \(\Омега\), соединенного параллельно с последовательной комбинацией резистора 1 кОм (\Омега\) и конденсатора \(-j400 \Омега\).
Самый разумный способ приблизиться к этому — начать с левого конца с простой комбинации последовательностей RC, а затем двигаться вправо, к интересующим узлам. Мы будем нумеровать компоненты слева направо для идентификации.
Мы будем нумеровать компоненты слева направо для идентификации.
\[Z_{left2} = R_1+(− jX_{C1}) \номер\]
\[Z_{left2} = 1k \Omega — j 400 \Omega \nonnumber\]
\[Z_{left2} = 1077\угол −21.{\circ} \Omega \nonumber\]
В прямоугольной форме это 1443 \(-j422,3 \Омега\), что означает, что эта цепь эквивалентна резистору 1443 \(\Омега\) с емкостным сопротивлением \(-j422,3 \Омега\). ).
Методы последовательно-параллельного упрощения не работают для всех цепей. Для некоторых сетей, таких как конфигурации «треугольник» или «мост», требуются другие методы, которые будут рассмотрены в последующих главах.
РЕАКТИВНАЯ МОЩНОСТЬ – Прикладное промышленное электричество
Рисунок 6.1 Чистая резистивная цепь переменного тока: напряжение и ток резистора совпадают по фазе.
Если бы мы построили график тока и напряжения для очень простой цепи переменного тока, состоящей из источника и резистора (рисунок выше), это выглядело бы примерно так: (рисунок ниже)
Рисунок 6.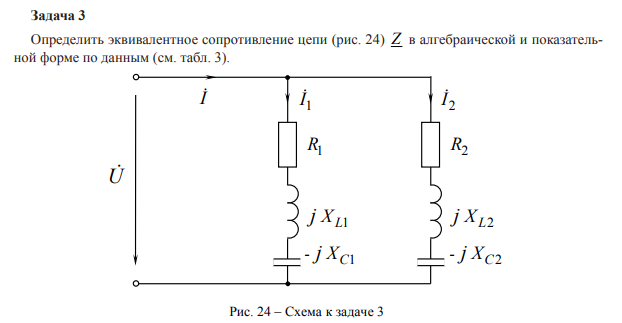 2 Напряжение и ток «в фазе» для резистивной цепи.
2 Напряжение и ток «в фазе» для резистивной цепи.
Поскольку резистор просто и напрямую сопротивляется протеканию тока во все периоды времени, форма сигнала падения напряжения на резисторе точно совпадает по фазе с формой сигнала тока через него.Мы можем посмотреть на любой момент времени вдоль горизонтальной оси графика и сравнить эти значения тока и напряжения друг с другом (любой «моментальный снимок» значений волны называется мгновенными значениями , что означает значения в этот момент во времени). Когда мгновенное значение тока равно нулю, мгновенное напряжение на резисторе также равно нулю. Точно так же в момент времени, когда ток через резистор достигает своего положительного пика, напряжение на резисторе также достигает своего положительного пика и так далее.В любой заданный момент времени на волнах закон Ома верен для мгновенных значений напряжения и тока.
Мы также можем рассчитать мощность, рассеиваемую этим резистором, и нанести эти значения на тот же график: (рисунок ниже)
Рисунок 6.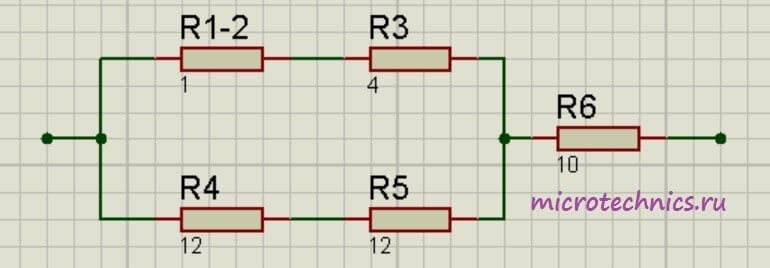 3. Мгновенная мощность переменного тока в чисто резистивной цепи всегда положительна.
3. Мгновенная мощность переменного тока в чисто резистивной цепи всегда положительна.
Резисторы и катушки индуктивности
Катушки индуктивности ведут себя не так, как резисторы. В то время как резисторы просто препятствуют протеканию через них тока (снижая напряжение, прямо пропорциональное току), катушки индуктивности препятствуют изменениям тока через них, понижая напряжение, прямо пропорциональное скорости изменения тока.В соответствии с Законом Ленца , это индуцированное напряжение всегда имеет такую полярность, чтобы пытаться поддерживать ток на его текущем значении. То есть, если ток увеличивается по величине, индуцированное напряжение будет «толкать» поток тока; если ток уменьшается, полярность изменится и «толкает» ток, чтобы противостоять уменьшению. Это противодействие текущим изменениям называется реактивным сопротивлением , а не сопротивлением. Выражаясь математически, отношение между падением напряжения на катушке индуктивности и скоростью изменения тока через катушку индуктивности выглядит следующим образом:
[латекс]e = L\frac{d_i}{d_t}[/латекс]
Переменный ток в простой индуктивной цепи
Выражение di/dt выводится из исчисления и означает скорость изменения мгновенного тока (i) во времени в амперах в секунду.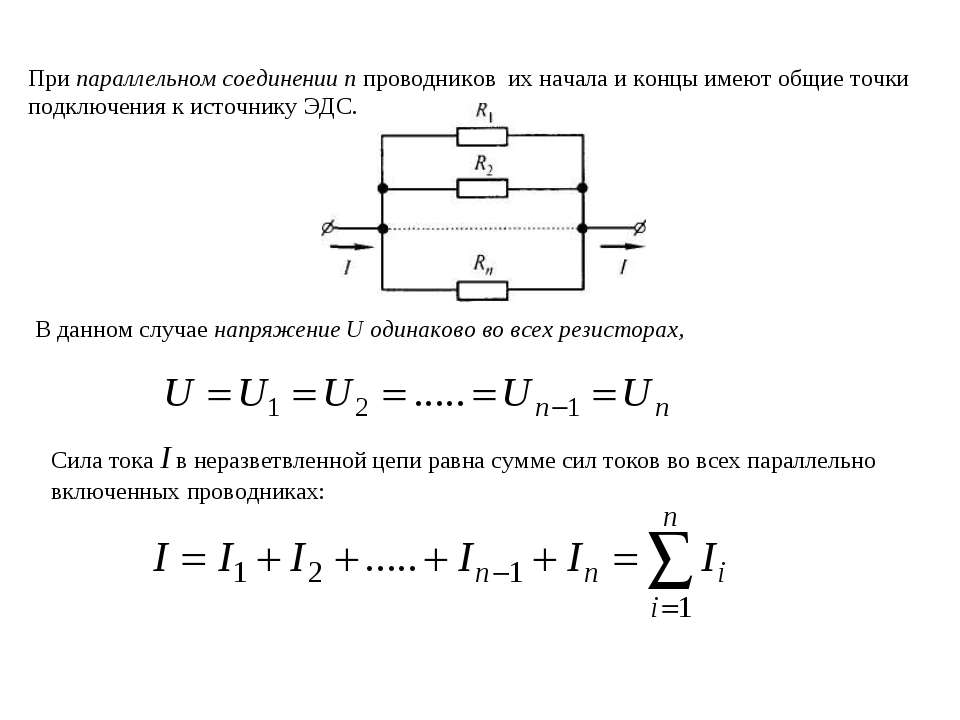 Индуктивность (L) в Генри, а мгновенное напряжение (e), разумеется, в вольтах. Иногда скорость мгновенного напряжения выражается как «v» вместо «e» (v = L di/dt), но это означает то же самое. Чтобы показать, что происходит с переменным током, давайте проанализируем простую цепь индуктивности:
Индуктивность (L) в Генри, а мгновенное напряжение (e), разумеется, в вольтах. Иногда скорость мгновенного напряжения выражается как «v» вместо «e» (v = L di/dt), но это означает то же самое. Чтобы показать, что происходит с переменным током, давайте проанализируем простую цепь индуктивности:
Рис. 6.4 Чистая индуктивная цепь: ток дросселя отстает от напряжения дросселя на 90°.
Если бы мы построили график тока и напряжения для этой очень простой схемы, это выглядело бы примерно так:
Рисунок 6.5 Чистая индуктивная цепь, формы сигналов.
Помните, что падение напряжения на катушке индуктивности является реакцией на изменение тока через нее. Следовательно, мгновенное напряжение равно нулю всякий раз, когда мгновенный ток имеет пиковое значение (нулевое изменение или наклон уровня на синусоиде тока), а мгновенное напряжение имеет пиковое значение всякий раз, когда мгновенный ток имеет максимальное изменение (точки самый крутой наклон на текущей волне, где она пересекает нулевую линию).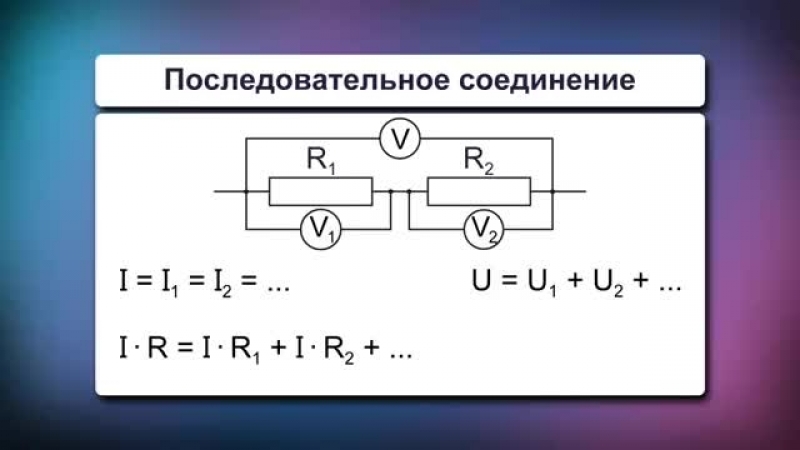 Это приводит к волне напряжения, которая на 90° не совпадает по фазе с волной тока. Глядя на график, кажется, что волна напряжения опережает волну тока; напряжение «опережает» ток, а ток «отстает» от напряжения.
Это приводит к волне напряжения, которая на 90° не совпадает по фазе с волной тока. Глядя на график, кажется, что волна напряжения опережает волну тока; напряжение «опережает» ток, а ток «отстает» от напряжения.
Ток отстает от напряжения на 90° в чисто индуктивной цепи.
Все становится еще интереснее, когда мы наносим мощность на эту схему:
Рисунок 6.6. В чисто индуктивной цепи мгновенная мощность может быть положительной или отрицательной.
Поскольку мгновенная мощность является произведением мгновенного напряжения и мгновенного тока (p=ie), мощность равна нулю всякий раз, когда мгновенный ток или напряжение равен нулю. Всякий раз, когда мгновенный ток и напряжение положительны (над линией), мощность положительна. Как и в примере с резистором, мощность также положительна, когда мгновенный ток и напряжение отрицательны (ниже линии). Однако, поскольку волны тока и напряжения сдвинуты по фазе на 90°, бывают моменты, когда одна положительна, а другая отрицательна, что приводит к одинаково частым случаям отрицательной мгновенной мощности .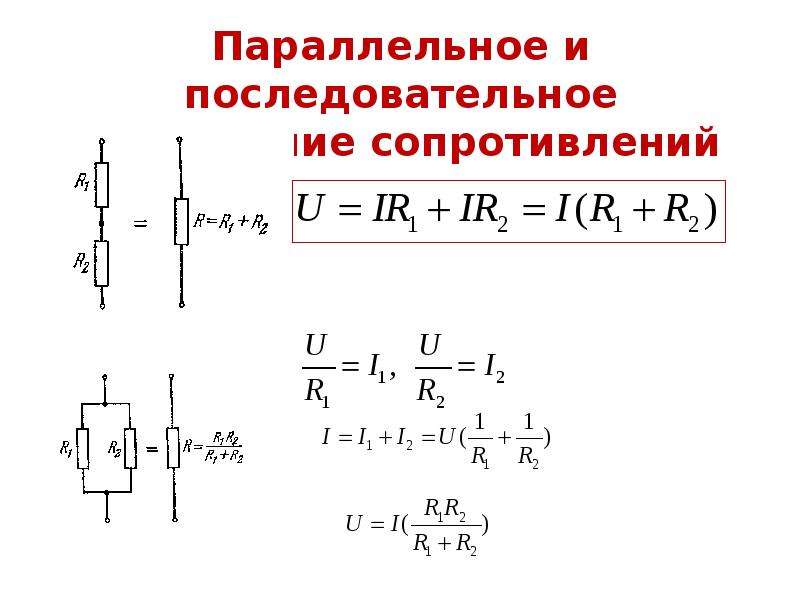
Что такое отрицательная сила?
Но что означает отрицательная мощность? Это означает, что катушка индуктивности отдает мощность обратно в цепь, а положительная мощность означает, что она поглощает мощность из цепи. Поскольку положительные и отрицательные циклы мощности равны по величине и продолжительности во времени, индуктор возвращает в цепь столько же энергии, сколько он поглощает в течение полного цикла. В практическом смысле это означает, что реактивное сопротивление индуктора рассеивает чистую энергию, равную нулю, в отличие от сопротивления резистора, который рассеивает энергию в виде тепла.Имейте в виду, это только для идеальных катушек индуктивности, которые не имеют сопротивления провода.
Реактивное сопротивление против сопротивления
Противодействие катушки индуктивности изменению тока переводится в противодействие переменному току в целом, который по определению всегда изменяется по мгновенной величине и направлению. Это противодействие переменному току похоже на сопротивление, но отличается тем, что оно всегда приводит к фазовому сдвигу между током и напряжением и рассеивает нулевую мощность.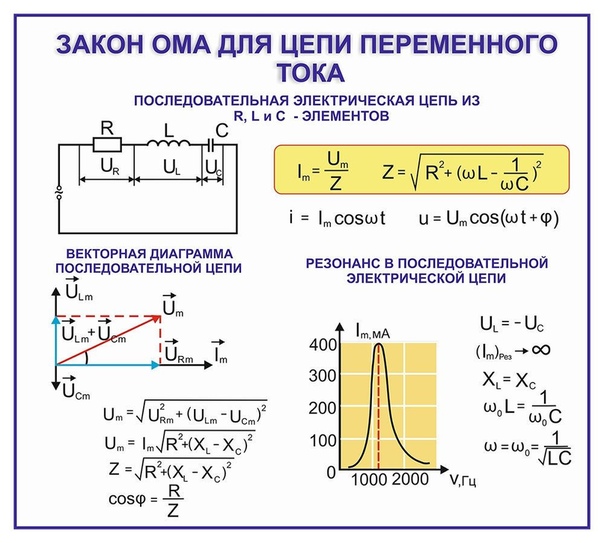 Из-за различий у него другое название: реактивное сопротивление .Реактивное сопротивление переменному току выражается в омах так же, как и сопротивление, за исключением того, что его математический символ — X вместо R. Чтобы быть точным, реактивное сопротивление, связанное с катушкой индуктивности, обычно обозначается заглавной буквой X с буквой L в качестве нижнего индекса, например это: X L .
Из-за различий у него другое название: реактивное сопротивление .Реактивное сопротивление переменному току выражается в омах так же, как и сопротивление, за исключением того, что его математический символ — X вместо R. Чтобы быть точным, реактивное сопротивление, связанное с катушкой индуктивности, обычно обозначается заглавной буквой X с буквой L в качестве нижнего индекса, например это: X L .
Поскольку на катушках индуктивности падает напряжение пропорционально скорости изменения тока, они будут падать больше напряжения для более быстро меняющихся токов и меньше напряжения для более медленных токов. Это означает, что реактивное сопротивление в омах для любой катушки индуктивности прямо пропорционально частоте переменного тока.Точная формула определения реактивного сопротивления выглядит следующим образом:
[латекс]X_L =2πfL[/латекс]
Если мы подвергнем индуктор 10 мГн воздействию частот 60, 120 и 2500 Гц, его реактивное сопротивление будет показано в таблице ниже.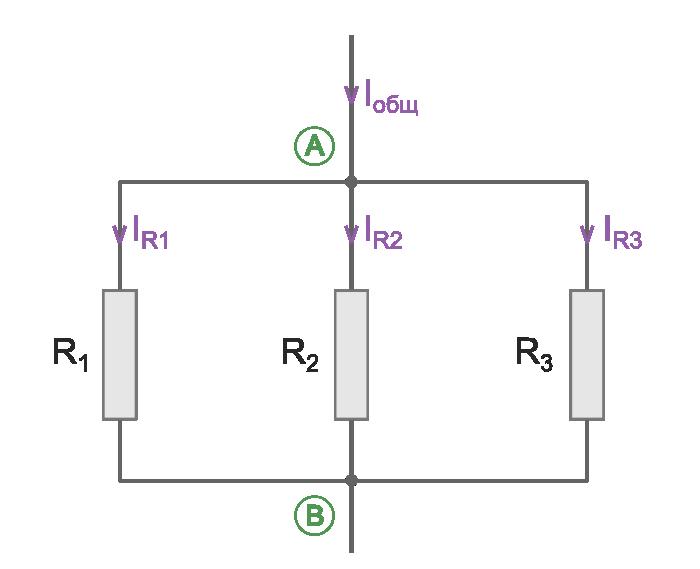
Реактивное сопротивление катушки индуктивности 10 мГн:
| Частота (Герц) | Реактивное сопротивление (Ом) |
| 60 | 3.7699 |
| 120 | 7,5398 |
| 2500 | 157.0796 |
В уравнении реактивного сопротивления термин «2πf» (все в правой части, кроме L) имеет особое значение сам по себе. Это число радиан в секунду, с которым «вращается» переменный ток, если вы представляете, что один цикл переменного тока представляет собой вращение по полной окружности. 90 743 радиан 90 744 – это единица измерения угла: в одном полном круге содержится 2π радиан, так же как в полном круге 360°.Если генератор переменного тока является двухполюсным устройством, он будет производить один цикл на каждый полный оборот вращения вала, что составляет каждые 2π радиан или 360 °.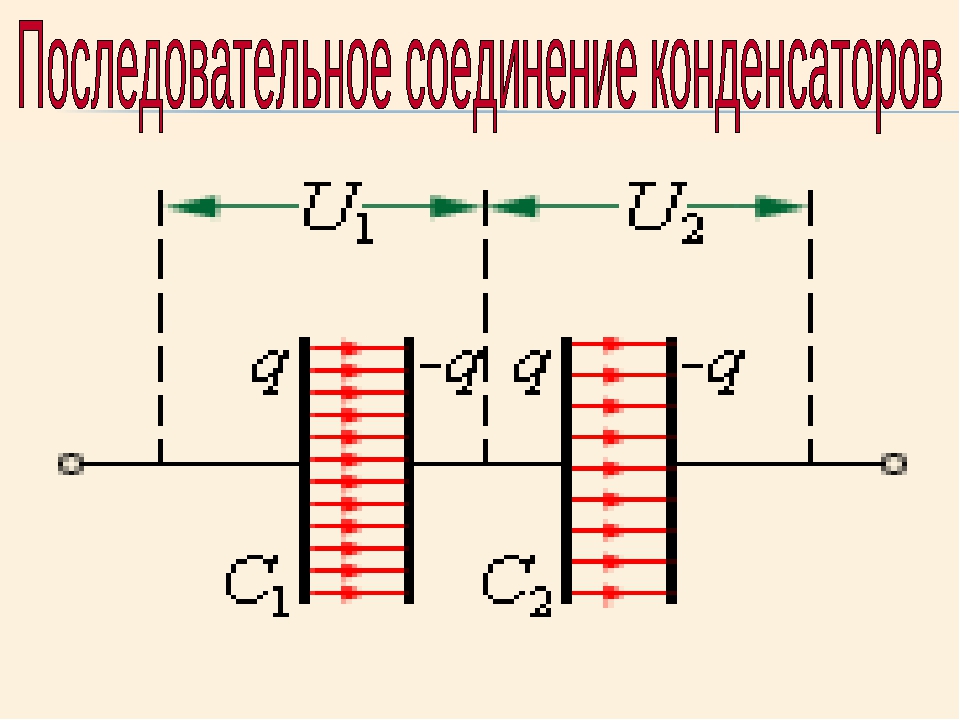 Если эту константу 2π умножить на частоту в герцах (количество циклов в секунду), результатом будет число в радианах в секунду, известное как угловая скорость системы переменного тока.
Если эту константу 2π умножить на частоту в герцах (количество циклов в секунду), результатом будет число в радианах в секунду, известное как угловая скорость системы переменного тока.
Угловая скорость в системах переменного тока
Угловая скорость может быть представлена выражением 2πf, или она может быть представлена своим собственным символом, строчной греческой буквой омега, которая похожа на нашу строчную римскую букву «w»: ω.Таким образом, формулу реактивного сопротивления X L = 2πfL также можно записать как X L = ωL.
Следует понимать, что эта «угловая скорость» является выражением того, насколько быстро меняются формы сигналов переменного тока, причем полный цикл равен 2π радианам. Это не обязательно отражает фактическую скорость вращения вала генератора переменного тока. Если генератор переменного тока имеет более двух полюсов, угловая скорость будет кратна скорости вращения вала. По этой причине ω иногда выражается в единицах электрических радиан в секунду, а не в (простых) радианах в секунду, чтобы отличить его от механического движения.
Как бы мы ни выражали угловую скорость системы, очевидно, что она прямо пропорциональна реактивному сопротивлению в индукторе. По мере увеличения частоты (или скорости вала генератора переменного тока) в системе переменного тока индуктор будет оказывать большее сопротивление прохождению тока, и наоборот. Переменный ток в простой индуктивной цепи равен напряжению (в вольтах), деленному на индуктивное сопротивление (в омах), точно так же, как переменный или постоянный ток в простой резистивной цепи равен напряжению (в вольтах), деленному на индуктивное сопротивление (в омах). сопротивление (в омах).Пример схемы показан здесь:
Индуктивное сопротивление
(индуктивное сопротивление катушки индуктивности 10 мГн при 60 Гц)
[латекс]X_L =3,7600 Ом[/латекс]
[латекс]I_{X_{L}} = \frac{E}{X}[/латекс]
[латекс] = \frac{10V}{3,7600 Ом}[/latex]
[латекс]\mathbf{= 2.6526A}[/латекс]
Фазовые углы
Однако мы должны иметь в виду, что напряжение и ток здесь не совпадают по фазе. Как было показано ранее, напряжение имеет фазовый сдвиг +90° по отношению к току.Если мы представим эти фазовые углы напряжения и тока математически в виде комплексных чисел, мы обнаружим, что противодействие катушки индуктивности току также имеет фазовый угол:
Как было показано ранее, напряжение имеет фазовый сдвиг +90° по отношению к току.Если мы представим эти фазовые углы напряжения и тока математически в виде комплексных чисел, мы обнаружим, что противодействие катушки индуктивности току также имеет фазовый угол:
[латекс]\текст{Оппозиция}= \фракция{\текст{Напряжение}}{\текст{Ток}}[/латекс]
[латекс]\текст{Оппозиция}= \фракция{10 В \угол \текст{90°}}{2,6526А \угол \текст{90°}}[/латекс]
[латекс]\begin{align} \text{Opposition } = & 3.7699 \Omega \angle \text{90°} \\ \text { or } & 0 + j3.7699 \Омега\конец{выравнивание}[/латекс]
Математически мы говорим, что фазовый угол сопротивления индуктора току равен 90°, а это означает, что сопротивление индуктора току является положительной мнимой величиной. Этот фазовый угол реактивного противодействия току становится критически важным при анализе цепей, особенно для сложных цепей переменного тока, где взаимодействуют реактивное сопротивление и сопротивление.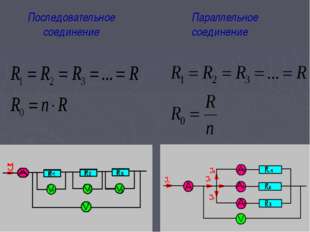 Будет полезно представить сопротивление любого компонента току в терминах комплексных чисел, а не скалярных величин сопротивления и реактивного сопротивления.
Будет полезно представить сопротивление любого компонента току в терминах комплексных чисел, а не скалярных величин сопротивления и реактивного сопротивления.
- Индуктивное реактивное сопротивление это противодействие, которое индуктор оказывает переменному току из-за сдвинутого по фазе накопления и высвобождения энергии в его магнитном поле. Реактивное сопротивление обозначается заглавной буквой «X» и измеряется в омах так же, как сопротивление (R).
- Индуктивное сопротивление можно рассчитать по следующей формуле: X L = 2πfL
- угловая скорость цепи переменного тока — это еще один способ выражения ее частоты в электрических радианах в секунду вместо циклов в секунду.Он обозначается строчной греческой буквой «омега» или ω.
- Индуктивное реактивное сопротивление увеличивается с увеличением частоты. Другими словами, чем выше частота, тем больше она противодействует потоку электронов переменного тока.

Возьмите эту схему в качестве примера для работы:
Цепь катушки индуктивности последовательного резистора: Ток отстает от приложенного напряжения на 0–90°.
Резистор будет обеспечивать сопротивление переменному току 5 Ом независимо от частоты, а индуктор — 3 Ом.7699 Ом реактивного сопротивления на переменный ток частотой 60 Гц.
Поскольку сопротивление резистора является действительным числом (5 Ом ∠ 0°, или 5 + j0 Ом), а реактивное сопротивление катушки индуктивности — мнимым числом (3,7699 Ом ∠ 90°, или 0 + j3,7699 Ом), комбинированный эффект из двух составляющих будет оппозиция тока, равная комплексной сумме двух чисел.
Это комбинированное противостояние будет векторной комбинацией сопротивления и противодействия. Чтобы кратко выразить эту оппозицию, нам нужен более широкий термин для оппозиции току, чем только сопротивление или реактивность.
Этот термин называется импедансом , его символом является Z, и он также выражается в омах, как сопротивление и реактивное сопротивление.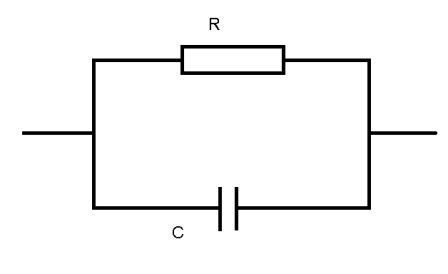 В приведенном выше примере полное сопротивление цепи составляет:
В приведенном выше примере полное сопротивление цепи составляет:
Сопротивление по закону Ома
Полное сопротивление связано с напряжением и током, как и следовало ожидать, аналогично сопротивлению в законе Ома:
На самом деле, это гораздо более полная форма Закона Ома , чем то, чему учили в электронике постоянного тока (E = IR), точно так же, как импеданс является гораздо более полным выражением сопротивления потоку тока, чем сопротивление. Любое сопротивление и любое реактивное сопротивление, по отдельности или в комбинации (последовательно/параллельно), могут и должны быть представлены как один импеданс в цепи переменного тока.
Чтобы рассчитать ток в приведенной выше цепи, нам сначала нужно задать опорный фазовый угол для источника напряжения, который обычно считается равным нулю. (Фазовые углы резистивного и индуктивного импеданса равны , всегда 0° и +90° соответственно, независимо от заданных фазовых углов для напряжения или тока).
Как и в чисто индуктивной цепи, волна тока отстает от волны напряжения (источника), хотя на этот раз отставание не столь велико: всего 37,016°, а не целых 90°, как это было в случае чисто индуктивной цепи. схема.
Ток отстает от напряжения в последовательной цепи L-R.
Для резистора и индуктора фазовые соотношения между напряжением и током не изменились.Напряжение на резисторе совпадает по фазе (сдвиг 0°) с протекающим через него током, а напряжение на катушке индуктивности сдвинуто по фазе на +90° с током, проходящим через него. Мы можем проверить это математически:
Напряжение на резисторе имеет тот же фазовый угол, что и ток через него, что говорит нам о том, что E и I совпадают по фазе (только для резистора).
Напряжение на катушке индуктивности имеет фазовый угол 52.984 °, в то время как ток через индуктор имеет фазовый угол -37,016 °, разница между ними составляет ровно 90 °.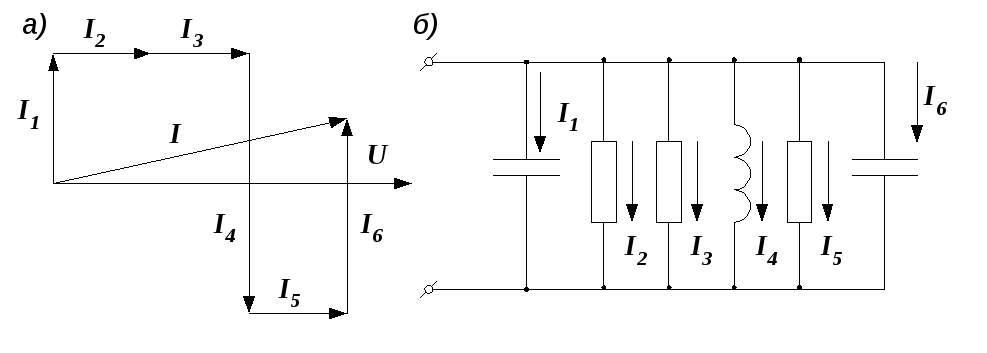 Это говорит нам о том, что E и I все еще сдвинуты по фазе на 90° (только для катушки индуктивности).
Это говорит нам о том, что E и I все еще сдвинуты по фазе на 90° (только для катушки индуктивности).
Используйте закон напряжения Кирхгофа
Мы также можем математически доказать, что эти комплексные значения складываются, чтобы получить общее напряжение, как и предсказывает закон Кирхгофа о напряжении:
Давайте возьмем одни и те же компоненты для нашей последовательной схемы и соединим их параллельно:
Рисунок 6.7 Параллельная цепь R-L.
Поскольку источник питания имеет ту же частоту, что и схема последовательного примера, а резистор и катушка индуктивности имеют одинаковые значения сопротивления и индуктивности соответственно, они также должны иметь одинаковые значения импеданса. Итак, мы можем начать нашу таблицу анализа с тех же «заданных» значений:
Таблица 6.2 Таблица анализа импеданса 1
Единственная разница в нашем методе анализа на этот раз заключается в том, что мы будем применять правила параллельных цепей вместо правил для последовательных цепей.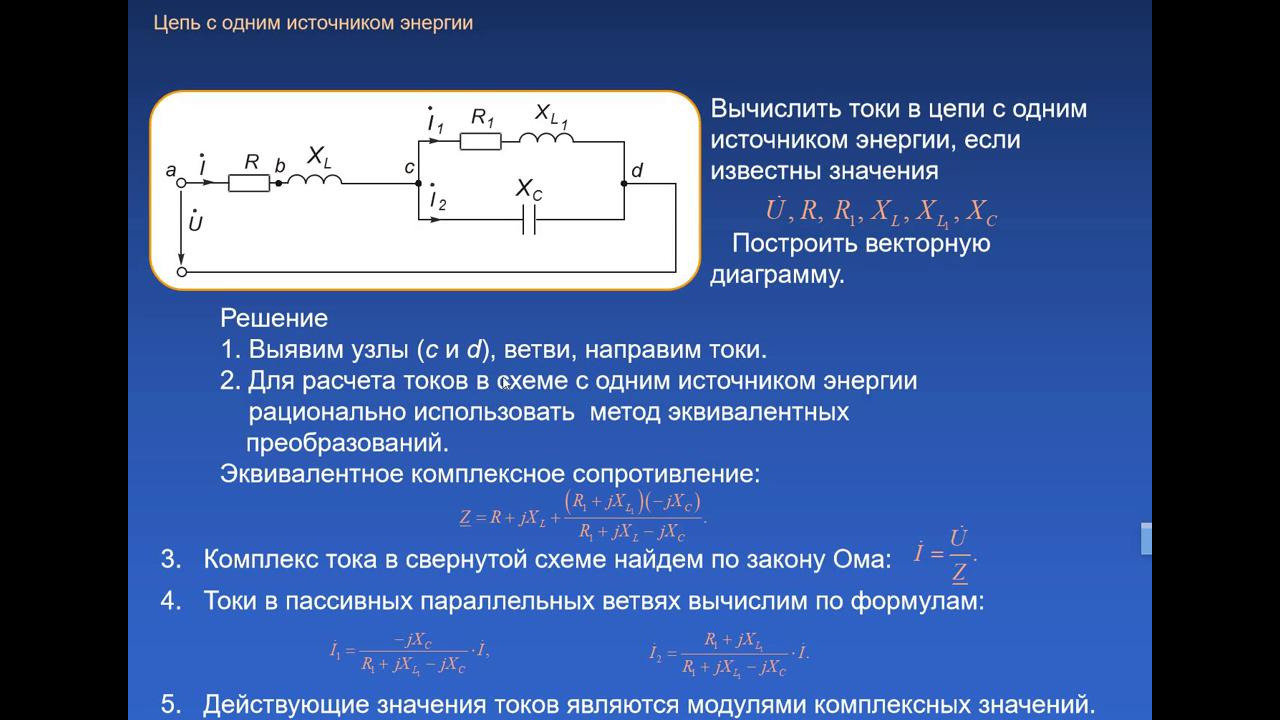 Подход в основном тот же, что и для DC. Мы знаем, что напряжение равномерно распределяется между всеми компонентами в параллельной цепи, поэтому мы можем перенести цифру полного напряжения (10 вольт ∠ 0°) во все столбцы компонентов:
Подход в основном тот же, что и для DC. Мы знаем, что напряжение равномерно распределяется между всеми компонентами в параллельной цепи, поэтому мы можем перенести цифру полного напряжения (10 вольт ∠ 0°) во все столбцы компонентов:
Таблица 6.3 Анализ импеданса, таблица 2
Теперь мы можем применить Закон Ома (I=E/Z) по вертикали к двум столбцам таблицы, вычислив ток через резистор и ток через индуктор:
Таблица 6.4 Анализ импеданса, таблица 3
Так же, как и в цепях постоянного тока, токи ветвей в параллельной цепи переменного тока суммируются, чтобы сформировать общий ток (закон тока Кирхгофа остается справедливым для переменного тока, как и для постоянного):
Таблица 6.5 Таблица анализа импеданса 4
Наконец, общий импеданс можно рассчитать с помощью закона Ома (Z=E/I) по вертикали в столбце «Общее». Между прочим, параллельное сопротивление также можно рассчитать, используя формулу обратной связи, идентичную той, которая используется при расчете параллельных сопротивлений.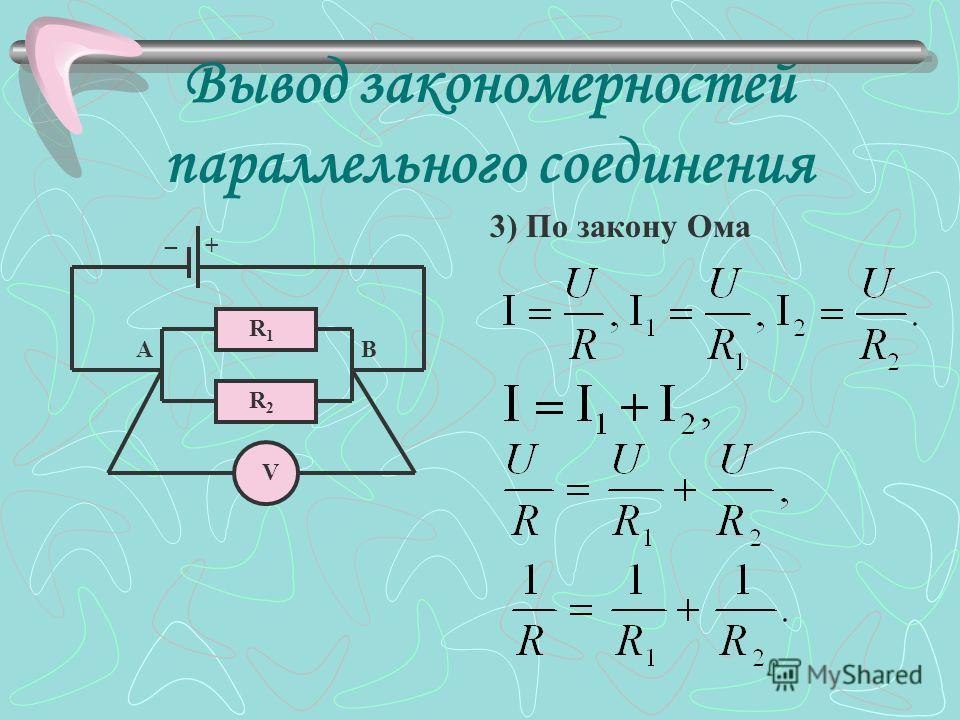
[латекс]\tag{6.1} Z_{parallel}=\frac{1}{\frac{1}{Z_1}+ \frac{1}{Z_2}+ \dots \frac{1}{Z_n}}[ /латекс]
Единственная проблема с использованием этой формулы заключается в том, что для ее выполнения обычно требуется много нажатий клавиш калькулятора.И если вы решили пробежаться по такой формуле «от руки», будьте готовы к очень большому объему работы! Но, как и в случае с цепями постоянного тока, у нас часто есть несколько вариантов расчета величин в наших аналитических таблицах, и этот пример ничем не отличается. Независимо от того, как вы вычисляете полное сопротивление (закон Ома или формула обратной связи), вы получите одно и то же число:
Таблица 6.6 Таблица анализа импеданса 5
- Импедансы (Z) управляются так же, как и сопротивления (R) при анализе параллельных цепей: параллельные импедансы уменьшаются для формирования общего импеданса по формуле обратной связи.Только обязательно выполняйте все вычисления в комплексной (не скалярной) форме!
[латекс]Z_{параллельный}=\frac{1}{(\frac{1}{Z1} + \frac{1}{Z2} + .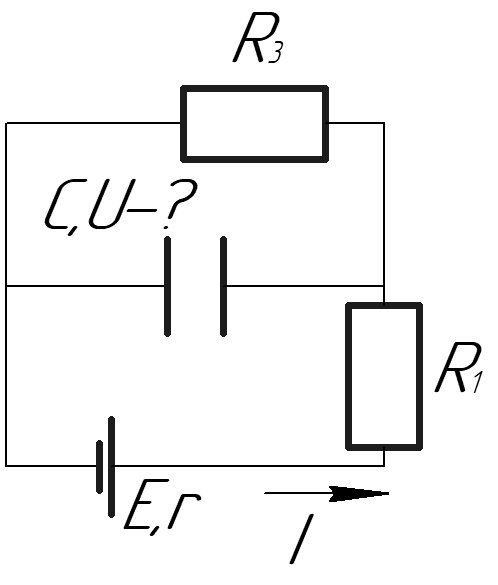 . . \frac{1}{Zn})}[/ латекс]
. . \frac{1}{Zn})}[/ латекс]
- Закон Ома для цепей переменного тока:
[латекс]E = {I}{Z}[/латекс] ; [латекс]I = \frac{E}{Z}[/latex] ; [латекс]Z =\frac{E}{I}[/латекс]
- Когда резисторы и катушки индуктивности соединены вместе в параллельных цепях (так же, как и в последовательных цепях), общий импеданс будет иметь фазовый угол где-то между 0° и +90°.Ток цепи будет иметь фазовый угол где-то между 0° и -90°.
- Параллельные цепи переменного тока обладают теми же фундаментальными свойствами, что и параллельные цепи постоянного тока: напряжение одинаково по всей цепи, токи ветвей складываются, образуя общий ток, а полное сопротивление уменьшается (согласно формуле обратной связи), образуя полное сопротивление.
В идеальном случае индуктор действует как чисто реактивное устройство. То есть его противопоставление переменному току основано строго на индуктивной реакции на изменение тока, а не на трении электронов, как в случае с резистивными элементами. Однако индукторы не столь чисты в своем реактивном поведении. Начнем с того, что они сделаны из проволоки, а мы знаем, что любая проволока обладает некоторым измеримым сопротивлением (кроме сверхпроводящей проволоки). Это встроенное сопротивление действует так, как если бы оно было соединено последовательно с идеальной индуктивностью катушки, например:
Однако индукторы не столь чисты в своем реактивном поведении. Начнем с того, что они сделаны из проволоки, а мы знаем, что любая проволока обладает некоторым измеримым сопротивлением (кроме сверхпроводящей проволоки). Это встроенное сопротивление действует так, как если бы оно было соединено последовательно с идеальной индуктивностью катушки, например:
Рисунок 6.8 Катушка индуктивности Эквивалентная схема реальной катушки индуктивности.
Следовательно, импеданс любой реальной катушки индуктивности всегда будет представлять собой сложную комбинацию сопротивления и реактивного сопротивления индуктивности.
Эта проблема усугубляется так называемым скин-эффектом , который представляет собой тенденцию переменного тока течь через внешние области поперечного сечения проводника, а не через его середину. Когда электроны движутся в одном направлении (DC), они используют для движения всю площадь поперечного сечения проводника. С другой стороны, электроны, переключающие направление потока, стремятся избежать прохождения через самую середину проводника, ограничивая доступную эффективную площадь поперечного сечения.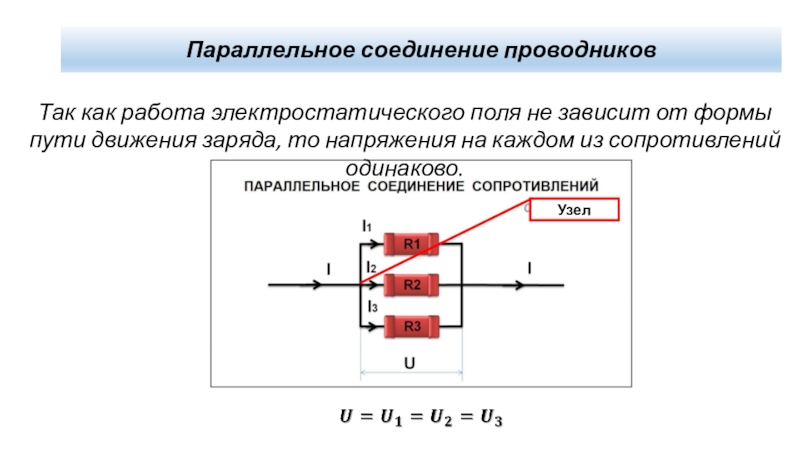 Скин-эффект становится более выраженным по мере увеличения частоты.
Скин-эффект становится более выраженным по мере увеличения частоты.
Кроме того, переменное магнитное поле индуктора, питаемого переменным током, может излучаться в космос как часть электромагнитной волны, особенно если переменный ток имеет высокую частоту. Эта излучаемая энергия не возвращается в индуктор, поэтому проявляется в виде сопротивления (рассеяния мощности) в цепи.
Вдобавок к резистивным потерям в проводе и излучению в катушках индуктивности с железным сердечником действуют и другие эффекты, которые проявляются в виде дополнительного сопротивления между выводами.Когда на катушку индуктивности подается переменный ток, создаваемые переменные магнитные поля имеют тенденцию индуцировать циркулирующие токи внутри железного сердечника, известные как вихревые токи . Эти электрические токи в железном сердечнике должны преодолевать электрическое сопротивление железа, которое не является таким хорошим проводником, как медь. Потери на вихревые токи в первую очередь противодействуют делению железного сердечника на множество тонких листов (слоев), каждый из которых отделен от другого тонким слоем электроизолирующего лака.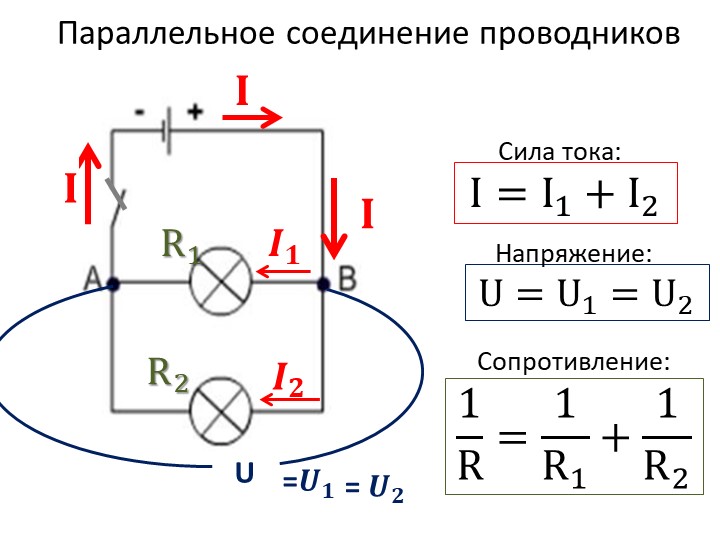 Поскольку поперечное сечение сердечника разделено на множество электрически изолированных участков, ток не может циркулировать в пределах этой площади поперечного сечения, и из-за этого эффекта не будет (или будет очень мало) резистивных потерь.
Поскольку поперечное сечение сердечника разделено на множество электрически изолированных участков, ток не может циркулировать в пределах этой площади поперечного сечения, и из-за этого эффекта не будет (или будет очень мало) резистивных потерь.
Как и следовало ожидать, потери на вихревые токи в металлических сердечниках катушек индуктивности проявляются в виде тепла. Эффект более выражен на более высоких частотах и может быть настолько экстремальным, что иногда используется в производственных процессах для нагревания металлических предметов! Фактически, этот процесс «индуктивного нагрева» часто используется в литейных операциях с высокой чистотой металлов, когда металлические элементы и сплавы необходимо нагревать в вакууме, чтобы избежать загрязнения воздухом, и, таким образом, стандартная технология нагрева путем сжигания бесполезна.Это «бесконтактная» технология, при которой нагретое вещество не должно касаться катушки (катушек), создающих магнитное поле.
В высокочастотном диапазоне вихревые токи могут возникать даже в поперечном сечении самого провода, способствуя дополнительным резистивным эффектам. Чтобы противодействовать этой тенденции, можно использовать специальную проволоку, изготовленную из очень тонких, индивидуально изолированных жил, называемую литцендратом (сокращение от Litzendraht ). Изоляция, отделяющая жилы друг от друга, предотвращает циркуляцию вихревых токов по всей площади поперечного сечения провода.
Чтобы противодействовать этой тенденции, можно использовать специальную проволоку, изготовленную из очень тонких, индивидуально изолированных жил, называемую литцендратом (сокращение от Litzendraht ). Изоляция, отделяющая жилы друг от друга, предотвращает циркуляцию вихревых токов по всей площади поперечного сечения провода.
Кроме того, любой магнитный гистерезис, который необходимо преодолевать при каждом изменении направления магнитного поля катушки индуктивности, представляет собой расход энергии, который проявляется как сопротивление в цепи. Некоторые материалы сердечника (например, феррит) особенно известны своим гистерезисным эффектом. Противодействие этому эффекту лучше всего достигается за счет правильного выбора материала сердечника и ограничения пиковой напряженности магнитного поля, создаваемого при каждом цикле.
В целом, паразитные резистивные свойства реального индуктора (сопротивление провода, радиационные потери, вихревые токи и гистерезисные потери) выражаются одним термином «эффективное сопротивление»:
Рис.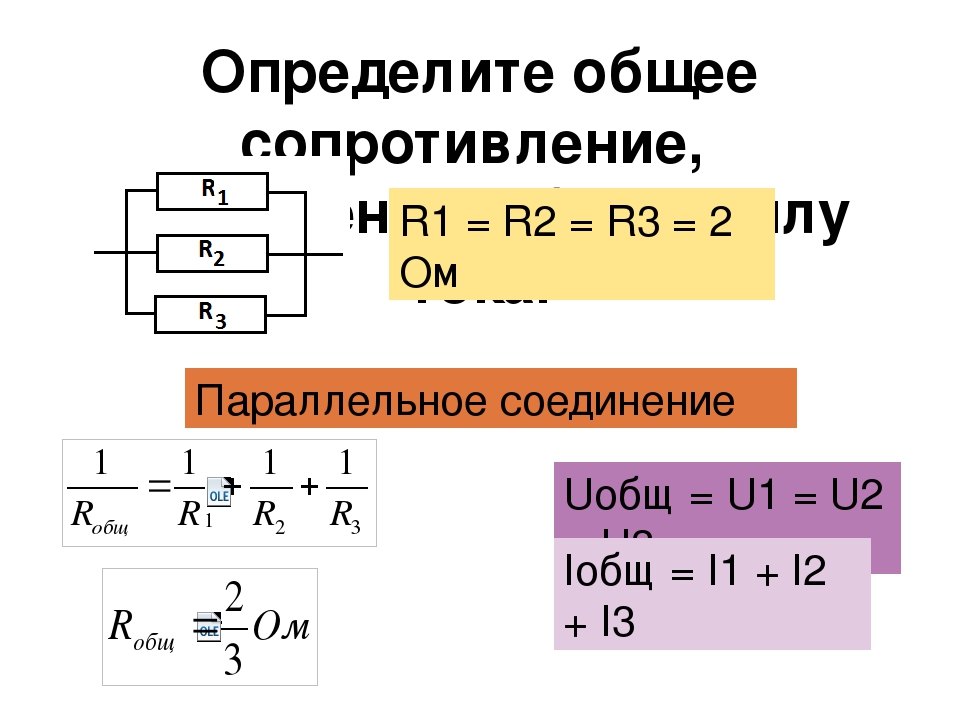 6.9 Эквивалентная схема реального индуктора со скин-эффектом, радиационными, вихретоковыми и гистерезисными потерями.
6.9 Эквивалентная схема реального индуктора со скин-эффектом, радиационными, вихретоковыми и гистерезисными потерями.
Следует отметить, что скин-эффект и радиационные потери применимы к прямым участкам провода в цепи переменного тока, как и к витому проводу. Обычно их совокупный эффект слишком мал, чтобы его можно было заметить, но на радиочастотах он может быть довольно большим. Антенна радиопередатчика, например, разработана специально для рассеивания наибольшего количества энергии в виде электромагнитного излучения.
Конденсаторы Против. Резисторы
Конденсаторы ведут себя не так, как резисторы. В то время как резисторы пропускают через себя поток электронов, прямо пропорциональный падению напряжения, конденсаторы противостоят изменениям напряжения, потребляя или подавая ток по мере того, как они заряжаются или разряжаются до нового уровня напряжения. Поток электронов «через» конденсатор прямо пропорционален скорости изменения напряжения на конденсаторе.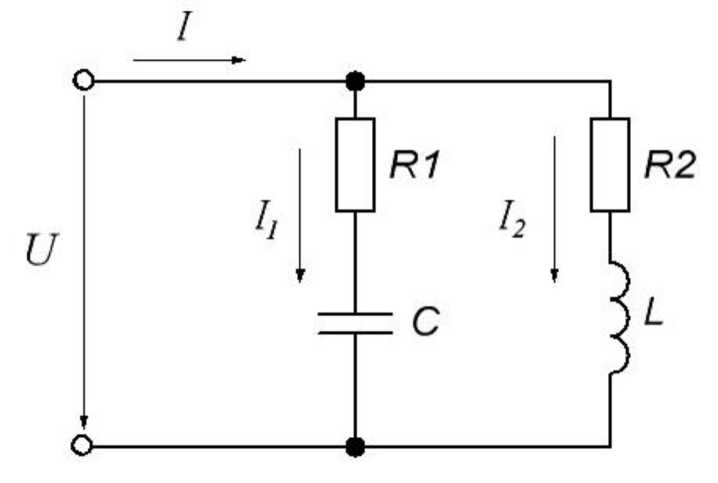 Это противодействие изменению напряжения является еще одной формой реактивного сопротивления , но прямо противоположной тому, что демонстрируют катушки индуктивности.
Это противодействие изменению напряжения является еще одной формой реактивного сопротивления , но прямо противоположной тому, что демонстрируют катушки индуктивности.
Характеристики цепи конденсатора
Математически выраженная зависимость между током, проходящим через конденсатор, и скоростью изменения напряжения на конденсаторе выглядит следующим образом:
[латекс]i=C\frac{d_e}{d_t}[/латекс]
Выражение de/dt выводится из исчисления и означает скорость изменения мгновенного напряжения (e) с течением времени в вольтах в секунду. Емкость (C) в фарадах, а мгновенный ток (i), разумеется, в амперах.Иногда скорость мгновенного изменения напряжения во времени выражается как dv/dt вместо de/dt: вместо этого используется строчная буква «v» или «e» для обозначения напряжения, но это означает то же самое. Чтобы показать, что происходит с переменным током, давайте проанализируем простую цепь конденсатора:
Рисунок 6.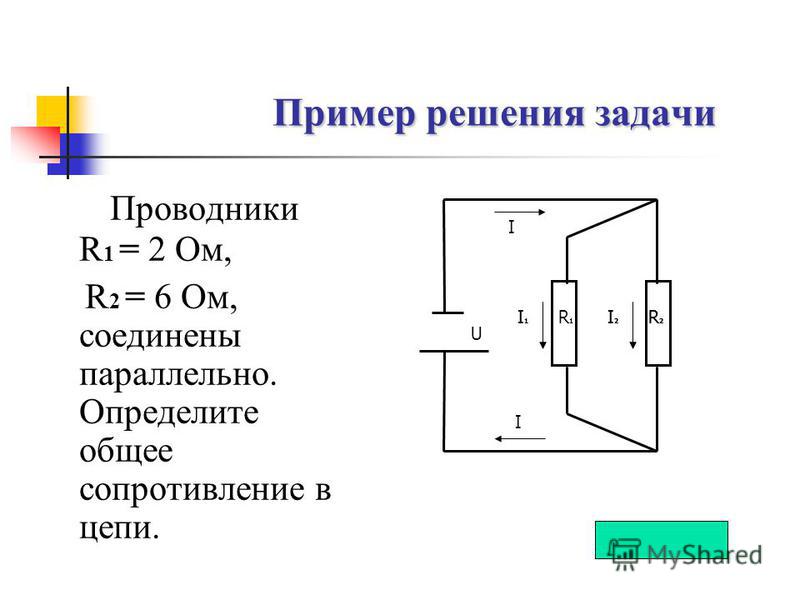 10 Чисто емкостная цепь: напряжение конденсатора отстает от тока конденсатора на 90°
10 Чисто емкостная цепь: напряжение конденсатора отстает от тока конденсатора на 90°
Если бы мы построили график тока и напряжения для этой очень простой схемы, это выглядело бы примерно так:
Рис. 6.11 Осциллограммы чисто емкостной цепи.
Помните, что ток через конденсатор является реакцией на изменение напряжения на нем. Следовательно, мгновенный ток равен нулю всякий раз, когда мгновенное напряжение имеет пиковое значение (нулевое изменение или наклон уровня на синусоиде напряжения), а мгновенный ток имеет пиковое значение всякий раз, когда мгновенное напряжение имеет максимальное изменение (точки самый крутой наклон волны напряжения, где она пересекает нулевую линию).Это приводит к тому, что волна напряжения не совпадает по фазе с волной тока на -90°. Глядя на график, кажется, что волна тока опережает волну напряжения; ток «опережает» напряжение, а напряжение «отстает» от тока.
Рисунок 6.12 Напряжение отстает от тока на 90° в чисто емкостной цепи.
Как вы могли догадаться, та же самая необычная волна мощности, которую мы видели в простой схеме с катушкой индуктивности, присутствует и в простой схеме с конденсатором:
Рис. 6.13 В чисто емкостной цепи мгновенная мощность может быть положительной или отрицательной.
Как и в случае с простой индукторной схемой, фазовый сдвиг на 90 градусов между напряжением и током приводит к волне мощности, которая в равной степени чередуется между положительной и отрицательной. Это означает, что конденсатор не рассеивает мощность, реагируя на изменения напряжения; он просто поглощает и высвобождает энергию попеременно.
Реактивное сопротивление конденсатора
Противодействие конденсатора изменению напряжения переводится в противодействие переменному напряжению в целом, которое по определению всегда изменяется по мгновенной величине и направлению.Для любой заданной величины переменного напряжения на заданной частоте конденсатор заданного размера будет «проводить» переменный ток определенной величины. Точно так же, как ток через резистор является функцией напряжения на резисторе и сопротивления резистора, переменный ток через конденсатор является функцией переменного напряжения на нем и реактивного сопротивления , создаваемого конденсатором. Как и в случае с катушками индуктивности, реактивное сопротивление конденсатора выражается в омах и обозначается буквой X (или X C , если быть более точным).
Точно так же, как ток через резистор является функцией напряжения на резисторе и сопротивления резистора, переменный ток через конденсатор является функцией переменного напряжения на нем и реактивного сопротивления , создаваемого конденсатором. Как и в случае с катушками индуктивности, реактивное сопротивление конденсатора выражается в омах и обозначается буквой X (или X C , если быть более точным).
Поскольку конденсаторы «проводят» ток пропорционально скорости изменения напряжения, они будут пропускать больший ток при более быстро меняющемся напряжении (поскольку они заряжаются и разряжаются до одинаковых пиков напряжения за меньшее время) и меньший ток при более медленно меняющемся напряжении. . Это означает, что реактивное сопротивление любого конденсатора в омах равно 90 743 обратно пропорционально 90 744 частоте переменного тока.
[латекс]X_C=\frac{1}{2πfC}[/латекс]
Реактивное сопротивление конденсатора 100 мкФ:
| Частота (Гц) | Реактивное сопротивление (Ом) |
| 60 | 26. 5258 5258 |
| 120 | 13,2629 |
| 2500 | 0,6366 |
Обратите внимание, что отношение емкостного сопротивления к частоте прямо противоположно отношению индуктивного сопротивления. Емкостное сопротивление (в омах) уменьшается с увеличением частоты переменного тока. И наоборот, индуктивное сопротивление (в омах) увеличивается с увеличением частоты переменного тока. Катушки индуктивности препятствуют более быстрому изменению тока, вызывая большее падение напряжения; конденсаторы противодействуют более быстрому изменению падения напряжения, пропуская большие токи.
Как и в случае с катушками индуктивности, член уравнения реактивного сопротивления 2πf может быть заменен строчной греческой буквой Омега (ω), которая обозначается как угловая скорость цепи переменного тока. Таким образом, уравнение X C = 1/(2πfC) также может быть записано как X C = 1/(ωC), где ω выражено в единицах радиан в секунду .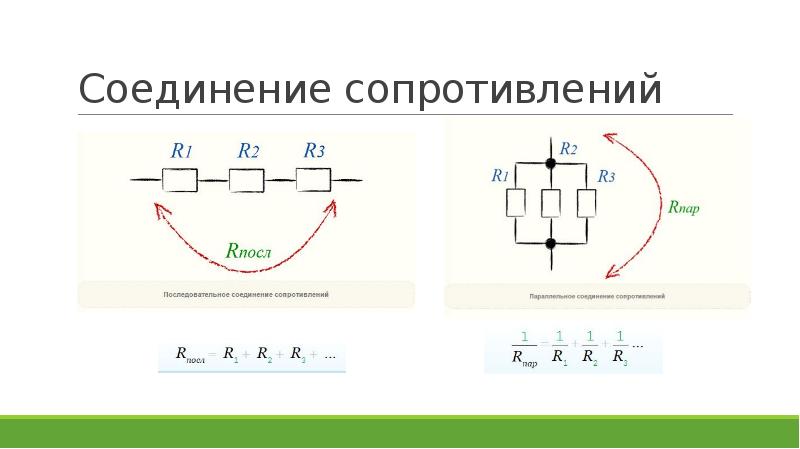
Переменный ток в простой емкостной цепи равен напряжению (в вольтах), деленному на емкостное сопротивление (в омах), точно так же, как переменный или постоянный ток в простой резистивной цепи равен напряжению (в вольтах), деленному на сопротивление (в омах).Следующая схема иллюстрирует это математическое соотношение на примере:
Емкостное реактивное сопротивление.
[латекс]X_C = 26,5258 Ом[/латекс]
[латекс]I=\frac{E}{X}[/латекс]
[латекс]I=\frac{10}{26,5258 Ом}[/латекс]
[латекс]I=0,3770А[/латекс]
Однако мы должны иметь в виду, что напряжение и ток здесь не совпадают по фазе. Как было показано ранее, ток имеет фазовый сдвиг +90° по отношению к напряжению.Если мы представим эти фазовые углы напряжения и тока математически, мы сможем вычислить фазовый угол реактивного сопротивления конденсатора току.
Напряжение отстает от тока на 90° в конденсаторе.
Математически мы говорим, что фазовый угол сопротивления конденсатора току равен -90°, а это означает, что сопротивление конденсатора току является отрицательной мнимой величиной. (См. рисунок выше.) Этот фазовый угол реактивного противодействия току становится критически важным при анализе цепей, особенно для сложных цепей переменного тока, где взаимодействуют реактивное сопротивление и сопротивление.Полезно будет представить сопротивление любого компонента току в терминах комплексных чисел, а не только скалярных величин сопротивления и реактивного сопротивления.
(См. рисунок выше.) Этот фазовый угол реактивного противодействия току становится критически важным при анализе цепей, особенно для сложных цепей переменного тока, где взаимодействуют реактивное сопротивление и сопротивление.Полезно будет представить сопротивление любого компонента току в терминах комплексных чисел, а не только скалярных величин сопротивления и реактивного сопротивления.
- Емкостное реактивное сопротивление является противодействием, которое конденсатор оказывает переменному току из-за сдвинутого по фазе накопления и высвобождения энергии в своем электрическом поле. Реактивное сопротивление обозначается заглавной буквой «X» и измеряется в омах так же, как сопротивление (R).
- Емкостное реактивное сопротивление можно рассчитать по следующей формуле: XC = 1/(2πfC)
- Емкостное сопротивление уменьшается с увеличением частоты.Другими словами, чем выше частота, тем меньше она противостоит (тем больше «проводит») переменному току.
Используя компоненты одинакового номинала в нашей последовательной примерной схеме, мы соединим их параллельно и посмотрим, что получится:
Рис. 6.14 Параллельная RC-цепь.
Резистор и конденсатор параллельно
Поскольку источник питания имеет ту же частоту, что и схема последовательного примера, а резистор и конденсатор имеют одинаковые значения сопротивления и емкости соответственно, они также должны иметь одинаковые значения импеданса.Итак, мы можем начать нашу таблицу анализа с тех же «заданных» значений:
Таблица 6.7
Теперь, когда это параллельная цепь, мы знаем, что напряжение распределяется поровну между всеми компонентами, поэтому мы можем поместить цифру общего напряжения (10 вольт ∠ 0°) во все столбцы:
Таблица 6.8 Расчет
по закону Ома
Теперь мы можем применить Закон Ома (I=E/Z) по вертикали к двум столбцам таблицы, вычислив ток через резистор и ток через конденсатор:
Таблица 6.9
Так же, как и в цепях постоянного тока, токи ветвей в параллельной цепи переменного тока в сумме образуют общий ток (снова закон Кирхгофа для тока):
Таблица 6.10
Наконец, общий импеданс можно рассчитать с помощью закона Ома (Z=E/I) по вертикали в столбце «Общий». Как мы видели в главе, посвященной индуктивности переменного тока, параллельное сопротивление также можно рассчитать, используя формулу обратной зависимости, идентичную той, что используется при расчете параллельных сопротивлений. Следует отметить, что это правило параллельного импеданса остается верным независимо от типа импеданса, помещенного параллельно.Другими словами, не имеет значения, рассчитываем ли мы цепь, состоящую из параллельных резисторов, параллельных катушек индуктивности, параллельных конденсаторов или какой-либо их комбинации: в форме импедансов (Z) все термины являются общими и могут применяться равномерно по одной и той же формуле. И снова формула параллельного импеданса выглядит так:
[латекс]Z_{параллельный}=\frac{1}{\frac{1}{Z_1}+ \frac{1}{Z_2}+ \dots \frac{1}{Z_n}}[/latex]
Единственным недостатком использования этого уравнения является значительный объем работы, необходимый для его расчета, особенно без помощи калькулятора, способного манипулировать сложными величинами.Независимо от того, как мы вычисляем полное сопротивление для нашей параллельной цепи (либо по закону Ома, либо по формуле обратной связи), мы придем к одной и той же цифре:
- Импедансы (Z) управляются так же, как и сопротивления (R) при анализе параллельных цепей: параллельные импедансы уменьшаются для формирования общего импеданса по формуле обратной связи. Просто убедитесь, что
- выполнять все вычисления в комплексной (не скалярной) форме! ZTotal = 1/(1/Z1 + 1/Z2 +… 1/Zn)
- Закон Ома для цепей переменного тока: E = IZ ; я = Э/З; Z = Э/И
- Когда резисторы и конденсаторы соединены вместе в параллельных цепях (так же, как и в последовательных цепях), общий импеданс будет иметь фазовый угол где-то между 0° и -90°.Ток в цепи будет иметь фазовый угол где-то между 0° и +90°.
- Параллельные цепи переменного тока обладают теми же фундаментальными свойствами, что и параллельные цепи постоянного тока: напряжение одинаково по всей цепи, токи ветвей складываются, образуя общий ток, а полное сопротивление уменьшается (согласно формуле обратной связи), образуя полное сопротивление.
(следующий раздел был адаптирован из: Уроки электрических цепей, том II, глава 5 – Реактивное сопротивление и импеданс – R, L и C)
Прежде чем мы начнем исследовать влияние резисторов, катушек индуктивности и конденсаторов, соединенных вместе в одних и тех же цепях переменного тока, давайте кратко рассмотрим некоторые основные термины и факты.
Сопротивление
По сути это трение против течения. В той или иной степени он присутствует во всех проводниках (кроме проводников super !), особенно в резисторах. Когда переменный ток проходит через сопротивление, возникает падение напряжения, синфазное с током. Сопротивление математически обозначается буквой «R» и измеряется в омах (Ом).
Реактивное сопротивление
По сути это инерция против течения тока.Он присутствует везде, где электрические или магнитные поля развиваются пропорционально приложенному напряжению или току соответственно; но особенно в конденсаторах и катушках индуктивности. Когда переменный ток проходит через чистое реактивное сопротивление, возникает падение напряжения, которое на 90° не совпадает по фазе с током. Реактивное сопротивление математически обозначается буквой «X» и измеряется в омах (Ом).
Полное сопротивление
Это исчерпывающее выражение любых и всех форм противодействия течению тока, включая как сопротивление, так и реактивное сопротивление.Он присутствует во всех цепях и во всех компонентах. Когда переменный ток проходит через импеданс, возникает падение напряжения, которое находится где-то между 0° и 90° в противофазе с током. Импеданс математически обозначается буквой «Z» и измеряется в омах (Ом) в комплексной форме.
Идеальные резисторы обладают сопротивлением, но не реактивным сопротивлением. Идеальные катушки индуктивности и идеальные конденсаторы обладают реактивным сопротивлением, но не обладают сопротивлением. Все компоненты обладают импедансом, и из-за этого универсального качества имеет смысл перевести все значения компонентов (сопротивление, индуктивность, емкость) в общие термины импеданса в качестве первого шага в анализе цепи переменного тока.
Рис. 6.15. Совершенные резистор, катушка индуктивности и конденсатор.
Фазовый угол импеданса для любого компонента представляет собой фазовый сдвиг между напряжением на этом компоненте и током через этот компонент. Для идеального резистора падение напряжения и ток 90 743 всегда 90 744 в фазе друг с другом, поэтому говорят, что угол импеданса резистора равен 0°. Для идеального индуктора падение напряжения всегда опережает ток на 90°, поэтому говорят, что фазовый угол импеданса индуктора равен +90°.Для идеального конденсатора падение напряжения всегда отстает от тока на 90°, поэтому говорят, что фазовый угол импеданса конденсатора равен -90°.
Полное сопротивление переменного тока ведет себя аналогично сопротивлению в цепях постоянного тока: они складываются последовательно и уменьшаются параллельно. Пересмотренная версия закона Ома, основанная на импедансе, а не на сопротивлении, выглядит так:
Закон Ома для цепи переменного тока
[латекс]\begin{align} \tag{6.2} \text{E }&={I}{Z} \\ \text{I } &=\frac{E}{Z}\\ \text{Z }&=\frac{E}{I} \end{align}[/latex]
Мы можем взять те же компоненты из последовательной схемы и переставить их в параллельную конфигурацию для простого примера схемы:
Рисунок 6.16 Пример R, L и C параллельная цепь.
Полное сопротивление в параллельных компонентах
Тот факт, что эти компоненты соединены параллельно, а не последовательно, теперь абсолютно не влияет на их индивидуальные импедансы. Пока источник питания имеет ту же частоту, что и раньше, индуктивное и емкостное сопротивления вообще не изменятся.
Рис. 6.17 Пример параллельной цепи R, L и C с импедансами, заменяющими номиналы компонентов.
Со значениями всех компонентов, выраженными в виде импедансов (Z), мы можем настроить таблицу анализа и действовать, как в последнем примере задачи, за исключением того, что на этот раз следуя правилам параллельных цепей вместо последовательных.
Зная, что напряжение распределяется поровну между всеми компонентами в параллельной цепи, мы можем перенести значение полного напряжения на все столбцы компонентов в таблице:
Таблица 6.11. Значения компонентов, выраженные в виде импеданса image 2
Теперь мы можем применить закон Ома (I=E/Z) по вертикали в каждом столбце, чтобы определить ток через каждый компонент:
Таблица 6.12. Значения компонентов, выраженные в виде импеданса image 3
Расчет полного тока и полного импеданса
Существует две стратегии расчета общего тока и полного сопротивления.Во-первых, мы могли бы рассчитать общий импеданс из всех отдельных импедансов параллельно (Z Total = 1/(1/Z R + 1/Z L + 1/Z C ), а затем вычислить общий ток путем деления напряжения источника на полное сопротивление (I=E/Z)
Однако работа над уравнением параллельного импеданса с комплексными числами — непростая задача со всеми обратными связями (1/Z). Это особенно верно, если вам не повезло, что у вас нет калькулятора, который обрабатывает комплексные числа, и вы вынуждены делать все это вручную (возвратить отдельные импедансы в полярную форму, затем преобразовать их все в прямоугольную форму для сложения, а затем преобразовать обратно). в полярную форму для окончательной инверсии, затем инвертировать).Второй способ рассчитать общий ток и полное сопротивление состоит в том, чтобы сложить все токи ветвей, чтобы получить общий ток (общий ток в параллельной цепи — переменного или постоянного тока — равен сумме токов ветвей), а затем использовать закон Ома. для определения общего импеданса по общему напряжению и полному току (Z=E/I).
Таблица 6.13 Расчет полного тока и полного сопротивления
Любой метод, выполненный должным образом, даст правильные ответы.
За заметным исключением расчетов мощности (P), все расчеты цепей переменного тока основаны на тех же общих принципах, что и расчеты цепей постоянного тока.Единственная существенная разница заключается в том, что в вычислениях переменного тока используются комплексные величины, а в вычислениях постоянного тока используются скалярные величины. Закон Ома, законы Кирхгофа и даже сетевые теоремы, изученные на постоянном токе, остаются верными для переменного тока, когда напряжение, ток и полное сопротивление выражаются комплексными числами. Те же стратегии устранения неполадок, которые применяются к цепям постоянного тока, применимы и к переменному току, хотя с переменным током, безусловно, может быть сложнее работать из-за фазовых углов, которые не регистрируются портативным мультиметром.
Сила — это совсем другая тема, и она будет рассмотрена в отдельной главе этой книги. Поскольку мощность в реактивной цепи одновременно поглощается и высвобождается, а не просто рассеивается, как в случае с резисторами, ее математическая обработка требует более прямого применения тригонометрии для решения.
При анализе цепи переменного тока первым шагом анализа является преобразование значений всех резисторов, катушек индуктивности и конденсаторов в импедансы (Z) на основе частоты источника питания.После этого выполните те же шаги и стратегии, которые вы изучили для анализа цепей постоянного тока, используя новую форму закона Ома: E = IZ; I=E/Z; и Z=E/I
Помните, что только расчетные значения, выраженные в полярной форме , применимы непосредственно к эмпирическим измерениям напряжения и тока. Прямоугольная запись — это просто полезный инструмент для сложения и вычитания комплексных величин. Полярная запись, где величина (длина вектора) напрямую связана с величиной измеряемого напряжения или тока, а угол напрямую связан со сдвигом фазы в градусах, является наиболее практичным способом выражения комплексных величин для анализа цепей.
РЕШЕНО:31.54. Параллельная схема L-R-C. Резистор, индуктивность. и конденсатор подключены параллельно к источнику переменного тока с амплитудой напряжения V и угловой частотой \omega . Пусть напряжение источника определяется выражением v=V cos\omegat. (a) Покажите, что мгновенные напряжения v_{R}, v_{L}, v_{L} и v_{C} в любой момент равны v и что i=i_{R}+i_{L}+ i_{O}, где i — ток через источник, а i_{R} . i_{L} и i_{C} — токи через резистор, катушку индуктивности и конденсатор соответственно.{2}}
Стенограмма видео
у вас четные или дальние во враче в столице подключены параллельно регистрируются в др На Gap Visitor подключены параллельно по институтам. C l R о, мы, например, это вы, мы знаем, и омега, что исходный бюллетень дается у него есть Тоби, не курс меня хорошо. Так что самобытность работы такова, что проведенный в своем мире тот, эээ, быть котом на ровне, я имею ввиду странный в этом нынешнем льду.Кал тох, ты, э-э, плюс я кричу менее ледяной и Б, но граница трудных мест это вверх. Какие красивые это еще я вижу. И я тебя со схемой так хвалю эти четыре резки, я да, я вижу тебя, и у нас есть хороший дроп. Он там. Они идут в c, но используют диаграмму. Итак, вы думаете, что повышение амплитуды — это диаграмма замораживания? Уверен, что я собирался носок У вас было имя кальмара может быть правильным. Я здесь. Джаред отрицательный. Приступайте к решению Так как l c r в пеланте, то потенциал по каждому значительно экономить, так как А r и C находятся в параллельной цепи, поэтому потенциал по округе будет равен Подножка.Г-н Равноногий введен в должность Часть тока, поступающего в цепь, Он разделится, как вы, э-э, мы с вами видим, применяя корень горечавки. Ага, какой-нибудь Окрент, что-нибудь мягкое должно быть равным, оставив doc current пропить ток No Well, так что мы можем писать. Я буду я Да, потому что я плюс Исаак, когда мы расстаемся, я чувствую странность, напряжение мантры, расстояние всегда в вере. Большой мир — это я Омега наверху Будь на мне, парень Следующие двойные свидания кусаются на 90 градусов Я вижу, будь на ху, что будет над Гарси, новые вещи.Болт на 90, так что мы можем нарисовать рокового Хагрупа. Это источник Вуди. Итак, он отредактировал, но это вы видите? И это ты на? Это будет желатиновый ток в цепи. Привет. Мгновенно Он получил это. Видеть? Но из пустыни я вырос. Я вонзился в него Наши года квадратные пули I c минусовые пули были и его можно вернуть. Я вижу, что это должно быть на площади статей. Будь Омега Пси минус. Будь готов ко мне, парень. Святая площадь, Оставь черным Этот вопрос может горечь Художников бросить. Отпусти меня, посмотри, и я все еще буду на ногах, так что один на ногах Джареда школы.Момент. Я должен сделать здесь поправку. Это все для этой проблемы.
Что это такое и как они работают?
Электрические цепи передают переменный или постоянный ток через замкнутые соединения между электрическими компонентами. Различное расположение и конфигурация этих компонентов создают разные виды цепей, и RLC-цепи — одна из них.
Каковы их основные характеристики и области применения? Какова роль RLC в электронике? В чем разница между последовательными и параллельными цепями RLC? На все эти вопросы есть ответ.
Распаковка RLC
RLC означает резистор (R), катушку индуктивности (L) и конденсатор (C). Это основные компоненты цепей RLC, соединенные в замкнутый контур.
Резистор изготовлен из резистивных элементов (таких как углерод), функция которых заключается в создании более высоких уровней электрического сопротивления, чем естественное сопротивление, влияющее на цепи. Это также снижает демпфирование и резонансную частоту в цепи (fr).
Катушка индуктивности накапливает энергию в магнитных полях, создаваемых электрическим током, протекающим по проводникам, в соответствии с законом Фарадея.
Конденсатор накапливает энергию в электрических полях через два или более проводников, чаще всего разделенных диэлектрической средой. Измерение этой «хранимости» называется емкостью.
Что такое параллельная цепь RLC?
В параллельной цепи RLC резистор, катушка индуктивности и конденсатор соединены параллельно и подключены к одному и тому же источнику напряжения. Это отличается от последовательного соединения.
В параллельных RLC-цепях переменного тока электрический ток разделяется, и все компоненты получают одинаковое напряжение, а ток делится в каждом компоненте в зависимости от его импеданса.Ток не протекает в параллельных цепях RLC с использованием источника постоянного тока с той же эффективностью, потому что индуктор действует как короткое замыкание, а конденсатор действует как разомкнутая цепь.
Чтобы рассчитать полный ток, общее напряжение и общее сопротивление RLC-цепи, мы можем использовать закон Ома, согласно которому ток (I), измеренный в амперах, равен напряжению (V), измеренному в вольтах. умножить на сопротивление (R), измеренное в омах (Ом):
V=IR или, в зависимости от единиц измерения: V = A x Ω
Если эту формулу применить к конденсатору цепи, R заменяется на Xc , где Xc — емкостное реактивное сопротивление.А применительно к катушкам индуктивности R заменяется на Xl, где Xl — индуктивное реактивное сопротивление.
V= IXc
V= IXl
Что такое импеданс?
Электрический импеданс — это измерение сопротивления току в цепи. Несмотря на их сходство, импеданс — это не то же самое, что сопротивление, потому что это понятие фактически охватывает как сопротивление, так и реактивное сопротивление, создаваемые в цепях переменного тока (реактивное сопротивление отсутствует в стабильном токе цепей постоянного тока).
При резонансе емкостное и индуктивное сопротивление будут равны друг другу.Катушка индуктивности и конденсатор также будут проводить больший ток на резонансной частоте.
Уравнение для параллельной цепи RLC дает комплексный импеданс для каждой параллельной ветви, поскольку каждый элемент становится обратной величиной импеданса ( 1/Z ). Величина, обратная импедансу, называется допуском (Y). Инверсия полного импеданса (ZRLC) представляет собой сумму обратных импедансов каждого компонента:
1/ ZRLC = 1/ZR + 1/ZL + 1/ZC. Другими словами, полная проводимость цепи представляет собой сумму проводимостей каждого компонента.
В противном случае формула для определения импеданса будет Z=V/I, где Z — импеданс, V — напряжение, а I — ток в цепи.
Инверсия полного полного сопротивления представляет собой сумму обратных импедансов каждого компонента. Другими словами, полная проводимость (мера того, насколько легко цепь или устройство пропускает ток) цепи представляет собой сумму проводимостей каждого компонента.
Какая польза от параллельной цепи RLC?
Цепи RLC часто используются в качестве схем генератора, поскольку они производят синусоидальные, прямоугольные или треугольные волны.Это колеблющиеся электронные сигналы, которые могут преобразовывать постоянный ток в переменный или работать как фильтр нижних частот, фильтр верхних частот, полосовой фильтр и полосовой фильтр.
В качестве полосового фильтра он используется для настройки, например, в телевизорах и аналоговых радиоприемниках, которые в основном позволяют вам найти определенный диапазон частот после сбора всех доступных окружающих радиоволн через антенну. Полосовые фильтры также используются для выравнивания звука, оформления звука и звукозаписи в студии.
Источник: Grooveaddicted/Pixabay
Как схема генератора, она должна иметь низкие значения демпфирования, чтобы работать эффективно. Другими словами, он должен иметь высокую добротность ( Q ). Коэффициент качества параллельной цепи RLC является обратным значением добротности последовательной цепи.
Q = R 𝐶 𝐿 = 𝑅 𝜔0 = 𝜔0 𝑅𝐶
Часто задаваемые вопросы о цепях RLC
Являются ли цепи LCR и RLC одинаковыми?
Да, меняется порядок символов.
Что такое реактивное сопротивление?
Реактивное сопротивление – это сопротивление компонента потоку тока из-за эффекта индуктивности или емкости, вызванного этим компонентом.
Как и в случае с сопротивлением, чем больше реактивное сопротивление в цепи, тем меньше ток, который она получает. Но, в отличие от сопротивления, реактивное сопротивление меняет фазу и не рассеивает электричество; вместо этого он сохраняет его.
Величина, обратная реактивному сопротивлению, представляет собой реактивную проводимость, которая измеряет легкость, с которой реактивное сопротивление (или набор реактивных сопротивлений) позволяет протекать переменному току при приложении напряжения заданной частоты.
Каковы различия между параллельными цепями RLC и последовательными цепями RLC?
Мало того, что существуют два разных типа цепей RLC, они также ведут себя противоположным образом:
- Если резистор, катушка индуктивности и конденсатор соединены параллельно в параллельных цепях RLC, Цепи серии RLC.

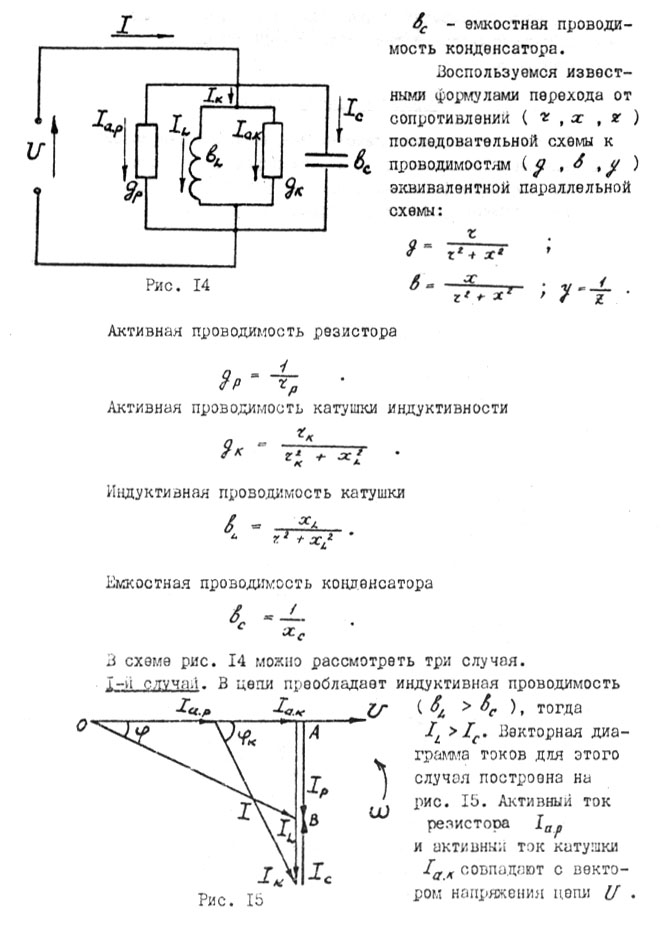 Электрические цепи постоянного тока.
Электрические цепи постоянного тока.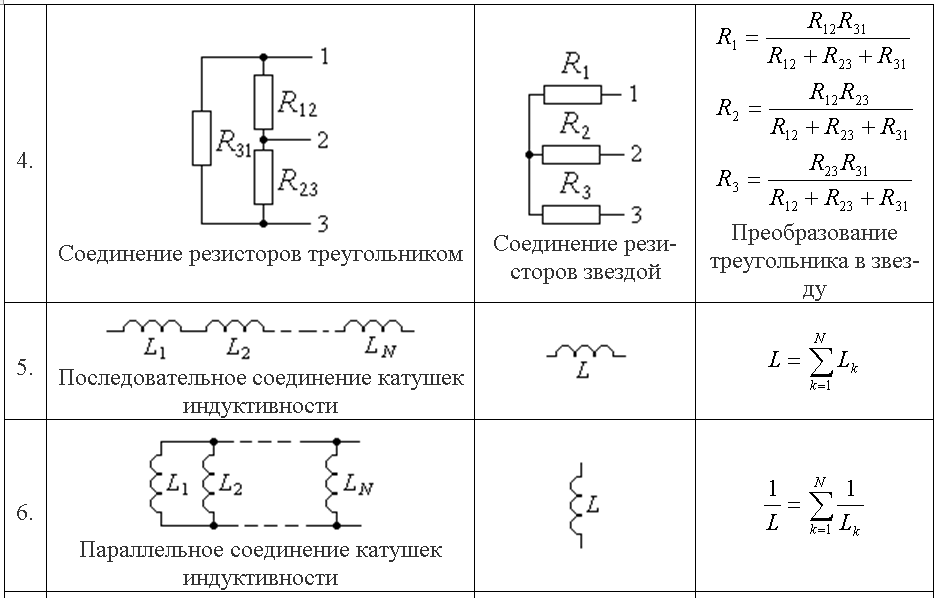
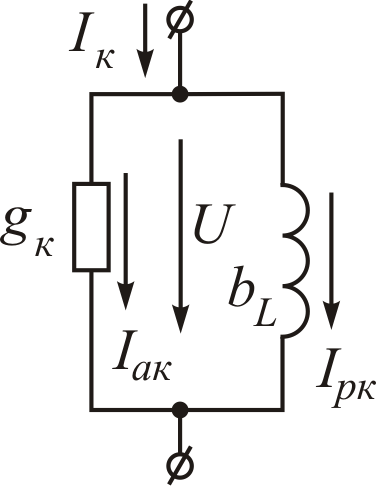
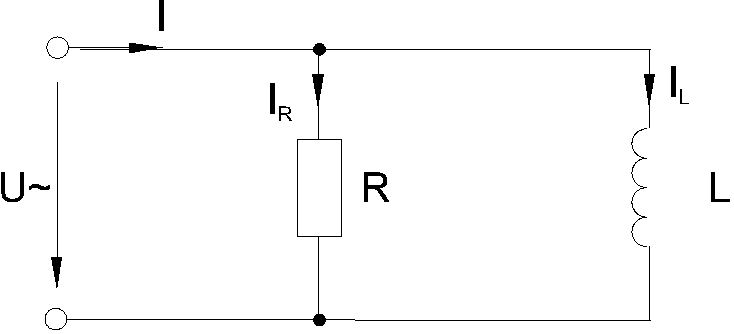
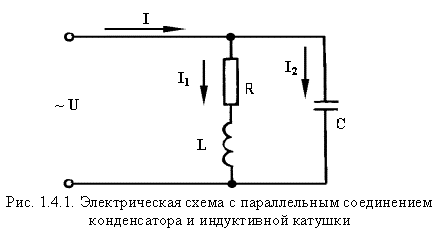
 Униполярные (полевые) транзисторы.
Униполярные (полевые) транзисторы.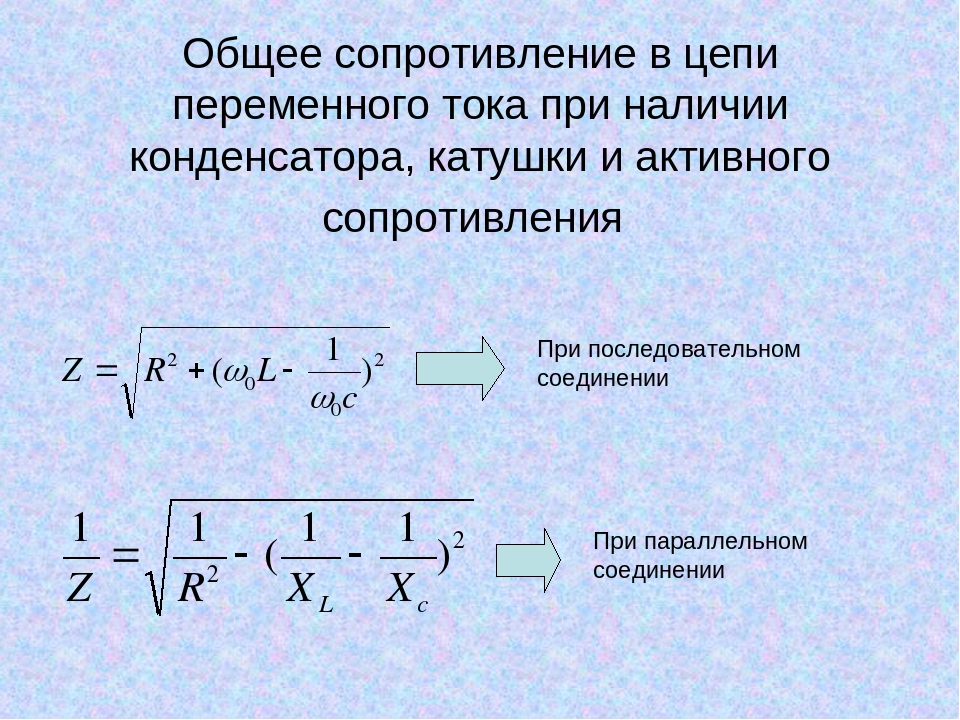 Трансформаторы.
Трансформаторы.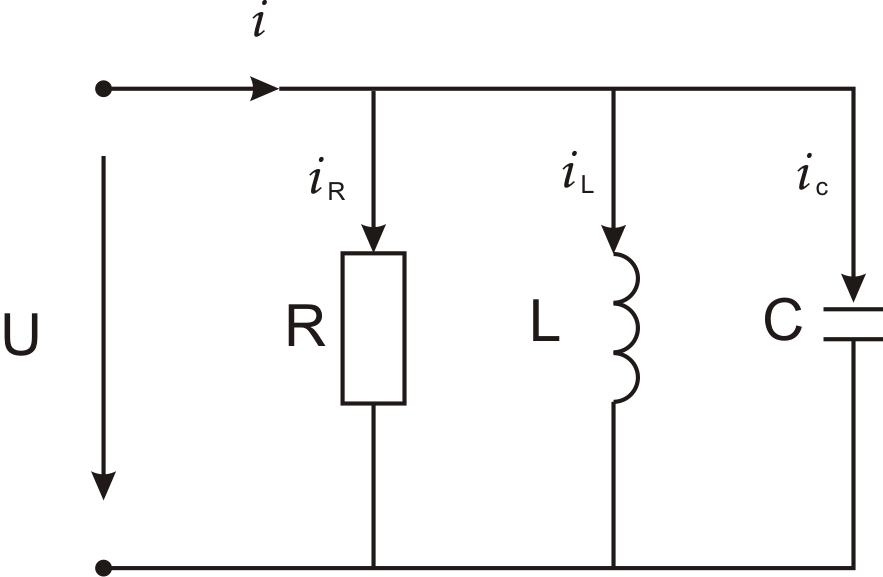 7. Регистрация и отображение на компьютере тока короткого замыкания на выводах вторичной обмотки однофазного трансформатора.
7. Регистрация и отображение на компьютере тока короткого замыкания на выводах вторичной обмотки однофазного трансформатора.
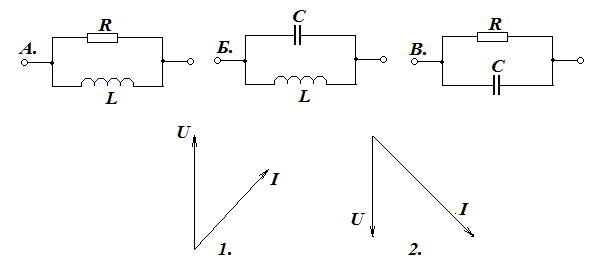
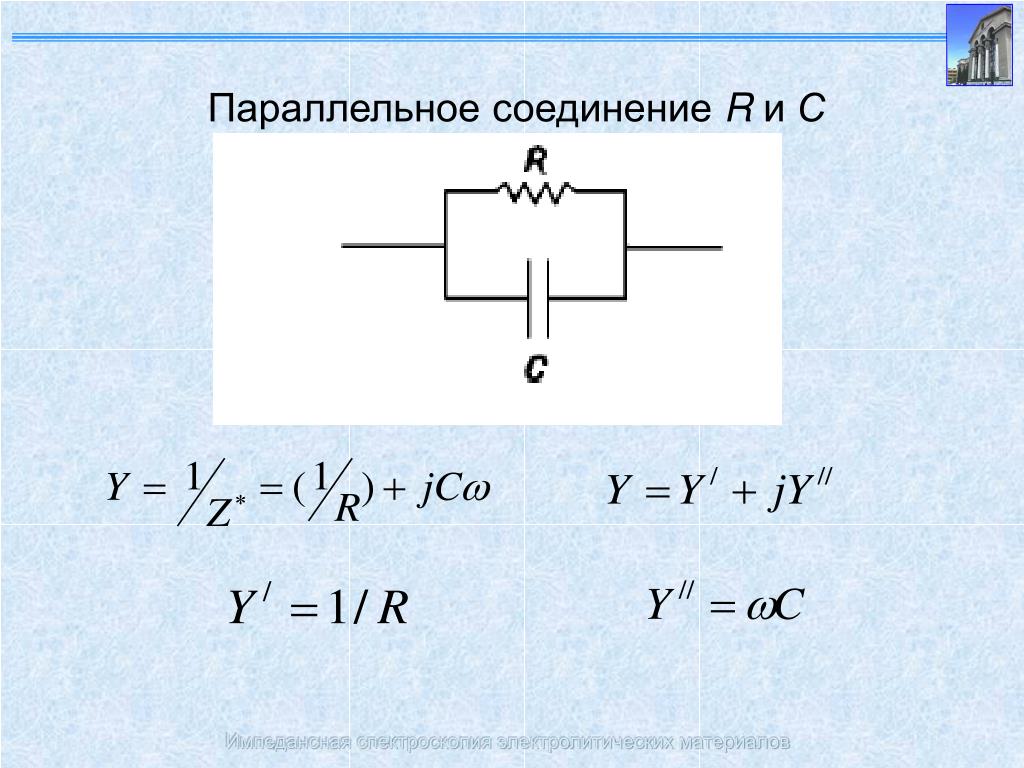



 2, асинхронным двигателем 106 и преобразователем углового перемещения) – 1 шт.
2, асинхронным двигателем 106 и преобразователем углового перемещения) – 1 шт.

