5. Переходные процессы в линейных электрических цепях. Переходные процессы в линейных электрических цепях
8. Переходные процессы в линейных электрических цепях
8.1. Общая характеристика переходных процессов
В электрических цепях возможны включения и отключения отдельных ветвей, короткие замыкания участков цепи, различного рода переключения. Любые изменения в электрических цепях можно представить в виде переключений или коммутаций. Характер коммутации указывается в схеме с помощью рубильника со стрелкой. По направлению стрелки можно судить, замыкается или размыкается рубильник.
При коммутации в цепи возникают переходные процессы, т.е. процессы перехода токов и напряжений от одного установившегося значения к другому. Изменения токов и напряжений вызывают одновременное изменение энергии электрического и магнитного полей, связанных с элементами цепи - емкостями и индуктивностями. Однако энергия электрического поля и энергия магнитного поля могут изменяться только непрерывно, так как скачкообразное изменение потребовало бы от источника бесконечно большой мощности. На этом рассуждении основаны законы коммутации.
Первый закон. В любой ветви с индуктивностью ток не может изменяться скачком и в момент коммутации сохраняет то значение, которое он имел непосредственно перед моментом коммутации
iL (0+) = iL (0-),
где iL(0+) - ток в ветви с индуктивностью в момент коммутации, сразу после коммутации. Знак "+" в формуле обычно не записывается. Время переходного процесса отсчитывается от момента коммутации;
iL(0-) - ток в индуктивности непосредственно перед коммутацией.
Второй закон. Напряжение на емкости сразу после коммутации сохраняет то значение, которое оно имело непосредственно перед моментом коммутации.
uC (0+) = uC (0-),
где uC(0+) - напряжение на емкости в момент коммутации;
uC(0-) - напряжение на емкости непосредственно перед моментом коммутации.
Допущения, применяемые при анализе переходных процессов:
Полагают, что переходный процесс длится бесконечно большое время.
Считают, что замыкание и размыкание рубильника происходит мгновенно, без образования электрической дуги.
Принимают, что к моменту коммутации предыдущие переходные процессы в цепи закончились.
В соответствии с классическим методом расчета, переходный ток в ветви схемы представляют в виде суммы принужденного и свободного токов.
.
где iпр(t) - принужденный ток, определяется в установившемся режиме после коммутации. Этот ток создается внешним источником питания. Если в цепь включен источник постоянной ЭДС, принужденный ток будет постоянным, если в цепи действует источник синусоидальной ЭДС, принужденный ток изменяется по периодическому, синусоидальному закону;
iсв(t) - свободный ток, определяется в схеме после коммутации, из которой исключен внешний источник питания. Свободный ток создается внутренними источниками питания: ЭДС самоиндукции индуктивности или напряжением заряженной емкости.
Свободный ток определяют по формуле:
.
Количество слагаемых в формуле равно числу реактивных элементов (индуктивностей и емкостей) в схеме.
P1, P2- корни характеристического уравнения.
А1, А2- постоянные интегрирования, определяются с помощью начальных условий.
Начальные условия - это переходные токи и напряжения в момент коммутации, в момент времени t, равный нулю.
Начальные условия могут быть независимыми или зависимыми.
Независимыми называют начальные условия, подчиняющиеся законам коммутации, законам постепенного, непрерывного изменения. Это напряжение на емкости uc(0) и ток в ветви с индуктивностью iL(0) в момент коммутации.
Остальные начальные условия: напряжение и ток в ветви с сопротивлением uR(0) и iR(0), напряжение на индуктивности uL(0) , ток в ветви с емкостью iC(0) - это зависимые начальные условия. Они не подчиняются законам коммутации и могут изменяться скачком.
studfiles.net
Переходные процессы в линейных электрических цепях
В электрических цепях возможны включения и отключения отдельных ветвей, короткие замыкания участков цепи, различного рода переключения. Любые изменения в электрических цепях можно представить в виде переключений или коммутаций. Характер коммутации указывается в схеме с помощью рубильника со стрелкой. По направлению стрелки можно судить, замыкается или размыкается рубильник. При коммутации в цепи возникают переходные процессы, т.е. процессы перехода токов и напряжений от одного установившегося значения к другому. Изменения токов и напряжений вызывают одновременное изменение энергии электрического и магнитного полей, связанных с элементами цепи - емкостями и индуктивностями. Однако энергия электрического поля и энергия магнитного поля могут изменяться только непрерывно, так как скачкообразное изменение потребовало бы от источника бесконечно большой мощности. На этом рассуждении основаны законы коммутации.
Первый закон. В любой ветви с индуктивностью ток не может изменяться скачком и в момент коммутации сохраняет то значение, которое он имел непосредственно перед моментом коммутации
iL (0+) = iL (0-),
где iL (0+) - ток в ветви с индуктивностью в момент коммутации, сразу после коммутации. Знак "+" в формуле обычно не записывается. Время переходного процесса отсчитывается от момента коммутации; iL (0-) - ток в индуктивности непосредственно перед коммутацией.Второй закон. Напряжение на емкости сразу после коммутации сохраняет то значение, которое оно имело непосредственно перед моментом коммутации.
uC (0+) = uC (0-),
где uC (0+) - напряжение на емкости в момент коммутации; uC (0-) - напряжение на емкости непосредственно перед моментом коммутации.Допущения, применяемые при анализе переходных процессов.
- Полагают, что переходный процесс длится бесконечно большое время.
- Считают, что замыкание и размыкание рубильника происходит мгновенно, без образования электрической дуги.
- Принимают, что к моменту коммутации предыдущие переходные процессы в цепи закончились.
В соответствии с классическим методом расчета, переходный ток в ветви схемы представляют в виде суммы принужденного и свободного токов.
.
где iпр(t) - принужденный ток, определяется в установившемся режиме после коммутации. Этот ток создается внешним источником питания. Если в цепь включен источник постоянной ЭДС, принужденный ток будет постоянным, если в цепи действует источник синусоидальной ЭДС, принужденный ток изменяется по периодическому, синусоидальному закону; iсв(t) - свободный ток, определяется в схеме после коммутации, из которой исключен внешний источник питания. Свободный ток создается внутренними источниками питания: ЭДС самоиндукции индуктивности или напряжением заряженной емкости.Свободный ток определяют по формуле:
.
Количество слагаемых в формуле равно числу реактивных элементов (индуктивностей и емкостей) в схеме. P1, P2 - корни характеристического уравнения. А1, А2 - постоянные интегрирования, определяются с помощью начальных условий. Начальные условия - это переходные токи и напряжения в момент коммутации, в момент времени t, равный нулю. Начальные условия могут быть независимыми или зависимыми. Независимыми называют начальные условия, подчиняющиеся законам коммутации, законам постепенного, непрерывного изменения. Это напряжение на емкости uc(0) и ток в ветви с индуктивностью iL(0) в момент коммутации. Остальные начальные условия: напряжение и ток в ветви с сопротивлением uR(0) и iR(0), напряжение на индуктивности uL(0) , ток в ветви с емкостью iC(0) - это зависимые начальные условия. Они не подчиняются законам коммутации и могут изменяться скачком.8.2. Переходные процессы в цепях с одним реактивным элементом
Короткое замыкание в R-L цепи
На рис. 8.1 изображена электрическая цепь, в которой включен источник постоянной ЭДС. В результате коммутации рубильник замыкается и образуется замкнутый на себя R-L контур.
До коммутации по индуктивности протекал ток Этот ток создавал постоянное магнитное поле в индуктивной катушке. Рис. 8.1
Определим закон изменения тока в индуктивности после коммутации. В соответствии с классическим методом
Принужденный ток после коммутации замыкается через рубильник, имеющий нулевое сопротивление, и через индуктивность не протекает. Индуктивный ток имеет только свободную составляющую
Магнитное поле, исчезая, индуктирует в индуктивной катушке ЭДС самоиндукции. Свободный ток в R-C контуре существует за счет этой электродвижущей силы. Запишем уравнение для свободного тока в R-L контуре, используя второй закон Кирхгофа.
(8.1)
Ищем решение этого уравнения в виде экспоненты
.
Производная
.
Подставим значения свободного тока и производной тока в уравнение (8.1)
(8.2)
Уравнение (8.2), полученное из уравнения (8.1), называется характеристическим.
- корень характеристического уравнения.
- постоянная времени переходного процесса, измеряется в секундах. Постоянная времени τ - это интервал времени, за который переходный ток уменьшается в e раз.
.
Постоянную интегрирования А определяем с помощью начального условия.
В соответствии с первым законом коммутации,
.
Получим
Напряжение на индуктивности .
На рис. 8.2 изображены кривые переходного тока в ветви с индуктивностью и переходного напряжения на индуктивности. Переходный ток и напряжение по экспоненте стремятся к нулю. В инженерных расчетах полагают, что через интервал времени, равный (4 ÷ 5)τ, переходный процесс заканчивается. Рис. 8.2
Подключение R-L цепи к источнику постоянной ЭДС
В схеме на рис. 8.3 до коммутации рубильник разомкнут. В результате коммутации рубильник замыкается и подключает R-L цепь к источнику постоянной ЭДС. Определим закон изменения тока i(t).
.
Принужденный ток в установившемся режиме после коммутации
.
В свободном режиме из схемы исключен внешний источник питания. Схема на рис. 8.3 без источника ЭДС ничем не отличается от схемы на
Свободный ток определяется по формуле . Запишем значение переходного тока для момента коммутации, (t = 0). , откуда . Рис. 8.3
До коммутации рубильник был разомкнут, и ток в схеме отсутствовал. Сразу после коммутации ток в индуктивности остается равным нулю.
.
.
.
Напряжение на индуктивности
.
На рис. 8.4 изображены кривые переходного, принужденного, свободного токов и переходного напряжения на индуктивности.
Свободный ток и напряжение на индуктивности плавно уменьшаются до нуля. В момент коммутации свободный и принужденный токи одинаковы по абсолютной величине. Переходный ток начинается при включении с нуля, затем возрастает, приближаясь к установившемуся постоянному значению. Рис. 8.4
Короткое замыкание в R-C цепи
В схеме на рис. 8.5 в результате коммутации рубильник замыкается, и образуется замкнутый на себя R-C контур. До коммутации емкость полностью зарядилась до напряжения, равного ЭДС источника питания, то есть uc(0-) = E. После коммутации емкость полностью разряжается, следовательно, принужденный ток в R-C цепи и принужденное напряжение на конденсаторе равны нулю.
В цепи существует только свободный ток за счет напряжения заряженного конденсатора. Запишем для R-C контура уравнение по второму закону Кирхгофа . Рис. 8.5
Ток через конденсатор .
Получим дифференциальное уравнение
. (8.3)
Решение этого уравнения .
Подставим значение свободного напряжения и производной от напряжения
в уравнение (8.3).
.
Уравнение называется характеристическим.
- корень характеристического уравнения;
- постоянная времени переходного процесса;
Переходный ток и переходное напряжение на конденсаторе по показательному закону уменьшаются до нуля (рис. 8.6). Рис. 8.6
Подключение R-C цепи к источнику постоянной ЭДС
Полагаем, что до коммутации конденсатор не заряжен, напряжение на нем uc(0-) = 0. В результате коммутации рубильник замыкается, и конденсатор полностью заряжается (рис. 8.7). Принужденное напряжение на емкости равно ЭДС источника питания ucпр= E.
Переходное напряжение
.
В момент коммутации .
Постоянная интегрирования . В соответствии со вторым законом коммутации . . Рис. 8.7
Переходное напряжение
.
Переходный ток
.
Кривые напряжений и тока изображены на рис. 8.8. Рис. 8.8
8.3. Переходные процессы в цепях с двумя реактивными элементами
При последовательном соединении сопротивления R, катушки индуктивности L и конденсатора С образуется электрический R-L-C контур (рис. 8.9). Дифференциальное уравнение для тока в контуре
.
После дифференцирования по t и деления на L получим
. (8.4)
Решение уравнения (8.4) равно сумме принужденной и свободной составляющих . В нашем случае принужденная составляющая переходного тока равна нулю, так как в схеме имеется емкость, являющаяся разрывом цепи для постоянного тока. Рис. 8.9
Свободная составляющая является общим решением уравнения
. (8.5)
Пусть , , .
После подстановки этих выражений в уравнение (8.5) получим характеристическое уравнение
.
Характеристическое уравнение имеет два корня
,
где - коэффициент затухания;
- угловая резонансная частота контура без потерь.
Получим
.
Вид корней зависит от отношения
,
где - характеристическое или волновое сопротивление контура;
- добротность контура.
Колебательный режим
Наиболее важен часто встречающийся случай, когда корни P1,2 - комплексные сопряженные с отрицательной вещественной частью, свободная составляющая имеет вид затухающих колебаний. В этом случае
, , , ,
где - угловая частота собственных колебаний в контуре;
- период собственных колебаний.
Ток в цепи
, (8.6)
где А и φ - постоянные интегрирования.
До коммутации ток в индуктивности равен нулю, сразу после коммутации остается равным нулю
.
Чтобы определить две постоянные интегрирования, необходимо иметь два начальных условия и составить два уравнения. Напряжение на индуктивности
. (8.7)
где - напряжение на индуктивности в момент коммутации, является зависимым начальным условием. Составим уравнение по второму закону Кирхгофа для момента коммутации, чтобы определить зависимое начальное условие .
.
До коммутации конденсатор был не заряжен, поэтому
.
Подставляя в (8.6) и (8.7) t = 0 и используя независимое и зависимое начальные условия, получим систему уравнений
(8.8)
Решив систему (8.8), определим
.
На рис. 8.10 приведена кривая изменения тока в контуре при подключении к нему источника постоянной ЭДС. Из рисунка видно, что колебания в контуре затухают по показательному закону из-за потерь электрической энергии в сопротивлении R. Затухание происходит тем медленнее, чем меньше коэффициент затухания α . Рис. 8.10
Постоянная времени переходного процесса .
При малом коэффициенте затухания величина ωС незначительно отличается от резонансной частоты ω0. Относительное затухание колебаний характеризуется декрементом затухания, представляющим отношение мгновенных значений тока через один период.
.
Натуральный логарифм этого оператора носит название логарифмического декремента затухания
.
Для контура с небольшим затуханием, когда
Апериодический режим в R-L-C контуре наблюдается при большом затухании, когда . В этом случае корни P1,2 вещественные, отрицательные, различные.
Свободный ток определяется по формуле
. (8.9)
Напряжение на индуктивности
. (8.10)
Подставив в уравнение (8.9) и (8.10) t = 0 и используя независимое и зависимое условия, получим систему уравнений
Решив эту систему, определим постоянные интегрирования
.
Выражение для тока в контуре
состоит из положительной, медленно затухающей экспоненты с коэффициентом затухания P1 и отрицательной, быстро затухающей экспоненты P2 (рис. 8.11).
Ток получается неколебательным, он не принимает отрицательных значений, то есть не меняет своего направления. На границе между колебательным и апериодическим режимом при наблюдается предельный случай апериодического процесса. Рис. 8.11
lections.tk
5. Переходные процессы в линейных электрических цепях.
23
Переходные процессы – процессы перехода от одного режима работы электрической цепи к другому, чем-либо отличающемуся от предыдущего (например, амплитудой, фазой, частотой).
Переходные процессы часто вызываются коммутацией в цепи (процессом замыкания или размыкания выключателей).
Обычно переходные процессы являются быстро протекающими, тем не менее, изучение переходных процессов важно, так как дает возможность установить, как деформируются сигналы по форме и амплитуде при прохождении их через цепи, фильтры и другие устройства, позволяет выявить превышение напряжения на отдельных участках цепи, которые могут оказаться опасными, а также определить длительность переходных процессов. Последнее также играет в электрических устройствах немаловажную роль, ведь из быстродействия отдельных элементов при суммировании складывается быстродействие всего устройства.
Переходные процессы, связанные с изменением топологии цепи или различными коммутациями пассивных элементов, присущи в основном устройствам производства, передачи и преобразования электрической энергии. Для радиотехнических устройств более характерен режим, когда топология цепи и параметры пассивных элементов неизменны, а внешнее воздействие на цепь меняется по произвольному (чаще всего непериодическому) закону.
Началом отсчета времени неустановившихся процессов, имеющих место в радиотехнических цепях, обычно называют моментом коммутации.
Этот момент времени непосредственно перед мгновенной коммутацией обозначим “0–“, а сразу после мгновенной коммутации – “0+”.
Задача о переходном процессе (с неизменными во времени R,L,C) можно привести к решению линейного дифференциального уравнения.
Рассмотрим, например, схему на рис. 5.1:
R L
E
Рис. 5.1
При замкнутом ключе по второму закону Кирхгофа:
uL+Ri=E или .
Таким образом, определение тока как функции времени по сути дела есть решение дифференциального уравнения.
Переход реальной электрической цепи от одного установившегося режима к другому не может происходить мгновенно, скачком. При этом соблюдаются 2 основных положения: ток через индуктивность и напряжение на емкости не могут измениться скачком.
Доказательство того, что ток через индуктивность не может измениться мгновенно приведем на примере вышеуказанной схемы. По второму закону Кирхгофа:
.
Допустим, что ток i может изменяться скачком. Скачек тока означает, что за бесконечно малый интервал времени t0 ток изменится на конечную величину i. При этом .
Левая часть уравнения не равна правой, второй закон Кирхгофа не выполняется. Следовательно, наше предположение неверно.
Доказательство того, что напряжение на емкости не может изменяться скачком, можно произвести аналогично.
Обратимся к простейшей цепи с емкостью (см. рис. 5.2).
R С
E
Рис. 5.2
Составим для нее уравнение по второму закону Кирхгофа:
, где
Е – эдс источника, конечная величина;
uc – напряжение на емкости.
Так как , то.
Если допустить, что напряжение uc может изменяться скачком, то
;
Левая часть не равна правой, что противоречит второму закону Кирхгофа.
Из доказанных двух основных положений следуют два закона (правила) коммутации.
I закон коммутации:
Ток через индуктивность непосредственно до коммутации iL(0–) равен току через туже индуктивность непосредственно после коммутации:
iL(0–) = iL(0+).
II закон коммутации:
uc(0–) = uc(0+).
В общем случае задача анализа переходных процессов заключается в определении мгновенных значений токов или напряжений всех или части ветвей электрической цепи в произвольный момент времени после коммутации и может быть сведена к решению дифференциального уравнения цепи при t>0.
Возвратимся к приведенному выше примеру (см. рис. 5.1).
–линейное дифференциальное уравнение.
Как известно из курса математики общее решение подобного уравнения равно сумме частного решения неоднородного уравнения и общего решения однородного уравнения.
Однородное уравнение получаем из исходного, если начальные условия нулевые. В нашем случае:
.
Можно разделить переменные, и общее решение будет иметь вид:
где
Дальнейшее решение можно произвести по готовым формулам или известным методам. В итоге будет получено общее решение неоднородного уравнения.
.
Принужденной составляющей тока (напряжения) называют составляющую, задаваемую действующими в цепи независимыми источниками энергии.
Проверка: .
Следовательно, решение верно.
Принужденная составляющая тока (напряжения) физически представляет собой составляющую, изменяющуюся с той же частотой, что и действующая в схеме принуждающая эдс.
Название “свободная” объясняется тем, что эта составляющая есть решение уравнения, свободного от вынуждающей силы (однородного уравнения без принуждающей части).
Свободная составляющая реакции цепи с течением времени затухает (стремится к нулю) при t, а принужденная составляющая представляет собой установившееся значение искомого тока или напряжения после коммутации.
studfiles.net
1. Переходные процессы в линейных электрических цепях
Министерство образования и науки Украины
Харьковский национальный университет радиоэлектроники
Факультет заочного обучения
Кафедра «Сети связи»
Курсовой проект
Пояснительная записка
Прохождение сигналов через линейные электрические цепи
(тема проекта)
Теория электрических сигналов и цепей
(дисциплина)
Руководитель ________________________________________
Студент гр. ИСС 27.10.2007
Харьков 2007
Содержание
Задание на курсовую работу………………………………………………………….1
Введение……………………………………………………………………………….3
1.Переходные процессы в линейных электрических цепях
1.1 Переходные характеристики ЛЭЦ с сосредоточенными элементами…..3
1.2 Законы коммутации…………………………………………………………5
1.3 Основы классического метода анализа переходных процессов………….6
1.4 Свободная и вынужденная составляющая переходных колебаний ( на
примере цепи 1-го порядка)…………………………………………..………7
1.5 Постоянная времени цепи и ее физический смысл……………………...10
2. Расчет прохождения сигнала через линейные электрические цепи……….….11
2.1Разложение импульсных колебаний на гармонические
составляющие………………………………………………………………….11
2.2 Расчет спектра выходного сигнала линейной электрической
цепи………………………………………………………………………..……15
2.2.1 Расчет прохождения сигнала через ЛЭЦ первого порядка………...…15
2.2.2. Расчет прохождения сигнала через идеальный источник напряжения, управляемый напряжением…………………………………………………..18
2.2.3 Расчет прохождения сигнала через ЛЭЦ второго порядка………..…20
Выводы……………………………………………………………………………….25
Список литературы…………………………………………………………………..25
Приложение 1. Графики сигналов воздействия и отклика ЛЭЦ …………………26
Введение
Задача анализа прохождения сигнала состоит в качественной и количественной оценках свойств электрической цепи и является одной из основных задач радиотехники, связи, измерительной техники.
При изучении электрических цепей рассматриваются установившиеся, стационарные значения токов и напряжений. Однако, наряду со стационарными режимами, большое значение имеют переходные процессы, происходящие в цепях в результате коммутации.
Переходные процессы обычно являются быстропротекающими процессами; длительность их составляет часто десятые, сотые, иногда даже миллионные доли секунды; сравнительно редко происходят переходные процессы, длительность которых составляет секунды и десятки секунд. Тем не менее, изучение переходных процессов весьма важно, так как оно позволяет выявить возможные превышения напряжения на отдельных участках цепи, которые могут оказаться опасными для изоляции установки, позволяет выяснить возможные увеличения амплитуд токов, которые могут в десятки раз превышать амплитуду тока установившегося периодического процесса.
Изучение переходных процессов позволяет решать и такие вопросы, как вопрос о том, как деформируются по форме и амплитуде сигналы при прохождении их через усилители, фильтры и другие радиотехнические устройства.
1.1.Переходные характеристики лэц
с сосредоточенными элементами.
Отношение реакции электрической цепи на ступенчатое воздействие к величине воздействия при нулевых начальных условиях называют переходной характеристикой цепи.
Переходные характеристики электрических цепей относятся к числу нормированных временных характеристик устойчивых линейных электрических цепей. При этом с неограниченным ростом времени значения переходной характеристики асимптотически приближаются к некоторой конечной величине, характеризующей относительную величину реакции электрической цепи в режиме постоянного тока. В частных случаях значение этого предела может быть равно нулю.
В зависимости от типа реакции и типа воздействия (ток или напряжение) различают четыре вида переходных характеристик (рис. 1.1):
переходная характеристика по напряжению
,
(1.1)
переходная характеристика по току
,
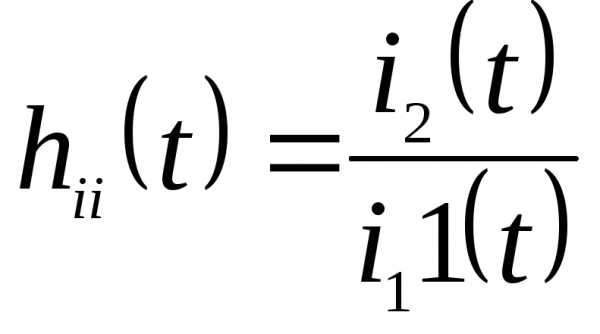
переходное сопротивление
;
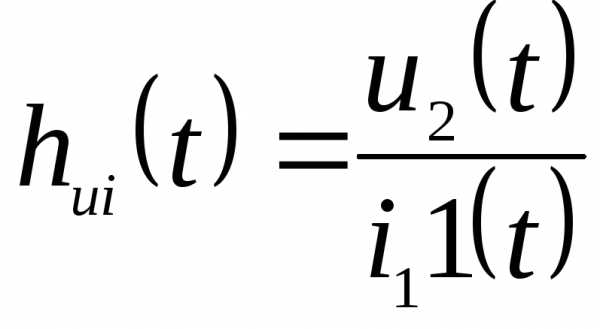
переходная проводимость
.
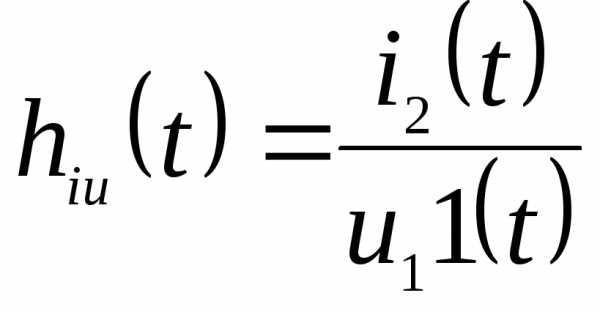
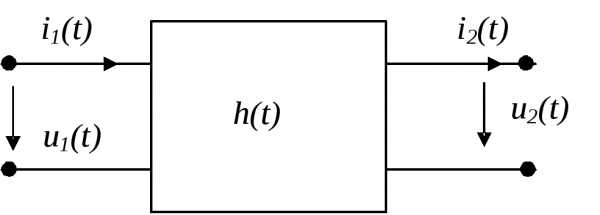
Рис. 1.1
Рассмотрим линейную электрическую цепь, не содержащую независимых источников тока и напряжения. Пусть внешнее воздействие на цепь представляет собой неединичный скачок x(t)=x1(t)=X*1(t-t0), а реакция цепи на это воздействие при нулевых начальных условиях y(t)=y1(t).
Тогда переходная характеристика цепи
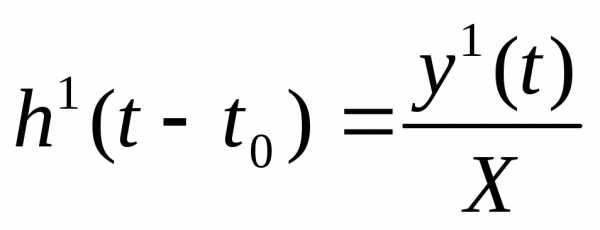(1.2)
Из выражения (1.1) видим, что h2(t-t0)=y1(t), если Х=1, следовательно, переходная характеристика цепи численно равна реакции цепи на воздействие единичного скачка тока или напряжения.
Пусть внешнее воздействие на цепь задается в виде произвольной функции х=х(t), равной нулю при t <t0 и непрерывной при всех t, за исключением точки t=t0. Эту функцию можно приближенно представить в виде суммы неединичных скачков. Тогда, в соответствии с определением переходной характеристики (1.2), реакция цепи на воздействие неединичного скачка, приложенного в момент времени t равна произведению высоты скачка на переходную характеристику цепи. Следовательно, реакция цепи на воздействие, представляемое суммой неединичных скачков, равна сумме произведений высот скачков на соответствующие переходные характеристики:
(1.3)
Точность представления входного воздействия в виде суммы неединичных скачков, как и точность представления реакции цепи в виде (1.3), возрастает с уменьшением шага разбиения по времени ∆τ. При ∆τ →0 суммирование заменяется интегрированием:
(1.4)
Используя это выражение, которое известно под названием интеграл Дюамеля, можно найти точное значение реакции цепи на заданное воздействие х=х(t) в любой момент времени t после коммутации
1.2.Законы коммутации
Неустановившиеся процессы, которые имеют место в цепи при переходе от одного установившегося режима к другому, называются переходными.
Переходные процессы, связанные с изменением топологии цепи или различными коммутациями пассивных элементов, присущи в основном устройствам производства, передачи и преобразования электрической энергии.
При анализе переходных процессов в цепи, как правило, можно пренебречь длительностью процесса коммутации, т.е. считать, что коммутация осуществляется практически мгновенно. Начало отсчета времени переходного процесса обычно совмещают с моментом коммутации, причем через t=0_ обозначают, момент времени, непосредственно предшествующий коммутации, а через t=0+, или t=0, момент времени, следующий непосредственно за коммутацией (начальный момент времени после коммутации).
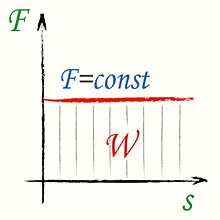
Переход реальной электрической цепи от одного установившегося соединения к другому не может происходить мгновенно, скачком. Это объясняется тем, что каждому установившемуся значению соответствует определенное значение энергии, запасенной в электрических и магнитных полях. Скачкообразный переход от одного установившегося режима к другому потребовал бы скачкообразного изменения запасенной энергии, что, учитывая выражение
, (1.5)
возможно только, если источники энергии обладают бесконечно большой мощностью, т. е. отдаваемые ими токи и напряжения могут принимать бесконечно большие значения. В связи с тем, что любой реальный источник энергии может отдавать только конечную мощность, суммарная энергия, запасенная в цепи, может изменяться только плавно, т.е. представляет собой непрерывную функцию времени.
Запасенная энергия цепи, содержащей реактивные элементы, определяется суммарным зарядом всех конденсаторов и потокосцеплением всех индуктивных катушек. Суммарные потокосцепление и заряд цепи также являются непрерывными функциями времени. В частности после коммутации они равны суммарному потокосцеплению и суммарному заряду цепи в момент коммутации.
(1.6)
В реальных цепях в момент коммутации возможны коммутационные потери энергии, например потери энергии за счет искры или электрической дуги между контактами переключателей, поэтому суммарная энергия цепи после коммутации может быть несколько меньше суммарной энергии цепи до коммутации.
Если коммутация идеализированной электрической цепи не затрагивает ветвей, содержащих реактивные элементы, т.е. в процессе коммутации не производиться подключения или отключения ветвей, содержащих емкости и индуктивности, и не происходит скачкообразного изменения их параметров, то из принципа непрерывности суммарных потокосцепления и заряда цепи следует непрерывность токов индуктивностей и напряжений емкостей. Вывод о непрерывности токов индуктивностей и напряжений емкостей формулируется в виде законов коммутации.
Первый закон коммутации: в начальный момент времени после коммутации ток индуктивности сохраняет такое же значение, как и непосредственно перед коммутацией:
(1.7)
а затем плавно изменяется, начиная с этого значения.
Второй закон коммутации: в начальный момент времени после коммутации напряжение на емкости сохраняет такое же значение, как и непосредственно перед коммутацией:
(1.8)
а затем плавно изменяется, начиная с этого значения.
Законы коммутации не накладывают ограничений на характер изменения токов емкостей, напряжений индуктивностей и токов или напряжений сопротивлений, которые могут изменяться произвольным образом, в том числе и скачкообразно.
studfiles.net
Переходные процессы в линейных электрических цепях
}Переходные процессы в линейных электрических цепях.
Определения
1. Коммутация это какое-либо включение, выключение, переключение пассивных и активных ветвей и элементов схемы, приводящее к изменению конфигурации схемы или ее параметров. Предполагается, что коммутация совершается мгновенно (время коммутации равно нулю). Момент времени непосредственно до коммутации называется: 0- (“минус ноль”, момент непосредственно после: 0+ (“плюс ноль”).
Для схемы до коммутации и после коммутации характерны некоторые установившиеся режимы. В результате коммутации в схеме возникает некий режим перехода от установившегося процесса до коммутации к установившемуся процессу после коммутации. Это и есть переходный процесс. Теоретически длительность переходного процесса равна бесконечности, т.е. режим в цепи асимптотически приближается к установившемуся. Практически малым отличием режима от установившегося пренебрегают, и считают, что длительность переходного процесса конечна.
Законы коммутации
- В индуктивном элементе ток и магнитный поток в момент коммутации не изменяются, т.е.
(1)
Ток индуктивности сразу после коммутации равен току индуктивности непосредственно перед коммутацией (то же для магнитных потоков). В переходном процессе ток индуктивности и ее магнитный поток изменяются, начиная с этого значения.
- Напряжение емкостного элемента и его заряд в момент коммутации не изменяются.
(2)
Напряжение на емкости и ее электрический заряд сразу после коммутации равны напряжению на емкости и электрическому заряду непосредственно перед коммутацией. В переходном процессе напряжение на емкости и ее электрический заряд изменяются, начиная с этого значения.
Обоснование законов коммутации
Если в момент коммутации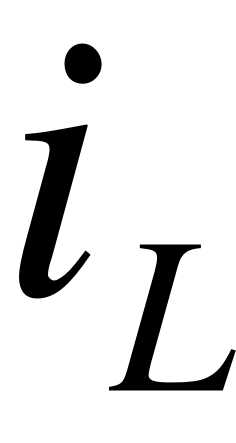 
меняется скачком, то и, следовательно, из-за чего нарушается второй закон Кирхгофа, чего не может быть.
Аналогично.
Если в момент коммутации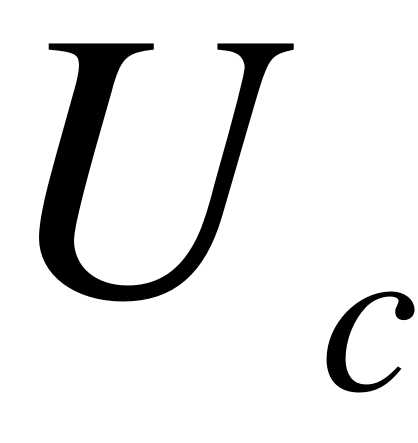 
меняется скачком, то и, следовательно, 
из-за чего нарушается первый закон Кирхгофа, чего не может быть.
Обоснование законов коммутации из закона сохранения энергии.
Энергия магнитного поля индуктивности:
Энергия электрического поля емкости:
,
- мощность.
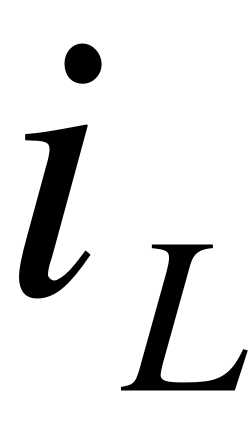, , если 
или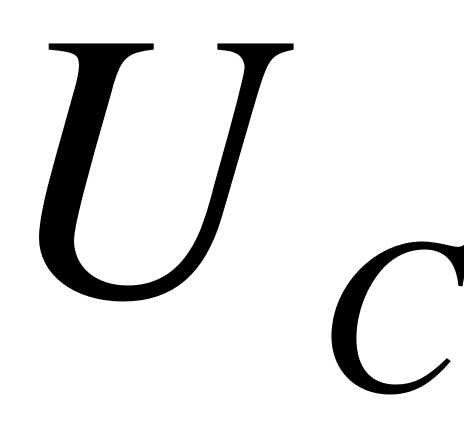 
меняются скачком, то соответствующая мощность 
и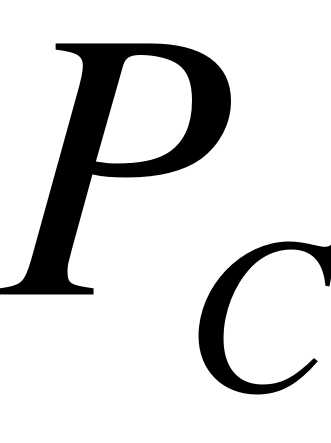 
стремятся к , следовательно, для скачкообразного изменения 
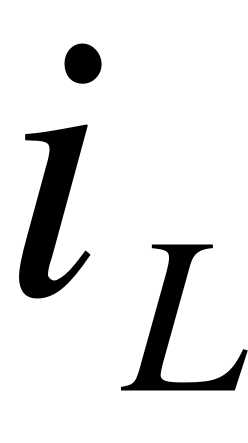или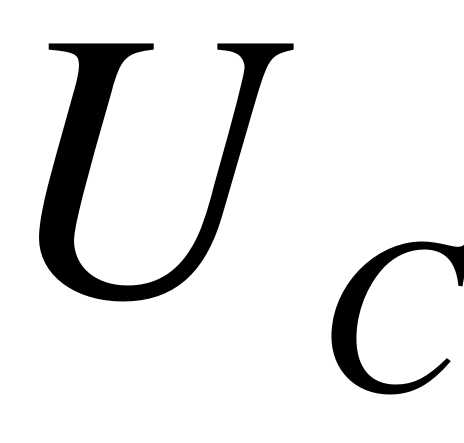 
схему надо подключить к источнику питания бесконечной мощности, чего быть не может.
Сформулированные законы коммутации не являются универсальными: существуют схемы, для которых они не выполняются. Эти схемы называются некорректными, для их расчета существуют специальные методы.
Значения в начальный момент времени токов индуктивностей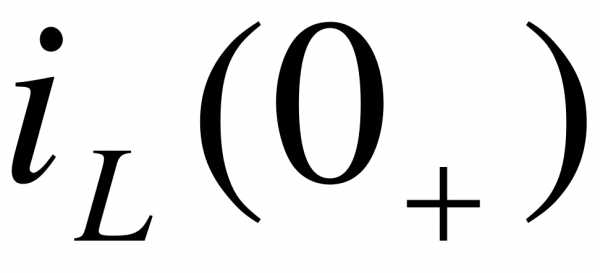 
и напряжений на ёмкостях 
называются независимыми начальными условиями. Значения других величин в начальный момент времени 
, 
, 
, 
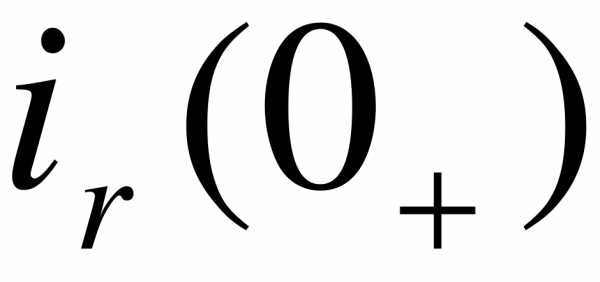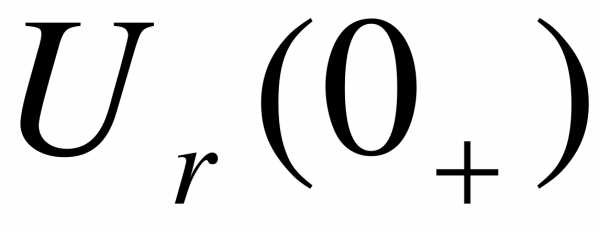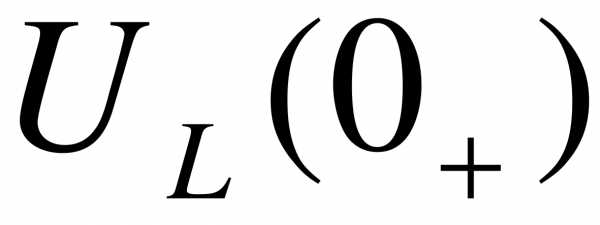называются зависимыми начальными условиями, они могут изменяться скачком в момент коммутации и определяются по независимым начальным условиям с помощью первого и второго закона Кирхгофа.
Зависимость токов и напряжений в схеме от времени представляем в виде суммы двух составляющих: принужденной и свободной:
, . (3)
Принужденная составляющая описывает установившийся режим цепи после коммутации, она определяется свойствами цепи и источника питания. Если источник постоянный, то установившийся режим постоянный и принужденная составляющая постоянная. Если источник периодический, то установившийся режим и принужденная составляющая - периодические.
Свободная составляющая отражает зависимость переходного процесса от свойств цепи конфигурации и параметров.
Математически переходный процесс в линейной схеме описывается линейным обыкновенным дифференциальным уравнением с постоянными коэффициентами n-ого порядка, где n число индуктивностей и емкостей в схеме, т.е. элементов, накапливающих энергию, источники напряжения и тока входят в правую часть этого ОДУ. Принужденная составляющая является частным решением неоднородного ОДУ, свободная составляющая общим решением однородного ОДУ. Для ОДУ n-ого порядка требуется n начальных условий. Они могут быть получены из n независимых условий: токов индуктивностей и напряжений емкостей в момент коммутации.
Метод расчета переходных процессов в линейных цепях состоящий в поиске решения ОДУ n-ого порядка называется классическим методом расчета переходных процессов. При этом само ОДУ в явном виде не записывается.
Пример 1
Включение RC-цепи на постоянное напряжение.
Найти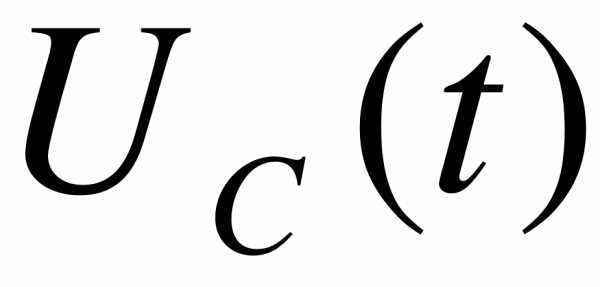 
, ключ замыкается
В замкнутом состоянии цепь является контуром, запишем для него второй закон Кирхгофа:
, т.к.
т.е.
Это ОДУ - линейное с постоянными коэффициентами.
Принужденное напряжение частное решение неоднородного ДУ - ищем в виде константы:
:
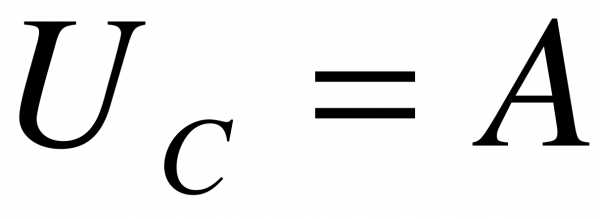Общее решение однородного уравнения будет иметь вид:
- постоянная времени.
Постоянная B ищется из нескольких условий: по закону коммутации , до коммутации ключ был разомкнут и все напряжения в схеме были равны нулю (она была отключена от источника)
Это и есть начальное условие для нашей задачи.
Решение ищем в виде:
отсюда
, 
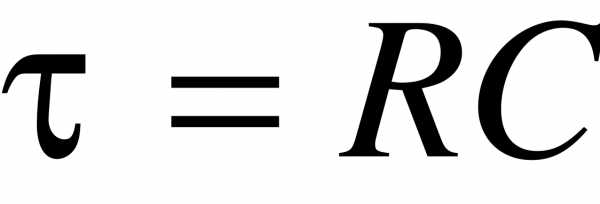(4)
Пример 2
Ключ замыкается
По законам Кирхгофа составим систему ОДУ:
;
(5)
,
откуда
подставим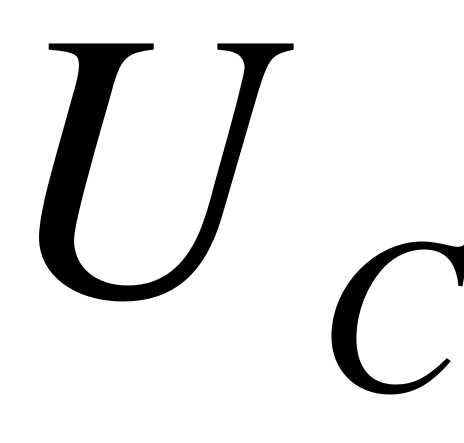 
в систему уравнений и продифференцируем по t:
(6)
Независимые начальные условия
;
определим из схемы до коммутации
ввиду того, что , , , постоянный ток через ёмкость не течет.
Запишем искомую величину в виде суммы свободной и принужденной составляющей:
Принужденная составляющая есть установившаяся составляющая после коммутации, когда переходный процесс закончился.
, 
Постоянный ток через емкость не течет.
Чтобы найти свободную составляющую переходного процесса, которая является общим решением однородного уравнения, необходимо записать характеристическое уравнение системы ОДУ (или ОДУ ей эквивалентного) и найти его корни. Из системы (6) можно исключить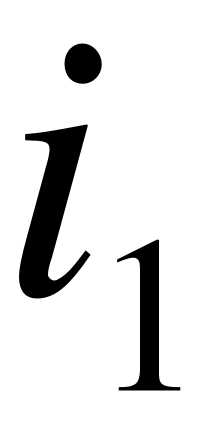 
и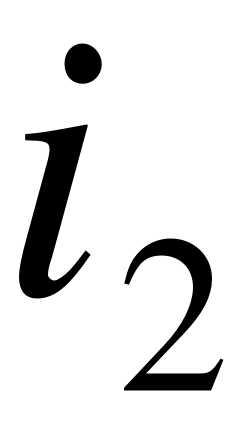 
, и для полученного ОДУ записать характеристическое уравнение. Но можно составить главный определитель системы (5) и приравнять его нулю:
отсюда
Корни характеристического уравнения:
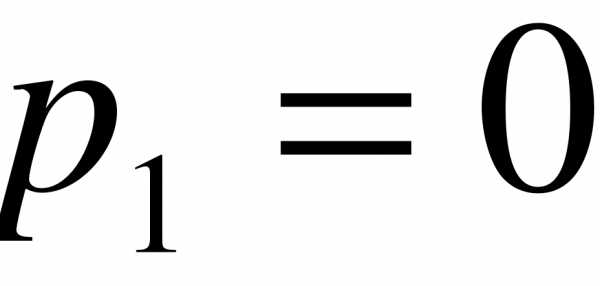- соответствует установившемуся режиму. Два других найдем из уравнения
или
Дискриминант этого квадратного уравнения имеет вид:
1) 
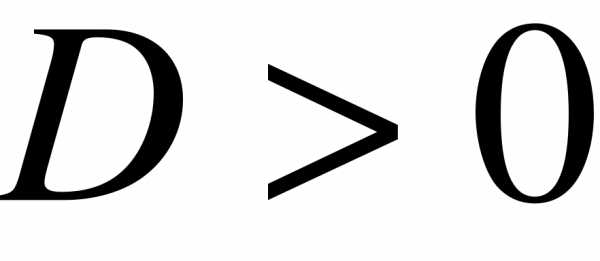- корни действительные, разные
) 
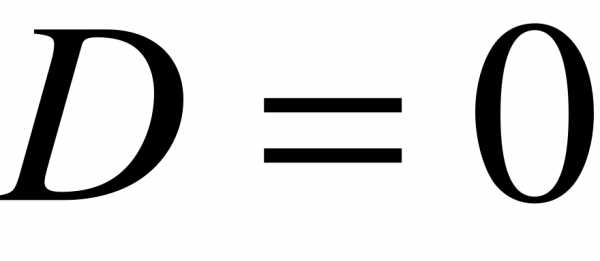- корни действительные, одинаковые
) 
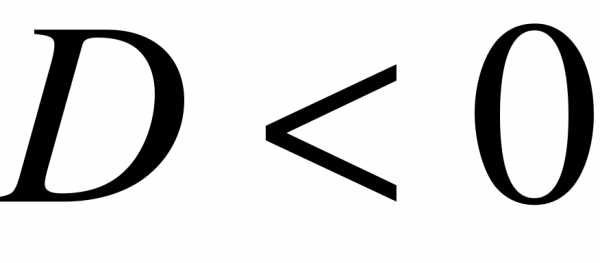- корни комплексные сопряженные
В первом случае свободная составляющая имеет вид
Во втором случае:
В третьем случае:
- есть действительная часть корней, св модуль мнимых частей корней.
Пусть в нашем случае корни действительные, различные, тогда, с учетом:
,
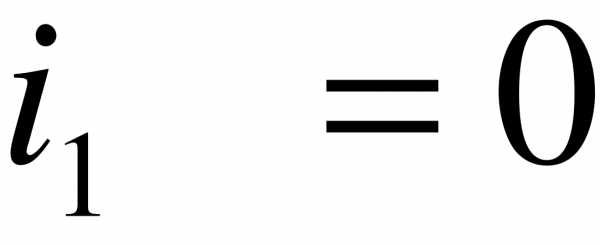решение примет вид:
Для определения постоянных интегрирования 
и 
, запишем значение и его производную в начальный момент времени:
значения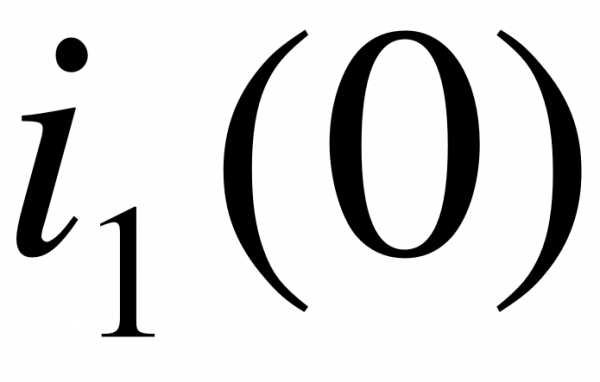 
и 
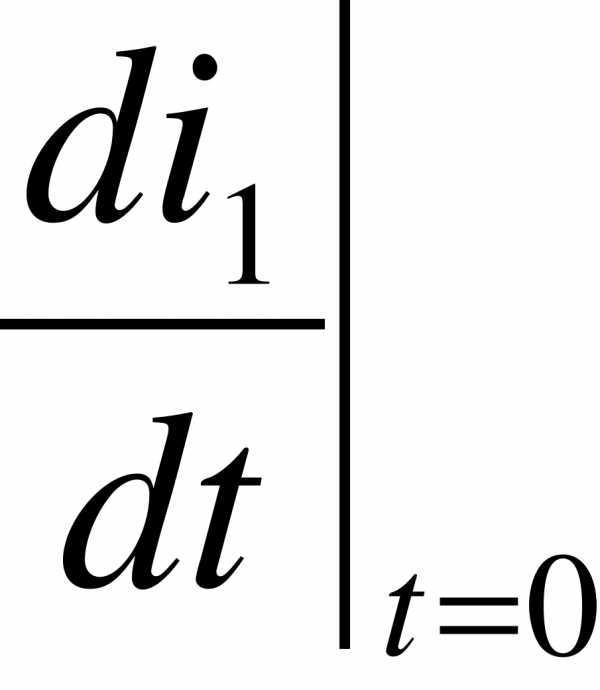определим из системы (5), записанной для начального момента времени 
:
.
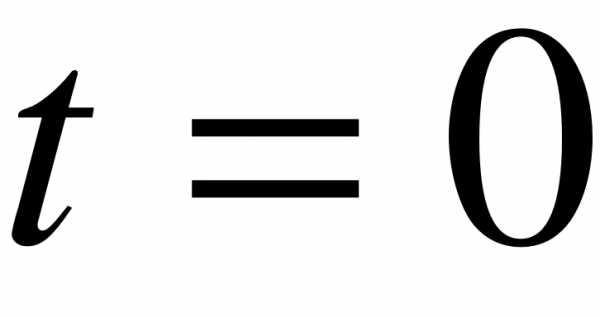Из законов коммутации:
,
тогда:
,
Для определения начального значения производной 
продифференцируем систему (5) и подставим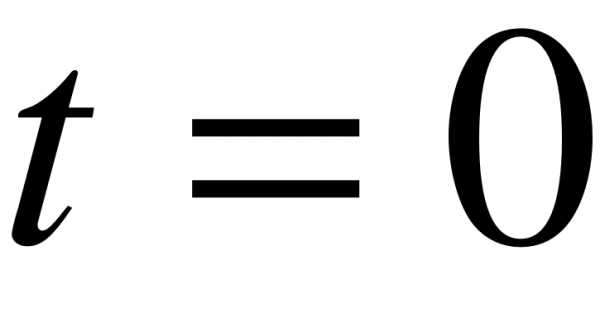 
отсюда
из второго уравнения исходной системы при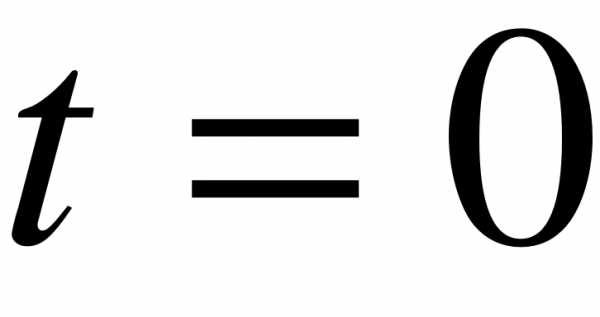 
Алгебраические уравнения для постоянных интегрирования:
refleader.ru
Тема №8. Переходные процессы в линейных электрических цепях.
13.1. Введение.
Рассматриваемые ранее процессы в электрических цепях относятся к установившимся. Это такие процессы, при которых напряжение и токи либо неизменны во времени ( цепи постоянного тока ), либо представляют собой периодические функции времени ( цепи переменного тока ).
Наступлению установившегося процесса, отличного от первоначального режима работы, предшествует, как правило, переходный процесс, при котором напряжения и токи изменяются непериодически. Таким образом, переходный процесс возникает в электрической цепи при переходе от одного установившегося состояния к другому. Известно, что определение напряжений и токов в установившемся режиме сводится к нахождению частных решений дифференциальных уравнений электрической цепи. Способы отыскания таких решений были рассмотрены ранее.
Переход от одного режима работы цепи к другому может быть вызван любыми переключениями в этой электрической цепи. Такие переключения называются в электротехнике коммутацией, причем считается, что сам процесс переключения производится мгновенно ( без затрат времени ). Однако, при любом внезапном изменении структуры электрической цепи, имеющиеся запасы энергии электрических и магнитных полей не соответствуют запасам энергии в новом установившемся режиме, после произошедших изменений в электрической цепи.
Но энергия не может измениться скачком ( на конечную величину за бесконечно малый промежуток времени )т.к. это приводит к бесконечно большой мощности ().
Поэтому новый режим в электрической цепи не устанавливается мгновенно. Время, затрачиваемое на возникновение нового установившегося состояния электрической цепи, называется временем переходного процесса.
Для завершения переходного процесса и наступления установившегося процесса теоретически требуется бесконечно большое время. Практически, время переходного процесса определяется малым интервалом, по истечении которого токи и напряжения настолько приближаются к установившимся, что разница оказывается почти неощутимой. Энергия, накопившаяся в реактивных элементах электрической цепи расходуется ( переходит в тепловую ) на сопротивлениях. Чем интенсивнее этот переход, тем быстрее протекает переходный процесс. Подбирая соответствующие параметры цепи ( элементы R,L,C ) можно ускорить или замедлить переходный процесс.
Переходные процессы могут быть нежелательным и опасными, например, при коротких замыканиях в энергетических системах. Однако, переходные процессы могут представлять собой естественный, нормальный режим работы цепи, например, в радиопередающих или радиоприёмных устройствах или системах автоматического регулирования.
13.2. Законы коммутации.
Введем следующие обозначения:
- Будем считать, что отсчет времени коммутации начинается с момента переключения, т.е. t=0.
- Величины токов, напряжений, их производных по времени к моменту, предшествующему коммутации, обозначим (0-), а сразу же после коммутации, обозначим (0+). Например iL(0-) – обозначает ток через индуктивность к моменту коммутации, uc(0+)- обозначает напряжение на емкости сразу же после коммутации.
Высказанные ранее положения о невозможности мгновенного изменения энергии электрических или магнитных полей выражают признаки непрерывности во времени потокосцепления индуктивности и электрического заряда емкости. 
. Если
потокосцепление изменяется скачком, то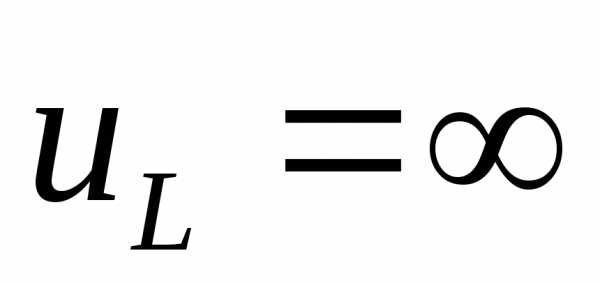
, что лишено физического смысла.
Но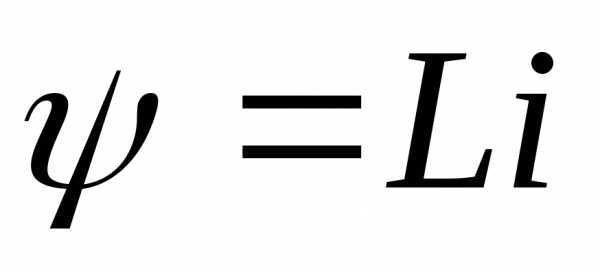 
, поэтому приL=const ток через индуктивность ( т.е. в цепи с индуктивностью ) не может измениться скачком. Таким образом, ток в цепи с индуктивностью, установившийся к моменту коммутации, равен току в цепи с индуктивностью, появившемуся сразу же после коммутации. Затем, с течением времени, этот ток плавно изменяется. Это можно записать так, используя рассматриваемые выше обозначения: .
Этот закон называется первым законом коммутации.
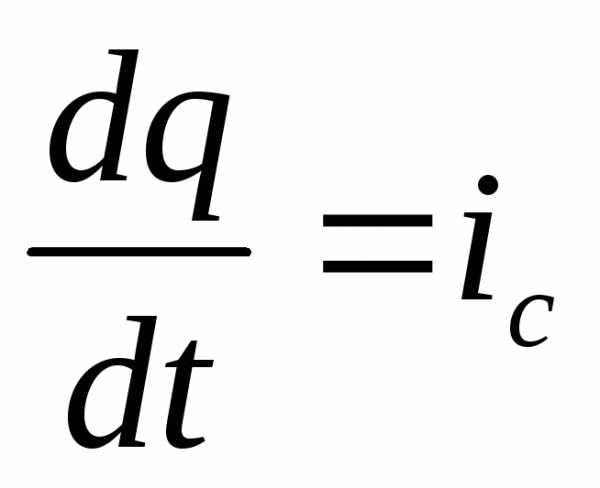если q меняется скачком, то 
, что лишено физического смысла. Так как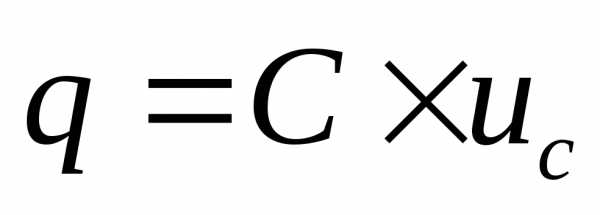
, где С – емкость - величина постоянная, то напряжение на емкости не может изменяться скачком. Поэтому, напряжение на емкости, установившееся к моменту коммутации, равно напряжению на емкости, имеющемуся сразу же после коммутации. Затем, с течением времени это напряжение плавно изменяется.
Используя введенные выше обозначения, запишем: . Этот закон называют вторым законом коммутации.
Сказанное ранее отнюдь не означает, что в электрических цепях невозможны скачкообразные изменения токов и напряжений. Например, напряжение на индуктивности и ток через емкость могут изменяться скачком. Возможны скачкообразные изменения токов и напряжений на резисторах.
studfiles.net
Переходные процессы в линейных электрических цепях
МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
(государственный технический университет)
ФИЛИАЛ «ВЗЛЕТ»
Кафедра РЭВС
РАЛДЫГИН И.К.
КОНСПЕКТ ЛЕКЦИЙ ПО КУРСУ
«Основы теории цепей». Часть 3.
Переходные процессы в линейных электрических цепях
Учебное пособие для студентов радиотехнической специальности.
Ахтубинск – 2004
Предисловие к 3-ей части
В третьей части конспекта по Основам теории цепей (ОТЦ) кратко изложены два метода расчета переходных процессов в линейных электрических цепях: Классический метод и Операторный метод. И классический и операторный методы расчета теоретически можно применять для решения задач любой сложности. Каким из них пользоваться определяется автором.
Однако классический метод физически более прозрачен, чем операторный, в котором решение уравнений во многом формализовано. Операторный метод имеет перед классическим явное преимущество если для расчета переходных процессов использовать прикладную программу Mathcad 2000, особенно в тех случаях, когда воздействующее напряжение является линейно возрастающее или в виде всплеска одной или несколько экспонент.
Глава 1. Основные сведения о переходных процессах в линейных электрических цепях
1.1 Возникновение и общая характеристика переходных процессов
Выше рассматривались цепи, в которых выполнялись два условия: 1) Источники энергии были подключены к цепи теоретически бесконечно давно; 2) Никаких изменений в состоянии цепи не производилось. Такой режим работы цепи называется установившимся или принужденным.
Переходным называют электромагнитный процесс, возникающий в электрической цепи, при переходе от одного установившегося режима к другому. Этот переход может происходить вследствие преднамеренного или случайного отключения цепи, а также подключения ее под напряжение, вследствие обрыва или короткого замыкания в цепи.
Любые изменения в цепи можно представить в виде переключений, которые называются коммутацией. Коммутация на схемах обозначается в виде ключа со стрелкой, обозначающей замыкание или размыкание:
Теоретически считается, что коммутация производится мгновенно.
Установившийся режим работы цепи при заданных и неизменных ее параметрах полностью определяется источником энергии: постоянный ток, переменный ток.
После коммутации, т.е. во время переходного процесса, токи и напряжения в цепи определяются не только внешними, но и внутренними источниками энергии, в качестве которых выступают индуктивности и емкости.
Дело в том, что в режиме, который существовал до коммутации, в катушках и конденсаторах было накоплено определенное количество энергии:
В момент коммутации (t=0) начинается перераспределение энергии между внутренними накопителями и внешними источниками; при этом часть энергии необратимо преобразуется в тепло.
По истечении какого-то времени после коммутации в цепи установится новый режим, который будет обусловлен только внешними источниками энергии. При отключении цепи от внешних источников переходной процесс будет существовать только за счет энергии накопленной в индуктивностях и емкостях, т.е. только за счет внутренней энергии. Новый установившийся режим, в этом случае, будет характеризоваться отсутствием тока в цепи.
Задача анализа переходного процесса заключается в том, чтобы установить по какому закону и как долго будет происходить переход от одного режима к другому.
В соответствии с законом непрерывности энергии напряжение на емкости и ток через индуктивность не могут изменяться скачком, т.к. в этом случае мощность, равная скорости изменения энергии обращалась бы в бесконечность, что физически невозможно.
На основании изложенного сформулированы два закона коммутации:
Заряд и напряжение на емкости в момент коммутации остаются такими же, какими они были непосредственно перед коммутацией, а затем плавно изменяются;
Ток через индуктивность в момент коммутации остается таким же, каким он был непосредственно перед коммуникацией, а затем плавно изменяется.
Математически законы коммутации записываются в следующем виде:
Ток через емкость и напряжение на индуктивности могут изменяться скачком.
1.2 Начальные условия
Значения токов, напряжений и их производных в момент коммутации называют начальными условиями.
Начальные условия подразделяются на зависимые и независимые.
Напряжение на емкости и ток через индуктивность, непосредственно перед коммутацией, называются независимыми начальными условиями, т.к. их значения не зависят от вида и места коммутации и определяются только энергетическим состоянием цепи непосредственно перед коммутацией.
Зависимыми начальными условиями являются токи через емкость и напряжение на индуктивности в момент коммутации. Они зависит от вида и места коммутации и в общем случае, в момент коммутации, могут изменяться скачком.
Независимые начальные условия определяются в цепи до коммутации, а зависимые начальные условия определяются в цепи образовавшейся в момент коммутации.
1.3 Математические основы анализа переходных процессов
Электромагнитные процессы в линейных электрических цепях в установившемся режиме описываются законами Кирхгофа для мгновенных или комплексных значений токов и напряжений.
Для определения законов изменения токов и напряжений в переходном режиме необходимо линейные уравнения, составленные по законам Кирхгофа для мгновенных значений, записать в виде дифференциальных уравнений, а затем решить эти уравнения относительно искомых токов и напряжений.
Таким образом, анализ переходных процессов сводится к решению обыкновенных дифференциальных уравнений с правой частью.
На практике для решения дифференциальных уравнений применяют классический и операторный методы расчета.
Суть классического метода расчета рассмотрим на конкретном примере.
Пусть задана электрическая цепь из последовательно соединенных RC элементов Рис.1.1.
Рис. 1.1. Цепь RC в момент t=0 при нулевых начальных условиях, Uc(0)=0, подключается к источнику постоянного напряжения
Определим, в общем виде, законы изменения напряжения на емкости и ток в цепи после коммутации.
Решение. При анализе переходных процессов классическим методом необходимо составить уравнения по законам Кирхгофа для мгновенных значений токов и напряжений. В данном случае можно составить только одно уравнение по второму закону Кирхгофа:
(1.1)
Поскольку исходное алгебраическое уравнение (1.1) можно записать в дифференциальной форме:
(1.2)
При анализе переходных процессов в качестве искомых функций могут выступать токи и напряжения на пассивных элементах цепи, образовавшейся после коммутации. Для общности обозначений, принятых в математике, условимся в дальнейшем искомую функцию обозначать Y(t).
ua.coolreferat.com
Видеоматериалы
Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше
Подробнее...С начала года из ветхого и аварийного жилья в республике были переселены десятки семей
Подробнее...Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе
Подробнее...Актуальные темы
ОТЧЕТ о деятельности министерства энергетики, ЖКХ и тарифной политики Кабардино-Балкарской Республики в сфере государственного регулирования и контроля цен и тарифов в 2012 году и об основных задачах на 2013 год
Подробнее...Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год
Подробнее...
КОНТАКТЫ
360051, КБР, г. Нальчик
ул. Горького, 4
тел: 8 (8662) 40-93-82
факс: 8 (8662) 47-31-81
e-mail:
Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.
