Закон ома для полной цепи и для участка цепи: варианты записи формулы, описание и объяснение
Закон Ома для участка цепи и полной цепи: формулы и определения
- Блог
- →
- Закон Ома для участка цепи и полной цепи: формулы и определения
Немецкий физик Георг Симон Ом (1787—1854) открыл основной закон электрической цепи.
Закон Ома для участка цепи:
Определение: Cила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.
- I — сила тока (в системе СИ измеряется — Ампер)
- Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
- Формула: I=frac{U}{R}
- U — напряжение (в системе СИ измеряется — Вольт)
- Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.
- Формула: U=IR
- Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.
- R — электрическое сопротивление (в системе СИ измеряется — Ом).
- Электрическое сопротивление R это отношение напряжения на концах проводника к силе тока, текущего по проводнику.
- Формула R=frac{U}{I}
Определение единицы сопротивления — Ом
1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1(Вольт) протекает ток 1 (Ампер).
Закон Ома для полной цепи
Определение: Сила тока в цепипропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника
Формула I=frac{varepsilon}{R+r}
- varepsilon — ЭДС источника напряжения, В;
- I — сила тока в цепи, А;
- R — сопротивление всех внешних элементов цепи, Ом;
- r — внутреннее сопротивление источника напряжения, Ом.
Как запомнить формулы закона Ома
Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.
.
- U — электрическое напряжение;
- I — сила тока;
- P — электрическая мощность;
- R — электрическое сопротивление
Смотри также:
- Первый закон Ньютона
- Второй закон Ньютона
- Третий закон Ньютона
Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.
Источник: https://bingoschool.ru/news/zakon-Oma-dlya-uchastka-i-polnoj-cepi:-formuly-i-opredeleniya/
Закон Ома простым языком
Для электрика и электронщика одним из основных законов является Закон Ома. Каждый день работа ставит перед специалистом новые задачи, и зачастую нужно подобрать замену сгоревшему резистору или группе элементов.
Электрику часто приходится менять кабеля, чтобы выбрать правильный нужно «прикинуть» ток в нагрузке, так приходится использовать простейшие физические законы и соотношения в повседневной жизни.
Значение Закона Ома в электротехники колоссально, к слову большинство дипломных работ электротехнических специальностей рассчитываются на 70-90% по одной формуле.
Историческая справка
Год открытия Закон Ома — 1826 немецким ученым Георгом Омом. Он эмпирически определил и описал закон о соотношении силы тока, напряжения и типа проводника.
Позже выяснилось, что третья составляющая – это не что иное, как сопротивление.
Впоследствии этот закон назвали в честь открывателя, но законом дело не ограничилось, его фамилией и назвали физическую величину, как дань уважения его работам.
Величина, в которой измеряют сопротивление, названа в честь Георга Ома. Например, резисторы имеют две основные характеристики: мощность в ваттах и сопротивление – единица измерения в Омах, килоомах, мегаомах и т.д.
Закон Ома для участка цепи
Для описания электрической цепи не содержащего ЭДС можно использовать закон Ома для участка цепи. Это наиболее простая форма записи.
Он выглядит так:
I=U/R
Где I – это ток, измеряется в Амперах, U – напряжение в вольтах, R – сопротивление в Омах.
Такая формула нам говорит, что ток прямопропорционален напряжению и обратнопропорционален сопротивлению – это точная формулировка Закона Ома. Физический смысл этой формулы – это описать зависимость тока через участок цепи при известном его сопротивлении и напряжении.
Внимание! Эта формула справедлива для постоянного тока, для переменного тока она имеет небольшие отличия, к этому вернемся позже.
Обратите внимание
Кроме соотношения электрических величин данная форма нам говорит о том, что график зависимости тока от напряжения в сопротивлении линеен и выполняется уравнение функции:
f(x) = ky или f(u) = IR или f(u)=(1/R)*I
Закон Ома для участка цепи применяют для расчетов сопротивления резистора на участке схемы или для определения тока через него при известном напряжении и сопротивлении.
Например, у нас есть резистор R сопротивлением в 6 Ом, к его выводам приложено напряжение 12 В. Необходимо узнать, какой ток будет протекать через него. Рассчитаем:
I=12 В/6 Ом=2 А
Идеальный проводник не имеет сопротивления, однако из-за структуры молекул вещества, из которого он состоит, любое проводящее тело обладает сопротивлением.
Например, это стало причиной перехода с алюминиевых проводов на медные в домашних электросетях. Удельное сопротивление меди (Ом на 1 метр длины) меньше чем алюминия.
Соответственно медные провода меньше греются, выдерживают большие токи, значит можно использовать провод меньшего сечения.
Еще один пример — спирали нагревательных приборов и резисторов обладают большим удельным сопротивлением, т.к. изготавливаются из разных высокоомных металлов, типа нихрома, кантала и пр.
Когда носители заряда движутся через проводник, они сталкиваются с частицами в кристаллической решетке, вследствие этого выделяется энергия в виде тепла и проводник нагревается.
Чем больше ток – тем больше столкновений – тем больше нагрев.
Чтобы снизить нагрев проводник нужно либо укоротить, либо увеличить его толщину (площадь поперечного сечения). Эту информацию можно записать в виде формулы:
Rпровод=ρ(L/S)
Где ρ – удельное сопротивление в Ом*мм2/м, L – длина в м, S – площадь поперечного сечения.
Закон Ома для параллельной и последовательной цепи
В зависимости от типа соединения наблюдается разный характер протекания тока и распределения напряжений. Для участка цепи последовательного соединения элементов напряжение, ток и сопротивление находятся по формуле:
I=I1=I2
U=U1+U2
R=R1+R2
Это значит, что в цепи из произвольного количества последовательно соединенных элементов протекает один и тот же ток.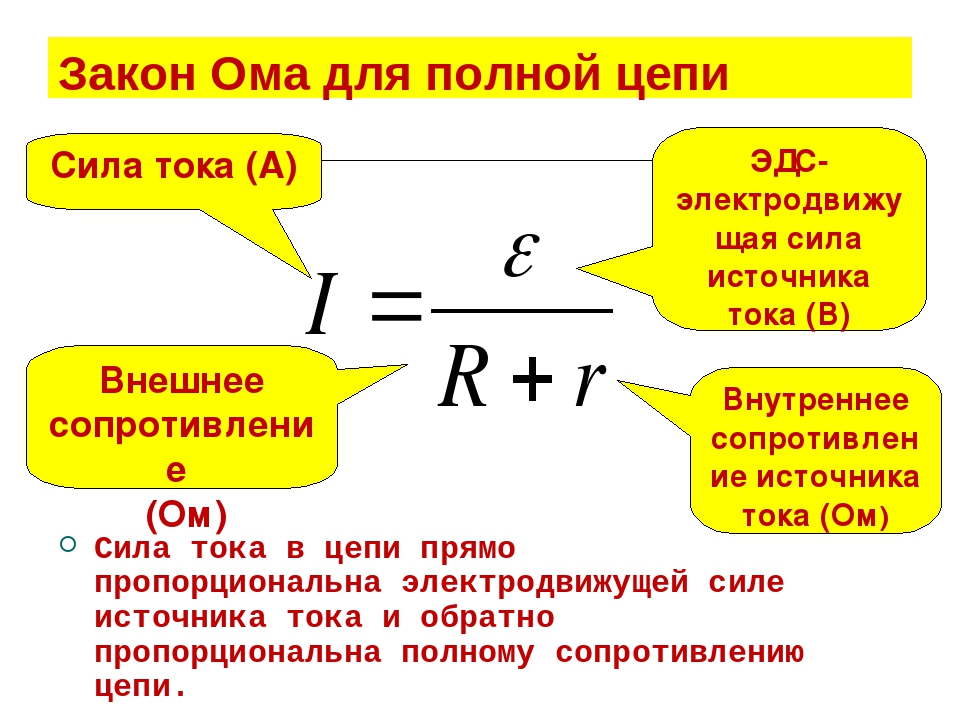
При этом напряжение, приложенное ко всем элементам (сумма падений напряжения), равно выходному напряжению источника питания. К каждому элементу в отдельности приложена своя величина напряжений и зависит от силы тока и сопротивления конкретного:
Uэл=I*Rэлемента
Сопротивление участка цепи для параллельно соединённых элементов рассчитывается по формуле:
I=I1+I2
U=U1=U2
1/R=1/R1+1/R2
Для смешанного соединения нужно приводить цепь к эквивалентному виду. Например, если один резистор соединен с двумя параллельно соединенными резисторами – то сперва посчитайте сопротивление параллельно соединенных. Вы получите общее сопротивление двух резисторов и вам остаётся сложить его с третьим, который с ними соединен последовательно.
Закон Ома д
варианты записи формулы, описание и объяснение
Закон Ома для участка цепи и полной цепи: формулы и определения
- Блог
- →
- Закон Ома для участка цепи и полной цепи: формулы и определения
Немецкий физик Георг Симон Ом (1787—1854) открыл основной закон электрической цепи.
Закон Ома для участка цепи:
Определение: Cила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.
- I — сила тока (в системе СИ измеряется — Ампер)
- Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
- Формула: I=frac{U}{R}
- U — напряжение (в системе СИ измеряется — Вольт)
- Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.
- Формула: U=IR
- R — электрическое сопротивление (в системе СИ измеряется — Ом).
- Электрическое сопротивление R это отношение напряжения на концах проводника к силе тока, текущего по проводнику.
- Формула R=frac{U}{I}
Определение единицы сопротивления — Ом
1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1(Вольт) протекает ток 1 (Ампер).
Закон Ома для полной цепи
Определение: Сила тока в цепипропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника
Формула I=frac{varepsilon}{R+r}
- varepsilon — ЭДС источника напряжения, В;
- I — сила тока в цепи, А;
- R — сопротивление всех внешних элементов цепи, Ом;
- r — внутреннее сопротивление источника напряжения, Ом.
Как запомнить формулы закона Ома
Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.
.
- U — электрическое напряжение;
- I — сила тока;
- P — электрическая мощность;
- R — электрическое сопротивление
Смотри также:
- Первый закон Ньютона
- Второй закон Ньютона
- Третий закон Ньютона
Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.
Закон Ома простым языком
Для электрика и электронщика одним из основных законов является Закон Ома. Каждый день работа ставит перед специалистом новые задачи, и зачастую нужно подобрать замену сгоревшему резистору или группе элементов.
Электрику часто приходится менять кабеля, чтобы выбрать правильный нужно «прикинуть» ток в нагрузке, так приходится использовать простейшие физические законы и соотношения в повседневной жизни.
Значение Закона Ома в электротехники колоссально, к слову большинство дипломных работ электротехнических специальностей рассчитываются на 70-90% по одной формуле.
Историческая справка
Год открытия Закон Ома — 1826 немецким ученым Георгом Омом. Он эмпирически определил и описал закон о соотношении силы тока, напряжения и типа проводника.
Позже выяснилось, что третья составляющая – это не что иное, как сопротивление.
Впоследствии этот закон назвали в честь открывателя, но законом дело не ограничилось, его фамилией и назвали физическую величину, как дань уважения его работам.
Величина, в которой измеряют сопротивление, названа в честь Георга Ома. Например, резисторы имеют две основные характеристики: мощность в ваттах и сопротивление – единица измерения в Омах, килоомах, мегаомах и т.д.
Закон Ома для участка цепи
Для описания электрической цепи не содержащего ЭДС можно использовать закон Ома для участка цепи. Это наиболее простая форма записи. Он выглядит так:
I=U/R
Где I – это ток, измеряется в Амперах, U – напряжение в вольтах, R – сопротивление в Омах.
Такая формула нам говорит, что ток прямопропорционален напряжению и обратнопропорционален сопротивлению – это точная формулировка Закона Ома. Физический смысл этой формулы – это описать зависимость тока через участок цепи при известном его сопротивлении и напряжении.
Внимание! Эта формула справедлива для постоянного тока, для переменного тока она имеет небольшие отличия, к этому вернемся позже.
Обратите внимание
Кроме соотношения электрических величин данная форма нам говорит о том, что график зависимости тока от напряжения в сопротивлении линеен и выполняется уравнение функции:
f(x) = ky или f(u) = IR или f(u)=(1/R)*I
Закон Ома для участка цепи применяют для расчетов сопротивления резистора на участке схемы или для определения тока через него при известном напряжении и сопротивлении.
Например, у нас есть резистор R сопротивлением в 6 Ом, к его выводам приложено напряжение 12 В. Необходимо узнать, какой ток будет протекать через него. Рассчитаем:
I=12 В/6 Ом=2 А
Идеальный проводник не имеет сопротивления, однако из-за структуры молекул вещества, из которого он состоит, любое проводящее тело обладает сопротивлением.
Например, это стало причиной перехода с алюминиевых проводов на медные в домашних электросетях. Удельное сопротивление меди (Ом на 1 метр длины) меньше чем алюминия.
Соответственно медные провода меньше греются, выдерживают большие токи, значит можно использовать провод меньшего сечения.
Еще один пример — спирали нагревательных приборов и резисторов обладают большим удельным сопротивлением, т.к. изготавливаются из разных высокоомных металлов, типа нихрома, кантала и пр.
Когда носители заряда движутся через проводник, они сталкиваются с частицами в кристаллической решетке, вследствие этого выделяется энергия в виде тепла и проводник нагревается.
Чем больше ток – тем больше столкновений – тем больше нагрев.
Чтобы снизить нагрев проводник нужно либо укоротить, либо увеличить его толщину (площадь поперечного сечения). Эту информацию можно записать в виде формулы:
Rпровод=ρ(L/S)
Где ρ – удельное сопротивление в Ом*мм2/м, L – длина в м, S – площадь поперечного сечения.
Закон Ома для параллельной и последовательной цепи
В зависимости от типа соединения наблюдается разный характер протекания тока и распределения напряжений. Для участка цепи последовательного соединения элементов напряжение, ток и сопротивление находятся по формуле:
I=I1=I2
U=U1+U2
R=R1+R2
Это значит, что в цепи из произвольного количества последовательно соединенных элементов протекает один и тот же ток.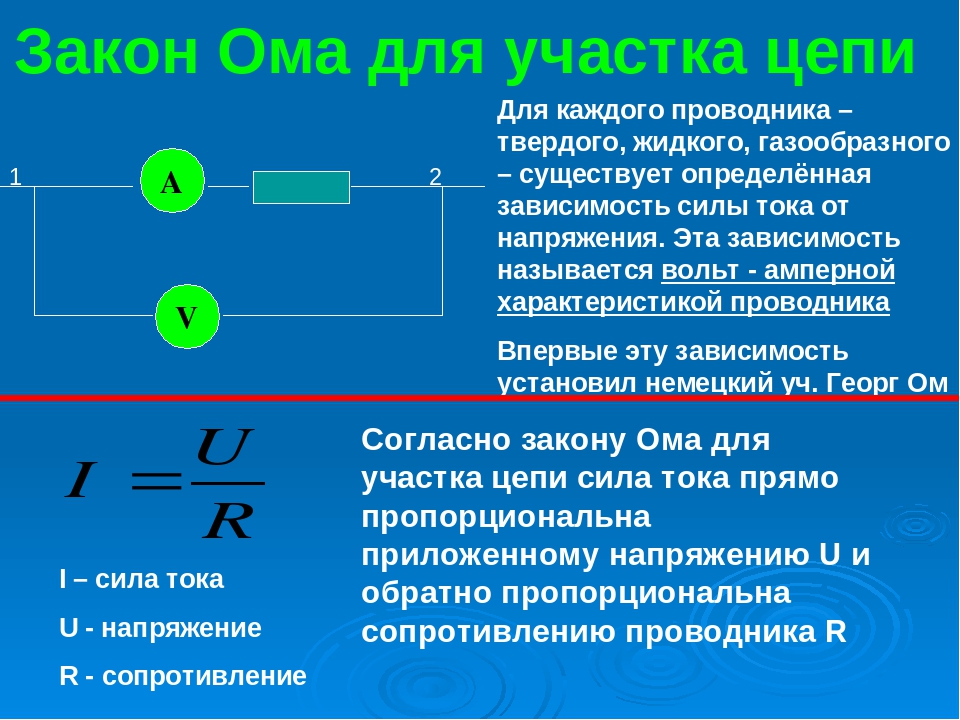
При этом напряжение, приложенное ко всем элементам (сумма падений напряжения), равно выходному напряжению источника питания. К каждому элементу в отдельности приложена своя величина напряжений и зависит от силы тока и сопротивления конкретного:
Uэл=I*Rэлемента
Сопротивление участка цепи для параллельно соединённых элементов рассчитывается по формуле:
I=I1+I2
U=U1=U2
1/R=1/R1+1/R2
Для смешанного соединения нужно приводить цепь к эквивалентному виду. Например, если один резистор соединен с двумя параллельно соединенными резисторами – то сперва посчитайте сопротивление параллельно соединенных. Вы получите общее сопротивление двух резисторов и вам остаётся сложить его с третьим, который с ними соединен последовательно.
Закон Ома для полной цепи
Полная цепь предполагает наличие источника питания. Идеальный источник питания – это прибор, который имеет единственную характеристику:
- напряжение, если это источник ЭДС;
- силу тока, если это источник тока;
Такой источник питания способен выдать любую мощность при неизменных выходных параметрах.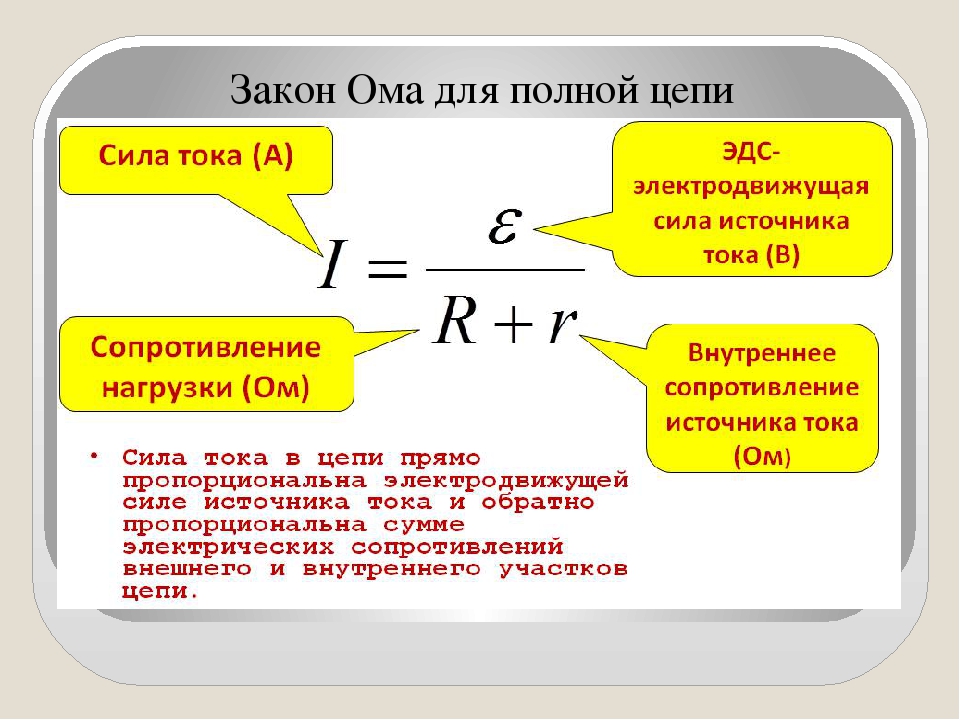
В реальном же источнике питания есть еще и такие параметры как мощность и внутреннее сопротивление. По сути, внутреннее сопротивление – это мнимый резистор, установленный последовательно с источником ЭДС.
Формула Закона Ома для полной цепи выглядит похоже, но добавляется внутренне сопротивление ИП. Для полной цепи записывается формулой:
I=ε/(R+r)
Где ε – ЭДС в Вольтах, R – сопротивление нагрузки, r – внутреннее сопротивление источника питания.
На практике внутреннее сопротивление является долями Ома, а для гальванических источников оно существенно возрастает. Вы это наблюдали, когда на двух батарейках (новой и севшей) одинаковое напряжение, но одна выдает нужный ток и работает исправно, а вторая не работает, т.к. проседает при малейшей нагрузке.
Закон Ома в дифференциальной и интегральной форме
Для однородного участка цепи приведенные выше форму
Закон Ома — Традиция
Материал из свободной русской энциклопедии «Традиция»
- Эта статья о физическом законе, относящемся к электромагнетизму. Для другого использования, см. Акустический закон Ома.
Для другого использования, см. Акустический закон Ома. V — напряжение,
I — сила тока,
R — сопротивление.
Георг Симон Ом.
Зако́н О́ма — закон, который открывает, что ток через проводник между двумя точками прямо пропорционален разности потенциалов между двумя точками. Вводя коэффициент пропорциональности, сопротивление,[1] приходим к обычному математическому уравнению, описывающего эту связь:[2]
$$I = \frac{V}{R},$$
где:
- \(I\) — ток через проводник в амперах,
- \(V\) — разность потенциалов, измеренная через проводник в вольтах,
- \(R\) — сопротивление проводника в омах. Конкретнее, в данном случае закон Ома гласит, что R в этом отношении является величиной постоянной, независимой от тока.[3]
Закон был назван в честь немецкого физика Георга Ома, который в трактате, опубликованном в 1827 году, описано измерения напряжения и тока с помощью простых электрических цепей, содержащих различные длины провода.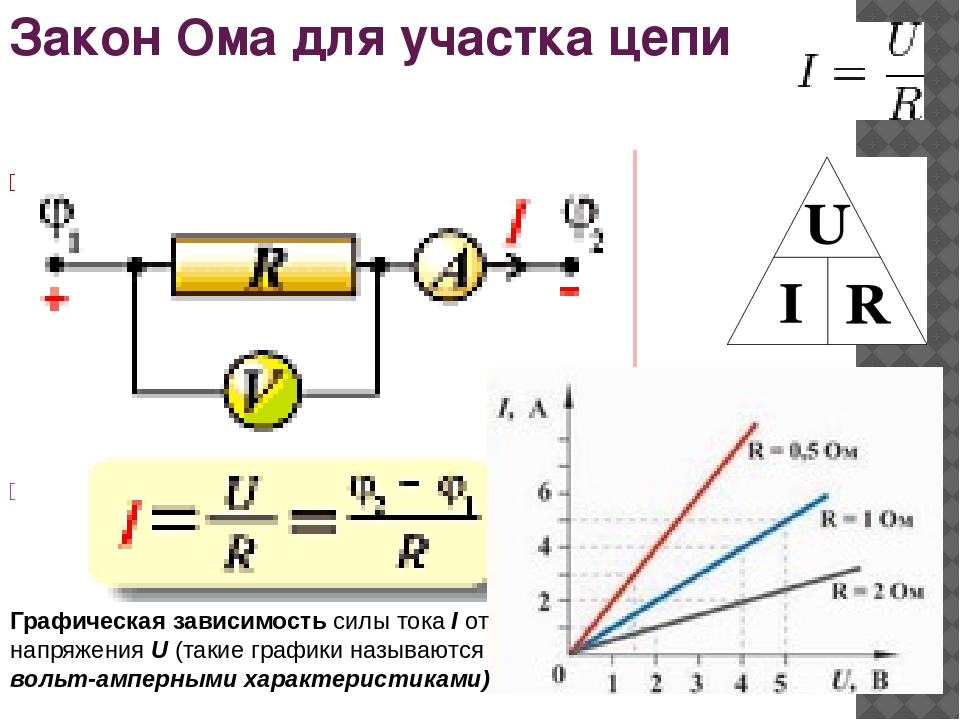
Он представил несколько более сложные уравнения, чтобы объяснить его экспериментальные результаты. Приведенное выше уравнение является современной формой закона Ома.
В физике термин «закон Ома» также применяется для обозначения различных обобщений закона, первоначально сформулированного Омом. Самый простой пример это:
$$\mathbf{J} = \sigma \mathbf{E},$$
где:
Эта переформулировка закона Ома принадлежит Густаву Кирхгофу.[4].
Мнемоническая диаграмма для Закона[править]
Схема, иллюстрирующая три составляющие закона Ома
Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления
В соответствии с этой диаграммой формально может быть записано выражение:
\(R\!= {U \over I}, \qquad(7)\)
которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно.
В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:
\(R\!= {\varrho l \over s}, \qquad(8) \)
где:
- \(\varrho \!\) — удельное сопротивление материала, из которого сделан проводник,
- \(l\!\) — его длина
- \(s\!\) — площадь его поперечного сечения
Закон Ома и
Закон Ома — Студопедия
ЗАКОН ОМА (по имени немецкого физика Г. Ома (1787-1854)) – единица электрического сопротивления. Обозначение Ом. Ом – сопротивление проводника, между концами которого при силе тока 1 А возникает напряжение 1 В.
Закон Ома гласит: Сила тока в однородном участке цепи прямо пропорциональна напряжению, приложенному к участку, и обратно пропорциональна электрическому сопротивлению этого участка.
И записывается формулой: R = U/ I.
(Где: I — сила тока (А), U — напряжение (В), R — сопротивление (Ом).)
Следует иметь в виду, что закон Ома является фундаментальным (основным) и может быть применён к любой физической системе, в которой действуют потоки частиц или полей, преодолевающие сопротивление. Его можно применять для расчёта гидравлических, пневматических, магнитных, электрических, световых, тепловых потоков и т. д., также, как и Законы Кирхгофа, однако, такое приложение этого закона используется крайне редко в рамках узко специализированных расчётов.
Взаимосвязь между падением напряжения на проводнике, его сопротивлением и силой тока легко запоминается в виде треугольника, в вершинах которого расположены символы U, I, R.
Законы Кирхгофа
Законы Кирхгофа (или правила Кирхгофа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи.
Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного и квазистационарного тока. Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач. Применение правил Кирхгофа к цепи позволяет получить систему линейных уравнений относительно токов, и соответственно, найти значение токов на всех ветвях цепи.
Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников и контуры — замкнутые пути из проводников. При этом каждый проводник может входить в несколько контуров.
В этом случае законы формулируются следующим образом.
Первый закон (ЗТК, Закон токов Кирхгофа) гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком):
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда.
Если цепь содержит p узлов, то она описывается p − 1 уравнениями токов. Этот закон может применяться и для других физических явлений (к примеру, водяные трубы), где есть закон сохранения величины и поток этой величины.
Второй закон (ЗНК, Закон напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю:
для постоянных напряжений:
для переменных напряжений:
Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит ветвей, из которых содержат источники тока ветви в количестве , то она описывается уравнениями напряжений. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи.
Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений.
На этом рисунке для каждого проводника обозначен протекающий по нему ток (буквой «I») и напряжение между соединяемыми им узлами (буквой «U»)
Например, для приведённой на рисунке цепи, в соответствии с первым законом выполняются следующие соотношения:
Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например здесь, токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.
В соответствии со вторым законом, справедливы соотношения:
Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), перепад напряжения считается положительным, в противном случае — отрицательным.
Законы Кирхгофа, записанные для узлов и контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и напряжения.
Существует мнение, согласно которому «Законы Кирхгофа» следует именовать «Правилами Кирхгофа», ибо они не отражают фундаментальных сущностей природы (и не являются обобщением большого количества опытных данных), а могут быть выведены из других положений и предположений.
20,2 Закон Ома: сопротивление и простые цепи — College Physics
20,2 Закон Ома: сопротивление и простые схемы — College Physics | OpenStaxSkip к контенту
- Предисловие
- 1 Введение: Природа науки и физики
- Введение в науку и область физики, физических величин и единиц измерения
- 1.1 Физика: введение
- 1.2 Физические величины и единицы измерения
- 1.3 Точность, прецизионность и значащие цифры
- 1.4 Приближение
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение в одномерную кинематику
- 2.1 Смещение
- 2.2 Векторы, скаляры, системы координат
и скорости и скорость
- 2.4 Ускорение
- 2.5 Уравнения движения для постоянного ускорения в одном измерении
- 2.6 Основы решения проблем для одномерной кинематики
- 2.7 падающих объектов
- 2.8 Графический анализ одномерного движения
- Глоссарий
- Сводка раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение в двумерную кинематику
- в двух измерениях: введение
- 3. 2 Сложение и вычитание векторов: графические методы
- 3.3 Сложение и вычитание векторов: аналитические методы
- 3.4 Движение снаряда
- 3.5 Добавление скоростей
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
2 Сложение и вычитание векторов: графические методы- Введение в динамику
- : законы Ньютона 4 4.1 Развитие концепции силы
- 4.2 Первый закон движения Ньютона: инерция
- 4.3 Второй закон движения Ньютона: концепция системы
- 4.4 Третий закон движения Ньютона: симметрия сил
- 4.5 Нормальные, растягивающие и другие примеры сил
- 4.6 Стратегии решения проблем
- 4.7 Дальнейшее применение законов движения Ньютона
- 4.8 Расширенная тема: Четыре основных силы — Введение
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение: Дальнейшие применения законов Ньютона
- 5. 1 Трение
- 5.2 Силы сопротивления
- 5.3 Упругость: напряжение и деформация
- Глоссарий
- Резюме раздела
- Концептуальные вопросы
- Задачи и упражнения
1 Трение- 6.1 Угол вращения и угловая скорость
- 6.2 Центростремительное ускорение
- 6.3 Центростремительная сила
- 6.4 Фиктивные силы и неинерциальные системы координат: сила Кориолиса
- 6.5 Универсальный закон тяготения Ньютона
- 6.6 Спутники и законы Кеплера: аргумент в пользу простоты
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Проблемы и упражнения
- Введение
- Работа, энергия и энергетические ресурсы
3 Гравитационная потенциальная энергияЗакон Ома отвечает на ваши вопросы — Блог о пассивных компонентах
- Дом
- Политика конфиденциальности
- Членство в EPCI
- Около
Нет результата
Просмотреть все результаты
НОВОСТНАЯ РАССЫЛКА
- Дом
- Новости по категориям
- Видеоканал с возможностью фильтрации
- Кто есть Whoin Пассивные
- События
- Обзоры рынка
Сопротивление и закон Ома
Введение
В этом уроке мы познакомим вас с идеей сопротивления.
Мы попытаемся объяснить, что такое электрическое сопротивление и что его вызывает.
Анимация показывает, что лампы с низким сопротивлением ярче и потребляют больший ток при заданном напряжении.
Мы увидим, как сопротивление связано с законом Ома, и проведем несколько экспериментов, чтобы увидеть, как изменяется сопротивление лампы, термистора, светозависимого резистора и диода при изменении тока через них.
Что такое электрическое сопротивление?
Есть несколько способов измерения электрического сопротивления.Мы собираемся взглянуть на это с точки зрения энергии.
Электрическое сопротивление говорит нам о том, сколько энергии вам нужно, когда вы перемещаете заряды через компонент, например лампочку. Если вам нужно много энергии, тогда сопротивление лампы будет высоким. Если вам не нужно много, значит, мало.
Сопротивление противоположно сопротивлению. Это означает, что если что-то имеет высокое сопротивление, оно имеет низкую проводимость.
Сопротивление и яркость лампочек
Другой способ взглянуть на сопротивление — представить себе три разных лампочки, подключенных к одному и тому же количеству батарей.На всех трех лампах будет одинаковое напряжение, но ток через них будет разным.
Анимация показывает, что лампы с низким сопротивлением ярче и потребляют больший ток при заданном напряжении.
Лампа, через которую протекает наибольший ток, будет самой яркой. Эта лампочка имеет самое низкое сопротивление, потому что вы получаете самый большой ток для данного напряжения.
Лампа с наименьшим током, протекающим через нее, будет самой тусклой. Эта лампа имеет самое высокое сопротивление, потому что вы получаете наименьший ток при заданном напряжении.
Распространенное заблуждение, что лампы с высоким сопротивлением — самые яркие.
Почему важно сопротивление лампочки?
В простой последовательной цепи мы предполагаем, что выводы и батарея имеют очень низкое сопротивление.
Сопротивление батареи мы называем внутренним сопротивлением, потому что вы не можете его изменить. Для упрощения часто игнорируется внутреннее сопротивление.
Нить лампы накаливания имеет большее сопротивление, чем провода. Это означает, что большая часть энергии преобразуется в нити накала, а не в выводах.Это также означает, что ток в цепи в основном зависит от сопротивления нити накала, а не проводов.
Анимация, поясняющая, что энергия преобразуется в точках цепи, которые имеют высокое относительное сопротивление.
Итак, мы хотим, чтобы нить лампы накаливания имела более высокое сопротивление, чем провода, но не настолько высокое, чтобы лампа была тусклой.
Чтобы понять, как мы проектируем нить накала лампы для обеспечения нужного сопротивления, будет полезно знать, как сопротивление куска провода зависит от того, из чего он сделан, его длины и толщины.
Как сопротивление зависит от материала, длины, толщины и температуры
Все металлы являются хорошими проводниками, поэтому все металлические провода имеют относительно низкое сопротивление.
Однако некоторые металлы являются лучшими проводниками, чем другие, например медь и серебро. Причина, по которой одни металлы являются лучшими проводниками, чем другие, заключается в том, как движутся их свободные электроны. Нити накаливания часто изготавливаются из вольфрама, который имеет очень высокую температуру плавления.
Анимация, объясняющая, как сопротивление зависит от материала, длины, площади поперечного сечения и температуры.
Чем длиннее кусок провода, тем выше его сопротивление. Удвоение длины означает удвоение сопротивления. Вы можете думать о длинном куске провода как о множестве последовательно соединенных резисторов, но есть и более формальное объяснение. Нить накала лампы может показаться довольно короткой, но если вы присмотритесь, вы увидите, что часто это очень тонкий кусок проволоки, который сильно скручен. В размотанном состоянии она может достигать полуметра.
Сопротивление куска проволоки также зависит от ее толщины.Удвоение площади означает половину сопротивления.
Тонкая проволока имеет более высокое сопротивление, чем такая же толстая проволока. Есть несколько неправильных представлений о сопротивлении и толщине. Самым важным моментом является то, что скорость заряда зависит только от напряжения, а не от толщины провода. Но с толстым проводом больше зарядов может двигаться бок о бок, поэтому заряд, проходящий через точку каждую секунду, больше.
Последнее, от чего зависит сопротивление куска проволоки, — это ее температура.Чем выше температура, тем выше сопротивление. Простое объяснение состоит в том, чтобы представить, что ионы вибрируют сильнее, поэтому электронам труднее попасть между ними. Более полное объяснение основано на рассуждениях, аналогичных представлениям о сопротивлении проводов, сделанных из разных металлов.
Игра У вас есть пары проводов, и вы должны стрелять в провод с большим сопротивлением.
Как рассчитать сопротивление
Когда вы рассчитываете сопротивление, вы действительно спрашиваете: «Какое напряжение мне нужно, чтобы поток в 1 ампер?»
Анимация, иллюстрирующая значение ома как единицы сопротивления.
Единица измерения сопротивления — ом, названная в честь немецкого физика начала 19 века Георга Ома. Символ ома — Ω (греческая заглавная буква омега). О для омега, о для ом, так что это имеет смысл. Поэтому, если вы видите «сопротивление было 40 Ом», прочтите это как «сопротивление было 40 Ом».
Если вам нужен 1 вольт для потока в 1 ампер, сопротивление будет 1 Ом. Если вам нужно 2 вольта, сопротивление будет 2 Ом и так далее. Если лампочке требуется 6 В для того, чтобы через нее протекали 2 А, сопротивление составляет 3 Ом.
Игра Вам даны напряжения и токи, и вам нужно рассчитать сопротивление. Направляйте космический вездеход над черной дырой, используя только квадраты с сопротивлением ровно 4 Ом.
Кривая зависимости тока от напряжения для лампы накаливания
Основное соотношение для всех проводников состоит в том, что большие напряжения вызывают большие токи.
Игра Правдивые или ложные утверждения о миллиамперах и амперах. Вы должны нацелить заявление на тележку для покупок или в мусорный бак.
Чтобы найти подробную взаимосвязь между напряжением и током, вам обычно нужно провести эксперимент, в котором вы изменяете напряжение на компоненте и измеряете ток через него.
Моделирование Эксперимент, в котором вы изменяете напряжение на лампе накаливания и измеряете ток через нее.
Когда мы строим график зависимости тока от напряжения для нити накала (а не люминесцентной), мы получаем кривую. Если мы рассчитаем сопротивление в каждой точке данных, используя сопротивление = напряжение / ток, мы обнаружим, что сопротивление увеличивается. Это связано с тем, что чем больше напряжение, тем горячее нить накала. Выше мы видели, что сопротивление металла увеличивается с повышением температуры.
Упражнение Постройте график зависимости тока от напряжения для лампы накаливания, перетащив крестики в нужное положение.
Тот факт, что график зависимости напряжения от тока имеет изогнутую форму, а не прямую линию, показывает, что сопротивление изменяется при изменении тока.
Иногда график строится в неправильном направлении: напряжение по оси y, а ток по оси x.
В этом случае более крутой склон означает большее сопротивление. Но вам нужно быть осторожным, потому что значение наклона численно не равно значению сопротивления, если линия является кривой.
Кривая зависимости тока от напряжения для резистора
Если вы проделаете тот же эксперимент с резистором, график будет прямой. Если вы посчитаете сопротивление, вы увидите, что оно не меняется. Резистор спроектирован так, что его сопротивление не меняется, пока напряжение на нем не слишком велико.
График, показывающий графики зависимости тока от напряжения для лампы накаливания и резистора.
Закон Ома
Если компонент подчиняется закону Ома, то ток через него пропорционален напряжению на нем. Другой способ осмыслить закон Ома — просто сказать, что сопротивление остается постоянным при изменении напряжения.
Другими словами, удвоение напряжения точно удваивает ток, утроение напряжения увеличивает ток и так далее. Провод подчиняется закону Ома, если не становится слишком горячим.
То же самое и с резисторами.
Анимация, поясняющая идею пропорций и прямолинейных графиков.
Закон Ома часто записывают как
В = ИК
напряжение = ток x сопротивление
Закон Ома и прямолинейные графики
Если ток пропорционален напряжению, тогда график зависимости тока отнапряжение должно давать прямую линию через начало координат.
Если вы построите график с осями в неправильном направлении (напряжение на оси Y), то чем круче прямая линия, тем больше сопротивление.
В этом случае градиент линии численно равен сопротивлению, но с этой идеей нужно быть очень осторожным.
Использование закона Ома для расчета напряжения и тока
Поскольку напряжение = ток x сопротивление, если вы знаете сопротивление компонента и ток через него, вы можете рассчитать, какое напряжение вам понадобится.
Анимация, демонстрирующая простой расчет напряжения с использованием уравнения закона Ома, V = IR.
Если вы измените уравнение, вы можете получить ток = напряжение / сопротивление, поэтому, если вы знаете напряжение и сопротивление, вы можете рассчитать ток.
Анимация показывает, как изменить уравнение закона Ома для расчета тока.
Зависимость тока от напряжения для диода
Моделирование. Объяснение функции диода и построение графика зависимости тока от напряжения.
Диод действует как вентиль для тока. Это позволяет току проходить через него в одном направлении, но не в другом. Это как если бы он имел бесконечное сопротивление в одну сторону и нулевое сопротивление при повороте.
Фактически вы обнаружите, что ток через диод быстро возрастает, когда вы приближаетесь к некоторому «пороговому» напряжению, обычно около 0,3 В. Если ток быстро растет при небольшом изменении напряжения, тогда сопротивление должно уменьшаться.
Сопротивление светозависимого резистора (LDR)
Чем больше света падает на него, тем меньше сопротивление LDR.Чтобы показать это, вы обычно поддерживаете постоянное напряжение, изменяете яркость света, падающего на LDR, и измеряете ток через него.
Анимация, показывающая, как сопротивление светозависимого резистора изменяется в зависимости от яркости падающего на него света.
LDR может иметь сопротивление несколько тысяч Ом в темноте и несколько десятков Ом при ярком свете.
Сопротивление падает, потому что фотоны света могут дать некоторым электронам достаточный импульс, чтобы вырваться из своих атомов.Чем больше свободных электронов, тем меньше сопротивление.
Сопротивление термистора
Сопротивление термистора изменяется в зависимости от температуры. Обычно более высокая температура означает меньшее сопротивление.
Анимация, показывающая, как сопротивление термистора изменяется в зависимости от температуры.
Опять же, типичный эксперимент включает поддержание постоянного напряжения, изменение температуры термистора и измерение тока через него.
Чем выше температура, тем больше свободных электронов раскачивается, и тем ниже сопротивление.Этот процесс подавляет любую тенденцию к увеличению сопротивления тем же способом, что и у металлов.
Игра Вы должны правильно ответить на вопросы о диодах, резисторах, светозависимых резисторах и термисторах.
Графическая сводка графиков для резистора, лампы накаливания, диода, LDR и термистора.
Вернуться к объяснению электроснабжения
Раздел 2. Первые законы: Законы Вавилона
ГЛАВА 1 МИРОВОЙ ЗАКОН
Блок 1.Необходимость закона
Текст Закон и общество
Задание 2. Найдите в тексте английские эквиваленты для следующих слов и выражений:
1. самозащита
2. — телохранитель
3. — общество
4. — правила поведения
5. Закон джунглей
6. несовершенные законы
7. средь бела дня
8.причинить вред
9. предоставить все возможности
10. — полагаться на кого-л.
11. требовать
Задача 3. Переведите следующий отрывок на английский язык.
, г. — Очевидно, что закон нужен в интересах всех.
. В противном случае мужчинам приходилось жить по закону джунглей.
, г. К сожалению, создать совершенные законы непросто.
, г. Поэтому каждое сообщество пытается установить собственные правила поведения.
, .- Однако закон не может удовлетворить всех.
, .- В любом случае несовершенные законы лучше, чем если бы у нас их вообще не было.
Задание 5. Какие части текста соответствуют следующим заголовкам?
1. шутка
2. Историческая справка
3. учитывая возможности
4.примеры
5. вывод
Раздел 2. Первые законы: законы Вавилона
Текст Рождение закона
Задание 1. Найдите в тексте слова, означающие следующее :.
Использование магической силы, особенно злых духов с помощью колдовства;
Наказание, назначенное за нарушение закона или правил наказания;
Общепринятые общественные обычаи или практические правила и законы;
Выплата за повреждение или утрату, реституционная компенсация;
Тот, от кого человек произошел от предка;
Вред или причиненный или понесенный ущерб — травмы
Задача 2.
Ответьте на следующие вопросы.
1. Трудно судить о самых ранних законах, потому что мы плохо знаем законы.
2. Первые законы появились до изобретения письма примерно в 3500 г. до н. Э. Самый ранний из известных юридических текстов был написан Ур-Намму, царем месопотамского города Ура, примерно в 2100 году н.э.
3. Ранние законы подчеркивали компенсацию за телесные повреждения и наказания за колдовство и беглых рабов, потому что эти вопросы были актуальны примерно в 2100 году до нашей эры.С.
Задание 3. Изучите все значения слова юридический. Выполните следующие английские выражения с их русскими эквивалентами.
1.Юридическая деятельность,;
2. юридический адрес;
3. юридическая консультация;
4. юридический возраст;
5. судебные издержки;
6. судебное решение;
7. юридический документ;
8. юридическое лицо;
9. юридическая этика;
10.
юрисконсульт; ;
11. история права;
12. юридический язык;
13. правообладатель;
14.правовая процедура;
15. юридическая защита;
16. юридические права;
17. правовой статус;
18. юридическая сила;
19. пользоваться законными правами;
20. поступить по профессии юриста.
Текст Законы Вавилона
Задача 4.Прочтите текст и напишите жирным шрифтом русские эквиваленты слов и выражений.
Самые подробные древние юридические коды —
Вырезан в большом каменном столбе —
Более обширный, чем все, что было раньше -, —
Жестокий принцип мести соблюден —
Получить в качестве наказания именно те травмы и повреждения, которые они нанесли своим жертвам -,
Приговорены к смертной казни
Чтобы потерять руку, нанесшую удар-,
Кодекс объявил частную кровную месть вне закона
Учтены обстоятельства правонарушителя
Гражданское дело проиграно
Получить меньше, если выиграет -,
Аванс на прежние племенные обычаи —
Наказание не могло быть жестче преступления -,
Задача 6.
1. Хаммурапи решил вырезать свои законы на столбе, чтобы их мог читать каждый гражданин.
2. Столп был установлен в храме, потому что все ходили туда регулярно и могли видеть законы.
3. Кодекс Хаммурабиса охватывал следующие сферы человеческой жизни: преступность, развод и брак, права рабовладельцев и рабов, урегулирование долгов, договоры о наследовании и собственности, положения о налогах и ценах на товары.Эти сферы были самыми обширными, чем все, что было раньше.
4. Я понимаю принцип око за око и зуб за зуб — получать в качестве наказания именно те травмы и повреждения, которые они нанесли своим жертвам.
5. Я считаю, что наказание не всегда было справедливым, я считаю, что оно было жестоким.
6. Разные чины по-разному трактовались кодексом Хаммурабиса, потому что это общество было разделено на чины с разными привилегиями и это касалось также системы наказаний.
Задание 7.
Код Хаммурабиса
В 1901 году каменный столб был обнаружен французскими археологами среди руин персидского города Сузы. Текст, вырезанный на столбе, был древнейшими сводами законов. Он был составлен Хаммурапи, царем Вавилонии, примерно в 1758 г. до н. Э.
Код Хаммурабиса
состоит из 282 абзацев. Колонна юридических кодексов была установлена в храме бога Вавилонии Мардука, чтобы служить правосудию и в то же время напоминать о том, что каждый гражданин должен знать законы.Кодекс охватывал все сферы жизни. Кодекс запрещал частную кровную месть, преступления и традицию, по которой мужчина мог похитить женщину, которую хотел для своей невесты. Наказание под кодой было суровым.
Кодекс был основан на принципе мести: получить в качестве наказания именно те травмы и повреждения, которые они нанесли своим жертвам: глаз за глаз и зуб за зуб. Ложным обвинителям грозит смертная казнь.
Кодекс охватывал вопросы собственности и наследования.Хаммурапи установил штраф с учетом правонарушения и ранга гражданина.
Закон Ома — Электронные вопросы и ответы
Почему для электроники действует закон Ома?
В этом разделе вы можете выучить и попрактиковаться в вопросах по электронике на основе «Закона Ома» и улучшить свои навыки, чтобы пройти собеседование, конкурсные экзамены и различные вступительные испытания (CAT, GATE, GRE, MAT, банковский экзамен, железнодорожный экзамен и т. Д.) с полной уверенностью.
Где я могу получить вопросы и ответы по закону Ома для электроники с пояснениями?
IndiaBIX предоставляет вам множество полностью решенных вопросов и ответов по электронике (закон Ома) с пояснениями. Решенные примеры с подробным описанием ответов, даны пояснения, которые легко понять. Все студенты, первокурсники могут загрузить вопросы викторины «Закон Ома по электронике» с ответами в виде файлов PDF и электронных книг.
Где я могу получить вопросы и ответы на собеседовании по закону Ома в области электроники (объективный тип, множественный выбор)?
Здесь вы можете найти вопросы и ответы по закону Ома объективного типа для собеседований и вступительных экзаменов.Также предусмотрены вопросы с множественным выбором и вопросы истинного или ложного типа.
Как решить проблемы с законом Ома в электронике?
Вы можете легко решить все вопросы по электронике, основанные на законе Ома, выполнив упражнения объективного типа, приведенные ниже, а также получите быстрые методы решения проблем, связанных с законом Ома в электронике.
Упражнение :: Закон Ома — общие вопросы
| 2. | Если удвоение напряжения на резисторе увеличивает вдвое ток через резистор, то | |||||||
|
Закон Ома | Электрические схемы
11.2 Закон Ома (ESBQ6)
Три основные величины для электрических цепей: ток, напряжение (разность потенциалов) и сопротивление . Напомним:
Электрический ток, \ (I \), определяется как скорость прохождения заряда через цепь.
Разность потенциалов или напряжение, \ (В \), — это количество энергии на единицу заряда, необходимое для перемещения этого заряда между двумя точками в цепи.
Сопротивление, \ (R \), является мерой того, насколько «трудно» протолкнуть ток через элемент схемы.
Теперь посмотрим, как эти три величины связаны друг с другом в электрических цепях.
Важная взаимосвязь между током, напряжением и сопротивлением в цепи была обнаружена Георгом Симоном Омом и называется законом Ома .
- Закон Ома
Величина электрического тока через металлический проводник при постоянной температуре в цепи пропорциональна напряжению на проводе и может быть описана с помощью
\ (I = \ frac {V} {R} \)
где \ (I \) — ток через проводник, \ (V \) — напряжение на проводнике, а \ (R \) — сопротивление проводника.Другими словами, при постоянной температуре сопротивление проводника постоянно, независимо от приложенного к нему напряжения или проходящего через него тока.
Закон Ома говорит нам, что если проводник имеет постоянную температуру, ток, протекающий по проводнику, прямо пропорционален напряжению на нем. Это означает, что если мы нанесем напряжение на ось x графика, а ток на ось y графика, мы получим прямую линию.
Наклон прямолинейного графика связан с сопротивлением проводника как
\ [\ frac {I} {V} = \ frac {1} {R}.\]
С точки зрения постоянного сопротивления это можно изменить как:
\ [R = \ frac {V} {I}. \]
Закон Ома
Цель
Для определения взаимосвязи между током, протекающим через резистор, и разностью потенциалов (напряжением) на том же резисторе.
Аппарат
4 ячейки, 4 резистора, амперметр, вольтметр, соединительные провода
Метод
Этот эксперимент состоит из двух частей. В первой части мы будем варьировать приложенное к резистору напряжение и измерять результирующий ток в цепи.Во второй части мы будем изменять ток в цепи и измерять результирующее напряжение на резисторе. После получения обоих наборов измерений мы проверим взаимосвязь между током и напряжением на резисторе.
Изменение напряжения:
Установите схему в соответствии со схемой 1), начиная с одной ячейки.
Нарисуйте следующую таблицу в своем лабораторном журнале.
Количество ячеек
Напряжение, В (\ (\ text {V} \))
Ток, I (\ (\ text {A} \))
\ (\ text {1} \)
\ (\ text {2} \)
\ (\ text {3} \)
\ (\ text {4} \) Попросите учителя проверить электрическую цепь перед включением питания.
Измерьте напряжение на резисторе с помощью вольтметра и ток в цепи с помощью амперметра.
Добавьте еще одну ячейку \ (\ text {1,5} \) \ (\ text {V} \) в схему и повторите измерения.
Повторяйте, пока не получите четыре ячейки и не заполните таблицу.
Изменение тока:
Установите схему в соответствии со схемой 2), начиная с одного резистора в цепи.
Нарисуйте следующую таблицу в своем лабораторном журнале.
Напряжение, В (\ (\ text {V} \))
Ток, I (\ (\ text {A} \))
Попросите учителя проверить вашу электрическую цепь перед включением питания.
Измерьте ток и напряжение на единственном резисторе.
Теперь добавьте еще один резистор последовательно в цепь и снова измерьте ток и напряжение только на исходном резисторе. Продолжайте добавлять резисторы, пока у вас не будет четырех последовательно, но не забывайте каждый раз измерять напряжение только на исходном резисторе. Введите измеренные вами значения в таблицу.
Анализ и результаты
Используя данные, записанные в первой таблице, нарисуйте график зависимости тока от напряжения.Поскольку напряжение — это переменная, которую мы изменяем напрямую, это независимая переменная, которая будет отложена по оси \ (x \). Ток является зависимой переменной и должен быть нанесен на ось \ (y \).
Используя данные, записанные во второй таблице, постройте график зависимости напряжения от тока. В этом случае независимой переменной является ток, который должен быть нанесен на ось \ (x \), а напряжение является зависимой переменной и должно быть нанесено на ось \ (y \).
Выводы
Изучите график, который вы построили из первой таблицы. Что происходит с током через резистор при увеличении напряжения на нем? т.е. увеличивается или уменьшается?
Изучите график, который вы построили на основе второй таблицы. Что происходит с напряжением на резисторе, когда ток через резистор увеличивается? т.е. увеличивается или уменьшается?
Подтверждают ли результаты ваших экспериментов закон Ома? Объясни.
Вопросы и обсуждение
- Для каждого из ваших графиков рассчитайте градиент и по нему определите сопротивление исходного резистора. Получаете ли вы одно и то же значение, когда рассчитываете его для каждого из ваших графиков?
Как вы можете найти сопротивление неизвестного резистора, используя только источник питания, вольтметр и известный резистор \ (R_0 \)?
Присоединяйтесь к тысячам учащихся, улучшающих свои научные оценки онлайн с помощью Siyavula Practice.
Зарегистрируйтесь здесь
Закон Ома
Упражнение 11.1
Постройте график напряжения (по оси X) и тока (по оси Y).
Какой тип графика вы получите (прямолинейный, парабола, другая кривая)
прямая линия
Рассчитайте градиент графика.
Градиент графика (\ (m \)) — это изменение тока, деленное на изменение напряжения:
\ begin {align *}
m & = \ frac {\ Delta I} {\ Delta V} \\
& = \ frac {(\ text {1,6}) — (\ text {0,4})} {(\ text {12}) — (\ text {3})} \\
& = \ текст {0,13}
\ end {выровнять *}
Подтверждают ли результаты ваших экспериментов закон Ома? Объясни.
Да. График с прямой линией получается, когда мы строим график зависимости напряжения от тока.
Как вы можете найти сопротивление неизвестного резистора, используя только источник питания, вольтметр и известный резистор \ (R_ {0} \)?
Вы начинаете с подключения известного резистора в цепь с источником питания. Теперь вы читаете напряжение источника питания и записываете его.
Затем вы последовательно подключаете два резистора.Теперь вы можете измерить напряжение на каждом из резисторов.
Итак, мы можем найти напряжения для двух резисторов. Теперь отметим, что:
\ [V = IR \]
Итак, используя это и тот факт, что для резисторов, включенных последовательно, ток везде одинаковый в цепи, мы можем найти неизвестное сопротивление.
\ begin {align *}
V_ {0} & = IR_ {0} \\
I & = \ frac {V_ {0}} {R_ {0}} \\
V_ {U} & = IR_ {U} \\
I & = \ frac {V_ {U}} {R_ {U}} \\
\ frac {V_ {U}} {R_ {U}} & = \ frac {V_ {0}} {R_ {0}} \\
\ поэтому R_ {U} & = \ frac {V_ {U} R_ {0}} {V_ {0}}
\ end {выровнять *}
Омические и неомические проводники (ESBQ7)
Проводники, которые подчиняются закону Ома, имеют постоянное сопротивление, когда на них изменяется напряжение или увеличивается ток, проходящий через них.Эти проводники называются омическими проводниками . График зависимости тока от напряжения на этих проводниках будет прямолинейным. Некоторые примеры омических проводников — резисторы цепи и нихромовая проволока.
Как вы видели, когда мы говорим о законе Ома, есть упоминание о постоянной температуре . Это связано с тем, что сопротивление некоторых проводников изменяется при изменении их температуры. Эти типы проводников называются неомическими проводниками , потому что они не подчиняются закону Ома.Лампочка — типичный пример неомического проводника. Другими примерами неомических проводников являются диоды и транзисторы.
В лампочке сопротивление нити накала резко возрастает по мере того, как она нагревается от комнатной до рабочей температуры. Если мы увеличим напряжение питания в реальной цепи лампы, то увеличение тока приведет к увеличению температуры нити накала, что приведет к увеличению ее сопротивления. Это эффективно ограничивает увеличение тока.В этом случае напряжение и ток не подчиняются закону Ома.
Явление изменения сопротивления при изменении температуры присуще почти всем металлам, из которых изготовлено большинство проводов. Для большинства приложений эти изменения сопротивления достаточно малы, чтобы их можно было игнорировать. При применении металлических нитей накаливания ламп, температура которых сильно повышается (примерно до \ (\ text {1 000} \) \ (\ text {℃} \) и начиная с комнатной температуры), изменение довольно велико.
В общем, для неомических проводников график зависимости напряжения от тока не будет прямолинейным, что указывает на то, что сопротивление не является постоянным для всех значений напряжения и тока.
Включен рекомендуемый эксперимент для неформальной оценки. В этом эксперименте учащиеся получат данные о токе и напряжении для резистора и лампочки и определят, какой из них подчиняется закону Ома. Вам потребуются лампочки, резисторы, соединительные провода, источник питания, амперметр и вольтметр. Учащиеся должны обнаружить, что резистор подчиняется закону Ома, а лампочка — нет.
Омические и неомические проводники
Aim
Чтобы определить, подчиняются ли два элемента схемы (резистор и лампочка) закону Ома
Аппарат
4 ячейки, резистор, лампочка, провода соединительные, вольтметр, амперметр
Метод
Две схемы, показанные на схемах выше, одинаковы, за исключением того, что в первой есть резистор, а во второй — лампочка.Настройте обе схемы, указанные выше, начиная с 1 ячейки. Для каждой цепи:
Измерьте напряжение на элементе схемы (резисторе или лампочке) с помощью вольтметра.
Измерить ток в цепи с помощью амперметра.
Добавьте еще одну ячейку и повторяйте измерения, пока в вашей цепи не будет 4 ячейки.
Результаты
Нарисуйте в своей книге две таблицы, которые выглядят следующим образом.У вас должна быть одна таблица для измерений первой цепи с резистором и другая таблица для измерений второй цепи с лампочкой.
Количество ячеек | Напряжение, В (\ (\ text {V} \)) | Ток, I (\ (\ text {A} \)) | |
\ (\ text {1} \) | |||
\ (\ text {2} \) | |||
\ (\ text {3} \) | |||
| \ (\ text {4} \) |
Анализ
Используя данные в ваших таблицах, нарисуйте два графика \ (I \) (\ (y \) — ось) vs.\ (V \) (\ (x \) — ось), один для резистора и один для лампочки.
Вопросы и обсуждение
Внимательно изучите свои графики и ответьте на следующие вопросы:
Как должен выглядеть график зависимости \ (I \) от \ (V \) для проводника, подчиняющегося закону Ома?
Один или оба ваших графика выглядят так?
Какой можно сделать вывод о том, подчиняются ли резистор и / или лампочка закону Ома?
Имеет ли лампочка омический или неомический провод?
Использование закона Ома (ESBQ8)
Теперь мы готовы увидеть, как закон Ома используется для анализа схем.
Рассмотрим схему с элементом и омическим резистором R. Если сопротивление резистора равно \ (\ text {5} \) \ (\ text {Ω} \), а напряжение на резисторе равно \ (\ text { 5} \) \ (\ text {V} \), то мы можем использовать закон Ома для расчета тока, протекающего через резистор. Наша первая задача — нарисовать принципиальную схему. Решая любую проблему с электрическими цепями, очень важно составить схему цепи, прежде чем производить какие-либо расчеты. Принципиальная схема для этой проблемы выглядит следующим образом:
Уравнение закона Ома:
\ [R = \ frac {V} {I} \]
, который можно преобразовать в:
\ [I = \ frac {V} {R} \]
Ток, протекающий через резистор:
\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {\ text {5} \ text {V}} {\ text {5} \ Omega} \\
& = \ текст {1} \ текст {А}
\ end {align *}
Рабочий пример 1: Закон Ома
Изучите принципиальную схему ниже:
Сопротивление резистора равно \ (\ text {10} \) \ (\ text {Ω} \), а ток, проходящий через резистор, равен \ (\ text {4} \) \ (\ text {A} \ ).Какова разность потенциалов (напряжение) на резисторе?
Определите, как подойти к проблеме
Нам задают сопротивление резистора и ток, проходящий через него, и просят вычислить напряжение на нем. Мы можем применить закон Ома к этой проблеме, используя:
\ [R = \ frac {V} {I}. \]
Решить проблему
Измените приведенное выше уравнение и замените известные значения на \ (R \) и \ (I \), чтобы найти \ (V \).
\ begin {align *}
R & = \ frac {V} {I} \\
R \ times I & = \ frac {V} {I} \ times I \\
V & = I \ раз R \\
& = \ текст {10} \ times \ text {4} \\
& = \ текст {40} \ текст {V}
\ end {align *}
Напишите окончательный ответ
Напряжение на резисторе равно \ (\ text {40} \) \ (\ text {V} \).
Присоединяйтесь к тысячам учащихся, улучшающих свои научные оценки онлайн с помощью Siyavula Practice.
Зарегистрируйтесь здесь
Закон Ома
Упражнение 11.2
Вычислите сопротивление резистора, разность потенциалов которого составляет \ (\ text {8} \) \ (\ text {V} \), когда ток равен \ (\ text {2} \) \ (\ text {A} \) протекает через него. Перед расчетом нарисуйте принципиальную схему.
Сопротивление неизвестного резистора составляет:
\ begin {align *}
R & = \ frac {V} {I} \\
& = \ frac {8} {2} \\
& = \ текст {4} \ текст {Ω}
\ end {выровнять *}
Какой ток будет проходить через резистор \ (\ text {6} \) \ (\ text {Ω} \) при разности потенциалов \ (\ text {18} \) \ (\ text {V} \) на концах? Перед расчетом нарисуйте принципиальную схему.
Сопротивление неизвестного резистора составляет:
\ begin {align *}
I & = \ frac {V} {R} \\
& = \ frac {18} {6} \\
& = \ текст {3} \ текст {А}
\ end {выровнять *}
Какое напряжение на резисторе \ (\ text {10} \) \ (\ text {Ω} \) при токе \ (\ text {1,5} \) \ (\ text {A} \) течет хоть это? Перед расчетом нарисуйте принципиальную схему.
