Переходные процессы в электрических цепях. Первый закон коммутации

1. Основные понятия. Законы коммутации

ЛЕКЦИЯ 15 КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА

ПЕРЕХОДНЫХ ПРОЦЕССОВ

План лекции

2. Суть классического метода расчета переходных процессов 3. Подключение реального конденсатора к источнику постоянного на-

пряжения 4. Определение длительности переходного процесса

1.Основныепонятия. Законыкоммутации

Вповседневной жизни мы постоянно наблюдаем явления, которые показывают, что не во всех электрических цепях возможно мгновенное изменение режима работы. Например, телевизор или радиоприемник продолжают некоторое время работать после отключения от источника энергии.

Вшкольном курсе физики обычно демонстрируют следующий опыт.

Кисточнику энергии подключают две параллельные ветви, в одной из которых находится лампочка накаливания, в другой – лампочка накаливания и индуктивная катушка. После замыкания ключа первая лампочка загорается мгновенно, вторая – постепенно.

Эти опыты свидетельствуют о том, что в цепях с реактивными элементами невозможно мгновенное изменение режима работы. Ранее мы изучали установившиеся режимы. Если в электрической цепи есть конденсаторы и индуктивные катушки, то при переходе от одного установившегося режима

кдругому наблюдается переходный процесс. Сам процесс изменения режима работы цепи (включение или выключение рубильника) в электротехнике называют коммутацией.

Последовательность событий такова: установившийся режим → коммутация → переходный процесс → новый установившийся режим.

Переходные процессы подчиняются двум законам коммутации. Первый закон коммутации: ток в ветви с индуктивной катушкой не

может измениться скачком.

Принято считать, что коммутация происходит мгновенно во время t = 0. Поэтому при рассмотрении переходных процессов различают два нулевых момента времени:t = 0−, когда коммутация еще не произошла, иt = 0+после коммутации.

Тогда первый закон коммутации можно сформулировать следующим образом: ток в индуктивной катушке до коммутации равен току в момент, наступивший сразу после коммутации, т. е. iL (0−)= iL (0+) .

Теоретические основы электротехники. Конспект лекций

-97-

ЛЕКЦИЯ 15. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ

1. Основные понятия. Законы коммутации

Второй закон коммутации: напряжение на конденсаторе не может измениться скачком.

Либо: uС (0−)= uС (0+) .

Можно дать энергетическое обоснование законов коммутации. Энергию магнитного поля индуктивной катушки определяют по формуле

W =	LiL2	. Мощность Р	М	=	dWМ	.
M	2				dt

Если ток iL изменится скачком, то иWM изменится скачком. Тогда

мощность магнитного поля катушки будет равна бесконечности, что невозможно, так как не существуют реальные источники энергии с бесконечно большой мощностью.

			Энергия электрического			поля конденсатора W =		CuС2	, мощность
						Э	2
			dWЭ
	Р	=		. Если напряжение u	С	изменится скачком, то W изменится скач-
	Э		dt				Э

ком, РЭ = ∞, что невозможно.

Можно провести доказательства исходя из противного и на основании формул uL = L dditL ,iС = C ddutС .

Изучение переходных процессов очень важно, так как они положены в основу принципа действия некоторых устройств и аппаратов. Быстродействие современных ЭВМ таково, что в них практически нет установившихся режимов.

Кроме того, во время переходного процесса могут возникать токи и напряжения большие, чем при установившемся режиме. Электрическая цепь, пригодная для номинального режима работы, может выйти из строя при подключении к источнику энергии.

2. Сутьклассическогометодарасчета переходныхпроцессов

Составим систему уравнений электрического состояния в дифференциальной форме для схемы замещения электрической цепи.

Как известно из математики, решение полученной системы линейных дифференциальных неоднородных уравнений есть сумма двух слагаемых: частного решения неоднородных уравнений и общего решения однородных уравнений.

В качестве частного решения берут принужденный режим, вызываемый внешними источниками энергии. Составляющие токов и напряжений, найденные в результате частного решения неоднородных уравнений, называют принужденными: iпр,uпр.

Теоретические основы электротехники. Конспект лекций

-98-

ЛЕКЦИЯ 15. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ

2. Суть классического метода расчета переходных процессов

Общее решение однородного уравнения характеризует процессы, происходящие в цепи при отсутствии внешних источников энергии. В учебниках и в лекциях можно встретить утверждение, что эти процессы происходят за счет энергии, запасенной в магнитном поле катушки и электрическом поле конденсатора. Но это неверно, так как переходные процессы происходят и при отсутствии этих запасов энергии. Например, при подключении незаряженного конденсатора к источнику энергии.

Эти процессы происходят за счет изменения энергии магнитного поля катушки и электрического поля конденсатора.

Составляющие токов и напряжений, найденные в результате общего решения однородных уравнений, называют свободными: iсв,uсв . Свободные

составляющие стремятся к нулю.

Классический метод расчета переходных процессов заключается в отыскании закона изменения любого тока и напряжения как суммы принужденной и свободной составляющих:

i = iпр+iсв; u = uпр+uсв.

Когда свободные составляющие станут равны нулю, переходный процесс закончится. Отсюда следует, что принужденный режим – это новый установившийся режим после переходного процесса.

Далее рассмотрим классический метод расчета переходных процессов на ряде конкретных примеров.

3.Подключениереальногоконденсатора кисточникупостоянногонапряжения

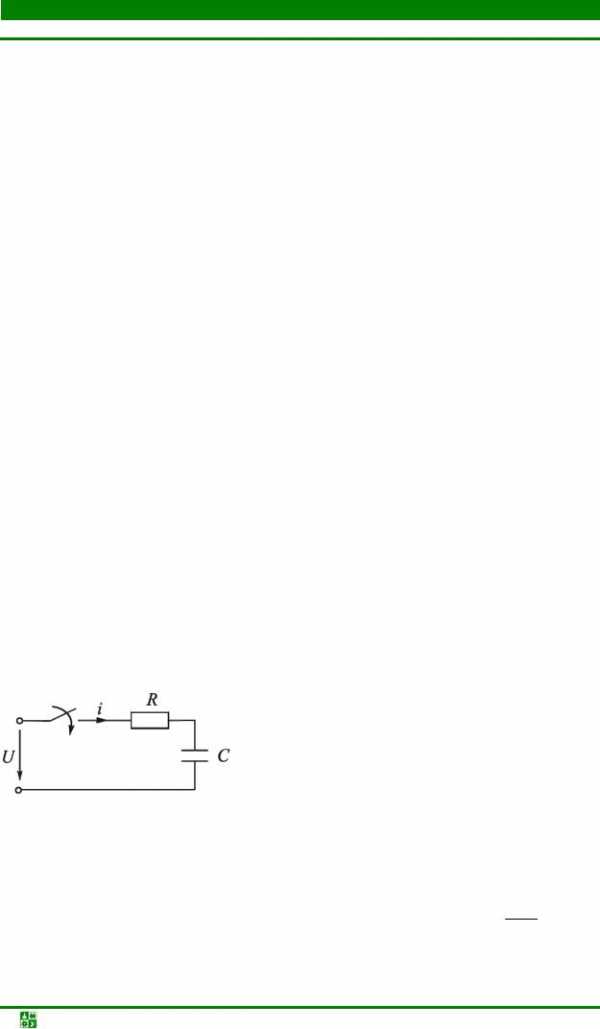
Схема замещения рассматриваемой цепи приведена на рис. 15.1.

1. Составим систему уравнений электрического состояния. Так как схема одноконтурная, то можно написать только одно уравнение по второму закону Кирхгофа:

Ri + uС =U.

Рис. 15.1

В этом уравнении во время переходного процесса происходит изменение двух величин: тока i и напряжения на емкостном элементеuС . НапряжениеuС подчиняется второму закону коммута-

ции, поэтому рационально выразить ток по закону Ома i = iС = C ddutС .

Теоретические основы электротехники. Конспект лекций

-99-

ЛЕКЦИЯ 15. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ

3. Подключение реального конденсатора к источнику постоянного напряжения

Тогда уравнение примет вид

RC ddutС +uС =U.

2. Ищем решение этого уравнения как сумму двух слагаемых:

uС = uСпр+uСсв.

3. Найдем uСпр.

Теоретически переходной процесс длится бесконечно долго, поэтому принужденный режим рассмотрим как новый установившийся режим при t = ∞. Конденсатор постоянный ток не пропускает (iпр = 0),Riпр = 0. Отсюда

uСпр=U.

4. Вычислим uСсв . Из математики известно, что свободные составляющие меняются по экспоненциальному закону:

uСсв= Аеpt .

1. Определим показатель степени р, который является корнем характеристического уравнения.

Запишем уравнение электрического состояния для свободной составляющей:

RC dudСtсв + uСсв = 0 .

Производной экспоненты является сама экспонента. Так как функция сложная, дифференцируем еще и показатель степени.

	В итоге производная	duСсв	= рАеpt . После подстановки в уравнение
		dt

электрического состояния получаем

RCpAept + Aept = 0.

Сократим на Aept :

RCp +1 = 0.

Сравнив уравнение электрического состояния с характеристическим, делаем вывод: для получения характеристического уравнения в уравнении электрического состояния правую часть нужно приравнять к нулю, перемен-

Теоретические основы электротехники. Конспект лекций

-100-

ЛЕКЦИЯ 15. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ

3. Подключение реального конденсатора к источнику постоянного напряжения

ную величину заменить единицей, ее производную – р, вторую производную –р2 и т. д.

Решение характеристического уравнения позволяет определить p = − RC1 .

Величину 1p = RC обозначают τ и называют постоянной времени.

Показатель p = −1τ. Так как[R]= Ом,[C]= Ф= Омс , то[τ]= с.

2. Определим постоянную интегрирования А.

Постоянные интегрирования определяют из начальных условий с использованием законов коммутации.

Уравнение, по которому проводим решение, справедливо для любого момента времени, следовательно, и для начального:

uС (0+)= uСпр(0+)+ uСсв(0+).

По второму закону коммутации uС (0+)= uС (0−) . До коммутации схема не была подключена к источнику энергии, поэтомуuС (0−)= 0 .

Принужденная составляющая в данном примере является постоянной величиной, значит uСпр(0+)=U.

Свободная составляющая uСсв = Аерt приt = 0+ равнаА. После подстановки получим 0=U + A. ОтсюдаA = −U .

− 1 t

Тогда закон изменения напряжения uС =U −UeRC .

Закон изменения тока можно получить как из уравнения по второму закону Кирхгофа, так и из закона Ома.

Из уравнения по второму закону Кирхгофа

−

1

t

U

−u

U

RC

i =

С

=

−U+Ue

R

R

du

С

U

−

1

t

U

−

1

t

либо i = C

= C

e

RC

=

e

RC .

RC

R

dt

Проиллюстрируем полученные уравнения графиками.

График напряжения uС (см.рис. 15.2) получаем суммированием графиковuСпр иuСсв . СоставляющаяuСпр =U = const . Свободная составляю-

Теоретические основы электротехники. Конспект лекций

-101-

ЛЕКЦИЯ 15. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ

3. Подключение реального конденсатора к источнику постоянного напряжения

щая изменяется по закону экспоненты и стремится к нулю. В начальный момент uСсв(0+)= −U .

t

uCсв

-U

Рис. 15.2

График подтверждает, что напряжение на конденсаторе меняется плавно, что принужденный режим – это новый установившийся режим после переходного процесса.

График изменения тока представлен на рис. 15.3.

iC

U

R

t

Рис. 15.3

При t = 0– тока не было, приt = 0+ токiС = UR , далее он стремится к

нулю по закону экспоненты.

Графики будут меняться при изменении параметров схемы R иС. Величина напряжения от них не зависит. Величина тока обратно пропорциональна сопротивлениюR и не зависит от емкостиС. Длительность переходного процесса прямо пропорциональна значениямR иС.

4. Определениедлительности переходногопроцесса

Теоретически переходный процесс длится бесконечно долго. Практически переходный процесс заканчивается через (3–5)ф.

Теоретические основы электротехники. Конспект лекций

-102-

ЛЕКЦИЯ 15. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ

4. Определение длительности переходного процесса

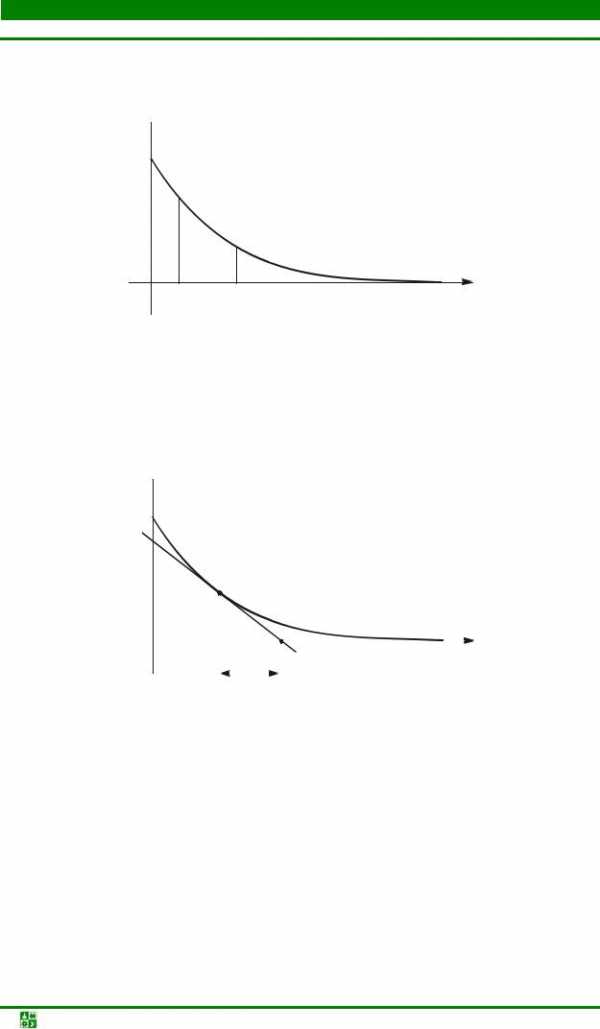
Постоянная времени ф – это время, в течение которого свободные составляющие уменьшаются в е раз (см. рис. 15.4).

iсв

			t1	t2
						Рис. 15.4
Время t	2	−t	= τ, если	it1		= e≈2,7 .
		1		it2
Постоянной			времени	можно дать геометрическую интерпретацию:

ф – это величина подкасательной к любой точке экспоненты (см. рис. 15.5).

iсв

		τ		t

Рис. 15.5

Поэтому можно определить постоянную времени по известному графику изменения свободной составляющей и неизвестных параметрах схемы.

Длительность переходного процесса, зависящая от параметров, может быть различной.

Если в схеме замещения R = 100 Ом,С = 100 мкФ, то при замыкании ключа конденсатор заряжается с постоянной времени τзар = 0,01 с. При раз-

мыкании ключа конденсатор будет разряжаться с τраз ≈ 28часов, т. е. кон-

денсатор будет сохранять напряжение на своих обкладках несколько суток и представлять собой опасность. Поэтому после окончания работы с конденсатором нужно использовать разрядное устройство.

Теоретические основы электротехники. Конспект лекций

-103-

ЛЕКЦИЯ 15. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ

Вопросыдлясамопроверки

1.Какие законы коммутации вы знаете?

2.Как доказывают законы коммутации?

3.В чем суть классического метода расчета переходных процессов?

4.За счет чего возникают принужденные составляющие токов и напряжений?

5.Какие процессы характеризует общее решение однородного урав-

нения?

6.По какому закону меняются свободные составляющие?

7.Как составить характеристическое уравнение для неразветвленной

цепи?

8.Сколько длится переходный процесс?

9.Каков физический смысл постоянной времени ф?

10.Как графически определить постоянную времени ф?

Теоретические основы электротехники. Конспект лекций

-104-

studfiles.net

Переходные процессы в электрических цепях — WiKi

Перехо́дные проце́ссы — процессы, возникающие в электрических цепях при различных воздействиях, приводящих их из стационарного состояния в новое стационарное состояние, то есть, — при действии различного рода коммутационной аппаратуры, например, ключей, переключателей для включения или отключения источника или приёмника энергии, при обрывах в цепи, при коротких замыканиях отдельных участков цепи и т. д.

Например, при подключении разряженного конденсатора C{\displaystyle C} к источнику напряжения U0{\displaystyle U_{0}} через резистор R{\displaystyle R}, напряжение на конденсаторе меняется от 0 до U0{\displaystyle U_{0}} по закону:

Uc(t)=U0(1−e−t/τ){\displaystyle U_{c}(t)=U_{0}(1-e^{-t/\tau })}[1]

τ=RC{\displaystyle \tau =RC} (постоянная времени).

Физическая причина возникновения переходных процессов в цепях — наличие в них катушек индуктивности и конденсаторов, то есть индуктивных и ёмкостных элементов в соответствующих схемах замещения. Объясняется это тем, что энергия магнитного и электрического полей этих элементов не может изменяться скачком при коммутации (процесс замыкания или размыкания выключателей) в цепи.

Стандартные идеализированные воздействия при анализе отклика математической модели цепи — это ступенчатая функция Хевисайда и импульсная функция Дирака.

Переходный процесс в цепи описывается математически дифференциальным уравнением

• неоднородным (однородным), если схема замещения цепи содержит (не содержит) источники ЭДС и тока,
• линейным (нелинейным) для линейной (нелинейной) цепи.

Время установления в новое стационарное состояние

Переходные процессы могут продолжаться от долей наносекунд до нескольких лет. Продолжительность зависит от конкретной цепи. Например, постоянная времени саморазряда конденсатора с полимерным диэлектриком может достигать тысячелетия. Длительность протекания переходного процесса определяется постоянной времени цепи.

Законы (правила) коммутации

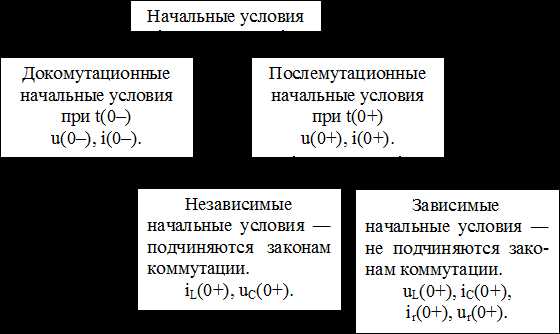
Начальные значения величин

Начальные значения (условия) — значения токов и напряжений в схеме при t=0.

Напряжения на индуктивных элементах и резисторах, а также токи, протекающие через конденсаторы и резисторы, могут изменяться скачком, то есть их значения после коммутации t=0+{\displaystyle t=0_{+}}  чаще всего оказываются не равными их значениям до коммутации t=0−{\displaystyle t=0_{-}} .

Независимые начальные значения — это значения токов, протекающих через индуктивные элементы, и напряжений на конденсаторах, известные из докоммутационного режима.

Зависимые начальные значения — это значения остальных токов и напряжений при t=0+{\displaystyle t=0_{+}}  в послекоммутационной схеме, определяемые по независимым начальным значениям из законов Кирхгофа.

Методы расчёта переходных процессов

• Классический метод (решение дифференциальных уравнений с постоянными параметрами методами классической математики).
• Операторный метод (перенос расчёта переходного процесса из области функций действительной переменной (времени t{\displaystyle t} ) в область функций комплексного переменного, в которой дифференциальные уравнения преобразуются в алгебраические).
• Метод переменных состояния (составление и решение системы дифференциальных уравнений первого порядка, разрешенной относительно производных. Число переменных состояний равно числу независимых накопителей энергии).

См. также

Литература

• Электротехника: Учеб. для вузов/А. С. Касаткин, М. В. Немцов.— 7-е изд., стер.— М.: Высш. шк., 2003.— 542 с.: ил. ISBN 5-06-003595-6

• Бессонов Л.А. Гл. 8. Переходные процессы в линейных электрических цепях // Теоретические основы электротехники. Электрические цепи: учебник. — 11-е изд., перераб. и доп.. — М.: "Гардарики", 2007. — С. 231, 235-236. — 701 с. — 5000 экз. — ISBN 5-8297-0046-8, ББК 31.21, УДК 621.3.013(078.5).

Ссылки

Примечания

ru-wiki.org

Законы коммутации и начальные условия.

Стр 1 из 4Следующая ⇒

Переходные процессы в линейных электрических цепях.

 

Переходным процессом называется переход электрической цепи из одного установившегося состояния в другое установившееся состояние. Только в частном случае цепей с чисто активными сопротивлениями такой переход совершается мгновенно.

 

Если цепь кроме активных сопротивлений содержит реактивные элементы (индуктивности и емкости), то переход цепи из одного установившегося состояния в другое совершается за конечное время.

 

Переходные процессы возникают при коммутациях электрической цепи. Коммутацией называется включение или отключение какой-либо ветви или группы ветвей.

Во всех случаях коммутацию будем считать мгновенной, т.е. будем полагать, что время на подключение или отключение ветвей не тратится. Кроме того, условимся, что коммутация происходит в момент времени t=0. В противном случае момент коммутации оговаривается особо.

 

Законы коммутации и начальные условия.

 

Законы коммутации устанавливают характер изменения физической величины в момент коммутации.

Для оценки тока (напряжения) в момент коммутации вводятся два значения: как предел слева, и как предел справа.

При коммутации ветвей с чисто активным сопротивлением токи в них могут изменяться скачком (рис. 4.4):

, .

 

Рис. 4.4

 

Запас энергии магнитного поля индуктивности не может изменяться скачком. Это выражает принцип непрерывности во времени потокосцепления индуктивности. Невозможность скачкообразного изменения потокосцепления объясняется в свою очередь тем, что в противном случае на индуктивности появилось бы бесконечно большое напряжение

,

что противоречит опыту.

Следствие равенства

принцип непрерывности потокосцепления означает, что ток индуктивности не может изменяться скачком:

 

– первый закон коммутации.

 

Запас энергии электрического поля емкости не может изменяться скачком. Это выражает принцип непрерывности во времени электрического заряда.

Невозможность скачкообразного изменения заряда объясняется в свою очередь тем, что в противном случае через емкость протекал бы бесконечно большой ток ,

что противоречит опыту.

Вследствие равенства

принцип непрерывности заряда означает, что напряжение на ёмкости не может измениться скачком:

– второй закон коммутации.

 

 

 

Следовательно: – величины, которые не могут изменяться скачком, – величины, которые могут изменяться скачком.

Значения функции в момент коммутации называются начальными условиями.

©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.

arhivinfo.ru

6.1.2. Законы коммутации. Начальные условия

Переходные процессы связаны с изменением магнитной энергии в индуктивности L и электрической энергии в емкостиСи запасом этих энергий на момент коммутации.

Энергия магнитного поля в индуктивности

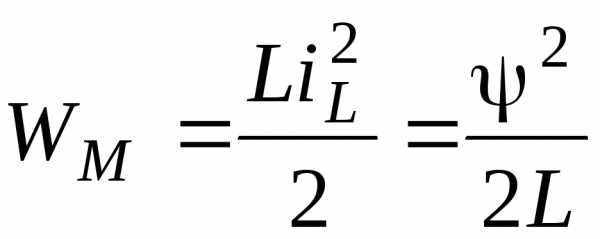(6.1)

и энергия электрического поля в емкости

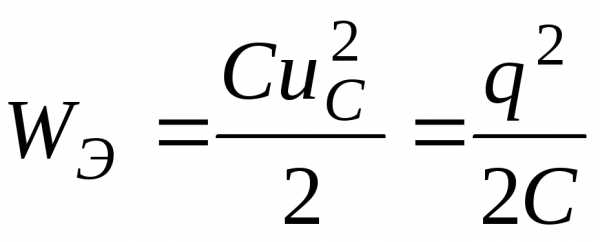(6.2)

не могут изменяться мгновенно, так как для мгновенного изменения энергии

потребовались бы бесконечно большие мощности источников, что физически невозможно.

Из соотношения (6.1) следует, что ток и потокосцепление в индуктивности не могут изменяться скачком (мгновенно). Это положение известно под названием первого закона коммутации.Из соотношения (6.2) следует, что напряжение на емкости и его заряд не могут изменяться скачком (мгновенно). Это положение называетсявторым законом коммутации.

Для учета влияния энергетического состояния цепи на момент коммутации и для записи законов коммутации введем понятие тока 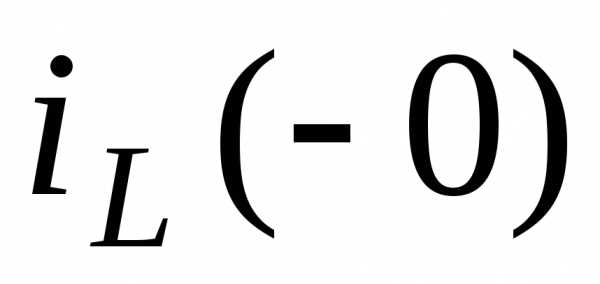в индуктивности и напряжения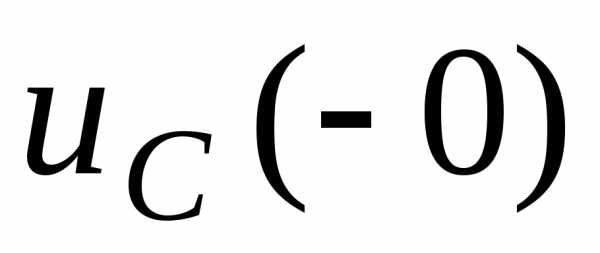на емкости в последний момент перед коммутацией, а также понятие токав индуктивности и напряженияна емкости в первый момент после коммутации. Напомним, что за момент коммутации принято времяt= 0. В соответствии с этим законы коммутации можно записать в виде:

первый закон коммутации или ; (6.3)

второй закон коммутации или . (6.4)

Заметим, что напряжение на индуктивности и ток в емкости могут изменяться мгновенно.

Если цепь содержит только активные сопротивления, то запасенная энергия электрического и магнитного полей несоизмеримо мала с выделяющейся тепловой энергией в сопротивлениях, что обусловливает отсутствие переходных процессов в таких цепях. При этом ток и напряжения изменяются мгновенно от первоначально установившегося режима до нового установившегося режима. Независимыми начальными условиямипринимают токиiL(–0) в индуктивностях и напряженияuC(–0) на емкостях, В дальнейшем для краткости будем их называть начальными условиями. ЕслиiL(–0)=0 иuC(–0)=0, то такие начальные условия называются нулевыми. Следует отметить, что характер переходного процесса зависит от начальных условий.

6.1.3. Расчет переходных процессов

Электромагнитные процессы в электрических цепях описываются дифференциальными уравнениями, составленными согласно первому и второму законам Кирхгофа с использованием уравнений элементов. Порядок дифференциального уравнения определяется тем, сколько в цепи имеется накопителей электрической и магнитной энергии. Если требуется найти ток ikвк-й ветви, то исключая последовательно все токи остальных ветвей, можно получить одно дифференциальное уравнение, содержащее только токik и его производные

(6.5)

Здесь - постоянные коэффициенты, значение которых зависит от конфигурации цепи. Правая частьf(t) содержит в себе заданные ЭДС.

Полный интеграл дифференциального уравнения с правой частью равен сумме частного решения этого уравнения и решения того же уравнения без правой части (однородного) [1].

Частное решениеуравнения (6.5) дает нам значение тока приt = ¥, т. е. при установившемся режиме, наступившем после коммутации. Характер и величина этой составляющей определяются внешними источниками. Поэтому ее часто называют принужденной составляющей и обозначают какiпр.Например, если источники постоянны, то и принужденный токiпр = const. Если же ЭДС заданы в виде синусоидальных функций, тоiпртакже будет синусоидальной функцией. Определениеiпрявляется задачей расчета установившегося режима в цепи, способы и методы которого рассматривались в предыдущих разделах дисциплины.

Общее решениефизически определяет электромагнитные процессы, происходящие в цепи при отсутствии внешних источников энергии, за счет запаса энергии в индуктивностях и емкостях, который был в начальный момент времени.

Так как в реальных цепях всегда имеет место рассеяние энергии (преобразование в тепло), то запас энергии будет со временем исчерпан и электромагнитные процессы в цепи прекратятся.

Из этого следует, что общее решение однородного уравнения должно стремиться к нулю при t ® ¥.Эта составляющая не зависит от внешних источников и поэтому ее часто называют свободной составляющей и обозначают какiсв.

Общее решение однородного дифференциального уравнения n-го порядка, как известно из курса математики в случае простых корней, имеет вид:

iсв=,

где t– время;Ak– постоянные интегрирования, определяемые из начальных условий;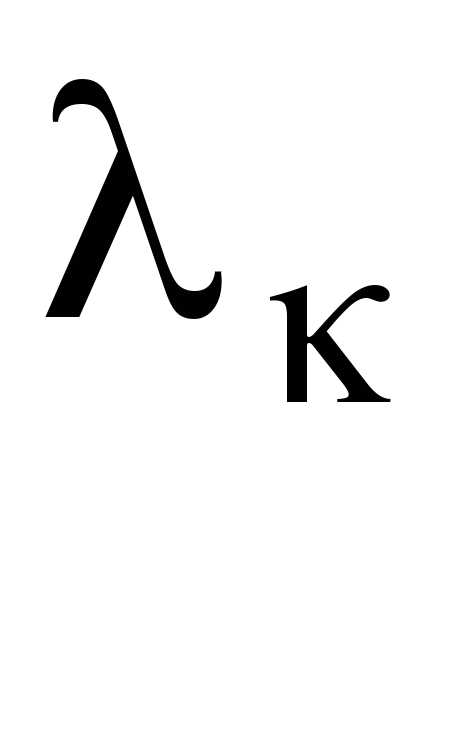– корень характеристического уравнения

ann + a n-1 n-1 + … + a 1 + a0 =0. (6.6)

Рассмотренный метод расчета переходных процессов называется классическим. Обратим внимание, что при составлении дифференциальных уравнений в качестве неизвестных необходимо принимать токiLв индуктивности и напряжениеuCна емкости. При таком выборе неизвестных достаточно легко на основании начальных условий и законов коммутации определить постоянные интегрирования.

studfiles.net

1 Переходные процессы и законы коммутации 2 Переходные

1 Переходные процессы и законы коммутации

2 Переходные процессы возникают при включении или отключении источников, элементов цепи, при коротких замыканиях и обрывах проводов, а также при различных импульсных воздействиях на цепь, например, при грозовых разрядах

3 Переходный процесс или переходный режим цепи – это изменение во времени напряжений и токов от одних установившихся значений к другим установившимся значениям

4 Установившиеся значения напряжений и токов характеризуют установившийся режим цепи и могут оставаться неизменными бесконечно долго, причем эти значения задаются источниками электрической энергии

5 При анализе и расчете переходных процессов будем считать, что переходные процессы возникают при включении или отключении элементов цепи посредством ключей, причем эта коммутация происходит мгновенно быстро в момент времени t=0

6 Ключ замыкается:

7 Ключ замыкается:

8 Ключ замыкается:

9 Ключ размыкается:

10 Ключ размыкается:

11 при времени t= переходный процесс теоретически заканчивается и наступает новый установившийся режим время t

12 момент времени t=0+ соответствует первому моменту времени после коммутации скачок – это мгновенное изменение напряжения или тока при t=0+

13 f(t) t Установившийся режим до коммутации Переходный режим Установившийся режим после коммутации 0

14 Законы коммутации

15 + 1. Первый закон коммутации

16 Ток в индуктивности не может измениться скачком

17 Это объясняется тем, что энергия магнитного поля индуктивного элемента WL=LiL2/2 , Дж не может измениться мгновенно, для чего потребовалась бы бесконечно большая мощность PL=dWL/dt= , Вт и бесконечно большое напряжение uL=d(LiL)/dt= , В а это не реально

18 - напряжение может измениться скачком

19 t 0

20 + 2. Второй закон коммутации

21 Напряжение на емкости не может измениться скачком

22 Это объясняется тем, что энергия электрического поля емкостного элемента WC=CuC2/2 , Дж не может измениться мгновенно, для чего потребовалась бы бесконечно большая мощность PC=dWC/dt= , Вт и бесконечно большой ток iC=d(CuC)/dt= , А а это не реально

23 - ток может измениться скачком

24 t 0

25 Переходный процесс обусловлен наличием в цепи L и C

26 К л а с с и ч е с к и й метод расчета переходных процессов

27 Используется для линейных цепей, которые характеризуются линейными дифференциальными уравнениями, составляемыми при помощи законов Кирхгофа для цепи после коммутации

28 - уравнение 1

29 это линейное неоднородное дифференциальное уравнение n- порядка для тока или напряжения f(t) переходного процесса при t>0 (схема после коммутации)

30 Где: постоянные коэффициенты, определяемые параметрами (R, L, C) и структурой цепи после коммутации

31 Где: функция, определяемая (независимыми) источниками цепи после коммутации

32 Решение уравнения 1:

33 Где: принужденная составляющая – это частное решение уравнения 1, зависящее от F(t)

34 Где: свободная составляющая – это общее решение однородного уравнения 1 при F(t) = 0

35 При постоянных и гармонических источниках это установившееся значение после коммутации

36 зависит от корней характеристического уравнения и начальных условий

37 Характеристическое уравнение 3:

38 а) если корни уравнения 3 вещественные, отрицательные и разные

39 То тогда

40 б) если корни уравнения 3 вещественные, отрицательные и одинаковые, т.е.

41 То тогда

42 в) если корни уравнения 3 комплексные и попарно сопряженные, т.е.

43 То тогда

44 Где: постоянные интегрирования, определяемые начальными условиями

45 Где: коэффициенты затухания свободных колебаний

46 Где: угловые частоты свободных колебаний

47 Различают: а) независимые начальные условия и

48 б) зависимые начальные условия и другие величины

49 в) принужденные значения, определяемые из расчета установившегося режима после коммутации

50 + + Пример:

51 Дано: Определить: начальные условия и принужденные составляющие

52 а) независимые начальные условия (схема до коммутации)

53 б) зависимые начальные условия (схема после коммутации при )

54 + +

55

56

57

58 в) принужденные составляющие (схема после коммутации при t = ) При постоянных источниках: L – закоротка, С – разрыв.

59

present5.com

---

• 
  Договор между управляющей организацией и ресурсоснабжающей организацией
• 
  Ток утечки как найти
• 
  Сварочный аппарат постоянка
• 
  Повторная аттестация по электробезопасности
• 
  Счетчик электроэнергии с пультом на столбе
• 
  Поверка электросчетчика или замена
• 
  Принцип работы контакторы
• 
  Как обозначается дифавтомат на схеме
• 
  7 августа 1986 ядерная катастрофа в сша
• 
  Условное обозначение электрических элементов на схеме
• 
  Принцип работы мтз