46. Полное сопротивление в цепи переменного тока.
Обычно
цепь переменного тока включает в себя
и активное сопротивление, и емкость, и
индуктивность.
Полное
сопротивление (Z)
— это векторная сумма всех сопротивлений:
активного, емкостного и индуктивного.
—
полное сопротивление цепи.
—
активное сопротивление.
—
индуктивное сопротивление.
—
полное сопротивление определяет силу
тока в цепи по закону Ома.
—
емкостное сопротивление.
I — действующее
значение силы тока (един.измер. А)
U— действующее
значение напряжения(един.измер. В)
XL
— индуктивное
сопротивление(един.измер. Ом)
ω — циклическая
частота переменного тока(един.измер.
рад/с)
L – индуктивность(ед.из.
Гн)
C – емкость (ед.из.
Ф)
XC
— индуктивное
сопротивление (ед.из. Ом)
Z — полное сопротивление
(Ом)
R — активное
сопротивление (Ом)
ρ — удельное
сопротивление проводника (Ом/м)
l
— длина проводника (м)
S
— площадь сечения проводника (м2
47.
 Импеданс тканей. Физические основы реографии.
Импеданс тканей. Физические основы реографии.
Импеданс –
основные понятия.
При прохождении
через ткани переменного тока, изменяющегося
по гармоническому закону
I(t)
=I0 cos
ωt,
падение напряжения
на биологической ткани изменяется по
закону
U
(t)=Uo⋅cos
(ωt+ϕ).
Величиной,
определяющей соотношение между
напряжением и силой переменного тока,
является импеданс
— полное электрическое сопротивление
цепи переменному току.
На опыте напряжение
отстает по фазе от тока (ϕ<0), что
характерно для электрических цепей,
состоящих из резисторов и конденсаторов.
Для биологического
объекта импеданс носит составной
(комплексный) характер Z=(R,X). Его активная
составляющая R связана, в первую очередь,
с проводимостью внутренних жидких сред,
являющихся электролитами. Различные
процессы в тканях, сопровождающиеся
необратимыми потерями энергии, также
дают вклад в величину активной составляющей
импеданса.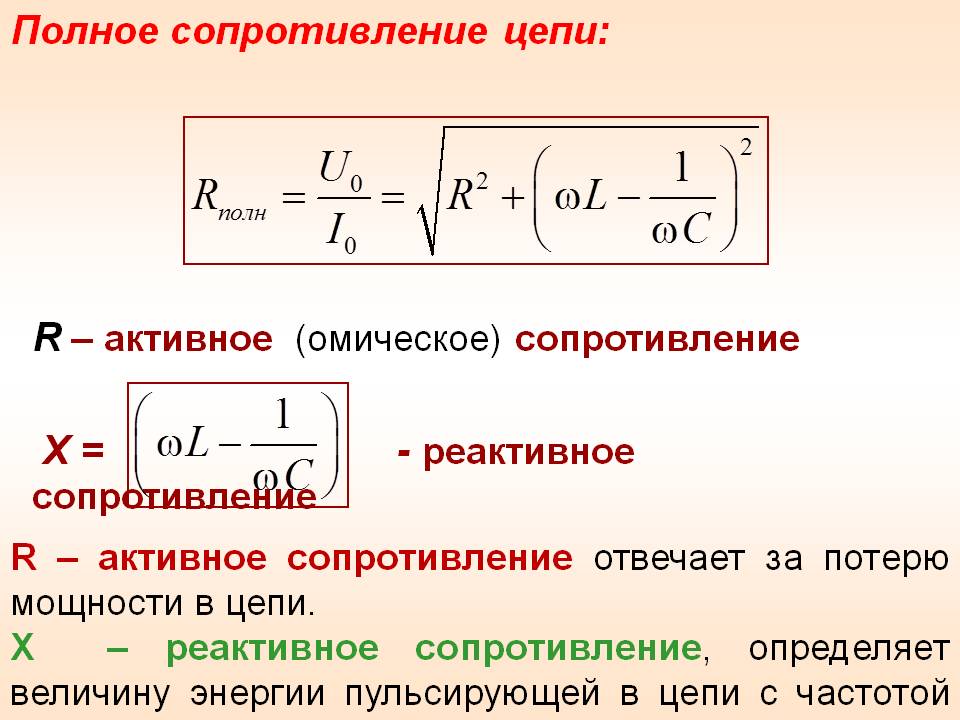 Реактивная компонента X
Реактивная компонента X
определяется емкостными свойствами
исследуемой ткани, в частности, емкостью
биологических мембран. Кроме того, в
емкостную составляющую импеданса дает
вклад и область контакта стимулирующих
электродов с биологическими тканями.
Абсолютная
величина (модуль) электрического
импеданса определяется выражением
.22XRZ+=
На
опыте величина импеданса может быть
определена по измерениям амплитудных
(или эффективных) значений напряжения
Uo и
силы тока Io
⏐Z⏐
= Uo/Io
(или ⏐Z⏐ =
Uэфф/Iэфф).
Фазовый сдвиг ϕ
определяет отношение реактивной и
активной составляющих импеданса
tg ϕ = X/R.
Значения угла
сдвига фаз, полученные при частоте 1 кГц
для различных биологических объектов,
приведены в таблице 1.
Таблица 1. Угол
сдвига фаз (в градусах) для различных
видов тканей.
Объект | ϕ |
Кожа человека, Нерв лягушки Мышцы | -55 -64 -65 |
Составную
(комплексную) величину Z принято изображать
в виде векторной диаграммы, на которой
ось абсцисс — величина активного
сопротивления, ось ординат — величина
реактивного сопротивления.
Абсолютная
величина импеданса ⏐Z⏐ и фазовый сдвиг
ϕ являются функциями частоты переменного
тока. Зависимость электрического
импеданса от частоты носит название
дисперсии
импеданса.
Физические основы
реологии.
Величина импеданса
тканей зависит от их физиологического
состояния, в частности от их кровоснабжения.
При кровенаполнении сосудов происходит
изменение величины импеданса в такт с
работой сердца. По величине изменений
импеданса можно судить о состоянии
сердечно-сосудистой системы.
Реология
— диагностический
метод, основанный на регистрации
изменения величины импеданса тканей в
процессе сердечной деятельности.
Величина
импеданса тканей |Z| состоит из двух
составляющих |Z| = |Zo|
+ |z(t)|: постоянной — |Zo|
и изменяющейся во времени в соответствии
с работой сердца – |z(t)|.
На
практике, на исследуемый участок тела
накладывают электроды площадью несколько
см2 и
пропускают переменный ток частотой ≈
30 − 40 кГц. Выбор частоты определяется
несколькими факторами: электробезопасностью,
исключением влияния электродов и емкости
их контакта с кожей, уменьшением
зависимости величины импеданса от
механических воздействий на исследуемую
ткань. Наполнение сосудов кровью изменяет
расстояния между отдельными участками
ткани, что должно приводить к изменению
ёмкостного сопротивления. Но вклад
Но вклад
макроскопических объемов тканей в
реактивную составляющую импеданса
существенен только в области α- дисперсии.
Следовательно, изменения импеданса во
времени обусловлены влиянием притока
и оттока крови на активную составляющую
полного сопротивления.
При
прохождении через ткани электрического
тока I = Io⋅cos
ωt величина напряжения будет изменяться
по закону
U
= Uο cos
(ωt + ϕ) = Io⋅(
⏐Zo⏐
+ ⏐z(t)⏐ )⋅cos
(ωt +ϕ ).
Электрическими
методами выделяют из регистрируемого
сигнала составляющую, пропорциональную
|z(t)|, содержащую информацию о состоянии
кровоснабжения изучаемого участка
тканей − реограмму.
Для парных
анатомических образований проводят
запись реограммы на правой и левой
стороне тела.
Полное сопротивление цепей переменного тока
При последовательном
соединении приборов с активным и индуктивным сопротивлениями полное сопротивление цепи нельзя находить арифметическим суммированием.
Полное сопротивление является геометрической суммой активного и реактивного сопротивлений. Для упрощения расчетов
полезно знать, что если одно из сопротивлений (r или xL) превосходит
другое в 10 или более раз, то можно пренебречь меньшим сопротивлением и
считать, что z равно большему сопротивлению. При параллельном соединении ветвей, имеющих активные и реактивные сопротивления …
При последовательном соединении приборов с активным и индуктивным сопротивлениями (рис. 1) полное сопротивление цепи нельзя находить арифметическим суммированием. Если обозначить полное сопротивление через z, то для его определения служит формула:
Как видно, полное сопротивление является геометрической суммой активного и реактивного сопротивлений. Так, например, если r = 30 Ом и XL = 40 Ом, то
т. е. z получилось меньше, чем r + XL = 30 + 40 = 70 Ом.
Для упрощения расчетов полезно знать, что если одно из сопротивлений (r или xL) превосходит другое в 10 или более раз, то можно пренебречь меньшим сопротивлением и считать, что z равно большему сопротивлению.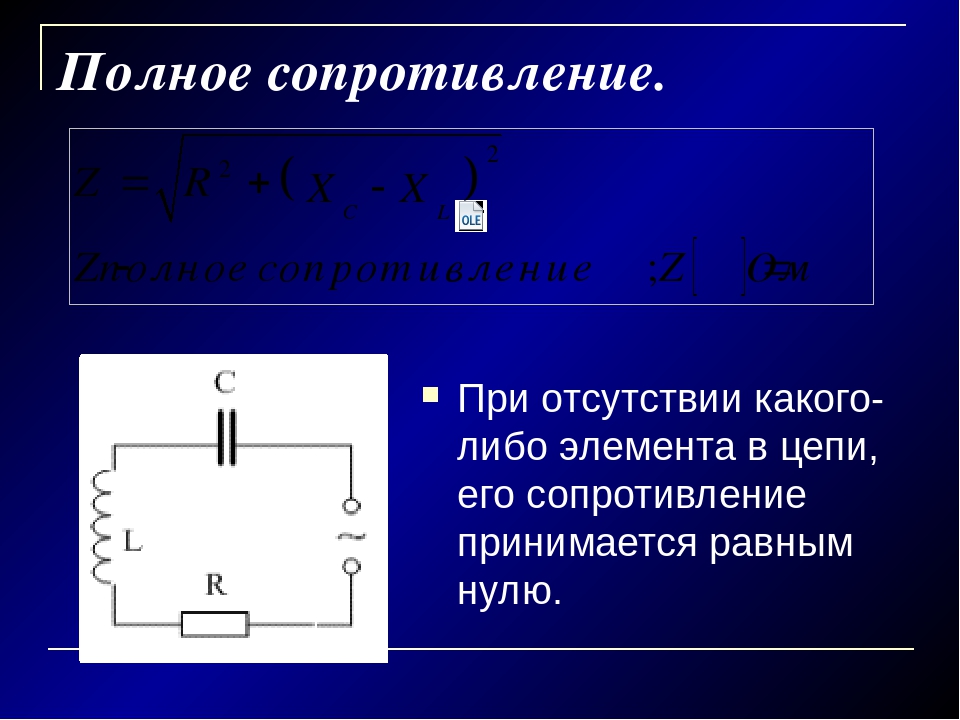 Ошибка весьма невелика.
Ошибка весьма невелика.
Например, если r = 1 Ом и xL = 10 Ом, то
Ошибка лишь 0,5 % вполне допустима, так как сами сопротивления r и х бывают известны с меньшей точностью.
Итак, если
То
а если
То
При параллельном соединении ветвей, имеющих активные и реактивные сопротивления (рис. 2), расчет полного сопротивления удобнее делать с помощью активной проводимости
и реактивной проводимости
Полная проводимость цепи у равна геометрической сумме, активной и реактивной проводимостей:
А полное сопротивление цепи является величиной, обратной у,
Если выразить проводимость через сопротивления, то нетрудно получить следующую формулу:
Эта формула напоминает известную формулу
но только в знаменателе стоит не арифметическая, а геометрическая сумма сопротивлений ветвей.
Пример. Найти полное сопротивление, если параллельно соединены приборы, имеющие r = 30 Он и xL = 40 Ом.
Решение.
При расчете z для параллельного соединения можно для упрощения пренебречь большим сопротивлением, если оно превосходит меньшее в 10 и более раз. Ошибка не будет превышать 0,5 %
Рис. 1. Последовательное соединение участков цепи с активным и индуктивным сопротивлением
Рис. 2. Параллельное соединение участков цепи с активным и индуктивным сопротивлением
Следовательно, если
То
а если
То
Принцип геометрического сложения применяется для цепей переменного тока также в случаях, когда надо складывать активные и реактивные напряжения или токи. Для последовательной цепи по рис. 1 складываются напряжения:
1 складываются напряжения:
При параллельном соединении (рис. 2) складываются токи:
Если же последовательно или параллельно соединены приборы, имеющие только одни активные или только одни индуктивные сопротивления, то сложение сопротивлений или проводимостей и соответствующих напряжений или токов, а также активных или реактивных мощностей производится арифметически.
При любой цепи переменного тока закон Ома можно писать в следующем виде:
где z — полное сопротивление, вычисляемое для каждого случая соединения так, как это было показано выше.
Коэффициент мощности cos для любой цепи равен отношению активной мощности Р к полной S. При последовательном соединении это отношение можно заменить отношением напряжений или сопротивлений:
При параллельном соединении получим:
10. 12.2016
12.2016
Без рубрики
Как определяется полное сопротивление цепи переменного тока
Импеданс (impedance) – комплексное, полное сопротивление переменному току электрической цепи с активным и реактивным сопротивлением.
Импеданс и общий сдвиг фаз для синусоидального тока можно рассчитать исходя из последовательного или параллельного соединения элементов цепи.
Последовательное соединение
При последовательном соединении, согласно Закону Ома для переменного тока, во всех элементах цепи ток будет общим I = U/Z, а значения напряжений на каждом элементе определятся пропорционально его сопротивлению:
на выводах резистора UR = IR; на выводах конденсатора UC = IXC; на выводах катушки UL = IXL.
Векторы индуктивной и ёмкостной составляющих напряжения направлены в противоположные стороны.
С учётом отрицательного ёмкостного сдвига, общее напряжение на реактивных элементах UX = UL — UC .
Пропорционально напряжению, получим общее реактивное сопротивление X = XL — XC .
Векторы напряжений на активной и реактивной составляющей импеданса имеют угол сдвига фаз 90 градусов.
U , UR и UX представим в виде прямоугольного треугольника напряжений с углом сдвига фаз φ.
Тогда получим соотношение, согласно Теореме Пифагора, U ² = UR² + UX² .
Следовательно, с учётом пропорциональности элементов R, L, C значениям напряжений на их выводах, определим импеданс, который будет равен квадратному корню из суммы квадратов активного и реактивного сопротивлений цепи.
XL = ωL = 2πfL — реактивное сопротивление индуктивности.
XC = 1/(ωC) = 1/(2πfC) — реактивное сопротивление ёмкости.
Угол сдвига фаз φ и его дополнение до 90° δ определятся тригонометрическими функциями из треугольника сопротивлений с катетами R, X и гипотенузой Z, как показано на рисунке:
Обычно, для облегчения расчётов, импеданс представляют в виде комплексного числа, где действительной его частью является активное сопротивление, а мнимой — реактивное.
Для последовательного соединения импеданс можно записать в комплексном виде следующим образом:
Тогда в тригонометрической интерпретации модулем этого числа будет импеданс, а аргументом — угол φ.
В соответствии с формулой Эйлера, запишем показательную форму комплексного импеданса:
Отсюда активная составляющая импеданса R = Zcosφ
Реактивная составляющая X = Zsinφ.
Параллельное соединение
Для вычисления импеданса при параллельном соединении активных и реактивных сопротивлений будем исходить из суммы обратных им величин — проводимостей y = 1/Z, G = 1/R, b = 1/X.
y = 1/Z = √(G 2 + b 2 )
Сдвиг фаз в этом случае будет определён треугольником сопротивлений следующим образом:
Комплексную проводимость, как величину, обратную комплексному импедансу, запишем в алгебраической форме:
Либо в показательной форме:
Здесь:
Y — комплексная проводимость.
G — активная проводимость.
b — реактивная проводимость.
y — общая проводимость цепи, равная модулю комплексной проводимости.
e — константа, основание натурального логарифма.
j — мнимая единица.
φ — угол сдвига фаз.
Онлайн-калькулятор расчёта импеданса и угла сдвига фаз
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Похожие страницы с расчётами:
Замечания и предложения принимаются и приветствуются!
При последовательном соединении приборов с активным и индуктивным сопротивлениями (рис. 1) полное сопротивление цепи нельзя находить арифметическим суммированием. Если обозначить полное сопротивление через z, то для его определения служит формула:
Как видно, полное сопротивление является геометрической суммой активного и реактивного сопротивлений. Так, например, если r = 30 Ом и XL = 40 Ом, то
т. е. z получилось меньше, чем r + XL = 30 + 40 = 70 Ом.
е. z получилось меньше, чем r + XL = 30 + 40 = 70 Ом.
Для упрощения расчетов полезно знать, что если одно из сопротивлений (r или xL) превосходит другое в 10 или более раз, то можно пренебречь меньшим сопротивлением и считать, что z равно большему сопротивлению. Ошибка весьма невелика.
Например, если r = 1 Ом и xL = 10 Ом, то
Ошибка лишь 0,5 % вполне допустима, так как сами сопротивления r и х бывают известны с меньшей точностью.
При параллельном соединении ветвей, имеющих активные и реактивные сопротивления (рис. 2), расчет полного сопротивления удобнее делать с помощью активной проводимости
и реактивной проводимости
Полная проводимость цепи у равна геометрической сумме, активной и реактивной проводимостей:
А полное сопротивление цепи является величиной, обратной у,
Если выразить проводимость через сопротивления, то нетрудно получить следующую формулу:
Эта формула напоминает известную формулу
но только в знаменателе стоит не арифметическая, а геометрическая сумма сопротивлений ветвей.
Пример. Найти полное сопротивление, если параллельно соединены приборы, имеющие r = 30 Он и xL = 40 Ом.
При расчете z для параллельного соединения можно для упрощения пренебречь большим сопротивлением, если оно превосходит меньшее в 10 и более раз. Ошибка не будет превышать 0,5 %
Рис. 1. Последовательное соединение участков цепи с активным и индуктивным сопротивлением
Рис. 2. Параллельное соединение участков цепи с активным и индуктивным сопротивлением
Принцип геометрического сложения применяется для цепей переменного тока также в случаях, когда надо складывать активные и реактивные напряжения или токи. Для последовательной цепи по рис. 1 складываются напряжения:
При параллельном соединении (рис. 2) складываются токи:
Если же последовательно или параллельно соединены приборы, имеющие только одни активные или только одни индуктивные сопротивления, то сложение сопротивлений или проводимостей и соответствующих напряжений или токов, а также активных или реактивных мощностей производится арифметически.
При любой цепи переменного тока закон Ома можно писать в следующем виде:
где z — полное сопротивление, вычисляемое для каждого случая соединения так, как это было показано выше.
Коэффициент мощности cosφ для любой цепи равен отношению активной мощности Р к полной S. При последовательном соединении это отношение можно заменить отношением напряжений или сопротивлений:
При параллельном соединении получим:
Вывод основных расчетных формул для последовательной цепи переменного тока, имеющей активное и индуктивное сопротивления, можно сделать следующим образом.
Проще всего построить векторную диаграмму для последовательной цепи (рис. 3).
Рис. 3. Векторная диаграмма для последовательной цепи с активным и индуктивным сопротивлением
На этой диаграмме показаны вектор тока I, вектор напряжения UA на активном участке, совпадающий по направлению с вектором I, и вектор напряжения UL на индуктивном сопротивлении. Это напряжение опережает ток на 90° (напомним, что векторы надо считать вращающимися против часовой стрелки). Полное напряжение U представляет собой суммарный вектор, т. е. диагональ прямоугольника со сторонами UA и UL. Иначе говоря, U есть гипотенуза, а UA и UL — катеты прямоугольного треугольника. Отсюда следует, что
Это напряжение опережает ток на 90° (напомним, что векторы надо считать вращающимися против часовой стрелки). Полное напряжение U представляет собой суммарный вектор, т. е. диагональ прямоугольника со сторонами UA и UL. Иначе говоря, U есть гипотенуза, а UA и UL — катеты прямоугольного треугольника. Отсюда следует, что
Т. е. что напряжения на активном и реактивном участках складываются геометрически.
Разделив обе части равенства на I2, найдем формулу для сопротивлений:
В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется активным, а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные.
Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.
Введем понятие полного сопротивления цепи переменному току — Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока
Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока
На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь.
Рисунок 1. Классификация цепей переменного тока.
Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи.
Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.
Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.
В любом сечении цепи, изображенной на рисунке 2,а, мгновенные значения тока должны быть одинаковыми, так как в противном случае наблюдались бы скопления и разрежения электронов в каких-либо точках цепи. Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения UL (напряжение на индуктивном сопротивлении) и напряжения UR (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.
Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения UL (напряжение на индуктивном сопротивлении) и напряжения UR (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.
Рисунок 2. Полное сопротивление цепи с активным сопротивлением и индуктивностью. а) — схема цепи; б) — сдвиг фаз тока и напряжения; в) — треугольник напряжений; д) — треугольник сопротивлений.
Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов UL и UR. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор UAB является гипотенузой прямоугольного треугольника.
Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.
По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление.
Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z 2 ) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е.
(1)
Извлекая квадратный корень из обеих частей этого равенства, получим,
(2)
Таким образом, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений
Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.
Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.
Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.
В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи.
Рисунок 3. Полное сопротивление цепи с активным сопротивлением и емкостью. а) — схема цепи; б) — треугольник сопротивлений .
Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его.
Для данного случая:
(3)
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.
Рисунок 4. Полное сопротивление цепи содержащей R, L и C. а) — схема цепи; б) — треугольник сопротивлений .
Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. е.
е.
(4)
Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (XL или XC преобладает).
После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.
(5)
(6)
Способ построения треугольника сопротивлений для этого случая изображен на рис. 4 б.
Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.
Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.
Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.
Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) — параллельное соединение R и L; б) — параллельное соединение R и C .
Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z
Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.
(7)
Приводя к общему знаменателю подкоренное выражение, получим:
(8)
(9)
Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.
Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.
Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно:
(10)
Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.
В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).
Рисунок 6. Эквивалентная схема колебательного контура.
Формула полного сопротивления для этого случая будет:
(11)
Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:
(12)
В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие
е. чтобы соблюдалось условие
(13)
При соблюдении этого условия полное сопротивление колебательного контура будет равно:
(14)
где L—индуктивность катушки в Гн;
С—емкость конденсатора в Ф;
R—активное сопротивление катушки в Ом.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Как найти полное сопротивление цепи
В любой цепи переменного тока наряду с чисто реактивным сопротивлением присутствует омическое (активное) сопротивление, которое нужно учитывать при определении полного сопротивления.
| Z | полное сопротивление, | Ом |
|---|---|---|
| R | омическое (активное) сопротивление, | Ом |
| X | реактивное сопротивление, | Ом |
| Y = 1/Z | полная проводимость, | сименс |
| G | активная проводимость, | сименс |
| B | реактивная проводимость, | сименс |
| U | полное напряжение (эффективное значение), | Вольт |
| I | полный ток (эффективное значение), | Ампер |
Полное сопротивление при последовательном соединении R и X
При последовательном соединении активное и реактивное сопротивления складываются геометрически
X определяется по формулам реактивного сопротивления и Величина Ux определяется, как произведение IX.
Сопротивление Z не зависит от времени. Вектор, изображающий сопротивление на векторной диаграмме, не вращается.
Полное сопротивление при параллельном соединение R и X
При параллельном соединении активная и реактивная проводимости складываются геометрически
Величина В = 1/Х определяется но формулам реактивного сопротивления. Ix определяется как произведение UB.
Величина Y не зависит от времени. Вектор, изображающий на векторной диаграмме проводимость, не вращается.
При последовательном соединении участков электрической цепи полное сопротивление всей цепи
(1.1)
и определяется из выражения (1.2)
где r — активное сопротивление всей цепи; x – реактивное сопротивление всей цепи.
Результаты измерений в неразветвленной цепи
| № п/п | Характер нагрузки | Измеренные величины | Примечание | |
| U, B | I, A | P, Вт | Uk, B | Uc, B |
| Катушка индуктивности и конденсатор | xk xc(Cmax= ) | |||
| Катушка индуктивности | ||||
| Конденсатор | Cmin= | |||
| Ламповый реостат |
Активное сопротивление катушки вычисляется по формуле:
(1. 3)
3)
где Рk — активная мощность, потребляемая катушкой индуктивности, в опытах 1, 2, 3 и 4 равная активной мощности всей цепи Р.
Реактивное (индуктивное) сопротивление катушки определяется следующим образом:
(1.4)
где – полное сопротивление катушки индуктивности.
Индуктивность катушки вычисляется по формуле:
(1.5)
где ω, с -1 — круговая частота напряжения питания; f = 50 Гц — циклическая частота напряжения питания.
Реактивное (емкостное) сопротивление конденсатора можно вычислить следующим образом:
(1.6)
Емкость конденсатора определяется по формуле:
. (1.7)
Коэффициенты мощности всей цепи cosφ и катушки индуктивности cosφк вычисляются по формулам:
(1.8)
(1.9)
Составляющие напряжения катушки Uak — активная и реактивная Upk — определяются по формулам:
(1.10)
Активное сопротивление лампового реостата определяется по данным опыта 6 как
(1. 11)
11)
Реактивное сопротивление всей цепи при последовательном соединении катушки индуктивности и конденсатора можно определить по формуле:
. (1.12)
Рассчитанные значения параметров цепи записать в табл. 1.3.
По результатам измерений и расчетным данным строятся векторные диаграммы. На рис. 1.2 приведен пример построения векторной диаграммы.
Рис. 1.2. Пример построения векторной диаграммы для последовательного соединения катушки индуктивности и конденсатора
Параметры неразветвленной цепи
| № п/п | Ламповый реостат | Катушка индуктивности | Конденса-тор | Вся цепь | |||||||||
| rr, Ом | rk, Ом | xk, Ом | zk, Ом | cosφk | L, мГн | Uak, B | Upk, B | xc,Ом | C, мкФ | r, Ом | x, Ом | z,Ом | cosφ |
. |
При построении векторных диаграмм для последовательного соединения элементов электрической цепи за исходный вектор принимается вектор тока. Векторы напряжений откладываются в масштабе, общем для всех напряжений. Вектор Ūr совпадает по направлению с вектором тока, а вектор Ūс отстает от вектора тока на угол π/2. Вектор напряжения Ūk строится как векторная сумма вектора активной составляющей Ūаk, совпадающего по фазе с вектором тока, и вектора индуктивной составляющей Ūpk, опережающего вектор тока на угол π/2.
Вектор приложенного к схеме напряжения Ū равен векторной сумме векторов напряжений на отдельных элементах цепи.
При последовательном соединении катушки индуктивности и конденсатора и условии
наступает резонанс напряжений.
В этом режиме цепь ведет себя как активное сопротивление:
(1.14)
При резонансе напряжений, если реактивные сопротивления катушки индуктивности и конденсатора значительно больше активного сопротивления цепи, на катушке индуктивности и конденсаторе возникают перенапряжения, величина которых существенно больше напряжения питания, что может привести к пробою изоляции и выходу из строя этих элементов.
В отчете привести:
– принципиальные схемы с необходимыми пояснениями;
– паспортные данные приборов;
– таблицы и расчетные формулы;
– векторные диаграммы для режимов, указанных преподавателем.
Вопросы для самоконтроля
2. Как найти полное сопротивление последовательной цепи, если известно сопротивление отдельных элементов?
3. Что такое коэффициент мощности?
4. Как можно изменить коэффициент мощности всей цепи?
5. Вследствие чего ток в цепи при резонансе напряжений имеет наибольшее значение?
6. Что такое резонанс напряжений и каковы его характерные особенности?
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9364 – | 7302 – или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
При последовательном соединении приборов с активным и индуктивным сопротивлениями (рис. 1) полное сопротивление цепи нельзя находить арифметическим суммированием. Если обозначить полное сопротивление через z, то для его определения служит формула:
Как видно, полное сопротивление является геометрической суммой активного и реактивного сопротивлений. Так, например, если r = 30 Ом и XL = 40 Ом, то
т. е. z получилось меньше, чем r + XL = 30 + 40 = 70 Ом.
Для упрощения расчетов полезно знать, что если одно из сопротивлений (r или xL) превосходит другое в 10 или более раз, то можно пренебречь меньшим сопротивлением и считать, что z равно большему сопротивлению. Ошибка весьма невелика.
Например, если r = 1 Ом и xL = 10 Ом, то
Ошибка лишь 0,5 % вполне допустима, так как сами сопротивления r и х бывают известны с меньшей точностью.
При параллельном соединении ветвей, имеющих активные и реактивные сопротивления (рис. 2), расчет полного сопротивления удобнее делать с помощью активной проводимости
и реактивной проводимости
Полная проводимость цепи у равна геометрической сумме, активной и реактивной проводимостей:
А полное сопротивление цепи является величиной, обратной у,
Если выразить проводимость через сопротивления, то нетрудно получить следующую формулу:
Эта формула напоминает известную формулу
но только в знаменателе стоит не арифметическая, а геометрическая сумма сопротивлений ветвей.
Пример. Найти полное сопротивление, если параллельно соединены приборы, имеющие r = 30 Он и xL = 40 Ом.
При расчете z для параллельного соединения можно для упрощения пренебречь большим сопротивлением, если оно превосходит меньшее в 10 и более раз. Ошибка не будет превышать 0,5 %
Рис. 1. Последовательное соединение участков цепи с активным и индуктивным сопротивлением
Рис. 2. Параллельное соединение участков цепи с активным и индуктивным сопротивлением
2. Параллельное соединение участков цепи с активным и индуктивным сопротивлением
Принцип геометрического сложения применяется для цепей переменного тока также в случаях, когда надо складывать активные и реактивные напряжения или токи. Для последовательной цепи по рис. 1 складываются напряжения:
При параллельном соединении (рис. 2) складываются токи:
Если же последовательно или параллельно соединены приборы, имеющие только одни активные или только одни индуктивные сопротивления, то сложение сопротивлений или проводимостей и соответствующих напряжений или токов, а также активных или реактивных мощностей производится арифметически.
При любой цепи переменного тока закон Ома можно писать в следующем виде:
где z — полное сопротивление, вычисляемое для каждого случая соединения так, как это было показано выше.
Коэффициент мощности cosφ для любой цепи равен отношению активной мощности Р к полной S. При последовательном соединении это отношение можно заменить отношением напряжений или сопротивлений:
При параллельном соединении получим:
Вывод основных расчетных формул для последовательной цепи переменного тока, имеющей активное и индуктивное сопротивления, можно сделать следующим образом.
Проще всего построить векторную диаграмму для последовательной цепи (рис. 3).
Рис. 3. Векторная диаграмма для последовательной цепи с активным и индуктивным сопротивлением
На этой диаграмме показаны вектор тока I, вектор напряжения UA на активном участке, совпадающий по направлению с вектором I, и вектор напряжения UL на индуктивном сопротивлении. Это напряжение опережает ток на 90° (напомним, что векторы надо считать вращающимися против часовой стрелки). Полное напряжение U представляет собой суммарный вектор, т. е. диагональ прямоугольника со сторонами UA и UL. Иначе говоря, U есть гипотенуза, а UA и UL — катеты прямоугольного треугольника. Отсюда следует, что
Т. е. что напряжения на активном и реактивном участках складываются геометрически.
Разделив обе части равенства на I2, найдем формулу для сопротивлений:
Как вычислить полное сопротивление цепи
Импеданс (impedance) – комплексное, полное сопротивление переменному току электрической цепи с активным и реактивным сопротивлением.
Импеданс и общий сдвиг фаз для синусоидального тока можно рассчитать исходя из последовательного или параллельного соединения элементов цепи.
Последовательное соединение
При последовательном соединении, согласно Закону Ома для переменного тока, во всех элементах цепи ток будет общим I = U/Z, а значения напряжений на каждом элементе определятся пропорционально его сопротивлению:
на выводах резистора UR = IR; на выводах конденсатора UC = IXC; на выводах катушки UL = IXL.
Векторы индуктивной и ёмкостной составляющих напряжения направлены в противоположные стороны.
С учётом отрицательного ёмкостного сдвига, общее напряжение на реактивных элементах UX = UL — UC .
Пропорционально напряжению, получим общее реактивное сопротивление X = XL — XC .
Векторы напряжений на активной и реактивной составляющей импеданса имеют угол сдвига фаз 90 градусов.
U , UR и UX представим в виде прямоугольного треугольника напряжений с углом сдвига фаз φ.
Тогда получим соотношение, согласно Теореме Пифагора, U ² = UR² + UX² .
Следовательно, с учётом пропорциональности элементов R, L, C значениям напряжений на их выводах, определим импеданс, который будет равен квадратному корню из суммы квадратов активного и реактивного сопротивлений цепи.
XL = ωL = 2πfL — реактивное сопротивление индуктивности.
XC = 1/(ωC) = 1/(2πfC) — реактивное сопротивление ёмкости.
Угол сдвига фаз φ и его дополнение до 90° δ определятся тригонометрическими функциями из треугольника сопротивлений с катетами R, X и гипотенузой Z, как показано на рисунке:
Обычно, для облегчения расчётов, импеданс представляют в виде комплексного числа, где действительной его частью является активное сопротивление, а мнимой — реактивное.
Для последовательного соединения импеданс можно записать в комплексном виде следующим образом:
Тогда в тригонометрической интерпретации модулем этого числа будет импеданс, а аргументом — угол φ.
В соответствии с формулой Эйлера, запишем показательную форму комплексного импеданса:
Отсюда активная составляющая импеданса R = Zcosφ
Реактивная составляющая X = Zsinφ.
Параллельное соединение
Для вычисления импеданса при параллельном соединении активных и реактивных сопротивлений будем исходить из суммы обратных им величин — проводимостей y = 1/Z, G = 1/R, b = 1/X.
y = 1/Z = √(G 2 + b 2 )
Сдвиг фаз в этом случае будет определён треугольником сопротивлений следующим образом:
Комплексную проводимость, как величину, обратную комплексному импедансу, запишем в алгебраической форме:
Либо в показательной форме:
Здесь:
Y — комплексная проводимость.
G — активная проводимость.
b — реактивная проводимость.
y — общая проводимость цепи, равная модулю комплексной проводимости.
e — константа, основание натурального логарифма.
j — мнимая единица.
φ — угол сдвига фаз.
Онлайн-калькулятор расчёта импеданса и угла сдвига фаз
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Похожие страницы с расчётами:
Замечания и предложения принимаются и приветствуются!
1. Находим полное сопротивление цепи
Z =
где R = R1 + R2 = 2 + 2 = 4 – арифметическая сумма всех активных сопротивлений, Ом;
Х L = Х L1 + Х L2 = 4 + 5 = 9, X C = X C1 + X C2 = 4 + 2 = 6 – арифметические суммы однотипных индуктивного и емкостного сопротивлений, Ом.
Подставляем полученные значения в формулу.
Z = = = 5 Ом
2. По закону Ома для цепи переменного тока определим ток в цепи:
I = U / Z = 220 / 5 = 44 А
3. Из треугольника сопротивлений следует: Сos φ = R / Z = 4 / 5 = 0,8 ;
Sin φ= =( 9 – 6) / 5 = 0,6
По таблицам тригонометрических величин найдем значения угла сдвига фаз: φ = 36 0
4. Подсчитываем мощности:
полная мощность S = U· I = 220 · 44 = 9680 ВА = 9,6 кВА
активная Р = S ·Сos φ = 9680 · 0,8 = 7744 Вт =7,744 кВт
реактивная Q = S· Sin φ = 9680· 0,6 = 5808 вар = 5,808 квар
При построении векторных диаграмм тока и напряжений следует исходить из следующих условий:
· ток одинаков для любого участка цепи, т. к. разветвлений в ней нет;
· на каждом сопротивлении при прохождении тока создается падение напряжения, значение которого определяют по закону Ома для цепи и называют напряжением на данном сопротивлении: UА = I ·R – на активном, UL = I ·Х L – на индуктивном; U С = I ·Х С – на емкостном.
Построение векторной диаграммы
1. Выписываем значение тока и напряжений: I= 44 А; U L1 = I ·Х L1 = 44· 4 = 176 В; U А1 = I· R1 = 44 · 2 = 88 В; UL2 = I ·Х L2 = 44 ·5 = 220 В; U А2 = I ·R2 =
44 · 2 = 88 В; Uc1 =I ·Х С1 = 44 · 4 = 176 В; U С2 = I· Х С2 = 44 · 2 = 88 В.
2. Исходя из размеров бумаги (миллиметровки, или тетрадного листа в клетку), задаемся масштабом по току и напряжению. Для рассматриваемого примера принимаем масштаб: по току m I= 10 А /см, по напряжению
m U =44 В/ см. Тогда длины векторов ℓ следующие:
длина вектора тока
ℓI = I / m I = 44 / 10 = 4,4 см;
длины векторов напряжений
ℓ UА 1 = U А1 / m U = 88 В / 44 В / см = 2 см
ℓ UА 2 = U А2 / m U = 88 В / 44 В / см = 2 см
ℓ UС 2 = U С 2 / m U = 88 В / 44 В см = 2 см
3. Выполняем построение диаграммы в такой последовательности:
Выполняем построение диаграммы в такой последовательности:
а) за начальный принимается вектор тока, так как ток имеет одинаковое значение для всех участков цепи.
Строим этот вектор горизонтально в масштабе (рисунок 15)
Далее следует строить векторы напряжений на каждом сопротивлении с учетом сдвига фаз относительно вектора тока.
При этом целесообразно придерживать схемной ( рисунок 14) последовательности расположения сопротивлений и напряжений на них.
б) вектор напряжения на первом индуктивном сопротивлении строим от начало вектора тока под углом 90 0 в сторону опережения этого вектора (вверх) ( рисунок 16)
Опережение или отставание вектора определяется характером нагрузки и принятым направлением вращения векторов против часовой стрелки;
в) вектор напряжения на первом активном сопротивлении UА1 строим от конца вектора UL1, параллельно вектору тока, т. к. между этими векторами I и UА1 сдвига фаз нет (рисунок 17)
m U = 44 В / см m U = 44 В / см
Рисунок 16 Рисунок 17
г) вектор напряжения на втором индуктивном сопротивлении UL2 строим от конца вектора UА1 в сторону опережения на 90 0 (вверх) (рисунок 18)
m U = 44 в / см m U = 44 в / см m U = 44 в / см
Рисунок 18 Рисунок 19 Рисунок 20
д) вектор напряжения на втором активном сопротивлении UА2 строим от конца вектора UL2 параллельно вектору тока аналогично построению вектора UА1 (рисунок 19) .
е) векторы напряжений на первом и втором емкостных сопротивлений UС1 и UС2 строим от конца вектора UА2 под углом 90 0 в сторону отставания от вектора тока (вниз) ( риcунок 20).
ж) вектор полного напряжения U находим геометрическим сложением векторов по правилу многоугольника; начало принятого за первый вектор UL1 соединением с концом последнего вектора UС2 (рисунок 21).
Угол между векторами тока I и общего ( приложенного) напряжения U обозначают φ и называют углом сдвига фаз данной цепи.
Следует проверить аналитическое решение и построение векторной диаграммы путем их сопоставления следующим образом.
1. Проверка угла φ производится с помощью транспортира и сравнением полученного угла в градусах с расчетным значением решения в данном случае по расчету φ = 36 0 по диаграмме этот угол также равен φ = 36 0 .
2. Проверка значения приложенного напряжения по диаграмме длина этого вектора ℓ U = 5 см, значение напряжения
U = ℓ U ·m U = 5 см · 44 В / см = 220 В,
что соответствует условием задачи. Значит , диаграмма построена верно. В случае значительных расхождений при такой проверке следует найти ошибку.
Значит , диаграмма построена верно. В случае значительных расхождений при такой проверке следует найти ошибку.
4 Экзаменационные вопросы
1. Определение и изображение электрического поля. Закон Кулона.
2. Напряженность электрического поля. Электрическое напряжение.
3. Электроизоляционные материалы.
4. Электрическая емкость. Плоский конденсатор. Соединение конденсаторов. Энергия электрического поля.
5. Преобразование электрической энергии в тепловую энергию.
6. Электрическая цепь, электрический ток, сила тока.
7. Проводниковые материалы. Зависимость сопротивления от температуры.
8. Закон Ома для участка и полной электрической цепи.
9. Способы соединения сопротивлений.
10. Законы Кирхгофа.
11. Электрическое сопротивление. Проводимость.
12. Энергия и мощность электрической цепи, их единицы измерения.
13. Магнитная индукция и магнитная проницаемость.
14. Магнитные материалы, применяемые в электрических приборах и машинах.
15. Действие магнитного поля на проводник с током.
16. Классификация измерительных приборов, классы точности.
17. Расширение пределов измерения приборов в цепях переменного и постоянного тока.
18. Измерение тока, напряжения, сопротивления.
19. Ваттметр, электрический счетчик, способ включения в цепь переменного тока.
20. Приборы электромагнитной системы ,устройство, принцип действия, достоинства и недостатки.
21. Приборы магнитоэлектрической системы, устройство, принцип действия, достоинства и недостатки.
22. Приборы электродинамической системы, устройство, принцип действия, достоинства и недостатки.
23. Получение однофазного переменного тока.
24. Переменный ток. Амплитудное, действующее и мгновенное значение величины переменного тока, период, частота, фаза, сдвиг фаз.
25. Цепь с последовательным соединением активного и индуктивного сопротивления.
26. Электрическая цепь с последовательным включением активного и емкостного сопротивления.
27. Цепь с последовательным соединением активного, индуктивного и емкостного сопротивлений. Условия резонанса напряжений.
28. Условия и принцип действия трехфазных синхронных электрических двигателей.
29. Треугольник сопротивления и мощности при последовательном соединении R,L,C.
30. Понятие об электроприводе, структурная схема. Режимы работы электродвигателей.
31. Электрическая цепь с параллельным включением активного, индуктивного и емкостного сопротивления. Резонанс токов.
32. Передача и распределение электрической энергии.
33. Активная, реактивная и полная мощность электрической цепи
34. Принципы получения трехфазной ЭДС
35. Транзистор. Устройство, назначение и принцип действия. Условное обозначение.
36. Соединение электроприемников в «звезду». Линейные, фазные токи и напряжения.
37.Двух – полупериодная схема выпрямления с использованием средней точки вторичной обмотки трансформатора.
38.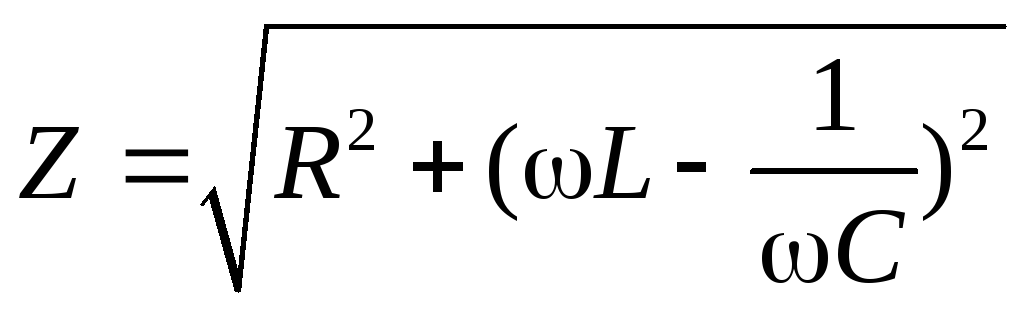 Соединение электроприемноков в «треугольник». Линейные и фазные токи и напряжения.
Соединение электроприемноков в «треугольник». Линейные и фазные токи и напряжения.
39. Устройство и принцип действия трансформаторов и автотрансформаторов.
40. Электрическая схема реверсивного магнитного пускателя.
41. Источники света и осветительная аппаратура на строительной площадке
42. действие электрического тока на организм человека.
43. Виды электрической сварки.
44. Использование сварочных аппаратов в строительных технологиях..
45. Особенности работы электрооборудования грузоподъемных машин.
46. Простейшие схемы электроснабжения.
47. Защитное заземление и зануление.
48. Требования к крановым электродвигателям.
49. Классификация электрических машин.
50. Классификация электрических сетей.
51. Трансформаторные подстанции и особенности их размещения на строительной площадке.
5 Список рекомендуемой литературы
1. Зайцев В.Е. Нестерова Т.А. Электротехника. Электроснабжение, электротехнология и электрооборудование строительных площадок. М.: Мастерство, 2001.
М.: Мастерство, 2001.
2. Данилов И.А., Иванов П.М. Общая электротехника с основами электроники. М.: Высшая школа, 1989.
3. Зайцев В.Е., Нестерова Т.А. «Задания на лабораторные работы по электронике». Смоленск, 1966.
4. Евдокимов Ф.Е. Общая электротехника. М.: Высшая школа.
5. Чикаев Д.С., Федуркина М.Д. Электрооборудование строительных машин и энергоснабжение строительных площадок.
6. Рабинович Э.А. Сборник задач по общей электротехнике. М.: Стройздат, 1981.
Дата добавления: 2015-05-06 ; Просмотров: 1098 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется активным, а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные.
Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.
То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.
Введем понятие полного сопротивления цепи переменному току — Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока
На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь.
Рисунок 1. Классификация цепей переменного тока.
Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи.
Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.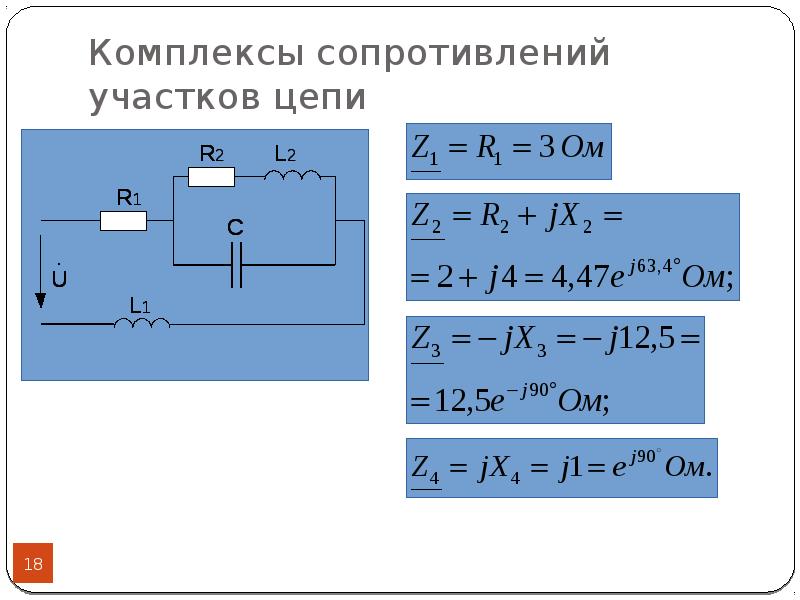
Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.
В любом сечении цепи, изображенной на рисунке 2,а, мгновенные значения тока должны быть одинаковыми, так как в противном случае наблюдались бы скопления и разрежения электронов в каких-либо точках цепи. Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения UL (напряжение на индуктивном сопротивлении) и напряжения UR (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.
Рисунок 2. Полное сопротивление цепи с активным сопротивлением и индуктивностью. а) — схема цепи; б) — сдвиг фаз тока и напряжения; в) — треугольник напряжений; д) — треугольник сопротивлений.
Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов UL и UR. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор UAB является гипотенузой прямоугольного треугольника.
Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.
По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление.
Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z 2 ) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е.
(1)
Извлекая квадратный корень из обеих частей этого равенства, получим,
(2)
Таким образом, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений
Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т.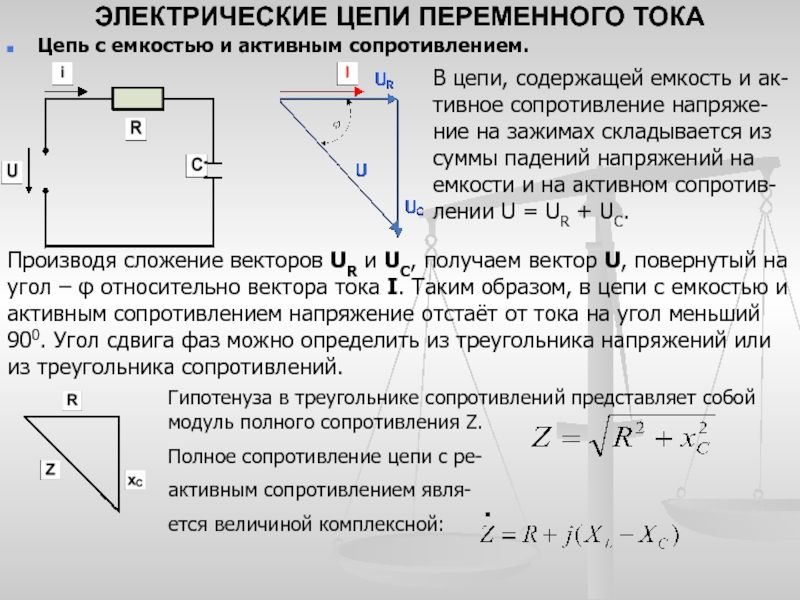 е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.
е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.
Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.
В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи.
Рисунок 3. Полное сопротивление цепи с активным сопротивлением и емкостью. а) — схема цепи; б) — треугольник сопротивлений .
Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его.
Для данного случая:
(3)
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.
Рисунок 4. Полное сопротивление цепи содержащей R, L и C. а) — схема цепи; б) — треугольник сопротивлений .
а) — схема цепи; б) — треугольник сопротивлений .
Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. е.
(4)
Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (XL или XC преобладает).
После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.
(5)
(6)
Способ построения треугольника сопротивлений для этого случая изображен на рис. 4 б.
Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.
Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.
Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.
Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) — параллельное соединение R и L; б) — параллельное соединение R и C .
Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z
Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.
(7)
Приводя к общему знаменателю подкоренное выражение, получим:
(8)
(9)
Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.
5а.
Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.
Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно:
(10)
Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.
В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).
Рисунок 6. Эквивалентная схема колебательного контура.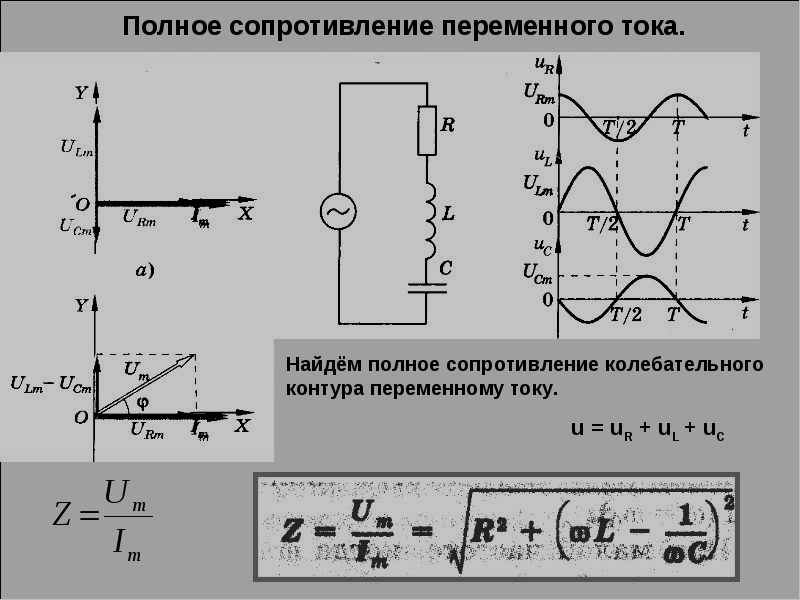
Формула полного сопротивления для этого случая будет:
(11)
Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:
(12)
В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие
(13)
При соблюдении этого условия полное сопротивление колебательного контура будет равно:
(14)
где L—индуктивность катушки в Гн;
С—емкость конденсатора в Ф;
R—активное сопротивление катушки в Ом.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Полное сопротивление цепи — Справочник химика 21
Полное сопротивление цепи равно [c.13]
Найдем импеданс (полное сопротивление) цепи (см. рис. 20,6). Так как реактивное сопротивление емкости с = 1//шс, то полная проводимость У параллельного участка R и i) составит [c.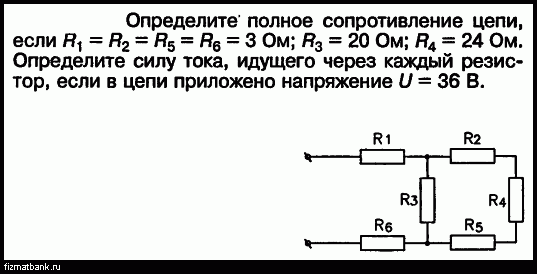 118]
118]
В системах, где не достигается защитного потенциала по той или иной причине, полное сопротивление цепи КСС с увеличением напряжения несколько увеличивается (рис. 18). [c.36]
Импеданс (полное сопротивление) цепи гфи влиянии внешних полей [c.674]
Разрядная емкость ХИТ (- р) [c.866]
Таким образом, наибольшая мощность дуги достигается при условии, что сопротивление дуги равно полному сопротивлению цепи. Значение максимальной мощности дуги Рд, акс и тока /2-1 можно получить при подстановке Гд = в формулы (2-27) и (2-18) [c.78]
Усилитель фирмы Листон—Беккер обычно не имеет цепи обратной связи. Следовательно, при изменении положения делителя на мостике становится другой и усиливаемая мощность, что является следствием изменения полного сопротивления цепи. В результате для применяемой системы следует калибровать коэффициенты деления. Усилитель с цепью обратной связи устраняет эту проблему. [c.139]
[c.139]
У—1- Полное сопротивление цепи, показанной на [c.67]
Из анализа выражения для полного сопротивления последовательной эквивалентной электрической схемы ячейки следует, что активная составляющая полного сопротивления цепи [Л. 1] [c.13]
При нагрузках до 10 Мн м тепловое сопротивление контактов составляет значительную часть (до 50% и более) от полного сопротивления цепи. [c.183]
Z n — полное сопротивление цепи фаза — нуль, Ом. [c.91]
Измерение полного сопротивления цепи фаза — нулевой защитный проводник способом амперметра — вольтметра. Этот способ применяют при отключенном испытуемом оборудовании. Измерение производится на переменном токе пониженного напряжения от трансформатора достаточной мощности. Для измерения делают искусственное замыкание одного из фазных проводов на корпус электрооборудования. После подачи напряжения в измерительную цепь измеряются ток / и напряжение 1/. Ток должен составлять 10—20 А. [c.65]
Ток должен составлять 10—20 А. [c.65]
Когда конденсатор включается последовательно с батареей, то полное сопротивление цепи определяется выражением [c.78]
Тогда полное сопротивление цепи будет [c.79]
Полное сопротивление цепи, показанной на рис. 13, б, равно сумме сопротивлений ее частей (последовательное соединение) [c.67]
Аналитический расчет основных параметров электродвигателя. Расчет характеристик электродвигателя проводится по схеме замещения (фиг. 41, 42). Вначале рассчитывается сопротивление двух параллельно включенных участков, а затем — полное сопротивление цепи. Таким образом, имеем общее сопротивление вторичного и намагничивающего контуров, равное [c.107]
И полное сопротивление цепи электродвигателя, равное [c.107]
Для определения тока в первичной цепи — в обмотке статора — необходимо подводимое напряжение разделить на модуль полного сопротивления цепи, следовательно, [c. 108]
108]
Сопротивление, обусловленное емкостью, как известно, равно 1//(оС, где С — емкость, со — частота переменного тока, / = 1/— 1. Полное сопротивление цепи, показанной на рис. 13,6, равно сумме сопротивлений ее частей (последовательное соединение) [c.59]
Полное сопротивление цепи,, равное отношению давления к потоку.— Прим. ред. [c.104]
I — средняя длина магнитной силовой линии, см Полное сопротивление цепи переменного тока с индуктивностью определяется формулой [c.141]
Импеданс — полное сопротивление цепи в переменном токе. [c.190]
Полное сопротивление цепи между точками аЪ является сопротивлением двух параллельных ветвей, для которых [c.18]
С повышением температуры энергетическая зависимость функции (4.14) становится более слабой, и максимум функции оказывается весьма размытым. При этом сопротивление нижней части всей цени, отвечающее колебательным переходам в нижней половине потенциальной ямы, делается сравнимым с сопротивлением верхней части цепи. Более того, при очень высоких температурах (Jir D/10) вклад нескольких первых членов суммы в полное сопротивление цепи становится определяющим. Это приводит к эффекту, выражающемуся в уменьшении константы скорости диссоциации при высоких температурах, вычисленной в лестничном приближении, по сравнению с результатом [c.23]
Более того, при очень высоких температурах (Jir D/10) вклад нескольких первых членов суммы в полное сопротивление цепи становится определяющим. Это приводит к эффекту, выражающемуся в уменьшении константы скорости диссоциации при высоких температурах, вычисленной в лестничном приближении, по сравнению с результатом [c.23]
После такой перенормировки полное сопротивление цепи р и константа скорости диссоциации вычисляются с помощью рекуррентных соотношений (6.6) и формулы (6.5). Соответственно в аналитических вариантах решений, изложенных в 6, в первом приближении следует перенормировать лишь сопротивление Рп по схеме [c.41]
В связи с тем, что ЭУР представляет собой электрохимическую ячейку, заполненную электролитом, в нем имеется гальваническая связь между цепями управления и считывания. Эквивалентную схему ЭУР при протекании переменного тока из цепи управления в цепь считывания можно представить в виде полного сопротивления цепи управления 2у, включенного в середину резистивного электрода, полное сопротивление которого равно 2р,э. Тогда при протекании переменного тока через выводы 5—3 (см. рис. 2.1) для режима генератора тока напряжение на выходах резистивного электрода 2 и 3 равно [c.63]
Тогда при протекании переменного тока через выводы 5—3 (см. рис. 2.1) для режима генератора тока напряжение на выходах резистивного электрода 2 и 3 равно [c.63]
Логен 2 считает, что практически невозможно гарантировать покрытие, которое осталось бы неизменным после нескольких лет нахождения в земле. Если в некоторых точках анодной части покрытой трубы сталь начинает подвергаться коррозии, то действие тока будет концентрироваться в этих точках, вызывая очень интенсивное анодное воздействие. Вполне правильно указание на то, что вследствие микроскопических размеров нарушений пленки электрическое сопротивление будет во многих случаях довольно значительно. ОднакО оно все же весьма мало по сравнению с полным сопротивлением цепи, и в таком случае наличие покрытия, мало уменьшающего весь ток, уходящий с трубы, сильно уменьшит площадь, на которой концентрируется коррозия. В результате,, вследствие наличия ненадежного покрытия интенсивность воздействия (коррозия на единицу площади) увеличится. Очевидно применением неподходящего покрытия анодной части трубопровода можно только ухудшить положение. Однако тот же тип покрытия может быть хорош в случае применения его в катодной части, так как будет уменьшать общую величину коррозии. [c.47]
Очевидно применением неподходящего покрытия анодной части трубопровода можно только ухудшить положение. Однако тот же тип покрытия может быть хорош в случае применения его в катодной части, так как будет уменьшать общую величину коррозии. [c.47]
При наладке катодной защиты. После окончания строительства i монтажа катодной защиты перед включением ее под напряжение тщательно лроверяют все элементы, производят измерение сопротивлений растекания анодного И защитных заземлений, переходного сопротивления защищаемое сооружение—земля, полного сопротивления цепи и полученные данные заносят в паспорт. Подают напряжение переменного тока на выпрямитель, включают нагрузку и, регулируя напряжение и ток источника защиты, устанавливают эффективную полноту катодной защиты по миллиамперметру в электрической цепи диод—миллиамперметр— 1И0Д. С этой целью наблюдают за показанием стрелки в процессе регулирования, [c.123]
Для определения правильного положения обеих ручек нам нужен некоторый индикатор согласования сопротивлений и достижения частоты резонанса. Эта проблема обычно решается двумя способами. Первый и лучший из них-реальное измерение отклика цепи с помощью радиочастотного моста. Его устройство аналогично обычному мосту сопротивлений мосту Уинстона), но модифицированному для работы с переменным током. Он имеет четыре вывода (обычно он представляет собой просто небольшую коробочку с четырьмя разъемами), два из которых используются для ввода сигнала опорной частоты и вывода ответа па измерительное устройство (лучше всего осциллограф). К одному из оставшихся двух подключается эталонное сопротивление (50 Ом), к другому-настраиваемый датчик (рис. 3.11). При равенстве полного сопротивления цепи датчика эталонному сопротивлению мост достигает баллаиса, и вывод на измерительное устройство становится минимальным. [c.90]
Эта проблема обычно решается двумя способами. Первый и лучший из них-реальное измерение отклика цепи с помощью радиочастотного моста. Его устройство аналогично обычному мосту сопротивлений мосту Уинстона), но модифицированному для работы с переменным током. Он имеет четыре вывода (обычно он представляет собой просто небольшую коробочку с четырьмя разъемами), два из которых используются для ввода сигнала опорной частоты и вывода ответа па измерительное устройство (лучше всего осциллограф). К одному из оставшихся двух подключается эталонное сопротивление (50 Ом), к другому-настраиваемый датчик (рис. 3.11). При равенстве полного сопротивления цепи датчика эталонному сопротивлению мост достигает баллаиса, и вывод на измерительное устройство становится минимальным. [c.90]
Ток, протекающий через электроды контактной пары, называется коррозионным током (/корр), а соответствующий ему потенциал (в первом приближении одинаковый у обоих электродов) — коррозионным потенциалом ( корр) (рис.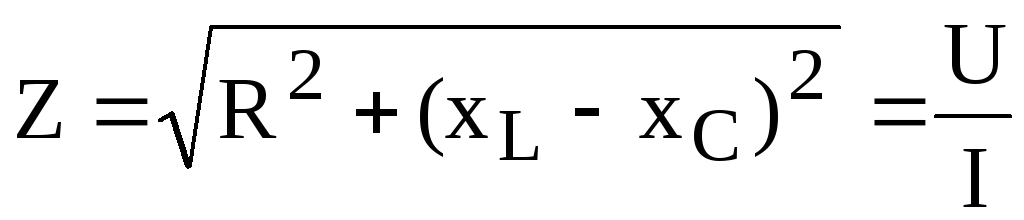 П-23). Точка пересечения поляризационных кривых соответствует максимальному коррозионному току (/корр. макс)> который имел бы место в коррозионном элементе, если бы полное сопротивление цепи было равно нулю (/ = 0). На практике всегда имеет место определенное сопротивление электролита, и истинный коррозионный ток приобретает несколько меньшее значение. [c.36]
П-23). Точка пересечения поляризационных кривых соответствует максимальному коррозионному току (/корр. макс)> который имел бы место в коррозионном элементе, если бы полное сопротивление цепи было равно нулю (/ = 0). На практике всегда имеет место определенное сопротивление электролита, и истинный коррозионный ток приобретает несколько меньшее значение. [c.36]
Максимальная чувствительность гальванометра, указанная в его паспорте, достигается лишь в том случае, если полное сопротивление / цепи гальванометра, представляющее собой сумму внутреннего сопротивления гальванометра и внешнего сопротивления цепи, равно его критическому сопротивлению / кр. При / = / кр катушка гальванометра с зеркальцем движется к положению равновесия при замыка- [c.104]
Гогда полное сопротивление цепи будет [c.357]
Обш ие свойства цепи, представленной на рис. 1, с сопротивлениями типа (4.14), (6.9) и (6.11) исследованы в [33]. Полное сопротивление цепи ро в основном определяется сопротивлением между точкой d и некоторой точкой п, отстоящей по энергии от границы диссоциации на (3 -ь 10)кТ (см. Значение п при неслишком высоких температурах определяется уравнением [33] [c.30]
Значение п при неслишком высоких температурах определяется уравнением [33] [c.30]
Полное сопротивление — электрическая цепь
Полное сопротивление — электрическая цепь
Cтраница 1
Полное сопротивление электрической цепи переменному току зависит не только от параметров цепи, но и от частоты переменного тока. Эта зависимость, выражаемая законом Ома (4.7) при последовательном включении элементов цепи переменного тока, имеет довольно сложный вид.
[1]
Так как полные сопротивления электрических цепей определяются параметрами составляющих их элементов, то проверка исправности контролируемой цепи сводится к сравнению токов, протекающих по контролируемой и образцовой цепям. Для уменьшения влияния на режим работы цепей эти сопротивления берут достаточно малыми и равными по величине.
[3]
Что называют полным сопротивлением электрической цепи переменного тока.
[4]
Какие параметры определяют полное сопротивление электрической цепи при переменном токе.
[5]
Из чего складывается полное сопротивление электрической цепи.
[6]
Эта величина характеризует полное сопротивление электрической цепи переменному току и называется импедансом.
[7]
В процессе контроля полные сопротивления электрических цепей изменяются от десятков ом до десятков мегом. Поэтому источники питания рассмотренных схем сравнения должны быть достаточно мощными и стабильными. Нестабильность этого напряжения увеличивает общую погрешность и, следовательно, не должна превышать допустимое значение.
[8]
Эта величина характеризует полное сопротивление электрической цепи переменному току и называется импедансом.
[9]
Какие параметры определяют полное сопротивление электрической цепи при переменном токе.
[10]
При выполнении условия (5.16) полное сопротивление электрической цепи принимает максимальное значение ZR. Максимальному значению полного сопротивления такой электрической цепи соответствует минимальное значение силы тока. Следовательно, при выполнении условия (5.16), называемого условием резонанса токов в колебательном контуре, сила тока в общей цепи минимальна.
[11]
От каких величин зависит полное сопротивление электрической цепи.
[12]
Из этого выражения следует, что полное сопротивление электрической цепи переменного тока зависит не только от параметров соответствующей цепи, но и от частоты питающего напряжения; причем для линейной цепи значение как полного сопротивления, так и его составляющих не зависит от значения подводимого напряжения.
[13]
Выходной трансформатор служит для согласования выходного полного электрического сопротивления каскада электронной аппаратуры с полным сопротивлением нагрузки, а согласующий-для согласования различных полных сопротивлений электрических цепей при передаче электрических сигналов от одного каскада электронной аппаратуры к другому.
[15]
Страницы:
1
2
серии R, L и C | Реактивное сопротивление и импеданс — R, L и C
Давайте рассмотрим следующую схему и проанализируем ее:
Пример цепи серии R, L и C.
Решение для реактивного сопротивления
Первым шагом является определение реактивного сопротивления (в омах) катушки индуктивности и конденсатора.
Следующий шаг — выразить все сопротивления и реактивные сопротивления в математически общей форме: импеданс. (Рисунок ниже)
(Рисунок ниже)
Помните, что индуктивное реактивное сопротивление переводится в положительный воображаемый импеданс (или импеданс при + 90 °), а емкостное реактивное сопротивление переводится в отрицательное воображаемое сопротивление (импеданс при -90 °). Сопротивление, конечно же, по-прежнему рассматривается как чисто «реальный» импеданс (полярный угол 0 °):
Пример последовательной цепи R, L и C с заменой значений компонентов на импедансы.
Таблица результатов:
Теперь, когда все величины противодействия электрическому току выражаются в общем формате комплексных чисел (как импедансы, а не как сопротивления или реактивные сопротивления), с ними можно обращаться так же, как с простыми сопротивлениями в цепи постоянного тока.
Это идеальное время, чтобы составить аналитическую таблицу для этой схемы и вставить все «заданные» цифры (общее напряжение и полное сопротивление резистора, катушки индуктивности и конденсатора).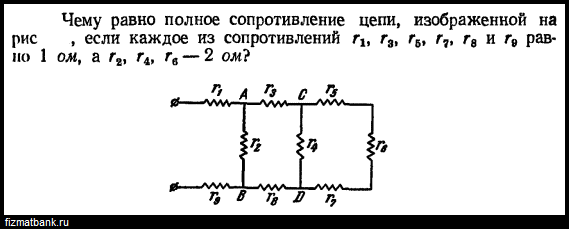
Если не указано иное, напряжение источника будет нашим опорным для фазового сдвига, поэтому оно будет записано под углом 0 °. Помните, что не существует такой вещи, как «абсолютный» угол фазового сдвига для напряжения или тока, поскольку это всегда величина относительно другой формы волны.
Фазовые углы для импеданса, однако (как и у резистора, катушки индуктивности и конденсатора), известны абсолютно, потому что фазовые отношения между напряжением и током в каждом компоненте абсолютно определены.
Обратите внимание, что я предполагаю идеально реактивные катушка индуктивности и конденсатор с фазовыми углами импеданса в точности +90 и -90 ° соответственно.
Хотя настоящие компоненты не могут быть идеальными в этом отношении, они должны быть довольно близкими. Для простоты я буду предполагать, что реактивные катушки индуктивности и конденсаторы с этого момента идеально подходят для расчетов в моем примере, если не указано иное.
Поскольку приведенный выше пример схемы является последовательной схемой, мы знаем, что полное сопротивление схемы равно сумме отдельных элементов, поэтому:
Вставив это число для общего импеданса в нашу таблицу:
Теперь мы можем применить закон Ома (I = E / R) по вертикали в столбце «Всего», чтобы найти общий ток для этой последовательной цепи:
Поскольку цепь является последовательной, ток должен быть одинаковым во всех компонентах.Таким образом, мы можем взять полученное значение полного тока и распределить его по каждой из других колонок:
Теперь мы готовы применить закон Ома (E = IZ) к каждому из столбцов отдельных компонентов в таблице, чтобы определить падение напряжения:
Обратите внимание на кое-что странное: хотя у нас напряжение питания всего 120 вольт, напряжение на конденсаторе 137,46 вольт! Как это может быть? Ответ заключается во взаимодействии индуктивного и емкостного сопротивлений.
Выражаясь в импедансах, мы можем видеть, что катушка индуктивности противодействует току точно противоположным образом, чем у конденсатора. Выраженный в прямоугольной форме, импеданс катушки индуктивности имеет положительный мнимый член, а конденсатор — отрицательный мнимый член.
Когда эти два противоположных импеданса складываются (последовательно), они имеют тенденцию уравновешивать друг друга! Хотя они по-прежнему составляют , сложенные вместе , чтобы получить сумму, на самом деле эта сумма на меньше , чем любое из отдельных (емкостных или индуктивных) импедансов по отдельности.
Это аналогично сложению положительного и отрицательного (скалярного) числа: сумма меньше индивидуального абсолютного значения любого из них.
Если полное сопротивление в последовательной цепи с индуктивными и емкостными элементами меньше, чем полное сопротивление любого элемента по отдельности, то общий ток в этой цепи должен быть на больше, чем , чем то, что было бы с только индуктивным или только емкостным. элементы там.
элементы там.
При таком аномально высоком токе, протекающем через каждый из компонентов, на некоторых отдельных компонентах могут быть получены напряжения, превышающие напряжение источника! Дальнейшие последствия противоположных реактивных сопротивлений катушек индуктивности и конденсаторов в одной и той же цепи будут рассмотрены в следующей главе.
После того, как вы освоите технику приведения всех значений компонентов к импедансу (Z), анализ любой цепи переменного тока будет примерно таким же трудным, как анализ любой цепи постоянного тока, за исключением того, что рассматриваемые величины являются векторными, а не скалярными.
За исключением уравнений, относящихся к мощности (P), уравнения в цепях переменного тока такие же, как и в цепях постоянного тока, с использованием импедансов (Z) вместо сопротивлений (R). Закон Ома (E = IZ) по-прежнему остается в силе, как и законы Кирхгофа по напряжению и току.
Чтобы продемонстрировать закон напряжения Кирхгофа в цепи переменного тока, мы можем взглянуть на полученные ответы для компонентных падений напряжения в последней цепи. KVL сообщает нам, что алгебраическая сумма падений напряжения на резисторе, катушке индуктивности и конденсаторе должна равняться приложенному напряжению от источника.
KVL сообщает нам, что алгебраическая сумма падений напряжения на резисторе, катушке индуктивности и конденсаторе должна равняться приложенному напряжению от источника.
Даже если на первый взгляд это может показаться неправдой, небольшое сложение комплексных чисел доказывает обратное:
За исключением небольшой ошибки округления, сумма этих падений напряжения действительно равна 120 вольт.Выполненный на калькуляторе (с сохранением всех цифр) ответ, который вы получите, должен быть ровно 120 + j0 вольт.
Мы также можем использовать SPICE для проверки наших цифр для этой схемы:
Пример цепи SPICE серии R, L и C.
г1 1 2 250 l1 2 3 650м c1 3 0 1.5u .ac lin 1 60 60 .print ac v (1,2) v (2,3) v (3,0) i (v1) .print ac vp (1,2) vp (2,3) vp (3,0) ip (v1) .конец частота v (1,2) v (2,3) v (3) i (v1) 6.000E + 01 1.943E + 01 1.905E + 01 1.375E + 02 7.773E-02 частота вп (1,2) вп (2,3) вп (3) ip (v1) 6.000E + 01 8.068E + 01 1.707E + 02 -9.320E + 00 -9.932E + 01
Моделирование SPICE показывает точность наших вычисленных вручную результатов.
Как видите, существует небольшая разница между анализом цепей переменного тока и анализом цепей постоянного тока, за исключением того, что все величины напряжения, тока и сопротивления (фактически, импеданс ) должны обрабатываться в комплексной, а не скалярной форме, чтобы учитывать для фазового угла.
Это хорошо, поскольку означает, что все, что вы узнали об электрических цепях постоянного тока, применимо к тому, что вы здесь изучаете. Единственным исключением из этой последовательности является вычисление силы, которое настолько уникально, что заслуживает главы, посвященной только этому предмету.
ОБЗОР:
- Полное сопротивление любого типа складывается последовательно: Z Итого = Z 1 + Z 2 +.
 . . Z n
. . Z n - Хотя импедансы складываются последовательно, общий импеданс для цепи, содержащей как индуктивность, так и емкость, может быть меньше одного или нескольких отдельных импедансов, поскольку последовательные индуктивные и емкостные импедансы имеют тенденцию компенсировать друг друга.Это может привести к падению напряжения на компонентах, превышающему напряжение питания!
- Все правила и законы цепей постоянного тока применимы к цепям переменного тока, если значения выражаются в сложной форме, а не в виде скаляра. Единственным исключением из этого принципа является расчет мощности и , что сильно отличается для переменного тока.
СВЯЗАННЫЙ РАБОЧИЙ ЛИСТ:
SPARKS: Расчет импеданса
Расчет импеданса
В цепях переменного тока Закон Ома принимает
более общая форма: E = I⋅Z , где E — напряжение, а I
актуален, как и раньше.Новый термин, Z , составляет импеданс ,
комбинация векторов:
- Сопротивление, R (в Ом), при падении напряжения синфазно с
электрический ток.
- Индуктивное сопротивление, X L (в Ом), с напряжением
опускает ведущий ток на 90 °. - Емкостное реактивное сопротивление, X C (в Ом) с напряжением
падает с отставанием ток на 90 °.
| f = 6,4 кГц R = 120 Ом L = 3,6 мГн C = 0,38 мкФ |
Рисунок 1. Пример цепи RLC |
| Рис. 2. Векторная сумма R и X L — X C дает Z |
Из формул для X L и X C , вы можете
видим, что реактивные сопротивления зависят от обоих значений компонентов L и C ,
а также частота переменного тока, f :
и
, где f — частота в
Герцы (или сек −1 ), L — индуктивность по Генри, а C —
емкость в фарадах. Потому что X L и X C
Потому что X L и X C
различаются по фазе на 180 °, общее реактивное сопротивление X последовательной цепи
составляет X L — X C .
Известные применения закона Ома, такие как последовательная и параллельная цепь.
расчеты, все еще применяются. Однако теперь вы должны рассмотреть конкурирующий вектор
вклады от сопротивлений и реактивных сопротивлений.
Фазовые углы и векторы
Давайте найдем полное сопротивление цепи на Рисунке 1.Используя формулы
выше:
Создавая импеданс Z , резистор вносит вклад в горизонтальную
компонент. Вертикальная составляющая — это разница реактивных сопротивлений: X L — X C .
Тогда Z — это векторная сумма R и X L — X C ,
как показано на рисунке 2.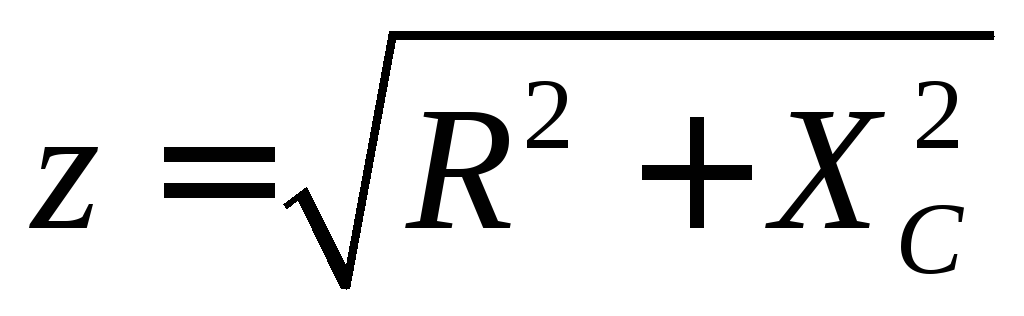
На рисунке 2 видно, что Z — гипотенуза прямоугольного треугольника,
мы можем использовать теорему Пифагора и геометрию прямоугольного треугольника, чтобы вычислить Z .
Итак, в этой схеме мы наблюдаем эффект импеданса
144 Ом, при отставании тока от напряжения питания на фазовый угол
33,5 °.
Как можно догадаться из обсуждения выше, вполне возможно, что
индуктивное и емкостное сопротивление для точной компенсации при правильной комбинации
из L , C и f
значения.Это очень важное условие, известное как резонанс .
Формула
EC — Импеданс
Где:
|
Электрический импеданс (Z) — это полное сопротивление цепи переменному току. Импеданс измеряется в омах и может включать сопротивление (R), индуктивное реактивное сопротивление (XL) и емкостное реактивное сопротивление (XC). Емкостное реактивное сопротивление обычно не присутствует при вихретоковом контроле, поэтому этот термин не включается в уравнение.
Импеданс измеряется в омах и может включать сопротивление (R), индуктивное реактивное сопротивление (XL) и емкостное реактивное сопротивление (XC). Емкостное реактивное сопротивление обычно не присутствует при вихретоковом контроле, поэтому этот термин не включается в уравнение.
Полный импеданс — это не просто алгебраическая сумма сопротивления и индуктивного реактивного сопротивления. Поскольку индуктивное реактивное сопротивление сдвинуто по фазе на 90 градусов с сопротивлением и, следовательно, их максимальные значения возникают в разное время, для расчета импеданса необходимо использовать сложение векторов.Это показано на изображении справа.
Если величина сопротивления представлена длиной горизонтальной линии, а величина индуктивного реактивного сопротивления представлена длиной вертикальной линии; тогда величина импеданса представлена длиной диагональной линии. Поскольку линии образуют прямоугольный треугольник, теорему Пифагора можно использовать для определения длины (значения) линии импеданса.
Теорема Пифагора записывается: c 2 = a 2 + b 2.
Для этого приложения переменная a равна сопротивлению, b равна индуктивному реактивному сопротивлению, а c равна импедансу. Итак, уравнение принимает следующий вид:
Z 2 = R 2 + X L 2
Когда это уравнение переписывается для решения относительно Z, уравнение импеданса создается в представленной форме.
Пример расчета:
Рассчитайте импеданс, когда сопротивление равно 0.6 Ом, а индуктивное сопротивление 0,4 Ом.
Просто введите значения и решите для Z.
Импеданс
Импеданс
Полное противодействие протеканию тока в цепи переменного тока называется импедансом и обозначается буквой Z. Комбинированные эффекты сопротивления, индуктивного реактивного сопротивления и емкостного реактивного сопротивления составляют полное сопротивление (полное противодействие к протеканию тока в цепи переменного тока).Чтобы точно рассчитать напряжение и ток в цепях переменного тока, необходимо учитывать влияние индуктивности и емкости наряду с сопротивлением. Импеданс измеряется в омах.
Комбинированные эффекты сопротивления, индуктивного реактивного сопротивления и емкостного реактивного сопротивления составляют полное сопротивление (полное противодействие к протеканию тока в цепи переменного тока).Чтобы точно рассчитать напряжение и ток в цепях переменного тока, необходимо учитывать влияние индуктивности и емкости наряду с сопротивлением. Импеданс измеряется в омах.
Рисунок 9-22. Применение постоянного и переменного тока в цепи.
Правила и уравнения для цепей постоянного тока применяются к цепям переменного тока только в том случае, если эта цепь содержит только сопротивление, а не индуктивность или емкость. Как в последовательной, так и в параллельной цепях, если цепь переменного тока состоит только из сопротивления, значение импеданса такое же, как сопротивление, а закон Ома для цепи переменного тока, I = E / Z, точно такой же, как для цепи постоянного тока. схема.На рис. 9-22 показана последовательная цепь, содержащая нагревательный элемент с сопротивлением 11 Ом, подключенный к источнику 110 В. Чтобы определить, какой ток протекает при подаче переменного тока 110 В, решается следующий пример:
Чтобы определить, какой ток протекает при подаче переменного тока 110 В, решается следующий пример:
Рисунок 9-23. Два значения сопротивления, подключенные параллельно к источнику переменного тока. Импеданс равен общему сопротивлению цепи.
Если есть два значения сопротивления, подключенных параллельно к переменному напряжению, как показано на рисунке 9-23, полное сопротивление равно общему сопротивлению цепи.Еще раз, вычисления будут производиться так же, как если бы это была цепь постоянного тока, и применимо следующее:
Так как это чисто резистивная цепь R T = Z (сопротивление = импеданс)
To Определите ток в цепи, используя уравнение:
Импеданс — это полное сопротивление току в цепи переменного тока. Если цепь имеет индуктивность или емкость, необходимо учитывать сопротивление (R), индуктивное реактивное сопротивление (X L ) и / или емкостное реактивное сопротивление (X C ) для определения полного сопротивления (Z). В этом случае Z не равно R T . Сопротивление и реактивное сопротивление (индуктивное или емкостное) нельзя сложить напрямую, но их можно рассматривать как две силы, действующие под прямым углом друг к другу. Таким образом, соотношение между сопротивлением, реактивным сопротивлением и импедансом можно проиллюстрировать прямоугольным треугольником. [Рис. 9-24] Поскольку эти величины могут быть связаны со сторонами прямоугольного треугольника, формулу для определения импеданса можно найти с помощью теоремы Пифагора. В нем говорится, что квадрат гипотенузы равен сумме квадратов двух других сторон.Таким образом, значение любой стороны прямоугольного треугольника можно найти, если известны две другие стороны.
В этом случае Z не равно R T . Сопротивление и реактивное сопротивление (индуктивное или емкостное) нельзя сложить напрямую, но их можно рассматривать как две силы, действующие под прямым углом друг к другу. Таким образом, соотношение между сопротивлением, реактивным сопротивлением и импедансом можно проиллюстрировать прямоугольным треугольником. [Рис. 9-24] Поскольку эти величины могут быть связаны со сторонами прямоугольного треугольника, формулу для определения импеданса можно найти с помощью теоремы Пифагора. В нем говорится, что квадрат гипотенузы равен сумме квадратов двух других сторон.Таким образом, значение любой стороны прямоугольного треугольника можно найти, если известны две другие стороны.
Рисунок 9-24. Треугольник импеданса Рисунок 9-25. Цепь, содержащая сопротивление и индуктивность.
На практике, если последовательная цепь переменного тока содержит сопротивление и индуктивность, как показано на рисунке 9-25, соотношение между сторонами может быть указано как:
Корень квадратный из обеих частей уравнения дает:
Эту формулу можно использовать для определения импеданса, если известны значения индуктивного реактивного сопротивления и сопротивления.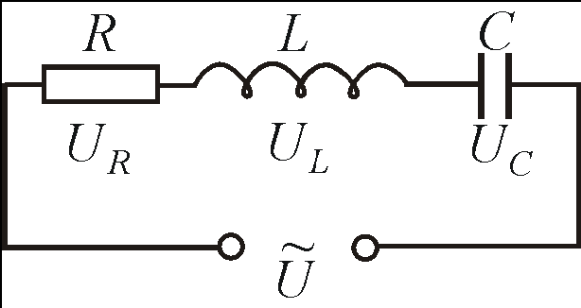 Его можно изменить для определения импеданса в цепях, содержащих емкостное реактивное сопротивление и сопротивление, подставив в формулу X C вместо X L . В цепях, содержащих сопротивление с индуктивным и емкостным сопротивлением, реактивные сопротивления можно комбинировать; но поскольку их эффекты в схеме прямо противоположны, они объединяются вычитанием (меньшее число всегда вычитается из большего):
Его можно изменить для определения импеданса в цепях, содержащих емкостное реактивное сопротивление и сопротивление, подставив в формулу X C вместо X L . В цепях, содержащих сопротивление с индуктивным и емкостным сопротивлением, реактивные сопротивления можно комбинировать; но поскольку их эффекты в схеме прямо противоположны, они объединяются вычитанием (меньшее число всегда вычитается из большего):
или
Пример 1 показан на рисунке 9-25.Здесь последовательная цепь, содержащая резистор и катушку индуктивности, подключена к источнику 110 вольт при 60 циклах в секунду. Резистивный элемент представляет собой простой измерительный элемент на 6 Ом, а индуктивный элемент — катушку с индуктивностью 0,021 Генри. Какое значение импеданса и тока в цепи?
Решение:
Сначала вычисляется индуктивное реактивное сопротивление катушки:
Затем вычисляется полное полное сопротивление:
Помните, что при расчетах для Z всегда используйте индуктивное реактивное сопротивление, а не индуктивность, и используйте емкостное сопротивление. , а не емкость.
, а не емкость.
После определения импеданса можно рассчитать общий ток.
Так как эта цепь резистивная и индуктивная, там есть фазовый сдвиг, когда напряжение ведет к току.
Пример 2 — это проиллюстрированная последовательная схема, в которой конденсатор емкостью 200 мкФ соединен последовательно с резистором 10 Ом. [Рисунок 9-26] Какое значение имеет импеданс, ток и падение напряжения на резисторе?
Рисунок 9-26. Цепь, содержащая сопротивление и емкость.
Решение:
Во-первых, емкость изменяется с микрофарад на фарады. Поскольку 1 миллион микрофарад равен 1 фараду, тогда 200 мкФ = 0,000200 фарад
Далее решаем емкостное реактивное сопротивление:
Чтобы найти полное сопротивление,
Поскольку эта цепь резистивная и емкостная, существует фазовый сдвиг, при котором ток напряжение на выводах:
Чтобы найти ток:
Чтобы найти падение напряжения на резисторе (E R ):
Чтобы найти падение напряжения на конденсаторе (E C ):
Сумма этих двух напряжений не равна приложенному напряжению, так как ток опережает напряжение. Используйте следующую формулу, чтобы найти приложенное напряжение:
Используйте следующую формулу, чтобы найти приложенное напряжение:
Если в цепи есть сопротивление, индуктивность и емкость, для определения импеданса используется следующее уравнение.
Пример 3: Каков импеданс последовательной цепи, состоящей из конденсатора с емкостным реактивным сопротивлением 7 Ом, катушки индуктивности с индуктивным сопротивлением 10 Ом и резистора с сопротивлением 4 Ом? [Рисунок 9-27] Рисунок 9-27. Цепь, содержащая сопротивление, индуктивность и емкость.
Решение:
Чтобы найти полный ток:
Помните, что индуктивное и емкостное реактивные сопротивления могут вызвать фазовый сдвиг между напряжением и током. В этом примере индуктивное реактивное сопротивление больше емкостного реактивного сопротивления, поэтому напряжение ведет к току.
Следует отметить, что, поскольку индуктивное реактивное сопротивление, емкостное реактивное сопротивление и сопротивление влияют друг на друга под прямым углом, падения напряжения в любой последовательной цепи переменного тока должны складываться с использованием векторного сложения. На рис. 9-28 показано падение напряжения в последовательной цепи переменного тока, описанной в примере 3 выше.
На рис. 9-28 показано падение напряжения в последовательной цепи переменного тока, описанной в примере 3 выше.
Рисунок 9-28. Падение напряжения.
Чтобы вычислить отдельные падения напряжения, просто используйте уравнения:
Чтобы определить общее приложенное напряжение для цепи, каждое отдельное падение напряжения должно быть добавлено с помощью векторного сложения.
Параллельные цепи переменного тока
При решении параллельных цепей переменного тока необходимо также использовать производную теоремы Пифагора.Уравнение для нахождения полного сопротивления в цепи переменного тока выглядит следующим образом:
Чтобы определить полное сопротивление параллельной цепи, показанной на рисунке 9-29, сначала нужно определить емкостное и индуктивное реактивные сопротивления. (Не забудьте перевести микрофарады в фарады.)
Рисунок 9-29. Полный импеданс параллельной цепи.
Затем можно найти полное сопротивление:
Для определения протекания тока в цепи:
Чтобы определить протекание тока через каждый параллельный путь цепи, рассчитайте I R , I L и I C .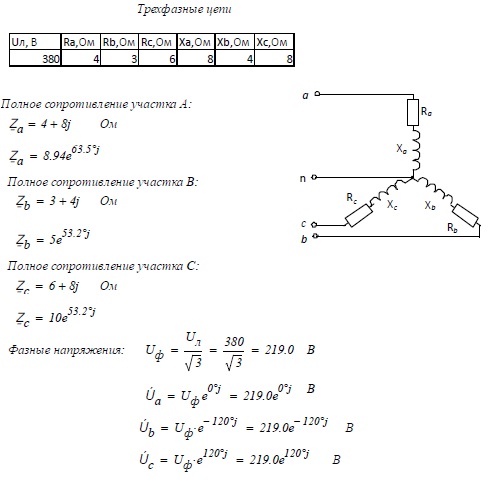
Следует отметить, что общий ток в параллельных цепях определяется с помощью векторного сложения отдельных потоков тока следующим образом:
Мощность в цепях переменного тока
Поскольку напряжение и ток определяют мощность , есть сходства в мощности, потребляемой цепями переменного и постоянного тока. Однако в переменном токе ток зависит как от сопротивления, так и от реактивного сопротивления цепи. Мощность, потребляемая любой цепью переменного тока, является функцией приложенного напряжения, а также сопротивления и реактивного сопротивления цепи.Цепи переменного тока имеют два различных типа мощности: один создается сопротивлением цепи, а другой — реактивным сопротивлением цепи.
Истинная мощность
Истинная мощность любой цепи переменного тока обычно называется рабочей мощностью цепи. Истинная мощность — это мощность, потребляемая участком сопротивления цепи, и измеряется в ваттах (Вт).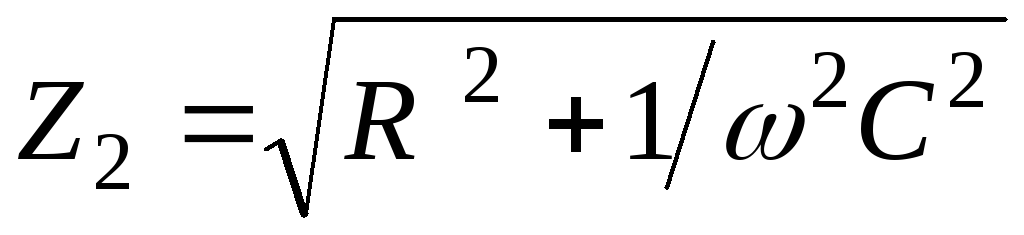 Истинная мощность обозначается буквой P и указывается любым ваттметром в цепи. Истинная мощность рассчитывается по формуле:
Истинная мощность обозначается буквой P и указывается любым ваттметром в цепи. Истинная мощность рассчитывается по формуле:
Полная мощность
Полная мощность в цепи переменного тока иногда называется реактивной мощностью цепи.Полная мощность — это мощность, потребляемая всей схемой, включая сопротивление и реактивное сопротивление. Полная мощность обозначается буквой S и измеряется в вольт-амперах (ВА). Полная мощность — это произведение действующего напряжения на эффективный ток. Полная мощность рассчитывается по формуле:
Коэффициент мощности
Как видно на Рисунке 9-30, резистивная мощность и реактивная мощность влияют на схему под прямым углом друг к другу.Коэффициент мощности в цепи переменного тока создается этим эффектом прямого угла.
Рисунок 9-30. Соотношения сил в цепи переменного тока.
Коэффициент мощности можно определить как математическую разницу между истинной мощностью и полной мощностью. Коэффициент мощности (PF) — это коэффициент и всегда измеряется в диапазоне от 0 до 100. Коэффициент мощности напрямую связан с фазовым сдвигом цепи. Чем больше фазовый сдвиг в цепи, тем ниже коэффициент мощности. Например, цепь переменного тока, которая является чисто индуктивной (содержит только реактивное сопротивление и не имеет сопротивления), имеет фазовый сдвиг 90 ° и коэффициент мощности 0.0. Цепь переменного тока, которая является чисто резистивной (без реактивного сопротивления), имеет фазовый сдвиг 0 и коэффициент мощности 100. Коэффициент мощности рассчитывается по следующей формуле:
Коэффициент мощности (PF) — это коэффициент и всегда измеряется в диапазоне от 0 до 100. Коэффициент мощности напрямую связан с фазовым сдвигом цепи. Чем больше фазовый сдвиг в цепи, тем ниже коэффициент мощности. Например, цепь переменного тока, которая является чисто индуктивной (содержит только реактивное сопротивление и не имеет сопротивления), имеет фазовый сдвиг 90 ° и коэффициент мощности 0.0. Цепь переменного тока, которая является чисто резистивной (без реактивного сопротивления), имеет фазовый сдвиг 0 и коэффициент мощности 100. Коэффициент мощности рассчитывается по следующей формуле:
Пример расчета коэффициента мощности: Рисунок 9-31 показана нагрузка переменного тока, подключенная к источнику питания на 50 В. Потребляемый в цепи ток составляет 5 ампер, а общее сопротивление цепи составляет 8 Ом. Определите истинную мощность, полную мощность и коэффициент мощности для этой цепи.
Рисунок 9-31. Нагрузка переменного тока подключена к источнику питания на 50 В.
Решение:
Коэффициент мощности также может быть представлен в процентах. Используя процентное соотношение для отображения коэффициента мощности, схема в предыдущем примере будет иметь коэффициент мощности 80 процентов.
Следует отметить, что низкий коэффициент мощности нежелателен. Цепи с более низким коэффициентом мощности создают избыточную нагрузку на источник питания и снижают эффективность системы. Генераторы переменного тока для самолетов обычно должны работать с коэффициентом мощности от 90 до 100 процентов.Поэтому очень важно тщательно учитывать коэффициент мощности при проектировании электрической системы самолета.
Flight Mechanic рекомендует
Почему импеданс имеет значение и как его контролировать — Royal Circuits Solutions
Цепь, работающая на высоких частотах, демонстрирует сопротивление или сопротивление потоку электрического тока из-за комбинации сопротивления, индуктивности и емкости, присутствующей в ней, когда на цепь подается переменное напряжение.Этот импеданс складывается из сложной суммы сопротивления цепи постоянному току и ее реактивного сопротивления. В то время как сопротивление постоянному току не зависит от частоты приложенного переменного напряжения, реактивное сопротивление зависит от того, является ли элемент схемы индуктивным или емкостным. При увеличении частоты приложенного напряжения индуктивное реактивное сопротивление цепи увеличивается, а ее емкостное реактивное сопротивление уменьшается — при уменьшении частоты происходит обратное.
В то время как сопротивление, связанное с цепью, не вызывает изменения фазового угла между приложенным переменным напряжением и результирующим током, реактивное сопротивление в цепи заставляет ток отставать или опережать напряжение, в зависимости от того, является ли цепь индуктивной или емкостной.
Для математических расчетов, точно так же, как сопротивление цепи представлено R, электрическое сопротивление представлено Z, емкостное реактивное сопротивление X C и индуктивное реактивное сопротивление X L . Как индуктивное, так и емкостное реактивное сопротивление выражается в омах, аналогично единицам измерения сопротивления, а, следовательно, и полного сопротивления.
Почему импеданс имеет значение в печатной плате
Для медной дорожки на печатной плате обратный путь может проходить через другую дорожку или через пластину заземления.В то время как сопротивление, с которым сталкивается ток, остается постоянным, когда он проходит через дорожку и ее обратный путь, импеданс, с которым сталкивается ток, зависит от природы дорожки и ее обратного пути. Например, независимо от того, следует ли обратная трасса или нет близко к первичной трассе, или плоскость возврата близко к основной трассе или далеко от нее, изменяется импеданс, с которым сталкивается ток.
Короче говоря, если разработчик тщательно не спроектировал трассу, ее обратный путь и их среду должным образом, значение импеданса, вероятно, будет варьироваться от точки к точке вдоль трассы.На высоких частотах приложенного напряжения дорожки на печатной плате редко ведут себя как простые соединения, а изменяющийся импеданс ухудшает сигнал при его перемещении по печатной плате.
Подобно тому, как наличие сопротивления в цепи служит для уменьшения или ослабления амплитуды тока, протекающего по цепи, импеданс дорожки печатной платы также ослабляет амплитуду тока, протекающего через нее. Однако, поскольку это затухание зависит от частоты, оно комплексно влияет на характеристики схемы.Например, идеальные прямоугольные волны на высоких частотах, проходя через дорожки печатной платы, могут больше не иметь возможности сохранять свои вертикальные края, или углы их формы волны могут стать закругленными.
Меандр представляет собой комбинацию нескольких синусоидальных волн на разных частотах, каждая из которых является целым кратным основной гармоники. По мере того, как эта комбинация перемещается по трассе, изменяющийся импеданс по трассе ослабляет более высокие частоты в большей степени, чем более низкие частоты.Следовательно, форма сигнала, достигающего другого конца трассы, больше не сохраняет исходную начальную резкость, а искажается описанным выше способом.
Этот искаженный сигнал вызывает непредсказуемые проблемы в работе схемы, принимающей его, и, следовательно, является неприемлемым. Решение состоит в том, чтобы управлять импедансом вдоль пути к печатной плате, чтобы искажение на конце было незначительным, а приемная цепь могла его компенсировать, обеспечивая тем самым воспроизводимые высокочастотные характеристики.
Управление характеристическим импедансом линии передачи, образованной проводниками печатной платы, называется управляемым импедансом. Это становится тем более важным, когда высокочастотные или высокоскоростные сигналы распространяются по линиям передачи печатных плат. Контроль импеданса необходим для целостности сигнала — распространения сигналов без искажений.
Управляющий импеданс
Факторы, влияющие на сопротивление, включают:
- Ширина и толщина медного следа сверху и снизу слоя
- Толщина препрега или материала сердцевины по обе стороны от медной дорожки
- Диэлектрическая проницаемость препрега или материала сердцевины
- Расстояние от других медных элементов
Следовательно, производителю печатной платы, возможно, придется изменить определенные спецификации, такие как ширина дорожки, ее толщина и толщина препрега или материала сердцевины, чтобы обеспечить достижение окончательного импеданса в пределах указанного допуска.
Материалы печатной платы, используемые производителем, также определяют импеданс дорожек. Производители называют импеданс материалов и ожидаемый импеданс на их основе контролируемым диэлектриком. Большинство производителей предлагают методы расчета импеданса на основе необходимого диэлектрического пространства между медными слоями в фабрике и позволяют прокладывать дорожки с правильной шириной и шагом. Это приводит к двум методам контроля импеданса:
Контролируемый диэлектрик: Разработчик указывает набор печатных плат, материал и толщину диэлектрика, а также допуски.Изготовитель фокусируется в первую очередь на создании платы с заданной толщиной от слоя к слою в пределах указанного допуска и не пытается контролировать импеданс.
Контроль импеданса: Разработчик определяет импеданс, а производитель достигает его, контролируя толщину диэлектрика, ширину дорожек и расстояние. Производитель использует купоны TDR, чтобы проверить, что они достигли желаемого импеданса. Перед выполнением всего заказа производитель обрабатывает первое изделие, чтобы оценить любые несоответствия.В зависимости от результатов первой статьи производитель регулирует параметры процесса, чтобы они соответствовали спецификациям проектировщика в пределах указанных допусков.
Путь с наименьшим импедансом и высокоскоростными сигналами
Хотя путь наименьшего сопротивления на печатной плате может быть короче, для высокоскоростных сигналов вместо этого предпочтительнее следовать путем наименьшего сопротивления. На низких частотах обратный ток в основном следует за заземляющим слоем непосредственно от нагрузки к источнику.Эта прямая линия между нагрузкой и источником представляет собой путь наименьшего сопротивления, и это путь наименьшего сопротивления для низких частот.
При увеличении частоты или скорости сигнала взаимная индуктивность между дорожкой на сигнальном слое и плоскостью меди под ней создает путь с низким импедансом, который позволяет обратным токам следовать за дорожкой на сигнальном слое.
Проектирование обратных путей в печатных платах
Разработчики печатных плат
обычно следуют лучшим практикам, которые позволяют правильно разводить сигналы и их обратные пути по пути с наименьшим импедансом.Вот некоторые из этих передовых практик:
- Обратный путь очень близко и параллельно или ниже трассы, несущей высокоскоростной сигнал
- Дифференциальные сигналы, исходящие от контактов пакета, должны немедленно сблизиться и оставаться близкими на протяжении всего пути
- Поместите переходные отверстия заземления рядом с переходными отверстиями дифференциальной пары
- Медная стяжка обливается вокруг межсоединений к заземляющей пластине ниже.
- Круглые тактовые импульсы и другие трассы сигналов с быстрым нарастанием / спадом с заливкой земли и использование полной непрерывной заземляющей поверхности под трассой сигнала для минимизации шума от EMI
- Конструкции, требующие тестирования FCC, могут направлять высокоскоростные сигналы между двумя заземляющими плоскостями, окруженными сшитыми переходными отверстиями.
Расчет контролируемого импеданса
Также можно рассчитать управляемый импеданс по физическим параметрам, упомянутым ранее. Однако уравнения основаны на сложной математике, и для решения уравнений необходимы такие методы решения полей, как анализ граничных элементов.
Тестирование печатных плат на контролируемый импеданс
Критические печатные платы с контролируемым импедансом проходят 100% тестирование. Однако фактические трассы, составляющие управляемый импеданс, не всегда могут быть доступны для тестирования.Кроме того, задействованные дорожки могут быть слишком короткими для проведения точных измерений, а также могут содержать переходные отверстия и ответвления, которые также затрудняют точное измерение импеданса. Добавление дополнительных переходных отверстий или контактных площадок для облегчения тестирования может повлиять на производительность и занять дополнительное место на плате.
Таким образом, производители проверяют управляемый импеданс не на самой печатной плате, а на нескольких тестовых купонах, которые они интегрируют в панель. Купон соответствует той же структуре слоев и дорожек, что и на основной плате.Поскольку дорожки на купоне имеют идентичный импеданс, что и на основной печатной плате, тестирование купона гарантирует производителю, что импеданс на плате будет правильным.
Измерение контролируемого импеданса
Рефлектометр или TDR является наиболее распространенным прибором для измерения контролируемого импеданса. Во время измерения TDR использует кабель и щуп для подачи быстрого скачка напряжения на дорожки на купоне. Кабель особого типа с жестко контролируемым импедансом.Любое изменение значения импеданса — прерывание — проявляется в виде отражений в выходном сигнале импульса, который отображает TDR. Соответствующее программное обеспечение в TDR преобразует данные измерений, чтобы указать масштаб и местоположение неоднородности. Программное обеспечение в рефлектометре также строит график импеданса по длине тестовой дорожки на купоне. Этот график представляет собой характеристический импеданс следа и позволяет проводить несколько сложных измерений.
Оборудование для измерения контролируемого импеданса
Некоторые производители оригинального оборудования производят различные типы оборудования для измерения контролируемого импеданса.Среди них два хорошо известных имени — Tektronix и Agilent. Например, модульные TDR от Tektronix позволяют пользователю смешивать и сопоставлять различные модули для достижения наилучшего сочетания, необходимого для их приложения. Серия TDR для анализа целостности сигнала от Agilent позволяет пользователям использовать несколько портов для измерения. Каждый инструмент имеет свои преимущества и недостатки, связанные с требованиями приложения.
Заключение
С увеличением рабочей скорости и частоты сигналов в современном оборудовании, в сочетании с их уменьшающимися размерами, достижение воспроизводимого и стабильного функционирования зависит от целостности сигнала и тщательного проектирования печатных плат.Для этого одним из критических факторов является контролируемый импеданс. Передовой опыт проектирования печатных плат и усовершенствования технологий производства с помощью современных инструментов помогает избавиться от большей части тайны в достижении желаемого контролируемого импеданса.
Что такое электрическое сопротивление? | EAGLE
Вы пытаетесь понять электрическое сопротивление? Скорее всего, если вы уже углублялись в эту тему в прошлом, то получили некоторый жаргон вроде фазоров, фазовых соотношений и даже воображаемого сопротивления.Что это вообще такое ?!
Не все из нас — инженеры-электрики с высшим образованием. Некоторые из нас просто возятся с электроникой в свободное время и никогда не сталкиваются со строгой математикой, с которой вы сталкиваетесь в университете. Но это не значит, что понимание импеданса должно быть препятствием. Если вы планируете работать с электронными устройствами с питанием от переменного тока, вам нужно знать, что такое импеданс и что он делает с вашей схемой.
Давай узнаем!
Не совсем яблоки в яблоки
Лучший способ понять электрический импеданс — это сравнить его с тем, с чем вы уже знакомы — сопротивлением.И здесь мы собираемся предложить краткое изложение импеданса в двух словах:
Электрический импеданс — это просто форма сопротивления, которая зависит от частоты.
Вот и все. Вы можете уйти прямо сейчас и добавить еще одно слово в свой словарь по электротехнике. Когда вы понижаете импеданс, он обеспечивает сопротивление току в зависимости от рабочей частоты цепи. Но, конечно, есть еще кое-что.
Резисторы
довольно легко работают в цепи постоянного тока; они сопротивляются току, протекающему через какой-то металл, например медь.Вы добавляете резистор 220 кОм в цепь постоянного тока, и вы получаете определенное уменьшение тока между одной стороной резистора и другой. Резисторы, как и другие нереактивные компоненты, меньше заботятся о таких вещах, как частота источника питания. Они просто будут продолжать делать то, что делают, все время сопротивляясь одной и той же силе тока.
Но что будет, если вы начнете работать с электроникой с питанием от переменного тока? С переменным током это не просто вопрос питания вашей цепи напряжением 5 В.Вместо этого у вас есть новые переменные, которые нужно учитывать, например, конкретную частоту вашего переменного тока. Здесь, в США, переменный ток перемещается вперед и назад со скоростью 60 циклов в секунду (60 Гц). Над прудом, в Европе, частота 50 Гц.
В отличие от прямого постоянного тока, переменный ток колеблется взад и вперед с заданным количеством циклов в секунду. (Источник изображения)
Суть всего в том, что в электронике с питанием от переменного тока вам нужны не только нереактивные компоненты, такие как резисторы для сопротивления току.Вам также потребуются компоненты, которые могут реагировать на изменения тока и частоты , например конденсаторы и катушки индуктивности; в противном случае ваша схема не будет работать должным образом. Сложите все это вместе, и вы почти сможете думать об импедансе как о старшем брате сопротивления. Импеданс включает в себя как сопротивление, так и реактивное сопротивление. Или выражается как отношение:
Импеданс = Сопротивление + Реактивное сопротивление
Но что такое реактивность?
Reactance бывает двух видов в зависимости от того, какой реактивный компонент вы используете, к ним относятся:
Индуктивное реактивное сопротивление
Вы увидите это в виде электромагнитов, которые изменяют магнитное поле в цепи, также называемой индуктором.Катушки индуктивности будут иметь низкий импеданс на низких частотах и высокий импеданс на высоких частотах.
Связка индукторов, обратите внимание на общность, катушка с медным проводом вокруг магнита. (Источник изображения)
Емкостное реактивное сопротивление
Вы увидите это в виде заряжающего электрического поля между двумя проводящими поверхностями, также называемого проводником. Проводники имеют высокий импеданс на низких частотах и низкий импеданс на высоких частотах.
Конденсаторы бывают всех форм и размеров.(Источник изображения)
Поместите резисторы, катушки индуктивности и конденсаторы в цепь переменного тока, и у вас будет не только возможность противостоять электричеству, но и способность накапливать и выделять энергию. В то время как резистор будет поддерживать постоянное сопротивление независимо от изменяющихся условий, катушки индуктивности и конденсаторы изменят свое сопротивление в зависимости от частоты сигнала, который они представляют. А когда конденсаторы и катушки индуктивности и сопротивляются накоплению / высвобождению энергии, тогда у вас есть мера импеданса.
Как измерить импеданс?
Давайте возьмем простую схему, чтобы связать все это вместе. Взгляните на первый ниже; это цепь с питанием от постоянного тока с током, протекающим через резистор. Довольно просто, правда? Чем выше сопротивление в этой цепи, тем меньше будет ток.
Простая цепь постоянного тока с резистором 100 Ом для ограничения тока.
Но что произойдет, если вы модернизируете эту схему с помощью источника переменного тока, катушки индуктивности и конденсатора? Теперь у вас есть два дополнительных компонента, обеспечивающих собственное сопротивление электрическому току.Как и резистор, они оба препятствуют потоку тока , а также реагируют на него . Когда вы объединяете сопротивление своего резистора, сопротивление и реактивное сопротивление конденсатора и катушки индуктивности вместе, вы получаете полное сопротивление.
Последовательная цепь переменного тока с резистором, катушкой индуктивности и конденсатором.
Но подождите, вычислить импеданс не так просто, как сложить ваше сопротивление и реактивное сопротивление вместе, и именно здесь большинство руководств начинается с набора математических формул.Так что давайте рассмотрим эту часть медленно.
Расчет импеданса конденсатора
Чтобы рассчитать импеданс нашего конденсатора, вы можете использовать приведенную ниже формулу. Здесь X C — это полное сопротивление, которое вы получите, которое измеряется в Ом (Ом). f — это частота сигнала через конденсатор, а C — это емкость.
Расчет импеданса индуктора
Чтобы рассчитать импеданс нашего индуктора, вы можете использовать формулу ниже.Здесь X L — это полное сопротивление, которое вы получите, которое снова измеряется в Ом (Ом). f — это частота сигнала, проходящего через вашу индуктивность, а L — это индуктивность.
Эти формулы хороши и хороши, если вам просто нужны измерения импеданса для отдельных компонентов, но что, если вы хотите знать полное сопротивление для всей вашей цепи? Здесь все становится сложнее.
Прежде чем мы перейдем к нашей последней формуле, мы хотим предложить вам калькулятор импеданса, который может облегчить вашу жизнь: Калькуляторы импеданса от Кейсана.
Расчет общего импеданса
Чтобы выполнить работу, вам понадобится помощь теоремы Пифагора. Как мы объясняли выше, в цепях переменного тока вы будете работать как с сопротивлением, так и с реактивным сопротивлением, которые вместе дают общее сопротивление. Но дело не просто в сложении сопротивления и реактивного сопротивления. Мы могли бы объяснить почему, но это позволило бы погрузиться в тонкости векторов и фазоров, а это уже целый блог.
Когда вы разбиваете процесс вычисления импеданса для всей цепи, вы получите так называемый треугольник импеданса, посмотрите это ниже:
Треугольник импеданса позволяет легко рассчитать импеданс для всей вашей цепи.(Источник изображения)
Наиболее важной частью этого треугольника является гипотенуза, которая дает вам полное сопротивление, основанное на квадратном корне из вашего реактивного сопротивления и сопротивления. Если вы поместите это в формулу, вы можете найти свой полный импеданс по формуле ниже. Здесь Z — ваше полное сопротивление, R — ваше полное сопротивление, а X — ваше полное реактивное сопротивление.
Практический импеданс
Видите ли, теперь понять электрический импеданс не так уж и сложно, не так ли? Есть масса бесплатных калькуляторов, которые помогут вам в работе.Что вам действительно нужно знать, так это то, что импеданс работает так же, как сопротивление, препятствуя протеканию тока в цепи с питанием от переменного тока.
Именно способность компонентов, таких как конденсаторы и катушки индуктивности, реагировать на постоянно меняющийся переменный ток, делает их уникальными. Из-за сопротивления у вас может быть что-то вроде блока предохранителей в вашем доме, который будет реагировать на неожиданный скачок напряжения, предотвращая перегорание электрической системы вашего дома. И вы также можете поблагодарить импеданс за возможность носить с собой портативный ноутбук, зная, что ваши батареи полностью заряжены и не взорвутся.
Когда дело доходит до работы с устройствами с питанием от переменного тока, будь то ваш ноутбук или блок предохранителей в вашем доме, вам нужно поблагодарить за сопротивление. И помните, что электрическое сопротивление — это просто старший брат сопротивления, объединяющий сопротивление и реактивное сопротивление в одной простой формуле.
Готовы приступить к разработке своей первой электроники с питанием от переменного тока? Попробуйте Autodesk EAGLE бесплатно сегодня!
Импеданс и реактивное сопротивление | Основы
Импеданс и реактивное сопротивление
Элемент в цепи постоянного тока можно описать, используя только его сопротивление.Сопротивление конденсатора в цепи постоянного тока рассматривается как разомкнутое соединение (бесконечное сопротивление), в то время как сопротивление индуктора в цепи постоянного тока рассматривается как короткое соединение (нулевое сопротивление). Другими словами, использование конденсаторов или катушек индуктивности в идеальной цепи постоянного тока было бы пустой тратой компонентов. Тем не менее, они все еще используются в реальных цепях, и причина в том, что они никогда не работают с идеально постоянными напряжениями и токами.
В отличие от цепей с постоянным напряжением, в цепях переменного тока полное сопротивление элемента является мерой того, насколько элемент противодействует протеканию тока, когда на него подается напряжение переменного тока.В основном это отношение напряжения к току, выраженное в частотной области. Импеданс — это комплексное число, состоящее из действительной и мнимой частей:
, где Z — комплексный импеданс. Действительная часть R представляет сопротивление, а мнимая часть X представляет реактивное сопротивление. Сопротивление всегда положительное, а реактивное сопротивление может быть положительным или отрицательным. Сопротивление в цепи рассеивает мощность в виде тепла, в то время как реактивное сопротивление сохраняет энергию в виде электрического или магнитного поля.
Импеданс резистора
Резисторы в цепях переменного тока ведут себя так же, как и в цепях постоянного тока. В основном импеданс резистора состоит только из действительной части, которая равна сопротивлению резистора. Следовательно, полное сопротивление резистора можно выразить как:
, где Z — полное сопротивление, а R — сопротивление резистора. Очевидно, что резистор не имеет реактивного сопротивления и, следовательно, не может накапливать энергию.Кроме того, когда на резистор подается напряжение, ток, протекающий через резистор, будет совпадать по фазе с напряжением, как видно на этой иллюстрации:
Импеданс конденсатора
Конденсаторы — это компоненты, которые вводят в цепь определенную емкость. Они используются для временного хранения электрической энергии в виде электрического поля. Хотя это определение технически верно, оно мало что значит для любителя или даже для большинства инженеров.Возможно, более уместно сказать, что конденсаторы используются для задержки напряжения на 90 градусов по сравнению с током во временной области. Этот эффект лучше описать графически:
Как видно из графика, напряжение конденсатора отстает от тока конденсатора. В качестве альтернативы можно сказать, что ток конденсатора опережает напряжение конденсатора на 90 градусов. Чтобы представить этот факт с помощью комплексных чисел, для импеданса конденсатора используется следующее уравнение:
, где Z C — импеданс конденсатора, ω — угловая частота (заданная как ω = 2πf , где f — частота сигнала), а C — емкость конденсатора.Несколько фактов очевидны только из этой формулы:
- Сопротивление идеального конденсатора равно нулю.
- Реактивное сопротивление идеального конденсатора и, следовательно, его полное сопротивление отрицательны для всех значений частоты и емкости.
- Эффективный импеданс (абсолютное значение) конденсатора зависит от частоты, и для идеальных конденсаторов всегда уменьшается с частотой.
Импеданс индуктора
Точно так же индукторы — это компоненты, которые вносят в цепь определенную индуктивность.Они используются для временного хранения электрической энергии в виде магнитного поля. Таким образом, индукторы используются для задержки тока на 90 градусов по сравнению с напряжением во временной области. Следующий график объясняет это явление:
Напряжение индуктора опережает ток конденсатора на 90 градусов. Следующее уравнение используется для импеданса катушки индуктивности:
, где Z L — полное сопротивление данной катушки индуктивности, ω — угловая частота, а L — индуктивность катушки индуктивности.Опять же, из этой формулы можно сделать несколько выводов:
- Сопротивление идеального индуктора равно нулю.
- Реактивное сопротивление идеальной катушки индуктивности и, следовательно, ее полное сопротивление положительно для всех значений частоты и индуктивности.
- Эффективный импеданс (абсолютное значение) индуктора зависит от частоты и для идеальных индукторов всегда увеличивается с частотой.
Закон Ома
Закон
Ома был первоначально сформулирован для цепей постоянного тока и гласит:
Чтобы иметь смысл для цепей переменного тока, он был позже расширен за счет использования комплексных чисел, и новая формулировка:
, где U — комплексное напряжение между двумя точками, I — комплексный ток, а Z — комплексный импеданс.Поскольку импеданс всегда рассматривается как комплексное число, мы опустили подчеркивание для импеданса по всему тексту.
Понятие сложных напряжений и токов поначалу может сбивать с толку, поэтому давайте сначала попробуем объяснить это. Цепи переменного тока часто находятся в установившемся режиме, когда один или несколько источников питания работают на одной и той же частоте, что дает синусоидальный выходной сигнал. В этом случае можно доказать, что все напряжения и токи в цепях также являются колебательными сигналами синусоидальной формы, причем все они колеблются с одной и той же угловой частотой, ω .Однако эти напряжения и токи, вообще говоря, не совпадают по фазе. Если напряжение в цепи переменного тока задано в виде косинусоидальной волны, такой как эта:
, где u (t) — напряжение между некоторыми двумя точками в цепи, заданное как функция времени, U M — амплитуда, ω — угловая частота и Φ U — фаза, то комплексное представление этого напряжения:
На шкале цепи шириной, то обычно используют один сигнал в качестве фазового опорного сигнала.Это означает, что предполагается, что фаза этого сигнала равна нуль, и фаза всех других сигналов (напряжения и тока) определяются в отношении этой ссылки.
Эквивалентные сопротивления
Последовательное соединение
Если два сопротивления соединены последовательно, эквивалентный импеданс получается простым сложением — Z e = Z 1 + Z 2 . Сложение двух комплексов легко осуществить так:
Например, резистор 10 Ом, соединенный последовательно с конденсатором 1 мФ на частоте 100 Гц, будет иметь эквивалентное сопротивление:
Эффективный импеданс, также называемый величиной импеданса, рассчитывается как:
В нашем примере величина импеданса равна:
Подключение параллельно
Чтобы получить эквивалентное сопротивление двух параллельно соединенных сопротивлений, мы сначала определим полную проводимость.Единица проводимости — сименс [1 S], и это мера того, насколько легко элемент пропускает ток, и его значение является обратной величиной импеданса:
Эквивалентная полная проводимость двух параллельно соединенных сопротивлений равна сумме индивидуальных проводимых сопротивлений:
Если мы используем те же значения, что и в предыдущем примере, мы легко можем получить:
Это дает величину импеданса:
.

 000E + 01 8.068E + 01 1.707E + 02 -9.320E + 00 -9.932E + 01
000E + 01 8.068E + 01 1.707E + 02 -9.320E + 00 -9.932E + 01
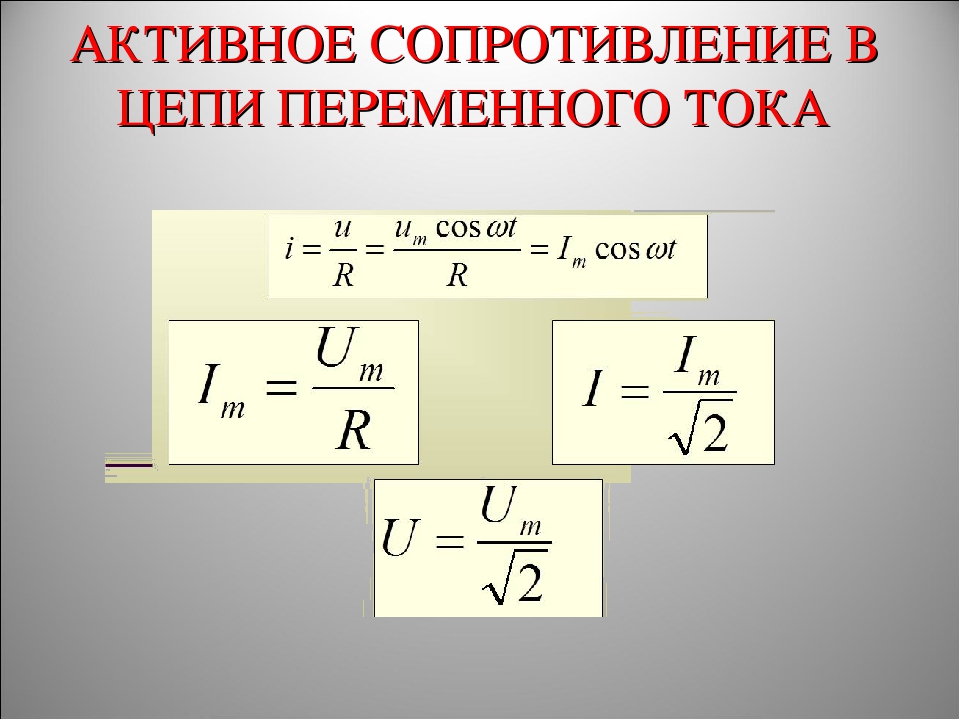 . . Z n
. . Z n 