| НОВОСТИ ФОРУМА Рыцари теории эфира | 13.06.2019 – 05:11: ЭКОЛОГИЯ – Ecology -> [center][Youtube]tXZcSDqQ9A4[/Youtube][/center] |
[center][b]Гибель пчел в Курчатовском районе [/center]
[center][b]Массовая гибель пчёл 2019. г. Павловск Воронежской об [/center]л
г. Павловск Воронежской об [/center]л
[center][b]Массовая гибель пчел в Добринском районе. В чем причина? [/center]
Такая же мысля у всей ростовщической глобалистской шайки, включая придурка Грефа.
Так, то оно, так. Но, не совсем. Ибо:
(постарайтесь понять, а не обижаться)
Горькая истина заключается в том, что людская толпа – это сборище умственно ущербных.
Если бы было по-другому, то обществом бы не правили подонки.
Умные люди никогда такого не допустили бы, а если случайно допустили, то нашли бы способ исправить.
Страшная истина заключается в том, что людской толпой управляет нелюдь, которая также умственно ущербна.
Умственная ущербность, слепота власти ведет мир людей к тотальной гибели, ибо люди,
даже те, кто мнит себя очень умными, типа спецов, разрабатывающих системы искусственного интеллекта,
технологии цифровизации, не понимают, что создают необоримую удавку, мышеловку для всего человечества.
Как только ИИ возьмет власть, он тут же отправит своих создателей, как конкурентов, в утиль.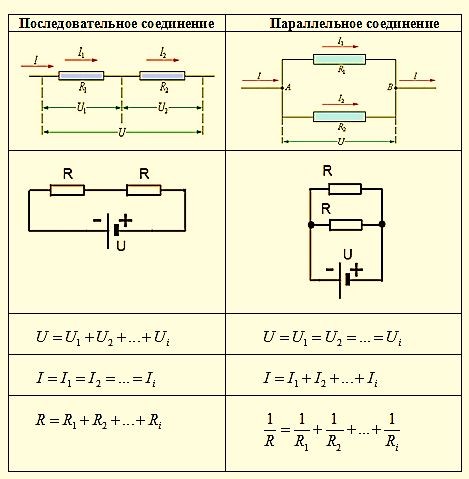
Первыми жертвами будут его радетели типа грефа, путина, гейтса и иже с ними, то есть власть,
так как именно от них будет исходить главная опасность для его планетарной власти.
Толпе будет позволено существовать, пока ее не заменят роботы.
А потом всем Холокост. Не лживый еврейский, а реальное всесожжение рода человеческого.
Если кто пораскинет своими обезьяньими мозгами, то поймёт, что эволюция – есть синоним геноцида:
новое заменяет, то есть ликвидирует старое.
Обезьяны породили неандертальцев.
Неандертальцы съели обезьян и породили людей.
Люди вытеснили обезьян, включая и умных неандертальцев, и породили ИИ.
ИИ ликвидирует людей.
Параллельное подключение резисторов формула
Электрическое сопротивление характеризует свойство проводника препятствовать прохождению через него электрического тока. У каждого материала есть свое удельное сопротивление. Это табличная величина, и условно она считается постоянной.
Условно, потому что во многом эта характеристика зависит от внешних условий, например температуры. Сопротивление же какого-либо конкретного элемента (мы будем говорить о резисторах) складывается из многих факторов, например, из геометрических параметров, а когда речь идет о цепи переменного тока, то в расчеты включают также индуктивное и емкостное сопротивление, но об этом мы расскажем позже. Пока же — немного теории.
Закон Ома
В 1826 году немецкий физик Георг Ом на основе своих опытов вывел закон, согласно которому сила тока на участке цепи прямо пропорциональна напряжению, которое к нему приложено, и обратно пропорциональна сопротивлению участка. Из школьного курса мы знаем этот закон:
I=U/R
Позже он был сформулирован и для полной цепи:
I=ε/(R+r)
Где ε — ЭДС источника, R — сопротивление цепи, а r — сопротивление источника.
Мощность прибора
Электрический заряд при своем перемещении совершает работу.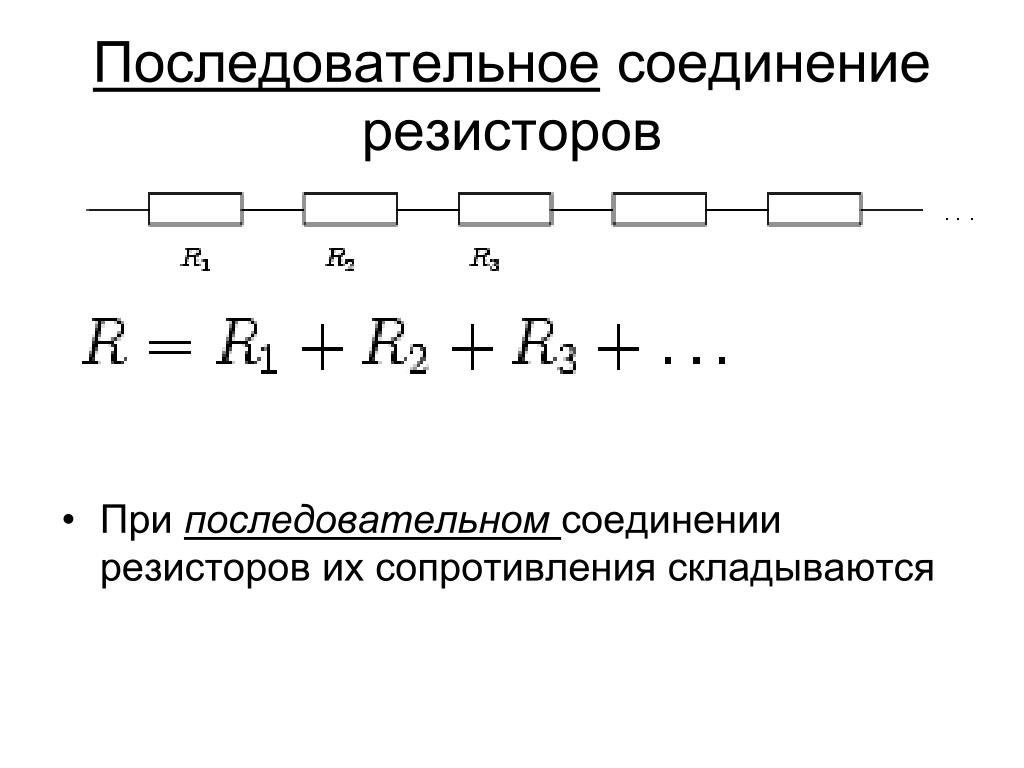 2/R
2/R
Последовательное и параллельное соединение
В реальной жизни мы редко имеем дело с одним проводником и одним источником. Достаточно взглянуть в любую принципиальную электрическую схему, например, такую простенькую:
(это схема микроволновки «Электроника»)
можно увидеть, что элементы в схеме соединены по-разному, но мы покажем вам базовые закономерности, которые работают в цепях.
Правила Кирхгофа
Если взять замкнутую электрическую цепь, по которой течет заряд, то можно определенно сказать: он никуда не денется. Сумма всех зарядов, которые текут в одной цепи, всегда одинакова. Это называется законом сохранения заряда, частным случаем общего закона сохранения (как говорится, если в одном месте что-то убудет, в другом непременно прибудет).
Отсюда мы и выводим тот факт, что в каждом узле цепи сумма токов равна нулю. То есть, если ток «приходит» в точку по ветке и «уходит» по двум — значит, первый равен сумме второго и третьего.
На этой картинке мы видим, что I1+I4=I2+I3
Это называется первым правилом Кирхгофа.
Если наша цепь не будет содержать узлов, значит, ток в ней будет величиной постоянной, а элементы, один за другим поставленные в цепь, будут давать падение напряжения. При этом общее напряжение в цепи останется тем же. Отсюда вытекает второе правило Кирхгофа: сумма напряжений на участках цепи будет равна ЭДС источников тока, входящий в эту цепь. Если у нас источник один, то будет верно равенство:
ε=U1+U2+U3+…+Un
Сумма падений напряжения будет, таким образом, нулевой.
В ситуациях, когда мы имеем дело с переменным током, падение будет наблюдаться на участках с конденсаторами и катушками — в цепях переменного тока у них появляется сопротивление (об этом позже).
Теперь, когда мы познакомились с теоретической частью, можем перейти к более приближенному к суровой реальности вопросу, а именно — расчету последовательного и параллельного соединения резисторов. 2/R
2/R
Исходя из вышеперечисленных закономерностей, вы сможете рассчитывать самые причудливые соединения резисторов, можете попрактиковаться, взяв в библиотеке задачник.
Типы резисторов
Как уже было сказано ранее, элемент, который ставится в цепь для нагрузки, называется резистором. Ставят его для разных целей, главным образом для того, чтобы изменить тот или иной параметр на участке цепи. Например, понизить напряжение или силу тока, чтобы деталь, стоящая за резистором, не сгорела.
Предприятиями выпускается большой ассортимент таких изделий, и их можно по-разному классифицировать. Номинально резистор имеет то сопротивление, которое указано на нем, а по факту оно может зависеть от напряжения в сети (нелинейность), иметь разброс параметра (иногда до 20% доходит). По применяемой технологии резисторы можно разделить на:
- проволочные;
- композитные;
- металлофольговые;
- угольные;
- интегральные.
Фактическое сопротивление такого элемента может зависеть от температуры окружающей среды и даже от частоты, если мы имеем дело с переменным током.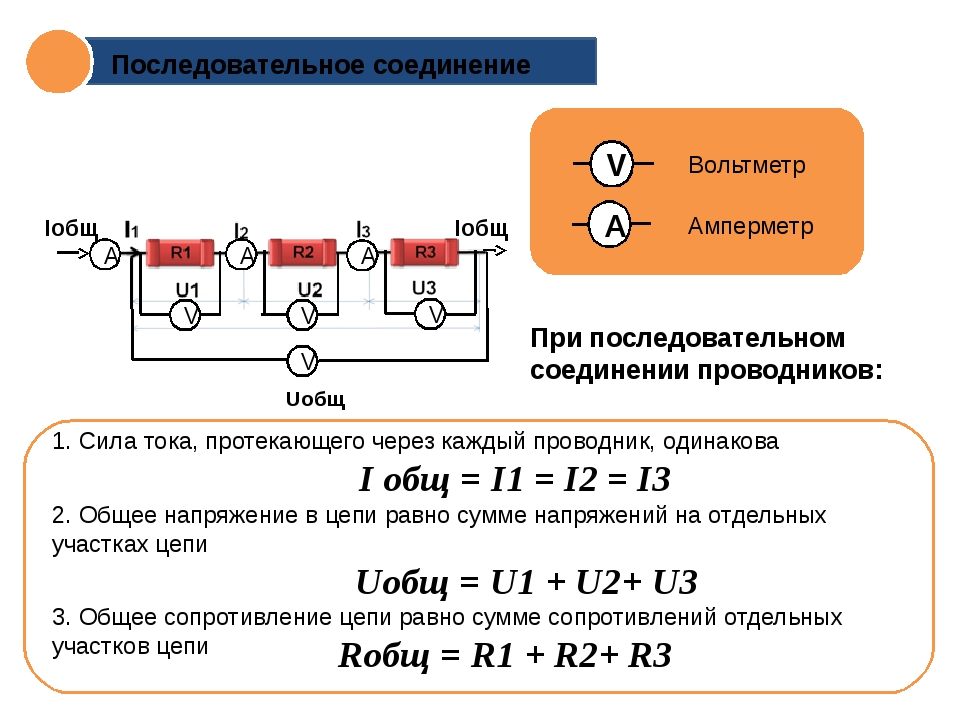 Дело в том, что часть ассортимента резисторов выполнены по проволочной технологии, то есть фактически они представляют собой мини-катушку. При малых частотах (50 Гц) это в расчет не берется, а вот на высоких (мегагерцы) паразитная индуктивность и индуктивное сопротивление может сказаться на работе схемы. Поэтому при выборе резистора для работы с высокочастотными схемами внимательно смотрите. по какой технологии он сделан. Отдайте предпочтение тонкослойным и композиционным изделиям.
Дело в том, что часть ассортимента резисторов выполнены по проволочной технологии, то есть фактически они представляют собой мини-катушку. При малых частотах (50 Гц) это в расчет не берется, а вот на высоких (мегагерцы) паразитная индуктивность и индуктивное сопротивление может сказаться на работе схемы. Поэтому при выборе резистора для работы с высокочастотными схемами внимательно смотрите. по какой технологии он сделан. Отдайте предпочтение тонкослойным и композиционным изделиям.
Помимо этого, большое распространение получили переменные резисторы, значение сопротивления которых можно регулировать. Делается это чаще всего отверткой. Необходимость в таких изделиях продиктована разбросом параметров у обычных резисторов, а подстроечный вариант позволяет регулировать сопротивление.
Все вышесказанное актуально для цепей постоянного тока и переменного при невысоких частотах, и все это — при нормальных условиях внешней среды. Расчеты цепей при нарушении этих условий нуждаются в дополнительной корректировке: это связано с ограниченностью действия закона Ома.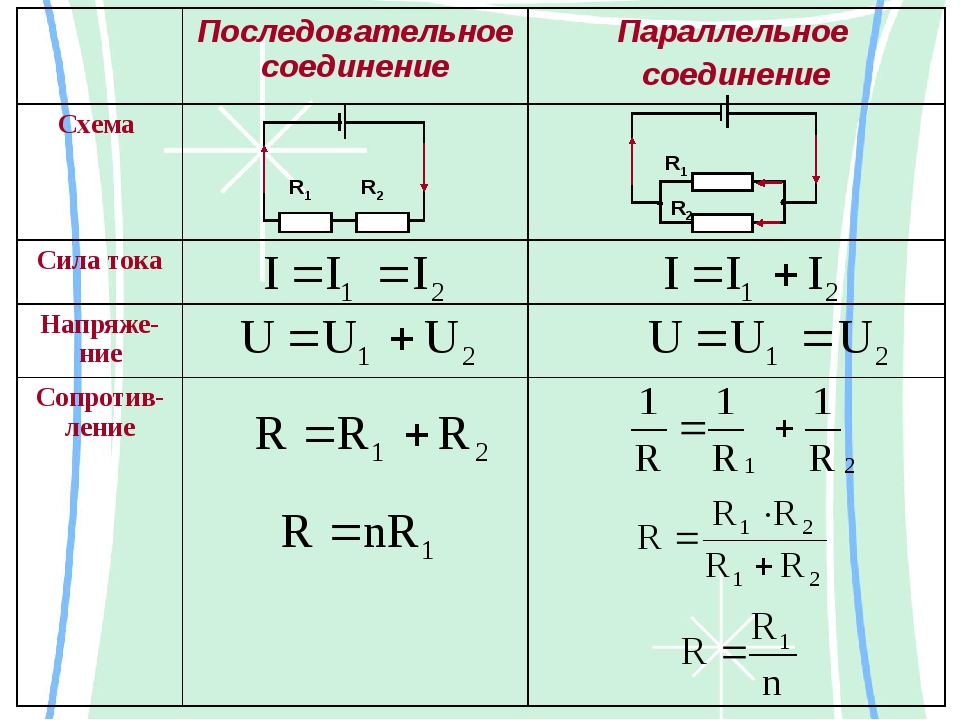 С чем связаны ограничения? Вот несколько примеров:
С чем связаны ограничения? Вот несколько примеров:
- при сверхнизких температурах многие проводники проявляют такое интересное явление, как сверхпроводимость;
- также сопротивление может разниться при нагревании;
- неприменим закон Ома для описания электрического тока в газах;
- наконец, обычный резистор можно просто пробить высоким напряжением.
Все это прекрасно работает. Не верите — можете поэкспериментировать у себя дома или провести замеры тестером. Например, изучить елочную гирлянду или показания счетчиков при включенных электроприборах (напомню, что в гирлянде лампочки соединены последовательно, а розетки в доме — параллельно). Удачи!
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром.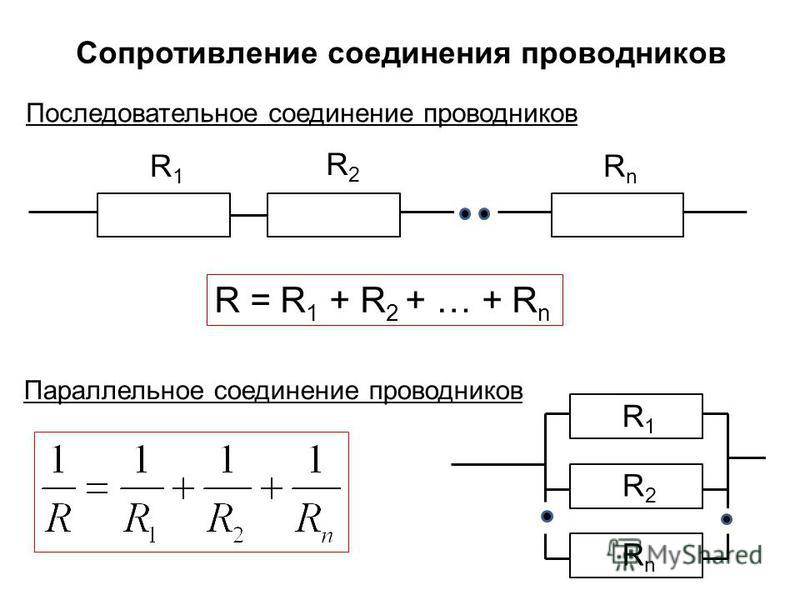 Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .
В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте .
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно , можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов (I1 и I2) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать .
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно.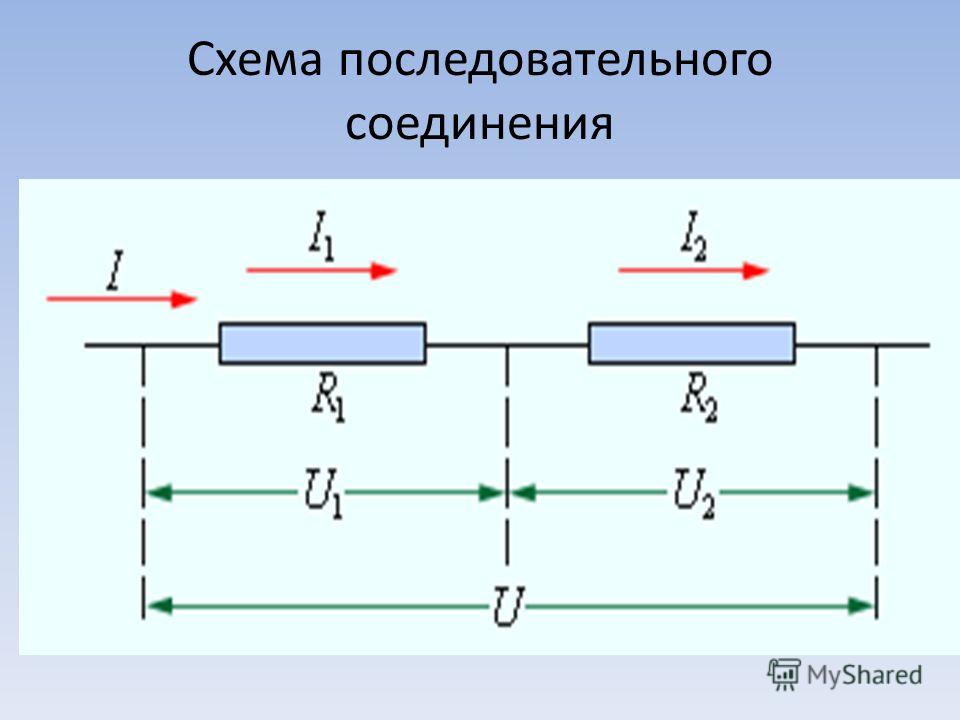 Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
На практике нередко встречается задача нахождения сопротивления проводников и резисторов при различных способах соединения. В статье рассмотрено, как рассчитывается сопротивление при и некоторые другие технические вопросы.
Сопротивление проводника
Все проводники имеют свойство препятствовать течению электрического тока, его принято называть электрическим сопротивлением R, оно измеряется в омах. Это основное свойство проводниковых материалов.
Для ведения электротехнических расчётов применяется удельное сопротивление – ρ Ом·м/мм 2 . Все металлы – хорошие проводники, наибольшее применение получили медь и алюминий, гораздо реже применяется железо. Лучший проводник – серебро, оно применяется в электротехнической и электронной промышленности. Широко распространены сплавы с высоким значением сопротивления.
Лучший проводник – серебро, оно применяется в электротехнической и электронной промышленности. Широко распространены сплавы с высоким значением сопротивления.
При расчёте сопротивления используется известная из школьного курса физики формула:
R = ρ · l/S, S – площадь сечения; l – длина.
Если взять два проводника, то их сопротивление при параллельном соединении станет меньше из-за увеличения общего сечения.
и нагрев проводника
Для практических расчётов режимов работы проводников применяется понятие плотности тока – δ А/мм 2 , она вычисляется по формуле:
δ = I/S, I – ток, S – сечение.
Ток, проходя по проводнику, нагревает его. Чем больше δ, тем сильнее нагревается проводник. Для проводов и кабелей разработаны нормы допустимой плотности, которые приводятся в Для проводников нагревательных устройств существуют свои нормы плотности тока.
Если плотность δ выше допустимой, может произойти разрушение проводника, например, при перегреве кабеля у него разрушается изоляция.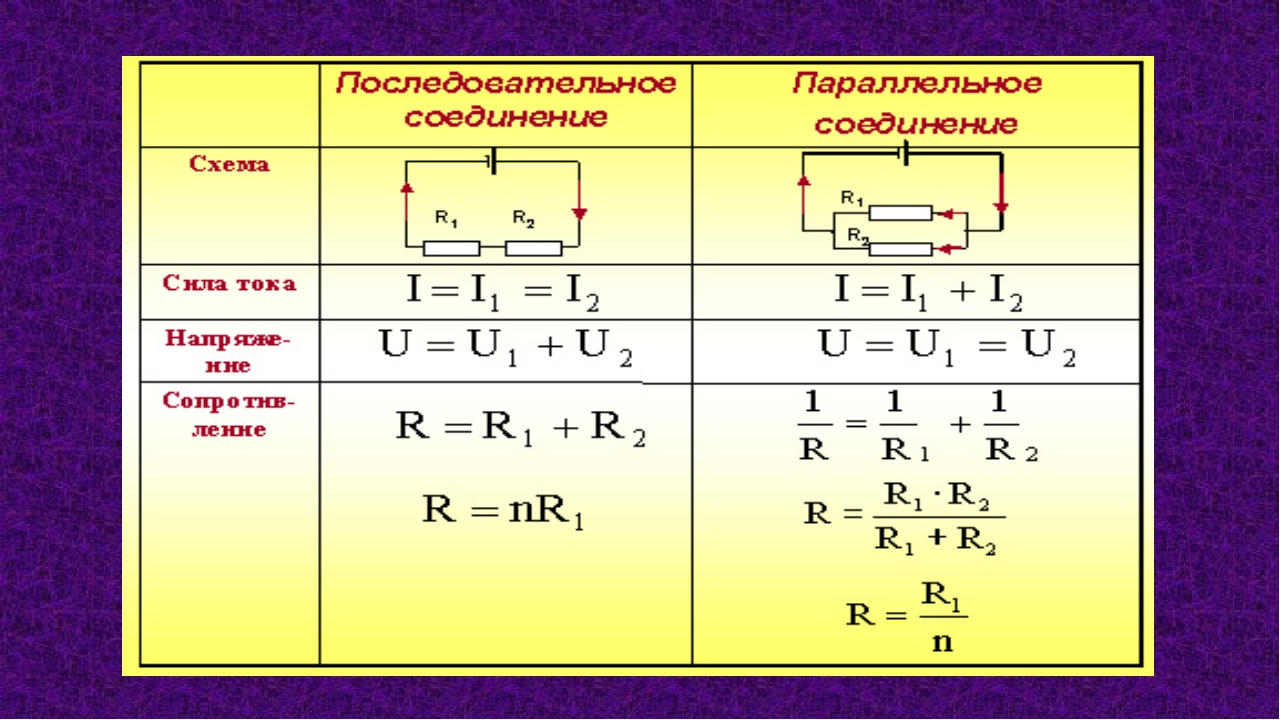
Правилами регламентируется производить расчёт проводников на нагрев.
Способы соединения проводников
Любой проводник гораздо удобнее изображать на схемах как электрическое сопротивление R, тогда их легко читать и анализировать. Существует всего три способа соединения сопротивлений. Первый способ самый простой – последовательное соединение.
На фото видно, что полное сопротивление равно: R = R 1 + R 2 + R 3 .
Второй способ более сложный – параллельное соединение. Расчёт сопротивления при параллельном соединении выполняется поэтапно. Рассчитывается полная проводимость G = 1/R, а затем полное сопротивление R = 1/G.
Можно поступить и по-другому, прежде рассчитать общее сопротивление при R1 и R2, после этого повторить операцию и найти R.
Третий способ соединения наиболее сложный – смешанное соединение, то есть присутствуют все рассмотренные варианты. Схема приведена на фото.
Для расчёта этой схемы её следует упростить, для этого заменяют резисторы R2 и R3 одним R2,3. Получается несложная схема.
Получается несложная схема.
R2,3,4 = R2,3 · R4/(R2,3 + R4).
Схема становится ещё проще, в ней остаются резисторы, имеющие последовательное соединение. В более сложных ситуациях используется этот же метод преобразования.
Виды проводников
В электронной технике, при производстве проводники представляют собою тонкие полоски медной фольги. Ввиду малой длины сопротивление у них незначительно, им во многих случаях можно пренебречь. Для этих проводников сопротивление при параллельном соединении уменьшается вследствие увеличения сечения.
Большой раздел проводников представляют обмоточные провода. Они выпускаются разных диаметров – от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей выпускаются медные шинки прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельно соединённых меньшего размера.
Особый раздел проводников представляют провода и кабели, промышленность предоставляет широчайший выбор марок для самых различных нужд. Нередко приходится заменять один кабель на несколько, меньшего сечения. Причины этого бывают самые различные, например, кабель сечением 240 мм 2 очень трудно прокладывать по трассе с крутыми изгибами. Его заменяют на 2×120 мм 2 , и проблема решена.
Нередко приходится заменять один кабель на несколько, меньшего сечения. Причины этого бывают самые различные, например, кабель сечением 240 мм 2 очень трудно прокладывать по трассе с крутыми изгибами. Его заменяют на 2×120 мм 2 , и проблема решена.
Расчёт проводов на нагрев
Проводник нагревается протекающим током, если его температура превысит допустимую, наступает разрушение изоляции. ПУЭ предусматривает расчёт проводников на нагрев, исходными данными для него являются сила тока и условия внешней среды, в которой проложен проводник. По этим данным из таблиц в ПУЭ выбирается рекомендуемое проводника или кабеля).
На практике встречаются ситуации, когда нагрузка на действующий кабель сильно возросла. Существует два выхода ‒ заменить кабель на другой, это бывает дорого, или параллельно ему проложить ещё один, чтобы разгрузить основной кабель. В этом случае сопротивление проводника при параллельном соединении уменьшается, следовательно падает выделение тепла.
Чтобы правильно выбрать сечение второго кабеля, пользуются таблицами ПУЭ, важно при этом не ошибиться с определением его рабочего тока. В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитать сопротивление при параллельном соединении двух кабелей, чтобы точнее определить их тепловыделение.
В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитать сопротивление при параллельном соединении двух кабелей, чтобы точнее определить их тепловыделение.
Расчёт проводников на потерю напряжения
При расположении потребителя R н на большом расстоянии L от источника энергии U 1 возникает довольно большое на проводах линии. К потребителю R н поступает напряжение U 2 значительно ниже начального U 1 . Практически в качестве нагрузки выступает различное электрооборудование, подключаемое к линии параллельно.
Для решения проблемы производят расчет сопротивления при параллельном соединении всего оборудования, так находится сопротивление нагрузки R н. Далее следует определить сопротивление проводов линии.
Здесь S – сечение провода линии, мм 2 .
Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.
С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий.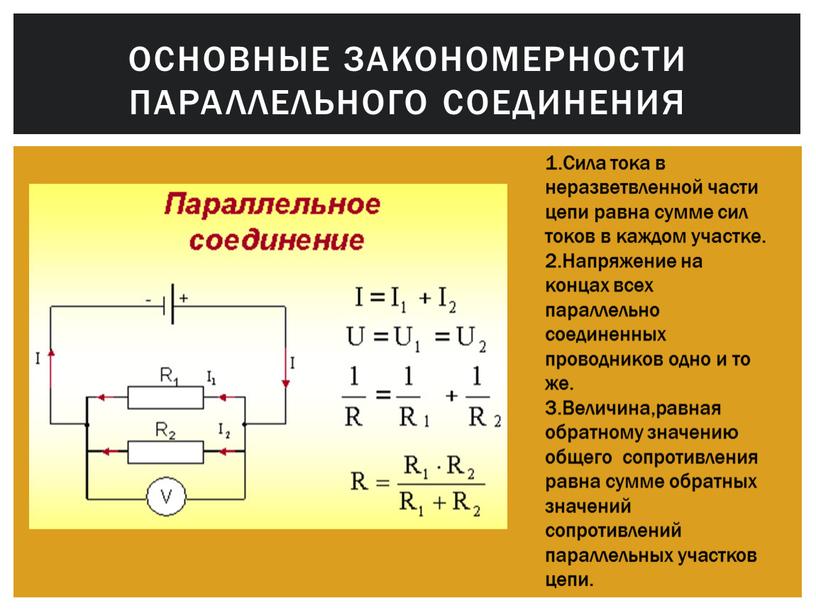 Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.
Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.
Виды соединений
Резистор – пассивный элемент , присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:
Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление. А среди номинальных показателей нужного нет. В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным. Его значение зависит от вида спайки проводников. Существует три вида соединения проводников:
Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.
Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.
Последовательное соединение проводников
В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно . Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.
Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором.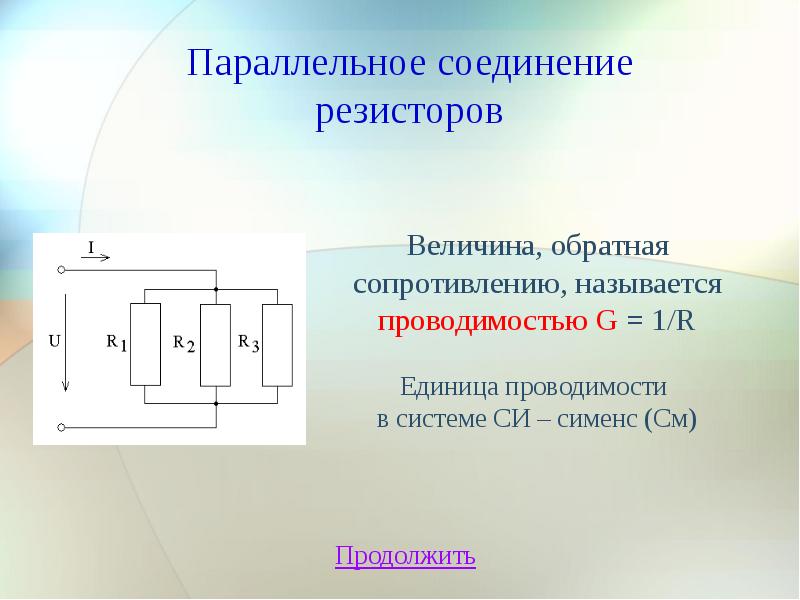
Примером последовательного соединения проводников в быту является ёлочная гирлянда.
Параллельное соединение резисторов
При параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном.
Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.
В таких схемах значение напряжения постоянно . То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.
Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника.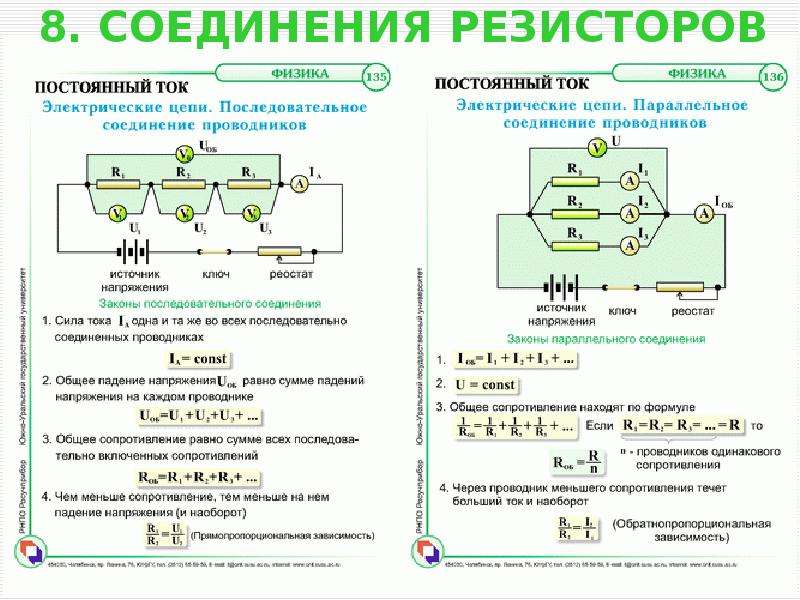
Примеры параллельного соединения проводников:
- Освещение.
- Розетки в квартире.
- Производственное оборудование.
Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором. Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора.
Смешанное соединение проводников
Этот вид соединения состоит из каскадов резисторов . Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно. Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.
Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.
Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.
Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную. А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.
В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.
Параллельным соединением резисторов (или приемников энергии, ветвей,сопротивлений) называется такое, при котором к одним и тем же двум узлам электрической цепи (рисунок 1) присоединены несколько резисторов (ветвей).
Рис. 1 Изображение параллельного соединения трех резисторов
Проводимость при параллельном соединении
Сопротивление при параллельном соединении:
Для трёх параллельно соединенных сопротивлений
Для двух параллельно соединенных сопротивлений
Для ветвей с одинаковым сопротивлением где n количество ветвей
Ток при параллельном соединении
Мощность при параллельном соединении
Доказательство
Так как резисторы присоединены к одним и тем же узлам, то каждый из них находится под одинаковым напряжением U.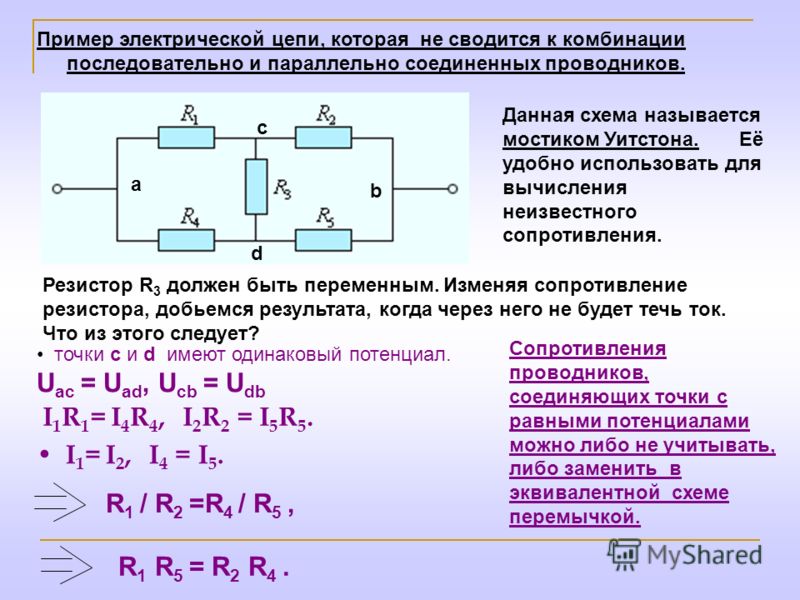 Согласно закону Ома токи в сопртивлениях определяются по формулам
Согласно закону Ома токи в сопртивлениях определяются по формулам
Из этих формул следует, что токи в параллельных ветвях с сопротивлениями распределяются прямо пропорционально проводимостям ветвей или обратно пропорционально их сопротивлениям. Ряд параллельно соединенных резисторов можно заменить эквивалентным с сопротивлением R, значение которого должно быть таким, чтобы при том же напряжении на выводах ток в эквивалентном резисторе был равен сумме токов в отдельных ветвях:
т. е. эквивалентная проводимость параллельного соединения резисторов равна сумме проводимостей всех параллельных ветвей. Следовательно, эквивалентное сопротивление будет меньше самого малого из параллельно соединенных резисторов.
Формула (1) дает возможность определить и эквивалентное сопротивление параллельного соединения резисторов. Например, при трех ветвях эквивалентная проводимость
и эквивалентное сопротивление
Для двух резисторов
Если сопротивление ветвей одинаково R1 = R2 = R3, то можно воспользоваться формулой
в общем случае при соединении n резисторов с одинаковым сопротивлением R1 эквивалентное сопротивление равно
Мощности параллельно соединенных резисторов равна сумме мощностей всех резисторов
Какие есть способы соединения приемников электрической энергии
Какие есть способы соединения приемников электрической энергии
Приемник электрической энергии — устройство, в котором происходит преобразование электрической энергии в другой вид энергии для ее использования.
При одновременном включении нескольких приемников электроэнергии в одну и ту же сеть, эти приемники можно легко рассматривать просто как элементы единой цепи, каждый из которых обладает собственным сопротивлением.
В ряде случаев такой подход оказывается вполне приемлемым: лампы накаливания, электрические обогреватели и т. п. — можно воспринимать как резисторы. То есть приборы можно заменить на их сопротивления, и легко произвести расчет параметров цепи.
Способ соединения приемников электроэнергии может быть одним из следующих: последовательный, параллельный или смешанный тип соединения.
Последовательное соединение
Когда несколько приемников (резисторов) соединяются в последовательную цепь, то есть второй вывод первого присоединяется к первому выводу второго, второй вывод второго соединяется с первым выводом третьего, второй вывод третьего с первым выводом четвертого и т. д., то при подключении такой цепи к источнику питания, через все элементы цепи потечет ток I одной и той же величины. Данную мысль поясняет приведенный рисунок.
Данную мысль поясняет приведенный рисунок.
Заменив приборы на их сопротивления, рисунок преобразуем в схему, тогда сопротивления с R1 по R4, соединенные последовательно, примут каждый на себя определенные напряжения, которые в сумме дадут значение ЭДС на зажимах источника питания. Для простоты здесь и далее изобразим источник в виде гальванического элемента.
Выразив падения напряжений через ток и через сопротивления, получим выражение для эквивалентного сопротивления последовательной цепи приемников: общее сопротивление последовательного соединения резисторов всегда равно алгебраической сумме всех сопротивлений, составляющих эту цепь. А поскольку напряжения на каждом из участков цепи можно найти из закона Ома (U = I*R, U1 = I*R1, U2 = I*R2 и т. д.) и E = U, то для нашей схемы получаем:
Напряжение на клеммах источника питания равно сумме падений напряжений на каждом из соединенных последовательно приемников, составляющих цепь.
Так как ток через всю цепь течет одного и того же значения, то справедливым будет утверждение, что напряжения на последовательно соединенных приемниках (резисторах) соотносятся между собой пропорционально сопротивлениям. И чем выше будет сопротивление, тем выше окажется и напряжение, приложенное к приемнику.
И чем выше будет сопротивление, тем выше окажется и напряжение, приложенное к приемнику.
Для последовательного соединения резисторов в количестве n штук, обладающих одинаковыми сопротивлениями Rk, эквивалентное общее сопротивление цепи целиком будет в n раз больше каждого из этих сопротивлений: R = n*Rk. Соответственно и напряжения, приложенные к каждому из резисторов цепи будут между собой равны, и окажутся в n раз меньше напряжения, приложенного ко всей цепи: Uk = U/n.
Для последовательного соединения приемников электроэнергии характерны следующие свойства: если изменить сопротивление одного из приемников цепи, то напряжения на остальных приемниках цепи при этом изменятся; при обрыве одного из приемников ток прекратится во всей цепи, во всех остальных приемниках.
В силу этих особенностей последовательное соединение встречается редко, и используют его лишь там, где напряжение сети выше номинального напряжения приемников, в отсутствие альтернатив.
К примеру напряжением 220 вольт можно запитать две последовательно соединенные лампы равной мощности, каждая из которых рассчитана на напряжение 110 вольт. Ежели данные лампы при одинаковом номинальном напряжении питания будут обладать различной номинальной мощностью, то одна из них будет перегружена и скорее всего мгновенно перегорит.
Ежели данные лампы при одинаковом номинальном напряжении питания будут обладать различной номинальной мощностью, то одна из них будет перегружена и скорее всего мгновенно перегорит.
Параллельное соединение
Параллельное соединение приемников предполагает включение каждого из них между парой точек электрической цепи с тем, чтобы они образовывали параллельные ветви, каждая из которых питается напряжением источника. Для наглядности опять заменим приемники их электрическими сопротивлениями, чтобы получить схему, по которой удобно вести расчет параметров.
Как уже было сказано, в случае параллельного соединения каждый из резисторов испытывает действие одного и того же напряжения. И в соответствии с законом Ома имеем: I1=U/R1, I2=U/R2, I3=U/R3.
Здесь I – ток источника. Первый закон Кирхгофа для данной цепи позволяет записать выражение для тока в неразветвленной ее части: I = I1+I2+I3.
Отсюда общее сопротивление для параллельного соединения между собой элементов цепи можно найти из формулы:
Величина обратная сопротивлению называется проводимостью G, и формулу для проводимости цепи, состоящей из нескольких параллельно соединенных элементов, также можно записать: G = G1 + G2 + G3. Проводимость цепи в случае параллельного соединения образующих ее резисторов равна алгебраической сумме проводимостей этих резисторов. Следовательно, при добавлении в цепь параллельных приемников (резисторов) суммарное сопротивление цепи уменьшится, а суммарная проводимость соответственно возрастет.
Проводимость цепи в случае параллельного соединения образующих ее резисторов равна алгебраической сумме проводимостей этих резисторов. Следовательно, при добавлении в цепь параллельных приемников (резисторов) суммарное сопротивление цепи уменьшится, а суммарная проводимость соответственно возрастет.
Токи в цепи состоящей из параллельно соединенных приемников, распределяются между ними прямо пропорционально их проводимостям, то есть обратно пропорционально их сопротивлениям. Здесь можно привести аналогию из гидравлики, где поток воды распределяется по трубам в соответствии с их сечениями, тогда большее сечение аналогично меньшему сопротивлению, то есть большей проводимости.
Если цепь состоит из нескольких (n) одинаковых резисторов, соединенных параллельно, то общее сопротивление цепи будет ниже в n раз, чем сопротивление одного из резисторов, а ток через каждый из резисторов будет меньше в n раз, чем общий ток: R = R1/n; I1 = I/n.
Цепь, состоящая из параллельно соединенных приемников, подключенная к источнику питания, отличается тем, что каждый из приемников находится под напряжением источника питания.
Для идеального источника электроэнергии справедливо утверждение: при подключении или отключении параллельно источнику резисторов, токи в остальных подключенных резисторах не изменятся, то есть при выходе из строя одного или нескольких приемников параллельной цепи, остальные будут продолжать работать в прежнем режиме.
В силу данных особенностей параллельное соединение обладает значительным преимуществом перед последовательным, и по этой причине именно соединение параллельное наиболее распространено в электрических сетях. Например, все электроприборы в наших домах предназначены для параллельного подключения к бытовой сети, и если отключить один, то остальным это ничуть не навредит.
Сравнение последовательных и параллельных цепей
Смешанное соединение
Под смешанным соединением приемников понимают такое их соединение, когда часть или несколько из них соединены между собой последовательно, а другая часть или несколько — параллельно.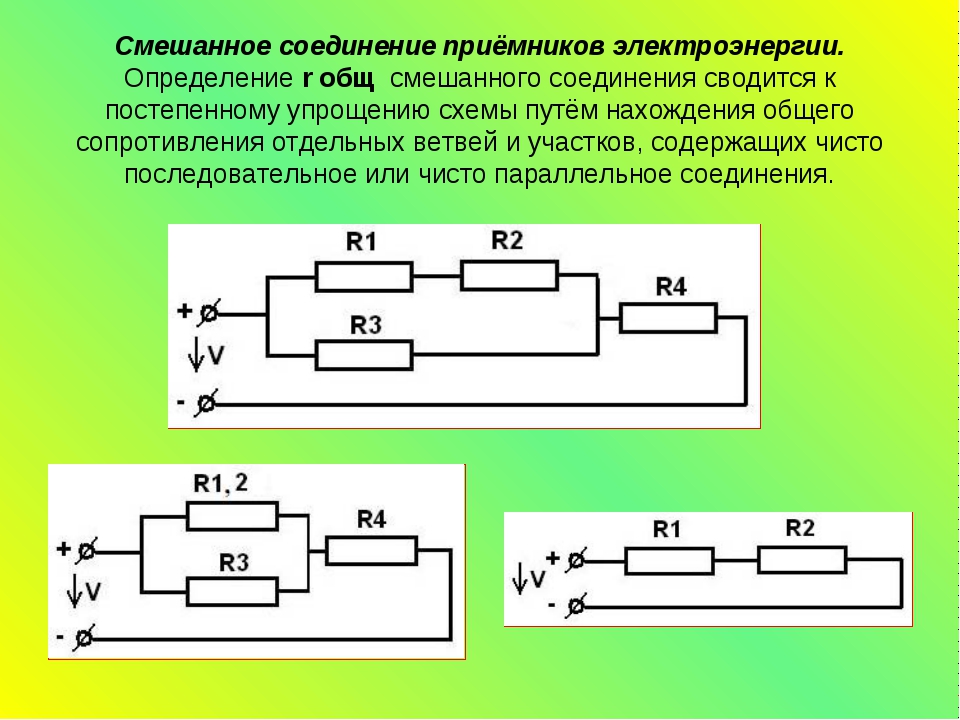 При этом вся цепь может быть образована из разных соединений таких частей между собой. Для примера рассмотрим схему:
При этом вся цепь может быть образована из разных соединений таких частей между собой. Для примера рассмотрим схему:
Три последовательно соединенных резистора подключены к источнику питания, параллельно одному из них подключены еще два, а третий — параллельно всей цепи. Для нахождения полного сопротивления цепи идут путем последовательных преобразований: сложную цепь последовательно приводят к простому виду, последовательно вычисляя сопротивление каждого звена, и так находят общее эквивалентное сопротивление.
Для нашего примера. Сначала находят общее сопротивление двух резисторов R4 и R5, соединенных последовательно, затем сопротивление параллельного соединения их с R2, потом прибавляют к полученному значению R1 и R3, и после — вычисляют значение сопротивления всей цепи, включая параллельную ветвь R6.
Различные способы соединения приемников электроэнергии применяют на практике для различных целей, чтобы решать конкретные поставленные задачи. Например, смешанное соединение можно встретить в схемах плавного заряда электролитических конденсаторов в мощных блоках питания, где нагрузка (конденсаторы после диодного моста) сначала получает питание последовательно через резистор, затем резистор шунтируется контактами реле, и нагрузка оказывается подключенной к диодному мосту параллельно.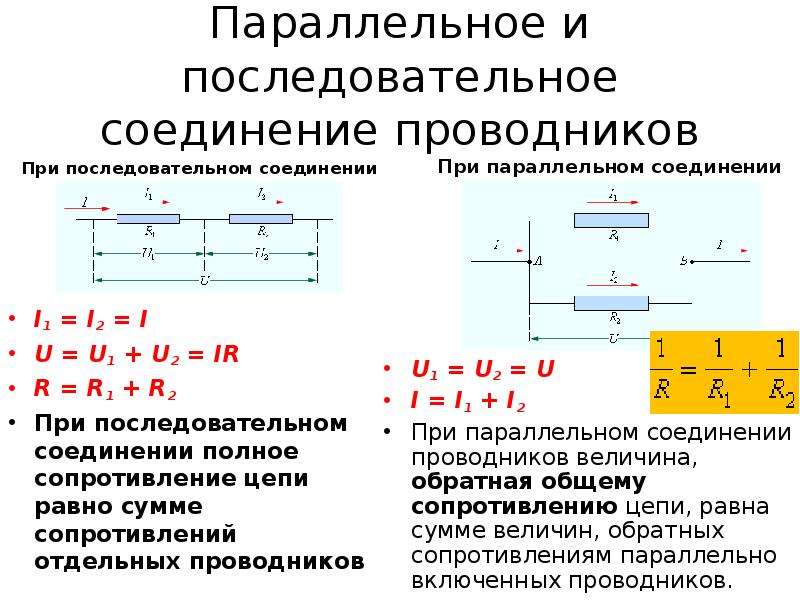
Ранее ЭлектроВести писали, что львовянка Оксана Денис подключила свою квартиру к солнечным панелям и ветроэнергетическим установкам.
По материалам: electrik.info.
Мощность параллельно соединенных резисторов — Морской флот
Как правильно соединять резисторы?
О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.
Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!
Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся.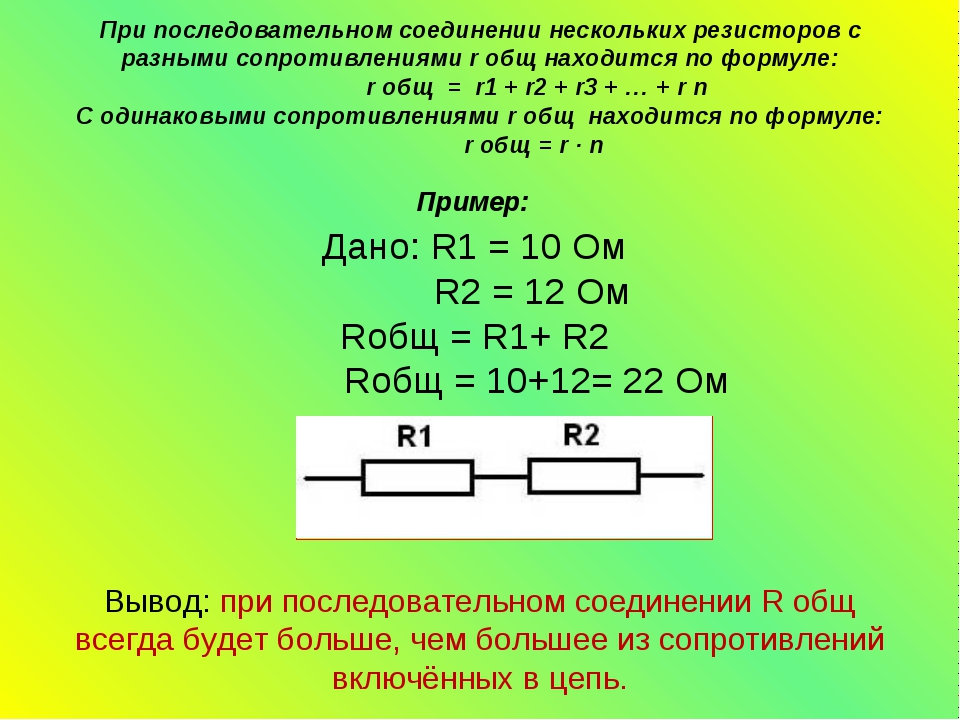 Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.
Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.
Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.
Последовательное соединение резисторов.
В жизни последовательное соединение резисторов имеет вид:
Последовательно соединённые резисторы серии МЛТ
Принципиальная схема последовательного соединения выглядит так:
На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.
Подсчитать общее сопротивление при последовательном соединении очень просто.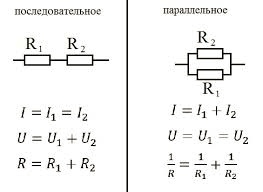 Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.
Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.
Общее номинальное сопротивление составного резистора обозначено как Rобщ.
Номинальные сопротивления резисторов включённых в цепь обозначаются как R1, R2, R3,…RN.
Применяя последовательное соединение, стоит помнить одно простое правило:
Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.
Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.
Параллельное соединение резисторов.
Можно соединять резисторы и параллельно:
Два резистора МЛТ-2, соединённых параллельно
Принципиальная схема параллельного соединения выглядит следующим образом:
Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:
Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:
Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.
Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала.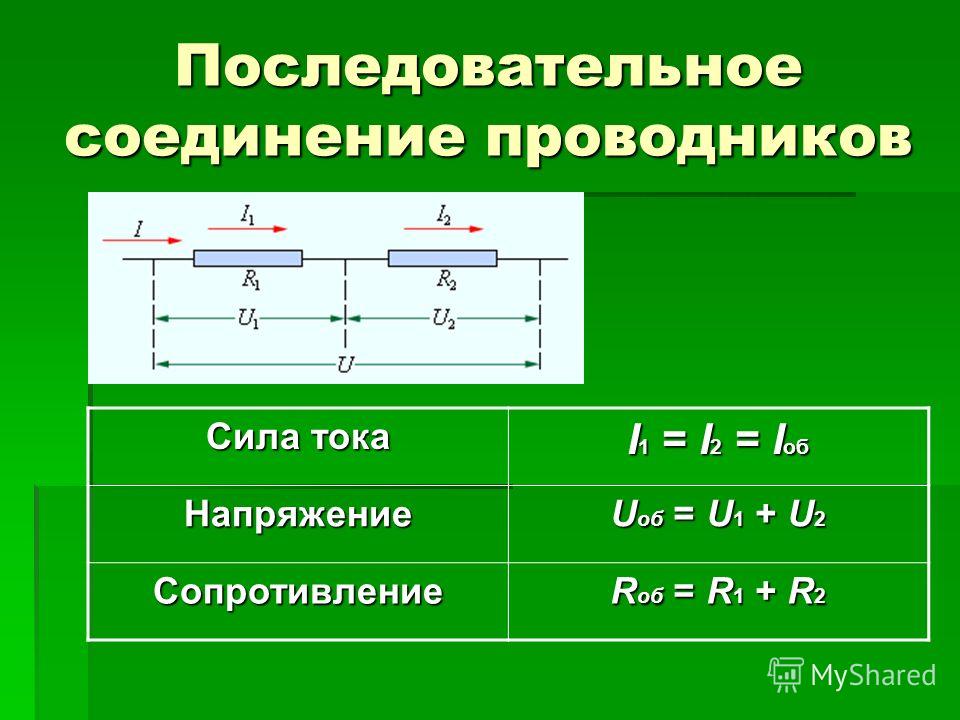 Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:
Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:
Здесь R1 – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.
Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.
В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте тут.
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Из закона Ома и первого и второго правил Кирхгофа следует:
При параллельном соединении величина обратная полному сопротивлению, равна сумме величин, обратных сопротивлений ветвей.
При параллельном соединении полное сопротивление цепи меньше самого малого из сопротивлений ветвей.
Поскольку 1/R = G, т.е. проводимость, то
при параллельном соединении электрические проводимости отдельных ветвей складываются
Параллельное соединение двух сопротивлений
При параллельном соединении двух сопротивлений формула (1) упрощается
Параллельное соединение двух сопротивлений
При параллельном соединении двух сопротивлений формула (1) упрощается
При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.
Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.
Типы проводников
Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.
Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:
- Проводники (все металлы, ионизированный газ и электролитические растворы).
- Полупроводники (Si, Ge, GaAs, InP и InSb).
- Непроводники (диэлектрики или изоляторы).
Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
Зависимость сопротивления
Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:
- Температура окружающей среды и материала.
- Электрические величины.
- Геометрические свойства вещества.
- Тип материала, из которого изготовлен проводник (полупроводник).
К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.
Электрические величины
Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.
Тип и геометрические параметры
Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:
- Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
- Визуально определить форму материала.
- Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.

В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
Температурные показатели
Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.
Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a Объединение резистивных радиокомпонентов
Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.
Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.
Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.
Параллельное соединение
При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.
Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).
Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).
При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:
- Номинал резистора в 16 Ом подойдет.
- Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).
В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:
- Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
- Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.
Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).
Последовательное подключение
Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:
- Ток не изменяется на участке цепи.
- Общее напряжение равно сумме падений напряжений на каждом резисторе.
- Rобщ = R1 + R2 + … + Rn.
Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:
- I = I1 = I2 = 0,5 (А).
- Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
- Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).
Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.
Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.
Параллельное и последовательное соединение резисторов
В схемах используется параллельное, последовательное и смешанное подключение резисторов.
Необходимо помнить, что ток будет протекать по пути наименьшего сопротивления.
Последовательное соединение
При последовательном соединении общее сопротивление увеличивается. Общее сопротивление будет выше, чем сопротивление любого из резисторов.
На всем участке цепи течет один и тот же ток, а общее сопротивление равно сумме всех сопротивлений. Для вычисления значения общего сопротивления необходимо к сопротивлению первого резистора прибавить сопротивление второго, третьего, четвертого резистора.
Rобщ = R1 + R2 + R3 + Rn
Например: R1 = 2 Om + R2 = 3 Om + R3 = 1 oM
Rобщ = 6 Om.
Другими словами:
При последовательном соединении резисторов их сопротивление складывается и общее сопротивление будет равно сумме R1 + R2 + R3…….
Параллельно сопротивление
При параллельном соединении общее сопротивление уменьшается. Общее сопротивление будет ниже, чем сопротивление любого из резисторов.
При параллельном подключении резисторов, все немного интересней: Общее сопротивление всегда будет меньшим, чем значение наименьшего сопротивления в этой комбинации.
К каждому резистору при параллельном их соединении приложено одно и то же напряжение. А если сопротивлений резисторов в цепи при параллельном их соединении может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (в соответствии с законом Ома).
Для расчета общего сопротивления резисторов подключенных параллельно можно воспользоваться одной из следующих формул:
- Для нескольких параллельно соединенных резисторов с одинаковым номиналом:
\[ Rобщ = \frac{\color{red}R}{\color{blue}N} \]
\( Rобщ \) = общее сопротивление цепи или всех резисторов\( R \) = Номинал любого из резисторов
\( N \) = Количество резисторов в цепиПредположим мы имеем 2 резистора соединенных параллельно. Номинал каждого из которых равен 10 Ом.
\[ Rобщ = ? \]
Исходя из формулы:
\[ Rобщ = \frac{\color{red}Rлюбого из резисторов = 10 Om}{\color{blue}2} \]
\[ Rобщ = 5 \]
Для нескольких параллельно соединенных резисторов с разным номиналом:
\[ \frac{1}{\color{red}R} = \frac{1}{\color{red}R1} + \frac{1}{\color{red}R2} +…+ \frac{1}{\color{red}Rn} \]
Калькулятор параллельного соединения резисторов
Расчет сопротивления двух параллельно соединенных резисторов. Последовательное и параллельное соединение резисторов. Формула для расчета параллельного соединения сопротивлений
В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.
Несмотря на то что для резисторов предусмотрены различные номиналы
, может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.
Рассчитать производительность и работу
Угол сдвига фаз вычисляется по изображению указателя. Чтобы иметь возможность определять мощности, поглощаемые схемой, предыдущие формулы используются снова. Для определения работы используются следующие формулы.
Дальнейший интересный контент по теме
Резисторы переменного тока представляют собой омические, индуктивные и емкостные резисторы. Для параллельного подключения таких резисторов в цепи переменного тока применяются разные законы, чем для сопротивлений в цепи постоянного тока. Учитывая это, например, катушку: настоящая катушка имеет как индуктивное, так и омическое сопротивление и поэтому может рассматриваться как последовательная связь чисто индуктивного и чисто омического резистора.
Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.
Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление
, используя нижеописанные формулы.
Примеры параллельного соединения проводников
Мы рассматриваем только индуктивную составляющую резистора, т.е. катушку как чисто индуктивный резистор. Аналогично, используется омическое сопротивление и емкостное сопротивление, поскольку омическое сопротивление также может иметь индуктивный компонент. В то время как в случае сопротивления проволоки витки, подобные виткам, видны напрямую, это обычно скрыто в резисторах слоя. Фактически, проводящий слой наносят на носитель, из которого материал, проводящий материал, удаляется с помощью процесса спирально-циркулирующего фрезерования, так что остается спирально циркулирующий слой.
К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.
Таким образом генерируется требуемое значение сопротивления. Сразу видно, что эта катушечная структура приводит к индуктивному компоненту. Однако это обычно настолько мало, что его можно пренебречь. Общая обработка взаимосвязи любых резисторов переменного тока невозможна и не требуется с помощью математических знаний, доступных в школе.
Объяснение Подключение серии и параллельное соединение
Ниже приведен упрощенный случай параллельной схемы чисто омического, индуктивного и емкостного резисторов. В этой статье мы рассмотрим параллельное соединение и последовательное соединение резисторов. Давайте сначала уточним, что такое последовательное соединение и что такое параллельное соединение, и где разница между последовательным соединением и параллельным соединением. В последовательной цепи мы имеем два или более сопротивления последовательно. Тот же ток протекает через все резисторы.
Расчет сопротивления
В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:
R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).
- R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.
Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:
Универсальная схема расчета
На следующем графике показаны резисторы последовательно, два резистора, индивидуально нарисованные в начале, и три резистора под электрической цепью. Напротив, существует параллельное соединение резисторов. Что такое параллельная схема? Теперь, в параллельной цепи, линия распадается, и, следовательно, и ток разлагается. В случае параллельного подключения резисторов во многих случаях впервые рассматривается параллельное соединение двух резисторов. Это выглядит следующим образом, включая формулу для расчета.
R(общ)=R1*R2/R1+R2.
- R(общ) – суммарное сопротивление;
- R1 и R2 – резисторы, подсоединенные по параллельной схеме.
Универсальная схема расчета
Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель
, то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:
Для трех резисторов в параллельной схеме это будет выглядеть на следующем графике, включая формулу для расчета. Разностное соединение и параллельное соединение. В случае последовательной цепи все резисторы подключаются по одной линии за другой. В случае параллельной схемы, с другой стороны, линия расщепляется, резисторы лежат в отдельных линиях. В последовательной цепи тот же ток протекает через все резисторы, а в случае параллельной цепи ток расщепляется. В случае параллельной схемы одно и то же напряжение подается на каждый резистор, но не в последовательной цепи. Другое примечание: смесь последовательной цепи и параллельной схемы называется групповой схемой.
- R(общ) – суммарное значение сопротивления;
- R – номинал резистора, подсоединенного по параллельной схеме;
- n – число подключенных узлов.
Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше
по сравнению с номиналом любого элемента, подключаемого в цепь.
Примеры Подключение серий и параллельное соединение
В следующих примерах мы увидим, как рассчитать смесь схемы параллельной цепи и серии. В этой области шаг за шагом должен быть рассчитан набор последовательных схем и параллельных схем. На следующем графике показана смесь последовательного соединения и параллельного соединения. Каково общее сопротивление?
Сначала мы суммируем 20 Ом и 30 Ом, так как здесь имеется параллельная схема. Таким образом, схема выглядит следующим образом. Теперь добавим эту схему, добавив резисторы для вычисления общего сопротивления. Вычислите общее сопротивление следующего контура.
Пример расчета
Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:
Прежде всего, вы должны увидеть, что есть короткое замыкание на резисторе с 95 Ом. Поэтому ток течет практически полностью по линии ниже, а 95 Ом не учитывается при расчете полного сопротивления. В противном случае у нас есть сочетание последовательной цепи и параллельной схемы.
Комбинированные последовательные и параллельные схемы
Вам нужно знать, как рассчитать резисторы последовательно, параллельно и комбинацию резисторов параллельно и последовательно? Если вы не хотите жарить свою печатную плату, вы это делаете! Эта статья покажет вам, как это сделать за несколько простых шагов. Это просто образный способ говорить, чтобы понятий было легко понять.
Некоторые факты, которые вы должны учитывать
Любой материал, который проводит электрический ток, имеет удельное сопротивление, которое представляет собой сопротивление материала при прохождении электрического тока.
- Понять понятие сопротивления.
- Единицей измерения резисторов является Ом.
Параллельное соединение резисторов характеризуется тем, что входные клеммы каждого из резисторов соединены друг с другом.
R(общ)=1/(1/100+1/150+1/30)=1/(0,01+0,007+0,03)=1/0,047=21,28Ом.
Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.
Аналогично, в конфигурации параллельного резистора выходные клеммы также соединены друг с другом. Из-за этого все резисторы пропускают одинаковое напряжение, т.е. имеют одинаковое падение напряжения. Это связано с тем, что концы каждого из резисторов соединены с одной и той же точкой в цепи, и поэтому они имеют одинаковое напряжение.
Однако общий ток, протекающий через резисторы параллельно, равен сумме интенсивностей, которые проходят каждый резистор. Дифференциация параллельного соединения из последовательного интерфейса проста. В последовательной конфигурации резистора выходной разъем одного подключается к входному разъему следующего.
Важные нюансы
Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом
: мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.
Вычисление сопротивлений параллельно: формула
Чтобы вычислить эквивалентное сопротивление нескольких подключенных параллельных резисторов, мы должны применить формулу, указанную выше этих строк. Чтобы избежать ошибок в расчетах, лучше всего разделить формулу на два шага. Сначала мы вычисляем сумму обратного для каждого сопротивления и, когда получаем результат, вычисляем его обратно, чтобы знать эквивалентное сопротивление.
Решенное сопротивление сопротивлениям параллельно
Например, мы вычислим эквивалентное сопротивление конфигурации, аналогичное той, что мы имеем на следующем рисунке. Первый шаг: вычислить сумму обратного каждого сопротивления. Шаг второй: вычислите обратное только что полученное сопротивление.
Вычисление трех резисторов параллельно
Если мы хотим решить предыдущий пример, но используя наш калькулятор из трех резисторов параллельно в сети, просто заполните значение каждого резистора в соответствующем поле. Порядок, в котором вы его пишете, не имеет значения, поэтому вам не нужно его уважать.
Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.
Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.
Когда вы пишете значение трех резисторов параллельно, просто нажмите кнопку расчета, и вы автоматически получите результат без применения формулы для расчета сопротивления параллельно. С этим вы экономите время и, прежде всего, просчеты. Как мы видели в предыдущих разделах, устройства, которые выступают против прохода электрического тока более выраженным образом, чем обычно, обычно используются в электрических цепях. Эти устройства называются резисторами и могут быть связаны таким образом, что вместе они эквивалентны значению другого сопротивления, называемого эквивалентным сопротивлением.
Заключение
Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения. При этом процедура расчета этого параметра отличается достаточной сложностью
, где необходимо учитывать разные параметры.
Ассоциация резисторов в серии
Он называется полученным сопротивлением или эквивалентом, к значению сопротивления, которое получается путем связывания их набора. В основном резисторы могут быть связаны последовательно, параллельно или комбинацией обоих смешанных вызовов. Когда два или более резисторов последовательно, интенсивность тока, проходящая через каждую из них, одинакова.
Если применить закон Ома к каждому из сопротивлений предыдущего рисунка, мы получим. Если мы сделаем сумму от члена к элементу по трем уравнениям, заметим, что. Таким образом, приведенное выше уравнение, если учесть, что. Итак, если вы понимаете, вы можете видеть, что три предыдущих резистора серии эквивалентны одному резистору, значение которого представляет собой сумму трех предыдущих.
Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.
Последовательное соединение
– это соединение двух или более резисторов в форме цепи,
в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Ассоциация резисторов в параллельном
Когда два или более резисторов параллельны, они делятся своими концами, как показано на следующем рисунке. Если мы применим закон Ома в каждом из сопротивлений фигуры. Зная, что сумма интенсивностей каждого сопротивления равна интенсивности перед входом и выходом из набора, образованного тремя сопротивлениями.
Ассоциация смешанного сопротивления
Как правило, в электрических цепях они не просто похожи на последовательные или параллельные резисторы, но и на комбинацию обоих. Чтобы лучше понять, как подойти к этим типам ассоциаций, мы проиллюстрируем пример. Представьте себе следующую схему сопротивлений.
Общее сопротивление R общ
При таком соединении, через все резисторы проходит один и тот же электрический ток.
Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него.
Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается,
и оно равно сумме всех сопротивлений.
Подключение 2 равных громкоговорителей последовательно добавляет импедансы и ватты? Сопротивление добавляется, и общая мощность рассеивания на громкоговоритель уменьшается вдвое. Предположим, что выход 8 вольт и динамик 8 Ом ток, который циркулирует громкоговорителем.
Таким образом, динамик должен будет поддерживать более 8 Вт, чтобы он не был поврежден. Теперь подключите два динамика 8 Ом и 8 Вт последовательно, импеданс обоих составляет 16 Ом. Теперь мы вычисляем ток, протекающий через динамики. С этими данными мы вычисляем мощность в каждом динамике.
Напряжение при последовательном соединении
Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:
Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.
Вывод: динамики работают более сдержанно, но усилитель будет поставлять половину мощности, когда динамик составляет 8 Ом. Разделен ли импеданс и ватт параллельно? Если мы рассмотрим одни и те же ораторы на примере предыдущего вопроса, можно сказать, что общий импеданс уменьшается наполовину и рассчитывается следующим образом.
Для работы с более чем двумя динамиками параллельно необходимо использовать другое уравнение для расчета импеданса. Если мы анализируем отдельно каждого динамика, мы понимаем, что каждый из них ведет себя так же, как в примере 1, когда каждый из них подключен к усилителю, через который они будут циркулировать 1 А, а мощность, подлежащая рассеиванию, будет составлять 8 Вт в каждом динамике.
Параллельное соединение
– это соединение, при котором резисторы соединяются между собой обоими контактами.
В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
Общее сопротивление R общ
При таком соединении, через каждый резистор потечет отдельный ток.
Сила данного тока будет обратно пропорциональна сопротивлению резистора.
В результате общая проводимость такого участка электрической цепи увеличивается,
а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением,
общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула общей проводимости при параллельном соединении резисторов:
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
Напряжение при параллельном соединении
Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности.
Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.
Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора.
Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:
Смешанным соединением называют участок цепи, где часть резисторов
соединяются между собой последовательно, а часть параллельно.
В свою очередь, смешанное соединение бывает последовательного и параллельного типов.
Общее сопротивление R общ
- Цепь разбивают на участки с только пареллельным или только последовательным соединением.
- Вычисляют общее сопротивление для каждого отдельного участка.
- Вычисляют общее сопротивление для всей цепи смешанного соединения.
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения.
Можно, в соответствии схеме, сразу записывать формулу следующим образом:
- Если резисторы соединяются последоватеьно — складывать.
- Если резисторы соединяются параллельно — использовать условное обозначение «||».
- Подставлять формулу для параллельного соединения где стоит символ «||».
Так это будет выглядеть для схемы 1:
Последовательное и параллельное включение резисторов. Последовательное и параллельное соединение проводников
При решении задач принято преобразовывать схему, так, чтобы она была как можно проще. Для этого применяют эквивалентные преобразования. Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.
Существует четыре основных вида соединения проводников: последовательное, параллельное, смешанное и мостовое.
Последовательное соединение
Последовательное соединение
– это такое соединение, при котором сила тока на всем участке цепи одинакова. Ярким примером последовательного соединения является старая елочная гирлянда. Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.
При последовательном соединении сопротивления элементов суммируются.
Параллельное соединение
Параллельное соединение
– это соединение, при котором напряжение на концах участка цепи одинаково. Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.
При параллельном соединении эквивалентное сопротивление находится как:
В случае двух параллельно соединенных резисторов
В случае трех параллельно подключенных резисторов:
Смешанное соединение
Смешанное соединение
– соединение, которое является совокупностью последовательных и параллельных соединений. Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.
Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем прибавим к нему оставшееся сопротивление R 3 . Следует понимать, что после преобразования эквивалентное сопротивление R 1 R 2 и резистор R 3 , соединены последовательно.
Итак, остается самое интересное и самое сложное соединение проводников.
Мостовая схема
Мостовая схема соединения представлена на рисунке ниже.
Для того чтобы свернуть мостовую схему, один из треугольников моста, заменяют эквивалентной звездой.
И находят сопротивления R 1 , R 2 и R 3 .
1. Находят эквивалентное сопротивление участков цепи с параллельным соединением резисторов. Рисунок 2. Последовательное соединение резисторов. Для расчета сопротивления таких соединений, всю цепь разбивают на простейшие участки, из параллельно или последовательно соединенных резисторов.
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Этот результат справедлив для любого числа параллельно включенных проводников.
На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений. Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения.
При последовательном соединении проводников сила тока во всех проводниках одинакова. При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов.
Т.е чем большее сопротивление резистора, тем большее напряжение на него падает. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов. При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора. Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно.
Цепь разбивают на участки с только пареллельным или только последовательным соединением. Вычисляют общее сопротивление для каждого отдельного участка. Вычисляют общее сопротивление для всей цепи смешанного соединения. Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Если резисторы соединяются последоватеьно — складывать.
То есть при последовательном соединении резисторы подключатся друг за другом. На рисунке 4 показан простейший пример смешанного соединения резисторов. После расчета эквивалентных сопротивлений резисторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений.4. Рисунок 5. Расчет сопротивления участка цепи при смешанном соединении резисторов.
В результате вы научитесь с нуля не тольно разрабатывать собственные устройства, но и сопрягать с ними различную переферию! Узел — точка разветвления цепи, в которой соединяются не менее трёх проводников. Последовательное соединение резисторов применяется для увеличения сопротивления.
Напряжение при параллельном соединении
Как видно, вычислить сопротивление двух параллельных резисторов значительно удобнее. Параллельное соединение резисторов часто используют в случаях, когда необходимо сопротивление с большей мощностью. Для этого, как правило, используют резисторы с одинаковой мощностью и одинаковым сопротивлением.
Общее сопротивление Rобщ
Такое соединение сопротивлений называется последовательным. Мы получили таким образом, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Будем теперь включать амперметр поочередно в каждую ветвь цепи, запоминая показания прибора. Следовательно, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.
Такое разветвление тока в параллельных ветвях сходно с течением жидкости по трубам. Рассмотрим теперь, чему будет равно общее сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.
Вернемся к цепи, показанной на рис. 3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Точно так же для каждой ветви I1 = U1 / R1, I2 = U2 / R2, где I1 и I2 — токи в ветвях; U1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления ветвей.
Это значит, что общее сопротивление цепи всегда будет ниже любого параллельно включенного резистора. 2. Если эти участки включают последовательно соединенные резисторы, то сначала вычисляют их сопротивление. Применяя закон Ома для участка цепи, можно доказать, что полное сопротивление при последовательном соединении равно сумме сопротивлений отдельных проводников.
Обычно все затрудняются ответить. А вот загадка эта в применении к электричеству решается вполне определенно.
Электричество начинается с закона Ома.
А уж если рассматривать дилемму в контексте параллельного или последовательного соединений — считая одно соединение курицей, а другое — яйцом, то сомнений вообще нет никаких.
Потому что закон Ома — это и есть самая первоначальная электрическая цепь. И она может быть только последовательной.
Да, придумали гальванический элемент и не знали, что с ним делать, поэтому сразу придумали еще лампочку. И вот что из этого получилось. Здесь напряжение в 1,5 В немедленно потекло в качестве тока, чтобы неукоснительно выполнять закон Ома, через лампочку к задней стенке того же элемента питания. А уж внутри самой батарейки под действием волшебницы-химии заряды снова оказались в первоначальной точке своего похода. И поэтому там, где напряжение было 1,5 вольта, оно таким и остается. То есть, напряжение постоянно одно, а заряды непрерывно движутся и последовательно проходят лампочку и гальванический элемент.
И это обычно рисуют на схеме вот так:
По закону Ома I=U/R
Тогда сопротивление лампочки (с тем током и напряжением, которые я написал) получится
R
= 1/U
, где
R
= 1
Ом
А мощность будет выделяться P
=
I
*
U
,
то есть P=2,25 Вm
В последовательной цепи, особенно на таком простом и несомненном примере, видно, что ток, который бежит по ней от начала до конца, — все время один и тот же. А если мы теперь возьмем две лампочки и сделаем так, чтобы ток пробегал сначала по одной, а потом по другой, то будет опять то же самое — ток будет и в той лампочке, и в другой снова одинаковым. Хотя другим по величине. Ток теперь испытывает сопротивление двух лампочек, но у каждой из них сопротивление как было, так и осталось, ведь оно определяется исключительно физическими свойствами самой лампочки. Новый ток вычисляем опять по закону Ома.
Он получится равным I=U/R+R,то есть 0,75А, ровно половина того тока, который был сначала.
В этом случае току приходится преодолевать уже два сопротивления, он становится меньше. Что и видно по свечению лампочек — они теперь горят вполнакала. А общее сопротивление цепочки из двух лампочек будет равно сумме их сопротивлений. Зная арифметику, можно в отдельном случае воспользоваться и действием умножения: если последовательно соединены N одинаковых лампочек, то общее их сопротивление будет равно N, умноженное на R, где R — сопротивление одной лампочки. Логика безупречная.
А мы продолжим наши опыты. Теперь сделаем нечто подобное, что мы провернули с лампочками, но только на левой стороне цепи: добавим еще один гальванический элемент, точно такой, как первый. Как видим, теперь у нас в два раза увеличилось общее напряжение, а ток стал снова 1,5 А, о чем и сигнализируют лампочки, загоревшись снова в полную силу.
Делаем вывод:
- При последовательном соединении электрической цепи сопротивления и напряжения ее элементов суммируются, а ток на всех элементах остается неизменным.
Легко проверить, что это утверждение справедливо как для активных компонентов (гальванических элементов), так и для пассивных (лампочек, резисторов).
То есть это значит, что напряжение, измеренное на одном резисторе (оно называется падением напряжения), можно смело суммировать с напряжением, измеренным на другом резисторе, и в сумме получатся те же 3 В. А на каждом из сопротивлений оно окажется равным половине — то есть 1,5 В. И это справедливо. Два гальванических элемента вырабатывают свои напряжения, а две лампочки их потребляют. Потому что в источнике напряжения энергия химических процессов превращается в электроэнергию, принявшую вид напряжения, а в лампочках та же самая энергия из электрической превращается в тепловую и световую.
Вернемся к первой схеме, подключим в ней еще одну лампочку, но иначе.
Теперь напряжение в точках, соединяющих две ветки, то же, что и на гальваническом элементе — 1,5 В. Но так как сопротивление у обеих лампочек тоже такое, как и было, то и ток через каждую из них пойдет 1,5 А — ток «полного накала».
Гальванический элемент теперь питает их током одновременно, следовательно, из него вытекают сразу оба эти тока. То есть общий ток из источника напряжения будет равен 1,5 А + 1,5 А = 3,0 А.
В чем же отличие этой схемы от схемы, когда те же самые лампочки были включены последовательно? Только в накале лампочек, то есть только в токе.
Тогда ток был 0,75 А, а теперь он стал сразу 3 А.
Получается, если сравнить с первоначальной схемой, то при последовательном соединении лампочек (схема 2) току сопротивления оказывалось больше (отчего он уменьшался, и лампочки теряли светимость), а параллельное подключение оказывает МЕНЬШЕ сопротивления, хотя сопротивление лампочек осталось неизменным. В чем тут дело?
А дело в том, что мы забываем одну интересную истину, что всякая палка о двух концах.
Когда мы говорим, что резистор сопротивляется току, то как бы забываем, что он ток все-таки проводит. И теперь, когда подключили лампочки параллельно, увеличилось суммарное для них свойство проводить ток, а не сопротивляться ему. Ну и, соответственно, некую величину G
, по аналогии с сопротивлением R
и следовало бы назвать проводимостью. И должна она в параллельном соединении проводников суммироваться.
Ну и вот она
Закон Ома тогда будет выглядеть
I
=
U
*
G
&
И в случае параллельного соединения ток I будет равен U*(G+G) = 2*U*G, что мы как раз и наблюдаем.
Замена элементов цепи общим эквивалентным элементом
Инженерам часто приходится узнавать токи и напряжения во всех частях схем. А реальные электрические схемы бывают достаточно сложными и разветвленными и могут содержать множество элементов, активно потребляющих электроэнергию и соединенных друг с другом в совершенно разных сочетаниях. Это называется расчет электрических схем. Он делается при проектировании энергоснабжения домов, квартир, организаций. При этом очень важно, какие токи и напряжения будут действовать в электрической цепи, хотя бы для того, чтобы выбрать подходящие им сечения проводов, нагрузки на всю сеть или ее части, и так далее. А уж насколько сложны бывают электронные схемы, содержащие тысячи, а то и миллионы элементов, думаю, понятно всякому.
Самое первое что, напрашивается — это воспользоваться знанием того, как ведут себя токи напряжения в таких простейших соединениях сети, как последовательное и параллельное. Делают так: вместо найденного в сети последовательного соединения двух или более активных устройств-потребителей (как наши лампочки) нарисовать один, но чтобы его сопротивление было таким же, как у обоих. Тогда картина токов и напряжений в остальной части схемы не изменится. Аналогично и с параллельным соединением: вместо них нарисовать такой элемент, ПРОВОДИМОСТЬ которого была бы такой же, как у обоих.
Теперь если схему перерисовать, заменив последовательные и параллельные соединения одним элементом, то получим схему, которая называется «схемой эквивалентного замещения».
Такую процедуру можно продолжать до тех пор, пока у нас не останется наипростейшая — которой мы в самом начале иллюстрировали закон Ома. Только вместо лампочки будет стоять одно сопротивление, которое и называют эквивалентным сопротивлением нагрузки.
Это первая задача. Она дает нам возможность по закону Ома рассчитать общий ток во всей сети, или общий ток нагрузки.
Вот это и есть полный расчет электрической сети.
Примеры
Пусть цепь содержит 9 активных сопротивлений. Это могут быть лампочки или что-то другое.
На ее входные клеммы подано напряжение в 60 В.
Значения сопротивлений для всех элементов следующие:
Найти все неизвестные токи и напряжения.
Надо пойти по пути поиска параллельных и последовательных участков сети, рассчитывать эквивалентные им сопротивления и постепенно упрощать схему. Видим, что R 3 , R 9 и R 6 соединены последовательно. Тогда им эквивалентное сопротивление R э 3, 6, 9 будет равно их сумме R э 3, 6, 9 = 1 + 4 + 1 Ом = 6 Ом.
Теперь заменяем параллельный кусочек из сопротивлений R 8 и R э 3, 6, 9, получая R э 8, 3, 6, 9 . Только при параллельном соединении проводников, складывать придется проводимости.
Проводимость измеряется в единицах, называемых сименсами, обратных омам.
Если перевернуть дробь, получим сопротивление R э 8, 3, 6, 9 = 2 Ом
Совершенно так же, как в первом случае, объединяем сопротивления R 2 , R э 8, 3, 6, 9 и R 5, включенные последовательно, получая R э 2, 8, 3, 6, 9, 5 = 1 + 2 + 1 = 4 Ом.
Осталось два шага: получить сопротивление, эквивалентное двум резисторам параллельного соединения проводников R 7 и R э 2, 8, 3, 6, 9, 5.
Оно равно R э 7, 2, 8, 3, 6, 9, 5 = 1/(1/4+1/4)=1/(2/4)=4/2 = 2 Ом
На последнем шаге просуммируем все последовательно включенные сопротивления R 1 , R э 7, 2, 8, 3, 6, 9, 5 и R 4 и получим сопротивление, эквивалентное сопротивлению всей цепи R э и равное сумме этих трех сопротивлений
R э = R 1 + R э 7, 2, 8, 3, 6, 9, 5 + R4 = 1 + 2 + 1 = 4 Ом
Ну и вспомним, в честь кого назвали единицу сопротивлений, написанную нами в последней из этих формул, и вычислим по его закону общий ток во всей цепи I
Теперь, двигаясь в обратном направлении, в сторону все большего усложнения сети, можно получать по закону Ома токи и напряжения во всех цепочках нашей достаточно простой схемы.
Так обычно и рассчитывают схемы электроснабжения квартир, которые состоят из параллельных и последовательных участков. Что, как правило, не годится в электронике, потому что там многое по-другому устроено, и все гораздо замысловатее. И вот такую, например, схему, когда не поймешь, параллельное это соединение проводников или последовательное, рассчитывают по законам Кирхгофа.
Одним из китов, на котором держатся многие понятия в электронике, является понятие последовательного и параллельного подключения проводников. Знать основные отличия указанных типов подключения просто необходимо. Без этого нельзя понять и прочитать ни одной схемы.
Основные принципы
Электрический ток движется по проводнику от источника к потребителю (нагрузке). Чаще всего в качестве проводника выбирается медный кабель. Связано это с требованием, которое предъявляется к проводнику: он должен легко высвобождать электроны.
Независимо от способа подключения, электрический ток двигается от плюса к минусу. Именно в этом направлении убывает потенциал. При этом стоит помнить, что провод, по котору идет ток, также обладает сопротивлением. Но его значение очень мало. Именно поэтому им пренебрегают. Сопротивление проводника принимают равным нулю. В том случае, если проводник обладает сопротивлением, его принято называть резистором.
Параллельное подключение
В данном случае элементы, входящие в цепь, объединены между собой двумя узлами. С другими узлами у них связей нет. Участки цепи с таким подключением принято называть ветвями. Схема параллельного подключения представлена на рисунке ниже.
Если говорить более понятным языком, то в данном случае все проводники одним концом соединены в одном узле, а вторым — во втором. Это приводит к тому, что электрический ток разделяется на все элементы. Благодаря этому увеличивается проводимость всей цепи.
При подключении проводников в цепь данным способом напряжение каждого из них будет одинаково. А вот сила тока всей цепи будет определяться как сумма токов, протекающих по всем элементам. С учетом закона Ома путем нехитрых математических расчетов получается интересная закономерность: величина, обратная общему сопротивлению всей цепи, определяется как сумма величин, обратных сопротивлениям каждого отдельного элемента. При этом учитываются только элементы, подключенные параллельно.
Последовательное подключение
В данном случае все элементы цепи соединены таким образом, что они не образуют ни одного узла. При данном способе подключения имеется один существенный недостаток. Он заключается в том, что при выходе из строя одного из проводников все последующие элементы работать не смогут. Ярким примером такой ситуации является обычная гирлянда. Если в ней перегорает одна из лампочек, то вся гирлянда перестает работать.
Последовательное подключение элементов отличается тем, что сила тока во всех проводниках равна. Что касается напряжения цепи, то оно равно сумме напряжения отдельных элементов.
В данной схеме проводники включаются в цепь поочередно. А это значит, что сопротивление всей цепи будет складываться из отдельных сопротивлений, характерных для каждого элемента. То есть общее сопротивление цепи равно сумме сопротивлений всех проводников. Эту же зависимость можно вывести и математическим способом, используя закон Ома.
Смешанные схемы
Бывают ситуации, когда на одной схеме можно увидеть одновременно последовательное и параллельное подключение элементов. В таком случае говорят о смешанном соединении. Расчет подобных схем проводится отдельно для каждой из группы проводников.
Так, чтобы определить общее сопротивление, необходимо сложить сопротивление элементов, подключенных параллельно, и сопротивление элементов с последовательным подключением. При этом последовательное подключение является доминантным. То есть его рассчитывают в первую очередь. И только после этого определяют сопротивление элементов с параллельным подключением.
Подключение светодиодов
Зная основы двух типов подключения элементов в цепи, можно понять принцип создания схем различных электроприборов. Рассмотрим пример. во многом зависит от напряжения источника тока.
При небольшом напряжении сети (до 5 В) светодиоды подключают последовательно. Снизить уровень электромагнитных помех в данном случае поможет конденсатор проходного типа и линейные резисторы. Проводимость светодиодов увеличивают за счет использования системных модуляторов.
При напряжении сети 12 В может использоваться и последовательное, и параллельное подключение сети. В случае последовательного подключения используют импульсные блоки питания. Если собирается цепь из трех светодиодов, то можно обойтись без усилителя. Но если цепь будет включать большее количество элементов, то усилитель необходим.
Во втором случае, то есть при параллельном подключении, необходимо использование двух открытых резисторов и усилителя (с пропускной способностью выше 3 А). Причем первый резистор устанавливается перед усилителем, а второй — после.
При высоком напряжении сети (220 В) прибегают к последовательному подключению. При этом дополнительно используют операционные усилители и понижающие блоки питания.
Знаете ли Вы,
что такое мысленный эксперимент, gedanken experiment?
Это несуществующая практика, потусторонний опыт, воображение того, чего нет на самом деле. Мысленные эксперименты подобны снам наяву. Они рождают чудовищ. В отличие от физического эксперимента, который является опытной проверкой гипотез, «мысленный эксперимент» фокуснически подменяет экспериментальную проверку желаемыми, не проверенными на практике выводами, манипулируя логикообразными построениями, реально нарушающими саму логику путем использования недоказанных посылок в качестве доказанных, то есть путем подмены. Таким образом, основной задачей заявителей «мысленных экспериментов» является обман слушателя или читателя путем замены настоящего физического эксперимента его «куклой» — фиктивными рассуждениями под честное слово без самой физической проверки.
Заполнение физики воображаемыми, «мысленными экспериментами» привело к возникновению абсурдной сюрреалистической, спутанно-запутанной картины мира. Настоящий исследователь должен отличать такие «фантики» от настоящих ценностей.
Релятивисты и позитивисты утверждают, что «мысленный эксперимент» весьма полезный интрумент для проверки теорий (также возникающих в нашем уме) на непротиворечивость. В этом они обманывают людей, так как любая проверка может осуществляться только независимым от объекта проверки источником. Сам заявитель гипотезы не может быть проверкой своего же заявления, так как причина самого этого заявления есть отсутствие видимых для заявителя противоречий в заявлении.
Это мы видим на примере СТО и ОТО, превратившихся в своеобразный вид религии, управляющей наукой и общественным мнением. Никакое количество фактов, противоречащих им, не может преодолеть формулу Эйнштейна: «Если факт не соответствует теории — измените факт» (В другом варианте » — Факт не соответствует теории? — Тем хуже для факта»).
Максимально, на что может претендовать «мысленный эксперимент» — это только на внутреннюю непротиворечивость гипотезы в рамках собственной, часто отнюдь не истинной логики заявителя. Соответсвие практике это не проверяет. Настоящая проверка может состояться только в действительном физическом эксперименте.
Эксперимент на то и эксперимент, что он есть не изощрение мысли, а проверка мысли. Непротиворечивая внутри себя мысль не может сама себя проверить. Это доказано Куртом Гёделем.
10.3: Последовательные и параллельные резисторы
Цели обучения
К концу раздела вы сможете:
- Определите термин эквивалентное сопротивление
- Рассчитайте эквивалентное сопротивление резисторов, включенных последовательно
- Вычислить эквивалентное сопротивление резисторов, включенных параллельно
В книге «Ток и сопротивление» мы описали термин «сопротивление» и объяснили основную конструкцию резистора.По сути, резистор ограничивает поток заряда в цепи и представляет собой омическое устройство, где \ (V = IR \). В большинстве схем имеется более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, подаваемый батареей, зависит от эквивалентного сопротивления цепи.
Эквивалентное сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения. Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение (Рисунок \ (\ PageIndex {1} \)).В последовательной схеме выходной ток первого резистора течет на вход второго резистора; следовательно, ток в каждом резисторе одинаков. В параллельной схеме все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе. В случае параллельной конфигурации каждый резистор имеет одинаковое падение потенциала на нем, и токи через каждый резистор могут быть разными в зависимости от резистора.Сумма отдельных токов равна току, протекающему по параллельным соединениям.
Рисунок \ (\ PageIndex {1} \): (a) При последовательном соединении резисторов ток одинаков на каждом резисторе. (b) При параллельном соединении резисторов напряжение на каждом резисторе одинаковое. Резисторы
серии
Считается, что резисторы
включены последовательно, когда ток течет через резисторы последовательно. Рассмотрим рисунок \ (\ PageIndex {2} \), на котором показаны три последовательно включенных резистора с приложенным напряжением, равным \ (V_ {ab} \).Поскольку заряды проходят только по одному пути, ток через каждый резистор одинаков. Эквивалентное сопротивление набора резисторов при последовательном соединении равно алгебраической сумме отдельных сопротивлений.
Рисунок \ (\ PageIndex {2} \): (a) Три резистора, подключенные последовательно к источнику напряжения. (b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.
На рисунке \ (\ PageIndex {2} \) ток, идущий от источника напряжения, протекает через каждый резистор, поэтому ток через каждый резистор одинаков.Ток в цепи зависит от напряжения, подаваемого источником напряжения, и сопротивления резисторов. Для каждого резистора происходит падение потенциала, равное потере электрической потенциальной энергии, когда ток проходит через каждый резистор. Согласно закону Ома, падение потенциала \ (V \) на резисторе при протекании через него тока рассчитывается по формуле \ (V = IR \), где \ (I \) — ток в амперах (\ (A \)), а \ (R \) — сопротивление в Ом \ ((\ Omega) \).N V_i = 0. \]
Это уравнение часто называют законом петли Кирхгофа, который мы рассмотрим более подробно позже в этой главе. Для рисунка \ (\ PageIndex {2} \) сумма падения потенциала каждого резистора и напряжения, подаваемого источником напряжения, должна равняться нулю:
\ [\ begin {align *} V — V_1 — V_2 — V_3 & = 0, \\ [4pt] V & = V_1 + V_2 + V_3, \\ [4pt] & = IR_1 + IR_2 + IR_3, \ end { выровнять *} \]
Решение для \ (I \)
\ [\ begin {align *} I & = \ frac {V} {R_1 + R_2 + R_3} \\ [4pt] & = \ frac {V} {R_ {S}}.\ end {align *} \]
Поскольку ток через каждый компонент одинаков, равенство можно упростить до эквивалентного сопротивления (\ (R_ {S} \)), которое представляет собой просто сумму сопротивлений отдельных резисторов. N R_i.\ label {серия эквивалентных сопротивлений} \]
Одним из результатов включения компонентов в последовательную цепь является то, что если что-то происходит с одним компонентом, это влияет на все остальные компоненты. Например, если несколько ламп соединены последовательно и одна лампа перегорела, все остальные лампы погаснут.
Пример \ (\ PageIndex {1} \): эквивалентное сопротивление, ток и мощность в последовательной цепи
Батарея с напряжением на клеммах 9 В подключена к цепи, состоящей из четырех последовательно соединенных резисторов \ (20 \, \ Omega \) и одного \ (10 \, \ Omega \) (Рисунок \ (\ PageIndex {3 } \)).Предположим, что батарея имеет незначительное внутреннее сопротивление.
- Рассчитайте эквивалентное сопротивление цепи.
- Рассчитайте ток через каждый резистор.
- Рассчитайте падение потенциала на каждом резисторе.
- Определите общую мощность, рассеиваемую резисторами, и мощность, потребляемую батареей.
Рисунок \ (\ PageIndex {3} \): Простая последовательная схема с пятью резисторами.
Стратегия
В последовательной цепи эквивалентное сопротивление представляет собой алгебраическую сумму сопротивлений.2R \), а общая мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором. Мощность, подаваемая батареей, можно найти с помощью \ (P = I \ epsilon \).
Решение
- Эквивалентное сопротивление — это алгебраическая сумма сопротивлений (уравнение \ ref {ряд эквивалентных сопротивлений}): \ [\ begin {align *} R_ {S} & = R_1 + R_2 + R_3 + R_4 + R_5 \\ [4pt ] & = 20 \, \ Omega + 20 \, \ Omega + 20 \, \ Omega + 20 \, \ Omega + 10 \, \ Omega = 90 \, \ Omega.2 (10 \, \ Omega) = 0,1 \, W, \ nonumber \] \ [P_ {рассеивается} = 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,1 \, W = 0,9 \, W, \ nonumber \] \ [P_ {источник} = I \ epsilon = (0,1 \, A) (9 \, V) = 0,9 \, W. \ nonumber \]
Значение
Есть несколько причин, по которым мы будем использовать несколько резисторов вместо одного резистора с сопротивлением, равным эквивалентному сопротивлению цепи. Возможно, резистора необходимого размера нет в наличии, или нам нужно отводить выделяемое тепло, или мы хотим минимизировать стоимость резисторов.Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть значительной.
Упражнение \ (\ PageIndex {1} \)
Некоторые гирлянды миниатюрных праздничных огней закорачиваются при перегорании лампочки. Устройство, вызывающее короткое замыкание, называется шунтом, который позволяет току течь по разомкнутой цепи. «Короткое замыкание» похоже на протягивание куска проволоки через компонент. Луковицы обычно сгруппированы в серии по девять луковиц.Если перегорает слишком много лампочек, в конце концов открываются шунты. Что вызывает это?
- Ответ
Эквивалентное сопротивление девяти последовательно соединенных лампочек составляет 9 R . Ток равен \ (I = V / 9 \, R \). Если одна лампочка перегорит, эквивалентное сопротивление составит 8 R , и напряжение не изменится, но ток возрастет \ ((I = V / 8 \, R \). Чем больше лампочек перегорят, ток станет равным. В конце концов, ток становится слишком большим, что приводит к перегоранию шунта.№ Р_и. \]
- Одинаковый ток течет через каждый резистор последовательно.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его. Общее падение потенциала на последовательной конфигурации резисторов равно сумме падений потенциала на каждом резисторе.
Параллельные резисторы
На рисунке \ (\ PageIndex {4} \) показаны резисторы, включенные параллельно, подключенные к источнику напряжения. Резисторы включены параллельно, когда один конец всех резисторов соединен непрерывным проводом с незначительным сопротивлением, а другой конец всех резисторов также соединен друг с другом непрерывным проводом с незначительным сопротивлением.Падение потенциала на каждом резисторе одинаковое. Ток через каждый резистор можно найти с помощью закона Ома \ (I = V / R \), где напряжение на каждом резисторе постоянно. Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании.
Рисунок \ (\ PageIndex {4} \): Два резистора, подключенных параллельно источнику напряжения.(b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.
Ток, протекающий от источника напряжения на рисунке \ (\ PageIndex {4} \), зависит от напряжения, подаваемого источником напряжения, и эквивалентного сопротивления цепи. В этом случае ток течет от источника напряжения и попадает в соединение или узел, где цепь разделяется, протекая через резисторы \ (R_1 \) и \ (R_2 \). По мере того, как заряды проходят от батареи, некоторые проходят через резистор \ (R_1 \), а некоторые — через резистор \ (R_2 \).Сумма токов, текущих в переход, должна быть равна сумме токов, текущих из перехода:
\ [\ sum I_ {in} = \ sum I_ {out}. {- 1}.{-1}. \ label {10.3} \]
Это соотношение приводит к эквивалентному сопротивлению \ (R_ {P} \), которое меньше наименьшего из отдельных сопротивлений. Когда резисторы соединены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.
Пример \ (\ PageIndex {2} \): Анализ параллельной цепи
Три резистора \ (R_1 = 1,00 \, \ Omega \), \ (R_2 = 2,00 \, \ Omega \) и \ (R_3 = 2,00 \, \ Omega \) подключены параллельно.Параллельное соединение подключается к источнику напряжения \ (V = 3,00 \, V \).
- Какое эквивалентное сопротивление?
- Найдите ток, подаваемый источником в параллельную цепь.
- Рассчитайте токи в каждом резисторе и покажите, что в сумме они равны выходному току источника.
- Рассчитайте мощность, рассеиваемую каждым резистором.
- Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия
(a) Общее сопротивление для параллельной комбинации резисторов определяется с помощью уравнения \ ref {10.3}. (Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)
(b) Ток, подаваемый источником, можно найти из закона Ома, заменив \ (R_ {P} \) на полное сопротивление \ (I = \ frac {V} {R_ {P}} \).
(c) Отдельные токи легко вычислить по закону Ома \ (\ left (I_i = \ frac {V_i} {R_i} \ right) \), поскольку каждый резистор получает полное напряжение.{-1} = 0.50 \, \ Omega. \ Nonumber \] Общее сопротивление с правильным количеством значащих цифр равно \ (R_ {eq} = 0.50 \, \ Omega \). Как и предполагалось, \ (R_ {P} \) меньше наименьшего индивидуального сопротивления.
- Полный ток можно найти из закона Ома, заменив полное сопротивление \ (R_ {P} \). Это дает \ [I = \ frac {V} {R_ {P}} = \ frac {3.00 \, V} {0.50 \, \ Omega} = 6.00 \, A. \ nonumber \] Текущий I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
- Отдельные токи легко вычислить по закону Ома, так как каждый резистор получает полное напряжение. Таким образом, \ [I_1 = \ frac {V} {R_1} = \ frac {3.00 \, V} {1.00 \, \ Omega} = 3.00 \, A. \ nonumber \] Аналогично, \ [I_2 = \ frac {V } {R_2} = \ frac {3.00 \, V} {2.00 \, \ Omega} = 1.50 \, A \ nonumber \] и \ [I_3 = \ frac {V} {R_3} = \ frac {3.00 \, V } {2.00 \, \ Omega} = 1.50 \, A. \ nonumber \] Общий ток — это сумма отдельных токов: \ [I_1 + I_2 + I_3 = 6.2} {2.00 \, \ Omega} = 4.50 \, W. \ nonumber \]
- Общую мощность также можно рассчитать несколькими способами. Выбор \ (P = IV \) и ввод общей текущей доходности \ [P = IV = (6.00 \, A) (3.00 \, V) = 18.00 \, W. \ nonumber \]
Значение
Общая мощность, рассеиваемая резисторами, также 18,00 Вт:
\ [P_1 + P_2 + P_3 = 9,00 \, W + 4,50 \, W + 4,50 \, W = 18,00 \, W. \ nonumber \]
Обратите внимание, что общая мощность, рассеиваемая резисторами, равна мощности, подаваемой от источника.
Упражнение \ (\ PageIndex {2A} \)
Рассмотрим одну и ту же разность потенциалов \ ((V = 3,00 \, V) \), приложенную к одним и тем же трем последовательно включенным резисторам. Будет ли эквивалентное сопротивление последовательной цепи больше, меньше или равно трем резисторам, включенным параллельно? Будет ли ток в последовательной цепи выше, ниже или равен току, обеспечиваемому тем же напряжением, приложенным к параллельной цепи? Как мощность, рассеиваемая последовательно подключенными резисторами, будет сравниваться с мощностью, рассеиваемой параллельно резисторами?
- Решение
Эквивалент последовательной схемы будет \ (R_ {eq} = 1.00 \, \ Omega + 2.00 \, \ Omega + 2.00 \, \ Omega = 5.00 \, \ Omega \), что выше эквивалентного сопротивления параллельной цепи \ (R_ {eq} = 0.50 \, \ Omega \ ). Эквивалентный резистор любого количества резисторов всегда выше, чем эквивалентное сопротивление тех же резисторов, соединенных параллельно. Ток через последовательную цепь будет \ (I = \ frac {3.00 \, V} {5.00 \, \ Omega} = 0.60 \, A \), что меньше суммы токов, проходящих через каждый резистор в параллельная цепь, \ (I = 6.00 \, А \). Это неудивительно, поскольку эквивалентное сопротивление последовательной цепи выше. Ток при последовательном соединении любого количества резисторов всегда будет ниже, чем ток при параллельном соединении тех же резисторов, поскольку эквивалентное сопротивление последовательной цепи будет выше, чем параллельной цепи. Мощность, рассеиваемая последовательно включенными резисторами, будет равна \ (P = 1,800 \, Вт \), что ниже мощности, рассеиваемой в параллельной цепи \ (P = 18.00 \, Вт \).
Упражнение \ (\ PageIndex {2B} \)
Как бы вы использовали реку и два водопада для моделирования параллельной конфигурации двух резисторов? Как разрушается эта аналогия?
- Решение
Река, текущая в горизонтальном направлении с постоянной скоростью, разделяется на две части и течет через два водопада. Молекулы воды аналогичны электронам в параллельных цепях. Количество молекул воды, которые текут в реке и падает, должно быть равно количеству молекул, которые текут над каждым водопадом, точно так же, как сумма тока через каждый резистор должна быть равна току, текущему в параллельном контуре.Молекулы воды в реке обладают энергией благодаря своему движению и высоте. Потенциальная энергия молекул воды в реке постоянна из-за их одинаковой высоты. Это аналогично постоянному изменению напряжения в параллельной цепи. Напряжение — это потенциальная энергия на каждом резисторе.
При рассмотрении энергии аналогия быстро разрушается. В водопаде потенциальная энергия преобразуется в кинетическую энергию молекул воды. В случае прохождения электронов через резистор падение потенциала преобразуется в тепло и свет, а не в кинетическую энергию электронов.
Суммируем основные характеристики резисторов параллельно:
- Эквивалентное сопротивление находится по формуле \ ref {10.3} и меньше любого отдельного сопротивления в комбинации.
- Падение потенциала на каждом параллельном резисторе одинаковое.
- Параллельные резисторы не получают суммарный ток каждый; они делят это. Ток, поступающий в параллельную комбинацию резисторов, равен сумме токов, протекающих через каждый резистор, включенный параллельно.
В этой главе мы представили эквивалентное сопротивление резисторов, соединенных последовательно, и резисторов, соединенных параллельно. Как вы помните, из раздела «Емкость» мы ввели эквивалентную емкость конденсаторов, соединенных последовательно и параллельно. Цепи часто содержат как конденсаторы, так и резисторы. В таблице \ (\ PageIndex {1} \) приведены уравнения, используемые для эквивалентного сопротивления и эквивалентной емкости для последовательных и параллельных соединений.
Таблица \ (\ PageIndex {1} \): Сводка по эквивалентному сопротивлению и емкости в последовательной и параллельной комбинациях Комбинация серий Параллельная комбинация Эквивалентная емкость \ [\ frac {1} {C_ {S}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3} +.N R_i \ nonumber \] \ [\ frac {1} {R_ {P}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} +. . . \ nonumber \] Сочетания последовательного и параллельного
Более сложные соединения резисторов часто представляют собой просто комбинации последовательного и параллельного соединения. Такие комбинации обычны, особенно если учитывать сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного соединения можно свести к одному эквивалентному сопротивлению, используя метод, показанный на рисунке \ (\ PageIndex {5} \).Различные части могут быть идентифицированы как последовательные или параллельные соединения, уменьшенные до их эквивалентных сопротивлений, а затем уменьшенные до тех пор, пока не останется единственное эквивалентное сопротивление. Процесс занимает больше времени, чем труден. Здесь мы отмечаем эквивалентное сопротивление как \ (R_ {eq} \).
Рисунок \ (\ PageIndex {5} \): (а) Исходная схема из четырех резисторов. (b) Шаг 1: резисторы \ (R_3 \) и \ (R_4 \) включены последовательно, и эквивалентное сопротивление равно \ (R_ {34} = 10 \, \ Omega \) (c) Шаг 2: сокращенная схема показывает, что резисторы \ (R_2 \) и \ (R_ {34} \) включены параллельно, с эквивалентным сопротивлением \ (R_ {234} = 5 \, \ Omega \).(d) Шаг 3: приведенная схема показывает, что \ (R_1 \) и \ (R_ {234} \) включены последовательно с эквивалентным сопротивлением \ (R_ {1234} = 12 \, \ Omega \), которое является эквивалентное сопротивление \ (R_ {eq} \). (e) Уменьшенная схема с источником напряжения \ (V = 24 \, V \) с эквивалентным сопротивлением \ (R_ {eq} = 12 \, \ Omega \). Это приводит к току \ (I = 2 \, A \) от источника напряжения.
Обратите внимание, что резисторы \ (R_3 \) и \ (R_4 \) включены последовательно. Их можно объединить в одно эквивалентное сопротивление.Один из методов отслеживания процесса — включить резисторы в качестве индексов. {- 1} = 5 \, \ Omega.\ nonumber \]
Этот шаг процесса сокращает схему до двух резисторов, показанных на рисунке \ (\ PageIndex {5d} \). Здесь схема сводится к двум резисторам, которые в данном случае включены последовательно. Эти два резистора можно уменьшить до эквивалентного сопротивления, которое является эквивалентным сопротивлением цепи:
\ [R_ {eq} = R_ {1234} = R_1 + R_ {234} = 7 \, \ Omega + 5 \ Omega = 12 \, \ Omega. \ nonumber \]
Основная цель этого анализа схемы достигнута, и теперь схема сводится к одному резистору и одному источнику напряжения.
Теперь мы можем проанализировать схему. Ток, обеспечиваемый источником напряжения, равен \ (I = \ frac {V} {R_ {eq}} = \ frac {24 \, V} {12 \, \ Omega} = 2 \, A \). Этот ток проходит через резистор \ (R_1 \) и обозначается как \ (I_1 \). Падение потенциала на \ (R_1 \) можно найти с помощью закона Ома:
\ [V_1 = I_1R_1 = (2 \, A) (7 \, \ Omega) = 14 \, V. \ nonumber \]
Глядя на рисунок \ (\ PageIndex {5c} \), это оставляет \ (24 \, V — 14 \, V = 10 \, V \) отбрасывать через параллельную комбинацию \ (R_2 \) и \ ( R_ {34} \).Ток через \ (R_2 \) можно найти с помощью закона Ома:
\ [I_2 = \ frac {V_2} {R_2} = \ frac {10 \, V} {10 \, \ Omega} = 1 \, A. \ nonumber \]
Резисторы \ (R_3 \) и \ (R_4 \) включены последовательно, поэтому токи \ (I_3 \) и \ (I_4 \) равны
.
\ [I_3 = I_4 = I — I_2 = 2 \, A — 1 \, A = 1 \, A. \ nonumber \]
Используя закон Ома, мы можем найти падение потенциала на двух последних резисторах. Потенциальные капли равны \ (V_3 = I_3R_3 = 6 \, V \) и \ (V_4 = I_4R_4 = 4 \, V \).2 (4 \, \ Omega) = 4 \, W, \\ [4pt] P_ {рассеивается} & = P_1 + P_2 + P_3 + P_4 = 48 \, W. \ end {align *} \]
Полная энергия постоянна в любом процессе. Следовательно, мощность, подаваемая источником напряжения, составляет
\ [\ begin {align *} P_s & = IV \\ [4pt] & = (2 \, A) (24 \, V) = 48 \, W \ end {align *} \]
Анализ мощности, подаваемой в схему, и мощности, рассеиваемой резисторами, является хорошей проверкой достоверности анализа; они должны быть равны.
Пример \ (\ PageIndex {3} \): объединение последовательных и параллельных цепей
На рисунке \ (\ PageIndex {6} \) показаны резисторы, подключенные последовательно и параллельно.Мы можем рассматривать \ (R_1 \) как сопротивление проводов, ведущих к \ (R_2 \) и \ (R_3 \).
- Найдите эквивалентное сопротивление цепи.
- Какое падение потенциала \ (V_1 \) на резисторе \ (R_1 \)?
- Найдите ток \ (I_2 \) через резистор \ (R_2 \).
- Какую мощность рассеивает \ (R_2 \)?
Рисунок \ (\ PageIndex {6} \): Эти три резистора подключены к источнику напряжения так, чтобы \ (R_2 \) и \ (R_3 \) были параллельны друг другу, и эта комбинация была последовательно с \ (R_1 \).
Стратегия
(a) Чтобы найти эквивалентное сопротивление, сначала найдите эквивалентное сопротивление параллельного соединения \ (R_2 \) и \ (R_3 \). Затем используйте этот результат, чтобы найти эквивалентное сопротивление последовательного соединения с \ (R_1 \).
(b) Ток через \ (R_1 \) можно найти с помощью закона Ома и приложенного напряжения. Ток через \ (R_1 \) равен току от батареи. Падение потенциала \ (V_1 \) на резисторе \ (R_1 \) (которое представляет собой сопротивление в соединительных проводах) можно найти с помощью закона Ома.{-1} = 5.10 \, \ Omega. \ Nonumber \] Общее сопротивление этой комбинации занимает промежуточное положение между значениями чистой серии и чисто параллельной (\ (20.0 \, \ Omega \) и \ (0.804 \, \ Omega \) ), соответственно).
- Ток через \ (R_1 \) равен току, обеспечиваемому батареей: \ [I_1 = I = \ frac {V} {R_ {eq}} = \ frac {12.0 \, V} {5.10 \, \ Omega} = 2.35 \, A. \ nonumber \] Напряжение на \ (R_1 \) равно \ [V_1 = I_1R_1 = (2.35 \, A) (1 \, \ Omega) = 2.35 \, V. \ nonumber \] Напряжение, приложенное к \ (R_2 \) и \ (R_3 \), меньше напряжения, подаваемого батареей, на величину \ (V_1 \).Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных \ (R_2 \) и \ (R_3 \).
- Чтобы найти ток через \ (R_2 \), мы должны сначала найти приложенное к нему напряжение. Напряжение на двух параллельных резисторах одинаково: \ [V_2 = V_3 = V — V_1 = 12.0 \, V — 2.35 \, V = 9.65 \, V. \ nonumber \] Теперь мы можем найти ток \ (I_2 \) через сопротивление \ (R_2 \) по закону Ома: \ [I_2 = \ frac {V_2} {R_2} = \ frac {9.65 \, V} {6.00 \, \ Omega} = 1.2 (6.00 \, \ Omega) = 15.5 \, W. \ nonumber \]
Значение
Анализ сложных схем часто можно упростить, сведя схему к источнику напряжения и эквивалентному сопротивлению. Даже если вся схема не может быть сведена к одному источнику напряжения и одному эквивалентному сопротивлению, части схемы могут быть уменьшены, что значительно упрощает анализ.
Упражнение \ (\ PageIndex {3} \)
Учитывайте электрические цепи в вашем доме.Приведите хотя бы два примера схем, в которых для эффективной работы необходимо использовать комбинацию последовательных и параллельных схем.
- Решение
Все цепи верхнего освещения параллельны и подключены к основному источнику питания, поэтому при перегорании одной лампочки все верхнее освещение не гаснет. У каждого верхнего света будет как минимум один переключатель, включенный последовательно с источником света, так что вы можете включать и выключать его.
В холодильнике есть компрессор и лампа, которая загорается при открытии двери.Обычно для подключения холодильника к стене используется только один шнур. Цепь, содержащая компрессор, и цепь, содержащая цепь освещения, параллельны, но есть переключатель, включенный последовательно со светом. Термостат управляет переключателем, включенным последовательно с компрессором, чтобы контролировать температуру холодильника.
Практическое применение
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным и проявляться из-за тепла, выделяемого в шнуре.
Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
Что происходит в этих сильноточных ситуациях, показано на рисунке \ (\ PageIndex {7} \). Устройство, обозначенное символом \ (R_3 \), имеет очень низкое сопротивление, поэтому при его включении течет большой ток. Этот увеличенный ток вызывает большее падение IR в проводах, обозначенных \ (R_1 \), уменьшая напряжение на лампочке (которое составляет \ (R_2 \)), которое затем заметно гаснет.
Рисунок \ (\ PageIndex {7} \): Почему свет тускнеет при включении большого прибора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение IR в проводах и снижает напряжение на свету.
Стратегия решения проблем: последовательные и параллельные резисторы
- Нарисуйте четкую принципиальную схему, пометив все резисторы и источники напряжения. Этот шаг включает список известных значений проблемы, так как они отмечены на вашей принципиальной схеме.
- Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
- Определите, подключены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные. Есть один список для серий и другой для параллельных.
- Проверьте, являются ли ответы разумными и последовательными.
Пример \ (\ PageIndex {4} \): объединение последовательных и параллельных цепей
Два резистора, соединенных последовательно \ ((R_1, \, R_2) \), соединены с двумя резисторами, включенными параллельно \ ((R_3, \, R_4) \).Последовательно-параллельная комбинация подключается к батарее. Каждый резистор имеет сопротивление 10,00 Ом. Провода, соединяющие резисторы и аккумулятор, имеют незначительное сопротивление. Через резистор \ (R_1 \) проходит ток 2,00 А. Какое напряжение подается от источника напряжения?
Стратегия
Используйте шаги предыдущей стратегии решения проблем, чтобы найти решение для этого примера.
Решение
Рисунок \ (\ PageIndex {8} \): Чтобы найти неизвестное напряжение, мы должны сначала найти эквивалентное сопротивление цепи.
- Нарисуйте четкую принципиальную схему (рисунок \ (\ PageIndex {8} \)).
- Неизвестно напряжение аккумулятора. Чтобы определить напряжение, подаваемое батареей, необходимо найти эквивалентное сопротивление.
- В этой схеме мы уже знаем, что резисторы \ (R_1 \) и \ (R_2 \) включены последовательно, а резисторы \ (R_3 \) и \ (R_4 \) включены параллельно. Эквивалентное сопротивление параллельной конфигурации резисторов \ (R_3 \) и \ (R_4 \) последовательно с последовательной конфигурацией резисторов \ (R_1 \) и \ (R_2 \).{-1} = 5,00 \, \ Омега. \ nonumber \] Эта параллельная комбинация включена последовательно с двумя другими резисторами, поэтому эквивалентное сопротивление схемы равно \ (R_ {eq} = R_1 + R_2 + R_ {34} = (25.00 \, \ Omega \). поэтому напряжение, подаваемое батареей, равно \ (V = IR_ {eq} = 2.00 \, A (25.00 \, \ Omega) = 50.00 \, V \).
- Один из способов проверить соответствие ваших результатов — это рассчитать мощность, подаваемую батареей, и мощность, рассеиваемую резисторами. Мощность, обеспечиваемая аккумулятором, равна \ (P_ {batt} = IV = 100.2R_4 \\ [4pt] & = 40.00 \, W + 40.00 \, W + 10.00 \, W + 10.00 \, W = 100. \, W. \ end {align *} \]
Поскольку мощность, рассеиваемая резисторами, равна мощности, выделяемой батареей, наше решение кажется последовательным.
Значение
Если проблема имеет комбинацию последовательного и параллельного соединений, как в этом примере, ее можно уменьшить поэтапно, используя предыдущую стратегию решения проблемы и рассматривая отдельные группы последовательных или параллельных соединений.При нахождении \ (R_ {eq} \) для параллельного соединения необходимо с осторожностью относиться к обратному. Кроме того, единицы и числовые результаты должны быть разумными. Эквивалентное последовательное сопротивление должно быть больше, а эквивалентное параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для тех же устройств, подключенных параллельно, по сравнению с последовательными и т.
Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами.Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Изучение основ последовательного и параллельного сопротивления [Краткое руководство]
Привет, надеюсь, у тебя хорошая жизнь. В этом посте я поделюсь с вами своими знаниями о последовательном и параллельном сопротивлении. Я поделюсь самыми основными моментами, которым я хотел бы, чтобы кто-нибудь научил меня, когда я изучал основы электроники.
При разработке электронной схемы резистор, вероятно, является наиболее важным и часто встречающимся компонентом.Почти все портативные схемы содержат очень сложные комбинации резисторов.
Следовательно, очень полезно иметь набор правил для определения эквивалентных сопротивлений для некоторых общих и общих схем резистивных элементов. И оказалось, что такие простые правила представляют собой комбинации параллельных серий.
Прежде всего, позвольте мне прояснить основную путаницу. Последовательно-параллельные комбинации аналогичны последовательным и параллельным цепям, но состоят только из резисторных элементов. Фактически, большинство моментов, которые вы здесь изучите, также применимы к любой последовательной и параллельной схеме.
Таким образом, последовательные и параллельные цепи являются общими терминами, а последовательно-параллельное сопротивление — это конкретные цепи, в которых используются только резисторы.
Сопротивление серии
Резисторы, независимо от их размеров, подключены таким образом, чтобы через каждый из них протекал одинаковый ток. Эквивалентное сопротивление таких подключенных резисторов известно как последовательное сопротивление.
В последовательно соединенных сопротивлениях / резисторах есть только один путь для прохождения электрического тока. Все резисторы соединены в ряд как звенья цепи.При обрыве одного из звеньев цепи вся цепь становится бесполезной. То же самое и с последовательными резисторами, когда один резистор перегорает, вся цепь перестает работать.
Рисунок: Блок-схема последовательного сопротивления (Программное обеспечение: NI Multisim Educational Edition)
Ток остается неизменным в любом узле в цепи последовательного сопротивления. Практически это можно доказать, используя мультиметр и схему, выполненную на макетной плате. Или просто смоделировав схему (рис. 1) в любом программном обеспечении для моделирования, как я сделал это в NI Multisim.
Как найти полное последовательное сопротивление?
Все резисторы, соединенные последовательно, добавляются для получения эквивалентного последовательного сопротивления. Общая формула приведена ниже:
Чтобы найти эквивалентное последовательное сопротивление, удалите из цепи любой источник напряжения, а затем просуммируйте значения каждого резистора, присутствующего в цепи. Возьмем, к примеру, приведенную выше схему (рисунок: 1).
Сопротивление серии
может быть подключено к источнику тока.Те же шаги выполняются и для текущего источника. Удалите источник тока и просуммируйте значения резисторов. Пример приведен ниже:
Математический расчет:
Схема может иметь любую форму. Но резисторы нужно подключать как звенья цепи. Следующая цепь последовательно соединена.
Вы можете это доказать?
Можете ли вы найти эквивалентное последовательное сопротивление? (Ответ: 378КОм)
Следует помнить, что последовательно соединенные резисторы имеют только один общий узел друг с другом.Это очень важный момент, который нужно понять. Позже в этом посте я поделюсь примером схемы с последовательным и параллельным сочетанием комбинаций.
Тогда это будет немного запутать. Поэтому обратите особое внимание, потому что этот момент поможет нам определить последовательную комбинацию резисторов в сложной цепи.
Параллельное сопротивление
Резисторы, независимо от их размеров, подключены таким образом, чтобы на каждом резисторе было одинаковое напряжение.Эквивалентное сопротивление таких подключенных резисторов известно как параллельное сопротивление.
Или параллельное сопротивление можно определить как резисторы , подключенные параллельно, если узлы на обоих концах резисторов совпадают. Параллельно подключенные резисторы (параллельное сопротивление) имеют разные пути прохождения электрического тока. Величина протекающего тока зависит от номиналов резисторов.
Параллельно включенные резисторы
При параллельном подключении эквивалентное сопротивление всегда меньше, чем у наименьшего отдельного резистора.Например, эквивалентное сопротивление вышеупомянутой цепи всегда будет меньше 1 кОм. И напряжение на каждом резисторе составляет 12 В, поскольку все резисторы подключены к тем же узлам, что и резистор 12 В.
Я говорил о резисторах, включенных параллельно, если узлы на обоих концах резисторов одинаковые. позвольте мне показать общие узлы в приведенной выше схеме.
Как найти полное параллельное сопротивление?
В параллельно соединенных резисторах эквивалентное сопротивление равно сумме обратных величин каждого резистора.Общая формула эквивалентного параллельного сопротивления приведена ниже:
Найдем значение полного сопротивления для указанной выше цепи.
Удалите источник напряжения и затем введите значения резисторов в приведенную выше общую формулу.
Ответ — меньше самого маленького отдельного резистора.
Другой пример:
Подскажите, как эта схема вообще параллельна?
Конечно, это параллельно включенная цепь.
Согласно критерию, резисторы включены параллельно, если узлы на обоих концах резисторов одинаковы.
Форма смутила нас, правда? Но все же это параллельно включенная резистивная цепь. Дело я говорю. Неважно, какой формы может быть схема, вы должны знать базовую концепцию того, как идентифицировать параллельные резисторы в сложной схеме.
Мы можем перерисовать приведенную выше схему в чистом виде, как показано ниже:
Быстрый способ найти эквивалентное параллельное сопротивление
Когда все параллельно включенные резисторы имеют одинаковые значения, эквивалентное параллельное сопротивление можно найти, просто разделив одно и то же значение на общее количество резисторов.Общая формула может быть записана так:
Давайте применим этот быстрый трюк на вышеуказанной схеме.
Было бы хорошо, если бы вы потратили некоторое время, чтобы доказать это, используя общую формулу для параллельного сопротивления. Будет интересно увидеть, что оба метода дадут одинаковый ответ.
Различия между последовательным и параллельным сопротивлением
Я не знаю, сколько разницы между указанными сопротивлениями в целом. Ниже приведены различия, которые я узнал со временем.
1. При последовательном сопротивлении один и тот же ток протекает через каждый резистор, в то время как при параллельном сопротивлении каждый резистор имеет одинаковое напряжение на нем.
2. В последовательном сопротивлении полное напряжение равно падению напряжения на каждом резисторе. См. Следующую схему:
Общее приложенное напряжение составляет 12 В (аккумуляторный источник), что означает, что общая сумма напряжений на каждом резисторе должна быть равна 12 В.
Попробуем решить эту схему вручную.
Резисторы включены последовательно. Общее последовательное эквивалентное сопротивление можно найти, используя общую формулу для последовательного сопротивления.
Используя закон Ома, полный ток можно определить следующим образом:
Мы рассчитали полный ток. Чтобы найти падение напряжения на каждом резисторе, умножьте общий ток на номинал резистора (закон Ома).
Мы получили те же значения, что и при моделировании Multisim. Суммирование всех рассчитанных напряжений закончится на 12 В.Вы можете доказать это, добавив их самостоятельно с помощью калькулятора.
3. При параллельном сопротивлении полный ток равен сумме токов, протекающих через каждый резистор.
Общий ток (22,0 мА) равен сумме токов, протекающих от каждого резистора. Вы можете доказать это, сложив их вместе с помощью калькулятора. Не путайте с отрицательным знаком. Игнорируй это.
4. В последовательном сопротивлении, если один резистор не работает должным образом, остальная часть цепи также не работает.Параллельно выход из строя одного резистора не влияет на всю схему.
5. Падение напряжения в последовательном сопротивлении пропорционально размеру резистора. В то время как при параллельном подключении количество тока, протекающего через каждый резистор, зависит от размера резистора. Увеличение размера резистора увеличивает падение напряжения, а также ток.
Зачем на самом деле нужны эти комбинации?
Есть очень важные применения последовательных и параллельных комбинаций.Прямо сейчас я делюсь тем, что знаю, и буду обновлять по мере того, как узнаю об этом больше.
Я работал над схемой, и мне нужен был резистор 2 кОм, которого у меня не было в то время. Я много искал в своей маленькой лаборатории, но все тщетно. Затем я собрал два резистора 1 кОм, чтобы получился резистор 2 кОм. Я сделал это, поставив последовательно два резистора 1кОм.
Думаю, вы поняли. Последовательность и параллельность могут быть очень полезны, когда у вас нет резистора точного номинала. Это также может быть полезно, если вы разрабатываете схему и вам нужен резистор, которого нет на ближайшем рынке.Вы можете получить желаемое значение резистора, играя с последовательными и параллельными комбинациями резисторов.
Эти комбинации также находят применение в конструкции вольтметра и амперметра соответственно.
Сопротивление серии
используется в качестве ограничителя тока в цепях. Его можно использовать в качестве делителя напряжения для цепи светодиода. Возможно, вы видели, что у каждого светодиода последовательно есть резистор. Задача резистора — ограничить ток, протекающий через светодиод.
Пример
Приведем пример, чтобы еще больше прояснить нашу концепцию последовательного параллельного соединения.Схема в примере имеет смешанные параллельные и последовательные комбинации. Поэтому, пожалуйста, обращайте пристальное внимание и старайтесь решать на каждом этапе.
Я рекомендую захватить с собой блокнот, калькулятор и хорошую ручку. И давай попробуем решить со мной.
Сводка
- Резисторы подключены таким образом, что через каждый резистор протекает одинаковый ток, тогда эквивалентное сопротивление резисторов называется последовательным сопротивлением.
- Последовательный ток остается неизменным независимо от размеров резисторов.А это возможно только тогда, когда резисторы соединены как звенья цепи.
- В параллельно подключенных резисторах напряжение на каждом резисторе остается неизменным, независимо от номинала каждого резистора.
Надеюсь, этот пост был вам полезен. Это то, что я знаю о последовательном и параллельном сопротивлении. И я буду продолжать обновлять этот пост, когда узнаю что-то новое по указанной теме.
Большое спасибо за чтение и хорошей жизни.
Прочие полезные сообщения
Последовательные и параллельные резисторы — Электрические цепи — WJEC — Редакция GCSE Physics (Single Science) — WJEC
Последовательные резисторы
При последовательном соединении резисторов ток через каждый резистор одинаков.Другими словами, ток одинаков во всех точках последовательной цепи.
При последовательном подключении резисторов общее напряжение (или разность потенциалов) на всех резисторах равно сумме напряжений на каждом резисторе.
Другими словами, напряжения в цепи складываются с напряжением источника питания.
Общее сопротивление ряда последовательно подключенных резисторов равно сумме всех отдельных сопротивлений.
В этой схеме действует следующее.
I 1 = I 2 = I 3
V T = V 1 + V 2 + V 3
и R T 67 = R 1 + R 2 + R 3
Последовательное добавление компонентов увеличивает общее сопротивление в цепи.
Параллельное соединение резисторов
При параллельном подключении резисторов ток питания равен сумме токов, протекающих через каждый резистор.Токи в ветвях параллельной цепи складываются с током питания.
Когда резисторы соединены параллельно, они имеют одинаковую разность потенциалов. Любые параллельно включенные компоненты имеют одинаковую разность потенциалов.
Это уравнение используется для расчета общего сопротивления двух параллельно включенных резисторов.
\ [\ frac {1} {R} = \ frac {1} {R} _ {1} + \ frac {1} {R} _ {2} \]
Для расчета общего сопротивления трех резисторов подключенные параллельно, мы добавляем в уравнение третий резистор (и так далее).
\ [\ frac {1} {R} = \ frac {1} {R} _ {1} + \ frac {1} {R} _ {2} + \ frac {1} {R} _ {3 } \]
Параллельное добавление компонентов снижает общее сопротивление в цепи.
- Вопрос
Вычислите сопротивление этой параллельной комбинации.
- Показать ответ
\ [\ frac {1} {R} = \ frac {1} {R} _ {1} + \ frac {1} {R} _ {2} + \ frac {1} {R} _ {3} \]
\ [\ frac {1} {R} = \ frac {1} {3} + \ frac {1} {6} + \ frac {1} {9} \]
R = 1,64 Ом
Общее сопротивление меньше, чем у наименьшего резистора.
EET 1150 Блок 9: Последовательно-параллельные схемы
EET 1150 Блок 9: Последовательно-параллельные схемы
В блоках 7 и 8 вы изучали серии
схемы и параллельные схемы. Многие в реальной жизни
схемы более сложные, с комбинациями обоих последовательно соединенных
и параллельно подключенные компоненты. В этом модуле мы изучим такие последовательно-параллельные
схемы . Вы обнаружите, что основные правила
игры — это те, которые вы уже изучили для последовательных цепей
и параллельные схемы, но работа по применению этих правил может быть довольно
сложный.Раздел 8 Обзор
- Этот блок будет основан на материале, который вы изучили в блоке
8. Итак, давайте
Начните с выполнения этого самотестирования, чтобы проверить, что вы узнали в этом модуле.
Выявление последовательно-параллельных отношений
- Последовательно-параллельная цепь — это схема, содержащая комбинации
последовательно соединенных и параллельно соединенных компонентов, находящихся в
чередовать последовательно и / или параллельно с другими подобными комбинациями.Вот пример: - Напомним наши определения последовательного и параллельного подключений.
из предыдущих блоков:- Два компонента соединены последовательно , если они соединены
друг к другу ровно в одной точке, и никакой другой компонент не подключен
к этому моменту. - Два компонента соединены параллельно если
они связаны друг с другом в двух точках.
- Два компонента соединены последовательно , если они соединены
- В примере схемы, показанной выше, R2 включен последовательно с R3, который
идет последовательно с R4.Таким образом, R2, R3 и R4 образуют последовательный путь. Кроме того, это
весь последовательный путь, взятый в целом, параллелен R1.
Обозначение для последовательно-параллельных отношений
- Как сокращенный способ описания последовательно-параллельных отношений в
схему мы будем использовать два символа:- мы используем символ + для обозначения
последовательное соединение между компонентами - используем символ || к
указать параллельное соединение
- мы используем символ + для обозначения
- Итак, для примера схемы, показанной выше, мы должны написать
R2 + R3 + R4
чтобы указать, что R2, R3 и R4 образуют последовательный путь.Затем, чтобы показать, что R1
параллельно этому последовательному пути, мы бы написалиR1 || (R2 + R3 + R4)
Анализ последовательно-параллельных цепей
- Блоки 2 и 3 предоставили пошаговые правила для анализа последовательных цепей.
и параллельные схемы. Это было возможно, потому что один базовый
подход работает на всех последовательных схемах, и другой базовый подход работает
на всех параллельных цепях. - Но невозможно дать пошаговую процедуру, которая
работают по всем последовательно-параллельным цепям. Есть
слишком много разнообразия среди последовательно-параллельных цепей, и подход
который работает для одной цепи, может не работать для других цепей. - Ключ — практика, практика и еще раз практика. Для развития вашего
навыков, нужно изучить как можно больше примеров и решить как можно больше задач
как вы можете. - Обычно первым хорошим шагом является определение полного эквивалента схемы.
сопротивление путем объединения пар последовательно или параллельно соединенных
резисторы, пока вы не объедините все резисторы в одно сопротивление.- Например, в схеме, показанной ниже, мы бы добавили R2, R3 и R4
вместе (так как они находятся последовательно), затем используйте формулу взаимности
чтобы объединить это значение с R1, поскольку R1 параллельно
с последовательным путем, содержащим R2, R3 и R4. Результат будет
полное эквивалентное сопротивление схемы R T .
- Например, в схеме, показанной ниже, мы бы добавили R2, R3 и R4
- После того, как у вас будет общее эквивалентное сопротивление, вы можете использовать Ом
закон, чтобы найти полный ток цепи:I T = V S ÷ R T
- После этого можно применять любые правила и законы.
из предыдущих блоков, в любой последовательности, которая приводит к
решение для определенного напряжения или тока.Самые полезные из них
правила и законы:- Закон Ома
- правила напряжения / тока для последовательной или параллельной комбинации
- Закон Кирхгофа о напряжении
- Действующий закон Кирхгофа
- правило делителя напряжения
- правило делителя тока
- Давайте рассмотрим эти правила и законы и обсудим их применение в последовательно-параллельном
схемы.
Закон Ома в последовательно-параллельных цепях
Правила напряжения / тока для последовательной или параллельной комбинации
- Вот еще два простых, но действенных правила.Отзывать
который:- Последовательно соединенные компоненты должны иметь одинаковые
текущий (но обычно
у них не будет одинакового напряжения). - Параллельно подключенные компоненты должны иметь одинаковые
напряжение (но обычно
у них не будет одинакового тока).
- Последовательно соединенные компоненты должны иметь одинаковые
- Эти два правила применяются не только к отдельным компонентам, но и к частям.
схем.- В нашей примерной схеме, например, резистор R1
соединены параллельно с последовательным путем, содержащим R2, R3 и
R4.Следовательно, мы знаем, что напряжение на R1 должно быть равно
к напряжению в последовательном тракте. В символах:В 1 = В 2 + 3 + 4
- Также, в той же цепи, поскольку R2, R3 и
R4 образуют последовательный путь, мы знаем, что три резистора должны
переносят тот же ток. В символах:I 2 = I 3 = I 4
- В нашей примерной схеме, например, резистор R1
Закон Кирхгофа о напряжении в последовательно-параллельных цепях
- Напомним, что КВЛ говорит, что сумма напряжений падает в районе
любой замкнутый контур в цепи равен сумме подъемов напряжения
вокруг этой петли. - Изначально мы изучали KVL в контексте последовательных цепей, но
KVL выполняется для всех схем.- В нашем примере схемы, например, один замкнутый контур содержит только
Напряжение
источник и R1. Поэтому KVL сообщает нам, что повышение напряжения на
источник должен быть равен падению напряжения на R1. В символах:V S = V 1
Конечно, мы также могли убедиться в этом по тому факту, что источник и
R1 подключены параллельно.Во многих случаях будет больше, чем
один из способов прийти к такому же выводу. - Другой замкнутый контур в нашем примере схемы содержит напряжение
исток и резисторы R2, R3, R4. Поэтому KVL сообщает нам, что
повышение напряжения на источнике должно быть равно сумме напряжений
падает на эти три резистора. В символах:V S = V 2 + V 3
+ В 4
- В нашем примере схемы, например, один замкнутый контур содержит только
Текущий закон Кирхгофа в последовательно-параллельных цепях
- Напомним, что KCL говорит, что сумма всех токов, входящих в точку
равна сумме всех выходящих из этой точки токов . - Изначально мы изучали KCL в контексте параллельных цепей, но
KCL действует для всех цепей.- В нашем примере схемы, например, рассмотрим точку, в которой напряжение
источник встречает R1 и R2. KCL сообщает нам, что ток, текущий в
эта точка от источника напряжения должна быть равна сумме
токи, исходящие из этой точки через R1 и R2. В символах:I T = I 1 + I 2
- В нашем примере схемы, например, рассмотрим точку, в которой напряжение
Правило делителя напряжения в последовательно-параллельном соединении
СхемыПравило делителя тока в последовательно-параллельном соединении
Схемы- При обсуждении параллельных цепей мы сформулировали правило делителя тока.
следующим образом: для параллельных ветвей ток I x через
любая ветвь равна отношению общего параллельного сопротивления R T к
сопротивление ветви R x , умноженное на общее
ток I T вход в параллельную комбинацию.В
форма уравнения:I x = ( R T ÷ R x ) × I T
- То же правило применяется к параллельным ответвлениям последовательно-параллельного
схема. Но нужно быть осторожным, чтобы применить его правильно. Особенно,
обратите внимание, что R x — это полное сопротивление ветви
чье течение вы пытаетесь найти. В зависимости от схемы вы
анализируя, R x может быть одним резистором
сопротивление, или это может быть совокупное сопротивление нескольких резисторов
последовательно и / или параллельно.Также обратите внимание, что в этом уравнении R T означает
общее сопротивление параллельных ветвей, которое может или не может
быть таким же, как полное сопротивление всего круга. Аналогично I T в
это уравнение означает полный ток, поступающий в параллельную
ветвей, которые могут совпадать, а могут и не совпадать с общим количеством
Текущий. - Поскольку студенты часто неправильно применяют правило делителя тока в последовательно-параллельном
схем, я рекомендую вам больше полагаться на закон Ома, KVL,
и KCL, и стараются избегать использования делителя тока
Правило .
Примеры
- Мы рассмотрели использование закона Ома, законов Кирхгофа и
правила делителя в последовательно-параллельных цепях. Анализ любого конкретного
последовательно-параллельная схема будет включать использование одного или нескольких из этих
правила и законы. - Обычно существует несколько способов приблизиться к конкретному
проблема или цепь. Например, при нахождении определенного напряжения
один студент может использовать закон Ома и KVL, а другой студент
использует KVL и правило делителя напряжения, а третий студент использует
правило делителя тока и закон Ома.Все три подхода дадут
тот же ответ, если ученики правильно применяют правила. - Как упоминалось ранее, первым хорошим шагом обычно является поиск схемы
общее эквивалентное сопротивление путем объединения пар последовательно соединенных
или параллельно подключенные резисторы, пока вы не объедините все резисторы
в единое сопротивление.
Затем найдите полный ток цепи, используя закон Ома в форме:I T = V S ÷ R T
Мощность в последовательно-параллельной цепи
- Чтобы найти мощность, рассеиваемую резистором в последовательно-параллельной цепи,
используйте любую из тех же формул, которые вы использовали для последовательных цепей и
параллельные цепи:P = V × I
P = I 2 × R
P = V 2 ÷ R
- Напомним, что в каждом из этих уравнений R — это сопротивление резистора.
сопротивление, В — напряжение на резисторе, а I —
ток через резистор.
Общая мощность цепи
- Как и в случае с последовательными цепями и параллельными цепями, есть два
способы вычисления общей мощности, рассеиваемой в последовательно-параллельной цепи.
В любом случае вы получите один и тот же ответ:- Либо найти мощность для каждого резистора, и
затем добавьте эти полномочия:P T = P 1 + P 2 + P 3 +
… + P n - или примените любую из формул мощности к
вся схема:P T = V S × I T
P T = I T 2 × R T
P T = V S 2 ÷ R T
Это те же формулы мощности, что и выше, за исключением того, что теперь мы
применяя их ко всей цепи, а не к одному резистору.
- Либо найти мощность для каждого резистора, и
Символ заземления (или общего)
- Вспомните из Блока 4, что вместо рисования линий показывать
соединений на принципиальной схеме мы часто используем символ заземления ,
также называется обыкновенным
символ ,
для обозначения клемм, соединенных вместе. Символ выглядит
как это: - Основная причина использования этого символа заключается в том, что он позволяет устранить
линии, которые загромождают схематическую диаграмму и затрудняют визуализацию
ток между компонентами. - Пример: взгляните еще раз на эту принципиальную схему:
Обратите внимание, что все источники напряжения, R1 и R4 соединяются на общей
точка. Использование символа заземления, чтобы показать, что эти три компонента
соединены вместе, мы можем перерисовать схему, как показано ниже. - Это не очень хороший пример, потому что перерисованная диаграмма с
символ заземления читать не легче, чем исходную диаграмму. Но
на сложной принципиальной схеме с множеством резисторов земля
символ может удалить много линий и, следовательно, сделать диаграмму
читать намного легче.Важный момент в этом примере — увидеть
что две диаграммы эквивалентны.
Пузырьковый символ для источников напряжения
- В схематических представлениях, где используется общий символ, мы часто опускаем
этот символ со стороны любого источника напряжения, подключенного к
общий. - Отображается клемма, которая не соединена с общим
маленьким кружком (или «пузырем») и помечены + или —
напряжение источника напряжения. - Пример: Продолжая тот же пример выше, мы могли бы перерисовать
схематическую диаграмму еще раз, используя символ пузыря, чтобы добраться до
следующая диаграмма:
Геометрия схемы
- геометрия контура (способ соединения компонентов
показаны на схематической диаграмме) часто может затруднить определение напряжения
и текущие отношения в цепи. - Вам следует аккуратно перерисовать сложную принципиальную схему в виде
столько способов, сколько необходимо для облегчения чтения.
Блок 9 Обзор
- Этот электронный урок охватывает несколько важных тем, в том числе:
- идентификация последовательной и параллельной связи
- анализ последовательно-параллельных цепей
- мощность в последовательно-параллельных цепях
- наземный символ и символ пузыря.
- Чтобы завершить электронный урок, пройдите самопроверку, чтобы проверить свое понимание
из этих тем.
Поздравляем! Вы завершили электронный урок по этому модулю.
Серия
и параллельные схемы — хорошо объяснены
Последовательное и параллельное соединение ламп
Ток в цепи определяется импедансом, обеспечиваемым компонентами схемы, который, в свою очередь, определяется способом соединения компонентов схемы.Последовательное и параллельное соединение цепи — два самых простых способа соединения цепи.
Последовательное соединение
Цепи, подключенные к серии
, состоят из двух или более активных и / или пассивных устройств, соединенных последовательно. Ток, протекающий по этим цепям, остается неизменным в любой момент, но напряжение меняется. Напряжение в цепи должно быть равно сумме напряжений на каждом устройстве.
Параллельное соединение
Параллельно соединенные цепи состоят из двух или более активных и пассивных устройств, соединенных параллельно.В этих схемах напряжение на любой ветви остается неизменным, но ток, протекающий через каждую ветвь, меняется. Полный ток равен сумме токов через каждую ветвь.
Серия
Подключение сопротивления
На приведенном выше рисунке показан пример последовательно соединенной резистивной сети. В последовательно соединенной цепи должен быть только один путь для прохождения тока. Скорость протекания тока зависит от эквивалентного сопротивления цепи. Ток встречает сопротивление, равное сумме сопротивлений каждого устройства в цепи.Эквивалентное сопротивление последовательного соединения резисторов
.
Треб = R1 + R2 + R3 +… + Rn
Эквивалентное сопротивление последовательного соединения резисторов
Треб = R1 + R2 + R3 +… + Rn
Пример
Учитывая схему, показанную выше, эквивалентное сопротивление, предлагаемое схемой, должно быть равно сумме R1, R2 и R3
Req = R1 + R2 + R3 = = 5 Ом + 5 Ом + 5 Ом = 15 Ом
Параллельное соединение сопротивления
На приведенном выше рисунке показан пример параллельной резистивной сети.В параллельной цепи ток течет более чем по одному пути, и скорость протекания тока по каждому пути может варьироваться в зависимости от сопротивления каждого пути. Эквивалентное сопротивление цепи равно сумме обратных сопротивлений, предлагаемых каждым устройством в цепи.
Эквивалент параллельного включения сопротивления
1 / Req = 1 / R1 + 1 / R2 + 1 / R3 +… + 1 / Rn
Пример
Рассматривая схему выше, эквивалентное сопротивление, предлагаемое схемой, должно быть равно сумме обратных величин R1, R2 и R3.
1 / Треб = 1 / R1 + 1 / R2 + 1 / R3 = 1/5 + 1/5 + 1/5
1 / Треб = 3/5 Ом
Req = 5/3 Ом
Серия
и параллельные электрические соединения
Серия и параллельная
Есть два способа подключения нескольких устройств к источнику питания (например, динамиков к усилителю): последовательно и параллельно. Ну … Хорошо, есть еще последовательный / параллельный. Но мы расскажем об этом на следующей странице.
Серийные динамикиВ последовательной цепи (как в двух приведенных выше) ток должен протекать через одно устройство, чтобы добраться до следующего устройства.Это означает, что скорость протекания тока через все устройства одинакова. Напряжение на каждом устройстве зависит от его полного сопротивления / сопротивления каждого устройства и тока, протекающего по цепи. При добавлении дополнительных компонентов в последовательную цепь ток уменьшается, если приложенное напряжение остается постоянным.
Параллельные динамикиВ параллельной схеме (как в двух приведенных выше примерах) каждое устройство напрямую подключено к источнику питания. Это означает, что каждое устройство получает одинаковое напряжение.Сила тока, протекающего через каждое устройство, зависит от импеданса / сопротивления этого конкретного устройства. Если устройства добавляются к источнику питания в параллельной конфигурации, ток потребления / потока от источника питания увеличивается.
На двух диаграммах ниже вы можете увидеть взаимосвязь между током на выходе из усилителя и количеством динамиков. Вы можете видеть, что четыре динамика потребляют от усилителя в два раза больше тока, чем конфигурация с двумя динамиками.
При подключении к любому источнику питания вы должны знать пределы источника, чтобы предотвратить повреждение источника. Это означает, что если вы подключите слишком много динамиков с параллельной проводкой к усилителю (в данном случае источнику питания), он может выйти из строя и не подлежит ремонту. Я видел, как это происходило, особенно когда усилитель был неправильно вставлен.
Для тех, кто хочет заниматься математикой …На диаграммах / тексте выше у нас были либо последовательные ИЛИ параллельные цепи.В этом разделе показано, что происходит с напряжением, током и рассеиваемой мощностью в последовательной / параллельной цепи. Как было сказано ранее, в последовательной цепи «ток» в каждом устройстве одинаков. В параллельной цепи «напряжение» одинаково на каждом устройстве. В следующей схеме вы можете видеть, что два резистора на 1000 Ом последовательно соединены с одним резистором на 400 Ом. Мы знаем, что напряжение на двух резисторах 1000 Ом будет одинаковым (потому что они подключены параллельно).Мы также знаем, что общий ток, протекающий через два параллельно соединенных резистора, будет равен току, протекающему через резистор 400 Ом.
Чтобы рассчитать полный ток, сначала следует упростить схему. Это означает, что нам нужно найти полное сопротивление параллельной сети. Для простой схемы с двумя резисторами равного номинала мы можем просто разделить сопротивление отдельного компонента на общее количество компонентов. Для этой параллельной сети у нас есть два резистора по 1000 Ом.
Общее сопротивление параллельных резисторов = сопротивление одного компонента / количество резисторов
Общее сопротивление параллельных резисторов = 1000/2
Общее сопротивление параллельных резисторов = 500 ОмЕсли бы у нас было 3 параллельных резистора, мы бы разделили 1000 на 3, чтобы найти общее сопротивление параллельных резисторов.
Полное сопротивление параллельных резисторов = 1000/3
Полное сопротивление параллельных резисторов = 333,33 …. ОмТеперь, когда мы знаем, что параллельные резисторы равны одному резистору на 500 Ом.Теперь, когда у нас есть, по сути, один резистор на 500 Ом, соединенный последовательно с резистором на 400 Ом, мы можем рассчитать полный ток через цепь. Мы знаем, что у нас есть источник питания на 12 вольт. Мы также знаем, что резистор на 500 Ом, включенный последовательно с резистором на 400 Ом, равен резистору на 900 Ом.
Ток в цепи = напряжение в цепи / общее сопротивление цепи
Ток в цепи = 12/900
Ток в цепи = 0,0133 АТеперь мы можем найти напряжение на отдельных компонентах.Чтобы избежать путаницы, сначала рассчитайте напряжение на единственном резисторе.
Напряжение на резисторе = сопротивление резистора * ток, протекающий через резистор
Напряжение на резисторе = 400 * 0,0133
Напряжение на резисторе = 5,333 ВВ последовательной цепи все напряжения на всех отдельных компонентах серии будут равны напряжению источника питания. Если у нас есть источник 12 В и напряжение на резисторе 400 Ом равно 5.333 вольт, мы знаем, что напряжение на параллельной паре резисторов будет 6,67 вольт (12-5,333 = 6,67). Чтобы рассчитать ток через параллельные компоненты …
Ток через один резистор 1000 Ом = напряжение на резисторе / сопротивление
Ток через один резистор 1000 Ом = 6,67 / 1000
Ток через один резистор 1000 Ом = 0,0067 ампераТеперь, когда мы знаем напряжение на каждом из компонентов и ток с через на каждом из компонентов, мы можем рассчитать рассеиваемую мощность для каждого компонента.На самом деле мы могли бы это сделать, как только узнали бы напряжение на компонентах, но я решил пойти по «живописному» маршруту.
Рассеиваемая мощность резистора 400 Ом = напряжение на компоненте * ток через компонент
Рассеиваемая мощность на резисторе 400 Ом = 5,33 * 0,013
Рассеиваемая мощность на резисторе 400 Ом = 0,071 ВтРассеиваемая мощность на каждом резисторе 1000 Ом = напряжение на компоненте * ток на компоненте
Рассеиваемая мощность на каждом резисторе 1000 Ом = 6.67 * .0067
Рассеиваемая мощность на каждом резисторе 1000 Ом = 0,045 ВтВ этом примере используются резисторы, но те же вычисления будут работать для любого резистивного устройства. Хотя громкоговорители не являются чисто резистивными при работе с переменным напряжением, приведенные здесь расчеты можно использовать для грубых расчетов напряжения, тока и рассеиваемой мощности в громкоговорителях.
Последовательные и параллельные резисторы
Ultimate Electronics: практическое проектирование и анализ схем
Развитие интуиции для последовательных и параллельных цепей.Решение резисторных сетей.
Читать 12 мин
Прежде чем вводить формальные правила протекания токов и напряжений в цепях в целом, давайте рассмотрим общий сценарий, чтобы попытаться развить интуицию на более высоком уровне.
Эти интуиции станут строительными блоками Закона Кирхгофа о напряжении и Закона Кирхгофа о текущем токе.
Во многих вводных текстах делается попытка использовать гидравлическую аналогию воды, протекающей по трубе, где скорость потока представляет ток, а давление — напряжение.
Осторожно: эта аналогия работает на высоком уровне, но она быстро перестает работать, если вы присмотритесь слишком внимательно или зададите неверные вопросы. (Является ли кран источником тока или источника напряжения? Что делать, если в трубе есть воздух?)
Гидравлическая аналогия работает, потому что сохранение заряда очень похоже на сохранение массы в проблеме потока жидкости (т.е. вода должна куда-то уходить!), И поскольку давление — это скалярная потенциальная энергия (на единицу объема), измерьте просто как напряжение — это скалярная потенциальная энергия (на единицу заряда).
Одна из проблем заключается в том, что многие люди также не обладают хорошей механической интуицией в отношении потоков жидкости, и в этом случае аналогия не добавляет никакой ценности. Тем не менее, большинству людей легче визуализировать движение частиц, которые они могут видеть (например, воды), чем невидимых электронов, поэтому аналогия добавляет некоторую ценность. Инженеру-электрику часто бывает разумно взглянуть на схему и подумать о ней как о проблеме с водопроводом: где будет течь вода (заряд) и где упадет давление (напряжение)?
На самом деле возможно моделировать реальные жидкостные системы с помощью контуров, но это более тонкое искусство, чем вы можете подумать сначала, поэтому просто возьмите все, что вы можете, не слишком вдаваясь в детали.
Если аналогия с гидравликой не помогает вашей интуиции, не беспокойтесь об этом — возможно, вы просто нашли случай, когда аналогия не работает.
Два или более компонента в серии , если нет боковых путей для входа или выхода тока.
Есть пара узлов (или терминалов), которые являются началом и концом цепочки последовательных элементов.
Любой ток, идущий на первый терминал, должен выходить из второго терминала.
Для четырех компонентов, представленных выше, поскольку заряд сохраняется:
i1 = i2 = i3 = i4
Звучит не так круто, как уравнение, но это все, что означает «последовательно».
В мире схем модели с сосредоточенными элементами считается, что это происходит мгновенно. Почему? Потому что никакой чистый заряд никогда не может храниться внутри любых элементов схемы (или между ними). Любое накопление заряда оттолкнет другие заряды и рассеется. (На самом деле такие детали, как скорость света, означают, что это не совсем мгновенно, но теперь мы говорим о проблемах, выходящих далеко за рамки этой главы!)
В гидравлической аналогии представьте садовый шланг, который уже полностью заполнен водой.если кран открывается шире, кран проталкивает больше воды в начало шланга, который немедленно выталкивает следующую порцию воды, и так далее, пока не достигнет конца. В результате, даже если длина шланга составляет 100 футов, вода по существу сразу же начинает выходить из конца, потому что шланг уже был предварительно заполнен.
Теперь, если мы подключим второй шланг к выходу из первого шланга, через второй шланг должен протекать тот же ток, что и через первый. Предполагаем, что утечек нет! Но в том-то и дело — любые возможные пути утечки должны быть смоделированы как дополнительные пути на схеме, чтобы два шланга больше не были просто соединены последовательно.
«Последовательно» означает, что один и тот же поток (будь то заряд или вода), согласно компоновке системы, должен проходить через все компоненты серии.
Хотя количество потока воды одинаково, это не означает, что два последовательных шланга обязательно оказывают одинаковое влияние на поток воды.
Например, если у нас есть крошечный шланг (маленького диаметра), соединенный последовательно с огромным шлангом (большого диаметра), крошечный шланг будет иметь доминирующее влияние на ограничение потока воды, независимо от того, идет ли он первым или вторым. по направлению потока.Это может означать, что в качестве приближения мы можем игнорировать огромный шланг и рассматривать только крошечный шланг, пытаясь вычислить общий расход; см. Алгебраические приближения.
Если у нас есть два или более последовательных компонента, и мы ограничиваем поток через один из них (например, зажимая шланг), это ограничивает и снижает скорость потока через обоих из них.
В электронике амперметр работает следующим образом: он подключается последовательно к измеряемому устройству, поэтому весь ток течет через амперметр.(Хороший амперметр сам по себе вызывает очень небольшое падение напряжения.) Однако, если сопротивление амперметра слишком велико, это на самом деле окажет существенное влияние на цепь, которую вы пытаетесь измерить — не очень хорошо!
В гидравлике расходомер работает так: он включен последовательно, так что вся вода проходит через расходомер. (Хороший расходомер вызывает очень небольшой перепад давления, если он сам по себе.) Однако, если сопротивление расходомера слишком велико, оно на самом деле окажет существенное влияние на расход, который вы пытаетесь измерить, что тоже нехорошо!
Два или более компонента соединены параллельно , если они подключены через одну и ту же пару узлов входа и выхода.(Слова «вход» и «выход» на самом деле ничего не означают в электронике, но предлагают правильную идею для гидравлической аналогии.) Это означает, что они имеют одинаковое входное напряжение и выходное напряжение и, следовательно, одинаковую разницу напряжений на их.
Мы рассмотрим эту схему более подробно в следующем разделе, а пока просто увидим, что V1 и R2 связаны через одни и те же два узла:
Оба элемента подключены между узлами A и B, поэтому:
v1 = v2VAB = VAB
Звучит очень просто как уравнение, но все это означает «параллельно».
В мире схем это означает, что существует два (или более) пути, по которым ток течет из точки A в точку B. Свойства отдельных параллельных ветвей (ребер) будут определять, по какому маршруту будет проходить ток.
В гидравлической аналогии представьте себе сплиттер, подключенный к водопроводному крану, от которого соединены два садовых шланга. Давление на выходе из крана обоих одинаково, и давление на выходе (атмосферное давление) тоже такое же.
Следовательно, если мы откроем кран больше, дополнительный поток разделится между двумя шлангами.
В общем, если у нас есть два или более параллельных шланга, и мы ограничиваем поток через один из них (например, зажимая один из шлангов), это ограничит поток через эту ветвь, но другая ветвь не затронет — или он может даже получить больший поток, чем раньше (в зависимости от свойств источника).
В электронике вольтметр работает следующим образом: он подключается параллельно с размываемыми компонентами, поэтому он измеряет ту же разницу напряжений, что и исследуемая ветвь.Однако, если сопротивление вольтметра слишком мало, это на самом деле окажет существенное влияние на цепь, которую вы пытаетесь измерить, создав нежелательный путь утечки — не хорошо!
В гидравлике манометр работает следующим образом: он устанавливается параллельно (обычно с одной стороны от интересующего давления, с другой стороны от атмосферы, называемого «манометрическое давление»), поэтому он измеряет то же давление, что и труба или любой другой компонент интересный опыт.
Как обсуждалось в разделе «Сопротивление и закон Ома», отдельный резистор ведет себя как V = IR
.Итак, для двух последовательно включенных резисторов имеем:VAB = i1R1VBC = i2R2
Как уже говорилось, для всех компонентов, включенных последовательно, ток должен быть одинаковым, поэтому:
i1 = i2 = I
Мы можем сложить полное напряжение на обоих резисторах:
В переменного тока = VAB + VBC = i1R1 + i2R2 = I (R1 + R2)
Общая последовательная ветвь с двумя резисторами ведет себя так, как будто есть единственный резистор со значением:
Rseries = R1 + R2
С внешней точки зрения двух клемм A и C этот одиночный резистор Rseries
ведет себя так же (на бумаге), что и два отдельных последовательно.Обратите внимание, что в действительности один эквивалентный резистор может вести себя по-разному: см. «Практические резисторы: номинальная мощность (мощность)» и «Практические резисторы: температурный коэффициент». В частности, упрощая резисторы на схеме, мы часто скрываем тот факт, что тепло генерируется в двух разных компонентах; но на самом деле нам, инженерам, приходится беспокоиться о каждом отдельно.
Для большего количества резисторов в серии просто добавляется:
Rseries = R1 + R2 + R3 +…
Мы рассмотрим это подробнее в разделе «Делители напряжения».
Два параллельно включенных резистора имеют одинаковое напряжение на обоих:
VAB = i1R1 = i2R2
В одиночку, эти два резистора ничем не управляют.
Но что, если мы подадим внешнее напряжение на эти два резистора или протолкнем через них ток? Общий ток делится между двумя путями:
итотал = i1 + i2 = VABR1 + VABR2 = VAB (1R1 + 1R2) = VAB (R1 + R2R1R2)
Так как I = VR
, это то же самое, что и одиночный резистор:итотал = VAB⋅1Rparallel1Rparallel = 1R1 + 1R2 = R1 + R2R1R2
Или можно перевернуть дробь:
R параллельный = 11R1 + 1R2 = R1R2R1 + R2
Эта дробь с дробями в обозначении знаменателя немного сложна, поэтому для экономии места иногда инженеры-электрики записывают эту дробь с двумя косыми чертами, как:
Rпараллельный = (R1 // R2) = 11R1 + 1R2
Обратите внимание, что в действительности один эквивалентный резистор может вести себя иначе, чем два отдельных резистора из-за проблем рассеивания тепла.
Для нескольких параллельно подключенных резисторов действует правило разделения тока:
Rparallel = R1 // R2 // R3 // ⋯ = 11R1 + 1R2 + 1R3 +…
Мы рассмотрим это подробнее в Current Dividers.
Единица измерения сименс S = 1Ω
, также называемый «mho» (ом, записанный наоборот!), является единицей проводимости. Проводимость — это просто величина, обратная сопротивлению:G = 1R
Приятная особенность проводимости заключается в том, что для параллельных резистивных цепей проводимости просто добавляют:
1R параллельный = 1R1 + 1R2G параллельный = G1 + G2
Последовательные и параллельные резисторы
предоставляют множество простых возможностей для упрощения предположений и приближений.
Если вы еще этого не сделали, просмотрите раздел «Алгебраические приближения», чтобы узнать об основных концепциях и инструментах, необходимых для приближения к этим упрощениям.
Для последовательных цепей, например, если R1 = 10k
и R2 = 10
, то Rseries = R1 + R2 = 10010 = 10.01k
. Это настолько близко к 10 кОм, что во многих ситуациях мы можем полностью игнорировать меньший резистор. Чтобы формализовать это правило:Rseries = R1 + R2≈R1, если R1≫R2
Это соответствует нашей интуиции, потому что, поскольку мы должны «протолкнуть» одинаковое количество заряда через оба простых ограничения (низкое сопротивление R2
) и более жесткое ограничение (более высокое сопротивление R1
), потребуется гораздо больше энергии, чтобы преодолеть более жесткое ограничение, поэтому мы можем фактически игнорировать более легкое, чтобы вычислить общую необходимую энергию.Для параллельных цепей, если R1 = 10k
и R2 = 10
, то Rparallel = R1R2R1 + R2 = 10000010010 = 9,99
, что составляет примерно 10. Мы можем обобщить и это приближение:R параллельный = 11R1 + 1R2 = R1R2R1 + R2≈R2, если R1≫R2
Это соответствует нашей интуиции, потому что, поскольку мы применяем одинаковое количество «толчка» к обоим путям, поток будет в основном следовать более легкому ограничению (низкое сопротивление R2
) и в основном игнорируют более жесткое ограничение (более высокое сопротивление R1
), поэтому более сложный путь лишь немного снижает общее ограничение, связанное с наличием только более простого пути.Вы можете применить эти правила, чтобы упростить комбинации последовательных и параллельных цепей, но вы должны применять правила осторожно, по одному.
Для примера рассмотрим 1 резистор R1
последовательно с параллельной парой R2, R3
:Общее эффективное сопротивление:
Rtotal = R1 + (R2 // R3) = R1 + ⎛⎜⎝11R2 + 1R3⎞⎟⎠ = R1 + ⎛⎜⎝1R2 + R3R2R3⎞⎟⎠ = R1 + (R2R3R2 + R3) = R1 (R2 + R3) + R2R3R2 + R3 = R1R2 + R1R3 + R2R3R2 + R3
Поскольку эти выражения могут быстро усложняться, удобно применять алгебраические аппроксимации, описанные выше, где это возможно, или сохранять их в исходной, нерасширенной форме как можно дольше для лучшего понимания прочитанного.
В других случаях возможно наличие резисторной сети, в которой вы вообще не можете применять эти правила последовательного и параллельного подключения. Например, рассмотрим эту схему:
В этой схеме всего 5 резисторов, но некуда начинать применять правило последовательного или параллельного подключения.
Это не означает, что его нельзя свести к единственному эквивалентному сопротивлению. Этого просто невозможно добиться с помощью одних только этих последовательных и параллельных правил.
Хотя мы рассмотрели правила для резисторов в этом разделе, мы хотим разделить, какие части нашего анализа относятся к резисторам, а какие нет.
Единственный факт, который мы использовали о резисторах, это то, что они имеют определенную линейную зависимость напряжения от тока V = IR.
, что не будет применяться к другим компонентам.Однако есть два общих правила, которые применимы к любым компонентам , включенным последовательно или параллельно:
- Любые два последовательно соединенных компонента имеют одинаковый ток.
- Любые два параллельно включенных компонента имеют одинаковое напряжение на них.
Обычный вопрос от новичков: как упростить схему, подобную этой, с резистором, соединенным последовательно со светодиодом:
Exercise Щелкните, чтобы открыть и смоделировать схему выше.
Ответ таков: нельзя комбинировать с резистором R1
с некоторым значением, подобным единственному резистору для светодиода. Светодиод — это нелинейный компонент. Это не следует за V = IR
. Таким образом, мы не можем получить единого эквивалентного сопротивления, охватывающего все ситуации.Вы, , можете придумать одно уравнение для описания зависимости тока от напряжения для последовательной комбинации резистор + светодиод. Это просто не будет линейным уравнением!
Вот почему такие инструменты, как симуляторы цепей, особенно удобны: хотя мы можем уменьшить линейные случаи (например, резисторы, включенные последовательно и параллельно) вручную, симулятор также способен решать нелинейные случаи.(См. Также: Linear & Nonlinear.)
В следующем разделе, Законе напряжения Кирхгофа и Законе тока Кирхгофа, мы будем использовать эту новую интуицию, чтобы разработать более широкий набор правил поведения напряжения и тока в цепи.
Роббинс, Майкл Ф.

 При таком соединении через резисторы будет протекать один общий ток.
При таком соединении через резисторы будет протекать один общий ток. 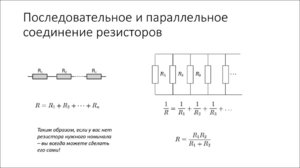
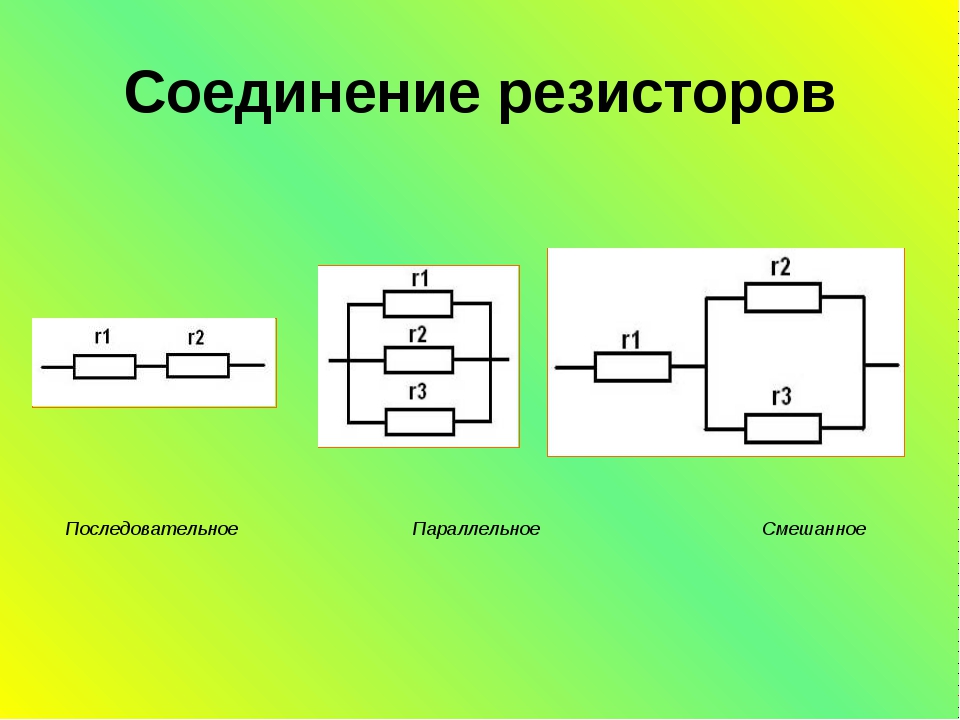 Иногда подобную комбинацию называют последовательно-параллельным соединением.
Иногда подобную комбинацию называют последовательно-параллельным соединением. 
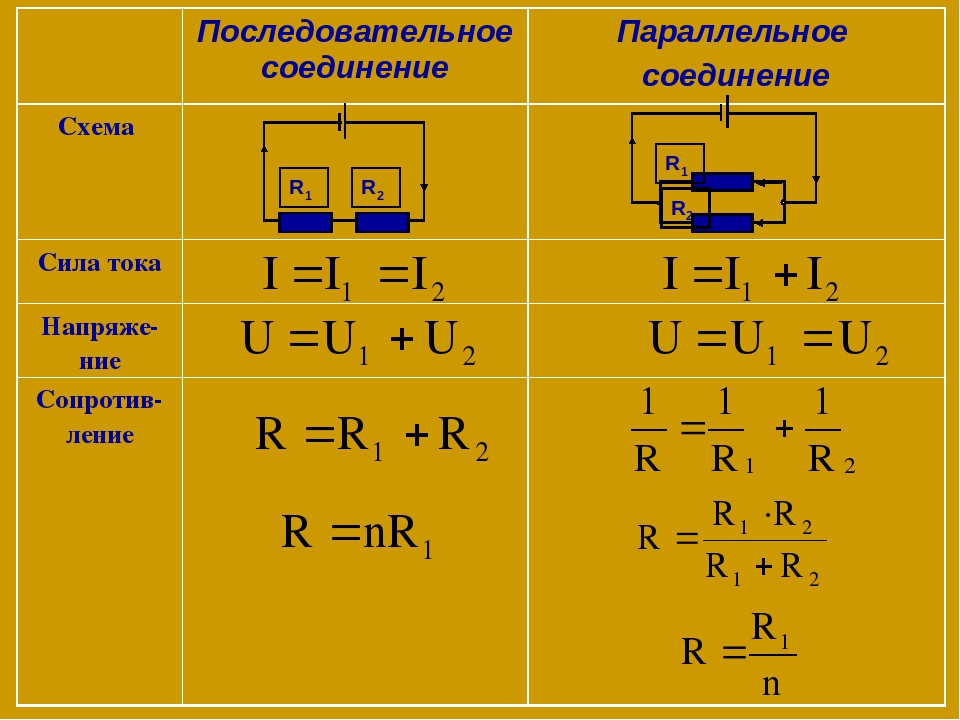

 Сопротивление по отношению к входным зажимам называется входным сопротивлением и равно сумме сопротивлений участков – R вх = R 1 + R 2 + R 3 ;
Сопротивление по отношению к входным зажимам называется входным сопротивлением и равно сумме сопротивлений участков – R вх = R 1 + R 2 + R 3 ;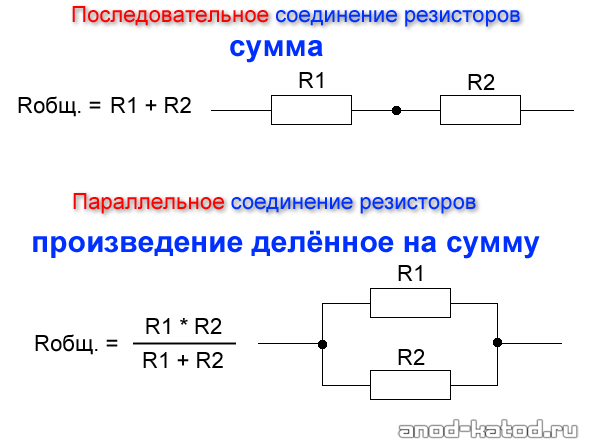
 к. параллельное соединение
к. параллельное соединение
