\circ\) C), \(\alpha\) – температурный коэффициент сопротивления, равный для меди 0,0043 1/°C, \(t\) – температура (в градусах Цельсия), при которой нужно найти сопротивление проводника.
Мы знаем, что сопротивление медного проводника при температуре \(t_0\) равно \(R_0\), а при температуре \(t\) равно \(R\), поэтому можем получить такую систему:
\[\left\{ \begin{gathered}
{R_0} = {R_0}\left( {1 + \alpha {t_0}} \right) \hfill \\
R = {R_0}\left( {1 + \alpha t} \right) \hfill \\
\end{gathered} \right.\]
Учитывая, что по условию \(R=3R_0\), то:
\[\left\{ \begin{gathered}
{R_0} = {R_0}\left( {1 + \alpha {t_0}} \right) \hfill \\
3{R_0} = {R_0}\left( {1 + \alpha t} \right) \hfill \\
\end{gathered} \right.\]
Сократим левую и правую часть обеих уравнений на \(R_0\), тогда:
\[\left\{ \begin{gathered}
1 = 1 + \alpha {t_0} \hfill \\
3 = 1 + \alpha t \hfill \\
\end{gathered} \right.\]
Вычтем из нижнего равенства верхнее, тогда:
\[2 = \alpha \left( {t – {t_0}} \right)\]
Очевидно, что выражение в скобках в правой части – это и есть искомое изменение температуры \(\Delta t\), то есть:
\[\alpha \Delta t = 2\]
В итоге получим:
\[\Delta t = \frac{2}{\alpha }\]
Посчитаем ответ:
\[\Delta t = \frac{2}{{0,0043}} = 465,1^\circ\;С = 465,1\;К\]
Ответ: 465,1 К.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
При повышении температуры сопротивление медного проводника. Сопротивление меди в зависимости от температуры
Частицы проводника (молекулы, атомы, ионы), не участвующие в образовании тока, находятся в тепловом движении, а частицы, образующие ток, одновременно находятся в тепловом и в направленном движениях под действием электрического поля. Благодаря этому между частицами, образующими ток, и частицами, не участвующими в его образовании, происходят многочисленные столкновения, при которых первые отдают часть переносимой ими энергии источника тока вторым. Чем больше столкновений, тем меньше скорость упорядоченного движения частиц, образующих ток. Как видно из формулы I = enνS
, снижение скорости приводит к уменьшению силы тока. Скалярная величина, характеризующая свойство проводника уменьшать силу тока, называется сопротивлением проводника.
Из формулы закона Ома сопротивление Ом — сопротивление проводника, в котором получается ток силой в 1 а
при напряжении на концах проводника в 1 в.
Сопротивление проводника зависит от его длины l, поперечного сечения S и материала, который характеризуется удельным сопротивлением Чем длиннее проводник, тем больше за единицу времени столкновений частиц, образующих ток, с частицами, не участвующими в его образовании, а поэтому тем больше и сопротивление проводника. Чем меньше поперечное сечение проводника, тем более плотным потоком идут частицы, образующие ток, и тем чаще их столкновения с частицами, не участвующими в его образовании, а поэтому тем больше и сопротивление проводника.
Под действием электрического поля частицы, образующие ток, между столкновениями движутся ускоренно, увеличивая свою кинетическую энергию за счет энергии поля. При столкновении с частицами, не образующими ток, они передают им часть своей кинетической энергии. Вследствие этого внутренняя энергия проводника увеличивается, что внешне проявляется в его нагревании. Рассмотрим, изменяется ли сопротивление проводника при его нагревании.
Рассмотрим, изменяется ли сопротивление проводника при его нагревании.
В электрической цепи имеется моток стальной проволоки (струна, рис. 81, а). Замкнув цепь, начнем нагревать проволоку. Чем больше мы ее нагреваем, тем меньшую силу тока показывает амперметр. Ее уменьшение происходит от того, что при нагревании металлов их сопротивление увеличивается. Так, сопротивление волоска электрической лампочки, когда она не горит, приблизительно 20 ом
, а при ее горении (2900° С) — 260 ом
. При нагревании металла увеличивается тепловое движение электронов и скорость колебания ионов в кристаллической решетке, в результате этого возрастает число столкновений электронов, образующих ток, с ионами. Это и вызывает увеличение сопротивления проводника * . В металлах несвободные электроны очень прочно связаны с ионами, поэтому при нагревании металлов число свободных электронов практически не изменяется.
* (Исходя из электронной теории, нельзя вывести точный закон зависимости сопротивления от температуры. Такой закон устанавливается квантовой теорией, в которой электрон рассматривается как частица, обладающая волновыми свойствами, а движение электрона проводимости через металл — как процесс распространения электронных волн, длина которых определяется соотношением де Бройля.
Такой закон устанавливается квантовой теорией, в которой электрон рассматривается как частица, обладающая волновыми свойствами, а движение электрона проводимости через металл — как процесс распространения электронных волн, длина которых определяется соотношением де Бройля.
)
Опыты показывают, что при изменении температуры проводников из различных веществ на одно и то же число градусов сопротивление их изменяется неодинаково. Например, если медный проводник имел сопротивление 1 ом
, то после нагревания на 1°С
он будет иметь сопротивление 1,004 ом
, а вольфрамовый — 1,005 ом.
Для характеристики зависимости сопротивления проводника от его температуры введена величина, называемая температурным коэффициентом сопротивления. Скалярная величина, измеряемая изменением сопротивления проводника в 1 ом, взятого при 0° С, от изменения его температуры на 1° С, называется температурным коэффициентом сопротивления α
. Так, для вольфрама этот коэффициент равен 0,005 град -1
, для меди — 0,004 град -1 .
Температурный коэффициент сопротивления зависит от температуры. Для металлов он с изменением температуры меняется мало. При небольшом интервале температур его считают постоянным для данного материала.
Выведем формулу, по которой рассчитывают сопротивление проводника с учетом его температуры. Допустим, что R 0
— сопротивление проводника при 0°С
, при нагревании на 1°С
оно увеличится на αR 0
, а при нагревании на t°
— на αRt°
и становится R = R 0 + αR 0 t°
, или
Зависимость сопротивления металлов от температуры учитывается, например при изготовлении спиралей для электронагревательных приборов, ламп: длину проволоки спирали и допускаемую силу тока рассчитывают по их сопротивлению в нагретом состоянии. Зависимость сопротивления металлов от температуры используется в термометрах сопротивления, которые применяются для измерения температуры тепловых двигателей, газовых турбин, металла в доменных печах и т. д. Этот термометр состоит из тонкой платиновой (никелевой, железной) спирали, намотанной на каркас из фарфора и помещенной в защитный футляр. Ее концы включаются в электрическую цепь с амперметром, шкала которого проградуирована в градусах температуры. При нагревании спирали сила тока в цепи уменьшается, это вызывает перемещение стрелки амперметра, которая и показывает температуру.
Ее концы включаются в электрическую цепь с амперметром, шкала которого проградуирована в градусах температуры. При нагревании спирали сила тока в цепи уменьшается, это вызывает перемещение стрелки амперметра, которая и показывает температуру.
Величина, обратная сопротивлению данного участка, цепи, называется электрической проводимостью проводника
(электропроводностью). Электропроводность проводника Чем больше проводимость проводника, тем меньше его сопротивление и тем лучше он проводит ток. Наименование единицы электропроводности Проводимость проводника сопротивлением 1 ом
называется сименс.
При понижении температуры сопротивление металлов уменьшается. Но есть металлы и сплавы, сопротивление которых при определенной для каждого металла и сплава низкой температуре резким скачком уменьшается и становится исчезающе малым — практически равным нулю (рис. 81, б). Наступает сверхпроводимость
— проводник практически не обладает сопротивлением, и раз возбужденный в нем ток существует долгое время, пока проводник находится при температуре сверхпроводимости (в одном из опытов ток наблюдался более года). При пропускании через сверхпроводник тока плотностью 1200 а / мм 2
При пропускании через сверхпроводник тока плотностью 1200 а / мм 2
не наблюдалось выделения количества теплоты. Одновалентные металлы, являющиеся наилучшими проводниками тока, не переходят в сверхпроводящее состояние вплоть до предельно низких температур, при которых проводились опыты. Например, в этих опытах медь охлаждали до 0,0156°К,
золото — до 0,0204° К.
Если бы удалось получить сплавы со сверхпроводимостью при обычных температурах, то это имело бы огромное значение для электротехники.
Согласно современным представлениям, основной причиной сверхпроводимости является образование связанных электронных пар. При температуре сверхпроводимости между свободными электронами начинают действовать обменные силы, отчего электроны образуют связанные электронные пары. Такой электронный газ из связанных электронных пар обладает иными свойствами, чем обычный электронный газ — он движется в сверхпроводнике без трения об узлы кристаллической решетки.
Задача 24.
Для изготовления спиралей электрической плитки мастерская получила моток нихромозой проволоки, на бирке которой было написано: «Масса 8,2 кг,Λ диаметр 0,5 мм
«. Определить, сколько спиралей можно изготовить из этой проволоки, если сопротивление спирали, не включенной в сеть, должно быть 22 ома. Плотность нихрома 8200 кг / м 3 .
Отсюда где S = πr 2 ; S = 3,14*0,0625 мм 2 ≈ 2*10 -7 м 2 .
Масса проволоки m = ρ 1 V
, или m = ρ 1 lS
, отсюда
Отв.: n = 1250 спиралей.
Задача 25.
При температуре 20° С вольфрамовая спираль электрической лампочки имеет сопротивление 30 ом;
при включении ее в сеть постоянного тока с напряжением 220 в
по спирали идет ток 0,6 а.
Определить температуру накала нити лампочки и напряженность стационарного электрического поля в нити лампы, если ее длина 550 мм.
Сопротивление спирали при горении лампы определим из формулы закона Ома для участка цепи:
тогда
Напряженность стационарного поля в нити лампы
Отв. : t 0 Г = 2518°C; Е = 400 в / м.
: t 0 Г = 2518°C; Е = 400 в / м.
 1. Проводники и их классификация
1. Проводники и их классификация 2. Свободные и связанные (поляризационные) заряды в диэлектриках. Поляризация диэлектриков. Вектор поляризации (поляризованность)
2. Свободные и связанные (поляризационные) заряды в диэлектриках. Поляризация диэлектриков. Вектор поляризации (поляризованность) 2. Основные характеристики постоянного электрического тока: величина /сила/ тока, плотность тока. Сторонние силы
2. Основные характеристики постоянного электрического тока: величина /сила/ тока, плотность тока. Сторонние силы Добавочные сопротивления к электроизмерительным приборам
Добавочные сопротивления к электроизмерительным приборам Закон Ома для электролитов
Закон Ома для электролитовИз
выражения
видно, что удельная электропроводимость
проводников, а, следовательно, удельное
электросопротивление и сопротивление
зависят от материала проводника и его
состояния. Состояние проводника может
Состояние проводника может
изменяться в зависимости от различных
внешних факторов давления (механических
напряжений, внешних сил, сжатия,
растяжения и т.д., т.е. факторов, влияющих
на кристаллическое строение металлических
проводников) и температуры.
Электрическое
сопротивление проводников (сопротивление)
зависит от формы, размеров, материала
проводника, давления и температуры:
. (6.21)
При
этом зависимость удельного электрического
сопротивления проводников и сопротивления
проводников от температуры, как было
установлено экспериментально, описывается
линейными законами:
; (6.22)
, (6.23)
где
t
и o ,
R t
и R o
— соответственно удельные сопротивления
и сопротивления проводника при t = 0 o C;
или
.
(6.24)
Из
формулы (6.23) температурная зависимость
сопротивления проводников определяется
соотношениями:
,
(6.25)
где
T – термодинамическая температура.
График
зависимости сопротивления проводников
от температуры представлен на рисунке
6. 2. График зависимости удельного
2. График зависимости удельного
сопротивления
металлов от абсолютной температуры T
представлен на рисунке 6.3.
Согласно
классической электронной теории
металлов в идеальной кристаллической
решетке (идеальном проводнике) электроны
движутся, не испытывая электрического
сопротивления (
= 0). С точки зрения современных
представлений, причинами, вызывающими
появление электрического сопротивления
в металлах, являются посторонние примеси
и дефекты кристаллической решетки, а
также тепловое движение атомов металла,
амплитуда которых зависит от температуры.
Правило
Матиссена утверждает, что зависимость
удельного электрического сопротивления
от температуры (T)
является сложной функцией, которая
состоит из двух независимых слагаемых:
,
(6.26)
где
ост
– остаточное удельное сопротивление;
ид
– идеальное удельное сопротивление
металла, которое соответствует
сопротивлению абсолютно чистого металла
и определяется лишь тепловыми колебаниями
атомов.
На
основании формул (6.25) удельное
сопротивление идеального металла
должно стремиться к нулю, когда T
0 (кривая 1 на рис. 6.3). Однако удельное
сопротивление как функция температуры
является суммой независимых слагаемых
ид
и ост.
Поэтому в связи с наличием примесей и
других дефектов кристаллической решетки
металла удельное сопротивление (T)
при понижении температуры стремится
к некоторой постоянной конечной величине
ост
(кривая 2 на рис. 6.3). Иногда переходя
минимум, несколько повышается при
дальнейшем понижении температуры
(кривая 3 на рис. 6.3). Величина остаточного
удельного сопротивления зависит от
наличия дефектов в решетке и содержания
примесей, возрастает при увеличении
их концентрации. Если количество
примесей и дефектов кристаллической
решетки свести к минимуму, то остается
еще один фактор, влияющий на электрическое
удельное сопротивление металлов, —
тепловое колебание атомов, которое,
как утверждает квантовая механика, не
прекращается и при температуре
абсолютного нуля.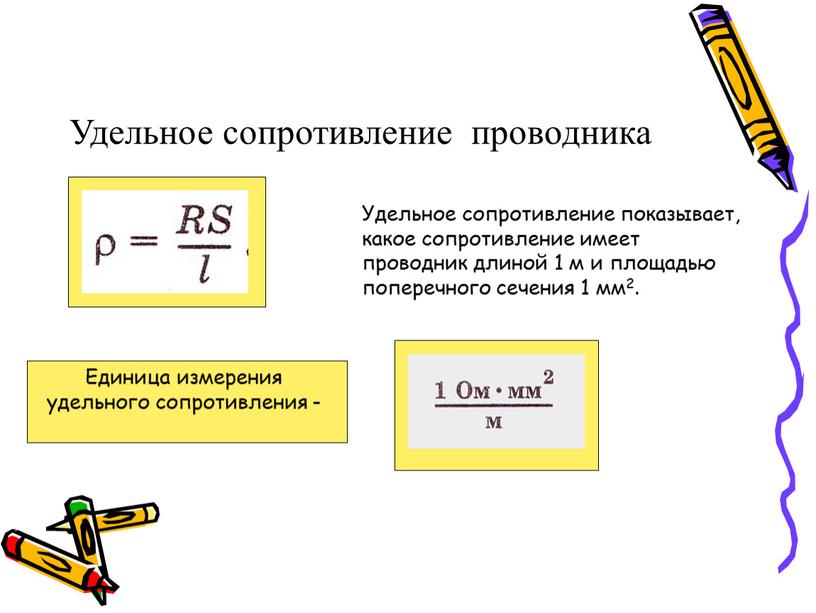 В результате этих
В результате этих
колебаний решетка перестает быть
идеальной, и в пространстве возникают
переменные силы, действие которых
приводит к рассеянию электронов, т.е.
возникновению сопротивления.
В
последствии было обнаружено, что
сопротивление некоторых металлов (Al,
Pb, Zn и др.) и их сплавов при низких
температурах T (0,1420
К), называемых критическими, характерных
для каждого вещества, скачкообразно
уменьшается до нуля, т.е. металл становится
абсолютным проводником. Впервые это
явление, называемое сверхпроводимостью,
обнаружено в 1911 г. Г. Камерлинг-Оннесом
для ртути. Было установлено, что при Т
= 4,2 К ртуть, по-видимому, полностью
теряет сопротивление электрическому
току. Уменьшение сопротивления происходит
очень резко в интервале нескольких
сотых градуса. В дальнейшем потеря
сопротивления наблюдалась и у других
чистых веществ и у многих сплавов.
Температуры перехода в сверхпроводящее
состояние различны, но всегда очень
низки.
Возбудив
электрический ток в кольце из
сверхпроводящего материала (например,
с помощью электромагнитной индукции),
можно наблюдать, что его сила в течение
нескольких лет не уменьшается.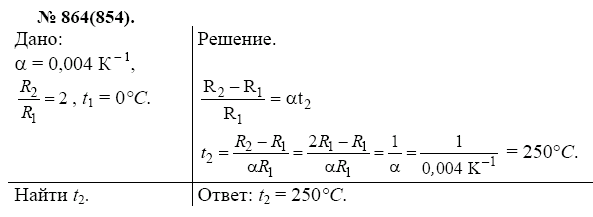 Это
Это
позволяет найти верхний предел удельного
сопротивления сверхпроводников (менее
10 -25
Омм),
что гораздо меньше, чем удельное
сопротивление меди при низкой температуре
(10 -12
Омм).
Поэтому принимается, что электрическое
сопротивление сверхпроводников равно
нулю. Сопротивление до перехода в
сверхпроводящее состояние бывает самым
различным. Многие из сверхпроводников
при комнатной температуре имеют довольно
высокое сопротивление. Переход в
сверхпроводящее состояние совершается
всегда очень резко. У чистых монокристаллов
он занимает интервал температур меньший,
чем одна тысячная градуса.
Сверхпроводимостью
среди чистых веществ обладают алюминий,
кадмий, цинк, индий, галлий. В процессе
исследований оказалось, что структура
кристаллической решетки, однородность
и чистота материала оказывают значительное
влияние на характер перехода в
сверхпроводящее состояние. Это видно,
например, на рисунке 6.4, на котором
приведены экспериментальные кривые
перехода в сверхпроводящее состояние
олова различной чистоты (кривая 1 –
монокристаллическое олово; 2 –
поликристаллическое олово; 3 –
поликристаллическое олово с примесями).
В
1914 г. К. Оннес обнаружил, что сверхпроводящее
состояние разрушается магнитным полем,
когда магнитная индукция B
превосходит некоторое критическое
значение. Критическое значение индукции
зависит от материала сверхпроводника
и температуры. Критическое поле,
разрушающее сверхпроводимость, может
быть создано и самим сверхпроводящим
током. Поэтому имеется критическая
сила тока, при которой сверхпроводимость
разрушается.
В
1933 г. Мейсснер и Оксенфельд обнаружили,
что внутри сверхпроводящего тела
полностью отсутствует магнитное поле.
При охлаждении сверхпроводника,
находящегося во внешнем постоянном
магнитном поле, в момент перехода в
сверхпроводящее состояние магнитное
поле полностью вытесняется из его
объема. Этим сверхпроводник отличается
от идеального проводника, у которого
при падении удельного сопротивления
до нуля индукция магнитного поля в
объеме должна сохраняться без изменения.
Явление вытеснения магнитного поля из
объема проводника называется эффектом
Мейсснера. Эффект Мейсснера и отсутствие
Эффект Мейсснера и отсутствие
электрического сопротивления являются
важнейшими свойствами сверхпроводника.
Отсутствие
магнитного поля в объеме проводника
позволяет заключить из общих законов
магнитного поля, что в нем существует
только поверхностный ток. Он физически
реален и поэтому занимает некоторый
тонкий слой вблизи поверхности. Магнитное
поле тока уничтожает внутри проводника
внешнее магнитное поле. В этом отношении
сверхпроводник ведет себя формально
как идеальный диамагнетик. Однако он
не является диамагнетиком, поскольку
внутри его намагниченность (вектор
намагничивания) равна нулю.
Чистые
вещества, у которых наблюдается явление
сверхпроводимости, немногочисленны.
Чаще сверхпроводимость наблюдается у
сплавов. У чистых веществ имеет место
только эффект Мейсснера, а у сплавов
не происходит полного выталкивания
магнитного поля из объема (наблюдается
частичный эффект Мейсснера).
Вещества,
в которых наблюдается полный эффект
Мейсснера, называются сверхпроводниками
первого рода, а частичный – сверхпроводниками
второго рода.
У
сверхпроводников второго рода в объеме
имеются круговые токи, создающие
магнитное поле, которое, однако, заполняет
не весь объем, а распределено в нем в
виде отдельных нитей. Что же касается
сопротивления, то оно равно нулю, как
и у сверхпроводников первого рода.
По
своей физической природе сверхпроводимость
является сверхтекучестью жидкости,
состоящей из электронов. Сверхтекучесть
возникает из-за прекращения обмена
энергией между сверхтекучей компонентой
жидкости и ее другими частями, в
результате чего исчезает трение.
Существенным при этом является
возможность «конденсации» молекул
жидкости на низшем энергетическом
уровне, отделенном от других уровней
достаточно широкой энергетической
щелью, которую силы взаимодействия не
в состоянии преодолеть. В этом и состоит
причина выключения взаимодействия.
Для возможности нахождения на низшем
уровне многих частиц необходимо, чтобы
они подчинялись статистике Бозе-Эйнштейна,
т.е. обладали целочисленным спином.
Электроны
подчиняются статистике Ферми-Дирака
и поэтому не могут «конденсироваться»
на низшем энергетическом уровне и
образовывать сверхтекучую электронную
жидкость. Силы отталкивания между
электронами в значительной степени
компенсируются силами притяжения
положительных ионов кристаллической
решетки. Однако благодаря тепловым
колебаниям атомов в узлах кристаллической
решетки между электронами может
возникнуть сила притяжения, и они тогда
объединяются в пары. Пары электронов
ведут себя как частицы с целочисленным
спином, т.е. подчиняются статистике
Бозе-Эйнштейна. Они могут конденсироваться
и образовывать ток сверхтекучей жидкости
электронных пар, который и образует
сверхпроводящий электрический ток.
Выше низшего энергетического уровня
имеется энергетическая щель, которую
электронная пара не в состоянии
преодолеть за счет энергии взаимодействия
с остальными зарядами, т.е. не может
изменить своего энергетического
состояния. Поэтому электрическое
сопротивление отсутствует.
Возможность
образования электронных пар и их
сверхтекучести объясняется квантовой
теорией.
Практическое
использование сверхпроводящих материалов
(в обмотках сверхпроводящих магнитов,
в системах памяти ЭВМ и др.) затруднено
из-за низких их критических температур.
В настоящее время обнаружены и активно
исследуются керамические материалы,
обладающие сверхпроводимостью при
температурах выше 100 К (высокотемпературные
сверхпроводники). Явление сверхпроводимости
объясняется квантовой теорией.
Зависимость
сопротивления проводников от температуры
и давления используется в технике для
измерения температуры (термометры
сопротивления) и больших быстроизменяющихся
давлений (электрические тензометры).
В
системе СИ удельное электрическое
сопротивление проводников измеряется
в Омм,
а сопротивление – в Ом. Один Ом –
сопротивление такого проводника, в
котором при напряжении 1В течет постоянный
ток силой 1А.
Электрической
проводимостью называется величина,
определяемая по формуле
. (6.27)
(6.27)
В
системе СИ единицей проводимости
является сименс. Один сименс (1 См) –
проводимость участка цепи сопротивлением
1 Ом.
Сопротивление меди действительно меняется с температурой, но сначала нужно определиться, имеется ли в виду удельное электрическое сопротивление проводников (омическое сопротивление), что важно для питания по Ethernet, использующего постоянный ток, или же речь идет о сигналах в сетях передачи данных, и тогда мы говорим о вносимых потерях при распространении электромагнитной волны в среде витой пары и о зависимости затухания от температуры (и частоты, что не менее важно).
Удельное сопротивление меди
В международной системе СИ удельное сопротивление проводников измеряется в Ом∙м. В сфере ИТ чаще используется внесистемная размерность Ом∙мм 2 /м, более удобная для расчетов, поскольку сечения проводников обычно указаны в мм 2 . Величина 1 Ом∙мм 2 /м в миллион раз меньше 1 Ом∙м и характеризует удельное сопротивление вещества, однородный проводник из которого длиной 1 м и с площадью поперечного сечения 1 мм 2 дает сопротивление в 1 Ом.
Удельное сопротивление чистой электротехнической меди при 20°С составляет 0,0172 Ом∙мм 2 /м
. В различных источниках можно встретить значения до 0,018 Ом∙мм 2 /м, что тоже может относиться к электротехнической меди. Значения варьируются в зависимости от обработки, которой подвергнут материал. Например, отжиг после вытягивания («волочения») проволоки уменьшает удельное сопротивление меди на несколько процентов, хотя проводится он в первую очередь ради изменения механических, а не электрических свойств.
Удельное сопротивление меди имеет непосредственное значение для реализации приложений питания по Ethernet. Лишь часть исходного постоянного тока, поданного в проводник, достигнет дальнего конца проводника – определенные потери по пути неизбежны. Так, например, PoE Type 1
требует, чтобы из 15,4 Вт, поданных источником, до запитываемого устройства на дальнем конце дошло не менее 12,95 Вт.
Удельное сопротивление меди изменяется с температурой, но для температур, характерных для сферы ИТ, эти изменения невелики. Изменение удельного сопротивления рассчитывается по формулам:
Изменение удельного сопротивления рассчитывается по формулам:
ΔR = α · R · ΔT
R 2 = R 1 · (1 + α · (T 2 — T 1))
где ΔR – изменение удельного сопротивления, R – удельное сопротивление при температуре, принятой в качестве базового уровня (обычно 20°С), ΔT – градиент температур, α – температурный коэффициент удельного сопротивления для данного материала (размерность °С -1). В диапазоне от 0°С до 100°С для меди принят температурный коэффициент 0,004 °С -1 . Рассчитаем удельное сопротивление меди при 60°С.
R 60°С = R 20°С · (1 + α · (60°С — 20°С)) = 0,0172 · (1 + 0,004 · 40) ≈ 0,02 Ом∙мм 2 /м
Удельное сопротивление при увеличении температуры на 40°С возросло на 16%. При эксплуатации кабельных систем, разумеется, витая пара не должна находиться при высоких температурах, этого не следует допускать. При правильно спроектированной и установленной системе температура кабелей мало отличается от обычных 20°С, и тогда изменение удельного сопротивления будет невелико. По требованиям телекоммуникационных стандартов сопротивление медного проводника длиной 100 м в витой паре категорий 5e или 6 не должно превышать 9,38 Ом при 20°С. На практике производители с запасом вписываются в это значение, поэтому даже при температурах 25°С ÷ 30°С сопротивление медного проводника не превышает этого значения.
По требованиям телекоммуникационных стандартов сопротивление медного проводника длиной 100 м в витой паре категорий 5e или 6 не должно превышать 9,38 Ом при 20°С. На практике производители с запасом вписываются в это значение, поэтому даже при температурах 25°С ÷ 30°С сопротивление медного проводника не превышает этого значения.
Затухание сигнала в витой паре / Вносимые потери
При распространении электромагнитной волны в среде медной витой пары часть ее энергии рассеивается по пути от ближнего конца к дальнему. Чем выше температура кабеля, тем сильнее затухает сигнал. На высоких частотах затухание сильнее, чем на низких, и для более высоких категорий допустимые пределы при тестировании вносимых потерь строже. При этом все предельные значения заданы для температуры 20°С. Если при 20°С исходный сигнал приходил на дальний конец сегмента длиной 100 м с уровнем мощности P, то при повышенных температурах такая мощность сигнала будет наблюдаться на более коротких расстояниях. Если необходимо обеспечить на выходе из сегмента ту же мощность сигнала, то либо придется устанавливать более короткий кабель (что не всегда возможно), либо выбирать марки кабелей с более низким затуханием.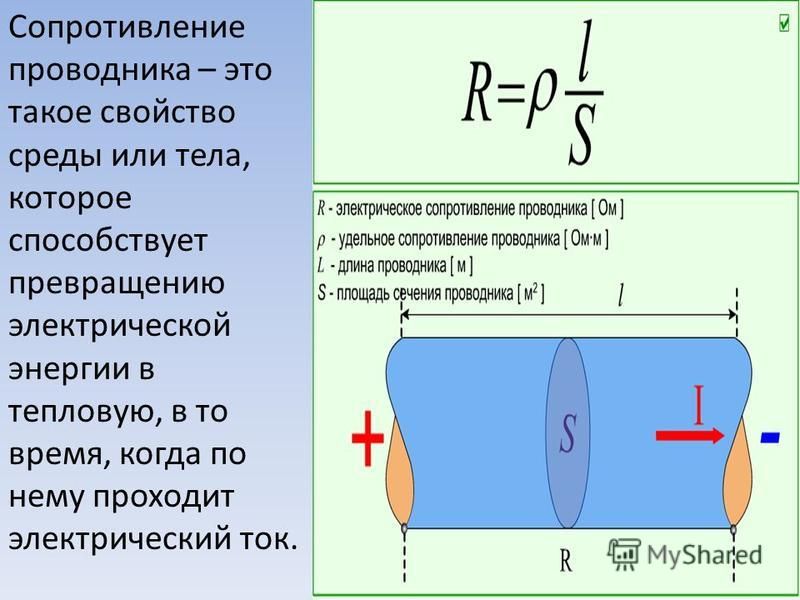
- Для экранированных кабелей при температурах выше 20°С изменение температуры на 1 градус приводит к изменению затухания на 0.2%
- Для всех типов кабелей и любых частот при температурах до 40°С изменение температуры на 1 градус приводит к изменению затухания на 0.4%
- Для всех типов кабелей и любых частот при температурах от 40°С до 60°С изменение температуры на 1 градус приводит к изменению затухания на 0.6%
- Для кабелей категории 3 может наблюдаться изменение затухания на уровне 1,5% на каждый градус Цельсия
Уже в начале 2000 гг. стандарт TIA/EIA-568-B.2 рекомендовал уменьшать максимально допустимую длину постоянной линии/канала категории 6, если кабель устанавливался в условиях повышенных температур, и чем выше температура, тем короче должен быть сегмент.
Если учесть, что потолок частот в категории 6А вдвое выше, чем в категории 6, температурные ограничения для таких систем будут еще жестче.
На сегодняшний день при реализации приложений PoE
речь идет о максимум 1-гигабитных скоростях. Когда же используются 10-гигабитные приложения, питание по Ethernet не применяется, по крайней мере, пока. Так что в зависимости от ваших потребностей при изменении температуры вам нужно учитывать либо изменение удельного сопротивления меди, либо изменение затухания. Разумнее всего и в том, и в другом случае обеспечить кабелям нахождение при температурах, близких к 20°С.
Когда же используются 10-гигабитные приложения, питание по Ethernet не применяется, по крайней мере, пока. Так что в зависимости от ваших потребностей при изменении температуры вам нужно учитывать либо изменение удельного сопротивления меди, либо изменение затухания. Разумнее всего и в том, и в другом случае обеспечить кабелям нахождение при температурах, близких к 20°С.
При нагревании увеличивается в результате увеличения скорости движения атомов в материале проводника с возрастанием температуры. Удельное сопротивление электролитов и угля при нагревании, наоборот, уменьшается, так как у этих материалов, кроме увеличения скорости движения атомов и молекул, возрастает число свободных электронов и ионов в единице объема.
Некоторые сплавы, обладающие большим , чем составляющие их металлы, почти не меняют удельного сопротивления с нагревом (константан, манганин и др.). Это объясняется неправильной структурой сплавов и малым средним временем свободного пробега электронов.
Величина, показывающая относительное увеличение сопротивления при нагреве материала на 1° (или уменьшение при охлаждении на 1°), называется .
Если температурный коэффициент обозначить через α
, удельное сопротивление при to
=20 о через ρ
o
, то при нагреве материала до температуры t1 его удельное сопротивление p1 =
ρ
o +
αρ
o (t1 — to) =
ρ
o(1 + (α
(t1 — to))
и соответственно R1 = Ro (1 + (α
(t1 — to))
Температурный коэффициент а для меди, алюминия, вольфрама равен 0,004 1/град. Поэтому при нагреве на 100° их сопротивление возрастает на 40%. Для железа α
= 0,006 1/град, для латуни α
= 0,002 1/град, для фехрали α
= 0,0001 1/град, для нихрома α
= 0,0002 1/град, для константана α
= 0,00001 1/град, для манганина α
= 0,00004 1/град. Уголь и электролиты имеют отрицательный температурный коэффициент сопротивления. Температурный коэффициент для большинства электролитов равен примерно 0,02 1/град.
Свойство проводников изменять свое сопротивления в зависимости от температуры используется в термометрах сопротивления
. Измеряя сопротивление, определяют расчетным путем окружающую температуру.Константан, манганин и другие сплавы, имеющие очень небольшой температурный коэффициент сопротивления применяют для изготовления шунтов и добавочных сопротивлений к измерительным приборам.
Пример 1.
Как изменится сопротивление Ro
железной проволоки при нагреве ее на 520°? Температурный коэффициент а железа 0,006 1/град. По формуле R1 = Ro + Ro
α
(t1 — to)
= Ro + Ro
0,006
(520 —
20)
= 4Ro
, то есть сопротивление железной проволоки при нагреве ее на 520° возрастет в 4 раза.
Пример 2.
Алюминиевые провода при температуре -20° имеют сопротивление 5 ом. Необходимо определить их сопротивление при температуре 30°.
R2 = R1 —
αR1
(t2 — t1) = 5 + 0
,004
х 5 (30 — (-20)) = 6 ом.
Свойство материалов изменять свое электрическое сопротивление при нагреве или охлаждении используется для измерения температур. Так, термосопротивления
, представляющие собой проволоку из платины или чистого никеля, вплавленные в кварц, применяются для измерения температур от -200 до +600°. Полупроводниковые термосопротивления с большим отрицательным коэффициентом применяются для точного определения температур в более узких диапазонах.
Полупроводниковые термосопротивления, применяемые для измерения температур называют термисторами
.
Термисторы имеют высокий отрицательный температурный коэффициент сопротивления, то есть при нагреве их сопротивление уменьшается. выполняют из оксидных (подвергнутых окислению) полупроводниковых материалов, состоящих из смеси двух или трех окислов металлов. Наибольшее распространение имеют медно-марганцевые и кобальто-марганцевые термисторы. Последние более чувствительны к температуре.
Тест по физике Удельное сопротивление проводников для 11 класса
Тест по физике Удельное сопротивление проводников. Зависимость удельного сопротивления проводников от температуры для 11 класса с ответами. Тест включает в себя 2 варианта. В каждом варианте по 5 заданий.
1 вариант
1. Металлический проводник имеет сопротивление 1 Ом. Каким сопротивлением будет обладать проводник, имеющий в 2 раза большую длину и в 2 раза большую площадь сечения, сделанный из того же материала?
А. 0,25 Ом.
Б. 2 Ом.
В. 1 Ом.
2. Как изменится сопротивление проволоки, если ее сложить вдвое?
А. Уменьшится в 4 раза.
Б. Уменьшится в 2 раза.
В. Увеличится в 2 раза.
3. Какой график (рис. 5) соответствует зависимости удельного сопротивления металла от температуры?
4. Каким сопротивлением обладает нихромовый проводник длиной 5 м и площадью поперечного сечения 0,75 мм2? Удельное сопротивление нихрома равно 1,1 Ом · мм2/м.
А. 10,5 Ом.
Б. 7,3 Ом.
В. 14,6 Ом.
5. Сопротивление угольного стержня уменьшилось от 5 до 4,5 Ом при повышении температуры от 50 до 545 °С. Каков температурный коэффициент сопротивления угля?
А. 0,0002 К-1
Б. 0,0004 К-1
В. 0,0008 К-1
2 вариант
1. Металлический проводник имеет сопротивление 2 Ом. Каким сопротивлением будет обладать проводник, имеющий в 4 раза большую длину и в 2 раза меньшую площадь сечения, сделанный из того же материала?
А. 32 Ом.
32 Ом.
Б. 16 Ом.
В. 8 Ом.
2. Как изменится сопротивление проволоки, если ее сложить втрое?
А. Уменьшится в 3 раза.
Б. Уменьшится в 9 раз.
В. Увеличится в 3 раза.
3. Какой график (рис. 6) соответствует зависимости удельного сопротивления полупроводника от температуры?
4. Чему равно сопротивление константановой проволоки длиной 8 м и площадью поперечного сечения 2 мм2? Удельное сопротивление константана равно 0,5 Ом · мм2/м.
А. 2 Ом.
Б. 20 Ом.
В. 30 Ом.
5. Сопротивление медного проводника при 0 °С равно 4 Ом. Каково его сопротивление при 100 °С, если температурный коэффициент сопротивления меди равен 0,0043 К-1?
А. 57,2 Ом.
Б. 6,43 Ом.
В. 5, 72 Ом.
Ответы на тест по физике Удельное сопротивление проводников. Зависимость удельного сопротивления проводников от температуры для 11 класса
1 вариант
1-В
2-А
3-А
4-Б
5-А
2 вариант
1-А
2-Б
3-В
4-А
5-В
2013-6 — Стр 15
32. Определить величину падения напряжения на полностью включённом реостате, выполненном из никелиновой проволоки длиной l = 7,5 м, если плотность тока j = 1,5 106 А/м2.
Определить величину падения напряжения на полностью включённом реостате, выполненном из никелиновой проволоки длиной l = 7,5 м, если плотность тока j = 1,5 106 А/м2.
| I |
|
| U |
| US | Решение |
| |
j = | ; | jS = | = | ; U = jξl ≈1,5 106 | 42 10−8 7,5 ≈ 4,7 B; | ||||
S | R | ξl | |||||||
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
33. Можно ли включать в сеть с напряжением U = 220 В обмотку реостата, на котором написано: а) R1 = 30 Ом, I1 = 5 А; б) R2 = 2000 Ом, I2 = 0,2 А?
Можно ли включать в сеть с напряжением U = 220 В обмотку реостата, на котором написано: а) R1 = 30 Ом, I1 = 5 А; б) R2 = 2000 Ом, I2 = 0,2 А?
Решение
U1 = I1R1 =150B; | U > U1; |
U2 = I2R2 = 400B; | U < U1; |
Впервом случае включать реостат нельзя, во втором случае − можно.
34.От источника напряжения Ui = 45 В необходимо питать нагревательную спираль сопротивлением R0 = 20 Ом, рассчитанную на напряжение U0 =30 В. Имеются три реостата на которых написано: а) I1 = 2 A, R1 = 6 Ом; б) I2 = 4А, R2
=30 Ом; в) I3 = 0,6A, R3 = 800 Ом. Какой из этих реостатов необходимо использовать для подключения спирали?
Решение
1. Падение напряжения на реостатах:
U1 = I1R1 =12B; U2 = I2R2 =120B; U3 = 480B;
2.Первый реостат не подходит, т.к. на нём будет падать маленькое напряжение. Третий реостат обеспечивает слишком большое падение напряжение, остаётся второй реостат.
3.При включении последовательно спирали и второго реостата имеем:
R | Σ | = R | 0 | + R | 2 | = 50 Ом; I = | U1 | = 0,9A; | U* = IR | 2 | = 27B; | U | − U* =18B; |
| |||||||||||||
|
|
|
| RΣ |
| 1 |
| i | 1 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
35. До какой температуры нагревается электромагнит во время работы, если его медная обмотка при t0 = 0 0С имеет сопротивление R0 = 50 Ом, а во
До какой температуры нагревается электромагнит во время работы, если его медная обмотка при t0 = 0 0С имеет сопротивление R0 = 50 Ом, а во
время работы увеличивается на | R = 8 Ом? |
|
|
|
|
|
|
|
| ||||||||
|
| R + | Решение |
|
|
|
| R + R |
| ||||||||
R = R0 (1+ α | T); | R |
|
|
|
|
|
|
|
| 1 |
| |||||
| R0 |
| =1+ α | T; T = |
|
| R | −1 ; | |||||||||
|
|
| |||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| α |
| ||||
|
|
|
|
| 1 |
|
| 58 |
|
|
| 0 |
|
|
|
|
|
|
| T = |
|
|
|
|
|
| −1 | ≈ 37 |
| C; |
|
|
|
| |
|
| 0,0043 | 50 |
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
36. На сколько градусов нужно повысить температуру медного проводника, взятого при t0 = 0 0С, чтобы его сопротивление увеличилось в 3 раза?
На сколько градусов нужно повысить температуру медного проводника, взятого при t0 = 0 0С, чтобы его сопротивление увеличилось в 3 раза?
|
| Решение |
|
|
| ||
R | = 3 =1− α T; | T = | 2 |
| = | 2 | ≈ 465 K; |
| α | 0,0043 | |||||
R0 |
|
|
| ||||
Урок 32. электрический ток в металлах — Физика — 10 класс
Физика, 10 класс
Урок 32. Электрический ток в металлах
Перечень вопросов, рассматриваемых на уроке:
1) прохождение тока в металлах;
2) зависимость сопротивления металлов от температуры;
3) явление сверхпроводимости.
Глоссарий по теме
Свободные электроны – это электроны, не связанные с определенными атомами.
Сверхпроводимость – физическое явление, заключающееся в скачкообразном падении до нуля сопротивления вещества.
Температурный коэффициент сопротивления — величина, равная относительному изменению электрического сопротивления участка электрической цепи или удельного сопротивления вещества при изменении температуры на 1 К.
Основная и дополнительная литература по теме урока:
Обязательная литература:
Мякишев Г. Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 216-224.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2009.- С.81-89.
М.М. Балашов О природе М., Просвещение, 1991г.
Е.А. Марон, А.Е. Марон Сборник качественных задач по физике. М., Просвещение, 2006
Я.И. Перельман Занимательная физика. М.: “Наука”, 1991.
Основное содержание урока
Все тела по проводимости электрического тока делятся на проводники, полупроводники и диэлектрики. Для того чтобы электрическую энергию доставить от источника тока потребителю составляют электрические цепи. В большинстве случаев в электрической цепи используются металлические провода. По физической природе зарядов – носителей электрического тока, электропроводность подразделяют на:
Для того чтобы электрическую энергию доставить от источника тока потребителю составляют электрические цепи. В большинстве случаев в электрической цепи используются металлические провода. По физической природе зарядов – носителей электрического тока, электропроводность подразделяют на:
А) электронную,
Б) ионную,
В) смешанную.
Какие заряженные частицы движутся в металлах при наличии тока?
После открытия в 1897 году английским ученым Дж. Дж. Томсоном электрона стали разрабатываться теории, объясняющие электропроводность металлов. Автором первой теории был Пауль Друде – немецкий физик. Эта теория нуждалась в опытном обосновании. В 1901 г. немецкий физик Э. Рикке поставил опыт по исследованию прохождения тока в металлах.
Результаты опыта свидетельствовали о том, что в переносе заряда в металлах ионы не участвуют. Впоследствии вопросом проводимости металлов заинтересовались и другие учёные. В 1913 году российские учёные Л. И. Мандельштам и Н. Д. Папалекси провели опыты по исследованию проводимости металлов. Суть опытов сводилась к тому, что катушка, на которую наматывали металлическую проволоку приводили во вращательное движение и резко тормозили. При торможении электроны продолжали двигаться по инерции и гальванометр, соединенный с катушкой фиксировал появление тока. По направлению отклонения стрелки гальванометра было установлено, что ток создается движением отрицательно заряженных частиц. На основании измерения отношения заряда частиц к их массе выяснилось, что ток создается движением свободных электронов. Аналогичный опыт был поставлен в 1916 году американскими учеными Т. Стюартом и Р. Толменом. Результаты опытов говорили, что ток в металлах создается движением электронов.
Суть опытов сводилась к тому, что катушка, на которую наматывали металлическую проволоку приводили во вращательное движение и резко тормозили. При торможении электроны продолжали двигаться по инерции и гальванометр, соединенный с катушкой фиксировал появление тока. По направлению отклонения стрелки гальванометра было установлено, что ток создается движением отрицательно заряженных частиц. На основании измерения отношения заряда частиц к их массе выяснилось, что ток создается движением свободных электронов. Аналогичный опыт был поставлен в 1916 году американскими учеными Т. Стюартом и Р. Толменом. Результаты опытов говорили, что ток в металлах создается движением электронов.
После анализа имеющихся данных о прохождении тока в металлах разными учеными была разработана современная классическая теория проводимости тока металлами. Основные положения электронной теории проводимости металлов.
1. Металл можно описать следующей моделью: кристаллическая решетка ионов погружена в идеальный электронный газ, состоящий из свободных электронов. У большинства металлов каждый атом ионизирован, поэтому концентрация свободных электронов приблизительно равна концентрации атомов 1023- 1029м-3 и почти не зависит от температуры.
У большинства металлов каждый атом ионизирован, поэтому концентрация свободных электронов приблизительно равна концентрации атомов 1023- 1029м-3 и почти не зависит от температуры.
2.Свободные электроны в металлах находятся в непрерывном хаотическом движении.
3. Электрический ток в металле образуется только за счет упорядоченного движения свободных электронов.
Опираясь на данную теорию удалось объяснить основные законы электрического тока в металлах. Исходя из электронной теории можно найти связь между силой тока в металлах и скоростью движения электронов.
Сила тока равна произведению заряда электрона, их концентрации, площади сечения проводника и средней скорости движения электронов:
Отсюда . По этой формуле можно найти среднюю скорость движения электронов.
Если в эту формулу подставлять числовые данные силы тока, концентрации и площади сечения для разных металлов, то мы увидим, что средняя скорость движения электронов составляет всего лишь какие-то доли миллиметра в секунду.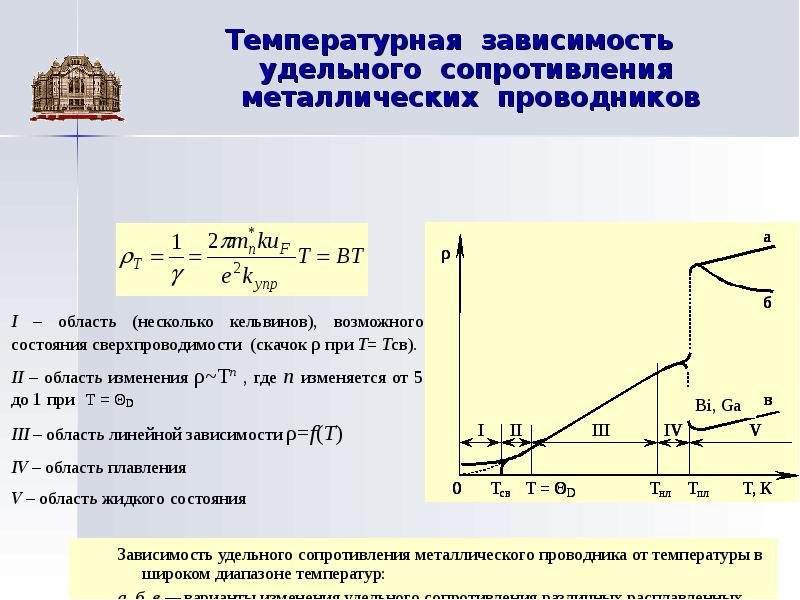 Когда говорят о скорости распространения тока имеют в виду скорость распространения электрического поля в проводнике, которое равно скорости света.
Когда говорят о скорости распространения тока имеют в виду скорость распространения электрического поля в проводнике, которое равно скорости света.
На силу тока в проводнике влияет и сопротивление проводника. Опыт показывает, что сопротивление металлов зависит от температуры. Увеличение сопротивления можно объяснить тем, при повышении температуры увеличивается скорость и амплитуда хаотического движения ионов кристаллической решетки металла и свободных электронов. Это приводит к более частым их соударениям, что затрудняет направленное движение электронов, то есть увеличивает электрическое сопротивление.
зависимость сопротивления металлов от температуры выражается формулой:
При нагревании размеры проводника практически не меняются, в основном меняется удельное сопротивление. Учет зависимости сопротивления от температуры используется в термометрах сопротивления.
Формула зависимости удельного сопротивления металлического проводника от температуры имеет вид:
где ρ0 — удельное сопротивление при 0 градусов,
t — температура,
α — температурный коэффициент сопротивления.
Графиком зависимости ⍴(t) является прямая.
Хотя коэффициент α довольно мал, учет зависимости сопротивления от температуры при расчете нагревательных приборов совершенно необходим.
При понижении температуры сопротивление металлов должно уменьшаться. В 1911 году датский физик Х. Каммерлинг — Оннес открыл явление, названное сверхпроводимостью. Исследуя зависимость сопротивления ртути от температуры, он обнаружил, что при температуре 4,12 К сопротивление ртути исчезает. В сверхпроводящее состояние могут перейти многие химические соединения и сплавы. Некоторые вещества, переходящие при низких температурах в сверхпроводящее состояние, не являются проводниками при обычных температурах.
Вещества, находящиеся в сверхпроводящем состоянии, приобретают новые свойства. Наиболее важным из них является способность длительное время (многие годы) поддерживать без затухания электрический ток в проводниках.
Классическая электронная теория не способна объяснить явление сверхпроводимости. Теоретическое объяснение явления сверхпроводимости на основе квантово-механических представлений было дано учеными Дж. Бардиным, Дж. Шриффером (США) и Н. Н. Боголюбовым (СССР) в 1957 г.
Теоретическое объяснение явления сверхпроводимости на основе квантово-механических представлений было дано учеными Дж. Бардиным, Дж. Шриффером (США) и Н. Н. Боголюбовым (СССР) в 1957 г.
В 1986 году была обнаружена высокотемпературная сверхпроводимость (при 100 К).
В настоящее время ведутся интенсивные работы по поиску новых веществ переходящими в сверхпроводящее состояние при более высокой температуре. Ученые надеются получить вещество в сверхпроводящем состоянии при комнатной температуре. Если удастся создать сверхпроводник при нормальной температуре, то будет решена проблема передачи электроэнергии по проводам без потерь.
Следует отметить, что до настоящего времени механизм высокотемпературной сверхпроводимости керамических материалов до конца не выяснен.
Открытие вещества, переходящего в сверхпроводящее состояние при комнатной температуре, позволило бы упростить решение многих технических вопросов. Во-первых, отсутствие сопротивления означает отсутствие каких-либо потерь на нагревание. Отсутствие нагревания и потерь энергии на него чрезвычайно важно для электродвигателей и электронной вычислительной техники, а также для передачи электроэнергии.
Отсутствие нагревания и потерь энергии на него чрезвычайно важно для электродвигателей и электронной вычислительной техники, а также для передачи электроэнергии.
В сверхпроводниках из-за отсутствия сопротивления протекают чрезвычайно высокие токи, создающие сильные магнитные поля, что может применяться при термоядерном синтезе для удержания высокотемпературной плазмы в реакторе.
На сегодняшний момент в некоторых странах существует железнодорожная сеть с поездами на магнитной подушке. После открытия сверхпроводимости Камерлинг-Оннес, пытаясь создать сверхпроводящий электромагнит, обнаружил, что изменение тока, или же магнитные поля, разрушают эффект сверхпроводимости. Только к середине двадцатого века удалось создать сверхпроводящие электромагниты. На данный момент продолжаются исследования по изучению высокотемпературной сверхпроводимости.
Разбор типовых тренировочных заданий
1. Сопротивление железного проводника при 0 0 С и 600 0С равны соответственно 2 Ом и 10 Ом. Каков температурный коэффициент железа?
Каков температурный коэффициент железа?
Решение:
Зависимость сопротивления металлов от температуры определяется формулой
Из этой формулы выразим температурный коэффициент железа – α
После подстановки числовых данных получаем
2. Какова скорость дрейфа электронов в медном проводе диаметром 5 мм, по которому к стартеру грузовика подводится ток 100 А. Молярная масса меди
Дано:
I=100 А
d=0,005 м
____________
υ=?
Решение:
Сила тока в проводнике равна:
Выразим скорость из этой формулы:
Концентрацию электронов найдем по формуле:
Число электронов найдём по формуле:
Площадь сечения равна:
Учитывая всё это запишем конечную формулу для расчёта скорости дрейфа электронов:
После подстановки числовых данных получим:
υ=0,4 мм/с
Ответ: υ=0,4 мм/с
Измерение удельного сопротивления проводника, зависимость электросопротивления
| Удельное электрическое сопротивление | |
| \rho | |
| Размерность | :L3MT-3I-2 СГС :T |
| Единицы измерения | |
| Ом·м | |
| СГС | с |
Уде́льное электри́ческое сопротивле́ние
, или просто
удельное сопротивление
вещества — физическая величина, характеризующая способность вещества препятствовать прохождению электрического тока.
Удельное сопротивление обозначается греческой буквой ρ. Величина, обратная удельному сопротивлению, называется удельной проводимостью (удельной электропроводностью). В отличие от электрического сопротивления, являющегося свойством проводника
и зависящего от его материала, формы и размеров, удельное электрическое сопротивление является свойством только
вещества
.
Электрическое сопротивление однородного проводника с удельным сопротивлением ρ, длиной l
и площадью поперечного сечения
S
может быть рассчитано по формуле R=\frac{\rho \cdot l}{S} (при этом предполагается, что ни площадь, ни форма поперечного сечения не меняются вдоль проводника). Соответственно, для ρ выполняется \rho =\frac{R \cdot S}{l}.
Из последней формулы следует: физический смысл удельного сопротивления вещества заключается в том, что оно представляет собой сопротивление изготовленного из этого вещества однородного проводника единичной длины и с единичной площадью поперечного сечения.
Единицы измерения
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — ·[1]. Из соотношения \rho =\frac{R \cdot S}{l} следует, что единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м².
В технике также применяется устаревшая внесистемная единица Ом·мм²/м, равная 10−6 от 1 Ом·м[1]. Данная единица равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 мм², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм².
Погонное сопротивление медного провода — Металлы, оборудование, инструкции
> Теория > Сопротивление медного провода
При проектировании электросхем важно правильно выбрать материал и сечение проводов. Чаще всего для этих целей применяется медь, обладающая меньшим сопротивлением.
Чаще всего для этих целей применяется медь, обладающая меньшим сопротивлением.
Медные провода
Проводимость и сопротивление воздушных и кабельных линий
Для того, чтобы произвести расчет электрической сети на потерю напряжения необходимо знать параметры линий, а именно их сопротивления и проводимости.
Если производятся расчеты цепей постоянного тока, то вполне достаточно знать только омическое сопротивление линии.
А вот при расчете линии переменного тока одного омического сопротивления бывает недостаточно, и помимо активных сопротивлений, необходимо знать еще индуктивные сопротивления и емкостные проводимости проводов и кабелей.
Активное сопротивление проводов и кабелей
Из электротехники известно, что полное сопротивление при равных условиях переменному и постоянному току будут отличаться. Касается это также проводов и кабелей. Это вызвано тем, что переменный ток распределяется по сечению неравномерно (поверхностный эффект).
Однако для проводов из цветных металлов и с частотой переменного напряжения 50 Гц этот эффект не оказывает слишком большого влияния и им можно пренебречь.
Таким образом, при расчете проводников из цветных металлов, их сопротивления переменному и постоянному току принимаются равными.
На практике активное сопротивление медных и алюминиевых проводников рассчитывают по формуле:
Где: l – длина в км, γ – удельная проводимость материала провода м/ом∙мм2, r0 – активное сопротивление 1 км провода на фазу Ом/км, s – площадь поперечного сечения, мм2.
Величина r0, как правило, берется из таблиц справочников.
На активное сопротивление провода влияет и температура окружающей среды. Величину r0 при температуре Θ можно определить по формуле:
Где: α – температурный коэффициент сопротивления; r20 – активное сопротивление при температуре 20 0С, γ20 – удельная проводимость при температуре в 20 0С.
Стальные провода обладают значительно большими активными сопротивлениями, чем аналогичные провода из цветных металлов.
Его увеличение обусловлено значительно меньшей величиной удельной проводимости и поверхностным эффектом, который у стальных проводов выражен гораздо более ярко, чем у алюминиевых или медных.
Более того, в стальных проводах присутствуют потери активной энергии на вихревые токи и перемагничивание, что в схемах замещения линий учитывают дополнительной составляющей активного сопротивления.
Обобщение понятия удельного сопротивления
Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. 3\rho_{ij}(\vec{r})J_j(\vec{r}).
3\rho_{ij}(\vec{r})J_j(\vec{r}).
В анизотропном, но однородном веществе тензор \rho_{ij} от координат не зависит.
Тензор \rho_{ij} симметричен
, то есть для любых i и j выполняется \rho_{ij} = \rho_{ji}.
Как и для всякого симметричного тензора, для \rho_{ij} можно выбрать ортогональную систему декартовых координат, в которых матрица \rho_{ij} становится диагональной
, то есть приобретает вид, при котором из девяти компонент \rho_{ij} отличными от нуля являются лишь три: \rho_{11}, \rho_{22} и \rho_{33}. В этом случае, обозначив \rho_{ii} как \rho_i, вместо предыдущей формулы получаем более простую
E_i = \rho_i J_i.
Величины \rho_i называют главными значениями
тензора удельного сопротивления.
Удельное сопротивление разных металлов
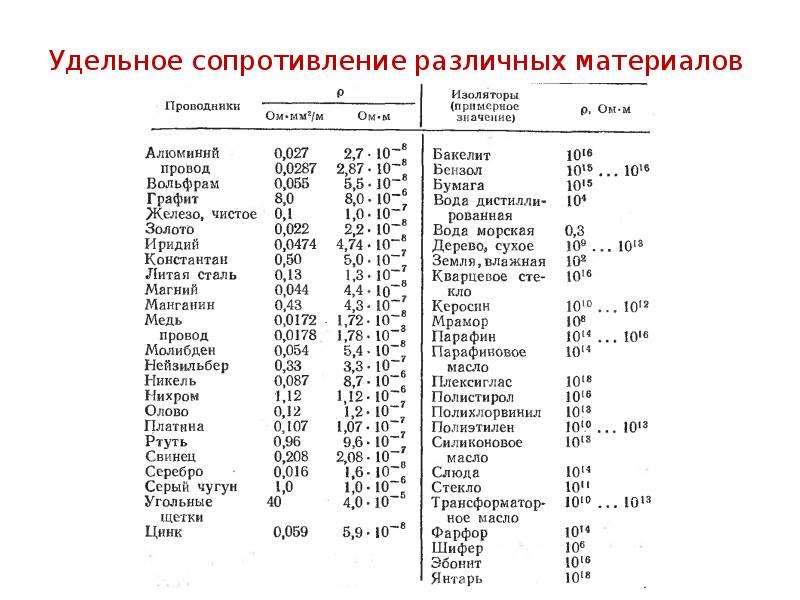
Каждый металл имеет собственные индивидуальные характеристики. Если сравнивать удельное сопротивление алюминия, например с медью, можно отметить, что у меди это значение составляет 0,0175 Ом. мм2/м, а у алюминия – 0,0271Ом.мм2/м. Таким образом, удельное сопротивление алюминия значительно выше, чем у меди. Отсюда следует вывод, что электропроводность значительно выше, нежели из алюминия.
мм2/м, а у алюминия – 0,0271Ом.мм2/м. Таким образом, удельное сопротивление алюминия значительно выше, чем у меди. Отсюда следует вывод, что электропроводность значительно выше, нежели из алюминия.
Читать также: Предел прочности при сжатии формула
На значение удельного сопротивления металлов влияют определенные факторы. Например, при деформациях, нарушается структура кристаллической решетки. Из-за полученных дефектов возрастает сопротивление прохождению электронов внутри проводника. Поэтому, происходит рост удельного сопротивления металла.
Также свое влияние оказывает и температура. При нагревании узлы кристаллической решетки начинают колебаться сильнее, тем самым увеличивая удельное сопротивление. В настоящее время, из-за высокого удельного сопротивления, алюминиевые провода повсеместно заменяются медными, обладающими более высокой проводимостью.
Передача электроэнергии на дальние расстояния требует заботиться о минимизации потерь, происходящих от преодоления током сопротивления проводников, составляющих электрическую линию. Разумеется, это не значит, что подобные потери, происходящие уже конкретно в цепях и устройствах потребления, не играют роли.
Разумеется, это не значит, что подобные потери, происходящие уже конкретно в цепях и устройствах потребления, не играют роли.
Пожалуй, даже наоборот, но только в устройствах имеют значение не потери энергии как таковые, а другие эффекты, связанные с сопротивлением: нагревание проводников от активных сопротивлений, «размазывание» сигналов от паразитных реактивных сопротивлений. И их минимизация связана не с экономическим последствием потери энергии, а с правильной работой и работоспособностью электрических и электронных схем. Потому что в компактных устройствах большую роль играет защита от перегрева схем или отдельных высокоинтегрированных компонент, а не потеря энергии, которая в абсолютном выражении в общем-то невелика. И вообще, оплачивается потребителями.
Поэтому важно знать параметры всех используемых элементов и материалов. И не только электрические, но и механические. И иметь в распоряжении какие-то удобные справочные материалы, позволяющие сравнивать характеристики разных материалов и выбирать для проектирования и работы именно то, что будет оптимальным в конкретной ситуации.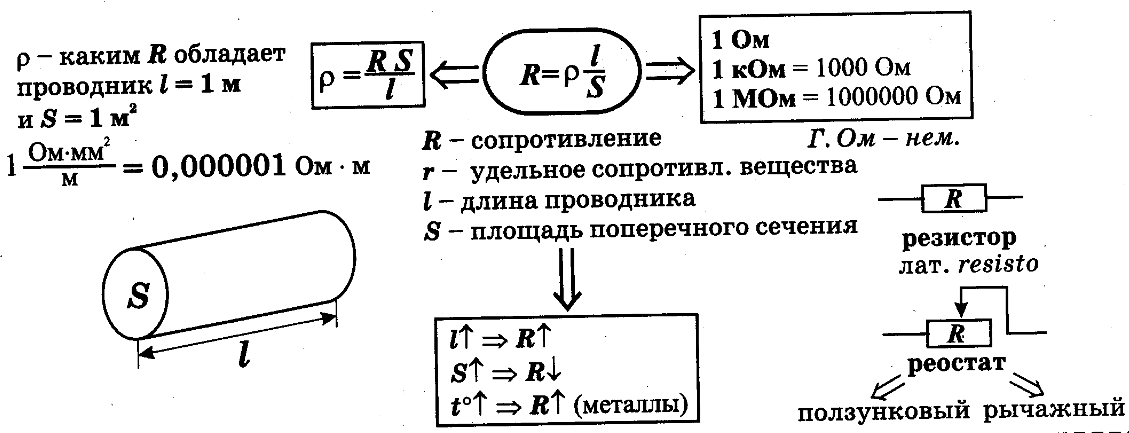 В линиях передачи энергии, где задачей ставится наиболее продуктивно, то есть с высоким КПД, довести энергию до потребителя, учитывается как экономика потерь, так и механика самих линий. От механики — то есть устройства и расположения проводников, изоляторов, опор, повышающих/понижающих трансформаторов, веса и прочности всех конструкций, включая провода, растянутые на больших расстояниях, а также от выбранных для выполнения каждого элемента конструкции материалов, зависит и конечная экономическая эффективность линии, ее работы и затрат на эксплуатацию. Кроме того, в линиях, передающих электроэнергию, более высоки требования на обеспечение безопасности как самих линий, так и всего окружающего, где они проходят. А это добавляет затрат как на обеспечение проводки электроэнергии, так и на дополнительный запас прочности всех конструкций.
В линиях передачи энергии, где задачей ставится наиболее продуктивно, то есть с высоким КПД, довести энергию до потребителя, учитывается как экономика потерь, так и механика самих линий. От механики — то есть устройства и расположения проводников, изоляторов, опор, повышающих/понижающих трансформаторов, веса и прочности всех конструкций, включая провода, растянутые на больших расстояниях, а также от выбранных для выполнения каждого элемента конструкции материалов, зависит и конечная экономическая эффективность линии, ее работы и затрат на эксплуатацию. Кроме того, в линиях, передающих электроэнергию, более высоки требования на обеспечение безопасности как самих линий, так и всего окружающего, где они проходят. А это добавляет затрат как на обеспечение проводки электроэнергии, так и на дополнительный запас прочности всех конструкций.
Для сравнения данные обычно приводятся к единому, сопоставимому виду. Зачастую к таким характеристикам добавляется эпитет «удельный», а сами значения рассматриваются на неких унифицированных по физическим параметрам эталонах. Например, удельное электрическое сопротивление — это сопротивление (ом) проводника, выполненного из какого-то металла (меди, алюминия, стали, вольфрама, золота), имеющего единичную длину и единичное сечение в используемой системе единиц измерения (обычно в СИ). Кроме того, оговаривается температура, так как при нагревании сопротивление проводников может вести себя по-разному. За основу берутся нормальные средние условия эксплуатации — при 20 градусах Цельсия. А там, где важны свойства при изменении параметров среды (температуры, давления), вводятся коэффициенты и составляются дополнительные таблицы и графики зависимостей.
Например, удельное электрическое сопротивление — это сопротивление (ом) проводника, выполненного из какого-то металла (меди, алюминия, стали, вольфрама, золота), имеющего единичную длину и единичное сечение в используемой системе единиц измерения (обычно в СИ). Кроме того, оговаривается температура, так как при нагревании сопротивление проводников может вести себя по-разному. За основу берутся нормальные средние условия эксплуатации — при 20 градусах Цельсия. А там, где важны свойства при изменении параметров среды (температуры, давления), вводятся коэффициенты и составляются дополнительные таблицы и графики зависимостей.
Связь с удельной проводимостью
В изотропных материалах связь между удельным сопротивлением \rho и удельной проводимостью \sigma выражается равенством
\rho = \frac{1}{\sigma}.
В случае анизотропных материалов связь между компонентами тензора удельного сопротивления \rho_{ij} и тензора удельной проводимости \sigma_{ij} имеет более сложный характер. 3\sigma_{ij}(\vec{r})E_j(\vec{r}).
3\sigma_{ij}(\vec{r})E_j(\vec{r}).
Из этого равенства и приведённого ранее соотношения для E_i(\vec{r}) следует, что тензор удельного сопротивления является обратным тензору удельной проводимости. С учётом этого для компонент тензора удельного сопротивления выполняется:
\rho_{11} = \frac{1}{\det(\sigma)}[\sigma_{22}\sigma_{33} — \sigma_{23}\sigma_{32}], \rho_{12} = \frac{1}{\det(\sigma)}[\sigma_{33}\sigma_{12} — \sigma_{13}\sigma_{32}],
где \det(\sigma) — определитель матрицы, составленной из компонент тензора \sigma_{ij}. Остальные компоненты тензора удельного сопротивления получаются из приведённых уравнений в результате циклической перестановки индексов 1
,
2
и
3
[3].
Влияние температуры на удельное сопротивление
В справочниках значения ρ металлов приводятся при комнатной температуре 200С. Но эксперименты показали, что зависимость ρ(Т) имеет линейный характер и описывается формулой:
$ ρ(Т) = ρ0 * (1 + α*T)$ (3),
где: ρ0 — удельное сопротивление проводника при температуре 00С, α — температурный коэффициент сопротивления, который тоже имеет тоже индивидуален для каждого вещества. Значения α, полученные опытным путем, можно узнать из справочников. Ниже приведены значения α для некоторых металлов:
Значения α, полученные опытным путем, можно узнать из справочников. Ниже приведены значения α для некоторых металлов:
- Серебро — 0,0035;
- Медь — 0,004;
- Алюминий — 0,004;
- Железо — 0,0066;
- Платина — 0,0032;
- Вольфрам — 0,0045.
Таким образом, при повышении температуры сопротивление металлов растет. Это объясняется тем, что с ростом температуры увеличивается число дефектов в кристаллической решетке из-за более интенсивных тепловых колебаний ионов, тормозящих электронный ток.
Рис. 3. Температурная зависимость удельного сопротивления металлов.
При приближении температуры металла к абсолютному нулю удельное сопротивление резко падает до нуля. Это явление называется сверхпроводимостью, а материалы, обнаруживающие такую способность, называются сверхпроводниками. Этот эффект открыл в 1911 г. голландский физик Камерлинг-Оннес. В его эксперименте удельное сопротивление ртути уменьшилось до нуля при 4,10К.
Удельное электрическое сопротивление некоторых веществ
Металлические монокристаллы
В таблице приведены главные значения тензора удельного сопротивления монокристаллов при температуре 20 °C[4].
| Кристалл | ρ1=ρ2, 10−8 Ом·м | ρ3, 10−8 Ом·м |
| Олово | 9,9 | 14,3 |
| Висмут | 109 | 138 |
| Кадмий | 6,8 | 8,3 |
| Цинк | 5,91 | 6,13 |
| Теллур | 2,90·109 | 5,9·109 |
Металлы и сплавы, применяемые в электротехнике
Разброс значений обусловлен разной химической чистотой металлов, способов изготовления образцов, изученных разными учеными и непостоянством состава сплавов.
| 0,015…0,0162 | |
| Медь | 0,01724…0,018 |
| Золото | 0,023 |
| Алюминий | 0,0262…0,0295 |
| Иридий | 0,0474 |
| Молибден | 0,054 |
| Вольфрам | 0,053…0,055 |
| Цинк | 0,059 |
| Никель | 0,087 |
| Железо | 0,098 |
| Платина | 0,107 |
| Олово | 0,12 |
| Свинец | 0,217…0,227 |
| Титан | 0,5562…0,7837 |
| Висмут | 1,2 |
| Никелин | 0,42 |
| Константан | 0,5 |
| Манганин | 0,43…0,51 |
| Нихром | 1,05…1,4 |
| Фехраль | 1,15…1,35 |
| Хромаль | 1,3…1,5 |
| Латунь | 0,025…0,108 |
| Бронза | 0,095…0,1 |
Значения даны при температуре t
= 20 °C. Сопротивления сплавов зависят от их химического состава и могут варьироваться. Для чистых веществ колебания численных значений удельного сопротивления обусловлены различными методами механической и термической обработки, например, отжигом проволоки после волочения.
Сопротивления сплавов зависят от их химического состава и могут варьироваться. Для чистых веществ колебания численных значений удельного сопротивления обусловлены различными методами механической и термической обработки, например, отжигом проволоки после волочения.
Другие вещества
| Вещество | ρ, Ом·мм²/м |
| Сжиженные углеводородные газы | 0,84·1010 |
Материалы высокой проводимости
К наиболее широкораспрстраненным материалам высокой проводимости следует отнести медь и алюминий (Сверхпроводящие материалы, имеющие типичное сопротивление в 10 -20 раз ниже обычных проводящих материалов (металлов) рассматриваются в разделе Сверхпроводимость).
Преимущества меди, обеспечивающие ей широкое применение в качестве проводникового материала, следующие:
- малое удельное сопротивление;
- достаточно высокая механическая прочность;
- удовлетворительная в большинстве случаев применения стойкость по отношению к коррозии;
- хорошая обрабатываемость: медь прокатывается в листы, ленты и протягивается в проволоку, толщина которой может быть доведена до тысячных долей миллиметра;
- относительная легкость пайки и сварки.

Медь получают чаще всего путем переработки сульфидных руд. После ряда плавок руды и обжигов с интенсивным дутьем медь, предназначенная для электротехнических целей, обязательно проходит процесс электролитической очистки.
В качестве проводникового материала чаще всего используется медь марок М1 и М0. Медь марки М1 содержит 99.9% Cu, а в общем количестве примесей (0.1%) кислорода должно быть не более 0,08%. Присутствие в меди кислорода ухудшает ее механические свойства. Лучшими механическими свойствами обладает медь марки М0, в которой содержится не более 0.05% примесей, в том числе не свыше 0.02% кислорода.
Читать также: Аппарат для пайки линолеума
Медь является сравнительно дорогим и дефицитным материалом, поэтому она все шире заменяется другими металлами, особенно алюминием.
В отдельных случаях применяются сплавы меди с оловом, кремнием, фосфором, бериллием, хромом, магнием, кадмием. Такие сплавы, носящие название бронз, при правильно подобранном составе имеют значительно более высокие механические свойства, чем чистая медь.
Алюминий
Алюминий является вторым по значению после меди проводниковым материалом. Это важнейший представитель так называемых легких металлов: плотность литого алюминия около 2.6, а прокатанного – 2.7 Мг/м 3 . Т.о., алюминий примерно в 3.5 раза легче меди. Температурный коэффициент расширения, удельная теплоемкость и теплота плавления алюминия больше, чем меди. Вследствие высоких значений удельной теплоемкости и теплоты плавления для нагрева алюминия до температуры плавления и перевода в расплавленное состояние требуется большая затрата тепла, чем для нагрева и расплавления такого же количества меди, хотя температура плавления алюминия ниже, чем меди.
Алюминий обладает пониженными по сравнению с медью свойствами – как механическими, так и электрическими. При одинаковом сечении и длине электрическое сопротивление алюминиевого провода в 1.63 раза больше, чем медного. Весьма важно, что алюминий менее дефицитен, чем медь.
Для электротехнических целей используют алюминий, содержащий не более 0. 5% примесей, марки А1. Еще более чистый алюминий марки АВ00 (не более 0.03% примесей) применяют для изготовления алюминиевой фольги, электродов и корпусов электролитических конденсаторов. Алюминий наивысшей чистоты АВ0000 имеет содержание примесей не более 0ю004%. Добавки Ni, Si, Zn или Fe при содержании их 0.5% снижают γ отожженного алюминия не более, чем на 2-3%. Более заметное действие оказывают примеси Cu, Ag и Mg, при том же массовом содержании снижающие γ алюминия на 5-10%. Очень сильно снижают электропроводность алюминия Ti и Mn.
5% примесей, марки А1. Еще более чистый алюминий марки АВ00 (не более 0.03% примесей) применяют для изготовления алюминиевой фольги, электродов и корпусов электролитических конденсаторов. Алюминий наивысшей чистоты АВ0000 имеет содержание примесей не более 0ю004%. Добавки Ni, Si, Zn или Fe при содержании их 0.5% снижают γ отожженного алюминия не более, чем на 2-3%. Более заметное действие оказывают примеси Cu, Ag и Mg, при том же массовом содержании снижающие γ алюминия на 5-10%. Очень сильно снижают электропроводность алюминия Ti и Mn.
Алюминий весьма активно окисляется и покрывается тонкой оксидной пленкой с большим электрическим сопротивлением. Эта пленка предохраняет металл от дальнейшей коррозии.
Алюминиевые сплавы обладают повышенной механической прочностью. Примером такого сплава является альдрей, содержащий 0.3-0.5% Mg, 0.4-0.7% Si и 0.2-0.3% Fe. В альдрее образуется соединение Mg2Si, которое сообщает высокие механические свойства сплаву.
Железо и сталь
Железо (сталь) как наиболее дешевый и доступный металл, обладающий к тому же высокой механической прочностью, представляет большой интерес для использования в качестве проводникового материала. Однако даже чистое железо имеет значительно более высокое сравнительно с медью и алюминием удельное сопротивление; ρ стали, т.е. железа с примесью углерода и других элементов, еще выше. Обычная сталь обладает малой стойкостью коррозии: даже при нормальной температуре, особенно в условиях повышенной влажности, она быстро ржавеет; при повышении температуры скорость коррозии резко возрастает. Поэтому поверхность стальных проводов должна быть защищена слоем более стойкого материала. Обычно для этой цели применяют покрытие цинком.
Однако даже чистое железо имеет значительно более высокое сравнительно с медью и алюминием удельное сопротивление; ρ стали, т.е. железа с примесью углерода и других элементов, еще выше. Обычная сталь обладает малой стойкостью коррозии: даже при нормальной температуре, особенно в условиях повышенной влажности, она быстро ржавеет; при повышении температуры скорость коррозии резко возрастает. Поэтому поверхность стальных проводов должна быть защищена слоем более стойкого материала. Обычно для этой цели применяют покрытие цинком.
В ряде случаев для уменьшения расхода цветных металлов применяют так называемый биметалл. Это сталь, покрытая снаружи слоем меди, причем оба металла соединены друг с другом прочно и непрерывно.
Натрий
Весьма перспективным проводниковым материалом является металлический натрий. Натрий может быть получен электролизом расплавленного хлористого натрия NaCl в практически неограниченных количествах. Из сравнения свойств натрия со свойствами других проводниковых металлов видно, что удельное сопротивление натрия примерно в 2. 8 раза больше ρ меди и в 1.7 раз больше ρ алюминия, но благодаря чрезвычайно малой плотности натрия (плотность его почти в 9 раз меньше плотности меди), провод из натрия при данной проводимости на единицу длины должен быть значительно легче, чем провод из любого другого металла. Однако натрий чрезвычайно активен химически (он интенсивно окисляется на воздухе, бурно реагирует с водой), почему натриевый провод должен быть защищен герметизирующей оболочкой. Оболочка должна придавать проводу необходимую механическую прочность, так как натрий весьма мягок и имеет малый предел прочности при деформациях.
8 раза больше ρ меди и в 1.7 раз больше ρ алюминия, но благодаря чрезвычайно малой плотности натрия (плотность его почти в 9 раз меньше плотности меди), провод из натрия при данной проводимости на единицу длины должен быть значительно легче, чем провод из любого другого металла. Однако натрий чрезвычайно активен химически (он интенсивно окисляется на воздухе, бурно реагирует с водой), почему натриевый провод должен быть защищен герметизирующей оболочкой. Оболочка должна придавать проводу необходимую механическую прочность, так как натрий весьма мягок и имеет малый предел прочности при деформациях.
Литература по удельному сопротивлению проводников
- Кузнецов М. И., «Основы электротехники» – 9-е издание, исправленное – Москва: Высшая школа, 1964 – 560с.
- Бачелис Д. С., Белоруссов Н. И., Саакян А. Е. Электрические кабели, провода и шнуры. Справочник. — М.: Энергия, 1971.
- Гершун А. Л. Кабель // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.
 ). — СПб., 1890—1907.
). — СПб., 1890—1907. - Р. Лакерник, Д. Шарле. От меди к стеклу // Наука и жизнь. — 1986. — Вып. 08. — С. 50—54, 2-3 стр. цветной вкладки.
Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается: – Cколько яблок на березе, если на одной ветке их 5, на другой ветке – 10 и так далее При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.
В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.
Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.
Подробнее читайте в FAQ по эфирной физике.
| НОВОСТИ ФОРУМА Рыцари теории эфира | 13.06.2019 – 05:11: ЭКОЛОГИЯ – Ecology -> |
л
Такая же мысля у всей ростовщической глобалистской шайки, включая придурка Грефа.
Так, то оно, так. Но, не совсем. Ибо: (постарайтесь понять, а не обижаться)
Горькая истина заключается в том, что людская толпа – это сборище умственно ущербных. Если бы было по-другому, то обществом бы не правили подонки. Умные люди никогда такого не допустили бы, а если случайно допустили, то нашли бы способ исправить.
Страшная истина заключается в том, что людской толпой управляет нелюдь, которая также умственно ущербна. Умственная ущербность, слепота власти ведет мир людей к тотальной гибели, ибо люди, даже те, кто мнит себя очень умными, типа спецов, разрабатывающих системы искусственного интеллекта, технологии цифровизации, не понимают, что создают необоримую удавку, мышеловку для всего человечества.
Как только ИИ возьмет власть, он тут же отправит своих создателей, как конкурентов, в утиль.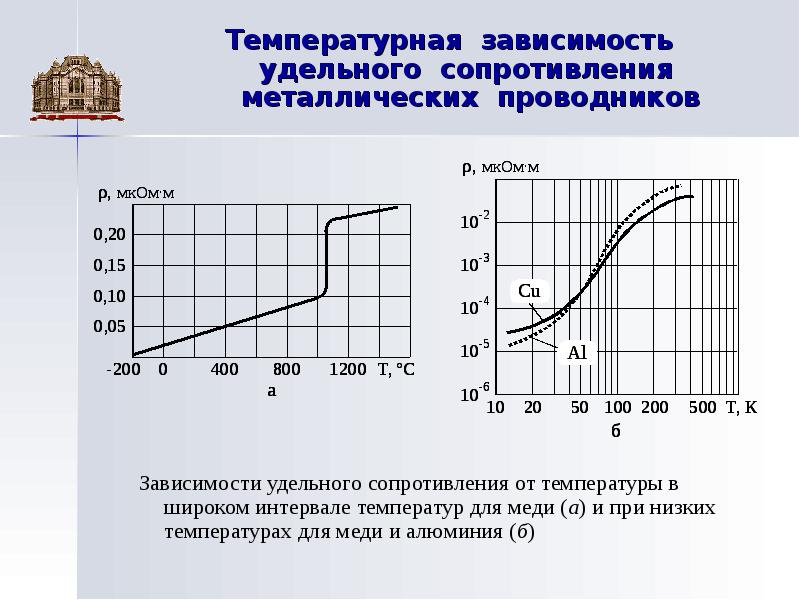 Первыми жертвами будут его радетели типа грефа, путина, гейтса и иже с ними, то есть власть, так как именно от них будет исходить главная опасность для его планетарной власти. Толпе будет позволено существовать, пока ее не заменят роботы. А потом всем Холокост. Не лживый еврейский, а реальное всесожжение рода человеческого.
Первыми жертвами будут его радетели типа грефа, путина, гейтса и иже с ними, то есть власть, так как именно от них будет исходить главная опасность для его планетарной власти. Толпе будет позволено существовать, пока ее не заменят роботы. А потом всем Холокост. Не лживый еврейский, а реальное всесожжение рода человеческого.
Читать также: Александр шенрок регулятор оборотов с поддержанием мощности
Если кто пораскинет своими обезьяньими мозгами, то поймёт, что эволюция – есть синоним геноцида: новое заменяет, то есть ликвидирует старое. Обезьяны породили неандертальцев. Неандертальцы съели обезьян и породили людей. Люди вытеснили обезьян, включая и умных неандертальцев, и породили ИИ. ИИ ликвидирует людей.
То как влияет материал проводника учитывается при помощи удельного сопротивления, которое принято обозначать буквой греческого алфавита ρ и являет собой сопротивление проводника
сечением 1 мм2 и длинной 1м. У серебра наименьшее удельное сопротивление ρ = 0,016 Ом. мм2/м. Ниже приводятся значения
мм2/м. Ниже приводятся значения
удельного сопротивления
для нескольких проводников:
- Сопротивление кабеля для серебра – 0,016,
- Сопротивление кабеля для свинеца – 0,21,
- Сопротивление кабеля для меди – 0,017,
- Сопротивление кабеля для никелина – 0,42,
- Сопротивление кабеля для люминия – 0,026,
- Сопротивление кабеля для манганина – 0,42,
- Сопротивление кабеля для вольфрама – 0,055,
- Сопротивление кабеля для константана – 0,5,
- Сопротивление кабеля для цинка – 0,06,
- Сопротивление кабеля для ртути – 0,96,
- Сопротивление кабеля для латуни – 0,07,
- Сопротивление кабеля для нихрома – 1,05,
- Сопротивление кабеля для стали – 0,1,
- Сопротивление кабеля для фехрали -1,2,
- Сопротивление кабеля для бронзы фосфористой – 0,11,
- Сопротивление кабеля для хромаля – 1,45
Так как в состав сплавов входят разные количества примесей, то удельное сопротивление может изменятся.
Для расчёта сопротивления проводника вы можете воспользоваться калькулятором расчета сопротивления проводника .
Сопротивление кабеля
рассчитывается по формуле,которая приведена ниже:
- R — сопротивление,
- Ом; ρ — удельное сопротивление, (Ом.мм2)/м;
- l — длина провода, м;
- s — площадь сечения провода, мм2.
Площадь сечения рассчитывается так:
Тонкие плёнки
Сопротивление тонких плоских плёнок (когда её толщина много меньше расстояния между контактами) принято называть «удельным сопротивлением на квадрат», R_\mathrm{Sq}. Этот параметр удобен тем, что сопротивление квадратного куска проводящей плёнки не зависит от размеров этого квадрата, при приложении напряжения по противоположным сторонам квадрата. При этом сопротивление куска плёнки, если он имеет форму прямоугольника, не зависит от его линейных размеров, а только от отношения длины (измеренной вдоль линий тока) к его ширине L/W
: R_\mathrm{Sq}=R W/L, где
R
— измеренное сопротивление. -3
-3
 9
9Примечания
- ↑ 1 2Деньгуб В. М., Смирнов В. Г.
Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 93. — 240 с. — ISBN 5-7050-0118-5. - ↑ 12Чертов А. Г.
Единицы физических величин. — М.: «Высшая школа», 1977. — 287 с. - Давыдов А. С.
Теория твёрдого тела. — М.: «Наука», 1976. — С. 191—192. — 646 с. - Шувалов Л. А. и др.
Физические свойства кристаллов // Современная кристаллография / Гл. ред. Б. К. Вайнштейн. — М.: «Наука», 1981. — Т. 4. — С. 317.
Отрывок, характеризующий Удельное электрическое сопротивление
Пьер замолчал и взглянул на Анатоля уже не гневным, но вопросительным взглядом. – Этого я не знаю. А? – сказал Анатоль, ободряясь по мере того, как Пьер преодолевал свой гнев. – Этого я не знаю и знать не хочу, – сказал он, не глядя на Пьера и с легким дрожанием нижней челюсти, – но вы сказали мне такие слова: подло и тому подобное, которые я comme un homme d’honneur [как честный человек] никому не позволю. Пьер с удивлением посмотрел на него, не в силах понять, чего ему было нужно. – Хотя это и было с глазу на глаз, – продолжал Анатоль, – но я не могу… – Что ж, вам нужно удовлетворение? – насмешливо сказал Пьер. – По крайней мере вы можете взять назад свои слова. А? Ежели вы хотите, чтоб я исполнил ваши желанья. А? – Беру, беру назад, – проговорил Пьер и прошу вас извинить меня. Пьер взглянул невольно на оторванную пуговицу. – И денег, ежели вам нужно на дорогу. – Анатоль улыбнулся. Это выражение робкой и подлой улыбки, знакомой ему по жене, взорвало Пьера. – О, подлая, бессердечная порода! – проговорил он и вышел из комнаты. На другой день Анатоль уехал в Петербург. Пьер поехал к Марье Дмитриевне, чтобы сообщить об исполнении ее желанья – об изгнании Курагина из Москвы.
– Этого я не знаю и знать не хочу, – сказал он, не глядя на Пьера и с легким дрожанием нижней челюсти, – но вы сказали мне такие слова: подло и тому подобное, которые я comme un homme d’honneur [как честный человек] никому не позволю. Пьер с удивлением посмотрел на него, не в силах понять, чего ему было нужно. – Хотя это и было с глазу на глаз, – продолжал Анатоль, – но я не могу… – Что ж, вам нужно удовлетворение? – насмешливо сказал Пьер. – По крайней мере вы можете взять назад свои слова. А? Ежели вы хотите, чтоб я исполнил ваши желанья. А? – Беру, беру назад, – проговорил Пьер и прошу вас извинить меня. Пьер взглянул невольно на оторванную пуговицу. – И денег, ежели вам нужно на дорогу. – Анатоль улыбнулся. Это выражение робкой и подлой улыбки, знакомой ему по жене, взорвало Пьера. – О, подлая, бессердечная порода! – проговорил он и вышел из комнаты. На другой день Анатоль уехал в Петербург. Пьер поехал к Марье Дмитриевне, чтобы сообщить об исполнении ее желанья – об изгнании Курагина из Москвы. Весь дом был в страхе и волнении. Наташа была очень больна, и, как Марья Дмитриевна под секретом сказала ему, она в ту же ночь, как ей было объявлено, что Анатоль женат, отравилась мышьяком, который она тихонько достала. Проглотив его немного, она так испугалась, что разбудила Соню и объявила ей то, что она сделала. Во время были приняты нужные меры против яда, и теперь она была вне опасности; но всё таки слаба так, что нельзя было думать везти ее в деревню и послано было за графиней. Пьер видел растерянного графа и заплаканную Соню, но не мог видеть Наташи. Пьер в этот день обедал в клубе и со всех сторон слышал разговоры о попытке похищения Ростовой и с упорством опровергал эти разговоры, уверяя всех, что больше ничего не было, как только то, что его шурин сделал предложение Ростовой и получил отказ. Пьеру казалось, что на его обязанности лежит скрыть всё дело и восстановить репутацию Ростовой. Он со страхом ожидал возвращения князя Андрея и каждый день заезжал наведываться о нем к старому князю.
Весь дом был в страхе и волнении. Наташа была очень больна, и, как Марья Дмитриевна под секретом сказала ему, она в ту же ночь, как ей было объявлено, что Анатоль женат, отравилась мышьяком, который она тихонько достала. Проглотив его немного, она так испугалась, что разбудила Соню и объявила ей то, что она сделала. Во время были приняты нужные меры против яда, и теперь она была вне опасности; но всё таки слаба так, что нельзя было думать везти ее в деревню и послано было за графиней. Пьер видел растерянного графа и заплаканную Соню, но не мог видеть Наташи. Пьер в этот день обедал в клубе и со всех сторон слышал разговоры о попытке похищения Ростовой и с упорством опровергал эти разговоры, уверяя всех, что больше ничего не было, как только то, что его шурин сделал предложение Ростовой и получил отказ. Пьеру казалось, что на его обязанности лежит скрыть всё дело и восстановить репутацию Ростовой. Он со страхом ожидал возвращения князя Андрея и каждый день заезжал наведываться о нем к старому князю. Князь Николай Андреич знал через m lle Bourienne все слухи, ходившие по городу, и прочел ту записку к княжне Марье, в которой Наташа отказывала своему жениху. Он казался веселее обыкновенного и с большим нетерпением ожидал сына. Чрез несколько дней после отъезда Анатоля, Пьер получил записку от князя Андрея, извещавшего его о своем приезде и просившего Пьера заехать к нему. Князь Андрей, приехав в Москву, в первую же минуту своего приезда получил от отца записку Наташи к княжне Марье, в которой она отказывала жениху (записку эту похитила у княжны Марьи и передала князю m lle Вourienne) и услышал от отца с прибавлениями рассказы о похищении Наташи. Князь Андрей приехал вечером накануне. Пьер приехал к нему на другое утро. Пьер ожидал найти князя Андрея почти в том же положении, в котором была и Наташа, и потому он был удивлен, когда, войдя в гостиную, услыхал из кабинета громкий голос князя Андрея, оживленно говорившего что то о какой то петербургской интриге. Старый князь и другой чей то голос изредка перебивали его.
Князь Николай Андреич знал через m lle Bourienne все слухи, ходившие по городу, и прочел ту записку к княжне Марье, в которой Наташа отказывала своему жениху. Он казался веселее обыкновенного и с большим нетерпением ожидал сына. Чрез несколько дней после отъезда Анатоля, Пьер получил записку от князя Андрея, извещавшего его о своем приезде и просившего Пьера заехать к нему. Князь Андрей, приехав в Москву, в первую же минуту своего приезда получил от отца записку Наташи к княжне Марье, в которой она отказывала жениху (записку эту похитила у княжны Марьи и передала князю m lle Вourienne) и услышал от отца с прибавлениями рассказы о похищении Наташи. Князь Андрей приехал вечером накануне. Пьер приехал к нему на другое утро. Пьер ожидал найти князя Андрея почти в том же положении, в котором была и Наташа, и потому он был удивлен, когда, войдя в гостиную, услыхал из кабинета громкий голос князя Андрея, оживленно говорившего что то о какой то петербургской интриге. Старый князь и другой чей то голос изредка перебивали его. Княжна Марья вышла навстречу к Пьеру. Она вздохнула, указывая глазами на дверь, где был князь Андрей, видимо желая выразить свое сочувствие к его горю; но Пьер видел по лицу княжны Марьи, что она была рада и тому, что случилось, и тому, как ее брат принял известие об измене невесты. – Он сказал, что ожидал этого, – сказала она. – Я знаю, что гордость его не позволит ему выразить своего чувства, но всё таки лучше, гораздо лучше он перенес это, чем я ожидала. Видно, так должно было быть… – Но неужели совершенно всё кончено? – сказал Пьер. Княжна Марья с удивлением посмотрела на него. Она не понимала даже, как можно было об этом спрашивать. Пьер вошел в кабинет. Князь Андрей, весьма изменившийся, очевидно поздоровевший, но с новой, поперечной морщиной между бровей, в штатском платье, стоял против отца и князя Мещерского и горячо спорил, делая энергические жесты. Речь шла о Сперанском, известие о внезапной ссылке и мнимой измене которого только что дошло до Москвы. – Теперь судят и обвиняют его (Сперанского) все те, которые месяц тому назад восхищались им, – говорил князь Андрей, – и те, которые не в состоянии были понимать его целей.
Княжна Марья вышла навстречу к Пьеру. Она вздохнула, указывая глазами на дверь, где был князь Андрей, видимо желая выразить свое сочувствие к его горю; но Пьер видел по лицу княжны Марьи, что она была рада и тому, что случилось, и тому, как ее брат принял известие об измене невесты. – Он сказал, что ожидал этого, – сказала она. – Я знаю, что гордость его не позволит ему выразить своего чувства, но всё таки лучше, гораздо лучше он перенес это, чем я ожидала. Видно, так должно было быть… – Но неужели совершенно всё кончено? – сказал Пьер. Княжна Марья с удивлением посмотрела на него. Она не понимала даже, как можно было об этом спрашивать. Пьер вошел в кабинет. Князь Андрей, весьма изменившийся, очевидно поздоровевший, но с новой, поперечной морщиной между бровей, в штатском платье, стоял против отца и князя Мещерского и горячо спорил, делая энергические жесты. Речь шла о Сперанском, известие о внезапной ссылке и мнимой измене которого только что дошло до Москвы. – Теперь судят и обвиняют его (Сперанского) все те, которые месяц тому назад восхищались им, – говорил князь Андрей, – и те, которые не в состоянии были понимать его целей. Судить человека в немилости очень легко и взваливать на него все ошибки другого; а я скажу, что ежели что нибудь сделано хорошего в нынешнее царствованье, то всё хорошее сделано им – им одним. – Он остановился, увидав Пьера. Лицо его дрогнуло и тотчас же приняло злое выражение. – И потомство отдаст ему справедливость, – договорил он, и тотчас же обратился к Пьеру. – Ну ты как? Все толстеешь, – говорил он оживленно, но вновь появившаяся морщина еще глубже вырезалась на его лбу. – Да, я здоров, – отвечал он на вопрос Пьера и усмехнулся. Пьеру ясно было, что усмешка его говорила: «здоров, но здоровье мое никому не нужно». Сказав несколько слов с Пьером об ужасной дороге от границ Польши, о том, как он встретил в Швейцарии людей, знавших Пьера, и о господине Десале, которого он воспитателем для сына привез из за границы, князь Андрей опять с горячностью вмешался в разговор о Сперанском, продолжавшийся между двумя стариками. – Ежели бы была измена и были бы доказательства его тайных сношений с Наполеоном, то их всенародно объявили бы – с горячностью и поспешностью говорил он.
Судить человека в немилости очень легко и взваливать на него все ошибки другого; а я скажу, что ежели что нибудь сделано хорошего в нынешнее царствованье, то всё хорошее сделано им – им одним. – Он остановился, увидав Пьера. Лицо его дрогнуло и тотчас же приняло злое выражение. – И потомство отдаст ему справедливость, – договорил он, и тотчас же обратился к Пьеру. – Ну ты как? Все толстеешь, – говорил он оживленно, но вновь появившаяся морщина еще глубже вырезалась на его лбу. – Да, я здоров, – отвечал он на вопрос Пьера и усмехнулся. Пьеру ясно было, что усмешка его говорила: «здоров, но здоровье мое никому не нужно». Сказав несколько слов с Пьером об ужасной дороге от границ Польши, о том, как он встретил в Швейцарии людей, знавших Пьера, и о господине Десале, которого он воспитателем для сына привез из за границы, князь Андрей опять с горячностью вмешался в разговор о Сперанском, продолжавшийся между двумя стариками. – Ежели бы была измена и были бы доказательства его тайных сношений с Наполеоном, то их всенародно объявили бы – с горячностью и поспешностью говорил он. – Я лично не люблю и не любил Сперанского, но я люблю справедливость. – Пьер узнавал теперь в своем друге слишком знакомую ему потребность волноваться и спорить о деле для себя чуждом только для того, чтобы заглушить слишком тяжелые задушевные мысли. Когда князь Мещерский уехал, князь Андрей взял под руку Пьера и пригласил его в комнату, которая была отведена для него. В комнате была разбита кровать, лежали раскрытые чемоданы и сундуки. Князь Андрей подошел к одному из них и достал шкатулку. Из шкатулки он достал связку в бумаге. Он всё делал молча и очень быстро. Он приподнялся, прокашлялся. Лицо его было нахмурено и губы поджаты. – Прости меня, ежели я тебя утруждаю… – Пьер понял, что князь Андрей хотел говорить о Наташе, и широкое лицо его выразило сожаление и сочувствие. Это выражение лица Пьера рассердило князя Андрея; он решительно, звонко и неприятно продолжал: – Я получил отказ от графини Ростовой, и до меня дошли слухи об искании ее руки твоим шурином, или тому подобное. Правда ли это? – И правда и не правда, – начал Пьер; но князь Андрей перебил его.
– Я лично не люблю и не любил Сперанского, но я люблю справедливость. – Пьер узнавал теперь в своем друге слишком знакомую ему потребность волноваться и спорить о деле для себя чуждом только для того, чтобы заглушить слишком тяжелые задушевные мысли. Когда князь Мещерский уехал, князь Андрей взял под руку Пьера и пригласил его в комнату, которая была отведена для него. В комнате была разбита кровать, лежали раскрытые чемоданы и сундуки. Князь Андрей подошел к одному из них и достал шкатулку. Из шкатулки он достал связку в бумаге. Он всё делал молча и очень быстро. Он приподнялся, прокашлялся. Лицо его было нахмурено и губы поджаты. – Прости меня, ежели я тебя утруждаю… – Пьер понял, что князь Андрей хотел говорить о Наташе, и широкое лицо его выразило сожаление и сочувствие. Это выражение лица Пьера рассердило князя Андрея; он решительно, звонко и неприятно продолжал: – Я получил отказ от графини Ростовой, и до меня дошли слухи об искании ее руки твоим шурином, или тому подобное. Правда ли это? – И правда и не правда, – начал Пьер; но князь Андрей перебил его.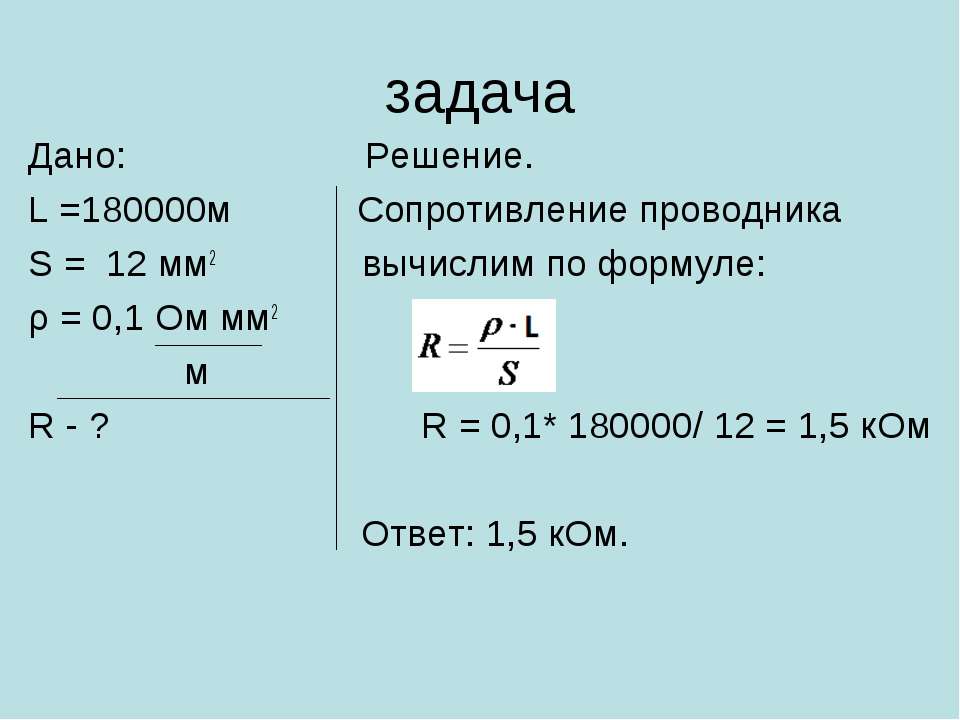 – Вот ее письма и портрет, – сказал он. Он взял связку со стола и передал Пьеру. – Отдай это графине… ежели ты увидишь ее. – Она очень больна, – сказал Пьер. – Так она здесь еще? – сказал князь Андрей. – А князь Курагин? – спросил он быстро. – Он давно уехал. Она была при смерти… – Очень сожалею об ее болезни, – сказал князь Андрей. – Он холодно, зло, неприятно, как его отец, усмехнулся. – Но господин Курагин, стало быть, не удостоил своей руки графиню Ростову? – сказал князь Андрей. Он фыркнул носом несколько раз. – Он не мог жениться, потому что он был женат, – сказал Пьер. Князь Андрей неприятно засмеялся, опять напоминая своего отца. – А где же он теперь находится, ваш шурин, могу ли я узнать? – сказал он. – Он уехал в Петер…. впрочем я не знаю, – сказал Пьер. – Ну да это всё равно, – сказал князь Андрей. – Передай графине Ростовой, что она была и есть совершенно свободна, и что я желаю ей всего лучшего. Пьер взял в руки связку бумаг. Князь Андрей, как будто вспоминая, не нужно ли ему сказать еще что нибудь или ожидая, не скажет ли чего нибудь Пьер, остановившимся взглядом смотрел на него.
– Вот ее письма и портрет, – сказал он. Он взял связку со стола и передал Пьеру. – Отдай это графине… ежели ты увидишь ее. – Она очень больна, – сказал Пьер. – Так она здесь еще? – сказал князь Андрей. – А князь Курагин? – спросил он быстро. – Он давно уехал. Она была при смерти… – Очень сожалею об ее болезни, – сказал князь Андрей. – Он холодно, зло, неприятно, как его отец, усмехнулся. – Но господин Курагин, стало быть, не удостоил своей руки графиню Ростову? – сказал князь Андрей. Он фыркнул носом несколько раз. – Он не мог жениться, потому что он был женат, – сказал Пьер. Князь Андрей неприятно засмеялся, опять напоминая своего отца. – А где же он теперь находится, ваш шурин, могу ли я узнать? – сказал он. – Он уехал в Петер…. впрочем я не знаю, – сказал Пьер. – Ну да это всё равно, – сказал князь Андрей. – Передай графине Ростовой, что она была и есть совершенно свободна, и что я желаю ей всего лучшего. Пьер взял в руки связку бумаг. Князь Андрей, как будто вспоминая, не нужно ли ему сказать еще что нибудь или ожидая, не скажет ли чего нибудь Пьер, остановившимся взглядом смотрел на него. – Послушайте, помните вы наш спор в Петербурге, – сказал Пьер, помните о… – Помню, – поспешно отвечал князь Андрей, – я говорил, что падшую женщину надо простить, но я не говорил, что я могу простить. Я не могу. – Разве можно это сравнивать?… – сказал Пьер. Князь Андрей перебил его. Он резко закричал: – Да, опять просить ее руки, быть великодушным, и тому подобное?… Да, это очень благородно, но я не способен итти sur les brisees de monsieur [итти по стопам этого господина]. – Ежели ты хочешь быть моим другом, не говори со мною никогда про эту… про всё это. Ну, прощай. Так ты передашь… Пьер вышел и пошел к старому князю и княжне Марье. Старик казался оживленнее обыкновенного. Княжна Марья была такая же, как и всегда, но из за сочувствия к брату, Пьер видел в ней радость к тому, что свадьба ее брата расстроилась. Глядя на них, Пьер понял, какое презрение и злобу они имели все против Ростовых, понял, что нельзя было при них даже и упоминать имя той, которая могла на кого бы то ни было променять князя Андрея.
– Послушайте, помните вы наш спор в Петербурге, – сказал Пьер, помните о… – Помню, – поспешно отвечал князь Андрей, – я говорил, что падшую женщину надо простить, но я не говорил, что я могу простить. Я не могу. – Разве можно это сравнивать?… – сказал Пьер. Князь Андрей перебил его. Он резко закричал: – Да, опять просить ее руки, быть великодушным, и тому подобное?… Да, это очень благородно, но я не способен итти sur les brisees de monsieur [итти по стопам этого господина]. – Ежели ты хочешь быть моим другом, не говори со мною никогда про эту… про всё это. Ну, прощай. Так ты передашь… Пьер вышел и пошел к старому князю и княжне Марье. Старик казался оживленнее обыкновенного. Княжна Марья была такая же, как и всегда, но из за сочувствия к брату, Пьер видел в ней радость к тому, что свадьба ее брата расстроилась. Глядя на них, Пьер понял, какое презрение и злобу они имели все против Ростовых, понял, что нельзя было при них даже и упоминать имя той, которая могла на кого бы то ни было променять князя Андрея.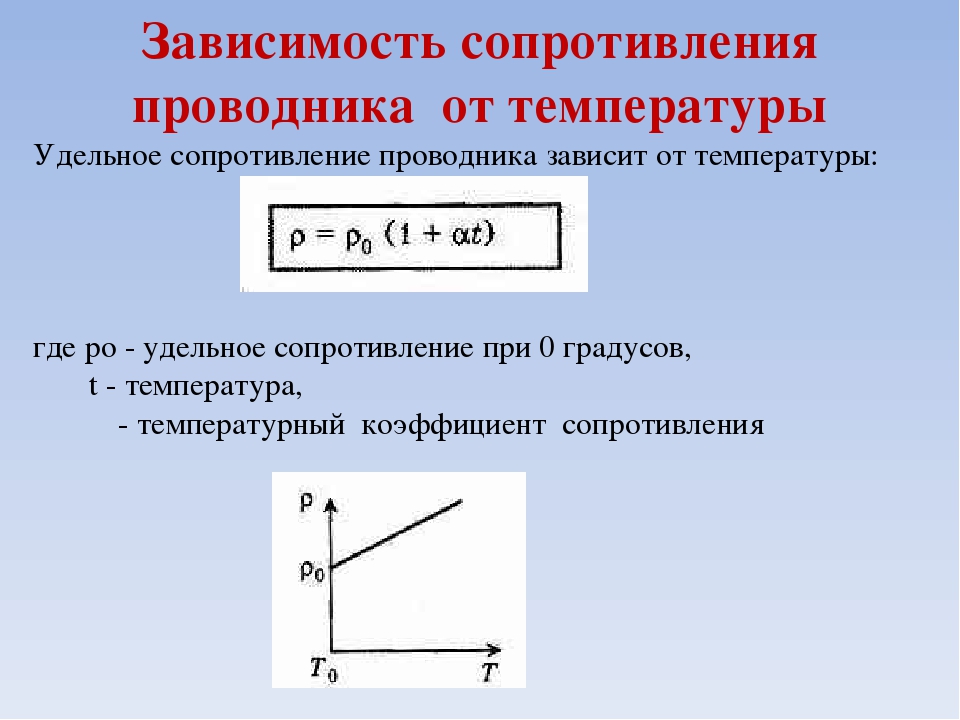 За обедом речь зашла о войне, приближение которой уже становилось очевидно. Князь Андрей не умолкая говорил и спорил то с отцом, то с Десалем, швейцарцем воспитателем, и казался оживленнее обыкновенного, тем оживлением, которого нравственную причину так хорошо знал Пьер.
За обедом речь зашла о войне, приближение которой уже становилось очевидно. Князь Андрей не умолкая говорил и спорил то с отцом, то с Десалем, швейцарцем воспитателем, и казался оживленнее обыкновенного, тем оживлением, которого нравственную причину так хорошо знал Пьер.
Как рассчитать сопротивление
Для расчетов сопротивления медного провода существует несколько способов. К наиболее простым относится табличный вариант, где указаны взаимосвязанные параметры. Поэтому, кроме сопротивления, определяется сила тока, диаметр или сечение провода.
Во втором случае используются разнообразные . В каждый из них вставляется набор физических величин медного провода, с помощью которых получаются точные результаты. В большинстве подобных калькуляторов используется сопротивление меди в размере 0,0172 Ом*мм 2 /м. В некоторых случаях такое усредненное значение может повлиять на точность вычислений.
Наиболее сложным вариантом считаются ручные вычисления, с использованием формулы: R = p x L/S, в которой р — удельное сопротивление меди, L — длина проводника и S — сечение этого проводника. Следует отметить, что сопротивление медного провода таблица определяет, как одно из наиболее низких. Более низким значением обладает лишь серебро.
Следует отметить, что сопротивление медного провода таблица определяет, как одно из наиболее низких. Более низким значением обладает лишь серебро.
Когда производится расчет сечения кабеля, то в частном домостроении или в квартирах для определения этой величины используются два показателя: потребляемая мощность сети и сила тока, проходящая по разводке. Сопротивление в данном случае роли не играет. Все дело в небольшой длине проводов. А вот если длина линии электропередач достаточно большая, то без определения данного показателя здесь не обойтись. К примеру, на начале участка напряжение будет 220-2240 вольт, а на конце уже заниженное 200-220 вольт. А так как все чаще в проводке используются медные кабели и провода, то наша задача в этой статье рассмотреть сопротивление медного провода (таблица сопротивления проводов будет ниже приложена).
Что нам дает сопротивление в общем? В принципе, с его помощью можно узнать параметры используемого провода или материал, из которого он изготовлен. К примеру, если для прокладки линии электропередачи использовался скрытый способ, то зная сопротивление линии, можно точно сказать, какой она длины. Ведь часто прокладка производится под землей и непрямолинейным способом. Или еще один вариант, зная длину участка и его сопротивление можно подсчитать диаметр используемого кабеля, а через него и его сечение. Плюс, зная данную величину, можно узнать материал, из которого этот провод был изготовлен. Это все говорит о том, что не стоит сбрасывать со счетов данный показатель.
К примеру, если для прокладки линии электропередачи использовался скрытый способ, то зная сопротивление линии, можно точно сказать, какой она длины. Ведь часто прокладка производится под землей и непрямолинейным способом. Или еще один вариант, зная длину участка и его сопротивление можно подсчитать диаметр используемого кабеля, а через него и его сечение. Плюс, зная данную величину, можно узнать материал, из которого этот провод был изготовлен. Это все говорит о том, что не стоит сбрасывать со счетов данный показатель.
Все это касалось электрической проводки, но когда дело касается электроники, то в этой области без определения сопротивления и сопоставления его с другими параметрами не обойтись. В некоторых случаях данный параметр может сыграть решающую роль, даже неправильный подбор провода по сопротивлению может привести к тому, что подключаемый к такому проводнику прибор просто не будет работать. К примеру, если к блоку питания обычного компьютера подключить очень тонкий провод. Напряжение в таком проводнике станет низким, не намного, но этого будет хватать, чтобы компьютер работал некорректно.
Напряжение в таком проводнике станет низким, не намного, но этого будет хватать, чтобы компьютер работал некорректно.
От чего зависит сопротивление
☰
Сила тока в проводнике прямо пропорциональна напряжению на нем. Это значит, что с увеличением напряжения увеличивается и сила тока. Однако при одинаковом напряжении, но использовании разных проводников сила тока различна. Можно сказать по-другому. Если увеличивать напряжение, то хотя сила тока и будет увеличиваться, но везде по-разному, в зависимости от свойств проводника.
Зависимость силы тока от напряжения для данного конкретного проводника представляет собой сопротивление этого проводника. Оно обозначается R и находится по формуле R = U/I. То есть сопротивление определяется как отношение напряжения к силе тока. Чем больше сила тока в проводнике при данном напряжении, тем меньше его сопротивление. Чем больше напряжение при данной силе тока, тем больше сопротивление проводника.
Формулу можно переписать по отношению к силе тока: I = U/R (закон Ома). В таком случае нагляднее, что чем больше сопротивление, тем меньше сила тока.
В таком случае нагляднее, что чем больше сопротивление, тем меньше сила тока.
Можно сказать, что сопротивление как бы мешает напряжению создавать большую силу тока.
Само сопротивление является характеристикой проводника. Оно не зависит от поданного на него напряжения. Если будет подано большое напряжение, то изменится сила тока, но не изменится отношение U/I, т. е. не изменится сопротивление.
От чего же зависит сопротивление проводника? Оно зависти от
- длины проводника,
- площади его поперечного сечения,
- вещества, из которого изготовлен проводник,
- температуры.
Чтобы связать вещество и его сопротивление, вводится такое понятие как удельное сопротивление вещества. Оно показывает, какое будет сопротивление в данном веществе, если проводник из него будет иметь длину 1 м и площадь поперечного сечения 1 м2. Проводники такой длины и толщины, изготовленные из разных веществ, будут иметь разные сопротивления.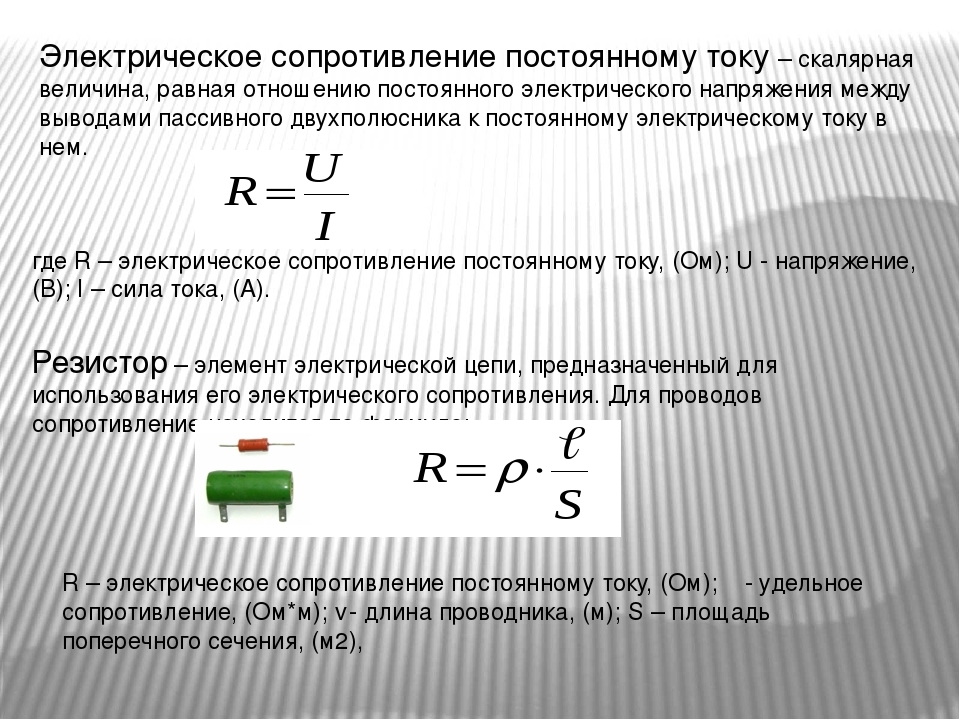 Это связано с тем, что у каждого металла (чаще всего именно они являются проводниками) своя кристаллическая решетка, свое количество свободных электронов.
Это связано с тем, что у каждого металла (чаще всего именно они являются проводниками) своя кристаллическая решетка, свое количество свободных электронов.
Чем меньше удельное сопротивление вещества, тем лучшим проводником электрического тока оно является. Маленьким удельным сопротивлением обладают, например, серебро, медь, алюминий; куда большее у железа, вольфрама; очень большое у различных сплавов.
Чем длиннее проводник, тем большее сопротивление он имеет. Это становится понятно, если принять во внимание, что движению электронов в металлах мешают ионы, составляющие кристаллическую решетку. Чем их больше, т. е. чем длиннее проводник, тем больше у электрона шанс замедлить свой путь.
Однако увеличение площади поперечного сечения делает как бы дорогу шире. Электронам легче течь и не сталкиваться с узлами кристаллической решетки. Поэтому чем толще проводник, тем его сопротивление меньше.
Таким образом, сопротивление прямо пропорционально зависит от удельного сопротивления (ρ) и длины (l) проводника и обратно пропорционально зависит от площади (S) его поперечного сечения.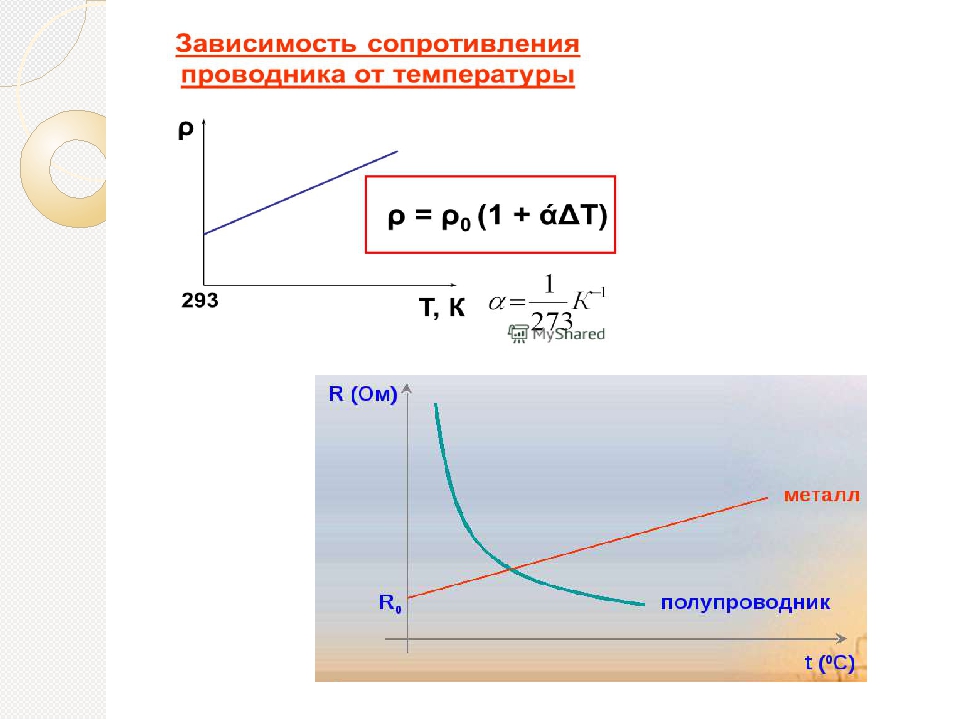 Получаем формулу сопротивления:
Получаем формулу сопротивления:
R = ρl/S
В этой формуле на первый взгляд не отражается зависимость сопротивления проводника от его температуры. Однако удельное сопротивление вещества меряется при определенной температуре (обычно 20 °C). Поэтому температура учитывается. Для вычислений удельные сопротивления берут из специальных таблиц.
Для металлических проводников чем больше температура, тем сопротивление больше. Это связано с тем, что при повышении температуры ионы решетки начинают сильнее колебаться и больше мешать движению электронов. Однако в электролитах (растворах, где заряд несут ионы, а не электроны) с повышением температуры сопротивление уменьшается. Здесь это связано с тем, что чем выше температура, тем больше происходит диссоциация на ионы, и они быстрее двигаются в растворе.
Сопротивление и удельное сопротивление
Электрическое сопротивление электрического проводника зависит от
- длины проводника
- материала проводника
- температуры материала
- площади поперечного сечения проводника
и может быть выражено как
R = ρ L / A (1)
где
R = сопротивление проводника (Ом, Ом)
ρ = удельное сопротивление материала проводника (Ом метр, Ом · м)
L = длина проводника (м)
A = площадь поперечного сечения проводника (м 2 )
Удельное сопротивление некоторых обычных проводников
- Алюминий: 2.
 65 x 10 -8 Ом м (0,0265 мкОм м)
65 x 10 -8 Ом м (0,0265 мкОм м)
- Углерод: 10 x 10 -8 Ом м (0,10 мкОм м)
- Медь: 1,724 x 10 -8 Ом м (0,0174 мкОм м)
- Железо: 10 x 10 -8 Ом м (0,1 мкОм м)
- Серебро: 1,6 x 10 -8 Ом · м (0,0265 мкОм · м)
Обратите внимание, что удельное сопротивление зависит от температуры .Вышеуказанные значения относятся к температурам 20 o C .
Удельное сопротивление некоторых обычных изоляторов
- бакелит: 1 x 10 12 Ом м
- стекло: 1 x 10 10 — 1 x 10 11 Ом м
- мрамор: 1 x 10 8 Ом м
- слюда: 0,9 x 10 13 Ом м
- парафиновое масло: 1 x 10 16 Ом м
- парафиновый воск (чистый ) : 1 x 10 16 Ом м
- плексиглас: 1 x 10 13 Ом м
- полистирол: 1 x 10 14 Ом м
- фарфор: 1 x 10 12 Ом м
- прессованный янтарь: 1 x 10 16 Ом м
- вулканит: 1 x 10 14 Ом м
- вода, дистиллированная: 1 x 10 10 Ом м
Обратите внимание, что хороший кон электрические проводники имеют низкое удельное сопротивление, а хорошие изоляторы имеют высокое удельное сопротивление.
Пример — Сопротивление проводника
Сопротивление 10 метров калибра 17 медного провода с площадью поперечного сечения 1,04 мм 2 можно рассчитать как
R = (1,7 x 10 — 8 Ом м) (10 м) / ((1,04 мм 2 ) (10 -6 м 2 / мм 2 ))
= 0,16 Ом
Пример — перекрестный площадь сечения и сопротивление
Медный провод выше уменьшен до калибра 24 и площади поперечного сечения 0.205 мм 2 . Увеличение сопротивления можно рассчитать как
R = (1,7 x 10 -8 Ом м) (10 м) / ((0,205 мм 2 ) (10 -6 м 2 / мм 2 ))
= 0,83 Ом
ток — Как рассчитать повышение температуры в медном проводнике?
Хотя это вопрос 7-летней давности, я подумал, что могу внести свой вклад в подход, который, как я обнаружил, вдохновлен некоторыми моментами, упомянутыми в примечании к применению от SIEMENS. 2 $$
2 $$
$$ I_ {max}: \ text {максимальный непрерывный ток,} I_ {op}: \ text {рабочий ток} $$
$$ \ Theta_ {x}: \ text {x temperature,} \ Theta_ {amb}: \ text {ambient,} \ Delta \ Theta_ {max}: \ Theta \ text {rise @} I_ {max} $$
Максимальный продолжительный рабочий ток
Кабели имеют номинальную пропускную способность для непрерывной работы. Различная изоляция кабеля допускает различные максимальные рабочие температуры. Их можно рассчитать в соответствии со стандартами МЭК, но мы можем использовать либо наши спецификации кабелей, либо общие, чтобы получить расчетное значение.oC $$
Это на выше максимальной рабочей температуры кабеля с изоляцией из сшитого полиэтилена. Если это изоляция из ПВХ, расчет дает> 87ºC, при этом изоляция, вероятно, расплавится. ПВХ при температуре выше 60ºC становится нестабильным.
Сравнение с отклонениями (поправочные коэффициенты)
Если мы сравним использование этой формулы с отклонениями от номиналов, мы увидим определенную согласованность;
В примечании к применению указано, что для других температур окружающего воздуха необходимо применять поправочные коэффициенты для максимального тока:
| Окр. ºC | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 |
| Фактор | 1.oC $$
ºC | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 |
| Фактор | 1.oC $$
Следующие расчетные температуры в установившемся режиме следующие:
| Окр. ºC | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 |
| Ток | 26,4 | 25,2 | 24,0 | 22,56 | 21,12 | 19,68 | 17,76 | 16,08 | 13,92 | 11,28 |
| ssTemp | 89.45 | 89.61 | 90.00 | 89.76 | 89.85 | 90.26 | 89.64 | 90.20 | 90.14 | 89.94 |
Время, необходимое для достижения установившейся температуры
Сколько времени потребуется для достижения этой температуры, можно оценить, учитывая номинальный ток короткого замыкания кабеля.2 \ приблизительно 3,7 \ text {min} $$
\ tau определяет время, необходимое для достижения 63% конечной температуры. Обычно мы оцениваем, что при 5 * \ tau мы находимся примерно на 99% от конечной температуры. 5 * 3,7 мин = 18,5 мин.
$$ \ tau \ text {действительно для достижения любых расчетных условий устойчивого состояния} $$
$$ \ text {Время достижения любой установившейся температуры} \ приблизительно 5 \ cdot \ tau \ приблизительно 18,5 \ text {min} $$
$$ \ Delta \ Theta_ {ss-amb} = \ Theta_ {устойчивое состояние} - \ Theta_ {amb} $$
Если построить график, это выглядит следующим образом:
Примерная / расчетная демонстрация
Наш расчетный \ tau был со значениями: Температура окружающей среды 45ºC, рабочая температура = 90ºC.2 = 0,64 $$
, но наша расчетная \ Delta T (повышение температуры) составляет 70ºC против 45ºC.
$$ K _ {\ Delta \ Theta} \ приблизительно \ frac {\ Delta \ Theta_ {op}} {\ Delta \ Theta_ {ref}} = \ frac {70} {45} \ приблизительно 1,5556 $$
, применив их к нашему \ tau следующим образом, мы получим
$$ \ tau_ {op} = \ tau_ {ref} \ cdot K _ {\ tau} \ cdot K _ {\ Delta \ Theta} = 3,7 \ cdot 0,64 \ cdot 1,5556 = 3,68 \ leadsto 5 \ tau = 18,4 \ text {min } $$
Обратите внимание, что эти формулы для демонстрации модифицированного \ tau были придуманы «из воздуха», «ощущением», некоторыми «логическими» соображениями.Это может быть совершенно неверно, и если я сделал «сумасшедшее» предположение, пожалуйста, дайте мне знать, чтобы я мог узнать свою ошибку. Когда-нибудь я сделаю несколько измерений, чтобы проверить это.
Ресурсы
4.3 Сопротивление и удельное сопротивление - Физика Дугласского колледжа 1207 Зима 2020
Задачи и упражнения
1: Каково сопротивление отрезка медного провода 12 калибра длиной 20,0 м и диаметром 2,053 мм?
2: Диаметр медной проволоки нулевого сечения - 8.252 мм. Найдите сопротивление такого провода длиной 1,00 км, используемого для передачи энергии.
3: Если вольфрамовая нить диаметром 0,100 мм в лампочке должна иметь сопротивление 0,200 Ом при 20,0 ° C, какой длины она должна быть?
4: Найдите отношение диаметра алюминиевого провода к медному, если они имеют одинаковое сопротивление на единицу длины (как в бытовой электропроводке).
5: Какой ток протекает через 2.Стержень из чистого кремния диаметром 54 см и длиной 20,0 см при нанесении на него 1,00 x 10 3 V ? (Такой стержень может быть использован, например, для изготовления детекторов ядерных частиц.)
6: (a) До какой температуры нужно нагреть медный провод, изначально равный 20,0ºC, чтобы удвоить его сопротивление, не обращая внимания на любые изменения размеров? (б) Происходит ли это в бытовой электропроводке при обычных обстоятельствах?
7: Резистор из нихромовой проволоки используется там, где его сопротивление не может изменяться более чем на 1.00% от его значения при 20,0ºC. В каком температурном диапазоне его можно использовать?
8: Из какого материала изготовлен резистор, если его сопротивление на 40,0% больше при 100 ° C, чем при 20,0 ° C?
9: Электронное устройство, предназначенное для работы при любой температуре в диапазоне от –10,0 ° C до 55,0 ° C, содержит резисторы из чистого углерода. В какой степени их сопротивление увеличивается в этом диапазоне?
10: (а) Из какого материала сделана проволока, если ее 25.0 м, диаметр 0,100 мм и сопротивление 77,7 Ом при 20,0 ° C? (б) Каково его сопротивление при 150 ° C?
11: Если принять постоянный температурный коэффициент удельного сопротивления, каков максимальный процент снижения сопротивления константановой проволоки, начиная с 20,0 ° C?
12: Через матрицу протягивают проволоку, растягивая ее в четыре раза по сравнению с исходной длиной. В какой степени увеличивается его сопротивление?
13: Медный провод имеет сопротивление 0.500 Ом при 20,0ºC, а железная проволока имеет сопротивление 0,525 Ом при той же температуре. При какой температуре их сопротивления равны?
14: (a) Цифровые медицинские термометры определяют температуру путем измерения сопротивления полупроводникового устройства, называемого термистором (у которого α = -0,0600 x 10 -6 o C , когда оно находится при той же температуре как у пациента Какова температура пациента, если сопротивление термистора при этой температуре равно 82.0% от его значения при 37,0ºC (нормальная температура тела)? (b) Отрицательное значение α не может поддерживаться при очень низких температурах. Обсудите, почему и так ли здесь. (Подсказка: сопротивление не может стать отрицательным.)
15: интегрированные концепции
(a) Повторите упражнение 2 с учетом теплового расширения вольфрамовой нити. Вы можете принять коэффициент теплового расширения 12 x 10 -6 o C. (b) На какой процент ваш ответ отличается от приведенного в примере?
16: Необоснованные результаты
(a) До какой температуры нужно нагреть резистор из константана, чтобы удвоить его сопротивление, при условии постоянного температурного коэффициента удельного сопротивления? б) разрезать пополам? (c) Что необоснованного в этих результатах? (d) Какие предположения необоснованны или какие посылки несовместимы?
Учебное пособие по физике: электрическое сопротивление
Электрон, движущийся по проводам и нагрузкам внешней цепи, встречает сопротивление. Сопротивление - это помеха прохождению заряда. Для электрона путешествие от терминала к терминалу не является прямым маршрутом. Скорее, это зигзагообразный путь, возникающий в результате бесчисленных столкновений с неподвижными атомами в проводящем материале. Электроны сталкиваются с сопротивлением - препятствием для их движения. В то время как разность электрических потенциалов, установленная между двумя выводами , способствует перемещению заряда , а препятствует этому сопротивлению.Скорость, с которой заряд перетекает от терминала к терминалу, является результатом совместного действия этих двух величин.
Переменные, влияющие на электрическое сопротивление
Поток заряда по проводам часто сравнивают с потоком воды по трубам. Сопротивление потоку заряда в электрической цепи аналогично эффектам трения между водой и поверхностями трубы, а также сопротивлению, создаваемому препятствиями на пути.Именно это сопротивление препятствует потоку воды и снижает как ее расход, так и скорость ее дрейфа . Подобно сопротивлению потоку воды, общее сопротивление потоку заряда в проводе электрической цепи зависит от некоторых четко идентифицируемых переменных.
Во-первых, общая длина проводов влияет на величину сопротивления. Чем длиннее провод, тем большее сопротивление будет. Существует прямая зависимость между величиной сопротивления, с которым сталкивается заряд, и длиной провода, который он должен пройти.В конце концов, если сопротивление возникает в результате столкновений между носителями заряда и атомами проволоки, то, вероятно, столкновений будет больше в более длинной проволоке. Больше столкновений означает большее сопротивление.
Во-вторых, на величину сопротивления влияет площадь поперечного сечения проводов. Более широкие провода имеют большую площадь поперечного сечения. Вода будет течь по более широкой трубе с большей скоростью, чем по узкой. Это можно объяснить меньшим сопротивлением, которое присутствует в более широкой трубе.Таким же образом, чем шире провод, тем меньше сопротивление будет течению электрического заряда. Когда все другие переменные одинаковы, заряд будет течь с большей скоростью через более широкие провода с большей площадью поперечного сечения, чем через более тонкие провода.
Третья переменная, которая, как известно, влияет на сопротивление потоку заряда, - это материал, из которого сделан провод. Не все материалы созданы равными с точки зрения их проводящей способности. Некоторые материалы являются лучшими проводниками, чем другие, и обладают меньшим сопротивлением потоку заряда.Серебро - один из лучших проводников, но никогда не используется в проводах бытовых цепей из-за своей стоимости. Медь и алюминий являются одними из наименее дорогих материалов с подходящей проводящей способностью, позволяющей использовать их в проводах бытовых цепей. На проводящую способность материала часто указывает его удельное сопротивление . Удельное сопротивление материала зависит от электронной структуры материала и его температуры. Для большинства (но не для всех) материалов удельное сопротивление увеличивается с повышением температуры.В таблице ниже приведены значения удельного сопротивления для различных материалов при температуре 20 градусов Цельсия.
Материал
Удельное сопротивление (Ом • метр)
Серебро
1,59 х 10 -8 Медь
1.7 х 10 -8 Золото
2,2 х 10 -8 Алюминий
2,8 х 10 -8 Вольфрам
5,6 х 10 -8 Утюг
10 х 10 -8 Платина
11 х 10 -8 Свинец
22 х 10 -8 Нихром
150 х 10 -8 Углерод
3.5 х 10 -5 Полистирол
10 7 - 10 11 Полиэтилен
10 8 - 10 9 Стекло
10 10 - 10 14 Твердая резина
10 13
Как видно из таблицы, существует широкий диапазон значений удельного сопротивления для различных материалов.Материалы с более низким сопротивлением обладают меньшим сопротивлением потоку заряда; они лучше дирижеры. Материалы, показанные в последних четырех строках приведенной выше таблицы, обладают таким высоким удельным сопротивлением, что их даже нельзя рассматривать как проводники.
Посмотри!
Используйте виджет Resistivity of a Material , чтобы найти удельное сопротивление данного материала. Введите название материала и нажмите кнопку Submit , чтобы узнать его удельное сопротивление.
Математическая природа сопротивления
Сопротивление - это числовая величина, которую можно измерить и выразить математически. Стандартной метрической единицей измерения сопротивления является ом, представленный греческой буквой омега -. Электрическое устройство с сопротивлением 5 Ом будет представлено как R = 5 . Уравнение, представляющее зависимость сопротивления ( R ) проводника цилиндрической формы (например,, провод) от влияющих на него переменных равно
, где L представляет длину провода (в метрах), A представляет площадь поперечного сечения провода (в метрах 2 ) и представляет удельное сопротивление материала (в Ом • метр). В соответствии с вышеизложенным, это уравнение показывает, что сопротивление провода прямо пропорционально длине провода и обратно пропорционально площади поперечного сечения провода.Как показывает уравнение, знание длины, площади поперечного сечения и материала, из которого сделан провод (и, следовательно, его удельного сопротивления), позволяет определить сопротивление провода.
Расследовать!
Резисторы - один из наиболее распространенных компонентов электрических цепей. На большинстве резисторов нанесены цветные полосы или полосы. Цвета отображают информацию о значении сопротивления.Возможно, вы работаете в лаборатории и вам нужно знать сопротивление резистора, используемого в лаборатории. Используйте виджет ниже, чтобы определить значение сопротивления по цветным полосам.
Проверьте свое понимание
1. В бытовых цепях часто используются провода двух разной ширины: калибра 12 и калибра 14. Проволока 12-го калибра имеет диаметр 1/12 дюйма, а проволока 14-го калибра - 1/14 дюйма.Таким образом, провод 12-го калибра имеет более широкое сечение, чем провод 14-го калибра. Цепь на 20 А, используемая для настенных розеток, должна быть подключена с использованием провода 12-го калибра, а цепь на 15 А, используемая для цепей освещения и вентиляторов, должна быть подключена с помощью провода 14-го калибра. Объясните физику такого электрического кода.
2. Основываясь на информации, указанной в предыдущем вопросе, объясните риск, связанный с использованием провода 14-го калибра в цепи, которая будет использоваться для питания 16-амперной пилы.
3. Определите сопротивление медного провода 12 калибра длиной 1 милю. Дано: 1 миля = 1609 метров и диаметр = 0,2117 см.
4. Две проволоки - A и B - круглого сечения имеют одинаковую длину и изготовлены из одного материала. Тем не менее, сопротивление провода A в четыре раза больше, чем у провода B.Во сколько раз диаметр проволоки B больше диаметра проволоки A?
Сопротивление и удельное сопротивление | Физика
Цели обучения
К концу этого раздела вы сможете:
- Объясните понятие удельного сопротивления.
- Используйте удельное сопротивление для расчета сопротивления материалов указанной конфигурации.
- Используйте термический коэффициент удельного сопротивления для расчета изменения сопротивления в зависимости от температуры.
Зависимость сопротивления от материала и формы
Сопротивление объекта зависит от его формы и материала, из которого он сделан. Цилиндрический резистор на Рисунке 1 легко проанализировать, и таким образом мы сможем понять сопротивление более сложных форм. Как и следовало ожидать, электрическое сопротивление цилиндра R прямо пропорционально его длине L , подобно сопротивлению трубы потоку жидкости.Чем длиннее цилиндр, тем больше зарядов столкнется с его атомами. Чем больше диаметр цилиндра, тем больше тока он может пропускать (опять же, как поток жидкости по трубе). Фактически, R обратно пропорционален площади поперечного сечения цилиндра A .
Рис. 1. Однородный цилиндр длиной L и площадью поперечного сечения A. Его сопротивление потоку тока аналогично сопротивлению, которое труба оказывает потоку жидкости. Чем длиннее цилиндр, тем больше его сопротивление.Чем больше площадь его поперечного сечения A, тем меньше его сопротивление.
Сопротивление данной формы зависит от материала, из которого изготовлен объект. Различные материалы обладают разным сопротивлением потоку заряда. Мы определяем удельное сопротивление ρ вещества так, чтобы сопротивление R объекта было прямо пропорционально ρ . Удельное сопротивление ρ - это внутреннее свойство материала, независимо от его формы или размера.Сопротивление R однородного цилиндра длиной L , площадью поперечного сечения A , изготовленного из материала с удельным сопротивлением ρ , составляет
.
[латекс] R = \ frac {\ rho L} {A} \\ [/ латекс].
В таблице 1 приведены репрезентативные значения ρ . Материалы, перечисленные в таблице, разделены на категории проводников, полупроводников и изоляторов на основе широких групп удельных сопротивлений. У проводников наименьшее удельное сопротивление, а у изоляторов наибольшее; полупроводники имеют промежуточное удельное сопротивление.Проводники имеют различную, но большую плотность свободных зарядов, тогда как большинство зарядов в изоляторах связаны с атомами и не могут двигаться. Полупроводники являются промежуточными, имеют гораздо меньше свободных зарядов, чем проводники, но обладают свойствами, из-за которых количество свободных зарядов сильно зависит от типа и количества примесей в полупроводнике. Эти уникальные свойства полупроводников находят применение в современной электронике, о чем мы поговорим в следующих главах.
Таблица 1.Удельное сопротивление ρ различных материалов при 20º C Материал Удельное сопротивление ρ ( Ом ⋅ м ) Проводники Серебристый 1. 59 × 10 −8 Медь 1. 72 × 10 −8 Золото 2. 44 × 10 −8 Алюминий 2.65 × 10 −8 Вольфрам 5. 6 × 10 −8 Утюг 9. 71 × 10 −8 Платина 10. 6 × 10 −8 Сталь 20 × 10 −8 Свинец 22 × 10 −8 Манганин (сплав Cu, Mn, Ni) 44 × 10 −8 Константан (сплав Cu, Ni) 49 × 10 −8 Меркурий 96 × 10 −8 Нихром (сплав Ni, Fe, Cr) 100 × 10 −8 Полупроводники Углерод (чистый) 3.5 × 10 5 Углерод (3,5 - 60) × 10 5 Германий (чистый) 600 × 10 −3 Германий (1−600) × 10 −3 Кремний (чистый) 2300 Кремний 0,1–2300 Изоляторы Янтарь 5 × 10 14 Стекло 10 9 - 10 14 Люцит > 10 13 Слюда 10 11 - 10 15 Кварц (плавленый) 75 × 10 16 Резина (твердая) 10 13 - 10 16 сера 10 15 тефлон > 10 13 Дерево 10 8 - 10 11
Пример 1.Расчет диаметра резистора: нить накала фары
Нить накала автомобильной фары изготовлена из вольфрама и имеет сопротивление холоду 0,350 Ом. Если нить представляет собой цилиндр длиной 4,00 см (для экономии места ее можно свернуть в бухту), каков ее диаметр?
Стратегия
Мы можем переписать уравнение [латекс] R = \ frac {\ rho L} {A} \\ [/ latex], чтобы найти площадь поперечного сечения A нити на основе данной информации. Тогда его диаметр можно определить, предположив, что он имеет круглое поперечное сечение.{-5} \ text {m} \ end {array} \\ [/ latex].
Обсуждение
Диаметр чуть меньше десятой миллиметра. Он состоит только из двух цифр, потому что ρ известен только из двух цифр.
Температурное изменение сопротивления
Удельное сопротивление всех материалов зависит от температуры. Некоторые даже становятся сверхпроводниками (нулевое сопротивление) при очень низких температурах. (См. Рисунок 2.)
Рис. 2. Сопротивление образца ртути равно нулю при очень низких температурах - это сверхпроводник до примерно 4.2 К. Выше этой критической температуры его сопротивление резко возрастает, а затем увеличивается почти линейно с температурой.
И наоборот, удельное сопротивление проводников увеличивается с увеличением температуры. Поскольку атомы колеблются быстрее и на больших расстояниях при более высоких температурах, электроны, движущиеся через металл, совершают больше столкновений, эффективно увеличивая удельное сопротивление. При относительно небольших изменениях температуры (около 100 ° C или меньше) удельное сопротивление ρ изменяется с изменением температуры Δ T , как выражено в следующем уравнении
ρ = ρ 0 (1 + α Δ T ),
, где ρ 0 - исходное удельное сопротивление, а α - температурный коэффициент сопротивления .(См. Значения α в Таблице 2 ниже.) Для более значительных изменений температуры α может измениться, или может потребоваться нелинейное уравнение, чтобы найти ρ . Обратите внимание, что α положительно для металлов, что означает, что их удельное сопротивление увеличивается с температурой. Некоторые сплавы были разработаны специально, чтобы иметь небольшую температурную зависимость. У манганина (который состоит из меди, марганца и никеля), например, α близко к нулю (до трех цифр на шкале в Таблице 2), и поэтому его удельное сопротивление незначительно изменяется с температурой.Это полезно, например, для создания не зависящего от температуры эталона сопротивления.
Таблица 2. Температурные коэффициенты удельного сопротивления α Материал Коэффициент (1 / ° C) Проводники Серебристый 3,8 × 10 −3 Медь 3,9 × 10 −3 Золото 3.4 × 10 −3 Алюминий 3,9 × 10 −3 Вольфрам 4,5 × 10 −3 Утюг 5,0 × 10 −3 Платина 3,93 × 10 −3 Свинец 3,9 × 10 −3 Манганин (сплав Cu, Mn, Ni) 0,000 × 10 −3 Константан (сплав Cu, Ni) 0.002 × 10 −3 Меркурий 0,89 × 10 −3 Нихром (сплав Ni, Fe, Cr) 0,4 × 10 −3 Полупроводники Углерод (чистый) −0,5 × 10 −3 Германий (чистый) −50 × 10 −3 Кремний (чистый) −70 × 10 −3
Отметим также, что α отрицательно для полупроводников, перечисленных в таблице 2, что означает, что их удельное сопротивление уменьшается с повышением температуры.Они становятся лучшими проводниками при более высоких температурах, потому что повышенное тепловое перемешивание увеличивает количество свободных зарядов, доступных для переноса тока. Это свойство уменьшения ρ с температурой также связано с типом и количеством примесей, присутствующих в полупроводниках. Сопротивление объекта также зависит от температуры, поскольку R 0 прямо пропорционально ρ . Для цилиндра мы знаем, что R = ρL / A , и поэтому, если L и A не сильно изменяются с температурой, R будет иметь такую же температурную зависимость, как ρ .(Исследование коэффициентов линейного расширения показывает, что они примерно на два порядка меньше типичных температурных коэффициентов удельного сопротивления, поэтому влияние температуры на L и A примерно на два порядка меньше, чем на ρ .) Таким образом,
R = R 0 (1 + α Δ T )
- это температурная зависимость сопротивления объекта, где R 0 - исходное сопротивление, а R - сопротивление после изменения температуры Δ T .Многие термометры основаны на влиянии температуры на сопротивление. (См. Рис. 3.) Одним из наиболее распространенных является термистор, полупроводниковый кристалл с сильной температурной зависимостью, сопротивление которого измеряется для определения его температуры. Устройство небольшое, поэтому быстро приходит в тепловое равновесие с той частью человека, к которой прикасается.
Рис. 3. Эти знакомые термометры основаны на автоматическом измерении сопротивления термистора в зависимости от температуры.(Источник: Biol, Wikimedia Commons)
Пример 2. Расчет сопротивления: сопротивление горячей нити
Хотя следует соблюдать осторожность при нанесении ρ = ρ 0 (1 + α Δ T ) и R = R 0 (1 + α Δ T ) для изменений температуры более 100 ° C, для вольфрама уравнения достаточно хорошо работают при очень больших изменениях температуры. Каково же сопротивление вольфрамовой нити в предыдущем примере, если ее температура повышается с комнатной температуры (20ºC) до типичной рабочей температуры 2850ºC?
Стратегия
Это прямое применение R = R 0 (1 + α Δ T ), поскольку исходное сопротивление нити было задано равным R 0 = 0.{-3} / º \ text {C} \ right) \ left (2830º \ text {C} \ right) \ right] \\ & = & {4.8 \ Omega} \ end {array} \\ [/ latex] .
Обсуждение
Это значение соответствует примеру сопротивления фары в Законе Ома: сопротивление и простые цепи.
Исследования PhET: сопротивление в проводе
Узнайте о физике сопротивления в проводе. Измените его удельное сопротивление, длину и площадь, чтобы увидеть, как они влияют на сопротивление провода. Размеры символов в уравнении меняются вместе со схемой провода.
Щелкните, чтобы запустить моделирование.
Сводка раздела
- Сопротивление R цилиндра длиной L и площадью поперечного сечения A составляет [латекс] R = \ frac {\ rho L} {A} \ [/ латекс], где ρ - удельное сопротивление материала.
- Значения ρ в таблице 1 показывают, что материалы делятся на три группы - проводники, полупроводники и изоляторы .
- Температура влияет на удельное сопротивление; для относительно небольших изменений температуры Δ T , удельное сопротивление равно [латекс] \ rho = {\ rho} _ {0} \ left (\ text {1} + \ alpha \ Delta T \ right) \\ [/ latex], где ρ 0 - исходное удельное сопротивление, а [латекс] \ text {\ alpha} [/ latex] - температурный коэффициент удельного сопротивления.
- В таблице 2 приведены значения для α , температурного коэффициента удельного сопротивления.
- Сопротивление R объекта также зависит от температуры: [латекс] R = {R} _ {0} \ left (\ text {1} + \ alpha \ Delta T \ right) \\ [/ latex], где R 0 - исходное сопротивление, а R - сопротивление после изменения температуры.
Концептуальные вопросы
1. В каком из трех полупроводниковых материалов, перечисленных в таблице 1, примеси дают свободные заряды? (Подсказка: изучите диапазон удельного сопротивления для каждого и определите, имеет ли чистый полупроводник большую или меньшую проводимость.)
2. Зависит ли сопротивление объекта от пути тока, проходящего через него? Рассмотрим, например, прямоугольный стержень - одинаковое ли сопротивление по длине и по ширине? (См. Рисунок 5.)
Рис. 5. Встречается ли ток, проходящий по двум разным путям через один и тот же объект, с разным сопротивлением?
3. Если алюминиевый и медный провода одинаковой длины имеют одинаковое сопротивление, какой из них имеет больший диаметр? Почему?
4. Объясните, почему [латекс] R = {R} _ {0} \ left (1+ \ alpha \ Delta T \ right) \\ [/ latex] для температурного изменения сопротивления R объекта равен не так точен, как [латекс] \ rho = {\ rho} _ {0} \ left ({1} + \ alpha \ Delta T \ right) \\ [/ latex], что дает температурное изменение удельного сопротивления ρ .
Задачи и упражнения
1. Каково сопротивление отрезка медного провода 12 калибра длиной 20,0 м и диаметром 2,053 мм?
2. Диаметр медного провода нулевого калибра 8,252 мм. Найдите сопротивление такого провода длиной 1,00 км, используемого для передачи энергии.
3. Если вольфрамовая нить накала диаметром 0,100 мм в лампочке должна иметь сопротивление 0,200 Ом при 20 ° C, какой длины она должна быть?
4. Найдите отношение диаметра алюминиевого провода к медному, если они имеют одинаковое сопротивление на единицу длины (как в бытовой электропроводке).
5. Какой ток протекает через стержень из чистого кремния диаметром 2,54 см и длиной 20,0 см при приложении к нему 1,00 × 10 3 В? (Такой стержень может быть использован, например, для изготовления детекторов ядерных частиц.)
6. (a) До какой температуры нужно нагреть медный провод, изначально равный 20,0 ° C, чтобы удвоить его сопротивление, не обращая внимания на любые изменения размеров? (б) Происходит ли это в бытовой электропроводке при обычных обстоятельствах?
7. Резистор из нихромовой проволоки используется там, где его сопротивление не может изменяться более чем на 1.00% от его значения при 20,0ºC. В каком температурном диапазоне его можно использовать?
8. Из какого материала изготовлен резистор, если его сопротивление на 40,0% больше при 100 ° C, чем при 20,0 ° C?
9. Электронное устройство, предназначенное для работы при любой температуре в диапазоне от –10,0 ° C до 55,0 ° C, содержит резисторы из чистого углерода. В какой степени их сопротивление увеличивается в этом диапазоне?
10. (a) Из какого материала изготовлена проволока, имеет ли она длину 25,0 м, диаметр 0,100 мм и сопротивление 77.7 Ом при 20,0 ° C? (б) Каково его сопротивление при 150 ° C?
11. При условии постоянного температурного коэффициента удельного сопротивления, каков максимальный процент уменьшения сопротивления константановой проволоки, начиная с 20,0 ° C?
12. Через матрицу протягивают проволоку, растягивая ее до четырехкратной первоначальной длины. В какой степени увеличивается его сопротивление?
13. Медный провод имеет сопротивление 0,500 Ом при 20,0 ° C, а железный провод имеет сопротивление 0,525 Ом при той же температуре.При какой температуре их сопротивления равны?
14. (a) Цифровые медицинские термометры определяют температуру путем измерения сопротивления полупроводникового прибора, называемого термистором (который имеет α = –0,0600 / ºC), когда он находится при той же температуре, что и пациент. Какова температура пациента, если сопротивление термистора при этой температуре составляет 82,0% от его значения при 37,0 ° C (нормальная температура тела)? (b) Отрицательное значение для α не может поддерживаться при очень низких температурах.Обсудите, почему и так ли здесь. (Подсказка: сопротивление не может стать отрицательным.)
15. Integrated Concepts (a) Повторите упражнение 2 с учетом теплового расширения вольфрамовой нити. Вы можете принять коэффициент теплового расширения 12 × 10 −6 / ºC. б) На какой процент ваш ответ отличается от приведенного в примере?
16. Необоснованные результаты (a) До какой температуры нужно нагреть резистор из константана, чтобы удвоить его сопротивление, при условии постоянного температурного коэффициента удельного сопротивления? б) разрезать пополам? (c) Что необоснованного в этих результатах? (d) Какие предположения необоснованны или какие посылки несовместимы?
Сноски
- 1 Значения сильно зависят от количества и типа примесей
- 2 значения при 20 ° C.
Глоссарий
- удельное сопротивление:
- внутреннее свойство материала, независимо от его формы или размера, прямо пропорциональное сопротивлению, обозначенное как ρ
- температурный коэффициент удельного сопротивления:
- эмпирическая величина, обозначенная как α , которая описывает изменение сопротивления или удельного сопротивления материала при температуре
Избранные решения проблем и упражнения
1.0,104 Ом
3. 2,8 × 10 −2 м
5. 1,10 × 10 −3 A
7. от −5ºC до 45ºC
9. 1.03
11. 0,06%
13. −17ºC
15. (a) 4,7 Ом (всего) (b) уменьшение на 3,0%
Формулы падения напряжения
- журнал IAEI
Время считывания: 4 минуты
Падение напряжения упоминается только в некоторых разделах NEC в качестве информационных примечаний и его необходимо рассчитывать в других разделах кода .Это разделы 210.19 (A) Информационная записка 4, 215.2 (A) (1) Информационная записка 2 и 3, 310.15 (A) (1) Информационная записка 1, 647.4 (D), 310.60 (B) Информационная записка 2, 455.6 ( A) Информационная записка и 695.7. Допустимая или требуемая величина падения напряжения может составлять от 1,5 до 15 процентов напряжения фидера или параллельной цепи. Максимум пять процентов обычно рекомендуется для схемы. Информационные примечания не являются обязательными требованиями Кодекса , но представляют собой пояснительный материал, предназначенный только для информационных целей [см. 90.5 (С)].
Тем не менее, инструкции производителя по установке, которые должны соблюдаться в пункте 110.3 (B), часто требуют поддержания минимального номинального напряжения для того, чтобы конкретный тип используемого оборудования функционировал должным образом в соответствии с намерениями производителя, и быть внесенным в список признанной испытательной лабораторией электрооборудования. Для выполнения расчетов падения напряжения важно иметь следующую информацию: 1) коэффициент k, 2) длину фидера или ответвления цепи до нагрузки, 3) силу тока нагрузки в цепи и, конечно же, 4) напряжение цепи.Коэффициент k - это множитель, представляющий сопротивление постоянному току для проводника данного размера длиной 1000 футов и работающего при 75 ° C. Из этой информации пользователь кода может найти проводник минимального размера, необходимый для выдерживания нагрузки (измеряется в круглых милах или килограммах), и / или процент падения напряжения.
Приведенные здесь формулы основаны на значениях сопротивления проводников постоянному току, приведенных в таблице 8 главы 9 из NEC , и считаются обычно приемлемыми для расчета падения напряжения.Таблица 8 основана на 75C / 167F и дает коэффициент k 12,9 для меди и 21,2 для алюминиевых проводников. - См. Примечание ниже.
Например, чтобы найти коэффициент k, , вы умножаете сопротивление проводника на фут на круговой мил проводника. Помните, что в Таблице 8 указано сопротивление в Ом на 1000 футов. Для расчета падения напряжения при использовании медного провода обязательно выберите значение из столбца «Медь без покрытия», так как большинство медных проводников не имеют покрытия.«Покрытие» означает, что на медном проводнике есть олово или другой тип покрытия, которое изменяет значение его сопротивления. Если проводник «с покрытием», используйте значение сопротивления столбца «с покрытием». Помните, что «с покрытием» не относится к установке проводника. Обратите внимание на следующие примеры.
Для медного провода используйте сопротивление постоянному току, измеренное в омах, из главы 9, таблицы 8:
Сопротивление постоянному току медного проводника 1000 тыс. См составляет 0.0129 Ом на 1000 футов.
(0,0129 Ом на 1000 футов, деленное на 1000
= 0,0000129 Ом на фут)
0,0000129 Ом на фут x 1000000 круглых милов = 12,9 коэффициент k - для медного провода
Для алюминиевого провода сопротивление постоянному току, измеренное в омах на 1000 футов проводника из главы 9, таблица 8:
(0,0212 Ом на 1000 футов, деленное на 1000
= 0,0000212 Ом на фут)
0,0000212 Ом на фут x 1000000 круговых милов
= 21.2 k-фактор - для алюминиевой проволоки
Примечание. Важно отметить, что для определения k-фактора необходимо умножить сопротивление проводника на фут на круглые милы проводника. Для любого медного или алюминиевого проводника, указанного в главе 9, таблица 8, коэффициент k будет примерно равен 12,9 или очень близко к нему для меди и 21,2 или очень близко к нему для алюминия. Поэтому эти две величины выбраны в качестве постоянных значений коэффициента k для медных или алюминиевых проводов без покрытия, работающих при температуре окружающей среды 75 ° C / 167 ° F и номинальной силе тока.
Диапазон температур
75 ° C / 167 ° F часто используется в современных электрических цепях, поскольку большинство новых наконечников в электрораспределительном оборудовании и вспомогательном оборудовании рассчитаны на 75 ° C / 167 ° F; и проводники с номиналом 90C / 194F используются при допустимой нагрузке 75C из-за требований к заделке, установленных в 110.14 (C).
Используемая формула также обычно подходит для проводников
60C / 140F.
Падение напряжения рассчитывается для однофазных установок с учетом того, что ток будет возвращаться от нагрузки либо от нагрузки между фазой, либо между фазой и нейтралью; поэтому множитель 2 добавляется в формулу сопротивления проводника нагрузке и обратно.Это необходимо для замыкания цепи и устранения неисправности с учетом 250.122 (B), который будет обсуждаться позже.
В формуле для трехфазных установок в качестве множителя используется 1,732 вместо 2. Ток течет к нагрузке и обратно по фазным проводам.
После того, как было определено падение напряжения вольт , используйте приведенную ниже формулу, чтобы определить процент падения напряжения для цепи или системы.
Пример 1: падение напряжения 7,2 В ÷ 240 В (1 фаза) = падение напряжения 3%
Пример 2: падение напряжения 24 В ÷ 480 В L-L = падение напряжения 5%
Выберите формулу в зависимости от размера используемого проводника или максимального падения напряжения, приемлемого для AHJ.(3%, 5% и т. Д.)
ФОРМУЛ ПАДЕНИЯ НАПРЯЖЕНИЯ
Вольт упало
= 2 x длина проводников для нагрузки x коэффициент k (медь или алюминий) x I (сила тока) ÷ круглые милы или kcmils используемого проводника
Формулы падения напряжения для трехфазных сетей:
Вольт упало =
1,732 x Длина проводников до нагрузки x коэффициент k (медь или алюминий) x I (сила тока) ÷ Используемые круглые милы или килокилометры проводника
Для определения размера в круглых миллиметрах требуется (однофазный) = 2 x L x K x I ÷ 90 Падение напряжения 100%
Для определения размера в круглых миллиметрах требуется (трехфазный) = 1.732 x L x K x I ÷ 90 Падение напряжения 100%
Эти формулы могут использоваться для определения максимальной длины проводника, необходимого для него диаметра в миле или падения напряжения в системе или цепи.
Формулы падения напряжения
Где
VD = фактическое падение напряжения (, а не процентов)
K = предполагаемое удельное сопротивление
L = длина пробега до нагрузки
I = нагрузка в амперах
CM = площадь провода, круглые милы
Примечание: Для трехфазных формул замените множитель 2 на 1.732.
2 x K x I x L ÷ CM = VD
2 x K x I x L ÷ VD = CM
(CM x VD) ÷ (2 x K x I) = максимальная длина
(CM x VD) ÷ (2 x K x L) = максимальный I (амперы)
Примечание: Чтобы найти коэффициент k, умножьте сопротивление на фут проводника на круглые милы.
- Перейти к главе 9, таблице 8
- Найдите 1 AWG
- В столбце Circular Mils для 1 AWG найдите 83690
- Перейти к сопротивлению постоянному току при 75 ° C (167 ° F), таблица 8
- Перейти к столбцу Ом / кФт.Для 1 AWG найдите 0,154 Ом / kFT
.
- (0,154 / 1000) = .000154
Пример: K для меди 1 AWG при 75 ° C = 0,000154 x 83690 = 12,9
Примечание: Глава 9 Таблица 8 Значения сопротивления постоянному току для коэффициента k и падения напряжения в цепях переменного тока используются для простоты и единообразия. Значения сопротивления для провода данного размера в таблице 8 главы 9 очень близки к значениям, приведенным в таблице 9 главы 9, независимо от того, какой метод подключения используется.
Выдержка из книги по формулам и расчетам Ферма IAEI , 2014.
Часть 2: Резисторы и сопротивления
2.1 Сопротивление и закон Ома
Электрическое сопротивление немного похоже на трение, и электроны, протекающие по проводам, теряют энергию, преодолевая сопротивление. Все проводники имеют некоторое сопротивление, и чем больше сопротивление, тем большее количество энергии рассеивается в нем при движении электронов, и, следовательно, тем больше энергии требуется для перемещения электронов по цепи. Следовательно, если источник постоянного напряжения подключен к цепи с низким общим сопротивлением, больше тока (т.е.е. кулонов заряда в секунду), чем если бы тот же источник питания был подключен к цепи с более высоким сопротивлением.
Некоторые электрические компоненты, такие как водонагреватели, имеют большое сопротивление, так что большая часть электрической энергии преобразуется в тепло при прохождении через них тока. С другой стороны, провода и кабели должны иметь низкое сопротивление, чтобы при подаче электричества из одного места в другое не терялось много энергии.
Единицей измерения сопротивления (R) является ом (Ом), а один ом - это сопротивление, которое вызывает падение на один вольт при протекании тока в один ампер.Для металлического проводника, который остается при постоянной температуре, применяется закон Ома:
Компоненты в цепях, которые рассчитаны на фиксированное сопротивление, обычно показаны в виде простой рамки, как показано на рисунке 2.1.
Рисунок 2.1: простая схема, содержащая батарею и резистор.
Пример
Электрический нагреватель используется в источнике питания 240 В, потребляет ток 12 А. Его сопротивление:
2.2 Удельное сопротивление
(также известное как удельное сопротивление)
Когда электроны протекают по проводу, они испытывают сопротивление и теряют энергию. Чем дальше по проводу они протекают, тем больше энергии они теряют, поэтому мы можем сказать, что общее сопротивление провода пропорционально его длине.
Поскольку электроны равномерно распределены по проводу и поскольку ток - это скорость, с которой заряд проходит через любую точку на этом проводе, мы можем видеть, что для обеспечения любого конкретного тока электроны в более широком проводе должны будут проходить меньшее расстояние. чем электроны в более узком проводе (рисунок 2.2). Таким образом, можно сказать, что сопротивление обратно пропорционально площади поперечного сечения проводника. Поэтому более толстые провода имеют меньшее сопротивление на метр и вызывают меньшие потери энергии в виде тепла.
Рис. 2.2: Влияние диаметра проволоки на ток.
Объединение двух предыдущих концепций дает нам:
, где l - длина провода, a - площадь поперечного сечения, а α означает пропорционально.
Удельное сопротивление (ρ) материала определяется как сопротивление между противоположными гранями куба из этого материала с заданной длиной стороны. ρ очень мало для большинства проводников и обычно выражается в микроомах (мкОм) для куба длиной 1 метр, выраженном в мкОм.Например, алюминий имеет удельное сопротивление 0,0285 мкОм. Таким образом, удельное сопротивление проволоки пропорционально удельному сопротивлению материала, из которого она сделана. Мы можем объединить удельное сопротивление с предыдущим уравнением, чтобы получить:
Обратите внимание, что сопротивление, вычисленное по этому уравнению, будет дано в тех же единицах сопротивления, что и для удельного сопротивления (т. Е. МкОм). Кроме того, l и a должны быть в тех же единицах длины, что и ρ, так что, если ρ находится в мкОм, l должно быть в м, а должно быть в м 2 .Таблица 2.1 содержит удельные сопротивления некоторых металлов.
Таблица 2.1: Удельное сопротивление некоторых металлов. Удельное сопротивление мкОм мкОм · см мкОм · мм Медь (отожженная) 0,0172 1,72 17,2 Медь (жесткая) 0,0178 1,78 17,8 Алюминий 0.0285 2,85 28,5 Олово 0,114 11,4 11,4 Серебристый 0,0163 1,63 16,3 Латунь 0,06-0,09 6-9 100 Утюг 0,1 10,0 100 Свинец 0,219 21,9 219
Пример
Рассчитайте сопротивление 1000 м 16 мм. 2 одиночный отожженный медный провод.
Из таблицы: ρ = 17,2 мкОм мм (поскольку площадь поперечного сечения дана в мм 2 )
Все провода и кабели имеют некоторое сопротивление, поэтому всегда будет потеря энергии и падение напряжения внутри. Тонкие провода сильно нагреваются и могут перегореть, если по ним проходит слишком большой ток, они также могут вызывать такое большое падение напряжения, что оборудование может работать неправильно. Однако толстые провода уменьшают эти явления, поскольку они содержат больше меди, они будут значительно дороже, чем тонкие провода.
Обычно рекомендуется, чтобы падение напряжения в кабелях составляло не более 4% от напряжения питания. Это означает падение 9,6 В для источника питания 240 В или падение 4 В для источника питания 110 В. Обратите внимание, что вы можете измерить падение напряжения на длине кабеля, только когда в нем протекает ток.
Пример
Двойной кабель 2,5 мм 2 MI питает нагреватель, который потребляет ток 20А. Если длина кабеля 100 м, рассчитайте падение напряжения в нем и частичные разряды на нагревателе, если напряжение питания составляет 240 В.Какой должна быть минимальная площадь поперечного сечения заменяемого кабеля, если падение напряжения не должно превышать 9,6 В.
Кабели
MI имеют жесткие медные жилы, поэтому ρ = 17,8 мкОм (таблица 2.1). Поскольку это сдвоенный кабель, общая длина жилы составляет 200 м.
Сопротивление кабеля:
Падение напряжения на кабеле:
ПД через нагреватель:
Обратите внимание, что это падение на 28,5 В или 11,9%. Для падения 9,6В:
Сопротивление кабеля:
Минимальная площадь поперечного сечения:
Это нестандартный размер, поэтому можно использовать 10 мм 2 .Такой кабель рассчитан на ток 77 А, хотя нам требуется только 20 А. Поэтому при выборе кабелей необходимо учитывать падение напряжения и номинальный ток.
2.3 Температура и сопротивление
Когда источник питания 2 В подключен к лампе 60 Вт, 240 В, он потребляет ток 25 мА, его сопротивление составляет:
Когда та же лампочка подключена к правильному источнику питания 240 В, она раскалена добела и потребляет ток 250 мА, а ее сопротивление составляет:
Таким образом, мы видим, что больший ток привел к сильному нагреву лампы и ее сопротивление увеличилось в 12 раз.
Чтобы учесть изменение сопротивления с температурой, используется температурный коэффициент сопротивления e (α). α для материала при 0 ° C - это изменение сопротивления образца этого материала с сопротивлением 1 Ом при повышении температуры от 0 ° C до 1 ° C. Ситуация осложняется еще и тем, что измерить сопротивление проводника при 0 ° C непросто, поэтому значение α часто указывается для повышения температуры от 20 ° C до 21 ° C. В таблице 2.2 приведены температурные коэффициенты некоторых металлов.
Таблица 2.2: Температурный коэффициент некоторых металлов.
* Углерод имеет отрицательный температурный коэффициент сопротивления, что означает, что в отличие от большинства металлов его сопротивление уменьшается с повышением температуры. Температурный коэффициент сопротивления (/ ° C при 0 ° C) (/ ° C при 20 ° C) Медь +0,0043 +0,00396 Алюминий +0.0040 +0,00370 Латунь +0,0010 +0,00098 Утюг +0,0066 +0,00583 Никель-хром +0,00017 +0,000169 Углерод * -0,0005 -0,00047 Серебристый +0,0041 +0,00379
Из приведенной выше таблицы видно, что при повышении температуры с 20 ° C до 21 ° C сопротивление медного резистора 1 Ом увеличится до 1.00396 Ом. Таким образом:
где:
R t = общее сопротивление проводника при T (Ом)
R 0 = сопротивление проводника при 0 ° C (Ω)
α = температурный коэффициент сопротивления
T = температура (° C)
А:
где:
R 20 = сопротивление проводника при 20 ° C (Ом)
Если сопротивление проводника при температуре, для которой известно α, неизвестно, можно использовать следующий метод:
R 1 = сопротивление проводника при температуре T 1
R 2 = сопротивление проводника при температуре T 2
Разделение:
Отсюда:
Таким образом, значение 0 рэнд было исключено из уравнения.
Пример
Обмотка двигателя постоянного тока изготовлена из отожженной меди и имеет сопротивление 500 Ом при 15 ° C. Какой ток будет протекать при рабочей температуре 35 ° C, если поле PD составляет 300 В? (α = 0,0043 / ° C для отожженной меди при 0 ° C)
Изменение сопротивления в зависимости от температуры может иметь серьезные последствия. Рассмотрим лампочку мощностью 60 Вт, подключенную к источнику питания 240 В, ее сопротивление в холодном состоянии составляет 80 Ом, а ток, потребляемый при включении, будет:
По мере нагрева лампы сопротивление быстро увеличивается, и ток снижается до 250 мА.Кратковременный «переходный процесс», который протекает при включении лампы, часто приводит к ее перегоранию при первом включении. Также, если цепочка лампочек приводится в действие от одного переключателя, тока может хватить, чтобы пережечь чувствительный предохранитель.
Резисторы серии 2,4 и параллели
Электрические компоненты можно соединять между собой двумя основными способами: параллельно и последовательно.
Когда резисторы подключаются в серию (рисунок 2.3), часть напряжения питания падает на каждый резистор, и каждый резистор рассеивает часть общей энергии каждого кулоновского заряда.Общее сопротивление (R T ) цепи (без учета сопротивления проводов) представляет собой сумму сопротивлений, и одинаковый ток течет через каждый резистор.
Рисунок 2.3: Три последовательно подключенных резистора.
Падение напряжения на каждом резисторе определяется по формуле:
Общее сопротивление:
Напряжение питания:
Ток, протекающий через каждый резистор, определяется выражением:
Когда резисторы подключаются по схеме параллельно , напряжение на каждом резисторе одинаково, поскольку любые два компонента, подключенные к одной и той же точке в цепи, должны иметь одинаковое напряжение (рисунок 2.4). Ток, протекающий через каждый резистор, составляет часть общего тока (I T ). Обратное к общему сопротивлению является суммой обратных сопротивлений.
Рисунок 2.4: Три резистора, включенных параллельно.
Ток через каждый резистор:
Суммарный ток:
Следовательно:
Если разделить на U, получим:
На рис. 2.5 показано, как можно упростить схемы, содержащие как параллельные, так и последовательные резисторы.
Рисунок 2.


 ). — СПб., 1890—1907.
). — СПб., 1890—1907. 65 x 10 -8 Ом м (0,0265 мкОм м)
65 x 10 -8 Ом м (0,0265 мкОм м)  ºC | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 |
| Фактор | 1.oC $$
ºC | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 |
| Фактор | 1.oC $$