Параллельное соединение элементов — Энциклопедия по машиностроению XXL
Система с параллельным соединением элементов (рис. 21, б). Такая система выходит из строя только в случае отказа всех ее элементов. При условии, что отказы элементов статистически независимы, надежность всей системы будет [17]
[c.80]
Р1з этих выражений видно, что при параллельном соединении элементов надежность системы выше надежности составляющих элементов. При смешанном соединении элементов системы при наличии взаимного влияния отказов на надежность остающихся работоспособных элементов выражения для подсчета надежности системы будут сложнее. [c.175]
Решение. Общий к. п. д. системы параллельно соединенных элементов по формуле (176)
[c.266]
Сравнение дуальных электрических цепей показывает, что последовательному соединению элементов цепи, построенной по первой системе электромеханических аналогий, соответствует параллельное соединение элементов цепи, построенной по второй системе электромеханических аналогий.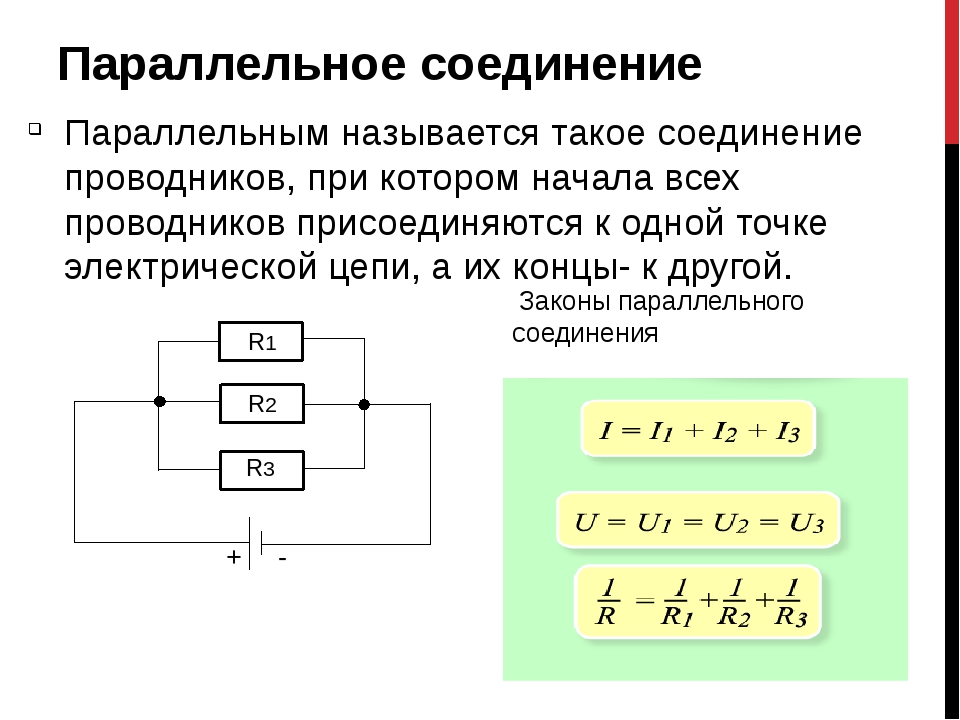 Напряжения в первой цепи распределяются подобно токам второй, а ток первой цепи аналогичен падению напряжения между узлами второй цепи.
[c.208]
Напряжения в первой цепи распределяются подобно токам второй, а ток первой цепи аналогичен падению напряжения между узлами второй цепи.
[c.208]
Параллельное соединение элементов н машин. Пусть п элементов или машин соединены параллельно и суммарная работа движущих сил Лдв распределяется между п элементами произвольно. Такое распределение энергии имеет место в групповом трансмиссионном приводе станков, веретен прядильных машин и т. п. Введем обозначения Агд , — работа дви- [c.97]
Подставляя в (5.55) значения (5.52) и (5.53), а затем определенные из (5.54) величины А, с и Л.дв, получим соответствующие равенства для определения общего КПД параллельного соединения элементов [c.97]
С помощью первого равенства (5.56) определим коэффициент потерь параллельного соединения элементов, подставив значения Ц = 1 — После упрощений найдем [c.97]
Сложное соединение элементов или машин. В машинах применяют как последовательные, так и параллельные соединения элементов. КПД сложных цепей невозможно представить единой формулой, как при однородных соединениях. Для определения КПД сложных цепей необходимо выделить в них параллельные и последовательные цепи и к каждой из них применить выведенные выше формулы.
[c.98]
КПД сложных цепей невозможно представить единой формулой, как при однородных соединениях. Для определения КПД сложных цепей необходимо выделить в них параллельные и последовательные цепи и к каждой из них применить выведенные выше формулы.
[c.98]
Аналогично устанавливается формула для определения приведенных параметров диссипации энергии п параллельно соединенных элементов [c.104]
Модель Фойгта (рис. 5.22) содержит параллельное соединение элементов упругости и вязкости, для которого общее усилие [c.139]
Для систем, в которых имеют место более сложные функциональные связи, чем последовательное или параллельное соединения элементов, можно использовать формулу полной вероятности (формула Байеса) для оценки безотказности их работы [9]. [c.190]
В 4.2 рассматриваются системы со стандартными структурами последовательное и параллельное соединение элементов. Такие структуры характерны, в частности, для различного оборудования систем энергетики. Как правило, это последовательное (в смысле надежности) соединение элементов, в котором лишь отдельные эле-148
[c.148]
Как правило, это последовательное (в смысле надежности) соединение элементов, в котором лишь отдельные эле-148
[c.148]
Пример расчета надежности электроэнергетической системы параллельным соединением элементов, т [c.184]
По типу структуры среди систем с временным резервированием различают (см. 1.6) системы с последовательным, параллельным, последовательно-параллельным соединением элементов, системы с сетевой структурой (структурно-сложные системы). В свою очередь последовательное соединение бывает двух типов основное и многофазное. При основном соединении нарушение работоспособности элемента приводит немедленно к нарушению работоспособности системы. При многофазном соединении в системе есть промежуточные накопители продукции и при отказе элемента нарушение работоспособности системы происходит не мгновенно, а через некоторое время, равное времени исчерпания запасов продукции в накопителях между отказавшим элементом и выходом системы. Параллельное соединение также имеет две разновидности резервное и многоканальное. При резервном соединении все элементы разделяются на две группы основные и резервные, причем последние не выполняют полезной работы, пока работоспособны основные элементы. При многоканальном соединении все параллельно включенные элементы выполняют полезную работу, создавая запас производительности.
[c.205]
Параллельное соединение также имеет две разновидности резервное и многоканальное. При резервном соединении все элементы разделяются на две группы основные и резервные, причем последние не выполняют полезной работы, пока работоспособны основные элементы. При многоканальном соединении все параллельно включенные элементы выполняют полезную работу, создавая запас производительности.
[c.205]
В модель, состоящую из двух элементов, входят пружина (упругий элемент) и элемент, обеспечивающий вязкое демпфирование. Как можно видеть из рис. 6.8, в рассматриваемых моделях указанные элементы соединяются последовательно и параллельно. Как известно, модель, в которой использовано последовательное соединение, служит для исследования ползучести. Рассмотрим модель с параллельным соединением элементов, полагая, что т) — коэффициент вязкого трения. Уравнение движения, соответствующее этой модели, имеет вид [c.152]
Алгоритм определения Тс условной системы при параллельном соединении элементов определяется выражением
[c. 108]
108]
Вывод формулы для расчета надежности системы облегчается, если подготовить наглядную картину анализа влияния отказов — так называемую блок-схему надежности. На этой блок-схеме определяются те части системы, отказ которых вызывает отказ системы (последовательные элементы), и те части системы, отказ которых приводит лишь к увеличению вероятности отказа системы (параллельные элементы). При параллельном соединении элементов отказ системы происходит лишь при совмещении отказов частей системы. Другими словами, блок-схема надежности представляет вероятностную задачу в виде схемы. Решением этой вероятностной задачи является выражение вероятности отказа системы через вероятности отказов рассматриваемых ее частей. [c.36]
К терминам Постоянное резервирование , Динамическое резервирование и Скользящее резервирование . Постоянное резервирование в простейшем случае представляет собой параллельное соединение элементов без переключающих устройств.
[c. 231]
231]
При параллельном соединении элементов (рис. 5, б) отказ всей системы возможен только при условии отказа каждой из параллельных ветвей.
[c.31]
Итак, чем больше будет в параллельно соединенных элементов, тем меньше [c.306]
Пример 2. Определение надежности при последовательном и параллельном соединении элементов. Для системы питания предложено две схемы, использующие аккумуляторы с напряжением 4 В (рис. 59). В первой схеме применяется последовательное соединение элементов, дающее напряжение 12 В (рис. 59, а), вторая — рассчитана на напряжение 4 В (рис. 59, 6). Вероятность безотказной [c.198]
Безотказность системы с параллельным соединением элементов возрастает с увеличением кратности резервирования. Так, уже при однократном резервировании (дублировании) в случае, когда показатель надежности элемента Pq = 0,99, для системы получаем Р =
[c. 29]
29]
Блок-схема, иллюстрирующая эти подсистемы, показана на рис. 1.3.5, б. Обратим внимание на то, что в парах параллельно соединенных элементов одни и те же стержни фермы (в разных комбинациях) появляются неоднократно. Нетрудно подсчитать, что число таких элементов равно 19, в то время как физическая система состоит только из 10 элементов. [c.30]
Рассмотрим систему, состоящую из параллельно соединенных элементов (рис. 9.8, б), дублирующих друг друга. В этом случае отказ системы произойдет только при отказе всех элементов. [c.380]
Например, если Я,- = 0,5, то общая надежность системы Я = 0,97. Вероятность безотказной работы системы с параллельно соединенными элементами выше, чем надежность ее элементов, т.е. можно существенно повысить Я системы, если вместо одного малонадежного элемента включить в общую систему блок из нескольких параллельно соединенных элементов. Например, в системе последовательно соединенных трех элементов имеется один элемент с малой надежностью (Я2) (рис. 9.9). Если Щ = 0,9, ifp = 0,3, Щ = 0,8, то общая надеж-
[c.380]
9.9). Если Щ = 0,9, ifp = 0,3, Щ = 0,8, то общая надеж-
[c.380]
В некоторых изделиях, преимущественно в электронной аппаратуре, для повышения надежности применяют не последователыюе, а параллельное соединение элементов и так называемое резервирование. При параллельном соединении элементов надежность системы значительно повышается, так как функцию отказавшего элемента принимает на себя параллельный ему или резервный элемент. В машиностроении параллельное соединение элементов и резервирование применяют редко, так как в большинстве случаев они приводят к значительному повышению массы, габаритов и стоимости изделий. Оправданным применением параллельного соединения могут служить самолеты с двумя и [c.13]
При более детальной классифиации в зависимости от схемы соединения элементов выделяют объекты с последовательным, параллельным и смешанным (последовательно-параллельным) соединением элементов, а также объекты с сетевой структурой в зависимости от
[c. 74]
74]
Уравнение (3.6) обобщает результаты испытаний с различными режимами нагружения материалов, не чувствительных к истории предшествующего деформирования, сопротивление которых полностью определяется только мгновеннымп значениями скорости пластической деформации и ее величины независимо от пути накопления последней во времени. Такому уравнению состояния соответствует реологическая модель, образованная последовательным соединением упругой и вязко-пластической ячеек, последняя из которых представляет собой параллельное соединение элемента трения, соответствующего сопротивлению деформации при начальной скорости ео (/ на рис. 57, б), элемента вязкости IV на рис. 57, б), характеризующего составляющую сопротивления, связанную с вязким демпфированием дислокаций, и ряда цепочек из элементов трения и нелинейной вязкости (цепочки // и III на рис. 57, б), каждая 113 которых отражает влияние на сопротивление термоактивируемого преодоления дислокациями барьеров одного типа. Сопротивление цепочки равно нулю при скорости деформации
[c. 139]
139]
Введение понятия о последовательном и параллельном соединении элементов и их графическое представление особенно удобны для линейных систем. В этом случае решение сравнительно просто получается в форме передаточных фикций, линейно связывающих изобр е-ние мходной величины с изображением входной Хг= = WXi. Из условия линейности непосредственно вытекает, что лри параллельном соединении объектов передаточные функции складываются
[c.55]
Этот результат можно получить проще, если вычислить вероятность противоположного события — отказ всех элементов одновременно. Тогда Л = Л1 Д Д ЛаДЛз и для независимых событий Р (Л)=Р A-i) Р (Л 2) Р (Лз) = (1—0,9) = = 0,001. В соответствии с этим Р (Л) = 1 — Р(Л) = 1—0,001 = 0,999. Из рассмотренного примера видно, что надежность параллельного соединения элементов существенно выше. Разумеется, что другие характеристики системы (например, масса, компактность и т.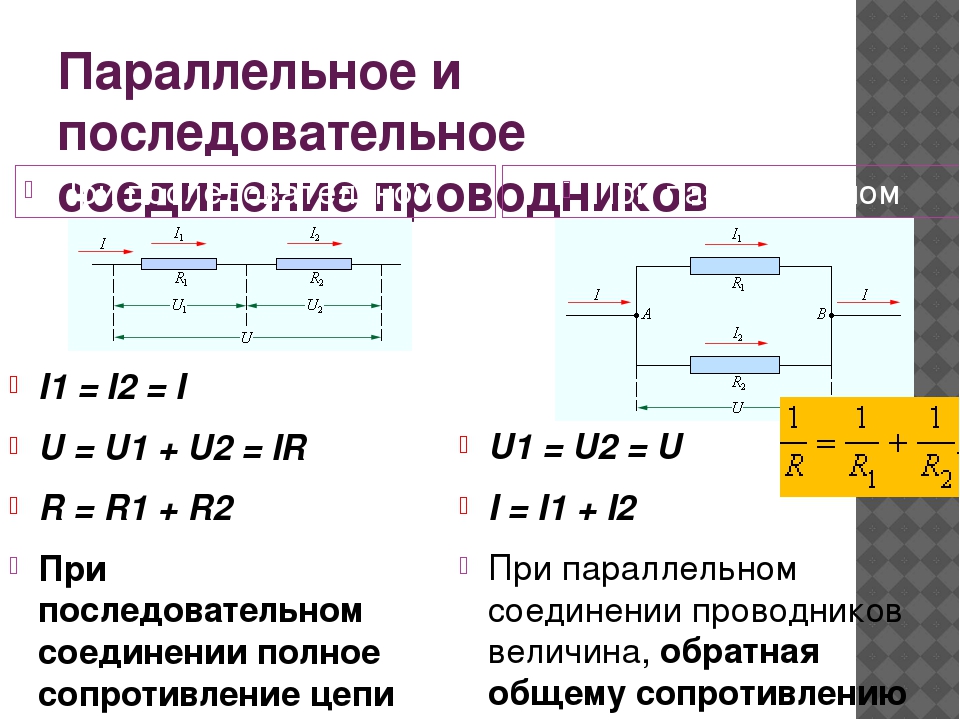 д.) в первой системе могут оказаться значительно лучше, чем во второй, и решение конструктора должно основываться на учете всех многообразных факторов.
[c.199]
д.) в первой системе могут оказаться значительно лучше, чем во второй, и решение конструктора должно основываться на учете всех многообразных факторов.
[c.199]
Тарельчатые пружины (Бельеилля) имеют малые габариты, большую нагрузочную способность и значительное демпфирование между отдельными тарелками, составляющими пакет последовательно или параллельно соединенных элементов
[c.199]
Одним из способов повышения надежности систем является резервирование элементов, которое широко используется на стадии про-екгарования. Система с параллельным соединением элементов построена таким образом, что отказ ее происходит лишь в случае отказа всех элементов, т.е. система исправна, если исправен хотя бы один элемент. При разработке технических систем в зависимости от выполняемой задачи применяют нагруженное (горячее) и ненагруженное (холодное) резервирование. [c.232]
Параллельное соединение — урок. Физика, 8 класс.
При параллельном соединении все потребители подключены к источнику тока независимо друг от друга и образуют разветвлённую цепь.
Рис. \(1\). Параллельное соединение
При параллельном соединении все потребители подключены к одному источнику тока, между клеммами которого имеется определённое напряжение.
Каждый потребитель получает полное напряжение цепи.
U=U1=U2=U3=…
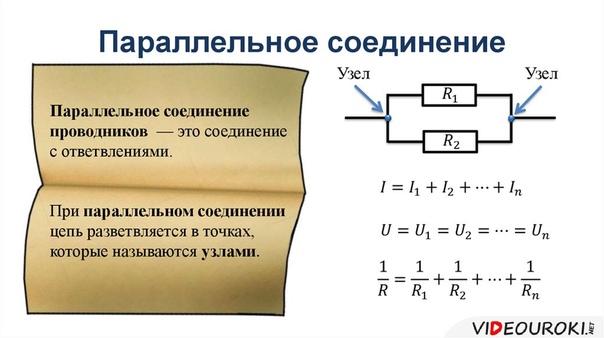
Рис. \(2\). Параллельное соединение, токи в различных потребителях
При параллельном соединении общий ток является суммой токов, протекающих через отдельные потребители.
I=I1+I2+I3+…
Общее сопротивление потребителей, находящихся в параллельном соединении, будет наименьшим (меньше, чем наименьшее из сопротивлений параллельно подключённых потребителей).
Если параллельно соединены \(n\) потребителей, а сопротивление каждого из них одинаково и равно \(R\), тогда общее сопротивление цепи будет равно \(R : n\).
Можно сделать вывод о том, что при увеличении числа потребителей общая сила тока неограниченно возрастает, что может привести к пожару.
Обрати внимание!
В одну розетку нельзя включать несколько мощных потребителей, так как перенагруженные провода нагреваются и могут загореться.
В квартире потребители включены в параллельное соединение. Подводка электричества, входящего в квартиру, состоит из нескольких проводов, которые проходят через счётчик, измеряющий потребление электроэнергии. Электрический ток течёт через предохранители, которые подключены последовательно и предусмотрены для определённой силы тока в цепи. Они размыкают цепь в случае опасной перегрузки.
Электрический кабель, который используется в электрической цепи квартиры, имеет три провода. Третий провод является заземлением.
Преимуществом параллельного соединения является то, что при отключении одного из потребителей, остальные продолжают работать.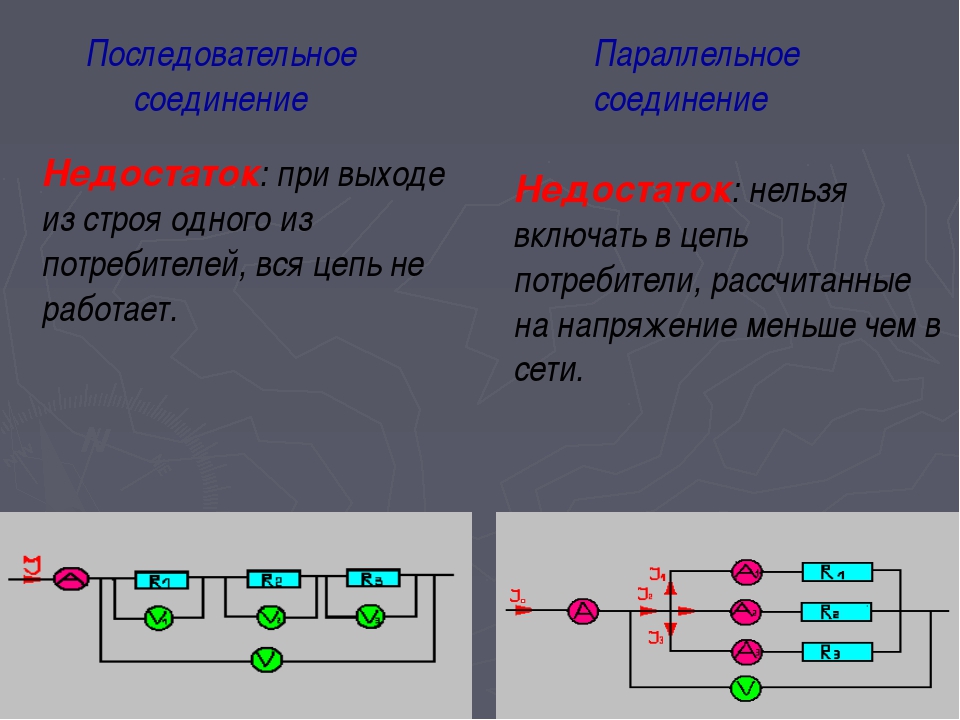
Источники:
Рис. 1. Параллельное соединение. © ЯКласс.
Рис. 2. Параллельное соединение, токи в различных потребителях. © ЯКласс.
3.1. Системы с последовательным соединением элементов
3.1. Системы с последовательным соединением элементов
Системой с последовательным соединением элементов называется система, в которой отказ любого элемента приводит к отказу всей системы (см. п. 2, рис 2.1). Такое со единение элементов в технике встречается наиболее часто, поэтому его называют основным соединением.
В системе с последовательным соединением для безотказной работы в течении некоторой наработки необходимо и достаточно, чтобы каждый из ее n элементов работал безотказно в течении этой наработки. Считая отказы элементов независимыми, вероятность одновременной безотказной работы n элементов определяется по теореме умножения вероятностей: вероятность совместного появления независимых событий равна произведению вероятностей этих событий:
(3. 1)
1)
(далее аргумент t в скобках, показывающий зависимость показателей надежности от времени, опускаем для сокращения записей формул). Соответственно, вероятность отказа такой ТС
(3.2)
Если система состоит из равнонадёжных элементов (рi = р), то
, (3.3)
Из формул (3.1) — (3.3) очевидно, что даже при высокой надежности элементов на- дежность системы при последовательном соединении оказывается тем более низкой, чем больше число элементов (например, при р = 0.95 и n =10 имеем Р = 0.60, при n=15 Р =0.46, а при n = 20 P = 0.36). Кроме того, поскольку все сомножители в правой части выражения (3.1) не превышают единицы, вероятность безотказной работы ТС при последовательном соединении не может быть выше вероятности безотказной работы самого ненадежного из ее элементов (принцип “хуже худшего”) и из малонадежных элементов нельзя создать высоконадежной ТС с последовательным соединением.
Рекомендуемые файлы
Если все элементы системы работают в периоде нормальной эксплуатации и имеет место простейший поток отказов (см. п. 1), наработки элементов и системы подчиняются экспоненциальному распределению (1.7) и на основании (3.1) можно записать
(3.4)
Люди также интересуются этой лекцией: 11. Плотность транспортного потока.
где
(3.5)
есть интенсивность отказов системы. Таким образом, интенсивность отказов системы при последовательном соединении элементов и простейшем потоке отказов равна сумме интенсивностей отказов элементов. С помощью выражений (1.8) и (1.9) могут быть определены средняя и g — процентная наработки.
Из (3.4) — (3.5) следует, что для системы из n равнонадёжных элементов (li = l)
L=nl , , (3. 6)
6)
т.е. интенсивность отказов в п раз больше, а средняя наработка в n раз меньше, чем у отдельного элемента.
Последовательное и параллельное соединение элементов электрической цепи. Последовательное и параллельное соединения проводников
На уроке рассматривается параллельное соединение проводников. Изображается схема такого соединения, показывается выражение для вычисления силы тока в такой цепи. Также вводится понятие эквивалентного сопротивления, находится его значение для случая параллельного соединения.
Соединения проводников бывают различные. Они могут быть параллельными, последовательными и смешанными. На данном уроке мы рассмотрим параллельное соединение проводников и понятие эквивалентного сопротивления.
Параллельным соединением проводников называется такое соединение, при котором начала и концы проводников соединяются вместе. На схеме такое соединение обозначается следующим образом (рис. 1):
Рис. 1. Параллельное соединение трех резисторов
На рисунке изображены три резистора (прибор, основанный на сопротивлении проводника) с сопротивлениями R1, R2, R3.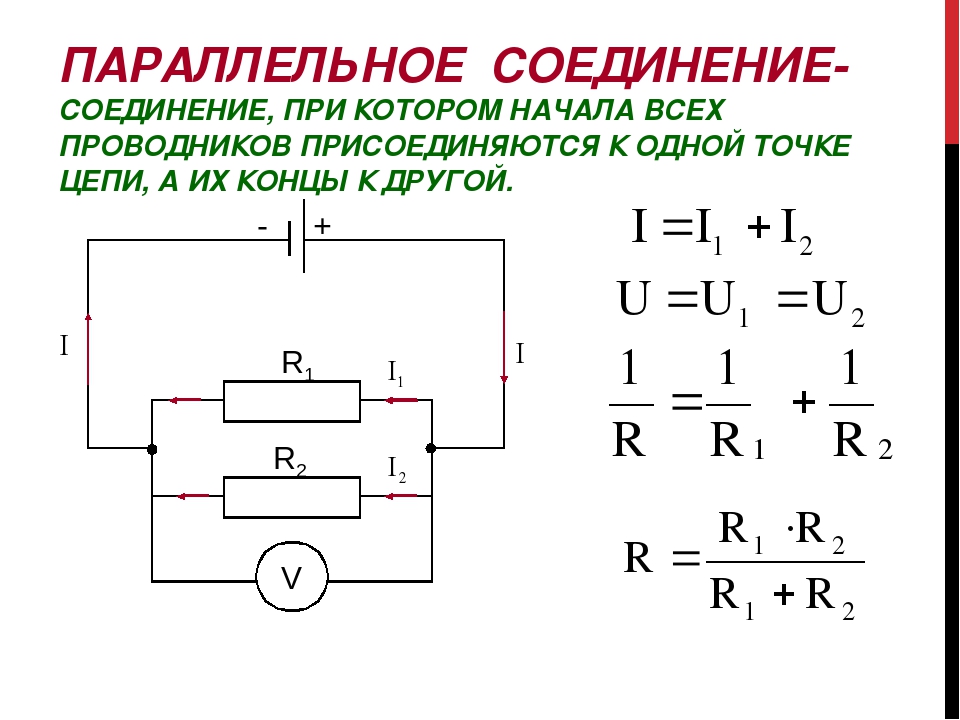 Как видим, начала этих проводников соединены в точке А, концы — в точке Б, а расположены они параллельно друг другу. Также в цепи может быть большее количество параллельно соединенных проводников.
Как видим, начала этих проводников соединены в точке А, концы — в точке Б, а расположены они параллельно друг другу. Также в цепи может быть большее количество параллельно соединенных проводников.
Теперь рассмотрим следующую схему (рис. 2):
Рис. 2. Схема для исследования силы тока при параллельном соединении проводников
В качестве элементов цепи мы взяли две лампы (1а, 1б). Они также имеют свое сопротивление, поэтому мы их можем рассматривать наравне с резисторами. Эти две лампы соединены параллельно, соединяются они в точках А и Б. К каждой лампе подсоединен свой амперметр: соответственно, А 1 и А 2 . Также есть амперметр А 3 , который измеряет силу тока во всей цепи. В цепь еще входит источник питания (3) и ключ (4).
Замкнув ключ, мы будем следить за показаниями амперметров. Амперметр А 1 покажет силу тока, равную I 1 , в лампе 1а, амперметр А 2 — cилу тока, равную I 2 , в лампе 1б. Что же касается амперметра А 3 , то он покажет силу тока, равную сумме токов в каждой отдельной взятой цепи, соединенных параллельно: I = I 1 + I 2 . То есть, если сложить показания амперметров А 1 и А 2 , то получим показания амперметра А 3 .
То есть, если сложить показания амперметров А 1 и А 2 , то получим показания амперметра А 3 .
Стоит обратить внимание, что если одна из ламп перегорит, то вторая будет продолжать работать. При этом весь ток будет проходить через эту вторую лампу. Это очень удобно. Так, например, электроприборы в наших домах включаются в цепь параллельно. И если один из них выходит из строя, то остальные остаются в рабочем состоянии.
Рис. 3. Схема для нахождения эквивалентного сопротивления при параллельном соединении
На схеме рис. 3 мы оставили один амперметр (2), но добавили в электрическую цепь вольтметр (5) для измерения напряжения. Точки А и Б являются общими и для первой (1а), и для второй лампы (1б), а значит, вольтметр измеряет напряжение на каждой из этих ламп (U 1 и U 2) и во всей цепи (U). Тогда U = U 1 = U 2 .
Эквивалентным сопротивлением называется сопротивление, которое может заменить все элементы, входящие в данную цепь. Посмотрим, чему же оно будет равно при параллельном соединении. Из закона Ома можно получить, что:
Из закона Ома можно получить, что:
В данной формуле R — эквивалентное сопротивление, R 1 и R 2 — сопротивление каждой лампочки, U = U 1 = U 2 — напряжение, которое показывает вольтметр (5). При этом мы используем то, что сумма токов в каждой отдельной цепи равна общей силе тока (I = I 1 + I 2). Отсюда можно получить формулу для эквивалентного сопротивления:
Если в цепи будет больше элементов, соединенных параллельно, то и слагаемых будет больше. Тогда придется вспомнить, как работать с простыми дробями.
Стоить отметить, что при параллельном соединении эквивалентное сопротивление будет достаточно малым. Соответственно, сила тока будет достаточно большой. Это стоит учитывать при включении в розетки большого количества электрических приборов. Ведь тогда сила тока возрастет, что может привести к перегреванию проводов и пожарам.
На следующем уроке мы рассмотрим другой тип соединения проводников — последовательное.
Список литературы
- Генденштейн Л.
 Э, Кайдалов А.Б., Кожевников В.Б. Физика 8 / Под ред. Орлова В.А., Ройзена И.И. — М.: Мнемозина.
Э, Кайдалов А.Б., Кожевников В.Б. Физика 8 / Под ред. Орлова В.А., Ройзена И.И. — М.: Мнемозина. - Перышкин А.В. Физика 8. — М.: Дрофа, 2010.
- Фадеева А.А., Засов А.В., Киселев Д.Ф. Физика 8. — М.: Просвещение.
- Физика ().
- Сверхзадача ().
- Интернет-портал Nado5.ru ().
Домашнее задание
- Стр. 114-117: вопросы № 1-6. Перышкин А.В. Физика 8. — М.: Дрофа, 2010.
- Могут ли быть параллельно соединены более трех проводников?
- Что случится, если одна из двух ламп, которые соединены параллельно, перегорит?
- Если к любой цепи параллельно подключить еще один проводник, всегда ли её эквивалентное сопротивление будет уменьшаться?
Одним из китов, на котором держатся многие понятия в электронике, является понятие последовательного и параллельного подключения проводников. Знать основные отличия указанных типов подключения просто необходимо. Без этого нельзя понять и прочитать ни одной схемы.
Основные принципы
Электрический ток движется по проводнику от источника к потребителю (нагрузке). Чаще всего в качестве проводника выбирается медный кабель. Связано это с требованием, которое предъявляется к проводнику: он должен легко высвобождать электроны.
Независимо от способа подключения, электрический ток двигается от плюса к минусу. Именно в этом направлении убывает потенциал. При этом стоит помнить, что провод, по котору идет ток, также обладает сопротивлением. Но его значение очень мало. Именно поэтому им пренебрегают. Сопротивление проводника принимают равным нулю. В том случае, если проводник обладает сопротивлением, его принято называть резистором.
Параллельное подключение
В данном случае элементы, входящие в цепь, объединены между собой двумя узлами. С другими узлами у них связей нет. Участки цепи с таким подключением принято называть ветвями. Схема параллельного подключения представлена на рисунке ниже.
Если говорить более понятным языком, то в данном случае все проводники одним концом соединены в одном узле, а вторым — во втором. Это приводит к тому, что электрический ток разделяется на все элементы. Благодаря этому увеличивается проводимость всей цепи.
Это приводит к тому, что электрический ток разделяется на все элементы. Благодаря этому увеличивается проводимость всей цепи.
При подключении проводников в цепь данным способом напряжение каждого из них будет одинаково. А вот сила тока всей цепи будет определяться как сумма токов, протекающих по всем элементам. С учетом закона Ома путем нехитрых математических расчетов получается интересная закономерность: величина, обратная общему сопротивлению всей цепи, определяется как сумма величин, обратных сопротивлениям каждого отдельного элемента. При этом учитываются только элементы, подключенные параллельно.
Последовательное подключение
В данном случае все элементы цепи соединены таким образом, что они не образуют ни одного узла. При данном способе подключения имеется один существенный недостаток. Он заключается в том, что при выходе из строя одного из проводников все последующие элементы работать не смогут. Ярким примером такой ситуации является обычная гирлянда. Если в ней перегорает одна из лампочек, то вся гирлянда перестает работать.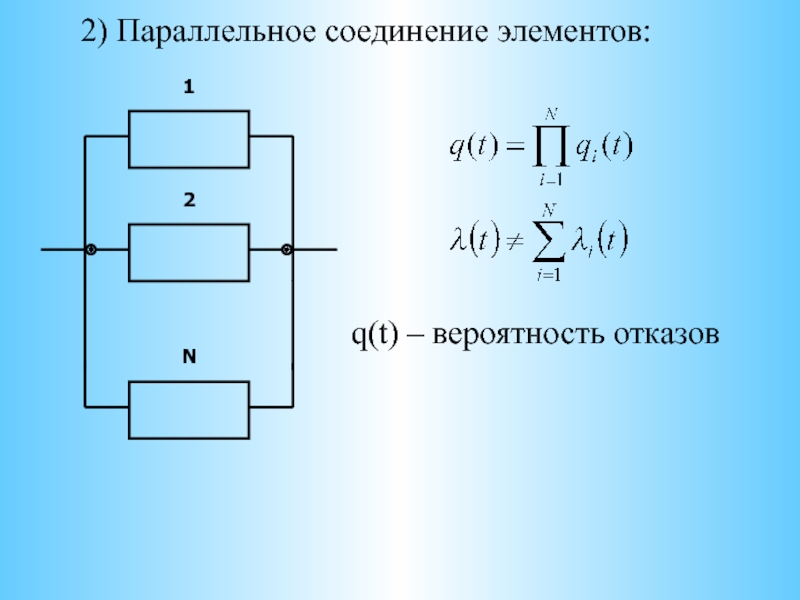
Последовательное подключение элементов отличается тем, что сила тока во всех проводниках равна. Что касается напряжения цепи, то оно равно сумме напряжения отдельных элементов.
В данной схеме проводники включаются в цепь поочередно. А это значит, что сопротивление всей цепи будет складываться из отдельных сопротивлений, характерных для каждого элемента. То есть общее сопротивление цепи равно сумме сопротивлений всех проводников. Эту же зависимость можно вывести и математическим способом, используя закон Ома.
Смешанные схемы
Бывают ситуации, когда на одной схеме можно увидеть одновременно последовательное и параллельное подключение элементов. В таком случае говорят о смешанном соединении. Расчет подобных схем проводится отдельно для каждой из группы проводников.
Так, чтобы определить общее сопротивление, необходимо сложить сопротивление элементов, подключенных параллельно, и сопротивление элементов с последовательным подключением. При этом последовательное подключение является доминантным. То есть его рассчитывают в первую очередь. И только после этого определяют сопротивление элементов с параллельным подключением.
То есть его рассчитывают в первую очередь. И только после этого определяют сопротивление элементов с параллельным подключением.
Подключение светодиодов
Зная основы двух типов подключения элементов в цепи, можно понять принцип создания схем различных электроприборов. Рассмотрим пример. во многом зависит от напряжения источника тока.
При небольшом напряжении сети (до 5 В) светодиоды подключают последовательно. Снизить уровень электромагнитных помех в данном случае поможет конденсатор проходного типа и линейные резисторы. Проводимость светодиодов увеличивают за счет использования системных модуляторов.
При напряжении сети 12 В может использоваться и последовательное, и параллельное подключение сети. В случае последовательного подключения используют импульсные блоки питания. Если собирается цепь из трех светодиодов, то можно обойтись без усилителя. Но если цепь будет включать большее количество элементов, то усилитель необходим.
Во втором случае, то есть при параллельном подключении, необходимо использование двух открытых резисторов и усилителя (с пропускной способностью выше 3 А).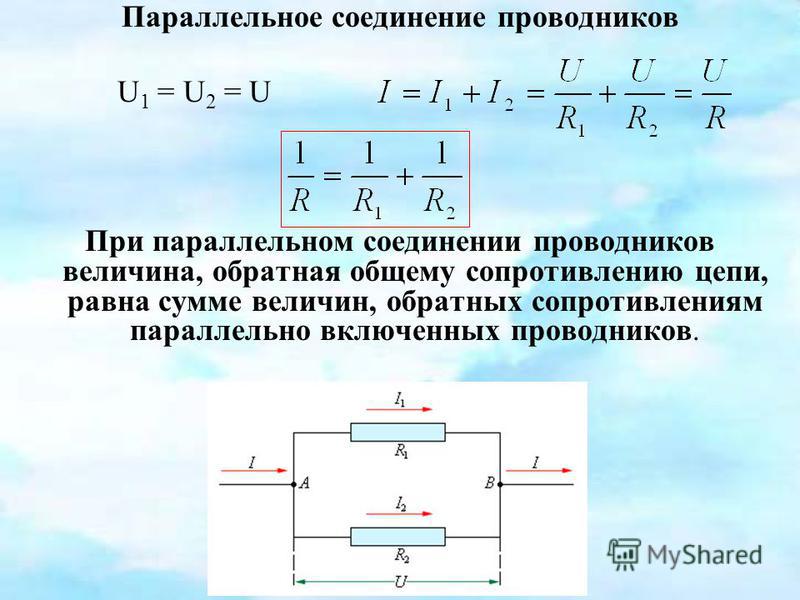 Причем первый резистор устанавливается перед усилителем, а второй — после.
Причем первый резистор устанавливается перед усилителем, а второй — после.
При высоком напряжении сети (220 В) прибегают к последовательному подключению. При этом дополнительно используют операционные усилители и понижающие блоки питания.
Всем доброго времени суток. В прошлой статье я рассмотрел , применительно к электрическим цепям, содержащие источники энергии. Но в основе анализа и проектирования электронных схем вместе с законом Ома лежат также законы баланса , называемым первым законом Кирхгофа, и баланса напряжения на участках цепи, называемым вторым законом Кирхгофа, которые рассмотрим в данной статье. Но для начала выясним, как соединяются между собой приёмники энергии и какие при этом взаимоотношения между токами, напряжениями и .
Приемники электрической энергии можно соединить между собой тремя различными способами: последовательно, параллельно или смешано (последовательно — параллельно). Вначале рассмотрим последовательный способ соединения, при котором конец одного приемника соединяют с началом второго приемника, а конец второго приемника – с началом третьего и так далее.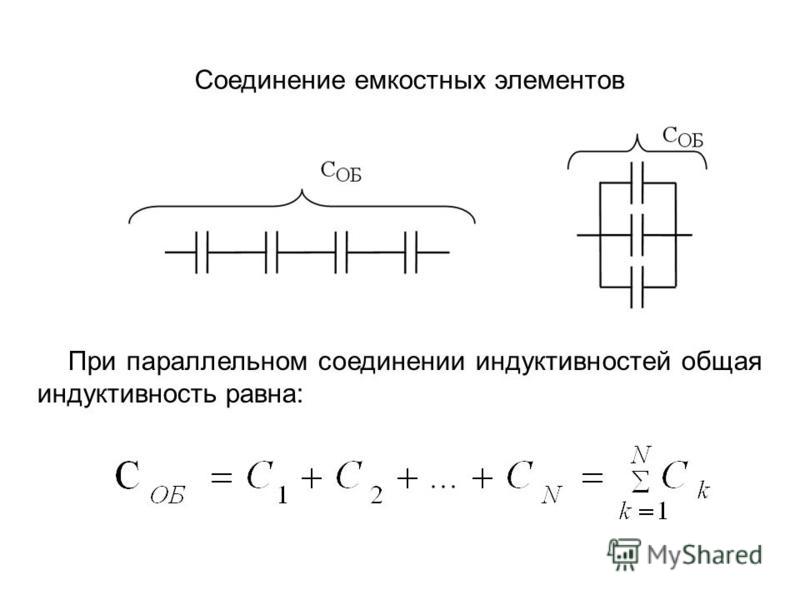 На рисунке ниже показано последовательное соединение приемников энергии с их подключением к источнику энергии
На рисунке ниже показано последовательное соединение приемников энергии с их подключением к источнику энергии
Пример последовательного подключения приемников энергии.
В данном случае цепь состоит из трёх последовательных приемников энергии с сопротивлением R1, R2, R3 подсоединенных к источнику энергии с U. Через цепь протекает электрический ток силой I, то есть, напряжение на каждом сопротивлении будет равняться произведению силы тока и сопротивления
Таким образом, падение напряжения на последовательно соединённых сопротивлениях пропорциональны величинам этих сопротивлений.
Из вышесказанного вытекает правило эквивалентного последовательного сопротивления, которое гласит, что последовательно соединённые сопротивления можно представить эквивалентным последовательным сопротивлением величина, которого равна сумме последовательно соединённых сопротивлений. Это зависимость представлена следующими соотношениями
где R – эквивалентное последовательное сопротивление.
Применение последовательного соединения
Основным назначением последовательного соединения приемников энергии является обеспечение требуемого напряжения меньше, чем напряжение источника энергии. Одними из таких применений является делитель напряжения и потенциометр
Делитель напряжения (слева) и потенциометр (справа).
В качестве делителей напряжения используют последовательно соединённые резисторы, в данном случае R1 и R2, которые делят напряжение источника энергии на две части U1 и U2. Напряжения U1 и U2 можно использовать для работы разных приемников энергии.
Довольно часто используют регулируемый делитель напряжения, в качестве которого применяют переменный резистор R. Суммарное сопротивление, которого делится на две части с помощью подвижного контакта, и таким образом можно плавно изменять напряжение U2 на приемнике энергии.
Ещё одним способом соединения приемников электрической энергии является параллельное соединение, которое характеризуется тем, что к одним и тем же узлам электрической цепи присоединены несколько преемников энергии.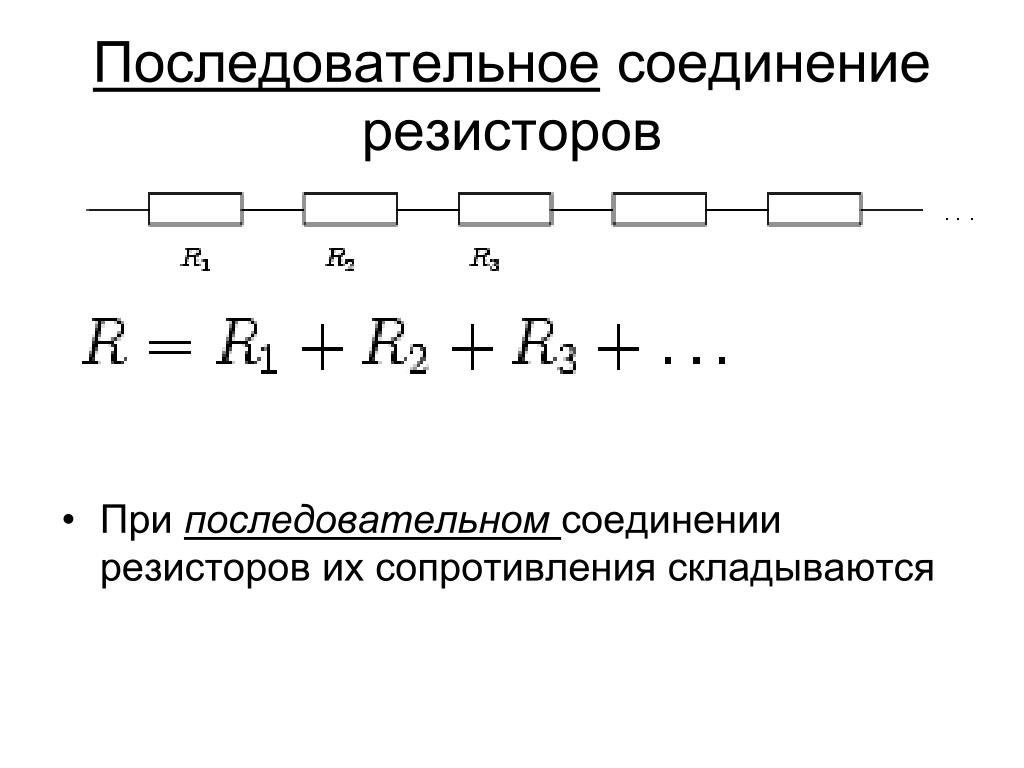 Пример такого соединения показан на рисунке ниже
Пример такого соединения показан на рисунке ниже
Пример параллельного соединения приемников энергии.
Электрическая цепь на рисунке состоит из трёх параллельных ветвей с сопротивлениями нагрузки R1, R2 и R3. Цепь подключена к источнику энергии с напряжением U, через цепь протекает электрический ток с силой I. Таким образом, через каждую ветвь протекает ток равный отношению напряжения к сопротивлению каждой ветви
Так как все ветви цепи находятся под одним напряжением U, то токи приемников энергии обратно пропорциональны сопротивлениям этих приемников, а следовательно параллельно соединённые приемники энергии можно заметь одним приемником энергии с соответствующим эквивалентным сопротивлением, согласно следующих выражений
Таким образом, при параллельном соединении эквивалентное сопротивление всегда меньше самого малого из параллельно включенных сопротивлений.
Смешанное соединение приемников энергии
Наиболее широко распространено смешанное соединение приемн
Формула общего сопротивления при последовательном соединении.
 Электрическая цепь с последовательным соединением элементов
Электрическая цепь с последовательным соединением элементов
Отдельные проводники электрической цепи могут быть соединены между собой последовательно, параллельно и смешанно. При этом последовательное и параллельное соединение проводников являются основными видами соединений, а смешанное соединение это их совокупность.
Последовательным соединением проводников называется такое соединение, когда конец первого проводника соединен с началом второго, конец второго проводника соединен с началом третьего и так далее (рисунок 1).
Рисунок 1. Схема последовательного соединения проводников
Общее сопротивление цепи, состоящее из нескольких последовательно соединенных проводников, равно сумме сопротивлений отдельных проводников:
r
= r
1 + r
2 + r
3 + … + r n
.
Ток на отдельных участках последовательной цепи везде одинаков:
I
1 = I
2 = I
3 = I
.
Видео 1. Последовательное соединение проводников
Пример
1.
На рисунке 2 представлена электрическая цепь, состоящая из трех последовательно включенных сопротивлений r
1 = 2 Ом, r
2 = 3 Ом, r
3 = 5 Ом. Требуется определить показания вольтметров V
1 , V
2 , V
3 и V
4 , если ток в цепи равен 4 А.
Сопротивление всей цепи
r
= r
1 + r
2 + r
3 = 2 + 3 + 5 =10 Ом.
Рисунок 2. Схема измерения напряжений на отдельных участках электрической цепи
В сопротивлении r
1 при протекании тока будет падение напряжения:
U
1 = I
× r
1 = 4 × 2 = 8 В.
Вольтметр V
1 , включенный между точками а
и б
, покажет 8 В.
В сопротивлении r
2 также происходит падение напряжения:
U
2 = I
× r
2 = 4 × 3 = 12 В.
Вольтметр V
2 , включенный между точками в
и г
, покажет 12 В.
Падение напряжения в сопротивлении r
3:
U
3 = I
× r
3 = 4 × 5 = 20 В.
Вольтметр V
3 , включенный между точками д
и е
, покажет 20 В.
Если вольтметр присоединить одним концом к точке а
, другим концом к точке г
, то он покажет разность потенциалов между этими точками, равную сумме падений напряжения в сопротивлениях r
1 и r
2 (8 + 12 = 20 В).
Таким образом, вольтметр V
, измеряющий напряжение на зажимах цепи и включенный между точками а
и е
, покажет разность потенциалов между этими точками или сумму падений напряжения в сопротивлениях r
1 , r
2 и r
3 .
Отсюда видно, что сумма падений напряжения на отдельных участках электрической цепи равна напряжению на зажимах цепи.
Так как при последовательном соединении ток цепи на всех участках одинаков, то падение напряжения пропорционально сопротивлению данного участка.
Пример 2.
Три сопротивления 10, 15 и 20 Ом соединены последовательно, как показано на рисунке 3. Ток в цепи 5 А. Определить падение напряжения на каждом сопротивлении.
Определить падение напряжения на каждом сопротивлении.
U
1 = I
× r
1 = 5 ×10 = 50 В,
U
2 = I
× r
2 = 5 ×15 = 75 В,
U
3 = I
× r
3 = 5 ×20 = 100 В.
Рисунок 3. К примеру 2
Общее напряжение цепи равно сумме падений напряжений на отдельных участках цепи:
U
= U
1 + U
2 + U
3 = 50 + 75 + 100 = 225 В.
Параллельное соединение проводников
Параллельным соединением проводников называется такое соединение, когда начала всех проводников соединены в одну точку, а концы проводников – в другую точку (рисунок 4). Начало цепи присоединяется к одному полюсу источника напряжения, а конец цепи – к другому полюсу.
Из рисунка видно, что при параллельном соединении проводников для прохождения тока имеется несколько путей. Ток, протекая к точке разветвления А
, растекается далее по трем сопротивлениям и равен сумме токов, уходящих от этой точки:
I
= I
1 + I
2 + I
3 .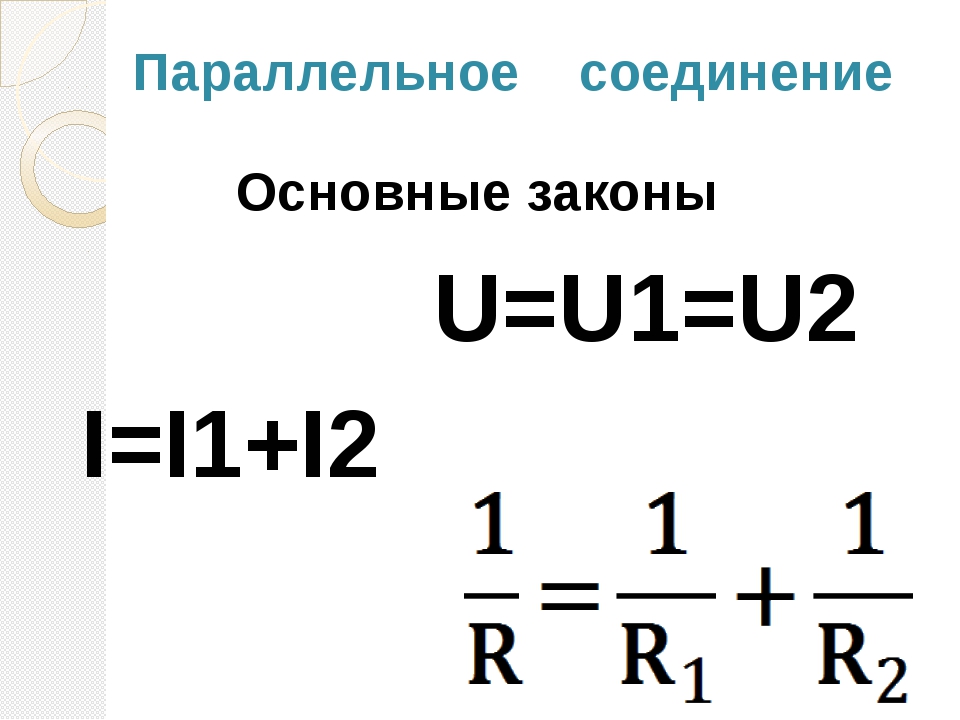
Если токи, приходящие к точке разветвления, считать положительными, а уходящие – отрицательными, то для точки разветвления можно написать:
то есть алгебраическая сумма токов для любой узловой точки цепи всегда равна нулю. Это соотношение, связывающее токи в любой точке разветвления цепи, называется первым законом Кирхгофа
. Определение первого закона Кирхгофа может звучать и в другой формулировке, а именно: сумма токов втекающих в узел электрической цепи равна сумме токов вытекающих из этого узла.
Видео 2. Первый закон Кирхгофа
Обычно при расчете электрических цепей направление токов в ветвях, присоединенных к какой либо точке разветвления, неизвестны. Поэтому для возможности самой записи уравнения первого закона Кирхгофа нужно перед началом расчета цепи произвольно выбрать так называемые положительные направления токов во всех ее ветвях и обозначить их стрелками на схеме.
Пользуясь законом Ома, можно вывести формулу для подсчета общего сопротивления при параллельном соединении потребителей.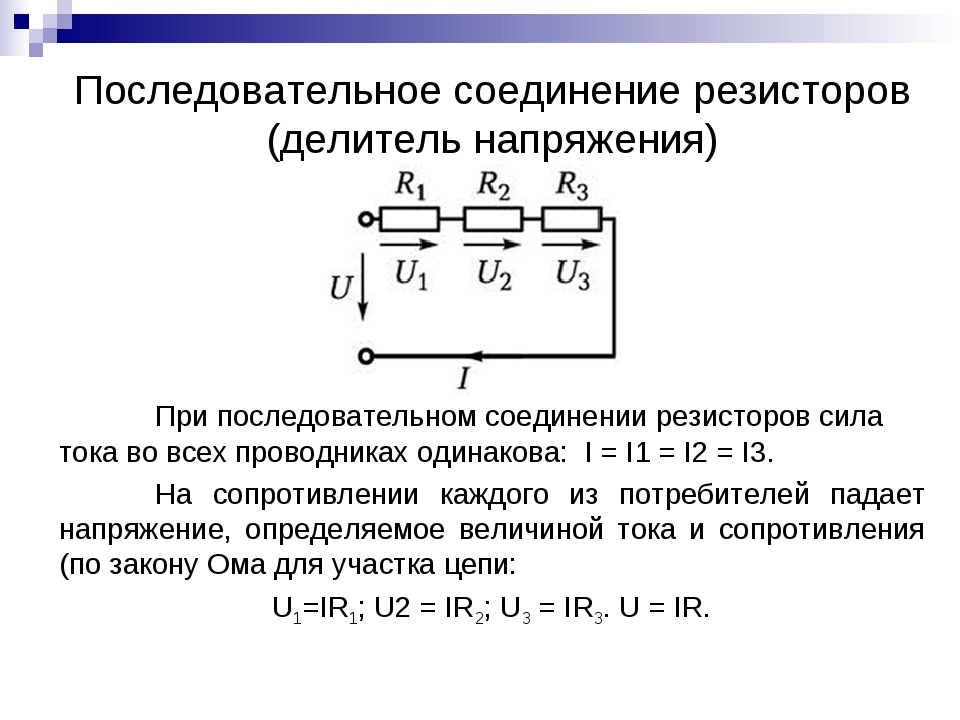
Общий ток, приходящий к точке А
, равен:
Токи в каждой из ветвей имеют значения:
По формуле первого закона Кирхгофа
I
= I
1 + I
2 + I
3
Вынося U
в правой части равенства за скобки, получим:
Сокращая обе части равенства на U
, получим формулу подсчета общей проводимости:
g = g 1 + g 2 + g 3 .
Таким образом, при параллельном соединении увеличивается не сопротивление, а проводимость .
Пример 3.
Определить общее сопротивление трех параллельно включенных сопротивлений, если r
1 = 2 Ом, r
2 = 3 Ом, r
3 = 4 Ом.
Пример 4.
Пять сопротивлений 20, 30 ,15, 40 и 60 Ом включены параллельно в сеть. Определить общее сопротивление:
Следует заметить, что при подсчете общего сопротивления разветвления оно получается всегда меньше, чем самое меньшее сопротивление, входящее в разветвление.
Если сопротивления, включенные параллельно, равны между собой, то общее сопротивление r
цепи равно сопротивлению одной ветви r
1 , деленному на число ветвей n
:
Пример 5.
Определить общее сопротивление четырех параллельно включенных сопротивлений по 20 Ом каждое:
Для проверки попробуем найти сопротивление разветвления по формуле:
Как видим, ответ получается тот же.
Пример 6.
Пусть требуется определить токи в каждой ветви при параллельном их соединении, изображенном на рисунке 5, а
.
Найдем общее сопротивление цепи:
Теперь все разветвления мы можем изобразить упрощенно как одно сопротивление (рисунок 5, б
).
Падение напряжения на участке между точками А
и Б
будет:
U
= I
× r
= 22 × 1,09 = 24 В.
Возвращаясь снова к рисунку 5, а видим, что все три сопротивления окажутся под напряжением 24 В, так как они включены между точками А
и Б
.
Рассматривая первую ветвь разветвления с сопротивлением r
1 , мы видим, что напряжение на этом участке 24 В, сопротивление участка 2 Ом. По закону Ома для участка цепи ток на этом участке будет:
Ток второй ветви
Ток третьей ветви
Проверим по первому закону Кирхгофа
Последовательное, параллельное и смешанное соединения резисторов.
Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление.
Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов
(приемников электрической энергии): последовательное, параллельное и смешанное.
Последовательное соединение резисторов
.
При последовательном соединении
нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.
Последовательное соединение приемников поясняет рис. 25, а.
.Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.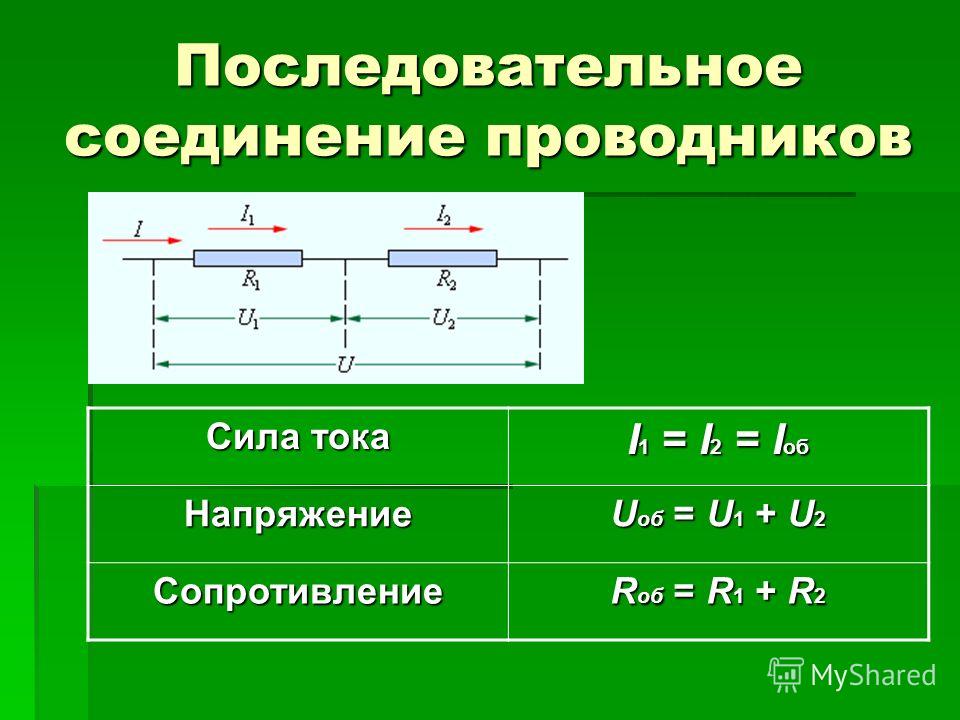
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:
E = IR 1 + IR 2 + IR 3 = I(R 1 + R 2 + R 3) = IR эк
(19)
где R
эк
=
R 1 + R 2 + R 3
.
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U 1 =IR 1 ; U 2 = IR 2 , U 3 = IR з и в данном случае E = U, то длярассматриваемой цепи
U = U 1 + U 2 +U 3
(20)
Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:
U 1: U 2: U 3 = R 1: R 2: R 3
(21)
т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.
В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:
При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Параллельное соединение резисторов
. При параллельном соединении
нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или
I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк
(23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/R эк
=
1/R 1 + 1/R 2 + 1/R 3
(24)
Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов
:
G эк = G 1 + G 2 +G 3
(25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3
(26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
R эк =R 1 R 2 /(R 1 +R 2)
при трех параллельно включенных резисторах
R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
R эк = R1 / n
(27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n
(28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных.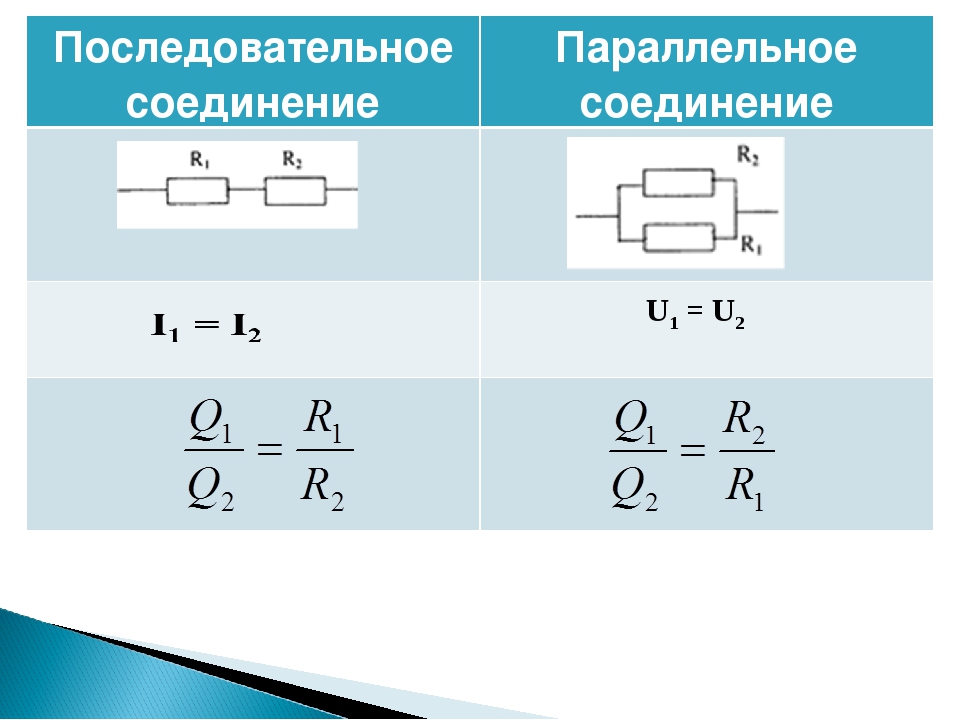 Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Смешанное соединение резисторов
. Смешанным соединением
называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле
R 123 =R 12 R 3 /(R 12 +R 3)=(R 1 +R 2)R 3 /(R 1 +R 2 +R 3).
При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:
R эк = R 123 + R 4 = (R 1 + R 2) R 3 / (R 1 + R 2 + R 3) + R 4
Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э.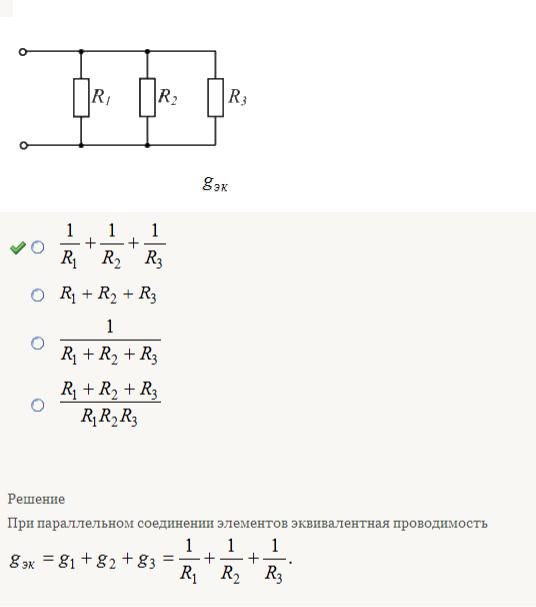 п. с. постоянного тока.
п. с. постоянного тока.
Параллельные соединения резисторов, формула расчёта которых выводится из закона Ома и правил Кирхгофа, являются наиболее распространённым типом включения элементов в электрическую цепь. При параллельном соединении проводников два или несколько элементов объединяются своими контактами с обеих из сторон соответственно. Подключение их к общей схеме осуществляется именно этими узловыми точками.
Gif?x15027″ alt=»Общий вид»>
Общий вид
Особенности включения
Включённые таким образом проводники нередко входят в состав сложных цепочек, содержащих, помимо этого, последовательное соединение отдельных участков.
Для такого включения типичны следующие особенности:
- Общее напряжение в каждой из ветвей будет иметь одно и то же значение;
- Протекающий в любом из сопротивлений электрический ток всегда обратно пропорционален величине их номинала.
В частном случае, когда все включённые в параллель резисторы имеют одинаковые номинальные значения, протекающие по ним «индивидуальные» токи также будут равны между собой.
Расчёт
Сопротивления ряда соединённых в параллель проводящих элементов определяются по общеизвестной форме расчёта, предполагающей сложение их проводимостей (обратных сопротивлению величин).
Протекающий в каждом из отдельных проводников ток в соответствие с законом Ома, может быть найден по формуле:
I= U/R (одного из резисторов).
После ознакомления с общими принципами обсчёта элементов сложных цепочек можно перейти к конкретным примерам решения задач данного класса.
Типичные подключения
Пример №1
Нередко для решения стоящей перед конструктором задачи требуется путём объединения нескольких элементов получить в итоге конкретное сопротивление. При рассмотрении простейшего варианта такого решения допустим, что общее сопротивление цепочки из нескольких элементов должно составлять 8 Ом. Этот пример нуждается в отдельном рассмотрении по той простой причине, что в стандартном ряду сопротивлений номинал в 8 Ом отсутствует (есть только 7,5 и 8,2 Ом).
Решение этой простейшей задачи удаётся получить за счёт соединения двух одинаковых элементов с сопротивлениями по 16 Ом каждое (такие номиналы в резистивном ряду существуют). Согласно приводимой выше формуле общее сопротивление цепочки в этом случае вычисляется очень просто.
Из неё следует:
16х16/32=8 (Ом), то есть как раз столько, сколько требовалось получить.
Таким сравнительно простым способом удаётся решить задачу формирования общего сопротивления, равного 8-ми Омам.
Пример №2
В качестве ещё одного характерного примера образования требуемого сопротивления можно рассмотреть построение схемы, состоящей из 3-х резисторов.
Общее значение R такого включения может быть рассчитано по формуле последовательного и параллельного соединения в проводниках.
Gif?x15027″ alt=»Пример»>
В соответствии с указанными на картинке значениями номиналов, общее сопротивление цепочки будет равно:
1/R = 1/200+1/220+1/470 = 0,0117;
R=1/0,0117 = 85,67Ом.
В итоге находим суммарное сопротивление всей цепочки, получаемой при параллельном соединении трёх элементов с номинальными значениями 200, 240 и 470 Ом.
Важно!
Указанный метод применим и при расчёте произвольного числа соединенных в параллель проводников или потребителей.
Также необходимо отметить, что при таком способе включения различных по величине элементов общее сопротивление будет меньше, чем у самого малого номинала.
Расчёт комбинированных схем
Рассмотренный метод может применяться и при расчёте сопротивления более сложных или комбинированных схем, состоящих из целого набора компонентов. Их иногда называют смешанными, поскольку при формировании цепочек используются сразу оба способа. Смешанное соединение резисторов представлено на размещенном ниже рисунке.
Gif?x15027″ alt=»Смешанная схема»>
Смешанная схема
Для упрощения расчета сначала разбиваем все резисторы по типу включения на две самостоятельные группы. Одна из них представляет собой последовательное соединение, а вторая – имеет вид подключения параллельного типа.
Из приведённой схемы видно, что элементы R2 и R3 соединяются последовательно (они объединены в группу 2), которая, в свою очередь, включена в параллель с резистором R1, принадлежащим группе 1.
Последовательным
называется такое соединение резисторов, когда конец одного проводника соединяется с началом другого и т.д. (рис. 1). При последовательном соединении сила тока на любом участке электрической цепи одинакова. Это объясняется тем, что заряды не могут накапливаться в узлах цепи. Их накопление привело бы к изменению напряженности электрического поля, а следовательно, и к изменению силы тока. Поэтому
\(~I = I_1 = I_2 .\)
Амперметр А
измеряет силу тока в цепи и обладает малым внутренним сопротивлением (R
A → 0).
Включенные вольтметры V
1 и V
2 измеряют напряжение U
1 и U
2 на сопротивлениях R
1 и R
2 . Вольтметр V
измеряет подведенное к клеммам Μ
и N
напряжение U
.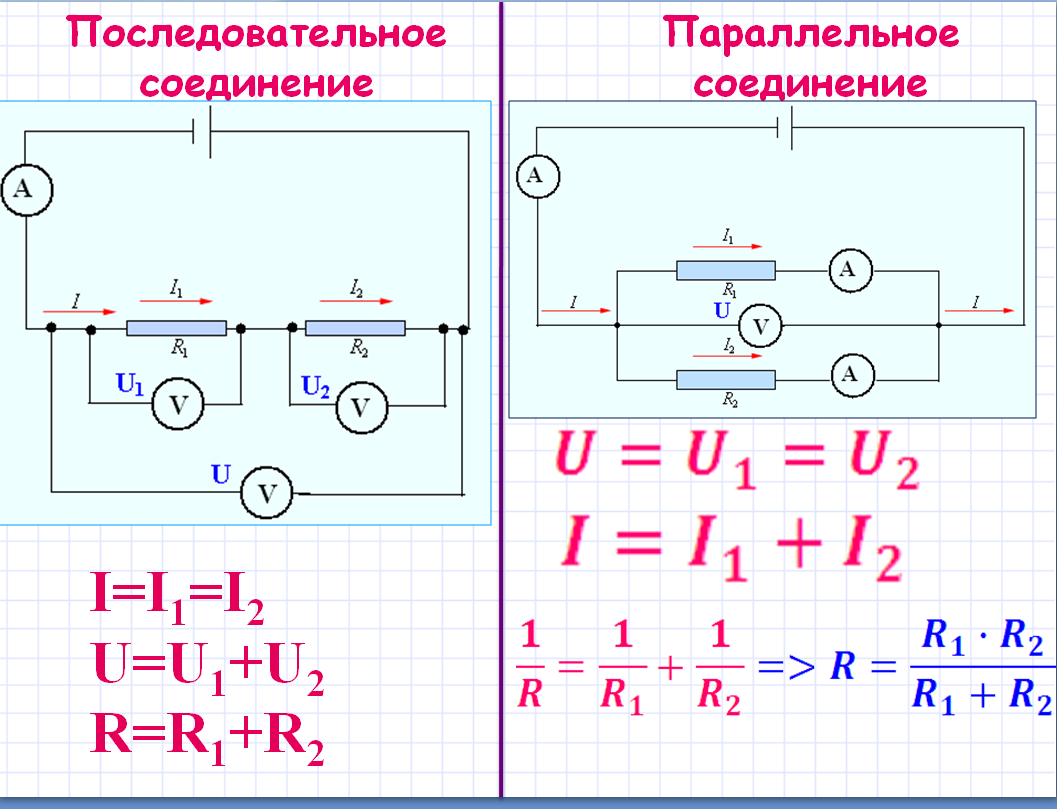 n R_i .\)
n R_i .\)
Если сопротивления отдельных резисторов равны между собой, т.е. R
1 = R
2 = … = R
n , то общее сопротивление этих резисторов при последовательном соединении в n
раз больше сопротивления одного резистора: R
= nR
1 .
При последовательном соединении резисторов справедливо соотношение \(~\frac{U_1}{U_2} = \frac{R_1}{R_2}\), т.е. напряжения на резисторах прямо пропорциональны сопротивлениям.
Параллельным
называется такое соединение резисторов, когда одни концы всех резисторов соединены в один узел, другие концы — в другой узел (рис. 2). Узлом называется точка разветвленной цепи, в которой сходятся более двух проводников. При параллельном соединении резисторов к точкам Μ
и N
подключен вольтметр. Он показывает, что напряжения на отдельных участках цепи с сопротивлениями R
1 и R
2 равны. Это объясняется тем, что работа сил стационарного электрического поля не зависит от формы траектории:
\(~U = U_1 = U_2 . n \frac{1}{R_i} .\)
n \frac{1}{R_i} .\)
Если сопротивления всех n
параллельно соединенных резисторов одинаковы и равны R
1 то \(~\frac 1R = \frac{n}{R_1}\) . Откуда \(~R = \frac{R_1}{n}\) .
Сопротивление цепи, состоящей из n
одинаковых параллельно соединенных резисторов, в n
раз меньше сопротивления каждого из них.
При параллельном соединении резисторов справедливо соотношение \(~\frac{I_1}{I_2} = \frac{R_2}{R_1}\), т.е. силы токов в ветвях параллельно соединенной цепи обратно пропорциональны сопротивлениям ветвей.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 257-259.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2
на 3
и 47 Ом
и соединим их последовательно.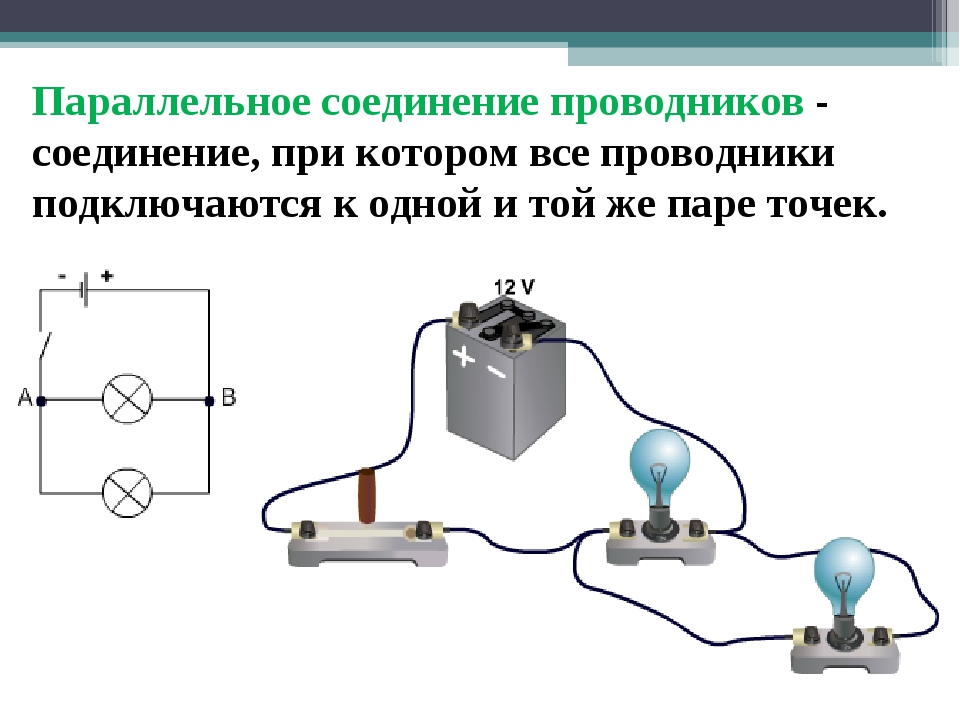 Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно
учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом
и мощностью 1 Вт
. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А
), а сопротивление каждого из них равно 50 Ом
, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт
. В результате на каждом из них выделится по 0,5 Вт
В результате на каждом из них выделится по 0,5 Вт
мощности. В сумме это и будет тот самый 1 Вт
.
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте .
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
1.5. Способы соединения элементов и преобразования цепей
1.5. Способы соединения элементов и преобразования цепей
При расчетах часто возникает необходимость упростить схему. В основе
различных методов преобразования электрических цепей лежит понятие эквивалентности. Согласно этому понятию напряжения и токи в ветвях цепи, не затронутых преобразованием, остаются неизменными. Наиболее часто электрические цепи представляют собой последовательное и паралельное соединение резистивных, емкостных, индуктивных элементов и источников питания.
Последовательное соединение резисторов показано на рис. 1.12.
Рис. 1.12. Последовательное соединение резисторов.
На основании второго закона Кирхгофа для цепи рис. 1.12 можно записать следующее выражение:
, где
Из полученного выражения видно, что при последовательном соединении резисторов их общее электрическое сопротивление равно сумме электрических сопротивлений всех резисторов цепи.
. (1.24)
Последовательное соединение емкостей показано на рис. 1.13
Рис. 1.13. Последовательное соединение емкостей.
Напряжение на каждой емкости в сумме дает напряжение, приложенное к батарее емкостей. Учитывая, что напряжение на емкости
для схемы рис. 1.13 можно записать:. (1.25)
Отношение u к q дает величину, обратную суммарной емкости CΣ. Следовательно
.
Т.е. при последовательном соединении величина, обратная суммарной емкости, равна сумме величин, обратных емкостям.
Последовательное соединение индуктивностей показано на рис. 1.14.
Рис. 1.14. Последовательное соединение индуктивностей.
Напряжение на каждой индуктивности в сумме дает напряжение, приложенное к суммарной индуктивности LΣ.
.
Разделив u на
получим общую индуктивность, т. е.. (1.26)
При последовательном соединении индуктивностей общая индуктивность равна сумме всех индуктивностей, включенных в электрическую цепь.
Последовательное соединение источников напряжения показано на рис. 1.15.
Рис. 1.15. Последовательное соединение источников напряжения.
Учитывая, что источники, действующие в одном направлении, суммируются, а в противоположных направлениях вычитаются; на основании рис. 1.15 имеем
. (1.27)
При последовательном соединении источников напряжения общая величина напряжения равна алгебраической сумме напряжений на каждом источнике.
Параллельное соединение резисторов показано на рис. 1.16,а.
1.16,а.
Рис. 1.16. Параллельное соединение резисторов (а), индуктивных (б) и емкостных (в) элементов.
Из рис. 1.16 видно, что при параллельном соединении элементов к ним приложено одно и тоже напряжение u. Согласно первому закону Кирхгофа для тока каждой из схем, изображенных на рис. 1.16 можно записать:
. (1.28)
На основании этого уравнения и учитывая, что для резистивного элемента
, получаем:, где . (1.29)
При параллельном соединении резистивных элементов общая проводимость цепи равна сумме проводимостей всех резистивных элементов, включенных в электрическую цепь.
Параллельное соединение индуктивностей показано на рис. 1.16,б. Ток в индуктивности равен
.Подставляя значение тока в выражение (1.28) будем иметь:, где . (1.30)
При параллельном соединении индуктивных элементов обратная величина индуктивности всей цепи равна сумме обратных величин каждой индуктивности, включенной в электрическую цепь.
Параллельное соединение емкостей показано на рис. 1.16,в.
Ток в емкостном элементе равен
. Подставляя значения тока в выражение (1.28) получаем, где . (1.31)
При параллельном соединении емкостных элементов общая емкость цепи равна сумме всех емкостей, включенных в электрическую цепь.
Следовательно, электрическую цепь, состоящую из n последовательно или параллельно соединенных резистивных, индуктивных или емкостных элементов можно заменить одним эквивалентным резистивным, индуктивным или емкостным элементом с параметрами, вычисленными по формулам (1.24÷1.26) и (1.29÷1.31).
2.2.3 Цепи с последовательными и параллельными элементами
Большинство энергосистем фактически настроено как «цепи» или контуры, и нам может потребоваться найти эквивалентное последовательно-параллельное сопротивление от начала контура до конца. На рисунке ниже показан особенно неприятный пример, но мы можем разбить его на несколько простых шагов.
Рисунок 2.7: Сложная последовательно-параллельная схема
Щелкните здесь, чтобы увидеть текстовое описание рисунка 2.7
Схема представлена прямоугольником, который разделен по вертикали на большую и меньшую секции.Слева находится закрашенный кружок со знаком плюс и минус, обозначенный как 120V. В цепи 4 резистора. Первый находится в верхней части большой части прямоугольника и обозначен как 4 Ом. Следующий находится в верхней части маленькой стороны схемы и обозначен как 3 Ом. В правой части прямоугольника есть резистор, обозначенный как 6 Ом. Последний резистор находится на делении и имеет маркировку 18 Ом. Под резистором 4 Ом находится стрелка, указывающая вправо, с надписью i s .Резистор на 18 Ом имеет направленную вниз стрелку, обозначенную i 1 , а резистор на 6 Ом имеет направленную вниз стрелку, обозначенную i 2 .
Источник: Сет Блумсак
На этом рисунке у нас есть источник 120 В (например, небольшая батарея), который передает ток через показанную сеть резисторов. Какое эквивалентное сопротивление во всей цепи, от положительной до отрицательной клеммы аккумулятора?
Какое эквивалентное сопротивление во всей цепи, от положительной до отрицательной клеммы аккумулятора?
Шаг 1. Возьмем резистор 3 Ом и резистор 6 Ом и вычислим эквивалентное последовательное сопротивление следующим образом: 3 Ом + 6 Ом = 9 Ом.Это дает новое представление схемы ниже.
Рисунок 2.8: Первый шаг упрощения сложной схемы
Щелкните здесь, чтобы увидеть текстовое описание рисунка 2.8
Схема представлена прямоугольником, который разделен по вертикали на большую и меньшую части. Слева находится закрашенный кружок со знаком плюс и минус, обозначенный как 120V. В цепи 3 резистора. Первый находится в верхней части большой части прямоугольника и обозначен как 4 Ом.В правой части прямоугольника есть резистор, обозначенный как 9 Ом. Последний резистор находится на делении и имеет маркировку 18 Ом.
Источник: Сет Блумсак
На шаге 2 мы вычислим эквивалентное параллельное сопротивление элементов 9 Ом и 18 Ом. Мы рассчитываем это как:
1 (19 + 118) = 1 (218 + 118) = 1 (16) = 6 Ом
Рисунок 2.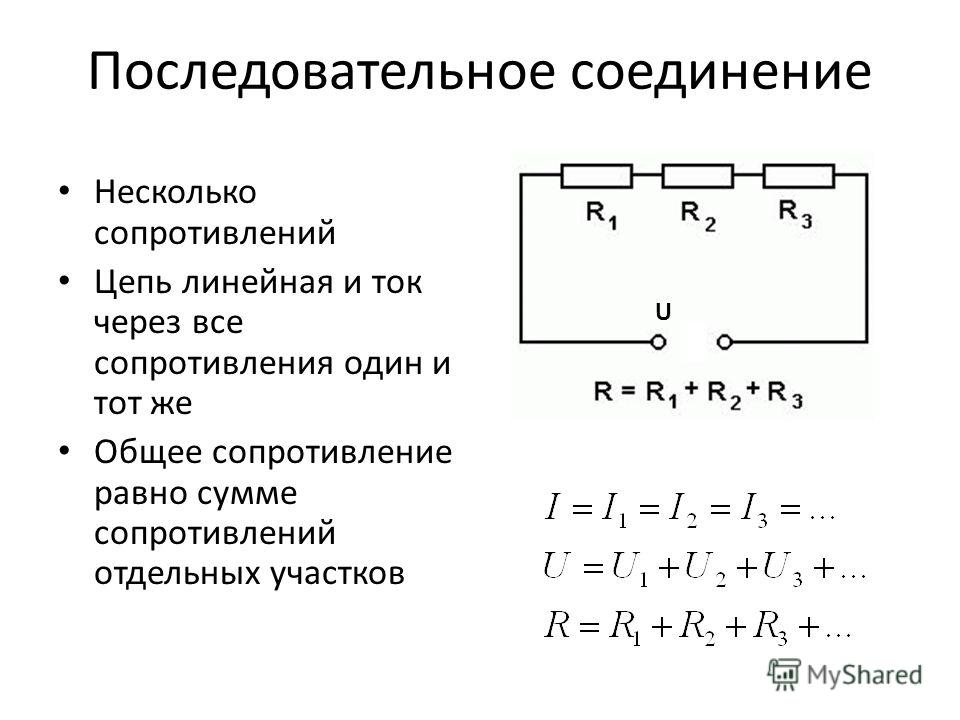 9: Второй шаг упрощения сложной схемы
9: Второй шаг упрощения сложной схемы
Щелкните здесь, чтобы увидеть текстовое описание рисунка 2.9
На схеме показана более простая схема, представленная прямоугольником со встроенным кружком с левой стороны.Внутри круга есть символы плюса и минуса, обозначенные как 120 В. В верхней части схемы находится резистор с маркировкой 4 Ом, а с правой стороны схемы — резистор с маркировкой 6 Ом
.
Источник: Сет Блумсак
На последнем этапе мы возьмем последовательное сопротивление элементов 4 Ом и 6 Ом: 4 Ом + 6 Ом = 10 Ом.
В этих нескольких шагах мы показали, что две цепи на рисунке ниже имеют точно такое же эквивалентное сопротивление.
Фигура 2.10. Сложная последовательно-параллельная схема (слева) и ее эквивалентная простая схема (справа)
Щелкните здесь, чтобы увидеть текстовое описание рисунка 2.10
Схема с рисунка 2.8 рядом с простой схемой. Простая схема представлена прямоугольником со встроенным кружком с левой стороны с символом плюс и минус внутри, обозначенным 120 В. На правой стороне схемы резистор с маркировкой 10 Ом.
На правой стороне схемы резистор с маркировкой 10 Ом.
Источник: Сет Блумсак
Добавление элементов в схемы — Обучающие подходы
Что такое действие для
Это демонстрационное задание помогает ученикам понять, как работают параллельные схемы.
Что приготовить
- 12 В, лампочки 24 Вт
- Источник питания постоянного тока 12 В
- с большим, легко читаемым дисплеем
Демонстрационный амперметр
Используя автомобильные лампы для фар на 12 В, 24 Вт, лабораторный источник питания на 12 В и демонстрационный аналоговый измеритель (0–5 ампер постоянного тока), вы, вероятно, будете измерять ток 1,4 ампера в каждой петле.
Что происходит во время этого действия
Часть 1: зажигание двух лампочек от одного источника питания
Для начала учитель собирает учеников вокруг и в порядке повторения демонстрирует знакомые моменты, которые:
- Одна лампочка, подключенная к источнику питания, имеет нормальную яркость.

- Две одинаковые лампы, соединенные последовательно, имеют одинаковую тусклость.
Затем задает вопрос:
Учитель: Как можно подключить две лампочки к одному источнику, чтобы обе лампы были нормальной яркости?
Ученики могут предложить: Просто подключите каждую лампочку к батарее, чтобы получилось две цепи
(а если они этого не сделают, вы можете предложить: вот простой способ сделать это
).
Подключите цепь и включите. Обе лампочки горят одинаково, нормальная яркость.
Просмотр параллельных цепей как двух контуров
Теперь, когда лампочки находятся перед глазами учеников, вы должны обратить внимание на явно странную природу этой схемы.
Учитель: Итак! Обе лампочки горят до нормальной яркости. Я не добавлял больше батареек или чего-то еще, но мы зажгли две лампочки, что вдвое больше энергии. Как это может быть? Это мечта йоркширца: вкратце! Что тут происходит?
В качестве отправной точки для выяснения того, что происходит, предложите измерить токи в каждой из цепей:
Учитель: Что ж, давайте посмотрим на токи в каждой из этих петель. Большая петля слева и маленькая петля справа.
Большая петля слева и маленькая петля справа.
Часть 2: рассмотрение параллельных цепей как двух контуров
Следующим шагом является реорганизация схемы так, чтобы она больше походила на стандартный формат параллельной схемы:
Учитель: Предположим, я просто поднимаю эту большую петлю поперек, чтобы она охватывала маленькую петлю.
Сосредоточьтесь на токе, затем на стандартной параллельной цепи
Учитель: У нас в малой цепи ток 1,4 ампера, идущий от источника питания, и 1.4 ампера в большой цепи, тоже от источника питания. Как вы думаете, какой будет суммарный ток от блока питания?
Самый простой способ измерить общий ток в источнике питания — использовать два дополнительных провода, от источника питания и к нему, и подключить их к обеим контурам. Измерьте ток в каждом из двух выводов источника питания:
Учитель: Итак, ток от батареи здесь 2,8 ампера, а обратно на батарею здесь 2,8 ампера.
Демонстрационная схема теперь выглядит как стандартный формат принципиальной схемы для параллельных цепей:
Все, что осталось, — это собрать все объяснения воедино.
Учитель: Хорошо, поэтому с одной батареей и одной лампочкой мы можем изобразить заряженные частицы, движущиеся через батарею к лампочке, и энергия смещается при каждом заряде. Когда параллельно добавляется вторая лампочка, образуется дополнительная петля, по которой движутся заряженные частицы. Таким образом, количество заряженных частиц, проходящих через батарею каждую секунду, удваивается, и такое же количество энергии смещается при каждом заряде. Таким образом, во втором контуре заряженные частицы перемещают энергию из накопителя, связанного с батареей, в два раза быстрее, и батарея разряжается быстрее.
Сопротивление
— Элементы схемы — Содержание MCAT
Согласно закону Ома, падение напряжения В на резисторе при протекании через него тока рассчитывается с помощью уравнения V = IR, где I — ток в амперах (А), а R — сопротивление в Ом (Ом).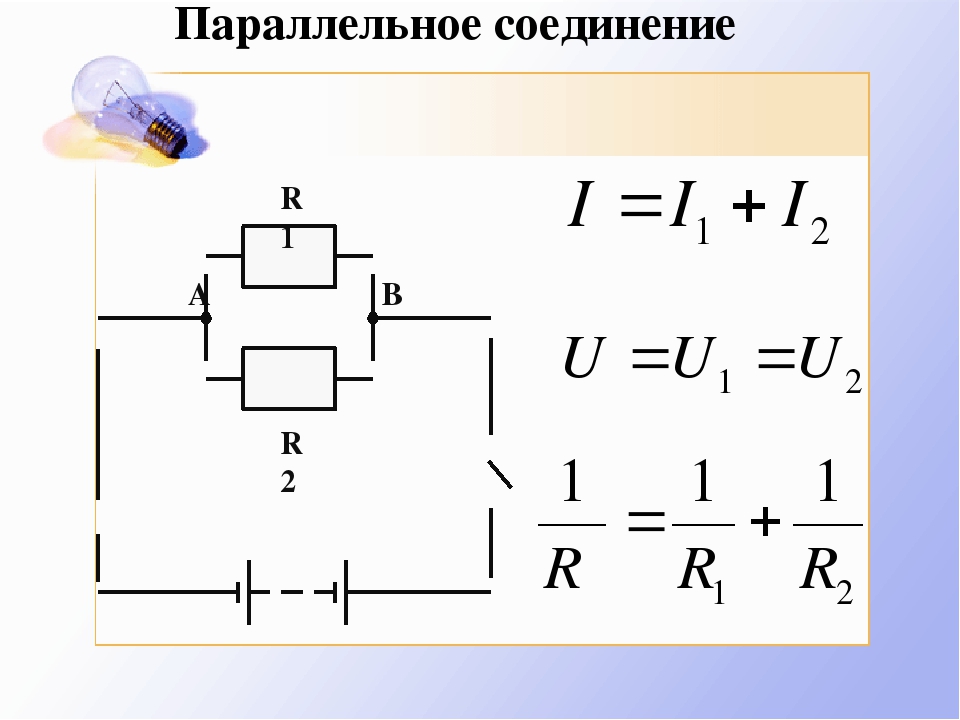
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению В. .Немецкий физик Георг Симон Ом (1787–1854) был первым, кто экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению. Многие вещества, для которых действует закон Ома, называются омическими. К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление R, которое не зависит от напряжения V и тока I. Объект с простым сопротивлением называется резистором, даже если его сопротивление невелико.
Резисторы серии
Резисторы
включены последовательно всякий раз, когда поток заряда или ток должен проходить через компоненты последовательно.
Общее сопротивление в цепи равно сумме отдельных сопротивлений.
Параллельные резисторы
Резисторы
включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения посредством соединения проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника.
Таким образом, к каждому резистору приложено полное напряжение источника.
На каждый резистор в цепи подается полное напряжение. По закону Ома токи, протекающие через отдельные резисторы, равны I1 = VR1
.
Общее сопротивление в параллельной цепи равно сумме обратных величин каждого отдельного сопротивления.
Удельное сопротивление — это свойство материала, которое количественно определяет, насколько сильно он сопротивляется или проводит электрический ток.Низкое удельное сопротивление указывает на материал, который легко пропускает электрический ток, и наоборот. Рассчитывается как:
ρ = R • A / L
R — электрическое сопротивление однородного образца материала
л — длина экземпляра
А — площадь поперечного сечения образца
Практические вопросы
Ханская академия
Анализ сигналов напряжения электрокардиограммы
Официальная подготовка MCAT (AAMC)
Physics online Flashcards Вопрос 1
Physics Question Pack Отрывок 9 Вопрос 54
Physics Question Pack Отрывок 9, вопрос 56
Пакет вопросов по физике, вопрос 117
Секция банка C / P Вопрос 15 секции
Раздел Банк C / P Вопрос 17
Образец теста C / P Раздел Отрывок 7 Вопрос 35
Практический экзамен 1 Секция C / P Отрывок 10 Вопрос 52
Практический экзамен 2 Раздел C / P, вопрос 59
Практический экзамен 3 Раздел C / P Отрывок 7 Вопрос 39
Ключевые точки
• Падение напряжения V на резисторе при протекании через него тока рассчитывается по формуле V = IR
• Общее сопротивление в цепи равно сумме отдельных сопротивлений.
• Общее сопротивление в параллельной цепи равно сумме обратных величин каждого отдельного сопротивления.
• Удельное сопротивление измеряет, насколько сильно материал сопротивляется или проводит электрический ток.
Ключевые термины
ток : количество заряда, перемещающегося через поперечное сечение за период времени.
напряжение : Разность электрических потенциалов, выраженная в вольтах
сопротивление : Сопротивление — это мера сопротивления току, протекающему в электрической цепи.
удельное сопротивление: свойство материала, которое количественно определяет, насколько сильно он сопротивляется или проводит электрический ток
Комбинированная серия
/ Параллельные схемы — Устранение неисправностей двигателей и органов управления
Кен Диксон-Селф
В простых последовательных цепях все компоненты соединены встык, образуя только один путь для прохождения электронов по цепи:
В простых параллельных цепях все компоненты подключаются между одними и теми же двумя наборами электрически общих точек, создавая несколько путей для прохождения электронов от одного конца батареи к другому:
Для каждой из этих двух базовых конфигураций схемы у нас есть определенные наборы правил, описывающих отношения напряжения, тока и сопротивления.
- Цепи серии:
- Падения напряжения прибавляются к общему напряжению.
- Все компоненты имеют одинаковый (равный) ток.
- Сопротивления добавляют к равному общему сопротивлению.
- Параллельные цепи:
- Все компоненты имеют одинаковое (равное) напряжение.
- Токи ответвления складываются с равным общим током.
- Сопротивления уменьшаются до полного сопротивления.
Однако, если компоненты схемы соединены последовательно в одних частях и параллельно в других, мы не сможем применить единый набор правил для каждой части этой цепи.Вместо этого нам придется определить, какие части этой цепи являются последовательными, а какие — параллельными, а затем выборочно применять правила последовательного и параллельного подключения, если это необходимо, чтобы определить, что происходит. Возьмем, к примеру, следующую схему:
Эта схема не является ни простой последовательной, ни простой параллельной. Скорее, он содержит элементы обоих. Ток выходит из нижней части батареи, разделяется, чтобы пройти через R 3 и R 4 , снова присоединяется, затем снова разделяется, чтобы пройти через R 1 и R 2 , затем снова присоединяется, чтобы вернуться к верх аккумуляторной батареи.Существует более одного пути прохождения тока (не последовательно), но в цепи более двух наборов электрически общих точек (не параллельных).
Скорее, он содержит элементы обоих. Ток выходит из нижней части батареи, разделяется, чтобы пройти через R 3 и R 4 , снова присоединяется, затем снова разделяется, чтобы пройти через R 1 и R 2 , затем снова присоединяется, чтобы вернуться к верх аккумуляторной батареи.Существует более одного пути прохождения тока (не последовательно), но в цепи более двух наборов электрически общих точек (не параллельных).
Поскольку схема представляет собой комбинацию как последовательной, так и параллельной, мы не можем применять правила для напряжения, тока и сопротивления «поперек стола», чтобы начать анализ, как мы могли бы, когда цепи были так или иначе. Например, если бы вышеприведенная схема была простой последовательной, мы могли бы просто сложить R 1 — R 4 , чтобы получить общее сопротивление, вычислить общий ток, а затем вычислить все падения напряжения.Точно так же, если бы вышеуказанная схема была простой параллельной, мы могли бы просто решить для токов ответвления, сложить токи ответвления, чтобы вычислить общий ток, а затем вычислить общее сопротивление из общего напряжения и общего тока. Однако решение этой схемы будет более сложным.
Однако решение этой схемы будет более сложным.
Таблица по-прежнему поможет нам управлять различными значениями для последовательно-параллельных комбинированных схем, но мы должны быть осторожны, как и где применять разные правила для последовательного и параллельного подключения. Закон Ома, конечно, по-прежнему работает точно так же для определения значений в вертикальном столбце таблицы.
Если мы можем определить, какие части схемы являются последовательными, а какие — параллельными, мы можем анализировать их поэтапно, подходя к каждой части по очереди, используя соответствующие правила для определения отношений напряжения, тока и сопротивления. . Остальная часть этой главы будет посвящена демонстрации техник для этого.
Процесс анализа последовательно-параллельной цепи резисторов
Цель анализа последовательно-параллельной цепи резисторов — определить все падения напряжения, токи и рассеиваемую мощность в цепи.Общая стратегия достижения этой цели следующая:
- Шаг 1.
 Определите, какие резисторы в цепи соединены вместе простым последовательным или простым параллельным соединением.
Определите, какие резисторы в цепи соединены вместе простым последовательным или простым параллельным соединением. - Шаг 2: Изобразите схему заново, заменив каждую из комбинаций последовательных или параллельных резисторов, определенных на шаге 1, одним резистором эквивалентного номинала. Если для управления переменными используется таблица, создайте новый столбец таблицы для каждого эквивалента сопротивления.
- Шаг 3: Повторяйте шаги 1 и 2, пока вся цепь не будет уменьшена до одного эквивалентного резистора.
- Шаг 4: Рассчитайте общий ток из общего напряжения и общего сопротивления (I = E / R).
- Шаг 5: Взяв значения общего напряжения и полного тока, вернитесь к последнему шагу в процессе сокращения цепи и вставьте эти значения, где это возможно.
- Шаг 6: Из известных значений сопротивления и значений полного напряжения / полного тока из шага 5 используйте закон Ома для вычисления неизвестных значений (напряжения или тока) (E = IR или I = E / R).

- Шаг 7: Повторяйте шаги 5 и 6, пока все значения напряжения и тока не будут известны в исходной конфигурации схемы.По сути, вы будете шаг за шагом переходить от упрощенной версии схемы к ее исходной сложной форме, вставляя значения напряжения и тока, где это необходимо, до тех пор, пока не будут известны все значения напряжения и тока.
- Шаг 8: Рассчитайте рассеиваемую мощность на основе известных значений напряжения, тока и / или сопротивления.
Это может показаться пугающим процессом, но его гораздо легче понять на примере, чем через описание.
В приведенном выше примере схемы R 1 и R 2 соединены простым параллельным соединением, как и R 3 и R 4 .После идентификации эти секции необходимо преобразовать в эквивалентные одиночные резисторы и заново нарисовать схему:
Символы двойной косой черты (//) обозначают «параллельность», чтобы показать, что эквивалентные значения резисторов были рассчитаны по формуле 1 / (1 / R). Резистор 71,429 Ом в верхней части схемы эквивалентен R 1 и R 2 , включенным параллельно друг другу. Резистор 127,27 Ом внизу эквивалентен R 3 и R 4 , включенным параллельно друг другу.
Резистор 71,429 Ом в верхней части схемы эквивалентен R 1 и R 2 , включенным параллельно друг другу. Резистор 127,27 Ом внизу эквивалентен R 3 и R 4 , включенным параллельно друг другу.
Наша таблица может быть расширена, чтобы включить эти эквиваленты резисторов в отдельные столбцы:
Теперь должно быть очевидно, что схема была уменьшена до простой последовательной конфигурации только с двумя (эквивалентными) сопротивлениями. Последний шаг в уменьшении — сложение этих двух сопротивлений, чтобы получить общее сопротивление цепи. Когда мы складываем эти два эквивалентных сопротивления, мы получаем сопротивление 198,70 Ом. Теперь мы можем перерисовать схему как единое эквивалентное сопротивление и добавить значение общего сопротивления в крайний правый столбец нашей таблицы.Обратите внимание, что столбец «Итого» был переименован (R 1 // R 2 —R 3 // R 4 ), чтобы указать, как он электрически связан с другими столбцами цифр. Символ «-» здесь используется для обозначения «серии», так же как символ «//» используется для обозначения «параллельности».
Символ «-» здесь используется для обозначения «серии», так же как символ «//» используется для обозначения «параллельности».
Теперь общий ток цепи можно определить, применив закон Ома (I = E / R) к столбцу «Всего» в таблице:
Вернемся к нашему рисунку эквивалентной схемы, наше общее текущее значение 120.Здесь показан только ток 78 миллиампер:
Теперь мы начинаем работать в обратном направлении в нашей прогрессии переделки схем до исходной конфигурации. Следующим шагом является переход к схеме, в которой последовательно соединены 1 // 2 и 3 // 4 рандов:
Поскольку R 1 // R 2 и R 3 // R 4 включены последовательно друг с другом, ток через эти два набора эквивалентных сопротивлений должен быть одинаковым.Кроме того, ток через них должен быть таким же, как и полный ток, поэтому мы можем заполнить нашу таблицу соответствующими текущими значениями, просто скопировав текущую цифру из столбца Total в R 1 // R 2 и R 3 // R 4 9000 8 столбцов:
Теперь, зная ток через эквивалентные резисторы R 1 // R 2 и R 3 // R 4 , мы можем применить закон Ома (E = IR) к двум правым вертикальным столбцам, чтобы найти падение напряжения на них:
Поскольку мы знаем, что R 1 // R 2 и R 3 // R 4 являются эквивалентами параллельных резисторов, и мы знаем, что падения напряжения в параллельных цепях одинаковы, мы можем передавать соответствующие падения напряжения в соответствующие столбцы таблицы для этих отдельных резисторов. Другими словами, мы делаем еще один шаг назад в нашей последовательности рисования к исходной конфигурации и заполняем таблицу соответствующим образом:
Другими словами, мы делаем еще один шаг назад в нашей последовательности рисования к исходной конфигурации и заполняем таблицу соответствующим образом:
Наконец, исходный раздел таблицы (столбцы R 1 — R 4 ) заполнен достаточным количеством значений для завершения. Применяя закон Ома к остальным вертикальным столбцам (I = E / R), мы можем определить токи через R 1 , R 2 , R 3 и R 4 по отдельности:
Размещение значений напряжения и тока на диаграммах
Найдя все значения напряжения и тока для этой цепи, мы можем показать эти значения на принципиальной схеме как таковые:
В качестве последней проверки нашей работы мы можем увидеть, складываются ли рассчитанные текущие значения должным образом в общую сумму.Поскольку R 1 и R 2 подключены параллельно, их комбинированные токи в сумме должны составить 120,78 мА. Аналогичным образом, поскольку R 3 и R 4 подключены параллельно, их комбинированные токи в сумме также должны составлять 120,78 мА. Вы можете проверить сами, чтобы убедиться, что эти цифры действительно совпадают.
Вы можете проверить сами, чтобы убедиться, что эти цифры действительно совпадают.
Эта глава является адаптацией книги Lessons in Electric Circuits Тони Р. Купхальда (на allaboutcircuits.com) и используется в соответствии с лицензией на научный дизайн.
Схемы с элементами последовательной и параллельной схемы
Примечание. Предполагается, что вы уже знакомы с порядком проведения расчетов с последовательными и параллельными цепями (с двумя резисторами и с более чем двумя резисторами). Если нет, просмотрите предыдущие страницы.
Вы встретите схемы, которые содержат элементы как последовательных, так и параллельных цепей, например, этот:
Хотя это может показаться сложным, на самом деле это действительно просто.Вот как бы вы ее решили:
1) Начнем с таблицы:
| сопротивление (в кОм) | ток, I (в миллиамперах, мА) | Падение напряжения: ∆V | Мощность, P, падение (в милливаттах, мВт) | |
| R1 | ||||
| R2 | ||||
| R3 | ||||
| всего |
2) Введите известные значения:
| сопротивление (в кОм) | ток, I (в миллиамперах, мА) | Падение напряжения: ∆V | Мощность, P, падение (в милливаттах, мВт) | |
| R1 | 6 | |||
| R2 | 4 | |||
| R3 | 10 | 20 | ||
| всего |
Примечание: причина, по которой мы знаем падение напряжения на резисторе 3, заключается в том, что это резистор, включенный параллельно; следовательно, падение напряжения на каждом параллельном резисторе такое же, как и напряжение от источника питания. Поскольку резисторы 1 и 2 включены последовательно, их падение напряжения не будет одинаковым; однако общее падение напряжения на этих двух резисторах будет равно 20 (если вы «упростите» эти два резистора в один с сопротивлением, эквивалентным сопротивлению двух вместе взятых, этот резистор будет включен параллельно резистору 3).
Поскольку резисторы 1 и 2 включены последовательно, их падение напряжения не будет одинаковым; однако общее падение напряжения на этих двух резисторах будет равно 20 (если вы «упростите» эти два резистора в один с сопротивлением, эквивалентным сопротивлению двух вместе взятых, этот резистор будет включен параллельно резистору 3).
3) Найдите полное сопротивление R1 и R2:
R1 + R2 = 6 кОм +4 кОм = 10 кОм
4) Теперь найдите эквивалентное сопротивление (R e ) в цепи:
R e = (10 кОм * 10 кОм) / (10 кОм + 10 кОм) = 5 кОм
5) Теперь рассчитайте общий ток в цепи:
В = ИК
20 В = (I) (5 кОм)
4 мА = I
6) Теперь вы можете рассчитать ток в отдельных резисторах.Помните, что в параллельной цепи ток разделяется между двумя ветвями цепи. Таким образом, мы можем рассчитать полный ток в каждой ветви цепи следующим образом (помните, что полное сопротивление на обоих составляет 10 кОм):
В = ИК
20 В = (I) (10 кОм)
2 мА = I
7) Теперь давайте сосредоточимся на резисторах 1 и 2. Ток на этой ветви схемы (с резисторами 1 и 2) составляет 2 мА, и, следовательно, ток в каждом резисторе составляет 2 мА.Используя это, мы можем рассчитать падение напряжения на обоих:
Ток на этой ветви схемы (с резисторами 1 и 2) составляет 2 мА, и, следовательно, ток в каждом резисторе составляет 2 мА.Используя это, мы можем рассчитать падение напряжения на обоих:
R1: V = (2 мА) (6 кОм) = 12 В
R2: V = (2 мА) (4 кОм) = 8 В
8) Наконец, мы можем рассчитать падение мощности:
P = IV
R1: P = (2 мА) (12 В) = 24 мВт
R2: P = (2 мА) (8 В) = 16 мВт
R3: P = (2 мА) (20 В) = 40 мВт
9) В самом конце можем заполнить таблицу:
| сопротивление (в кОм) | ток, I (в миллиамперах, мА) | Падение напряжения ∆V (в вольтах В) | Мощность, P, падение (в милливаттах, мВт) | |
| R1 | 6 | 2 | 12 | 24 |
| R2 | 4 | 2 | 8 | 16 |
| R3 | 10 | 2 | 20 | 40 |
| всего | R e = 5 | 4 | 20 | 80 |
<< Параллельные схемы с более чем двумя резисторами ответы и пояснения | Цепи Clossary >>
Нравится:
Нравится Загрузка. ..
..
Резисторы
в схемах — Резюме — Гипертекст по физике
Резисторы в схемах — Резюме — Гипертекст по физике
Сводка
- Основными компонентами простой схемы являются…
- Источник напряжения или разности потенциалов ( В, ), такой как аккумулятор, источник питания, солнечная батарея и т. Д.
- устройство с сопротивлением ( R ), такое как свет, обогреватель, двигатель, телевизор и т. Д., Обозначенное общим названием резистор .
- провода с незначительным сопротивлением для передачи тока ( I ) по замкнутому контуру от источника напряжения до резистора и обратно.
- Сохранение заряда в цепи
- Ток, текущий в компонент, равен текущему току.
- Сохранение энергии в цепи
- Когда ток течет через источник напряжения, он испытывает повышение напряжения.

- Когда через резистор протекает ток, на нем падает напряжение.
- Когда ток течет по цепи, напряжение не изменяется.
- Когда ток течет через источник напряжения, он испытывает повышение напряжения.
- Компоненты в последовательной цепи соединены по единому пути.
- В последовательной цепи ток везде одинаковый .
I с = I 1 = I 2 = I 3 =… = I i
- В последовательной цепи напряжение делится на , так что увеличение напряжения, подаваемое источником напряжения, равно сумме падений напряжения на резисторах.
В с = В 1 + В 2 + В 3 +… = ∑ В i
- В последовательной цепи общее сопротивление равно сумме отдельных сопротивлений.
R с = R 1 + R 2 + R 3 +… = ∑ R i
- Сопротивление увеличивается (и уменьшается ток), когда резисторы добавляются последовательно к источнику постоянного напряжения.

- Сопротивление увеличивается (и уменьшается ток), когда резисторы добавляются последовательно к источнику постоянного напряжения.
- В последовательной цепи ток везде одинаковый .
- Компоненты параллельной цепи лежат в независимых ветвях.
- Метров в цепях
- Ток измеряется амперметром .
- Амперметр подключается последовательно к проверяемому элементу цепи или участку цепи.
- Идеальный амперметр имеет нулевое сопротивление, поэтому он не увеличивает сопротивление и не снижает ток.
- Обозначение амперметра — заглавная A⃝ в кружке.
- Напряжение измеряется вольтметром .
- Вольтметр подключается параллельно элементу цепи или участку исследуемой цепи.
- Идеальный вольтметр имеет бесконечное сопротивление, чтобы не уменьшать сопротивление и не увеличивать ток (чтобы не происходило короткое замыкание).
- Обозначение вольтметра — заглавная буква V⃝ в кружке.
- Сопротивление измеряется омметром .
- Омметр объединяет блок питания с амперметром и вольтметром.
- Омметр «вычисляет» сопротивление по отношению напряжения к току.

- Символ омметра — греческая заглавная буква Ω⃝ (омега) в круге.
- Ток измеряется амперметром .
Нет постоянных условий.
- Механика
- Кинематика
- Движение
- Расстояние и перемещение
- Скорость и скорость
- Разгон
- Уравнения движения
- Свободное падение
- Графики движения
- Кинематика и расчет
- Кинематика в двух измерениях
- Снаряды
- Параметрические уравнения
- Dynamics I: Force
- Силы
- Сила и масса
- Действие-реакция
- Вес
- Динамика
- Статика
- Трение
- Силы в двух измерениях
- Центростремительная сила
- Кадры ссылки
- Энергия
- Работа
- Энергия
- Кинетическая энергия
- Потенциальная энергия
- Сохранение энергии
- Мощность
- Простые станки
- Dynamics II: Импульс
- Импульс и импульс
- Сохранение импульса
- Импульс и энергия
- Импульс в двух измерениях
- Вращательное движение
- Кинематика вращения
- Инерция вращения
- Динамика вращения
- Вращательная статика
- Угловой момент
- Энергия вращения
- Прокатный
- Вращение в двух измерениях
- Сила Кориолиса
- Планетарное движение
- Геоцентризм
- Гелиоцентризм
- Вселенская гравитация
- Орбитальная механика I
- Гравитационная потенциальная энергия
- Орбитальная механика II
- Плотность вытянутых тел
- Периодическое движение
- Пружины
- Генератор простых гармоник
- Маятники
- Резонанс
- Эластичность
- Жидкости
- Плотность
- Давление
- Плавучесть
- Расход жидкости
- Вязкость
- Аэродинамическое сопротивление
- Режимы потока
- Кинематика
- Теплофизика
- Тепло и температура
- Температура
- Тепловое расширение
- Атомная природа материи
- Закон о газе
- Кинетико-молекулярная теория
- Фазы
- Калориметрия
- Явное тепло
- Скрытое тепло
- Химическая потенциальная энергия
- Теплопередача
- Проводимость
- Конвекция
- Радиация
- Термодинамика
- Тепло и работа
- Диаграммы давление-объем
- Двигатели
- Холодильники
- Энергия и энтропия
- Абсолютный ноль
- Тепло и температура
- Волны и оптика
- Волновые явления
- Природа волн
- Периодические волны
- Интерференция и суперпозиция
- Интерфейсы и барьеры
- Звук
- Природа звука
- Интенсивность
- Эффект Доплера (звук)
- Ударные волны
- Дифракция и интерференция (звук)
- Стоячие волны
- ударов
- Музыка и шум
- Физическая оптика
- Природа света
- Поляризация
- Эффект Доплера (световой)
- Черенковское излучение
- Дифракция и интерференция (свет)
- Тонкопленочная интерференция
- Цвет
- Геометрическая оптика
- Отражение
- Преломление
- Зеркала сферические
- Сферические линзы
- Аберрация
- Волновые явления
- Электричество и магнетизм
- Электростатика
- Электрический заряд
- Закон Кулона
- Электрическое поле
- Электрический потенциал
- Закон Гаусса
- Проводников
- Электростатические приложения
- Конденсаторы
- Диэлектрики
- Батареи
- Электрический ток
- Электрический ток
- Электрическое сопротивление
- Электроэнергия
- Цепи постоянного тока
- Резисторы в цепях
- Батареи в цепях
- Конденсаторы в цепях
- Правила Кирхгофа
- Магнитостатика
- Магнетизм
- Электромагнетизм
- Закон Ампера
- Электромагнитная сила
- Магнитодинамика
- Электромагнитная индукция
- Закон Фарадея
- Закон Ленца
- Индуктивность
- Цепи переменного тока
- Переменный ток
- RC цепи
- Цепи RL
- LC цепи
- Электромагнитные волны
- Уравнения Максвелла
- Электромагнитные волны
- Электромагнитный спектр
- Электростатика
- Современная физика
- Теория относительности
- Пространство-время
- Масса-энергия
- Общая теория относительности
- Quanta
- Излучение черного тела
- Фотоэффект
- Рентгеновские снимки
- Антиматерия
- Волновая механика
- Волны материи
- Атомарные модели
- Полупроводники
- Конденсированное вещество
- Ядерная физика
- Изотопы
- Радиоактивный распад
- Период полураспада
- Энергия связи
- Деление
- Fusion
- Нуклеосинтез
- Ядерное оружие
- Радиобиология
- Физика элементарных частиц
- Квантовая электродинамика
- Квантовая хромодинамика
- Квантовая динамика вкуса
- Стандартная модель
- Модель сверх стандартной
- Теория относительности
- Фундаменты
- шт.

- Международная система единиц
- Гауссова система единиц
- Британо-американская система единиц
- Единицы разного назначения
- Время
- Преобразование единиц
- Измерение
- Значащие цифры
- По порядку величины
- Графики
- Графическое представление данных
- Линейная регрессия
- Подгонка кривой
- Исчисление
- Векторы
- Тригонометрия
- Сложение и вычитание векторов
- Векторное разрешение и компоненты
- Умножение вектора
- ссылку
- Специальные символы
- Часто используемые уравнения
- Физические константы
- Астрономические данные
- Периодическая система элементов
- Люди в физике
- шт.
- Назад дело
- Предисловие
- Об этой книге
- Связаться с автором
- гленнелерт.
 нас
нас - Behance
- Твиттер
- YouTube
- гленнелерт.
- Аффилированные сайты
- hypertextbook.com
- midwoodscience.org
- Предисловие
2 подхода к анализу и решению последовательных параллельных сетей
Последовательные параллельные сети
Твердое понимание основных принципов, связанных с последовательными и параллельными цепями, является достаточным основанием для начала исследования любой сети постоянного тока с одним источником, имеющей комбинацию последовательные и параллельные элементы или ответвления.Как правило, последовательно-параллельные сети — это сети, которые содержат конфигурации как последовательных, так и параллельных цепей.
2 подхода к анализу и решению последовательных параллельных сетей
Специалисты в области анализа последовательно-параллельных сетей могут стать специалистами только при наличии опыта, практики и опыта .
Со временем путь к желаемому неизвестному становится более очевидным, поскольку вспоминаются похожие конфигурации и разочарование, вызванное неправильным подходом.
Начало работы //
Есть несколько шагов , которые могут быть полезны для начала работы первых нескольких упражнений, хотя ценность каждого станет очевидна только с опытом.
Шаг № 1 Найдите минутку, чтобы изучить проблему «в целом» и сделать краткий мысленный набросок общего подхода, который вы планируете использовать. В результате могут быть сокращены время и энергия.
Шаг № 2 Затем исследуйте каждую область сети независимо, прежде чем связывать их вместе в последовательно-параллельные комбинации. Обычно это упрощает сеть и, возможно, открывает прямой подход к получению одного или нескольких желаемых неизвестных.
Он также устраняет многие ошибки , которые могут возникнуть из-за отсутствия систематического подхода.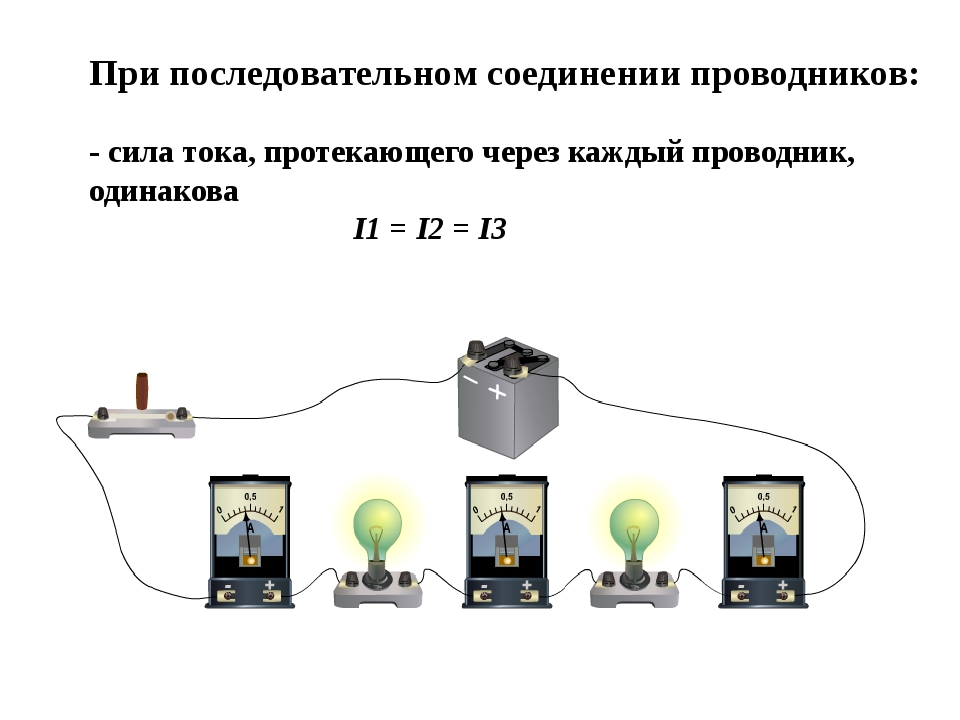
Шаг № 3 Перерисовывайте сеть как можно чаще с уменьшенными ветвями и неизменными неизвестными величинами, чтобы сохранить ясность и обеспечить сокращенные сети для возврата к неизвестным величинам от источника.
Шаг № 4 Когда у вас есть решение, проверьте его разумность, учитывая величины источника энергии и элементов в сети. Если это не кажется разумным, либо решите схему, используя другой подход, либо очень внимательно проверьте свою работу.
Подход с уменьшением и возвратом //
Для многих последовательных параллельных сетей с одним источником используется анализ, который возвращается к источнику, определяет ток источника, а затем находит путь к желаемому неизвестному.
Рисунок 1 — Представление подхода уменьшения и возврата
Например, на Рисунке 1 (а) требуется напряжение V 4 . Отсутствие единственного последовательного или параллельного пути к V 4 от источника сразу показывает, что методы, представленные в последних двух главах, здесь не применимы. Во-первых, необходимо объединить последовательные и параллельные элементы, чтобы получить сокращенную схему на рис. 1 (b). Затем элементы серии объединяются, чтобы сформировать простейшую конфигурацию, показанную на рис. 1 (c).
Во-первых, необходимо объединить последовательные и параллельные элементы, чтобы получить сокращенную схему на рис. 1 (b). Затем элементы серии объединяются, чтобы сформировать простейшую конфигурацию, показанную на рис. 1 (c).
Теперь ток источника можно определить с помощью закона Ома, и мы можем вернуться в сеть, как показано на рис. 1 (d) справа.
Напряжение V 2 может быть определено, а затем исходная сеть может быть перерисована, как показано на рис. 1 (е). Поскольку теперь известно V 2 , можно использовать правило делителя напряжения , чтобы найти желаемое напряжение V 4 .Из-за сходства между сетями на рисунках 1 (a) и 1 (e), а также между схемами 1 (b) и 1 (d), сети, нарисованные во время фазы сокращения, часто используются для обратного пути.
Хотя все детали анализа не были описаны выше, общая процедура для ряда проблем последовательно-параллельной сети использует процедуру, описанную выше: Неизвестно .
Не каждая проблема решит этот путь.У некоторых найдутся более простые и прямые решения. Однако подход с уменьшением и возвратом решает один тип проблем, которые возникают снова и снова.
Подход с блок-схемой //
Для решения последовательно-параллельных сетей будет использоваться подход блок-схемы, чтобы подчеркнуть тот факт, что комбинации элементов, а не просто отдельные резистивные элементы, могут быть включены последовательно или параллельно . Этот подход также позволит выявить количество, казалось бы, разных сетей, которые имеют одинаковую базовую структуру и, следовательно, могут включать аналогичные методы анализа.
Рисунок 2 — Представление подхода с использованием блок-схемы
Первоначально будет некоторая озабоченность по поводу того, что идентифицирует последовательные и параллельные элементы и ветви и выберет наилучшую процедуру для решения.
Однако по мере того, как вы продвигаетесь по примерам и решаете несколько проблем, вы обнаружите общий путь к большинству решений, которые действительно могут сделать анализ таких систем интересным и приятным занятием 🙂
На рисунке 2, блоки B и C подключены параллельно (точки b и c общие), а источник напряжения E включен последовательно с блоком A (точка a общая).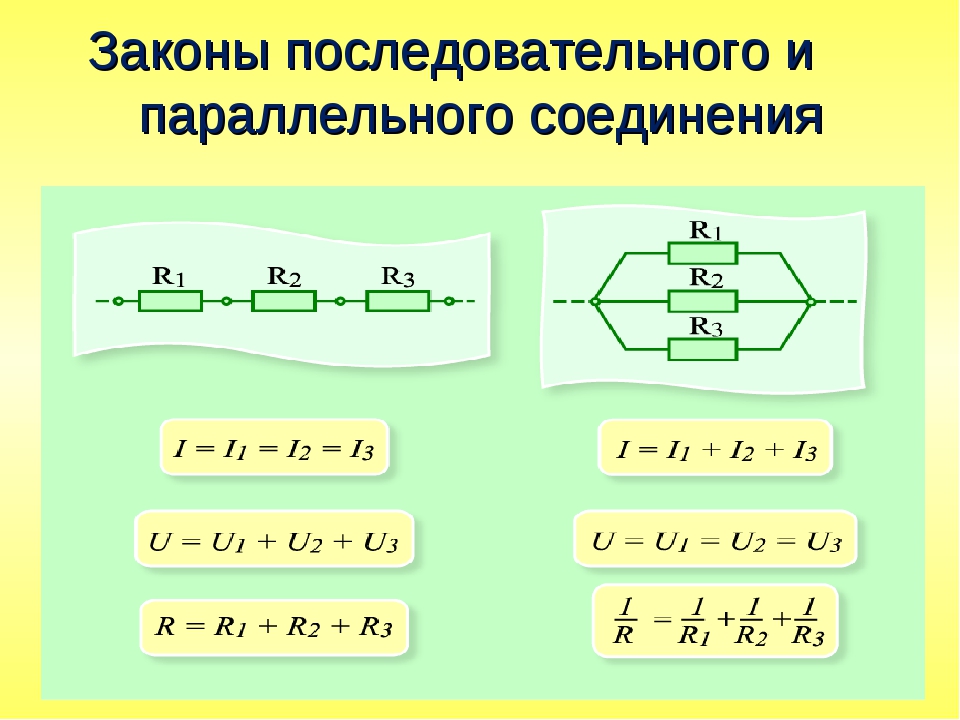 Параллельная комбинация B и C также включена последовательно с A и источником напряжения E из-за общих точек b и c соответственно.
Параллельная комбинация B и C также включена последовательно с A и источником напряжения E из-за общих точек b и c соответственно.
Чтобы последующий анализ был как можно более ясным и незагроможденным, следующие обозначения будут использоваться для последовательных и параллельных комбинаций элементов .
Для резисторов серии R 1 и R 2 между их индексами будет вставлена запятая, как показано здесь //
Для параллельных резисторов R 1 и R 2 , параллельный символ будет вставлен между их индексными обозначениями, как показано ниже //
Анализ параллельных и последовательных цепей резисторов
Эта процедура утомительна, но требует очень мало математических вычислений, а это концептуально красиво .Вы должны иметь возможность взглянуть на готовый продукт и объяснить, ПОЧЕМУ значения падений напряжения и токов для каждого резистора и комбинации резисторов имеют те отношения, которые они имеют.

 Э, Кайдалов А.Б., Кожевников В.Б. Физика 8 / Под ред. Орлова В.А., Ройзена И.И. — М.: Мнемозина.
Э, Кайдалов А.Б., Кожевников В.Б. Физика 8 / Под ред. Орлова В.А., Ройзена И.И. — М.: Мнемозина.
 Определите, какие резисторы в цепи соединены вместе простым последовательным или простым параллельным соединением.
Определите, какие резисторы в цепи соединены вместе простым последовательным или простым параллельным соединением.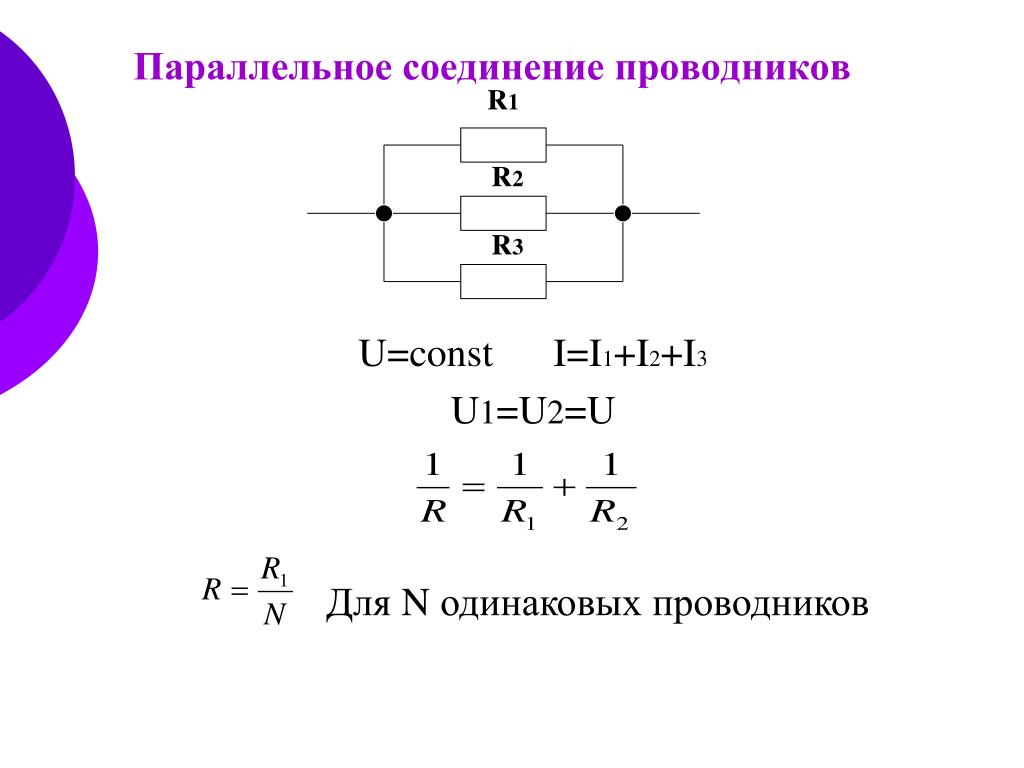

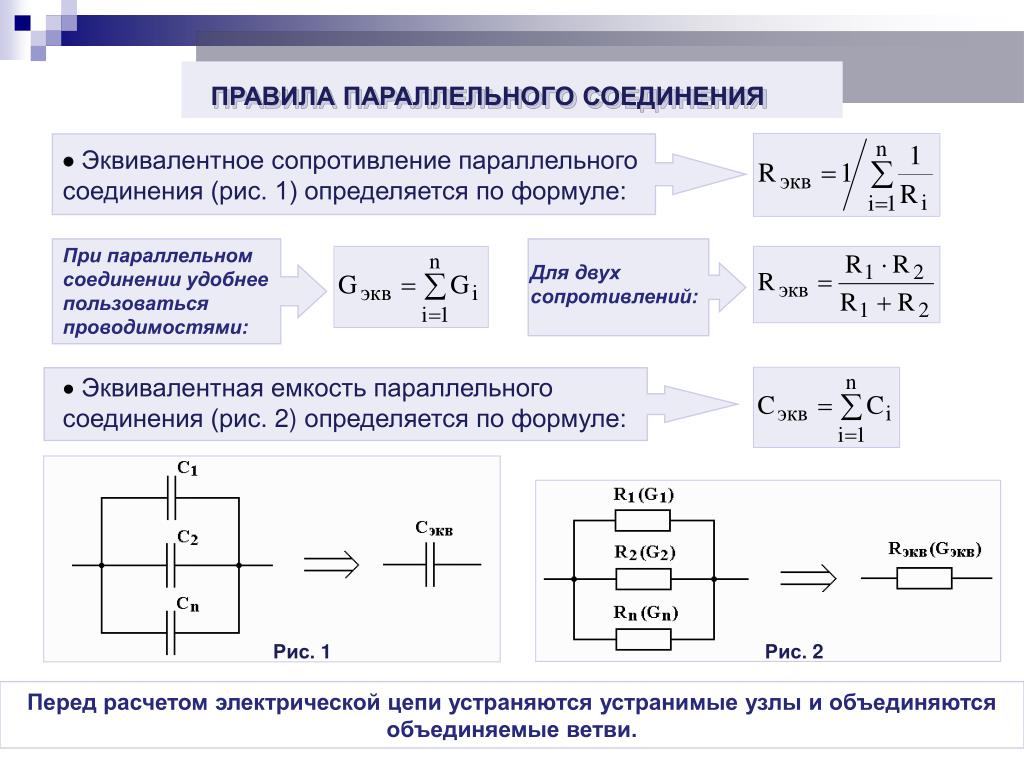

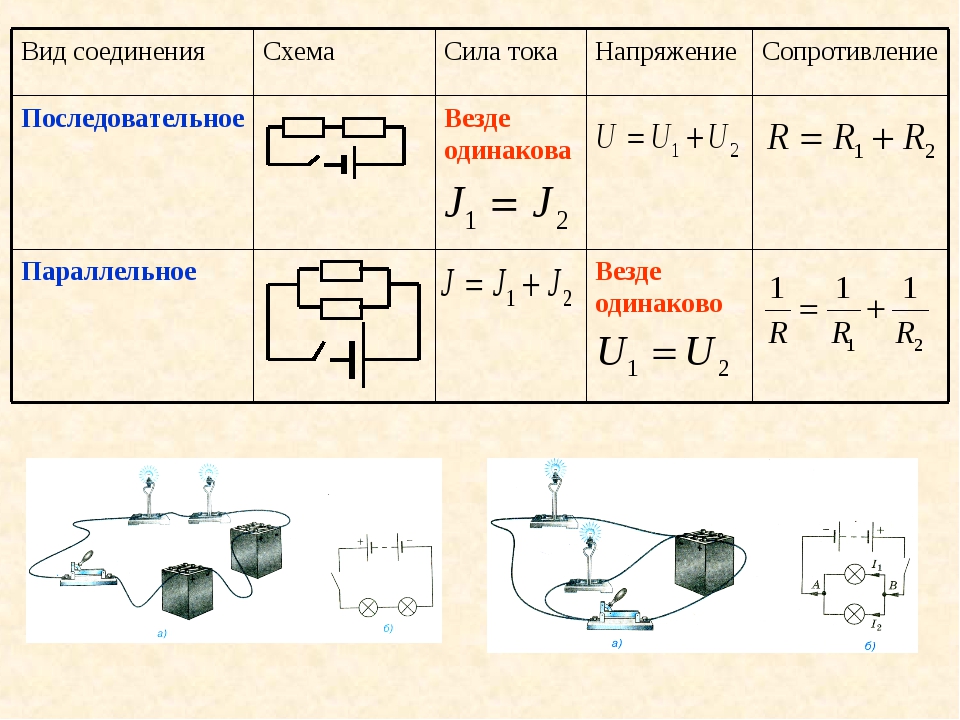
 нас
нас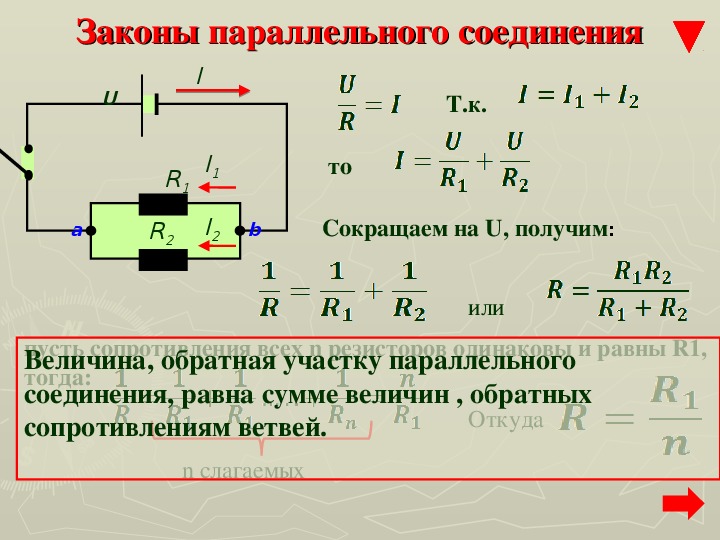 Со временем путь к желаемому неизвестному становится более очевидным, поскольку вспоминаются похожие конфигурации и разочарование, вызванное неправильным подходом.
Со временем путь к желаемому неизвестному становится более очевидным, поскольку вспоминаются похожие конфигурации и разочарование, вызванное неправильным подходом.