Электромагнетизм — учебный материал — Каталог статей
Электромагинтная индукция – это явление возникновения
индукционного тока в замкнутом контуре при изменении магнитного потока через
него.
Магнитный поток – это величина, численно равная
количеству линий магнитной индукции, пересекающих контур площадью S.
Магнитный поток вычисляется по
формуле: Ф = BS cos α, где α – угол между нормалью к контуру и вектором магнитной
индукции. Измеряется в веберах (Вб).
Таким образом, явление магнитной
индукции возникает при любом изменении магнитного потока через контур:
— при изменении магнитной индукции В:
ΔФ = ΔBS cos α (движение магнита, движение вторичной катушки
с током, изменение силы тока во вторичной катушке при перемещении ползунка
реостата или включении/выключении тока в обмотке)
— площади контура S : ΔФ = BΔS cos α
— угла между нормалью и вектором магнитной
индукции α: ΔФ = BS(cos α2 – cos α1).
Закон Фарадея: ЭДС индукции, возникающая в контуре при
изменении магнитного потока, пересекающего этот контур, равна по модулю
скорости изменения магнитного потока:
Формула применима, если за промежуток
времени Δt магнитный поток изменяется на одну и
ту же величину, т.е. когда скорость изменения магнитного потока ΔФ/Δt постоянна.
Причины возникновения ЭДС индукции:
—
в замкнутом контуре изменение магнитного потока через него создает
вихревое электрическое поле, которое в свою очередь совершает работу по
перемещению электрического заряда, которая характеризуется ЭДС индукции;
— в проводнике, движущемся в
магнитном поле с постоянной скоростью v, на заряд действует сила Лоренца,
которая создает направленное движение заряженных частиц по проводнику.
Поэтому ЭДС индукции в движущемся в
магнитном поле проводнике равно ℰi = BvL sin α, где α – угол между направлением вектора
магнитной индукции и направлением скорости при движении проводника.
Так как в проводнике возникает ЭДС
индукции и соответственно индукционный ток, то силу тока можно найти по закону
Ома:
Направление индукционного тока:
— в замкнутом
контуре определяется правилом Ленца: индукционный ток всегда направлен так,
что своим магнитным полем он препятствует изменению магнитного потока,
вызывающего этот ток.
— в проводнике, который движется в
магнитном поле, направление индукционного тока определяется правилом левой
руки: если расположить левую руку так, чтобы четыре пальца показывали
направление движения проводника, магнитные линии входили в ладонь, то большой
палец покажет направление индукционного тока в проводнике.
Если ток в контуре по какой-то
причине будет изменяться, что созданное током магнитное поле создаст в той же
катушке индукционный ток, т.е. будет наблюдаться явление самоиндукции.
Магнитный поток в катушке пропорционален
силе тока в ней: Ф = LI, где L –
величина, называемая индуктивностью катушки L. Индуктивность
зависит от свойств катушки: ее длины, числа витков, наличия сердечника и
материала, из которого изготовлен сердечник (ферромагнетик, диамагнетик или
парамагнетик). Единица измерения индуктивности – генри (Гн).
При самоиндукции ЭДС, возникающая в
катушке при равномерном изменении силы тока в ней, равна:
Магнитное поле катушки обладает
энергией:
феномен возникающий в индуцированном поле
Явление электромагнитной индукции – это то, что заставляет работать электрические двигатели, позволяет генераторам вырабатывать электричество. Именно его открытие в начале XIX века привело к активному развитию таких отраслей, как энергетика, станкостроение, транспорт. Также данное явление широко применяется в медицине, радиовещании, при производстве расходомеров – счетчиков учета электроэнергии.

Практическое значение электромагнитной индукции
О том, в чем суть этого явления, когда и кто его открыл, что такое индуктивность и самоиндукция, какой энергией характеризуется совокупность магнитных силовых линий, будет рассказано в этой статье.
Явление электромагнитной индукции
Классическое определение этого явления гласит, что оно представляет собой появление упорядоченного движения заряженных частиц в замкнутом проводящем ток контуре (проводнике) при изменении проходящей через него, создаваемой постоянным магнитом совокупности силовых магнитных линий.
На заметку. Впервые обнаружить описываемое в статье явление экспериментальным путем получилось в 1831 году у известного ученого-физика Майкла Фарадея. Для своих опытов он использовал железное кольцо с намотанными с двух противоположных сторон витками медного провода, которые были соединены с гальваническим элементом и магнитной стрелкой. При подключении к первой обмотке гальванического элемента стрелка некоторое время двигалась, после чего останавливалась, после его отключения – плавно возвращалась в первоначальное положение. Подобные движения стрелки позволили предположить, что упорядоченное движение носителей электрических зарядов может возникать под воздействием совокупности силовых магнитных линий, источником которых служит первая обмотка.

Майкл Фарадей
Магнитный поток
Данное явление представляет собой совокупность силовых линий, проходящих через определённое сечение проводника или замкнутого токопроводящего контура.
Рассчитывается модуль этой величины Ф по следующей формуле:
Ф= B×S×Cos α, где:
- В – модуль вектора создаваемой силовыми линиями индукции;
- S – площадь поверхности, через которую проходит поток силовых линий;
- α – угол между векторами силовых линий индукции и нормали (т.е. перпендикуляром к пронизываемой силовыми магнитными линиями плоскости).
Измеряется данная величина в Веберах (Вб).
Закон электромагнитной индукции Фарадея
Данный фундаментальный закон имеет следующую формулировку: при любых изменениях магнитного потока, проходящего через проводящий контур, происходит возникновение электродвижущей силы (сокращенно ЭДС), значение которой прямо пропорционально скорости, с которой изменяется магнитный поток.
Отображением данной закономерности является следующая формула:
Ɛi = – ΔФ/Δt, где:
- Ɛi – появляющаяся в токопроводящем контуре электродвижущая сила индукции;
- ΔФ/Δt – скорость, с которой изменяется проходящий через замкнутый контур магнитный поток.
Таким образом, сила индукционного тока, образующегося в токопроводящем замкнутом контуре при воздействии на него электродвижущей силы, будет зависеть от того, с какой скоростью изменяется проходящий через него поток силовых линий магнита.
Векторная форма
В векторной форме этот закон выражается следующей формулой:
rot E= ΔB/Δt.
Согласно этой записи, напряжённость (E) электрического поля индукционного тока возрастает при увеличении скорости изменения потока B с силовыми линиями, пересекающими замкнутый контур.
Потенциальная форма
При помощи векторного потенциала закон электромагнитной индукции имеет следующую запись:
E =ΔA/Δt, где:
- Е – напряженность электрического поля, порождаемого индукционным током;
- ΔA/Δt – изменение векторного потенциала магнитного поля, проходящего через замкнутый контур, являющийся частью замкнутой цепи проводника.
Правило Ленца
Как гласит данное правило, на направление индукционного тока влияют вызвавшие его причины (факторы). Если значение Ф возрастает, то порождаемый им ток препятствует его увеличению. Если значение Ф убывает, происходит обратное: индукционный ток меняет направление, начиная препятствовать уменьшению плотности проходящих через контур силовых линий магнитного поля. Поэтому в формуле закона Фарадея содержится знак « минус».
Взаимодействие магнита с контуром
В качестве наглядного примера взаимодействия магнита и контура в сделанную из медного провода катушку помещают магнит. Если магнит медленно вставлять внутрь катушки, происходит постепенное увеличение пересекающего ее витки создаваемого магнитом потока. Появляющееся вследствие такой манипуляции упорядоченное движение частиц в катушке будет направлено по часовой стрелке, создавая собственное магнитное поле, ослабляющее поле магнита, отталкивая его тем самым от катушки.
Если магнит отдаляют от контура, его поток уменьшается, а заряженные частицы начинают двигаться против часовой стрелки, вследствие чего возникающая совокупность силовых магнитных линий будет притягивать магнит.
На заметку. В случае с незамкнутым (открытым) контуром: металлическим или алюминиевым кольцом, имеющим прорезь; катушкой, витки которой не замкнуты через амперметр, источник питания, данная закономерность, как и правило Ленца, не работает.
Вихревое электрическое поле
Изменяющееся во времени и пространстве магнитное поле является источником появления вихревого имеющего замкнутые силовые линии электрического поля. Его воздействие объясняет упорядоченное перемещение единичных зарядов в проводнике, находящемся в (статичном) неподвижном состоянии.
Направление силовых линий электрического поля подчиняется правилу Ленца и правилу «буравчика».
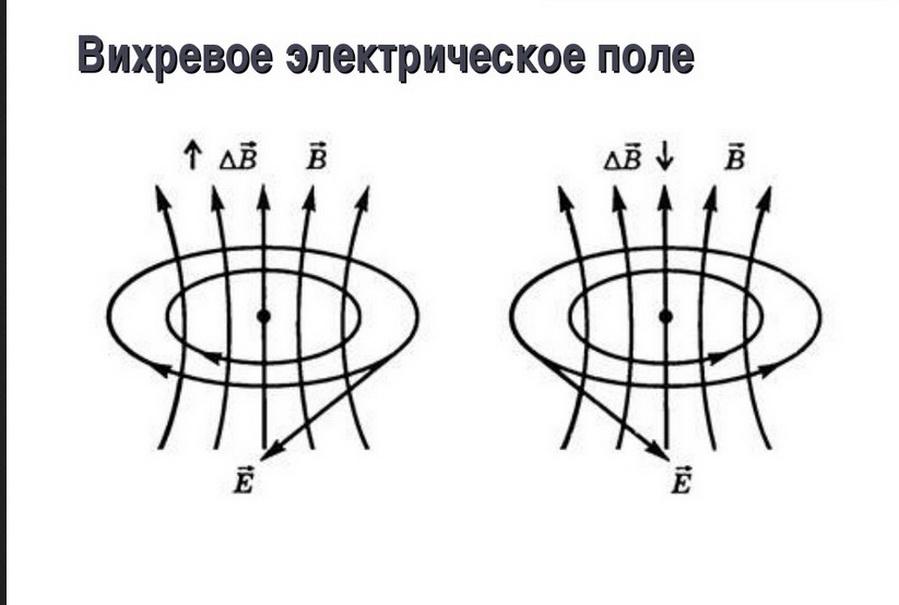
Вихревые силовые линии
Индуктивность
Проходя по контуру, электрический ток способствует образование вокруг него совокупности магнитных силовых линий. Согласно формуле Ф = L×I, создаваемый магнитом поток Ф пропорционально зависит от силы тока I.
Таким образом, под индуктивностью L понимают коэффициент соотношения магнитного потока Ф и силы тока I, протекающего по контуру. Рассчитывают данную величину по следующей формуле:
L=Ф/I.
Единицей измерения этой физической величины является Генри (Гн). 1 Гн – это индуктивность, образующаяся в замкнутом контуре, в котором сила тока изменяется на 1 Ампер, а величина напряжения в нем составляет 1 Вольт.
Самоиндукция
При изменениях значения силы тока в проводнике либо токопроводящей катушке происходит изменение магнитного потока, пронизывающего его. В результате в проводнике появляется электродвижущая сила самоиндукции, значение которой определяется по следующей формуле:
ƐiS = – ΔФ/Δt= –L(ΔI/Δt).
Энергия магнитного поля
Совокупность магнитных силовых линий имеет определенный запас энергии. Так как данное явление в контуре обусловлено протеканием по нему электрического тока, то и количество такой энергии зависит от величины затрат источников (генераторов, гальванических элементов) на создание тока. Рассчитывается эта величина (Wмаг.п) по следующей математической формуле:
Wмаг.п= (L×I2)/2.
На заметку. С практической точки зрения, значение данной величины оказывает влияние на мощность электрических агрегатов: электродвигателей, генераторов. Чем больше мощность силовых линий, образуемых обмотками или постоянными магнитами статора и ротора, тем выше крутящий момент и мощность двигателя, больше его КПД.
Основные формулы
Основные формулы для явления магнитной индукции указаны на рисунке ниже.

Основные формулы, описывающие явление электромагнитной индукции
Поняв, в чем заключается суть явления электромагнитной индукции, можно разобраться в том, как работают электродвигатели, генераторы. Эти знания, помимо большой теоретической ценности, имеет достаточно полезное практическое применение, позволяя самостоятельно находить, в ряде случаев и устранять, неисправности агрегатов, не прибегая к дорогостоящим услугам специалистов.
Видео
Более подробно и наглядно об описанном в данной статье явлении можно узнать в следующем видео.
Электродвижущая сила электромагнитной индукции — Студопедия
Причиной возникновения тока в замкнутом контуре является электродвижущая сила, возбуждаемая сторонней силой. Если контур 2 на рис. 8.1 разомкнуть, то гальванометр покажет отсутствие индукционного тока. Однако э.д.с. электромагнитной индукции в контуре 2 при изменении магнитного потока через его сечение все равно возникнет. Опыты Фарадея позволили ему сформулировать закон электромагнитной индукции:
При всяком изменении магнитного потока , охватывающего контур, в нем возникает э.д.с. электромагнитной индукции, величина которой пропорциональна скорости изменения магнитного потока:
(8.1)
где знак минус соответствует правилу Ленца: э.д.с. индукции противодействует причине, вызвавшей эту причине.
Пусть постоянное магнитное поле создано в лабораторной системе отсчета. Пусть движение контура с постоянной скоростью приводит к изменению магнитного потока через сечение, охватываемое контуром. Наблюдатель в лабораторной системе отсчета видит причину возникновении сторонней силы в действии силы Лоренца на носители тока в контуре (см. рис. 8.2).
Рис. 8.2
Выразим э.д.с. электромагнитной индукции в контуре :
где — напряженность поля сторонних сил,
и — сила Лоренца, действующая на свободный заряд в элементе контура , который движется со скоростью .
Отсюда получим выражение э.д.с. электромагнитной индукции для наблюдателя в лабораторной системе отсчета:
(8.2)
Учтем векторное тождество:
и перепишем выражение (8.2):
(8.3)
Вектор смещения элемента контура за время равен . Изменение вектора площади сечения контура за время составит . Изменение магнитного потока через сечение, охватываемое контуром, за время составит
. (8.4)
Сопоставляя (8.3) и (8.4), получим формулу закона электромагнитной индукции:
(8.1)
Перейдем в систему отсчета, движущуюся вместе с контуром . В этой системе контур неподвижен, и объяснить возникновение э.д.с. электромагнитной индукции за счет действия силы Лоренца нельзя. Наблюдатель в подвижной системе отсчета связывает возникновение э.д.с. с появлением вихревого электрического поля при переходе из лабораторной системы в подвижную систему отсчета.
Вывод: Электрическое поле, как и магнитное, проявляет относительные свойства (изменяется) при переходе из одной системы отсчета в другую.
Напряженность вихревого электрического поля служит напряженностью поля сторонних сил в подвижной системе отсчета: . Э.д.с. как скалярная величина, не зависит от выбора системы отсчета. В подвижной системе
Сопоставляя последнее выражение с (8.2) и учитывая произвольность выбора контура , получим выражение для напряженности вихревого электрического поля через индукцию магнитного поля и скорость движения контура:
(8.5)
При протекании индукционного тока в контуре выделяется джоулево тепло. Эта энергия равна работе механических сил, приводящих контур в движение.
Баллистический метод измерения индукции магнитного поля разработал А.Г. Столетов (изучить самостоятельно).
Пусть контур образован не одним витком, а образует соленоид из витков. Так как витки соединены последовательно, то э.д.с., возбуждаемые в отдельных витках, складываются. Полная э.д.с. индукции в катушке
(8.6)
где — потокосцепление или полный магнитный поток катушки,
и — магнитный поток через — ый виток; если все эти потоки одинаковы, то
Индукционные токи могут возбуждаться не только в проволочных контурах, но и в сплошных массивных проводниках. Тогда их называют индукционными токами или токами Фуко. Эти токи могут достигать больших значений, так как сплошные проводники имеют небольшое сопротивление. В соответствии с правилом Ленца индукционные токи противодействуют причине, их вызвавшей. Поэтому при движении массивных проводников в сильном магнитном поле эти проводники испытывают сильное торможение. Торможение вызывается силой, действующей на токи Фуко со стороны магнитного поля.
В технике токи Фуко могут оказывать полезное действие. Например, в измерительных приборах на оси стрелки закрепляется металлическая пластина, которая вводится в зазор между полюсами магнита. При движении пластины в ней возникают индукционные токи, вызывающие торможение всей системы. Торможение не препятствует приходу стрелки в равновесие.
Тепловое действие токов Фуко используют в индукционных печах. Печь образуется катушкой, которая питается высокочастотным током большой силы. Можно плавить металлы и получать химически чистые образцы.
До появления ферритов приходилось изготавливать ферромагнитные сердечники электромагнитов из пластин. Это позволяло уменьшить интенсивность токов Фуко в сердечниках и, соответственно, потери энергии на нагрев сердечников при их перемагничивании.
По мере повышения частоты переменный ток все больше концентрируется в поверхностном слое проводника (скин-эффект). Переменные токи Фуко направлены так, что ослабляют ток внутри провода, но усиливают у поверхности. Поверхностный эффект, приводящий к вытеснению тока в поверхностный слой проводника, позволяет применять полые трубчатые проводники в высокочастотных цепях.
Еще одним техническим применением явления электромагнитной индукции служат генераторы переменного тока (изучить самостоятельно).
Электромагнитная индукция. Правило Ленца
Явление электромагнитной индукции было открыто выдающимся английским физиком М.Фарадеем в 1831 г. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур.
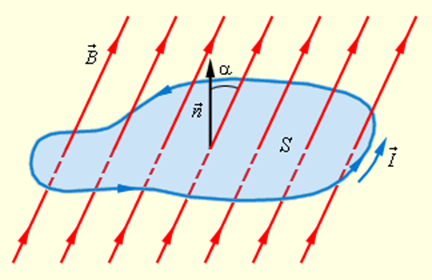
Магнитным потоком Φ через площадь S контура называют величину
Φ = B · S · cos α, |
где B – модуль вектора магнитной индукции, α – угол между вектором 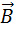 и нормалью
и нормалью 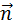 к плоскости контура (рис. 1.20.1).
к плоскости контура (рис. 1.20.1).
|
Рисунок 1.20.1. Магнитный поток через замкнутый контур. Направление нормали |
Определение магнитного потока нетрудно обобщить на случай неоднородного магнитного поля и неплоского контура. Единица магнитного потока в системе СИ называется Вебером (Вб). Магнитный поток, равный 1 Вб, создается магнитным полем с индукцией 1 Тл, пронизывающим по направлению нормали плоский контур площадью 1 м2:
1 Вб = 1 Тл · 1 м2. |
Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции 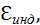 равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
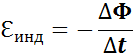
Эта формула носит название закона Фарадея.
Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Это утверждение, сформулированное в 1833 г., называется правилом Ленца.
Рис. 1.20.2 иллюстрирует правило Ленца на примере неподвижного проводящего контура, который находится в однородном магнитном поле, модуль индукции которого увеличивается во времени.
|
Рисунок 1.20.2. Иллюстрация правила Ленца. В этом примере |
Правило Ленца отражает тот экспериментальный факт, что 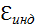 и
и 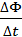 всегда имеют противоположные знаки (знак «минус» в формуле Фарадея). Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
всегда имеют противоположные знаки (знак «минус» в формуле Фарадея). Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам.
1. Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
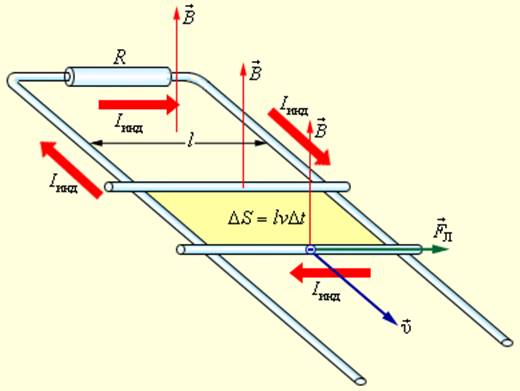
Рассмотрим в качестве примера возникновение ЭДС индукции в прямоугольном контуре, помещенном в однородное магнитное поле 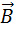 перпендикулярное плоскости контура. Пусть одна из сторон контура длиной l скользит со скоростью
перпендикулярное плоскости контура. Пусть одна из сторон контура длиной l скользит со скоростью 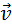 по двум другим сторонам (рис. 1.20.3).
по двум другим сторонам (рис. 1.20.3).
|
Рисунок 1.20.3. Возникновение ЭДС индукции в движущемся проводнике. Указана составляющая силы Лоренца, действующей на свободный электрон |
На свободные заряды на этом участке контура действует сила Лоренца. Одна из составляющих этой силы, связанная с переносной скорость 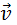 зарядов, направлена вдоль проводника. Эта составляющая указана на рис. 1.20.3. Она играет роль сторонней силы. Ее модуль равен
зарядов, направлена вдоль проводника. Эта составляющая указана на рис. 1.20.3. Она играет роль сторонней силы. Ее модуль равен
Работа силы FЛ на пути l равна
По определению ЭДС
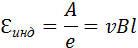
В других неподвижных частях контура сторонняя сила равна нулю. Соотношению для 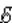 инд можно придать привычный вид. За время Δt площадь контура изменяется на ΔS = lυΔt. Изменение магнитного потока за это время равно ΔΦ = BlυΔt. Следовательно,
инд можно придать привычный вид. За время Δt площадь контура изменяется на ΔS = lυΔt. Изменение магнитного потока за это время равно ΔΦ = BlυΔt. Следовательно,
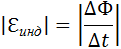
Для того, чтобы установить знак в формуле, связывающей 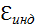 и
и 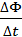 нужно выбрать согласованные между собой по правилу правого буравчика направление нормали
нужно выбрать согласованные между собой по правилу правого буравчика направление нормали 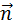 и положительное направление обхода контура
и положительное направление обхода контура 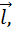 как это сделано на рис. 1.20.1 и 1.20.2. Если это сделать, то легко прийти к формуле Фарадея.
как это сделано на рис. 1.20.1 и 1.20.2. Если это сделать, то легко прийти к формуле Фарадея.
Если сопротивление всей цепи равно R, то по ней будет протекать индукционный ток, равный 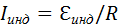 . За время Δt на сопротивлении R выделится джоулево тепло
. За время Δt на сопротивлении R выделится джоулево тепло
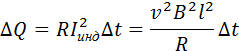
Возникает вопрос: откуда берется эта энергия, ведь сила Лоренца работы не совершает! Этот парадокс возник потому, что мы учли работу только одной составляющей силы Лоренца. При протекании индукционного тока по проводнику, находящемуся в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, связанная с относительной скоростью движения зарядов вдоль проводника. Эта составляющая ответственна за появление силы ампера 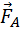 . Для случая, изображенного на рис. 1.20.3, модуль силы Ампера равен FA = I B l. Сила Ампера направлена навстречу движению проводника; поэтому она совершает отрицательную механическую работу. За время Δt эта работа Aмех равна
. Для случая, изображенного на рис. 1.20.3, модуль силы Ампера равен FA = I B l. Сила Ампера направлена навстречу движению проводника; поэтому она совершает отрицательную механическую работу. За время Δt эта работа Aмех равна
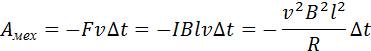
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю. Джоулево тепло в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
2. Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике. Следовательно, электрическое поле, порожденное изменяющимся магнитным полем, не является потенциальным. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Джеймсом Максвеллом в 1861 г.
Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея. Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной: в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца; в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
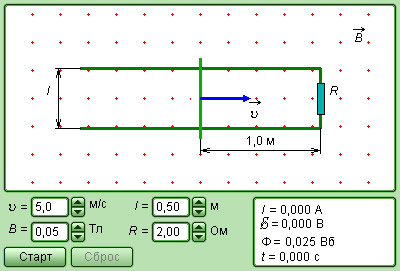 |
Модель. Электромагнитная индукция |
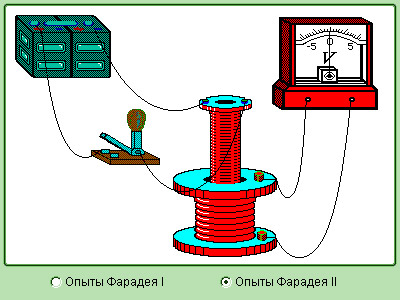 |
Модель. Опыты Фарадея |
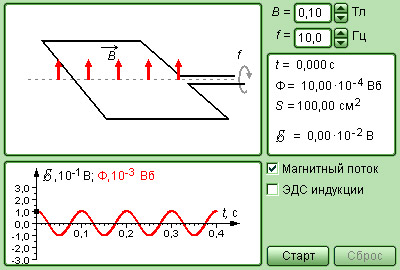 |
Модель. Генератор переменного тока |
ЭДС индукции в движущихся проводниках. Электродинамический микрофон
ЭДС индукции в движущихся проводниках. Электродинамический микрофон
- Подробности
- Просмотров: 360
«Физика — 11 класс»
ЭДС индукции в движущихся проводниках
Пусть проводник MN длиной l движется с постоянной скоростью V по проводящим направляющим в однородном магнитном поле.
Вектор магнитной индукции поля перпендикулярен проводнику и составляет угол α с направлением его скорости.
Проводник MN вместе с направляющими образует контур MNCD.
При движении проводника его свободные заряды движутся вместе с ним, поэтому на заряды со стороны магнитного поля действует сила Лоренца.
Fл = | q |υ B sin α
Сила Лоренца, совершает работу по перемещению зарядов по всей длине проводника.
А = Fлl = | q | υ Bl sin α
Возникающая здесь за счет действия на заряды силы Лоренца ЭДС индукции имеет магнитное происхождение.
Электродвижущая сила индукции в проводнике MN равна отношению работы по перемещению заряда q к этому заряду:
Эта формула справедлива для любого проводника длиной l, движущегося со скоростью V в однородном магнитном поле.
В других проводниках контура MNCD ЭДС равна нулю, так как эти проводники неподвижны.
Следовательно, ЭДС во всем контуре MNCD равна и остается неизменной, если скорость движения V постоянна.
Электродинамический микрофон
Электродинамический громкоговоритель преобразует колебания электрического тока в звуковые колебания.
Обратный процесс превращения звуковых колебаний воздуха в колебания электрического тока осуществляется с помощью микрофона.
Действие электродинамического микрофона основано на явлении электромагнитной индукции.
Как устроен этот микрофон?
Диафрагма 2 из тонкой полистирольной пленки или алюминиевой фольги жестко связана со звуковой катушкой 1 из тонкой проволоки. Катушка помещается в кольцевом зазоре сильного постоянного магнита 3. Линии магнитной индукции перпендикулярны к виткам катушки.
Звуковая волна вызывает колебания диафрагмы и связанной с ней катушки, в результате в катушке возникает меняющийся индукционный ток.
Подробнее:
при движении витков катушки в магнитном поле в них возникает переменная ЭДС индукции и переменное напряжение на зажимах катушки, которое вызывает колебания электрического тока в цепи микрофона.
Эти колебания после усиления могут быть поданы на громкоговоритель и т. д.
В телефонных аппаратах применяют менее совершенные, но зато более дешевые угольные микрофоны.
Диафрагма в таких микрофонах действует на угольный порошок и создает в нем периодические сжатия и разрежения.
От этого меняются сопротивление порошка и сила тока в электрической цепи микрофона.
Существуют и другие типы микрофонов.
Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин
Электромагнитная индукция. Физика, учебник для 11 класса — Класс!ная физика
Электромагнитная индукция. Магнитный поток —
Направление индукционного тока. Правило Ленца —
Закон электромагнитной индукции —
ЭДС индукции в движущихся проводниках. Электродинамический микрофон —
Вихревое электрическое поле —
Самоиндукция. Индуктивность. Энергия магнитного поля тока —
Электромагнитное поле —
Примеры решения задач —
Краткие итоги главы
Самоиндукция простыми словами: определение, формулы, примеры
Явление электромагнитной индукции очень часто наблюдается в электротехнике. Взаимное влияние электрических и магнитных полей иногда приводит к интересным результатам. Самоиндукция – частный случай электромагнитной индукции.
Общеизвестно, что причиной порождения электрического тока является переменное магнитное поле. Именно этот принцип реализован в конструкциях современных генераторов. Природа самоиндукции также связана с электромагнетизмом, но это явление проявляется она по-другому.
Определение
Рассмотрим схему катушки, по обмоткам которой протекает электрический ток (рис. 1). Так как вокруг проводника, который находится под током, всегда существует связанное с ним магнитное поле, то силовые линии этого поля пронизывают плоскости витков. В результате такого взаимодействия соленоиды образуют собственное магнитное поле, магнитные линии которого замыкаются за его пределами.
 Рис. 1. Магнитное поле катушки
Рис. 1. Магнитное поле катушки
Частным случаем катушки является замкнутый контур (один виток). В нём, как и в катушке, образуется собственное магнитное поле (см. рис. 2). Если ток постоянный, то в контуре никаких изменений не происходит.
Но при изменении параметров, например, в результате размыкания цепи, изменяется магнитный поток, создаваемый электрическим полем, что является причиной возникновения ЭДС индукции. Аналогичное изменение произойдёт и в случае замыкания цепи.
Изменение параметров магнитного поля вызывает появление вихревого электрического поля, что в свою очередь приводит к возбуждению индуктивной электродвижущей силы. Возникновение ЭДС индукции, в результате изменения ток в замкнутом контуре, называется самоиндукцией.
Магнитный поток, ограниченный поверхностью контура, меняется прямо пропорционально изменению тока, циркулирующего в нём.
 Рис. 2. Явление самоиндукции
Рис. 2. Явление самоиндукции
Направление вектора ЭДС самоиндукции не совпадает с направлением тока в период его возрастания (при замыкании цепи), но он сонаправлен с ним в период убывания (разъединения цепи). Такое действие проявляется в замедлении появления тока в соленоиде при замыкания цепи, или в его задержке на какое-то время после разрыва цепи.
Описанное явление можно наблюдать на опыте с лампочками, одна из которых подключена последовательно с индуктивностью (см. рис. 3).
 Рис. 3. Схема опыта с лампочками
Рис. 3. Схема опыта с лампочками
Как видно на рисунке слева, ток от источника питания, проходящий через лампочку 2, при замыкании контактов встретит сопротивление вихревых токов, поскольку они противоположно направлены. Поэтому зажигание этой лампочки произойдёт с задержкой.
На время включения лампочки 1 вихревые токи повлияют, но сила тока в её цепи уменьшится после зажигания лампы 2. При отключении цепи от источника питания произойдёт обратный процесс: лампочка в цепи индуктивности некоторое время будет медленно угасать, а вторая лампа потухнет сразу после разъединения контактов.
График на рисунке 4 красноречиво объясняет эффект задержки.
 Рис. 4. Иллюстрация задержки изменения тока в цепи индуктивности
Рис. 4. Иллюстрация задержки изменения тока в цепи индуктивности
Обратите внимание на нелинейность изменения силы тока по времени.
Аналогичные процессы происходят в цепи, состоящей из одной катушки. На рисунке 5 изображена такая схема и график изменения силы тока.
 Рис. 5. Возникновение самоиндукции
Рис. 5. Возникновение самоиндукции
Остаётся добавить, что скорость изменение величины ЭДС зависит от количества витков соленоида. Чем больше витков, тем больше влияние вихревых токов, на параметры цепи.
В случае с переменным током амплитуда ЭДС самоиндукции пропорциональна амплитуде синусоиды питания, её частоте и индуктивности катушки.
Синусоидальный ток, проходя через катушку индуктивности, сдвигается по фазе на величину π/2. Именно этот сдвиг является причиной отставания собственного тока катушки от тока, вырабатываемого источником питания.
Формулы
Собственный магнитный поток контура (Ф) связан прямо пропорциональной зависимостью с индуктивностью (L) этого контура и величиной тока в нём (i). Данная зависимость выражается формулой: Ф = L×i. Коэффициент пропорциональности L принято называть коэффициентом самоиндукции или же просто индуктивностью контура.
При этом индуктивность контура пребывает в зависимости от его геометрии, площади плоскости ограниченной витком и магнитной проницаемости окружающей среды. Но этот коэффициент не зависит от силы тока в контуре. Если же форма, линейные размеры и магнитная проницаемость не изменяются, то для определения величины индуктивной ЭДС применяется формула:

где Eсамоинд. – ЭДС самоиндукции, Δi – изменение силы тока за время Δt.
Индуктивность
Выше мы отметили, что индуктивность контура зависит от его геометрии и размеров, а также от магнитной проницаемости среды. Если речь идёт о катушке, то эти утверждения справедливы и для неё. На индуктивность катушки влияет её диаметр и количество витков. Индуктивность существенно повышается, если в катушку добавить ферромагнитный сердечник.
Магнитные поля отдельных витков катушки складываются. Если витков достаточно много, то ток, протекающий через катушку, образует вокруг неё сильное магнитное поле, реагирующее на изменения электрического поля. Индуктивность является той величиной, которая характеризует то, насколько сильно проводник, из которого состоят витки, противодействует электрическому току.
Чем больше индуктивность катушки и чем выше скорость прерывания её цепи, тем больший всплеск ЭДС произойдёт в цепи. При этом полярность вихревых токов на выводах катушки противоположна направлению тока источника питания.
Индуктивность (то есть коэффициент пропорциональности) является важной характеристикой катушек, дросселей и других контурных элементов. Этот параметр можно сравнить с ёмкостью конденсаторов. Тем более что действие катушки индуктивности и конденсатора в электрических цепях очень похожи. RL и RC цепочки часто используют для сглаживания всплесков напряжений в различных фильтрах.
Единицей измерения индуктивности в международной системе СИ является генри. Величина размеров в 1 Гн – это такая индуктивность, при которой ЭДС составляет 1 В, при скорости изменения тока на 1 А за секунду.
Индуктивность определяет количество энергии, выделяющейся в результате действия собственного магнитного поля при самоиндукции. Эту энергию легко рассчитать по формуле: Wм = LI2/2.
Собственная энергия катушки численно равна работе, которую необходимо выполнить источником питания при преодолении ЭДС самоиндукции.
Важно знать, что в результате резкого разрыва цепи с большой индуктивностью, энергия высвобождается в виде искры или даже с образованием дугового разряда.
Примеры использования на практике
Явление самоиндукции нашло широкое практическое применение. Автолюбители прекрасно знают, что такое катушка зажигания. Без неё карбюраторный двигатель не запустится.
Работает этот важный узел следующим образом:
- На катушку с большой индуктивностью подаётся бортовое напряжение 12 В.
- Электрическая цепь резко обрывается специальным прерывателем.
- Накопленная энергия самоиндукции поступает по высоковольтным проводам на свечу и образует на её электродах мощную искру.
- Искровой разряд зажигает топливную смесь, приводя в движение поршень.
В современных автомобилях разрыв цепи выполняет электроника, но суть от этого не меняется – для образования искры по-прежнему используется энергия самоиндукции.
Мы уже упоминали о сетевых фильтрах, в которых используется явление самоиндукции. RL цепочка реагирует на любое изменение параметров. При его возрастании она задерживает во времени пиковые скачки и заполняет собственными вихревыми токами провалы. Таким образом, происходит сглаживание напряжения в электрически цепях.
В блоках питания электронной аппаратуры таким же способом убирают:
- шумы:
- пульсации;
- нежелательные частоты.
Самоиндукция дросселей используется в люминесцентных лампах для розжига электродов. После срабатывания стартера происходит разрыв контактов, в результате чего в дросселе наводится ЭДС самоиндукции. Энергия дросселя разжигает дугу на электродах, и люминесцентная лампа начинает светиться.
Перечисленные примеры демонстрируют полезное применение самоиндукции. Однако, как это всегда бывает, индуктивная ЭДС может наносить вред. При разъединении контактов выключателей, нагрузкой которых являются цепи с большой индуктивностью, возможны дуговые разряды. Они разрушают контакты, замедляют время защиты и т.п. С целью снижения риска от негативных влияний самоиндукции автоматические выключатели оборудуют дугогасительными камерами.
В таких случаях приходится принимать меры для нейтрализации энергии ЭДС самоиндукции. Ещё большая потребность в рассеянии энергии самоиндукции возникает в полупроводниковых ключах, чувствительных к пробоям.
В промышленности и энергетике самоиндукция является серьёзной проблемой. При отключении нагруженных линий ЭДС самоиндукции может достигать опасных для жизни величин. Это требует дополнительных затрат на принятие мер предосторожности. В частности, необходимо устанавливать на линиях устройства, препятствующие молниеносному размыканию цепи.
Видео в помощь
3.15. Природа электромагнитной индукции
В
предыдущих разделах мы рассмотрели
закон электромагнитной индукции и
различные его проявления. Возникновение
ЭДС индукции и индукционного тока в
замкнутом проводящем контуре при
изменении магнитного потока через этот
контур означает, что на электроны в
контуре действуют какие-то сторонние
силы, заставляющие электроны двигаться
упорядоченно. Рассмотрим природу этих
сил.
Как
уже обсуждалось в п. 3.10, явление
возникновения ЭДС индукции наблюдается
либо при изменении магнитного поля во
времени, либо при движении контура или
его частей во внешнем магнитном поле.
В соответствии с этим существует и две
различных причины возникновения ЭДС
индукции.

Рассмотрим
первый случай, когда контур или его
часть движется в магнитном поле. Вновь
обратимся к опыту, изображенному на
рис. 3.22. Пусть перемычка CD
длиной
 движется со скоростью
движется со скоростью в однородном магнитном поле, индукция
в однородном магнитном поле, индукция которого перпендикулярна плоскости
которого перпендикулярна плоскости
контураABCD.
Формально магнитный поток изменяется
вследствие изменения площади контура,
в результате чего в контуре действует
ЭДС индукции и течет индукционный ток
(см. пример 3.13). Разберём ситуацию более
детально (рис. 3.25). Так как перемычка
движется со скоростью
 вправо, электроны внутри неё движутся
вправо, электроны внутри неё движутся
вправо точно с такой же скоростью.
Индукционный ток по перемычкеCD
течет сверху вниз, следовательно,
электроны движутся упорядоченно снизу
вверх с некоторой скоростью
 относительно проводника. В итоге
относительно проводника. В итоге
результирующая скорость электрона направлена под некоторым углом к
направлена под некоторым углом к
проводнику. На электрон, движущийся
в магнитном поле, действует сила Лоренца ,
,
перпендикулярная скорости .
.
Силу Лоренца можно разложить на две
составляющие, действующие вдоль провода
и перпендикулярно ему: .
.
Сила направлена перпендикулярно проводу
направлена перпендикулярно проводу
против направления его
перемещения. Такая сила действует
на каждый электрон в проводе. По сути,
сумма всех сил ,
,
действующих на различные электроны,
представляет собой силу Ампера (см.
пример 3.13). Она стремится затормозить
проводник и совершает отрицательную
работу. Составляющая направлена вдоль проводника, разгоняет
направлена вдоль проводника, разгоняет
электроны и совершает положительную
работу, работа составляющей отрицательна. Полная работа силы Лоренца,
отрицательна. Полная работа силы Лоренца,
как всегда, равна нулю. Сила привела бы к остановке перемычкиCD,
привела бы к остановке перемычкиCD,
если бы на перемычку не действовала еще
одна сила, совершающая положительную
работу, — сила тяги. И в конечном итоге
именно за счет механических усилий,
т.е. работы силы тяги, вырабатывается
электроэнергия (по контуру ABCD
течет ток и контур нагревается).
Составляющая
силы Лоренца
 обусловлена движением проводника со
обусловлена движением проводника со
скоростью (рис. 3.25). Поэтому
(рис. 3.25). Поэтому .
.
Работа по перемещению одного электрона
от одного полюса перемычкиCD
к другому
 ,
,
работа по перемещениюN
электронов
 ,
,
где
суммарный заряд, прошедший вдоль
перемычки. Тогда ЭДС индукции (см. формулу
(2.12))
 .
.
Этот результат совпадает с результатом
(3.32) примера 3.13, полученным формально
из закона электромагнитной индукции.
Если
движущаяся перемычка CD
незамкнута, то индукционного тока не
будет, но один из концов перемычки под
действием силы Лоренца зарядится
отрицательно, а другой положительно,
т.е. между концами перемычки возникнет
разность потенциалов, которая и будет
равна ЭДС индукции, определяемой
выражением (3.32). Можно сказать, что в
этом случае движущаяся в магнитном
поле перемычка будет представлять собой
незамкнутую «батарейку». Небольшая
разность потенциалов возникает, например,
на концах крыльев самолетов, осей машин
и т.п. при движении в магнитном поле
Земли.
Таким
образом, роль
сторонних сил, вызывающих появление
ЭДС индукции в случае движения контура
или его части в магнитном поле играет
сила Лоренца,
или точнее её составляющая, направленная
вдоль проводника. Именно сила Лоренца,
например, действует на электроны во
вращающемся в магнитном поле якоре,
приводя к возникновению электродвижущей
силы генератора. Можно сказать, что
возникновение индукционного тока в
случае движения контура или его частей
не представляет собой принципиально
нового физического явления. Похожим
образом, например, объясняется эффект
Холла, рассмотренный в п. 3.5.
Рассмотрим
второй случай возникновения, когда ЭДС
индукции и индукционный ток возникают
в неподвижном контуре, находящемся в
переменном магнитном поле. Понятно, что
в этом случае сила Лоренца на свободные
заряды не действует. Какая же сторонняя
сила приводит в упорядоченное движение
электроны в этом случае? Максвелл
предположил, что имеет место совершенно
новое физическое явление: изменяющееся
во времени магнитное поле приводит к
появлению в пространстве вихревого
электрического поля.
Возникновение
индукционного тока в контуре, находящимся
в переменном магнитном поле можно
объяснить следующим образом. Переменное
магнитное поле порождает в пространстве
вихревое электрическое поле. Как и любое
электрическое поле, вихревое электрическое
поле действует на свободные электроны
контура с силой, и электроны движутся
упорядоченно, т.е. возникает ток. Отметим,
однако, что само вихревое электрическое
поле возникает в пространстве, где есть
переменное магнитное поле вне всякой
зависимости от наличия проводящего
контура. Проводящий контур играет роль
своеобразного индикатора, «лакмусовой
бумажки», указывающей на существование
в пространстве вихревого электрического
поля. В этом существенная разница
трактовки закона электромагнитной
индукции Фарадея и Максвелла. Фарадей,
на опыте открывший этот закон, видел
его суть в возникновении индукционного
тока. По Максвеллу, суть закона в
возникновении вихревого электрического
поля. (В дальнейшем Максвелл постулировал
факт, в то время не подкрепленный никакими
экспериментами, что, в свою очередь,
переменное электрическое поле порождает
магнитное поле). Эта гениальная догадка
Максвелла является важнейшим законом
физики, открытым в 19 веке. Фарадей и
Максвелл внесли грандиозный вклад в
развитие теории электромагнетизма. Их
работы заложили основы нового раздела
физики – волновой оптики (теории света
как электромагнитной волны).
Термин
вихревое
поле означает,
что силовые линии такого поля замкнуты.
Вихревое электрическое поле существует
вне прямой связи с зарядами – его
источником является переменное магнитное
поле. Работа по перемещению заряда в
потенциальном электрическом поле,
источником которого являются какие-то
заряды, равна нулю (см. п. 1.12). Работа же
вихревого электрического поля по
замкнутому контуру отлична от нуля.
Работа силы, действующей со стороны
вихревого электрического поля, по
перемещению положительного единичного
заряда по замкнутому контуру и представляет
собой ЭДС индукции в контуре:
 (см. формулу 2.12). Работа вихревого поля
(см. формулу 2.12). Работа вихревого поля по перемещению заряда по замкнутому
по перемещению заряда по замкнутому
контуруL
(см. также п. 1.12):
 .
.
Тогда:
 .
.
(3.39)
Если
ЭДС индукции представить как произведение
некоторого среднего значения напряженности
вихревого электрического поля на длину
контура
 ,
,
то для оценки величины напряженности
вихревого поля, направленного вдоль
провода, получим .
.
По
закону электромагнитной индукции
(3.25,а) из уравнения (3.39) получаем:
 .
.
(3.40)
Учитывая
выражение для магнитного потока (3.19,
а), уравнение (3.40) можно представить в
виде:
 ,
,
(3.40,а)
где
S
может быть любой поверхностью, натянутой
на контур L.
Уравнение
(3.40,а) представляет собой одно из уравнений
Максвелла. Его смысл в том, что источником
электрического поля может быть переменное
магнитное поле. Или буквально: переменное
магнитное поле создаёт отличную от нуля
циркуляцию электрического поля.
В
соответствии с принципом относительности
Эйнштейна все
явления природы происходят одинаково
во всех инерциальных системах отсчета.
Принципа относительности мы уже касались
в п. 3.1, когда говорили о том, что в любой
инерциальной системе отсчета действующая
на заряд электромагнитная сила одна и
та же, хотя ее электрическая и магнитная
составляющие могут изменяться.
На
первый взгляд может показаться, что
закон электромагнитной индукции
описывает принципиально два различных
физических явления: возникновение ЭДС
индукции и индукционного тока в контуре
в результате действия силы Лоренца
(т.е. действия самого магнитного поля)
и в результате действия вихревого
электрического поля, порождаемого
переменным магнитным полем. Сам же закон
(3.25) одинаков в обоих случаях! Выясним
причины этого «совпадения». Рассмотрим
вновь опыт Фарадея, представленный на
рис. 3.18. Представим себе двух наблюдателей,
один из которых «сидит» на магните, а
другой – на кольце. Если в контур кольца
включить гальванометр, то оба наблюдателя
увидят отклонение его стрелки. Первый
наблюдатель, находящийся на кольце,
будет утверждать, что переменное
магнитное поле порождает вихревое
электрическое, которое действует на
электроны кольца с силой, в результате
по кольцу идет ток. Для второго наблюдателя,
находящегося на магните, магнит
неподвижен, а движется кольцо. Поэтому
он скажет, что причиной тока является
сила Лоренца, действующая со стороны
магнитного поля на электроны кольца.
Обоих наблюдателей «примиряет» принцип
относительности Эйнштейна. Важно, что
они, находясь в разных системах отсчета,
наблюдают одно и то же физическое
явление: одинаковый индукционный ток
в кольце, а значит и одинаковую ЭДС
индукции. Поэтому и сам закон Фарадея
(3.25) должен выглядеть одинаково для
обоих случаев.
Важным
следствием принципа относительности
Эйнштейна является относительность
магнитного и электрического полей.
Нельзя утверждать, что в пространстве
имеется магнитное или электрическое
поля, не указывая, относительно какой
системы отсчёта ведется наблюдение.
Если для первого наблюдателя вихревое
электрическое поле существует, то для
второго наблюдателя его нет.
Относительность
электрического и магнитного полей
следует также из того факта, что в любой
инерциальной системе отсчета ускорение
заряда и электромагнитная сила (обобщенная
сила Лоренца – см. формулу (3.2)) одни и
те же.
Motional Emf | Электромагнитная индукция и цепи переменного тока
ЭДС движения
Как мы видели, любое изменение магнитного потока индуцирует ЭДС, противодействующую этому изменению — процесс, известный как индукция. Движение — одна из основных причин индукции. Например, магнит, перемещенный к катушке, индуцирует ЭДС, а катушка, перемещенная к магниту, создает аналогичную ЭДС. В этом разделе мы сконцентрируемся на движении в магнитном поле, которое является стационарным относительно Земли, производя то, что в общих чертах называется ЭДС движения .
Одна ситуация, когда возникает двигательная ЭДС, известна как эффект Холла и уже была исследована. Заряды, движущиеся в магнитном поле, испытывают действие магнитной силы \ (F = \ text {qvB} \ phantom {\ rule {0.25em} {0ex}} \ text {sin} \ phantom {\ rule {0.25em} {0ex}} \ theta \), который перемещает противоположные заряды в противоположных направлениях и производит \ (\ text {emf} = \ mathrm {B \ ell v} \). Мы увидели, что эффект Холла имеет приложения, включая измерения \ (B \) и \ (v \). Теперь мы увидим, что эффект Холла является одним из аспектов более широкого явления индукции, и мы обнаружим, что ЭДС движения может использоваться как источник энергии.
Рассмотрим ситуацию, показанную на этом рисунке. Стержень движется со скоростью \ (v \) по паре проводящих рельсов, разделенных расстоянием \ (\ ell \) в однородном магнитном поле \ (B \). Рельсы неподвижны относительно \ (B \) и подключены к стационарному резистору \ (R \). Резистором может быть что угодно, от лампочки до вольтметра. Рассмотрим площадь, ограниченную подвижным стержнем, рельсами и резистором. \ (B \) перпендикулярно этой области, и площадь увеличивается по мере движения стержня. Таким образом, увеличивается магнитный поток между рельсами, стержнем и резистором.Когда поток изменяется, возникает ЭДС согласно закону индукции Фарадея.


(a) Движущийся v \ (\ text {emf} = \ mathrm {B \ ell v} \) индуцируется между рельсами, когда этот стержень перемещается вправо в однородном магнитном поле. Магнитное поле \ (B \) находится внутри страницы, перпендикулярно движущемуся стержню и рельсам и, следовательно, к области, окружающей их. (б) Закон Ленца определяет направления индуцированного поля и тока, а также полярность наведенной ЭДС. Поскольку поток увеличивается, индуцированное поле направлено в противоположном направлении или за пределы страницы.RHR-2 дает указанное направление тока, и полярность стержня будет управлять таким током. RHR-1 также указывает на такую же полярность стержня. (Обратите внимание, что символ E, используемый в эквивалентной схеме в нижней части части (b), представляет собой ЭДС.)
Чтобы найти величину ЭДС, индуцированную вдоль движущегося стержня, мы используем закон индукции Фарадея без знака:
\ (\ text {emf} = N \ cfrac {\ Delta \ Phi} {\ Delta t} \ text {.} \)
Здесь и ниже «эдс» означает величину эдс.В этом уравнении \ (N = 1 \) и поток \ (\ Phi = \ text {BA} \ phantom {\ rule {0.25em} {0ex}} \ text {cos} \ phantom {\ rule {0.25em } {0ex}} \ theta \). У нас есть \ (\ theta = 0º \) и \ (\ text {cos} \ phantom {\ rule {0.25em} {0ex}} \ theta = 1 \), поскольку \ (B \) перпендикулярно \ (A \). Теперь \ (\ Delta \ Phi = \ Delta (\ text {BA}) = B \ Delta A \), поскольку \ (B \) равномерно. Обратите внимание, что область, выметаемая стержнем, равна \ (\ Delta A = \ ell \ Delta x \). Ввод этих величин в выражение для ЭДС дает
\ (\ text {emf} = \ cfrac {B \ Delta A} {\ Delta t} = B \ cfrac {\ ell \ Delta x} {\ Delta t} \ text {.} \)
Наконец, обратите внимание, что \ (\ Delta x / \ Delta t = v \), скорость стержня. Ввод этого в последнее выражение показывает, что
\ (\ text {emf} = \ mathrm {B \ ell v} \ phantom {\ rule {3.00em} {0ex}} \ text {(} B, \ phantom {\ rule {0.25em} {0ex}} \ mathrm {\ ell и} \ phantom {\ rule {0.25em} {0ex}} v \ phantom {\ rule {0.25em} {0ex}} \ text {перпендикулярно)} \)
— двигательная ЭДС. Это то же самое выражение, которое было дано ранее для эффекта Холла.
Установление связей: объединение сил
Между электрической и магнитной силой существует множество связей.Тот факт, что движущееся электрическое поле создает магнитное поле, и, наоборот, движущееся магнитное поле создает электрическое поле, является частью того, почему электрические и магнитные силы теперь считаются различными проявлениями одной и той же силы. Это классическое объединение электрических и магнитных сил в так называемую электромагнитную силу является источником вдохновения для современных усилий по объединению других основных сил.
Чтобы найти направление индуцированного поля, направление тока и полярность наведенной ЭДС, мы применяем закон Ленца, как это объясняется в Законе индукции Фарадея: Закон Ленца.(См. Этот рисунок (b).) Поток увеличивается, так как увеличивается ограниченная площадь. Таким образом, индуцированное поле должно противостоять существующему и быть вне страницы. Таким образом, RHR-2 требует, чтобы I вращались против часовой стрелки, что, в свою очередь, означает, что верхняя часть стержня положительна, как показано.
ЭДС движения также возникает, если магнитное поле движется и стержень (или другой объект) неподвижен относительно Земли (или некоторого наблюдателя). Мы видели пример этого в ситуации, когда движущийся магнит индуцирует ЭДС в неподвижной катушке.Важно относительное движение. В этих наблюдениях обнаруживается связь между магнитным и электрическим полями. Движущееся магнитное поле создает электрическое поле за счет наведенной ЭДС. Мы уже видели, что движущееся электрическое поле создает магнитное поле: движущийся заряд подразумевает движущееся электрическое поле, а движущийся заряд создает магнитное поле.
ЭДС движения в слабом магнитном поле Земли обычно не очень велики, иначе мы могли бы заметить напряжение вдоль металлических стержней, таких как отвертка, во время обычных движений.{-5} \ phantom {\ rule {0.25em} {0ex}} \ text {T}) (1 \ text {.} 0 м) (3 \ text {.} 0 м / с) = \ text {150 мкВ} \). Это небольшое значение согласуется с опытом. Однако есть впечатляющее исключение.
В 1992 и 1996 годах с космическим челноком были предприняты попытки создать большие двигательные ЭДС. Привязанный спутник должен был быть выпущен на проводе длиной 20 км, как показано на этом рисунке, для создания ЭДС 5 кВ за счет движения с орбитальной скоростью через поле Земли. Эту ЭДС можно было бы использовать для преобразования некоторой кинетической и потенциальной энергии шаттла в электрическую, если бы можно было создать полную цепь.Чтобы замкнуть цепь, неподвижная ионосфера должна была обеспечить обратный путь для прохождения тока. (Ионосфера — это разреженная и частично ионизированная атмосфера на орбитальных высотах. Она проводит из-за ионизации.
Ионосфера выполняет ту же функцию, что и неподвижные рельсы и соединительный резистор на этом рисунке, без которых не было бы полной цепи. ) Затяните ток в кабеле из-за магнитной силы B \ (F = \ mathrm {I \ ell B} \ phantom {\ rule {0.25em} {0ex}} \ text {sin} \ phantom {\ rule { 0.25em} {0ex}} \ theta \) выполняет работу, уменьшающую кинетическую и потенциальную энергию шаттла и позволяющую преобразовывать ее в электрическую. Оба теста были неудачными. В первом случае кабель зависал, и его можно было протянуть только на пару сотен метров; во втором трос оборвался при почти полном растяжении. этот пример показывает выполнимость в принципе.
Пример: Расчет большой ЭДС движения объекта на орбите


ЭДС движения как преобразование электроэнергии для космического челнока является мотивацией для эксперимента с привязанным спутником.{3} \ phantom {\ rule {0.25em} {0ex}} \ text {V.} \ End {array} \)
Обсуждение
Полученное значение больше измеренного напряжения 5 кВ для шаттла эксперимент, поскольку реальное орбитальное движение троса не перпендикулярно полю Земли. Значение 7,80 кВ — это максимальная ЭДС, полученная при \ (\ theta = \ text {90º} \) и \ (\ text {sin} \ phantom {\ rule {0.25em} {0ex}} \ theta = 1 \).
.
индукция | Infoplease
индукция, электричество и магнетизм, общее название для трех различных явлений. Электромагнитная индукция — это производство электродвижущей силы (ЭДС) в проводнике в результате изменения магнитного поля вокруг проводника и является наиболее важным из трех явлений. Он был открыт в 1831 году Майклом Фарадеем и независимо Джозефом Генри. Изменение поля вокруг проводника может быть произведено за счет относительного движения между проводником и источником магнитного поля, как в электрическом генераторе, или путем изменения силы всего поля, так что поле вокруг проводника также изменяется. .Поскольку магнитное поле создается вокруг проводника с током, такое поле можно изменить, изменив ток. Таким образом, если проводник, в котором должна быть индуцирована ЭДС, является частью электрической цепи, индукция может быть вызвана изменением тока в этой цепи; это называется самоиндукцией. Индуцированная ЭДС всегда такова, что она противодействует вызывающему ее изменению, согласно закону Ленца. Изменение тока в данной цепи может также вызвать ЭДС в другой, соседней цепи, не связанной с исходной схемой; Этот тип электромагнитной индукции, называемый взаимной индукцией, лежит в основе трансформатора.Электростатическая индукция — это создание несбалансированного электрического заряда на незаряженном металлическом теле в результате того, что заряженное тело подносят к нему, не касаясь его. Если заряженное тело заряжено положительно, электроны незаряженного тела будут притягиваться к нему; если противоположный конец тела затем заземлен, электроны будут течь на него, чтобы заменить те, которые притягиваются к другому концу, тело, таким образом, приобретает отрицательный заряд после разрыва заземления. Аналогичную процедуру можно использовать для создания положительного заряда на незаряженном теле, когда к нему подносят отрицательно заряженное тело.Смотрите электричество. Магнитная индукция — это создание магнитного поля в куске немагнитного железа или другого ферромагнитного вещества при приближении к нему магнита. Магнит заставляет отдельные частицы железа, которые действуют как крошечные магниты, выстраиваться в линию, так что образец в целом становится намагниченным. Большая часть этого наведенного магнетизма теряется при удалении вызывающего его магнита. См. Магнетизм.
Колумбийская электронная энциклопедия, 6-е изд. Авторские права © 2012, Columbia University Press.Все права защищены.
См. Другие статьи в энциклопедии по адресу: Электротехника
.
Электромагнитная индукция — Energy Education
 Рис. 1. Одно из первых устройств Майкла Фарадея для демонстрации индукции. [1]
Рис. 1. Одно из первых устройств Майкла Фарадея для демонстрации индукции. [1]
Электромагнитная индукция — это производство электродвижущей силы (ЭДС), создаваемой в результате относительного движения между магнитным полем и проводником. Он был открыт в 1831 году Майклом Фарадеем, [2] и закладывает основу для выработки электроэнергии на электростанциях, электродвигателях и схемах переменного тока, которые питают электросети, трансформаторы и многие другие явления.
Уравнение, которое математически описывает электромагнитную индукцию , закон Фарадея , который гласит, что любое изменение магнитной среды витого провода вызывает индуцирование напряжения (ЭДС). [3] Фарадей нашел много способов, чтобы это произошло, например, изменение напряженности магнитного поля, перемещение магнита через катушку с проволокой и перемещение катушки через магнитное поле, и это лишь некоторые из них. Напряжение (ЭДС), генерируемое в катушке с проволокой, можно описать следующим уравнением: [3]
[математика] EMF = -N \ frac {\ Delta (BA)} {\ Delta t} [/ math]
где
- [math] N [/ math] — количество витков в проводе.
- [math] \ Delta (BA) [/ math] — изменение магнитного потока.
- [math] \ Delta t [/ math] — это изменение во времени.
. Все способы, которые Фарадей нашел для изменения этого потока, как указано выше, могут быть представлены в этом уравнении.Причина, по которой это уравнение отрицательно, заключается в законе Ленца, который требует, чтобы любое изменение магнитного потока воспроизводилось проводом с одинаковой силой, но в противоположном направлении.
Закон Фарадея важен для многих электромагнитных приложений в мире, включая автомобили. Система зажигания в двигателе внутреннего сгорания автомобиля потребляет от аккумулятора всего 12 вольт и увеличивает его до 40000 вольт! Посетите Hyperphysics, чтобы узнать, как это сделать.
PhET Моделирование индукции
PhET любезно позволил нам использовать их модели, а приведенное ниже демонстрирует закон электромагнитной индукции Фарадея.Видно, что напряжение изменяется по мере изменения магнитного потока через него.
Для дальнейшего чтения
Для получения дополнительной информации см. Соответствующие страницы ниже:
Ссылки
.
23.2 Закон индукции Фарадея: Закон Ленца — Физика колледжа
23.2 Закон индукции Фарадея: Закон Ленца — Физика колледжа | OpenStaxSkip к содержанию
- Предисловие
- 1 Введение: Природа науки и физики
- Введение в науку и область физики, физических величин и единиц измерения
- 1.1 Физика: введение
- 1.2 Физические величины и единицы измерения
- 1.3 Точность, прецизионность и значащие цифры
- 1.4 Приближение
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение в одномерную кинематику
- 2.1 Смещение
- 2.2 Векторы, скаляры, системы координат
и скорости. и скорость
- 2.4 Ускорение
- 2.5 Уравнения движения для постоянного ускорения в одном измерении
- 2.6 Основы решения проблем для одномерной кинематики
- 2.7 падающих объектов
- 2.8 Графический анализ одномерного движения
- Глоссарий
- Сводка раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение в двумерную кинематику
- в двух измерениях: введение
- 3.2 Сложение и вычитание векторов: графические методы
- 3.3 Сложение и вычитание векторов: аналитические методы
- 3.4 Движение снаряда
- 3.5 Добавление скоростей
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение в динамику
- : законы Ньютона 4 4.1 Развитие концепции силы
- 4.2 Первый закон движения Ньютона: инерция
- 4.3 Второй закон движения Ньютона: концепция системы
- 4.4 Третий закон движения Ньютона: симметрия сил
- 4.5 Нормальные, растягивающие и другие примеры сил
- 4.6 Стратегии решения проблем
- 4.7 Дальнейшие применения законов движения Ньютона
- 4.8 Расширенная тема: Четыре основных силы — Введение
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение: Дальнейшие применения законов Ньютона
- 5.1 Трение
- 5.2 Силы сопротивления
- 5.3 Упругость: напряжение и деформация
- Глоссарий
- Резюме раздела
- Концептуальные вопросы
- Задачи и упражнения
- 6.1 Угол вращения и угловая скорость
- 6.2 Центростремительное ускорение
- 6.3 Центростремительная сила
- 6.4 Фиктивные силы и неинерциальные системы координат: сила Кориолиса
- 6.5 Универсальный закон тяготения Ньютона
- 6.6 Спутники и законы Кеплера: аргумент в пользу простоты
- Глоссарий
- Резюме раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение Работа, энергия и энергетические ресурсы
- Введение в линейный импульс и столкновения
- 8.1 Линейный импульс и сила
- 8.2 Impulse
- 8.3 Сохранение импульса
- 8.4 Упругие столкновения в одном измерении
- 8.5 Неупругие столкновения в одном измерении
- 8.6 Столкновения точечных масс в двух измерениях
- 8.7 Введение в ракетное движение
- Глоссарий
- 000 Краткое содержание раздела Концептуальные вопросы
- Задачи и упражнения
- Введение в статику и крутящий момент
- 9.1 Первое условие равновесия
- 9.2 Второе условие равновесия
- 9.3 Стабильность
- 9.4 Приложения статики, включая стратегии решения проблем
- 9.5 Простые механизмы
- 9.6 Силы и моменты в мышцах и суставах
- Глоссарий
- Резюме раздела
- Концептуальные вопросы Задачи и упражнения
- Введение в вращательное движение и угловой момент
- 10.1 Угловое ускорение
- 10.2 Кинематика вращательного движения
- 10.3 Динамика вращательного движения: вращательная инерция
- 10.4 Кинетическая энергия вращения: новый взгляд на работу и энергию
- 10,5 Угловой момент и его сохранение
- 10,6 Столкновения 9000 протяженных тел 4
- 10.7 Гироскопические эффекты: векторные аспекты углового момента
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение в статику жидкостей
- 11.1 Что такое жидкость?
- 11.2 Плотность
- 11.3 Давление
- 11.4 Изменение давления по глубине в жидкости
- 11,5 Принцип Паскаля
- 11,6 Измерение манометрического давления, абсолютного давления и давления
- 11,7 Принцип Архимеда
- 11,8 : Поверхностное натяжение и капиллярное действие
- 11.9 Давления в теле
- Глоссарий
- Резюме раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение в динамику жидкости и ее использование Биологические и медицинские приложения
- 12.1 Расход и его связь со скоростью
- 12.2 Уравнение Бернулли
- 12.3 Наиболее общие приложения уравнения Бернулли
- 12.4 Вязкость и ламинарный поток; Закон Пуазейля
- 12.5 Начало турбулентности
- 12.6 Движение объекта в вязкой жидкости
- 12.7 Явления молекулярного переноса: диффузия, осмос и связанные процессы
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Концептуальные вопросы
- Введение в температуру, кинетическую теорию и законы газа
- 13.1 Температура
- 13.2 Термическое расширение твердых тел и жидкостей
- 13.3 Закон идеального газа
- 13.4 Кинетическая теория: атомное и молекулярное объяснение давления и температуры
- 13,5 Фазовые изменения
- 13,6 Влажность, испарение и кипение
- Введение в методы теплопередачи
- 14.1 Тепло
- 14.2 Изменение температуры и теплоемкость
- 14.3 Фазовое изменение и скрытая теплота
- 14.4 Методы теплопередачи
- 14,5 Проводимость
- 14,6 Конвекция
- 14,7 Излучение
- Глоссарий
- Краткое содержание раздела
- Вопросы по концепции
И упражнения
- Введение в термодинамику
- 15.1 Первый закон термодинамики
- 15.2 Первый закон термодинамики и некоторые простые процессы
- 15.3 Введение во второй закон термодинамики: тепловые двигатели и их эффективность
- 15.4 Идеальный тепловой двигатель Карно: пересмотр второго закона термодинамики
- 15.5 Приложения термодинамики: тепловые насосы и холодильники
- 15,6 Энтропия и второй закон термодинамики: Беспорядок и недоступность энергии
- 15.7 Статистическая интерпретация энтропии и второй закон термодинамики: основное объяснение
- Глоссарий
- Резюме раздела
- Концептуальные вопросы
- Задачи и упражнения
- 16 Колебания и движения Введение в колебательное движение и волны
- 16.1 Закон Гука: новый взгляд на напряжение и деформацию
- 16.2 Период и частота колебаний
- 16.3 Простое гармоническое движение: особое периодическое движение
- 16.4 Простой маятник
- 16.5 Энергия и простой гармонический осциллятор
- 16.6 Простое круговое движение и простое равномерное движение Гармоническое движение
- 16,7 Затухающее гармоническое движение
- 16,8 Принудительные колебания и резонанс
- 16,9 Волны
- 16,10 Суперпозиция и интерференция
- 16.11 Энергия в волнах: интенсивность
- Глоссарий
- Резюме раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение в физику слуха
- 17.1 Звук
- 17.2 Скорость звука
- 17.3 Интенсивность звука и уровень звука
- 17.4 Эффект Доплера и звуковые удары
- 17.5 Звуковые помехи и резонанс: стоячие волны в столбе воздуха
- 17.6 Слух
- 17.7 Ультразвук
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Задачи и упражнения
и частота, скорость звука, частота
- Введение в электрический заряд и электрическое поле
- 18.1 Электробезопасность. заряда
- 18.2 Проводники и изоляторы
- 18.3 Закон Кулона
- 18.4 Электрическое поле: новая концепция поля
- 18.5 линий электрического поля: множественные заряды
- 18.6 Электрические силы в биологии
- 18.7 Проводники и электрические поля в статическом равновесии
- 18.8 Применение электростатики
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Введение в электрический потенциал и электрическую энергию
- 19.1 Электрическая потенциальная энергия: разница потенциалов
- 19.2 Электрический потенциал в однородном электрическом поле
- 19.3 Электрический потенциал из-за точечного заряда
- 19.4 Эквипотенциальные линии
- 19,5 Конденсаторы и диэлектрики
- 19,6 Последовательные и параллельные конденсаторы
- 19,7 Энергия, накопленная в конденсаторах
- Резюме
- Концептуальные вопросы
- Задачи и упражнения
Задачи и упражнения 19 Электрический потенциал и электрическое поле
- Введение в электрический ток, сопротивление и закон Ома
- 20.1 Ток
- 20,2 Закон Ома: сопротивление и простые схемы
- 20,3 Сопротивление и удельное сопротивление
- 20,4 Электроэнергия и энергия
- 20,5 Сравнение переменного и постоянного тока
- 20,6 Опасности поражения электрическим током и человеческое тело
- 20,7 Нервная проводимость — 9000 кардиограмм
- Глоссарий
- Краткое содержание раздела
- Концептуальные вопросы
- Проблемы и упражнения
- Введение в схемы и приборы постоянного тока
- 21.1 Последовательные и параллельные резисторы
- 21.2 Электродвижущая сила: напряжение на клеммах
- 21.3 Правила Кирхгофа
- 21.4 Вольтметры и амперметры постоянного тока
- 21,5 Измерения нуля
- 21,6 Цепи постоянного тока, содержащие резисторы и конденсаторы Раздел
0003
000 Глоссарий Вопросы
- Введение в магнетизм
- 22.1 Магниты
- 22.2 Ферромагнетики и электромагниты
- 22.3 Магнитные поля и линии магнитного поля
- 22.4 Напряженность магнитного поля: сила, действующая на движущийся заряд в магнитном поле
- 22,5 Сила, действующая на движущийся заряд в магнитном поле: примеры и приложения
- 22,6 Холла Влияние
- 22.7 Магнитная сила на токопроводящий проводник
- 22.8 Крутящий момент на токовой петле: двигатели и измерители
- 22.9 Магнитные поля, создаваемые токами: закон Ампера
- 22.10 Магнитная сила между двумя параллельными проводниками
- 22.11 Другие применения магнетизма
- Глоссарий
- Сводка раздела
- Концептуальные вопросы
- Задачи и упражнения
- Введение в электромагнитную индукцию , Цепи переменного тока и электрические технологии
- 23.1 Индуцированная ЭДС и магнитный поток
- 23.2 Закон индукции Фарадея: закон Ленца
- 23.3
.

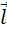 обхода контура связаны правилом правого буравчика
обхода контура связаны правилом правого буравчика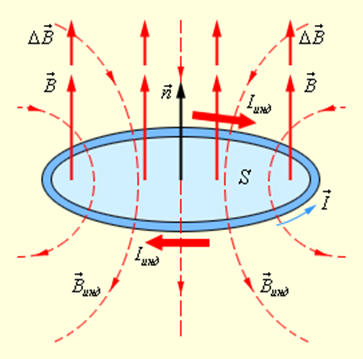
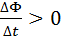 , а
, а 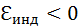 . Индукционный ток Iинд течет навстречу выбранному положительному направлению
. Индукционный ток Iинд течет навстречу выбранному положительному направлению 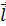 обхода контура
обхода контура