Принцип кирхгофа: Законы Кирхгофа простыми словами ⋆ diodov.net

Законы Кирхгофа простыми словами ⋆ diodov.net

Два закона Кирхгофа вместе с законом Ома составляют тройку законов, с помощью которых можно определить параметры электрической цепи любой сложности. Законы Кирхгофа мы будем проверять на примерах простейших электрических схем, собрать которые не составит никакого труда. Для этого понадобится несколько резисторов, пара источников питания, в качестве которых подойдут гальванические элементы (батарейки) и мультиметр.

Первый закон Кирхгофа

Первый закон Кирхгофа говорит, что сумма токов в любом узле электрической цепи равна нулю. Существует и другая, аналогичная по смыслу формулировка: сумма значений токов, входящих в узел, равна сумме значений токов, выходящих из узла.

Давайте разберем сказанное более подробно. Узлом называют место соединения трех и более проводников.

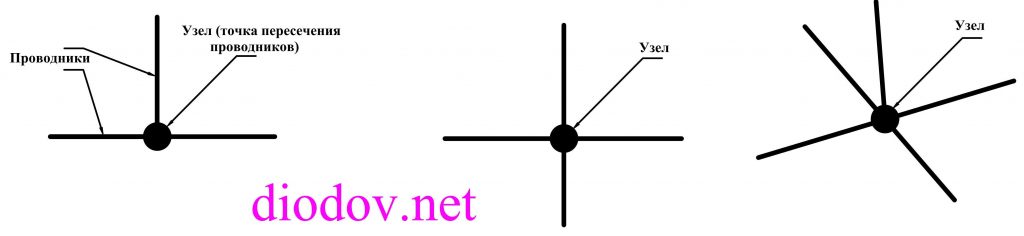
Ток, который втекает в узел, обозначается стрелкой, направленной в сторону узла, а выходящий из узла ток – стрелкой, направленной в сторону от узла.

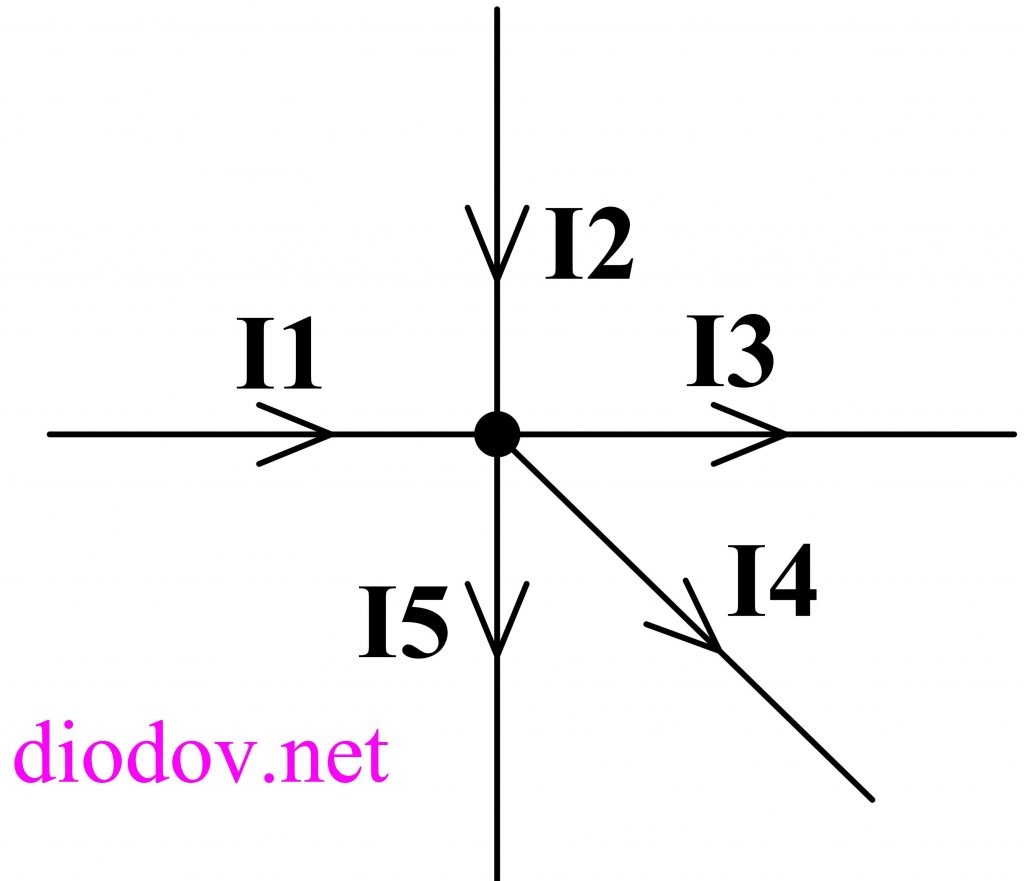
Согласно первому закону Кирхгофа

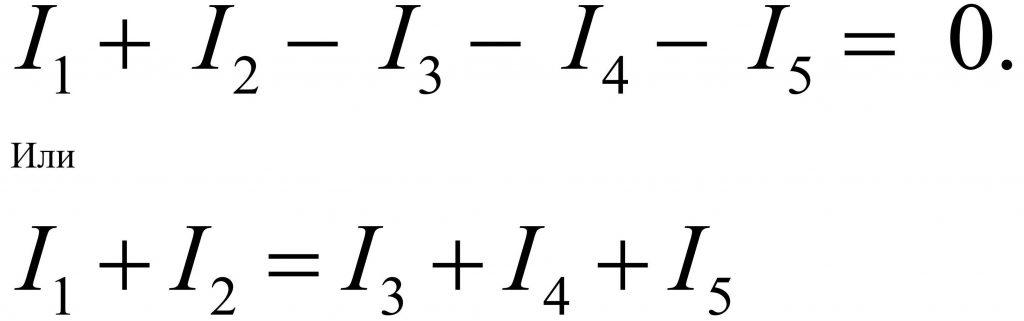
Условно присвоили знак «+» всем входящим токам, а «-» ‑ все выходящим. Хотя это не принципиально.

1 закон Кирхгофа согласуется с законом сохранения энергии, поскольку электрические заряды не могут накапливаться в узлах, поэтому, поступающие к узлу заряды покидают его.

Убедиться в справедливости 1-го закона Кирхгофа нам поможет простая схема, состоящая из источника питания, напряжением 3 В (две последовательно соединенные батарейки по 1,5 В), три резистора разного номинала: 1 кОм, 2 кОм, 3,2 кОм (можно применять резисторы любых других номиналов). Токи будем измерять мультиметром в местах, обозначенных амперметром.

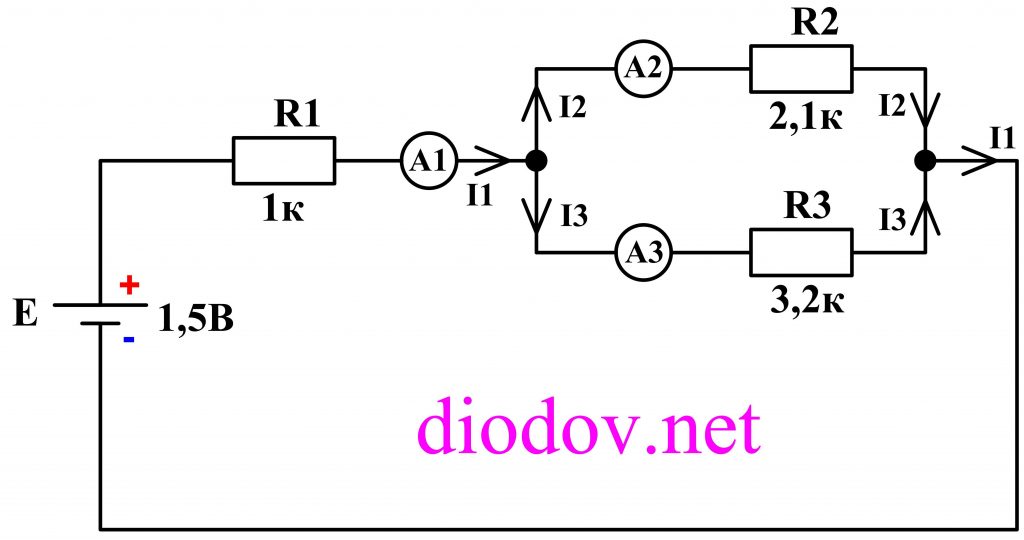
Если сложить показания трех амперметров с учетом знаков, то, согласно первому закону Кирхгофа, мы должны получить ноль:

I₁ — I₂ — I₃ = 0.

Или показания первого амперметра А1 будет равняться сумме показаний второго А2 и третьего А3 амперметров.

Второй закон Кирхгофа

Второй закон Кирхгофа воспринимается начинающими радиолюбителями гораздо сложнее, нежели первый. Однако сейчас вы убедитесь, что он достаточно прост и понятен, если объяснять его нормальными словами, а не заумными терминами.

Упрощенно 2 закон Кирхгофа говорит: сумма ЭДС в замкнутом контуре равна сумме падений напряжений

ΣE = ΣIR

Самый простой случай данного закона разберем на примере батарейки 1,5 В и одного резистора.

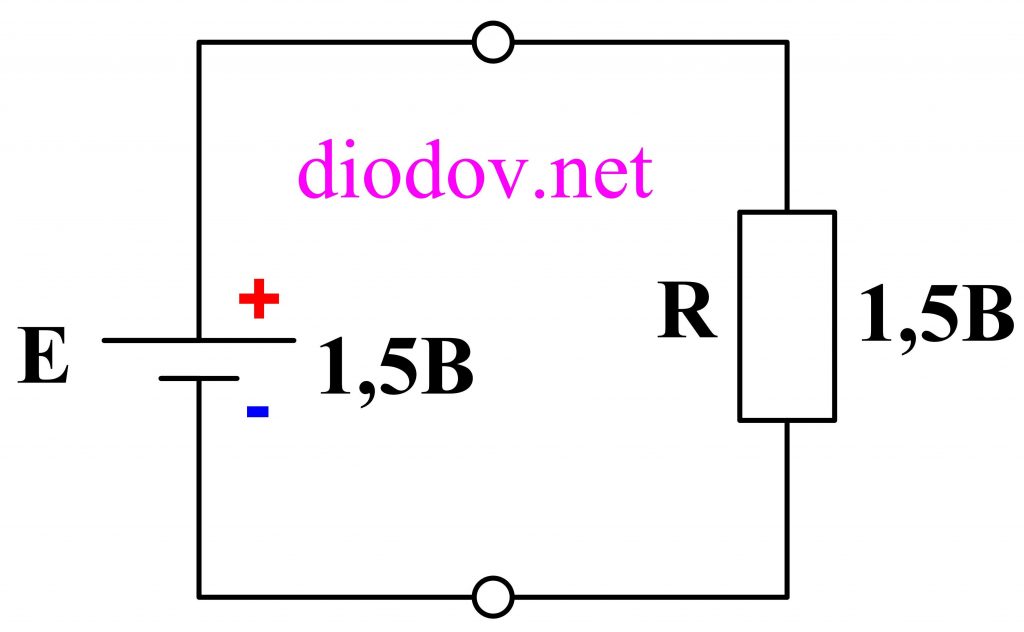
Поскольку резистор всего один и одна батарейка, то ЭДС батарейки 1,5 В будет равна падению напряжения на резисторе.

Если мы возьмем два резистора одинакового номинала и подключим к батарейке, то 1,5 В распределятся поровну на резисторах, то есть по 0,75 В.

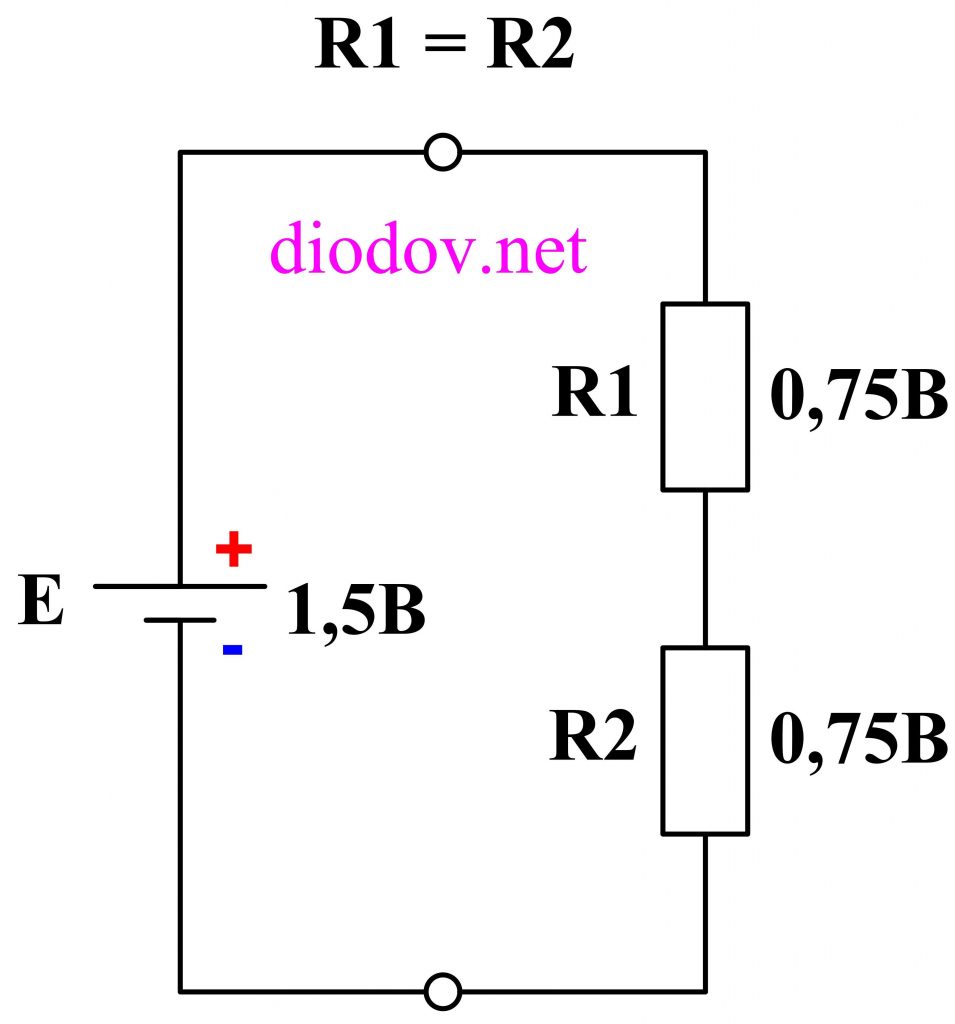
Если возьмем три резистора снова одинакового номинала, например по 1 кОм, то падение напряжения на них будет по 0,5 В.

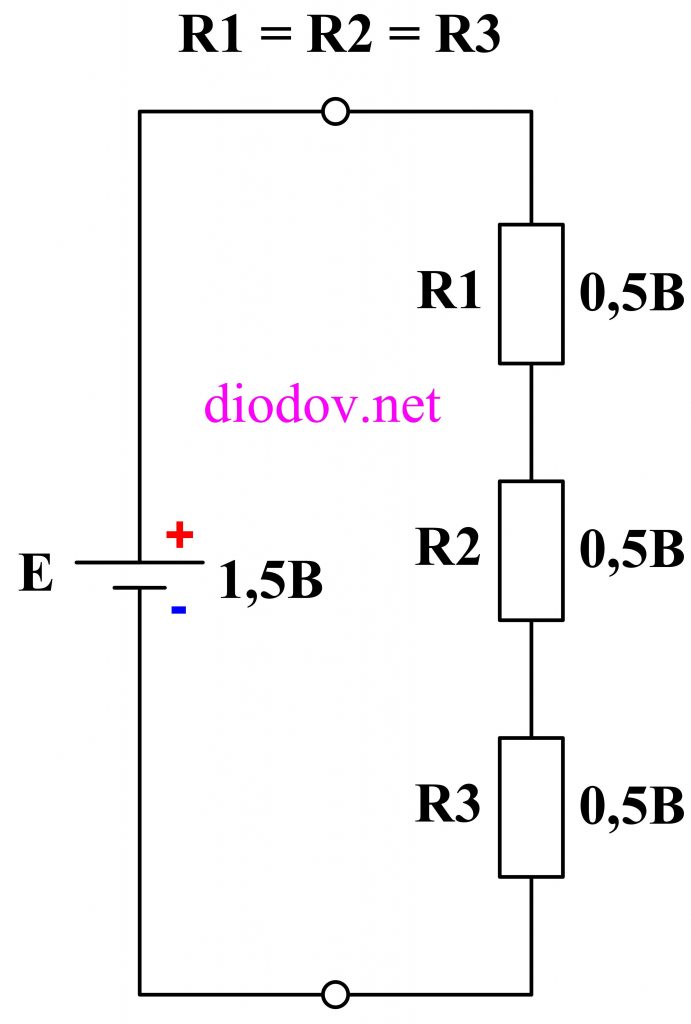
Формулой это будет записано следующим образом:

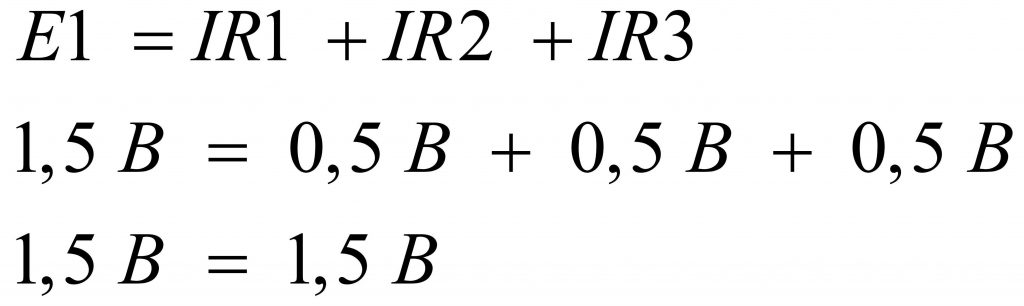
Рассмотрим условно более сложный пример. Добавим в последнюю схему еще один источник питания E2, напряжением 4,5 В.

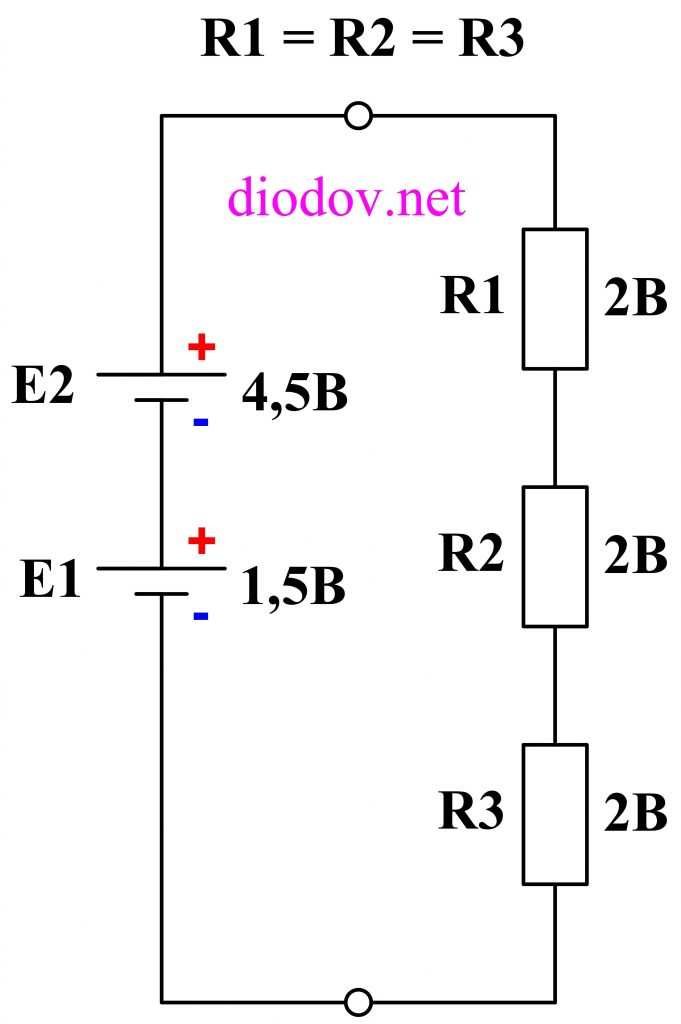
Обратите внимание, что оба источника соединены последовательно и согласно, то есть плюс одной батарейки соединяется с минусом другой батарейки или наоборот. При таком способе соединения гальванических элементов их электродвижущие силы складываются: E1 + E2 = 1,5 + 4,5 = 6 В, а падение напряжения на каждом сопротивлении составляет по 2 В. Формулой это описывается так:

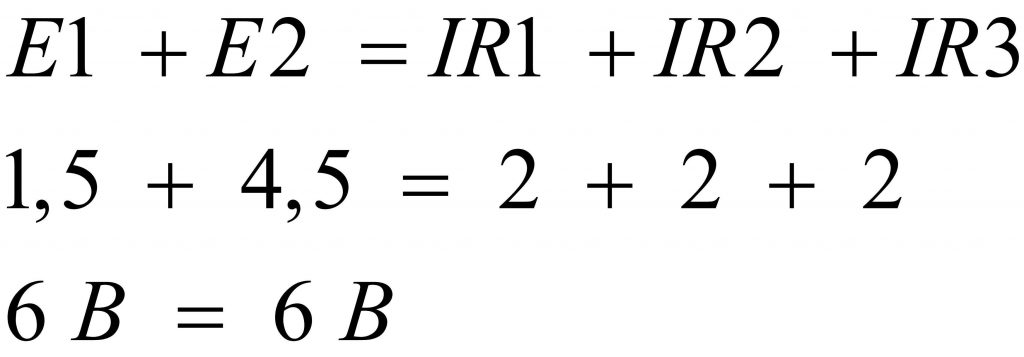
И последний отличительный вариант, который мы рассмотрим в данной статье, предполагает последовательное встречное соединение гальванических элементов. При таком соединении источников питания из большей ЭДС отнимается значение меньшей ЭДС. Следовательно к резисторам R1…R3 будет приложена разница E1 – E2, то есть 4,5 – 1,5 = 3 В, — по одному вольту на каждый резистор.

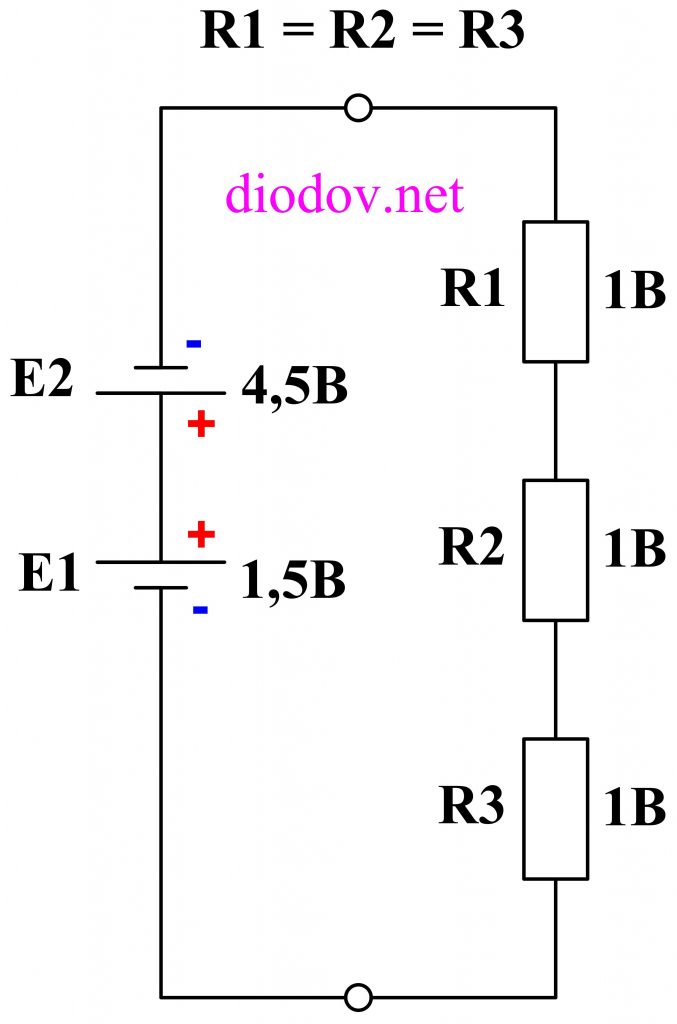
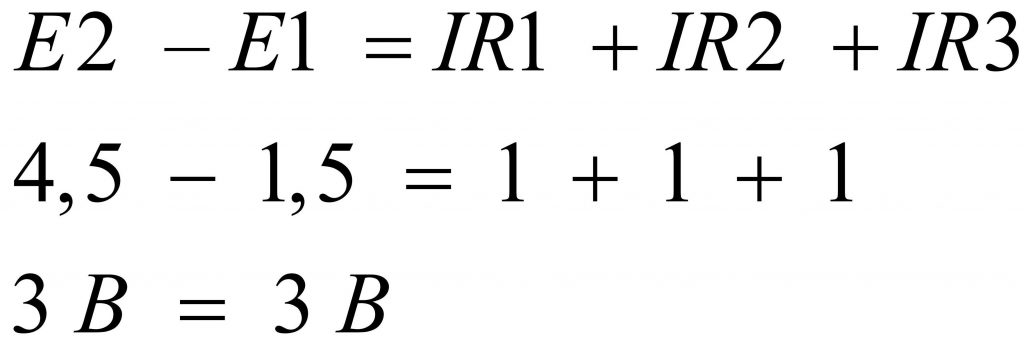
Второй закон Кирхгофа работает не зависимо от количества источников питания и нагрузок, а также независимо от места их расположения в контуре схемы. Полезно будет собрать рассмотренные схемы и выполнить соответствующие измерения с помощью мультиметра.

Законы Кирхгофа действуют как для постоянного, так и для переменного тока.

Еще статьи по данной теме

Правила Кирхгофа — Википедия

Пра́вила Кирхго́фа (часто в литературе ошибочно называются Зако́нами Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи.
Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока^[1]. Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей.
Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений, и соответственно, найти значения токов на всех ветвях цепи и все межузловые напряжения.

Сформулированы Густавом Кирхгофом в 1845 году^[2].

Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (третье уравнение Максвелла при неизменном магнитном поле).
Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.

Формулировка правил

Определения

Для формулировки правил Кирхгофа вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют участок электрической цепи с одним и тем же током, например, на рис. отрезок, обозначенный R₁, I₁ есть ветвь. Узлом называют точку соединения трех и более ветвей (на рис. обозначены жирными точками). Контур — замкнутый путь, проходящий через несколько ветвей и узлов разветвлённой электрической цепи. Термин замкнутый путь означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам.

В терминах данных определений правила Кирхгофа формулируются следующим образом.

Первое правило

Сколько тока втекает в узел, столько из него и вытекает.
i₂ + i₃ = i₁ + i₄

Первое правило Кирхгофа гласит, что алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи, равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным: Алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла.

∑j=1nIj=0.{\displaystyle \sum \limits _{j=1}^{n}I_{j}=0.}

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.

Второе правило

Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:

для постоянных напряжений ∑k=1nEk=∑k=1mUk=∑k=1mRkIk;{\displaystyle \sum _{k=1}^{n}E_{k}=\sum _{k=1}^{m}U_{k}=\sum _{k=1}^{m}R_{k}I_{k};}

для переменных напряжений ∑k=1nek=∑k=1muk=∑k=1mRkik+∑k=1muLk+∑k=1muCk.{\displaystyle \sum _{k=1}^{n}e_{k}=\sum _{k=1}^{m}u_{k}=\sum _{k=1}^{m}R_{k}i_{k}+\sum _{k=1}^{m}u_{L\,k}+\sum _{k=1}^{m}u_{C\,k}.}

Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.

Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).

Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.

Особенности составления уравнений для расчёта токов и напряжений

Если цепь содержит p{\displaystyle p} узлов, то она описывается p−1{\displaystyle p-1} уравнениями токов. Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.

Если цепь содержит m{\displaystyle m} ветвей, из которых содержат источники тока ветви в количестве mi{\displaystyle m_{i}}, то она описывается m−mi−(p−1){\displaystyle m-m_{i}-(p-1)} уравнениями напряжений.

• Правила Кирхгофа, записанные для p−1{\displaystyle p-1} узлов или m−(p−1){\displaystyle m-(p-1)} контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и все напряжения.
• Перед тем, как составить уравнения, нужно произвольно выбрать:
  • положительные направления токов в ветвях и обозначить их на схеме, при этом не обязательно следить, чтобы в узле направления токов были и втекающими, и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;
  • положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке).
• Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в противном случае — отрицательным.
• При записи линейно независимых уравнений по второму правилу Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие).
• В сложных непланарных графах электрических цепей человеку трудно увидеть независимые контуры и узлы, каждый независимый контур (узел) при составлении системы уравнений порождает ещё 1 линейное уравнение в определяющей задачу системе линейных уравнений. Подсчёт количества независимых контуров и их явное указание в конкретном графе развит в теории графов.

Пример

На этом рисунке для каждой ветви обозначен протекающий по ней ток (буквой «I») и напряжение между соединяемыми ею узлами (буквой «U»)

Количество узлов: 3.

p−1=2{\displaystyle p-1=2}

Количество ветвей (в замкнутых контурах): 4. Количество ветвей, содержащих источник тока: 0.

m−mi−(p−1)=2{\displaystyle m-m_{i}-(p-1)=2}

Количество контуров: 2.

Для приведённой на рисунке цепи, в соответствии с первым правилом, выполняются следующие соотношения:

{I1−I2−I6=0I2−I4−I3=0{\displaystyle {\begin{cases}I_{1}-I_{2}-I_{6}=0\\I_{2}-I_{4}-I_{3}=0\end{cases}}}

Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например, здесь токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.

Решение полученной линейной системы алгебраических уравнений позволяет определить все токи узлов и ветвей, такой подход к анализу цепи принято называть методом контурных токов.

В соответствии со вторым правилом, справедливы соотношения:

{U2+U4−U6=0U3+U5−U4=0{\displaystyle {\begin{cases}U_{2}+U_{4}-U_{6}=0\\U_{3}+U_{5}-U_{4}=0\end{cases}}}

Полученные системы уравнений полностью описывают анализируемую цепь, и их решения определяют все токи и все напряжения ветвей. Такой подход к анализу цепи принято называть методом узловых потенциалов.

О значении для электротехники

Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простоте формулировки уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).

Закон излучения Кирхгофа

Закон излучения Кирхгофа гласит — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.

Закон Кирхгофа в химии

Закон Кирхгофа гласит — температурный коэффициент теплового эффекта химической реакции равен изменению теплоёмкости системы в ходе реакции.

Примечания

Литература

• Матвеев А. Н. Электричество и магнетизм : учебное пособие. — М.: Высшая школа, 1983. — 463 с.
• Калашников С. Г. Электричество : учебное пособие. — М.: Физматлит, 2003. — 625 с.
• Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — 11-е издание. — М.: Гардарики, 2007.
• Герасимов В. Г., Кузнецов Э. В., Николаева О. В. Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. — М.: Энергоатомиздат, 1996. — 288 с. — ISBN 5-283-05005-X.

Правила Кирхгофа — Википедия. Что такое Правила Кирхгофа

Пра́вила Кирхго́фа (часто в литературе ошибочно называются Зако́нами Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи.
Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока^[1]. Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей.
Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений, и соответственно, найти значения токов на всех ветвях цепи и все межузловые напряжения.

Сформулированы Густавом Кирхгофом в 1845 году^[2].

Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (третье уравнение Максвелла при неизменном магнитном поле).
Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.

Формулировка правил

Определения

Для формулировки правил Кирхгофа вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют участок электрической цепи с одним и тем же током, например, на рис. отрезок, обозначенный R₁, I₁ есть ветвь. Узлом называют точку соединения трех и более ветвей (на рис. обозначены жирными точками). Контур — замкнутый путь, проходящий через несколько ветвей и узлов разветвлённой электрической цепи. Термин замкнутый путь означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам.

В терминах данных определений правила Кирхгофа формулируются следующим образом.

Первое правило

Сколько тока втекает в узел, столько из него и вытекает.
i₂ + i₃ = i₁ + i₄

Первое правило Кирхгофа гласит, что алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи, равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным: Алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла.

∑j=1nIj=0.{\displaystyle \sum \limits _{j=1}^{n}I_{j}=0.}

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.

Второе правило

Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:

для постоянных напряжений ∑k=1nEk=∑k=1mUk=∑k=1mRkIk;{\displaystyle \sum _{k=1}^{n}E_{k}=\sum _{k=1}^{m}U_{k}=\sum _{k=1}^{m}R_{k}I_{k};}

для переменных напряжений ∑k=1nek=∑k=1muk=∑k=1mRkik+∑k=1muLk+∑k=1muCk.{\displaystyle \sum _{k=1}^{n}e_{k}=\sum _{k=1}^{m}u_{k}=\sum _{k=1}^{m}R_{k}i_{k}+\sum _{k=1}^{m}u_{L\,k}+\sum _{k=1}^{m}u_{C\,k}.}

Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.

Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).

Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.

Особенности составления уравнений для расчёта токов и напряжений

Если цепь содержит p{\displaystyle p} узлов, то она описывается p−1{\displaystyle p-1} уравнениями токов. Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.

Если цепь содержит m{\displaystyle m} ветвей, из которых содержат источники тока ветви в количестве mi{\displaystyle m_{i}}, то она описывается m−mi−(p−1){\displaystyle m-m_{i}-(p-1)} уравнениями напряжений.

• Правила Кирхгофа, записанные для p−1{\displaystyle p-1} узлов или m−(p−1){\displaystyle m-(p-1)} контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и все напряжения.
• Перед тем, как составить уравнения, нужно произвольно выбрать:
  • положительные направления токов в ветвях и обозначить их на схеме, при этом не обязательно следить, чтобы в узле направления токов были и втекающими, и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;
  • положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке).
• Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в противном случае — отрицательным.
• При записи линейно независимых уравнений по второму правилу Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие).
• В сложных непланарных графах электрических цепей человеку трудно увидеть независимые контуры и узлы, каждый независимый контур (узел) при составлении системы уравнений порождает ещё 1 линейное уравнение в определяющей задачу системе линейных уравнений. Подсчёт количества независимых контуров и их явное указание в конкретном графе развит в теории графов.

Пример

На этом рисунке для каждой ветви обозначен протекающий по ней ток (буквой «I») и напряжение между соединяемыми ею узлами (буквой «U»)

Количество узлов: 3.

p−1=2{\displaystyle p-1=2}

Количество ветвей (в замкнутых контурах): 4. Количество ветвей, содержащих источник тока: 0.

m−mi−(p−1)=2{\displaystyle m-m_{i}-(p-1)=2}

Количество контуров: 2.

Для приведённой на рисунке цепи, в соответствии с первым правилом, выполняются следующие соотношения:

{I1−I2−I6=0I2−I4−I3=0{\displaystyle {\begin{cases}I_{1}-I_{2}-I_{6}=0\\I_{2}-I_{4}-I_{3}=0\end{cases}}}

Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например, здесь токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.

Решение полученной линейной системы алгебраических уравнений позволяет определить все токи узлов и ветвей, такой подход к анализу цепи принято называть методом контурных токов.

В соответствии со вторым правилом, справедливы соотношения:

{U2+U4−U6=0U3+U5−U4=0{\displaystyle {\begin{cases}U_{2}+U_{4}-U_{6}=0\\U_{3}+U_{5}-U_{4}=0\end{cases}}}

Полученные системы уравнений полностью описывают анализируемую цепь, и их решения определяют все токи и все напряжения ветвей. Такой подход к анализу цепи принято называть методом узловых потенциалов.

О значении для электротехники

Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простоте формулировки уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).

Закон излучения Кирхгофа

Закон излучения Кирхгофа гласит — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.

Закон Кирхгофа в химии

Закон Кирхгофа гласит — температурный коэффициент теплового эффекта химической реакции равен изменению теплоёмкости системы в ходе реакции.

Примечания

Литература

• Матвеев А. Н. Электричество и магнетизм : учебное пособие. — М.: Высшая школа, 1983. — 463 с.
• Калашников С. Г. Электричество : учебное пособие. — М.: Физматлит, 2003. — 625 с.
• Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — 11-е издание. — М.: Гардарики, 2007.
• Герасимов В. Г., Кузнецов Э. В., Николаева О. В. Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. — М.: Энергоатомиздат, 1996. — 288 с. — ISBN 5-283-05005-X.

Правила Кирхгофа — Википедия

Пра́вила Кирхго́фа (часто в литературе ошибочно называются Зако́нами Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи.
Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока^[1]. Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей.
Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений, и соответственно, найти значения токов на всех ветвях цепи и все межузловые напряжения.

Сформулированы Густавом Кирхгофом в 1845 году^[2].

Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (третье уравнение Максвелла при неизменном магнитном поле).
Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.

Формулировка правил

Определения

Для формулировки правил Кирхгофа вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют участок электрической цепи с одним и тем же током, например, на рис. отрезок, обозначенный R₁, I₁ есть ветвь. Узлом называют точку соединения трех и более ветвей (на рис. обозначены жирными точками). Контур — замкнутый путь, проходящий через несколько ветвей и узлов разветвлённой электрической цепи. Термин замкнутый путь означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам.

В терминах данных определений правила Кирхгофа формулируются следующим образом.

Первое правило

Сколько тока втекает в узел, столько из него и вытекает.
i₂ + i₃ = i₁ + i₄

Первое правило Кирхгофа гласит, что алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи, равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным: Алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла.

∑j=1nIj=0.{\displaystyle \sum \limits _{j=1}^{n}I_{j}=0.}

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.

Второе правило

Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:

для постоянных напряжений ∑k=1nEk=∑k=1mUk=∑k=1mRkIk;{\displaystyle \sum _{k=1}^{n}E_{k}=\sum _{k=1}^{m}U_{k}=\sum _{k=1}^{m}R_{k}I_{k};}

для переменных напряжений ∑k=1nek=∑k=1muk=∑k=1mRkik+∑k=1muLk+∑k=1muCk.{\displaystyle \sum _{k=1}^{n}e_{k}=\sum _{k=1}^{m}u_{k}=\sum _{k=1}^{m}R_{k}i_{k}+\sum _{k=1}^{m}u_{L\,k}+\sum _{k=1}^{m}u_{C\,k}.}

Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.

Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).

Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.

Особенности составления уравнений для расчёта токов и напряжений

Если цепь содержит p{\displaystyle p} узлов, то она описывается p−1{\displaystyle p-1} уравнениями токов. Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.

Если цепь содержит m{\displaystyle m} ветвей, из которых содержат источники тока ветви в количестве mi{\displaystyle m_{i}}, то она описывается m−mi−(p−1){\displaystyle m-m_{i}-(p-1)} уравнениями напряжений.

• Правила Кирхгофа, записанные для p−1{\displaystyle p-1} узлов или m−(p−1){\displaystyle m-(p-1)} контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и все напряжения.
• Перед тем, как составить уравнения, нужно произвольно выбрать:
  • положительные направления токов в ветвях и обозначить их на схеме, при этом не обязательно следить, чтобы в узле направления токов были и втекающими, и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;
  • положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке).
• Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в противном случае — отрицательным.
• При записи линейно независимых уравнений по второму правилу Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие).
• В сложных непланарных графах электрических цепей человеку трудно увидеть независимые контуры и узлы, каждый независимый контур (узел) при составлении системы уравнений порождает ещё 1 линейное уравнение в определяющей задачу системе линейных уравнений. Подсчёт количества независимых контуров и их явное указание в конкретном графе развит в теории графов.

Пример

На этом рисунке для каждой ветви обозначен протекающий по ней ток (буквой «I») и напряжение между соединяемыми ею узлами (буквой «U»)

Количество узлов: 3.

p−1=2{\displaystyle p-1=2}

Количество ветвей (в замкнутых контурах): 4. Количество ветвей, содержащих источник тока: 0.

m−mi−(p−1)=2{\displaystyle m-m_{i}-(p-1)=2}

Количество контуров: 2.

Для приведённой на рисунке цепи, в соответствии с первым правилом, выполняются следующие соотношения:

{I1−I2−I6=0I2−I4−I3=0{\displaystyle {\begin{cases}I_{1}-I_{2}-I_{6}=0\\I_{2}-I_{4}-I_{3}=0\end{cases}}}

Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например, здесь токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.

Решение полученной линейной системы алгебраических уравнений позволяет определить все токи узлов и ветвей, такой подход к анализу цепи принято называть методом контурных токов.

В соответствии со вторым правилом, справедливы соотношения:

{U2+U4−U6=0U3+U5−U4=0{\displaystyle {\begin{cases}U_{2}+U_{4}-U_{6}=0\\U_{3}+U_{5}-U_{4}=0\end{cases}}}

Полученные системы уравнений полностью описывают анализируемую цепь, и их решения определяют все токи и все напряжения ветвей. Такой подход к анализу цепи принято называть методом узловых потенциалов.

О значении для электротехники

Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простоте формулировки уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).

Закон излучения Кирхгофа

Закон излучения Кирхгофа гласит — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.

Закон Кирхгофа в химии

Закон Кирхгофа гласит — температурный коэффициент теплового эффекта химической реакции равен изменению теплоёмкости системы в ходе реакции.

Примечания

Литература

• Матвеев А. Н. Электричество и магнетизм : учебное пособие. — М.: Высшая школа, 1983. — 463 с.
• Калашников С. Г. Электричество : учебное пособие. — М.: Физматлит, 2003. — 625 с.
• Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — 11-е издание. — М.: Гардарики, 2007.
• Герасимов В. Г., Кузнецов Э. В., Николаева О. В. Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. — М.: Энергоатомиздат, 1996. — 288 с. — ISBN 5-283-05005-X.

Теория по физике для ЕГЭ, пособия по подготовке и справочные материалы в Москве

Первое правило Кирхгофа

Алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи, равна нулю.

Также можно легко запомнить первый закон Кирхгофа следующим образом: сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.

Здесь ток \(I_1\) — ток, втекающий в узел, а токи \(I_2\) и \(I_3\) — токи, вытекающие из узла. Тогда можно записать:

\(I_1 = I_2 + I_3,\ (1)\)

Перенесем токи \(I_2\) и \(I_3\) в левую часть выражения (1), тем самым получим:

\(I_1 — I_2 — I_3 = 0,\ (2)\)

Знаки «минус» в выражении (2) и означают, что токи вытекают из узла.

Знаки для втекающих и вытекающих токов можно брать произвольно, однако в основном всегда втекающие токи берут со знаком «+», а вытекающие со знаком «—».

Второе правило Кирхгофа

Алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур.

Термин «алгебраическая сумма» означает, что как величина ЭДС, так и величина падения напряжения на элементах может быть как со знаком «+», так и со знаком «—». При этом определить знак можно по следующему алгоритму:

1. Выбираем направление обхода контура (два варианта: либо по часовой стрелке, либо против).

2. Произвольно выбираем направление токов через элементы цепи.

3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:

— ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура, записываются со знаком «+», в противном случае ЭДС записываются со знаком «—».

— напряжения, падающие на элементах цепи, записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «—».

Например, рассмотрим цепь на рисунке и запишем выражение согласно второму закону Кирхгофа, обходя контур по часовой стрелке и выбрав направление токов через резисторы, как показано на рисунке.

Получим:

\(E_1- E_2 = -UR_1 — UR_2\) или \(E_1 = E_2 — UR_1 — UR_2\)

Принцип Кирхгофа — это… Что такое Принцип Кирхгофа?



Принцип Кирхгофа

Принцип Кирхгофа

Принцип Кирхгофа — принцип построения криптографических алгоритмов, согласно которому в секрете держится только определенный набор параметров алгоритма (ключ), а остальные детали могут быть открыты без снижения стойкости алгоритма ниже допустимой величины.

См. также:  Криптографические алгоритмы  

Финансовый словарь Финам.

.

• Принцип единства кассы
• Принцип локомотива

Смотреть что такое «Принцип Кирхгофа» в других словарях:

• Принцип Кирхгофа — Словосочетание принцип Кирхгофа может подразумевать: Правила Кирхгофа для электрической цепи Закон излучения Кирхгофа Принцип Керкгоффса для криптографических систем …   Википедия

• Принцип Гюйгенса — Френеля — Рефракция волн по Гюйгенсу …   Википедия

• Принцип транслинейности — (англ. translinear principle, от англ. transconductance  проводимость, крутизна передаточной характеристики) в анализе и проектировании аналоговых интегральных схем  правило (уравнение), определяющее соотношения токов,… …   Википедия

• КИРХГОФА ФОРМУЛА — Кирхгофа интеграл, формула которая выражает значение и( х, t )решения неоднородного волнового уравнения в любой точке х=( х 1, х 2, x3 )ОWв момент времени tчерез запаздывающий объемный потенциал с плотностью f и через значения функции и( у, t )и… …   Математическая энциклопедия

• Принцип Гюйгенса — Рефракция волн по Гюйгенсу …   Википедия

• Принцип Гюйгенса-Френеля — Рефракция волн по Гюйгенсу Дифракция волн по Гюйгенсу Принцип Гюйгенса  Френеля  основной постулат волновой теории, описывающий и объясняющий механизм распространения волн, в частности световых. Принцип Гюйгенса  Френеля является развитием… …   Википедия

• Принцип Гюйгенса–Френеля — Рефракция волн по Гюйгенсу Дифракция волн по Гюйгенсу Принцип Гюйгенса  Френеля  основной постулат волновой теории, описывающий и объясняющий механизм распространения волн, в частности световых. Принцип Гюйгенса  Френеля является развитием… …   Википедия

• Принцип Гюйгенса—Френеля — Рефракция волн по Гюйгенсу Дифракция волн по Гюйгенсу Принцип Гюйгенса  Френеля  основной постулат волновой теории, описывающий и объясняющий механизм распространения волн, в частности световых. Принцип Гюйгенса  Френеля является развитием… …   Википедия

• Принцип Керкгоффса — Не следует путать с Законы Кирхгофа. Принцип Керкгоффса  правило разработки криптографических систем, согласно которому в засекреченном виде держится только определённый набор параметров алгоритма, называемый ключом, а сам алгоритм… …   Википедия

• Правило Кирхгофа — Правила Кирхгофа в физике  правила, устанавливающие соотношения для токов и напряжений в разветвленных электрических цепях постоянного или квазистационарного тока. См. также Закон излучения Кирхгофа в физике, описывающий отношение… …   Википедия

Электричество и магнетизм

Приведем пример расчета токов в разветвленной цепи (рис. 4.25).

Рис. 4.25. Пример разветвленной цепи 

Направления действия ЭДС показаны синими стрелками. В этой цепи у нас имеется два узла — точки b и d (m = 2), и три ветви — участок b–а–d с током I₁, участок b–d с током I₂ и участок b–c–d с током I₃ (n = 3). Значит, мы можем написать одно (m – 1 = 2 – 1 = 1) уравнение на основе первого правила Кирхгофа и два (n – m + 1 = 3 – 2 + 1 = 2) уравнения на основе второго правила Кирхгофа. Как же это делается на практике? 

Шаг первый. Выберем направления токов, текущих в каждой из ветвей цепи. Как эти направления выбрать — совершенно неважно. Если мы угадали, в окончательном результате значение этого тока получится положительным, если нет и направление должно быть обратным — значение этого тока получится отрицательным. В нашем примере мы выбрали направления токов как показано на рисунке. Важно подчеркнуть, что направления действия ЭДС не произвольны, они определяются способом подключения полюсов источников тока (см. рис. 4.25). 

Шаг второй. Записываем первое правило Кирхгофа для всех узлов кроме одного (в последнем узле, выбор которого произволен, это правило будет выполняться автоматически). В нашем случае мы можем записать уравнение для узла b, куда входит ток I₂ и выходят токи I₁ и I₃

Шаг третий. Нам осталось написать уравнения (в нашем случае — два) для второго правила Кирхгофа. Для этого надо выбрать два независимых замкнутых контура. В рассматриваемом примере имеются три такие возможности: путь по левому контуру b–a–d–b, путь по правому контуру b–c–d–b и путь вокруг всей цепи b–a–d–c–b. Достаточно взять любые два из них, тогда для третьего контура второе правило Кирхгофа будет выполнено автоматически. Направление обхода контура роли не играет, но при обходе ток будет браться со знаком плюс, если он течет в направлении обхода, и со знаком минус, если ток течет в противоположном направлении. Это же относится к знакам ЭДС.

Возьмем для начала контур b–a–d–b. Мы выходим из точки b и движемся против часовой стрелки. На нашем пути встретятся два тока, I₁ и I₂, направления которых совпадают с выбранным направлением обхода. ЭДС также действует в этом же направлении. Поэтому второе правило Кирхгофа для этого участка цепи записывается как

В качестве второго замкнутого пути для разнообразия выберем путь b–a–d–c–b вокруг всей цепи. На этом пути мы встречаем два тока I₁ и I₃, из которых первый войдет со знаком плюс, а второй — со знаком минус. Мы встретимся также с двумя ЭДС, из которых  войдет в уравнения со знаком плюс, а  — со знаком минус. Уравнение для этого замкнутого пути имеет вид

Шаг четвертый. Мы нашли три уравнения для трех неизвестных токов в цепи. Решение произвольной системы линейных уравнений описывается в курсе математики. Для наших целей (цепь достаточна проста) можно просто выразить I₃ через I₁ из уравнения (4.47)

I₂ через I₁ с помощью уравнения (4.46)

и подставить (4.48), (4.49) в уравнение первого правила Кирхгофа (4.45). Это уравнение содержит лишь неизвестное I₁, которое находится без труда

Подставляя это выражение в (4.48), (4.49), находим соответственно токи I₂, I₃

Закон Кирхгофа для сложных схем | EAGLE

Закон

Ома — ваш золотой билет для расчета напряжения, тока или сопротивления в простой последовательной или параллельной цепи, но что происходит, когда ваша схема более сложная? Возможно, вы разрабатываете электронику, которая имеет как параллельное, так и последовательное сопротивление, и закон Ома начинает падать. Или что, если у вас нет источника постоянного тока? В таких ситуациях, когда нельзя использовать только V = IR, пора встать на плечи Ома и применить закон Кирхгофа.Здесь мы рассмотрим, что такое Закон Кирхгофа и как его использовать для анализа напряжения и тока сложных электрических цепей.

Что такое Окружной закон Кирхгофа?

Когда вы строите сложную схему, включающую мосты или тройники, вы не можете полагаться только на закон Ома, чтобы найти напряжение или ток. Здесь пригодится закон Кирхгофа, который позволяет рассчитывать как ток, так и напряжение для сложных цепей с помощью системы линейных уравнений.Существует два варианта закона Кирхгофа, в том числе:

• Закон Кирхгофа: Для анализа полного тока сложной цепи
• Закон Кирхгофа о напряжении : для анализа полного напряжения сложной цепи
• Когда вы объединяете эти два закона, вы получаете Окружной закон Кирхгофа

Как и любой другой научный или математический закон, названный в честь их создателя, Закон Кирхгофа был изобретен немецким физиком Густавом Кирхгофом.Густав был известен многими достижениями при жизни, в том числе теорией спектрального анализа, которая доказала, что элементы излучают уникальный световой узор при нагревании. Когда Кирхгоф и химик Роберт Бунзен проанализировали эти световые узоры через призму, они обнаружили, что каждый элемент периодической таблицы имеет свою уникальную длину волны. Открытие этого паттерна позволило дуэту открыть два новых элемента, цезий и рубидий.

Густав Кирхгоф (слева) и Роберт Бунзен (справа)

Кирхгоф позже применил свою теорию спектрального анализа для изучения состава Солнца, где он обнаружил множество темных линий в спектре длин волн Солнца.Это было вызвано тем, что газ Солнца поглощает световые волны определенной длины, и это открытие ознаменовало начало новой эры исследований и исследований в области астрономии.

Немного ближе к дому в мире электроники, Кирхгоф объявил свой свод законов для анализа тока и напряжения в электрических цепях в 1845 году, известный сегодня как Закон Кирхгофа о цепях. Эта работа строится на основе, изложенной в законе Ома, и помогла проложить путь для анализа сложных схем, на который мы полагаемся сегодня.

Первый закон — Действующий закон Кирхгофа

Закон Кирхгофа по току гласит, что величина тока, поступающего в узел, равна величине тока, выходящего из узла. Почему? Потому что, когда ток входит в узел, ему некуда идти, кроме выхода. То, что входит, должно выйти. Вы можете определить узел, в котором два или более пути соединены общей точкой. На схеме это будет точка соединения, соединяющая две пересекающиеся сетевые соединения.

Взгляните на изображение ниже, чтобы визуально понять этот Закон.Здесь у нас есть два тока, входящие в узел, и три тока, выходящие из узла. Согласно Закону Кирхгофа, взаимосвязь между этими токами, входящими в узел и выходящими из него, может быть представлена ​​как I 1 + I 2 = I 3 + I 4 + I 5 .

Текущий закон Кирхгофа, ток на входе должен равняться току на выходе. (Источник изображения)

Когда вы уравновешиваете это уравнение как алгебраическое выражение, вы делаете вывод, что ток на входе и выходе из узла всегда будет равен 0, или I 1 + I 2 + (-I 3 + -I 4 + -I 5 ) = 0 Все должно уравновешиваться, и Кирхгоф назвал этот принцип Сохранением заряда .

Давайте посмотрим на пример схемы, чтобы увидеть, как это работает. Ниже представлена ​​схема с четырьмя узлами: A, C, E и F. Сначала ток течет от источника напряжения и отделяется в узле A, а затем протекает через резисторы R1 и R2. Оттуда ток рекомбинирует в узле C и снова разделяется, чтобы течь через резисторы R3, R4 и R5, где он встречается с узлом E и узлом F.

(Источник изображения)

Чтобы подтвердить закон Кирхгофа в этой цепи, нам необходимо предпринять следующие шаги:

1. Рассчитать полный ток цепи
2. Рассчитать ток, протекающий через каждый узел
3. Сравните входные и выходные токи в определенных узлах, чтобы подтвердить текущий закон Кирхгофа.

1. Рассчитайте общий ток

Здесь мы используем закон Ома, чтобы получить полный ток нашей цепи с I = V / R . У нас уже есть общее напряжение 132 В, и теперь нам просто нужно найти общее сопротивление во всех наших узлах. Для этого требуется простой метод расчета общего сопротивления резисторов, подключенных параллельно, которое составляет:

Начиная с узла AC, получаем следующее сопротивление для параллельных резисторов R1 и R2:

И переходя к узлу CEF, мы получаем следующее сопротивление для параллельных резисторов R3, R4 и R5:

Теперь у нас есть общее сопротивление 11 Ом для всей цепи, которое мы можем затем подключить к закону Ома I = V / R , чтобы получить общий ток в нашей цепи:

2.Расчет узловых токов

Теперь, когда мы знаем, что из нашей цепи выходит 12 ампер, мы можем рассчитать ток в каждом наборе узлов. Мы снова воспользуемся помощью закона Ома в форме I = V / R , чтобы получить ток для каждой ветви узла.

Во-первых, нам нужны напряжения для узловых ветвей AC и CF:

Затем мы можем рассчитать ток для каждой ветви узла:

3. Подтвердите действующий закон Кирхгофа

После вычисления тока для каждой ветви узла у нас теперь есть две отдельные контрольные точки, которые мы можем использовать для сравнения наших входных и выходных токов.Это позволит нам проанализировать нашу схему и подтвердить текущий закон Кирхгофа следующим образом:

Второй закон — Закон Кирхгофа о напряжении

Закон Кирхгофа о напряжении гласит, что в любой цепи с замкнутым контуром полное напряжение всегда будет равно сумме всех падений напряжения в контуре. Вы обнаружите, что при протекании тока через пассивный компонент, такой как резистор, происходит падение напряжения, и Кирхгоф назвал этот закон Сохранением энергии .Опять же, то, что входит, должно выходить наружу.

Взгляните на изображение ниже, чтобы понять это визуально. В этой схеме у нас есть источник напряжения и четыре области в цепи, где напряжение столкнется с пассивным компонентом, что вызовет заметное падение напряжения.

Поскольку эти пассивные компоненты соединены последовательно, вы можете просто сложить общее падение напряжения и сравнить его с общим напряжением, чтобы получить соотношение, которое выглядит следующим образом:

Давайте начнем с простой схемы, чтобы продемонстрировать, как это работает.В приведенном ниже примере у нас есть две известные переменные: полное напряжение и падение напряжения на R1.

(Источник изображения)

Что нам нужно выяснить, так это падение напряжения на R2, и мы можем использовать закон напряжения Кирхгофа, чтобы выяснить это со следующей зависимостью:

Поскольку полное падение напряжения в цепи должно равняться общему напряжению источника, это обеспечивает простой способ вычисления нашей недостающей переменной. Если бы вы хотели выразить это соотношение в виде правильного алгебраического выражения, вы бы получили сумму всех падений напряжения и общее напряжение, равное нулю, как показано здесь:

Давайте посмотрим на другой пример.В схеме ниже у нас есть три резистора, подключенных последовательно к батарее на 12 В.

Чтобы проверить закон напряжения Кирхгофа в этой цепи, нам необходимо предпринять следующие шаги:

1. Вычислить общее сопротивление цепи
2. Вычислить полный ток цепи
3. Рассчитайте ток через каждого резистора
4. Рассчитайте падение напряжения на каждого резистора

Сравните источник напряжения с общим падением напряжения , чтобы подтвердить закон Кирхгофа о напряжении

1.Рассчитайте общее сопротивление

Поскольку все наши резисторы соединены последовательно, мы можем легко найти общее сопротивление, просто сложив все значения сопротивления вместе:

2. Рассчитайте общий ток

Теперь, когда мы знаем наше полное сопротивление, мы снова можем использовать закон Ома, чтобы получить полный ток нашей цепи в виде I = V / R, , который выглядит так:

3. Рассчитайте ток через каждый резистор

Поскольку все наши резисторы соединены последовательно, через них будет проходить одинаковый ток, который мы можем выразить как:

4.Рассчитайте падение напряжения на каждом резисторе

.

Наш окончательный расчет снова будет использовать закон Ома, чтобы получить полное падение напряжения для каждого резистора в виде В = IR , которое выглядит следующим образом:

5. Подтвердите закон Кирхгофа о напряжении

Теперь у нас есть все необходимые данные, включая полное напряжение нашей цепи, а также каждое падение напряжения на каждом из наших резисторов. Собирая все это вместе, мы можем легко проверить закон напряжения Кирхгофа с помощью следующего соотношения:

Это также можно выразить как:

Как видите, полное напряжение равно общему падению напряжения в нашей цепи.То, что входит, должно выйти наружу, и закон Кирхгофа снова работает!

Процесс использования закона Кирхгофа о схемах

Поняв, как работает закон Кирхгофа, в вашем наборе инструментов теперь есть новый инструмент для анализа напряжения и тока в полных цепях. При использовании этих Законов в дикой природе рассмотрите возможность использования следующего пошагового процесса:

1. Во-первых, начните с маркировки всех известных напряжений и сопротивлений на вашей цепи.
2. Затем назовите каждую ветвь в вашей цепи текущей меткой, например I1, I2, I3 и т. Д.Ветвь — это один или группа компонентов, соединенных между двумя узлами.
3. Затем найдите закон Кирхгофа для каждого узла в вашей цепи.
4. Затем найдите закон напряжения Кирхгофа для каждой из независимых петель в вашей цепи.

После расчета законов Кирхгофа по току и напряжению вы можете использовать свои уравнения, чтобы найти недостающие токи. Готовы попробовать это самостоятельно? Взгляните на схему ниже и посмотрите, сможете ли вы подтвердить закон Кирхгофа по току и закон напряжения с небольшой помощью Ома!

Напишите свои ответы в комментариях ниже!

Стоя на плечах Ома

Имея в руках Закон Кирхгофа о цепях, теперь у вас есть все инструменты, необходимые для анализа напряжения и тока в сложных цепях.Как и многие другие научные и математические принципы, закон Кирхгофа стоит на плечах того, что было раньше — закона Ома. Вы обнаружите, что используете закон Ома для расчета отдельных сопротивлений, напряжений или токов, а затем, основываясь на этих расчетах с законом Кирхгофа, увидите, соответствует ли ваша схема этим принципам тока и напряжения.

Готовы применить закон Кирхгофа в вашем собственном проекте электронного дизайна? Попробуйте Autodesk EAGLE бесплатно сегодня!

.

Закон Кирхгофа о напряжении и Закон Кирхгофа

Ultimate Electronics: практическое проектирование и анализ схем

Как написать фундаментальные уравнения, описывающие структуру любой схемы из первых принципов.

Читать 14 мин

В предыдущем разделе, посвященном последовательным и параллельным резисторам, мы выработали много интуитивного представления о том, как думать о токе и напряжении в цепи. (Если вы не читали этот раздел, вернитесь и сделайте это сейчас.)

Специальные правила комбинации резисторов для последовательно включенных и параллельных резисторов не распространяются на другие элементы схемы. Однако есть два основных принципа, которые можно обобщить:

1. Два последовательно соединенных компонента будут иметь одинаковый ток через . Мы сделаем это заявление немного шире, и оно станет Текущим законом Кирхгофа .
2. Два параллельно включенных компонента будут иметь одинаковое напряжение на . Мы сделаем это заявление немного шире, и оно станет Законом о напряжении Кирхгофа .

Эти два закона Кирхгофа станут нашей основой для написания уравнений, описывающих, как ток и напряжение ведут себя в любой электронной схеме .

В этом разделе нас интересует только то, как написать этих уравнений. В других разделах, включая раздел «Системы уравнений» из предыдущей главы, мы обсудим, как решить этих уравнений после того, как они были написаны.

Текущий закон Кирхгофа — это заявление о сохранении заряда: то, что входит, должно выходить на каждом соединении (узле) в коммутационной сети.

В рамках модели сосредоточенных элементов заряд не может храниться ни в одном узле схемы, поэтому, если заряд вытекает из одного элемента в узле A, то же количество тока должно мгновенно течь на вывод подключенного элемента в узле A.

Чтобы понять, почему это должно быть правдой, помните, что электроны не могут никуда входить в систему или выходить из нее (нет никаких «утечек»), и электроны не могут нигде «скапливаться», потому что они отталкиваются друг от друга.

Это аналогично гидравлической аналогии с потоком воды в трубопроводной сети: на любом стыке труб имеется 2 или более соединений, и любая поступающая вода должна уходить!

Направление тока тоже важно: мы должны определить токи с помощью входящих или исходящих стрелок и тщательно их пометить.(Мы обсудим это подробнее в следующем разделе, Маркировка напряжений, токов и узлов.)

Рассмотрим схему сети с тремя узлами и четырьмя элементами:

В схеме выше у нас есть три узла. Мы можем записать Текущий закон Кирхгофа как на каждую из трех узлов.

Математически один способ записать это в каждом узле:

∑i = 0

Это говорит о том, что сумма всех токов в узле равна нулю.

Мы должны отслеживать и использовать знак положительный , если ток течет в узел, и отрицательный знак , если ток течет из .

В приведенном выше примере, проходя через каждый узел, уравнения KCL:

i1 − i2 = 0 Узел Ai2 − i3 + i4 = 0 Узел B − i1 + i3 − i4 = 0 Узел C

Другой способ сформулировать действующий закон Кирхгофа:

∑ini = ∑outi

В приведенном выше примере три уравнения будут:

i1 = i2Node Ai2 + i4 = i3Node Bi3 = i1 + i4Node C

В этой формулировке мы говорим, что сумма токов в узле равна сумме токов из этого узла.

Это математически идентично первому способу определения KCL, потому что эти токи просто имеют отрицательный знак.

Будьте внимательны при выборе направления! Не имеет особого значения, какое направление вы выберете для маркировки каждого потока, но абсолютно важно, чтобы оно было последовательным; ток в одном узле является током из другого.

Мы можем записать KCL на каждом узле схемы. Узел — это просто место, где элементы соединяются.

Обратите внимание, что узлы могут быть больше, чем кажется на первый взгляд: мы можем назвать узлы A, B, C
и ссылаться на эти имена в нескольких местах на схеме, даже если между ними нет явно проведенных проводов.Кроме того, наземный узел является частным случаем именованного узла и также повсюду соединен вместе.

Мы можем написать уравнения KCL, ничего не зная о компонентах; он только определяет топологию (форму) того, как вещи соединяются друг с другом.

Вот немного более сложный пример с 5 узлами и 7 ребрами. Обратите внимание, что мы помечаем все узлы, а затем помечаем все токи и их направления:

Вот уравнения KCL для каждого узла, которые получаются при суммировании всех токов до нуля:

i1 − i2 = 0 Узел Ai2 − i3 − i4 = 0 Узел Bi3 − i5 − i6 = 0 Узел Ci4 + i5 − i7 = 0 Узел Di6 + i7 − i1 = 0 Узел E

И, для полноты, вот уравнения KCL для каждого узла, которые получаются, когда вы суммируете все токи, равные всем выходным токам:

i1 = i2Node Ai2 = i3 + i4Node Bi3 = i5 + i6Node Ci4 + i5 = i7Node Di6 + i7 = i1Node E

Эти две системы уравнений алгебраически одинаковы.Присмотритесь к тому, что имеет для вас больше смысла, и понаблюдайте, как вы можете преобразовать одно в другое.

В следующем разделе мы поговорим о маркировке токов, чтобы они выполнялись последовательно по направлению и знаку — обычная ловушка для новичков.

Как мы уже указывали в статьях «Линейные и нелинейные» и «Системы уравнений», полезно развить некоторую интуицию в линейной алгебре. Вышеприведенная серия уравнений KCL для примера с пятью узлами может быть записана как:

⎡⎢
⎢
⎢
⎢
⎢
⎢⎣1−10000001−1−10000010−1−10000110−1−1000011⎤⎥
⎥
⎥
⎥
⎥
⎥⎦⎡⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢⎣i1i2i3i4i5i6i7⎤⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥⎦ = 0

Сама по себе это еще не решаемая система уравнений, однако она вносит значительный вклад в общую систему уравнений, составляющих решаемую схему.

Из действующего закона Кирхгофа нет никаких исключений — по определению.

Обратите внимание, что в то время как электроны в проводниках будут отталкиваться друг от друга, для изолятора электроны могут «застрять» — статический заряд. Статический заряд может накапливаться внутри и внутри цепи; однако вместо того, чтобы рассматривать KCL как нарушенный, этот эффект лучше всего моделировать путем добавления емкостей в рассматриваемых узлах.

Если у нас есть n
узлов в нашей схеме, мы можем написать n
Уравнения KCL — по одному на каждый узел.

Однако эти уравнения не будут линейно независимыми . (Чтобы узнать о линейной независимости и о том, почему она так важна, см. «Системы уравнений».)

Рассмотрим эту простую схему с двумя узлами:

Мы можем записать KCL в узле A:

i1 − i2 + i3 = 0

И теперь мы можем записать KCL в узле B:

−i1 + i2 − i3 = 0

Должно быть очевидно, что на самом деле это одно и то же уравнение, записанное дважды; мы только что умножили одно из них на -1.

Запись дважды (по одному на узел) фактически не добавила никакой информации. Второе уравнение не добавляло никаких новых ограничений, которые еще не были включены в первое уравнение.

Это потому, что каждое ребро на графике добавляет текущий член в уравнение KCL одного узла и вычитает этот текущий член из другого уравнения KCL. Мы дважды считаем входящие и исходящие потоки везде, даже если весь заряд сохраняется, что приводит к этому бесполезному дополнительному уравнению.

Это относится и к более сложным примерам.Снова рассмотрим пример с тремя узлами, который мы рассмотрели выше:

Мы можем записать KCL на каждом узле, как делали выше:

i1 − i2 = 0 Узел Ai2 − i3 + i4 = 0 Узел B − i1 + i3 − i4 = 0 Узел C

В этом немного более сложном случае менее «очевидно», что они не являются линейно независимыми, но это все же верно. Чтобы убедиться в этом, сложите уравнение №1 и уравнение №2, затем умножьте его на -1, и вы получите уравнение №3.

Это обычная ловушка для начинающих решать проблемы, поэтому следите за ней.

На практике решением является не писать уравнение KCL для узла, выбранного в качестве наземного узла . Мы поговорим об этом подробнее в следующем разделе.

Закон Кирхгофа о напряжении можно сформулировать несколькими разными способами с тем же основным смыслом.

Мы уже обсуждали в разделе «Напряжение и ток», как напряжение всегда является разницей в двух точках . Даже когда мы для удобства определяем узел заземления, мы все равно смотрим на разницу напряжений относительно этого произвольно определенного заземления.

Первый способ сформулировать закон Кирхгофа о напряжении состоит в том, что общая разница напряжений между двумя точками A и B одинакова, независимо от того, какой путь вы выберете.

Это все равно что сказать, что разница между человеком ростом 5 футов и человеком ростом 6 футов всегда будет составлять 1 фут. Неважно, если мы:

1. Поместите двух людей спиной к спине и измерьте разницу от макушки одной головы до другой, или
2. Измерьте расстояние от головы до пят и выполните вычитание, или
3. Измерьте их оба от потолка и выполните вычитание,
4. Попросите обоих встать на коробку, измерить от нижней части коробки и выполнить вычитание.

Во всех четырех случаях мы получаем разницу в высоте в 1 фут.

Давайте поместим этих двух людей в комнату и скажем, что плоскость x-y — это пол, а ось z направлена ​​к потолку.

Теперь представьте себе, что все четыре способа измерения представляют собой разные пути в пространстве между точками A (верхняя часть головы первого человека) и B (верхняя часть головы второго человека). Мы собираемся пройти по кривой каждого пути и сложить только расстояние по оси Z по вертикали, отслеживая положительное и отрицательное, когда мы идем по этим четырем путям.У нас всегда будет разница в 1 фут, независимо от того, какой путь мы выберем между A и B.

Мы можем игнорировать движение в других направлениях, потому что имеет значение только разница в высоте. (И точно так же для напряжений имеют значение только электрические поля , параллельные пути .)

Это может показаться простым, но это все, что есть в Законе напряжения Кирхгофа.

Существует второй распространенный способ определения KVL: сумма напряжений на любом контуре равна нулю.Цикл определяется как любой путь, который начинается и заканчивается в одной и той же точке.

Чтобы применить к нашей аналогии с ростом, теперь говорится, что если вы начнете с вершины головы человека ростом 5 футов и сделаете любую петлю в пространстве, и вы сложите изменения высоты (ось z) по мере продвижения , вы получите ноль, когда вернетесь в исходную точку.

Утверждения «каждый цикл суммируется до нуля» и «каждый путь между A и B имеет одинаковую разницу напряжений» математически идентичны, потому что вы всегда можете выбрать путь от A до некоторой точки Q, а затем добавить любой путь обратно от Q обратно к A, чтобы сделать петлю.

Если вы изучали многомерное исчисление, то это версия линейного интеграла в векторном поле — в данном случае электрическом поле — и существует потенциальная функция (само напряжение), поэтому линейный интеграл не зависит от пути, и электрическое поле — это градиент потенциальной функции. (Мы обсуждали это подробнее в разделе «Электроны в состоянии покоя».)

Мы только что говорили об измерении роста людей, но какое это имеет отношение к электронике?

Ну, точно так же, как высота является способом измерения гравитационной потенциальной энергии массы в гравитационном поле , аналогично напряжение является способом измерения электрической потенциальной энергии заряда в электрическом поле .

Допустим, у нас есть высота A (выше) и высота B (ниже) и несколько маленьких стальных шарикоподшипников. Слева мы построили ящик, который принимает шары с высоты B и поднимает их на высоту A. Справа шары, выходящие из ящика, спускаются по пандусу с высоким коэффициентом трения, где они скатываются вниз и в конце концов останавливаются внизу, на высоте B. Оттуда они возвращаются в ящик слева, чтобы продолжить свой цикл.

Если мы сопоставим массы с зарядами, а высоту — с напряжениями, мы только что описали что-то вроде этой очень простой схемы с одним источником напряжения и одним резистором:

Закон Кирхгофа о напряжении гласит, что разница напряжений между двумя точками, обозначенными нами как A и B, одинакова, независимо от того, идем ли мы по пути через источник напряжения или по пути через резистор.Вот несколько взаимозаменяемых определений в математических терминах:

v

.