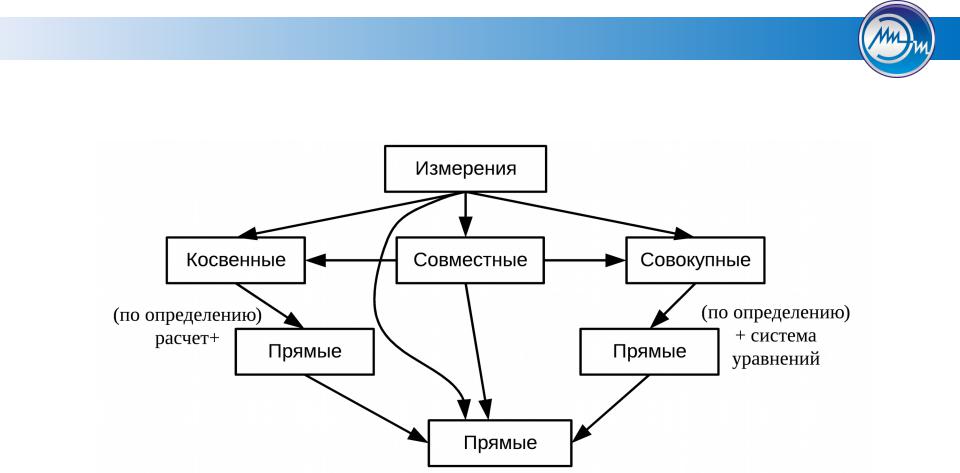
Прямые, косвенные, совместные и совокупные измерения
В зависимости от способа получения результата измерения делят на прямые, косвенные, совместные и совокупные. Прямые измерения, в свою очередь делят на измерения методом непосредственной оценки и измерения методом сравнения с мерой. Каждый метод имеет свой предельный уровень точности и области применения.
[c.69]
Методы обработки результатов экспериментальных данных зависят от вида измерений (прямые, косвенные, совместные и совокупные). Соответственно для каждого вида измерений существует свой метод обработки. [c.160]
Измерения могут быть классифицированы но ряду признаков. Наибольшее распространение получила классификация по общим приемам получения результатов измерений. Согласно этому признаку, измерения делятся на прямые, косвенные, совместные и совокупные. [c.27]
[c.27]
При косвенных измерениях результат находят на основании известной зависимости между определяемой величиной и некоторыми другими величинами, которые, в свою очередь, находят с помощью прямых, а иногда и косвенных, совместных или совокупных измерений. Примером косвенного измерения является определение расхода жидкости с помощью сужающего устройства. [c.134]
При совместных и совокупных измерениях искомые величины определяют в результате решения системы уравнений. При этом числовые коэффициенты и некоторые члены уравнений, входящие в эту систему, находят в результате прямых или косвенных измерений. Отличие между совместными и совокупными измерениями заключается в том, что в первом случае при определении искомой величины измеряют несколько других разноименных величин, а во втором — несколько других одноименных величин. Примером сов- [c.134]
Примерами косвенного измерения могут служить определение расхода питательной воды сужающим устройством, измерение температуры ТС и т.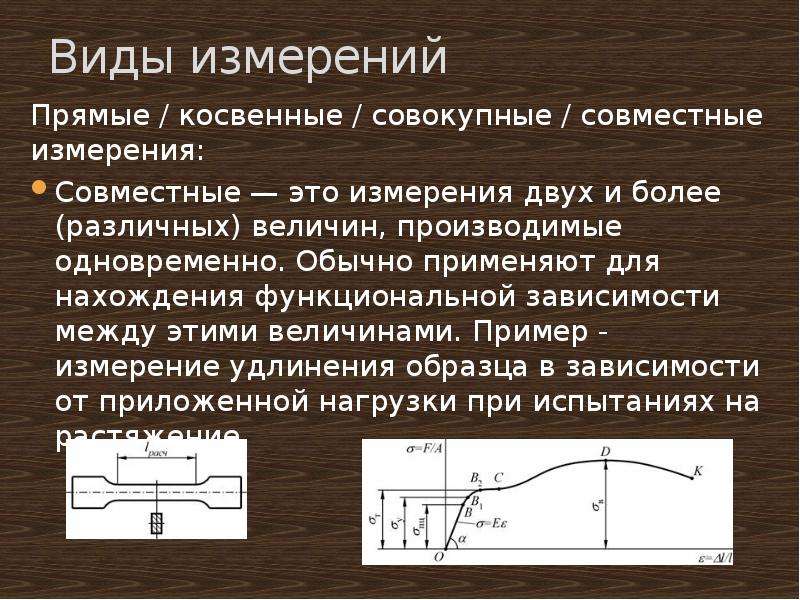 д. Совместные и совокупные измерения по способам нахождения искомых значений очень близки, и в том и другом случае их находят рещением системы уравнений, в которых коэффициенты и отдельные члены получены в результате измерений (обычно прямых). Основное отличие состоит в том, что при совокупных измерениях одновременно проводят несколько одноименных измерений, а при совместных — разноименных. К совокупным относятся измерения, состоящие из совокупности ряда прямых и косвенных измерений. Искомые числовые значения определяют из так называемых условных уравнений
[c.373]
д. Совместные и совокупные измерения по способам нахождения искомых значений очень близки, и в том и другом случае их находят рещением системы уравнений, в которых коэффициенты и отдельные члены получены в результате измерений (обычно прямых). Основное отличие состоит в том, что при совокупных измерениях одновременно проводят несколько одноименных измерений, а при совместных — разноименных. К совокупным относятся измерения, состоящие из совокупности ряда прямых и косвенных измерений. Искомые числовые значения определяют из так называемых условных уравнений
[c.373]
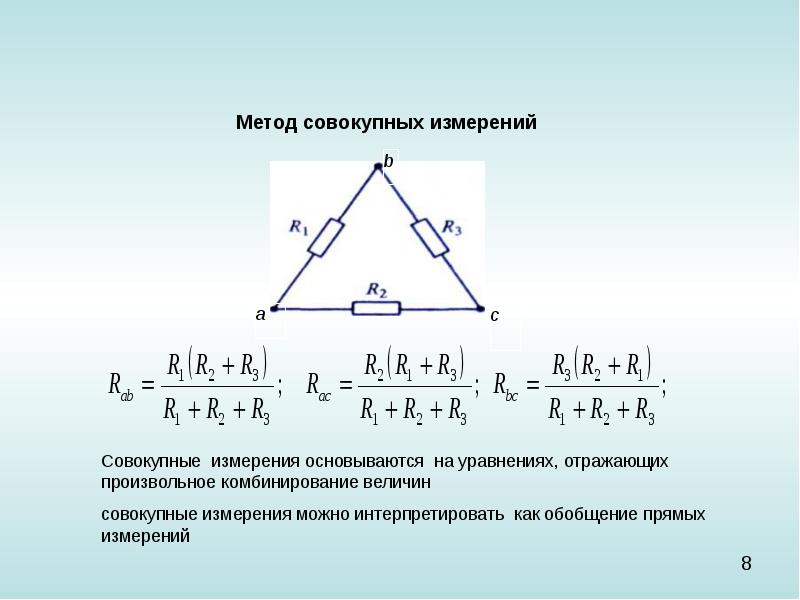
Рассмотрим наиболее общий случай — осуществление совокупных измерений. Как известно, при таких измерениях значения искомых величин Ух, ут рассчитываются по системе уравнений, связывающих их с величинами, измеряемыми прямыми или косвенными методами. Для получения каждого уравнения измеряется одна из комбинаций этих величин. Частным случаем совокупных измерений являются совместные измерения. Различие между этими двумя способами проведения измерений заключается в том, что при совокупных измерениях при переходе от одного уравнения к другому меняются условия проведения измерений, а следовательно, и значения величин. . ., Х/, измеряемых прямыми или косвенными методами. При совокупных измерениях изменяется при этом и вид уравнений системы
[c.45]
. ., Х/, измеряемых прямыми или косвенными методами. При совокупных измерениях изменяется при этом и вид уравнений системы
[c.45]
По способу получения результатов измерений (виду уравнения измерений) их разделяют на прямые, косвенные, совокупные и совместные.
[c.7]
В соответствии со сложившимися в метрологии подходами следует различать несколько видов лабораторных измерений по характеру зависимости измеряемых величин от времени (статические и динамические измерения) по виду уравнения измерений (прямые, косвенные, совокупные или совместные измерения) по условиям, определяющим точность результата (измерения максимально возможной точности, контрольно-поверочные и технические) по способам выражения результатов измерений (абсолютные и относительные). [c.62]
По способу получения значений физической величины измерения могут быть прямыми, косвенными, совокупными и совместными. При прямом измерении искомое значение величины находят непосредственно из опытных данных. Примерами прямых измерений являются измерения длины с помощью линейных мер или температуры термометром. Прямые измерения составляют основу более сложных косвенных, совокупных и совместных измерений. При косвенном измерении искомое значение величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям, например тригонометрические методы измерения углов, при которых острый угол прямоугольного треугольника определяют по измеренным длинам катетов и гипотенузы (см. 29), или измерение среднего диаметра резьбы методом трех проволочек (см. 66). Косвенные измерения в ряде случаев позволяют получить более точные результаты, чем прямые измерения. Например, погрешности прямых измерений углов угломерами на порядок выше погрешностей косвенных измерений углов с помощью синусных линеек.
[c.15]
При прямом измерении искомое значение величины находят непосредственно из опытных данных. Примерами прямых измерений являются измерения длины с помощью линейных мер или температуры термометром. Прямые измерения составляют основу более сложных косвенных, совокупных и совместных измерений. При косвенном измерении искомое значение величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям, например тригонометрические методы измерения углов, при которых острый угол прямоугольного треугольника определяют по измеренным длинам катетов и гипотенузы (см. 29), или измерение среднего диаметра резьбы методом трех проволочек (см. 66). Косвенные измерения в ряде случаев позволяют получить более точные результаты, чем прямые измерения. Например, погрешности прямых измерений углов угломерами на порядок выше погрешностей косвенных измерений углов с помощью синусных линеек.
[c.15]
Числовое значение величины находят путем измерения, т. е. узнают, во сколько раз значение данной величины больше или меньше значения величины, принятого равным единице. По способу получения числового значения измеряемой величины все измерения делят на прямые, косвенные, совокупные и совместные.
[c.902]
е. узнают, во сколько раз значение данной величины больше или меньше значения величины, принятого равным единице. По способу получения числового значения измеряемой величины все измерения делят на прямые, косвенные, совокупные и совместные.
[c.902]
В настояшее время существует множество видов измерений, различаемых физическим характером измеряемой величины и факторами, определяющими разнообразные условия и режимы измерений. Основными видами измерений физических величин, в том числе и линейно-угловых (ГОСТ 16263—70), являются прямые, косвенные, совокупные, совместные, абсолютные и относительные. [c.262]
В-четвертых, в классификации, описываемой в литературе, косвенные измерения рассматриваются наравне с совокупными и совместными измерениями. Иначе говоря, подразумевается, что имеются три на одном классификационном уровне группы измерений косвенные, совокупные, совместные. Однако сравнивая между собой эти три группы измерений (см., например, [9]), можно заключить, что они объединяются принципиально общим свойством результат (результаты) измерений определяется путем расчета по известным функциональным зависимостям между измеряемой величиной (измеряемыми величинами) и некоторыми величинами, подвергаемыми прямым измерениям. Различие между этими тремя группами измерений заключается только в виде упомянутой функциональной зависимости. При косвенных измерениях эта зависимость выражается одним уравнением в виде
[c.53]
Различие между этими тремя группами измерений заключается только в виде упомянутой функциональной зависимости. При косвенных измерениях эта зависимость выражается одним уравнением в виде
[c.53]
При совокупных и совместных измерениях функциональная зависимость измеряемых величин от аргументов, подвергаемых прямым измерениям, выражается системой неявных уравнений. Более подробно на совокупных и совместных измерениях мы не останавливаемся, так как они многократно описаны в литературе (например, в [9]). Нас интересует лишь тог факт, что при совокупных и совместных измерениях могут возникать методические погрешности, обусловленные алгоритмами решения уравнений. Следовательно, они соответствуют тому признаку, который позволяет четко отделить прямые измерения от косвенных и выделить определенный источник погрешностей измерений прн анализе и синтезе МВИ. [c.53]
Поэтому представляется целесообразной классификация, несколько отличающаяся от общепринятой прямые и косвенные измерения косвенные подразделяются на несколько групп, различающихся между собой количеством и видом уравнений, представляющих функциональные зависимости между измеряемыми величинами и величинами, подвергаемыми прямым измерениям. Частные виды таких групп представляют совокупные и совместные измерения. Целесообразность рассмотрения совокупных и совместных измерений как частных случаев косвенных уже отмечалась в [37].
[c.53]
Частные виды таких групп представляют совокупные и совместные измерения. Целесообразность рассмотрения совокупных и совместных измерений как частных случаев косвенных уже отмечалась в [37].
[c.53]
При совокупных и совместных измерениях искомые значения физических величин Ql, Са, Qm и полученные в -м опыте в результате прямых или косвенных измерений значения физических величин А , связаны между собой уравнениями вида [c.100]
По способу получения числового значения измеряемой величины все технические измерения можно разделить на прямые и косвенные. В лабораторной практике и научных исследованиях имеют место также совокупные и совместные измерения. Прямыми измерения называются такие, при которых искомое значение величины находят непосредственно из опытных данных. Например, измерение температуры термометром, давления — манометром. Результат измерения может быть получен также путем косвенных измерений, когда численное значение находят на основании прямых измерений величин, связанных с измеряемой величиной определенной зависимостью
[c.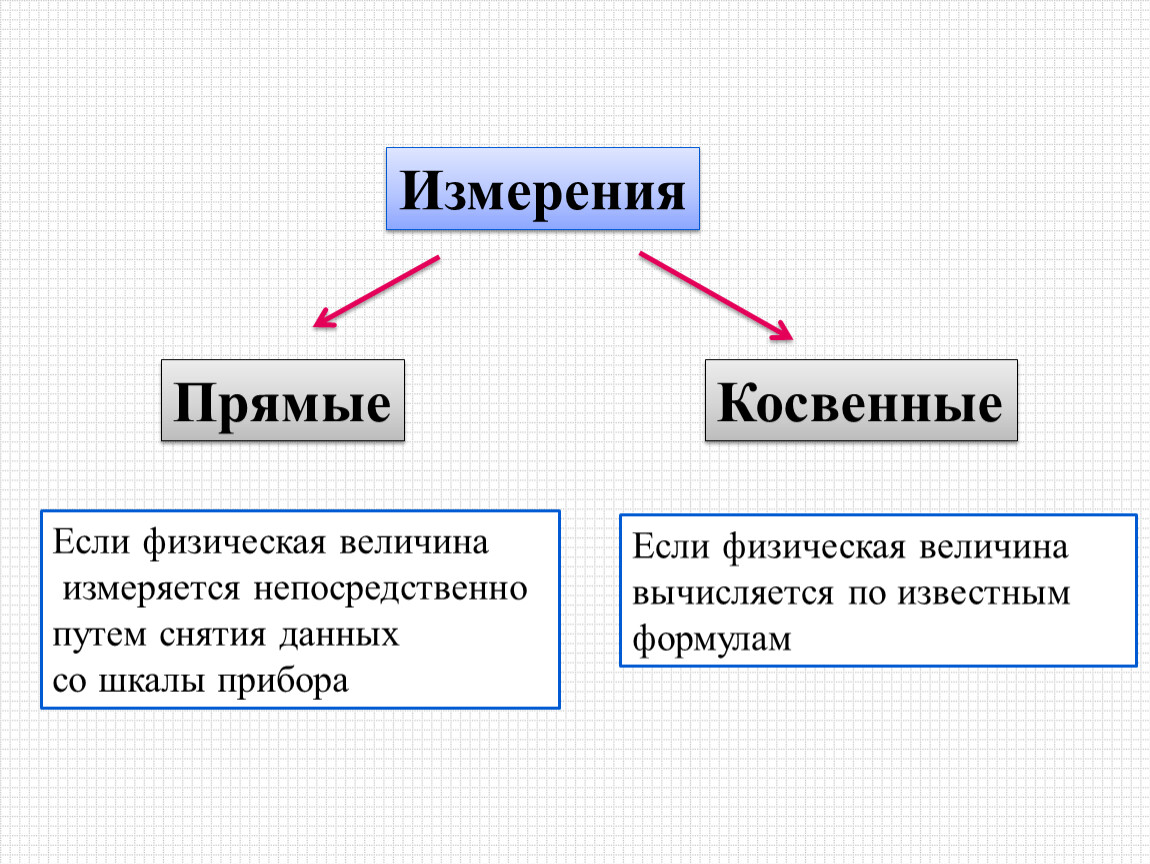 4]
4]
Измерения подразделяются на прямые, косвенные, совместные и совокупные, что обусловлено пpиeмa лп получения результатов измерений. Каждая категория измерений связана с определенным способом обработки экспериментальных данных для нахождения результата измерения и оценивания его погрешностей. [c.125]
По способу получения результатов измерения разделяют на прямые, косвенные, Совокупные и совместные. Пряное — измерение, при котором искомое чначе-ние величины находят непосредственно из опыта. Косвенное — измерение, при котором искомое значение величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям. Совокупные — производимые одновременно измерения нескольких величин, при которых искомые значения величин на .одят решением системы уравнений, получаемых при прямых измерениях и включающих в себя измеряемые величины. Совместные — производимые одновременно измерения двух или несксльких величин для нахождения зависимости между ними Г2]. [c.11]
[c.11]
По способу получения измеряемой величины (результата измерения) измерения разделяют на прямые, косвенные, совокупные и совместные (см. раздел 1 гл. ) Примерами косвенных измерений являются измерения мощности, модуля и фазы импеданса через сигналы скорости и силы. Примером совокупных измерений явля- [c.108]
Результаты измерений — прямых, косвенных, совокупных и совместных широко используются при эксплуатации сложных изделии либо непосредственно при формировании оценок их состояния, либо в качестве исходных данных для решения задач статистического оценивания — сглаживания, фильтрации и прогно-ьирования. При оценивании используются классические методы обработки измерительной информации — максимального правдоподобия, наименьших квадратов и др. [c.38]
Методы измерений и измерительные средства.
Методы и средства измерений физических величин
Как и чем производят измерения?
В результате измерения определяют числовое значение измеряемой величины, равное отношению измеряемой величины к единице измерения или эталону.
В зависимости от конкретных условий, применяемых измерительных средств и приемов их использования измерения могут производиться различными способами или методами. С точки зрения общих приемов получения результатов измерения различают измерения непосредственные, т. е. прямые и косвенные.
Прямые измерения
При прямых измерениях искомая величина определяется непосредственно показаниями прибора или измерительной шкалы инструмента.
К прямым измерениям относятся измерения длин линейками, штангенинструментом, микрометрами, широкодиапазонными инкрементными измерительными головками с цифровым отсчетом, высотомерами, измерения углов — угломерами и др.
Косвенные измерения
При косвенных измерениях искомая величина (размер или отклонение) определяется по результатам прямых измерений одной или нескольких величин, связанных с искомой величиной определенной функциональной зависимостью, т. е. после определения косвенных величин, влияющих на искомую, определяют искомую величину, используя математические методы вычислений или преобразований.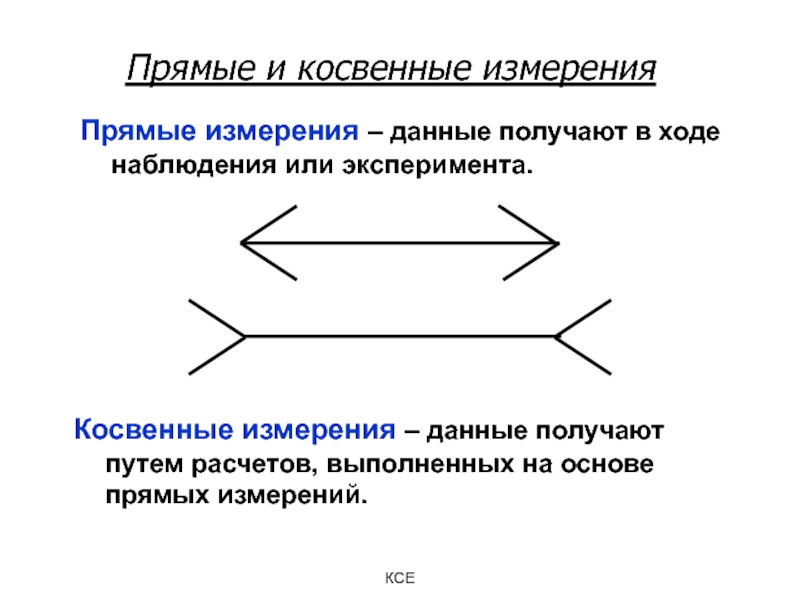
Примером косвенных измерений могут служить измерения диаметра вала по длине его окружности с помощью рулетки или обкатного ролика, измерения на координатно-измерительных машинах (КИМ), и др.
На рисунке представлен пример косвенного измерения диаметра вала с помощью рулетки, при этом измеряется длина окружности и с помощью известной зависимости D = L/π определяется ее диаметр.
Прямые измерения более просты и сразу приводят к результату измерения, поэтому они имеют преимущественное распространение в машиностроении.
Однако в ряде случаев прямые измерения не могут быть осуществлены, например, при измерении штангенциркулем расстояния между осями отверстий, при измерениях на КИМ, при измерении валов большого диаметров и др.
Прямые измерения иногда уступают по точности косвенным измерениям, как это имеет место при измерении углов угломерами, погрешности которых в десятки раз превышают погрешности синусных линеек.
Косвенные измерения широко применяют при координатных измерениях, потому что результат измерения всегда получают расчетом по определенным при измерении координатам двух или нескольких точек.
Каждое измерение может производиться абсолютным или относительным методом.
Абсолютный метод измерения
При абсолютном методе весь измеряемый размер определяется непосредственно по показаниям прибора. В настоящее время большинство приборов и инструментов измеряют абсолютным методом – штангенинструмент, микрометры, широкодиапазонные индикаторы и преобразователи, высотомеры, КИМ, угловые энкодеры и др.
Относительный метод измерения
Относительный (сравнительный) метод измерения дает только отклонение размера от установочной меры или образца, по которым прибор был установлен на ноль. Определение размера в этом случае производится алгебраическим суммированием размера установочной меры и показаний прибора при измерении.
Приборы для относительных измерений требуют дополнительной затраты времени для предварительной настройки прибора по установочной мере, что существенно снижает производительность измерений при небольших партиях проверяемых деталей. Снижение производительности становится несущественным, если после настройки прибором производят большое число измерений.
Снижение производительности становится несущественным, если после настройки прибором производят большое число измерений.
Приборы для относительных измерений в ряде случаев позволяют получить более высокую точность, а при измерении больших партий деталей и более высокую производительность контроля, благодаря удобству отсчета отклонений размера по шкале прибора.
Относительный метод измерения применяется на контрольных приспособлениях и автоматах, в приборах активного контроля.
Кроме того, методы измерения делятся на комплексные и дифференцированные.
Комплексный метод измерения
Комплексный метод измерения заключается в сопоставлении действительного контура проверяемого объекта с его предельными контурами, определяемыми величинами и расположением полей допусков отдельных элементов этого объекта.
Комплексный метод измерения обеспечивает проверку накопленных погрешностей взаимосвязанных элементов объекта, ограниченных суммарным допуском. Этот метод измерения является наиболее надежным с точки зрения обеспечения взаимозаменяемости и обычно осуществляется проходными калибрами, сконструированными по принципу подобия.
Этот метод измерения является наиболее надежным с точки зрения обеспечения взаимозаменяемости и обычно осуществляется проходными калибрами, сконструированными по принципу подобия.
Примером комплексного метода измерения может служить проверка резьбы гайки проходной резьбовой пробкой.
Дифференцированный метод измерения
Дифференцированный метод измерения сводится к независимой проверке каждого элемента отдельно. Этот метод не может непосредственно гарантировать взаимозаменяемости изделий.
Например, при дифференцированной проверке среднего диаметра, шага и половины угла профиля резьбы необходимо дополнительно подсчитать приведенный средний диаметр резьбы, включающий отклонения перечисленных выше элементов резьбы, и убедиться, что он находится в заданных пределах.
Комплексный метод измерения применяется преимущественно при проверке изделий, а дифференцированный метод — при проверке инструментов, настройке станков и при выявлении причин размерного брака изделий.
При проверке изделий предельными калибрами обычно сочетаются комплексные и дифференцированные методы измерений.
Каждый из перечисленных выше методов измерения может осуществляться контактным или бесконтактным способом.
Контактный метод измерения
Контактный метод измерения осуществляется путем непосредственного соприкосновения измерительных поверхностей (наконечников) прибора или инструмента с поверхностью контролируемого объекта.
Бесконтактный метод измерения
Бесконтактный метод измерения характеризуется отсутствием измерительного контакта прибора с проверяемым объектом (например, при пневматическом методе измерения, при измерении на проекторах, микроскопах, лазерных приборах, лазерных итерферометрах и т.п.).
В последнее время получил большое распространение бесконтактный метод измерения с помощью лазерного сканирования, в том числе 3D сканирования и лазерных триангуляционных измерениях.
***
Измерительные средства
Измерительные средства, применяемые в металлообрабатывающей промышленности, можно разделить на три основные группы:
- меры и калибры;
- универсальные инструменты и приборы, специальные средства измерений — контрольные приспособления, контрольные автоматы, приборы активного контроля;
- координатно-измерительные машины.

Мерами называются средства измерения, служащие для воспроизведения одного или нескольких известных значений данной величины.
Калибрами называются меры, служащие для проверки правильности размеров, форм и взаимного расположения частей изделия.
Калибры долгое время являлись одними из наиболее распространенных измерительных средств, но с повышением точности металлообработки, распространением станков с ЧПУ, появлением индикаторов, электронных приборов и инструментов с цифровым отсчетом и КИМ применение калибров существенно снизилось.
Универсальные инструменты и приборы служат для определения значений измеряемой величины.
Они различаются по конструктивным признакам, по целевому назначению, по степени механизации, пределам измерения, цене деления аналогового или цифрового отсчета и прочим показателям.
Классификация средств измерения
Универсальные измерительные инструменты и приборы классифицируются по конструктивным признакам на:
- механические инструменты, снабженные штриховой шкалой и нониусом — штангенинструменты и (штангенциркули, штангенглубиномеры, штангенрейсмасы и др.
 ) и универсальные угломеры;
) и универсальные угломеры; - электронные штангенинструменты с цифровым отсчетом (штангенциркули, штангенглубиномеры, штангенрейсмасы);
- микрометрические инструменты, основанные на применении микропар (микрометры, микрометрические нутромеры, глубиномеры и др.);
- электронные микрометрические инструменты с цифровым отсчетом (микрометры, нутромеры, глубиномеры и др.);
- механические индикаторы со шкалой и стрелкой;
- электронные индикаторы с цифровым отсчетом;
- оптические приборы (длиномеры, интерферометры, проекторы, микроскопы, лазерные приборы и др.);
- индуктивные приборы;
- широкодиапазонные приборы (емкостные, индуктивные и фотоэлектрические);
- пневмоиндуктивные приборы;
- высотомеры;
- координатно-измерительные машины (КИМ).
Кроме того, существуют специальные приборы — контрольные приспособления, контрольные автоматы и приборы активного контроля, предназначенные для контроля одной или нескольких однотипных деталей после их обработки на станке или в процессе обработки.
По числу одновременно проверяемых размеров приборы разделяются на одномерные и многомерные.
По установившейся на производстве терминологии простейшие измерительные средства — калибры, линейки, штангенинструмент, микрометры, уровни — именуются измерительным инструментом.
***
Основные характеристики средств измерения
Главная страница
Дистанционное образование
Специальности
Учебные дисциплины
Олимпиады и тесты
Определения и классификация измерений
Измерение – нахождение значения физической величины опытным путем с помощью специальных технических средств. Под измерением понимается процесс физического сравнения данной величины с некоторым её значением, принятым за единицу измерения.
Измерение – познавательный процесс, заключающийся в сравнении опытным путём измеряемой величины с некоторым значением, принятым за единицу измерения.
Из определения измерений следуют признаки измерений:
1) измеряются только физические величины, т.е. параметры реальных объектов;
2) измерение требует проведения опытов;
3) для проведения опытов требуются особые технические средства- средства измерений;
4) результатом измерения является значение физической величины.
Основное уравнение измерения имеет следующий вид:
А = а Х , (2.1)
где А – измеряемая величина, а – единица измерения; Х – численное значение измеряемой величины при выбранной единице измерения. Из уравнения следуют слагаемые процесса измерения:
1) воспроизведение единицы физической величины в виде меры;
2) преобразование измеряемого сигнала;
3) сравнение измеряемой величины с мерой;
4) фиксация результата измерения.
В зависимости от способа нахождения значения измеряемой величины измерения делят на:
1) прямые;
2) косвенные;
3) совокупные;
4) совместные.
Прямым называется измерение, когда искомое значение физической величины находится непосредственно из опытных данных. Следует отметить, что часто под прямыми понимаются такие измерения, при которых не производится промежуточных преобразований. Это, например, измерение напряжения и силы тока известными электроизмерительными приборами – вольтметрами и амперметрами. Прямые измерения очень распространены в метрологической практике. Математически прямые измерения можно охарактеризовать элементарной формулой
А = х, (2.2)
где х – значение величины, найденное путём её измерения и называемое результатом измерения.
Косвенным
называется измерение, при котором искомое значение величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям. Косвенные измерения можно охарактеризовать следующей формулой:
Косвенные измерения можно охарактеризовать следующей формулой:
A = f(x1 , x2 ,…, xm), (2.3)
где x1 , x2 ,…, xm – результаты прямых измерений величин, связанных известной функциональной зависимостью f с искомым значением измеряемой величины А.
Косвенные измерения характерны для практики измерений в телекоммуникационных системах, например, измерение мощности методом амперметра-вольтметра, определение резонансной частоты колебательного контура по результатам прямых измерений ёмкости и индуктивности контура, определение расстояния до места неоднородности в оптическом кабеле методом обратного рассеяния и т.д.
При совокупных измерениях одновременно измеряют несколько одноимённых величин, а их искомые значения находят решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин. Например, измерения, при которых размер ёмкости набора конденсаторов находят по известному значению ёмкости одного конденсатора и результатам прямых сравнений размеров ёмкостей различных сочетаний конденсаторов.
Например, измерения, при которых размер ёмкости набора конденсаторов находят по известному значению ёмкости одного конденсатора и результатам прямых сравнений размеров ёмкостей различных сочетаний конденсаторов.
Совместные измерения состоят в одновременном измерении двух или нескольких неодноимённых величин для нахождения зависимости между ними.
Пример совместных измерений – определение зависимости сопротивления резистора от температуры.
Похожие материалы:
Лекция 7 Виды и методы измерений Обработка
Лекция № 7 Виды и методы измерений. Обработка результатов косвенных измерений. 1
Виды измерений В зависимости от способа обработки экспериментальных данных для получения результата различают следующие виды измерений прямые, косвенные, совместные, совокупные и измерения корреляционно связанных величин. 1. Прямые измерения — это измерения, при которых значения величин находят непосредственно из опытных данных в результате выполнения измерений. Различают однократные и многократные прямые измерения. Примеры: измерение напряжения вольтметром, измерение тока амперметром, сопротивления – омметром. 2
Различают однократные и многократные прямые измерения. Примеры: измерение напряжения вольтметром, измерение тока амперметром, сопротивления – омметром. 2
2. Косвенные измерения это измерения, при которых искомое значение величины Y находят на основании известной зависимости F между этой величиной и другими величинами xj, подвергаемыми прямым измерениям. Примеры: Rx = F(U, I) = U/I Px= F(U, I) = UI Px = F(U, R) = U 2/R Px = F(I, R) = I 2 R 3
3. Совместные измерения одновременные измерения значений нескольких неодноименных величин для определения зависимости между ними. Пример – температурные измерения для определения R 0, A, B измеряется RT при трех температурах и решается система из трех уравнений 4
4. Совокупные измерения одновременные измерения нескольких значений одноименных величин, при которых искомое значение находят решением системы уравнений, составленных по результатам прямых измерений различных сочетаний значений этих величин. 5
5
Обработка результатов косвенных измерений 1. Определяется линейность зависимости, если функция линейна, можно записать: 2. Дисперсия результата определяется выражением: — коэффициент взаимного влияния аргументов xj rkl — коэффициент корреляции аргументов xj 6
Дисперсии аргументов определяются выражением: Коэффициент корреляции: Если rkl 1, то имеется тесная связь между аргументами и ее необходимо учитывать. Если rkl 0, то связи между аргументами нет и ее можно не учитывать. 7
3. Наилучшей оценкой результата является выражение: 4. Результат линейных косвенных измерений записывается в виде: где — при условии rkl 0. 8
5. Если функциональная зависимость F не линейна, можно записать в виде ряда Тейлора: где xj – абсолютные погрешности измерения аргументов; R — остаточный член, который для функции двух аргументов: Остаточным членом пренебрегают, если выполняется условие: R
Дисперсия результата определяется выражением: 6. Результат нелинейных косвенных измерений записывается в виде: где 10
Результат нелинейных косвенных измерений записывается в виде: где 10
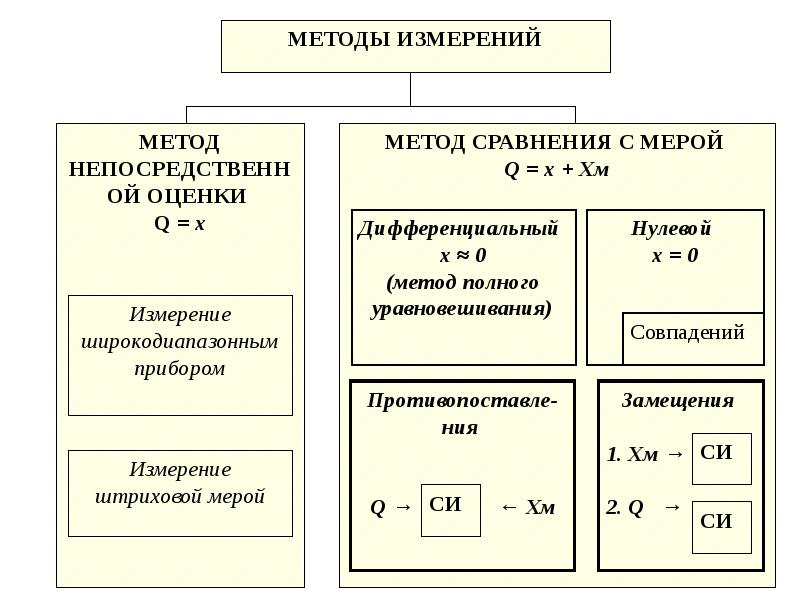
Методы измерения выделяются в зависимости от их взаимодействия с мерой, их классификация показана на рисунке МЕТОДЫ ИЗМЕРЕНИЯ Непосредственной оценки Дифференциальный Совпадения Сравнения с мерой Нулевой Замещения 11
При нулевом методе измерения разность измеряемой и известной величин сводится к нулю, что фиксируется нуль-индикатором – высокочувствительным прибором. Уравнение равновесия моста: Мост постоянного тока для измерения сопротивлений, Г – гальванометр. n = R 1 / R 2 – десятичный множитель 12
При методе замещения производится поочередное подключение на вход прибора измеряемой и известной величин, по двум показаниям прибора оценивается значение известной величины r. Д SA 1 T ˜ rx r 0 V r 1=100 OM Метод замещения 2 N k Измерение сопротивлений методом замещения. N – осциллограф. 13
При дифференциальном методе разность измеряемой величины известной определяется при помощи измерительного прибора. Дифференциальный метод ΔUx V Ux U 0 R U Схема измерения напряжения дифференциальным методом 14
Дифференциальный метод ΔUx V Ux U 0 R U Схема измерения напряжения дифференциальным методом 14
Примеры расчета неопределенности измерений — Profilab.by
Примеры расчета неопределенности измерений
Оценивание неопределенности измерений (количественных величин) – одна из важных задач, стоящих перед каждой лабораторией. Требование к оцениванию неопределенности измерений заложено в межгосударственном стандарте ГОСТ ISO/IEC 17025-2019, а также политике ILAC-G17:2002.
Чтобы получить предварительную информацию по теме Неопределенность измерений, посмотрите, пожалуйста, наше обучающее видео:
Международное метрологическое сообщество давно уже разработало и приняло основные принципы концепции неопределенности, закрепив их в серии международных документов JCGM (Joint Committee for Guides in Metrology), а также документах ISO/IEC Guide 98. Разработано много дополнительных руководств по различных подходам оценивания неопределенности измерений в конкретных областях испытаний/измерений (EA, EURACHEM, Nordtest, EUROLAB и т.д.).
Разработано много дополнительных руководств по различных подходам оценивания неопределенности измерений в конкретных областях испытаний/измерений (EA, EURACHEM, Nordtest, EUROLAB и т.д.).
ОНЛАЙН-КАЛЬКУЛЯТОР
Расчет составляющей неопределенности измерений из-за построения градуировочного графика
ПОДРОБНЕЕ
Несмотря на хорошо разработанные и представленные в документах свободного доступа теоретические принципы и подходы оценивания, и даже наличия конкретных примеров, у специалистов лабораторий все еще остаются вопросы по практической реализации этих принципов и подходов для измерений, проводимых в их лаборатории.
Ближайшие семинары:
«Внутренний аудит системы менеджмента в испытательных и калибровочных лабораториях» — 25 января (онлайн)
Программа семинара рассчитана на специалистов, ответственных за планирование и проведение внутренних аудитов систем менеджмента, а также участвующих во внутренних аудитах. Семинар также будет полезен для специалистов, ответственных за разработку, внедрение и актуализацию системы менеджмента…
Семинар также будет полезен для специалистов, ответственных за разработку, внедрение и актуализацию системы менеджмента…
ПОДРОБНЕЕ
«Микробиологические исследования: валидация и верификация методов микробиологического анализа. Контроль качества» — 26-27 января (онлайн)
В соответствии с требованиями ГОСТ ISO/IEC 17025-2019 компетентная лаборатория должна использовать валидированные методы измерений, оценивать неопределенность измерений количественных величин и проводить периодический контроль качества измерений. Эти требования касаются и деятельности микробиологических лабораторий, которые могут испытывать трудности с практической реализацией упомянутых процедур, в частности с правильным применением статистических методов обработки данных…
ПОДРОБНЕЕ
«Неопределенность измерения величин: основные принципы и подходы к оцениванию (при проведении химических и био-аналитических измерений)» — 2-3 февраля (онлайн)
Оценивание неопределенности измерения является одним из требований ГОСТ ISO/IEC 17025-2019.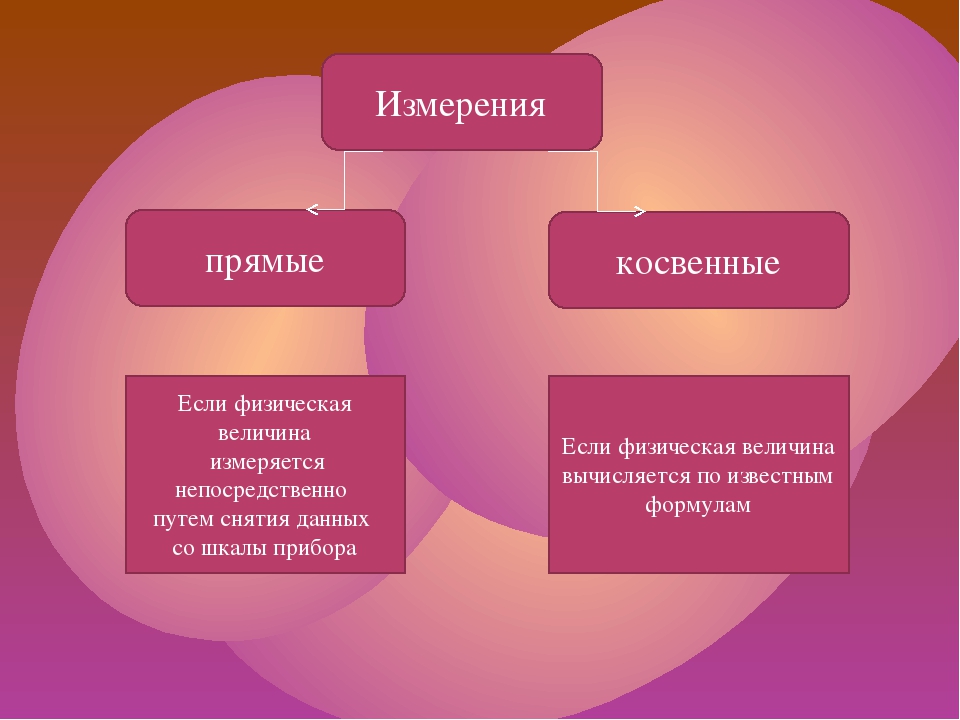 Не смотря на то, что требование к оцениванию неопределенности измерения предъявляется уже более 10 лет и лаборатории имеют большой опыт, все еще остаются вопросы, связанные с практической реализацией процедуры оценивания неопределенности…
Не смотря на то, что требование к оцениванию неопределенности измерения предъявляется уже более 10 лет и лаборатории имеют большой опыт, все еще остаются вопросы, связанные с практической реализацией процедуры оценивания неопределенности…
ПОДРОБНЕЕ
С целью наглядного представления основных принципов концепции неопределенности измерений и подхода моделирования предлагаем Вашему вниманию решение нескольких несложных, но часто встречающейся в практике многих испытательных лабораторий, задач:
Пример 1. Оценивание неопределенности измерений массовой доли влаги
Пример 2. Оценивание неопределенности измерений сопротивления изоляции
Пример 3. Оценивание неопределенности измерений коэффициента поправки титрованного раствора
Пример 4. Оценивание неопределенности измерений pH воды
Пример 5. Оценивание неопределенности измерений относительного удлинения эластичного герметика
Пример 6.
 Оценивание неопределенности измерений прочности бетона на растяжение при изгибе
Оценивание неопределенности измерений прочности бетона на растяжение при изгибе
Пример 7. Оценивание неопределенности измерений твердости по Бриннелю
Пример 1. Оценивание неопределенности измерений массовой доли влаги
Исходные данные:
- Объект измерений – углекислый барий
- Измеряемая величина – массовая доля влаги
- Единицы измерений – процент (%)
- Методика выполнения измерения – ГОСТ 2149-75 «Барий углекислый технический. Технические условия»
- Метод измерений – метод высушивания пробы до постоянной массы
Этап 1. Составление функции измерений
Функция измерений для измеряемой величины составляется на основании принципа измерений, заложенного в методе измерений, и описанного для реализации в методике выполнения измерений.
Массовую долю влаги бария углекислого Х в процентах вычисляют на основании ГОСТ 2149 (п. 3.5) в соответствии с функцией измерений:
3.5) в соответствии с функцией измерений:
где Хi – массовая доля влаги i-ой пробы углекислого бария, %;
m1 – масса стаканчика для взвешивания с навеской до высушивания, г;
m2 – масса стаканчика для взвешивания с навеской после высушивания, г;
m – масса навески углекислого бария, г;
mcт – масса стаканчика для взвешивания, г;
i – номер параллельной пробы, i = 1, 2;
F – поправочный множитель, учитывающий допускаемое расхождение между параллельными определениями.
Разработка/Валидация МЕТОДИК
Выполним работы по разработке Методик измерений
ПОДРОБНЕЕ ОБ УСЛУГЕ
МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ
В комплекте с автоматизированным расчетом
ПОДРОБНЕЕ ОБ УСЛУГЕ
Этап 2.
 Анализ входных величин
Анализ входных величин
1) Масса стаканчика для взвешивания с навеской до высушивания, m1
Масса стаканчика для взвешивания с навеской до высушивания определяется путем взвешивания на весах лабораторных AV264C. При измерении влажности двух проб бария углекислого были получены следующие значения входной величины:
- для первой пробы m1(1) = 41,0055 г,
- для второй пробы m1(2) = 41,3842 г.
Неопределенность, связанную с величиной m1, оцениваем, используя данные производителя на весы. В паспорте на весы лабораторные AV264C для диапазона измерений до 50 г указаны пределы погрешности взвешивания ± 0,001 г. Поскольку значение дано без доверительной вероятности, принимаем прямоугольное распределение значений погрешности взвешивания в этих границах. Стандартная неопределенность массы стаканчика для взвешивания с навеской до высушивания m1 оценивается по типу В и составляет:
2) Масса стаканчика для взвешивания, mcт
Масса стаканчика для взвешивания определяется путем взвешивания на весах лабораторных AV264C. При измерении влажности двух проб бария углекислого были получены следующие значения входной величины:
При измерении влажности двух проб бария углекислого были получены следующие значения входной величины:
- для первой пробы mст(1) = 21,0034 г,
- для второй пробы mст(2) = 21,3822 г.
Неопределенность массы стаканчика для взвешивания после высушивания обусловлена двумя факторами:
- погрешностью взвешивания стаканчика на весах;
- возможными отклонениями массы стаканчика после высушивания вследствие нечеткого определения в методике выполнения измерений момента, в который масса стаканчика после высушивания будет являться постоянной величиной.
Стандартная неопределенность u1(mcт), связанная с погрешностью взвешивания, оценивается на основании данных производителя на весы лабораторные AV264C, определяется аналогично неопределенности величины m1 и составляет u1(mcт) = 0,00058 г.
Стандартную неопределенность u2(mcт), обусловленную отклонениями массы стаканчика для взвешивания после высушивания, можно определить на основании информации о том, что разность между двумя последующими взвешиваниями стаканчика для взвешивания после сушки не должна превышать 0,002 г (принято лабораторией, поскольку ГОСТ 2149-75 четко не устанавливает момент, в который масса стаканчика после высушивания будет являться постоянной величиной). Это значение можно рассматривать как 95-% доверительный интервал для разности двух оценок величины, распределенной по нормальному закону распределения (предел повторяемости по СТБ ИСО 5725-6). Стандартная неопределенность u2(mcт) будет равна стандартному отклонению, рассчитанному на основании указанного интервала по типу В по формуле:
Это значение можно рассматривать как 95-% доверительный интервал для разности двух оценок величины, распределенной по нормальному закону распределения (предел повторяемости по СТБ ИСО 5725-6). Стандартная неопределенность u2(mcт) будет равна стандартному отклонению, рассчитанному на основании указанного интервала по типу В по формуле:
Суммарную стандартную неопределенность величины mcт находим путем суммирования квадратов стандартных неопределенностей перечисленных выше двух вкладов:
3) Масса стаканчика для взвешивания с навеской после высушивания, m2
Масса стаканчика для взвешивания с навеской после высушивания определяется путем взвешивания на весах лабораторных AV264C. При измерении влажности двух проб бария углекислого были получены следующие значения входной величины:
- для первой пробы m2(1) = 40,9850 г,
- для второй пробы m2(2) = 41,3638 г.

Неопределенность массы стаканчика для взвешивания с навеской после высушивания обусловлена двумя факторами:
- погрешностью взвешивания пробы на весах;
- возможными отклонениями массы пробы после высушивания вследствие нечеткого определения в методе испытаний момента, в который масса пробы после высушивания будет являться постоянной величиной.
Стандартная неопределенность u1(m2), связанная с погрешностью взвешивания, оценивается на основании данных производителя на весы лабораторные AV264C, определяется аналогично неопределенности величины m2 и составляет u1(m2) = 0,00058 г.
Стандартную неопределенность u2(m2), обусловленную отклонениями массы стаканчика для взвешивания с навеской после высушивания, можно определить на основании информации о том, что разность между двумя последующими взвешиваниями стаканчика для взвешивания с навеской пробы бария углекислого после сушки не должна превышать 0,002 г (принято лабораторией, поскольку ГОСТ 2149-75 четко не устанавливает момент, в который масса пробы после высушивания будет являться постоянной величиной). Это значение можно рассматривать как 95-% доверительный интервал для разности двух оценок величины, распределенной по нормальному закону распределения (предел повторяемости по СТБ ИСО 5725-6). Стандартная неопределенность u2(m2) будет равна стандартному отклонению, рассчитанному на основании указанного интервала по типу В по формуле:
Это значение можно рассматривать как 95-% доверительный интервал для разности двух оценок величины, распределенной по нормальному закону распределения (предел повторяемости по СТБ ИСО 5725-6). Стандартная неопределенность u2(m2) будет равна стандартному отклонению, рассчитанному на основании указанного интервала по типу В по формуле:
Суммарную стандартную неопределенность величины m2 находим путем суммирования квадратов стандартных неопределенностей перечисленных выше двух вкладов:
4) Поправочный множитель, учитывающий допускаемое расхождение между параллельными определениями, F
Значение оценки величины принимается равным единице: F = 1.
Стандартная неопределенность поправочного множителя рассчитывается на основании информации о допускаемом расхождении между параллельными определениями влажности, приведенными в ГОСТ 2149-75 (п.3.5.2). Приведенное допускаемое относительное расхождение составляет r = 20 % и рассматривается как 95-% доверительный интервал для разности двух оценок величины, распределенной по нормальному закону распределения.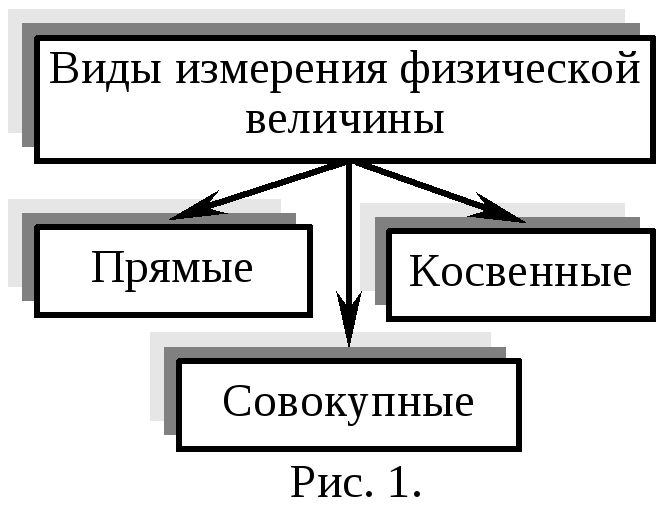 Стандартная неопределенность поправочного множителя будет равна стандартному отклонению, рассчитанному на основании указанного интервала, с учетом того, что за результат измерения принимают среднее арифметические определений двух параллельных проб, по типу В по формуле:
Стандартная неопределенность поправочного множителя будет равна стандартному отклонению, рассчитанному на основании указанного интервала, с учетом того, что за результат измерения принимают среднее арифметические определений двух параллельных проб, по типу В по формуле:
Этап 3. Анализ корреляций
Все входные величины рассматриваются как некоррелированные, поскольку получены независимо друг от друга в различных экспериментах.
ОБУЧЕНИЕ ПРОЦЕДУРЕ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ (химия и аналитика)
Семинар: «Неопределенность измерения величин: основные принципы и подходы к оцениванию»
ПОДРОБНЕЕ О СЕМИНАРЕ
ОБУЧЕНИЕ ПРОЦЕДУРЕ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ (прямые методы измерений)
Семинар: «Неопределенность измерения величин: основные принципы и подходы к оцениванию»
ПОДРОБНЕЕ О СЕМИНАРЕ
Этап 4. Измеренное значение величины
Массовая доля влаги i-ой пробы углекислого бария рассчитывается по формуле (2):
Расхождение между результатами измерений двух параллельных проб не превышает допускаемого значения, установленного в ГОСТ 2149-75 (п. 3.5.2):
3.5.2):
Массовая доля влаги бария углекислого Х в процентах вычисляется в соответствии с функцией измерений (1):
Измеренное значение (оценку измеряемой величины) округляют до четырех знаков после запятой (принято лабораторией, поскольку ГОСТ 2149-75 четко не устанавливает требования к округлению результата измерения).
Этап 5. Суммарная стандартная неопределенность
Стандартную неопределенность измеряемой величины Х получаем по закону распространения неопределенностей путем суммирования квадратов произведений стандартных неопределенностей всех влияющих величин, входящих в функции измерений (1) и (2), на соответствующие коэффициенты чувствительности:
где коэффициенты чувствительности рассчитываются как частные производные функции измерений по входным величинам:
Примечание – Для вычисления коэффициентов чувствительности можно использовать либо минимальные значения масс, полученные при измерении массовой доли влаги i-ой пробы бария углекислого, либо результаты измерений масс, полученные на определенной пробе бария углекислого. В данном примере коэффициенты чувствительности рассчитываются на основании результатов измерений масс для первой пробы.
В данном примере коэффициенты чувствительности рассчитываются на основании результатов измерений масс для первой пробы.
Суммарная стандартная неопределенность составит
Этап 6. Бюджет неопределенности
В таблице представлен бюджет неопределенности для измеряемой величины.
Вклад в неопределенность от j-ой входной величины рассчитывается как произведение стандартной неопределенности этой величины на соответствующий коэффициент чувствительности.
Этап 7. Расширенная неопределенность
Расширенную неопределенность U получаем умножением суммарной стандартной неопределенности на коэффициент охвата k, который выбирается равным 2 при уровне доверия приблизительно 95 % в предположении нормального распределения вероятностей измеряемой величины:
Этап 8. Представление результата измерения
Результат измерения массовой доли влаги углекислого бария представляют в виде:
«Массовая доля влаги бария углекислого составила (0,1022 ± 0,0150) %, где число, следующее за знаком ±, является численным значением расширенной неопределенности, которая получена умножением суммарной стандартной неопределенности на коэффициент охвата k = 2, основанный на предполагаемом нормальном распределении, и определяет интервал, соответствующий вероятности охвата приблизительно 95 %».
Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.
Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.
УЗНАТЬ СТОИМОСТЬ РАЗРАБОТКИ МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ…
Пример 2. Оценивание неопределенности измерений сопротивления изоляции
Исходные данные:
- Объект измерений – кабель силовой АВБбШв
- Измеряемая величина – сопротивления изоляции
- Единицы измерений – МОм
- Измерение сопротивления изоляции выполняется методом непосредственной оценки с помощью мегаомметра Е6-24
Измерения проведены в диапазоне измерений мегаомметра Е6-24 от 100 до 999 МОм при температуре окружающего воздуха 22 °С и относительной влажности воздуха 65 %.
Этап 1. Составление функции измерений
Сопротивление изоляции определяется в соответствии со следующей функцией измерений
где R – сопротивление изоляции, МОм;
Rind – среднее арифметическое повторных измерений сопротивления изоляции, МОм;
FΔ – поправка, учитывающая допускаемую основную погрешность измерения сопротивления мегаомметра Е6-24, МОм;
Fс – поправка, учитывающая единицу младшего разряда, выдаваемых мегаомметром Е6-24 показаний сопротивления, МОм.
Примечание – В функции измерений не учитываются поправки FΔt и FΔφ на дополнительные погрешности измерения сопротивления мегаомметра Е6-24, вызванные отклонением соответственно температуры и влажности окружающей среды от нормальных условий в рабочем диапазоне. Поправки будут вводиться только в случае, если измеренные значения температуры и/или относительной влажности окружающей среды находятся в рабочем диапазоне, но выходят за диапазон нормальных условий эксплуатации мегаомметра Е6-24 (значения нормальных и рабочих условий эксплуатации указаны в руководстве по эксплуатации мегаомметра Е6-24).
Этап 2. Анализ входных величин
1) Среднее арифметическое повторных измерений сопротивления изоляции Rind, МОм.
При проведении измерений сопротивления изоляции кабеля силового АВБбШв получены следующие результаты повторных измерений: R1 = 124 МОм; R2 = 131 МОм; R3 = 137 МОм.
Значение оценки величины Rind определяется по формуле
где Ri – результат i-го повторного измерения сопротивления изоляции, определяемый как показание, снимаемое с дисплея мегаомметра Е6-24, МОм;
n – количество повторных измерений, n = 3.
Стандартная неопределенность измерений величины Rind, МОм, рассчитывается в предположении нормального распределения вероятностей по формуле
2) Поправка, учитывающая допускаемую основную погрешность измерения сопротивления мегаомметра Е6-24, FΔ
Значение оценки величины FΔ принимается равным 0,0 МОм.
Стандартная неопределенность u(FΔ), МОм, оценивается на основании информации о пределах допускаемой основной абсолютной погрешности измерения сопротивления мегаомметра Е6-24 ± Δ, МОм. В предположении прямоугольного распределения вероятностей значений погрешности в границах ± Δ определяется по формуле
Примечание — согласно [1] пределы допускаемой основной погрешности измерения сопротивления приведены в виде ± (% + е.м.р.) т. е. для получения пределов абсолютной погрешности измерения Δ нужно воспользоваться формулой
где δ» – допускаемая относительная погрешность измерения сопротивления, которая принимается равной первому числу, стоящему в [1] в записи пределов допускаемой основной погрешности измерения сопротивления, %;
100 – коэффициент перехода от долей к процентам, %;
m – второе число стоящее в [1] в записи пределов допускаемой основной погрешности измерения сопротивления, определяющее количество единиц младшего разряда;
с – единица младшего разряда выдаваемого мегаомметром Е6-24 показания сопротивления, МОм.
3) Поправка, учитывающая единицу младшего разряда выдаваемых мегаомметром Е6-24 показаний сопротивления, Fс
Значение оценки величины Fc принимается равным 0,0 МОм.
Стандартная неопределенность u(Fc), МОм, определяется на основании информации о единице младшего разряда выдаваемого мегаомметром Е6-24 показания сопротивления c = 1 МОм (для диапазона измерений мегаомметра Е6-24 от 100 до 999 МОм). В предположении прямоугольного распределения вероятностей значений величины c в границах ± c/2 определяется по формуле
Этап 3. Анализ корреляций
Все величины, входящие в функцию измерений (1), рассматриваются как некоррелированные.
Этап 4. Оценка измеряемой величины
Значение оценки величины R, МОм, «сопротивление изоляции» рассчитывается по формуле (1)
Значение сопротивления изоляции (МОм) округляют до одного знака после запятой.
Этап 5. Суммарная стандартная неопределенность
Суммарная стандартная неопределенность измерений сопротивления изоляции силового кабеля u(R), МОм, определяется по формуле
Процентные вклады неопределенностей влияющих величин в суммарную стандартную неопределенность u(R) определяются по формулам
Этап 6. Бюджет неопределенности
Бюджет неопределенности измерений сопротивления изоляции силового кабеля представлен в таблице 1.
Таблица 1 – Бюджет неопределенности измерений сопротивления изоляции силового кабеля
Этап 7. Расширенная неопределенность
Расширенная неопределенность измерений сопротивления изоляции силового кабеля U(R), МОм, определяется для вероятности 95 % в предположении распределения Стьюдента по формуле
где коэффициент охвата k = 2,26, выбирается в зависимости от числа эффективных степеней свободы veff, которое рассчитывается по формуле
Этап 8.
 Результат измерения
Результат измерения
Сопротивление изоляции силового кабеля АВБбШв составило
(130,7 ± 12,5) МОм (k = 2,26, veff = 9,14, Р = 95 %).
Библиография
[1] РЛПА 411218.001 РЭ Руководство по эксплуатации. Мегаомметры Е6-24, E6-24/1 и E6-24/2.
Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.
Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.
УЗНАТЬ СТОИМОСТЬ РАЗРАБОТКИ МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ…
Пример 3. Оценивание неопределенности измерений коэффициента поправки титрованного раствора
Исходные данные:
- Объект измерений – раствор серной кислоты концентрации моль/дм3
- Измеряемая величина – коэффициента поправки 0,1 моль/дм3 раствора серной кислоты
- Единицы измерений – безразмерная величина
- Методика измерений – ГОСТ 25794.
 1 83 «Реактивы. Методы приготовления титрованных растворов для кислотно-основного титрования»
1 83 «Реактивы. Методы приготовления титрованных растворов для кислотно-основного титрования» - Метод измерений – титриметрический по безводному углекислому натрию
Этап 1. Составление функции измерений
Значение оценки коэффициента поправки 0,1 моль/дм3 раствора серной кислоты Ki, при единичном определении рассчитывается по формуле:
где m – масса навески безводного углекислого натрия, г;
P – чистота реактива безводного углекислого натрия, P = 1;
M – молярная масса эквивалента безводного углекислого натрия, г/моль;
с – заданная молярная концентрация серной кислоты в 0,1 моль/дм3 растворе серной кислоты, с = 0,1 моль/дм3, рассматривается как постоянная и не учитывается при расчете неопределенности измерений коэффициента K;
V – объем 0,1 моль/дм3 раствора серной кислоты, израсходованный на титрование, см3.
1000 – коэффициент перехода единицы измерения объема см3 в дм3.
Значение оценки коэффициента K вычисляется как среднее арифметическое трех повторных определений коэффициента поправки раствора серной кислоты по формуле:
где F – поправочный коэффициент, учитывающий расхождение между результатами повторных определений коэффициента поправки раствора серной кислоты, F = 1.
Расхождение между результатами трех повторных определений коэффициента поправки раствора серной кислоты не должно превышать значения 0,001, установленного ГОСТ 25794.1 (п. 1.11).
Этап 2. Анализ входных величин
2.1 Масса навески безводного углекислого натрия, m
Значение массы навески безводного углекислого натрия, m, г, определяется как разность показаний весов при взвешивании стаканчика с навеской установочного вещества и пустого стаканчика.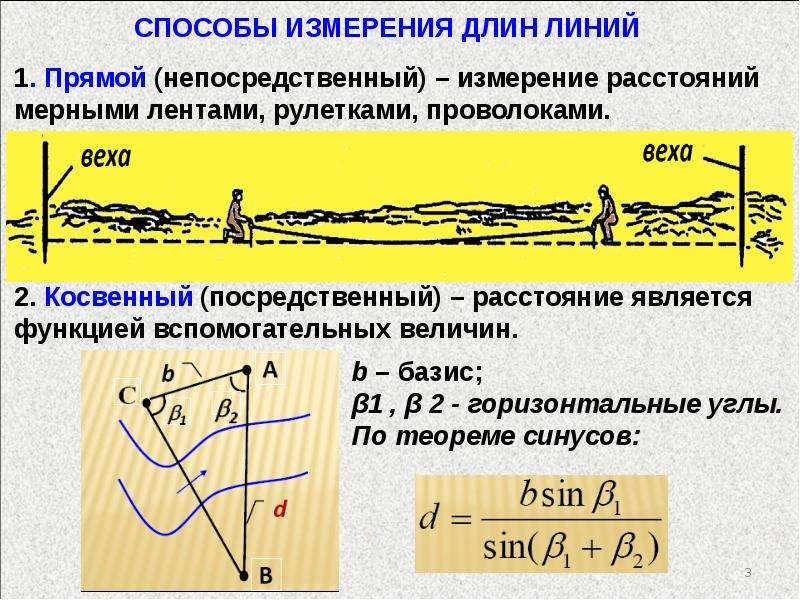 При выполнении измерения были получены следующие значения выходной величины для трех повторных определений коэффициента поправки: m1 = 0,1648 г; m2 = 0,1643 г; m3 = 0,1649 г.
При выполнении измерения были получены следующие значения выходной величины для трех повторных определений коэффициента поправки: m1 = 0,1648 г; m2 = 0,1643 г; m3 = 0,1649 г.
Стандартная неопределенность измерений массы навески установочного вещества, u(m), г, оценивается на основании информации о пределах допускаемой погрешности используемых весов ВСЛ-200/0,1А ± Δm = ± 0,001 г в диапазоне измерений от 0,01 до 50 г, и дискретности отсчета весов d = 0,0001 г, установленных в технической документации на весы. В предположении прямоугольного распределения вероятностей значений погрешности и дискретности в границах ± Δm и ± d/2 соответственно и учитывая двойное взвешивание (пустого стаканчика и стаканчика с навеской установочного вещества) стандартная неопределенность u(m) рассчитывается по формуле:
2.2 Чистота реактива безводного углекислого натрия, P
Значение оценки величины P принимается равным 1.
Стандартная неопределенность измерений степени чистоты реактива углекислого натрия u(P) оценивается на основании информации о том, что согласно ГОСТ 83-79 «Реактивы. Натрий углекислый. Технические условия» массовая доля углекислого натрия в реактиве безводного углекислого натрия составляет не менее 99,8 %. Неопределенность измерений u(P) рассчитывается исходя из отклонения значения чистоты реактива от 1 в предположении прямоугольного распределения величины Р в границах ± (1 – 0,998) по формуле:
2.3 Молярная масса эквивалента безводного углекислого натрия, M
Значение оценки величины M, г/моль, определяется как произведение фактора эквивалентности безводного углекислого натрия fэ = 1/2 на молярную массу установочного вещества M0, г/моль, по формуле:
где молярная масса безводного углекислого натрия (Na2CO3) рассчитывается на основании значений атомных масс натрия, углерода и кислорода A, взятых из таблиц атомных масс IUPAC (//www. sbcs.qmul.ac.uk/iupac/AtWt/), и количества атомов этих элементов в молекуле безводного углекислого натрия n (ANa ≈ 22,98976928, Aс = 12,011, A0 = 15,999, nNa= 2, nс = 1, n0 = 3):
sbcs.qmul.ac.uk/iupac/AtWt/), и количества атомов этих элементов в молекуле безводного углекислого натрия n (ANa ≈ 22,98976928, Aс = 12,011, A0 = 15,999, nNa= 2, nс = 1, n0 = 3):
Стандартная неопределенность измерений молярной массы эквивалента безводного углекислого натрия, u(M), г/моль, определяется на основании возможных разбросов значений атомных масс углерода и кислорода ΔА = Amax – Amin и неопределенности последней цифры атомной массы натрия ΔA, а также количества атомов этих элементов в молекуле безводного углекислого натрия n. Данные по разбросам значений атомных масс углерода и кислорода и неопределенности последней цифры атомной массы натрия выбираются из таблиц атомных масс IUPAC (//www.sbcs.qmul.ac.uk/iupac/AtWt/). Стандартная неопределенность значений атомных масс химических элементов рассчитывается в предположении прямоугольного распределения вероятностей атомных масс элементов в границах ± ΔА/2 (для углерода и кислорода) и в границах ± ΔA (для натрия). Неопределенность для вклада атомов одного элемента рассчитывается умножением стандартной неопределенности атомной массы элемента на количество атомов элемента. Стандартная неопределенность измерений молярной массы эквивалента безводного углекислого натрия, u(M), г/моль, определяется по формуле:
Неопределенность для вклада атомов одного элемента рассчитывается умножением стандартной неопределенности атомной массы элемента на количество атомов элемента. Стандартная неопределенность измерений молярной массы эквивалента безводного углекислого натрия, u(M), г/моль, определяется по формуле:
2.4 Объем раствора серной кислоты, израсходованный на титрование, V
Значение оценки величины V, см3, определяется по шкале бюретки номинальной вместимостью 25 см3 2-го класса точности по ГОСТ 29251-91 «Посуда лабораторная стеклянная. Бюретки. Часть 1. Общие требования». При выполнении измерения были получены следующие значения выходной величины для трех повторных определений коэффициента поправки: V1= 31,1 см3; V2= 31,0 см3; V3= 31,1 см3.
Стандартная неопределенность измерений объема 0,1 моль/дм3 раствора серной кислоты, израсходованного на титрование, u(V), см3, состоит из следующих основных вкладов:
- стандартная неопределенность, обусловленная погрешностью измерения объема сливаемой жидкости используемой бюретки, u(VΔ), см3;
- стандартная неопределенность, обусловленная ценой наименьшего деления шкалы используемой бюретки, u(Vc), см3;
- стандартная неопределенность, обусловленная отличием температуры, при которой проводятся измерения, от температуры, при которой нормируется погрешность измерения объема сливаемой жидкости бюретки, u(Vt), см3.

Стандартная неопределенность u(VΔ), см3, рассчитывается на основании информации о пределах погрешности измерения сливаемой жидкости бюреткой ± ΔV = 0,1 см3, установленных ГОСТ 29251 в предположении треугольного распределения погрешности в установленных пределах по формуле:
Стандартная неопределенность u(Vc), см3, рассчитывается на основании информации о цене наименьшего деления шкалы используемой бюретки см3, в предположении прямоугольного распределения вероятностей цены деления в пределах ± dV/2 по формуле:
Стандартная неопределенность u(Vt), см3, рассчитывается в предположении прямоугольного распределения исходя из возможных пределов изменения объема жидкости при условии колебания температуры в лаборатории при измерении в пределах (20 ± 5) °С (Δt = 5 °С) и коэффициента объемного расширения жидкости kV, ºС-1, равного 0,00021 ºС-1 для воды (основное вещество в растворе) по формуле:
Примечание – Для оценивания стандартной неопределенности u(Vt) используется измеренное значение объема раствора серной кислоты, пошедшего на титрование, полученное для первой навески безводного углекислого натрия.
Суммарная стандартная неопределенность измерений объема 0,1 моль/дм3 раствора серной кислоты, израсходованного на титрование, u(V), см3 вычисляется путем суммирования стандартных неопределенностей перечисленных выше вкладов по формуле:
2.5 Поправочный коэффициент, учитывающий расхождение между результатами повторных определений коэффициента поправки раствора серной кислоты, F
Значение оценки величины F принимается равным 1.
Стандартная неопределенность измерений поправочного коэффициента, учитывающего расхождение между результатами повторных определений коэффициента поправки раствора серной кислоты, u(F), определяется на основании установленного ГОСТ 25794.1 (п. 1.11) допускаемого расхождения между результатами повторных определений коэффициента поправки r = 0,001, которое рассматривается как предел повторяемости согласно СТБ ИСО 5725-6-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике». С учетом того, что за результат измерения принимается среднее арифметическое трех определений, стандартная неопределенность u(F) определяется по формуле:
Часть 6. Использование значений точности на практике». С учетом того, что за результат измерения принимается среднее арифметическое трех определений, стандартная неопределенность u(F) определяется по формуле:
Этап 3. Анализ корреляций
Все входные величины рассматриваются как некоррелированные, поскольку получены независимо друг от друга в различных экспериментах.
Этап 4. Оценка измеряемой величины
Значения коэффициента поправки раствора серной кислоты при i-ом определении согласно формуле (1) составляют:
Максимальное расхождение между результатами трех определений не превышает допускаемого значения, установленного ГОСТ 25794.1:
Значение коэффициента поправки раствора серной кислоты определяется по формуле (2) на основании результатов параллельных определений, которые рассчитываются по формуле (1):
Коэффициент поправки вычисляют с точностью до четвертого десятичного знака. Полученное значение коэффициента поправки раствора серной кислоты удовлетворяет требованию ГОСТ 25794.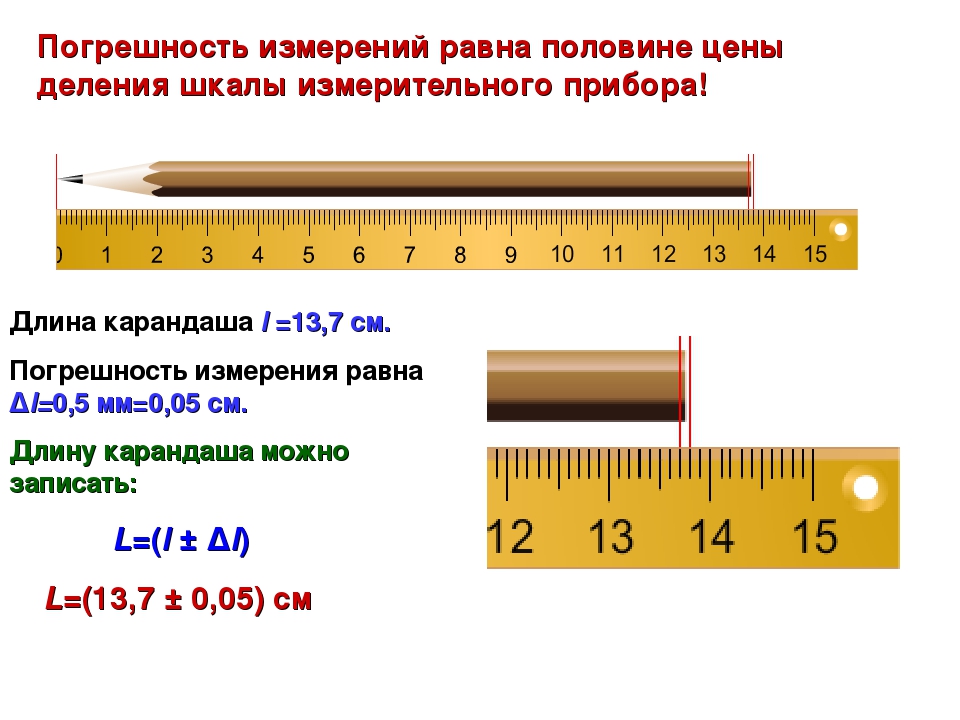 1 (п. 1.11) о том, что значение коэффициента поправки должно соответствовать диапазону .
1 (п. 1.11) о том, что значение коэффициента поправки должно соответствовать диапазону .
Этап 5. Суммарная стандартная неопределенность
Суммарная стандартная неопределенность измерений коэффициента поправки K определяется по закону распространения неопределенностей путем суммирования относительных стандартных неопределенностей всех влияющих величин, входящих в функции измерений (1) и (2), по формуле:
Примечание — Для оценивания суммарной стандартной неопределенности u(K) используются значения оценок влияющих величин (измеренные значения), полученные для первой навески безводного углекислого натрия.
Значения относительных стандартных неопределенностей влияющих величин рассчитываются как отношение стандартной неопределенности влияющей величины к значению оценки влияющей величины.
Значения процентных вкладов неопределенностей влияющих величин в суммарную стандартную неопределенность рассчитываются как умноженное на 100 % отношение квадрата относительной стандартной неопределенности влияющей величины к квадрату относительной суммарной стандартной неопределенности.
Этап 6. Бюджет неопределенности
В таблице представлен бюджет неопределенности измерений коэффициента поправки серной кислоты.
Этап 7. Расширенная неопределенность
Расширенная неопределенность измерений коэффициента поправки серной кислоты, U(K), получается умножением суммарной стандартной неопределенности, u(K), на коэффициент охвата k, который выбирается равным 2 при уровне доверия приблизительно 95 % в предположении нормального распределения вероятностей измеряемой величины:
Этап 8. Результат измерения
Коэффициент поправки раствора серной кислоты концентрации c(H2SO4) = 0,1 моль/дм3 составляет (1,0001 ± 0,0108), где число, следующее за знаком ±, является численным значением расширенной неопределенности, которая получена умножением суммарной стандартной неопределенности на коэффициент охвата k = 2, основанный на предполагаемом нормальном распределении, и определяет интервал, соответствующий вероятности охвата приблизительно 95 %.
Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.
Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.
УЗНАТЬ СТОИМОСТЬ РАЗРАБОТКИ МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ…
Пример 4. Оценивание неопределенности измерений pH воды
Измерительная задача
Метод основан на измерении разности потенциалов гальванического элемента с использованием соответствующего рН-метра. Измерения проводят рН-метром/иономером ИТАН. Перед измерением пробы воды про-водится двухточечная калибровка по буферным растворам. Температура пробы питьевой воды и температура буферных растворов измеряется термодатчиком, встроенным в рН-метр.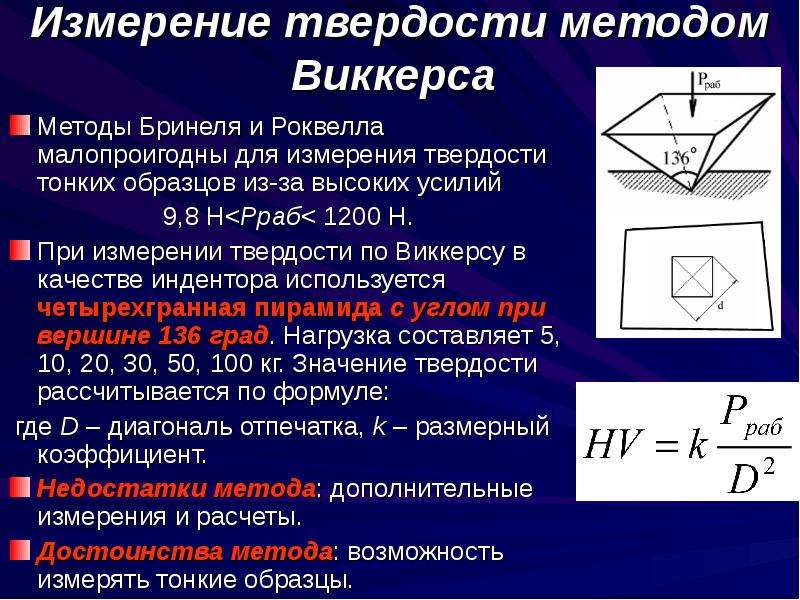 рН-метр автоматически учитывает разность температур буферных растворов и пробы питьевой воды в выдаваемых показаниях.
рН-метр автоматически учитывает разность температур буферных растворов и пробы питьевой воды в выдаваемых показаниях.
Этап 1. Составление функции измерений
Измеряемой величиной является рН пробы питьевой воды, ед. рН, которая определяется согласно функции измерений:
где рНизм – показания рН-метра, ед. рН;
δкал – поправка на погрешность калибровки рН-метра, ед. рН;
δсх – поправка на повторяемость измерений, ед. рН.
Измеренное значение величины округляют до одного десятичного знака.
Результаты измерений
Температура пробы питьевой воды, измеренная термодатчиком рН-метра, составила 10 °С. При измерении пробы питьевой воды с цифрового дисплея рН-метра было снято показание рН равное 6,52 ед. рН.
Этап 2. Анализ входных величин
2.1 Показания рН-метра (рНизм)
Показание рН-метра составило рНизм = 6,52 ед. рН.
Стандартная неопределенность величины рНизм рассчитывается на основании информации о пределах основной допускаемой абсолютной погрешности рН-метра в предположении прямоугольного распределения вероятностей. В паспорте на рН-метр/иономер ИТАН указаны пределы основной допускаемой абсолютной погрешности измерения рН (измерительным преобразователем в комплекте с электродной системой в растворах с температурой от 10 °С до 60 °С) ± Δ = ± 0,050 ед. рН. Стандартная неопределенность величины рНизм рассчитывается по формуле:
В паспорте на рН-метр/иономер ИТАН указаны пределы основной допускаемой абсолютной погрешности измерения рН (измерительным преобразователем в комплекте с электродной системой в растворах с температурой от 10 °С до 60 °С) ± Δ = ± 0,050 ед. рН. Стандартная неопределенность величины рНизм рассчитывается по формуле:
Примечание – Неопределенностью измерений, обусловленной разрешающей способностью цифрового дисплея рН-метра пренебрегаем, поскольку данная составляющая неопределенности значительно ниже составляющей, обусловленной основной допускаемой абсолютной погрешностью рН-метра.
2.2 Поправка на погрешность калибровки рН-метра (δкал)
Поправка на погрешность калибровки рН-метра оценивается значением «нуль»
δкал = 0 ед. рН.
Стандартная неопределенность измерений величины δкал рассчитывается на основании информации о допускаемом отклонении значений рН, при проверке калибровки, от значений рН буферных растворов в контрольных точках ± Δк = ± 0,03 ед. рН. Стандартная неопределенность величины δкал рассчитывается в предположении прямо-угольного распределения вероятностей в указанных границах по формуле:
рН. Стандартная неопределенность величины δкал рассчитывается в предположении прямо-угольного распределения вероятностей в указанных границах по формуле:
Примечание – Неопределенностью измерений рН буферных растворов пренебрегаем, т.к. значения расширенных неопределенностей измерений рН буферных растворов не превышают 1/3 от допускаемого отклонения Δк.
2.3 Поправка на повторяемость измерений (δсх)
Поправка на повторяемость измерений рН оценивается значением «нуль» δсх = 0 ед. рН.
Стандартная неопределенность измерений величины δсх рассчитывается на основании информации о стандартном отклонении повторяемости в предположении нормального распределения вероятностей. Для питьевой воды в диапазоне рН от 6,35 до 6,46 ед. рН при межлабораторном исследовании метода измерений рН было установлено значение стандартного отклонения повторяемости σr = 0,011 ед. рН. В лаборатории при внедрении метода измерений установленное значение показателя повторяемости было подтверждено и распространено на диапазон измерений, содержащий измеренное значение рН в исследуемой пробе питьевой воды. Стандартная неопределенность величины δсх рассчитывается по формуле:
Стандартная неопределенность величины δсх рассчитывается по формуле:
Этап 3. Анализ корреляций
Все входные величины рассматриваются как некоррелированные.
Этап 4. Измеренное значение величины
рН пробы питьевой воды будет оцениваться в соответствии с выражением (1) и составит:
Этап 5. Суммарная стандартная неопределенность
Суммарная стандартная неопределенность измерений величины рН рассчитывается по формуле:
Коэффициенты чувствительности для всех влияющих величин, входящих в функцию измерений (1), будут равны 1.
Этап 6. Бюджет неопределенности
В таблице представлен бюджет неопределенности для измеряемой величины и произведены соответствующие расчеты для нахождения ее стандартной неопределенности.
Таблица – Бюджет неопределенности для рН пробы питьевой воды
Этап 7. Расширенная неопределенность
Расширенная неопределенность U получается умножением суммарной стандартной неопределенности на коэффициент охвата k, который выбирается равным 2 при уровне доверия 95 % в предположении нормального распределения вероятностей измеряемой величины:
Этап 8.
 Представление результата измерения
Представление результата измерения
Результат измерения записывается в виде:
«рН пробы воды составила (6,5 ± 0,1) ед. рН, k = 2, P = 95 %».
Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.
Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.
УЗНАТЬ СТОИМОСТЬ РАЗРАБОТКИ МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ…
Пример 5. Оценивание неопределенности измерений относительного удлинения эластичного герметика
Измерительная задача
Относительное удлинение герметика полиуретанового определяется по ГОСТ 21751-76 «Герметики. Метод определения условной прочности относительного удлинения при разрыве и относительной остаточной деформации после разрыва» с применением разрывной машины РМ-30-1 методом растяжения образцов с постоянной скоростью при заданной температуре до разрыва с последующим измерением геометрических параметров образца.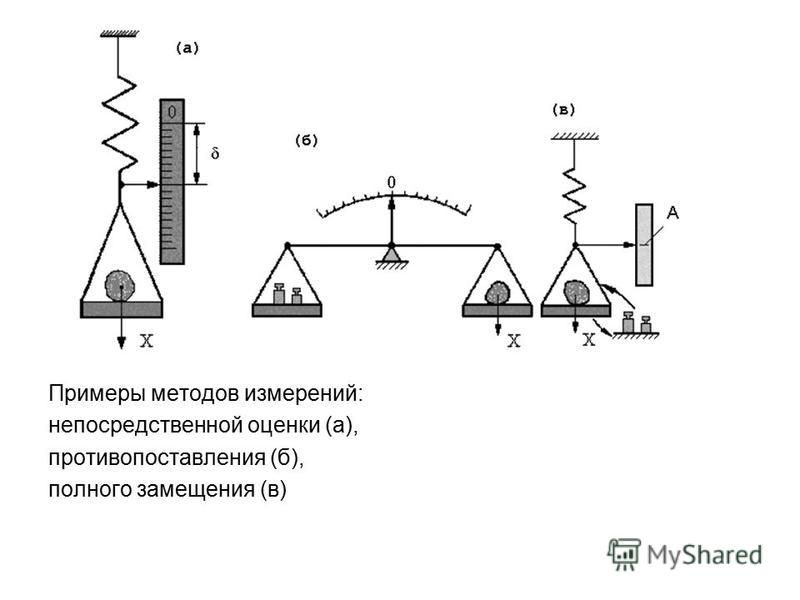 Длина рабочего участка образца до и после приложения нагрузки измеряется линейкой металлической по ГОСТ 427-75 с пределом измерений 300 мм и ценой деления 1 мм.
Длина рабочего участка образца до и после приложения нагрузки измеряется линейкой металлической по ГОСТ 427-75 с пределом измерений 300 мм и ценой деления 1 мм.
Образцы герметика для испытаний типа 1 вырезают длиной (115 ± 1) мм специальным ножом согласно ГОСТ 21751 (пп. 1.3, 2.1-2.4). Общее количество испытываемых образцов – 5. Испытания проводят при температуре окружающего воздуха (20 ± 3) ºС и относительной влажности (65 ± 5) %.
Этап 1. Составление функции измерений
Относительное удлинение каждого испытываемого образца, εрi, в процентах рассчитывается на основании функции измерений:
где lpi – длина рабочего участка образца в момент разрыва, мм;
l0 – первоначальная длина рабочего участка образца, мм.
Относительное удлинение герметика полиуретанового рассчитывается как среднее арифметическое относительных удлинений, εрi, полученных для каждого из испытываемых образцов:
где – среднее арифметическое измерений относительного удлинения пяти образцах, %;
t – количество испытанных образцов герметика;
Fr – поправка на рассеяние результатов измерений относительных удлинений, полученных на всех испытанных образцах, %.
Результат измерения округляется до целых чисел.
Результаты измерений
При определении относительного удлинение герметика полиуретанового было испытано 5 образцов. Результаты испытаний представлены в таблице 1.
Таблица 1 – Результаты испытаний образов герметика полиуретанового на относительное удлинение
Этап 2. Анализ входных величин
2.1 Среднее арифметическое измерений относительного удлинения пяти образцах ()
Значение оценки рассчитывается по формуле
Возможное рассеяние результатов измерений относительного удлинения на пяти единичных образцах герметика учитывается через влияющую величину F.
2.2 Первоначальная длина рабочего участка образца (l0i)
Тип оценивания неопределенности: В
Вид распределения: трапецеидальное
Значение оценки: получают путем снятия показаний со шкалы линейки при прямых измерениях длины рабочего участка образца до проведения испытаний, мм; значения для каждого образца представлены в таблице 1
Стандартная неопределенность: u(l0i) = 0,294 мм
Неопределенность, связанная с величиной l0i, оценивается на основании информации о допускаемом отклонении от номинальных значений длины шкалы используемой линейки с пределом измерений 300 мм ±Δl = ±0,10 мм и цене деления линейки d = 1 мм. Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:
Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:
2.3 Длина рабочего участка образца в момент разрыва (lpi)
Вид распределения: трапецеидальное
Значение оценки: получают путем снятия показаний со шкалы линейки при прямых измерениях длины рабочего участка образца после проведения испытаний, мм; значения для каждого образца представлены в таблице 1
Стандартная неопределенность: u(lpi) = 0,294 мм
Неопределенность, связанная с величиной lpi, оценивается на основании информации о допускаемом отклонении от номинальных значений длины шкалы используемой линейки с пределом измерений 300 мм ±Δl = ±0,10 мм и цене деления линейки d = 1 мм. Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:
Стандартная неопределенность оценивается по типу В и составляет:
2.4 Поправка на рассеяние результатов измерений относительных удлинений, полученных на всех испытанных образцах (Fr )
Тип оценивания неопределенности: А
Вид распределения: нормальное
Значение оценки: Fr = 0,0 %
Стандартная неопределенность: u(Fr) = 22,80 %
Стандартная неопределенность поправки рассчитывается как стандартное отклонение среднего арифметического измерений относительного удлинения пяти образцах по типу А в предположении нормального распределения и составляет:
Этап 3. Анализ корреляций
Все входные величины рассматриваются как некоррелированные.
Этап 4. Измеренное значение величины
Оценка измеряемой величины – относительное удлинение герметика, εр, в процентах, рассчитывается по формуле (1) используя полученные в Этапе 2 значения оценок входных величин:
Этап 5.
 Суммарная стандартная неопределенность
Суммарная стандартная неопределенность
Стандартную неопределенность измеряемой величины εр, %, рассчитываем по закону распространения неопределенностей путем суммирования квадратов произведений стандартных неопределенностей влияющих величин, входящих в функции измерений (1) и (2), на соответствующие коэффициенты чувствительности:
Коэффициенты чувствительности рассчитываются как частные производные функции измерений (1) по входным величинам:
Примечание – Для расчета коэффициентов чувствительности используются значения параметров, полученные при испытаниях первого образца герметика.
Вклад в неопределенность от j-ой входной величины рассчитывается как произведение стандартной неопределенности этой величины на соответствующий коэффициент чувствительности. Процентный вклад рассчитывается как отношение квадрата вклада входной величины к квадрату суммарной стандартной неопределенности (выражается в процентах):
Этап 6.
 Бюджет неопределенности
Бюджет неопределенности
Бюджет неопределенности для относительного удлинения герметика представлен в таблице 3.
Таблица 3 – Бюджет неопределенности для относительного удлинения
Этап 7. Расширенная неопределенность
Расширенную неопределенность U получаем умножением суммарной стандартной неопределенности на коэффициент охвата k. Поскольку в бюджете неопределенности доминирует составляющая, распределенная по нормальному закону распределения и рассчитанная на малом объеме экспериментальных данных (менее 10), то значение коэффициента охвата выбирается в предположении распределения Стьюдента для измеряемой величины как квантиль распределения Стьюдента при вероятности 95 % и числе эффективных степеней свободы, которые рассчитываются по формуле Уэлча-Саттертуэта
Значение коэффициента охвата принимается равным k = 2,57. Расширенная неопределенность будет рассчитываться по формуле:
Этап 8. Представление результата измерения
Результат измерения представляют в виде:
«Относительное удлинение герметика полиуретанового составило (580 ±63) %, где число, следующее за знаком ±, является численным значением расширенной неопределенности, которая получена умножением суммарной стандартной неопределенности на коэффициент охвата k = 2,78, основанный на предполагаемом распределении Стьюдента и числе эффективных степеней свободы νeff = 5, и определяет интервал, соответствующий вероятности охвата 95 %».
Библиография
ГОСТ 21751-76 Герметики. Метод определения условной прочности относительного удлинения при разрыве и относительной остаточной деформации после разрыва
ГОСТ 427-75 Линейки измерительные металлические. Технические условия
Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.
Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.
УЗНАТЬ СТОИМОСТЬ РАЗРАБОТКИ МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ…
Пример 6. Оценивание неопределенности измерений прочности бетона на растяжение при изгибе
Измерительная задача
Прочность на растяжение при изгибе бетона класса прочности на растяжение при изгибе Вtb3,6 определяется по ГОСТ 10180-2012 «Бетоны. Методы определения прочности по контрольным образцам» путем разрушающих кратковременных статических испытаний специально изготовленных контрольных образцов бетона. В качестве контрольных образцов используются изготовленные согласно ГОСТ 10180 (п. 4) образцы бетона в форме призмы квадратного сечения 100×100×400 мм. Количество контрольных образцов в серии – три.
Методы определения прочности по контрольным образцам» путем разрушающих кратковременных статических испытаний специально изготовленных контрольных образцов бетона. В качестве контрольных образцов используются изготовленные согласно ГОСТ 10180 (п. 4) образцы бетона в форме призмы квадратного сечения 100×100×400 мм. Количество контрольных образцов в серии – три.
Испытания контрольных образцов на прочность на растяжение при изгибе проводят на универсальной испытательной машине C093-03A. Линейные размеры образцов измеряют линейкой металлической по ГОСТ 427-75 с пределом измерений 500 мм и ценой деления 1 мм.
Этап 1. Составление функции измерений
Прочность бетона на растяжение при изгибе для i-го образца в серии Rtb,i, МПа, вычисляется в соответствии со следующей функцией измерений:
где δ – масштабный коэффициент для приведения прочности бетона к прочности бетона в образцах базовых размера и формы;
Fi – разрушающая нагрузка для i-го контрольного образца, Н;
ai – ширина поперечного сечения призмы для i-го контрольного образца, мм;
bi – высота поперечного сечения призмы для i-го контрольного образца, мм;
l – расстояние между опорами, мм.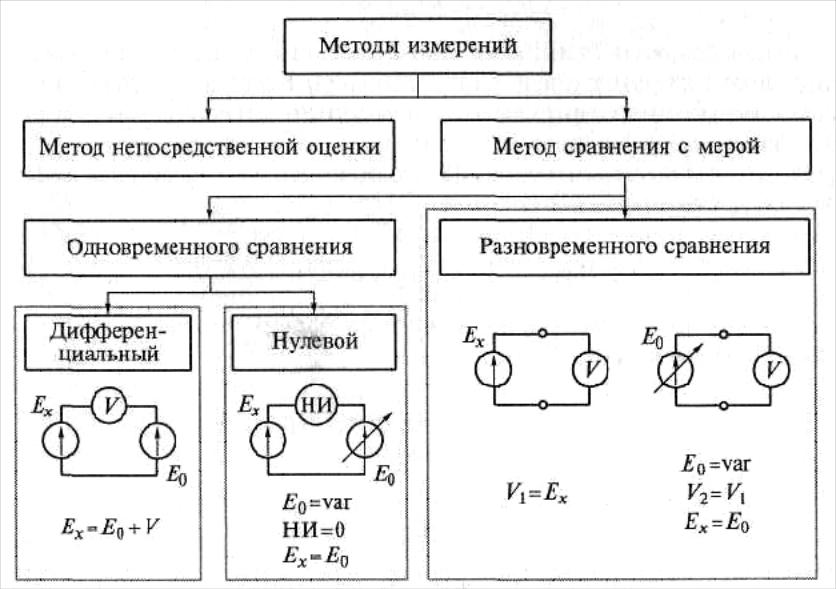
Прочность бетона на растяжение при изгибе Rtb, МПа, вычисляется в соответствии со следующей функцией измерений:
где Fr – поправочный коэффициент, учитывающий расхождение между результатами измерений прочности n образцов, Fr = 1;
n – количество образцов в серии, n = 3.
Измеренное значение прочности бетона на растяжение при изгибе округляется с точностью до 0,01 МПа.
Результаты измерений
При проведении испытаний трех контрольных образцов бетона на растяжение при изгибе были получены значения параметров, представленные в таблице 1.
Таблица 1 – Результаты испытаний контрольных образцов бетона на прочность на растяжение при изгибе
Этап 2. Анализ входных величин
2.1 Масштабный коэффициент для приведения прочности бетона к прочности бетона в образцах базовых размера и формы (δ)
Значение оценки выбирается согласно ГОСТ 10180 (таблица 1) и составляет δ = 0,92.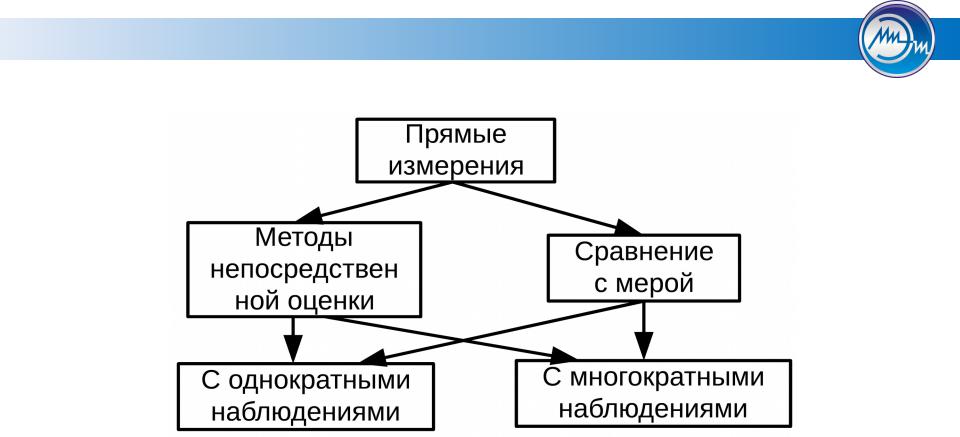
Величина рассматривается как постоянная.
2.2 Разрушающая нагрузка для i-го контрольного образца (Fi)
Значение оценки величины Fi для каждого контрольного образца определяется по шкале отсчетного устройства испытательной машины и представлено в таблице 1
Тип оценивания неопределенности: В
Вид распределения: трапецеидальное
Стандартная неопределенность: u(F) = 164,04 Н
Неопределенность, связанная с величиной F, оценивается на основании информации о пределах допускаемой относительной погрешности показания силы ± δF = ± 1 % и цене деления шкалы стрелочного индикатора d = 500 Н. Поскольку значения приведены без вероятности, принимаем прямоугольное распределение значений погрешности показаний силы и ошибки оператора при снятии показаний со шкалы индикатора в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:
Примечание – Для расчета стандартной неопределенности разрушающей нагрузки используется значение параметра, полученное при испытаниях первого контрольного образца.
2.3 Ширина поперечного сечения призмы для i-го контрольного образца (ai)
Значение оценки величины аi для каждого контрольного образца определяется по шкале линейки металлической и представлено в таблице 1
Тип оценивания неопределенности: В
Вид распределения: трапецеидальное
Стандартная неопределенность: u(а) = 0,301 мм
Неопределенность, связанная с величиной а, оценивается на основании информации о допускаемом отклонении от номинальных значений длины шкалы используемой линейки с пределом измерений 500 мм ±Δl = ±0,15 мм и цене деления линейки dl = 1 мм. Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:
2.4 Высота поперечного сечения призмы для i-го контрольного образца (bi)
Значение оценки величины bi для каждого контрольного образца определяется по шкале линейки металлической и представлено в таблице 1
Тип оценивания неопределенности: В
Вид распределения: трапецеидальное
Стандартная неопределенность: u(b) = 0,301 мм
Неопределенность, связанная с величиной b, оценивается на основании информации о допускаемом отклонении от номинальных значений длины шкалы используемой линейки с пределом измерений 500 мм ±Δl = ±0,15 мм и цене деления линейки dl = 1 мм. Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:
Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:
2.5 Расстояние между опорами (l)
Значение оценки величины l = 300 мм и определяется по шкале линейки металлической
Тип оценивания неопределенности: В
Вид распределения: трапецеидальное
Стандартная неопределенность: u(l) = 0,301 мм
Неопределенность, связанная с величиной l, оценивается на основании информации о допускаемом отклонении от номинальных значений длины шкалы используемой линейки с пределом измерений 500 мм ±Δl = ±0,15 мм и цене деления линейки dl = 1 мм. Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:
Стандартная неопределенность оценивается по типу В и составляет:
2.6 Поправочный коэффициент, учитывающий расхождение между результатами измерений прочности n образцов (Fr)
Значение оценки: Fr = 1
Тип оценивания неопределенности: B
Вид распределения: нормальное
Стандартная неопределенность: u(Fr) = 0,06
Стандартная неопределенность поправки рассчитывается на основании среднего внутрисерийного коэффициента вариации прочности бетона, установленного в лаборатории согласно ГОСТ 10180 (Приложение А) и равного 6 %. Стандартная неопределенность оценивается по типу В в предположении нормального распределения и составляет:
Примечание – Для использования в расчетах установленного в лаборатории среднего внутрисерийного коэффициента вариации следует проверить соответствие реального разброса результатов измерений прочности бетона на растяжение при изгибе, полученного на испытанных контрольных образцах, установленному среднему внутрисерийному коэффициенту вариации используя положения СТБ ИСО 5725-6 и следующее неравенство:
где f(n) – коэффициент критического размаха, выбирается в зависимости от количества контрольных образцов в серии n по СТБ ИСО 5725-6 (таблица 1).
Для нашего примера f(n=3) = 3,3 и неравенство (8) выполняется:
Этап 3. Анализ корреляций
При измерении величин а и b, близких по измеренным значением, присутствуют корреляционные эффекты, связанные с применением одного средства измерений (линейки металлической) в одной точке диапазона измерений (узком диапазоне измерений) и вызванные погрешностью применяемого средства измерений. Однако, учитывая, что вклад этой составляющей в стандартные неопределенности величин а и b незначителен (в процентном выражении составляет 8,3 %), существующей корреляцией пренебрегаем и не учитываем при расчете суммарной стандартной неопределенности измеряемой величины: прочности бетона на растяжение при изгибе.
Все остальные входные величины рассматриваются как некоррелированные.
Этап 4. Измеренное значение величины
Оценка измеряемой величины – прочности бетона на растяжение при изгибе, Rtb, МПа, рассчитывается по формуле (2) используя полученные в таблице 1 значения оценок входных величин:
Этап 5.
 Суммарная стандартная неопределенность
Суммарная стандартная неопределенность
Стандартную неопределенность измеряемой величины Rtb, МПа, рассчитываем по закону распространения неопределенностей путем суммирования квадратов относительных стандартных неопределенностей влияющих величин, входящих в функции измерений (1) и (2):
и составляет для нашего примера
Примечание – Для расчета относительных стандартных неопределенностей входных величин используются значения величин, полученные для первого контрольного образца.
Значения процентных вкладов неопределенностей влияющих величин в суммарную стандартную неопределенность рассчитываются как умноженное на 100 % квадрат отношения относительной стандартной неопределенности влияющей величины к относительной суммарной стандартной неопределенности:
Этап 6. Бюджет неопределенности
Бюджет неопределенности для прочности бетона на растяжение при изгибе представлен в таблице 3.
Таблица 3 – Бюджет неопределенности для прочности бетона на растяжение при изгибе
Этап 7.
 Расширенная неопределенность
Расширенная неопределенность
Расширенную неопределенность U получаем умножением суммарной стандартной неопределенности на коэффициент охвата k = 2 в предположении нормального распределения при уровне доверия приблизительно 95 %:
Этап 8. Представление результата измерения
Результат измерения представляют в виде:
«Прочность бетона на растяжение при изгибе бетона класса прочности на растяжение при изгибе Вtb3,6 составила (3,65 0,45) МПа, где число, следующее за знаком ±, является численным значением расширенной неопределенности, которая получена умножением суммарной стандартной неопределенности на коэффициент охвата k = 2, основанный на предполагаемом нормальном распределении, и определяет интервал, соответствующий вероятности охвата приблизительно 95 %».
Библиография
ГОСТ 10180-2012 Бетоны. Методы определения прочности по контрольным образцам
ГОСТ 427-75 Линейки измерительные металлические. Технические условия
Технические условия
СТБ ИСО 5725-6-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике
Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.
Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.
УЗНАТЬ СТОИМОСТЬ РАЗРАБОТКИ МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ…
Пример 7. Оценивание неопределенности измерений твердости по Бриннелю
Измерительная задача
Измерение твердости трубопровода из Стали 10Г2СД по шкале Бриннеля выполняется твердомером ТКМ-459
Условия проведения измерений:
- температура окружающего воздуха +15 ºС;
- относительная влажность 60 %;
- толщина контролируемого участка детали 10 мм;
- шероховатость поверхности, на которой производится измерение Rа 1,2.

Этап 1. Составление функции измерений
Измеряемой величиной является твердость контролируемого участка объекта контроля по шкале Бринелля, Н, которая определяется как:
где Низм – показания твердомера, НВ;
δт – поправка на погрешность твердомера, НВ;
δр – поправка на разрешающую способность дисплея твердомера, НВ.
Результаты измерений
На контролируемом участке были получены следующие единичные результаты наблюдения твердости по шкале Бринелля:
h2 = 180 НВ
h3 = 184 НВ
h4 = 175 НВ
h5 = 172 НВ
H5 = 183 НВ
Этап 2. Анализ входных величин
2.1 Показания твердомера (Низм)
Показания твердомера оцениваются как среднее арифметическое из 5 единичных результатов наблюдений твердости контролируемого участка объекта контроля по формуле:
Стандартная неопределенность величины Низм рассчитывается как среднее квадратическое отклонение среднего арифметического из 5 единичных результатов наблюдений по формуле:
Примечание – Данная составляющая может не учитываться, если отклонение максимального единичного показания твердости от минимального не превышает предела основной допускаемой погрешности твердомера.
2.2 Поправка на погрешность твердомера (δт)
Поправка на погрешность твердомера оценивается значением «нуль». В паспорте на твердомер установлены пределы абсолютной погрешности ± Δ = ± 15 НВ при измерении по шкале Бринелля (НВ). Стандартная неопределенность поправки определяется по типу В на основании установленных пределов абсолютной погрешности твердомера в предположении прямоугольного закона распределения: 2.3 Поправка на разрешающую способность дисплея твердомера (δр)
Поправка на разрешающую способность дисплея твердомера оценивается значением «нуль». Стандартная неопределенность поправки определяется через величину единицы наименьшего разряда дисплея (а = 1 НВ).
Стандартная неопределенность поправки на разрешающую способность дисплея твердо-мера оценивается по типу В в предположении прямоугольного распределения из выражения:
Этап 3. Анализ корреляций
Все входные величины рассматриваются как некоррелированные.
Этап 4. Измеренное значение величины
Твердость контролируемого участка трубопровода будет оцениваться в соответствии с выражением (1) и составит:
Этап 5. Суммарная стандартная неопределенность
Суммарная стандартная неопределенность, приписываемая результату измерения Н, рас-считывается по формуле:
Коэффициенты чувствительности для всех влияющих величин, входящих в функцию измерений (1), будут равны 1.
Этап 6. Бюджет неопределенности
В таблице представлен бюджет неопределенности для измеряемой величины и произведены соответствующие расчеты для нахождения ее стандартной неопределенности.
Таблица – Бюджет неопределенности для твердости по шкале Бриннеля Н
Этап 7. Расширенная неопределенность
Суммарное распределение измеряемой величины предполагаем прямоугольным (по-скольку доминирует составляющая неопределенности от величины δт, процентный вклад составляет более 90 %). Коэффициент охвата для уровня доверия 95 % принимается равным k = 1,65. Расширенную неопределенность рассчитываем по формуле:
Коэффициент охвата для уровня доверия 95 % принимается равным k = 1,65. Расширенную неопределенность рассчитываем по формуле:
Этап 8. Представление результата измерения
Результат измерения записывается в виде:
«Твердость по Бринеллю контролируемого участка трубопровода из Стали 10Г2СД со-ставила (180 ± 15) НВ, k = 1,65, P = 95 %».
Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.
Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.
УЗНАТЬ СТОИМОСТЬ РАЗРАБОТКИ МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ…
Прямые и косвенные измерения в физике — видео и стенограмма урока
Прямые измерения
Прямые измерения — более простые из двух типов измерений, которые мы рассмотрим в этом уроке. Прямое измерение происходит, когда вы производите измерение явно той характеристики объекта, которую хотите измерить. Например, вы можете напрямую измерить свой рост с помощью рулетки, вы можете напрямую измерить температуру в духовке с помощью термометра, и вы можете напрямую измерить продолжительность утренней пробежки с помощью секундомера.
Одним из распространенных примеров прямого измерения в физике является измерение тока. Когда мы хотим измерить ток, протекающий по проводу в физике, мы используем амперметр, подключенный к цепи, чтобы напрямую измерить его. Это прямое измерение, потому что амперметр измеряет ток в проводе без необходимости предварительно знать какую-либо другую информацию.
Косвенные измерения
Хотя прямые измерения — это те виды измерений, с которыми вы, возможно, наиболее знакомы, на самом деле они менее распространены в физике, чем косвенные измерения.Косвенное измерение выполняется, когда вы измеряете что-то еще и преобразуете его в измерение рассматриваемой характеристики. Концепция косвенных измерений может показаться вам странной, но вы будете делать это постоянно, работая с физикой.
Например, давайте посмотрим на определение напряжения ( В, ) в цепи с одним резистором 200 Ом ( R ) путем косвенного измерения. Вы можете измерить ток ( I ) непосредственно с помощью амперметра, а затем найти напряжение, используя закон Ома, В = IR .В этом примере мы скажем, что измерили ток в цепи амперметром и составили 0,025 А.
Итак, напрямую измерив ток, а затем преобразовав его в напряжение по закону Ома, мы провели косвенное измерение напряжения. Хотя этот пример довольно прост, это именно то, что физики постоянно делают в своих экспериментах. Они проводят прямые измерения и преобразовывают их для получения других косвенных измерений. Вы даже сделаете это сами, работая над физическими задачами в курсе физики.Информация, которую дает вам проблема, подобна прямому измерению, а информация, которую вы получаете при решении проблемы, подобна косвенному измерению.
Итоги урока
Давайте рассмотрим. Умение проводить измерения — важнейший аспект работы физика. Измерения, которые проводят физики, бывают двух разных форм: прямые и косвенные измерения.
Прямое измерение выполняется, когда вы явно измеряете характеристику рассматриваемого объекта.Например, если вы хотите узнать свой рост, вы точно измеряете его с помощью рулетки. Это тип измерения, с которым вы, вероятно, наиболее знакомы, но он менее распространен в физике.
Непрямое измерение выполняется, когда вы находите измерение характеристики объекта путем преобразования из другого измерения. Физики делают это постоянно, работая с формулами. Они находят прямые измерения в эксперименте, а затем используют формулу для преобразования их в косвенные измерения различных характеристик.
Методы измерения и ошибки измерения
Несколько недель назад мы рассмотрели историческое развитие измерительной техники. Сегодня мы хотели бы обсудить различные методы и методы измерения, которые помогают определять различные параметры измеряемой детали. Давайте начнем с нескольких основных терминов, прежде чем мы дадим краткий обзор наиболее распространенных методов измерения.
Метрология
Основы метрологии описаны в стандарте DIN 1319-1: 1995-01.Методы измерения основаны на так называемой «метрологии», которая изучает научные основы разработки средств измерений и их применения. Метрологические находки воплощены в технике средств измерений и их использовании.
Прямые и косвенные методы измерения
В прямом методе измерения измеряемая величина напрямую сравнивается со стандартом (согласованная единица измерения), то есть значение определяется непосредственно на измеряемой части.Примерами в этом контексте являются сравнение длины со шкалой или сравнение массы с балансировочными грузами, такими как балансирные весы. Другими типичными примерами процедур прямого измерения являются измерение напряжения или электрического тока и измерение температуры с помощью ртутного термометра.
Следовательно, процедура прямого измерения является прямым сравнением и поэтому также называется методом сравнения. Необходимые международные «базовые единицы» определены в Международной системе единиц (французский язык: SI, Système international d’unités ).Это метрическая система единиц, охватывающая следующие основные единицы, от которых происходят все остальные единицы:
- Длина (1 м)
- Масса (1 кг)
- Время (1 с)
- Электрический ток (1 А)
- Температура (1К)
- Сила света (1 кд)
- Количество вещества (1 моль).
В определения основных единиц в прошлом были внесены изменения. Например, до 1960 г. первичный счетчик использовался в качестве прототипа для прибора счетчик .Все остальные единицы, кроме килограмма, при этом определяются неизменными естественными константами. Поскольку масса первичного килограмма теоретически может измениться (и, вероятно, изменится), проводятся исследования, чтобы однозначно определить единицу килограмма таким образом.
Если прямое измерение невозможно, используется метод косвенного измерения . Измеряемая величина получается путем измерения других величин, при этом должно быть известно соотношение между физическими величинами.(Пример: определение скорости по формуле «скорость = путь / время»). Поскольку этот вид измерения основан на эталоне, метод косвенного измерения также называется сравнительным измерением.
Аналоговые и цифровые методы измерения
Также проводится различие между аналоговым измерением и цифровым измерением. В аналоговом методе измерение выполняется непрерывно, и размер сигнала аналогичен измеренному значению. Измеренное значение отображается на стрелочном приборе со шкалой (например,г. напряжение, сопротивление). Другой пример аналогового измерения — это измерение температуры с помощью ртутного термометра, как упоминалось выше.
В отличие от этого, в цифровом методе измеренное значение преобразуется в двоичный формат и отображается в числовой форме. Измерение скорости путем подсчета количества оборотов за определенный период времени также является цифровой процедурой измерения.
Хотя цифровые индикаторы позволяют получать более точные показания, чтобы можно было предотвратить ошибки или неточности считывания — как это может случиться с аналоговыми индикаторами — последние обычно считаются более легкими для восприятия людьми, чем цифровые индикаторы.
Непрерывный и прерывистый метод
Как следует из терминов, фактор времени здесь находится на переднем плане, а измерительный сигнал может быть как аналоговым, так и цифровым. Если измеряемая величина постоянно фиксируется, например, с помощью самописца непрерывного действия, это называется непрерывным измерением.
Однако при прерывистом методе путь прохождения сигнала между точкой измерения и измерительным выходом (например, строковым самописцем) активируется только периодически.Измеряемый параметр фиксируется с периодическими прерываниями, например с записывающим устройством с пунктирной линией. Таким образом, значения измеряемого параметра могут быть представлены за более длительный период.
Метод измерения прогиба
Как сказано выше, измерение — это процесс сравнения измеряемой величины с известной величиной, то есть параметром калибровки. В методе измерения отклонения это может быть удлинение, обозначенное на шкале, и вес объекта может быть легко определен, например, с помощью пружинных весов.В этом случае известной величиной является сила пружины, которая увеличивается пропорционально ее прогибу.
Порядок компенсации
В качестве наглядного примера можно использовать балансир. В этом методе измеряемый объект сравнивается с калиброванными эталонами (т. Е. Гирями).
Если гравитационная постоянная изменится, это повлияет на обе стороны баланса.Для определения веса измеряемого объекта выполняется нулевое измерение: то есть эталонный эталон изменяется до тех пор, пока он не будет соответствовать измеренной величине — в примере балансировки балок это выполняется путем добавления или удаления весов.
Погрешности измерения
Абсолютно правильное определение количества невозможно — всегда есть некоторая вариация: погрешность измерения. Это называется разницей между измеренным значением величины и ее истинным значением.Есть несколько причин ошибок измерения. К ним относятся ошибки прибора, ошибки окружающей среды или ошибки человека. Кроме того, проводится различие между «систематическими ошибками» и «случайными ошибками».
Систематические ошибки — это последовательные и, следовательно, воспроизводимые ошибки. Они могут быть вызваны самим измерительным прибором (например, из-за износа, старения или влияния окружающей среды), а также процедурой измерения. Поэтому систематические ошибки можно исправить, приняв соответствующие меры.
Случайные ошибки, напротив, являются несистематическими ошибками, которые могут быть связаны с неправильно откалиброванными приборами, условиями окружающей среды (например, температурой) или оператором (ошибкой считывания). Такие ошибки в конечном итоге можно компенсировать повторными измерениями и определением среднего значения (всегда при условии, что прибор правильно откалиброван).
Расчет ошибки
Поскольку точные измерения невозможны, отклонения измеренных значений от их фактических значений всегда влияют на результат измерения.Следовательно, оно также будет отклоняться от своего истинного значения. Чтобы свести к минимуму такие ошибки, принят метод расчета ошибок. На самом деле этот термин вводит в заблуждение, потому что ошибки не могут быть вычислены, а их можно только оценить реалистично. Следовательно, цель вычисления ошибки состоит в том, чтобы определить наилучшую оценку истинного значения (результата измерения) и величины отклонения (неопределенности измерения).
Существует историческое развитие технологии измерения, которое подробно описано в отдельной статье в блоге.
Источники:
Поведение в отношении здоровья и санитарное просвещение
Введение
TRA / TPB — одна из наиболее часто используемых теорий, которая применяется к поведению в отношении здоровья на протяжении почти 40 лет. Таким образом, измерение конструкций TRA / TPB хорошо установлено.
В этом разделе будет представлено краткое введение с подробным описанием общих характеристик измерения TRA / TPB, таких как типы используемых шкал, необходимость проведения исследований, а также различия в прямых и косвенных измерениях.После введения эти характеристики измерения TRA / TPB будут обсуждаться более подробно и применительно к каждой конструкции.
- 5- или 7-балльная шкала
- Биполярные или двунаправленные шкалы (также известные как шкалы семантического дифференциала): маловероятно / вероятно, не согласен / согласен, хорошо / плохо.
- Униполярные или однонаправленные весы: очень слабый контроль / полный контроль, совсем не беспокоит / очень беспокоит.
- Оценка от -3 до +3 таких, что:
- Вера в то, что поведение приведет к положительному результату, положительно влияет на оценку.
- Убеждение, что поведение приведет к отрицательному результату, отрицательно влияет на оценку.
- Выявительные исследования: исследования, проведенные для выявления и выбора содержания для построения показателей.
- Прямое измерение относится к измерению основного конструкта (например, отношения, субъективных норм, воспринимаемого поведенческого контроля).Обычно они сильнее связаны с результатами, чем косвенные показатели. Продемонстрируйте эти ассоциации, прежде чем переходить к косвенным мерам.
- Косвенное измерение относится к измерению второстепенных конструктов, составляющих основную конструкцию, с последующим вычислением этих оценок по результатам поведения.
- Пример:
- основной конструкт = отношение, косвенные меры измерения
второстепенные конструкты = поведенческие убеждения, оценка
поведенческие исходы; расчет обсуждается позже
- основной конструкт = отношение, косвенные меры измерения
- Важно показать тесную связь между этими показателями и основной конструкцией, чтобы гарантировать, что соответствующие убеждения были измерены.Если так продемонстрировано, они представляют наибольший интерес.
- Пример:
- Оценка надежности прибора путем повторного тестирования и / или надежности внутренней согласованности
Прямые и косвенные измерения с использованием ТТ и ТН
Прямые и косвенные измерения
Для того, чтобы измерял электрические величины , измерительные приборы должны быть подключены к линиям безопасно, с максимальной простотой и удобством.Как правило, основными параметрами, подлежащими обнаружению, являются напряжение и ток, которые, соответственно, требуют параллельного и последовательного подключения к линии, на которой проводятся измерения.
Прямые и косвенные измерения с использованием ТТ и ТН (фото предоставлено frbiz.com)
Вообще говоря, есть два подхода, когда вы хотите проводить измерения:
- Прямые измерения
- Косвенные измерения
Прямые измерения
Прямое подключение к линии определяет прямое измерение количества, поскольку прибор подключается к точке измерения без использования переходников.
Прямое измерение возможно только тогда, когда измеряемая величина имеет уровень, который находится в пределах возможностей прибора !
Например, если необходимо измерить напряжение 230 В, прибор должен иметь емкость, превышающую это значение (например, 300 В). Это также относится к измерениям тока: если необходимо измерить токи до 5 А, потребуется прибор с емкостью не менее 5 А и входом 0-5 А .
Панельные и шкафные приборы для прямых измерений обычно состоят из приборов с очень ограниченной пропускной способностью (измерение малых значений тока и напряжения) с одним или несколькими дополнительными сопротивлениями, вставленными внутри для вольтметров и / или одним или несколькими шунтами для амперметров.
Когда в прибор вставлены емкостные сопротивления, прибор можно подключить непосредственно к линиям, на которых проводится измерение.
Квадратный амперметр и вольтметр, используемые для прямого измерения (фото предоставлено ABB)
Вернуться к измерениям ↑
Косвенные измерения
Когда измеряемая величина превышает емкость измерительного прибора, необходимо вставить трансформатор который уменьшает количество и передает количество в инструмент со значениями, совместимыми с его емкостью.Эта методология определяется как косвенное измерение.
Измерение, проводимое с помощью измерительного трансформатора, определяется как косвенное измерение, поскольку оно не выполняется непосредственно на исследуемой линии.
Например, если ток до 100 A должен быть измерен с током, который имеет емкость 5 A , должен быть вставлен трансформатор тока (CT) с коэффициентом трансформации 100/5. .
Если трансформатор тока является трансформатором с обмоткой первичной обмотки, он последовательно подключается непосредственно к проводнику, на котором необходимо измерить ток.С другой стороны, если это тип со сквозной первичной обмоткой, изолированный или неизолированный провод вставляется внутрь отверстия устройства.
Трансформатор тока имеет выход, который будет подавать ток, который в 20 раз меньше тока, циркулирующего в измеряемом проводе, к которому подключен ток с мощностью 5 А . В трансформаторах тока первичная обмотка предназначена для последовательного подключения к цепи, через которую проходит измеряемый ток, в то время как вторичная обмотка питает один или несколько измерительных приборов (все последовательно соединены друг с другом).
На схеме подключения на Рисунке 1 показаны эти трансформаторы.
Рисунок 1 — Схема подключения трансформатора тока (ТТ)
По сравнению с принципом работы обычного трансформатора, ТТ разработан таким образом, чтобы минимизировать ток намагничивания I 0 , необходимый для создания потока Φ дюйма. ядро.
В этих условиях первичный и вторичный токи находятся в точном противофазе, и их соответствующие эффективные значения находятся в соотношении друг к другу, обратном количеству катушек N 1 и N 2 .Другими словами:
откуда:
Соотношение n катушки между вторичной и первичной обмотками, таким образом, является идеальным коэффициентом трансформации между первичным и вторичным током.
Фактически, магнитный сердечник трансформатора не может иметь нулевого реактивного сопротивления, и стандарты IEC 38-1 определяют для каждого отдельного трансформатора первичные и вторичные опорные токи, которые составляют номинальные токи I Pn и I Sn трансформатора.Отношение между этими двумя токами составляет номинальное отношение :
, которое указывается постоянным указанием числителя и знаменателя: трансформатор тока, например, имеет номинальное отношение от 75 до 5 А, и Для краткости написано как CT 75 A / 5 A .
В таблице 1 показаны коэффициенты и угловые погрешности (разность фаз между первичным и вторичным током), разрешенные стандартами IEC для трансформаторов тока.
Таблица 1 — Коэффициент трансформации трансформатора тока и угловые погрешности, разрешенные стандартом IEC.
| Класс точности | Ток в% от номинального значения | Ошибки соотношения% | Угловые ошибки | |
| в угловых минутах | в сотых долях или в процентах | |||
| 0,1 | 10 | ± 0,25 | ± 10 | ± 0,3 |
| 10 | ± 0,20 | ± 8 | ± 0.24 | |
| 100 | ± 0,1 | ± 5 | ± 0,15 | |
| 120 | ± 0,1 | ± 5 | ± 0,15 | |
| 0,2 | 10 | ± 0,5 | ± 20 | ± 0,6 |
| 20 | ± 0,35 | ± 15 | ± 0,45 | |
| 100 | ± 0,2 | ± 10 | ± 0,3 | |
| 120 | ± 0 .2 | ± 10 | ± 0,3 | |
| 0,5 | 10 | ± 1 | ± 60 | ± 1,8 |
| 20 | ± 0,75 | ± 45 | ± 1,35 | |
| 100 | ± 0,5 | ± 30 | ± 0,9 | |
| 120 | ± 0,5 | ± 30 | ± 0,9 | |
| 1 | 10 | ± 2 | ± 120 | ± 3.6 |
| 10 | ± 1,5 | ± 90 | ± 2,7 | |
| 100 | ± 1 | ± 60 | ± 1,8 | |
| 120 | ± 1 | ± 60 | ± 1,8 | |
| 3 | 50 | ± 3 | без рецепта | |
| 120 | ± 3 | |||
| 5 | 50 | ± 5 | без рецепта | |
| 120 | ± 5 | |||
Когда возникает проблема измерения высокого напряжения или напряжения, превышающего емкость прибора, используются трансформаторы напряжения (обозначаются буквами VT ), на первичную обмотку которого подается измеряемое напряжение U P , в то время как трансформаторы используют вторичную обмотку для питания измерительного прибора. (все параллельно друг другу) при напряжении U S .
На схеме подключения на Рисунке 2 показаны эти трансформаторы.
Рисунок 2 — Схема подключения трансформатора напряжения (ТН)
Аналогично трансформаторам тока, теоретическое соотношение n между количеством катушек двух обмоток (идеальный коэффициент трансформации) определяется формулами:
Однако , на практике падение омического и индуктивного напряжения двух обмоток означает, что отношение U P / U S отличается от отношения n катушек, что приводит к ошибке отношения ηV% .Соответственно, для каждого отдельного трансформатора производитель устанавливает номинальные первичные и вторичные напряжения, которые соответствуют заданному состоянию нагрузки: два определенных напряжения составляют номинальные напряжения трансформатора, которые должны обозначаться соответственно символами U Pn и U Sn .
Соотношение между этими двумя напряжениями — это номинальное отношение трансформатора:
, которое должно всегда указываться с указанием двух терминов: трансформатор напряжения, например, имеет номинальное отношение от 10 000 до 100 В. и для краткости записано как VT 10 000 V / 100 V .Также для ТН в таблице 2 показаны относительные и угловые погрешности, указанные в стандарте IEC.
Таблица 2 — Передаточное отношение и угловые погрешности, разрешенные стандартом IEC.
| Классы | Ошибки отношения% | Угловые ошибки | |
| в угловых минутах | в сотых долях | ||
| 0,1 | ± 0,1 | ± 5 | ± 0,15 |
| 0,2 | ± 0.2 | ± 10 | ± 0,3 |
| 0,5 | ± 0,5 | ± 20 | ± 0,6 |
| 1,0 | ± 1 | ± 40 | ± 1,2 |
| 3,0 | ± 3 | без рецепта | без рецепта |
В заключение этого обсуждения средств измерения напряжения и тока напомним читателю, что при допустимой погрешности измерения, погрешность прибора всегда должна добавляться к погрешности трансформатора.
Например // Если рейтинг точности прибора равен 1,5, а рейтинг точности трансформатора равен 0,5, предел погрешности может составлять ± 2% от считываемого значения (рейтинг точности 2).
Вернуться к измерениям ↑
Ссылка // Практическое руководство по электрическим измерениям в низковольтных распределительных щитах от ABB
Прямое и косвенное измерение физической активности у пожилых людей: систематический обзор литературы | Международный журнал поведенческого питания и физической активности
Группа Всемирного банка: Мировое население. Таблицы прогнозов по странам и группам. 2011, Вашингтон, округ Колумбия: Группа Всемирного банка
Google Scholar
Национальный институт старения и Национальный институт здоровья: Почему старение населения имеет значение: глобальная перспектива. Книга Почему старение населения имеет значение: глобальная перспектива. 2007, Bethesda, MD: Национальный институт старения,
Национальные институты здравоохранения и Департамент здравоохранения и социальных служб
США.
Google Scholar
Haub C: Книга Старение населения мира: часы показывают рост населения в возрасте от 5 до 65 лет. Старение населения мира: часы показывают рост населения в возрасте от 5 до 65 лет. 2011, Вашингтон, округ Колумбия: Справочник по народонаселению Бюро
Google Scholar
Канадское физиологическое общество: Книга канадских рекомендаций по физической активности для пожилых людей — 65 лет и старше.Канадские рекомендации по физической активности для пожилых людей — 65 лет и старше. 2011 г., Оттава, Онтарио: Общественное здравоохранение
Агентство Канады.
Google Scholar
Физическая активность для всех. Сколько физической активности нужно пожилым людям?
http://www.cdc.gov/physicalactivity/everyone/guidelines/olderadults.html
.
Nelson ME, Rejeski WJ, Blair SN, Duncan PW, Judge JO, King AC, Macera CA, Castaneda-Sceppa C: Физическая активность и общественное здоровье у пожилых людей: Рекомендация Американского колледжа спортивной медицины и Американская кардиологическая ассоциация (ACSM / AHA).Тираж. 2007, 116: 1094-1105.
Артикул
Google Scholar
Канадский научно-исследовательский институт фитнеса и образа жизни: Книжный бюллетень 2: Уровни физической активности канадцев. Бюллетень 2: Уровни физической активности канадцев. 2009, Оттава, Онтарио: Канадский научно-исследовательский институт фитнеса и образа жизни
Google Scholar
Ходзко-Зайко В.Дж., Проктор Д.Н., Сингх МАФ, Минсон К.Т., Нигг С.Р., Салем Г.Дж., Скиннер Дж.С.: Упражнения и физическая активность для пожилых людей.Медико-спортивные упражнения. 2009, 41: 1510-1530. 10.1249 / MSS.0b013e3181a0c95c.
Артикул
Google Scholar
Warburton DER, Nicol CW, Bredin SSD: Польза для здоровья от физической активности: доказательства. Кан Мед Асс Дж. 2006, 174: 801-809. 10.1503 / cmaj.051351.
Артикул
Google Scholar
Министерство здравоохранения Канады: Книга «Здоровое старение: физическая активность и пожилые люди».Здоровое старение: физическая активность и пожилые люди. 2002, Оттава, Онтарио: министерство
общественных работ и государственных услуг Канада, 1-14.
Google Scholar
Патерсон Д.Х., Джонс Г.Р., Рис CL: Старение и физическая активность: данные для разработки рекомендаций по упражнениям для пожилых людей. Канадский J. Преп. Общественного здравоохранения Кан де Санте Публик. 2007, 98 (Приложение 2): S69-S108.
Google Scholar
Rikli RE: Надежность, обоснованность и методологические вопросы оценки физической активности у пожилых людей. Res Q Exerc Sport. 2000, 71: 89-96.
Артикул
Google Scholar
Национальный совет по вопросам старения: Книга для пожилых людей в Канаде, табель успеваемости за 2006 год. Табель успеваемости пожилых людей в Канаде за 2006 год. 2006 г., Оттава, Онтарио: Национальный совет по
Старение (NACA).
Google Scholar
Casperen CJ, Powell KE, Christenson GM: Физическая активность, упражнения и физическая подготовка: определения и различия для исследований, связанных со здоровьем. Public Health Rep.1985, 100: 126-131.
Google Scholar
Wilcox S, Ainsworth BE: Глава 17. Измерение физической активности. Справочник по изменению поведения в отношении здоровья. Под редакцией: Шумакер С.А., Окене Дж.К., Рикерт К.А. 2009, Нью-Йорк, Нью-Йорк: Springer Publshing
Компания, ООО, 327-346.3.
Google Scholar
Харада Н.Д., Чиу В., Кинг А.С., Стюарт А.Л.: оценка трех инструментов самоотчета о физической активности для пожилых людей. Медико-спортивные упражнения. 2001, 33: 962-970. 10.1097 / 00005768-200106000-00016.
CAS
Статья
Google Scholar
Shephard RJ: Ограничения измерения обычной физической активности с помощью анкет.Br J Sports Med. 2003, 37: 197-206. 10.1136 / bjsm.37.3.197.
CAS
Статья
Google Scholar
Shephard RJ: Измерение физической активности у пожилых людей: некоторые значения для питания. Может J Aging. 1990, 9: 188-203. 10.1017 / S0714980800013167.
Артикул
Google Scholar
Мерфи С.Л.: Обзор измерения физической активности с помощью акселерометров у пожилых людей: соображения по дизайну и проведению исследования.Предыдущая Мед. 2009, 48: 108-114. 10.1016 / j.ypmed.2008.12.001.
Артикул
Google Scholar
Adamo KB, Prince SA, Tricoo AC, Connor-Gorber S, Tremblay M: Сравнение косвенных и прямых измерений для оценки физической активности в педиатрической популяции: систематический обзор. Int J Pediatr Obes. 2009, 4: 2-27. 10.1080 / 17477160802315010.
Артикул
Google Scholar
Dale D, Welk GJ, Matthews CE: Оценка физической активности для исследований, связанных со здоровьем. Под редакцией: Welk GJ. 2002, Шампейн, Иллинойс: кинетика человека
Издатели.
Prince SA, Adamo KB, Hamel ME, Hardt J, Gorber SC, Tremblay M: Сравнение прямых и самоотчетных показателей для оценки физической активности у взрослых: систематический обзор. Закон Int J Behav Nutr Phys. 2008, 5: 56-10.1186 / 1479-5868-5-56.
Артикул
Google Scholar
Дишман РК: Измерение физической активности. В активном образе жизни, когнитивном функционировании и старении. Под редакцией: Пун Л.В., Ходзко-Зайко В., Томпоровски П.Д. 2006, Шампейн, Иллинойс, США: Human Kinetics, 91–111. Серия статей о старении, упражнениях и познании (Том 1)]
Google Scholar
Тюдор-Локк CE, Майерс AM: Проблемы и возможности измерения физической активности у взрослых, ведущих малоподвижный образ жизни. Sports Med. 2001, 31: 91-100. 10.2165 / 00007256-200131020-00002.
CAS
Статья
Google Scholar
Garatachea N, Luque GT, Gallego JG: Измерения физической активности и расхода энергии с помощью акселерометров у пожилых людей. Nutr Hosp. 2010, 25: 224-230.
CAS
Google Scholar
Динджер М.К., Оман Ф., Тейлор Э.Л., Веселы С.К., Эйбл Дж .: Стабильность и конвергентность шкалы физической активности для пожилых людей (PASE).J Sports Med Phys Fitness. 2004, 44: 186-192.
CAS
Google Scholar
Forsén L, Loland NW, Vuillemin A, Chinapaw MJM, van Poppel MNM, Mokkink LB, van Mechelen W., Terwee CB: Самостоятельно заполняемые анкеты по физической активности для пожилых людей: систематический обзор свойств измерения. Sports Med. 2010, 40: 601-623. 10.2165 / 11531350-000000000-00000.
Артикул
Google Scholar
Hagstromer M, Bowles H: измерение активного и малоподвижного поведения: устранение пробелов в методах самоотчета. Контрольный список для оценки обоснованности и пригодности существующих инструментов физической активности и сидячего поведения. 2010, Бетстеда, Мэриленд: Национальные институты здравоохранения
Google Scholar
Даунс Ш., Блэк Н: Возможность создания контрольного списка для оценки методологического качества рандомизированных и нерандомизированных исследований медицинских вмешательств.J Epidemiol Community Health. 1998, 52: 377-384. 10.1136 / jech.52.6.377.
CAS
Статья
Google Scholar
Фишер Р.А.: О вероятной ошибке коэффициента корреляции, выведенной из небольшой выборки. Метрон. 1921, 1: 1-32.
Google Scholar
Всесторонний мета-анализ: Энглвуд. 2006, Нью-Джерси: Biostat, Inc.
Google Scholar
Bonnefoy M, Normand S, Pachiaudi C, Lacour JR, Laville M, Kostka T. Одновременная проверка десяти анкет по физической активности у пожилых мужчин: исследование воды с двойной маркировкой. J Am Geriatr Soc. 2001, 49: 28-35. 10.1046 / j.1532-5415.2001.49006.x.
CAS
Статья
Google Scholar
Конн В.С., Минор М.А., Мехр Д.Р., Буркс К.Дж.: Запись активности пожилых женщин с помощью TriTrac. Am J Health Behav. 2000, 24: 370-378. 10.5993 / AJHB.24.5.5.
Артикул
Google Scholar
Гердхем П., Денкер М., Рингсберг К., Акессон К.: Ежедневная физическая активность восьмидесятилетнего возраста, измеренная акселерометром: результаты и ассоциации с другими показателями физической работоспособности и плотности костей. Eur J Appl Physiol. 2008, 102: 173-180.
Артикул
Google Scholar
Джайлс К., Маршалл А.Л.: Воспроизводимость и точность CHAMPS как показателя физической активности в выборке пожилых австралийских людей.J Phys Закон о здоровье. 2009, 6: 221-229.
Google Scholar
Джилл Д.П., Джонс Г.Р., Цзоу Дж., Спичли М: Phone-FITT: краткое интервью о физической активности для пожилых людей. Закон J Aging Phys. 2008, 16: 292-315.
Google Scholar
Хагивара А., Ито Н., Савай К., Казума К.: Достоверность и надежность шкалы физической активности для пожилых людей (PASE) у пожилых людей в Японии.Гериатр Геронтол Инт. 2008, 8: 143-151. 10.1111 / j.1447-0594.2008.00463.x.
Артикул
Google Scholar
Харрис Т.Дж., Оуэн К.Г., Виктор К.Р., Адамс Р., Экелунд У., Кук Д.Г.: Сравнение анкеты, акселерометра и шагомера: измерения у пожилых людей. Медико-спортивные упражнения. 2009, 41: 1392-1402. 10.1249 / MSS.0b013e31819b3533.
Артикул
Google Scholar
Heesch KC, Hill RL, van Uffelen JGZ, Brown WJ: Действительны ли вопросы о физической активности в Австралии для пожилых людей ?. J Sci Med Sport. 2011, 14: 233-237. 10.1016 / j.jsams.2010.11.004.
Артикул
Google Scholar
Хуртиг-Веннлоф А., Хагстромер М., Олссон Л.А.: Международный опросник по физической активности, модифицированный для пожилых людей: аспекты достоверности и выполнимости. Public Health Nutr. 2010, 13: 1847-1854. 10.1017 / S1368980010000157.
Артикул
Google Scholar
Морио Б., Ритц П., Вердье Э, Монтаурье С., Бофрер Б., Верморель М.: Критическая оценка факторных методов и методов регистрации сердечного ритма для определения расхода энергии у свободно живущих пожилых людей. Br J Nutr. 1997, 78: 709-722. 10.1079 / BJN19970189.
CAS
Статья
Google Scholar
Прюитт Л.А., Глинн Н.В., Кинг А.С., Гуральник Дж.М., Айкен Е.К., Миллер Дж., Хаскелл В.Л.: Использование акселерометрии для измерения физической активности у пожилых людей с риском нарушения подвижности. Закон J Aging Phys. 2008, 16: 416-434.
Google Scholar
Rutgers CJ, Klijn MJC, Deurenberg P: Оценка суточного расхода энергии у пожилых женщин с помощью поминутного мониторинга сердечного ритма. Энн Нутр Метаб. 1997, 41: 83-88. 10.1159 / 000177982.
CAS
Статья
Google Scholar
Сил Дж. Л., Кляйн Дж., Фридманн Дж., Дженсен Г.Л., Митчелл Д.К., Смициклас-Райт Х .: Энергозатраты, измеренные с помощью воды с двойной маркировкой, воспоминаний о физической активности и диетических данных у сельских пожилых людей. Питание. 2002, 18: 568-573. 10.1016 / S0899-9007 (02) 00804-3.
Артикул
Google Scholar
Stel VS, Smit JH, Pluijm SMF, Visser M, Deeg DJH, Lips P: Сравнение опросника физической активности LASA с 7-дневным дневником и шагомером.J Clin Epidemiol. 2004, 57: 252-258. 10.1016 / j.jclinepi.2003.07.008.
Артикул
Google Scholar
Washburn RA, Ficker JL: Шкала физической активности для пожилых людей (PASE): взаимосвязь с активностью, измеряемой портативным акселерометром. J Sports Med Phys Fitness. 1999, 39: 336-340.
CAS
Google Scholar
Washburn RA, Smith KW, Jette AM, Janney CA: Шкала физической активности для пожилых людей (Pase) — разработка и оценка.J Clin Epidemiol. 1993, 46: 153-162. 10.1016 / 0895-4356 (93) -4.
CAS
Статья
Google Scholar
Washburn RA, Jette AM, Janney CA: Использование не зависящих от возраста вопросников по физической активности в исследованиях с участием пожилых людей. J Старение здоровья. 1990, 2: 341-356. 10.1177 / 08982643
00304.
Артикул
Google Scholar
Ясунага А., Парк Х, Ватанабэ Э, Того Ф, Парк С., Шепард Р. Дж., Аояги Ю.: Разработка и оценка опросника физической активности для пожилых японцев: исследование наканодзё.Закон J Aging Phys. 2007, 15: 398-411.
Google Scholar
Залевски К.Р., Смит Дж. К., Мальцан Дж., ВанХарт М., О’Коннелл Д.: Измерения физических способностей не связаны с объективно измеряемым поведением при физической активности пожилых людей, проживающих в сообществах пенсионеров, находящихся под постоянным уходом. Arch Phys Med Rehabil. 2009, 90: 982-986. 10.1016 / j.apmr.2008.12.013.
Артикул
Google Scholar
Dominguez-Berjon F, Borrell C, Nebot M, Plasencia A: Оценка физической активности в обследованиях населения: можно ли ее упростить ?. Int J Epidemiol. 1999, 28: 53-57. 10.1093 / ije / 28.1.53.
CAS
Статья
Google Scholar
О’Брайен-Казинс S: Опись состояния упражнений пожилых людей: надежность и достоверность. J Sports Behav. 1996, 19: 288.
Google Scholar
Резник Б., Кинг А., Рибе Д., Ори М.: Измерение физической активности у пожилых людей — использование модельной программы мероприятий общественного здравоохранения для анкеты физической активности пожилых людей и обследования физической активности Йельского университета в трех исследованиях Консорциума по изменению поведения. West J Nurs Res. 2008, 30: 673-689. 10.1177 / 0193945
1320.
Артикул
Google Scholar
Weiss TW, Slater CH, Green LW, Kennedy VC, Albright DL, Wun CC: Достоверность отдельных вопросов для самооценки как показателя физической активности взрослых.J Clin Epidemiol. 1990, 43: 1123-1129. 10.1016 / 0895-4356 (90) -Ф.
CAS
Статья
Google Scholar
Аябе М., Исии К., Такаяма К., Аоки Дж., Танака Х .: Сравнение разницы в измерениях шагомеров между устройствами у молодых и пожилых людей. Br J Sports Med. 2010, 44: 95-99. 10.1136 / bjsm.2007.045179.
CAS
Статья
Google Scholar
Бергман Р.Дж., Бассетт Д.Р., Кляйн Д.А.: Допустимость 2 устройств для измерения шагов, предпринимаемых пожилыми людьми в учреждениях для престарелых. J Phys Закон о здоровье. 2008, 5: S166-S175.
Google Scholar
Cyarto EV, Myers AM, Tudor-Locke C: Точность шагомера в домах престарелых и пожилых людях в общественных местах. Медико-спортивные упражнения. 2004, 36: 205-209. 10.1249 / 01.MSS.0000113476.62469.98.
Артикул
Google Scholar
Fehling PC, Smith DL, Warner SE, Dalsky GP: Сравнение акселерометров с потреблением кислорода у пожилых людей во время упражнений. Медико-спортивные упражнения. 1999, 31: 171-175. 10.1097 / 00005768-1990-00026.
CAS
Статья
Google Scholar
Грант П.М., Далл П.М., Митчелл С.Л., Гранат М.Х.: Точность монитора активности при измерении количества шагов и частоты вращения педалей у пожилых людей, проживающих в сообществах. Закон J Aging Phys. 2008, 16: 201-214.
Google Scholar
Hooker SP, Feeney A, Hutto B, Pfeiffer KA, McIver K, Heil DR, Vena JE, LaMonte MJ, Blair SN: Валидация монитора активной активности у людей среднего и старшего возраста. J Phys Закон о здоровье. 2011, 8: 372-381.
Google Scholar
Кохерсбергер Дж., МакКоннелл Е: Надежность, достоверность и стабильность показателя физической активности у пожилых людей.Arch Phys Med Rehabil. 1996, 77: 793-795. 10.1016 / S0003-9993 (96)
-0.
CAS
Статья
Google Scholar
Leaf DA, Macrae H: достоверность 2 косвенных показателей расхода энергии во время ходьбы у пожилых людей. Закон J Aging Phys. 1995, 3: 97-106.
Google Scholar
Марш А.П., Вэнс Р.М., Фредерик Т.Л., Хессельманн С.А., Рейески В.Дж.: Объективная оценка активности пожилых людей с риском инвалидности опорно-двигательного аппарата.Медико-спортивные упражнения. 2007, 39: 1020-1026. 10.1249 / mss.0b013e3180423ac3.
Артикул
Google Scholar
Резник Б., Нахм Э. С., Орвиг Д., Циммерман С. С., Магазин Дж .: Измерение активности у пожилых людей: надежность и достоверность монитора шаговой активности. J Nurs Meas. 2001, 9: 275-290.
CAS
Google Scholar
Сторти К.Л., Петти К.К., Брач Дж. С., Тальковск Дж. Б., Ричардсон К. Р., Криска А. М.: Скорость походки и точность отслеживания количества шагов у пожилых людей, проживающих в сообществе.Медико-спортивные упражнения. 2008, 40: 59-64.
Артикул
Google Scholar
Набор инструментов для измерения диеты и физической активности.
http://toolkit.s24.net/index.html
.
Нилсон HK, Робсон П.Дж., Friedenreich CM, Csizmadi I: Оценка расхода энергии при физической активности: насколько достоверны анкеты по физической активности ?. Am J Clin Nutr. 2008, 87: 279-291.
CAS
Google Scholar
Дишман Р.К., Вашберн Р.А., Шоллер Д.А.: Измерение физической активности. Квест. 2001, 53: 295-309. 10.1080 / 00336297.2001.10491746.
Артикул
Google Scholar
Габриэль К.П., Макклейн Дж. Дж., Шмид К.К., Сторти К.Л., Высокий Р.Р., Андервуд Д.А., Куллер Л.Х., Криска А.М.: Проблемы методологии акселерометра: роль продолжительности эпохи в оценке физической активности и взаимосвязь с результатами для здоровья у женщин с избыточным весом в постменопаузе.Закон Int J Behav Nutr Phys. 2010, 7: 53-53. 10.1186 / 1479-5868-7-53.
Артикул
Google Scholar
Колли Р.К., Гарригет Д., Янссен И., Крейг К.Л., Кларк Дж., Тремблей М.С.: Физическая активность взрослых канадцев: результаты акселерометра по результатам обследования показателей здоровья в Канаде с 2007 по 2009 год. Health Rep / Stat Can, Can Center Health Inf = Rapports sur la santé / Statistique Canada, Канадский информационный центр по санте. 2011, 22: 7.
Google Scholar
Tudor-Locke C, Brashear MM, Johnson WD, Katzmarzyk PT: Акселерометрические профили физической активности и бездействия при нормальном весе, избыточном весе и ожирении у мужчин и женщин в США. Закон Int J Behav Nutr Phys. 2010, 7: 60-60. 10.1186 / 1479-5868-7-60.
Артикул
Google Scholar
Коупленд Дж. Л., Эслигер Д. В.: Акселерометрическая оценка физической активности у активных, здоровых пожилых людей.Закон J Aging Phys. 2009, 17: 17-30.
Google Scholar
Горман Э., Ян П., Хан К.М., Лю-Амброуз Т., Эш М.К.: Контрольные точки акселерометрии и пожилые люди: систематический обзор. 2011
Google Scholar
Эслигер Д., Тремблей М.: Профилирование физической активности и бездействия: новое поколение. Appl Physiol Nutr Metab. 2007, 32: S195-S207. 10.1139 / H07-107.
Артикул
Google Scholar
Коупленд Дж. Л., Эслигер Д. В. Насколько активны пожилые люди? Результаты исследования с использованием акселерометров. Обновление исследования. 2007, 14: 1-1.
Google Scholar
Бланд Дж. М., Альтман Д. Г.: Статистические методы для оценки соответствия между двумя методами клинических измерений. Ланцет. 1986, 1: 307-310.
CAS
Статья
Google Scholar
Terwee CB, Mokkink LB, van Poppel MNM, Chinapaw MJM, van Mechelen W., de Vet HCW: Качественные атрибуты и параметры измерения анкет по физической активности: контрольный список.Sports Med. 2010, 40: 525-537. 10.2165 / 11531370-000000000-00000.
Артикул
Google Scholar
Прямые и косвенные измерения — FlatEarth.ws
Измерение может быть прямым, как измерение длины непосредственно лентой или линейкой. Но он также может быть косвенным, например, измерение расстояния путем испускания звука, его прослушивания и измерения задержки звука, полученного после отражения от объекта.
Плоскоземельцы любят дискредитировать результаты измерений — например, расстояние до Солнца — упоминая, что это просто результаты вычислений, а не измерения напрямую.На самом деле многие повседневные инструменты измеряют косвенно. Они измеряют другое значение, а затем используют вычисления, чтобы получить желаемый расчет.
Например, чтобы определить скорость поверхности Земли на экваторе из-за вращения Земли, мы можем сначала определить окружность экватора и период вращения Земли. Радиус Земли на экваторе составляет 6378137 м, а звездный период вращения Земли составляет 23 часа 56 минут 4 секунды. Исходя из этих значений, мы можем вычислить, что скорость поверхности Земли на экваторе из-за вращения Земли составляет 2 × π × 6378137 м / (23 часа + 56 минут + 4 секунды) = 1674.4 км / час.
Плоскоземельцы любят отвергать такое измерение, потому что оно не было сделано напрямую, а получено косвенно из двух разных переменных. Они утверждают, что никакой инструмент не может измерить скорость вращения Земли.
На самом деле многие результаты измерений определяются косвенно. Электронный спидометр в автомобиле измеряет скорость, измеряя частоту вращения карданного вала автомобиля. Скорость самолета определяется разницей высот жидкости в разных столбах в результате разницы в давлении внутри трубки Пито.Анемометр косвенно измеряет скорость ветра, измеряя скорость вращения инструмента.
Большинство измерительных приборов, которые мы используем каждый день, показывают конечный результат в той единице, которую мы хотим видеть. Однако в большинстве случаев они получают результаты косвенно, так же, как мы определяем скорость вращения Земли, как описано выше. Тот факт, что измерение является косвенным, не означает, что оно «неверно», как часто утверждают сторонники теории плоской Земли.
Список литературы
Прямая и косвенная оценка
Прямая оценка включает изучение реальных образцов студенческих работ, созданных в рамках наших программ.Сюда входят замковые проекты, дипломные работы, выставки или выступления (см. Ниже).
Косвенная оценка — это сбор информации с помощью иных средств, чем просмотр реальных образцов.
студенческой работы. К ним относятся опросы, интервью при выходе и фокус-группы (см. Ниже).
Каждый служит определенной цели. Косвенные меры могут быстро предоставить нам информацию,
но не может предоставить реальных доказательств обучения учащихся.Студенты могут подумать, что они
хорошо выучили или говорят, что учили, но это не значит, что их восприятие
правильный.
Например, когда я впервые иду к врачу, мне выдают форму, в которой нужно заполнить мое имя,
адрес, страховая компания и ответы на различные вопросы, например: Кто-нибудь
в моей семье когда-нибудь был рак? Принимаю ли я различные лекарства, например? У меня аллергия
ни к чему? Переносили ли я когда-нибудь серьезную операцию, и если да, то с какой целью?
Это опрос, косвенная оценка .
Меня также могут спросить, почему я иду к врачу и каковы мои симптомы? Это тоже,
это опрос, и мои ответы — это мое восприятие моего состояния. Я могу или не могу
быть правильным. Это косвенная оценка моего здоровья .
Затем я иду к врачу, и он говорит мне: «Как ты себя чувствуешь?» Я всегда отвечаю,
«Отлично.«Я всегда отвечаю« отлично », независимо от того, как я себя чувствую: я не хочу раскрывать
ничего слишком личного. Моя жена говорит мне, что я глуп. Врач только что провел
интервью: косвенная оценка .
Он до сих пор не знает, здоров я или нет.
Итак, он слушает мое сердце, он бьет меня по колену (ничего), и он смотрит мне в уши
и глаза.Затем он просит меня оставить образец мочи. Он просит медсестру взять образцы крови.
Он заказывает колоноскопию. Это все прямых оценок.
Короче говоря, его косвенные оценки дали ему некоторые указания, но не свидетельства. Он
пришлось действительно смотреть или слушать вещественные доказательства, чтобы иметь прямую оценку.
То же самое и с нашей оценкой учебной программы.У студентов могут быть определенные представления
о том, что они узнали или нет, но, пока мы не рассмотрим доказательства — реальные образцы
их работы — мы действительно не можем быть уверены.
| ПРЯМЫЕ МЕРЫ | КОСВЕННЫЕ МЕРЫ | |
| Курс |
|
|
| Программа |
|
|
| Институциональные |
|
|
[1] Комиссия по высшему образованию Средних штатов. Оценка успеваемости учащихся: варианты и ресурсы. Глава 3, Оценка ученика
Обучение: 27-53; 2007 г.
.


 ) и универсальные угломеры;
) и универсальные угломеры;
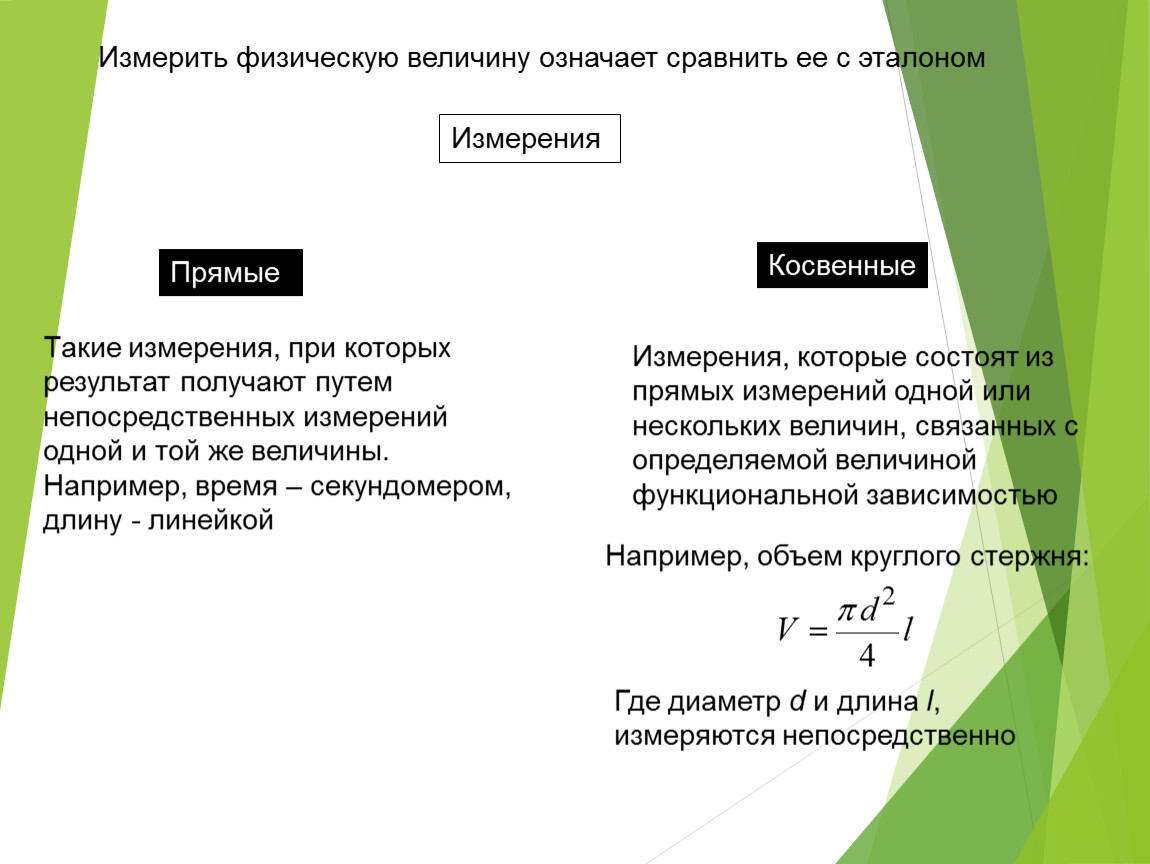 1 83 «Реактивы. Методы приготовления титрованных растворов для кислотно-основного титрования»
1 83 «Реактивы. Методы приготовления титрованных растворов для кислотно-основного титрования»