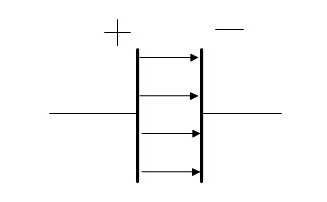
11 Работа и мощность тока. Работа и мощность тока
Работа и мощность тока
При упорядоченном движении заряженных частиц в проводнике электрическое поле совершает работу. Эту работу принято называть работой тока.
Пусть за время t через поперечное сечение проводника проходит заряд q. Тогда электрическое поле совершит работу А = Uq, где U – напряжение на данном участке цепи. Так как q = It , то A = UIt.
По закону сохранения энергии эта работа должна быть равна изменению энергии рассматриваемого участка цепи. В случае, если на участке не совершается механическая работа (проводник неподвижен) и ток не производит химических действий, происходит только нагревание проводника. Нагретый проводник отдает теплоту окружающим телам. Следовательно, .
Закон, определяющий количество теплоты, которое проводник с током выделяет в окружающую среду, был экспериментально установлен английским ученым Джоулем и русским ученым Ленцем. Закон Джоуля-Ленца был сформулирован следующим образом: количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени: .
Любой электрический прибор рассчитан на потребление определенной энергии в единицу времени. Поэтому важное значение имеет понятие мощности тока. Мощность тока равна работе тока за единицу времени: .
При соединении приборов или проводников необходимо помнить следующее:
при параллельном соединении напряжение на всех приборах одинаковое и наибольшую мощность будет потреблять и, соответственно, выделять большее количество теплоты прибор с наименьшим сопротивлением.
при последовательном соединении наибольшую мощность будет потреблять прибор с наибольшим сопротивлением (т.к. ток одинаковый).
От формулы, определяющей тепло, выделяющееся во всем проводнике, можно перейти к формуле, характеризующей выделение тепла в различных местах проводника. Выделим в проводнике объем в виде цилиндра. За время dt в этом объеме, согласно закону Джоуля-Ленца, выделится теплота dQ = I2Rdt = (jdS)2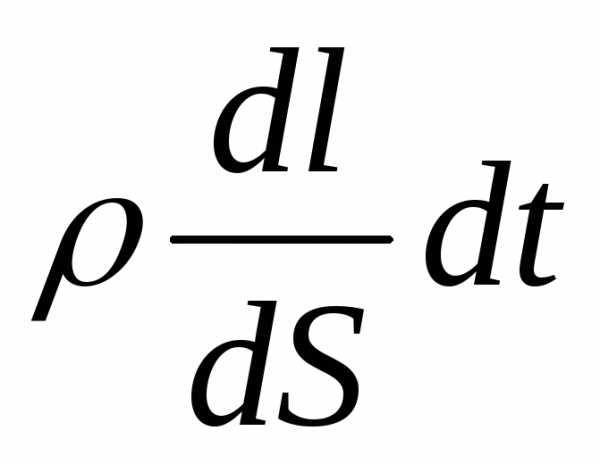 = ρj2dSdldt = ρj2dVdt.
= ρj2dSdldt = ρj2dVdt.
Qуд = 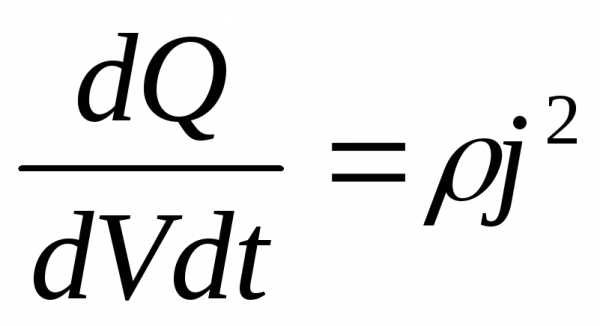 ,
,  Qуд = ρj2 - закон Джоуля-Ленца в дифференциальной форме. Qуд – удельная тепловая мощность тока (тепло, выделяющееся в единице объема в единицу времени). Так как j = σE, то Qуд = ρ(σE)2 = σE2.
Qуд = ρj2 - закон Джоуля-Ленца в дифференциальной форме. Qуд – удельная тепловая мощность тока (тепло, выделяющееся в единице объема в единицу времени). Так как j = σE, то Qуд = ρ(σE)2 = σE2.
Лекция 7 Закон Ома для замкнутой цепи
Если в проводнике создать электрическое поле и не принять меры для его поддержания, то перемещение носителей заряда приведет к тому, что разность потенциалов между концами проводника будет уменьшаться и электрическое поле быстро исчезнет. Для того, чтобы поддерживать ток длительное время, нужно от одного конца проводника отводить приносимые туда заряды, а к противоположному концу непрерывно их подводить. Т.е., необходимо осуществить круговорот зарядов, при котором они двигались бы по замкнутому пути. В этом случае в замкнутой цепи всегда будет участок, на котором перенос зарядов происходит против сил электростатического поля. Перемещение зарядов на этом участке возможно лишь с помощью сил не электростатического происхождения, называемых сторонними силами. Сторонние силы действуют в источниках тока.
П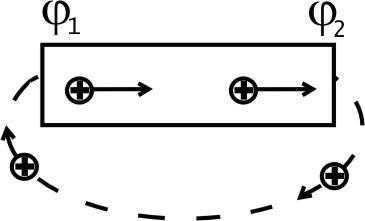 рирода сторонних сил может быть различной. В электрофорной машине разделение зарядов происходит за счет механической работы. В гальванических элементах и аккумуляторах – за счет энергии химической реакции. В фотоэлементах – за счет энергии света. В генераторах заряды разделяются силами магнитного поля.
рирода сторонних сил может быть различной. В электрофорной машине разделение зарядов происходит за счет механической работы. В гальванических элементах и аккумуляторах – за счет энергии химической реакции. В фотоэлементах – за счет энергии света. В генераторах заряды разделяются силами магнитного поля.
Действие сторонних сил характеризуется физической величиной, называемой электродвижущей силой (ЭДС). ЭДС в замкнутом контуре численно равна работе сторонних сил по перемещению единичного положительного заряда вдоль этого контура:  =
= 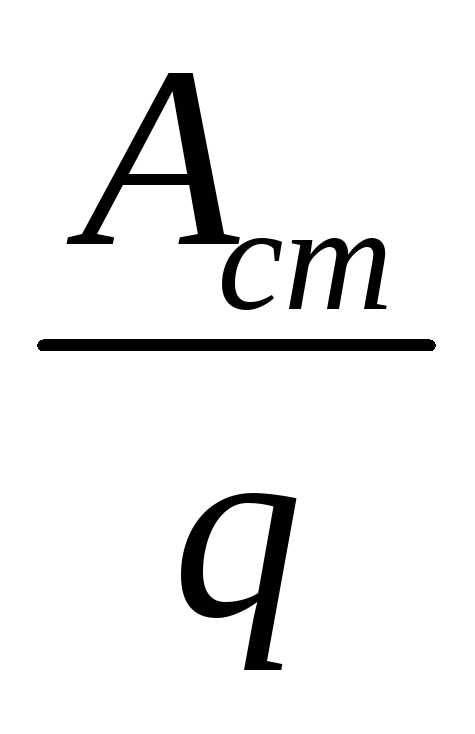 .
.
Рассмотрим простейшую цепь, состоящую из источника тока и резистора сопротивлениемR. Источник тока имеет ЭДС и внутреннее сопротивление r. За время t через поперечное сечение проводника пройдет заряд Dq. Тогда работа сторонних сил будет . При совершении этой работы на внешнем и внутреннем сопротивлении выделяется теплота. По закону Джоуля-Ленца:. По закону сохранения энергии Аст = Q.
или , 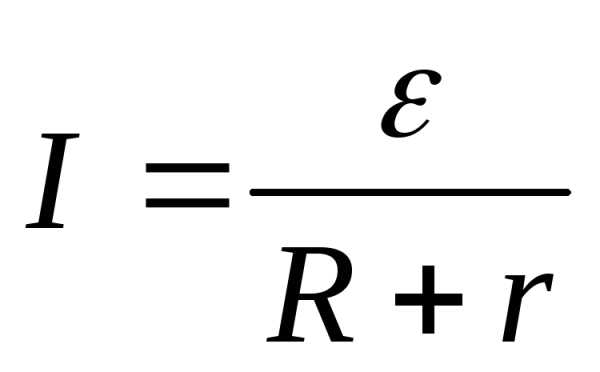 . Сила тока в замкнутой цепи равна отношению ЭДС цепи к ее полному сопротивлению. Это закон Ома для замкнутой цепи.
. Сила тока в замкнутой цепи равна отношению ЭДС цепи к ее полному сопротивлению. Это закон Ома для замкнутой цепи.
Если цепь содержит несколько источников ЭДС, то полная ЭДС цепи равна алгебраической сумме ЭДС отдельных источников. Если ЭДС способствует движению положительных носителей заряда в выбранном направлении, то ЭДС считается положительной, если препятствует – то ЭДС отрицательна. На рисунке показано, при каком направлении ЭДС считается положительной.
Для внешней цепи U = IR =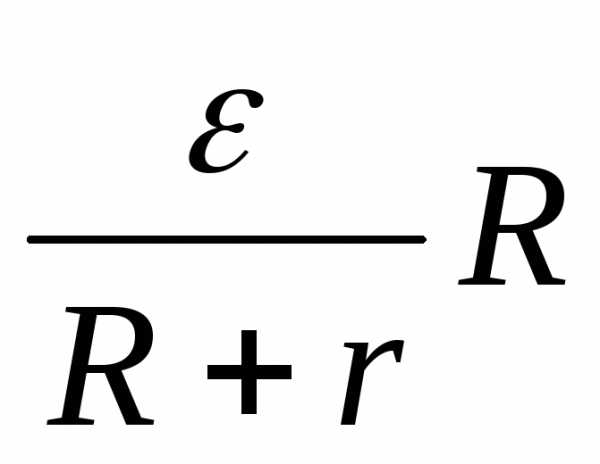 . ПриR = 0 (короткое замыкание) U = 0, ток короткого замыкания
. ПриR = 0 (короткое замыкание) U = 0, ток короткого замыкания 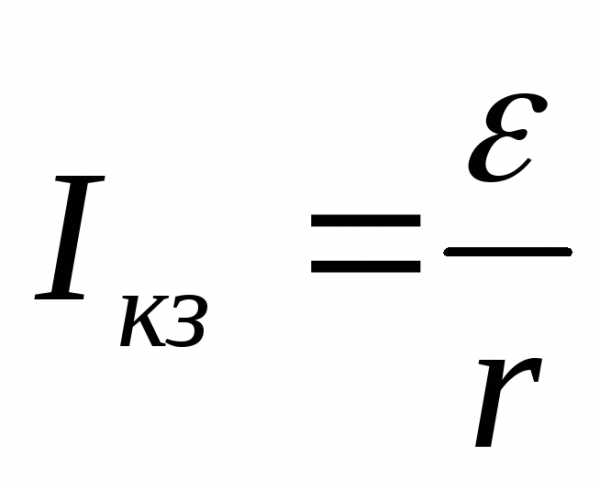 . ПриR = ∞, U = ε.
. ПриR = ∞, U = ε.
studfiles.net
Работа и мощность тока
Электрический ток снабжает нас энергией. Сейчас мы будем учиться эту энергию вычислять. Откуда вообще берётся эта энергия? Она возникает за счёт работы электрического поля по передвижению свободных зарядов в проводнике. Поэтому нахождение работы поля наша
первая задача.
11.1Работа тока
Рассмотрим участок цепи, по которому течёт ток I. Напряжение на участке обозначим U, сопротивление участка равно R (рис. 42).
I
R
U
Рис. 42. Участок цепи
За время t по нашему участку проходит заряд q = It. Заряд перемещается стационарным электрическим полем, которое совершает при этом работу:
За счёт работы (51) на рассматриваемом участке может выделяться тепловая энергия или совершаться механическая работа; могут также протекать химические реакции. Короче говоря, данная работа идёт на увеличение энергии нашего участка цепи.
Работа (51) называется работой тока. Термин крайне неудачный ведь работу совершает не ток, а электрическое поле. Но с укоренившейся терминологией, увы, ничего не поделаешь.
Если участок цепи является однородным, т. е. не содержит источника тока, то для этого участка справедлив закон Ома: U = IR. Подставляя это в формулу (51), получим:
A = I2Rt: | (52) | ||
Теперь подставим в (51) вместо тока его выражение из закона Ома I = U=R: |
| ||
| U2 | (53) | |
A = |
| t: | |
| |||
| R |
| |
Подчеркнём ещё раз: формула (51) получена из самых общих соображений, она является основной и годится для любого участка цепи. А вот формулы (52) и (53) получены из основной формулы с дополнительным привлечением закона Ома и потому годятся только для однородного участка.
11.2Мощность тока
Как вы помните, мощностью называется отношение работы ко времени её совершения. В частности, мощность тока это отношение работы тока ко времени, за которое эта работа совер-
шена:
P = At :
studfiles.net
16) Работа и мощность тока
При протекании тока по однородному участку цепи электрическое поле совершает работу. За время Δt по цепи протекает заряд Δq = I Δt. Электрическое поле на выделенном участке совершает работу
| ΔA = (φ1 – φ2) Δq = Δφ12 I Δt = U I Δt, |
где U = Δφ12– напряжение. Эту работу называют работой электрического тока.
Если обе части формулы
выражающей закон Ома для однородного участка цепи с сопротивлением R, умножить на IΔt, то получится соотношение
| R I2 Δt = U I Δt = ΔA. |
Это соотношение выражает закон сохранения энергии для однородного участка цепи.
Работа ΔA электрического токаI, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в тепло ΔQ, выделяющееся на проводнике.
|
Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж. Джоулем и Э. Ленцем и носит название закона Джоуля–Ленца (количество выделившейся в проводнике теплоты пропорционально его сопротивлению , квадрату силы тока и времени ).
Мощность электрического токаравна отношению работы тока ΔA к интервалу времени Δt, за которое эта работа была совершена:
| |
Работа электрического тока в СИ выражается в джоулях (Дж), мощность – в ваттах (Вт).
Соотношение (1) выражает закон Джоуля-Ленца в интегральной форме. Введем плотность тепловой мощности , равную энергии выделенной за единицу время прохождения тока в каждой единице объема проводника
где S - поперечное сечение проводника, - его длина. Используя (1.13) и соотношение, получим:
Но - плотность тока, а, тогда
с учетом закона Ома в дифференциальной форме , окончательно получаем
| (17.14) |
Формула (17.14) выражает закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля.
17) Магнитное поле в вакууме
Взаимодействие электрических токов между собой осуществляется через поле, называемое магнитным. В опыте Эрстеда ( первый опыт с магнитным полем ) проволока, по которой шел ток, была натянута над магнитной стрелкой, вращающейся на игле. При включении тока стрелка устанавливалась перпендикулярно к проволоке. Изменение направления тока взывало поворот стрелки в противоположную сторону. Из опыта Эрстеда следует, что магнитное поле имеет направленный характер и должно характеризоваться векторной величиной. Магнитное поле в отличии от электрического не оказывает действия на покоящийся заряд. Сила возникает лишь тогда, когда заряд движется. Магнитное поле порождается движущимися зарядами.
Магнитная индукция — это векторная физическая величина, являющаяся силовой характеристикой магнитного поля, численно равная максимальному вращающему моменту, действующему на контур с единичным магнитным моментом, и направленная вдоль положительной нормали к контуру.
Модуль магнитной индукции равен
Единицей магнитной индукции в СИ является тесла (Тл).
1 Тл = Н·м/(А·м2) = Н/(А·м) .
1 Тл — магнитная индукция такого однородного поля, в котором на контур с магнитным моментом 1 А·м2 действует вращающий момент 1 Н·м.
Магнитная индукция B⃗ полностью характеризует магнитное поле. В каждой точке может быть найден ее модуль и направление.
Поле, в каждой точке которого модуль и направление магнитной индукции одинаковы ( B⃗ =const) , называется однородным магнитным полем.
Если магнитное поле образовано системой n проводников с токами, то, имеет место принцип суперпозиции магнитных полей: магнитная индукция поля системы токов равна геометрической сумме магнитных индукцией полей каждого из токов в отдельности:
B⃗ =B⃗ 1+B⃗ 2+…+B⃗ n=∑ni=1B⃗ i.
Индукция в вакууме или воздухе равна
, где.
studfiles.net
Constant-Current - Электрический ток в физике
Электрическая энергия легко преобразуется в другие виды энергии — механическую, химическую, световую, внутреннюю энергию вещества, что широко применяется в промышленности и в быту.
Мерой изменения энергии электрического тока служит работа источника тока, создающего и поддерживающего электрическое поле в цепи.
Стационарное электрическое поле, перемещающее заряды по проводнику, совершает работу. Эту работу называют работой тока. Работа электрического тока на участке цепи, как следует из определения напряжения,
где q — электрический заряд, проходящий по участку цепи, а U — напряжение на участке.
Учитывая, что q = It, где I — сила тока в проводнике, а t — время прохождения электрического тока, для работы тока получим
Если R — сопротивление однородного участка цепи, то, используя закон Ома для участка цепи, можно получить формулу для расчета работы тока:
Если участок цепи не является однородным, то работу совершает не только стационарное электрическое поле, но и сторонние силы, и полная работа определяется по формуле
По вышеприведенным формулам можно рассчитать полную работу тока на данном участке цепи.
Если в цепи есть электродвигатель, то энергия электрического тока, во-первых, расходуется на совершение механической работы — полезная работа Ameh, во-вторых, затрачивается на нагревание обмоток электродвигателя и соединительных проводов — теряемая энергия. В этом случае коэффициент полезного действия можно рассчитать как
Говоря о коэффициенте полезного действия источника тока, под полезной работой подразумевают работу, совершаемую во внешней цепи постоянного тока:
Затраченная же работа источника тока равна работе сторонних сил:
где .
Тогда .
КПД источника , где U — напряжение во внешней цепи (напряжение на полюсах источника тока). Графическая зависимость η = f(R) при r = const приведена на рис. 1.
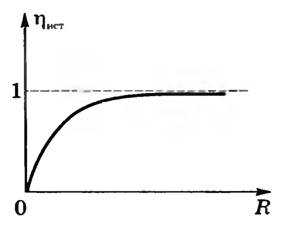 Рис. 1
Рис. 1Единица работы электрического тока в СИ — джоуль (Дж). 1 Дж представляет работу тока, эквивалентную механической работе в 1 Дж. 1 Дж = Кл·В = А·В·с.
Измеряют работу электрического тока счетчиками.
Скорость совершения работы тока на данном участке цепи характеризует мощность тока. Мощность тока определяют по формуле или P = IU.
Используя закон Ома для участка цепи, можно записать иначе формулу для мощности тока: . В этом случае речь идет о тепловой мощности.
Единица мощности тока — ватт: 1 Вт = Дж/с. Отсюда Дж = Вт·с.
Кроме того, применяют внесистемные единицы: киловатт-час или гектоватт-час: 1 кВт·ч = 3,6·106 Дж = 3,6 МДж; 1 гВт·ч = 3,6·105 Дж = 360 кДж.
Для измерения мощности тока существуют специальные приборы — ваттметры.
constant-current.narod.ru
Работа и мощность тока – HomeWork.net.ua
При протекании тока по однородному участку цепи электронное поле совершает работу. За время Δt по цепи протекает заряд Δq = IΔt. Электронное поле на выделенном учестке совершает работу
| ΔA = (φ1 – φ2)Δq = Δφ12IΔt = UIΔt, |
где U = Δφ12 – напряжение. Эту работу именуют работой электронного тока. Если обе части формулы
выражающей закон Ома для однородного участка цепи с сопротивлением R, помножить на IΔt, то получится соотношение
Это соотношение выражает закон сохранения энергии для однородного участка цепи. Работа ΔA электронного тока I, протекающего по недвижному проводнику с сопротивлением R, преобразуется в тепло ΔQ, выделяющееся на проводнике.
Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж. Джоулем и Э. Ленцем и носит заглавие закона Джоуля–Ленца. Мощность электронного тока равна отношению работы тока ΔA к интервалу времени Δt, за которое эта работа была совершена:
| |
Работа электронного тока в СИ выражается в джоулях (Дж), мощность – в ваттах (Вт). Разглядим сейчас полную цепь неизменного тока, состоящую из источника с электродвижущей силой и внутренним сопротивлением r и наружного однородного участка с сопротивлением R. Закон Ома для полной цепи записывается в виде
| (R + r)I = . |
Умножив обе части этой формулы на Δq = IΔt, мы получим соотношение, выражающее закон сохранения энергии для полной цепи неизменного тока:
| RI2Δt + rI2Δt = IΔt = ΔAст. |
1-ый член в левой части ΔQ = RI2Δt – тепло, выделяющееся на наружном участке цепи за время Δt, 2-ой член ΔQист = rI2Δt – тепло, выделяющееся снутри источника за то же время. Выражение IΔt равно работе посторониих сил ΔAст, действующих снутри источника. При протекании электронного тока по замкнутой цепи работа посторониих сил ΔAст преобразуется в тепло, выделяющееся во наружной цепи (ΔQ) и снутри источника (ΔQист).
. |
Следует направить внимание, что в это соотношение не заходит работа электронного поля. При протекании тока по замкнутой цепи электронное поле работы не совершает; потому тепло делается одними только посторонними силами, действующими снутри источника. Роль электронного поля сводится к перераспределению тепла меж разными участками цепи. Наружняя цепь может представлять собой не только лишь проводник с сопротивлением R, да и какое-либо устройство, потребляющее мощность, к примеру, электродвигатель неизменного тока. В данном случае под R необходимо осознавать эквивалентное сопротивление нагрузки. Энергия, выделяемая во наружной цепи, может отчасти либо стопроцентно преобразовываться не только лишь в тепло, на и в другие виды энергии, к примеру, в механическую работу, совершаемую электродвигателем. Потому вопрос об использовании энергии источника тока имеет огромное практическое значение. Полная мощность источника, другими словами работа, совершаемая посторонними силами за единицу времени, равна
Во наружной цепи выделяется мощность
Отношение равное
| |
именуется коэффициентом полезного деяния источника. На рис. 4.11.1 графически представлены зависимости мощности источника Pист , полезной мощности P, выделяемой во наружной цепи, и коэффициента полезного деяния η от тока в цепи I для источника с ЭДС, равной , и внутренним сопротивлением r. Ток в цепи может изменяться в границах от I = 0 (при ) до (при R = 0).
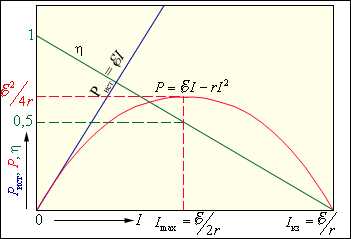 1 1 |
| Набросок 4.11.1. Зависимость мощности источника Pист, мощности во наружной цепи P и КПД источника η от силы тока. |
Из приведенных графиков видно, что наибольшая мощность во наружной цепи Pmax , равная
достигается при R = r. При всем этом ток в цепи
а КПД источника равен 50 %. Наибольшее значение КПД источника достигается при I → 0, другими словами при R → ∞. В случае недлинного замыкания нужная мощность P = 0 и вся мощность выделяется снутри источника, что может привести к его перегреву и разрушению. КПД источника при всем этом обращается в нуль.
homework.net.ua
Работа и мощность тока
Допустим, что между токами с напряжением U переносится заряд величины dq, в таком случае работа, которая совершается равна:
Если по проводнику течет ток $I$, рассмотрим его участок, между концами которого напряжение $U$. За время $dt$ на участке проводника перемещается заряд величины:
Если мы работу определили формулой (3), то мощность, которую развивает ток на том же участке, будет равна:
где $\left({\varphi }_1-{\varphi }_2\right)$- разность потенциалов между точками проводника, $\mathcal E_{12}$- ЭДС источника на данном участке.
Данная мощность может идти на совершение участком цепи работы над внешними телами при перемещении участка в пространстве. Или на химические реакции и нагревание выделенного участка.
Это отношение:
\[P_{ud}=\frac{\triangle P}{\triangle V}\left(5\right),\]где $\triangle P$ изменения мощности в объеме проводника $\triangle V$.
На неоднородном участке цепи на носители тока действуют электростатические силы: ${\overrightarrow{F}}_q=q\overrightarrow{E}$ и сторонние силы: ${\overrightarrow{F}}_{st}=q\overrightarrow{E_{st}}$. Эти силы при движении носителя тока развивают мощность, которая равна:
\[P'=q\left(\overrightarrow{E}+\overrightarrow{E_{st}}\right)\left(\overrightarrow{v}+\overrightarrow{u}\right)\left(6\right),\]где $\overrightarrow{v}$ -- скорость теплового движения молекул, $\overrightarrow{u}$ -- скорость упорядоченного движения носителей тока при наличии поля, $(\overrightarrow{v}+\overrightarrow{u})$- скорость носителей тока в поле, $q$ -- заряд носителя тока (электрона).
Проведем усреднение уравнения (6) по носителям тока, которые находятся в объеме $\triangle V$. В пределах выделенного объема будем считать $\overrightarrow{E},\overrightarrow{E_{st}}$ постоянными, получим:
\[\left\langle P'\right\rangle =q\left(\overrightarrow{E}+\overrightarrow{E_{st}}\right)\left\langle \overrightarrow{v}+\overrightarrow{u}\right\rangle =q\left(\overrightarrow{E}+\overrightarrow{E_{st}}\right)\left\langle \overrightarrow{v}\right\rangle +q\left(\overrightarrow{E}+\overrightarrow{E_{st}}\right)\left\langle \overrightarrow{u}\right\rangle =q\left(\overrightarrow{E}+\overrightarrow{E_{st}}\right)\left\langle \overrightarrow{u}\right\rangle \left(7\right),\]где $\left\langle \overrightarrow{v}\right\rangle =0$. При этом изменение мощности $\triangle P\ $ в$\ \triangle V$ объеме можно найти как произведение:
\[\triangle P=\left\langle P'\right\rangle n\triangle V\ \left(8\right),\]где n∆V -- число носителей тока в заданном объеме. Следовательно, получим:
\[\triangle P=q\left(\overrightarrow{E}+\overrightarrow{E_{st}}\right)\left\langle \overrightarrow{u}\right\rangle n∆V=\overrightarrow{j}\left(\overrightarrow{E}+\overrightarrow{E_{st}}\right)\triangle V\ \left(9\right),\]где $\overrightarrow{j}=q\left\langle \overrightarrow{u}\right\rangle n$ -- вектор плотности тока.
Получено, что удельная мощность проводника с током равна:
\[P_{ud}=\overrightarrow{j}\left(\overrightarrow{E}+\overrightarrow{E_{st}}\right)\left(10\right).\]Выражение (10) является дифференциальной формой уравнения (4).
Пример 1
Задание: Цепь состоит из источника тока и внешнего сопротивления (рис.1). В первом случае подключено сопротивление $R_1$, во втором сопротивление $R_2.\ $ Мощность, выделяющаяся во внешней цепи в обоих случаях равна P. Найдите внутренне сопротивление источника тока.
Рис. 1
Решение:
За основу решения задачи примем определение мощности для цепи с током:
\[P=IU=I^2R\ \left(1.1\right),\]где по закону Ома для замкнутой цепи можно записать, что:
\[I=\frac{\mathcal E}{R+r}\left(1.2\right),\]где $\mathcal E$ - ЭДС источника тока, $r$ -- внутреннее сопротивление источника тока.
Согласно условиям задачи мощность тока для цепи с первым сопротивлением и вторым сопротивлением равны, поэтому используем для двух сопротивлений уравнения (1.1) и (1.2), запишем:
\[P={I_1}^2R_1={I_2}^2R_2\to \frac{\mathcal E^2}{{\left(R_1+r\right)}^2}R_1=\frac{\mathcal E^2}{{\left(R_2+r\right)}^2}R_2\left(1.3\right).\]Из (1.3) выразим внутреннее сопротивление r, получим:
\[R_1{\left(R_2+r\right)}^2=R_2{\left(R_1+r\right)}^2\to r=\sqrt{R_1R_2}\left(1.4\right).\]Ответ: $r=\sqrt{R_1R_2}$.
Пример 2
Задание: Три одинаковых сопротивления подключены к источнику постоянного тока (рис.2) внутреннее сопротивление которого равно r. Каким должно быть сопротивление R, для того чтобы мощность, выделяемая на участке AB была максимальной?
Рис. 2
Решение:
Преобразуем электрическую схему, изображенную на рис.2, получим эквивалентную схему (рис.3):
Рис. 3
Результирующее сопротивление ($R_{AB}$) между точками A и B можно найти как:
\[\frac{1}{R_{AB}}=\frac{1}{R}+\frac{1}{R}+\frac{1}{R}\to R_{AB}=\frac{R}{3}\left(2.1\right).\]В таком случае мощность может быть найдена по формуле:
\[P=IU=I^2R_{AB}\ \left(2.2\right),\]где по закону Ома для замкнутой цепи можно записать, что:
\[I=\frac{\mathcal E}{R_{AB}+r}\left(2.3\right),\]где $\mathcal E$ - ЭДС источника тока, $r$ -- внутреннее сопротивление источника тока.
Функция достигает своего экстремума в точке, где ее производная равна нулю. Поэтому найдем производную $\frac{dP}{dR}$ и приравняем ее к нулю:
\[\frac{dP}{dR}={\left[{\left(\frac{\mathcal E}{R_{AB}+r}\right)}^2R_{AB}\right]}'={\left[\mathcal E^2R_{AB}{\left(R_{AB}+r\right)}^{-2}\right]}'=\frac{?^2}{{\left(R_{AB}+r\right)}^2}+\frac{\mathcal E^2R_{AB}\left(-2\right)}{{\left(R_{AB}+r\right)}^3}=\frac{\mathcal E^2\left(R_{AB}+r\right)-2 \mathcal E^2R_{AB}}{{\left(R_{AB}+r\right)}^3}=0\left(2.4\right),\]где ${\left(R_{AB}+r\right)}^3\ne 0$. Следовательно, приравняем числитель к нулю, выразим внешнее сопротивление, получим:
\[\mathcal E^2\left(R_{AB}+r\right)-2 \mathcal E^2R_{AB}=0\to \mathcal E^2r-\mathcal E^2R_{AB}=0\to R_{AB}=r\ \left(2.5\right).\]Используем (2.1), подставим в (2.5), получим:
\[\frac{R}{3}=r\to R=3r.\]Ответ: Мощность максимальна при $R=3r.$
spravochnick.ru
Работа и мощность тока | Практическая электроника
Работа и мощность тока — важный параметр в электронике. Проще всего измерить мощность и работу постоянного тока. Но пока что не будем далеко заходить и рассмотрим простую аналогию с гидравликой.
Работа тока
Давайте же представим себе нашу водобашню, которая одиноко стоит где-нибудь на горке.

Не долго думая, сделаем пробоину прямо сбоку у подножия водобашни. У нас потечет ручей. Скорость течения ручья, как вы поняли, будет зависеть от того, насколько у нас большая пробоина и много ли воды в башне. Предположим, что у нас на фото этот ручей. Сбоку ручья приделаем вот такое колесо с лопастями:

Чем сильнее бежит ручей, тем быстрее будет крутиться колесо, и наоборот. Это колесо можно заставить работать, приделав к его оси, скажем, электрогенератор, или какой-нибудь механизм. И чем дольше по времени оно будет крутиться, тем больше полезной работы оно сделает. Раньше, до появления электричества, использовали энергию воды именно так (для тех, кто не в курсе).
Так вот, работа электрического тока определяется точно также! Чем выше сила тока (сила скорости течения воды в ручье), напряжение (давление в башне), и чем дольше по времени все это будет продолжаться, тем больше работы будет совершать электрический ток!
где, А — работа электрического тока (выражается в Джоулях), U — напряжение (Вольты), I — сила тока (Амперы), t — время (секунды), в течение которого все это происходит.
Мощность тока
Рассмотрим две картинки:


Как вы думаете, у кого из них бОльшая мощность? Допустим, они оба пришли в спортзал и нашли боксерскую грушу. Ботаник, ударяя по груше, ее даже не шелохнул, но травмировал руку))). Дядя-качок, ударяя по груше, выбил из нее всю дурь. Следовательно, мощность качка намного больше, чем мощность ботаника. Мощность определяется как действие в мгновенный момент времени.
То же самое обстоит и с электрическим током. В такой-то момент времени мощность такая-то. Вот формула для мощности:
где, P — это мощность, I — сила тока, U — напряжение. Мощность измеряется в Ваттах (Вт).
В статье блок питания мы вычисляли мощность вентилятора. Она составила P=UхI=12х0,18=2,16 Ватт. Мда, мощный вентилятор 🙂

Все, что мы описали выше — это формулы для постоянного тока. Для переменного тока работа и мощность вычисляются по таким же формулам, но при условии, что если они питают только активную нагрузку, которая не имеет реактивных составляющих. Пример активной нагрузки в этом случае — это лампа накаливания, электроплитка, утюг и тд. В это случае нам бывает достаточно просто замерить переменное напряжение в розетке, потребляемую силу тока и вычислить по формуле
Нормальный китайский электрочайник потребляет мощность около 2 кВт. Следовательно, за час работы он съест 2 кВт х час. Это уже и есть работа. Так уж повелось, что ее привыкли измерять в Вт х час, а не в Джоулях. У меня в селе кВт х час на данный момент 2,4 рубля. Если я буду кипятить воду в течение часа, то с меня Россети сдерут 2,4 рубля ;-).
www.ruselectronic.com
Видеоматериалы
Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше
Подробнее...С начала года из ветхого и аварийного жилья в республике были переселены десятки семей
Подробнее...Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе
Подробнее...Актуальные темы
ОТЧЕТ о деятельности министерства энергетики, ЖКХ и тарифной политики Кабардино-Балкарской Республики в сфере государственного регулирования и контроля цен и тарифов в 2012 году и об основных задачах на 2013 год
Подробнее...Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год
Подробнее...
КОНТАКТЫ
360051, КБР, г. Нальчик
ул. Горького, 4
тел: 8 (8662) 40-93-82
факс: 8 (8662) 47-31-81
e-mail:
Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.